DOI:10.32604/cmc.2020.014232

| Computers, Materials & Continua DOI:10.32604/cmc.2020.014232 |  |
| Article |
A Parallel Approach to Discords Discovery in Massive Time Series Data
Department of Computer Science, South Ural State University, Chelyabinsk, 454080, Russian
*Corresponding Author: Mikhail Zymbler. Email: mzym@susu.ru
Received: 08 September 2020; Accepted: 30 September 2020
Abstract: A discord is a refinement of the concept of an anomalous subsequence of a time series. Being one of the topical issues of time series mining, discords discovery is applied in a wide range of real-world areas (medicine, astronomy, economics, climate modeling, predictive maintenance, energy consumption, etc.). In this article, we propose a novel parallel algorithm for discords discovery on high-performance cluster with nodes based on many-core accelerators in the case when time series cannot fit in the main memory. We assumed that the time series is partitioned across the cluster nodes and achieved parallelization among the cluster nodes as well as within a single node. Within a cluster node, the algorithm employs a set of matrix data structures to store and index the subsequences of a time series, and to provide an efficient vectorization of computations on the accelerator. At each node, the algorithm processes its own partition and performs in two phases, namely candidate selection and discord refinement, with each phase requiring one linear scan through the partition. Then the local discords found are combined into the global candidate set and transmitted to each cluster node. Next, a node performs refinement of the global candidate set over its own partition resulting in the local true discord set. Finally, the global true discords set is constructed as intersection of the local true discord sets. The experimental evaluation on the real computer cluster with real and synthetic time series shows a high scalability of the proposed algorithm.
Keywords: Time series; discords discovery; computer cluster; many-core accelerator; vectorization
Currently, the discovery of anomalous subsequences in a very long time series is a topical issue in a wide spectrum of real-world applications, namely medicine, astronomy, economics, climate modeling, predictive maintenance, energy consumption, and others. For such applications, it is hard to deal with multi-terabyte time series, which cannot fit into the main memory.
Keogh et al. [1] introduced HOTSAX, the anomaly detection algorithm based on the discord concept. A discord of a time series can informally be defined as a subsequence that has the largest distance to its nearest non-self match neighbor subsequence. A discord looks attractive as an anomaly detector because it only requires one intuitive parameter (the subsequence length), as opposed to most anomaly detection algorithms, which typically require many parameters [2]. HOTSAX, however, assumes that time series reside in main memory.
Further, Yankov, Keogh et al. proposed a disk-aware algorithm (for brevity, referred to as DADD, Disk-Aware Discord Discovery) based on the range discord concept [3]. For a given range  , DADD finds all discords at a distance of at least
, DADD finds all discords at a distance of at least 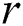 from their nearest neighbor. The algorithm requires two linear scans through the time series on a disk. Later, Yankov, Keogh et al. [4] discussed parallelization of DADD based on the MapReduce paradigm. However, in the experimental evaluation, the authors just simulated the above-mentioned parallel implementation on up to eight computers.
from their nearest neighbor. The algorithm requires two linear scans through the time series on a disk. Later, Yankov, Keogh et al. [4] discussed parallelization of DADD based on the MapReduce paradigm. However, in the experimental evaluation, the authors just simulated the above-mentioned parallel implementation on up to eight computers.
Our research is devoted to parallel and distributed algorithms for time series mining. In the previous work [5], we parallelized HOTSAX for many-core accelerators. This article continues our study and contributes as follows. We present a parallel implementation of DADD on the high-performance cluster with the nodes based on many-core accelerators. The original algorithm is extended by a set of index structures to provide an efficient vectorization of computations on each cluster node. We carried out the experiments on the real computer cluster with the real and synthetic time series, which showed a high scalability of our approach.
The rest of the article is organized as follows. In Section 2, we give the formal definitions along with a brief description of DADD. Section 3 provides the brief state of the art literature review. Section 4 presents the proposed methodology. In Section 5, the results of the experimental evaluation of our approach have been provided. Finally, Section 6 summarizes the results obtained and suggests directions for a further research.
2 Problem Statement and the Serial Algorithm
Below, we follow [4] to give some formal definitions and the statement of the problem.
A time series 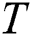 is a sequence of real-valued elements:
is a sequence of real-valued elements: 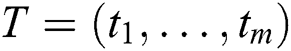 ,
, 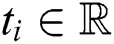 . The length of a time series is denoted by
. The length of a time series is denoted by 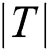 .
.
A subsequence 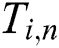 of a time series
of a time series 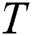 is its contiguous subset of
is its contiguous subset of 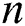 elements that starts at position
elements that starts at position 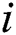 :
: 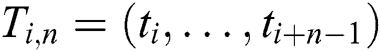 ,
, 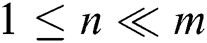 ,
, 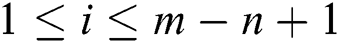 . We denote the set of all subsequences of length
. We denote the set of all subsequences of length 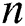 in
in 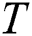 by
by 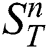 . Let
. Let 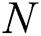 denotes the number of subsequences in
denotes the number of subsequences in 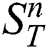 , i.e.,
, i.e., 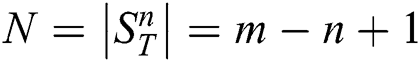 .
.
A distance function for any two subsequences is a nonnegative and symmetric function 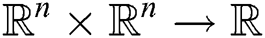 .
.
Two subsequences 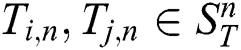 are non-trivial matches [6] with respect to a distance function
are non-trivial matches [6] with respect to a distance function 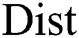 , if
, if 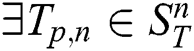 ,
, 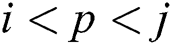 , and
, and 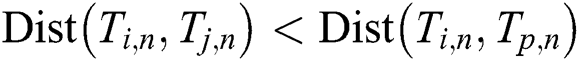 . Let us denote a non-trivial match of a subsequence
. Let us denote a non-trivial match of a subsequence 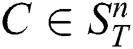 by
by 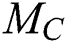 .
.
A subsequence 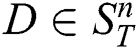 is said to be the most significant discord in
is said to be the most significant discord in 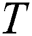 if the distance to its nearest non-trivial match is the largest. That is,
if the distance to its nearest non-trivial match is the largest. That is,
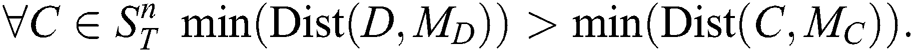
A subsequence 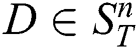 is called the most significant
is called the most significant 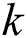 -th discord in
-th discord in 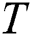 if the distance to its
if the distance to its 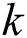 -th nearest non-trivial match is the largest.
-th nearest non-trivial match is the largest.
Given a positive parameter 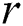 , the discord at a distance at least
, the discord at a distance at least 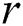 from its nearest neighbor is called the range discord, i.e., for discord
from its nearest neighbor is called the range discord, i.e., for discord 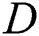
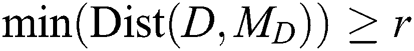 .
.
DADD, the original serial disk-based algorithm [4] addresses discovering range discords, and provides researchers with a procedure to choose the 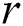 parameter. To accelerate the above-mentioned procedure, our parallel algorithm [5] for many-core accelerators can be applied, which discovers discords for the case when time series fit in the main memory.
parameter. To accelerate the above-mentioned procedure, our parallel algorithm [5] for many-core accelerators can be applied, which discovers discords for the case when time series fit in the main memory.
When computing distance between subsequences, DADD demands that the arguments have been previously z-normalized to have mean zero and a standard deviation of one. Here, 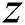 -normalization of a subsequence
-normalization of a subsequence 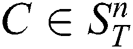 is defined as a subsequence
is defined as a subsequence 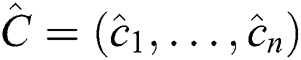 in which
in which
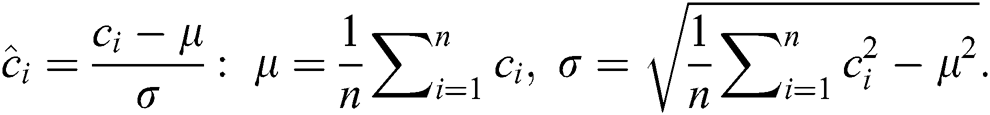
In the original DADD algorithm, the Euclidean distance is used as a distance measure yet the algorithm can be utilized with any distance function, which may not necessarily be a metric [4]. Given two subsequences  , the Euclidean distance between them is calculated as
, the Euclidean distance between them is calculated as

The DADD algorithm [4] performs in two phases, namely the candidate selection and discord refinement, with each phase requiring one linear scan through the time series on disk. Algorithm 1 depicts a pseudo code of DADD (up to the replacement of the Euclidean distance by an arbitrary distance function). The algorithm takes time series  and range
and range  as an input and outputs set of discords
as an input and outputs set of discords 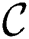 . For a discord
. For a discord 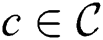 , we denote the distance to its nearest neighbor as
, we denote the distance to its nearest neighbor as 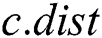 .
.
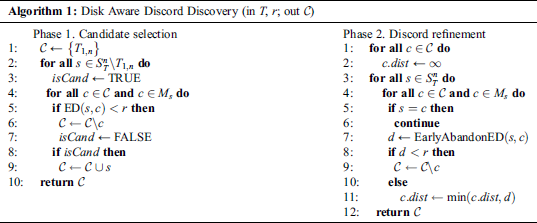
At the first phase, the algorithm scans through the time series 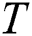 , and for each subsequence
, and for each subsequence 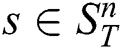 it validates the possibility for each candidate
it validates the possibility for each candidate  already in the set
already in the set  to be discord. If a candidate
to be discord. If a candidate 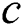 fails the validation, then it is removed from this set. In the end, the new
fails the validation, then it is removed from this set. In the end, the new 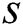 is either added to the candidates set, if it is likely to be a discord, or it is discarded. The correctness of this procedure is proved in Yankov et al. [4].
is either added to the candidates set, if it is likely to be a discord, or it is discarded. The correctness of this procedure is proved in Yankov et al. [4].
At the second phase, the algorithm initially sets distances of all candidates to their nearest neighbors to infinity. Then, the algorithm scans through the time series 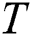 , calculating the distance between each subsequence
, calculating the distance between each subsequence 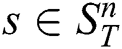 and each candidate
and each candidate 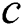 . Here, when calculating
. Here, when calculating 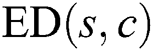 , the
, the 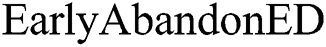 procedure stops the summation of
procedure stops the summation of 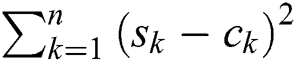 if it reaches
if it reaches 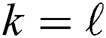 , such that
, such that 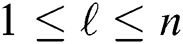 for which
for which 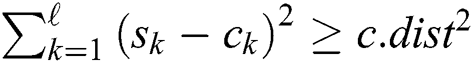 . If the distance is less than
. If the distance is less than 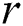 then the candidate is false positive and permanently removed from
then the candidate is false positive and permanently removed from 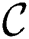 . If the above-mentioned distance is less than the current value of
. If the above-mentioned distance is less than the current value of 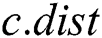 (and still greater than
(and still greater than 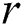 , otherwise it would have been removed) then the current distance to the nearest neighbor is updated.
, otherwise it would have been removed) then the current distance to the nearest neighbor is updated.
Being introduced in Keogh et al. [1], currently, time-series discords are considered one of the best techniques for the time series anomaly detection [7].
The original HOTSAX algorithm [1] is based on the SAX (Symbolic Aggregate ApproXimation) transformation [8]. Among the improvements of HOTSAX, we can mention the following algorithms, namely iSAX [9] and HOT-iSAX [10] (indexable SAX), WAT [11] (Haar wavelets instead of SAX), HashDD [12] (use of a hash table instead of the prefix trie), HDD-MBR [13] (application of R-trees), and BitClusterDiscord [14] (clustering of the bit representation of subsequences). However, the above-mentioned algorithms are able to discover discords if the time series fits in the main memory, and have no parallel implementations, to the best of our knowledge.
Further, Yankov, Keogh et al. [3] overcame the main memory size limitation having proposed a disk-aware discord discovery algorithm (DADD) based on the range discord concept. For a given range 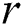 , DADD finds all discords at a distance of at least
, DADD finds all discords at a distance of at least 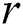 from their nearest neighbor. The algorithm performs in two phases, namely the candidate selection and discord refinement, with each phase requiring one linear scan through the time series on the disk.
from their nearest neighbor. The algorithm performs in two phases, namely the candidate selection and discord refinement, with each phase requiring one linear scan through the time series on the disk.
There are a couple of worth-noting works devoted to parallelization of DADD. The DDD (Distributed Discord Discovery) algorithm [15] parallelizes DADD through a Spark cluster [16] and HDFS (Hadoop Distributed File System) [17]. DDD distributes time series onto the HDFS cluster and handles each partition in a memory of a computing node. As opposed to DADD, DDD computes the distance without taking advantage of an upper bound for early abandoning, which would increase the algorithm’s performance.
The PDD (Parallel Discord Discovery) algorithm [18] also utilizes a Spark cluster but employs transmission of a subsequence and its non-trivial matches to one or more computing nodes to calculate the distance between them. A bulk of continuous subsequences is transmitted and calculated in a batch mode to reduce the message passing overhead. PDD is not scalable since intensive message passing between the cluster nodes leads to a significant degradation of the algorithm’s performance as the number of nodes increases.
In their further work [4], Yankov, Keogh et al. discussed the parallel version of DADD based on the MapReduce paradigm (hereinafter referred to as MR-DADD), and the basic idea is as follows. Let the input time series 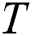 be partitioned evenly across
be partitioned evenly across 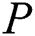 cluster nodes. Each node performs the selection phase on its own partition with the same
cluster nodes. Each node performs the selection phase on its own partition with the same 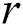 parameter and produces distinct candidate set
parameter and produces distinct candidate set 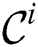 . Then the combined candidate set
. Then the combined candidate set 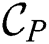 is constructed as
is constructed as  and transmitted to each cluster node. Next, a node performs the refinement phase on its own partition taking
and transmitted to each cluster node. Next, a node performs the refinement phase on its own partition taking 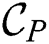 as an input, and produces the refined candidate set
as an input, and produces the refined candidate set 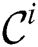 . The final discords are given by the set
. The final discords are given by the set  . In the experimental evaluation, the authors, however, just simulated the above-mentioned scheme on up to eight computers resulting in a near-to-linear speedup.
. In the experimental evaluation, the authors, however, just simulated the above-mentioned scheme on up to eight computers resulting in a near-to-linear speedup.
Concluding this brief review, we should also mention the matrix profile (MP) concept proposed by Keogh et al. [19]. MP is a data structure that annotates a time series, and can be applied to solve an impressively large list of time series mining problems including discords discovery but at computational cost of 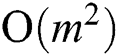 where
where 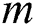 is the time series length [19,20]. Recent parallel algorithms of the MP computation include GPU-STAMP [19] and MP-HPC [21], which are implementations for graphic processors through CUDA (Compute Unified Device Architecture) technology and computer cluster through MPI (Message Passing Interface) technology, respectively.
is the time series length [19,20]. Recent parallel algorithms of the MP computation include GPU-STAMP [19] and MP-HPC [21], which are implementations for graphic processors through CUDA (Compute Unified Device Architecture) technology and computer cluster through MPI (Message Passing Interface) technology, respectively.
4 Discords Discovery on Computer Cluster with Many-Core Accelerators
The parallelization employs a two-level parallelism, namely across cluster nodes and among threads of a single node. We implemented these levels through partitioning of an input time series and MPI technology, and OpenMP technology, respectively. Within a single node, we employed the matrix representation of data to effectively parallelize computations through OpenMP. Below, we will show an approach to the implementation of these ideas.
4.1 Time Series Representation
To provide parallelism at the level of the cluster nodes, we perform time series partitioning across the nodes as follows. Let 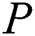 be the number of nodes in the cluster, then
be the number of nodes in the cluster, then 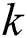 -th partition (
-th partition (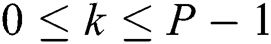 ) of the time series is defined as
) of the time series is defined as 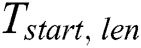 where
where
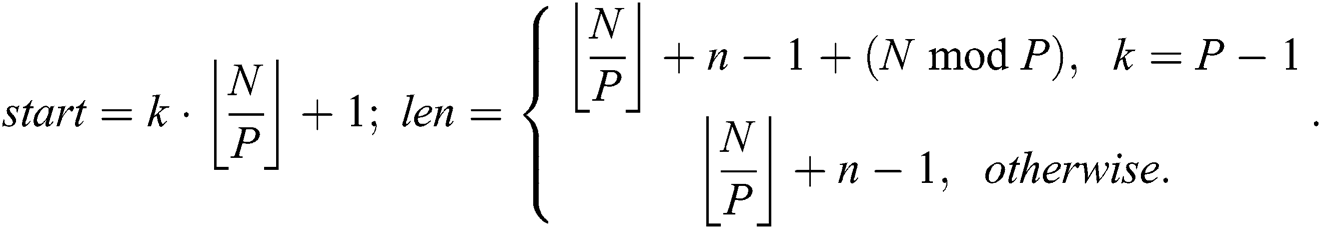
This means the head part of every partition except the first overlaps with the tail part of the previous partition in 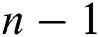 data points. Such a technique prevents us from a loss of the resulting subsequences in the junctions of two neighbor partitions. To simplify the presentation of the algorithm, hereinafter in this section, we use symbol
data points. Such a technique prevents us from a loss of the resulting subsequences in the junctions of two neighbor partitions. To simplify the presentation of the algorithm, hereinafter in this section, we use symbol 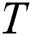 and the above-mentioned related notions implying a partition on the current node but not the whole input time series.
and the above-mentioned related notions implying a partition on the current node but not the whole input time series.
The time series partition is stored as a matrix of aligned subsequences to enable computations over aligned data with as many auto-vectorizable loops as possible. We avoid the unaligned memory access since it can cause an inefficient vectorization due to time overhead for the loop peeling [22].
Let us denote the number of floats stored in the VPU (vector processing unit of the many-core accelerator) by 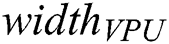 . If the discord length
. If the discord length 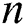 is not a multiple of
is not a multiple of 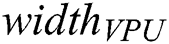 , then each subsequence is padded with zeroes where the number of zeroes is calculated as
, then each subsequence is padded with zeroes where the number of zeroes is calculated as 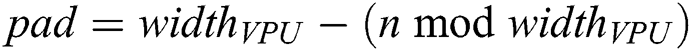 . Thus, the aligned (and previously z-normalized) subsequence
. Thus, the aligned (and previously z-normalized) subsequence 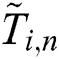 is defined as follows:
is defined as follows:
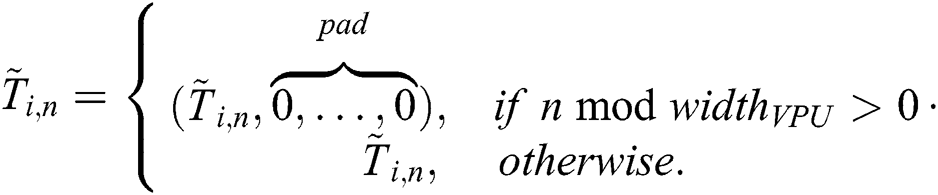
The subsequence matrix 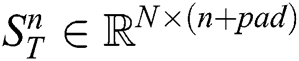 is defined as
is defined as
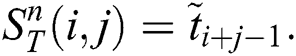
The parallel algorithm employs the data structures depicted in Fig. 1. Defining structures to store data in the main memory of a cluster node, we suppose that each structure is shared by all threads the algorithm is running on, and each thread processes its own data segment independently. Let us denote the amount of threads employing by the algorithm on a cluster node by 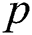 , and let
, and let 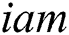 (
(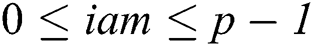 ) denotes the number of the current thread.
) denotes the number of the current thread.
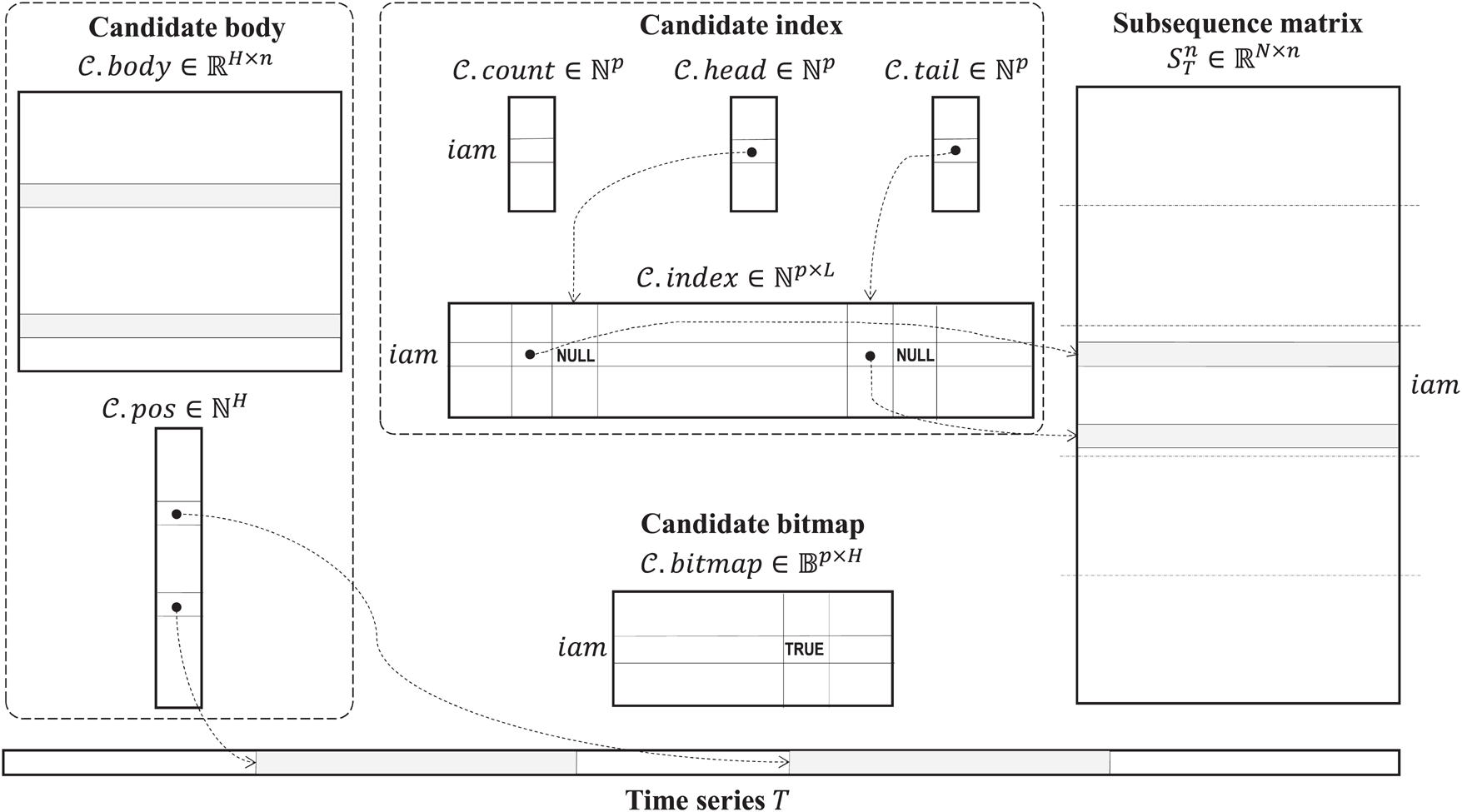
Figure 1: Data layout of the algorithm
Set of discords 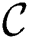 is implemented as an object with two basic attributes, namely candidate index and candidate body, to store indices of all potential discord subsequences and their values themselves, respectively.
is implemented as an object with two basic attributes, namely candidate index and candidate body, to store indices of all potential discord subsequences and their values themselves, respectively.
Let us denote a ratio of candidates selected at a cluster node and all subsequences of the time series by 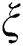 . The exact value of the
. The exact value of the 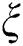 parameter is a subject of an empirical choice. In our experiments,
parameter is a subject of an empirical choice. In our experiments, 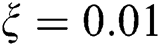 was enough to store all candidates. Thus, we denote the number of candidates as
was enough to store all candidates. Thus, we denote the number of candidates as 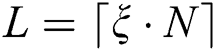 and assume that
and assume that 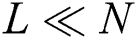 .
.
The candidate index is organized as a matrix 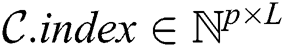 , which stores indices of candidates in the subsequence matrix
, which stores indices of candidates in the subsequence matrix 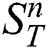 found by each thread, i.e.,
found by each thread, i.e., 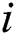 -th row keeps indices of the candidates that have been found by
-th row keeps indices of the candidates that have been found by 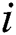 -th thread. Initially, the candidate index is filled by NULL values.
-th thread. Initially, the candidate index is filled by NULL values.
To provide a fast access to the candidate index during the selection phase, it is implemented as a deque (double-ended queue) with three attributes, namely 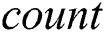 ,
, 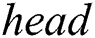 , and
, and 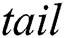 . The deque count is an array
. The deque count is an array 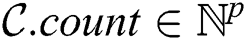 , which for each thread keeps the amount of non-NULL elements in the respective row of the candidate index matrix. The deque head and tail are arrays
, which for each thread keeps the amount of non-NULL elements in the respective row of the candidate index matrix. The deque head and tail are arrays  and
and 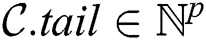 , respectively, which represent the second-level indices that for each thread keep a number of column in
, respectively, which represent the second-level indices that for each thread keep a number of column in 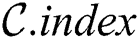 with the most recent NULL value, and with the least recent non-NULL value, respectively.
with the most recent NULL value, and with the least recent non-NULL value, respectively.
Let 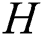 (
(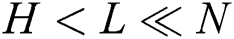 ) be the number of candidates selected at a cluster node during the algorithm’s first phase. Then the candidate body is the matrix
) be the number of candidates selected at a cluster node during the algorithm’s first phase. Then the candidate body is the matrix 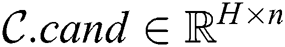 , which represents the candidate subsequences itself. The candidate body is accompanied by an array
, which represents the candidate subsequences itself. The candidate body is accompanied by an array  , which stores starting points of candidate subsequences in the input time series.
, which stores starting points of candidate subsequences in the input time series.
After the selection phase, all the nodes exchange the candidates found to construct the combined candidate set, so at each cluster node the candidate body will contain potential discords from all the nodes. At the second phase, the algorithm refines the combined candidate set comparing the parameter 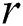 and distances between each element of the candidate body and each element of the subsequence matrix.
and distances between each element of the candidate body and each element of the subsequence matrix.
To parallelize this activity, we process rows of the subsequence matrix in the segment-wise manner and employ an additional attribute of the candidate body, namely bitmap. The bitmap is organized as a matrix 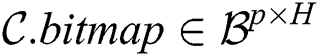 , which indicates the fact that an element of the candidate body has been successfully validated against all elements in a segment of the subsequence matrix. Thus, after the algorithm’s second phase,
, which indicates the fact that an element of the candidate body has been successfully validated against all elements in a segment of the subsequence matrix. Thus, after the algorithm’s second phase, 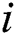 -th element of the candidate body is successfully validated if
-th element of the candidate body is successfully validated if 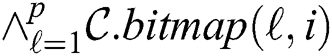 is true.
is true.
4.3 Parallel Implementation of the Algorithm
In the implementation, we apply the following parallelization scheme at the level of the cluster nodes. Let the input time series 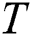 be partitioned evenly across
be partitioned evenly across 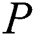 cluster nodes. Each node performs the selection phase on its own partition with the same threshold parameter
cluster nodes. Each node performs the selection phase on its own partition with the same threshold parameter  and produces distinct candidate set
and produces distinct candidate set 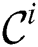 .
.
Next, as opposed to MR-DADD [4], each node refines its own candidate set 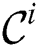 with respect to the
with respect to the 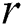 value. Indeed, a candidate cannot be the true discord if it is pruned in the refinement phase in at least one cluster node. Thus, by the local refinement procedure, we try to reduce each candidate set
value. Indeed, a candidate cannot be the true discord if it is pruned in the refinement phase in at least one cluster node. Thus, by the local refinement procedure, we try to reduce each candidate set 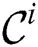 and, in turn, the combined candidate set
and, in turn, the combined candidate set 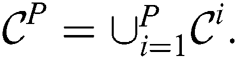 In the experiments, this allows us to reduce the size of the combined candidate set at times.
In the experiments, this allows us to reduce the size of the combined candidate set at times.
Then the combined candidate set  is constructed and transmitted to each cluster node. Next, a node refines
is constructed and transmitted to each cluster node. Next, a node refines 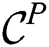 over its own partition, and produces the result
over its own partition, and produces the result 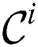 . Finally, the true discords set is constructed as
. Finally, the true discords set is constructed as 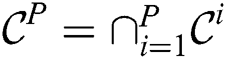 .
.
The parallel implementation of the candidate selection and refinement phases is depicted in Algorithm 2 and Algorithm 3, respectively. To speed up the computations at a cluster node, we omit the square root calculation since this does not change the relative ranking of the candidates (indeed, the 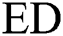 function is monotonic and concave).
function is monotonic and concave).


In the selection phase, we parallelize the outer loop along the rows of the subsequence matrix while in the inner loop along the candidates, each thread processes its own segment of the candidate index. By the end of the phase, the candidates found by each thread are placed into the candidate body, and all the cluster nodes exchange the resulting candidate bodies by the MPI_Send and MPI_Recv functions to form the combined candidate set, which serves as an input for the second phase.
In the refinement phase, we also parallelize the outer loop along the rows of the subsequence matrix, and in the inner loop along the candidates, each thread processes its own segments of the candidate body and bitmap. In this implementation, we do not use the early abandoning technique for the distance calculation relying on the fact that vectorization of the square of the Euclidean distance may give us more benefits. By the end of the phase, the column-wise conjunction of the elements in the bitmap matrix will result in a set of true discords found by the current cluster node. An intersection of such sets is implemented by one of the cluster nodes where the rest nodes send their resulting sets.
We evaluated the proposed algorithm during the experiments conducted on the Tornado SUSU computer cluster [23] with the nodes based on the Intel MIC accelerators [24]. Each cluster node is equipped by the Intel Xeon Phi SE10X accelerator with a peak performance 1.076 TFLOPS (60 cores at 1.1 GHz with hyper-threading factor 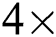 ). In the experiments, we investigated scalability of our approach and compared it with analogs, and the results are given below in Sections 5.1 and 5.2, respectively.
). In the experiments, we investigated scalability of our approach and compared it with analogs, and the results are given below in Sections 5.1 and 5.2, respectively.
5.1 The Algorithm’s Scalability
In the first series of the experiments, we assessed the algorithm’s scaled speedup, which is defined as the speedup obtained when the problem size is increased linearly with the number of the nodes added to the computer cluster [25]. Being applied to our problem, the algorithm’s scaled speedup is calculated as
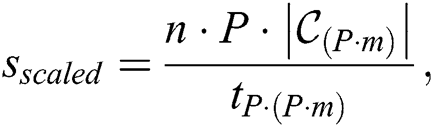
where 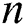 is the discord length,
is the discord length, 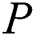 is the number of the cluster nodes,
is the number of the cluster nodes, 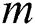 is a factor of the time series length,
is a factor of the time series length, 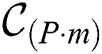 is a set of all the candidate discords selected by the algorithm at its first phase from a time series of length
is a set of all the candidate discords selected by the algorithm at its first phase from a time series of length 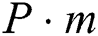 and
and 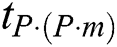 is the algorithm’s run time when the time series is processed on
is the algorithm’s run time when the time series is processed on 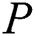 nodes.
nodes.
For the evaluation, we took ECG time series [26] (see Tab. 1 for the summary of the data involved). In the experiments, we discovered discords on up to 128 cluster nodes with the time series factor 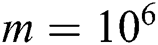 , and varied the discord’s length
, and varied the discord’s length  while the range parameter
while the range parameter 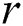 was chosen empirically to provide the algorithm’s best performance.
was chosen empirically to provide the algorithm’s best performance.
Table 1: Time series involved in the experiments on the algorithm’s scalability
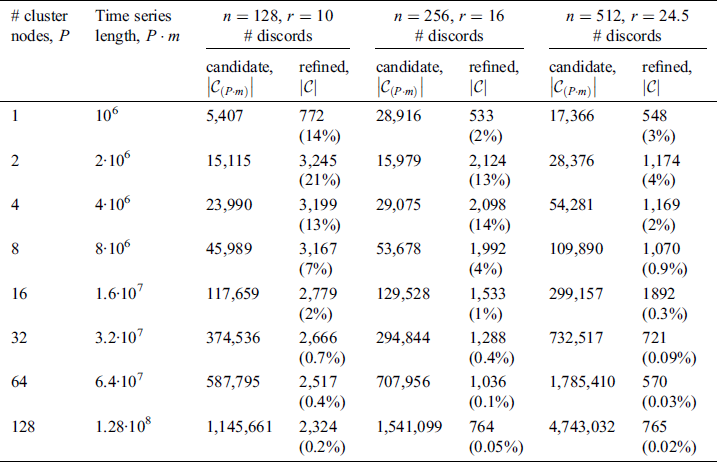
The results of the experiments are depicted in Fig. 2. As can be seen, our algorithm adapts well to increasing both the time series length and number of cluster nodes, and demonstrates the linear scaled speedup. As expected, the algorithm shows a better scalability with larger values of the discord length because this provides a higher computational load.
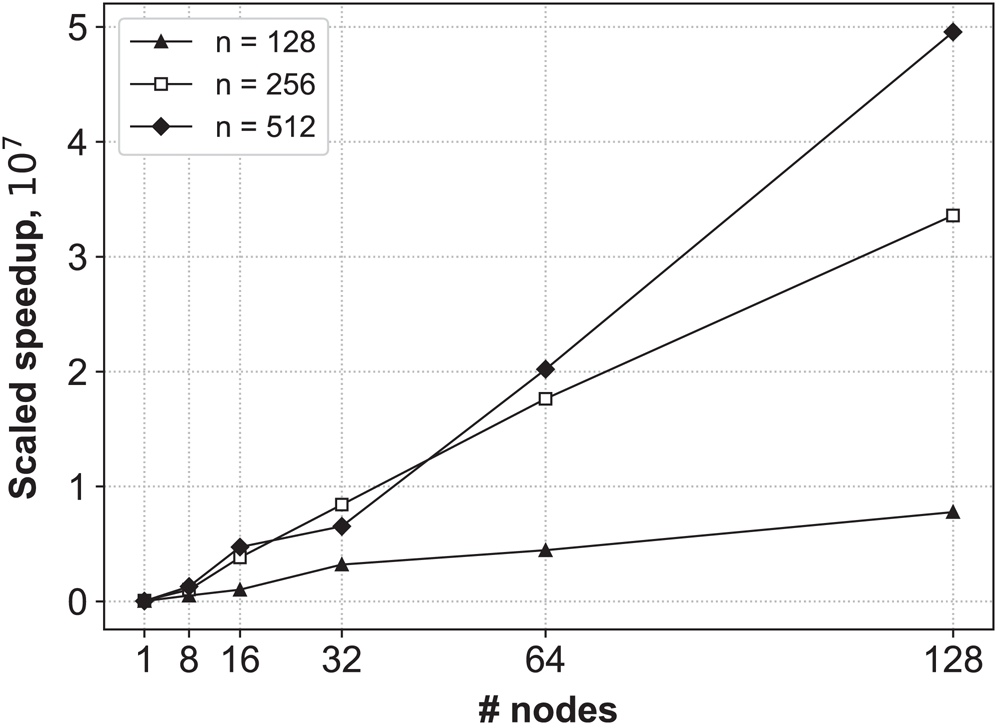
Figure 2: The scaled speedup of the algorithm
In the second series of the experiments, we compared the performance of our algorithm against the analogs we have already considered in Section 3, namely DDD [15], MR-DADD [4], GPU-STAMP [19], and MP-HPC [21]. We omit the PDD algorithm [18] since in our previous experiments [5], PDD was substantially far behind our parallel in-memory algorithm due to the overhead caused by the message passing among the cluster nodes.
Throughout the experiments, we used the synthetic time series generated according the Random Walk model [27] as that ones were employed for the evaluation by the competitors. For comparison purposes, we used the run times reported by the authors of the respective algorithms. To perform the comparison, we ran our algorithm on Tornado SUSU with a reduced number of nodes and cores at a node to make the peak performance of our hardware platform approximately equal to that of the system on which the corresponding competitor was evaluated.
Tab. 2 summarizes the performance of the proposed algorithm compared with the analogs. We can see that our algorithm outruns its competitors. As expected, direct analogs DDD and MR-DADD are inferior to our algorithm since they do not employ parallelism within a single cluster node. Additionally, indirect analogs GPU-STAMP and MP-HPC are behind our algorithm since they initially aim to solve a computationally more complex problem of computing the matrix profile, which can also be used for discords discovery among many other time series mining problems.
Table 2: Comparison of the proposed algorithm with analogs

In this article, we addressed the problem of discovering the anomalous subsequences in a very long time series. Currently, there is a wide spectrum of real-world applications where it is typical to deal with multi-terabyte time series, which cannot fit in the main memory: medicine, astronomy, economics, climate modeling, predictive maintenance, energy consumption, and others. In the study, we employ the discord concept, which is a subsequence of the time series that has the largest distance to its nearest non-self match neighbor subsequence.
We proposed a novel parallel algorithm for discords discovery in very long time series on the modern high-performance cluster with the nodes based on many-core accelerators. Our algorithm utilizes the serial disk-aware algorithm by Yankov, Keogh et al. [4] as a basis. We achieve parallelization among the cluster nodes as well as within a single node. At the level of the cluster nodes, we modified the original parallelization scheme that allowed us to reduce the number of candidate discords to be processed. Within a single cluster node, we proposed a set of the matrix data structures to store and index the subsequences of a time series, and to provide an efficient vectorization of computations on the many-core accelerator.
The experimental evaluation on the real computer cluster with the real and synthetic time series shows the high scalability of the proposed algorithm. Throughout the experiments on real computer cluster over real and synthetic time series, our algorithm showed the linear scalability, increasing in the case of a high computational load due to a greater discord length. Also, the algorithm’s performance was ahead of the analogs that do not employ both computer cluster and many-core accelerators.
In further studies, we plan to elaborate versions of the algorithm for computer clusters with GPU nodes.
Funding Statement: This work was financially supported by the Russian Foundation for Basic Research (Grant No. 20-07-00140) and by the Ministry of Science and Higher Education of the Russian Federation (Government Order FENU-2020-0022).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. J. Keogh, J. Lin and A. W. Fu. (2005). “HOT SAX: Efficiently finding the most unusual time series subsequence,” in Proc. ICDM, Houston, TX, USA, pp. 226–233. [Google Scholar]
2. E. J. Keogh, S. Lonardi and C. A. Ratanamahatana. (2004). “Towards parameter-free data mining,” in Proc. KDD, Seattle, WA, USA, pp. 206–215. [Google Scholar]
3. D. Yankov, E. J. Keogh and U. Rebbapragada. (2007). “Disk aware discord discovery: Finding unusual time series in terabyte sized datasets,” in Proc. ICDM, Omaha, NE, USA, pp. 381–390. [Google Scholar]
4. D. Yankov, E. J. Keogh and U. Rebbapragada. (2008). “Disk aware discord discovery: Finding unusual time series in terabyte sized datasets,” Knowledge and Information Systems, vol. 17, no. 2, pp. 241–262. [Google Scholar]
5. M. Zymbler, A. Polyakov and M. Kipnis. (2019). “Time series discord discovery on Intel many-core systems,” in Proc. PCT, Kaliningrad, Russia, pp. 168–182. [Google Scholar]
6. B. Y. Chiu, E. J. Keogh and S. Lonardi. (2003). “Probabilistic discovery of time series motifs,” in Proc. KDD, Washington, D.C., USA, pp. 493–498. [Google Scholar]
7. V. Chandola, D. Cheboli and V. Kumar. (2009). “Detecting anomalies in a time series database.” Technical Report, Department of Computer Science and Engineering, University of Minnesota, Minneapolis, MN, USA. [Google Scholar]
8. J. Lin, E. J. Keogh, S. Lonardi and B. Y. Chiu. (2003). “A symbolic representation of time series, with implications for streaming algorithms,” in Proc. DMKD, San Diego, California, USA, pp. 2–11. [Google Scholar]
9. J. Shieh and E. J. Keogh. (2008). “iSAX: Indexing and mining terabyte sized time series,” in Proc. KDD, Las Vegas, Nevada, USA, pp. 623–631. [Google Scholar]
10. H. T. Q. Buu and D. T. Anh. (2011). “Time series discord discovery based on iSAX symbolic representation,” in Proc. KSE, Hanoi, Vietnam, pp. 11–18. [Google Scholar]
11. A. W. Fu, O. T. Leung, E. J. Keogh and J. Lin. (2006). “Finding time series discords based on Haar transform,” in Proc. ADMA, Xi’an, China, pp. 31–41. [Google Scholar]
12. H. T. T. Thuy, D. T. Anh and V. T. N. Chau. (2016). “An effective and efficient hash-based algorithm for time series discord discovery,” in Proc. NICS, Danang, Vietnam, pp. 85–90. [Google Scholar]
13. P. M. Chau, B. M. Duc and D. T. Anh. (2018). “Discord detection in streaming time series with the support of R-tree,” in Proc. ACOMP, Ho Chi Minh City, Vietnam, pp. 96–103. [Google Scholar]
14. G. Li, O. Bräysy, L. Jiang, Z. Wu and Y. Wang. (2013). “Finding time series discord based on bit representation clustering,” Knowledge-Based Systems, vol. 54, pp. 243–254. [Google Scholar]
15. Y. Wu, Y. Zhu, T. Huang, X. Li, X. Liu et al. (2015). , “Distributed discord discovery: Spark based anomaly detection in time series,” in Proc. HPCC, Proc. CSS, Proc. ICESS, New York, NY, USA, pp. 154–159. [Google Scholar]
16. M. Zaharia, M. Chowdhury, M. J. Franklin, S. Shenker and I. Stoica. (2010). “Spark: Cluster computing with working sets,” in Proc. HotCloud, Boston, MA. [Google Scholar]
17. S. Ghemawat, H. Gobioff and S. Leung. (2003). “The Google file system,” in Proc. SOSP, Bolton Landing, NY, USA, pp. 29–43. [Google Scholar]
18. T. Huang, Y. Zhu, Y. Mao, X. Li, M. Liu et al. (2016). , “Parallel discord discovery,” in Proc. PAKDD, Auckland, New Zealand, pp. 233–244. [Google Scholar]
19. C. M. Yeh, Y. Zhu, L. Ulanova, N. Begum, Y. Ding et al. (2018). , “Time series joins, motifs, discords and shapelets: A unifying view that exploits the matrix profile,” Data Mining and Knowledge Discovery, vol. 32, no. 1, pp. 83–123. [Google Scholar]
20. Y. Zhu, C. M. Yeh, Z. Zimmerman, K. Kamgar and E. J. Keogh. (2018). “Matrix profile XI: SCRIMP++: Time series motif discovery at interactive speeds,” in Proc. ICDM, Singapore, pp. 837–846. [Google Scholar]
21. G. Pfeilschifter. (2019). “Time series analysis with matrix profile on HPC systems,” Ph.D. dissertation. Department of Informatics, Technical University of Munich, Munich, Bavaria, Germany. [Google Scholar]
22. D. F. Bacon, S. L. Graham and O. J. Sharp. (1994). “Compiler transformations for high-performance computing,” ACM Computing Surveys, vol. 26, no. 4, pp. 345–420. [Google Scholar]
23. P. Kostenetskiy and P. Semenikhina. (2018). “SUSU supercomputer resources for industry and fundamental science,” in Proc. GloSIC, Chelyabinsk, Russia, 8570068. [Google Scholar]
24. G. Chrysos. (2012). “Intel® Xeon Phi coprocessor (codename Knights Corner),” in Proc. HCS, Cupertino, CA, USA, pp. 1–31. [Google Scholar]
25. A. Grama, A. Gupta, G. Karypis and V. Kumar. (2003). Introduction to Parallel Computing. 2nd ed. Boston, MA, USA: Addison-Wesley. [Google Scholar]
26. A. L. Goldberger, L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. C. Ivanov et al. (2000). , “PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals,” Circulation, vol. 101, no. 23, pp. e215–e220. [Google Scholar]
27. K. Pearson. (1905). “The problem of the random walk,” Nature, vol. 72, no. 1865, pp. 294. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |