DOI:10.32604/cmc.2020.013355
| Computers, Materials & Continua DOI:10.32604/cmc.2020.013355 | |
| Article |
Efficient Routing Protection Algorithm in Large-Scale Networks
1School of Software Engineering, Shanxi University, Taiyuan, 030006, China
22Institute of Big Data Science and Industry, Shanxi University, Taiyuan, 030006, China
3School of Cyber Space and Technology, Beihang University, Beijing, 100191, China
4College of Engineering Northeastern University, Boston, 02115, USA
*Corresponding Author: Haijun Geng. Email: ghj123025449@163.com
Received: 04 August 2020; Accepted: 20 September 2020
Abstract: With an increasing urgent demand for fast recovery routing mechanisms in large-scale networks, minimizing network disruption caused by network failure has become critical. However, a large number of relevant studies have shown that network failures occur on the Internet inevitably and frequently. The current routing protocols deployed on the Internet adopt the reconvergence mechanism to cope with network failures. During the reconvergence process, the packets may be lost because of inconsistent routing information, which reduces the network’s availability greatly and affects the Internet service provider’s (ISP’s) service quality and reputation seriously. Therefore, improving network availability has become an urgent problem. As such, the Internet Engineering Task Force suggests the use of downstream path criterion (DC) to address all single-link failure scenarios. However, existing methods for implementing DC schemes are time consuming, require a large amount of router CPU resources, and may deteriorate router capability. Thus, the computation overhead introduced by existing DC schemes is significant, especially in large-scale networks. Therefore, this study proposes an efficient intra-domain routing protection algorithm (ERPA) in large-scale networks. Theoretical analysis indicates that the time complexity of ERPA is less than that of constructing a shortest path tree. Experimental results show that ERPA can reduce the computation overhead significantly compared with the existing algorithms while offering the same network availability as DC.
Keywords: Large-scale network; shortest path tree; time complexity; network failure; real-time and mission-critical applications
In recent years, the Internet has become a widely used platform for various network applications. With the rapid development of the Internet, several real-time and mission-critical applications, such as VoIP and video and online games, are deployed [1]. These applications are susceptible to network delay and interruption, which stress strict requirements on network availability [2]. Moreover, even a few seconds of network discontinuity would have an adverse effect on these applications [3]. However, network failures are common on the Internet. The IP networks need to reconverge when network failure occurs. The convergence time for the currently deployed intra-domain routing protocol is the order of seconds when network components are invalid. During this period, several packets may be dropped because of the inconsistent routing information [4]. The Internet service provider (ISP) has strong motivations to enhance the network survivability when network failures occur [5]. Therefore, improving the Internet routing availability has become an urgent problem that needs to be solved.
To improve the availability of intra-domain routing, the routing protection scheme is usually applied in the academia and industry [6]. The routing protection aims to prove fast convergence when network failures have been detected [7]. Existing routing protection schemes can be divided into two sub-categories depending on whether or not special cooperation between routers is required for packet forwarding. Cooperation-free schemes compute multiple next-hops for each destination, and each router selects an appropriate next-hop for standard packet forwarding independently, where care must be taken such that the induced forwarding paths are loop-free. The benefit is that they can provide not only redundant backup links but also other features, such as load balancing and high throughput. The other sub-category of schemes computes for a link to protect a multihop repair path that is agreed by all routers on that path. Thus, special cooperation mechanisms have to be used to reroute packets along that path.
In this work, we focus on the first type of scheme. We also confine our work in link-state routing networks. Most ISPs prefer link-state routing instead of distance-vector routing in their intra-domain system because of its merits, such as fast convergence and good support for metrics. Layer2 networks also incorporate link-state routing into their network architecture, such as the standardized transparent interconnection of lots of links. Furthermore, during topology changes caused by link or node failure, millisecond-level fast convergence, which poses stringent performance requirement to route computation, is preferred.
Among all of the hop-by-hop routing protection schemes, downstream path criterion (DC) [8] has been favored by the industry because of its simplicity in coping with all the single-link failure scenarios. All of the existing implementation algorithms about DC are time consuming and require a large amount of router CPU resources in large-scale networks.
However, the deployment of DC in real ISP networks is difficult because of the substantial computational overhead. Therefore, an efficient DC-based algorithm is required to be easily deployed in ISP. Thus, a lightweight IPFRR scheme is desired to provide cost-efficient routing protection effectively. Therefore, this study investigates the application of incremental shortest path first algorithm to reduce the computational overhead of the DC implementation. In particular, our contributions can be summarized as follows:
• We propose an efficient intra-domain routing protection algorithm (ERPA) in large-scale networks.
• Theoretical analysis indicates that the computation complexity of ERPA is less than that of constructing a shortest path tree (SPT).
• Theoretical analysis indicates that ERPA can provide the same network availability as DC.
• In terms of computation overhead and network availability, the theoretical analysis and experimental results are consistent.
Nowadays, network failures have become routine events rather than exceptions [9]. Many schemes for enhancing robustness against network failures have been proposed. Existing approaches fall in either one of the two categories: reactive and proactive approaches. The former studies the reduction of convergence time of routing protocol after the occurrence of failures, whereas the latter addresses the pre-calculating backup paths before the failures. Reactive approaches are applicable to all kinds of network failure scenarios regardless whether they are single or multiple failures. However, reactive approaches are subject to the risk of routing flap. Therefore, proactive approaches are preferred by the academia and industry. The idea of multitopology configuration method is that each router saves multiple configurations, and each configuration can protect some links to adapt to different link failures. However, the more configurations the router keeps, the more overhead it will introduce. Path splicing [10] is a classical multitopology configuration method that calculates multiple SPTs by adjusting link weights. Each spanning tree corresponds to a routing path, and packets can be forwarded among multiple spanning trees. However, a routing loop may be observed in path splitting, thereby degrading network performance. Dispath [11], which can protect all possible single fault cases in the network, is proposed in the literature. By constructing a directed acyclic graph with three disjoint edges [12], any two links in the network can be protected from failure. This study [13] investigates and proves that single- and double-fault protection algorithms are not restricted by network topology. Among the hop-by-hop proactive schemes, DC has been favored by the industry because of its simplicity in coping with all the single-link failure scenarios. However, all of the existing DC-based implementation algorithms are time consuming and require a large amount of router CPU resources. Authors propose an efficient algorithm called TBFH [14], which provides greater path diversity than ECMP with a very low overhead. In particular, TBFH computes the two best first hop disjoint paths efficiently. We also propose a SPT-based multipath routing algorithm called DMPA [15]. DMPA guarantees the loop-freeness of the induced routing path by maintaining a partial order of the routers underpinning it implicitly. The time complexity of DMPA does not depend on the degree of the calculating router. However, the network availability of TBFH and DMPA is lower than that of the DC. Unlike the aforementioned studies, our main concerns include computational efficiency and network availability, which are critical for the algorithm. Based on the existing work on this research area, we propose an algorithm whose complexity is less than that of constructing a SPT and without degrading the network availability for the first time.
3 Network Model and Problem Description
In this section, we will first show the network model and then describe the key problems that need to be solved in this work. For ease of reading, some of the symbols used in this paper are summarized in Tab. 1. A network can be expressed as a undirected graph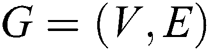
, where
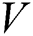and
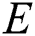denote the set of nodes and the set of edges in the network, respectively. For any node 
, we use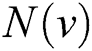
to denote all the neighbors of node
; 
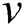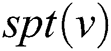represents a SPT rooted at
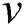; and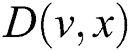 
is the descendant of node 
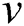in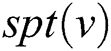
. Each link 
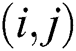in the network has a weight 
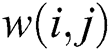and a failure probability 
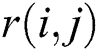. For any node pair 
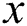and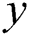 
, we use 
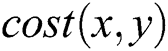to indicate the shortest cost from node
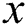to node
; 
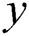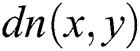is the default next-hop from node
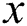to node
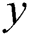; and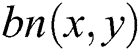 
is the backup next-hop set from node 
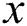to node
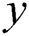. We will use a simple example to explain the aforementioned concepts. For example, Fig. 1 presents a SPT rooted at node 
,
,
, 
, 
,
, 
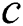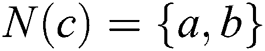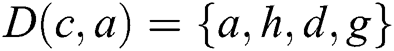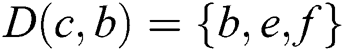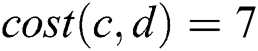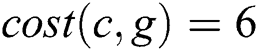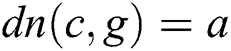, and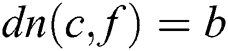 
.
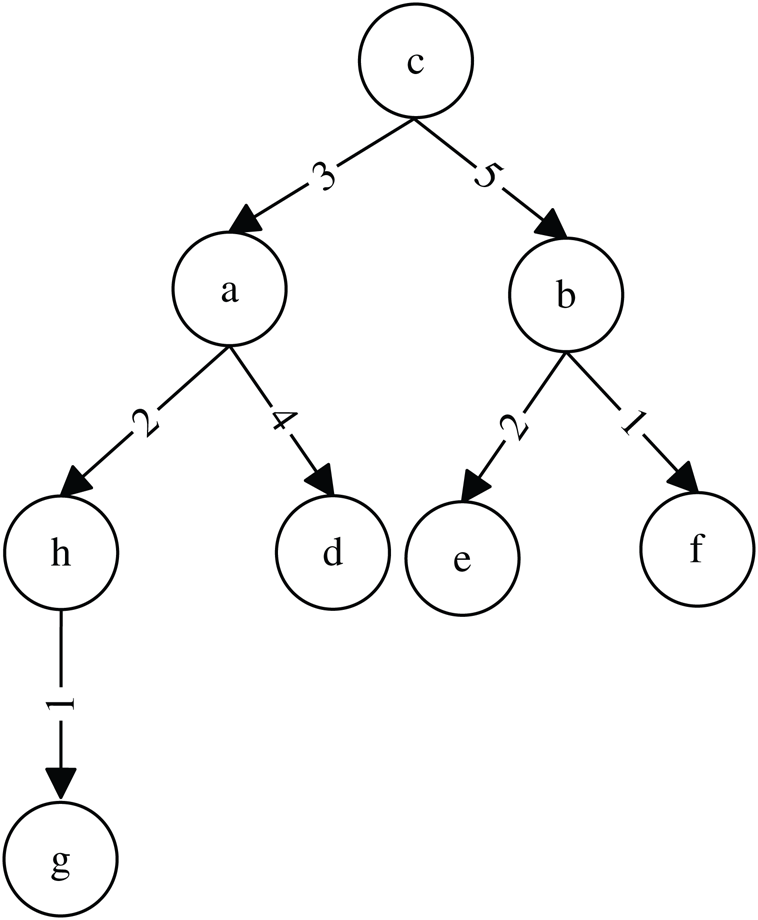
Figure 1: SPT rooted at node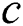 
The currently deployed intra-domain routing protocols (e.g., OSPF and IS-IS) only employ the shortest paths to forward packets. Thus, they need to reconverge when network component failures occur. The packets may be dropped because of invalid routing information. These protocols never exploit the inherent diversity of Internet topology and cannot handle network failure flexibly. Therefore, DC has been proposed to cope with all the single-link failure scenarios. The DC can be expressed as follows:
DC: For packets forwarded to a destination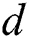
, node 
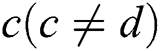can forward them to any of its neighboring node
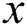when 
, and no forwarding loop will exist in the induced forwarding path.
To implement DC rule at node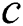
, node 
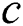should obtain the values of 
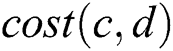and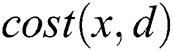
. The value of 
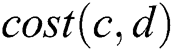can be achieved easily via
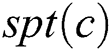. However, to obtain 
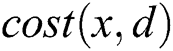, node 
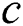needs to compute a SPT for each of its neighbor. Computational complexity increases with the number of network node degree, which is particularly high when a node has a high degree in large-scale networks. Therefore, implementing the DC rule in real ISP networks is not considered a scalable method. For the actual deployment on the Internet, a DC-based scheme should introduce a small additional burden on the current deployed routing protocol. This paper is dedicated to finding an efficient DC-based scheme that is suitable for an ISP network. In particular, we focus on addressing the following problems:
Given a computing node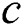 
and its SPT 
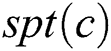, we can find an efficient DC-based algorithmic technique in large-scale networks, and the algorithm conforms to the two following conditions:
1. The time complexity of the algorithm is less than that of constructing a SPT.
2. It can provide the same network availability with DC.
ERPA will be discussed in detail to solve the above problem in this section. The problem can be presented to compute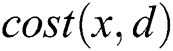 
in the 
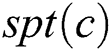. We first provide two theorems before formally describing the details of ERPA. The two following theorems describe how to compute the backup next-hop set that satisfies the DC Rule. Moreover, the computation overhead can be reduced dramatically by lessening the times of the operation.
Theorem 1: Given a computing node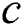 
and 
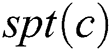, for any node 
, 
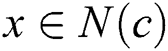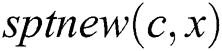is the new SPT rooted at node 
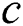when the weight of link 
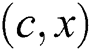is changed to 0. For any node
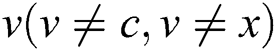, if 
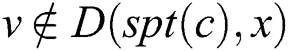and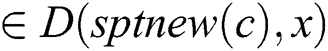 
, then we can obtain 
.
Proof: Assuming that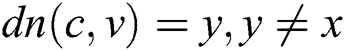 
in the 
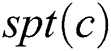, we have
.
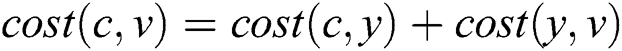Given that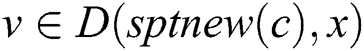
, we can obtain 
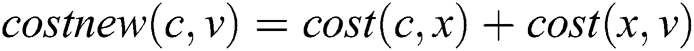., where 
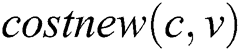is the cost from node 
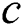to node 
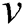in the 
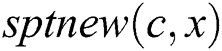. Because 
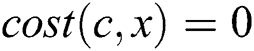in the 
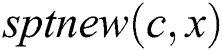, we can get 
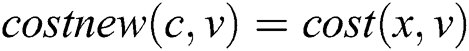(1). According to that 
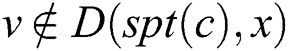and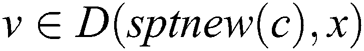
, we can obtain 
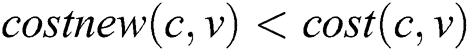(2). Combining Eqs. (1) and (2), we have
.
Theorem 2: Given a computing node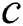
and 
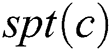, for any node
, 
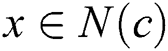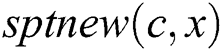is the new SPT rooted at node
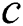when the weight of link 
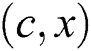is changed to 0. For any node 
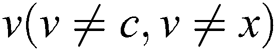, if
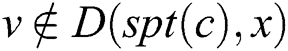and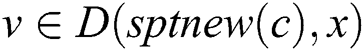
, then we can obtain 
.
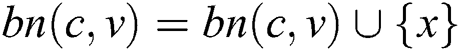Proof: As seen in Theorem 1 and DC rule, node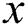 
is a viable backup next-hop from node 
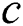to node
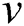; therefore, we can obtain 
.
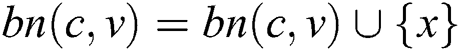We will use an example to explain Theorems 1 and 2. Fig. 1 shows a SPT rooted at node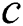
, whereas Figs. 2 and 3 represent the new SPT when links 
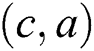and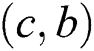 
are changed to 0, respectively. Because
, 
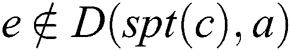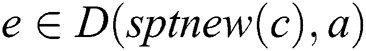, node 
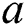can be a viable backup next-hop from 
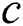to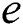 
. Given that 
, 
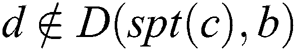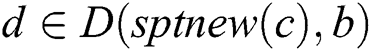, node 
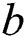can be a viable backup next-hop from 
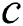to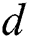 
. Considering that 
,
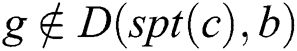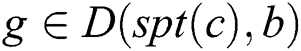, node 
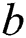can be a viable backup next-hop from 
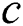to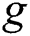 
.
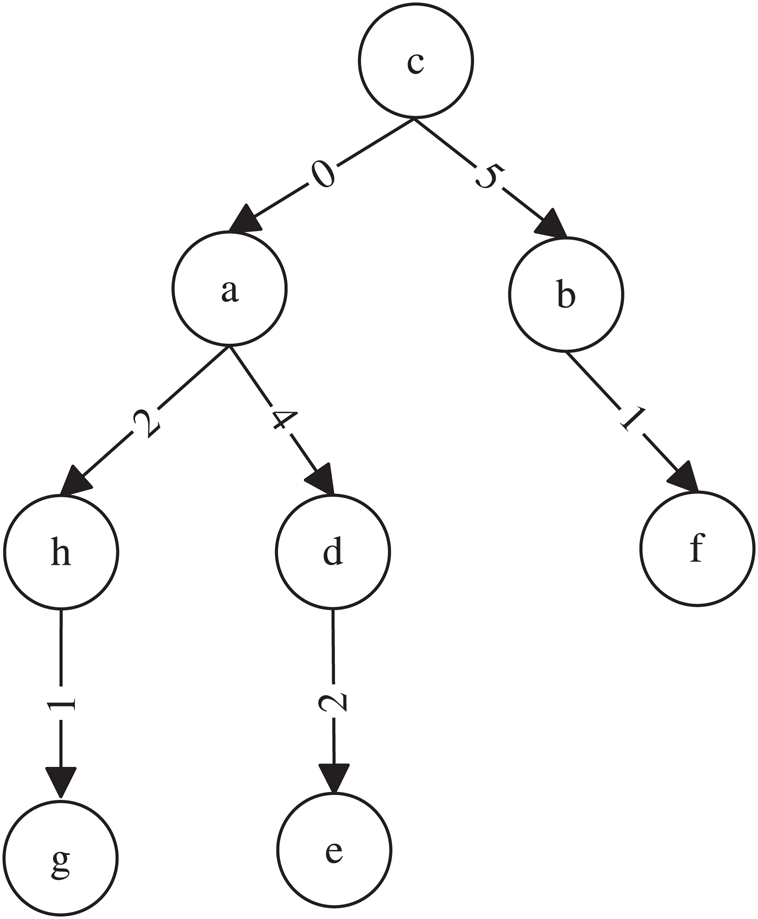
Figure 2: SPT rooted at node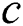 
when the weight of link 
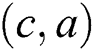is changed to 0
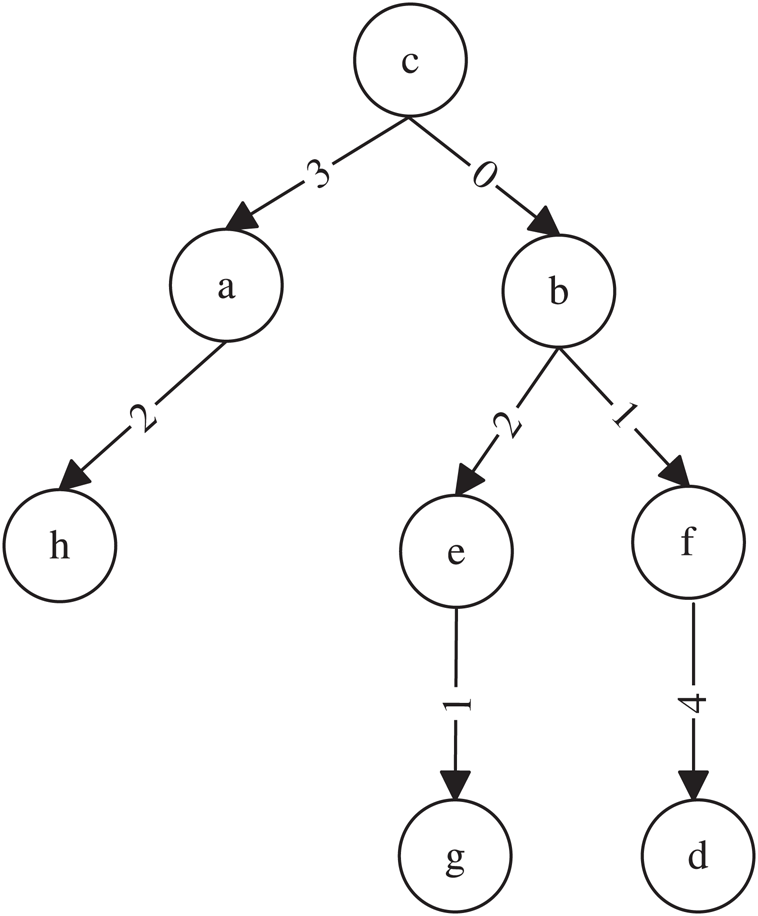
Figure 3: SPT rooted at node c when the weight of link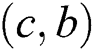 
is changed to 0
According to the above discussions, ERPA is proposed to compute the backup next-hop set that satisfies the DC rule. The inputs of ERPA include the network topology 
and
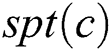, and the output is the backup next-hop set from node 
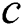to all the other nodes in the network. First, for each neighbor 
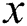of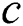 
, the weight of the link 
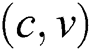is changed into 0 (lines 2–3), and then a new SPT is built by employing i-SPF (line 4). For any node
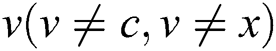, if
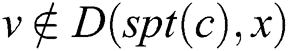and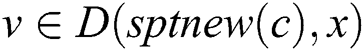
, then the node 
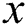can be a viable backup next-hop from 
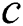to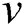 
(lines 5–9). At last, the weight of the link 
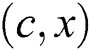is adjusted to its original value (line 10).
4.2 Algorithm Performance and Discussion
In this section, we will show the performance of the algorithm, including the time complexity and the number of backup next-hop computed by ERPA. Theorem 3 suggests that the computational complexity of ERPA is less than that of constructing a SPT. In Theorem 4, ERPA can compute all the backup next-hop sets that satisfy the DC Rule. We will describe Theorems 3 and 4 in detail and prove their correctness.
Theorem 3: Computational complexity of ERPA is less than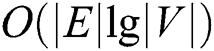
.
Proof: To compute all the backup next-hop set from node c to other nodes in the network. ERPA needs to run the i-SPF algorithm k times, where k is the number of neighbors of node c. Let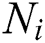 
and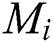 
indicate the number of nodes that must adjust their costs or parents and the number of edges attached to these nodes when the weight of link 
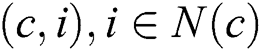is changed to 0, respectively. Therefore, the computational complexity of ERPA is
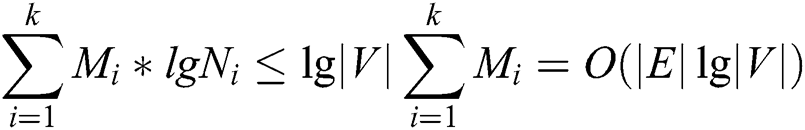
Considering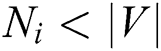 
, the computational complexity of ERPA is less than that of SPF.
Theorem 4: ERPA can compute all the backup next-hop set that satisfies the DC Rule.
Proof: We will prove the theorem by contradiction. Supposing that node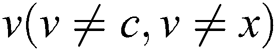
,
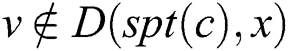and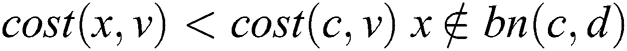 
exist when ERPA is terminated. For any node 
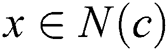, if
, then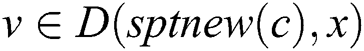
. Therefore, according to Theorem 2, we can obtain. Thus, 
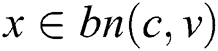contradicts the assumptions.
In this section, we will evaluate ERPA in terms of computation overhead and network availability. To indicate the performance of ERPA, we compare the results with TBFH, DMPA, and DC. All the algorithms are implemented on a PC (Intel i7, 3.7 GHz CPU, and 8G memory). All of the experimental results correspond to the average values of 15 random experiments. To truly reflect the link failure distribution, the failure probability of links in this paper adopts Weibull distribution
We conduct the simulations on a wide space of relevant topologies, including real, inferred, and synthetic ones. The real topology includes Abilene, USLD, ITALY, NJLATA, and TORONTO [16], as well as six ISP topologies that are inferred from the measurement results from Rocketfuel [17]. The parameters for real and Rocketfuel topology are summarized in Tab. 2. We also use BRITE [18] to generate some topologies, the numbers of nodes range from 100 to 1000, and the average node degree ranges from 5 to 40. The detailed parameters for BRITE are shown in Tab. 3.
Table 2: Parameters for Rocketfuel Topology
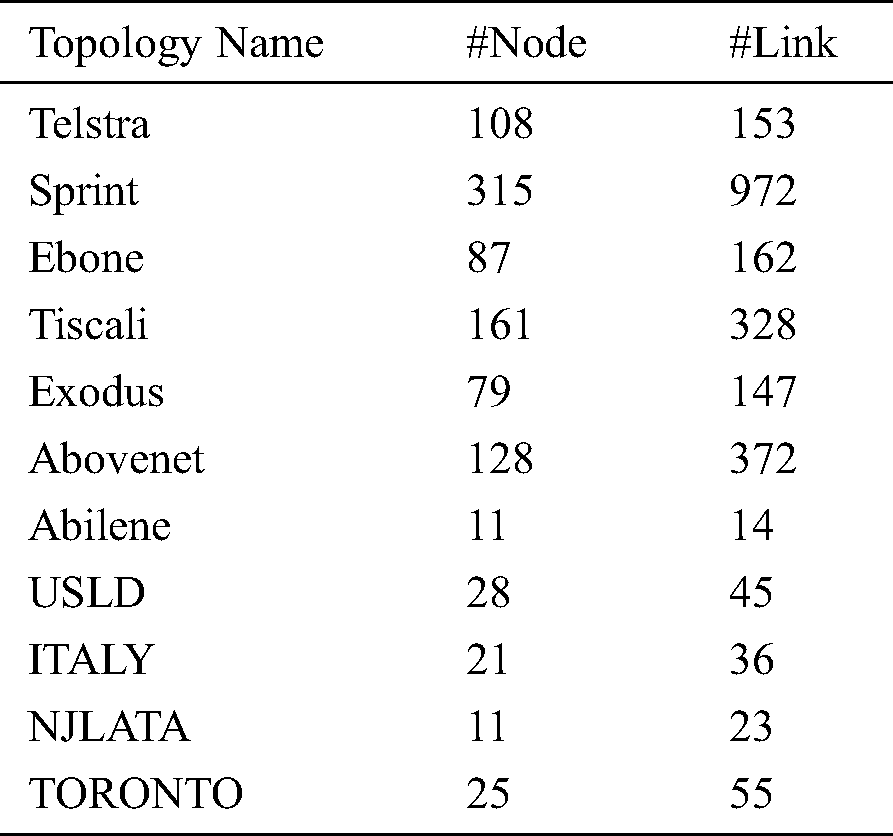
Table 3: Parameters for BRITE Topology
Theoretical analysis has indicated that the time complexity of ERPA is less than that of constructing a SPT, which has a great advantage over DC, TBFH, and DMPA. To further verify computational performance, we make simulations on different types of topologies. In this section, we evaluate the computational overhead of different algorithms on three types of topologies to avoid the uncertain impact of factors on the algorithm’s performance. The computational overhead of an algorithm is defined as the ratio of computation time of the algorithm to that of constructing a SPT.
Fig. 4 indicates the computational overhead obtained by different algorithms on real and Rocketfuel topologies. Fig. 4 shows that ERPA has the lowest computation overhead among all the algorithms. The computation overhead of ERPA is less than building a SPT, whereas DMPA need to construct a SPT, and TBFH need to compute two SPTs. The computation overhead of DC is proportional to the degree of the network average node degree.
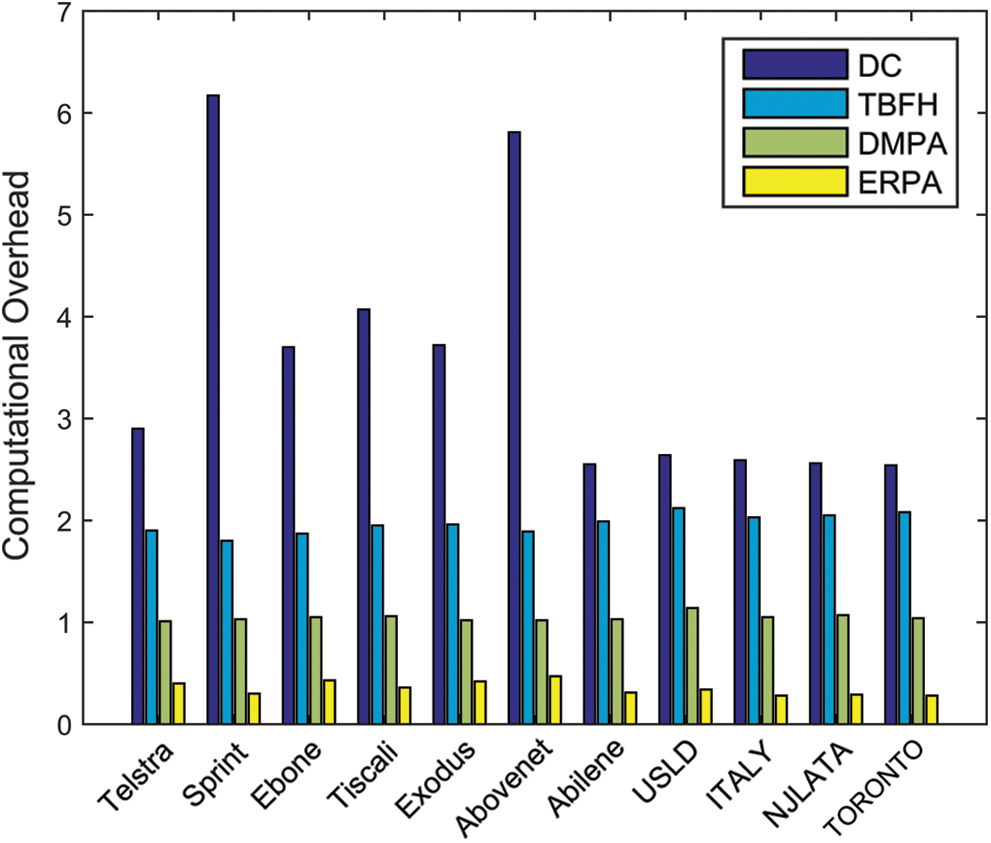
Figure 4: Computational overhead on Real and Rocketfuel topologies
Fig. 5 illustrates the relationship between the computation overhead and topology size on generated topologies when the average node degree is 8. In Fig. 5, the computation overhead does not depend on the topology size for all the four simulated algorithms. The computation overhead of ERPA is lowest in the four algorithms among all the topologies.
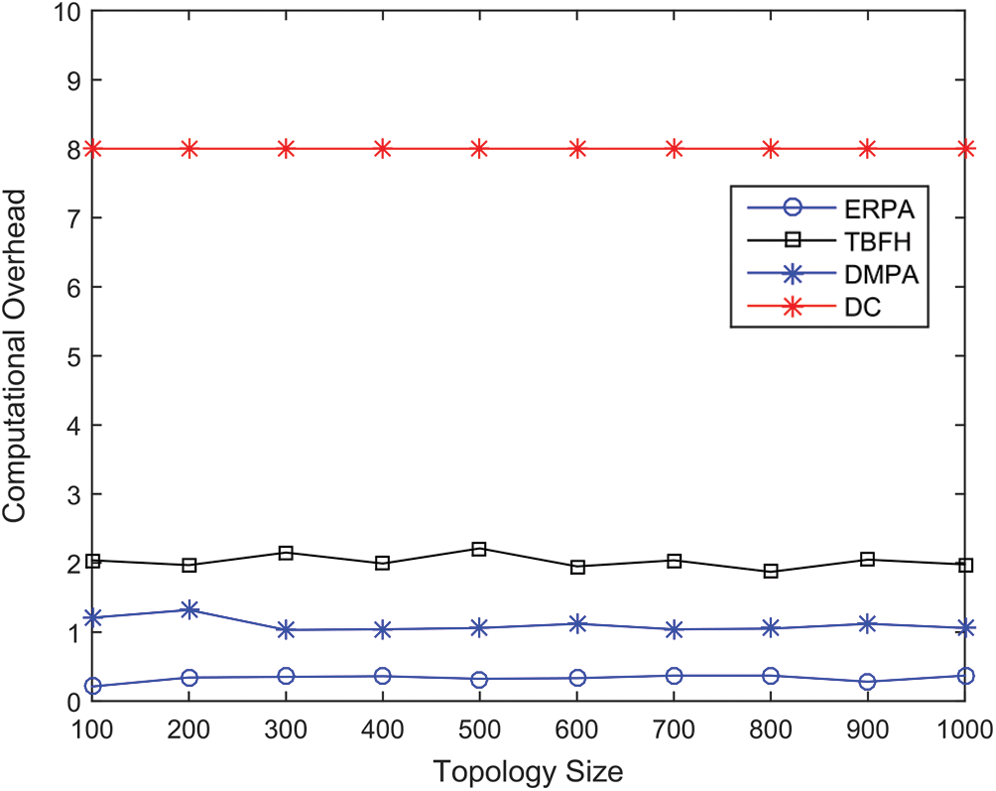
Figure 5: Computational overhead on Brite topologies
Fig. 6 shows the relationship between the computation overhead and average node degree on Brite topologies when the topology size is 1000. As the average node degree increases, the computation overhead of DC rises accordingly. Also, ERPA has exhibited the best performance among all of the tested algorithms. Therefore, the above experiment results are consistent with the theoretical analysis on computational complexity.
Figure 6: Computational overhead on Brite topologies
In this section, we will employ network availability as our main evaluation criterion to assess the reliability of the network. Network availability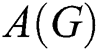 
can be formally defined as:
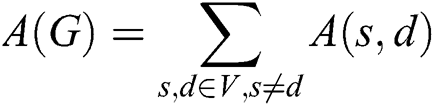
where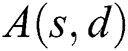 
is the availability of source–destination 
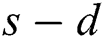pairs. We will describe the computation of 
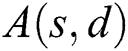in the following. Supposing that 
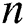different paths exist from 
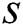to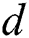 
, we use 
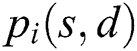to denote the i-th path in them. We use 
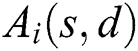to indicate 
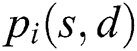works. The probability of 
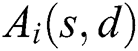can be written as:
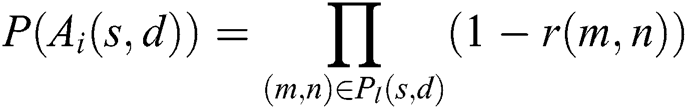
According to the inclusion–exclusion principle,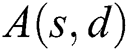 
be expressed as:
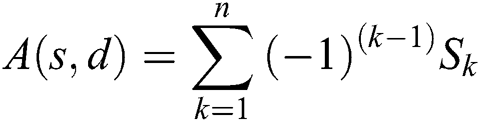
where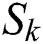 
is the total sum of the probabilities that a unique set of 
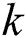paths from 
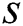to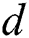 
are working simultaneously and can be expressed as:
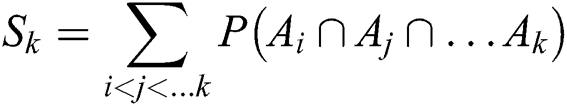
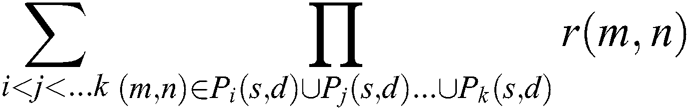
Tab. 4 provides the network availability provided by each protection scheme on real and inferred network topologies. The results show that ERPA has a clear advantage over TBFH and DMPA and has the same performance as DC. Therefore, the experimental results of network availability are consistent with those of the theoretical analysis.
Table 4: Network availability on Abilene and Rocketfuel topologies
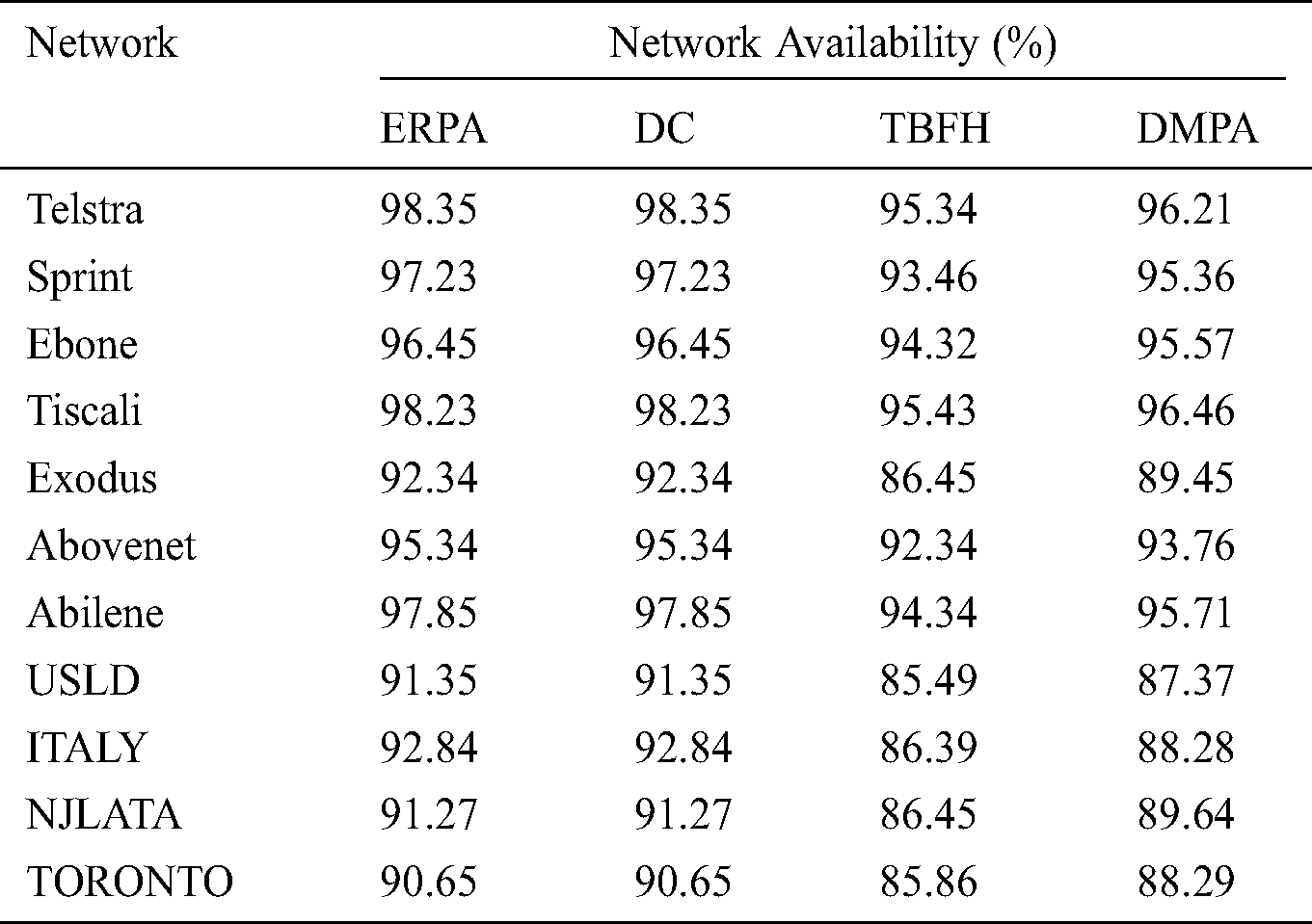
Fig. 7 illustrates the relationship between the network availability and the average node degree. The network availability increases with the average node degree. Notably, when the average node degree increases, all schemes provide better network availability results, whereas ERPA and DC are always better than those of DMPA and TBFH. Fig. 8 shows the relationship between network availability and topology size on generated topologies when the average node degree is 6. Fig. 8 shows that the network availability performance of ERPA and DC is obviously better than the two other algorithms. From the experiment, we can conclude that ERPA not only reduces the complexity of DC implementation greatly but also has the same routing availability as DC.
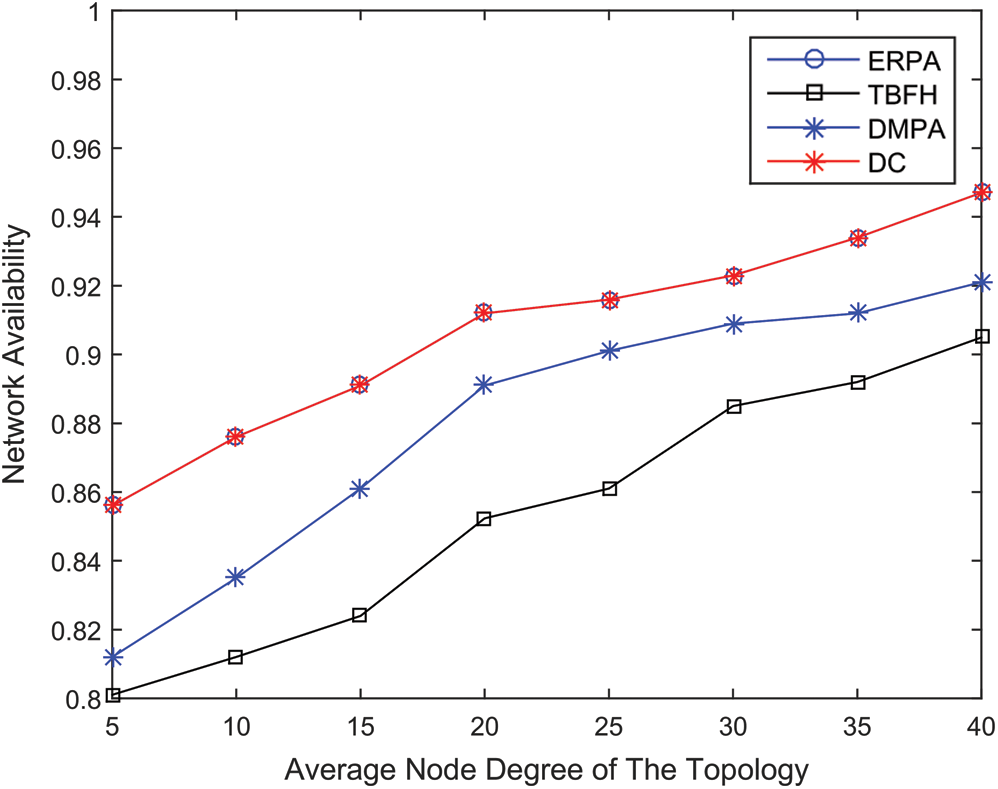
Figure 7: Network availability on Brite topologies
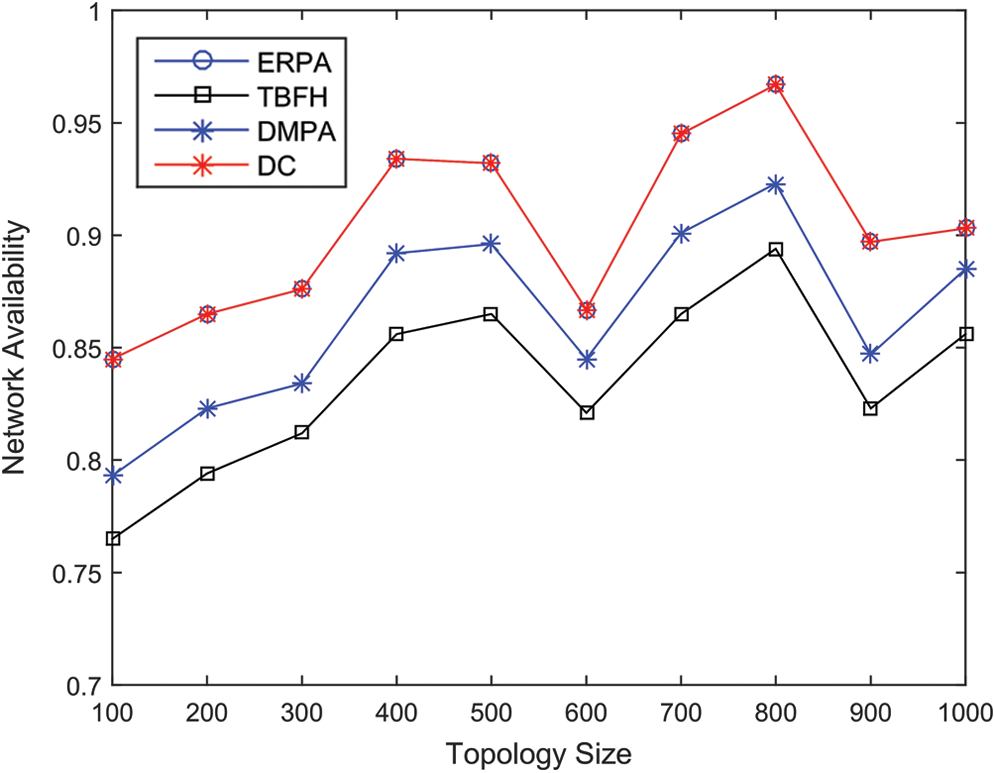
Figure 8: Network availability on Brite topologies
This study proposed an efficient scheme called ERPA to implement DC-based hop-by-hop routing protection. The computation complexity of ERPA is irrespective of the degree of the calculating router and is less than a full SPT calculation. We simulate ERPA on numerous topologies in comparison with DC, DMPA, and TBFH. The theoretical and experimental results show that ERPA can reduce the computational overhead and can provide the same network availability as DC dramatically. We are convinced that our proposed scheme ERPA takes a big step toward actual deployment.
Funding Statement: This work is supported by the National Natural Science Foundation of China (No. 61702315), the Key R&D program (international science and technology cooperation project) of Shanxi Province China (No. 201903D421003), the National Key Research and Development Program of China (No. 2018YFB1800401).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. F. Klaus-Tycho, P. Yvonne-Anne, S. Stefan and T. Gilles. (2018). “Local fast failover routing with low stretch,” ACM Sigcomm Computer Communication Review, vol. 48, no. 1, pp. 35–41. [Google Scholar]
2. Z. Yang and K. L. Yeung. (2020). “SDN candidate selection in hybrid IP/SDN networks for single link failure protection,” IEEE/ACM Transactions on Networking, vol. 28, no. 1, pp. 312–321. [Google Scholar]
3. S. Petale and J. Thangaraj. (2020). “Link failure recovery mechanism in software defined networks,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 7, pp. 1285–1292. [Google Scholar]
4. S. G. Kulkarni, G. Liu, K. K. Ramakrishnan, M. Arumaithurai, T. Wood et al. (2020). , “REINFORCE: Achieving efficient failure resiliency for network function virtualization-based services,” IEEE/ACM Transactions on Networking, vol. 28, no. 2, pp. 695–708. [Google Scholar]
5. T. Liu and J. C. S. Lui. (2020). “FAVE: A fast and efficient network flow availability estimation method with bounded relative error,” IEEE/ACM Transactions on Networking, vol. 28, no. 2, pp. 505–518. [Google Scholar]
6. Y. Wang, S. X. Feng, H. T. Guo, X. S. Qiu and H. B. An. (2019). “A single-link failure recovery approach based on resource sharing and performance prediction in SDN,” IEEE Access, vol. 7, pp. 174750–174763. [Google Scholar]
7. J. Q. Zheng, H. Xu, X. J. Zhu, G. H. Chen and Y. H. Geng. (2019). “Sentinel: Failure recovery in centralized traffic engineering,” IEEE/ACM Transactions on Networking, vol. 27, no. 5, pp. 1859–1872. [Google Scholar]
8. X. W. Yang and D. Wetherall. (2006). “Source selectable path diversity via routing deflections,” in Proc. of the SIGCOMM, Pisa, Italy, pp. 159–170. [Google Scholar]
9. H. J. Geng, X. G. Shi, Z. L. Wang, X. Yin and S. P. Yin. (2017). “Algebra and algorithms for multipath QoS routing in link state networks,” Journal of Communications and Networks, vol. 19, no. 2, pp. 189–200. [Google Scholar]
10. M. Motiwala, M. Elmore, N. Feamster and S. Vempala. (2008). “Path splicing,” in Proc. of the SIGCOMM, Seattle, WA, USA, pp. 27–38. [Google Scholar]
11. S. Antonakopoulos, Y. Bejerano and P. Koppol. (2015). “Full protection made easy: The DisPath IP fast reroute scheme,” IEEE/ACM Transactions on Networking, vol. 23, no. 4, pp. 1229–1242. [Google Scholar]
12. S. Cho, T. Elhourani and S. Ramasubramanian. (2012). “Independent directed acyclic graphs for resilient multipath routing,” IEEE/ACM Transactions on Networking, vol. 20, no. 1, pp. 153–162. [Google Scholar]
13. Y. Yang, M. W. Xu and Q. Li. (2018). “Fast re-routing against multi-link failures without topology constraint,” IEEE/ACM Transactions on Networking, vol. 26, no. 1, pp. 384–397. [Google Scholar]
14. P. Mérindol, P. Francois, O. Bonaventure, S. Cateloin and J. J. Pansiot. (2011). “An efficient algorithm to enable path diversity in link state routing networks,” Computer Networks, vol. 55, no. 5, pp. 1132–1149. [Google Scholar]
15. H. J. Geng, X. G. Shi, Z. L. Wang and X. Yin. (2018). “A hop-by-hop dynamic distributed multipath routing mechanism for link state network,” Computer Communications, vol. 116, no. 4, pp. 225–239. [Google Scholar]
16. W. Braun and M. Menth. (2015). “Loop-free alternates with loop detection for fast reroute in software-defined carrier and data center networks,” Journal of Network and Systems Management, vol. 24, no. 3, pp. 470–490. [Google Scholar]
17. N. Spring, R. Mahajan, D. Wetherall and T. Anderson. (2004). “Measuring ISP topologies with Rocketfuel,” IEEE/ACM Transactions on Networking, vol. 12, no. 1, pp. 2–16. [Google Scholar]
18. H. J. Geng, J. Y. Yao and Y. Y. Zhang. (2020). “Single failure routing protection algorithm in the hybrid SDN network,” Computers, Materials & Continua, vol. 64, no. 1, pp. 665–679. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |