DOI:10.32604/cmc.2020.012677
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012677 | |
| Article |
Darcy-Forchheimer Hybrid Nano Fluid Flow with Mixed Convection Past an Inclined Cylinder
1Department of Mathematics, City University of Science and Information Technology, Peshawar, 25000, Pakistan
2Department of Basic Sciences and Humanities, College of Computer and Information Sciences, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
3Department of Information Technology, Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, 80261, Saudi Arabia
4Basic Sciences Department, Deanship of Preparatory Year, King Faisal University, Al Ahsa, 31982, Saudi Arabia
5Center of Excellence in Theoretical and Computational Science (TaCS-CoE), SCL 802 Fixed Point Laboratory, Science Laboratory Building, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, 10140, Thailand
*Corresponding Author: Taza Gul. Email: tazagul@cusit.edu
Received: 08 July 2020; Accepted: 01 October 2020
Abstract: This article aims to investigate the Darcy Forchhemier mixed convection flow of the hybrid nanofluid through an inclined extending cylinder. Two different nanoparticles such as carbon nanotubes (CNTs) and iron oxide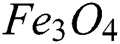 
have been added to the base fluid in order to prepare a hybrid nanofluid. Nonlinear partial differential equations for momentum, energy and convective diffusion have been changed into dimensionless ordinary differential equations after using Von Karman approach. Homotopy analysis method (HAM), a powerful analytical approach has been used to find the solution to the given problem. The effects of the physical constraints on velocity, concentration and temperature profile have been drawn as well for discussion purpose. The numerical outcomes have been carried out for the drag force, heat transfer rate and diffusion rate etc. The Biot number of heat and mass transfer affects the fluid temperature whereas the Forchhemier parameter and the inclination angle decrease the velocity of the fluid flow. The results show that hybrid nanofluid is the best source of enhancing heat transfer and can be used for cooling purposes as well.
Keywords: Mixed convection; similarity transformation; HAM; hybrid nanofluid; CNTs; Darcy Forchhemier; inclined cylinder
The study of the hybrid nanofluid in the existence of mass and heat transfer has received special attention from many scientists and researchers because of its essential role in the field of science and technology [1]. The convection of the hybrid nanofluid flow, together with heat and mass transfer, has several important applications in industry such as oil reservoir, suspension and colloidal solution, bioengineering, nuclear industries, polymer solution, paper production, geophysics, chemical industries and exotic lubricants etc. [2–6]. The fluid like kerosene oil, water, acetone, engine oil and ethylene glycol has low thermal conductivity. In the era of modern science and technology, the extensive need for thermal energy cannot be fulfilled through commonly used fluids. However, a significant enhancement in thermal characteristics was noted when these base liquids were synthesized with the addition of small sized particles [7]. Thus, this rise in the thermal properties of ordinary fluids developed the keen curiosity of scientists for further investigations. Numerous researches on nanoparticles and carbon nanotubes CNTs, both single walled carbon nanotubes and multi-walled carbon nanotubes (SWCNTs and MWCNTs) have been carried out by the researchers. CNTs are the allotropes of carbon with a nano cylindrical structure. The CNTs are frequently used in the energy sector and Nanoscience [8]. The mixture of copper oxide and water was examined by Animasaun [9]. The water based nanofluid fluid flow of CNTs was analyzed by Aman et al. [10]. The enhancement of the heat transfer rate using the nanofluid of carbon nanotubes was examined by Raza et al. [11]. The impact of the nanofluid using Arrhenius activation energy was examined by Muhammad et al. [12]. The water based iron oxide nanofluid flow was studied by Qasim et al. [13]. The nanofluid of magnetite-ferrium oxide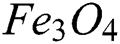 
was examined by Hussanan et al. [14]. The water based aluminum oxide (
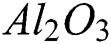) nanofluid was studied by Sheikholeslami et al. [15]. The nanofluid flow through a stirring surface has been studied by Haq et al. [16]. The mixed convection flow of hybrid nanofluid consisting CNTs over a stretching inclined cylinder has tremendous use in the field of mechanical engineering. The mass and heat transfer of nanofluid through an inclined surface is affected due to the buoyancy forces. This type of phenomena plays an important role in the cooling of electronic devices, automobile demister, boilers, defroster system and in solar energy system [17]. The effects of slip flow over time dependent stretching sheet including mixed convection were explored by Makinde et al. [18]. Rashad et al. [19] minutely examined the micropolar fluid flow using double stratified medium. Turkyilmazoglu [20] scrutinized viscoelastic fluid flow with mixed convection over a stretching porous surface. Ashraf et al. [21] investigated the 3D Maxwell fluid flow with mixed convection over an extending inclined surface. The mixed convection flow with double effect of stratification of a Jeffrey fluid past on an extending inclined cylinder has been scrutinized by Hayat et al. [22]. The analytic solution of the nanofluid flow including natural convection over a linearly extending sheet has been presented by Hammad [23]. A survey article has been published by Buongiorno [24] on convection transport through nanofluid. The Darcy-Forchheimer model is the most well-known extension to Darcian flow usually in resemblance with the effects of inertia. The effect of inertia is considered by the insertion of squared terms of the velocity in the momentum equation known as Forchheimer modification. This new term has been named as Forchheimer factor by Muskat [25]. Mondal et al. [26,27] examined non-Darcy Forchheimer model in their research articles over a stretching surface. The Darcy Forchheimer (DF) flow over an upright surface has been studied by Anwar et al. [28]. In order to understand better the problems occurred in the field of physics, it is essential to involve non-Darcy effects in convective transport analysis. The Darcy Forchheimer mixed convective flow in porous media has been examined by Seddek [29]. The DF mixed convection flow of the hybrid nanofluid consisting CNTs through the impermeable inclined cylinder has been investigated minutely in this study. It will lead the researchers to new investigations. The mixed convection flow and heat transfer have several useful applications such as storage and food processing, underground disposing of nuclear wastes and geophysical system [30]. This versatility makes several applications to be studied through the fluid flow over an inclined cylinder for the enhancement of heat and mass transfer. Keep in view the importance and applications of this work, we have extended the idea of [17] and revealed this problem. The results have been achieved through HAM.
The mixed convection Darcy-Forchhimier fluid flow over an inclined stretching cylinder has been examined in this research. The flow has been considered steady and axisymmetric. The physical sketch of the flow has been illustrated in Fig. 1. The analysis of heat and mass transfer has been considered for the hybrid nanofluid consisting CNTs and iron oxide. The analysis of the hybrid nanofluid flow past an extended cylinder has been considered. In the coordinate system, the x-axis and r-axis are considered along the axial and normal direction to the cylinder respectively. After using the boundary layer approximations, the laws have been reduced to the form as follows [17]. The basic flow equations are:
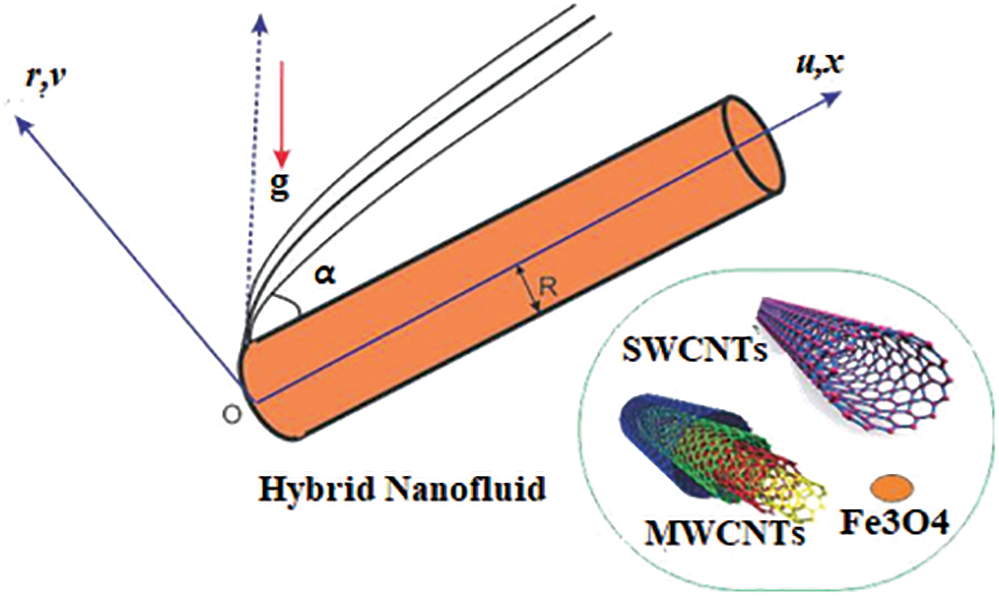
Figure 1: Geometry of the problem
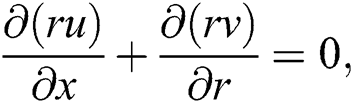
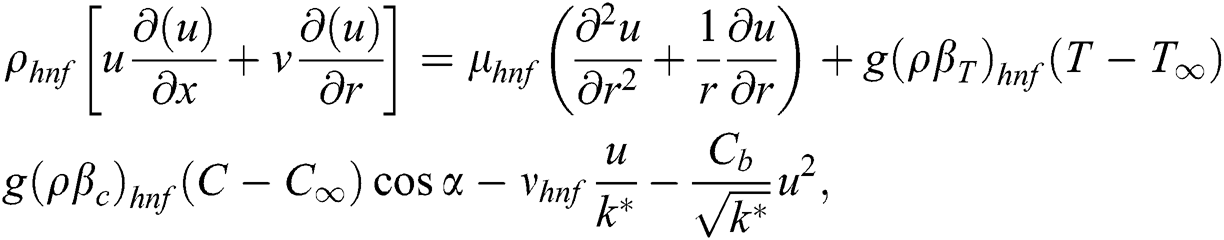
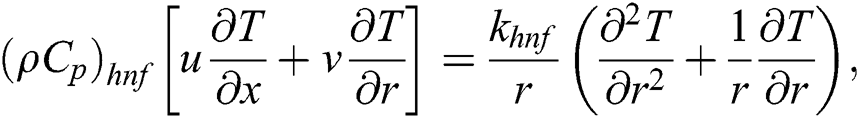
The physical conditions for the governing equations are:
The velocity components u and v have been taken along the axial and normal directions of the cylinder.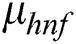 
, 
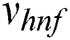and 
demonstrate the dynamic, kinematic and density of hybrid nanoflui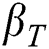d. 
and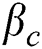 
show the thermal expansion coefficient and the concentration expansion coefficient respectively. Whereas 
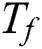and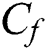 
represents the convective fluid temperature and concentration respectively.
The appropriate transformations are:
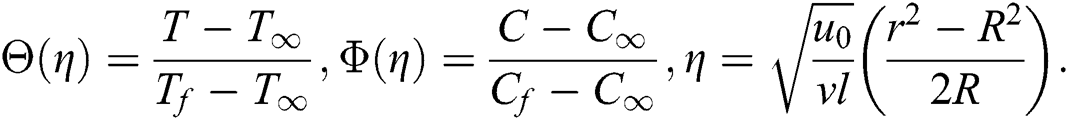
By using Eq. (6) in Eqs. (1)–(5), we get
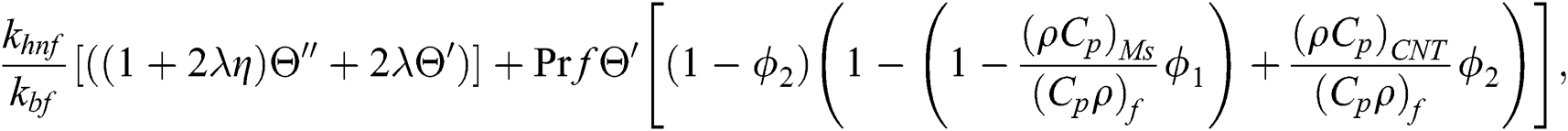
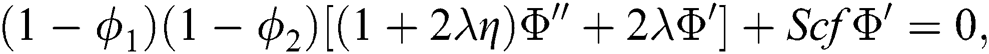
The transformed conditions for nonlinear differential equations are as follows:
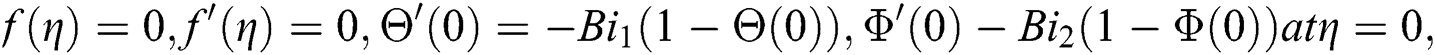
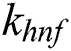is the thermal conductivity and 
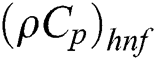is the volumetric heat capacity of hybrid nanofluid as stated in [31]:
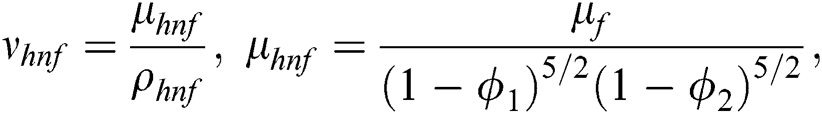
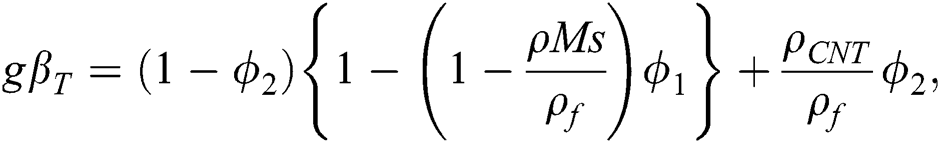
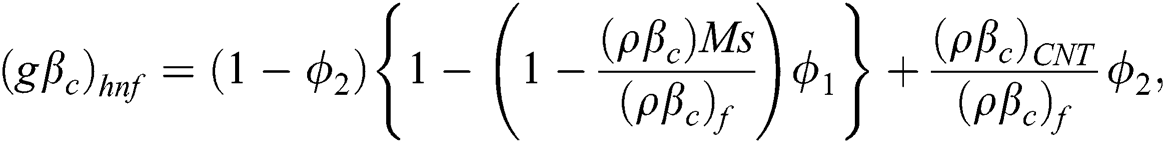
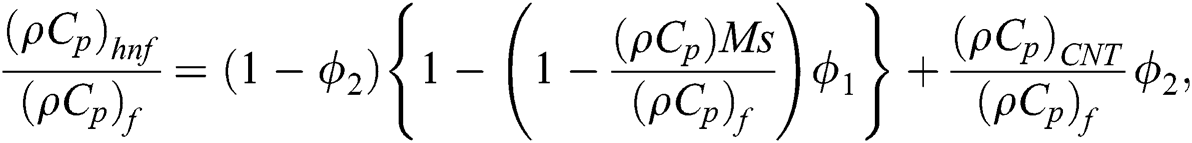
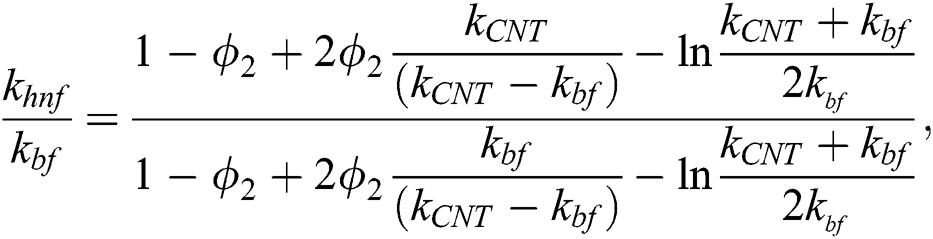
where
The volumetric concentrations of 
and CNTs have been denoted by 
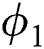and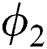 
. Each and every abbreviation has been defined individually. Furthermore, 
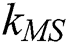and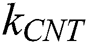 
imply the thermal conductivities of 
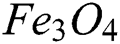and CNTs. 
is the density, 
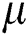is the viscosity and 
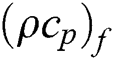is the specific heat of the 
. 
, 
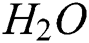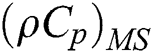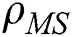, and 
at constant pressure indicate specific heat capacities and densities of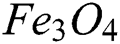 
and CNTs. The Deborah number, Prandtl number and Schmidt number have been denoted by 
, Pr and Sc.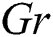 
and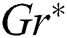 
denote temperature Grashof number and mass Grashof number respectively. Biot numbers 
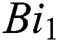and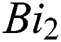 
are for the heat and mass transfer.
The physical constraints have been defined in [17]:
, 
, 
, 
,
, 
, 
, 
.
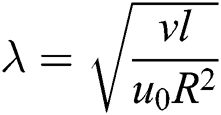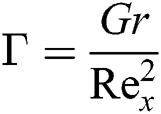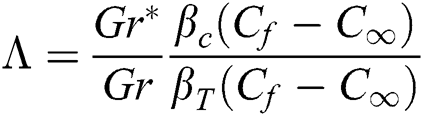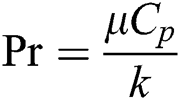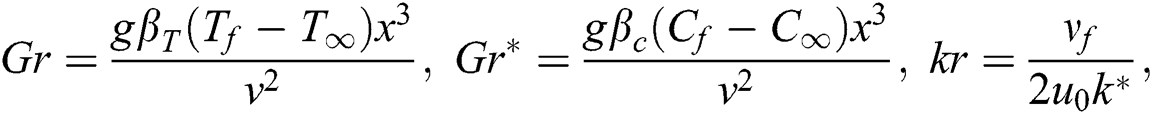
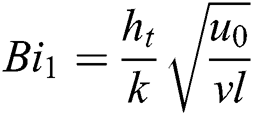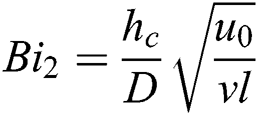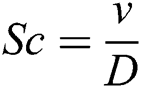The Sherwood number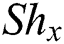 
, the local Nusselt number 
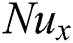and skin friction coefficient have been expressed in dimensional form as follows:
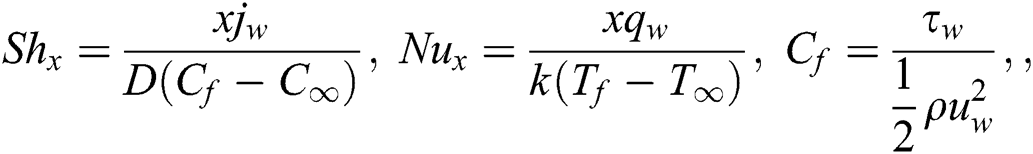
In which surface mass flux, surface heat flux and surface shear stress have been represented by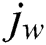
, 
and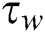 
:
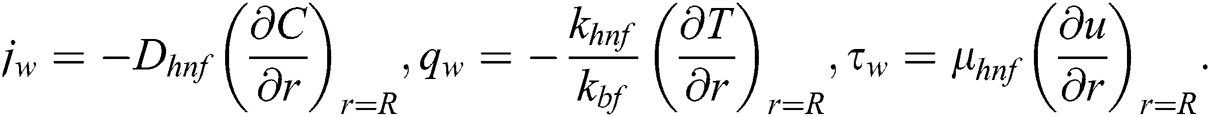
Local Sherwood number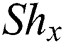 
, the local Nusselt number 
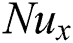and Skin friction coefficient 
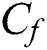are:
The local Reynolds number is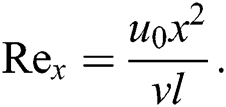 
The current problem has been solved by using HAM technique that was initiated by Liao [32–34]. BVPh 2.0 package [35–42] has been used for the convergence of the modeled problem. The initial approximations for velocity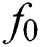 
, temperature 
and concentration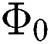 
are given as:
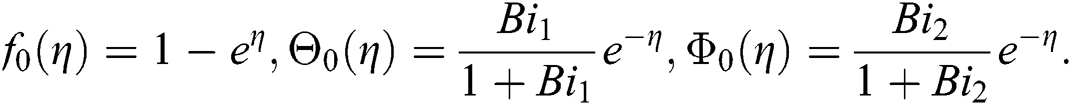
The linear operators 
, 
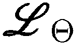and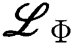 
presented as:
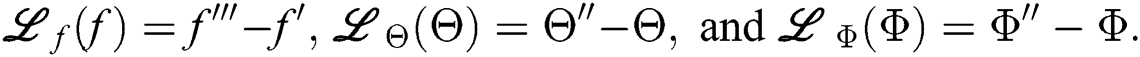
The solved form of 
, 
and 
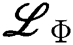are:
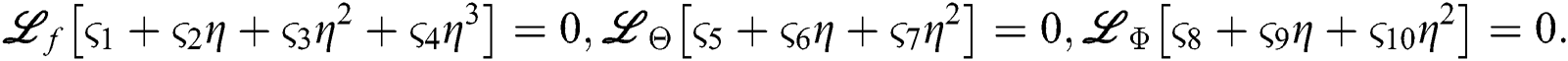
The series introduced by Taylor’s has been used as:
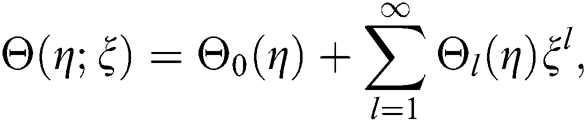
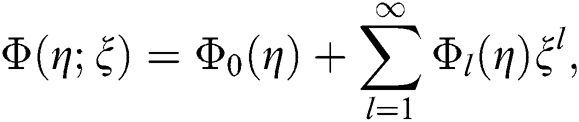
Now
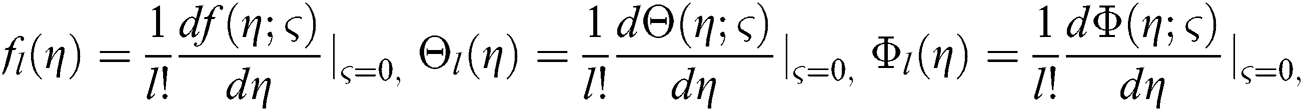
The equations have been further concluded in the form of a system as:
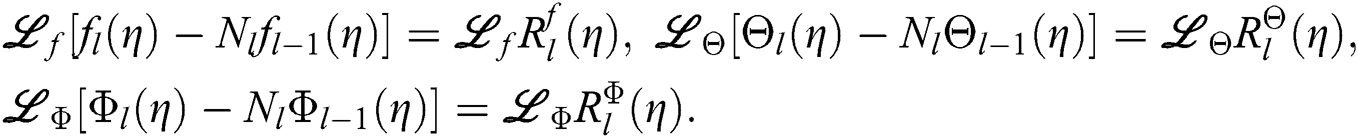
This study aims to use the hybrid nanofluids flow over a stretching cylinder for the rapid heating and cooling applications in the field of thermal engineering. The hybrid nanofluid contains solid particles of the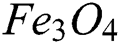 
, 
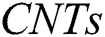and base liquid of 
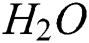. The solid particles disperse in the base liquid and as a result the hybrid nanofluid is prepared. The analytical solution of the system has been obtained through the Homotopy analysis method (HAM). The influence of the constraints has been demonstrated in Figs. 2–16. Fig. 2 reveals the influence of the Farchemmier’s parameter 
on velocity profile. When 
increases, it enhances the transfer of mass in fluid flow which results in a decrease in the velocity of fluid flow. Fig. 3 intends to perceive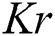 
effects on the velocity field. The rising value of
results in an increase in the fluid kinematic viscosity and consequently declines the velocity of the hybrid nanofluid. The kinematic viscosity of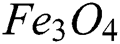 
is greater than the CNTs. Thus, the influence of 
is comparatively large using the iron oxide.
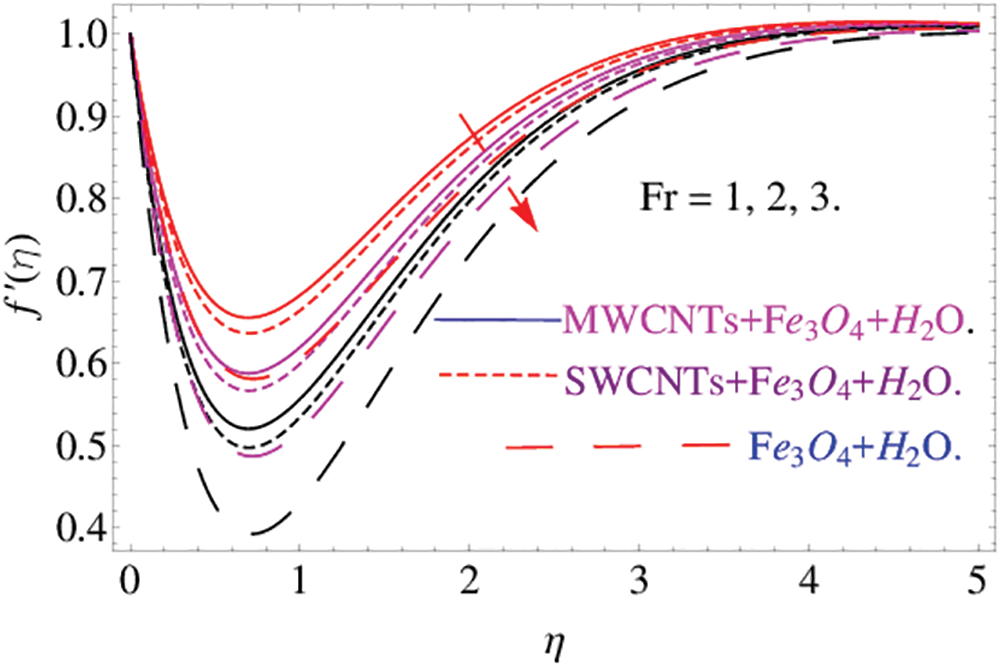
Figure 2: The effects of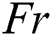 
on velocity profile
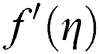when 
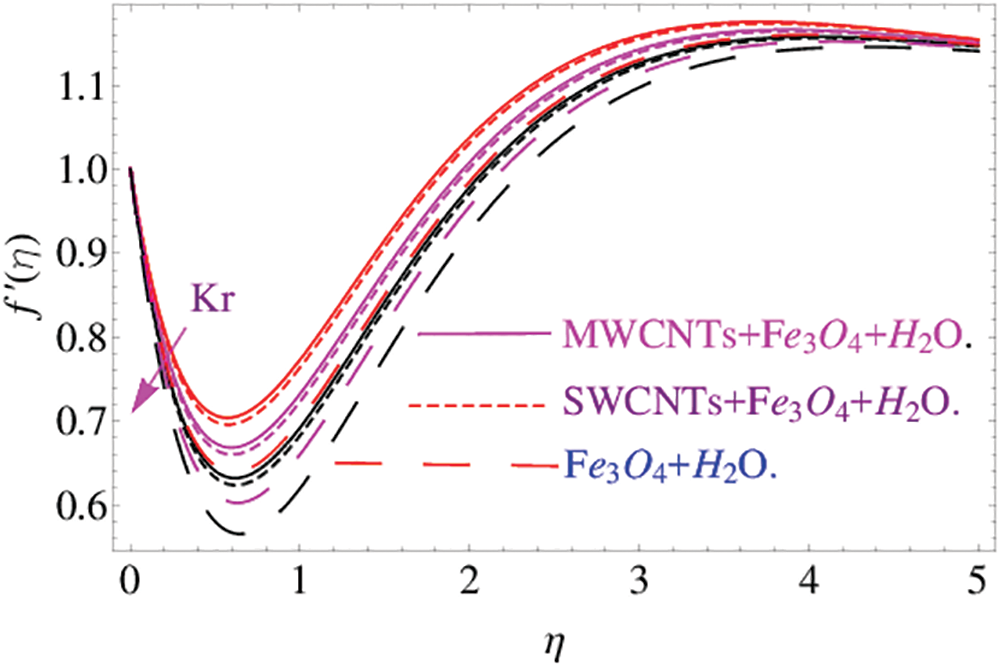
Figure 3: The effects of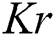 
on velocity profile
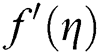when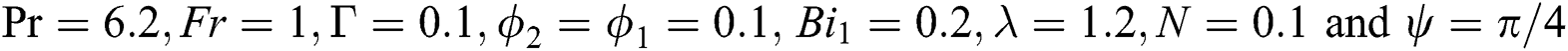 
Fig. 4 has been sketched to reveal the influences of 
(angle of inclination) on both CNTs and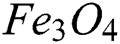 
nanofluid with velocity 
. The increase in the value of the parameter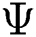 
decreases the velocity field. In fact, decreasing the effect of gravity decreases velocity profile. The decreasing effect of gravity decreases velocity profile. The essential performance of the velocity field 
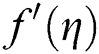with the rising values of 
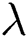has been shown in Fig. 5. As 
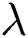is the ratio of relaxation to retardation time, thus, the increase in the values of 
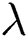(i.e., extending the relaxation time) provides some additional resistance to the flow field. That’s why fluid velocity decreases.
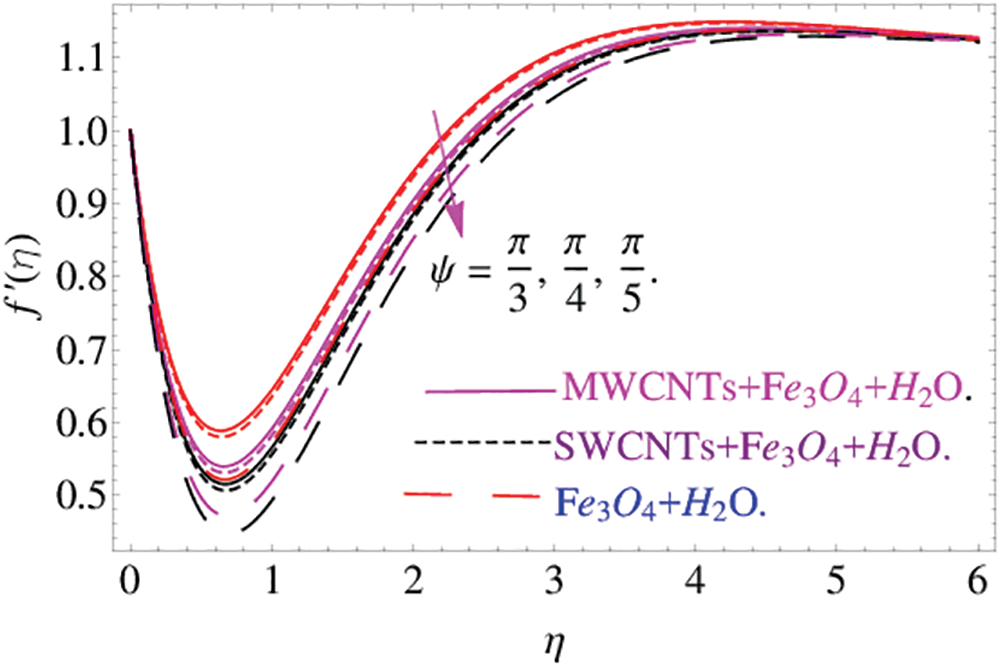
Figure 4: The effects of 
on velocity profile
when
Figure 5: The effects of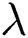 
on velocity profile
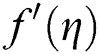when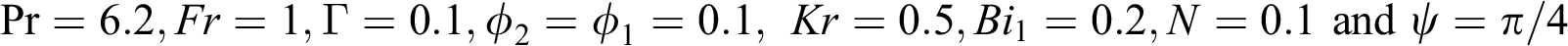
The additional resistance due to relaxation time also enhances the fluid temperature presented in Fig. 6. Fig. 7 shows the effects of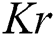
parameter on temperature distribution. The fluid temperature decreases while increasing 
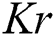. In fact, the kinematic viscosity of the fluid increases which drops the temperature normally.
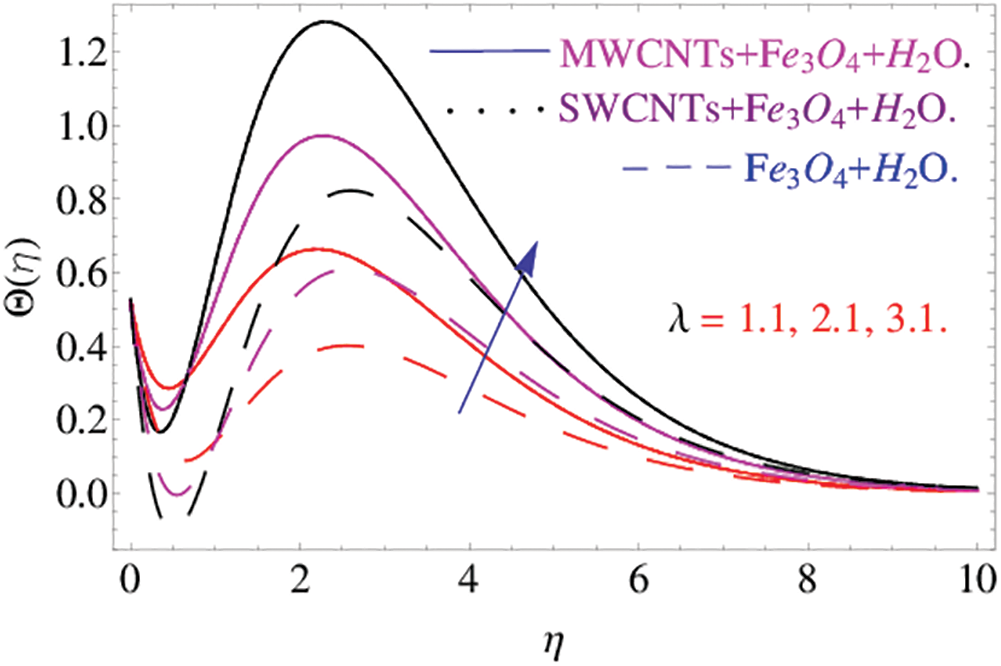
Figure 6: The effects of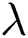 
on temperature distribution
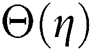when
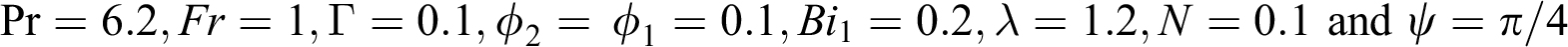
Figure 7: The effects of 
on temperature distribution 
when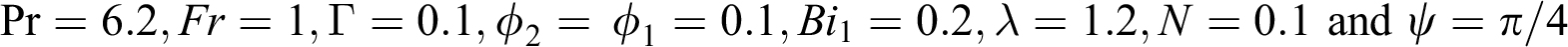
Figs. 8 and 9 demonstrate the variation of temperature distribution with Biot numbers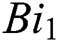 
and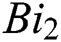 
respectively. Both Biot numbers consist of heat and mass transfer coefficient 
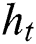and
respectively. Thus, the increase in the values of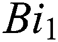 
and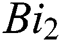 
enriches the thermal boundary layer and concentration field. Which results in an increase in the fluid temperature.
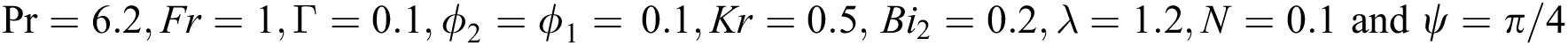
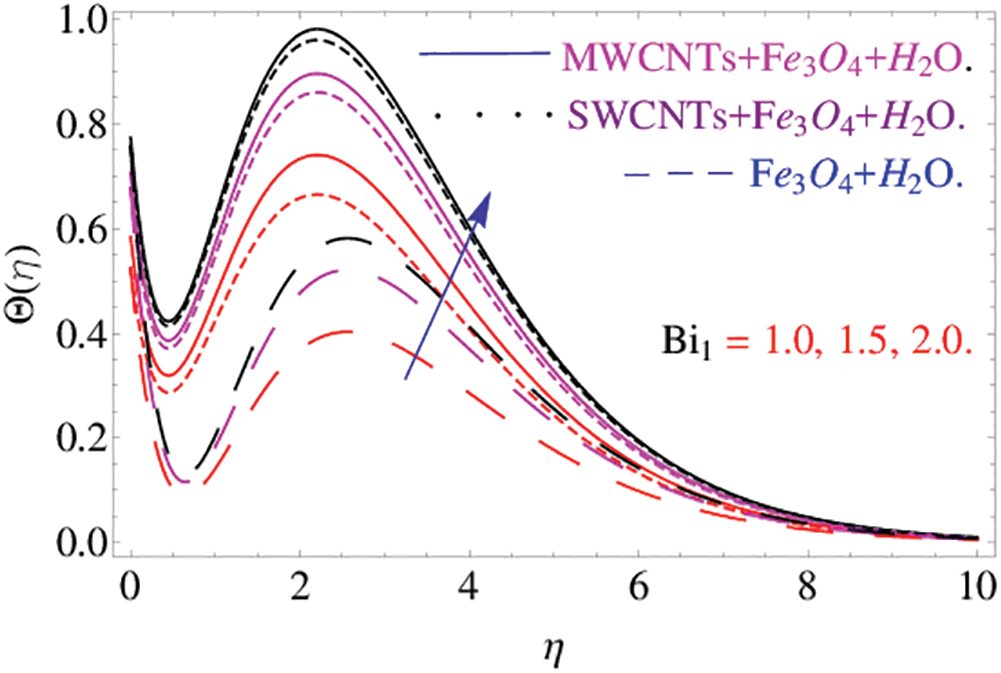
Figure 8: The effects of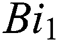 
on temperature distribution 
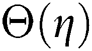when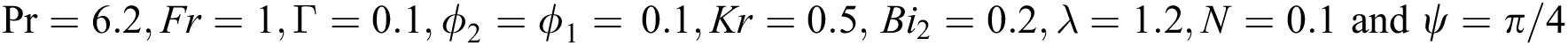
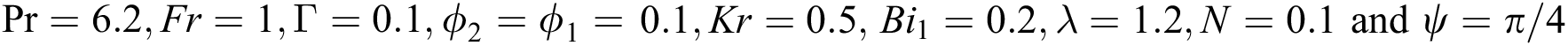
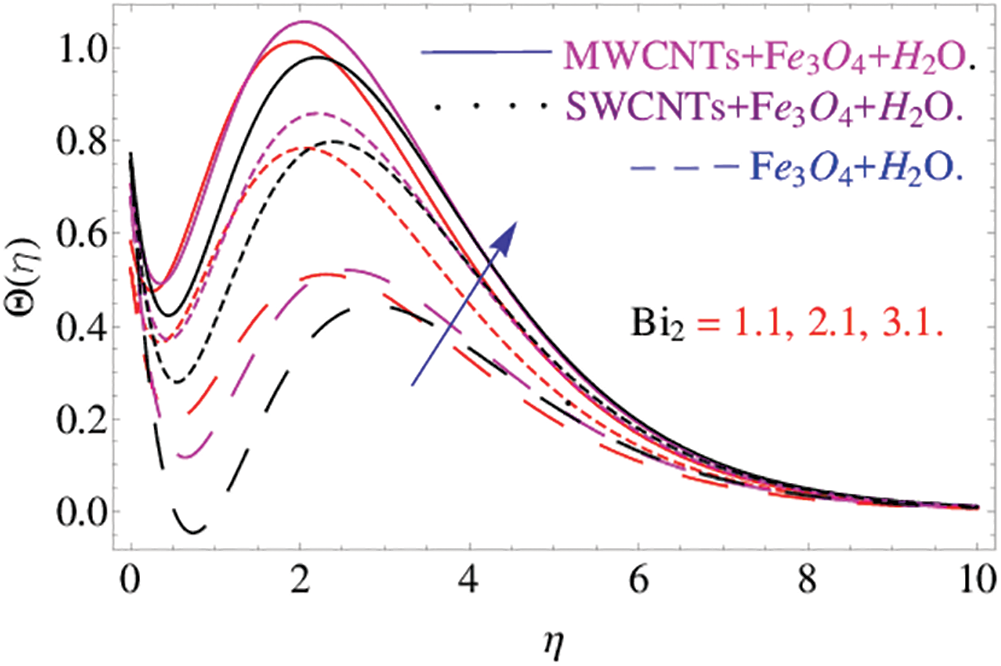
Figure 9: The effects of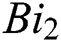 
on temperature distribution 
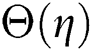when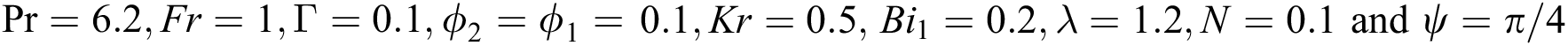
Figs. 10 and 11 describe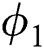 
and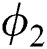 
(volume fraction parameters) of the mentioned nanoparticles that affect the temperature distribution. The volume fraction constraints 
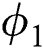and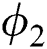 
boost up the temperature field. It has been noticed that the adequate amount of volume fraction can increase thermal property of the base fluid and consequently the temperature of the fluid increases.
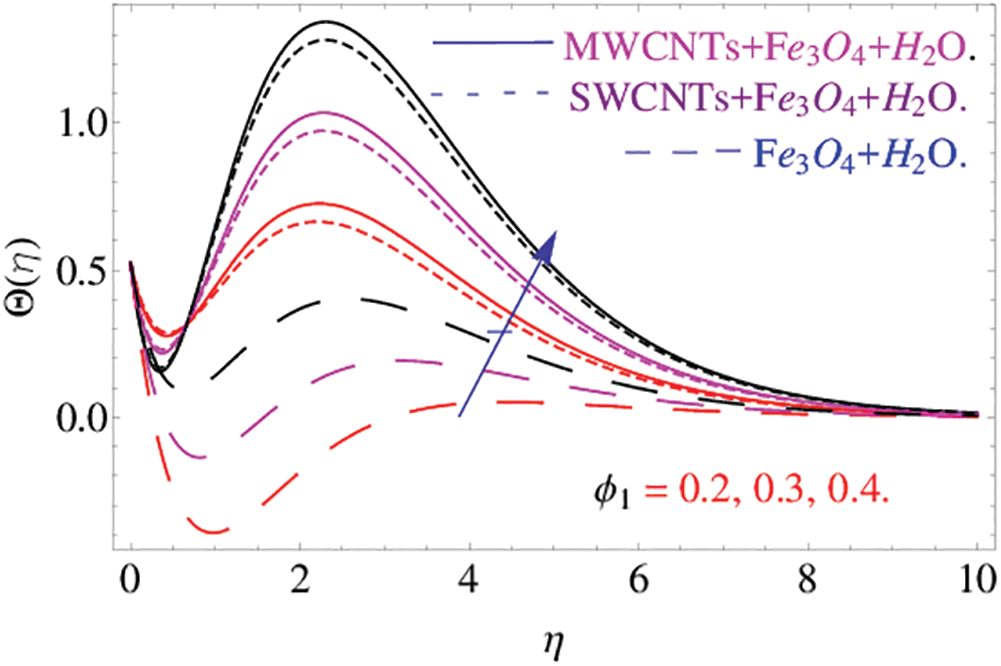
Figure 10: The effects of 
on temperature distribution 
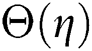when
Figure 11: The effects of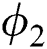 
on temperature distribution 
when
Fig. 12 establishes the changes in the temperature field versus 
. The increasing value of 
reduces the thermal diffusivity, consequently it drops the fluid temperature. Fig. 13 illustrates the Schmidt number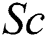 
and its effects on the concentration distribution respectively. It has been observed that Schmidt number is used to increase the thickness of associated boundary layer and concentration.
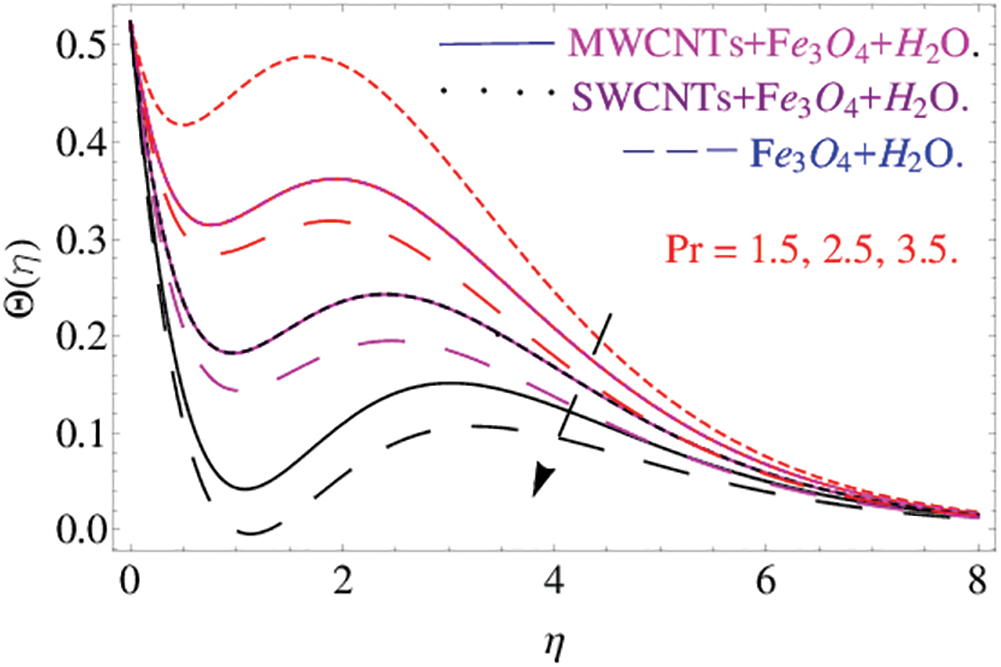
Figure 12: The effects of 
on temperature distribution 
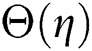when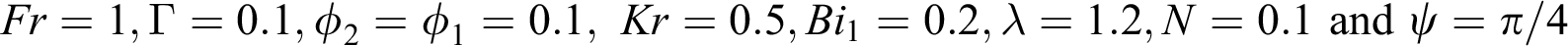
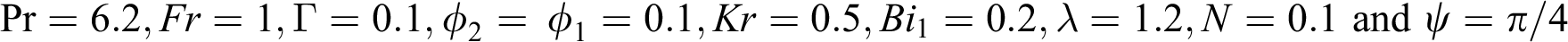
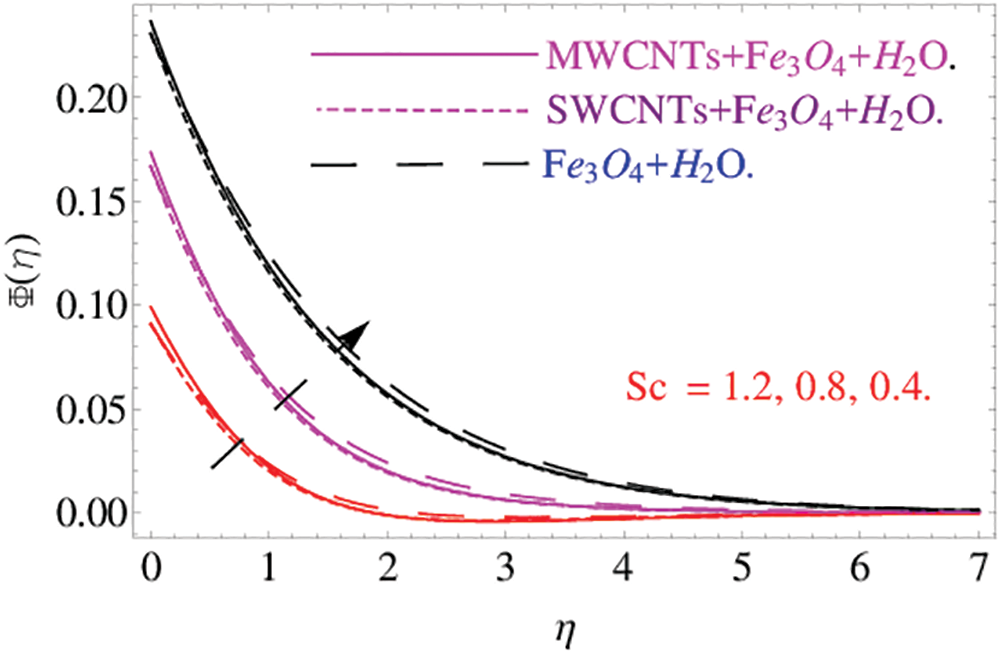
Figure 13: The effects of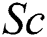 
on concentration distribution 
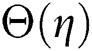when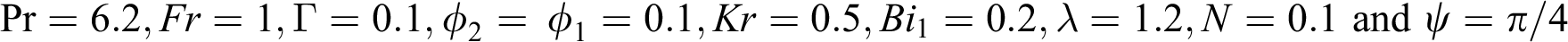
Table 1: Thermo-physical properties of water,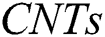 
and 
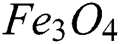nanoparticles
Tab. 1 shows the thermophysical properties of the base fluid and nanoparticles. Tab. 2 shows the effect of the parameters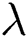 
and 
. It has been observed that skin friction increases due to the resistivity created by the mentioned parameters.
Table 2: Presents the numerical outcomes of skin friction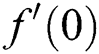 
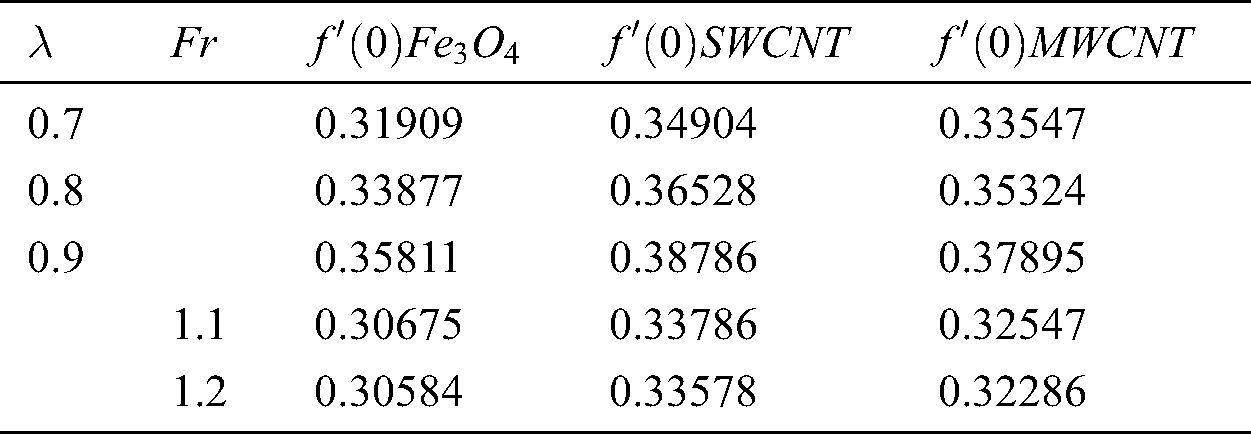
Tab. 3 shows the effects of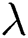 
and 
. It has been noticed that both parameters jointly increase Nusselt number due to the rise in the numerical values of these parameters during the thermal process. Moreover, SWNCTs offer excellence behavior to MWCNTs.
Table 3: Exhibits the numerical outcomes of Nusselt number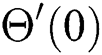 
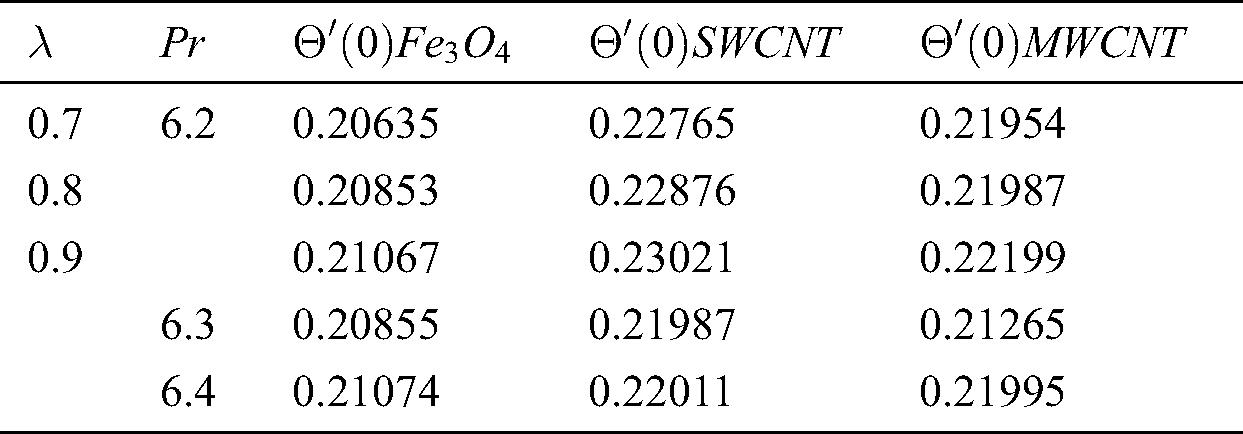
Tab. 4 shows the way 
behaves to Sherwood number. It is mainly found that as the Sherwood number decreases, it results in increasing in Schmidt number. The dominant impact of the SWCNTs is still observed on MWCTs.
Table 4: Shows the numerical outcomes of Sherwood number 
In this work, we have addressed the Darcy Forchhemie’r hybrid nanofluid flow past a stretched and inclined cylinder. The solid nanoparticles of the CNTs and iron oxide have been used for the preparation of hybrid nanofluid. The main findings are as below:
• It has been noticed that increase in the values of the curvature parameter results in an increase in the profiles of the temperature, concentration and velocity of the hybrid nanofluid.
• The Biot numbers are used to improve the concentration and temperature transfer rates.
• In temperature distribution, the role of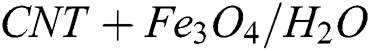 
is more dominant than 
.
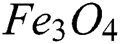• The variation in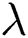 
(mixed convection parameter) increases the velocity profile while the rise in the Skin friction coefficient decreases the velocity field.
• The use of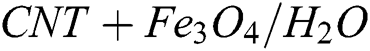 
is more significant to increase the thermal efficiency of the base fluid as compared to the common fluid.
Funding Statement: This research has received no specific funding.
Conflict of Interest: The authors of this research have no conflict of interest.
1. A. Hussanan, M. Z. Salleh, I. Khan and Z. M. Chen. (2019). “Unsteady water functionalized oxide and non-oxide nanofluids flow over an infinite accelerated plate,” Chinese Journal of Physics, vol. 6, no. 2, pp. 115–131. [Google Scholar]
2. J. A. Eastman, U. S. Choi, S. Li, L. J. Thompson and S. Lee, “Enhanced thermal conductivity through the development of nanofluids, Argonne National Lab, IL (United States1996. [Google Scholar]
3. J. A. Eastman, S. U. S. Cho, S. Li, G. Soyez, L. J. Thompson et al. (1999). , “Novel thermal properties of nanostructured materials,” Journal of Metastable Nanocrystal Materials, vol. 2, pp. 629–637.
4. G. M. Moldoveanu, A. A. Minea, G. Huminic and A. Huminic. (2019). “Al2O3/TiO2 hybrid nanofluids thermal conductivity,” Journal of Thermal Analysis and Calorimetry, vol. 13, no. 7, pp. 583–592.
5. K. A. Kumar, N. Sandeep, V. Sugunamma and I. L. Animasaun. (2020). “Effect of irregular heat source/sink on the radiative thin film flow of MHD hybrid ferrofluid,” Journal of Thermal Analysis and Calorimetry, vol. 139, no. 3, pp. 2145–2153.
6. A. Wakif, A. Chamkha, T. Thumma, I. L. Animasaun and R. Sehaqui. (2020). “Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina-copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model,” Journal of Thermal Analysis and Calorimetry, vol. 2, no. 1, pp. 1–20. [Google Scholar]
7. J. Buongiorno, D. C. Venerus, N. Prabhat, T. Mckrell, J. Townsend et al. (2009). , “A benchmark study on the thermal conductivity of nanofluids,” Journal of Applied Physics, vol. 106, no. 9, pp. 294–312. [Google Scholar]
8. R. Kandasamy, R. Mohamad and M. Ismoen. (2016). “Impact of chemical reaction on Cu, Al2O3 and SWCNTs–nanofluid flow under slip conditions,” Engineering Science and Technology, an International Journal, vol. 19, no. 2, pp. 700–709. [Google Scholar]
9. I. L. Animasaun, B. Mahanthesh, A. O. Jagun, T. D. Bankole, R. Sivaraj et al. (2019). , “Significance of Lorentz force and thermoelectric on the flow of 29 nm CuO-water nanofluid on an upper horizontal surface of a paraboloid of revolution,” Journal of Heat Transfer, vol. 141, no. 2, pp. 384–402. [Google Scholar]
10. S. Aman, I. Khan, Z. Ismail, M. Z. Salleh and Q. M. Al-Mdallal. (2017). “Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids,” Scientific Reports, vol. 7, no. 2, pp. 24–45. [Google Scholar]
11. M. Raza, R. Ellahi, S. Sait, M. M. Sarafraz, M. S. Shadloo et al. (2019). , “Enhancement of heat transfer in peristaltic flow in a permeable channel under induced magnetic field using different CNTs,” Journal of Thermal Analysis and Calorimetry, vol. 3, no. 1, pp. 1–15. [Google Scholar]
12. T. Muhammad, H. Waqas, S. A. Khan, R. Ellahi and S. M. Sait. (2020). “Significance of nonlinear thermal radiation in 3D eyring-powell nanofluid flow with arrhenius activation energy,” Journal of Thermal Analysis and Calorimetry, vol. 10, no. 2, pp. 1–16. [Google Scholar]
13. M. Qasim, Z. H. Khan, W. A. Khan and I. A. Shah. (2014). “MHD boundary layer slip flow and heat transfer of ferrofluid along a stretching cylinder with prescribed heat flux,” PLoS One, vol. 9, no. 1, pp. 912–930. [Google Scholar]
14. A. Hussanan, M. Z. Salleh and I. Khan. (2018). “Microstructure and inertial characteristics of a magnetite ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model,” Journal of Molecular Liquids, vol. 255, pp. 64–75. [Google Scholar]
15. M. Sheikholeslami, H. R. Kataria and A. S. Mittal. (2017). “Radiation effects on heat transfer of three dimensional nanofluid flow considering thermal interfacial resistance and micro mixing in suspensions,” Chinese Journal of Physics, vol. 55, no. 6, pp. 2254–2272. [Google Scholar]
16. R. U. Haq, I. Rashid and Z. H. Khan. (2017). “Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface,” Journal of Molecular Liquids, vol. 24, no. 3, pp. 682–688. [Google Scholar]
17. T. Hayat, S. Qayyum, A. Alsaedi and S. Asghar. (2017). “Radiation effects on the mixed convection flow induced by an inclined stretching cylinder with non-uniform heat source/sink,” PLoS One, vol. 12, no. 4, pp. 175–194. [Google Scholar]
18. G. Singh and O. D. Makinde. (2015). “Mixed convection slip flow with temperature jump along a moving plate in presence of free stream,” Thermal Science, vol. 19, no. 1, pp. 119–128. [Google Scholar]
19. A. M. Rashad, S. Abbasbandy and A. J. Chamkha. (2014). “Mixed convection flow of a micropolar fluid over a continuously moving vertical surface immersed in a thermally and solutally stratified medium with chemical reaction,” Journal of the Taiwan Institute of Chemical Engineers, vol. 45, no. 5, pp. 2163–2169. [Google Scholar]
20. M. Turkyilmazoglu. (2013). “The analytical solution of mixed convection heat transfers and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface,” International Journal of Mechanical Sciences, vol. 7, no. 7, pp. 263–268. [Google Scholar]
21. M. B. Ashraf, T. Hayat, S. A. Shehzad and A. Alsaedi. (2015). “Mixed convection radiative flow of three dimensional Maxwell fluid over an inclined stretching sheet in presence of thermophoresis and convective condition,” American Institute of Physics Advances, vol. 5, no. 2, pp. 117–134. [Google Scholar]
22. T. Hayat, S. Qayyum, M. Farooq, A. Alsaedi and M. Ayub. (2017). “Mixed convection flow of Jeffrey fluid along an inclined stretching cylinder with double stratification effect,” Thermal Science, vol. 2, no. 2, pp. 849–862. [Google Scholar]
23. M. A. A. Hamad. (2011). “Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field,” International Communications in Heat and Mass Transfer, vol. 38, no. 4, pp. 487–492. [Google Scholar]
24. J. Buongiorno. (2006). “Convective transport in nanofluids,” Journal of Heat Transfer, vol. 128, no. 3, pp. 240–250. [Google Scholar]
25. M. Muskat. (1938). “The flow of homogeneous fluids through porous media,” Soil Science, vol. 46, no. 2, pp. 1–19. [Google Scholar]
26. D. Pal and H. Mondal. (2011). “Effects of soret dufour, chemical reaction and thermal radiation on MHD non-Darcy unsteady mixed convective heat and mass transfer over a stretching sheet,” Communications in Nonlinear Science and Numerical Simulation, vol. 6, no. 4, pp. 1942–1958. [Google Scholar]
27. D. Pal and H. Mondal. (2014). “Effects of temperature-dependent viscosity and variable thermal conductivity on MHD non-Darcy mixed convective diffusion of species over a stretching sheet,” Journal of the Egyptian Mathematical Society, vol. 22, no. 1, pp. 123–133. [Google Scholar]
28. O. A. Bég, J. Zueco and H. S. Takhar. (2008). “Laminar free convection from a continuously-moving vertical surface in thermally-stratified non-Darcian high-porosity medium: Network numerical study,” International Communications in Heat and Mass Transfer, vol. 35, no. 7, pp. 810–816. [Google Scholar]
29. M. A. Seddeek. (2006). “Influence of viscous dissipation and thermophoresis on Darcy-Forchheimer mixed convection in a fluid saturated porous media,” Journal of Colloid and Interface Science, vol. 293, no. 1, pp. 137–142. [Google Scholar]
30. M. Rabeti. (2014). “Mixed convection heat transfer of nanofluids about a horizontal circular cylinder in porous media, Sop Trans,” Sop Transactions on Nano-Technology, vol. 23, no. 10, pp. 237–246. [Google Scholar]
31. F. Saba, N. Ahmed, U. Khan and S. T. Mohyud-Din. (2019). “A novel coupling of (CNT-Fe3O4/H2O) hybrid nanofluid for improvements in heat transfer for flow in an asymmetric channel with dilating/squeezing walls,” International Journal of Heat and Mass Transfer, vol. 1, no. 36, pp. 186–195. [Google Scholar]
32. S. J. Liao. (1992). “The proposed homotopy analysis technique for the solution of nonlinear problems, Doctoral dissertation,” Ph. D. thesis, Shanghai Jiao Tong University. [Google Scholar]
33. S. Liao and Y. Tan. (2007). “A general approach to obtain series solutions of nonlinear differential equations,” Studies in Applied Mathematics, vol. 119, no. 4, pp. 297–354.
34. S. Liao and S. A. Sherif. (2004). “Beyond perturbation: Introduction to the homotopy analysis method”. Applied Mechanics Reviews, vol. 57, no. 5, pp. 25. [Google Scholar]
35. T. Gul, W. Noman, M. Sohail and M. A. Khan. (2019). “Impact of the Marangoni and thermal radiation convection on the graphene-oxide-water-based and ethylene-glycol-based nanofluids,” Advances in Mechanical Engineering, vol. 11, no. 6, pp. 168–178. [Google Scholar]
36. T. Hayat, R. S. Saif, R. Ellahi, T. Muhammad and B. Ahmad. (2017). “Numerical study for Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions,” Results in Physics, vol. 7, pp. 2886–2892.
37. T. Hayat, R. S. Saif, R. Ellahi, T. Muhammad and A. Alsaedi. (2018). “Simultaneous effects of melting heat and internal heat generation in stagnation point flow of Jeffrey fluid towards a nonlinear stretching surface with variable thickness,” International Journal of Thermal Sciences, vol. 12, no. 3, pp. 344–354.
38. N. Shehzad, A. Zeeshan, R. Ellahi and K. Vafai. (2016). “Convective heat transfer of nanofluid in a wavy channel: Buongiorno’s mathematical model,” Journal of Molecular Liquids, vol. 222, no. 2, pp. 446–455.
39. R. Ellahi and R. Riaz. (2010). “Analytical solutions for MHD flow in a third-grade fluid with variable viscosity,” Mathematical and Computer Modelling, vol. 52, no. 10, pp. 1783–1793.
40. T. Gul. (2019). “Scattering of a thin layer over a nonlinear radially extending surface with Magneto hydrodynamic and thermal dissipation,” Surface Review and Letters, vol. 26, no. 1, pp. 1850123.
41. V. Ali, T. Gul, S. Afridi, F. Ali, S. O. Alharbi et al. (2019). , “Thin film flow of micropolar fluid in a permeable medium,” Coatings, vol. 9, no. 2, pp. 83–98.
42. S. Liao. (2014). Advances in the Homotopy Analysis Method, vol. 427. Singapore: World Scientific. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |