DOI:10.32604/cmc.2020.012659

| Computers, Materials & Continua DOI:10.32604/cmc.2020.012659 |  |
| Article |
Entanglement and Sudden Death for a Two-Mode Radiation Field Two Atoms
1Department of Mathematics, Faculty of Science,University of Jeddah, Jeddah, Saudi Arabia
2Mathematics Department, Faculty of Science, Taif University, Taif City, Saudi Arabia
3Department of Mathematics, Faculty of Science,Al-Azhar University, Cairo, Egypt
4Department of Mathematics, Faculty of Science,Sohag University, Sohag, Egypt
*Corresponding Author: E. M. Khalil. Email: eiedkhalil@yahoo.com
Received: 08 July 2020; Accepted: 14 August 2020
Abstract: The effect of the field–field interaction on a cavity containing two qubit (TQ) interacting with a two mode of electromagnetic field as parametric amplifier type is investigated. After performing an appropriate transformation, the constants of motion are calculated. Using the Schrödinger differential equation a system of differential equations was obtained, and the general solution was obtained in the case of exact resonance. Some statistical quantities were calculated and discussed in detail to describe the features of this system. The collapses and revivals phenomena have been discussed in details. The Shannon information entropy has been applied for measuring the degree of entanglement (DE) between the qubits and the electromagnetic field. The normal squeezing for some values of the parameter of the field–field interaction is studied. The results showed that the collapses disappeared after the field–field terms were added and the maximum values of normal squeezing decrease when increasing of the field–field interaction parameter. While the revivals and amplitudes of the oscillations increase when the parameter of the field–field interaction increases. Degree of entanglement is partially more entangled with increasing of the field-field interaction parameter. The relationship between revivals, collapses and the degree of entanglement (Shannon information entropy) was monitored and discussed in the presence and absence of the field–field interaction.
Keywords: Field–field interaction; su(1,1) Lie group; degree of entanglement; normal squeezing
The entanglement between the atom-field (AF) interaction for Jaynes–Cummings model (JCM) [1] has been discussed by [2]. This simple model represents the interacting between qubit (Q) and the field placed individually in a high-Q space. It is known that, this model is simple and analytically solvable, which helps to effectively understand quantum optics and information problems. The entanglement between TQ has been studied in one and two JCM and one-photon [3]. The influence of the amplifier terms (two-photon degenerate and non-degenerate case) on the two two-level atoms has been investigated by [4,5]. The effect of atom-atom cross interaction has been studied with a maximally entangled state, the occurrence of sudden birth of entanglement has been studied by [6]. The problem of TQ interaction with one mode has been studied by [7–10]. On the other hand, the system of TQ and a system represented by su(1,1) in existence of classical field has been studied by [6]. However, the generalization of the model from one atom to two atoms with classical field or Stark shift has been investigated by [8,9]. The interaction between the TQ and a one field leads to more entanglement between the subsystem, such that the atoms in general entangled and after adding the field due to the interaction is more increases [10]. The effectiveness of the squeezed state on the TQ system interacting with a field in frame 2-photon has been studied by [11,12]. The degree of entanglement of two atoms with a linear interaction prepared initially in thermal state has been studied by [13].
In this communication, consider a two mode of the electromagnetic field as parametric amplifier interacting with a TQ as well as the field–field interaction as follows:
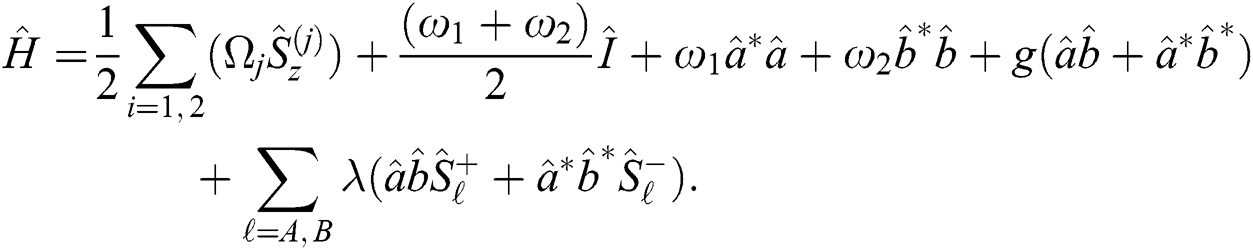
where, 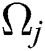 represents the TQ frequency. While
represents the TQ frequency. While 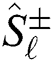 and
and  are the Pauli matrices. The
are the Pauli matrices. The 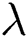 is the coupling of the TQ-EMF interaction and
is the coupling of the TQ-EMF interaction and 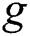 is a coupling of the field-field interaction. If we set
is a coupling of the field-field interaction. If we set 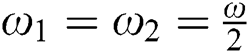 and introducing the su(1,1) generators,
and introducing the su(1,1) generators, 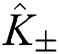 and
and  as follows:
as follows:
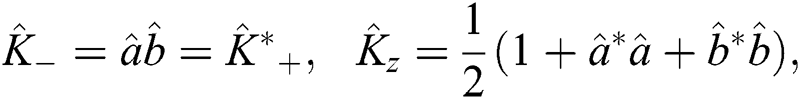
which satisfy the relations: 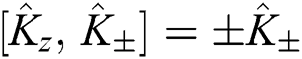 and
and 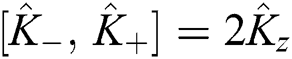 . Therefore, we find that:
. Therefore, we find that: 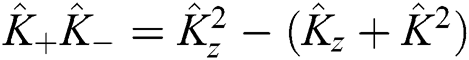 . The
. The 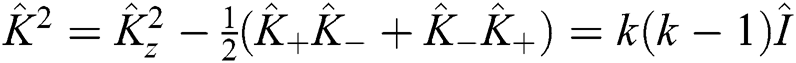 is the Casimier operator and
is the Casimier operator and 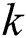 is the Bargmann number. The Hamiltonian of Eq. (1) can be governed by an su(1,1) and su(2) Lie algebra as:
is the Bargmann number. The Hamiltonian of Eq. (1) can be governed by an su(1,1) and su(2) Lie algebra as:
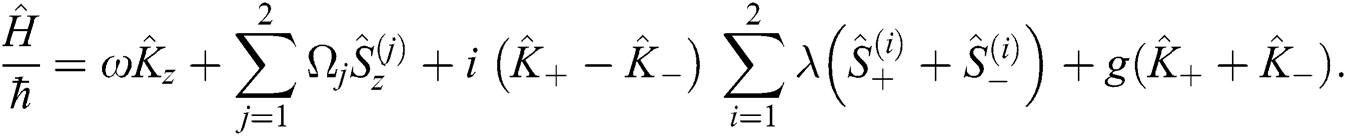
So the su(1,1) operators in the number state representation takes the following form,
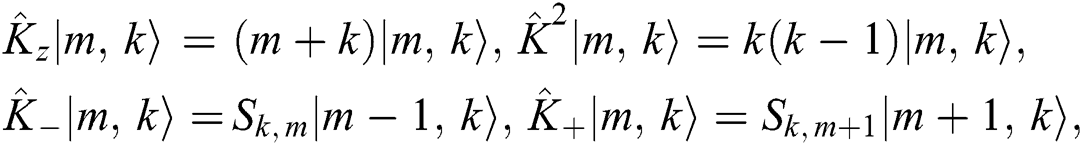
where 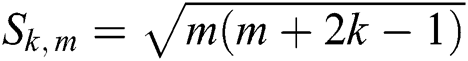 . It is noted that the connection between
. It is noted that the connection between  and the photon number of the field modes is
and the photon number of the field modes is 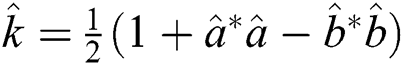 and
and 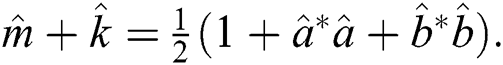
The basic aim of this work is to study the behavior of the system Eq. (3) besides to see the influence of the external terms (field–field interaction), which represented the linear combination between  and
and  terms on the interaction of the present system. The derivation of the Schrödinger differential equations and their solution will be done in the next Section 2. The relative inversion will be discussed in Section 3 and the degree of entanglement in Section 4. The normal squeezing is considered in Section 5. In Section 6 some brief remarks will be presented.
terms on the interaction of the present system. The derivation of the Schrödinger differential equations and their solution will be done in the next Section 2. The relative inversion will be discussed in Section 3 and the degree of entanglement in Section 4. The normal squeezing is considered in Section 5. In Section 6 some brief remarks will be presented.
To calculate the wave function for the present system Eq. (3), we must solve the Schrödinger differential equations. It is necessary to calculate the constants of the motion, which facilitates the process solution. In the presence of field–field interaction, we cannot obtain the constants of motion. So we apply the following transformations to remove these terms.
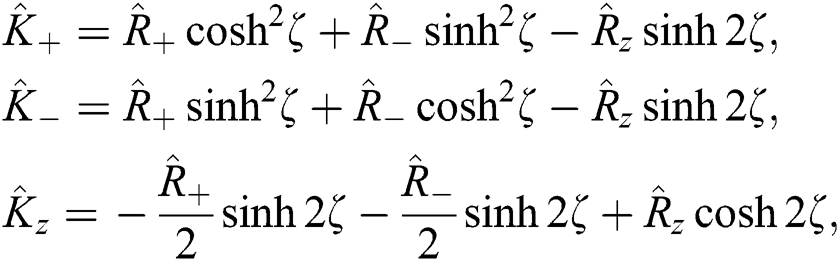
where the operators 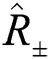 ,
, 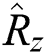 are generators of the su(1,1) group with
are generators of the su(1,1) group with 
Now if we substitute Eq. (5) into the Hamiltonian Eq. (3), the Hamiltonian becomes t
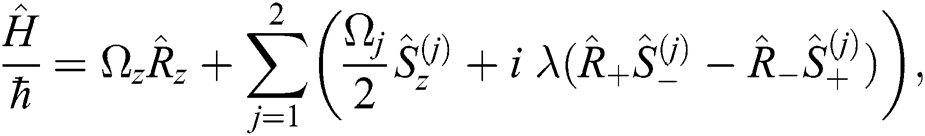
With 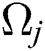 is the transition frequency for each qubit and
is the transition frequency for each qubit and 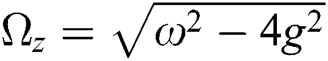 indicates to the artificial frequency of the quantum system. The Heisenberg equation of motion is applied to calculate the dynamical operators
indicates to the artificial frequency of the quantum system. The Heisenberg equation of motion is applied to calculate the dynamical operators  and
and 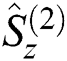 as follows:
as follows:

Therefore we introduce the constant operator 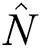 as
as
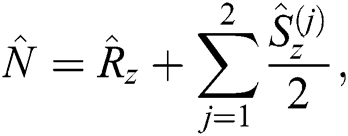
By applying Eq. (8), the Hamiltonian Eq. (6) becomes
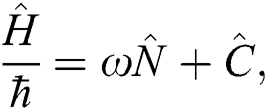
where 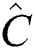 is defined as
is defined as
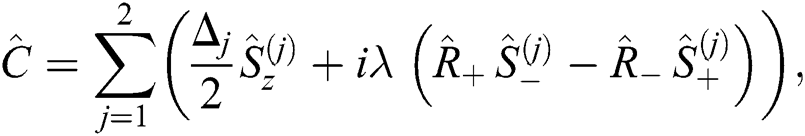
where the quantity 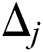 refers to the detuning parameter which is represented by
refers to the detuning parameter which is represented by
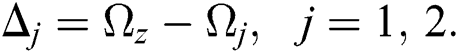
Consider that the initial condition for the su(1,1) system is the Barut–Girardello coherent state and TQ are in excited states. Therefore, the initial conditions state for the wave function takes the following equation,
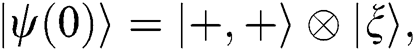
where 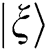 is given by
is given by
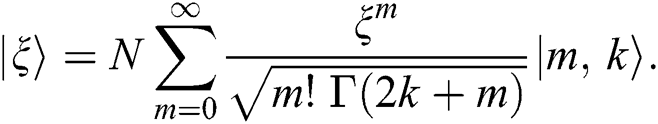
where the quantity 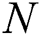 is the normalized factor. Therefore the time dependence of the state
is the normalized factor. Therefore the time dependence of the state 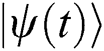 takes the form,
takes the form,
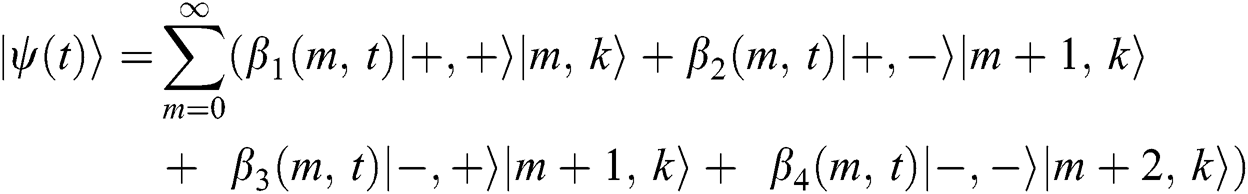
with 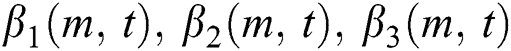 and
and 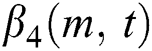 are the solutions of Schrodinger equation
are the solutions of Schrodinger equation 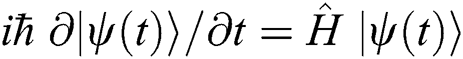 which take the following form,
which take the following form,

The coefficients 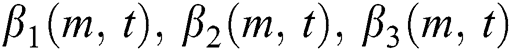 and
and  are given by the following equations,
are given by the following equations,
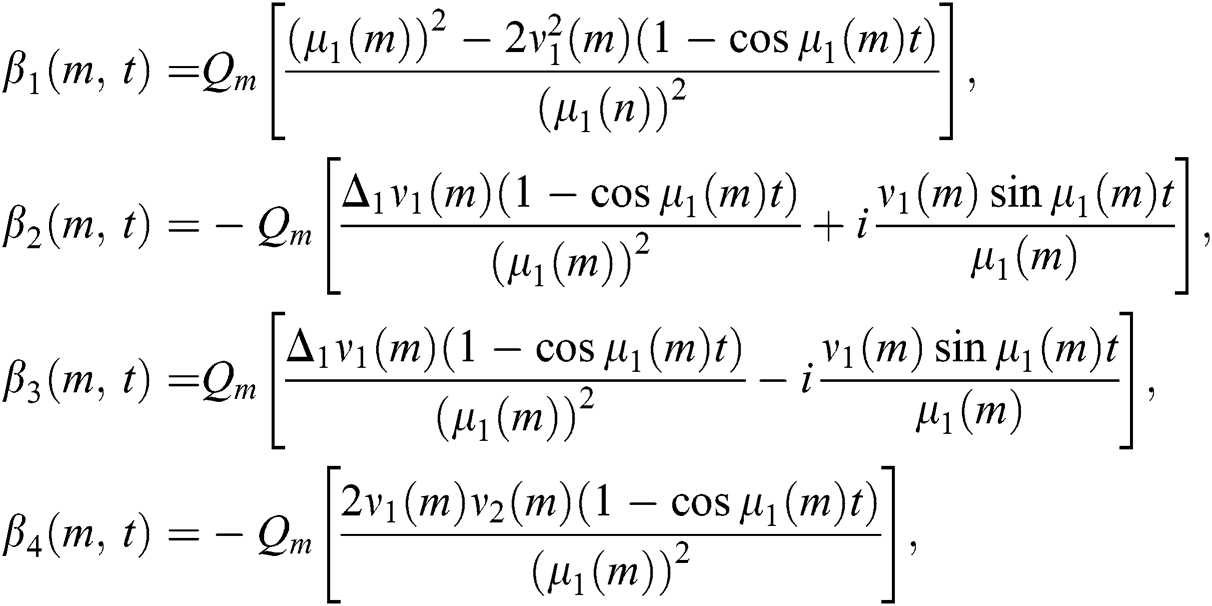
where 
with
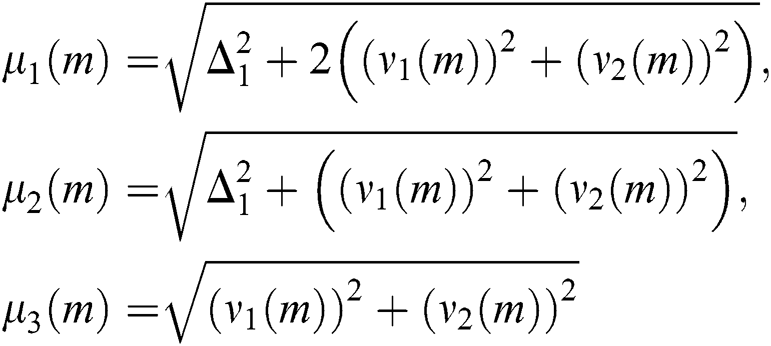
Now we can measure some physical quantities that help us to understand the behavior of the Hamiltonian Eq. (3). The relative inversion, degree of entanglement and normal squeezing will be discussed in forthcoming.
In quantum optics, the phenomena of collapses and revivals provide us more measures for the system and its connection to the process of entanglement. Therefore, it is known that there are relations between the photon number and the phenomena of collapses and revivals, so we will study the effective of the field-field interaction on the population inversion. Through the two Eqs. (5) and (8), the change in the sum of photons is defined as follows
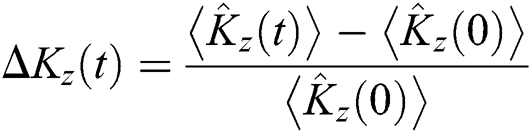
where 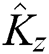 is given by Eq. (5). The obtained results are shown in Fig. 1. regarding the population function
is given by Eq. (5). The obtained results are shown in Fig. 1. regarding the population function  for the fixed parameters
for the fixed parameters 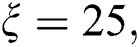
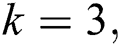
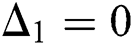 and varying the field-field interaction parameter
and varying the field-field interaction parameter 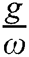 . For example, in Fig. 1a in absence of the field-field interaction
. For example, in Fig. 1a in absence of the field-field interaction  In this case, the function of the population since beginning of the interaction revealed a periodic behavior of the collapse followed by revival. This behavior repeated regularly through the time of interaction consideration with period
In this case, the function of the population since beginning of the interaction revealed a periodic behavior of the collapse followed by revival. This behavior repeated regularly through the time of interaction consideration with period 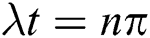 (
( 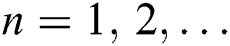 ). The symmetry of the function
). The symmetry of the function 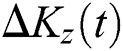 around the horizontal axis is washed after adding the field–field terms into account (
around the horizontal axis is washed after adding the field–field terms into account (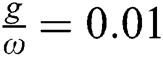 ). In general, the lower values of the function
). In general, the lower values of the function 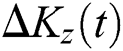 decreased, in contrast the higher values increased with the continuation of the interaction time see Fig. 1b. For increases of the parameter
decreased, in contrast the higher values increased with the continuation of the interaction time see Fig. 1b. For increases of the parameter  , the fluctuations between the lower values and the higher values increased and the collapses phenomena does not occur as seen in Fig. 1c. More increasing the field-field interaction parameter
, the fluctuations between the lower values and the higher values increased and the collapses phenomena does not occur as seen in Fig. 1c. More increasing the field-field interaction parameter 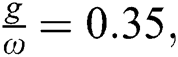 due to more raising in the fluctuation through the periods of revivals with shift upward of the collapses regions.
due to more raising in the fluctuation through the periods of revivals with shift upward of the collapses regions.

Figure 1: The relative inversion with 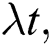 where
where 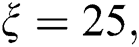

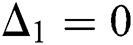 (a)
(a) 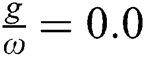 (b)
(b) 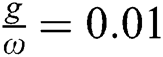 (c)
(c) 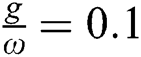 (d)
(d) 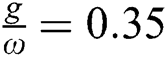
Entanglement is one of the mainstays of many vital applications of quantum information [14–19]. In addition, it forms the support of experiments in quantum information. On the other hand, there are many uses and applications of the disentanglement quantum system [2]. Through dynamic analyzes and conclusions we can describe the behavior of the DF for the system contains the A-F interaction via Shannon information entropies [14] which is defined by
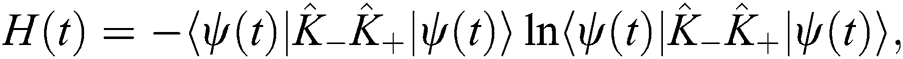
where  and
and 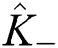 are defined in Eq. (5). From Eqs. (5) and (19) it is easy to calculate the operator
are defined in Eq. (5). From Eqs. (5) and (19) it is easy to calculate the operator 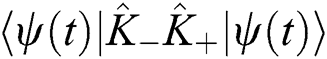 and takes the follows form,
and takes the follows form,
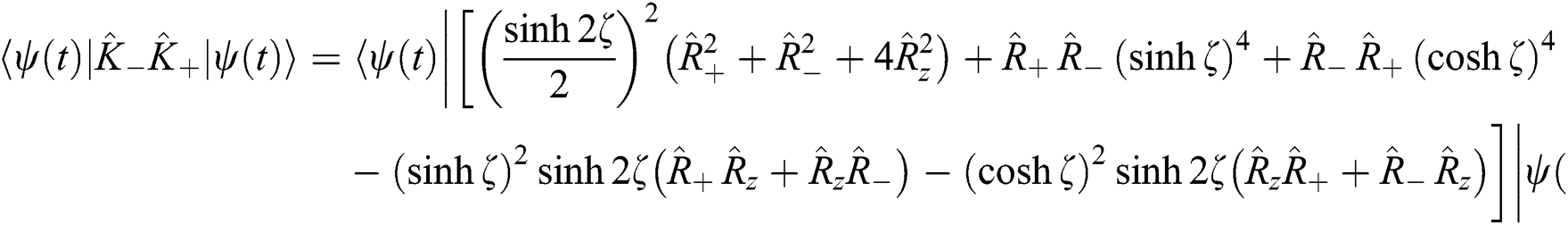
Now we examine the DF between the interaction of the TQ and the QS with including the field-field interaction which are represented in Eq. (3). Depending on the same condition as mentioned in the previous section. In the first case with excluding the field-field interaction (i.e., 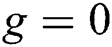 ), the entropy indicates that the system begins to disentanglement followed by partial entanglement and the entropy function
), the entropy indicates that the system begins to disentanglement followed by partial entanglement and the entropy function  shows periodic and regular oscillations with a period
shows periodic and regular oscillations with a period 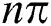
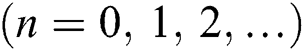 . The system approaches to zero value (pure state) at the lower values of
. The system approaches to zero value (pure state) at the lower values of 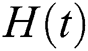 namely (
namely (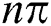 ) as shown in Fig. 2a. After adding the field–field interaction into account (i.e.,
) as shown in Fig. 2a. After adding the field–field interaction into account (i.e., 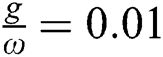 ) the lower and higher values of the entropy increases, the system becomes more partial entanglements, the oscillations grow and the maxima holds in centre of the collapses and the revivals regions as comparison between the relative inversion and the degree of entanglement, see Figs. 1b and 2b. It is pointed out the entropy function is symmetric about the value
) the lower and higher values of the entropy increases, the system becomes more partial entanglements, the oscillations grow and the maxima holds in centre of the collapses and the revivals regions as comparison between the relative inversion and the degree of entanglement, see Figs. 1b and 2b. It is pointed out the entropy function is symmetric about the value 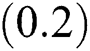 in the preceding case, this symmetry vanished after adding the field–field interaction into the interaction cavity, the higher values of the entropy increase and the system still in partial entanglement state. By increasing the parameter field–field interaction adjust
in the preceding case, this symmetry vanished after adding the field–field interaction into the interaction cavity, the higher values of the entropy increase and the system still in partial entanglement state. By increasing the parameter field–field interaction adjust 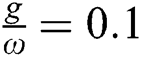 , the oscillations increase and the extreme values of the entropy function increase too as the time of interaction goes on, see Fig. 2c. With more increase of the parameter
, the oscillations increase and the extreme values of the entropy function increase too as the time of interaction goes on, see Fig. 2c. With more increase of the parameter 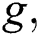 we see that the lower values which occurs in the collapses regions decrease and the DF approaches the pure state, see Fig. 2d.
we see that the lower values which occurs in the collapses regions decrease and the DF approaches the pure state, see Fig. 2d.

Figure 2: The DE with 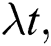 where
where 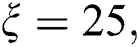
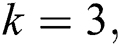
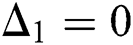 , (a)
, (a) 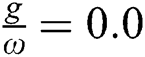 (b)
(b) 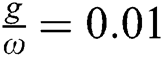 (c)
(c) 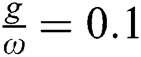 (d)
(d) 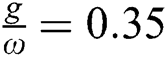
One of the fundamentals of quantum mechanics is normal squeezing, which is completely related to the Heisenberg uncertainty principle, which has been suggested by [20–28]. A fundamental assumption in the study of quantum mechanics for any two observable 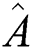 and
and  that are not commute (i.e.,
that are not commute (i.e., 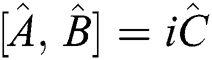 ), cannot be determined with the same precision. The uncertainty relation for the observable
), cannot be determined with the same precision. The uncertainty relation for the observable 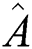 and
and 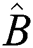 achieves the following inequality,
achieves the following inequality,
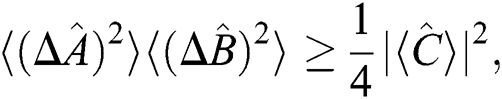
For the case 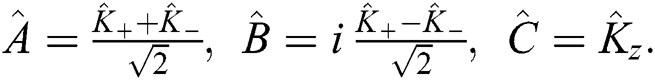 Therefore, the uncertainty inequality becomes
Therefore, the uncertainty inequality becomes

The quantities 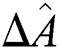 and
and 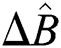 are estimated by the following relationships,
are estimated by the following relationships,
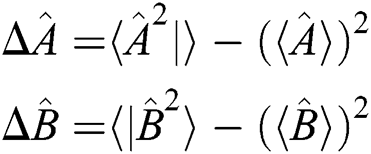
To analyze the normal squeezing behavior, consider the same conditions as in the above sections. In the absence of the field–field interaction (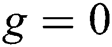 ), the regular squeezing appears in
), the regular squeezing appears in 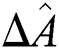 and never occurs in
and never occurs in 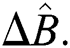 The oscillations of the squeezing repeated periodically with period (
The oscillations of the squeezing repeated periodically with period (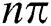 ,
, 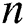 is nonnegative integer number) and the oscillations reduced gradually as observed in Fig. 3a. To visualize the field–field interaction by setting
is nonnegative integer number) and the oscillations reduced gradually as observed in Fig. 3a. To visualize the field–field interaction by setting  , we see that the squeezing regions in the quadrature
, we see that the squeezing regions in the quadrature 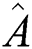 reduced and the maximum values of the oscillations decreased, see Fig. 3b. By increasing the parameter
reduced and the maximum values of the oscillations decreased, see Fig. 3b. By increasing the parameter  adjust
adjust 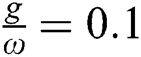 , the squeezing more reduced for the first quadrature
, the squeezing more reduced for the first quadrature  (may takes the minimum values), while for the second quadrature
(may takes the minimum values), while for the second quadrature 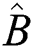 the squeezing began to grow gradually as the time increasing, Fig. 3c.
the squeezing began to grow gradually as the time increasing, Fig. 3c.

Figure 3: The normal squeezing with 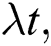 where
where 
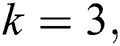
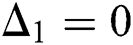 , (a)
, (a) 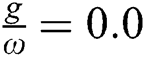 (b)
(b)  (c)
(c) 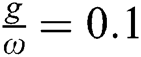 (d)
(d) 
Finally, with more increases of the 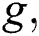 adjust
adjust 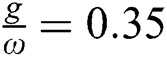 , the squeezing regions for
, the squeezing regions for 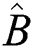 more increases as the time increases, see Fig. 2d. Moreover, there is exchange for squeezing phenomena between the two quadrature
more increases as the time increases, see Fig. 2d. Moreover, there is exchange for squeezing phenomena between the two quadrature 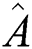 and
and 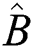 which dependence on the field–field interaction parameter
which dependence on the field–field interaction parameter 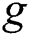 .
.
The effect of a field–field interaction on a cavity containing a pair of qubit interacting with a two-mode field of parametric amplifier is studied. The electromagnetic field transformed into a su(1,1) Lee group. Appropriate transformations have also been used to determine the constants of motion by calculating the equations of motion for some operators by using the Heisenberg differential formula. The wave function is calculated by solving the Schrödinger differential equation. The relative population, Shannon information entropy as well as the normal squeezing are discussed. The influence of the field-field interaction terms due to reduce of the frequency of the su(1,1) term in the system Hamiltonian are also presented. The results indicated that the collapses phenomena are reduced by increasing of the ratio 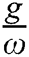 . The entanglement between the parties of the system started in separated state and becomes partially entangled, the lower and higher values of the modified Shannon information entropy are related to the periods of collapses and the revivals regions. The periods of squeezing estimated, in the exclude of the field–field interaction terms, the squeezing occurs in quadrature
. The entanglement between the parties of the system started in separated state and becomes partially entangled, the lower and higher values of the modified Shannon information entropy are related to the periods of collapses and the revivals regions. The periods of squeezing estimated, in the exclude of the field–field interaction terms, the squeezing occurs in quadrature 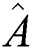 and after adding the ratio
and after adding the ratio 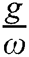 the squeezing grows in the quadrature
the squeezing grows in the quadrature 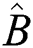 and reduced for the quadrature
and reduced for the quadrature 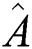 .
.
Funding Statement: This work was funded by the University of Jeddah, Saudi Arabia, under Grant No. UJ-02-082-DR. The authors, therefore, acknowledge with thanks the University technical and financial support.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. T. Jaynes and F. W. Cummings. (1963). “Comparison of quantum and smiclassical radiation theories with application to the beam maser,” Proc. IEEE, vol. 51, no. 10, pp. 89–109. [Google Scholar]
2. S. J. D. Phoenix and P. L. Knight. (1991). “Establishment of an entangled atom-field state in the Jaynes–Cummings model,” Physical Review A, vol. 44, no. 9, pp. 6023–6029. [Google Scholar]
3. M. S. Kim, J. Y. Lee, D. Ahn and P. L. Knight. (2002). “Entanglement induced by a single-mode heat environment,” Physical Review A, vol. 65, no. 4, 040101. [Google Scholar]
4. E. M. Khalil, M. S. Abdalla and A. S. F. Obada. (2010). “Pair entanglement of two-level atoms in the presence of a nondegenerate parametric amplifier,” Journal of Physics B: Quantum and Semiclassical Optics, vol. 43, no. 9, 095507. [Google Scholar]
5. E. M. Khalil, M. S. Abdalla, A. S. F. Obada and J. Perina. (2010). “Entropic uncertainty in two two-level atoms interacting with a cavity field in presence of degenerate parametric amplifier,” Journal of the Optical Society of America B, vol. 27, no. 2, pp. 266–276. [Google Scholar]
6. M. S. Abdalla, E. M. Khalil, A. S. F. Obada, J. Perina, J. K. Repelka. (2015). et al., “Quantum statistical characteristics of the interaction between two two-level atoms and radiation field,” European Physical Journal Plus, vol. 130, no. 11, pp. 227. [Google Scholar]
7. H. S. Alqannas and E. M. Khalil. (2018). “Quantum interaction of su(1,1) Lie group with entangled a two 2-level atoms,” Physica A, vol. 489, no. 1, pp. 1–8. [Google Scholar]
8. E. M. Khalil and S. Abedel-Khalek. (2018). “Entangled two two-level atom in the presence of external classical fields,” International Journal of Theoretical Physics, vol. 57, no. 9, pp. 2615–2627. [Google Scholar]
9. M. A. E. Hilal and E. M. Khalil. (2018). “Quantum statistical aspects of interactions between the radiation field and two entangled two-level atoms in the presence of stark shift terms,” Journal of Russian Laser Research, vol. 39, no. 3, pp. 207–215. [Google Scholar]
10. Y. Al-Hadeethi, B. M. Raffah, N. Almalky and E. M. Khalil. (2019). “Entropy squeezing, nonlocal correlation and purification properties of two-trap ion interaction with laser field in the presence of Stark shift effect,” International Journal of Modern Physics B, vol. 33, no. 12, 1950118. [Google Scholar]
11. E. M. A. Hilal, S. Alkhateeb, S. Abdel-Khalek, E. M. Khalil and A. A. Almowalled. (2020). “Quantum scheme for N-level atom interacting with a two two-level atom: Atomic Fisher information and entropy squeezing,” Alexandria Engineering Journal, vol. 59, no. 3, pp. 1259–1264. [Google Scholar]
12. L. Zhou, H. S. Song and C. Li. (2002). “Entanglement induced by a single-mode thermal field and the criteria for entanglement,” Journal of Optics B: Quantum and Semiclassical Optics, vol. 4, no. 6, pp. 425–429. [Google Scholar]
13. L. Zhou, X. X. Yi, H. S. Song and Y. Q. Quo. (2004). “Entanglement of two atoms through different couplings and thermal noise,” Journal of Optics B: Quantum and Semiclassical Optics, vol. 6, no. 9, pp. 378–382. [Google Scholar]
14. H. Y. Yoo and J. H. Eberly. (1985). “Dynamical theory of an atom with two or three levels interacting with quantized cavity fields,” Physics Reports, vol. 118, no. 5, pp. 239–337. [Google Scholar]
15. B. W. Shore and P. L. Knight. (1993). “The Jaynes–Cummings model,” Journal of Modern Optics, vol. 40, no. 7, pp. 1195–1238.
16. C. H. Bennet and S. J. Weisner. (1992). “Communication via one- and two-particle operators on Einstein–Podolsky–Rosen states,” Physical Review Letters, vol. 69, no. 20, pp. 2881–2884.
17. S. F. Huelga, C. Macchiavello, T. Pellizzari, A. K. Ekert, M. B. Plenio. (1997). et al., “ Improvement of frequency standards with quantum entanglement,” Physical Review Letters, vol. 79, no. 20, pp. 3865–3868.
18. S. Bose, V. Vedral and P. L. Knight. (1998). “Multiparticle generalization of entanglement swapping,” Physical Review A, vol. 57, no. 2, pp. 822–829.
19. M. Murao, M. B. Plenio, S. Popescue, V. Vedral and P. L. Knight. (1998). “Multiparticle entanglement purification protocols,” Physical Review A, vol. 57, no. 6, pp. R4075–R4078. [Google Scholar]
20. A. Carlson, M. Koashi and N. Imoto. (1999). “Quantum entanglement for secret sharing and secret splitting,” Physical Review A, vol. 59, no. 1, pp. 162–168. [Google Scholar]
21. P. W. Shor. (1995). “Scheme for reducing decoherence in quantum computer memory,” Physical Review A, vol. 52, no. 4, pp. R2493–R2496.
22. P. L. Knight and P. M. Radamore. (1982). “Quantum revivals of a two-level system driven by chaotic radiation,” Physics Letters A, vol. 90, no. 7, pp. 342–346.
23. E. M. Khalil. (2007). “Generation of a nonlinear two-mode stark shift via nondegenerate Raman transition,” International Journal of Modern Physics B, vol. 21, no. 30, pp. 5143–5154.
24. M. S. Abdalla, E. M. Khalil and A. S. F. Obada. (2007). “Statistical properties of a two-photon cavity mode in the presence of degenerate parametric amplifier,” Annals of Physics, vol. 322, no. 11, pp. 2554–2568.
25. E. M. Khalil, M. S. Abdalla and A. S. F. Obada. (2006). “Entropy and variance squeezing of two coupled modes interacting with a two-level atom: Frequency converter type,” Annals of Physics, vol. 321, no. 2, pp. 421–434.
26. S. Abdel-Khalek. (2015). “Entanglement of atom-field interaction for nonlinear optical fields,” Open Systems & Information Dynamics, vol. 22, no. 3, pp. 1550015.
27. T. M. El-Shahat, S. Abdel-Khalek and A. S. F. Obada. (2005). “Entropy squeezing of a driven two-level atom in a cavity with injected squeezed vacuum,” Chaos Solitons & Fractals, vol. 26, no. 5, pp. 1293–1307.
28. M. S. Abdalla, A. S. F. Obada and S. Abdel-Khalek. (2008). “Entropy squeezing of time dependent single-mode Jaynes–Cummings model in presence of non-linear effect,” Chaos Solitons & Fractals, vol. 36, no. 2, pp. 405–417. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |