DOI:10.32604/cmc.2020.012611
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012611 | |
| Article |
Application of Modified Extended Tanh Technique for Solving Complex Ginzburg–Landau Equation Considering Kerr Law Nonlinearity
1Department of Mathematics, Huzhou University, Huzhou, 313000, China
2Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, Changsha University of Science & Technology, Changsha, 410114, China
3Mathematics Department, College of Science, University of Kirkuk, Kirkuk, Iraq
4Department of Mathematics, Payame Noor University, Tehran, Iran
5Amol University of Special Modern Technologies, Amol, Iran
6Department of Mathematics, COMSATS University Islamabad, Chak Shahzad Islamabad, 45550, Pakistan
7Department of Mathematics, Cankaya University, Ankara, Turkey
8Institute of Space Sciences, Magurele-Bucharest, Romania
*Corresponding Author: Shumaila Javeed. Email: Shumaila_javeed@comsats.edu.pk
Received: 06 July 2020; Accepted: 17 July 2020
Abstract: The purpose of this work is to find new soliton solutions of the complex Ginzburg–Landau equation (GLE) with Kerr law non-linearity. The considered equation is an imperative nonlinear partial differential equation (PDE) in the field of physics. The applications of complex GLE can be found in optics, plasma and other related fields. The modified extended tanh technique with Riccati equation is applied to solve the Complex GLE. The results are presented under a suitable choice for the values of parameters. Figures are shown using the three and two-dimensional plots to represent the shape of the solution in real, and imaginary parts in order to discuss the similarities and difference between them. The graphical representation of the results depicts the typical behavior of soliton solutions. The obtained soliton solutions are of different forms, such as, hyperbolic and trigonometric functions. The results presented in this paper are novel and reported first time in the literature. Simulation results establish the validity and applicability of the suggested technique for the complex GLE. The suggested method with symbolic computational software such as, Mathematica and Maple, is proven as an effective way to acquire the soliton solutions of nonlinear partial differential equations (PDEs) as well as complex PDEs.
Keywords: Modified extended tanh technique; soliton solution; complex Ginzburg–Landau equation; Riccati equation
Exact traveling wave solutions of nonlinear PDEs has become imperative in the study physical phenomena. NPDEs are used to express different real-world phenomena of applied sciences, such as, fluid and solid mechanics, quantum theory, shallow water waves, plasma physics, and chemical reaction diffusion models etc.
Many semi-analytical and analytical techniques have been studied to solve nonlinear PDEs, for example the auxiliary equation technique [1], the expansion (G′/G) technique [2], the exponential function technique [3,4], the generalized Kudryashov technique [5], the first integral technique [6,7], the Jacobi elliptic technique [8], the tan(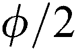
)–expansion technique [9], the Bernoulli sub-equation technique [10], the sine-Gordon technique [11,12], the sub-equation technique [13], the Liu group technique [14] and the new extended direct algebraic technique [15–17], etc.
The complex GLE is an imperative PDE in the field of physics. The applications of complex GLE can be found in optics, plasma and other related fields. Different techniques have been suggested to acquire the solutions of NPDEs. These techniques are the first integral and (G′/G)-expansion [18], the new extended direct algebraic [19], the generalized exponential function [20] and the ansatz functions [21], etc.
The focus of this study is to acquire the soliton solutions of complex GLE with Kerr law nonlinearity employing the modified extended tanh technique with Riccati equation. This paper is presented in the following manner: In Section 2, the proposed technique is described. In Section 3, the solutions of complex GLE are presented. In Section 4, the conclusions and future recommendations are discussed.
The NPDE is generally defined as follows:
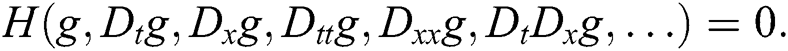
Implementing the transformation:
where 
and 
are nonzero constants. Applying the above transformation, we convert Eq. (1) into a nonlinear ordinary differential equation (ODE) as follows:
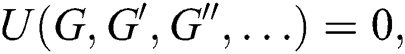
where the derivatives are with respect to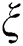 
. The solutions of Eq. (2) is presented as follows
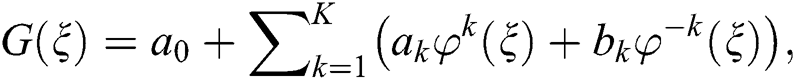
where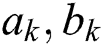 
, 
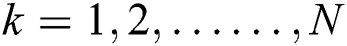denote the constants that are required to be calculated.
Moreover,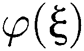 
satisfies the following Riccati equation
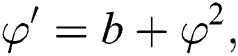
where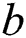
is a constant, Eq. (4) has the following solutions:
(i) For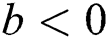 
, we get
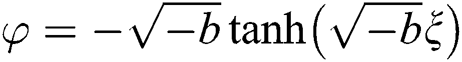, or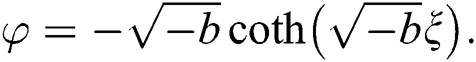 
(ii) For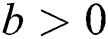 
, we get
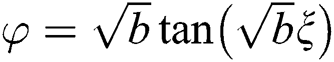, or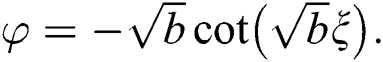 
(iii) For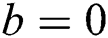
, we get
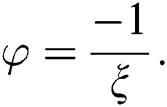
The value of K can be computed to balance the nonlinear and linear terms of highest orders (c.f. Eq (2)). Then, substitute Eq. (3) with its derivatives into Eq. (2) yields:
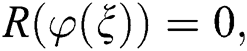
where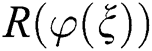 
denotes a polynomial in 
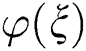. Afterwards, we equate the coefficients of each power of 
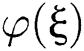in Eq. (5) to zero, and a system of algebraic equations is acquired. Thus, the solution of obtained algebraic equations will provide the exact solutions of Eq. (1).
3 Application of the Technique on CGLE
This study comprises of several solutions of the CGLE using the proposed method (c.f. Section 2).
Consider the CGLE with Kerr law nonlinearity [22,23]:
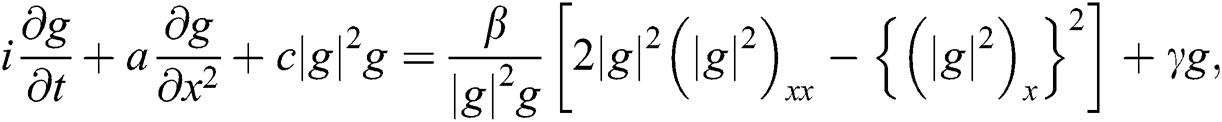
where x is the distance along the fibers and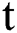 
is the dimensionless time. Moreover, 
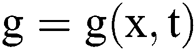is a complex function which represents the wave profile occur in many phenomena such as, plasma physics and nonlinear optics. The real valued parameters 
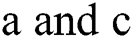relates to the velocity dispersion and the nonlinearity coefficient, respectively. Furthermore, β is the perturbation parameter and γ represents the detuning effects. In order to find the solution (c.f. Eq. (6)), we employ the wave transformation as given below:
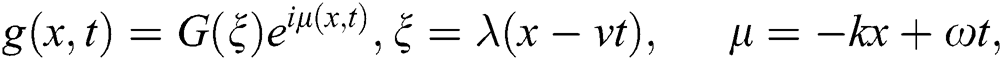
where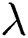 
and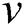 
. are the constants. Moreover, 
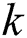describes the wave frequency and the 
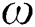expresses the wave number.
From (7), we obtain:
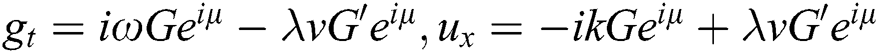
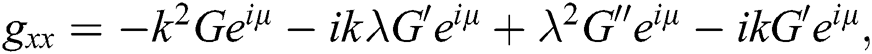
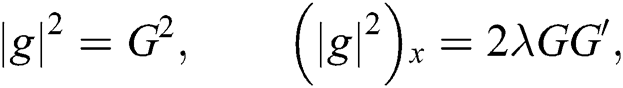
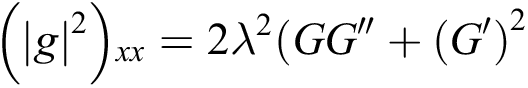
Now, substitute Eq. (8) and Eq. (7) into Eq. (6), we get:
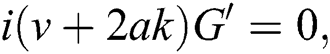
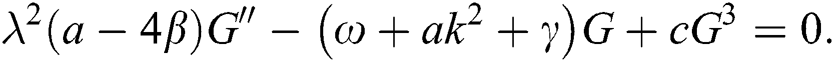
From Eq. (9), we obtain:
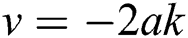
Balancing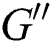 
and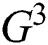 
in Eq. (10) results 
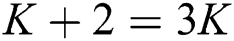, and so 
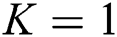. Thus, we acquire the form as given below:
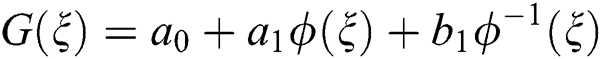
Now, substitute Eq. (11) into Eq. (10). Thus, the following system is acquired by equating the coefficients of each power of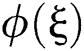 
to zero:
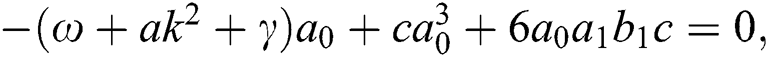
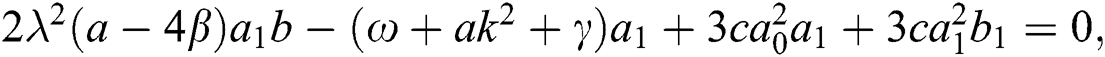
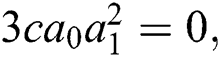
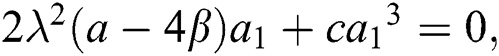
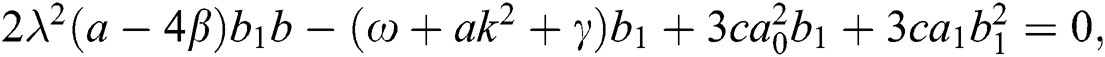
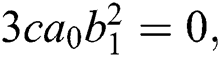
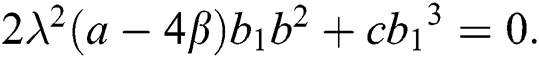
After solving the above system, we acquire the following solutions.
Case 1.
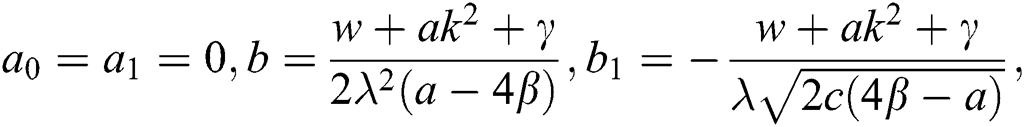
hence, the solution is formed as:
If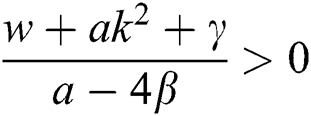 
, then
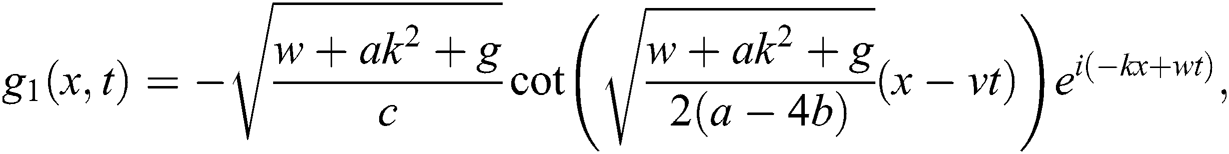
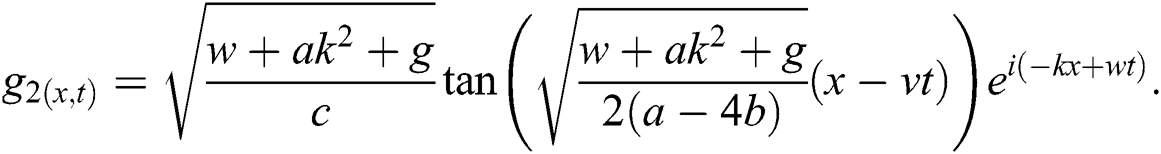
If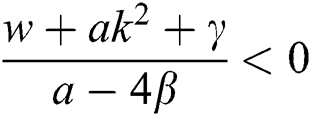 
, then
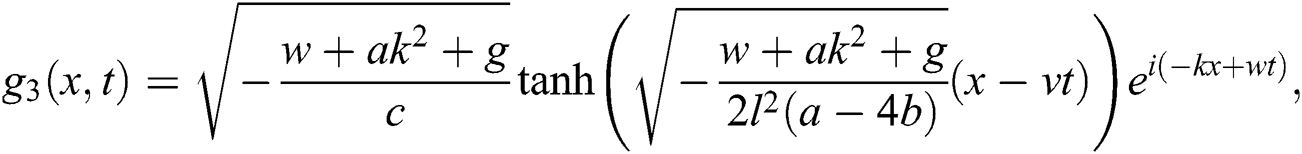
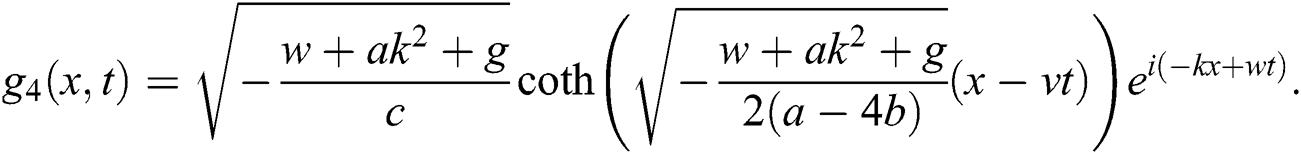
Case 2.
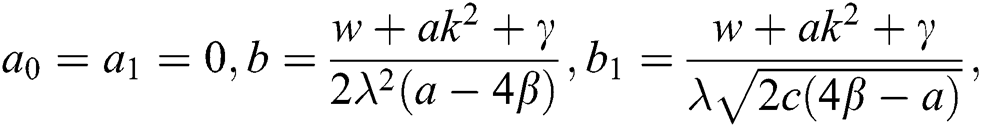
hence, the solution is formed as:
If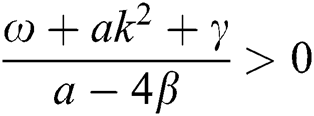 
, then
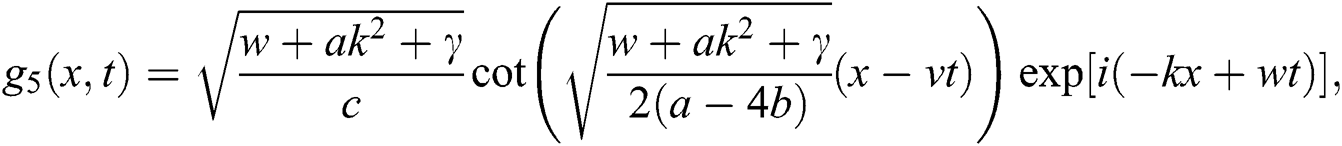
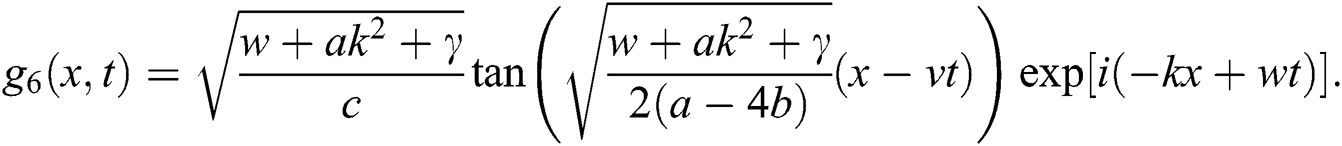
If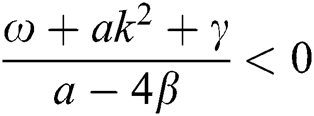 
, then
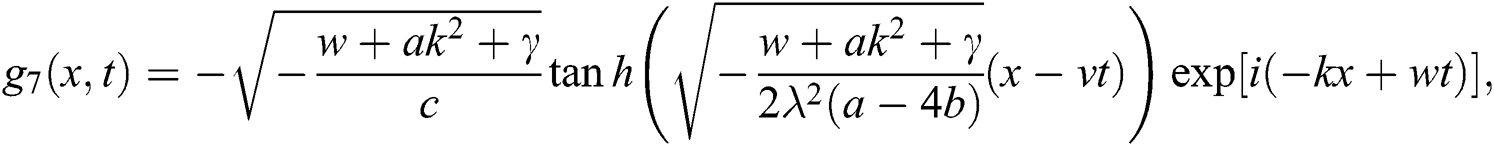
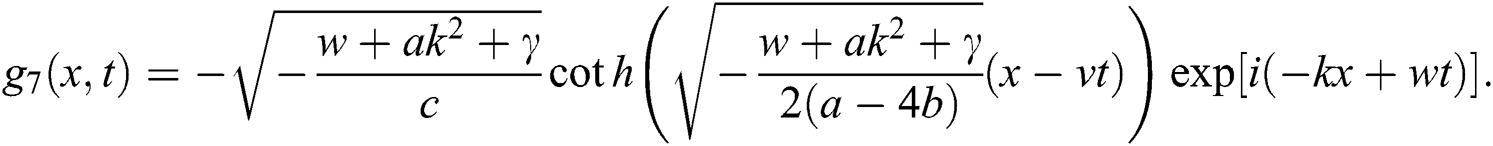
Case 3.
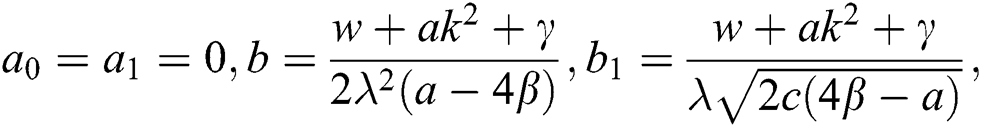
hence, the solution is formed as:
If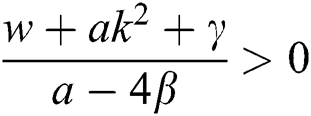 
, then
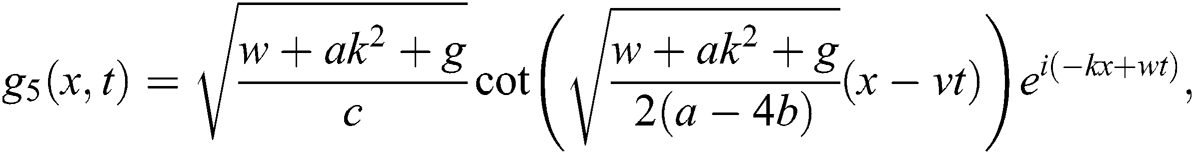
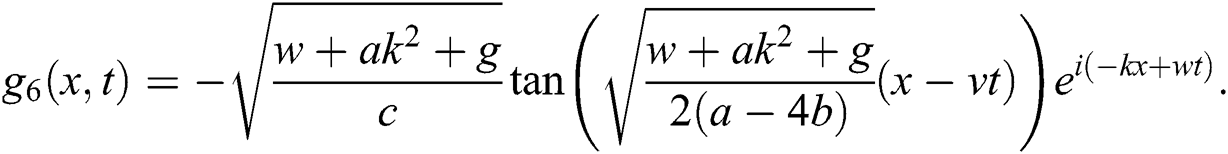
If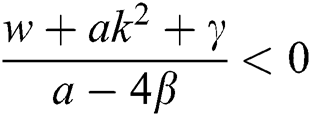 
, then
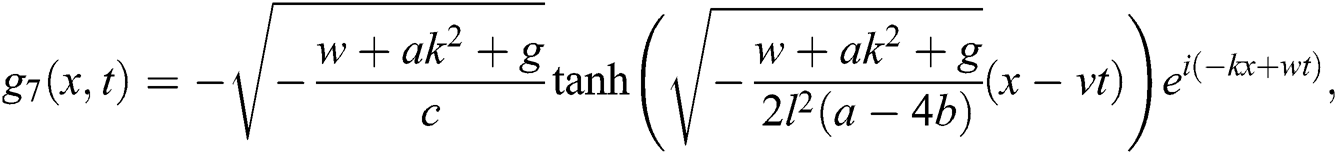
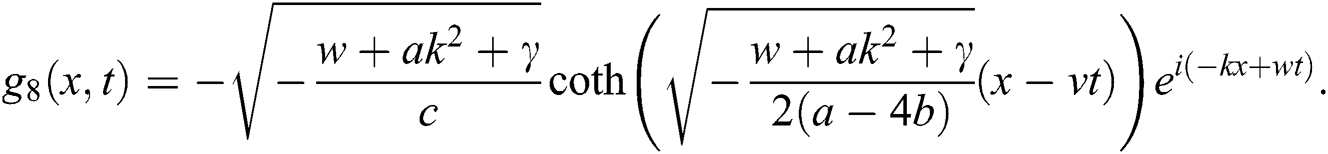
Case 4.
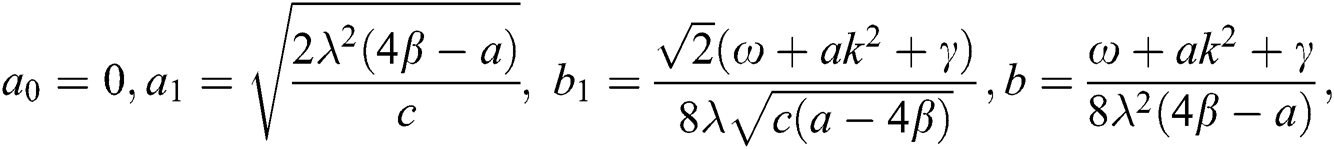
therefore, the solution is formed as:
If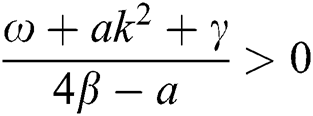 
, then
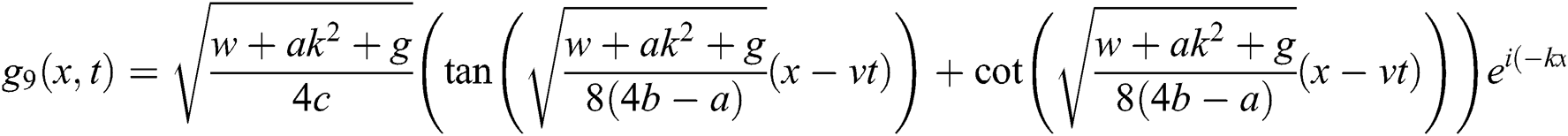
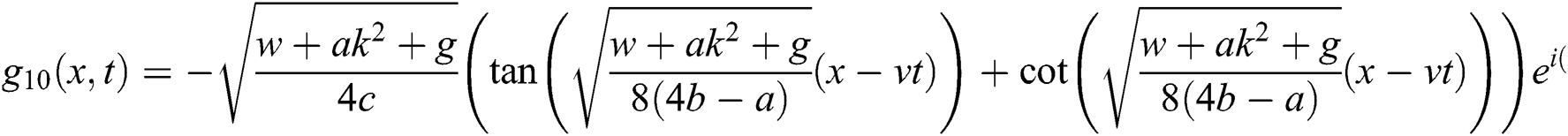
If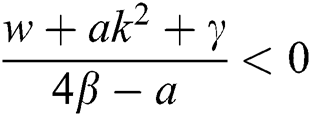 
, then
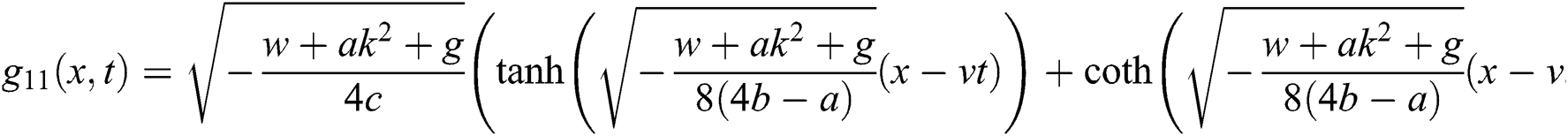
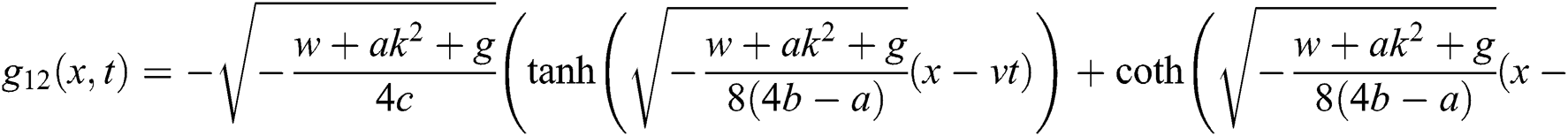
4 Representation of Obtained Solutions
This part studies the physical interpretation of obtained solutions under a suitable choice for the values of parameters. It represents each one of the selected solutions by three and two-dimensional plots, we represent the shape of the solution in real, and imaginary plots to show the similarities and difference between them in these cases. We have plotted each of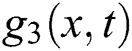 
in Figs. 1–3 considering the following conditions:
Figure 1: Plotting the real part of 
with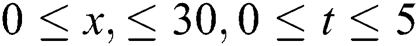 
Figure 2: Plotting the imaginary part of 
with 
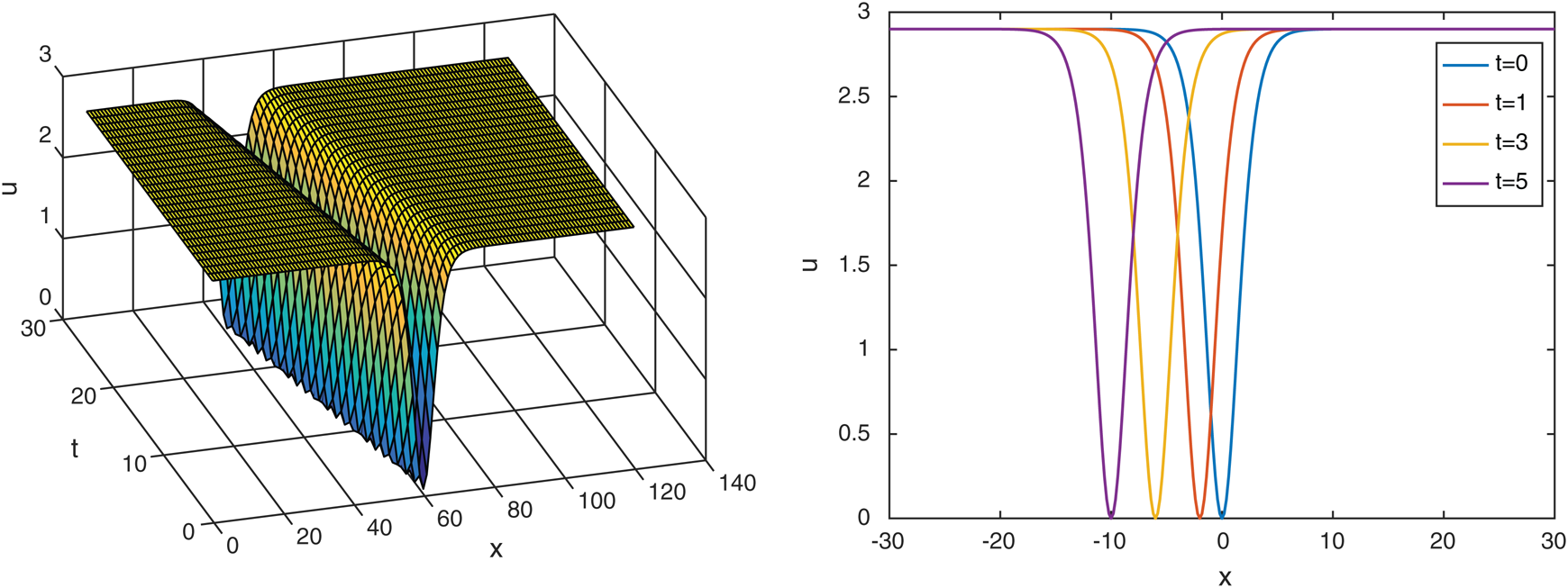
Figure 3: Plotting of 
with 
Wave solution of 
in three and two dimensional when,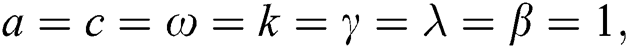 
in the next interval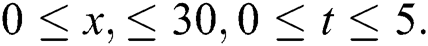 
Furthermore, we have plotted each of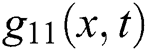 
in Figs. 4–6 considering the following conditions: Wave solution of 
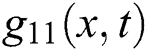in three and two dimensional when, 
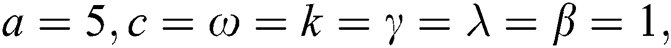in the next interval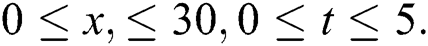 
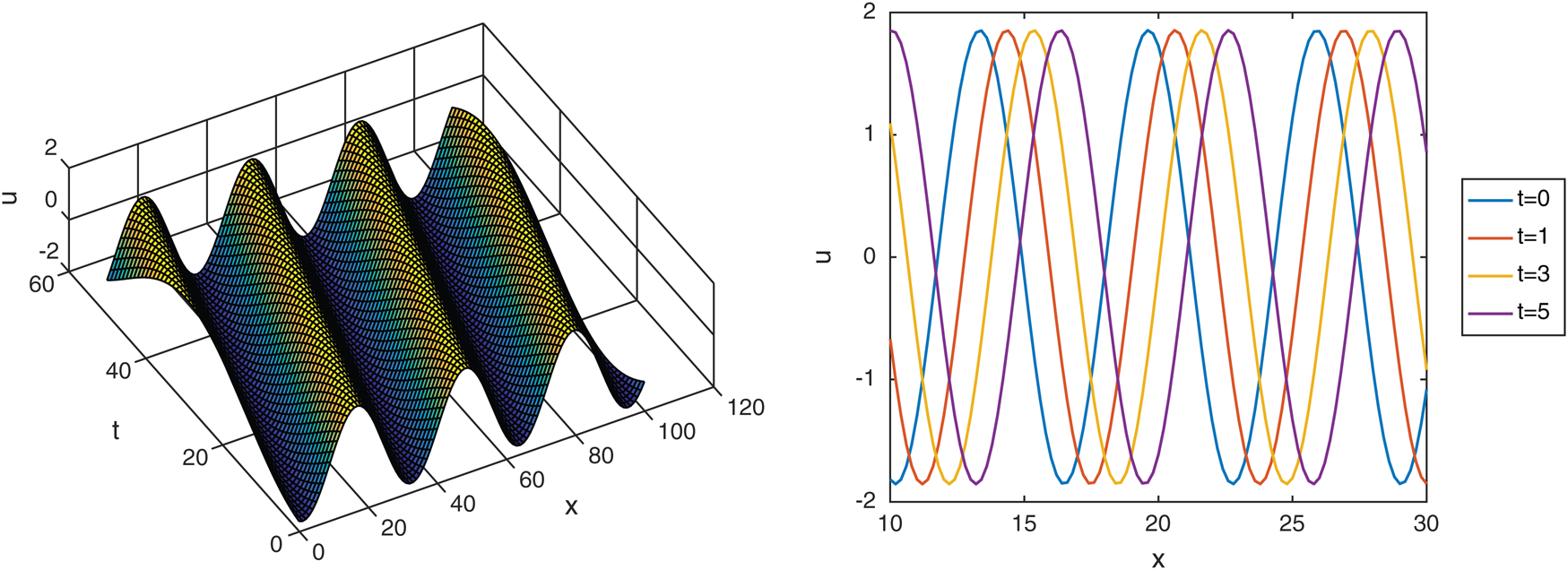
Figure 4: Plotting the real part of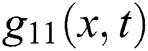 
with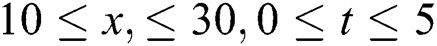 
Figure 5: Plotting the imaginary part of 
with 
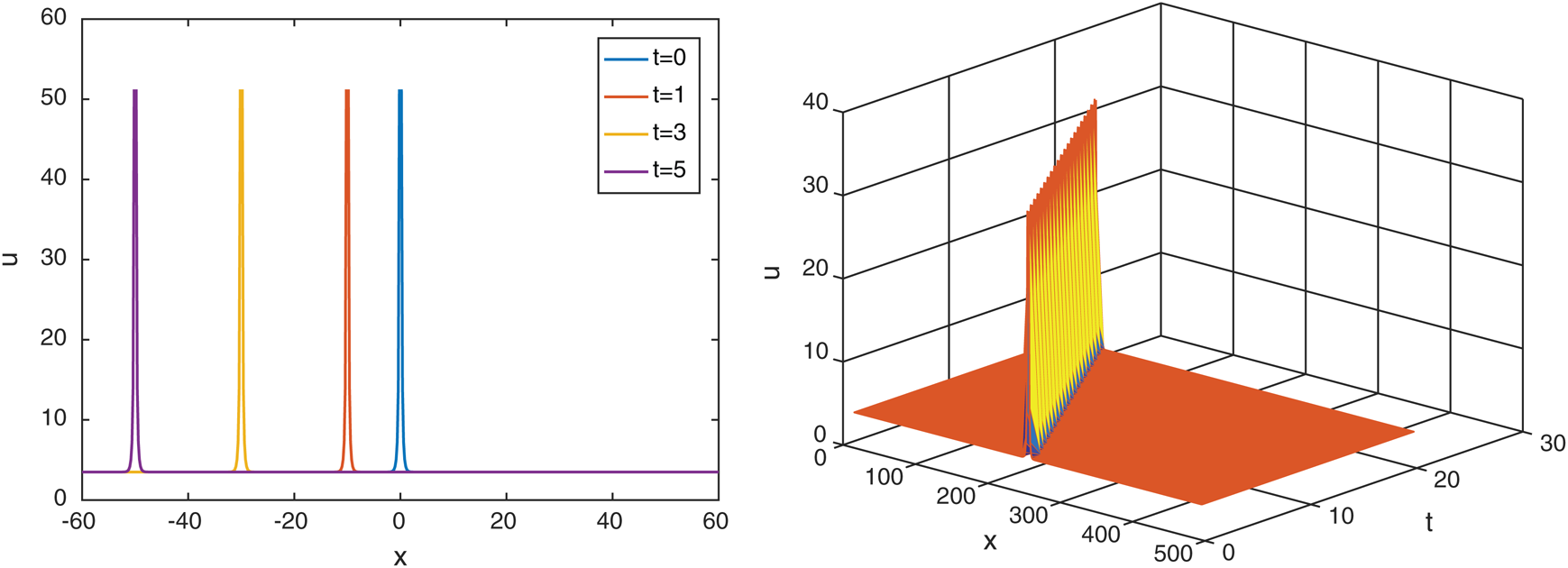
Figure 6: Plotting of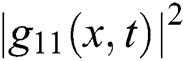 
with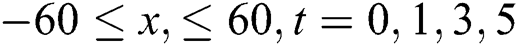 
In this work, new generalized travelling wave solutions of the Complex GLE with Kerr law non-linearity were obtained. The modified extended tanh method with Riccati equation was implemented. The acquired results are represented by trigonometric and hyperbolic functions. The results depict the typical soliton behavior of the solution. The suggested technique is a powerful and efficient way to discuss complex NPDEs. The results presented in this paper are novel and reported first time in the literature. Simulation results establish the validity and applicability of the suggested technique.
Acknowledgement: The authors are thankful to the anonymous reviewers for improving this manuscript.
Funding Statement: The research was supported by the National Natural Science Foundation of China (Grant Nos. 11971142, 11871202, 61673169, 11701176, 11626101, 11601485). YMC received the grant for this work.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. I. Sirendaorej. (2004). “New exact travelling wave solutions for the Kawahara and modified Kawahara equations,” Chaos Solitons Fractals, vol. 19, no. 1, pp. 147–150. [Google Scholar]
2. J. Zhang, F. Jiang and X. Zhao. (2010). “An improved (G′/G)–expansion method for solving nonlinear evolution equations,” International Journal of Computer Mathematics, vol. 87, no. 8, pp. 1716–1725. [Google Scholar]
3. M. M. A. Khater and X. J. Yang. (2016). “Exact traveling wave solutions for the generalized Hirota–Satsuma couple KdV system using the exp (–φ(ξ))-expansion method,” Cogent Mathematics, vol. 3, no. 1, pp. 1–16. [Google Scholar]
4. S. Javeed, K. S. Alimgeer, S. Nawaz, A. Waheed, M. Suleman et al. (2020). , “Soliton solutions of mathematical physics models using the exponential function technique,” Symmetry, vol. 12, no. 1, pp. 176. [Google Scholar]
5. M. S. Islam, K. Khan and A. H. Arnous. (2015). “Generalized Kudryashov method for solving some (3+1)-dimensional nonlinear evolution equations,” New Trends Mathemaics Science, vol. 3, no. 3, pp. 46–57. [Google Scholar]
6. S. Javeed, S. Saif, A. Waheed and D. Baleanu. (2018). “Exact solutions of fractional mBBM equation and coupled system of fractional Boussinesq–Burgers,” Results in Physics, vol. 9, pp. 1275–1281. [Google Scholar]
7. S. Javeed, S. Riaz, K. S. Alimgeer, M. Atif, A. Hanif et al. (2019). , “First integral technique for finding exact solutions of higher dimensional mathematical physics models,” Symmetry, vol. 11, no. 6, pp. 783. [Google Scholar]
8. M. Mirzazadeh, M. Ekici, A. Sonmezoglu, S. Ortakaya, M. Eslami et al. (2016). , “Soliton solutions to a few fractional nonlinear evolution equations in shallow water wave dynamics,” Europen Physics Journal Plus, vol. 131, no. 166, pp. 1–11. [Google Scholar]
9. H. Rezazadeh, J. Manafian, S. S. Khodadad and F. Nazari. (2018). “Traveling wave solutions for density-dependent conformable fractional diffusion-reaction equation by the first integral method and the improved tan(φ(ξ)/2)-expansion,” Optical and Quantum Electronics, vol. 50, pp. 121. [Google Scholar]
10. H. M. Baskonus, D. A. Koc and H. Bulut. (2016). “New travelling wave prototypes to the nonlinear Zakharov–Kuznetsov equation with power law nonlinearity,” Nonlinear Science Letter A, vol. 7, pp. 67–76. [Google Scholar]
11. A. Korkmaz, O. E. Hepson, K. Hosseini, H. Rezazadeh and M. Eslami. (2020). “Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class,” Journal of King Saud University-Science, vol. 32, no. 1, pp. 567–574. [Google Scholar]
12. H. Rezazadeh, M. Mirzazadeh, S. M. Mirhosseini-Alizamini, A. Neirameh, M. Eslami et al. (2018). , “Optical solitons of Lakshmanan–Porsezian–Daniel model with a couple of nonlinearities,” Optik, vol. 164, pp. 414–423. [Google Scholar]
13. H. Aminikhah, A. R. Sheikhani and H. Rezazadeh. (2016). “Sub-equation method for the fractional regularized long-wave equations with conformable fractional derivatives,” Scientia Iranica Transaction B Mechanical Engineering, vol. 23, no. 3, pp. 1048. [Google Scholar]
14. K. R. Raslan, K. K. Ali and M. A. Shallal. (2017). “The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations,” Chaos Solitons & Fractals, vol. 103, pp. 404–409. [Google Scholar]
15. Q. Zhou, A. Pan, S. M. Mirhosseini-Alizamini, M. Mirzazadeh, W. Liu et al. (2017). , “Group analysis and exact soliton solutions to a new (3+1)-dimensional generalized Kadomtsev–Petviashvili equation in fluid mechanics,” Acta Physica Polonica A, vol. 134, no. 2, pp. 564–569. [Google Scholar]
16. H. Rezazadeh, S. M. Mirhosseini-Alizamini, M. Eslami, M. Rezazadeh, M. Mirzazadeh et al. (2018). , “New optical solitons of nonlinear conformable fractional Schrodinger–Hirota equation,” Optik-International Journal of Light and Electron Optics, vol. 172, pp. 545–553.
17. H. Rezazadeh, H. Tariq, M. Eslami, M. Mirzazadeh and Q. Zhou. (2018). “New exact solutions of nonlinear conformable time-fractional Phi-4 equation,” Chinese Journal of Physics, vol. 56, no. 6, pp. 2805–2816. [Google Scholar]
18. F. Batool and G. Akram. (2017). “On the solitary wave dynamics of complex Ginzburg–Landau equation with cubic nonlinearity,” Optical and Quantum Electronics, vol. 49, no. 1, pp. 1–9. [Google Scholar]
19. H. Rezazadeh. (2018). “New solitons solutions of the complex Ginzburg–Landau equation with Kerr law nonlinearity,” Optik, vol. 167, pp. 218–227. [Google Scholar]
20. M. S. Osman, B. Ghanbari and J. A. T. Machado. (2019). “New complex waves in nonlinear optics based on the complex Ginzburg–Landau equation with Kerr law nonlinearity,” Europen Physics Journal Plus, vol. 134, no. 20, pp. 1–10. [Google Scholar]
21. I. Ahmed, A. R. Seadawy and D. Lu. (2019). “Combined multi-waves rational solutions for complex Ginzburg–Landau equation with Kerr law of nonlinearity,” Modern Physics Letters A, vol. 1, no. 34, pp. 1–16. [Google Scholar]
22. A. I. Aliyu, A. Yusuf and D. Baleanu. (2017). “Optical solitons for complex Ginzburg–Landau model in nonlinear optics,” Optik-International Journal of Light and Electron Optics, vol. 158, pp. 368–375. [Google Scholar]
23. A. H. Arnous, A. R. Seadawy, R. T. Alqahtani and A. Biswas. (2017). “Optical solitons with complex Ginzburg–Landau equation by modified simple equation method,” Optik-International Journal of Light and Electron Optics, vol. 144, pp. 475–480. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |