DOI:10.32604/cmc.2020.012457
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012457 | |
| Article |
An Unsteady Oscillatory Flow of Generalized Casson Fluid with Heat and Mass Transfer: A Comparative Fractional Model
1Department of Mathematics, City University of Science and Information Technology, Peshawar, 25000, Pakistan
2Computational Analysis Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam
3Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
4Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
5Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Al-Dawaser, 11991, Al Kharj, Saudi Arabia
*Corresponding Author: Aamina Aamina. Email: aamina@tdtu.edu.vn
Received: 01 July 2020; Accepted: 10 September 2020
Abstract: It is of high interest to study laminar flow with mass and heat transfer phenomena that occur in a viscoelastic fluid taken over a vertical plate due to its importance in many technological processes and its increased industrial applications. Because of its wide range of applications, this study aims at evaluating the solutions corresponding to Casson fluids’ oscillating flow using fractional-derivatives. As it has a combined mass-heat transfer effect, we considered the fluid flow upon an oscillatory infinite vertical-plate. Furthermore, we used two new fractional approaches of fractional derivatives, named AB (Atangana–Baleanu) and CF (Caputo–Fabrizio), on dimensionless governing equations and then we compared their results. The Laplace transformation technique is used to get the most accurate solutions of oscillating motion of any generalized Casson fluid because of the Cosine oscillation passed over the infinite vertical-plate. We obtained and analyzed the distribution of concentration, expressions for the velocity-field and the temperature graphically, using various parameters of interest. We also analyzed the Nusselt number and the skin friction due to their important engineering usage.
Keywords: AB and CF fractional derivatives; generalized Casson fluid; heat and mass transfer; oscillation
Flows in oscillating bodies play an important role in engineering and the industrial field. It is of high interest to study unsteady flows of fluids, which are incompressible non-Newtonian created by oscillatory flat-plates, because of their applications in the assessment of numerical methods performance while computing transient flows have various industrial applications. These flows have generated theoretical and fundamental interest, in addition to their usability in biological-industrial processes such as fluctuating unsteady boundary layer blood flow (quasi-periodic), cardio-vascular systems and an oscillating body surrounded by acoustic streaming.
Focusing on the advantages of viscoelastic flows, several studies have been carried out and published. Ross [1] was the first to investigate the history of fractional calculus and studied the pioneers of fractional calculus, because the viscoelastic fluids have an elastic nature, while fractional calculus is more convenient to discuss the memory effect. Choudhury et al. [2] observed the viscoelastic behavior of the fluid with the help of fractional calculus. Zheng et al. [3] used generalized derivatives and studied the slip effects of the viscoelastic fluid. Meral et al. [4] researched the use of a viscoelastic fluid with fractional calculus in the medical field. Cao et al. [5] investigated the fractional Maxwell model for second grade viscoelastic fluid. They discussed the parametric influence of various embedded parameters on the velocity profile of viscoelastic fluid. Sheikh et al. [6] investigated the idea of the CF derivatives of fractional order on MHD flow of second-grade fluid, while radiative heat transfer has been taken into account.
The exact work becomes rare if one considers the analytical solution of the Casson fluid model through a fractional derivative. When it comes to the comparison between fractional calculus and classical, it has been observed that for several fluids between elastic and viscous materials, the fractional constitutive relationship model is much more important as compared to the customary constitutive relationship model. The fractional derivative has very fruitful result when it comes to describing more complex dynamics. Ali et al. [7] studied the properties of MHD for the blood flow when blood is characterized as an example of Casson fluid, together with magnetic particles in a horizontal cylinder. Vázquez [8] used the time-fractional derivative and obtained a diffusion equation for fractional, which has had very fruitful results in the field of computational fluid dynamics. It has been reported that Vieru et al. [9] conducted very interesting research using the time-fractional derivative to study the free convection flow of an incompressible viscous fluid when the fluid is flowing near the vertical plate; moreover, the Newtonian heating and mass diffusion has been taken in the presence of chemical reaction. Sin et al. [10] has studied viscoelastic properties. The constitutive equations have been solved with fractional derivatives, and the exact solutions have been calculated for the generalized Maxwell model. Research has discovered that rest state stability of a target fractional calculus model has been built up, which is a significant finding that invigorates the physical premise of these fractional models [11]. Furthermore, the study has found that when fractional derivatives are used for constitutive equations, one can obtain better experimental data. Khan et al. [12] investigated Casson fluid over an oscillating plate with the help of Caputo time-fractional derivative.
In the new world of fractional calculus, different methods are used but the most common fractional calculus to be found are Caputo and Riemann–Liouville fractional calculus operators, while Riemann–Liouville and Caputo operators come up with some deficiencies i.e., in the world of calculus, it is very common that whenever the derivative of a constant is taken, it always gives zero, but in case of Riemann–Liouville fractional derivatives, this property was not satisfied and the derivative was not zero. At the same time, Caputo has investigated a kernel for the fractional derivatives, which is a singular function. In 2015, Michele Caputo and Mauro Fabrizio heightened the need to put an end to this deficiency and introduced another fractional method in which the kernel is in exponential order and this exponential kernel is having no singularities [13]. Khan et al. [14] utilized the possibility of the CF fractional calculus to generalize the starting solutions of the flow of second-grade fluid over a vertical plate and acquired the exact answers to the utilization of the Laplace model approach. In other papers, Ali et al. [15] examined the influence of various shapes for MoS2 nanoparticles on engine oil taking the study of generalized Brinkman-type fluid model into account with the non-singular kernel. The CF time-fractional derivatives are useful in the application of the Laplace transform. Zafar et al. [16] studied incompressible viscous fluid that was flowing on an infinite plate and the non-integer order derivative, in which the kernel was taken non-singular. Atangana et al. [17] together used the idea of the non-local and non-singular kernel of fractional derivatives and solved a model known as the Cattaneo-Hristov model. Alkahtani et al. [18] used CF fractional derivative and studied different wave motions that take place on the surface of low water. Atangana [19] used the interesting properties of Caputo and Fabrizio fractional-order derivative and brought very interesting modifications in Fisher’s reaction for diffusion equation. Atangana et al. [20] applied the Caputo–Fabrizio derivative to investigate the behavior of groundwater flow within the confined aquifer. However, some problems rose when one of the fractional calculus methods, named Caputo–Fabrizio fractional approach, was used because the kernel in the integral for the mentioned approach was non-singular as well as non-local. To overcome the lack of non-locality of the kernel, two mathematicians, Atangana and Baleanu, introduced a very fruitful work in the field of fractional calculus. The new fractional derivative was similar to w the Caputo and Riemann-Liouville fractional model and based on the generalized Mittag-Leffler function. Machado et al. [21] made a very good research on fractional dynamics and used the idea for mathematical physics, which is still the center of interest of many physicists and mathematicians. Saqib et al. [22] studied Caputo–Fabrizio time-fractional derivative and obtained closed-form solutions for Jeffery fluid. Reddy et al. [23] studied Casson ferrofluid over an upper convective surface having a parabolic revolution, in which the fluid is studied in the presence of viscous dissipation and non-linear thermal radiation. Reddy et al. [24] made a research on transitive radiative free convective hydro-magnetic Casson fluid in the presence of entropy heat generation. Ajayi et al. [25] investigated the two dimensional Casson fluid, which is flowing in a horizontal melting surface; moreover, the fluid is taken in a thermally arranged medium. Ali et al. [26] investigated Cattaneo-Christov heat flux model in the presence of a variable source and non-linear radiation effect. Sandeep et al. [27] studied the nature of magneto-hydrodynamic Casson fluid in the presence of heat and mass transfer and came up with some theoretical results about the Brownian moment of the fluid particles. Mehmood et al. [28] investigated Casson fluid and studied a micro-rotation in the presence of mixed convection flow of the fluid. Ali et al. [29] investigated Casson fluid, coupled with the energy equation with the help of the fractional derivative.
Fractional calculus unlocked new research areas and enabled researchers to study high complex physical phenomena in daily life. Ali et al. [30] researched the effects of magneto-hydrodynamics on the oscillating blood flow in a cylinder. Algahtani [31] carried out a comparison between two different kernels of AB and CF fractional operators to get a solution of the Allen–Cahn model, which is based on Crank–Nicholson scheme. Ullah et al. [32] studied the effect of slip condition on magnetic-hydrodynamics free convective flow in the presence of Newtonian heating. Sheikh et al. [33] studied comparison on a coupled fractional derivatives, which are based on the exponential kernel suggested by Caputo and Fabrizio. Tateishi et al. [34] carried out a detailed study on the behavior of anomalous diffusion with the help of the fractional derivative and ended with a fruitful investigation. A comparative investigation of RL and RC electrical current has been carried out by Abro et al. [35] using Atangana-Baleanu and Caputo-Fabrizio derivative. Sheikh et al. [36] obtained a generalized nanofluid model using the AB and CF fractional approach to enhance the performance of solar collectors. Sheikh et al. [37] carried out a comparison between two different fractional models, namely as AB and CF fractional models, and studied the chemical reaction for the flow of Casson fluid. Abro et al. [38] obtained the same results for the generalized second-grade fluid model along with heat and mass transfer. Jassim et al. [39] investigated the second kind Volterra integrodifferential equation with the help of the local fractional Adomian decomposition method and obtained the analytical solution through fractional approach.
Motivated by the above literature, this research paper studies the comparative analysis of CF and AB fractional derivatives to the convective heat transfer in Casson fluid. Exact solutions for velocity and temperature are obtained for both cases via the Laplace transformation. Graphs for both cases are formed with the help of Mathcad software, which shows the behavior of Casson fluid.
In the current problem, the flow of Casson fluid along with heat as well as mass transfer over an infinite vertical flat plate has been considered. The x-axis is the direction of the fluid’s flow, while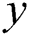 
-axis is considered normal to the plate. At first, the fluid and plate are static having constant physical properties i.e., temperature and concentration 
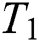and 
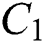respectively. After some time 
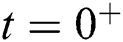, the plate starts the to move in its plane with uniform velocity U as illustrated by Fig. 1. The temperature and concentration levels of the plate increased linearly to 
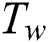and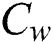 
with time 
.
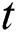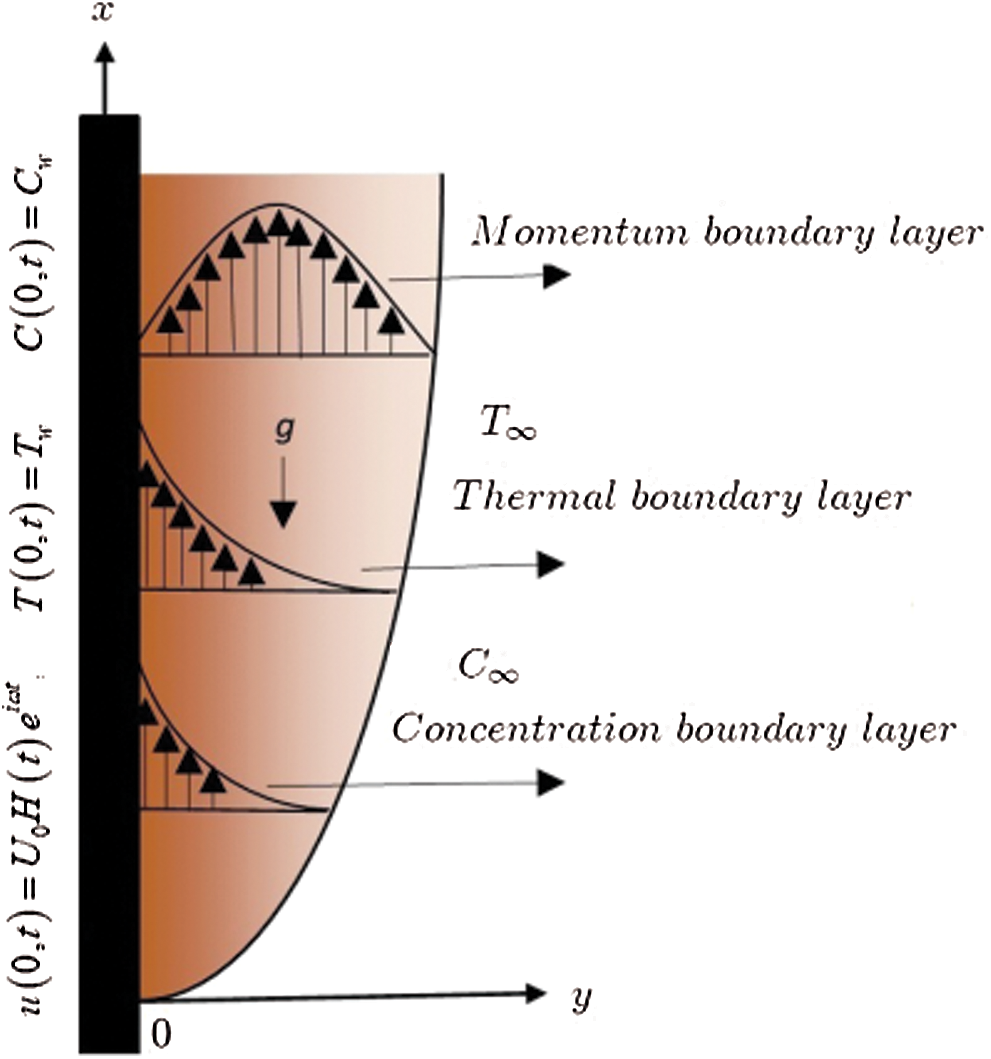
Figure 1: Geometry of the flow
Since incompressible Casson fluid is considered [4], for which the rheological equation is as below.
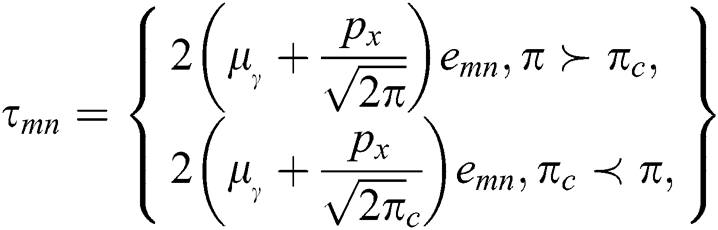
where μ is the dynamic viscosity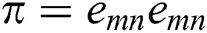 
and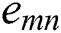 
is the 
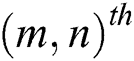component of deformation rate. For the non-Newtonian fluid, 
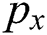is known as the yield stress, 
is known as the product of the component of deformation rate,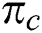 
is the critical value considered for this product, which is based on the non-Newtonian model and 
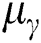is the symbol for the plastic dynamic viscosity. Since the physical quantities i.e., velocity, temperature and concentration, are functions of 
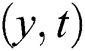only, then by the normal Boussinesq estimation, the free convection flow of the Casson fluid together with the heat as well as the mass transfer is governed by the following partial differential equations [20]:
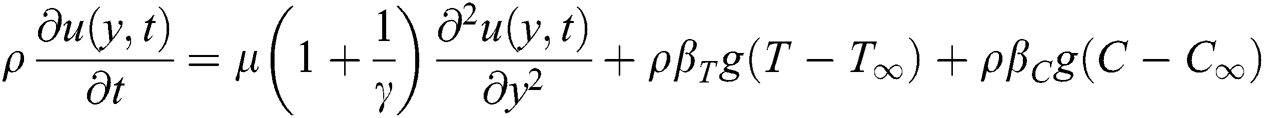
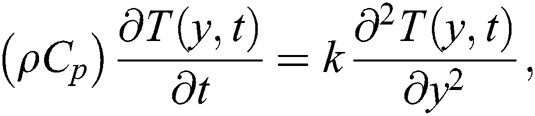
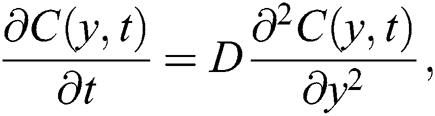
subjected to the following initial and boundary conditions:
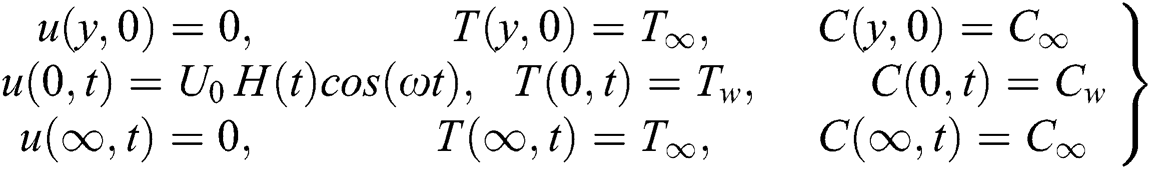
where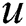 
denotes the fluid velocity in the 
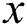-direction, 
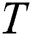is the temperature, 
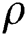is the fluid density, 
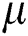is the dynamic viscosity of fluids, 
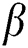is the material parameter of the Casson fluid, 
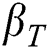is the thermal expansion coefficient, 
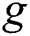is the acceleration due to gravity, 
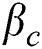is the coefficient of concentration, 
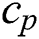is the specific heat capacity of fluids, 
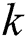is the thermal conductivity and 
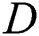is the thermal diffusivity.
Using the following dimensionless variables:
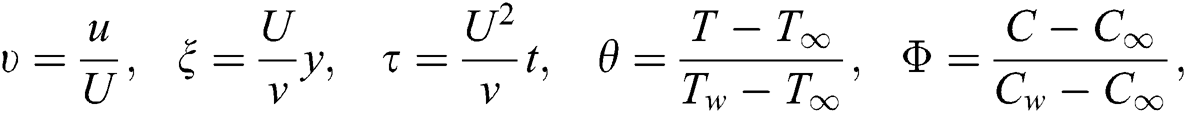
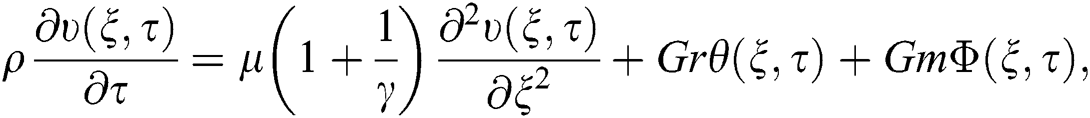
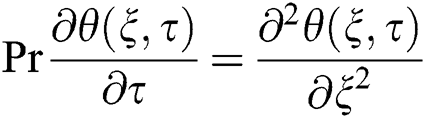
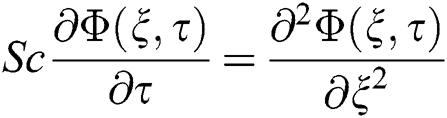
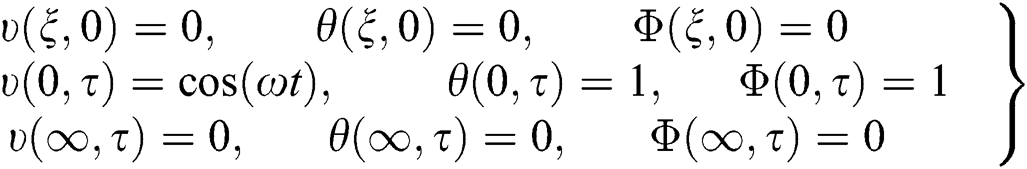
where
, 
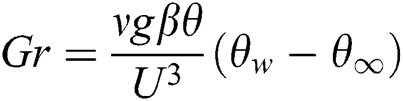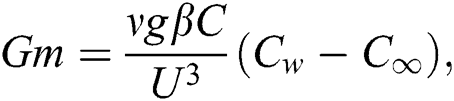
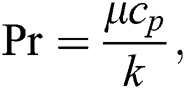
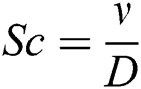represents the thermal Grashof number, mass Grashof number, Prandtl number and Schmidt number, respectively.
2.1 Solution with Atangana-Baleanu Derivatives
To develop the AB fractional model for a generalized Casson fluid, we introduce 
:
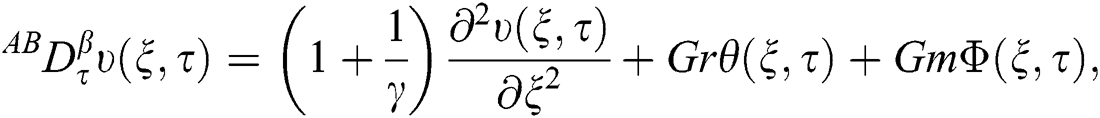
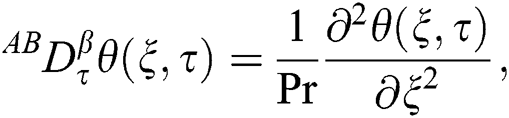
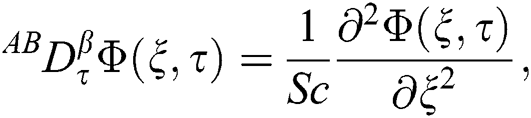
where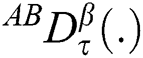 
is known as AB time fractional operator of order 
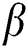and is defined as [11]:
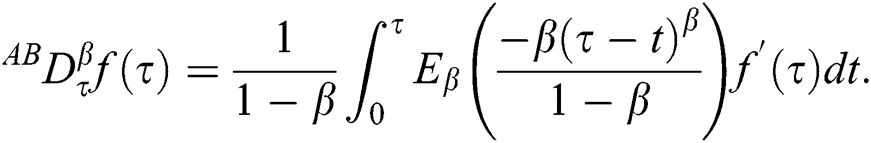
where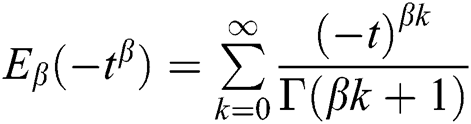 
is the generalized Mittag-Leffler function.
Applying the Laplace transformation on Eqs. (11)–(12) and using the corresponding initial conditions from Eq. (9), we get:
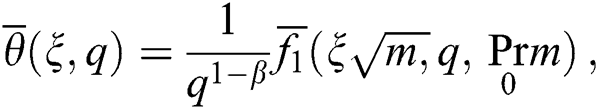
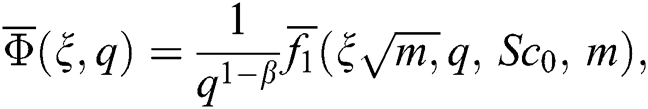
Using the Laplace transform of Eq. (10) and incorporating Eqs. (14)–(15) in it gives the following equation:
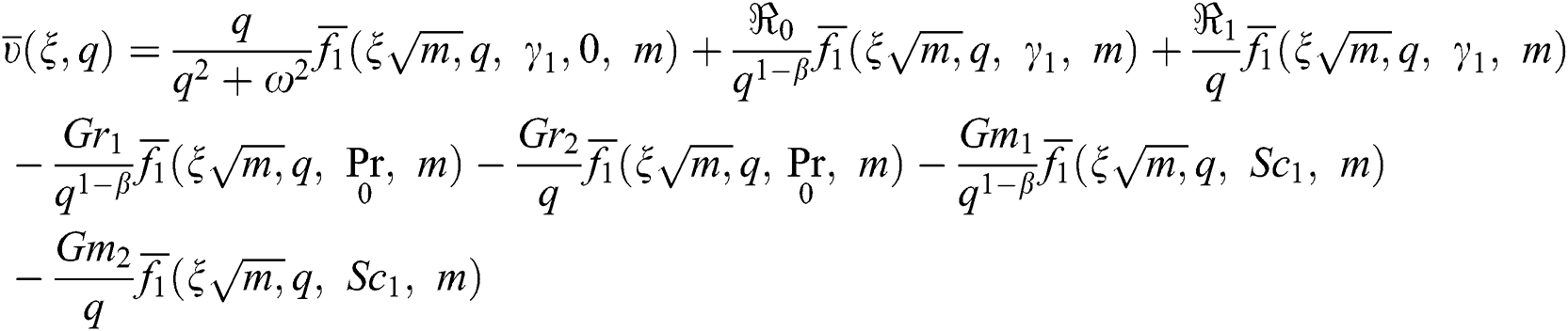
where
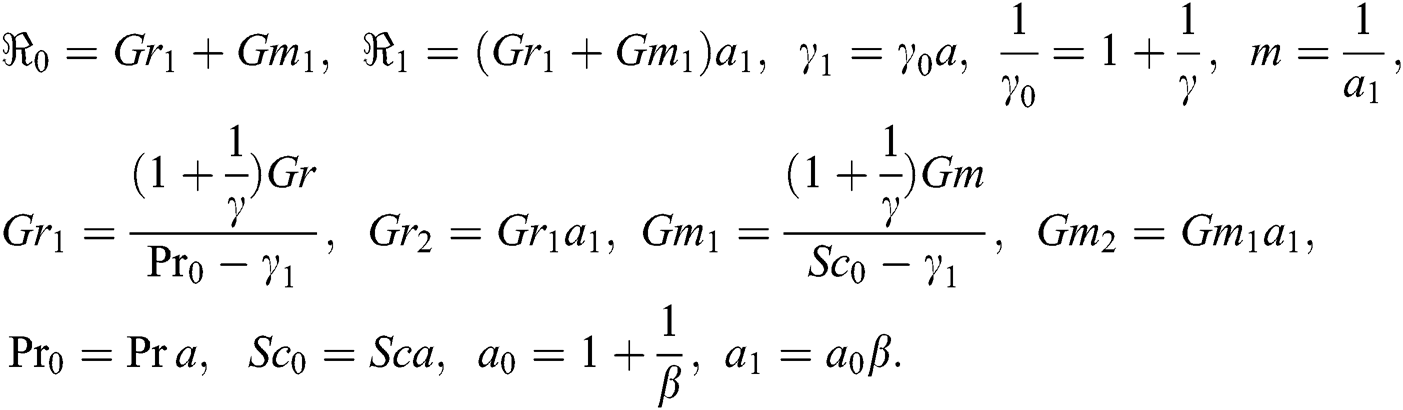
Applying inverse Laplace transform on Eqs. (14)–(16), we get:
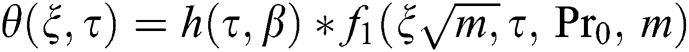
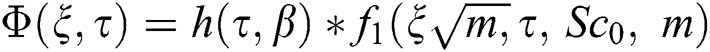
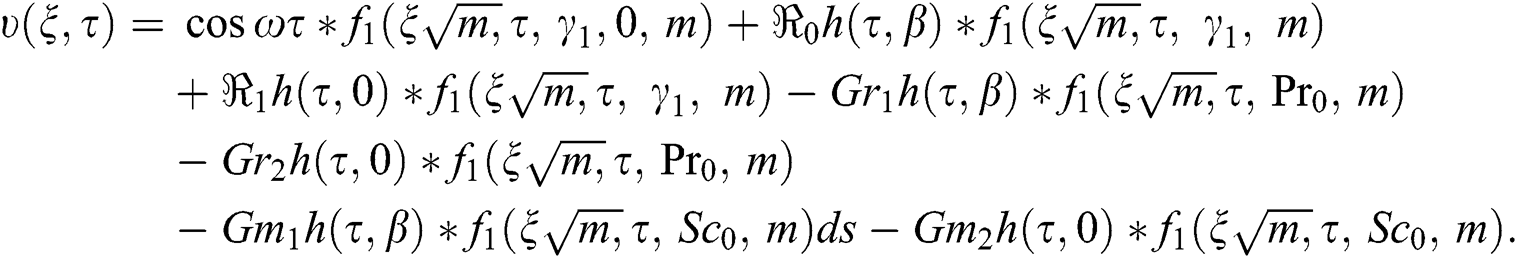
where the formula for special functions are as follows:
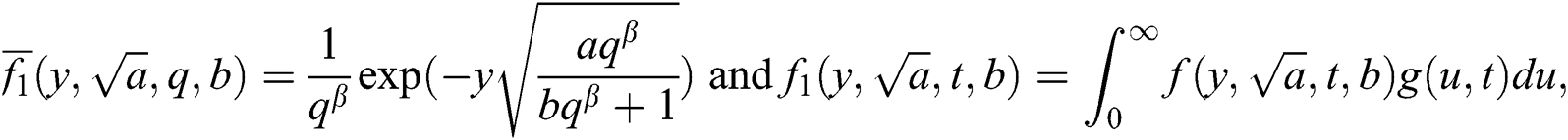
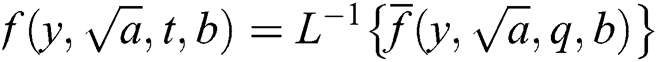
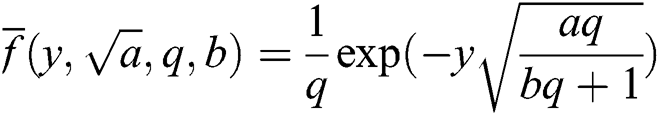
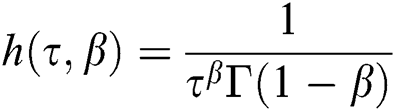
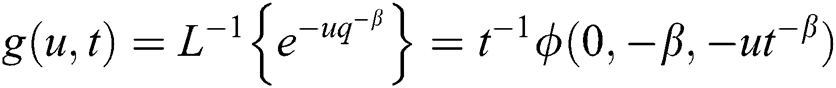
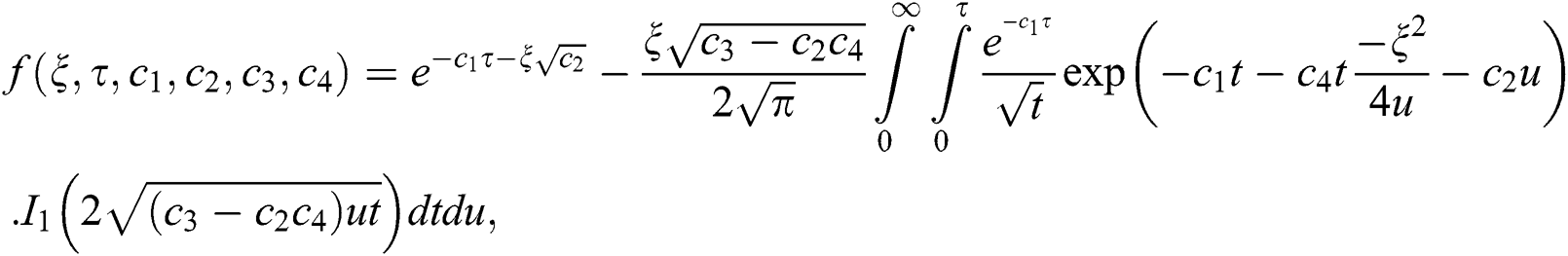
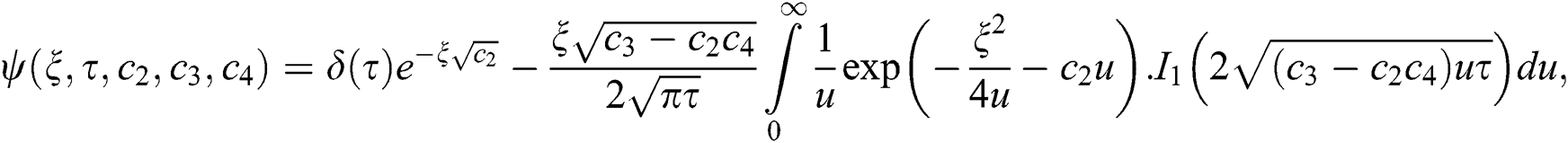
where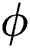 
the Wright function and is defined as
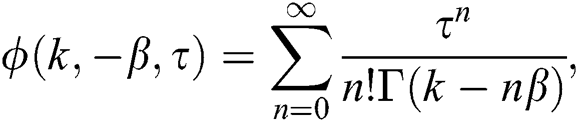
For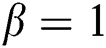 
the above-obtained solution can be reduced to a classical solution with the help of the following properties:
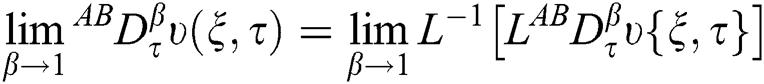
2.2 Solution with Caputo–Fabrizio Derivatives
To develop CF fractional model for generalized Casson fluid, we replace partial derivatives concerning s by CF fractional operator of order a, and Eqs. (6)–(8) becomes as:
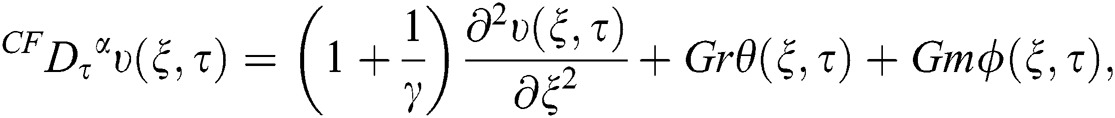
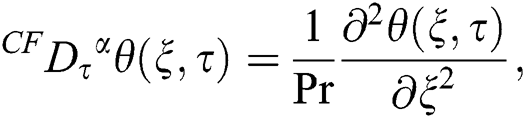
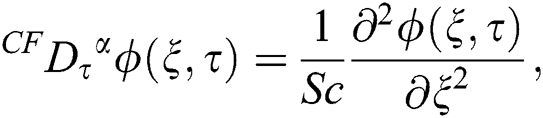
where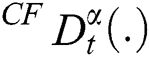 
stands for the CF time-fractional operator of order 
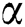and is defined as [10]:
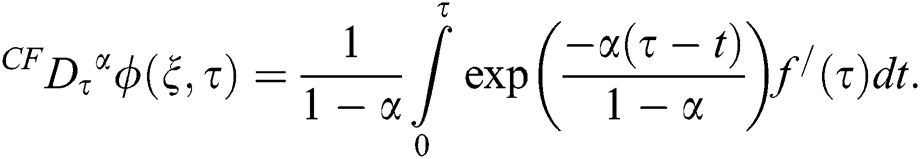
Using the Laplace transformation on Eqs. (21)–(22) and using the corresponding initial conditions from Eq. (9), we get:
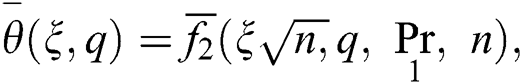
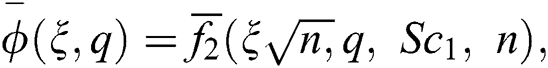
Taking the Laplace transform of Eq. (20) and incorporating Eqs. (23)–(24) in it gives the following equation.
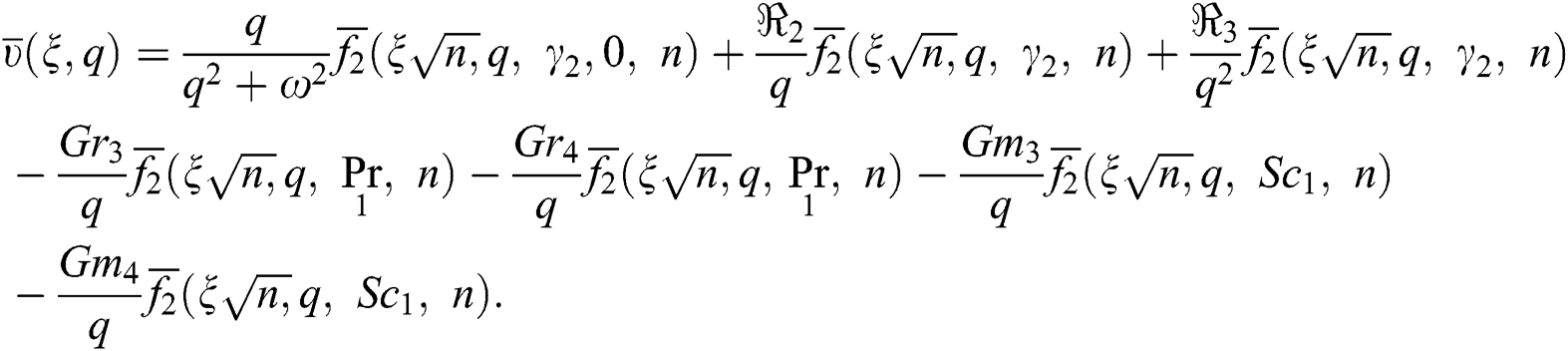
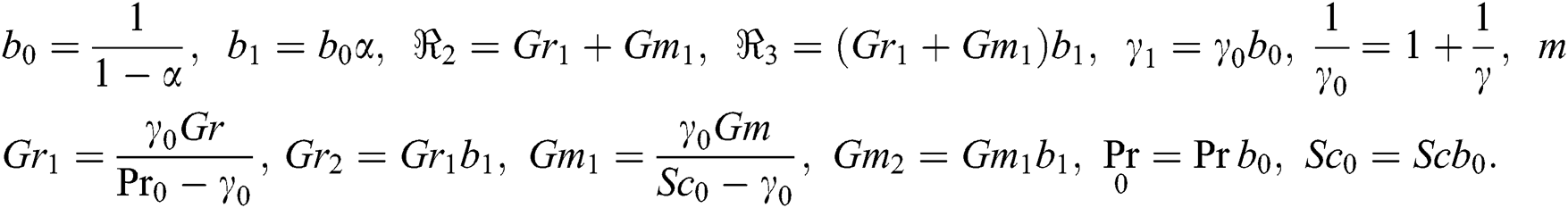
Applying inverse Laplace transform on Eqs. (23)–(25), we get:
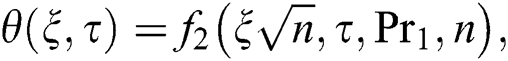
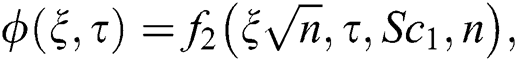
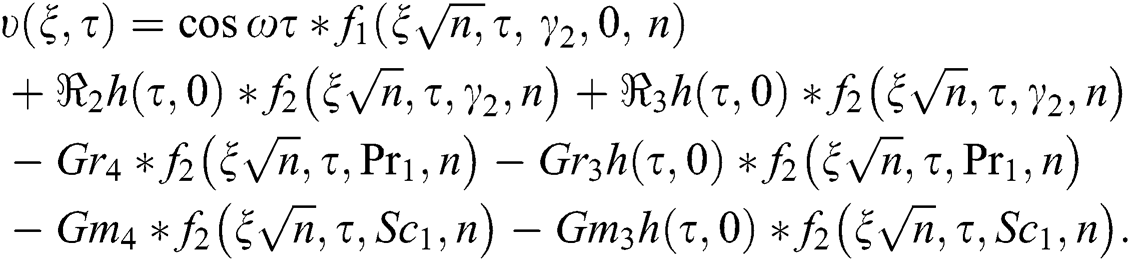
The expression for the rate of heat transfer is given as:
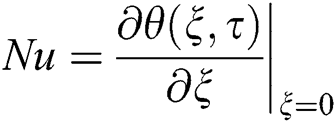
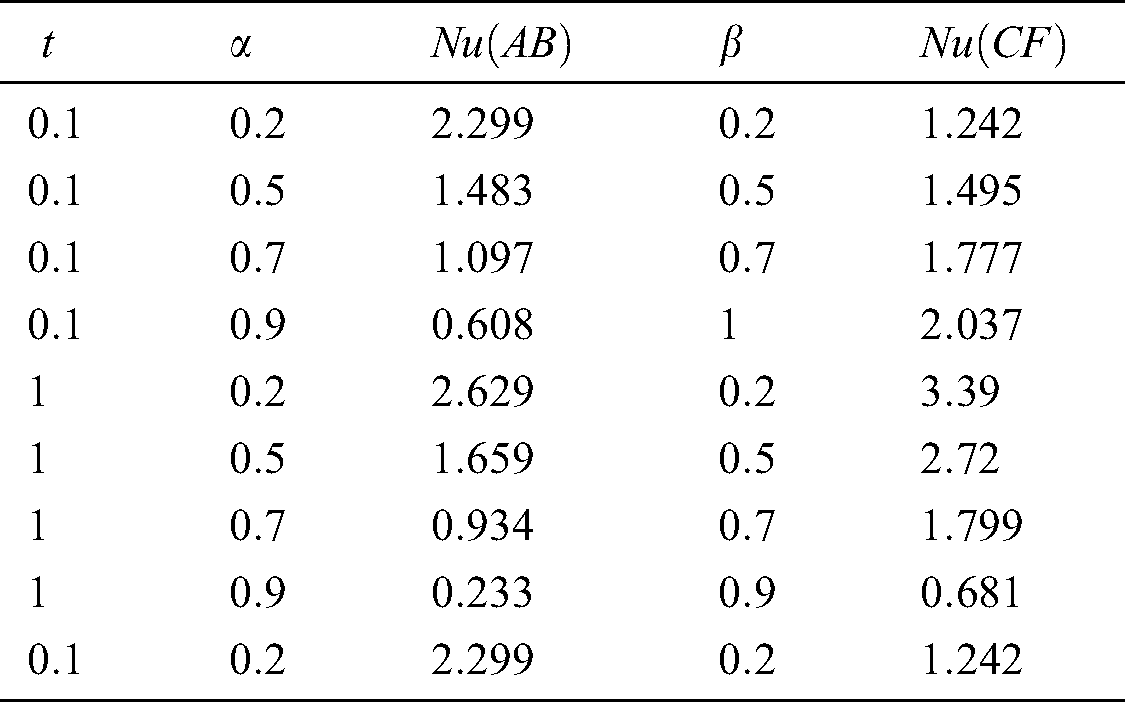
The convergence of the fractional model to the classical model is shown in Tab. 1. The Nusselt number gradually decreases for a small value of time in AB fractional derivatives, while in CF fractional derivatives it increases. Put another way, for a larger value of time, both fractional models gradually decrease when we converge to the classical model. This is because the Nusselt number is the ratio of convective heat transfer to conductive heat transfer.
Table 1: Comparison of rate of heat transfer for time and fractional parameters
The focus of our study is the achievement of accurate solutions, using Laplace transform technique, free convection flow of Casson fluid (generalized) on a vertical-plate having infinite oscillation. We analyzed the combined effect of mass and heat transfer. To apply the recently introduced fractional calculus definitions, two pairs of mathematicians, Caputo and Fabrizio and Baleanu and Atangana, took Casson fluid’s generalized fraction-model in 2015 and 2016, respectively. Both pairs used graphs and tables to compare the accuracy of solutions in each case. Moreover, various embedded parameters such as thermal Grashof number (Gr), Casson fluid (γ), number of mass Grashof (Gm), Schmidt number (Sc), and Prandtl number (Pr) for the obtained solutions of Casson fluid’s AB fractional-model are represented graphically. Fig. 2 shows a fluid motion comparative study between CF and AB. We observed greater velocity for less time (τ = 0.02) using the AB approach than the CF approach, while for the case of greater time (τ = 5), we observed greater velocity using the CF approach than the AB approach. However, we found the two velocities identical via both approaches for unit time (τ = 1).
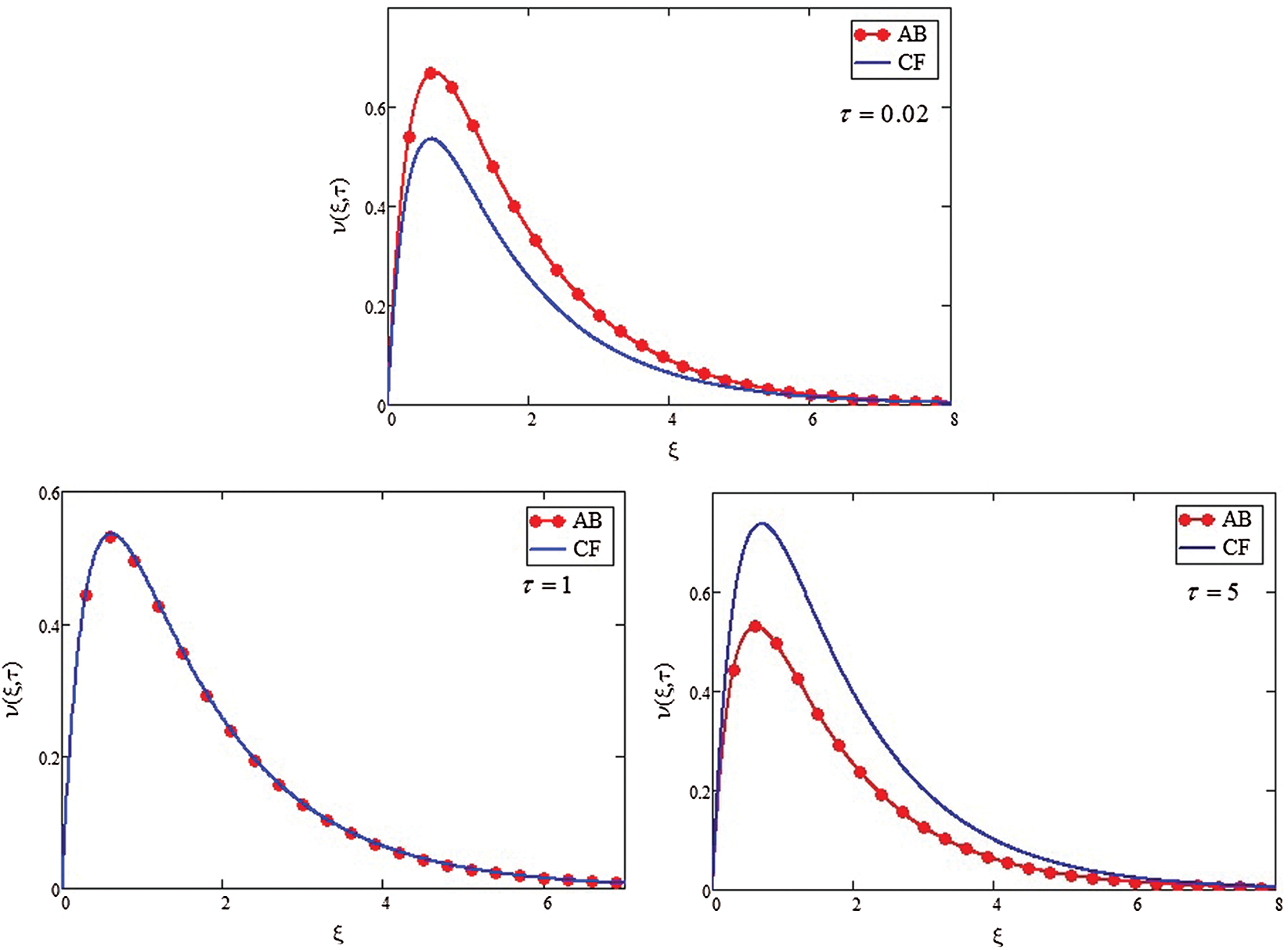
Figure 2: Comparing the velocities of AB and CF for different 
values
Fig. 3 shows parameter γ of Casson fluid influencing v(ξ, τ). The velocity shows a direct relation with the values of γ due to the reduction of the thickness of the boundary layer with the reduction in γ values.
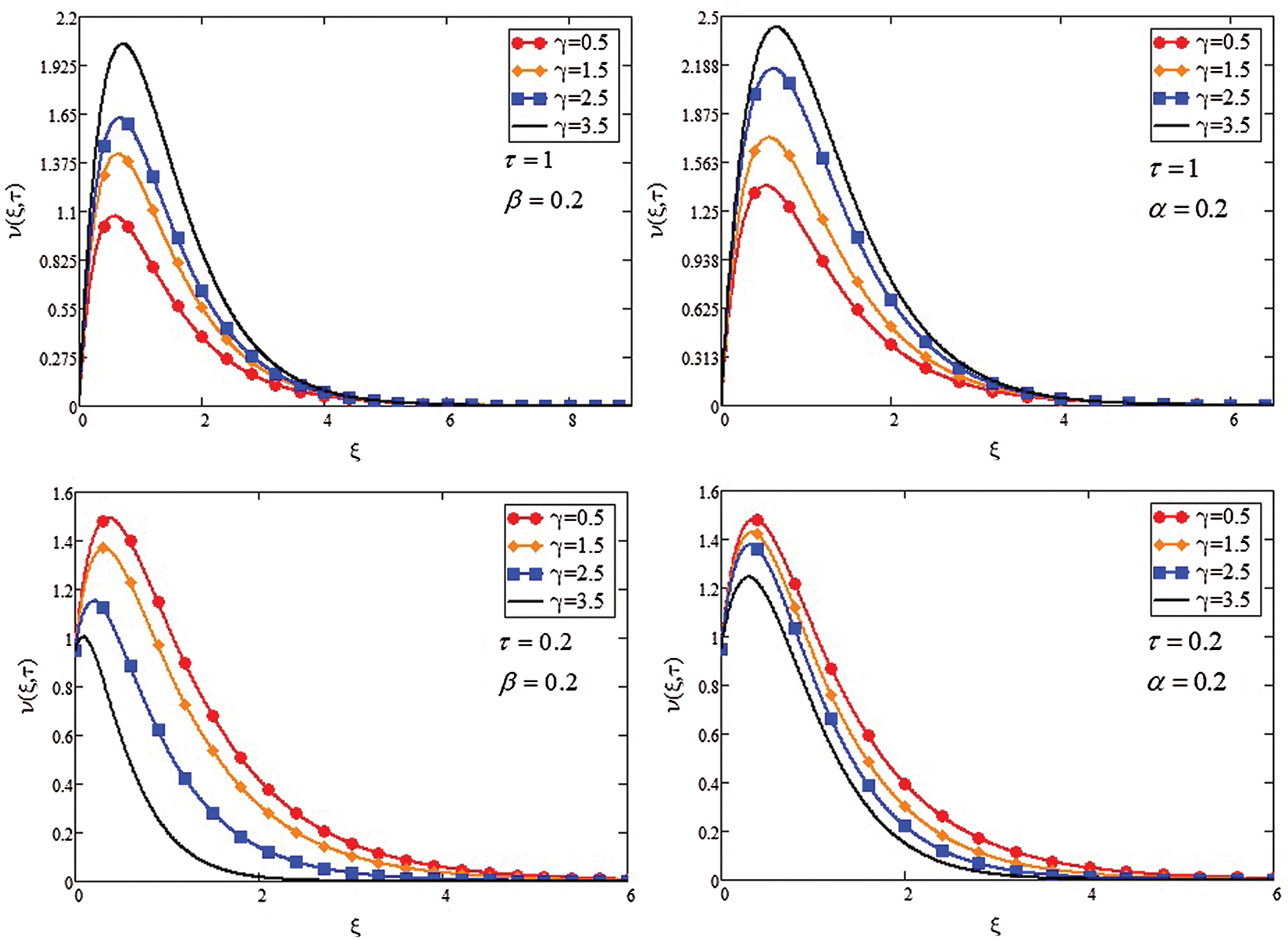
Figure 3: Profile of velocity for (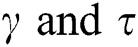
)
The effect of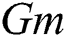 
and 
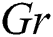on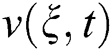 
is represented in Figs. 4 and 5. An increase in 
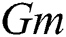and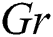 
increases 
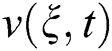due to buoyancy force enhancement, which is caused by concentration gradients and temperature. Physically, 
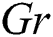and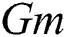 
signify the relative effect of buoyancy forces concentration and thermal on the viscous hydrodynamic force, respectively. An increase in 
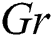and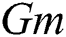 
values increase concentration gradients and temperature, which signifies buoyancy contribution near the plate, hence, causes a short rise in 
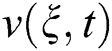value near the plate.
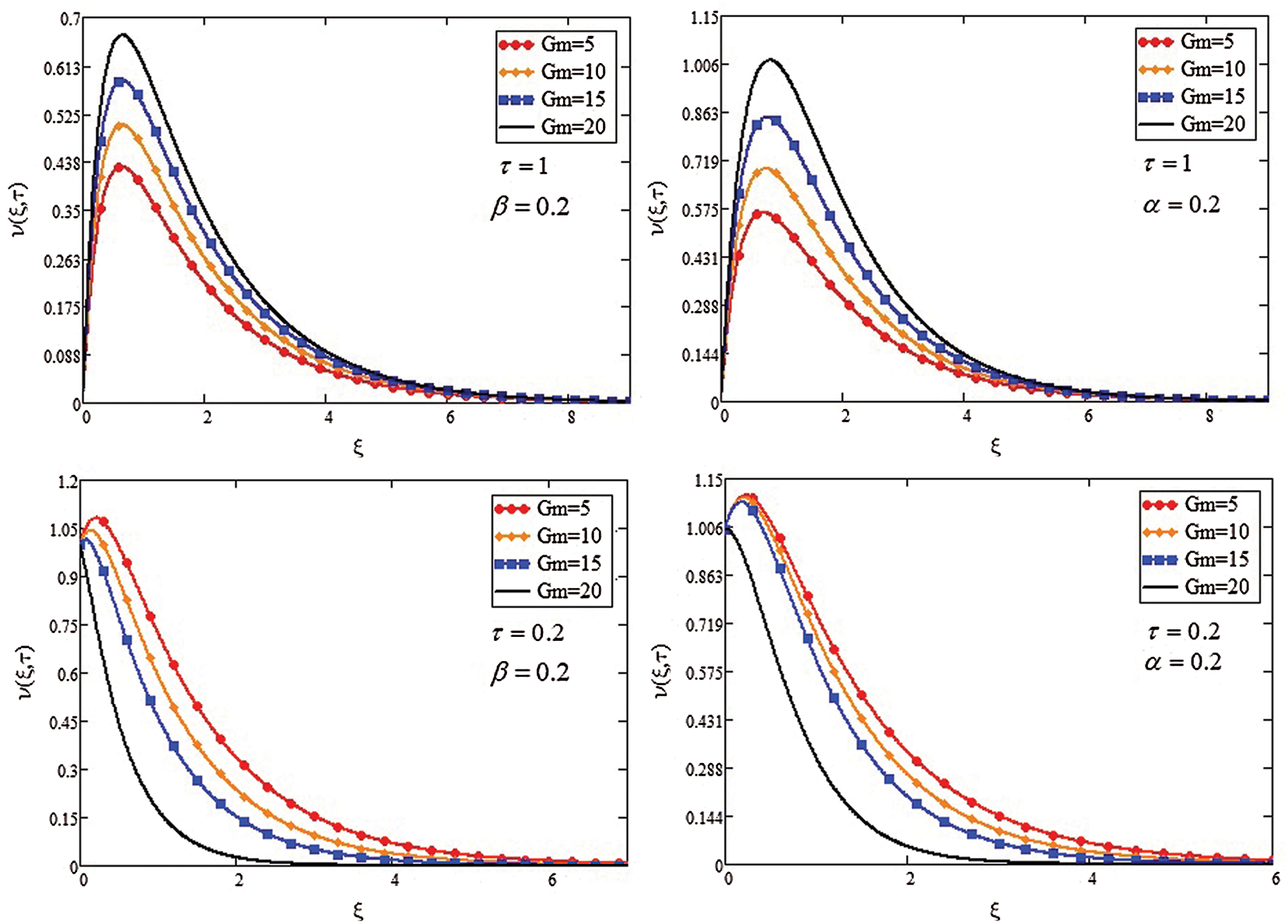
Figure 4: Velocity profile for (
)
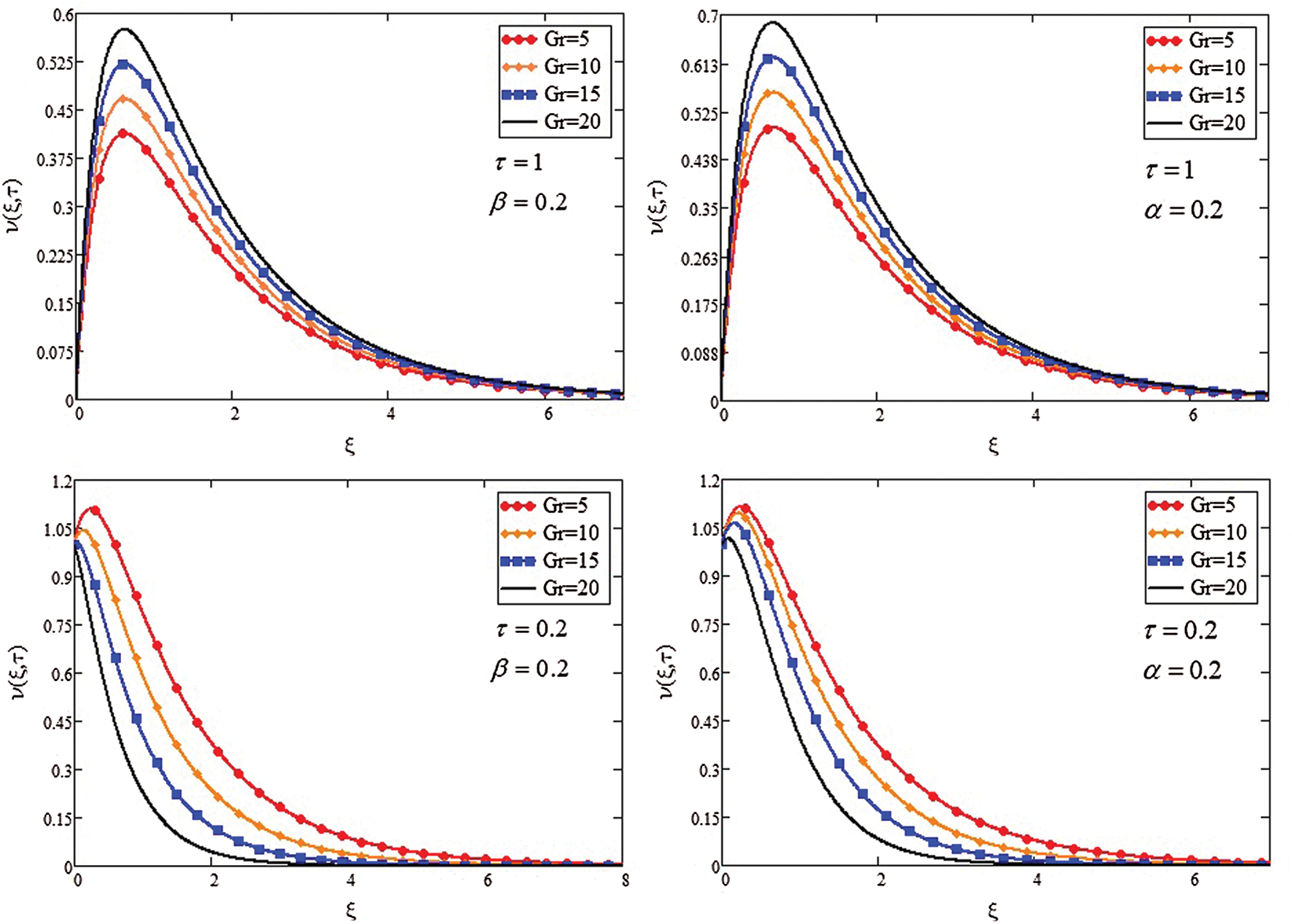
Figure 5: Velocity profile for (Gr and τ)
Figs. 6–7 show 
that and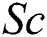 
has an inverse relation with 
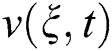. Increase in values of 
and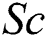 
reduces thermal and concentration boundary layer thickness, respectively. The ratio of thermal and momentum diffusivity is signified by the 
. Thermal boundary layers and 
controls relative thickening of the momentum in heat transfer problems. Therefore, we can use 
it to increase the cooling rate.
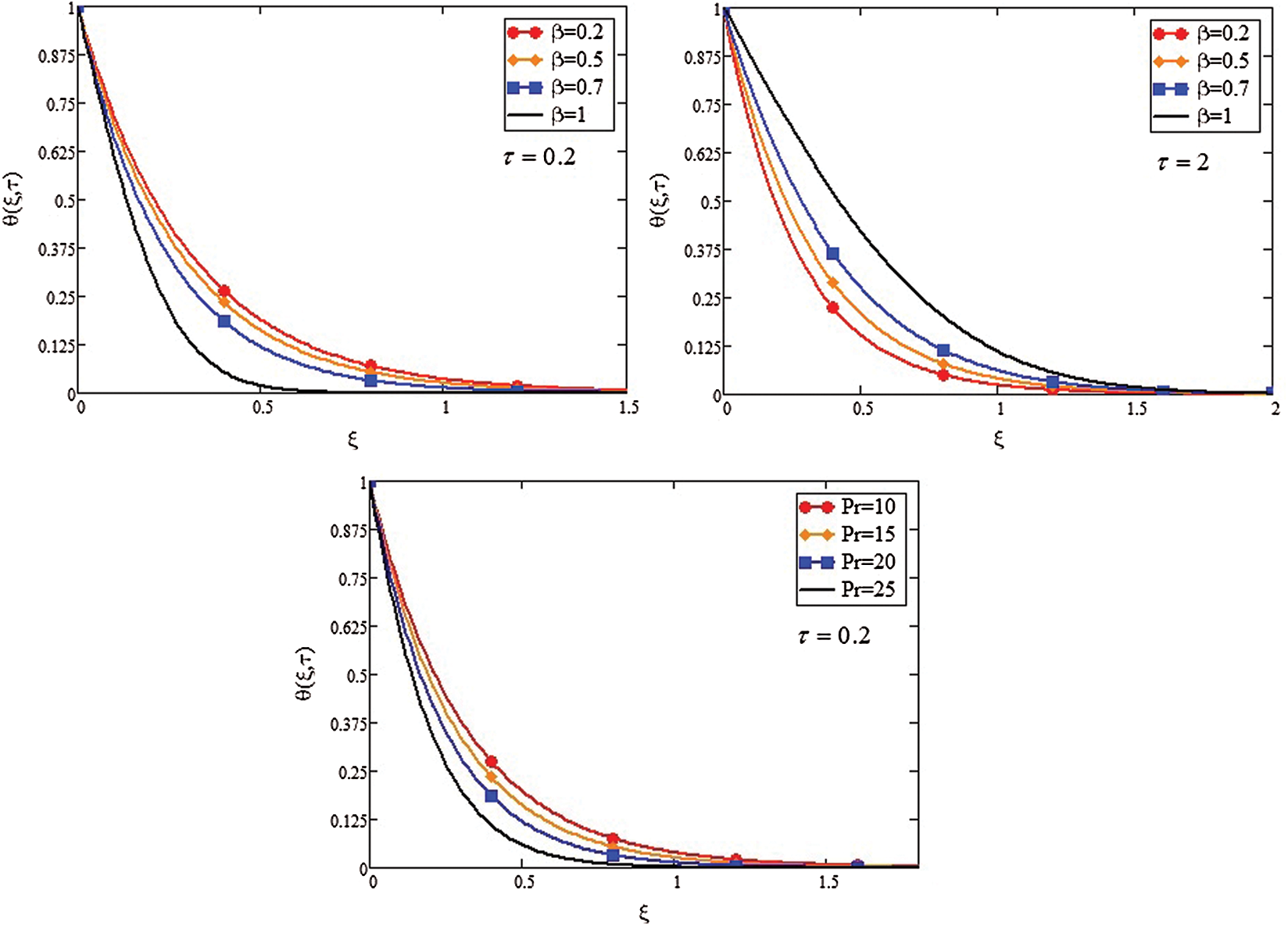
Figure 6: Temperature profile for different values of Pr and two different times
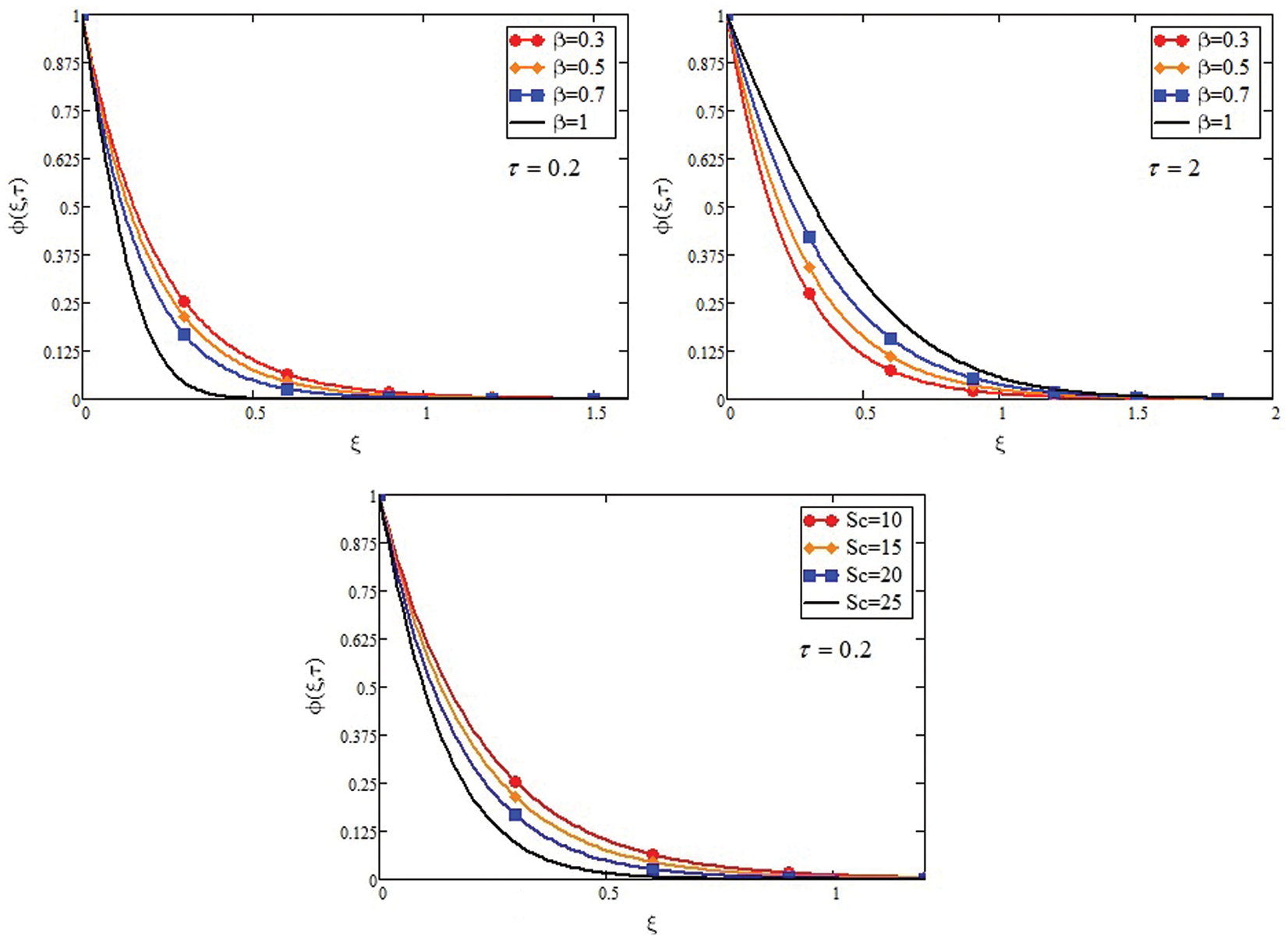
Figure 7: Velocity profile for (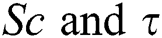
)
Using AB and CF approaches, we carried out a comparative analysis for generalized Casson fluid flow with mass and heat transfer. We summarized that the behavior of fluid velocity is opposite for different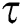 
values using AB and CF approaches where (
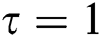) is the point of transition. An increase in the values of 
, 
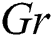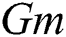, and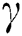 
increases the fluid velocity, while a increases in the values of 
and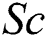 
decreases the fluid velocity.
An increase in the values of 
and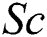 
decreases the temperature and the levels of concentration, respectively.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. Ross. (1977). “The development of fractional calculus 1695–1900,” Historia Mathematica, vol. 4, no. 1, pp. 75–89. [Google Scholar]
2. M. D. Choudhury, S. Chandra, S. Nag, S. Das and S. Tarafdar. (2012). “Forced spreading and rheology of starch gel: Viscoelastic modeling with fractional calculus,” Colloids and Surfaces A: Physicochemical and Engineering Aspects, vol. 407, pp. 64–70. [Google Scholar]
3. L. Zheng, Y. Liu and X. Zhang. (2012). “Slip Effects on MHD flow of a generalized Oldroyd-B fluid with fractional derivative,” Nonlinear Analysis: Real World Applications, vol. 13, no. 2, pp. 513–523. [Google Scholar]
4. F. C. Meral, T. J. Royston and R. Magin. (2010). “Fractional calculus in viscoelasticity: An experimental study,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, no. 4, pp. 939–945. [Google Scholar]
5. Z. Cao, J. Zhao, Z. Wang, F. Liu and L. Zheng. (2016). “MHD flow and heat transfer of fractional Maxwell viscoelastic nanofluid over a moving plate,” Journal of Molecular Liquids, vol. 222, pp. 1121–1127. [Google Scholar]
6. N. A. Sheikh, F. Ali, I. Khan and M. Saqib. (2018). “A modern approach of Caputo–Fabrizio time-fractional derivative to MHD free convection flow of generalized second-grade fluid in a porous medium,” Neural Computing and Applications, vol. 30, no. 6, pp. 1865–1875. [Google Scholar]
7. F. Ali, N. A. Sheikh, I. Khan and M. Saqib. (2017). “Magnetic field effect on blood flow of Casson fluid in an axisymmetric cylindrical tube: A fractional model,” Journal of Magnetism and Magnetic Materials, vol. 423, pp. 327–336. [Google Scholar]
8. J. L. Vázquez. (2017). “The mathematical theories of diffusion: Nonlinear and fractional diffusion,” in Nonlocal and Nonlinear Diffusions and Interactions: New Methods and Directions, pp. 205–278, . [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-319-61494-6_5. [Google Scholar]
9. D. Vieru, C. Fetecau and C. Fetecau. (2015). “Time-fractional free convection flow near a vertical plate with Newtonian heating and mass diffusion,” Thermal Science, vol. 19, no. 1, pp. 85–98. [Google Scholar]
10. C. S. Sin, L. Zheng, J. S. Sin, F. Liu and L. Liu. (2017). “Unsteady flow of viscoelastic fluid with the fractional K-BKZ model between two parallel plates,” Applied Mathematical Modelling, vol. 47, pp. 114–127. [Google Scholar]
11. N. Shahid. (2015). “A study of heat and mass transfer in a fractional MHD flow over an infinite oscillating plate,” SpringerPlus, vol. 4, no. 1, pp. 640–661. [Google Scholar]
12. I. Khan, N. A. Shah and D. Vieru. (2016). “Unsteady flow of generalized Casson fluid with fractional derivative due to an infinite plate,” European Physical Journal Plus, vol. 131, no. 6, pp. 181–193. [Google Scholar]
13. M. Caputo and M. Fabrizio. (2015). “A new definition of fractional derivative without singular kernel,” Progress in Fractional Differentiation and Applications, vol. 1, no. 2, pp. 1–13. [Google Scholar]
14. N. A. Shah and I. Khan. (2016). “Heat transfer analysis in a second-grade fluid over an oscillating vertical plate using fractional Caputo-Fabrizio derivatives,” European Physical Journal C, vol. 76, no. 7, pp. 362–373. [Google Scholar]
15. F. Ali, M. Saqib, I. Khan and N. A. Sheikh. (2016). “Application of Caputo–Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model,” European Physical Journal Plus, vol. 131, no. 10, pp. 377–387. [Google Scholar]
16. A. A. Zafar and C. Fetecau. (2016). “Flow over an infinite plate of a viscous fluid with non-integer order derivative without singular kernel,” Alexandria Engineering Journal, vol. 55, no. 3, pp. 2789–2796. [Google Scholar]
17. A. Atangana and I. Koca. (2016). “On the new fractional derivative and application to nonlinear Baggs and Freedman model,” Journal of Nonlinear Sciences and Applications, vol. 9, pp. 2467–2480. [Google Scholar]
18. B. S. T. Alkahtani and A. Atangana. (2016). “Controlling the wave movement on the surface of shallow water with the Caputo–Fabrizio derivative with fractional order,” Chaos Solitons & Fractals, vol. 89, pp. 539–546. [Google Scholar]
19. Atangana, A. (2016). “On the new fractional derivative and application to nonlinear Fisher’s reaction-diffusion equation,” Applied Mathematics and Computation, vol. 273, pp. 948–956. [Google Scholar]
20. A. Atangana and D. Baleanu. (2017). “Caputo-Fabrizio derivative applied to groundwater flow within a confined aquifer,” Journal of Engineering Mechanics, vol. 143, no. 5, pp. 1–5. [Google Scholar]
21. J. T. Machado, A. M. Galhano and J. J. Trujillo. (2013). “Science metrics on fractional calculus development since 1966,” Fractional Calculus and Applied Analysis, vol. 16, no. 2, pp. 479–500. [Google Scholar]
22. M. Saqib, F. Ali, I. Khan, N. A. Sheikh and S. A. A. Jan. (2018). “Exact solutions for free convection flow of generalized Jeffrey fluid: A Caputo-Fabrizio fractional model,” Alexandria Engineering Journal, vol. 57, no. 3, pp. 1849–1858. [Google Scholar]
23. J. R. Reddy, V. Sugunamma and N. Sandeep. (2017). “Enhanced heat transfer in the flow of dissipative non-Newtonian Casson fluid flow over a convectively heated upper surface of a paraboloid of revolution,” Journal of Molecular Liquids, vol. 229, pp. 380–388. [Google Scholar]
24. G. J. Reddy, B. Kethireddy, M. Kumar and M. M. Hoque. (2018). “A molecular dynamics study on transient non-Newtonian MHD Casson fluid flow dispersion over a radiative vertical cylinder with entropy heat generation,” Journal of Molecular Liquids, vol. 252, pp. 245–262. [Google Scholar]
25. T. M. Ajayi, A. J. Omowaye and I. L. Animasaun. (2017). “Viscous dissipation effects on the motion of Casson fluid over an upper horizontal thermally stratified melting surface of a paraboloid of revolution: Boundary layer analysis,” Journal of Applied Mathematics, vol. 2017, no. 3805, pp. 1–13. [Google Scholar]
26. M. E. Ali and N. Sandeep. (2017). “Cattaneo-Christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: A numerical study,” Results in Physics, vol. 7, pp. 21–30. [Google Scholar]
27. G. Kumaran and N. Sandeep. (2017). “Thermophoresis and Brownian moment effects on the parabolic flow of MHD Casson and Williamson fluids with cross-diffusion,” Journal of Molecular Liquids, vol. 233, pp. 262–269. [Google Scholar]
28. Z. Mehmood, R. Mehmood and Z. Iqbal. (2017). “Numerical investigation of micropolar Casson fluid over a stretching sheet with internal heating,” Communications in Theoretical Physics, vol. 67, no. 4, pp. 443–450. [Google Scholar]
29. F. Ali, N. A. Sheikh, I. Khan and M. Saqib. (2017). “Solutions with Wright function for time-fractional free convection flow of Casson fluid,” Arabian Journal for Science and Engineering, vol. 42, no. 6, pp. 2565–2572. [Google Scholar]
30. F. Ali, N. A. Sheikh, I. Khan and M. Saqib. (2017). “Magnetic field effect on blood flow of Casson fluid in an axisymmetric cylindrical tube: A fractional model,” Journal of Magnetism and Magnetic Materials, vol. 423, pp. 327–336. [Google Scholar]
31. O. J. J. Algahtani. (2016). “Comparing the Atangana-Baleanu and Caputo-Fabrizio derivative with fractional order: Allen Cahn model,” Chaos Solitons & Fractals, vol. 89, pp. 552–559. [Google Scholar]
32. I. Ullah, S. Shafie and I. Khan. (2017). “Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium,” Journal of King Saud University—Science, vol. 29, no. 2, pp. 250–259. [Google Scholar]
33. N. A. Sheikh, F. Ali, M. Saqib, I. Khan and S. A. A. Jan. (2017). “A comparative study of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid,” European Physical Journal Plus, vol. 132, no. 1, pp. 54–68. [Google Scholar]
34. A. A. Tateishi, H. V. Ribeiro and E. K. Lenzi. (2017). “The role of fractional time-derivative operators on anomalous diffusion,” Frontiers in Physics, vol. 5, pp. 52–61. [Google Scholar]
35. K. A. Abro, A. A. Memon and M. A. Uqaili. (2018). “A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives,” European Physical Journal Plus, vol. 133, no. 3, pp. 113–122. [Google Scholar]
36. N. A. Sheikh, F. Ali, I. Khan, M. Gohar and M. Saqib. (2017). “On the applications of nanofluids to enhance the performance of solar collectors: A comparative analysis of Atangana-Baleanu and Caputo-Fabrizio fractional models,” European Physical Journal Plus, vol. 132, no. 12, pp. 540–551. [Google Scholar]
37. N. A. Sheikh, F. Ali, M. Saqib, I. Khan, S. A. A. Jan. (2017). et al., “Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction,” Results in Physics, vol. 7, pp. 789–800. [Google Scholar]
38. A. Khan, K. Ali Abro, A. Tassaddiq and I. Khan. (2017). “Atangana–Baleanu and Caputo Fabrizio analysis of fractional derivatives for heat and mass transfer of second-grade fluids over a vertical plate: A comparative study,” Entropy, vol. 19, no. 8, pp. 279–291. [Google Scholar]
39. H. K. Jassim. (2016). “Extending application of adomian decomposition method for solving a class of volterra integro-differential equations within local fractional integral operators,” Journal of College of Education for Pure Science, vol. 6, no. 1, pp. 146–155. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |