DOI:10.32604/cmc.2020.012326
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012326 | |
| Article |
Al2O3 and γAl2O3 Nanomaterials Based Nanofluid Models with Surface Diffusion: Applications for Thermal Performance in Multiple Engineering Systems and Industries
1Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif, 12080, Pakistan
2Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
3Department of Mathematics, Faculty of Sciences, HITEC University, Taxila Cantt, 47070, Pakistan
4University of Multan, Multan, 66000, Pakistan
5Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, 72915, Vietnam
6Department of Mathematics, Cankaya University, Ankara, Turkey
7Institute of Space Sciences, Magurele, 077125, Romania
8Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
9Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, 11991, Saudi Arabia
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 25 June 2020; Accepted: 14 September 2020
Abstract: Thermal transport investigation in colloidal suspensions is taking a significant research direction. The applications of these fluids are found in various industries, engineering, aerodynamics, mechanical engineering and medical sciences etc. A huge amount of thermal transport is essential in the operation of various industrial production processes. It is a fact that conventional liquids have lower thermal transport characteristics as compared to colloidal suspensions. The colloidal suspensions have high thermal performance due to the thermophysical attributes of the nanoparticles and the host liquid. Therefore, researchers focused on the analysis of the heat transport in nanofluids under diverse circumstances. As such, the colloidal analysis of H2O composed by γAl2O3 and Al2O3 is conducted over an elastic cylinder. The governing flow models of γAl2O3/H2O and Al2O3/H2O is reduced in the dimensionless form by adopting the described similarity transforms. The colloidal models are handled by implementing the suitable numerical technique and provided the results for the velocity, temperature and local thermal performance rate against the multiple flow parameters. From the presented results, it is shown that the velocity of Al2O3–H2O increases promptly against a high Reynolds number and it decreases for high-volume fraction. The significant contribution of the volumetric fraction is examined for thermal enhancement of nanofluids. The temperature of Al2O3–H2O and γAl2O3–H2O significantly increases against a higher ϕ. Most importantly, the analysis shows that γAl2O3–H2O has a high local thermal performance rate compared to Al2O3–H2O. Therefore, it is concluded that γAl2O3–H2O is a better heat transfer fluid and is suitable for industrial and technological uses.
Keywords: Thermal performance; Al2O3 and γAl2O3 nanomaterials; thermophysical attributes of nanomaterials; stretching cylinder; suction/blowing; numerical scheme; nusselt number
The analysis of heat transfer had been a major problem for engineers, industrialists, and scientists. For many industrial productions, a large amount of heat is essential to complete the production processes. Unfortunately, regular liquids are not capable to provide the required heat transfer. This major problem economically affected the industrialists and engineers. So, scientists and engineers thought to gathered and focus to resolve this major problem. Finally, they developed a new sort of fluids known as “Nanofluids” [1,2]. These fluids are the composition of nanosized metallic particles and the base liquids. The base liquids and the metallic particles are thermally in equilibrium. These fluids became very productive for industrialists and engineers.
Due to the remarkable thermal performance rate, these fluids attained much popularity among the researcher’s and engineers in a very short period. The applications of these fluids found in medical sciences, chemical and mechanical engineering, in the detection of cancer cells, aerodynamics, home appliances, paint industry, electronics, computer chips, manufacturing of air crafts parts, various industrial productions and in many more. In view of these applications, the researchers and industrialists focused on the analysis of nanofluids under various flow conditions.
The investigation of heat transfer in the nanofluids over a stretching cylinder is significant from the industrial point of view. In 2017, Pandey et al. [3] reported the heat transfer investigation in the nanofluid over a stretching cylinder. They studied the heat transfer in the additives of water and Cu nanoparticles by considering the slip effects and thermal radiations. They revealed that the temperature of the nanofluid rises due to high volume fraction and the momentum boundary layer region decreases. In 2017, Salahuddin et al. [4] presented the heat transfer investigation in Carreau nanofluid over a stretchable cylinder. They considered the effects of generalized slip flow conditions over the cylinder surface. Further, the finite-difference algorithm is implemented for the mathematical analysis and studied the behavior of the velocity and heat transfer by varying the particular flow parameters.
The analysis of the heat transport and the velocity for different nanofluids in the presence of Lorentz forces over a stretchable cylinder was investigated in [5]. A novel thermal analysis in the nano bioconvection model over a stretchable sheet was presented by Zheng et al. [6]. They studied the effects of thermal radiations, velocity and thermal jump conditions in the governing model. They presented a comprehensive discussion on the behavior of the velocity and the temperature against various flow parameters. The temperature behavior of water suspended by Cu nanomaterial over a stretching/shrinking cylinder was reported by Sulochana et al. [7] in 2016. They studied the flow characteristics for different values of the flow parameters. Bakar et al. [8] discussed the stability analysis in the nanofluid over a shrinking/stretching cylinder. They discussed the influence of the suction parameter in the flow field. The flow of nanofluid by considering the influence of corner radius over a square cylinder was presented in [9].
The analysis of the heat and mass transfer in the presence of porosity parameter over a horizontal cylinder was reported by Reddy et al. [10]. A comprehensive discussion was provided on the flow behavior against the particular flow parameters. The influence of uniform suction and injection on the heat and mass transfer were described in [11]. Recently, Mohyud-Din et al. [12] reported the temperature analysis in a hybrid colloidal model by incorporating the effects of Cattaneo Christov model in the energy equation. They considered the flow of hybrid host liquid (H2O–C2H6O2) saturated by hybrid tiny particles of GO–MoS2. From the analysis, they concluded that the particular hybrid nanoliquid have a high thermal transport rate and reliable for the industrial and engineering applications. The analysis of gyrotactic microorganism’s boundary layer flow was presented by Aziz et al. [13]. They tackled the model numerically and presented the results for the flow fields. Furthermore, the significant studies related to the flow fields and relevant analysis was reported in [14–23].
The thermal performance in Al2O3 and γAl2O3 based hybrid suspensions over a cylinder is significant from the industrial and engineering point of view. It is investigated that the thermal transport in Al2O3–H2O and γAl2O3–H2O colloidal suspensions was not reported so far. Therefore, the analysis is presented to fill this significant research gap. The two nanofluid models are considered over a cylinder and treated numerically. Then, graphical results for the velocity and the temperature profiles are plotted by altering the particular parameters and discussed in detail. Finally, the major findings of the analysis are incorporated in the last section.
2 Statement Geometry and Nanofluid Models Formulation
The flow of Al2O3–H2O and γAl2O3–H2O nanoliquids over a cylinder with uniform suction/blowing is considered. It is assumed that the nano particles dispersed continuously in the host liquid and there is no slip between them. The study is conducted in cylindrical coordinates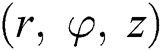 
and corresponding velocity components are 
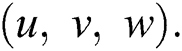Further, length of the cylinder is infinite and 
denotes the cylinders radius. The flow is an inward direction which forms the stagnation circle with 
and 
. Fig. 1 presents the flow configuration.
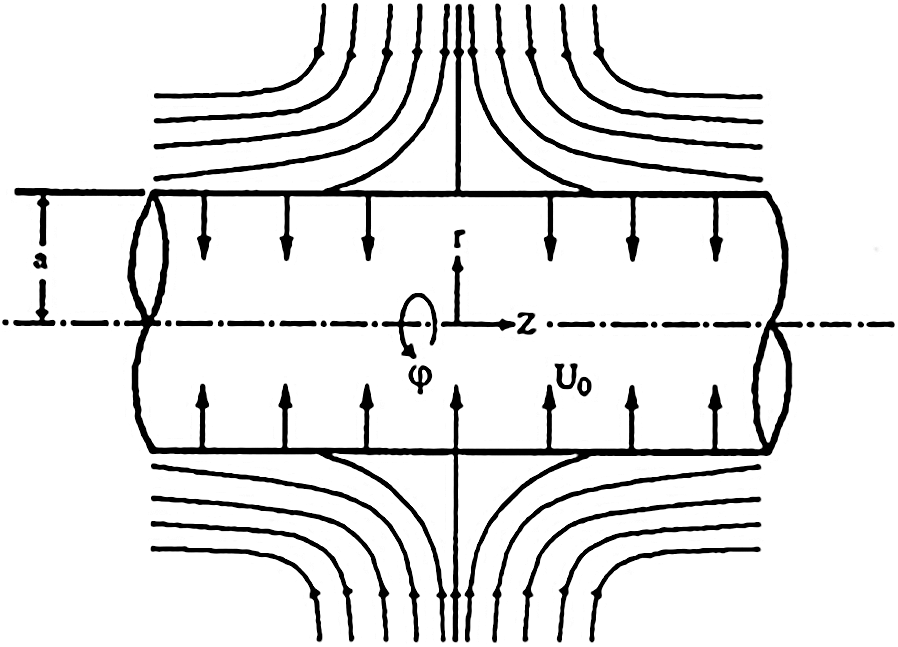
Figure 1: Flow configuration of the nanofluids
The axisymmetric nanofluid model which governs the flow over a cylinder is described as [24]:
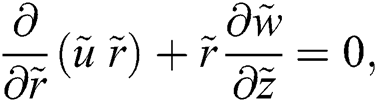
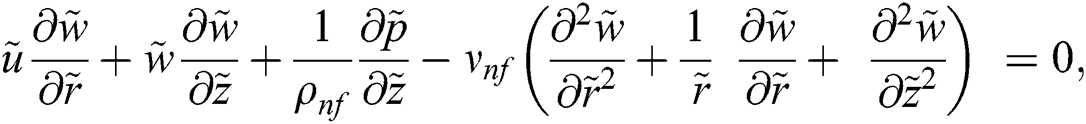
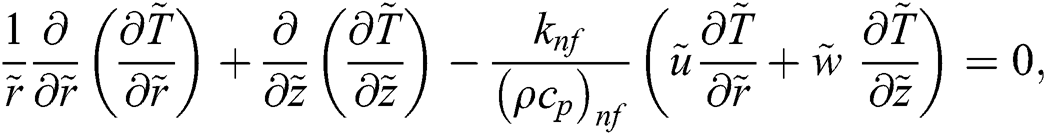
The associated flow conditions described by the following equations:
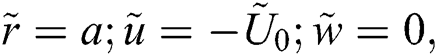
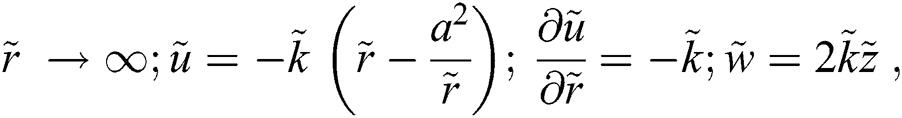
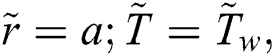
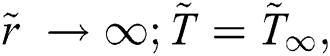
The associated invertible transformations that reduced the nanofluid model into a self-similar form are described in the Eqs. (9)–(13):
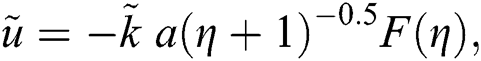
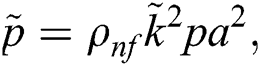
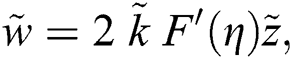
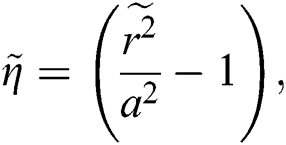
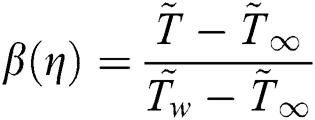
2.2 Adopted Models for Nanofluids Thermal Performance
The following nanofluid models are adopted for thermal performance in Al2O3–H2O and γAl2O3–H2O nanofluids [25]:
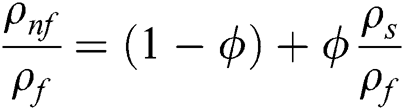
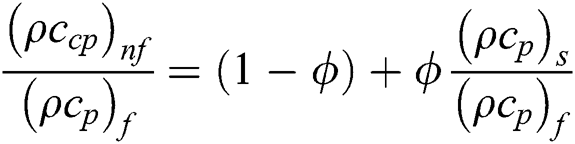
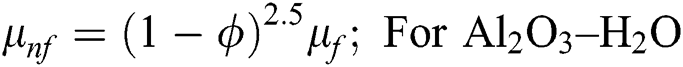
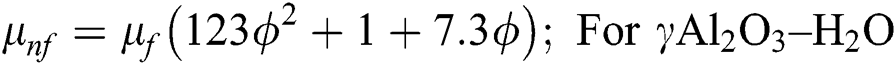
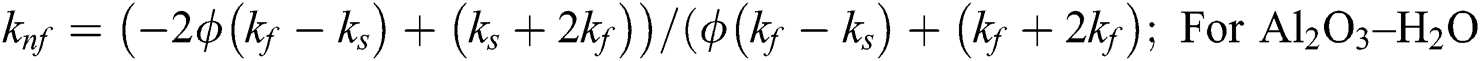
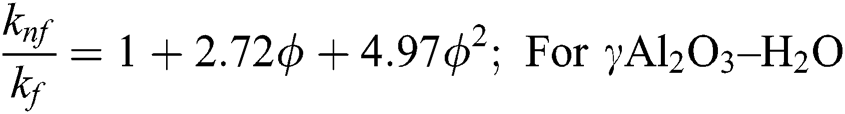
After using the invertible transformations labeled in Eqs. (9)–(13), the associated flow conditions labeled in Eqs. (5)–(8) and the thermal performance models labeled in Eqs. (14)–(19) in the governing model labeled in Eqs. (1)–(4), the following dimensionless form of the models are obtained:
By using the effective nanofluid models, the following nonlinear model is attained for Al2O3–H2O:
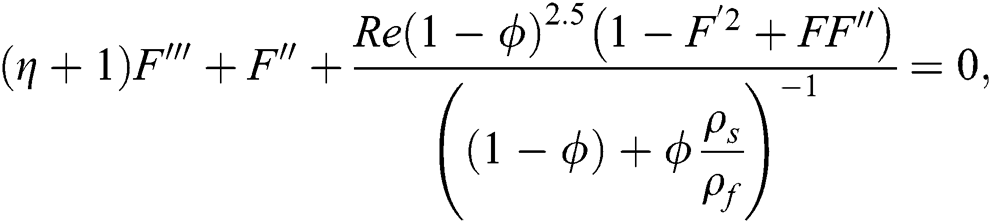
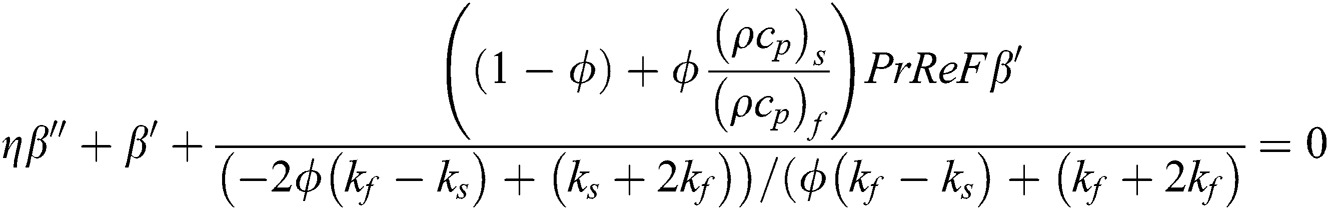
By using the effective models labeled in Eqs. (14)–(19), the following model is obtained for γAl2O3–H2O:
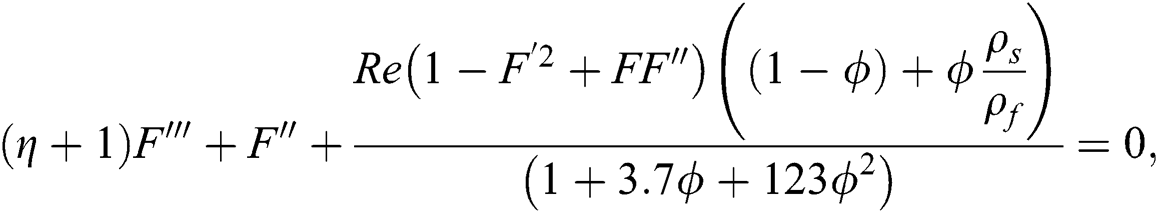
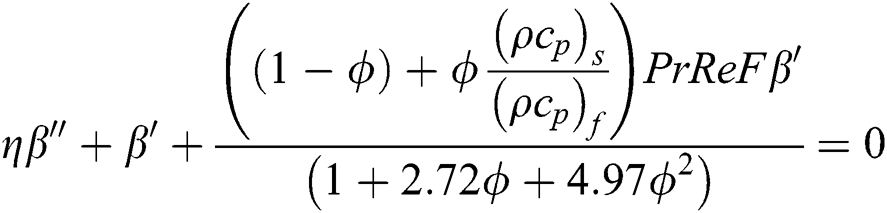
The associated flow conditions at the surface and far from the cylinder surface are labeled in the following equations:
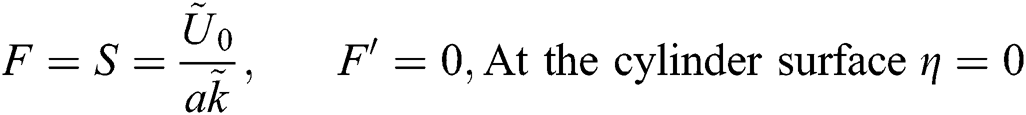
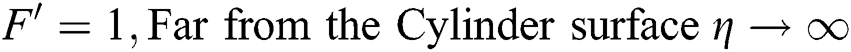
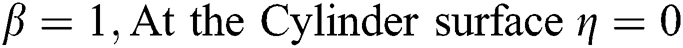
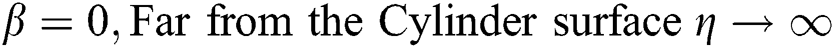
2.5 Quantity for Thermal Performance
The local heat transfer is significant from an engineering, technological, and industrial point of view. The mathematical relation describing the quantity is labeled in the following equations:
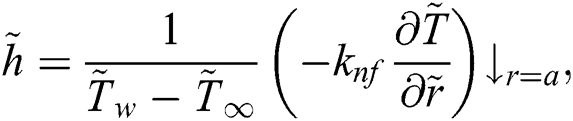
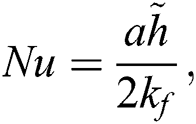
By using the values from Eq. (28) in Eq. (29), the following self-similar formulas are obtained for the local heat transfer coefficient:
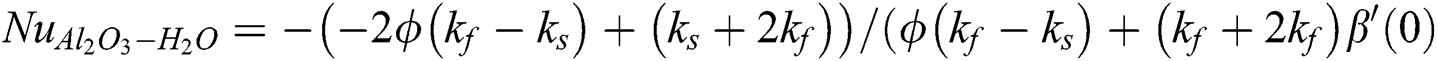
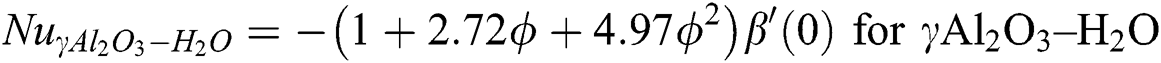
3 Mathematical Analysis of the Models
The nanofluid models labeled in Eqs. (20)–(23) associated with the flow conditions described in Eqs. (24)–(27) are nonlinear over a semi-infinite domain. It is not easy to tackle such models for exact solutions. Therefore, we treated the models numerically. For said purpose, Runge–Kutta algorithm is adopted with the coupling of shooting technique. The algorithm is applied to the Initial Value Problem (IVP). For this, firstly, we transformed the models into IVP. The following transformations are introduced according to the models:
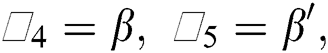
By using the transformations described in Eqs. (32) and (33) in the models given in (20)–(23), the following systems are obtained:
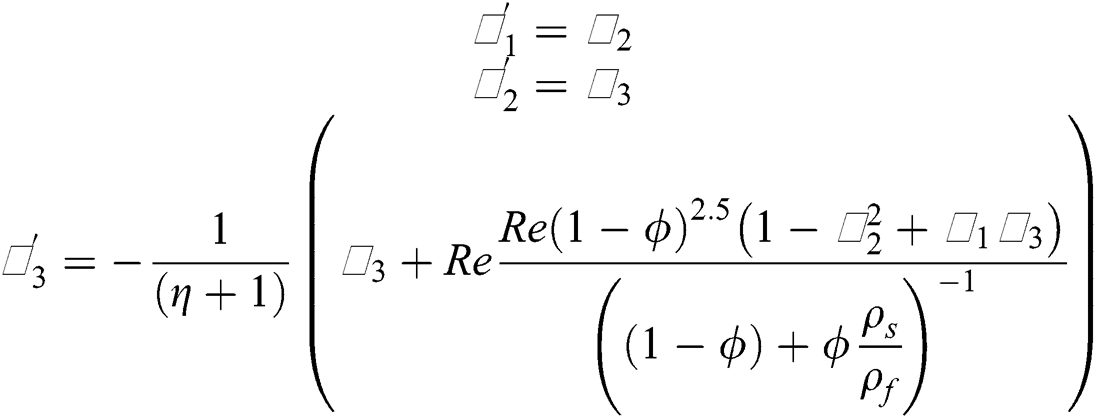
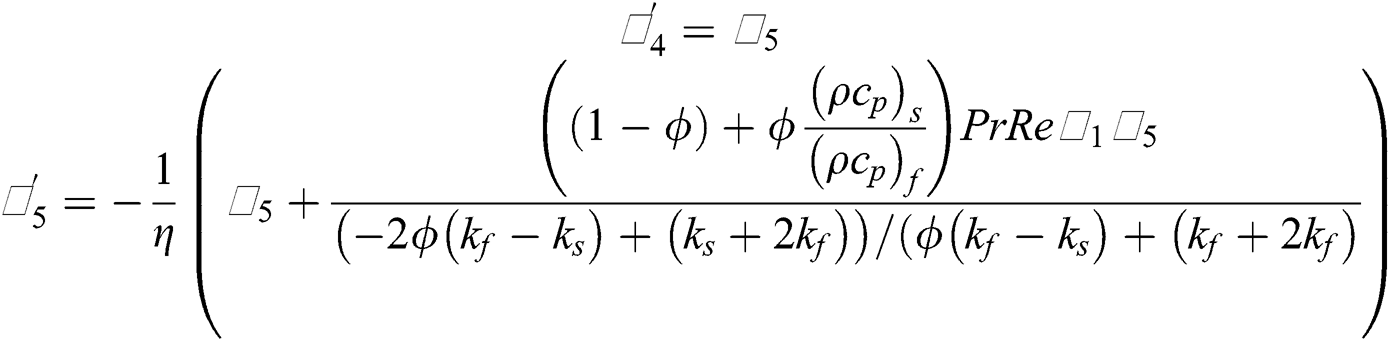
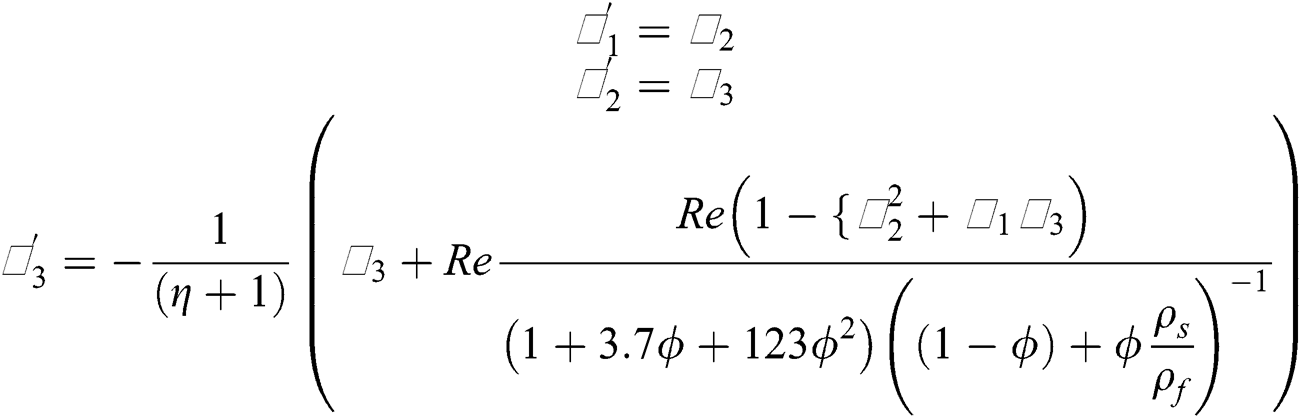
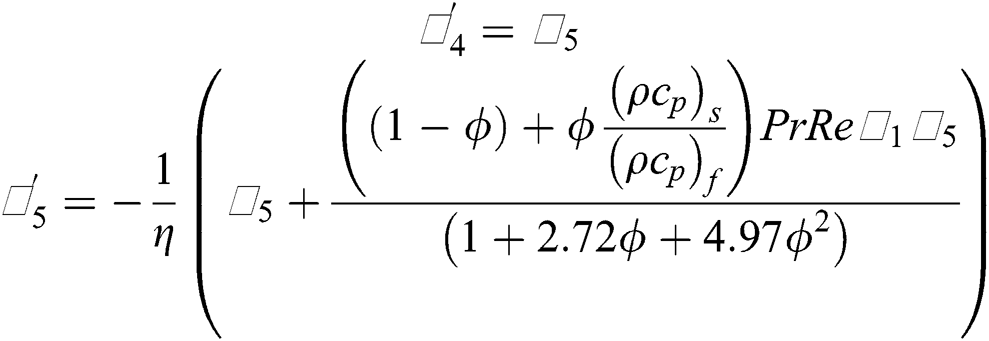
The reduced models are then solved by using aforementioned techniques and plotted the results for the flow regimes by varying the particular parameters embedded in the models.
4 Physical Interpretation of the Results
The behavior of the velocity and heat transfer by changing the particular flow parameters are decorated in this section over the feasible domain.
4.1 The Velocity against Preeminent Parameters
The velocity behavior in Al2O3–H2O and γAl2O3–H2O due to varying Reynolds number is plotted in Fig. 2 for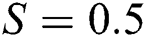 
and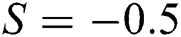 
, respectively. It is perceived that the velocity rises due to injecting fluid from the cylinder surface. Near the surface, rapid changes in the velocity are observed. Physically, injecting fluid from the cylinder surface disturbed the fluid particles adjacent to the surface that causes the rapid changes in the fluid motion. Furthermore, a rapid increment in the velocity of Al2O3–H2O is observed. Physically, in the view of thermophysical characteristics, Al2O3–H2O becomes less dense as compared to that of γAl2O3–H2O. Therefore, the particles of Al2O3–H2O freely moving in comparison with γAl2O3–H2O. Apart from the surface of the cylinder, the effects of injecting fluid become minimal, therefore, increment in the velocity becomes slow. The suction effects of the fluid velocity are decorated in Fig. 2b. Although, the velocity rises for suction of the fluid from the cylinder surface and these changes are quite slow in comparison with injecting case. Physically, due to suction, more fluid particles get stuck to the surface of the cylinder that opposes the fluid motion. Therefore, the fluid particles move slowly.
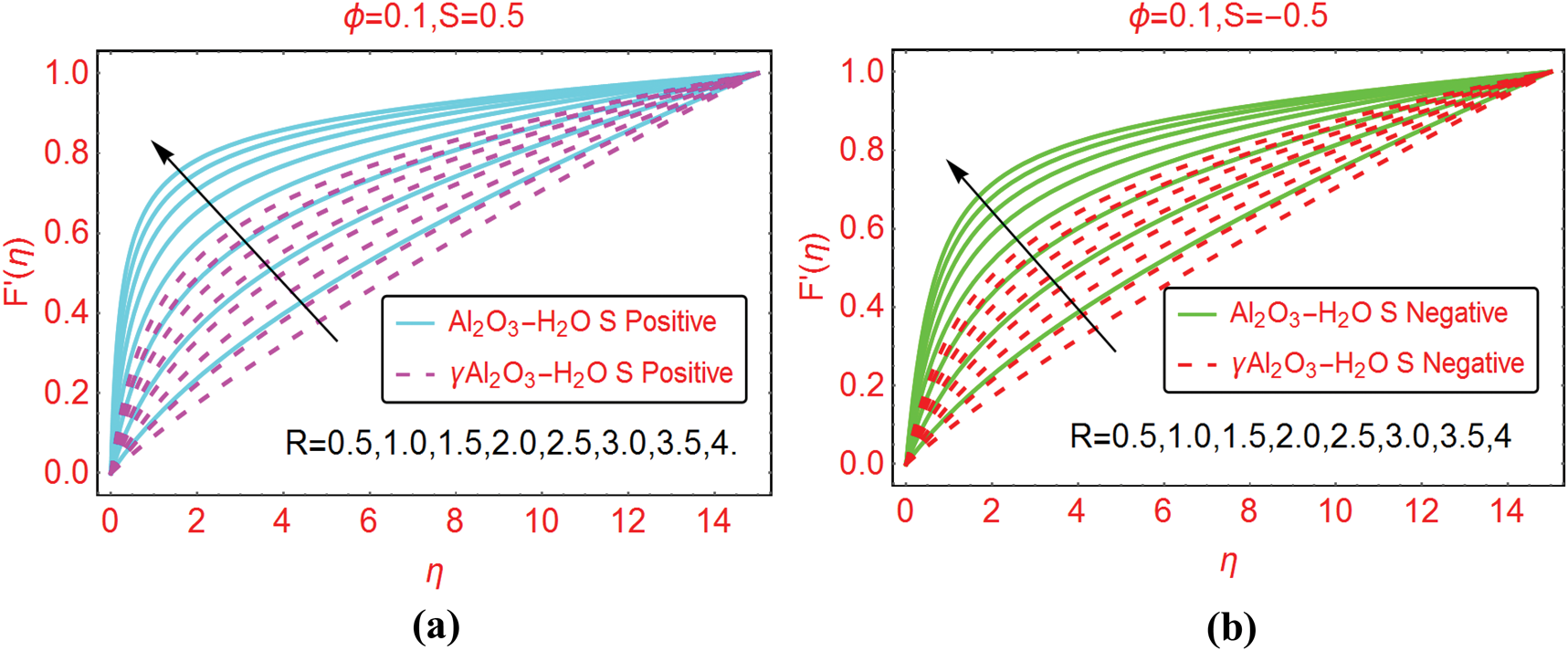
Figure 2: The velocity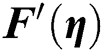 
against varying Re (a) 
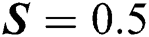and (b)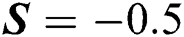 
In the analysis of nanofluids, the volumetric fraction 
is a significant parameter that effectively alters the fluid characteristics. The velocity of Al2O3–H2O and γAl2O3–H2O against multiple values of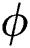 
are elaborated in Figs. 3a and 3b for injection and suction, respectively. The volume fraction 
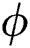resists the motion of Al2O3–H2O and γAl2O3–H2O colloidal suspensions. It is detected that for γAl2O3–H2O nanofluid, the velocity decrement is very rapid due to high dynamic viscosity. Physically, due to high dynamic viscosity and injection of the fluid from the cylinder surface, rapid decrement in the velocity is occurred. Almost inconsequential decrement in the velocities is detected for both injection and suction of the fluid from the cylinder surface for γAl2O3–H2O nanofluid.
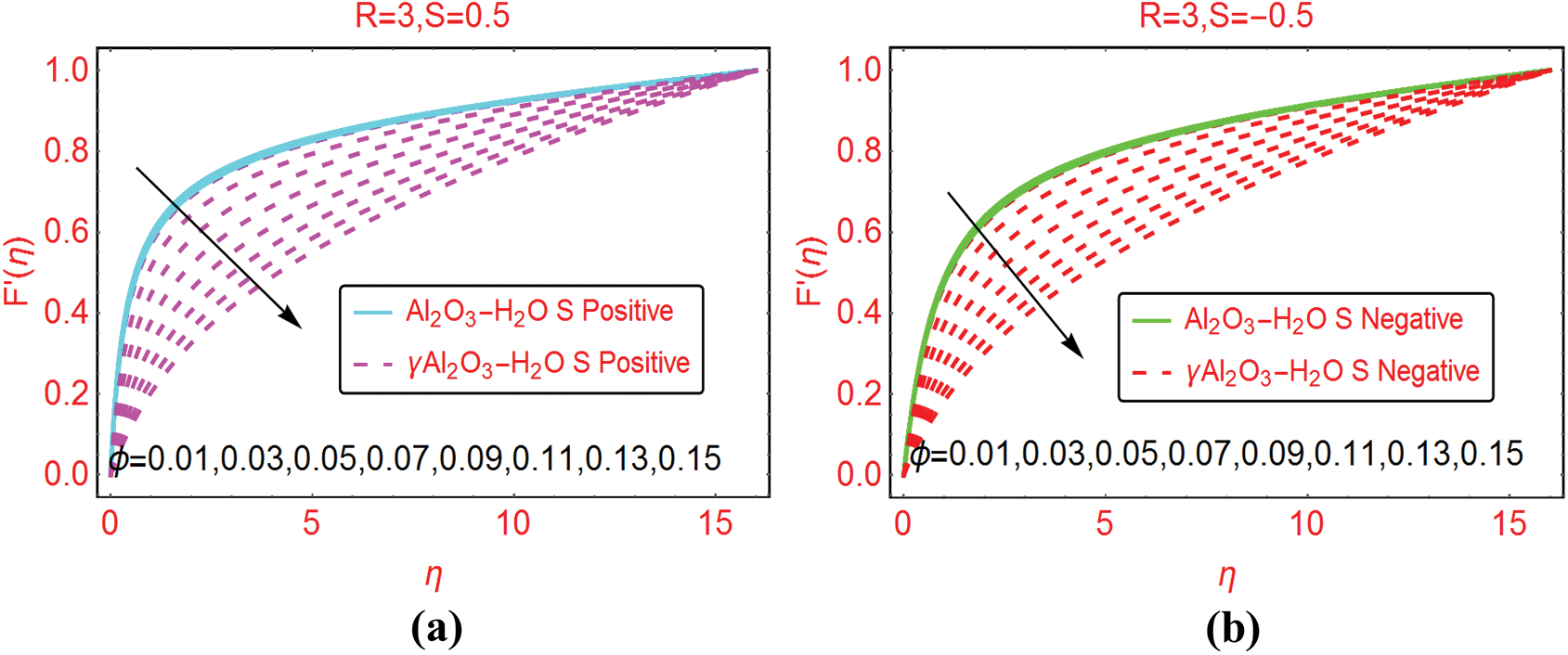
Figure 3: The velocity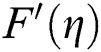 
against varying 
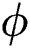(a)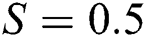 
and (b)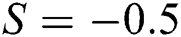 
The velocity trends for variable injection and suction values are decorated in Figs. 4a and 4b, respectively. The velocity for both colloidal suspensions increases significantly near the cylinder surface. Further, it is examined that the velocity of Al2O3–H2O prevailed for both suction and injection of the fluid from the cylinder surface. Physically, for injection of the fluid, the velocity rises rapidly because injecting fluid disturbed the fluid particles therefore, the particles move rapidly.
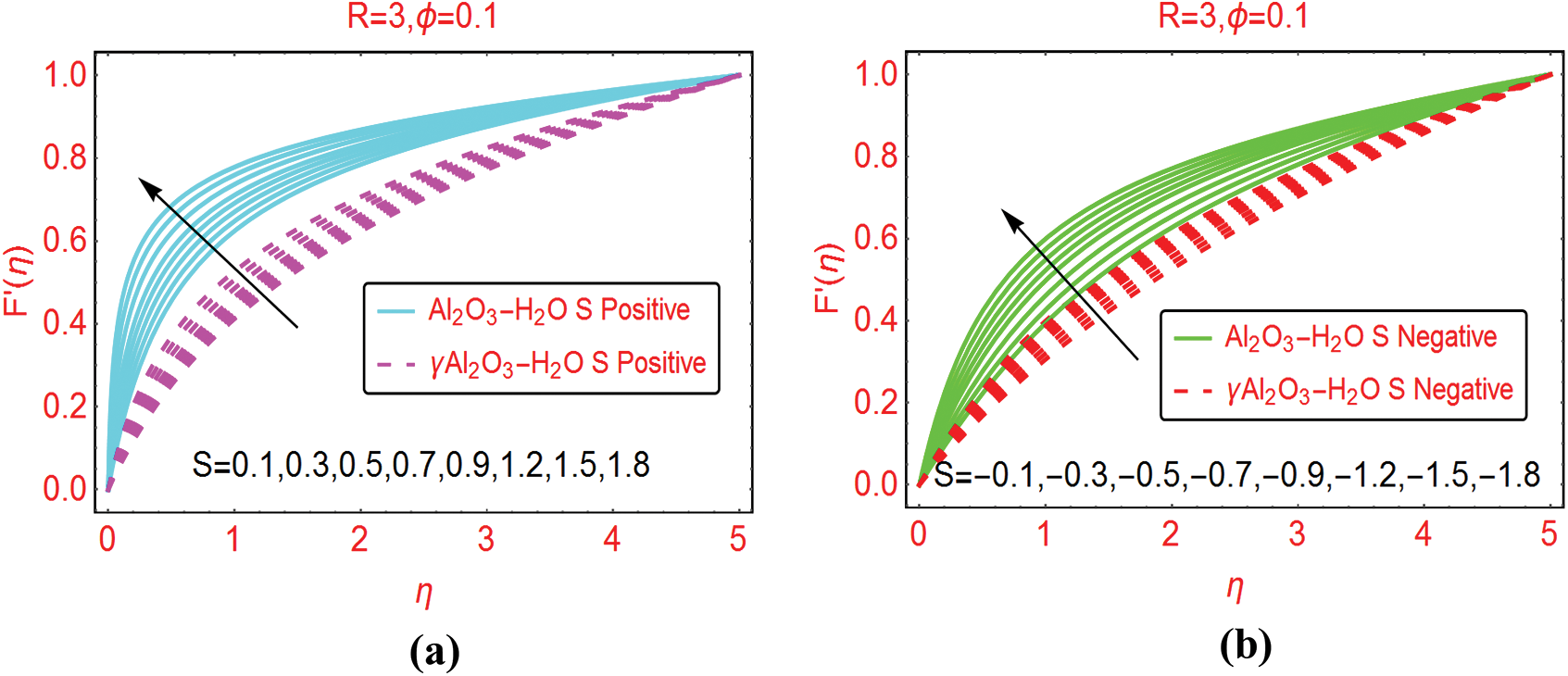
Figure 4: The velocity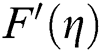 
against varying (a) 
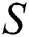Positive and (b) 
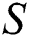Negative
4.2 The Temperature against Preeminent Parameters
Fig. 5 portraying the behavior of temperature for different Reynolds number. It is noted that the temperature of γAl2O3–H2O drops slowly due to high thermal conductivity and varying Reynolds number. For injecting fluid, the temperature declines quite rapidly in comparison with suction case. Near the cylinder surface, the temperature declines slowly for both injection and suction.
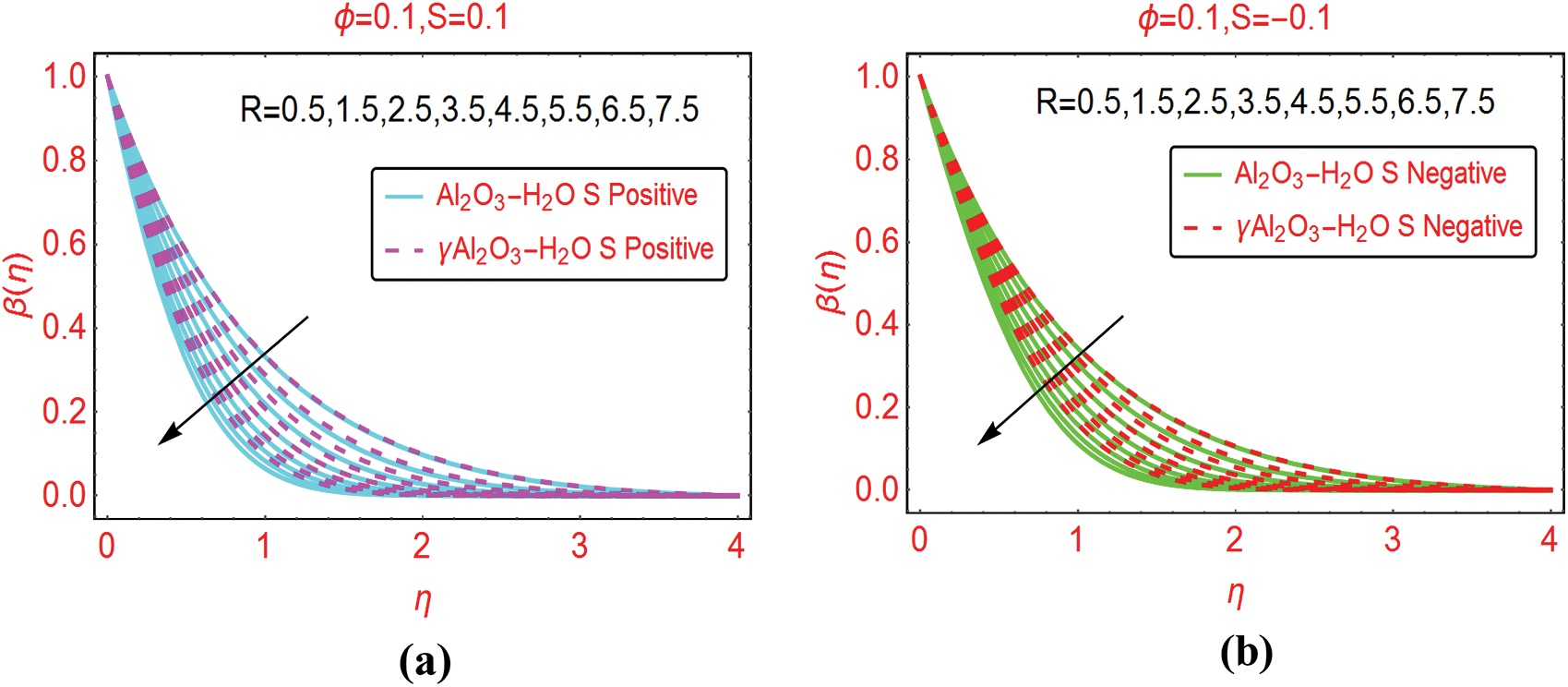
Figure 5: The temperature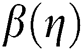 
against varying 
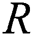(a)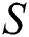 
Positive and (b) 
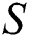Negative
A pertinent parameter known as the volumetric fraction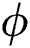 
of the tiny particles is significant in the thermal analysis of the nanofluids. The trends against 
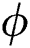are decorated in Fig. 6 for both injection and suction, respectively. It can be seen that the thermal performance of the nanofluids enhances due to increasing volumetric fraction of the tiny particles. From the analysis, it is examined that the thermal performance of γAl2O3–H2O nanofluid dominated.
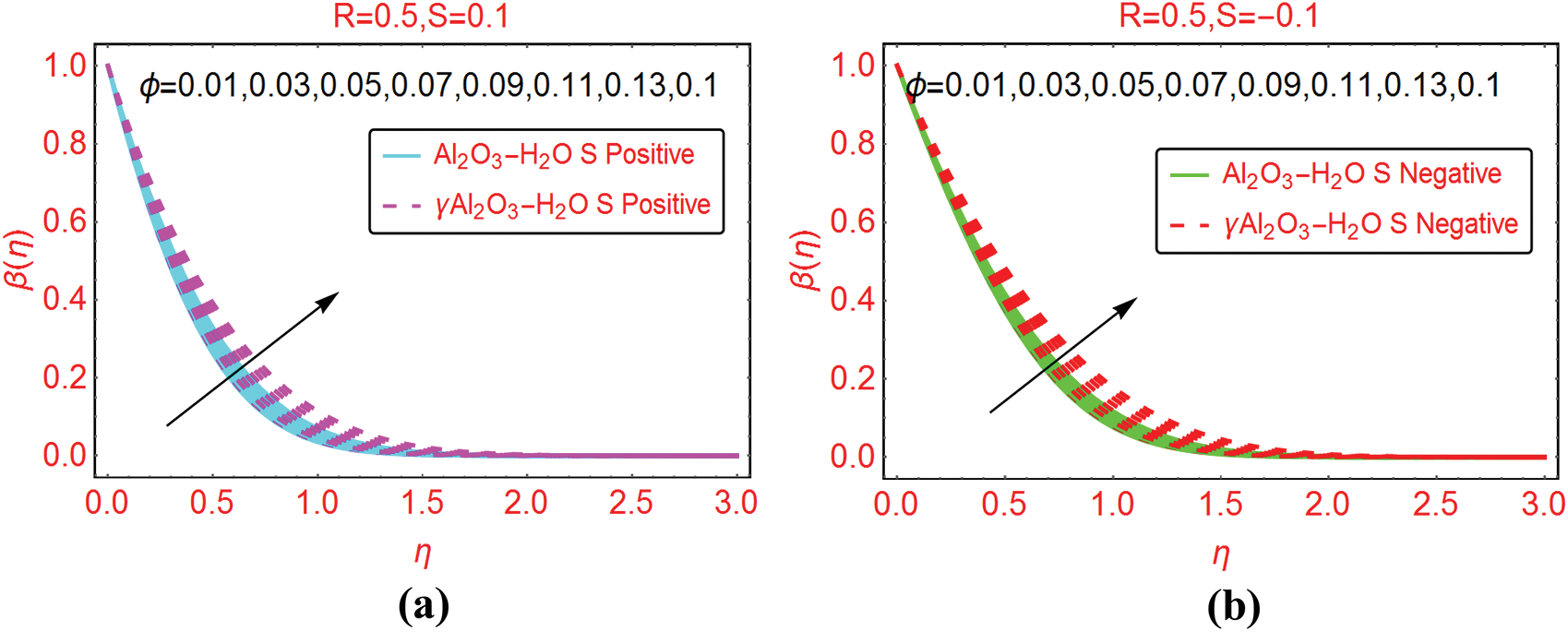
Figure 6: The velocity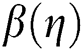 
against varying 
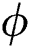(a)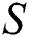 
Positive and (b) 
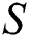Negative
4.3 Local Thermal Performance Rate
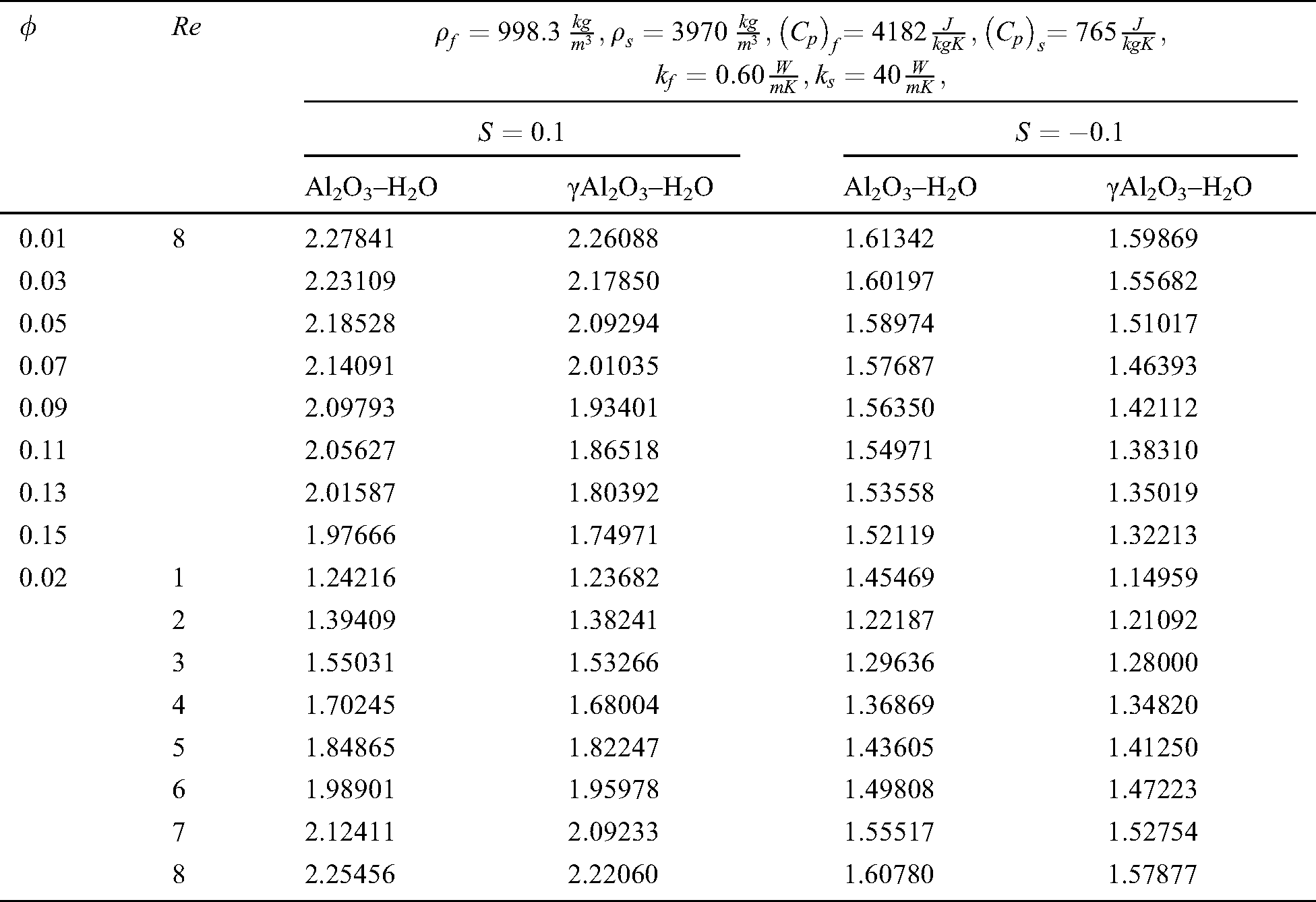
The local thermal performance rate (local heat transport) against multiple values of the volumetric fraction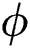 
, Reynolds number, injection and suction of the fluid are described in Tab. 1. From the analysis, it is observed that the local thermal performance rate of the nanofluids rises against the high-volume fraction of the tiny particles. However, in the current scenario, the thermal performance rate of Al2O3–H2O is higher than γAl2O3–H2O. For injecting fluid, thermal performance rises abruptly in comparison with suction case. Similarly, it is examined that for higher Reynolds number, the local heat transfer rase for both sorts of nanofluids under the injection and suction effects.
Table 1: Impacts of multiple values of preeminent parameters on the local thermal performance rate
The preeminent flow parameters that appeared in the flow models are significantly change the flow patterns and isotherms over the domain of interest. Fig. 7 describes the flow pattern against varying Reynolds number. It is investigated that for higher Reynolds values, the streamlines pattern expanded around the cylinder surface. Similarly, the streamlines pattern for multiple injecting fluid parameters decorated in Fig. 8. Figs. 9 and 10 portraying the isotherms profiles for multiple Reynolds range at constant injection of the fluid.
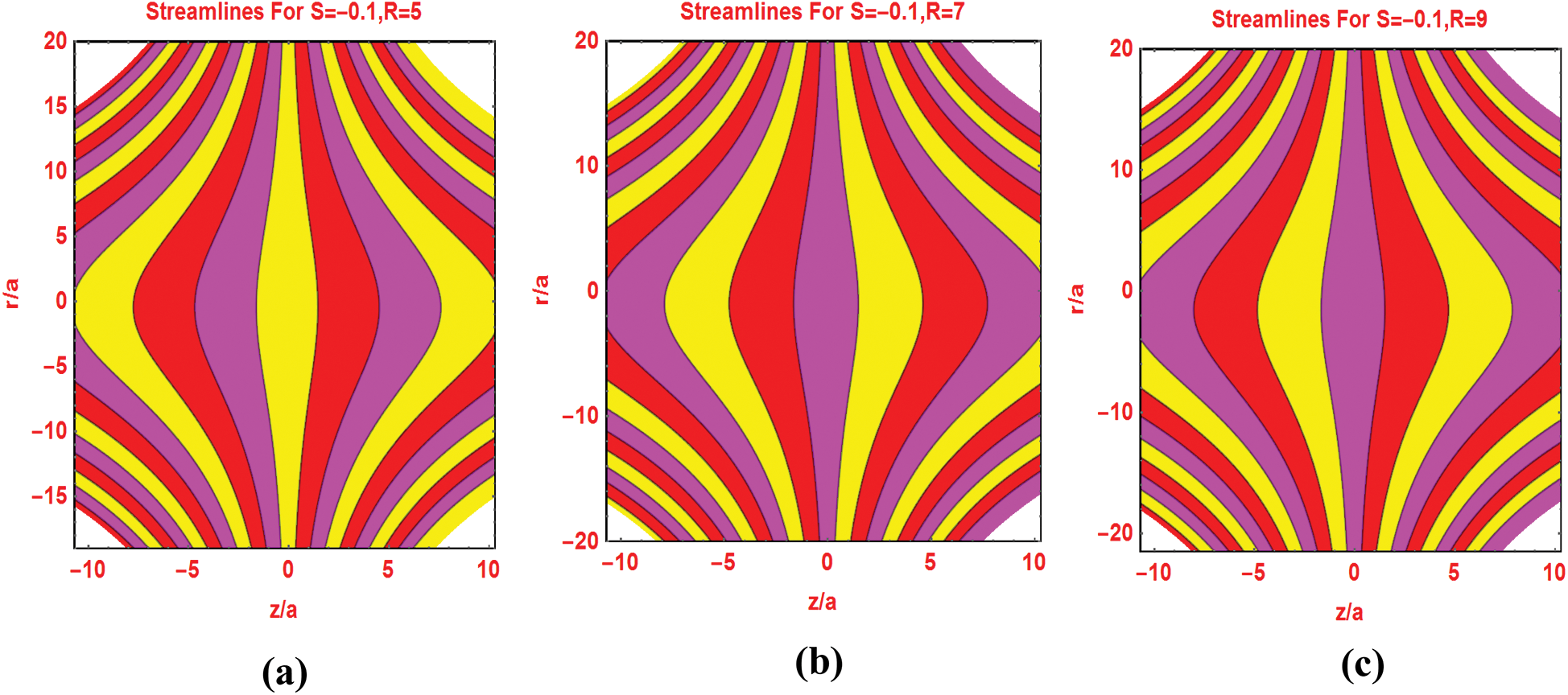
Figure 7: Streamlines pattern for different Reynolds number
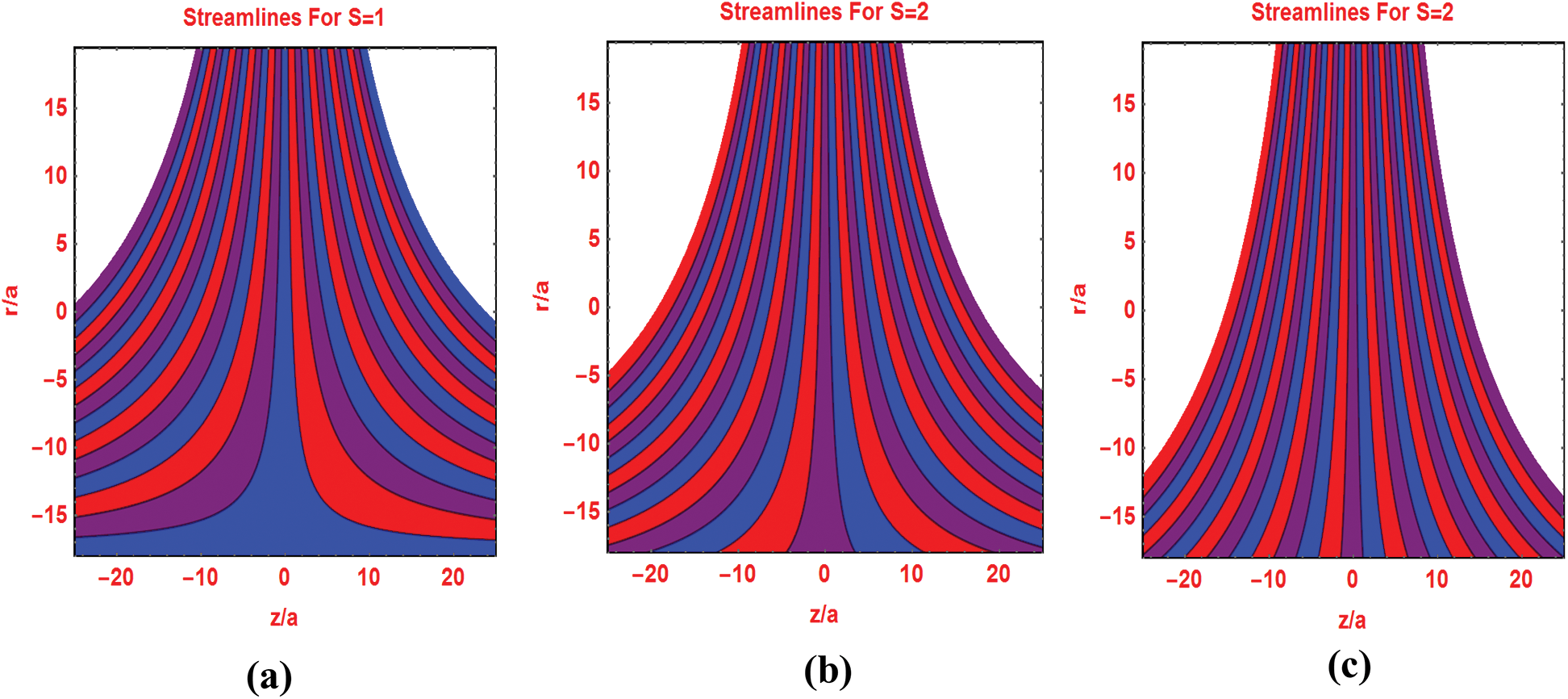
Figure 8: Streamlines pattern for different S
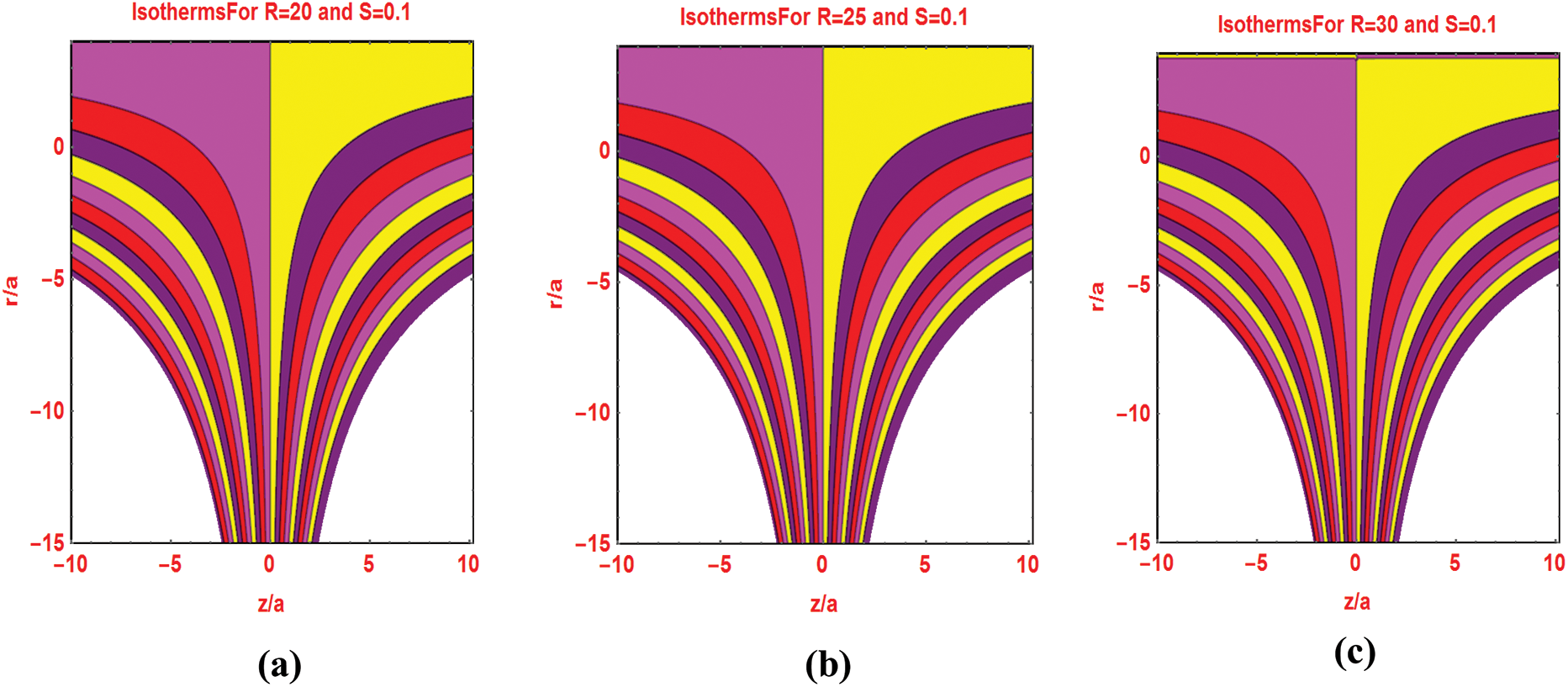
Figure 9: Isotherms pattern for different Reynolds number
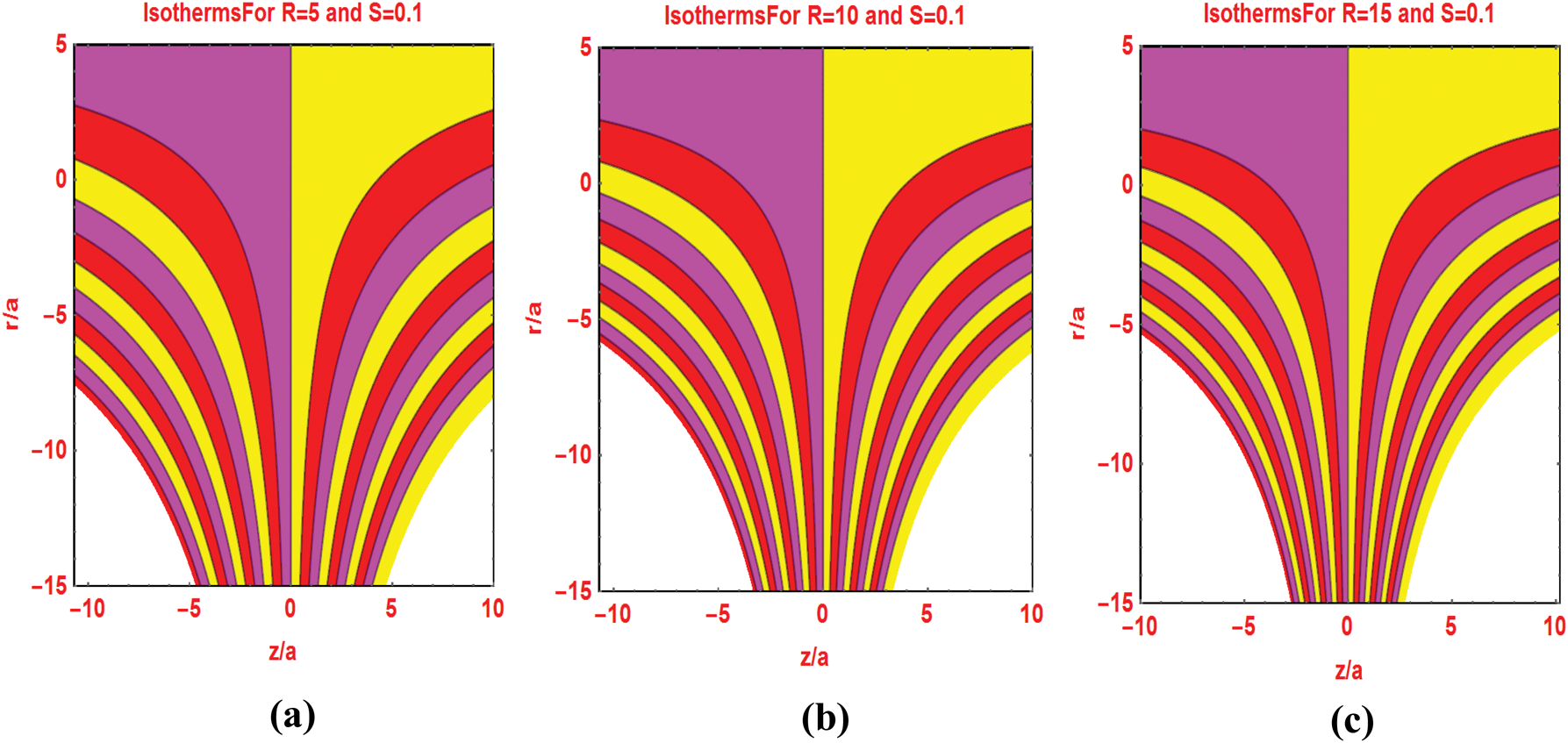
Figure 10: Isotherms pattern for different Reynolds number fixed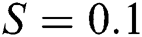 
The thermal performance rate and the behavior of flow regimes for Al2O3–H2O and γAl2O3–H2O are conducted over a cylinder. The effective nanofluid characteristics are implemented and obtained the dimensionless flow models. The invertible transforms are used for nondimensionalization of the problem. The impacts of the flow quantities on the fluid velocity, temperature, and local thermal performance rate are plotted and explained in detail. It is observed that the velocity of Al2O3–H2O rises promptly it prevailed throughout the analysis. The volumetric fraction of the tiny particles resists the nanofluids motion. it is perceived that the temperature enhances against the volumetric fraction. It is also noticed that the thermal performance rate of both the nanofluids increases. Therefore, these nanofluids are reliable for the industrial, engineering and technological purposes, where high thermal performance rate is required to accomplish the production processes.
Funding Statement: Authors declare no specific funding received for this work.
Conflict of Interest: There is no financial or competing interest regarding to this work.
1. Adnan, S. Z. A. Zaidi, U. Khan, N. Ahmed, S. T. Mohyud-Din. (2020). et al., “Impacts of freezing temperature based thermal conductivity on the heat transfer gradient in nanofluids: Applications for a curved riga surface,” Molecules, vol. 25, no. 9, pp. 2152. [Google Scholar]
2. N. Ahmed, Adnan, U. Khan, S. T. Mohyud-Din, I. Khan. (2020). et al., “Radiative colloidal investigation for thermal transport by incorporating the impacts of nanomaterial and molecular diameters (dnanoparticles, dfluidApplications in multiple engineering systems,” Molecules, vol. 25, no. 8, pp. 1896. [Google Scholar]
3. A. K. Pandey and M. Kumar. (2017). “Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip,” Alexandria Engineering Journal, vol. 56, no. 4, pp. 671–677. [Google Scholar]
4. T. Salahuddin, A. Hussain, M. Y. Malik, M. Awais and M. Khan. (2017). “Carreau nanofluid impinging over a stretching cylinder with generalized slip effects: using finite difference scheme,” Results in Physics, vol. 7, pp. 3090–3099. [Google Scholar]
5. H. R. Ashorynejad, M. Sheikholeslami, I. Pop and D. D. Ganji. (2012). “Nanofluid flow and heat transfer due to a stretching cylinder in the presence of magnetic field,” Heat and Mass Transfer, vol. 49, no. 3, pp. 427–436. [Google Scholar]
6. L. Zheng, C. Zhang, X. Zhang and J. Zhang. (2013). “Bioconvection heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump,” Journal of the Franklin Institute, vol. 350, no. 5, pp. 990–1007. [Google Scholar]
7. C. Sulochana and N. Sandeep. (2016). “Stagnation point flow and heat transfer behavior of Cu-water nanofluid towards horizontal and exponentially stretching/shrinking cylinders,” Applied Nanoscience, vol. 6, no. 3, pp. 451–459. [Google Scholar]
8. N. A. A. Bakar, N. Bachok, N. D. Arifin and I. Pop. (2018). “Stability analysis on the flow and heat transfer of nanofluid past a stretching/shrinking cylinder with suction effect,” Results in Physics, vol. 9, pp. 1335–1344. [Google Scholar]
9. P. Dey and A. K. Das. (2017). “Analysis of fluid flow and heat transfer characteristics over a square cylinder: Effect of corner radius and nanofluid volume fraction,” Arabian Journal for Science and Engineering, vol. 42, no. 5, pp. 1687–1698. [Google Scholar]
10. P. S. Reddy and A. J. Chamkha. (2016). “Heat and mass transfer characteristics of nanofluid over horizontal circular cylinder,” Ain Shams Engineering Journal, vol. 9, no. 4, pp. 707–716. [Google Scholar]
11. E. M. A. Elbashbeshy, T. G. Emam, M. S. E. Azab and K. M. Abdelgaber. (2016). “Slip effects on flow, heat and mass transfer of nanofluid over stretching horizontal cylinder in the presence of suction/injection,” Thermal Science, vol. 20, no. 6, pp. 1813–1824. [Google Scholar]
12. S. T. Mohyud-Din, Adnan, U. Khan, N. Ahmed and I. Khan. (2020). “Thermal transport investigation in magneto-radiative GO-MoS2/H2O-C2H6O2 hybrid nanofluid subject to Cattaneo–Christov model,” Molecules, vol. 25, no. 11, pp. 2592. [Google Scholar]
13. M. A. E. Aziz and A. M. Aly. (2020). “MHD boundary layer flow of a power-law nanofluid containing gyrotactic microorganisms over an exponentially stretching surface,” Computers, Materials & Continua, vol. 62, no. 2, pp. 525–549. [Google Scholar]
14. M. A. E. Aziz and A. M. Aly. (2020). “Entropy generation for flow and heat transfer of Sisko-fluid over an exponentially stretching surface,” Computers, Materials & Continua, vol. 62, no. 1, pp. 37–59. [Google Scholar]
15. I. S. Awaludin, A. Ishak and I. Pop. (2019). “Stagnation point flow over a permeable stretching/shrinking sheet with chemical reaction and heat source/sink,” Computer Modeling in Engineering & Sciences, vol. 120, no. 1, pp. 203–214.
16. K. G. Kumar, S. Manjunatha and N. G. Rudraswamy. (2020). “MHD flow and nonlinear thermal radiative heat transfer of dusty prandtl fluid over a stretching sheet,” Fluid Dynamics & Materials Processing, vol. 16, no. 2, pp. 131–146.
17. B. Xiong, K. Yang, J. Zhao, W. Li and K. Li. (2016). “Performance evaluation of open flow-based software-defined networks based on queueing model,” Computer Networks, vol. 102, pp. 172–185.
18. X. L. Xu, C. Su, J. C. Lin, S. M. He and Z. J. Fu. (2017). “De-cloaking malicious activities in smartphones using http flow mining,” KSII Transactions on Internet & Information Systems, vol. 11, no. 6, pp. 3230–3253.
19. J. Y. Zhao, Z. H. Hu, B. Xiong and K. Q. Li. (2018). “Accelerating packet classification with counting bloom filters for virtual open flow switching,” China Communications, vol. 15, no. 10, pp. 117–128.
20. H. S. Yu, H. Qi, K. Q. Li, J. H. Zhang, P. Xiao. (2018). et al., “Open flow based dynamic flow scheduling with multipath for data center networks,” Computer Systems Science and Engineering, vol. 33, no. 4, pp. 251–258.
21. J. L. Zhang, X. C. Liu, J. Wan, Y. J. Ren and B. L. Xu. (2019). “Numerical optimization algorithm for unsteady flows of rotor based on web service,” Intelligent Automation and Soft Computing, vol. 25, no. 3, pp. 527–546.
22. B. Yin, S. Y. Zhou, Y. P. Lin, Y. H. Liu and Y. P. Hu. (2014). “Efficient distributed skyline computation using dependency-based data partitioning,” Journal of Systems and Software, vol. 93, pp. 69–83.
23. P. Zhang, W. J. Li and H. Sun. (2016). “Cost-efficient and multi-functional secure aggregation in large scale distributed application,” PLoS One, vol. 11, no. 8, pp. 0159605. [Google Scholar]
24. R. Zahmatkesh, H. Mohammadiun, M. Mohammadiun and M. H. D. Bonab. (2019). “Investigation of entropy generation in nanofluid’s axisymmetric stagnation flow over a cylinder with constant wall temperature and uniform surface suction-blowing,” Alexandria Engineering Journal, vol. 58, no. 4, pp. 1483–1498. [Google Scholar]
25. M. M. Rashidi, N. V. Ganesh, A. K. A. Hakeem, B. Ganga and G. Lorenzini. (2016). “Influences of an effective prandtl number model on nano boundary layer flow of Al2O3–H2O and Al2O3–C2H6O2 over a vertical stretching sheet,” International Journal of Heat and Mass Transfer, vol. 98, pp. 616–623. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |
Al
Al