DOI:10.32604/cmc.2020.011976
| Computers, Materials & Continua DOI:10.32604/cmc.2020.011976 | |
| Article |
Temporal Stability Analysis of Magnetized Hybrid Nanofluid Propagating through an Unsteady Shrinking Sheet: Partial Slip Conditions
1School of Quantitative Sciences, Universiti Utara Malaysia, 06010, Sintok, Kedah, Malaysia
2KCAET Khairpur Mir’s, Sindh Agriculture University, Tandojam Sindh, 70060, Pakistan
3IICT, University of Sindh, Jamshoro, 76080, Pakistan
4Department of Mathematics, Huzhou University, Huzhou, 313000, China
5Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, Changsha University of Science & Technology, Changsha, 410114, China
6Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
7Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, Saudi Arabia
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 08 June 2020; Accepted: 10 July 2020
Abstract: The unsteady magnetohydrodynamic (MHD) flow on a horizontal preamble surface with hybrid nanoparticles in the presence of the first order velocity and thermal slip conditions are investigated. Alumina (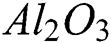
) and copper (Cu) are considered as hybrid nanoparticles that have been dispersed in water in order to make hybrid nanofluid (
/water). The system of similarity equations is derived from the system of partial differential equations (PDEs) by using variables of similarity, and their solutions are gotten with shooting method in the Maple software. In certain ranges of unsteadiness and magnetic parameters, the presence of dual solutions can be found. Further, it is examined that layer separation is deferred due to the effect of the hybrid nanoparticles. Moreover, the capacity of the thermal enhancement of 
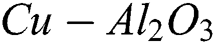/water hybrid nanofluid is higher as compared to 
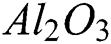/water based nanofluid and enhancements in 
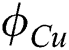are caused to rise the fluid temperature in both solutions. In the last, solutions stability analyzes were also carried out and the first solution was found to be stable.
Keywords: Cu − Al2O3/H2O; hybrid nanofluid; magnetic field; slip conditions; dual solutions
The topic of research in various engineering and industrial fields, such as air-conditioning, microelectronic, and power generation is energy sustainability and the optimizations of thermal systems performance. For energy sustainability, an inventive variety in thermodynamics was important [1]. Throughout such engineering processes, the cooling systems operate on a fluid medium through a forced flux in the absence and presence of convective heat transfer. The thermal conductivity of the liquid is therefore worthwhile to be enhanced for a better engineering process. The nanofluid formation is created through scattering single nanoparticle into the normal fluids, for example, vegetable oil, glycol, water, or the combination of glycol with water. The nanoparticles can be classified as carbon (CNTs, MWCNT), metal oxides (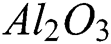
, 
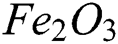, CuO), metal (Cu, Ag), and metal carbide and nitride. Many researchers dealt with the various kind of nanoparticle combinations for example metal oxides (
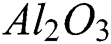, CuO), metals (Al, Cu, Fe), and semiconductors (
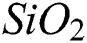, T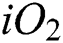
) nanoparticles. The important references on nanofluid can be seen in the books of [2,3]. On the other hand, comprehensive review papers on the nanofluid were written by [4–12].
Recently, researchers introduced a new type of nanofluid, and they call it Hybrid nanofluid. Hybrid nanofluid helps the regular nanofluids to improve its thermal properties. It can be described as the hybrid nanofluid, which consists of two different kinds of nanoparticles together with new chemical and thermophysical properties that can improve the rate of heat transfer due to synergistic properties (see [13]). Esfe et al. [14] stated that the good heat transfer rate is gotten by hybridizing the small amount of the nanoparticles volume fraction in the base fluid. Yan et al. [15] stated that the rate of heat transfer of the hybridized nanofluid is more as compared to the normal water-based nanofluid during the examination of the Cu-Al2O3/water nanofluid. They found ranges of the existence of multiple solutions and also performed stability analysis of the solutions. Lund et al. [16] examined the MHD flow of Cu-Fe3O4/H2O hybrid nanofluid over non-linear stretching and shrinking parameters in the presence of the joule heating. Two solutions were found, and an unstable solution was recognized by without doing stability analysis due to the existence of the singularity in the second solution. Further, Waini et al. [17] obtained two solutions during the examination of the hybrid nanofluid over vertical sheet embedded in a permeable medium. They claimed that the non-uniqueness of solutions depends on the ranges of the mixed convection parameter. Waini et al. [18] continued the problem of [19] for the hybrid nanofluid and successfully found dual solutions in the ranges of the unsteadiness parameter. Due to various practical applications of the unsteady flow, the research of [19] was also extended by the [20] for the nanofluid by using of the double phase model and successfully found the dual solutions. The same paper was also extended by the [21] for the MHD unsteady flow of the Casson type nanofluid with effects of the slip conditions and Stefan blowing and noticed that dual solutions are also possible for the accelerated surface. Further, Lund et al. [22] considered the revised model of [18,19] for the unsteady incompressible MHD flow of the hybrid nanofluid in the existence of thermal radiation effects. It is now clear the importance of the unsteady model for the practical point of view. In this paper, we also extended the work of [18] and [22] for the hybrid nanofluid in the absence of the viscous dissipation and thermal radiation effect. To date, numerous review publications are present in the literature on the synthesis and preparation and hybrid nanofluids, such as [23–30]. Besides, some significant research articles of hybrid nanofluids are also available in these references [31–38].
The main objective of the current article is, therefore, to extend the works of [18,22] of MHD flow of the hybrid nanofluid on a shrinking sheet with the effect of the magnetic field, velocity, and thermal slip conditions. The alumina (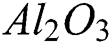
) and copper (Cu) are known to be hybrid nanoparticles here. The nanoparticles are then dispersed in order to develop the hybrid nanofluid (
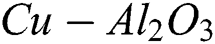/water). In order to validate the present results, current results are compared with the results of the previously published.
Let us take the MHD unsteady flow of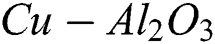 
/water hybrid nanofluid over the shrinking sheet. The coordinate system and the physical representation of the problem are shown in Fig. 1. Further, velocity and thermal partial slip conditions are also taken into account where 
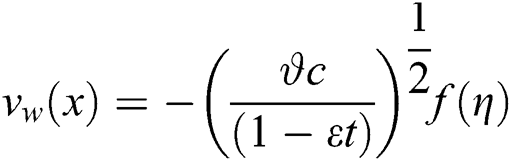is the mass transfer. Besides, the flow is assumed to be subject to a transverse magnetic field 
, where constant magnetic field is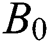 
. The influence of 
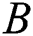on the shrinking sheet is applied perpendicular (see Fig. 1). Tiwari and Das’s model are expressed as follows based on the considered assumptions [18,22]:
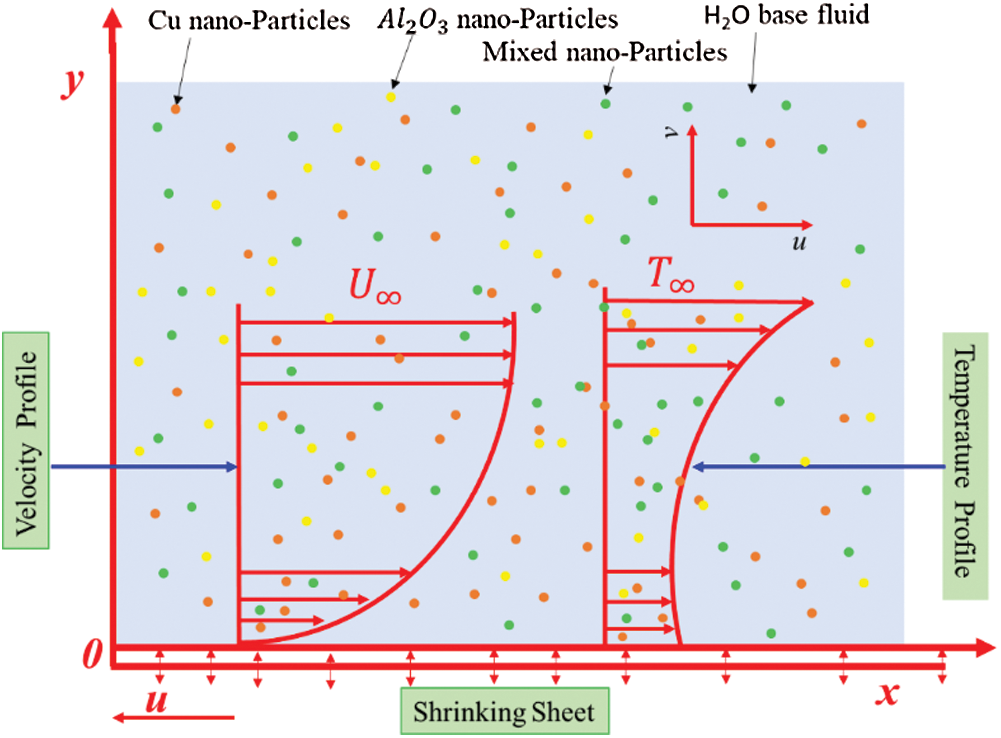
Figure 1: Physical models and coordinate systems
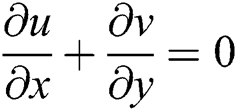
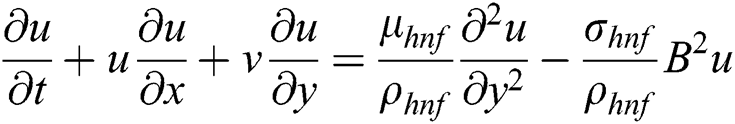
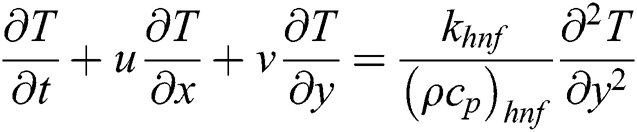
The subject to boundary conditions [21]
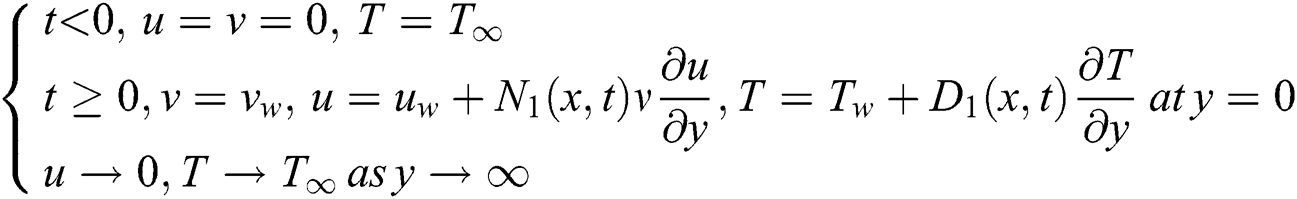
where velocity of surface is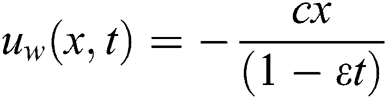 
. The thermophoresis property of Yan et al. [15] are followed in the present analysis.
Further, 
is velocity slip factor and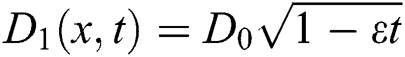 
is thermal slip factor where 
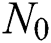and 
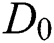are the slip factors. Tabs. 1 and 2 demonstrate these features of hybrid nanofluid.
Table 1: Thermophysical properties of hybrid nanofluid [22]
Table 2: The thermo physical properties of the base fluid (water) and the nanoparticles [18,22]
We employ the following variable of similarity transformation to convert the Eqs. (1)–(3) into a system of ODEs.
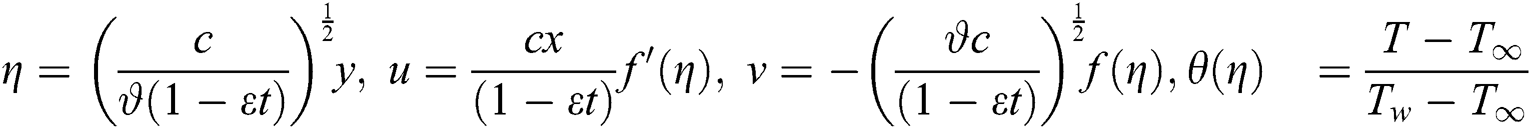
By applying Eq. (5) into Eqs. (1)–(3) then we have following non-dimensional form of ODEs
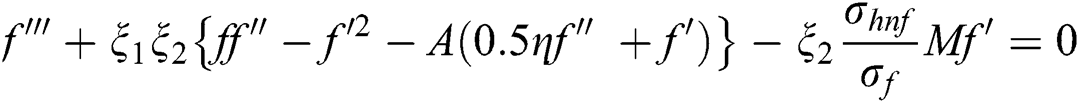
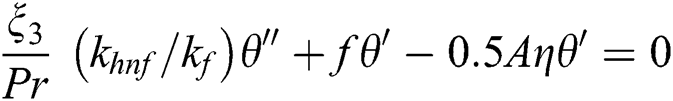
Along with the boundary conditions
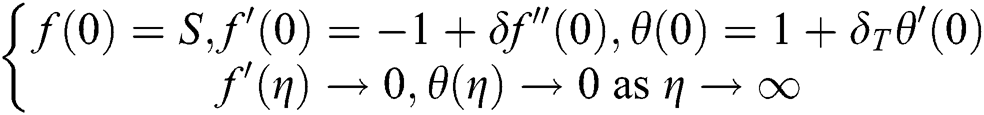
The non-dimensional quantities are given as 
.
The coefficient of skin friction 
and local Nusselt number 
are given as
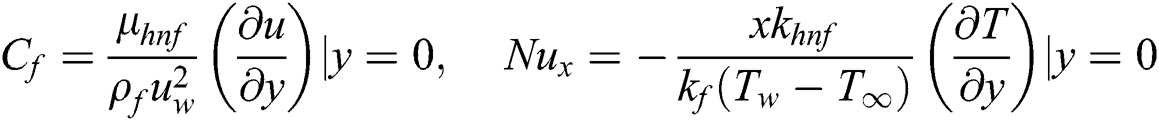
By employing Eq. (9) in Eq. (10), we get
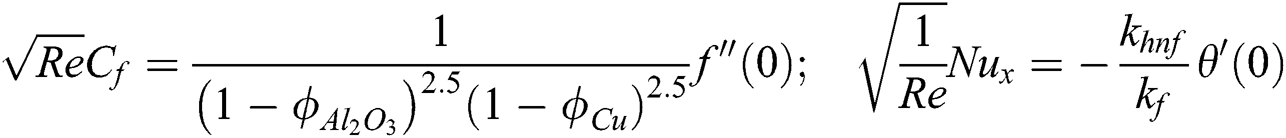
where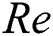 
is local Reynold number.
Merkin et al. [39–43] suggested for the stability analysis that the new non-dimensional variables of similarity transformation need to be introduced by considering 
, therefore, following new similarity transformation variables are introduced.
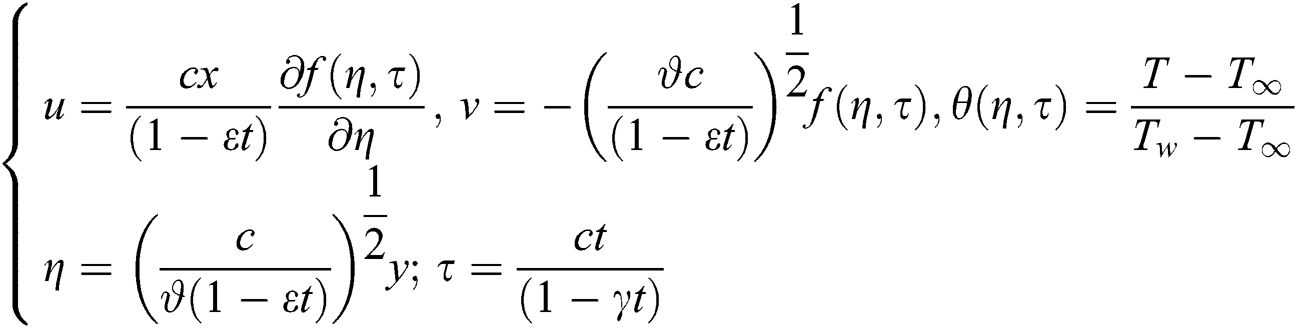
By putting Eq. (12) in Eqs. (2) and (3), we get
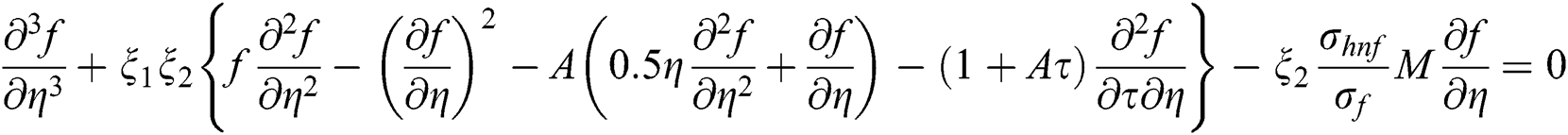
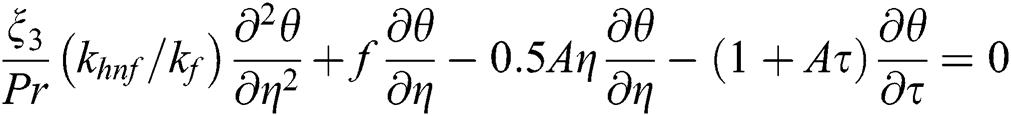
Along with boundary conditions
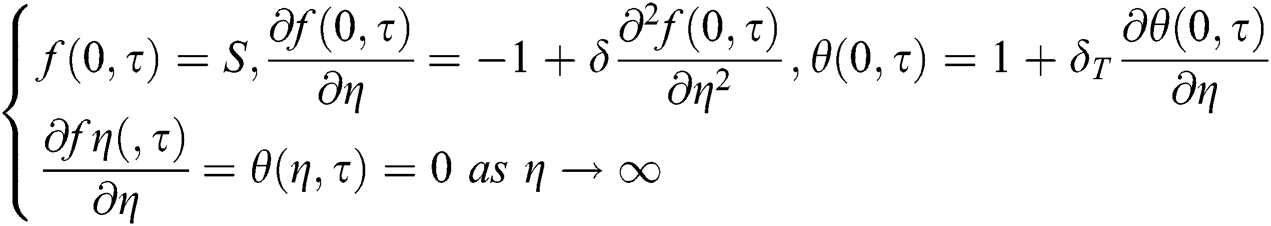
According to Lund et al. [41], “to check the stability of steady flow solutions where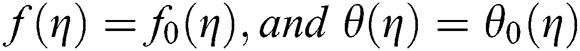 
of satisfying the boundary value problem Eqs. (6)–(8)”, we have
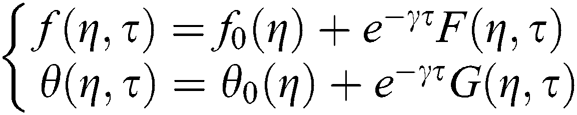
where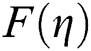 
and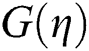 
are relatively small to 
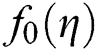and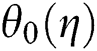 
and Y is called as unknown parameter of eigenvalue which need to be determined. Thus, we have the following linearized problems of eigenvalue, by replacing Eq. (16) in Eqs. (13) and (14) with 
.
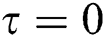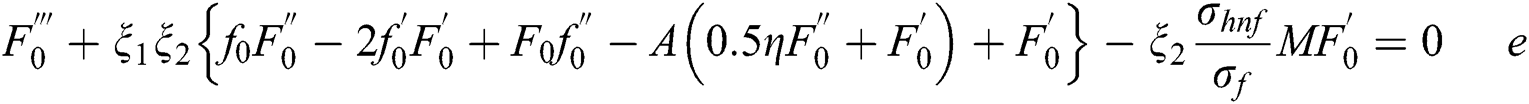
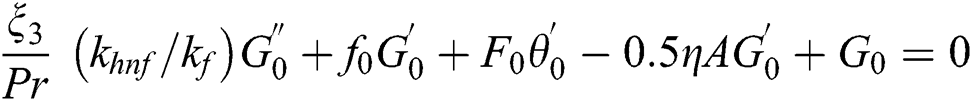
Subject to the boundary conditions
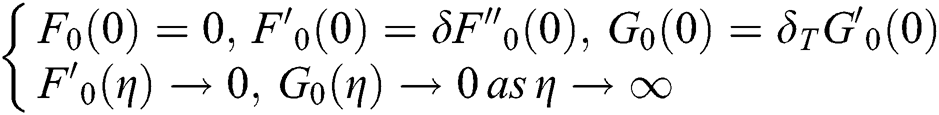
According to Dero et al. [44–46], one boundary condition from two should be converted to initial boundary condition (relaxed) in order to achieve the smallest values of eigenvalue. Therefore,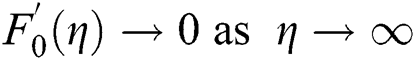 
is relaxed into 
.
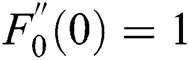The shooting method in Maple code with add of shootlib function has been employed to solve unsteady flow equations and bvp4c code in MATLAB software is used to solve the normalizing stability equations. The results of these codes are compared graphically and numerically with previously published works and found in the excellent agreements. In this study,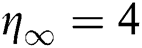 
is kept fixed during the computations but it is also noticed that 
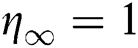and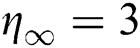 
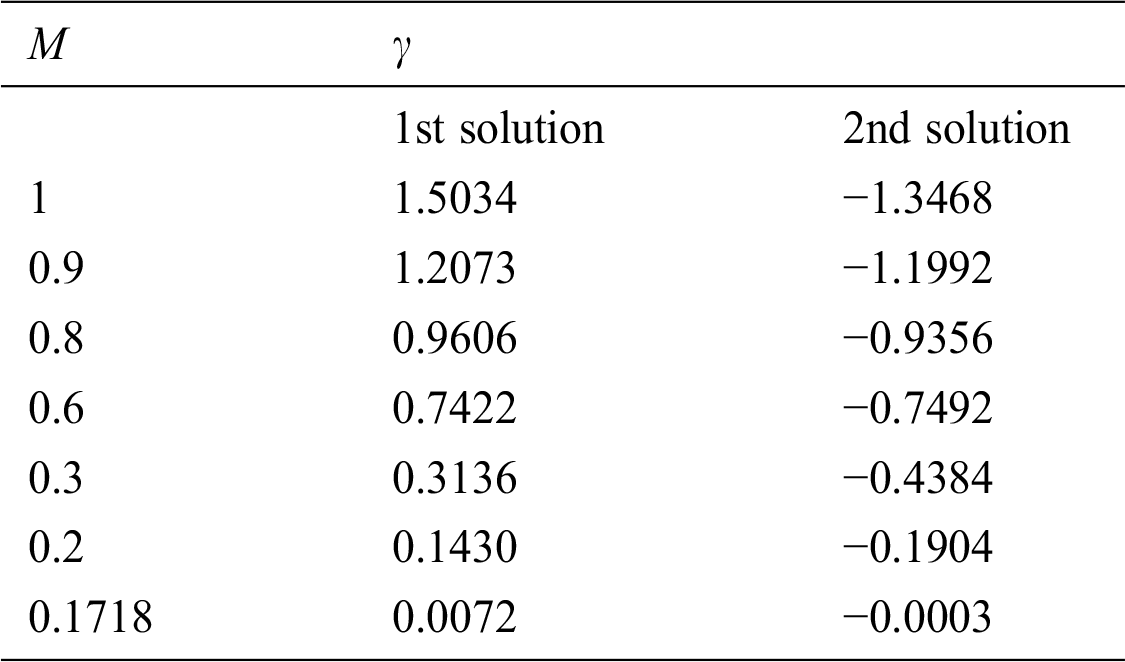
are tolerable for temperature and velocity profiles in order to satisfy the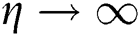 
as shown in Figs. 9 and 10, respectively. For the numerical compression, Tab. 3 is construction for the magnitude of 
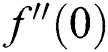and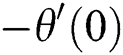 
with previously available results of [22]. It is found that our results are showing a favorable agreement. Further, it can be observed from Tab. 4 that the first (second) solution is stable (unstable) as the values of 
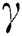are positive (negative). The positive (negative) magnitude of 
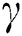should be noted as indicating an initial decay (growth) of disturbance.
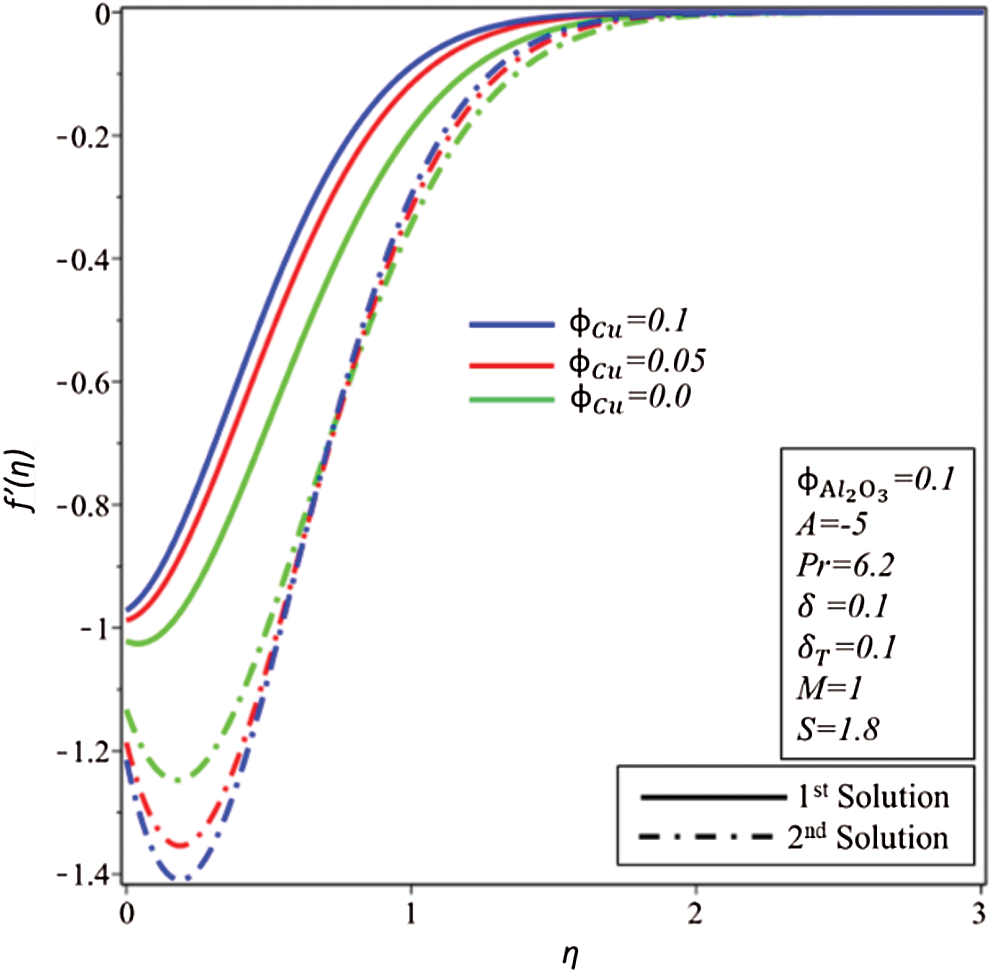
Figure 9: Variation of f″ (η) for φCu
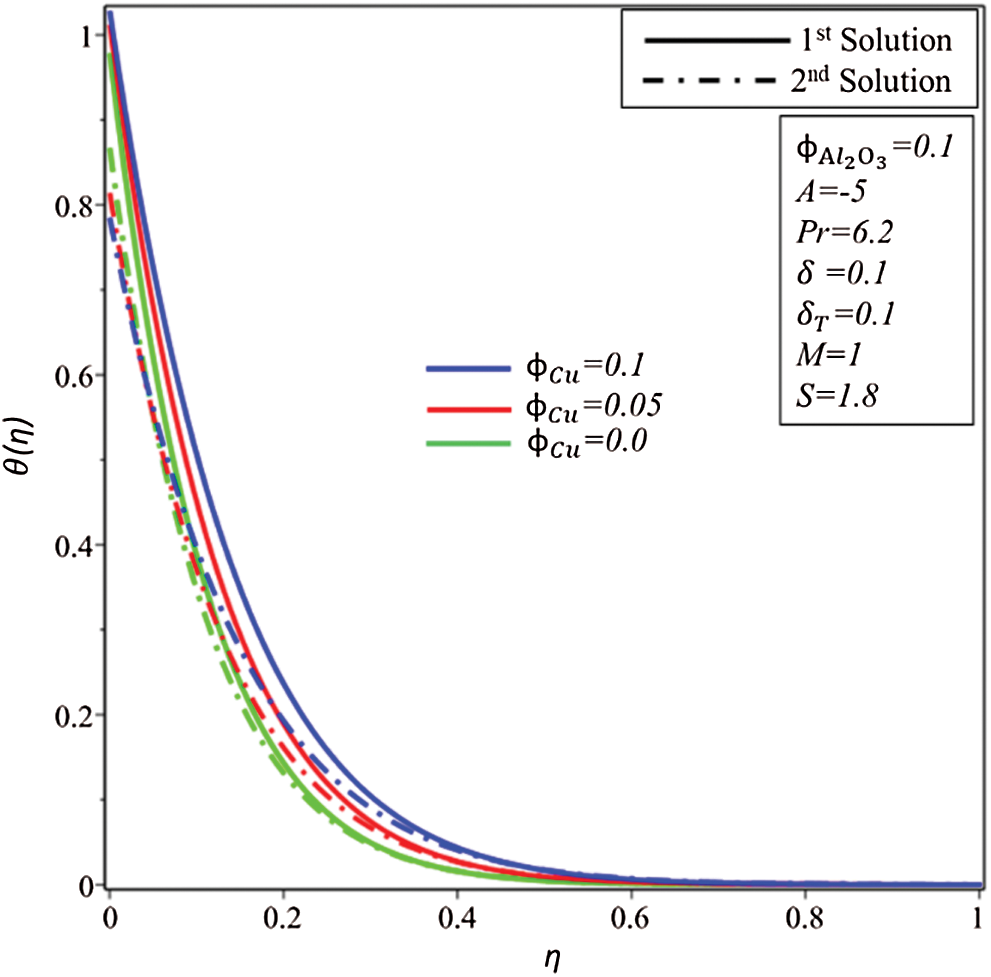
Figure 10: Variation of θ (η) for φCu
Table 3: Values of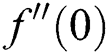 
and 
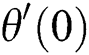for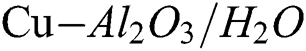 
hybrid nanofluid for 
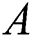when 
, 
, 
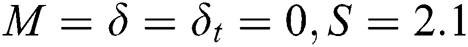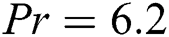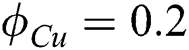and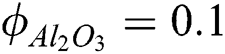 
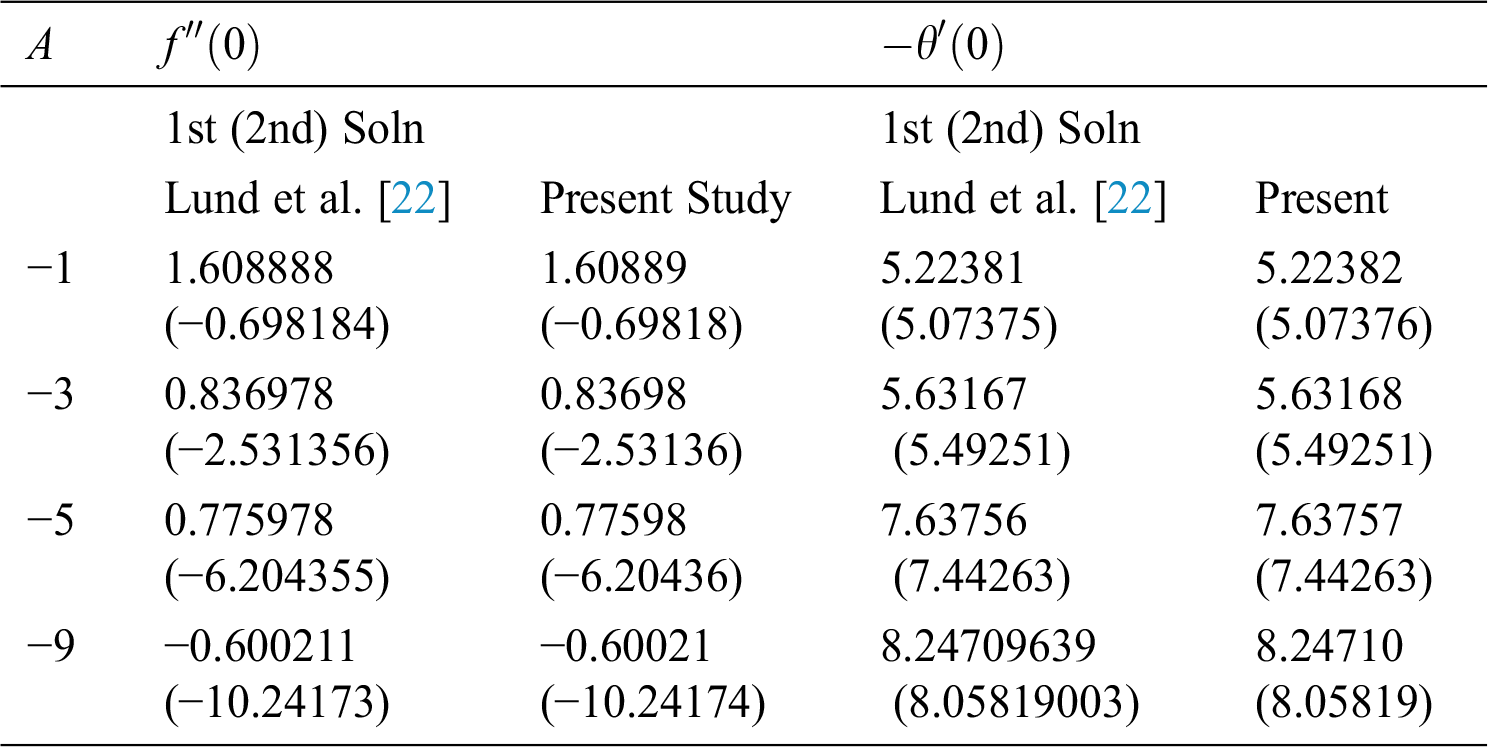
Table 4: The smallest eigenvalues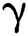 
for the numerous values of magnetic parameter 
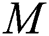at 
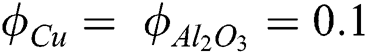
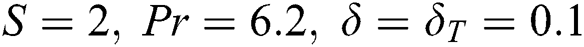and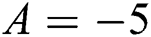 
The preparation of a hybrid nanofluid has been shown in the studies of [15,17,22]. They originally considered nanoparticles of alumina (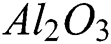
) into water base fluid and then, nanoparticles of copper (Cu) were mixed with the alumina (
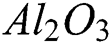) by considering the distant fractions of solid volume in order to make a hybrid nanofluid. This kind of hybrid nanofluid was called as 
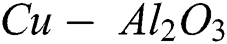/water. We also follow their works by keeping the 
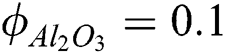as constant in the whole article while the range of 
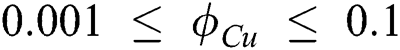was kept for copper nanoparticles.
We have water as a base fluid so Pr = 6.2 is kept as constant for the room temperature of 25°C. The graphical contrast with the sixth graph of [18] is demonstrated in Fig. 2 in order to validate our numerical coding and its results. It can be concluded that our numerical coding is working properly and can be used in this study as the critical values of our figure is the same as given in the article of [18].
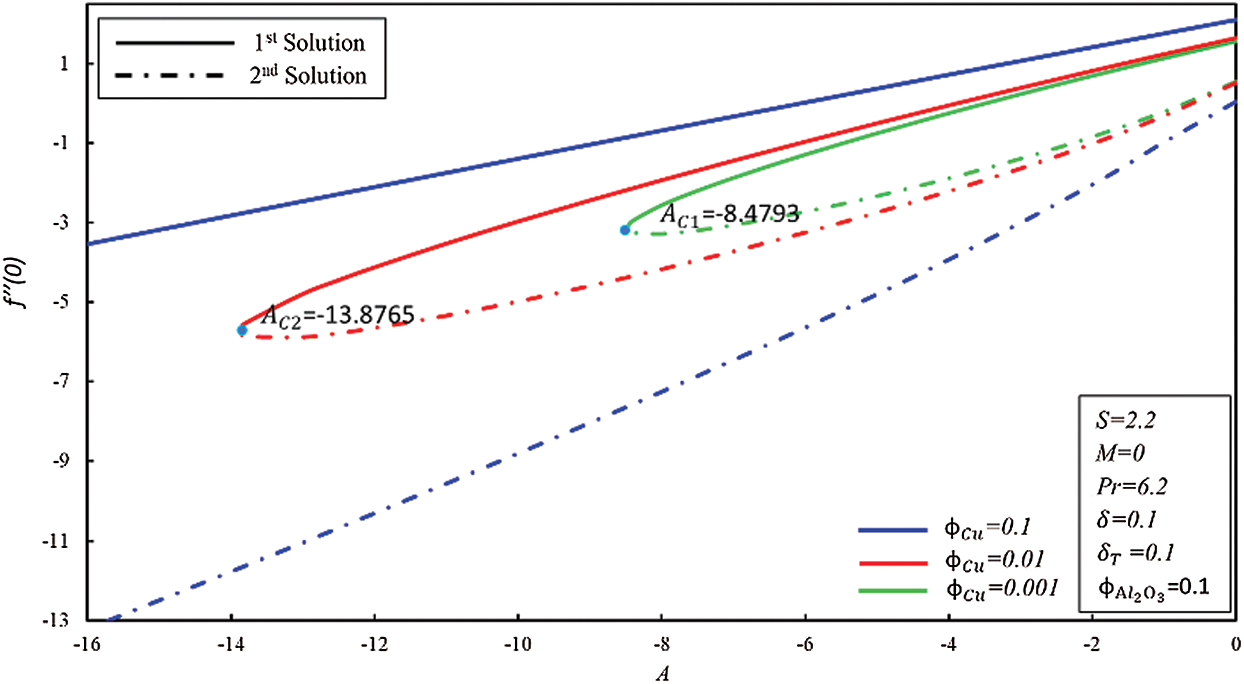
Figure 2: Conmparison with the 6th Fig. of [18]
Figs. 3 and 4 display the coefficient of skin friction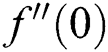 
and rate of heat transfer 
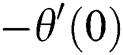of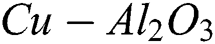 
/water nanofluid to 
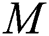for numerous estimations of 
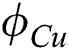, respectively. Range of first and second solutions is 
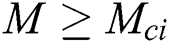where 
where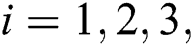as range of no solution is 
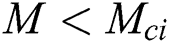where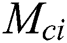 
shows the critical values of magnetic field for respective 
.
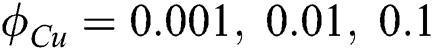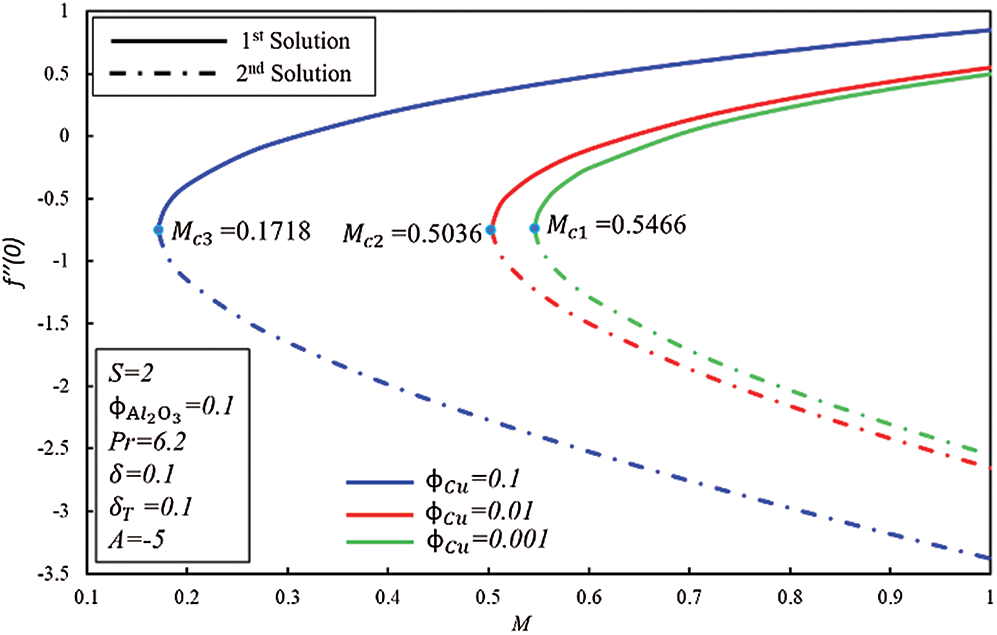
Figure 3: Variation of f″ (0) for ϕCu along with various values of M
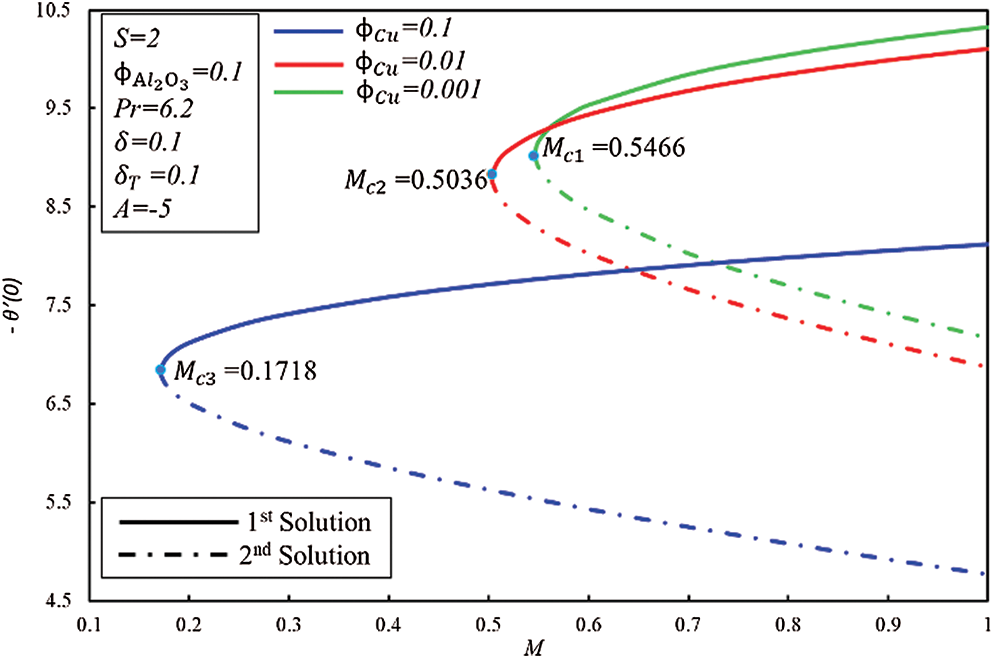
Figure 4: Variation of −θ′ (0) for ϕCu along with various values of M
It should be noted that at the pint of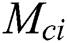 
, fluid flow of boundary layer initiates converting from laminar flow to turbulent flow and it is noticed from the previous studies that this is possible only when fluid is flowing over the shrinking surface. Further, it is observed that dual solutions exist when the flow is deaccelerated which means that values of the unsteadiness parameter are negative. Moreover, the rate of heat transfer increases in the first solution for the rising effect of the magnetic field, while it decreases in the second solution.
Figs. 5 and 6 show the significance of unsteadiness parameter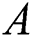 
for different values of suction parameter 
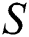on 
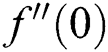and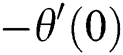 
, respectively. The coefficient of skin friction 
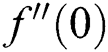improves in the first solution as suction increases, whereas it decreases in the second solution. The enhancement in the 
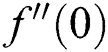is since suction generates the drag force inside the boundary layer. At the same time, the skin friction coefficient increases in both solutions as the unsteadiness parameter increases. Decreasing and increasing behavior of heat transfer rate observed in two solutions as unsteadiness parameter enhances. Further, the rate of heat transfer enhances in the first solution as suction increases, while dual nature is observed in the second solution.
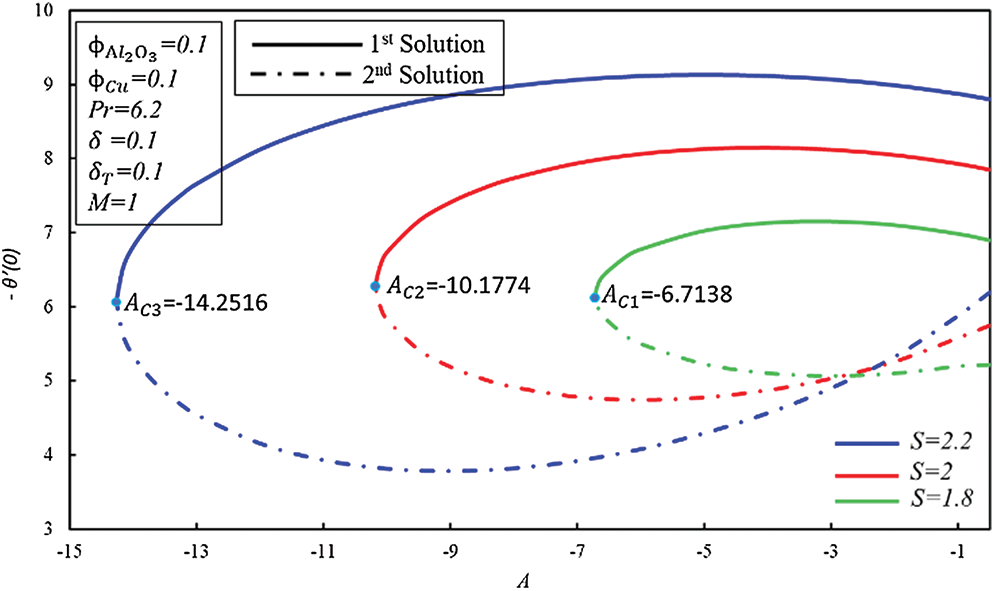
Figure 5: Variation of f″ (0) for S along with various values of A
Figure 6: Variation of −θ′ (0) for S along with various values of A
Variations of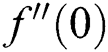 
against velocity slip factor 
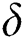for numerous values of 
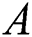is revealed in Fig. 7. It is noticed that the dual solutions can be found in a specific range of 
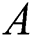which is 
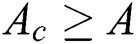, while no solution is obtained as 
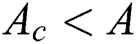, where 
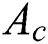is known as the critical points where existences of solutions are possible. It is perceived that the presence of slip effect delay the boundary layer separation where 
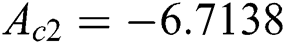and 
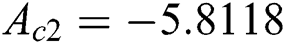are the critical values of the 
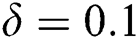and 
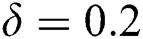, respectively. At the same time, magnitudes of 
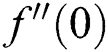increase when 
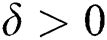in the second solution, whereas there exist dual behaviors in the second solution. Fig. 8 demonstrates the variation of 
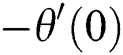versus thermal slip condition 
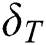for many values of 
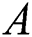. It can be detected that dual behavior is noticed in the magnitude of the rate of heat transfer in the first solution as thermal slip condition 
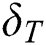is enhanced, while the rate of heat transfer declines in the second solution when 
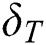increases. It is also noticed that 
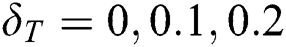has the same critical value which means that increments in the thermal slip do not affect boundary-layer separation.
Figure 7: Variation of f″ (0) for δ along with various values of A
Figure 8: Variation of −θ′ (0) for δ T along with various values of A
Effects of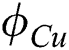 
on profiles of velocity 
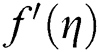and temperature 
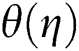are illustrated in Figs. 9 and 10, respectively. In comparison, the capacity of the thermal enhancement of 
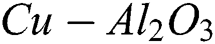/water hybrid nanofluid is more to 
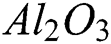/water-based nanofluid.
It is gained that fluid velocity declines in the first solution as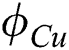 
enhances and as a resulting thickness of the hydrodynamic layer decreases. After all, velocity increases at first and then starts to decrease in the second solution. Further, enhancements in 
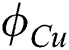are caused to raise the temperature of the fluid in both solutions as shown in Fig. 10.
In the current examination, the papers of [18,22] are extended in order to inspect the effects of MHD and slip for a hybrid nanofluid case. The current findings were checked for verification with previously reported data and an agreement between those findings is outstanding. Dual solutions have been found in some ranges of magnetic and unsteadiness parameter. The range of the first and second solutions is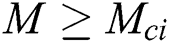 
where 
where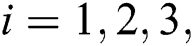as range of no solution is 
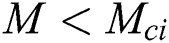where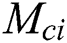 
shows magnetic critical values for respective values of 
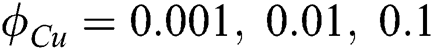. Further, the magnitude of the rate of heat transfer is increased in the first solution as thermal slip condition 
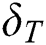is enhanced, while the heat transfer rate declines in the second solution as 
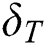increases. The coefficient of skin friction 
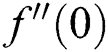enhances in the first solution as suction increases, while it decreases in the second solution. Stability analyzes are carried out and the results suggest that the first solution is stable.
Funding Statement: This project was supported by the Natural Science Foundation of China (Grant Nos. 61673169, 11701176, 11626101, 11601485).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. A. Lund, Z. Omar, I. Khan and S. Dero. (2019). “Multiple solutions of Cu-C6H9 NaO7 and Ag- C6H9 NaO7 nanofluids flow over nonlinear shrinking surface,” Journal of Central South University, vol. 26, no. 5, pp. 1283–1293. [Google Scholar]
2. A. A. Minea. (2017). Advances in new heat transfer fluids: From numerical to experimental techniques. Broken Sound Parkway NW, USA, CRC Press. [Google Scholar]
3. W. J. Minkowycz, E. Sparrow and J. P. Abraham. (2016). Nanoparticle heat transfer and fluid flow. Broken Sound Parkway NW, USA, CRC Press. [Google Scholar]
4. G. Rasool, A. Shafiq and I. Tlili. (2020). “Marangoni convective nanofluid flow over an electromagnetic actuator in the presence of first-order chemical reaction,” Heat Transfer-Asian Research, vol. 49, no. 1, pp. 274–288. [Google Scholar]
5. J. Fan and L. Wang. (2011). “Review of heat conduction in nanofluids,” Journal of Heat Transfer, vol. 133, no. 4, pp. 99.
6. O. Mahian, A. Kianifar, S. A. Kalogirou, I. Pop and S. Wongwises. (2013). “A review of the applications of nanofluids in solar energy,” International Journal of Heat and Mass Transfer, vol. 57, no. 2, pp. 582–594.
7. O. Mahian, L. Kolsi, M. Amani, P. Estellé, G. Ahmadi. (2019). et al., “Recent advances in modeling and simulation of nanofluid flows-part I: Fundamentals and theory,” Physics Reports, vol. 790, pp. 1–48.
8. O. Mahian, L. Kolsi, M. Amani, P. Estellé, G. Ahmadi. (2019). et al., “Recent advances in modeling and simulation of nanofluid flows-Part II: Applications,” Physics Reports, vol. 791, pp. 1–59.
9. M. Sheikholeslami and D. D. Ganji. (2016). “Nanofluid convective heat transfer using semi analytical and numerical approaches: A review,” Journal of the Taiwan Institute of Chemical Engineers, vol. 65, pp. 43–77.
10. J. Buongiorno, D. C. Venerus, N. Prabhat, T. McKrell, J. Townsend. (2016). et al., “A benchmark study on the thermal conductivity of nanofluids,” Journal of Applied Physics, vol. 106, no. 9, 094312.
11. T. G. Myers, H. Ribera and V. Cregan. (2017). “Does mathematics contribute to the nanofluid debate?,” International Journal of Heat and Mass Transfer, vol. 111, pp. 279–288.
12. S. Kakac and A. Pramuanjaroenkij. (2019). “Review of convective heat transfer enhancement with nanofluids,” International Journal of Heat and Mass Transfer, vol. 52, no. 13–14, pp. 3187–3196. [Google Scholar]
13. J. Sarkar, P. Ghosh and A. Adil. (2016). “A review on hybrid nanofluids: Recent research, development and applications,” Renewable and Sustainable Energy Reviews, vol. 43, pp. 164–177. [Google Scholar]
14. M. H. Esfe, A. Alirezaie and M. Rejvani. (2017). “An applicable study on the thermal conductivity of SWCNT-MgO hybrid nanofluid and price-performance analysis for energy management,” Applied Thermal Engineering, vol. 111, pp. 1202–1210. [Google Scholar]
15. L. Yan, S. Dero, I. Khan, I. A. Mari, D. Baleanu. (2020). et al., “Dual solutions and stability analysis of magnetized hybrid nanofluid with joule heating and multiple slip conditions,” Processes, vol. 8, no. 3, pp. 332. [Google Scholar]
16. L. A. Lund, Z. Omar, J. Raza and I. Khan. (2020). “Magnetohydrodynamic flow of Cu-Fe3O4/H2O hybrid nanofluid with effect of viscous dissipation: dual similarity solutions,” Journal of Thermal Analysis and Calorimetry, vol. 142, pp. 1–13. [Google Scholar]
17. I. Waini, A. Ishak, T. Groşan and I. Pop. (2020). “Mixed convection of a hybrid nanofluid flow along a vertical surface embedded in a porous medium,” International Communications in Heat and Mass Transfer, vol. 114, 104565. [Google Scholar]
18. I. Waini, A. Ishak and I. Pop. (2019). “Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid,” International Journal of Heat and Mass Transfer, vol. 136, pp. 288–297. [Google Scholar]
19. A. M. Rohni, S. Ahmad and I. Pop. (2012). “Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids,” International Journal of Heat and Mass Transfer, vol. 55, no. 7–8, pp. 1888–1895. [Google Scholar]
20. S. Dero, M. J. Uddin and A. M. Rohni. (2019). “Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions,” Heat Transfer—Asian Research, vol. 48, no. 6, pp. 2047–2066. [Google Scholar]
21. L. L. Ali, Z. Omar, J. Raza, I. Khan and E. S. M. Sherif. (2020). “Effects of stefan blowing and slip conditions on unsteady MHD Casson nanofluid flow over an unsteady shrinking sheet: Dual solutions,” Symmetry, vol. 12, no. 3, pp. 487. [Google Scholar]
22. L. A. Lund, Z. Omar, I. Khan and E. S. M. Sherif. (2020). “Dual solutions and stability analysis of a hybrid nanofluid over a stretching/shrinking sheet executing MHD flow,” Symmetry, vol. 12, no. 2, pp. 276. [Google Scholar]
23. N. A. C. Sidik, I. M. Adamu, M. M. Jamil, G. H. R. Kefayati, R. Mamat. (2016). et al., “Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review,” International Communications in Heat and Mass Transfer, vol. 78, pp. 68–79. [Google Scholar]
24. N. A. C. Sidik, M. M. Jamil, W. M. A. A. Japar and I. M. Adamu. (2017). “A review on preparation methods, stability and applications of hybrid nanofluids,” Renewable and Sustainable Energy Reviews, vol. 80, pp. 1112–1122.
25. J. R. Babu, K. K. Kumar and S. S. Rao. (2017). “State-of-art review on hybrid nanofluids,” Renewable and Sustainable Energy Reviews, vol. 77, pp. 551–565.
26. M. U. Sajid and H. M. Ali. (2018). “Thermal conductivity of hybrid nanofluids: A critical review,” International Journal of Heat and Mass Transfer, vol. 126, pp. 211–234.
27. D. K. Devendiran and V. A. Amirtham. (2016). “A review on preparation, characterization, properties and applications of nanofluids,” Renewable and Sustainable Energy Reviews, vol. 60, pp. 21–40.
28. H. Ibrahim, N. Sazali, A. S. Jamaludin, W. N. W. Salleh and M. H. D. Othman. (2018). “A brief review on utilization of hybrid nanofluid in heat exchangers: Theoretical and experimental,” in Proc. of the Int. Manufacturing Engineering Conf. & the Asia Pacific Conf. on Manufacturing Systems, Putrajaya, Malaysia, pp. 416–422.
29. L. Yang, W. Ji, M. Mao and J. N. Huang. (2020). “An updated review on the properties, fabrication and application of hybrid-nanofluids along with their environmental effects,” Journal of Cleaner Production, vol. 55, 120408.
30. M. H. Ahmadi, M. Ghazvini, M. Sadeghzadeh, M. A. Nazari and M. Ghalandari. (2019). “Utilization of hybrid nanofluids in solar energy applications: A review,” Nano-Structures & Nano-Objects, vol. 20, 100386. [Google Scholar]
31. S. S. Ghadikolaei, M. Gholinia, M. E. Hoseini and D. D. Ganji. (2019). “Natural convection MHD flow due to MoS2-Ag nanoparticles suspended in C2H6O2H2O hybrid base fluid with thermal radiation,” Journal of the Taiwan Institute of Chemical Engineers, vol. 97, pp. 12–23. [Google Scholar]
32. A. J. Chamkha, A. S. Dogonchi and D. D. Ganji. (2019). “Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating,” AIP Advances, vol. 9, no. 2, 025103.
33. N. S. Khashi’ie, N. M. Arifin, R. Nazar, E. H. Hafidzuddin, N. Wahi. (2020). et al., “Magnetohydrodynamics (MHD) axisymmetric flow and heat transfer of a hybrid nanofluid past a radially permeable stretching/shrinking sheet with Joule heating,” Chinese Journal of Physics, vol. 64, pp. 251–263.
34. L. A. Lund, Z. Omar, I. Khan, A. H. Seikh, E. S. M. Sherif. (2020). et al., “Stability analysis and multiple solution of Cu-Al2O3/H2O nanofluid contains hybrid nanomaterials over a shrinking surface in the presence of viscous dissipation,” Journal of Materials Research and Technology, vol. 9, no. 1, pp. 421–432.
35. S. Das, R. N. Jana and O. D. Makinde. (2017). “MHD flow of Cu-Al2O3/water hybrid nanofluid in porous channel: Analysis of entropy generation,” Defect and Diffusion Forum, vol. 377, pp. 42–61.
36. S. S. U. Devi and S. A. Devi. (2016). “Numerical investigation of three-dimensional hybrid Cu-Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating,” Canadian Journal of Physics, vol. 94, no. 5, pp. 490–496.
37. M. Hassan, M. Marin, R. Ellahi and S. Z. Alamri. (2018). “Exploration of convective heat transfer and flow characteristics synthesis by Cu-Ag/water hybrid-nanofluids,” Heat Transfer Research, vol. 49, no. 18, pp. 1837–1848.
38. G. Huminic and A. Huminic. (2020). “Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review,” Journal of Molecular Liquids, vol. 302, 112533. [Google Scholar]
39. J. H. Merkin. (1986). “On dual solutions occurring in mixed convection in a porous medium,” Journal of Engineering Mathematics, vol. 20, no. 2, pp. 171–179. [Google Scholar]
40. L. A. Lund, Z. Omar, I. Khan, D. Baleanu and S. K. Nisar. (2020). “Triple solutions and stability analysis of micropolar fluid flow on an exponentially shrinking surface,” Crystals, vol. 10, no. 4, pp. 283.
41. L. A. Lund, Z. Omar, I. Khan, J. Raza, E. S. M. Sherif. (2020). et al., “Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and joule heating over an exponential shrinking sheet: Triple solutions and stability analysis,” Symmetry, vol. 12, no. 1, pp. 142. [Google Scholar]
42. L. A. Lund, Z. Omar, I. Khan, S. Kadry, S. Rho. (2019). et al., “Effect of viscous dissipation in heat transfer of MHD flow of micropolar fluid partial slip conditions,” Dual Solutions and Stability Analysis, Energies, vol. 12, no. 24, pp. 4617.
43. N. S. Khashi’ie, N. M. Arifin, I. Pop, R. Nazar, E. H. Hafidzuddin. (2020). et al., “Non-axisymmetric Homann stagnation point flow and heat transfer past a stretching/shrinking sheet using hybrid nanofluid,” International Journal of Numerical Methods for Heat & Fluid Flow. [Google Scholar]
44. S. Dero, A. M. Rohni and A. Saaban. (2020). “Stability analysis of Cu− C6H9NaO7 and Ag− C6H9NaO7 nanofluids with effect of viscous dissipation over stretching and shrinking surfaces using a single-phase model,” Heliyon, vol. 6, no. 3, e03510. [Google Scholar]
45. S. Dero, A. M. Rohni and A. Saaban. (2020). “Effects of the viscous dissipation and chemical reaction on Casson nanofluid flow over the permeable stretching/shrinking sheet,” Heat Transfer, vol. 49, no. 4, pp. 1736–1755.
46. L. A. Lund, Z. Omar and I. Khan. (2019). “Quadruple solutions of mixed convection flow of magnetohydrodynamic nanofluid over exponentially vertical shrinking and stretching surfaces: Stability analysis,” Computer Methods and Programs in Biomedicine, vol. 182, 105044. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |