DOI:10.32604/cmc.2020.012468

| Computers, Materials & Continua DOI:10.32604/cmc.2020.012468 |  |
| Article |
Peristaltic Flow of Dusty Nanofluids in Curved Channels
1Mathematics Department, Jouf University, Qurayyat, Saudi Arabia
2Department of Mathematics, King Khalid University, Abha, Saudi Arabia
*Corresponding Author: Sameh E. Ahmed. Email: sehassan@kku.edu.sa
Received: 01 July 2020; Accepted: 12 August 2020
Abstract: In this paper, numerical investigations for peristaltic motion of dusty nanofluids in a curved channel are performed. Two systems of partial differential equations are presented for the nanofluid and dusty phases and then the approximations of the long wave length and low Reynolds number are applied. The physical domain is transformed to a rectangular computational model using suitable grid transformations. The resulting systems are solved numerically using shooting method and mathematical forms for the pressure distributions are introduced. The controlling parameters in this study are the thermal buoyancy parameter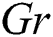 , the concentration buoyancy parameter
, the concentration buoyancy parameter 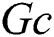 , the amplitude ratio
, the amplitude ratio 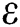 , the Eckert number
, the Eckert number 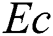 , the thermophoresis parameter
, the thermophoresis parameter 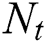 and the Brownian motion parameter
and the Brownian motion parameter 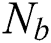 and the dusty parameters
and the dusty parameters 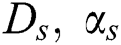 . The obtained results revealed that an increase in the Eckert number enhances the temperature of the fluid and dusty particles while the nanoparticle volume fraction is reduced. Also, both of the temperature and nanoparticles volume fraction are supported by the growing of the Brownian motion parameter.
. The obtained results revealed that an increase in the Eckert number enhances the temperature of the fluid and dusty particles while the nanoparticle volume fraction is reduced. Also, both of the temperature and nanoparticles volume fraction are supported by the growing of the Brownian motion parameter.
Keywords: Peristaltic motion; dusty particles; nanofluid; curved channels
Study of the peristalsis flow has many applications such as movement of the food in the intestine tract, the urine passage from a kidney to the bladder blood flow in small veins and arteries of the blood circulation, transferring the ovum in the Fallopian tube and the movement of sperm in the channels. Also, there are many applications of peristaltic motion in the biomedical devices, such as blood pumps and heart lung machines. The physiology of the gastrointestinal tract discussed by Latham [1], Mishra et al. [2]. Also, many studies interested with peristaltic flow in a curved channel [3–11]. Sato et al. [3] discussed the peristaltic flow in a curved channel. Ali et al. [4] studied the peristaltic flow in a curved channel with a long wavelength approximation. Ali et al. [5,6] examined effects of the heat transfer and fluid flow of a non-Newtonian third grade fluid in a curved channel. Hayat et al. [7] discussed the Newtonian fluid peristaltic flow, heat and mass transfer in a curved channel with compliant walls. The investigation in [7] was extended by Hayat et al. [8] and Hina et al. [9] to include case of a third grade fluid. Hina et al. [9] considered case of the peristaltic motion in curved channels contain compliant walls using Johnson-Segalman fluid. Hina et al. [10,11] studied the combined heat and mass transfer effects as well as the influence of wall properties on the peristaltic flow of Johnson-Segalman and the peristaltic flow of pseudoplastic fluid, respectively.
In the recent years, the researchers focused on studying the nanofluids due to their applications in various fields. The first study was introduced by Choi [12] who studied the pure fluids with suspended nanoparticles. He discussed the substantial augmentation of the heat transported in suspensions of copper or aluminum nanoparticles in water or other liquids. Buongiorno [13] takes into his account the Brownian diffusion as well as thermophoresis in writing the transport equations. The literature survey indicates that attempts on peristalsis of the nanofluid model in a curved channel are little. Hina et al. [14] discussed numerically the peristaltic flow of a nanofluid in a curved channel. Ayub et al. [15] studied the mixed convection in the presence of a thermal radiation and a chemical reaction, analytically. The results indicated that the heat transfer rate decreases with the increase in thermophoresis parameter. Narla et al. [16] studied the peristaltic transport of a Jeffrey nanofluid in a curved channel and examined effects of various parameters on the fluid flow and the temperature distributions. Noreen et al. [17] discussed the induced magnetic field effects on the peristaltic flow in a curved channel. They found that an increase in the Brownian motion and thermophoresis parameters causes an increase in the temperature profiles. Hayat et al. [18] studied the peristaltic motion of a copper-water based nanoliquid with the thermal slip conditions. Hayat et al. [19] studied the MHD peristaltic flow of Sisko nanofluids with the Joule heating effects. They used a numerical treatment for the governing equations. They found that the increasing values of the curvature parameter results in symmetric behaviors at the centerline of the channel for the velocity, temperature and concentration distributions. Tanveer et al. [20] studied the peristaltic motion of a Sisko fluid with homogeneous-heterogeneous reaction effects. The results revealed that the lower velocity, temperature and concentration profiles are obtained in case of the higher bending. Tanveer et al. [21] studied the peristaltic flow of Eyring-Powell nanofluids in a curved channel with compliant walls. They found that the Eyring-Powell parameters tend to decrease the velocity and temperature of the nanofluid while the concentration bears a dual response. Hayat et al. [22] discussed the peristalsis of MHD Jeffery nanofluids in a curved channel with a porous medium.
On the other hand, the practical applications of the dusty fluid flow can be found in atmospheric, engineering and physiological fields, for example, conveying of powdered materials, purification of crude oil, environmental pollutants, dust in gas cooling systems, petroleum industry. Many other applications are included in the valuable book written by Rudinger [23]. Farbar et al. [24] studied the heat transfer by flow of the gas-solid mixtures in a circular tube. Saffman [25] presented a dusty fluid model in the laminar flow. Many researchers [26–33] extended the dusty fluid topic with different physical circumstance. Recently, this topic is generalized to case of the dusty nanofluid by many researchers. Siddiqa et al. [34] conducted an analysis of a two-phase natural convection flow of dusty nanofluid along a vertical wavy surface. They found that presence of the dust particles have a notable influence on the temperature distribution as the isotherms get stronger for the dusty water. Begum et al. [35] studied the gyrotactic bioconvection of the dusty nanofluid along an isothermally heated vertical wall. They applied a numerical treatment for the mathematical model using the two-point implicit finite difference method. Gireesha et al. [36], Gireesha et al. [37] studied the Hall effect on a two-phase transient flow with stretching sheet using KVL model and irregular heat generation/consumption, respectively. Good recently studies in the nanofluid topics are found in [38–43].
The authors in all the mentioned papers disregarded case of the peristaltic motion of the dusty nanofluids in complex shapes. Therefore the main objective of this paper is to study the peristaltic flow in a curved channel using the dusty nanofluids. The two-phase nanofluid model is used to simulate this case and approximations of the long wave length and low Reynolds number are applied. Also, one of the objectives of this study is to express the pressure distributions in the flow domain and examining effects of the dusty and geometry parameters on the nanofluid flow, heat and nanoparticles distributions.
2 Discerption of the Problem and Mathematical Formulation
Consider an unsteady two dimensional peristaltic motion of a dusty nanofluid inside a curved channel. Fig. 1 shows conditions of the problem and coordinates system. In this figure, the 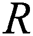 -axis is taken normal to surface of the channel and the
-axis is taken normal to surface of the channel and the 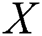 -axis is taken along walls of the channel. Width of the channel is 2d1 surrounded in a circle of a radius
-axis is taken along walls of the channel. Width of the channel is 2d1 surrounded in a circle of a radius 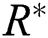 and a center
and a center  . Boundaries of the channel walls are determined as:
. Boundaries of the channel walls are determined as: 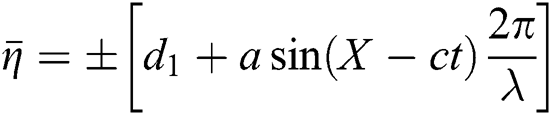 ; where
; where 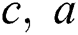 and
and 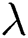 are the speed, amplitude and length of the wave. In addition, the nanofluid is modeled using the two-phase model in which effects of the Brownian motion and thermophoresis are included. The base fluid, dusty particles and nanoparticles are in a thermal equilibrium model. Viscous dissipation effect is considered and a linear Boussinesq approximation is taken into account. A uniform size of the dusty particles is assumed and they distribute equally in the mixture.
are the speed, amplitude and length of the wave. In addition, the nanofluid is modeled using the two-phase model in which effects of the Brownian motion and thermophoresis are included. The base fluid, dusty particles and nanoparticles are in a thermal equilibrium model. Viscous dissipation effect is considered and a linear Boussinesq approximation is taken into account. A uniform size of the dusty particles is assumed and they distribute equally in the mixture.
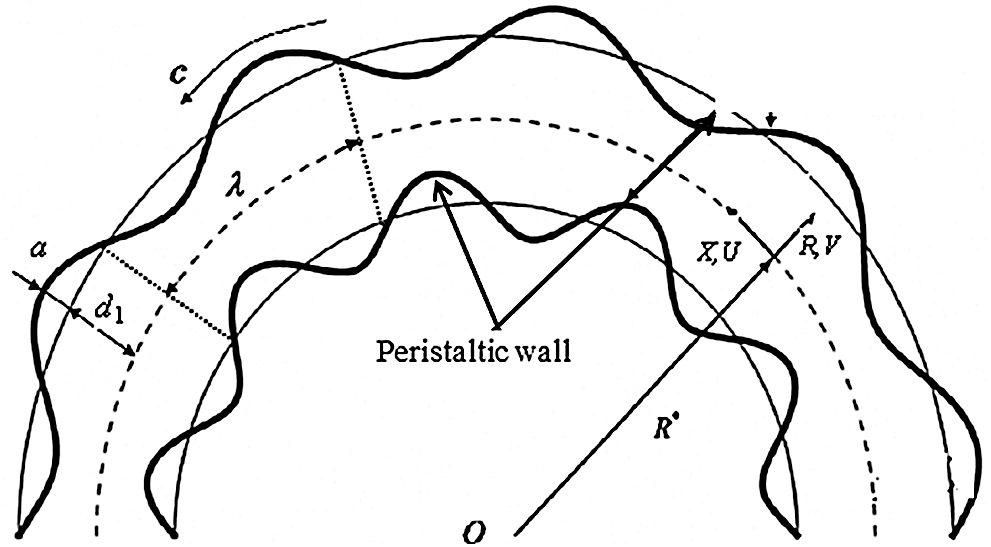
Figure 1: The physical model of the channel
Under all the mentioned assumptions, the governing equations of the problem are introduced as, see [14,26,27]

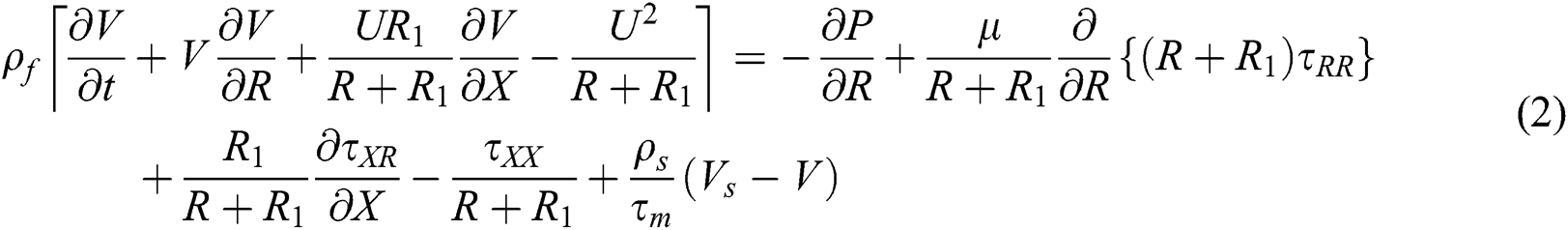
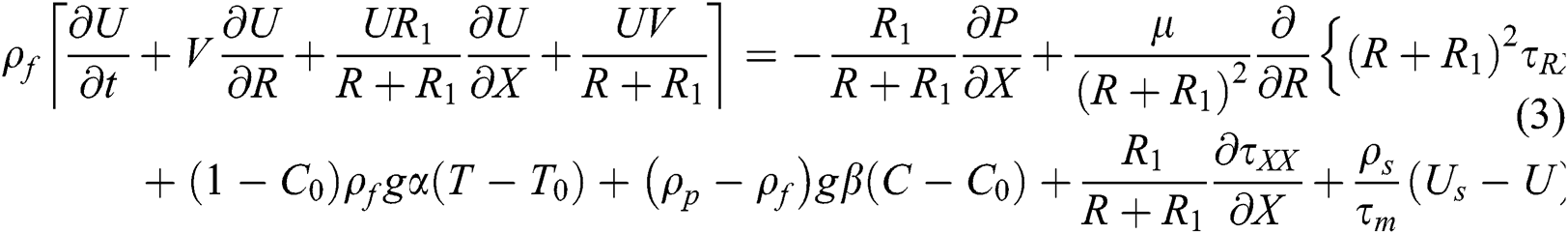
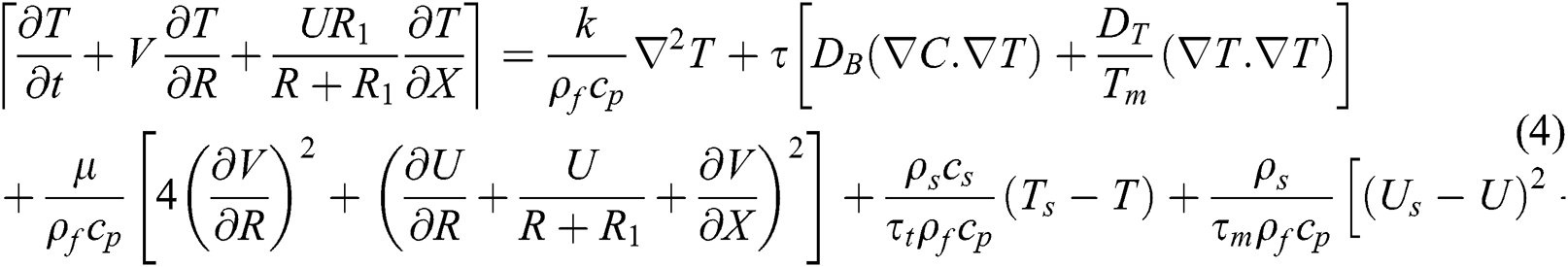
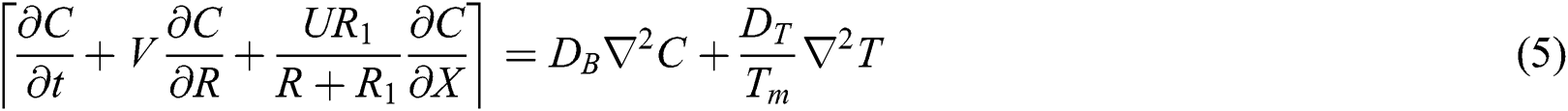

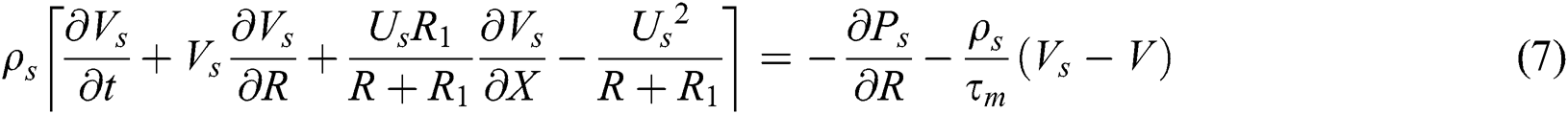
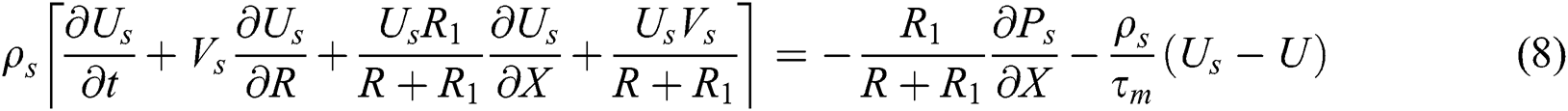
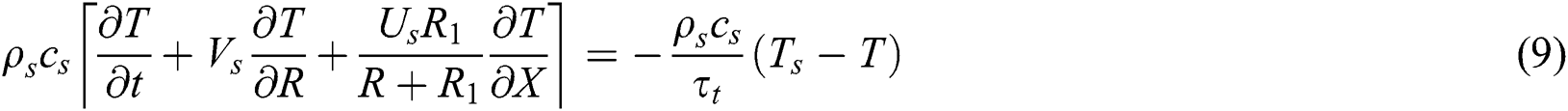
where
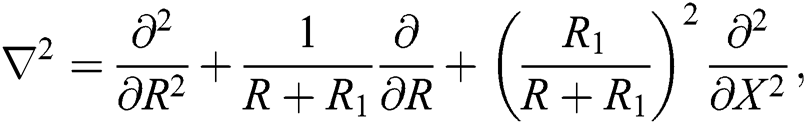
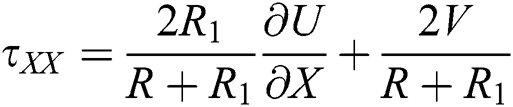
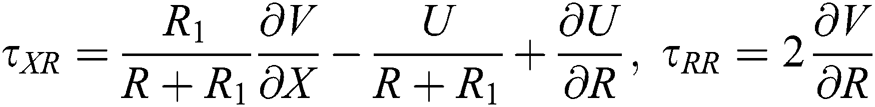
In Eqs. (1)–(9), 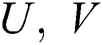 ,
, 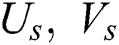 are the velocity components of the fluid and dust phase, in the laboratory frame
are the velocity components of the fluid and dust phase, in the laboratory frame 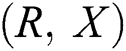 ;
; 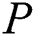 ,
, 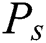 is the pressure, of the fluid and dust phase,
is the pressure, of the fluid and dust phase, 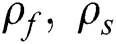 is density of the fluid and dust phase,
is density of the fluid and dust phase, 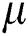 is the dynamic Viscosity,
is the dynamic Viscosity, 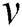 is the kinematic viscosity,
is the kinematic viscosity, 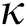 is the thermal conductivity,
is the thermal conductivity, 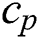 is the specific heat at constant pressure,
is the specific heat at constant pressure, 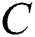 is the concentration and
is the concentration and 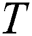 is the temperature of the fluid,
is the temperature of the fluid, 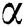 is the coefficient of linear thermal expansion of the fluid,
is the coefficient of linear thermal expansion of the fluid, 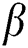 is the coefficient of expansion with concentration, and
is the coefficient of expansion with concentration, and 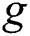 is acceleration due to gravity, If
is acceleration due to gravity, If 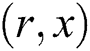 and
and 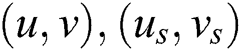 are the coordinates and velocity components in the wave frame then
are the coordinates and velocity components in the wave frame then
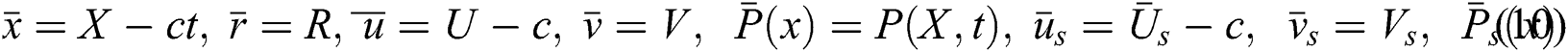
Also, the following non-dimensional quantities are introduced:
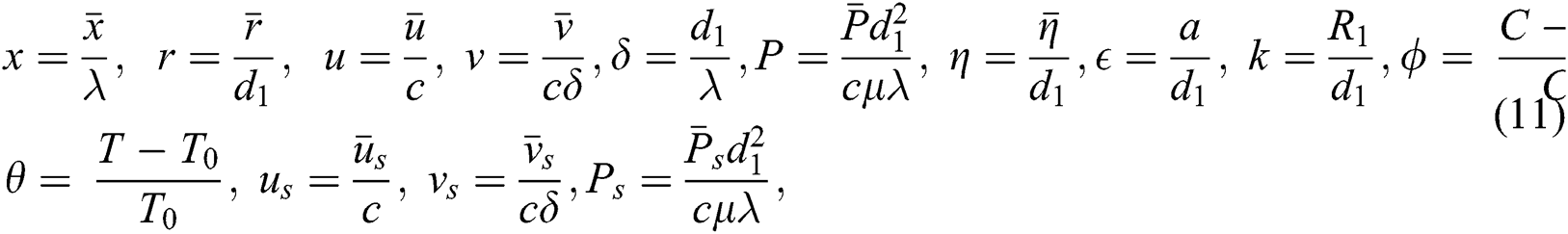
In Eq. (11), the subscript 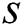 refers to the dusty phase and
refers to the dusty phase and 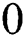 refers to the conditions at the channels walls. Moreover, definitions the stream function for the nanofluid phase
refers to the conditions at the channels walls. Moreover, definitions the stream function for the nanofluid phase 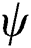 and the dusty particles phase
and the dusty particles phase 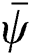 are expressed as:
are expressed as:
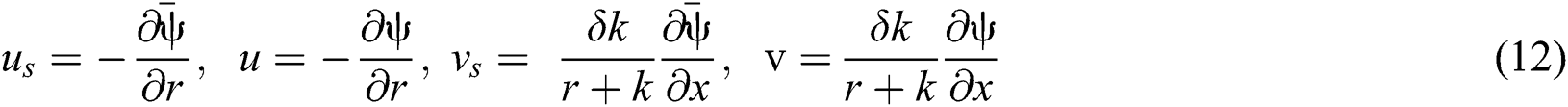
Substituting Eqs. (10)–(12) in the systems of Eqs. (1)–(5) and (6)–(9) and applying the approximations of the low Reynolds number and long of the wave length, the governing equations become:

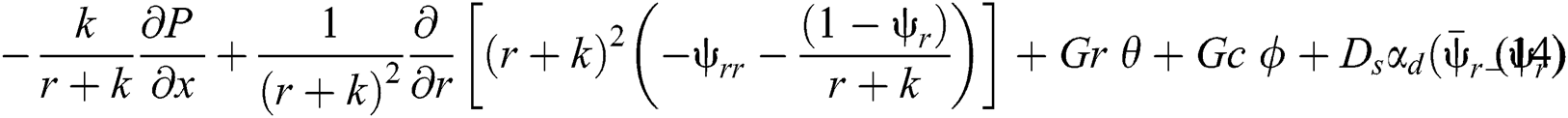
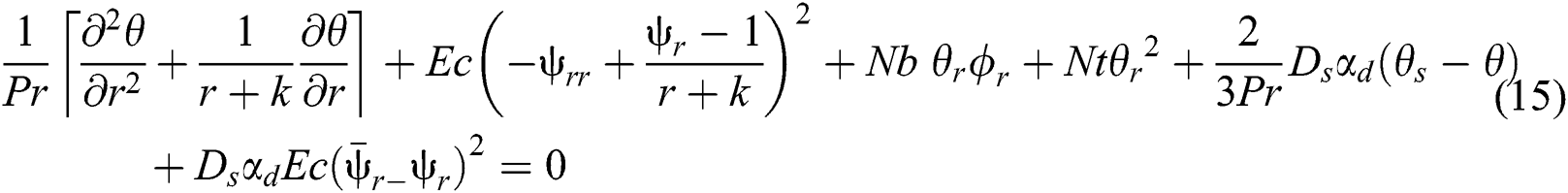
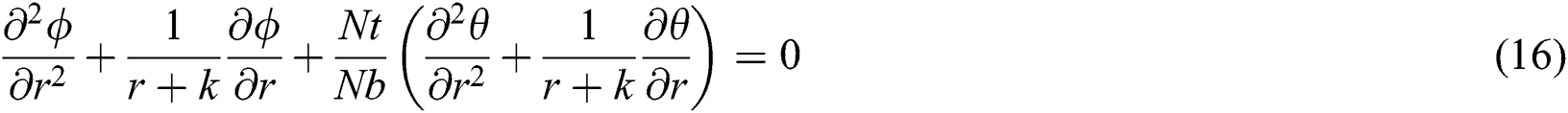



where
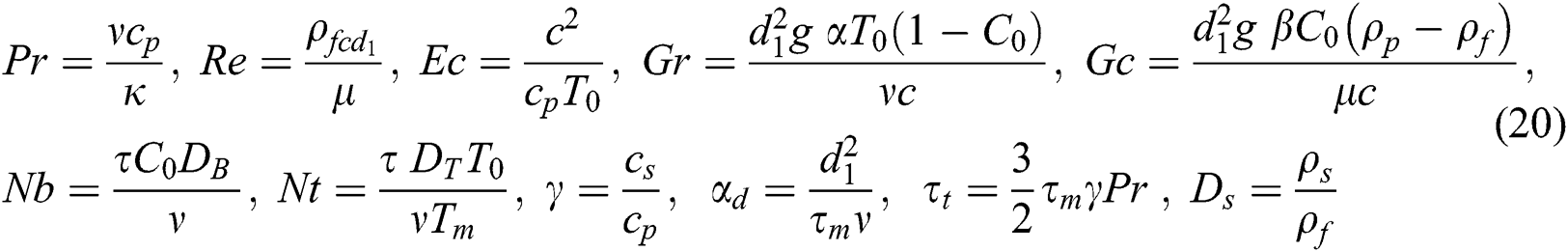
In Eq. (20), 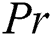 is the Prandtl number,
is the Prandtl number, 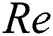 is the Reynolds number,
is the Reynolds number, 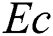 is the Ekert number,
is the Ekert number, 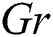 is the thermal buoyancy parameter,
is the thermal buoyancy parameter, 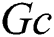 is the concentration buoyancy parameter,
is the concentration buoyancy parameter, 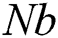 is the dimensionless Brownian motion,
is the dimensionless Brownian motion, 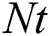 is the dimensionless thermophores parameter,
is the dimensionless thermophores parameter, 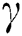 is the specific heat ratio of the mixture,
is the specific heat ratio of the mixture, 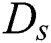 is the mass concentration of particle phase and
is the mass concentration of particle phase and 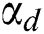 is the dust parameter.
is the dust parameter.
Eqs. (13), (14), (17) and (18) after eliminating the pressure terms are written as:
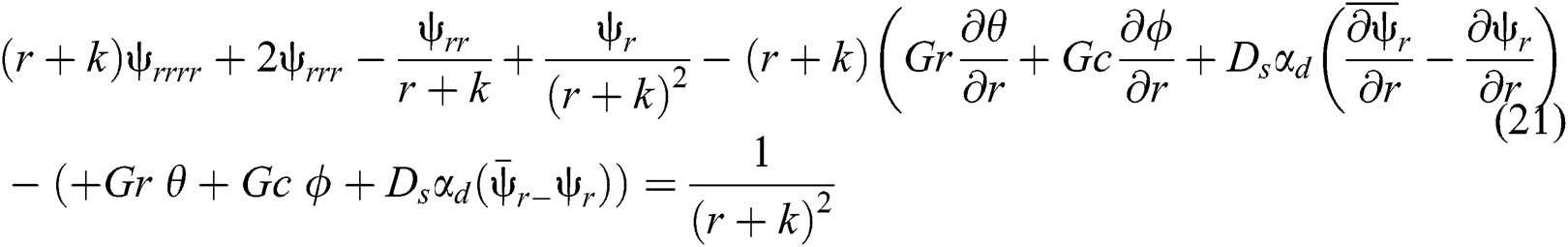

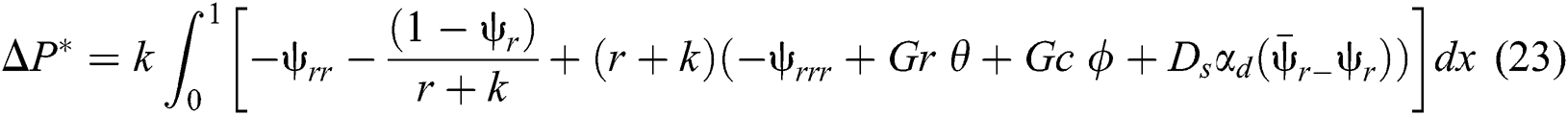
The corresponding boundary conditions are given by:
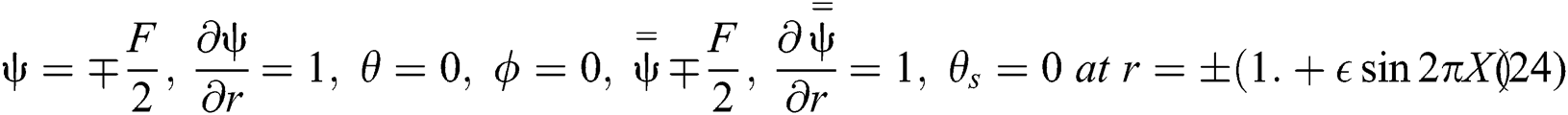
On the other hand, rate of the volume flows in the laboratory frame and in the wave frame are, respectively, given by:


The dimensionless mean flows in the laboratory  and in the wave frame
and in the wave frame  are defined as:
are defined as:

where  is the time averaged flow over a period
is the time averaged flow over a period  and it is given by:
and it is given by:

From the previous equations, the following relations are obtained:


To solve the governing Eqs. (15), (16), (19), (21) and (22), it is needed to map the wavy boundaries into a rectangular computational domain. Therefore, the following new independent variables are introduced:

The partial derivatives for the dependent variables are obtained as follows:

Where 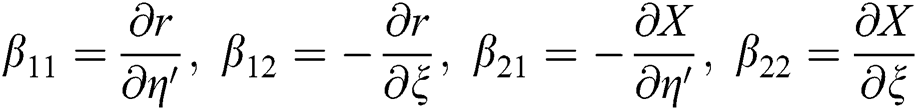 and
and 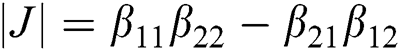
Using Eqs. (31), (32), the computational domain is transformed to 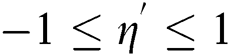 which makes the applying of the numerical method is available. Here the Runge-Kutta method with shooting technique is used to solve the resulting system of the equations. The number of the grid points are taken to be equal 401 and the convergence criteria is
which makes the applying of the numerical method is available. Here the Runge-Kutta method with shooting technique is used to solve the resulting system of the equations. The number of the grid points are taken to be equal 401 and the convergence criteria is 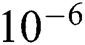 . In addition, a validation test consisting of comparisons with previously published results is performed and presented in Fig. 2. It is found very good agreements are observed between the presented study (in special cases) and those obtained by Hina et al. [14].
. In addition, a validation test consisting of comparisons with previously published results is performed and presented in Fig. 2. It is found very good agreements are observed between the presented study (in special cases) and those obtained by Hina et al. [14].
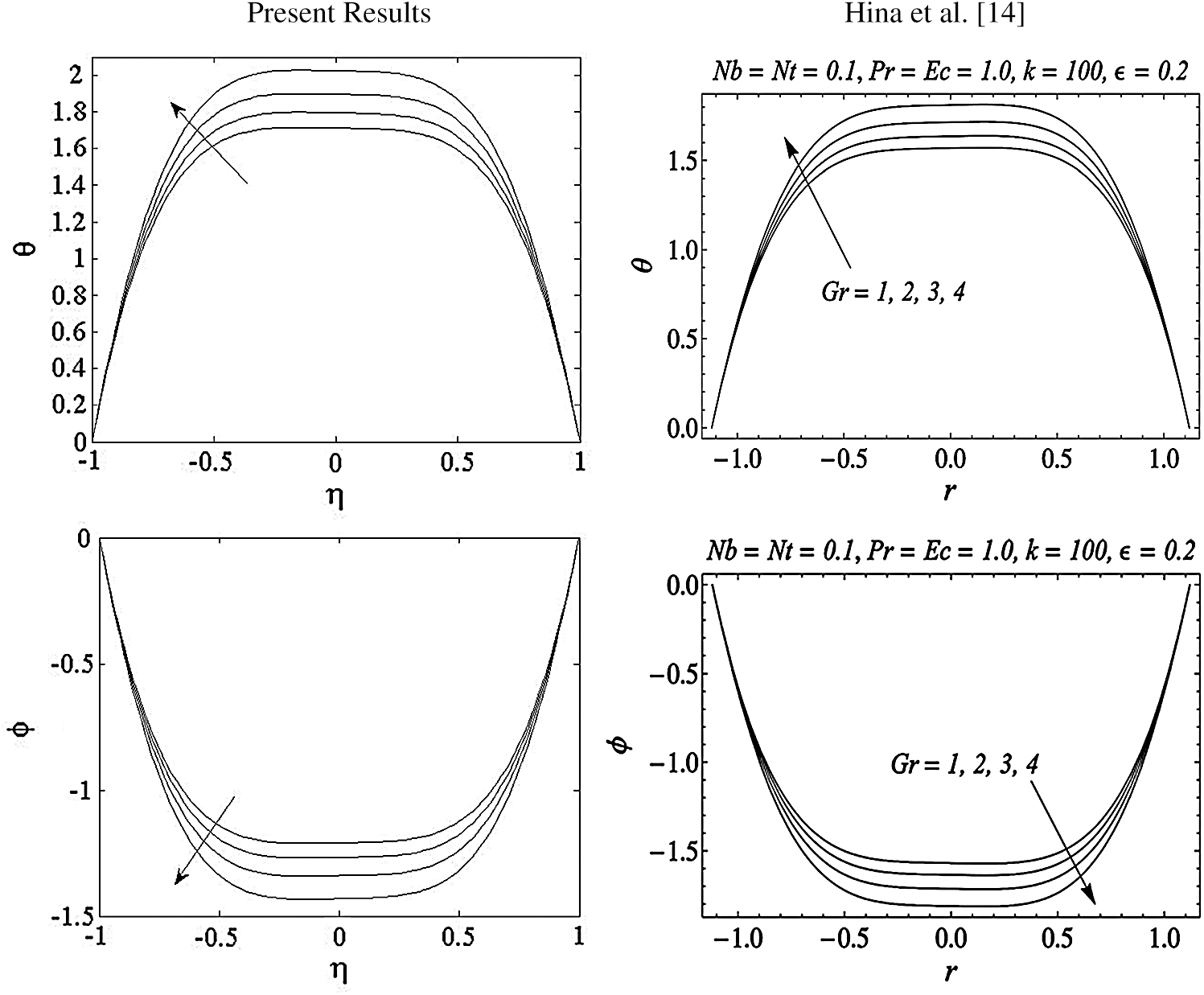
Figure 2: Validation tests at 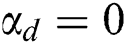 and
and 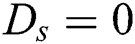
Discussion of the obtained results is notified in this section. A set of graphical results in terms of the velocity profiles for the dusty particles, temperature distributions and nanoparticle volume fraction are presented in Figs. 3–15. During these computations, the governing parameters are considered in wide ranges, i.e., range of the thermal buoyancy parameter 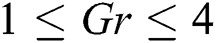 , range of the concentration buoyancy parameter
, range of the concentration buoyancy parameter 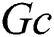 is
is 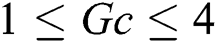 , range of amplitude ratio
, range of amplitude ratio 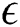 is
is 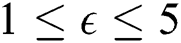 , range the Eckert number is
, range the Eckert number is 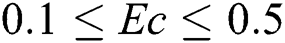 , range of the thermophoresis parameter
, range of the thermophoresis parameter 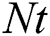 is
is 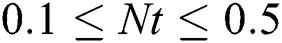 and the Brownian motion parameter
and the Brownian motion parameter 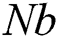 is varying from 0.1 to 0.5. Here it should be mentioned that from Eq. (19), the profiles of the temperature of the dusty particles are the same of nanofluid temperature. Also, values of the mass concentration of the dusty particles
is varying from 0.1 to 0.5. Here it should be mentioned that from Eq. (19), the profiles of the temperature of the dusty particles are the same of nanofluid temperature. Also, values of the mass concentration of the dusty particles 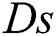 and the dusty parameters
and the dusty parameters 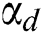 are assumed 0.1 and 10, respectively.
are assumed 0.1 and 10, respectively.
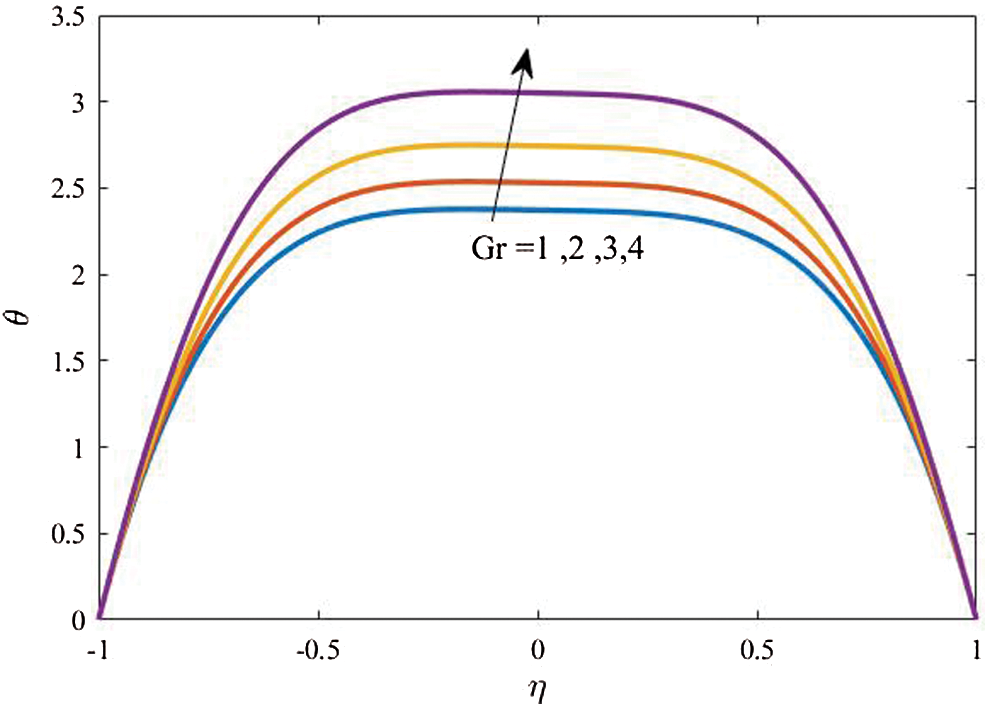
Figure 3: Profiles of the fluid temperature for variations of 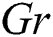 at
at 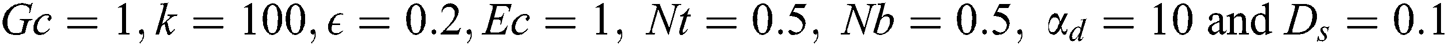
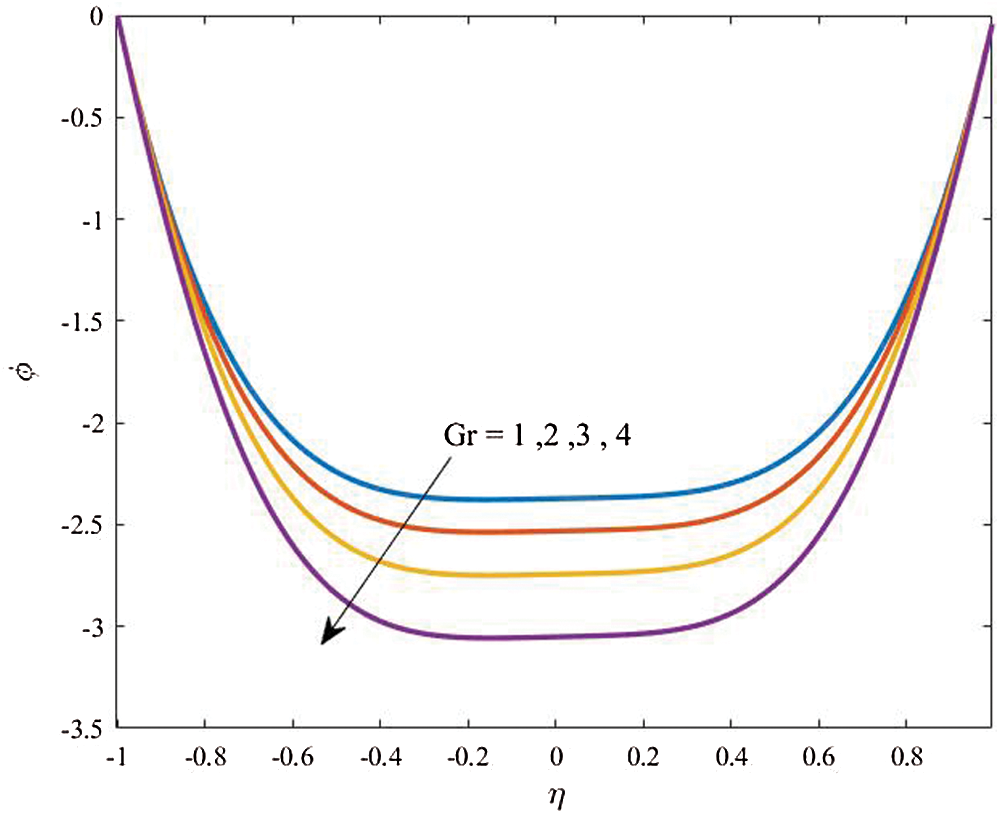
Figure 4: Profiles of the nanoparticles volume fraction for variations of 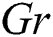 at
at 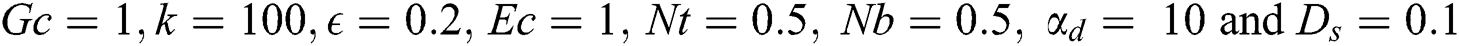
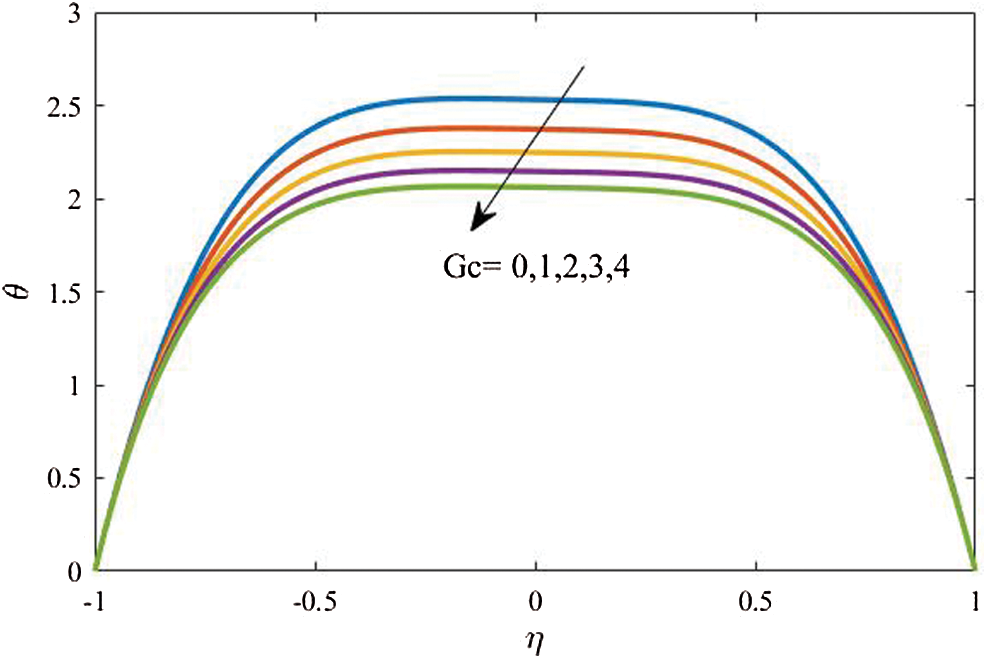
Figure 5: Profiles of the fluid temperature for variations of  at
at 
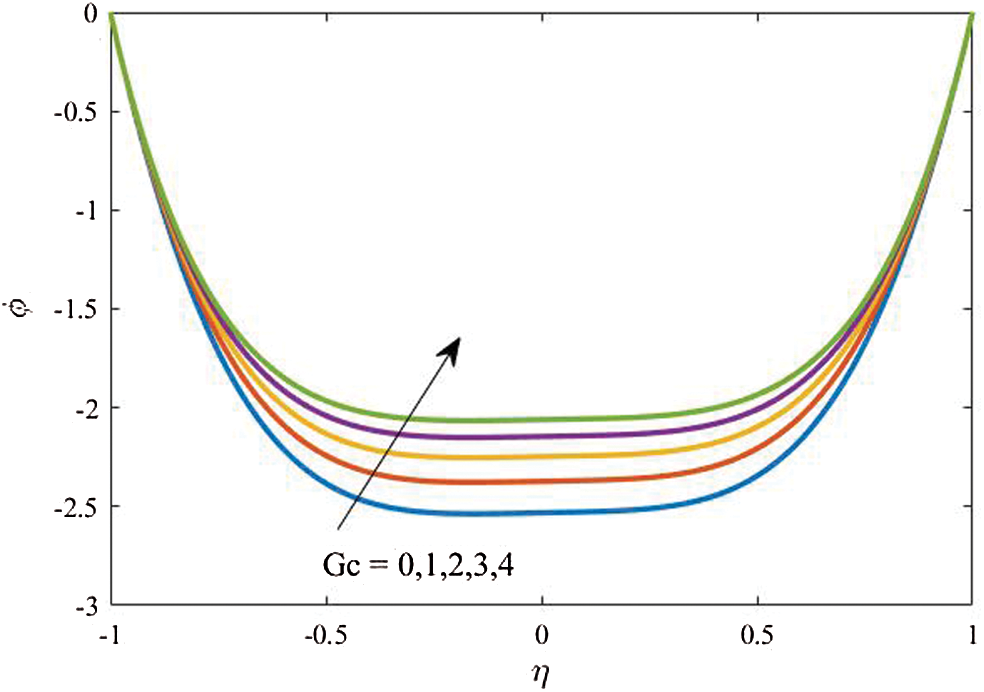
Figure 6: Profiles of the fluid temperature for variations of 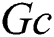 at
at 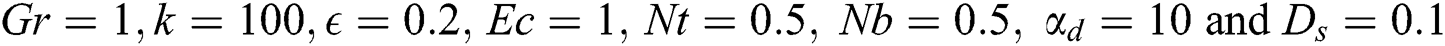
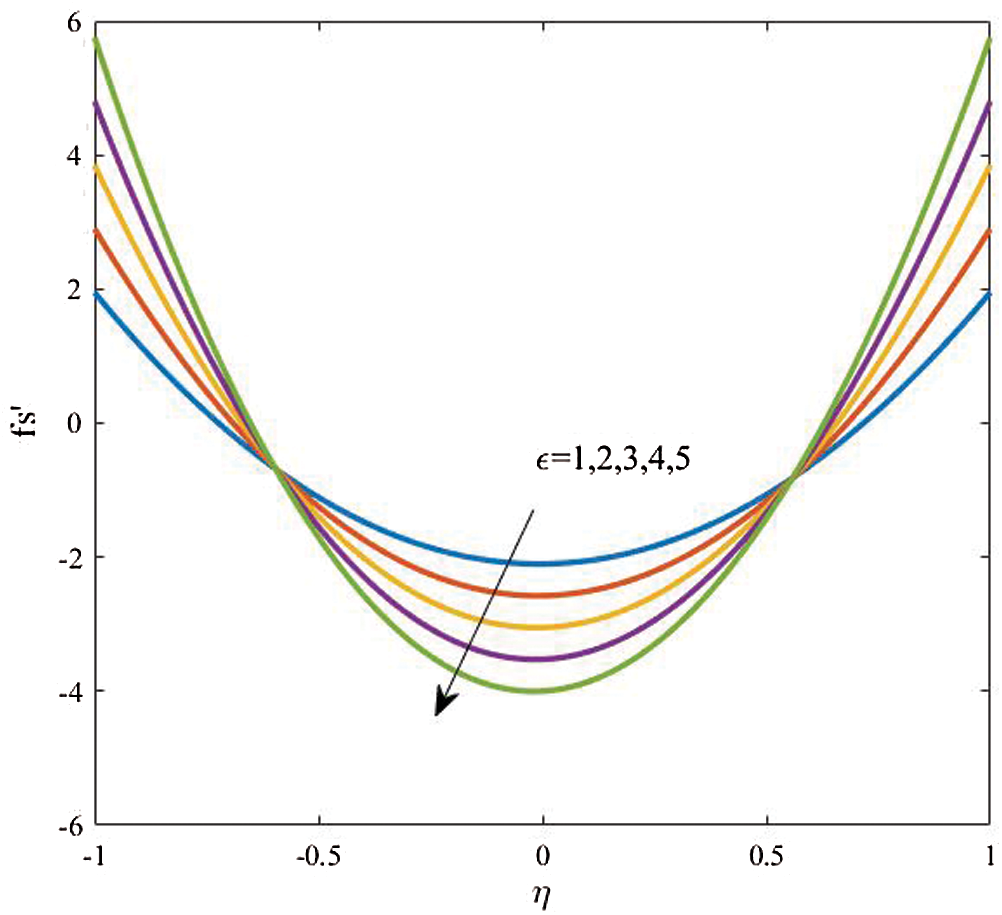
Figure 7: Dusty velocity for different values of 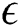 at
at 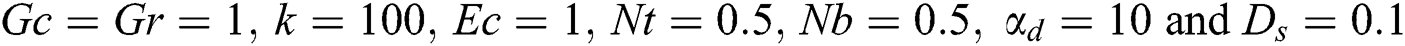
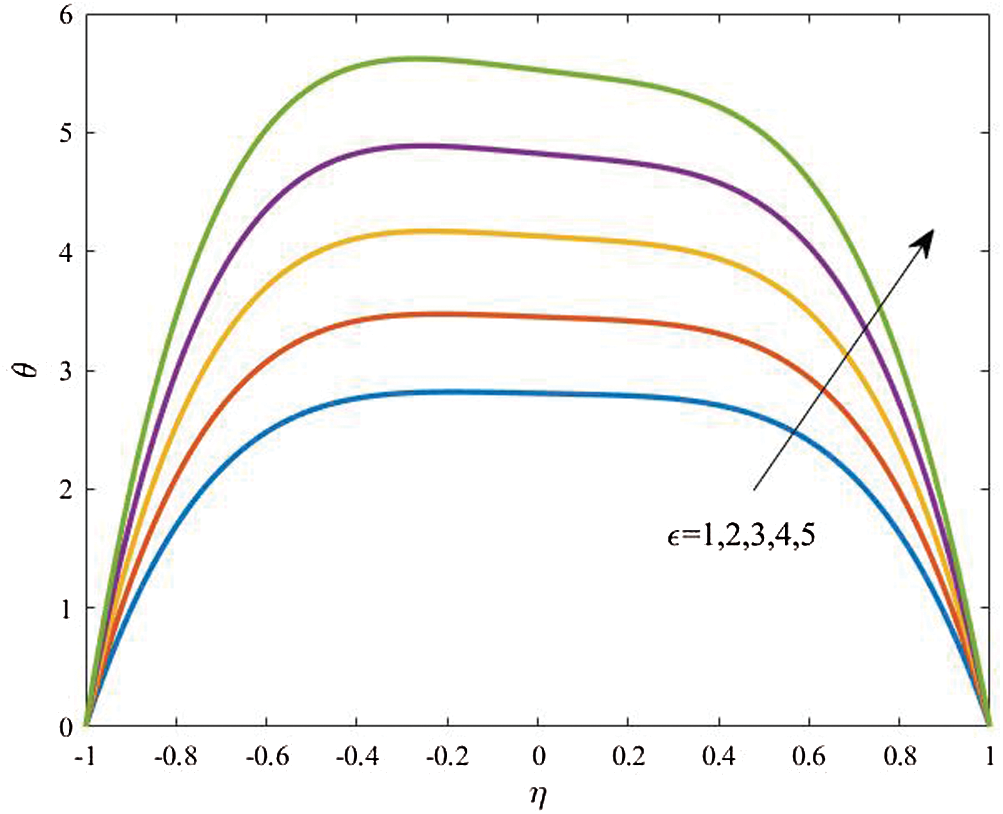
Figure 8: Profiles of the temperature for variations of 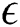 at
at 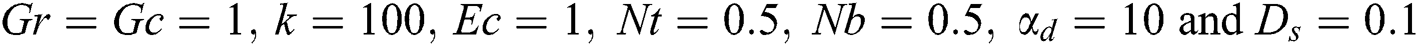
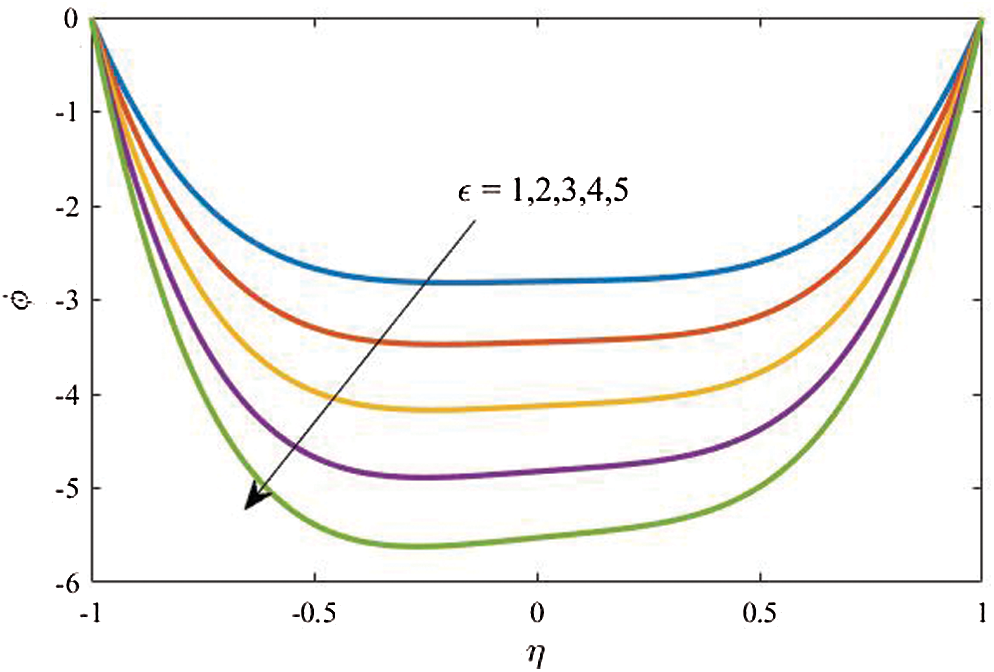
Figure 9: Profiles of the nanoparticles volume fraction for variations of  at
at 
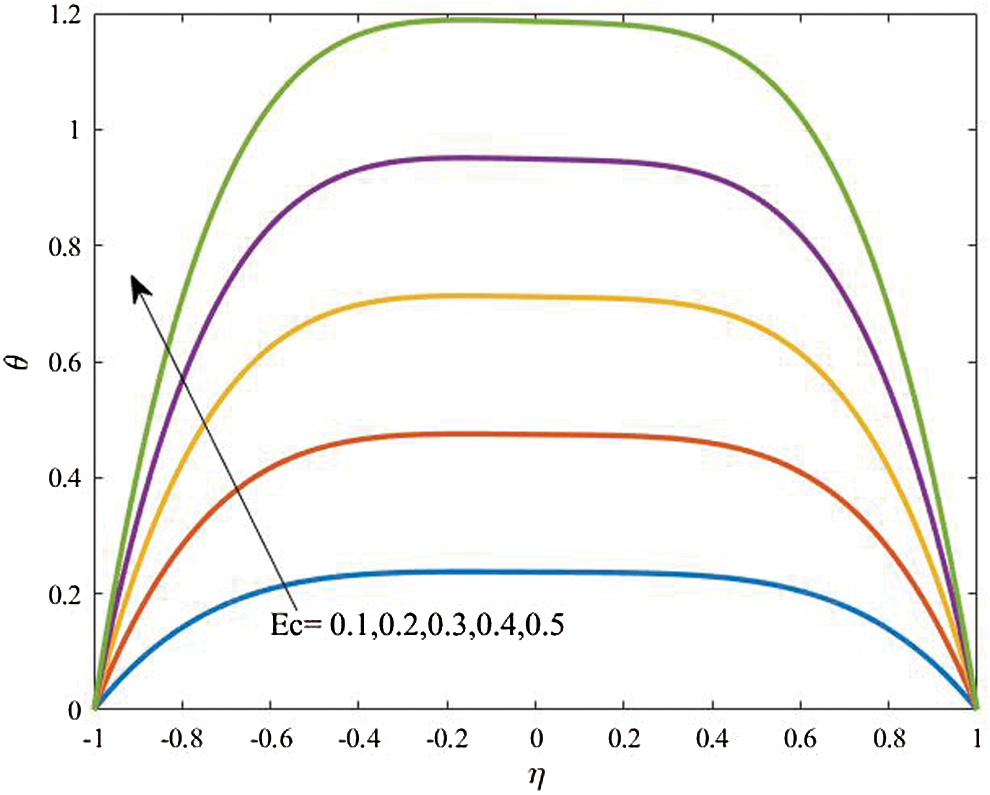
Figure 10: Profiles of the temperature for variations of 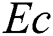 at
at
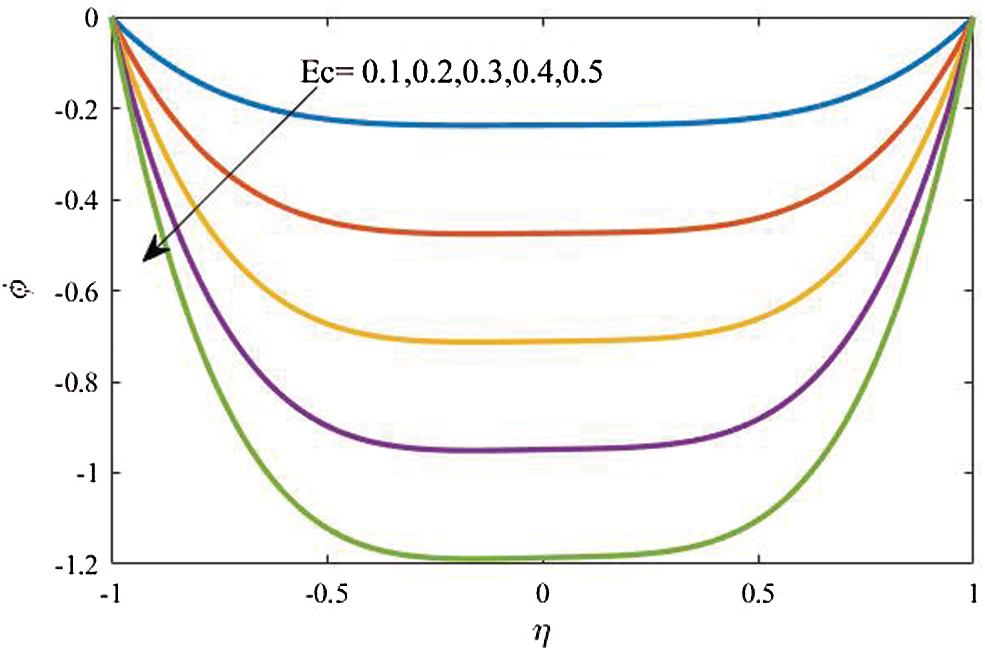
Figure 11: Profiles of the nanoparticles volume fraction for variations of Ec at 
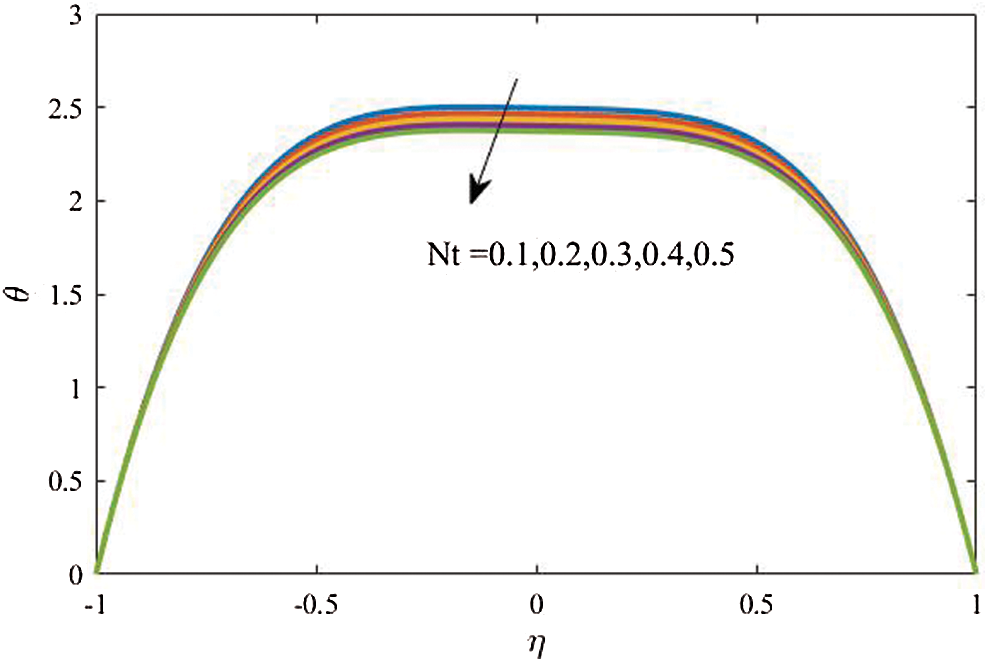
Figure 12: Profiles of the temperature for variations of  at
at
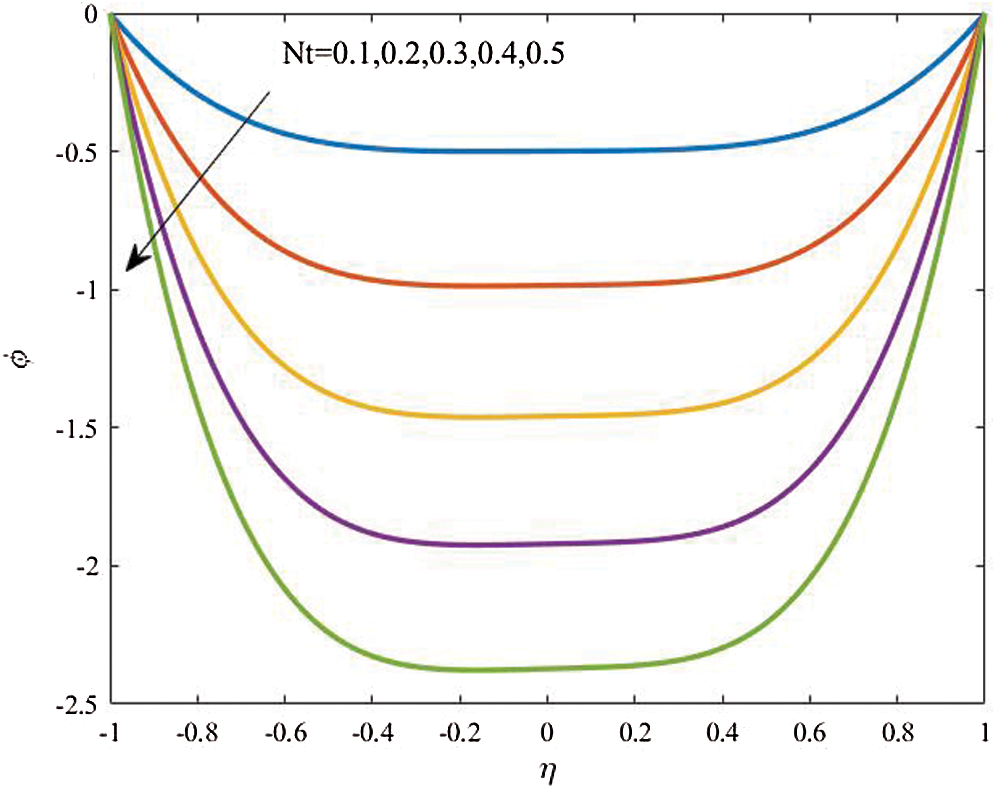
Figure 13: Profiles of the nanoparticles volume fraction for variations of 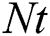 at
at 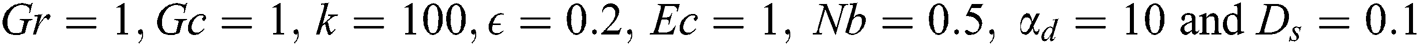
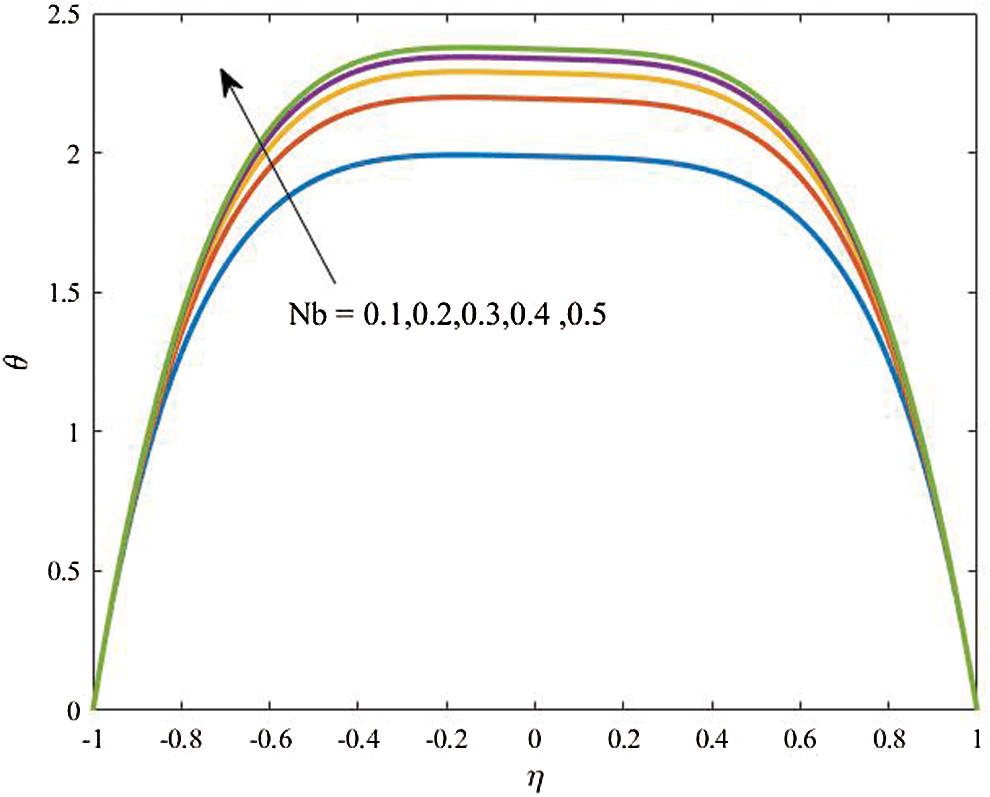
Figure 14: Profiles of the temperature for variations of 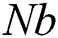 at
at 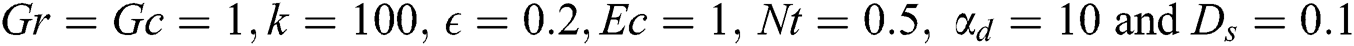
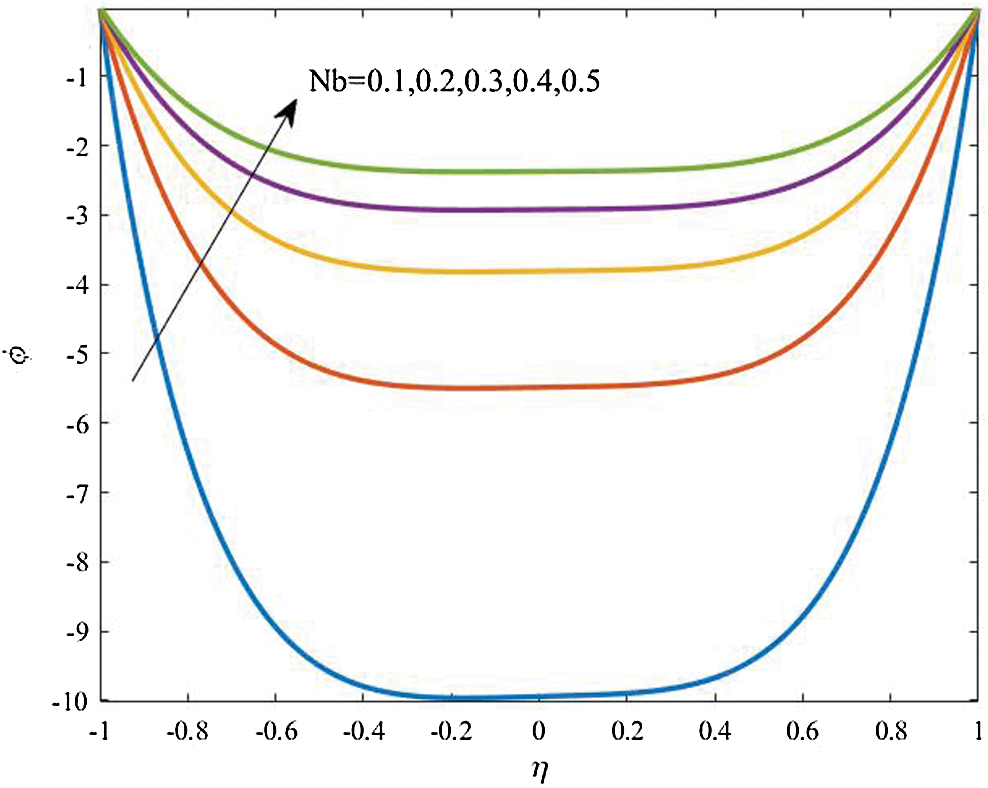
Figure 15: Profiles of the nanoparticles volume fraction for variations of 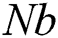 at
at 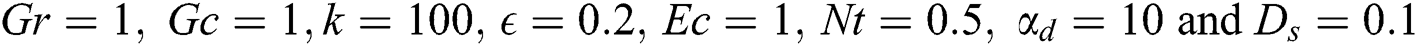
Figs. 3 and 4 display profiles of the temperature distributions for both fluid and dusty particles and nanoparticles volume fraction for different values of the thermal buoyancy parameters 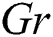 at
at 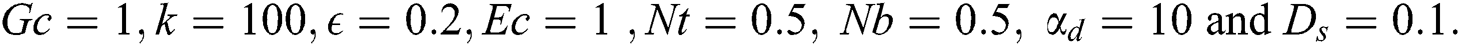 It is found that, in the curvature domain, the temperature distributions are enhanced as the thermal buoyancy parameter increases. The interpretation of this behavior, physically, related to the temperature differences inside the flow domain that is enhanced as
It is found that, in the curvature domain, the temperature distributions are enhanced as the thermal buoyancy parameter increases. The interpretation of this behavior, physically, related to the temperature differences inside the flow domain that is enhanced as 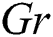 increases and hence the fluid and dusty particles temperature are supported. In addition, it is noted that profiles of the nanoparticles volume fraction are reduced as
increases and hence the fluid and dusty particles temperature are supported. In addition, it is noted that profiles of the nanoparticles volume fraction are reduced as 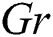 is growing due to the fact that the increase in the temperature differences diminishes the concentration distributions.
is growing due to the fact that the increase in the temperature differences diminishes the concentration distributions.
In Figs. 5 and 6, variations of the concentration buoyancy parameter 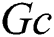 and their effects on the dusty particles and fluid temperature and nanoparticles volume fraction are presented. The other parameters are fixed at
and their effects on the dusty particles and fluid temperature and nanoparticles volume fraction are presented. The other parameters are fixed at 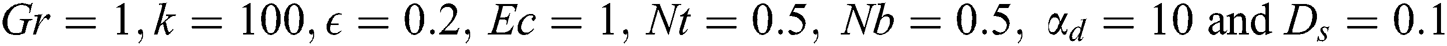 . The results revealed that the increase in
. The results revealed that the increase in 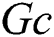 causes a clear reduction in the temperature distributions. The physical explanation of this behavior is due to the buoyancy forces due to the concentration differences that minimize profiles of the temperature. However, an obvious enhancement in the nanoparticles volume fraction is seen as
causes a clear reduction in the temperature distributions. The physical explanation of this behavior is due to the buoyancy forces due to the concentration differences that minimize profiles of the temperature. However, an obvious enhancement in the nanoparticles volume fraction is seen as 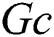 increases due to the support in concentration differences in the curvature domain.
increases due to the support in concentration differences in the curvature domain.
Profiles of velocity of the dusty particles, the fluid and dusty particles temperature and the nanoparticles volume fraction for different values of the amplitude ratio 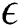 at
at 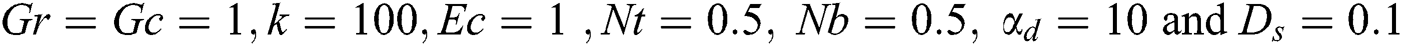 are shown in Figs. 7, 8 and 9, respectively. It is observed that an obvious reduction in the velocity profiles is seen as
are shown in Figs. 7, 8 and 9, respectively. It is observed that an obvious reduction in the velocity profiles is seen as 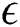 is increased due to an increase in area of the channel. Also, based on the fact that the decrease in the fluid velocity enhances the fluid temperature, the fluid temperature is supported as
is increased due to an increase in area of the channel. Also, based on the fact that the decrease in the fluid velocity enhances the fluid temperature, the fluid temperature is supported as 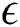 increases. Additionally, the nanoparticles volume fraction distributions are wasted as the amplitude ratio increases due to the increase in the temperature difference inside the flow domain.
increases. Additionally, the nanoparticles volume fraction distributions are wasted as the amplitude ratio increases due to the increase in the temperature difference inside the flow domain.
Effects of the viscous dissipation represented by variation of the Eckert number 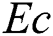 on the temperature distributions and nanoparticles volume fraction are examined with help of Figs. 10 and 11. These figures are plotted at
on the temperature distributions and nanoparticles volume fraction are examined with help of Figs. 10 and 11. These figures are plotted at 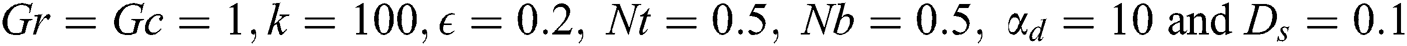 . As it expected, a clear enhancement in profiles of the temperature is obtained as
. As it expected, a clear enhancement in profiles of the temperature is obtained as 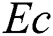 increases. Physically, the fluid is heated up as
increases. Physically, the fluid is heated up as 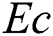 increases due to the kinetic energy in the flow area. On the other hand, the temperature differences are increased and hence the nanoparticles volume fraction is detracted as
increases due to the kinetic energy in the flow area. On the other hand, the temperature differences are increased and hence the nanoparticles volume fraction is detracted as 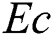 is growing.
is growing.
Figs. 12 and 13 analyzed effects of the thermophoresis parameter 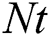 on the temperature distributions and nanoparticles volume fraction at
on the temperature distributions and nanoparticles volume fraction at 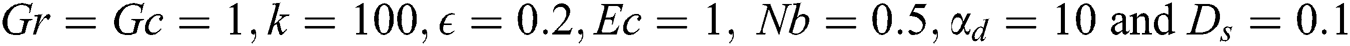 The results show that effects of
The results show that effects of 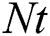 on the temperature are clearer than the nanoparticles volume fraction. In addition, both the temperature and concentration profiles are reduced as
on the temperature are clearer than the nanoparticles volume fraction. In addition, both the temperature and concentration profiles are reduced as 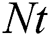 increases. In fact, this outcome agrees with the previous study reported by Hina et al. [14].
increases. In fact, this outcome agrees with the previous study reported by Hina et al. [14].
Effects of the Brownian motion parameter 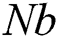 on the temperature distributions and profiles of the nanoparticles volume fraction are displayed in Figs. 14 and 15. It is found that the increase in
on the temperature distributions and profiles of the nanoparticles volume fraction are displayed in Figs. 14 and 15. It is found that the increase in 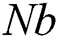 results in an increase in both of the temperature and nanoparticles volume fraction. Also, the results revealed that the concentration distribution is higher at the walls in comparison with the central part of the curved channel. All these effects are examined the a referenced case
results in an increase in both of the temperature and nanoparticles volume fraction. Also, the results revealed that the concentration distribution is higher at the walls in comparison with the central part of the curved channel. All these effects are examined the a referenced case 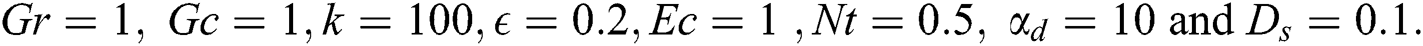
In this investigation, a peristaltic flow of a dusty nanofluid in a curved channel was, numerical studied. Approximations of the low Reynolds number and the long wave length are considered. Two systems of the equations are presented for the nanofluid phase and the dusty particles phase. A mathematical form for the pressure distributions is introduced and validation tests with previously published results are performed. The following findings can be summarized:
•Values of the dusty temperature are equal values of the nanofluid temperature regardless variations of the governing parameter.
•An increase in the thermal buoyancy parameter causes an enhancement in the temperature distributions while a clear reduction in profiles of the nanoparticles volume fraction is noted.
•The nanoparticles volume fractions are supported by the increase in the concentration buoyancy parameter but the both the nanofluid and the dusty particles are decreased.
•The viscous dissipation helps in the increase of temperature of the nanofluid and the dusty particles while it decreases the nanoparticles volume fraction.
•Velocity of the dusty particles is reduced as the amplitude ratio increases (particularly at the mid-section of the channel.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant Number (R.G.P2/72/41).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. T. Latham. (1966). “Fluid motions in a peristaltic pump,” M.S. Thesis, MIT, Cambridge, MA.
2. J. Misra and S. Pandey. (2006). “Peristaltic transport of physiological fluids,” in Biomathematics, J. C. Misra, London, USA, Singapore: Modelling and Simulation, World Scientific, pp. 167–193.
3. H. Sato, T. Kawai, T. Fujita and M. Okabe. (2000). “Two dimensional peristaltic flow in curved channels,” Transactions of the Japan Society of Mechanical Engineers Series B, vol. 66, no. 99, pp. 679–685.
4. N. Ali, M. Sajid and T. Hayat. (2010). “Long wavelength flow analysis on curved channel,” Zeitschrift Für Naturforschung, vol. 65, no. 3, pp. 191–196.
5. N. Ali, M. Sajid, T. Javed and Z. Abbas. (2010). “Heat transfer analysis of peristaltic flow in a curved channel,” International Journal of Heat and Mass Transfer, vol. 53, no. 15–16, pp. 3319–3325.
6. N. Ali, M. Sajid, Z. Abbas and T. Javed. (2010). “Non-Newtonian fluid flow induced by peristaltic waves in a curved channel,” European Journal of Mechanics-B/Fluids, vol. 29, no. 5, pp. 387–594.
7. T. Hayat, M. Javed and A. Hendi. (2011). “Peristaltic transport of viscous fluid in a curved channel with compliant walls,” International Journal of Heat and Mass Transfer, vol. 54, no. 7–8, pp. 1615–1621.
8. T. Hayat, S. Hina, A. Hendi and S. Asghar. (2011). “Effect of wall properties on the peristaltic flow of a third grade fluid in a curved channel with heat and mass transfer,” International Journal of Heat and Mass Transfer, vol. 54, no. 23–24, pp. 5126–5136.
9. S. Hina, T. Hayat and S. Asghar. (2012). “Peristaltic transport of Johnson-Segalman fluid in a curved channel with wall compliant properties,” Nonlinear Analysis: Modelling and Control, vol. 17, no. 3, pp. 297–311.
10. S. Hina, T. Hayat and A. Alsaedi. (2012). “Heat and mass transfer effects on the peristaltic flow of Johnson-Segalman fluid in a curved channel with compliant walls,” International Journal of Heat and Mass Transfer, vol. 55, no. 13–14, pp. 3511–3521.
11. S. Hina, M. Mustafa, T. Hayat and A. Alsaedi. (2013). “Peristaltic flow of pseudoplastic fluid in a curved channel with wall properties,” Journal of Applied Mechanics, vol. 80, no. 2, pp. 275.
12. S. Choi. (1995). “Enhancing thermal conductivity of fluids with nanoparticles,” in Developments and Applications of Non-Newtonian Flows, D. A. Singer, H. P. Wang, New York: American Society of Mechanical Engineers, pp. 99–105.
13. J. Buongiorno. (2006). “Convective transport in nanofluids,” ASME Journal of Heat Transfer, vol. 128, no. 3, pp. 240–250.
14. S. Hina, M. Mustafa, S. Abbasbandy, T. Hayat and A. Alsaedi. (2014). “Peristaltic motion of nanofluid in a curved channel,” Journal of Heat Transfer-ASME, vol. 136, no. 5, pp. 052001.
15. S. Ayub, T. Hayat, S. Asghar and B. Ahmad. (2017). “Thermal radiation impact in mixed convective peristaltic flow of third grade nanofluid,” Results in Physics, vol. 7, pp. 3687–3695.
16. V. Narla, K. Prasad and J. Ramanamurthy. (2015). “Peristaltic transport of Jeffrey nanofluid in curved channels,” Procedia Engineering, vol. 127, pp. 869–876.
17. S. Noreen, M. Qasim and Z. Khan. (2015). “MHD pressure driven flow of nanofluid incurved channel,” Journal of Magnetism and Magnetic Materials, vol. 393, pp. 490–497.
18. T. Hayat, S. Farooq and A. Alsaedi. (2017). “Mixed convection peristaltic motion of copper-water nanomaterial with velocity slip effects in a curved channel,” Computer Methods and Programs in Biomedicine, vol. 142, pp. 117–128.
19. T. Hayat, N. Aslam, A. Alsaedi and M. Rafiq. (2017). “Numerical study for MHD peristaltic transport of Sisko nanofluid in a curved channel,” International Journal of Heat and Mass Transfer, vol. 109, pp. 1281–1288.
20. A. Tanveer, T. Hayat, A. Alsaed and B. Ahmad. (2017). “Mixed convective peristaltic flow of Sisko fluid in curved channel with homogeneous-heterogeneous reaction effects,” Journal of Molecular Liquids, vol. 233, pp. 131–138.
21. A. Tanveer, T. Hayat, F. Alsaadi and A. Alsaedi. (2017). “Mixed convection peristaltic flow of Eyring-Powell nanofluid in a curved channel with compliant walls,” Computers in Biology and Medicine, vol. 82, pp. 71–79.
22. T. Hayata, A. Tanveera and A. Alsaedi. (2016). “Numerical analysis of partial slip on peristalsis of MHD Jeffery nanofluid in curved channel with porous space,” Journal of Molecular Liquids, vol. 224, pp. 944–953.
23. G. Rudinger. (1980). Fundamentals of Gas-Particle Flow. Amsterdam: Elsevier Scientific Publishing Co.
24. L. Farbar and M. Morley. (1957). “Heat transfer to flowing gas-solid mixtures in a circular tube,” Industrial & Engineering Chemistry, vol. 49, no. 7, pp. 1143–1150.
25. P. Saffman. (1962). “On the stability of laminar flow of a dusty gas,” Journal of Fluid Mechanics, vol. 13, pp. 120–128.
26. M. Turkyilmazoglu. (2017). “Magnetohydrodynamic two-phase dusty fluid flow and heat model over deforming isothermal surfaces,” Physics of Fluids, vol. 29, no. 1, pp. 013302.
27. M. Jalil, S. Asghar and S. Yasmeen. (2017). “An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface,” Mathematical Problems in Engineering, vol. 2017, no. 4, pp. 1–5.
28. B. Gireesha, C. Bagewadi and B. Prasannakumar. (2007). “Study of unsteady dusty fluid flow through rectangular channel in frenet frame field system,” International Journal of Pure and Applied Mathematics, vol. 34, pp. 525–534.
29. B. Gireesha, C. Bagewadi and B. Prasannakumar. (2009). “Pulsatile flow of an unsteady dusty fluid through rectangular channel,” Communications in Nonlinear Science and Numerical Simulation, vol. 14, pp. 2103–2110.
30. P. Manjunatha, B. Gireesha and B. Prasannakumar. (2014). “Thermal analysis of conducting dusty fluid flow in a porous medium over a stretching cylinder in the presence of non-uniform source/sink,” International Journal of Mechanical and Materials Engineering, vol. 24, pp. 1–13.
31. B. Prasannakumar, B. Gireesha and P. Manjunatha. (2015). “Melting phenomenon in MHD stagnation point flow of dusty fluid over a stretching sheet in the presence of thermal radiation and non-uniform heat source/sink,” International Journal of Computational Methods in Engineering Science and Mechanics, vol. 16, pp. 265–274.
32. C. Bagewadi, P. Venkatesh, N. Shashikumar and B. Prasannakumar. (2017). “Boundary layer flow of dusty fluid over a radiating stretching surface embedded in a thermally stratified porous medium in the presence of uniform heat source,” Nonlinear Engineering, vol. 6, pp. 31–41.
33. R. Muthuraj, K. Nirmala and S. Srinivas. (2016). “Influences of chemical reaction and wall properties on MHD peristaltic transport of a dusty fluid with heat and mass transfer,” Alexandria Engineering Journal, vol. 55, pp. 597–611.
34. S. Siddiqa, N. Begum, M. A. Hossain, R. S. R. Gorla and A. Al-Rashed. (2018). “Two-phase natural convection dusty nanofluid flow,” International Journal of Heat and Mass Transfer, vol. 118, pp. 66–74.
35. N. Begum, S. Siddiqa, M. Sulaiman, S. Islam, M. A. Hossain et al. (2017). , “Numerical solutions for gyrotactic bioconvection of dusty nanofluid along a vertical isothermal surface,” International Journal of Heat and Mass Transfer, vol. 113, pp. 229–236.
36. B. Gireesha, B. Mahanthes, G. Thammanna and P. Sampathkumar. (2018). “Hall effects on dusty nanofluid two-phase transient flow past a stretching sheet using KVL model,” Journal of Molecular Liquids, vol. 256, pp. 139–147.
37. B. Gireesha, B. Mahanthesh and K. Krupalakshmi. (2017). “Hall effect on two-phase radiated flow of magneto-dusty-nanoliquid with irregular heat generation/consumption,” Results in Physics, vol. 7, pp. 4340–4348.
38. S. E. Ahmed. (2017). “Modeling natural convection boundary layer flow of micropolar nanofluid over vertical permeable cone with variable wall temperature,” Applied Mathematics and Mechanics-English Edition, vol. 38, no. 8, pp. 1171–1180.
39. S. E. Ahmed. (2020). “Effect of fractional derivatives on natural convection in a complex-wavy–wall surrounded enclosure filled with porous media using nanofluids,” Zeitschrift Für Angewandte Mathematik und Mechanik, vol. 100, e201800323.
40. S. E. Ahmed. (2020). “Non-Darcian natural convection of a nanofluid due to triangular fins within trapezoidal enclosures partially filled with a thermal non-equilibrium porous layer,” Journal of Thermal Analysis and Calorimetry.
41. S. E. Ahmed. (2020). “Natural convection of dusty hybrid nanofluids in diverging-converging cavities including volumetric heat sources,” Journal of Thermal Science and Engineering Applications, vol. 13, no. 1, pp. 011018.
42. S. E. Ahmed. (2020). “FEM-CBS algorithm for convective transport of nanofluids in inclined enclosures filled with anisotropic non-Darcy porous media using LTNEM,” International Journal of Numerical Methods for Heat & Fluid Flow.
43. S. E. Ahmed. (2020). “Caputo fractional convective flow in an inclined wavy vented cavity filled with a porous medium using Al2O3–Cu hybrid nanofluids,” International Communications in Heat and Mass Transfer, vol. 116, pp. 104690.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |