DOI:10.32604/cmc.2020.012464
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012464 | |
| Article |
Optimizing Bidders Selection of Multi-Round Procurement Problem in Software Project Management Using Parallel Max-Min Ant System Algorithm
1Institute of Research and Development, Duy Tan University, Da Nang, 550000, Vietnam
2Faculty of Information Technology, Duy Tan University, Da Nang, 550000, Vietnam
3Faculty of Information Technology, Haiphong University, Haiphong, 180000, Vietnam
4Graduate School, Duy Tan University, Da Nang, 550000, Vietnam
5School of Mathematics, Thapar Institute of Engineering and Technology, Patiala, 147004, India
6Hanoi University of Science and Technology, Hanoi, 100000, Vietnam
7Hanoi University, Hanoi, 100000, Vietnam
8Department of ICT, Ministry of Education and Training, Hanoi, 100000, Vietnam
*Corresponding Author: Dac-Nhuong Le. Email: ledacnhuong@duytan.edu.vn
Received: 3 June 2020; Accepted: 25 July 2020
Abstract: This paper presents a Game-theoretic optimization via Parallel Min-Max Ant System (PMMAS) algorithm is used in practice to determine the Nash equilibrium value to resolve the confusion in choosing appropriate bidders of multi-round procurement problem in software project management. To this end, we introduce an approach that proposes: (i) A Game-theoretic model of multi-round procurement problem (ii) A Nash equilibrium strategy corresponds to multi-round strategy bid (iii) An application of PSO for the determination of global Nash equilibrium. The balance point in Nash Equilibrium can help to maintain a sustainable structure not only in terms of project management but also in terms of future cooperation. As an alternative of procuring entities subjectively, a methodology to support decision making has been studied using Nash equilibrium to create a balance point on benefit in procurement where buyers and suppliers need multiple rounds of bidding. Our goal focus on the balance point in Nash Equilibrium to optimizing bidder selection in multi-round procurement which is the most beneficial for both investors and selected tenderers. Our PMMAS algorithm is implemented based on MPI (message passing interface) to find the approximate optimal solution for the question of how to choose bidders and ensure a path for a win-win relationship of all participants in the procurement process. We also evaluate the speedup ratio and parallel efficiency between our algorithm and other proposed algorithms. As the experiment results, the high feasibility and effectiveness of the PMMAS algorithm are verified.
Keywords: Parallel min-max ant system; multi-objective; multi-round procurement; software project management; project conflicts; Nash equilibrium; game theory; MPI
Project planning consists of refining the project scope, defining tasks and activities to achieve the goals, establishing a sequence of activities to further develop a schedule, cost estimation, and budget. One of the key problems in software project planning is the scheduling, which involves resource allocation and scheduling activities on time, optimizing the cost and/or duration of the project. The scheduling is a complex constrained optimization problem, because for the optimization of resources, time and cost, it is necessary to consider a combination of variables, rules, and restrictions that cause the problem to be NP-hard Search-based software engineering (SBSE) is an emerging area focused on solving software engineering problems by using search-based optimization algorithms. SBSE has been applied to several problems which arise during the software life cycle. The software project scheduling problem (SPSP) consists in finding a suitable assignment of employees to tasks, such that the project can be delivered in the shortest possible time and with the minimum cost [1]. Since these objectives are in conflict, that is, the minimization of one of them leads to the deterioration of the other, the result of the optimization process is a set of solutions which represents the trade-offs between both objectives [2]. Risk and conflict management are a very important in implementing software projects. Since 1990s, many risk managements processes have been proposed, such as: PMBOK (Project Management Body of Knowledge), PRAM (Project Risk Analysis and Management), and RAMP (Risk Analysis and Management for Projects). Many methods do not apply any mathematical theory or model in risk assessment and calculate their quantitative effects. Therefore, we need to have a more scientific approach to managing the risks of software development projects, thereby increasing the success and results of the project. We summarize generalizations of the activity concept, the precedence relations and of the resource constraints. Alternative objectives and approaches for scheduling multiple projects are discussed as well. In addition to popular variants and extensions such as multiple modes, minimal and maximal time lags, and net present value-based objectives, such as: PSP, SBSE, SPSP, RCPSP, RCPSP/max, RCPSP-GPR, RCPSPCF, MRCPSP, MRCPSP/max, RACP, RIP/max, RCMPS, WBS, TSPMP, etc. [1,2] As we can see, the RCPSP can be classified by preemptive scheduling, resource requests varying with time, setup times, multiple modes, tradeoff problems, minimal time lags, maximal time lags, release dates and deadlines, time-switch constraints, etc. The RCPSP is a general problem in scheduling that has a wide variety of applications in manufacturing, production planning, project management, and various other areas. In this study, we aim to identify the key aspects of procurement in the software project management context and their relation to project success.
Multi-round procurement is a process of self-taking advantages of the investor and the bidders. It includes several participants join negotiating, persuading to gain the most benefit while their relationship is still preserved. In the specification, the investor wants to reap high yield while choosing trustful bidders with the minimum prices, make the project cost the least as well as not losing the faith of other providers. On the contrary, purveyors have the first target is to be chosen. Hence, they need to give a suitable requirement and acceptable cost. Their goal is profit obtaining at the end of the project after being selected [3–5]. The problem is if each participant always tries to get the best advantage, it will create an endless loop. The stakeholder will always put effort into constraining contractors to lower their prices. The contractors want to have the contract and keep long-term business will lower their product prices to compete with others. They could probably suffer losses or reduce their product quality to sign the deal at the moment but later increase the next product's cost to erase the loss. Continuously, those trusty and quality suppliers may give up. The remaining will be the cheaper but high risk of product quality decreased. In this case, the project owner has lost all worthy suppliers. Bidders may accept to suffer loss or they can collaborate to push the price higher. Thus, it does not benefit if the investor is too greedy or auction-goers are too competitive [6–8]. The problems facing can be listed as follow:
•Project time: The longer the project takes, the higher the cost raise. We all know that a dollar at the moment will be more valuable than a dollar in the future. As inflation increasing, changes in the exchange rate will lead to decreasing in the value of the original money. As a consequence, the material price will higher or lower after time.
•Material cost: The number of needed materials also affect the profit of both sides.
•Discount rate: This depends on the strategies of the contractors. Will they give a discount or intensify the price?
•Selection: Usually, we tend to choose the cheapest price. The question is how do we ensure it won't be risky. The quality can be low and the bidders who suffer the detriment can raise higher price next time to afford their loss.
Procurement is viewed as a strategic function working to improve the organization's profitability. In recent years, it is shown that there are many challenges and difficulties in procurement, especially in multi-round procurement which is the result of selecting bidders in one round will affect bidder's bidding behavior in another round [3]. The first challenge is the difficulty in choosing the right bidders to maximize profits while making sure project completeness, which is more and more challenging when the procurement process is divided into many stages with several bidders. The material depends on each company and their pricing policies refer to how they can maximize their business earnings (Quality and Cost-based Selection). Therefore, the buyer cannot assure the quality of goods and services afterward [4]. This implies many risks as there is no measure or evidence to prove the chosen bidder is the most proper one. Moreover, a win-win relationship requires the fairest auctioning environment possible, which is ideal when all bidders granted the highest profits. Secondly, dividing the project into many stages affects the project’s total cost that is time-related. Good sustainability strategies are required to cut costs and also develop a closer relationship with bidders, the negotiation process becomes one of reaching on goods or services in a cooperative model. This enables buyers to lower profits as a sustainability strategy by selecting higher value bidders in the early stages of the procurement to get more profits from these bidders in later stages or future. In summary, a scientific and applicable method is necessary to make the last decision of auction [5–8].
Apart from that, the questions for the problem are: (1) When is the best time to open a bid? (2) Who are the most suitable bidders? (3) What are the most suitable quality and the price at each stage? (4) How can we solve this? This problem can be modeled to a perfect informed game. Each member will take part and offer methodologies to locate the most fitting answer for keep up their relationship and lead the most benefit [9]. There is a list of necessary material divided in many packages as the plan of the bidders. The project will occur in a certain time. In that time, several rounds will be held, each time the investor will by one or many packages necessary for the project. The project has many bidders join, including the long-term partners and new collaborators. Each supplier is capable of providing some material based on their ability. They have their own tactics with information about the price, discount after time. Summarized, to calculate the Nash equilibrium point for this real-world problem to archive sustainability strategy, this paper sought to provide more parameters to the game model. That is to say, we could analyze the data from the problems mentioned above, the data is then represented by a model element.
The software project management was being an NP-Hard problem, solution methods are primarily meta-heuristics. We classify and present the state-of-the-art hybrid meta-heuristics for software project management and multi-round procurement problems in Tab. 1. These methods can be categorized based on local search meta-heuristics, evolutionary and population-based, learning meta-heuristics and our proposed algorithms [10–29]. In [6], Rao et al. designed a new approach to find out a winner in a multiple-attribute auction. The new method can help to address a mechanism for decision making in dealing with multiple-attribute and multiple-sourcing procurement. Multiple-sourcing is usually proposed to prevent a variety of procurement risk and uncertainty. Yang et al. [7] developed a model to assist participants in multiple-attribute procurement in inferring their preference based on the difficulty of elicitation. Bichler et al. [8] analyzed the ability to use Bayesian equilibrium to predict human behavior in sealed-bid split-award procurement auctions. The auction type is a multi-object extension in which bidders may require more than one unit. Authors applied Bayes Nash equilibrium in the expanded game to forecast strategies of participants. Then, they experimented with the accuracy of the equilibrium with computerized bidders. The result showed that the complexity of the multi-object does not have much effect on the result of procurement rather than the risk aversion does. In game theory, Nash Equilibrium has been used to analyze the outcome of strategic interaction and also how conflict may be mitigated in competitive environments. A Nash solution is a mixed strategy profile with the property that no single player can obtain a higher value of expected utility by deviating unilaterally from this profile. It means all players obtain more revenue under cooperation, and thereby promoting sustainability. The above questions are already answered by some researchers using the Genetic algorithm and the Nash equilibrium [30–32]. However, when the number of a threshold is changed, the performance of each algorithm is different. Furthermore, there are many meta-heuristic algorithms were proposed, such as GDE3 [11],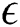
-MOEA [15], 
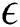-NSGA-II [14], NSGA-III [13], SPEA2 [14], ACO [9], PSO [16], Water drops [17], ACO Parallel (PACO) [18], PSO Parallel (PPSO) [19].
Table 1: Summary of the classification algorithms for the software project management problems
In [20], we proposed a genetic algorithm model to infer the Nash equilibrium model of a multi-round procurement problem in which the buyer not only focuses on the revenue with the first-price bidder strategy but also considers a variety of properties of bidders such as the relationship between buyer and bidder, offer for future promotion, and the business credit score of the bidder. The chromosome in the genetic algorithm represents the Nash equilibrium point that includes all characteristics of the solution for the problem. An iterative genetic algorithm is said to converge when, as the iterations proceed, the fitness value gets closer to specific values, and we discovered a balance point for all sides in procurement. In [21], we introduced a Bayesian critical path method for managing common risks in software project scheduling. We also presented a Nash equilibrium model for conflicts in project management in [22]. In [23,24], we proposed a Unified Game-based model based on the concept of game theory and Nash equilibrium. This scientific model can help the decision-maker to recognize, and define all characteristics of the conflict problems in project management. The model can be solved by a variety of multi-objective evolutionary algorithms. Our previous work introduced some important conflicts in project management and proposed a mathematical model addressing these problems. Experimental results show that the Unified Game-based model is useful to address these problems and effective in generating a near-optimal balance point. In [25], we presented a novel Min-Max Ant System (MMAS) algorithm for multi-round procurement.
3 Multi-round Procurement Problem Formulation
Project management is the core process of most current business activities, which include projects that have the goal of creating products, services, or original results. Project management tasks include project scope management, quality, project schedule, budget, resources, and risks. Still, there are more internal problems affecting the project which is out of the management of risk management parts such as the conflicts between the project partners or the conflicts in risk management itself. Therefore, detecting and analyzing these problems brings a necessary supplement for the project management tasks, thus ensuring all matters arising to be controlled and also enhancing the quality and chances of success of the project [3–5]. Based on various factors such as the source, cause, role, or function of conflicts in the project, conflicts can be classified into several categories as follows:
•By source of conflict, conflicts are classified as (i) conflict from plan scheduling, (ii) conflict from determining the priority in performing project task, (iii) conflict from the power sources, (iv) conflict from technical problems, (v) conflict from administrative procedure, (vi) conflict from the private issue and (vii) conflict from the expenditure.
•By cause of conflict, conflicts are classified as: (i) conflict from different goals, (ii) conflict from resource disparity, (iii) conflict by other people’s obstruction, (iv) conflict due to stress and psychological pressure from many people, (v) conflict due to ambiguity of jurisdiction and (vi) conflict due to misleading communication.
•By role, conflicts are classified as (i) positive conflict and (ii) negative conflict.
•By function, conflicts are classified as (i) functional conflict and (ii) dysfunctional conflict.
Multi-round procurement with many bidders is the process of the project owner, and other bidders join negotiation, persuasion to bring benefits to themselves [20,21]. Bidding is a process whereby an investor chooses a contractor who meets his or her requirements. The buyer organizes the tender so that the seller (the contractor) can compete for each other. Indeed, for large projects, time-stretching is usually divided into smaller categories. The project owner (investor) will not find the contractor for the whole project at a single time but will hold the bid for each item at different times. The purpose is to maximize the benefits to the contractor while minimizing risks during project implementation. The contractor will select the time of bidding and choose the significant level of the tender package. Since the raw material prices fluctuate over time, the contractor must ensure that they have sufficient capacity to implement the tender package. The investor will choose to distribute the parts of the package to the appropriate contractor [22,23,25].
Conflict occurs when both builders and contractors participating in the bidding will try to get the most significant benefit for themselves from the tender package. Specifically, for the contractors, the benefit that they wish to receive from the tender package is to find a reliable investor with the most reasonable price to reduce the cost of the project, minimize the cost of the project but it does not offend their partners. For the investors, the critical goal is to be selected. To achieve that they should provide the most suitable conditions and prices for the offered goods; their last benefit is the profit from the project after winning the bid. The problem is to solve the Multi-round procurement problem, ensure the benefits for both the contractor and the investor, that is, help to resolve conflicts between the contractor and the project owner during the Multi-round procurement engagement based on the available information of the project, the project owner and the contractor. In most cases, any decision to gain profit results in the disagreements of the other. According to Nash equilibrium [26], solving this problem brings the balance result for all contestants. The strategies to reach this point is modeled as a group of tactics:
in which,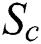 
and 
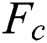are a complete plan of action and benefit function of a first player, project owner, respectively; 
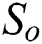and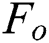 
are a complete plan of action and benefits function of a second player: project bidder;
where,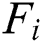 
is quantifying of player's net benefit; 
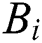is quantifying of a player's net revenue; 
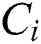is the total of the best possible price for round i (in a period of time 
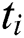) in multi-round procurement; At the beginning of 
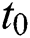, it is necessary to use the discount rate to calculate the decrement of the cash 
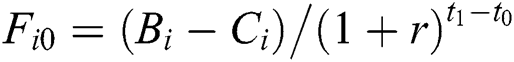, where r is discount rate; 
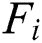is the net benefit from 
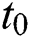to 
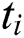. Set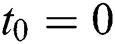 
, we have: 
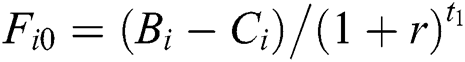. When the project is separated into many stages, the net benefit is calculated by:
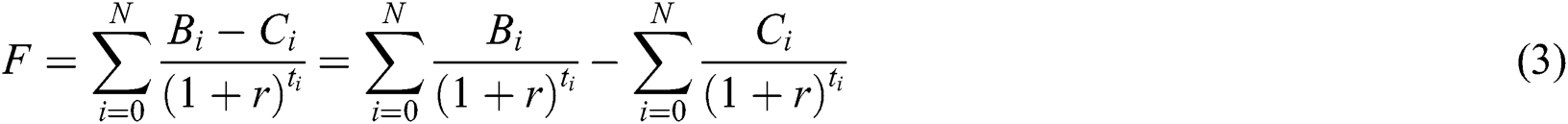
Since 
, the string Taylor of 
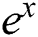will give the approximately number:
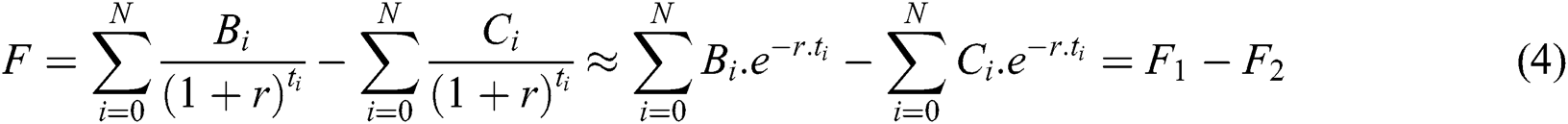
where,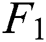 
is the benefit function; 
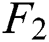is the cost function.
The utility function is calculated as:
3.1 The Benefit of Project Owner
Assume that the estimated cost for the whole project is A; the actual cost is B (usually B<A). The profit of the project owner is: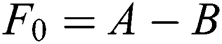 
; B is calculated as 
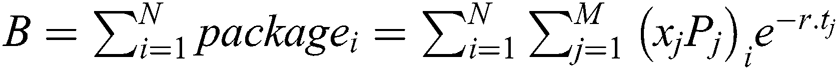where, 
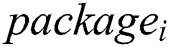is the total cost for package i; 
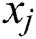is the number of material i at time j; 
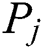is the cost of material i at stage j after deducting the discount; N is the number of package; M is the number of stage.
The profit of the project owner according to first calculation is:
The higher the value of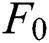 
, the higher the benefit the project owner get.
For each material, based on the sale price, original price, and discount to customers, we have different profit values. The benefit of each bidder follows the formula:
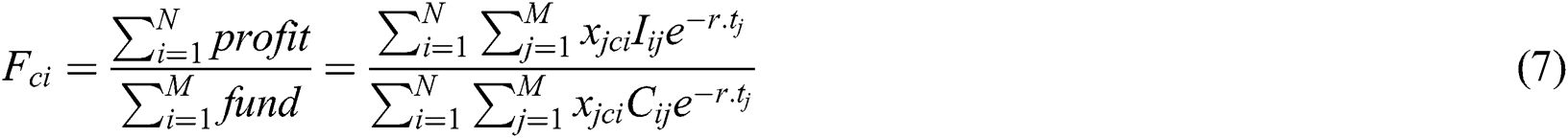
where,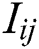 
is the profit and 
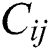is the base price for each unit of item I at the time j;
The profit of each contractor should be big enough to keep the same interest in the project. To balance the benefit, the total subtraction of each providers' profit is taken into account:
in which, h is the number of contractors. The balance is defined when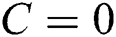 
, then all contractors will have the same profit in return.
The profit gained is calculated by the sum of all profits from the materials for the project.
where, p is the total number of bidders. The higher the value of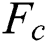 
, the bigger the benefit the bidders get.
4 Parallel MMAS Algorithm with Nash Equilibrium Theory for Multi-Round Procurement
4.1 Nash Equilibrium Theory for Multi-Round Procurement
Game theory is “The study of mathematical models of conflict and cooperation between intelligent rational decision-makers.” It has applications in a variety of fields of social science as well as in computer science [27]. In this research, we present a decision-supporting approach based on game theory. Multi-round procurement as a process relating to many participants requires a balance of harms and benefits of the decision. Using game theory, real-world conflicts for such situations as pricing competition and relationship negotiation can be laid out [28]. We study infinite games of perfect information played by multiple players, all players of a game pick and join to create a blended procedure, which is a combination of beliefs about probabilities over strategies and the choices of the other player. Technically, a Nash equilibrium is a set of mutual strategies that is considered as most beneficial by all parties and no player will defer from it. As mentioned in John Nash's theory, the systems or joined moves are no mystery. The benefit value represents the quality of each player's profile of action in terms of players cooperatively trying to reach an agreement [26].
Nash equilibrium is one of the most important tools to comprehend the contention between various players. For example, in the Prisoner's dilemma, two detainees are scrutinized for the same crime. Provided that player A defects to the police and confesses that player B committed the crime, A gets his sentence removed and B gets full jail time. If both defect from each other, they get equally long prison sentences, and if both parties cooperate and remain silent, they each get reduced jail time. On the off chance that both parties blame each other, which implies a conundrum both will be placed in prison for a long time. Nash equilibrium is a widely utilized model to comprehend the contention between numerous players. For example, the two detainees’ question, if two detainees are scrutinized a similar interest that on the off chance that he concedes the other individual has made the wrongdoing, he can have ten years rebuff by detainment diminished or else both will be placed in prison for a long time. On the off chance that every one of the two blames the other, that implies a conundrum, both will be placed in prison for a long time. On the off chance that one denounces, the other stay silent, the tranquil individual will get longer discipline. The conditions of the problem are shown in Tab. 2.
Table 2: The problem circumstances
By far the best strategy for the prisoners is cooperating to get a short jail term for them both. By contrast, receiving a long jail term is a bad strategy. As it has been pointed out, the problem draws a conflict for each individual in which they do not want to cooperate. It is a choice between competition and cooperation. The agreement to cooperate can guarantees that both wins. By contrast, in a non-cooperative situation, even a more attractive strategy can lead to worse results.
4.2 Parallel MMAS Algorithm Proposed for Multi-Round Procurement
In our approach, we apply the decision-supporting suggested based on game theory. The game comprises of numerous players and moves that players can pick just as the reward for each combination of moves. This ensures that a solution with the probability of success from a variety of strategies will be created [28]. The multi-stage procurement has a lot of cases and possibilities that can happen with extra conditions given by bidders and investors in order to gain satisfying benefits. Hence, constraints are considered as follows: The whole project is divided into many stages, the total time of each round equals the project length, each round lasts at least 1 month. Bidders joined must provide sufficient materials and participate until the end of the project. Moreover, they can join any stage they want within their capability.
The MMAS algorithm is a variant from Ant System (AS) algorithm [29–31]. Each ant k is encoded by a real vector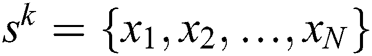 
where 
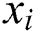is the is number of material i at time j and 
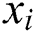is generated as uniformly distributed random number within the interval [0,1] corresponding sets of N different types of material. The ant population are fully random initialized.
The pheromone matrix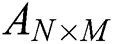 
(N is number of packages; M is number of stage) is generated. Let 
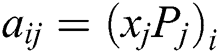is the cost of package i at the stage j. Each ant can choose the direction of movement based on probability defined by 
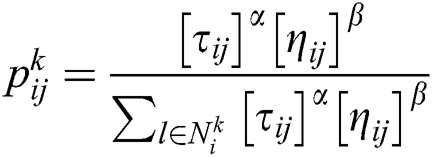. In which, 
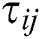is the pheromone on the edge (
,
); 
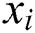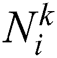is the number of neighboring verticals can visit by the ant k from vertical 
; 
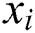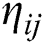is the desirability of the bidder 
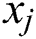, and it depends on optimization goal so it can be the fitness function. The impact of the pheromone awareness of the probability value is presented by
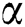, while 
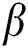does the same for the desirability. Both lower pheromone (
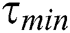) and upper pheromone (
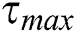) bounds (
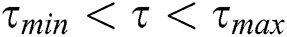) are initialized by 
.
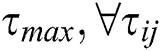Parallel MMAS (PMMAS) evolves from the original MMAS [31–34], and it can be looked as a parallelization implementation of MMAS basing on MPI [35–39]. The pheromone of paths update when all ants complete a search of the graph, rather than any ant finishes one step of searching moving. The algorithm structure of MMAS has potential parallelism. We can be separated into many computing nodes to enhance computational efficiency. Assigning all ants averagely to each computing node is more conducive for parallel implementation and can reduce communication between processors thereby improve the algorithm parallelism better. When we select parallel granularity, the coarse-grained parallel strategy is more effective. We have complete information, including the pheromone matrix, distance matrix, iterative optimal solution, upper limit time, lower limit time, and so on. These sub-ant colonies construct solutions independently under the guidance of local information on their own processor, and different sub-ant colonies from different nodes collaborate through information exchange.
According to the frequency of information exchange, PMMAS algorithm mainly has two kinds of implementation modes on the master node and the slave node (see Fig. 1).
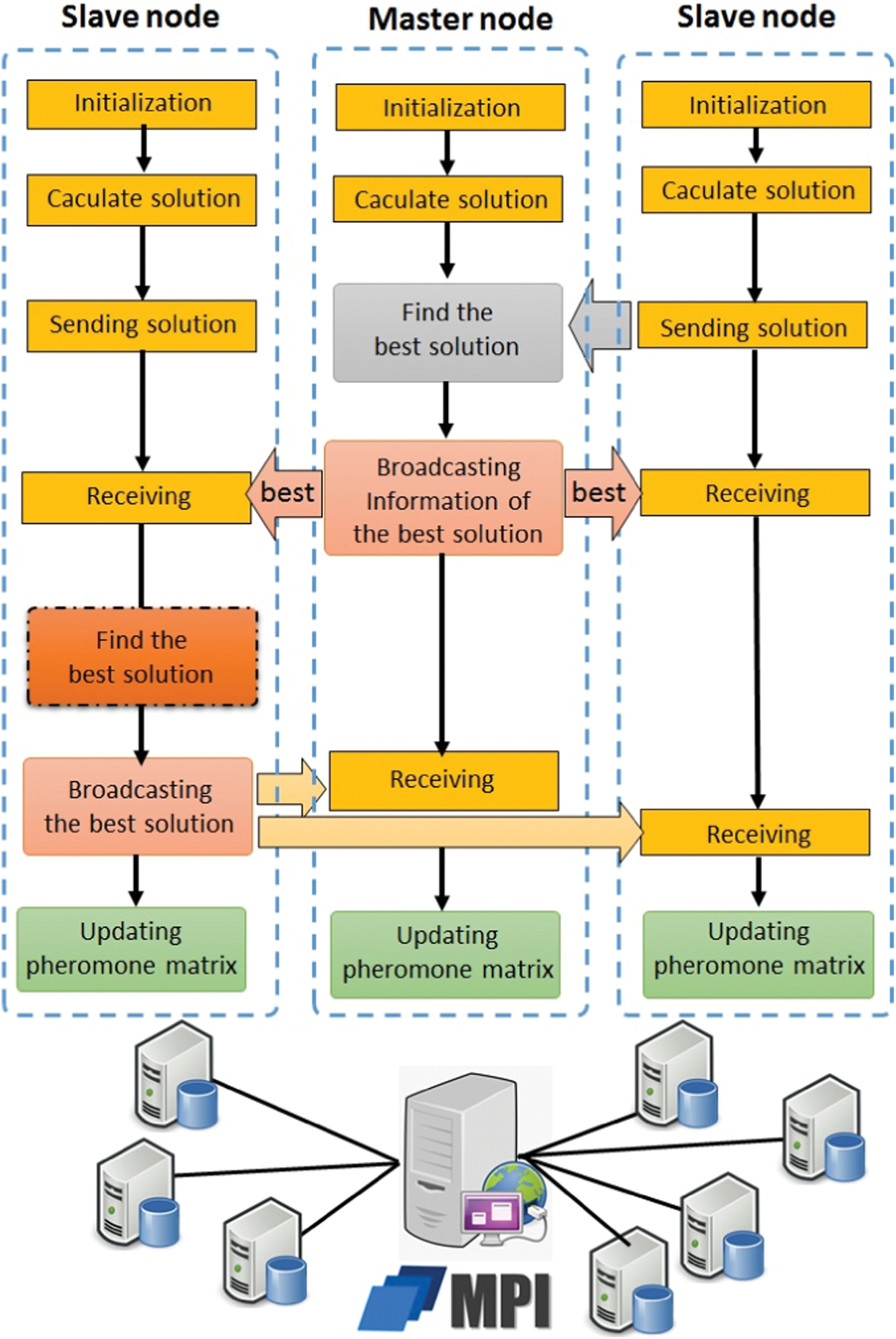
Figure 1: Parallel MMAS algorithm proposed for multi-round procurement
The parallel strategy is to distribute the ant colony to different CPU processes in a relatively average way. Differences in ant numbers among CPU processes cannot be larger than 1. So, each CPU process is allocated with a much smaller ant colony. Several techniques are introduced for the parallel implementation to optimize the parallel process. The detail of our algorithms implemented below:
Algorithm 1: PMMAS implemented in the master node
Algorithm 2: PMMAS implemented in the slave node
5 Experimental Evaluation and Results Analysis
5.1 Datasets and Testing Environment
A decision support system based on PMMAS is developed to define the Nash equilibrium point of the multi-round procurement issue. The system was written in Java and MySQL. In a real-world project, since most of the procurement data is kept secret, a large-scale data set for an evolutionary algorithm such as PMMAS is a big obstacle in the experiment. We found 4 sample data sets for multi-round procurement in big Vietnamese government-funded projects. The experimental result can prove that a Game-theoretic model and PMMAS are suitable in solving a critical and real-world problem in this research.
Dataset structure: Data is organized in a .json file (see the supplementary material files). Dataset 1 (The project “IT application investment project in party agencies of Nghe An province”) starts from 2015-2020. Project funded with development investment from the provincial budget, the investment limit is 39.8 billion. The equipment category has 46 items (H01–H46) with 6 bidders. Dataset 2 (The project “IT application investment project in party agencies of Haiphong city”) start from 2018-2020. Project funded with development investment from the provincial budget, the investment limit is 168 billion. The equipment category has 100 items (H01 – H100) with 15 bidders. Dataset 3 (The project “IT application investment project in party agencies of Hanoi city”) has a total estimated cost of 27,654,400 VND. During the project duration from 1/1/2019 to 21/6/2019, it divided into 6 main packages auctioned in different stages. There are 43 products assessed in the unit. Five contractors joined the project: the information contains their company name, their qualities, their relationship with the investor, the discount rate and its time-line, the price contractors bought the products, and the price they sell them. Dataset 4 (The project “IT application investment project in agencies of Haiphong city (2019-2020)”) is a large-scale project which needs a large number of bidders, resources, items, proposals, and budget. Project has 4787 items in procurement, 45 bidders joining in the auction of 1248 rounds, and each round includes several items in the auction. In total, the problem contains 2584 proposals for 8715 items in packages.
Testing Environment: Our experiments are conducted on a computer configured with CPU Intel Core i5 6200U (Skylake), 2.7GHz, 8GB RAM. The programming language is Java 11, json-simple-1.1.1.jar
In the first experiment, we installed and compared the performance of eleven algorithms, such as GDE3 [11], 
-MOEA [15], SPEA2 [14], NSGA-II [14], NSGA-III [13], ACO [9], PSO [16], PACO [18], PPSO [19], MMAS [25] and our PMMAS algorithm on dataset 1 and 2. We compared two criteria: the payoff value of the solution and the runtime. The payoff of the solution is calculated by summing the goodness at each corresponding weighting goal. Thus, the payoff value is within [0,1], and the closer to 0 the better the solution. After testing the program 100 times, there are 1000 randomly initialized individuals within the population, the maximum number of individuals created for each runtime is 10000. The comparison of the payoff parameter and the runtime on the dataset 1 and 2 are shown in Figs. 2 and 3.
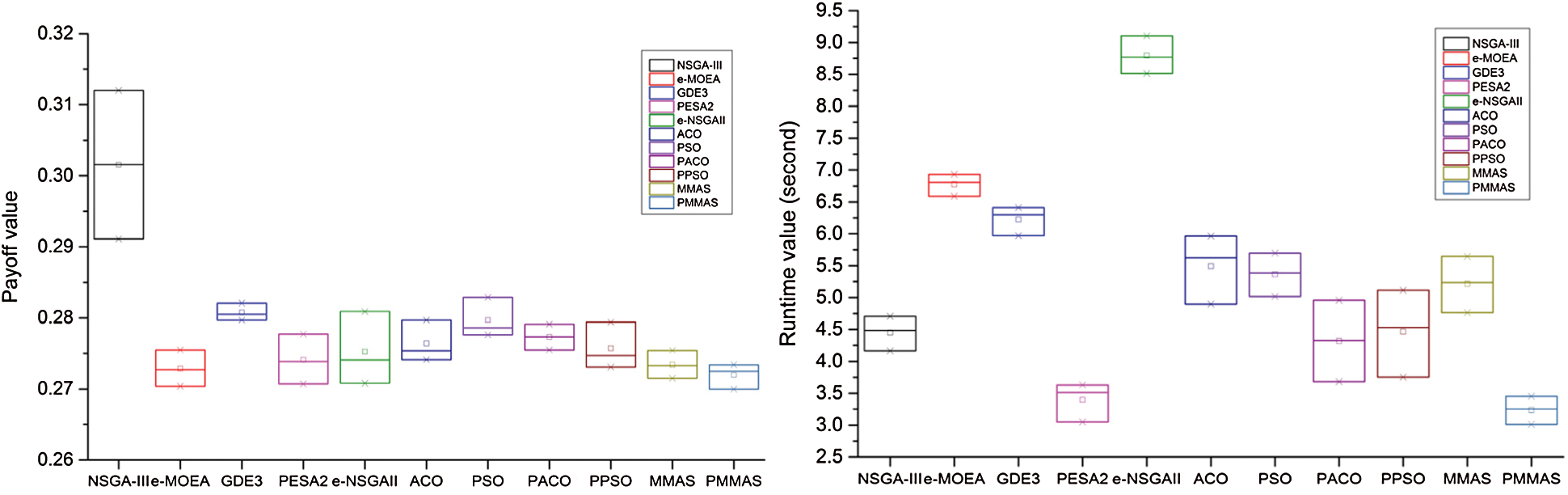
Figure 2: The comparison of payoff and runtime (second) in the best, average, and worst in dataset 1
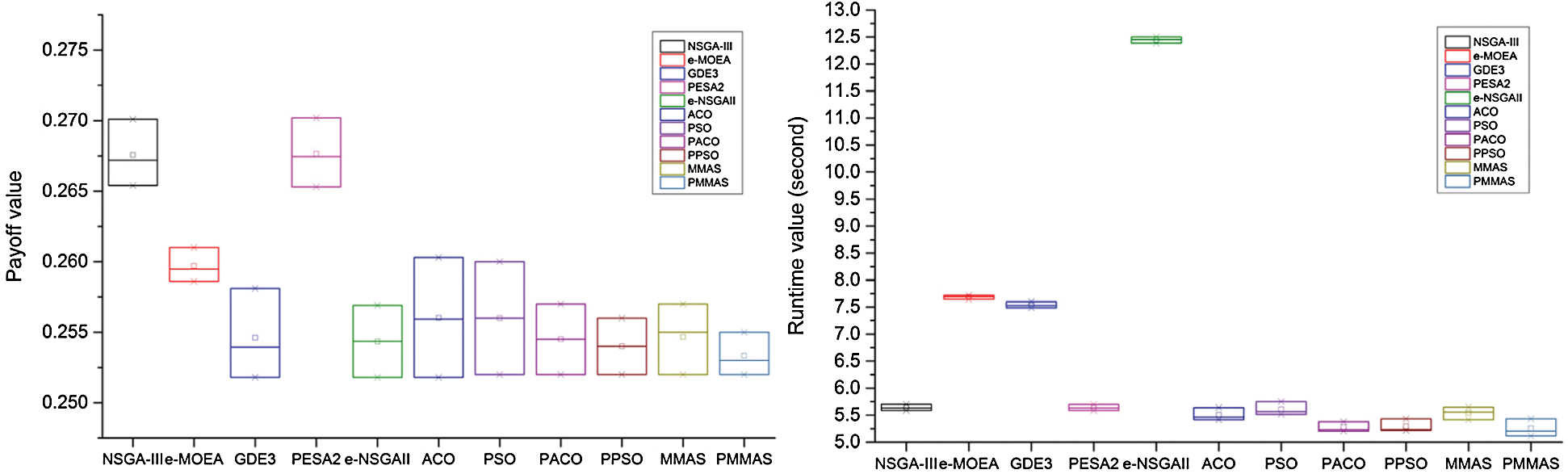
Figure 3: The comparison of payoff and runtime (second) in the best, average, and worst in dataset 1
We compare the performance of our algorithm and other algorithms of in the best, worst, and average. The figures show the differences in convergence, leading to the stability of algorithms. The PMMAS proposed algorithm shows that meeting both criteria is a convergence in fitness function and fast execution time. We also executed the PMMAS algorithm 100 times with 500 ants are random initialization, the maximum number of individuals is created for each runtime is 10000. We evaluate the stability of the algorithm based on parameters, such as the minimum (Min), maximum (Max), mean, variance and standard deviation (Std) of fitness, time cost in Tab. 3.
Table 3: Analysis and statistical evaluation of payoff and runtime of PMMAS algorithm in dataset 1 and 2
The comparison of fitness and runtime of PMMA algorithm’s on dataset 3 is showed in Tab. 4. Our proposed algorithm shows the stability and convergence of values estimated cost and payment in different experiments. Through experiments shows that the values of estimated cost (27,654,400), investor payment (13,181,444), and benefit of project owner (14,472,956) are not changed. However, the distribution of the bidder values will fluctuate, resulting in a fluctuation in the fitness function (see Tab. 5).
Table 4: The comparison of fitness and runtime (minutes) of PMMAS on the dataset 3
Table 5: Analysis and statistical evaluation of time, fitness, bidders’ value of PMMAS algorithm in dataset 3
To evaluate the performance and convergence of our algorithm on both the fitness and time functions, we execute and compare the performance between different meta-heuristic algorithms on a large-scale project in dataset 4 which has a large number of bidders, resources, items, proposals, and budget. The experiment results show that our algorithm has the best in performance and quality of Nash equilibrium point when the fitness values are lowest. Tab. 6 and Fig. 4 show the differences in convergence, the stability of algorithms. The PMMAS proposed algorithm has the best both runtime and fitness.
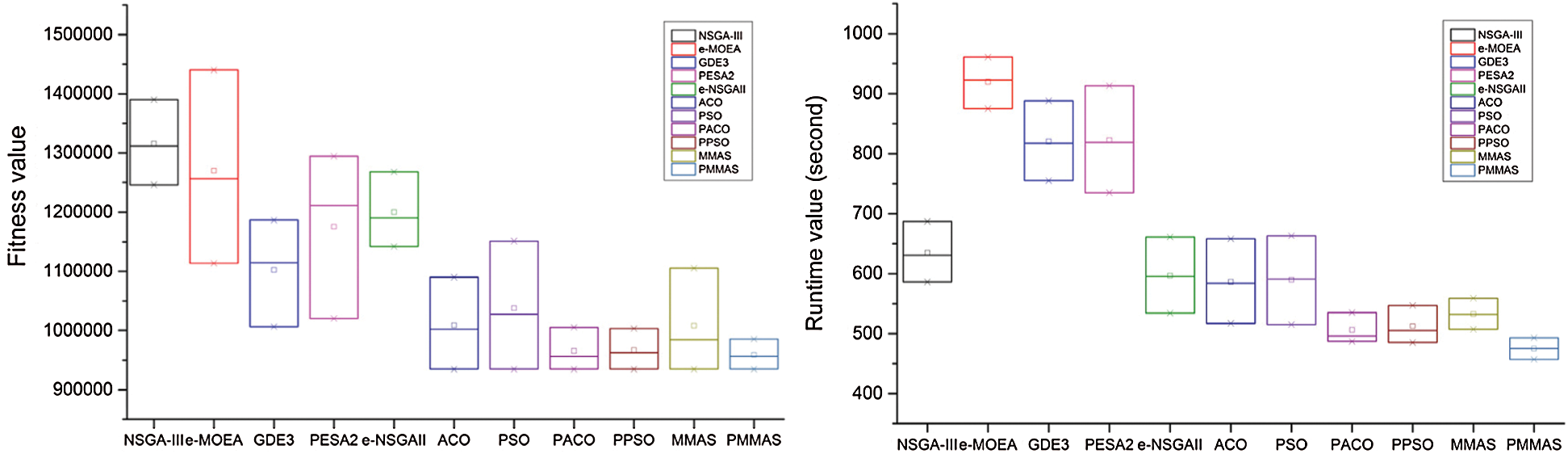
Figure 4: The comparison of payoff and runtime (second) in the best, average, and worst in dataset 4
Table 6: Analysis and statistical evaluation of fitness optimal and time of algorithm PMMAS in dataset 4
To evaluate the performance on the PMMAS algorithm proposed, we expand the variety concerning computing nodes, the running time over PMMAS reduces significantly with dataset 4. It is obvious that PMMAS algorithm obtains nice parallel performance for small-scale examples.
The speedup ratio and parallel efficiency results are computed as flows:
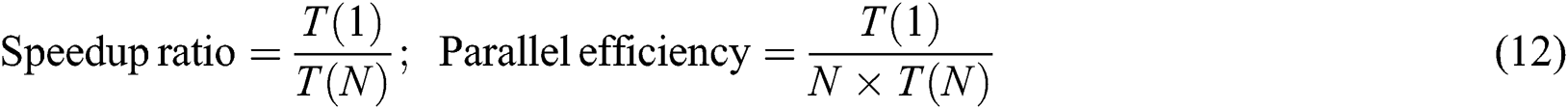
According to the experiment data in Fig. 5 shows that while the number of compute nodes is becoming larger, the parallel rate will become larger, but speed acceleration is becoming smaller. Because when the number of nodes increases, more slave nodes are taking part in the computation, so it takes less computer time and accelerates development. However, communication between nodes becomes more and more time-consuming, so the acceleration rate decreases.
Figure 5: The computation time, speedup ratio and parallel efficiency of PMMAS algorithm in dataset 4
From the experiment results, we have some comments and evaluations as follows: The NSGA-III algorithm gives the worst results because it is very easy to focus on local solutions with the fast runtime. Both 
-MOEA and 
-NSGA-II algorithms are the poor performing algorithms, which 
-MOEA being the worst due to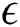 
-dominate calculations taking much more time than conventional dominates. The 
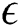-NSGA-II algorithm has good results, so using 
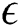-dominate instead of dominant is often costly in terms of time, but it has significant efficiency. Both 
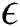-MOEA and PESA2 have in common that dividing the target space into hyperboxes, the algorithm efficiency depends on the width of the target space. This results in the differences in the order compared to the other algorithms on two datasets. The GDE3 have in common that the selection is not through mating but based on the individual transformation (mutation, or change in rules). Thus, the resulting order has similarities to 
-NSGA-II. The ACO, PSO, PACO, and PPSO algorithms can found the best solutions. However, the average and worst solutions are not good. From overall observation, the author comes to some conclusion for case study 3. The result after each run is a convergence to a similar solution. Contractors are likely to have similar interests. The choosing decision is based on many other criteria such as the price, the relationship, and the quality of each bidder. However, more trustworthy contractors are more likely to be chosen. Especially as bidder 3 does not have any relationship with the investor. The program took some time and depends on the number of the swarm population and the max running fold. The PMMAS proposed algorithm shows that meeting both criteria is a convergence in fitness function and fast execution time. Our algorithm can give the best performance in terms of payoff and time taken with limited iterations in case study 3 and 4. For some small size datasets such as dataset 1, 2, and 3: Both qualities of solution (fitness value) and time was taken are slightly different, but for the large-scale dataset 4, there are enormous differences between our approach and another algorithm. The PMMAS is parallelized and optimized with improved judging strategies for the iteration number and time reduction and parallel strategies to reduce communication costs using calculations instead of communications.
In this paper, the parallel MMAS (PMMAS) algorithm is implemented with the Nash Equilibrium theory to solve the problem of decision-making in the many stages of the auction. The approach helped proved the potential of the methodology in practical application in multi-stage procurement. The PMMAS algorithm is implemented in MPI to find the approximate optimal solution for the question of how to choose bidders and ensure a path for a win-win relationship of all participants in the procurement process. The numerical studies are compared to GDE3 [11], 
-MOEA [15], SPEA2 [14], NSGA-II [14], NSGA-III [13], ACO [9], PSO [16], PACO [18], PPSO [19], MMAS [25] to evaluate the effects of payoff and time. We also evaluate the speedup ratio and parallel efficiency between MMAS and PMMAS algorithms. Therefore, our approach is currently among the best-performing algorithms for this problem. The parallel performance is tested and studied by numerical examples with different scales. As the experiment results, the high feasibility and effectiveness of the PMMAS algorithm are verified.
Funding Statement: This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.03-2019.10.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Issa and Y. Tu. (2020). “A survey in the resource-constrained project and multi-project scheduling problems,” Journal of Project Management, vol. 5, no. 2, pp. 117–138.
2. H. Sönke and D. Briskorn. (2010). “A survey of variants and extensions of the resource-constrained project scheduling problem,” European Journal of Operational Research, vol. 207, no. 1, pp. 1–14.
3. S. S. Nagabhushan and D. S. Swamny. (2013). “Design of two-stage bidding model for supplier selection,” International Journal of Innovative Research in Science, vol. 2, no. 7, pp. 2676–2681.
4. L. Ji and T. Li. (2008). “Multi-round procurement auctions with secret reserve prices: theory and evidence,” Journal of Applied Econometrics, vol. 23, no. 7, pp. 897–923.
5. D. Wu. (2015). “Estimation of Procurement Auctions with Secret Reserve Prices,” Ph.D. dissertation. Clemson University, South Carolina.
6. C. Rao, Y. Zhao and S. Ma. (2012). “Procurement decision making mechanism of divisible goods based on multi-attribute auction,” Electronic Commerce Research and Applications, vol. 11, no. 4, pp. 397–406.
7. N. Yang, X. Liao and W. W. Huang. (2014). “Decision support for preference elicitation in multi-attribute electronic procurement auctions through an agent-based intermediary,” Decision Support Systems, vol. 57, pp. 127–138.
8. M. Bichler, K. Guler and S. Mayer. (2015). “Split-award procurement auctions—Can Bayesian equilibrium strategies predict human bidding behavior in multi-object auctions?,” Production and Operations Management, vol. 24, no. 6, pp. 1012–1027.
9. J. Xiao, X. T. Ao and Y. Tang. (2013). “Solving software project scheduling problems with ant colony optimization,” Computers & Operations Research, vol. 40, no. 1, pp. 33–46.
10. R. Zamani. (2017). “An evolutionary implicit enumeration procedure for solving the resource-constrained project scheduling problem,” International Transactions in Operational Research, vol. 24, no. 6, pp. 1525–1547.
11. K. Quresh, S. Rahnamayan, Y. He and R. Liscano. (2019). “Enhancing LQR controller using optimized real-time system by GDE3 and NSGA-II algorithms and comparing with conventional method, ” in 2019 IEEE Congress on Evolutionary Computation, pp. 2074–2081.
12. E. Gholizadeh and N. B. Afshar. (2018). “Solving a Bi-objective resource constrained multi-mode project scheduling problem with regard to payment planning using the NSGA-II algorithm,” Journal of Optimization in Industrial Engineering, vol. 21, pp. 165–187.
13. W. Mkaouer, M. Kessentini, A. Shaout, P. KoligheuS. Bechikh et al. (2015). , “Many-objective software remodularization using NSGA-III,” ACM Transactions on Software Engineering and Methodology, vol. 24, no. 3, pp. 1–45.
14. B. Gadhvi, V. Savsani and V. Patel. (2016). “Multi-objective optimization of vehicle passive suspension system using NSGA-II, SPEA2 and PESA-II,” Procedia Technology, vol. 23, pp. 361–368.
15. D. Hadka. (2015). “Moea framework-a free and open source java framework for multiobjective optimization,” version 2.11, . http://www.moeaframework.org.
16. V. Zeighami, R. Akbari and K. Ziarati. (2013). “Development of a method based on particle swarm optimization to solve resource constrained project scheduling problem,” Scientia Iranica, vol. 20, no. 6, pp. 2123–2137.
17. B. Crawford, R. Soto, G. Astorga, C. Castro, F. Paredes et al. (2018). , “Solving the software project scheduling problem using intelligent water drops,” Tehnički vjesnik, vol. 25, no. 2, pp. 350–357.
18. R. Zamani. (2010). “A parallel complete anytime procedure for project scheduling under multiple resource constraints,” International Journal of Advanced Manufacturing Technology, vol. 50, no. 1-4, pp. 353–362.
19. A. Fahmy, T. M. Hassan and H. Bassioni. (2014). “Improving RCPSP solutions quality with stacking justification−Application with particle swarm optimization,” Expert Systems with Applications, vol. 41, no. 13, pp. 5870–5881.
20. B. N. Trinh, H. Q. Thang and T. L. Nguyen. (2017). “Research on genetic algorithm and nash equilibrium in multi-round procurement, ” in SoMeT, pp. 51–64.
21. N. T. Nguyen, H. Q. Thang and T. H. G. Vu. (2018). “A Bayesian critical path method for managing common risks in software project scheduling,” in Proc. of the Ninth Int. Sym. on Information and Communication Technology, pp. 382–388.
22. H. Q. Thang, B. N. Trinh and T. X. Nguyen. (2019). “Nash Equilibrium model for conflicts in project management,” Journal of Computer Science and Cybernetics, vol. 35, no. 2, pp. 167–184.
23. B. N. Trinh, H. Q. Thang, T. X. Nguyen, P. C. Luong and K. H. Ho. (2019). “Applying a unified game-based model in a payment scheduling problem and design of experiments using MOEA framework, ” in SoMeT, pp. 55–68.
24. H. Q. Thang and N. T. Nguyen. (2020). “Probabilistic method for managing common risks in software project scheduling based on program evaluation review technique,” International Journal of Information Technology Project Management, vol. 11, no. 3, pp. 77–97.
25. D. N. Le, G. N. Nguyen, B. N. Trinh, N. T. NguyenH. Q. Thang et al. (2020). , “Min-max ant system algorithm and nash equilibrium to solve multi-round procurement problem,” in Proc. of ETAEERE 2020, Advances in Power Systems and Energy Management, Springer, 690.
26. A. B. Leoneti and G. A. Prataviera. (2020). “Entropy-norm space for geometric selection of strict Nash equilibria in n-person games,” Physica A: Statistical Mechanics and its Applications, vol. 546, pp. 124407.
27. M. K. Sohrabi and H. Azgomi. (2020). “A survey on the combined use of optimization methods and game theory,” Archives of Computational Methods in Engineering, vol. 27, no. 1, pp. 59–80.
28. G. Schuh and S. Runge. (2014). “Applying game theory in procurement. An approach for coping with dynamic conditions in supply chains,” Contributions to Game Theory and Management, vol. 7, pp. 326–340.
29. A. Nayyar, D. N. Le and N. G. Nguyen. (2018). Advances in Swarm Intelligence for Optimizing Problems in Computer Science, CRC Press.
30. D. N. Le. (2017). “A new ant algorithm for optimal service selection with end-to-end QoS constraints,” Journal of Internet Technology, vol. 18, no. 5, pp. 1017–1030.
31. D. N. Le, V. Bhateja and N. G. Nguyen. (2017). “A parallel max-min ant system algorithm for dynamic resource allocation to support QoS requirements,” in 2017 4th IEEE Uttar Pradesh Section Int. Conf. on Electrical, Computer and Electronics, pp. 697–700.
32. D. N. Le. (2014). “Applied MMAS algorithm to optimal resource allocation to support QoS requirements in NGNs,” in Int. Wireless Internet Conference, Springer, pp. 209–216.
33. D. N. Le, N. G. Nguyen, C. V. Le and N. Dey. (2017). “MMAS algorithm for features selection using 1D-DWT for video-based face recognition in the online video contextual advertisement user-oriented system,” Journal of Global Information Management, vol. 25, no. 4, pp. 103–124.
34. D. N. Le, N. G. Nguyen, V. Bhateja and S. C. Suresh. (2017). “Optimizing feature selection in video-based recognition using max-min ant system for the online video contextual advertisement user-oriented system,” Journal of Computational Science, vol. 21, pp. 361–370.
35. H. Garg. (2016). “A hybrid PSO-GA algorithm for constrained optimization problems,” Applied Mathematics and Computation, vol. 274, pp. 292–305.
36. B. Barker. (2015). “Message passing interface, ” in Workshop: High Performance Computing on Stampede. vol. 262.
37. M. Starzec, G. Starzec, A. Byrski, W. Turek and K. Pietak. (2020). “Desynchronization in distributed Ant Colony Optimization in HPC environment,” Future Generation Computer Systems, vol. 109, pp. 125–133.
38. Q. Tan, Q. He and Z. Shi. (2012). “Parallel max-min ant system using mapreduce,” in Int. Conf. in Swarm Intelligence, Berlin, Heidelberg: Springer, pp. 182–189.
39. R. Skinderowicz. (2020). “Implementing a GPU-based parallel MAX-MIN ant system,” Future Generation Computer Systems, vol. 106, pp. 277–295.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |