Computers, Materials & Continua DOI:10.32604/cmc.2020.012593
Article

Recommender Systems Based on Tensor Decomposition

Zhoubao Sun1,*, Xiaodong Zhang1, Haoyuan Li1, Yan Xiao2 and Haifeng Guo3

1School of Information Engineering, Nanjing Audit University, Nanjing, 211815, China
2School of Computing, National University of Singapore, 117417, Singapore
3Jiangsu Key Laboratory of Data Science and Smart Software, Jinling Institute of Technology, Nanjing, 211169, China
*Corresponding Author: Zhoubao Sun. Email: sunzhoubao@sina.com
Received: 05 July 2020; Accepted: 31 July 2020

Abstract: Recommender system is an effective tool to solve the problems of information overload. The traditional recommender systems, especially the collaborative filtering ones, only consider the two factors of users and items. While social networks contain abundant social information, such as tags, places and times. Researches show that the social information has a great impact on recommendation results. Tags not only describe the characteristics of items, but also reflect the interests and characteristics of users. Since the traditional recommender systems cannot parse multi-dimensional information, in this paper, a tensor decomposition model based on tag regularization is proposed which incorporates social information to benefit recommender systems. The original Singular Value Decomposition (SVD) model is optimized by mining the co-occurrence and mutual exclusion of tags, and their features are constrained by the relationship between tags. Experiments on real dataset show that the proposed algorithm achieves superior performance to existing algorithms.

Keywords: Recommender system; social information; tensor decomposition; tag regularization

1  Introduction

In recent years, recommender systems have become popular and attracted much attention. A recommender system is an effective tool to solve the problem of information overload. It builds models according to the interest and historical behavior of the target users to predict the interest of them, generate recommendation lists, and meet the personalized needs of target users in specific situations [1].

The concept of recommendation system was first proposed by Resnick [2], from then on, many scholars have begun to research recommendation algorithms to improve the performance of recommender systems. The traditional ones [2], which only consider the relationships between users and items, ignoring the social interactions among users, are no longer suitable for the social tagging system with the ternary relationship of users, items and tags. In fact, the accompanying social information plays a very important role in recommendation process. Hence, in order to provide more accuracy and personalized recommendation results, the accompanying information should be taken into consideration.

In order to solve the problem mentioned above, we focus on the social-based recommender system and propose an algorithm named RSboTD (Recommender Systems based on Tensor Decomposition) that integrates social network information to improve the prediction accuracy of recommender systems. In the process of recommendation, we mainly propose a tensor decomposition model based on tag regularization. It mainly analyses the co-occurrence and mutual exclusion between tags, which are added as a regularization item of the tensor decomposition model to mine the potential association among users, items and tags, and improve the performance of tag recommendation by using tag information in the social tagging system. We have conducted experiments on real dataset to evaluate the performance of the proposed model on the predict accuracy.

The remainder of the paper is organized as follows. The related work is presented in Section 2. The problem and the details of the proposed approach are shown in Section 3. Section 4 shows the experiments results. Finally, we draw the conclusion in Section 5.

2  Related Work

In this section, we review the algorithms to traditional recommender systems and social-based recommender systems.

2.1 Traditional Recommender Systems

Collaborative filtering may be the most commonly-used recommender systems. The existing approaches include memory-based [3,4], model-based [5,6] and content-based approaches [7,8]. Memory-based algorithms mine recommender items by finding the nearest neighbor from a rating matrix based on other similar users’ tastes. Model-based algorithms use the ratings to build a model to make rating predictions. The data sparsity is the key drawback of collaborative filtering algorithms. Therefore, the recommender system cannot recommend the item until it is rated by a substantial number of users. Content-based algorithms take the tags into consideration to recommend the user items similar to the ones the user preferred in the past. The limitation is that two different items are indistinguishable if they are represented by the same tags, another problem is that, if there is a new user, its’ recommender accuracy is not credible.

Each kind of recommendation algorithms have its own defects. In order to alleviate this problem, hybrid recommendation algorithm is proposed. By combining the advantages of different kinds of algorithms, the recommendation results are better. Different ways of combining recommendation algorithms can produce different results.

2.2 Social-Based Recommender Systems

The traditional recommendation algorithms are mature, but assume the users are independent and rarely use social tag information. However, the fact is that, the relationships among users and the accompanying social information, are useful for improving the accuracy of recommender systems. In this paper, the concept “social-based recommender system” is defined as combining the social network information, such as tags. With the development of social network, how to utilize tags has become a hot issue and been studied in many applications. Hunag et al. [9] used an adaptive model to calculate the relationship between users and tag-related items. A hybrid model is established to recommend tags by combining the similarity between tags to improve the accuracy [10,11]. Although these models are helpful to improve recommendation performance, they only consider the relationship between users and tags or items and tags, ignoring the relationship among users, items and tags. Therefore, Symeonidis et al. [12] proposed the model based on tensor to solve the problems; Rendle et al. [13] proposed a pairwise interaction tensor factorization model for tag recommendation; Ifada et al. [14] used social tagging information for tensor decomposition, and then Bayesian estimation is used to calculate user preferences for items. Ma et al. [15,16] proposed a socialized recommendation algorithm based on probability matrix decomposition, which considers user’s potential feature matrix is determined by user preferences and user's trust relationship. Ren et al. [17] proposed a random walk model to spread trust among users in order to solve the problem of data sparsity. Both of the above models are based on the trust relationships among users. In addition, a social regularization method which combines the social relationship of users with matrix decomposition was proposed in [18]. Liu et al. [19] employed the influence of context on the basis of [18], and proposed a recommendation algorithm combining social network and context. Because context has a certain impact on social recommendation, tensor decomposition has become a hot issue in social recommendation [20].

However, the social recommendation problem is not well studied in the above work. They assumed that a user’s preference should be similar to that of him/her social network, and tags are not used effectively. Compared with the mentioned work, in this paper, the tags are taken into consideration and tensor decomposition is used to calculate the similarity between users, which can improve the accuracy of recommendation results.

3  The Proposed Social-Based Recommender Algorithm

The traditional recommender systems ignore the importance of tags. They just employ the user-item matrix to generate recommendation. In fact, the tagged ternary relation has higher accuracy in sparse dataset than binary metadata under the same conditions. So, more and more scholars begin to study tag-based recommender model. For the high-dimensional data with tag information, tensor decomposition becomes an efficient research method.

3.1 High Order Singular Value Decomposition (HOSVD)

HOSVD is the most widely used decomposition method in Tucker decomposition. HOSVD can also be regarded as a high-order extension of SVD. Consider a third-order tensor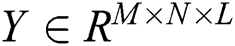, as Fig. 1, HOSVD can decompose the third-order tensor into three low-rank matrices and one core tensor, 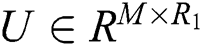represents the potential feature matrix of user, 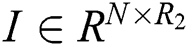represents the potential feature matrix of item, 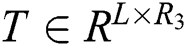represents the potential feature matrix of tag, 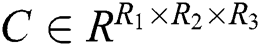is the core tensor,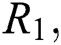 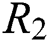and 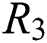represents the potential feature dimensions of users, resources and tags respectively.

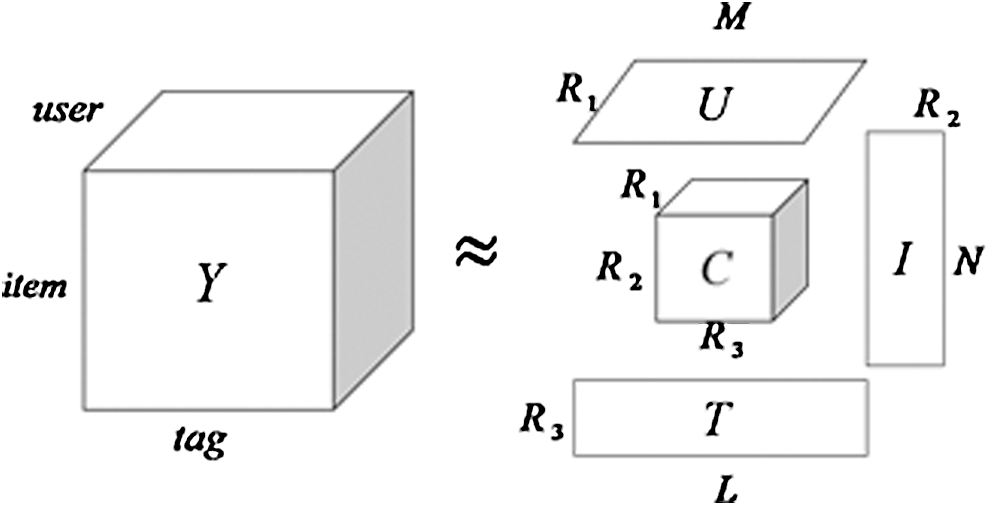
Figure 1: The HOSVD model

Assuming that the decomposed tensor is ,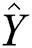

In this paper, the parameters of decomposed tensors in Eq. (1) are calculated by defining quaternions 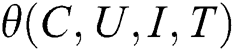, , 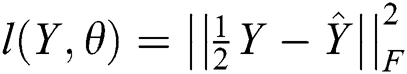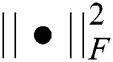is the F-norm. Because the elements in a tensor are very sparse, only the items with values need to be computed, in order to avoid over-fitting, a regularization term is added after the loss function to avoid this situation:

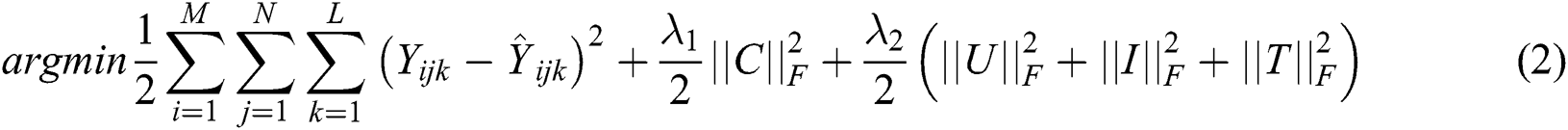
In Eq. (2), 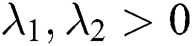, represent the penalty weight of regularization term for loss function. The optimization problem of each parameter can be solved by least square method or random gradient descent method.

3.2 Tensor Decomposition Model Based on Tag Regularization

As the most widely used method in tensor decomposition, HOSVD has been successfully applied in social tagging system. However, the decomposition model based on the original data model is defective. Firstly, the original tensor may be very sparse due to users only tag few items. Under these circumstances, the traditional HOSVD model is ineffective. Secondly, there are correlations among tags, for example, tags with similar semantics usually appear at the same time, so the accuracy of recommendation will be reduced if we ignore the intrinsic relationships between tags. In order to alleviate the problem, we use topic model to map the original sparse tensor to high-dimensional space, and propose a tensor decomposition based on the co-occurrence and mutual exclusion of tags.

Assuming that and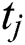 are two tags, the measurement of correlation between them as follows, 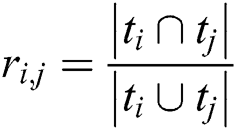, 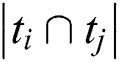represents the number of items are jointly tagged, 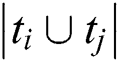represents the number of total items are tagged, 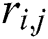represents the tightness between tags, So for tag 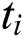, all tag sets associated with tag 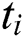can be represented as 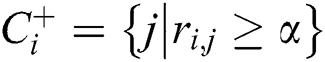, , 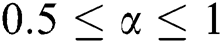if , , 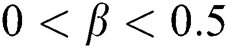represents the two tags seldom co-occurrences and can be considered mutually exclusive, the relations can be represented as 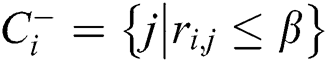, according to the above information, the HOSVD-based tag regularization model is as follows,

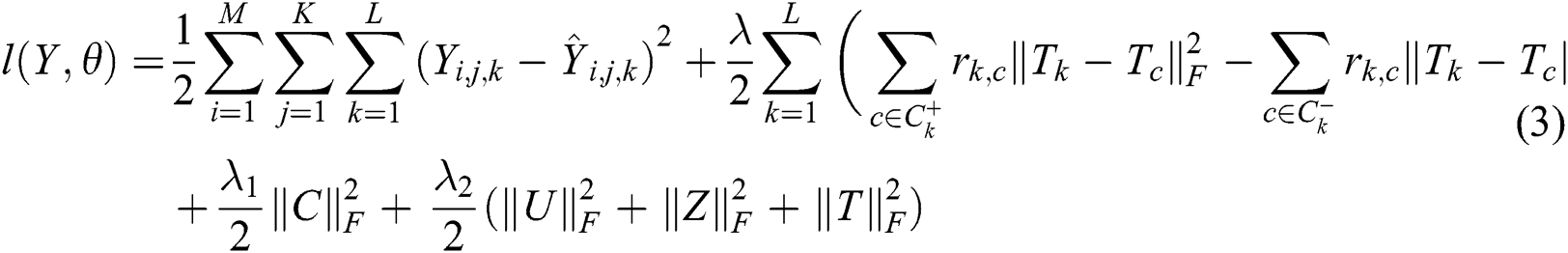
In Eq. (3), 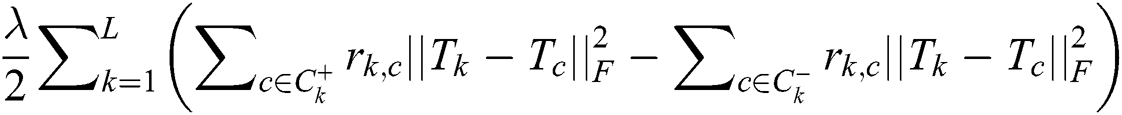is the regularization term. Here, the stochastic gradient descent method is used to minimize the loss function. The local optimal solution of the parameters can be obtained, and the final optimal value of the parameters can be obtained by iteration method. Therefore, for a given third-order tensor of <user-item-tag>, the stochastic gradient descent method is used to update the core tensor , user , topic and label until the objective function converges and the final result is obtained. The calculation formula is as follows,

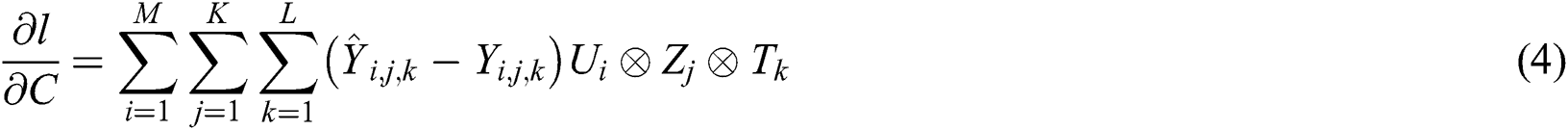
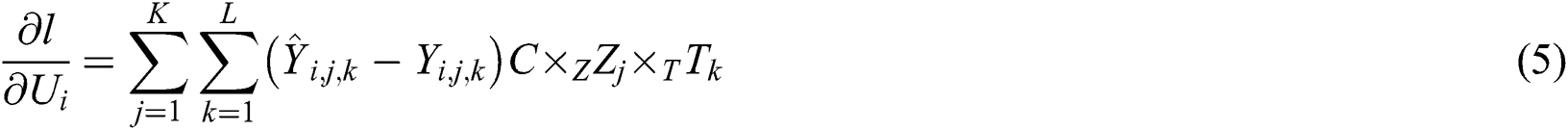
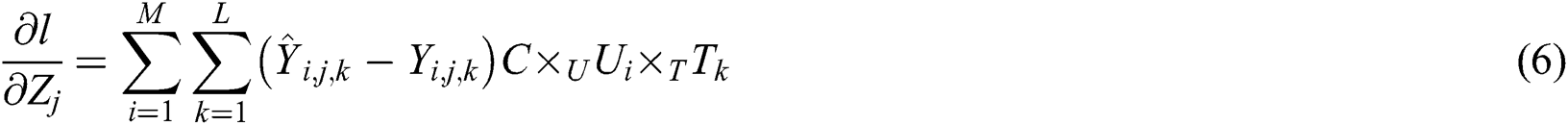
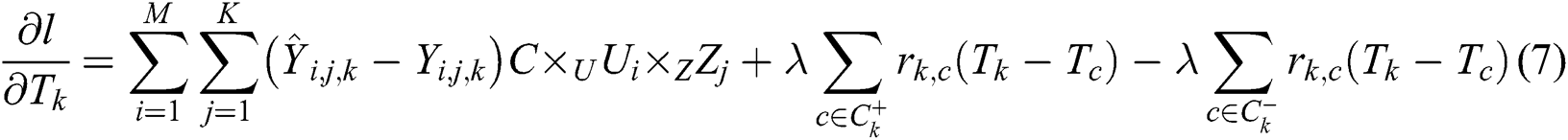
The parameters in the tensor diversity model can be solved as follows.

According to Eqs. (4)–(7), the gradient method is used to calculate the parameter values, it can iteratively solve the values of each parameter in the process of tensor decomposition. The first to third actions are initialization operations, and the fifth to ninth lines are iterative execution steps. 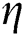is the learning ratio, 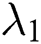, 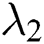are the regularization parameters. The time complexity of the algorithm is 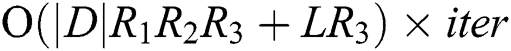. The scale of the algorithm depends on the number of observations in the tensor and the eigenvector dimensions of users, items and tags, 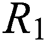, 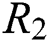and 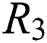is related to the number of iterations. With the updating of tag features, the co-occurrence and mutual exclusion of tags need to be recalculated, so the time complexity is also dominated by the number of tags.

4  Experimental Analysis

In this section, we conduct experiments on real dataset to validate the effectiveness of tag regularization algorithm. All the experiments are conducted on a Linux virtual machine with Intel processors (3.0 GHz) and 4 GB memory.

4.1 Dataset

With the rapid development of Web 2.0 technology, a lot of data has been produced on the internet every day. People influence each other through social network services. In this paper, Del.icio.us dataset, which is a well-known tool that is easy and free to save, organize and discover interesting links on the web, is used for the experiments. The users can share the interesting resource and get in touch with other users who have the same interests. The users in the same community can easily get the new tags of the other users without the need to access them. The dataset from Del.icio.us contains social network information, item and tag. Social network information contains 1867 users. The data density is 0.44%. There are 437593 <USER, URL, Tags> information entries, with 64305 tags, 69225 items (URLs) and 1867 users. At last, we collect 99499 pieces of information. By random extraction, 80% of the data set is selected as training set and 20% as test set.

We use the training data to learn model and predict Top-N tags for each user’s tagging tendency of resources. Therefore, in this paper, we use the popular metrics, precision and recall, to measure the prediction quality of the proposed approach. The precision and recall are defined as follows,

where 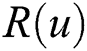denotes the tags that user 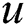may label, and 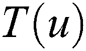denotes the actual tags that user 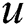labeled. The precision refers to the number of items which 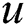labeled takes the proportion of the entire recommendation items. It reflects the possibility that 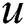is interested in recommender item. The recall refers to the number of items which 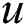labeled takes the proportion of all the items. It reflects the possibility that an item which 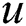labeled may be recommended. As usual, with the increasing number of recommender items, the precision decreases. According to the calculation method above mentioned, we use precision@N indicates the accuracy of recommended labels and recall@N indicates the recall rate of the recommended label.

4.2 Comparisons

In order to discuss the advantages and disadvantages of the proposed algorithm and other algorithms in accuracy and validity, we compare our algorithm with the other two existing algorithms:

1.HOSVD [21]: The traditional decomposition model of HOSVD, which directly uses the original HOSVD to decompose tensors based on <user-item-tag>.

2.T-HOSVD [21]: A traditional tensor decomposition algorithm based on tag regularization. A tensor model based on <user-item-tag> is constructed by the traditional 0/1 model, and then decomposed by the tag regularization tensor decomposition method.

3.RSboTD: A tag regularization tensor decomposition algorithm, mapping items to latent semantic space by topic, builds a tensor model based on <user-item-tag> and decomposes it by tag regularization tensor decomposition method.

4.3 Experimental Results

The experiment is conducted on Del.icio.us dataset. HOSVD, T-HOSVD, RSboTD stands for the three kinds of algorithms mentioned above. The dimension of latent factor characteristic matrix for each order of HOSVD is set respectively 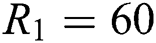, , 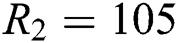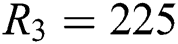. Setting learning rate 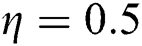, the regularization parameters 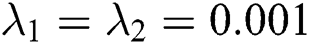, the tag regularization parameters 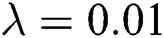, the tag co-occurrence threshold 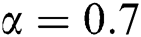, the tag exclusion threshold 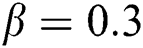, 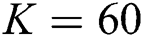. Fig. 2 shows the experimental results of various algorithms in precision.

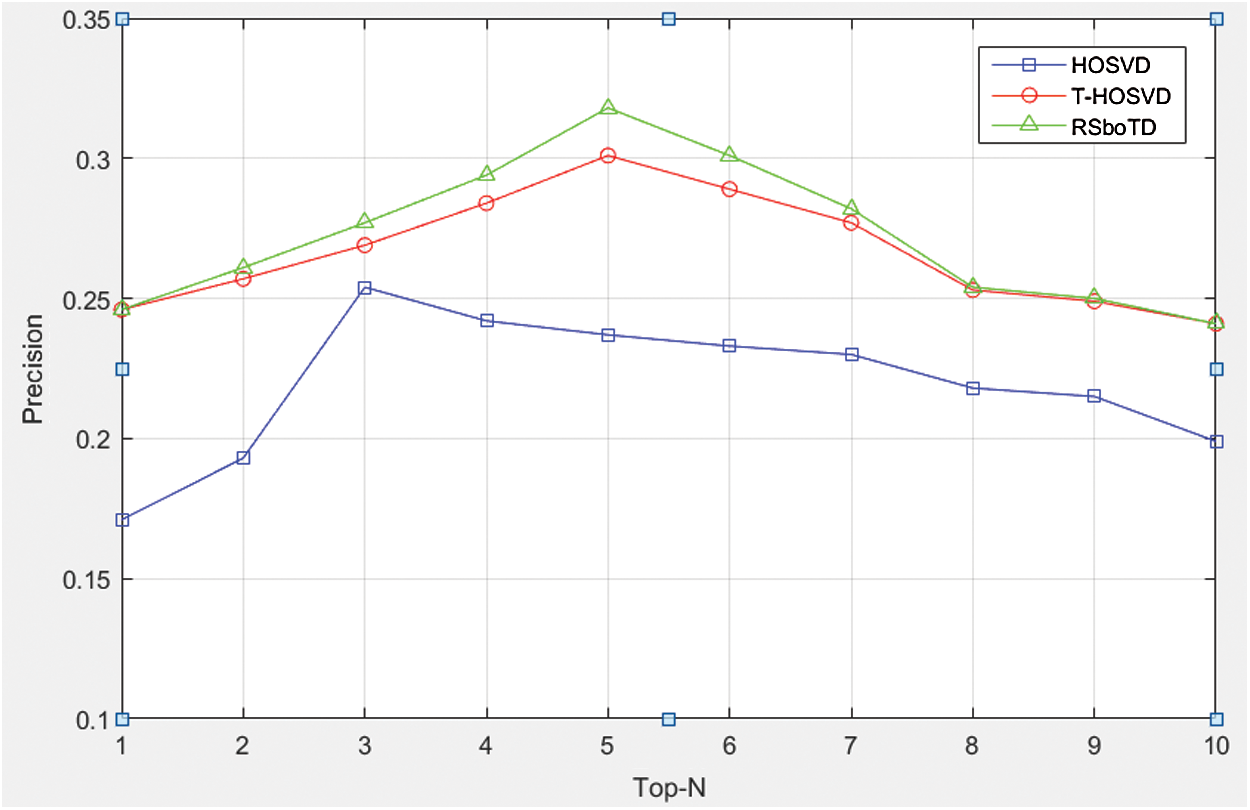
Figure 2: The precision of the compared algorithm

Fig. 3 shows the experiment results of the compared algorithms in recall rate. It is obvious that RSboTD performs better than the other existing algorithms, the reason is that it takes advantage of the intrinsic relationships between tags. It can be seen that when recommending the number of tags between 3 and 5, the efficiency is better.

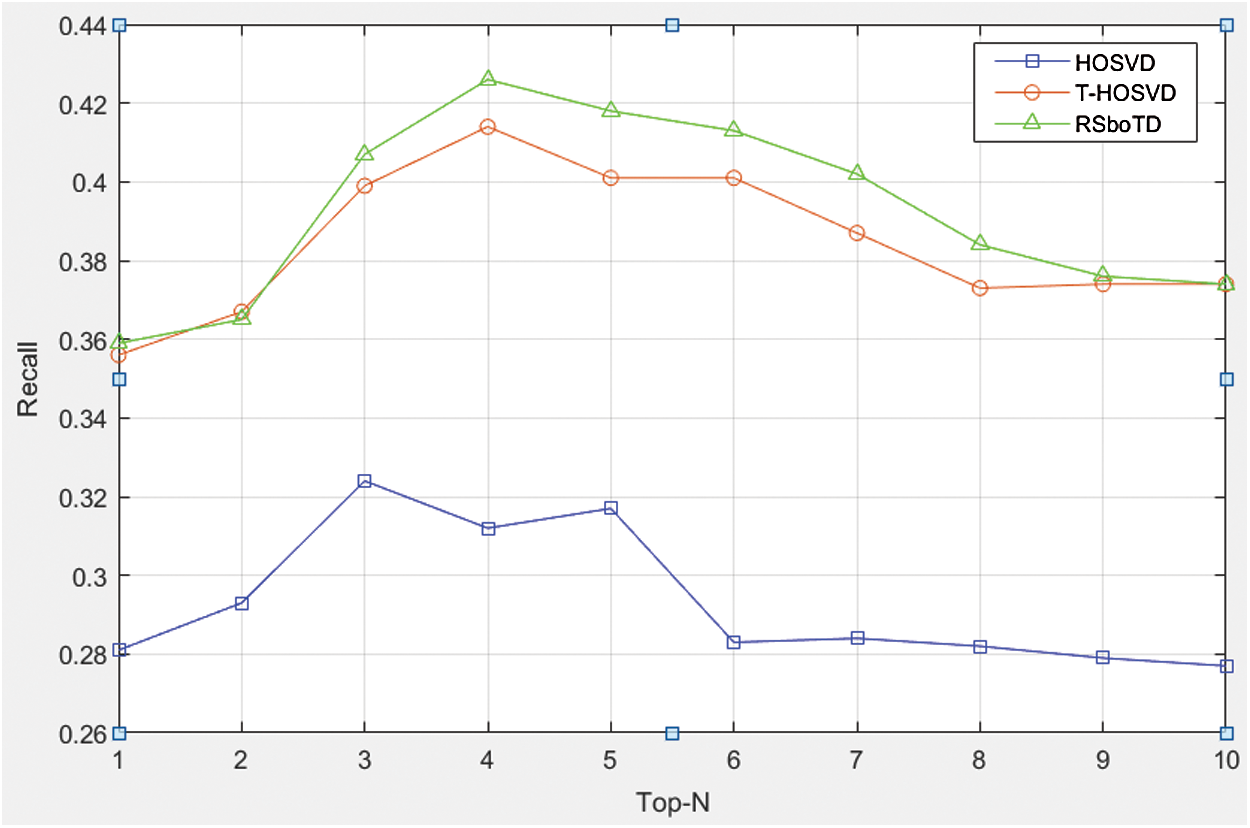
Figure 3: The recall rate of the comparison algorithms

When recommending two tags or even few, the recall rate of RSboTD is slightly lower than that of T-HOSVD. This is because the advantages of item content cannot be reflected when the number of recommendations is too small, but the recall rate of RSboTD is higher than that of TR-HOSVD when recommend more tags. Therefore, it can be inferred that recommendation based on item content can better discover the items that users are interested in. So, we can consider that the RSboTD algorithm proposed in this paper has better recommendation effect than the other two algorithms.

Tag regularization terms have certain impacts on the performance of the algorithm, but how to measure the constraints of the tag regularization term on the loss function is what we need to study. The threshold parameters 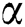and 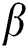are used to measure the degree of co-occurrence and mutual exclusion between tags in tag regularization items, 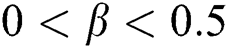, 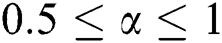. In order to express the relationship between these two thresholds more intuitively, we set 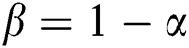, Fig. 4 shows the trends of accuracy and recall rate with varying parameters.

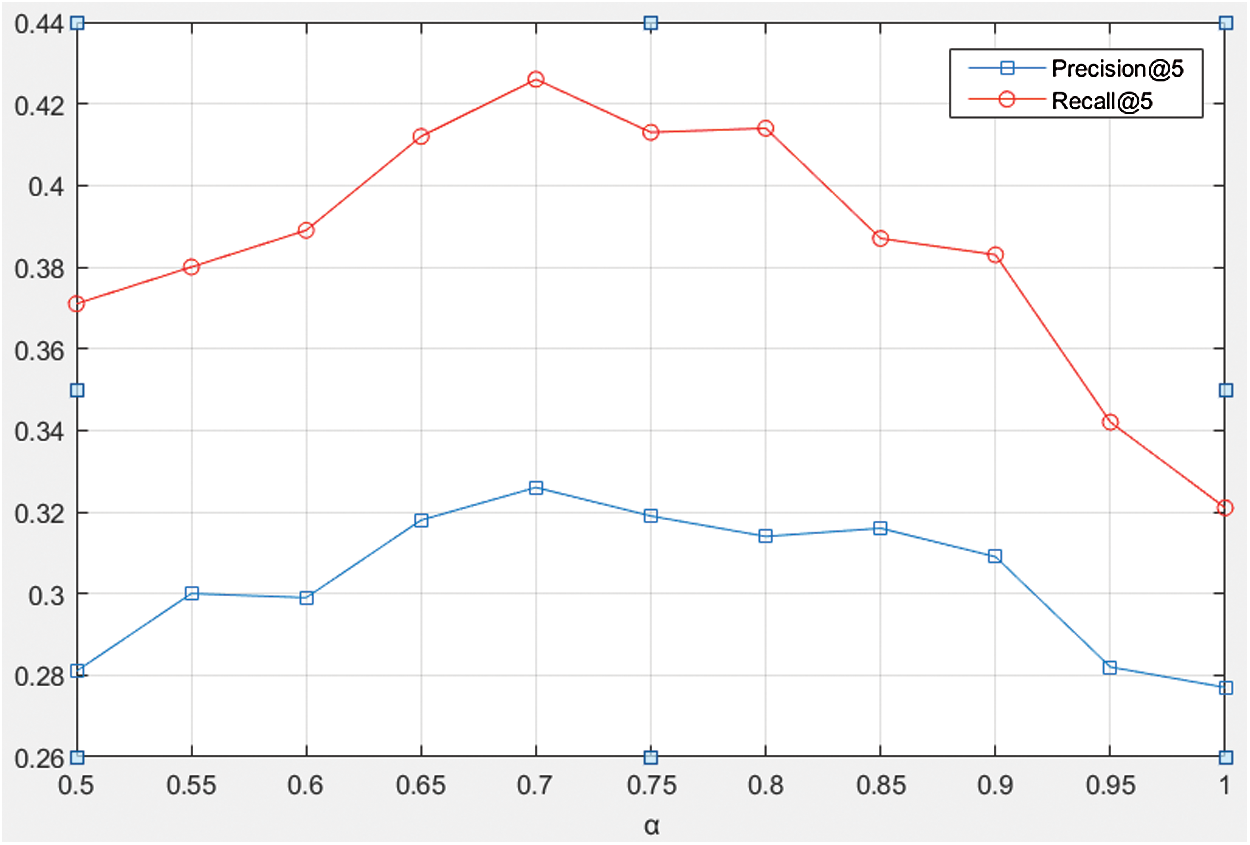
Figure 4: The impacts of parameters

It can be seen from the Fig. 4 that when the value of parameter 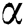is between 0.65 and 0.8, which means the value of parameter 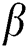is between 0.2 and 0.35, the recommendation performance is better, if the value of parameter 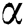is too small, there are too many co-occurrence and mutually exclusive relations of tags, which will reduce the recommendation performance. When the value of parameter 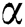is too large, there are too few co-occurrence and mutually exclusive relations of tags which will also reduce recommendation performance. From the Fig. 4, we can see that 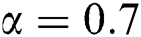, the accuracy and recall rate can achieve the optimal results in this dataset.

Fig. 5 shows the effect of parameter 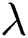. It can be seen that when the value of 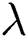is too large, the recommendation accuracy and recall rate are almost zero. This is because the tag regularization item is only used to assist recommendation. If it is too large, the training result will be distorted. Therefore, setting the parameter 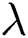in a relatively small range can improve the recommendation performance. In this paper, the accuracy and recall rate can achieve the best results when 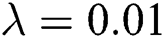. If 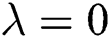, the proposed RSboTD algorithm will degenerate into the ordinary HOSVD algorithm.

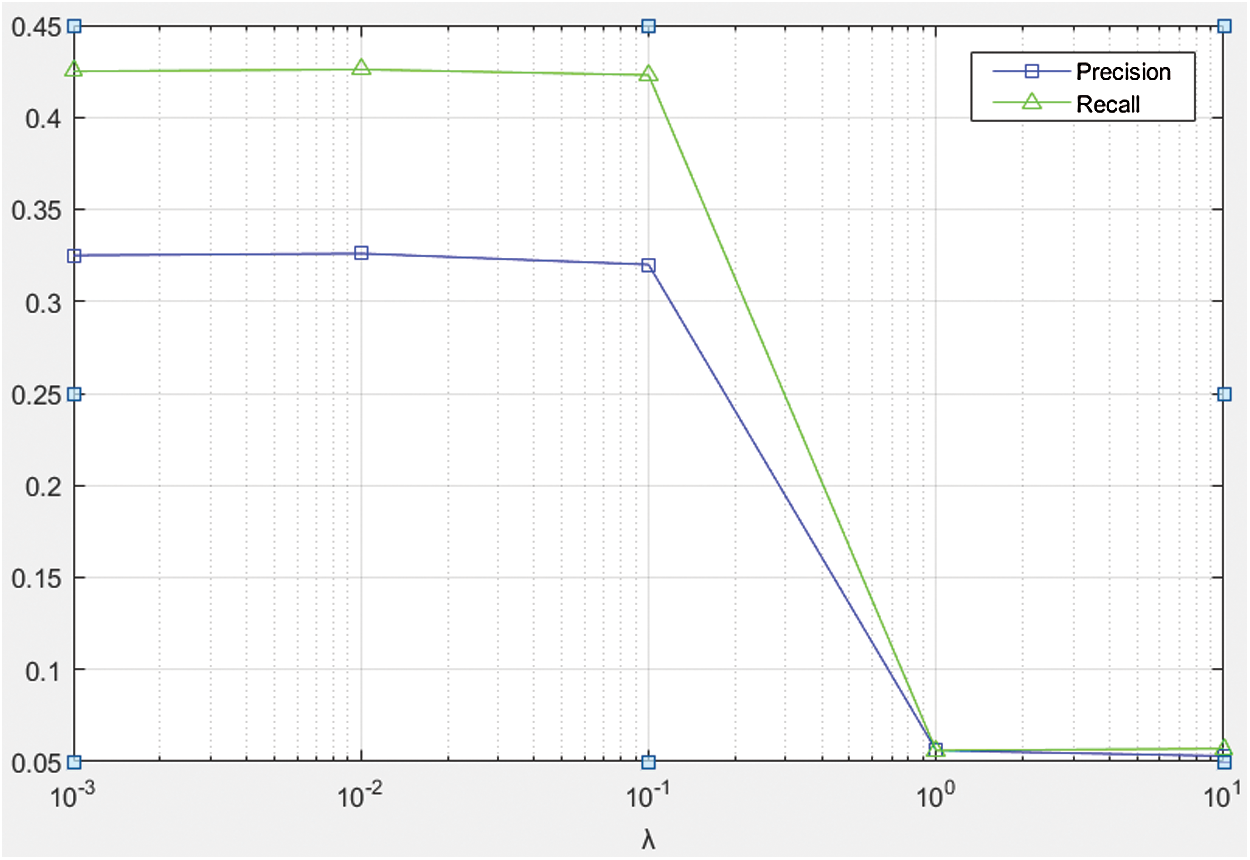
Figure 5: The impacts of parameter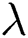

5  Conclusion

In this paper, based on the observation that the tags can improve the prediction quality, we propose a social regularization algorithm which incorporates tags to benefit recommender systems. Tensor decomposition is employed in designing social regularization terms. The experiments on real dataset show that the proposed approach outperforms the other existing algorithms.

With the development of social networks, the social-based recommender systems become more important. In this paper, we fuse tags on the basis of tensor decomposition to improve recommendation quality, however, we need to investigate the following problems: the cold-start problem, the time-series information, the place information and so on. These are many interesting works to be explored in the future.

Acknowledgement: Many thanks are expressed to Jinjin Zhang for his kind help during the preparation of the manuscript and to Congdong Lv for assistant with the experiments.

Funding Statement: The work is supported by the following grants: The National Key Research and Development Program of China (No. 2019YFB1404602, X.D. Zhang); The Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 17KJB520017, Z.B. Sun); The Young Teachers Training Project of Nanjing Audit University (No. 19QNPY017, Z.B. Sun); The Opening Project of Jiangsu Key Laboratory of Data Science and Smart Software (No. 2018DS301, H.F. Guo, Jinling Institute of Technology); and Funded by Government Audit Research Foundation of Nanjing Audit University.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1.   P. Brusilovsky and N. David. (2013). “Preface to the special issue on personalization in social web systems,” User Modeling and User-Adapted Interaction, vol. 23, no. 2, pp. 83–87.

2.   P. Resnick and H. R. Varian. (1997). “Recommender systems,” Communications of the ACM, vol. 40, no. 3, pp. 56–58.

3.   A. Bellogin, P. Castells and I. Cantado. (2013). “Improving memory-based collaborative filtering by neighbor selection based on user preference overlap,” in Proc. ORAIR, Lisbon, Portugal, pp. 145–148.

4.   M. Jiang and L. N. Xu. (2019). “Collaborative filtering recommendation algorithm based on multi-relationship social network,” Computers, Materials & Continua, vol. 60, no. 2, pp. 659–674.

5.   P. Symeonidis. (2015). “ClustHOSVD: Item recommendation by combining semantically enhanced tag clustering with tensor HOSVD,” IEEE Transactions on Systems Man & Cybernetics Systems, vol. 46, no. 9, pp. 1–12.

6.   Y. Bergner, S. Droschler and G. Kortemeyer. (2012). “Model-based collaborative filtering analysis of student response data: Machine-learning item response theory,” in Proc. EDM, Chania, Greece, pp. 95–102.

7.   J. Illig, A. Hotho and R. Jäschke. (2011). “A comparison of content-based tag recommendations in folksonomy systems,” Knowledge Processing and Data Analysis, vol. 65, no. 81, pp. 136–149.

8.   A. B. Barragáns-Martínez, E. Costa-Montenegro and J. C. Burguillo. (2011). “A hybrid content-based and item-based collaborative filtering approach to recommend TV programs enhanced with singular value decomposition,” Information Sciences, vol. 180, no. 22, pp. 4290–4311.

9.   J. Hunag, X. Yuan and N. Zhong. (2015). “Modeling tag-aware recommendations based on user preferences,” International Journal of Information Technology & Decision Making, vol. 14, no. 5, pp. 947–970.

10. X. Xia, D. Lo and X. Wang. (2013). “Tag recommendation in software information sites,” in Proc. MSR, San Francisco, CA, USA, pp. 287–296.

11. S. Wang and B. Vasilescu. (2018). “EnTagRec: An enhanced tag recommendation system for software information sites,” Empirical Software Engineering, vol. 23, no. 2, pp. 800–832.

12. P. Symeonidis, A. Nanopoulos and Y. Manolopoulos. (2008). “Tag recommendations based on tensor dimensionality reduction,” in ACM Conf. on Recommender Systems, New York, NY, USA, pp. 43–50.

13. S. Rendle and L. Schmidt-Thieme. (2010). “Pairwise interaction tensor factorization for personalized tag recommendation,” in Proc. WSWDM, New York, NY, USA, pp. 81–90.

14. N. Ifada and R. Nayak. (2014). “Tensor-based item recommendation using probabilistic ranking in social tagging systems,” in Proc. WCNC, Istanbul, Turkey, pp. 805–810.

15. Z. Sun, L. Han, W. Huang, X. Wang,X. Zeng et al. (2015). , “Recommender systems based on social networks,” Journal of Systems and Software, vol. 99, no. 1, pp. 109–119.

16. H. Ma, I. King and M. R. Lyu. (2009). “Learning to recommend with social trust ensemble,” in Proc. RDIR, Tokyo, Japan, pp. 203–210.

17. Y. J. Ren, Y. P. Chen and J. Wang. (2019). “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892.

18. H. Ma, D. Zhou and C. Liu. (2011). “Recommender systems with social regularization,” in Proc. WSWDM, Hong Kong, China, pp. 287–296.

19. X. Liu and K. Aberer. (2013). “SoCo: A social network aided context-aware recommender system,” in Proc. WWW, Rio de Janeiro, Brazil, pp. 781–802.

20. C. Zheng and M. Song. (2016). “CMPTF: Contextual modeling probabilistic tensor factorization for recommender systems,” Neurocomputing, vol. 205, no. 4, pp. 141–151.

21. L. D. Lathauwer, B. D. Moor and J. Vandewalle. (2000). “A multilinear singular value decomposition,” SIAM Journal on Matrix Analysis & Applications, vol. 21, no. 4, pp. 1253–1278.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.