DOI:10.32604/cmc.2020.011907
| Computers, Materials & Continua DOI:10.32604/cmc.2020.011907 | |
| Article |
Computer Methodologies for the Comparison of Some Efficient Derivative Free Simultaneous Iterative Methods for Finding Roots of Non-Linear Equations
1Department of Mathematics, Huzhou University, Huzhou, 313000, China
2Department of Mathematics, National University of Modern Languages, Islamabad, Pakistan
3Department of Mathematics and Statistics, Riphah International University I-14, Islamabad, 44000, Pakistan
4Center for Advanced Studies in Pure and Applied Mathematics Bahauddin Zakariya University, Multan, Pakistan
5School of Mathematical Sciences, Zhejiang University, Hanghou, 310027, China
*Corresponding Author: Mudassir Shams. Email: mudassir4shams@gmail.com
Received: 04 June 2020; Accepted: 02 July 2020
Abstract: In this article, we construct the most powerful family of simultaneous iterative method with global convergence behavior among all the existing methods in literature for finding all roots of non-linear equations. Convergence analysis proved that the order of convergence of the family of derivative free simultaneous iterative method is nine. Our main aim is to check out the most regularly used simultaneous iterative methods for finding all roots of non-linear equations by studying their dynamical planes, numerical experiments and CPU time-methodology. Dynamical planes of iterative methods are drawn by using MATLAB for the comparison of global convergence properties of simultaneous iterative methods. Convergence behavior of the higher order simultaneous iterative methods are also illustrated by residual graph obtained from some numerical test examples. Numerical test examples, dynamical behavior and computational efficiency are provided to present the performance and dominant efficiency of the newly constructed derivative free family of simultaneous iterative method over existing higher order simultaneous methods in literature.
Keywords: Non-linear equation; iterative method; simultaneous method; basins of attractions; computational efficiency
One of the ancient problems in mathematics is the estimations of roots of non-linear equation
There are number of applications of non-linear equation in science and engineering. Newton’s method is a numerical iterative scheme which finds a single root at a time. The simultaneous iterative method (SIM) such as, Weirstrass [1] method is used to find all the distinct roots of Eq. (1). The iterative methods for finding single root of non-linear polynomial equation have been studied by [2–4] and many others. On the other hand, there are lot of numerical iterative methods devoted to approximate all roots of Eq. (1) simultaneously (see, e.g., [1,5–8] and the references therein). The SIM are popular as compared to single root finding methods due to their wider range of convergence, reliability and their applications for parallel computing as well. Further details on SIM, their convergence analysis, efficiency and parallel implementations can be seen in [9,10–13] and references cited there in. The main objective of this article is to construct SIM which have more efficient and higher convergence order for approximating all distinct roots of Eq. (1). For the analysis and comparison of convergence behavior of simultaneous iterative methods, we use the techniques of dynamical plane with CAS MATLAB (R2011b).
2 Constructions of Simultaneous Method
Here, we construct a ninth order derivative free simultaneous method which is more efficient than the similar methods existing in literature.
2.1 Construction of Simultaneous Methods for Distinct Roots
Consider eighth order derivative free Kung–Traub’s [4] family of iterative method (abbreviated as KF):
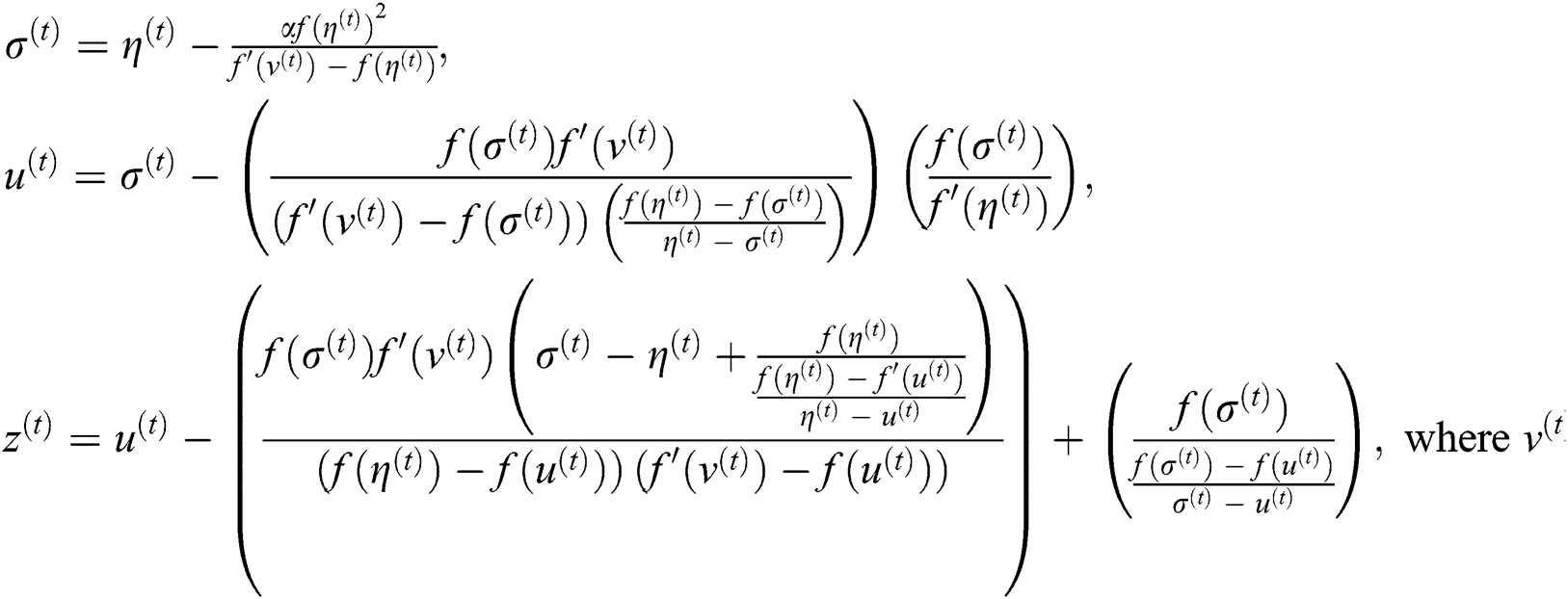
Using well known Weierstrass [1] method, abbreviated as (WKD), we have:
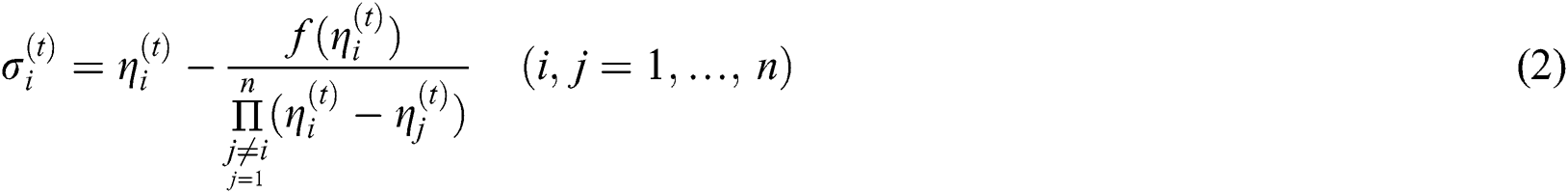
Replacing 
by 
in Eq. (2), we get new simultaneous iterative method (abbreviated as SIM1),
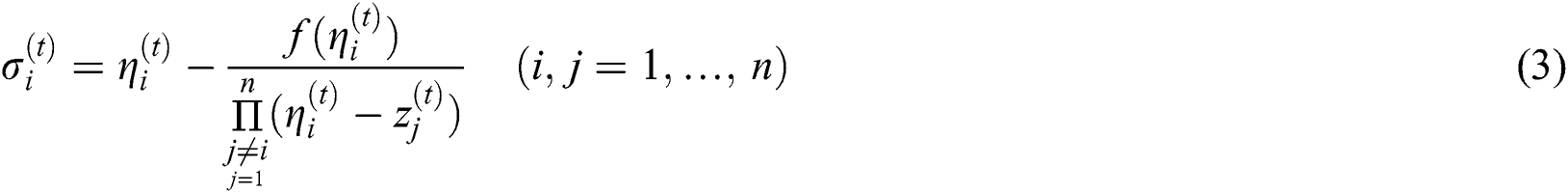
where
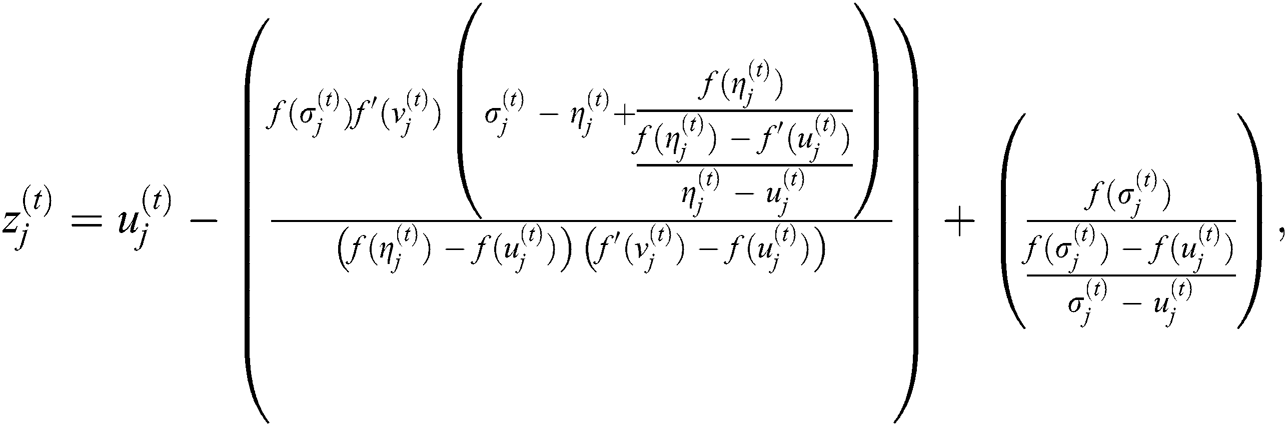
Thus, we have a new derivative free family of simultaneous method Eq. (3), abbreviated as SIM1, for approximating all the distinct roots of Eq. (1).
Here, we discuss the convergence of iterative method SIM1:
Theorem: Let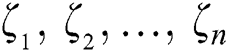 
be n simple roots of Eq. (1). If 
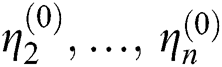be the sufficiently close initial approximations to actual roots, then the order of convergence of SIM1 is nine.
Proof: Let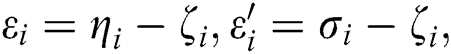 
be the errors in 
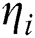and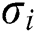 
approximations respectively. For simplification, we omit iteration index 
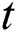. From SIM1, we have:
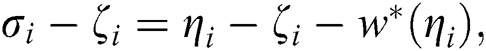where 
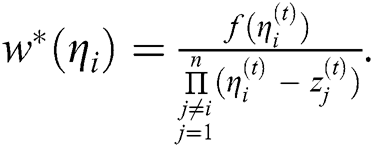
where
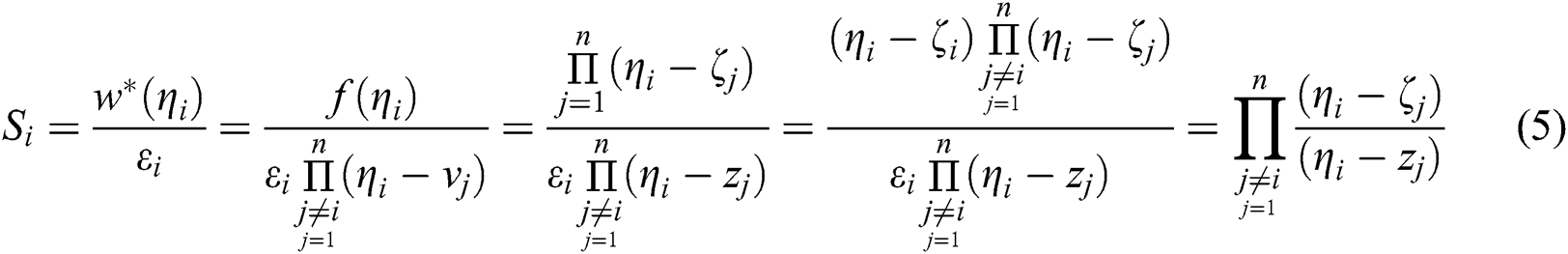
Now, if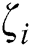 
is a simple root, then for a small enough 
, 
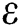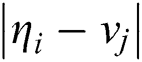is bounded away from zero, and so
where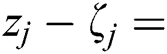 
Õ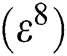 
, see [4]:
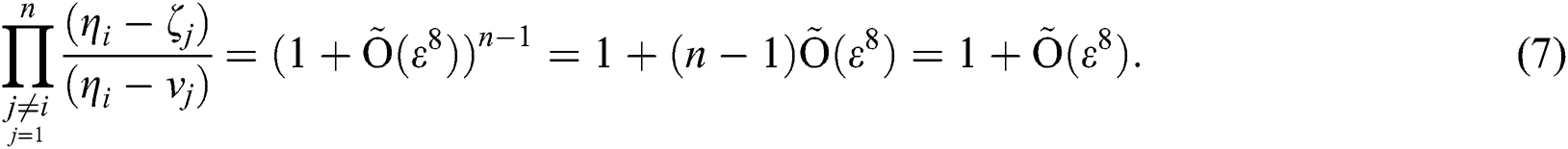
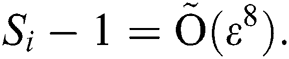
Thus, Eq. (4) gives:
Hence, the theorem is proved.
3 Dynamical Studies of KF, SIM1 and SPJ1
In this section, we discuss the dynamical study of KF, SIM1 and [14] method (abbreviated as SPJ1). We have discussed the dynamical behavior of simultaneous methods to show global convergence as dynamical planes of single root finding methods may have divergence regions which do not exist in simultaneous methods. Let us recall some basic concepts of this study. For more details on the dynamical behavior of the iterative methods one can consult [2] and [15]. Taking a rational map 
, where 
is a complex plane, the orbit 
defines a set such as,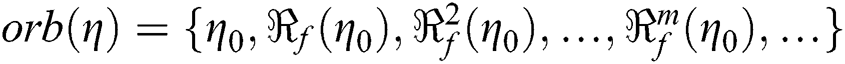 
. The convergence 
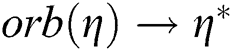is understood in the sense if 
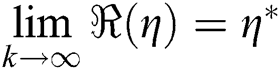exist. A point 
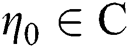known as attracting, if 
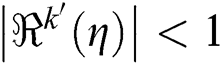. An attracting point 
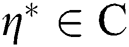defines basins of attraction 
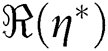as the set of starting points whose orbit tends to 
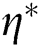. To generate basins of attraction, we take grid 
of square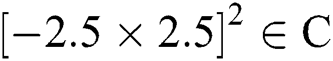 
. To each root of Eq. (1), we assign a color to which the corresponding orbit of the iterative methods starts and converges to a fixed point. Take color map as Jet. We take 
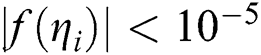and maximum numbers of iterations are chosen as 5 due to wider convergence region of simultaneous methods. Dark black points are assigned, if the orbit of the iterative methods does not converge to root after 5 iterations. We obtained basins of attractions for the following three test function 
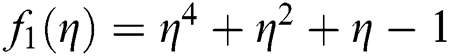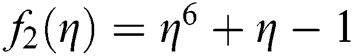and 
and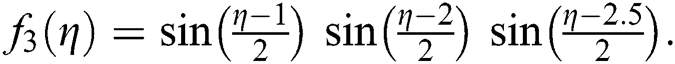 
The root of 
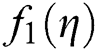are 0.2 + 1.3i, 0.2 − 1.3i, −1, 0.5, roots of 
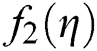are −1.1, −0.4 + 1i, −0.4 − 1i, 0.6 + 0.7i, 0.6 − 0.7i, 0.7 and root of 
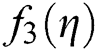are 1, 2, 2.5 correct up to 1-decimal place. Brightness in color in Figs. 1–9 means less number of iterations. Finally, in Fig. 10, we present Elapsed time of basins of attraction corresponding to iterative map KF, SIM1 and SPJ1 using tic-toc command in MATLAB (R2011b).
Here, we discuss the computational efficiency and convergence behavior of the [14] method (abbreviated as SPJ1) and the new method SIM1. As presented in [14], the efficiency index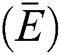 
is used to estimate the efficiency of iterative method as:
where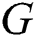 
in [14], denotes the cost of computation and r, the order of convergence.
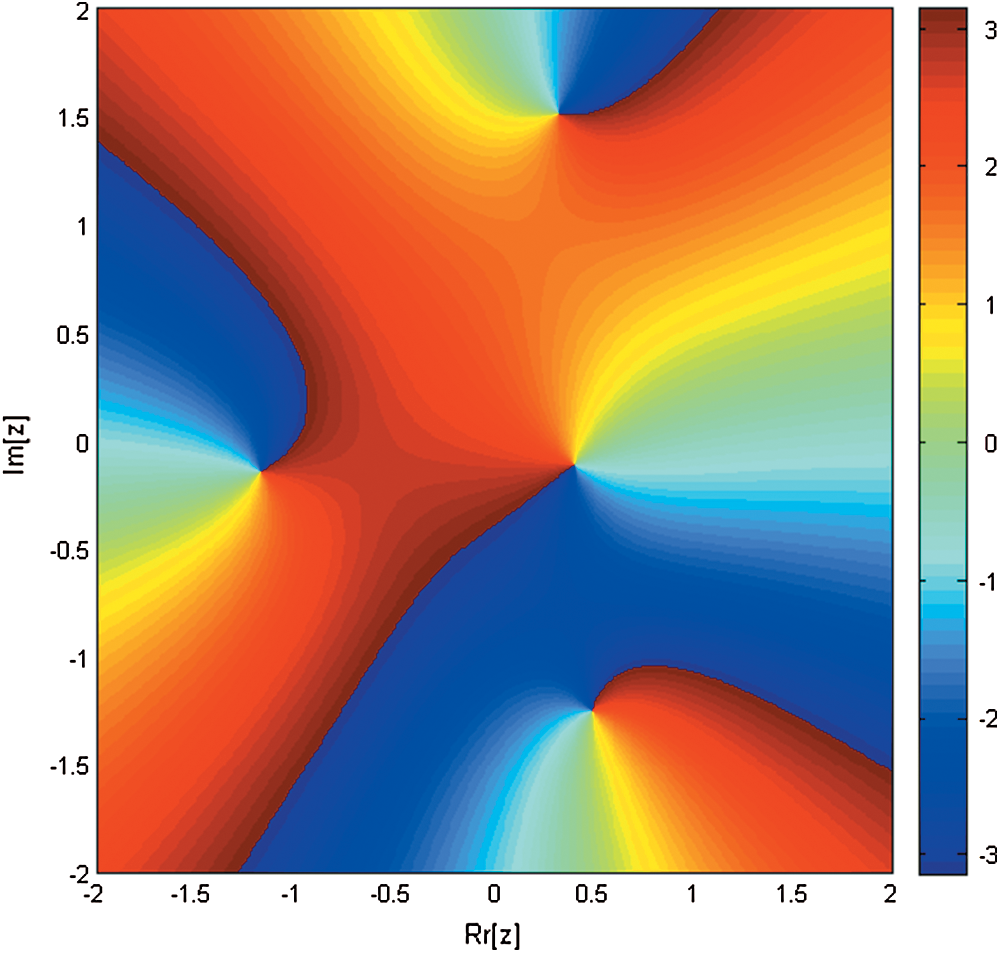
Figure 1: Basin of attraction of iterative method SIM1 for non-linear equation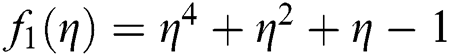 
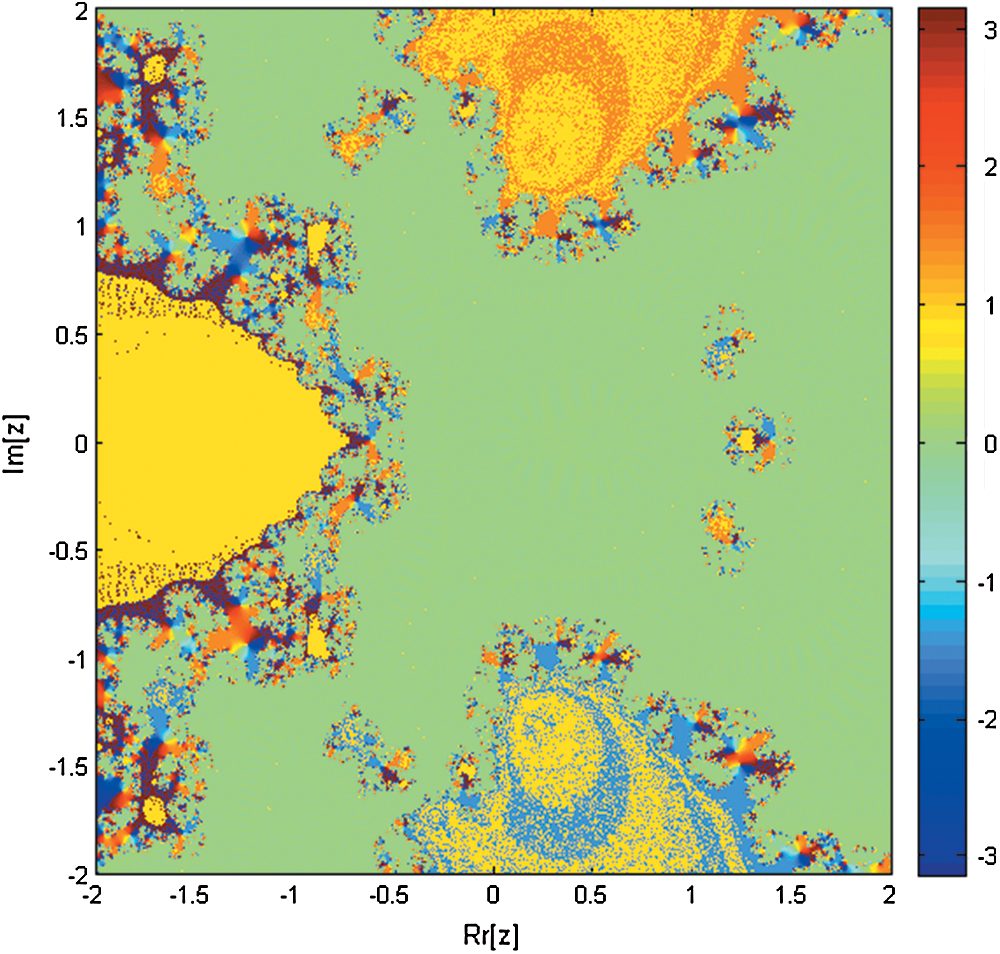
Figure 2: Basin of attraction of iterative method KF for non-linear equation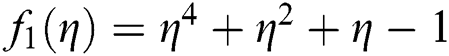 
Thus, Eq. (9) becomes:
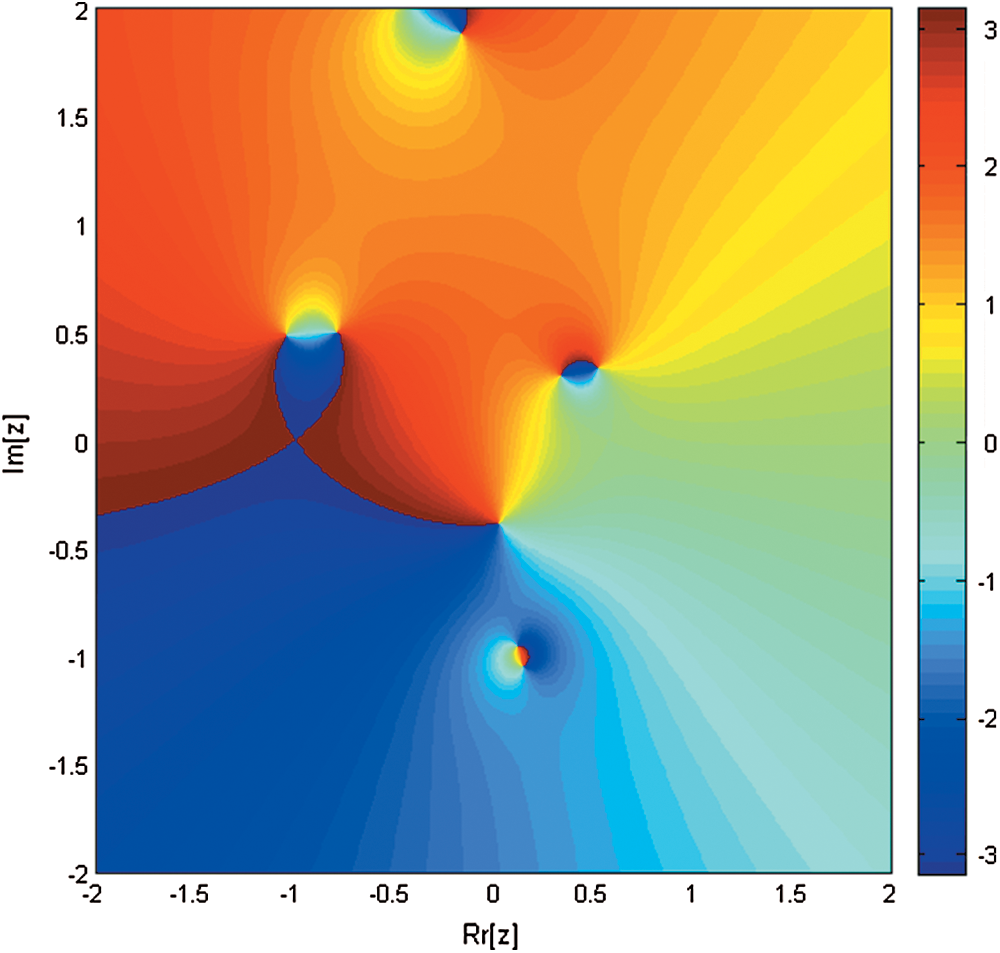
Figure 3: Basin of attraction of iterative method SPJ1 for non-linear equation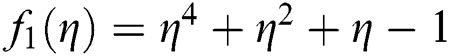 
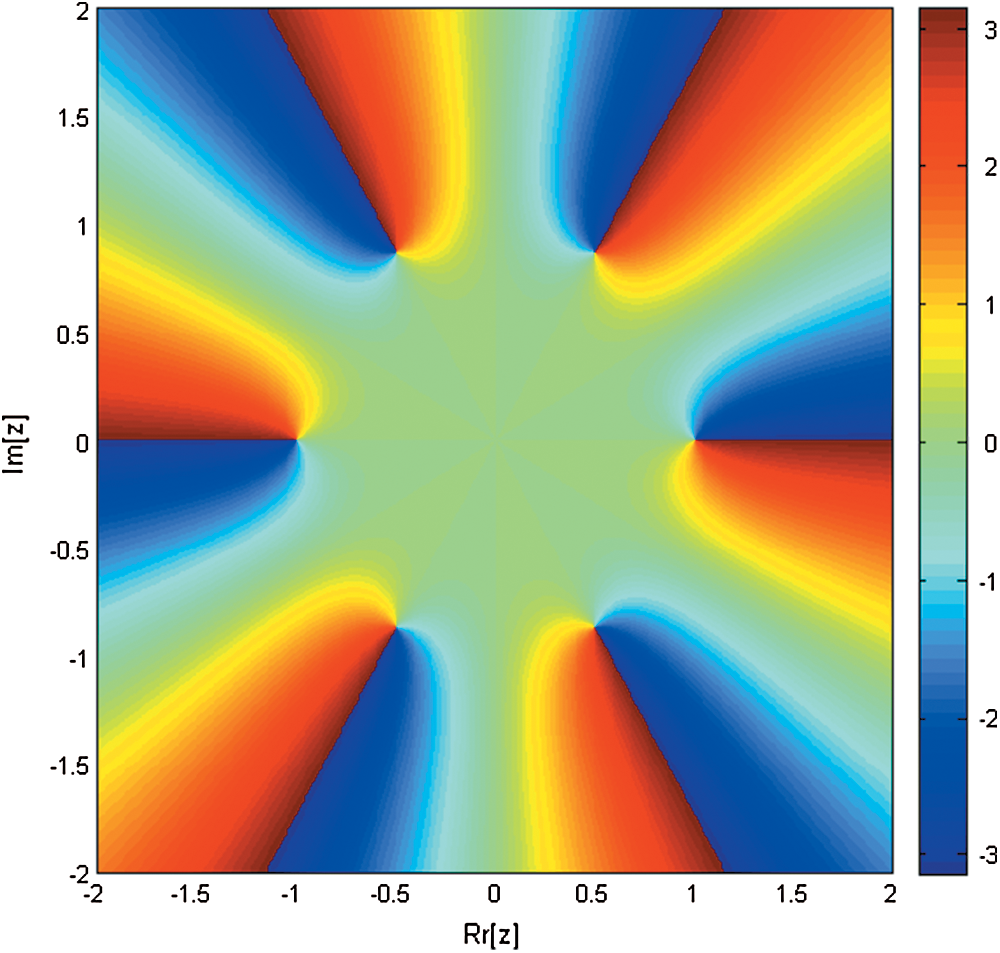
Figure 4: Basin of attraction of iterative method SIM1 for non-linear equation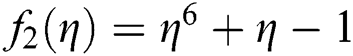 
Using Eq. (11) and data in Tab. 1, we find the percentage ratio 
[14] as:
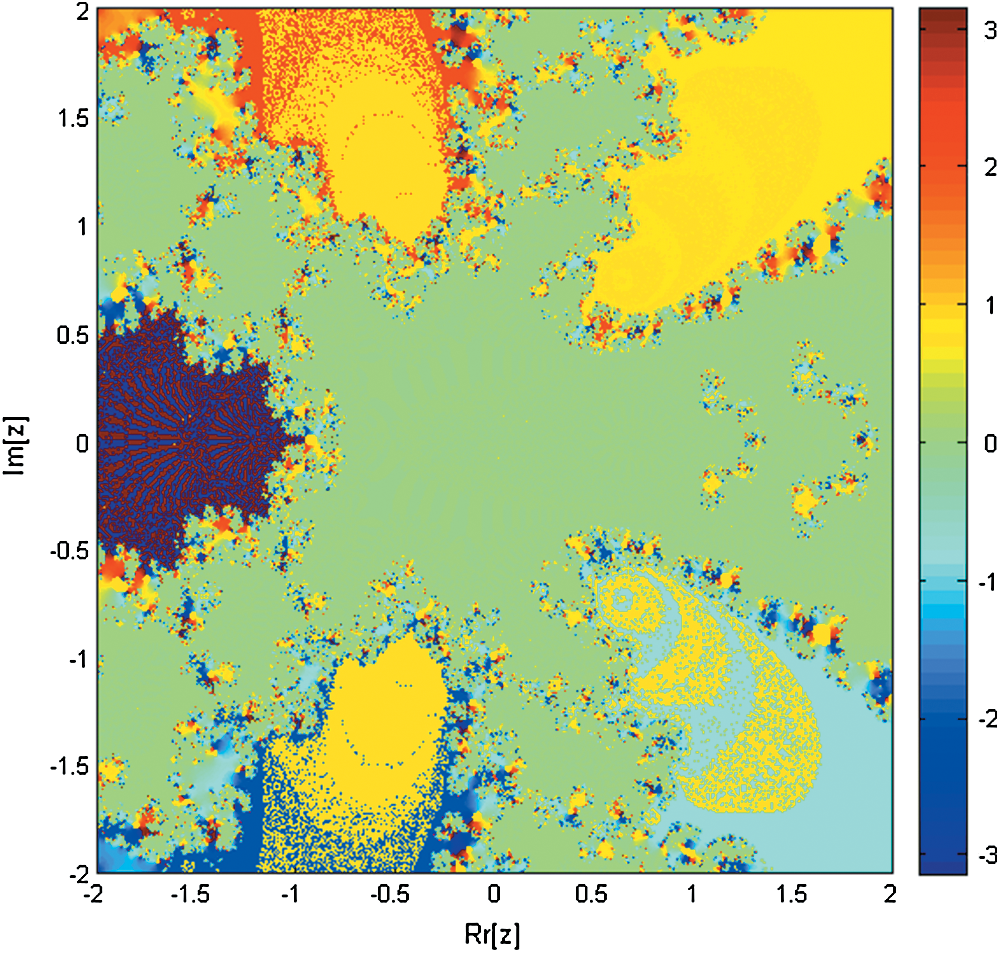
Figure 5: Basin of attraction of iterative method KF for non-linear equation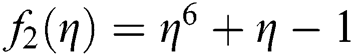 
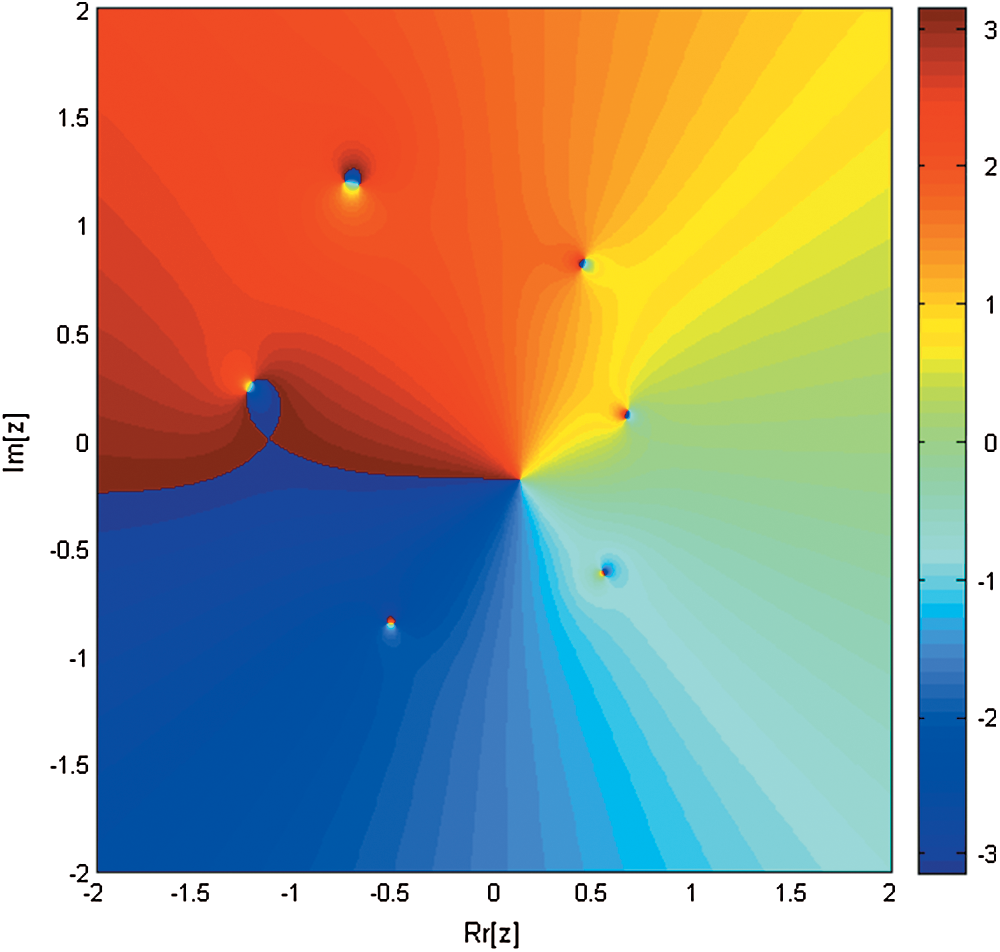
Figure 6: Basin of attraction of iterative method SPJ1 for non-linear equation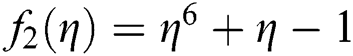 
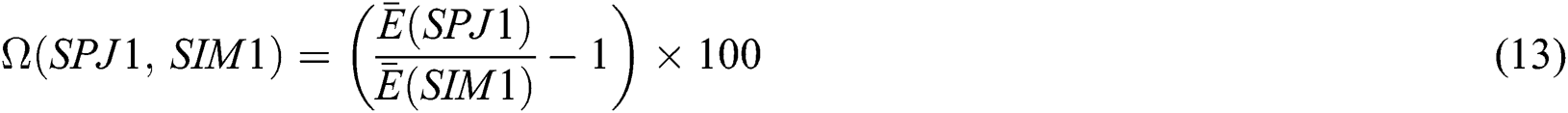
Figs. 11–12, graphically illustrates these percentage ratios. Figs. 11–12, clearly show that the newly constructed simultaneous method SIM1 is more efficient as compared to Petkovic method (SPJ1).
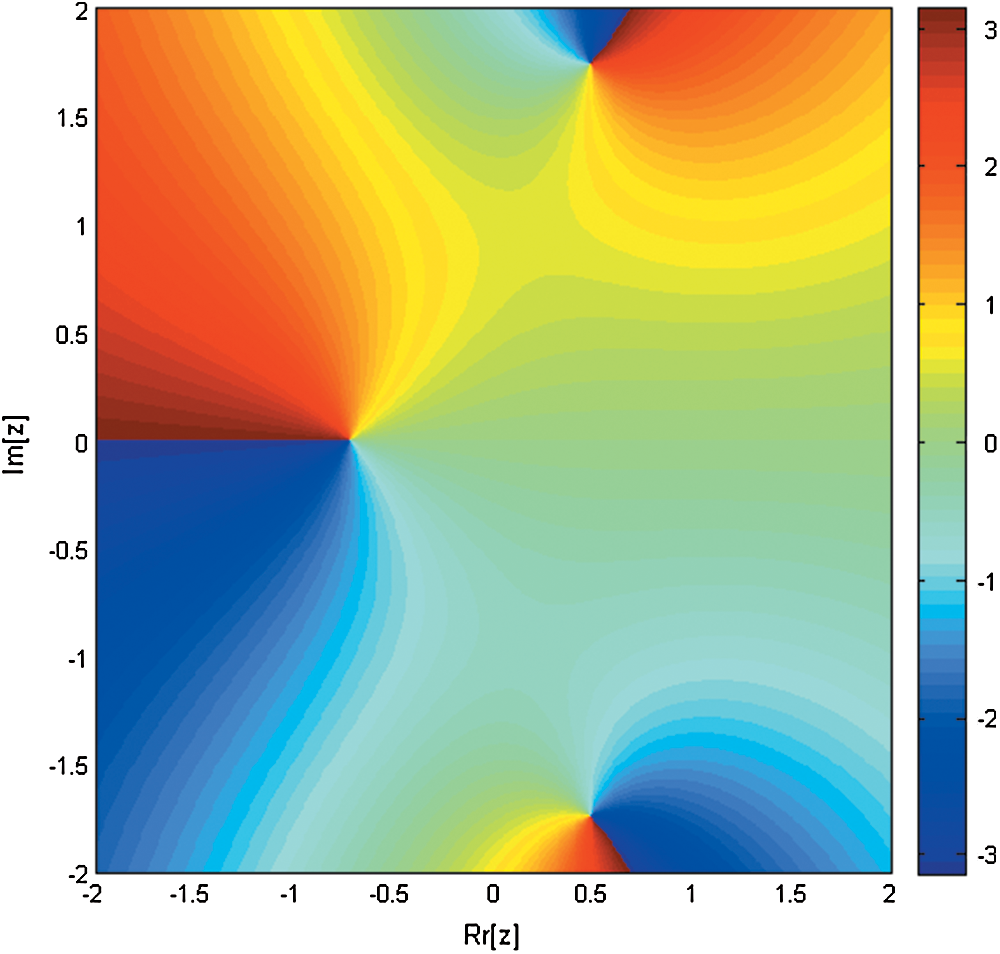
Figure 7: Basin of attraction of iterative method SIM1 for non-linear equation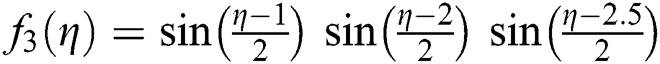 
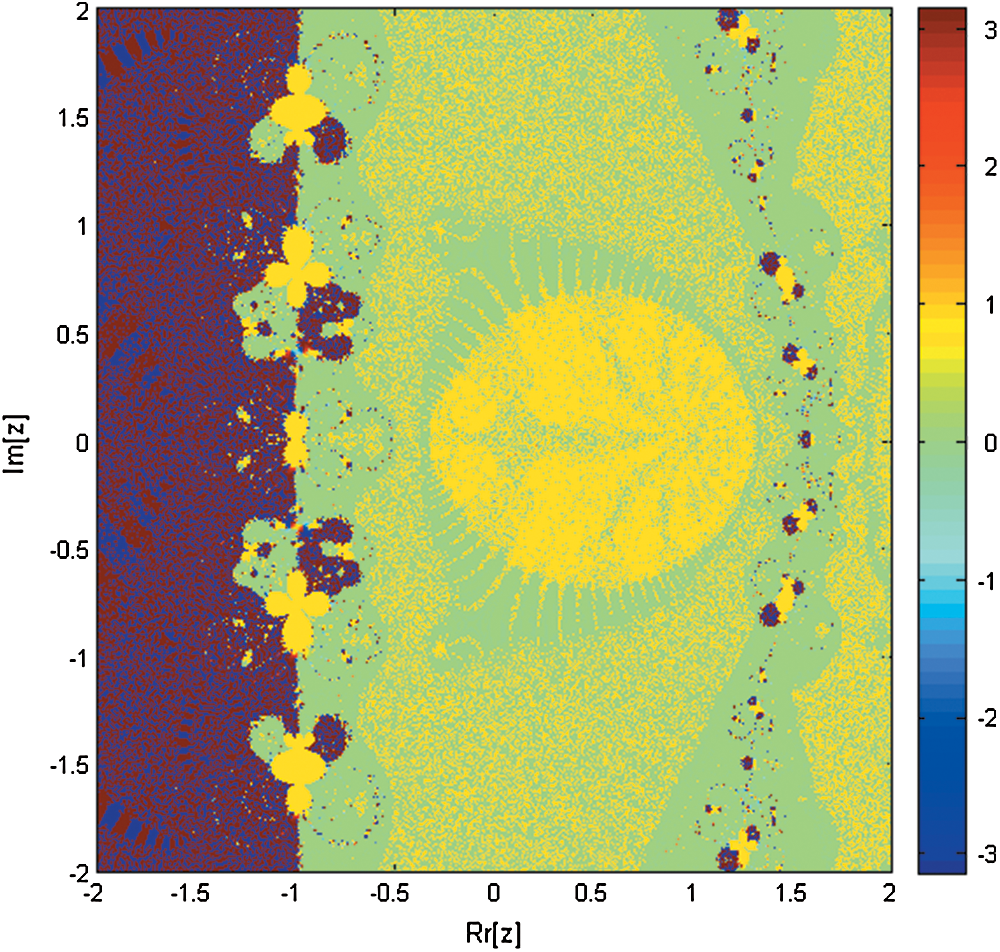
Figure 8: Basin of attraction of iterative method KF for non-linear equation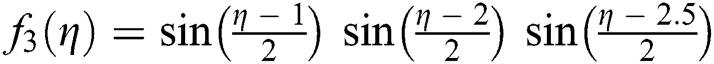 
Here, some numerical test examples are considered in order to show the performance of simultaneous ninth order derivative free method SIM1. We compare our method with [14] method (SPJ1) of convergence order ten for distinct roots. All the numerical calculations are done by using Maple 18 with 64 digits floating point arithmetic. We take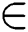 
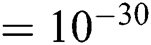as tolerance and use as a stopping criteria.
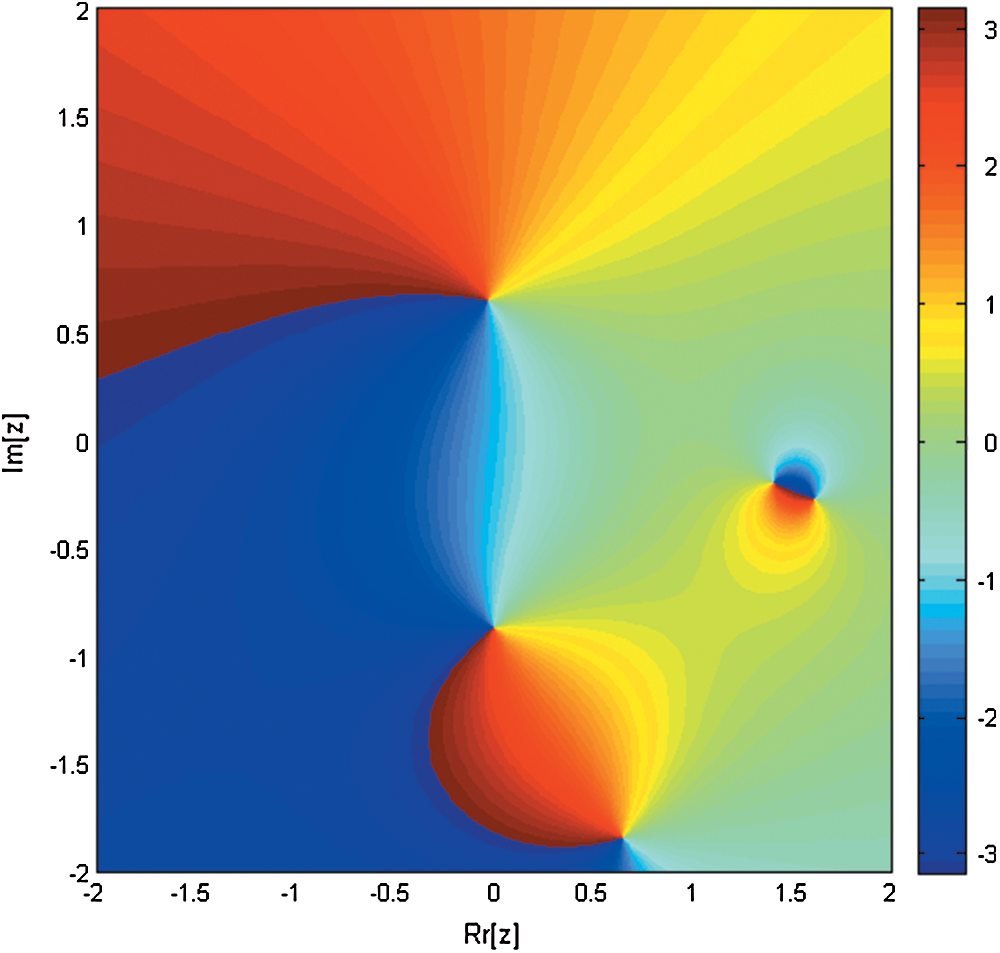
Figure 9: Basin of attraction of iterative method SPJ1 for non-linear equation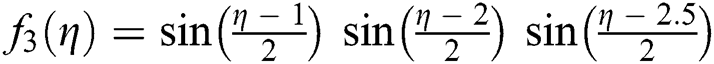 
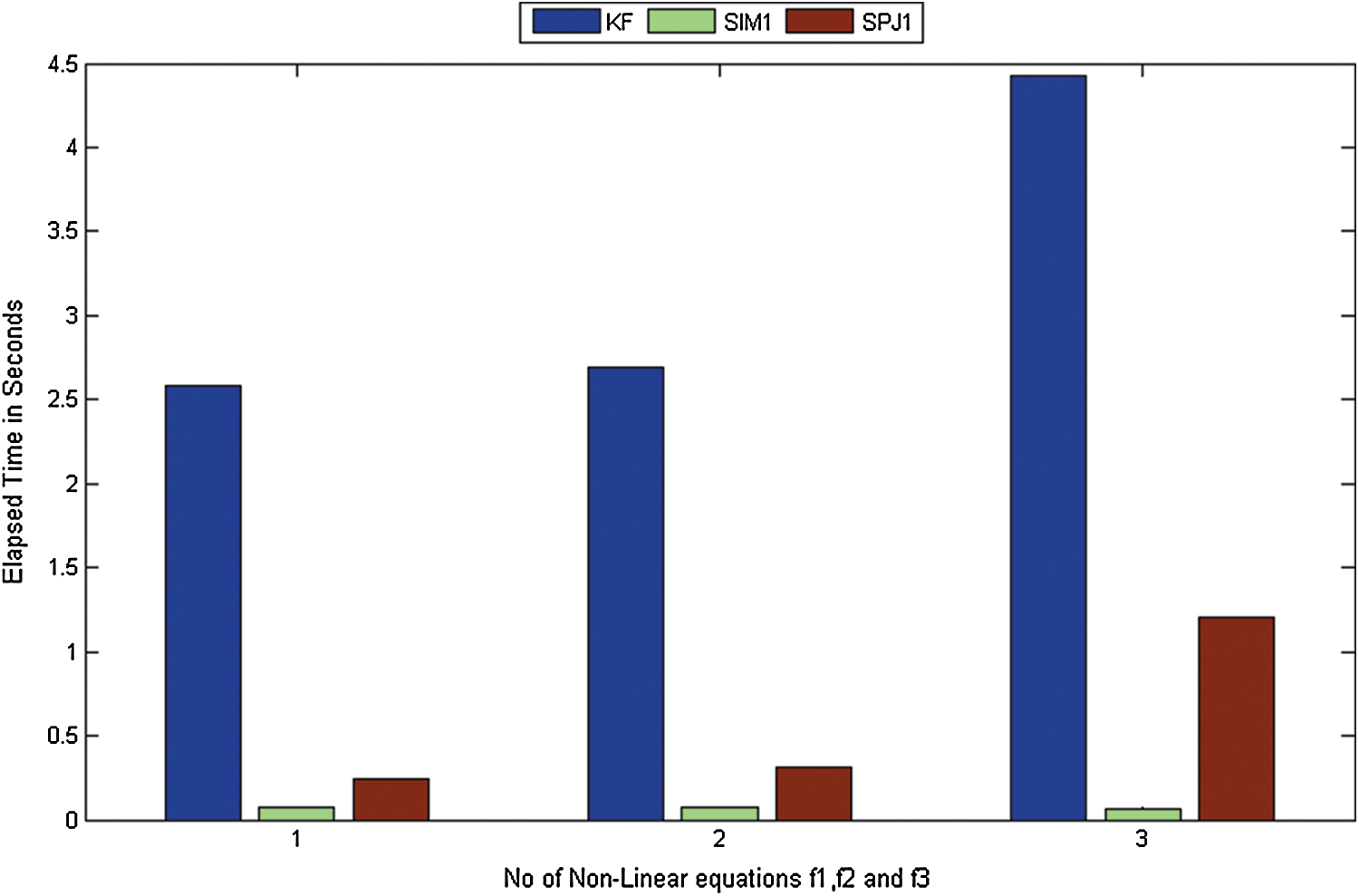
Figure 10: Elapsed time of iterative methods SIM1, KF, SPJ1 in seconds for non-linear function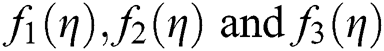 
respectively
Table 1: The number of basic arithmetic operations
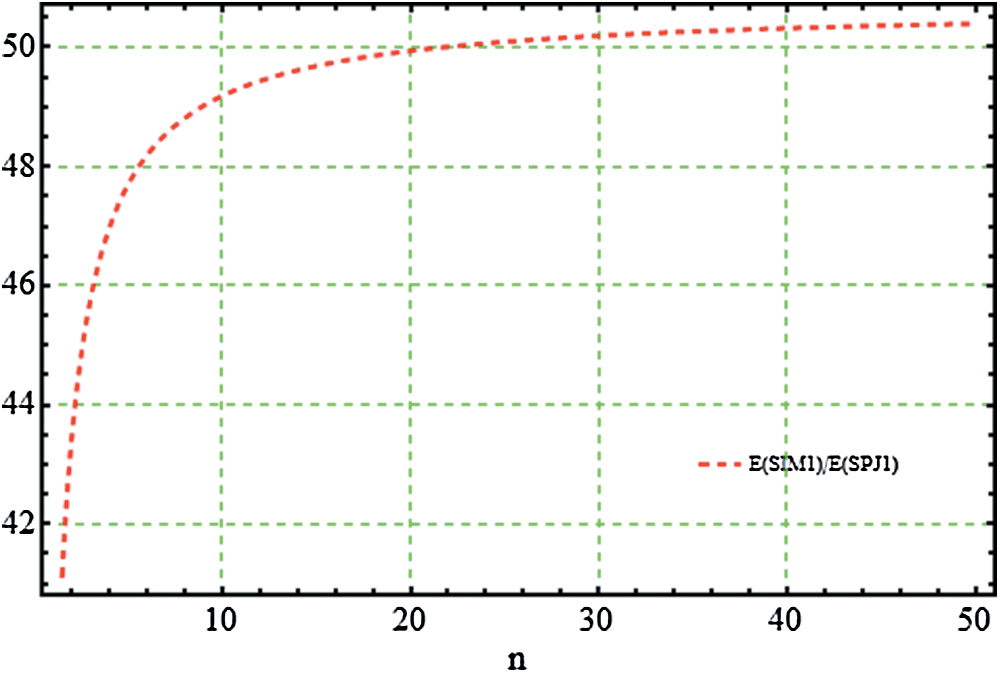
Figure 11: Computation efficiency of SIM1 w.r.t. SPJ1
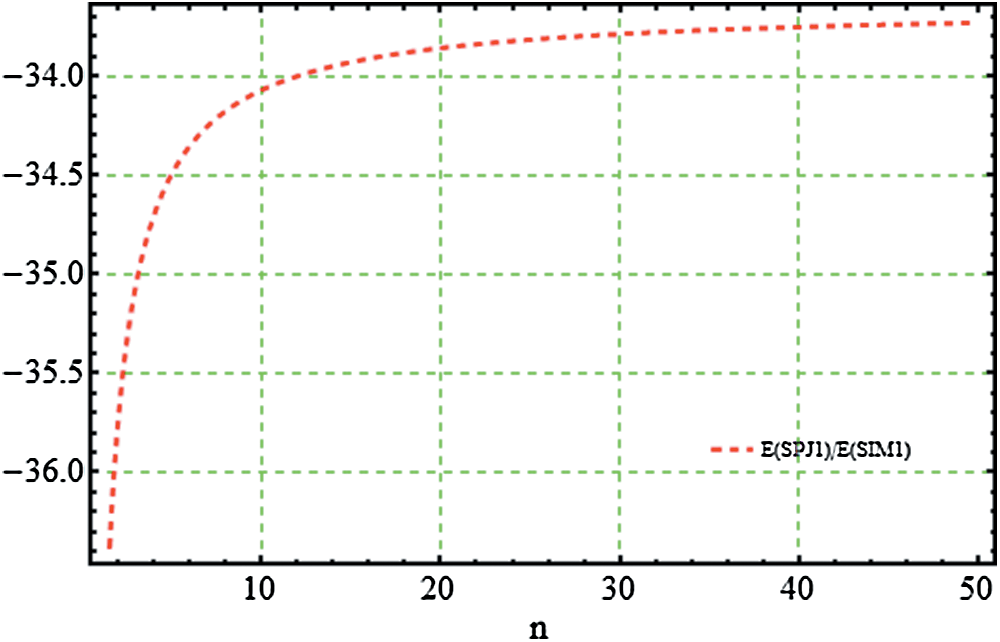
Figure 12: Computation efficiency of SPJ1 w.r.t. SIM1
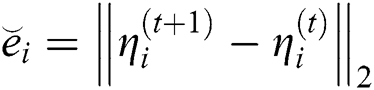
Tests examples from [16–18] are provided in Tabs. 2–3. In all Tables, CO denotes the order of convergence, 
, parameter valued in SIM1, 
the number of iterations and 
, execution time in seconds. Figs. 13–16, show that residue fall of the methods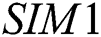 
and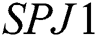 
for the numerical test examples 
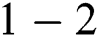, shows that method 
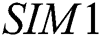is more efficient as compared to 
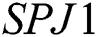. We observe that numerical results of the method 
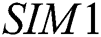are comparable with 
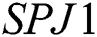method on same number of iteration.
Table 2: Simultaneous determination of all roots f4 η
Table 3: Simultaneous determination of all roots f5 η
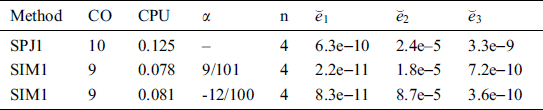
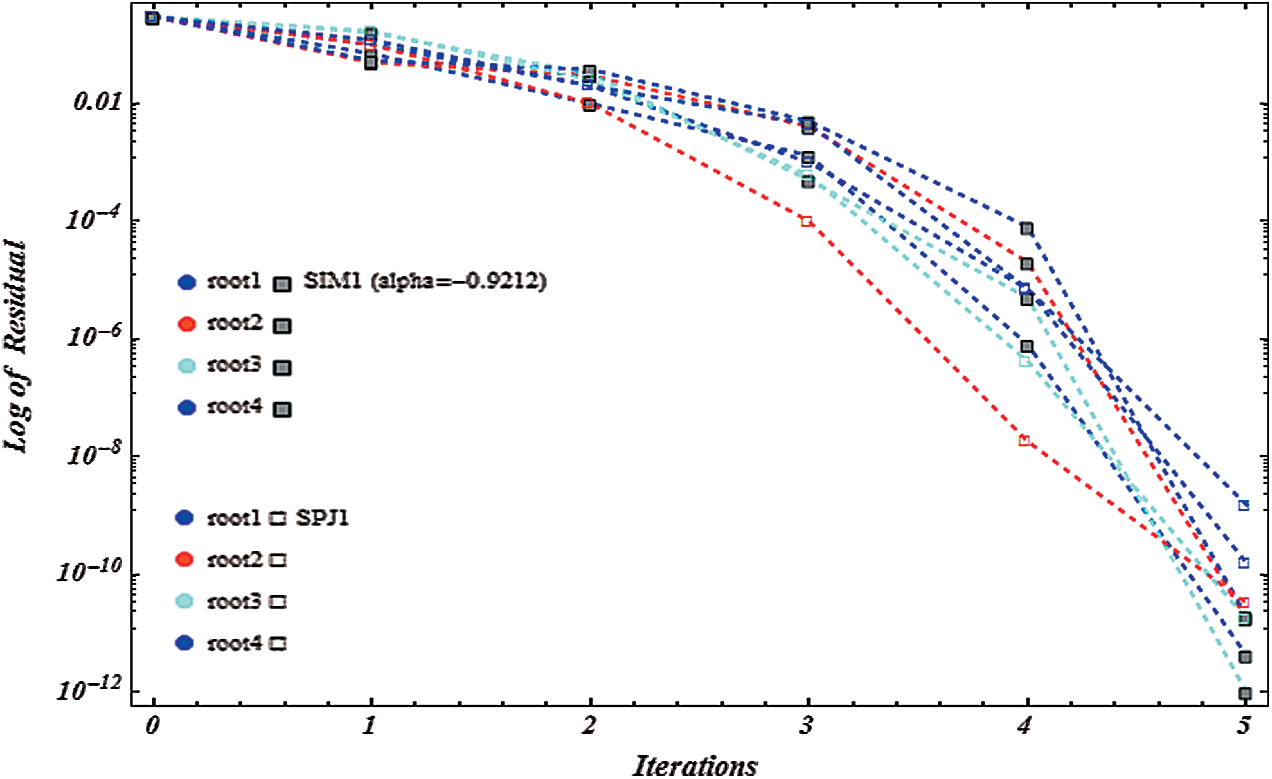
Figure 13: Shows residual graph of SIM1 
and SPJ1 for non-linear function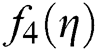 
Figure 14: Shows residual graph of SIM1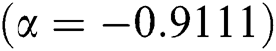 
and SPJ1 for non-linear function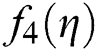 
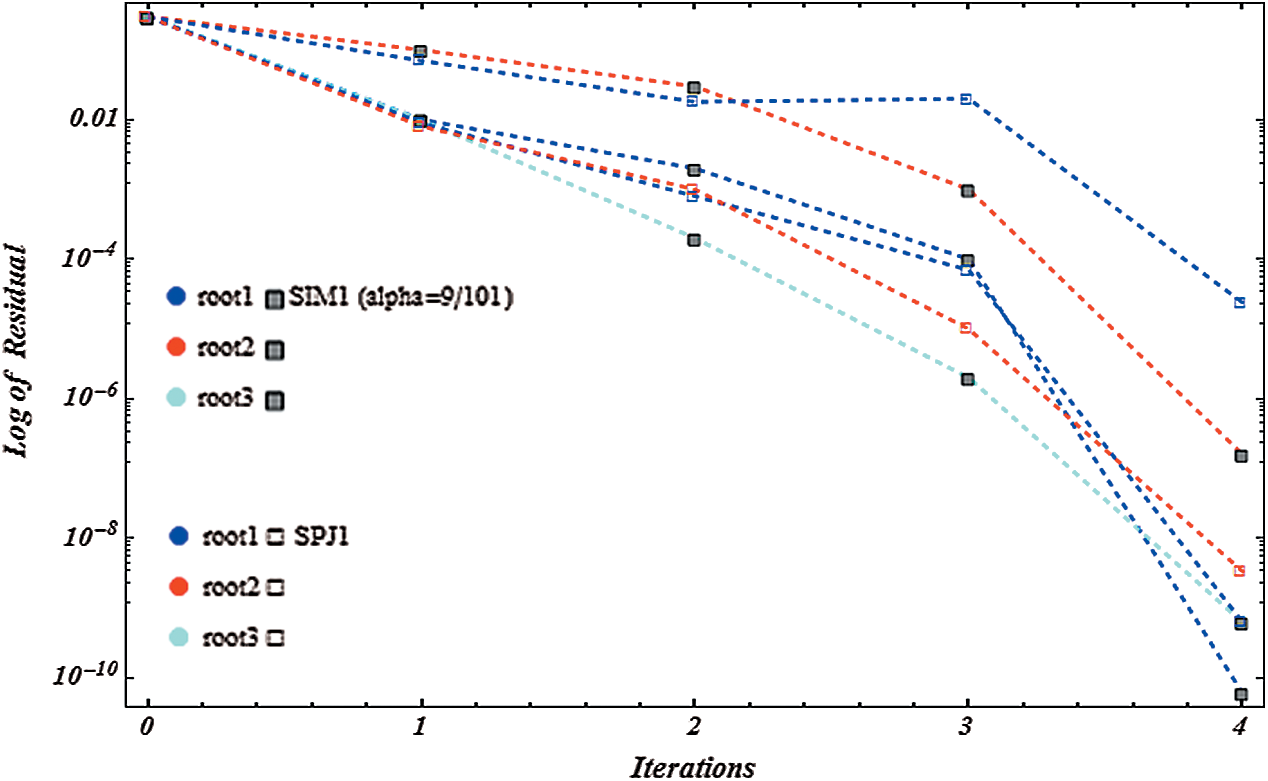
Figure 15: Shows residual graph of SIM1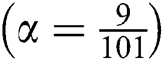 
and SPJ1 for non-linear function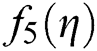 
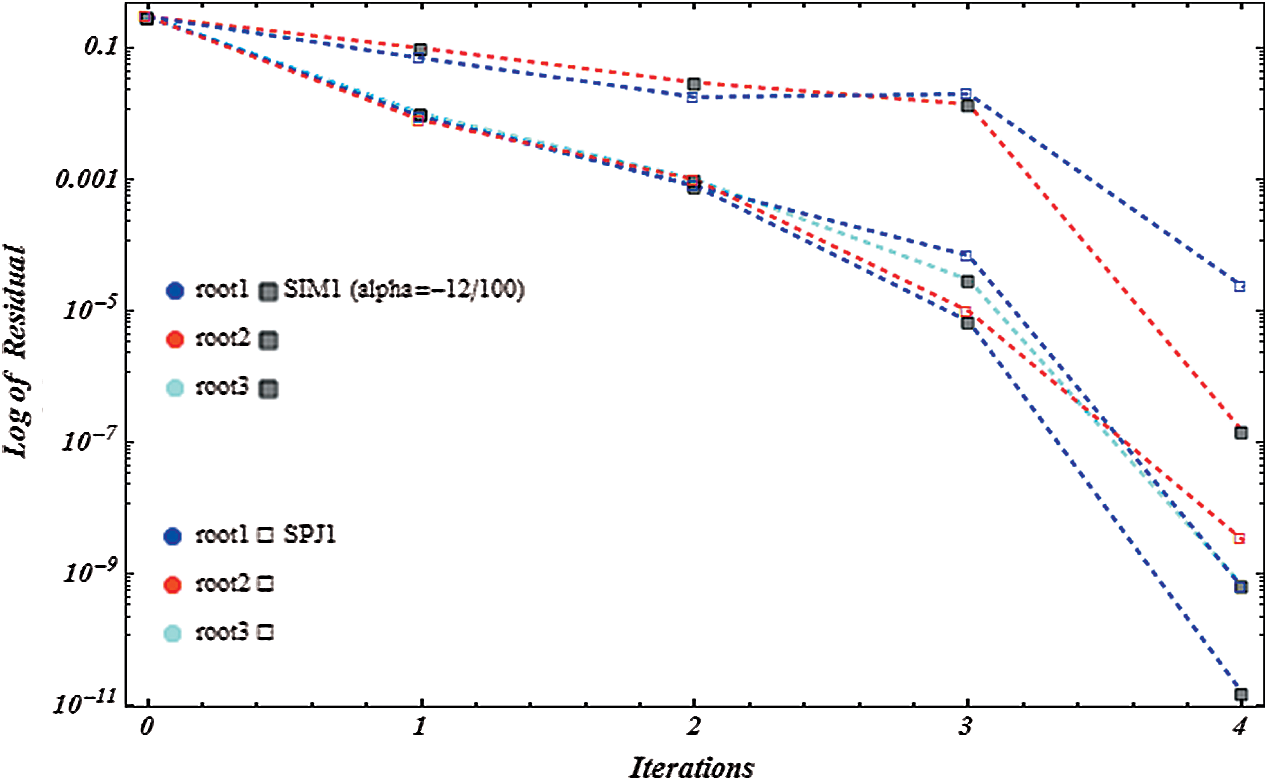
Figure 16: Shows residual graph of SIM1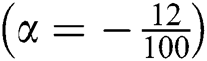 
and SPJ1 for non-linear function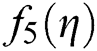 
We also calculate the CPU execution time, as all the calculations are done using Maple 18 on (Processor Intel(R) Core(TM) i3-3110m CPU@2.4 GHz with 64-bit Operating System). We observe from Tables that CPU time of the methods SIM1 is comparable or better than method SPJ1, showing the efficiency of our family of derivative free methods SIM1 as compared to them.
Algorithm for simultaneous iterative method
Step 1: Given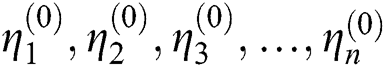 
for t = 0, such that
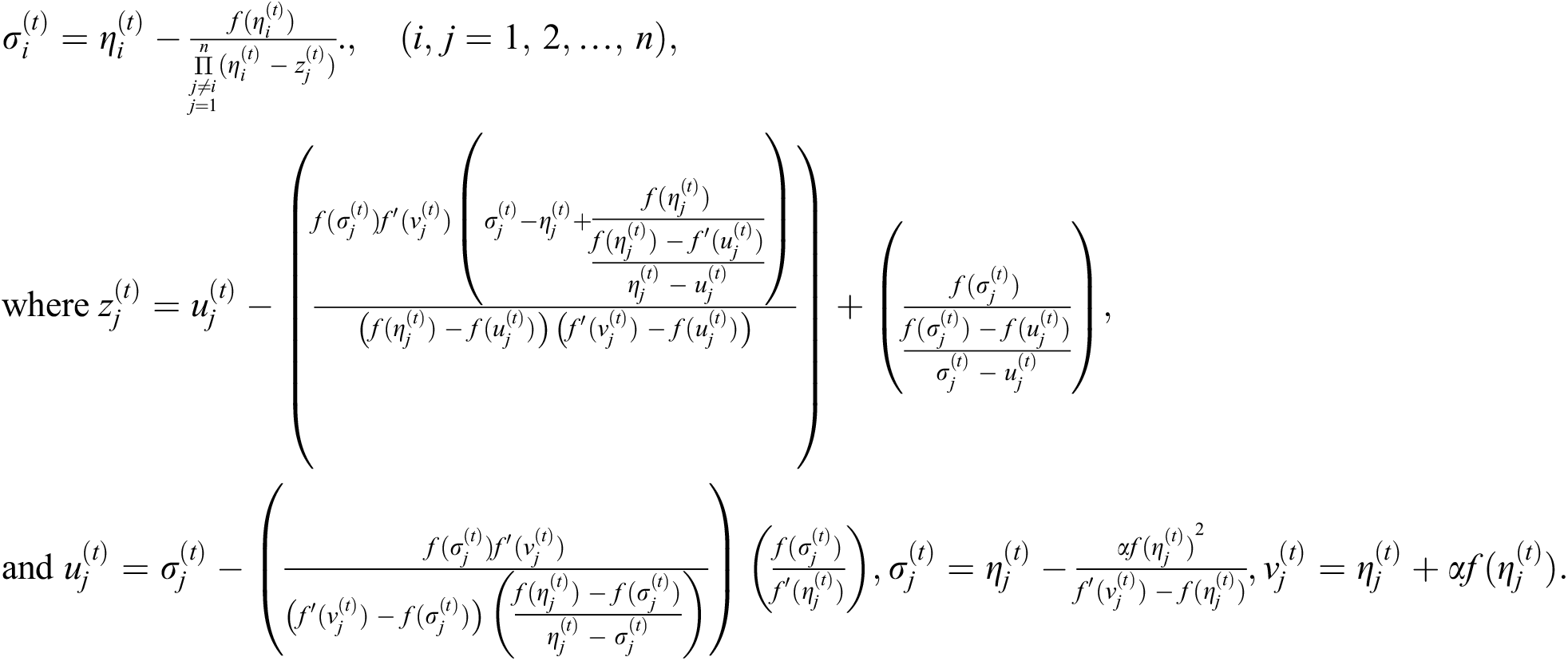
Step 2: Set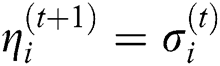 
Step 3: For a given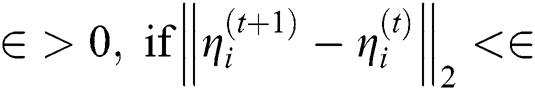 
, then stop.
Step 4: Set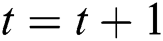 
and go to Step 1.
Example 1 [18]:
Consider
with exact roots:
The initial estimates have been taken as:
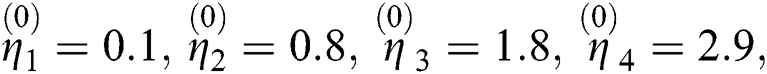
Example 2 [17]:
Consider
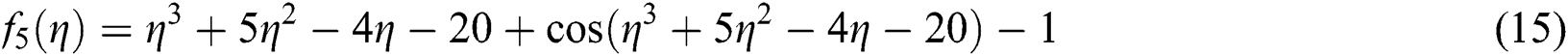
with exact roots are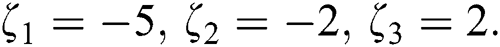 
The initial estimates have been taken as:
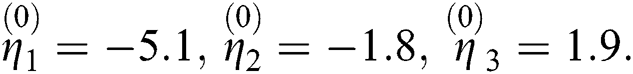
Example 3 [16]:
The acidity of a saturated solution of magnesium hydroxide in hydrochloric acid HCl is given by
for the hydronium ion concentration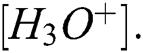 
If we set 
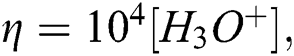we obtained the following non-linear equation
with exact roots are 
, 
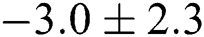up to one decimal places. The initial estimates have been taken as: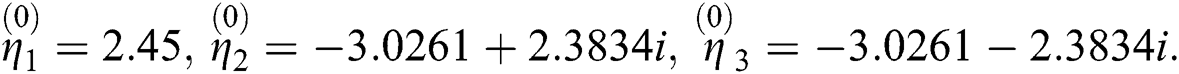 
Table 4: Simultaneous determination of all roots f6 η
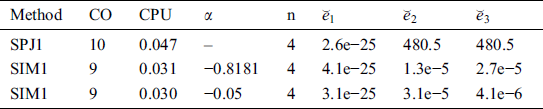
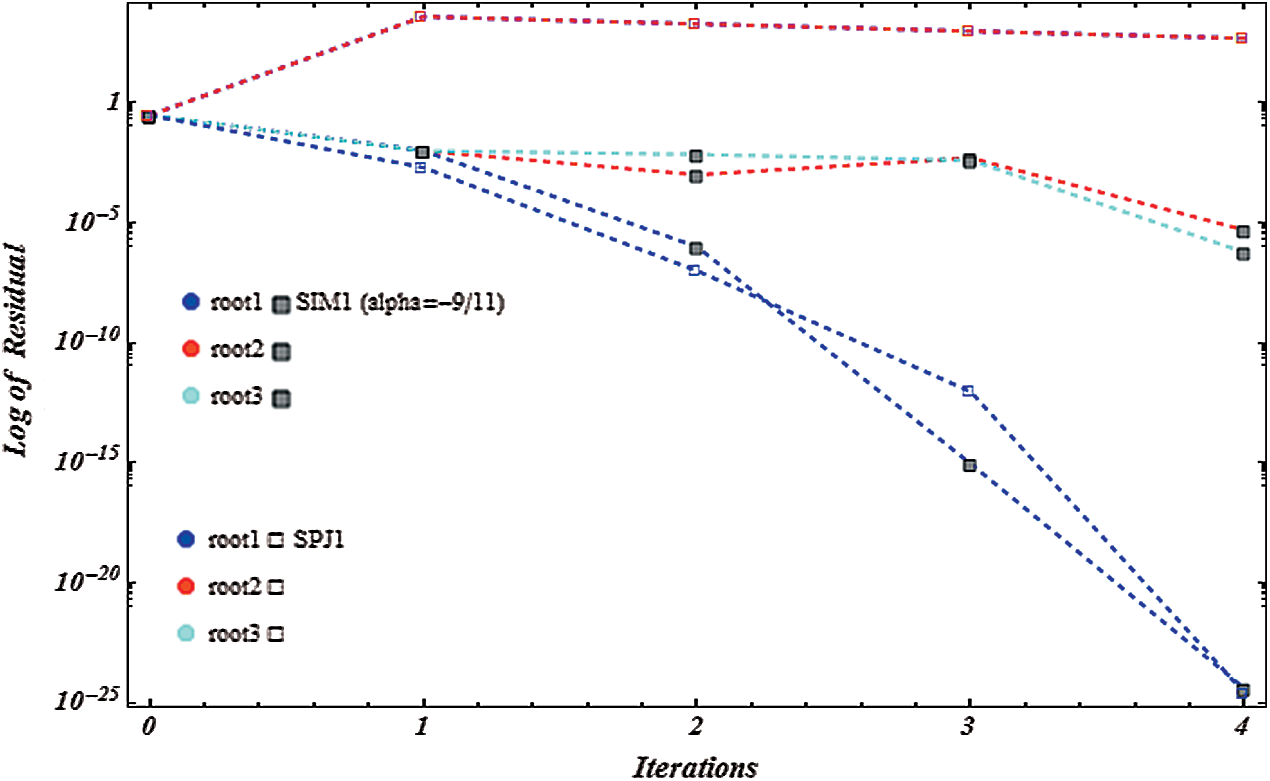
Figure 17: Shows residual graph of SIM1 
and SPJ1 for non-linear function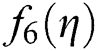 
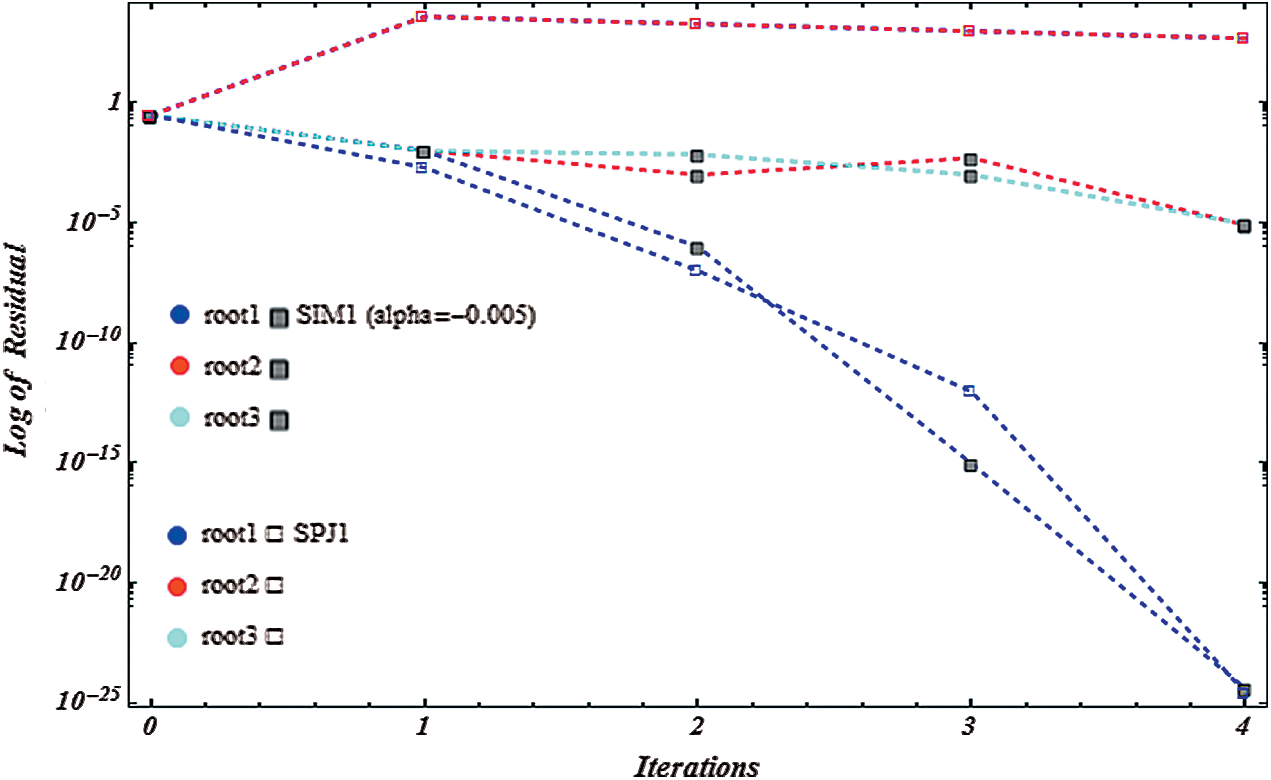
Figure 18: Shows residual graph of SIM1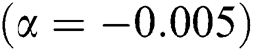 
and SPJ1 for non-linear function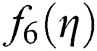 
We have developed here derivate free family of simultaneous methods of order nine for determining all the roots of non-linear equations. It must be pointed out that so far there exists derivative free method of order four only in the literature. We have made here comparison with method SPJ1 of order 10 involving derivative. The dynamical behavior/basins of attractions of our family of simultaneous methods SIM1 is also discussed here to show the global convergence. An example of single root finding derivative free method of order 8 of King–Traub is discussed to show that the single root finding methods may have divergence region. The computational efficiency of our method SIM1 is very large as compare to the method SPJ1 as given in Tabs. 2–4, which is also obvious from Figs. 11–12. We have made the numerical comparison with SPJ1 method. From Tabs. 2–4 and Figs. 1, 4, 7, 13–18, we observe that our numerical results are comparable or better in term of absolute error, number of iterations and CPU time and for log of residual graphs and lapsed time of dynamical planes.
Acknowledgement: The work is supported by the Natural Science Foundation of China (Grant Nos. 61673169, 11301127, 11701176, 11626101, and 11601485) and The Natural Science Foundation of Huzhou City (Grant No. 2018YZ07).
Funding Statement: The article processing charges (APC) will be paid by Natural Science Foundation and Natural Science Foundion of Huzhou City, China.
Confilcts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1P. D. Proinov and M. D. Petkova. (2014), “A new semilocal convergence theorem for the Weierstrass method for finding zeros of a polynomial simultaneously. ,” Journal of Complexity, vol. 30, no. (3), pp, 366–380,.
2F. I. Chicharro, A. Cordero, N. Garrido and J. R. Torregrosa. (2018), “Stability and applicability of iterative methods with memory. ,” Journal of Mathematical Chemistry, vol. 57, no. (5), pp, 1282–1300,. [Google Scholar]
3C. Chun and M. Y. Lee. (2013), “A new optimal eight-order family of iterative methods for the solution of nonlinear equations. ,” Applied Mathematics and Computation, vol. 223, pp, 506–519,. [Google Scholar]
4T. Lotfi, S. Sharifi, M. Salimi and S. Siegmund. (2015), “A new class of three-point methods with optimal convergence order eight and its dynamics. ,” Numerical Algorithms, vol. 68, no. (2), pp, 261–288,. [Google Scholar]
5V. K. Kyncheva, V. V. Yotov and S. I. Ivanov. (2017), “Convergence of Newton, Halley and Chebyshev iterative methods as methods for simultaneous determination of multiple polynomial zeros. ,” Applied Numerical Mathematics, vol. 112, pp, 146–154,. [Google Scholar]
6P. D. Proinov, S. I. Ivanov and M. S. Petkovi’c. (2019), “On the convergence of Gander’s type family of iterative methods for simultaneous approximation of polynomial zeros. ,” Applied Mathematics and Computation, vol. 349, pp, 168–183,.
7N. A. Mir, M. Shams, N. Rafiq, S. Akram and M. Rizwan. (2020), “Derivative free iterative simultaneous method for finding distinct roots of polynomial equation. ,” Alexandria Engineering Journal, vol. 59, no. (3), pp, 1629–1636,.
8N. A. Mir, R. Muneer and I. Jabeen. (2011), “Some families of two-step simultaneous methods for determining zeros of non-linear equations. ,” ISRN Applied Mathematics, vol. 2011, pp, 1–11,. [Google Scholar]
9F. Peng, Q. Long, Z. X. Lin and M. Long. (2019), “A reversible watermarking for authenticating 2D CAD engineering graphics based on iterative embedding and virtual coordinates. ,” Multimedia Tools and Applications, vol. 78, no. (19), pp, 26885–26905,. [Google Scholar]
10P. D. Proinov, S. I. Ivanov and M. S. Petkovi’c. (2019), “On the convergence of Gander’s type family of iterative methods for simultaneous approximation of polynomial zeros. ,” Applied Mathematics and Computation, vol. 349, pp, 168–183,. [Google Scholar]
11P. D. Proinov and S. I. Ivanov. (2015), “On the convergence of Halley’s method for multiple polynomial zeros. ,” Mediterranean Journal of Mathematics, vol. 12, no. (2), pp, 555–572,.
12F. Yu, L. Liu, L. Xiao, K. L. Li and S. Cai. (2019), “A robust and fixed-time zeroing neural dynamics for computing time-variant nonlinear equation using a novel nonlinear activation function. ,” Neurocomputing, vol. 350, pp, 108–116,.
13L. L. Zhou, F. Tan, F. Yu and W. Liu. (2019), “Cluster synchronization of two-layer nonlinearly couple multiplex networks with multi-links and time delays. ,” Neurocomputing, vol. 359, pp, 264–275,. [Google Scholar]
14M. S. Petkovic, L. D. Petkovic and J. Džunic. (2014), “On an efficient simultaneous method for finding polynomial zeros. ,” Applied Mathematics Letters, vol. 28, pp, 60–65,. [Google Scholar]
15F. Chicharro, A. Cordero, J. M. Gutierrez and J. R. Torregrosa. (2013), “Complex dynamics of derivative-free methods for nonlinear equations. ,” Applied Mathematics and Computation, vol. 219, no. (12), pp, 7023–7035,. [Google Scholar]
16S. C. Chapra. (2010), Applied Numerical Methods with MATLAB® for Engineers and Scientists. 6th Ed. New York: ,. [Google Scholar]
17M. R. Farmer. (2014), “Computing the zeros of polynomials using the divide and conquer approach. ,” Ph.D thesis. Department of Computer Science and Information Systems, Birkbeck, University of London,. [Google Scholar]
18G. H. Nedzhibov. (2013), “Iterative methods for simultaneous computing arbitrary number of multiple zeros of nonlinear equations. ,” International Journal of Computer Mathematics, vol. 90, no. (5), pp, 994–1007,. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |