DOI:10.32604/cmc.2020.012234

| Computers, Materials & Continua DOI:10.32604/cmc.2020.012234 |  |
| Article |
Numerical Treatment of MHD Flow of Casson Nanofluid via Convectively Heated Non-Linear Extending Surface with Viscous Dissipation and Suction/Injection Effects
1Department of Mathematics, Faculty of Science, Taif University, Taif, 888, Saudi Arabia
2Department of Mathematics, Faculty of Science, New Valley University, Al-Kharga, Al-Wadi Al-Gadid, 72511, Egypt
3Department of Mathematics, Faculty of Science, Northern Border University, Arar, 1321, Saudi Arabia
4Sohag Technical Industrial Institute, Ministry of Higher Education, Egyptian Technical College, Sohag, Egypt
*Corresponding Author: Hammad Alotaibi. Email: hm.alotaibi@tu.edu.sa
Received: 21 June 2020; Accepted: 06 July 2020
Abstract: This paper introduces the effect of heat absorption (generation) and suction (injection) on magnetohydrodynamic (MHD) boundary-layer flow of Casson nanofluid (CNF) via a non-linear stretching surface with the viscous dissipation in two dimensions. By utilizing the similarity transformations, the leading PDEs are transformed into a set of ODEs with adequate boundary conditions and then resolved numerically by (4–5)th-order Runge-Kutta Fehlberg procedure based on the shooting technique. Numerical computations are carried out by Maple 15 software. With the support of graphs, the impact of dimensionless control parameters on the nanoparticle concentration profiles, the temperature, and the flow velocity are studied. Other parameters of interest, such as the skin friction coefficient, heat, and mass transport at the diverse situation and dependency of various parameters are inspected through tables and graphs. Additionally, it is verified that the numerical computations with the reported earlier studies are in an excellent approval. It is found that the heat and mass transmit rates are enhanced with the increasing values of the power-index and the suction (blowing) parameter, whilst are reduced with the boosting Casson and the heat absorption (generation) parameters. Also, the drag force coefficient is an increasing function of the power-index and a reduction function of Casson parameter.
Keywords: Casson nanofluid; viscous dissipation; MHD; heat generation; suction/injection
Due to its large number of applications, the study of non-Newtonian fluids over an extending surface has attained great attention. In fact, the impacts of non-Newtonian behavior can be assessed by its elasticity, but their constitutive equations sometimes identify the rheological properties of the fluid. Provided the rheological parameters, the constitutive equations in the non-Newtonian fluids are more complex and thus giving rise to the complicated equations than the Navier–Stokes equations. Many of the liquids utilized in the oil sector, multiplex networks, cooling processes of micro-ships, open-flow switching, and simulating reservoirs are considerable non-Newtonian [1–5]. They show shear-dependent viscosity in different degrees. The concerted impacts of yield stress and boundary absorption on the flow of Casson fluid in a tube were checked by [6]. Casson fluid has special characteristics in the class of non-Newtonian fluids, which are commonly used in food manufacturing, metallurgy, drilling, and bio-engineering activities, etc. The definition of mixed convection stagnation-point flow of Casson fluid was proposed by [7] under the influence of convective boundary condition (CBC). Mukhopadhyay et al. [8] introduced the influence of the mass transfer in the presence of a chemical reaction on the MHD flow of the power-law fluids. Pramanik [9] explored the impact of the flow and heat transfer on Casson fluid’s boundary-layer flow ahead of an asymmetric wedge. Mahantha et al. [10] tested the boundary-layer movement of a non-Newtonian fluid in the existence of suction (blowing) at the interface followed by heat transmission to an exponentially expanding plate. Khalid et al. [11] decided to the study of CBC mechanism for 3D hydro-magnetic flow of CNF and Casson fluid induced by linear and nonlinear elongating surfaces. Whereas, MHD Casson fluid of the time-dependent natural convection flowing over a movable vertical surface in a porous medium was observed by [12]. Nadeem et al. [13] inspected the effect of the magnetic parameter on CNF over a non-linearly extending plate.
A large number of examinations on the boundary-layer flow of CNF with various geometries have been carried out in recent years. The analytical solution of CNF in the existence of CBC results in the expanding surface was scrutinized by [14]. Wahiduzzaman et al. [15] deliberated the steady laminar flowing and heat transport of a CNF through a non-linearly expanding vertical cylinder numerically. Sulochana et al. [16] presented a computational problem of the boundary-layer flow over a non-isothermal porous surface of the 3D Casson fluid. The numerical computations of the radiation and the viscous dissipation impacts utilizing CBC for the issue of MHD Casson fluid of 3D flow via an elongating plate in a porous substance with a chemical reaction were intended by [17]. Khalid et al. [18] explored the influence of the magnetic field and the heat supply on a CNF steady flow and heat transmit over an exponentially expanding cylinder over its radial path. Besthapu et al. [19] tested in a porous substance with wall temperature, MHD time-dependent Casson fluid running over a vertical surface. Imtiaz et al. [20] probed CNF mixed convection magneto flow via a non-linear permeable extending plate with the viscous dissipation. Oyelakin et al. [21] looked at the CNF mixed convective flow created by an expanding cylinder under the impact of CBC. Afify [22] analyzed numerically, by using the spectral relaxation process, the impacts of radiation, heat source, and the concerted effect of the Soret and Dufour numbers on the Casson nanofluid via a time-dependent stretchable plate. Ibrahim et al. [23] numerically examined the effects of a chemical reactive flow and a viscous dissipation on CNF and heat transmission across an expanding area. Shah et al. [24] researched CNF mixed convective flowing with the chemically reactive species and heat source. Some neoteric researches related to a study of CNF flow can be found in [25–28].
All of the above studies are related to the examination of the influences of fluid motions over the diverse surfaces in Newtonian and non-Newtonian types. However, numerous studies have been performed to explore different types of flow and thermal impacts of nanofluid flow over various forms of surfaces. Eid et al. [29] investigated the analytical problem of 3D Oldroyd-B magneto nanofluid flow past an extending surface with CBC. Eid et al. [30] debated the concerted impacts of the magnetic field and the heat source (sink) on time-dependent convective heat and mass transmission past a permeable expanding wall of a power-law nanofluid. The heat transfer features of gold-based nanofluid flowing past a power-law expanding sheet were addressed by [31]. Eid et al. [32] inspected the impacts of the slip and heat source (sink) on the unsteady stagnation point flow and heat transport of a nanofluid over an extending plate in a porous material. Eid et al. [33] addressed the steady Sisko nanofluid flow and heat transport past a non-linearly expanding plate with the heat generation (absorption) in a porous material. With the suction (injection) and the radiation, Hady et al. [34] checked the impact of the magnetic parameter on the two-phase Carreau nanofluid via a permeable non-linearly expanding plate. More related works in relation to these elements can be found in [35–45].
The goal of the current research is to present an inclusive numerical analysis of the impact of the heat absorption (generation) and the suction (blowing) on 2D Casson nanofluid hydro-magneto flow past a non-linear extending plate with the viscous dissipation. Consideration is granted to CBC on temperature. Similar solutions are implemented to transform nonlinear PDEs into ODEs. The outcomes are obtain by using the technique of Runge-Kutta Fehlberg of (4–5)th-order (RFK4-5). Embedded parameter behaviors are accentuated through graphical and tabular results.
Consider MHD CNF flow in the region 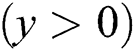 over an exponentially extendable surface as 2D viscous, steady, and incompressible with the influence of the viscous dissipation and the heat source (sink). The Cartesian coordinates
over an exponentially extendable surface as 2D viscous, steady, and incompressible with the influence of the viscous dissipation and the heat source (sink). The Cartesian coordinates 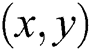 select wherein the
select wherein the 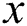 -axis of the surface is measured while the
-axis of the surface is measured while the 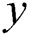 -axis is perpendicular to it. The extendable sheet is expected to have a global velocity profile of the power-law
-axis is perpendicular to it. The extendable sheet is expected to have a global velocity profile of the power-law 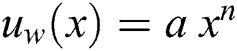 where
where 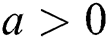 ,
, 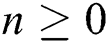 are constants. The action of the magnetic field is subjected to varying strength
are constants. The action of the magnetic field is subjected to varying strength 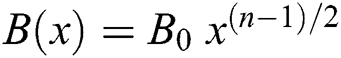 . There is no electrical field, but the induced magnetic field is ignored by the weak magnetic number of Reynolds. The temperature of the surface is designated by a relation
. There is no electrical field, but the induced magnetic field is ignored by the weak magnetic number of Reynolds. The temperature of the surface is designated by a relation 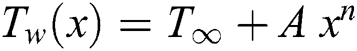 where
where  is a fixed value,
is a fixed value, 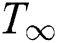 is the free stream temperature and
is the free stream temperature and 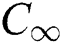 is the ambient nanoparticles concentration. The flow model and coordinate scheme are shown in Fig. 1.
is the ambient nanoparticles concentration. The flow model and coordinate scheme are shown in Fig. 1.
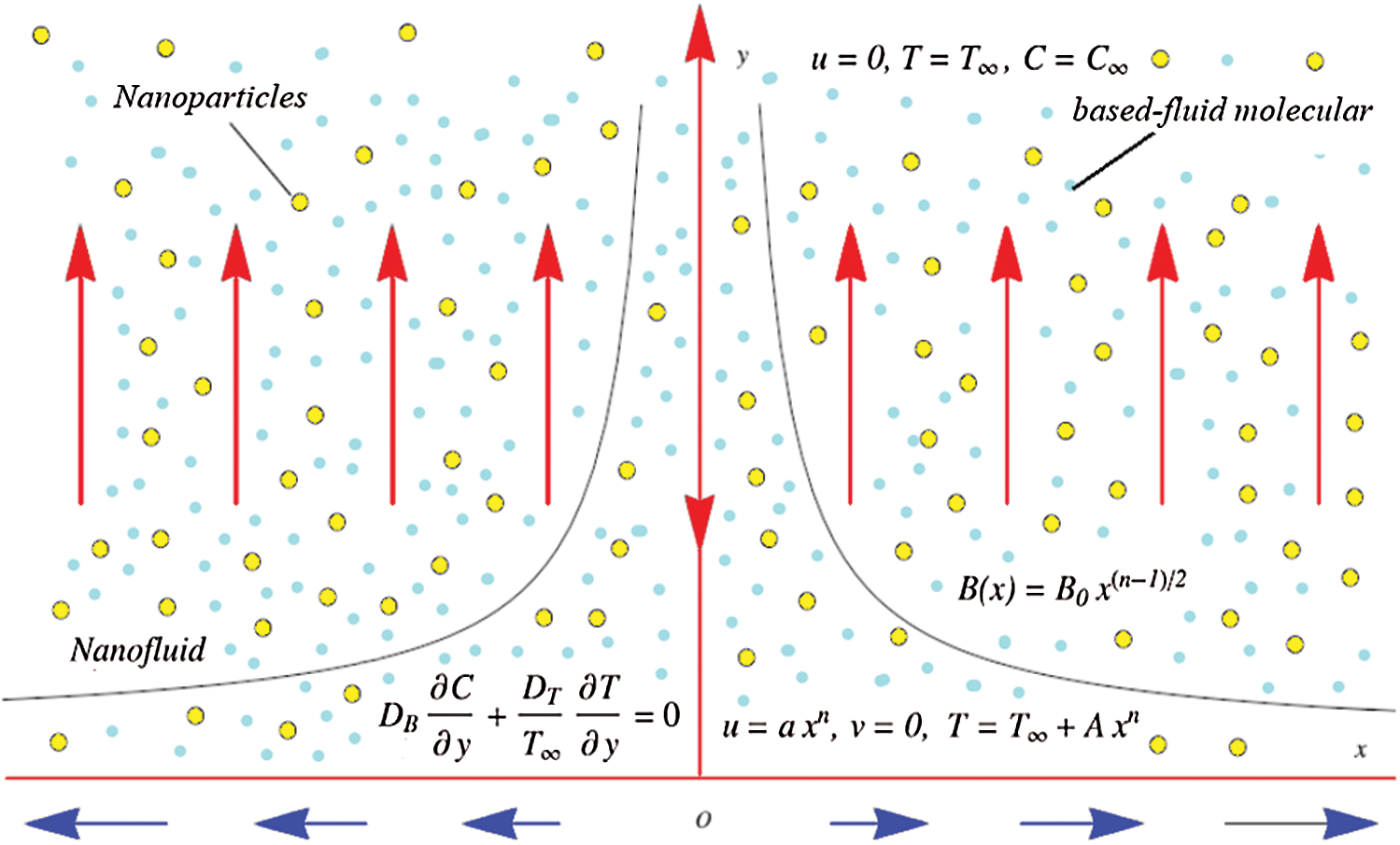
Figure 1: Geometry of flow scheme
The rheological state equation for a Casson fluid isotropic fluid is [13,15]:

where 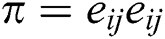 and
and 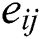 symbols for the
symbols for the 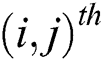 deformation component rate,
deformation component rate,  is the deformation component rate product,
is the deformation component rate product, 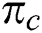 signifies to the non-Newtonian fluid critical value of this multiple,
signifies to the non-Newtonian fluid critical value of this multiple, 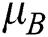 mentions to Casson fluid plastic viscosity and
mentions to Casson fluid plastic viscosity and 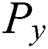 the fluid yield stress. Let us consider the components of velocity
the fluid yield stress. Let us consider the components of velocity 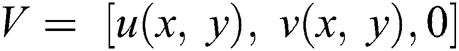 , the temperature relation
, the temperature relation 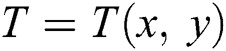 and nanoparticle concentration
and nanoparticle concentration 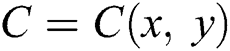 . The momentum, temperature and the concentration equations in a Casson nanofluid following above-mentioned conditions are written as
. The momentum, temperature and the concentration equations in a Casson nanofluid following above-mentioned conditions are written as


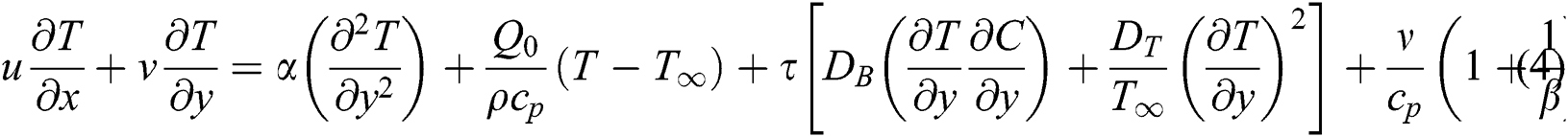

where 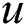 and
and 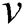 are the components of velocity over the
are the components of velocity over the 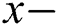 and
and 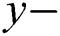 coordinates respectively,
coordinates respectively, 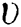 is the kinematic viscosity,
is the kinematic viscosity, 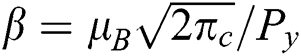 is the parameter of Casson,
is the parameter of Casson, 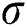 is the conductivity electrical field,
is the conductivity electrical field, 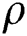 is the density, the thermal diffusivity is denoted by
is the density, the thermal diffusivity is denoted by 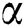 ,
,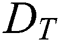 and
and 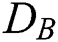 are the coefficients of the thermophoresis and Brownian diffusions,
are the coefficients of the thermophoresis and Brownian diffusions, 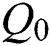 is the coefficient of the heat source (sink) in dimensional form,
is the coefficient of the heat source (sink) in dimensional form, 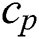 stands for the specific heat, and
stands for the specific heat, and  indicates the nanoparticle material’s ratio of the effective heat capacity to efficient liquid heat capacity. The related boundary-conditions of the current problem are
indicates the nanoparticle material’s ratio of the effective heat capacity to efficient liquid heat capacity. The related boundary-conditions of the current problem are
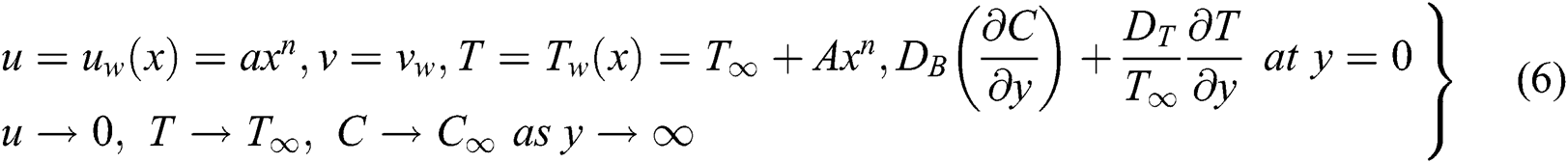
The system of Eqs. (2)–(5) and the concerning conditions (6) are non-dimensionalised by the following conversion
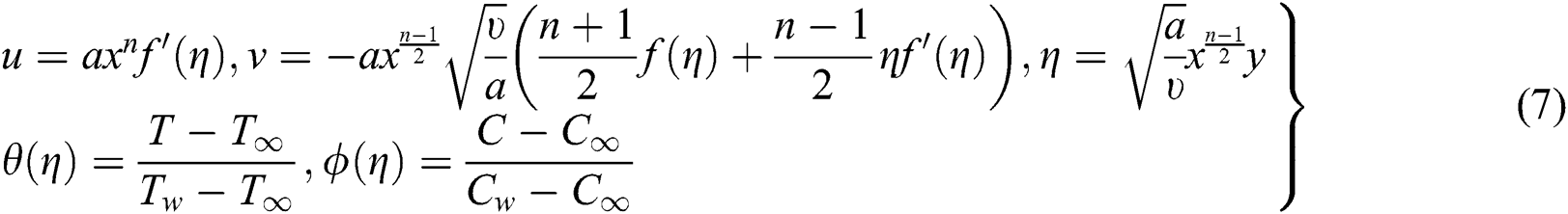
Eq. (2) is identically verified and Eqs. (3)–(6) converted to

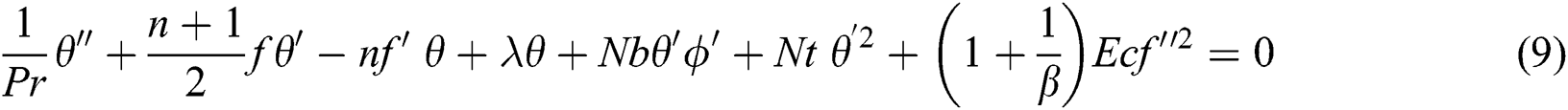

The related conditions are

In the overhead formulas 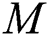 is the parameter of the magnetic field,
is the parameter of the magnetic field, 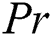 symbols to the number of Prandtl,
symbols to the number of Prandtl, 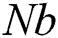 is the Brownian motion parameter,
is the Brownian motion parameter, 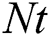 is the thermophoresis diffusion,
is the thermophoresis diffusion, 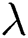 is the heat generation
is the heat generation 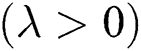 or absorption
or absorption 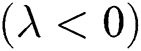 ,
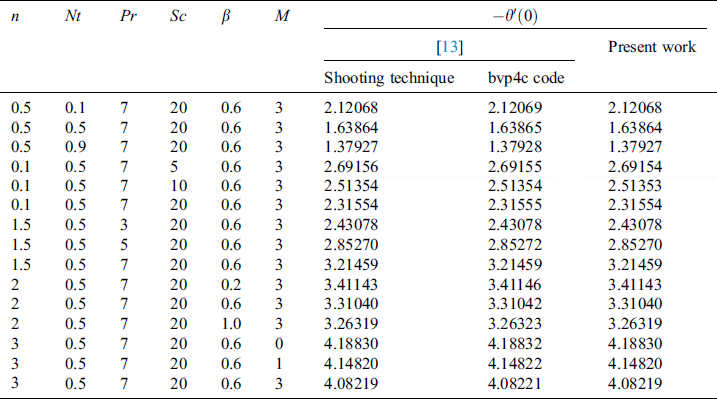
, 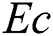 is Eckert number,
is Eckert number,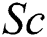 is the Schmidt number,
is the Schmidt number, 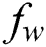 is the suction (blowing) parameter (
is the suction (blowing) parameter (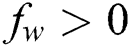 for suction and
for suction and 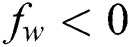 for blowing). These are defined as below:
for blowing). These are defined as below:

The amounts of practical attention include the drag force coefficient 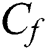 , local Nusselt
, local Nusselt 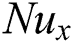 and local Sherwood
and local Sherwood 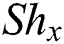 numbers, are known as follows:
numbers, are known as follows:
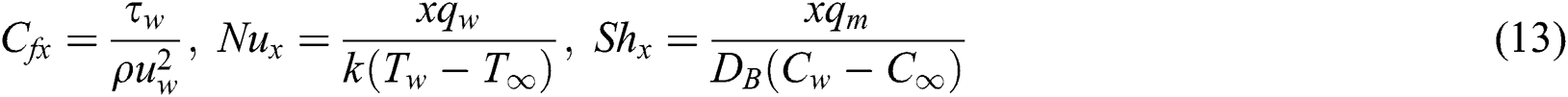
where 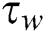 is the wall shear stress,
is the wall shear stress,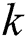 signalizes to the thermal nanofluid conductivity and
signalizes to the thermal nanofluid conductivity and 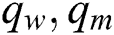 are the surface heat and mass flux, which are specified by
are the surface heat and mass flux, which are specified by
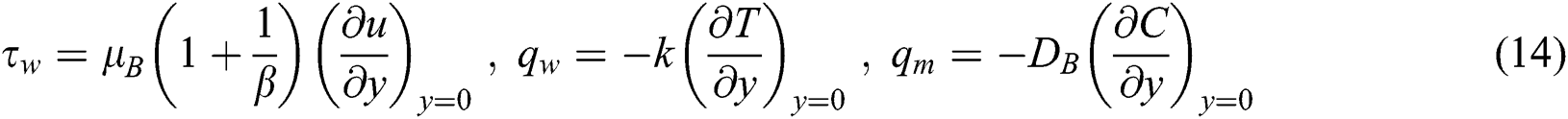
Substituting Eqs. (7) and (14) into Eq. (13), we obtain
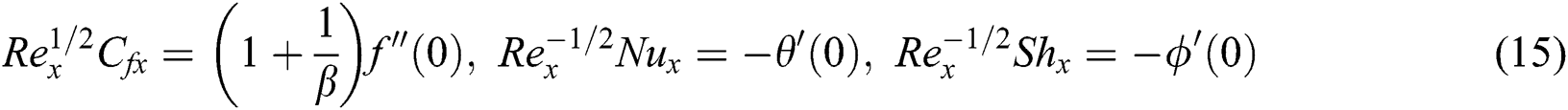
wherever 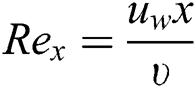 is the local Reynolds number.
is the local Reynolds number.
The effects of the different physical parameters values in order to have a physical understanding of the problem like, the magnetic 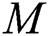 , suction (blowing)
, suction (blowing) 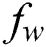 , Casson
, Casson 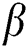 , Eckert number
, Eckert number 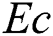 , heat source (sink) parameter
, heat source (sink) parameter 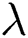 , thermophoretic diffusion
, thermophoretic diffusion 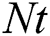 , Brownian diffusion
, Brownian diffusion 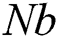 , the Prandtl number
, the Prandtl number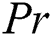 and power-law index
and power-law index 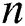 on the profiles of velocity
on the profiles of velocity  , temperature
, temperature 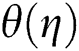 , the volume fraction
, the volume fraction 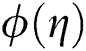 , drag force
, drag force 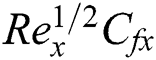 , local Nusselt
, local Nusselt 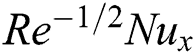 and local Sherwood
and local Sherwood 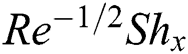 numbers are examined numerically and showed through Figs. 2–17. The validity of the developed code is checked for special cases to evaluate the accuracy of the current results with the previously published results of [13] for the rate of heat transfer at the plate
numbers are examined numerically and showed through Figs. 2–17. The validity of the developed code is checked for special cases to evaluate the accuracy of the current results with the previously published results of [13] for the rate of heat transfer at the plate 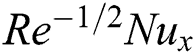 for different values of
for different values of  ,
, 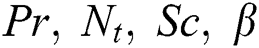 and
and 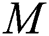 when
when 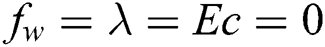 , and
, and 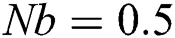 (Tab. 1) and established a very excellent accordance. This allows us to ensure our numerical findings. Figs. 2 and 3 depict the effects of magnetic parameter
(Tab. 1) and established a very excellent accordance. This allows us to ensure our numerical findings. Figs. 2 and 3 depict the effects of magnetic parameter 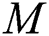 , suction (blowing)
, suction (blowing) 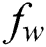 and Casson parameter
and Casson parameter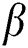 on velocity profile
on velocity profile 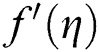 for other parameters fixed values. It is detected that the increment in
for other parameters fixed values. It is detected that the increment in 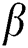 increases the fluid viscosity due to applied stress that at the latest decelerates the flow of a nanofluid along the
increases the fluid viscosity due to applied stress that at the latest decelerates the flow of a nanofluid along the 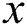 -direction. Therefore, the velocity of flow and the thickness of momentum-layer are reduced. Similar result is shown in Fig. 2 when the parameter of the magnetic M increases. Physically, the impact of the magnetic value
-direction. Therefore, the velocity of flow and the thickness of momentum-layer are reduced. Similar result is shown in Fig. 2 when the parameter of the magnetic M increases. Physically, the impact of the magnetic value 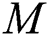 rises due to the Lorentz forces become a stronger along the direction perpendicular to
rises due to the Lorentz forces become a stronger along the direction perpendicular to  -axis that offers more resistance in the fluid flows as a result in the velocity profile is reduced. It is noted that the flow velocity of nanofluid is diminished with a rising different estimations of
-axis that offers more resistance in the fluid flows as a result in the velocity profile is reduced. It is noted that the flow velocity of nanofluid is diminished with a rising different estimations of 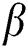 and M. Fig. 3 reveals the flow velocity of a nanofluid is reduced with an upsurge in
and M. Fig. 3 reveals the flow velocity of a nanofluid is reduced with an upsurge in 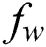 . Fig. 4 represents the influence of
. Fig. 4 represents the influence of 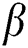 on the velocity for both taking values of
on the velocity for both taking values of 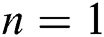 and
and 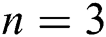 . It is seen that an upsurge in
. It is seen that an upsurge in 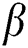 leads to a reduction in nanofluid movement. That velocity of Casson nanofluid when
leads to a reduction in nanofluid movement. That velocity of Casson nanofluid when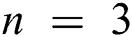 is greater than the Newtonian fluid when
is greater than the Newtonian fluid when 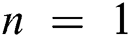 .
.
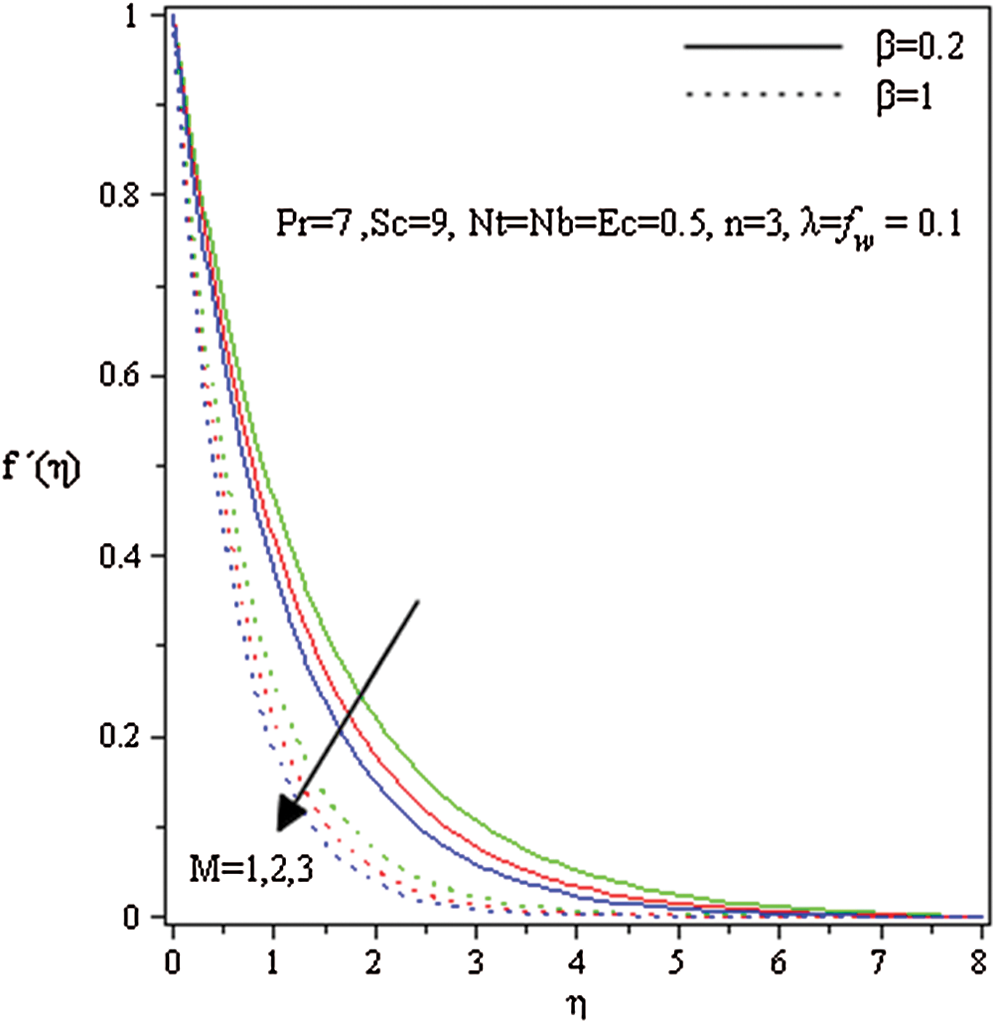
Figure 2: Influence of 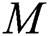 and
and 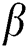 on
on 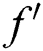
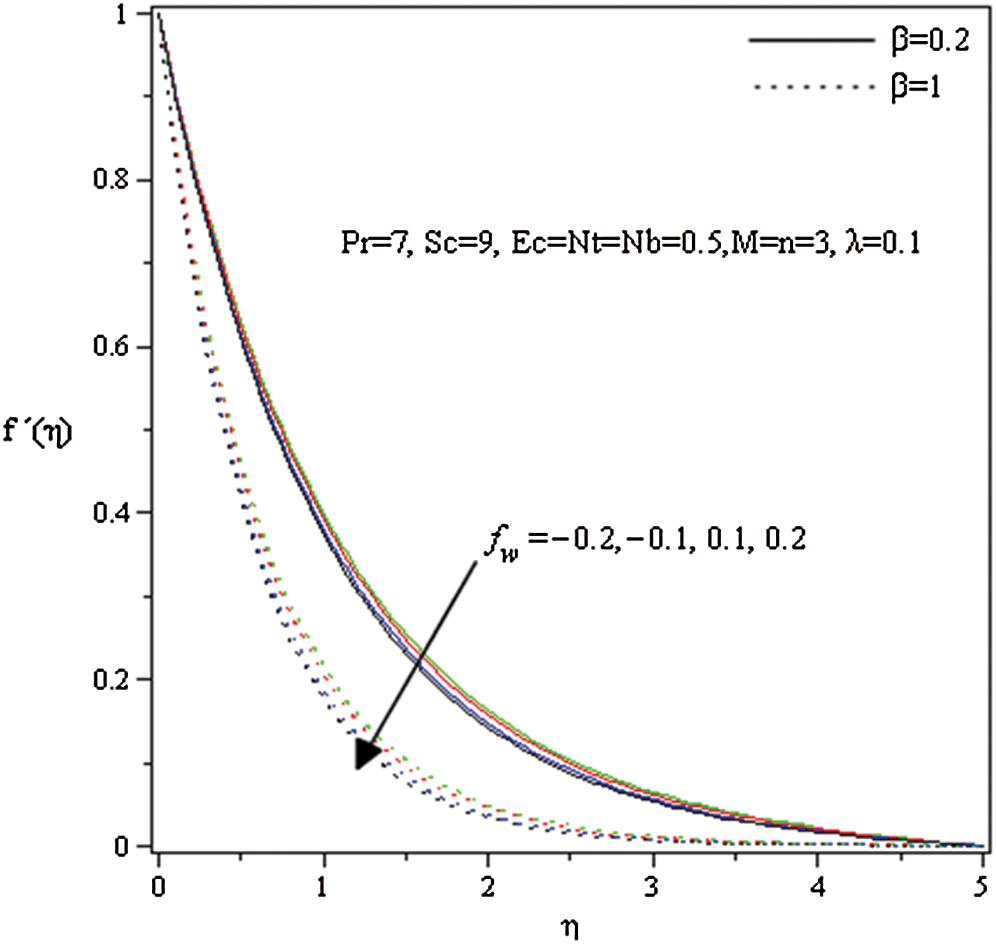
Figure 3: Influence of 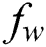 and
and 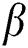 on
on 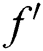
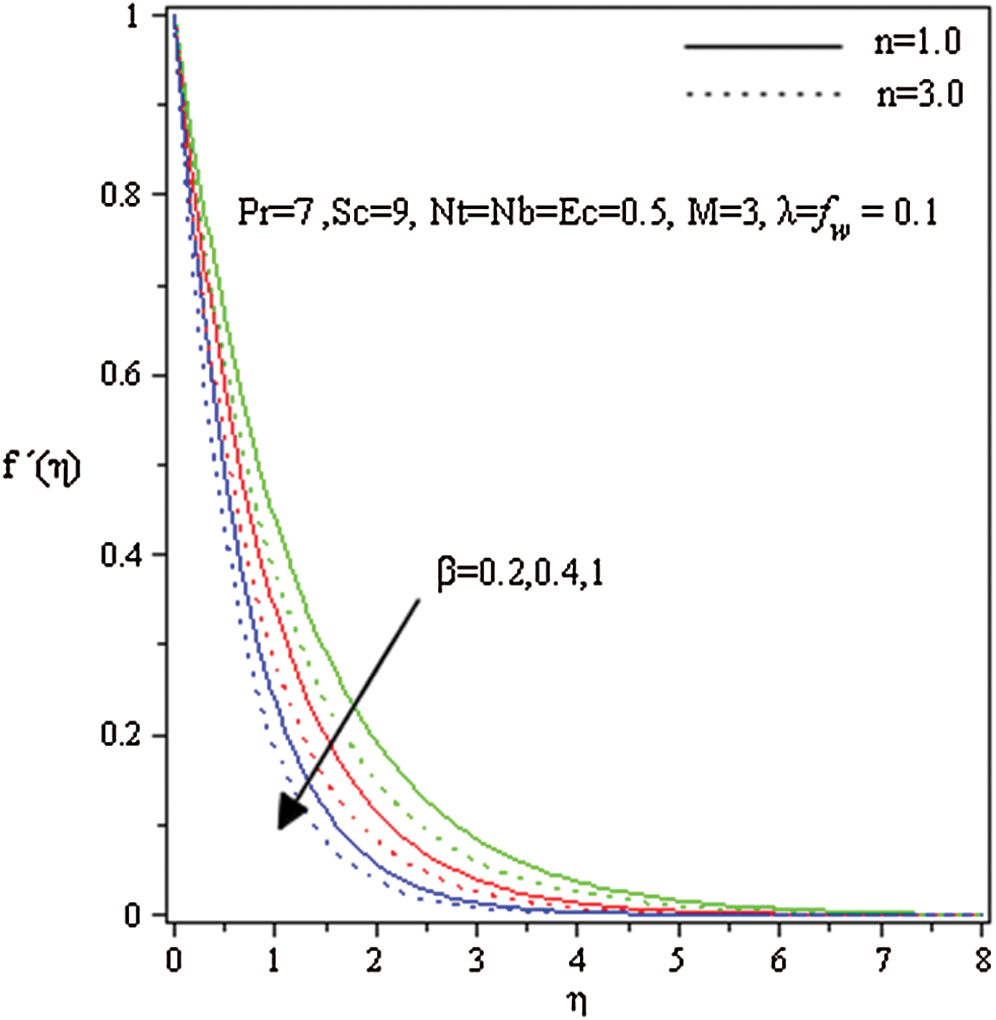
Figure 4: Influence of 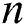 and
and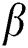 on
on 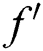
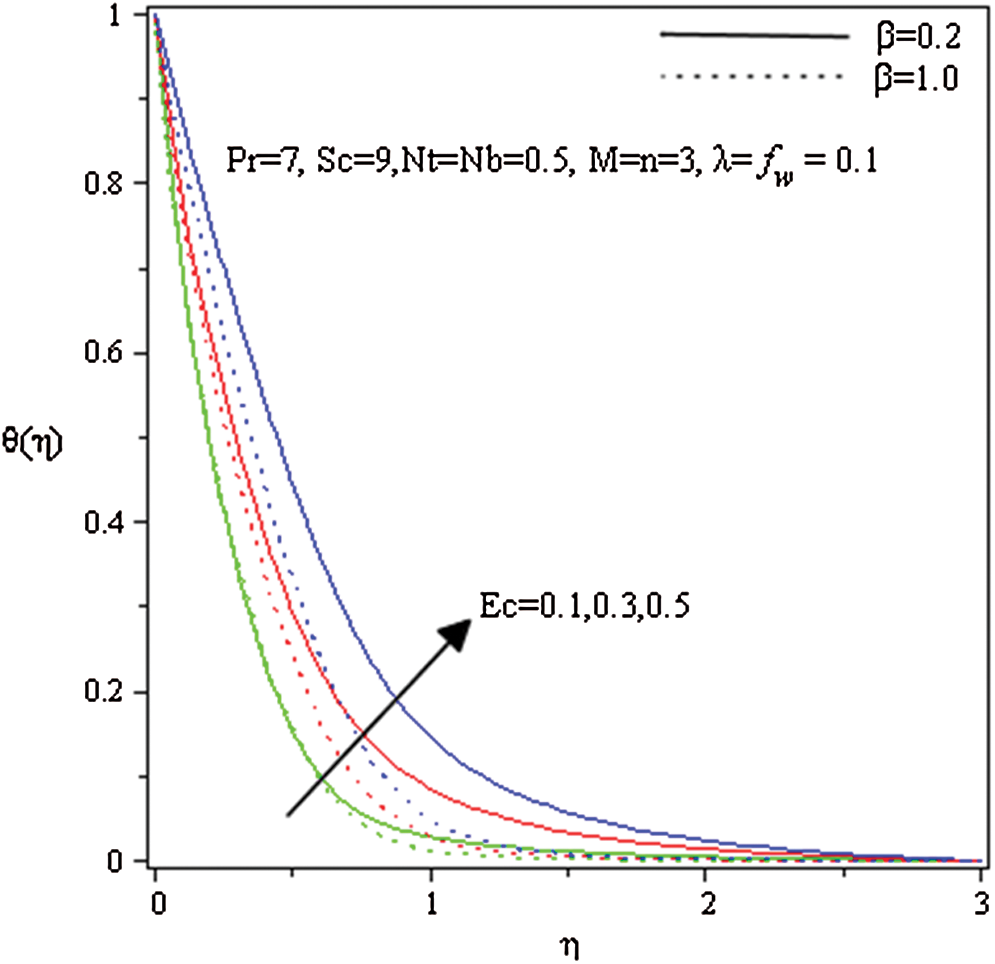
Figure 5: Influence of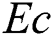 and
and 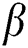 on
on 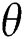
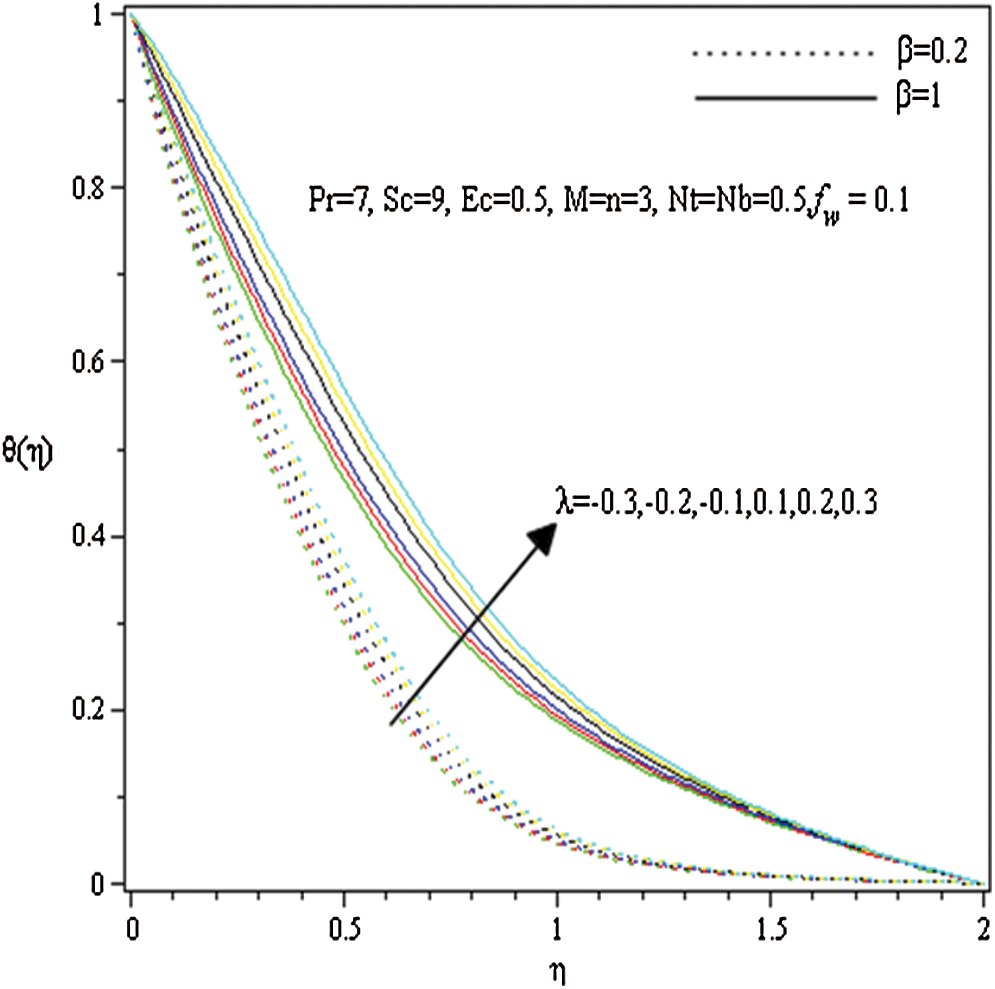
Figure 6: Influence of 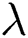 and
and 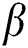 on
on 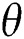
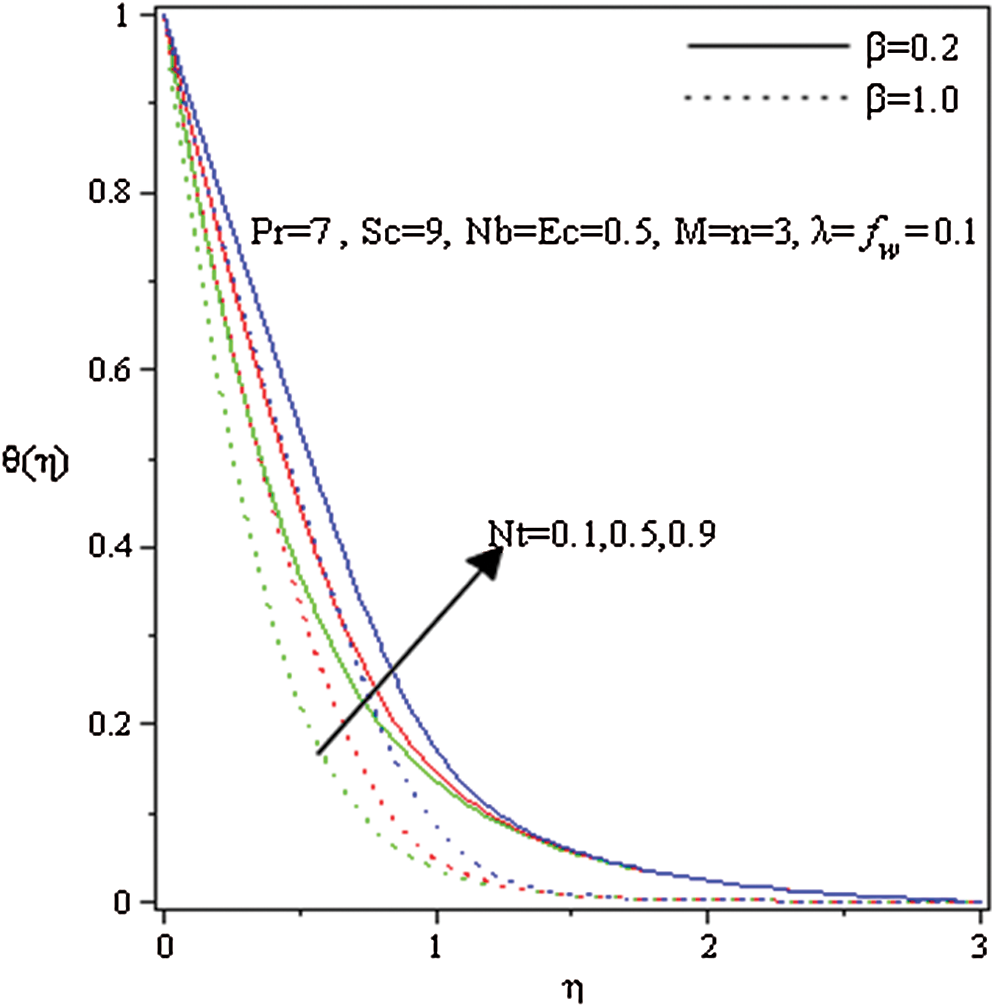
Figure 7: Influence of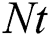 and
and 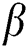 on
on 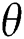
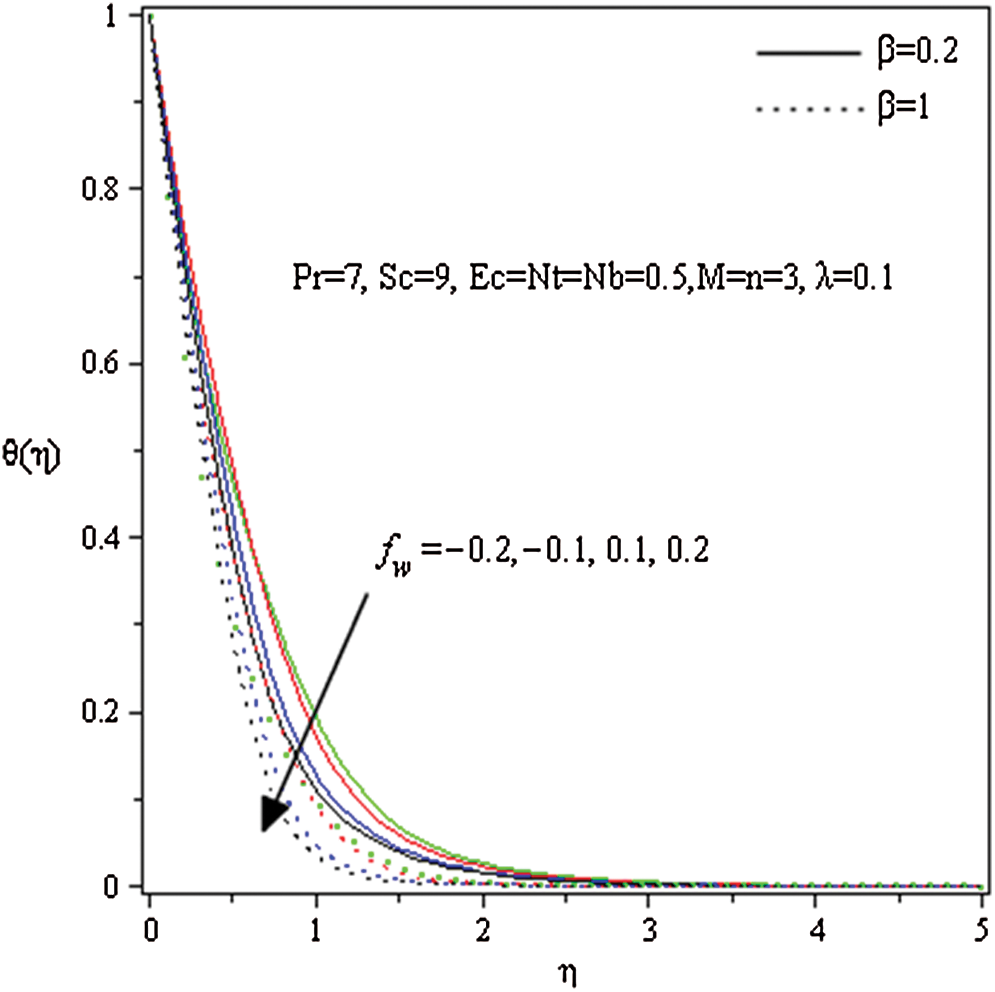
Figure 8: Influence of 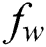 and
and 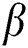 on
on 
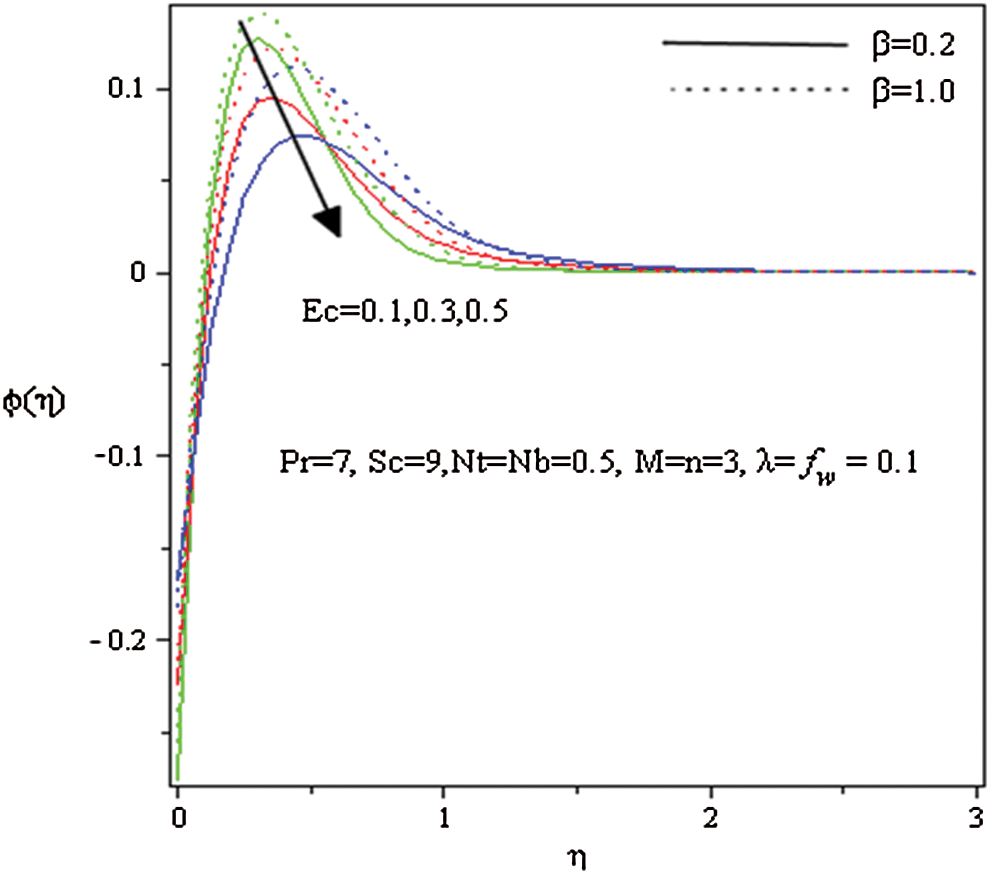
Figure 9: Influence of 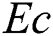 and
and 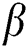 on
on 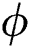
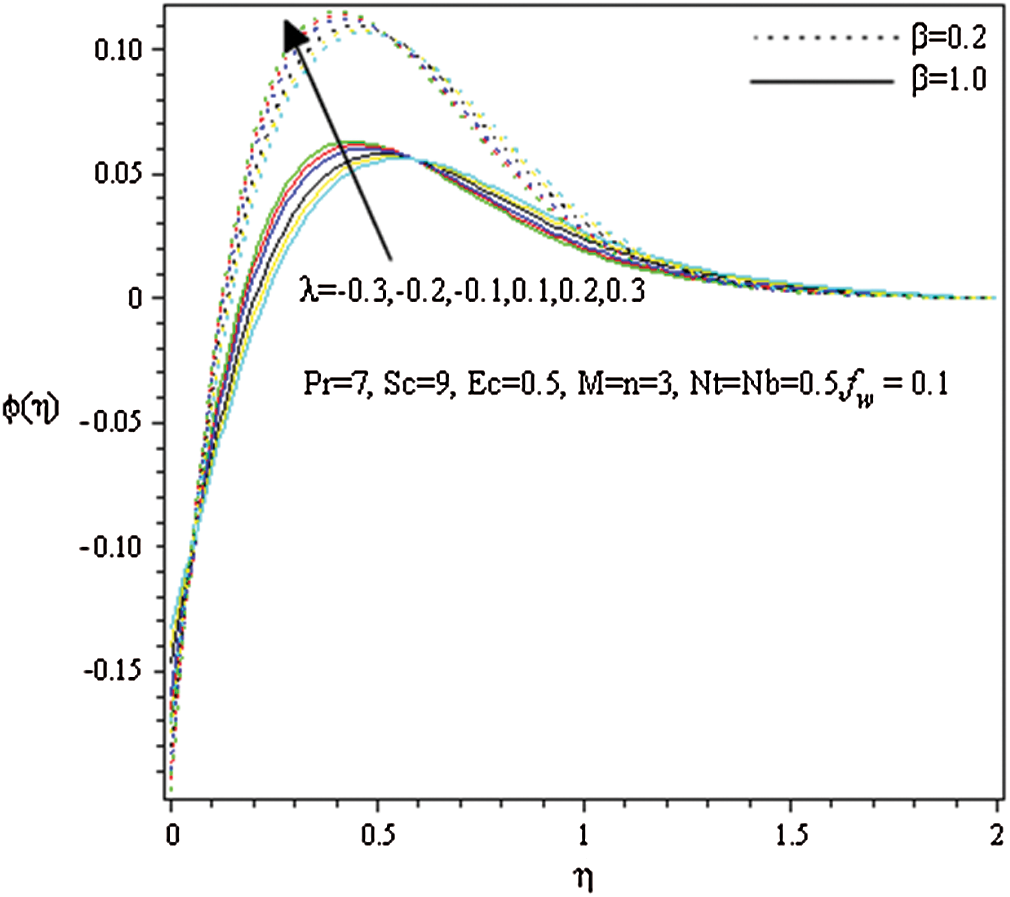
Figure 10: Influence of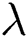 and
and 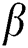 on
on 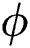
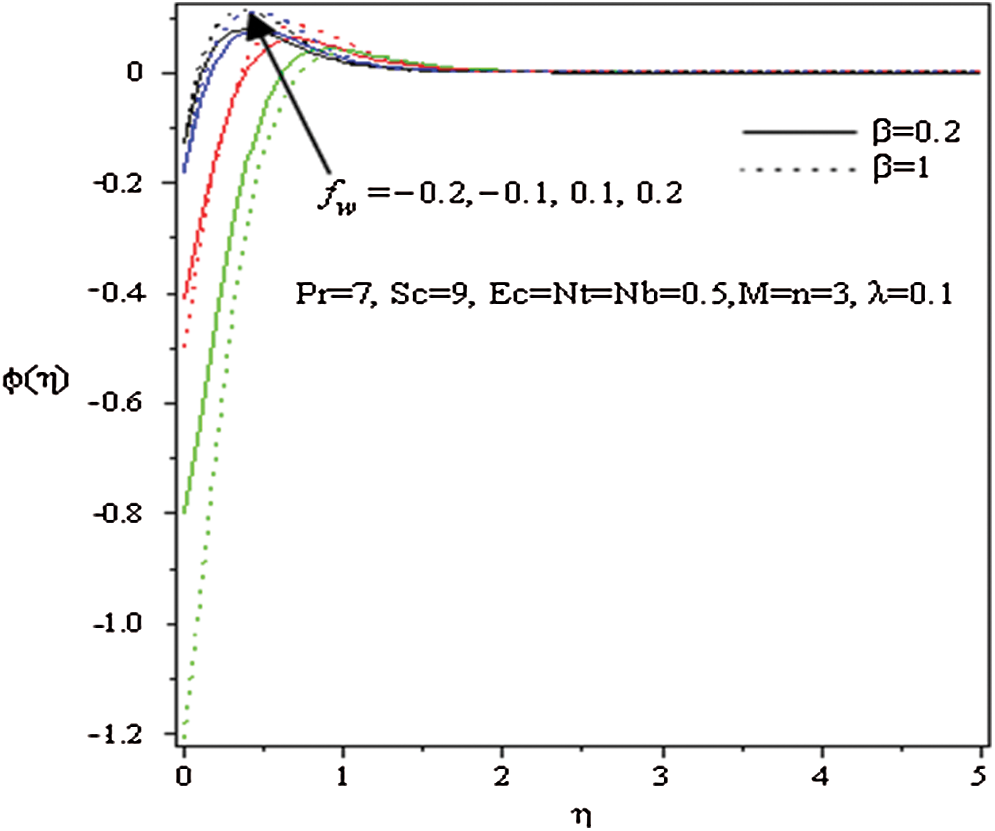
Figure 11: Influence of 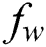 and
and 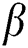 on
on 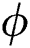
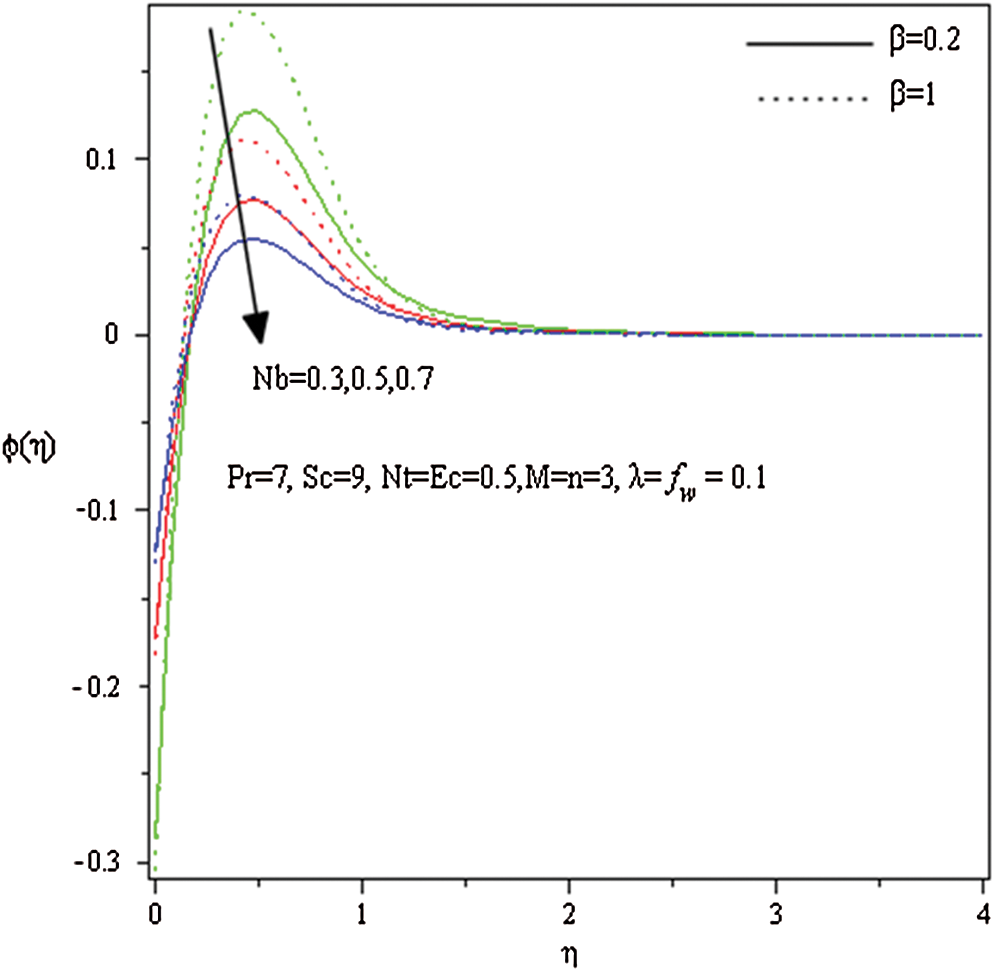
Figure 12: Influence of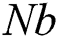 and
and 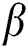 on
on 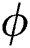
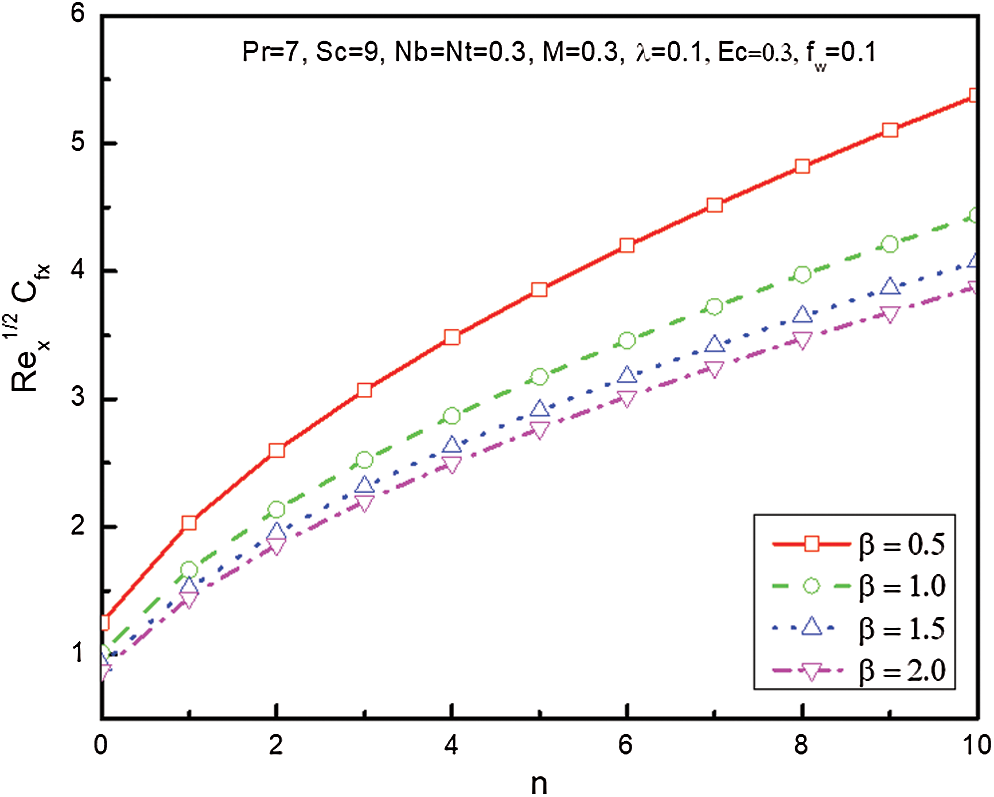
Figure 13: Influence of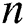 and
and 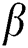 on
on 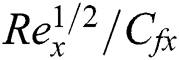
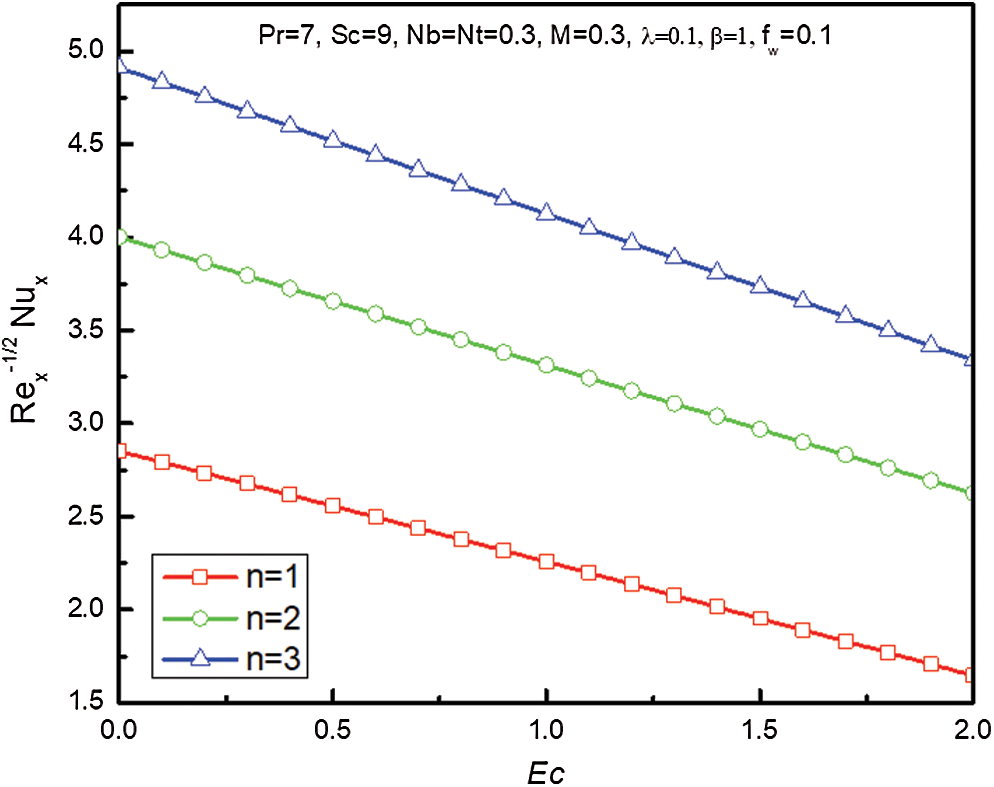
Figure 14: Influence of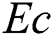 and
and 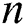 on
on 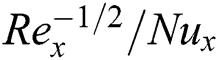
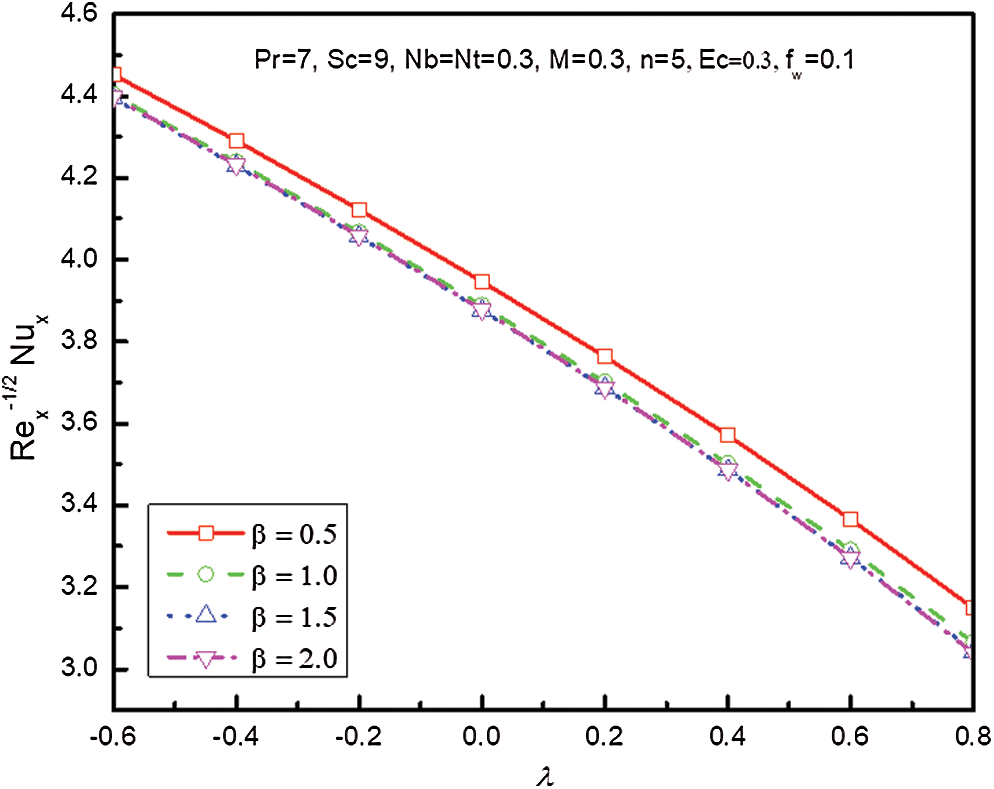
Figure 15: Influence of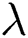 and
and 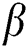 on
on 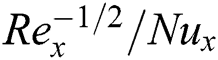
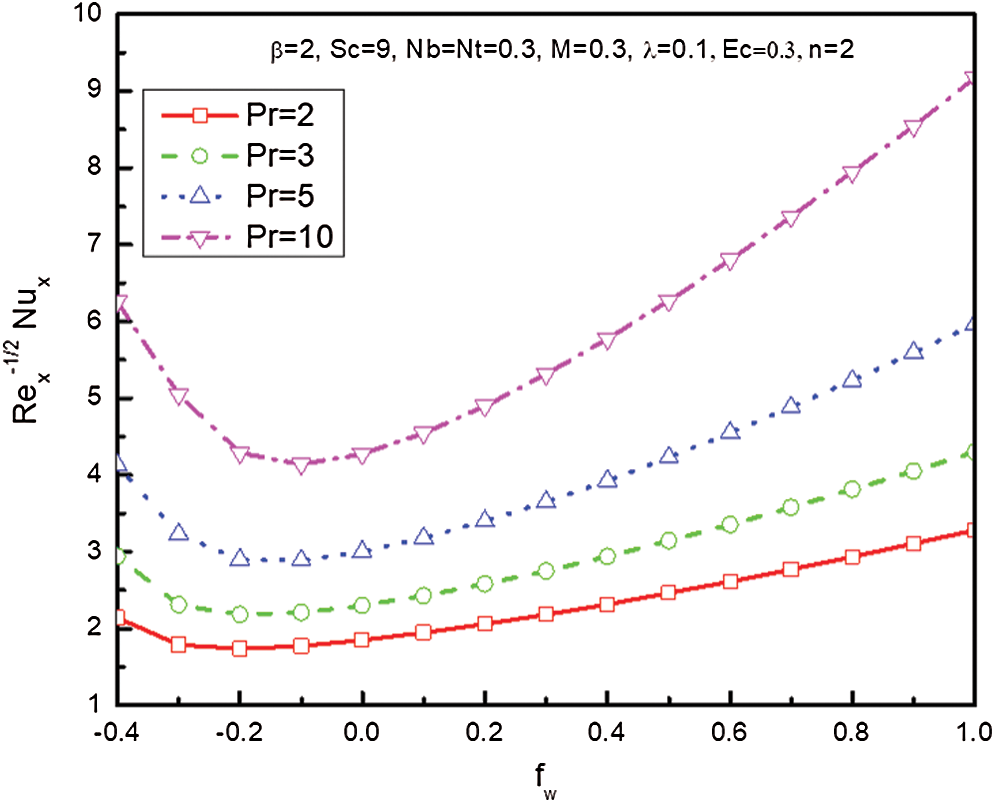
Figure 16: Influence of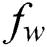 and
and 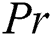 on
on 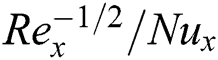

Figure 17: Influence of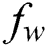 and
and 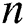 on
on 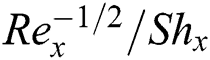
Table 1: 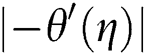 for distinct values of
for distinct values of 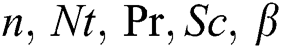 and
and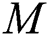 when
when 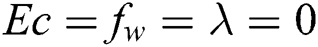
Figs. 5–8 depict the influences of Eckert number 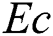 , heat source (sink) parameter
, heat source (sink) parameter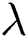 , thermophoresis parameter
, thermophoresis parameter 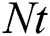 and suction (blowing) parameter
and suction (blowing) parameter 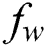 , respectively on temperature profile
, respectively on temperature profile 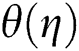 for two cases
for two cases 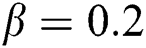 and
and 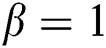 , whilst the further parameters are constant. In fact, it is clear that a growth in the value of
, whilst the further parameters are constant. In fact, it is clear that a growth in the value of 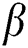 leads to an increase in the temperature outline. Physically, this happened due to high values of
leads to an increase in the temperature outline. Physically, this happened due to high values of 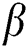 indicating stronger molecular motion as well as interactions that ultimately increase the fluid temperature. Fig. 5 prepares to perceive the influence of Eckert number on temperature distribution
indicating stronger molecular motion as well as interactions that ultimately increase the fluid temperature. Fig. 5 prepares to perceive the influence of Eckert number on temperature distribution 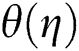 . It is showed that the fluid’s temperature significantly is raised as Eckert number
. It is showed that the fluid’s temperature significantly is raised as Eckert number 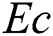 increases. Physically, the viscosity of the fluid in a viscous flow absorbs the kinetic energy from the fluid’s motion and transforms it into internal energy which is heated the fluid. This operation is partly irreversible and is known as the viscous dissipation. Fig. 6 elaborates
increases. Physically, the viscosity of the fluid in a viscous flow absorbs the kinetic energy from the fluid’s motion and transforms it into internal energy which is heated the fluid. This operation is partly irreversible and is known as the viscous dissipation. Fig. 6 elaborates 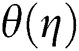 variation with the different amounts of heat source (sink)
variation with the different amounts of heat source (sink) 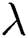 in a constant worth case of other parameters. It is displayed that the heat source upsurges the temperature and correspondence thermal-layer thickness. This is due to the heat source (sink) raises extra heat to the surface, which defines that the produced heat in the boundary layer is increased and contributes to a higher temperature area.
in a constant worth case of other parameters. It is displayed that the heat source upsurges the temperature and correspondence thermal-layer thickness. This is due to the heat source (sink) raises extra heat to the surface, which defines that the produced heat in the boundary layer is increased and contributes to a higher temperature area.
Fig. 7 includes the effect of thermophoresis parameter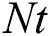 on the temperature distribution
on the temperature distribution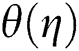 . It is noticed that the temperature outline with the thickness of the thermal-layer is increased with the snowballing values of
. It is noticed that the temperature outline with the thickness of the thermal-layer is increased with the snowballing values of 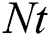 . Physically, in the thermophoretic effect, due to the temperature pattern control, the nanoparticles migrate from the hot stretch board to the cold fluid in the ambient. The influence of suction (blowing) parameter
. Physically, in the thermophoretic effect, due to the temperature pattern control, the nanoparticles migrate from the hot stretch board to the cold fluid in the ambient. The influence of suction (blowing) parameter 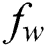 on the heat profile is displayed in Fig. 8. It is noteworthy that an upsurge in
on the heat profile is displayed in Fig. 8. It is noteworthy that an upsurge in 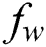 decreases the nanofluid heat and thermal-layer thickness. This is because of the suction; the hot nanofluid is pulled near to surface.
decreases the nanofluid heat and thermal-layer thickness. This is because of the suction; the hot nanofluid is pulled near to surface.
Figs. 9–12 represent the effects of Eckert number 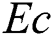 , heat source (sink) parameter
, heat source (sink) parameter 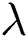 , suction (blowing) parameter
, suction (blowing) parameter 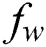 and Brownian diffusion
and Brownian diffusion 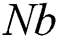 on the volume fraction
on the volume fraction 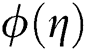 for both the cases
for both the cases 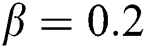 and
and 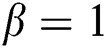 , when the other parameters are fixed. The impact of Eckert parameter on the volume fraction profile is plotted in Fig. 9. It is clearly noted that the concentration distribution is improved with the snowballing of
, when the other parameters are fixed. The impact of Eckert parameter on the volume fraction profile is plotted in Fig. 9. It is clearly noted that the concentration distribution is improved with the snowballing of 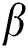 values. It is also noticed that
values. It is also noticed that 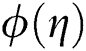 is declined with the increasing of Eckert number. Fig. 10 illustrates the impact of
is declined with the increasing of Eckert number. Fig. 10 illustrates the impact of  on
on 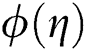 . It is observed that
. It is observed that 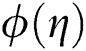 is declined with the increasing values of
is declined with the increasing values of 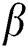 while it is increased with the increment of
while it is increased with the increment of 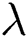 . The suction (blowing) effect on the distribution of
. The suction (blowing) effect on the distribution of 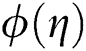 is portrayed in Fig. 11. It is observed that
is portrayed in Fig. 11. It is observed that 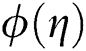 outline is raised with the swelling values of both
outline is raised with the swelling values of both 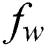 and
and 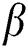 . Fig. 12 reveals the effect of the Brownian
. Fig. 12 reveals the effect of the Brownian 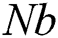 parameter on
parameter on 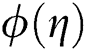 . It is observed that
. It is observed that 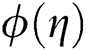 is decreased with
is decreased with 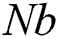 while it is increased with the parameter
while it is increased with the parameter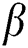 .
.
Figs. 13–17 demonstrate the influences of the diverse parameters on the drag force coefficient 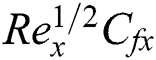 , Nusselt
, Nusselt 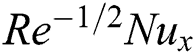 , and Sherwood
, and Sherwood 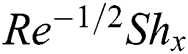 numbers. Fig. 13 elucidates the effects of
numbers. Fig. 13 elucidates the effects of 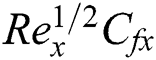 against
against 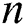 for different values of
for different values of 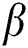 . It is found that
. It is found that 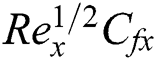 is increased when
is increased when 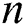 increases while it is reduced with an increment in
increases while it is reduced with an increment in 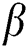 . Fig. 14 depicts the variation of
. Fig. 14 depicts the variation of 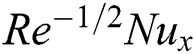 with Eckert number
with Eckert number 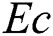 for diverse values of
for diverse values of 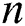 . It is remarked that the heat transfer rate is increased with the snowballing values of
. It is remarked that the heat transfer rate is increased with the snowballing values of 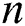 , whilst an upsurge in Eckert number
, whilst an upsurge in Eckert number 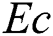 occurs a diminish in the magnitude heat transport rate. Fig. 15 demonstrates the variation of
occurs a diminish in the magnitude heat transport rate. Fig. 15 demonstrates the variation of 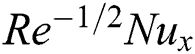 with
with 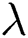 for various amounts of
for various amounts of 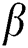 . It is found that an upsurge in both parameters
. It is found that an upsurge in both parameters 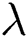 and
and 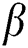 leads to a reduction in the scale of the Nusselt number. Fig. 16 depicts the Nusselt number differences with
leads to a reduction in the scale of the Nusselt number. Fig. 16 depicts the Nusselt number differences with 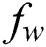 for different values of
for different values of 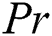 . It is simple to understand from the figure that the heat transport rate is boosted with the increment values of both
. It is simple to understand from the figure that the heat transport rate is boosted with the increment values of both 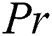 and
and 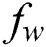 . Fig. 17 shows the variation of
. Fig. 17 shows the variation of 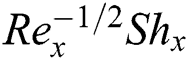 with
with 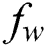 for different power index values
for different power index values 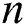 . It is remarked that a rise in both
. It is remarked that a rise in both 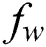 and
and 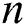 occurs an upsurge in the magnitude of
occurs an upsurge in the magnitude of 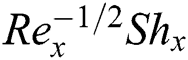 .
.
A numerical solution of the effect on the MHD boundary layer flux of CNF on a non-linear extending plate with the viscous dissipation in two dimensions with the heat absorption (generation) and the suction (blowing) are scrutinized. The numerical computations are performed by the assist of 4–5th-order Runge-Kutta Fehlberg technique depends on the shooting process. The significant findings of the study are next:
•Velocity profile is reduced with the growing of 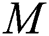 ,
, 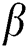 ,
, 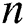 , and
, and 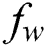 values.
values.
•Temperature profile is improved with the growing of 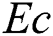 ,
, 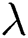 and
and 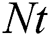 values while decreases when
values while decreases when 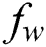 increases.
increases.
•Concentration distribution is enhanced with the increasing of 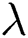 and
and 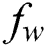 values while decreases when
values while decreases when 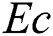 and
and 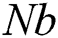 increase.
increase.
•Nusselt number is boosted when 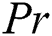 ,
, 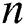 , and
, and 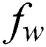 increase while, it is diminished when
increase while, it is diminished when 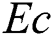 ,
, 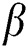 , and
, and 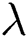 increase.
increase.
•Sherwood number is enhanced when 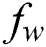 and
and 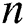 increase.
increase.
•Drag force coefficient is boosted when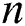 increases, while it decreases when
increases, while it decreases when 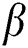 increases.
increases.
Funding Statement: This research was funded by the Deanship of Scientific Research, Taif University, KSA [Research Project Number 0-440-6166].
Conflicts of Interest: The authors declare that they have no conflicts of interest.
References
1B. Xiong, K. Yang, J. Zhao, W. Li and K. Li. (2016), “Performance evaluation of OpenFlow-based software-defined networks based on queueing model. ,” Computer Networks, vol. 102, pp, 172–185, .
2J. Y. Zhao, Z. G. Hu, B. Xiong and K. Q. Li. (2018), “Accelerating packet classification with counting bloom filters for virtual OpenFlow switching. ,” China Communications, vol. 15, no. (10), pp, 117–128, .
3H. S. Yu, H. Qi, K. Q. Li, J. H. Zhang, P. Xiao et al.. (2018). , “Openflow based dynamic flow scheduling with multipath for data center networks. ,” Computer Systems Science and Engineering, vol. 33, no. (4), pp, 251–258, .
4J. L. Zhang, X. C. Liu, J. Wan, Y. J. Ren, B. L. Xu et al.. (2019). , “Numerical optimization algorithm for unsteady flows of rotor based on web service. ,” Intelligent Automation and Soft Computing, vol. 25, no. (3), pp, 527–546, .
5L. L. Zhou, F. Tan, F. Yu and W. Liu. (2019), “Cluster synchronization of two-layer nonlinearly coupled multiplex networks with multi-links and time-delays. ,” Neurocomputing, vol. 359, pp, 264–275, . [Google Scholar]
6T. Hayat, S. A. Shehzad, A. Alsaedi and M. S. Alhothuli. (2012), “Mixed convective stagnation point flow of Casson fluid with convective boundary condition. ,” Chinese Physics Letters, vol. 29, pp, 256–307, . [Google Scholar]
7S. A. Shehzad, T. Hayat, M. Qasim and S. Asghar. (2013), “Effects of mass transfer on MHD flow of Casson fluid with chemical reaction and suction. ,” Brazilian Journal of Chemical Engineering, vol. 30, no. (1), pp, 187–195, . [Google Scholar]
8S. Mukhopadhyay, I. C. Mondal and A. J. Chamkha. (2013), “Casson fluid flow and heat transfer past a symmetric wedge. ,” Heat Transfer-Asian Research, vol. 42, no. (8), pp, 665–675, . [Google Scholar]
9S. Pramanik. (2014), “Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. ,” Ain Shams Engineering Journal, vol. 5, no. (1), pp, 205–212, . [Google Scholar]
10G. Mahantha and S. Shaw. (2015), “3D Casson fluid flow past a porous linearly stretching sheet with convective boundary conditions. ,” Alexandria Engineering Journal, vol. 54, no. (3), pp, 653–659, . [Google Scholar]
11A. Khalid, I. Khan, A. Khan and S. Shafie. (2015), “Unsteady MHD free convection flow of Casson fluid past over a no oscillating vertical plate embedded in a porous medium. ,” Engineering Science and Technology, vol. 18, pp, 309–317, . [Google Scholar]
12M. Mustafa and J. A. Khan. (2015), “Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. ,” AIP Advances, vol. 5, 077148, . [Google Scholar]
13S. Nadeem, R. Mehmood and N. S. Akbar. (2014), “Optimized analytical solution for oblique flow of a Casson nanofluid with convective boundary conditions. ,” International Journal of Thermal Sciences, vol. 78, pp, 90–100, . [Google Scholar]
14M. Y. Malik, M. Naseer, S. Nadeem and A. Rehman. (2014), “The boundary layer flow of Casson nanofluid over a vertical exponentially stretching cylinder. ,” Applied Nanoscience, vol. 4, no. (7), pp, 869–873, . [Google Scholar]
15M. Wahiduzzaman, M. M. Miah, M. B. Hosssain, F. Johora and S. Mistri. (2014), “MHD Casson fluid flow past a non-isothermal porous linearly stretching sheet. ,” Nonlinear Dynamics and Chaos, vol. 2, pp, 61–69, . [Google Scholar]
16C. Sulochana, M. Kumar and N. Sandeep. (2015), “Non-linear thermal radiation and chemical reaction effects on MHD 3D Casson fluid flow in porous medium. ,” Chemical and Process Engineering Research, vol. 37, pp, 225, . [Google Scholar]
17G. Sarojamma and K. Vendabai. (2015), “Boundary layer flow of a Casson nanofluid past a vertical exponentially stretching cylinder in the presence of a transverse magnetic field with internal heat generation/absorption. ,” International Journal of Aerospace and Mechanical Engineering, vol. 9, pp, 138–141, . [Google Scholar]
18A. Khalid, I. Khan, A. Khan and S. Shafie. (2015), “Unsteady MHD free convection flow of Casson fluid past over a no oscillating vertical plate embedded in a porous medium. ,” Engineering Science and Technology, vol. 18, pp, 309–317, . [Google Scholar]
19P. Besthapu and S. Bandari. (2015), “Mixed convection MHD flow of a Casson nanofluid over a nonlinear permeable stretching sheet with viscous dissipation. ,” Applied Mathematics and Physics, vol. 3, no. (12), pp, 1580–1593, . [Google Scholar]
20M. Imtiaz, T. Hayat and A. Alsaedi. (2016), “Mixed convection flow of Casson nanofluid over a stretching cylinder with convective boundary conditions. ,” Advanced Powder Technology, vol. 27, no. (5), pp, 2245–2256, . [Google Scholar]
21I. S. Oyelakin, S. Mondal and P. Sibanda. (2016), “Unsteady Casson nanofluid over a stretching sheet with thermal radiation, convective and slip boundary conditions. ,” Alexandria Engineering Journal, vol. 55, no. (2), pp, 1025–1035, . [Google Scholar]
22A. A. Afify. (2017), “The influence of slip boundary condition on Casson nanofluid flow over a stretching sheet in the presence of viscous dissipation and chemical reaction. ,” Mathematical Problems in Engineering, vol. 2017, 3804751, . [Google Scholar]
23S. M. Ibrahim, G. Lorenzini, P. Vijaya Kumar and C. S. K. Raju. (2017), “Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. ,” International Journal of Heat and Mass Transfer, vol. 11, pp, 346–355, . [Google Scholar]
24Z. Shah, P. Kumam and W. Deebani. (2020), “Radiative MHD Casson nanofluid flow with activation energy and chemical reaction over past nonlinearly stretching surface through entropy generation. ,” Scientific Reports, vol. 10, no. (1), pp, 1–14, . [Google Scholar]
25A. S. Butt, K. Maqbool, S. M. Imran and B. Ahmad. (2020), “Entropy generation effects in MHD Casson nanofluid past a permeable stretching surface. ,” International Journal of Exergy, vol. 31, no. (2), pp, 150–171, . [Google Scholar]
26F. A. Alwawi, H. T. Alkasasbeh, A. Rashad and R. Idris. (2020), “MHD natural convection of Sodium Alginate Casson nanofluid over a solid sphere. ,” Results in Physics, vol. 16, pp, 102818, .
27M. Nayak, J. Prakash, D. Tripathi, V. Pandey, S. Shaw et al.. (2020). , “3D Bioconvective multiple slip flow of chemically reactive Casson nanofluid with gyrotactic microorganisms. ,” Heat Transfer-Asian Research, vol. 49, no. (1), pp, 135–153, .
28S. A. Shehzad, Z. Abdullah, F. M. Abbasi, T. Hayat and A. Alsaedi. (2016), “Magnetic field effect in three-dimensional flow of an Oldroyd-B nanofluid over a radiative surface. ,” Journal of Magnetism and Magnetic Materials, vol. 399, pp, 97–108, . [Google Scholar]
29M. R. Eid and K. L. Mahny. (2017), “Unsteady MHD heat and mass transfer of a non-Newtonian nanofluid flow of a two-phase model over a permeable stretching wall with heat generation/absorption. ,” Advanced Powder Technology, vol. 28, no. (11), pp, 3063–3073, . [Google Scholar]
30M. R. Eid, A. Alsaedi, T. Muhammad and T. Hayat. (2017), “Comprehensive analysis of heat transfer of gold-blood nanofluid (Sisko-model) with thermal radiation. ,” Results in Physics, vol. 7, pp, 4388–4393, . [Google Scholar]
31M. R. Eid. (2017), “Time-dependent flow of water-NPs over a stretching sheet in a saturated porous medium in the stagnation-point region in the presence of chemical reaction. ,” Journal of Nanofluids, vol. 6, no. (3), pp, 550–557, . [Google Scholar]
32M. R. Eid and K. L. Mahny. (2018), “Flow and heat transfer in a porous medium saturated with a Sisko nanofluid over a nonlinearly stretching sheet with heat generation. ,” Heat Transfer-Asian Research, vol. 47, no. (1), pp, 54–71, . [Google Scholar]
33M. R. Eid, K. L. Mahny, T. Muhammad and M. Sheikholeslami. (2018), “Numerical treatment for Carreau nanofluid flow over a porous nonlinear stretching surface. ,” Results in Physics, vol. 8, pp, 1185–1193, . [Google Scholar]
34F. M. Hady, F. S. Ibrahim, S. M. Abdel-Gaied and M. R. Eid. (2012), “Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. ,” Nanoscale Research Letters, vol. 7, no. (1), pp, 229, . [Google Scholar]
35M. R. Eid. (2016), “Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. ,” Journal of Molecular Liquids, vol. 220, pp, 718–725, . [Google Scholar]
36M. R. Eid and O. Makinde. (2018), “Solar radiation effect on a magneto nanofluid flow in a porous medium with chemically reactive species. ,” International Journal of Chemical Reactor Engineering, vol. 16, no. (9), pp, 20170212, .
37T. Muhammad, D. C. Lu, B. Mahanthesh, M. R. Eid, M. Ramzan et al.. (2018). , “Significance of Darcy-Forchheimer porous medium in nanofluid through carbon nanotubes. ,” Communications in Theoretical Physics, vol. 70, no. (3), pp, 361, .
38A. F. Al-Hossainy, M. R. Eid and M. Sh. Zoromba. (2019), “SQLM for external yield stress effect on 3D MHD nanofluid flow in a porous medium. ,” Physica Scripta, vol. 94, 105208, .
39M. R. Eid, A. F. Al-Hossainy and M. Sh. Zoromba. (2019), “FEM for blood-based SWCNTs flow through a circular cylinder in a porous medium with electromagnetic radiation. ,” Communications in Theoretical Physics, vol. 71, no. (12), pp, 1425–1434, .
40N. Boumaiza, M. Kezzar, M. R. Eid and I. Tabet. (2019), “On numerical and analytical solutions for mixed convection Falkner-Skan flow of nanofluids with variable thermal conductivity. ,” Waves in Random and Complex Media, vol. 12, no. (2), pp, 1–20, .
41S. Lahmar, M. Kezzar, M. R. Eid and M. R. Sari. (2020), “Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. ,” Physica A: Statistical Mechanics and Its Applications, vol. 540,
42M. R. Eid, K. Mahny, A. Dar and T. Muhammad. (2020), “Numerical study for Carreau nanofluid flow over a convectively heated nonlinear stretching surface with chemically reactive species. ,” Physica A: Statistical Mechanics and Its Applications, vol. 540, 123063, .
43N. Khan, I. Riaz, M. S. Hashmi, S. A. Musmar, S. U. Khan et al.. (2020). , “Aspects of chemical entropy generation in flow of Casson nanofluid between radiative stretching disks. ,” Entropy, vol. 22, no. (5), 495, .
44M. R. Eid. (2020), “Effects of NP shapes on non-Newtonian bio-nanofluid flow in suction/blowing process with convective condition: Sisko model. ,” Journal of Non-Equilibrium Thermodynamics, vol. 45, no. (2), pp, 97–108, .
45F. Faraz, S. Haider and S. M. Imran. (2020), “Study of magneto-hydrodynamics (MHD) impacts on an axisymmetric Casson nanofluid flow and heat transfer over unsteady radially stretching sheet. ,” SN Applied Sciences, vol. 2, no. (1), 14, . [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |