DOI:10.32604/cmc.2020.012946
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012946 | |
| Article |
Fault Tolerant Suffix Trees
1Department of Computer Science and Information Technology, University of Engineering and Technology, Peshawar, 25120, Pakistan
2Department of Computer Science, Shaheed Benazir Bhutto Women University, Peshawar, 25000, Pakistan
3Department of Information Technology, FCIT, King Abdulaziz University, Jeddah, Saudi Arabia
4Department of Electrical Engineering, University of Engineering and Technology, Peshawar, 25120, Pakistan
*Corresponding Author: Iftikhar Ahmad. Email: ia@uetpeshawar.edu.pk
Received: 18 July 2020; Accepted: 19 August 2020
Abstract: Classical algorithms and data structures assume that the underlying memory is reliable, and the data remain safe during or after processing. However, the assumption is perilous as several studies have shown that large and inexpensive memories are vulnerable to bit flips. Thus, the correctness of output of a classical algorithm can be threatened by a few memory faults. Fault tolerant data structures and resilient algorithms are developed to tolerate a limited number of faults and provide a correct output based on the uncorrupted part of the data. Suffix tree is one of the important data structures that has widespread applications including substring search, super string problem and data compression. The fault tolerant version of the suffix tree presented in the literature uses complex techniques of encodable and decodable error-correcting codes, blocked data structures and fault-resistant tries. In this work, we use the natural approach of data replication to develop a fault tolerant suffix tree based on the faulty memory random access machine model. The proposed data structure stores copies of the indices to sustain memory faults injected by an adversary. We develop a resilient version of the Ukkonen’s algorithm for constructing the fault tolerant suffix tree and derive an upper bound on the number of corrupt suffixes.
Keywords: Resilient data structures; fault tolerant data structures; suffix tree
Computer memory plays an important role in all Turing-based computational platforms. Modern systems are using memories at multiple levels which consequently increases the need of its correctness [1]. However, memories, at any level, are fragile and can be error-prone, so some sort of healing mechanism is necessary. A fault is an underlying cause of an error, such as a stuck-at bit or high energy particle strike. Faults can be active (causing errors) or dormant (not causing errors) [1]. An error is an incorrect portion of state resulting from an active fault, such as an incorrect value in memory. Faults are predicted to become more frequent in future systems that contain many times more DRAM and SRAM than found in current systems.
Memory faults can compromise the correctness of results. During the execution of an algorithm or during the lifetime of a data structure, it is assumed that the data stored, and data structures built in memory locations are correct and the processing is taking place exactly according to the directions of the algorithm. When memory faults occur, data items stored on memory locations get altered and algorithm is compelled to take wrong steps. Consequently, the results are quite different from the expected results. This can lead to financial loss or even result in more disastrous situations such as in case of avionics applications [2]. The errors can be contained by using the error detection and correction circuitry. But this is an expensive solution in terms of price and performance as additional computational overhead is also added. Another solution can be the use of high performance and reliable memory like memory registers. However, it is too expensive to be used for large applications. Hence these faults need to be taken care of at application level instead of hardware level. Therefore, some recovery or tolerance mechanism is required to guard against these memory faults and ensure the reliability of processing. For this purpose, resilient algorithms or fault-tolerant data structures are designed. A resilient algorithm is the one which can compute a correct output based on uncorrupted values [3]. During the last fifty years several resilient algorithms and fault-tolerant data structures have been presented by the algorithmic community [2].
Suffix tree is an important data structure used for performing substring queries on a given string. Several classical algorithms are available for creating suffix tree for a given string. These algorithms fail when a few memory faults occur. Therefore, in this work, we design a fault tolerant suffix tree based on the natural technique of data replication. We use the Faulty-Memory random access machine model introduced by Finocchi and Italiano [3] to construct a Fault-Tolerant Suffix Tree (FTST). We use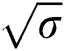 
as duplication function, where 
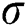is an upper bound on memory faults. Instead of duplication actual characters of the string, only the starting index of each edge is duplicated 
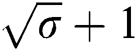times. The proposed FTST can tolerate 
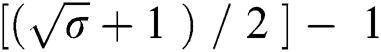faults on each edge of the suffix tree.
Rest of the paper is organized as follows. Section 2 provides a brief overview of the state of the art. Formal problem statement is presented in Section 3. Section 4 presents the proposed Fault Tolerant Suffix Tree (FTST) model, and analysis of the model is performed in the same section. Section 4 concludes the work and provides directions for future research.
A lot of work has been done in the field of fault-tolerant data structures and resilient algorithms. Large-scale applications process massive data which requires large amount of low-cost memory. Hence fault-tolerance is an important consideration in large systems, safety critical systems and financial institutions’ systems etc. Computing with unreliable information is a new and interesting area of research. Investigations and explorations have been carried out for coping with the problem of computing with unreliable information in a variety of different settings. For example, liar model [4], fault-tolerant persistent memory programming [5], fault tolerant main memory file systems [6], parallel models of computation with faulty memories [7], and others [8–11]. In the following, we summarize key works in the area of fault tolerant algorithms and systems.
Zhang [5] presented Pangolin, which is a fault tolerant persistent object library for NVMM. The proposed library uses a variety of techniques such as parity, checksums and micro-buffering to protect and preserve the objects from errors introduced due to media failure or due to software bugs. Xu et al. [6] proposed a novel non-volatile main memory (NVMM) based file system called NOVA-Fortis. The proposed file system is capable of performing well even in the presence of faulty storage (errors introduced due to corruption) or software bugs. Wang et al. [11] considered the problem of massive health data generation, transmission and collection using various devices, and proposed a interest matching mechanism for efficient, fault tolerant data collection. Jia [12] criticised the stability of traditional systems in the era of big data processing. The author proposed a fault tolerant model using spark application framework for big data clustering in distributed environment.
Finocchi [3] introduced a faulty-memory random access machine model, in which the storage locations may suffer from storage faults. In this model an adversary can alter up to σ storage locations throughout the execution of an algorithm. This model is used to produce correct output based on uncorrupted values [3,8]. Aumann [9] proposed fault-tolerant Stack, Linked List and General Tree. In their work they have used reconstruction technique. When the faults are detected, the data structure is reconstructed. Finocchi et al. [10] presented resilient search trees to obtain optimal time and space bounds while tolerating up to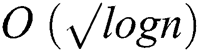 
memory faults, where 
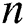is the size of search tree.
Weidendorfer et al. [13] proposed LAIK (Lightweight Application-Integration data distribution for parallel worKers) to support fault tolerant features in parallel programming. LAIK has access to data and has the ability to perform various operations such as freeing up the node before failure and assisting in replication for roll back schemes. The authors presented an example by integrating LAIK with other application.
Wang et al. [14] considered the high computational cost and I/O costs incurred during the archiving phase of large graph computation systems and proposed to dynamically adjust checkpoint interval. The resultant procedure not only achieves the required key property of fault tolerance but significantly reduces the high I/O costs as well.
Traditionally, wireless sensor network nodes have low energy storage capacity, resulting in the failure of routing and communication protocols. This can result in power outage in some sensor networks resulting in loss of communication among nodes. Lu [15] addressed the problem by proposing a new algorithm using the structured directional de Brujin graph to improve the fault tolerance of communication protocols in wireless sensor networks. The intuition behind the proposed algorithm is to deploy nodes with high energy to act as super nodes responsible for formation of redundant routing tables.
We have a string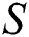 
containing 
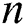number of characters including 
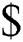symbol as its last character. String 
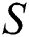is constituted over a set of alphabets of size 
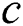. A pattern 
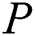is any other string of length 
. 
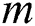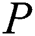is to be checked for substring of 
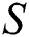. The suffix tree data structure can be used for substring queries. The suffix tree built for 
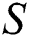contains 
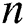number of suffixes or leaf nodes and 
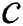number of root-originating edges. The total number of edges of suffix tree are represented by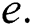 
We are using faulty-memory random access machine model for constructing the Fault Tolerant Suffix Tree. In this model resilient variables are used to achieve resilience capability. A resilient variable duplicates values for safety purpose. This duplication is based on a function of number of corruptions, such as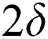 
or 
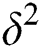, where 
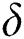is an upper bound on the number of corruptions that can be introduced by an adversary. The duplication function 
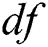, if not selected cautiously, can decrease the performance of resilient data structures or algorithms in terms of space and running time. Therefore, we have carefully selected 
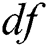for our 
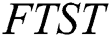model as 
.
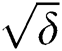Fact 1: The minimum number of edges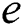 
in a suffix tree is given by 
.
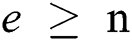Fact 2: The maximum number of edges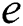 
in a suffix tree is given by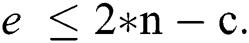 
Lemma 1: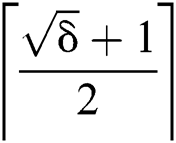 
corruptions on a single edge of a suffix tree will leave the value of that edge irreparable.
Proof: To sustain adversarial faults on an edge, the edge value is duplicated so that if some values are altered, we may still have some correct values remaining. But if half or more of the values are altered, then majority of the values are corrupted and hence the edge value cannot be repaired.
Theorem 1: The minimum numbers of uncorrupted edges are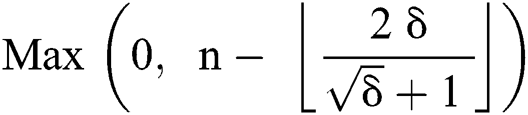 
Proof: We know that the minimum number of edges in a suffix tree is at least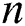 
. From Lemma 1, the maximum number of corrupt edges because of 
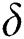corruptions, are upper bounded by 
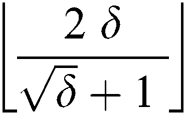, therefore, the minimum number of uncorrupted edges are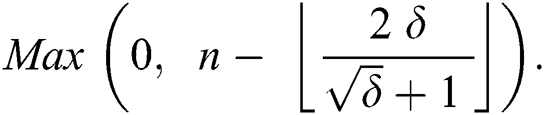 
Theorem 2: For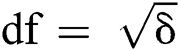 
, 
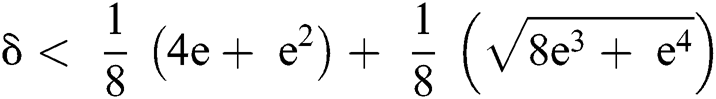as otherwise an adversary can corrupt all edges beyond repair.
Proof; From Lemma 1, we know that to corrupt the value of an edge, an adversary needs to corrupt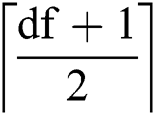 
copies. Therefore, to corrupt 
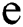number of edges, the number of corruptions required is 
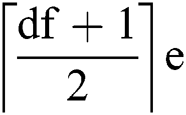, i.e., 
.
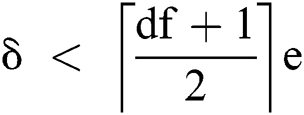Replacing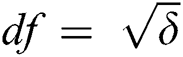 
, we obtain;
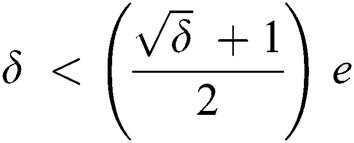
Solving we get;
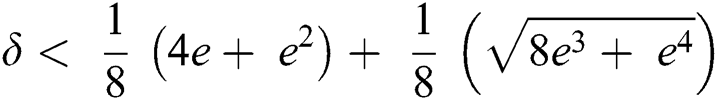
4 Proposed Fault Tolerant Suffix Tree Algorithms
In this section, we present the proposed fault tolerant suffix tree construction and traversing algorithms. The construction algorithm (Algorithm 1) is used to construct a fault tolerant suffix tree for string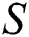 
of length 
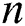. Algorithm 2 and Algorithm 3 are used to find a pattern 
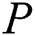in string 
.
:
:
:
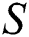4.1 Construction of Fault Tolerant Suffix Tree
Algorithm 1 describes the steps required for the construction of a fault tolerant suffix tree. Algorithm 1 receives string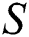 
as input where 
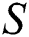contains $ symbol as its terminating character. 
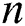represents the size of string 
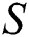and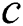 
the size of its alphabets. These two values 
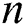and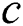 
are used for calculating the possible number of edges 
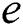of the 
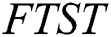by using Fact 1. By using Theorem 2, maximum number of corruptions, 
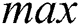are calculated beyond which all edges can be corrupted by adversary. Actual number of corruptions 
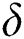are then randomly selected between 
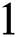and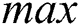 
. The number of actual corruptions 
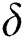defines the value of our duplication function 
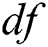. We are aware that data replication can be very costly in terms of running time and space, therefore, we have carefully selected the 
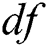as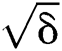 
. r represents the duplicate copies plus the original value which will be used to decide the size of array which stores start index of every node of 
.
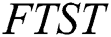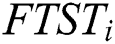is the Fault Tolerant Suffix Tree of 
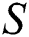which contains characters of 
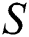from 
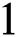to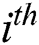 
character. 
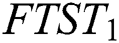is the Fault Tolerant Suffix Tree which contains only the first character of 
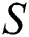. Then by using all the five heuristics of Ukkonen’s algorithm, the whole 
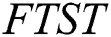is constructed. Each child node stores the 
and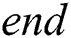 
index which links it to its parent node. This 
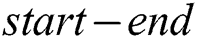pair shows the length of the edge which connects this child to its parent. Each 
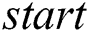index is a resilient variable which stores the value 
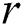number of times to provide the resilience capability. The majority of 
index values decide its correctness or otherwise.
4.2 Searching for Pattern P in Fault Tolerant Suffix Tree
Algorithm 2 and Algorithm 3 are proposed to search for pattern P in the fault tolerant suffix tree constructed by Algorithm 1. The algorithms and the required explanation is provided in the text below.
Algorithm 2 (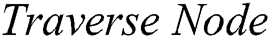
) receives three parameters, a node 
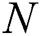of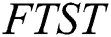 
, a pattern 
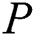and an integer value 
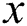which is used as index of pattern 
. 
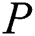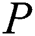is another string of length 
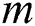and is globally accessible in all algorithms. P is to be searched within 
. 
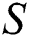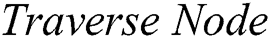algorithm traverses its edge and stores the returned value in result. A 
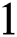shows success while 
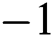shows failure of search. Variable 
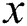is incremented by the length of edge. The character of 
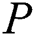at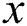 
is used as index for identifying among children nodes of 
. 
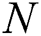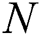recursively calls its valid child node and proceeds.
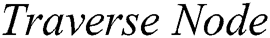algorithm calls 
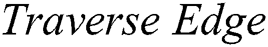(Algorithm 3) to explore the edge which links 
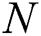to its parent node. During this exploration, corresponding characters of the pattern 
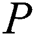are compared with characters stored on this edge. If 
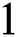is received from 
algorithm, then it shows that pattern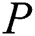 
is successfully found in string 
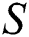. If 
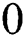is received from 
algorithm, then it means that comparison is successful on this edge but is incomplete and the remaining part needs to be explored further. To explore the deeper edge, linking this child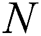 
to its sub-child, 
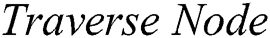algorithm recursively calls itself. Any value other than 
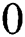or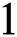 
indicates that pattern 
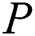is not a substring of 
.
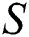Algorithm 3 (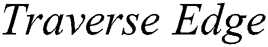
) receives four parameters, a pattern 
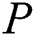to be searched, an integer 
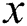which represents the index of pattern 
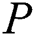, an array of integers 
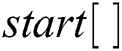representing the starting index of node and integer variable 
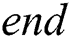representing end index of node. Integer variable 
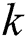is used as index of string 
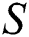and 
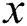of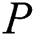 
. If corresponding characters are not equal, -1 is returned indicating failure of searching. Every node of 
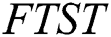stores a pair of indices start and end, which stores the start and end index of the edge linking this node to its parent node, respectively. In order to achieve resilience capability, the 
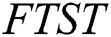stores the start index value 
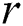times in an array, 
, of size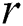 
. 
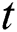stores the start index value. 
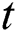receives its value by calling 
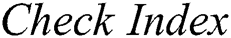algorithm which finds a value in majority.
After the while loop,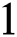 
is returned to indicate that comparison has remained successful till the end of pattern 
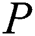, hence 
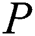is a substring of 
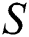. If comparison between the corresponding characters remained successful but the end of pattern 
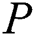has not reached so far, then it means that further match must be searched in the sub-child of this node. To signal this phenomenon, 0 is returned.
4.3 Analysis of the Proposed Model
In this section, we compute the maximum number of edges that can be corrupted by an adversary, as well as the number of corruptions required by an adversary to corrupt root-originating edges.
Theorem 3: If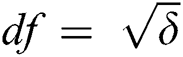 
, then the maximum number of edges that can be corrupted by an adversary is no more than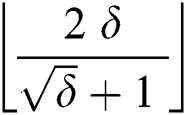 
Proof: We know that a single edge can be corrupted beyond repair if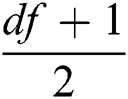 
copies are corrupted. In our case, 
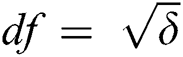, which means 
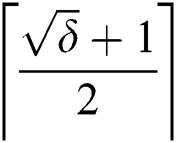corruptions will leave an edge value irreparable (Lemma 3). Alternatively, 
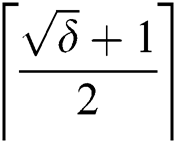corruptions cause a single edge corruption, therefore, by using basic mathematics, 
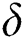corruptions will cause at maximum 
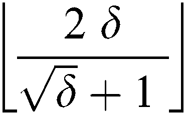edges beyond repair.
Since a suffix can consists of more than one edges, therefore, at maximum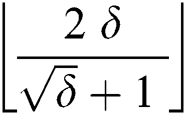 
suffixes can be corrupted in a suffix tree with 
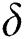number of memory faults.
Theorem 4: To corrupt all root-originating edges, a minimum of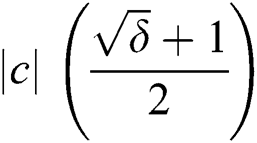 
corruptions are required, provided that 
.
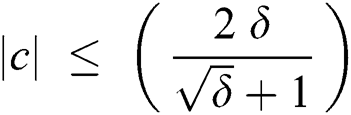Proof: We know that the number of root-originating edges is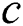 
. To corrupt a single edge, we need 
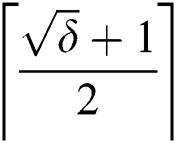number of corruptions. Then to corrupt 
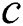edges, we need 
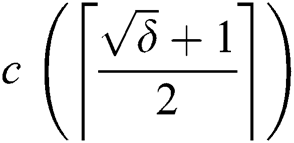number of corruptions. Thus, to corrupt all root-originating edges, we need a minimum of 
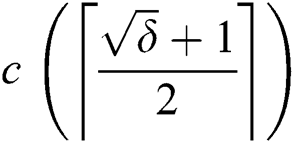corruptions.
But total corruptions cannot exceed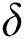 
, therefore,
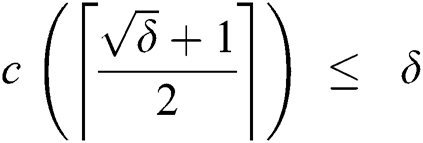
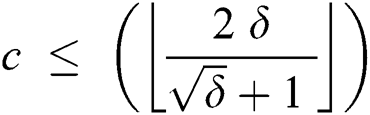
In this work, we designed a Fault Tolerant Suffix Tree (FTST) data structure which is used for applying substring queries. FTST is very useful specially in situations where memory faults can occur frequently, such as large-scale data processing systems which require low price high capacity memory or systems used at high altitudes and are susceptible to cosmic radiation. We used the natural concept of data replication for the construction of FTST. We also proposed resilient algorithm for sub-string query in FTST and derived an upper bound on the number of maximum corruptions that FTST can sustain.
The proposed FTST construction and sub-string query algorithms can be used in a variety of applications where fault tolerance is a key design requirement. The proposed technique can also be used to design other fault tolerant data structures such as AVL trees, Red-Black trees and Splay trees etc.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. V. Sridharan, N. DeBardeleben, S. Blanchard, K. B. Ferreira, J. Stearley et al. (2015). , “Memory errors in modern systems: the good, the bad, and the ugly,” ACM SIGPLAN Notices, vol. 50, no. 4, pp. 297–310.
2. U. Ferraro-Petrillo, I. Finocchi and G. F. Italiano. (2010). “Experimental study of resilient algorithms and data structures,” in Proc. Int. Sym. on Experimental Algorithms, Berlin, Heidelberg: Springer, pp. 1–12.
3. I. Finocchi and G. F. Italiano. (2004). “Sorting and searching in the presence of memory faults (without redundancy),” in Proc. 36th ACM Sym. on Theory of Computing, New York, NY, USA, pp. 101–110.
4. A. Dhagat, P. Gács and P. Winkler. (1992). “On playing twenty questions with a liar,” in Proc. 3rd ACM-SIAM Sym. on Discrete Algorithms. Society for Industrial and Applied Mathematics, USA, pp. 16–22.
5. L. Zhang and S. Swanson. (2019). “Pangolin: a fault-tolerant persistent memory programming library,” in Proc. 2019 USENIX Annual Technical Conference, Berkeley, CA, USA, pp. 897–912.
6. J. Xu, L. Zhang, A. Memaripour, A. Gangadharaiah, A. Borase et al. (2017). , “NOVA-Fortis: a fault-tolerant non-volatile main memory file system,” in Proc. 26th Sym. on Operating Systems Principles, New York, NY, USA, pp. 478–496.
7. Y. Xie, C. Yang, C. A. Mao, H. Chen and Y. Z. Xie. (2017). “A novel low-overhead fault tolerant parallel-pipelined FFT design,” in Proc. 2017 IEEE Int. Sym. on Defect and Fault Tolerance in VLSI and Nanotechnology Systems, Cambridge, UK, pp. 1–4.
8. I. Finocchi and G. F. Italiano. (2008). “Sorting and searching in faulty memories,” Algorithmica, vol. 52, no. 3, pp. 309–332.
9. Y. Aumann and M. A. Bender. (1996). “Fault-tolerant data structures,” in Proc. 37th IEEE Sym. on Foundations of Computer Science, Burlington, VT, USA, pp. 580–589.
10. I. Finocchi, F. Grandoni and G. F. Italiano. (2007). “Resilient search trees,” in Proc. of the 8th Annual ACM-SIAM Sym. on Discrete Algorithms, vol. 7, no. 9, pp. 547–553.
11. K. Wang, Y. Shao, L. Shu, C. Zhu and Y. Zhang. (2016). “Mobile big data fault-tolerant processing for ehealth networks,” IEEE Network, vol. 30, no. 1, pp. 36–42.
12. Z. Jia, Z. Hou and C. Shen. (2020). “Fault-tolerant technology for big data cluster in distributed flow processing system,” Web Intelligence, vol. 18, no. 2, pp. 101–110.
13. J. Weidendorfer, D. Yang and C. Trinitis. (2017). “Laik: a library for fault tolerant distribution of global data for parallel applications,” PARS-Mitteilungen, vol. 34, no. 1, pp. 140–150.
14. Z. Wang, Y. Gu, Y. Bao, G. Yu and L. Gao. (2017). “An I/O-efficient and adaptive fault-tolerant framework for distributed graph computations,” Distributed and Parallel Databases, vol. 35, no. 2, pp. 177–196.
15. C. Lu and D. Hu. (2016). “A fault-tolerant routing algorithm for wireless sensor networks based on the structured directional de Bruijn graph,” Cybernetics and Information Technologies, vol. 16, no. 2, pp. 46–59.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |