Generating Synthetic Data for Machine Learning Models from the Pediatric Heart Network Fontan I Dataset

1 Introduction

Over the next 20 years, the global population of patients with the Fontan circulation is projected to double [1]. Unfortunately, there are no predictive models for estimating time-to-Fontan failure in this population. Fontan failure is defined as the overt failure of the single ventricle or organs. Researchers have identified predictors for Fontan failure [2,3,4,5,6]. However, the high variance in surgical procedures and patient characteristics has led to few prognostic models that quantify dynamic risk throughout a patient’s life. In addition, the lack of large, publicly available data on patients with the Fontan circulation represents a bottleneck in the use of machine learning and deep learning models for this population.

The Fontan circulation is the culmination of a series of staged surgical procedures that reroute the circulation of patients born with single ventricle anatomy. The goal of the Fontan circulation is to make the single ventricle the sole pumping source of the systemic and pulmonary circulations. More specifically, most single ventricle patients undergo a three-staged surgical procedure which starts with the Blalock-Taussig shunt, which occurs immediately after birth. This initial surgery is followed by a, Bidirectional Glenn shunt, which occurs approximately 3–6 months after birth. Finally, the Fontan procedure, which occurs approximately 2–5 years after birth results in the final Fontan circulation [7]. While the series of procedures has saved many lives, patients with the Fontan circulation still face short-term and long-term medical complications, like a progressive decrease in ventricular systolic and diastolic function. Predicting adverse medical events in this population continues to be a challenge. The use of artificial intelligence to predict health outcomes in the broader congenital heart disease community is gaining traction but has yet to directly benefit patients with the Fontan circulation.

The use of artificial intelligence (AI) to predict health outcomes in the congenital heart disease community, a broader population including Fontan patients, has increased in the last five years. AI includes machine learning and deep learning models that can be used to classify, stratify, and predict various outcomes in a population given an array of features. For example, Mayourian et al. developed a convolutional neural network (a deep learning model) to detect biventricular pathophysiology in congenital heart disease patients using electrocardiogram (ECG) signals [8]. Similarly, Mayourian et al. also developed a convolutional neural network trained on ECG data to predict 5-year mortality in pediatric and adult CHD patients [9]. Both studies relied on ECG data collected internally at Boston Children’s Hospital. Zeng et al. created a k-means clustering model that considered blood pressure, patient surgical information, and demographics to predict post-operative complications in CHD patients after surgery [10]. Lastly, Smith et al. developed a machine learning-based survival model to predict five-year transplant-free survival among infants with hypoplastic left heart syndrome using data from the Pediatric Heart Network (PHN) [11]. This represents the only model trained on publicly accessible data for the congenital heart disease community.

Publicly available medical data on patients with the Fontan circulation is scarce but needed to train machine learning and deep learning models that estimate the timing of Fontan failure or for adverse event detection. The PHN Fontan I dataset [12] is the only freely available Fontan patient dataset in the United States. The cohort consists of 546 Fontan patients with multiple categorical, serological, exercise testing and hemodynamic measurements. In subsequent studies, the Fontan 2 [13] and Fontan 3 [14] datasets would represent the only freely accessible longitudinal Fontan dataset, once released. Researchers have already demonstrated that early-stage catheterization measurements predict short-term post-Fontan surgery outcomes [15]. More broadly, researchers have also demonstrated that longitudinal data is more critical for predicting long-term outcomes compared to cross-sectional data alone [16]. Given that most studies that identify predictors of Fontan circulatory failure are limited to single-center data or meta-analysis studies, the lack of longitudinal data for this population is a problem that deters the development of machine and deep learning models. Generative algorithms can address the scarcity of data needed for the development of Fontan-specific models.

Generative algorithms, AI models that can synthesize data in the form of images or tabular data, can generate large amounts of records representative of real longitudinal Fontan endogenous measurements. There are numerous methods to achieve this, with one method being the use of generative adversarial networks (GANs) [17]. GANs use two competing neural networks, a generator and a discriminator, which use real data samples to create synthetic samples with similar probability distributions. GANs have been developed to create synthetic electronic health records [18]. Time-series GANs have also been used to create dynamic and the time-dependent clinical measurements [19]. As a result, generating longitudinal hemodynamic, exercise, and serological data that closely resembles the statistical distribution of Fontan patient measurements is feasible and can be leveraged for training data-hungry models. To date, studies have relied on identifying covariates that are associated with Fontan’s failure to quantify the risk that a patient will need a medical intervention.

In this study, the generation of synthetic data from a subset of features in the PHN Fontan I dataset is described. The overall goal of this study is to demonstrate the method by which to generate synthetic data from any of the PHN databases to encourage the training of predictive models in the congenital heart disease field. A secondary goal is to create a synthetic training dataset that contains commonly measured doppler echocardiography features that can be used to classify ventricular dysfunction in Fontan patients.

2 Methods

2.1 Data Source

The PHN Fontan I dataset comes from a cross-sectional study in which Fontan patients were enrolled from seven hospitals in the United States between 2003–2004 [12]. The study enrolled a total of 546 Fontan patients with an age range between 6–8 years old. The study includes parental and child functional health questionnaires and hemodynamic measures of ventricular health taken by Doppler echocardiography (Doppler Echo), ECG, cardiac magnetic resonance imaging (MRI), maximal exercise testing, and resting B-type natriuretic peptide (BNP) concentration. In addition, medical records that include ventricular morphology, pre-Fontan cardiac anatomic diagnosis, and age at various staged surgical procedures are also included.

2.2 Data Pre-Processing

All data files were downloaded in comma-separated values (CSV) format and imported into R and R Studio. The primary goal of this study was to demonstrate the generation of synthetic data from a public database from the PHN. To demonstrate this, synthetic data was generated from a portion of the Fontan I dataset. Specifically, synthetic data was generated on the Doppler echo measurements since these are measurements commonly taken during routine cardiovascular monitoring visits. The secondary goal of this study was to use the synthetic dataset to predict the ventricular functional status of Fontan patients, to demonstrate utility. As a result, a new subset of data, which included 24 features (shown in Table 1) and one classifier, the presence or absence of ventricular dysfunction was created. Missing data was handled in two ways: (1) imputation using Multiple Imputation by Chained Equations (MICE) and (2) dropping subjects that had missing data. The imputation algorithm went through 10 iterations. For each iteration, imputed values were updated based on the latest estimates from the other variables’ distributions. All tests for fidelity and utility yielded two separate results, one for synthetic data created from real data samples (referred to as synthetic data from real imputed samples) in which the missing values were imputed and one for synthetic data created from real data in which subjects with missing values were dropped from the dataset (referred to as synthetic data from real dropped samples). A block diagram of this process is shown in Fig. 1.

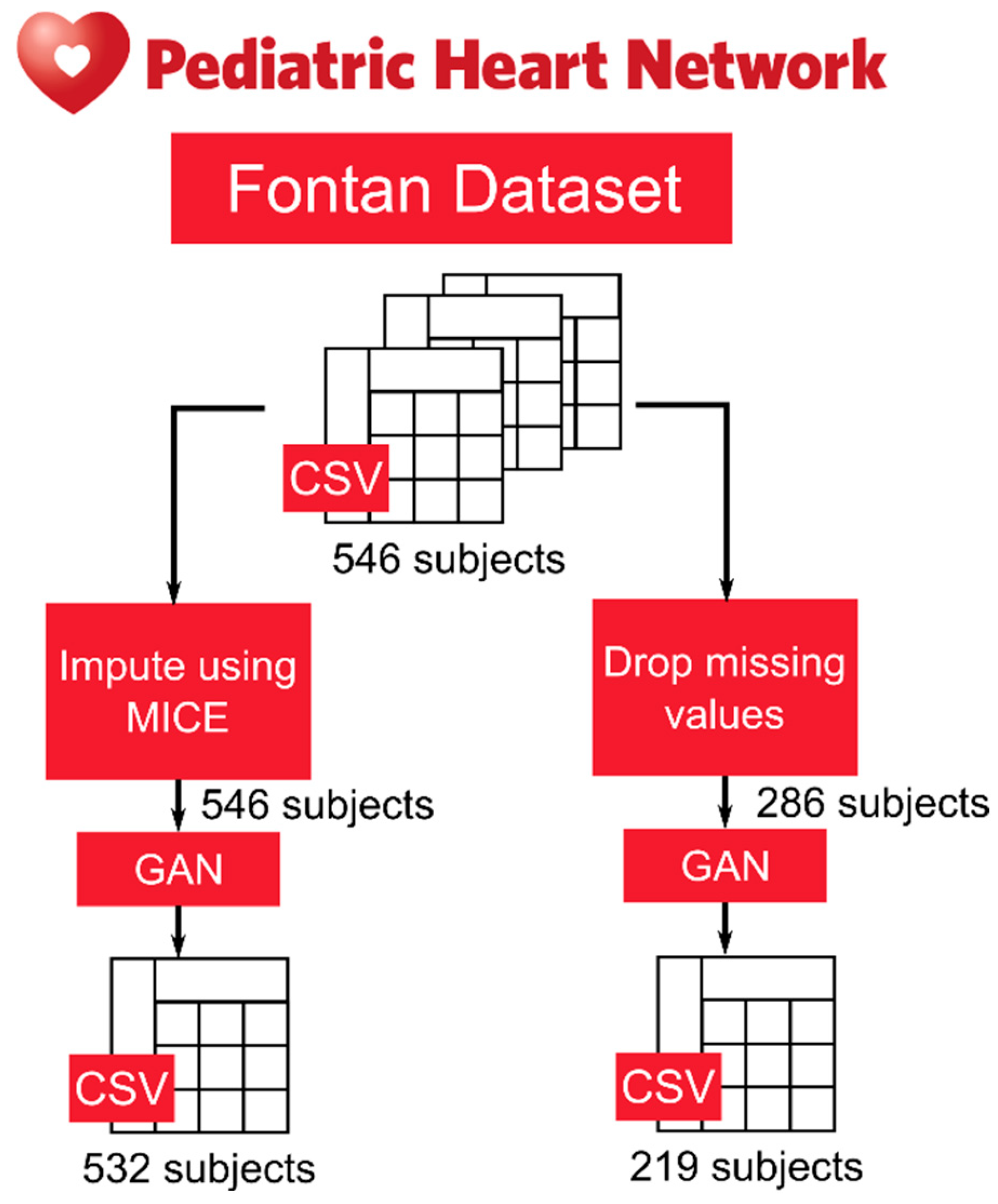
Figure 1: Block diagram showing the two methods that synthetic data was generated from the Fontan public use dataset on the Pediatric Heart Network.

Table 1: Features used in generating synthetic data from PHN Fontan I.

Feature	Description
Age @ Enrollment	Age of patient at PHN enrollment
Age @ Fontan Surgery	Age of patient at Fontan surgery
Number of Associations	Number of significant associated anatomic diagnoses
Number of Procedures	Number of cardiac surgical procedures prior to most recent Fontan
Fenestration (Y/N)	Presence of fenestrations in Fontan circulation
Cardiac Surgery (Y/N)	Patient has undergone cardiac surgery
Number of Cardiac Surgeries	Number of cardiac surgeries
Post-Fontan Catheterizations (Y/N)	Patient has undergone a cardiac catheterization procedure
Stroke Events (Y/N)	Patient has experienced a stroke event
Number of Stroke Events	Number of stroke events the patient has experienced
Seizure (Y/N)	Patient has experienced a seizure
Thrombosis (Y/N)	Patient has experienced a thrombosis event
Number of Thrombosis	Number of thrombosis events the patient has experienced
PLE (Y/N)	Patient has been diagnosed with protein losing enteropathy (PLE)
Arythmias (Y/N)	Patient has an arrythmia
Number Arythmias	Number of arrythmia events experienced by the patient
Echo BSA	Body surface area (BSA) take at the echocardiography procedure, units: m2
Echo SV	Ventricular stroke volume measured during the echocardiography procedure, units: mL
Echo dpdt	Derivative of left ventricular pressure with respect to time, dP/dt, units: mmHg/s
Echo tde	Tissue Doppler peak early diastolic velocity, units: cm/s
Echo tda	Tissue Doppler peak late diastolic velocity, units: cm/s
BNP	BNP assay result, units: pg/mL
Dominant Ventricle	Ventricular dominance in patient

2.3 Synthetic Data Generation

Synthetic data was generated using a tabular generative adversarial network (tabGAN) on Python. For synthetic data from real imputed samples, the real dataset contained 546 subjects. For synthetic data from real dropped samples, the real dataset contained 286 subjects (after dropping subjects with missing values). To train the discriminator of the GAN, 80% of the real data, in both scenarios, was used for training while 20% was used for testing. The hyperparameters for the GAN are shown in Table 2. The gen_x_times parameter, which is a parameter used to indicate how many synthetic samples to generate, was varied for this study but was set to 1 for the results shown in this research. In total, the synthetic data from real imputed samples totaled to 532 synthetic subjects. The synthetic data from real dropped samples totaled 219 synthetic subjects. The final synthetic datasets were then combined with their respective real datasets and each subject was labeled “Synthetic” and “Real” for testing synthetic data fidelity and utility. These mixed datasets were saved as CSV files.

Table 2: Hyperparameters of the tabGAN.

Hyperparameter	Value
gen_x_times	1
bottom filter quantile	0.001
top filter quantile	0.999
pregeneration fraction	0.2
batch size	500
epochs	500
early stopping patience	25
Adversarial model parameters
metrics	rmse (root mean squared error)
max depth	2
max bin	100
learning rate	0.02
random seed	42
n estimators	500

2.4 Synthetic Data Fidelity

Synthetic data fidelity, defined as having similar probability distribution as the real data, was measured both qualitatively and quantitatively. Qualitatively, histograms and probability density functions for each feature, both real and synthetic, were also plotted and visually compared. In addition, the principal component analysis plots (PCA) were also used to visualize the resemblance of the synthetic data to real data. Quantitative measures of fidelity were carried out in two ways (1) comparing synthetic and real data using Kolmogorov-Smirnov test to evaluate the similarity of two distributions and (2) using a post-hoc classifier in which a generic neural network (128 layers) was used to classify if samples were real or synthetic. The neural network was trained on 80% of the mixed dataset and tested on 20% of the rest of the data. The classification error was used as the quantitative measure of fidelity. Scores near 50% were indicative of synthetic data that is indistinguishable from real data.

2.5 Synthetic Data Utility

Synthetic data utility, defined as data being as useful as real samples in making predictions (for example, training a model with synthetic and testing that model with real data), was measured quantitatively. Synthetic data should resemble the predictive characteristics of real data. This was demonstrated by training a generic neural network (128 layers) to classify if patients had ventricular dysfunction based solely on 24 features (shown in Table 1). The neural network is a deep feedforward network (designed for regression tests) consisting of five layers: An input layer that matches the dimensionality of the input features, three hidden layers with 64, 32, and 16 neurons, respectively, and an output layer. Each of the hidden layers Rectified Linear Unit (ReLU) activation function. The training process for the neural network is set with a patience level of 500 epochs and a minimum delta of 0.001 to restore the best weights once convergence is detected. Table 3 contains the hyperparameters used on the neural network.

Table 3: Hyperparameters Neural Network.

Hyperparameter	Value
Number of hidden layers	3
Number of neurons per hidden layer
1st layer	64
2nd layer	32
3rd layer	16
Dropout rate	0.3
Optimizer	32
Loss Function	Mean Squared Error
Batch size	32
Number of epochs	1000
Early stopping patience	500 epochs
Minimum delta for early stopping	0.001

The neural network was trained with synthetic data and tested with real data (train on synthetic test on real). A total of 100% of the synthetic data was used to train the neural network and 100% of the real data was used to test the model. The classification error was used as the quantitative measure of utility. A low classification error signifies a model that the synthetic data acts as a useful surrogate for real samples in training a machine learning model.

3 Results

The histograms and probability density functions of synthetic data generated from real imputed samples are shown in Fig. 2. The histograms include the distribution of eight continuous features. The histograms and probability density functions of synthetic data generated from real dropped samples is shown in Fig. 3. The density functions in black represent the real data with imputed values and the red probability density functions represent the associated synthetic data generated by the tabGAN. In addition, the PCA plots of the real and synthetic data in both imputed and dropped cases are shown in Fig. 4a and Fig. 4b, respectively, with real data samples in black and synthetic data samples in red.

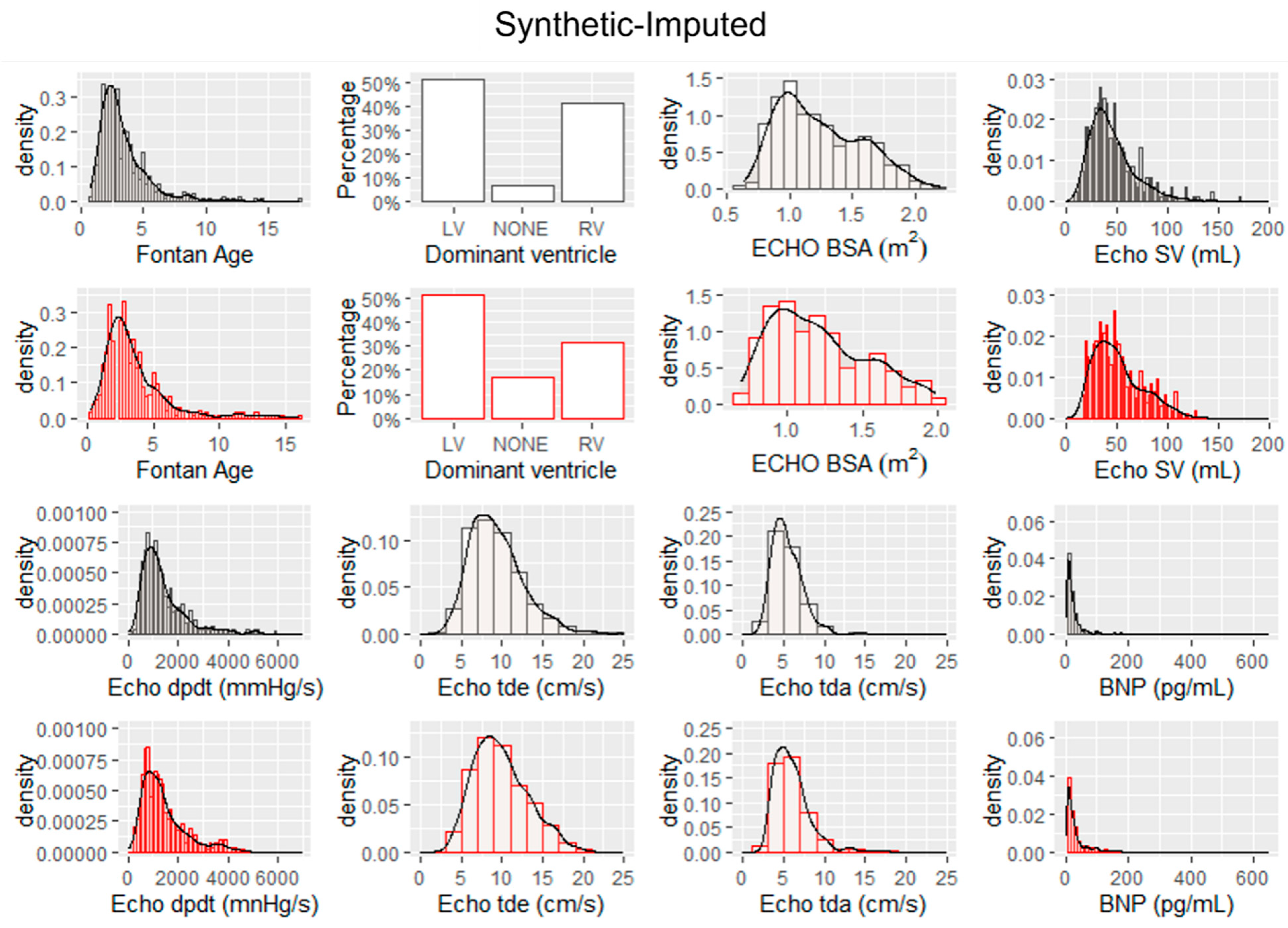
Figure 2: Histograms and probability density functions for real data with imputed values for missing data (shown in black) and histograms and probability density functions for synthetic data generated by the tabGAN (in red).

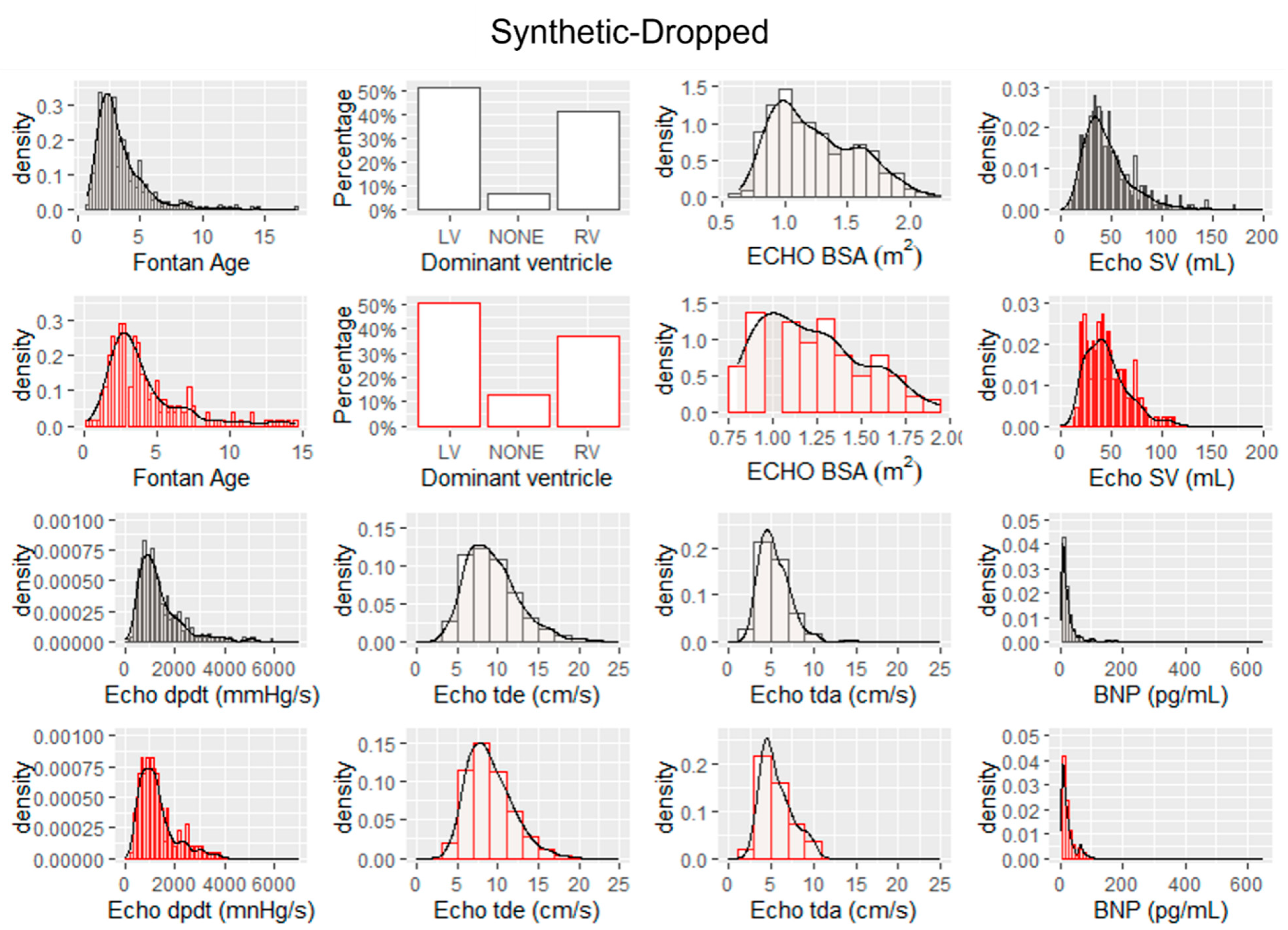
Figure 3: Histograms and probability density functions for real data in which missing data was dropped (shown in black) and histograms and probability density functions for synthetic data generated by the tabGAN (in red).

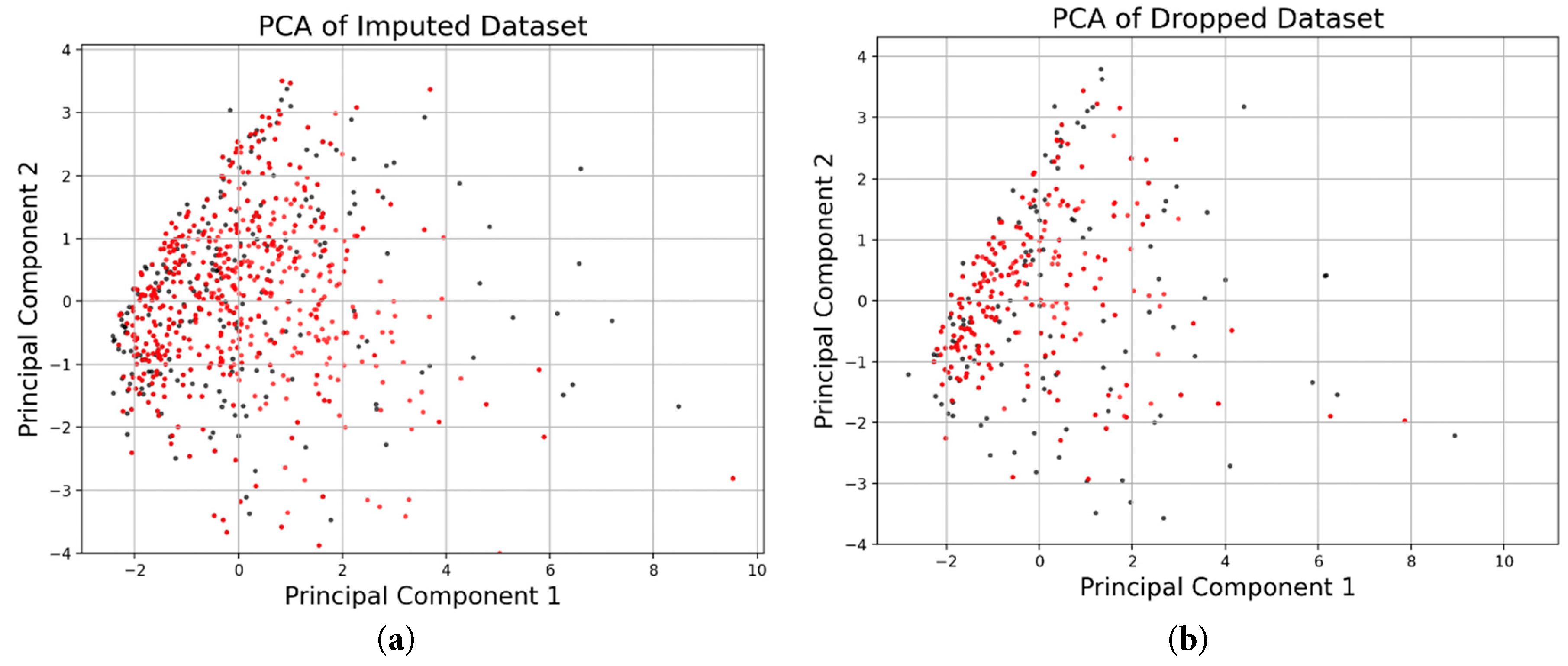
Figure 4: (a) PCA plots overlaying the distribution along the two principal components for synthetic samples generated from real data in which the missing values were imputed and (b) PCA plots overlaying the distribution along the two principal components for synthetic samples generated from real data in which the missing values were dropped.

Similarity of both synthetic data samples and real samples using the two-sample Kolmogorov-Smirnov test are shown for each continuous feature in Table 4. The bold signifies a KS-Statistic value that rejects the null hypothesis that the data samples came from the same distribution and the bold with an asterisk signifies a p-value that is less than 0.05.

Table 4: Two-sample Kolmogorov-Smirnov Test to Evaluate Similarity of Two Distributions.

	Imputed Real Data		Dropped Real Data
Feature	Kolmogorov–Smirnov statistic (D)	p-value	Kolmogorov–Smirnov statistic (D)	p-value
Age @ Fontan Surgery	0.0389	0.8111	0.1339	0.0075*
Echo BSA	0.0460	0.6221	0.0680	0.4673
Echo SV	0.1177	0.0032*	0.0606	0.6714
Echo dpdt	0.0304	0.9783	0.0690	0.4874
Echo tde	0.0777	0.1046	0.0626	0.6114
Echo tda	0.1123	0.0048*	0.0596	0.6796
BNP	0.1375	0.0001*	0.0528	0.7882

The misclassification error for the neural network trained on identifying real data (with missing values imputed) versus synthetic data is 65.2% as shown in the confusion matrix in Fig. 5a. The misclassification error for a neural network trained on identifying ventricular dysfunction in Fontan patients with synthetic data, derived from real data in which the missing data was imputed, as the primary training set is 10.99%. The confusion matrix for this experiment is shown in Fig. 5b. The false positive rate for this model is 4.8% and the false negative rate is 6.2%. The F1 score is 93.44%.

The misclassification error for the neural network trained on identifying real data (with missing values dropped) versus synthetic data is 49.3% as shown in the confusion matrix in Fig. 6a. The misclassification error for a neural network trained on identifying ventricular dysfunction in Fontan patients with synthetic data, derived from real data in which the missing data was dropped, as the primary training set is 9.44%. The confusion matrix for this experiment is shown on Fig. 6b. The false positive rate for this model is 3.1% and the false negative rate is 6.3%. The F1 score is 94.36%.

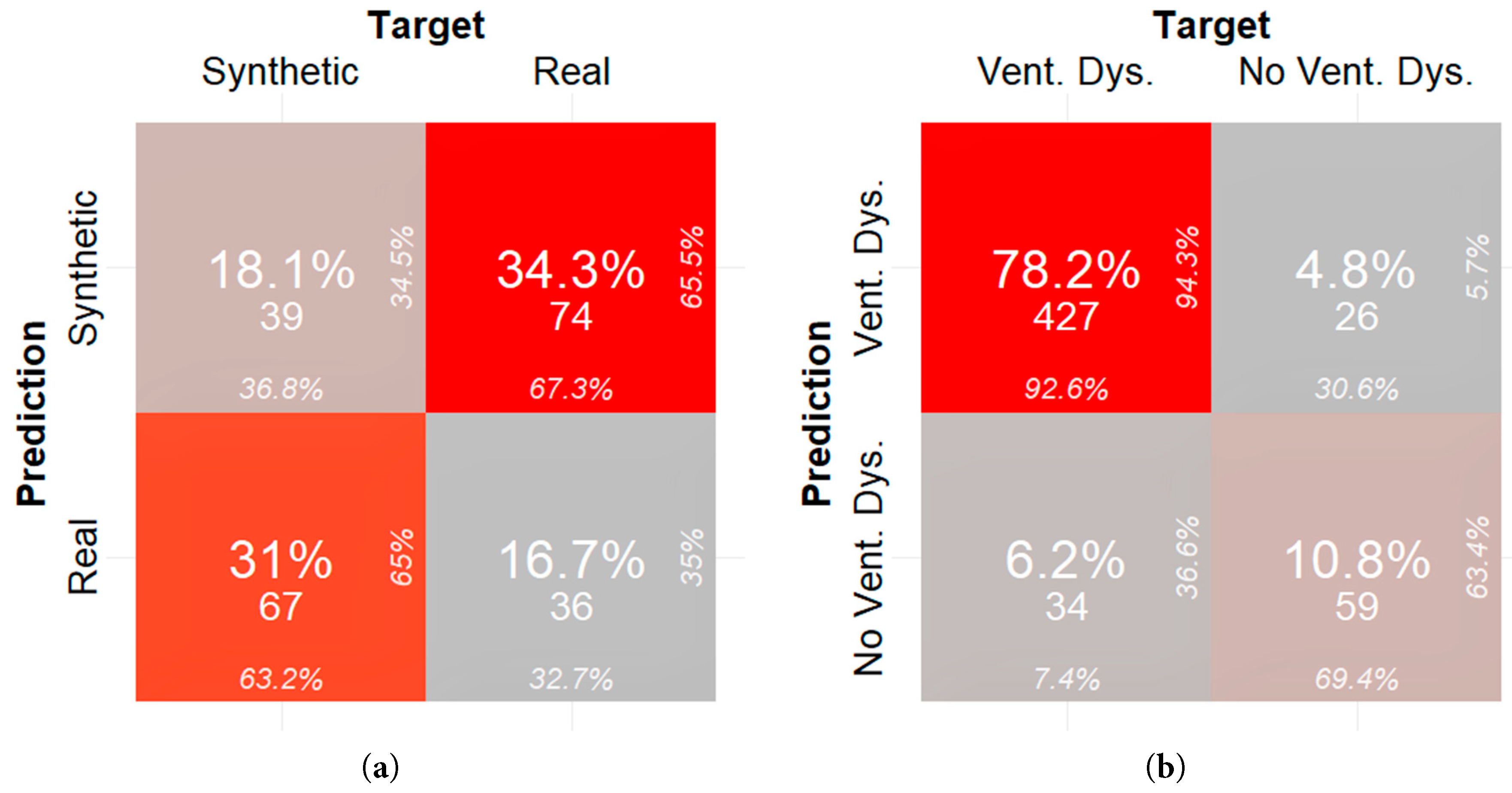
Figure 5: (a) Confusion matrix quantifying fidelity of synthetic samples generated from real data in which the missing data was imputed and (b) confusion matrix quantifying utility of synthetic samples generated from real data in which the missing data was imputed.

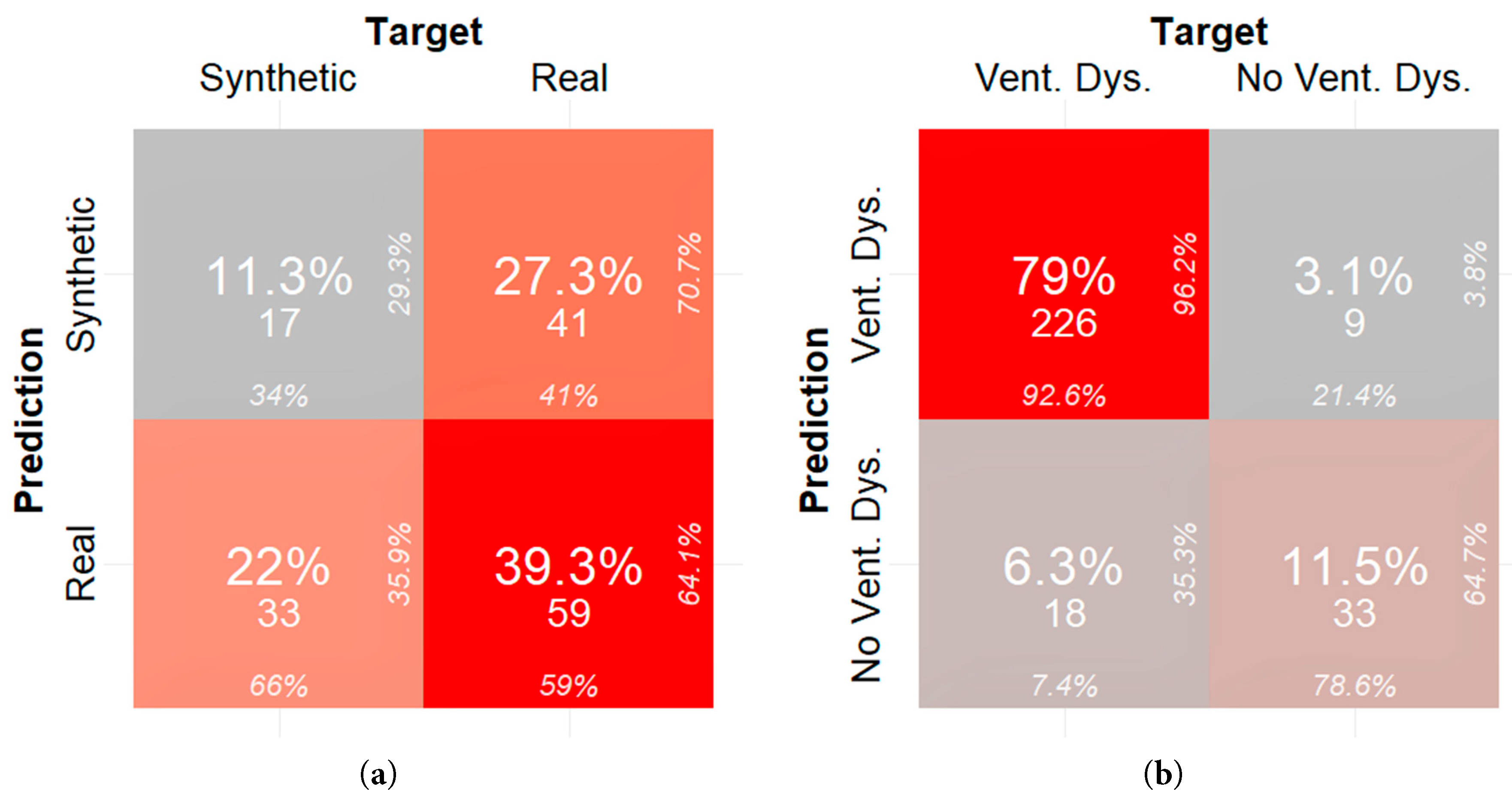
Figure 6: (a) Confusion matrix quantifying fidelity of synthetic samples generated from real data in which the missing data was dropped and (b) confusion matrix quantifying utility of synthetic samples generated from real data in which the missing data was dropped.

4 Discussion

Synthetic Fontan I data generated from tabGAN, is similar and as useful as real data from the PHN database in classifying ventricular dysfunction. As demonstrated qualitatively, the synthetic data generated has a similar probability density function for key features as evidenced by Fig. 2. In addition, the PCA plots show sample distribution along the first two principal components that are similar for both real and synthetic data. More specifically, when comparing the histogram plots of synthetic data from real imputed samples, the variance is preserved when compared to the histogram plots of synthetic data from dropped real samples. For example, Echo dpdt, a measure of ventricular contractility, shows a larger range in the synthetic data from imputed samples (Fig. 2) than the synthetic data from dropped samples (Fig. 3). This is in large part because when samples were dropped in the latter case, it constituted 47.6% of the data dropped. The reduced variance is also confirmed in the PCA plots shown in Fig. 4, where the variance along principal component 2 is more pronounced for synthetic data from imputed real samples. As a result, if the variance of the data is an important feature to preserve, imputing missing real data appears to be a better option than dropping missing values.

Quantitively, the synthetic-real classifier demonstrated a classification rate of 65.28% when the synthetic data was derived from real data in which the missing values were imputed. The synthetic-real classifier demonstrated a classification rate of 49.3% when the synthetic data was derived from real data in which the missing values were dropped. As a benchmark, a trained neural network that cannot distinguish between real and synthetic data samples would perform at a 50% classification error. Given the limited availability of national-level Fontan patient cardiovascular data, using GANs to generate synthetic data are promising surrogates for use in creating datasets with many samples for use in machine learning and deep learning models. Specifically, when the synthetic data is generated from real data in which the missing values are dropped, trained classifiers have a harder time distinguishing real from synthetic data.

At least for the Fontan I dataset, dropping missing values versus imputing missing values with MICE is more advantageous for mimicking the probability distribution of the original data. As seen in Table 4, only the “Age at Fontan” feature resulted in a Kolmogorov–Smirnov statistic (D), 0.1339 (p-value = 0.0075), in which the similarity of the synthetic data was not statistically like the real data. When missing values are imputed using the MICE algorithm, the synthetic data generated becomes more dissimilar than the real data. If imputation must be used, various imputation algorithms should be compared.

The usefulness of synthetic data generated from tabGAN is promising, at least with respect to classifying patients with ventricular dysfunction given standard echocardiography measures, BNP measurements, and the number of surgical procedures. In fact, a neural network trained on only synthetic data derived from real data in which the missing values were imputed and tested only on real data was able to achieve an accuracy of 89.01% (taken as 100%-classification error). A neural network trained on only synthetic data derived from real data in which the missing values were dropped and tested only on real data was able to achieve an accuracy of 90.56% (taken as 100%-classification error%). These classification errors demonstrate the utility of synthetic data in training machine learning classifiers.

In terms of clinical significance, researchers and clinicians can use synthetic data generated from in-house or internal databases to train complex machine learning and deep learning models. In this study, a neural network was trained on synthetic data with the goal to classify if a patient had ventricular dysfunction solely based on echocardiographic measures and BNP serological measures. When the neural network was trained with synthetic data, there was a difference in performance of the neural network dependent on how the synthetic data was derived. The neural network trained with dropped real data had a better false positive rate (3.1% versus 4.8%), higher specificity (78.6% versus 69.4%), and improved precision (96.2% versus 94.3%) when compared to when it was trained with imputed real data. This demonstrates that synthetic data acts as an adequate surrogate for real data in training machine learning models and that these models can predict Fontan patient functional status from a limited pool of commonly measured features.

There were some limitations to this study. First, only a subset of the vast dataset available on PHN was used. Echocardiographic measures were the focus of this study. However, Fontan patient data is complex, containing information about cardiovascular anatomical diagnosis, information about post-Fontan cardiovascular procedures, medication, valve issues, and much more. Data on maximal exercise capacity, which contain measures that have been shown to be very predictive of ventricular dysfunction, were also omitted. In addition, ventricular dysfunction was simplified as a binary variable. In fact, ventricular dysfunction in Fontan patients has many phenotypes. As a result, future research should focus on including more of these features, to approximate the medical records more accurately.

5 Conclusions

In this paper, the generation of two synthetic datasets from the Pediatric Heart Network Fontan I dataset was demonstrated. A dataset of 546 real subjects was used and missing values were handled in two ways: (1) imputing using MICE and (2) dropping the missing values. Upon generation of the synthetic data from these two scenarios, fidelity and utility of the synthetic datasets was calculated. Using histograms, probability density functions, and PCA, similarity in the distribution between synthetic data and real data were visually alike. Quantitatively, the synthetic data approximated a coin-flip guess in classifying real from synthetic samples (as evidenced by the 65.28% and 49.3% classification error). In addition, the utility of both synthetic datasets was shown. Specifically, a neural network trained on synthetic data was able to classify ventricular dysfunction from echocardiographic measures and BNP with misclassification rates of 10.99% and 9.44%. The classification error for this model trained on synthetic data derived from real data in which the missing values were imputed was 10.99%. The classification error for this model trained on synthetic data derived from real data in which the missing values were dropped was 9.44%. Overall, this represents the first attempt at generating synthetic data for cross-sectional data for the Fontan population.