 Open Access
Open Access
ARTICLE
Preliminary Evaluation of Hemodynamic Effects of Fontan Palliation on Renal Artery Using Computational Fluid Dynamics
1 Institute of Pediatric Translational Medicine, Shanghai Children’s Medical Center, School of Medicine, Shanghai Jiao Tong University, Shanghai, China
2 Shanghai Engineering Research Center of Virtual Reality of Structural Heart Disease, Shanghai Children’s Medical Center, School of Medicine, Shanghai Jiao Tong University, Shanghai, China
3 Department of Imaging Diagnosis Center, Shanghai Children's Medical Center, School of Medicine, Shanghai Jiao Tong University, Shanghai, China
* Corresponding Authors: Jun Du. Email: ; Qian Wang. Email:
# Jinlong Liu and Jing Shi contributed equally to this work
Congenital Heart Disease 2023, 18(1), 41-55. https://doi.org/10.32604/chd.2023.025005
Received 17 June 2022; Accepted 05 September 2022; Issue published 09 January 2023
Abstract
Background: The assessment of renal function is important to the prognosis of patients needing Fontan palliation due to the reconstructed compromised circulation. To know the relationship between the kidney perfusion and hemodynamic characteristics during surgical design could reduce the risk of acute kidney injury (AKI) and the postoperative complications. However, the issue is still unsolved because the current clinical evaluation methods are unable to predict the hemodynamic changes in renal artery (RA). Methods: We reconstructed a three-dimensional (3D) vascular model of a patient requiring Fontan palliation. The technique of computational fluid dynamics (CFD) was utilized to explore the changes of RA hemodynamics under different possible blood flow rates. The relationship between the kidney perfusion and hemodynamic characteristics was investigated. Results: The calculated results indicated the declined tendency of the pressure and pressure drop as the flow rate decreased. When the flow rate decreased to two-thirds of its baseline, both the pressure of left renal artery (LRA) and the pressure of right renal artery (RRA) dipped below 50%, and the pressure of RRA fell more quickly than that of LRA. Uneven distribution of WSS was observed on the trunk of RA, and the lowest WSS was found at the distal of RA. The average WSS in RA dropped to around 50% as the flow rate reached one-third of its baseline. Conclusions: As a promising approach, CFD can be utilized to quantitatively evaluate the hemodynamic characteristics of RA and contribute to offsetting the drawbacks of clinical assessments of renal function, to help realize better prognosis for the patients with Fontan palliation.Graphic Abstract

Keywords
Nomenclature
| AA | abdominal aorta |
| AKI | acute kidney injury |
| BSA | body surface area |
| bpm | beat per minute |
| CFD | computational fluid dynamics |
| CPB | cardiopulmonary bypass |
| CRF | chronic renal failure |
| d | characteristic length |
| EBS | Ebstein’s anomaly |
| EDV | end diastolic velocity |
| GS | Glenn shunt |
| HR | heart rate |
| HRV | hypoplastic right ventricle |
| Lh | hilum of the left kidney |
| LRA | left renal artery |
| PSV | peak systolic velocity |
| M | male |
| MAP | mean arterial pressure |
| p | pressure |
| Re | Reynolds number |
| Rh | hilum of the right kidney |
| RI | resistance index |
| RRA | right renal artery |
| WSS | wall shear stress |
| t | time |
| ux | velocity along the vascular wall |
| v | velocity |
| y | height above the wall |
| μ | viscosity |
| ρ | blood density |
| τwall | wall shear stress |
Kidney, as one of the important organs, has a great major role in filtration, metabolism and excretion of compounds [1]. The blood flow of kidney received takes up approximately 20%–25% of total cardiac output [2]. Because of its role, renal function has a great impact on the systemic circulation and prognosis of patients with cardiovascular diseases, which is a common focused indication during cardiovascular perioperative period consequently [3,4]. Fontan palliation is the commonly acceptable operation for patients born with functionally univentricular circulation for whom double ventricular circulation cannot be achieved. The palliation usually constructs an anastomosis with system venous and pulmonary arteries for restoring the in-series circulation. Owing to the peculiar anatomy of Fontan circulation, renal function of Fontan patients was more significant than that of other cardiac malformations, even as a determinant of their prognosis [5]. Of these, the application of intraoperative cardiopulmonary bypass, the frequent use of perioperative cardiotonic drugs and the geometric change of postoperative blood vessel morphology led to fluctuations in systemic circulation hemodynamics in Fontan patients [6], as well as that in renal artery (RA). Hemodynamic disturbance could bring a negative influence on renal function subsequently [7], which may lead to acute kidney risk or injury. However, there are few studies on the hemodynamic evaluation of RA currently because of the limitation of measurement methods [8]. Early detection of the alterations of RA hemodynamics and recognition of the deterioration of renal function would contribute to better outcomes for Fontan patients.
Computational fluid dynamics (CFD) has been emerging in many medical fields as a technological approach [9]. It can be used for simulating blood flow movements under different pathological or physiological situations by utilizing reconstructed individualized vascular models of patients and calculating the flow domain with corresponding blood boundary conditions. Compared with traditional imaging technologies, it can realize quantitative evaluation and prediction of blood flow movements intuitively in three dimensions (3D) for knowing the hemodynamic characteristics [10], rather than a sole vessel cross-section in the ultrasound measurements. Based on the preponderance of CFD technology, it has been applied a lot in the surgical design of Fontan palliation. However, most of them focused on these issues, like various geometries of cavopulmonary shunts and different fenestration forms or so [11–15]. Except for the above, Trusty et al. [16] also attempted to explore the relationship between hepatic fibrosis and Fontan hemodynamics. Whereas there are fewer studies on the hemodynamic effects of Fontan palliation on the renal arteries, which may lead to the hemodynamic alterations of RA, relate to surgical design, and affect the prognosis of Fontan patients as well. Fontan palliation changed the primary circulation actually and caused the fluctuation of cardiac output, as results as the changeable perfusion of kidney and related complications were prone to occur. Whether these hemodynamic alterations of RA are into the adjustable physiology range is unclear. Besides, the employment of cardiopulmonary bypass (CPB) which provides a bloodless field during the operative period, replaced the function of heart pumping and changed primary pulsative effects. Surgeons always drained the venous blood through the intravenous cannulation and placed the arterial conduit in the ascending aorta to maintain systemic circulation, and the maintained blood pressure was lower than the primary one consequently [17]. All these above factors can bring unknown hemodynamic influence on RA through various renal perfusion during the Fontan palliation period. A better comprehension of the relationship between blood flow perfusion and RA hemodynamics may help to accomplish a well-thought-out surgical design.
In order to figure out the effects of different renal perfusion on RA hemodynamics of Fontan patients, we utilized CFD technology to penetrate into the alterations of RA hemodynamic characteristics under different blood flow rates. We reconstructed a patient-specific 3D model of RA, rendered degressive flow rates to the abdominal aorta (AA), and analyzed hemodynamic alterations of RA. The aim of the present study is to provide not only local hemodynamic evaluations by CFD, but also quantitative information to the clinicians for a better surgical design.
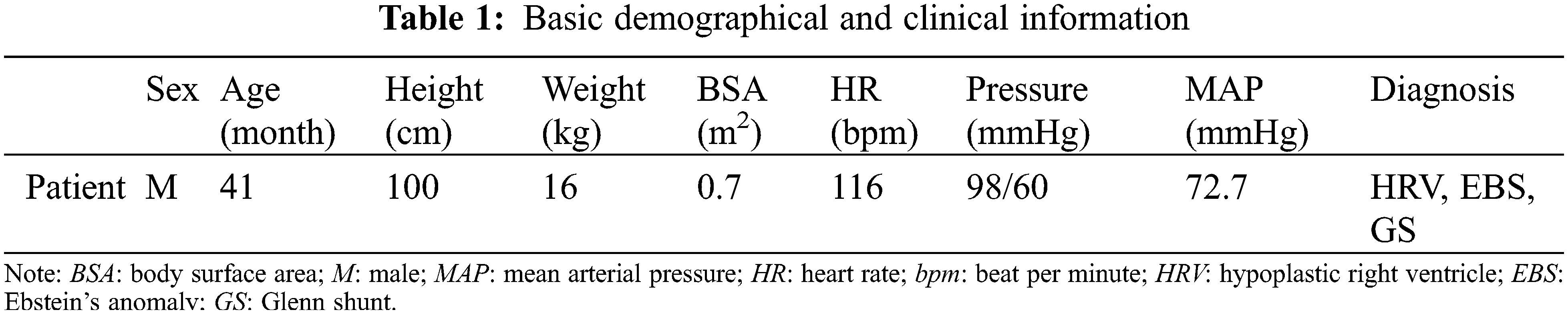
2.1 Patient Data and Model Reconstruction
The current study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). It was carried out with the approval of the local institutional review board and regional research ethics committee of Shanghai Children’s Medical Center (SCMC) Affiliated Shanghai Jiao Tong University School of Medicine (SCMCIRB-K2021052-1), and written informed consent was obtained from the patient’s parents. The diagnosis of the patient was hypoplastic right ventricle (HRV), and he was going to perform Fontan palliation. The basic demographic and clinical information were shown in Table 1. The abdominal vascular imaging data of the patient before Fontan palliation were acquired by a 64-slice multi-detector row enhanced computed tomography (CT) scanner (Bright Speed Elite, GE Medical System, General Electric, Fairfield, Connecticut, USA). Meanwhile, related ultrasound blood flow data of these vessels were collected by color Doppler flow imaging (CDFI) measurement, including the peak systolic velocity (PSV), the end diastolic velocity (EDV) and the resistance index (RI), and so on. Table 2 collected patient-specific ultrasound data about renal arteries.
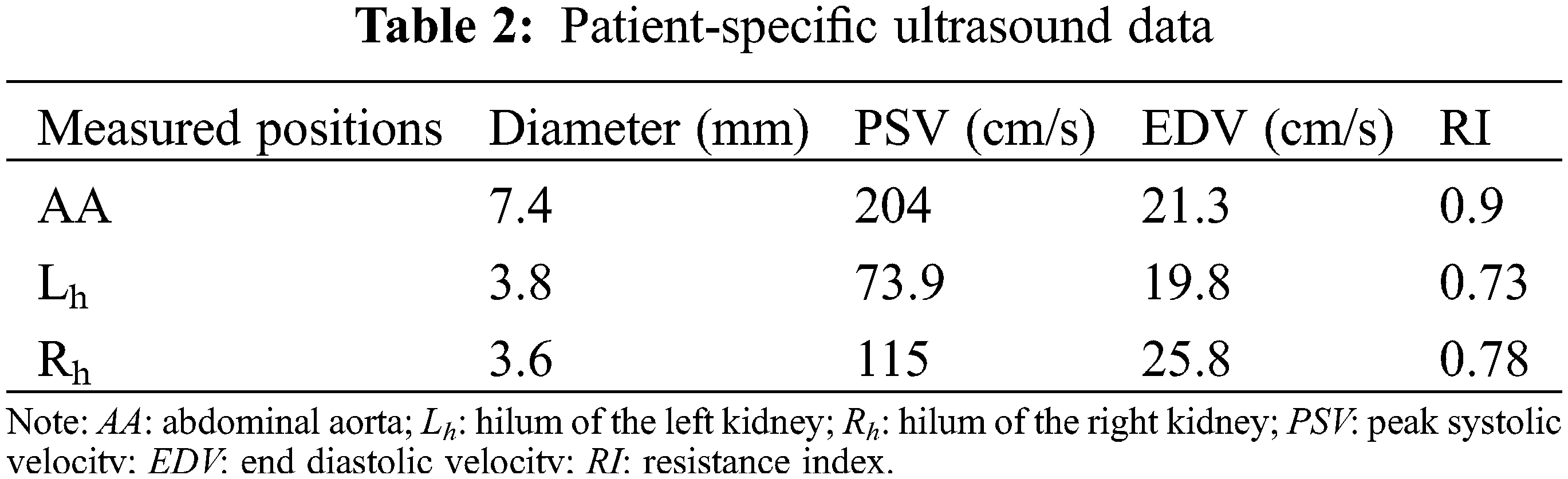
The highly integrated medical image processing software, Materialise®-Mimics Innovation Suite 20.0 (Materialise NV. Leuven, Belgium) and Materialise®-3-Matic 12.0 (Materialise NV. Leuven, Belgium), were utilized to perform 3D reconstruction of AA, RA and other vascular branches. Fig. 1 showed the reconstruction of patient-specific 3D vascular model. The model remained AA, hepatic artery (HA), splenetic artery (SA), left renal artery (LRA) and right renal artery (RRA), which were exported in stereolithography interface format (STL) for CFD analysis.
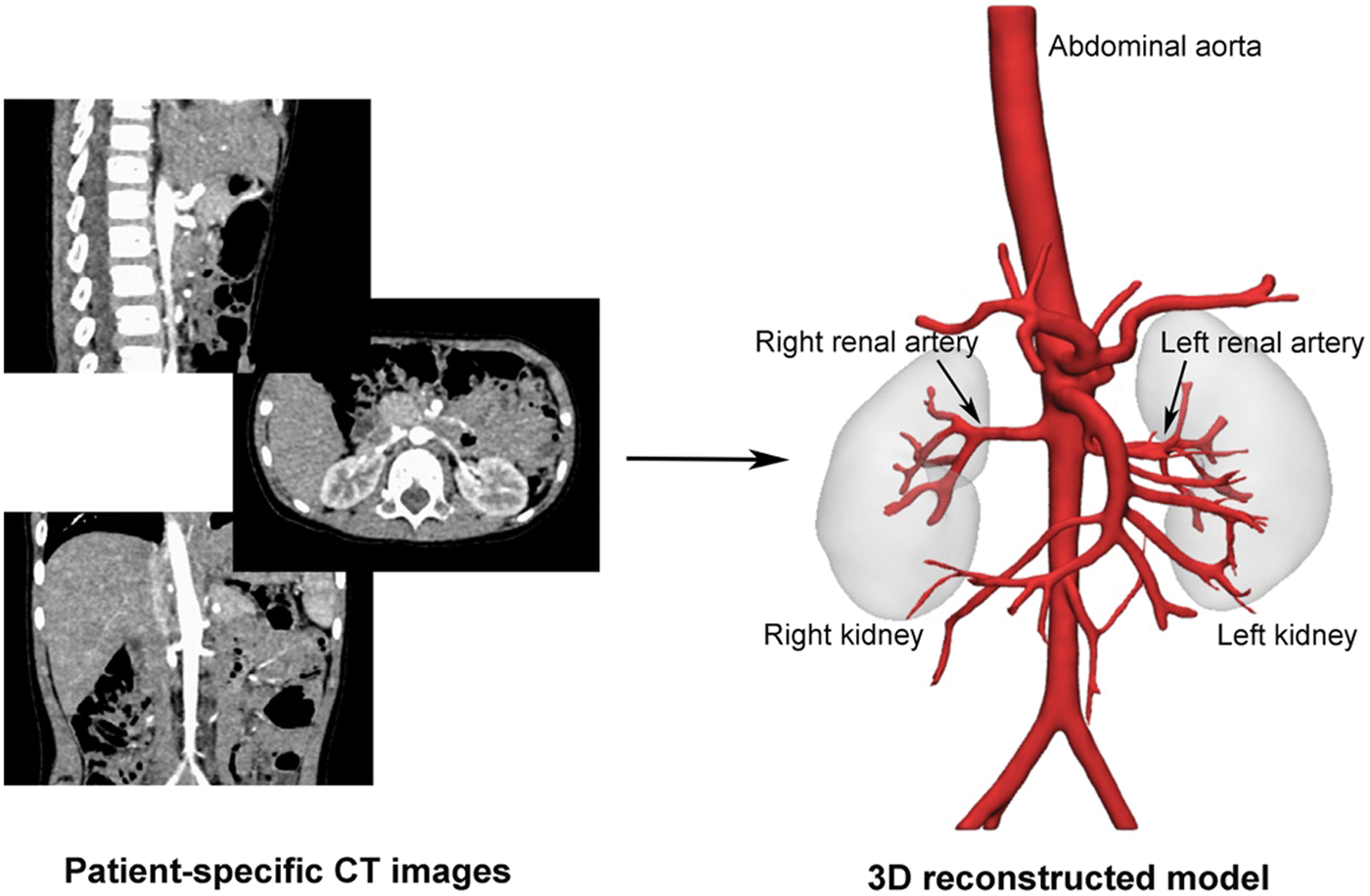
Figure 1: The reconstruction of the patient-specific 3D model
2.2 Numerical Simulation and Hemodynamic Parameters
ANSYS®-ICEM CFD 2020 (ANSYS Inc. Houston, Texas, USA), as the mesh-generation software, was applied for the tetrahedral mesh generation in the interior of the model and five layers of body-fitted prism mesh generation in the near-wall region. Concerning the complex geometry of the vascular model, especially in the connection area of branches with different diameters, the self-adaptive refinement was used to be optimized globally. We found that sensitivity analysis of the grid refinement showed the most efficient when the total number of mesh elements achieved 1.0 million.
Assuming that the vascular wall was rigid and had no slip, and the blood flow was Newtonian fluid [18] with a density of 1060 kg/m3 and a dynamic viscosity of 3.5 × 10−3 Pa⋅s. The numerical simulation software ANSYS®-Fluent 2020 (ANSYS Inc. Houston, Texas, USA) was used to analyze the hemodynamic performance of the 3D reconstructed RA model based on the continuity and Navier-Stokes (N-S) equations. They were as follows (Eqs. (1) and (2)):
∇⋅v=0 (1)
ρDvDt+ρv⋅∇v=−∇p+μ∇2v (2)
where ρ is the blood density, v is the velocity vector of a point in the fluid domain, μ is the viscosity, t is the time, and p is the pressure.
To explore the effects of fluctuated blood perfusion on RA hemodynamics, we assumed the actual ultrasound data as the boundary conditions of “Q” for illustrating the primary state. According to the common practices of cardiopulmonary bypass (CPB) in our hospital SCMC, we found one-third of the flow rate in “Q” close to the lowest available value during CPB operation. And we multiplied the flow rate by 2/3 and 1/3, respectively, and set “2/3 Q” and “1/3 Q” to represent different blood fluctuations in Fontan palliation process consequently.
In view of the three states, we adopted the clinical measurement values to figure out the dimensionless unit, the Reynolds number (Re), for detecting the blood flow movement of RA. It was defined as the following (Eq. (3)):
Re=ρνdμ (3)
where v was the velocity, and d was the characteristic length. Accordingly, the Re numbers of the three states were all smaller than the critical value (2300 generally) [19]. Meantime, lots of numerical simulation research about AA conducted the laminar model for solving these blood flows [20–22], and we herein chose the laminar model.
To simulate the actual blood flow of aorta under the application of CPB, we measured the vessel length from the implanted site of aortic conduit to the inlet, which is approximately equal to 20 times the diameter of the abdominal aorta. Hence, the inlet was added a 20 times extension of the diameter in the upstream direction. The velocity of the inlet was acquired by the patient-specific ultrasound data, and the flow rates of bilateral RA were also obtained. Depending on the patient-specific ultrasound data, we got these blood flow fractions among the vascular branches of AA. Compared with the blood flow fractions utilized by Qin et al. [23] for detecting the hemodynamics of AA, our obtained data about fractions were in its range. Herein, the blood flow fractions were adopted, and we assumed the constant values in three situations, given that kidney had a regulating function in a certain range of blood pressure [24,25]. The SIMPLE algorithm and the second-order upwind scheme were used to solve the blood flow domain, and the convergence criterion was set to 10−5.
In the process of Fontan palliation, the reconstruction of cardiovascular circulation, the application of CPB and the frequent employment of vasoactive drugs would change the cardiac output and pressure of inferior vena cava directly, inducing the fluctuations of blood perfusion for RA finally. And these parameters, such as pressure, pressure drop%, velocity, streamlines and wall shear stress (WSS), were supposed to reveal the alteration of hemodynamic characteristics initially. This study thereupon mainly discussed the above parameters.
Pressure drop% was the ratio of pressure drop between the inlet and outlets of RA to the inlet blood pressure of RA, which was defined as follows (Eq. (4)):
Pressuredrop%=Pinlet−PoutletPinlet×100% (4)
where Pinlet and Poutlet are the average blood pressure of RA inlet (the connection area of RA and AA) and outlets (the ends of RA branches of the reconstructed model), respectively. The pressure drop% of LRA and RRA were both calculated.
WSS is the interaction force formed by the flowing blood on the wall of vessels. It was proven to be relevant to vascular endothelial dysfunction [26]. It was given by (Eq. (5)):
τwall=−μ∂ux∂y∣∣∣y=0 (5)
where μ is the viscosity, ux is the velocity of the blood flow along the vascular wall, and y is the height above the wall.
3.1 Pressure and Pressure Drop%
Fig. 2 displayed the pressure distribution of patient-specific 3D models under different blood flow rates. When the blood flow rate maintained the original level, as “Q”, the average pressure of AA was about 75.2 mmHg, higher than the value of mean arterial pressure (MAP = 72.7 mmHg) due to the neglection of the elastic artery wall in simulation. As the flow rate of inlet cut down to “1/3 Q”, the average pressure of AA (48.1 mmHg) was near the minimum value of the physiologically affordable blood pressure (50 mmHg) [27]. Hence, we presumed the kidney of the patient could still adjust the decreased pressure within the physiological range, and the primary proportions of blood flow fractions hold the same when setting the boundary conditions of outlets in “2/3 Q” and “1/3 Q”. From “Q” to “1/3 Q”, blood pressure of the main trunk of AA was decreasing gradually. However, for RA, the decreasing tendency only exited in the region close to the main body of AA. The pressure changes in distal vessels of RA were not obvious.
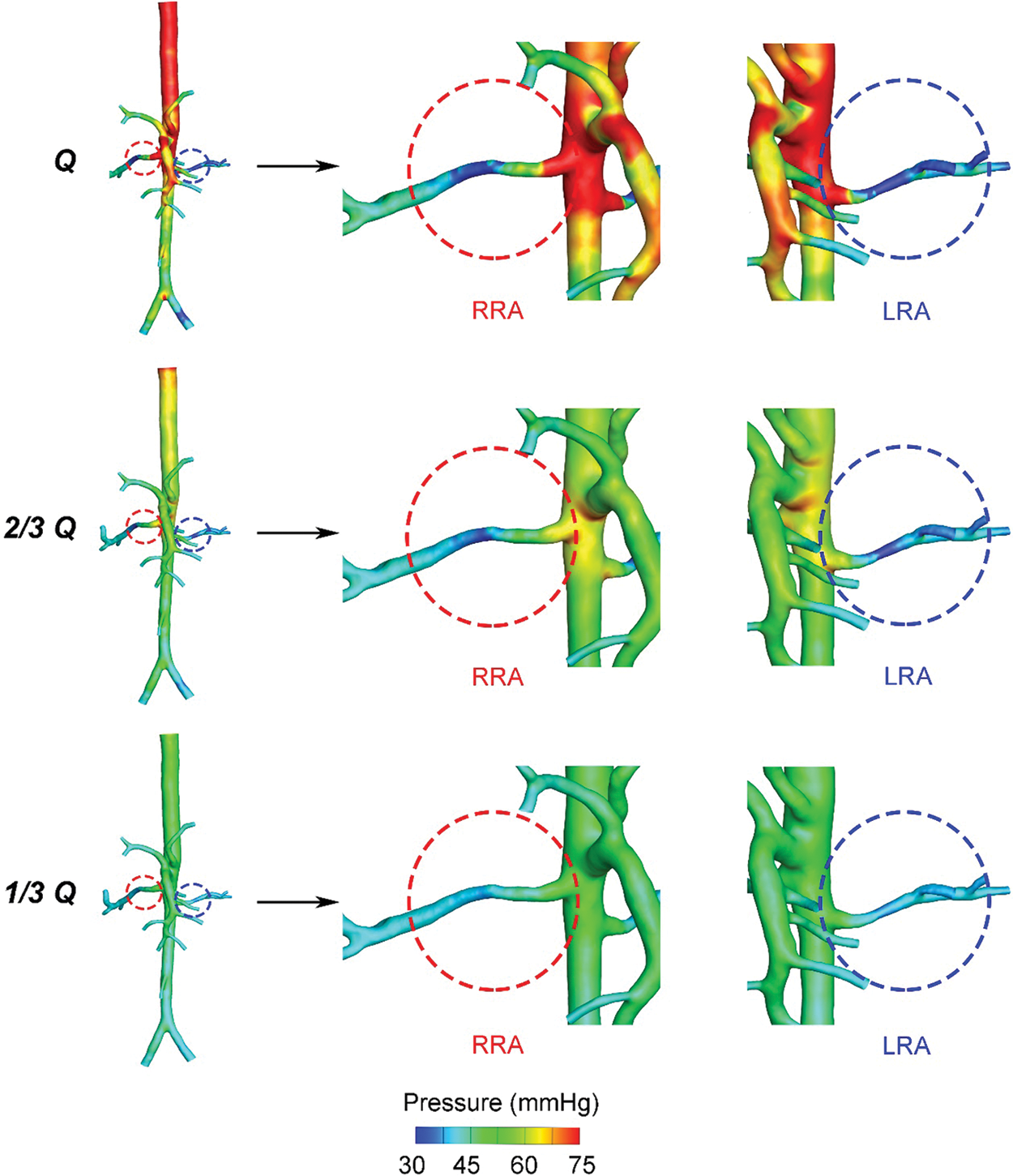
Figure 2: Pressure contour plots of the three states
Fig. 3 demonstrated the tendency of pressure drop% from “Q” to “1/3 Q”, which represents the descendent tendency of pressure in LRA and RRA, respectively. The value of pressure drop% in RRA was higher than LRA. The difference was caused by the primary unbalance of resistance index (RI) between LRA (0.73) and RRA (0.78). What’s more, the pressure drop% of RRA fell more quickly than LRA. A more significant decreasing tendency was observed from “Q” to “2/3 Q” than that from “2/3 Q” to “1/3 Q”. In “2/3 Q”, the pressure drop% of LRA and RRA both dipped below 50%. The gap of LRA and RRA shown in Fig. 3 was getting smaller as the decreasing flow rates.
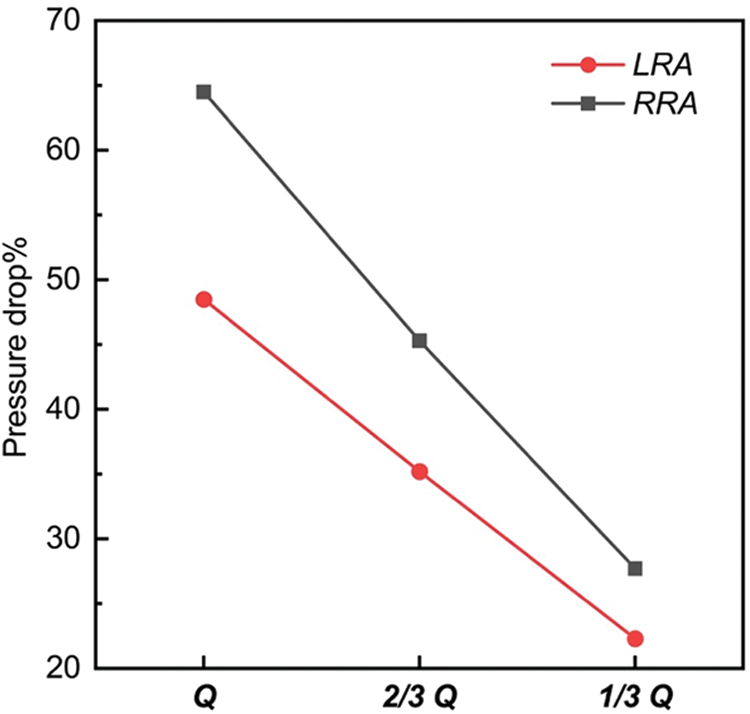
Figure 3: Tendence of pressure drop% in the three states
As shown in Fig. 4, a decreased tendency about the value of velocity was observed from “Q” to “1/3 Q”. The streamlines of the whole flow domain were flat, with no obvious turbulence flow. In every state, it was noted that a higher velocity region was observed on the main trunk of RA. The higher velocity region gradually faded as the reduced flow rates. The velocity distribution showed that the average velocity of “Q” was around 2.5 m/s, and the average of “1/3 Q” did not even reach 1.5 m/s.
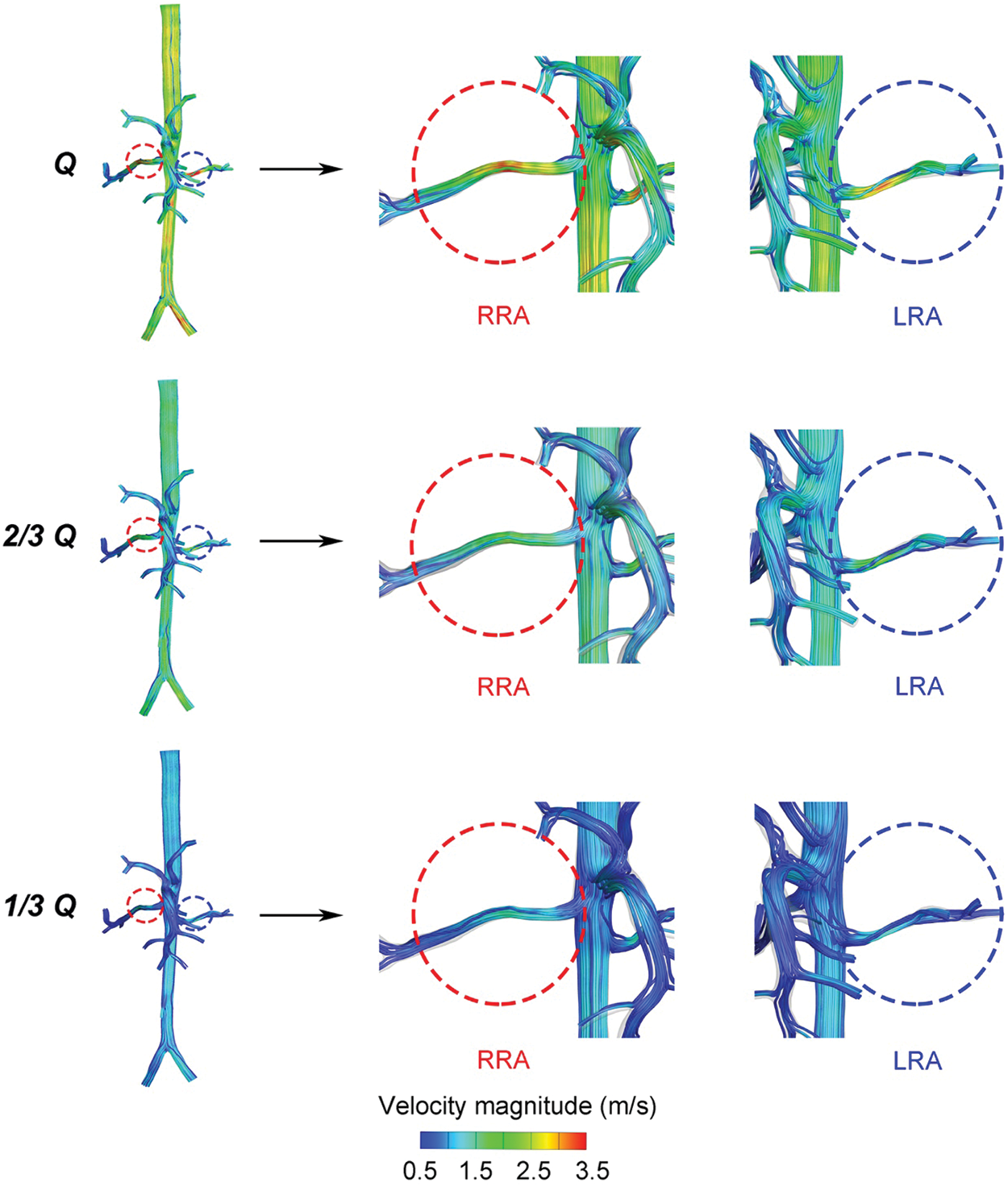
Figure 4: The velocity distribution of the three states
WSS of RA were displayed in Fig. 5. A higher WSS region was observed bilaterally near the entrance of RA, and a lower region near the distal vessel, respectively. With the decrease of flow rates, the area of higher WSS region was becoming smaller, and the lower one bigger. From “Q” to “1/3 Q”, the difference of the average WSS between LRA and RRA, displayed in Fig. 6, was getting smaller and smaller as well. It was ranged from 20.4 to 4.4 Pa. As for RRA, the average value of WSS dropped 52.3 Pa in “Q” from 11.8 Pa in “1/3 Q”. While the alterations were more dramatic in LRA (56.7 Pa). Likewise, the distribution of higher regions was found like a little more uneven than other vascular areas in RA.
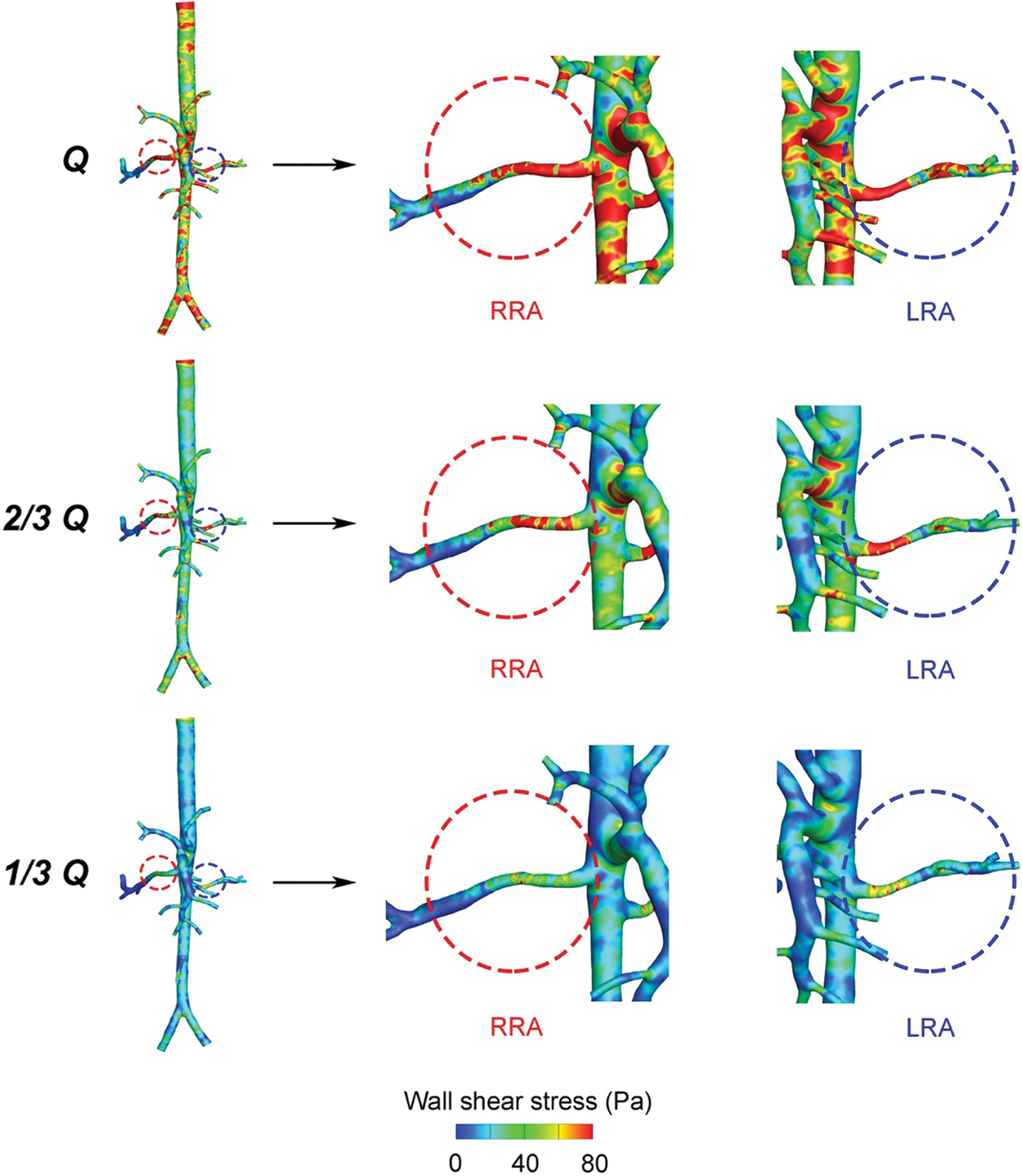
Figure 5: Wall shear stress distribution in the three states
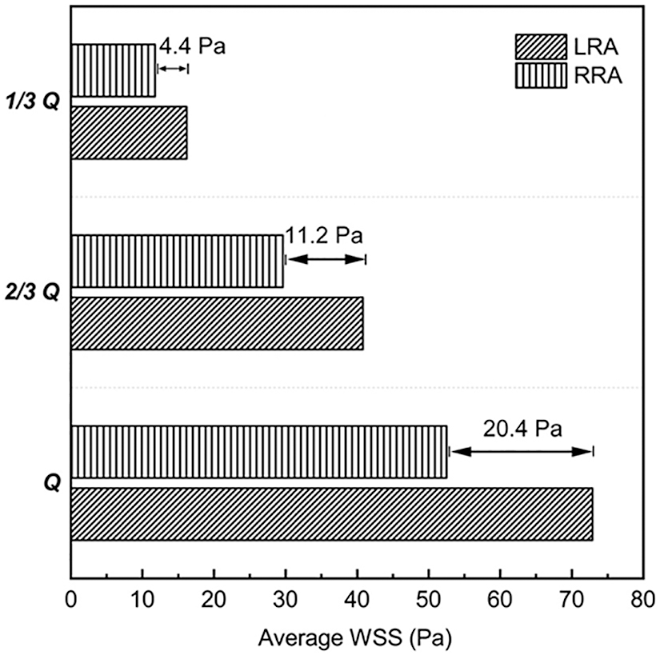
Figure 6: Average WSS of the three states
Renal function is a commonly examined indication for cardiothoracic surgeries, which can reflect the fluctuation of systemic circulation indirectly. When postoperative patients occur kidney injuries, such as acute kidney injury (AKI) or chronic renal failure (CRF), the later the kidney injury is diagnosed, the worse the prognosis for patients [28]. Most biochemical examined indications, like serum creatinine and urine output, usually lack certain sensibility and specificity [29,30]. Moreover, the etiology of kidney injury is usually complex, not monopolistic. Among these risk factors, there are plenty of definite risk factors about AKI, for example, the duration of CPB, the complexity of cardiac surgery, low cardiac output syndrome, ischemia-reperfusion injury and so on [27].
Furthermore, Fontan operation is the common palliative procedure for patients with a single ventricle, whose surgical procedures are more complicated than other congenital heart diseases [6,31]. The complexity and particularity of Fontan palliation make the renal function of Fontan patients more susceptible to these risk factors. These factors above can interact with each other and cause the hemodynamic alterations of RA essentially along the continuum of the Fontan palliation process. It is supposed that the alterations of RA hemodynamics have superior to the emergence of biochemical blood markers for renal dysfunction.
Meantime, the employment of CPB technology is quite necessary for Fontan palliation. During the operative period, CPB technology needs to clamp the aorta and replace the systemic circulation to a form like extracorporeal circulation, consisting of an oxygenator and a blood pump. When clamping the aorta, the blood flow of coronary artery would decrease sharply, and the myocardium would not get enough perfusion. Consequently, the function of heart pumping got impaired and patients with cardiac surgeries can develop various complications, like low cardiac output syndrome. As a result, the cardiac output got affected and the whole systemic perfusion got decreased, as well as the poor perfusion of organs, which were relevant to the time of aorta clamping. When the successful work of this extracorporeal circulation was established, the optimal perfusion pressure and flow rates of the blood pump for Fontan patients were still controversial. The detailed control of the blood pump always depended on the experiences of CPB operator. During the working time of CPB, the mean artery pressure is used to maintain the constant value between 50 to 70 mmHg for providing basic life activities [27]. Although the blood pressure maintained the blood perfusion requirements of major organs, like the brain and kidney, it was still a low perfusion pressure, and non-pulsative blood flow differed from physiological pulsation [32]. And there was little known about what hemodynamic alterations the low perfusion and non-pulsative blood flow would bring to the kidney. Hence, it is necessary to elucidate the hemodynamic alterations of RA.
CFD technology, as a promising tool, can analyze the blood flow movements through reconstructed 3D vasular models for a more comprehensive evaluation, rather than a sole vessel cross-section in the ultrasound measurements. More than that, CFD can realize the prediction of hemodynamic characteristics according to different boundary conditions corresponding to research objectives.
This current study performed a steady blood flow to simulate the non-pulsative blood flow, and changed different possible blood flow rates, for figuring out the tendency of hemodynamic alterations of RA. The calculated results were expected for predicting the appropriate perfusion of kidney during the Fontan palliation process and reducing the risks of renal dysfunction in patients with Fontan for better surgical design.
From our calculated results, the average blood pressure of “Q” and “1/3 Q” was near the actual value of mean arterial pressure, MAP (72.7 mmHg) and the minimum adjustive value of CPB (50 mmHg), and these results confirmed the rationality of our simulation. Along with the opening of CPB, the blood pump started to work and pumped blood into the kidney for keeping renal perfusion. The opening period resembled the alteration turning “Q” into “1/3 Q” which was accomplished in CFD simulation. It is easy to find the lower pressure with the decreasing blood flow rate. The velocity of blood flow was decreasing either. When the blood flow rates cut down to “2/3 Q”, the pressure of RA and AA decreased sharply. Within the physiologically affordable blood flow range, kidney started to regulate the fluctuated blood flow through augment of RI. And the ability of regulation would get worsen with the lower perfusion, like the condition as “1/3 Q”. It explained the lowest value of pressure drop% in “1/3 Q” among the three conditions, which meant the increased RI [33,34].
Of note, we found the disturbance of WSS, which was mainly found in the region near the entrance of RA. In this region, blood flow went through the bifurcation of AA and RA firstly, and then turned the corners to renal branches. The complex anatomy shape caused the hemodynamic characteristics changeable, as WSS. The sudden increase of WSS was also observed, as same as the findings of Sughimoto et al. [35]. In the bigger size of blood vessels, as the aorta, the main trunk of hepatic artery and renal artery, WSS means the shear force formed by flowing blood acting on the vessel wall surface. The higher values of WSS predicated the higher shear forces the region suffered and may cause higher risks of the endothelial dysfunction of RA [25]. The long-term risk that renal hilum section suffered may trigger the process of proliferation of the inner membrane [36], which was also found in the development of renal hypertension [37]. More than that, the uneven distribution of WSS suggested a more disorganized flow domain existed in that region, led to endothelial dysfunction and induced kidney function lesion eventually. After Fontan palliation, the anastomosis of cave vein and pulmonary artery, unlike normal venous return, caused the systemic venous pressure to increase. This was equivalent to the increase of the distal pressure and contributed to the poor renal perfusion. The decreasing process of renal perfusion during the postoperative period was also simulated by cutting off the blood flow rate gradually. And the diminishing pressure drop and flow rates proved to the poor renal perfusion either. It was worth noting that the lowest WSS was found in the distal renal arteries. Other than the bigger size vessels, WSS in small size vessels preferred the interforce of blood cells, like red blood cells, white blood cells, or lymphocytes [38,39]. The lower the value of WSS, the slower the velocity change of those vessels. The velocity of blood flow in those distal vessels was also the minimum. Within the almost motionless blood flow, blood cells silted up the whole lumen, and the risk of thrombosis increased dramatically once the hypercoagulable state of Fontan patients occurred [40,41]. Consequently, the perfusion of the posterior renal corpuscle declined sharply, which would make kidney function drastically impacted [42]. And the occurrence of various complications associated with kidney for Fontan patients was apparently higher than in other cardiac surgery patients, owing to the changeable and complex hemodynamics of RA. The hemodynamic alterations of RA illuminated the suspectable tendency of worse renal function in patients with Fontan surgery better.
Herein, investigating the hemodynamic characteristics of RA is necessary for predicting the appropriate renal perfusion of Fontan patients. CFD, as an approach, integrates with strong computational capability and patient-specific investigation. It has the advantage of non-invasion, accuracy and personalization, and provides various hemodynamic parameters which cannot be obtained by clinical measurements [9]. By comparing with the simulation results under different blood flow rates during Fontan palliation procedure, we can predict the alterations of hemodynamic characteristics in RA through CFD analysis. It may contribute to the early detection of kidney lesions for Fontan patients and allow for more quantitative and personalized information for clinicians to make Fontan patients a better outcome in surgical design. Further works will be done to explore the interrelationship between the biomechanical markers and the hemodynamic parameters in the future. What’s more, traditional examined methods, like MRI and ultrasound, combined with CFD, are supposed to establish an emerging evaluation standard about renal kidney for reducing risks of Fontan patients in expectations.
The present study was a preliminary exploration about the application of CFD in estimating the renal function in patients with Fontan palliation under different states. Previous studies indicated a certain relationship between microcirculation and renal function [43]. Taking into account the safety of pediatric radiation exposure, the use of low-dose contrast media for children’s CT examinations also resulted in a slightly lower resolution of pediatric CT images than adult CT images and the difficulty of the reconstruction of small-size vessels about the kidney [44]. Hence, the image quality was not enough to show the distal vessels clearly. It was technically and ethically inevitable to miss some microvascular structures. The hemodynamic analysis of the microcirculation of RA was not considered in the present study. Additionally, this study assumed the rigid artery wall and the simulation combined with fluid-structure interaction would be applied in the future, considering the elasticity of the artery wall.
In this study, CFD was used to investigate the hemodynamic characteristics of RA under different flow rates for imitating the blood flow alterations during the Fontan palliation process. In view of the direct influence caused by blood flow fluctuations, we discussed the pressure, pressure drop%, velocity, streamlines and WSS of RA. With the blood flow rates decreasing, it was remarkably observed that the declined tendency of pressure was consistent with that of the velocity on each side of the renal artery, but the pressure of RRA reduced more quickly than LRA. And the disorganized WSS distribution may contribute to worse renal function and induce complications in Fontan patients. Through the analysis of CFD results, hemodynamic alterations of RA, which were likely caused by the Fontan palliation, would trigger the renal function lesion eventually, related to various complications. Within the physiological adjustive range, the application of CFD technology can contribute to predicting the possible hemodynamic states, and it is worthy of surgical design in clinical practice. In the future, more large-scale investigations will be done on the clinical practice of CFD to realize the intrinsic hemodynamic alteration of RA in Fontan patients and on the coherence of the hemodynamics of RA and traditional examined methods for providing more information to improve the surgical design.
Authorship: The authors confirm contribution to the paper as follows: study conception and design: Jinlong, L., Jing, S.; administrative support: Qian, W., Jun, D. and Jinlong, L.; provision of study materials or patients: Lefei, Y., Jing, S.; collection and assembly of data: Peixuan, S., Tianyi, L. and Jun, D.; data analysis and interpretation: Weiru, L., Zhirong, T. and Qian, W.; draft manuscript preparation: Jinlong, L., Weiru, L. and Jing, S. All authors reviewed the results and approved the final version of the manuscript.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013), and prior informed consent was obtained from surrogate decision-makers. This study was carried out with the approval of the local institutional review board and regional research ethics committee of Shanghai Children’s Medical Center (SCMC) Affiliated Shanghai Jiao Tong University School of Medicine (SCMCIRB-K2021052-1) and the written informed consent from the parents of a patient.
Availability of Data and Materials: These datasets used and analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgement: The authors acknowledge the support from the Department of Cardiothoracic Surgery and the Department of Radiology of Shanghai Children’s Medical Center.
Funding Statement: This study was supported by National Natural Science Foundation of China (No. 81970439), Natural Science Foundation of Shanghai (No. 19ZR1432700), Fund of the Shanghai Committee of Science and Technology (Nos. 19411965400, 17DZ2253100) and the Development Fund of Shanghai Talents (No. 2020114).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Wallace, M. A. (1998). Anatomy and physiology of the kidney. AORN Journal, 68(5), 799–820. DOI 10.1016/S0001-2092(06)62377-6. [Google Scholar] [CrossRef]
2. Basile, D. P., Anderson, M. D., Sutton, T. A. (2012). Pathophysiology of acute kidney injury. Comprehensive Physiology, 2(2), 1303–1353. DOI 10.1002/cphy. [Google Scholar] [CrossRef]
3. Yuan, S. M. (2019). Acute kidney injury after pediatric cardiac surgery. Pediatrics and Neonatology, 60(1), 3–11. DOI 10.1016/j.pedneo.2018.03.007. [Google Scholar] [CrossRef]
4. Amann, K., Wanner, C., Ritz, E. (2006). Cross-talk between the kidney and the cardiovascular system. Journal of the American Society of Nephrology, 17(8), 2112–2119. DOI 10.1681/ASN.2006030204. [Google Scholar] [CrossRef]
5. Byrne, R. D., Weingarten, A. J., Clark, D. E., Huang, S., Perri, R. E. et al. (2019). More than the heart: Hepatic, renal, and cardiac dysfunction in adult Fontan patients. Congenital Heart Disease, 14(5), 765–771. DOI 10.1111/chd.12820. [Google Scholar] [CrossRef]
6. de Lange, C. (2020). Imaging of complications following Fontan circulation in children—diagnosis and surveillance. Pediatric Radiology, 50(10), 1333–1348. DOI 10.1007/s00247-020-04682-5. [Google Scholar] [CrossRef]
7. Zafar, F., Lubert, A. M., Katz, D. A., Hill, G. D., Opotowsky, A. R. et al. (2020). Long-term kidney function after the Fontan operation: JACC review topic of the week. Journal of the American College of Cardiology, 76(3), 334–341. DOI 10.1016/j.jacc.2020.05.042. [Google Scholar] [CrossRef]
8. Suarez, J., Busse, L. W. (2020). New strategies to optimize renal haemodynamics. Current Opinion in Critical Care, 26(6), 536–542. DOI 10.1097/MCC.0000000000000774. [Google Scholar] [CrossRef]
9. Salavitabar, A., Armstrong, A. K. (2020). Personalized interventions: A reality in the next 20 years or pie in the sky. Pediatric Cardiology, 41(3), 486–502. DOI 10.1007/s00246-020-02303-4. [Google Scholar] [CrossRef]
10. Mittal, R., Seo, J. H., Vedula, V., Choi, Y. J., Liu, H. et al. (2016). Computational modeling of cardiac hemodynamics: Current status and future outlook. Journal of Computational Physics, 305(4), 1065–1082. DOI 10.1016/j.jcp.2015.11.022. [Google Scholar] [CrossRef]
11. Bove, E. L., de Leval, M. R., Migliavacca, F., Balossino, R., Dubini, G. (2007). Toward optimal hemodynamics: Computer modeling of the Fontan circuit. Pediatric Cardiology, 28(6), 477–481. DOI 10.1007/s00246-007-9009-y. [Google Scholar] [CrossRef]
12. Hong, H., Dur, O., Zhang, H., Zhu, Z., Pekkan, K. et al. (2013). Fontan conversion templates: Patient-specific hemodynamic performance of the lateral tunnel versus the intraatrial conduit with fenestration. Pediatric Cardiology, 34(6), 1447–1454. DOI 10.1007/s00246-013-0669-5. [Google Scholar] [CrossRef]
13. de Zelicourt, D. A., Kurtcuoglu, V. (2016). Patient-specific surgical planning, Where do we stand? The example of the Fontan procedure. Annals of Biomedical Engineering, 44(1), 174–186. DOI 10.1007/s10439-015-1381-9. [Google Scholar] [CrossRef]
14. Ono, M., Burri, M., Mayr, B., Anderl, L., Cleuziou, J. et al. (2020). Flow dynamics of bilateral superior cavopulomonary shunts influence outcomes after Fontan completion. Pediatric Cardiology, 41(4), 816–826. DOI 10.1007/s00246-020-02318-x. [Google Scholar] [CrossRef]
15. Wei, Z. A., Johnson, C., Trusty, P., Stephens, M., Wu, W. et al. (2020). Comparison of Fontan surgical options for patients with apicocaval juxtaposition. Pediatric Cardiology, 41(5), 1021–1030. DOI 10.1007/s00246-020-02353-8. [Google Scholar] [CrossRef]
16. Trusty, P. M., Wei, Z., Rychik, J., Russo, P. A., Surrey, L. F. et al. (2018). Impact of hemodynamics and fluid energetics on liver fibrosis after Fontan operation. Journal of Thoracic and Cardiovascular Surgery, 156(1), 267–275. DOI 10.1016/j.jtcvs.2018.02.078. [Google Scholar] [CrossRef]
17. Tolwani, A., Paganini, E., Joannidis, M., Zamperetti, N., Verbine, A. et al. (2008). Treatment of patients with cardiac surgery associated-acute kidney injury. International Journal of Artificial Organs, 31(2), 190–196. DOI 10.1177/039139880803100212. [Google Scholar] [CrossRef]
18. Ou, J., Tang, A. Y. S., Chiu, T. L., Chow, K. W., Chan, Y. C. et al. (2017). Haemodynamic variations of flow to renal arteries in custom-made and pivot branch fenestrated endografting. European Journal of Vascular and Endovascular Surgery, 53(1), 133–139. DOI 10.1016/j.ejvs.2016.10.022. [Google Scholar] [CrossRef]
19. Weddell, J. C., Kwack, J., Imoukhuede, P. I., Masud, A. (2015). Hemodynamic analysis in an idealized artery tree: Differences in wall shear stress between Newtonian and non-Newtonian blood models. PLoS One, 10(4), e0124575. DOI 10.1371/journal.pone.0124575. [Google Scholar] [CrossRef]
20. Nerem, R. M., Seed, W. A., Wood, N. B. (1972). An experimental study of the velocity distribution and transition to turbulence in the aorta. Journal of Fluid Mechanics, 52(1), 137–160. DOI 10.1017/S0022112072003003. [Google Scholar] [CrossRef]
21. Bonert, M., Leask, R. L., Butany, J., Ethier, C. R., Myers, J. G. et al. (2003). The relationship between wall shear stress distributions and intimal thickening in the human abdominal aorta. Biomedical Engineering Online, 2(1), 18. DOI 10.1186/1475-925X-2-18. [Google Scholar] [CrossRef]
22. Qian, Y., Liu, J. L., Itatani, K., Miyaji, K., Umezu, M. (2010). Computational hemodynamic analysis in congenital heart disease: Simulation of the Norwood procedure. Annals of Biomedical Engineering, 38(7), 2302–2313. DOI 10.1007/s10439-010-9978-5. [Google Scholar] [CrossRef]
23. Qin, S., Chen, R., Wu, B., Shiu, W. S., Cai, X. C. (2021). Numerical simulation of blood flows in patient-specific abdominal aorta with primary organs. Biomechanics and Modeling in Mechanobiology, 20(3), 909–924. DOI 10.1007/s10237-021-01419-7. [Google Scholar] [CrossRef]
24. Lee, D., Chen, J. Y. (2002). Numerical simulation of steady flow fields in a model of abdominal aorta with its peripheral branches. Journal of Biomechanics, 35(8), 1115–1122. DOI 10.1016/S0021-9290(02)00044-1. [Google Scholar] [CrossRef]
25. Mortazavinia, Z., Arabi, S., Mehdizadeh, A. R. (2014). Numerical investigation of angulation effects in stenosed renal arteries. Journal of Biomedical Physics and Engineering, 4(1), 1–8. [Google Scholar]
26. Ballermann, B. J., Dardik, A., Eng, E., Liu, A. (1998). Shear stress and the endothelium. Kidney International Supplements, 67, S100–S108. [Google Scholar]
27. Yang, P. L., Wong, D. T., Dai, S. B., Song, H. B., Ye, L. et al. (2009). The feasibility of measuring renal blood flow using transesophageal echocardiography in patients undergoing cardiac surgery. Anesthesia and Analgesia, 108(5), 1418–1424. DOI 10.1213/ane.0b013e3181923d2e. [Google Scholar] [CrossRef]
28. Hobson, C. E., Yavas, S., Segal, M. S., Schold, J. D., Tribble, C. G. et al. (2009). Acute kidney injury is associated with increased long-term mortality after cardiothoracic surgery. Circulation, 119(18), 2444–2453. DOI 10.1161/CIRCULATIONAHA.108.800011. [Google Scholar] [CrossRef]
29. Ratanarat, R., Skulratanasak, P., Tangkawattanakul, N., Hantaweepant, C. (2013). Clinical accuracy of RIFLE and Acute Kidney Injury Network (AKIN) criteria for predicting hospital mortality in critically ill patients with multi-organ dysfunction syndrome. Journal of the Medical Association of Thailand, 96(Suppl 2), S224–231. [Google Scholar]
30. Wang, Y., Bellomo, R. (2017). Cardiac surgery-associated acute kidney injury: Risk factors, pathophysiology and treatment. Nature Reviews Nephrology, 13(11), 697–711. DOI 10.1038/nrneph.2017.119. [Google Scholar] [CrossRef]
31. Sharma, S., Ruebner, R. L., Furth, S. L., Dodds, K. M., Rychik, J. et al. (2016). Assessment of kidney function in survivors following Fontan palliation. Congenital Heart Disease, 11(6), 630–636. DOI 10.1111/chd.12358. [Google Scholar] [CrossRef]
32. Murkin, J. M. (2019). Monitoring and optimization of the microcirculation during CPB. Journal of Thoracic Disease, 11(Suppl 10), S1489–S1491. DOI 10.21037/jtd.2019.02.100. [Google Scholar] [CrossRef]
33. Alwaidh, M. H., Cooke, R. W., Judd, B. A. (1998). Renal blood flow velocity in acute renal failure following cardiopulmonary bypass surgery. Acta Paediatrica, 87(6), 644–649. DOI 10.1111/j.1651-2227.1998.tb01524.x. [Google Scholar] [CrossRef]
34. Ardalan, M. R., Tarzamani, M. K., Mortaazavi, M., Bahloli, A. (2003). Relation between resistive index and serum creatinine level in first month after renal transplantation. Transplantation Proceedings, 35(7), 2628–2629. DOI 10.1016/j.transproceed.2003.09.054. [Google Scholar] [CrossRef]
35. Sughimoto, K., Shimamura, Y., Tezuka, C., Tsubota, K., Liu, H. et al. (2016). Effects of arterial blood flow on walls of the abdominal aorta: Distributions of wall shear stress and oscillatory shear index determined by phase-contrast magnetic resonance imaging. Heart and Vessels, 31(7), 1168–1175. DOI 10.1007/s00380-015-0758-x. [Google Scholar] [CrossRef]
36. Long, Q., Xu, X. Y., Bourne, M., Griffith, T. M. (2000). Numerical study of blood flow in an anatomically realistic aorto-iliac bifurcation generated from MRI data. Magnetic Resonance in Medicine, 43(4), 565–576. DOI 10.1002/(sici)1522-2594(200004)43:4<565::aid-mrm11>3.0.co;2-l. [Google Scholar] [CrossRef]
37. Wang, D. H., Prewitt, R. L., Reilly, C. K. (1993). Altered local regulation of blood flow and shear rate in renal hypertension. American Journal of Hypertension, 6(10), 851–856. DOI 10.1093/ajh/6.10.851. [Google Scholar] [CrossRef]
38. Yin, X., Zhang, J. (2012). Cell-free layer and wall shear stress variation in microvessels. Biorheology, 49(4), 261–270. DOI 10.3233/BIR-2012-0608. [Google Scholar] [CrossRef]
39. Hogan, B., Shen, Z., Zhang, H., Misbah, C., Barakat, A. I. (2019). Shear stress in the microvasculature: Influence of red blood cell morphology and endothelial wall undulation. Biomechanics and Modeling in Mechanobiology, 18(4), 1095–1109. DOI 10.1007/s10237-019-01130-8. [Google Scholar] [CrossRef]
40. Chiu, J. J., Chien, S. (2011). Effects of disturbed flow on vascular endothelium: Pathophysiological basis and clinical perspectives. Physiological Reviews, 91(1), 327–387. DOI 10.1152/physrev.00047.2009. [Google Scholar] [CrossRef]
41. Koskinas, K. C., Chatzizisis, Y. S., Antoniadis, A. P., Giannoglou, G. D. (2012). Role of endothelial shear stress in stent restenosis and thrombosis: Pathophysiologic mechanisms and implications for clinical translation. Journal of the American College of Cardiology, 59(15), 1337–1349. DOI 10.1016/j.jacc.2011.10.903. [Google Scholar] [CrossRef]
42. Sakamaki, Y., Konishi, K., Hayashi, K., Hashiguchi, A., Hayashi, M. et al. (2013). Renal thrombotic microangiopathy in a patient with septic disseminated intravascular coagulation. BMC Nephrology, 14(1), 260. DOI 10.1186/1471-2369-14-260. [Google Scholar] [CrossRef]
43. Guerci, P., Ergin, B., Ince, C. (2017). The macro- and microcirculation of the kidney. Best Practice and Research Clinical Anaesthesiology, 31(3), 315–329. DOI 10.1016/j.bpa.2017.10.002. [Google Scholar] [CrossRef]
44. Goodman, T. R., Mustafa, A., Rowe, E. (2019). Pediatric CT radiation exposure: Where we were, and where we are now. Pediatric Radiology, 49(4), 469–478. DOI 10.1007/s00247-018-4281-y. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
