DOI:10.32604/biocell.2021.015301

| BIOCELL DOI:10.32604/biocell.2021.015301 |  |
| Article |
Two approaches for calculating female fetal DNA fraction in noninvasive prenatal testing based on size analysis of maternal DNA fragments
1Human Genetics Resource Center, National Research Institute for Family Planning, Beijing, 100081, China
2Graduate School, Peking Union Medical College, Beijing, 100730, China
3Beijing University of Technology, Beijing, 100124, China
*Address correspondence to: Jianbo Lu, jblu@lsec.cc.ac.cn; Xu Ma, genetic88@126.com
#These authors contributed equally to this work
Received: 07 December 2020; Accepted: 03 February 2021
Abstract: The concentration of cell-free fetal DNA fragments should be detected before noninvasive prenatal testing (NIPT). The fetal DNA molecules have significant clinical potential in determining the overall performance of NIPT and clinical interpretation. It is important to measure fetal DNA fraction before NIPT. However, there is still little research on how to calculate the concentration of female fetuses. Two estimation approaches were proposed to calculate fetal DNA fraction, including the fragments size-based approach, aneuploid-based approach, which are all approaches based on chromosome segments. Based on high-throughput sequencing data, two approaches to calculate the DNA fraction of male fetuses were tested and obtained the experiment values, which were close to the actual values. The correlation coefficient of fragments size-based approach was 0.9243 (P < 0.0001) and the aneuploid-based approach reached 0.9339 (P < 0.0001). We calculated the concentration of female fetuses and obtained remarkable experimental results. We came up with two approaches for calculating the fetal DNA fraction of female fetuses. It provides an important theoretical basis for the detection of female fetal concentration in future clinical diagnosis.
Keywords: Fetal DNA fraction; Noninvasive prenatal testing; Cell-free fetal DNA; Female fetus
Cell-free fetal DNA (cffDNA) has been confirmed to be present in the plasma of pregnant women. Many studies show that the detection of cffDNA in maternal plasma has significant clinical potential for the noninvasive prenatal diagnosis of fetal genetic disorders and pregnancy-associated diseases (Jahr et al., 2001). The cffDNA in the maternal plasma accounts for about 5–20% of the total cell-free DNA fragments (Lo et al., 1999). The cffDNA from maternal plasma accounts for about 3.4% in early gestation and comprises a mean of 6.2% in late gestation (Lo et al., 1998). As the gestation time increases, the concentration of cffDNA rises sharply in the last 8k of pregnancy (Lo et al., 2007).
Noninvasive prenatal testing (NIPT) has been widely used in clinical practice. When NIPT is used to detect fetal chromosome aneuploidy, low cffDNA concentration will lead to a false negative. Therefore, cffDNA concentration ≥4% is considered an important quality control indicator for noninvasive prenatal testing (Liu et al., 2018). In addition, the accurate estimation of the fetal DNA concentration is particularly important in the detection of noninvasive single-gene diseases (Canick et al., 2013; Nygren et al., 2010). The cell fetal DNA concentration is an important parameter for analyzing site variation. Therefore, the concentration of cffDNA must be determined before NIPT (Tsui et al., 2011). The cell-free DNA fragments are mainly below 200 bp in maternal plasma (Chan et al., 2004). The maternal plasma’s cell-free fetal DNA fragments are much shorter than the DNA fragments derived maternal DNA molecules. The fractional fetal DNA concentration is a paramount factor for determining the overall performance of NIPT based on the analysis of DNA in maternal plasma (Sun et al., 2019). Based on the different regional distributions derived from the length of fetal and maternal DNA-free fragments, it is possible to further explore the relationship between the two based on this principle.
The use of massively parallel sequencing (MPS) of cell-free DNA in maternal plasma for noninvasive prenatal testing has become widely adopted in prenatal care (Yu et al., 2017). The massively parallel sequencing is an approach to quantify DNA sequences for the noninvasive prenatal diagnosis of fetal chromosomal aneuploidy (Fan et al., 2010). It is a counting-based method analyzing the DNA fragments mapped to different regions of the genome in maternal plasma. The count-based methods of fetal fraction determination calculate the proportion of the number of reads mapped to chromosomes that differ in mother and fetus genotypes. They are quite reliable and can be used on samples with male or trisomic fetuses (Gazdarica et al., 2019). It can calculate fetal chromosome concentration and detect fetal chromosomal abnormalities and other related diseases through appropriate bioinformatics analysis. To determine the size distribution of DNA fragments in maternal plasma, Chan et al. (2004) developed nine real-time PCR assays to amplify different-sized amplicons targeting the leptin gene in 2004. The data generated from their study indicate that the DNA fragments in the plasma of pregnant women are significantly longer than the fetal-derived ones. The fetal DNA, which has a shorter size distribution than maternal DNA, becomes detectable (Chan et al., 2004). The research of Li et al. indicates that most maternally derived DNA molecules are considerably larger than fetal DNA molecules (Li et al., 2004). The explanation for this may be that cffDNA appears to come exclusively derived from the placenta, whereas most normal maternal cell-free DNA is a hematopoietic source (Guibert et al., 2003; Lui et al., 2002). The selective enrichment of fetal DNA sequences can be achieved by size-dependent separation.
There are a number of existing methods for the determination of fetal DNA fraction, such as the method of fetal DNA fragment estimation based on Y chromosome sequence (Chiu et al., 2011; Hudecova et al., 2014). The approach of the fetal DNA fraction determined from the proportion of chromosome Y sequences in the maternal plasma samples is simple and accurate for male fetuses but not suitable for pregnancies with female fetuses (Chen et al., 2019).
If the genotype of the biological father is available, the fetal DNA fraction can be detected by the ratio of fetal-specific alleles to the total alleles in maternal plasma DNA (Liao et al., 2011; Lo et al., 2010). However, the genotype of the biological father is not obtainable in many cases. The FetalQuant, which is an approach to estimate the fetal DNA fraction, does not need the parental genotype information (Jiang et al., 2012; Jiang et al., 2016). Its limitation is the sequencing depth is required to be very high. The cell-free fragments size ratio-based approach has been developed to directly determine fetal fraction from the plasma sequencing data because maternal plasma and fetal DNA exhibit different fragmentation patterns (Chen et al., 2019; Yu et al., 2014). In this paper, two approaches of calculating the female fetal DNA fraction are based on the DNA molecule fragments’ size and counts. These approaches can directly estimate fetal DNA fraction from the high throughput sequencing data of NIPT without other operations.
Two sample sets were used, which were collected by the team of Y. M. Dennis Lo in this study (Yu et al., 2014). The first sample set includes 69 maternal plasma samples with a male fetus. These included 9 cases each with a trisomy 13 fetus, 7 cases each with a trisomy 18 fetus, 17 cases each with a trisomy 21 fetus, and 36 cases each with a euploid fetus. The second sample set 68 maternal plasma samples with a female fetus, including 8 cases each with a trisomy 13 fetus, 18 cases each with a trisomy 18 fetus, 19 cases each with a trisomy 21 fetus, and 23 cases each with a euploid fetus. Maternal peripheral blood was collected in EDTA-containing tubes before invasive obstetrics procedures. All blood samples were collected before performing any invasive procedures (Sun et al., 2019).
All maternal plasma DNA samples were analyzed by paired-end massively parallel sequencing. The sample data contain significant information about all chromosomes (autosomes and sex chromosomes) and the counts of corresponding segments from 36 to 600 bp per chromosome. The data information is shown in Appendix 1.
Calculating the most suitable range of ratio
To calculate the ratio, we first determine the range of values in the denominator. Generally, the fragment length from maternal cell-free DNA is longer than cell-free fetal DNA. We have shown that cell-free DNA fragments are mainly concentrated between 40–200 bp. We determined the overall plasma DNA size distribution for 69 male maternal plasma DNA samples. We took four samples with different fetal DNA fractions in Fig. 1. The rest of the samples are shown in Appendix 2.
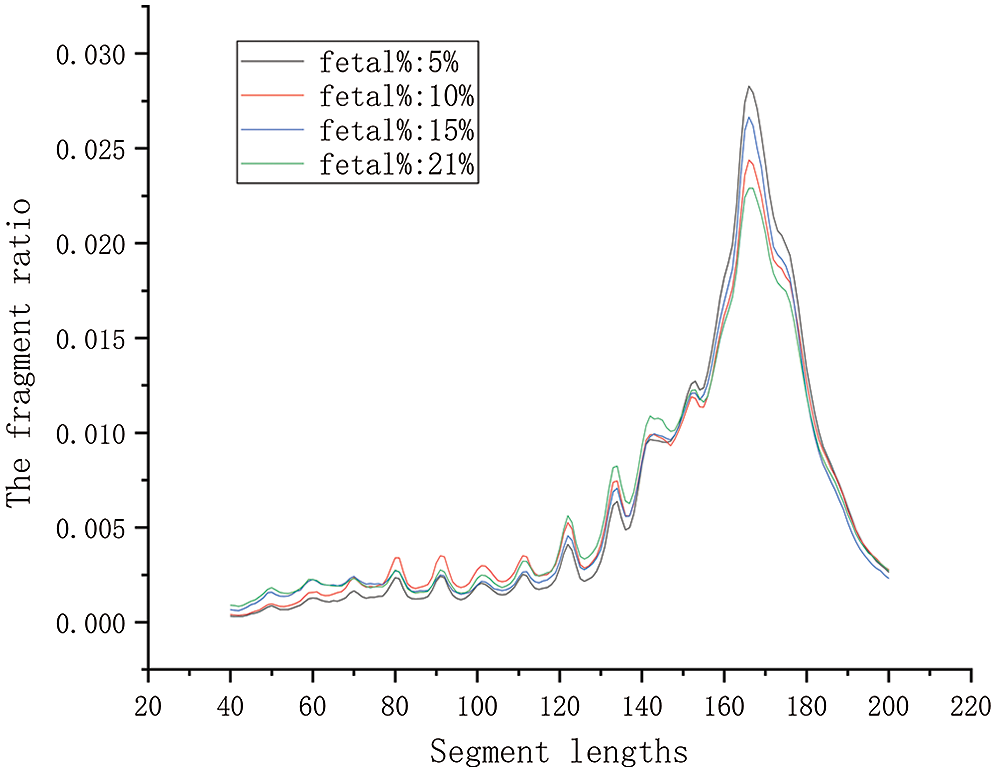
Figure 1: The contrast curve of different fetal concentrations. There are four maternal plasma samples with a euploid male fetus. Their corresponding fetal DNA fraction are 5.0, 10, 15, 21%, respectively.
In Fig. 1, the plasma sample with a higher fetal DNA fraction had a higher proportion of short fragments from 80 bp to 150 bp. It has been shown that includes the big peak at 166 bp. The plasma sample with a higher fetal DNA fraction had a lower proportion of fragments of 166 bp compared with the sample with a lower fetal DNA fraction. Therefore, we initially set the value calculation range of the ratio at 80–150 bp. We gradually narrowed the range of the interval via a traversing algorithm and finally settled on a range of DNA fragment lengths. Based on biological principles and existing research, the range of the ratio should not be too small. According to the calculation results, the maximum value of the lower boundary was set to 115 bp, and the minimum value of the upper boundary was set to 125 bp. We extended the maximum value of the upper boundary to 160 bp for proving that the value of correlation decreases as the value range increases.

The first sample set includes 69 maternal plasma samples with a male fetus. We divided it into a training set and a test set, 35 and 34 samples, respectively. We calculated corresponding the size ratio of the lower boundary from 80 to 115 in 5 bp increments and the upper boundary from 125 to 160 in 5 bp increments (Suppl. Tab. S1). We found a correlation between size ratios and fetal DNA fractions for the 35 male samples in the training group. The test results are consistent with the training results. It was shown in Tab. 1 that the fetal DNA fraction was highly consistent with the fetal concentration determined by the proportion of the Y chromosome sequence (the correlation coefficients were greater than 0.85). The calculated ratio was fitted linearly with fetal concentration, and the best fitting range was 115–140 bp. The highest value of the correlation coefficient in Tab. 1 is 0.924 (P < 0.0001, linear regression). In Tab. 1, the value of each row increased with the increase of fragment length and decreased with the increase of fragment length when reaching a certain value. In the first five rows, the maximum value of each row corresponds to 150 bp. It implied that the longer the number of fragments after 150 bp, the more likely it was to be derived from the DNA fragment in maternal peripheral blood.

Figure 2: The difference curve of two samples in segment lengths. The curve represents the difference in the proportion of each segment between two samples (5% and 21%).
The higher the fetal DNA fraction expresses, the more cell-free fetal fragments in maternal plasma. Conversely, the lower the fetal score, the more maternal free DNA fragments are present in maternal plasma. We obtained the difference between the number of segments corresponding to two samples of different concentrations (Fig. 2). To make the effect obvious, we selected samples with fetal concentrations of 5% and 21%, respectively. As shown in Fig. 2, the cell-free fetal DNA fragments from maternal plasma are roughly between 160 and 170. The optimal value interval is determined by further analysis. In Fig. 2, the curve showed a big peak, which represents the range of maternal cell-free DNA fragments. Using a cutoff value of >0.0035, we obtained the range of maternal DNA fragments size of 163 to 170 bp. Combined with the above calculation results, we determined the calculation formula of the ratio.
where size radio denotes the proportion of the sum of two segment lengths, sum (lower-upper) denotes the sum of fragments originating from 115–140 bp, and sum (163–170) denotes the sum of fragments originating from 163–170 bp.
Calculation methods of chromosome proportion
We calculated the proportion of chromosome 13, chromosome 18, chromosome 21 in each sample though using three methods. In the first method (M1), the ratio is the sum of each chromosome over the sum of the total number of all chromosomes, as Eq. (2).
where P1 denotes the proportion of target chromosome fragments in all chromosome fragments using the first method
The second method (M2) is first to calculate the product of the size of the target chromosome fragments and the corresponding number. Eq. (3) shows the proportion of every chromosome.
where P2 denotes the proportion of target chromosome fragments in all chromosome fragments using the second method.
The third method (M3) is to calculate the proportion of chromosomes by the size ratio. The following Eq. (4) was used to calculate the ratio per chromosome.
where P3 denotes the proportion of target chromosome fragments in all chromosome fragments using the third method.
The ratio of chromosomes calculated by the three methods was analyzed and detected, and it was concluded that the ratio calculated by the first method had the best effect. Therefore, in the following calculation, the ratio of chromosomes is calculated by the first method.
Calculating estimate female concentration by the size of fragments
Through the above series of calculations, we concluded that the optimal range of the ratio is 115–140 bp for the fetal DNA fragments and 163–170 bp for the maternal DNA fragments. The results of calculating the fetal DNA fractions of 69 male fetuses by the size-ratio were highly concordant with the fetal DNA fractions determined from the proportion of chromosome Y sequences in the maternal plasma samples with male fetuses. In both male and female fetuses, the length of cell-free fetal DNA fragments was shorter than that of maternal cell-free DNA fragments. The fetal and maternal segments were distributed over a range of areas. Therefore, we can use this fragment size-based approach to calculate the concentration of female fetuses.
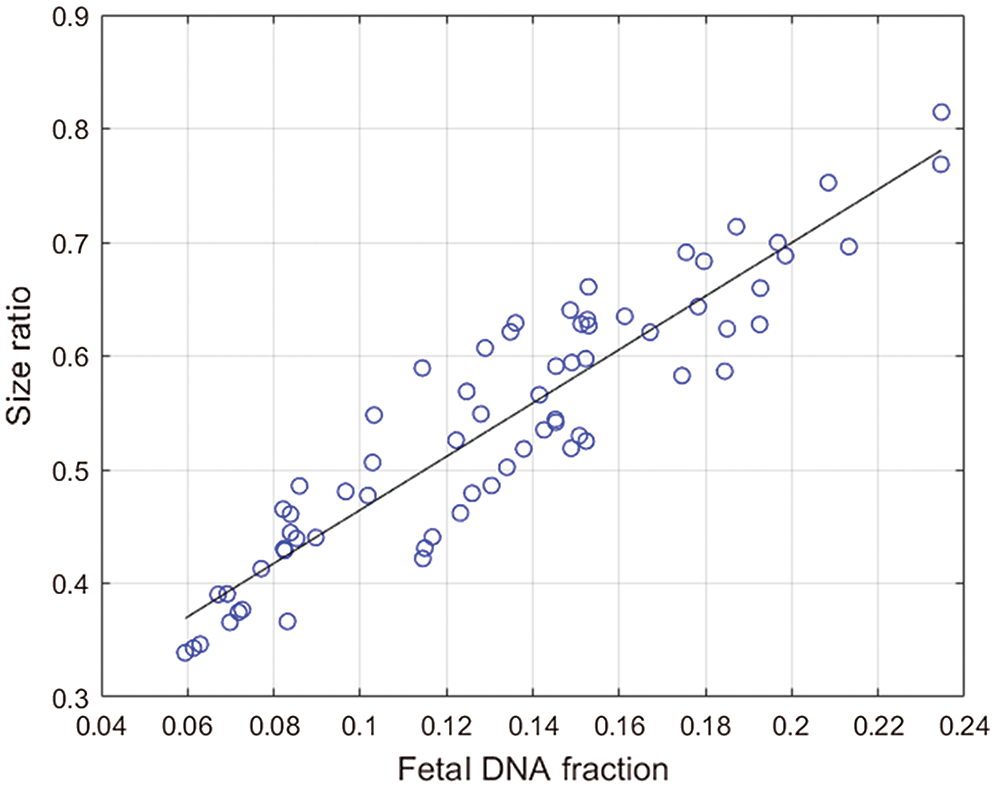
Figure 3: The solid line is the linear regression line through the data, and the corresponding regression equation is given on the graph.The x-coordinate is the fetal concentration, and the y-coordinate is the size ratio.
The approach based on the size of fragments was used to calculate the fetal DNA fraction in 68 female cases. We found a positive correlation between the size ratio obtained from the fetal concentration and the fetal DNA fraction determined from the proportion of chromosome Y sequences in the maternal plasma samples. The calculation formula is as shown in Fig. 3. The correlation coefficient is 0.9243 (P < 0.0001, linear regression). The regression equation (Eq. (5)) obtained from the 69 male maternal plasma samples is used to calculate fetal DNA fraction in 68 female maternal plasma samples:
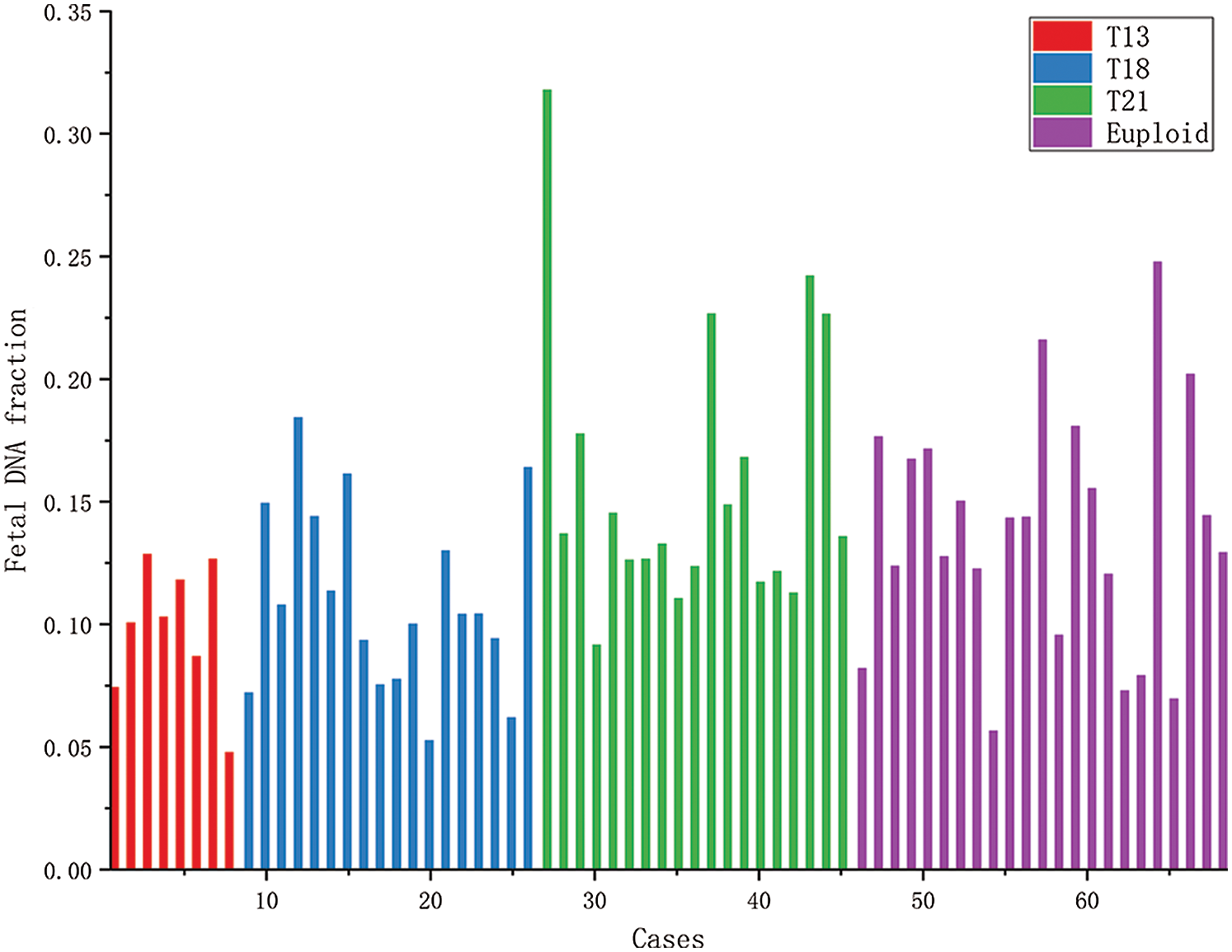
Figure 4: The histogram of fetal concentrations of 68 female fetuses. The horizontal axis represents the fetal sample code; the vertical axis represents the fetal fraction corresponding to each sample.
Fig. 4 shows the concentrations of 68 female fetal samples with a trisomy 21 fetus, most of which range from 5% to 30%. The first 8 samples were the maternal plasma samples, each with a trisomy 13 female fetus. The 18 blue bars were the maternal plasma samples, each with a trisomy 18 female fetus. The 19 green bars were the maternal plasma samples, each with a trisomy 21 female fetus. And then, the last 23 samples were the maternal plasma samples, each with a euploid female fetus.
Calculating fetal DNA fraction by aneuploid
The three most common autosomal aneuploidies are trisomy 21 syndrome (Down syndrome), trisomy 13 syndrome (Patau syndrome), and trisomy 18 syndrome (Edwards syndrome). Normally, fetal chromosomes should be diploid, meaning the number of autosomes per chromosome is two. If the embryo is triploid through chromosome testing, there is one more chromosome than normal fetus. We can use this property to calculate fetal DNA fraction of an aneuploidy fetus. We have 33 aneuploid male maternal plasma samples included 9 cases each with a trisomy 13 fetus, 7 cases each with a trisomy 18 fetus, 17 cases each with a trisomy 21 fetus. We used the following equation to calculate fetal DNA fraction, the results are shown in Fig. 5.
where
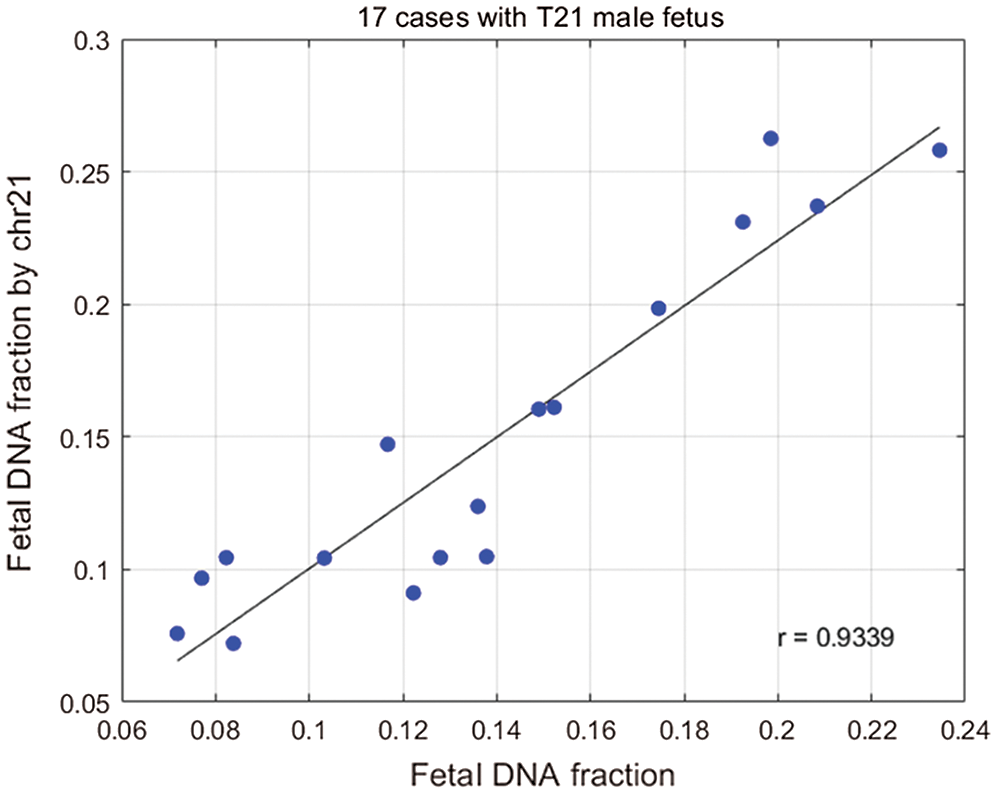
Figure 5: Plot of the fetal DNA fraction deduced from the size ratio using the above regression equation against that determined from the proportion of chromosome Y sequences for the 17 samples.
We calculated fetal concentrations for 33 male samples with aneuploid fetuses using Eq. (6). The analysis verified that there was a high correlation between fetal concentration calculated using chromosome 21 and fetal concentration calculated using chromosome Y. We calculated the relationship between the concentration of 21 chromosome and fetal DNA fraction in male fetuses (Chu et al., 2009) (Fig. 5). We found a positive correlation between the fetal DNA fraction through the fragments size-based approach and the fetal DNA fraction through the aneuploid-based approach (r = 0.9339, P < 0.0001, linear regression). When a fetus had autosome aneuploidy, its corresponding chromosome ratio would increase. We know that if there are extra or missing chromosomes, the number of corresponding fetal DNA fragments will increase or decrease. The fetal DAN fractions by aneuploid are highly accurate, so we can use this principle to predict fetal concentration.
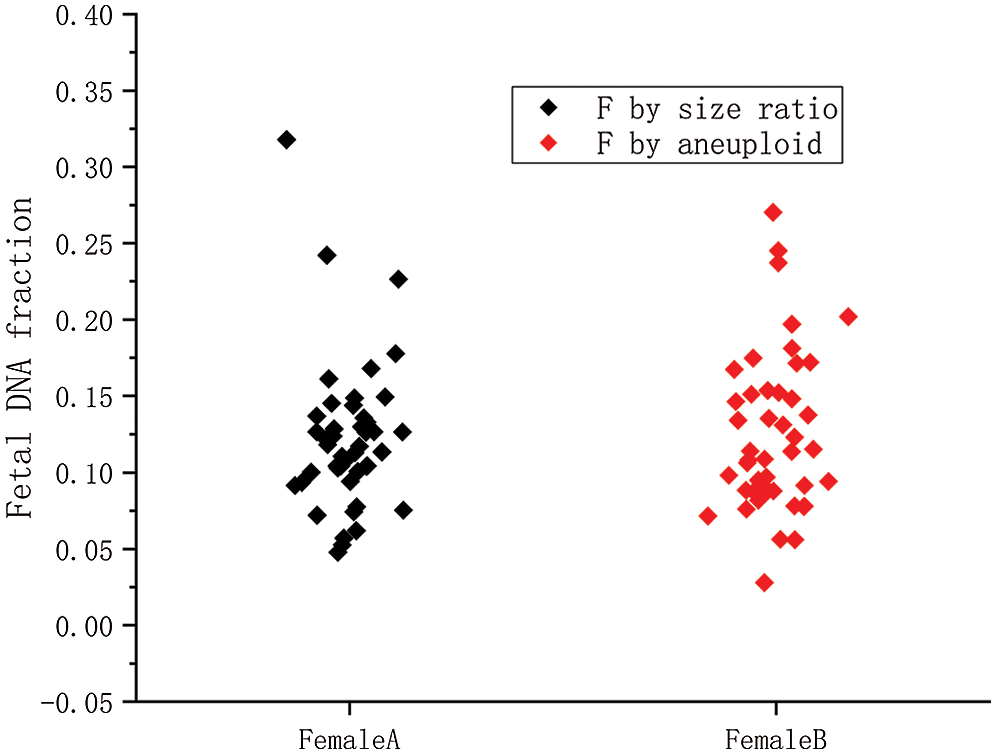
Figure 6: The fetal concentration distributions of 45 female fetuses by two methods.
Female A is the fetal concentration based on the size ratio of 45 female samples; Female B is the fetal concentration based on aneuploidy of 45 female samples.
We used the aneuploidy-based method to calculate 45 female cases with aneuploid fetuses. The calculation results were shown in Fig. 6. It can also be seen from the scatter diagram that fetal concentration is mainly concentrated at 5–20%, which is consistent with early studies (Lo et al., 1999). The black squares represent fetal concentrations determined from the fragments size-based approach. The red squares represent fetal concentrations determined from the aneuploidy-based approach. In Fig. 7A, Pearson’s correlation coefficient of the two sets of data is 0.8263 (P < 0.0001, linear regression). Fig. 7B shows that the residuals are normally distributed, zero centered, and with a standard deviation equal to 0.0504.
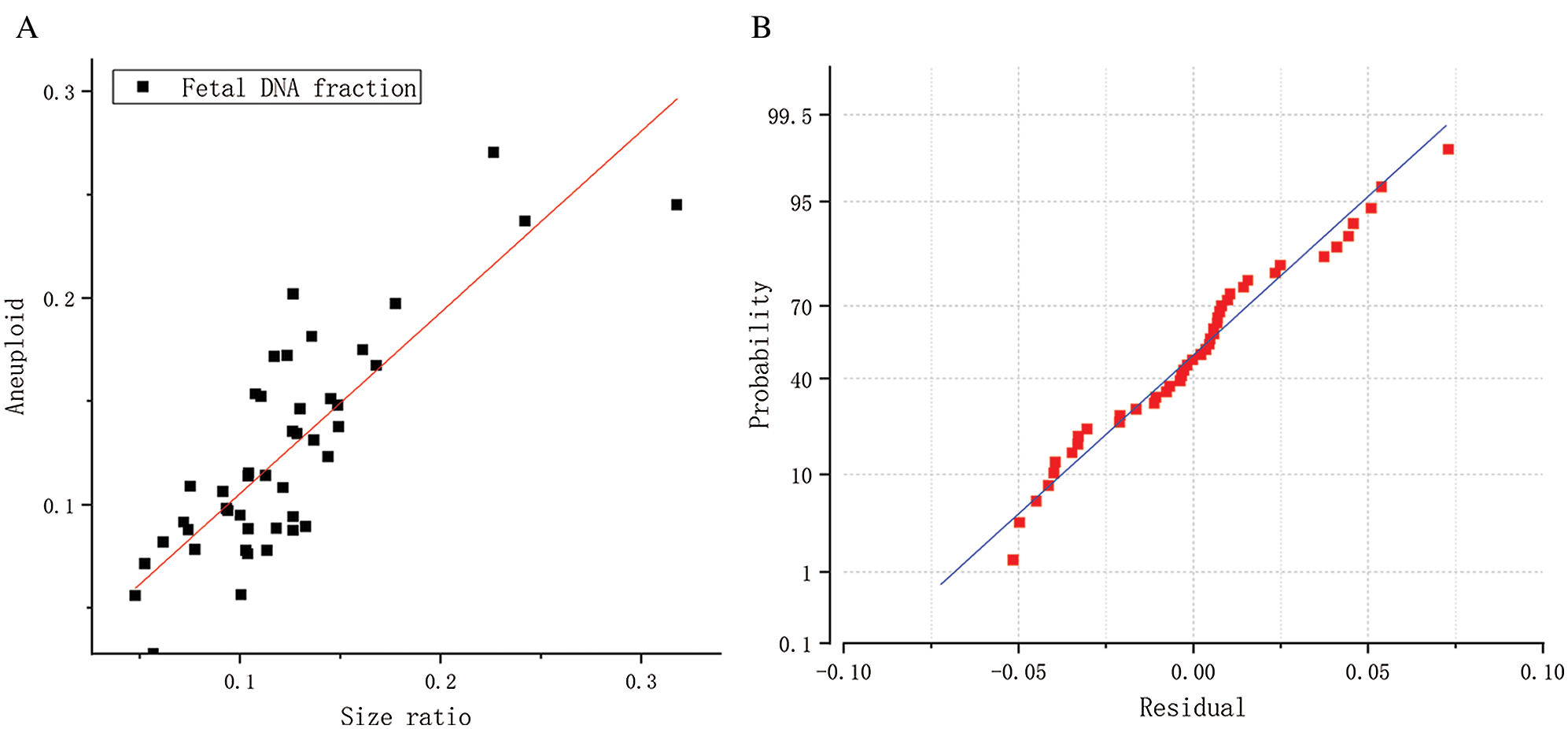
Figure 7: (A) Correlation between the fetal DNA fractions determined from the fragments size-based approach and aneuploidy-based approach for the 45 female samples. (B) A normal probability graph of residuals.
Among the 45 samples, the fetal DNA fraction of 19 female samples with a trisomy 21 fetus obtained the best result by using Eq. (6). We compared the calculation results with 19 female samples with a trisomy 21 fetus in 3. 2. When the two sets of data are compared, the results show that they are very similar. Fig. 8 shows that the percentages of the two results are close to 50%, which indicates that the two results are close to each other. We can apply the aneuploid-based method to calculating fetal fraction with an aneuploid female fetus. The fetal DNA fraction of the euploid female fetus is calculated by the size of fragments.
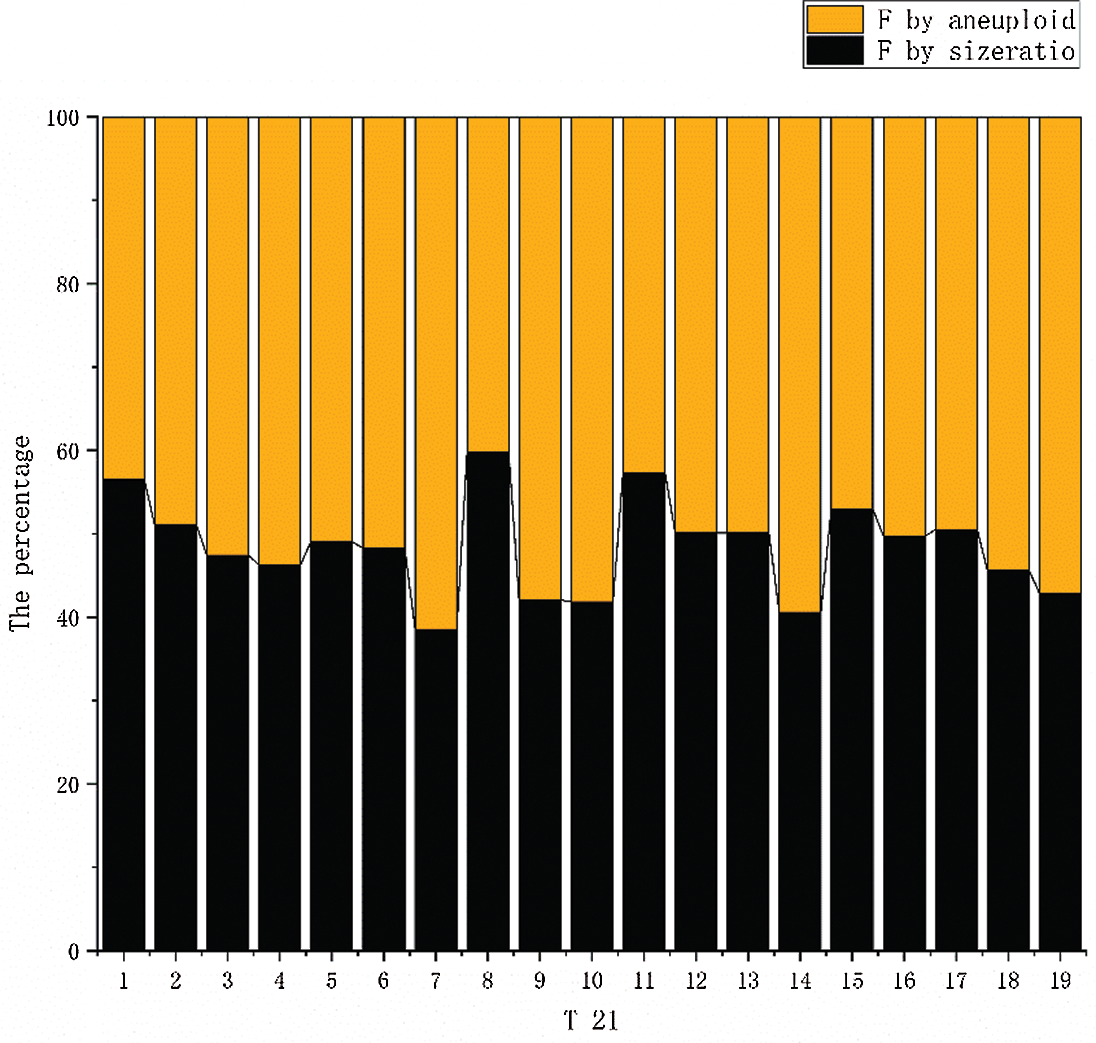
Figure 8: The results of the two calculation methods are compared. The orange columnar represents the fetal fraction calculated using aneuploidy. The blue columnar represents the fetal fraction calculated using the size ratio.
The use of cffDNA could in theory reduce the number of invasive prenatal diagnostic procedures by 50% (Chiu and Lo, 2002). For pregnant women, this greatly reduces the risk of miscarriage and other problems. In general, the concentration of cell-free fetal DNA fragments should be measured before NIPT is performed. Detection of fetal aneuploidy and autosomal recessive diseases with cffDNA is particularly challenging because only a small proportion of cell-free DNA in maternal plasma is derived from the fetus (Fan et al., 2010). The maternal DNA background has significant practical limitations on sensitivity for almost all prenatal diagnostic assays, and thus the proportion of fetal DNA in the maternal plasma is a key parameter. Due to the development of multiple detection methods, fetal DNA has many potential clinical applications in maternal plasma (Lui et al., 2002). Fetal DNA in maternal plasma is a convenient source of fetal genetic material, which can be safely obtained by collecting maternal peripheral blood samples (Li et al., 2004). An efficient fetal DNA fraction estimation method is necessary for NIPT. It is particularly important for the future development of NIPT that is the clinical application of noninvasive single-gene disease (Peng and Jiang, 2017). Cell-free DNA in maternal plasma consists of a mixture of fetal and maternal DNA. The counting approach enumerates both fetal and maternal DNA molecules in a maternal plasma sample. By using the difference in the length distribution of the cffDNA and the maternal DNA, the non-positiveness of the chromosome can be distinguished accordingly such as Down syndrome (Chan et al., 2016). For instance, the ratio of the concentration of the sequences from the Y chromosome to that of an autosome was used for the determination of fetal DNA fraction (Mckanna et al., 2019; Straver et al., 2016).
In the context of NIPT using massively parallel sequencing, the proportion of all sequence reads from the Y chromosome can be translated to the fetal DNA fraction. The concentration of cffDNA can affect the accuracy of NIPT results and has potential clinical diagnostic value. In this paper, we used various cffDNA concentration estimation methods (Bestor, 2000; Chu et al., 2010). Many methods have been used to calculate the fetal fraction of male fetuses, but there are few methods for calculating female fetuses. In this paper, we verified two calculation methods of female fetal DNA fraction. Cell-free DNA size ratio-based approach and aneuploid-based approach were used to calculate the fetal DNA fraction of females. The results of these two methods are well-validated.
In the study, we calculated the proportion of different chromosome segments. It was found that the length of chromosome fragments was mainly concentrated between 40 and 200 bp. Through data analysis, we concluded that fetal segment length was mainly concentrated in the range of 115–140 bp and maternal segment length was mainly concentrated in the range of 163–170 bp. It provided a theoretical basis for the calculation of female fetal concentration. We calculated female fetal DNA fraction based on it and used the fragments size-based approach and aneuploid-based approach to calculate female fetal concentration.
The determination of female fetal concentration is still an urgent problem. Our method verifies the accuracy of the method by calculating the concentration of male fetuses, which is the premise of our work for calculating the concentration of female fetuses. The approaches are applied to calculate the concentration of female fetuses based on chromosome fragments and have a simple operation. The amount of cell-free fetal DNA in maternal plasma is extremely small, and the length of the pregnancy may affect the accuracy of fetal concentration assessment. The accuracy of our method is affected by fetal concentration. The amount of data is insufficient, and we expect to verify our method with more data in the future. In the future, further verification and clinical experiments will be required to improve our method.
This paper not only calculates and verifies the DNA fraction of a male fetus but also puts forward the calculation method of female fetus DNA euploid and aneuploid. The research of fetal DNA fraction is important for the performance of NIPT and its clinical assessment. Before NIPT is performed, a certain concentration is generally required to ensure the accuracy of the results. The fetal concentration can be estimated from fetal cell-free DNA fragments in maternal plasma. It has a valuable reference point for fetal clinical diagnosis.
Acknowledgement: Thanks to Professor LO and his team for the data used in this article.
Authors’ Contributions: Conceptualization: Xiaohan Sun, Jianbo Lu, Xu Ma. Data curation: Xiaohan Sun. Formal analysis: Xiaohan Sun. Funding acquisition: Jianbo Lu, Xu Ma. Investigation: Jianbo Lu. Methodology: Xiaohan Sun, Jianbo Lu. Project administration: Jianbo Lu, Xu Ma. Resources: Jianbo Lu, Xu Ma. Supervision: Jianbo Lu. Validation: Xu Ma. Visualization: Xiaohan Sun. Writing—original draft: Xiaohan Sun. Writing—review & editing: Xiaohan Sun, Jianbo Lu, Xu Ma.
Availability of Data and Materials:All data generated or analyzed during this study are included in this published article.
Supplementary Material: The supplementary material is available online at DOI: https://10.32604/biocell.2021.015301.
Funding Statement: This project was supported by the National Key Research and Development Program of China 2016YFC1000307. The sub-project of National Key Research and Development Program of China 2016YFC1000307-10, the Program of National Research Institute for Family Planning (2017GJM04, 2018CNV).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
Bestor TH (2000). The DNA methyltransferases of mammals. Human Molecular Genetics 9: 2395–2402. DOI 10.1093/hmg/9.16.2395. [Google Scholar] [CrossRef]
Canick JA, Palomaki GE, Kloza EM, Lambert-Messerlian GM, Haddow JE (2013). The impact of maternal plasma DNA fetal fraction on next generation sequencing tests for common fetal aneuploidies. Prenatal Diagnosis 33: 667–674. DOI 10.1002/pd.4126. [Google Scholar] [CrossRef]
Chan KCA, Jiang P, Sun K, Cheng YKY, Tong YK, Cheng SH, Wong AIC, Hudecova I, Leung TY, Chiu RWK, Lo YMD (2016). Second generation noninvasive fetal genome analysis reveals de novo mutations, single-base parental inheritance, and preferred DNA ends. Proceedings of the National Academy of Sciences of the United States of America 113: E8159–E8168. DOI 10.1073/pnas.1615800113. [Google Scholar] [CrossRef]
Chan KA, Zhang J, Hui AB, Wong N, Lau TK, Leung TN, Lo KW, HuangDWS (2004). Size distributions of maternal and fetal DNA in maternal plasma. Clinical Chemistry 50: 88–92. DOI 10.1373/clinchem.2003.024893. [Google Scholar] [CrossRef]
Chen M, Jiang F, Guo Y, Yan H, Wang J, Zhang L, Zeng XJ, Li S, Li Y, Li N, Zhang C, Zhu W, Du B, Wang Y, Lan Z, Luo X, Luo F, Chen D (2019). Validation of fetal DNA fraction estimation and its application in noninvasive prenatal testing for aneuploidy detection in multiple pregnancies. Prenatal Diagnosis 39: 1273–1282. DOI 10.1002/pd.5597. [Google Scholar] [CrossRef]
Chiu RWK, Akolekar R, Zheng YWL, Leung TY, Sun H, Chan KCA, Lun FMF, Go ATJI, Lau ET, To WWK, Leung WC, Tang RYK, Au-Yeung SKC, Lam H, Kung YY, Zhang X, van Vugt JMG, Minekawa R, Tang MHY, Wang J, Oudejans CBM, Lau TK, Nicolaides KH, Lo YMD (2011). Non-invasive prenatal assessment of trisomy 21 by multiplexed maternal plasma DNA sequencing: Large scale validity study. BMJ 342: c7401. DOI 10.1136/bmj.c7401. [Google Scholar] [CrossRef]
Chiu RW, Lo YD (2002). Application of fetal DNA in maternal plasma for noninvasive prenatal diagnosis. Expert Review of Molecular Diagnostics 2: 32–40. DOI 10.1586/14737159.2.1.32. [Google Scholar] [CrossRef]
Chu T, Bunce K, Hogge WA, Peters DG (2009). Statistical model for whole genome sequencing and its application to minimally invasive diagnosis of fetal genetic disease. Bioinformatics 25: 1244–1250. DOI 10.1093/bioinformatics/btp156. [Google Scholar] [CrossRef]
Chu T, Bunce K, Hogge WA, Peters DG (2010). A novel approach toward the challenge of accurately quantifying fetal DNA in maternal plasma. Prenatal Diagnosis 30: 1226–1229. DOI 10.1002/pd.2656. [Google Scholar] [CrossRef]
Fan HC, Blumenfeld YJ, Chitkara U, Hudgins L, Quake SR (2010). Analysis of the size distributions of fetal and maternal cell-free DNA by paired-end sequencing. Clinical Chemistry 56: 1279–1286. DOI 10.1373/clinchem.2010.144188. [Google Scholar] [CrossRef]
Gazdarica J, Hekel R, Budis J, Kucharik M, Duris F, Radvanszky J, Turna J, Szemes T (2019). Combination of fetal fraction estimators based on fragment lengths and fragment counts in non-invasive prenatal testing. International Journal of Molecular Sciences 20: 3959. DOI 10.3390/ijms20163959. [Google Scholar] [CrossRef]
Guibert J, Benachi A, Grebille AG, Ernault P, Zorn JR, Costa JM (2003). Kinetics of SRY gene appearance in maternal serum: Detection by real time PCR in early pregnancy after assisted reproductive technique. Human Reproduction 18: 1733–1736. DOI 10.1093/humrep/deg320. [Google Scholar] [CrossRef]
Hudecova I, Sahota D, Heung MM, Jin Y, Lee WS, Leung TY, Lo YMD, Chiu RWK, Chavatte-Palmer P (2014). Maternal plasma fetal DNA fractions in pregnancies with low and high risks for fetal chromosomal aneuploidies. PLoS One 9: e88484. DOI 10.1371/journal.pone.0088484. [Google Scholar] [CrossRef]
Jahr S, Hentze H, Englisch S, Hardt D, Fackelmayer FO, Hesch RD, Knippers R (2001). DNA fragments in the blood plasma of cancer patients: quantitations and evidence for their origin from apoptotic and necrotic cells. Cancer Research 61: 1659–1665. [Google Scholar]
Jiang P, Chan KA, Liao GJ, Zheng YW, Leung TY, Chiu RW, Lo YM, Sun H (2012). FetalQuant: Deducing fractional fetal DNA concentration from massively parallel sequencing of DNA in maternal plasma. Bioinformatics 28: 2883–2890. DOI 10.1093/bioinformatics/bts549. [Google Scholar] [CrossRef]
Jiang P, Peng X, Su X, Sun K, Yu SCY, Chu WI, Leung TY, Sun H, Chiu RWK, Lo YMD, Chan KCA (2016). FetalQuant SD: accurate quantification of fetal DNA fraction by shallow-depth sequencing of maternal plasma DNA. NPJ Genomic Medicine 1: 1–7. DOI 10.1038/npjgenmed.2016.13. [Google Scholar] [CrossRef]
Li Y, Zimmermann B, Rusterholz C, Kang A, Holzgreve W, Hahn S (2004). Size separation of circulatory DNA in maternal plasma permits ready detection of fetal DNA polymorphisms. Clinical Chemistry 50: 1002–1011. DOI 10.1373/clinchem.2003.029835. [Google Scholar] [CrossRef]
Liao GJ, Lun FM, Zheng YW, Chan KA, Leung TY, Lau TK, Chiu RW, Lo YM (2011). Targeted massively parallel sequencing of maternal plasma DNA permits efficient and unbiased detection of fetal alleles. Clinical Chemistry 57: 92–101. DOI 10.1373/clinchem.2010.154336. [Google Scholar] [CrossRef]
Liu S, Huang S, Chen F, Zhao L, Yuan Y, Francis SS, Fang L, Li Z, Lin L, Liu R, Zhang Y, Xu H, Li S, Zhou Y, Davies RW, Liu Q, Walters RG, Lin K, Ju J, Korneliussen T, Yang MA, Fu Q, Wang J, Zhou L, Krogh A, Zhang H, Wang W, Chen Z, Cai Z, Yin Y, Yang H, Mao M, Shendure J, Wang J, Albrechtsen A, Jin X, Nielsen R, Xu X (2018). Genomic analyses from non-invasive prenatal testing reveal genetic associations, patterns of viral infections, and Chinese population history. Cell 175: 347–359. DOI 10.1016/j.cell.2018.08.016. [Google Scholar] [CrossRef]
Lo YM, Tein MS, Lau TK, Haines CJ, Leung TN, Poon PM, Wainscoat JS, Johnson PJ, Chang AM, Hjelm NM (1998). Quantitative analysis of fetal DNA in maternal plasma and serum: Implications for noninvasive prenatal diagnosis. American Journal of Human Genetics 62: 768–775. [Google Scholar]
Lo YMD, Chan KCA, Sun H, Chen EZ, Jiang P, Lun FMF, Zheng YW, Leung TY, Lau TK, Cantor CR, Chiu RWK (2010). Maternal plasma DNA sequencing reveals the genome-wide genetic and mutational profile of the fetus. Science Translational Medicine 2: 61ra91. DOI 10.1126/scitranslmed.3001720. [Google Scholar] [CrossRef]
Lo YMD, Lun FMF, Chan KCA, Tsui NBY, Chong KC, Lau TK, Leung TY, Zee BCY, Cantor CR, Chiu RWK (2007). Digital PCR for the molecular detection of fetal chromosomal aneuploidy. Proceedings of the National Academy of Sciences of the United States of America 104: 13116–13121. DOI 10.1073/pnas.0705765104. [Google Scholar] [CrossRef]
Lo YD, Zhang J, Leung TN, Lau TK, Chang AM, Hjelm NM (1999). Rapid clearance of fetal DNA from maternal plasma. American Journal of Human Genetics 64: 218–224. DOI 10.1086/302205. [Google Scholar] [CrossRef]
Lui YY, Chik KW, Chiu RW, Ho CY, Lam CW, Lo YD (2002). Predominant hematopoietic origin of cell-free DNA in plasma and serum after sex-mismatched bone marrow transplantation. Clinical Chemistry 48: 421–427. DOI 10.1093/clinchem/48.3.421. [Google Scholar] [CrossRef]
McKanna T, Ryan A, Krinshpun S, Kareht S, Marchand K, Grabarits C, Ali M, McElheny A, Gardiner K, LeChien K, Hsu M, Saltzman D, Stosic M, Martin K, Benn P (2019). Fetal fraction-based risk algorithm for non-invasive prenatal testing: screening for trisomies 13 and 18 and triploidy in women with low cell-free fetal DNA. Ultrasound in Obstetrics and Gynecology 53: 73–79. DOI 10.1002/uog.19176. [Google Scholar] [CrossRef]
Nygren AO, Dean J, Jensen TJ, Kruse S, Kwong W, van den Boom D, Ehrich M (2010). Quantification of fetal DNA by use of methylation-based DNA discrimination. Clinical Chemistry 56: 1627–1635. DOI 10.1373/clinchem.2010.146290. [Google Scholar] [CrossRef]
Peng XL, Jiang P (2017). Bioinformatics approaches for fetal DNA fraction estimation in noninvasive prenatal testing. International Journal of Molecular Sciences 18: 453. DOI 10.3390/ijms18020453. [Google Scholar] [CrossRef]
Straver R, Oudejans CB, Sistermans EA, Reinders MJ (2016). Calculating the fetal fraction for noninvasive prenatal testing based on genome-wide nucleosome profiles. Prenatal Diagnosis 36: 614–621. DOI 10.1002/pd.4816. [Google Scholar] [CrossRef]
Sun X, Lu J, Ma X (2019). An efficient method for noninvasive prenatal diagnosis of fetal trisomy 13, trisomy 18, and trisomy 21. PLoS One 14: e0215368. DOI 10.1371/journal.pone.0215368. [Google Scholar] [CrossRef]
Tsui NB, Kadir RA, Chan KCA, Chi C, Mellars G, Tuddenham EG, Leung TY, Lau TK, Chiu RWK, Lo YMD (2011). Noninvasive prenatal diagnosis of hemophilia by microfluidics digital PCR analysis of maternal plasma DNA. Blood 117: 3684–3691. DOI 10.1182/blood-2010-10-310789. [Google Scholar] [CrossRef]
Yu SCY, Chan KCA, Zheng YWL, Jiang P, Liao GJW, Sun H, Akolekar R, Leung TY, Go AT JI, van Vugt JMG, Minekawa R, Oudejans CBM, Nicolaides KH, Chiu RWK, Lo YMD (2014). Size-based molecular diagnostics using plasma DNA for noninvasive prenatal testing. Proceedings of the National Academy of Sciences of the United States of America 111: 8583–8588. DOI 10.1073/pnas.1406103111. [Google Scholar] [CrossRef]
Yu SC, Jiang P, Chan KA, Faas BH, Choy KW, Leung WC, Leung TY, Lo YM, ChiuRW (2017). Combined count-and size-based analysis of maternal plasma DNA for noninvasive prenatal detection of fetal subchromosomal aberrations facilitates elucidation of the fetal and/or maternal origin of the aberrations. Clinical Chemistry 63: 495–502. DOI 10.1373/clinchem.2016.254813. [Google Scholar] [CrossRef]
Appendix 1. Sample set. The sample set contained 69 maternal plasma samples with a male fetus and 68 maternal plasma samples with a female fetus, including 17 cases each with a trisomy 13 fetus, 25 cases each with a trisomy 18 fetus, 36 cases each with a trisomy 21 fetus, and 59 cases each with a euploid fetus.
Appendix 2. The fragments ratio. The overall plasma DNA size distribution for 69 maternal plasma DNA samples.
Supplementary Table S1. Size ratio. The size ratio of the lower boundary from 80 to 115 in 5 bp increments and the upper boundary from 125 to 160 in 5 bp increments.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |