 Open Access
Open Access
ARTICLE
Proposition de modélisation de la dynamique du système urbain : vitesse/densité/espace perçu Simulation de l’Ile de France
Proposal of Modeling of Urban’s System Dynamics Speed, Density, Perceived Space Simulation of Ile de France
Independent Researcher, Val d’Oise, 95000, France
* Corresponding Author: Cyril Enault. Email:
Revue Internationale de Géomatique 2024, 33, 273-293. https://doi.org/10.32604/rig.2024.053490
Received 01 May 2024; Accepted 15 July 2024; Issue published 26 August 2024
RÉSUMÉ
La question environnementale est devenue un enjeu majeur de société dans les pays occidentaux et principalement en France. L’Ile de France est aujourd’hui au cœur de cette nouvelle politique de maitrise de l’expansion des agglomérations. Aussi l’étalement urbain et plus particulièrement sa mesure et son évaluation actuelle et future présente un véritable enjeu de société. L’exploration de l’étalement urbain est donc au cœur de la géographie et de l’Economie Géographique depuis le début des années 1980, période où s’amorcent les grands développements du périurbain. Fort de ces enjeux, cet article s’intéresse à la question de l’’étalement urbain dans son rapport à la question de la vitesse et de l’espace sous une forme non euclidienne. Il prend essentiellement l’outil mathématique comme support de la dynamique et étudie les formes de la ville en termes de cartographie dans un système d’information géographique. Il met en lumière une méthodologie qui combine, par le calcul, différentes hypothèses issues du monde de la physique, de la psychologie de l’espace, de l’urbanisme et des sciences de l’ingénieur. In fine, la construction d’un système repose donc sur l’introduction progressive de différentes hypothèses urbaines: gravitation des populations, mécanique des fluides (modèle de circulation), mécanique générale du mouvement et de la perception de l’espace. Par le biais de simulations informatiques, il met en évidence les grandes tendances de l’étalement urbain au sein de la région Ile-de-France et vise à prévoir si les résultats sont conformes aux attendus des politiques publiques.Abstract
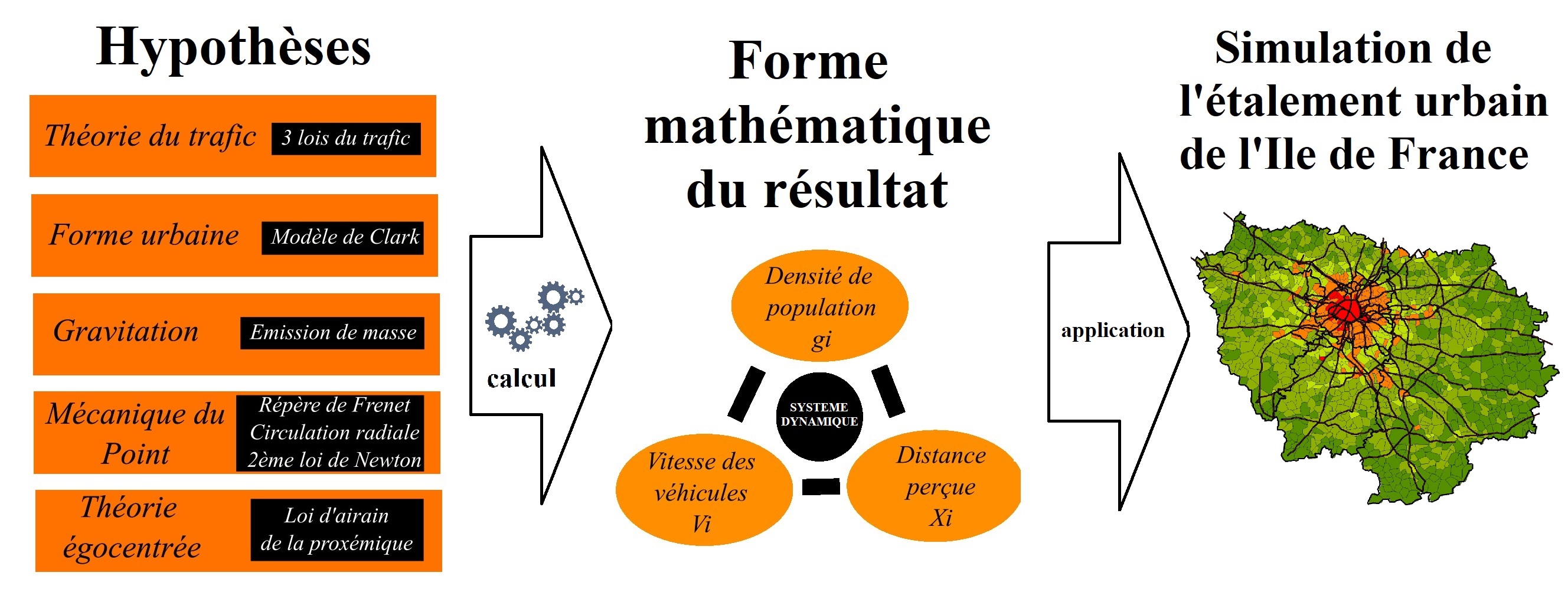
The environment has become a major social issue in Western countries, especially in France. Today, the Ile-de-France region is at the heart of this new policy to control urban sprawl. Urban sprawl, and more specifically its current and future measurement and evaluation, is a real social issue. The exploration of urban sprawl has therefore been at the heart of geography and Geographic Economics since the early 1980s, when the great developments of the peri-urban area began. With these issues in mind, this article takes a non-Euclidean look at the question of urban sprawl as it relates to speed and space. Essentially, it uses mathematical tools to support dynamics and studies the forms of the city in terms of cartography in a geographic information system. It highlights a methodology that combines, through calculation, different hypotheses from the worlds of physics, spatial psychology, urban planning and engineering sciences. Ultimately, the construction of a system is based on the progressive introduction of various urban hypotheses: population gravitation, fluid mechanics (circulation model), general mechanics of movement and perception of space. By means of computer simulations, it highlights the major trends in urban sprawl within the Ile-de-France region, and aims to predict whether the results are in line with public policy expectations.Graphic Abstract
MOTS CLÉS
Keywords
Depuis de nombreuses années, la question environnementale est au cœur des problématiques de la ville. Aussi, maitriser l’étalement urbain devient un enjeu de société et principalement en Ile de France. En 2013, la région Ile de France, met en place le Schéma directeur régional de l’Ile de France (SDRIF) qui vise à réglementer la consommation d’espace pour la région Ile de France. Avec le ZAN (zéro artificialisation nette), la loi climat résilience (loi du 22 août 2021 portant lutte contre le dérèglement climatique et renforcement de la résilience face à ses effets) renforce encore un peu plus cette réglementation et en conséquence met en place un nouveau SDRIF E (environnemental) plus restrictif. Au regard de ces politiques publiques, l’étude de l’étalement urbain devient fondamental pour se documenter sur la consommation réelle et possible des surfaces urbanisées et donc être utilisée par les politiques publiques pour vérifier l’application des lois dans les territoires.
La question de l’étalement urbain est souvent considérée d’un point de vue pratique plutôt que théorique. Souvent, les études visent à explorer les formes de l’étalement dans l’espace, ainsi que les conditions de cet étalement.
Les formes de périurbanisation sont aujourd’hui relativement bien connues et peuvent être modélisées. Il existe plusieurs types d’études dans ce sens. Le premier est l’approche par la densité de population, approche pionnière dans l’analyse des formes urbaines. A partir des travaux fondateurs d’Alonso [1], cette question a d’abord été rattachée au modèle concentrique [2–6], avant de trouver une nouvelle issue polycentrique avec le développement de l’Economie Géographique dans les années 1980 et 1990 [7–11]. Il existe d’autres types d’approches comme les fractals [12,13], permettant d’intégrer la notion d’échelle dans la description même des formes. Des études systémiques plus récentes ont apporté une contribution encore plus significative à notre compréhension de l’environnement urbain. Il s’agit notamment d’études utilisant les équations différentielles et les automates cellulaires.
Elles peuvent être utilisés pour suivre les évolutions à l’échelle d’une ville (Lajoie et al.), voire pour simuler les dynamiques d’occupation des sols au niveau du pixel [14–17].
Notre approche par équations différentielles ne fait pas appel à de tels logiciels1, mais adopte une approche plus théorique. Elle vise à simuler l’étalement urbain non plus par le bâti mais par les densités, la dynamique des populations. En cela, elle se trouve complémentaire des études par automates cellulaires ou systèmes multi agents. Quatre hypothèses ont été retenues.
1) La première suppose que les densités de population sont à l’origine du flux. Dans sa forme la plus simple, le modèle gravitaire est basé sur une analogie avec la loi de la gravitation universelle. Le modèle utilisé ici en est une généralisation.
2) La deuxième hypothèse ajoute la mécanique des flux (modèle de trafic macroscopique). Là encore, il s’agit d’une analogie avec la physique. Ce modèle introduit le trafic dans les réseaux.
3) La troisième hypothèse est à nouveau une analogie avec les lois de la physique. Elle apporte une réponse simple à la dynamique des populations, en supposant que le mouvement est, au fil du temps, le résultat des forces d’attraction présentes dans notre espace.
4) Enfin, la dernière hypothèse considère un espace non euclidien sur lequel repose notre dynamique2. Elle est basée sur la psychologie de l’espace, et principalement sur des questions de proxémique. Ces quatre hypothèses servent de base à la constitution d’un système différentiel.
Qu’obtient-on si l’on prend en compte ces hypothèses ? Comment appliquer cette dynamique à l’échelle communale d’une région (Ile-de-France) ? Comment ces dynamiques s’exercent-elles dans cette région ? Les dynamiques simulées de la région Ile de France sont elles conformes aux objectifs du ZAN3 ? Cet article est divisé en quatre parties :
- La première présente le contexte général de cette étude.
- La deuxième partie définit l’espace proxémique urbain. Cet espace a été récemment décrit pour définir les processus de déformation cartographique (Enault [23])4.
- La troisième partie rassemble les hypothèses relatives aux populations sélectionnées, pour aboutir à une proposition de modélisation du système dynamique urbain.
- Enfin, la dernière partie propose de spatialiser notre modèle à travers une simulation en 2040, et de discuter deux scénarios.
2 Contexte général de cette modélisation
L’ambition de réunir des domaines aussi vastes que la perception de l’espace, le trafic ou la question de l’urbanisme avec la densité de population semble difficile. Au-delà de l’aspect purement technique de ce pari, se pose aussi la question de l’intérêt d’une telle entreprise. Pourquoi créer un pont entre ces différents domaines ? Pour deux raisons majeures : la première concerne la question de la perception. Puisque l’être humain perçoit le monde d’une certaine manière, il semble logique qu’il conçoive ses créations en fonction de cette même perception. Le monde observé ne pourrait que résulter de cette déformation, avec une métrique à définir. Pour comprendre la dynamique de ce territoire perçu, il faut raisonner sur cet espace perçu.
Notre deuxième réponse est la suivante : pour comprendre la question de l’urbanisme, il faut aussi comprendre la question des transports. La vitesse semble être un facteur clé dans la compréhension de la forme urbaine. Ainsi, pour étudier et projeter la forme urbaine (et donc étudier la question de l’étalement urbain), il faut un support sur lequel les dynamiques se réalisent : l’espace perçu, et un vecteur pour expliquer ces dynamiques : la question de la vitesse via le trafic. Le rapprochement de ces trois champs est donc un défi majeur, mais une issue intéressante pour comprendre les dynamiques de la forme urbaine.
Mais avant de se pencher strictement sur un système possible, il faut se pencher sur l’histoire de ces questions. Au départ, et encore aujourd’hui, les trois domaines restent assez éloignés les uns des autres, parfois même cloisonnés. C’est sans doute la question de la perception qui est la plus spécifique. Les études sur cette question forment un bloc isolé. Historiquement, les premières études sur la psychologie de l’espace datent des années 1960. Pour Piaget et alii [25], la perception est avant tout égocentrée (le corps est la référence principale) et les objets peuvent être définis par la distance au corps. Les individus ont une “cognition spatiale” ou “taille des espaces” spécifique. Des mesures ont montré qu’il existe des lois de la proxémique. En France, Moles et al. [26] suggèrent que le monde est la conséquence d’une boucle phénoménologique de la perception, comme nous l’avons suggéré. De plus, ces auteurs ont été les premiers à produire un graphique dont l’abscisse est la distance au corps et l’ordonnée la perception de la métrique. Ce travail reste une référence pour les géographes et les psychologues de l’espace. Plutôt que d’offrir de véritables solutions techniques, Moles a préféré proposer des hypothèses.
A côté de ces travaux, se posent les questions de la forme urbaine. Les travaux les plus anciens datent de 1951 (Clark) [2], où l’auteur montre qu’il existe une relation statistique entre le logarithme de la densité de population et la distance au centre des villes. Ces études seront ensuite complétées par les travaux comparatifs de Mills Tan [27]. Enfin, d’autres études seront proposées pour adapter la fonction utilisée pour la densité [3–5].
Enfin, le troisième domaine à aborder est celui des déplacements ou du trafic. Sur cette question, de nombreux travaux ont été produits depuis les premières études routières de Greenshields [28]. Aussi, les études les plus remarquables datent de 1956 avec le modèle LWR [29,30] qui reste encore aujourd’hui une référence pour les modèles macroscopiques de trafic de premier ordre. A noter que ceux-ci sont divisés en 3 sections :
la relation caractéristique, première équation commune à tous les modèles macroscopiques du trafic :
Avec Qi trafic en i, Ki concentration ou nombre de véhicules par unité de distance et Vi vitesse en kilomètres par heure.
la relation dite d’équilibre ou dynamique où la somme des flux entrant dans un lieu i est égale à la somme des flux qui en sortent.
enfin, le diagramme fondamental qui relie le trafic à la concentration. Il met en évidence une partie fluide et une partie saturée.
Ainsi, chacun de ses trois domaines a pu suivre son chemin individuellement. Cependant, depuis le XIXe siècle, des ponts ont été jetés entre deux de ces volets : la question de l’urbanisme avec les densités de population ou les populations et celle des transports avec les trafics. On parle alors de modèle d’interaction spatiale.
Cette histoire relativement ancienne remonte à Ravenstien [31] qui a été le premier à initier ces analogies entre la physique et les Sciences Sociales. D’autres modèles ont été proposés (pour un article de présentation D’aubigny et al. [32]). Nous retiendrons l’expression, la plus simple, issue directement de la physique.
Avec :
Qi le flux routier ou le trafic émis par le lieu i
G une constante
Mi la population du lieu i.
Nous préférons cependant une forme développée contenant le modèle de Clark) [2].
Le lien entre trafic et densité est donc ancien, mais, dans les années 1960, la question du lien entre vitesse et densité reste entière. Il s’agit donc d’un défi majeur. Il a fallu attendre les études approfondies de Newman et al. ([33,34]) pour qu’un lien statistique émerge sur un vaste panel de villes du monde entier. Il semblerait qu’il s’agisse d’une relation inverse. Il est vrai que, jusqu’à une date récente, il était difficile de collecter des données sur les vitesses urbaines. En l’absence de données, de nombreux auteurs ont dû recourir à des études qualitatives de cette relation [35–38]5. Avec l’avènement des SIG, une tentative a été faite pour établir cette relation [41], mais elle n’a pas abouti à une relation dynamique.
Il est vrai que si l’enjeu d’un lien entre ces deux grandeurs est important, les preuves apportées resteront longtemps statiques, toujours par manque de données, jusqu’à ce qu’un lien dynamique de ce couple soit proposé [42]. Il en résulte un modèle de simulation de l’étalement urbain et de prédiction de l’évolution de la vitesse de déplacement.
Si le principe de la modélisation du couple est connu, le défi reste d’associer un espace qui rendra mieux compte de la dynamique des centres-villes et des périphéries.
Il s’agit de construire un trio interactif et dynamique liant densité de population, vitesse et espace perçu.
Cette recherche implique un certain nombre d’hypothèses que nous nous proposons de présenter ici.
3 Recherche d’hypothèses de travail sur l’espace de perception
3.1 Hypothèses générales sur l’espace
Nous avons identifié quatre hypothèses principales :
- Un espace non euclidien basé sur la perception de n individus6;
- Chaque lieu i est caractérisée par une densité de population gi (que nous considérerons par la densité) sans lien avec la position géographique ;
- Nous supposerons également que la ville est composée de i centres urbains : ville polycen trique ;
- La vitesse routière envisagée Vi constitue une moyenne au point i, ce qui, pour un espace vide, conduit à un plan.
L’espace proxémique utilisé dans cet article est basé sur les hypothèses de Moles [44]. Casti [45] notait, à ce titre, que la proxémique pourrait constituer une évolution importante dans la pensée géographique. Dans cette théorie, on considère alors que le monde qui nous entoure est perçu de manière égocentrée à partir du corps (voir Fig. 1).
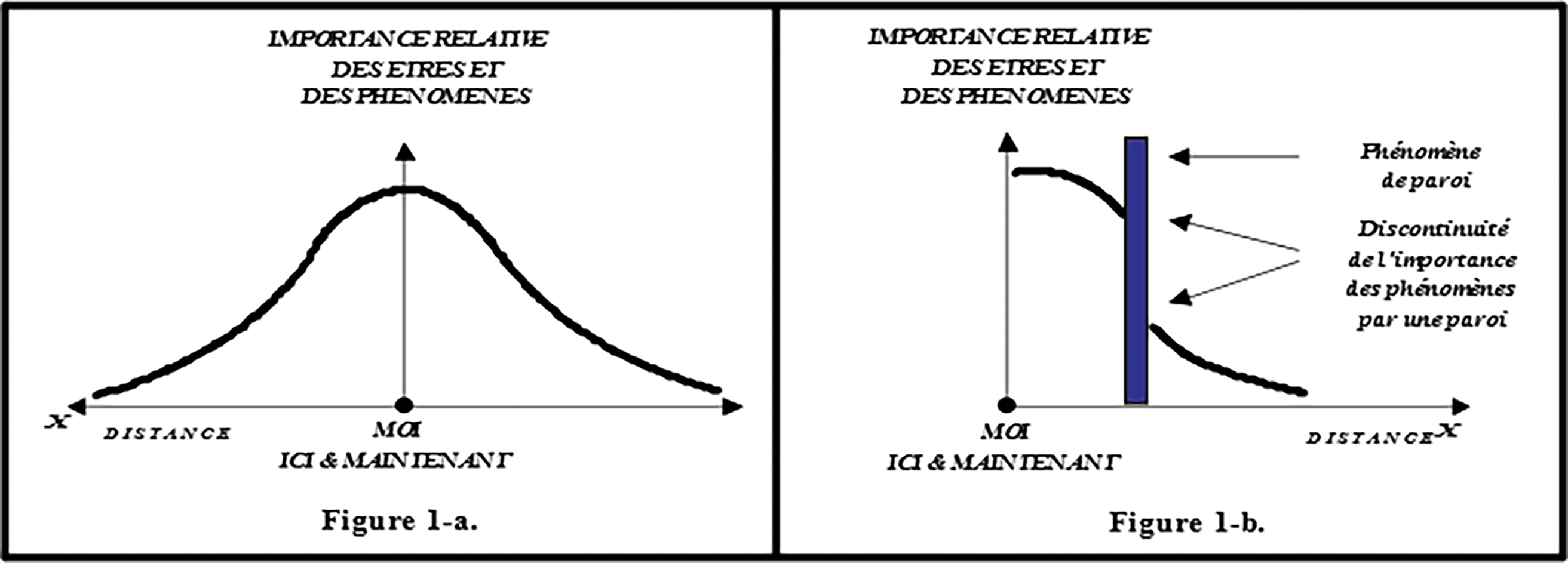
Figure 1: La loi proxémique (1-a) et le phénomène de paroi (1-b) de Moles et Rohmer
La perception de la valeur de l’espace, ou de la taille des espaces, diminue donc au fur et à mesure que l’on s’éloigne de l’individu (point ici). Cette loi est connue sous le nom de loi d’airain de la proxémique, et a été envisagée sous la forme mathématique suivante [19] :
Avec L(x) la taille d’un espace ou la métrique du mètre physique, L le mètre physique, r un facteur de réduction et x la distance physique au point de vue ici, c’est-à-dire à l’individu.
Diverses opérations mathématiques permettent ensuite de passer de cette loi de base à la notion de distance proxémique ou distance perçue, qui correspond à la distance perçue entre l’individu et un objet situé à une distance physique x.
3.3 Distance proxémique urbaine
Sur la base de cette distance proxémique, les individus peuvent être regroupés en anneaux concentriques pour former une ville. Ce calcul implique alors la densité de population sous sa forme exponentielle [2].
Avec D(x) la densité de population à la distance x du centre, D, la densité extrapolée au centre et α, le gradient de densité.
Nous obtenons une forme hybride mêlant densité et proxémique :
Avec X distance proxémique ou perçue du centre ville, A paramètre à ajuster α, r paramètres des équations précédentes et x distance physique au centre ville.
Cette loi reflète donc la valeur de la distance proxémique séparant le centre d’une distance physique x de la ville. Naturellement, dans le cas de villes polycentriques, il s’agirait de mesurer la distance proxémique des périphéries aux n centres urbains.
Un des intérêts de cette distance proxémique est d’offrir la possibilité de calculer la distance réellement perçue par un individu se déplaçant du centre de la ville vers la périphérie. Ce résultant intéressant pour déformer les cartes ne peut toutefois pas servir dans le cadre de la construction de modèles plus généraux faisant intervenir les densités ou la vitesse. Aussi, il convient de mettre cette expression (5) sous une forme de type métrique au sens mathématique du terme.
Or, l’expression (5) ne peut pas être transformée en une forme différentielle en supprimant le terme x. Il faut proposer une autre solution.
Au final, nous proposons donc d’appliquer le modèle suivant7 (somme de (3) du centre à x) qui est proche de (5) en termes de forme graphique :
Cela correspond plus ou moins à notre modèle (5). La forme mathématique différentielle résultante est alors8:
Avec Xi la distance proxémique au centre i, xi la distance physique au centre i et β et α deux paramètres à évaluer. Notez que la forme (7) est beaucoup plus simple que (5). Après avoir exprimé mathématiquement notre espace perçu, voyons comment le relier à l’occupation de l’espace.
3.4 Le lien mécanique espace de perception-occupation de l’espace
La règle classique de distribution des densités de population est le modèle de Clark [2]. Cependant, nous avons précisé que notre espace de base, sur lequel se déroule notre dynamique à long terme, sera non euclidien, il est donc possible de montrer l’existence d’un lien mécanique entre la densité et l’espace proxémique. Dans ce cas, la distance physique de la formule de Clark (généralisée aux centres i) doit être remplacée par la distance perçue Xi, soit :
En sens inverse, on obtient donc une expression de la proxémique en fonction de la densité, soit :
Par souci de simplicité, nous appelons X(xi), Xi et D(X(xi)), D(Xi).
Notons que les dynamiques de vitesse ou de trafic se déroulent sur une courte période et ne nécessitent donc pas l’introduction de la distance perçue dans les calculs. Avec cette partie, nous clôturons notre exposé sur les hypothèses de travail sur l’espace de perception. Ce dernier peut maintenant être intégré comme variable (ou fonction) pour nos futurs calculs de dynamique de population et de vitesse. La suite de notre discussion s’attachera à trancher sur l’hypothèse de gravitation et la question des flux et du trafic, et ce afin d’aboutir à notre modèle final.
4 Hypothèses concernant les populations, leurs mouvements et la conception du modèle final
4.1 Une attraction gravitaire des populations
Notre hypothèse est que la population d’un point i de l’espace est à l’origine d’un trafic Qi. L’espace global des flux, dans une perspective polycentrique, se trouve donc être une somme d’interactions gravitaires (en suivant pour partie le modèle de Wilson 1970) [46], que nous avions envisagées dans la première partie comme :
4.2 Un phénomène d’écoulement du trafic selon les lois de l’écoulement des fluides
Sur la base de cette hypothèse, nous supposons que le flux peut également être exprimé par des modèles de trafic. Tout d’abord, nous choisissons le modèle de Greenshieds comme diagramme fondamental. La relation caractéristique (Qi = Ki * Vi) est naturellement prise comme hypothèse. Enfin, il reste la deuxième relation dont le principe doit être discuté.
De manière général, les flux sont équilibrés dans un réseau donné. Cependant, si l’on considère la diffusion d’un flux dans un espace poreux, cela implique des gains ou des pertes aléatoires dans le réseau routier. On suppose alors que le flux entrant dans un réseau correspond au flux qui en sort, avec une fonction de perte ou de gain.
Avec L(x, t) fonction de gain ou de perte de flux externe dans l’agglomération que nous définissons par une fonction linéaire où, pour une surface donnée, s émet un flux L(x) = Rx.
R une constante à définir. Sur une distance xi
Le flux L est donc :
En fait, on obtient le modèle simplifié suivant selon les expressions (11) et (12) :
En conséquence, le système suivant sera retenu :
Avec Qi le trafic en i, Ki la concentration de véhicules en i et Vi la vitesse en i et R une constante, a et b des paramètres9.
4.3 Forces et exercice des forces sur les déplacements
Dans ce territoire, nous supposons que le deplacement (l’accélération a) derive de la distribution des densités de population. Il en découle un système basée sur le principe de Clark [2], mais aussi une logique de mouvements complexes régis par une quantité n de forces. Ces forces dérivent des densités de population. On en déduit que la vitesse ou le flux interagit avec la densité selon les lois habituelles du mouvement dans un espace que l’on peut d’abord définir comme lisse. La deuxième loi de Newton fournit la clé ou le lien entre la vitesse d’une part et la gravitation d’autre part.
Soit :
Pi représente la gravitation agissant à un moment t donné et en un lieu i sur l’individu en deplacement dans notre espace et
4.4 Le modèle général : démonstration du système différentiel
Dans ce paragraphe, nous rechercherons l’expression de la vitesse dynamique. Pour ce faire, nous partons d’un schéma fondamental du type Greenshields 193510 [25]. En divisant Qi par la vitesse, nous montrons que :
Où Vi est la vitesse moyenne, Ki la concentration de véhicules et a et b les paramètres à déterminer. Cherchons alors la dynamique de la vitesse par la dérivée, c’est-à-dire :
La concentration peut être exprimée par l’introduction de (13)11.
Calculons maintenant Qi/xi. Dans cette expression, nous introduisons également gi = Mi exp(−αXi).
en introduisant (7) :
Nous fixons finalement αGL = λ, Lnr/L = −β et aR = Γ12; nous obtenons la première expression de notre système vitesse-densité.
4.4.2 Définition de la gravitation des populations et de la dynamique des flux
Pour chaque lieu i de l’espace, nous définissons un repère de Frenet avec des coordonnées curvilignes, ce qui nous permet de démontrer le lien entre la densité et la vitesse par le biais de la deuxième loi de Newton. Dans une logique d’attraction gravitaire, tout flux est considéré comme convergeant ou divergeant vers l’ensemble des points i (selon un principe polycentrique). La trajectoire alors suivie par un objet en mouvement sera fonction de la distribution de la masse gravitaire de la population pour tous les lieux i. En fait, le mouvement observé oscille entre différentes trajectoires autour des points i. Le schéma suivant explique la trajectoire de l’individu en mouvement (voir Fig. 2) dans le référentiel de Frenet (voir encadré 1) :
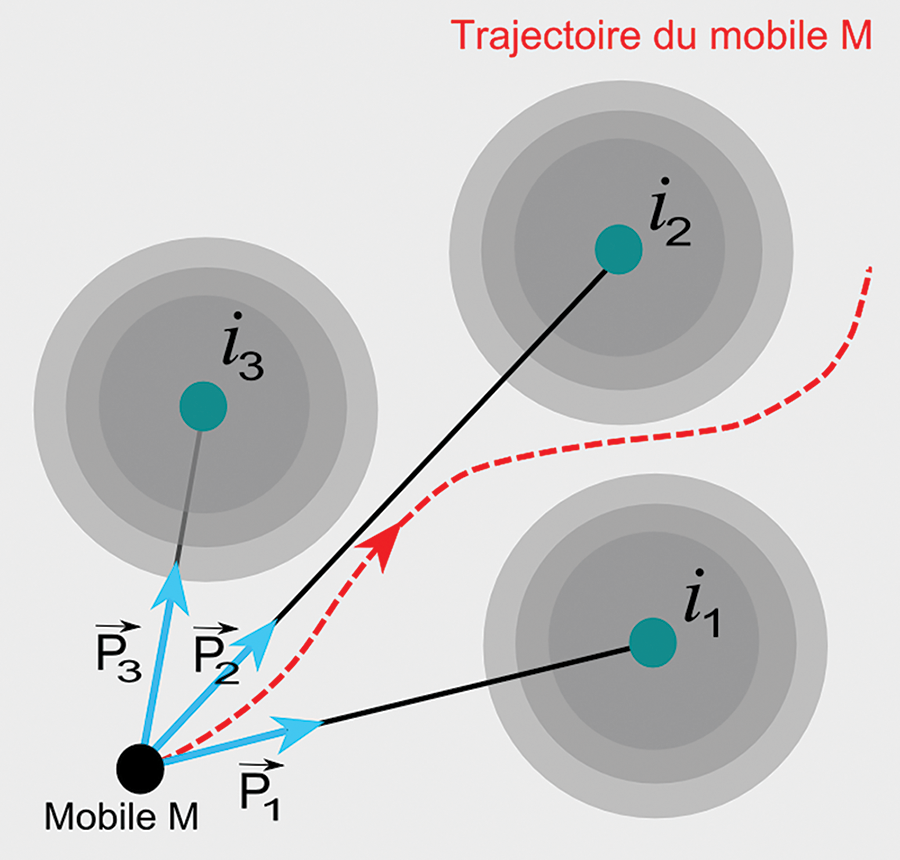
Figure 2: Mouvement et attraction gravitaire (Copyright © 2012 Cybergeo)
Encadré 1 : repère de Frenet
Le repère de Frenet (voir Fig. 3) est un repère individu centré pour exprimer les coordonnées des trajectoires curvilignes. En un Point P (individu), située à une distance R du centre de la ville c, on prend la tangente et sa perpendiculaire. On définit alors un repère en P avec en coordonnées radiale r = V2/R et en coordonnée tangentielle t = dV/dt (avec V vitesse de l’individu)
Pour notre cas, la coordonnée tangentielle est nulle. Car les mouvements sont uniquement radiaux du centre vers les périphéries et inversement. Si la coordonnée tangentielle est conservée le mouvement devient spiralé.
On exprime donc l’accélération (a) sous cette forme réduite :
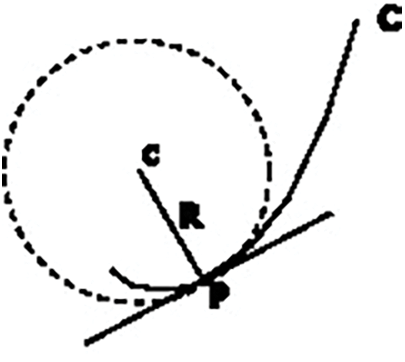
Figure 3: Repère de Frenet
Dans ce modèle, la composante radiale est par définition égale à
La somme des forces Pi est exprimée selon le modèle de gravitation14.
D’où, selon (15), (22) et (23) :
Nous fixons ensuite 2λ/Gxi = ξ et 2Γ/Gxi = Φ.15.
Nous retenons l’expression suivante pour le couple vitesse-densité :
4.4.3 Calcul de l’espace proxémique dynamique
Il nous reste donc une autre équation à évaluer : la dynamique de l’espace proxémique dXi/dt. Pour ce faire, nous nous référons à la formule (8)16 et calculons la dynamique.
Nous avons :
Soit en dérivant d’après (25) :
Nous concluons donc que :
Ou en fixant 1/α = Λ, on obtient le système suivant :
Le résultat que nous obtenons ici est un système de trois équations différentielles reliant directement la densité de population gi à la vitesse routière Vi et à la distance proxémique urbaine Xi au moyen de variables d’ajustement. En pratique, cela signifie que l’évolution de la vitesse interagit avec l’évolution de la densité et de la distance moyenne perçue Xi.
Le système n’a pas de solution analytique, car les trois fonctions Vi, Xi et gi sont liées de manière non linéaire dans le temps par leurs dérivées. Le paramètre τi représente le taux d’évolution de la densité de la population locale ; il sera calculé selon la formule suivante :
Ainsi, le modèle suit l’évolution du trio vitesse/densité/espace perçu, pour un lieu i indéfini dans l’espace. Par conséquent, lorsqu’il est appliqué à de multiples entités géographiques, il nous permet de suivre les trajectoires différenciées des espaces. À cet égard, on peut dire que notre modèle s’apparente mathématiquement au champ de vecteurs tridimensionnel d’un espace géographique. Au-delà de son expression purement mathématique, le système (29) peut être parfaitement ajusté aux données et aux vitesses réelles des populations. Il peut alors être utilisé pour simuler la dynamique du trio vitesse/espace urbain perçu/densité de population. Dans la suite de ce texte, nous proposons d’appliquer le modèle dans le contexte de la région Ile-de-France, et de découvrir ainsi le visage de la région capitale en 2040.
5 Application de la dynamique urbaine : l’exemple de l’Ile de France
5.1 Ajustement du système de modalité
5.1.1 Calibrer les densités de population gi
L’idée est alors de simuler la dynamique en modifiant les paramètres jusqu’à ce que la régression linéaire “Données réelles = a * données simulées + b” donne un a proche de 1 et un b proche de 0.
A l’issue de la calibration de notre modèle, nous obtenons le graphique suivant (Fig. 4) pour l’année 2007.
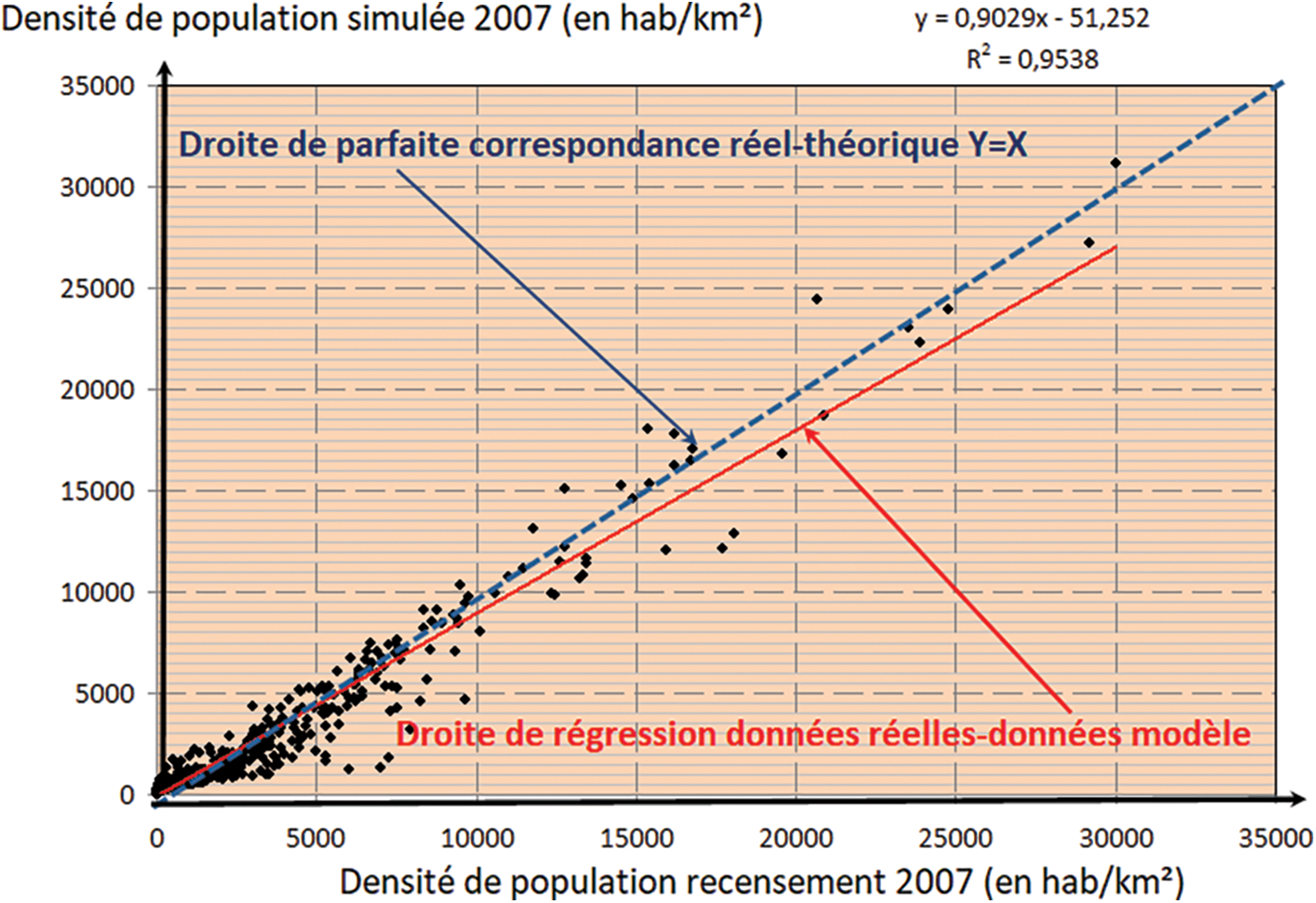
Figure 4: Ajustement des données de densité de population
En effectuant la simulation, nous nous sommes aperçus que les valeurs de vitesse Vi calculées à partir des densités de population ne correspondaient pas directement aux valeurs de vitesse MODUS17. Il existe donc une transformation permettant de passer de la vitesse calculée à la vitesse “réelle”.
Pour le calcul (initialisation en 1968), nous utilisons une dérivée du BPR18 soit :
Pour le traitement, nous utilisons la logistique suivante :
Nous en déduisons que19 :
En réalisant les vitesses moyennes agrégées par distance au centre de la ville, il est possible d’approcher les valeurs de vitesse “réelles” Vi en 2007.
Notons que la question de la perception peut également être traitée dans cette partie ajustement. En effet, la proxémique ou distance perçue Xi peut se rapprocher du temps généralisé (temps utilisé pour ajustement des modèles à 4 étapes dont MODUS). Le temps servant à calibrer les trafics est en réalité un temps perçu. La distance perçue est donc le temps perçu sur la vitesse soit : Ti/Vi. Les résultats donnent un nuage de points s’étirant le long d’une droite parfaitement calée avec celle de notre modèle (voir Fig. 5).
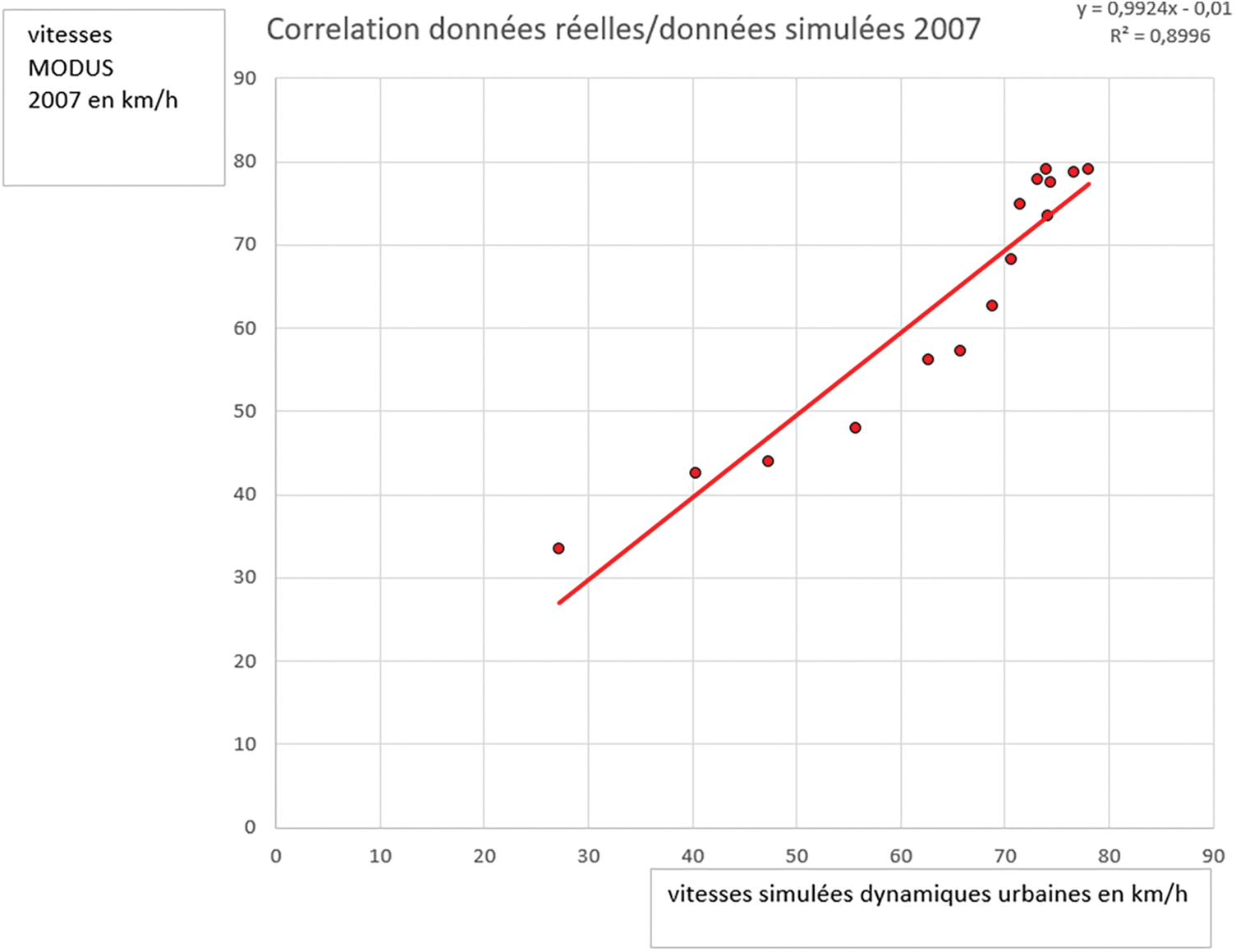
Figure 5: Ajustement des données de vitesse agrégées
5.1.3 Résultat de l’ajustement
Pour les trois variables gi, Xi et Vi, on constante que pour une simulation donnée à la date t = 2007, les résultats sont conformes à la réalité (quasiment Y = X ou valeur modélisée = valeur réelle). En partant de la date initiale, il nous a été possible de simuler le vecteur M (gi, Vi, Xi) et cela pour toutes les communes. On obtient une cartographie des densités des communes de l’Ile de France quasiment conforme aux valeurs réelles.
5.2 Présentation de la simulation 2040 en Ile-de-France à partir des projections de l’INSEE
5.2.1 Présentation de la situation de comparaison et justification du choix de la date de départ de 1968
Dans un premier temps, nous avons effectué une simulation sur la base du recensement de 1968. Ce faisant, nous avons opté pour une date qui coïncide avec la fin du baby-boom, c’est-à-dire la fin des grands programmes de développement de la région Ile-de-France. En effet, une date antérieure n’aurait pas permis de calibrer notre modèle, puisqu’une rupture a été observée à la fin des années 1950. La date de 1968 permet donc de suivre l’évolution des densités sans trop d’accidents (voir Fig. 6). En 2007, date de comparaison de notre modèle, l’Ile-de-France suit une logique de densité assez comparable à celle des villes occidentales, c’est-à-dire une logique de cratère de densité. Les densités du centre (Paris) forment un “cratère” par rapport aux densités des banlieues les plus proches, qui ont les densités les plus élevées. Plus on s’éloigne du centre, plus les densités glissent vers la périphérie, jusqu’à atteindre un seuil bas, une sorte de plateau périurbain avec des densités faibles qui déclinent très lentement vers les limites de l’Ile-de-France. Cette logique correspond à un modèle bien connu en économie urbaine : le modèle du cratère de densité de Newling (1969). Au-delà de cette logique radiale, les formes urbaines présentent un aspect anisotrope, où les densités s’étalent en doigts de gant le long des principales vallées (Seine, Oise, Marne) et le long des corridors du RER.
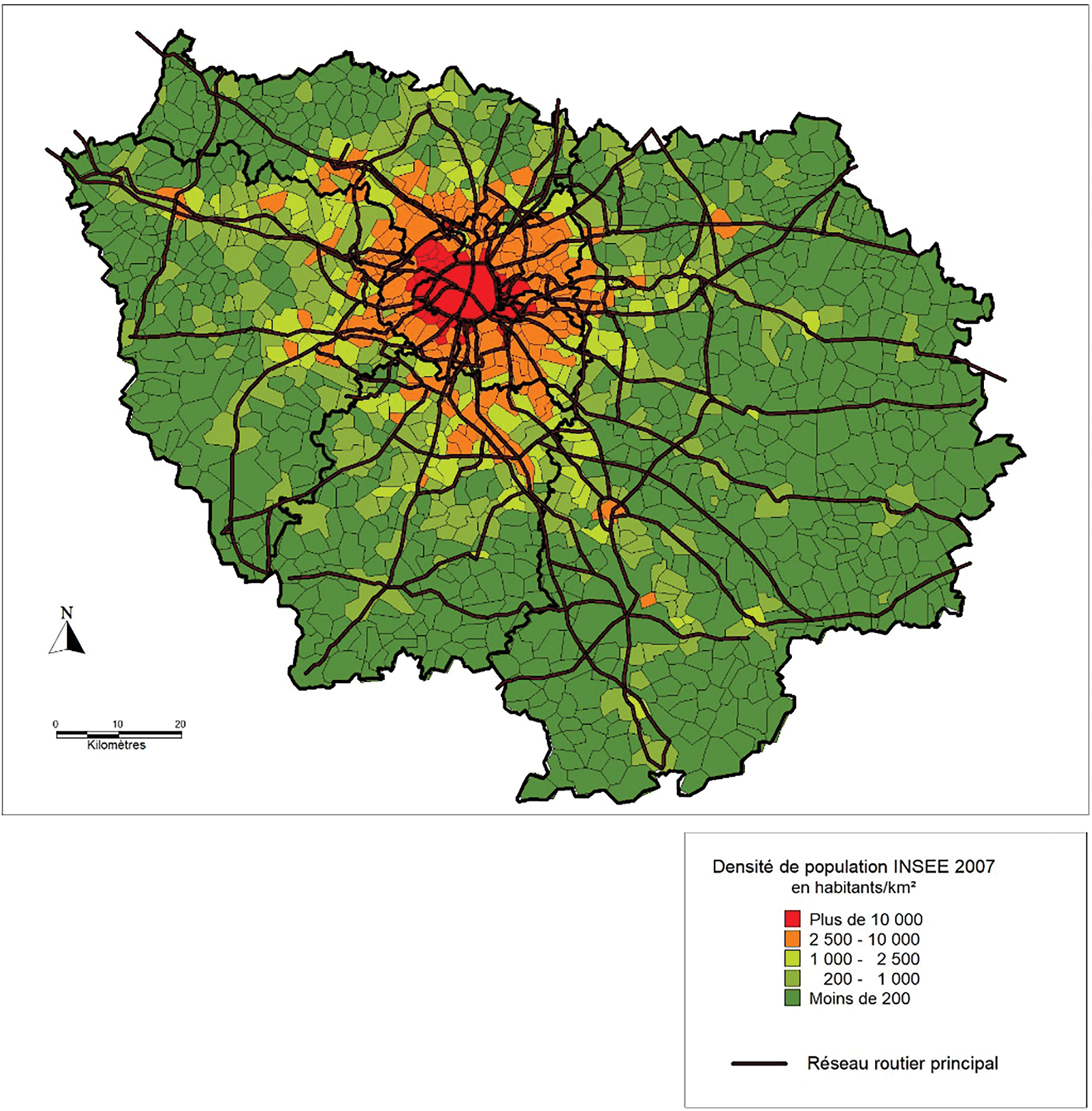
Figure 6: Densité de la population de l'INSEE en 2007
Enfin, il existe également des pôles de densité secondaire, soit en périphérie de l’agglomération parisienne (villes nouvelles de Melun-Senart, Marne-la-Vallée, Cergy-Pontoise et Saint-Quentin-en-Yvelines, Evry), soit en dehors de l’agglomération parisienne, avec des villes comme Mantes-la-Jolie, Meaux, Fontainebleau et Provins.
Cette situation perdurera-t-elle en 2040 ?
5.2.2 Scénario 1 : croissance modérée
Ce scénario suppose une augmentation du coût de l’essence et une politique volontariste de développement des communes de l’agglomération parisienne.
Cette carte (Fig. 7) montre un territoire qui conserve globalement les mêmes logiques de formes urbaines qu’en 2007 (densité en forme de cratère), mais avec des variations assez marquées dans le détail. Tout d’abord, la zone centrale (conurbation) est quasiment inchangée, alors que la périphérie est en pleine mutation. Le tissu urbain progresse en s’éloignant de Paris, généralement en anneaux concentriques légèrement décalés vers le flanc sud-ouest. L’extension se fait le long des lignes de RER dans toutes les directions, avec une moindre ampleur vers la Seine-et-Marne. Globalement, y compris dans les espaces intermédiaires des corridors du RER, les densités augmentent dans l’ensemble de la banlieue parisienne, de sorte que l’effet “corridor fluvial” tend à s’estomper au profit des lignes de RER. On peut donc dire que, dans un scénario modéré, la région parisienne continue à s’urbaniser, la limite urbaine passant de 40 km à 60 km du centre de Paris. Si l’on affine la classe des moins de 200 habitants/km2, on constate également que les densités les plus faibles se maintiennent aux marges de l’Ile-de-France dans sa partie extrême orientale.
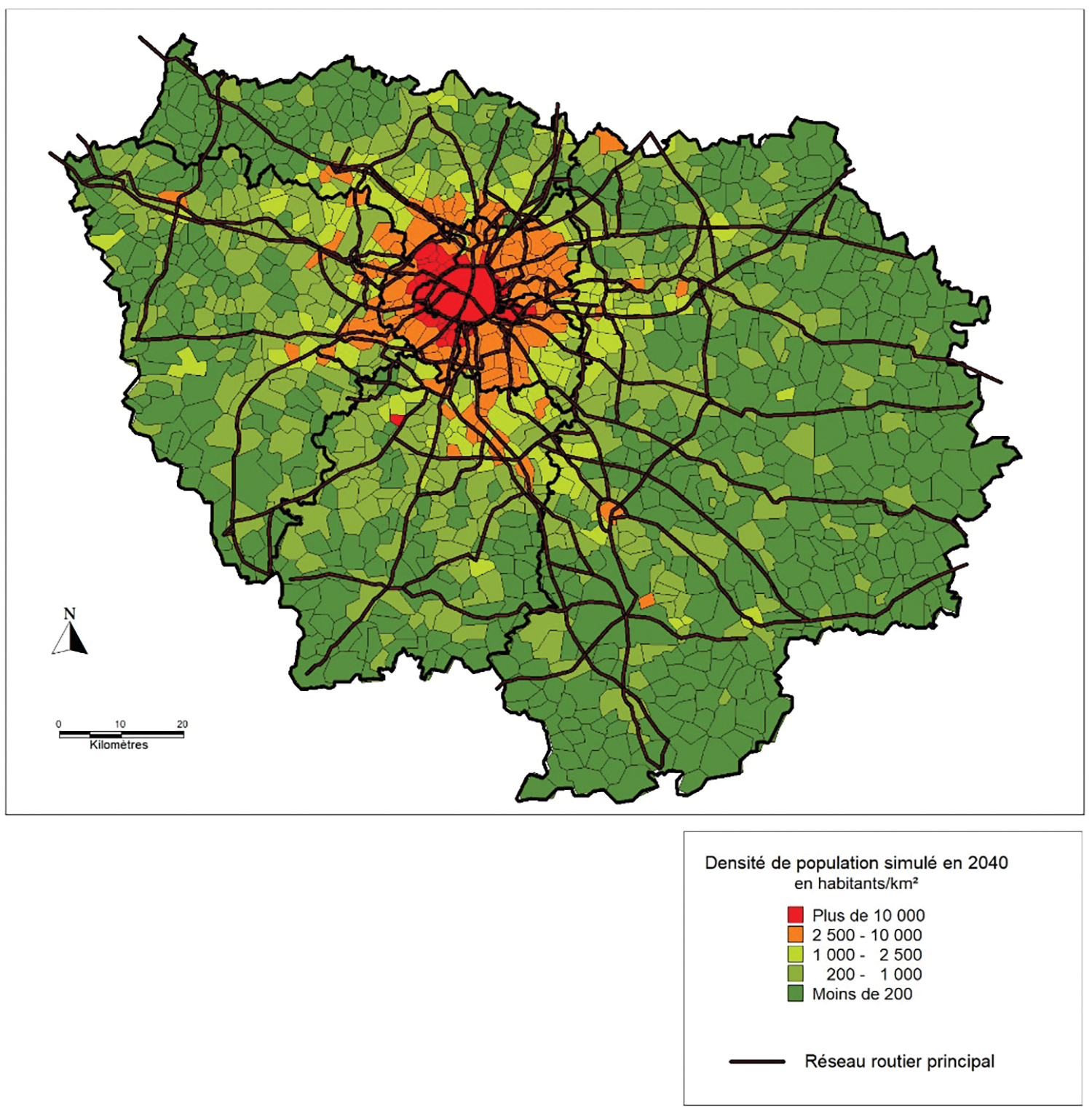
Figure 7: Simulation en 2040 des densités de population, scénario 1
5.2.3 Scénario 2 : croissance plus forte
Ce scénario (Fig. 8) suppose une évolution modérée du prix de l’essence et une large ouverture de l’offre de terrains à bâtir dans les banlieues de la région Ile-de-France.
Notons que ce modèle pour les deux scénarios présentés, diffère des résultats précédents de l’étalement urbain qui étaient plus permissifs au niveau des gains surfaciques. Toutefois la simulation OMPHALE20 de l’INSEE prévoit depuis de nombreuses années une stabilisation de l’étalement urbain, ce qui va dans le sens de notre étude.
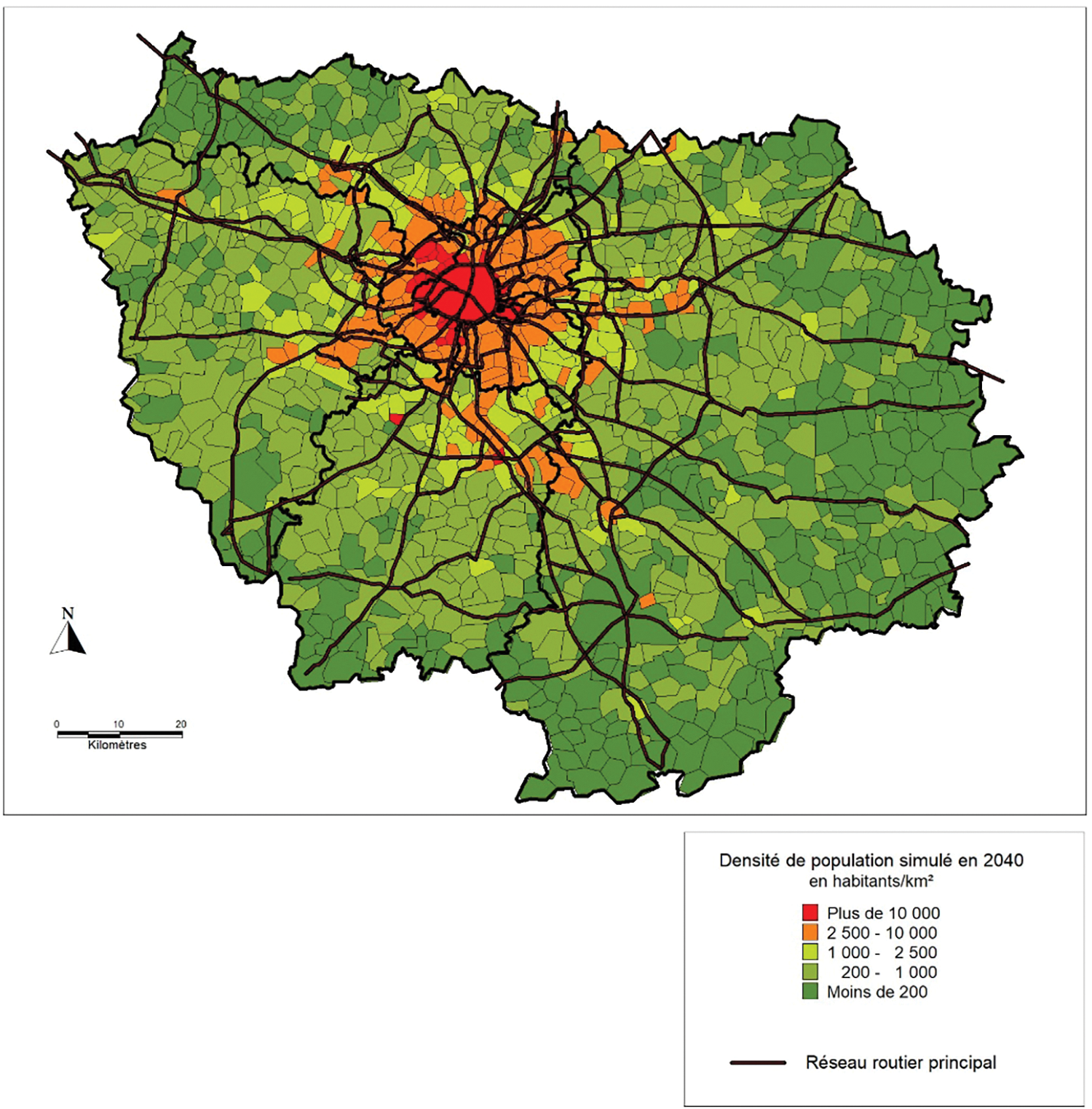
Figure 8: Simulation en 2040 des densités de population, scénario 2
Cette carte, fondamentalement différente de la précédente, montre une agglomération en progression sur ses marges par trois aspects :
Une progression des densités dans la partie centrale ;
Une progression de la première couronne de haute densité ;
L’apparition de pôles marginaux à proximité de l’agglomération.
En périphérie, l’agglomération progresse en doigts de gant, toutefois moins visibles que sur la carte précédente. L’auréole urbaine de Paris passe alors à 80 km de Paris en moyenne. L’urbanisation se fait dans toutes les directions, souvent en contournant les couloirs du RER et les grandes vallées. Enfin, comme dans la carte précédente, la partie Sud-Ouest s’urbanise beaucoup plus vite que la partie Est. Dans cette dernière partie, les doigts de gant sont alors plus marqués. C’est là que l’on trouve les densités les plus faibles. Ce scénario confère à l’Ile-de-France un caractère beaucoup plus urbain en 2040 ; cependant, compte tenu des évolutions économiques actuelles, il semble beaucoup moins probable que le précédent21. Si les évolutions globales des densités sont modérées dans les deux scénarios, on assiste néanmoins à une redistribution importante des populations au sein de l’Ile-de-France. En effet, la petite couronne et Paris semblent stagner, voire régresser en termes de densité, alors que la grande couronne progresse. Ce sont surtout les communes de banlieue qui bénéficient de cette redistribution. La grande couronne, moins dense, se réduit au contraire à la périphérie de la région parisienne.
Comment montrer l’étalement urbain ?
Peut-être en décrivant les formes pour les différentes périodes observées. Mais l’étalement urbain est avant tout dynamique et doit être envisagé de manière comparative. L’approche la plus simple est de proposer une analyse diachronique des périodes les unes après les autres. Cette approche simple est cependant limitée car elle ne permet pas de se projeter dans l’avenir. La solution la plus appropriée est de modéliser ces dynamiques. C’est ce que nous nous avons montré dans ce document.
A partir d’hypothèses aussi variées que la théorie de l’espace proxémique, la mécanique générale et plus particulièrement la mécanique des fluides, et la gravitation universelle, nous avons pu construire une dynamique originale combinant trois éléments : la densité de population, la vitesse et la distance proxémique urbaine. Pour ces hypothèses, l’apport de ce papier aux précédents est celui de l’espace proxémique. Nous avions déjà formé une dynamique mêlant gravitation, trafic et étalement urbain, mais l’espace dans lequel se déroulaient ces évolutions était physique. Il en résultait des dynamiques moyennement fiables au centre de l’agglomération et sur les franges périurbaines. L’introduction d’un espace proxémique permet de pallier ces insuffisances.
L’autre apport de ce document provient de la méthode utilisée pour construire le modèle. Les hypothèses seules ne suffisent pas à créer une simulation. Il faut les combiner, et pour cela, le calcul est un bon outil. Nous produisons ainsi un système de trois équations différentielles : espace proxémique, vitesse, densité (Vi, Xi, gi) qui, en utilisant le principe de discrétisation d’Euler, nous permet de produire un calcul incrémental facilement programmable dans un algorithme. L’objet mathématique constitué par ce système est intéressant en ce qu’il permet de suivre simultanément trois variables, chacune d’entre elles étant dynamiquement liée aux deux autres. Cette approche s’inscrit clairement dans les travaux de la synergétique ou de la systémique au sens le plus formel. Au-delà des simples équations, ce système est aussi un outil puissant pour simuler la forme urbaine et la dynamique des vitesses et de l’espace perçu à des échelles fines comme la commune. Il fournit une carte représentant les vitesses à l’échelle de la commune, ainsi que les densités de population et l’espace perçu, toujours à la même échelle. L’analyse de ces résultats donne au géographe la dimension de la croissance urbaine, à l’échelle souhaitée.
L’application à l’Ile-de-France met en évidence la force des dynamiques urbaines futures. Nous montrons que les dynamiques globales à l’œuvre ne changeront pas fondamentalement, avec un cœur régional qui pourrait conserver sa physionomie actuelle, en revanche une possible croissance significative de l’Ile-de-France aux marges de l’agglomération. L’un des scénarios les plus pessimistes prévoit même un doublement de la taille de l’aire métropolitaine de Paris en 2040. Cela reste toutefois très peu probable. Malgré ses atouts, ce modèle présente néanmoins des faiblesses. Le plus gros écueil est sans doute l’absence de facteurs “transports publics” dans la composante transport22. Nous répondrons tout de même que les conséquences des transports publics sont présentes dans la dynamique des densités. La congestion routière prend ici tout son sens dans la mesure où elle est en concurrence avec le métro, le RER, le tramway ou ses propres sites. Observerait-on les mêmes tendances de densité avec l’introduction de modèles pondérés par les transports en commun ? Probablement pas. Cette question mérite sans doute la plus grande attention et pourrait apparaître comme la principale évolution de ce type de modélisation. Enfin, nous conclurons en étendant le champ d’application de notre système à d’autres types de formalisation que la densité de population. Avec les fonctions de transfert et la densité bâtie, il serait relativement simple de projeter l’évolution de la morphologie urbaine au sens propre du terme. Naturellement, cela ne serait possible que dans l’hypothèse d’une réallocation probabiliste des masses de bâtiments construits entre deux dates.
Remerciements/Acknowledgement: Les auteurs tiennent à exprimer leur profonde gratitude envers tous ceux qui les ont soutenus et encouragés tout au long de ce travail de recherche.
Financements/Funding Statement: Les auteurs n’ont reçu aucun financement spécifique pour cette étude.
Disponibilité des données et du matériel/Availability of Data and Materials: Les principales données sont issues de data.gouv.fr et de l’INSEE.
Avis éthiques/Ethics Approval: Not applicable.
Conflits d’intérêt/Conflicts of Interest: Les auteurs déclarent qu’ils n’ont pas de conflits d’intérêts à signaler en ce qui concerne la présente étude.
1Cette approche théorique a pu être initiée par les travaux de Pumain (1982) [18].
2Les géographes ont investi depuis les années 70, ce type d’espace notamment avec la distance temps. L’Hostis et al. [19] a fait une démonstration d’un de ces types d’espace sous forme de cône. Kloeckner et al. [20] propose un exposé mathématique des différentes métriques utilisées en géographie.
3Zéro artificialisation nette voir Charme [21] et Rieutort [22].
4Les déformations cartographiques sont de plusieurs ordre comme le montre Bronner (2022) [24].
5Des études ont pu être publiées récemment sur cette thématique transversale de la forme urbaine et du transport (par exemple Rodrigues 2020 [39]). Au niveau local, il existe de nombreux travaux récents sur le continent africain, fortement impacté par l’étalement urbain non encadré. On retiendra, à ce titre, la thèse marocaine de S. Acherard Epse Filali [40].
6Que l’on peut rapprocher de la géométrie hyperbolique correspondant notamment au disque de Poincaré. Notons que dans cette géométrie est basée sur un seul centre donc se rapproche de la déformation autour d’un unique individu. Pour n individus, cela revient à une généralisation d’un espace hyperbolique à n centres. Un exposé récent du disque de Poincaré et de ses métriques est en fait pour les spécialistes dans Marle [43].
7Il s’agit de la distance proxémique à partir d’un unique individu vers une distance physique x. La forme graphique de ce modèle est quasiment identique à celle du modèle (5) d’où ce choix.
8Pour obtenir cette expression (6), nous avons dérivé X en fonction de la distance x et ensuite on remplace le reste de l’expression par X. Cela donne un lien entre la dérivée de X et X.
9Qi s’exprime en nombre de véhicules par heure, Ki est en nombre de véhicules par km et Vi en distance par heure.
10Dans le diagramme fondamental, le débit Qi =
11Sachant que
12λ estime la part de la densité de population qui explique la variation de la vitesse. Γ estime la part constante de la diminution de la variation de la vitesse.
13Selon les lois de l’accélération gravitaire.
14La gravitation est la seule force s’exerçant sur l’individu et s’exprime par ΣPi = Ggi avec gi densité de population. Il suffit ensuite de passer G de l’autre côté de l’expression et de dériver gi.
15ξ estime la force du lien entre la vitesse et la densité dans la variation de la densité de population. Φ, exprime la part de l’augmentation de la variation de densité liée à la vitesse.
16Dans ce calcul, nous raisonnerons sur un unique individu et donc nous éliminerons la somme de (9) pour se rattacher à une version à une version monocentrique. La version polycentrique est comparable.
17MODUS : acronyme de Modèle de Déplacements Urbains et Périurbains. MODUS est le modèle de prévision de trafic de la Direction Régionale et Interdépartementale de l’Equipement et de l’Aménagement d’Ile de France. Il s’agit d’un modèle qui existe depuis 1990 et qui fait partie des outils macroscopiques et statiques de prévision de trafic appelés modèle à 4 étapes. Nous définissons ensuite 4 étapes successives qui se caractérisent comme une série de modèles mathématiques permettant, à partir d’enquêtes ménages, de prévoir les trafics sur les principaux tronçons routiers de la région Ile-de-France.
-La première étape consiste à générer le nombre d’individus qui peuvent potentiellement se déplacer depuis et vers les zones (IRIS);
-La deuxième étape consiste à définir la matrice origine/destination entre les zones. C’est ce qu’on appelle la distribution. Dans MODUS, cette étape est réalisée par le modèle gravitaire.
-La troisième étape crée, à partir de la matrice origine/destination, plusieurs matrices : “Camion”, “Véhicules légers avec ventilation”, “Heure de pointe du matin”, “Heure de pointe du soir”.
-Enfin, la dernière étape est l’affectation réalisée à l’aide de l’algorithme du chemin le plus court. Le réseau est progressivement rempli par itération successive en bouclant sur l’étape précédente. Ce modèle est aujourd’hui largement utilisé par l’Etat et les collectivités locales dans une version affinée aux territoires concernés.
Pour plus de détails, se référer à : Modélisation des déplacements en IDF avec MODUS 3.1, scénarios prospectifs et résultats, DRIEA, Paris 2010.
18Note d’information du SETRA, Approche de la congestion routière, méthode de calcul du temps incommodé, 2009, Bagneux.
19Par cette transformation (33), calculée en remplaçant Vinitiale, on exprime la vitesse Vréelle à comparer avec les données MODUS en partant des densités gi à une date t simulée. Cela donne donc le lien statique à une date t entre la vitesse Vi et la densité gi.
20OMPHALE est une simulation statistique qui prévoit à l’échelle de la France les grandes tendances de population en des termes purement démographiques. Cette simulation est globale et ne peut être transposée à des échelles fines comme la commune.
21Voire fortement improbable du fait de la mise en place du SDRIF (schéma directeur régional de l’Ile-de-France) en 2013. On peut retrouver un exposé de ces politiques d’aménagement dans les ouvrages de Delattres [47] et Desjardins [48]. Les schémas prévoient, entre autre, un zéro artificialisation nette (ZAN) en 2050. Notons qu’une surface artificialisée retourne rarement en situation de terres non artificialisées sauf rares exceptions. Le ZAN prévoit justement le calcul de la différence entre les espaces consommés et les espaces reconvertis en espaces naturels et agricoles. A l’échelle globale, cette tendance à contrôler l’urbanisation en Ile-de-France va se poursuivre avec la mise en place en place du SDRIF E (environnement) qui devrait encore un peu plus renforcer les contraintes pour l’urbanisation. Cependant, le schéma global reste à appliquer et toutes les communes ne respectent pas exactement la loi climat résilience (LOI n° 2021-1104 du 22 août 2021) dans laquelle s’inscrit le SDRIF E largement plus restrictif que le SDRIF.Au titre de ce ZAN, l’IPR interroge les modes d’artificialisation du sol fortement consommateur d’espace et les met en perspective avec une densification (IPR 2019) [49] souhaitable des territoires urbains.
22A ce titre, Stransky [50] a pu montrer en quoi la périurbanisation pouvait être en lien avec les transports en commun au niveau morphologique.
References
1. Alonso W. Localisation and land use. Harvard University Press; 1964. [Google Scholar]
2. Clark C. Urban population densities. J Royal Stat Soc Serie A. 1951;114:490–6. doi:10.2307/2981088. [Google Scholar] [CrossRef]
3. Newling BE. The spatial variation of urban population densities. Geograph Rev. 1969;59:242–52. doi:10.2307/213456. [Google Scholar] [CrossRef]
4. Mills ES. Urban density functions. Urban Stud. 1970;7:5–20. doi:10.1080/00420987020080011. [Google Scholar] [CrossRef]
5. Bussière R. Interaction urbaines. In: Le modèle de la CRU. Paris: Centre de recherche d’urbanisme; 1975 (In French). [Google Scholar]
6. Peguy PY. Analyse économique des configurations urbaines et de leur étalement, thèse de doctorat en Sciences Economique sous la direction A. Bonnafous, Université de Lyon II : France; 2000 (In French). [Google Scholar]
7. Anas A, Arnott R, Small KA. Urban spatial structure. J Econ Lit. 1998;36:1426–64. [Google Scholar]
8. Small KA, Song S. Population and employment densities: structure and change. J Urban Econ. 1994;36:292–313. doi:10.1006/juec.1994.1037. [Google Scholar] [PubMed] [CrossRef]
9. Mc Donald J, Prather P. Suburban employment centres: the case of Chicago. Urban Stud. 1994;3:20–8. [Google Scholar]
10. Mc Donald J. The identification of urban employment subcenters. J Urban Econ. 1987;2:242–58. doi:10.1016/0094-1190(87)90017-9. [Google Scholar] [CrossRef]
11. Mahmassani HS, Baaj MM, Tong CC. Characterization and evolution of spatial density patterns in urban areas. Transportation. 1988;15(3):233–56. doi:10.1007/BF00837583. [Google Scholar] [CrossRef]
12. Batty M, Longley P. The fractal simulation of urban structure. Environ Plann A. 1986;18:1143–79. doi:10.1068/a181143. [Google Scholar] [CrossRef]
13. Frankhauser P. L’approche fractale : un nouvel outil de réflexion dans l’analyse spatiale des agglomérations urbaines. Population. 1997;4:1005–40 (In French). [Google Scholar]
14. Dubos-Paillard E, Guermond Y, Langlois P. Analyse de l’évolution urbaine par automate cellulaire : le modèle SpaCelle. L’espace géographique. 2003 Tome 32;4:357–78 (In French). [Google Scholar]
15. Antoni JP. Modélisation dynamique de l’étalement urbain : aspects conceptuels et gestionnaires : application à Belfort, doctorat en géographie sous la direction de C. Cauvin. Université de Strasbourg : France; 2003 (In French). [Google Scholar]
16. Lajoie G, Hagen Zanker A. La simulation de l’étalement urbain à la Réunion : apport de l’automate cellulaire métronamica pour la prospective territoriale. Cybergeo : Systèmes, Modélisation, Géostatistiques. 2007;405 (In French). doi:10.4000/cybergeo.11882. [Google Scholar] [CrossRef]
17. Vairet T. Ilot de chaleur, croissance urbaine et climat urbain : simulations sur Dijon Métropole, thèse de géographie sous la direction de Thomas Thevenin. Université de Bourgogne : France; 2020. p. 216. [Google Scholar]
18. Pumain D. La dynamique des villes. Paris: Economica; 1982 (In French). [Google Scholar]
19. L’Hostis A, Abdou F. What is the shape of geographical time-space? A three-dimensional model made of curves and cones. ISPRS Int J Geo-Inf. 2021;10(5):340–57. doi:10.3390/ijgi10050340. [Google Scholar] [CrossRef]
20. Kloeckner BR, L’Hostis A, Richard T. Contextual metrics a mathematical definition for a comprehensive approach of geographical distances. Geogr Anal. 2020;53(1):736–66. doi:10.1111/gean.12260. [Google Scholar] [CrossRef]
21. Charmes É. De quoi le ZAN (zéro artificialisation nette) est-il le nom ? Fonciers en débat; 2021 (In French). [Google Scholar]
22. Rieutort L. Sobriété foncière et territoires, d’autres approches du ZAN justifiées par la géographie. Population et Avenir. 2024;768:4–7 (In French). [Google Scholar]
23. Enault C. Vers une transformation géométrique géocentrique des espaces urbains : la ville vue à partir du ou des centre(s). Revue Internationale de Géomatique. 2024;33(1):77–92 (In French). doi:10.32604/rig.2024.046591. [Google Scholar] [CrossRef]
24. Bronner AC. Cartogrammes, anamorphoses : des territoires transformés. In: Cunty C, Mathian H, editors. Traitements et cartographie de l’information géographique. France: ISTE Sciences, Géographie et Démographie/cartographie; 2020. p. 231–71 (In French). [Google Scholar]
25. Piaget J, Inhelder B. The child’s conception of space. New York: Norton; 1967. [Google Scholar]
26. Moles A, Rohmer E. Psychologie de l’espace. Tournai: Casterman; 1976 (In French). [Google Scholar]
27. Mills ES, Tan JP. A comparison of urban density functions in developed and developing countries. Urban Stud. 1980;17:313–21. doi:10.1080/00420988020080621. [Google Scholar] [CrossRef]
28. Greenshields BD. A study of traffic capacity. Highway Res Board Proc. 1935;14:448–77. [Google Scholar]
29. Lighthill MJ, Whitham GB. On kinematic waves : a theory of traffic flow on long crowded roads. Proc R Soc. 1955;1178:145–317. [Google Scholar]
30. Richards PI. Shockwaves on the highway. Operat Res. 1956;4(1):42–51. doi:10.1287/opre.4.1.42. [Google Scholar] [PubMed] [CrossRef]
31. Ravenstein E. The law of migration. J Royal Stat Soc. 1885;167–235. [Google Scholar]
32. D’aubigny G, Calzada C, Grasland C, Robert D, Viho G Et Vincent J-M. Approche poissonnienne des modèles d’interaction spatiale. Cybergeo : Systèmes, Modélisation, Géostatistiques. 2007 Juin 07; 126 (In French). [Google Scholar]
33. Newman P, Kenworthy JR. Cities and automobile dependence, an international Sourcebook. Brookfield; 1989. [Google Scholar]
34. Newman P, Kenworthy JR. Transport and urban form in thirty two of the world’s principal cities. Trans Rev. 1991;11(3):249–72. doi:10.1080/01441649108716787. [Google Scholar] [CrossRef]
35. Dupuy G. Les territoires de l’automobile. Anthropos: Economica Paris; 1995a (In French). [Google Scholar]
36. Dupuy G. La ville et l’automobile. Paris: Flammarion; 1995b (In French). [Google Scholar]
37. Wiel M. La transition urbaine ou le passage de la ville pédestre à la ville motorisée. édition Margada; 1999 (In French). [Google Scholar]
38. Wiel M. Villes et automobile. édition Descartes et Cie, collection Les urbanités; 2002 (In French). [Google Scholar]
39. Rodrigue J-P. The geography of transport systems. 5th ed. Routledge; 2020. [Google Scholar]
40. Acherard Epse Filali S. Interactions entre formes urbaines et formes de mobilité. Cas du groupement de Constantine, thèse de doctorat es science aménagement urbain, sous la direction de Osni Boukerzaza, Université de Constantine, p. 411; 2022 (In French). [Google Scholar]
41. Enault C. Vitesse, accessibilité et étalement urbain; analyse et application à l’aire urbaine dijonnaise, thèse de doctorat sous la direction de Jean Jacques Bavoux, université de Bourgogne: Dijon; 2003 (In French). [Google Scholar]
42. Enault C. Simulation de l’étalement urbain de Dijon en 2030: approche systémique de la dynamique gravitaire ville-transport. Cybergeo : Eur J Geogr, Systèmes, Modélisation, Géostatistiques. 2012; 592 (In French). doi:10.4000/cybergeo.25157. [Google Scholar] [CrossRef]
43. Marle CM. Projection stereographique et moments. Université Pierre et Marie Curie : France; 2021 (In French). [Google Scholar]
44. Moles A. Vers une psycho-géographie. In: Bailly A, Ferras R, Pumain D, editors. Encyclopédie de la géographie. Paris: Economica; 1992. p. 177–205 (In French). [Google Scholar]
45. Casti E. Le tournant proxémique: de la représentation à la spatialité cartographique (In French). Available from: http://www.espacestemps.net/articles/le-tournant-proxemique-de-la-representation-a-la-patialite-cartographique/. [Accessed 2024]. [Google Scholar]
46. Wilson AG. Entropy in urban and regional modelling. Pion, Londres: Grande-Bretagne; 1970. [Google Scholar]
47. Delattre R. Réguler l’étalement urbain: les services de l’Etat français face aux projets d’urbanisme locaux. Espace et Société; 2024 (In French). [Google Scholar]
48. Desjardins X. Planification Urbaine, la ville en devenir. Armand Colin; 2020. p. 234 (In French). [Google Scholar]
49. IPR. Les espaces urbains au défi de la densification. Note rapide; 2020 (In French). [Google Scholar]
50. Stránský V. Périurbain et transit-oriented development: un couple invraisemblable ? Flux. 2019;(115):33–57 (In French). [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools