 Open Access
Open Access
SHORT COMMUNICATION
New Definitions of the Isometric Latitude and the Mercator Projection
Faculty of Geodesy, University of Zagreb, Zagreb, HR-10000, Croatia
* Corresponding Author: Miljenko Lapaine. Email:
Revue Internationale de Géomatique 2024, 33, 155-165. https://doi.org/10.32604/rig.2024.052258
Received 27 March 2024; Accepted 20 May 2024; Issue published 10 June 2024
Abstract
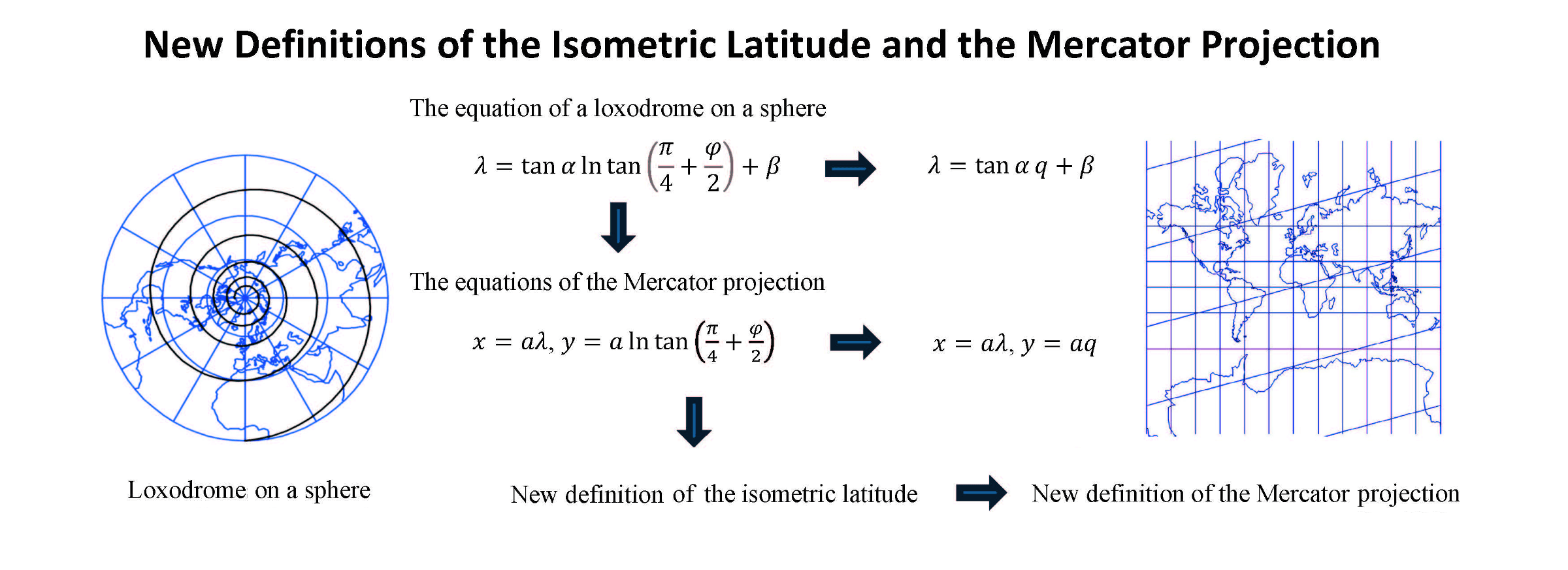
The short communication discusses the interrelationships of loxodromes, isometric latitudes and the normal aspect of Mercator projection. It is shown that by applying the isometric latitude, a very simple equation of the loxodrome on the sphere is reached. The consequence of this is that the isometric latitude can be defined using the generalized longitude, and not only using the latitude, as was common until now. Generalized longitude is the longitude defined for every real number; modulo 2π of generalized and usual longitude are congruent. Since the image of the loxodrome in the plane of the Mercator projection is a straight line, the isometric latitude can also be defined using this projection. Finally, a new definition of the Mercator projection is given, according to which it is a normal aspect cylindrical projection in which the images of the loxodromes on the sphere are straight lines in the plane of the projection that, together with the images of the meridians in the projection, form equal angles, as do the loxodromes with the meridians on the sphere. The short communication provides additional knowledge to all those who are interested in the theory of maps in navigation and have a piece of requisite mathematical knowledge, as well as an interest in map projections. It will be useful for teachers and students studying cartography and GIS, navigation or applied mathematics.Graphic Abstract
Keywords
We encounter the loxodrome in mathematics, cartography and seafaring. According to Britannica et al. [1], a loxodrome is a line on the globe that intersects all meridians at the same angle. A loxodrome is also the route a ship sails when it keeps the same course. The loxodrome at latitude φ = 0°, with a course of 90° or 270°, is the great circle of the Earth (equator). The loxodromes at other northern or southern latitudes, with a course of 90° or 270°, are small circles (parallels). Loxodromes with a course of 0° or 180° are great circles (meridians). In all other cases, loxodromes are spirals that twist toward the poles.
There is relatively detailed cartographic literature on loxodromes, isometric latitude and Mercator projection [2–5].
Loxodrome and Mercator projection are closely related to navigation [6–9]. The loxodrome was specially investigated by Alexander [10], Kos et al. [11,12], Elhashash [13], Petrović [14,15], Weintrit et al. [16], Babaarslan et al. [17], Kovalchuk et al. [18] and Lambrinos et al. [19]. Alexander [10] mainly deals with the historical development and connection of the loxodrome with the Mercator projection. Petrović [14] considers the loxodrome on the ellipsoid of revolution, but only gives equations without a more detailed derivation and without concrete applications.
Isometric latitude (see details in Section 3) appears in conformal mappings [20,21]. The Mercator projection is one of the most famous map projections. Even in recent times, it has been researched and written about by many, e.g., Kawase [22], Abee [23], Lapaine et al. [24], Pápay [25] and Viličić et al. [26]. Lapaine et al. [24] investigate a new variant of the Mercator projection, the web-Mercator projection. Viličić et al. [26] deal with the transverse Mercator projection and the problem of secant cylinders.
In this short communication, we start with the derivation of the loxodrome equation on the sphere in the geographic parameterization. Then, instead of geographic latitude, we introduce isometric latitude as a parameter. This shows how to arrive at a very simple equation of the loxodrome. It is a linear relationship between the isometric latitude and geographic longitude, with the fact that the longitude should be taken in a generalized sense, i.e., from the interval
After that, we consider the normal aspect Mercator projection of the sphere in the usual way and using the isometric latitude. Then we derive the equation of the loxodrome image in that projection. This gives us the possibility of a new interpretation of isometric latitude using the Mercator projection. Finally, the idea to approach the Mercator projection in a new way is presented. We define it as a normal aspect cylindrical projection in which the images of loxodromes on the sphere are straight lines in the plane of the projection that make the same angles as the images of the meridians in the projection as loxodromes with the meridians on the sphere.
2 The Equation of a Loxodrome on the Sphere
Let us recall that for R = const.
Defines a sphere with its center at the origin of the coordinate system and the radius R. Curves on the sphere for which
The coefficients of the first differential form of this mapping are
The differential expressions for any curve on the sphere are
where

If we accept the relations from Table 1, and the fact that the length of the arc of the curve must be positive, then in Eqs. (4) and (5), it is sufficient to take only the positive sign.
Let it be
Which after integration gives
and it is the equation of the loxodrome connecting the latitude
Loxodromes on a sphere are generally spiral curves that wrap around each pole an infinite number of times (Fig. 1) and never reach it, although their length is finite. The length of the loxodrome from pole to pole is equal to the length of the arc of the meridian divided by the cosine of the angle α. Indeed, in Eq. (6) we should put

Figure 1: Loxodrome on a sphere
If we start with the differential Eq. (4) we cannot integrate it immediately. First we should express
After integration we get
We note that according to (8)
If we want the loxodrome to pass through the point with geographical coordinates
Finally, if we want the relationship between
If
3 Isometric Latitude and Loxodrome
The isometric latitude q on the sphere is defined in the theory of map projections by the geographic latitude
The purpose of the isometric latitude is to give a parametrization, in which the Gaussian fundamental coefficients E and G are equal to each other. The solution of differential Eq. (11) is
with the assumption that we took for the integration constant the value that gives
Note that
These relations are easily derived from the definition of isometric latitude
Furthermore, the differential Eq. (7) written by using the isometric latitude q becomes very simple and reads
After integration, we get the equation of the loxodrome on the sphere in the form
where
where
If we want the loxodrome to pass through the point with coordinates
Meridians and parallels are special cases of loxodromes. For meridians,
Indeed, if we take
3.2 The Equation of a Loxodrome on a Sphere Expressed Using Isometric Latitude
The equation of the loxodrome on the sphere expressed using geographic coordinates is (8). Considering the relation between geographic and isometric latitudes (12), (8) can be written in the form
For constant values of
4 Mercator Projection of the Sphere
The Mercator projection is a conformal cylindrical projection. This means that the basic equations of the normal aspect projection are
where
where h and k are local linear scale factors along the meridian and parallel, respectively. From the expression [2,3]:
It follows according to (21):
i.e.,
and from there
where K is the constant of integration. The constants a and K can be chosen in different ways. For example, if we set the conditions
Let us note at the end that the equations of the Mercator projection (26) can be written in a very simple form using the isometric latitude q (12).
4.1 Loxodrome in the Normal Aspect Mercator Projection
The equation of the loxodrome on the sphere is (19). If we substitute (19) in (27), we will get the equation of the loxodrome in the Mercator projection.
Eq. (28) represents the straight line equation in parametric form. The parameter here is the isometric latitude q. By eliminating that parameter, we can obtain the equation of the straight line in an explicit, implicit or any other form.
From (19) we can get
and then from (27)
Eq. (30) again represents the straight line equation in parametric form. The parameter is now the generalized longitude
Fig. 2 shows the loxodrome in the normal aspect Mercator projection with the assumptions

Figure 2: Loxodrome in the normal aspect Mercator projection
Although the geometric interpretations of latitude and longitude and geocentric and reduced latitude are well known, a similar interpretation of isometric latitude is not easy to find. For example, Heck [28] says in his famous monograph: “While the latitude
Now we will give a new definition of the isometric latitude q on the sphere using the Mercator projection.
Definition. The isometric latitude of any point on the sphere is proportional to the ordinate y of the image of that point in the normal aspect Mercator projection,
5 A New Approach to Normal Aspect Mercator Projection
A common approach to deriving the equations of the normal aspect Mercator projection is to look for a cylindrical projection that satisfies the conformality condition (Section 4 in this short communication). When we have the equations of the normal aspect Mercator projection, then we derive from them the equation of the loxodrome in that projection and show that it is always a straight line. The new approach to the derivation of the equations of this projection does not start with setting the conformality condition. Instead, we set the condition that each loxodrome in the normal aspect cylindrical projection is mapped as a straight line. The equations of the normal aspect Mercator projection will emerge from this condition. Let us remind that when Mercator made his famous map, he had in mind the rectilinearity of loxodromes, not conformality.
Let us start from the equations of any normal aspect cylindrical projection (20) where
For (31) to be straight line equations in parametric form with the parameter q, which form the angle
where b is a constant. Considering (12), we have
Therefore, the equations of the normal aspect cylindrical projection, which has the property that every loxodrome on the sphere that forms an angle
In addition to the usual condition in map projections that
where we recognize the equations of the normal aspect Mercator projection.
It is known that instead of geographic latitude, it is convenient to introduce isometric latitude as a parameter when it comes to the issue of preserving angles [2,30–32]. We have shown that in this way, we arrive at a very simple equation of the loxodrome on the sphere. It is a linear relationship between the isometric latitude and geographic longitude, with the fact that longitude should be taken in a generalized sense, i.e., from the interval
The normal aspect of the Mercator projection of the sphere can be defined in the usual way or using isometric latitude. We have shown that the introduction of the isometric latitude is very clever when deriving the equation of the loxodrome image in that projection. Furthermore, it enabled a new definition of isometric latitude using the normal aspect Mercator projection.
When Mercator made his map, he had in mind the rectilinearity of the loxodrome, not conformality. The Mercator projection is usually defined as a cylindrical conformal projection, and the novelty of this paper is that this is a consequence of the new definition. Namely, this projection can also be defined as a normal aspect cylindrical projection in which the images of the loxodromes from the sphere are straight lines in the plane of the projection that form the same angles as the images of the meridians in the projection as the loxodromes with the meridians on the sphere. Thus, the article, in a certain way, connects Mercator’s original idea with today’s usual approach to his projection, as a conformal cylindrical projection. In this way, we enrich the theory of map projections and expand the horizons of the user’s knowledge.
Acknowledgement: The author would like to thank the anonymous reviewers for their useful comments.
Funding Statement: The author received no specific funding for this study.
Author Contributions: All the work was done by Miljenko Lapaine.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
References
1. Britannica. loxodrome. Available from: https://www.britannica.com/topic/ loxodrome. [Accessed 2024]. [Google Scholar]
2. Snyder JP. Map projections–a working manual. Washington DC, USA: U.S. Government Printing Office; 1987. [Google Scholar]
3. Bugaevsky LM, Snyder JP. Map projections: a reference manual. London, Bristol: Taylor & Francis; 1995. [Google Scholar]
4. Deakin RE. 3-D coordinate transformations. Surv Land Inf Syst. 1998;58(4):223–34. doi:10.1017/S0373463315000181. [Google Scholar] [CrossRef]
5. Bian SF, Li HP. Mathematical analysis in cartography by means of computer algebra system. In: Bateira C, editor. Cartography: a tool for spatial analysis. Rijeka: InTech; 2012. [Google Scholar]
6. Lenart AS. Orthodromes and loxodromes in marine navigation. J Navig. 2017;70(2):432–9. doi:10.1017/S0373463316000552. [Google Scholar] [CrossRef]
7. Gao M, Shi GY. Ship-handling behavior pattern recognition using AIS sub-trajectory clustering analysis based on the T-SNE and spectral clustering algorithms. Ocean Eng. 2020;205:106919. [Google Scholar]
8. Nicolai R. The map projection of portolan charts. Nieuw Archief Voor Wiskunde. 2021;5(1):33–41. [Google Scholar]
9. Jiao C, Wan X, Li H, Bian S. Dynamic projection method of electronic navigational charts for polar navigation. J Mar Sci Eng. 2024;12(4):577. [Google Scholar]
10. Alexander J. Loxodromes: a rhumb way to go. Math Mag. 2004;77(5):349–56. doi:10.1080/0025570X.2004.11953279. [Google Scholar] [CrossRef]
11. Kos S, Filjar R, Hess M. Differential equation of the loxodrome on a rotational surface. In: Proceedings of the 2009 International Technical Meeting of the Institute of Navigation; 2009; Anaheim, CA, USA. p. 958–960. [Google Scholar]
12. Kos S, Vranić D, Zec D. Differential equation of a Loxodrome on a sphere. J Navig. 1999;52(3):418–20. doi:10.1017/S0373463399008395. [Google Scholar] [CrossRef]
13. Elhashash A. Existence, uniqueness and angle computation for the loxodrome on an ellipsoid of revolution. J Geom Symmetry Phys. 2009;13:75–88. doi:10.7546/jgsp-13-2009-75-88. [Google Scholar] [CrossRef]
14. Petrović M. Differential equation of a loxodrome on the spheroid. Naše More. 2007;54(3–4):87–9. [Google Scholar]
15. Petrović M. Orthodrome-loxodrome correlation by the middle latitude rule. J Navig. 2014;67(3):539–43. doi:10.1017/S037346331300074X. [Google Scholar] [CrossRef]
16. Weintrit A, Kopcz P. Loxodrome (Rhumb lineorthodrome (Great circlegreat ellipse and geodetic line (Geodesic) in Navigation. Boca Raton: CRC Press, Inc.; 2014. [Google Scholar]
17. Babaarslan M, Yayli Y. Differential equation of the loxodrome on a helicoidal surface. J Navig. 2015;68(5):962–70. doi:10.1017/S0373463315000181. [Google Scholar] [CrossRef]
18. Kovalchuk V, Mladenov IM. λ-spheres as a new reference model for geoid: explicit solutions of the direct and inverse problems for loxodromes (Rhumb lines). Mathematics. 2022;10(18):3356. doi:10.3390/math10183356. [Google Scholar] [CrossRef]
19. Lambrinos N, Repanidou I, Intzidou G. A didactical approach of rhumb line vs. great circle in web mercator projection for 6th grade pupils. In: Didactic strategies and resources for innovative geography teaching. IGI Global; 2022. p. 168–202. [Google Scholar]
20. Bermejo-Solera M, Otero J. Simple and highly accurate formulas for the computation of Transverse Mercator coordinates from longitude and isometric latitude. J Geod. 2009;83(1):1–12. doi:10.1007/s00190-008-0224-y. [Google Scholar] [CrossRef]
21. Li H, Bian S, Chen L. The direct calculating formulae for transformations between authalic latitude function and isometric latitude. Geom Inf Sci Wuhan Univ. 2011;36(7):843–6. [Google Scholar]
22. Kawase K. Concise derivation of extensive coordinate conversion formulae in the Gauss-Krüger projection. Bulletin Geospat Inform Auth Japan. 2013;60:1–6. [Google Scholar]
23. Abee M. The spread of the mercator projection in western european and united states cartography. Cartogr: Int J Geogr Inf Geovis. 2021;56(2):151–65. doi:10.3138/cart-2019-0024 [Google Scholar] [PubMed] [CrossRef]
24. Lapaine M, Frančula N. Web mercator projection-one of cylindrical projections of an ellipsoid to a plane. Cartogr Geoinf. 2021;20(35):31–47. doi:10.32909/kg.20.35.2. [Google Scholar] [CrossRef]
25. Pápay G. Mercator’s geometric method in the construction of his projection from 1569. KN-J Cartogr Geogr Inform. 2022;72(4):261–7. doi:10.1007/s42489-022-00115-5. [Google Scholar] [CrossRef]
26. Viličić M, Lapaine M. Loxodrome and isometric latitude. Cartogr. Geoinf. 2024;32(41). [Google Scholar]
27. Heck B. Rechenverfahren und auswertemodelle der landesvermessung. Karlsruhe: Herbert Wichmann Verlag; 1987 (In German). [Google Scholar]
28. Kerkovits K. Secant cylinders are evil−A case study on the standard lines of the universal transverse mercator and universal polar stereographic projections. ISPRS Int J Geo Inf. 2024;13(2):56. doi:10.3390/ijgi13020056. [Google Scholar] [CrossRef]
29. Lapaine M. Izometrijska širina i loksodroma. Geodetski List; 1993. 1:5–14 (In Croatian). [Google Scholar]
30. Adams OS. Latitude developments connected with geodesy and cartography with tables, including a table for lambert equal-area meridional projections. Am Math Mon. 1921;28(11/12):454. doi:10.2307/2972482. [Google Scholar] [CrossRef]
31. Lee LP. The computation of conformal projections. Surv Rev. 1974;172(22):245–56. doi:10.1179/sre.1974.22.172.245. [Google Scholar] [CrossRef]
32. Lee LP. Conformal projections based on elliptic functions. Toronto, Canada: University of Toronto Press; 1976. vol. 13, pp. 1–128. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools