 Open Access
Open Access
ARTICLE
Vers une transformation géométrique géocentrique des espaces urbains : la ville vue à partir du ou des centre(s)
Towards a Geocentric Geometric Transformation of Urban Spaces: The City Seen from the Centre(s)
Ministère de Transition Écologique et de la Cohésion des Territoires, Direction Départementale des Territoires du Val d’Oise, Service d’urbanisme et d’aménagement durable, Pôle d'étude et d’analyse territoriale, Val d’Oise, 95000, France
* Corresponding Author: Cyril Enault. Email:
Revue Internationale de Géomatique 2024, 33, 77-92. https://doi.org/10.32604/rig.2024.046591
Received 08 October 2023; Accepted 04 March 2024; Issue published 18 April 2024
RÉSUMÉ
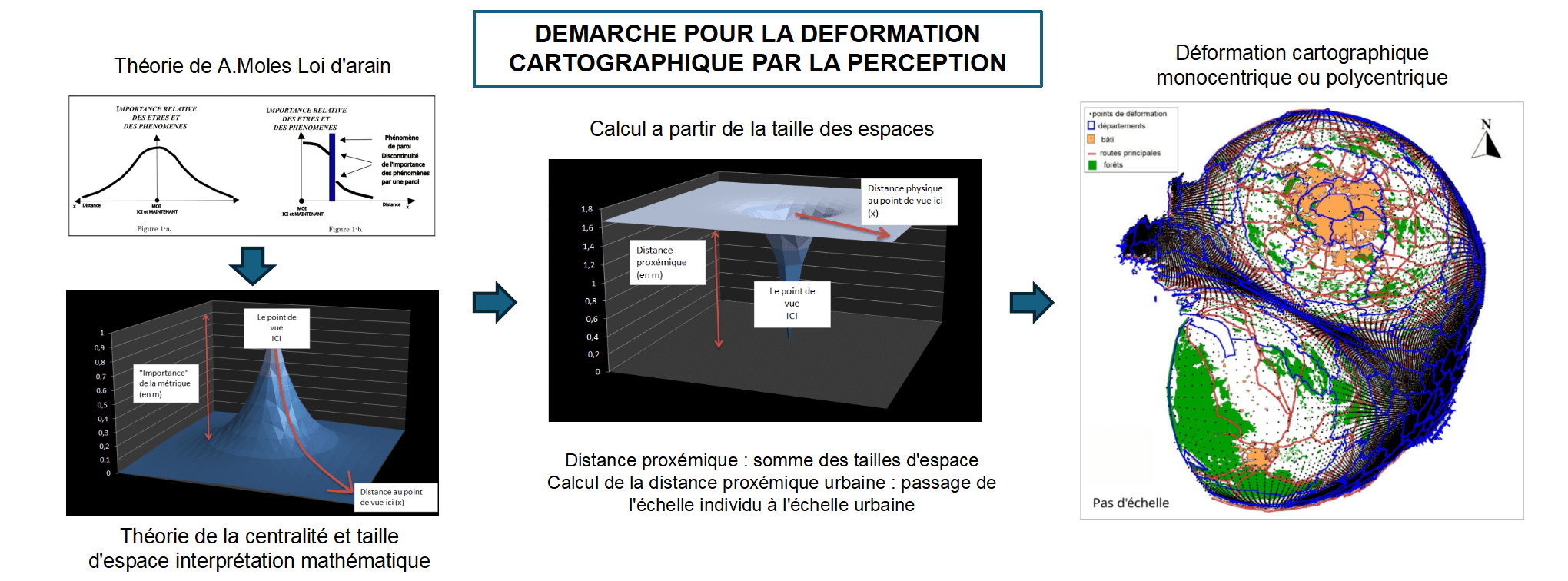
La théorie égocentrée est aujourd’hui bien connue des éthologues et des psychologues mais moins diffusée chez les géographes car elle reste encore à l’état de théorie abstraite. Ce papier se propose dans un premier temps de rendre opérationnel cette approche dans le cadre de travaux géographiques à l’échelle de l’individu. Puis, elle envisage d’établir le lien entre l’échelle individu et l’échelle de la ville avec comme objectif de produire des cartes déformées de la ville.Abstract
The egocentred theory is now well known to ethologists and psychologists but less spread among geographers because it still stays in the state of abstract theory. This paper suggests at first making this approach operational within the framework of geographical works on the scale of the individual. Then, it intends to establish the link between the individual scale and the city scale, with the aim of producing deformation maps of the city.Graphic Abstract
MOTS CLÉS
Keywords
Depuis la « time Géography » avec comme précurseur T. Hagerstrand, la mesure de l’espace n’est plus une donnée euclidienne. On parle alors plus volontiers de distance temps pour signifier le plus souvent la métrique géographique. De nombreux auteurs ont pu depuis proposer des méthodes de déformation cartographique pour représenter ce nouvel espace. A ce titre, on citera les travaux très récents de L’Hostis et al. 1 [1] (qui reprennent pour partie la thèse de L’Hostis sur les représentations de la distance temps en en améliorant les principes). On pourra également citer les travaux de déformation des réseaux (distance temps centrée) par Kaiser et al. [2]. Dans cet article, les auteurs agrandissent les zones à grande distance temps et réduisent les réseaux à petite distance temps. Enfin, on pourra également faire référence aux travaux plus anciens de Spiekermann et al. [3] portant sur les déformations cartographiques en distance temps en Europe.
Cette entrée de l’espace par les distances temps, fondamentale et dominante, ne doit cependant pas nous interdire d’autres approches selon d’autres critères que le temps de trajet [4,5]. Pour cerner notre propos, on peut alors commencer par une citation.
« L’homme est la mesure de toutes choses », cette citation est attribuée à Protagoras (−490−420) et marque le début du relativisme qui encore aujourd’hui persiste dans la une très large partie des sciences humaines. Il est vrai que le scepticisme et la subjectivité tiennent une place importante en donnant comme référence de notre monde l’homme. Cette base a donné lieu en particulier, en éthologie (discipline appliquée à l’homme), à la théorie proxémique que nous proposons ici d’analyser.
La théorie proxémique est née au milieu des années 60. Considérée par la suite comme une branche de la psychologie, elle sera reprise dans le cadre des théories d’ Moles et al. [6] en micro-psychologie puis en psycho-géographie. Tuan [7] émet alors l’idée que la distance est une expérience de l’individu et que ce dernier est au cœur de l’espace et intervient dans sa définition.
La géographie a tout à gagner à intégrer ce type de théorie alors comme le souligne l’article d'espace-temps.net (2012) d’ Casti [8], se pourrait-il que la proxémique représente possiblement un tournant dans l’évolution disciplinaire géographique ?
Avec le développement des modèles dits individus, la Géographie rentrerait ainsi parfaitement dans cette logique de psychologie environnementale. La question en suspens reste alors le lien à entretenir entre l’échelle de l’individu et le méso ou macro espace. Au regard des approches sur la « time géography », les nouveautés de ce type d’entrée sont de deux ordres.
• On propose ainsi d’intégrer l’homme à la métrique que l’on va mesurer. Il est alors au cœur de cette nouvelle mesure de l’espace, l’espace, en tant que mesure, devient par nature humain ; l’individu se trouve alors au cœur de cette nouvelle définition de l’espace.
• La déformation de l’espace dépend de l’individu. Aussi l’espace est non euclidien, centré sur l’individu et distordu en fonction de ce dernier.
Des similitudes pourraient être trouvées avec la géométrie hyperbolique de H. Poincaré du début du 20ième siècle2 (disque de Poincaré).
Pour ce faire, dans cet article, nous nous proposons d’élaborer une expression quantifiée applicable de la loi de la Proxémique de Moles, restée qualitative. Par ailleurs, plus intéressant encore serait de proposer un passage de cette loi proxémique relative à l’individu à une loi valable pour un collectif, la ville. Enfin, la proposition d’une méthode de cartographie de la ville fondée sur cette distance proxémique globale pourrait présenter un intérêt et cela dans le cadre de la ville monocentrique ou polycentrique.
Avant de répondre à cette question, nous nous proposons d’expliciter ce qu’est la théorie proxémique, puis de dégager des « lois » individus pour cette dernière, ce qui nous permettra d’aller vers des « lois » à l’échelle de ville et enfin de terminer par notre question initiale : Quelle visualisation pour la ville en partant de la théorie égocentrée.
1.1 la théorie égocentrée : un rapide expose
D’un point de vue théorique, l’éthologie est la première science qui a reconnu la théorie égocentrée. Elle est alors étudiée comme sous ensemble de la notion de proxémique. Pour Hall (1971) [9], la proxémique est, d’un point de vue global, « l’ensemble des observations et théories que l’Homme fait de l’espace en tant que produit culturel spécifique ». Dans ce cadre, la notion de distance apparaît importante. La théorie égocentrée se présente comme un produit de cette interaction de plus ou moins grande proximité des individus. Selon chaque individu, chaque culture, cette distance proxémique est différente. Il apparaît alors que des affinités entre individus de langage, discours peuvent réduire cette distance. De la même manière, on se tient plus loin d’une personne présentant un handicap ou une différence quelconque.
Plus généralement et pour tous, le territoire3 est un lieu de perception où chaque individu se trouve au centre d’une « bulle ». Il apprécie alors le lieu en fonction de ses mouvements, le geste pour les espaces les plus proches et la vision pour les zones les plus lointaines. Les comportements des individus sont régulés les uns par rapport aux autres en fonction d’une distance sociale.
Il distingue ainsi plusieurs grandes bulles en fonction de la distance au corps :
La distance intime (entre 15 et 45 cm) : zone qui s’accompagne d’une grande implication physique et d’un échange sensoriel élevé.
La distance personnelle (entre 45 et 135 cm) : est utilisée dans les conversations particulières.
La distance sociale (entre 1,20 et 3,70 m) : est utilisée au cours de l’interaction avec des amis et des collègues de travail.
La distance publique (supérieure à 3,70 m) : est utilisée lorsqu’on parle à des groupes.
E. T. Hall détaille plus loin, dans son ouvrage, les 4 sphères ou « bulles ».
Plus intéressant pour le géographe et plus concret est le modèle dit de A. Moles où l’espace valorise la proximité, l’enracinement, l’immobilité. L’auteur développe le concept des « coquilles du Moi », organisation des individus de manière concentrique selon un gradient de familiarité de l’espace proche au vaste monde (Moles et Rohmer 1999). Le rapport à la familiarité décroit avec la distance au lieu de résidence.
V. Schwach écrivait en 1993 à propos des travaux de A. Moles : la « philosophie de la centralité correspond au point de vue “Ici et Maintenant” de l’individu en situation… il éprouve son propre rapport à l’environnement. Dans cette perspective, l’être, c’est-à-dire chacun de nous, s’éprouve comme le centre du monde, et celui-ci s’étend autour de lui ».
Ainsi la caractéristique principale de cette théorie est la proxémique, où l’importance des êtres et des choses, des événements diminuent avec la distance (Moles et al., 1999) [6] (voir Fig. 1). Dans cette logique, il existe une primauté du concept d’Ici et du phénomène d’atténuation avec la distance. Selon les auteurs, « fondamentalement, axiomatiquement, ce qui est proche est, toutes choses étant égales par ailleurs, plus important que ce qui est loin, qu’il s’agisse d’un événement, d’un objet, d’un phénomène ou d’un être ».
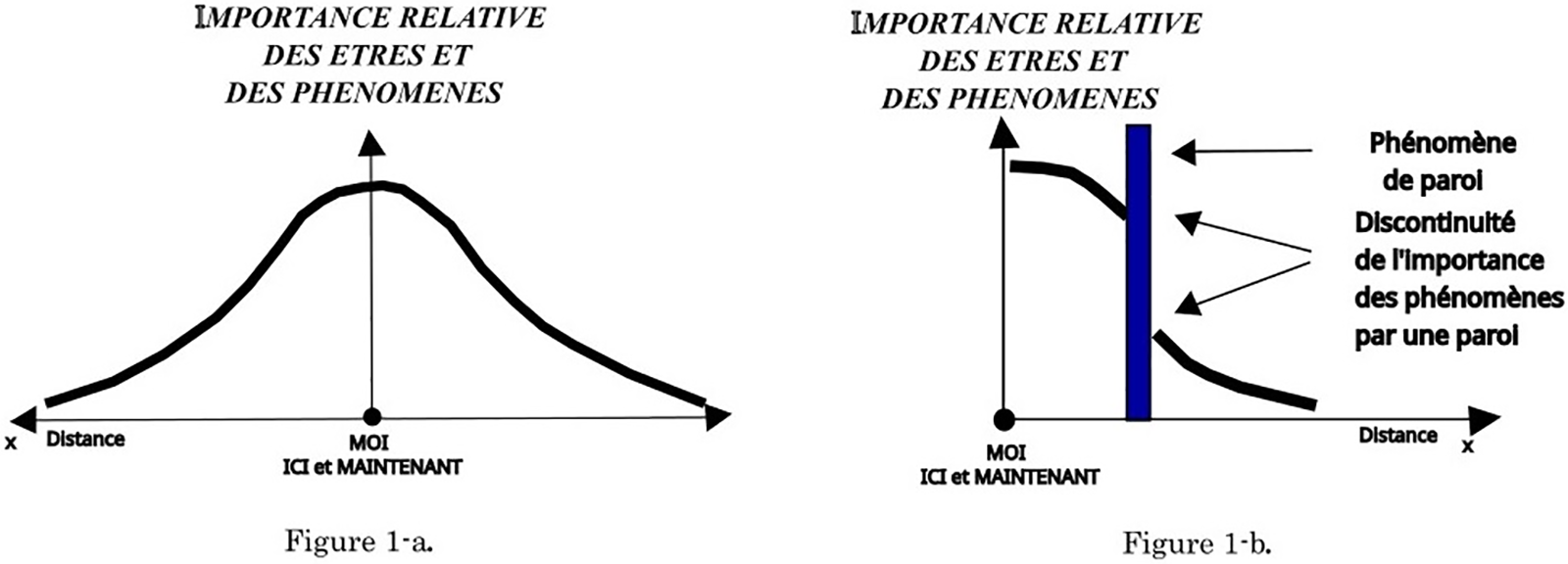
Figure 1: La Loi proxémique (1-a) et le phénomène de paroi (1-b) de Moles et Rohmer
En partant du modèle d’A. Moles, il peut sembler raisonnable d’imaginer l’espace comme égocentré, centré sur l’individu ou les individus. Cette approche proxémique semble par conséquent un point d’entrée tout à fait intéressant pour représenter l’espace. Il reste à en extraire les principes mathématiques et à les introduire au sein des métriques4.
1.2 De la « loi » individu a la « loi » collective : la théorie égocentrée applicable aussi à l’échelle de l’espace urbain
Découlant directement des théories d’A. Moles, il est possible de construire la loi dite d’airain de la proxémique.
A. Moles par sa formation de physicien propose une loi quasi physique pour la « philosophie de la centralité ».
Schwach [12] observe dans un hommage à A. Moles : qu’il s’agit d’une loi-psycho-socio-physique que l’auteur nomme loi d’airain de la proxémique.
Dans cette loi d’airain, il semble a priori important de définir ce que l’on entend par « ici » et sur ce point A. Moles propose « le lieu où l’on se situe ».
« L’importance » de la taille d’espace signifie dans ce cas précis une taille d’espace décroissante de la distance en fonction du point du vue Ici. Par Ici, on peut considérer qu’il s’agit du lieu où se situe l’individu. L’annexe I présente le volet technique de cette « loi ». L’idée globale de ces calculs part de la taille d’espace décroissante de la distance au point de vue ici. On somme alors l’ensemble de ces taille d’espace du point de vue ici à l’infini de l’individu pour former le concept de distance proxémique représenté sur la Fig. 2.
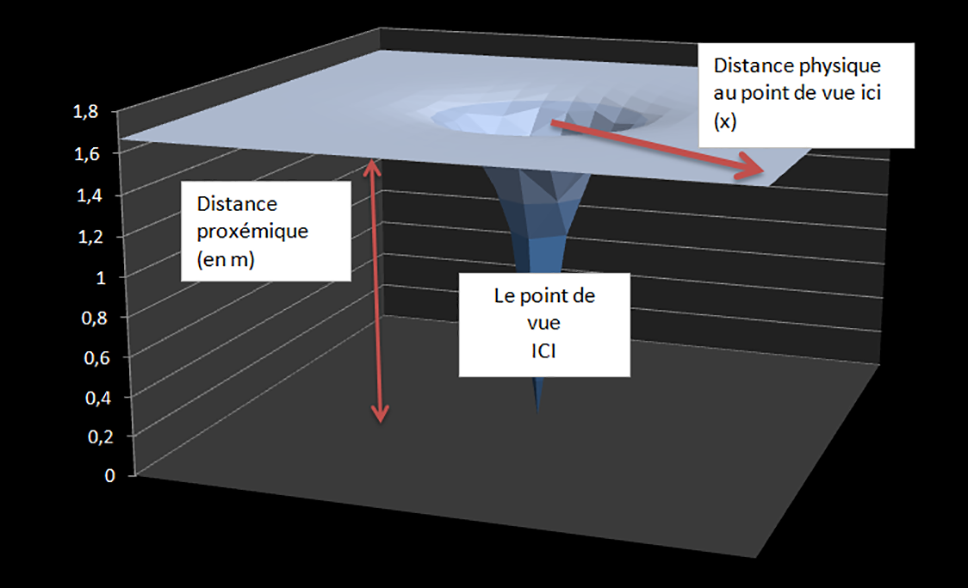
Figure 2: Représentation 3D de la distance proxémique au point de vue ici
En appliquant cette loi, on peut déformer des cartes (nous présenterons les procédés mathématiques de déformation dans l’annexe II) à partir de la localisation d’un individu voire de plusieurs. Prenons d’abord comme exemple la déformation à partir de Bordeaux (Fig. 3).
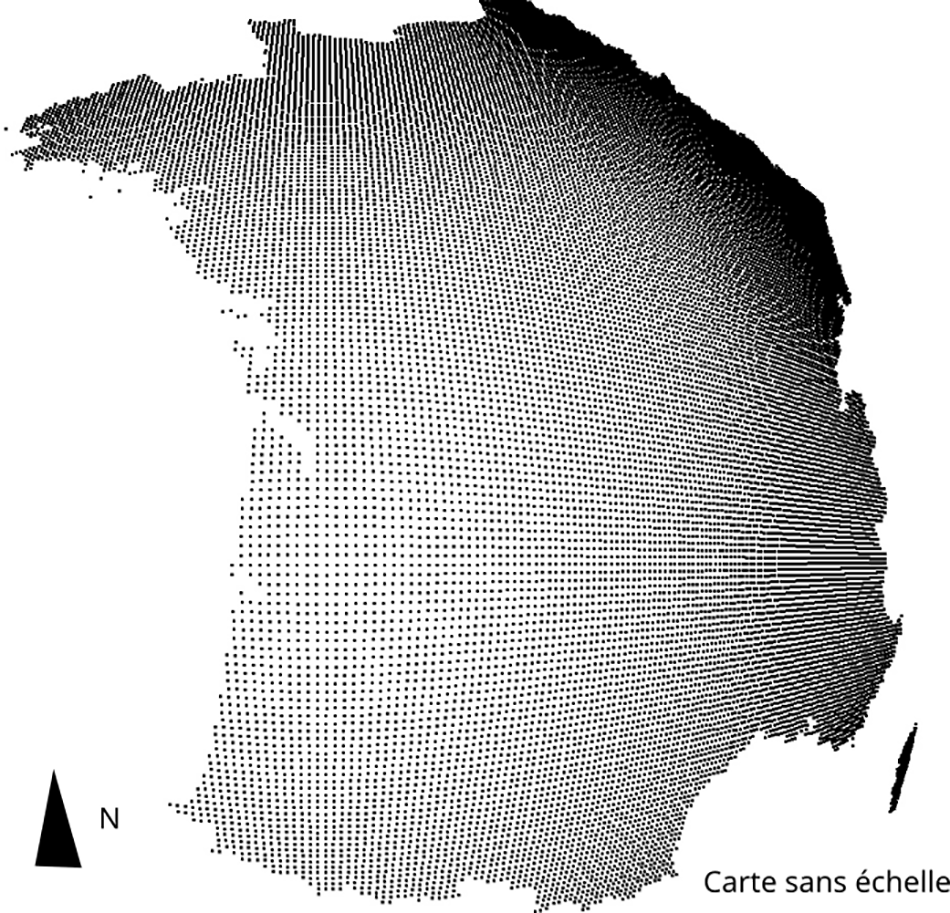
Figure 3: Déformation de la France à partir d’un individu localisé à Bordeaux
Pour les cartes à plusieurs individus, on obtiendrait par exemple la Fig. 4.
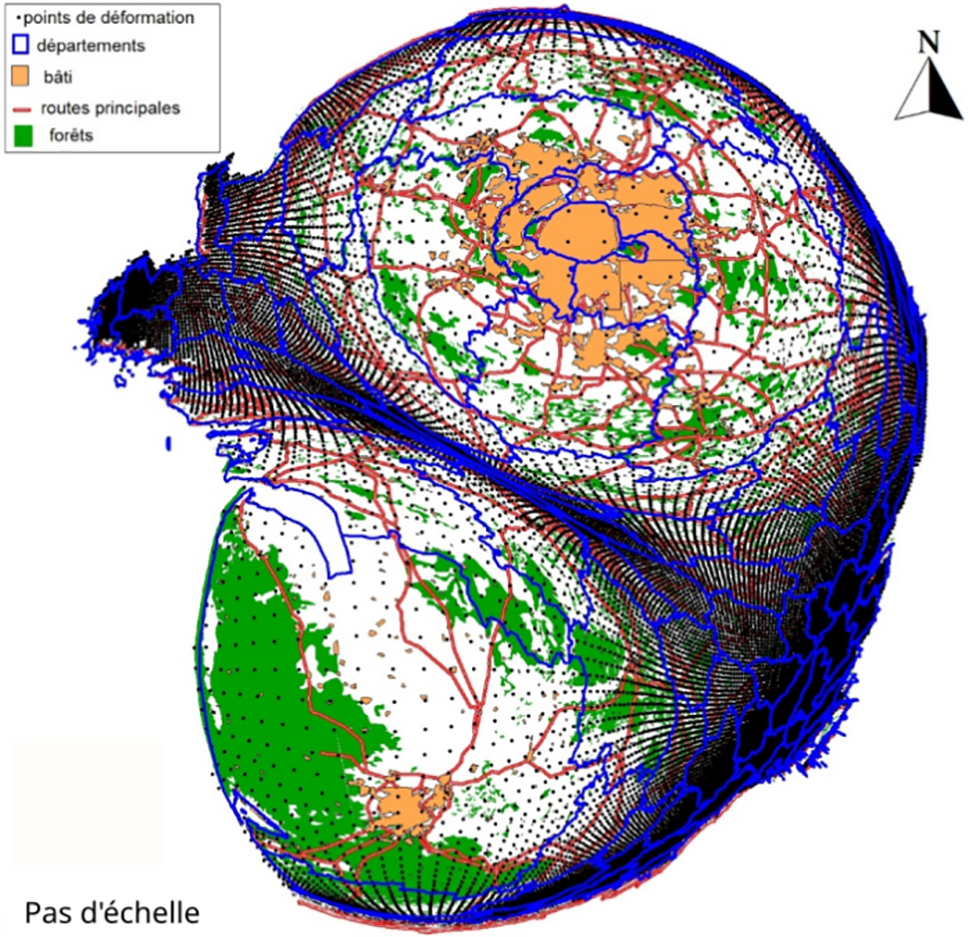
Figure 4: Représentation de « l’effet tunnel » entre Paris et Bordeaux
Un individu localisé à Paris déforme mentalement l’espace mais on peut imaginer qu’il perçoit également la ville de Bordeaux tout en déformant aussi l’espace. Le résultat est une carte en deux hémisphères : Paris et Bordeaux et un espace aplati entre les deux villes.
Voyons à présent comment passer de l’individu à l’échelle collective, la ville.
Pour que l’opération soit réalisable, il est nécessaire de sommer les individus, de les rassembler en groupe.
Prenons d’abord comme hypothèse que la ville est de centre O et de rayon x. Alors, il devient possible de projeter la densité de population sur un segment radial pour retrouver une courbe indiquant la densité de population en fonction de la distance au centre x (voir Fig. 5).
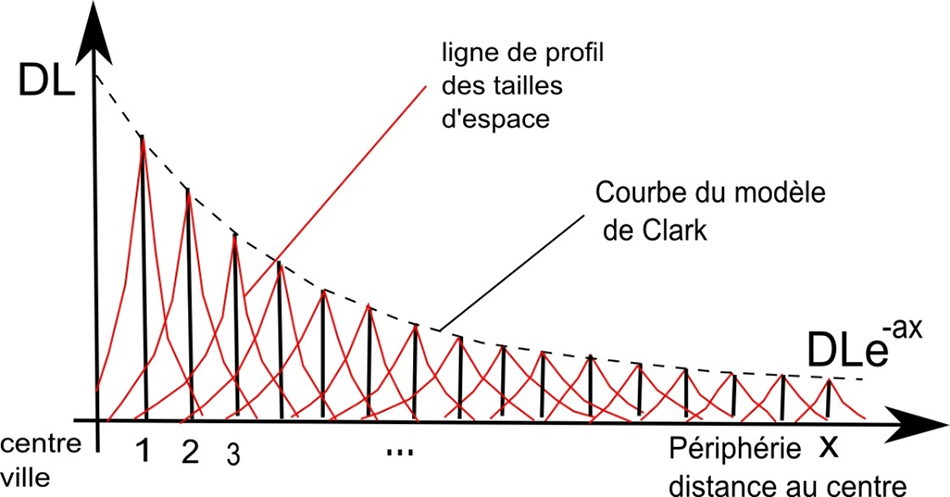
Figure 5: Tailles d’espace et modèle de Clark
S’il existe de nombreuses lois pour mettre en relation la distance avec la densité dans les villes, la plus courante reste celle du modèle dit de Clark (1951) (Mills 1970) [13,14].
Avec D(x) densité de population à une distance x du centre, D, densité extrapolée au centre et α, gradient de densité.
Les tailles d’espace représentent les valeurs de l’unité de distance du collectif pour une distance donnée du centre-ville.
Pour chaque couronne de distance x, soit à chaque unité de distance, on somme le nombre d’individus.
Ainsi, le groupe d’individus à une distance x du centre est par nature :
Il est à noter que cette simplification est une des seules possibles pour pouvoir combiner le collectif avec la taille d’espace individuelle, elle-même radiale. Par ailleurs, la solution du modèle de Clark est largement déployée dans la littérature économique pour analyser les formes urbaines. En cela, la ville est simplifiée mais représentative dans sa morphologie. D’autres options non formelles n’offriraient pas la possibilité d’aller vers une modélisation de la forme urbaine. Quant au choix du modèle de Clark au regard d’autres solutions plus complexes comme le modèle à cratère de densité de Newling [15], nous le justifions par l’usage du modèle de Clark étendue (en version polynucléaire) pour les villes polycentriques qui forment aujourd’hui les types urbains les plus courants dans le monde.
Pour poursuivre notre démonstration, pour chaque couronne, il existe une taille d’espace décroissante de la distance au centre qui décroit ensuite à la distance x−1 et x+1 selon Lr.
En somme, si l’on désire obtenir la somme des métriques pour une distance x, il faut sommer toutes les métriques des autre distance x + ou −i.
Soit :
On obtient alors :
Ainsi S représente la taille d’espace décroissante d’un groupe d’individus pour une distance x du centre de la ville.
Comme dans l’annexe I, il est possible de trouver ensuite la distance dite égocentrée ou proxémique séparant le centre-ville à la distance physique x du centre.
Pour cela il faut sommer toutes les tailles d’espace du centre de la ville vers la périphérie. L’opération est plus complexe que précédemment.
On obtient avec sommes des termes d’une suite géométrique :
On retiendra alors, en simplifiant par A = DL/(1 − r)
De ce fait, ce groupe est représentatif du collectif, l’échelle urbaine, la courbe résultante l’est donc aussi.
La représentation graphique de cette fonction urbaine synthèse est alors :
On observera, dans la Fig. 6, que le profil de la distance proxémique urbaine est sensiblement différent de l’échelle individuelle pour la partie centrale. En effet, ce profil tend vers une asymptote en moins l’infini, ce qui n’était pas le cas pour la courbe dite « individu ». Par ailleurs, l’expression mathématique (2) n’est plus aussi triviale que le modèle initial même si l’on retrouve certains éléments.
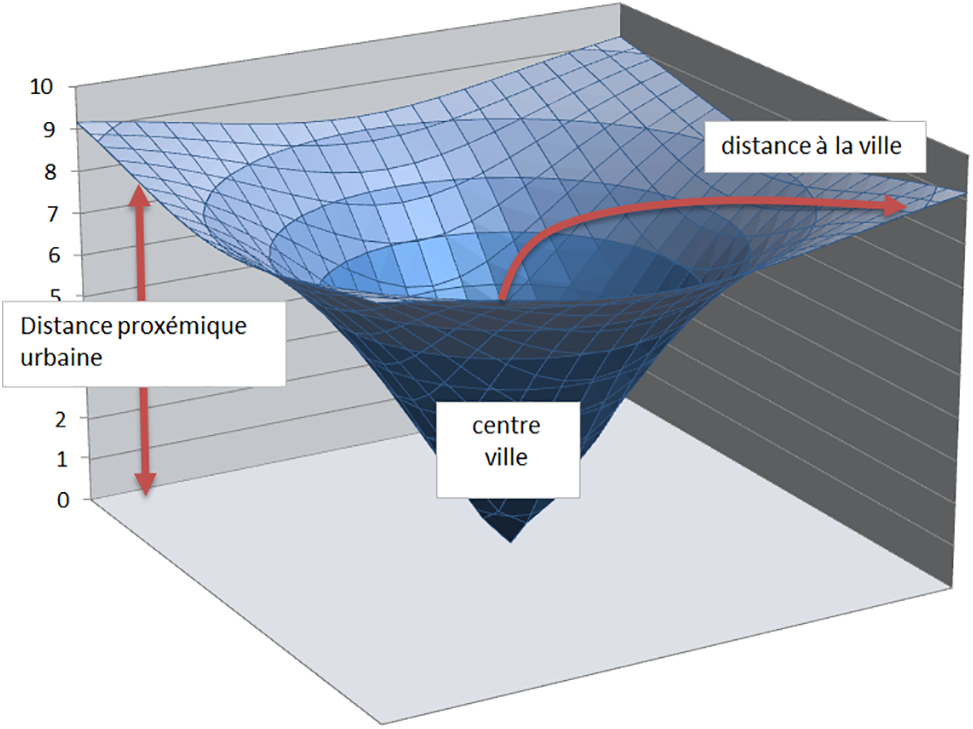
Figure 6: Représentation graphique de la fonction de distance égocentrée urbaine
La signification d’une telle fonction est alors la suivante :
La distance proxémique au centre de la ville augmente plus que linéairement dans la partie centrale de la ville (un espace euclidien donnerait une ligne droite centre périphérie). Cela a pour conséquence que le riverain perçoit l’espace urbain central comme plus grand, mieux connu, mieux appréhendé que la périphérie.
Plus on s’éloigne, plus le gradient de perception décroit, cela signifie que l’habitant dispose d’une connaissance de moins en moins précise de son espace à mesure que l’on s’éloigne de la ville. Au bout d’un moment, sa connaissance du territoire n’évolue plus et il perçoit de la même manière un territoire périurbain de frange que l’infini. Sa représentation du lieu est alors floue.
Suivant ce principe, on peut imaginer que la structure du territoire repose pour partie sur cette géométrie, ce qui nous conduit à envisager une application directe de cette métrique : substituer la distance physique conventionnelle par le modèle (2) dans les profils de densité ville campagne (voir encadré).
1.2.1 Encadré : caler les paramètres dans le modèle (6) ou tenter de s’affranchir de la frontière ville campagne
La quasi-totalité des auteurs des études sur les relations ville campagne plaident en la faveur d’une rupture entre l’agglomération et le périurbain. Cette rupture est clairement marquée au sol avec une morphologie qui évolue à mesure que l’on s’éloigne de la ville. Certains auteurs notent toutefois la possibilité d’un continuum urbain rural (David 1985) [16]. Ce papier explore une possibilité de faire apparaitre ce phénomène par l’intermédiaire de la distance égocentrée. Il faut voir ce type d’analyse comme une application directe de la théorie proxémique. En cela, l’espace urbain et périurbain n’est-il en réalité pas proxémique dans ses métriques sous-jacentes.
Pour ce faire, réalisons les moyennes de densité de population par couronnes autour d’une ville (exemple de l’aire urbaine de Dijon) et appliquons le modèle de Clark (voir Enault 2003) [17]. On voit apparaitre une rupture dans le modèle à 7 km du centre. On a donc deux fonctions discontinues de densité (ici les logarithmes de densité voir Fig. 7). A présent, si l’on substitue la distance euclidienne par la distance proxémique (2) dans le modèle de Clark, on peut ajuster l’urbain et le périurbain par une courbe continue bleue. Le paramètre r peut être trouvé ainsi en fixant D et α. Le coefficient résultant calculé de la courbe est de 0,8891, bien plus que la moyenne des deux coefficients de détermination urbain et périurbain Le calcul du coefficient de la courbe reste inchangé.
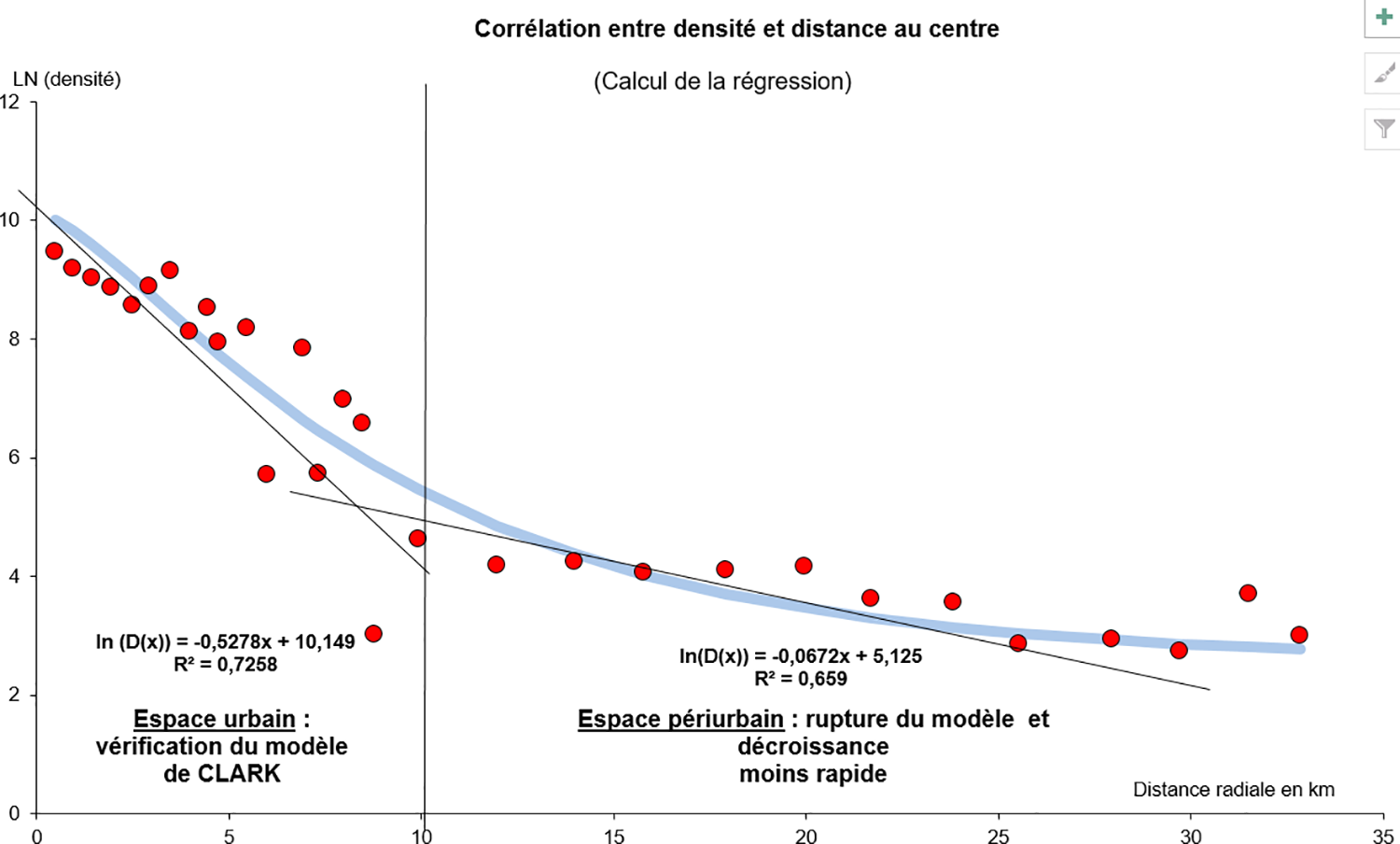
Figure 7: Continuum ou rupture ville campagne dans l’aire urbaine dijonnaise
1.3 La déformation cartographique égocentrée à l’échelle d’une ville
La question de la déformation urbaine découle directement de la notion de perception de l’espace pour un ou des groupe(s) d’individus. En effet, passer de l’échelle d’un individu (avec la loi d’airain (annexe I)) à celle d’une ville implique des opérations de regroupement. Cela suppose également une certaine forme conforme de ville.
La ville est-elle monocentrique5 ou polycentrique6 ? En fonction du cas, la résolution du problème géométrique est différente.
Commençons par le cas le plus évident (la ville monocentrique). On considère alors que la ville comporte un unique CBD et que les densités de population décroissent à partir de la distance au centre selon une fonction exponentielle ; le cas le plus évident étant le modèle dit de Clark [13].
On considère alors que pour chaque couronne, il existe un nombre d’individus défini par le modèle de Clark qui dispose tous d’une même loi d’airain. Or chaque couronne dispose de cette même loi d’airain. En conséquence pour savoir quelle est la perception globale du groupe à une distance x du centre, il faut sommer toutes les distances des lois d’airain des autres couronnes. On obtient une somme de taille d’espace de groupe d’individus. Il faut donc ensuite traduire cela en distance proxémique. On obtient alors une équation (2) qui permet d’exprimer la distance proxémique urbaine en fonction de la distance physique au centre de la ville, du gradient de densité, de la densité extrapolée au centre et du facteur de réduction r.
Pour enfin pouvoir déformer les cartographies, on utilise la méthodologie exposée dans l’annexe II. Cette dernière se base sur un calcul de géométrie analytique qui transforme l’ensemble des points de la carte en des points images selon une pseudo-homothétie.
L’application de ces opérations pour un modèle de Clark ajusté à partir des densités de population par ilots de 1999 est la suivante :
La cartographie initiale de l’agglomération de Dijon se déforme à partir du point central (le centre-ville) pour laisser apparaitre des espaces dont les métriques sont conformes à la carte source vers le centre et totalement aplaties vers les périphéries (voir Fig. 8). De fait, la carte se transforme en « boule » calquée sur les densités de population modélisées par le modèle de Clark.
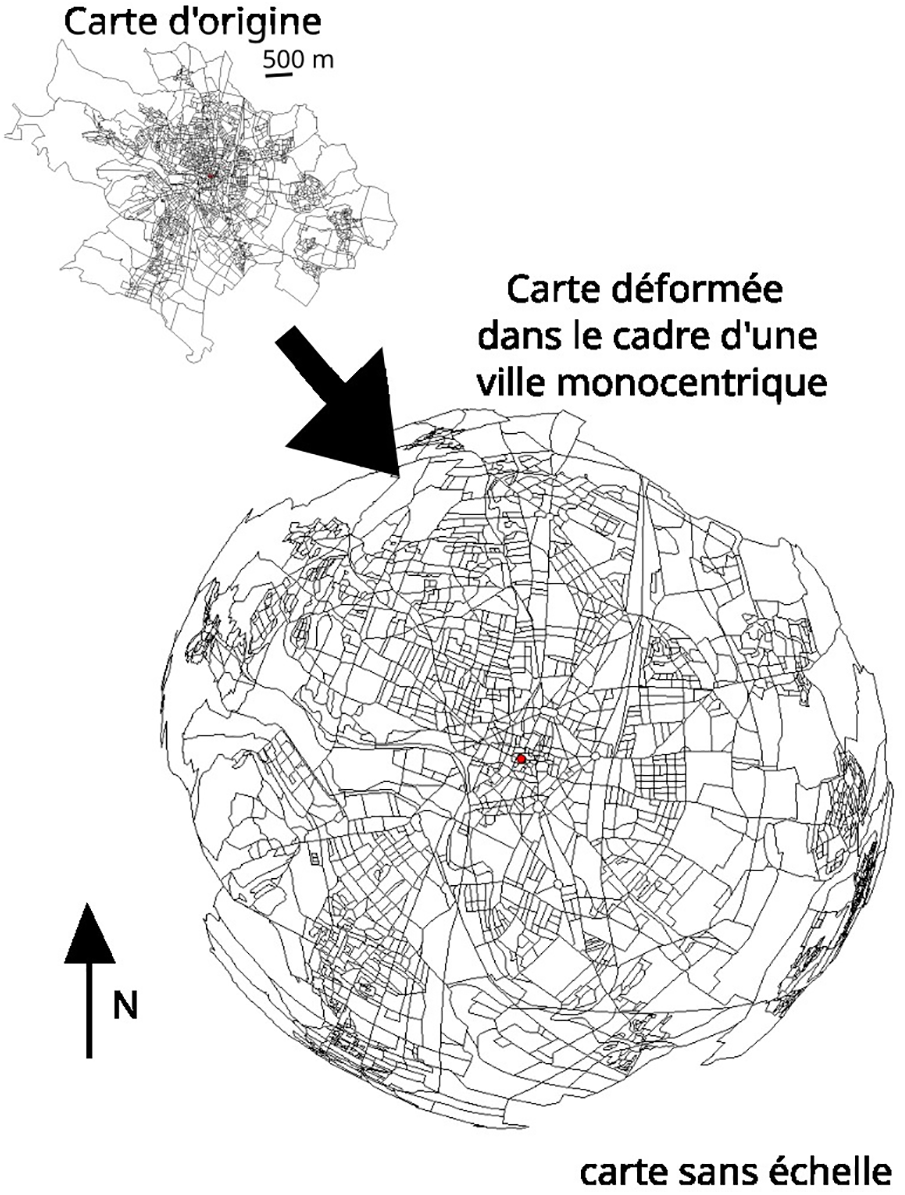
Figure 8: Déformation de la carte des îlots 1999 de la communauté d’agglomération dijonnaise à partir du centre-ville
Imaginons à présent les villes plus complexes (les villes polycentriques) [19,20]. On utilise à la base le même principe mathématique de regroupement pour former la distance proxémique à la différence près que l’on considère l’existence d’une infinité de centre. Par conséquent, on doit au préalable définir le modèle de densité polycentrique. Nous prendrons la loi suivante qui est aussi la plus courante (Anas et al., 1998) [21].
ou Di(xi) est la densité en un lieu i de la carte, xi la distance à un centre i, Di la densité extrapolée au centre i et α le gradient de densité au centre i.
Nous avons alors pris une couronne de 3 km pour le centre-ville et de 2 km pour les autres centres afin d’ajuster notre modèle de densité. Nous obtenons la Fig. 9.
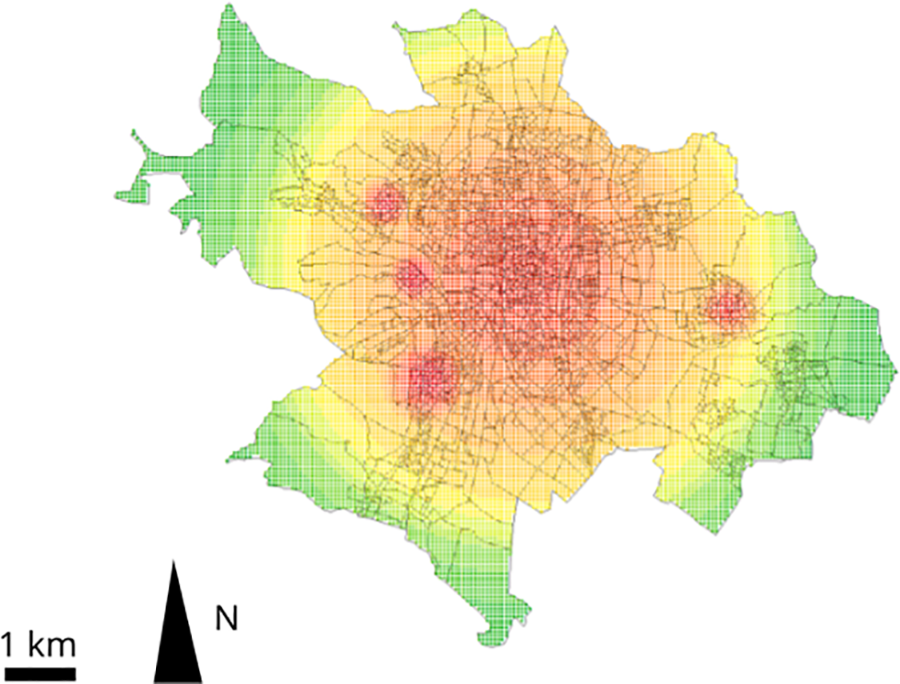
Figure 9: Modèle de densité polycentrique ajusté à l’agglomération de Dijon (5 centres)
A partir de cette configuration de densité, on obtient la carte « multidéformée » suivante (voir Fig. 10).
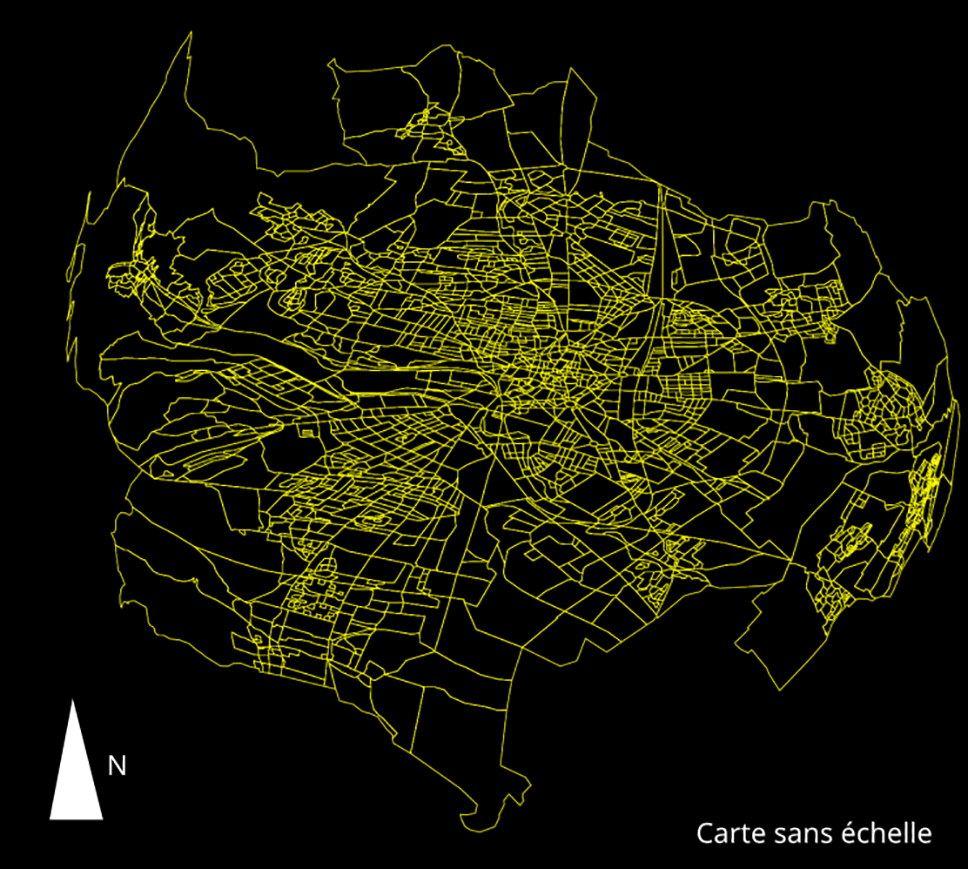
Figure 10: Déformation de la carte des îlots 1999 de la communauté d’agglomération dijonnaise à partir de 5 centres
Suivant le modèle de densité à 5 centres, on aboutit à une carte déformée où le centre-ville et ses proches périphéries conservent une métrique quasi normale. Certaines périphéries comme Fontaine d’Ouche ou Chenôve sont légèrement « grossies ». A contrario, les espaces les plus lointains sont quasiment absents de la carte.
Encore relativement confidentielle dans les travaux de géographes, la théorie égocentrée est souvent traitée d’un point de vue qualitatif. Disposant d’un socle solide à l’échelle de l’individu, on envisage assez facilement que l’usage d’une telle approche soit plus orientée vers l’éthologie ou la psychologie (micro-psychologie).
Néanmoins A. Moles, reste, en la matière, un passeur pour cette théorie vers la Géographie.
En nous appuyant sur ses travaux, nous avons proposé un cadre technique pour la théorie égocentrée. Cette visée plus pragmatique que Moles nous a permis de proposer tout un corpus de « lois » applicables à l’échelle de l’individu.
Un des intérêts pourrait être alors la déformation de cartes géographiques comme nous l’avons proposé ici. Ces nouvelles visualisations apportent un éclairage différent sur la ville et la manière dont cette dernière est perçue par un groupe d’individus.
In fine, l’approche décrite ne représente qu’une petite partie des applications possibles de la théorie égocentrée. On peut envisager la distance proxémique comme alimentant des modèles spatiaux, ce qui implique de très nombreuses autres applications. L’application dans le modèle de Clark, nous en a donné un bref aperçu.
Si l’on se réfère aux travaux de R. Hong and al.7 [22], une des applications possibles pourrait être l’utilisation de ces nouvelles cartes déformées pour remplacer les cartes réelles et ainsi permettre une meilleure évaluation de métriques par les utilisateurs. Par exemple, en offrant un regard des espaces perçus, l’utilisateur pourrait voir instantanément les lieux contractés qu’il ne connait pas et donc les explorer en priorité. On pense en particulier à une application pour les jeux vidéos.
2.1 Annexe I : loi d’airain de la proxémique (voir Fig. 11)
Nous proposons de modéliser cette loi par la formule suivante :
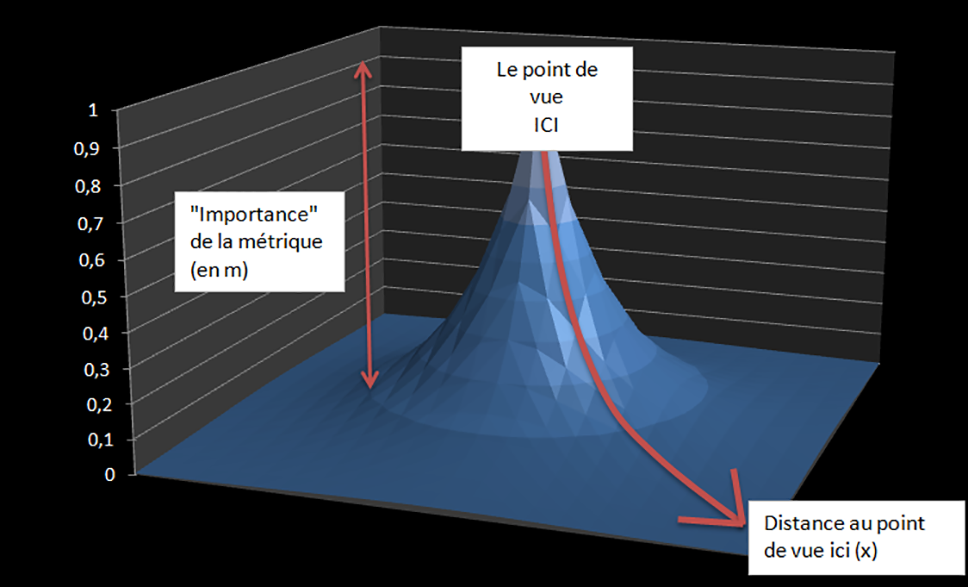
Figure 11: Représentation 3D de la loi d’airain de la proxémique
Avec L(x) taille d’un espace ou métrique du mètre physique, L le mètre physique, r un facteur de réduction et x distance physique au point de vue Ici donc à l’individu.
Ainsi dans la théorie de A. Moles, les tailles d’espace décroissent de l’individu vers ce que l’auteur nomme « le vaste monde ». En l’état, cette « loi » est peu opérationnelle.
Pour que « la loi » soit pleinement géographique, il est nécessaire de raisonner sur la notion de distance et donc de définir la distance dite proxémique.
On passe alors à l’étape suivante, celle du calcul aboutissant à une forme mathématique éloignée des travaux d’A. Moles.
Dans la version de la loi d’airain, un mètre proche du point de vue ici est différent d’un mètre loin du point de vue ici.
Dans ces conditions, la distance séparant le point de vue ici et l’infini peut être calculée ; elle est égale à la somme des mètres de la loi d’airain soit :
Cette somme est une somme remarquable de terme d’une suite géométrique. Elle peut donc être calculée de la manière suivante :
Avec X(x) distance proxémique au point de vue ici, L le mètre physique, r un facteur de réduction et x distance physique au point de vue Ici.
La distance proxémique X(x) au point de vue Ici est aussi la distance perçue au point de vue Ici.
Cette dernière, contrairement à une distance euclidienne, augmente plus rapidement jusqu’à un point donné puis tend vers une valeur fixe qui vaut :
Ainsi l’espace proxémique est lui-même centré sur le point de vue Ici. La perception de la distance proxémique est quasi-uniforme égale à notre constante (6) à l’exception des lieux proches au point de vue Ici. Il existe alors un gradient dans les perceptions passant de (6) à 0.
Ainsi, la distance proxémique se différencie de la distance physique par la constante L/(1 − r). Dans le cas de l’euclidien, on s’éloigne d’un mètre de l’individu et la distance est bien de 1.
A l’infini, la distance physique croit selon une droite. Dans le cas de la proxémique, la croissance de la distance est, au départ, plus importante et ensuite tend à se limiter. A l’infini, la distance tend vers la constante (6). Il y a donc une saturation de cette distance proxémique.
2.2 Annexe II : méthodologie de déformations des cartes a partir des points de vue ici
Notons O le centre du repère et x et y respectivement les coordonnées Lambert en latitude et en longitude. (à noter qu’est ici représenté un espace très petit pour lequel le repère fonctionne comme du cartésien, pour les grandes distances, le principe que nous proposons par la suite fonctionne également mais les distances sont courbes).
On note A, le point central à partir duquel, on veut déformer la carte (Le point de vue Ici), M un point de l’espace et M’ son image dans la transformation cartographique. Les coordonnées cartésiennes dans le système Lambert sont respectivement xA, yA, xO, yO, xM, yM et xM′, yM′.
Par construction (voir Fig. 12)
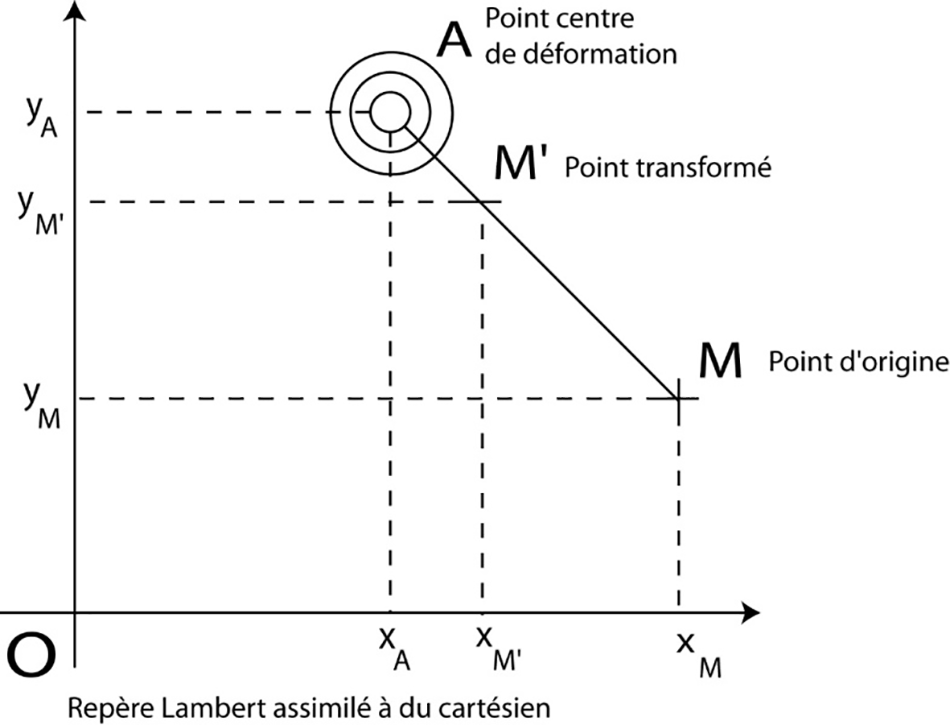
Figure 12: Transformation de coordonnées cartésiennes par le point A Réalisation
On en déduit donc que
On introduit alors le point O pour obtenir les coordonnées de l’image M’ (changement de repère) soit
D’où
On en déduit alors que
Par définition, la distance transformée de AM est AM’ et cette dernière se calcule selon la formule [2] de la seconde partie d’où
On obtient ainsi pour tout point M (xM, yM) de l’espace, les coordonnées xM’ et yM’ après transformation. Dans le cas, d’une transformation à partir d’un point A, on utilise le système [5]. Dans le cas, d’une déformation multicentrique, on procède à une définition moyennée soit la mise en place d’un barycentre à partir des coordonnées définies en [5]. Cela se traduit par une moyenne des coordonnées xM’ et yM’. Notons que les distances AM sont facilement calculables dans le SIG.
Remerciements/Acknowledgement: Les auteurs tiennent à exprimer leur profonde gratitude envers tous ceux qui les ont soutenus et encouragés tout au long de ce travail de recherche.
Financements/Funding Statement: Les auteurs n’ont reçu aucun financement spécifique pour cette étude.
Contributions des auteurs/Author Contributions: conception de l’étude : C.Enault ; collecte des données : C.Enault ; analyse et interprétation des résultats : C.Enault ; préparation du projet de manuscrit : C.Enault. Tous les auteurs ont examiné les résultats et approuvé la version finale du manuscrit.
Disponibilité des données et du matériel/Availability of Data and Materials: Les principales données sont issues de data.gouv.fr et de l’INSEE.
Conflits d’intérêt/Conflicts of Interest: Les auteurs déclarent qu’ils n’ont pas de conflits d’intérêts à signaler en ce qui concerne la présente étude.
1Dans ce nouvel article, les auteurs proposent une représentation de l’espace basée sur des cônes qui se touchent, ayant pour sommet une ville (pour représenter l’espace terrestre). On calcule alors le rapport entre la distance aérienne entre les villes et la distance sur les faces de ces cônes. Cet assemblage donne une représentation de la distance temps et donc produit une carte déformée de l’espace en 3 dimensions.
2Le disque de Poincaré représente un monde imaginaire dont les grandeurs se réduisent du centre du disque vers la périphérie pour tendre vers un infiniment petit au bord du disque. Cette construction purement mathématique a donné lieu à toute une géométrie dite hyperbolique. Nous verrons dans la suite de notre propos que cette construction qui peut paraitre éloignée de la Géographie ressemble à la géométrie de la proxémique.
3Contrairement à l’espace égocentré, le territoire est essentiellement réel et visuel, il est habité, transformé et partagé. Cela signifie qu’il est fondamentalement humanisé, ce qui suppose qu’il résulte du travail de l’homme comme le suggère C.Raffestin.
A contrario, l’espace égocentré est un espace relevant de l’immatériel et du travail de l’esprit à partir de la perception du réel. Il apporte un éclairage sur le psychisme humain et la manière dont nous percevons globalement notre environnement. Il procède essentiellement par l’appui de notre corps comme unique référence et par les distances qui nous éloignent des objets que nous percevons.
Quand le territoire laisse apparaître l’œuvre de l’action humaine, l’espace égocentré montre la manière dont ce territoire est perçu par l’esprit.
4Par métrique il faut entendre la définition géographique qui désigne la mesure de la distance entre les unités spatiales. « Cette mesure conventionnelle de la distance, le plus souvent comptée en mètres ou en kilomètres, n’est pas la seule possible. Depuis une trentaine d’années, d’autres systèmes ont peu à peu émergé comme la distance-temps et la distance-coût. De même, les anamorphoses, ou encore les cartes mentales, utilisent d’autres métriques que la classique mesure euclidienne » tiré de l’article métrique de Géoconfluence. (suivre le lien : http://geoconfluences.ens-lyon.fr/glossaire/metrique). A noter que A.l’Hostis (2014) détaille largement cette notion de métrique en s’appuyant autant sur les distances temps que d’autres types de distance [10,11].
Cette notion de métrique n’est pas à confondre avec la notion de taille d’espace qui désigne la valeur infinitésimale d’une unité de mesure métrique, cela correspond plus à la définition mathématique du terme métrique.
5Une ville définie au sens de la nouvelle économie urbaine (NEU), c’est-à-dire la ville monocentrique, circulaire, de centre O et de rayon x disposant de rentes d’enchère des terrains décroissantes de la distance au centre. Le fondateur de cette NEU est Alonso [18].
6Ville définie par l’économie géographique, c’est-à-dire polycentrique, vue comme une généralisation de la ville de la NEU. Elle dispose d’une infinité de centres urbains ainsi que de courbe d’enchère multiples en équilibre en fonction des différents centres.
7Dans le cas de cette article, l’utilisation de ces cartes déformées par les distances temps (cartogramme DC) a été testée sur un panel de 20 personnes. 50% des utilisateurs avouaient avoir privilégié ces cartogrammes pour évaluer les distances pour se déplacer.
References
1. L’Hostis A, Abdou F. What is the shape of geographical time-space? A three-dimensional model made of curves and cones. ISPRS Int J Geo-Inf. 2021;10(5):340–57. doi: 10.3390/ijgi10050340. [Google Scholar] [CrossRef]
2. Kaiser C, Walsh F, Farmer QCJ, Pozdnoukhov A. User-centric time-distance representation of road networks. In: International Conference on Geographic Information Science, 2010; Zurich, Switzerland, Berlin, Heidelberg, Springer-Verlag; p. 85–99. 10.1007/978-3-642-15300-6_7. [Google Scholar] [CrossRef]
3. Spiekermann K, Wegener M. The shrinking continent: new time-space maps of Europe. Environ Plann B.: Plann Design. 1994;21(6):653–73. doi:10.1068/b210653. [Google Scholar] [CrossRef]
4. Bahoken F, Lambert N. Le cartogramme par points. Cybergeo: European J Geogr. Available from: https://neocarto.hypotheses.org/20094. [Accessed 2024]. [Google Scholar]
5. Bronner AC. Cartogrammes, anamorphoses : des territoires transformés. In: Cunty C, Mathian H, editors. Traitements et cartographie de l’information géographique. France: ISTE Sciences, Géographie et Démographie/cartographie; 2020. p. 231–71. [Google Scholar]
6. Moles A, Rohmer E. Psychosociologie de l’espace. L’Information Géographique. 2000;64(2):191. [Google Scholar]
7. Tuan YF. Space and place: The perspective of experience. Minneapolis: U of Minnesota Press; 1977. [Google Scholar]
8. Casti E. Le tournant proxémique : de la représentation à la spatialité cartographique. Available from: http://www.espacestemps.net/articles/le-tournant-proxemique-de-la-representation-a-la-patialite-cartographique/. [Accessed 2024]. [Google Scholar]
9. Hall ET. La dimension cachée. Fait partie d’un numéro thématique. 1971;13(1–2):258–60. Available from: https://www.persee.fr/issue/hom_0439-4216_1973_num_13_1?sectionId=hom_0439-4216_1973_num_13_1_367350. [Accessed 2024]. [Google Scholar]
10. Kloeckner BR, L’Hostis A, Richard T. Contextual metrics a mathematical definition for a comprehensive approach of geographical distances. Geogr Anal. 2020;53(1):736–66. doi: 10.1111/gean.12260. [Google Scholar] [CrossRef]
11. L’Hostis A. Le Détour, La Pause et l’optimalité, Essai Sur La Distance et Ses Apports Au Transport et à l’urbanisme, Habilitation à diriger des recherches. Université de Paris Marne la Vallée: France; 2014. [Google Scholar]
12. Schwach V. Phénoménologie et proxémique La méthode d’Abraham Moles. Bull Micropsychol. 1993;24. [Google Scholar]
13. Clark C. Urban population densities. J R Stat Soc Series A. 1951;114(4):490–6. [Google Scholar]
14. Mills ES. Urban density functions. Urban Stud. 1970;7(1):5–20. doi: 10.1080/00420987020080011. [Accessed 2024]. [Google Scholar] [CrossRef]
15. Newling BE. The spatial variation of urban population densities. Geogr Rev. 1969;59(2):242–52. doi: 10.2307/213456. [Google Scholar] [CrossRef]
16. David J. Les périphéries urbaines : nouvel espace ou discours ? Acte de colloque Angers, géographie sociale. 1985;259–62. [Google Scholar]
17. Enault C. Vitesse, accessibilité et étalement urbain, analyse et application à l’aire urbaine dijonnaise (Thèse de doctorat). Université de Bourgogne: France; 2003. [Google Scholar]
18. Alonso W. Location and land use: toward a general theory of land rent. Cambridge, MA and London, England: Harvard University Press; 1964. doi: 10.4159/harvard.9780674730854. [Google Scholar] [CrossRef]
19. Baumont C. Analyse des espaces urbains multicentriques : la localisation résidentielle. Centre national de la recherche scientifique, Université de Bourgogne: France; 1993. [Google Scholar]
20. Garreau J. Edge city: life on the new frontier. New York, Doubleday, United States: AnchorBooks; 1991. [Google Scholar]
21. Anas A, Arnott R, Small KA. Urban Spatial Structure. J Econ Lit. 1998;36(3):1426–64. [Google Scholar]
22. Hong S (RayYoo MJ, Chinh B, Han A, Battersby S, Kim J. To distort or not to distort: distance cartograms in the wild. In: Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, 2018 Apr; Montreal QC, Canada, USA: Association for Computing Machinery; p. 1–12. doi: 10.1145/3173574.3174202. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools