1  Introduction

L'analyse hydro-morphométrique, qui constitue la première étape de la compréhension des bassins versants, permet de décrire les principaux facteurs naturels qui influent sur les processus d'écoulement en surface. Ces facteurs incluent les caractéristiques de relief, de morphologie, de lithologie, de climat et de biogéographie. L'interaction entre ces facteurs est cruciale pour comprendre le comportement hydrologique des bassins (Baba-Hamed et al. [1]).

Les écoulements dans un bassin versant, qu'ils soient intenses ou moins importants, ont des effets différents. D'une part, ils peuvent contribuer de manière positive à l'alimentation en eau des réserves. D'autre part, lorsqu'ils deviennent excessifs, ils peuvent causer des inondations et des écoulements intenses (Hocine et al. [2]). Le long du réseau hydrographique, l'intensité des écoulements varie considérablement de l'amont vers l'aval, selon la configuration topographique de chaque zone.

L’impact des indices géomorphologiques sur le transfert des volumes d’eau jusqu’à l’exutoire d’un bassin versant a été examiné par plusieurs auteurs, notamment (Rodriguez-Iturbe et al. et al. [3], Gupta et al. [4], Ambroise [5]. L’estimation du ruissellement pour un bassin versant non jaugé peut être réalisée à l’aide de modèles géomorphologiques d’hydrogrammes, comme étudié par White et al. [6], Kumar et al. [7], Singh et al. [8]. Dans le but de prédire les pics de crue, les études de Bhadra et al. [9], Lee et al. [10], Moussa [11]) ont été axées sur l’analyse quantitative des réseaux hydrographiques pour examiner l’incidence de leur structure et de leurs caractéristiques physiques (longueur, pente, largeur, microtopographie) sur la forme des hydrogrammes mesurés à la sortie des bassins étudiés.

Le bassin versant est considéré comme un ensemble complexe d'unités fonctionnelles spécifiques, dont les échanges sont régis par des caractéristiques hydro-géomorphologiques locales (Maréchal et al. [12]). L'analyse seule de l'hydrogramme à l'exutoire ne suffit pas à expliquer la variabilité des réponses hydrologiques à l'intérieur du bassin, en particulier pour les bassins soumis à des précipitations particulièrement intenses.

Pour mesurer l'influence de la morphologie sur la dynamique de la réponse hydrologique à chaque point de l'espace, Douvinet et al. [13] ont proposé des indices morphométriques basés sur la simulation théorique des écoulements. En général, l'approche morphométrique appliquée à un bassin versant permet une description quantitative de sa géométrie ainsi que des caractéristiques du réseau de drainage. Cette approche repose sur des techniques quantitatives qui sont utiles pour comprendre le drainage et hiérarchiser les bassins versants en termes de fonctionnement hydrologique (Idrissi [14]).

Contrairement à la revue de littérature existante, dans cet article nous analysons l'influence des paramètres hydro-morphométriques sur l'écoulement des eaux dans les sous-bassins versants de la Tshopo. L'accent est mis sur la compréhension des interactions entre ces paramètres et leur impact sur la vitesse d'écoulement des eaux de surface. En effet, le bassin versant de la rivière Tshopo est sujet à plusieurs risques naturels, tels que l'érosion hydrique des formations meubles de la cuvette centrale et les inondations catastrophiques qui menacent la ville de Kisangani.

Situé dans une région équatoriale où les précipitations sont fréquentes tout au long de l'année, ce bassin versant est confronté à de fortes crues causées par des pluies diluviennes. Ces crues entraînent souvent des débordements de la rivière et des inondations dans de nombreux quartiers de Kisangani et dans les villages riverains. Cependant, peu d'études scientifiques ont été réalisées pour évaluer ces risques qui menacent la ville de Kisangani. Jusqu'à présent, les paramètres hydro-morphométriques les plus caractéristiques qui influencent l'écoulement des eaux dans le bassin versant de la Tshopo n'ont pas encore été déterminés.

L'objectif de cet article est de parvenir à identifier les paramètres qui ont une influence significative sur la vitesse d'écoulement des eaux et de regrouper les sous-bassins versants présentant des similarités physiques. Cette étude aborde deux points, à savoir : (1) les relations entre les paramètres hydro-morphométriques et l'écoulement des eaux de surface, et (2) la classification des sous-bassins versants de la Tshopo en fonction de leur similitude.

2  Milieu d’étude, Matériels et Méthodes

2.1 Présentation du Milieu d’étude

Le bassin versant étudié est drainé par la rivière Tshopo dans la partie centre nord-est de la République démocratique du Congo. Il est situé entre les latitudes −0,23°S et 1,24°N et les longitudes 25,12° et 27, 45°E. Il est entouré par le bassin versant de la Maïko au sud, celui de la Lindi au nord et par la vallée du Fleuve Congo au sud-ouest. La Tshopo est cette rivière qui a donné son nom à la province. Sa source se situe dans la province même, en territoire de Bafwasende, et elle se jette dans la Lindi sans jamais sortir non plus de cet espace provincial (Otemikongo et al. [15]).

La situation de la Tshopo sous l’équateur dans une région continentale où les deux saisons de pluies et les deux saisons sèches sont très peu marquées ainsi que la nature de la végétation recouvrant son bassin fait que le débit de cette rivière soit relativement assez constant. Les basses eaux, plus ou moins marquées selon les années, se situent dans les mois de février, mars, et juin, juillet, août. Les hautes eaux sont atteintes fin avril-mai et surtout en octobre, novembre et décembre. L’amplitude maximum de la variation du niveau des eaux est de l’ordre de 4 à 5 m. Le débit annuel moyen de la rivière se situe aux environs de 300 à 450 m3/seconde avec un minimum de 30 m3/seconde et un maximum de 1.100 m3/seconde.

D’après Léonard [16], ce bassin de forme allongée est couvert principalement de forêts ombrophiles guinéo-congolaises. Au total 8 sous-bassins versants ont été délimités sur une superficie d’environ 19.335 km2 (Fig. 1).

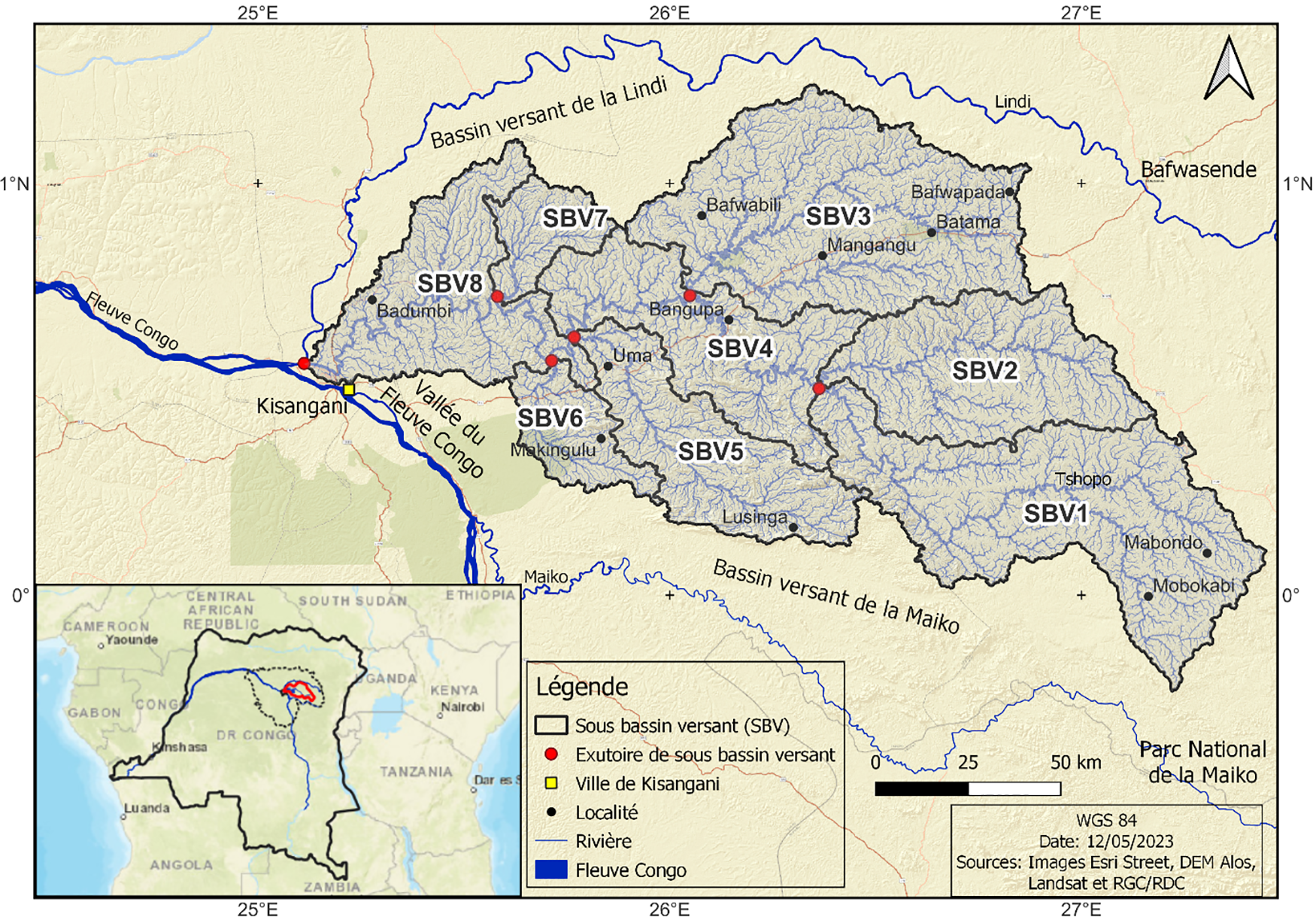
Figure 1: Localisation des sous-bassins versants de la rivière Tshopo

2.2 Données et Matériels

Dans le cadre de cette recherche, nous avons exploité et interprété les données altimétriques (DEM Alos World 3D-30 m), des données OSM (Open Street Map) et les images Google Earth dans le but de cartographier le réseau hydrographique et de délimiter les sous-bassins versants Lasri [17], et par la suite déterminer les différents paramètres géométriques, topographiques et hydrographiques des sous-bassins étudiés. Dans le processus de délimitation des sous-bassins versants de la Tshopo à partir du Modèle Numérique de Terrain (MNT), nous avons considéré conformément à la hiérarchisation de (Strahler [18]), les sous-bassins versants d’ordres (5, 6 et 7) comme étant les plus représentatifs pour les analyses hydro-morphométriques quantitatives, car les petits bassins versants d’ordres (1,2,3 et 4) affichent généralement une distribution spatiale non équilibrée des cours d’eau sur les deux rives de leurs principales rivières.

Les outils SIG (Système d’Information Géographique) ont été utilisés pour traiter et analyser les données altimétriques afin d’élaborer le MNT dérivé du DEM Alos World 3D-30 m et d’effectuer une quantification automatique des caractéristiques hydro-morphométriques des sous-bassins versants de la Tshopo. Plusieurs chercheurs ont utilisé cette technique pour des analyses morphométriques de bassins versants, tels que Manojkumar et al. [19], Prakash et al. [20], Gautam et al. [21]. L’analyse morphométrique à l’aide de MNT et de SIG a été un outil précieux pour étudier les caractéristiques géomorphologiques des bassins versants, comme en témoignent les travaux de Guerbouz et al. [22], Faye et al. [23].

L’approche spatiale multicritère basée sur le SIG pour la caractérisation des micro-bassins versants, telle qu’illustrée par les travaux de Balasubramani et al. [24], Jain et al. [25], Ghosh et al. [26], s’est révélée être un outil précieux pour mieux appréhender la topographie, la répartition des eaux et d’autres aspects importants des bassins versants. Les travaux réalisés par Ganie et al. [27], Ganie et al. [28] ont utilisé les outils SIG pour effectuer une caractérisation hydro-morphométrique et une hiérarchisation des bassins versants. Par ailleurs, Gallo et al. [29] ont employé ces outils pour mettre en évidence l'érosion hydrique à l’échelle d’un bassin versant dans le contexte Sahélien. Enfin, Ganie et al. [30] ont utilisé ces méthodes pour modéliser le bassin fluvial des montagnes en utilisant des approches hydro-morphologiques.

Les logiciels comme Tanagra, Rstudio et Excel ont permis de créer des bases de données, réaliser les analyses statistiques des paramètres étudiés ainsi que la représentation graphique des résultats obtenus.

Les données hydro-morphométriques utilisées pour caractériser les sous-bassins versants de la Tshopo sont représentées dans les Tableaux 1–3.

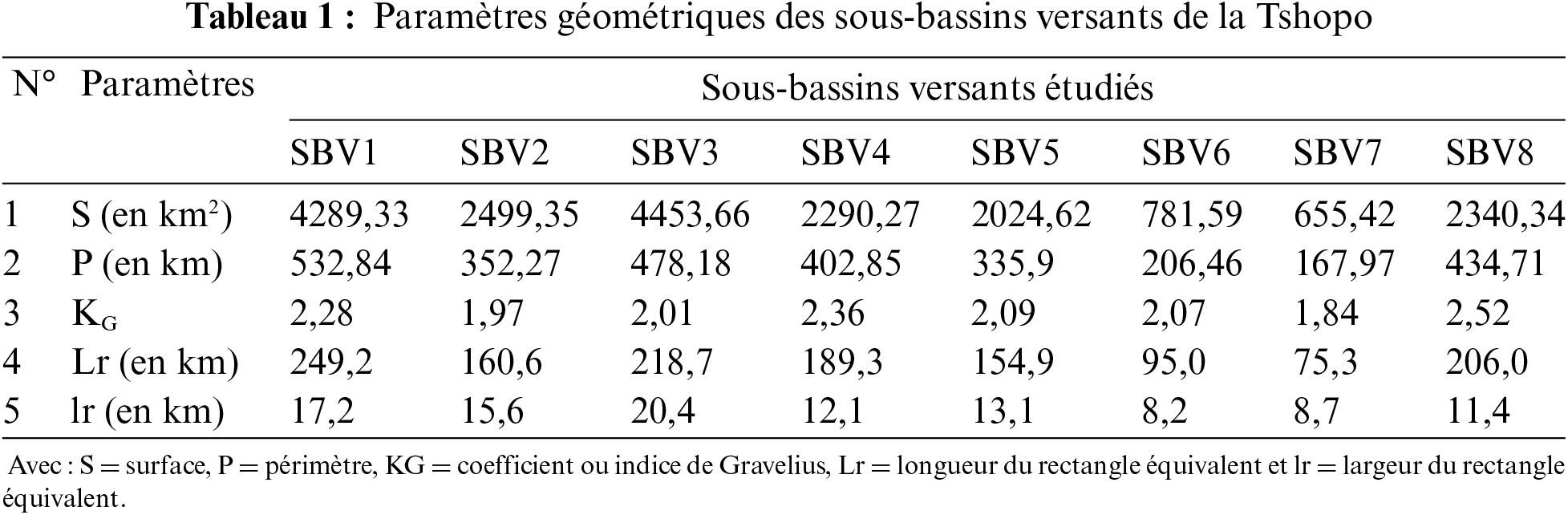
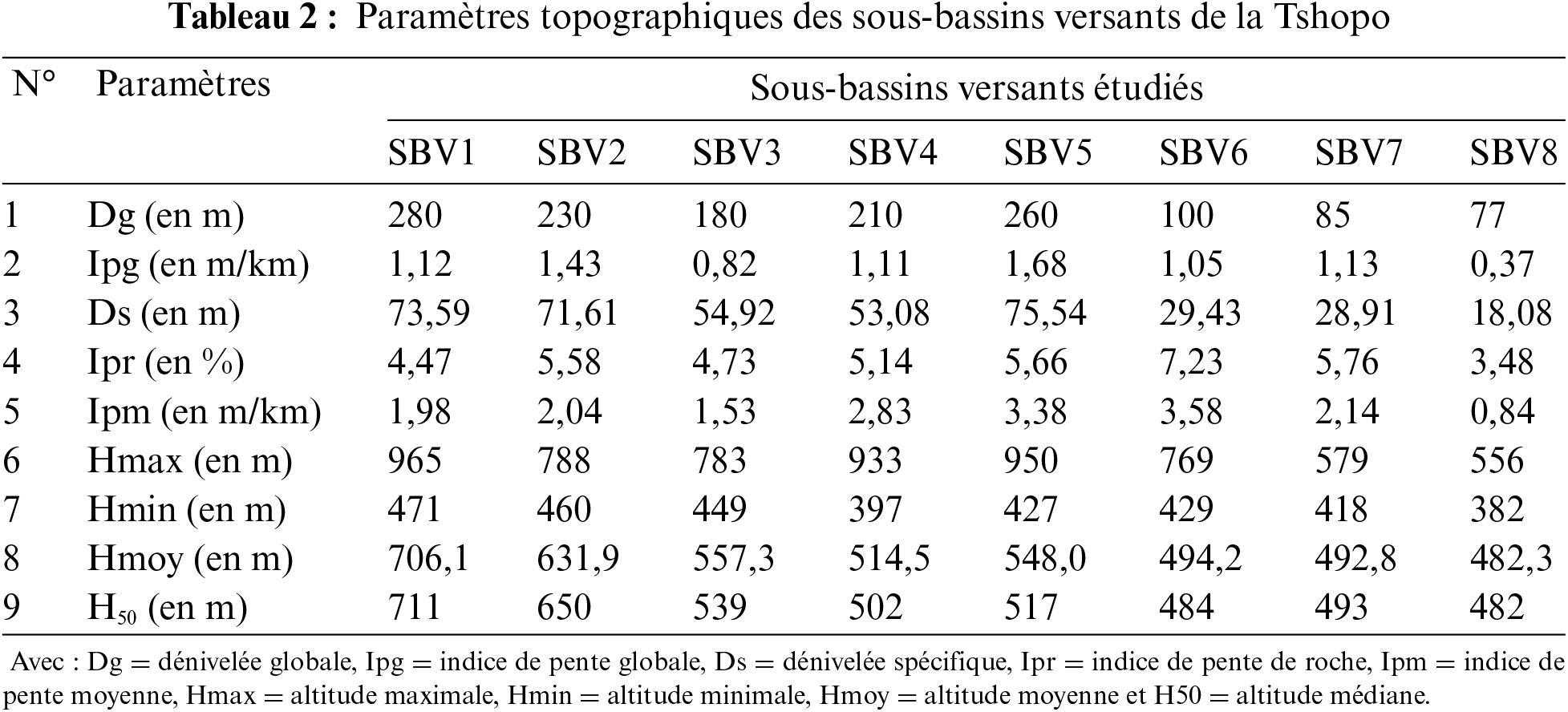
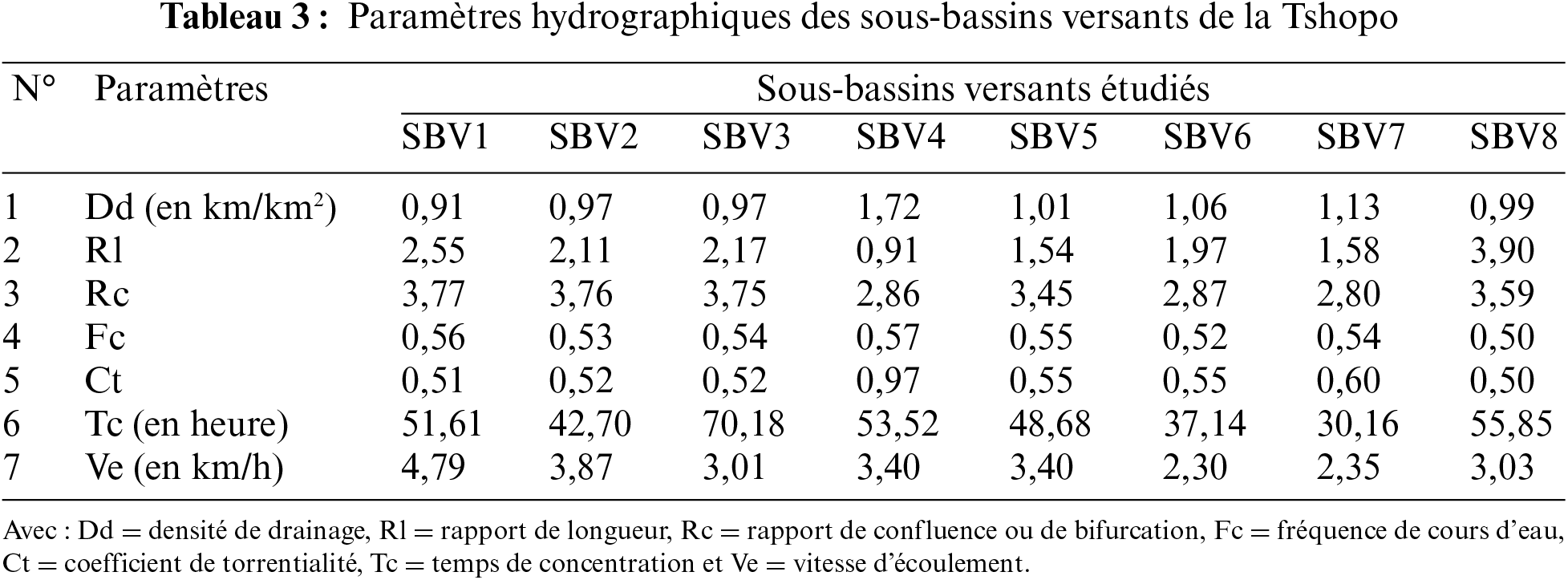
La surface et le périmètre des sous-bassins versants de la Tshopo ont été déterminés automatiquement à l’aide du logiciel QGIS 3.22.13 Berteaux [31]. L’indice de compacité de Gravelius KG Roche [32] est appelé également coefficient de forme du bassin versant Strahler [33]. Il est défini comme le rapport du périmètre du bassin versant au périmètre d’un cercle de même superficie. Cet indice a été calculé par la formule (1) (Bentoumi et al. [34], Bourafa et al. [35]) :

KG=P2π⋅S=0,28×PS(1)

Avec : KG = Coefficient ou indice de compacité de Gravelius ; P = Périmètre du bassin versant en km; S = Superficie du bassin versant en km² et π = constant 3,14.

La longueur et largeur du rectangle équivalent sont utilisées comme indicateur de la compacité ou de l'allongement de la forme d'un bassin versant (Benzougagh et al. [36]). Elles ont été calculées par les formules (2) et (3) (Thiaw [37]) :

Lr=KGS1,12×[1+1−(1,12KG)2](2)

lr=KGS1,12×[1−1−(1,12KG)2](3)

Avec : Lr = longueur du rectangle (km) ; lr = largeur du rectangle (km) ; KG = coefficient de Gravelius et S = surface du bassin versant (km2).

Les altitudes minimales et maximales ont été obtenues directement à partir des MNT de différents sous-bassins versants de la Tshopo à l’aide du logiciel QGIS 3.22.13. L’altitude médiane d’un bassin versant correspond à l’altitude lue au point d’abscisse 50% de la surface totale du bassin sur la courbe hypsométrique (Rayane et al. [38]). L’altitude moyenne a été calculée par la formule (4), à partir des courbes hypsométriques (Ameur et al. [39]).

Hmoy=∑Si.HiS(4)

Avec : Hmoy = altitude moyenne (m), Si = surface de chaque tranche d’altitude (km2); Hi = altitude moyenne de chaque tranche (m)et S : surface totale du bassin (km2).

L’indice de pente moyenne a été calculé à partir de la formule (5). C’est le quotient de la différence entre les hauteurs extrêmes par la longueur du rectangle équivalent (Benzougagh et al. [36]).

Ipm=Hmax−HminLr(5)

Avec : Ipm = indice de pente moyenne (en m/km ou %); Hmax = altitude maximale (en m); Hmin = altitude minimale (en m) et Lr = longueur de rectangle équivalent (en km).

L’indice de pente globale est défini comme étant le rapport entre la dénivellation et la longueur de rectangle équivalent (Ameur et al. [39]). Il a été calculé à partir de la formule (6).

Ipg=DgLr(6)

Avec : Ipg = indice de pente globale (en m/km); Dg = dénivelée globale (en m) et Lr = longueur de rectangle équivalent (en km).

L’indice de pente de roche est égal à la somme des racines carrées des pentes moyennes de chaque élément partiel compris entre deux courbes de niveau, pondéré par la surface partielle qui lui est associée et mesurées sur le rectangle équivalent. Il s’exprime par la formule (7).

Ipr=1Lr∑ai.di(7)

Avec : Ipr = indice de pente de roche (en %); Lr = longueur de rectangle équivalent (en km); ai = pourcentage de la superficie entre les courbes de niveau et di = distance entre les courbes de niveau appelée aussi dénivelée (m).

La dénivelée globale a été calculée à partir de la formule (8). Elle donne une idée sur la différence d'altitudes entre l’amont et l’aval d'un bassin versant. Ces altitudes ont été extraites sur les courbes hypsométriques (Nihad et al. [40]).

Dg=H5% −H95% (8)

Avec : Dg = dénivelée globale (en m); H95% = altitude correspondante à 95% de la superficie totale du bassin versant (en m) et H5% = altitude correspondante à 5% de la superficie totale du bassin versant (en m).

La dénivelée spécifique permet de comparer le relief des bassins versants de taille différente. Elle est définie comme étant le produit de l’indice de pente globale par la racine carrée de la surface du bassin versant. La formule (9) a été utilisée pour calculer ce paramètre (Ameur et al. [39]).

Ds=IpgS(9)

Avec : Ds = dénivelée spécifique (en m); Ipg = indice de pente globale (m/km) et S = surface du bassin versant (km2).

La densité de drainage correspond au rapport de la longueur totale des thalwegs par la surface du bassin (Benzougagh et al. [36]). Elle a été calculée à partir de la formule (10).

Dd=∑i=1nLiS(10)

Avec : Dd = densité de drainage en (km/km2); Li = somme des longueurs de tous les thalwegs y compris le thalweg principal (km)et S = superficie du bassin versant (km2).

Rapport de longueur correspond au rapport de longueur moyenne des thalwegs d’ordre « n + 1 » sur la longueur moyenne des thalwegs d’ordre « n ». Ce rapport est calculé par la formule (11) (Barbot et al. [41]).

Rl=L(n+1)L(n)(11)

Avec : Rl = rapport de longueur; L (n+ 1) = longueur moyenne des cours d’eau d’ordre « n+ 1 » en (km) et L (n) = longueur moyenne des cours d’eau d’ordre « n » en (km).

Rapport de confluence est défini comme un rapport du nombre de cours d’eau d’ordre « n » sur le nombre de cours d’eau d’ordre « n + 1 », formule (12).

Rc=N(n)N(n+1)(12)

Avec : Rc = rapport de confluence des cours d'eau (``bifurcation ratio") ; N(n) = nombre des cours d'eau d'ordre « n »; N (n+ 1) = nombre des cours d'eau d'ordre suivant « n+ 1 ».

La fréquence des cours d’eau est définie comme le nombre total de thalwegs de tous les ordres par unité de surface (Horton [42]). Elle a été calculer à partir de la formule (13).

Fc=NtS(13)

Avec : Fc = fréquence des cours d’eau ; Nt = nombre total des talwegs de tous les ordres et S = surface du bassin versant.

Le coefficient de torrentialité est le produit de la densité de drainage par la fréquence des cours d’eau élémentaire (d’ordre 1) (Benzougagh et al. [36]). Il s’exprime par la formule (14).

Ct=Dd×Fc1=Dd×N1S(14)

Avec : Ct = coefficient de torrentialité; Dd = densité de drainage (km/km2); Fc1 = Fréquence des cours d’eau d’ordre « 1 »; N1 = nombre des cours d’eau d’ordre « 1 »et S = surface du bassin versant (km2).

Le temps de concentration correspond au temps que met la particule d’eau provenant de la partie la plus éloignée du bassin pour arriver à l’exutoire (Ameur et al. [39], Belazreg [43]). Nous l’avons calculé à partir de la formule de Giandotti adaptée par Grimaldi et al. [44], Pale et al. [45], formule (15). La formule a été calibrée sur 12 bassins d'une superficie variant entre 170 et 70 000 km2. Cependant, les détails concernant le nombre et les types d'événements d'inondation utilisés lors de la procédure de calibrage ne sont pas spécifiés. Ce temps de concentration est très important pour l’alerte d’un risque de crue dans un bassin versant (Chanyour et al. [46]).

Tc=4S+1,5Lt0,8H(15)

Avec : Tc = temps de concentration (en heure); S = surface du bassin versant (km2); Lt = longueur du thalweg principal (km)et H = différence entre l'altitude moyenne du bassin et l'altitude de l'exutoire (m).

La vitesse d’écoulement de l’eau représente la distance qu’une masse d’eau parcourt par unité de temps (Guerbouz et al. [22], Bensaad et al. [47]). Elle est donnée par la formule (16).

Ve=LtTc(16)

Avec : Ve = vitesse d’écoulement de l’eau(km/h) ; Lt = longueur du thalweg principal (km)et Tc = temps de concentration (en heure).

2.3 Méthodes D’analyse Statistique Multivariée

2.3.1 Analyse de Corrélation, Modélisation et Tests Statistiques

L'analyse de corrélation est un outil statistique utilisé pour évaluer la relation entre deux variables. Elle nous a permis de déterminer si les variations d'une variable sont associées aux variations de l'autre variable. Nous avons calculé les coefficients de corrélation (r) afin d’évaluer la force et le sens du lien statistique entre les paramètres hydro-morphométriques. La régression linéaire multiple (RLM) quand elle, a été utilisée pour modéliser la relation linéaire entre les différents paramètres hydro-morphométriques analysés et déduire les variables les plus caractéristiques qui influencent significativement l’écoulement des eaux dans les sous-bassins versants de la rivière Tshopo. Cette technique est couramment utilisée dans les littératures scientifiques pour prédire et expliquer la variation d’une variable dépendante en fonction des plusieurs variables indépendantes, comme démontré par (D’Arcy [48], Kribes et al. [49], El Badaoui et al. [50], Amiri et al. [51], Alonso et al. [52,53], Abdellatif et al. [54]).

Dans le cadre de cette étude, la recherche du modèle optimal qui prédit la vitesse d’écoulement des eaux de surface a été réalisée avec le logiciel Tanagra 1.4.50 intégré comme option complémentaire dans Excel. Cette opération se fonde sur une approche itérative d’ajout et de retrait de chacune des variables explicatives dans le modèle final. Ce dernier devrait répondre aux critères basés sur les hypothèses suivantes : la linéarité de la relation, l’indépendance des résidus, l'homoscédasticité et l’absence de multicolinéarité entre les variables explicatives. Pour minimiser le nombre de variables explicatives tout en maximisant R2, nous avons procédé à l’identification à partir d’une matrice de corrélation, les variables explicatives corrélées entre elles. La réduction de la complexité du modèle s’est faite en éliminant les variables explicatives moins pertinentes par une approche de régression pas à pas (Backward stepwise). Cette technique nous a permis d’éliminer séquentiellement une par une les variables explicatives qui ont moins d’impact sur le modèle prédictif d’écoulement des eaux en se basant sur un critère statistique prédéfini, telle qu’une valeur de probabilité p-value inférieur ou égale au seuil de 0,05. L’équation générale pour le modèle de régression multiple est représentée par la formule (17).

Y=b0+b1∗X1+b2∗X2+⋯+bn∗Xn(17)

Avec : Y = variable à expliquer ou dépendante que l'on cherche à prédire; X1, X2, ..., Xn = variables explicatives ou indépendantesqui sont utilisées pour prédire Y; b0, b1, b2,..., bn = coefficients de régression estimés pour chaque variable explicative.

Nous avons effectué des tests statistiques pour évaluer la significativité des variables explicatives et l’ajustement global du modèle. Deux tests ont été utilisés, à savoir : le test de significativité globale (test F de Fisher) pour évaluer si le modèle dans son ensemble est significatif et des tests individuels (test t) pour évaluer la significativité des coefficients de régression pour chaque variable explicative. Le seuil statistique de comparaison adopté est α = 0,05. Ainsi, une valeur de probabilité p-value supérieure à 0,05 indique une différence ou relation non significative, p-value comprise entre 0,05 et 0,01 caractérise une différence ou relation significative, p-value comprise entre 0,01 et 0,001 caractérise une différence ou relation hautement significative et lorsque p-value est inférieure ou égale à 0,001, la différence ou relation est très hautement significative.

2.3.2 Regroupement des Sous-bassins Versants

Une technique couramment utilisée en statistique exploratoire des données, la classification ascendante hiérarchique (CAH) a été appliquée à 8 individus (sous-bassins versants) et 21 variables (paramètres hydro-morphométriques) pour former des groupes homogènes (cluster) des sous-bassins versants de la Tshopo en fonction de leurs similarités. Chaque groupe contient des individus similaires en termes de caractéristiques hydro-morphométriques analysées.

La CAH commence par considérer chaque observation comme un cluster individuel, puis fusionne itérativement les clusters les plus similaires jusqu'à ce qu'un seul cluster global soit formé. Elle utilise des mesures de similarité et de dissimilarité pour regrouper les observations en fonction de leurs caractéristiques communes. Cette méthode permet de créer une structure hiérarchique de clusters qui peut être représentée sous forme de dendrogramme. La distance euclidienne a été choisie comme mesure de similarité entre les sous-bassins versants afin de former des groupes plus ou moins homogènes et physiquement distincts dans le dendrogramme (Güler et al. [55]). Ainsi, les individus qui sont proches les uns des autres sont plus similaires que ceux qui sont éloignés. Pour déterminer le nombre de groupes d’individus à former, nous avons choisi un seuil de 5 comme hauteur de coupe appropriée afin de regrouper les sous-bassins versants de la rivière Tshopo.

3  Résultats

3.1 Relation Interparamètres et leur Influence sur l’écoulement des Eaux

Pour mieux appréhender le degré de dépendance entre les variables hydro-morphométriques afin de déterminer leur influence sur l’écoulement des eaux de surface, nous avons calculé les coefficients de corrélations. Le Tableau 4 ci-dessous donne sous forme de matrice, les valeurs de coefficients de corrélations (r) calculés sur les 21 variables prises deux à deux.

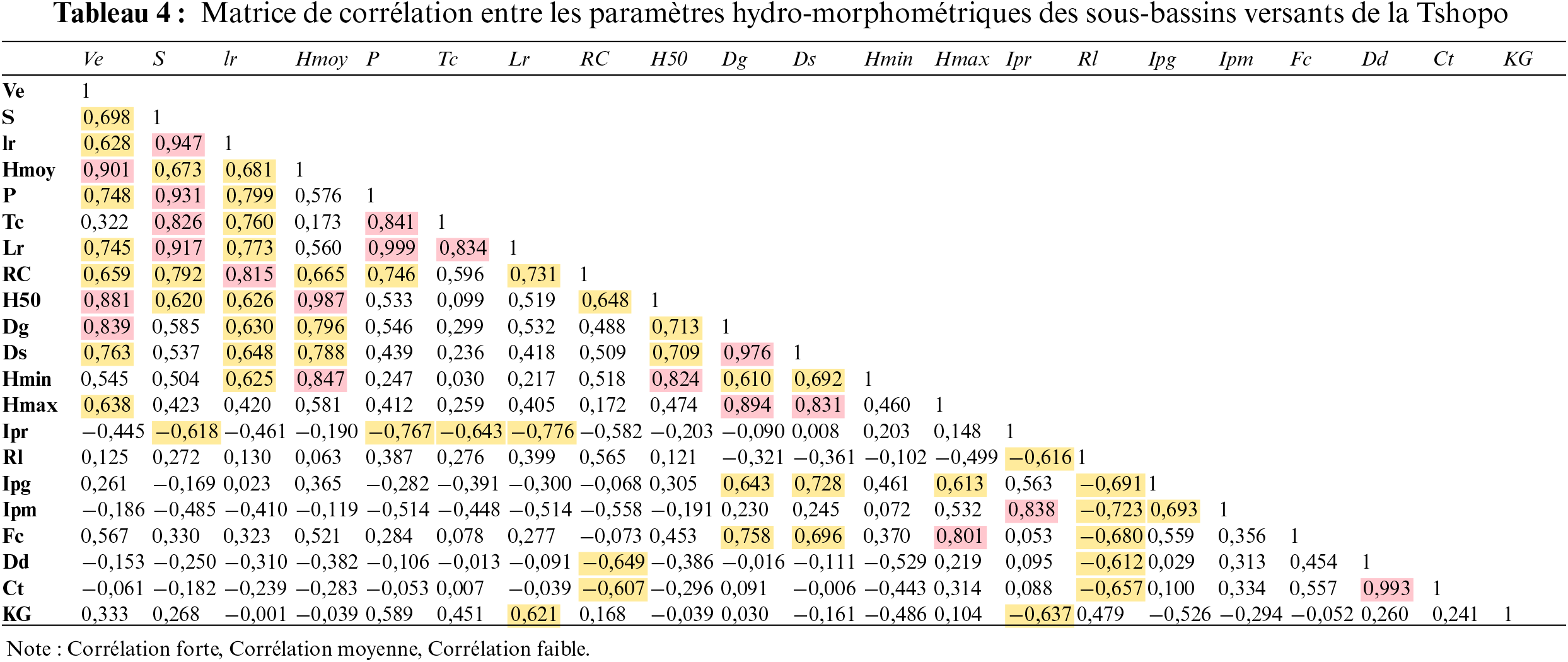
Au vu du résultat de ce tableau, nous constatons qu’il existe une forte corrélation positive entre certains paramètres topographiques comme l’altitude moyenne (Hmoy, r = 0,9), l’altitude médiane (H50, r = 0,881) et la dénivelée globale (Dg, r = 0,839) avec la vitesse d’écoulement des eaux (Ve). En revanche, elle est corrélée moyennement de manière positive avec la dénivelée spécifique (Ds, r = 0,763), le périmètre (P, r = 0,748), la longueur du rectangle équivalent (Lr, r = 0,748), la surface (S, r = 0,698), le rapport de confluence des cours d'eau (Rc, r = 0,659), l’altitude maximale (Hmax, r = 0,638) et la largeur du rectangle équivalent (lr, r = 0,628).

La régression linéaire multiple (RLM) nous a permis de modéliser la relation linéaire entre les différents paramètres hydro-morphométriques et déduire, grâce à l’approche de régression pas à pas (Backward stepwise) les variables les plus caractéristiques qui influencent significativement la vitesse d’écoulement des eaux dans les sous-bassins versants de la rivière Tshopo.

Les paramètres d’évaluation de la significativité du modèle dans son ensemble et la quantification de son ajustement aux données ainsi que les coefficients du modèle ajusté prédisant la vitesse d’écoulement en fonction des variables explicatives topographiques les plus pertinentes sont consignés dans les Tableaux 5 et 6. La significativité statistique a été considérée au risque p-value ≤ 0,05 (*) pour une relation significative et p-value ≤ 0,01 (**) pour celle qui est hautement significative.

Le Tableau 5 montre que le modèle obtenu est hautement significatif statistiquement (p-value = 0,0039) et bien ajusté aux données (R2 ajusté = 0,92). Cette valeur élevée du coefficient de détermination exprime 92% de la variabilité de la vitesse d’écoulement (Ve) prédite par certaines variables topographiques incluses dans le modèle.

Les résultats présentés dans le Tableau 6 fournissent des informations sur l'impact de chaque variable indépendante sur l'écoulement des eaux, tout en tenant compte des autres variables pertinentes incluses dans le modèle de l'équation (18). Ainsi, il a été démontré que trois variables topographiques, à savoir l'altitude médiane (H50 : p-value = 0,02), la dénivelée globale (Dg : p-value = 0,03) et la dénivelée spécifique (Ds : p-value = 0,05), ont une influence significative sur la vitesse d'écoulement des eaux dans les sous-bassins versants de la Tshopo.

Ve=−0,518+0,006∗H50+0,018∗Dg−0,049∗Ds(18)

Cette équation générale du modèle de prédiction de la vitesse d’écoulement a une allure linéaire. Les droites de régression correspondantes sont représentées sur les Figs. 2–4.

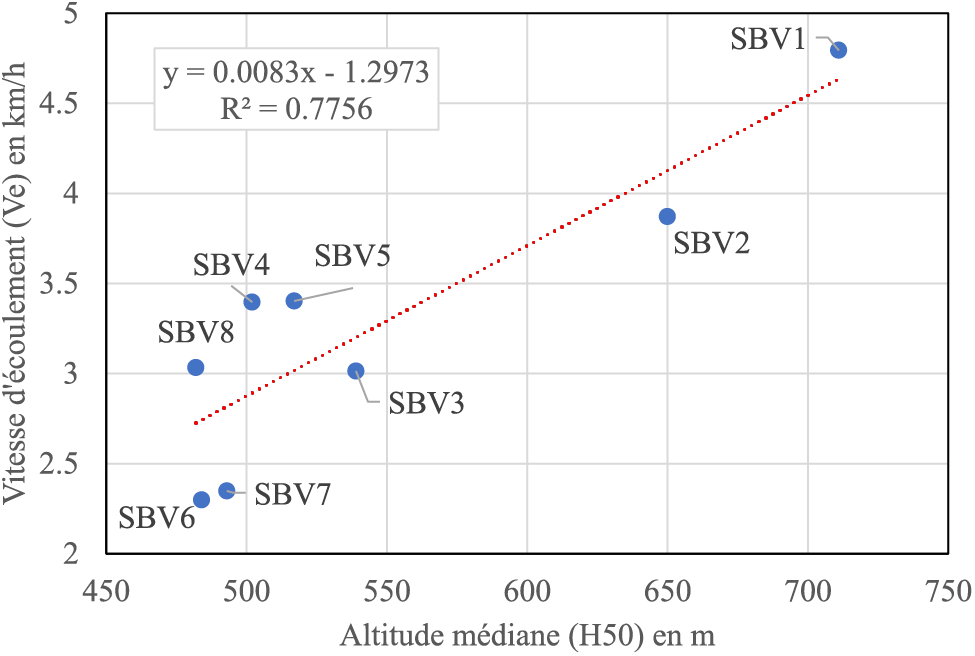
Figure 2: Relation linéaire entre la vitesse d’écoulement (Ve) et l’altitude médiane (H50)

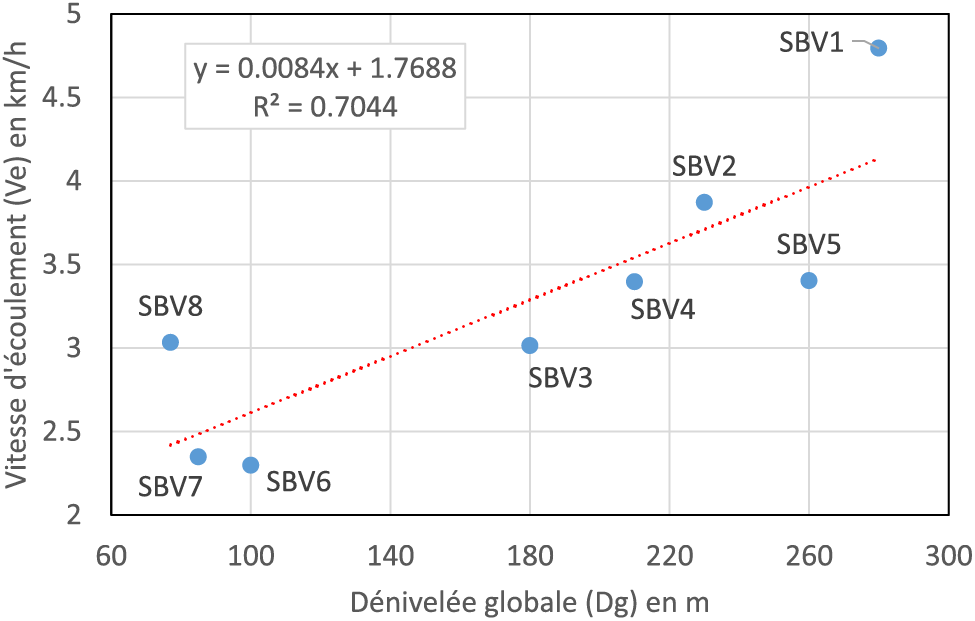
Figure 3: Relation linéaire entre la vitesse d’écoulement (Ve) et la dénivelée globale (Dg)

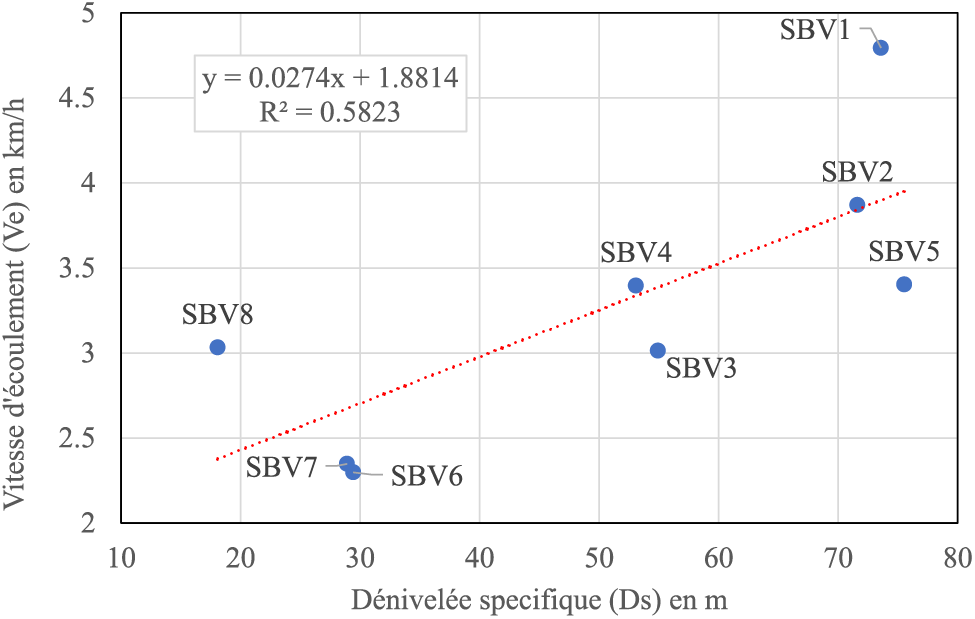
Figure 4: Relation linéaire entre la vitesse d’écoulement (Ve) et la dénivelée spécifique (Ds)

Il ressort des Figs. 2–4 que l’altitude médiane (H50), la dénivelée globale (Dg), et la dénivelée spécifique (Ds) présentent une relation linéaire positive avec la vitesse d’écoulement (Ve).

3.2 Regroupement des Sous-Bassins Versants de la Tshopo

La classification ascendante hiérarchique (CAH) a permis d’individualiser les sous-bassins versants de la Tshopo en groupes homogènes physiquement. Ainsi, deux groupes (G1 et G2) opposés des sous-bassins versants ont été mis en évidence, d’un côté les sous-bassins versants appartenant au cours supérieur et moyen de la Tshopo (SBV1, SBV2, SBV3 et SBV5) et de l’autre les sous-bassins versants du cours inférieur (SBV6, SBV7 et SBV8). Le premier groupe est caractérisé par un relief modéré alors que pour le second groupe, le relief est faible. De plus, nous pouvons observer des corrélations spatiales, où les sous-bassins versants géographiquement proches appartiennent au même groupe identifié par le dendrogramme (Fig. 5). En conclusion, nous pouvons affirmer que le relief et la proximité géographique sont les facteurs les plus représentatifs pour la répartition des sous-bassins versants de la rivière Tshopo entre le cours supérieur-moyen et le cours inférieur.

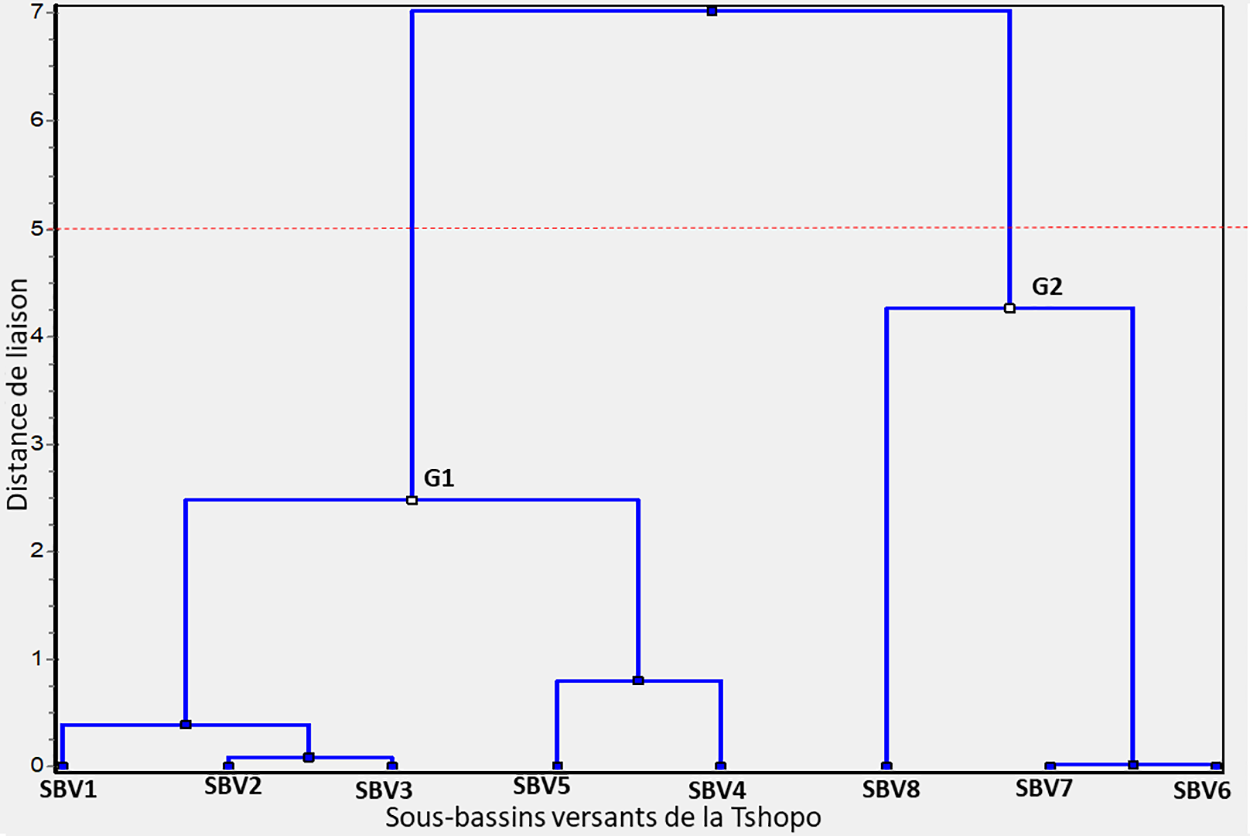
Figure 5: Dendrogramme montrant le regroupement des sous-bassins versants de la Tshopo selon leur ressemblance et dissemblance physique

Il est important de noter que l'influence du relief sur l'écoulement varie d'un secteur à l'autre, comme indiqué dans le Tableau 7.

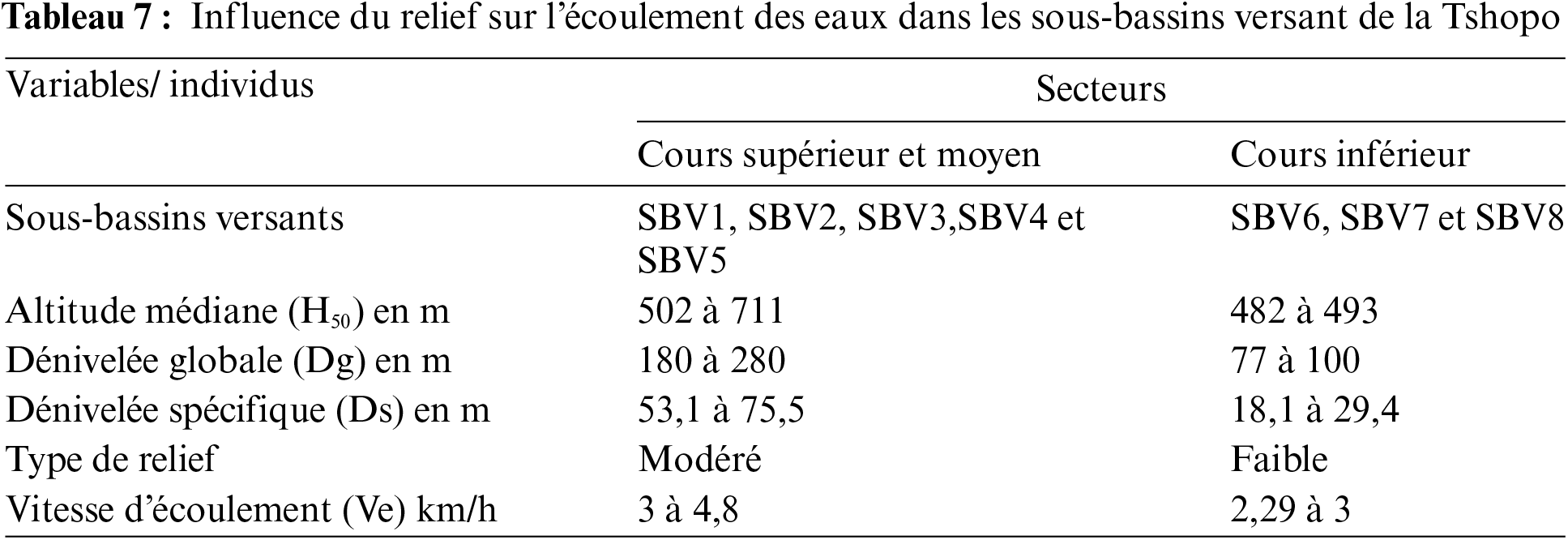
L'analyse du Tableau 7 révèle que dans le secteur à relief modéré, l'écoulement est assez intense (avec une vitesse d'écoulement comprise entre 3 et 4,8 km/h). En revanche, dans le secteur à relief faible, l'influence de la topographie sur l'écoulement diminue progressivement, entraînant des valeurs de vitesse d'écoulement des eaux de surface plus faibles (entre 2,29 et 3 km/h). Par conséquent, l'intensité de l'écoulement de la rivière diminue progressivement jusqu'à atteindre un calme relatif au niveau de Kisangani.

4  Discussion

4.1 Relation Interparamètres et Leur Influence sur L’écoulement des Eaux

Pour améliorer notre compréhension du niveau de relation entre les différentes variables, nous avons utilisé une matrice de coefficients de corrélation pour les 21 variables hydro-morphométriques analysées (Faye [56], Baba-Hamed et al. [1], Faye [57]).

Au regard des résultats de l'analyse de corrélation (Tableau 4), il est observé une forte corrélation positive entre certains paramètres topographiques tels que l'altitude moyenne (Hmoy, r = 0,9), l'altitude médiane (H50, r = 0,881) et la dénivelée globale (Dg, r = 0,839) avec la vitesse d'écoulement des eaux (Ve). En revanche, il est constaté une corrélation positive de niveau moyen entre la vitesse d'écoulement des eaux et d'autres paramètres tels que la dénivelée spécifique (Ds, r = 0,763), le périmètre (P, r = 0,748), la longueur du rectangle équivalent (Lr, r = 0,748), la surface (S, r = 0,698), le rapport de confluence des cours d'eau (Rc, r = 0,659), l’altitude maximale (Hmax, r = 0,638) et la largeur du rectangle équivalent (lr, r = 0,628). Ces résultats indiquent que ces paramètres jouent un rôle déterminant dans l'écoulement des eaux de surface dans les sous-bassins versants de la Tshopo.

Les résultats obtenus par la régression linéaire multiple (RLM) confirment l'importance de la dépendance de l'écoulement par rapport à la topographie. Le modèle prédictif obtenu par cette analyse statistique est hautement significatif (p-value = 0,0039). Certaines variables, telles que l'altitude médiane (H50), la dénivelée globale (Dg) et la dénivelée spécifique (Ds) exercent une influence significative sur la vitesse d'écoulement (Ve) des eaux de surface dans les sous-bassins versants de la rivière Tshopo. Les valeurs élevées du test de Fisher (F = 27,67) et du coefficient de détermination ajusté (R2 = 0,92) indiquent que les variables indépendantes (H50, Dg, et Ds) incluses dans notre modèle (formule (18)) ont une forte capacité à expliquer une proportion importante de la variabilité de la vitesse d'écoulement, avec une faible erreur-type (0,23) (Tableau 5). La forte corrélation (r > 0,8) (Tableau 4) entre ces variables topographiques (Dg, H50, Dg et Ds) et la vitesse d'écoulement (Ve) n'est pas surprenante dans le bassin versant de la Tshopo, étant donné la relation qui existe entre les conditions d'écoulement et ces variables topographiques. De plus, les résultats des Figs. 2–4 montrent une corrélation linéaire positive entre l'altitude médiane (H50), la dénivelée globale (Dg) et la dénivelée spécifique (Ds) avec la vitesse d'écoulement (Ve). Ces trois variables topographiques (H50, Dg et Ds) expliquent respectivement 77,56%, 70,44% et 58,23% de la variabilité de la vitesse d'écoulement des eaux de surface dans les sous-bassins versants de la Tshopo.

4.2 Regroupement des Sous-Bassins Versants de la Tshopo

Il existe différentes approches pour regrouper les données, cependant, la classification ascendante hiérarchique (CAH) est couramment employée dans la littérature scientifique (Steinhorst et al. [58], Davis [59], Schot et al. [60]). L’analyse des groupes (clusters) est d’une importance capitale, comme le soulignent Ribeiro et al. [61]. Cette méthode permet de détecter des regroupements naturels au sein des données. L'analyse CAH effectuée sur les 8 sous-bassins versants de la Tshopo a conduit à la construction d'un dendrogramme (Fig. 4). Dans cette étude, la distance euclidienne a été sélectionnée comme mesure de similarité entre les sous-bassins versants, dans le but de former des groupes homogènes et physiquement distincts. Dans l'étude menée par Güler et al. [55], il a également été observé que l'utilisation de la distance euclidienne permettait d'obtenir les groupes les plus séparés et distincts.

La classification des sous-bassins versants en groupes est basée sur une observation visuelle du dendrogramme. Dans notre cas, une ligne de classification a été tracée à une distance de liaison d'environ 5 à travers le dendrogramme. Ainsi, les sous-bassins versants dont la distance de liaison est inférieure à 5 sont regroupés ensemble. Cette ligne de classification a permis de diviser le dendrogramme en deux groupes de sous-bassins versants, appelés G1 et G2. Globalement, le groupe G1 est caractérisé par un relief modéré (Ds, de l’ordre de 53,19 à 73,6 m) tandis que le groupe G2 présente un relief faible (Ds comprise entre 18,1 à 29,43 m).

Il est essentiel de souligner que le nombre de groupes peut être modifié en ajustant la position de la ligne de classification sur le dendrogramme, comme relevé par Güler et al. [55]. Cette évaluation subjective confère à la méthode CAH une nature semi-objective, selon les observations de (Cloutier et al. [62]). Dans cette étude, le classement en deux groupes a donné les résultats les plus satisfaisants pour former des groupes physiquement distincts.

5  Conclusion

Cette étude repose sur l'analyse statistique multivariée des paramètres hydro-morphométriques mesurés dans l'ensemble des sous-bassins versants de la Tshopo. Son objectif est de déterminer les variables qui influencent significativement l'écoulement des eaux de surface et de regrouper les sous-bassins versants en fonction de leur similitude physique. Pour ce faire, plusieurs méthodes ont été utilisées, notamment l'analyse de corrélation, la régression linéaire multiple (RLM) et la classification ascendante hiérarchique (CAH).

Les résultats obtenus mettent en évidence l'importance de la topographie sur l'écoulement des eaux. Plus précisément, trois variables topographiques, à savoir l'altitude médiane (H50), le dénivelé global (Dg) et le dénivelé spécifique (Ds), ont une influence significative sur la vitesse d'écoulement (Ve) des eaux de surface dans les sous-bassins versants de la Tshopo. En analysant les données, nous avons identifié deux groupes de sous-bassins versants. Le premier groupe est composé des sous-bassins versants SBV1, SBV2, SBV3, SBV4 et SBV5, situés dans la partie supérieure et moyenne de la Tshopo, et se caractérise par un relief modéré. Le second groupe est formé des sous-bassins versants SBV6, SBV7 et SBV8, situés dans la partie inférieure, qui présentent un relief faible. Ainsi, nous pouvons conclure que la proximité géographique et les caractéristiques topographiques pertinentes sont à l'origine du regroupement et de la distinction entre les sous-bassins versants de la Tshopo.

Il convient de noter que l'analyse des variables hydro-morphométriques est intéressante, mais qu'elle ne suffit pas à comprendre les réponses hydrologiques d'un grand bassin versant comme la Tshopo. Dans de futures études, il sera nécessaire d'analyser d'autres facteurs tels que la géologie, les sols, la couverture végétale, les formes d'occupation humaine de l'espace, ainsi que l'évaluation des débits des cours d'eau.

Acknowledgement: Nous tenons à exprimer nos sincères remerciements à la société SNEL (Société Nationale d'Électricité) à Kisangani pour avoir mis à notre disposition leur base de données sur le débit de la rivière Tshopo dans le cadre de notre article.

Financements/Funding Statement: Les auteurs n'ont pas reçu de financement spécifique pour cette étude.

Contributions des auteurs/Author Contributions: La conception et design de l'étude, collecte des données, analyse et interprétation des résultats ainsi que la préparation du projet de manuscrit ont été réalisées par Faidance Mashauri. Les auteurs Mokili Mbuluyo et Nsalambi Nkongolo ont examiné les résultats et approuvé la version finale du manuscrit.

Disponibilité des données et du matériel/Availability of Data and Materials: Les données et le matériel utilisés dans cette étude sont disponibles sur demande auprès des auteurs. Les détails spécifiques concernant l'accès aux données et au matériel peuvent être obtenus en contactant cette adresse E-mail : mashaurifaidance@gmail.com.

Conflits d'intérêts/Conflicts of Interest: Les auteurs déclarent qu'ils n'ont aucun conflit d'intérêts en relation avec cette recherche.

References

1. Baba-Hamed, K., Bouanani, A. (2016). Caractérisation d’un bassin versant par analyse statistique des paramètres morphométriques : Cas du bassin versant de la Tafra (Nord-ouest Algerien). Géo-Eco-Trop, 40(4), 277–286. [Google Scholar]

2. Hocine, F., Belhadj-Aissa, M., Haddoud, F., Ouarzeddine, M., Belhadj-Aissa, A. (2008). Simulation du comportement des écoulements d’eau en utilisant le réseau hydrographique d’un bassin versant : Cas de l’Oued Benimessous. Algerie Revue Télédétection, 8(1), 179–191. [Google Scholar]

3. Rodriguez-Iturbe, I., Valdès, J. B. (1979). The geomorphologic structure of hydrologic response. Water Resources Research, 15(6), 1409–1419. https://doi.org/10.1029/WR015i006p01409 [Google Scholar] [CrossRef]

4. Gupta, V. K., Waymire, E., Wang, C. T. (1980). A representation of an instantaneous unit hydrograph from geomorphology. Water Resources Research, 16(5), 855–862. https://doi.org/10.1029/WR016i005p00855 [Google Scholar] [CrossRef]

5. Ambroise, B. (1998). Genèse des débits dans les petits bassins versants ruraux en milieu tempéré : Processus et facteurs. Revue des sciences de l’eau, 4(4), 475–495. https://doi.org/10.7202/705317ar [Google Scholar] [CrossRef]

6. White, A. B., Kumar, P., Saco, P. M., Rhoads, B. L., Yen, B. C. (2004). Hydrodynamic and geomorphologic dispersion: Scale effects in the Illinois River Basin. Journal of Hydrology, 288(3–4), 237–257. https://doi.org/10.1016/j.jhydrol.2003.10.019 [Google Scholar] [CrossRef]

7. Kumar, R., Chatterjee, C., Singh, R. D., Lohani, A. K., Kumar, S. (2007). Runoff estimation for an ungauged catchment using geomorphological instantaneous unit hydrograph (GIUH) models. Hydrological Processes, 21(14), 1829–1840. https://doi.org/10.1002/hyp.6318 [Google Scholar] [CrossRef]

8. Singh, P. K., Bhunya, P. K., Mishraa, S. K., Chaube, U. C. (2007). An extended hybrid model for synthetic unit hydrograph derivation. Journal of Hydrology, 336(3–4), 247–360. [Google Scholar]

9. Bhadra, A., Panigrahy, N., Singh, R., Raghuwanshi, N. S., Mal, B. C. et al. (2008). Development of a geomorphological instantaneous unit hydrograph model for scantily gauged watersheds. Environmental Modelling & Software, 23(8), 1013–1025. [Google Scholar]

10. Lee, K. T., Chen, N. C., Chung, Y. R. (2008). Derivation of variable IUH corresponding to time-varying rainfall intensity during storms. Journal of Hydrological Sciences, 53(2), 323–337. [Google Scholar]

11. Moussa, R. (2009). Definition of new equivalent indices of Horton-Strahler ratios for the derivation of the geomorphological instantaneous unit hydrograph. Water Resources Research, 45(9), 24. https://doi.org/10.1029/2008WR007330 [Google Scholar] [CrossRef]

12. Maréchal, D., Ayral, P. A., Bailly, J. S., Puech, C., Sauvagnargues-Lesage, S. (2013). Sur l’origine morphologique des écoulements par l’analyse d’observations hydrologiques distribuées. Application à deux bassins versants cévenols (Gard, France). Géomorphologie : Relief, Processus, Environnement, 19(1), 47–62. https://doi.org/10.4000/geomorphologie.10120 [Google Scholar] [CrossRef]

13. Douvinet, J., Delahaye, D., et Langlois, P. (2008). Modélisation de la dynamique potentielle d’un bassin versant et mesure de son efficacité structurelle. Cybergeo : European Journal of Geography, Systèmes, Modélisation, Géostatistiques, Document, 412. https://doi.org/10.4000/cybergeo.16103 [Google Scholar] [CrossRef]

14. Idrissi, S., Taous, A. (2022). Analyse morphométrique et hydrographique du bassin versant du Beht et de ses principaux affluents en utilisant le système d’information géographique. Revue Marocaine de Géomorphologie, (6), 83–103. https://revues.imist.ma/index.php/Remageom/article/view/36440 [Google Scholar]

15. Otemikongo, J., Omasombo, J., Stroobant, E., Obotela, N., Bolakonga, B. et al. (2020). Tshopo : Laborieuse construction politico-administrative coloniale muée en bastion du nationalisme congolais. Monographies des provinces de la RD Congo, vol. 14. Belgique: Musée royal de l’Afrique centrale. [Google Scholar]

16. Léonard, J. (1993). Etude phytosociologique des chutes de la Tshopo (Kisangani-Zaire). Bulletin du Jardin Botanique National de Belgique, 62(1/4), 283–347. [Google Scholar]

17. Lasri, M. (2019). La cartographie de l’aléa d’inondation dans l’agglomération de Fès : De la modélisation hydrologique à la simulation hydraulique. EWASH & TI Journal, 3(2), 113–123. [Google Scholar]

18. Strahler, A. N. (1957). Quantitative analysis of watershed geomorphology. Transactions, American Geophysical Union, 38(6), 913–1920. [Google Scholar]

19. Manojkumar, P. D., Nitin, N. M., Akshada, H. K., Ganesh, M. D. (2019). Morphometric analysis of Kolavadi sub-watershed in Bhor Tahsil using GIS techniques. Journal of Geographical Studies, 3(1), 1–10, 87–96. [Google Scholar]

20. Prakash, K., Rawat, D., Singh, S., Chaubey, K., Kanhaiya, S. et al. (2019). Morphometric analysis using SRTM and GIS in synergy with depiction: A case study of the Karmanasa River basin, North central India. Applied Water Science, 9(1), 1. https://doi.org/10.1007/s13201-018-0887-3 [Google Scholar] [CrossRef]

21. Gautam, P. K., Singh, D. S., Kumar, D., Singh, A. K. (2020). A GIS-based approach in drainage morphometric analysis of Sai River Basin, Uttar Pradesh. India Journal of the Geological Society of India, 95, 366–376. [Google Scholar]

22. Guerbouz, Y., Mohammed, B. H. (2020). Apport du SIG et de l’MNT-ASTER à l’étude morphometrique d’un bassin versant en zone aride : Cas de l’Oued Zegrir/Guerrara (Mémoire de Master). Université de Ghardaïa, Algérie. [Google Scholar]

23. Faye, C., Dièye, S., Faye, G. (2021). Analyse morphométrique et hydrologique du sous-bassin versant du Niaoule (bassin de la Gambie) à l'aide de techniques SIG. Algerian Journal of Arid Environment, 11(1), 54–75. [Google Scholar]

24. Balasubramani, K., Gomathi, M., Bhaskaran, G., Kumaraswamy, K. (2019). GIS-based spatial multi-criteria approach for characterization and prioritization of micro-watersheds: A case study of semi-arid watershed, South India. Applied Geomatics, 11(3), 289–307. [Google Scholar]

25. Jain, P., Ramsankaran, R. A. A. J. (2019). GIS-based integrated multi-criteria modelling framework for watershed prioritisation in India—a demonstration in Marol watershed. Journal of Hydrology, 578(12), 124–131. [Google Scholar]

26. Ghosh, M., Gope, D. (2021). Hydro-morphometric characterization and prioritization of sub-watersheds for land and water resource management using fuzzy analytical hierarchical process (FAHPA case study of upper Rihand watershed of Chhattisgarh State, India. Applied Water Science, 11(2), 1–20. [Google Scholar]

27. Ganie, P. A., Posti, R., Kunal, K., Kunal, G., Sarma, D. et al. (2022). Insights into the morphometric characteristics of the Himalayan River using remote sensing and GIS techniques: A case study of Saryu basin, Uttarakhand, India. Applied Geomatics, 14, 707–730. [Google Scholar]

28. Ganie, P. A., Posti, R., Bharti, V. S., Sehgal, V. K., Sarma, D. et al. (2023b). Striking a balance between conservation and development: A geospatial approach to watershed prioritisation in the himalayan basin. Conservation, 3(4), 460–490. [Google Scholar]

29. Gallo, N., Abdoulaye, F., Guilgane, F. (2023). L’érosion Hydrique dans le Contexte Sahélien : Cas du Bassin Versant du Ferlo. ESI Preprints. https://doi.org/10.19044/esipreprint.9.2023.p73 [Google Scholar] [CrossRef]

30. Ganie, P. A., Posti, R., Kunal, K., Kunal, G., Bharti, V. S. et al. (2023a). Modelling of the Himalayan Mountain river basin through hydro-morphological and compound factor-based approaches using geoinformatics tools. Modeling Earth Systems and Environment, 9(3), 3053–3084. [Google Scholar]

31. Berteaux, A. (2022). Modélisation hydrologique du ruissellement des eaux de surface de petits bassins versants lors d'événements de précipitations extrêmes (Mémoire de Master). École Polytechnique Fédérale de Lausanne, Suisse. [Google Scholar]

32. Roche, M. (1963). Hydrologie de surface. Paris : Edition Gauthier-Villars et ORSTOM. [Google Scholar]

33. Strahler, A. N. (1964). Quantitative geomorphology of drainage basins and channel networks. In: Chow, V. T. (Ed.Handbook of applied hydrology, pp. 4–76. New York: McGraw Hill Book Company. [Google Scholar]

34. Bentoumi, O., Hammou, W. (2021). L’apport de la télédétection et des SIG dans l’étude de l’évolution du couvert végétal du sous bassin Oued Soummam (Mémoire de Master). Université de M’sila, Algérie. [Google Scholar]

35. Bourafa, A., Laadjroud, M. (2022). Etude par approche numérique des caractéristiques morphologiques du sous bassin versant de la Soummam/Algérie Nord-Est (Mémoire de Master). Université Mohammed Seddik Benyahia-Jijel, Algérie. [Google Scholar]

36. Benzougagh, B., Dridri, A., Boudad, L., Sdkaoui, D., Baamar, B. (2019). Apport des SIG et télédétection pour l’évaluation des caractéristiques physiques du bassin versant d’Oued Inaouene (Nord-est Maroc) et leurs utilités dans le domaine de la gestion des risques naturels. American Journal of Innovative Research and Applied Sciences, 8(4), 120–130. [Google Scholar]

37. Thiaw, I. (2020). Caractérisation et valorisation des ressources en eau des bas-fonds du bassin versant du Diarha (Thèse de doctorat). Université Cheikh Anta Diop, Sénégal. [Google Scholar]

38. Rayane, C., Amira, T. (2023). L’utilisation de SIG et télédétection à la cartographie et à l’étude les sous bassins versants au niveau de la wilaya de Bordj Bou Arreridj (Mémoire de Master). Université Mohammed El Bachir El Ibrahimi B.B.A, Algérie. [Google Scholar]

39. Ameur, N., Saidi, S. (2020). Utilisation d’un SIG pour l’évaluation des caractéristiques morphométriques d’un sous—bassin versant et leurs influences sur l’écoulement des eaux : Sous—bassin versant d'Oued Bou saâda—Algérie (Mémoire de master). Université Mohamed Boudiaf–M’sila, Algérie. [Google Scholar]

40. Nihad, M., Hicham, M. (2022). Etude du fonctionnement hydrologique du bassin versant d’oued El-Agrem/Jijel, NE Algérien (Mémoire de Master). Université de Jijel, Algérie. [Google Scholar]

41. Barbot, A., Hilali, M., Mahboub, A., Boudad, L., Rachid, L. et al. (2019). Caractérisation morphologique et hydrodynamique du bassin de Tazarine (Anti Atlas Oriental du Maroc). EWASH & TI Journal, 3(3), 198–208. [Google Scholar]

42. Horton, R. E. (1932). Drainage basin characteristics. Trans Am Geophys Union, 13(1), 350–361. [Google Scholar]

43. Belazreg, N. (2019). Fonctionnement hydrologique des bassins versants à réseaux hydrographiques différents (Mémoire de Master). Université Mohamed Khider-Biskar, Algérie. [Google Scholar]

44. Grimaldi, S., Petroselli, A., Tauro, F., Profiri, M. (2012). Time of concentration: A paradox in modern hydrology. Hydological Sciences Journal, 57(2), 217–228. [Google Scholar]

45. Pale, S., Kekele, A., Da, D. E. C. (2020). Caractérisation géomorphométrique des formes de relief dans le bassin versant du Poni, au Burkina Faso. Afrique Science, 17(3), 62– 77. [Google Scholar]

46. Chanyour, Y., Obda, K., El Achari, O. (2020). Hydrologie des bassins versants présahariens: Exemple du bassin versant de l’oued Daoura (sud-est Marocain). Revue Espace Géographique et Société Marocaine, (37/38), 99–117. https://revues.imist.ma/index.php/EGSM/article/view/22394/12011 [Google Scholar]

47. Bensaad, S., Boudrouaya, A. (2022). Caractéristiques hydrologiques du bassin versant du Bas Sébaou/W.Boumerdès (Mémoire de Master). Université Mouloud Mammeri de Tizi-Ouzou, Algérie. [Google Scholar]

48. D’Arcy, P. (1993). Relations entre les propriétés du bassin versant, la morphométrie du Lac et la qualité des eaux (Mémoire de Master). Université du Québec, Canada. [Google Scholar]

49. Kribes, N., Ouelaa, N., Yallese, M. A., Belhadi, S. (2007). Analyse de l’impact des paramètres de coupe et des vibrations sur la rugosité des pièces usinées en tournage à partir de la méthode de régression linéaire multiple. Matériaux & Techniques, 95(3), 197–203. https://doi.org/10.1051/mattech:2008004 [Google Scholar] [CrossRef]

50. El Badaoui, H., Abdallaoui, A., Lancelot, L. (2012). Application des réseaux de neurones artificiels et des régressions linéaires multiples pour la prédiction des concentrations des métaux lourds dans les sédiments fluviaux marocains. 20e édition du colloque Journées Information Eaux, Université de Poitiers, Poitiers, France. [Google Scholar]

51. Amiri, S. S., Mottahedi, M., Asadi, S. (2015). Development of multi-linear regression model to predict energy consumption in the early stages of building design. Architectural Engineering National Conference 2015: Birth and Life of the Integrated Building, AEI 2015, vol. 85, no. 3, pp. 54–65. https://doi.org/10.1061/9780784479070.006 [Google Scholar] [CrossRef]

52. Alonso, L., Renard, F. (2019). Integrating satellite-derived data as spatial predictors in multiple regression models to enhance the knowledge of air temperature patterns. Urban Science, 3(4), 101. [Google Scholar]

53. Alonso, L., Renard, F., (2020). Compréhension du microclimat urbain lyonnais par l’intégration de prédicteurs complémentaires à différentes échelles dans des modèles de régression. Climatologie, 17(3), 2. https://doi.org/10.1051/climat/202017002 [Google Scholar] [CrossRef]

54. Abdellatif, M., Chamoin, J., Nianga, J. M., Defer, D. (2020). Prédiction par régression linéaire multiple : Application au comportement thermique d’un bâtiment. 38ème Rencontre Universitaire de Genie Civil (RUGC 2020), pp. 77–80. Marrakech, Maroc. [Google Scholar]

55. Güler, C., Thyne, G. D., McCray, J. E., Turner, A. K. (2002). Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeology Journal, 10, 455–474. [Google Scholar]

56. Faye, C. (2014). Méthode d’analyse statistique de données morphométriques : Corrélation de paramètres morphométriques et influence sur l’écoulement des sous-bassins du fleuve Sénégal. Cinq Continents, 4(10), 80–108. [Google Scholar]

57. Faye, C. (2018). Caractérisation d’un bassin versant par l’analyse statistique des paramètres morphométriques : Cas du bassin versant de la Gambie (bassin continental Guineo-Sénégalais). ReMaGéom, (2), 110–127. [Google Scholar]

58. Steinhorst, R. K., Williams, R. E. (1985). Discrimination of groundwater sources using cluster analysis, MANOVA, canonical analysis and discriminant analysis. Water Resources Research, 21, 1149–1156. [Google Scholar]

59. Davis, J. C. (1986). Statistics and data analysis in geology. New York: John Wiley & Sons Inc. [Google Scholar]

60. Schot, P. P., van der Wal, J. (1992). Human impact on regional groundwater composition through intervention in natural flow patterns and changes in land use. Journal of Hydrology, 134, 297–313. [Google Scholar]

61. Ribeiro, L., Macedo, M. E. (1995). Application of multivariate statistics, trend and cluster analysis to groundwater quality in the Tejo and Sado aquifer. Groundwater Quality: Remediation and Protection. Proceedings of the Prague Conference, pp. 39–47. Prague. [Google Scholar]

62. Cloutier, V., Lefebvre, R., Therrien, R., Savard, M. (2008). Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system. Journal of Hydrology, 353(3–4), 294–313. [Google Scholar]