Research on Parking Path Planing Based on A-Star Algorithm

1  Introduction

In recent years, with the acceleration of urbanization and the improvement of road construction level in China, the number of cars has grown from 10 million in 2000 to 417 million in 2022, ranking first in the world. Although the rapid increase in the number of cars has improved people’s living convenience, it has also brought problems such as traffic congestion and environmental pollution. Due to the increasingly complex internal structure of parking lots and the insufficiently clear signage inside the parking lots, congestion often occurs in parking lots during peak periods. Providing reliable optimal parking navigation routes for car drivers has become crucial. This approach can not only save parking costs, reduce fuel consumption and environmental pollution, but also reduce internal congestion in parking lots, thereby greatly improving the utilization efficiency of parking spaces, and to a large extent, alleviating the problem of parking difficulties in cities.

Currently, methods for solving the single-source shortest path planning problem mainly include ant colony algorithm, Dijkstra algorithm, bee algorithm, A-star algorithm, particle swarm algorithm, genetic algorithm, etc. [1]. Through comparison and analysis of various path planning algorithms, A-star algorithm and Dijkstra algorithm are good methods for calculating the optimal path between two points in parking path planning problems. Although Dijkstra algorithm has high accuracy, its search scope is large. Compared with Dijkstra algorithm, A-star algorithm greatly reduces its search scope for finding the shortest path by adding heuristic function, and its search time is shorter, thus improving the search efficiency of the algorithm. In the peak period of parking, the requirement for algorithm search performance is high, therefore, this paper selects A-star algorithm as the basic algorithm for optimal path planning. A-star algorithm is widely used due to its high search efficiency, and ability to obtain optimal or near-optimal solutions, and is recognized as the most complete classical algorithm for calculating the single-source shortest path.

Traditional single-source shortest path algorithms only consider the shortest distance or time without taking into account the dynamic traffic conditions of the road network. To address this issue, this paper proposes an improved path planning model that integrates the theory of road impedance functions to calculate path travel time, and uses a fusion function of path length and travel time as the weight matrix for the A-star algorithm to achieve optimal path planning. This method solves the problem of requiring a long time to travel the optimal path when only considering the shortest distance, as well as the problem of having a very long optical path length when only considering the shortest time.

2  Related Work

Currently, many works are studying the improvements and practical applications of the A-star algorithm. Erke et al. [2] developed a heuristic function based on criteria generated by humans or global planning, and introduced a new variable step-size A-star algorithm that reduces computation time and increases robustness. Ma et al. [3] proposed three new concepts, including bidirectional search, guiding path, and critical point list, to optimize the A-star algorithm and gratify indoor environment modeling methods to reduce memory usage. Xiangrong et al. [4] proposed an algorithm designed using a cell decomposition method and map updating method, which solves the problem of insufficient continuity and high-precision environmental modeling. By task decomposition and dynamic map updating, the shortcomings of local optimization of the A-star algorithm are effectively overcome. Li et al. [5] proposed an approach to eliminate the restriction of node movement direction in traditional A-star algorithms by extending the search neighborhood and designed a process to remove redundant sub-node expansions caused by neighborhoods in the same direction. Zheng et al. [6] improved the node search method and search speed by using the characteristics of jump point search, and added an angle evaluation cost function to the cost function of the A-star algorithm to find the path with the least number of inflection points, thereby improving the speed of path search. Wang et al. [7] introduced the factor of turning and used an edge removal method based on an improved A-star algorithm to solve the k-shortest path problem. It can effectively search for the shortest time path and avoid collisions. Chen et al. [8] processed concave obstacles into convex ones and extended obstacles. They limited the search direction of each node in the A-star algorithm based on the position of the target point relative to the starting point, which can effectively reduce the number of nodes that need to be searched during algorithm execution.

There are also many applications related to path planning in parking navigation systems. Dokur et al. [9] used an embedded system based on Arduino to test sensors. After analyzing the initial test results, they developed detection logic to identify a vehicle. This logic was extended to trigger a camera to capture an image of the vehicle for verification purposes. The system consists of Arduino, ultrasonic sensors, and a temperature sensor. Shin et al. [10] proposed a neural network-based predictive control method to dynamically find suitable weights for multiple factors, thereby achieving optimal performance of an intelligent parking guidance system Liu et al. [11] used an adaptive genetic algorithm to induce and simulate drivers, obtaining the optimal path and shortest time for the driver to reach each parking lot from the current location. They proposed a wavelet neural network model and used a particle swarm optimization algorithm to optimize the wavelet neural network model Ren et al. [12] proposed a new parking guidance system by integrating ZigBee, geomagnetic sensors, and RNN technology. This system uses RNN for the first time in geomagnetic vehicle detection to detect the status of parking spaces Khanna et al. [13] proposed a cloud-integrated intelligent parking system based on the Internet of Things. It includes an on-site deployed IoT module for monitoring and displaying the availability status of each parking space, a mobile application that allows end-users to check parking availability and reserve parking spaces accordingly, and a high-level view of the system architecture. In conclusion, there are many factors added to the research of path planning algorithms.

3  Implementation of Path Planning Algorithm

3.1 A-Star Algorithm

The A-star algorithm is a common heuristic algorithm. heuristic search is a search in the state space that evaluates the position of each search to get the best position, and then searches from this position until the target. the A-star algorithm is often used to calculate the shortest path between two nodes, which is implemented by the valuation function f(k):

f(k)=g(k)+h(k)(1)

The above equation g(k) represents the cost spent from the start point to node k and h(k) represents the estimated distance from node k to the goal point. f(k) is the sum of g(k) and h(k), and optimal path planning is the search for a minimum value of f(k). The A-star algorithm needs to maintain two lists, the open list, and the closed list.

The process of the A-star algorithm is shown in Fig. 1. The specific steps are as follows:

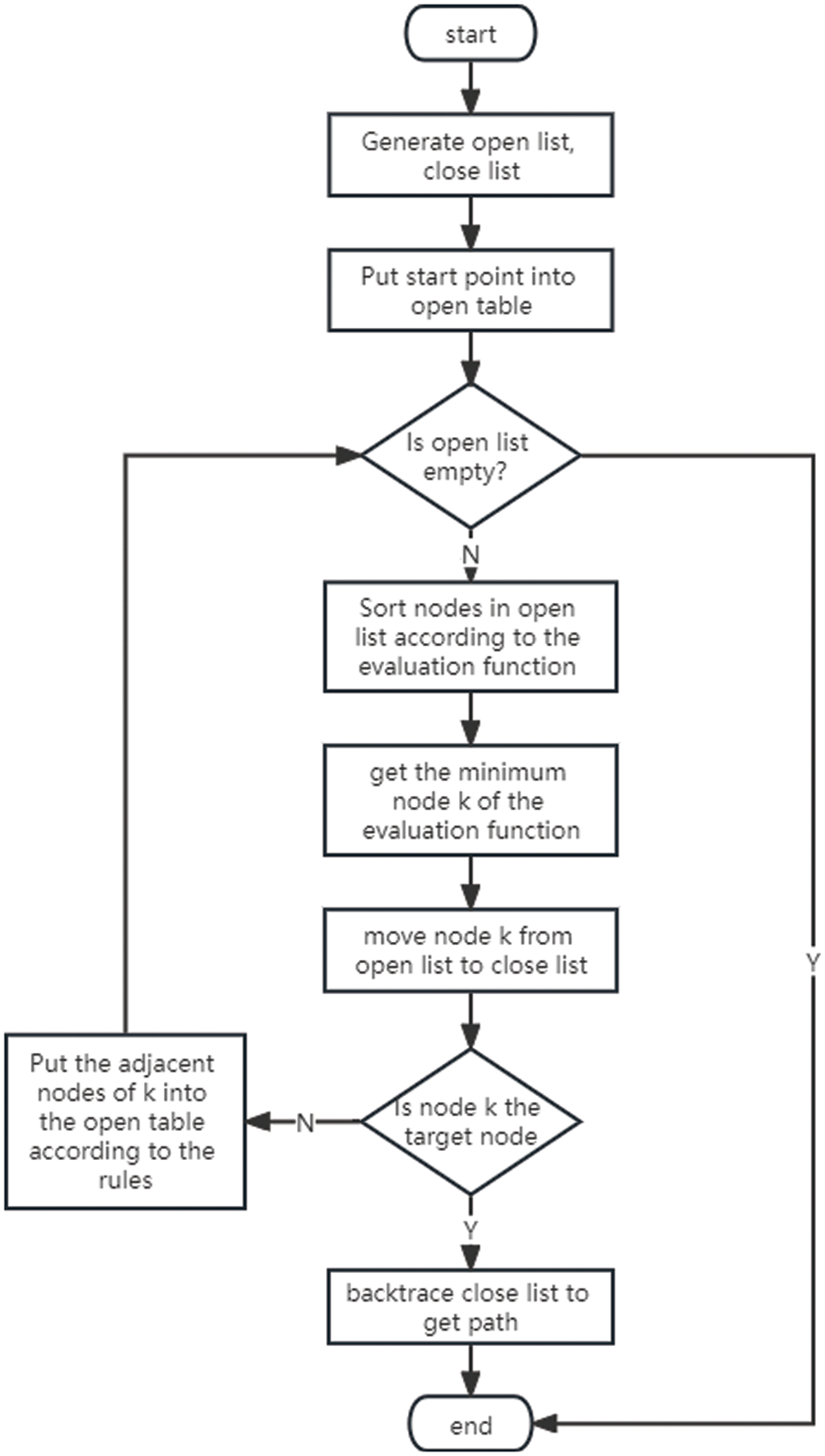
Figure 1: The A-star algorithm flow diagram

(1) First, add the starting point to the open list, then traverse the open list, find the node with the minimum f(k) value, and move it to the close list as the current node to be processed.

(2) Check each adjacent node of the current node one by one. If the adjacent node is unreachable or in the close list, ignore it. Otherwise, if it is not in the open list, add it to the open list, and set the current square as its parent square. If it is in the open list, check if this path is closed. If it is closer, set its parent square as the current square and recalculate g(k) and f(k).

(3) If the target point is added to the open list, it means that the shortest path has been found and the search is stopped. If the search for the target point fails and the open list is empty, it means that there is no path.

(4) From the target point, move each square along the parent square until the starting point is reached to form the shortest path.

3.2 Impedance Function Model

The road impedance function is a fundamental technique that plays a critical role in transportation planning and control. It represents the operational distance, time, comfort, or a combination of these factors between paths on a transportation network. The road impedance function refers to the functional relationship between traffic load, travel time, and driving speed during travel. The principles of traffic distribution in transportation planning are applied based on the road impedance function.

The solution method for the road impedance function adopts a combination of empirical and theoretical approaches. The main idea of this solution method is to determine the theoretical model of the road impedance function based on the relationship between the three parameters of traffic flow theory: traffic volume Q, speed V, and density K. Traffic volume refers to the number of participants in the traffic passing through a certain path on the road in a unit of time. The value of traffic volume is the product of speed and density. The calculation process of the road impedance function model is as follows:

T(p,q)=S(p,q)V(p,q)(2)

In the formula, T(p,q) represents the time it takes for a motor vehicle to pass through the path (p,q), where V(p,q) represents the speed of the vehicle passing through the path (p,q), and S(p,q) represents the length of the path (p,q).

K=1D(3)

In the formula, K represents the traffic density of the path, and D represents the distance between two vehicles on the path, which is the distance between the current vehicle’s front bumper and the next vehicle’s front bumper.

V(p,q)=V2±(v2)2−Q(p,q)∗VK(4)

In the formula, V(p,q) represents the speed of a motor vehicle passing through the path (p,q), where V represents the driving speed of a vehicle on the path in a non-congested state, and Q(p,q) represents the traffic volume on the path (p,q). When calculating the speed of a motor vehicle passing through the path (p,q), if Q≤VK/10, it represents that the path (p,q) is unobstructed and a positive sign is taken. If Q>VK/10, it represents that the path is congested and a negative sign is taken. If Q≥VK/4since a negative value cannot appear under the square root, the value under the square root is zero. The value of T(p,q) is used as the weight of the path in the A-star algorithm, which can obtain a time-optimal path planning considering the congestion status.

3.3 Fusion Function

This paper proposes a fusion function that comprehensively considers the impact of path length and path duration consumption on the weight in the A-star algorithm, and the degree to which they affect the path weight can be represented by the fusion function.

W(p,q)=S(p,q)+δT(p,q)(5)

In the above formula, W(p,q) represents the weight of path (p,q) when considering both path length and path duration consumption comprehensively.

δ=O1O2(6)

The value of δ in the above formula is the ratio of the average path length to the average path duration consumption in the map, which can make the impact of path duration consumption and path length on the weight of the path (p,q) equal.

O1=∑p=1N∑q=1NS(p,q)N2(7)

In the above formula, O1 represents the average length of each path segment in the path planning, and N represents the number of nodes in the path planning.

O2=∑p=1N∑q=1NT(p,q)N2(8)

In the above formula, O2 represents the average time consumption of each path segment in the path planning, and N represents the number of nodes in the path planning.

4  Simulation Experiment and Result Analysis

4.1 Creating Parking Lot Map Model

Obtaining data for vehicles driving in an underground parking lot is difficult. To visually compare and analyze the effectiveness of different path planning algorithm models, this paper creates an underground parking lot map as shown in Fig. 2. The map depicts a 35-m long and 15-m wide wall surrounding the parking lot.

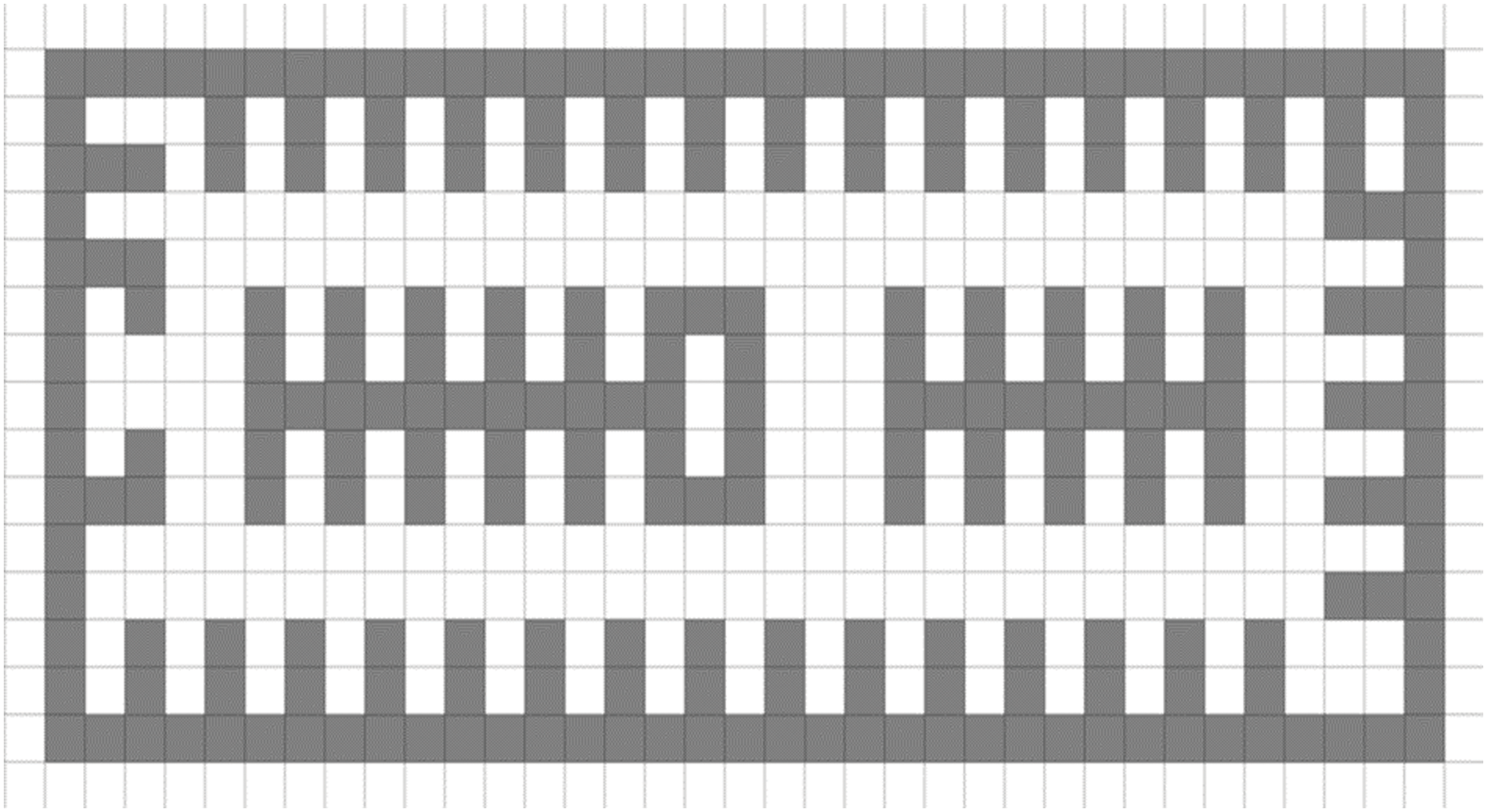
Figure 2: Underground parking lot floor plan map

The obstacles in an underground parking lot are significantly different from those found outdoors. To increase the realism of the environment, the map simulates obstacles such as parking spaces, staircases, and elevators found in underground parking lots, as shown in Fig. 3. The leftmost shape represents a parking space in the underground parking lot map. The middle shape represents a staircase, and the rightmost shape represents an elevator. The underground parking lot map includes a total of 52 parking spaces, 1 staircase, and 2 elevator shafts.

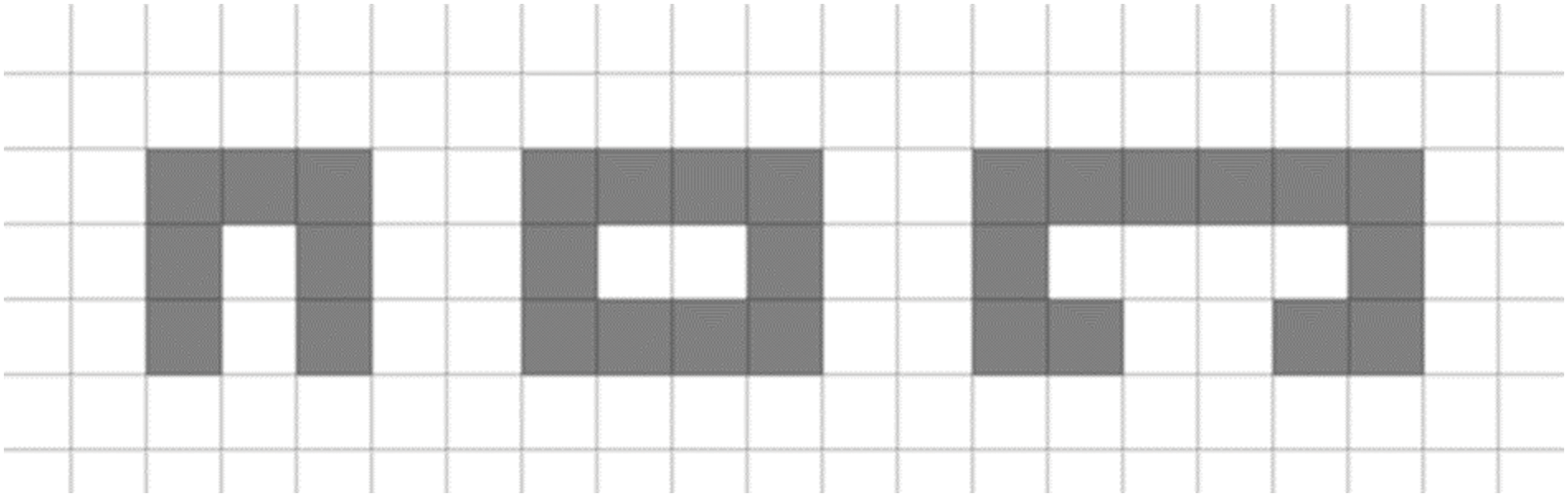
Figure 3: Obstacles in underground parking lot floor plan map

We can create a directed graph containing the entrance of the parking lot, the exit of the parking lot, parking spaces, road nodes, and obstacles based on the plan of the underground parking lot. At the same time, we can also construct other data about the N-order matrix S(p,q), Vm, Q(p,q) and D.

4.2 Simulation and Analysis

To compare and analyze the effectiveness of path planning algorithms, this paper takes the staircase entrance of a parking lot as the starting point and a certain parking space in the parking lot as the target point. The weight matrix representing the path distance, denoted as S(p,q), is used as the weight matrix for path planning. Similarly, the weight matrix representing the path duration, denoted as T(p,q), is also used for path planning. In addition, a joint function of path distance S(p,q) and path duration T(p,q) is used as the weight matrix for path planning. Based on the above three situations, the simulation results are shown in Table 1.

To compare and analyze the effectiveness of using path distance matrix and path duration matrix as weight matrices, the former representing path distance and the latter representing path duration, simulations were conducted for the optimal path from the starting point (shown in dark green in the figure) to the destination point (shown in red in the figure). When using the path distance matrix as the weight matrix, the simulation result in Fig. 4 shows that the path length from the starting point to the destination point is 108 m, and it takes 31 s to complete. When using the path duration matrix as the weight matrix, the simulation result in Fig. 5 shows that the path length from the starting point to the destination point is 111 m, and it takes 19 s to complete. The former path has a shorter length but takes 12 s longer than the latter path. Therefore, using the path duration matrix as the weight matrix is better for path planning than using the path distance matrix as the weight matrix, with less time cost. Meanwhile, the results of using the fusion matrix as the weight matrix were compared with using only the path duration matrix as the weight matrix. The former simulation result in Fig. 6 shows that the path length from the starting point to the destination point is 108 m, and it takes 20 s to complete. The former path takes only 1 s less than the latter path but is 3 m longer. It can be seen that using the fusion matrix as the weight matrix for path planning is more efficient and cost-effective than using only the path duration matrix as the weight matrix.

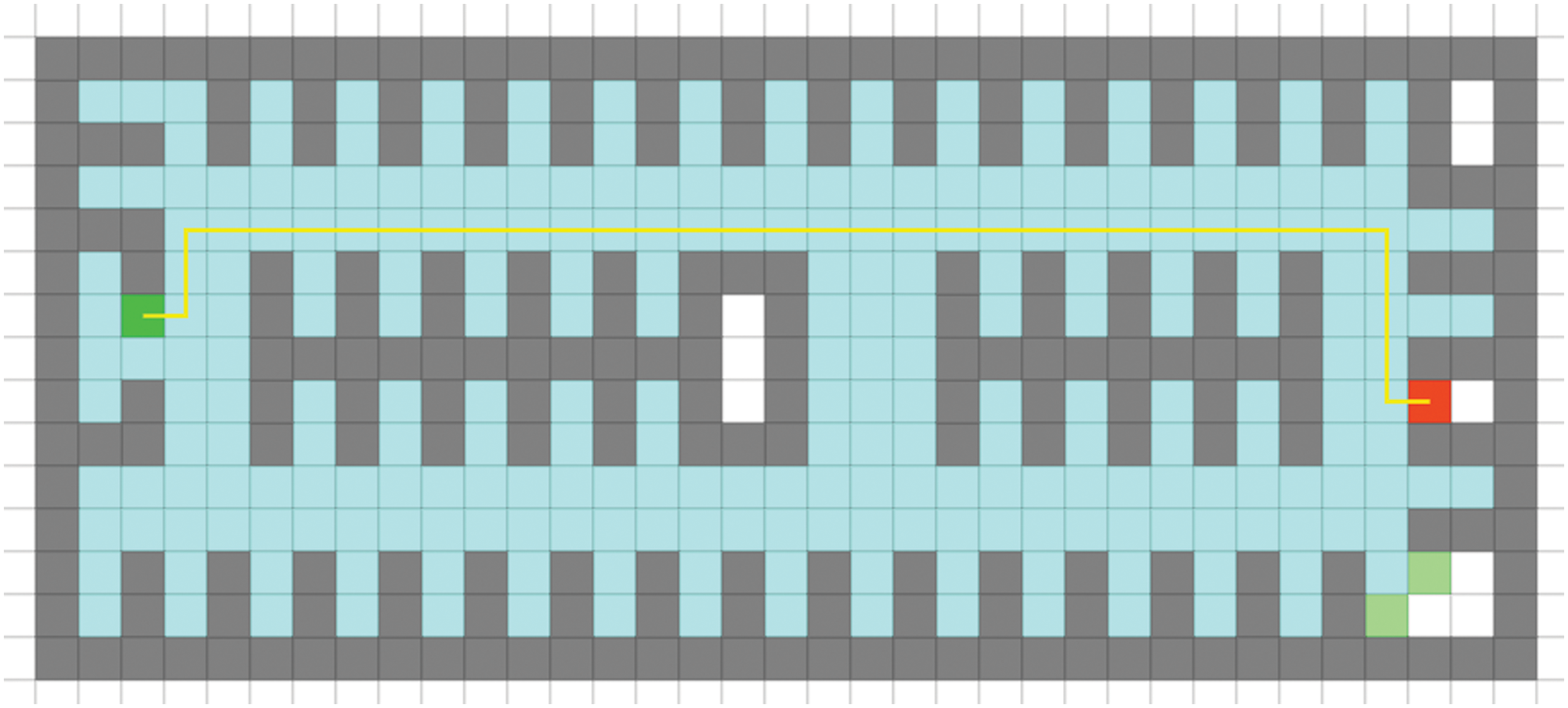
Figure 4: Simulation results of using path length matrix as weight matrix for path planning

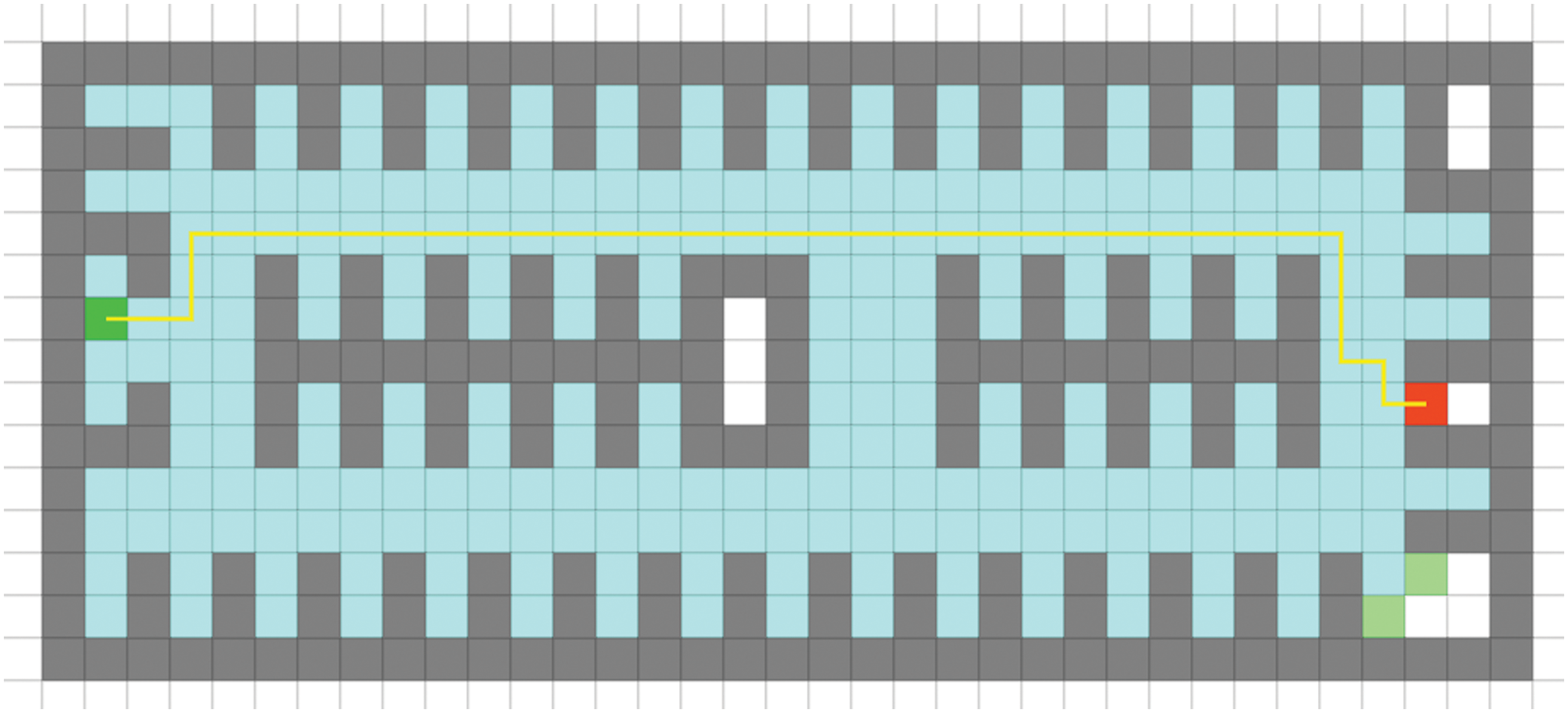
Figure 5: Simulation results of using path duration matrix as weight matrix for path planning

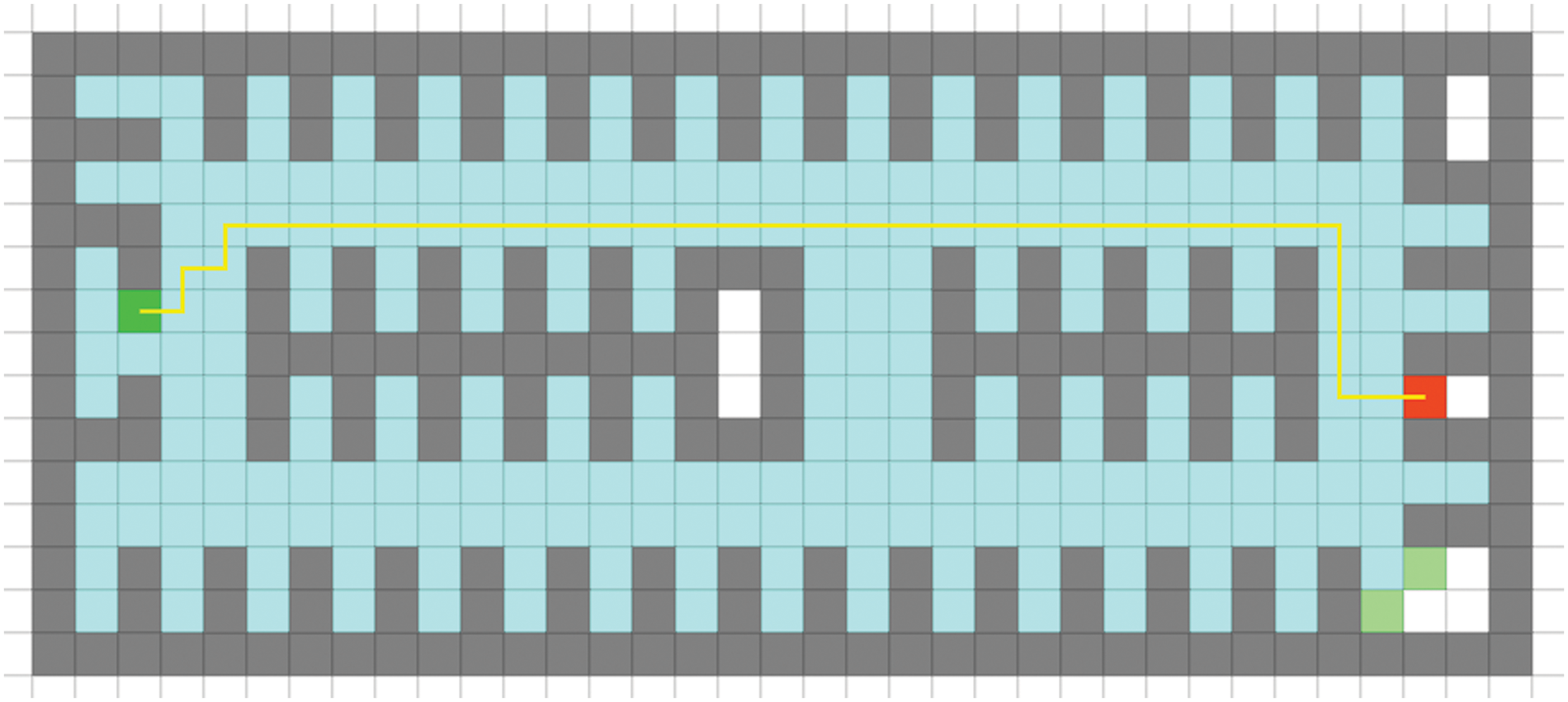
Figure 6: Simulation results of using fusion matrix as weight matrix for path planning

5  Conclusion

Currently, the internal structure of parking lots in cities is complex, and the signage inside the lots is not clear enough, leading to traffic congestion during the parking process. In this paper, we propose an improved A-star algorithm to solve the path planning problem in parking lots, and combine an impedance function model to use a fusion matrix composed of path length and path duration as the weight matrix of the A-star algorithm to improve the traffic efficiency of vehicles in the parking lot. Simulation results show that considering the fusion function of both distance and travel time results in more reasonable paths than considering only one factor. The improved A-star algorithm can be used for parking lot path planning, reducing congestion during the parking process, improving user convenience, and reducing parking lot management costs, and will have practical value in the field of intelligent parking.

Acknowledgement: Thanks to Professor Zhang and Professor Deng for their guidance in the process of completing this article.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the previous study.

References

1. A. Fahim, M. Hasan and M. A. Chowdhury, “Smart parking systems: Comprehensive review based on various aspects,” Heliyon, vol. 7, no. 5, pp. e07050, 2021. [Google Scholar] [PubMed]

2. S. Erke, D. Bin, N. Yiming, Z. Qi, X. Liang et al., “An improved A-star based path planning algorithm for autonomous land vehicles,” International Journal of Advanced Robotic Systems, vol. 17, no. 5, pp. 1729881420962263, 2020. [Google Scholar]

3. Y. Ma, Y. Zhao, Z. Li, X. Yan, H. Bi et al., “A new coverage path planning algorithm for unmanned surface mapping vehicle based on A-star based searching,” Applied Ocean Research, vol. 123, no. 3, pp. 103163, 2022. [Google Scholar]

4. T. XiangRong, Z. Yukun and J. XinXin, “Improved A-star algorithm for robot path planning in static environment,” Journal of Physics: Conference Series, vol. 1792, no. 1, pp. 12067, IOP Publishing, 2021. [Google Scholar]

5. X. Li, X. Hu, Z. Wang and Z. Du, “Path planning based on combination of improved A-STAR algorithm and DWA algorithm,” in 2020 2nd Int. Conf. on Artificial Intelligence and Advanced Manufacture (AIAM), Piscataway, IEEE, pp. 99–103, 2020. [Google Scholar]

6. T. Zheng, Y. Xu and D. Zheng, “AGV path planning based on improved A-star algorithm,” in 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conf. (IMCEC), Piscataway, IEEE, pp. 1534–1538, 2019. [Google Scholar]

7. C. Wang, L. Wang, J. Qin, Z. Wu, L. Duan et al., “Path planning of automated guided vehicles based on improved A-Star algorithm,” in 2015 IEEE Int. Conf. on Information and Automation, Piscataway, IEEE, pp. 2071–2076, 2015. [Google Scholar]

8. G. Chen, T. Wu and Z. Zhou, “Research on ship meteorological route based on A-star algorithm,” Mathematical Problems in Engineering, vol. 2021, no. 7, pp. 1–8, 2021. [Google Scholar]

9. O. Dokur, S. Katkoori and N. Elmehraz, “Embedded system design of a real-time parking guidance system,” in 2016 Annual IEEE Systems Conf. (SYSCON), IEEE, pp. 1–8, 2016. [Google Scholar]

10. J. -H. Shin, H. -B. Jun and J. -G. Kim, “Dynamic control of intelligent parking guidance using neural network predictive control,” Computers & Industrial Engineering, vol. 120, no. 9, pp. 15–30, 2018. [Google Scholar]

11. J. Liu, J. Wu and L. Sun, “Control method of urban intelligent parking guidance system based on Internet of Things,” Computer Communications, vol. 153, no. 4, pp. 279–285, 2020. [Google Scholar]

12. C. Ren, S. Lee, D. Jeong, H. Chen and Y. Xiao, “Parking guidance system based on geomagnetic sensors and recurrent neural networks,” Journal of Sensors, vol. 2022, pp. 1–12, 2022. [Google Scholar]

13. A. Khanna and R. Anand, “IoT based smart parking system,” in 2016 Int. Conf. on Internet of Things and Applications (IOTA), Piscataway, IEEE, pp. 266–270, 2016. [Google Scholar]