 Open Access
Open Access
ARTICLE
Securing Electronic Health Records with Cryptography and Lion Optimization
Department of Mathematics, Open Educational College, Kirkuk Branch, Kirkuk, 36001, Iraq
* Corresponding Author: Arkan Kh Shakr Sabonchi. Email:
Journal of Cyber Security 2025, 7, 21-43. https://doi.org/10.32604/jcs.2025.059645
Received 14 October 2024; Accepted 21 January 2025; Issue published 18 February 2025
Abstract
With the internet and modern mobile technologies, health-related information is readily available, and thus, the security aspect of health information is at great risk. Confidentiality and protection of medical information regarding patients are of prime concern in the context of sharing such data with different healthcare providers. On one hand, Electronic Health Record Systems (EHRS) and online sites have proved to be hassle-free ways of exchanging medical information between health professionals. On the other hand, data security issues remain a concern. The proposed paper presents an improvement in the security mechanism of EHRS by utilizing the Lion Optimization Algorithm (LOA) and the Secure Hash Algorithm (SHA-256) algorithm, which is a better security mechanism, and elliptic curve cryptography. This design will use LOA for the generation of an Elliptic Curve Cryptography (ECC) private key to improve the security of data storage in EHRs. The design will be further justified by comparing the encoding and decoding time against the other techniques such as ECC-GA-SHA-256. The results depict that the proposed model indeed gives faster encoding and decoding times. It also outperforms other encryption methods, as it presents encoding and decoding times higher by more than 18.89% when compared to those methods. This means there is great potential for the proposed approach to boost both the security and performance of EHRS. That is, this work could be one of the effective solutions to the security-related challenges of the EHR systems, as it was designed using LOA with SHA-256 and ECC.Keywords
Abbreviations
| FPA | Flower Pollination Algorithm |
| RSA | Rivest-Shamir-Adleman |
| A-BRSA | Attribute-Based Encryption |
| AES | Advanced Encryption Standard |
| BHS-ALOHDL | Blockchain Assisted Healthcare System Using Ant Lion Optimizer with Hybrid Deep Learning |
| CNN | Convolutional Neural Network |
| CPU | Central Processing Unit |
| CS | Cuckoo Search Algorithm |
| ECC | Elliptic Curve Cryptography |
| ECG | Electrocardiogram |
| EHRS | Electronic Health Record Systems |
| GA | Genetic Algorithm |
| GDPR | General Data Protection Regulation |
| HE | Homomorphic Encryption |
| HIPAA | Health Insurance Portability and Accountability Act |
| HO | Hostile Orchestration |
| IoT | Internet of Things |
| LOA | Lion Optimization Algorithm |
| LSTM | Long Short-Term Memory |
| LSTM-RNN | Long Short-Term Memory-Recurrent Neural Network |
| OBBO | Obstruction Bloom Breeding Optimization |
| RSA-AM | Rivest–Shamir–Adleman-Based Arnold Map |
| SALO | Salp-Ant Lion Optimisation Algorithm |
| SHA | Secure Hash Algorithm |
| SVD | Singular Value Decomposition |
EHRS is a complete electronic repository of the patient’s health information, such as medical history, diagnoses, medications, allergies, immunization records, laboratory results, and all other relevant clinical data, as explained in [1]. An EHR contains real-time, up-to-date, accurate patient information for the healthcare professional to make informed decisions on diagnosis, treatment, and follow-up care.
EHRs play a critical role in enhancing communication and coordination among healthcare practitioners, significantly improving patient safety and care quality. By streamlining administrative tasks such as reducing paperwork and eliminating redundant testing, EHRs alleviate the burden on healthcare professionals while promoting efficiency [2]. These records are securely maintained in electronic databases, ensuring access is restricted to authorized personnel directly involved in patient care. Moreover, EHRs enable data sharing across different healthcare facilities, facilitating seamless integration and coordination of care delivery, ultimately optimizing patient outcomes [3]. However, standardization of electronic usage protocols and practices is required for the realization of universal usability and interoperability. Strong mechanisms for access control, storage, transmission, and regulatory obligations are required to ensure patient privacy and the security of the data [4]. In this regard, a hybrid model has been proposed that will integrate the SHA-256 hashing algorithm, elliptic curve cryptography, and Lion Optimization Algorithm [5]. In this model, the ECC private key will be generated by LOA to optimize key generation to enhance the overall security of the system. LOA is a metaphorical optimization algorithm, taking inspiration from the behavior and social organization of lions. It improves the candidate solutions through exploration and exploitation, using the territorial defense and hunting nature of the lions to reach the optimal solution in a given population. As time goes on, the solution using the algorithm tends to converge to the best possible one, hence improving the security performance of the system. The public-key encryption method of ECC utilizing elliptic curves over finite fields has widely been recognized as having strong security combined with computational efficiency and shorter key length in contrast to the more traditional encryption methods. Due to these advantages, ECC finds a wide range of applications in secure messaging, digital signatures, and exchanging keys. The smaller key sizes of ECC will offer better computational and memory efficiency without compromising security [6]. In addition, SHA-256 is a hash function in cryptocurrency, taken to involves fixed-size 256-bit output that keeps data integrity to detect even slight changes during transmission [7]. Even when the input of the data alters slightly, the value of the hash completely changes, hence an indication of tampering [8]. Key exchange with ECC and digital signature, along with integrity using SHA-256, makes the communication and data exchange secure over the Internet. Using such hybrid techniques, namely LOA for the generation of keys, ECC for encryption, and SHA-256 for integrity verification, healthcare systems can ensure more security for EHRs. It ensures the privacy of patients while still allowing the sharing of information to take place, thus improving effective, efficient, and secure health delivery.
Security concerns of EHRS data from unauthorized access are very basic issues related to any information of patients concerning confidentiality and integrity. The breaches in EHRS data without authorized access can easily lead to a situation with serious consequences, such as compromising the confidentiality of patients and even manipulation of sensitive health data. For that, methods for strong encryption of storage and transportation of data need to be developed. The most important strategies to protect this information involve encrypting it before any transmission is made, so only trusted personnel would be able to read such information. This paper will present a method of increasing EHRS data security by making use of LOA for generating a private key for ECC. Further, it embeds the SHA-256 algorithm for cryptographic hashing to enhance data security. Conclusively, LOA, ECC, and SHA-256 provide an integrated solution in this proposed work for holistic fortification in strengthening EHRS security from unauthorized access, and also for reliable transmission and storage of data.
The contribution this paper makes to the security of EHRS is done in four important ways. First, it introduces a new concept in EHRS security by integrating Elliptic Curve Cryptography, the Lion Optimization Algorithm, and the SHA-256 cryptographic hashing algorithm. Second, it creates an effective generation method of private keys in ECC with the LOA for optimized key generation. It refines the study of security in data by performing encryption on ciphertext with ECC and LOA, which is further strengthened by the SHA-256 algorithm. Finally, empirical evaluation models the proposed approach along with other existing approaches for a performance study of encryption speed and security strength.
The rest of the paper is organized as follows: Section 2 presents some related works in this field. Section 3 explains LOA and ECC. Section 4 proposes the model of EHRS that will be implemented. Section 5 compares the proposed approach to other existing approaches. Section 6 discusses how the proposed model could be integrated into existing EHRS or its impact on system usability. Section 7 includes a discussion on compliance with data protection laws and ethical considerations in healthcare. Finally, Section 8 concludes the study and outlines the future directions.
In the last decade, the security and privacy challenges in EHRS have emerged as a serious health concern; therefore, many innovative methodologies have been proposed, keeping in mind confidentiality, the integrity and availability of medical data are critical in healthcare systems. For instance, the study presented in [9] introduces robust authentication mechanisms and anonymity-focused security measures aimed at safeguarding user privacy in telecare medical information systems. That method uses biometri LOA and pseudonyms, which ensure the confidentiality of the patients’ identities, while the healthcare providers can obtain the medical data. In the same context, reference [10] proposes a data aggregation scheme in a manner that ensures the preservation of privacy, which uses the bilinear ElGamal cryptosystem in order to protect the sensitive information of patients when their medical data are aggregated. Another novel approach was presented in [11] in order to secure ECG data in telecare medical information systems. It is an approach that makes use of SVD in encryption and data compression; this goes a long way in adding security to the data without tampering with the quality of the data while in transmission. The integrity of the data would thus be intact. A fragile watermarking scheme for detecting medical images when tampered with is also supported in. Using the embedding of marks, done through a combination of discrete wavelet transform and singular value decomposition on medical images, this mechanism identifies any modification and hence can maintain data integrity [12]. It also proposes two methods in for protecting patient privacy in IoT-based healthcare systems [13] a mechanism called PrivacyProtector, which does not disclose the patients’ identity and allows data collection; and a quantum information hiding approach based on quantum entanglement and quantum teleportation that sets a secure channel for transmitting medical images across an unsecured channel. In [14], the authors propose a cancelable finger-vein biocryptosystem that leverages smart card technology to improve security in mobile healthcare data while ensuring the preservation of user privacy. A cancelable biometric template is generated from the finger-vein pattern of a user.enabling secure and reliable authentication without revealing or compromising sensitive identity information. Similarly, the study in [15] introduces an efficient public-key cryptosystem implemented on a NanoPi Fire platform, designed to safeguard medical data. This system ensures robust security while offering fast encryption and decryption processes, facilitating real-time protection of sensitive medical information. Another state-of-the-art approach, proposed in [16], has been oriented toward the secure audio transmission of medical reports for processing visas with a view to mitigating the spread of communicable diseases among the immigrant population. This would improve the security and privacy of data while providing better health access to immigrants through the secure transmission of sensitive information regarding patients’ medical data. The idea in proposes a secure cloud-based medical data processing methodology that involves watermarking and encryption of the medical data as a way of ensuring confidentiality and integrity, and at the same time allowing for efficient and secure sharing of the data. All these cumulatively have attained milestones in securing medical data sharing while keeping patients’ privacy [17]. Various advanced techniques have been implemented to address the security and privacy challenges of EHRs. Various methodologies have been proposed to enhance security and privacy, including biometric-based authentication systems, techniques for secure data aggregation, approaches integrating compression and encryption, the application of watermarking methods, advancements in quantum information hiding, and the utilization of cancelable biometric templates [18]. Furthermore, the study in [19] proposes a novel approach integrating the CS, SHA-256, and ECC to enhance EHR system security. By utilizing CS to generate ECC private keys, this method significantly improves the security of data storage while achieving faster encoding and decoding times compared to conventional techniques. In another significant contribution, reference [20] investigates the security of medical images in IoT healthcare using cryptographic and optimization approaches. The framework utilizes RSA-AM, HO, and OBBO to optimize key management for enhanced encryption and decryption. Similarly, research in [21] explores the potential of HE to secure EHR systems, enabling data processing on encrypted information without compromising privacy. The study demonstrates the feasibility of HE in enhancing both data confidentiality and system performance for healthcare analytics and machine learning. Additionally, reference [22] discusses the safeguarding of medical images in IoT healthcare through lightweight cryptographic techniques, incorporating deep learning-based encryption and decryption networks. This approach enhances the confidentiality, integrity, and availability of medical images, providing a secure framework for medical imaging in connected healthcare environments.
The work in [23] proposed the Blockchain-Assisted IoT Healthcare System, BHS-ALOHDL, which combines the Ant Lion Optimizer for feature selection, a hybrid deep learning model comprising CNN and LSTM for intrusion detection, along with the FPA for hyperparameter optimization. This approach has been able to show superior detection accuracy with enhanced system security on benchmark datasets. Similarly, reference [24] proposed a secured cloud-based medical data-sharing system using a hybrid A-BRSA encryption model that integrates attribute-based encryption with B-RSA. It utilized the SALO to select the best key value and demonstrated that it improves the performance of this system in secure medical data sharing within cloud-assisted environments. Finally, IoT-based patient monitoring was proposed by [25] integrating a hybrid LSTM-RNN with the Lion Optimization for feature selection. It achieved 99.99% accuracy regarding the prediction of cardiac health conditions based on real-time data for early detection and personalized interventions. These studies together reveal the potentials of optimization algorithms along with advanced computational models to resolve some key security, efficiency, and prediction issues related to IoT healthcare systems.
This section presents an overview of the LOA and ECC algorithms.
3.1 Meta-Heuristic Lion Optimization Algorithm
The LOA is a metaheuristic stochastic approach designed for solving optimization problems [5]. Algorithms based on metaheuristics are effective in giving good solutions in each iteration. An LOA typically generates a random population in the solution space. Each solution here is called a “lion,” modeled as Eq. (1):
(1)
Here, are dimensional positions of individual lions, while presents the number of dimensions in the search space. A fraction P of the population consists of nomadic lions that are generated randomly, and the rest may be resident lions. The position of every lion denoted by y has n elements as: y = . It represents the position of the candidate solution in the search space. Further, the algorithm calculates the fitness value of each lion. The fitness function specifies how the candidate solution will deserve to fit concerning the problem it will be applied to. Then, LOA goes into the following process:
Step 1: Initialization: The population is initialized randomly throughout the solution space, and the position of the lions is kept in a matrix. An objective function calculates the fitness value for every lion and then sorts and stores it in a matrix as Eq. (2):
(2)
where is the fitness value and represents the dimensional space.
Step 2: Mating: The generation of new solutions through the combination of the existing ones, with operations like mutation and crossover. Eliminate worse solutions to retain better ones only.
Step 3: Territorial Defense: This step compares the fitness values for nomadic lions against those of resident lions. If a better fitness value of a nomadic lion within the resident lion exists, it replaces the resident lion.
Step 4: Territory Takeover: In this phase, all resident lions are sorted according to their fitness values. The weak males get expelled to become nomads, and the stronger ones continue as resident lions.
The LOA does a good job in feature selection and enhancing the generalization of classification models.
3.2 Balancing Exploration and Exploitation in LOA
A critical aspect of the Lion Optimization Algorithm (LOA) is balancing exploration and exploitation within the solution space. This balance ensures that the algorithm effectively searches for potential solutions (exploration) while converging on the optimal ones (exploitation).
LOA achieves this balance by the following mechanisms:
1. Population Division: The population of the lions falls into two portions: The resident lions and the nomadic lions. The resident lion optimizes the solution in his territory by refining the solutions, while the nomadic lion increases exploration through the search for new areas in the solution space to maintain the diversity and avoid premature convergence.
2. Territorial Defense and Takeover: The strong resident lions replace the weaker ones to defend their territories. If the nomadic lions are superior, they can take over the territories, hence introducing better solutions and maintaining dynamic balance between local refinement and global search.
3. Crossover and Mutation: Mating introduces diversity into the gene pool, exploits superior characteristics, and passes those on to new generations; adjustable probabilities for mutation are ways one can manage the intensity of exploration.
4. Parameter Tuning: Parameters like the number of prides, pride size, and the probability of nomadic replacement directly affect the balance. For instance, increasing nomadic replacement promotes exploration, while a larger number of prides increases local exploitation.
5. Dynamics of Iteration: While in the early iterations, exploration dominates in order to have a broad search in the solution space, in later stages, the focus shifts toward exploitation to refine the best solutions in order to converge on the optimal result.
These mechanisms guarantee LOA adaptability and effectiveness in a wide range of optimization tasks. In the context of this work, this balance is fundamental for the generation of secure and optimized private keys: while exploration will provide randomness to robustly populate cryptographic properties, exploitation will tune the keys toward optimal security properties.
3.3 Elliptic-Curve Cryptography
ECC is a powerful technique of cryptographic that leverages the mathematics of elliptic curves over finite fields to achieve secure communication. ECC is renowned for its efficiency, offering strong security with relatively short key lengths, making it faster than many traditional encoding techniques. The security of ECC is rooted in the computational complexity of the discrete logarithm problem over elliptic curves, which ensures resistance to cryptographic attacks [6].
In ECC, two parameters, and , are selected from a finite field , and the elliptic curve is defined as a set of points satisfying the equation:
(3)
The curve includes a set of points, often known as , with being an example of a point on the curve. The ECC encryption process involves the following steps:
1. Parameter Initialization: This step establishes the necessary parameters and initializes data structures, including the elliptic curve , a base point , and the prime . Additionally, random values or initial parameters may be generated as needed.
2. Key Pair Generation: ECC employs a key pair, which is comprised of two distinct but mathematically related keys: a public key and a private key. The private key, denoted as , is a randomly selected number from the finite field in the range . The corresponding public key, , is computed by
3. The public key is primarily utilized for encoding information conversely, the private key plays a crucial role in decoding the encrypted data. The key pair is generated through a process designed to ensure that deriving the private key from the public key is computationally infeasible.
4. Encoding: The encoding process begins by converting plaintext data into a binary format and mapping it onto the elliptic curve as a set of points . Encryption is then performed using the public key, rendering the information unreadable without the corresponding private key. The ciphertext consists of two components, as shown in the equation:
(4)
Here, is a randomly chosen number used to enhance encryption security.
Decoding: Decoding involves recovering the original data using the private key . The ciphertext is decrypted through the equation: .
Substituting the values yields:
(5)
This would ensure that only the owner of the private key successfully decrypts the encrypted data, and confidentiality and security remain paramount during communication. If the elliptic curve algorithms are used properly, their mathematical difficulty ensures that unauthorized access is not gained, and sensitive information is available to the recipient it was intended for. This is a strong mechanism and one of the backbones of secure systems: it protects data integrity and builds trust in digital interactions.
A random private key generation is considered paramount to the secure encryption and decryption of data in ECC. This paper aims at proposing a method where LOA could be used for generating such a key. The randomness within a private key is actually one of the critical keys that decide upon the quality of sensitive data encryption on ECC. These optimization techniques include LOA, which essentially function to find the optimal set of solutions available within a pre-defined search space. In this regard, the goal of LOA would be to determine the optimal privet key (Pr) for ECC so that the ciphertext can effectively be decrypted back into its original plaintext securely and accurately.
The fitness degree of the solution of a private key might be obtained by a comparison with the decrypted plaintext against its original plaintext. The fitness function could be based on security and accuracy in the process of decryption. The objective function of LOA here may, therefore, be formulated as Eq. (6):
(6)
In this model, the ciphertext represents the encrypted output generated after the encryption process, while corresponds to the original plaintext. The decryption process, denoted as , involves decrypting using the private key . The similarity or distance between the original plaintext and the decrypted plaintext is computed using the function . To frame the problem as a minimization task, a negative sign is introduced in the objective function, aiming to minimize the discrepancy between the original text and its decrypted counterpart.
The proposed model comprises a series of structured steps designed to achieve optimal results, detailed as follows:
1. Initialization: The Lion Optimizaton Algorithm (LOA) is initialized by defining key parameters, including the number of prides (n), the size of each pride (m), the detection probability of foreign solutions (p_a), the step size (α = 0.01), and the maximum number of iterations. These parameters establish the foundation for the optimization process.
2. Optimization Process: During every iteration of LOA, both the exploration and exploitation strategies create new candidate private keys or solutions. The quality of each candidate solution is evaluated based on the objective function as given by Eq. (6). Hence, the inferior solution would be replaced by the better one, which serves to help the process incrementally refine the private key candidates.
3. Elimination of Inferior Solutions: “Weak” prides are identified by generating random numbers and comparing them against the detection probability . If a pride’s fitness falls below a defined threshold, it is replaced with a newly generated result. This iterative process continues until either the maximum number of iterations is reached or an optimal solution is identified.
4. Termination: The process concludes when the best-performing pride achieves the desired solution quality. Experimentation determines the optimal values for parameters such as and , further refining the algorithm’s performance.
The proposed scheme significantly enhances the efficiency of automating the assignment of private key strings, eliminating the need for manual input. In this approach, the Level of Assurance (LOA) mechanism is responsible for generating private keys for users (e.g., User 1 and User 2), while the corresponding public key is derived from the private key and a computed point on the ECC curve. The algorithm is designed to perform up to 150 iterations to optimize the solution.
Algorithm Overview:
• Initialization: The equation of ECC curve should be defined, and public key point Q calculated.
• Private Key Generation: LOA computes the optimal value of private key.
• Encryption: The SHA-256 algorithm is run over the plaintext after private key generation, followed by encryption with ECC.
• Decryption: In the process of decryption, the hashed values are tempered using XOR and left-shift operations, and then decrypted by ECC to retrieve the original plain text.
It offers a variety of major advantages: time-saving, security in communications, and generation of a private key automatically. Increased security in the encryption process through LOA-based private key optimization is one of the benefits. SHA-256 hashing and the incorporation of extra operations like XOR and shift-left contribute to the toughening of security mechanisms in the model.
In general, the proposed model represents an efficient and secure model for private key assignment and, respectively, data transmission. The encoding and decoding operations in the design with ECC, in combination with the XOR and shift-left techniques, have strong encryption that can transmit messages securely between different users. Fundamentally, the four phases—Encoding (1), Encoding (2), Decoding (1), and Decoding (2) strengthen the core of the model through the integration of ECC, sealing in confidence and integrity of data to be transmitted. Then the decryption will operate the ciphertext by XOR and shift left operations before final decryption using ECC for complete coverage in the entire process. As shown in Algorithm 1, and Fig. 1.

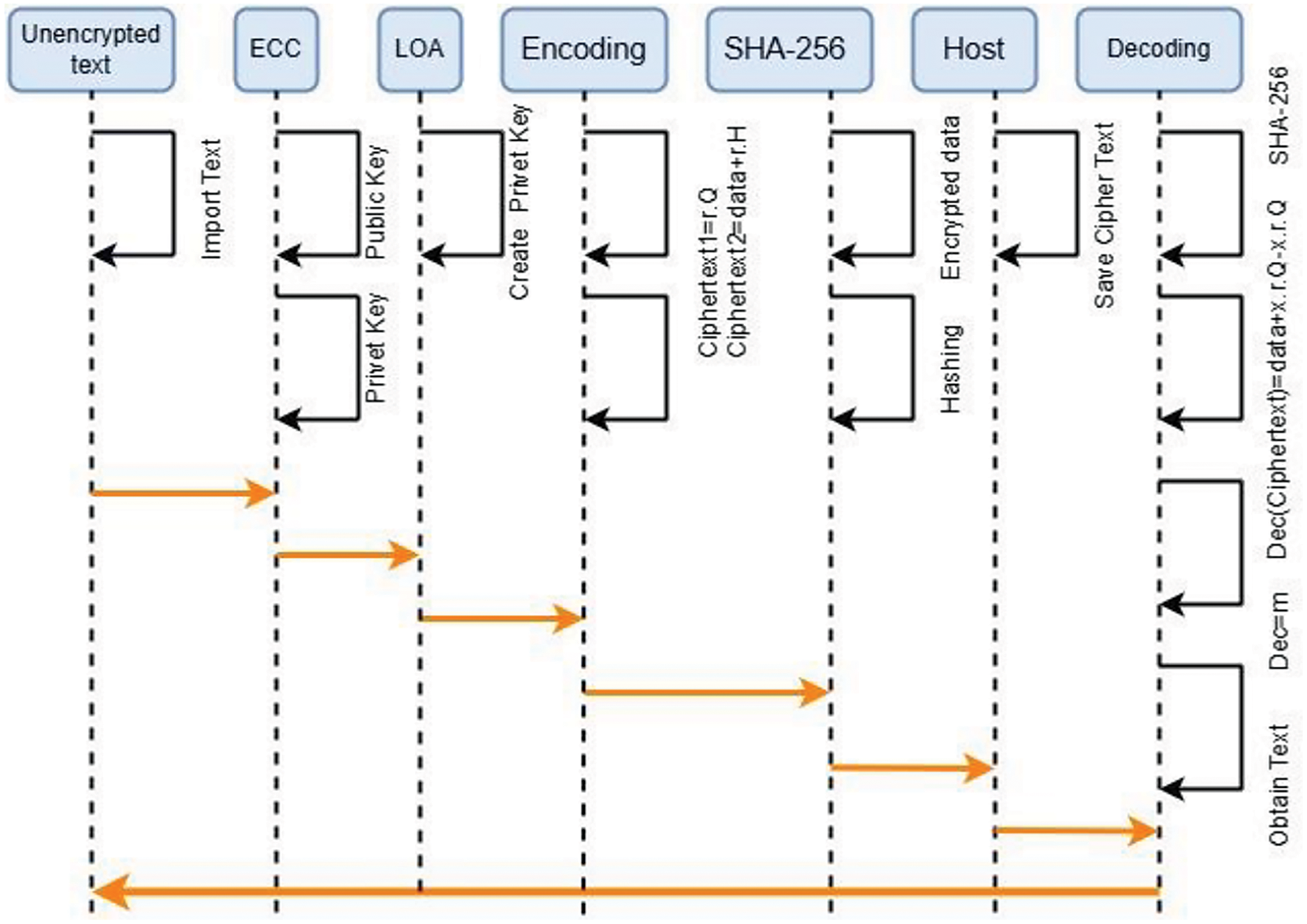
Figure 1: Diagram of the proposed model
This section analyzes the encoding and decoding throughput of the proposed model, focusing on its processing efficiency. The analysis examines performance across varying file sizes and iterations, highlighting the model’s speed, scalability, and resource optimization compared to existing techniques. This provides insights into its practicality for real-world applications. The experimental evaluation was conducted on a Windows 10 Pro system using a custom implementation developed in C# within the Microsoft Visual Studio 2012 development environment. The test setup featured an AMD E-350 processor operating at 1.60 GHz, paired with 4 GB of RAM.
An initial population size was selected depending on the key length. In this experiment, random integers varying from 0 to 127 were used for the selection of the initial size of the population, and perhaps necessary to note directly affected the performance of the system both in encoding and decoding operations. Therefore, the evaluation of performances for the platform was done based on this experimental setup.
Besides, this evaluation tried to look at the model, in respect of efficiency in handling the cryptographic operations, to get insights about its performance in terms of throughput, and computing speed in different scenarios, hence such results are important for our decision on practicality and scalability of the model in different scenes.
While the proposed model demonstrates significant improvements in encoding and decoding times, it is also crucial to evaluate its security robustness against potential vulnerabilities:
Resistance to Side-Channel Attacks
Side-channel attacks exploit physical information leaks, such as timing, power consumption, or electromagnetic emissions, to extract cryptographic keys or sensitive data. Although the proposed model integrates ECC and SHA-256, it does not explicitly address resistance to these attacks. Simulations or experimental setups testing such conditions would provide valuable insights into its robustness. Countermeasures such as constant-time implementations, noise addition, or masking techniques could be incorporated to strengthen the system further.
Quantum Computing Threats
The traditional cryptographic schemes, like ECC, are under threat with the advancement in quantum computing due to algorithms like Shor’s, which solves discrete logarithm problems efficiently. Though this work is on optimizing the ECC using LOA, the future work would be to incorporate quantum-resistant cryptography techniques, such as lattice-based or hash-based cryptography into the system for long-term security.
Attack Scenarios Simulated
For example, stimulation attacks-such as differential power analysis or timing attacks-or simply fault injection may provide deep insights into the aspects of the performance of the model that are exposed to adversarial conditions. Interaction testing, such as measuring system response to injected faults related to encoding and decoding techniques, may serve to highlight and ensure the mitigation of potential “weak links”.
Decoding and Encoding times
This section discusses the encoding and the decoding speeds of the proposed model. The results are represented as Figs. 2 and 3, respectively. Fig. 2 describes the encoding time in millisecond units for the proposed model based on different iteration types with an initial population of size 20. Based on the data, the number of iterations will decide the encoding time, and the minimum encoding time is at 50 iterations. For instance, a file of 10.000 KB takes 1.523 ms for 20 iterations to encode, 1.403 ms at 50 iterations, and 1.499 ms for 70 iterations. Likewise, and in the same stride, a file of 50.000 KB would encode for: at 20 iterations, 5.608 ms; at 50 iterations, 4.245 ms; and, finally, at 70 iterations, 4.583 ms. The findings are substantiated by the data illustrated in the accompanying figures, derived from a comprehensive experimental evaluation of the proposed model.
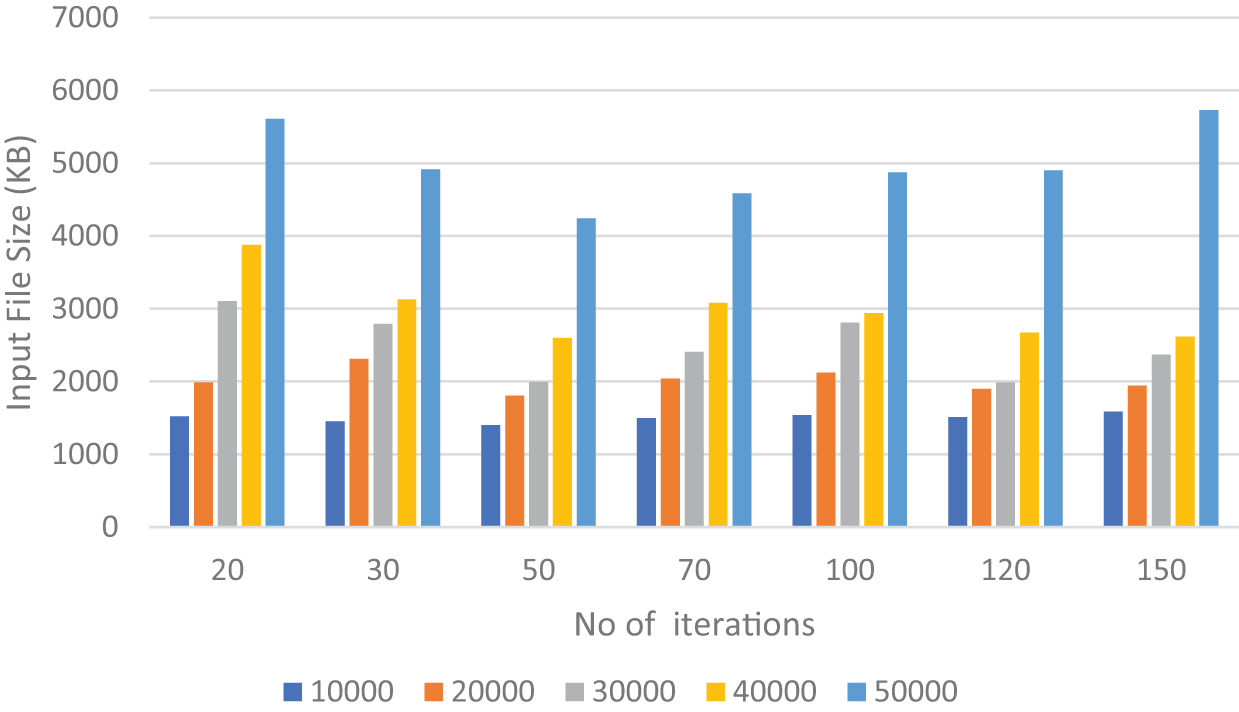
Figure 2: Encoding time against no. of iterations
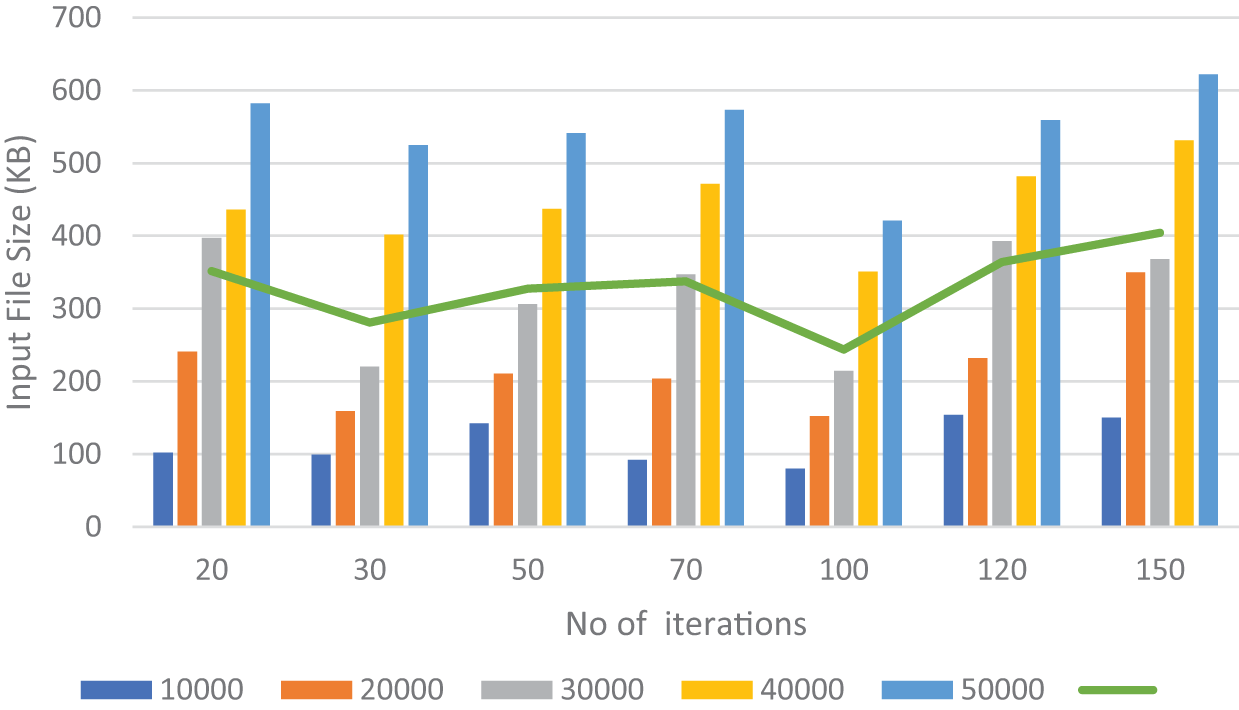
Figure 3: Decoding time as a function of iterations
Fig. 3 depicts the decoding time in milliseconds at different iterations of the proposed model. It should be considered that the target is always to have a decoding time less than the encoding time to make the system more efficient and responsive. This can be observed from the results, where the decoding time has its minimum at an iteration of 100. For instance, the decoding time for a file of 10.000 KB is 102.139 ms when iterations are 20, 92.152 ms at 70 iterations, and 80.005 ms at 100 iterations. In the same manner as above, for a file of 50.000 KB, decoding time is 582.091 ms at 20 iterations, 541.249 ms at 50 iterations, and 421.102 ms at 100 iterations. These values show the best performance of the proposed model by increasing iteration number up to 100 and, after that, it improves for higher iterations.
Fig. 4 illustrates the variation in mean encoding and decoding times across iterations for the proposed model. The results indicate that the most efficient encoding time occurs at the 50th iteration, measured at 2602.2 ms, while the most efficient decoding time is observed at the 100th iteration, with a value of 2509.101 ms. These findings demonstrate that the proposed model achieves the desired security level while optimizing execution time.

Figure 4: Average encoding and decoding times through different iterations
Based on this, one might have come to a conclusion that the suggested model is appropriate for the data encoding process in an unprotected environment. The second point the findings obtained within this test relate to the efficacy of the proposed model as for the speed of data encoding/decoding. From that very perspective, the number of iterations for optimal value represents 50 iterations from encoding time and 100 from the decoding time. The obtained results provide insight into how more efficient encoding algorithms could be designed in the future. This contribution is, of course, great to cryptography. Besides, the better execution time for the proposed model provides practical benefits related to the processing of large sizes of files for applications.
The experiments were conducted with the aid of Visual Studio, for a key length of 128 bits. In this section, a comparative study between the RSA [26] vs. proposed model depending on the evaluation of 14 different sizes files is presented.
The study primarily compares the proposed model with traditional cryptographic methods like AES and RSA. Future work should include comparisons with modern advancements, such as lightweight and post-quantum cryptography, to provide a comprehensive evaluation of the model’s performance and adaptability in diverse scenarios.
5.2.1 Encoding and Decoding Based on Proposed Model and AES
In this regard, the main objective of the present study was set to investigate the efficiency of the proposed model and AES by encoding and decoding times. The results derived from the study depicted that the proposed model always outperformed AES, especially at large data sizes. A 50 MB size is shown in Table 1. For example, at a file size of 50 MB, the encoding time of AES is 7.011 s, while in the proposed model, it requires only 4.69 s. This depicts that as far as the processing time is concerned, huge improvement has been achieved. Fig. 5 depicts that the encoding time of the proposed model is far lesser compared to AES, which accounts for approximately 33.11% reduction in execution time to encode a 50 MB file. In addition, performances of the proposed model have always outperformed those from AES so far; hence, it established its efficiency advantage over the current approach of AES.


Figure 5: Comparison of encoding times between the proposed model and AES
The time comparison for decoding is shown in Fig. 6, where the proposed model, compared to AES, takes less time for decryption. As rules and table-wise, the numbers of computation required to encode or decode by the proposed model are lower in number compared to that of AES; thus, the proposed is faster. These findings showed that the encoding time taken by the proposed model is much lesser, which achieved about 12.92% faster execution time for a 50 MB-sized file in the process of encoding.
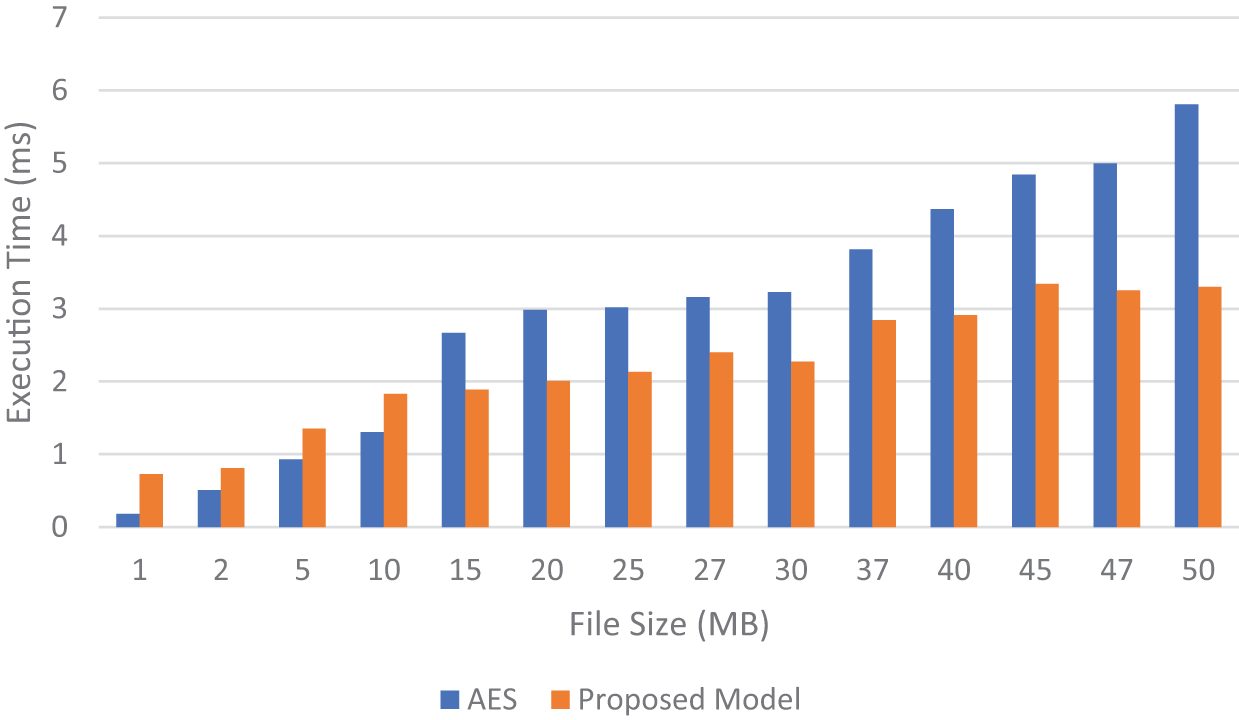
Figure 6: Timing comparison between proposed and AES decoding
Its encoding and decoding are way faster than those of the AES, making this model much more efficient and feasible for cryptographic applications, especially under resource-poor circumstances. The contribution of ECC thus provides the suggested model with less computational complexity; hence, it makes it speedier and suitable under conditions where immediacy is required. In fact, this presents the model as promising for secure data chatting.
In a nutshell, the proposed model has proved better performance than AES by a factor of encoding and decoding time, which makes it stronger and more practical in actual cryptographic applications, especially when resources are limited. The model, with an integration of ECC, has demonstrated effective reduction in computational overhead hence improving its operating efficiency. Therefore, with this model, real-time applications will be highly convenient, providing a strong as well as efficient solution toward secure data communication.
5.2.2 Encoding and Decoding Based on the Proposed Model and RSA
This section presents a comparative study of the proposed model against the RSA algorithm as referred to in [26]. The main aim of the evaluation is to determine the performance of the proposed model in comparison with RSA using the time consumed in encoding and decoding.
The results for the above are shown in Table 2, where one can appreciate how the proposed model outperforms RSA with a large margin, considering the huge dataset of 50 MB.

Taking the case of the RSA encoding time of a file sized about 50 MB, the encoding time is 460.918 s; for the proposed model, it takes only 4.88 s, and as observed, this forms a great advantage in decreasing the processing time. With a huge key size, RSA has a huge computational cost. An alternate efficient approach comes with ECC as under discussion in [27]. With ECC, higher processing speed is achievable with much smaller key size and less memory usage. The proposed model and other models based on ECC may be more applicable to the resource-poor device hence allowing for higher speed real time computation.
Fig. 7 presents a comparison of the encoding time between the proposed model and the RSA method, revealing that the proposed model achieves significantly shorter encoding times. Specifically, it reduces the encoding execution time by approximately 98.94% for a file size of 50 MB. Furthermore, the proposed model consistently outperforms RSA, highlighting its superior efficiency.

Figure 7: Encoding time comparison of the proposed model against RSA
Fig. 8: Performance comparison between the proposed model and RSA during decoding. From this figure, it can be seen that the proposed model possesses very high performance in terms of speed. This is attributed to its efficient key generation mechanism and efficient decryption mechanisms. It is suitable for applications requiring fast processing, such as those involving big data sets or tasks where timing is critical.

Figure 8: Comparison of decoding time between RSA and proposed model
This is because the fact that RSA applies complex encryption and decryption procedures could be an important factor contributing to its slowness, considering the algorithms make heavy computation of modular exponentiation together with calculation of a private key exponent, hence making them slower than other models. While, on the other hand, the encoding and decoding processes proposed by the model require fewer computations. Hence, it can assure faster processing speeds than in RSA. Therefore, the computational requirements are relatively smaller in the proposed model, which explains its better performance.
In brief, the model proposed in this work is faster compared with AES-RSA in both encoding and decoding, hence more efficient and viable for cryptographic applications, especially under scarce resources. ECC used in the proposed model reduces computational overhead; thus, it is faster and suitable for real-time applications. With regard to the discussion above. The proposed model demonstrates superior decoding speed and efficiency, making it ideal for high-performance applications.
5.2.3 Encoding and Decoding Based on GA, and Proposed Model
This section compares the performance of the metaheuristic Genetic Algorithm [28] with that of the proposed model in generating the keys in ECC. Both algorithms employ selection, crossover, and mutation operators to optimize ECC solutions, enabling efficient key generation and improved cryptographic performance.
As per the results represented in the Table 3, the proposed model outperforms GA by showing better solutions with enhanced search efficiency and power convergence. In fact, for a 5.000 KB file, the time taken to encode and decode using GA-ECC-SHA-256 is 701 and 693 ms, respectively, but the proposed model reduced them to 667 and 602 ms, respectively. Also, for the file size of 23.750 KB, encoding time taken by GA-ECC-SHA256 is of 3.239 ms, and decoding time taken is 3.153 ms, while in the proposed model, encoding time is taken of 2.928 ms, and decoding time is taken of 2.652 ms. Results conclude with no doubt that the proposed model would support an even faster and more effective solution than Genetic Algorithm.

It also further details how Figs. 9 and 10 depict further proof of the proposed model with better execution time and efficiency of encoding, in comparison to previous methods. These further emphasize the model effectiveness in the generation of the ECC keys within the LOA algorithm framework. These results clearly show that the LOA algorithm, implemented according to the proposal developed in this work, significantly improves efficiency and security in cryptographic systems, making it a more robust and reliable solution compared to traditional ones.

Figure 9: Comparison based on encoding time between proposed model and GA

Figure 10: Decoding time comparison between the genetic algorithm (GA) and the proposed model
This study aimed to evaluate the coding and decoding capabilities of the proposed model by applying a speed benchmark defined through Eqs. (7) and (8) [29], where higher reading speeds indicate superior performance. To test the model’s efficiency, a file size of 23,750 KB was utilized, and the results were compared with those of the ECC-GA-SHA-256 model. The encoding and decoding throughputs achieved by the proposed model were approximately 8.111 and 8.956 ms, respectively. In comparison, the ECC-GA-SHA-256 model exhibited encoding and decoding throughputs of 7.333 ms for both processes. These findings highlight the performance of the proposed model, indicating its capability to process data efficiently while maintaining competitive speed relative to existing models. Such performance improvements are essential for real-time applications requiring fast and secure encryption and decryption processes.
(7)
(8)
The results of these experiments are presented to testify that the performance of the model proposed, once applied, increased by about 10.62% with respect to encoding throughput and about 18.89% related to decoding throughput, comparing to the ECC-GA-SHA-256 model. These results depict efficiency and effectiveness of the model proposed in this work to provide a more secure and fast way of encoding and decoding data when compared with other models.
6 Practical Integration with Existing EHRS
The integration of the proposed cryptographic model into existing electronic health record systems (EHRS) requires careful consideration of several factors, including compatibility, computational overhead, and user-interface implications. This section outlines how the proposed model can be effectively embedded into current systems and the potential impact on system usability.
Compatibility with Existing EHRS
The proposed model is designed to be modular and adaptable, making it compatible with most existing EHRS architectures. By leveraging standard cryptographic protocols such as elliptic curve cryptography (ECC) and SHA-256, the model can seamlessly integrate into systems that already utilize similar encryption standards. Additionally, the use of a lightweight optimization algorithm (LOA) ensures that the model does not impose significant architectural changes, allowing for straightforward implementation.
Potential Overhead
The computational efficiency of the proposed model minimizes the overhead introduced to existing systems. The encoding and decoding times, as demonstrated in the evaluation, are competitive even for larger datasets, suggesting that the model can handle typical EHRS workloads without noticeable latency. However, real-world deployment scenarios may reveal additional processing overhead, particularly in resource-constrained environments, which could be addressed through further optimization.
Impact on User Interface
The proposed model focuses on the backend cryptographic processes and does not directly interfere with the user interface of EHRS. Nonetheless, the inclusion of advanced security measures might introduce additional authentication steps or data encryption layers. To ensure usability, any new features must be designed to be intuitive and minimally intrusive for healthcare providers. Training modules and documentation should accompany the integration process to help users adapt seamlessly to the enhanced security protocols.
Scalability and Maintenance
The modular nature of the model simplifies its scalability and maintenance. Updates to the cryptographic algorithms or optimization techniques can be applied independently without disrupting the entire EHRS infrastructure. This flexibility ensures that the system remains secure and up-to-date with emerging threats.
7 Compliance with Ethical Standards and Regulations
Healthcare data security is governed by stringent ethical standards and regulatory frameworks, such as the General Data Protection Regulation (GDPR) in Europe and the Health Insurance Portability and Accountability Act (HIPAA) in the United States. These frameworks emphasize patient privacy, data integrity, and accountability in the collection, storage, and transmission of sensitive health information.
Alignment with GDPR and HIPAA Standards
The proposed cryptographic model aligns with key principles of these regulations in the following ways:
1. Data Confidentiality: By leveraging robust encryption techniques (ECC and SHA-256) and optimizing private key generation through LOA, the model ensures that patient data remains confidential and accessible only to authorized personnel.
2. Data Integrity: The integration of SHA-256 ensures that any unauthorized tampering or alteration of data during transmission or storage can be detected, satisfying the GDPR and HIPAA requirements for maintaining data integrity.
3. Minimization of Data Exposure: The model supports secure storage and transmission, reducing the risk of unauthorized access or data breaches, which aligns with GDPR’s principle of data minimization and HIPAA’s technical safeguard standards.
Ethical Considerations
The model’s focus on enhancing security aligns with ethical obligations to protect patient privacy and prevent misuse of sensitive data. However, it is important to consider the following:
- Transparency: Healthcare providers should inform patients about the encryption measures used to protect their data.
- Access Control: Proper policies must be in place to manage decryption keys, ensuring that only authorized personnel can access sensitive information.
Health information is more available and accessible through better means like the internet and health information is more available and accessible through better means like the internet and cell phones when compared to old ways. However, confidentiality within knowledge related to the patient remains an important issue to be taken care of when that very information is shared among the doctors involved. While the usage of electronic records, along with the internet, makes access to medical information rather much more convenient and quick, the issues regarding security are not fully abolished. To enhance the security of medical information, certain methods have proven to be more efficient than others. This research introduces a novel approach to securing Electronic Health Records (EHRs) by integrating Elliptic Curve Cryptography (ECC) and SHA-256 with the LOA algorithm.
The efficiency of the proposed method is depicted in the speed, with reduced encoding and decoding time. Therefore, this work returns the best results by using 50 iterations in encoding and 100 iterations in decoding through simulations. It provides an improvement of 18.89% as compared to other techniques while being secure from various types of attacks. Thus, the result proves feasible on low-resource devices. Meanwhile, the following two aspects should be pointed out. This research has made stimulating efforts to improve EHR data security. However, there are a few limitations that have to be mentioned: The evaluation was accomplished considering various assumed scenarios; therefore, the proposed method might work in a different scenario in other environments or real-world implementation. Furthermore, the study has chosen sets of security algorithms, which may have many alternative ways of encryption and key generation.
One limitation of the current study is that the proposed model was evaluated within a controlled experimental environment. While this approach allows for precise assessment of performance under fixed parameters, it does not account for the variability and complexity present in real-world healthcare settings, such as fluctuating network conditions, diverse healthcare infrastructures, or varying levels of user expertise.
Limitations: These relate to areas that would require possible future work in terms of clinical trials in actual or daily healthcare environments. Potential studies would need to be about implementing the model across diversified health systems, under heterogeneous states of the network, especially with regard to the tests on its robustness, versatility, and general performance under typical operational constraints.
Besides scalability issues, interoperability with existing systems and compliance with various healthcare regulations of different regions should also be considered. Until these real-world validations are
conducted, the results of this study should be interpreted with caution as a promising but initial step toward enhancing the security and efficiency of electronic health record systems.
Furthermore, the current study does not particularly talk to or incorporate considerations on scalability and resource consumptions that are required by handling large volumes of datasets or a high volume of users. Additional work to be done would be performing the test using larger sets of data, as well as in simulated high-traffic conditions that validate both its performance and efficiency in the use of resources. Metrics around memory usage, CPU consumption, and response times among other indicators give validity to model scalability and usability in diversified healthcare settings.
While this paper illustrates the feasibility of LOA for cryptographic key generation, further research can be done to optimize encryption schemes like adaptive parameter tuning, hybridization with lightweight cryptographic schemes, dynamic updating of keys, and integration with post-quantum cryptographic techniques. For all such enhancements, extensive testing regarding various security metrics will be necessary, such as resistance to different cryptanalytic and side-channel attacks, to ensure that the process of encryption remains robust and efficient.
The studies presented here should be extended to other encoding techniques and new methods of generating private keys for EHRs. Some of the promising avenues that could be further explored in enhancing data security and privacy in EHRs include blockchain and secure multi-party computation. Future systems can be more robust in safeguarding sensitive information with the integration of such advanced technologies. Besides, real-life trials and assessments across various healthcare settings will yield valuable information on the effectiveness and feasibility of the proposed methods, which also helps in the validation of practical applicability.
Future research should be channeled into overcoming the current limitations in EHR security and exploring new methods of enhancing confidentiality, integrity, and availability. Ensuring these core principles is central to protecting patient privacy, maintaining the accuracy and reliability of health data, and ensuring timely access by authorized users. Such advancements will go a long way in enhancing not only the trustworthiness of EHR systems but also, very importantly, the general advancement of secure healthcare data management.
Acknowledgement: We would like to express our greatest thanks to the Mathematics Department, Open Educational College, Kirkuk Branch, for its support of this research.
Funding Statement: This study was not funded by any specific public, commercial or not-for-profit funding agencies.
Availability of Data and Materials: The data and materials associated with this study are available upon request. Application should be made to Arkan Kh Shakr Sabonchi, as the disposition of data and privacy provisions and access are under his consideration and may be limited due to confidentiality regarding ethical and legal considerations.
Ethics Approval: Not applicable.
Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.
References
1. Seymour T, Frantsvog D, Graeber T. Electronic health records (EHR). Am J Health Sci AJHS. 2012;3(3):201–10. doi:10.19030/ajhs.v3i3.7139. [Google Scholar] [CrossRef]
2. Hoover R. Benefits of using an electronic health record. Nursing. 2016;46(7):21–2. doi:10.1097/01.NURSE.0000484036.85939.06. [Google Scholar] [PubMed] [CrossRef]
3. Keshta I, Odeh A. Security and privacy of electronic health records: concerns and challenges. Egypt Inform J. 2021;22(2):177–83. doi:10.1016/j.eij.2020.07.003. [Google Scholar] [CrossRef]
4. Chanal PM, Kakkasageri MS. Security and privacy in IoT: a survey. Wirel Pers Commun. 2020;115(2):1667–93. doi:10.1007/s11277-020-07649-9. [Google Scholar] [CrossRef]
5. Yazdani M, Jolai F. Lion optimization algorithm (LOAa nature-inspired metaheuristic algorithm. J Comput Des Eng. 2016;3(1):24–36. doi:10.1016/j.jcde.2015.06.003. [Google Scholar] [CrossRef]
6. Miller VS. Use of elliptic curves in cryptography. In: Advances in Cryptology—CRYPTO ’85 Proceedings; 2007; Berlin/Heidelberg: Springer. p. 417–26. doi:10.1007/3-540-39799-x_31. [Google Scholar] [CrossRef]
7. Yoshida H, Biryukov A. Analysis of a SHA-256 variant. In: Selected Areas in Cryptography: 12th International Workshop, SAC 2005; 2006; Kingston, ON, Canada: Springer. p. 245–60. [Google Scholar]
8. Prasanna SR, Premananda BS. Performance analysis of MD5 and SHA-256 algorithms to maintain data integrity. In: 2021 International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT); 2021 Aug 27–28; Bangalore, India: IEEE. Vol. 2021, p. 246–50. doi:10.1109/rteict52294.2021.9573660. [Google Scholar] [CrossRef]
9. Xiong H, Tao J, Yuan C. Enabling telecare medical information systems with strong authentication and anonymity. IEEE Access. 2017;5:5648–61. doi:10.1109/ACCESS.2017.2678104. [Google Scholar] [CrossRef]
10. Ara A, Al-Rodhaan M, Tian Y, Al-Dhelaan A. A secure privacy-preserving data aggregation scheme based on bilinear ElGamal cryptosystem for remote health monitoring systems. IEEE Access. 2017;5:12601–17. doi:10.1109/ACCESS.2017.2716439. [Google Scholar] [CrossRef]
11. Liu TY, Lin KJ, Wu HC. ECG data encryption then compression using singular value decomposition. IEEE J Biomed Health Inform. 2018;22(3):707–13. doi:10.1109/JBHI.2017.2698498. [Google Scholar] [PubMed] [CrossRef]
12. Shehab A, Elhoseny M, Muhammad K, Sangaiah AK, Yang P, Huang H, et al. Secure and robust fragile watermarking scheme for medical images. IEEE Access. 2018;6:10269–78. doi:10.1109/ACCESS.2018.2799240. [Google Scholar] [CrossRef]
13. Luo E, Bhuiyan MZA, Wang G, Rahman MA, Wu J, Atiquzzaman M. PrivacyProtector: privacy-protected patient data collection in IoT-based healthcare systems. IEEE Commun Mag. 2018;56(2):163–8. doi:10.1109/MCOM.2018.1700364. [Google Scholar] [CrossRef]
14. Abd El-Latif AA, Abd-El-Atty B, Hossain MS, Rahman MA, Alamri A, Gupta BB. Efficient quantum information hiding for remote medical image sharing. IEEE Access. 2018;6:21075–83. doi:10.1109/ACCESS.2018.2820603. [Google Scholar] [CrossRef]
15. Yang W, Wang S, Hu J, Zheng G, Chaudhry J, Adi E, et al. Securing mobile healthcare data: a smart card based cancelable finger-vein bio-cryptosystem. IEEE Access. 2018;6:36939–47. doi:10.1109/ACCESS.2018.2844182. [Google Scholar] [CrossRef]
16. Abbasinezhad-Mood D, Nikooghadam M. Efficient design of a novel ECC-based public key scheme for medical data protection by utilization of NanoPi fire. IEEE Trans Reliab. 2018;67(3):1328–39. doi:10.1109/TR.2018.2850966. [Google Scholar] [CrossRef]
17. Datta B, Pal PK, Bandyopadhyay SK. Audio transmission of medical reports for visa processing: a solution for the spread of communicable diseases by the immigrant population. IEEE Consum Electron Mag. 2018;7(5):27–33. doi:10.1109/MCE.2018.2835898. [Google Scholar] [CrossRef]
18. Boussif M, Aloui N, Cherif A. Secured cloud computing for medical data based on watermarking and encryption. IET Netw. 2018;7(5):294–8. doi:10.1049/iet-net.2017.0180. [Google Scholar] [CrossRef]
19. Kh Shakr Sabonchi A, Hashim Obaid Z. Ensuring information security in electronic health record system using cryptography and cuckoo search algorithm. J Inf Hiding Priv Prot. 2023;5(1):61–8. doi:10.32604/jihpp.2023.041972. [Google Scholar] [CrossRef]
20. Selvaraj J, Lai WC, Kavin BP, Kavitha C, Seng GH. Cryptographic encryption and optimization for Internet of Things based medical image security. Electronics. 2023;12(7):1636. doi:10.3390/electronics12071636. [Google Scholar] [CrossRef]
21. Chirra BR. Enhancing healthcare data security with homomorphic encryption: a case study on electronic health records (EHR) systems. Revista de Inteligencia Artificial en Medicina. 2023;14(1):549–59. [Google Scholar]
22. Nadhan AS, Jeena Jacob I. Enhancing healthcare security in the digital era: safeguarding medical images with lightweight cryptographic techniques in IoT healthcare applications. Biomed Signal Process Contr. 2024;88(4):105511. doi:10.1016/j.bspc.2023.105511. [Google Scholar] [CrossRef]
23. Alamro H, Marzouk R, Alruwais N, Negm N, Aljameel SS, Khalid M, et al. Modeling of blockchain assisted intrusion detection on IoT healthcare system using ant lion optimizer with hybrid deep learning. IEEE Access. 2023;11:82199–207. doi:10.1109/ACCESS.2023.3299589. [Google Scholar] [CrossRef]
24. Binbusayyis A, Alanazi A, Alsubai S, Alasiry A, Marzougui M, Alqahtani A, et al. A secured cloud-medical data sharing with A-BRSA and salp-ant lion optimisation algorithm. CAAI Trans Intel Tech. 2024;12(13):367. doi:10.1049/cit2.12305. [Google Scholar] [CrossRef]
25. Kabila R, Balaji SS, Vikraam V, Kumar SR, Praveen R. Hybrid LSTM-RNN and lion optimization algorithm for IoT-based proactive healthcare data management. In: 2024 International Conference on Knowledge Engineering and Communication Systems (ICKECS); 2024 Apr 18–19; Chikkaballapur, India: IEEE. Vol. 2024, p. 1–7. doi:10.1109/ICKECS61492.2024.10616709. [Google Scholar] [CrossRef]
26. Zou L, Ni M, Huang Y, Shi W, Li X. Hybrid encryption algorithm based on AES and RSA in file encryption. In: Frontier computing. Singapore: Springer Singapore; 2020. p. 541–51. doi:10.1007/978-981-15-3250-4_68. [Google Scholar] [CrossRef]
27. Bafandehkar M, Yasin SM, Mahmod R, Hanapi ZM. Comparison of ECC and RSA algorithm in resource constrained devices. In: 2013 International Conference on IT Convergence and Security (ICITCS); 2013 Dec 16–18; Macao, China: IEEE. Vol. 2013, p. 1–3. doi:10.1109/ICITCS.2013.6717816. [Google Scholar] [CrossRef]
28. Holland JH. Genetic algorithms. Sci Am. 1992;267(1):66–72. doi:10.1038/scientificamerican0792-66. [Google Scholar] [CrossRef]
29. Lemma A, Tolentino M, Mehari G. Performance analysis on the implementation of data encryption algorithms used in network security. Int J Comput Inf Technol. 2015;4(4):711–7. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
