Nonlinear Post-Buckling Stability of Graphene Origami-Enabled Auxetic Metamaterials Plates

1  Introduction

Auxetic metamaterials increase in the lateral direction when elongated axially, contract laterally, and compressed axially, thereby resulting in a negative Poisson’s ratio. Auxetic word is originally from the Greek word “auxetos” that means “tends to expand”. It was first defined by Evans and colleagues in 1991 [1]. Auxetic metamaterials have lower densities, reduction in material usage, high shear resistance, high energy absorption capacity, good acoustic behavior, and crashworthiness [2]. These merits make them very favorable in many applications such as aerospace, biomedical scaffold, and defense areas [3,4].

Wen et al. [5] proved the microstructural hierarchy of pristine chemically modified graphene films renders remarkable negative Poisson’s ratios ranging from −0.25 to −0.55. Dutta et al. [6] developed single cell auxetic beams with different geometries using a finite element (FE) approach. Meng et al. [7] investigated the self-folding of 2D graphene into 3D graphene Miura origami helped by hydrogenation and identified the origin of their deviation. Zhao et al. [8] conducted bending tests and numerical simulations to study the static bending behavior of the sandwich auxetic honeycomb beams. Wu et al. [9] presented a review article for metallic metamaterials focusing on design process, fabrication and property testing and classification. Fang et al. [10] presented a comprehensive review of bi/multi-stable phenomenon of composite origami metamaterial structures. Liu et al. [11] presented yield area, yield criterion, and loading history as design tools of plasticity in modifying buckling load and sequence in metamaterials. Jiang et al. [12] estimated crushing response of 3D reentrant circular auxetic metamaterials under quasi-static loads. Lu et al. [13] and Wang et al. [14] studied the quasi-static bending response and energy absorption of sandwich beam with auxetic core. Francisco et al. [15] examined the vibration and bending of sandwich auxetic tubes. They noticed that the vertical length of cell has effects on natural frequencies and buckling loads. Wu et al. [16] exploited the gradient-free method to get the topology optimization of metamaterial microstructures for negative Poisson’s ratio under large deformation. Lv et al. [17] explored analytically mechanical and thermal post-buckling of FG-GOEMA auxetic metamaterials plates. Du et al. [18] developed a new approach for the layout design of cuts in kirigami metamaterials attain desired deformation patterns under buckling and post-buckling behaviors. Li et al. [19] studied the nonlinear vibration of the sandwich beam with auxetic honeycomb core under thermal shock. Vineyard et al. [20] employed the asymptotic homogenization approach to obtain the effective thermoelastic properties of the multiphase metamaterials.

Response of a structure regarding its load bearing capacity may fall into two general categories: stable or unstable. Buckling and post-buckling are unstable responses of thin structures those must be understood comprehensively by researchers. The long history of buckling theory for structures begins with the studies by Euler in 1744 of the stability of flexible compressed beams [21]. In 1993, Wang et al. [22] studied the buckling response of rectangular Mindlin plates with internal line supports. Shariyat et al. [23] investigated uniaxial and biaxial postbuckling behaviors of the longitudinally graded plates by using the exact 3D elasticity theory. Wehmeyer et al. [24] presented reduced-order numerical solutions to describe nonlinear buckling of elastic struts inclined relative to the loading direction. Eltaher et al. [25] illustrated the influence of periodic/nonperiodic imperfections modes on buckling and postbuckling of beam with nonlinear elastic foundations. Mao et al. [26] examined buckling and postbuckling of FG piezoelectric plate under the effect of electrical and mechanical loads. Mehrabi et al. [27] examined post buckling of the composite eccentric annular sector auxetic metamaterial plate under a thermal load. Derveni et al. [28] explored buckling response of plate-lattice architectures under uniaxial compression. Moradi-Dastjerdi et al. [29] examined the biaxial buckling of an active sandwich plate. Liu et al. [30] studied nonlinear vibration response of auxetic honeycomb plates via Galerkin and multiple scale methods. Abbaspour et al. [31] predicted the thermal buckling of sandwich microshell with piezoelectric layers. Long et al. [32] studied the nonlinear stability of porous FG spherical caps and circular plates. Yan et al. [33] presented a comprehensive overview of recent articles related to snapping metamaterials and their design strategies.

Based on refined plate theory, Ezzati et al. [34] investigated free vibration GOAM plate rested on Winkler–Pasternak elastic substrate analytically. Mahinzare et al. [35] proposed DQM to examine the nonlinear vibration of GOAM sandwich pates numerically. Mohamed et al. [36] developed a novel mathematical model for nonlinear buckling, postbuckling, and snap-through of bidirectional FG porous plates rested on elastic foundation. He et al. [37] investigated buckling and postbuckling of anisogrid lattice-core sandwich plates with nanocomposite skins. Milazzo et al. [38] exploited Ritz method to study buckling and postbuckling responses of variable stiffness plates with cutouts. Vaghefi [39] used meshless approach to analyze the elastoplastic postbuckling of porous FG plates with elastic foundations. Dai et al. [40] exploited the Floquet exponent method to study dynamic stability characteristics of rotating truncated conical shells under periodic axial loads. Nasri et al. [41] studied nonlinear bending and buckling stability of curved metamaterial beam and optimized the results by using the response surface methodology.

Post-buckling behavior of metamaterial structures has received limited attention from researchers. Shen et al. [42] illustrated the effect of in-plane negative Poisson’s ratio on the post-buckling response of graphene-reinforced metal matrix composite plates. An et al. [43] studied bending and buckling response of FG-GOAMs irregular plates using generalized finite difference method. Murari et al. [44,45] investigated nonlinear vibration and post-buckling responses of GOAMs tapered beams in fluid by using physics-embedded machine learning model. Ghasemi et al. [46] presented the small/large amplitude vibration of the pre/post-buckled geometrically imperfect re-entrant auxetic tube modeled by von-Kármán nonlinear strain and Timoshenko beam theory. Based on the first order shear deformation and the two-step perturbation method, Lv et al. [17] examined the mechanical and thermal post-buckling of FG-GOAMs. Sengar et al. [47] presented stability of FG skew sandwich plates having temperature-dependent properties and a re-entrant auxetic core. Ghasemi et al. [48] investigated analytically nonlinear postbuckling and static bending behaviors of 3D auxetic tubes.

To our knowledge, this study presents the first application of the numerical differential quadrature method (DQM) to investigate the nonlinear post-buckling behavior of FG auxetic metamaterial higher-order plates. The primary objective is to determine the optimal combination of graphene content, folding degree, and distribution patterns to enhance the postbuckling performance of FG-GOAM plates. In the following sections, the problem formulation will be presented by including the high shear deformation theory, von Karman nonlinear strain, and micromechanical models used to evaluate material properties of the FG-GOAM. DQM, linearization and novel iterative approaches used in the solution of developed models are discussed through Section 3. Model validation with previous respectable works is proved through Section 4. Numerical parametric studies to present the effects of graphene content, folding degree and GO distribution patterns on the postbuckling responses of GOAM plates are discussed in Section 5. Observations and concluding remarks are summarized in Section 6.

2  Problem Formulation

2.1 Mechanical Properties of Metamaterials

The considered GOAM plate consists of an even number of layers 𝒩 arranged symmetrically about its mid surface. Each layer is composed of cupper (Cu) matrix enforced by graphene origami (GO) material. The GO content is constant within each layer but it changes in different layers according to a specified distribution of GO weight fraction (WGr).

Three GO distribution patterns are considered [44,45]:

U−type:VGO(l)=V¯GOX−type:VGO(l)=2V¯GO|2l−NL−1|/NLO−type:VGO(l)=2V¯GO(1−|2l−NL−1|/NL)(1)

U-type where the same GO content in all layers, X-type where higher GO content at the top and bottom layers and O-type where higher GO content near the mid surface. Where V¯GO is the average GO volume fraction in the lth layer that is related to the weight fraction WGO by [44]:

V¯GO=WGoWGo+(ρGr/ρCu)(1−WGo)(2)

meanwhile ρGr and ρCu are the densities of graphene and cupper, respectively.

These types are schematically represented in Fig. 1 where the darker color stands for a higher GO content. The plate has length a, width b and thickness h. The plate is described in a rectangular coordinate system in which the x- and y-axes lie in the mid-plane (z = 0) while the z-axis is perpendicular to the mid-plane.

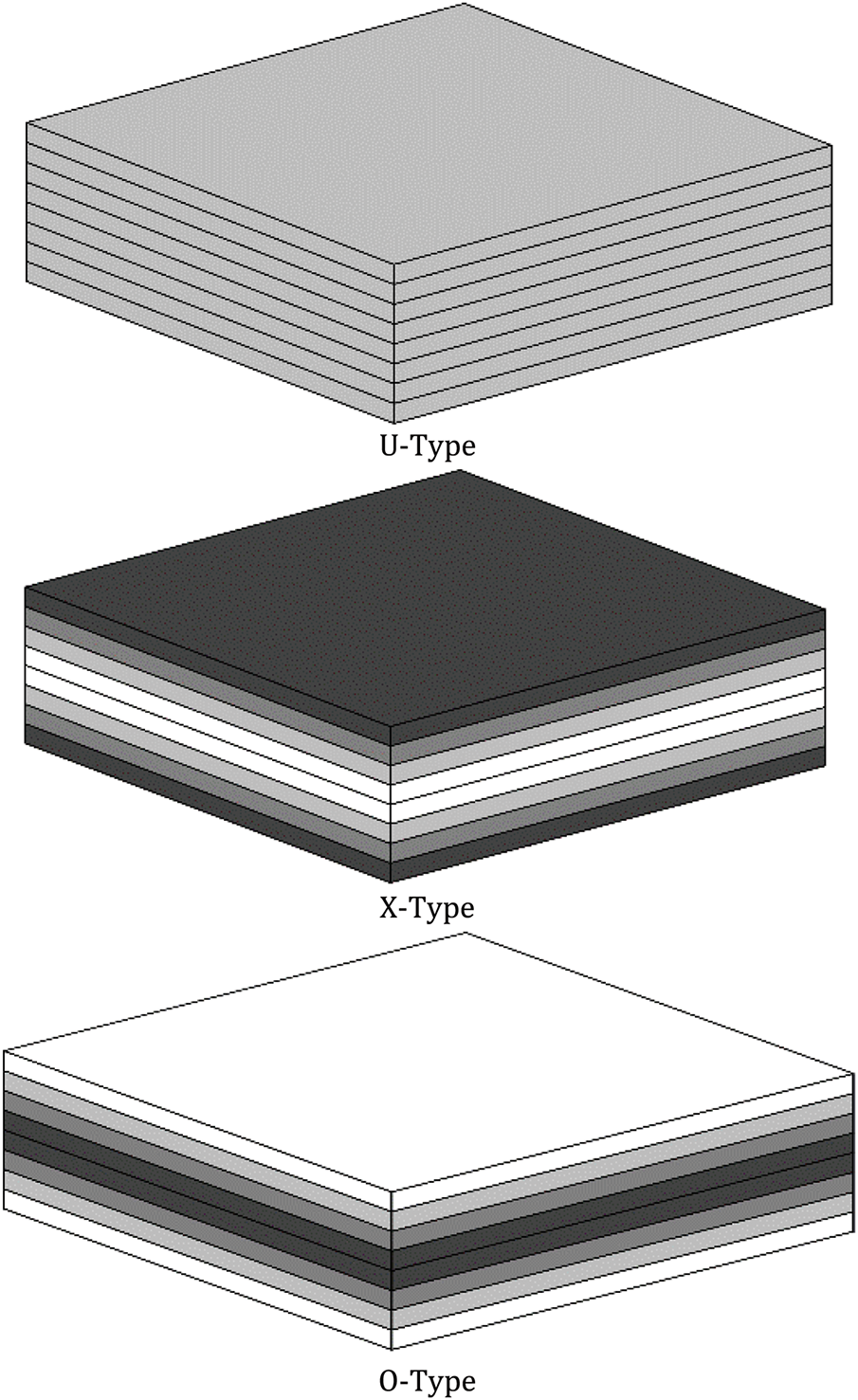
Figure 1: Schematic of considered three GO distribution types of GOAM plates

The composite Young’s modulus Ec and Poisson’s ration νc of GOAM at temperature T are evaluated by genetic micromechanical model [49] as:

Ec=1+ξηVGO1−ηVGOECu(1.11−1.22VGO−0.134TT0+0.559VGOTT0−5.5HGOVGO+38HGOVGO2−20.6HGO2VGO2)νc=(νGOVGO+νCuVCu)(1.01−1.43VGO+0.165TT0−16.8HGOVGO−1.1HGOVGOTT0+16HGO2VGO2)(3)

where ξ=2(lGr/tGr),η=(EGr/ECu)−1(EGr/ECu)+ξ, T0=300K, lGr and tGr are the length and thickness of graphene, respectively, and HGO is the H atom coverage quantify the folding degree of GO.

2.2 Kinematic and Constitutive Equations

The displacement field of four variables shear deformation theory without shear correction is portrayed by [50–53]:

u1(x,y,z)=u(x,y)−z∂wb∂x−F(z)∂ws∂xu2(x,y,z)=v(x,y)−z∂wb∂y−F(z)∂ws∂yu3(x,y,z)=w¯(x,y)=wb(x,y)+ws(x,y)(4)

where the von Karman strains are:

{εxxεyyγxy}={∂u∂x+12(∂w¯∂x)2∂v∂y+12(∂w¯∂y)2∂u∂y+∂v∂x+∂w¯∂x∂w¯∂y}+z{−∂2wb∂x2−∂2wb∂y2−2∂2wb∂x∂y}+F(z){−∂2ws∂x2−∂2ws∂y2−2∂2ws∂x∂y}=ε0+zεb+F(z)εs(5a)

{γyzγxz}=G(z){∂ws∂y∂ws∂x}=G(z)ε¯(5b)

According to Reddy theorem, F(z)=4z33h2 and G(z)=1−dF(z)dz=1−4z2h2. Based on equivalent single layer theory, that lowers 3D to 2D shear deformation theory (εz=0), the stress–strain relationships for the kth layer can be characterized by:

[σxσyτxyτyzτxz](k)=[Q11Q12000Q12Q2200000Q6600000Q4400000Q55](k)[εxxεyyγxyγyzγxz](k)(6a)

where plane stress stiffnesses at layer k are:

Q11(k)=Q22(k)=Ec(k)1−(vc(k))2,Q12(k)=vc(k)2Ec(k)1−(vc(k))2,Q44(k)=Q55(k)=Q66(k)(k)=Ec(k)2(1+vc(k))(6b)

and Ec(k) and vc(k) are computed by Eq. (3).

2.3 Nonlinear Governing Equation

Nonlinear governing equilibrium equations of composite-GOAM plates in terms of stress resultants are drew by the virtual work principle as follows:

δuo:∂Nx∂x+∂Nxy∂y=0(7a)

δvo:∂Nxy∂x+∂Ny∂y=0(7b)

δwb:∂2Mxb∂x2+2∂2Mxyb∂x∂y+∂2Myb∂y2+N¯o+N¯(w¯)=0(7c)

δws:∂2Mxs∂x2+2∂2Mxys∂x∂y+∂2Mys∂y2+∂Syzs∂y+∂Sxzs∂x+N¯o+N¯(w¯)=0(7d)

where the nonlinear term N¯(w¯) and the in-plane force N¯o terms are defined as:

N¯(w¯)=∂∂x(Nx∂w¯∂x+Nxy∂w¯∂y)+∂∂y(Nxy+Ny∂w¯∂y)(8a)

N¯o=Nx0∂2w¯∂x2+Ny0∂2w¯∂y2(8b)

The present work considers composite GOAM plates consisting of symmetrically arranged layers in the thickness direction (Eq. (1)). Accordingly, the stress resultants can be expressed by:

[NxNyNxy]=[A11A120A12A22000A66]ε0,(9a)

[MxbMybMxyb]=[D11D120D12D22000D66]εb+[D11sD12s0D12sD22s000D66s]εs(9b)

[MxsMysMxys]=[D11sD12s0D12sD22s000D66s]εb+[H11sH12s0H12sH22s000H66s]εs(9c)

[SyzsSxzs]=[A44s00A55s]ε¯(9d)

where {ε0,εb,εs,ε¯} are defined in Eq. (5). The rigidity terms are obtained as [54]:

[Aij,Dij,Dijs,Hijs]=∫−h/2h/2Qij(z)[1,z2,zF(z),(F(z))2]dz,ij=11,12,22,66(10a)

Aijs=∫−h/2h/2Qij(z)(G(z))2dz,ij=44,55(10b)

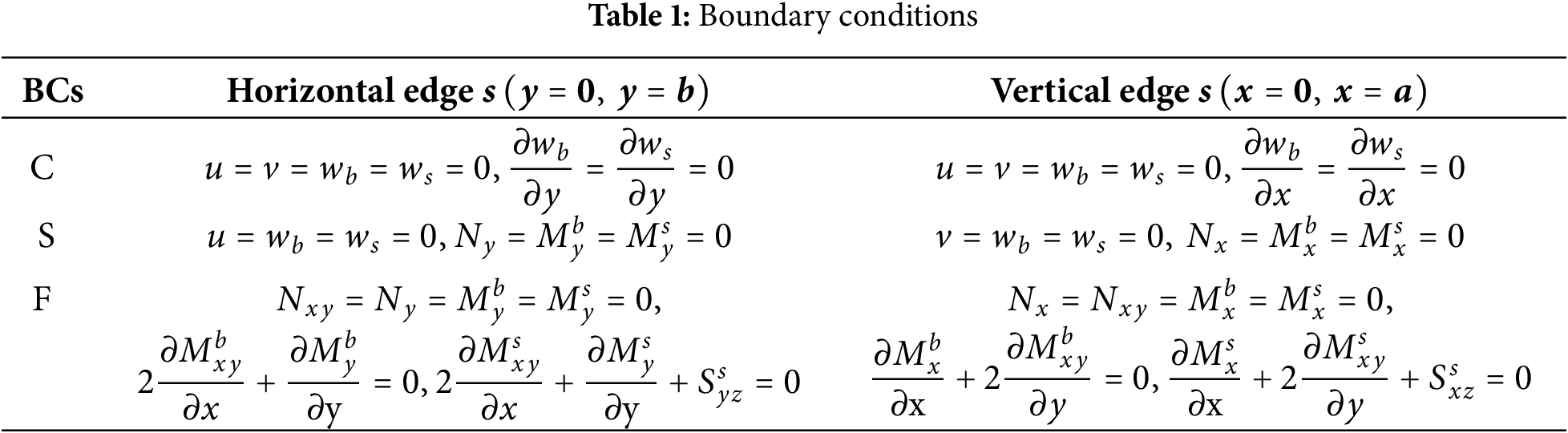
The present study investigates the responses of rectangular GOAM plate s(0≤x≤a,0≤y≤b) with different boundary conditions (BCs). Each edge of the plate is symbolized by: C, S, or F, to denote, respectively: clamped, simply supported, or free edge with the BCs defined in Table 1.

3  Solution Methodology

3.1 DQM Discretization of Partial Differential Equations

Several research [25,28,29,32] demonstrated that the DQM can effectively solve systems of differential equations with a relatively small number of grid points, which leads to less computational cost. Furthermore, DQM provides matrix-based operators to approximate the solution’s derivatives. This transforms the original system of differential equations into a system of algebraic equations, which can be readily solved.

Based on DQM [55], a function f(x) with domain a≤x≤b is discretized such that the domain and function are represented as vectors: x=[x1=a,x2,⋯,xN=b]T and f=[f1,f2,⋯,fp]T, respectively. Additionally, the approximation of its first derivative f′=[f1′,f2′,⋯,fp′]T is computed as f′=cf, where c is the weighting (p×p) matrix of the first order derivative. Higher order derivatives are derived using matrix multiplication: f′′=c2f,f′′′=c3f,⋯.

The DQM is developed here to discretize the governing set of partial differential equations (Eq. (7)). The plate domain (Ω:0<x<a,0<y<b) is discretized in the x- and y-directions using p- and q-nodes, respectively. The discrete values of an unknown function u(x,y) is generally arranged as a two-dimensional array uij=u(xj,yi) but can be rearranged as a (pq×1)-vector constructed from the array vectors one after another such that U=[u11,u21,⋯uq1,u12,u22,⋯uq2,⋯,⋯,u1p,u2p,⋯uqp]T. According to this vector representation of the unknowns, partial derivative s∂u(x,y)/∂x and ∂u(x,y)/∂y are approximated by vectors Ux=𝒞xU and Uy=𝒞yU, respectively, such that

𝒞x=Kron(cx,I(q)),𝒞y=Kron(I(p),cy)(11)

where I(n) is the identity matrix of dimension (n×n), cx(p×p)andcy(q×q) are the first order derivative matrices of single variable functions in x and y, respectively, and Kron indicates Kronecker product. The resulting partial derivative matrices 𝒞x and 𝒞y have dimensions (pq×pq). Approximation of higher and mixed partial derivatives such as ∂2u∂x2,∂2u∂y2, ∂2u∂x∂y are computed as Uxx=𝒞xxU,Uyy=𝒞yyU and Uxy=𝒞xyU, respectively, where 𝒞xx=𝒞x2,𝒞yy=𝒞y2, and 𝒞xy=𝒞x𝒞y.

The governing equations for the GOAM plate, see Eqs. (5), (7) and (9), consist of four nonlinear partial differential equations in the unknowns u(x,y),v(x,y),wb(x,y) and ws(x,y). They are discretized by DQM as the unknown vectors U,V,Wb and Ws each of dimension (pq×1) and arranged as global unknown (4pq×1) vector 𝒴=[UT,VT,WbTWsT]T.

3.2 Linearization and Iterative Approach

Since the governing nonlinear set of partial differential equations for the GOAM plate is homogeneous (without any external transversal force), it is a nonlinear eigenvalue problem. Investigation of the plate response is based on critical buckling load λcr and postbuckling paths that describe the relation between the applied axial load and buckling deflection. In the present study, the axial load intensity λ is plotted vs. the maximum buckling deflection of the plate.

A simple linearization approach is adopted to solve Eq. (7). The nonlinear terms in the strain ε0, Eq. (5a), and the nonlinear function N(w¯), Eq. (8a), are discretized by DQM and linearized such that

(∂w¯∂x)2≜(𝒞xW0)∘(𝒞xW),(∂w¯∂y)2≜(𝒞yW0)∘(𝒞yW),∂w¯∂x∂w¯∂y≜(𝒞xW0)∘(𝒞yW)(12)

where W0=Wb0+Ws0 is an approximate pq-vector. Through an iterative procedure, W0 is computed from the previous iteration. According to the above data structure and using the notation: Wx0=𝒞xW0,Wy0=𝒞yW0 and applying the DQM, the linearized stress resultants can be written as:

[Nx¯Ny¯Nxy¯MxbMybMxybMxsMysMxys]=[A11𝒞xA12𝒞yA12𝒞xA22𝒞yA66𝒞yA66𝒞xA11(12Wx0∘𝒞x)+A12(12Wy0∘𝒞y)A11(12Wx0∘𝒞x)+A12(12Wy0∘𝒞y)A12(12Wx0∘𝒞x)+A22(12Wy0∘𝒞y)A12(12Wx0∘𝒞x)+A22(12Wy0∘𝒞y)A66(Wx0∘𝒞y)A66(Wx0∘𝒞y)OOOOOO−(D11𝒞xx+D12𝒞yy)−(D11s𝒞xx+D12s𝒞yy)−(D12𝒞xx+D22𝒞yy)−(D12s𝒞xx+D22s𝒞yy)−2D66𝒞xy−2D66s𝒞xyOOOOOO−(D11s𝒞xx+D12s𝒞yy)−(H11s𝒞xx+H12s𝒞yy)−(D12s𝒞xx+D22s𝒞yy)−(H12s𝒞xx+H22s𝒞yy)−2D66s𝒞xy−2H66s𝒞xy][UVWbWs](13)

where an overbar indicate a linearized stress, O is the zero square matrix of dimension (pq) and operator ‘∘’ is defined for a vector V and matrix A, each with the same number of rows, such that S=V∘A implies that Sij=ViAij.

Now, the linearized discrete governing algebraic system for Eq. (7) is written in an iteration step ‘i’ as a linear generalized eigenvalue problem

𝒦(i)𝒴(i)=λ(i)𝒫𝒴(i)(14)

where 𝒦(i) and 𝒫 are presented in Appendix A. Upon application of the boundary conditions to Eq. (14), the resulting linear eigenvalue problem has to be solved for the unknown deflection vector 𝒴(i)=[UTVTWbTWsT]T(i) as well as the compressive load λ(i). The iteration procedure is described in the following Algorithm 1 in which the maximum of a buckling deflection 𝒴 is computed as max(Wb+Ws).

4  Model Validation

For GOAM plates, the material properties of matrix Cu and graphene are presented in Table 2 while the geometric parameters of graphene are lGr=83.76×10−10m,tGr=3.4×10−10m.

First, an isotropic plate is considered. Table 3 compares the values of dimensionless critical buckling loads of a square plate under uniaxial and biaxial compression assuming simply supported boundary conditions and Poisson’s ratio v = 0.3. Different solution methods are compared: DQM [26], analytical solution based on Mindlin plate theory [22] and the two-step perturbation method [17]. The results demonstrate good consistency for different thickness to length ratios.

Comparisons with Prakash et al. [56] and Mohamed et al. [36] of the dimensionless postbuckling equilibrium paths of a square isotropic plate are depicted in Fig. 2. The dimensionless deflection w¯=wmax/h is plotted vs. dimensionless axial pressure Λ=λ(a2π2Dc),where Dc=Eh312(1−ν2). The material properties are: E=380 GPa,ν=0.3. Good agreement is observed especially with those of [36,56].

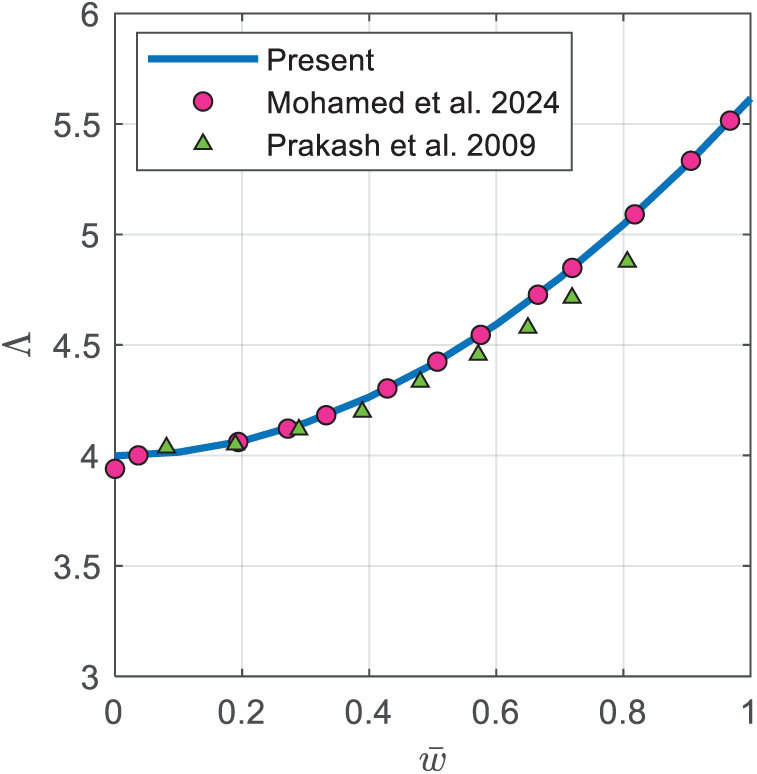
Figure 2: Comparison with [36,56] for postbuckling paths of simply supported isotropicsquare plate under uniaxial compression. (E=380GPa;ν=0.3;a/h=100)

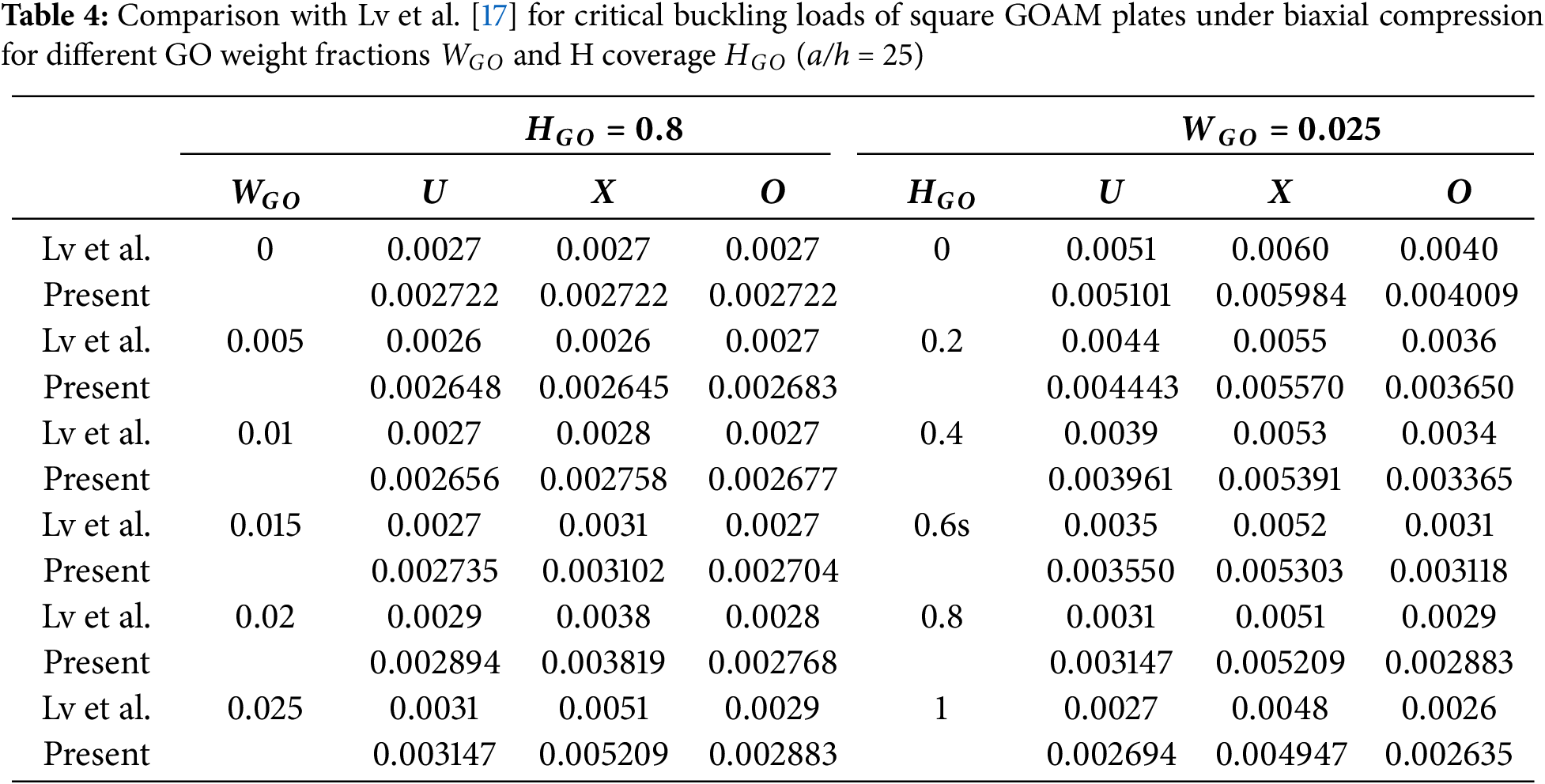
Next, to validate the present formulation and solution methodology of GOAM plates, critical buckling loads of square GOAM plates under biaxial compression are compared with [17]. For different GO folding degrees HGO and weight fractions WGO under three distribution patterns, the critical buckling loads are compared in Table 4. It is clear that the current research results are in good agreement with those of [17].

The postbuckling response of an X-type GOAM plate under biaxial loading is compared with Lv et al. [17] in Fig. 3 showing good agreement.

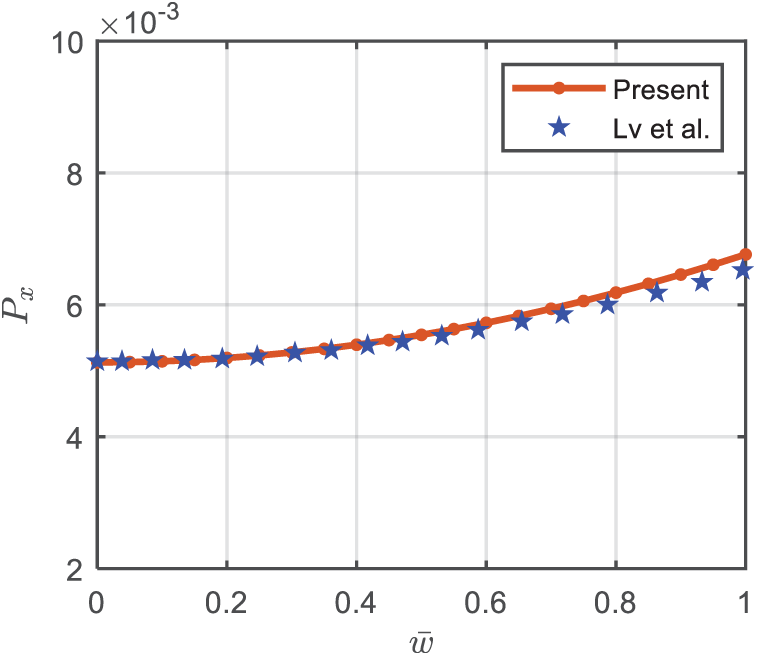
Figure 3: Comparison with Lv et al. [17] The postbuckling response of the X-type GOAM plates under biaxial loading. (a/h=25,a/b=1,WGO=0.025,HGO=0.8). Px=Ncr(1−νCu2)ECuhb

5  Numerical Parametric Studies

5.1 Influence of Graphene Origami Parameters {WGO,HGO} on the Material Mechanical Properties

Fig. 4 illustrates the mutual effect of graphene origami contents (WGO) and folding degrees parameter (HGO) on material mechanical characteristics of the studied GOAM plate: (a)Ec,(b)νc,(c)Q11,(d)Q12 and (e)Q66. As observed from Fig. 4a, Young’s modulus of GO/Cu composite material is generally increased with the increase of WGO and/or reduction of the folding degree HGO. However the rate of this increase is not uniform but depends on the values of both WGO and HGO. For example, for small graphene origami content (WGO<0.5%), Ec has no significant change while it increases significantly for higher values of WGO especially for smaller folding degree HGO values. Fig. 4b illustrates that increasing either of WGO or HGO reduces the Poisson’s ratio, which can reach negative values leading the GO/Cu composite to be transformed into an auxetic metamaterial. The influence of WGO and HGO on the plane stress stiffnesses Q11,Q12,Q44=Q55=Q66, defined in Eq. (6b), are shown in Fig. 4c–e, respectively.

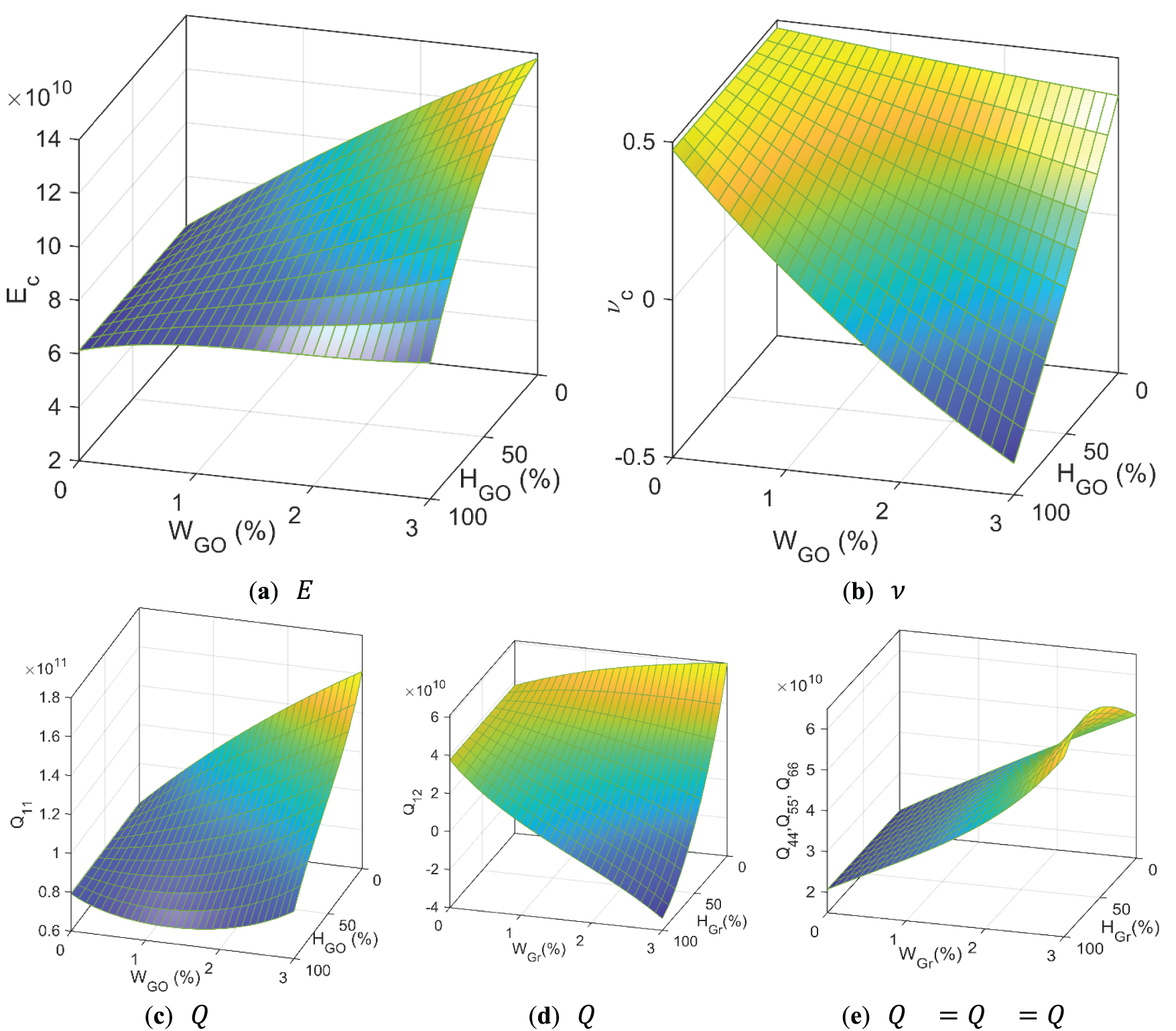
Figure 4: Influence of Graphene Origami parameters {WGO,HGO} on the mechanical properties of a single layer

5.2 Influence of GO Volume Fraction Distribution Types

Herein, the effect of GO distribution patterns defined in Eq. (1) on the postbuckling response of GOAM plates are examined. Fig. 5 presents the postbuckling curves of simply supported GOAM plates under biaxial compression. The plate is composed of 10 layers and arranged according to different distribution types. Compared with other distribution types of GO volume fraction, the GOAM plate with X-distribution type exhibits the greatest critical buckling load and best postbuckling performance, followed by the U-type, then the O-type GOAM plate. This performance demonstrates that dispersing more GO near the surfaces of the plate is an effective way to achieve good structural performance of the metamaterial plate.

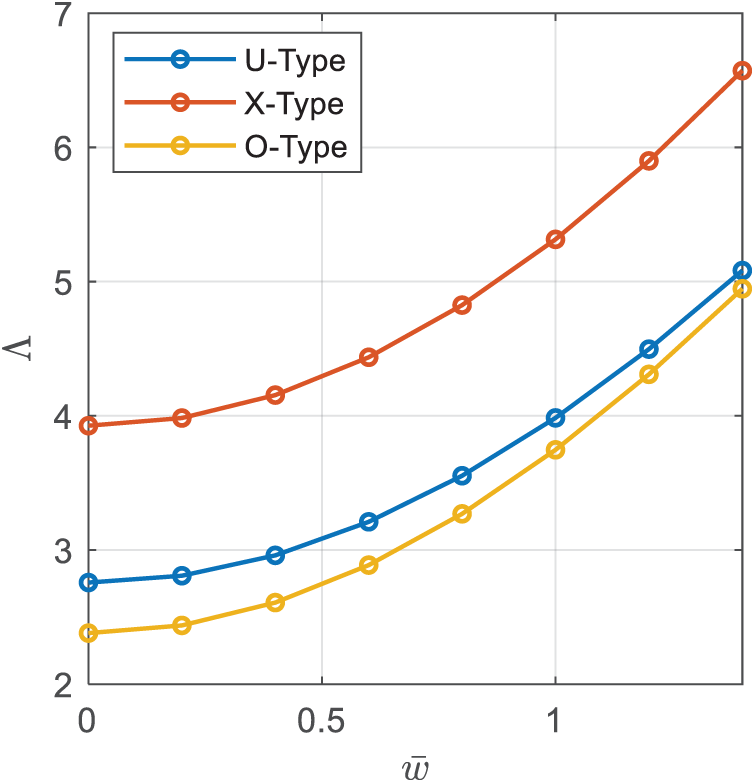
Figure 5: Influence of GO volume fraction distribution types on postbuckling behavior of a SSSS GOAM plate under biaxial compression (ah=25,WGO=2.5%,HGO=50%,Λ=λ(a2ECuh3),w¯=wm/h)

5.3 Influence of Graphene Folding Degrees HGO

Fig. 6 highlights the influences of graphene folding degree HGO on the dimensionless buckling and postbuckling behavior of FG-GOAM composite plates, assuming constant GO weight fraction WGO=2% . A simply supported square GOAM plate under uniaxial and biaxial compression is considered. Fig. 6 demonstrates that the buckling loads in case of uniaxial compression are double those computed in case of biaxial loading. Furthermore, the figure reveals that increasing HGO results in decreasing the postbuckling loads. This behavior is understood since the stiffness of GOAM composite decreases with increasing HGO due to the reduction of Young’s modulus, Poisson’s ration, and stiffness coefficient Q11 as can be observed from Fig. 4. In general, increasing folding degree (HGO) gives rise to the transformation of GO/Cu composite into GOAM with NPR and reduced Young’s modulus, making the metamaterial structure more flexible.

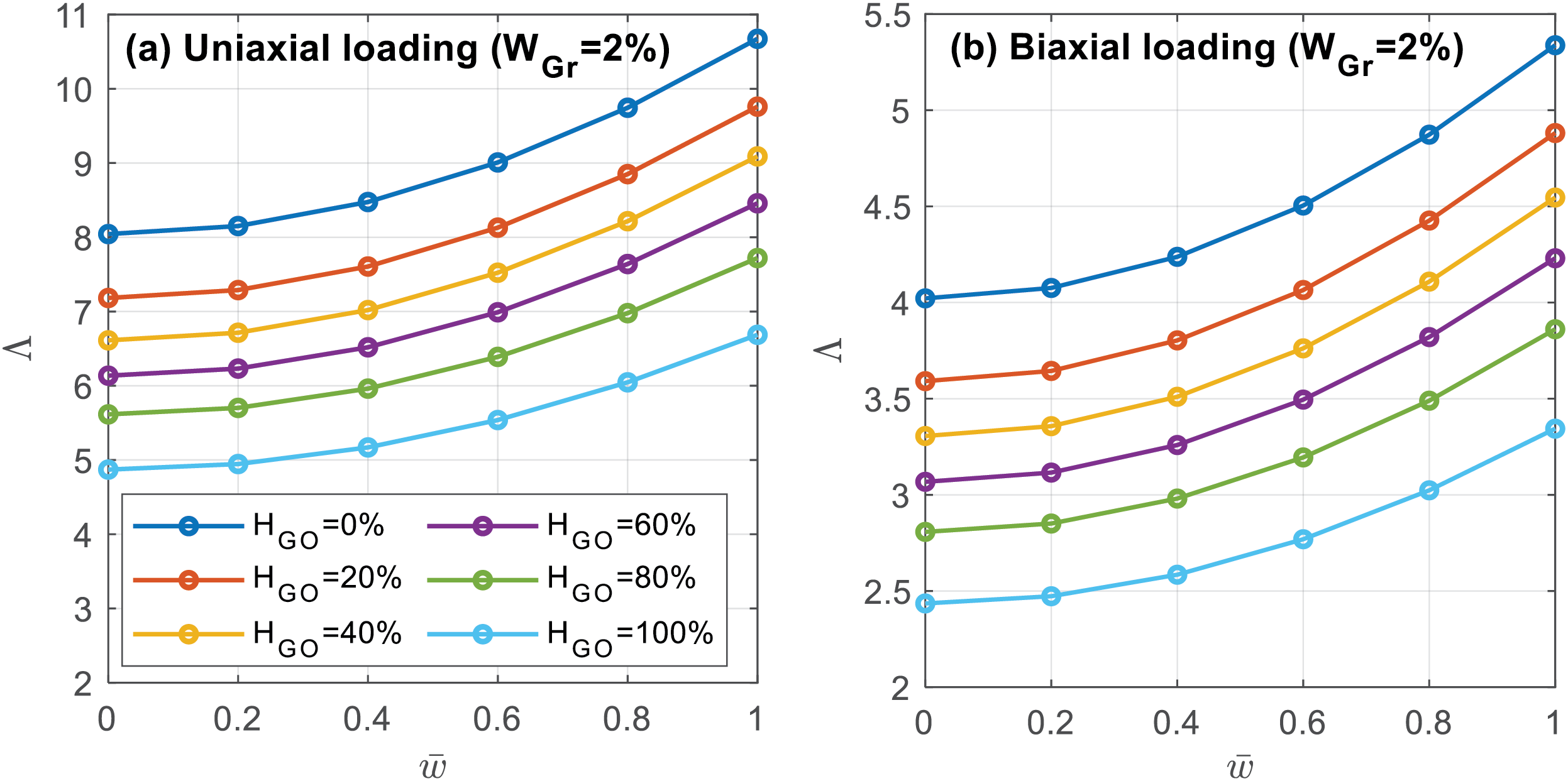
Figure 6: Influence of GO folding degrees HGO on postbuckling behavior of GOAM plate under (a) uniaxial and (b) biaxial compression for X-distribution type (ah=25,WGO=2% ,Λ=Ncr(a2ECuh3),w¯=wm/h)

5.4 Influence of Graphene Weight Fraction WGO

Fig. 7 plots the postbuckling paths of X-type GOAM simply supported square plate under uniaxial and biaxial compression for different values of graphene-origami weight fraction WGO. In the current parametric study, the folding degree is assumed constant (HGO=0.8). As can be seen from Fig. 7, for large graphene origami content WGO≥1.5% , a rise in GO content results in increased postbuckling loads. However, this characteristic is violated for GOAM plates when GO weight fraction increases in the range 0≤WGO<1.5%  where the buckling loads change slowly and may even reduce. This can be interpreted since, as can be noticed from Fig. 4a,b in the range WGO≥1.5%  the increased graphene content leads to a larger Young’s modulus Ec and smaller negative Poisson’s ratio νc (or greater νc2). This results in larger values of (Q11=Ec/(1−νc2)). Accordingly, increasing graphene-origami weight fraction in the range WGO≥1.5% leads to increased plate stiffness and higher postbuckling loads. On the other side, in the smaller range 0≤WGO<1.5% , the GO/Cu composite cannot show NPR features. The increased graphene content leads to a larger Young’s modulus but smaller (positive) Poisson’s ratio, giving rise to the nearly constant or even decreased value of Q11.

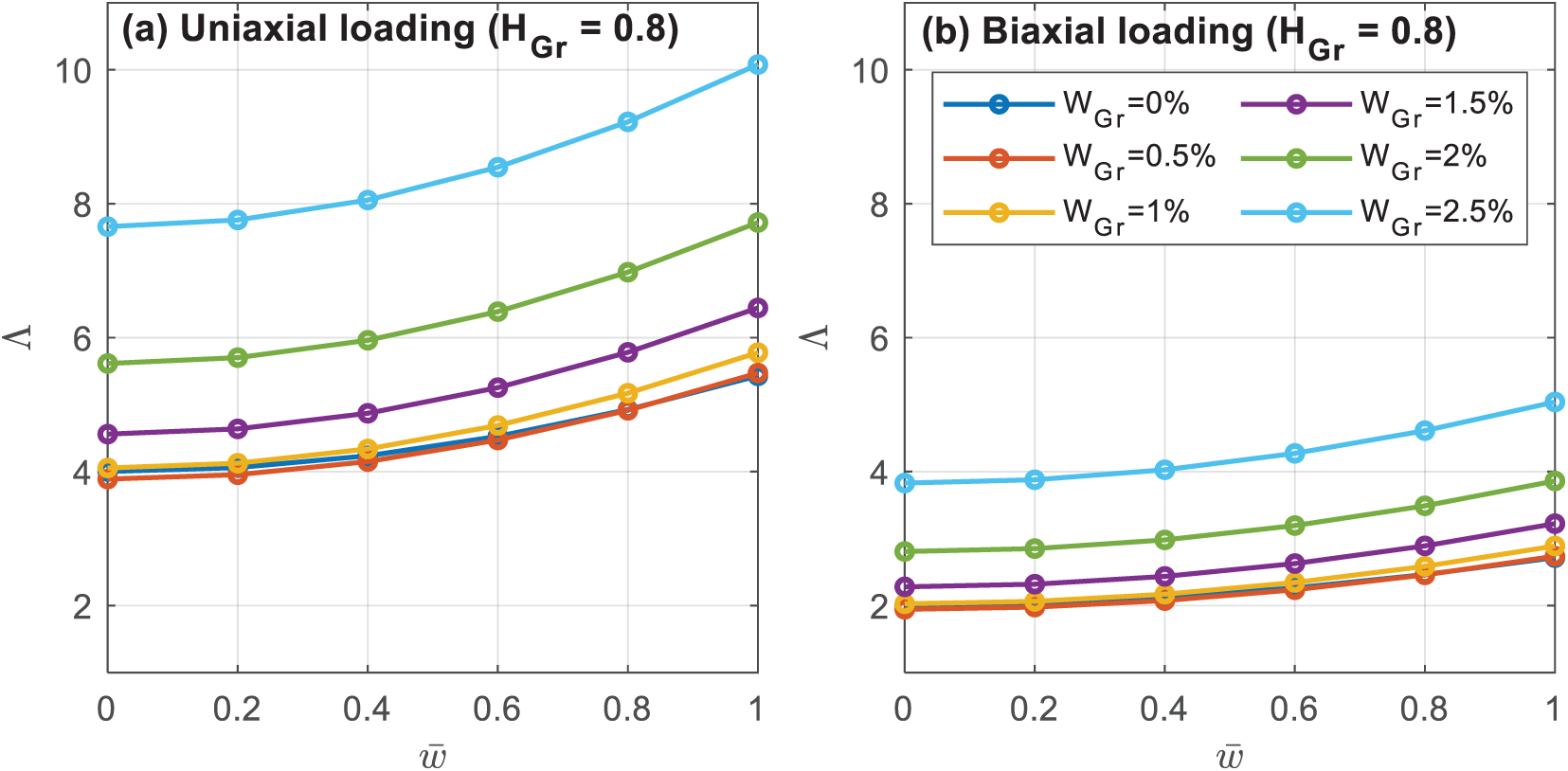
Figure 7: Influence of Graphene weight fraction W_Gr on postbuckling behavior of GOAM plate under (a) uniaxial and (b) biaxial compression for X-distribution type (ah=25,HGr=0.8,Λ=λ(a2ECuh3),w¯=wm/h)

5.5 Mutual Influence of GO Properties {WGr,HGr}

In order to investigate the mutual influence of Cu\GO parameters WGO and HGO on postbuckling behavior of GOAM plate, a simply supported U-type square plate under biaxial compression is considered. The postbuckling paths for different WGO={0%,0.5%,1%,1.5%,2%,2.5%} and HGO={0%,25%,50%,100%} are presented in Fig. 8. As can be observed, at WGO=0, the postbuckling paths are identical and as expected are independent on the value HGO. Another observation is driven form Fig. 8a–c for HGO={0%,25%,50%} that the postbuckling loads considerably increase with increasing the WGO content. The rate of this increase reduces as the folding degrees increase. Alternative behavior is observed in Fig. 8d for HGO=100%. The postbuckling loads decrease with increasing WGO from 0% up to 1% but they increase as WGO increases from 1.5% up to 2.5%. To understand these responses and theoretically investigate mutual influences of WGr and HGr on postbuckling behavior, the mechanical properties Ec,νc of the Cu/GO composite are computed based on Eq. (3) and plotted in Fig. 9a,b. Fig. 9a indicates that Young’s modulus Ec increases with the increase of WGO but it decreases with the increase of HGO. With respect to Poisson’s ratio, Fig. 9b shows that νc increases with increasing WGO, but it decreases as HGO increases. The most important is to notice that νc becomes negative at some specific values of WGO and HGO. For example, in the considered range (0≤WGO≤2.5% ), νc is always positive in cases of HGO={0%,25%,50%}, however it reaches negative values in cases of HGO={75%,100%}. Since (Q11=Ec/(1−νc2)) is a reasonable measure of plate stiffness, we plot 1/(1−νc2) and Q11 in Fig. 9c,d, respectively. It is clear that, νc=0 is a critical value that can reverse the performance of GOAM plates. Fig. 9d indicates that the plate stiffness increases as WGOincreases in the cases of HGO={0%,25%,50%}. However, in case of HGO=100%, the plate stiffness decreases in the range of WGO, where νc≥0 but it increases as νc becomes negative. These theoretical conclusions are consistent with the numerical results shown in Fig. 7 and interpret mutual influence of Cu\GO parameters WGO and HGO on postbuckling behavior of GOAM plates.

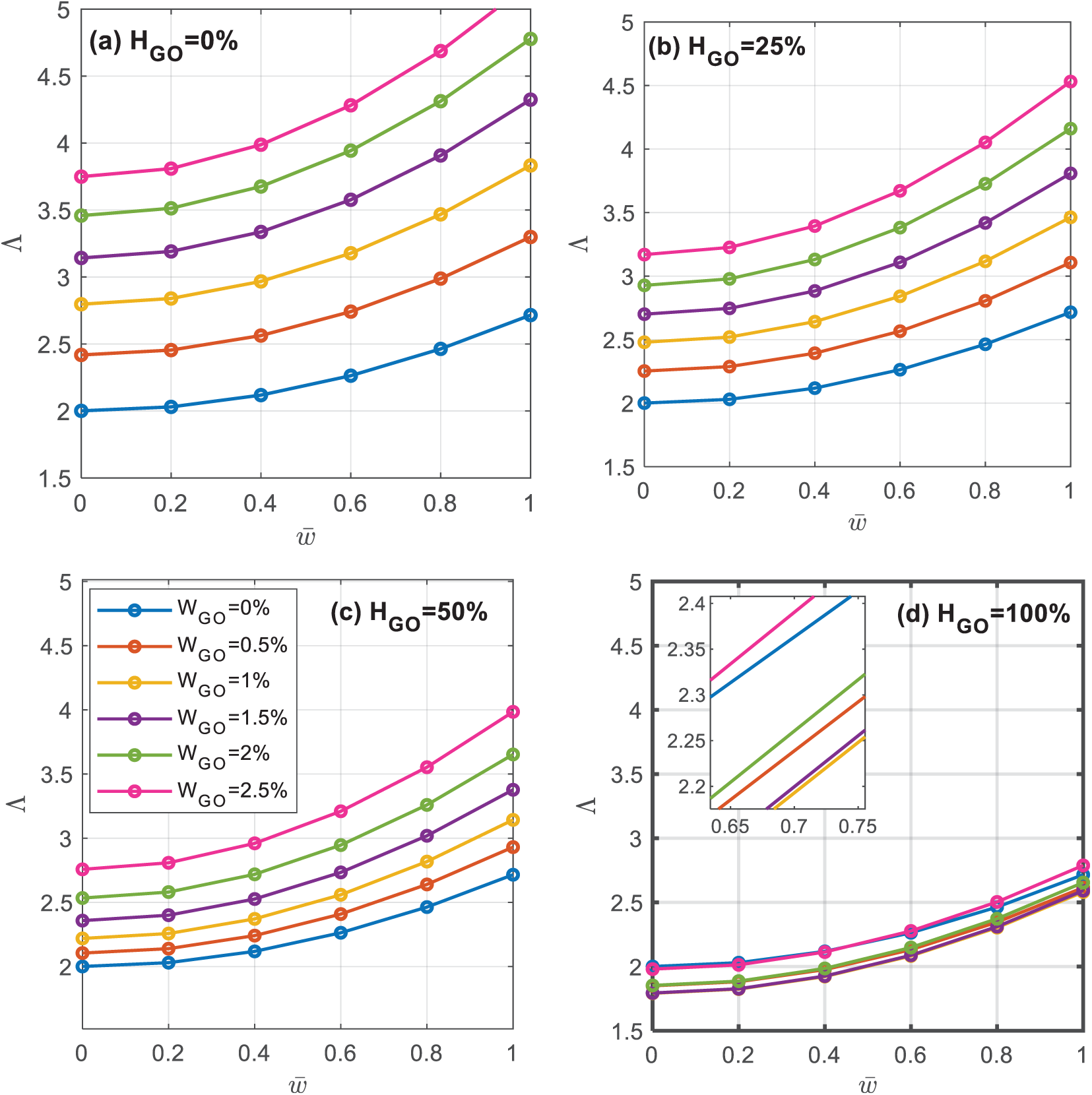
Figure 8: Mutual influence of GO properties {WGO,HGO} on postbuckling behavior of GOAM plate under biaxial compression for U-distribution type (ah=25,Λ=λ(a2ECuh3),w¯=wm/h)

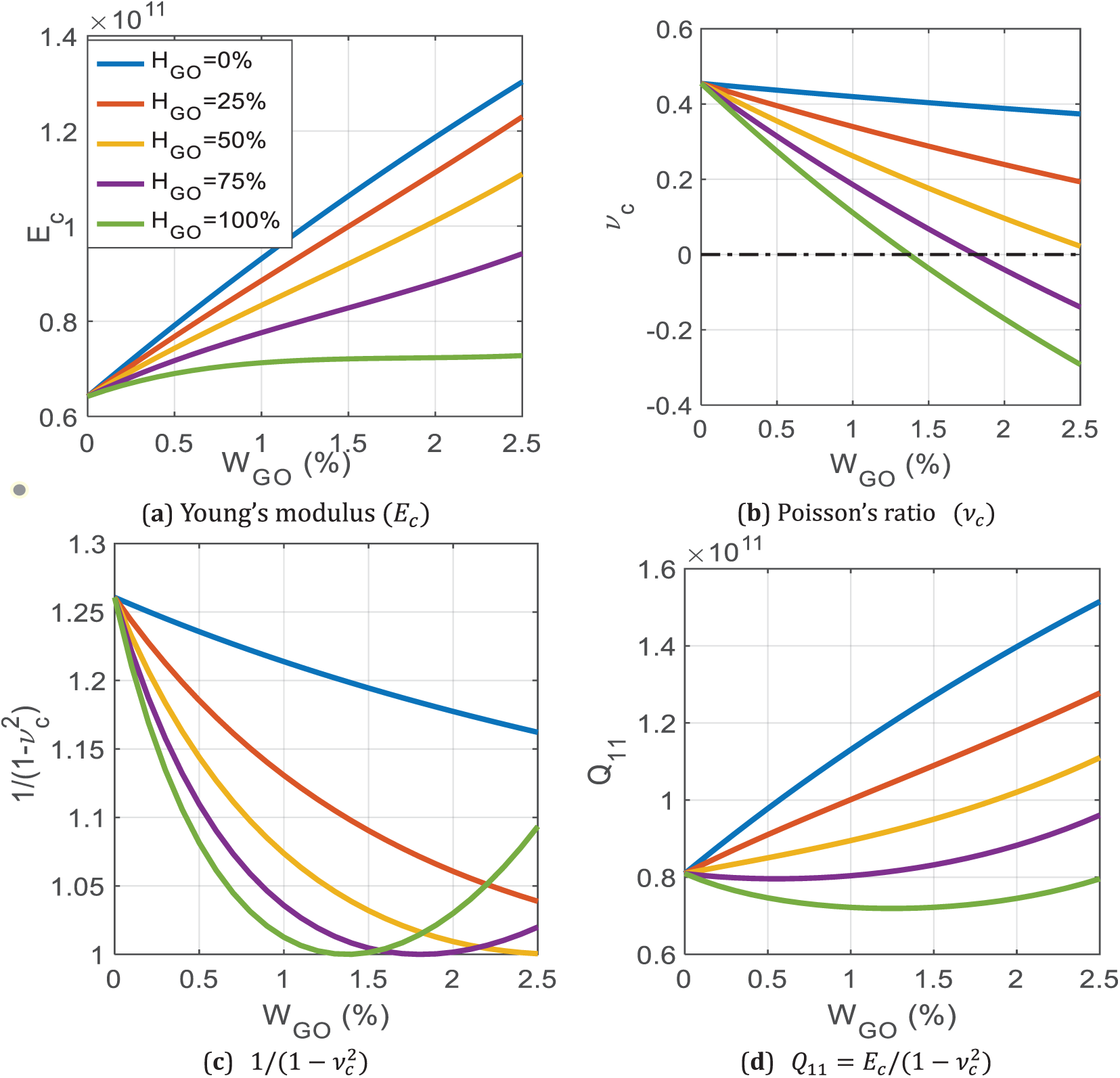
Figure 9: Mutual influence of GO parameters {WGO,HGO} on mechanical properties of GOAM plate (U-distribution type)

As can be observed from Figs. 5–8, the postbuckling paths are of the pitchfork bifurcation type, which is characterized by zero lateral deflection whenever the axial load is less than a critical value λcr. The dimensionless critical buckling load Λcr=λcr(a2ECuh3) corresponds to w¯=0 in these figures. Table 5 reports values of Λcr of simply supported GOAM square plates under uni/bi-axial compression for different values of WGO,HGO and different FG-distribution types.

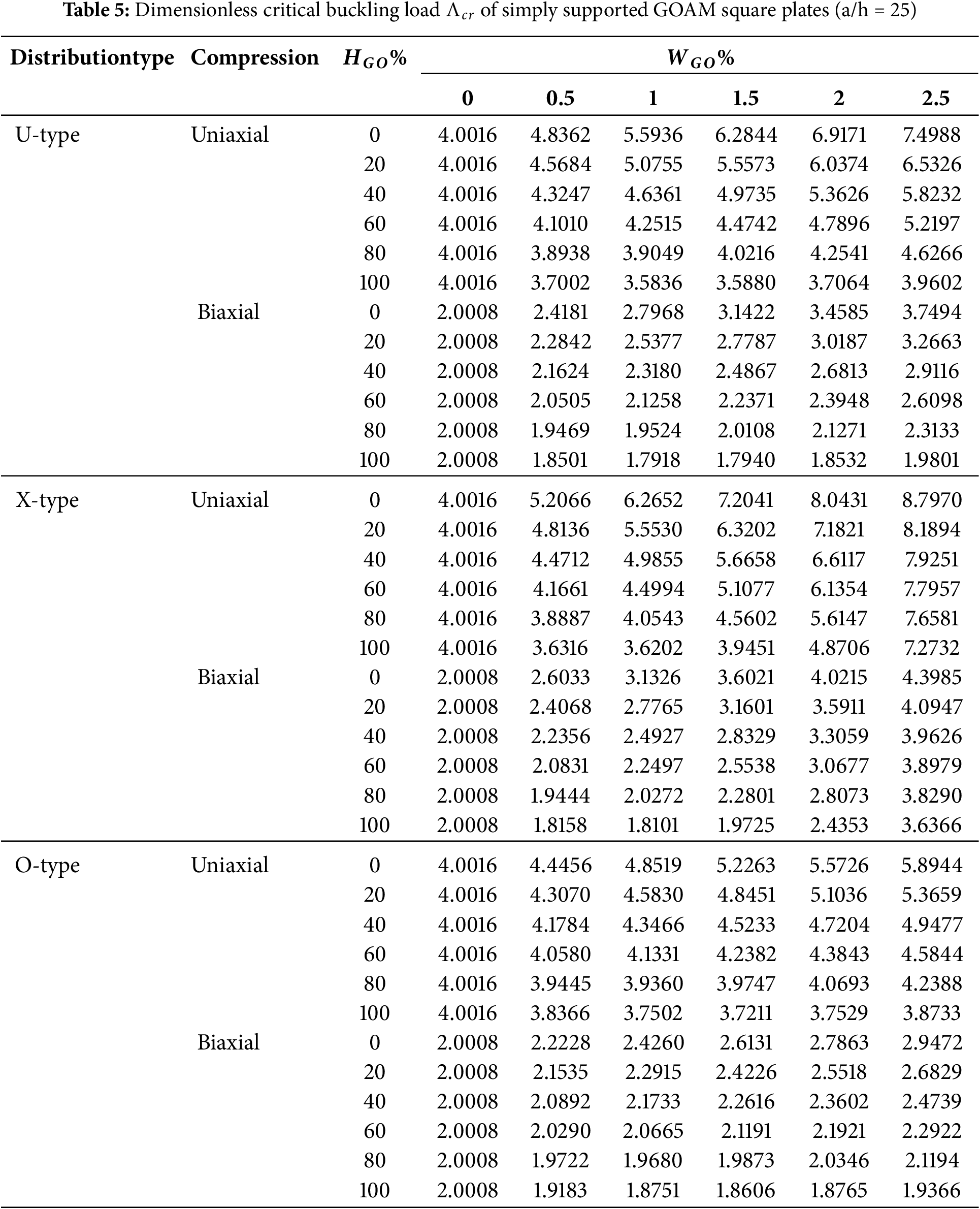
Results in Table 5 demonstrate that, for both of uniaxial and biaxial loading, for all material distribution types, and for WGO>0, increasing the GO folding degree (HGO) decreases the critical buckling load. Influence of GO content (WGO) on critical buckling load depends on the value of HGO. At HGO={0%,20%,40%,60%} the critical buckling increases as WGO increases. However, at higher folding degrees (HGO={80%,100%}) the critical buckling reduces then rises as WGO increases.

5.6 Influence of GOAM Plate Thickness

To study influence of GOAM plate thickness h on postbuckling behavior, a different normalization of the axial load is defined as Λ¯=λ(100/ECua) to excludeh from the previous normalization. A simply supported GOAM plate (WGO=2.5%,HGO=50%) under biaxial compression is considered. Fig. 10 presents the postbuckling paths of plates with different thicknesses assuming two different GO distribution types. As the figure reveals, the postbuckling loads considerably increase with the increase of plate thickness. Moreover, X-type GOAM plate exhibits better postbuckling performance compared with the U-type. Table 6 reports the normalized buckling loads Λ¯ of simply supported (SSSS) and fully clamped (CCCC) X-type GOAM plates with different thickness and different GO parameters (WGO,HGO).

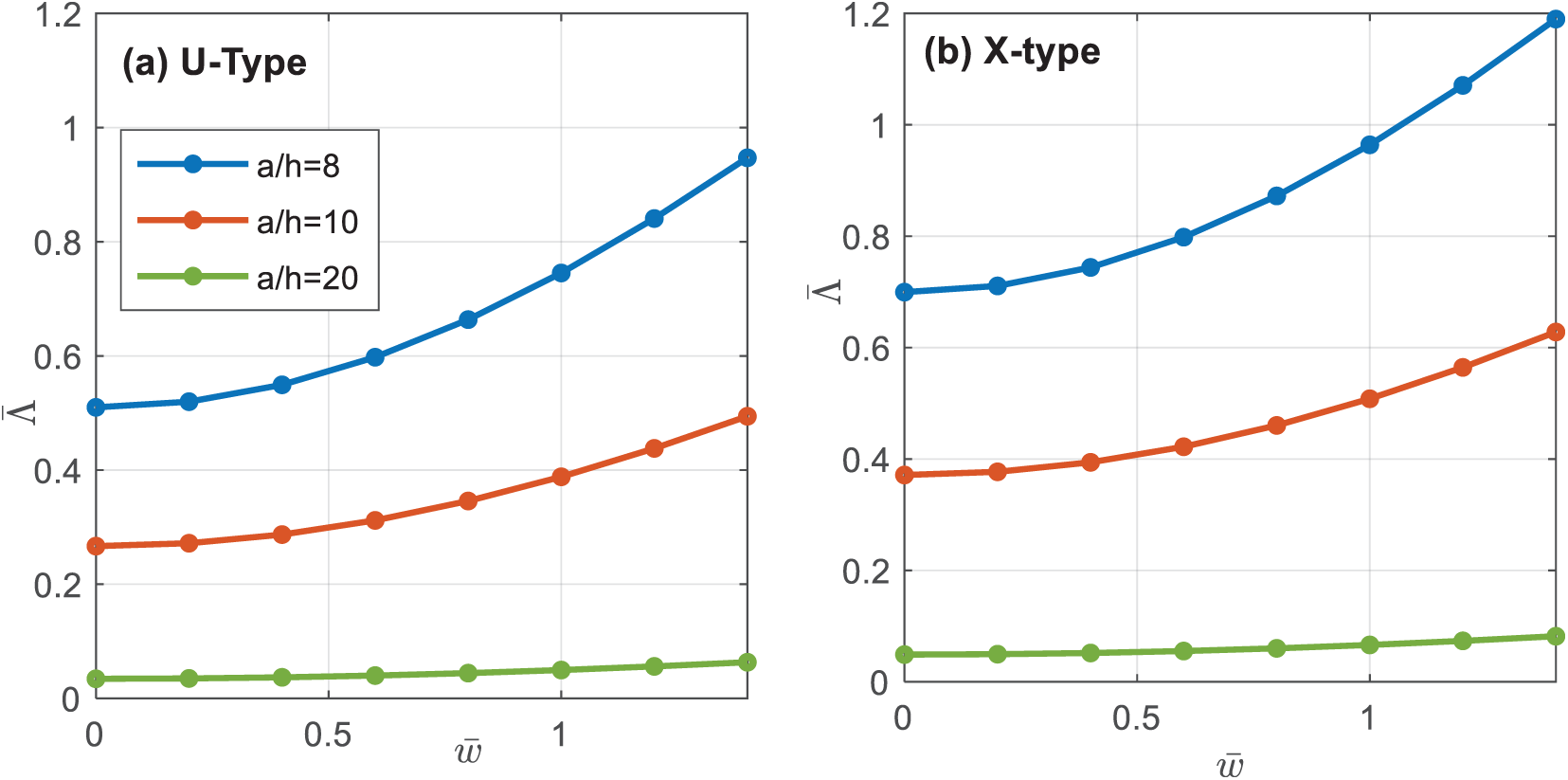
Figure 10: Influence of plate thickness on postbuckling behavior of GOAM plate under biaxial compression for GO distribution patterns: (a) U-type and (b) X-type (a=b=0.1,WGr=2.5%,HGr=50%,Λ¯=λ(100ECua),w¯=wm/h)

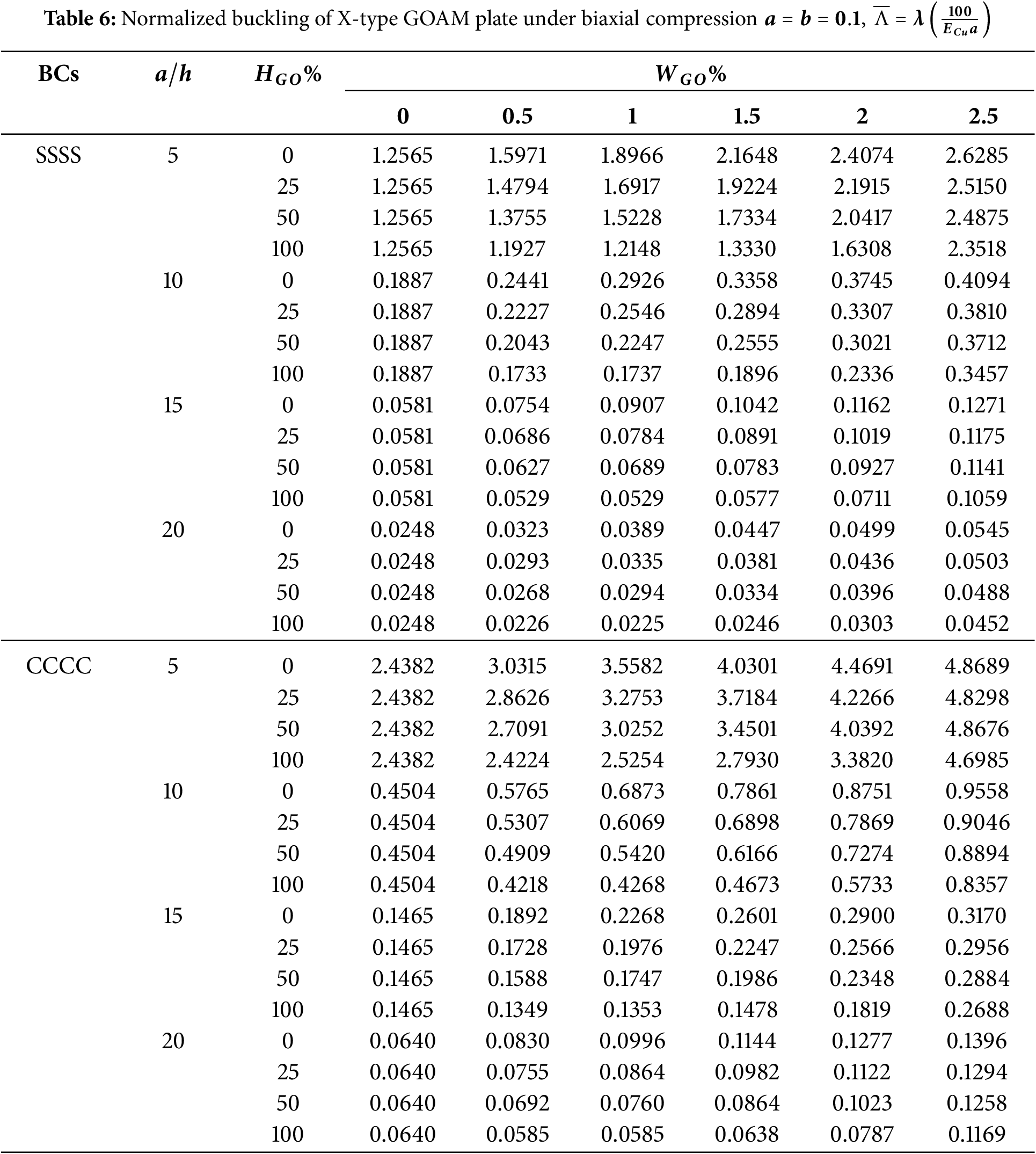
5.7 Influence of Boundary Conditions

In almost all previous results, a simply supported GOAM plates was considered. Only Table 6 presents comparison of first critical buckling loads Λ¯ of SSSS and CCCC corresponding to different values of: a/h ratio, WGO% and HGO% . In the current subsection, the first four critical buckling loads with the associated buckling modes of GOAM plates are presented in Figs. 11–13 for different boundary conditions. In these figures, U-type GOAM plates (ah=25,WGO=2.5%,HGO=50%) are considered and the critical buckling loads are normalized by Λ=λ(a2ECuh3). The first four modes entitled by the values of corresponding normalized critical buckling load Λ are shown for: (1) simply supported GOAM plate under biaxial loading in Fig. 11, (2) CCCC plate under uniaxial compression in Fig. 12, and (3) a CFCF plate with two opposite sides clamped and other two opposite sides free under uniaxial loading in Fig. 13.

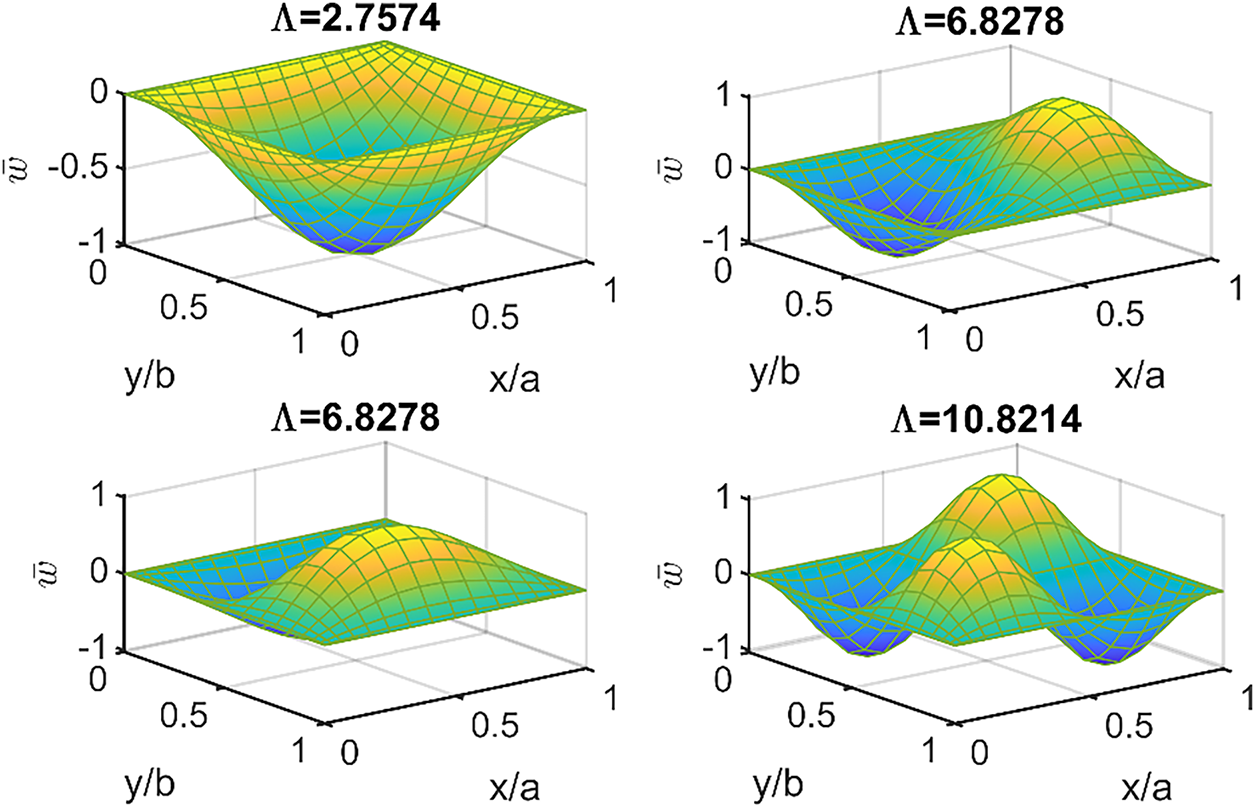
Figure 11: First four linear mode shapes of U-type GOAM SSSS plate under biaxial loading (ah=25,WGO=2.5%,HGO=50%)

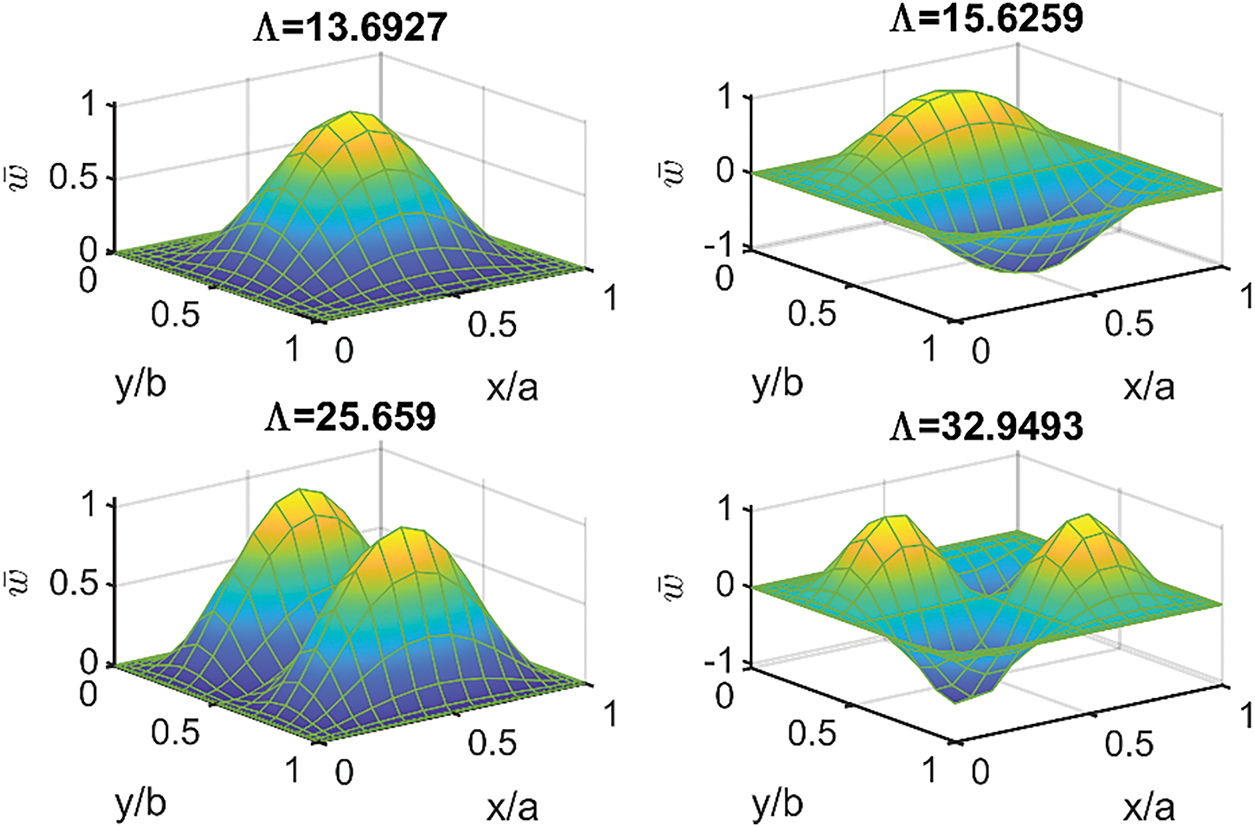
Figure 12: First four linear mode shapes of U-type GOAM CCCC plate under uniaxial loading (a/h=25,WGO=0.025,HGO=0.5)

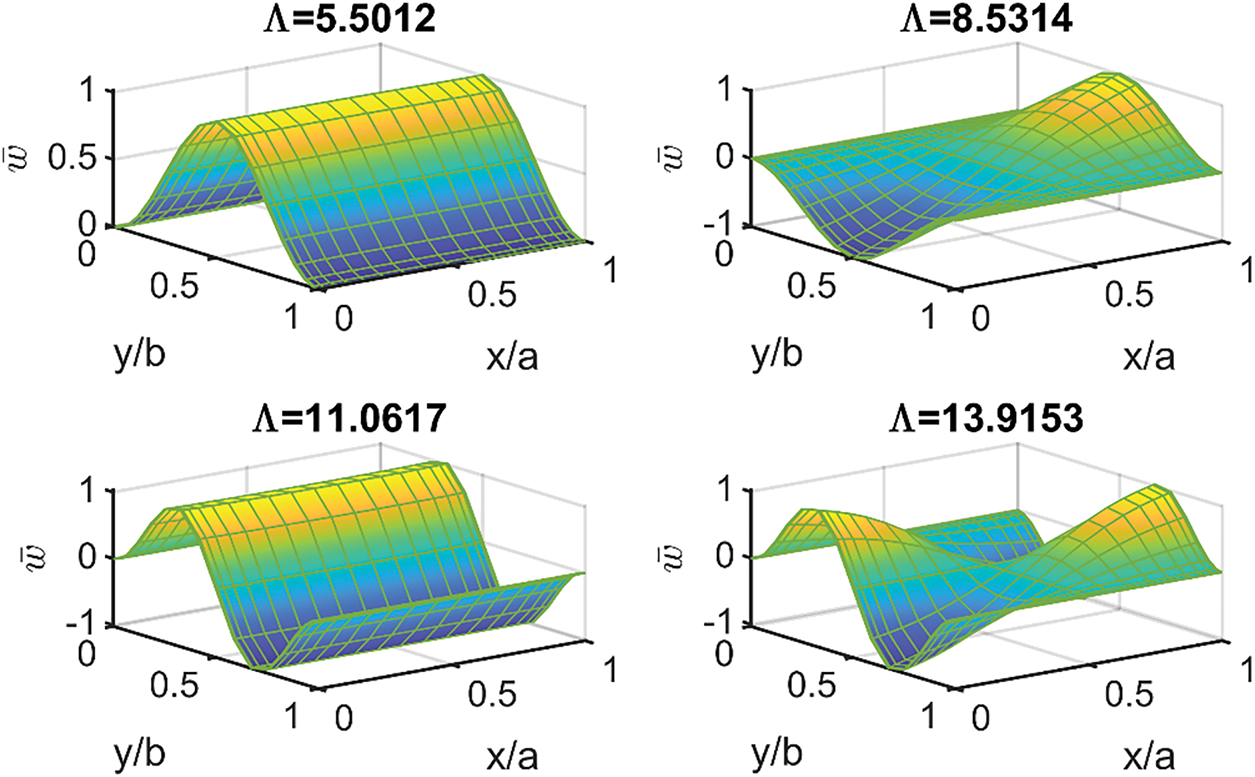
Figure 13: First four linear mode shapes of U-type GOAM CFCF plate under uniaxial loading (ah=25,WGO=0.025,HGO=0.5)

6  Conclusions

This paper studies the characteristics of critical-buckling, and nonlinear post-buckling behavior of multi-layer GOAM plate, subjected to uniaxial or biaxial compressive loads. The mechanical properties, within each layer, are modeled as a function of graphene origami content, and the folding degree. Three symmetric distributions of GOAM (i.e., U-pattern, X-pattern, and O-pattern) are considered in the analysis. Based on four variables of nonlinear high shear deformation theory, the virtual work principle is implemented to derive the governing equations assets of nonlinear eigenvalue problems. DQM is applied to discretize the governing equations, and the resulting algebraic nonlinear eigenvalue problem is solved iteratively. Theoretical and numerical analyses present the effects of graphene origami content, degree of folding, and distribution pattern on the post-buckling response of GOMA plates. The main remarks from the following analysis can be summarized as follows:

•   Increasing the folding degree increases the transformation of GO/Cu composite into GOAM with NPR, and reduces Young’s modulus, thus making the metamaterial structure more flexible.

•   For different folding degrees HGO, a rise in graphene origami content WGO results in increasing Young’s modulus and decreasing Poisson’s ratio.

•   For a smaller range of the folding degrees, where the composite Poisson’s ratio is still positive (νc≥0), the critical and post-buckling loads of the plate with any GO distributions are increased by increasing WGO. In contrast, as the folding degree increases, the negative Poisson’s ratio is reached and the GOAM plate exhibits a counter-intuitive buckling behavior.

•   Buckling loads under uniaxial compression are twice those calculated for biaxial loading.

•   The GOAM plate with an X-distribution type demonstrates the greatest resistance to buckling and the most favorable post-buckling behavior.

•   Thicker plates demonstrate the higher-load-bearing capacity

•   The following model is limited to flat plates without curvature and imperfections.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Salwa A. Mohamed: Validation, Supervision, Resources, Methodology, Investigation, Formal analysis. Mohamed A. Eltaher: Conceptualization, Validation, Investigation, Formal analysis. Nazira Mohamed: Resources, Conceptualization, Investigation, Formal analysis. Rasha Abo-bakr: Visualization, Validation, Investigation, Formal analysis. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data can be provided according to reasonable requirements.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

𝒦(i)𝒴(i)=[𝒞xNx¯+𝒞yNxy¯𝒞xNxy¯+𝒞yNy¯𝒞xxMxb+2𝒞xyMxyb+𝒞yyMyb+𝒩¯𝒞xxMxs+2𝒞xyMxys+𝒞yyMys+𝒞ySyzs+𝒞xSxzs+𝒩¯]𝒫=[OOOOOOOOOOOOγ1𝒞xx+γ2𝒞yyγ1𝒞xx+γ2𝒞yyγ1𝒞xx+γ2𝒞yyγ1𝒞xx+γ2𝒞yy](A1)

𝒩¯=𝒞x(Wx0∘Nx¯+Wy0∘Nxy¯)+𝒞y(Wx0∘Nx¯+Wy0∘Ny¯)(A2)

Syzs=[OOOA44s𝒞y],Sxzs=[OOOA55s𝒞x],λγ1=Nxo,λγ2=Nyo(A3)

References

1. Balan M, Mertens J, Bahubalendruni MR. Auxetic mechanical metamaterials and their futuristic developments: a state-of-art review. Mater Today Commun. 2023;34:105285. doi:10.1016/j.mtcomm.2022.105285. [Google Scholar] [CrossRef]

2. Momoh EO, Jayasinghe A, Hajsadeghi M, Vinai R, Evans KE, Kripakaran P, et al. A state-of-the-art review on the application of auxetic materials in cementitious composites. Thin-Walled Struct. 2024;196:111447. doi:10.1016/j.tws.2023.111447. [Google Scholar] [CrossRef]

3. Huang C, Chen L. Negative Poisson’s ratio in modern functional materials. Adv Mater. 2016;28(37):8079–96. doi:10.1002/adma.201601363. [Google Scholar] [PubMed] [CrossRef]

4. Contreras N, Zhang X, Hao H, Hernández F. Application of elastic metamaterials/meta-structures in civil engineering: a review. Compos Struct. 2024;327:117663. doi:10.1016/j.compstruct.2023.117663. [Google Scholar] [CrossRef]

5. Wen Y, Gao E, Hu Z, Xu T, Lu H, Xu Z, et al. Chemically modified graphene films with tunable negative Poisson’s ratios. Nat Commun. 2019;10(1):2446. doi:10.1038/s41467-019-10361-3. [Google Scholar] [PubMed] [CrossRef]

6. Dutta S, Menon HG, Hariprasad MP, Krishnan A, Shankar B. Study of auxetic beams under bending: a finite element approach. Mater Today Proc. 2021;46:9782–7. doi:10.1016/j.matpr.2020.10.479. [Google Scholar] [CrossRef]

7. Meng F, Chen S, Zhang W, Ou P, Zhang J, Chen C, et al. Negative Poisson’s ratio in graphene Miura origami. Mech Mater. 2021;155:103774. doi:10.1016/j.mechmat.2021.103774. [Google Scholar] [CrossRef]

8. Zhao X, Wei L, Wen D, Zhu G, Yu Q, Ma ZD. Bending response and energy absorption of sandwich beams with novel auxetic honeycomb core. Eng Struct. 2021;247:113204. doi:10.1016/j.engstruct.2021.113204. [Google Scholar] [CrossRef]

9. Wu X, Yan H, Zhou Y, Zhang P, Lu Q, Shi H. Review of additive manufactured metallic metamaterials: design, fabrication, property and application. Opt Laser Technol. 2025;182:112066. doi:10.1016/j.optlastec.2024.112066. [Google Scholar] [CrossRef]

10. Fang S, Zhou S, Yurchenko D, Yang T, Liao WH. Multistability phenomenon in signal processing, energy harvesting, composite structures, and metamaterials: a review. Mech Syst Signal Process. 2022;166:108419. doi:10.1016/j.ymssp.2021.108419. [Google Scholar] [CrossRef]

11. Liu W, Ennis B, Coulais C. Tuning the buckling sequences of metamaterials using plasticity. J Mech Phys Solids. 2025;196:106019. doi:10.1016/j.jmps.2024.106019. [Google Scholar] [CrossRef]

12. Jiang F, Yang S, Qi C. Quasi-static crushing response of a novel 3D re-entrant circular auxetic metamaterial. Compos Struct. 2022;300:116066. doi:10.1016/j.compstruct.2022.116066. [Google Scholar] [CrossRef]

13. Lu H, Wang X, Chen T. Quasi-static bending response and energy absorption of a novel sandwich beam with a reinforced auxetic core under the fixed boundary at both ends. Thin-Walled Struct. 2023;191:111011. doi:10.1016/j.tws.2023.111011. [Google Scholar] [CrossRef]

14. Wang H, Shao J, Zhang W, Yan Z, Huang Z, Liang X. Three-point bending response and energy absorption of novel sandwich beams with combined re-entrant double-arrow auxetic honeycomb cores. Compos Struct. 2023;326:117606. doi:10.1016/j.compstruct.2023.117606. [Google Scholar] [CrossRef]

15. Francisco MB, Pereira JL, da Cunha SS Jr, Gomes GF. Design optimization of a sandwich composite tube with auxetic core using multiobjective lichtenberg algorithm based on metamodelling. Eng Struct. 2023;281:115775. doi:10.1016/j.engstruct.2023.115775. [Google Scholar] [CrossRef]

16. Wu W, Wang Y, Gao Z, Liu P. Topology optimization of metamaterial microstructures for negative poisson’s ratio under large deformation using a gradient-free method. Comput Model Eng Sci. 2024;139(2):2001–26. doi:10.32604/cmes.2023.046670. [Google Scholar] [CrossRef]

17. Lv Y, Zhang J, Wu J, Li L. Mechanical and thermal postbuckling of functionally graded graphene origami-enabled auxetic metamaterials plates. Eng Struct. 2024;298:117043. doi:10.1016/j.engstruct.2023.117043. [Google Scholar] [CrossRef]

18. Du C, Wang Y, Kang Z. Cut layout optimization for design of kirigami metamaterials under large stretching. Theor Appl Mech Lett. 2024;14(6):100528. doi:10.1016/j.taml.2024.100528. [Google Scholar] [CrossRef]

19. Li PQ, Wang KF, Wang BL. Nonlinear vibration of the sandwich beam with auxetic honeycomb core under thermal shock. Thin-Walled Struct. 2024;196:111479. doi:10.1016/j.tws.2023.111479. [Google Scholar] [CrossRef]

20. Vineyard E, Gao XL. Topology and shape optimization of 2-D and 3-D micro-architectured thermoelastic metamaterials using a parametric level set method. Comput Model Eng Sci. 2021;127(3):819–54. doi:10.32604/cmes.2021.015688. [Google Scholar] [CrossRef]

21. Bloom F, Coffin D. Handbook of thin plate buckling and postbuckling. Boca Raton, FL, USA: CRC Press; 2000. [Google Scholar]

22. Wang CM, Liew KM, Xiang Y, Kitipornchai S. Buckling of rectangular Mindlin plates with internal line supports. Int J Solids Struct. 1993;30(1):1–7. doi:10.1016/0020-7683(93)90129-U. [Google Scholar] [CrossRef]

23. Shariyat M, Asemi K. Uniaxial and biaxial post-buckling behaviors of longitudinally graded rectangular plates on elastic foundations according to the 3D theory of elasticity. Compos Struct. 2016;142:57–70. doi:10.1016/j.compstruct.2016.01.065. [Google Scholar] [CrossRef]

24. Wehmeyer S, Zok FW, Eberl C, Gumbsch P, Cohen N, McMeeking RM, et al. Post-buckling and dynamic response of angled struts in elastic lattices. J Mech Phys Solids. 2019;133:103693. doi:10.1016/j.jmps.2019.103693. [Google Scholar] [CrossRef]

25. Eltaher MA, Mohamed N, Mohamed SA, Seddek LF. Periodic and nonperiodic modes of postbuckling and nonlinear vibration of beams attached to nonlinear foundations. Appl Math Model. 2019;75:414–45. doi:10.1016/j.apm.2019.05.026. [Google Scholar] [CrossRef]

26. Mao JJ, Zhang W. Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos Struct. 2019;216:392–405. doi:10.1016/j.compstruct.2019.02.095. [Google Scholar] [CrossRef]

27. Mehrabi P, Mortazavi M, Far H. Axisymmetric thermal post-buckling of the eccentric annular sector plate made of Gori-metamaterials: introducing DNN-RF algorithm for solving the post-buckling problems. Thin-Walled Struct. 2025;208:112795. doi:10.1016/j.tws.2024.112795. [Google Scholar] [CrossRef]

28. Derveni F, Gross AJ, Peterman KD, Gerasimidis S. Postbuckling behavior and imperfection sensitivity of elastic-plastic periodic plate-lattice materials. Extrem Mech Lett. 2022;50:101510. doi:10.1016/j.eml.2021.101510. [Google Scholar] [CrossRef]

29. Moradi-Dastjerdi R, Behdinan K. Biaxial buckling analysis of an innovative active sandwich plate. Mech Based Des Struct Mach. 2024;52(1):275–88. doi:10.1080/15397734.2022.2107539. [Google Scholar] [CrossRef]

30. Liu Y, Qin Z, Chu F. Nonlinear vibrations of auxetic honeycomb thin plates based on the modified Gibson functions. Thin-Walled Struct. 2023;193:111259. doi:10.1016/j.tws.2023.111259. [Google Scholar] [CrossRef]

31. Abbaspour F, Hosseini S. Thermal buckling of piezoelectric graphene platelets reinforced cylindrical microshells using Navier’s and meshless methods. Mech Based Des Struct Mach. 2024;52(8):5653–72. doi:10.1080/15397734.2023.2260466. [Google Scholar] [CrossRef]

32. Long VT, Tung HV. Postbuckling responses of porous FGM spherical caps and circular plates including edge constraints and nonlinear three-parameter elastic foundations. Mech Based Des Struct Mach. 2023;51(8):4214–36. doi:10.1080/15397734.2021.1956327. [Google Scholar] [CrossRef]

33. Yan S, Wu L, Wen Y, Sun J, Zhou J. Snap-through instability in mechanical metamaterials. Responsive Mater. 2025;94:e20240035. doi:10.1002/rpm.20240035. [Google Scholar] [CrossRef]

34. Ezzati H, Pashalou S, Rastgoo A, Ebrahimi F. Vibration analysis of multilayer graphene origami-enabled metamaterial plates. Acta Mech. 2024;235:7623–40. doi:10.1007/s00707-024-04117-4. [Google Scholar] [CrossRef]

35. Mahinzare M, Rastgoo A, Ebrahimi F. Nonlinear vibration of FG graphene origami auxetic sandwich plate including smart hybrid nanocomposite sheets. J Eng Mech. 2024;150(4):04024007. doi:10.1061/JENMDT.EMENG-7398. [Google Scholar] [CrossRef]

36. Mohamed SA, Assie AE, Eltaher MA, Abo-bakr RM, Mohamed N. Nonlinear postbuckling and snap-through instability of movable simply supported BDFG porous plates rested on elastic foundations. Mech Based Des Struct Mach. 2024;52:528789–816. doi:10.1080/15397734.2024.2328339. [Google Scholar] [CrossRef]

37. He L, Maalla A, Zhou X, Tang H. Buckling and post-buckling of anisogrid lattice-core sandwich plates with nanocomposite skins. Thin-Walled Struct. 2024;199:111828. doi:10.1016/j.tws.2024.111828. [Google Scholar] [CrossRef]

38. Milazzo A, Guarino G, Gulizzi V. Buckling and post-buckling of variable stiffness plates with cutouts by a single-domain Ritz method. Thin-Walled Struct. 2023;182:110282. doi:10.1016/j.tws.2022.110282. [Google Scholar] [CrossRef]

39. Vaghefi R. Three-dimensional elastoplastic post-buckling analysis of porous FG plates resting on Winkler/Pasternak foundation using meshless RRKPM. Thin-Walled Struct. 2024;200:111915. doi:10.1016/j.tws.2024.111915. [Google Scholar] [CrossRef]

40. Dai Q, Liu Y. Dynamic stability analysis of periodic loaded rotating conical shells using Floquet exponent method. Mech Based Des Struct Mach. 2024;52(3):1399–413. doi:10.1080/15397734.2022.2147082. [Google Scholar] [CrossRef]

41. Nasri MR, Salari E, Salari A, Vanini SA. Nonlinear bending and buckling analysis of 3D-printed meta-sandwich curved beam with auxetic honeycomb core. Aerosp Sci Technol. 2024;152:109339. doi:10.1016/j.ast.2024.109339. [Google Scholar] [CrossRef]

42. Shen HS, Xiang Y, Reddy JN. Effect of negative Poisson’s ratio on the post-buckling behavior of FG-GRMMC laminated plates in thermal environments. Compos Struct. 2020;253:112731. doi:10.1016/j.compstruct.2020.112731. [Google Scholar] [CrossRef]

43. An J, Wang A, Zhang K, Zhang W, Song L, Xiao B, et al. Bending and buckling analysis of functionally graded graphene origami metamaterial irregular plates using generalized finite difference method. Results Phys. 2023;53:106945. doi:10.1016/j.rinp.2023.106945. [Google Scholar] [CrossRef]

44. Murari B, Zhao S, Zhang Y, Ke L, Yang J. Vibrational characteristics of functionally graded graphene origami-enabled auxetic metamaterial beams with variable thickness in fluid. Eng Struct. 2023;277:115440. doi:10.1016/j.engstruct.2022.115440. [Google Scholar] [CrossRef]

45. Murari B, Zhao S, Zhang Y, Yang J. Graphene origami-enabled auxetic metamaterial tapered beams in fluid: nonlinear vibration and postbuckling analyses via physics-embedded machine learning model. Appl Math Model. 2023;122:598–613. doi:10.1016/j.apm.2023.06.023. [Google Scholar] [CrossRef]

46. Ghasemi F, Salari E, Rastgoo A, Li D, Deng J. Nonlinear vibration analysis of pre/post-buckled 3D-printed tubular metastructures. Eng Anal Bound Elem. 2024;165:105777. doi:10.1016/j.enganabound.2024.105777. [Google Scholar] [CrossRef]

47. Sengar V, Watts G, Kumar R, Patel SN, Kumar A. Tunable thermal postbuckling response of imperfect skew sandwich plates with auxetic core and FGCNTRC facings using isogeometric approach. Eng Struct. 2024;305:117706. doi:10.1016/j.engstruct.2024.117706. [Google Scholar] [CrossRef]

48. Ghasemi F, Salari E, Salari A, Rastgoo A, Li D, Deng J. Integrating analytical and machine learning methods for investigating nonlinear bending and post-buckling behavior of 3D-printed auxetic tubes. Eng Comput. 2024;353:1–38. doi:10.1007/s00366-024-02091-y. [Google Scholar] [CrossRef]

49. Zhao S, Zhang Y, Zhang Y, Zhang W, Yang J, Kitipornchai S. Genetic programming-assisted micromechanical models of graphene origami-enabled metal metamaterials. Acta Mater. 2022;228:117791. doi:10.1016/j.actamat.2022.117791. [Google Scholar] [CrossRef]

50. Babaei H, Eslami MR. Nonlinear analysis of thermal-mechanical coupling bending of FGP infinite length cylindrical panels based on PNS and NSGT. Appl Math Model. 2021;91:1061–80. doi:10.1016/j.apm.2020.10.004. [Google Scholar] [CrossRef]

51. Chu L, Dui G, Zheng Y. Thermally induced nonlinear dynamic analysis of temperature-dependent functionally graded flexoelectric nanobeams based on nonlocal simplified strain gradient elasticity theory. Eur J Mech—A/Solids. 2020;82:103999. doi:10.1016/j.euromechsol.2020.103999. [Google Scholar] [CrossRef]

52. Shahverdi H, Barati MR. Vibration analysis of porous functionally graded nanoplates. Int J Eng Sci. 2017;120:82–99. doi:10.1016/j.ijengsci.2017.06.008. [Google Scholar] [CrossRef]

53. Zhang DG. Modeling and analysis of FGM rectangular plates based on physical neutral surface and high order shear deformation theory. Int J Mech Sci. 2013;68:92–104. doi:10.1016/j.ijmecsci.2013.01.002. [Google Scholar] [CrossRef]

54. Melaibari A, Mohamed SA, Assie AE, Shanab RA, Eltaher MA. Static response of 2D FG porous plates resting on elastic foundation using midplane and neutral surfaces with movable constraints. Mathematics. 2022;10(24):4784. doi:10.3390/math10244784. [Google Scholar] [CrossRef]

55. Shu C. Differential quadrature and its application in engineering. Berlin/Heidelberg, Germany: Springer Science & Business Media; 2012. [Google Scholar]

56. Prakash T, Singha MK, Ganapathi M. Influence of neutral surface position on the nonlinear stability behavior of functionally graded plates. Comput Mech. 2009;43:341–50. doi:10.1007/s00466-008-0309-8. [Google Scholar] [CrossRef]