IDCE: Integrated Data Compression and Encryption for Enhanced Security and Efficiency

1  Introduction

Data contains symbols that can manifest sequences, segments, or blocks, and are either stored or transmitted. Data finds its application in various contexts, such as insertion into communication channels or storage on dedicated devices. However, data, whether stored on physical storage devices or transmitted across networks, often contains substantial redundancy. Data compression is a basic approach to address this issue by reducing redundancy, thereby saving storage space, and minimizing transmission time through the conversion of data into more compact forms that require fewer bits.

However, achieving robust data security requires addressing a variety of additional considerations. Compression algorithms depend on a pattern library to achieve optimal performance when both the sender and receiver have a thorough understanding of the same method. This dependence on a pattern library can assist authorized access while preserving information secrecy. However, a notable deficiency arises in many compression algorithms, such as their lack of incorporation of secret keys or password-based restrictions during both compression and decompression processes. This gap dents the overall level of security, potentially exposing sensitive data to unauthorized access. Though it is important to recognize that while data compression does offer a limited level of security, its primary objective remains the reduction of data redundancy.

More importantly, the contemporary environment of data security presents a serious challenge. The proliferation of interconnected computers, coupled with the exponential growth of data often reaching Exabyte-scale magnitudes [1], increases the urgency of data security. To reinforce data security comprehensively, it becomes necessary to enforce robust data encryption measures where digital assets are valuable. Data encryption is a widely adopted approach to ensure data security. Encryption algorithms typically manipulate data using pseudorandom generated keystreams with key control, thereby effectively achieving data encryption. Decrypting the data involves a straightforward reversal of this process, allowing the retrieval of plaintext from ciphertext. Despite their distinct advantages, both compression and encryption are intricate disciplines that demand substantial computational power when dealing with extensive data. Moreover, the intricacy arises because compression and encryption are distinct operations applied to the same data.

In the context of data manipulation, compression and encryption algorithms interact with data, either for compressing or encrypting it. Two established approaches are commonly employed for the sequential compression and encryption of data. The first approach involves compressing the data before encrypting it, while the second encrypts the data prior to compression (as illustrated in Figs. 1 and 2). Data compression serves a primary purpose in eliminating redundancy by identifying patterns, a practice that also enhances encryption security by reducing susceptibility to statistical cryptanalysis rooted in redundancy. A secondary reason for employing compression lies in situations where a correctly implemented encryption algorithm generates substantial random data while minimizing redundancy, rendering the data essentially uncompressible [2,3]. Although the sequential execution of compression and encryption provides significant benefits, such as reduced data storage demands, enhanced data transmission bandwidth, and heightened security, this duality adds complexity and increases processing time, presenting an area ripe for further exploration and innovation.

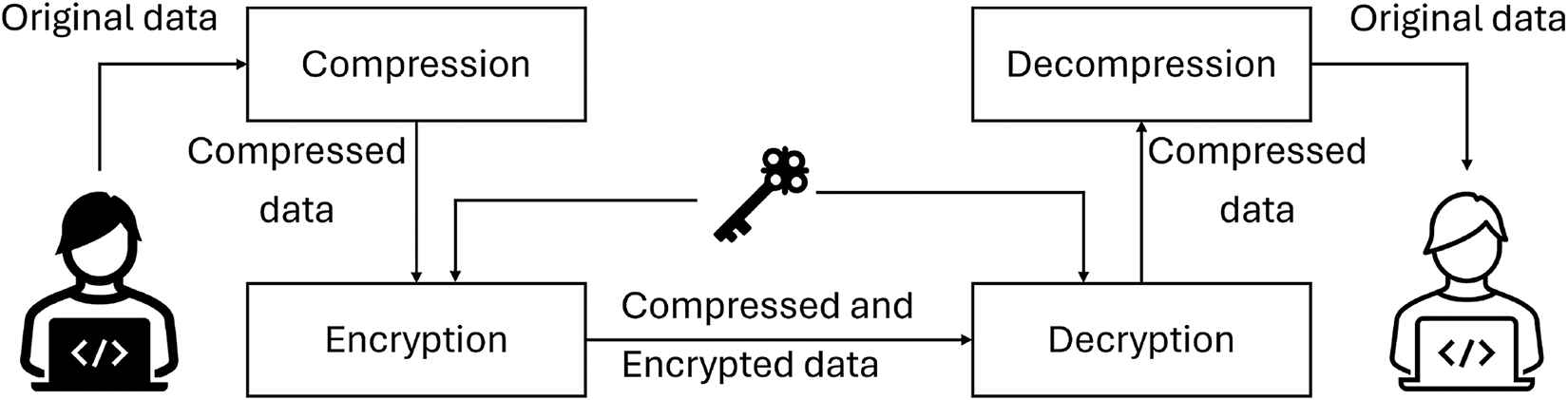
Figure 1: Traditional approach to apply compression-first

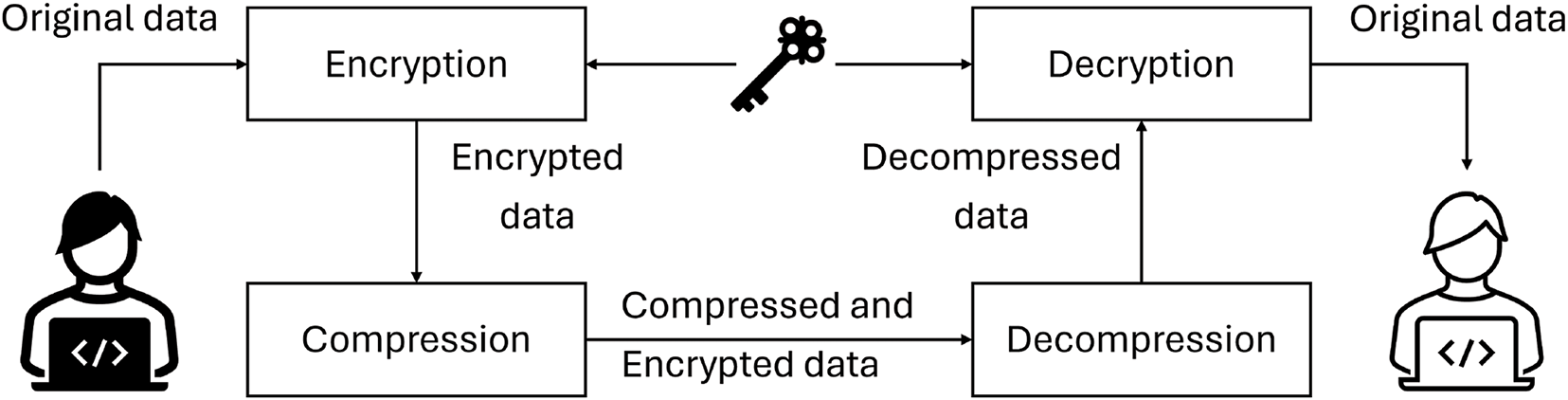
Figure 2: Traditional method to apply encryption first

Building upon the complexities and challenges highlighted in the preceding discussion, it becomes evident that concurrent data compression and encryption using a single algorithm is a challenging task. Contemporary endeavors in this direction often grapple with compromises between compression ratios and security levels. As such, there is a promising interest in exploring integrated data compression and encryption algorithms that can enhance data storage and transmission capacity while preserving data integrity and security. Leveraging insights from chaos theory, cryptography, and compression studies, this research embarks on the development of a tightly integrated compression and encryption scheme, aiming to unpredictably vary data compression while upholding data integrity.

The subsequent sections of this paper are structured as follows to provide a comprehensive understanding of the proposed approach. Section 2 investigates a review of related work in the field. In Section 3, the proposed algorithm is explained in detail. Section 4 presents the results of an experimental analysis of the proposed algorithm’s performance. Finally, Section 5 offers conclusions drawn from the study’s findings, summarizing its contributions and implications.

2  Related Work

The realms of data and file management commonly employ both compression and encryption algorithms, finding applications in a wide array of contexts, including networks, multimedia, medical, and military systems. Traditionally, these techniques have been executed separately, necessitating substantial computational resources to manage the substantial data flow between the two operations. Recognizing the potential advantages of integrating data compression and encryption into a unified approach, the aim is twofold: to optimize data storage and transmission efficiency through compression while bolstering resistance to statistical methods of cryptanalysis [4]. Previous attempts to integrate these operations have been made, but they have encountered formidable challenges. The primary obstacle lies in striking a balance between achieving an efficient compression ratio along with data security. This stability is crucial to ensure compact, reliable, and secure data storage and transmission while safeguarding against unauthorized access and misuse. Yet, the urgency of addressing this challenge cannot be overstated, especially in the contemporary era marked by ever-expanding data sizes, widespread online storage, and the escalating threat of network attacks.

Classical cryptography has historically drawn upon a rich set of mathematical tools, encompassing number theory, algebra, algebraic geometry, and combinatory techniques [5]. However, in recent decades, there has been a significant shift towards incorporating chaos theory from dynamical systems into the construction of cryptosystems. Chaos theory’s distinctive attributes and features, particularly those exhibited by discrete dynamic systems (chaotic maps), have rendered it exceptionally practical and valuable in the realm of cryptography [6–8]. The property of sensitivity to initial conditions is of particular significance, as it implies that each point within the system is intricately linked, in a random or arbitrary manner, to other points with substantial disparities in their trajectories. In the context of cryptosystems, this sensitivity becomes a fundamental building block for generating secret keys. Another vital characteristic is topological transitivity, which guarantees the ergodicity of a chaotic map. Also, this attribute is intimately connected with the diffusion aspect, which is pivotal for the operation of cryptosystems.

The intrinsic properties of chaotic systems bear a direct relevance to the field of cryptography, and their integration with data compression represents a relatively novel avenue of research. Within this emerging field, several approaches have been put forth [9–11]. These approaches can broadly be categorized into two distinct groups: compression-oriented and encryption-oriented schemes [11,12]. In encryption-oriented algorithms, compression is integrated within the framework of encryption, while in compression-oriented algorithms, encryption is incorporated into the compression process. However, it’s important to note that encryption-oriented algorithms often exhibit relatively poor compression ratios and performance when compared to conventional compression techniques [13]. Typically, these algorithms yield compression ratios in the range of 10%–17% [12]. The rationale behind this lies in the fundamental disparity in objectives between data compression and encryption. Data compression primarily aims to eliminate redundancy by identifying and exploiting patterns within the data, whereas a well-implemented encryption process generates data that is essentially random, with entropy approaching the ideal value of 8. This divergence in objectives underscores the inherent challenge of simultaneously optimizing compression and encryption within a single framework.

In the context of compression-oriented schemes, the body of research has been comparatively limited. Two noteworthy instances are found in [14,15]. However, it’s worth noting that both of these approaches are relatively dated, and their security vulnerabilities to known-plaintext attacks have been exposed in subsequent investigations [16]. Building upon the foundation laid by [14], a notable improvement was introduced in [17]. This work eliminated the constraints related to intervals by subdividing the Arithmetic Coding (AC) interval and incorporating two permutations to enhance diffusion. In a separate research direction, the randomized arithmetic coding (RAC) algorithm was presented in [18] as an enhancement for the JPEG 2000 standard. This method incorporated randomization into the conventional arithmetic coding process to improve encryption capabilities. However, as revealed in [16], this method has been found to produce output of lower quality when compared to the standard approach. In the domain of non-linear chaotic dynamical systems, reference [19] proposed the utilization of a Generalized Luroth Series (GLS) as a foundational framework. Conversely, reference [20,21] introduced a novel approach that simultaneously combined arithmetic coding and encryption based on chaotic maps to generate pseudorandom bit-streams. In this latter approach, the chaotic system serves primarily as a pseudorandom bit-stream generator, seamlessly incorporating key control into the encryption process [22,23].

Moreover, A study conducted on integrated encryption in dynamic arithmetic compression embedded into adaptive arithmetic coding cryptography features being performed simultaneously for encryption and compression. The proposed method indeed enhanced security at no performance cost, reducing computational overhead along with storage risks [24]. Another technique among them is a watermarking method that joins encryption and compression. This included hashing the document through SHA-256 encryption, compressing the document with Lempel-Ziv-Welch (LZW), and adding multiple watermarks to it. Such a method not only improved copyright ownership but also improved compression efficiency [25]. However, the review on different levels of encryption through compression is that there is more need for hybrid approaches with improved encryption/decryption times, optimizing storage being two major benefits [26].

Additionally, the incorporation of encryption capabilities within Huffman coding has primarily revolved around the manipulation of tree branches through the utilization of secret keys [15,27–31]. The integrated approach was presented in [15] for compression and encryption. This approach involved the manipulation of Huffman tree branches by swapping them to the left and right based on a certain key. Subsequently, enhancements were proposed, such as the introduction of chaotically mutated Huffman trees [27]. These modifications were designed to address challenges related to multiple code-word issues, thereby expanding the key space and rectifying security vulnerabilities inherent in the earlier approach [15]. Building upon these advancements, further refinements were put forth in [28–30], where the combination of two chaotic functions was utilized to prevent known-plaintext attacks. However, it is imperative to acknowledge that this category of algorithms continues to contend with significant security concerns [16,31–33]. Consequently, there remains a compelling need for further improvements and innovations in this domain to enhance the overall security and robustness of these approaches.

3  Proposed Work

In this work, an innovative approach called an Integrated Data Compression and Encryption algorithm is introduced, aiming to enhance both security and efficiency in a generalized computational context. IDCE is designed to address the specific challenges posed by systems with limited resources when handling extensive datasets. The core focus of IDCE revolves around the essential principles of efficiency and reliability, particularly in the realms of both data compression and encryption. IDCE employs a block cipher methodology that seamlessly integrates data compression into the encryption process as shown in Fig. 3. The compression strategy relies on Huffman coding, while security is fortified through a combination of chaotic-key expansion, multiple rounds, and scrambling functions.

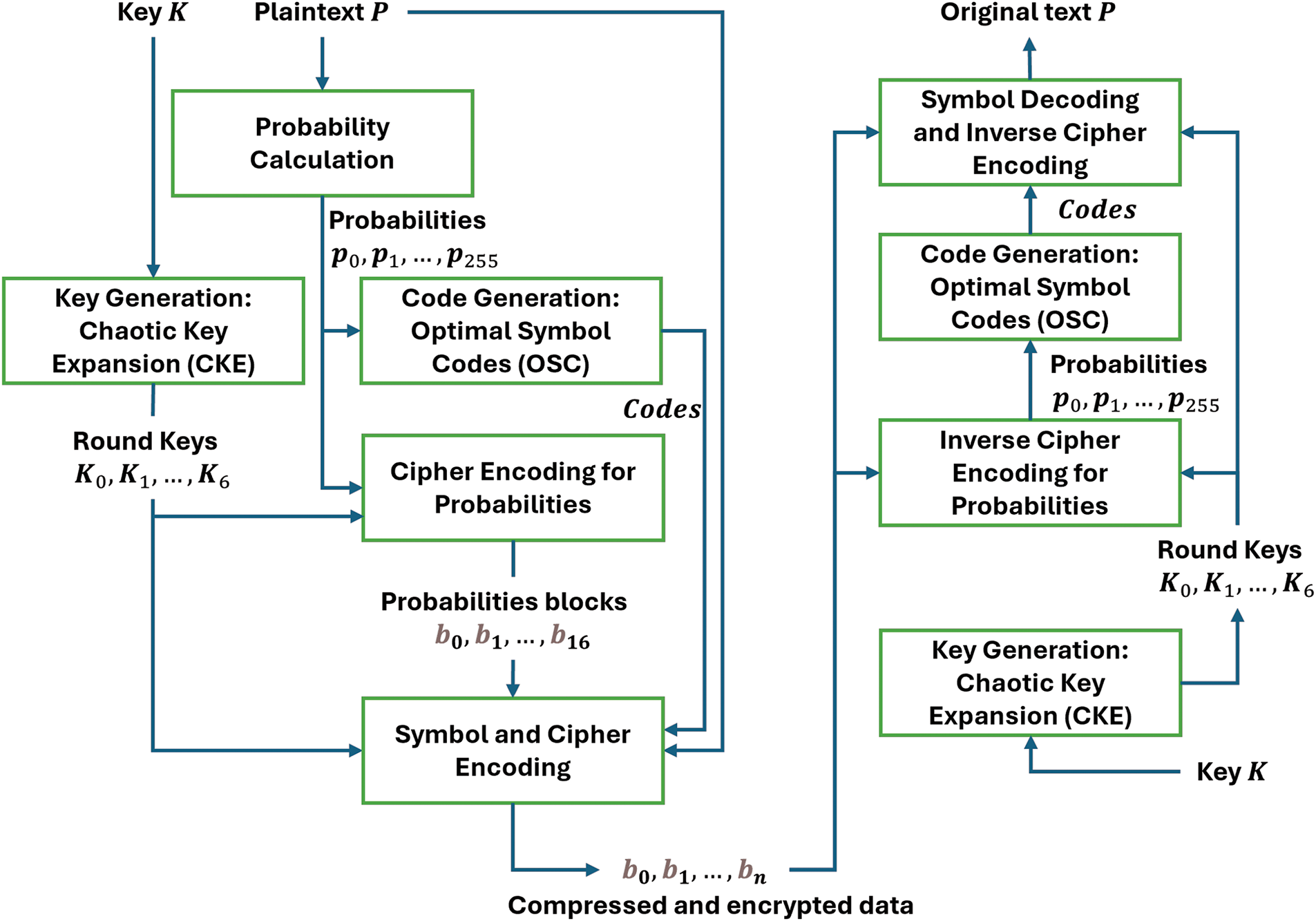
Figure 3: Proposed integrated data compression and encryption algorithm

The process of chaotic-key expansion defines how expanded keys are derived from the secret key, resulting in an expanded key size equal to the block size multiplied by seven rounds. Each round necessitates a unique round key, and a single round constitutes a sequence of scrambling functions within the cipher encoding, as explained in Section 3.2. The encryption of block data occurs by merging it with a round key through a straightforward XOR operation, which inherently possesses its own inverse operation. Subsequent subsections will provide in-depth details of each of these critical functions.

3.1 The IDCE Function

The IDCE function, denoted as , operates with two primary inputs: the first input is the secret key (a -bit data), and the second input is the plaintext (an -bit data). It yields an output, which is the ciphertext (an -bit data). Here, , , and are size parameters, where has a fixed length of 256 bits, while and have variable lengths. It’s crucial to note that must function as an encoding transformation on , effectively serving as both a compression and encryption function from to . The function is further detailed in Algorithm 1.

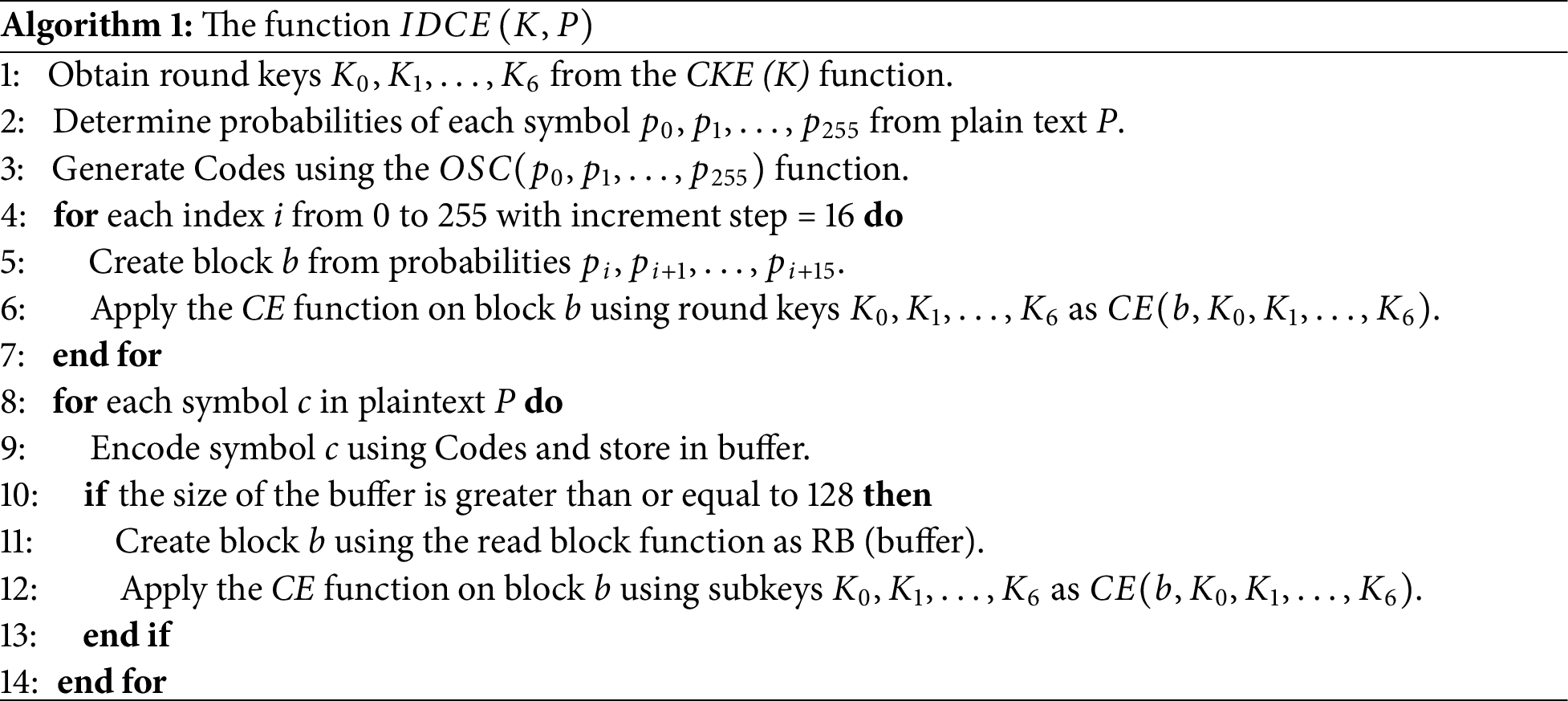
To initiate the process, we begin by deriving seven round keys, denoted as , from the provided key K. This key expansion is executed using the Chaotic Key Expansion function, as discussed in Section 3.4. Additionally, we compute the probabilities for each of the 256 ASCII symbols present in the plaintext P. This step serves as the compression header and results in a fixed-size header of 256 bytes, organized into 16 blocks.

Subsequently, these blocks undergo the encryption process and are saved as part of the output. Then, the Optimal Symbol Codes function comes into play, constructing the Huffman tree in a bottom-up manner to determine the optimal codes. TheOSC function operates iteratively, selecting and merging the two least probable symbols in each cycle, as outlined in Algorithm 2. This process is repeated a total of times, where , culminating in the final tree of optimal codes.

With the Huffman tree established, we proceed to encode each symbol from the plaintext P sequentially. This encoding process employs an encoding function, taking two inputs: the symbol and the determined optimal codes, and generating the corresponding optimal code in bits. These bits are then appended to a buffer, which has a maximum size of 136 bits. As the buffer accumulates bits, its size is regularly checked. If the buffer reaches a size equal to or exceeding 128 bits, the read block (RB) function comes into action, creating a 128-bit block for the subsequent cipher encoding. This block is then processed through the Cipher Encoding function, which encrypts it and stores the result in the output, as explained in Section 3.2. This sequential reading and encoding of plaintext symbols persists until the last symbol is processed.

As a natural complement to , we introduce its inverse, denoted as . This inverse function maps back to . Hence, , and its functionality is defined in Algorithm 3. Likewise, the function reverses the operations performed by . It commences by deriving the round keys, , and decrypting the 16 blocks of the compression header to recover the probabilities for each symbol. The OSC function is then employed to reconstruct the Huffman tree. Subsequently, each block within the ciphertext is read sequentially and decrypted through the Inverse Cipher Encoding function, as explained in Section 3.2. Furthermore, the decoding of each symbol within a block is executed using the decoding function, which serves as the inverse of the encoding function. This process operates bitwise on the input symbol and generates the encoded symbol using the provided Codes input. The sequential reading of blocks persists until the last block is processed.

3.2 Cipher Encoding (CE)

The functionality of the CE function is explained in Algorithm 4. CE commences by initializing the state variable to . This initialization stage involves a straightforward XOR operation between the first-round key and the block . The encoding process is organized into a series of iterations, each referred to as a “round,” and the algorithm encompasses a total of seven rounds.

It’s worth noting that the operations within each round are identical, except for the variation in the final round key. The final round, however, excludes the Chaotic Scrambling CS function call. CS is based on the Arnold cat map, as detailed in Section 3.3. In each round, the corresponding round key is incorporated into the state variable through a simple XOR operation: , where is the round counter variable, whereas the CS function is introduced to ensure optimal confusion during the encryption. The CS function effectively permutes the block data by preserving the actual data values but altering their arrangement via the Arnold cat map.

On the reverse side of the encryption process, the function performs inverse operations in a precisely reversed sequence, as outlined in Algorithm 5. It’s important to note that the XOR operation is self-inverse. Additionally, the individual inverse function, inverse chaotic scrambling function, is comprehensively described in Section 3.3.

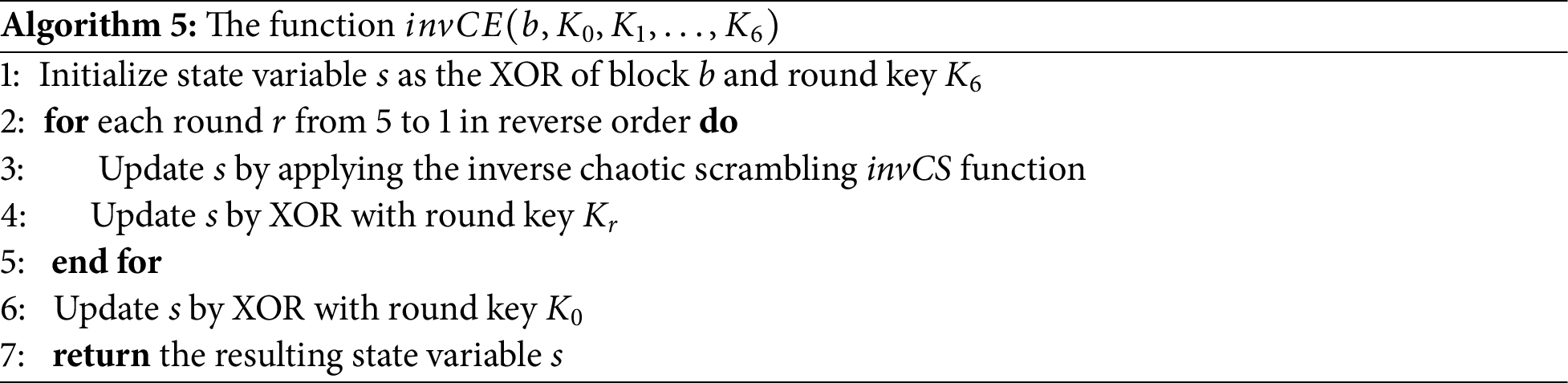
It’s worth noting that the operations within each round are identical, except for the variation in the final round key. The final round, however, excludes the CS function call. CS is based on the Arnold cat map, as detailed in Section 3.3. In each round, the corresponding round key is incorporated into the state variable through a simple XOR operation: , where is the round counter variable, whereas the CS function is introduced to ensure optimal confusion during the encryption. The CS function effectively permutes the block data by preserving the actual data values but altering their arrangement via the Arnold cat map.

On the reverse side of the encryption process, the function performs inverse operations in a precisely reversed sequence, as outlined in Algorithm 5. It’s important to note that the XOR operation is self-inverse. Additionally, the individual inverse function, inverse chaotic scrambling function, is comprehensively described in Section 3.3.

3.3 Chaotic Scrambling (CS)

The chaotic scrambling function operates by transforming a 128-bit input to another 128-bit output while applying chaotic transformations to each of the four columns, as expressed in Eq. (1):

(1)

This function’s fundamental form is designed for 2 bytes but is extended to accommodate 16 bytes. To achieve this extension, the Arnold Cat Map was selected due to its simplicity and established security properties. The Arnold Cat Map achieves data permutation or shuffling by rearranging the positions of bytes within the block [34]. The generalized form of the two-dimensional Arnold cat map is expressed as follows:

(2)

In Eq. (2), and serve as control parameters and are set to and for the proposed algorithm. Data positions undergo scrambling through the iterative application of this map across multiple rounds. The individual byte elements are shuffled using Eq. (2), which involves simple multiplication. The bytes within a column are replaced according to Eqs. (3) and (4) as follows:

(3)

(4)

On the inverse side, the inverse chaotic scrambling function conducts straightforward inverse multiplication according to Eq. (5):

(5)

It’s important to note that this transformation is unkeyed, and when repeatedly composed with itself, it ultimately results in the identity map [35]. The key cryptographic attribute of the Arnold cat map is its ability to rearrange data positions, which is highly valuable in cryptographic applications [35]. However, it is worth noting that after a certain number of iterations, this map can return the data positions to their original state, effectively restoring the original data block [35]. As an example, the matrix presented in Eq. (2) necessitates 191 iterations to revert to the identity map, a value determined through experimental computation.

3.4 Chaotic Key Expansion (CKE) Function

The Tent map was chosen as the foundational chaotic map for key expansion due to its favorable properties, including adherence to uniform distribution and invariant density characteristics [36–38]. It operates as an iterative function, defined by Eq. (6):

(6)

Here, serves as a control parameter, represents the state at step , and denotes the initial value (at ). Further, the inputs and are considered as a secret key, where value is used to generate pseudorandom keystream by setting threshold value . In proposed algorithm, the threshold value was set to (according to uniform probability model) as per Eq. (7):

(7)

However, it is important to investigate the Tent map chaotic behavior, particularly in scenarios where initial conditions and parameter values can lead to undesirable outcomes and vulnerabilities. The chaotic dynamics of the Tent map rely on . Specifically, when , the interval encompasses both periodic and non-periodic behavior. However, all orbits within this regime remain unstable, as nearby points diverge from the orbits instead of converging towards them. As increases, orbits with extended lengths emerge. Within the interval, there are periodic points of varying orbit lengths, alongside non-periodic points. Notably, the periodic points densely populate the range, signifying that the map has indeed achieved chaotic behavior, as illustrated in Figs. 4 and 5. Evaluation has confirmed that the Tent map behaves in a chaotic manner, which is advantageous for generating pseudorandom keystreams. Consequently, the proposed keystream generator is restricted to the parameter range of [22], where parameters and serve as a secret key.

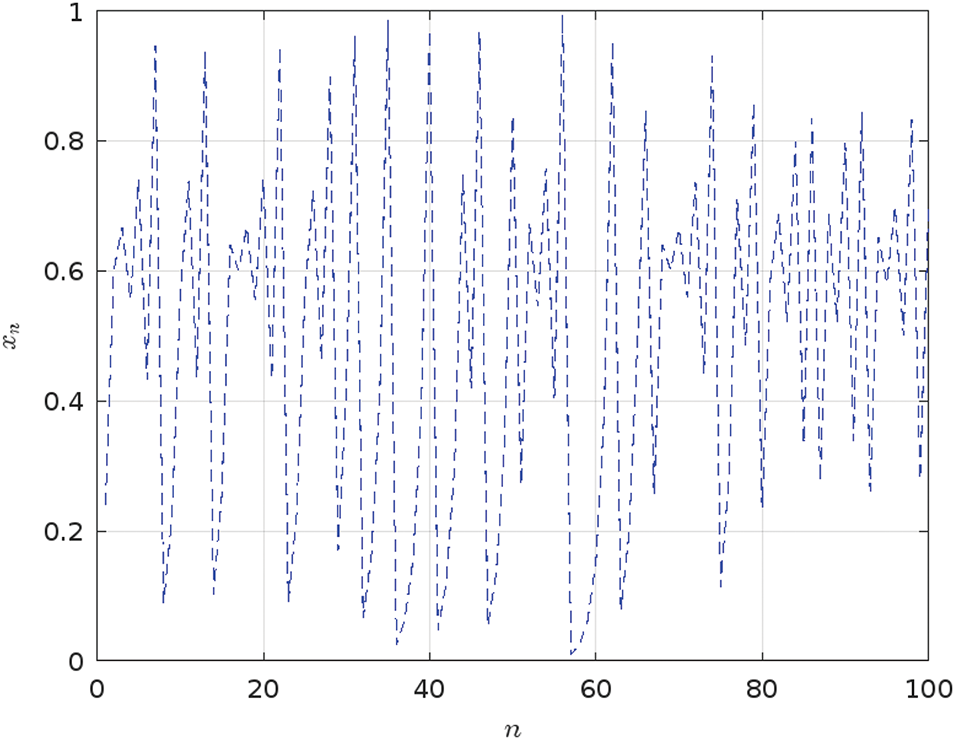
Figure 4: Analysis of the iterative behavior of the tent map for

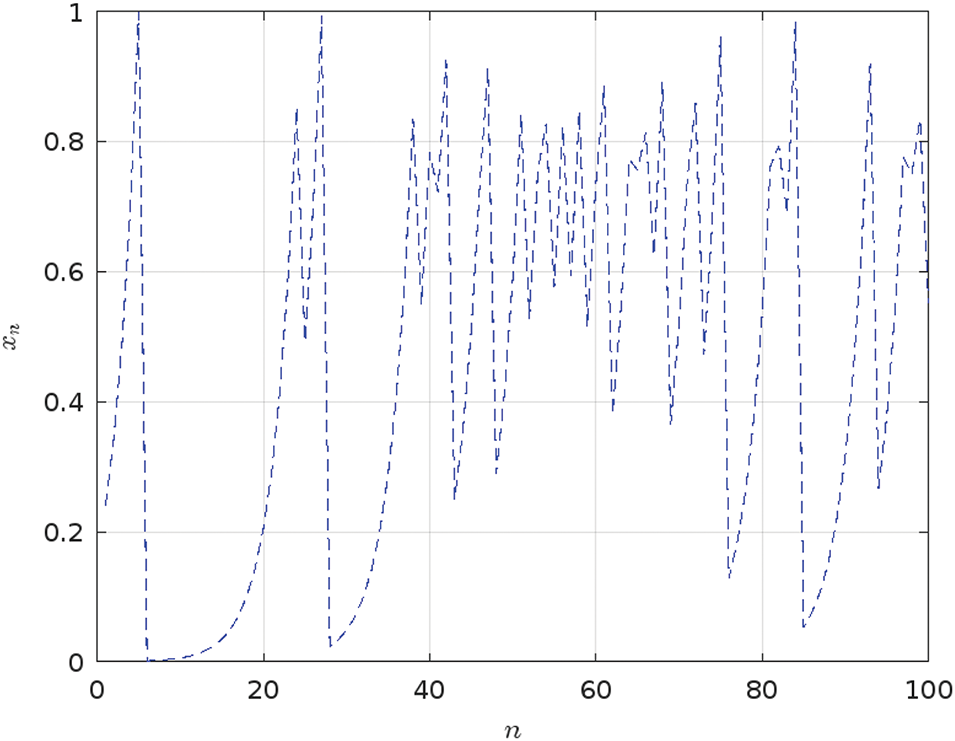
Figure 5: Analysis of the iterative behavior of the Tent map for

The adoption of the Tent map for key expansion represents a relatively better approach. It has been introduced to enhance the diffusion and non-linearity aspects within the expanded keys. The CKE function requires a 256-bit string as a secret key to derive seven subkeys, denoted as . These subkeys are converted into decimal values and employed as the initial values for the tent map function, generating pseudorandom keystreams of size 128 bits each, serving as seven round keys. These round keys are subsequently utilized in the CE and functions for masking and unmasking through a straightforward XOR operation with the corresponding block . The expression for the seven round keys is given by , where , as detailed in Eq. (6).

4  Experiment Analysis

The performance, compression ratio, and security features of the proposed algorithm underwent thorough evaluation on a computer system consisting of a Pentium-IV processor clocked at 2.4 MHz, running the Windows 7 operating system, and equipped with 3 GB of RAM. For a thorough comparative analysis, six established methods, namely Huffman coding [39], Advanced Encryption Standard (AES) [40], chaotically mutated Huffman trees (CHT) [27], and Chaotically Mutated Adaptive Huffman Tree (CMAHT) [28], were coded and executed in the Java programming language. The experimental dataset consisted of files from the standard Calgary corpus [41]. The Calgary Corpus, with its diverse collection of text and binary files, serves as a standard benchmark for evaluating proposed algorithm and existing techniques. Its variety of data types allows for testing the efficiency and compatibility of such algorithms in handling both compression and encryption processes effectively. The ensuing subsections present the outcomes of various experiments conducted to demonstrate the algorithm’s effectiveness in terms of compression, performance, and security.

4.1 Randomness Analysis

The proposed algorithm’s ciphertexts underwent a comprehensive assessment of their randomness using the NIST statistical test suite [42]. The NIST statistical test suite includes 16 distinct types of statistical tests, each providing a probability -value ranging from zero to one. A -value of 1 implies that the binary sequence exhibits perfect randomness, while a -value of 0 suggests complete non-randomness. The significance level, denoted as , can be adjusted to suit the analysis. In this experiment, a significance level of was chosen, ensuring a 99% confidence level in the randomness of the ciphertexts. In the NIST statistical test suite, a -value near the significance level (in this case, ) can be considered borderline. Specifically, a -value of indicates that there is a small but noticeable deviation from perfect randomness. This can be attributed to the inherent limitations of statistical testing when applied to finite datasets, as random noise or slight irregularities may cause such small deviations. However, a -value of still falls within the acceptable range for randomness, especially given the variety of tests performed and their collective results.

The calculated -value are shown in Table 1 for specific files selected from the Calgary corpus. Importantly, the ciphertexts produced by the proposed algorithm pass all statistical tests with a confidence level of 99%, affirming their randomness, while the Binary Matrix Rank test for the bib dataset yielded a -value of , other datasets like news produced a -value of , which is very close to 1, indicating strong randomness. The consistency of the results across different datasets further reassures us that the algorithm’s randomness is robust and reliable. Although a -value of is marginally below the threshold, it does not undermine the overall performance of the proposed algorithm. The results across other datasets, combined with the fact that the algorithm passes all tests with a high degree of consistency, support the conclusion that the ciphertexts exhibit strong randomness. This contributes to the algorithm’s resilience against ciphertext-only attacks (COA), as there are no discernible patterns or repetitions in the ciphertexts.

4.2 Number of Rounds Analysis

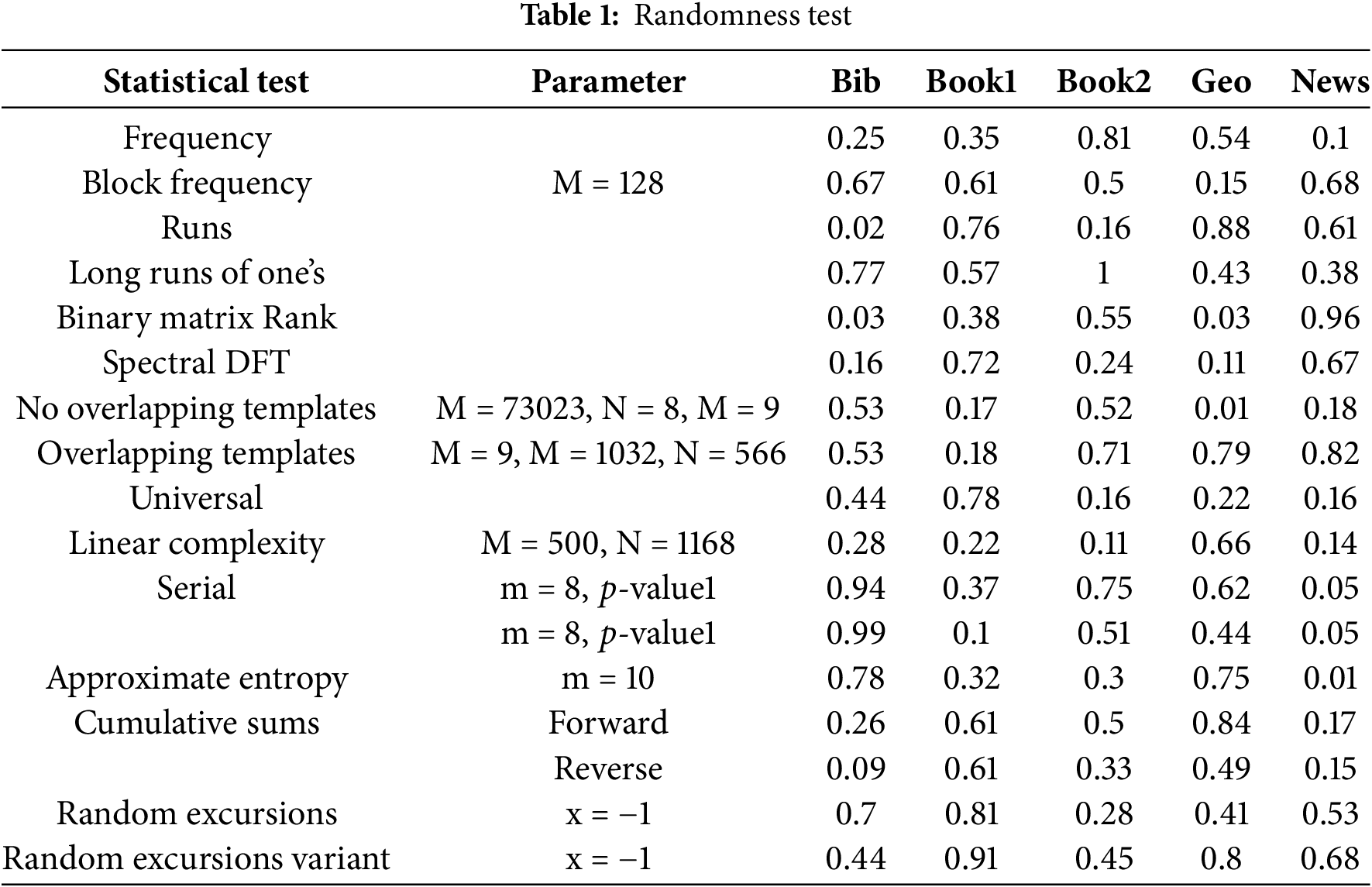
Recent advancements in cryptanalysis have underscored the pivotal role of the number of rounds in enhancing the security of iterative block ciphers [40]. Leveraging this insight, the proposed algorithm was meticulously crafted, considering the optimal number of rounds required to render cryptanalytic attacks inconsequential. To evaluate the algorithm’s robustness, a randomness test was conducted on the ciphertext generated by a reduced version featuring four rounds. The resulting computed -values, specifically for the “book1” file from the Calgary corpus, are presented in Table 2. The experimental outcomes unequivocally validate the presence of complete confusion and diffusion within the encryption process, given a 128-bit block size and 256-bit key length. In pursuit of heightened security and bolstered resistance against linear and differential cryptanalysis, an additional three rounds were judiciously incorporated as a security margin.

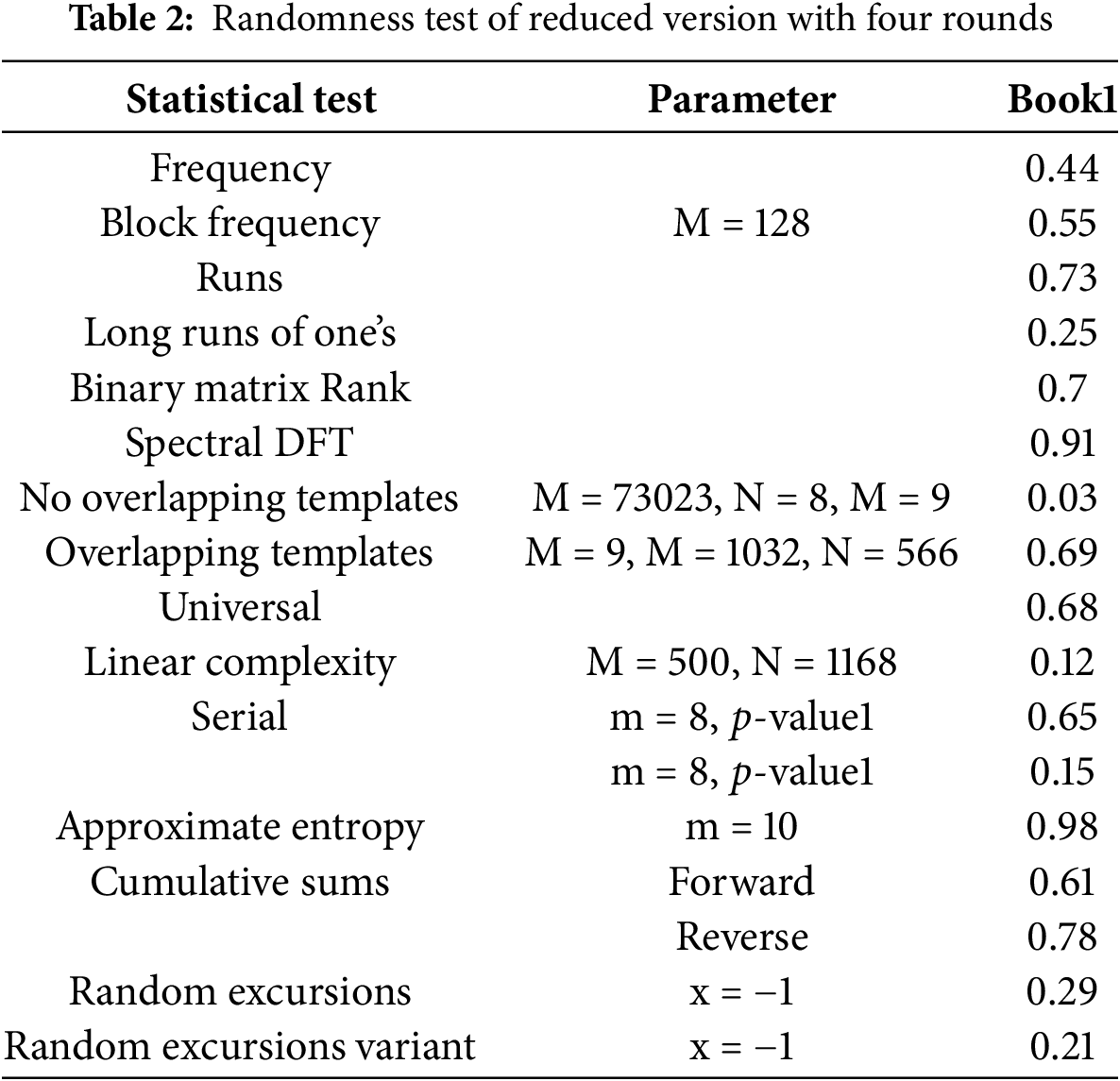
The inclusion of additional rounds also enhances the algorithm’s resistance to known-plaintext attacks (KPA). In a KPA scenario, the attacker has access to both the plaintext and corresponding ciphertext and attempts to derive the encryption key. By incorporating an adequate number of rounds and ensuring strong confusion and diffusion properties, the algorithm prevents the attacker from correlating patterns between plaintext and ciphertext. Furthermore, the algorithm demonstrates resilience against chosen-ciphertext attacks (CCA). In CCA, an attacker manipulates ciphertext to study the corresponding plaintext or encryption key. The optimal number of rounds, combined with robust key schedule algorithms and a highly nonlinear encryption process, ensures that even with controlled ciphertext inputs, no exploitable relationships emerge.

4.3 Compression Ratio

The compression ratio is a critical metric that reflects the effectiveness of an algorithm. In this context, we conducted experiments using the standard Calgary Corpus files to provide a comprehensive evaluation of the compression capabilities of the proposed algorithm in comparison to previously suggested algorithms. The compression ratios were calculated using Eq. (8), where the ratio is defined as the quotient of ciphertext length to plaintext length, expressed as a percentage.

(8)

The obtained compression ratios are presented in Table 3, encompassing results for 5 distinct Calgary Corpus files. It is noteworthy that the compression ratio achieved by the arithmetic coding approach surpasses that of the proposed algorithm, although it aligns closely with the performance of Huffman-based techniques. Minor variations in compression ratios were observed for certain files, primarily attributed to negligible padding within the cipher encoding process.

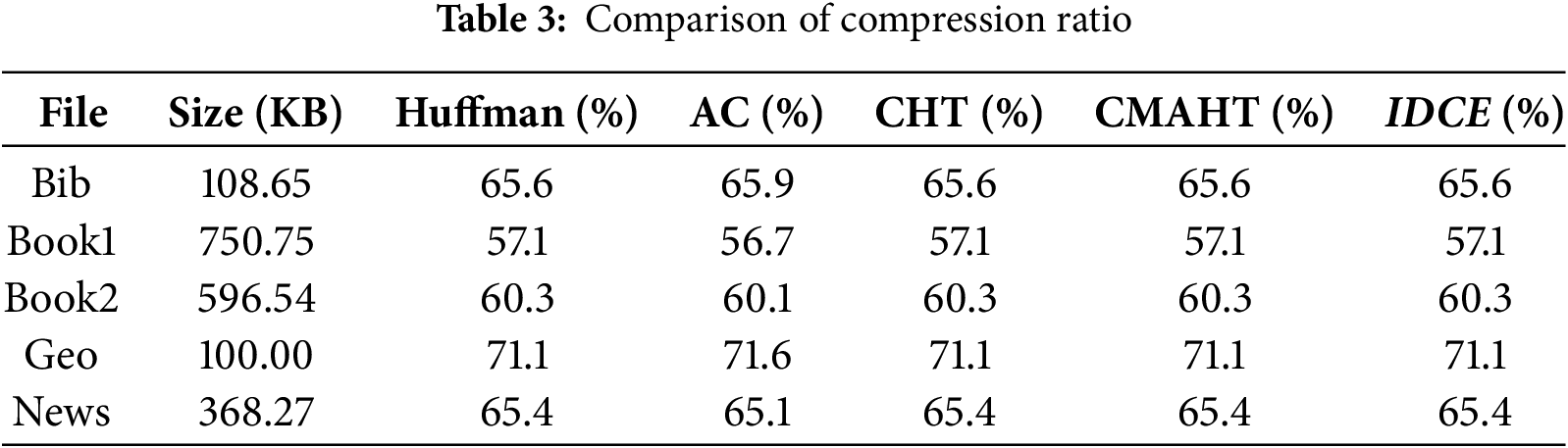
Morover, the proposed IDCE algorithm relies on compression to reduce data redundancy before encryption. For data that is inherently low in redundancy, such as random or already compressed data, the compression phase of IDCE has limited effectiveness. This may result in minimal or no reduction in data size, making IDCE less optimal for such cases, which required further research to adapt IDCE for such data types, potentially through advanced preprocessing techniques or hybrid compression methods.

4.4 Key Space Analysis

Ensuring the security of an encryption algorithm demands a key space of sufficient size to withstand various brute force attacks. The proposed algorithm distinguishes itself by supporting a robust 256-bit key size, which proves more than sufficient for practical and reliable cryptographic applications, especially when compared to previously known algorithms. To aid in comparisons, Table 4 provides a key space analysis that contrasts the proposed algorithm with these established alternatives.

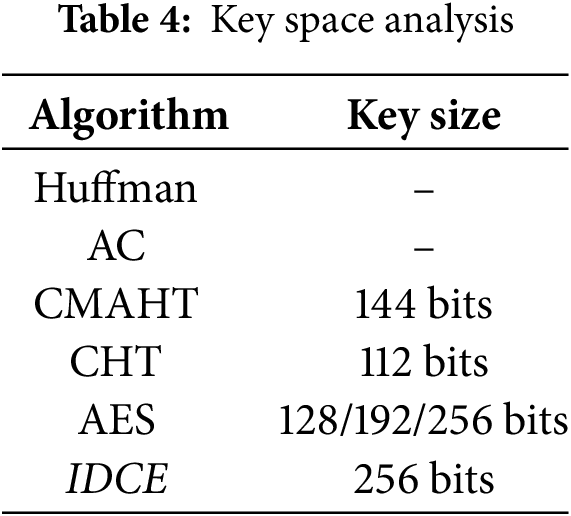
The large key space also enhances resistance to KPA. In KPA, the attacker uses pairs of known plaintext and corresponding ciphertext to derive the encryption key. The 256-bit key size ensures that even with multiple plaintext-ciphertext pairs, the computational resources required for a brute-force attack are astronomically high, making such attacks infeasible. Furthermore, the algorithm’s strong diffusion and nonlinearity characteristics eliminate exploitable patterns between plaintext and ciphertext, further securing against KPA. For COA, where the attacker has access only to the ciphertext and attempts to deduce the key or plaintext, the vast key space makes brute force practically impossible. Additionally, the randomness and entropy of the ciphertext (validated in 4.1) ensure that any statistical analysis by the attacker yields no useful information. These features collectively establish robust defense mechanisms against COA, ensuring the security and reliability of the proposed encryption system.

4.5 Key Sensitivity and Plaintext Sensitivity

An exemplary encryption algorithm must exhibit sensitivity concerning both the key and plaintext components. Even a minor alteration of a single bit within either the key or the plaintext should yield entirely distinct outcomes. This characteristic serves as a important test for evaluating the algorithm’s resistance level against brute-force attacks. To assess key sensitivity, the Calgary Corpus files were encrypted using the key “abcdefghijklmnopqrstuvwxyz123456”. Subsequently, the same set of files was encrypted once more, this time with a slight modification to the key, altering the most significant bit to “abcdefghijklmnopqrstuvwxyz123457”. The key sensitivity is calculated as the average percentage of different bits using Eq. (9):

(9)

where is the number of blocks in plaintext, is the length of each ciphertext block in bits, is the counter, is the block encrypted with the (“abcdefghijklmnopqrstuvwxyz123456”) key, is the block encrypted with the modified key (“abcdefghijklmnopqrstuvwxyz123457”), and the computes the number of different bits between and ciphertext files. The comparison percentages of selected Calgary Corpus files is tabulated in Table 5. Notably, the observed percentage of bit changes in the two ciphertexts closely approximates the ideal value of 50%. This outcome underscores the algorithm’s exceptional key sensitivity, reaffirming its robust security characteristics.

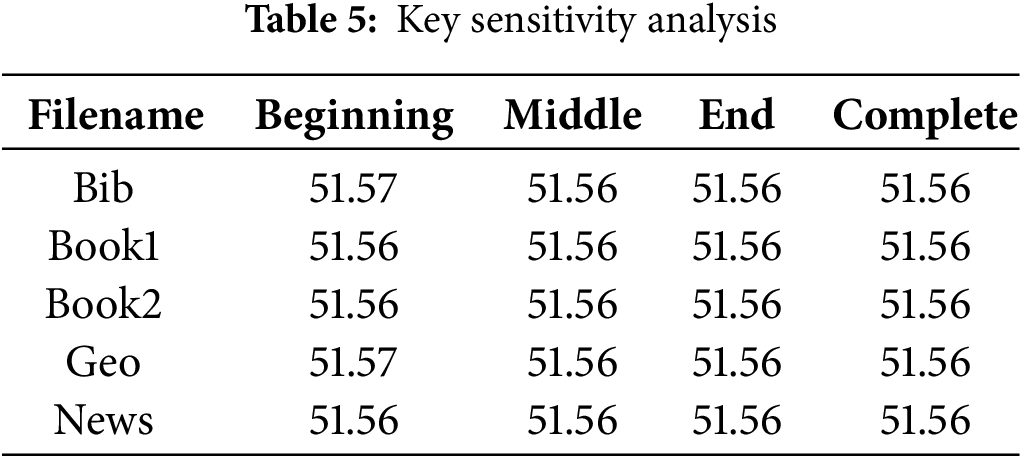
To evaluate the plaintext sensitivity of the proposed algorithm, a systematic approach was employed, involving the random toggling of one bit within each block of plaintext. Subsequently, encryption was carried out using the same cryptographic key. The resulting pair of ciphertext files underwent a thorough bit-by-bit comparison. The plaintext sensitivity is calculated as the average percentage of different bits using Eq. (9). The corresponding comparison percentages have been detailed in Table 6. Remarkably, the observed percentage of bit changes in the two ciphertexts closely approximates the expected value of approximately 50%. This outcome serves as compelling evidence of the algorithm’s robust plaintext sensitivity. Taken together with its key sensitivity, experimental results confirm that the proposed algorithm excels in both aspects, making it highly responsive to changes in both the key and plaintext.

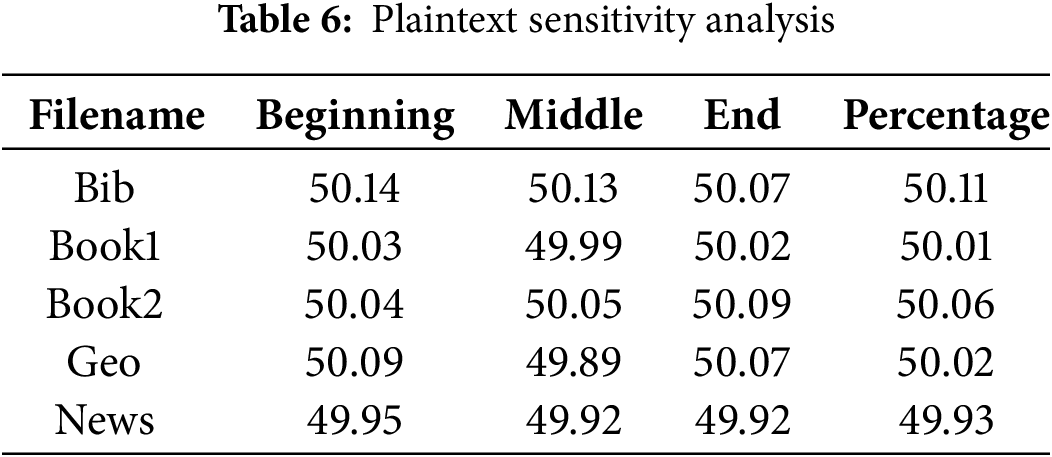
The algorithm’s sensitivity to both key and plaintext changes enhances its resistance to KPA, where an attacker possesses pairs of plaintext and corresponding ciphertext. High key and plaintext sensitivity ensure that even with such pairs, no patterns are discernible to infer the key or predict future ciphertexts. The nonlinearity and diffusion properties prevent exploitation of relationships between plaintext and ciphertext, thwarting KPA attempts. Moreover, The proposed algorithm mitigates CCA threat through its strong sensitivity and diffusion mechanisms, ensuring that any modification to the ciphertext results in an unpredictable plaintext. Additionally, the algorithm’s robust design and key space of 256 bits make reverse-engineering or leveraging ciphertext modifications computationally infeasible. Taken together, the experimental results confirm that the proposed algorithm excels in both key and plaintext sensitivity, making it highly responsive to changes and resistant to advanced cryptanalytic attacks, including KPA and CCA.

4.6 Processing Time

In addition to the comprehensive analysis encompassing compression and security, there are other critical considerations to address, notably the algorithm’s processing time. Here, the processing time of an proposed algorithm refers to the amount of time taken to perform compression and encryption simultaneously using (10) as:

(10)

Typically, compression and encryption algorithms tend to be optimized for either speed or compression/encryption efficiency, rarely excelling in both aspects simultaneously. Tables 7 and 8 summarize the processing time comparison, comparing the proposed algorithm with prior algorithms, based on trials conducted with the standard Calgary Corpus files. Furthermore, for the sake of comparison, test files underwent sequential compression and encryption operations, first with Huffman and Arithmetic Coding followed by AES encryption. This allowed for an assessment of the proposed algorithm’s effectiveness relative to the sequential execution of compression and encryption algorithms.

The results unequivocally confirm that the proposed algorithm boasts the highest processing speed when compared to AES, Huffman + AES, and AC + AES combinations. Additionally, it significantly reduces the time required for the simultaneous execution of data compression and encryption in contrast to performing these operations separately. It’s worth noting that while Huffman, AC, CHT, and CMAHT exhibit faster processing times, this is largely due to their limited security measures, where integration of chaotic maps, such as Arnold Cat and Tent maps, enhances the security but also introduces computational overheads. Moreover, the need for precise chaotic computations can pose challenges in real-time or resource-constrained environments.

5  Conclusion

This paper introduces a data encoding algorithm named IDCE, designed to seamlessly integrate data compression and encryption within a block cipher framework. By incorporating compression into the encryption process, the proposed algorithm achieves optimal data storage and transmission efficiency while ensuring robust security through secret key control. The proposed algorithm adopts Huffman coding for compression, utilizes the Tent map for pseudorandom keystream generation, and incorporates the Arnold Cat map for data scrambling with a multiple rounds structure, thereby enhancing security. The use of a structured round design in the proposed algorithm guarantees resistance against various attacks, while a substantial key space provides formidable resistance against brute-force attacks. We conducted a thorough implementation and critical analysis of the proposed algorithm, utilizing a standard set of Calgary Corpus files. The results of experiments bring forth several noteworthy findings. Notably, the ciphertexts generated by the proposed algorithm successfully passed all tests within the NIST statistical test suite, establishing their randomness with a high degree of confidence (99%). Furthermore, experiments revealed several prominent attributes, including an acceptable compression ratio and performance. However, the study has certain limitations. The proposed algorithm is primarily evaluated on standard datasets, and its performance on diverse real-world datasets, including multimedia files, remains to be explored. Additionally, while the algorithm balances security and efficiency, the computational overhead compared to traditional compression-only methods needs further optimization. Future research could focus on reducing processing time and expanding the algorithm’s adaptability to various data types and practical applications. In summary, the proposed algorithm represents a promising advancement in the research area of data encoding, offering a complete solution that integrates data compression and encryption without compromising on security or efficiency. Experimental findings emphasize the proposed algorithm’s robustness and its potential to address the important challenges of secure data storage and transmission in current computing environments.

Acknowledgement: This work was supported by the Deanship of Scientific Research, Qassim University, which funded the publication of this project.

Funding Statement: The researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2025).

Author Contributions: The authors confirm their contribution to the paper: study conception and design: Muhammad Usama; data collection: Muhammad Usama, Arshad Aziz; draft manuscript preparation: All authors; funding acquisition: Suliman A. Alsuhibany. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this study are publicly available benchmark datasets. Specifically, the standard Calgary Corpus [41] has been utilized, which can be accessed online at http://www.data-compression.info/Corpora/CalgaryCorpus/ (accessed on 25 February 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Armstrong K. Big data: a revolution that will transform how we live, work, and think. Inform, Commun Soc. 2014 Nov;17(10):1300–2. doi:10.1080/1369118X.2014.923482. [Google Scholar] [CrossRef]

2. Jridi M, Alfalou A. Real-time and encryption efficiency improvements of simultaneous fusion, compression and encryption method based on chaotic generators. Opt Lasers Eng. 2018;102:59–69. doi:10.1016/j.optlaseng.2017.10.007. [Google Scholar] [CrossRef]

3. Wong K-W, Lin Q, Chen J. Simultaneous arithmetic coding and encryption using chaotic maps. IEEE Transact Circ Syst II: Express Bri. 2010;57(2):146–50. doi:10.1109/TCSII.2010.2040315. [Google Scholar] [CrossRef]

4. Bose R, Pathak S. A novel compression and encryption scheme using variable model arithmetic coding and coupled chaotic system. IEEE Transact Circ Syst I: Regul Pap. 2006 Apr;53(4):848–57. doi:10.1109/TCSI.2005.859617. [Google Scholar] [CrossRef]

5. Coutinho SC. The mathematics of ciphers: number theory and RSA cryptography. 1st ed. New York: A K Peters/CRC Press; 1999. doi:10.1201/9781439863893. [Google Scholar] [CrossRef]

6. Baptista MSS. Cryptography with chaos. Phys Lett A. 1998;240(1–2):50–4. doi:10.1016/S0375-9601(98)00086-3. [Google Scholar] [CrossRef]

7. Yang D, Liao X, Wang Y, Yang H, Wei P. A novel chaotic block cryptosystem based on iterating map with output-feedback. Chaos Solit Fract. 2009 Jan;41(1):505–10. doi:10.1016/j.chaos.2008.02.017. [Google Scholar] [CrossRef]

8. Moses Setiadi DRI, Rijati N, Muslikh AR, Vicky Indriyono B, Sambas A. Secure image communication using galois field, hyper 3D Logistic Map, and B92 quantum protocol. Comput Mater Contin. 2024;81(3):4435–63. doi:10.32604/cmc.2024.058478. [Google Scholar] [CrossRef]

9. Calcagnile LM, Galatolo S, Menconi G. Non-sequential recursive pair substitutions and numerical entropy estimates in symbolic dynamical systems. J Nonlinear Sci. 2010;20(6):723–45. doi:10.1007/s00332-010-9071-0. [Google Scholar] [CrossRef]

10. Grassberger P. Data compression and entropy estimates by non-sequential recursive pair substitution; 2002. [cited 2025 Feb 25]. Available from: http://arxiv.org/abs/physics/0207023. [Google Scholar]

11. Lahdir M, Hamiche H, Kassim S, Tahanout M, Kemih K, Addouche S-A. A novel robust compression-encryption of images based on SPIHT coding and fractional-order discrete-time chaotic system. Opt Laser Technol. 2019 Jan;109(4):534–46. doi:10.1016/j.optlastec.2018.08.040. [Google Scholar] [CrossRef]

12. Zhang Y, Xiao D, Liu H, Nan H. GLS coding based security solution to JPEG with the structure of aggregated compression and encryption. Commun Nonlinear Sci Numer Simul. 2014;19(5):1366–74. doi:10.1016/j.cnsns.2013.09.019. [Google Scholar] [CrossRef]

13. Wong KW, Yuen CH. Embedding compression in chaos-based cryptography. IEEE Transact Circ Syst II: Express Bri. 2008;55(11):1193–7. doi:10.1109/TCSII.2008.2002565. [Google Scholar] [CrossRef]

14. Wen JG, Kim H, Villasenor JD. Binary arithmetic coding with key-based interval splitting. IEEE Signal Process Lett. 2006;13(2):69–72. doi:10.1109/LSP.2005.861589. [Google Scholar] [CrossRef]

15. Wu CP, Kuo CCJ. Design of integrated multimedia compression and encryption systems. IEEE Trans Multimedia. 2005;7(5):828–39. doi:10.1109/TMM.2005.854469. [Google Scholar] [CrossRef]

16. Jakimoski G, Subbalakshmi KP. Cryptanalysis of some multimedia encryption schemes. IEEE Trans Multimedia. 2008 Apr;10(3):330–8. doi:10.1109/TMM.2008.917355. [Google Scholar] [CrossRef]

17. Kim H, Wen J, Villasenor JD. Secure arithmetic coding. IEEE Trans Signal Process. 2007;55(5 II):2263–72. doi:10.1109/TSP.2007.892710. [Google Scholar] [CrossRef]

18. Grangetto M, Magli E, Olmo G. Multimedia selective encryption by means of randomized arithmetic coding. IEEE Trans Multimedia. 2006 Oct;8(5):905–17. doi:10.1109/TMM.2006.879919. [Google Scholar] [CrossRef]

19. Nagaraj N, Vaidya PG, Bhat KG. Arithmetic coding as a non-linear dynamical system. Commun Nonlinear Sci Numer Simul. 2009;14(4):1013–20. doi:10.1016/j.cnsns.2007.12.001. [Google Scholar] [CrossRef]

20. Darwish SM. A modified image selective encryption-compression technique based on 3D chaotic maps and arithmetic coding. Multimed Tools Appl. 2019 Jul;78(14):19229–52. doi:10.1007/s11042-019-7256-6. [Google Scholar] [CrossRef]

21. Huang YM, Liang YC. A secure arithmetic coding algorithm based on integer implementation. In: 11th International Symposium on Communications and Information Technology (ISCIT); 2011; Hangzhou, China: IEEE. p. 518–21. doi:10.1109/ISCIT.2011.6092162. [Google Scholar] [CrossRef]

22. Usama M, Zakaria N. Chaos-based simultaneous compression and encryption for Hadoop. PLoS One. 2017;12(1):e0168207. doi:10.1371/journal.pone.0168207. [Google Scholar] [PubMed] [CrossRef]

23. Fu S,. RHS-TRNG: a resilient high-speed true random number generator based on STT-MTJ device. IEEE Transact Very Large Scale Integr Syst. 2023;31(10):1–14. doi:10.1109/TVLSI.2023.3298327. [Google Scholar] [CrossRef]

24. Klein ST, Shapira D. Integrated encryption in dynamic arithmetic compression. Inf Comput. 2021;279:104617. doi:10.1016/j.ic.2020.104617. [Google Scholar] [CrossRef]

25. Singh AK, Thakur S, Jolfaei A, Srivastava G, Elhoseny MD, Mohan A. Joint encryption and compression-based watermarking technique for security of digital documents. ACM Trans Internet Technol. 2021;21(1):1–20. doi:10.1145/3414474. [Google Scholar] [CrossRef]

26. Gadhiya N, Tailor S, Degadwala S. A review on different level data encryption through a compression techniques. In: 2024 International Conference on Inventive Computation Technologies (ICICT); 2024; Lalitpur, Nepal: IEEE. p. 1378–81. doi:10.1109/ICICT60155.2024.10544803. [Google Scholar] [CrossRef]

27. Hermassi H, Rhouma R, Belghith S. Joint compression and encryption using chaotically mutated Huffman trees. Commun Nonlinear Sci Numer Simul. 2010;15(10):2987–99. doi:10.1016/j.cnsns.2009.11.022. [Google Scholar] [CrossRef]

28. Zhu ZL, Tang Y, Liu Q, Zhang W, Yu H. A chaos-based joint compression and encryption scheme using mutated adaptive huffman tree. In: 2012 Fifth International Workshop on Chaos-fractals Theories and Applications; 2012; Dalian, China: IEEE. p. 212–6. doi:10.1109/IWCFTA.2012.52. [Google Scholar] [CrossRef]

29. Sekar JG, Arun C, Rushitha S, Bhuvaneswari B, Sowmya CS, Prasuna NS. An improved two-dimensional image encryption algorithm using Huffman coding and hash function along with chaotic key generation. AIP Conf Proc. 2022;2676:030105. doi:10.1063/5.0114663. [Google Scholar] [CrossRef]

30. Adeniji OD,. Text encryption with advanced encryption standard (AES) for near field communication (NFC) using Huffman compression. In: International Conference on Applied Informatics; 2022; Cham: Springer International Publishing. [Google Scholar]

31. Hidayat T, Zakaria MH, Pee ANC. Increasing the Huffman generation code algorithm to equalize compression ratio and time in lossless 16-bit data archiving. Multimed Tools Appl. 2023;82(16):24031–68. doi:10.1007/s11042-022-14130-1. [Google Scholar] [CrossRef]

32. Zhou J, Au OC, Wong PHW. Adaptive chosen-ciphertext attack on secure arithmetic coding. IEEE Trans Signal Process. 2009;57(5):1825–38. doi:10.1109/TSP.2009.2013901. [Google Scholar] [CrossRef]

33. Khashman MA, Marzouk HKAAA, Alshaykh MR. Comments on A novel compression and encryption scheme using variable model arithmetic coding and coupled chaotic system. IEEE Transact Circ Syst I: Regul Pap. 2008 Nov;55(10):3368–9. doi:10.1109/TCSI.2008.924117. [Google Scholar] [CrossRef]

34. Zhang B, Liu L. Chaos-based image encryption: review, application, and challenges. Mathematics. 2023 Jun;11(11):2585. doi:10.3390/math11112585. [Google Scholar] [CrossRef]

35. Rickus A, Pfluegel E, Atkins N. Chaos-based image encryption using an AONT mode of operation. In: 2015 International Conference on Cyber Situational Awareness, Data Analytics and Assessment (CyberSA); 2015; London, UK: IEEE. p. 1–5. doi:10.1109/CyberSA.2015.7166113. [Google Scholar] [CrossRef]

36. Zhang L, Liao X, Wang X. An image encryption approach based on chaotic maps. Chaos Solit Fract. 2005;24(3):759–65. doi:10.1016/j.chaos.2004.09.035. [Google Scholar] [CrossRef]

37. Lawnik M, Berezowski M. New chaotic system: m-map and its application in chaos-based cryptography. Symmetry. 2022 Apr;14(5):895. doi:10.3390/sym14050895. [Google Scholar] [CrossRef]

38. Usama M, Khan MK, Alghathbar K, Lee C. Chaos-based secure satellite imagery cryptosystem. Comput Mathema Applicat. 2010 Jul;60(2):326–37. doi:10.1016/j.camwa.2009.12.033. [Google Scholar] [CrossRef]

39. Huffman DA. A method for the construction of minimum-redundancy codes. Proc IRE. 1952;40(9):1098–101. doi:10.1109/JRPROC.1952.273898. [Google Scholar] [CrossRef]

40. Daemen J, Rijmen V. The design of Rijndael: AES-the advanced encryption standard. Berlin/Heidelberg: Springer; 2002. doi:10.1007/978-3-662-04722-4. [Google Scholar] [CrossRef]

41. Witten J, Bell I, Cleary T. “Calgary Corpus,” University of Calgary, Canada; 1990. [cited 2025 Feb 25]. Available from: http://www.data-compression.info/Corpora/CalgaryCorpus/. [Google Scholar]

42. BasshamL, Rukhin A, Soto J, NechvatalJ, Smid M, Leigh S, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications. Vol. 800. Gaithersburg, MD, USA: Special Publication (NIST SPNational Institute of Standards and Technology; 2010. 131 p. [cited 2025 Feb 25]. Available from: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=906762. [Google Scholar]