A Bioinspired Method for Optimal Task Scheduling in Fog-Cloud Environment

1  Introduction

The application areas of Internet of Things (IoT) systems are increasing daily [1,2]. These systems have a network side where devices collect data and communicate with other devices, and another layer is the server (cloud) side for processing this collected data [3]. Since these systems usually work with different devices that do not have many resources in a distributed architecture, efficient and effective management has become more important. This is among the topics researchers focus on both the network and the server sides. In addition, since processing large volumes of data increases costs on a single cloud, researchers are directed to fog-cloud solutions. Therefore, one of the critical issues in fog and cloud-based environments is the efficient use of available resources with optimum task distribution [4]. In addition, task scheduling in these systems affects resource usage, operating costs, and end-user experience. So, in IoT-based systems, it is important to plan well to figure out which resources will be used, the order in which tasks will be done, and the times at which they will be done [5]. A general schema of an IoT system in a fog-cloud environment is represented in Fig. 1.

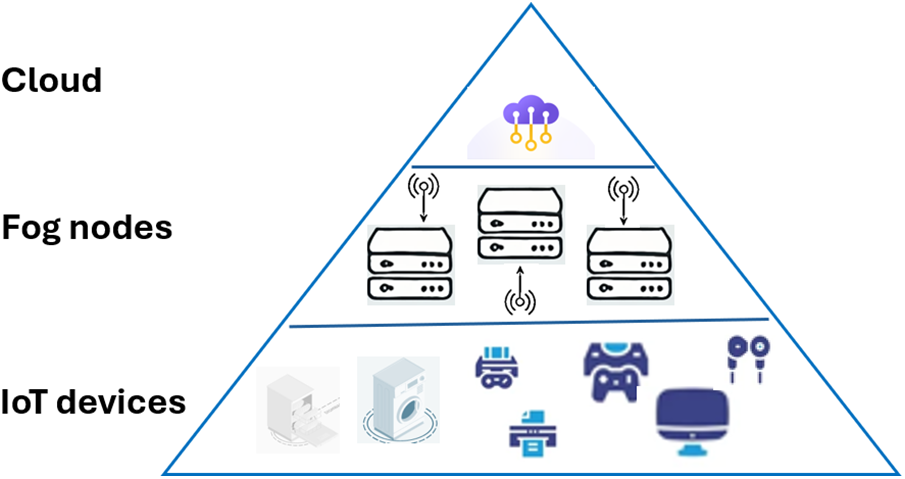
Figure 1: A General schema of fog-cloud computing

Tasks in the IoT system are generally assigned to Virtual Machines (VMs) on the server (cloud) side, and the efficiency of running times and resource consumption is ensured [6]. Although the proposed solutions and algorithms vary based on the planning criteria and the structure of the cloud system, efficiently matching these assignments and scheduling tasks is a complex Non-deterministic Polynomial-time (NP) hard problem type [7]. Especially as the number of tasks and VMs increases, the problem becomes more complex and difficult. Therefore, classical algorithms such as First-Come-First-Served (FCFS) and round-robin (RR) cannot provide very optimal results, and in this regard, the approach frequently used by researchers for such problems is Meta-Heuristic (MH) algorithms. An effective task-scheduling mechanism should be able to shorten the execution and construction time of fog-cloud applications in IoT systems. It also reduces energy consumption and provides efficient resource utilization. In other words, when task-scheduling problems are generally considered optimization problems, the focus is on optimizing these three parameters (makespan time, execution time, and energy consumption) [8]. Therefore, algorithms that provide multi-objectives in one place are needed rather than a classical single-objective MH.

During task planning, it is necessary to propose a solution with the knowledge that various constraints exist [9]. One of them is considering the limits of physical resources such as memory, bandwidth, and processor power. Another challenge is to define the precursor tasks. The third issue is to know whether the tasks are preconditional to each other. The last and fourth constraints define the tasks that must be completed within a specific certain time frame. These four conditions must be considered and implemented regardless of what algorithm is designed [10]. In addition to these constraints, more restrictions can occur depending on the needs of the system and the user. A similar scenario is valid for output objectives. Providing all these together means finding a solution to a complex problem. Therefore, MH algorithms have become better than a good option over classical and precise approaches. Accordingly, an optimal task scheduling mechanism is needed in a fog-cloud-based IoT system to provide efficient resource utilization, balanced load distribution, and high-quality service quickly with minimum cost, time, and energy. Detailed explanations about the problem are included in Section 3.

This study proposes a new task scheduling algorithm that provides the makespan time, execution time, and energy consumption at the most optimal level, especially considering the minimum latency requirement suitable for real-time IoT applications, to cope with the described problems. Accordingly, the MH-based Artificial Rabbits Optimization (ARO) [11] algorithm is enhanced in a way compatible with the problem by using Chaotic maps and Levy flight strategies (CLARO). This proposed algorithm addresses some of ARO’s weaknesses and tries to optimally solve the task scheduling problem in fog-cloud environments. In this regard, the efficiency of the exploration phase of the algorithm is improved with the approach based on chaos theory, while the efficiency of the exploitation phase is strengthened with the Levy flight strategy. In addition, a multi-objective fitness function is defined to address the problem, prioritizing the parameters of makespan, energy consumption, and execution cost, and the weights of these parameters are also set at the optimum level. The proposed algorithm is expected to exhibit superior performance using this admissible and consistent heuristic function. The ARO algorithm, published in 2023, is one of the best and strongest MH-based algorithms in recent times, and it works effectively and quickly with few parameters in solving complex problems. Another strength of this algorithm is its balanced and rapid changes between the exploration and exploitation phases. It is also a suitable choice for the problem considered in this study since it will quickly find suitable solutions for time-sensitive problems. However, since the population distribution of the ARO algorithm is random, it can have difficulty in the exploration phase and, therefore, in the exploitation phase in similar problems. In order to solve this issue, the aim is to increase the population diversity with the chaotic map and make the algorithm work efficiently. The levy flight strategy allows search agents to move beyond the local optimal with significant steps and fast convergence while hunting. As a result, the growing amount and volume of data in IoT systems raises the cost of computing and processing, which causes delays that cannot be avoided. It is necessary to use the best task-scheduling method possible. The key contributions of this study can be outlined as follows:

•   It addresses the shortcomings of ARO and improves its performance.

•   An improved and adaptive ARO algorithm based on chaotic map and levy flight strategies is proposed to ensure effective task scheduling and maximize Quality of Service (QoS) and IoT end-users’ satisfaction.

•   Exploration and exploitation phases and the transition between them becomes even more effective.

•   A fitness function is designed for the problem, incorporating makespan time, execution time, and energy consumption as key parameters.

•   It shows superior performance and achieves the best results compared to known metaheuristic-based algorithms in 30 cases and two special cases.

The remainder of this paper is structured as follows: Section 2 reviews the relevant literature. Section 3 explained the problem statement. Section 4 provides a concise overview of the operational mechanism of the ARO algorithm. In Section 5, an appropriate fitness function is introduced, along with a comprehensive explanation of the proposed algorithm. Section 6 discusses the simulation results and their analysis. Section 7 discusses the constraints and challenges of the proposed method, while the final section concludes the study and suggests directions for future research.

2  Related Works

This section discusses recent studies focusing on task and workflow scheduling challenges in fog-cloud environments. Classical and deterministic approaches, such as Earliest Time First (ETF), Join Shortest Queue (JSQ), and Heterogeneous Earliest Finish-Time (HEFT) algorithms, serve as well-known examples. Due to the complex nature of this problem with numerous parameters, these traditional methods fail to ensure efficient resource utilization and tend to elevate transaction costs. As explained before, the task scheduling problem, which is one of the most critical issues for efficient resource utilization, falls into the class of NP-hard problems, and therefore, MH-based approaches have been used more frequently by researchers recently. Studies in literature based on this category are examined in this section.

Bacanin et al. [12] proposed a modified Firefly Algorithm (FA) method to solve the workflow scheduling problem in a fog-cloud environment with minimum cost and throughput time. This method used the original FA algorithm, genetic operators, and a semi-reflection-based learning procedure. The results indicated that it has a faster convergence performance than FA and is successful in finding the best solutions compared to the other algorithms. Abohamama et al. [13] introduced a modified Genetic Algorithm (GA) to enhance task scheduling in a real-time fog-cloud environment, emphasizing minimizing cost and makespan. This study aimed to obtain minimum makespan and execution time by assigning tasks in the most appropriate order. Jing et al. [14] proposed a discrete PSO-based scheduling algorithm to fulfill the QoS requirements (time, reliability, and cost) and improve the IoT system’s fault tolerance. However, this method finds good results for minimal cases and situations. Xie et al. [15] suggested the Non-Local Convergent PSO (DNCPSO) algorithm to solve the workflow scheduling problem by focusing on the throughput time and cost parameters in a cloud-based environment. This method added selection and mutation operations to the directed search process. This way, the probability of falling into local optima was reduced with a faster convergence. Kakkottakath et al. [16] described a hybrid ACO-PSO algorithm that improves security using the Data Encryption Standard (DES) algorithm to schedule work more efficiently in the cloud. The fitness function was designed solely around cost, load, and makespan considerations. Natesan et al. [17] introduced a hybrid algorithm that combines the GA with the Whale Optimization Algorithm (WOA) to minimize costs and decrease makespan time. However, a shortcoming of these studies was their exclusive focus on the cloud environment. All these studies share the common shortcoming of ignoring the energy parameter.

Nikravan et al. [18] proposed an advanced PSO-based framework utilizing a proximal gradient approach to solve the task scheduling problem in an IoT system. This method effectively addressed the challenges associated with nondifferentiable convex optimization. However, this method has difficulty finding good answers because it occasionally faces local optima problems. Yadav et al. [19] presented the Opposition-Based Chemical Reaction (OBCR) method for task scheduling within fog computing networks. This novel algorithm integrated heuristic upward ranking and Chemical Reaction Optimization (CRO) techniques with Opposition-Based Learning (OBL). By employing its four operators, OBCR enhances exploration and exploitation within the solution space, reducing uptime delays and improving device stability. Cho et al. [20] developed a hybrid algorithm that integrates Ant Colony Optimization (ACO) and Particle Swarm Optimization (PSO) to tackle the task scheduling challenge. This algorithm effectively utilized historical data to adapt to complex environments while requiring minimal domain expertise, allowing it to forecast the workload of incoming requests. In addition, it eliminates requests that only become viable when the scheduling process aims to reduce processing time. Hasan et al. [21] proposed a Canonical PSO-based method to minimize resource allocation problems and optimal makespan time in an IoT-based system. Although it outperforms traditional list-based scheduling algorithms in comparison, it often falls into the local optimum trap. Khezri et al. [22] introduced the Data-Locality Aware Job Scheduling in Fog-Cloud (DLJSF) algorithm for job scheduling in fog-cloud environments, emphasizing data locality to reduce makespan, improve load balancing, and minimize unnecessary data transfers. A prevalent limitation across all studies within this category is their insufficient emphasis on execution time and energy consumption parameters.

Saif et al. [23] focused on enhancing delays and energy efficiency by addressing the QoS objectives for diverse IoT tasks, proposing the Multi-Objectives Grey Wolf Optimizer (MGWO) algorithm to achieve this goal. Djemai et al. [24] employed the Discrete PSO algorithm to reduce energy consumption and service delay within the fog environment. Therefore, a simple decision mechanism featuring a discrete structure was developed to assess whether resources are allocated to the intended process. A key limitation of this proposed model is its applicability solely to discrete structures. Movahedi et al. [25] proposed an improved WOA (OppoCWOA) method by focusing on energy consumption and time parameters for optimal task scheduling. However, this method is not efficient in terms of time computation. Milan et al. [26] introduced a novel task-scheduling algorithm using Bacterial Foraging Optimization (BFO) to minimize idle time in VMs. This approach utilizes the principles of chemotaxis, reproduction, and elimination-dispersal observed in bacterial behavior to dynamically assign tasks to suitable VMs within the cloud environment. Ijaz et al. [27] proposed an Energy-Makespan Multi-Objective Optimization (EM-MOO) algorithm for workflow scheduling in fog-cloud environments, optimizing energy consumption and makespan. It achieved up to 50% energy reduction with minimal impact on completion times through adaptive bi-objective optimization and frequency scaling. Kurkreja [28] explored task scheduling in cloud computing and IoT networks using metaheuristic algorithms. Multiswarm PSO outperforms other methods by reducing memory costs and energy consumption, making it ideal for dynamic IoT environments with efficient resource allocation and energy-aware solutions. The common shortcoming of all the studies described in this category is that they do not focus on the task execution cost parameter.

Gowri et al. [29] proposed a hybrid metaheuristic algorithm, OSS-GSA, inspired by the Oppositional Sparrow Search and Gravitational Search Algorithms to balance system load and enhance overall system performance. This approach improved energy consumption and response time, demonstrating better effectiveness in optimizing response time than energy metrics. Mangalampalli et al. [30] proposed a WOA-based task scheduling method focusing on energy and execution time parameters. Although the results are promising, its early convergence sometimes causes local traps. These studies did not address the aspects of QoS and makespan parameters.

Bitam et al. [31] presented an algorithm based on bees’ behavioral patterns to tackle the task allocation challenge within a fog computing environment. They aimed to achieve an optimal equilibrium between the time required to complete tasks and the storage demands of fog services created by mobile users. However, a limitation of this research is its exclusive focus on the fog layer, neglecting the collaboration between fog and cloud layers. In addition, the fitness function is constructed around a single objective. Subramoney et al. [32] proposed a Multi-Swarm PSO (MSPSO) algorithm to tackle the scheduling problem within a fog architecture, optimizing energy, cost, delay, and load balancing parameters. These studies overlook QoS and user satisfaction issues while failing to address dynamic task scheduling and prioritization.

In addition to the current shortcomings, most of the studies in the literature were conducted on a small number of scenarios and data. On the other hand, instead of the actual dataset, some studies used datasets that were either private datasets or created by researchers. This study proposes a new method on a comprehensive real dataset, focusing on all parameters and considering users’ satisfaction. The characteristics of some of the existing MH-based studies in literature are summarized in Table 1.

3  Problem Statement

Task scheduling involves the optimal execution of a collection of tasks on designated processors or resources, factoring in the QoS parameters provided to users during task distribution in a fog-cloud environment. Efficient allocation of these resources can maximize the utilization of network parameters such as bandwidth and energy, preventing resource failures due to excessive workloads while upholding the QoS guarantees. Therefore, the optimal task scheduling method will minimize the makespan and execution time, and the energy consumption costs, thus ensuring efficient resource utilization and increasing user satisfaction by maximizing the QoS rate. Metrics including makespan, execution time, and energy consumption characterize this NP-hard problem. Given that a simple and comprehensive solution mechanism can greatly enhance resource utilization, this study presents an improved ARO algorithm to efficiently allocate and schedule tasks within the system. When defining the relevant problem, it is essential to consider specific inherent constraints and conditions, as these will underpin effective problem-solving. The devices involved have particular limitations regarding RAM, CPU, and storage capacity. Therefore, the cumulative RAM, CPU, and storage requirements for all scheduled tasks must remain within the devices’ available resources. In addition, the total execution time for each task must comply with its specified deadline, ensuring it does not exceed this limit. Mathematically, the task scheduling problem can be formulated as follows.

3.1 Definition of Makespan Time Parameter

A primary objective of task scheduling is to minimize the total completion time, commonly referred to as makespan, or to enhance resource efficiency. Makespan is defined as the total duration of a task from its initiation to its conclusion, encompassing the complete time taken to execute a sequence of tasks. This parameter is critical in task scheduling, as minimizing makespan directly correlates with maximizing resource utilization. The makespan comprises several components, including processing time, queuing delays, and transmission time, and its calculation is articulated through Eq. (1). In addition, the overall completion time for a given schedule is denoted by ‘Mt’, which is derived using Eq. (2), drawing inspiration from the methodology outlined in [35].

(1)

(2)

where ‘Te’ is the time necessary to compute the ‘ith’ task, ‘yi’ is the computing power of the ‘jth’ VM. ‘Tc’ is the time required to transfer and receive a service from the ‘ith’ node on the ‘jth’ VM, ‘Tq’ is the anticipated duration for resource allocation to the task, which is assumed to be zero in this study, and ‘B’ is the network bandwidth available between the resources where tasks are allocated.

3.2 Definition of Execution Time Parameter

Another key evaluation parameter is execution time (cost). This parameter represents the service cost for executing various tasks within an IoT application. The total cost of service execution is calculated based on the transaction costs incurred in the fog-cloud layer, the makespan time, and the resource cost. This calculation employs hours as the time unit, as outlined in Eq. (3).

(3)

where ‘ypj’ and ‘tpj’ are the costs associated with the processing and transmission units on the resource ‘j’ under observation.

3.3 Definition of Energy Parameter

Another critical parameter examined in this study is energy consumption. In IoT systems, architecture typically employs inexpensive and compact devices designed for specific application domains. Therefore, these devices often face power constraints, making efficient energy usage paramount. Therefore, monitoring the energy consumption of VMs is essential to ensure optimal performance and resource efficiency. This analysis is conducted in accordance with Eq. (4), as outlined in the literature [36]. It is vital to consider the machines’ busy and idle states, as articulated in Eqs. (5) and (6), emphasizing the need for minimal energy consumption during idle periods to ensure accurate calculations.

(4)

(5)

(6)

where ‘d’ is a constant associated with the device’s dynamic power usage, which depends on its capacity, ‘V2j,s’ and ‘fj,s’ are the voltage and frequency at the ‘sth’ level of the ‘jth’ virtual machine, ‘V2j,min’ and ‘fj,min’ are the minimum voltage and frequency for the same machine, and ‘ICt’ is the idle duration of the relevant fog resource.

4  ARO: Artificial Rabbits Optimization

The Artificial Rabbits Optimization (ARO) algorithm is an MH optimization algorithm inspired by the hiding and foraging behavior of rabbits. Although it was introduced recently, it has been used in many studies based on its special characteristics and multipurpose compatible model [37–39]. This algorithm is inspired by three behavioral models of rabbits. It uses the foraging properties of rabbits in nature for the exploration phase, hiding features for the exploitation phase, and an energy shrink strategy for transitions between the two phases. This study section outlines the ARO algorithm’s working mechanism using mathematical models.

4.1 Initialization Phase

In this algorithm, the initial distribution of the population is generated randomly. Each individual (rabbit) in the population seeks optimal solutions using a fitness function designed for the problem during every iteration. The agent that identifies the best solution in each iteration leads the others, enhancing the quality of the solutions as the iterations advance. The role of each agent in the corresponding function is detailed in Eq. (7). Therefore, there is a matrix consisting of agents and problem’s parameters. Fig. 2 illustrates the ARO algorithm with a two-dimensional matrix comprising agents and problem dimensions.

(7)

where ‘n’ is the number of rabbits, ‘m’ is the dimensions of the problem, ‘Xij’ is the position of rabbit ‘i’ in dimension ‘j’, [Xi1, Xi2, ..., Xim] is the positions of the ‘ith’ agent, and the f [Xi1, Xi2, ..., Xim] is the value found by the agent based on the fitness function.

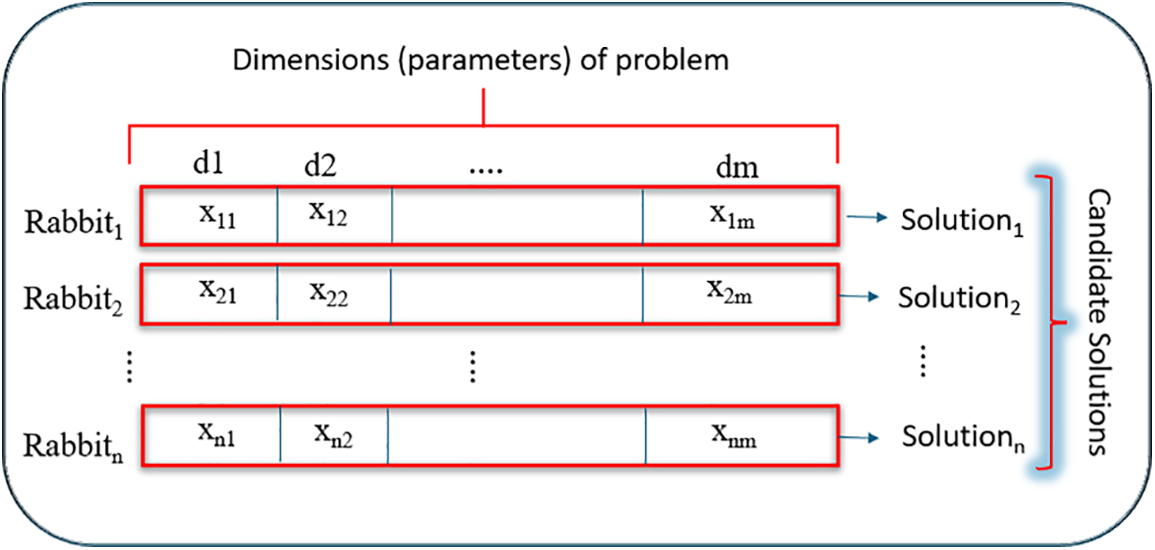
Figure 2: Matrix of ARO algorithm

4.2 Exploration Phase

The algorithm’s exploration phase is based on rabbits’ foraging strategies. In nature, rabbits stealthily eat grass near the burrows of other rabbits while hunting, which makes them difficult to be found by predators. Using this feature, the algorithm updates the position of each agent by comparing it to another randomly selected individual, which introduces a disturbance factor. The working model of this structure is mathematically presented in Eq. (8). This stage helps the ARO algorithm escape local optima and conduct a more effective global search across the search space.

(8)

where ‘Vi(t + 1)’ is the candidate position of the ‘ith’ rabbit at the time ‘t + 1’ (the next iteration), ‘Xi’ and ‘Xj’ are the positions of the ‘ith’ and ‘jth’ rabbits, respectively, ‘t’ is the current iteration, ‘T’ is the total number of iterations allowed, ‘r1’, ‘r2’, and ‘r3’ are uniformly distributed random numbers ranging from 0 to 1. In addition, ‘n1’ adheres to a standard normal distribution, and ‘round’ signifies the operation of rounding to the closest integer. The parameter ‘R’ simulates the running behavior of rabbits, which is calculated based on Eq. (9).

(9)

(10)

(11)

where R is the running operator. ‘L’ specifies the movement speed (running length) during the position update process, determined based on Eq. (10). As iterations proceed, this parameter decreases, allowing individuals to take shorter steps. ‘C’ is the mutation process that individuals undergo during foraging, which allows some individuals to randomly select regions, aiding the global search (Eq. (11)). Also, the ‘randperm’ generates a random permutation of the integers from 1 to ‘d’.

4.3 Exploitation Phase

The ARO algorithm generates random nests for individuals in every direction during each iteration, drawing inspiration from the rabbits’ natural behavior of building continuous and random burrows. In this process, the rabbits randomly select one of the ‘d’ burrows to hide in and create additional tunnels for further passage. Thanks to this feature, rabbits try to escape from predators. A simple example of the model, where the ‘ith’ rabbit moves to the ‘jth’ nest, is shown in Eq. (12). This model establishes ‘d’ burrows across each dimension within the rabbit’s surrounding area.

(12)

where ‘bi,j’ is a randomly selected hiding burrow, ‘H’ and ‘gu’ are calculated based on Eqs. (13) and (14), and the parameter ‘H’ is the hiding factor, which decreases linearly from 1 to 1/T with a random disturbance applied for iterations [40].

(13)

(14)

In this regard, although the number of slots is significant in the first iterations, the number of neighborhoods decreases inversely as the iterations progress. Therefore, at this stage, the ‘nth’ individual randomly chooses one of the ‘d’ slots and updates its position based on Eq. (15).

(15)

Therefore, once one of the stealthy foraging or random hiding techniques is effectively executed, the position update for the ‘nth’ rabbit is conducted using Eq. (16). If the fitness value associated with a rabbit’s candidate location surpasses that of its current position, the candidate location is selected as the following position for that rabbit. In such cases, either Eqs. (8) or (14) will be utilized, contingent upon the specific circumstances. In contrast, the rabbit will retain its existing position if the candidate location does not yield a superior fitness value.

(16)

4.4 Transition between Phases

In the ARO algorithm, the most obvious and specially designed model is that the real-life characteristics of rabbits inspire the transition between phases. For this, the Energy Shrink feature is defined. In the real world, rabbits change their status due to energy loss while grazing or hiding, and they do the opposite. Thanks to this feature, the algorithm is provided with a balance between the exploration and exploitation stages. In the algorithm, the ‘L’ and ‘C’ parameters are used. In addition, the ‘A’ parameter (energy factor) presented in Eq. (17) is an important metric. This factor is inversely proportional to the number of iterations. So, if A(t) > 1, rabbits will be forced to explore; otherwise, they will try to exploit. where ‘r6’ is a random number in [0, 1]. The working of this concept is depicted in Fig. 3.

(17)

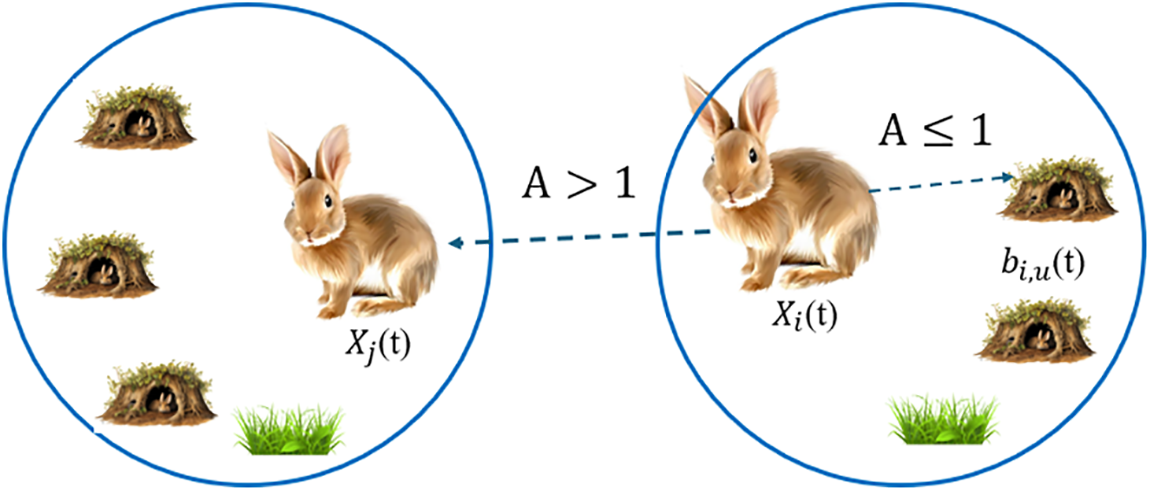
Figure 3: Exploration and exploitation behavior of ARO based on energy shrink [40]

5  Proposed Method

This section presents various dynamic strategies for improving the ARO algorithm, and a fitness function is defined under the problem defined in the previous section. Accordingly, it is planned to solve the task scheduling problem with an admissible and consistent heuristic function defined by the novel proposed improved ARO algorithm.

5.1 Chaotic Levy Flight ARO: CLARO

This section proposes an improved ARO algorithm by adding the chaotic map and levy strategies to amend is proposed in terms of amending the hiding and foraging mechanisms to increase exploration capability, reduce the possibility of local optima trapping, and increase the convergence speed. In this regard, each strategy and its role in the proposed algorithm and its mathematical model are explained. The general working schematic of the proposed method is presented in Fig. 4. It illustrates architecture addressing the task scheduling problem in an IoT-based system. The architecture consists of two main components: the network (IoT device) side and the server (cloud) side. On the network side, tasks are generated and collected from IoT devices and transmitted to the server side. On the server side, incoming tasks (Task1, Task2, ..., Taskn) are allocated to virtual machines (VM1, VM2, ..., VMm) for processing. The assigned tasks to VMs are managed by the proposed algorithm, which leverages chaotic maps and Levy flight strategies. This approach involves two primary phases: the initialization phase and the exploration-exploitation phase. In the initialization phase, the solution space is organized by helping the chaotic maps to establish an initial distribution between VMs and tasks. Adaptive search and refinement processes are employed during the exploration and exploitation phase to identify the optimal task-virtual machine assignment using the Levy flight strategy.

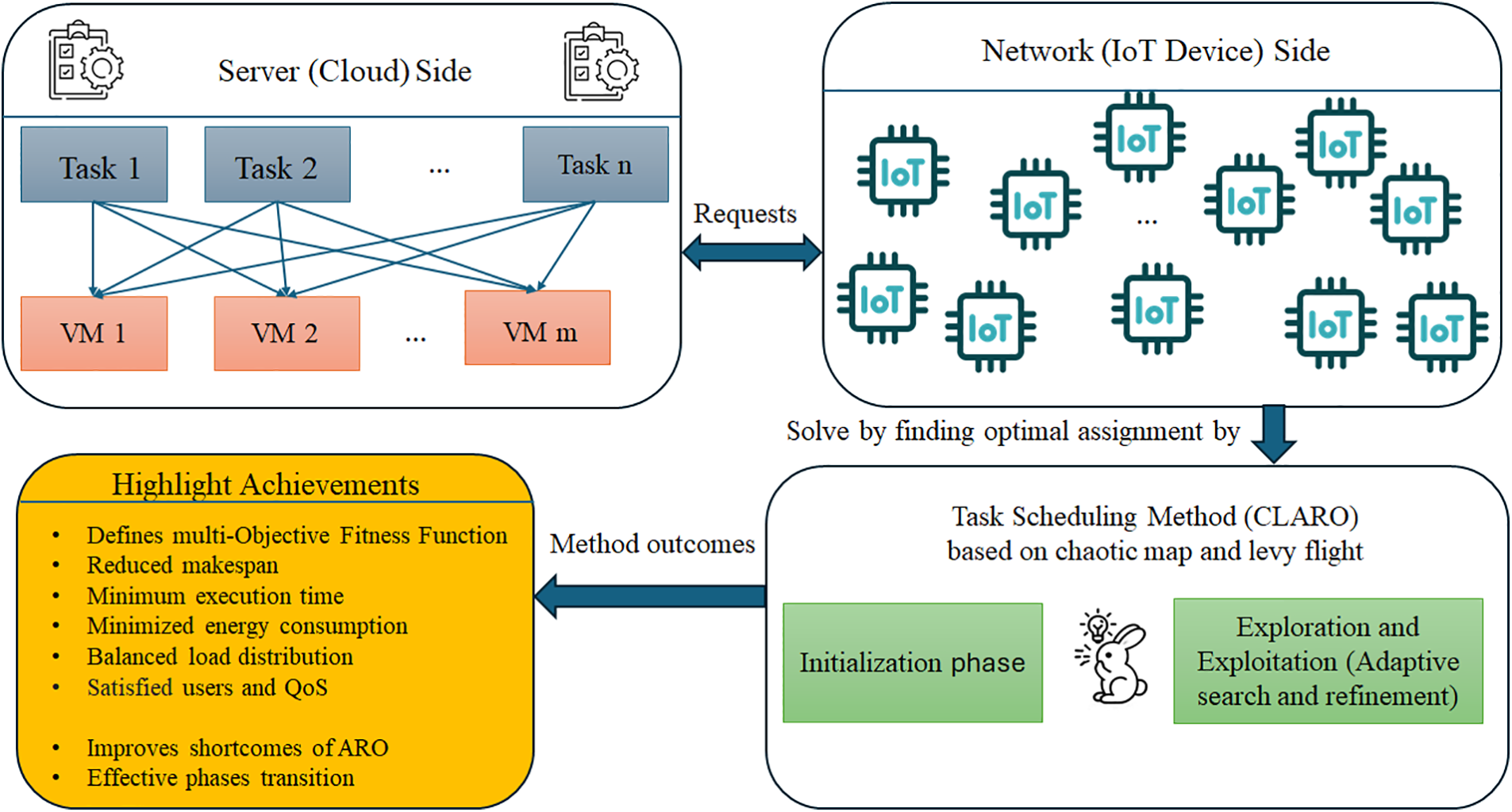
Figure 4: Working mechanism of CLARO

5.1.1 Gauss/Mouse Chaotic Map

The concept of chaos refers to the unpredictable behavior of a complex system, yet it has a form of internal harmony [41]. From a mathematical perspective, chaos refers to deterministic randomness exhibited by nonlinear, dynamic systems that do not converge to a stable state. This concept is introduced into the ARO algorithm to ensure that the algorithm performs a good scan in the global space, effectively realizes the initial population formation, and avoids the local optimum trap. Enhancing population diversity improves the likelihood of exploring the global search space, safeguarding the algorithm from getting trapped in local optima. Chaotic maps are based on this theory and help ensure equal population distribution. In this study, Gauss/Mouse chaotic map was determined that the map most compatible with the working nature of ARO is the Gauss/Mouse map after various experiments and also inspired by [42]. This chaotic map has been chosen after various experimental evaluations and is inspired by its robust performance in enhancing exploration capabilities. The Gauss/Mouse map is particularly effective in ensuring a well-distributed initial population across the search space, which is crucial for the algorithm’s success in solving complex optimization problems. The mathematical expression of this map is represented in Eq. (18). A large portion of the search area can be scanned with this map, providing more compatibility and better performance for ARO than other maps. It is important to highlight that during the initial population generation using the chaos map, careful consideration must be given to the problem’s upper and lower bound limits. This mitigates the risk of agents clustering in suboptimal regions, which can hinder performance. In addition, the exploration phase is refined by dynamically adjusting the population distribution, allowing the algorithm to adapt to various problem complexities. In this regard, Eq. (8), presented for the exploration phase, is revised to Eq. (19). This adjustment reflects the integration of chaos theory into the agent’s positional updates, ensuring enhanced global search capabilities. Implementing the chaotic map introduces an element of randomness that is deterministic yet non-repetitive, further reinforcing the algorithm’s ability to navigate complex solution landscapes.

(18)

(19)

5.1.2 Levy Flight Strategy

Levy flight is a random walk methodology defined by a combination of short steps and occasional long jumps, adhering to a probability distribution referred to as the levy distribution. This strategy draws inspiration from natural foraging behaviors observed in animals, where sporadic long-distance movements allow for a broader exploration of the environment. This strategy aims to facilitate rapid convergence in ARO while ensuring efficient exploration through a balanced interaction between the two phases. Short steps ensure the algorithm performs local searches around promising solutions, while infrequent long jumps enable the search agents to escape local optima and explore distant regions of the search space. This dynamic approach helps maintain diversity in the population and accelerates convergence toward the global optimum. In addition, this strategy aims to increase the flexibility of the exploitation phase. Eq. (20) expresses Lévy distribution.

(20)

(21)

This strategy allows agents to traverse vast areas of the search space, identifying high-quality solutions more rapidly by incorporating long-distance jumps. In addition, the stochastic nature of Levy flight prevents agents from clustering around local optima, fostering continuous exploration throughout the optimization process. In addition, the flexible step size adapts to the current iteration, providing larger jumps in the early stages of optimization and finer adjustments in later stages.

5.1.3 Flowchart, Pseudocode, and Time Complexity of CLARO

This section presents the flowchart and pseudocode of the proposed algorithm. Also, the time complexity analysis of the CLARO algorithm is depicted. The flowchart of the proposed algorithm is illustrated in Fig. 5, and its pseudocode is presented in Algorithm 1.

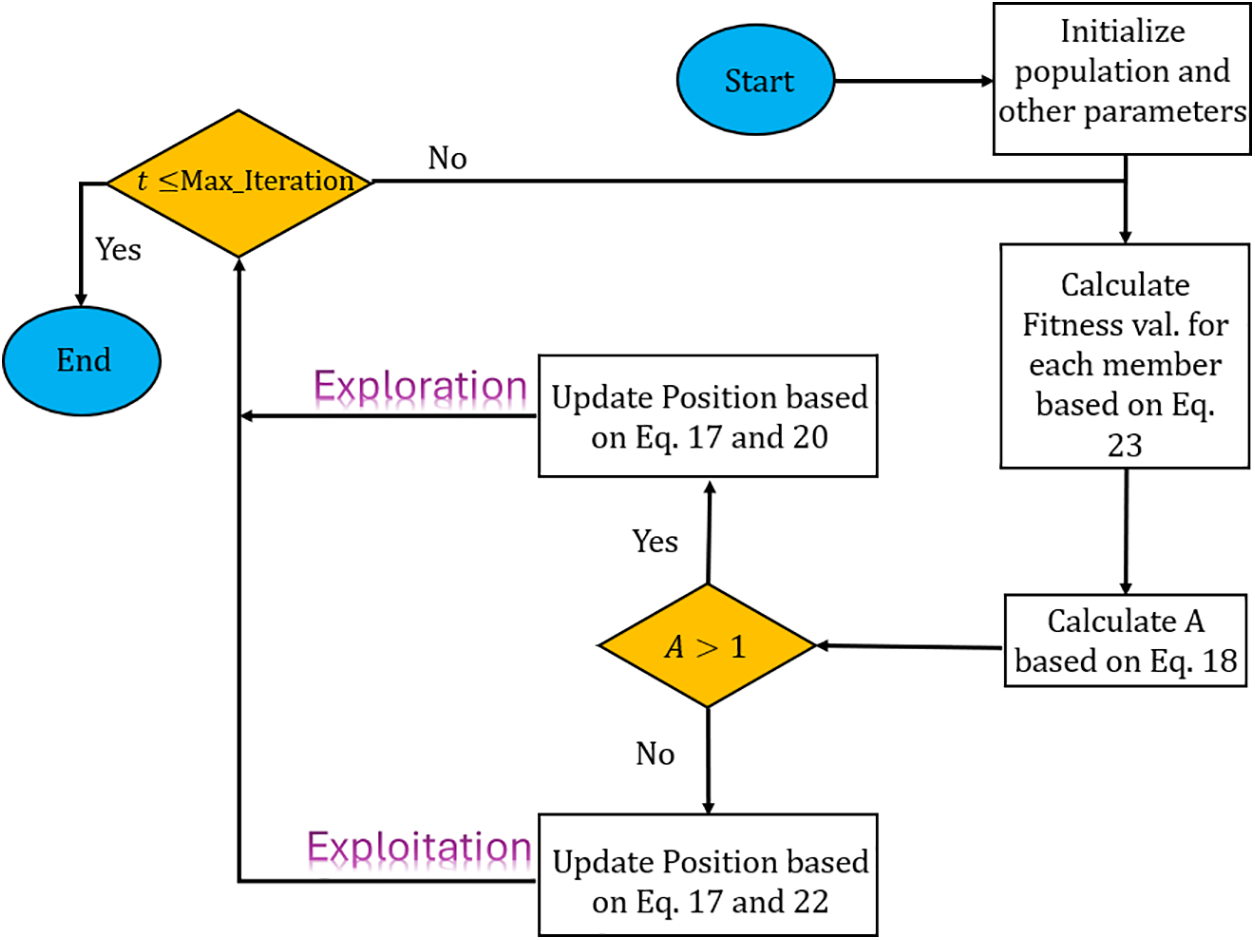
Figure 5: The flowchart of the CLARO algorithm

The complexity of CLARO is related to the initialization of search agents and the evaluation of the fitness function. These metrics are affected by the chaotic map and levy flight strategy involved in the proposed algorithm. The complexity of the initialization phase is O(nm); where ‘n’ is the number of search agents and ‘m’ is the dimension of the problem. The computational cost associated with assessing the fitness functions of all search agents is O(nT); where ‘T’ is the maximum iteration. The complexity of the location update process is equivalent to O(nmT). The complexity of the chaotic map and levy flight strategies are O(nT). Therefore, there is no negative impact on the overall complexity of the algorithm. As a result, the overall complexity cost of CLARO is calculated as O(nmT).

5.2 Fitness Function Definition

Once the problem is defined and the relevant uncertain parameters identified, it is essential to establish a fitness function designed for the specific challenges. This function will guide the proposed method and serve as a crucial metric for effectively evaluating the algorithm’s performance. The optimization challenge explored in this study seeks to simultaneously reduce makespan time, execution time cost, and energy consumption. In order to facilitate this, an appropriate fitness function was established (see Eq. (22)), incorporating weight coefficients for the relevant parameters to reflect their relative importance. Turning methods or metaheuristic approaches are necessary to determine these weights in an optimized manner. The tuning method developed and presented in the literature [43] was utilized to find the optimal weights of the defined parameters. The results obtained after application were as follows: α1 = 0.41, α2 = 0.24, and α3 = 0.35.

(22)

6  Simulation Results and Analysis

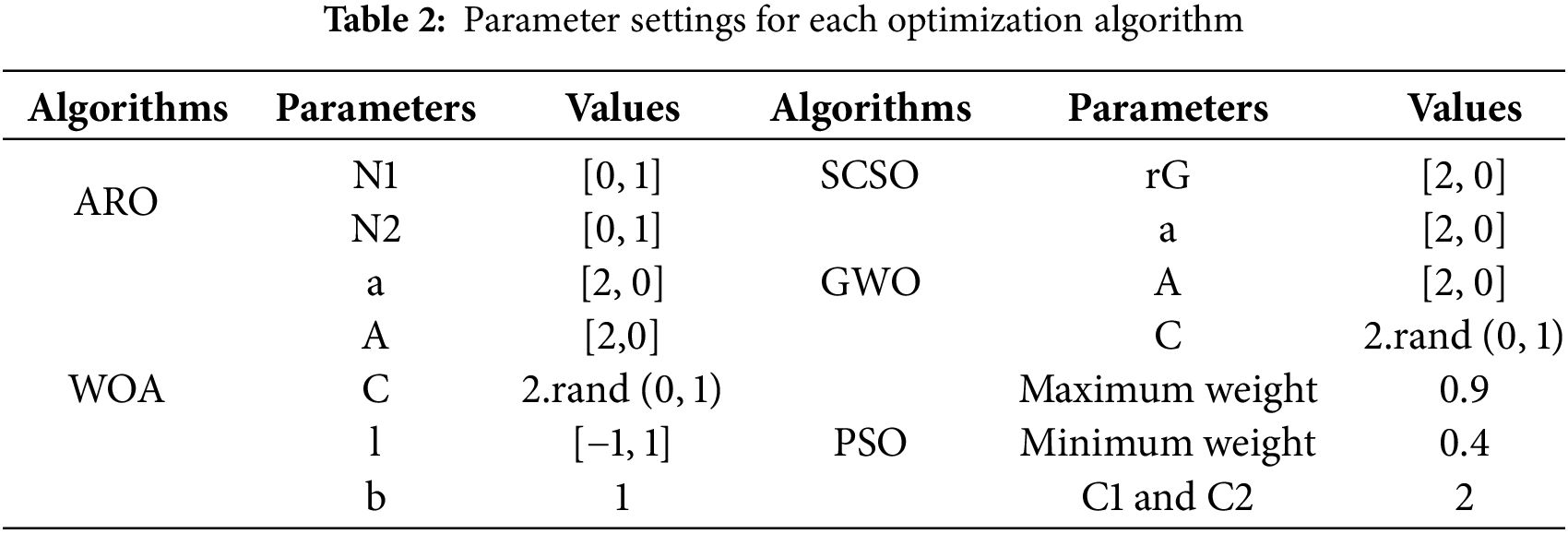
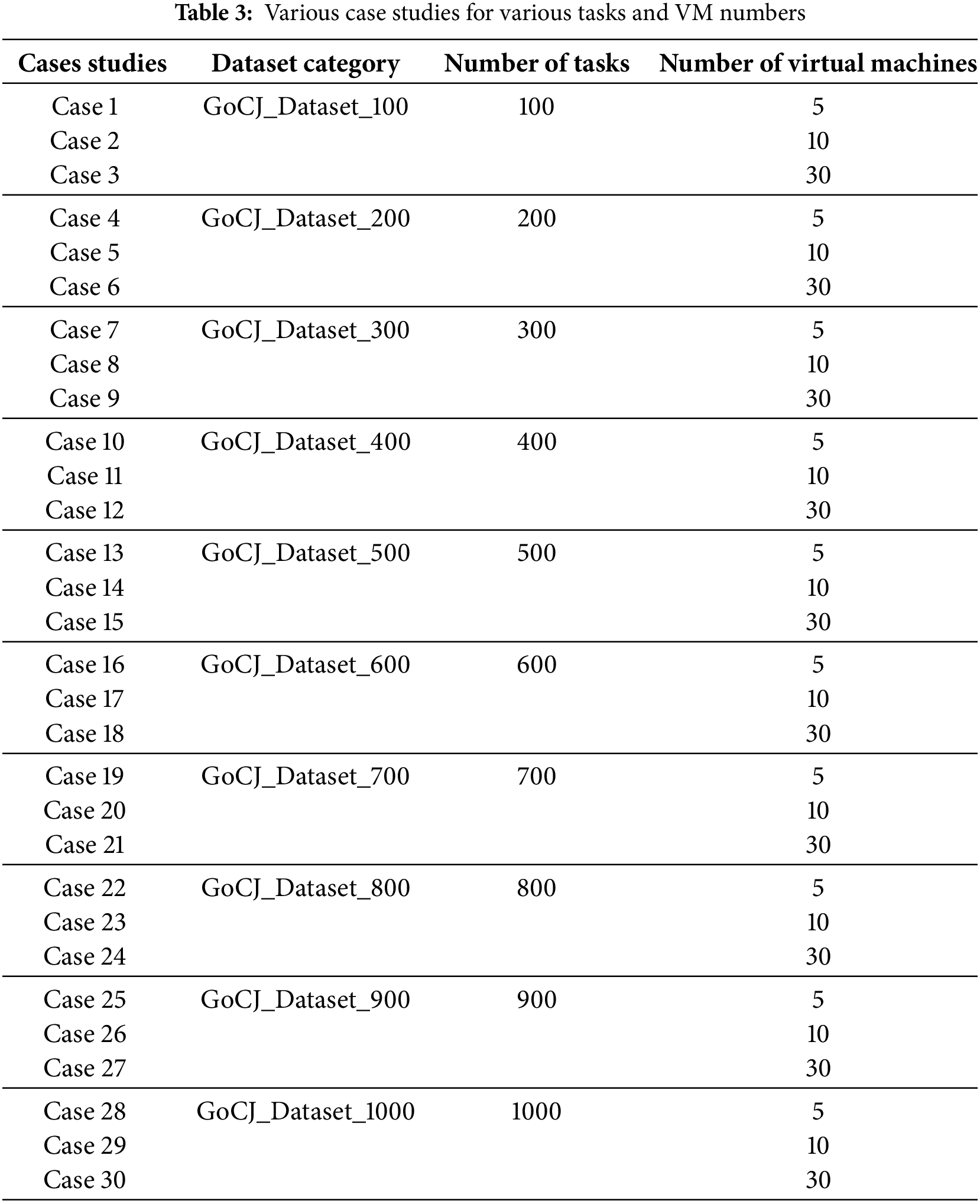
This section analyzes the performance of the proposed algorithm (CLARO) on the optimal task scheduling problem on the parameters makespan, execution time, and energy consumption. In this regard, the Google Cloud Jobs Dataset (GoCJ_Dataset) [44], which consists of publicly available and real-world examples, is utilized to demonstrate the algorithm’s effectiveness. A comparison is made with the well-known Sand Cat Swarm Optimization (SCSO) [45], Grey Wolf Optimizer (GWO) [24], Artificial Rabbits Optimizer (ARO) [11], Particle Swarm Optimization (PSO) [32], and Whale Optimization Algorithm (WOA) [30] to discuss the results. The algorithms used for comparison, except for the standard ARO, are methods that are specifically proposed and adapted to the problem addressed in this study. Therefore, the comparisons made will be more reliable and acceptable. All algorithms are implemented under identical conditions and designed to solve the problem to ensure reliable comparisons. All algorithms in this study are simulated on the same PC with a Core i7-11800 U 2.3 processor and 16 GB of RAM. In these studies, all analyses are performed in MATLAB. Accordingly, the population size is assumed to be 30, the total number of iterations is 100, and the total number of runs is 10. The parameter setting of each algorithm is listed in Table 2. Accordingly, analyses are conducted on 30 different case studies. Information on these cases is presented in Table 3. Small, medium, and large numbered tasks are in 10 different datasets. In this regard, VM numbers are evaluated in three different scenarios. In addition, in another analysis, allocations are made, assuming that VM numbers are 10% and 20% of the task numbers.

6.1 Analysis Based on Makespan Parameter

In this section, the performances of all algorithms for 30 different case studies and scenarios created on the considered data set are performed on the makespan parameter. The results obtained are listed in Table 4. Accordingly, the CLARO algorithm ranked first in 28 cases by finding the best answer (minimum makespan). Although it occasionally won this first place by a small margin, it caught up with other MH algorithms in most cases by a wide margin. It was not ranked first in cases 8 and 28, and it ranked first in cases 4, 11, 13, 16, 19, and 22, jointly with other MH algorithms. Based on the general performance analysis, SCSO ranked 2nd, and ARO ranked 3rd in this parameter. The other rankings belong to GWO, PSO, and WOA-based methods.

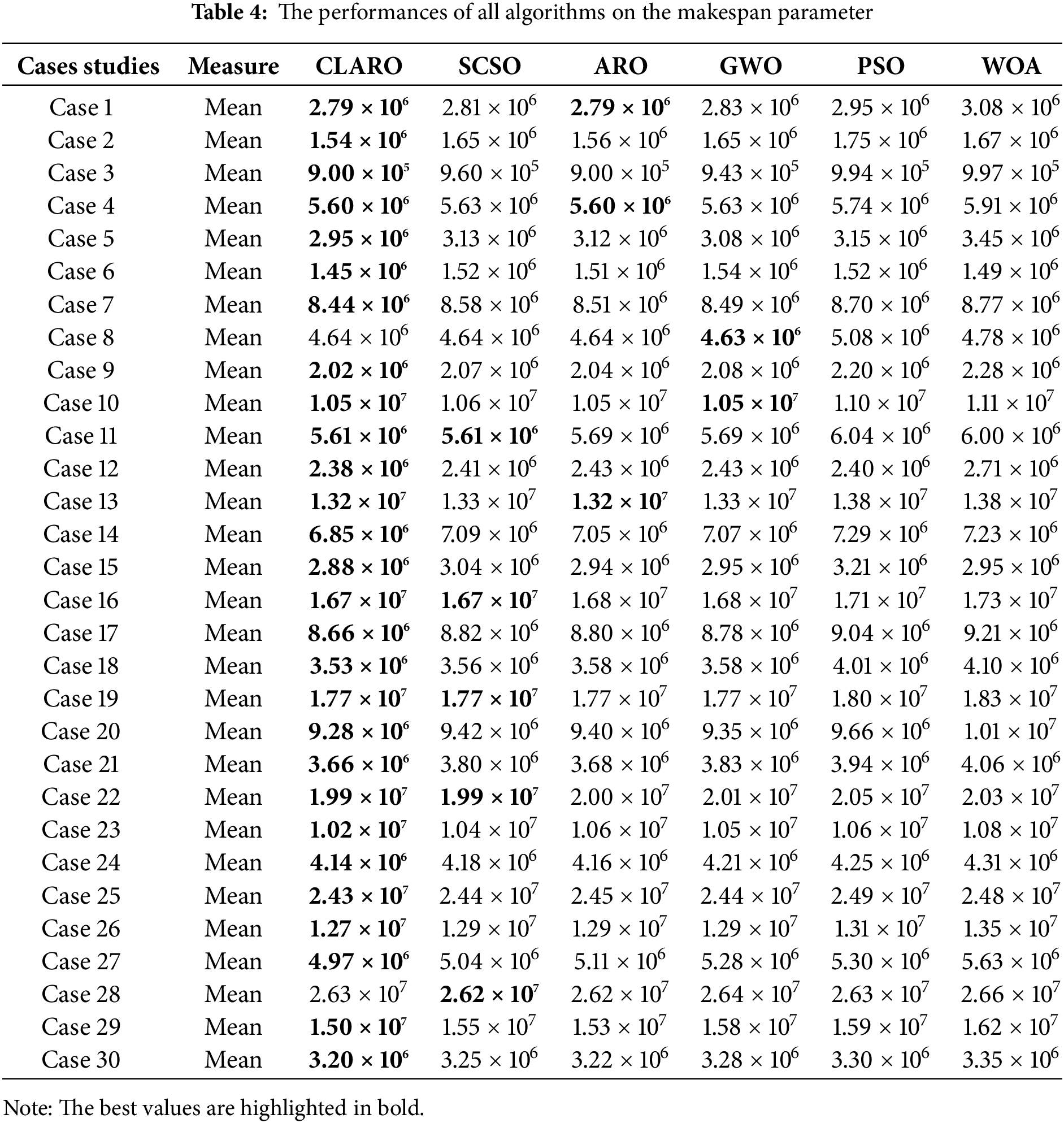
The ranking performances of the algorithms are also presented in percentages in Fig. 6. This figure is based only on the cases ranked first. Although the method ranked first alone received a full score (1), the score was equally divided among those ranked first jointly. This success rate is 80% for CLARO.

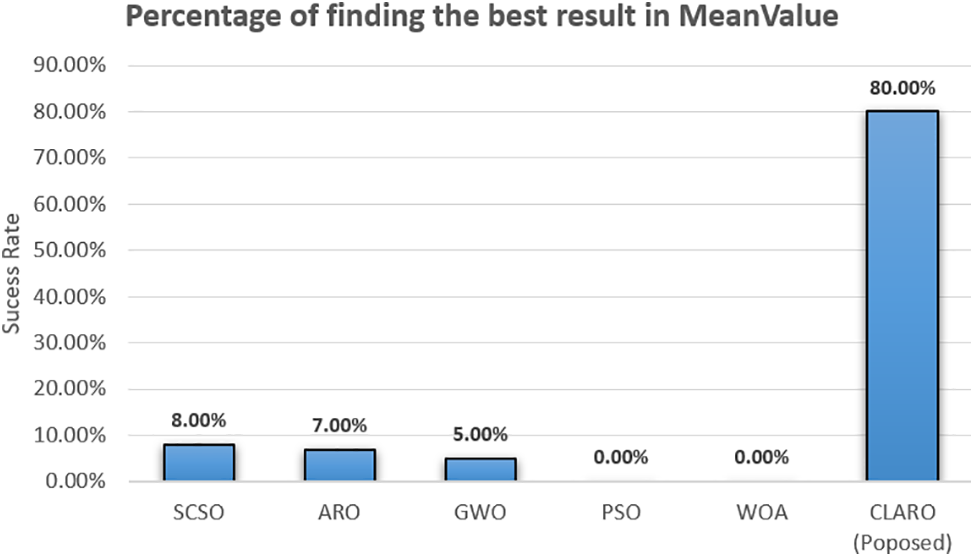
Figure 6: Percentage of success in ranking first based on makespan parameter analysis

6.2 Analysis Based on the Execution Time (Cost) Parameter

In this section, the performance of each method is evaluated through the execution time parameter. In some studies, this parameter is defined with the name cost. Based on the results (Table 5), the CLARO algorithm took first place by obtaining the best answer from 24 cases. The second place belongs to the standard ARO-based task scheduling method. The other places are SCSO, GWO, PSO, and WOA. The proposed algorithm cannot take first place in cases 7, 14, 15, 16, 19, and 26. When we calculate the rankings based on the score distribution in the previous section, the proposed algorithm achieved a success of 61% in catching first place. This information is presented in Fig. 7.

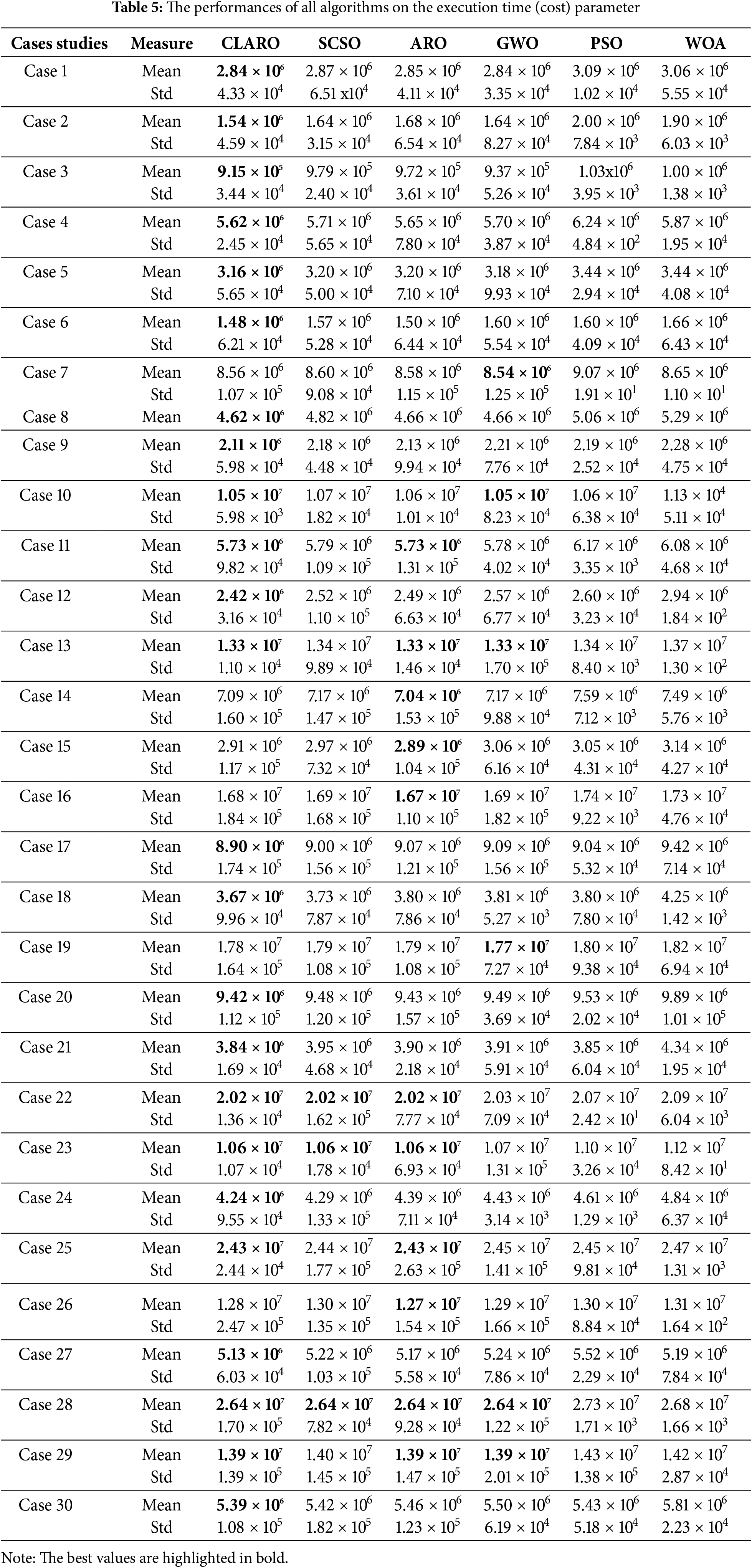
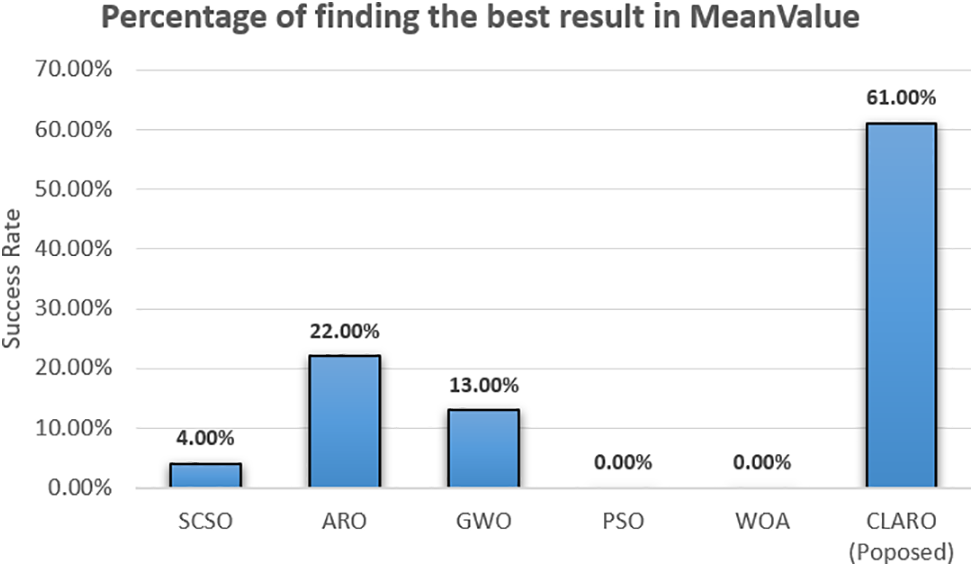
Figure 7: Percentage of success in ranking first based on execution time (cost) parameter analysis

6.3 Analysis Based on Energy Consumption Parameter

Another critical evaluation parameter is energy consumption, which refers to the amount of power utilized by resources during the execution of tasks. The results of the analysis are listed in Table 6. Based on the results, the CLARO method managed to take the first place except for 4 cases. These cases are cases 3, 15, 25, and 26, and in these scenarios, the SCSO, GWO, SCSO, and ARO methods took the first place, respectively. In addition, in 10 cases, the proposed algorithm took the first place jointly with other methods. The second place belongs to the SCSO-based task scheduling method. The other places are ARO, GWO, PSO, and WOA.

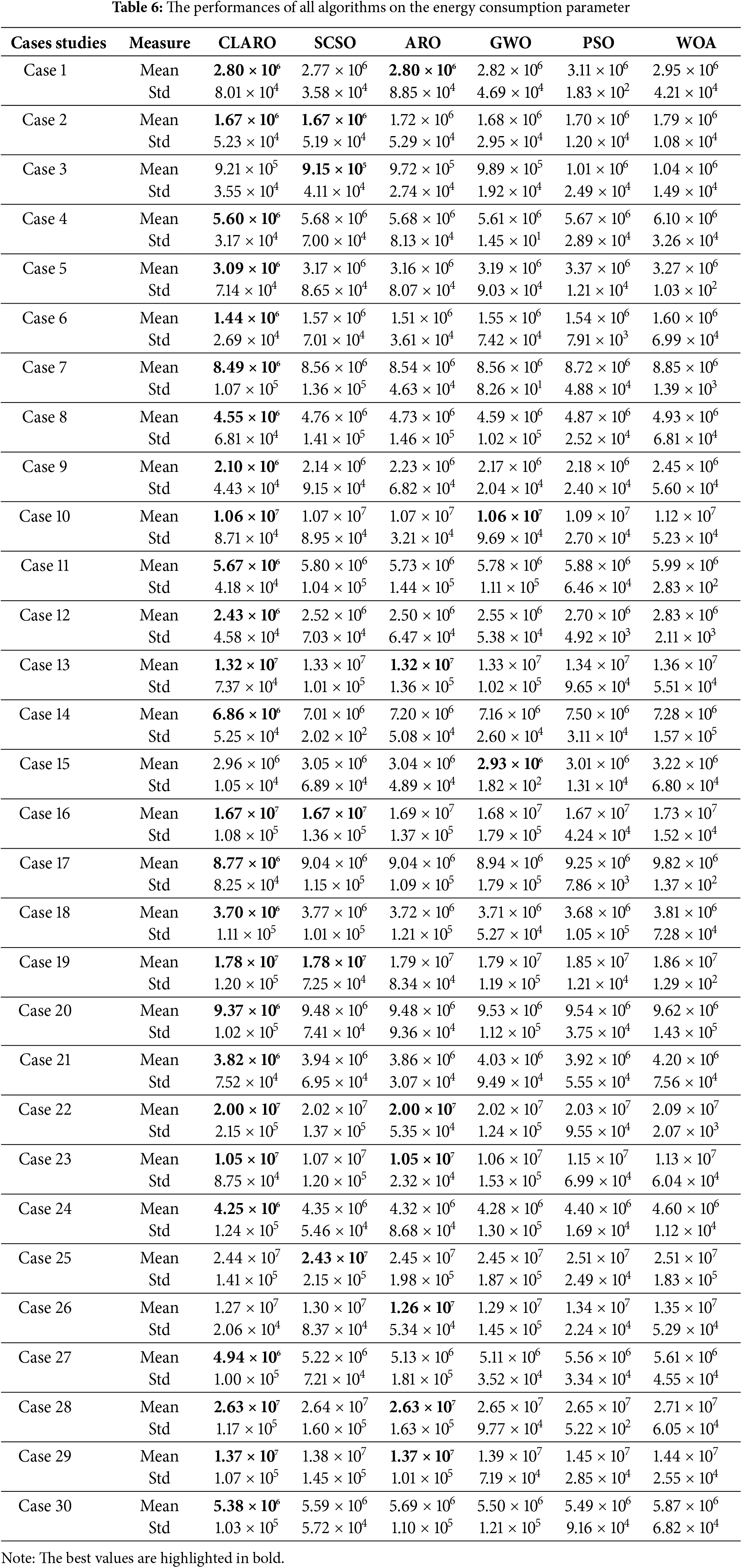
In addition, the ranking performances of the algorithms on the energy consumption parameter are presented as percentages in Fig. 8, based on the first-ranked cases. Accordingly, the success rate of the proposed algorithm is 69%. The proposed algorithm runs tasks with the best performance even with few resources. This inference is also understood from the analyses of the other two parameters. Our algorithm can perform well in all three parameters and will be able to work with a balanced load.

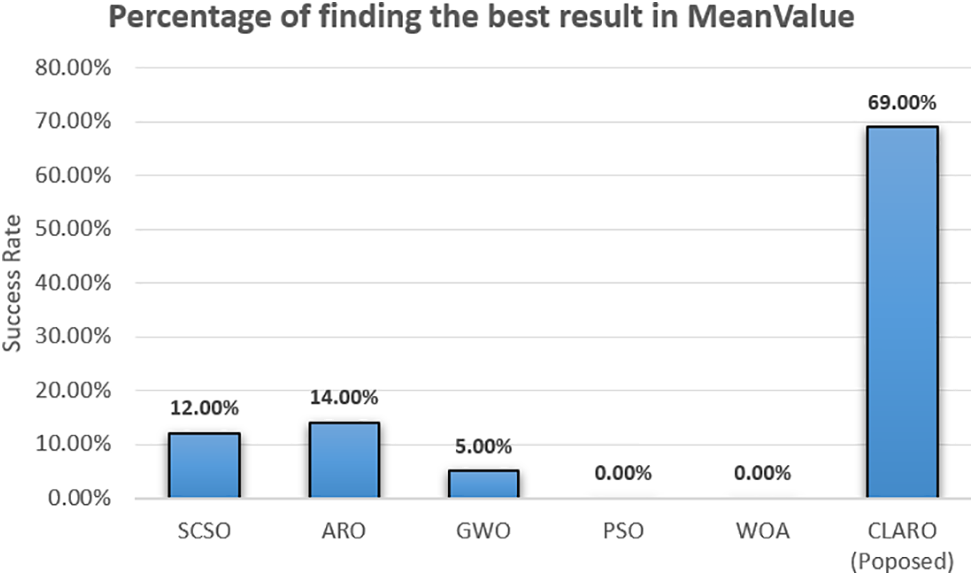
Figure 8: Percentage of success in ranking first based on energy consumption parameter analysis

6.4 Analysis Based on Multi-Objective Fitness Function

In this section, the performance evaluation of each algorithm on the multi-objective fitness function is performed (Fig. 9). In this analysis, the algorithm with the lowest fitness value is the method that finds the best result and shows the best performance. The tuning process of the weights in the function used, as mentioned before, was conducted using the method developed and presented in [43]. Based on the results obtained, CLARO is 2.52% better than ARO, 3.95% better than SCSO, 5.06% better than GWO, 8.15% better than PSO, and 9.41% better than WOA.

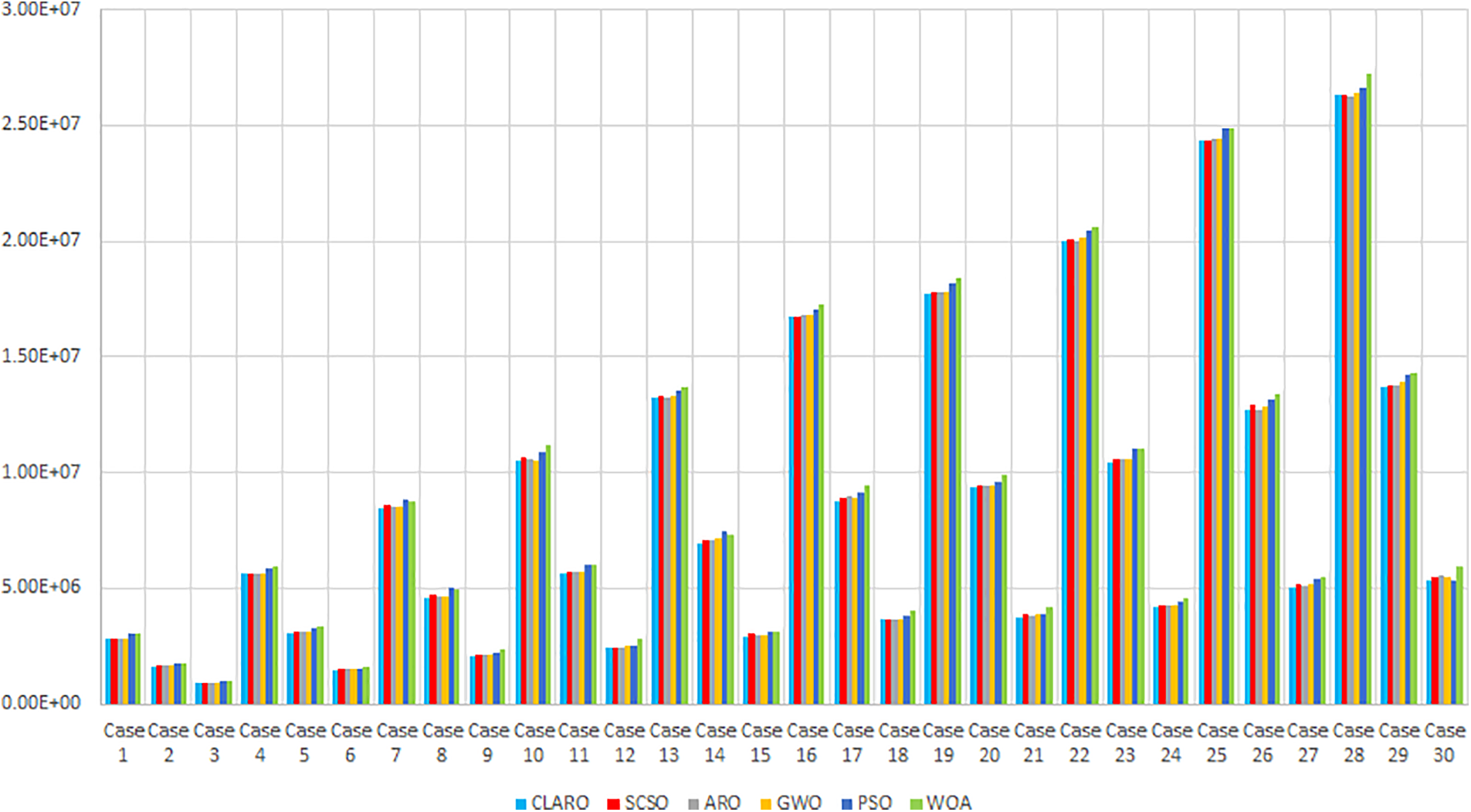
Figure 9: Performance of algorithms on multi-objective fitness function in all case studies

6.5 Analysis Based on Convergence Behavior

As the analysis progresses, the performance of all algorithms is assessed using the convergence curve. It is widely recognized in literature [46,47] that intelligent agents in optimization algorithms often exhibit unpredictable behavior in the initial stages, which is a normal occurrence. This shift in motion leads to a broader exploration of the search space, enabling more effective exploitation of its resources. The innovative strategies integrated into the CLARO algorithm, particularly the implementation of the chaotic map, significantly reduce the inefficiencies associated with this previously erratic working model. As a result, the algorithm exhibits robust performance right from the outset and maintains this consistency throughout its execution. In addition, fluctuations and variations diminish in the final iterations, facilitated by the levy strategy, ultimately leading to convergence at a specific local optimum. The analysis results are presented for all evaluation parameters on GoCJ_Dataset_100 and GoCJ_Dataset_1000, as shown in Figs. 10 and 11. The analysis results for other datasets are available in the supplementary file shared with the study.

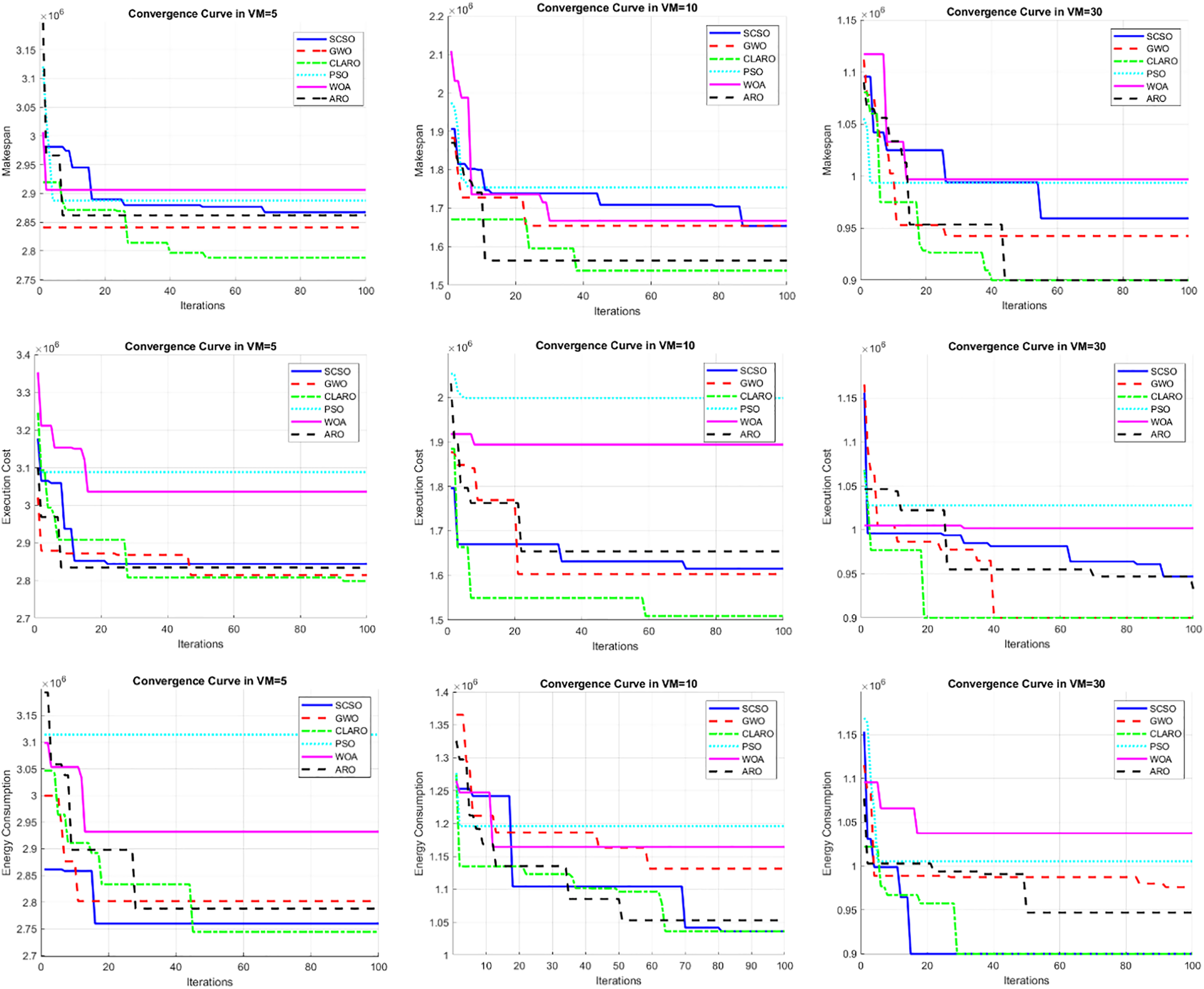
Figure 10: Convergence curve for all analysis parameters on GoCJ_Dataset_100 with various VMs

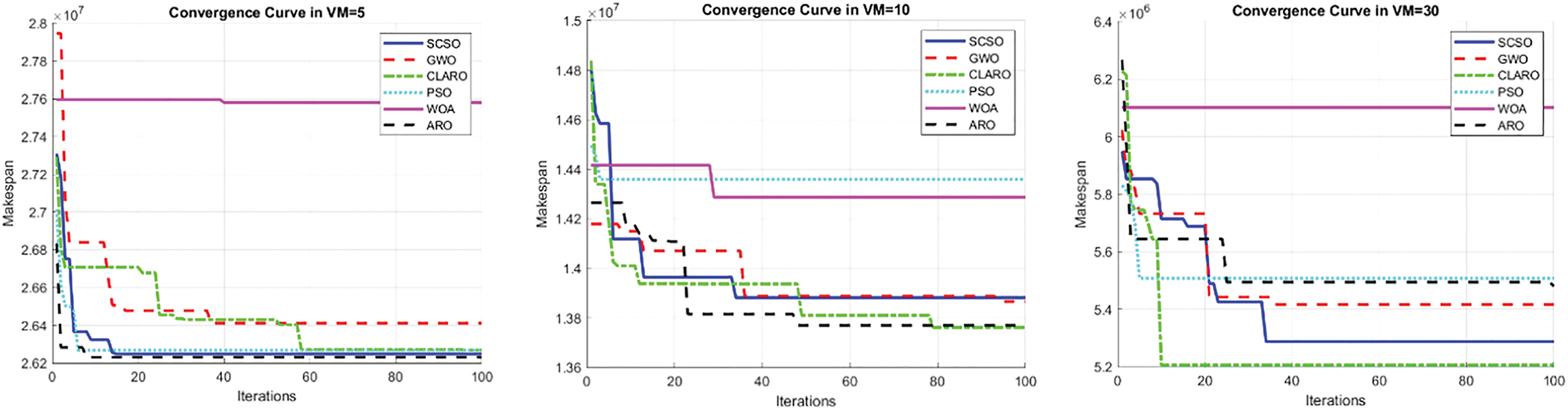
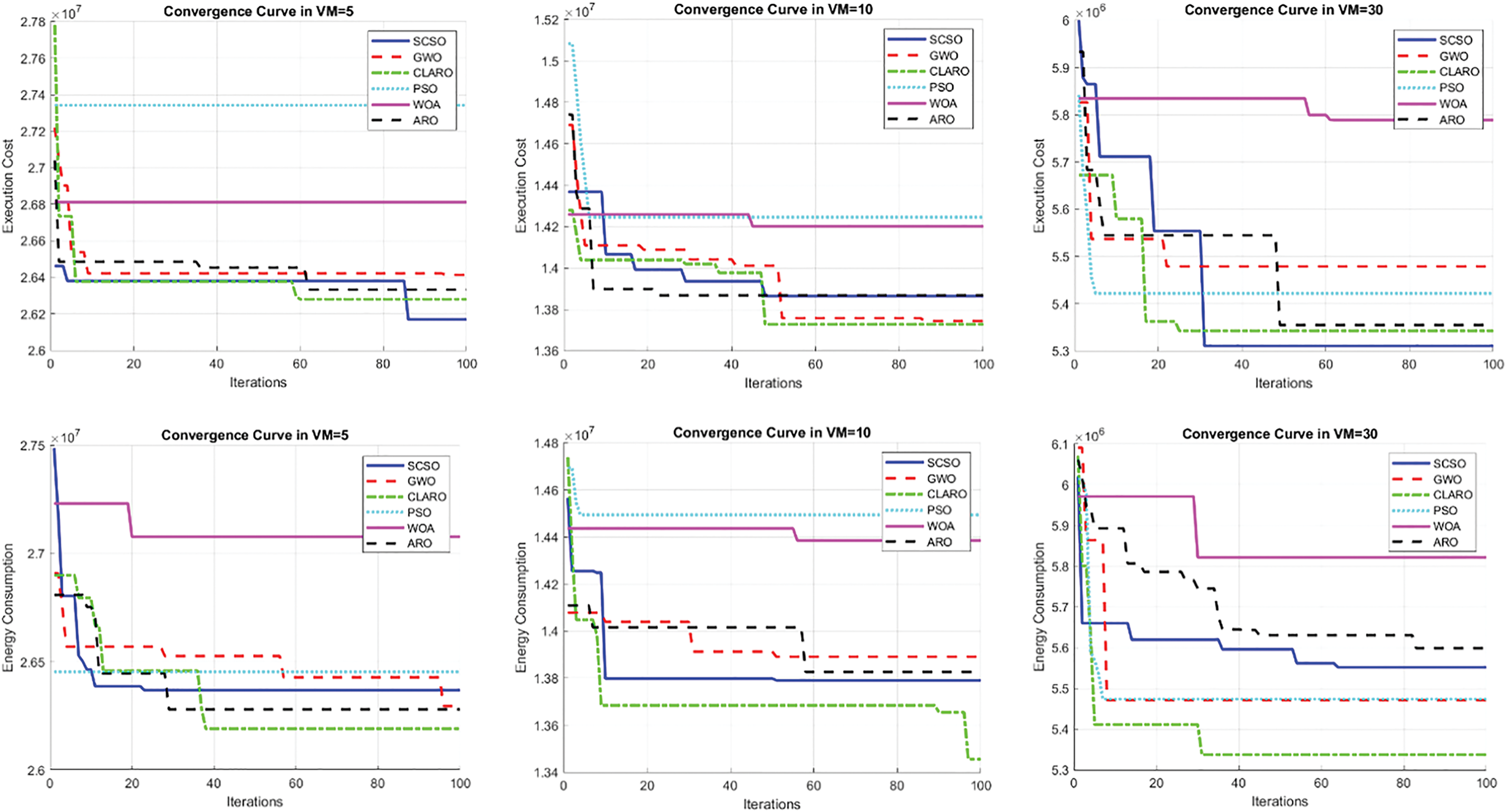
Figure 11: Convergence curve for all analysis parameters on GoCJ_Dataset_1000 with various VMs

6.6 Analysis Based on Proportional VM-Task Numbers

In this section, experiments are repeated with different numbers of VMs for all dataset categories depending on the number of tasks in each dataset category. This analysis has recently become the focus of many scientific studies [48,49]. The number of VMs for each dataset is assumed to be 10% and 20% of its tasks. This study aims to examine the performance of each algorithm at proportional VM numbers. The performance of the proposed algorithm on all datasets for both scenarios is presented in detail in Figs. 12 and 13.

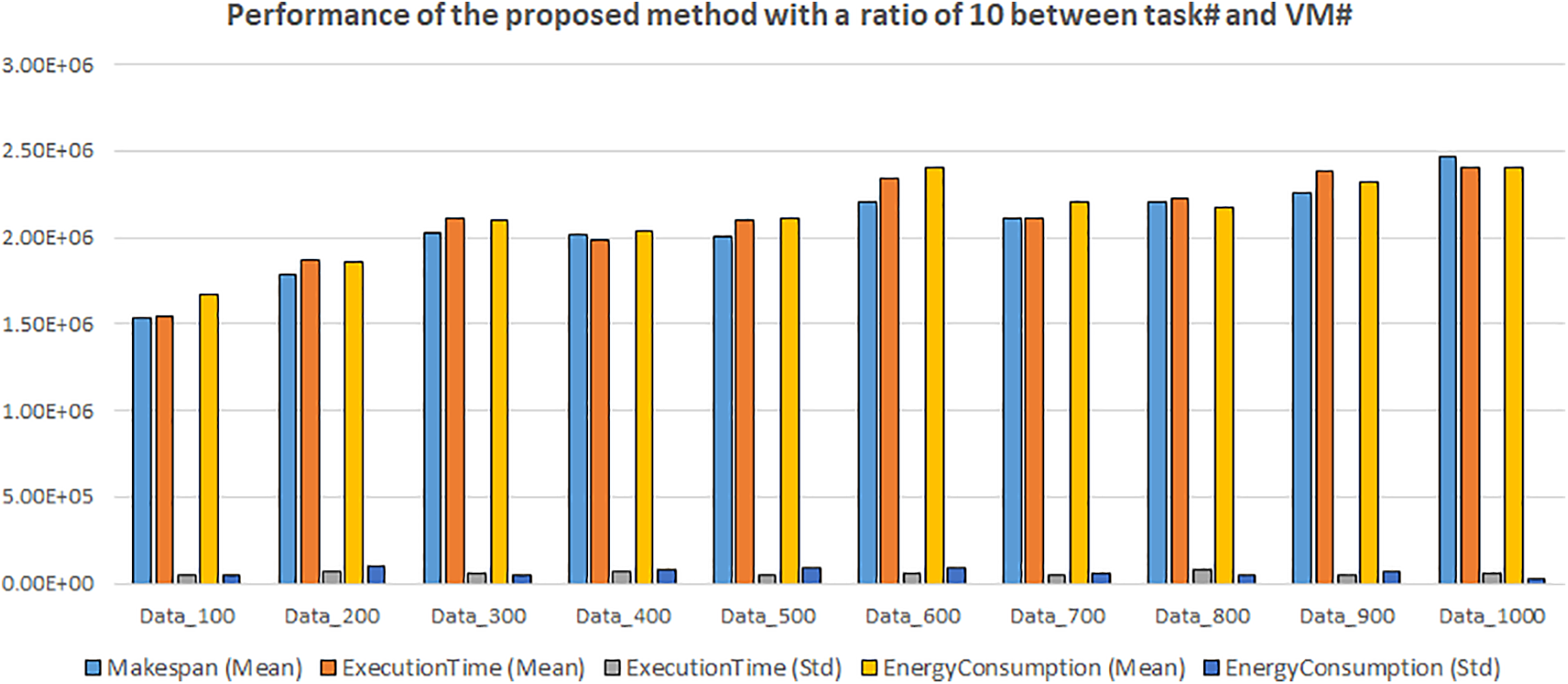
Figure 12: Performance of CLARO algorithm over all datasets in 10% task-VM ratio

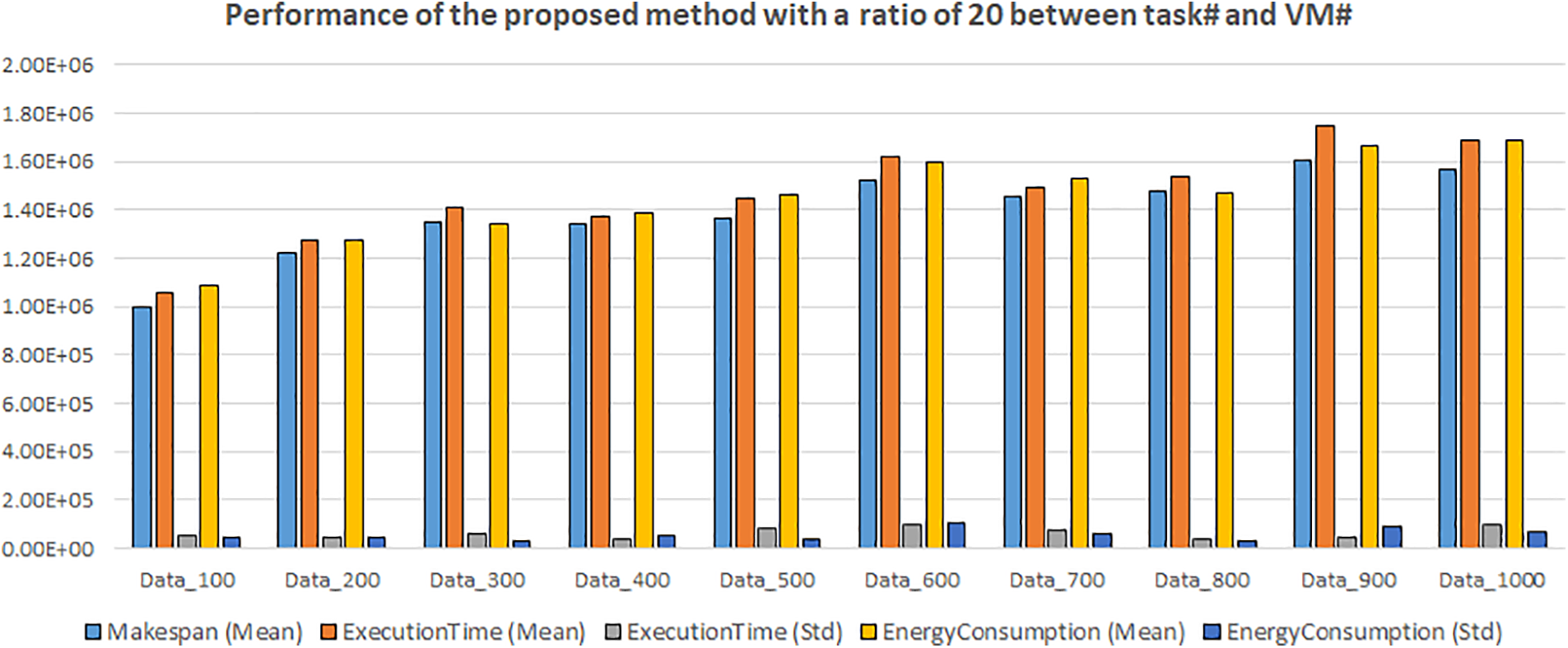
Figure 13: Performance of CLARO algorithm over all datasets in 20% task-VM ratio

In addition, the performance analysis of the methods is shown by convergence curves (Figs. 14 and 15). These analyses are presented on four different datasets, but analyses and information on other datasets can be obtained from our supplementary document. Based on the analysis of these behaviors, the proposed algorithm has a good convergence curve in this scenario, and the convergence rate is also accelerated compared to traditional ARO in general cases. Therefore, the search agents thoroughly investigate the solution space during the initial iterations and subsequently shift their focus to exploiting the identified areas after a certain number of iterations.

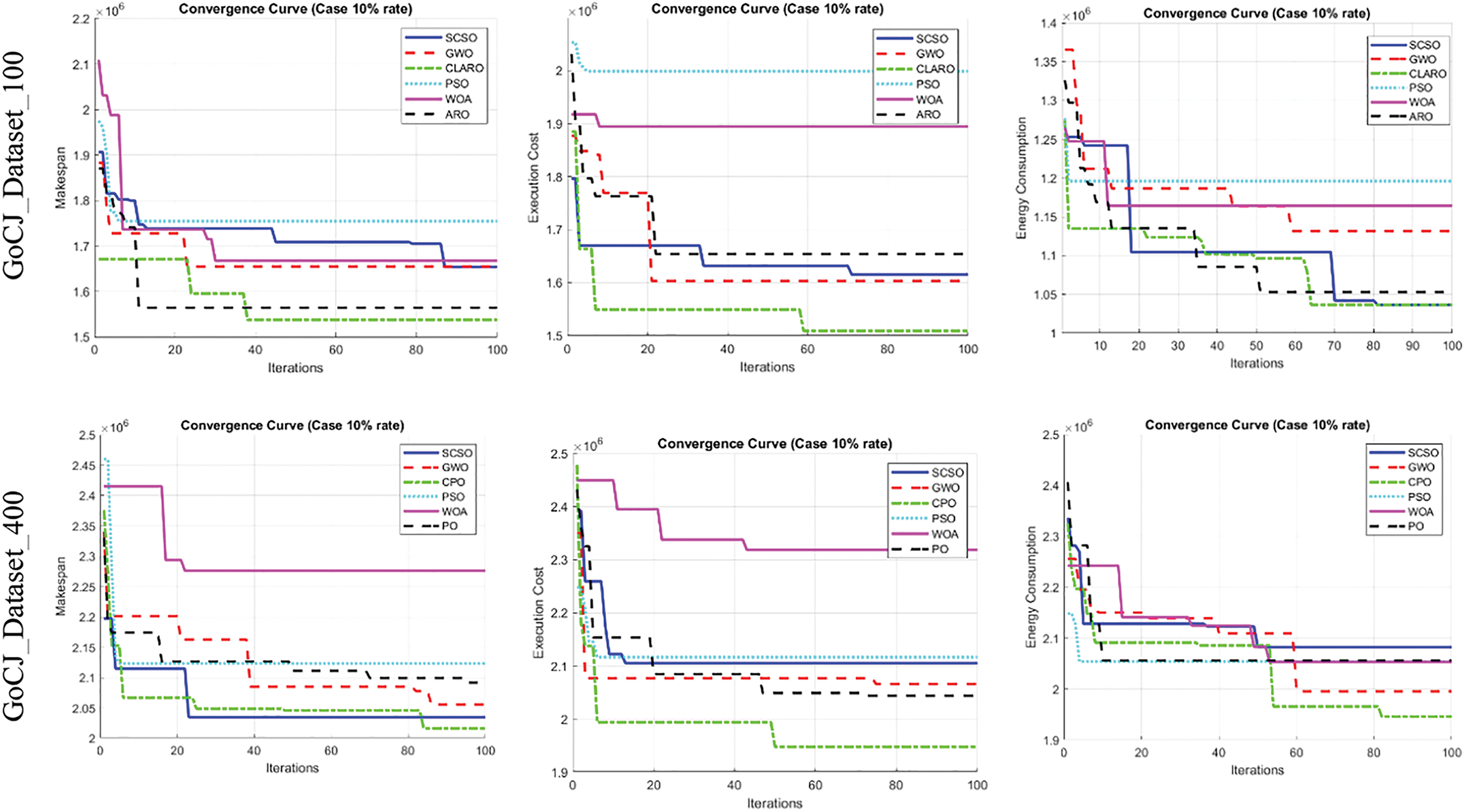
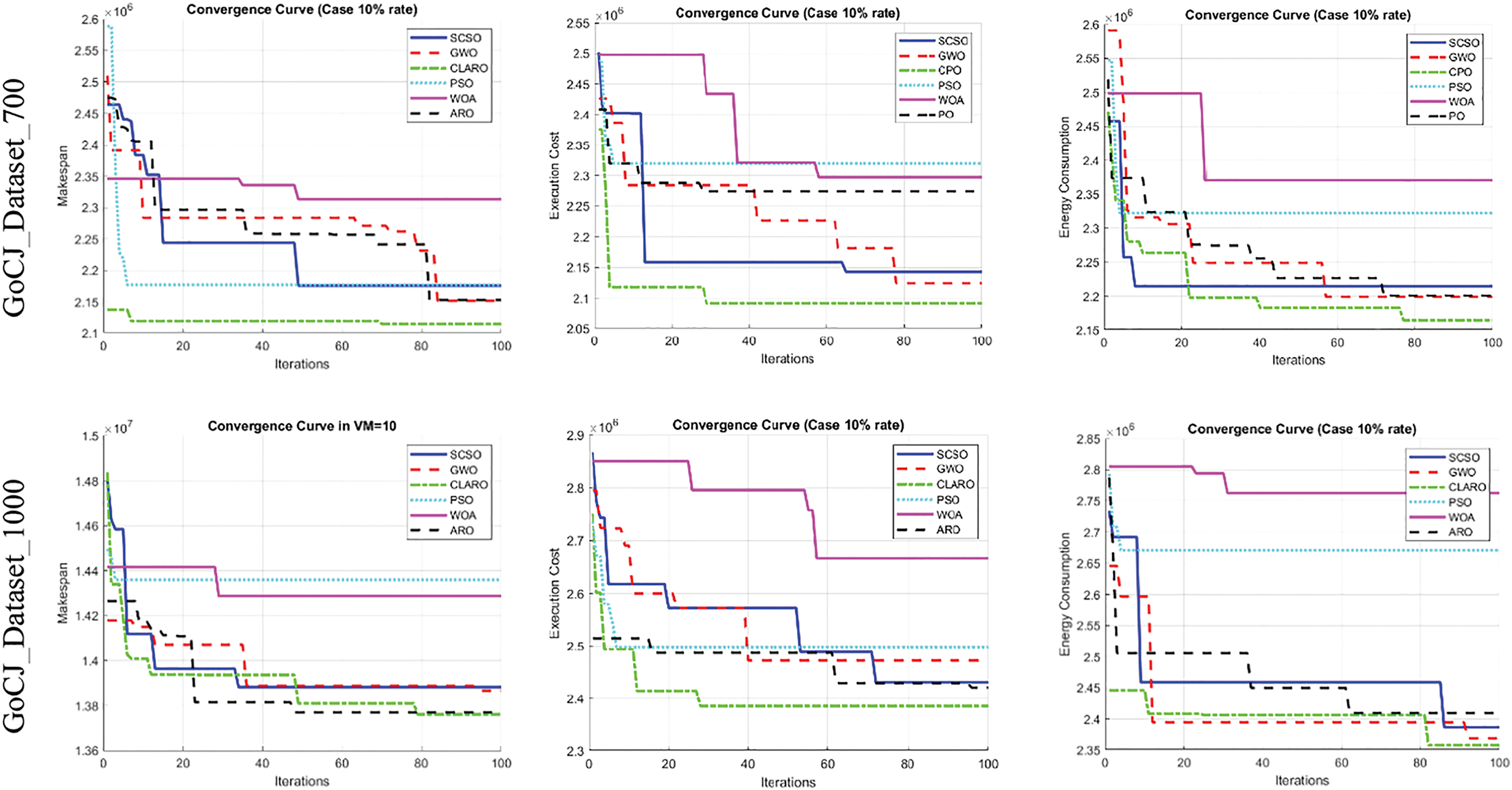
Figure 14: Convergence curve at a 10% rate for all analysis parameters (makespan, execution time, and energy consumption) over different datasets

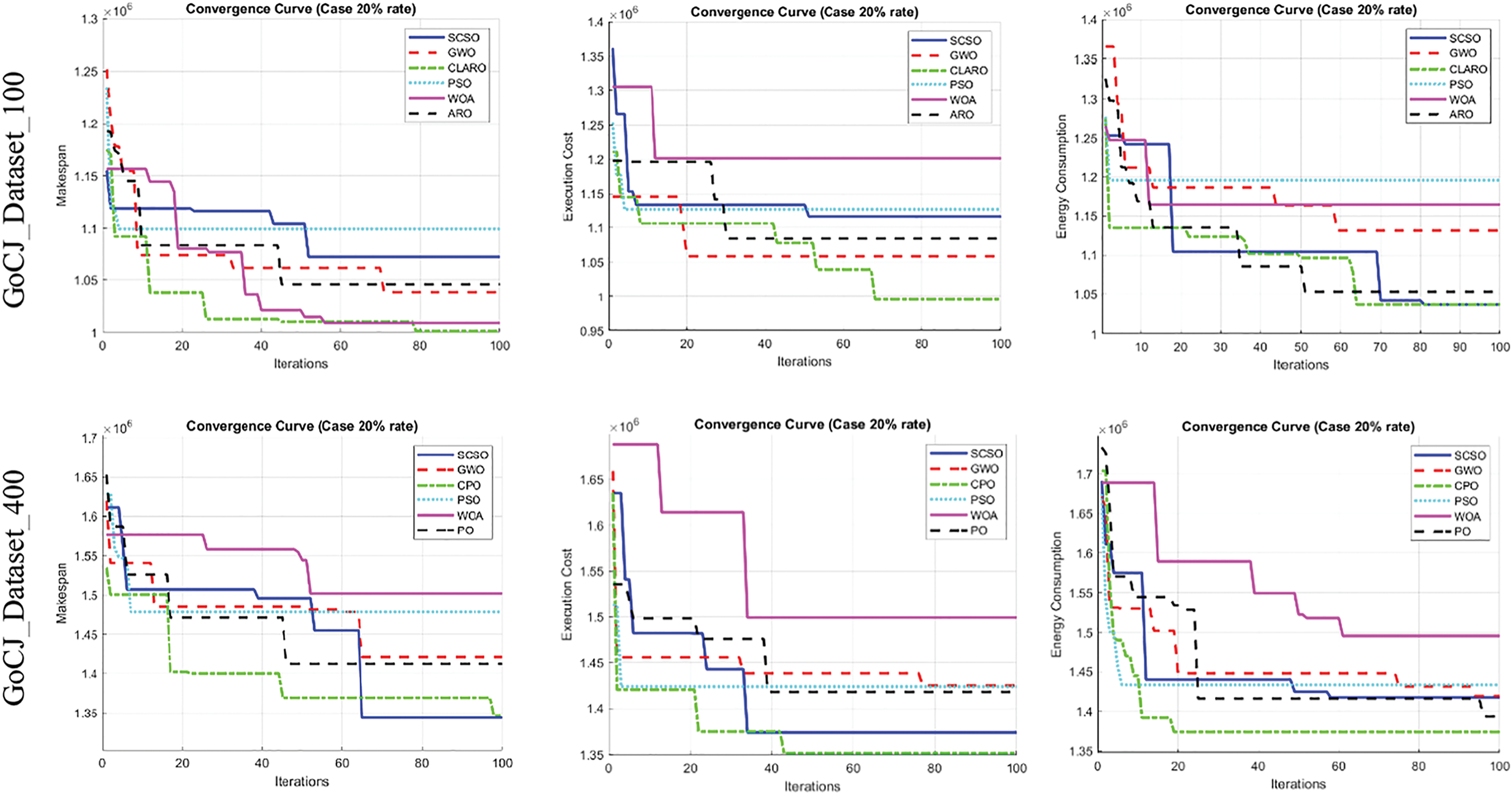
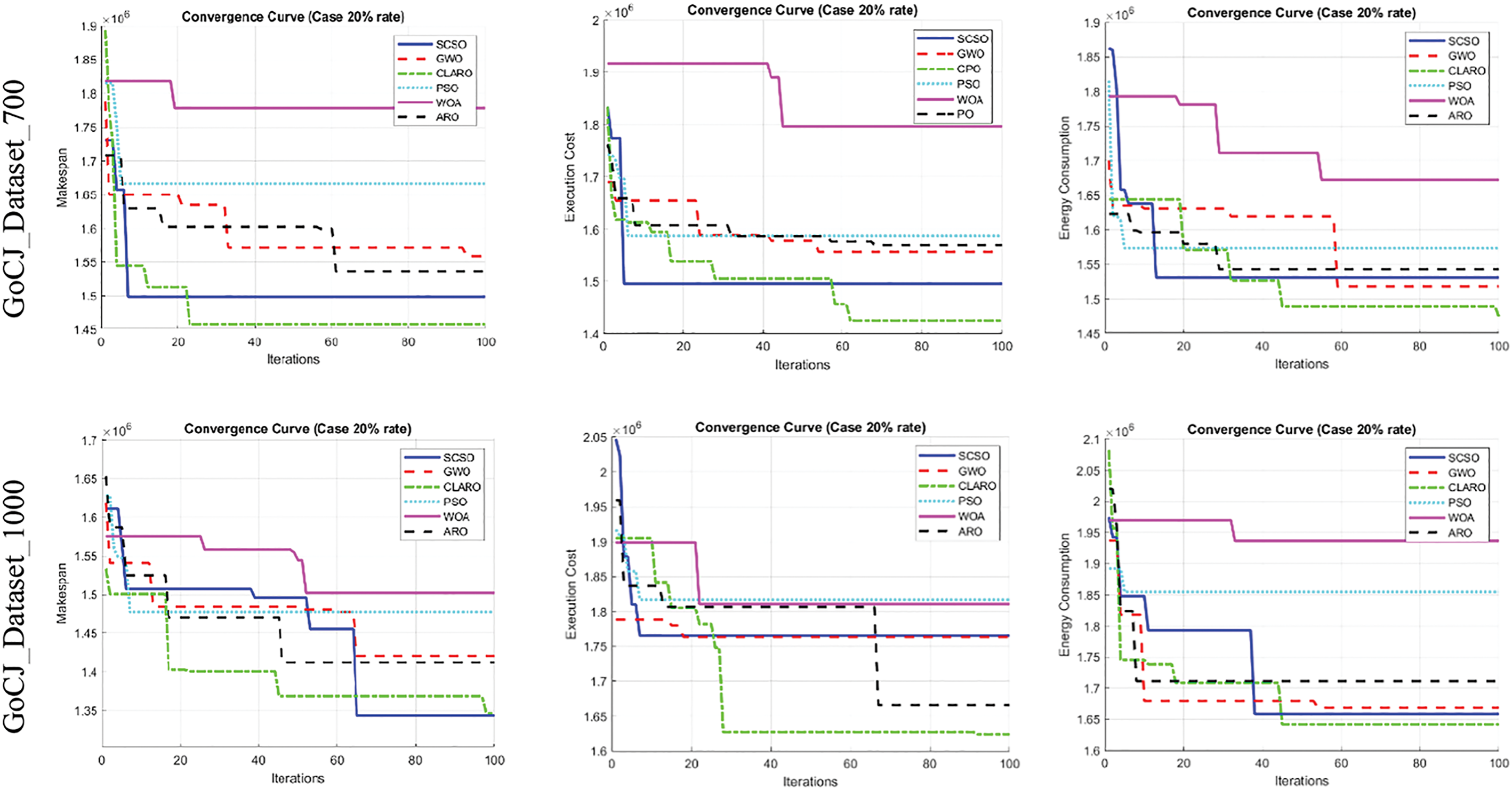
Figure 15: Convergence curve at a 20% rate for all analysis parameters (makespan, execution time and energy consumption) over different datasets

A comparative analysis of the results reveals that the proposed algorithm demonstrates superior performance, particularly in the execution time parameter, when contrasted with other algorithms. Although CLARO does not consistently match this level of superiority across all parameters, it still outperforms alternative methods. As the number of tasks and VMs increases, energy consumption inevitably rises, a trend observed across all algorithms [50–52]. Therefore, regardless of the savings achieved, energy consumption tends to escalate, leading to the performance of the more effective methods converging. However, the proposed method continues to exhibit the highest performance.

7  Constraints and Challenges

In real-world fog-cloud environments, task scheduling is constrained by multiple factors, which significantly influence algorithmic design and implementation. These constraints can be categorized as follows:

•   Resource Limitations: Physical resources such as CPU, memory, and bandwidth are finite, and their availability can vary over time. For example, devices within fog layers can have limited computational power compared to centralized cloud resources. Overcoming this constraint requires dynamic allocation strategies and efficient resource utilization to avoid bottlenecks.

•   Task Dependencies: Some tasks have precursor requirements, meaning they cannot begin until specific prior tasks are completed. This creates interdependencies that must be carefully managed to prevent delays and ensure logical execution order.

•   Deadlines and QoS Requirements: Many IoT applications are time-sensitive, necessitating strict adherence to task deadlines to maintain QoS. Algorithms must prioritize tasks to avoid penalties associated with latency or missed deadlines.

•   Scalability Challenges: As the number of tasks and devices increases, scheduling becomes more complex, making scalability a critical challenge. Metaheuristic algorithms, while effective, must be tuned to ensure their efficiency even in large-scale systems.

•   Uncertainty and Dynamic Changes: Real-world systems are often affected by dynamic conditions, such as fluctuating network bandwidth, sudden resource failures, or changing workloads. Algorithms must be robust enough to adapt to these uncertainties.

In addition, implementing the proposed task scheduling approach in real-world scenarios entails additional challenges:

•   Heterogeneity of Devices: Fog and cloud layers comprise highly heterogeneous devices with varying computational capabilities and energy consumption rates. Balancing workloads across these devices without overloading specific resources is critical.

•   Energy Efficiency: Energy consumption is a key consideration, particularly for IoT edge devices powered by batteries. Ensuring energy-efficient scheduling is essential to prolong device lifespans while maintaining QoS.

•   Security and Privacy Concerns: Data transmission and processing in fog-cloud environments can raise privacy concerns. Secure scheduling mechanisms must be incorporated to protect sensitive information, especially when tasks involve personal or confidential data.

•   Algorithm Complexity: Although the proposed algorithm demonstrates strong performance metrics, its computational overhead must remain manageable for real-time implementations. Balancing complexity with efficiency is crucial.

•   Interoperability: Real-world systems often require integration with existing hardware and software frameworks. Ensuring compatibility with different systems and protocols poses an additional layer of complexity.

8  Conclusions and Future Works

This study examines the fog-cloud environment for processing large volumes of data in real-time IoT systems. In this regard, allocating and scheduling tasks to fog nodes or VMs is crucial. The objective is to utilize system resources efficiently by focusing on key parameters such as completion (makespan) time, energy consumption, and execution time (cost). An enhanced version of the ARO algorithm is developed to achieve this aim, integrating a chaotic map and Lévy flight strategies (CLARO). A suitable fitness function is also defined in this study by recognizing the interrelationship among these three parameters. A real public dataset, comprising a range of small, medium, and large datasets and tasks, was utilized, consisting of a total of 10 sub-datasets. Simulations are conducted with three different numbers of VMs for each dataset, resulting in a total of 30 case studies. In addition, VM and task quantities were distributed in ratios of 10% and 20%, allowing for an assessment of each method’s performance under these scenarios. The results indicate that the proposed method outperformed other approaches across numerous case scenarios.

Future studies based on the findings and limitations of the current study can be listed as follows:

•   It is planned to run the proposed algorithm on more complex and different types of datasets and network configurations and to make necessary improvements.

•   Exploring the integration of multi-objective optimization techniques to balance conflicting parameters such as energy consumption and execution time more effectively.

•   Extending the proposed algorithm to handle dynamic environments with real-time changes in task loads and resource availability.

•   As discussed earlier, user satisfaction metrics are incorporated into the optimization framework through surveys or user studies.

•   Validating the algorithm’s performance using additional real-world case studies across various IoT domains.

Acknowledgement: The authors express their gratitude to the reviewers for their insightful feedback, which has greatly enhanced the quality of this paper.

Funding Statement: The authors extend appreciation to the Deanship of Postgraduate Studies and Scientific Research at Majmaah University for funding this research work through the project number (R-2025-1567).

Author Contributions: Ferzat Anka: Conceptualization, methodology, software, validation, formal analysis, resources, investigation, writing—review and editing, project administration. Ghanshyam G. Tejani: Conceptualization, validation, formal analysis, resources, investigation, writing—review and editing, project administration, funding acquisition. Sunil Kumar Sharma: Software, validation, formal analysis, resources, investigation, writing—review and editing, funding acquisition. Mohammed Baljon: Investigation, writing—review and editing, funding acquisition. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: It is provided based on request by corresponding authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Amin U, Myhammad AS, Li J, Lubna N, Tariq M, Amjad R, et al. Smart cities: the role of Internet of Things and machine learning in realizing a data-centric smart environment. Complex Intell Syst. 2023;10(1):1607–37. doi:10.1007/s40747-023-01175-4. [Google Scholar] [CrossRef]

2. Duan T, Liu Y, Li J, Lian Z, Li Q. DuFNet: dual flow network of real-time semantic segmentation for unmanned driving application of Internet of Things. Comput Model Eng Sci. 2023;136(1):223–39. doi:10.32604/cmes.2023.024742. [Google Scholar] [CrossRef]

3. Dadmehr R. Analyzing meta-heuristic algorithms for task scheduling in a fog-based IoT application. Algorithms. 2022;15(11):397. doi:10.3390/a15110397. [Google Scholar] [CrossRef]

4. Rajashekar KJ, Channakrishnaraju, Gowda PC, Jayachandra AB. SCEHO-IPSO: a nature-inspired meta heuristic optimization for task-scheduling policy in cloud computing. Appl Sci. 2023;13(19):10850. doi:10.3390/app131910850. [Google Scholar] [CrossRef]

5. Hilal AM, Abdalla Hashim AH, Obayya M, Gaddah A, Mohamed A, Yaseen I, et al. Metaheuristics based energy efficient task scheduling scheme for cyber-physical systems environment. Sustainability. 2022;14(24):16539. doi:10.3390/su142416539. [Google Scholar] [CrossRef]

6. Zhang S, Chi C, Ji K, Liu Z, Zhang F, Song P, et al. A new meta-heuristic task scheduling algorithm for optimizing energy efficiency in data centers. In: 2021 IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom); 2021 Sep 30–Oct 3; New York City, NY, USA: IEEE; 2021. p. 947–57. doi:10.1109/ispa-bdcloud-socialcom-sustaincom52081.2021.00133 [Google Scholar] [CrossRef]

7. Kumar M, Sharma SC, Goel A, Singh SP. A comprehensive survey for scheduling techniques in cloud computing. J Netw Comput Appl. 2019;143(2):1–33. doi:10.1016/j.jnca.2019.06.006. [Google Scholar] [CrossRef]

8. Khan ZA, Aziz IA, Osman NAB, Ullah I. A review on task scheduling techniques in cloud and fog computing: taxonomy, tools, open issues, challenges, and future directions. IEEE Access. 2023;11:143417–45. doi:10.1109/ACCESS.2023.3343877. [Google Scholar] [CrossRef]

9. Moid SM, Sara K, Raja J, Marius P. Task scheduling for energy-harvesting-based IoT: a survey and critical analysis. IEEE Internet Things J. 2021;8(18):13825–48. doi:10.1109/JIOT.2021.3086186. [Google Scholar] [CrossRef]

10. Jamil B, Ijaz H, Shojafar M, Munir K, Buyya R. Resource allocation and task scheduling in fog computing and Internet of everything environments: a taxonomy, review, and future directions. ACM Comput Surv. 2022;54(11s):1–38. doi:10.1145/3513002. [Google Scholar] [CrossRef]

11. Wang L, Cao Q, Zhang Z, Mirjalili S, Zhao W. Artificial rabbits optimization: a new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng Appl Artif Intell. 2022;114(4):105082. doi:10.1016/j.engappai.2022.105082. [Google Scholar] [CrossRef]

12. Bacanin N, Zivkovic M, Bezdan T, Venkatachalam K, Abouhawwash M. Modified firefly algorithm for workflow scheduling in cloud-edge environment. Neural Comput Appl. 2022;34(11):9043–68. doi:10.1007/s00521-022-06925-y. [Google Scholar] [PubMed] [CrossRef]

13. Abohamama AS, El-Ghamry A, Hamouda E. Real-time task scheduling algorithm for IoT-based applications in the cloud-fog environment. J Netw Syst Manag. 2022;30(4):54. doi:10.1007/s10922-022-09664-6. [Google Scholar] [CrossRef]

14. Jing W, Zhao C, Miao Q, Song H, Chen G. QoS-DPSO: Qos-aware task scheduling for cloud computing system. J Netw Syst Manag. 2020;29(1):5. doi:10.1007/s10922-020-09573-6. [Google Scholar] [CrossRef]

15. Xie Y, Zhu Y, Wang Y, Cheng Y, Xu R, Sani A, et al. A novel directional and non-local-convergent particle swarm optimization based workflow scheduling in cloud-edge environment. Future Gener Comput Syst. 2023;97(2):361–78. doi:10.1016/j.future.2019.03.005. [Google Scholar] [CrossRef]

16. Kakkottakath Valappil Thekkepuryil J, Suseelan DP, Keerikkattil PM. An effective meta-heuristic based multi-objective hybrid optimization method for workflow scheduling in cloud computing environment. Clust Comput. 2021;24(3):2367–84. doi:10.1007/s10586-021-03269-5. [Google Scholar] [CrossRef]

17. Natesan G, Chokkalingam A. Multi-objective task scheduling using hybrid whale genetic optimization algorithm in heterogeneous computing environment. Wirel Pers Commun. 2020;110(4):1887–913. doi:10.1007/s11277-019-06817-w. [Google Scholar] [CrossRef]

18. Nikravan M, Haghi Kashani M. A review on trust management in fog/edge computing: techniques, trends, and challenges. J Netw Comput Appl. 2022;204(30):103402. doi:10.1016/j.jnca.2022.103402. [Google Scholar] [CrossRef]

19. Yadav AM, Tripathi KN, Sharma SC. An opposition-based hybrid evolutionary approach for task scheduling in fog computing network. Arab J Sci Eng. 2023;48(2):1547–62. doi:10.1007/s13369-022-06918-y. [Google Scholar] [CrossRef]

20. Cho KM, Tsai PW, Tsai CW, Yang CS. A hybrid meta-heuristic algorithm for VM scheduling with load balancing in cloud computing. Neural Comput Appl. 2015;26(6):1297–309. doi:10.1007/s00521-014-1804-9. [Google Scholar] [CrossRef]

21. Hasan MZ, Al-Rizzo H. Task scheduling in Internet of Things cloud environment using a robust particle swarm optimization. Concurr Comput. 2020;32(2):e5442. doi:10.1002/cpe.5442. [Google Scholar] [CrossRef]

22. Khezri E, Yahya RO, Hassanzadeh H, Mohaidat M, Ahmadi S, Trik M. DLJSF: Data-Locality Aware Job Scheduling IoT tasks in fog-cloud computing environments. Results Eng. 2024;21(2):101780. doi:10.1016/j.rineng.2024.101780. [Google Scholar] [CrossRef]

23. Saif FA, Latip R, Hanapi ZM, Shafinah K. Multi-objective grey wolf optimizer algorithm for task scheduling in cloud-fog computing. IEEE Access. 2023;11:20635–46. doi:10.1109/ACCESS.2023.3241240. [Google Scholar] [CrossRef]

24. Djemai T, Stolf P, Monteil T, Pierson JM. A discrete particle swarm optimization approach for energy-efficient IoT services placement over fog infrastructures. In: 2019 18th International Symposium on Parallel and Distributed Computing (ISPDC); 2019 Jun 3–7; Amsterdam, Netherlands: IEEE; 2019. p. 32–40. doi:10.1109/ispdc.2019.00020 [Google Scholar] [CrossRef]

25. Movahedi Z, Defude B, Hosseininia AM. An efficient population-based multi-objective task scheduling approach in fog computing systems. J Cloud Comput. 2021;10(1):53. doi:10.1186/s13677-021-00264-4. [Google Scholar] [CrossRef]

26. Milan ST, Rajabion L, Darwesh A, Hosseinzadeh M, Navimipour NJ. Priority-based task scheduling method over cloudlet using a swarm intelligence algorithm. Clust Comput. 2011;23(2):663–71. doi:10.1007/s10586-019-02951-z. [Google Scholar] [CrossRef]

27. Ijaz S, Munir EU, Ahmad SG, Rafique MM, Rana OF. Energy-makespan optimization of workflow scheduling in fog-cloud computing. Computing. 2021;103(9):2033–59. doi:10.1007/s00607-021-00930-0. [Google Scholar] [CrossRef]

28. Richa, Kurkreja D. Optimizing task scheduling for energy aware networks. In: 2024 14th International Conference on Cloud Computing, Data Science & Engineering (Confluence); 2024 Jan 18–19; Noida, India: IEEE; 2024. p. 297–302. doi:10.1109/Confluence60223.2024.10463370 [Google Scholar] [CrossRef]

29. Gowri V, Baranidharan B. Multi objective hybrid load balancing based optimization algorithm for improving fog computing performance. 2023. doi:10.21203/rs.3.rs-1851406/v1. [Google Scholar] [CrossRef]

30. Mangalampalli S, Swain SK, Mangalampalli VK. Prioritized energy efficient task scheduling algorithm in cloud computing using whale optimization algorithm. Wirel Pers Commun. 2022;126(3):2231–47. doi:10.1007/s11277-021-09018-6. [Google Scholar] [CrossRef]

31. Bitam S, Zeadally S, Mellouk A. Fog computing job scheduling optimization based on bees swarm. Enterp Inf Syst. 2018;12(4):373–97. doi:10.1080/17517575.2017.1304579. [Google Scholar] [CrossRef]

32. Subramoney D, Nyirenda CN. Multi-swarm PSO algorithm for static workflow scheduling in cloud-fog environments. IEEE Access. 2022;10:117199–214. doi:10.1109/ACCESS.2022.3220239. [Google Scholar] [CrossRef]

33. Ghafari R, Mansouri N. An efficient task scheduling in fog computing using improved artificial hummingbird algorithm. J Comput Sci. 2023;74:102152. doi:10.1016/j.jocs.2023.102152. [Google Scholar] [CrossRef]

34. Jafari V, Rezvani MH. Joint optimization of energy consumption and time delay in IoT-fog-cloud computing environments using NSGA-II metaheuristic algorithm. J Ambient Intell Humaniz Comput. 2023;14(3):1675–98. doi:10.1007/s12652-021-03388-2. [Google Scholar] [CrossRef]

35. Apat HK, Sahoo B, Goswami V, Barik RK. A hybrid meta-heuristic algorithm for multi-objective IoT service placement in fog computing environments. Decis Anal J. 2024;10(1):100379. doi:10.1016/j.dajour.2023.100379. [Google Scholar] [CrossRef]

36. Khaledian N, Khamforoosh K, Azizi S, Maihami V. IKH-EFT: an improved method of workflow scheduling using the krill herd algorithm in the fog-cloud environment. Sustain Comput Inform Syst. 2023;37(4):100834. doi:10.1016/j.suscom.2022.100834. [Google Scholar] [CrossRef]

37. Khan IR, Sangari MS, Shukla PK, Aleryani A, Alqahtani O, Alasiry A, et al. An automatic-segmentation- and hyper-parameter-optimization-based artificial rabbits algorithm for leaf disease classification. Biomimetics. 2023;8(5):438. doi:10.3390/biomimetics8050438. [Google Scholar] [PubMed] [CrossRef]

38. Barut C, Yildirim G, Tatar Y. An intelligent and interpretable rule-based metaheuristic approach to task scheduling in cloud systems. Knowl Based Syst. 2024;284:111241. doi:10.1016/j.knosys.2023.111241. [Google Scholar] [CrossRef]

39. Wang Y, Huang L, Zhong J, Hu G. LARO: opposition-based learning boosted artificial rabbits-inspired optimization algorithm with lévy flight. Symmetry. 2022;14(11):2282. doi:10.3390/sym14112282. [Google Scholar] [CrossRef]

40. Anka F, Agaoglu N, Nematzadeh S, Torkamanian-afshar M, Gharehchopogh FS. Advances in artificial rabbits optimization: a comprehensive review. Arch Comput Meth Eng. 2024;117(1):105622. doi:10.1007/s11831-024-10202-7. [Google Scholar] [CrossRef]

41. Kiani F, Nematzadeh S, Anka FA, Findikli MA. Chaotic sand cat swarm optimization. Mathematics. 2023;11(10):2340. doi:10.3390/math11102340. [Google Scholar] [CrossRef]

42. Özbay FA, Özbay E, Gharehchopogh FS. An improved artificial rabbits optimization algorithm with chaotic local search and opposition-based learning for engineering problems and its applications in breast cancer problem. Comput Model Eng Sci. 2024;141(2):1067–110. doi:10.32604/cmes.2024.054334. [Google Scholar] [CrossRef]

43. Nematzadeh S, Kiani F, Torkamanian-Afshar M, Aydin N. Tuning hyperparameters of machine learning algorithms and deep neural networks using metaheuristics: a bioinformatics study on biomedical and biological cases. Comput Biol Chem. 2022;97(3):107619. doi:10.1016/j.compbiolchem.2021.107619. [Google Scholar] [PubMed] [CrossRef]

44. Hussain A, Aleem M. GoCJ: google cloud jobs dataset for distributed and cloud computing infrastructures. Data. 2018;3(4):38. doi:10.3390/data3040038. [Google Scholar] [CrossRef]

45. Jayalakshmi P, Ramesh SS. Multi-strategy improved sand cat optimization algorithm-based workflow scheduling mechanism for heterogeneous edge computing environment. Sustain Comput Inform Syst. 2024;43(8):101014. doi:10.1016/j.suscom.2024.101014. [Google Scholar] [CrossRef]

46. Nematzadeh S, Torkamanian-Afshar M, Seyyedabbasi A, Kiani F. Maximizing coverage and maintaining connectivity in WSN and decentralized IoT: an efficient metaheuristic-based method for environment-aware node deployment. Neural Comput Appl. 2023;35(1):611–41. doi:10.1007/s00521-022-07786-1. [Google Scholar] [CrossRef]

47. Houssein EH, Gad AG, Wazery YM, Suganthan PN. Task scheduling in cloud computing based on meta-heuristics: review, taxonomy, open challenges, and future trends. Swarm Evol Comput. 2021;62(3):100841. doi:10.1016/j.swevo.2021.100841. [Google Scholar] [CrossRef]

48. Huang X, Xie M, An D, Su S, Zhang Z. Task scheduling in cloud computing based on grey wolf optimization with a new encoding mechanism. Parallel Comput. 2024;122(3):103111. doi:10.1016/j.parco.2024.103111. [Google Scholar] [CrossRef]

49. Garmendia-Orbegozo A, Nunez-Gonzalez JD, Anton MA. Task offloading in edge computing using GNNs and DQN. Comput Model Eng Sci. 2024;139(3):2649–71. doi:10.32604/cmes.2024.045912. [Google Scholar] [CrossRef]

50. Zhang Q, Geng S, Cai X. Survey on task scheduling optimization strategy under multi-cloud environment. Comput Model Eng Sci. 2023;135(3):1863–900. doi:10.32604/cmes.2023.022287. [Google Scholar] [CrossRef]

51. Mahdizadeh M, Montazerolghaem A, Jamshidi K. Task scheduling and load balancing in SDN-based cloud computing: a review of relevant research. J Eng Res. 2024;22(12):14718. doi:10.1016/j.jer.2024.11.002. [Google Scholar] [CrossRef]

52. Seifhosseini S, Hosseini Shirvani M, Ramzanpoor Y. Multi-objective cost-aware bag-of-tasks scheduling optimization model for IoT applications running on heterogeneous fog environment. Comput Netw. 2024;240(10):110161. doi:10.1016/j.comnet.2023.110161. [Google Scholar] [CrossRef]