Progress on Multi-Field Coupling Simulation Methods in Deep Strata Rock Breaking Analysis

1  Introduction

The process of rock fracture in deep strata is characterized by intricate interactions across multiple physical fields, encompassing mechanical, thermal and hydraulic forces. This is exemplified in Fig. 1, which draws upon the findings of references [1–3]. These physical fields collectively influence the failure mechanisms and mechanical behavior of rocks under extreme high-pressure and high-temperature conditions, as evidenced by studies [4,5]. The advancement of deep geoengineering projects, including energy extraction [6], geological engineering [7], nuclear waste storage [8], and CO₂ geological sequestration [9], has highlighted the growing need for in-depth research into the failure mechanisms of deep rock masses. However, the complexity of the deep strata environment and the nonlinear effects of multi-field coupling present significant challenges to fully revealing the underlying physical mechanisms through experiments or theoretical analyses alone.

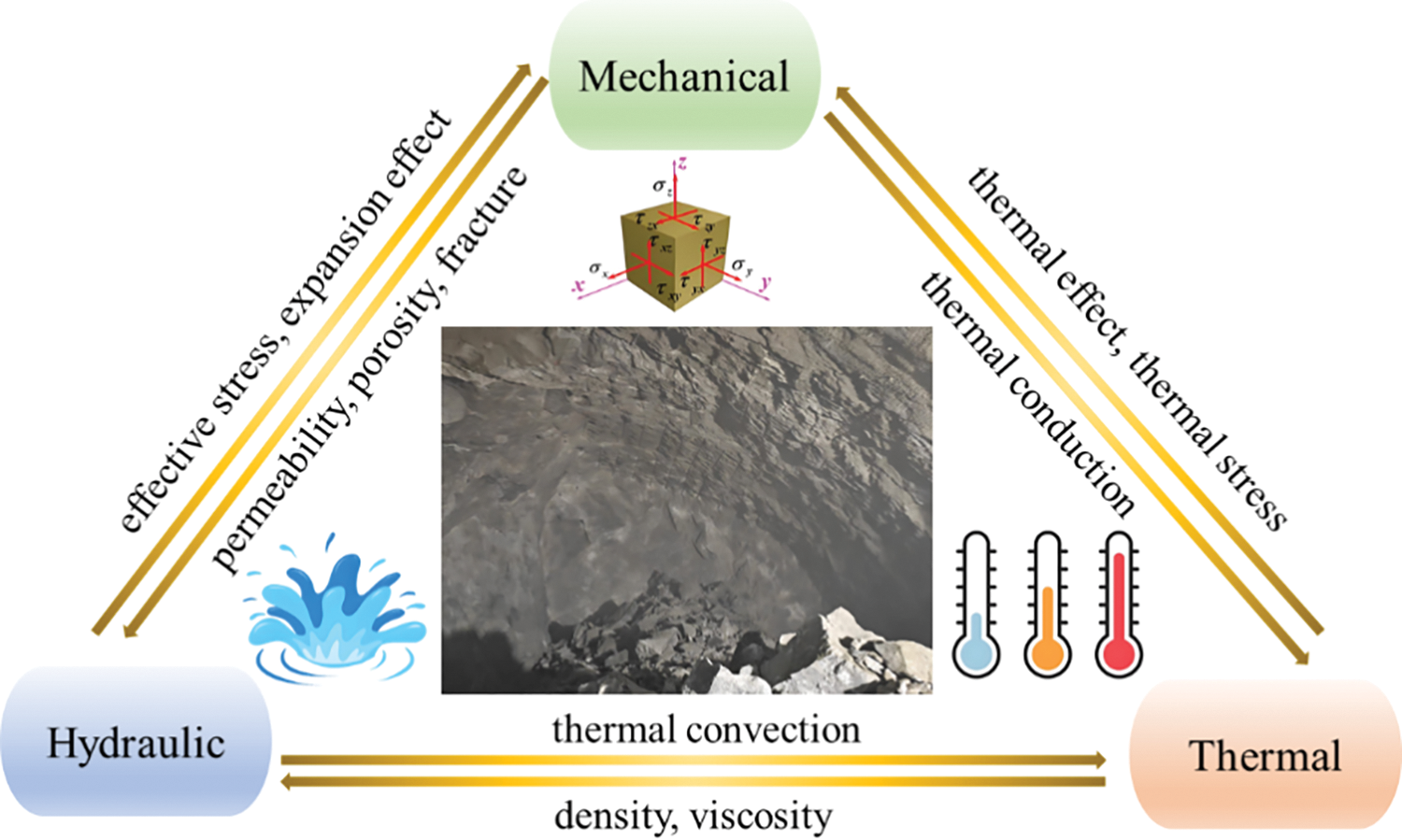
Figure 1: Multi-field coupling mechanism of underground rock breaking

In recent years, multi-field coupling simulation technology has emerged as a vital tool for addressing rock fracturing challenges in deep strata. Through numerical simulation methods, researchers can model the initiation and propagation of rock fractures and the evolution of seepage pathways under the interaction of multiple physical fields. This facilitates the prediction of mechanical and seepage behavior during the fracturing process, offering valuable scientific support for engineering design and optimization. Currently, multi-field coupling simulations can be broadly categorized into three approaches: continuum-based methods, such as the Finite Element Method (FEM) [10]; discontinued-based methods, including the Discrete Element Method (DEM) [11], Computational Fluid Dynamics (CFD) [12], and Smoothed Particle Hydrodynamics (SPH) [13]; and coupled continuum-discontinuum methods [14,15]. The primary coupling strategies include fully coupled and iterative coupling methods [16]. Fully coupled approaches integrate the governing equations of multiple physical fields into a unified global system for simultaneous solving, while iterative coupling methods solve each physical field separately and achieve coupling through information exchange. Leveraging these simulation techniques, researchers have conducted comprehensive analyses of rock masses under multi-field coupling [17]. These studies have elucidated the damage evolution mechanisms of engineering rock masses [18], deepened the understanding of rock failure processes [19,20], and effectively guided geotechnical engineering projects. This progress has significantly advanced both the theoretical and practical aspects of geotechnical engineering. Nonetheless, the deformation and failure behaviors of rock masses under multi-field coupling across varying spatial and temporal scales remain exceedingly complex. Existing research faces challenges in fully accounting for the spatiotemporal scale effects of multi-field coupling and addressing the discontinuities inherent in the rock fracturing process.

This review provides an overview of the current state of research on multi-field coupling in rock masses, focusing on coupling mechanisms, research methods, and rock damage characteristics. It systematically analyzes the scale effects and spatiotemporal discontinuities inherent in multi-field coupling and provides a detailed explanation of methods for characterizing rock fracturing. Finally, the review summarizes the key scientific challenges and future research directions in the study of multi-scale discontinuous fracturing of rock masses under multi-field coupling.

2  Mathematical Models in Multi-Field Coupling Simulations

2.1 Fundamental Governing Equations

In rock fracturing multi-field coupling analysis, the governing equations include the stress equilibrium equation, mass conservation equation, energy conservation equation, and constitutive relations for rocks. For rock-like materials, the stress equilibrium equation is typically based on the poroelastic theory of multi-phase flow in porous media [21,22]. The flow of fluids within rock masses generally adheres to Darcy’s law. However, for low-speed non-Darcian flow and high-speed non-Darcian flow, the linear relationship between seepage velocity and hydraulic gradient described by Darcy’s law no longer holds [23]. In cases of high-speed non-Darcian flow within fractures, Forchheimer’s law can be used for description [24]. The energy conservation equations in multi-field coupling analysis encompass both the solid energy conservation equation and the fluid energy conservation equation, which describe the transfer of heat within the rock mass and fluid flow, respectively.

Rock masses are inherently complex and heterogeneous materials. In long-term engineering computations, traditional strength calculation theories based on material mechanics and structural mechanics are commonly used. These approaches typically assume that complex rock masses are homogeneous, continuous, and isotropic materials [25], which contradicts the reality of naturally fractured rock masses with inherent defects. Rock strength theories can be broadly categorized into theoretical strength theories and empirical strength theories. Theoretical strength theories are derived from the principles of material mechanics and elasticity theory. They include four classical strength theories: the maximum normal stress theory, maximum shear stress theory, maximum normal strain theory, and octahedral shear stress theory, as well as the Mohr–Coulomb strength theory, Griffith and modified Griffith theories, and the twin shear strength theory [26]. Empirical strength theories, on the other hand, are derived from rock mechanics experiments and are used to approximate the rock failure process. Notable examples include the Hoek–Brown empirical strength criterion [27].

In the field of rock fracturing analysis, the construction of a mathematical model to represent the mechanical behavior of fractures formed after rock failure represents a significant challenge. The mechanical properties of these fractures are markedly distinct from those of the rock matrix. The mechanical parameters and permeability of fractures are subject to dynamic change in response to the application of normal load to the fracture walls. This necessitates the utilization of a fracture compliance matrix to establish the relationship between displacements on the fracture walls and the stress in the rock, thereby enabling the update of parameters such as fracture porosity and permeability [28]. Tang et al. [29] put forth a theoretical model for forecasting the closure characteristics of rock joints, which effectively encapsulates the behavior of joint closure. In a study conducted by Nguyen et al. [30], a thermo–mechanical coupled joint mathematical model was developed based on macroscopic formulations within an elasto–plastic framework. This model was designed to describe the deformation process of natural fractures under normal loading.

2.2 Coupling Methods

In multi-field coupling simulations, coupling methods involve the mathematical description and numerical handling of interactions between different physical fields. Effective coupling methods can significantly enhance simulation accuracy and computational efficiency. Based on the coupling strength and the characteristics of the coupled fields (as shown in Fig. 2), coupling methods can be classified into the following five categories:

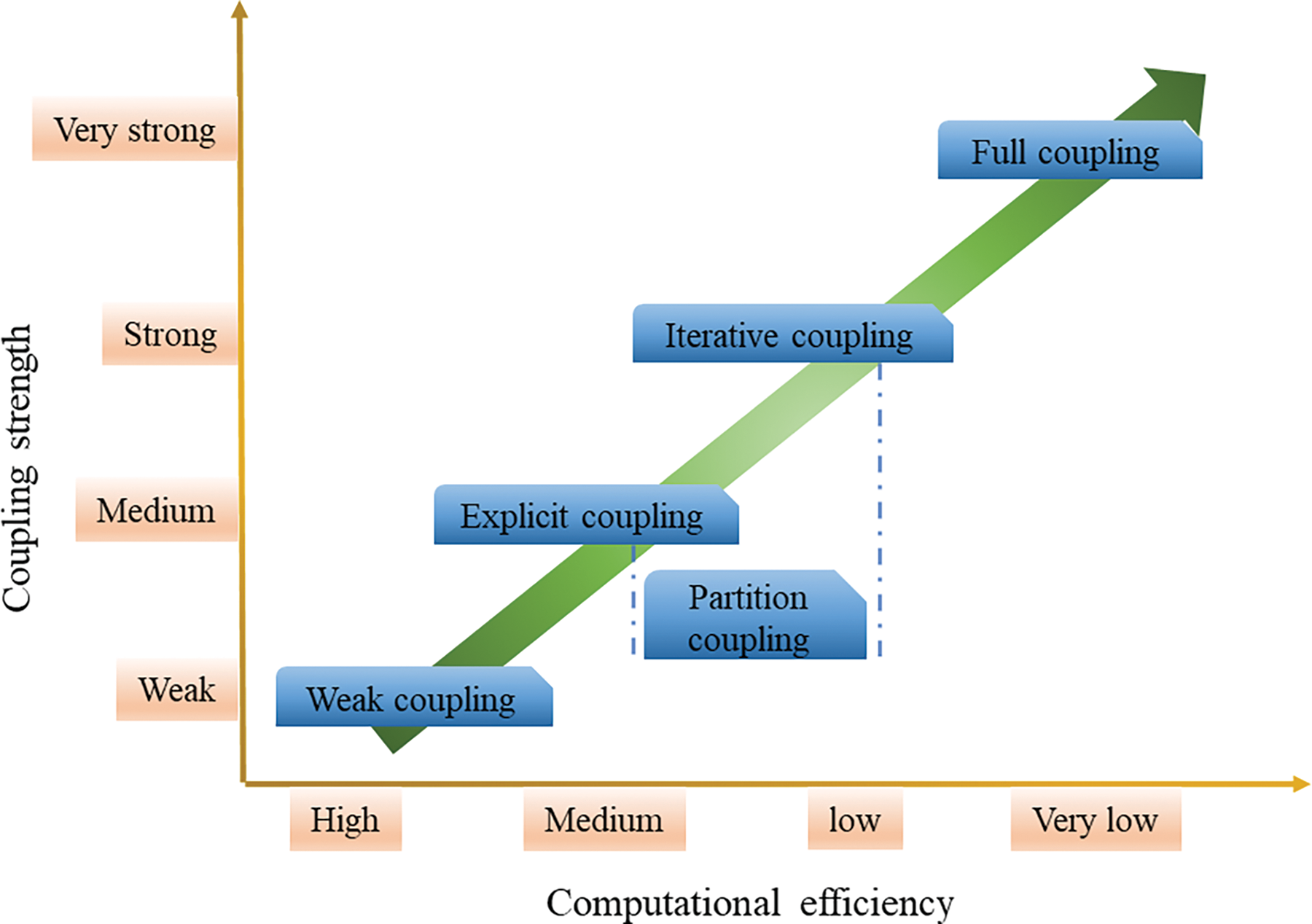
Figure 2: Coupling strength and coupling efficiency of various coupling methods

Full coupled models integrate the governing equations of multiple physical fields into a single global system for solving [31,32]. In this approach, the interactions between different fields are expressed through a unified mathematical model. All the equations are solved together, allowing for the direct capture of strong coupling effects between the fields. Fully coupled models can accurately describe the intense interactions between different physical fields, offer good numerical stability, and are suitable for highly coupled systems. The real-time interaction of multiple fields is solved simultaneously, enabling the simulation results to more accurately reflect the actual trends and coupling effects of the physical fields. This method can capture various nonlinear behaviors, such as crack propagation, fluid migration, and temperature gradients. However, it is important to note that fully coupled models are highly complex, computationally expensive, and numerically challenging, especially when dealing with large-scale problems, which can lead to significant computational burdens.

Iterative coupling involves solving different physical fields separately, with each field having its own governing equations and numerical solution process. However, coupling between the fields is achieved through information exchange over a set time step or iteration cycle [33]. In iterative coupling, the solutions of each physical field are adjusted through multiple iterations within each time step until a coupling equilibrium between the fields is reached. For thermo–hydro–mechanical (THM) coupling analysis, during each time step’s Newton iteration, the mass and energy conservation equations are solved implicitly first. The calculated average pore pressure is then passed to the stress equilibrium equation to solve for rock deformation. Based on the degree of deformation, key physical parameters such as porosity and permeability are updated, and the next iteration cycle begins. The mass conservation equation, energy conservation equation, and stress equilibrium equation are computed sequentially until convergence is achieved, and the process proceeds to the next time step. Compared to the fully coupled method, iterative coupling significantly improves computational efficiency.

Compared to iterative coupling, the information transfer in explicit coupling analysis is further reduced [32,34]. In each time step, information is only transferred once from the seepage field and temperature field to the stress field, meaning that only one calculation of the stress equilibrium equation and parameter update is performed per time step. However, the information from the stress field is not fed back into the seepage and temperature fields. Explicit coupling is a method with a lower degree of coupling, resulting in reduced computational accuracy. However, it offers high computational efficiency and good convergence, making it suitable for large-scale simulations, complex geological conditions, and mechanical modeling of rock mass with intricate constitutive models.

The weak coupling method further reduces the frequency of stress equilibrium equation calculations based on the explicit method [35,36]. In each time step, the seepage-temperature field and the stress field are calculated independently, and the stress equilibrium equation and parameter updates are performed only after several time steps, with the process iterating until completion. Compared to explicit coupling, this method results in lower computational accuracy but offers faster computation speed, good convergence, and a wide range of applicability. It can couple different types of programs, but weak coupling may lead to the accumulation of coupling errors and is unable to capture complex interactions.

In addition, when multi-field coupling simulations involve the coupling of two or more fields, partition coupling methods can be used to improve computational efficiency [37]. Wu et al. [38] employed an explicit partition scheme to couple the THM equations. The modular nature of the partition scheme provides flexible and efficient code management. During the analysis steps, hydraulic and thermal conduction calculations are performed simultaneously, with multiple mechanical calculations carried out to ensure quasi-static conditions. In this partition coupling method, the hydraulic and mechanical processes are mutually influential (fully coupled), while the coupling between the thermal and mechanical processes is unidirectional (temperature changes may induce thermal stresses, but the influence of mechanical changes on thermal conduction can be negligible in certain cases). Hydraulic and thermal conduction processes are partially coupled. Therefore, compared to other coupling methods, partition coupling allows for a flexible choice of coupling strategies based on the characteristics of different analysis objects, thereby improving both computational efficiency and accuracy.

3  The Scale Characteristics of Multi-Field Coupling Simulations in Rock-Breaking

3.1 Spatial Scale

The physical phenomena and interaction mechanisms within rock masses often change significantly with spatial scale. The characteristics of stress, fractures, seepage paths, and other factors vary at different scales. The coupling models at different spatial scales have their analytical characteristics, as shown in Table 1 Therefore, a reasonable division of scales can improve simulation accuracy and reduce computational complexity. Based on the main research objectives, as shown in Fig. 3, spatial scales can be classified into the following categories:

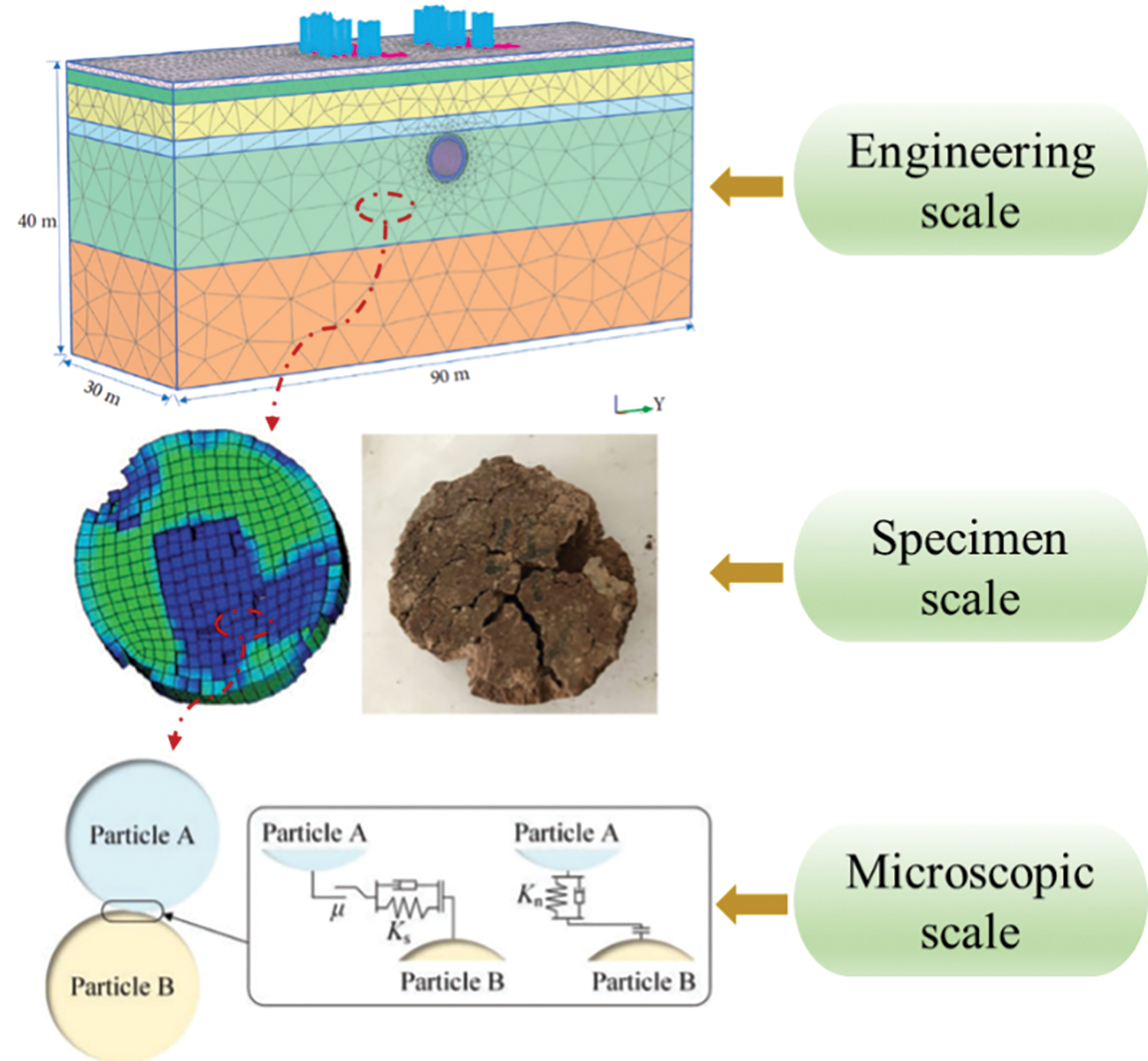
Figure 3: Spatial scale division in multi-field coupled simulation for deep formation rock fracture analysis

(1) Engineering scale

The analysis of rock fracture characteristics under multi-field coupling is essential for ensuring the safety and smooth operation of engineering projects. All multi-field coupling analyses must consider the overall geological environment and engineering context. Therefore, the damage issues of the rock mass at the engineering scale should be clarified first. The engineering scale involves the overall behavior of the entire project or research area, typically ranging from meters to hundreds of meters, focusing on the global characteristics and responses of the rock mass. The macro scale plays an important role in rock-breaking multi-field coupling simulations and directly affects the design and optimization of the project. By gaining a deeper understanding of the macro-scale characteristics and influencing factors, researchers can more effectively predict rock-breaking behavior and flow characteristics, promoting the sustainability of resource development and environmental protection.

The simulation models at the engineering scale are relatively large, usually employing continuum media simulation methods to ensure computational efficiency and simulation accuracy [39], as shown in Fig. 4. It is not feasible to consider all characteristics of the engineering rock mass, so simplifications must be made in the models [40–43]. Small-scale fractures and defects in the rock mass are equivalently treated, and mechanical responses follow the small deformation elastoplastic theory model. The internal temperature of the rock mass follows Fourier’s law, and the fluid flow is governed by Darcy’s law, among other simplifications. Wang et al. [44] constructed a thermo-hydro-mechanical analysis model at the engineering scale based on iterative coupling and Flac3D. Kang et al. [45] analyzed the thermo-hydro-mechanical coupling process of deep tunnels passing through composite strata and dense fault zones under high pressure, high temperature, and high seepage pressure conditions.

Figure 4: Analysis of engineering scale coupling model (a) Simplified model; (b) Response of stress, temperature, and water pressure (Reprinted from Ref. [39] with permission from Springer)

(2) Specimen scale

The vast range of factors involved in engineering problems presents significant challenges for conducting rigorous and precise scientific research. Therefore, to better study the influence of a few dominant factors, idealized laboratory model experiments can be conducted to address the main issues. The specimen scale lies between the micro and macro scales. It can reflect the true physical and mechanical properties of materials and capture the effects of the interaction between different physical fields on material behavior. At this spatial scale, researchers typically simulate small-scale models and test specimens [46,47] and compare them with experimental results to verify the applicability and accuracy of the simulation methods [48], as shown in Fig. 5. Since the specimen scale can both reflect the local characteristics of microstructures and the overall mechanical properties, it is the most commonly used scale for simulation methods. Xian et al. [49] used a coupled fluid-solid model based on Particle Flow Code in 3 Dimensions-Computational Fluid Dynamics (PFC3D-CFD) to simulate the scouring and water inrush process of tunnels connected to fracture zones, and the morphology of water inrush under increasing water pressure. They comprehensively analyzed the migration of filling particles, the movement trajectory of individual particles, particle mass loss, particle contact relationships, porosity, and permeability. Wang et al. [50] proposed a heterogeneous multi-field coupling modeling method that can better simulate irregularly shaped natural fractures.

Figure 5: Analysis of specimen scale coupling model. (a) Specimen scale model; (b) Simulation results of fracture geometry in rocks with various injected temperature differences (Reprinted from Ref. [48] with permission from Springer)

(3) Microscopic scale

The microscopic scale refers to the detailed description and simulation of materials or structures at the nanoscale to the microscale to study the interactions between different physical fields and their effects on the mechanical, thermal, and physical properties of materials. This analysis primarily reveals the local behavior of materials, such as crack propagation, pore flow, and particle interactions, as shown in Fig. 6, thus helping to predict their overall mechanical performance at larger scales.

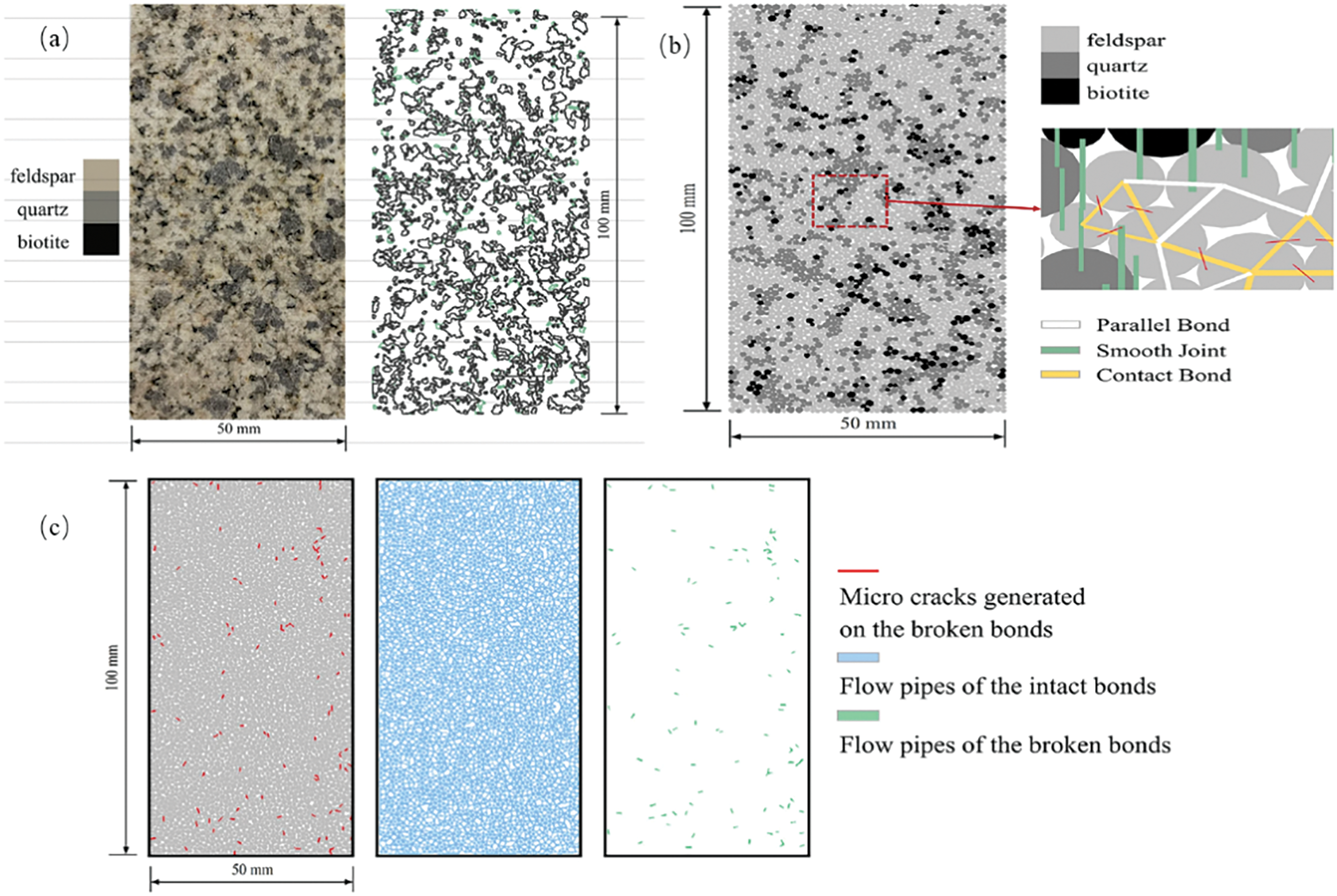
Figure 6: Microstructure modeling process. (a) The physical properties of the meso-structure of granite in the experiment; (b) The meso-structurebased model of the granite; (c) Distribution of different sets of flow pipes in the granite specimen specimen (Reprinted from Ref. [53] with permission from Springer)

In simulating the microscopic scale, the FEM primarily relies on high-precision meshing [51], solving the physical fields efficiently within each element to accurately describe the local response of materials. FEM is well-suited for handling complex boundary conditions, especially in heterogeneous materials or porous media with multi-field coupling simulations, as it can effectively capture the changes in local fields. However, the simulation accuracy of FEM highly depends on the mesh refinement. Coarse meshes may fail to capture fine microscopic structural features, while overly refined meshes significantly increase computational effort.

Particles are the fundamental units that make up materials such as rocks and soils at the microscopic scale. The DEM simulates the interactions between particles and analyzes their behaviors under force, temperature, and fluid effects, including movement, sliding, and rotation. DEM can capture the initiation and propagation of cracks between particles, making it especially useful for simulating the expansion of micro-cracks under the combined action of mechanical, thermal, and fluid fields and their impact on macroscopic strength [52,53]. However, the particle models in DEM often require idealization, which may cause deviations from actual conditions in some complex materials. Additionally, as the number of particles increases, the computational load in DEM grows exponentially, particularly in three-dimensional simulations, resulting in high computational resource demands.

Molecular dynamics (MD) is an advanced computational simulation method for analyzing the physical movements of atoms and molecules. It has been widely applied in materials science [54] and allows researchers to build simulation models to compute the interactions between particles. Through MD simulations, the movement of particles, lattice changes, and the propagation of microscopic defects such as dislocations can be observed [55,56]. This method is useful for analyzing the mechanical properties and damage mechanisms of various materials. In recent years, it has expanded from the medical field to mineral materials research, effectively solving some scientific problems in rock mechanics and mining engineering. It plays an important role in exploring the wettability of coal and clay minerals, gas flow in micropores, and geothermal energy extraction [57,58].

The cellular automaton (CA) method is a discrete model used to simulate local interactions and spatiotemporal evolution processes in complex systems. CA updates local units in both time and space by defining simple rules, thereby simulating the overall behavior and evolution of the system [59]. Due to its simplicity and ability to model complex phenomena, CA can be used to simulate the initiation and propagation of cracks. By defining rules for crack propagation, CA can study the evolution behavior of cracks under different stress states [60,61]. However, to make CA more realistic, the rule settings may become complex with numerous parameters. Additionally, CA is a highly abstract model that sometimes struggles to reflect real physical phenomena, particularly when the system exhibits complex nonlinear behavior.

The phase field method (PFM) is a continuum medium model widely applied to handle issues such as crack propagation, phase transitions, and grain growth in materials, especially for studying the initiation and propagation of cracks at the microscopic scale [62]. PFM describes the evolution of phase interfaces by defining continuous phase variables, avoiding the explicit crack modeling problems found in traditional fracture mechanics [63]. The phase field method can accurately simulate the propagation paths of micro-cracks under multi-field coupling, making it especially suitable for fracture problems in thermo-mechanical or fluid-mechanical coupling. However, the definition and evolution of different phase variables require complex parameterization based on specific issues, which can increase the model’s complexity and uncertainty.

3.2 Time Scale

Time scale refers to the characteristic time of the response and evolution of rock materials under different physical field interactions during simulations. In multi-field coupling simulations for rock breaking, the time scale problem involves the temporal evolution of interactions between different physical fields. Proper division and handling of time scales are crucial in multi-field coupling simulations, as they directly affect the accuracy and computational efficiency of the simulations. The coupling models of different time scales have their own analysis characteristics, as shown in Table 2. During the rock breaking process, the evolution rates of different physical fields, such as the mechanical field, temperature field, and fluid field, vary, and correspondingly, their time scales differ, as shown in Fig. 7. The coupled fields transition from non-equilibrium to equilibrium, generating a relaxation process. Each coupled field has its own specific characteristic time under certain conditions. Through reasonable modeling and analysis, these coupled dynamic processes can be coordinated and balanced, reflecting real-world phenomena correctly over different time windows.

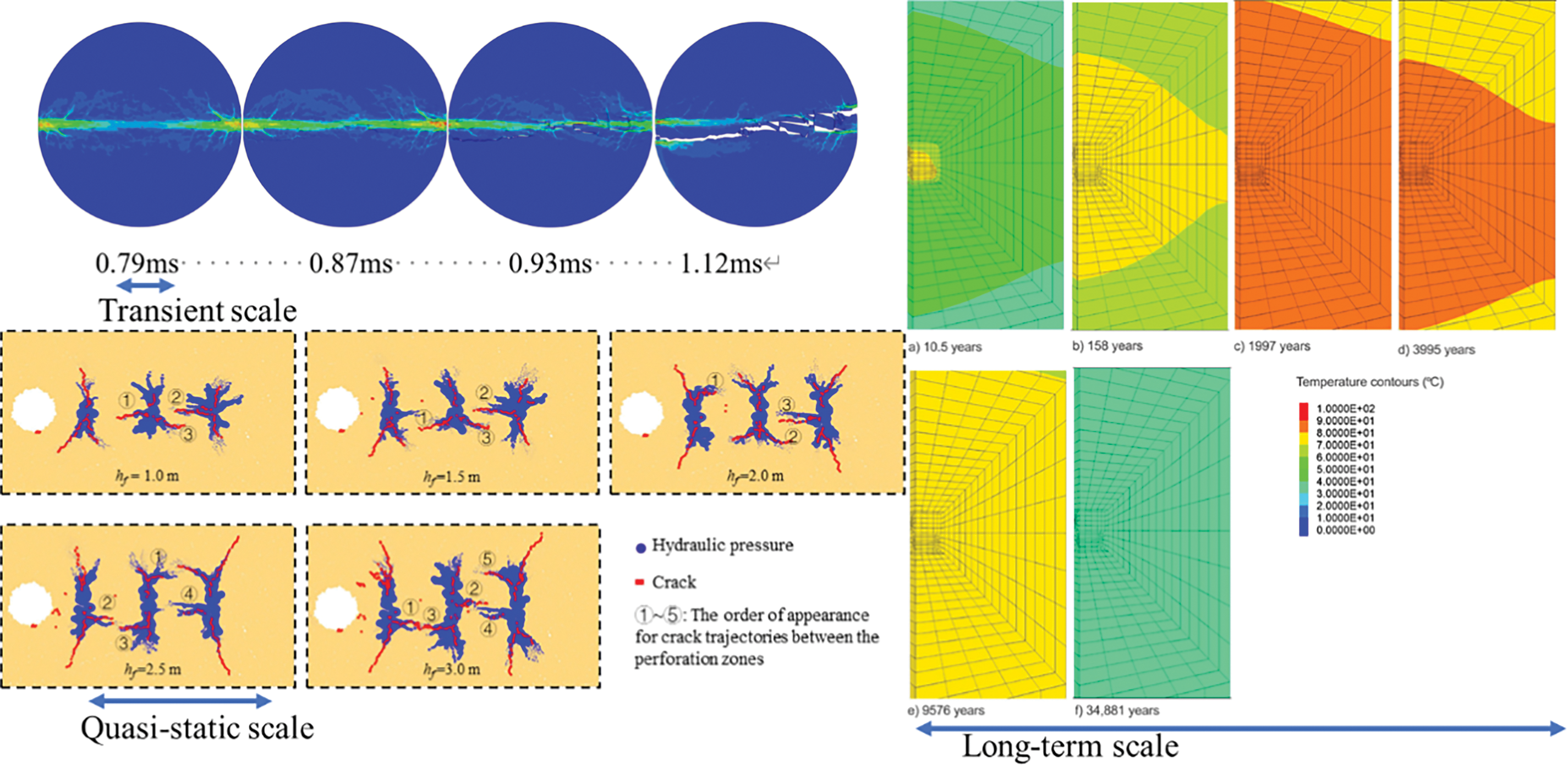
Figure 7: Time scale division in multi-field coupling simulation for rock breaking in deep strata

(1) Transient scale

In multi-field coupling simulations, the transient scale refers to processes in which physical phenomena change rapidly over time, typically involving intense dynamic responses over a short duration. Transient scale simulations are critical in engineering applications such as rock breaking, blasting, and stress wave propagation, as they can capture the sudden responses of rock masses under high stress and energy states. In stress fields, the time scale for blasting and impact-induced rock breaking typically ranges from milliseconds to seconds, requiring extremely small time steps (microseconds) to capture transient stress wave propagation and crack extension [64,65], as shown in Fig. 8.

Figure 8: Comparison of failure patterns of samples under different impact pressures

Simulations at the transient scale often employ explicit solution methods. The explicit method is suitable for simulating rapidly changing mechanical fields, such as seismic wave propagation, blasting, and impact problems [66]. Since the explicit method does not require iterative solutions, it can handle small time steps, but the computational load is relatively large [67], requiring substantial computational resources. To improve computational speed, parallel computing and GPU acceleration are often used to reduce computation time.

(2) Quasi-static scale

For hydraulic and temperature fields, fluid permeability, pressure, and heat diffusion processes are generally slower, and physical state changes take a longer time to manifest. The quasi-static time scale refers to the process where the changes in the system occur over a relatively long period, allowing the assumption that the system is in equilibrium or near-equilibrium at each time step [68–71]. The quasi-static scale lies between the transient scale and long-term processes, and it plays an important role in multi-field coupling, as it is suitable for describing gradual changes in rock masses under small external forces, such as slow deformation, gradual groundwater seepage and diffusion, and heat transfer.

At the quasi-static scale, it is often assumed that there are no significant inertial effects, so static equilibrium equations are used to describe the stress state within the rock mass. Fluid migration and temperature distribution are typically described using steady-state flow and heat conduction equations. The implicit integration method is usually applied in quasi-static problems, which is suitable for stable solutions with larger time steps, effectively reducing computational load and maintaining numerical stability. However, the strong nonlinearity between field variables in multi-field coupling can lead to divergence during equation solving, especially in areas with large temperature and stress gradients, which may cause local numerical instability. To ensure overall convergence and result accuracy, complex parameter adjustments and numerical tuning are often necessary.

(3) Long-term scale

With the effects of different fields, rock masses experience phenomena such as creep, stress relaxation, and fatigue failure [72]. The long-term time scale focuses on the cumulative changes in the system over an extended evolution process, such as the impact of creep deformation on rock structures. During simulation, it may be necessary to consider slowly changing dynamic effects. Due to the long time span, larger time steps are typically used, but adjustments to the time step may be needed to capture certain long-term trends and critical points of gradual changes [73], as shown in Fig. 9. For such slow-varying multi-field coupling problems, implicit methods are well-suited for handling larger time steps, especially for simulations involving steady-state or quasi-steady-state problems [74].

Figure 9: Evolution of damage in the crystalline rock (Reprinted from Ref. [73] with permission from Elsevier)

In long-term scale analysis, a large number of time steps are required to simulate gradual processes. Even though the error in each time step is small, the cumulative effect over a long period can cause significant errors, potentially deviating from actual results. This error accumulation effect is particularly significant in coupled processes such as thermal-mechanical and fluid-solid interactions, affecting the accuracy of the final numerical solution. Additionally, many key parameters, such as long-term rock mass creep parameters or deep fluid parameters, are difficult to obtain through short-term experiments and often rely on long-term monitoring or accelerated laboratory experiments. This leads to high data acquisition costs and large errors, which impact the model’s accuracy.

3.3 Cross-Space Scale Methods

Cross-scale numerical simulation is an important approach to solving complex system problems, especially in rock-breaking multi-field coupling simulations, where physical phenomena at different scales interact with each other. To ensure effective connections between different scales and the overall accuracy of the simulation, the information transfer mechanism plays a core role in cross-scale numerical simulations. Information transfer enables models at different scales to be organically combined, providing more comprehensive and accurate predictions. In cross-scale simulations, information transfer is typically bottom-up (from micro to macro), and it generally includes both material property transfer and field information transfer.

Material property transfer refers to the transfer of material microstructural information (e.g., crystal structure, crystalline properties, pore and microcrack distributions) obtained from the micro scale to the macro model [75], to determine the macroscopic mechanical properties of the rock mass [76] (such as elastic modulus, strength parameters, permeability coefficient, etc.). Field information transfer involves passing the stress field, strain field, fracture field, seepage field, and temperature field calculated from the micro-scale simulation model to the macro model, in order to obtain the analysis results for the entire engineering model. Common methods of information transfer include the following, and their main advantages and disadvantages are shown in Table 3.

(1) Homogenization method

Homogenization theory derives equivalent macroscopic properties by processing the local fields of the microstructure [77], as shown in Fig. 10. Different mineral phases within the rock have different mechanical properties, which need to be obtained through microstructural observation techniques (such as scanning electron microscopy and X-ray CT). In the homogenization process, the first step is to determine the representative volume element (RVE), which includes all the key microstructural features of the rock, such as mineral grains, pores, and fractures [78–80]. Then, methods like progressive homogenization, sparse methods, Mori-Tanaka method, self-consistent methods, generalized self-consistent methods, and differential methods [81–84] are used to derive the equivalent macroscopic mechanical properties of the rock.

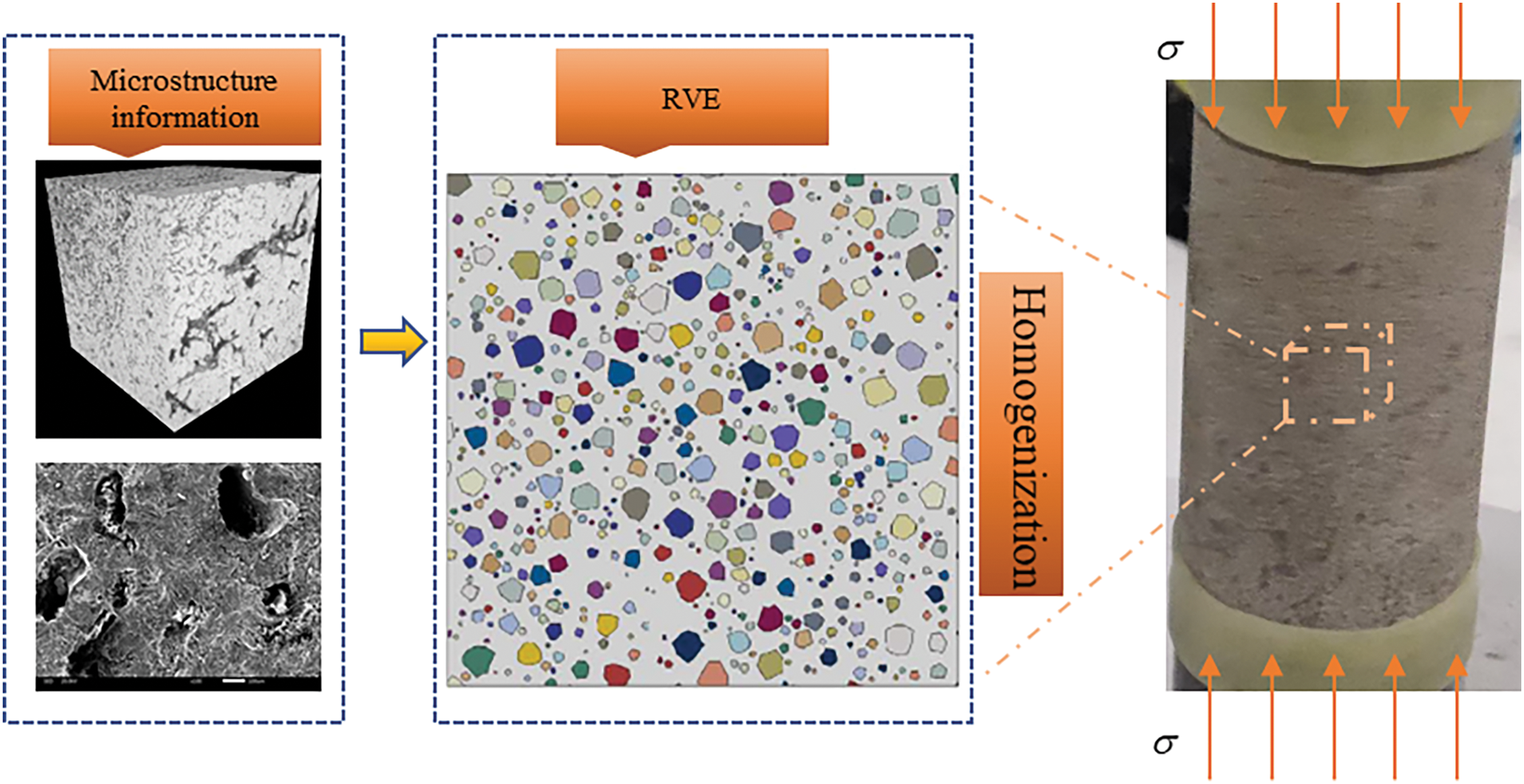
Figure 10: Homogenization method for equivalent macroscopic properties from microstructure local fields

The homogenization method simplifies microstructural information into macroscopic equivalent parameters, significantly reducing the computational effort. This is especially advantageous in simulating complex systems, as there is no need to model all the microscopic details, thereby reducing computational costs and time, and improving overall computational efficiency. At the same time, it can ensure high accuracy, as shown in Fig. 11. However, the simplifications made at the micro scale in the homogenization method may fail to capture the subtle local structural responses, particularly for complex or irregular microstructures, leading to a loss of precision. Furthermore, the effectiveness of the homogenization method depends on the assumption of homogeneity, which may not hold true for many materials such as rock or soil that have non-periodic structures, limiting the applicability of homogenization results for non-homogeneous materials.

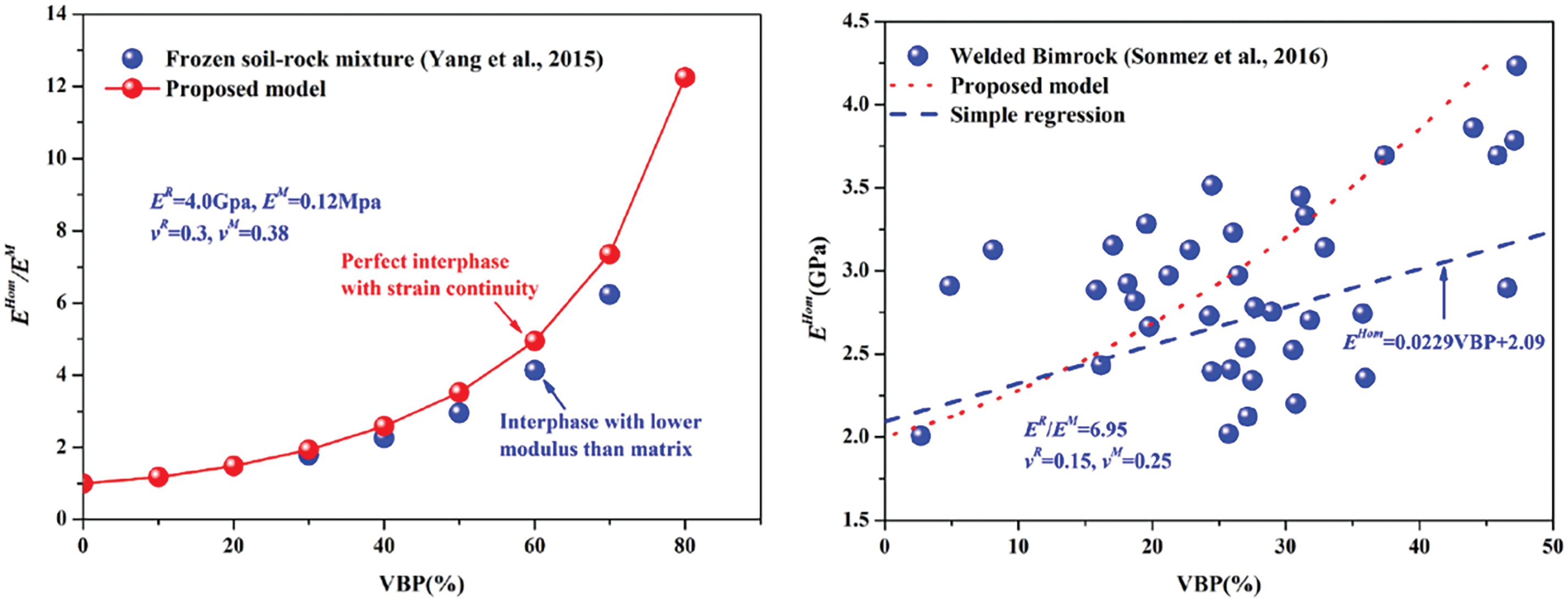
Figure 11: Comparison between prediction generated by proposed solution and experimental results (Reprinted from Ref. [77] with permission from Elsevier)

(2) Nested coupling method

The nested multi-scale coupling model embeds the micro-scale model within the macro-scale model, allowing models at different scales to run synchronously within the same computational process. The basic principle of this method is to use the macro-scale model to capture overall trends, while the micro-scale model captures local details. The two models are interdependent and provide feedback to achieve comprehensive coupling of multi-scale physical fields. In the simulation, the micro-scale model provides high-precision solutions in regions of local analysis, while the macro-scale model controls the overall boundary conditions and external loading [85], as shown in Fig. 12.

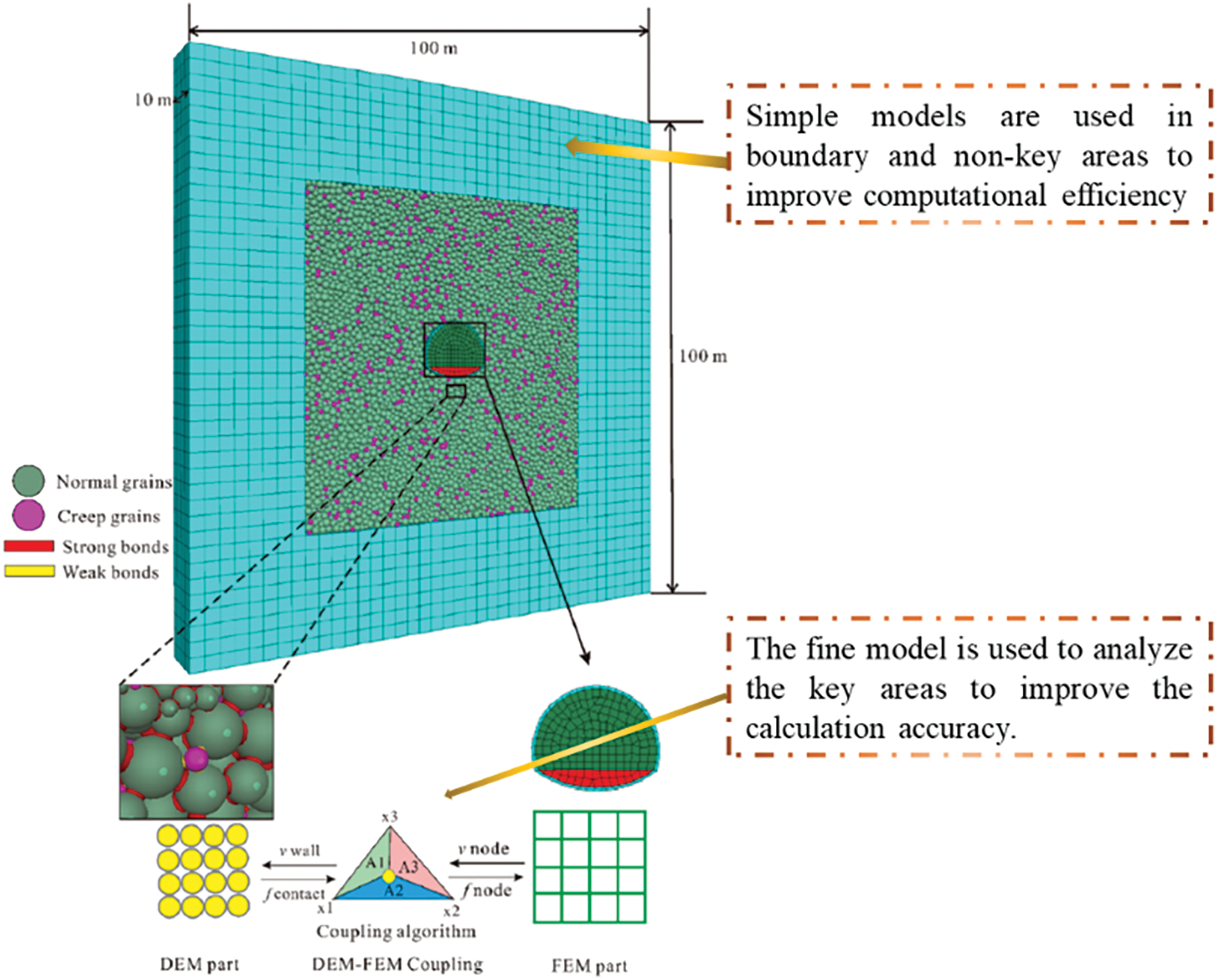
Figure 12: Nested coupling model (Reprinted from Ref. [85] with permission from Springer)

Nested coupling can flexibly adapt to various multi-field coupling scenarios, and by appropriately adjusting feedback parameters and hierarchical scales, it is suitable for the complex coupling of multiple physical fields [86,87]. The nested coupling method improves the accuracy of local details while maintaining overall computational efficiency, as shown in Fig. 13. The macro-scale model can use larger time steps, while the micro-scale model provides high-precision details, avoiding the significant computational cost required by pure micro-scale models. In the multi-field coupling analysis of rock fracture processes, the macro-scale typically describes the overall stress field, temperature field, and so on, while the micro-scale reflects details such as fracture propagation, particle sliding, and pore fluid seepage.

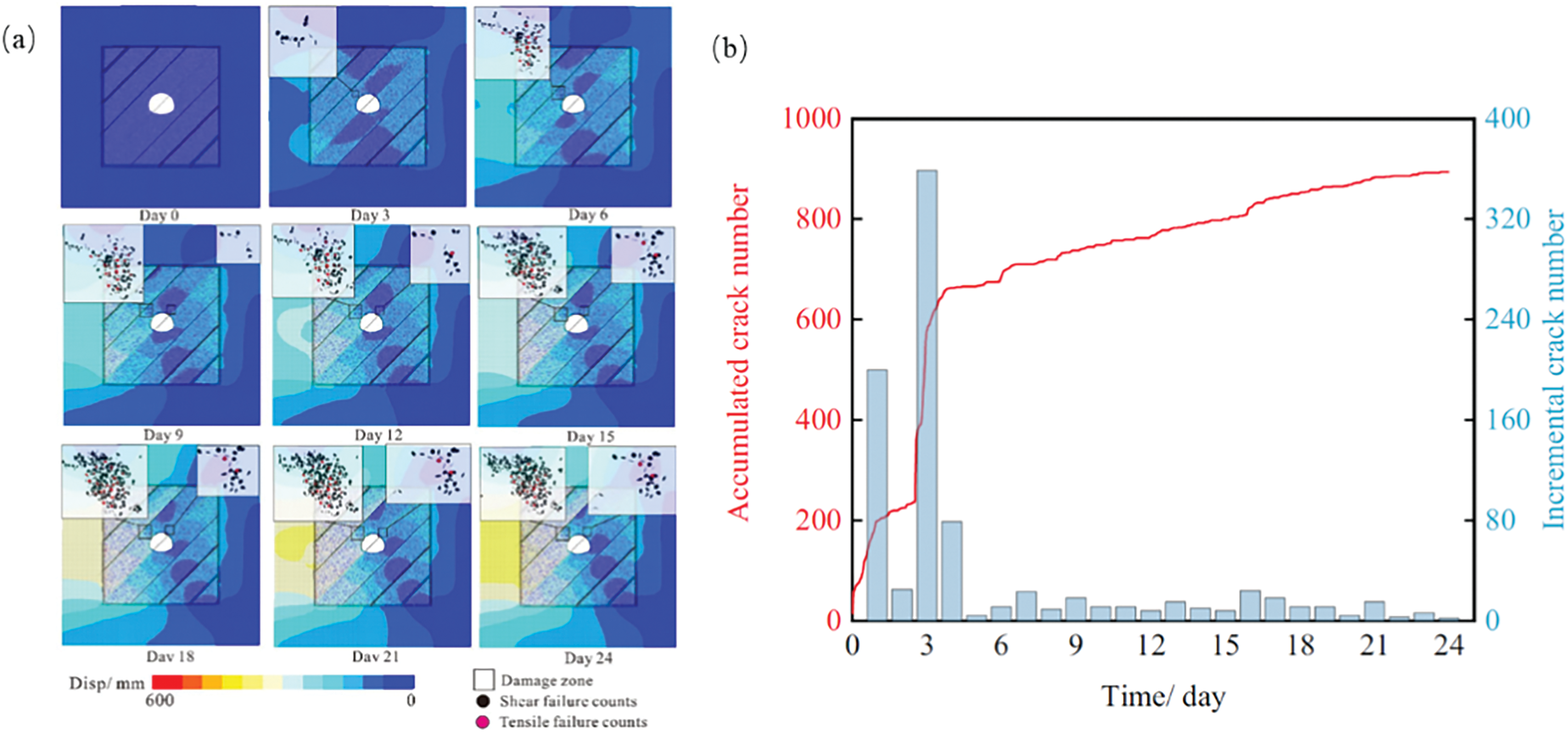
Figure 13: The soft rock tunnel surrounding rock at different phases. (a) Deformation map sand damage zones captured on different days, (b) counted crack numbers in the modeling process (Reprinted from Ref. [85] with permission from Springer)

(3) Data-driven methods

With the development of big data and machine learning (ML), data-driven approaches have begun to be utilized in information transfer for cross-scale simulations [38,88]. By analyzing large volumes of simulation data, machine learning models can learn and predict the relationships between different scales [89–91]. This approach can significantly improve the efficiency of information transfer, especially for complex nonlinear systems [92,93]. The process begins by analyzing the macro-mechanical properties of rock through extensive micro-scale models [94], then training and comparing different machine learning algorithms to select the optimal one for extensive training and validation. This allows the effective mapping of micro-scale features to macro-scale strength, as shown in Fig. 14. Machine learning encompasses many algorithms, with common ones used in multi-field coupling analysis including Support Vector Regression (SVR), Kernel Ridge Regression (KRR), Decision Tree Regression (DTR), and Gaussian Process Regression (GPR). SVR introduces an error margin to ensure model generalization while achieving precise regression, making it suitable for handling small sample, nonlinear data in complex regression problems. KRR combines ridge regression and kernel methods, enabling nonlinear regression in high-dimensional spaces. It has good generalization ability and robustness to multicollinearity. DTR recursively partitions the data space to form piecewise predictions, making it intuitive and easy to interpret. It is effective for modeling nonlinear relationships but can be prone to overfitting. GPR uses a Bayesian approach, providing predicted means and uncertainty estimates, making it well-suited for small sample, high-uncertainty nonlinear regression tasks.

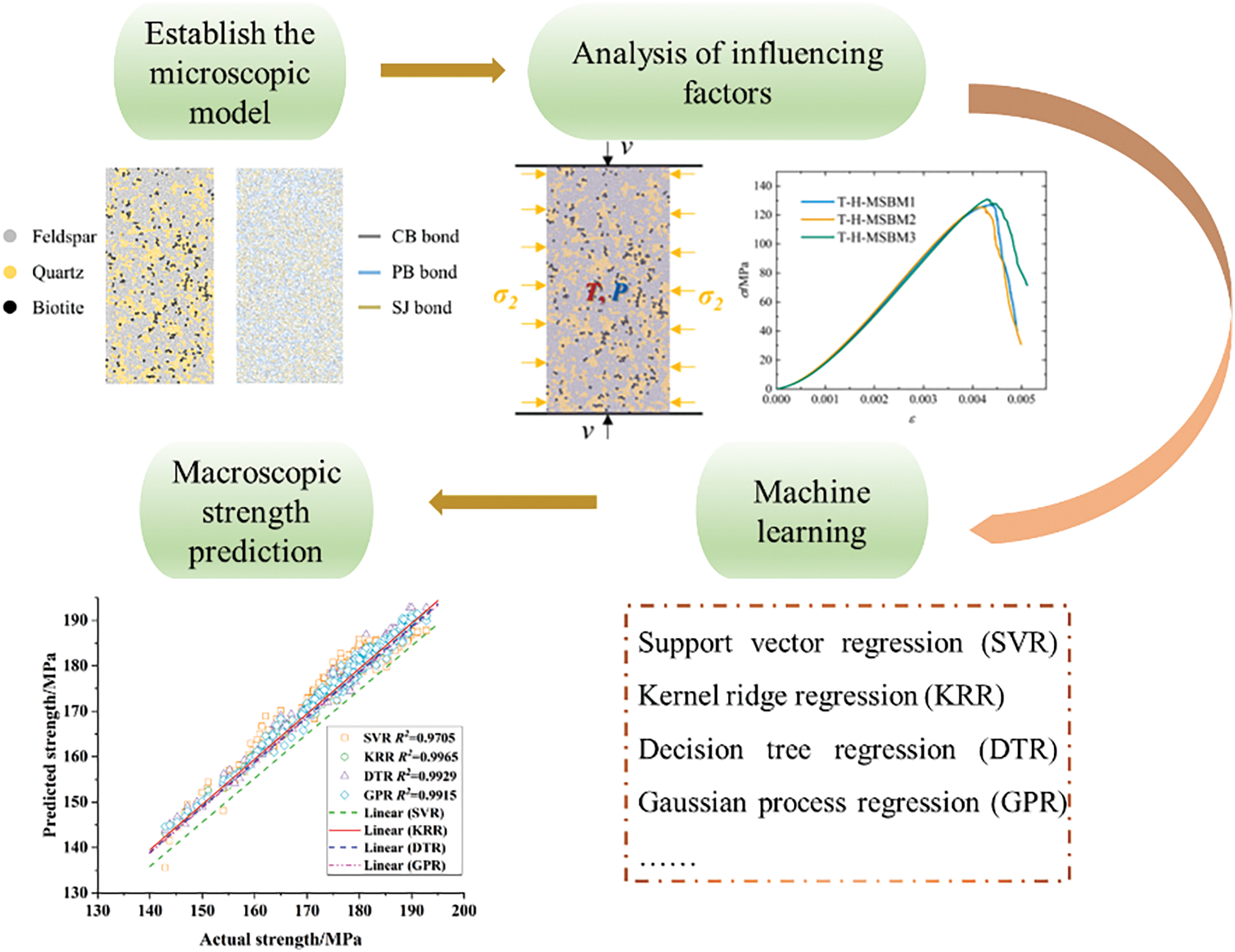
Figure 14: Machine learning approach to predicting rock macro-strength (Reprinted from Ref. [95] with permission from Elsevier)

Li et al. [95] based on our improved coupled thermo-hydro-mechanical-based DEM model, the THM responses of varying mineral grains, micro-defects, and cracks were explicitly distinguished and characterized in fractured granite. A reasonable correlation information database of rock macro-mechanical strength and THM factors was established through machine learning algorithms, and subsequently applied to large-scale engineering models, enabling information transfer from micro-scale to engineering scale, and compared the characteristics of different machine learning methods, as shown in Fig. 15. Gudala et al. [96] upgraded the THM model, incorporating dynamic characteristics of fluids, rocks, and fractures, along with machine learning (ML)-response surface model (RSM) and autoregressive integrated moving average (ARIMA) models to enhance the heat production capacity of geothermal reservoirs. Numerical investigations on a geothermal reservoir were conducted using full coupled THM simulations that integrated RSM, machine learning, and ARIMA models, aiming to provide more accurate predictions and optimize reservoir performance.

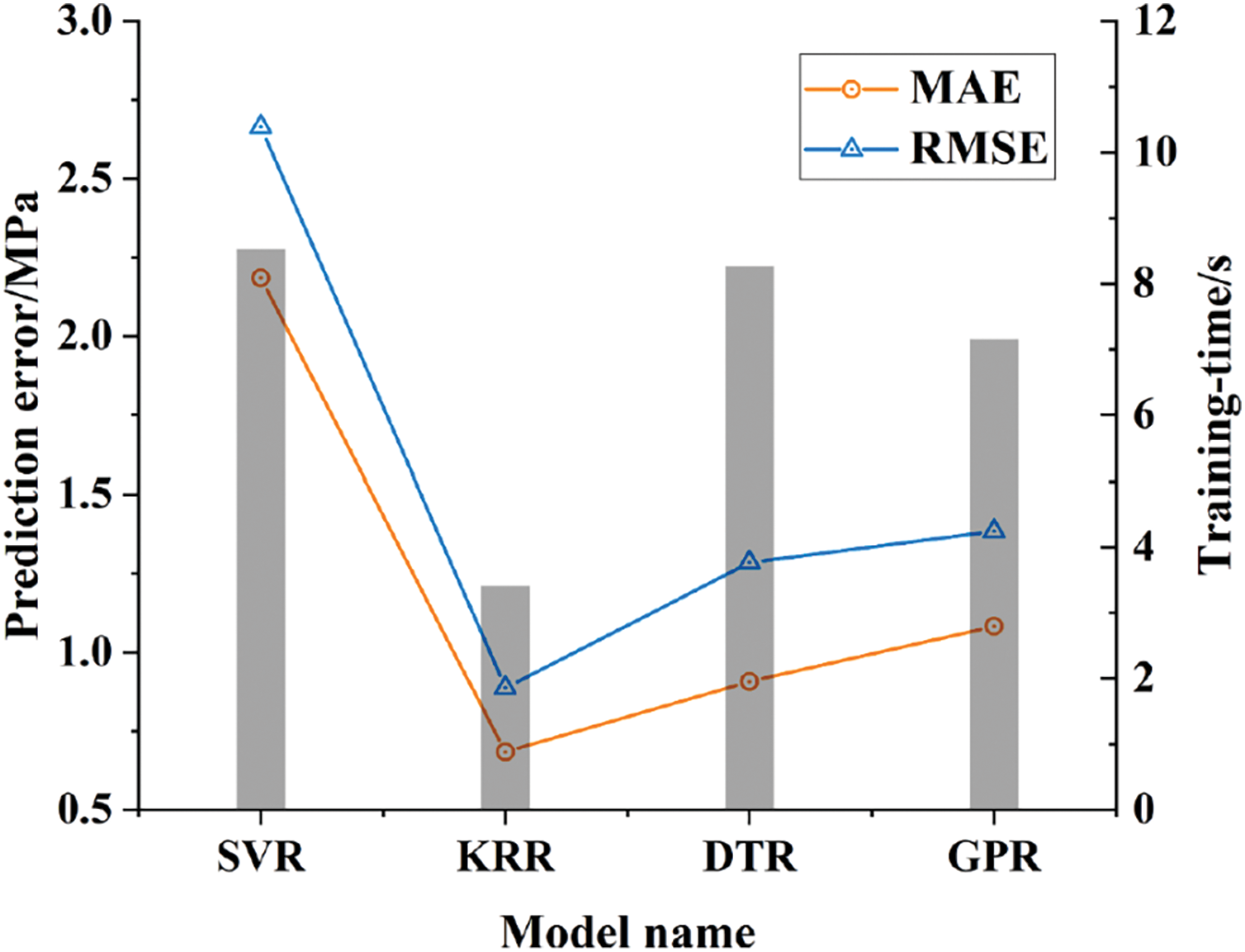
Figure 15: Comparisons of the performance evaluation index between different machine learning models (Reprinted from Ref. [95] with permission from Elsevier)

4  Discontinuity of Multi-Field Coupling Simulation of Rock Breaking

4.1 Spatial Discontinuity of Rock Mass

Spatial discontinuities formed by rock fracture are one of the key challenges in rock-breaking multi-field coupling simulations. At the microscopic scale, different minerals, micro-cracks, and pores in the rock generate interface effects, where stress concentrations occur, leading to the initiation of discontinuities [97,98]. At the specimen scale, cracks within the rock material begin to expand from microscopic pores or weak planes, promoting local crack initiation and propagation. This localized damage gradually spreads across the whole structure, forming a through-going crack that ultimately causes the instability and failure of the specimen [99]. Meanwhile, these discontinuous regions alter the overall heat flow and seepage pathways in the model. The permeability of cracks is much higher than that of the matrix regions, leading to significant inhomogeneities in the flow and thermal fields. These discontinuous distributions of heat flow and seepage further induce uneven local thermal expansion, significantly altering the stress and deformation fields of the rock, which accelerates the development of cracks [100]. At the engineering scale, discontinuous regions mainly refer to natural fractures, joints, and tectonic surfaces in the rock mass, which are easier to model due to their larger size. These discontinuities primarily cause large-scale instability in the rock structure [101], which is crucial for the design and safety of underground engineering projects such as tunnels and mines.

The key challenge in multi-field coupling analysis involving spatial discontinuities lies in how to handle the initiation, propagation, and fracture processes of rock cracks. It is very difficult to address discontinuities in continuous media. Adaptive Mesh Refinement (AMR) is commonly used to approximate the treatment of discontinuities. AMR dynamically adjusts the mesh density, using higher resolution grids in critical areas such as crack tips and stress concentration regions to accurately capture the crack propagation process. Dai et al. [102] employed an adaptive mesh refinement technique based on a prediction-correction method, which effectively improved the computational efficiency of crack propagation simulations in multi-field coupling models.

The DEM has inherent advantages in analyzing spatial discontinuities by simulating the mechanical interactions between particles in rock materials. When stress exceeds a certain threshold, the connections between particles break, simulating crack propagation and material fracture. DEM is suitable for simulating the discontinuous behavior of rocks during fracture processes [103,104]. DEM has high computational efficiency and accuracy at the specimen scale, which is why many researchers have used it to analyze discontinuities in rock at the specimen level. Li et al. [105] developed a coupled DEM and pore network model based on grain structure to study the interaction between hydraulic fractures and the inherent microstructure of rock. Zhang et al. [106] used DEM to study the effects of triaxial stress states, fracture width, and inclination angles on the mechanical properties of rocks.

The Extended Finite Element Method (XFEM) [107,108] is a powerful tool for handling crack propagation problems. XFEM introduces special displacement functions based on traditional finite element methods, adding special functions near the crack tip to describe stress concentration effects. This allows crack propagation to be handled without the need to remesh near the crack faces, making it highly effective for capturing spatial discontinuities and suitable for simulating complex crack networks and multi-crack interactions. Cheng et al. [109] developed a hydromechanical coupled XFEM method, which shows good results in simulating 3D non-planar hydraulic fracturing, crack-pore interactions, and natural fracture intersections.

4.2 Coupling of Discontinuity and Continuity

The FEM is commonly used to simulate the continuous behavior of rock materials, while the DEM is employed to handle cracks, fractures, and discontinuities. The coupling of FEM and DEM can effectively address the spatial discontinuity issues in the rock fracturing process [110]. FEM is used to describe the continuum mechanical behavior before local damage occurs in the rock, and once local fractures and crack propagation begin, the simulation switches to DEM to model the development of these cracks. This approach combines the high accuracy of FEM with the natural fracture handling capabilities of DEM, making it well-suited for simulating complex fracturing processes.

In the coupled FEM-DEM method, the elements can undergo elastic deformation, rotation, interaction, and translation, and fractures occur when specific fracture criteria are met. This leads to the formation of new discrete bodies or regions, which then undergo further displacement, deformation, interaction, and fracture. The method uses FEM to study solid deformation and assess fracture damage criteria, while DEM detects new contacts and describes the translation, rotation, and interaction of the discrete bodies. This method integrates FEM, based on continuous media, with DEM, based on discontinuous media. Finite Discrete Element Method (FDEM) not only simulates damage in brittle materials before fracturing but also models the complex interactions between cracks, as shown in Fig. 16. Insert zero thickness cohesive elements into each solid element during simulation modeling, and batch insert cohesive elements through Python programming. When the damage of the cohesive force element reaches 1 during calculation, the element is deleted, indicating material fracture and the formation of cracks. After the formation of the crack surface, the interaction between the crack surfaces also plays an important role in the subsequent crack propagation. In order to prevent mutual invasion of crack surfaces, a suitable contact model is adopted for the crack surface after the cohesive force is removed, as shown in the Fig. 17.

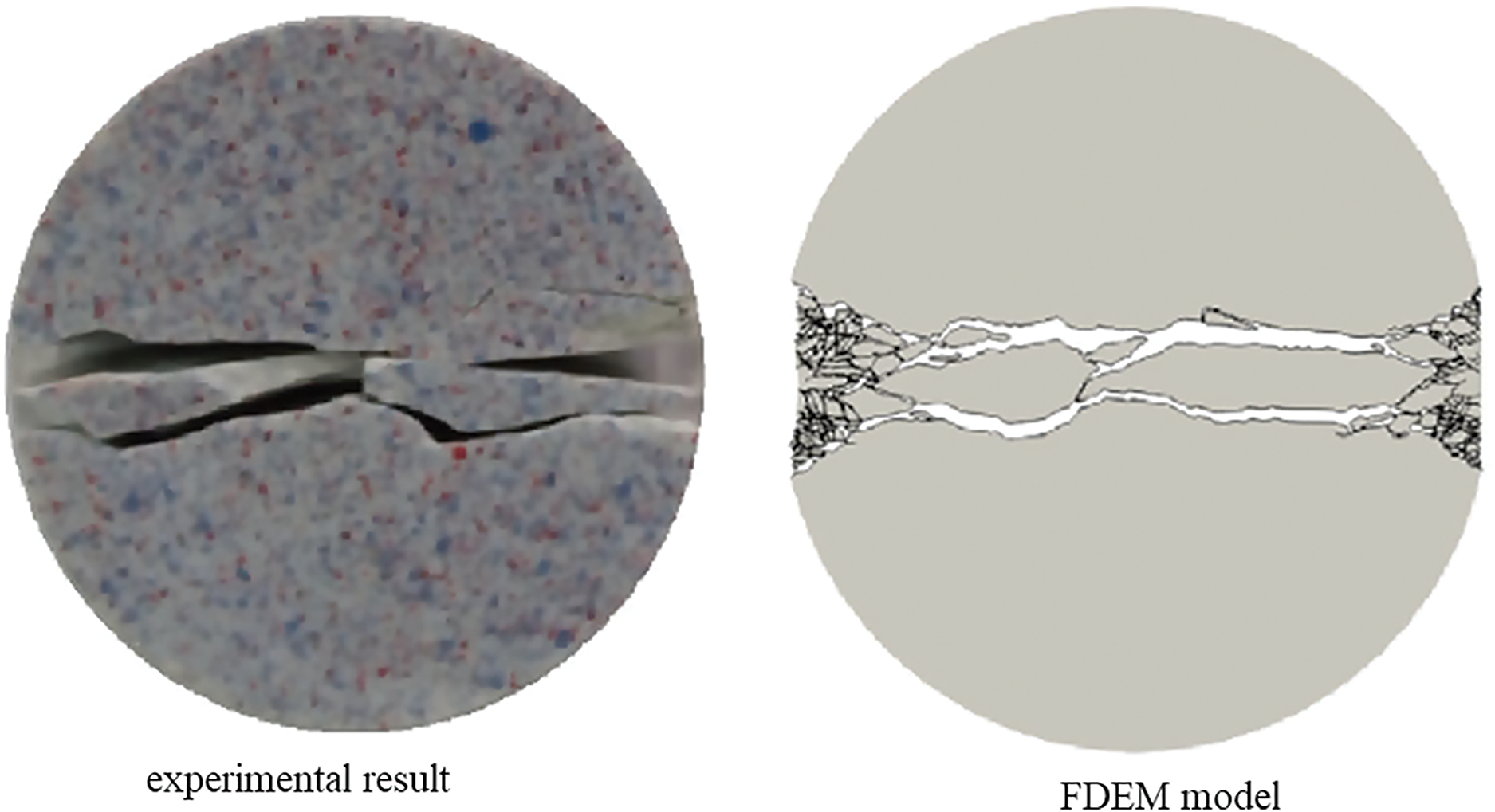
Figure 16: FDEM coupling analysis process (Reprinted from Ref. [64] with permission from Elsevier)

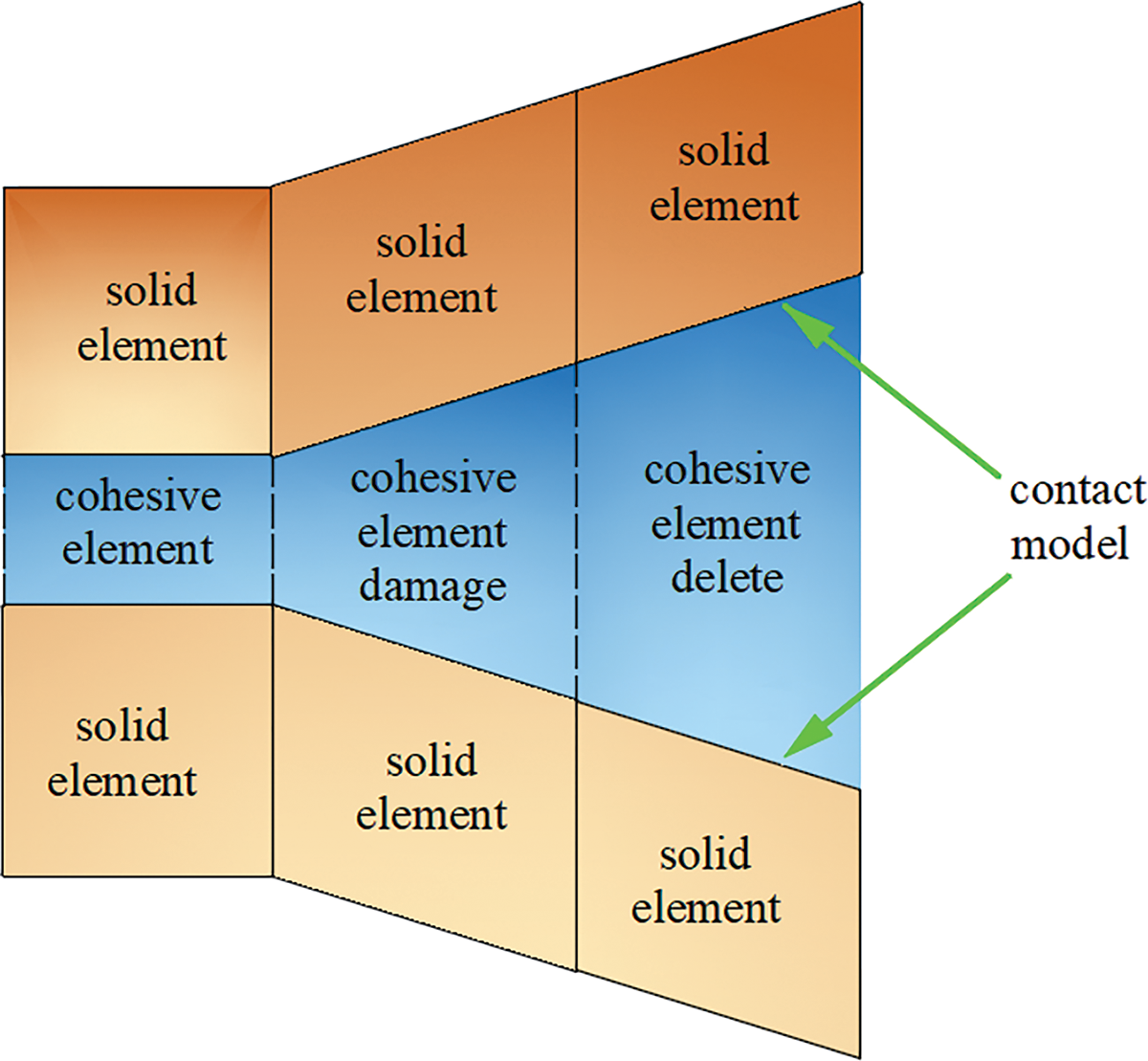
Figure 17: Crack growth model

FDEM can also be easily coupled with force, heat, and water physical fields. Flow and heat can not only be transmitted within the solid elements but also across the cracks, as shown in Fig. 18. When the rock is subjected to the combined effects of fluid flow, heat, and stress, and when the tensile or shear strength at the interface reaches the damage strength, a Fracture Process Zone (FPZ) begins to form. Once the interface reaches the maximum fracture energy or maximum displacement, visible cracks are formed. After crack formation, these cracks continue to carry loads, and the conditions for crack initiation and interaction can be conveniently defined.

Figure 18: FDEM coupling analysis process (Reprinted from Ref. [112] with permission from Springer)

Cui et al. [111] developed a 3D cohesive unit coupled with force, heat, and water physical fields, which is highly compatible with finite elements. Sharafisafa et al. [112] used FDEM to model hydraulic fracture propagation and studied the effects of controlling factors such as reservoir flow velocity, fluid viscosity, and rock pore aperture. Wu et al. [113] established a force-heat-water physical field coupling formulation based on a 2D FDEM and investigated rock deformation and fracturing behavior driven by the coupled physical fields in rock masses. The coupling scheme consists of three sub-solvers: a hydraulic solver, a thermal solver, and a mechanical solver. These solvers are iterated through an explicit partitioning scheme to achieve the coupled solution.

5  Conclusions and Prospects

This study begins with an introduction to the mathematical models and coupling strategies in multi-field coupled simulations for rock fracturing. It then delves into simulation techniques across different spatial and temporal scales, discusses methods for establishing cross-scale models and current scale information transfer technologies, and concludes with an overview of continuous-discontinuous coupling methods for addressing discontinuities in the fracturing process. The future directions and challenges for multi-field coupled simulations of rock fracturing are as follows:

(1) Characterization of simulation parameters

The accurate characterization of material parameters is challenging. At the microscale, precise parameters (grain size, microcracks and pore structures) are required, which often rely on experimental techniques or high-resolution imaging, incurring high costs. Crack propagation is highly nonlinear, making the development of precise fracture mechanics models difficult.

(2) Scale matching

The relationship between microstructural features and macroscopic mechanical properties is complex. Effectively transferring microscale information to the macroscale remains a challenge. In particular, how microscale damage influences macroscopic material performance requires further study. Significant differences in physical characteristics and numerical scales between the micro- and macro-scales pose difficulties in achieving effective scale matching. Establishing appropriate mapping relationships to represent microscale features in the macroscale without information loss or distortion is critical. Additionally, in multi-field coupling simulations, the coupling strength between fields may vary across scales, making the accurate transmission of coupling information across scales another challenge.

(3) Computational efficiency

Cross-scale simulations involve substantial computational demands, particularly for detailed microscale models, which are resource-intensive. Improving computational efficiency while ensuring accurate information transfer is a pressing issue in cross-scale simulations. Advances in high-performance computing and cloud computing provide opportunities to enhance simulation efficiency. The application of technologies such as large-scale parallel computing, cloud computing, and distributed computing could enable simulations of large-scale and high-resolution rock fracturing problems with improved efficiency.

(4) Intelligent simulation

The increasing maturity of artificial intelligence and machine learning offers promising avenues for advancing multi-field coupled simulations of rock fracturing. Introducing these technologies may facilitate automatic model optimization and intelligent processing. By integrating traditional physical models with data-driven models through hybrid modeling approaches, it is possible to retain the interpretability of physical processes while leveraging the predictive power of data-driven models. This combination can improve the accuracy of simulations for complex coupling problems.

In summary, while substantial progress has been made in the multi-field coupled simulation of rock fracturing, significant challenges remain in parameter characterization, scale matching, computational efficiency, and intelligent simulation. Addressing these challenges will pave the way for more accurate, efficient, and insightful simulations of rock fracturing processes.

Acknowledgement: The authors would like to express their heartful gratitude to the journal editor and anonymous reviewers for their valuable feedback, which helped us improve the content and quality of our paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Nos. 42477185, 41602308), the Zhejiang Provincial Natural Science Foundation of China (Grant No. LY20E080005), and the Postgraduate Course Construction Project of Zhejiang University of Science and Technology (Grant No. 2021yjskj05).

Author Contributions: Baoping Zou: Writing—review & editing, Methodology, Project administration, Resources, Conceptualization. Chenhao Pei: Writing original draft, Software, Methodology, Formal analysis. Qizhi Chen: Writing—review & editing, Conceptualization. Yansheng Deng: Writing—review & editing. Yongguo Chen: Methodology, Conceptualization. Xu Long: Writing—review & editing, Project administration, Conceptualization. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting this study’s findings are available on request from the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zou B, Yin J, Liu Z, Long X. Transient rock breaking characteristics by successive impact of shield disc cutters under confining pressure conditions. Tunnelling Undergr Space Technol. 2024;150:105861. doi:10.1016/j.tust.2024.105861. [Google Scholar] [CrossRef]

2. Yang X, Chu T, Yu M, Wang L, Chao J, Han X. Evolution characteristics of bulking factor in the multi-field loading of broken coal: an experimental study. Rock Mech Rock Eng. 2021;54(3):1481–99. doi:10.1007/s00603-020-02333-7. [Google Scholar] [CrossRef]

3. Lin Z, Zhang B, Guo J. Analysis of a water-inrush disaster caused by coal seam subsidence karst collapse column under the action of multi-field coupling in taoyuan coal mine. Comput Model Eng Sci. 2021;126(1):311–30. doi:10.32604/cmes.2021.011556. [Google Scholar] [CrossRef]

4. Zhang Y, Yu S, Deng H. Peridynamic model of deformation and failure for rock material under the coupling effect of multi-physical fields. Theor Appl Fract Mech. 2023;125:103912. doi:10.1016/j.tafmec.2023.103912. [Google Scholar] [CrossRef]

5. Ye D, Liu G, Yu B, Zhou Z, Gao C, Gao F. Study on microstructural evolution of rock fractures under multi-field interactions. Fractals-Complex Geome Patt Scal Nat Soc. 2022;30(3):1–16. doi:10.1142/S0218348X2250058X. [Google Scholar] [CrossRef]

6. Liu S, Wang W, Jia Y, Bian H, Shen W. Modeling of hydro-mechanical coupled fracture propagation in quasi-brittle rocks using a variational phase-field method. Rock Mech Rock Eng. 2024;57(9):7079–101. doi:10.1007/s00603-024-03896-5. [Google Scholar] [CrossRef]

7. Yi W, Huang S, Rao Q, Li Z, Huang D, Ma Y, et al. Cracking behaviors and mechanism of pre-cracked rock specimens under coupled THM fields with chemical processes. Case Stud Constr Mater. 2024;20(7):e02758. doi:10.1016/j.cscm.2023.e02758. [Google Scholar] [CrossRef]

8. Wu Y, Hu L, Yu J, Li X, Yang L, Xue S, et al. The sensitivity of mechanical properties and pore structures of Beishan granite to large variation of temperature in nuclear waste storage sites. Environ Sci Pollut Res. 2023;30(30):75195–212. doi:10.1007/s11356-023-27510-3. [Google Scholar] [PubMed] [CrossRef]

9. Qi S, Zheng B, Wang Z, Zhao H, Cui Z, Huang T, et al. Geological evaluation for the carbon dioxide geological utilization and storage (CGUS) site: a review. Sci China-Earth Sci. 2023;66:P1917–36. doi:10.1007/s11430-022-1107. [Google Scholar] [CrossRef]

10. Li X, Liu X, Chai X, He H, Zhang B, Zhang T. Multi-physics coupling simulation of small mobile nuclear reactor with finite element-based models. Comput Phys Commun. 2023;293(7):108900. doi:10.1016/j.cpc.2023.108900. [Google Scholar] [CrossRef]

11. Zhu Y, Liu C, Liu H, Kou Y, Shi B. A multi-field and fluid-solid coupling method for porous media based on DEM-PNM. Comput Geotech. 2023;154(1):105118. doi:10.1016/j.compgeo.2022.105118. [Google Scholar] [CrossRef]

12. Dai Y, Zhao J, Zhang X, Bai F, Tao W, Wang Y. Thermal full-field prediction of an air-cooled data center using a novel multi-scale approach based on POD and CFD coupling. Energy Build. 2024;307:113992. doi:10.1016/j.enbuild.2024.113992. [Google Scholar] [CrossRef]

13. Yu S, Ren X, Zhang J, Sun Z. An improved form of SPH method for simulating the thermo-mechanical-damage coupling problems and its applications. Rock Mech Rock Eng. 2022;55(3):1633–48. doi:10.1007/s00603-021-02753-z. [Google Scholar] [CrossRef]

14. Cheng H, Thornton AR, Luding S, Hazel AL, Weinhart T. Concurrent multi-scale modeling of granular materials: role of coarse in FEM-DEM. Comput Methods Appl Mech Eng. 2023;403(5):115651. doi:10.1016/j.cma.2022.115651. [Google Scholar] [CrossRef]

15. Malendowski M, Glema A. Development and implementation of coupling method for CFD-FEM analyses of steel structures in natural fire. Modern Build Mat, Struct Techn. 2017;172:692–700. doi:10.1016/j.proeng.2017.02.082. [Google Scholar] [CrossRef]

16. Reppas N, Gui Y, Wetenhall B, Davie CT, Ma J. A fully coupled thermo-hydro-mechanical elastoplastic damage model for fractured rock. Geomech Geophys Geo-Energy Geo-Resour. 2024;10(1):1–33. doi:10.1007/s40948-024-00753-1. [Google Scholar] [CrossRef]

17. Hu Y, Liu G, Luo N, Gao F, Yue F, Gao T. Multi-field coupling deformation of rock and multi-scale flow of gas in shale gas extraction. Energy. 2022;238(4):121666. doi:10.1016/j.energy.2021.121666. [Google Scholar] [CrossRef]

18. Liu W, Zheng L, Zhang Z, Liu G, Wang Z, Yang C. A micromechanical hydro-mechanical-damage coupled model for layered rocks considering multi-scale structures. Int J Rock Mech Min Sci. 2021;142(7):104715. doi:10.1016/j.ijrmms.2021.104715. [Google Scholar] [CrossRef]

19. Li Z, Liu X, Sun Y, Jiang X. Numerical simulation of frost heaving damage of earth-rock dam berms in cold regions with thermo-hydro-mechanical coupling. Cold Reg Sci Technol. 2024;223(S2):104207. doi:10.1016/j.coldregions.2024.104207. [Google Scholar] [CrossRef]

20. Mu D, Zhang K, Ma Q, Wang J. A coupled hydro-thermo-mechanical model based on TLF-SPH for simulating crack propagation in fractured rock mass. Geomech Geophys Geo-Energy Geo-Resour. 2024;10(1):1–38. doi:10.1007/s40948-024-00756-y. [Google Scholar] [CrossRef]

21. Yin S, Dusseault MB, Rothenburg L. Coupled THMC modeling of CO2 injection by finite element methods. J Pet Sci Eng. 2011;80(1):53–60. doi:10.1016/j.petrol.2011.10.008. [Google Scholar] [CrossRef]

22. Yin S, Towler BF, Dusseault MB, Rothenburg L. Fully coupled THMC modeling of wellbore stability with thermal and solute convection considered. Transp Porous Media. 2010;84(3):773–98. doi:10.1007/s11242-010-9540-9. [Google Scholar] [CrossRef]

23. Xie Y, Liao J, Zhao P, Xia K, Li C. Effects of fracture evolution and non-Darcy flow on the thermal performance of enhanced geothermal system in 3D complex fractured rock. Int J Min Sci Technol. 2024;34(4):443–59. doi:10.1016/j.ijmst.2024.03.005. [Google Scholar] [CrossRef]

24. Zhong Z, Meng X, Hu Y, Zhang F, Wu F, Wang G. Quantitative assessments on fluid flow through fractures embedded in permeable host rocks: experiments and simulations. Eng Geol. 2023;327(4):107341. doi:10.1016/j.enggeo.2023.107341. [Google Scholar] [CrossRef]

25. Espada M, Lamas L. Back analysis procedure for identification of anisotropic elastic parameters of overcored rock specimens. Rock Mech Rock Eng. 2017;50(3):513–27. doi:10.1007/s00603-016-1129-3. [Google Scholar] [CrossRef]

26. Saurav R, Kumar SN. Strength behaviour of sandstone subjected to polyaxial state of stress. Int J Min Sci Technol. 2017;27(6):889–97. doi:10.1016/j.ijmst.2017.06.022. [Google Scholar] [CrossRef]

27. Xiao J, Liu J, Xu Y, Li X, Liu A, Xia K. An improved three-dimensional extension of Hoek-Brown criterion for rocks. Geomech Geophys Geo-Energy Geo-Resour. 2024;10(1):1–24. doi:10.1007/s40948-024-00841-2. [Google Scholar] [CrossRef]

28. Shin H, Santamarina JC. An implicit joint-continuum model for the hydro-mechanical analysis of fractured rock masses. Int J Rock Mech Min Sci. 2019;119(3):140–8. doi:10.1016/j.ijrmms.2019.04.006. [Google Scholar] [CrossRef]

29. Tang ZC, Jiao YY. A self-consistent model with asperity interaction for the mechanical behavior of rock joints under compressive loading. Int J Rock Mech Min Sci. 2017;100(1442):23–7. doi:10.1016/j.ijrmms.2017.10.009. [Google Scholar] [CrossRef]

30. Nguyen TS, Kolditz O, Yoon JS, Zhuang L. Modelling the thermo-mechanical behaviour of a rock joint. Geomech Energy Environ. 2024;37(26):100520. doi:10.1016/j.gete.2023.100520. [Google Scholar] [CrossRef]

31. Zareidarmiyan A, Salarirad H, Vilarrasa V, Kim K, Lee J, Min K. Comparison of numerical codes for coupled thermo-hydro-mechanical simulations of fractured media. J Rock Mech Geotechnical Eng. 2020;12(4):850–65. doi:10.1016/j.jrmge.2019.12.016. [Google Scholar] [CrossRef]

32. Gudala M, Govindarajan SK, Tariq Z, Yan B, Sun S. Numerical investigations and evaluation of a puga geothermal reservoir with horizontal wells using a fully coupled thermo-hydro-geomechanical model (THM) and EDAS associated with AHP. Geoener Sci Eng. 2023;228(1–12):212035. doi:10.1016/j.geoen.2023.212035. [Google Scholar] [CrossRef]

33. Longuemare P, Mainguy M, Lemonnier P, Onaisi A, Gérard C, Koutsabeloulis N. Geomechanics in reservoir simulation: overview of coupling methods and field case study. Oil Gas Sci Technol-Revue D Ifp Energies Nouvelles. 2002;57(5):471–83. doi:10.2516/ogst:2002031. [Google Scholar] [CrossRef]

34. Akanji LT, Ibrahim A, Hamidi H, Matthai S, Akisanya A. A new explicit sequentially coupled technique for chemo-thermo-poromechanical modelling and simulation in shale formations. Energies. 2023;16(3):1543. doi:10.3390/en16031543. [Google Scholar] [CrossRef]

35. Preisig M, Prevost JH. Coupled multi-phase thermo-poromechanical effects. Case study: CO2 injection at in Salah. Algeria Int J Greenhouse Gas Control. 2011;5(4):1055–64. doi:10.1016/j.ijggc.2010.12.006. [Google Scholar] [CrossRef]

36. Rutqvist J, Wu YS, Tsang CF, Bodvarsson G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int J Rock Mech Min Sci. 2002;39(4):429–42. doi:10.1016/S1365-1609(02)00022-9. [Google Scholar] [CrossRef]

37. Zhou X, Zhang Y. Implementation and verification of a user-defined element (UEL) for coupled thermal-hydraulic-mechanical-chemical (THMC) processes in saturated geological media. Int J Numer Anal Methods Geomech. 2023;47(11):2153–90. doi:10.1002/nag.3556. [Google Scholar] [CrossRef]

38. Wu Z, Wu Y, Weng L, Li M, Wang Z, Chu Z. Machine learning approach to predicting the macro-mechanical properties of rock from the meso-mechanical parameters. Comput Geotech. 2024;166:105933. doi:10.1016/j.compgeo.2023.105933. [Google Scholar] [CrossRef]

39. Mclean ML, Espinoza DN. Thermo-poromechanical rock response around operating deep closed-loop geothermal wellbores. Rock Mech Rock Eng. 2024;57(10):8759–75. doi:10.1007/s00603-024-04002-5. [Google Scholar] [CrossRef]

40. Liu N, Liang S, Wang S, Song Z. THM model of rock tunnels in cold regions and numerical simulation. Sci Rep. 2024;14(1):3465. doi:10.1038/s41598-024-53418-0. [Google Scholar] [PubMed] [CrossRef]

41. Feng W, Were P, Li M, Hou Z, Zhou L. Numerical study on hydraulic fracturing in tight gas formation in consideration of thermal effects and THM coupled processes. J Pet Sci Eng. 2016;146(10):241–54. doi:10.1016/j.petrol.2016.04.033. [Google Scholar] [CrossRef]

42. Aliyu MD, Archer RA. A thermo-hydro-mechanical model of a hot dry rock geothermal reservoir. Renew Energy. 2021;176(3):475–93. doi:10.1016/j.renene.2021.05.070. [Google Scholar] [CrossRef]

43. Zhao Y, Feng Z, Feng Z, Yang D, Liang W. THM (Thermo-hydro-mechanical) coupled mathematical model of fractured media and numerical simulation of a 3D enhanced geothermal system at 573 K and buried depth 6000-7000 M. Energy. 2015;82(3):193–205. doi:10.1016/j.energy.2015.01.030. [Google Scholar] [CrossRef]

44. Wang Y, Zhang F, Liu F. Thermo-hydro-mechanical (THM) coupled simulation of the land subsidence due to aquifer thermal energy storage (ATES) system in soft soils. J Rock Mech Geotechnical Eng. 2024;16(6):1952–66. doi:10.1016/j.jrmge.2023.05.019. [Google Scholar] [CrossRef]

45. Kang Y, Liu Q, Xi H. Numerical analysis of THM coupling of a deeply buried roadway passing through composite strata and dense faults in a coal mine. Bull Eng Geol Environ. 2014;73(1):77–86. doi:10.1007/s10064-013-0506-3. [Google Scholar] [CrossRef]

46. Krzaczek M, Tejchman J. Hydraulic fracturing process in rocks-small-scale simulations with a novel fully coupled DEM/CFD-based thermo-hydro-mechanical approach. Eng Fract Mech. 2023;289(4):109424. doi:10.1016/j.engfracmech.2023.109424. [Google Scholar] [CrossRef]

47. Manda MSB, Rejab MRBM, Hassan SA, Wahit MUB, Binoj JS, Mansingh BB, et al. Tin slag polymer concrete strengthening by basalt and aramid fiber reinforced polymer confinement. J Polymer Mat. 2023;39(3-4):241–53. doi:10.32381/JPM.2022.39.3-4.5. [Google Scholar] [CrossRef]

48. Jiao K, Han D, Wang D, Chen Y, Li J, Gong L, et al. Investigation of thermal-hydro-mechanical coupled fracture propagation considering rock damage. Comput Geosci. 2022;26(5):1167–87. doi:10.1007/s10596-022-10155-5. [Google Scholar] [CrossRef]

49. Xian M, Xu Z, Chen B. Numerical investigation of variable-mass seepage mechanism of broken rock mass in faults. Comput Geotech. 2023;160(2):105527. doi:10.1016/j.compgeo.2023.105527. [Google Scholar] [CrossRef]

50. Wang F, Zhou M, Shen W, Huang H, He J. Fluid-solid-phase multi-field coupling modeling method for hydraulic fracture of saturated brittle porous materials. Eng Fract Mech. 2023;290:109231. doi:10.1016/j.engfracmech.2023.109501. [Google Scholar] [CrossRef]

51. Blaheta R, Kohut R, Kolcun A, Soucek K, Stas L, Vavro L. Digital image based numerical micromechanics of geocomposites with application to chemical grouting. Int J Rock Mech Min Sci. 2015;77(5):77–88. doi:10.1016/j.ijrmms.2015.03.012. [Google Scholar] [CrossRef]

52. Cui G, Feng X, Ning F, Chen Z, Tian H. Micro-cracks evolution process and borehole stability analysis in deep pebbly sandstone based on THM coupling method. Geoene Sci Eng. 2024;240(4):213000. doi:10.1016/j.geoen.2024.213000. [Google Scholar] [CrossRef]

53. Li M, Wu Z, Weng L, Liu Q, Chu Z. Modelling thermo-hydro-mechanical (THM) effect on the hydro-mechanical properties of granite in disposal system using an improved meso-structure-based DEM model. Rock Mech Rock Eng. 2024;57(7):5129–54. doi:10.1007/s00603-024-03779-9. [Google Scholar] [CrossRef]

54. Xiong Q, Kitamura T, Li Z. Nanocrystallization in single-crystal copper under laser shock compression: a molecular dynamics study. Mat Sci Eng A-Struct Mat Propert Microstruct Process. 2019;752(21):115–27. doi:10.1016/j.msea.2019.02.086. [Google Scholar] [CrossRef]

55. Xiao J, Zhu L, Wang R, Deng C, Wu Z, Zhu Y. Unveiling deformation twin nucleation and growth mechanisms in BCC transition metals and alloys. Mater Today. 2023;65:90–9. doi:10.1016/j.mattod.2023.03.028. [Google Scholar] [CrossRef]

56. Lu Y, Zhang Y, Ma E, Han W. Relative mobility of screw versus edge dislocations controls the ductile-to-brittle transition in metals. Proc Natl Acad Sci U S A. 2021;118(37):1–6. doi:10.1073/pnas.2110596118. [Google Scholar] [PubMed] [CrossRef]

57. Yu T, Hu H, Li Q, Tan Y, Xu L, Cao X. CO2 gas stripped off membranous residual oil from pore surfaces: effects of temperature, pressure and wettability. J Rock Mech Geotechnical Eng. 2023;15(12):3209–20. doi:10.1016/j.jrmge.2023.07.007. [Google Scholar] [CrossRef]

58. Choi JH, Kawamura K, Kimoto K, Ichikawa Y, Chae B. Multi-species diffusion analysis in porous media under various dry density and temperature conditions: molecular dynamics simulation, homogenization analysis, and finite element method. Int J Numer Anal Methods Geomech. 2014;38(16):1744–60. doi:10.1002/nag.2303. [Google Scholar] [CrossRef]

59. Gorsevski PV, Onasch CM, Farver JR, Ye X. Detecting grain boundaries in deformed rocks using a cellular automata approach. Comput Geosci. 2012;42:136–42. doi:10.1016/j.cageo.2011.09.008. [Google Scholar] [CrossRef]

60. Hou W, Pan P, Wang Z. Modeling of rock multiple fractures system with a new contact algorithm and a novel approach for complex topology construction. Theor Appl Fract Mech. 2023;124(8):103778. doi:10.1016/j.tafmec.2023.103778. [Google Scholar] [CrossRef]

61. Pan P, Feng X, Hudson JA. Study of failure and scale effects in rocks under uniaxial compression using 3D cellular automata. Int J Rock Mech Min Sci. 2009;46(4):674–85. doi:10.1016/j.ijrmms.2008.11.001. [Google Scholar] [CrossRef]

62. Zhou Z, Bi J, Zhao Y, Wang C, Zhang Y. Thermal-mechanical coupling smooth particle hydrodynamics-phase field method modelling of cracking in rocks. Comput Geotech. 2024;173(1):106476. doi:10.1016/j.compgeo.2024.106476. [Google Scholar] [CrossRef]

63. Yu Z, Sun Y, Vu M, Shao J. Modeling of mixed cracks in rock-like brittle materials under compressive stresses by a double-phase-field method. Rock Mech Rock Eng. 2023;56(4):2779–92. doi:10.1007/s00603-022-03196-w. [Google Scholar] [CrossRef]

64. Wu Di, Li H, Fukuda D, Liu H. Development of a finite-discrete element method with finite-strain elasto-plasticity and cohesive zone models for simulating the dynamic fracture of rocks. Comput Geotech. 2023;156:105271. doi:10.1016/j.compgeo.2023.105271. [Google Scholar] [CrossRef]

65. Wang Z, Wang H, Wang J, Tian N. Finite element analyses of constitutive models performance in the simulation of blast-induced rock cracks. Comput Geotech. 2021;135(10):104172. doi:10.1016/j.compgeo.2021.104172. [Google Scholar] [CrossRef]

66. Tan F, You M, Zuo C, Jiao Y, Tian H. Simulation of rock-breaking process by drilling machine and dynamic classification of surrounding rocks. Rock Mech Rock Eng. 2022;55(1):423–37. doi:10.1007/s00603-021-02659-w. [Google Scholar] [CrossRef]

67. Han H, Fukuda D, Liu H, Salmi EF, Sellers E, Liu T, et al. FDEM simulation of rock damage evolution induced by contour blasting in the bench of tunnel at deep depth. Tunnelling Undergr Space Technol. 2020;103:103495. doi:10.1016/j.tust.2020.103495. [Google Scholar] [CrossRef]

68. Huang G, Li M, Zhou F, Chu J, Xiong Z. A new numerical simulation method for multi-stage in-fracture temporary plugging and diverting fracturing: based on the modified cohesive zone model. Rock Mech Rock Eng. 2024;57(10):8723–40. doi:10.1007/s00603-024-04006-1. [Google Scholar] [CrossRef]

69. Chen Z, Qiu J, Chen Q, Li X, Ma B, Huang X. Influence of multi-perforations hydraulic fracturing on stress and fracture characteristics of hard rock mass under excavation condition. Eng Fract Mech. 2022;276(9):108925. doi:10.1016/j.engfracmech.2022.108925. [Google Scholar] [CrossRef]

70. Chen Y, Xie B, Long J, Kuang Y, Chen X, Hou M, et al. Interfacial laser-induced graphene enabling high-performance liquid-solid triboelectric nanogenerator. Adv Mater Deerfield. 2021;33(44):e2104290. doi:10.1002/adma.202104290. [Google Scholar] [PubMed] [CrossRef]

71. Liu Z, Li J, Liu X. Novel functionalized BN nanosheets/epoxy composites with advanced thermal conductivity and mechanical properties. ACS Appl Mat Interf. 2020;12(5):6503–15. doi:10.1021/acsami.9b21467. [Google Scholar] [PubMed] [CrossRef]

72. Zhang W, Lin S, Wang L, Wang L, Jiang X, Wang S. A novel creep contact model for rock and its implement in discrete element simulation. Comput Geotech. 2024;167(12):106054. doi:10.1016/j.compgeo.2023.106054. [Google Scholar] [CrossRef]

73. Radakovic-Guzina Z, Damjanac B, Lam T, Kasani HA. Numerical simulation of long-term performance of deep geological repository placement rooms in crystalline and sedimentary rocks. Comput Geotech. 2023;157:105348. doi:10.1016/j.compgeo.2023.105348. [Google Scholar] [CrossRef]

74. Wang W, Shao H, Rink K, Fischer T, Kolditz O, Nagel T. Analysis of coupled thermal-hydro-mechanical processes in Callovo-Oxfordian clay rock: from full-scale experiments to the repository scale. Eng Geol. 2021;293(1):106265. doi:10.1016/j.enggeo.2021.106265. [Google Scholar] [CrossRef]

75. Li G, Tang C. A statistical meso-damage mechanical method for modeling trans-scale progressive failure process of rock. Int J Rock Mech Min Sci. 2015;74(6):133–50. doi:10.1016/j.ijrmms.2014.12.006. [Google Scholar] [CrossRef]

76. Ip SCY, Borja RI. Hydromechanical coupling in unsaturated clayey rocks with double porosity based on a multiscale homogenization procedure. Comput Geotech. 2024;171(3):106380. doi:10.1016/j.compgeo.2024.106380. [Google Scholar] [CrossRef]

77. Ren M, Zhao G, Zhou Y. Elastic stress transfer model and homogenized constitutive equation for the multi-phase geomaterials. Eng Geol. 2022;306:106631. doi:10.1016/j.enggeo.2022.106631. [Google Scholar] [CrossRef]

78. Ren C, Yu J, Zhang C, Liu X, Zhu Y, Yao W. Micro-macro approach of anisotropic damage: a semi-analytical constitutive model of porous cracked rock. Eng Fract Mech. 2023;290(5):109483. doi:10.1016/j.engfracmech.2023.109483. [Google Scholar] [CrossRef]

79. Yu Di, Liu E, Xiang B, He Y, Luo F, He C. A micro-macro constitutive model for rock considering breakage effects. Int J Min Sci Technol. 2023;33(2):173–84. doi:10.1016/j.ijmst.2022.09.027. [Google Scholar] [CrossRef]

80. Liang S, Liu H. An equivalent strain based multi-scale damage model of concrete. Comput Model Eng Sci. 2020;122(3):1015–38. doi:10.32604/cmes.2020.07799. [Google Scholar] [CrossRef]

81. Yan B, Li C, Tariq Z, Zhang K. Estimation of heterogeneous permeability using pressure derivative data through an inversion neural network inspired by the Fast Marching Method. Geoene Sci Eng. 2023;228(3):211982. doi:10.1016/j.geoen.2023.211982. [Google Scholar] [CrossRef]

82. Zhang F, Guo H, Hu D, Shao J. Characterization of the mechanical properties of a claystone by nano-indentation and homogenization. Acta Geotechnica. 2018;13(6):1395–404. doi:10.1007/s11440-018-0691-0. [Google Scholar] [CrossRef]

83. Dormieux L, Lemarchand E, Kondo D, Brach S. Strength criterion of porous media: application of homogenization techniques. J Rock Mech Geotechnical Eng. 2017;9(1):62–73. doi:10.1016/j.jrmge.2016.11.010. [Google Scholar] [CrossRef]

84. Zhu Q, Shao J. Micromechanics of rock damage: advances in the quasi-brittle field. J Rock Mech Geotechnical Eng. 2017;9(1):29–40. doi:10.1016/j.jrmge.2016.11.003. [Google Scholar] [CrossRef]

85. Xia C, Liu Z, Zhou C, Zhang L. A meso/macroscale theoretical model for investigating the large deformation of soft rock tunnels considering creep and anisotropic effects. Rock Mech Rock Eng. 2023;56(7):4901–22. doi:10.1007/s00603-023-03306-2. [Google Scholar] [CrossRef]

86. Wang J, Zhang Y, Qin Z, Song S, Lin P. Analysis method of water inrush for tunnels with damaged water-resisting rock mass based on finite element method-smooth particle hydrodynamics coupling. Comput Geotech. 2020;126(4):103725. doi:10.1016/j.compgeo.2020.103725. [Google Scholar] [CrossRef]

87. Sun L, Grasselli G, Liu Q, Tang X. Coupled hydro-mechanical analysis for grout penetration in fractured rocks using the finite-discrete element method. Int J Rock Mech Min Sci. 2019;124(2):104138. doi:10.1016/j.ijrmms.2019.104138. [Google Scholar] [CrossRef]

88. Zhao Z, Shou Y, Zhou X. Microscopic cracking behaviors of rocks under uniaxial compression with micro-scopic multiphase heterogeneity by deep learning. Int J Min Sci Technol. 2023;33(4):411–22. doi:10.1016/j.ijmst.2022.12.008. [Google Scholar] [CrossRef]

89. Zhu D, Yu B, Wang D, Zhang Y. Fusion of finite element and machine learning methods to predict rock shear strength parameters. J Geophys Eng. 2024;21(4):1183–93. doi:10.1093/jge/gxae064. [Google Scholar] [CrossRef]

90. Wang H, Zhang C, Zhou B, Xue S, Jia P, Zhu X. Prediction of triaxial mechanical properties of rocks based on mesoscopic finite element numerical simulation and multi-objective machine learning. J King Saud Univ Sci. 2023;35(7):102846. doi:10.1016/j.jksus.2023.102846. [Google Scholar] [CrossRef]

91. Ishola O, Vilcaez J. Machine learning modeling of permeability in 3D heterogeneous porous media using a novel stochastic pore-scale simulation approach. Fuel. 2022;321(2):124044. doi:10.1016/j.fuel.2022.124044. [Google Scholar] [CrossRef]

92. Guan S, Qu T, Feng YT, Ma G, Zhou W. A machine learning-based multi-scale computational framework for granular materials. Acta Geotechnica. 2023;18(4):1699–720. doi:10.1007/s11440-022-01709-z. [Google Scholar] [CrossRef]

93. Suryawanshi A, Behera N. Application of machine learning for prediction dental material wear. J Poly Mate. 2024;40(3–4):305–16. doi:10.32381/JPM.2023.40.3-4.11. [Google Scholar] [CrossRef]

94. Zhao J, Li D, Jiang J, Luo P. Uniaxial compressive strength prediction for rock material in deep mine using boosting-based machine learning methods and optimization algorithms. Comput Model Eng Sci. 2024;140(1):275–304. doi:10.32604/cmes.2024.046960. [Google Scholar] [CrossRef]

95. Li M, Wu Z, Weng L, Zhang F, Zhou Y, Wu Y. Cross-scale analysis for the thermo-hydro-mechanical (THM) effects on the mechanical behaviors of fractured rock: integrating mesostructure-based DEM modeling and machine learning. Eng Fract Mech. 2024;306(3):110204. doi:10.1016/j.engfracmech.2024.110204. [Google Scholar] [CrossRef]

96. Gudala M, Govindarajan SK. Numerical investigations on a geothermal reservoir using fully coupled thermo-hydro-geomechanics with integrated RSM-machine learning and ARIMA models. Geothermics. 2021;96(1–12):102174. doi:10.1016/j.geothermics.2021.102174. [Google Scholar] [CrossRef]

97. Lin C, Jia X, Deng S, Mao J, Chen X, He J, et al. The roles of micro pores and minerals in shale during hydraulic fracturing. Rock Mech Rock Eng. 2024;57(11):10177–86. doi:10.1007/s00603-024-04063-6. [Google Scholar] [CrossRef]

98. Xiao ZM, Pae KD. The interaction between a penny-shaped crack and a spherical inhomogeneity in an infinite solid under uniaxial tension. Acta Mech. 1991;90(1–4):91–104. doi:10.1007/BF01177402. [Google Scholar] [CrossRef]

99. Dong Z, Cai M, Ma C, Wang P, Li P. Rock damage and fracture characteristics considering the interaction between holes and joints. Theor Appl Fract Mech. 2024;133(2):104628. doi:10.1016/j.tafmec.2024.104628. [Google Scholar] [CrossRef]

100. Guo T, Tang S, Liu S, Liu X, Zhang W, Qu G. Numerical simulation of hydraulic fracturing of hot dry rock under thermal stress. Eng Fract Mech. 2020;240:107350. doi:10.1016/j.engfracmech.2020.107350. [Google Scholar] [CrossRef]

101. Hu C, Gong S, Chen B, Zong Z, Bao X, Ru X. Finite element simulations of the localized failure and fracture propagation in cohesive materials with friction. Comput Model Eng Sci. 2024;140(1):997–1015. doi:10.32604/cmes.2024.048640. [Google Scholar] [CrossRef]

102. Dai Y, Hou B, Lee S, Wick T. A thermal-hydraulic-mechanical-chemical coupling model for acid fracture propagation based on a phase-field method. Rock Mech Rock Eng. 2024;57(7):4583–605. doi:10.1007/s00603-024-03769-x. [Google Scholar] [CrossRef]

103. Song H, Chen X, Zhu C, Yin Q, Wang W, Meng Q. RB-DEM modeling and simulation of non-persisting rough open joints based on the IFS-enhanced method. Comput Model Eng Sci. 2024;139(1):337–59. doi:10.32604/cmes.2023.031496. [Google Scholar] [CrossRef]

104. Zhang Y, Xia Z, Jiang Y, Chen M, Liu J, Yin Q. Effect of hole density and confining pressure on mechanical behavior of porous specimens: an insight from discrete element modeling. Comput Model Eng Sci. 2020;125(1):259–80. doi:10.32604/cmes.2020.011076. [Google Scholar] [CrossRef]

105. Li M, Wu J, Li J, Zhuang L, Wang S, Zhang F. Modeling of hydraulic fracturing in polymineralic rock with a grain-based DEM coupled with a pore network model. Eng Fract Mech. 2022;275(12):108801. doi:10.1016/j.engfracmech.2022.108801. [Google Scholar] [CrossRef]

106. Zhang D, Liu Z, Song Y, Huang J, Wu B, Ranjith PG, et al. DEM simulation on the damage of sandstone with a three-dimensional embedded rough fracture with different width and inclination angle under true-triaxial stress conditions. Theor Appl Fract Mech. 2024;133(8):104528. doi:10.1016/j.tafmec.2024.104528. [Google Scholar] [CrossRef]

107. Gupta P, Duarte CA, Dhankhar A. Accuracy and robustness of stress intensity factor extraction methods for the generalized/eXtended Finite Element Method. Eng Fract Mech. 2017;179(15):120–53. doi:10.1016/j.engfracmech.2017.03.035. [Google Scholar] [CrossRef]

108. Gordeliy E, Peirce A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM. Comput Methods Appl Mech Eng. 2013;253(6):305–22. doi:10.1016/j.cma.2012.08.017. [Google Scholar] [CrossRef]

109. Cheng L, Xie Y, Luo Z, Wu L. Numerical analysis of 3D nonplanar hydraulic fracture propagation in fractured-vuggy formations using a hydromechanical coupled XFEM approach. Comput Geotech. 2024;170(5):106267. doi:10.1016/j.compgeo.2024.106267. [Google Scholar] [CrossRef]

110. Yan C, Zhao Z, Yang Y, Zheng H. A three-dimensional thermal-hydro-mechanical coupling model for simulation of fracturing driven by multiphysics. Comput Geotech. 2023;155(3):105162. doi:10.1016/j.compgeo.2022.105162. [Google Scholar] [CrossRef]

111. Cui W, Potts DM, Zdravkovic L, Gawecka KA, Tsiampousi A. Formulation and application of 3D THM-coupled zero-thickness interface elements. Comput Geotech. 2019;116(18):103204. doi:10.1016/j.compgeo.2019.103204. [Google Scholar] [CrossRef]

112. Sharafisafa M, Aliabadian Z, Sato A, Shen L. Coupled thermo-hydro-mechanical simulation of hydraulic fracturing in deep reservoirs using finite-discrete element method. Rock Mech Rock Eng. 2023;56(7):5039–75. doi:10.1007/s00603-023-03325-z. [Google Scholar] [CrossRef]

113. Wu Z, Cui W, Weng L, Liu Q. A 2D FDEM-based THM coupling scheme for modeling deformation and fracturing of the rock mass under THM effects. Comput Geotech. 2022;152:361–82. doi:10.1016/j.compgeo.2022.105019. [Google Scholar] [CrossRef]