Thermal Performance of Entropy-Optimized Tri-Hybrid Nanofluid Flow within the Context of Two Distinct Non-Newtonian Models: Application of Solar-Powered Residential Buildings

1  Introduction

In recent years, significant advancements have been made in understanding heat and mass transfer across different disciplines, including technology, engineering, and environmental science. Heat and mass transfer are the basic modes of transmission that play significant roles in the behavior of different systems in engineering, physics, and other sciences. These processes play a crucial role in understanding how energy and matter move through different media. They are fundamental to designing and optimizing applications across various fields, including mechanical systems, equipment, biological processes, and environmental phenomena. Heat transfer refers to the movement of thermal energy from one location to another, while mass transfer deals with the movement of substances between different phases [1,2]. Heat transfer occurs whenever two materials at different temperatures come into contact and continue until they reach the same temperature. There are three methods through which heat can move: conduction, convection, and radiation [3]. Every heat transfer mode is from a high-temperature material to a lower-temperature substrate, and each mode depends on the presence of a temperature differential. Any exchange of energy between bodies takes place via one or more of these mechanisms. Heat is transferred through solids or stationary fluids by conduction. Also, heat is transferred by convection, which makes use of fluid movement. A good example of radiation is solar radiation, which is the most abundant alternative energy source on Earth. Solar radiation is the electromagnetic energy emitted by the sun. It is a crucial factor for photovoltaics, solar-thermal systems, and passive solar design. The radiation from the sun is composed of three elements: direct, also referred to as beam, diffused, and reflected, also referred to as albedo. The various elements of radiation from the sun are displayed in Fig. 1 [4]. Direct radiation refers to the type of radiation that hits the Earth’s outermost layer directly. In contrast, diffuse radiation is the energy that reaches the surface after being scattered by the Earth’s atmosphere, altering its path [5]. Diffuse radiation is influenced by the quantity of molecules, contaminants, or clouds present in the atmosphere. The portion of solar energy that is reflected off the surface of the Earth is known as reflected radiation. The reflected radiation is highly dependent on the surface’s structure and state. The total solar radiation value is a combination of the solar radiation that is reflected, diffused, and direct [6–8].

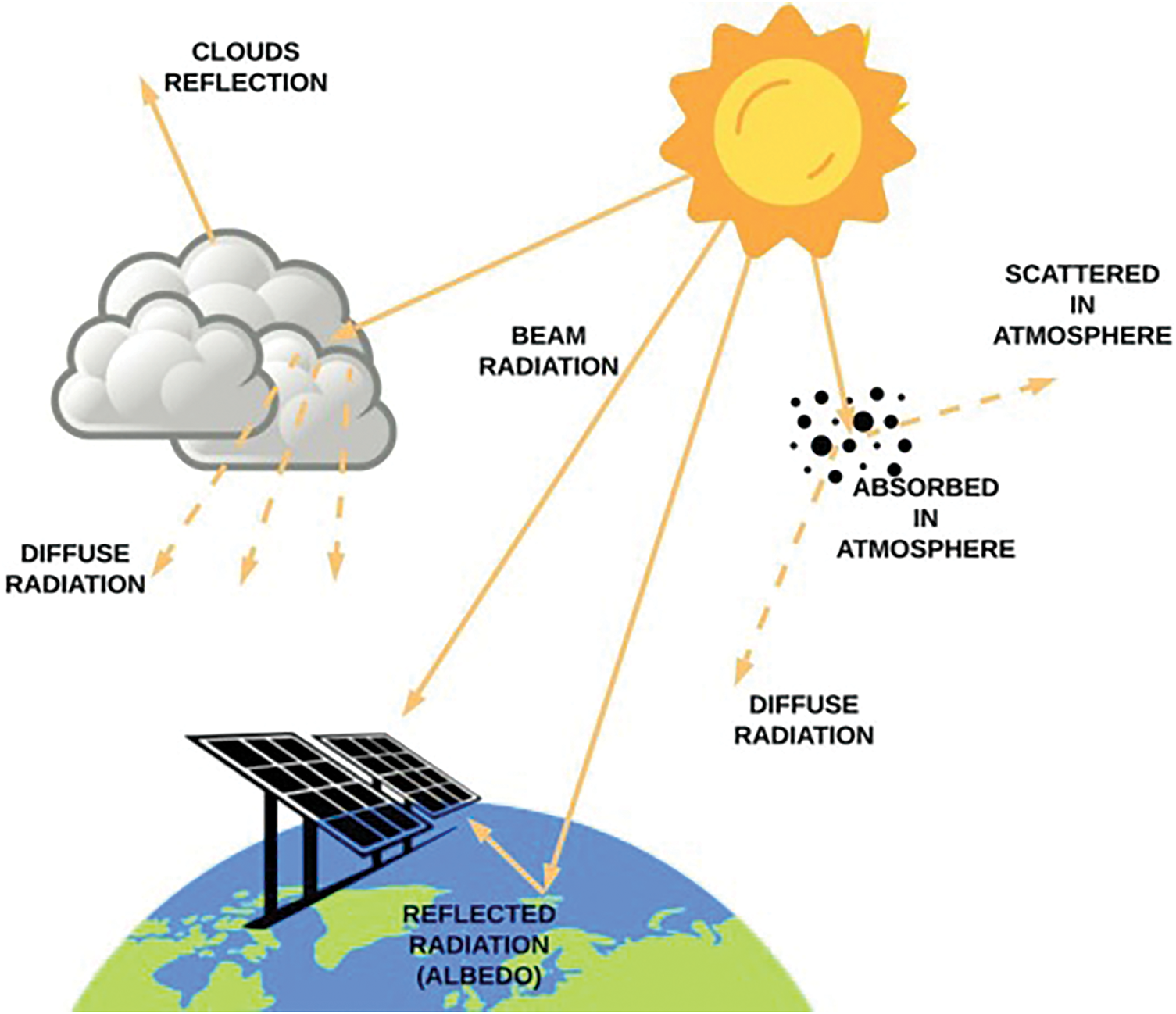
Figure 1: Components of solar radiation and its transmission method

Parabolic trough collectors (PTSC) are a kind of solar energy collector that comprises mirrors, which are coated silver or polished aluminum [9]. To reduce heat loss, a glass tube will be placed around the reception tube. Also, to capture the maximum amount of solar energy, the trough collectors can be rotated using a sun monitoring system and aligned along a north-south axis. Alternatively, they can also be positioned in an east-west direction without a sun monitoring device, as this orientation only needs to be adjusted periodically for less efficient alignment. Additionally, nanofluids are used in the reception tube of a Parabolic Trough Solar Collector (PTSC) as a synthetic oil to enhance heat absorption.

Tri-Hybrid Nanofluids (THNF) have emerged as a promising advancement in thermal management and energy systems due to their enhanced thermophysical properties and improved heat transfer capabilities. These fluids, consisting of three distinct nanoparticles dispersed in a base fluid, offer synergistic effects that surpass traditional mono and binary nanofluids. Over the past decade, significant efforts have been directed toward understanding and optimizing the behavior of THNF through theoretical analyses, experimental investigations, and computational simulations. THNF is a recently developed class of nanofluids created by suspending three different types of nanoparticles in a base liquid [10]. These advanced fluids are specifically engineered to optimize heat and mass transfer, outperforming traditional fluids in efficiency. THNF consist of three key components: a base fluid, nanoparticles, and surfactants. The synergistic interaction among these components significantly enhances thermophysical properties, including thermal conductivity, density, viscosity, and specific heat capacity [11]. The innovation of THNF has led to several potentials for heat transfer applications mainly in environmentally sensitive areas which include energy sectors, electronics appliances, and biomedical equipment. Recent studies on ternary nanofluids focus more on the interactions between the particles, base fluid, nanoparticles, and their concentrations. These fluids have been found to offer better thermal conductivity, making them ideal for next-generation heating and cooling applications. A laboratory investigation on ternary hybrid nanofluids, composed of water mixed with nanoparticles of aluminum oxide, copper oxide, and titanium oxide, was carried out by Sahoo et al. [12]. The impact of concentration and temperature on the THNF of dynamical viscosity was considered. According to the experimental results, the dynamic viscosity decreases with rising temperatures and increases with increasing solid volume fractions. Also, their work investigates how solar light and variable characteristics affect THNF flow and the impact of double diffusion. Several authors worldwide have recently studied hybrid nanofluids in many different scenarios. Cao et al. [13] investigated ternary hybrid nanofluid flows caused by force convection, free convection, and mixed convection to better understand the effects of non-linear thermal radiation and partial slip situations. Their results demonstrated that, while friction at the wall diminishes with partial slip, the lowest decreasing rate occurs at greater buoyancy force levels when free convection is responsible for inducing the transport phenomena. Further, Sarfraz et al. [14] solved the ternary hybrid nanofluid (silica, copper and cadmium selenide quantum dots) with ethanol-base fluid for the cases of Hiemenz (planar) and Homann (axisymmetric) flows normal to the stagnation point. Besides, the influence of a magnetic dipole in conjunction with nonlinear thermal radiation on a tri-hybrid nano-liquid was studied by Nasir et al. [15]. Using Mathematica software, the transformed issue was solved using the homotopy analysis approach. The outcome showed that while the temperature distribution is improved, the flow velocity is decreased when the volume fraction parameter is increased. Heat gain and loss on a flow of tri-hybrid nanofluids with magnetic flux and convective heating were examined by Animasaun et al. [16]. Using a finite difference approach, the three phases of the Labatto Illa integration formula were used to numerically solve the resolved governing equation. According to analysis, for both the heat acquisition and loss scenarios taken into consideration, the convective heating parameter is an increasing function of the temperature distribution. Some of the important participants are. Arif et al. [17] examined the application and thermal analysis of platelet-shaped grapheme, cylindrical carbon nanotubes, and spherical aluminium oxide dissolved in water. Numerical analysis of the study was performed using the computer program MATHCAD. According to the author’s results, the rate of heat transfer may be increased by up to 33.67% by utilizing water-based tri-hybrid nanofluids. Very recent, Usafzai et al. [18] found multiple algebraic-type solutions with the addition of injection parameter, and surprisingly, single solution with the consideration of suction parameter. Another numerical studies on ternary hybrid nanofluids were conducted by [19,20], Jamrus et al. [21,22] Mahmood et al. [23–25], Ouyang et al. [26] and Hussein et al. [27].

Non-Newtonian fluids are unique because their viscosity does not remain constant but changes depending on the shear stress or force applied. In contrast, Newtonian fluids maintain a consistent viscosity regardless of shear rate. This dynamic flow behavior allows non-Newtonian fluids to respond differently under varying conditions of force or pressure. These fluids play a crucial role in industries such as chemical engineering, pharmaceuticals, food production, cosmetics, and biomedical engineering. Common examples include ketchup, toothpaste, blood, paints, and polymer solutions. Their distinctive flow properties make them ideal for applications requiring precise control over fluid movement [28]. Non-Newtonian fluids can be tailored to meet specific application needs based on their unique flow properties. For example, shear-thinning fluids experience a decrease in viscosity when stress is applied, making them easier to pump and spread. This property is particularly useful in products like coatings and adhesives. In contrast, shear-thickening fluids become more viscous or denser under stress, which makes them ideal for applications such as protective gear and impact-resistant materials. Additionally, in many applications, the use of non-Newtonian fluids helps reduce energy consumption, enhancing efficiency in industrial processes. For instance, in some fluids, where the property known as steady shear thinning is manifested, the resistance in pumping is reduced, hence; energy consumption in transportation and processing systems. The Maxwell–Cross is one of the rheological models employed to determine the flow characteristic of non-Newtonian fluids. It is especially applicable in polymers biological fluids, and other industries’ fluids where viscosity is not a constant value, but it depends on the rate of shear.

1.1 Problem Statement

The rising demand for sustainable and efficient energy solutions has led to extensive research on nanofluids, particularly with solar energy systems. The effectiveness of traditional nanofluids in enhancing thermal conductivity and thermal energy storage is still limited by factors such as irreversible processes and heat loss. These issues ultimately reduce the efficiency of thermal systems. Optimizing all these factors is challenging, but tri-hybrid nanofluids have been introduced as a solution. This approach enhances the properties of the nanoparticles by combining the characteristics of the various materials. Although the roles of these nanoparticles, thermal radiation, and the process of irreversibility are important, research in this area has been limited, particularly regarding the sustainable use of solar energy in residential buildings.

1.2 Novelty of the Newly Proposed Model

This research aims to examine the entropy generation and heat transport in a tri-hybrid radiative binary nanofluid. The focus is on its potential applications in renewable energy systems for residential buildings. Furthermore, we study the thermophysical characteristics, Cattaneo–Christov heat fluxing, thermal radiation mechanism, and overall performance of the nanofluid in improving energy systems. The comparative investigation of Cu-TiO2-Ag/Ethylene Glycol tri-hybrid nanofluid and Cu-TiO2/Ethylene Glycol hybrid nanofluid on velocity and temperature boundary layer is considered. The present work also examines the double diffusion phenomenon to enhance thermal conductivity and improve the fluid’s heat transfer properties. Furthermore, the investigation compares how various parameters affect irreversibility and energy conversion mechanisms. The non-linear ODEs with boundary conditions are solved using the Galerkin-weighted residual method with the assistance of MATHEMATICA 11.3 software.

2  The Operation of Shingles Powered by Solar Energy

2.1 Solar Shingles

Harnessing solar energy is achieved through a highly effective method known as solar radiation. Solar shingles have photovoltaic cells on their surface that harvest energy from the sun directly. Below these cells, a nanofluid comprising tri-hybrid nanoparticles circulates through the solar tiles’ stretched sheet. It is a nanofluid that flows over the stretching plate that is placed below the PV cells. Solar radiation that passes through the photovoltaic panel reaches the stretched surface. As such, the solar panel acquires more heat through the integration of these tri-hybrid nanoparticles in the solar panel sheet.

2.2 Power Supply Regulator

A charge controller is employed alongside the battery to manage the voltage and current supplied by the solar panel, thereby safeguarding the battery from overcharging and ensuring its stability. Additionally, the inclusion of maximum power point tracking enables the battery to be charged up to 30% more quickly each day using the solar panel. This device functions with a capacity of 15 A/200 W.

2.3 Solar Inverter

An inverter is a device that transforms direct current (DC) power which is produced by solar panels or solar tiles into alternating current (AC) power which could be used by home appliances. This makes the inverter one of the essential elements of a solar power system. In a residential solar power system, a converter usually performs multiple functions simultaneously. It serves as a host that can connect to other networks and also oversees the whole system and at the same time convert solar power into AC electricity. The capacity of the devices powered by solar energy and battery storage to run during a power outage without the grid intervention is due to the application of advanced inverters as shown in Fig. 2.

Figure 2: The mechanism for harnessing solar energy involves the use of solar shingles

2.4 Batteries Equipped with Devices

Solar shingles harvest energy from the sun and convert it to electricity, this electricity is stored in inbuilt batteries thus no need for fuel. These batteries have the ability to store energy which enables them to discharge or supply power when needed. The photovoltaic technology that is used in the system is responsible for the collection of the solar energy that is used to provide electricity which is stored in the batteries. It shows that when the electrical system of the homes is charged during the day when exposed to sun the chances of developing problems at night are minimized. This stored energy enables the following applications: power residential living, garden or any outside space, garage use, security lighting, etc.

3  Mathematical Formulation

The mathematical analysis investigates the flow of a two-dimensional, incompressible, laminar binary fluid over a surface that is expanding. The expansion of the surface is characterized by the equation uw=ax, where a is a positive constant, indicating the rate at which the surface is expanding. The nanoparticles Cu (Copper), TiO2 (Titanium Dioxide), and Ag (Silver) are immersed in base fluid EG (Ethylene Glycol) resulting in tri-hybrid nanofluid (THNF) (Cu + TiO2 + Ag/Ethylene Glycol). As illustrated in Fig. 3, the stretching sheet is positioned below the photovoltaic sheet of the solar shingles, and the THNF flows over the stretching sheet. The Soret effects are explored to understand the impact of temperature variations on concentration and how concentration changes, in turn, affect temperature. Additionally, fluid flow through porous media is examined using Darcy’s law, with attention to the permeability of the medium. The Eqs. (2)–(5) are derived using the Navier-Stokes equations, the second law of thermodynamics, and Fick’s second law concerning diffusion processes.

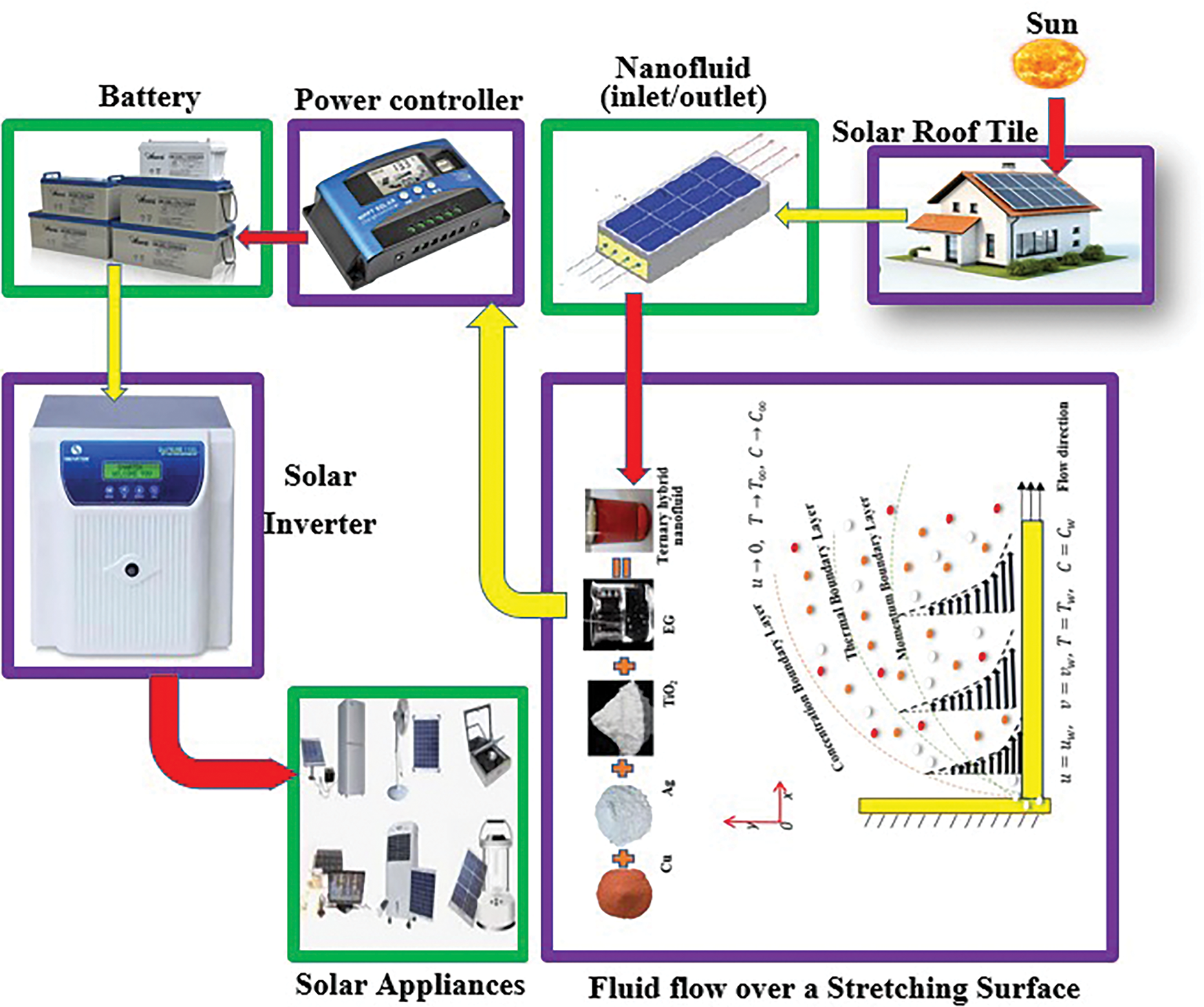
Figure 3: Fluid configuration

The temperature-based heat conduction is defined as:

k[3]nf(T)=k[3]nf[1+ε(T−T∞Tw−T∞)].(1)

Taking into account the previously mentioned assumptions, the expression that describes the tri-hybrid radiative binary nanofluid and double diffusion can be formulated as follows:

∂u∂x+∂v∂y=0,(2)

u∂u∂x+v∂u∂y+λ1(u2∂2u∂x2+v2∂2u∂y2+2uv∂2u∂x∂y)=μ[3]nfρ[3]nf∂∂y[∂u∂y1+(Γ(∂u∂y))n]−v[3]nfK1u−1ρ[3]nfFu2,(3)

(u∂∂x+v∂∂y)T=1(ρcp)[3]nf[∂∂y[k[3]nf(T)]∂T∂y]+τ[DB∂C∂y∂T∂y+DTT∞(∂T∂y)2]+DBKTcpCs∂2C∂y2−1(ρcp)[3]nf∂qr∂y,(4)

(u∂∂x+v∂∂y)C=DB∂2C∂y2+DTT∞∂2T∂y2+DCT∂2T∂y2,(5)

u=uwx,v=vw,T=Tw,C=Cw at y=0,u→0,T→T∞,,C→C∞ as y→∞.}.(6)

The description and symbols used in governing equations are listed below:

3.1 Mathematical Relations for Thermophysical Properties

The values for the thermo-physical properties can be found in Table 1 [19]. The theoretical details of the preparation and synthesis process for the THNF are illustrated in Fig. 4.

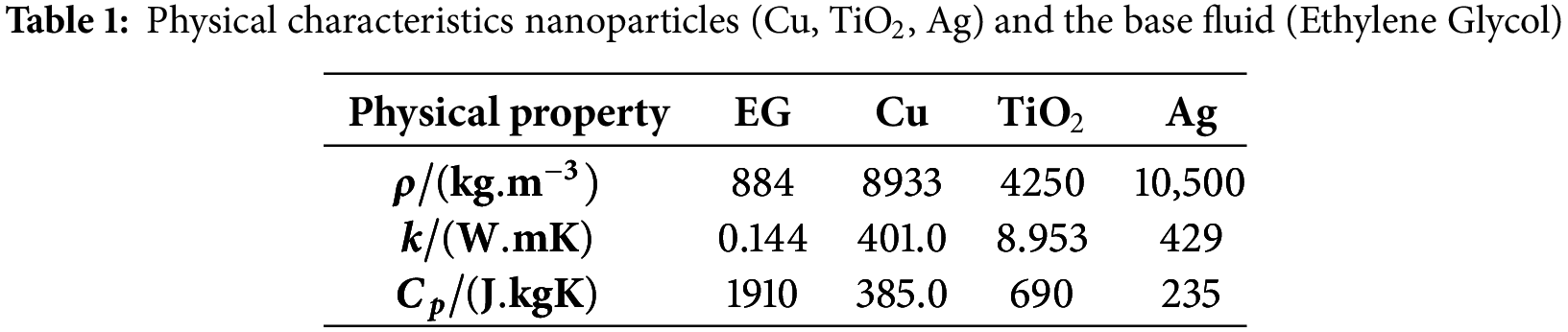
Figure 4: Theoretical depiction of the setup used for the preparation and synthesis of THNF

Here are the meanings and roles of the nanoparticles specifically related to solar power systems are defined below:

EG (Ethylene Glycol): Ethylene glycol refers to an organic compound that is mostly being used as a basis fluid in solar power systems. In solar power applications, EG is useful when combined with nanoparticles, as it serves as a heat transfer medium. This combination enhances the fluid’s ability to collect and transport heat in solar collectors, ultimately improving the efficiency of solar thermal systems.

Copper: Copper is one of the best conductors of heat and electricity among all the metals. Copper nanoparticles improve solar power systems by enhancing the thermal conductivity of the fluid used in them. When these nanoparticles are added to a base fluid, specifically ethylene glycol (EG), they increase the heat transfer rate in solar collectors. This leads to a better ability to collect and convert solar energy into usable thermal energy.

TiO2 (Titanium Dioxide): Titanium dioxide (TiO2) is a white crystalline compound that has a high refractive index and strong absorption of ultraviolet light. TiO2 nanoparticles are used in solar energy technology, particularly in photocatalytic processes. They help improve the ability of solar cells to absorb light and increase overall energy conversion efficiency. Additionally, TiO2 nanoparticles can be employed for surface functionalization to enhance light trapping in photovoltaic applications.

Ag (Silver): Silver (Ag) is a well-known precious metal, recognized for its excellent electrical and thermal conductivity. Silver nanoparticles are utilized in solar power systems to improve heat transfer and the efficiency of solar collectors. In photovoltaic (PV) cells, these nanoparticles enhance electrical conductivity and light absorption, leading to better conversion of solar energy. Additionally, silver nanoparticles can be included in coatings to reduce radiation losses and overall increase the efficiency of solar panels. The variable properties for Tri-hybrid nanofluid are listed below:

Dynamic viscosity:

μ[3]nf=μf(1−ϕ1)2.5(1−ϕ2)2.5(1−ϕ3)2.5.

Density:

ρ[3]nf=ρf{(1−ϕ1)[(1−ϕ2)(1−ϕ3)[(1−ϕ4)+ϕ4ρ4ρf]+ϕ3ρ3ρf+ϕ2ρ2ρf]+ϕ1ρ1ρf}.

Thermal conductance:

k[3]nfkf=k3+2k[2]nf−2ϕ3(k[2]nf−k3)ks+2k[2]nf+ϕ3(k[2]nf−k3),

k[2]nfkf=k2+2k[1]nf−2ϕ2(k[1]nf−k2)k2+2k[1]nf+ϕ2(k[1]nf−k2),

k[1]nfkf=k1+2kf−2ϕ1(kf−k1)k1+2kf+ϕ1(kf−k1).

Specific heat:

(ρcp)[3]nf=(1−ϕ3)(1−ϕ2){(1−ϕ1)(ρCp)f+(ρCp)s1ϕ1}+(ρCp)s2ϕ2+(ρCp)s3ϕ3.

3.2 Similarity Transformations

The following similarity transformations are:

χ=avy,Θ=T−T∞Tw−T∞,(7)

ψ=avxp(χ),φ=C−C∞Cw−C∞.

The governing equations mentioned above have been simplified to:

[(1−(n−1)(Wep″)n)]p″′+Z1Z2(1+(Wep″)n)2(pp″−p′2−Frp′2)−ΛZ1Z2(p2p″′−2pp′p″)−λp′=0,(8)

((1+εΘ)+43Z4Nr)Θ′′+εΘ′2+Z4Pr(NbΘ′φ′+NtΘ′2)+Z3Pr(Dp″+pΘ′)=0,(9)

φ″+NtNbΘ″+Scpφ′+ScSrΘ″=0.(10)

The simplified BCs are as follows:

p′(χ)=1,p(χ)=0,Θ(χ)=1,φ(χ)=1, at χ=0,p′(χ)→0,Θ(χ)→0,φ(χ)→0, as χ→∞.}.(11)

3.3 The Interest Physical Quantities

The physical quantities Cf and Nux are described as:

Cf=2τwρfuw2,(12)

and

Nux=xqwkf(Tw−T∞),

CfRex12=1Z1(p″1+(Wep″)n+(1+Λ)p″),(13)

NuxRex−1/2=−Z4Θ′.

here

shear stresses τwc=μ[3]nf[∂u∂y[11+(Γ∂u∂y)n]+(1+Λ)∂u∂y], heat flux qw=−k[3]nf∂T∂y,

Soret number Sr=DCT(TWT∞)DSM(CWC∞), Maxwell parameter Λ=λ1a, λ=caK1 porosity,

Dufour number D=DTC(CwC∞)v(TwT∞), Prandtl number Pr=μCpK∗. Weissenberg number we=aΓRex1/2, Radiation parameter Nr=16σT∞33k∗K∞, Brownian motion parameter Nb=τDB(Cw−C∞)νf, Thermophoresis parameter Nt=τDT(Tw−T∞)νfT∞, Schmidt number Sc=νfDB, Local Reynolds number Rex=Uwxνf, Forchheimer parameter Fr=aF,

Z1=1(1−ϕ1)2.5(1−ϕ2)2.5(1−ϕ3)2.5,

Z2=(1−ϕ1)[(1−ϕ2)(1−ϕ3)+ϕ3ρ3ϕf+ϕ2ρ2ϕf]+ϕ1ρ1ϕf,

Z3=(1−ϕ1)(1−ϕ2){(1−ϕ3)+(ρCp)s3(ρCp)fϕ3+(ρCp)s2(ρCp)fϕ2}+(ρCp)s1(ρCp)fϕ1,

Z4=k[3]nfkf.

4  Minimization of Entropy Generation (NS)

In fluid dynamics, entropy is a technique to measure how much energy is lost or wasted. This energy loss occurs due to factors like friction, heat conduction, and turbulence. via reducing the generation of entropy, scientist can improve the efficiency of heat exchange in systems like cooling and thermal management. For a fluid system, the production of entropy can be stated as:

Sg=kfT∞2[k[3]nfkg+16σ∗3k∗kf(∂T∂y]2]+μ[3]nfT∞(∂u∂y)2[11+(Γ∂u∂y)n]+μ[3]nfKT∞u2+(NrC∞(∂C∂y)2+NrT∞(∂C∂y)(∂T∂y))(14)

NG=Sgkf/x2ΩT2.(15)

Using the nondimensional formulation, the (Ns) is characterized by

(Z4+Nr)Θ′2+(BrZ1ΩT)(1+1(Wep″)n)p″2+(BrΩT)kZ1kP′2+Θ′φ′+GΩCΩTφ′2,(16)

here

Br=μfue2kf(Tw−T∞),ΩC=(Cw−C∞)C∞, ΩT=(Tw−T∞)T∞,Rex=uexvf.

The Bejan number (Be) is mathematically expressed as:

Be=(Z4+Nr)Θ′2ΩT(Z4+Nr)+(BrZ1ΩT)(1+1(Wep″)n)p″2+(BrΩT)kZ1kp′2+GΘ′φ′+GΩcΩTφ′2.(17)

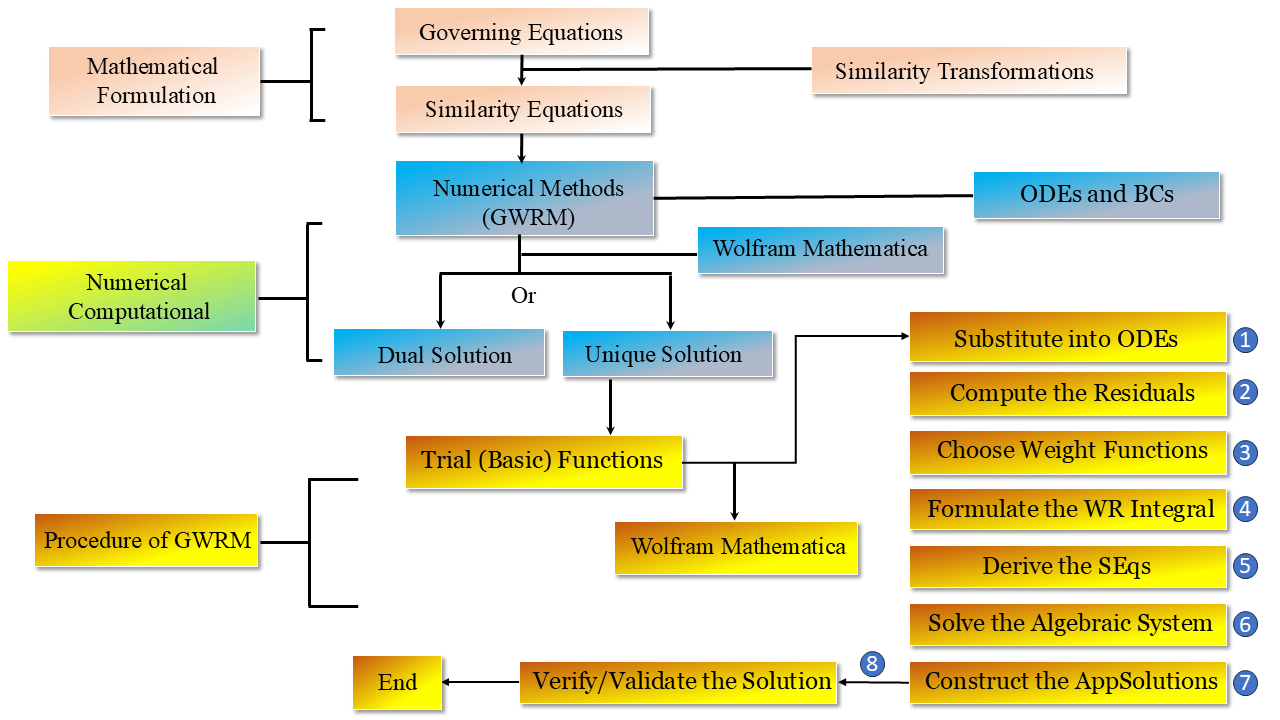
5  Application of Galerkin-Weighted Residual Method

Weighted residuals are used in a numerical method known as the Galerkin-weighted residual approach to solve PDEs. When it comes to tackling BC problems that other numerical schemes would find challenging, this one work fairly well. The critical stages of the GWRM are as follows: The first step is to look at Eqs. (8) through (10). In Step 2, the Galerkin-weighted residual technique simulates the numerical outcome of the equations using a trail function, which can be expressed as:

p~(χ)=q∗0+q∗1e−χ3+q∗2e−2χ3+q∗3e−2χ+…+q∗ne−nχ3=∑j=0nq∗je−jχ3,(18)

Θ~(χ)=r∗0+r∗1e−χ3+r∗2e−2χ3+r∗3e−2χ…+r∗ne−nχ3=∑j=0nr∗je−jχ3,(19)

φ~(χ)=s∗0+s∗1e−χ3+s∗2e−2χ3+s∗3e−2χ…+s∗ne−nχ3=∑j=0ns∗je−jχ3.(20)

Step 1 method and the reduced trial solutions are used in the fourth stage to construct residual vectors for temperature and velocity.

(ddη∑j=0nq∗je−jχ3−1)χ=0=0,(∑j=0nq∗je−jχ3)χ=0=0,(∑j=0nr∗je−jχ3−1)χ=0=0,(∑j=0ns∗je−jχ3−1)χ=0=0,(∑j=0nq∗je−jχ3−1)χ=0=0.(21)

In the third step of the procedure, the boundary conditions of Eq. (12) and the BCs for the issue are checked using the GWRM trial solutions. These are the following:

Rp=[(1−(n−1)(Wep~″)n)]p~′″+Z1Z2(1+(Wep~″)n)2(p~p~″−p~′2−Frp~′2)−ΛZ1Z2(p~2p~″′−2p~p~′p~″)−λp~′≅0,(22)

RΘ=((1+εΘ~)+43Z4Nr)Θ~″+εΘ~′2+Z4Pr(NbΘ~′φ~′+NtΘ~′2)+Z3Pr(Dp~″+p~Θ~′)≅0,(23)

Rφ=φ~″+NtNbΘ~″+Scpφ~′+ScSrΘ~″≅0.(24)

To examine the constants, step five indicates that the residual must be zero throughout the subsequent domain:

∫0∞Rpe−jχ3dχ≈∑k=1j[Ak(eχRpe−jχ3)χ=xk]=0,∫0∞RΘe−jχ3dχ≈(25)

∑k=1j[Ak(eχRΘe−jχ3)χ=xk]=0,∫0∞Rφe−jχ3dχ≈∑k=1j[Ak(eχRφe−jχ3)χ=xk]=0,Forj=0,1,2,…,N−2,l=0,12,…,N−2tozero,(26)

Ak=1Lj′(xk)∫0∞Lj(x)e−xx−xkdx=(j!)2xk(Lj′(xk))2,Lj=exdjdxj(e−xxj).(27)

To minimize the residual errors, the weight functions Rpe−jχ3, RΘe−jχ3, Rφe−jχ3 and residues product were integrated. The flow chart for the GWRM system is shown in Fig. 5.

Figure 5: The GWRM flow chart

6  Results and Discussion

This research focuses on studying the effects of double diffusion, Maxwell fluid behavior, solar radiation mechanisms, and porous media on a stretching sheet. Additionally, it examines the influences of Soret and Dufour effects in a tri-hybrid radiative binary nanofluid system. Also, three several kinds of nanoparticles Cu-TiO2-Ag with base fluid Ethylene Glycol (EG) are employed. In this section, each figure includes these two distinct sets of curves. The first set of curves represents the Cu-TiO2-Ag/EG tri-hybrid nanofluid is depicted in red whereas the second set displays the Cu-TiO2/EG hybrid nanofluid with a dashing black color. Table 2 exhibits how the Nux responds to the controlling operational variable.

Weissenberg number (We): We is a dimensionless number used in the scientific field of fluid dynamics to quantitatively express the relative proportions of elastic forces and viscous forces in a viscoelastic fluid. it can be described as the product of the characteristic time of the fluid which is usually the relaxation time and the characteristic shear rate. As displayed in Fig. 6, with growing of the We, the material becomes more and more elastic, in other words, the liquid resists deformation and stores energy like a solid and not like a viscous fluid. Thus, at a higher We, the fluid can be more elastic. The fluid was observed to store elastic energy each time it was subjected to shear, and this acted as a barrier against further deformation hence the slowdown of the p′(χ). Physically, in solar energy applications, the Weissenberg number is a critical parameter in defining the behavior of non-Newtonian fluids. It is therefore possible to control the Weissenberg number and in turn control the p′(χ), heat transfer rates the systems thus improving the efficiency of the solar energy systems. The use of elasticity together reform of solar energy is as vital in the operations of solar thermal collectors, heat storage systems desalination, and energy harvesting.

Figure 6: Effect of We on p′(χ)

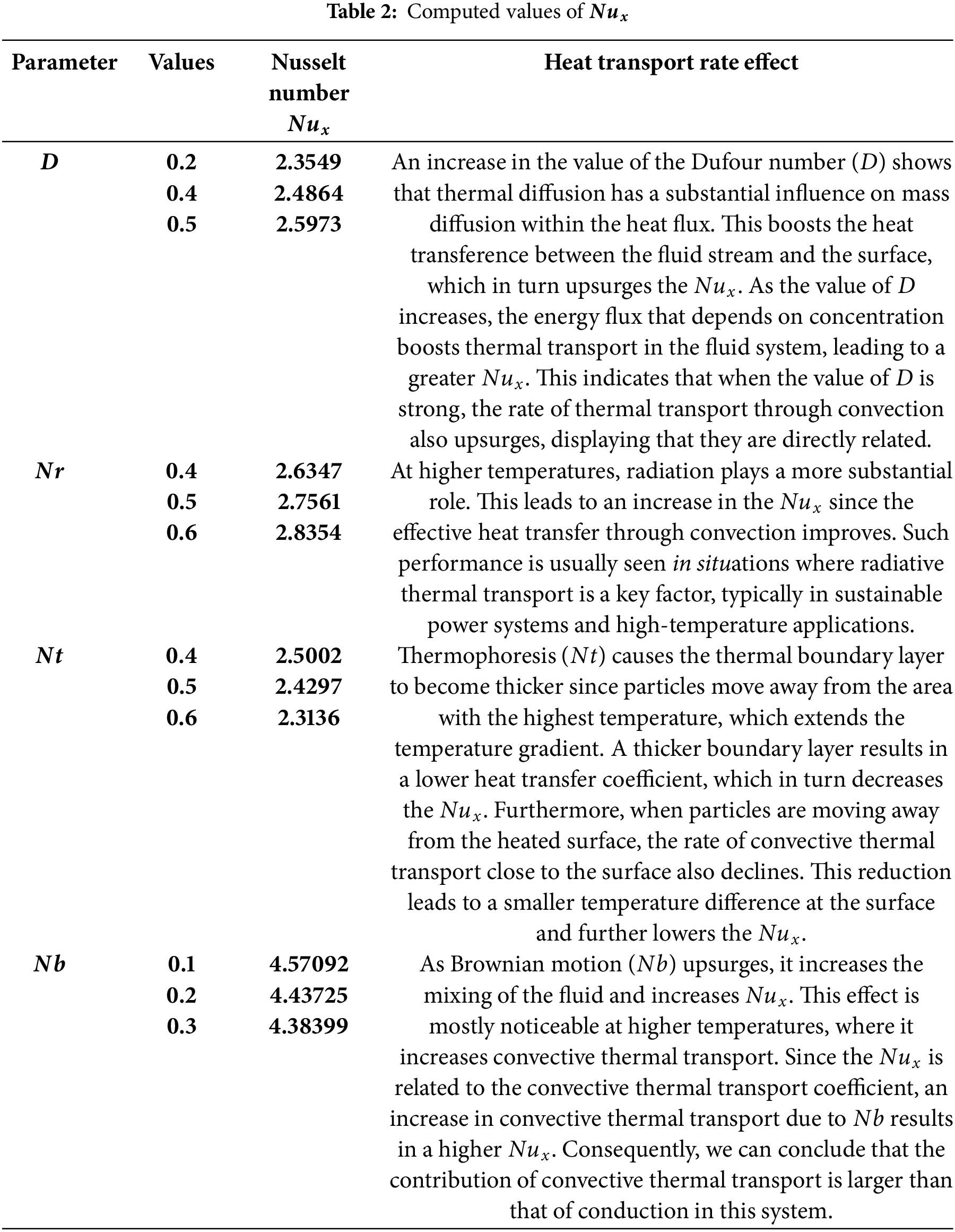
Forchheimer number (Fr): The Fr is a measure of the relative importance of the inertial effects in a porous media flow. It is the ratio of two important dimensionless groups of the fluid flow, inertial forces, and viscous forces. Fr has a property for which an increase in its value implies that inertial factors are playing a role in the flow through the porous media. It means that there has to be an added resistance to the flow of the fluid as has been described by Darcy’s law. Thus, the pressure drop for the whole porous area increases and so the velocity of the fluid reduces this performance is displayed in Fig. 7. Physically, optimizing thermal management can be achieved by designing the flow of coolant through a porous medium located beneath the photovoltaic (PV) cells in hybrid solar energy systems that integrate photovoltaic cells with thermal absorbers, known as PVT systems. Controlling the Forchheimer number ensures that the coolant flows at the right speed to reduce heat and prevent high pressure.

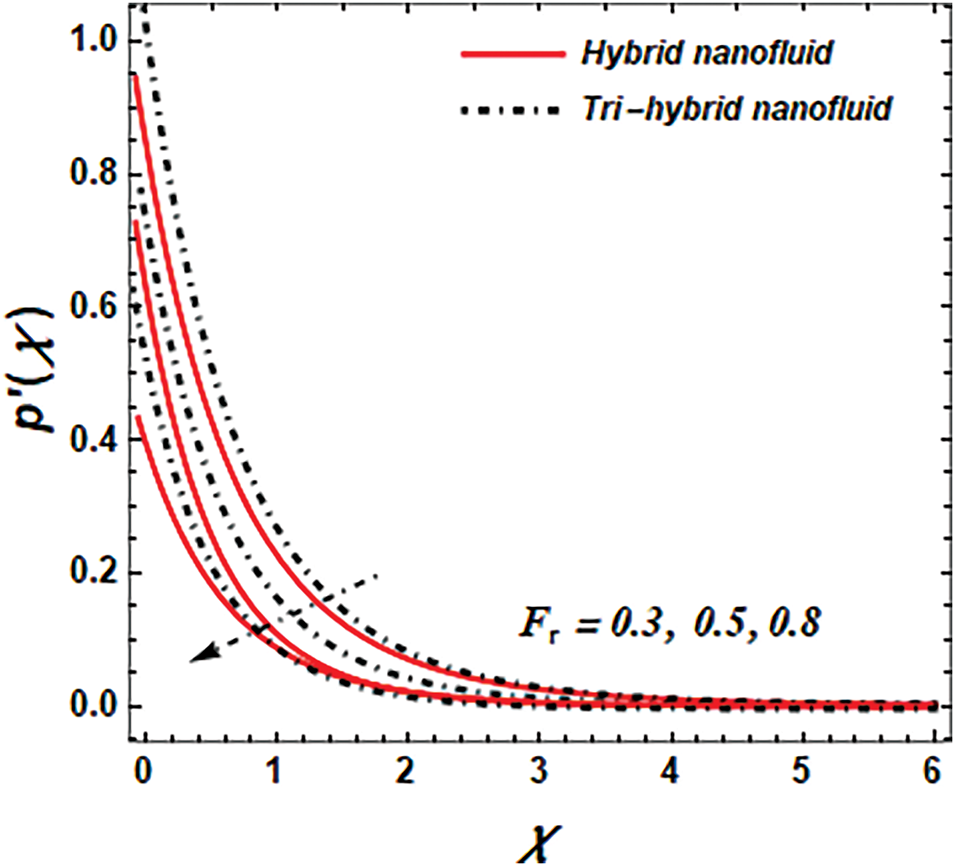
Figure 7: Effect of Fr on p′(χ)

Power index (n): The power index is usually employed to describe the flow behavior of non-Newtonian fluid (NNF). The NNF power law model is the connection between shear rate and shear stress. If n is less than 1, the fluid is shearing thinning, here the viscosity of the fluid reduces with the increase in shear rate. When n is larger than 1, the fluid exhibits a behavior known as shear thickening, where its viscosity increases as the shear rate increases. This results in reduced flow velocities because, as the shear rate rises, the fluid resists flow more strongly. But when n is equal to 1, it is referred to as Newtonian fluid or the fluid in which viscosity is the same whether high or low shear rate. For shear-thickening fluids, when the power index (n) is greater than one, a higher power index results in greater resistance to deformation. This behavior is displayed in Fig. 8.

Figure 8: Effect of Fr on p′(χ)

Porosity parameter (λ): Fig. 9 shows the impact of the λ on fluid flow. When fluid moves through a porous medium, it encounters resistance because of the pores that create obstacles in its path. The fluid is required to flow in the proximity of solid bodies hence there are shear losses. As the λ parameter reduces this resistance improves and slows down the p′(χ). When fluid flows through a porous medium, the presence of pores negatively affects its movement. As the fluid moves through solid materials, it encounters resistance, which leads to energy losses due to friction. In solar energy systems, especially in solar collectors, heat transfer enhancement of porous structure is usually employed. For instance, in solar thermal collectors, porous absorbers or heat exchangers can effectively capture and transfer significant amounts of heat due to their large surface area.

Figure 9: Effect of λon p′(χ)

Thermal radiation (Nr): The thermal radiation parameter is effective in thermal transport processes involving radiation. It determines the impact of thermal radiation in the transfer of energy in a fluid material with an increase in the Nr parameter, the temperature distribution becomes higher (see Fig. 10). Higher Nr parameter values indicate a stronger radiation effect, which leads to more energy being exchanged through radiation. This, in turn, causes an increase in the temperature of the medium. In solar thermal collectors, nanofluids contain nanoparticles and it used as working fluids to improve thermal performances. The enhancement in thermal radiation parameters as a result of solar radiation is said to raise the temperature of the nanofluid hence enhancing the ability of the solar collector to collect heat from the sun.

Figure 10: Effect of Nr on Θ(χ)

Thermophoresis diffusion (Nt): Thermophoresis diffusion Nt is a phenomenon of migration of particles within a fluid as a result of applied temperature difference. Fig. 11 displays the outcome of the Nt influence on the Θ(χ). The Nt parameter characterizes this effect and represents how strongly particles are moved from one temperature region to another. As the value of the Nt parameter rises, then the particles are further driven by the temperature gradient. This leads to an increase in the concentration of particles in cooler zones as well as a decrease in the concentration of the particles in the warmer zones. Therefore, the temperature in the heated region increases in intensity due to the reduced cooling effect of particles, which is caused by their lower concentration.

Figure 11: Effect of Nt on Θ(χ)

Brownian diffusion parameter (Nb): In dynamics of nanofluids especially in heat and mass transfer, the Nb is a factor of great importance. Fig. 12 shows the outcome of the Nb effect on the Θ(χ). It was observed that the Nb increases the Θ(χ). Greater value of Nb indicates that nanoparticles will be more active and will be moving more in the fluid system. The rate of the nanofluid improves as a result of improved thermal conductivity, which is enhanced by an increased rate of conduction. To enhance heat absorption and transfer, nanofluids are utilized in solar thermal collectors. An increased value of Nb contributes to an improvement in the thermal conduction of the nanofluid and, therefore, heat absorption from sunlight and efficient conversion to a storage system or the direct heating fluid.

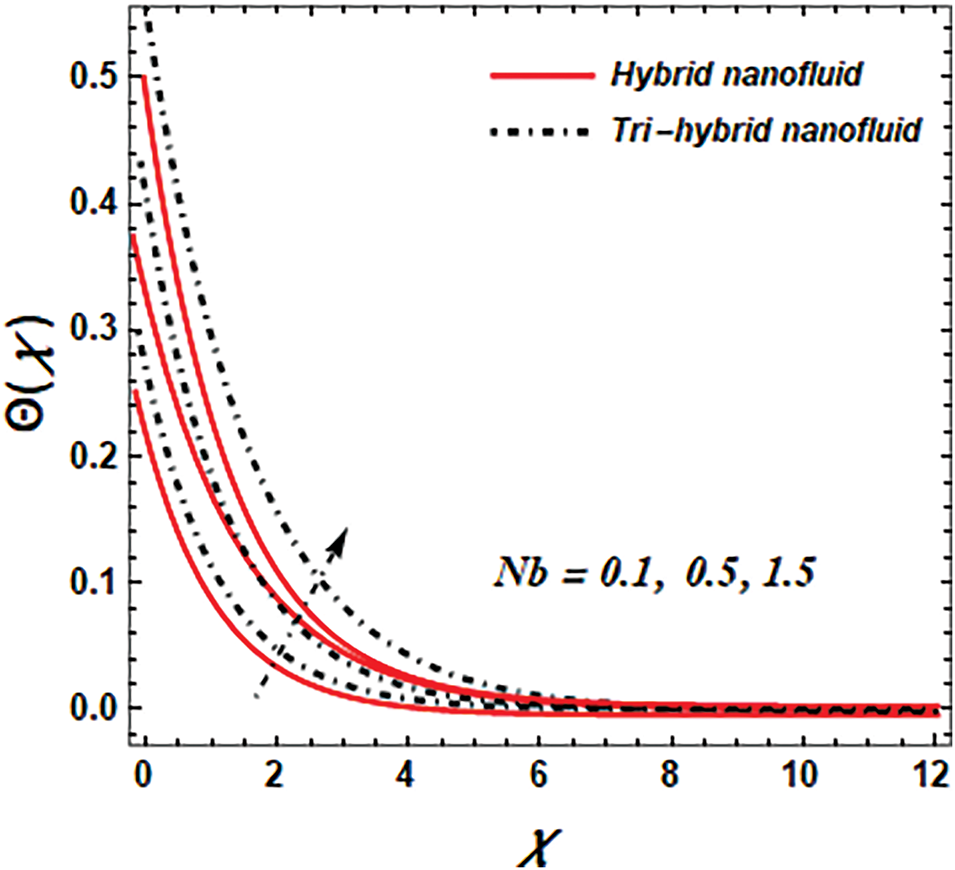
Figure 12: Effect of Nb on Θ(χ)

Dufour number (D) and thermal conductivity (ε): The Dufour number (D) is a non-dimensional quantity that expresses how concentration differences influence thermal transport as a result of the thermos diffusion, also identified as the Soret effect. The effect of Dufour number (D) on Θ(χ) is displayed in Fig. 13. As the value of D rises, the relationship between the concentration field and the temperature field becomes stronger. This leads to higher energy transport within the fluid system through heat exchange by mass diffusion, compared to convection and radiation. This enhanced flow of energy transfer raises the temperature of the fluid, resulting in a greater Θ(χ). In other words, with a higher value of Dufour number, there will be a higher amount of heat in the regions of high concentration gradients making the temperature of those regions high. Physically, when particles move from areas of high concentration to areas of low concentration, the thermal field’s effect causes an increase in local temperature. This is especially true in systems where thermos diffusion is active. Furthermore, it was observed in Fig. 14, that the effect of thermal conductivity reduces the Θ(χ).

Figure 13: Outcome of D on Θ(χ)

Figure 14: Impact of ε on Θ(χ)

Schmidt and Soret numbers (Sc, Sr): Figs. 15 and 16 indicate the effect of Schmidt and Soret numbers on the concentration profile. A positive fluctuation in Sc and Sr increases the concentration of the liquid. Soret number or temperature-diffusion number (Sr) is a dimensionless number that characterizes the influence of a temperature gradient on the diffusion of mass in a fluid mixture. Soret number is defined as the ratio of gradient force acting on the temperature gradient, which induces the transport of species from a high temperature to a low temperature. As displayed in Figs. 15 and 16, the density of the boundary layer increases as the Schmidt number and Soret number are raised, respectively. The rapid diffusion of the mass arises when the magnification in Schmidt number is increased. The concentration is closely associated with mass, and an increase in Schmidt number results in a positive change in mass profile. As the Soret number increases, the rate of mass transmission also upsurges.

Figure 15: Effect of Sc on concentration profile

Figure 16: Impact of Sr on concentration profile

Reynolds number (Re): Fig. 17 shows the influences of Reynolds number (Re) on the entropy production. The flow regime in a fluid system is characterized by the (Re), which is a dimensionless quantity generally employed in fluid mechanics to differentiate between laminar and turbulent flow. Greater values of Re, viscous effects are added and help in the dissipation of the liquid. All this dissipation transmutes mechanical energy into thermal energy, raising the temperature of the fluid, and thus augmenting its entropy. Also, the thickness of the boundary layer (BL) reduces as the Re increases. This signifies a larger velocity gradient close to the walls of the flow domain. As a result, this leads to higher shear stresses and energy dissipation in the BL, which in turn causes an increase in entropy production.

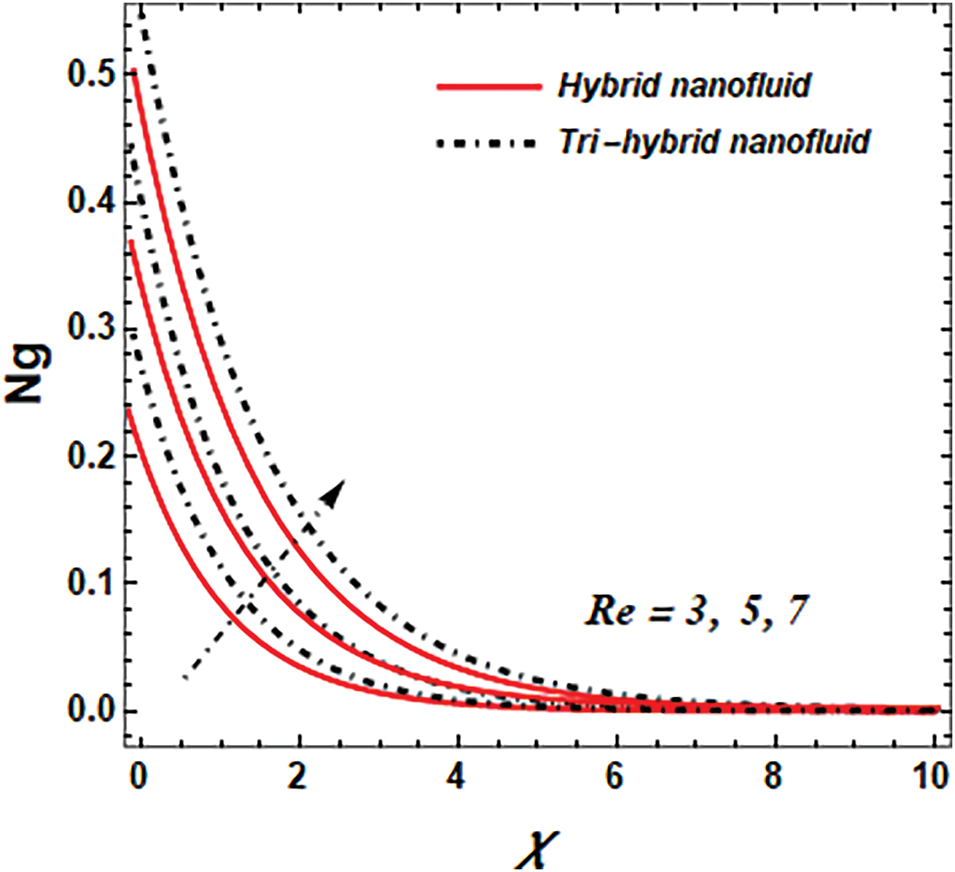
Figure 17: Impact of Re on entropy production

Brickman number (Br):The Br is a non-dimensional number used in fluid mechanics and thermal transport. It describes the influence of viscous forces in a fluid system. The effectiveness of the Brickman number on entropy generation is displayed in Fig. 18. With the rise of Br, there is more viscous dissipation within the fluid, and hence entropy generation is elevated. At high operating conditions of Br, the heat developed due to viscous dissipation is not easily conductively transmitted to the fluid. These cause localized temperature rises and hence a rise in the entropy generation rate in the process. Physically, the high Br, the heat generated from viscous dissipation is not easily transferred to the fluid through conduction. This leads to localized temperature increases, which in turn raises the rate of entropy generation in the process. The three-dimensional graphic illustration of Bejan number, with increased values of Br, is shown in Fig. 19. It is noteworthy that the Bejan number of Ag–trihybrid is higher than that of nano−hybrid fluid.

Figure 18: Influence of Br on entropy production

Figure 19: Effect of Br on Bejan number

7  Conclusions

In conclusion, this study provides significant theoretical contributions to the field THNF, advancing our understanding of their heat and mass transfer properties, as well as the irreversibility process. By integrating the Buongiorno and Tiwari–Das models, the research explores the unique interactions between various nanoparticles, such as Copper (Cu), Titanium Dioxide (TiO2), and Silver (Ag), suspended in Ethylene Glycol (EG), and their effects on the fluid’s thermal and electrical properties. These modifications enhance key characteristics like viscosity, heat capacity, electrical conductivity, thermal conductivity, and density, which collectively optimize the overall performance of the nanofluid. This theoretical exploration provides a deeper understanding of how THNF can be engineered for more efficient solar energy applications. By incorporating factors such as Cattaneo–Christov heat flux, porosity, double diffusion, and thermal radiation in an expandable surface setting, the study lays the groundwork for developing advanced systems that improve energy conversion and efficiency in solar capture technologies. The findings offer valuable insights into the potential of THNFs in promoting sustainable energy solutions, with applications in solar thermal engineering and other renewable energy systems, thus contributing to the broader goal of reducing environmental impacts while enhancing the performance of solar-based technologies. With the assistance of the Galerkin-weighted residual method, the boundary value problem is solved numerically. The major conclusions are:

•   The fluid temperature outlines improve with the upshot of the Brownian diffusion and thermophoresis diffusion.

•   The Bejan number, which represents the irreversibility ratio, decreases with higher Be and Re values.

•   By increasing the values of thermal radiation, the temperature of THNF is elevated.

•   The fluid temperature is boosted by the Dufour number and thermal conductivity.

•   An improvement in both the Brinkman number (Br), and Reynolds number (Re) leads to a growth in the entropy generation of the THNF.

•   The velocity profile gradually drops by increasing the values of porosity and Forchheimer number.

•   The Soret number and Schmidt numbers reduce mass profile.

•   The rate of thermal transport increases with the greater amount of thermal radiation. Moreover, prominent outcomes are presented via employing the THNF.

While this study provides significant insights into the thermal performance and entropy optimization of tri-hybrid nanofluids in non-Newtonian models, several limitations should be acknowledged:

•   The current research is based on numerical simulations and theoretical modelling, may not fully capture the complexities encountered in real-world experimental conditions. The assumptions made regarding fluid homogeneity, steady-state conditions, and negligible external disturbances may influence the generalizability of the findings.

•   This study focuses on specific thermophysical properties and heat transfer characteristics under controlled boundary conditions, which may not be directly applicable to all engineering scenarios. The influence of factors such as phase change, turbulent flow regimes, and long-term stability of nanofluids is beyond the scope of this work and requires further investigation.

•   Alternative numerical techniques or machine learning-based approaches may offer different perspectives on solution accuracy and computational efficiency.

•   Future research should incorporate experimental validation to reinforce the theoretical results and explore the impact of environmental factors on heat transfer efficiency. Expanding the study to consider varying nanoparticle concentrations, different base fluids, and hybrid configurations could further enhance the applicability of the proposed model in renewable energy and industrial applications.

Acknowledgement: We acknowledge the research supports from Universiti Teknikal Malaysia Melaka and Prince Sattam bin Abdulaziz University.

Funding Statement: The APC is funded by Universiti Teknikal Malaysia Melaka through the Tabung Penerbitan Jurnal (S11017).

Author Contributions: The authors confirm contribution to the paper as follows: Study Conception and Mathematical Formulation: Ahmed Mohamed Galal, Adebowale Martins Obalalu, Akintayo Oladimeji Akindele, Umair Khan; Data Collection: Abdulazeez Adebayo Usman, Olalekan Adebayo Olayemi; Analysis and Interpretation of Results: Ahmed Mohamed Galal, Adebowale Martins Obalalu, Akintayo Oladimeji Akindele, Najiyah Safwa Khashi’ie; Draft Manuscript Preparation: Adebowale Martins Obalalu, Akintayo Oladimeji Akindele, Umair Khan, Abdulazeez Adebayo Usman, Olalekan Adebayo Olayemi, Najiyah Safwa Khashi’ie. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zalba B, Marın JM, Cabeza LF, Mehling H. Review on thermal energy storage with phase change: materials, heat transfer analysis and applications. Appl Therm Eng. 2003;23(3):251–83. doi:10.1016/S1359-4311(02)00192-8. [Google Scholar] [CrossRef]

2. Afshar O, Saidur R, Hasanuzzaman M, Jameel M. A review of thermodynamics and heat transfer in solar refrigeration system. Renew Sustain Energy Rev. 2012;16(8):5639–48. doi:10.1016/j.rser.2012.05.016. [Google Scholar] [CrossRef]

3. Usman M, Gul T, Khan A, Alsubie A, Ullah MZ. Electromagnetic couple stress film flow of hybrid nanofluid over an unsteady rotating disc. Int Commun Heat Mass Transf. 2021;127:105562. doi:10.1016/j.icheatmasstransfer.2021.105562. [Google Scholar] [CrossRef]

4. Lipiński W, Abbasi-Shavazi E, Chen J, Coventry J, Hangi M, Iyer S, et al. Progress in heat transfer research for high-temperature solar thermal applications. Appl Therm Eng. 2021;184:116137. doi:10.1016/j.applthermaleng.2020.116137. [Google Scholar] [CrossRef]

5. Mushtaq A, Mustafa M, Hayat T, Alsaedi A. Nonlinear radiative heat transfer in the flow of nanofluid due to solar energy: a numerical study. J Taiwan Inst Chem Eng. 2014;45(4):1176–83. doi:10.1016/j.jtice.2013.11.008. [Google Scholar] [CrossRef]

6. Kalay MŞ, Kılıç B, Sağlam Ş. Systematic review of the data acquisition and monitoring systems of photovoltaic panels and arrays. Sol Energy. 2022;244:47–64. doi:10.1016/j.solener.2022.08.029. [Google Scholar] [CrossRef]

7. de Souza MB, Tonolo ÉA, Yang RL, Tiepolo GM, Urbanetz Jr. J. Determination of diffused irradiation from horizontal global irradiation—study for the city of Curitiba. Braz Arch Biol Technol. 2019;62:e19190014. doi:10.1590/1678-4324-smart-2019190014. [Google Scholar] [CrossRef]

8. Fernández-García A, Zarza E, Valenzuela L, Pérez M. Parabolic-trough solar collectors and their applications. Renew Sustain Energy Rev. 2010;14(7):1695–721. doi:10.1016/j.rser.2010.03.012. [Google Scholar] [CrossRef]

9. Bellos E, Tzivanidis C. Alternative designs of parabolic trough solar collectors. Prog Energy Combust Sci. 2019;71:81–117. doi:10.1016/j.pecs.2018.11.001. [Google Scholar] [CrossRef]

10. Oreyeni T, Oladimeji Akindele A, Martins Obalalu A, Olakunle Salawu S, Ramesh K. Thermal performance of radiative magnetohydrodynamic Oldroyd-B hybrid nanofluid with Cattaneo–Christov heat flux model: solar-powered ship application. Numer Heat Transf Part A Appl. 2024;85(12):1954–72. doi:10.1080/10407782.2023.2213837. [Google Scholar] [CrossRef]

11. Adun H, Kavaz D, Dagbasi M. Review of ternary hybrid nanofluid: synthesis, stability, thermophysical properties, heat transfer applications, and environmental effects. J Clean Prod. 2021;328:129525. doi:10.1016/j.jclepro.2021.129525. [Google Scholar] [CrossRef]

12. Sahoo RR, Kumar V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Int Commun Heat Mass Transf. 2020;111:104451. doi:10.1016/j.icheatmasstransfer.2019.104451. [Google Scholar] [CrossRef]

13. Cao W, Animasaun IL, Yook SJ, Oladipupo VA, Ji X. Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: ternary-hybrid nanofluid. Int Commun Heat Mass Transf. 2022;135:106069. doi:10.1016/j.icheatmasstransfer.2022.106069. [Google Scholar] [CrossRef]

14. Sarfraz M, Khan M. Heat transfer efficiency in planar and axisymmetric ternary hybrid nanofluid flows. Case Stud Therm Eng. 2023;44:102857. doi:10.1016/j.csite.2023.102857. [Google Scholar] [CrossRef]

15. Nasir S, Sirisubtawee S, Juntharee P, Berrouk AS, Mukhtar S, Gul T. Heat transport study of ternary hybrid nanofluid flow under magnetic dipole together with nonlinear thermal radiation. Appl Nanosci. 2022;12(9):2777–88. doi:10.1007/s13204-022-02583-7. [Google Scholar] [CrossRef]

16. Animasaun IL, Yook SJ, Muhammad T, Mathew A. Dynamics of ternary-hybrid nanofluid subject to magnetic flux density and heat source or sink on a convectively heated surface. Surf Interfaces. 2022;28:101654. doi:10.1016/j.surfin.2021.101654. [Google Scholar] [CrossRef]

17. Arif M, Kumam P, Kumam W, Mostafa Z. Heat transfer analysis of radiator using different shaped nanoparticles water-based ternary hybrid nanofluid with applications: a fractional model. Case Stud Therm Eng. 2022;31:101837. doi:10.1016/j.csite.2022.101837. [Google Scholar] [CrossRef]

18. Usafzai WK, Wahid NS, Arifin NM, Aly EH. MHD flow and heat transfer of nanotriple (Cu–Al2O3–Agexact solutions. Chin J Phys. 2025;93:56–74. doi:10.1016/j.cjph.2024.11.029. [Google Scholar] [CrossRef]

19. Wahid NS, Zamri NE, Jamaludin SZM, Norzawary NHA, Kasihmuddin MSM, Mansor MA, et al. Melting ternary hybrid nanofluid stagnation point flow with velocity slip past a stretching/shrinking sheet: numerical simulation and validation via P2SATRA. Alex Eng J. 2025;112:74–83. doi:10.1016/j.aej.2024.10.082. [Google Scholar] [CrossRef]

20. Ali F, Zaib A, Abbas M, Anitha G, Loganathan K, Ravindranath Reddy G. Radiative flow of cross ternary hybrid nanofluid (MoS2, TiO2, Ag/CMC-water) in a Darcy Forchheimer porous medium over a stretching cylinder with entropy minimization. Heliyon. 2024;10(14):e34048. doi:10.1016/j.heliyon.2024.e34048. [Google Scholar] [CrossRef]

21. Jamrus FN, Ishak A, Waini I. Stability scrutinization of time depending flow of a ternary hybrid nanofluid past a shrinking sheet with wall mass suction effect. Mal J Fund Appl Sci. 2024;20(3):528–43. doi:10.11113/mjfas.v20n3.3334. [Google Scholar] [CrossRef]

22. Jamrus FN, Waini I, Ishak A. Time-depending flow of ternary hybrid nanofluid past a stretching sheet with suction and magnetohydrodynamic (MHD) effects. J Adv Res Fluid Mech Therm Sci. 2024;117(2):15–27. doi:10.37934/arfmts.117.2.1527. [Google Scholar] [CrossRef]

23. Mahmood Z, Khan U, Saleem S, Rafique K, Eldin SM. Numerical analysis of ternary hybrid nanofluid flow over a stagnation region of stretching/shrinking curved surface with suction and Lorentz force. J Magn Magn Mater. 2023;573:170654. doi:10.1016/j.jmmm.2023.170654. [Google Scholar] [CrossRef]

24. Mahmood Z, Ahammad NA, Alhazmi SE, Khan U, Bani-Fwaz MZ. Ternary hybrid nanofluid near a stretching/shrinking sheet with heat generation/absorption and velocity slip on unsteady stagnation point flow. Int J Mod Phys B. 2022;36(29):2250209. doi:10.1142/S0217979222502095. [Google Scholar] [CrossRef]

25. Mahmood Z, Iqbal Z, Alyami MA, Alqahtani B, Yassen MF, Khan U. Influence of suction and heat source on MHD stagnation point flow of ternary hybrid nanofluid over convectively heated stretching/shrinking cylinder. Adv Mech Eng. 2022;14(9):16878132221126278. doi:10.1177/16878132221126278. [Google Scholar] [CrossRef]

26. Ouyang Y, Md Basir MF, Naganthran K, Pop I. Dual solutions in Maxwell ternary nanofluid flow with viscous dissipation and velocity slip past a stretching/shrinking sheet. Alex Eng J. 2024;105:437–48. doi:10.1016/j.aej.2024.07.093. [Google Scholar] [CrossRef]

27. Hussein UN, Khashi’ie NS, Arifin NM, Pop I. Magnetohydrodynamics (MHD) flow of ternary nanofluid and heat transfer past a permeable cylinder with velocity slip. Chin J Phys. 2025;93:328–39. doi:10.1016/j.cjph.2024.12.002. [Google Scholar] [CrossRef]

28. Wang Y, Yu L, Obalalu AM, Khan U, Waqas M, Elrashidi A, et al. Dissipative heat transfer in blood-based ternary hybrid nanofluids through a parallel channel with entropy optimization: the case of biomedical applications. Alex Eng J. 2025;115:252–63. doi:10.1016/j.aej.2024.12.026. [Google Scholar] [CrossRef]