 Open Access
Open Access
REVIEW
Advanced Computational Modeling and Mechanical Behavior Analysis of Multi-Directional Functionally Graded Nanostructures: A Comprehensive Review
Department of Mathematics, National Institute of Technology Rourkela, Odisha, 769008, India
* Corresponding Author: S. Chakraverty. Email:
(This article belongs to the Special Issue: Theoretical and Computational Modeling of Advanced Materials and Structures-II)
Computer Modeling in Engineering & Sciences 2025, 142(3), 2405-2455. https://doi.org/10.32604/cmes.2025.061039
Received 15 November 2024; Accepted 22 January 2025; Issue published 03 March 2025
Abstract
This review explores multi-directional functionally graded (MDFG) nanostructures, focusing on their material characteristics, modeling approaches, and mechanical behavior. It starts by classifying different types of functionally graded (FG) materials such as conventional, axial, bi-directional, and tri-directional, and the material distribution models like power-law, exponential, trigonometric, polynomial functions, etc. It also discusses the application of advanced size-dependent theories like Eringen’s nonlocal elasticity, nonlocal strain gradient, modified couple stress, and consistent couple stress theories, which are essential to predict the behavior of structures at small scales. The review covers the mechanical analysis of MDFG nanostructures in nanobeams, nanopipes, nanoplates, and nanoshells and their dynamic and static responses under different loading conditions. The effect of multi-directional material gradation on stiffness, stability and vibration is discussed. Moreover, the review highlights the need for more advanced analytical, semi-analytical, and numerical methods to solve the complex vibration problems of MDFG nanostructures. It is evident that the continued development of these methods is crucial for the design, optimization, and real-world application of MDFG nanostructures in advanced engineering fields like aerospace, biomedicine, and micro/nanoelectromechanical systems (MEMS/NEMS). This study is a reference for researchers and engineers working in the domain of MDFG nanostructures.Graphic Abstract
Keywords
With the advancement of new manufacturing techniques, material science has moved from traditional metals to advanced materials and smart materials. Though these materials have great properties, they have limitations in their applications. To deal with this a new class of advanced composite materials, known as functionally graded (FG) materials, has gained much attention due to their superior mechanical performance. These materials, which have a smooth variation in composition or structure, have advantages over traditional composites, especially in mechanical, thermal, and environmental resistance. FG materials are being used in industries like aerospace, biomedical, automotive, and defense as they can withstand extreme conditions without compromising the inherent properties [1]. The first use of FG materials were reported in Japan in the 1980s to overcome the limitations of conventional composite materials, which often suffer from delamination failures when subjected to high temperatures or high-stress conditions [2]. These failures occur due to the differences in thermal expansion properties of the constituent materials. In FG materials, the composition of constituents changes gradually, which helps to reduce stress concentrations and enhance material performance. These materials are called advanced engineering materials, as they show improved durability and function in harsh environments, like aerospace and defense applications, and high-temperature scenarios like thermal barrier coatings and fire retardants [3].
Conventional FG materials have been extensively utilized for their ability to mitigate abrupt property changes across interfaces. Multi-directional functionally graded (MDFG) materials, which are graded in more than one direction, surpass conventional FG materials by offering enhanced mechanical, structural, and energy transfer properties. For instance, bi-directional FG (BDFG) materials alleviate stress concentration and cracking issues, improving stiffness and lightweight characteristics, especially in dynamic and structural applications [4]. In tribological settings, multi-directional forging improves hardness and wear rate, and alters wear mechanisms, reducing friction coefficients and fostering beneficial microstructures [5]. Similarly, in metallurgical contexts, such as AlAl 6061 alloys, multi-directional forging enhances grain refinement, leading to increased hardness and yield strength, though with some brittleness [6]. Furthermore, anisotropic multi-layer FG materials, like black phosphorus, enable precise control of energy transfer rates in specific directions, which is a significant advantage over isotropic materials for energy applications [7]. These innovations demonstrate their potential to optimize performance in industries ranging from aerospace to electronics.
The lifecycle and ecological implications of MDFG nanostructures are crucial for their sustainable development. While their advanced properties, such as reduced weight and enhanced performance, improve efficiency and extend lifespan during use, the energy-intensive fabrication processes and resource consumption pose environmental challenges. To address this, sustainable manufacturing methods like green synthesis and additive manufacturing should be adopted, supported by life cycle assessments to evaluate and minimize environmental impacts. End-of-life management remains a challenge due to the complex, multi-material composition and nanoscale features, highlighting the need for eco-friendly recycling, upcycling, and disposal strategies. Additionally, the potential ecotoxicity of nanoscale particles must be studied to ensure environmental safety. A circular economy approach that prioritizes renewable resources, efficient recycling, and responsible disposal is essential to mitigate ecological risks while maximizing the benefits of MDFG nanostructures for advanced applications [8–10].
However, recent advancements in nanotechnology have enabled the development of MDFG structures at the nanoscale, offering enhanced control over spatially varying properties. This progression bridges the gap between macroscale FG materials and the sophisticated capabilities of nano-engineered MDFG structures, highlighting a continuous evolution in design and application. MDFG nanostructures are a significant advancement in material engineering, enabling more complex and efficient designs in micro/nanodevices like atomic force microscopes [11] and micro/nano electro-mechanical systems (MEMS/NEMS) [12]. These systems benefit from the size-dependent behavior of FG nanostructures, which cannot be explained by classical continuum theory. Instead, advanced theories like Eringen’s nonlocal elasticity theory (ENET) [13,14], nonlocal strain gradient theory (NSGT) [15,16], modified couple stress theory (MCST) [17,18], and consistent couple stress theory (CCST) [19,20] are being used to understand the unique mechanical behavior of these materials at small scales. These theories are thoroughly explained in Section 3. By incorporating size effects, these theories enable a more accurate analysis of stress distribution, deformation patterns, and structural responses in FG materials. This is especially significant for FG nanostructures, where small-scale effects strongly influence stiffness, strength, and stability. The insights provided by size-dependent theories are instrumental in optimizing the design and performance of FG materials in advanced applications, such as aerospace, biomedical devices, and nanotechnology. Various MDFG nanostructures are presented in Fig. 1 and the advancement of MDFG nanostructures is shown in Fig. 2.
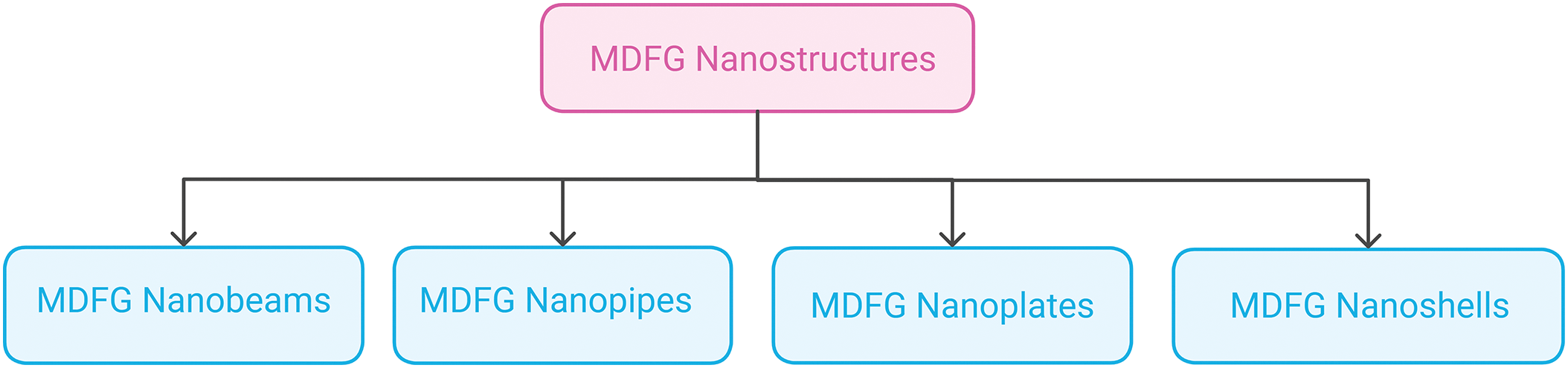
Figure 1: Various MDFG nanostructures
Figure 2: Advancement of MDFG nanostructures
Researchers have extensively applied nonlocal theories to analyze size-dependent effects in FG structures such as FG beams, FG plates, FG shells, and FG pipes. In vibration problems, governing equations are typically transformed into generalized eigenvalue problems [21–25] and solved using various analytical, semi-analytical, and numerical methods. The Finite Difference Method (FDM) [26–28] discretizes differential equations into finite difference equations, making it suitable for FG materials with spatially varying properties, though it is limited by its dependence on grid resolution. The Finite Element Method (FEM) [29–31], a powerful and versatile technique, divides structures into elements, allowing precise analysis of FG materials with complex geometries and varying boundary conditions. Semi-analytical methods like the Adomian Decomposition Method (ADM) [32–34] and Homotopy Perturbation Method (HPM) [35–37] provide fast, convergent solutions for nonlinear problems, especially in dynamic and thermal contexts. Numerical techniques such as the Differential Quadrature Method (DQM) [38–40] and Collocation Method [41–43] offer computationally efficient and precise solutions for high-order differential equations in FG materials. Energy-based approaches like the Rayleigh-Ritz Method [44–46] and weighted residual techniques such as the Galerkin Method [47–49] are particularly effective for vibration and stability analyses of FG materials. Meanwhile, the Boundary Element Method (BEM) [50–52] focuses on boundaries, making it ideal for FG structures in infinite or semi-infinite domains. For simply supported structures, analytical approaches like the Navier method [53,54], suitable for cases where all edges are simply supported, and the Levy method [55,56], ideal for plates simply supported on two opposite edges, remain popular choices. These methods collectively enable a deeper understanding of the dynamic behavior and size-dependent characteristics of FG materials, contributing to their optimization in engineering applications.
The computational and experimental findings on MDFG nanostructures play a critical role in advancing their practical applications. Computational models provide precise predictions of mechanical, thermal, and dynamic behaviors, enabling the optimized design of lightweight aerospace components, biocompatible biomedical implants, and high-performance MEMS/NEMS devices. Experimental validations confirm the accuracy of these models and demonstrate the feasibility of fabricating MDFG structures with precise material gradation, ensuring reliability, durability, and superior performance under real-world conditions. These combined insights highlight the ability of MDFG nanostructures to enhance stiffness, stability, and vibration resistance while extending operational lifespans, making them highly suitable for cutting-edge engineering and technological applications [9,57,58].
Markworth et al. [59] discussed modeling studies on FG materials. They highlighted the diverse microstructures in FG materials and recommended further studies using advanced techniques such as lattice models, fuzzy logic, percolation theory, fractal analysis, neural networks, and the renormalization group. Chakraverty [60] provided a comprehensive introduction to plate vibration theory, and introduced new methodologies and the concept of Boundary Characteristic Orthogonal Polynomials (BCOPs), offering valuable insights for analyzing plate dynamics in engineering structures. Nie et al. [61] studied the mechanical behavior of MDFG annular plates using DQM. They derived frequency equations for free vibration with varying material properties. Their findings suggest that MDFG materials are a promising alternative to unidirectional FG materials. BDFG material with varying elastic modulus was analyzed by Zhao et al. [62]. Their results highlighted the significance of eigenvalues in understanding local material behavior and failure, with numerical examples showing stress distributions in FG beams. Behera et al. [63–66] studied the vibration, bending, and buckling of nanobeams and nanoplates using ENET. They used the Rayleigh-Ritz method to solve vibration problems under different boundary conditions. Their results showed that nonlocal effects reduce frequency parameters and are more prominent in higher modes, especially in nonuniform structures on Winkler-Pasternak foundations. Şimşek [67] investigated the BDFG Timoshenko beams under moving loads. The dynamic responses were analyzed using the Newmark-ββ method. Pradhan et al. [68–71] solved FG beams and plates problems using efficient computational techniques, including FEM, DQM, and Rayleigh-Ritz methods. Their study examined the effects of material properties, volume fractions, and external factors such as thermal environments and elastic foundations, with applications in aerospace, nuclear, and automotive fields. Razavi et al. [72] analyzed electromechanical vibrations in FG piezoelectric material cylindrical nanoshells using the size-dependent CCST. Their study highlighted the influence of parameters such as length scale, length-to-radius ratio, and radius-to-thickness ratio on vibration behavior. The vibration characteristics of MDFG cellular materials inspired by natural structures was investigated by Niknam et al. [73]. Using homogenization and FEM, they demonstrated that optimized cell variation, especially through thickness, significantly enhances structural properties like bending stiffness in MDFG cellular plates. Ghayesh et al. [74] reviewed the mechanical behavior of FG nanostructures and microstructures, discussing fabrication advancements, studies on buckling, vibration, and deformation, and suggesting future applications in MEMS and NEMS. The effect of various homogenization models on the FG curved microbeams was analyzed by Karami et al. [75]. They concluded that the Mori-Tanaka and Voigt models overestimate frequencies, while the Local Representative Volume Elements (LRVE) model provides a good balance of accuracy and simplicity, especially for high-stiffness FG materials. Qin et al. [76] studied the traveling wave motions of rotating multi-layered FG-graphene platelet-reinforced composite cylindrical shells under various boundary conditions. They used the Donnell shell theory and the Rayleigh-Ritz method, considering centrifugal and Coriolis effects. Their results emphasized the influence of boundary spring stiffness, GPL weight fraction, total layer number, and geometric parameters on vibration characteristics, with consistent frequency trends across different conditions. Abbaspour et al. [77] investigated the free and forced vibrations, as well as the thermal buckling behavior, of three-layered centrosymmetric piezoelectric microplates. They utilized the CCST and examined the effects of material length scale, flexoelectricity, and circuit conditions on the outcomes. Ghatage et al. [78] reviewed on modeling and analysis of MDFG structures, focusing on beams, plates, and shells. While most FG composite studies address unidirectional gradation, they emphasize the need for multi-directional grading to meet complex application demands. The nonlinear vibration characteristics of BDFG plates with global and localized imperfections under harmonic excitation was analyzed by Chen et al. [79]. Using von Kármán’s nonlinearity and a reduced-order model, they analyzed how material gradients, imperfections, and excitation parameters impact vibrational responses, including resonant nonlinearity, bifurcations, and chaotic motions. Truong et al. [80] presented a deep feedforward neural network optimization technique to model the BDFG beams under static load. This method effectively saves computation resources while optimizing material distribution. The vibrations of FG porous nanobeams and microbeams were investigated by Jena et al. [81–83] using Euler-Bernoulli beam theory (EBT). Also, Jena et al. [84,85] considered the single-walled carbon nanotubes (CNTs) utilizing one-variable shear deformation beam theory (SDT), considering effects of axial magnetic fields, thermal, and hygroscopic environments. They applied NSGT for size effects and analyzed the impact of nonlocal parameters, magnetic fields, and environments on natural frequencies, and also investigated armchair, chiral, and zigzag single-walled CNTs embedded in a Winkler substrate, addressing surface energy, residual stresses, and temperature effects. Tang et al. [86,87] studied BDFG and TDFG material nanobeams on Pasternak foundations under magneto-electro-elastic (MEE) fields. Using Hamilton’s principle and GDQM, they found that BDFG MEE nanobeams display asymmetric modes, while TDFG beams enhance load-bearing capacity and flexibility with distinct nonlinear behaviors. Gao et al. [88] presented a model to analyze wave propagation in GPL-reinforced FG metal foam plates with piezoelectric layers under magneto-electro-thermo conditions. They studied the effects of material viscoelasticity, porosity, GPL distribution, and external fields on wave behavior, providing insights for tunable control in smart sandwich plates. Karmakar et al. [89–92] investigated the vibration behavior of nanobeam using NSGT with methods like ADM, HPM and DQM. They investigated thermal vibration on Winkler and Winkler-Pasternak foundations, piezoelectric and flexoelectric effects on nanobeam with different elastic foundations, and magnetic fields on FG nanobeam. Their results show the effect of foundation parameters, small-scale effects, and thermal and magnetic environments on vibration frequencies, which is helpful for complex nanobeam applications. Nuhu et al. [93] presented a comprehensive review of advancements in the vibration analysis of micro- and nanoplates using nonclassical continuum theories, including ENET, NSGT, and micro-continuum theories. Their work examined a range of small-scale structures, such as graphene sheets and metallic nanosheets, categorizing them into types like piezoelectric, viscoelastic, and composite-based systems. They concluded by highlighting future research opportunities, with a focus on integrating machine learning and optimization techniques to advance the analysis of small-scale structures. Wu et al. [94] reviewed mechanical analyses of rectangular nanobeams and CNTs using ENET. They covered bending, vibration, buckling, thermo-elastic effects, instability, wave propagation, and nonlinear behaviors. The survey includes the development of nonlocal beam/shell theories, strong- and weak-form formulations of the nonlocal Timoshenko beam theory (TBT) for the free vibration analysis of CNTs, and a comparative study of the results obtained using different nonlocal beam and shell theories. Mathew et al. [95] also explored different homogenization methods, such as the rule of mixtures and the Mori-Tanaka scheme, to estimate the effective properties of FG plates, which follow distributions like power-law, sigmoid, or exponential across the thickness. Zheng et al. [96] reviewed the recent advancements in tailoring the mechanical properties of FG piezoelectric micro/nanostructures, emphasizing their role in improving the performance of MEMS/NEMS. The review covers the size-dependent mechanical behaviors of these structures, including bending, buckling, vibration, and energy harvesting.
Though there is a lot of research on FG materials, BDFG and TDFG materials are still in the early stages of development. These complex structures are required for applications that involve multi-axial stress and temperature gradients, like modern aerospace vehicles where the stresses and environmental conditions vary in multiple directions. However, the study on MDFG nanostructures is still an under-explored area due to the challenges in modeling and simulation, especially with the need for robust and efficient numerical tools.
This article provides the first comprehensive review of the size-dependent mechanics of MDFG nanostructures. The review is organized into eight sections. In the first section, a general background and literature survey on the nanostructures and FG nanostructures are presented. Section 2 defines different types of FG materials and presents various homogenization models. In Section 3, size-dependent theories suitable for analyzing the FG structures at the nanoscale are discussed. Sections 4.1–4.4 review studies on the nonlocal behaviors of MDFG nanobeams, nanopipes, nanoplates, and nanoshells, focusing on vibration, buckling, and bending, respectively. Finally, Section 5 presents a summary of the main insights from this review and outlines potential directions for future research on the mechanics of FG nanoscale structures.
2 Different Types of FG Materials
FG materials are a unique class of nonhomogeneous engineered materials, characterized by a gradual variation in composition or structure. This results in a continuous change in material properties throughout their volume. This gradual transition enables FG materials to perform effectively under diverse environmental conditions, making them ideal for a wide range of applications. Key differences, advantages, and applications of various material property variations are summarized in Table 1 and a visual representation is presented in Fig. 3. There are several types of FG materials based on how the material properties change:
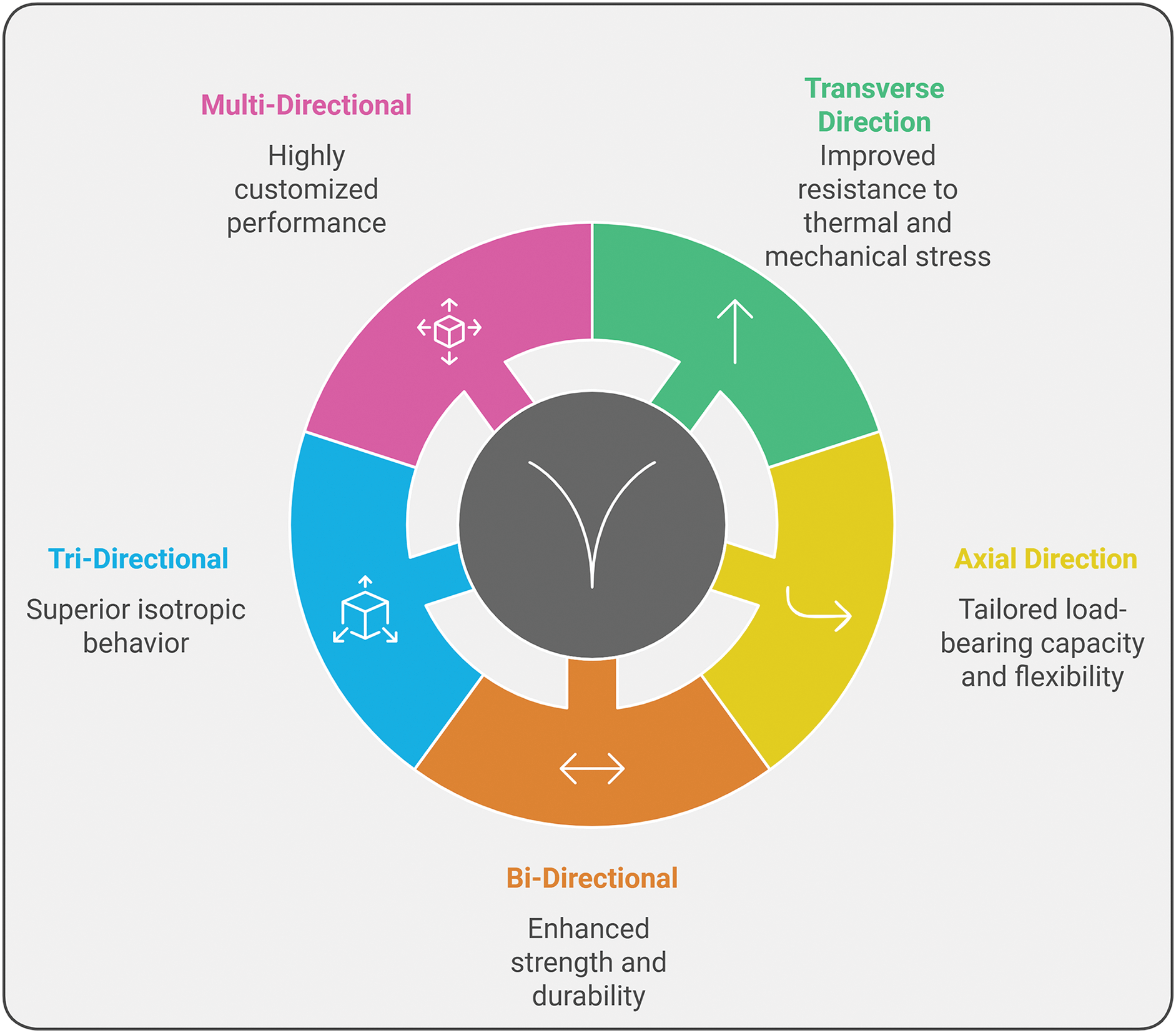
Figure 3: Variation of material properties in FG nanostructures
In conventional FG materials, the material properties are typically considered to vary along the thickness direction. This type of variation is most commonly employed due to its effectiveness in enhancing performance under external loading conditions. These materials are specifically designed for applications that require high thermal resistance on one side and high strength or toughness on the other. The advantages and applications of conventional FG materials are shown in Table 1. Typically, the variation in material properties, such as thermal conductivity, Young’s modulus, mass density, and Poisson’s ratio, is modeled using some specific mathematical functions. The choice of function depends on the nature of the application and the material behavior required.
The primary objective in the mechanics of FG materials is to predict their behavior by estimating their effective material properties, a process commonly known as Homogenization. Several homogenization techniques are used to determine the effective material properties. Below, a few commonly used homogenization models are discussed.
This model is widely recognized for describing FG materials composed of metal and ceramic constituents. In such materials, the volume fractions vary continuously along the thickness direction. For an FG material with a ceramic-rich upper surface and a metal-rich bottom, this distribution ensures a smooth transition between the two constituents, resulting in improved material properties. The variation in material properties of the FG material follows a specific power-law function, as defined by the following Rule of Mixture (also known as Voigt Model) [70,97,99,106,107]:
P(z)=(PU−PL)Vf(z)+PL,P(z)=(PU−PL)Vf(z)+PL,(1)
where, P(z)P(z) represents the effective material property, PUPU and PLPL are the material properties of upper surface (ceramic) and lower surface (metal), respectively. The volume fraction, VfVf, follows a power-law, given by:
Vf(z)=(zh+12)k,Vf(z)=(zh+12)k,(2)
where, kk is the power-law exponent, or material in-homogeneity constant (non-negative), hh is height, and zz denotes the transverse direction of the material.
When k=0k=0 or z=h2z=h2, then P(z)=PUP(z)=PU, indicating that the material property corresponds to the upper surface (ceramic). Conversely, if k→∞k→∞ or z=−h2z=−h2, then P(z)=PLP(z)=PL, signifying that the material property corresponds to the lower surface (metal). The effect of z/hz/h and kk on Young’s modulus E(z)E(z), according to Eqs. (1) and (2), is presented in Fig. 4. For all the plots, Alumina is considered ceramic and Aluminium is considered a metal constituent. So, EU=380EU=380 (Alumina) and EL=70EL=70 (Aluminium) [16,107].
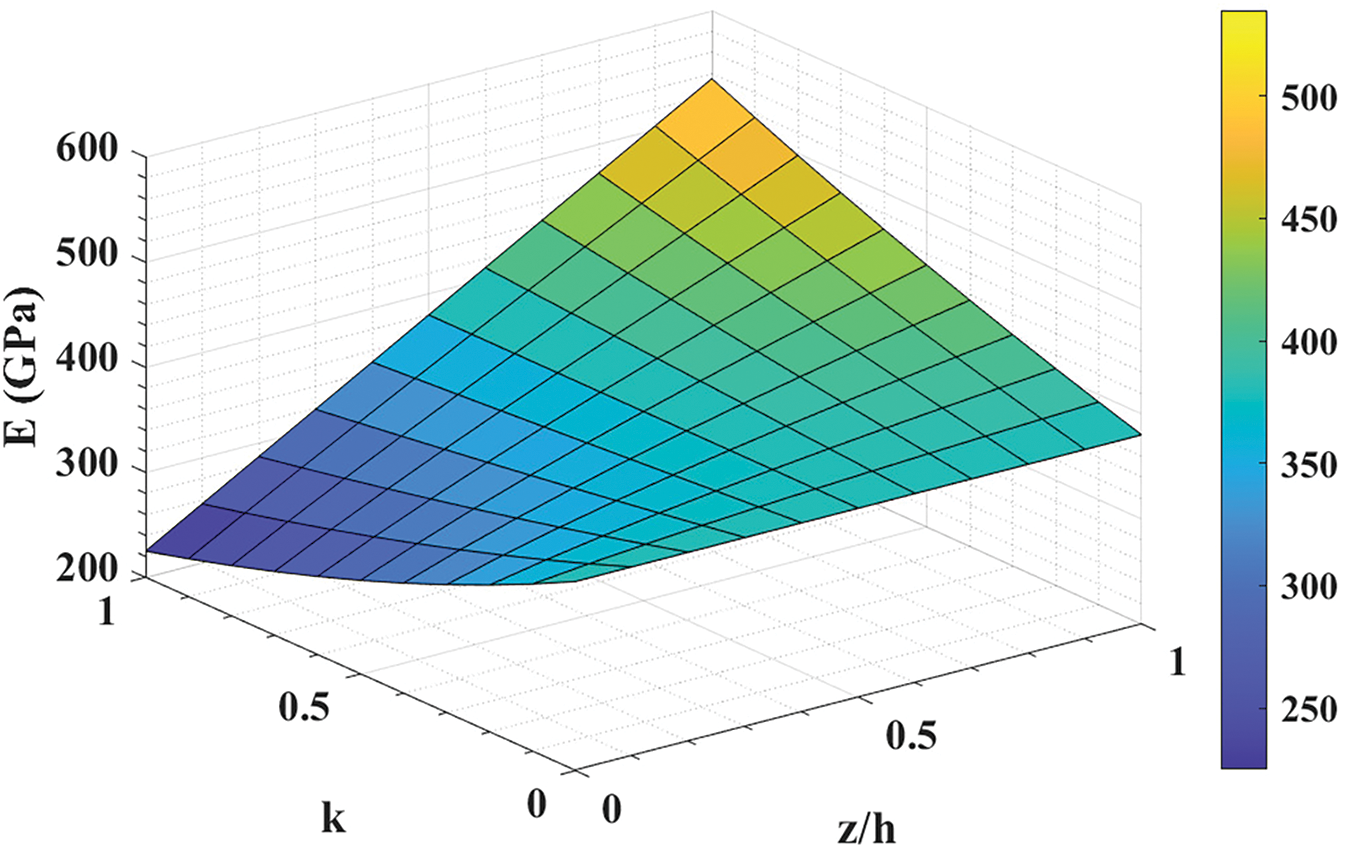
Figure 4: Effect of z/hz/h and kk on E(z)E(z) in power-law model
It is important to note that the effective mass density is determined using the rule of mixtures (Eq. (1)), regardless of the homogenization models applied.
FG materials with exponential variation create smooth transitions in properties like thermal conductivity, stiffness, and strength, reducing stress concentrations and enhancing performance, making them useful for fracture studies. These materials are commonly used in thermal barrier coatings, aerospace structures, biomedical implants, and wear-resistant surfaces to optimize thermal and mechanical behavior under extreme conditions. The effective material property, P(z)P(z), based on the exponential law is given by [108–112]:
P(z)=PUe−δ(1−2zh),P(z)=PUe−δ(1−2zh),(3)
where, δ=12ln(PUPL)δ=12ln(PUPL). Similarly, at z=h2z=h2, P(z)=PUP(z)=PU, and at z=−h2z=−h2, P(z)=PLP(z)=PL.
In the power-law variation of FG materials, the volume fraction changes rapidly near the bottom when k<1k<1 and near the top when k>1k>1. To achieve a smoother variation in material properties, two power-law functions are used. The volume fractions of ceramic and metal are defined using the rule of mixtures, ensuring a more gradual and controlled variation throughout the material. The sigmoid law of variation is expressed as [113–117]:
P(z)={(PU−PL)[12(1+2zh)k]+PL,for −h2≤k≤0,(PU−PL)[1−12(1−2zh)k]+PL,for 0≤k≤h2.(4)
When k=0, the Sigmoid-FG material behaves as a homogeneous material, with equal volume fractions of ceramic and metal constituents throughout its thickness. At k=1, the sigmoid model aligns with the power-law model.
This model offers the most diverse range of material variations compared to the power-law model. Its formulation allows for the selection of material mixtures at either the bottom or top surface of an FG structure. The model is further divided into three-parameter and four-parameter versions, as described below [98,118–121]:
P(z)={(PU−PL)[12−zh+c2(12+zh)k1]k2+PL,(Viola-Tornabene Three-Parameter Model)(PU−PL)[1−c1(12−zh)+c2(12+zh)k1]k2+PL,(Viola-Tornabene Four-Parameter Model)(5)
where, the constant parameters c1,c2,k1, and k2 dictate the propagation of material along the thickness direction in the FG structure.
In this model, the volume fraction of FG materials is considered in terms of trigonometric functions. The effective material property is written as [98,121]:
P(z)=(PU−PL) c1[12−c22sin(c3πzh+c4)]k+PL,(6)
where, c1,c2,c3,c4, and k are the controlling parameters that define the pattern of material variation within the FG structure.
The design optimization of FG materials involves determining the optimal variation in material composition to improve structural performance. For greater flexibility in the design, this variation is often represented using B-Splines, which offer smooth and precise control over the material distribution throughout the structure. The effective material property is given by [122–126]:
P(z)=(PU−PL)[∑ncpi=1Bi,p(ξ) Vi(z)]+PL,ξ∈[0,1],(7)
where, ncp denotes the number of control points. The term Vi(z) corresponds to the volume fraction at the i-th control point, and Bi,p is the B-Spline basis function associated with that point. Here, p is the degree of the B-Spline basis, and γ is the parametric coordinate, which ranges from 0 to 1.
The B-Spline basis Bi,p is constructed using a knot vector, which consists of non-negative and non-decreasing parametric values. These values are bounded by the parametric interval in which the B-Spline is defined. For a given knot vector Ξ={γ1,γ2,…,γn+p+1}, the basis functions are computed using the recursive Cox-de Boor formula [122,126]:
Bi,p(γ)=γ−γiγi+p−γi Bi,p−1(γ)+γi+p+1−γγi+p+1−γi+1 Bi+1,p−1(γ),(8)
Bi,0(γ)={1,for γi≤γ<γi+1,0,otherwise.(9)
2.1.7 Piece-Wise Cubic Interpolation Function
In this model, the material properties are determined using a non-monotonic variation function, which means the volume fraction at any point is computed using piecewise cubic interpolation. In this case, the effective material property is defined as [127,128]:
P(z)=(PU−PL)[ViH1(z)+SiH2(z)+Vi+1H3(z)+Si+1H4(z)]+PL,z∈[zi,zi+1],(10)
where, Vi and Si are the volume fraction and the slope of the volume fraction at the i-th control point in the thickness direction, respectively. The values of Vi, Si, and the Hermite basis functions Hk(z), (k=1,2,3,4) are provided in the study by Vel et al. [127].
This homogenization model is widely used to estimate the effective material properties of FG structures, where a continuous isotropic matrix is reinforced with randomly distributed particles. It calculates the effective shear moduli (G) and bulk moduli (K), which are then used to derive properties such as E and ν. Its simplicity, computational efficiency, and capability to manage both particulate and discontinuous phases make it a reliable tool for designing advanced graded structures. In this model, E(z) and ν(z) are given by [129–133]:
E(z)=9K(z)G(z)3K(z)+G(z),(11)
ν(z)=3K(z)−2G(z)2(3K(z)+G(z)),(12)
where,K(z)=(KL−KU)(Vf(z)1+(1−Vf(z)) KL−KUKU+43GU)+KU,(13)
G(z)=(GL−GU)(Vf(z)1+(1−Vf(z)) GL−GUGU+fU)+GU,(14)
where,Vf(z)=(zh+12)k fU=GU(9KU+8GU)6(KU+2GU).(15)
2.1.9 Tamura-Tomota-Ozawa Model
This model introduces an experimental parameter, denoted as q, which represents the stress-to-strain transfer. It is determined by coupling the average stress and strain values in a two-phase composite material under uni-axial uniform loading. The parameter q is mathematically expressed as [134–138]:
q=σU−σL|ϵU−ϵL|,0<q<∞,(16)
where, σU,σL are the average stresses, and ϵU,ϵL represent the average strains of the upper and lower surfaces of the FG material, respectively. Here, E(z) is represented as [138]:
E(z)=EUVf(z)+EL(1−Vf(z)) q+EUq+ELVf(z)+(1−Vf(z)) q+EUq+EL,(17)
where, Vf(z)=(zh+12)k. G(z) is determined using E(z) and ν(z). ν(z) is calculated using the formula ν(z)=νUVf(z)+νL(1−Vf(z)). It can be verified that when the parameter q approaches ±∞, Eq. (17) simplifies to the expression for E(z) in the Voigt model.
This model, also known as the inverse of the Voigt model, assumes that, at the macroscopic level, the average stress is the same in every phase of a material when subjected to uniform stress. In simple terms, the Reuss model predicts the effective properties of a composite material by considering that all phases experience equal stress under an external load. Based on this, the E(z) and ν(z) of the material are [139–143]:
E(z)=EUELEU(1−Vf(z))+ELVf(z),(18)
ν(z)=νUνLνU(1−Vf(z))+νLVf(z),(19)
where, Vf(z)=(zh+12)k. Hill [144] reported that the Voigt and Reuss models provide the upper and lower bounds, respectively, for the effective elastic properties of a material. Fig. 5 illustrates the effect of z/h and k on E(z) for EU=380 and EL=70.
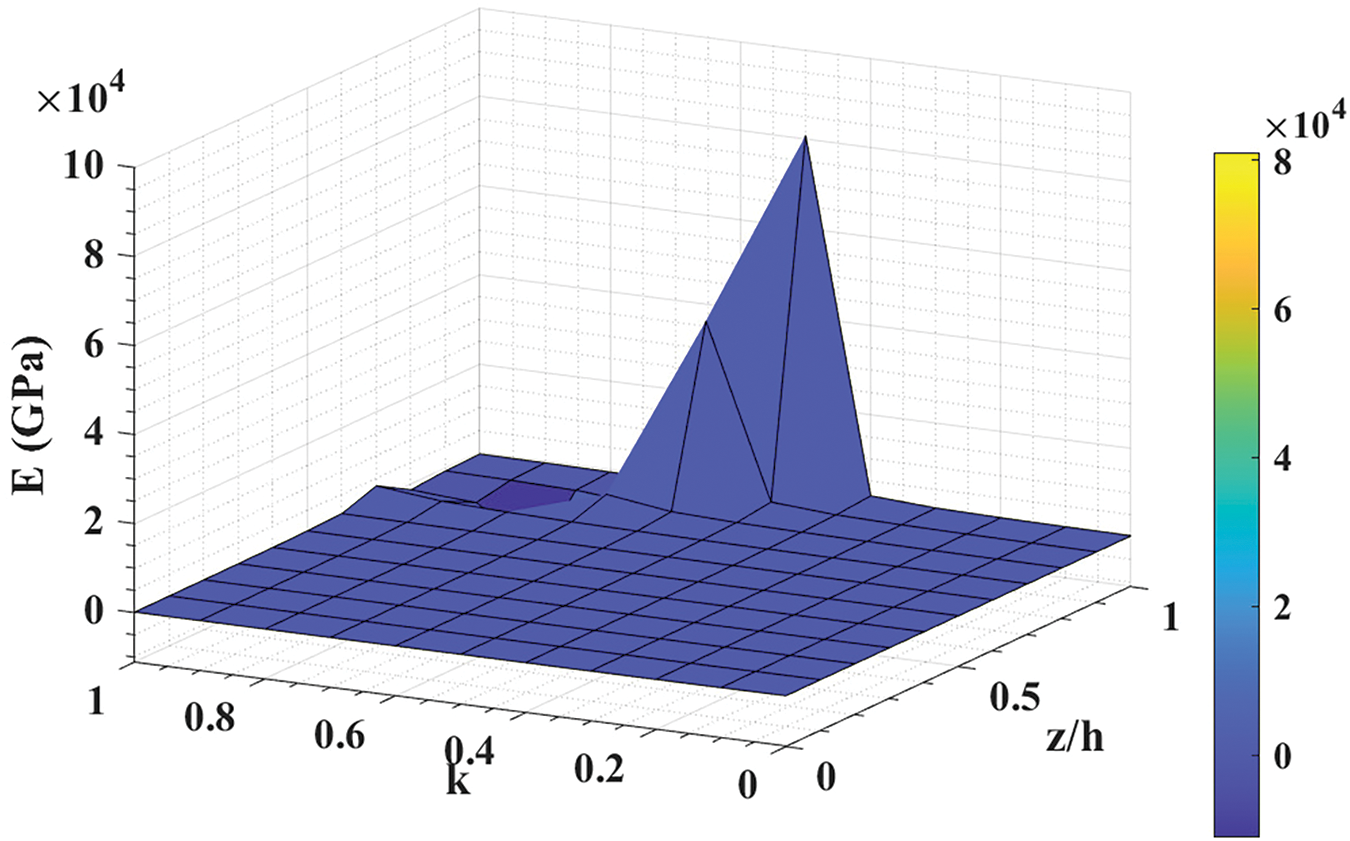
Figure 5: Effect of z/h and k on E(z) in Reuss model
2.1.11 Self-Consistent Estimation Model
This model is effective for determining the bulk and shear moduli in regions with interconnected skeletal microstructures. It assumes that each reinforcement inclusion is embedded in a continuous material possessing the composite’s effective properties, without differentiating between matrix and reinforcement phases. As a result, composites with identical constituents, even in different roles, will have the same moduli. To calculate the shear modulus, G(z), of the FG material, the following quadratic equation needs to be solved at each surface [145–149]:
3GUVf(z)3GU+4G(z)+3GL(1−Vf(z))3GL+4G(z)+5Vf(z)GLG(z)−GL+5(1−Vf(z))GUG(z)−GU+2=0.(20)
An auxiliary function η(z) is introduced in the form:
η(z)=G(z) Vf(z)G(z)−GL+G(z) (1−Vf(z))G(z)−GU.(21)
The bulk modulus, K(z), is now written in terms of G(z) and η(z) as:
K(z)=4 G(z) (3−5η(z))15 η(z)−6.(22)
The Mori-Tanaka model is then used to calculate the elastic modulus and Poisson’s ratio. According to Kiani et al. [149], the material properties determined using the Voigt, Mori-Tanaka, and Self-Consistent models differ by about 3%. It was found that the Mori-Tanaka model is more accurate when there is a continuous matrix, while the Self-Consistent model is more accurate and better suited for materials with a skeletal microstructure [146].
2.1.12 Cubic Local Representative Volume Elements Model
Gasik et al. [150] introduced this model, which is designed to estimate the effective properties of two-phase composite materials, where the second phase is considered as an inclusion [75,139,151]. The effective Young’s modulus of the composite is expressed as [150,152]:
E(z)=EL[1−3√(Vf(z))2(1−11−3√Vf(z)(1−ELEU))].(23)
The effect of z/h and k on E(z) is shown in Fig. 6 for EU=380 and EL=70. The Voigt homogenization model is used to determine the effective Poisson’s ratio of FG materials.

Figure 6: Effect of z/h and k on E(z) in cubic LRVE model
2.1.13 Hashin-Shtrikman Bounds Model
This model, also known as the Composite Sphere Assemblage Model, is developed by Hashin et al. [153], using a variational approach to heterogeneous linear elasticity, to calculate the effective elastic properties of two-phase materials. This model provides upper and lower bounds for the shear modulus (G) and bulk modulus (K) of materials with randomly distributed spherical inclusions. The upper bounds for the effective moduli are [153–157]:
G+(z)=GU+1−Vf(z)1GL−GU+6(KU+2GU)Vf(z)5GU(3KU+4GU),(24)
K+(z)=KU+1−Vf(z)1KL−KU+3Vf(z)3KU+4GU.(25)
Similarly, the lower bounds for the effective moduli are:
G−(z)=GL+Vf(z)1GU−GL+6(KL+2GL)(1−Vf(z))5GL(3KL+4GL),(26)
K−(z)=KL+Vf(z)1KU−KL+3(1−Vf(z))3KL+4GL.(27)
In these equations, + and − represent the upper and lower bounds, respectively. With these shear and bulk moduli, the effective Young’s modulus and Poisson’s ratio can be obtained by using the Mori-Tanaka method. Notably, the lower bound given by the Hashin-Shtrikman model aligns with the results obtained from the Mori-Tanaka method.
2.1.14 Wakashima-Tsukamoto Model
Wakashima et al. [158] calculated K(z) and G(z) of macroscopically isotropic dual-phase composite materials, accounting for arbitrary phase geometries. It models the composite as having randomly dispersed ellipsoidal inclusions and uses a mean-field approach to determine the effective mechanical properties [159,160]. In this model, K(z) and G(z) are expressed as [161,162]:
K(z)=KL+aVf(z)KL(KU−KL)(1−Vf(z))KU+aVf(z)KL,(28)
G(z)=GL+bVf(z)GL(GU−GL)(1−Vf(z))GU+bVf(z)GL,(29)
where,a=KU(3KL+4GL)KL(3KU+4GU),b=(1+e)GUGL+eGU,e=9KL+8GL6KL+12GL.(30)
Then, the Mori-Tanaka model is used to determine the E(z) and ν(z) of FG materials.
This modeling approach assumes that the reinforcement particles are spherical and are embedded in a uniform, isotropic material (which means the material has the same properties in every direction). It also assumes that the reinforcement particles and the surrounding material are perfectly bonded, with no gaps or imperfections at the interface [152,163,164]. The effective bulk and shear moduli are given as [159,165]:
K(z)=KUVf(z)3KU+4GU+KL(1−Vf(z))3KL+4GUVf(z)3KU+4GU+1−Vf(z)3KL+4GU,(31)
G(z)=GU[GL(1−Vf(z))(7−5νU)GU+(8−10νU)GL+Vf(z)15(1−νU)GU(1−Vf(z))(7−5νU)GU+(8−10νU)GL+Vf(z)15(1−νU)].(32)
Similarly, the Mori-Tanaka model is applied further to obtain the E(z) and ν(z).
2.1.16 Coherent Potential Approximation Model
The Coherent Potential Approximation model is also utilized to obtain the effective material properties of FG materials. A notable advantage of this method is that it can be applied regardless of whether the material phases are continuous or particulate in nature. This model leads to a set of coupled implicit equations, which is expressed as [159,165,166]:
Vf(z)(KU−K(z)3KU+4G(z))+(1−Vf(z))(KL−K(z)3KL+4G(z))=0,(33)
Vf(z)(GU−G(z)GU+G(z)(9K(z)+8G(z))6K(z)+12G(z))+(1−Vf(z))(GL−G(z)GL+G(z)(9K(z)+8G(z))6K(z)+12G(z))=0.(34)
The K(z) and G(z) can be derived from Eqs. (33) and (34). Then, the E(z) and ν(z) are obtained using the Mori-Tanaka model.
Axially FG materials are a type of advanced composite materials where the material properties, such as Young’s modulus, thermal conductivity, mass density, or Poisson’s ratio, vary continuously along the axial direction. This gradation is designed to optimize the material’s performance under varying conditions like thermal loads, mechanical stress, or environmental factors. By gradually changing the properties along the structure, axially FG materials reduce stress concentrations, improve durability, and enhance thermal resistance compared to homogeneous materials. They are used in applications like aerospace, biomedical implants, and mechanical components where tailored performance is crucial. The key differences between conventional and axially FG materials, along with their advantages and applications, are presented in Table 1. Some homogenization models related to axial variation are presented below.
In this model, the material properties of FG material are considered to vary in axial direction according to a power-law function. The effective material property is given by [167–171]:
P(x)=(PR−PL)(xL)k+PL.(35)
In some literature [46,172–174], the effective material property in Power-Law model is also considered as:
P(x)=(PL−PR)(1−xL)k+PR.(36)
Here, PL and PR are material properties on the left and right sides, respectively, of the FG structure. k is the power-law exponent, and x is the axial direction of the FG material. It is noted that P(x)=PL when x=0, and P(x)=PR when x=L. But, at k=0, P(x)=PR in Eq. (35) and P(x)=PL in Eq. (36). The effects of x/L and k on Young’s modulus E(x) according to Eqs. (35) and (36) are presented in Figs. 7 and 8. Here, the left side is considered as ceramic and right side is considered as metal. So, EL=380 (Alumina) and ER=70 (Aluminium).
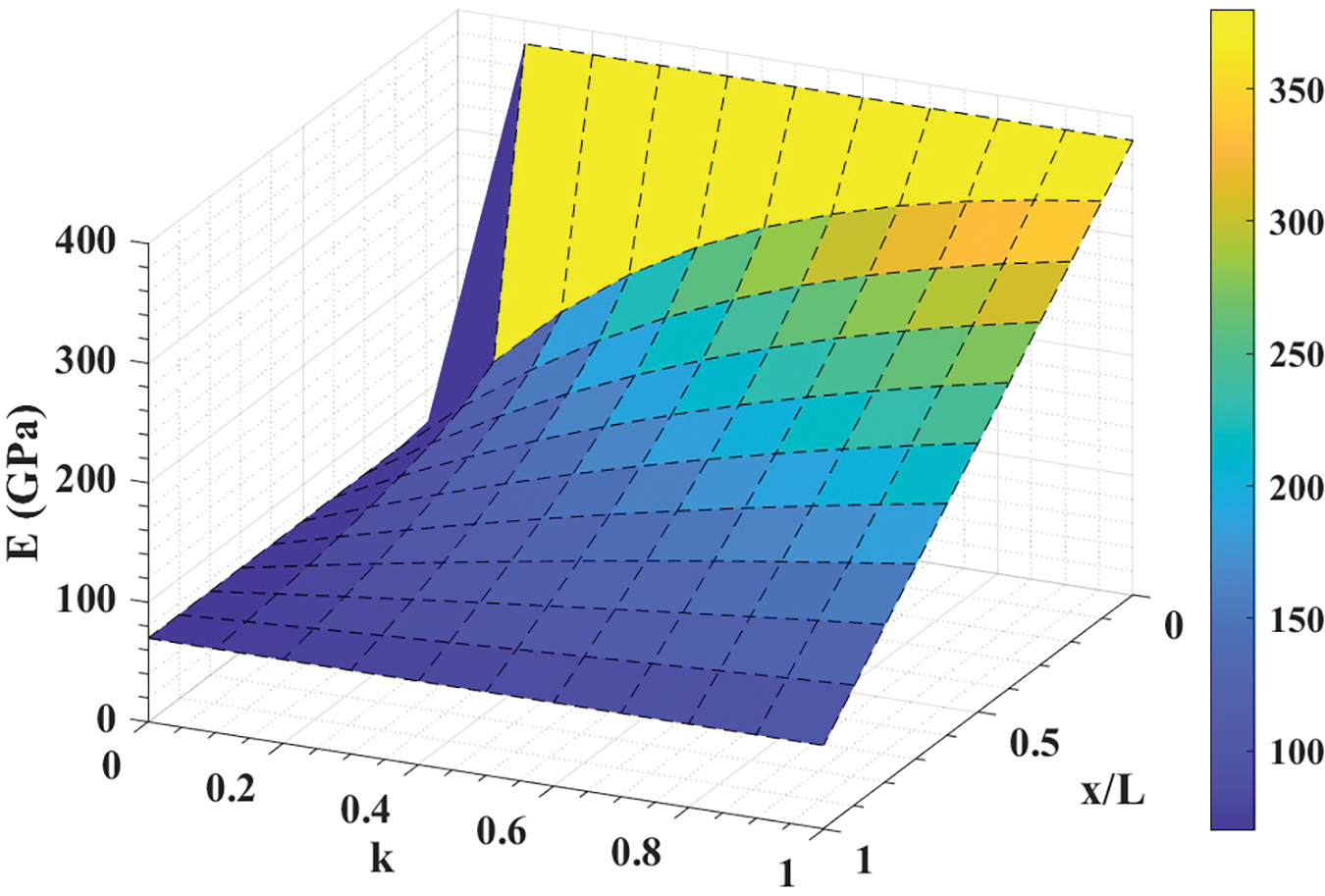
Figure 7: Effect of x/L and k on E(x) in power-law variation (35)
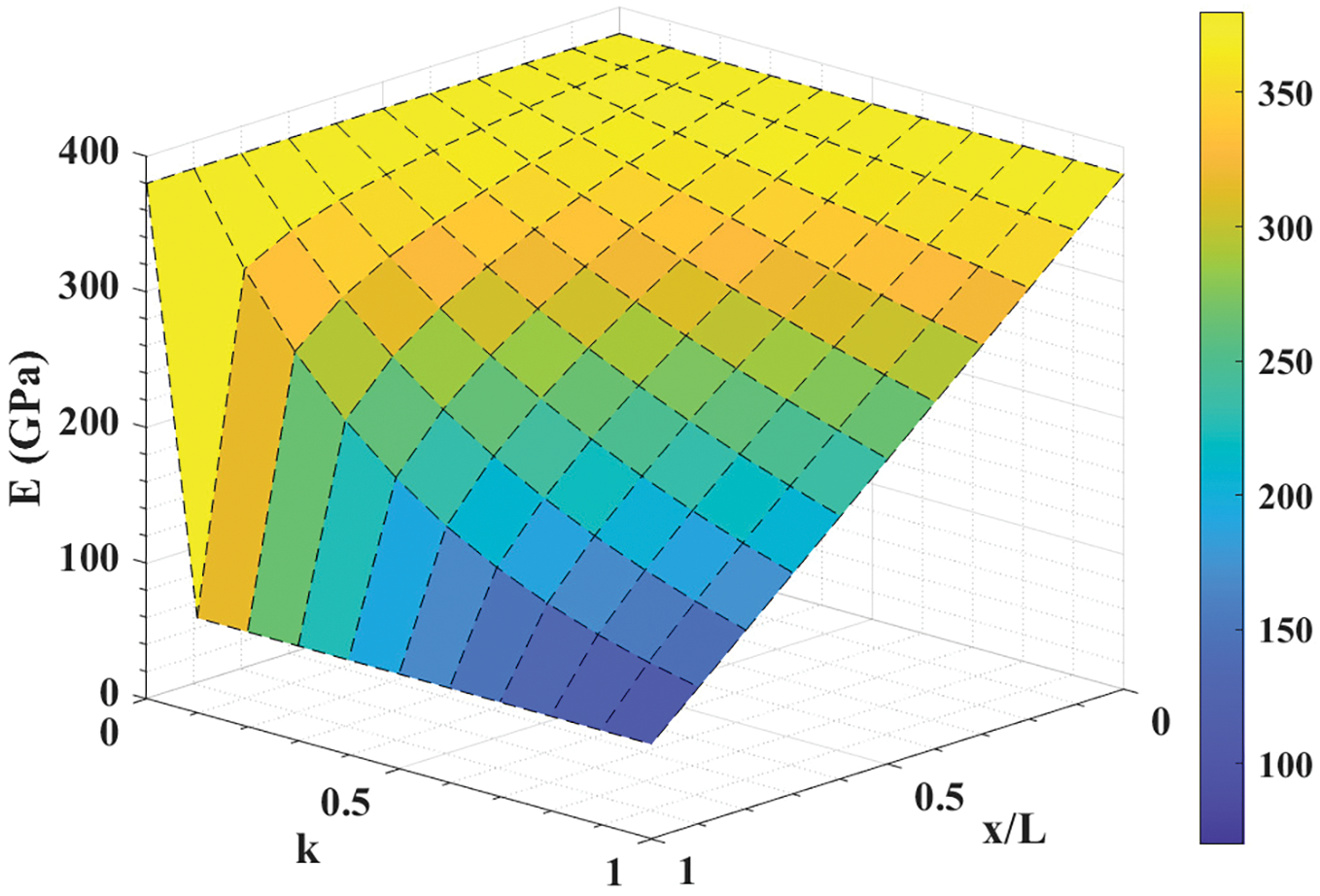
Figure 8: Effect of x/L and k on E(x) in power-law variation (36)
An exponent function is considered in this model to vary the material properties in the axial direction of the FG material. The effective material property with exponential variation is represented as [175–178]:
P(x)={(PR−PL)(ekxL−1ek−1)+PL,if k≠0,(PR−PL)(xL)+PL,if k=0,(37)
where, k is the gradient parameter, which describes the change in volume fraction between the two constituents of the FG material. Similarly, at x=0, P(x)=PL, and at x=L, P(x)=PR. Fig. 9 demonstrates the effect of x/L and k on the Young’s modulus E(x), considering EL=380 and ER=70.
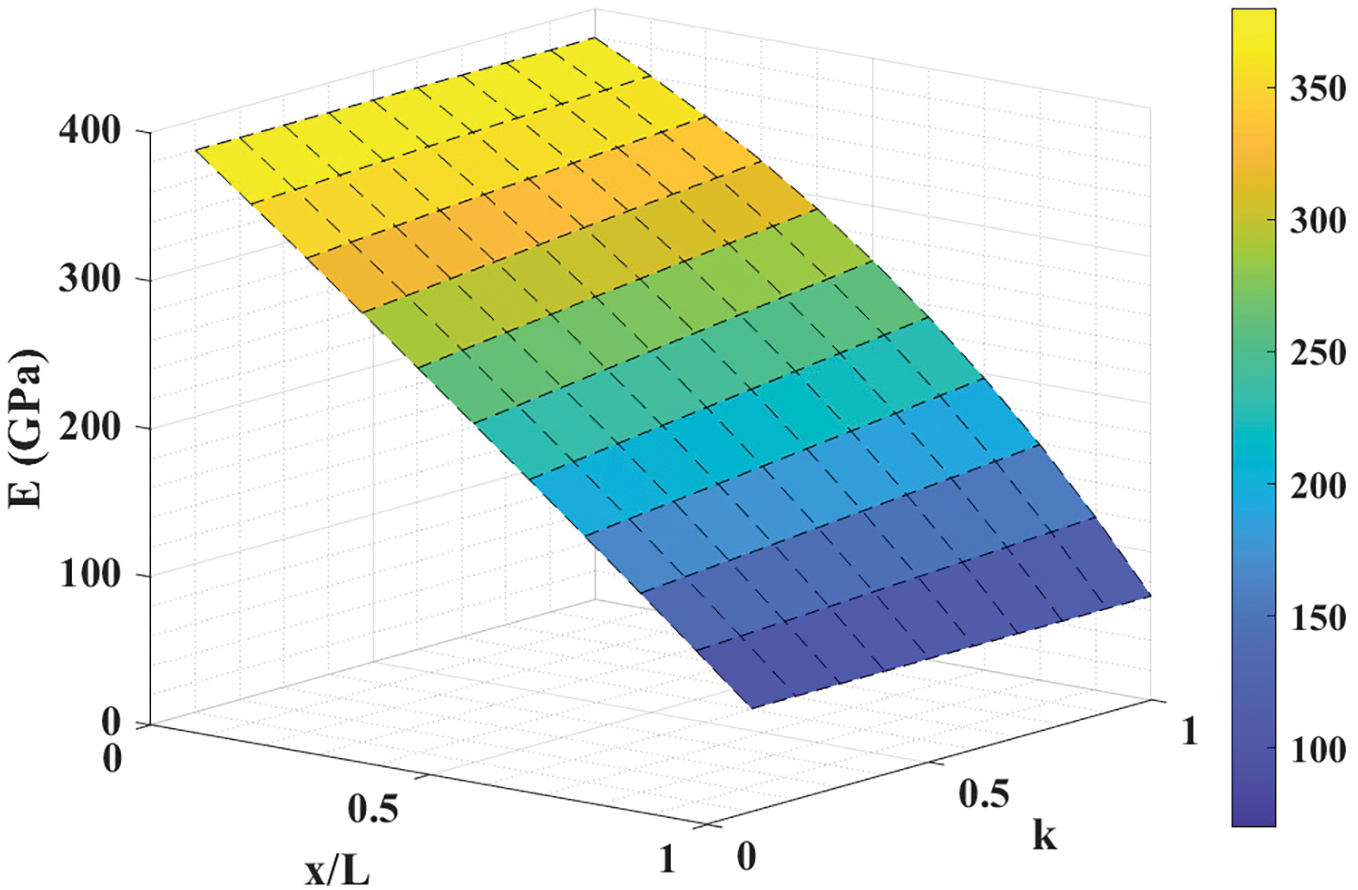
Figure 9: Effect of x/L and k on E(x) in exponential variation
The material properties of the FG material are considered to vary according to a trigonometric law along the axial direction, and the effective material property is given by [179]:
P(x)=(PR−PL) sin2(xL−α)+PL,(38)
where, α is an optional parameter. In Fig. 10, the plot for the effect of x/L and α on E(x) is illustrated, taking EL=380 and ER=70.
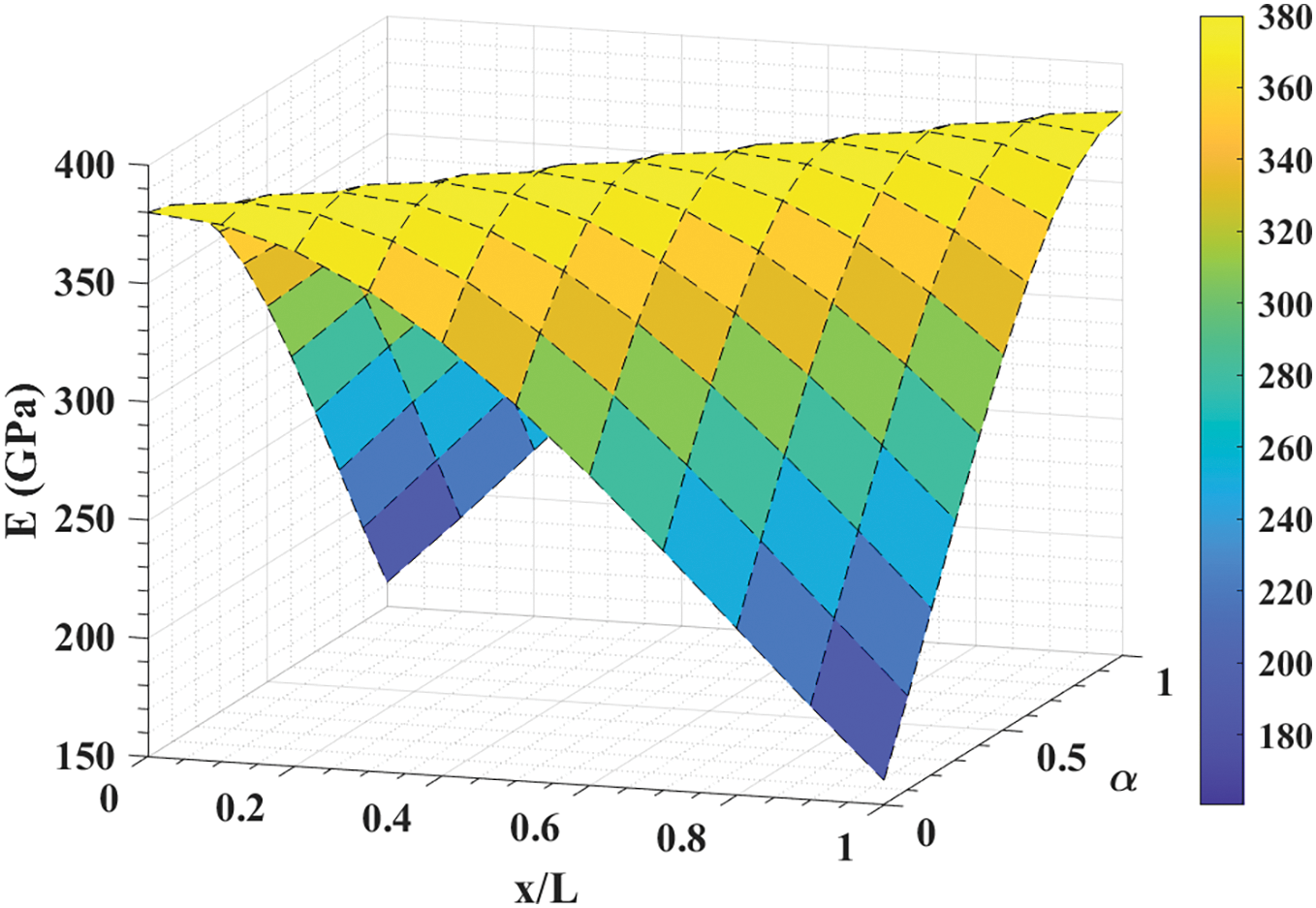
Figure 10: Effect of x/L and α on E(x) in trigonometric law model
2.2.4 Four-Parameter Power-Law Distribution
A power-law distribution function involving four parameters is used to describe the material properties of FG material in the axial direction. The effective material property, in this case, is given by [100,180]:
P(x)=(PL−PR) c1[1−(xL)+c2(xL)k1]k2+PR,(39)
where, the unknown parameters c1, c2, k1, and k2 control the variation of the material properties. These parameters are selected such that 0≤c1[1−(xL)+c2(xL)k1]k2≤1. When c1=1 and k2=0, P(x)=PL, and when c1=0, P(x)=PR. Also, when c1=1 and c2=0, it reduces to the general power-law variation, as defined in Eq. (36).
2.2.5 Four-Parameter Trigonometric Distribution
In this model, the material properties are also assumed to vary along the axial direction following a trigonometric distribution. However, this time, four parameters are used in the trigonometric distribution function. The effective material property of the FG material is determined as [181]:
P(x)=(PL−PR) c1[1+cos(c2x+c3)]k+PR,(40)
where, c1, c2, c3, and k are the design variables that regulate the variation of material properties. These parameters are chosen to ensure that 0≤c1[1+cos(c2x+c3)]k≤1.
2.2.6 Five-Parameter Trigonometric Distribution
A trigonometric distribution consisting of five different parameters is considered in this model to vary the material properties of the FG material along the axial direction. Here, the effective material property is represented as [100,180]:
P(x)=(PL−PR) c1[12−c22sin(c3πxL+c4)]k+PR,(41)
where, c1, c2, c3, c4, and k are parameters that control the material variation, and the values of these parameters are considered such that 0≤c1[12−c22sin(c3πxL+c4)]k≤1.
This model is based on the principle of averaging stress and strain in heterogeneous materials. According to this model, the effective material property of the axially FG material is expressed as [101,182–184]:
P(x)=12[(PR−PL)(xL)k+PL+PLPR(PL−PR)(xL)k+PR].(42)
It is noted that when k=0, P(x)=PR. The effect of x/L and k on E(x) is plotted in Fig. 11, considering EL=380 and ER=70.
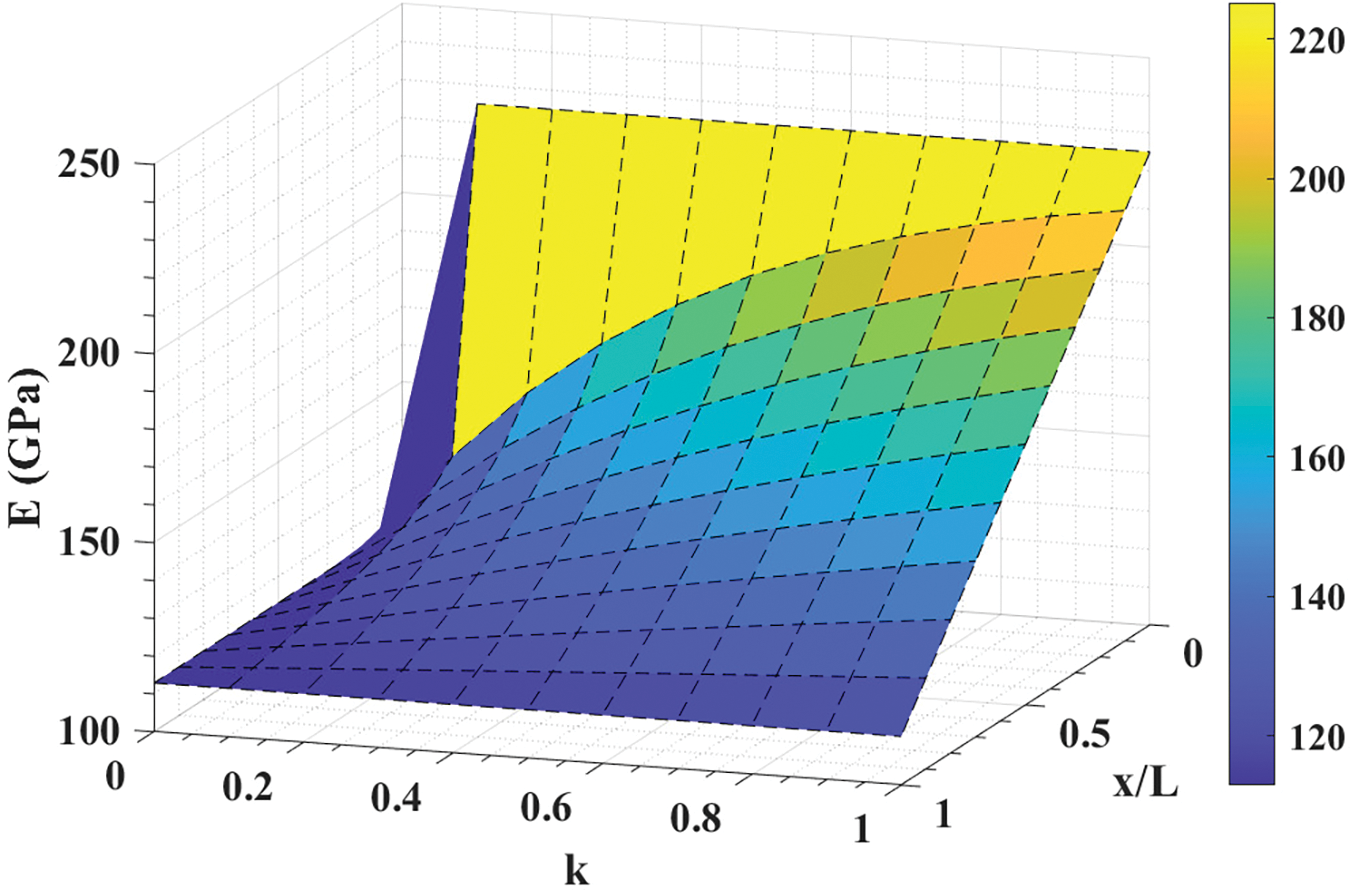
Figure 11: Effect of x/L and k on E(x) in Voigt-Reuss-Hill model
The Voigt, Reuss, Tamura, Mori-Tanaka, Local Representative Volume Element, and Hashin-Shtrikman bounds models for axially FG materials are similar to those used for conventional FG materials. The main difference is that Vf(z) (which represents the volume fraction in conventional FG materials) is replaced by Vf(x), where x denotes the axial direction. Additionally, the subscript U is replaced by R, where R and L correspond to the right and left sides, respectively, of the FG material. In this context, the material variation follows a power-law distribution function given by Vf(x)=(xL)k, where k is the power-law exponent [101].
2.3 Bi-Directional FG Materials
BDFG materials are designed with properties that vary along both the thickness and length (axial) directions. This unique variation makes them highly valuable for use in NEMS and MEMS. By customizing the material properties in two directions, BDFG materials can significantly improve structural performance while reducing material consumption and weight, making them a highly efficient choice for advanced engineering applications [16]. The advantages and applications of BDFG materials are outlined in Table 1.
Two power-law distribution functions are considered in the thickness and axial directions to vary the material properties of the BDFG materials. The effective material property, P(x,z), is expressed as:
P(x,z)=(Pc−Pm) Vf(x,z)+Pm,(43)
where, Pc and Pm are the material properties of the ceramic and metal constituents, respectively. The volume fraction, Vf(x,z), is given by [78,102,185–187]:
Vf(x,z)=(xL)k1(zh+12)k2.(44)
The effect of x/L and z/h on Young’s modulus E(x,z) according to Eqs. (43) and (44) is shown in Fig. 12 with fixed values of k1=1 and k2=2. Here, Ec=380 and Em=70 are considered for this plot.
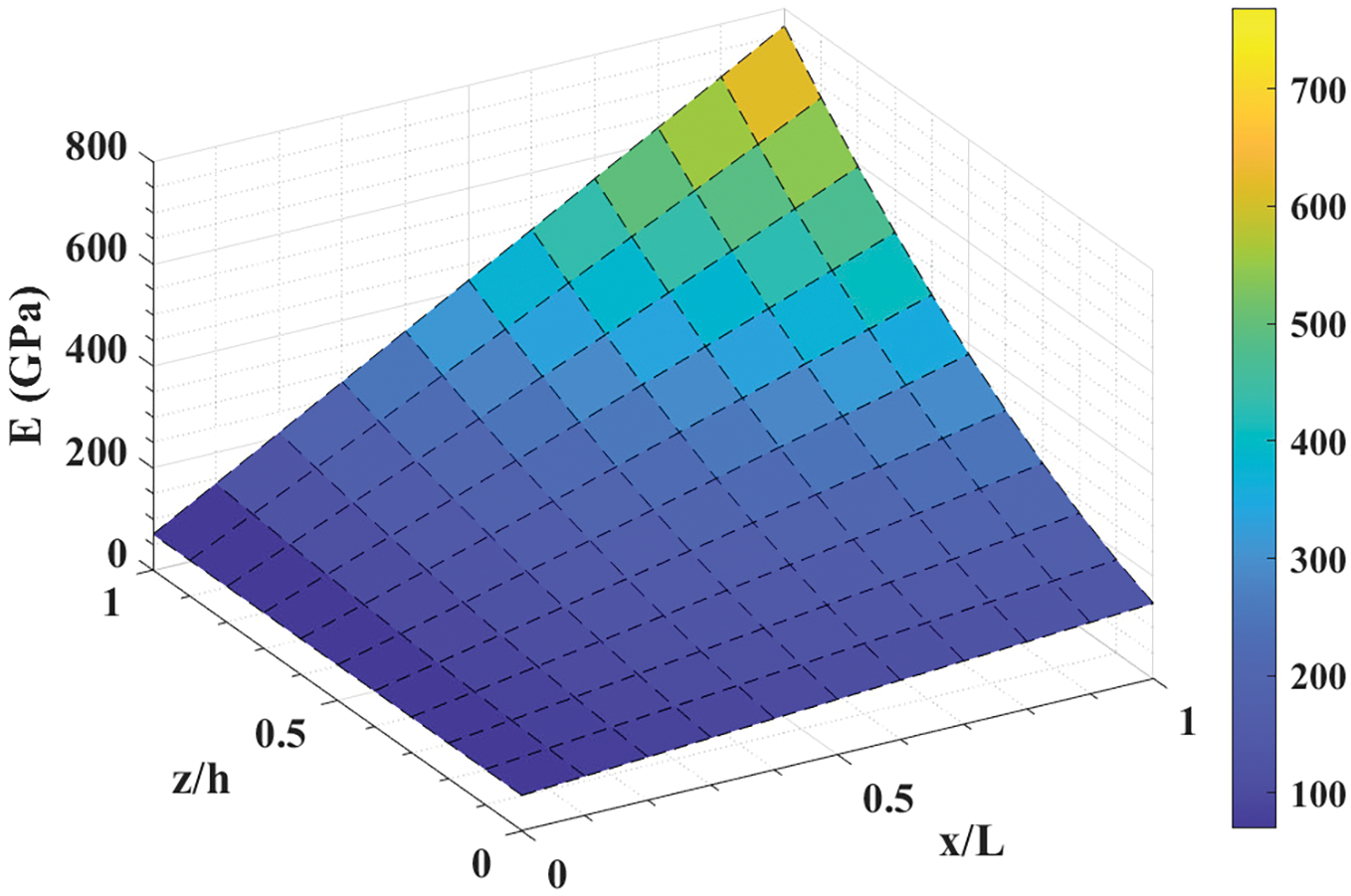
Figure 12: Effect of x/L and z/h on E(x,z) in power-law variation (k1=1, k2=2)
In some literature [188,189], the volume fraction in a power-law variation of BDFG materials is also defined by:
Vf(x,z)=(xL+12)k1(zh+12)k2.(45)
Chen et al. [190] reported the volume fraction as:
Vf(x,z)={(xL)k1(1+2zh)k2,0≤x≤L, −h2≤z≤0,(xL)k1(1−2zh)k2,0≤x≤L, 0≤z≤h2.(46)
While, Li et al. [191] and Thang et al. [192] presented the volume fraction as:
Vf(x,z)=(1−x2L)k1(zh+12)k2.(47)
Here, k1 and k2 are the power-law exponents in the axial and thickness directions, respectively. If k1=k2=0, then P(x,z)=Pc, which shows that the BDFG material has uniform material properties.
Additionally, in BDFG materials, the variation of material properties following a power-law distribution can be considered along the axial (x-axis) and lateral (y-axis) directions. The effective material property, P(x,y), in this case, is expressed as [79,193,194]:
P(x,y)=(Pc−Pm) V1(x) V2(y)+Pm,(48)
where, V1(x) and V2(y) are volume fractions of constituents in the axial and lateral directions, respectively. Three different types of variations are presented here.
Type I:
V1(x)=(xL)k1,0≤x≤L,(49a)
V2(y)=(yb)k2,0≤y≤b.(49b)
Type II:
V1(x)=(xL)k1,0≤x≤L,(50a)
V2(y)={(2yb)k2,0≤y≤b2,(2−2yb)k2,b2≤y≤b.(50b)
Type III:
V1(x)={(2xL)k1,0≤x≤L2,(2−2xL)k1,L2≤x≤L,(51a)
V2(y)={(2yb)k2,0≤y≤b2,(2−2yb)k2,b2≤y≤b,(51b)
in which, k1 and k2 are power-law exponents in x and y directions, respectively.
In this model, the material properties of BDFG materials change exponentially along both the axial direction (x-axis) and the lateral direction (y-axis). The effective material property, P(x,y), is given by [195,196]:
P(x,y)=(Pc−Pm) ec1x+c2yec1+c2+Pm,(52)
where, c1 and c2 are the material gradient indices, which dictate the material properties along the x and y directions.
2.3.3 Exponential and Power-Law Variations
The material properties of the BDFG material are varied using an exponential function along the axial direction and a power-law function along the thickness direction. The resulting effective material property is expressed as [16,197–200]:
P(x,z)=ecLx[(Pc−Pm)(zh+12)k+Pm],(53)
where, c is the axial FG index, and k is the thickness FG index. In Fig. 13, the effect of x/L and z/h on Young’s modulus E(x,z) is plotted for c=1 and k=2, considering Ec=380 and Em=70.

Figure 13: Effect of x/L and z/h on E(z) in power-law model
2.3.4 Polynomial Function Variation
In this model, the material properties of BDFG materials are varied using two polynomial functions along the axial and lateral directions. The effective material property is described as [195,196,201]:
P(x,y)=(Pc−Pm)[∑mi=0c1(xL)i∑nj=0c2(yb)j]+Pm,(54)
where, c1 and c2 are control parameters, m and n are orders of polynomials in x and y directions, respectively.
2.3.5 BDFG Materials with Three Material Constituents
In this model, the BDFG material consists of three distinct constituents, with at least one being ceramic and the other two being metals. This is different from conventional BDFG materials, which usually consist of only two material constituents. The material properties are designed to vary in both the axial and lateral directions. The effective material property for this type of BDFG material is described as [202,203]:
P(x,y)=P1[(1−(xL)k1)(1−(yb)k2)]+P2[(xL)k1(1−(yb)k2)]+P3(yb)k2,(55)
where, k1 and k2 are the gradient indices that represent the composition variation in the axial and lateral directions, respectively. These indices are independent of one another.
2.3.6 BDFG Materials with Four Material Constituents
The BDFG material is assumed to be composed of two ceramic and two metal constituents. The volume fraction of these materials varies in both the axial and transverse directions. Here, P(x,z) is represented by [191]:
P(x,z)=Pc1Vc1+Pc2Vc2+Pm1Vm1+Pm2Vm2,(56)
where,
Vc1=[1−(xL)k1](zh+12)k2,(57a)
Vc2=(xL)k1(zh+12)k2,(57b)
Vm1=[1−(xL)k1][1−(zh+12)k2],(57c)
Vm2=(xL)k1[1−(zh+12)k2].(57d)
Here, the subscripts c1, c2, m1, and m2 denote the ceramic 1, ceramic 2, metal 1, and metal 2, respectively. Pi represents the material property, and Vi denotes the volume fraction of the corresponding material constituent, where i=c1,c2,m1,m2.
The Mori-Tanaka and Voigt models applied to BDFG materials operate similarly to those used for conventional or axially FG materials. The key difference is that in the BDFG models, the standard volume fraction is replaced with the volume fractions of BDFG material [185].
2.4 Tri-Directional FG Materials
Tri-directional functionally graded (TDFG) materials are a type of advanced composites with properties that gradually vary in three directions: length (x-axis), width (y-axis), and thickness (z-axis). This design provides precise control over thermal, elastic, and mechanical properties throughout the material, making TDFG materials ideal for use in aerospace, automotive, and biomedical applications where they can withstand complex, multi-directional stresses. The key differences, advantages, and applications of TDFG materials compared to other materials are summarized in Table 1.
The effective material property of TDFG materials, characterized by power-law variations in the x, y, and z directions, is expressed as [104,105,204]:
P(x,y,z)=(Pc−Pm)[(xL)k1(yb)k2(zh+12)k3]+Pm.(58)
For TDFG materials, an additional type of power-law variation is considered in the literature [205], where the effective material property is:
P(x,y,z)=(Pc−Pm)[V1(x) V2(y)(zh+12)k3]+Pm,(59)
where,
V1(x)={(2xL)k1,0≤x≤L2,(2−2xL)k1,L2≤x≤L,(60a)
V2(y)={(2yb)k2,0≤y≤b2,(2−2yb)k2,b2≤y≤b.(60b)
Here, k1, k2 and k3 are power-law indexes in the x, y and z directions, respectively.
The effective material property of TDFG materials, where properties vary exponentially along the x direction and follow a power-law variation in the y and z directions, is written as [86,103]:
P(x,y,z)=ec1xL[(1−c2)(yb+12)k1+c2][(Pc−Pm)(zh+12)k2+Pm],(61)
where, c2 is the material constant, and c1, k1 and k2 are the axial, lateral, and transverse FG indexes, respectively.
3 Size-Dependent Theories for FG Nanostructures
The nonlocal/size-dependent theory provides a more accurate framework for describing the mechanical behavior of FG nanostructures by accounting for both the intrinsic material nonhomogeneity and the influence of small-scale effects on the overall response [206]. Unlike classical continuum mechanics, nonlocal theories incorporate the long-range interactions and size effects inherent in nanostructures, leading to a more precise analysis of their structural performance and enabling valuable insights into the underlying mechanisms governing the behavior of FG nanomaterials [207]. Incorporating nonlocal theory into the analysis of FG nanostructures enhances the understanding of stress distribution and deformation patterns, particularly in systems where size effects play a significant role. This approach allows for improved predictions of key mechanical properties, such as stiffness, strength, and stability, as well as the structural integrity of FG nanomaterials under various loading and boundary conditions [208]. Moreover, nonlocal models provide deeper insights into the influence of nanoscale phenomena, such as surface effects and scale-dependent stiffness, which are critical for the design and optimization of advanced FG materials. By leveraging nonlocal theories, researchers can bridge the gap between nanoscale physics and macroscopic material behavior, advancing the development of FG nanostructures for applications in cutting-edge fields such as nanoelectronics, biomedical engineering, and aerospace systems. Several well-established nonlocal models commonly used in the literature to analyze FG nanostructures are shown in Fig. 14 and discussed in detail below.

Figure 14: Various size-dependent theories for FG nanostructures
3.1 Eringen’s Nonlocal Elasticity Theory
The ENET is an extension of classical elasticity theory that incorporates nonlocal effects into the constitutive equations to account for interactions between material points not only at the same spatial location but also at neighboring points. This modification provides a more accurate representation of material behavior at small scales, particularly in nanoscale systems where atomic-scale interactions are significant [209,210]. By averaging stress and strain fields over a finite spatial domain, ENET captures size-dependent behaviors that classical theories often neglect. This theory is particularly valuable for analyzing materials with microstructural heterogeneities or addressing phenomena such as wave propagation, dislocation motion, and flexural rigidity in nanostructures [14]. For instance, ENET has been successfully applied to study the forced vibration of nanorods, where nonlocal effects enhance dynamic displacements and frequencies compared to classical models [211]. Additionally, it has been used in the buckling analysis of nano-scale plates, providing analytical solutions that align with observed size effects in experiments [212]. Furthermore, ENET has proven effective in addressing elastic properties in granular and nanoscale systems, emphasizing the limitations of standard continuum mechanics at small scales [213]. By integrating atomic-scale considerations, ENET bridges the gap between molecular dynamics and continuum mechanics, offering improved models for nanoindentation and other applications [214]. This theory is foundational for understanding mechanical behaviors in nanoscale systems and remains a critical tool in advancing nanotechnology and material science.
In ENET, the nonlocal stress tensor σij(x) at a point x is defined by integrating over the entire volumeV of the material to account for the strain at all points x′ within that neighborhood [215,216]:
σij(x)=∫Vα(|x′−x|,τ) tij(x) dV(x′),(62)
where, tij(x) is the local stress tensor at x, and α(|x′−x|,τ) is a kernel function that describes the nonlocal interaction between points based on the distance |x′−x| and a scaling factor τ. The kernel function α can take different forms depending on the dimensionality of the problem, and τ=e0aL. Here, L and a are external and internal characteristic lengths, respectively, and e0 is material constant. The components of the classical local stress tensor for a Hookean material are expressed as [216]:
tij=Cijkl εkl,(63)
where, Cijkl is the fourth order elasticity tensor, and εkl is the strain tensor.
To simplify practical application, Eringen developed an equivalent differential form that relates the nonlocal stress tensor σij to the local stress tensor tij via the Laplacian operator ∇2 [13,217]:
(1−(e0a)2∇2)σij=tij.(64)
This differential form is more computationally convenient for modeling stress distributions in various dimensions, capturing the size effect by introducing terms related to the second gradient of strain. By applying this theory, researchers gain an enhanced understanding of stress and deformation behaviors, particularly at the micro- and nanoscale, making it widely applicable in the analysis of FG materials, thin films, and other structures sensitive to nonlocal effects. Eringen’s theory thus extends the predictive power of elasticity models by incorporating essential nonlocal interactions, leading to more accurate descriptions of material behavior under diverse loading conditions.
3.2 Nonlocal Strain Gradient Theory
The NSGT provides a more accurate description of material behavior at small scales by incorporating both the nonlocal and strain gradient effects [15]. This theory is particularly useful in determining the mechanical properties of materials with microstructural features, such as thin films or nanomaterials [218]. Furthermore, this theory offers a comprehensive framework for analyzing the deformation and failure mechanisms of these advanced materials, taking into account the interactions between nonlocal effects and strain gradients [219].
According to NSGT, the total stress field t is defined to account for both classical nonlocal stress σ and higher-order strain gradient stress σ(1), formulated as [15,220]:
t=σ−∇σ(1),(65)
where, ∇ is the Laplacian operator, capturing the effect of spatial stress variations, and
σ=∫Vα0(x′,x,e0a) C:ε′ dV′,(66)
σ(1)=l2∫Vα1(x′,x,e1a) C:∇ε′ dV′,(67)
where, C is the fourth-order elasticity tensor and ε and ∇ε represent the strain tensor and strain gradient tensor, respectively. The terms e0 and e1 are nonlocal parameters describing the significance of nonlocal effects, and l is the material length scale parameter capturing strain gradient effects. The kernel functions α0 and α1 are assumed to satisfy the differential operator form suggested by Eringen [13]:Li=1−(eia)2∇2for i=0,1.(68)
Substituting these into the total stress expression results in the generalized NSGT constitutive relation, we get [220]:
(1−(e1a)2∇2)(1−(e0a)2∇2)t=(1−(e1a)2∇2)C:ε−l2(1−(e0a)2∇2)∇C:∇ε.(69)
To simplify this, we often assume e0=e1=e, yielding:
(1−(ea)2∇2)t=C:ε−l2∇C:∇ε.(70)
Setting l=0, we get the ENET, as proposed by Eringen [13,217]:
(1−(ea)2∇2)t=C:ε,(71)
while, setting ea=0 yields the pure strain gradient theory [221–223], represented by:
t=(1−l2∇2)C:ε.(72)
The NSGT model effectively explains size-dependent behavior in nanostructures, such as CNTs, showing strong agreement with molecular dynamics simulations. Its incorporation of both nonlocal and gradient effects provides a robust framework for capturing the unique mechanical properties observed at the nanoscale.
3.3 Modified Couple Stress Theory
The modified couple stress theory (MCST) [17] is an extension of classical continuum mechanics designed to account for size-dependent behaviors observed in micro- and nanoscale materials. Unlike classical theories, which assume that stress at a point is solely determined by deformation, MCST introduces a material length-scale parameter and incorporates rotational effects through couple stresses. This approach captures the influence of microstructural elements, such as grain boundaries or particle interactions, by allowing moments and higher-order deformation gradients to contribute to the material response [18,224]. MCST is particularly relevant in applications involving microbeams, nanoplates, and other small-scale structures, where classical mechanics often fails to predict mechanical behavior accurately [225,226].
The strain energy U in a deformed isotropic linear elastic material occupying a volume V is expressed by [227–229]:
U=12∫V(σ:ε+m:χ)dv,(73)
where, σ represents the Cauchy (classical) stress tensor, conjugated with the strain tensor ε, and m is the deviatoric part of the couple stress tensor, conjugated with the symmetric curvature tensor χ. The kinematic relations for strain and curvature are defined in terms of the displacement vector u and the rotation vector θ (related to the displacement gradient) as follows [228]:
ε=12(∇u+(∇u)T)andχ=12(∇θ+(∇θ)T),(74)
with the rotation vector θ defined by:θ=12∇×u.(75)
The constitutive relations for stress and couple stress are expressed using Lamé constants λ and μ, along with the length-scale parameter l, as [230]:
σ=λtr(ε)I+2μεandm=2μl2χ.(76)
Here, λ and μ are related to the material’s Young’s modulus E and Poisson’s ratio ν, while l characterizes the material’s resistance to couple stresses. The theory necessitates positive definiteness of the strain energy density function w, requiring that:
E>0,−1<ν<0.5,andl2>0.(77)
This ensures that the material response remains stable and unique in boundary value problems. The length-scale parameter l introduces a dependency on the material’s microstructure, distinguishing this model from classical elasticity. The value of l can be empirically determined through torsion or bending tests on slender structures, making the theory particularly useful for materials with pronounced side effects.
3.4 Consistent Couple Stress Theory
The consistent couple stress theory (CCST), proposed by Hadjesfandiari et al. [19,231], provides a robust framework for addressing the size-dependent mechanical behavior of materials at micro- and nanoscales. This theory refines classical continuum mechanics by introducing additional measures of deformation, particularly the couple-stress tensor and the curvature tensor, to account for microstructural effects. These additions allow CCST to capture phenomena that are otherwise inaccessible using traditional methods, such as size-dependent stiffness and strength in small-scale structures.
A central achievement of CCST is the introduction of the skew-symmetric couple-stress tensor, μij, defined by [20]:
μji=−μij.(78)
This tensor represents the internal moment per unit area caused by microstructural rotations. Unlike classical stress tensors, the force-stress tensor σij in CCST is asymmetric and is decomposed into symmetric and antisymmetric parts [20,232]:
σij=σ(ij)+σ[ij],(79)
where, σ(ij)=12(σij+σji) represents the symmetric part and σ[ij]=12(σij−σji) represents the antisymmetric part.
The surface forces and moments are described using the force-stress tensor and the couple-stress tensor, respectively [19,20]:
t(n)i=σjinj,m(n)i=μjinj,(80)
where, t(n)i and m(n)i are the force and moment traction vectors, and nj is the normal unit vector.
The equilibrium conditions in CCST extend those of classical mechanics to incorporate couple-stresses [19]:
σji,j+fi=0,(81a)
μji,j+ϵijkσjk+Ci=0.(81b)
Here, fi and Ci are the body force and body couple per unit volume, respectively, and εijk is the permutation tensor.
CCST introduces the rotation tensor ωij and the curvature tensor κij as measures of deformation. The displacement gradient tensor is decomposed as [20]:
ui,j=εij+ωij,(82)
where, εij=12(ui,j+uj,i) is the strain tensor, and ωij=12(ui,j−uj,i) is the rotation tensor. The curvature tensor is derived as [20,233]:
κij=ω[i,j]=12(ωi,j−ωj,i).(83)
These tensors describe the antisymmetric parts of the deformation and rotation fields.
For isotropic materials, CCST defines the stress and couple-stress tensors as [19,233]:
σ(ij)=λεkkδij+2Gεij,(84a)
μij=−4η(ωi,j−ωj,i),(84b)
where λ and G are the Lamé constants, δij is the Kronecker delta, and η=Gl2 is the couple-stress material constant, with l being the material length-scale parameter. The relation between η and l highlights that CCST requires only one additional material parameter.
The strain energy density function under CCST accounts for both symmetric and antisymmetric contributions [233]:
Us=∫Ω[12σ(ij)εij+μijκij]dΩ.(85)
These mathematical formulations enable CCST to effectively model phenomena such as bending, vibration, and stability in micro- and nanoscale structures. By addressing the limitations of classical mechanics and earlier couple-stress theories, CCST provides a unified and physically consistent approach for analyzing the mechanical behavior of small-scale materials. It plays a critical role in the design and analysis of advanced engineering systems, including FG materials and multilayered microstructures.
MDFG nanobeams are advanced materials with graded properties in multiple directions for enhanced resilience under complex loading and environmental changes. These FG materials are very important in nanotechnology where stability, vibration control, and resistance to thermal and mechanical stresses are crucial. Studies have shown that BDFG and TDFG materials outperform uni-directional materials as they can resist multi-directional forces and extreme temperature variations. Bi-directional grading enhances nanobeam performance by improving static deflection, load-bearing capacity, and stability along two axes, making it suitable for simpler applications. Tri-directional grading, with an additional material gradient, provides better vibration resistance, dynamic stability, and post-buckling performance, especially under complex multi-field conditions, making it ideal for advanced applications [234].
Nejad et al. [197,199] studied buckling and free vibration of BDFG nanobeams using ENET to capture nanoscale effects. By varying properties along both thickness and length, they reported that material length scale and gradation parameters affect critical buckling loads and frequencies. Using GDQM and Hamilton’s principle, they proved that bi-directional grading and nonlocal effects are important in nanoscale beam design. Yang et al. [235] presented a nonlinear model for BDFG nanobeams with exponential distribution of material in thickness and length. Using ENET and DQM, they studied size-dependent nonlinear bending, buckling, and vibration, and showed the effect of gradation, boundary conditions, and size effect on critical loads and frequencies. Hadi et al. [103] analyzed free vibration in TDFG Euler-Bernoulli nanobeams using NSGT. By grading material properties along axial, thickness, and width directions (excluding Poisson’s ratio) and using GDQM, they showed that natural frequencies could vary from classical results. Lal et al. [236] examined the vibrational behavior of BDFG Timoshenko nanobeams using ENET and first-order shear deformation theory (FSDT). With material composition graded by a power-law in thickness and exponentially in the axial direction, they demonstrated the effects of temperature, nonlocal parameters, and gradient indices on vibration characteristics. Dangi et al. [237] analyzed the nonlocal free vibration of BDFG nanobeams with material properties graded axially and through thickness. Using ENET, Hamilton’s principle, and FEM, they calculated the natural frequencies of the primary modes of vibration. Nazmul et al. [238] presented an analytical approach for bending analysis of BDFG nanobeams using ENET. By applying the Laplace transform, the authors derived explicit solutions for bending displacements under various loads and boundary conditions, considering material variation along thickness and axial directions. Khoram et al. [239] studied the bending behavior of BDFG nanobeams under mechanical and magnetic loads including the Winkler-Pasternak foundation. Applying ENET and TBT, they studied the effects of material gradation, aspect ratio, magnetic fields, and elastic foundation on buckling load. Malik et al. [240] studied the rotating BDFG nanobeams for free vibrations using ENET and EBT. The composition of the beam changes along length and thickness, and the governing equations derived from Hamilton’s principle and solved as an eigenvalue problem using the Ritz method. This paper focuses on flapping and lead-lag motions and provides nondimensional frequency-speed plots to understand the influence of nonlocality, length and thickness, root radius, and aspect ratio. Gholami et al. [241] studied the nonlinear free vibration of BDFG nanobeams with fixed boundary conditions using EBT. It was observed that nonlinear frequencies are higher than linear frequencies for the same oscillation amplitude and investigated the impacts of nonlocal parameters, vibration amplitude, and material gradient on the frequency behavior. Dangi et al. [242,243] modeled BDFG Euler-Bernoulli nanobeams with ENET, NSGT, and Gurtin-Murdoch surface elasticity theories, showing how combined nonlocal, strain gradient, and surface stresses affect natural frequencies, especially at low thicknesses. Also, Lal et al. [244] used nonlocal TBT to analyze the vibration response of BDFG nanobeams. The governing equations were solved with DQM, and the study highlights that surface and nonlocal effects are essential in accurately predicting the vibration behavior of shear-deformable nanobeams. Tang et al. [86] studied the nonlinear behavior of slender beams made of TDFG materials to resist multi-directional loads, particularly for aerospace and marine applications. Assuming the material properties vary continuously in three directions, they derived the governing equation using Hamilton’s principle and geometric nonlinearity. Using GDQM and homotopy analysis method (HAM), they calculated the nonlinear critical buckling load and frequency and found that TDFG indexes can increase the load-carrying capacity and dynamic flexibility more than FG and BDFG materials. Ohab-Yazdi [245] used ENET to analyze the mechanical vibration of rotating BDFG Euler-Bernoulli nanobeam. They varied the material properties for thickness and axial directions as a power-law to investigate the effects of hub ratio, rotation speed, and power indexes on natural frequencies. The results demonstrate that the natural frequency reduction is heavily influenced by different parameter adjustments, especially at high rotation speeds. Using a two-phase local/NSGT, Wang et al. [246] investigated the buckling behavior of porous BDFG Timoshenko nanobeams under hygro-thermo-mechanical loadings. The GDQM is employed and the results demonstrate softening/hardening behaviors in terms of critical buckling load against parameter variations including nonlocality, strain gradient, aspect ratio, and hygrothermal loadings under different boundary conditions. Barati et al. [247] studied the transverse vibrations of BDFG nanobeams under a longitudinal magnetic field using ENET. The equations of motion are solved with the GDQM. The study shows that parameters such as BDFG properties, size-dependent factors, and magnetic field strength significantly affect vibration frequencies, which can be controlled by adjusting the magnetic field. Zhao et al. [248] studied vibration frequency and wave propagation in MDFG nanobeams reinforced with CNTs, using an NSGT to account for size-dependent effects. The study separates bending and shear responses and considers nonlinear moisture and thermal effects. Analytical solutions revealed that changes in FG indexes influence the impact of the strain gradient coefficient on the vibration frequency. Shanab et al. [249] investigated the bending, buckling, and vibration characteristics of the BDFG nanobeams. Based on Gurtin-Murdoch’s surface elasticity theory and MCST, they analyzed the surface energy and microstructure of the tapered BDFG beams and established an EBT for the tapered BDFG beams. It includes the thickness and length dependency of material properties and linearly varying cross-section of the beam. They illustrated that nonuniformity, aspect ratio, and microstructural parameters sharply influenced the nanobeam’s static and dynamic behavior. Gartia et al. [16] investigated the free vibration of simply supported BDFG nanobeams, using EBT and NSGT to account for small-scale effects. Modeling material variations in axial and thickness directions, they analyzed the nanobeam on a Winkler-Pasternak foundation, finding that material inhomogeneity, nonlocal parameters, and foundation constants significantly influence vibration frequencies. In BDFG porous nanobeams subjected to moving loads, forced and free vibrations were analyzed by Majdi et al. [250] considering thickness effects using NSGT. Porosity is modeled as even, uneven, and asymmetric, and these properties are distributed differently on transverse and axial directions. The authors derived mathematical expressions for dynamic phenomena (such as resonance and cancellation effects) and pointed out a particular double-cancellation effect using a combination of analytical and numerical approaches. Parametric studies indicate that the system stiffness is thickness dependent and critical load speed is very sensitive to the porosity distribution and the thickness power index. A summary of the important studies on MDFG nanobeams is provided in Table 2 and the advancement of research is shown in Fig. 15.

Figure 15: Research advancement of MDFG nanobeams
Future work on MDFG nanobeams may focus on dynamic loading under various environmental conditions and advanced beam theories for complex geometries. Experimental validation along with multi-scale modeling and optimization will help to fine tune these materials for specific applications. Multi-physics and machine learning will help to streamline the design process and studies on durability and fatigue under cyclic loading will improve reliability and will open the way for their wider use in high performance nanotechnology and MEMS devices.
MDFG nanopipes are nanostructures with properties that vary in multiple directions. This design optimizes strength, thermal conductivity, and corrosion resistance. For example, outer layers can be corrosion-resistant, and inner layers can be stronger or better at heat management. These nanopipes are good for electronics where thermal control is crucial, and biomedical where durability and bio-compatibility are important. The tailored material distribution gives better performance in harsh environments.
Deng et al. [251] examined the size effect and stability of viscoelastic FG nanopipes with fluid flow, employing ENET to predict natural frequencies. They demonstrate that stability reduces as the nonlocal parameter increases, as depicted in Fig. 16, and enhances as the volume fraction exponent increases, suggesting that FG design can modulate natural frequencies. Liu et al. [252] investigated the nonlinear vibration and instability of fluid-conveying FG nanopipes containing initial imperfection based on NSGT and Von-Karman nonlinearity. They analyzed how oscillator amplitude, initial imperfection, and power-law index influence the frequency response and critical fluid velocity, which can be useful for the FG nanopipe design in micro/nanofluidic systems. Lyu et al. [253] presented a thermo-mechanical model for a size-dependent pipe made of BDFG materials conveying fluid. The model, based on NSGT and Hamilton’s principle, incorporates varying material properties and pipe-fluid interactions. Using the GDQM, they analyzed the frequency response and critical flow velocity, showing that the BDFG design improves pipe stability, with implications for advanced micro/nanofluidic devices in bioengineering. Zhang et al. [254] developed a multi-physics simulation to study the stability of a BDFG curved nanopipe conveying a liquid-gas flow. Using higher order shear deformation theory (HSDT), NSGT, FEM, and DQM, they analyzed the nanopipe’s frequency response to flow-induced forces. Their parametric study explored the effects of fluid velocity, aerodynamic pressure, yaw angle, and gas volume fraction, providing insights into controlling flow-induced vibration in nanoscale applications. Table 3 provides a summary of key studies on MDFG nanopipes, and Fig. 17 illustrates the advancements in this research field.
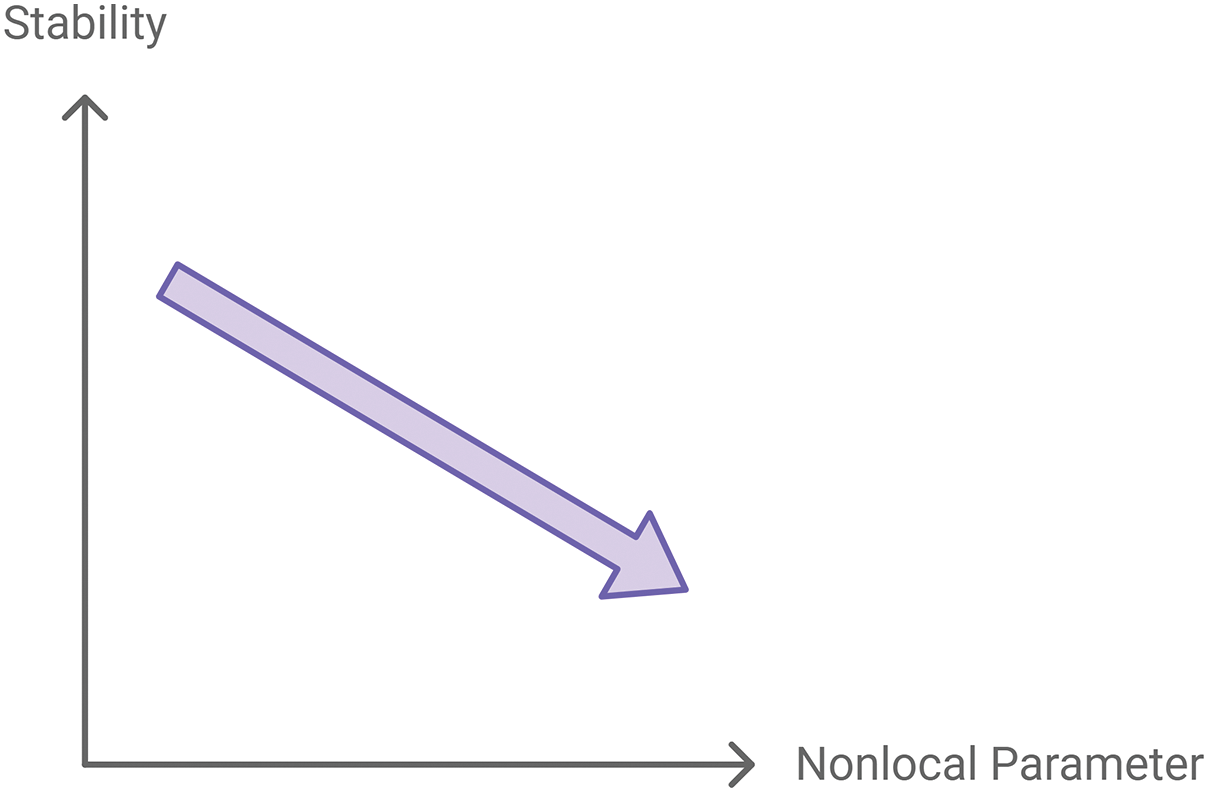
Figure 16: Stability vs. Nonlocal parameter for MDFG nanopipes
Figure 17: Research advancement of MDFG nanopipes
Possible future studies on MDFG nanopipes could be aimed at using new materials including nanocomposites and employing new fabrication technologies including 3D printing for the precise control of material characteristics. It will also be important to investigate how these nano pipes behave under conditions such as temperature variation and fluid flows, particularly in multiphase systems. Studying their nonlinear characteristics like vibration and stability will enable their enhancement in real-life usage. Also, improving computational models and thinking about the environmental implications of these materials will expand their applications in the aerospace, bioengineering, and energy industries.
MDFG nanoplates are advanced materials with properties varying in multiple directions, thickness, length and width. They are designed to perform optimally in applications where stress, thermal fields or other conditions vary in different axes. Usually made of ceramics, metals or composites, FG nanoplates gradate in properties like strength or flexibility. Analysis of their behavior requires advanced methods like FEM and HSDT to account for material gradients and size effects. These FG nanoplates are especially useful in applications like nanoelectronics, aerospace, and flexible devices.
Xie et al. [255] studied vibrations in BDFG nanoplates using an advanced HSDT that accounts for material property variations and small-scale effects via ENET. Their findings show that FG parameters increase natural frequency when the size effect parameter is less than 0.5 nm, as shown in Fig. 18, but decrease when it exceeds this value. Daikh et al. [256] studied the buckling behavior of bilayer FG porous nanoplates with consideration of thickness stretching and microstructure. Quasi-3D SDT was used to reduce displacement variables and to predict how microstructure, geometry, and material properties affect the critical buckling load for designing stable nanostructures. Saffari et al. [257] studied wave propagation in porous, MDFG nanoplates in a Kerr-elastic medium using FSDT and enhanced NSGT. They found that as the volume fraction index increases, phase velocity and wave frequency decrease, and porosity always decreases these values. This work shows how material gradients and porosity affect wave dispersion in FG nanoplates. Also, Roodgar Saffari et al. [258] studied the free and forced vibration behavior of sandwich magneto-electro-elastic nanoplates with an FG porous core, considering the varying thickness and initial electric and magnetic potentials. Using advanced shear deformation and NSGT, they examined the effects of porosity patterns, taper constants, initial potentials, and material gradients on the nanoplates’ vibration responses. Thi et al. [259] presented a three-node triangular plate element to study static bending, free vibration, and forced vibration in MDFG porous nanoplates using an improved FSDT and ENET. Their model, based on Mixed Interpolation of Tensorial Components 3+ (MITC3+) elements, handles material properties varying in three directions and diverse porosity distributions, with features to eliminate shear correction factors and avoid shear-locking. Nguyen et al. [187] discussed the analysis of static bending of BDFG nanoplates with internal pores, including geometric nonlinearity. In order to analyze stiffness-softening and hardening behaviors, they employed the FSDT, the von-Kármán assumption, and NSGT to investigate the deflection and other nonlinear properties for advanced engineering applications. In Table 4, a summary of significant research on MDFG nanoplates is presented, and in Fig. 19, the progression of research is illustrated.

Figure 18: Natural frequency vs. Size effect for MDFG nanoplates
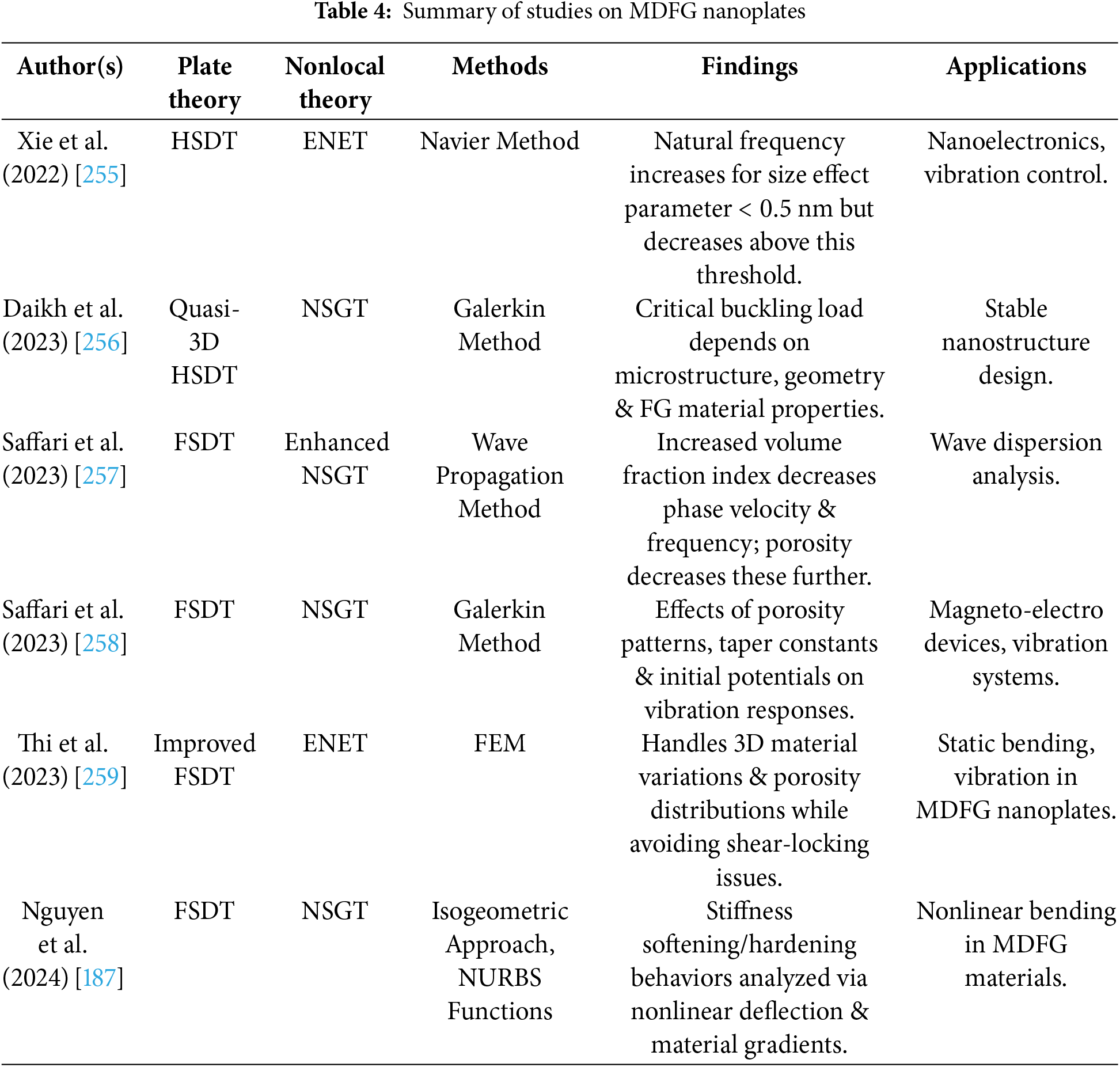
Figure 19: Research advancement of MDFG nanoplates
MDFG nanoplates are exciting across all engineering fields. Dynamic load and impact resistance studies are important for aerospace and automotive applications, and analysis of thermo-mechanical behavior under extreme environmental conditions is useful in space and nuclear engineering. Models for complex geometry and coupling multi-physics effects (like electromagnetic or piezoelectric) will boost smart material applications. AI-driven optimization and experimental validation will help targeted design improvements, and innovations in material grading will make FG nanoplates suitable for use in biomedical, electronic, and wearable technologies, resulting in more resilient and high-performance materials.
MDFG nanoshells are complex materials with properties that vary gradually in multiple directions at the nano level. These nanoshells are made using techniques like chemical vapor deposition (CVD) and atomic layer deposition (ALD), and the concentric layers possess distinct characteristics. MDFG nanoshells are more suitable for applications in energy storage, biomedical, optoelectronics, and structural composites because of their controlled properties. For the design and optimization of these materials, techniques like finite element analysis (FEA), molecular dynamics simulations, etc., are used to understand the response of the material under different conditions.
Cao et al. [260] analyzed the free vibration of TDFG nanoplates and nanoshells, with properties varying along length, width, and thickness (except for Poisson’s ratio). Using ENET and the Galerkin method, they derived natural frequencies for FG nanostructures, including spherical and cylindrical nanoshells. Their study examined the effects of nonlocal parameters and grading indexes on these frequencies. Cuong-Le et al. [261] investigated the natural frequency and critical buckling load of MDFG nanoshells with size effects using 3D isogeometric analysis based on ENET. They found out that as size effect parameters increased, the frequencies and critical buckling loads of the nanoshells reduced, as illustrated in Fig. 20. Their approach, which was based on non-uniform rational B-splines (NURBS) basis functions, gave reliable results without any assumptions made on deformation or stress distributions. Wang et al. [262] presented a quadratic hexahedral solid element for predicting the static and dynamic characteristics of porous MDFG nanoshell in MCST. Their method uses penalty unsymmetric FEM to impose C1 continuity in a weak form and adds independent rotation to improve the C0 continuity of test functions. They discovered that the out-of-plane vibrations are suppressed by increasing the material length scale parameter (MLSP) and the mode frequencies and order can be controlled by MLSP, a finding with significant implications for FG material design. A summary of key studies on MDFG nanoshells is presented in Table 5, with research advancements depicted in Fig. 21.

Figure 20: Natural frequency vs. Size effect for MDFG nanoshells
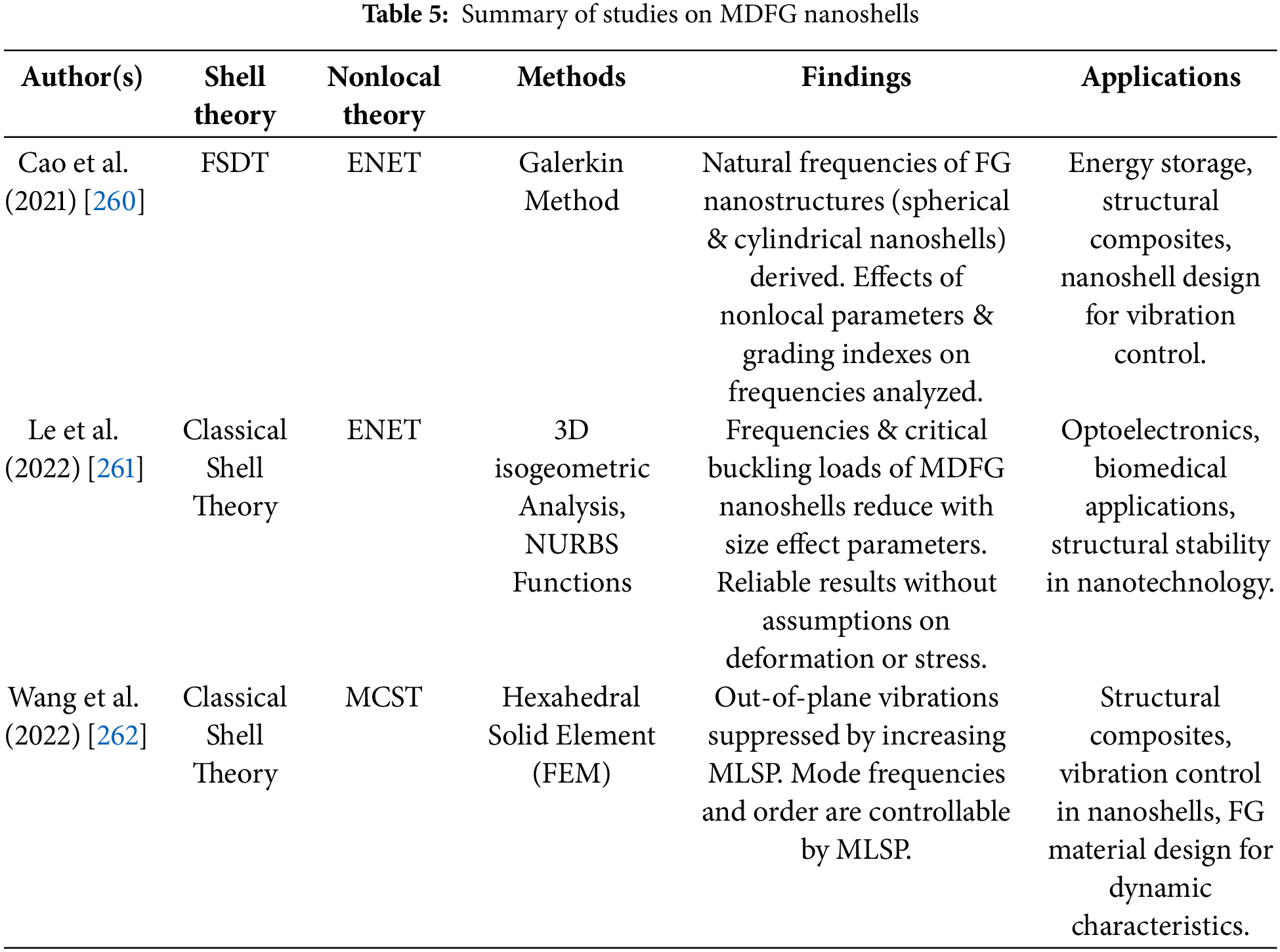
Figure 21: Research advancement of MDFG nanoshells
The future of MDFG nanoshells is in advancing computational methods like higher-order FEA, isogeometric analysis, and machine learning to predict their mechanical behavior. Multi-physics simulations and advanced techniques like meshless methods and molecular dynamics will give us insight into their performance under different conditions. With these scalable fabrication methods, we can design and optimize FG nanoshells for nanotechnology, biomedicine, aerospace, and energy and drive innovation in smart materials and adaptive structures.
This paper is a comprehensive review of MDFG nanostructures covering material distribution models, size-dependent elasticity theories, and the mechanical behavior of these structures. Although a lot of work has been done on FG nanostructures and MDFG structures, there is limited work on MDFG nanostructures, especially with various complicating effects. The importance of advanced size-dependent theories like ENET, NSGT, MCST, and CCST in capturing nanoscale behavior has been emphasized. This review also explores the mechanical responses of MDFG nanobeams, nanopipes, nanoplates, and nanoshells under both static and dynamic loading conditions, while underscoring the need for more robust analytical, semi-analytical, and numerical methods to address the complex vibration problems inherent to MDFG nanostructures.
To advance the research on MDFG nanostructures, several critical directions need to be explored. Developing more advanced modeling techniques, including machine learning-based and hybrid analytical-numerical approaches, will enable efficient analysis of static, dynamic, and vibrational behaviors under multi-directional material gradation and small-scale effects. Further investigation into the interplay between various size-dependent theories, such as ENET, NSGT, and MCST, is essential for creating a unified framework for nanoscale modeling. Additionally, coupled multi-physics effects, including thermomechanical, piezoelectric, and magnetoelastic responses, require comprehensive exploration to expand the practical applicability of MDFG structures. Experimental validation and material characterization are equally crucial to validate theoretical and numerical models. This includes the precise fabrication of MDFG nanostructures and rigorous testing to ensure real-world feasibility.
Moreover, research on optimization strategies tailored to real-world applications is necessary to bridge the gap between theoretical advancements and practical implementation, particularly in aerospace, biomedicine, and MEMS/NEMS. Investigating the dynamic and stability responses of MDFG nanostructures under complex loading conditions, while incorporating nonlinear effects and large deformations, is essential. Innovations in material design and synthesis, including novel material distribution models and advanced manufacturing techniques like additive manufacturing and nanolithography, will further enable the realization of precise MDFG structures. Finally, exploring the integration of MDFG nanostructures into emerging technologies such as soft robotics, flexible electronics, and nanomedicine will unlock their multi-functional potential and lead to groundbreaking applications.
In conclusion, advancing these research directions is crucial for the effective design, optimization, and practical implementation of MDFG nanostructures. This review serves as a valuable resource for researchers and engineers working on MDFG nanostructures and provides a clear roadmap for addressing existing challenges and driving innovations in this evolving field.
Acknowledgement: The first author is thankful to the Council of Scientific & Industrial Research (CSIR), India, for the fellowship to carry out this research.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Study conception and design: Akash Kumar Gartia, S. Chakraverty; analysis and interpretation of results: Akash Kumar Gartia, S. Chakraverty; draft manuscript preparation: Akash Kumar Gartia. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Zhao N, Qiu PY, Cao LL. Development and application of functionally graded material. In: Materials engineering and automatic control. Wollerau, Switzerland: Trans Tech Publications Ltd.; 2012. Vol. 562, p. 371–5. [Google Scholar]
2. Zhang N, Khan T, Guo H, Shi S, Zhong W, Zhang W. Functionally graded materials: an overview of stability, buckling, and free vibration analysis. Adv Mater Sci Eng. 2019;2019(5):1354150. doi:10.1155/2019/1354150. [Google Scholar] [CrossRef]
3. Ma Z, Liu W, Li W, Liu H, Song J, Liu Y, et al. Additive manufacturing of functional gradient materials: a review of research progress and challenges. J Alloys Comp. 2024;971:172642. doi:10.1016/j.jallcom.2023.172642. [Google Scholar] [CrossRef]
4. Karamanli A, Aydogdu M. Structural dynamics and stability analysis of 2D-FG microbeams with two-directional porosity distribution and variable material length scale parameter. Mech Based Des Struct Mach. 2020;48(2):164–91. doi:10.1080/15397734.2019.1627219. [Google Scholar] [CrossRef]
5. Djavanroodi F, Ebrahimi M, Nayfeh J. Tribological and mechanical investigation of multi-directional forged nickel. Sci Rep. 2019;9(1):241. doi:10.1038/s41598-018-36584-w. [Google Scholar] [PubMed] [CrossRef]
6. Bahat B, Yapici G. Comparison of static and dynamic mechanical response of Aluminum 6061 subjected to multi-directional forging. Mater Sci Forum. 2024;1120:21–8. doi:10.4028/p-1ijzJX. [Google Scholar] [CrossRef]
7. Nayem S, Sikder B, Uddin S. Anisotropic energy transfer near multi-layer black phosphorus. 2D Mater. 2023;10(4):045022. doi:10.1088/2053-1583/acf052. [Google Scholar] [CrossRef]
8. Şengül H, Theis TL, Ghosh S. Toward sustainable nanoproducts. J Ind Ecol. 2008;12(3):329–59. doi:10.1111/j.1530-9290.2008.00046.x. [Google Scholar] [CrossRef]
9. Li Y, Feng Z, Hao L, Huang L, Xin C, Wang Y, et al. A review on functionally graded materials and structures via additive manufacturing: from multi-scale design to versatile functional properties. Adv Mater Technol. 2020;5(6):1900981. doi:10.1002/admt.201900981. [Google Scholar] [CrossRef]
10. Zhao S, Zhao Z, Yang Z, Ke L, Kitipornchai S, Yang J. Functionally graded graphene reinforced composite structures: a review. Eng Struct. 2020;210:110339. doi:10.1016/j.engstruct.2020.110339. [Google Scholar] [CrossRef]
11. Rahaeifard M, Kahrobaiyan MH, Ahmadian MT. Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials. In: ASME Power Transmission and Gearing Conference; 3rd International Conference on Micro- and Nanosystems; 11th International Conference on Advanced Vehicle and Tire Technologies of International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; 2009; San Diego, CA, USA. Vol. 6. [Google Scholar]
12. Witvrouw A, Mehta A. The use of functionally graded Poly-SiGe layers for MEMS applications. In: Functionally graded materials VIII. Wollerau, Switzerland: Trans Tech Publications Ltd.; 2005. Vol. 492, p. 255–60. [Google Scholar]
13. Eringen AC. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys. 1983;54(9):4703–10. doi:10.1063/1.332803. [Google Scholar] [CrossRef]
14. Arda M, Aydogdu M. Torsional wave propagation in multiwalled carbon nanotubes using nonlocal elasticity. Appl Phys A. 2016;122(3):219. doi:10.1007/s00339-016-9751-1. [Google Scholar] [CrossRef]
15. Lim CW, Zhang G, Reddy JN. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J Mech Phys Solids. 2015;78(3):298–313. doi:10.1016/j.jmps.2015.02.001. [Google Scholar] [CrossRef]
16. Gartia AK, Chakraverty S. Free vibration of Bi-directional functionally graded nanobeams resting on Winkler–Pasternak foundations. J Vib Eng Technol. 2024;12(S2):1929–45. doi:10.1007/s42417-024-01511-z. [Google Scholar] [CrossRef]
17. Yang F, Chong ACM, Lam DCC, Tong P. Couple stress based strain gradient theory for elasticity. Int J Solids Struct. 2002;39(10):2731–43. doi:10.1016/S0020-7683(02)00152-X. [Google Scholar] [CrossRef]
18. Qi Z, Peng W, He T. Investigation on the thermoelastic response of a nanobeam in modified couple stress theory considering size-dependent and memory-dependent effects. J Therm Stresses. 2022;45(10):773–92. doi:10.1080/01495739.2022.2109543. [Google Scholar] [CrossRef]
19. Hadjesfandiari AR, Dargush GF. Couple stress theory for solids. Int J Solids Struct. 2011;48(18):2496–510. doi:10.1016/j.ijsolstr.2011.05.002. [Google Scholar] [CrossRef]
20. Alavi SE, Sadighi M, Pazhooh MD, Ganghoffer JF. Development of size-dependent consistent couple stress theory of Timoshenko beams. Appl Math Model. 2020;79:685–712. doi:10.1016/j.apm.2019.10.058. [Google Scholar] [CrossRef]
21. Bathe KJ, Wilson EL. Solution methods for eigenvalue problems in structural mechanics. Int J Numer Methods Eng. 1973;6(2):213–26. doi:10.1002/nme.1620060207. [Google Scholar] [CrossRef]
22. Vlase S, Marin M, Öchsner A. Eigenvalue and eigenvector problems in applied mechanics. Cham: Springer; 2019. doi:10.1007/978-3-030-00991-5. [Google Scholar] [CrossRef]
23. Sahoo M, Chakraverty S. Linear eigenvalue problems in dynamic structure with uncertainty: an expectation-based approach. In: Mathematical methods in dynamical systems.Boca Raton: CRC Press; 2023. p. 315–38. [Google Scholar]
24. Liu H, Zhong H. Free vibration analysis of thin plates with side cracks by the weak form quadrature element method. Comput Struct. 2023;289(1):107186. doi:10.1016/j.compstruc.2023.107186. [Google Scholar] [CrossRef]
25. Rao P, Roy D, Chakraverty S. Vibration analysis of single-link flexible manipulator in an uncertain environment. J Vib Eng Technol. 2023;12(2):2677–94. doi:10.1007/s42417-023-01007-2. [Google Scholar] [CrossRef]
26. Aksu G, Ali R. Free vibration analysis of stiffened plates using finite difference method. J Sound Vib. 1976;48(1):15–25. doi:10.1016/0022-460X(76)90367-9. [Google Scholar] [CrossRef]
27. Hosseini SM. Application of a hybrid mesh-free method based on generalized finite difference (GFD) method for natural frequency analysis of functionally graded nanocomposite cylinders reinforced by carbon nanotubes. Comput Model Eng Sci. 2013;95(1):1–29. [Google Scholar]
28. Ali S, Hawwa MA. Dynamics of axially moving beams: a finite difference approach. Ain Shams Eng J. 2023;14(1):101817. doi:10.1016/j.asej.2022.101817. [Google Scholar] [CrossRef]
29. Zheng DY, Kessissoglou NJ. Free vibration analysis of a cracked beam by finite element method. J Sound Vib. 2004;273(3):457–75. doi:10.1016/S0022-460X(03)00504-2. [Google Scholar] [CrossRef]
30. Friswell M, Adhikari S, Lei Y. Vibration analysis of beams with non-local foundations using the finite element method. Int J Numer Methods Eng. 2007;71(11):1365–86. doi:10.1002/nme.2003. [Google Scholar] [CrossRef]
31. Petyt M. Introduction to finite element vibration analysis. Cambridge, UK: Cambridge University Press; 2010. [Google Scholar]
32. Baghdadi S, Ahammad N. A comparative study of adomian decomposition method with variational iteration method for solving linear and nonlinear differential equations. J Appl Math Phys. 2024;12(8):2789–819. doi:10.4236/jamp.2024.128166. [Google Scholar] [CrossRef]
33. Chen Y, Chen G. Chained spatial beam adomian decomposition model: a novel model of flexible slender beams for large spatial deflections. J Mech Robot. 2025;17(5):051010. doi:10.1115/1.4067023. [Google Scholar] [CrossRef]
34. Al-Lehaibi EAN. Power law modeling of functionally graded Adomian’s decomposition method for thermoelastic materials in heat transfer and thermal stress analysis. Waves Random Complex Media. 2024;34(5):3832–46. doi:10.1080/17455030.2021.1985184. [Google Scholar] [CrossRef]
35. Wang L, Han X, Xie Y. A new homotopy perturbation method for solving an Ill-posed problem of multi-source dynamic loads reconstruction. Comput Model Eng Sci. 2011;82(3&4):179–94. doi:10.32604/cmes.2011.082.179. [Google Scholar] [CrossRef]
36. Sahoo M, Chakraverty S. Sawi transform based homotopy perturbation method for solving shallow water wave equations in fuzzy environment. Mathematics. 2022;10(16):2900. doi:10.3390/math10162900. [Google Scholar] [CrossRef]
37. Roy T, Soqi A, Maiti DK, Wannan R, Asad J. Pendulum attached to a vibrating point: semi-analytical solution by optimal and modified homotopy perturbation method. Alex Eng J. 2025;111(5):396–403. doi:10.1016/j.aej.2024.10.086. [Google Scholar] [CrossRef]
38. Behera L, Chakraverty S. Application of Differential Quadrature method in free vibration analysis of nanobeams based on various nonlocal theories. Comput Math Appl. 2015;69(12):1444–62. doi:10.1016/j.camwa.2015.04.010. [Google Scholar] [CrossRef]
39. Li H, Hao YX, Zhang W, Yang SW, Cao YT. Vibration analysis of the porous metal cylindrical curved panel by using the differential quadrature method. Thin-Walled Struct. 2023;186(3):110694. doi:10.1016/j.tws.2023.110694. [Google Scholar] [CrossRef]
40. Gu X, He J, Wang Z, Li M, Habibi M, Hashemabadi D. Application of hyperbolic differential quadrature method for vibration responses of the electrorheological disk. Eng Anal Bound Elem. 2023;155(5083):599–615. doi:10.1016/j.enganabound.2023.05.035. [Google Scholar] [CrossRef]
41. C-P, Wu, J-S Wang, Y-MWang. A DRK interpolation-based collocation method for the analysis of functionally graded piezoelectric hollow cylinders under electro-mechanical loads. Comput Model Eng Sci. 2009;52(1):1–38. doi:10.3970/cmes.2009.052.001. [Google Scholar] [CrossRef]
42. Huang Z, Peng L. A coordinate transformation based barycentric interpolation collocation method and its application in bending, free vibration and buckling analysis of irregular Kirchhoff plates. Int J Numer Methods Eng. 2023;124(22):5069–101. doi:10.1002/nme.7338. [Google Scholar] [CrossRef]
43. Jiang W, Gao X. Review of collocation methods and applications in solving science and engineering problems. Comput Model Eng Scie. 2024;140(1):41–76. doi:10.32604/cmes.2024.048313. [Google Scholar] [CrossRef]
44. Guo X, Zhang Y, Luo Z, Cao D. Nonlinear dynamics analysis of a graphene laminated composite plate based on an extended Rayleigh–Ritz method. Thin-Walled Struct. 2023;186:110673. doi:10.1016/j.tws.2023.110673. [Google Scholar] [CrossRef]
45. Kumar A, Kumar S, Choudhary P, Gupta A, Narayan A. Free vibration characteristics of elastic foundation-supported porous functionally graded nanoplates using Rayleigh-Ritz approach. Int J Struct Integr. 2024;15(2):298–321. doi:10.1108/IJSI-11-2023-0114. [Google Scholar] [CrossRef]
46. Gartia AK, Chakraverty S. Chebyshev polynomials based Rayleigh–Ritz method for free vibration analysis of axially functionally graded cantilever nanobeam. In: Advances in modelling and analysis of functionally graded micro- and nanostructures. Bristol, UK: IOP Publishing; 2024. p. 5-1–5-19. [Google Scholar]
47. Rao P, Chakraverty S, Roy D. Vibration analysis of single-link robotic manipulator by polynomial based Galerkin method in uncertain environment. In: Polynomial paradigms. Bristol, UK: IOP Publishing; 2022. p. 9-1–9-18. [Google Scholar]
48. Sihar I, Yang J, Hornikx M. Discontinuous Galerkin method for vibration of structures with piecewise constant material properties. Appl Acoust. 2024;216(2):109793. doi:10.1016/j.apacoust.2023.109793. [Google Scholar] [CrossRef]
49. Meng B, Lian C, Wang J, Jing H, Wu R, Lin J, et al. The approximate analysis of higher-order frequencies of nonlinear vibrations of a cantilever beam with the extended galerkin method. J Comput Nonlinear Dyn. 2024;19(4):041005. doi:10.1115/1.4064724. [Google Scholar] [CrossRef]
50. Ali A, Rajakumar C. The boundary element method: applications in sound and vibration. London: CRC Press; 2004. [Google Scholar]
51. Sheng X, Jones C, Thompson D. Modelling ground vibration from railways using wavenumber finite-and boundary-element methods. Proc Royal Soc A: Math, Phys Eng Sci. 2005;461(2059):2043–70. doi:10.1098/rspa.2005.1450. [Google Scholar] [CrossRef]
52. Dondero M, Cisilino AP, Tomba JP. Numerical design of random micro-heterogeneous materials with functionally-graded effective thermal conductivities using genetic algorithms and the fast boundary element method. Comput Model Eng Sci. 2011;78(3&4):225–46. doi:10.3970/cmes.2011.078.225. [Google Scholar] [CrossRef]
53. Chaudhuri RA, Kabir HRH. Vibration of clamped moderately thick general cross-ply plates using a generalized Navier approach. Compos Struct. 1993;24(4):311–21. doi:10.1016/0263-8223(93)90025-L. [Google Scholar] [CrossRef]
54. Jena S, Chakraverty S, Malikan M. Application of shifted chebyshev polynomial based Rayleigh-Ritz method and Navier’s technique for vibration analysis of a functionally graded porous beam embedded in Kerr foundation. Eng Comput. 2021;37(4):3569–89. doi:10.1007/s00366-020-01018-7. [Google Scholar] [CrossRef]
55. Palardy RF, Palazotto AN. Buckling and vibration of composite plates using the Levy method. Compos Struct. 1990;14(1):61–86. doi:10.1016/0263-8223(90)90059-N. [Google Scholar] [CrossRef]
56. Aksencer T, Aydogdu M. Levy type solution method for vibration and buckling of nanoplates using nonlocal elasticity theory. Physica E: Low-Dimens Syst Nanostruct. 2011;43(4):954–9. doi:10.1016/j.physe.2010.11.024. [Google Scholar] [CrossRef]
57. Nguyen NT, Hui D, Lee J, Nguyen-Xuan H. An efficient computational approach for size-dependent analysis of functionally graded nanoplates. Comput Methods Appl Mech Eng. 2015;297:191–218. doi:10.1016/j.cma.2015.07.021. [Google Scholar] [CrossRef]
58. Garg A, Chalak HD, Zenkour A, Belarbi MO, Houari MSA. A review of available theories and methodologies for the analysis of nano isotropic, nano functionally graded, and CNT reinforced nanocomposite structures. Arch Comput Methods Eng. 2021;29(4):2237–70. doi:10.1007/s11831-021-09652-0. [Google Scholar] [CrossRef]
59. Markworth A, Ramesh K, Parks W. Modelling studies applied to functionally graded materials. J Mater Sci. 1995;30(9):2183–93. doi:10.1007/BF01184560. [Google Scholar] [CrossRef]
60. Chakraverty S. Vibration of plates. Boca Raton: CRC Press; 2008. [Google Scholar]
61. Nie G, Zhong Z. Dynamic analysis of multi-directional functionally graded annular plates. Appl Math Model. 2010;34(3):608–16. doi:10.1016/j.apm.2009.06.009. [Google Scholar] [CrossRef]
62. Zhao L, Chen WQ, Lü CF. Symplectic elasticity for bi-directional functionally graded materials. Mech Mater. 2012;54(7):32–42. doi:10.1016/j.mechmat.2012.06.001. [Google Scholar] [CrossRef]
63. Behera L, Chakraverty S. Free vibration of Euler and Timoshenko nanobeams using boundary characteristic orthogonal polynomials. Appl Nanosci. 2014;4(3):347–58. doi:10.1007/s13204-013-0202-4. [Google Scholar] [CrossRef]
64. Chakraverty S, Behera L. Free vibration of rectangular nanoplates using Rayleigh–Ritz method. Physica E: Low-Dimens Syst Nanostruct. 2014;56:357–63. doi:10.1016/j.physe.2013.08.014. [Google Scholar] [CrossRef]
65. Chakraverty S, Behera L. Small scale effect on the vibration of non-uniform nanoplates. Struct Eng Mech. 2015;55(3):495–510. doi:10.12989/sem.2015.55.3.495. [Google Scholar] [CrossRef]
66. Chakraverty S, Behera L. Static and dynamic problems of nanobeams and nanoplates. Singapore: World Scientific; 2016. [Google Scholar]
67. Şimşek M. Bi-directional functionally graded materials (BDFGMs) for free and forced vibration of Timoshenko beams with various boundary conditions. Compos Struct. 2015;133(1):968–78. doi:10.1016/j.compstruct.2015.08.021. [Google Scholar] [CrossRef]
68. Pradhan KK, Chakraverty S. Effects of different shear deformation theories on free vibration of functionally graded beams. Int J Mech Sci. 2014;82:149–60. doi:10.1016/j.ijmecsci.2014.03.014. [Google Scholar] [CrossRef]
69. Pradhan K, Chakraverty S. Free vibration of functionally graded thin elliptic plates with various edge supports. Struct Eng Mech. 2015;53(2):337–54. doi:10.12989/sem.2015.53.2.337. [Google Scholar] [CrossRef]
70. Chakraverty S, Pradhan KK. Vibration of functionally graded beams and plates. London, UK: Academic Press; 2016. [Google Scholar]
71. Pradhan K, Chakraverty S, Panigrahi S. Implementation of numerical approximations in studying vibration of functionally graded beams. Int J Dyn Control. 2018;6(3):1023–46. doi:10.1007/s40435-017-0375-x. [Google Scholar] [CrossRef]
72. Razavi H, Babadi AF, Tadi Beni Y. Free vibration analysis of functionally graded piezoelectric cylindrical nanoshell based on consistent couple stress theory. Compos Struct. 2017;160(1):1299–309. doi:10.1016/j.compstruct.2016.10.056. [Google Scholar] [CrossRef]
73. Niknam H, Akbarzadeh AH, Rodrigue D, Therriault D. Architected multi-directional functionally graded cellular plates. Mater Des. 2018;148(1):188–202. doi:10.1016/j.matdes.2018.02.058. [Google Scholar] [CrossRef]
74. Ghayesh MH, Farajpour A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int J Eng Sci. 2019;137(4):8–36. doi:10.1016/j.ijengsci.2018.12.001. [Google Scholar] [CrossRef]
75. Karami B, Shahsavari D, Janghorban M, Li L. Influence of homogenization schemes on vibration of functionally graded curved microbeams. Compos Struct. 2019;216(1–3):67–79. doi:10.1016/j.compstruct.2019.02.089. [Google Scholar] [CrossRef]
76. Qin Z, Safaei B, Pang X, Chu F. Traveling wave analysis of rotating functionally graded graphene platelet reinforced nanocomposite cylindrical shells with general boundary conditions. Results Phys. 2019;15(3):102752. doi:10.1016/j.rinp.2019.102752. [Google Scholar] [CrossRef]
77. Abbaspour F, Arvin H. Vibration and thermal buckling analyses of three-layered centrosymmetric piezoelectric microplates based on the modified consistent couple stress theory. J Vib Control. 2020;26(15–16):1253–65. doi:10.1177/1077546320924273. [Google Scholar] [CrossRef]
78. Ghatage PS, Kar VR, Sudhagar PE. On the numerical modelling and analysis of multi-directional functionally graded composite structures: a review. Compos Struct. 2020;236(3):111837. doi:10.1016/j.compstruct.2019.111837. [Google Scholar] [CrossRef]
79. Chen X, Chen L, Huang S, Li M, Li X. Nonlinear forced vibration of in-plane bi-directional functionally graded materials rectangular plate with global and localized geometrical imperfections. Appl Math Model. 2021;93(26):443–66. doi:10.1016/j.apm.2020.12.033. [Google Scholar] [CrossRef]
80. Truong TT, Lee J, Nguyen-Thoi T. Multi-objective optimization of multi-directional functionally graded beams using an effective deep feedforward neural network-SMPSO algorithm. Struct Multidiscipl Optim. 2021;63(6):2889–918. doi:10.1007/s00158-021-02852-z. [Google Scholar] [CrossRef]
81. Jena S, Chakraverty S, Malikan M, Sedighi HM. Implementation of Hermite-Ritz method and Navier’s technique for vibration of functionally graded porous nanobeam embedded in Winkler-Pasternak elastic foundation using bi-Helmholtz nonlocal elasticity. J Mech Mater Struct. 2020;15(3):405–34. doi:10.2140/jomms.2020.15.405. [Google Scholar] [CrossRef]
82. Jena SK, Chakraverty S, Mahesh V, Harursampath D. Application of Haar wavelet discretization and differential quadrature methods for free vibration of functionally graded micro-beam with porosity using modified couple stress theory. Eng Anal Bound Elem. 2022;140(8):167–85. doi:10.1016/j.enganabound.2022.04.009. [Google Scholar] [CrossRef]
83. Jena SK, Chakraverty S. Structural dynamics in uncertain environments: micro, nano, and functionally graded beam analysis. Boca Raton: CRC Press; 2024. [Google Scholar]
84. Jena SK, Chakraverty S, Malikan M, Mohammad-Sedighi H. Hygro-magnetic vibration of the single-walled carbon nanotube with nonlinear temperature distribution based on a modified beam theory and nonlocal strain gradient model. Int J Appl Mech. 2020;12(5):2050054. doi:10.1142/S1758825120500544. [Google Scholar] [CrossRef]
85. Jena SK, Chakraverty S, Malikan M, Tornabene F. Effects of surface energy and surface residual stresses on vibro-thermal analysis of chiral, zigzag, and armchair types of SWCNTs using refined beam theory. Mech Based Des Struct Mach. 2022;50(5):1565–79. doi:10.1080/15397734.2020.1754239. [Google Scholar] [CrossRef]
86. Tang Y, Wang G, Ren T, Ding Q, Yang T. Nonlinear mechanics of a slender beam composited by three-directional functionally graded materials. Compos Struct. 2021;270(1):114088. doi:10.1016/j.compstruct.2021.114088. [Google Scholar] [CrossRef]
87. Tang Y, Ma ZS, Ding Q, Wang T. Dynamic interaction between bi-directional functionally graded materials and magneto-electro-elastic fields: a nano-structure analysis. Compos Struct. 2021;264(8):113746. doi:10.1016/j.compstruct.2021.113746. [Google Scholar] [CrossRef]
88. Gao W, Liu Y, Qin Z, Chu F. Wave propagation in smart sandwich plates with functionally graded nanocomposite porous core and piezoelectric layers in multi-physics environment. Int J Appl Mech. 2022;14(7):2250071. doi:10.1142/S1758825122500715. [Google Scholar] [CrossRef]
89. Karmakar S, Chakraverty S. Differential quadrature and Adomian decomposition methods for solving thermal vibration of Euler nanobeam resting on Winkler-Pasternak foundation. J Mech Mater Struct. 2021;16(4):555–72. doi:10.2140/jomms. [Google Scholar] [CrossRef]
90. Karmakar S, Chakraverty S. Thermal vibration of nonhomogeneous Euler nanobeam resting on Winkler foundation. Eng Anal Bound Elem. 2022;140(10):581–91. doi:10.1016/j.enganabound.2022.04.020. [Google Scholar] [CrossRef]
91. Karmakar S, Chakraverty S. Vibration of a piezoelectric nanobeam with flexoelectric effects by Adomian decomposition method. Acta Mech. 2023;234(6):2445–60. doi:10.1007/s00707-023-03512-7. [Google Scholar] [CrossRef]
92. Karmakar S, Chakraverty S. The torsional vibration of functionally graded nanobeams. In: Functionally graded structures. Bristol, UK: IOP Publishing; 2023. p. 9-1–9-13. [Google Scholar]
93. Nuhu AA, Safaei B. A comprehensive review on the vibration analyses of small-scaled plate-based structures by utilizing the nonclassical continuum elasticity theories. Thin-Walled Struct. 2022;179:109622. doi:10.1016/j.tws.2022.109622. [Google Scholar] [CrossRef]
94. Wu CP, Yu JJ. A review of mechanical analyses of rectangular nanobeams and single-, double-, and multi-walled carbon nanotubes using Eringen’s nonlocal elasticity theory. Arch Appl Mech. 2019;89(9):1761–92. doi:10.1007/s00419-019-01542-z. [Google Scholar] [CrossRef]
95. Mathew C, Ejiofor O. Mechanics and computational homogenization of effective material properties of functionally graded (Composite) material plate FGM. Int J Sci Res Publications. 2023;13(9):128. doi:10.29322/IJSRP.13.09.2023.p14120. [Google Scholar] [CrossRef]
96. Zheng S, Zhang N, Zhao X, Chen D, Wang H. Size-dependent mechanical analysis of porous functionally graded piezoelectric micro/nanoscale structures: a literature review. Smart Mater Struct. 2024;33(9):093002. doi:10.1088/1361-665X/ad5809. [Google Scholar] [CrossRef]
97. Woo J, Meguid SA, Ong LS. Nonlinear free vibration behavior of functionally graded plates. J Sound Vib. 2006;289(3):595–611. doi:10.1016/j.jsv.2005.02.031. [Google Scholar] [CrossRef]
98. Nikbakht S, Kamarian S, Shakeri M. A review on optimization of composite structures part II: functionally graded materials. Compos Struct. 2019;214(3):83–102. doi:10.1016/j.compstruct.2019.01.105. [Google Scholar] [CrossRef]
99. Chakraverty S, Kumar Jena S, Civalek O, editors. Functionally graded structures. Bristol, UK: IOP Publishing; 2023. [Google Scholar]
100. Alshabatat NT, Naghshineh K. Optimization of natural frequencies and sound power of beams using functionally graded material. Adv Acoust Vib. 2014;2014(1):75236. doi:10.1155/2014/752361. [Google Scholar] [CrossRef]
101. Yee K, Ong OZS, Ghayesh MH, Amabili M. Various homogenisation schemes for vibration characteristics of axially FG core multilayered microbeams with metal foam face layers based on third order shear deformation theory. Appl Math Model. 2024;125:189–217. doi:10.1016/j.apm.2023.08.037. [Google Scholar] [CrossRef]
102. Qian LF, Batra RC. Design of bidirectional functionally graded plate for optimal natural frequencies. J Sound Vib. 2005;280(1):415–24. doi:10.1016/j.jsv.2004.01.042. [Google Scholar] [CrossRef]
103. Hadi A, Nejad MZ, Hosseini M. Vibrations of three-dimensionally graded nanobeams. Int J Eng Sci. 2018;128(9):12–23. doi:10.1016/j.ijengsci.2018.03.004. [Google Scholar] [CrossRef]
104. Do DTT, Nguyen-Xuan H, Lee J. Material optimization of tri-directional functionally graded plates by using deep neural network and isogeometric multimesh design approach. Appl Math Model. 2020;87(3):501–33. doi:10.1016/j.apm.2020.06.002. [Google Scholar] [CrossRef]
105. Tang H, Nguyen NV, Lee J. Accelerating tri-directional material distribution optimization in functionally graded plates with an adaptive design control point variable selection. Comput Methods Appl Mech Eng. 2024;418:116474. doi:10.1016/j.cma.2023.116474. [Google Scholar] [CrossRef]
106. Sina SA, Navazi HM, Haddadpour H. An analytical method for free vibration analysis of functionally graded beams. Mater Des. 2009;30(3):741–7. doi:10.1016/j.matdes.2008.05.015. [Google Scholar] [CrossRef]
107. Pradhan KK, Chakraverty S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh–Ritz method. Compos Part B: Eng. 2013;51(4):175–84. doi:10.1016/j.compositesb.2013.02.027. [Google Scholar] [CrossRef]
108. Chakraborty A, Gopalakrishnan S, Reddy JN. A new beam finite element for the analysis of functionally graded materials. Int J Mech Sci. 2003;45(3):519–39. doi:10.1016/S0020-7403(03)00058-4. [Google Scholar] [CrossRef]
109. Aydogdu M, Taskin V. Free vibration analysis of functionally graded beams with simply supported edges. Mater Des. 2007;28(5):1651–6. doi:10.1016/j.matdes.2006.02.007. [Google Scholar] [CrossRef]
110. ŞimŞek M, Kocatürk T. Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Compos Struct. 2009;90(4):465–73. doi:10.1016/j.compstruct.2009.04.024. [Google Scholar] [CrossRef]
111. Chakraverty S, Pradhan KK. Free vibration of exponential functionally graded rectangular plates in thermal environment with general boundary conditions. Aerosp Sci Technol. 2014;36(2):132–56. doi:10.1016/j.ast.2014.04.005. [Google Scholar] [CrossRef]
112. Kumar V, Singh SJ, Saran VH, Harsha SP. Vibration response of the exponential functionally graded material plate with variable thickness resting on the orthotropic Pasternak foundation. Mech Based Des Struct Mach. 2024;52(5):2841–68. doi:10.1080/15397734.2023.2193623. [Google Scholar] [CrossRef]
113. Jung WY, Han SC. Analysis of sigmoid functionally graded material (S-FGM) nanoscale plates using the nonlocal elasticity theory. Math Probl Eng. 2013;2013(1):476131. doi:10.1155/2013/476131. [Google Scholar] [CrossRef]
114. Hamed M, Eltaher MA, Sadoun A, Almitani K. Free vibration of symmetric and sigmoid functionally graded nanobeams. Appl Phys A. 2016;122(9):829. doi:10.1007/s00339-016-0324-0. [Google Scholar] [CrossRef]
115. Ramteke PM, Mehar K, Sharma N, Panda SK. Numerical prediction of deflection and stress responses of functionally graded structure for grading patterns (Power-Law, Sigmoid, and Exponential) and variable porosity (Even/Uneven). Sci Iran. 2021;28(2):811–29. doi:10.24200/sci.2020.55581.4290. [Google Scholar] [CrossRef]
116. Van Vinh P. Nonlocal free vibration characteristics of power-law and sigmoid functionally graded nanoplates considering variable nonlocal parameter. Physica E: Low-Dimens Syst Nanostruct. 2022;135:114951. doi:10.1016/j.physe.2021.114951. [Google Scholar] [CrossRef]
117. Kumar P, Harsha SP. Dynamic analysis of porosity dependent functionally graded sigmoid piezoelectric (FGSP) plate. Structures. 2022;46(6):1737–52. doi:10.1016/j.istruc.2022.11.021. [Google Scholar] [CrossRef]
118. Viola E, Tornabene F. Free vibrations of three parameter functionally graded parabolic panels of revolution. Mech Res Commun. 2009;36(5):587–94. doi:10.1016/j.mechrescom.2009.02.001. [Google Scholar] [CrossRef]
119. Tornabene F, Viola E. Free vibrations of four-parameter functionally graded parabolic panels and shells of revolution. Eur J Mech—A/Solids. 2009;28(5):991–1013. doi:10.1016/j.euromechsol.2009.04.005. [Google Scholar] [CrossRef]
120. Nicholas Fantuzzi FT, Viola E. Four-parameter functionally graded cracked plates of arbitrary shape: a GDQFEM solution for free vibrations. Mech Adv Mater Struct. 2016;23(1):89–107. doi:10.1080/15376494.2014.933992. [Google Scholar] [CrossRef]
121. Boggarapu V, Gujjala R, Ojha S, Acharya S, babu Venkateswara P, Chowdary S, et al. State of the art in functionally graded materials. Compos Struct. 2021;262(5):113596. doi:10.1016/j.compstruct.2021.113596. [Google Scholar] [CrossRef]
122. Piegl L, Tiller W. The NURBS book. Berlin/Heidelberg: Springer Science & Business Media; 2012. [Google Scholar]
123. Lieu QX, Lee J, Lee D, Lee S, Kim D, Lee J. Shape and size optimization of functionally graded sandwich plates using isogeometric analysis and adaptive hybrid evolutionary firefly algorithm. Thin-Walled Struct. 2018;124:588–604. doi:10.1016/j.tws.2017.11.054. [Google Scholar] [CrossRef]
124. Do DTT, Lee D, Lee J. Material optimization of functionally graded plates using deep neural network and modified symbiotic organisms search for eigenvalue problems. Compos Part B: Eng. 2019;159(4):300–26. doi:10.1016/j.compositesb.2018.09.087. [Google Scholar] [CrossRef]
125. Wang C, Yu T, Curiel-Sosa J, Xie N, Bui TQ. Adaptive chaotic particle swarm algorithm for isogeometric multi-objective size optimization of FG plates. Struct Multidiscipl Optim. 2019;60(2):757–78. doi:10.1007/s00158-019-02238-2. [Google Scholar] [CrossRef]
126. Ribeiro LG, Maia MA, Parente EJr, de Melo AMC. Surrogate based optimization of functionally graded plates using radial basis functions. Compos Struct. 2020;252(4):112677. doi:10.1016/j.compstruct.2020.112677. [Google Scholar] [CrossRef]
127. Vel SS, Pelletier JL. Multi-objective optimization of functionally graded thick shells for thermal loading. Compos Struct. 2007;81(3):386–400. doi:10.1016/j.compstruct.2006.08.027. [Google Scholar] [CrossRef]
128. Nguyen TT, Lee J. Optimal design of thin-walled functionally graded beams for buckling problems. Compos Struct. 2017;179(5):459–67. doi:10.1016/j.compstruct.2017.07.024. [Google Scholar] [CrossRef]
129. Mori T, Tanaka K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metallurgica. 1973;21(5):571–4. doi:10.1016/0001-6160(73)90064-3. [Google Scholar] [CrossRef]
130. Bayat M, Sahari BB, Saleem M, Dezvareh E, Mohazzab AH. Analysis of functionally graded rotating disks with parabolic concave thickness applying an exponential function and the Mori-Tanaka scheme. IOP Conf Ser: Mater Sci Eng. 2011;17(1):012005. doi:10.1088/1757-899X/17/1/012005. [Google Scholar] [CrossRef]
131. Shen HS, Wang ZX. Assessment of Voigt and Mori–Tanaka models for vibration analysis of functionally graded plates. Compos Struct. 2012;94(7):2197–208. doi:10.1016/j.compstruct.2012.02.018. [Google Scholar] [CrossRef]
132. Singam S, Kumar B, Gupta R, Rajagopal A, Reddy J. Influence of the homogenization scheme on the bending response of functionally graded plates. Acta Mech. 2018;229(10):4071–89. doi:10.1007/s00707-018-2223-2. [Google Scholar] [CrossRef]
133. Eker M, Yarımpabuç D, Yıldırım A, Çelebi K. Elastic solutions based on the Mori-Tanaka scheme for pressurized functionally graded cylinder. J Appl Math Comput Mech. 2020;19(4):57–68. doi:10.17512/jamcm.2020.4.05. [Google Scholar] [CrossRef]
134. Tamura I, Tomota Y, Ozawa M. Strength and ductility of fe-ni-c alloys composed of austenite and martensite with various strength. In: Proceedings of the Third International Conference on Strength of Metals and Alloys; 1973. Vol. 1, p. 611–5. [Google Scholar]
135. Jin ZH, Paulino GH, Dodds RH. Cohesive fracture modeling of elastic–plastic crack growth in functionally graded materials. Eng Fract Mech. 2003;70(14):1885–912. doi:10.1016/S0013-7944(03)00130-9. [Google Scholar] [CrossRef]
136. Nayak P, Armani A. Optimal three-dimensional design of functionally graded parts for additive manufacturing using Tamura–Tomota–Ozawa model. Proc Inst Mech Eng, Part L: J Mater: Des Appl. 2021;235(9):1993–2006. doi:10.1177/14644207211011638. [Google Scholar] [CrossRef]
137. Arslan K, Gunes R, Apalak MK, Reddy JN. Evaluation of geometrically nonlinear and elastoplastic behavior of functionally graded plates under mechanical loading–unloading. Mech Adv Mater Struct. 2022;29(11):1587–600. doi:10.1080/15376494.2020.1829760. [Google Scholar] [CrossRef]
138. Nguyen D, Hoai B, Tran TH, Alexandrov S. Large deflections of functionally graded sandwich beams with influence of homogenization schemes. Arch Appl Mech. 2022;92(6):1757–75. doi:10.1007/s00419-022-02140-2. [Google Scholar] [CrossRef]
139. Akbarzadeh AH, Abedini A, Chen ZT. Effect of micromechanical models on structural responses of functionally graded plates. Compos Struct. 2015;119(6):598–609. doi:10.1016/j.compstruct.2014.09.031. [Google Scholar] [CrossRef]
140. Fan F, Lei B, Sahmani S, Safaei B. On the surface elastic-based shear buckling characteristics of functionally graded composite skew nanoplates. Thin-Walled Struct. 2020;154:106841. doi:10.1016/j.tws.2020.106841. [Google Scholar] [CrossRef]
141. Shahsavari D, Karami B. Assessment of Reuss, Tamura, and LRVE models for vibration analysis of functionally graded nanoplates. Arch Civil Mech Eng. 2022;22(2):92. doi:10.1007/s43452-022-00409-5. [Google Scholar] [CrossRef]
142. Billel R, Mansouri K, Mourad C, Berkia A, Messas T, Khadraoui F, et al. Effect of idealization models on deflection of functionally graded material (FGM) plate. J Nano Electron Phys. 2023;15:1022. [Google Scholar]
143. Billel R. Contribution to study the effect of (Reuss, LRVE, Tamura) models on the axial and shear stress of sandwich FGM plate (Ti–6A1–4V/ZrO2) subjected on linear and nonlinear thermal loads. AIMS Mater Sci. 2023;10(1):26–39. doi:10.3934/matersci.2023002. [Google Scholar] [CrossRef]
144. Hill R. Theory of mechanical properties of fibre-strengthened materials: I. elastic behaviour. J Mech Phys Solids. 1964;12(4):199–212. [Google Scholar]
145. Hill R. A self-consistent mechanics of composite materials. J Mech Phys Solids. 1965;13(4):213–22. doi:10.1016/0022-5096(65)90010-4. [Google Scholar] [CrossRef]
146. Reiter T, Dvorak GJ, Tvergaard V. Micromechanical models for graded composite materials. J Mech Phys Solids. 1997;45(8):1281–302. doi:10.1016/S0022-5096(97)00007-0. [Google Scholar] [CrossRef]
147. Kim JH, Paulino GH. An accurate scheme for mixed-mode fracture analysis of functionally graded materials using the interaction integral and micromechanics models. Int J Numer Methods Eng. 2003;58(10):1457–97. doi:10.1002/nme.819. [Google Scholar] [CrossRef]
148. Goupee AJ, Vel SS. Multi-objective optimization of functionally graded materials with temperature-dependent material properties. Mater Des. 2007;28(6):1861–79. doi:10.1016/j.matdes.2006.04.013. [Google Scholar] [CrossRef]
149. Kiani Y, Eslami MR. Thermal postbuckling of imperfect circular functionally graded material plates: examination of Voigt, Mori–Tanaka, and self-consistent schemes. J Press Vessel Technol. 2014;137(2):021201. [Google Scholar]
150. Gasik MM, Lilius RR. Evaluation of properties of W-Cu functional gradient materials by micromechanical model. Comput Mater Sci. 1994;3(1):41–9. doi:10.1016/0927-0256(94)90151-1. [Google Scholar] [CrossRef]
151. Shabana YM, Noda N. Numerical evaluation of the thermomechanical effective properties of a functionally graded material using the homogenization method. Int J Solids Struct. 2008;45(11):3494–506. doi:10.1016/j.ijsolstr.2008.02.012. [Google Scholar] [CrossRef]
152. Gasik MM. Micromechanical modelling of functionally graded materials. Comput Mater Sci. 1998;13(1):42–55. doi:10.1016/S0927-0256(98)00044-5. [Google Scholar] [CrossRef]
153. Hashin Z, Shtrikman S. A variational approach to the theory of the elastic behaviour of multiphase materials. J Mech Phys Solids. 1963;11(2):127–40. doi:10.1016/0022-5096(63)90060-7. [Google Scholar] [CrossRef]
154. Hashin Z. Analysis of composite materials—A survey. J Appl Mech. 1983;50(3):481–505. doi:10.1115/1.3167081. [Google Scholar] [CrossRef]
155. Mishnaevsky LL Jr. Computational mesomechanics of composites. West Sussex, England: John Wiley & Sons; 2007. [Google Scholar]
156. Loja MAR, Barbosa JI, Mota Soares CM. A study on the modeling of sandwich functionally graded particulate composites. Compos Struct. 2012;94(7):2209–17. doi:10.1016/j.compstruct.2012.02.015. [Google Scholar] [CrossRef]
157. Song G, Zou Y, Nie Y, Habibi M, Albaijan I, Toghroli E. Application of Hashin–Shtrikman bounds homogenization model for frequency analysis of imperfect FG bio-composite plates. J Mech Behav Biomed Mater. 2024;151(1):106321. doi:10.1016/j.jmbbm.2023.106321. [Google Scholar] [PubMed] [CrossRef]
158. Wakashima K, Tsukamoto H. Mean-field micromechanics model and its application to the analysis of thermomechanical behaviour of composite materials. Mater Sci Eng: A. 1991;146(1):291–316. doi:10.1016/0921-5093(91)90284-T. [Google Scholar] [CrossRef]
159. Zuiker JR. Functionally graded materials: choice of micromechanics model and limitations in property variation. Compos Eng. 1995;5(7):807–19. doi:10.1016/0961-9526(95)00031-H. [Google Scholar] [CrossRef]
160. Kapuria MBS, Kumar AN. Theoretical modeling and experimental validation of thermal response of metal-ceramic functionally graded beams. J Therm Stresses. 2008;31(8):759–87. doi:10.1080/01495730802194292. [Google Scholar] [CrossRef]
161. Cho JR, Ha DY. Averaging and finite-element discretization approaches in the numerical analysis of functionally graded materials. Mater Sci Eng: A. 2001;302(2):187–96. doi:10.1016/S0921-5093(00)01835-9. [Google Scholar] [CrossRef]
162. Chen B, Tong L. Thermomechanically coupled sensitivity analysis and design optimization of functionally graded materials. Comput Methods Appl Mech Eng. 2005;194(18):1891–911. doi:10.1016/j.cma.2004.07.005. [Google Scholar] [CrossRef]
163. Kerner EH. The elastic and thermo-elastic properties of composite media. Proc Phys Soc B. 1956;69(8):808–13. doi:10.1088/0370-1301/69/8/305. [Google Scholar] [CrossRef]
164. Miyamoto Y, Kaysser WA, Rabin BH, Kawasaki A, Ford RG. Functionally graded materials: design, processing and applications. New York: Springer Science & Business Media; 1999. [Google Scholar]
165. Zaidi M, Joshi KK, Shukla A, Cherinet B. A review of the various modelling schemes of unidirectional functionally graded material structures. AIP Conf Proc. 2021;2341(1):020021. doi:10.1063/5.0050306. [Google Scholar] [CrossRef]
166. Debnath A, Prokash RJ, Das SC, Afsar AM. An analysis of stress intensity factor of four equally spaced edge cracks in a functionally graded material cylinder. AIP Conf Proc. 2018;1980(1):030027. doi:10.1063/1.5044306. [Google Scholar] [CrossRef]
167. Nguyen DK. Large displacement response of tapered cantilever beams made of axially functionally graded material. Compos Part B: Eng. 2013;55(6):298–305. doi:10.1016/j.compositesb.2013.06.024. [Google Scholar] [CrossRef]
168. Li X, Li L, Hu Y, Ding Z, Deng W. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos Struct. 2017;165(1):250–65. doi:10.1016/j.compstruct.2017.01.032. [Google Scholar] [CrossRef]
169. Huang Y, Wang T, Zhao Y, Wang P. Effect of axially functionally graded material on whirling frequencies and critical speeds of a spinning Timoshenko beam. Compos Struct. 2018;192(11):355–67. doi:10.1016/j.compstruct.2018.02.039. [Google Scholar] [CrossRef]
170. Lin X, Huang Y, Zhao Y, Wang T. Large deformation analysis of a cantilever beam made of axially functionally graded material by homotopy analysis method. Appl Math Mech. 2019;40(10):1375–86. doi:10.1007/s10483-019-2515-9. [Google Scholar] [CrossRef]
171. Singh R, Sharma P. Vibration analysis of an axially functionally graded material non-prismatic beam under axial thermal variation in humid environment. J Vib Control. 2022;28(23–24):3608–21. doi:10.1177/10775463211037150. [Google Scholar] [CrossRef]
172. Babilio E. Dynamics of an axially functionally graded beam under axial load. Eur Phys J Special Topics. 2013;222(7):1519–39. doi:10.1140/epjst/e2013-01942-8. [Google Scholar] [CrossRef]
173. Akbas SD. Forced vibration responses of axially functionally graded beams by using ritz method. J Appl Computat Mech. 2021;7(1):109–15. [Google Scholar]
174. Simsek M, Kocaturk T, Akbas S. Dynamic behavior of an axially functionally graded beam under action of a moving harmonic load. Compos Struct. 2012;94(8):2358–64. doi:10.1016/j.compstruct.2012.03.020. [Google Scholar] [CrossRef]
175. Huang Y, Li XF. A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. J Sound Vib. 2010;329(11):2291–303. doi:10.1016/j.jsv.2009.12.029. [Google Scholar] [CrossRef]
176. Cao D, Gao Y, Yao M, Zhang W. Free vibration of axially functionally graded beams using the asymptotic development method. Eng Struct. 2018;173:442–8. doi:10.1016/j.engstruct.2018.06.111. [Google Scholar] [CrossRef]
177. Dai J, Liu Y, Liu H, Miao C, Tong G. A parametric study on thermo-mechanical vibration of axially functionally graded material pipe conveying fluid. Int J Mech Mater Des. 2019;15(4):715–26. doi:10.1007/s10999-018-09439-5. [Google Scholar] [CrossRef]
178. Rajasekaran S, Khaniki HB. Finite element static and dynamic analysis of axially functionally graded nonuniform small-scale beams based on nonlocal strain gradient theory. Mech Adv Mater Struct. 2019;26(14):1245–59. doi:10.1080/15376494.2018.1432797. [Google Scholar] [CrossRef]
179. Bednarik M, Cervenka M, Groby JP, Lotton P. One-dimensional propagation of longitudinal elastic waves through functionally graded materials. Int J Solids Struct. 2018;146(13):43–54. doi:10.1016/j.ijsolstr.2018.03.017. [Google Scholar] [CrossRef]
180. Tsiatas GC, Charalampakis AE. Optimizing the natural frequencies of axially functionally graded beams and arches. Compos Struct. 2017;160:256–66. doi:10.1016/j.compstruct.2016.10.057. [Google Scholar] [CrossRef]
181. Alshabatat NT. Natural frequencies optimization of thin-walled circular cylindrical shells using axially functionally graded materials. Materials. 2022;15(3):698. doi:10.3390/ma15030698. [Google Scholar] [PubMed] [CrossRef]
182. Voigt W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann Phys. 1889;274(12):573–87. doi:10.1002/andp.18892741206. [Google Scholar] [CrossRef]
183. Reuss A. Berechnung der Fliebgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM—J Appl Math Mech/Zeitschrift Für Angewandte Mathematik Und Mechanik. 1929;9(1):49–58. doi:10.1002/zamm.19290090104. [Google Scholar] [CrossRef]
184. Hill R. The elastic behaviour of a crystalline aggregate. Proc Phys Soc A. 1952;65(5):349. doi:10.1088/0370-1298/65/5/307. [Google Scholar] [CrossRef]
185. Ebrahimi MJ, Najafizadeh MM. Free vibration analysis of two-dimensional functionally graded cylindrical shells. Appl Math Model. 2014;38(1):308–24. doi:10.1016/j.apm.2013.06.015. [Google Scholar] [CrossRef]
186. Sahmani S, Safaei B. Nonlinear free vibrations of bi-directional functionally graded micro/nano-beams including nonlocal stress and microstructural strain gradient size effects. Thin-Walled Struct. 2019;140:342–56. doi:10.1016/j.tws.2019.03.045. [Google Scholar] [CrossRef]
187. Nguyen NV, Phan DH. A size-dependent nonlinear isogeometric approach of bidirectional functionally graded porous plates. Structures. 2024;68(4):107097. doi:10.1016/j.istruc.2024.107097. [Google Scholar] [CrossRef]
188. ŞimŞek M. Buckling of Timoshenko beams composed of two-dimensional functionally graded material (2D-FGM) having different boundary conditions. Compos Struct. 2016;149(1):304–14. doi:10.1016/j.compstruct.2016.04.034. [Google Scholar] [CrossRef]
189. Chen X, Zhang X, Lu Y, Li Y. Static and dynamic analysis of the postbuckling of bi-directional functionally graded material microbeams. Int J Mech Sci. 2019;151(3):424–43. doi:10.1016/j.ijmecsci.2018.12.001. [Google Scholar] [CrossRef]
190. Chen X, Lu Y, Zhu B, Zhang X, Li Y. Nonlinear resonant behaviors of bi-directional functionally graded material microbeams: one-/two-parameter bifurcation analyses. Compos Struct. 2019;223(3):110896. doi:10.1016/j.compstruct.2019.110896. [Google Scholar] [CrossRef]
191. Li J, Wang G, Guan Y, Zhao G, Lin J, Naceur H, et al. Meshless analysis of bi-directional functionally graded beam structures based on physical neutral surface. Compos Struct. 2021;259(1):113502. doi:10.1016/j.compstruct.2020.113502. [Google Scholar] [CrossRef]
192. Thang PT, Nguyen-Thoi T, Lee J. Modeling and analysis of bi-directional functionally graded nanobeams based on nonlocal strain gradient theory. Appl Math Comput. 2021;407(1–2):126303. doi:10.1016/j.amc.2021.126303. [Google Scholar] [CrossRef]
193. Lieu QX, Lee S, Kang J, Lee J. Bending and free vibration analyses of in-plane bi-directional functionally graded plates with variable thickness using isogeometric analysis. Compos Struct. 2018;192:434–51. doi:10.1016/j.compstruct.2018.03.021. [Google Scholar] [CrossRef]
194. Chen X, Lu Y, Wu Z, Shao Y, Xue X, Wu Y. Free vibration of in-plane bi-directional functionally graded materials rectangular plates with geometric imperfections and general elastic restraints. Aerosp Sci Technol. 2023;132(1):108045. doi:10.1016/j.ast.2022.108045. [Google Scholar] [CrossRef]
195. Wang C, Koh JM, Yu T, Xie NG, Cheong KH. Material and shape optimization of bi-directional functionally graded plates by GIGA and an improved multi-objective particle swarm optimization algorithm. Comput Methods Appl Mech Eng. 2020;366(12):113017. doi:10.1016/j.cma.2020.113017. [Google Scholar] [CrossRef]
196. Ma L, Wang C, Chong Y, Hu W, Zeng L. Isogeometric material optimization for shape control of bi-directional functionally graded plates with piezoelectric layers. Thin-Walled Struct. 2024;202(1):112067. doi:10.1016/j.tws.2024.112067. [Google Scholar] [CrossRef]
197. Nejad MZ, Hadi A. Non-local analysis of free vibration of bi-directional functionally graded Euler–Bernoulli nano-beams. Int J Eng Sci. 2016;105(9):1–11. doi:10.1016/j.ijengsci.2016.04.011. [Google Scholar] [CrossRef]
198. Nejad MZ, Hadi A. Eringen’s non-local elasticity theory for bending analysis of bi-directional functionally graded Euler–Bernoulli nano-beams. Int J Eng Sci. 2016;106(9):1–9. doi:10.1016/j.ijengsci.2016.05.005. [Google Scholar] [CrossRef]
199. Nejad MZ, Hadi A, Rastgoo A. Buckling analysis of arbitrary two-directional functionally graded Euler–Bernoulli nano-beams based on nonlocal elasticity theory. Int J Eng Sci. 2016;103(9):1–10. doi:10.1016/j.ijengsci.2016.03.001. [Google Scholar] [CrossRef]
200. Tang Y, Lv X, Yang T. Bi-directional functionally graded beams: asymmetric modes and nonlinear free vibration. Compos Part B: Eng. 2019;156(1):319–31. doi:10.1016/j.compositesb.2018.08.140. [Google Scholar] [CrossRef]
201. Hussein O, Mulani S. Multi-dimensional optimization of functionally graded material composition using polynomial expansion of the volume fraction. Struct Multidiscipl Optim. 2017;56(2):271–84. doi:10.1007/s00158-017-1662-z. [Google Scholar] [CrossRef]
202. Nemat-Alla M. Reduction of thermal stresses by developing two-dimensional functionally graded materials. Int J Solids Struct. 2003;40(26):7339–56. doi:10.1016/j.ijsolstr.2003.08.017. [Google Scholar] [CrossRef]
203. Attia MA, El-Shafei AG, Gad SI. Investigation of indentation response of bi-directional functionally graded materials. Proc Inst Mech Eng, Part J: J Eng Tribol. 2021;235(8):1641–58. doi:10.1177/1350650120971078. [Google Scholar] [CrossRef]
204. Nguyen-Ngoc H, Cuong-Le T, Nguyen KD, Nguyen-Xuan H, Abdel-Wahab M. Three-dimensional polyhedral finite element method for the analysis of multi-directional functionally graded solid shells. Compos Struct. 2023;305(6):116538. doi:10.1016/j.compstruct.2022.116538. [Google Scholar] [CrossRef]
205. Thai S, Nguyen VX, Lieu QX. Bending and free vibration analyses of multi-directional functionally graded plates in thermal environment: a three-dimensional Isogeometric Analysis approach. Compos Struct. 2022;295:115797. doi:10.1016/j.compstruct.2022.115797. [Google Scholar] [CrossRef]
206. Rezaiee-Pajand M, Rajabzadeh-Safaei N. Nonlocal static analysis of a functionally graded material curved nanobeam. Mech Adv Mater Struct. 2018;25(7):539–47. doi:10.1080/15376494.2017.1285463. [Google Scholar] [CrossRef]
207. Chakraverty S, Pradhan KK. Computational structural mechanics: static and dynamic behaviors. London, United Kingdom: Academic Press; 2018. [Google Scholar]
208. Berghouti H, Bedia EA, Benkhedda A, Tounsi A. Vibration analysis of nonlocal porous nanobeams made of functionally graded material. Adv Nano Res. 2019;7:351–64. [Google Scholar]
209. Barretta R, Luciano R, Marotti de Sciarra F, Ruta G. Stress-driven nonlocal integral model for Timoshenko elastic nano-beams. Eur J Mech—A/Solids. 2018;72(3):275–86. doi:10.1016/j.euromechsol.2018.04.012. [Google Scholar] [CrossRef]
210. Aydogdu M. Longitudinal wave propagation in multiwalled carbon nanotubes. Compos Struct. 2014;107:578–84. doi:10.1016/j.compstruct.2013.08.031. [Google Scholar] [CrossRef]
211. Aydogdu M, Arda M. Forced vibration of nanorods using nonlocal elasticity. Adv Nano Res. 2016 12;4(4):265–79. doi:10.12989/anr.2016.4.4.265. [Google Scholar] [CrossRef]
212. Lee WH, Han SC, Park WT. Application of nonlocal elasticity theory for buckling analysis of nano-scale plates. J Korea Acad Ind Coop Soc. 2012 11;13:5542–50. [Google Scholar]
213. Goldhirsch I, Goldenberg C. Granular and nano-elasticity. 2002. doi:10.48550/arXiv.cond-mat/0201081. [Google Scholar] [CrossRef]
214. Chiroiu V, Munteanu L, Dumitriu D, Teodorescu P. On the nonlocal simulation of nanoindentation problems. Proc SPIE—Int Soc Optical Eng. 2009;7297:72971R. doi:10.1117/12.823674. [Google Scholar] [CrossRef]
215. Eringen AC, Edelen DGB. On nonlocal elasticity. Int J Eng Sci. 1972;10(3):233–48. doi:10.1016/0020-7225(72)90039-0. [Google Scholar] [CrossRef]
216. Aranda-Ruiz J, Loya J, Fernández-Sáez J. Bending vibrations of rotating nonuniform nanocantilevers using the Eringen nonlocal elasticity theory. Compos Struct. 2012;94(9):2990–3001. doi:10.1016/j.compstruct.2012.03.033. [Google Scholar] [CrossRef]
217. Eringen AC. Nonlocal polar elastic continua. Int J Eng Sci. 1972;10(1):1–16. doi:10.1016/0020-7225(72)90070-5. [Google Scholar] [CrossRef]
218. Chen ZW, Lai JKL, Shek CH. Insights into microstructural evolution from nanocrystalline SnO2 thin films prepared by pulsed laser deposition. Phys Rev B. 2004;70:165314. doi:10.1103/PhysRevB.70.165314. [Google Scholar] [CrossRef]
219. Thai CH, Ferreira AJM, Phung-Van P. A nonlocal strain gradient isogeometric model for free vibration and bending analyses of functionally graded plates. Compos Struct. 2020;251:112634. doi:10.1016/j.compstruct.2020.112634. [Google Scholar] [CrossRef]
220. Lu L, Guo X, Zhao J. Size-dependent vibration analysis of nanobeams based on the nonlocal strain gradient theory. Int J Eng Sci. 2017;116:12–24. doi:10.1016/j.ijengsci.2017.03.006. [Google Scholar] [CrossRef]
221. Mindlin RD. Micro-structure in linear elasticity. Arch Ration Mech Anal. 1964;16(1):51–78. doi:10.1007/BF00248490. [Google Scholar] [CrossRef]
222. Mindlin RD. Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct. 1965;1(4):417–38. doi:10.1016/0020-7683(65)90006-5. [Google Scholar] [CrossRef]
223. Aifantis EC. On the role of gradients in the localization of deformation and fracture. Int J Eng Sci. 1992;30(10):1279–99. doi:10.1016/0020-7225(92)90141-3. [Google Scholar] [CrossRef]
224. Tang F, He S, Shi S, Xue S, Dong F, Liu S. Analysis of size-dependent linear static bending, buckling, and free vibration based on a modified couple stress theory. Materials. 2022;15(21):7583. doi:10.3390/ma15217583. [Google Scholar] [PubMed] [CrossRef]
225. Rahmani A, Faroughi S, Friswell MI, Babaei A. Eringen’s nonlocal and modified couple stress theories applied to vibrating rotating nanobeams with temperature effects. Mech Adv Mater Struct. 2022;29(26):4813–38. doi:10.1080/15376494.2021.1939468. [Google Scholar] [CrossRef]
226. Zhou Y, Fang Zheng Y, Wang F, ping Chen C. Size-dependent nonlinear free vibration of magneto-electro-elastic nanobeams by incorporating modified couple stress and nonlocal elasticity theory. Phys Scr. 2024;99(9):095217. doi:10.1088/1402-4896/ad67b6. [Google Scholar] [CrossRef]
227. Park SK, Gao XL. Bernoulli–Euler beam model based on a modified couple stress theory. J Micromech Microeng. 2006;16(11):2355. doi:10.1088/0960-1317/16/11/015. [Google Scholar] [CrossRef]
228. Ma HM, Gao XL, Reddy JN. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J Mech Phys Solids. 2008;56(12):3379–91. doi:10.1016/j.jmps.2008.09.007. [Google Scholar] [CrossRef]
229. Tsiatas GC. A new Kirchhoff plate model based on a modified couple stress theory. Int J Solids Struct. 2009;46(13):2757–64. doi:10.1016/j.ijsolstr.2009.03.004. [Google Scholar] [CrossRef]
230. Park S, Gao XL. Variational formulation of a modified couple stress theory and its application to a simple shear problem. Zeitschrift Für Angewandte Mathematik Und Physik. 2008;59(5):904–17. doi:10.1007/s00033-006-6073-8. [Google Scholar] [CrossRef]
231. Hadjesfandiari AR, Dargush GF. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int J Solids Struct. 2013;50(9):1253–65. doi:10.1016/j.ijsolstr.2012.12.021. [Google Scholar] [CrossRef]
232. Wu CP, Hu HX. A unified size-dependent plate theory for static bending and free vibration analyses of micro- and nano-scale plates based on the consistent couple stress theory. Mech Mater. 2021;162:104085. doi:10.1016/j.mechmat.2021.104085. [Google Scholar] [CrossRef]
233. Zhang R, Bai H, Chen X. The consistent couple stress theory-based vibration and post-buckling analysis of bi-directional functionally graded microbeam. Symmetry. 2022;14(3):602. doi:10.3390/sym14030602. [Google Scholar] [CrossRef]
234. Chen X. Hygro-thermo-magneto-elastic vibration of multidirectional graded porous nanobeams with axial motion by considering rotary inertia and thickness effects. Int J Struct Stab Dyn. 2024. doi:10.1142/S0219455425501305. [Google Scholar] [CrossRef]
235. Yang T, Tang Y, Li Q, Yang XD. Nonlinear bending, buckling and vibration of bi-directional functionally graded nanobeams. Compos Struct. 2018;204(5):313–9. doi:10.1016/j.compstruct.2018.07.045. [Google Scholar] [CrossRef]
236. Lal R, Dangi C. Thermomechanical vibration of bi-directional functionally graded non-uniform timoshenko nanobeam using nonlocal elasticity theory. Compos Part B: Eng. 2019;172(9):724–42. doi:10.1016/j.compositesb.2019.05.076. [Google Scholar] [CrossRef]
237. Dangi C, Saini S, Lal R, Vir Singh I. Size dependent FEM model for Bi-directional functionally graded nano-beams. Mater Today: Proc. 2020;24:1302–11. doi:10.1016/j.matpr.2020.04.445. [Google Scholar] [CrossRef]
238. Nazmul IM, Devnath I. Exact analytical solutions for bending of bi-directional functionally graded nanobeams by the nonlocal beam theory using the Laplace transform. Forces Mech. 2020;1(9):100002. doi:10.1016/j.finmec.2020.100002. [Google Scholar] [CrossRef]
239. Khoram MM, Hosseini M, Hadi A, Shishehsaz M. Bending analysis of bidirectional FGM timoshenko nanobeam subjected to mechanical and magnetic forces and resting on Winkler–Pasternak foundation. Int J Appl Mech. 2020;12(8):2050093. doi:10.1142/S1758825120500933. [Google Scholar] [CrossRef]
240. Malik M, Das D. Study on free vibration behavior of rotating bidirectional functionally graded nano-beams based on Eringen’s nonlocal theory. Proc Inst Mech Eng Part L: J Mater: Des Appl. 2020;234(9):1203–17. doi:10.1177/1464420720929375. [Google Scholar] [CrossRef]
241. Gholami M, Zare E, Alibazi A. Applying Eringen’s nonlocal elasticity theory for analyzing the nonlinear free vibration of bidirectional functionally graded Euler–Bernoulli nanobeams. Arch Appl Mech. 2021;91(7):2957–71. doi:10.1007/s00419-021-01939-9. [Google Scholar] [CrossRef]
242. Dangi C, Lal R, Sukavanam N. Effect of surface stresses on the dynamic behavior of bi-directional functionally graded nonlocal strain gradient nanobeams via generalized differential quadrature rule. Eur J Mech—A/Solids. 2021;90:104376. doi:10.1016/j.euromechsol.2021.104376. [Google Scholar] [CrossRef]
243. Dangi C, Lal R. Surface effect on vibration characteristics of bi-directional functionally graded nanobeam using Eringen’s nonlocal theory. Phys Scr. 2021;96(11):115703. doi:10.1088/1402-4896/ac14e2. [Google Scholar] [CrossRef]
244. Lal R, Dangi C. Dynamic analysis of bi-directional functionally graded Timoshenko nanobeam on the basis of Eringen’s nonlocal theory incorporating the surface effect. Appl Math Comput. 2021;395:125857. doi:10.1016/j.amc.2020.125857. [Google Scholar] [CrossRef]
245. Ohab-Yazdi SMK, Kadkhodayan M. Application of bi-directional functionally graded material model for free vibration analysis of rotating Euler-Bernoulli nanobeams. Mech Adv Compos Struct. 2021;8(2):389–99. [Google Scholar]
246. Wang S, Kang W, Yang W, Zhang Z, Li Q, Liu M, et al. Hygrothermal effects on buckling behaviors of porous bi-directional functionally graded micro-/nanobeams using two-phase local/nonlocal strain gradient theory. Eur J Mech—A/Solids. 2022;94:104554. doi:10.1016/j.euromechsol.2022.104554. [Google Scholar] [CrossRef]
247. Barati A, Hadi A, Nejad MZ, Noroozi R. On vibration of bi-directional functionally graded nanobeams under magnetic field. Mech Based Des Struct Mach. 2022;50(2):468–85. doi:10.1080/15397734.2020.1719507. [Google Scholar] [CrossRef]
248. Zhao J, Li X, Li S, Liu Y, Mohammadi R. Size-dependent investigation of the 2D-FG CNTRC nanobeams using nonlocal strain gradient beam theory subjected to hygro-thermo conditions. Waves Random Complex Media. 2022. doi:10.1080/17455030.2022.2070682. [Google Scholar] [CrossRef]
249. Shanab RA, Attia MA. Semi-analytical solutions for static and dynamic responses of bi-directional functionally graded nonuniform nanobeams with surface energy effect. Eng Comput. 2022;38(3):2269–312. doi:10.1007/s00366-020-01205-6. [Google Scholar] [CrossRef]
250. Majdi A, Yasin Y, Altalbawy FMA, Al-Timami AMS, Mashhadani ZIA, Albahash ZF, et al. Size-dependent vibrations of bi-directional functionally graded porous beams under moving loads incorporating thickness effect. Mech Based Des Struct Mach. 2024;52(4):1943–74. doi:10.1080/15397734.2023.2165098. [Google Scholar] [CrossRef]
251. Deng J, Liu Y, Zhang Z, Liu W. Size-dependent vibration and stability of multi-span viscoelastic functionally graded material nanopipes conveying fluid using a hybrid method. Compos Struct. 2017;179(2):590–600. doi:10.1016/j.compstruct.2017.07.084. [Google Scholar] [CrossRef]
252. Liu H, Lv Z, Tang H. Nonlinear vibration and instability of functionally graded nanopipes with initial imperfection conveying fluid. Appl Math Model. 2019;76:133–50. doi:10.1016/j.apm.2019.06.011. [Google Scholar] [CrossRef]
253. Lyu Z, Tang H, Xia H. Thermo-mechanical vibration and stability behaviors of bi-directional FG nano-pipe conveying fluid. Thin-Walled Struct. 2023;188(8):110784. doi:10.1016/j.tws.2023.110784. [Google Scholar] [CrossRef]
254. Zhang L, Zhang W, Chen F. Two-phase flow-induced vibration of tilted curved bi-directional functionally graded nanopipe in supersonic airflow. Mech Adv Mater Struct. 2024. doi:10.1080/15376494.2024.2354532. [Google Scholar] [CrossRef]
255. Xie J, Li J, Zhen L, Zhang C, Mohammadi R. A novel nonlocal higher-order theory for the accurate vibration analysis of 2D FG nanoplates. Pro Inst Mech Eng Part C: J Mech Eng Sci. 2022;236(5):2161–71. doi:10.1177/09544062211024688. [Google Scholar] [CrossRef]
256. Daikh AA, Belarbi MO, Khechai A, Li L, Ahmed H, Eltaher MA. Buckling of bi-coated functionally graded porous nanoplates via a nonlocal strain gradient quasi-3D theory. Acta Mech. 2023;234(8):3397–420. doi:10.1007/s00707-023-03548-9. [Google Scholar] [CrossRef]
257. Saffari PR, Thongchom C, Jearsiripongkul T, Saffari PR, Keawsawasvong S, Kongwat S. Porosity-dependent wave propagation in multi-directional functionally graded nanoplate with nonlinear temperature-dependent characteristics on Kerr-type substrate. Int J Thermofluids. 2023;20:100408. doi:10.1016/j.ijft.2023.100408. [Google Scholar] [CrossRef]
258. Roodgar Saffari P, Sirimontree S, Thongchom C, Jearsiripongkul T, Saffari P, Keawsawasvong S, et al. Free and forced vibration of sandwich FGM porous variable thickness nanoplates integrated with magneto-electro-elastic layers via nonlocal strain gradient theory. Eng Sci. 2023;24:918. doi:10.30919/es918. [Google Scholar] [CrossRef]
259. Thi TT, Ke T, Hoa P. Static and dynamic analyses of multi-directional functionally graded porous nanoplates with variable nonlocal parameter using MITC3 + element. J Vib Eng Technol. 2023;12(3):5147–71. doi:10.1007/s42417-023-01189-9. [Google Scholar] [CrossRef]
260. Cao Y, Khorami M, Baharom S, Assilzadeh H, Hassan Dindarloo M. The effects of multi-directional functionally graded materials on the natural frequency of the doubly-curved nanoshells. Compos Struct. 2021;258(8):113403. doi:10.1016/j.compstruct.2020.113403. [Google Scholar] [CrossRef]
261. Cuong-Le T, Nguyen KD, Lee J, Rabczuk T, Nguyen-Xuan H. A 3D nano scale IGA for free vibration and buckling analyses of multi-directional FGM nanoshells. Nanotechnol. 2022;33(6):065703. doi:10.1088/1361-6528/ac32f9. [Google Scholar] [PubMed] [CrossRef]
262. Wang S, Shang Y, Qian ZH. Size-dependent analysis of porous multi-directional FG shell structures based on the modified couple stress theory using the unsymmetric finite element method. Acta Mech. 2022;233(12):5105–36. doi:10.1007/s00707-022-03362-9. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF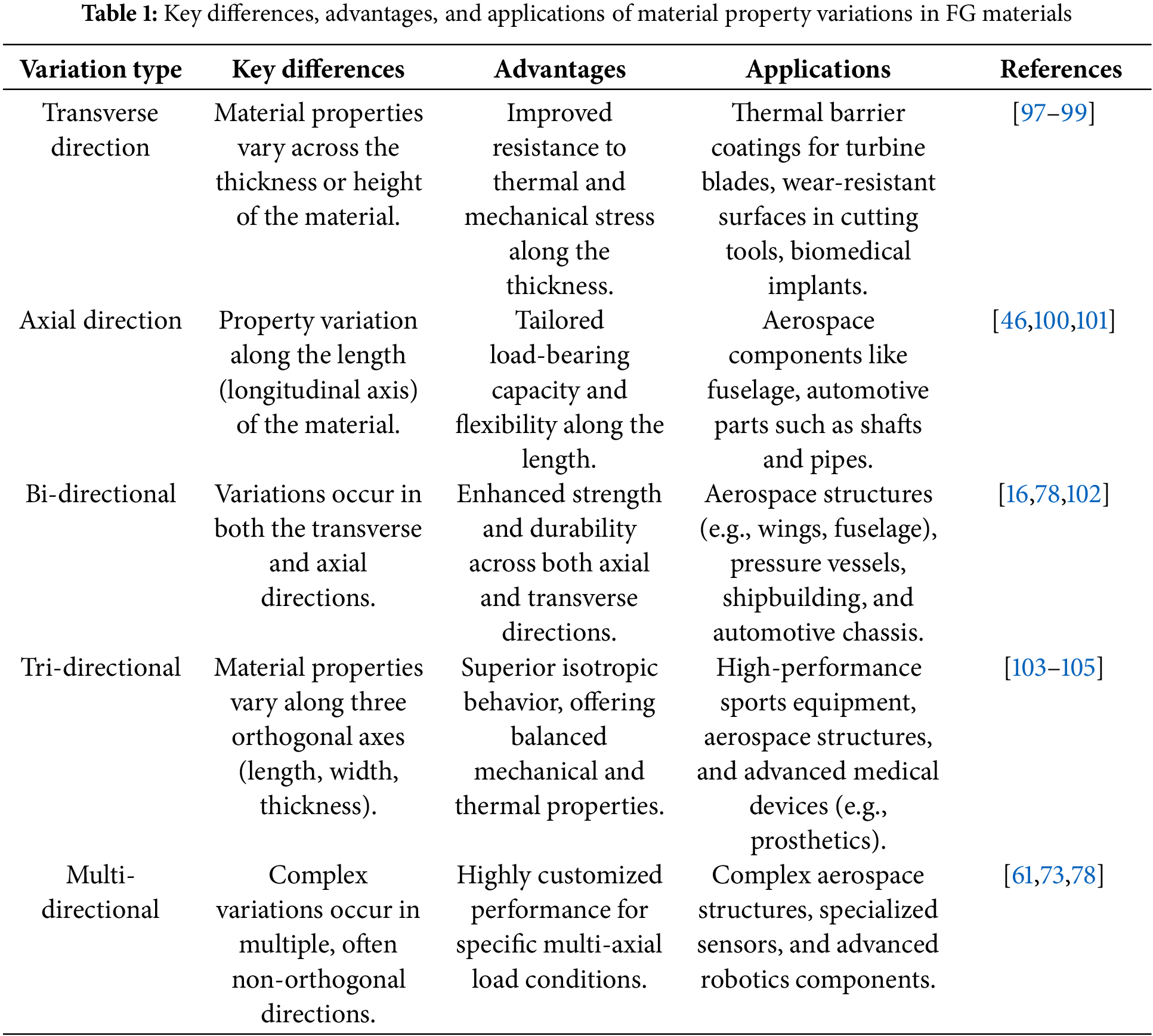
 Downloads
Downloads
 Citation Tools
Citation Tools
