Fine Tuned Hybrid Deep Learning Model for Effective Judgment Prediction

1  Introduction

With the development of big data and AI technologies, the use of computers to assist judgment decisions in legal cases has become a significant study area [1,2]. Legal Judgment Prediction (LJP) uses deep learning approaches to automatically forecast the judgment outcome of a case based on its fact description. The goal of LJP development is to increase the efficiency of legal practitioners [3,4]. Normally, judges use factual evidence to deal with criminal cases, but they also consider outside data, such as the defendant’s profile and the court’s perspective. Most current works ignore outside data and use the fact description as their only input for LJP [5,6]. LJP predicts the decision based on both statute (as created by the legislature) and case law (as developed by the courts) to find what is relevant for some specific case at hand. The binary classification method uses textual information taken from a case as input for the classifiers, and the final result is a determination of whether an article of the Convention on Human Rights has been violated [7]. Existing works consider LJP as a text classification cum prediction using Machine Learning classifier models. The core functions of machine intelligence research are learning, optimization, and search. Most of the research work considers judgment prediction as a text classification cum prediction concept using a deep learning model with conventional optimization algorithms. Nowadays, metaheuristic optimization algorithms are mostly utilized to fine-tune the weights of deep learning models for judgment prediction. Some limitations of Natural Language Processing (NLP) in the legal domain in terms of case facts include lexical and semantic ambiguity, the presence of complex and misspelled words, and the use of informal language and idiomatic expressions. Additionally, homonyms and context-dependent vocabulary pose challenges. Legal documents are often very lengthy, and collecting relevant case materials can be difficult. Furthermore, retrieving useful information from raw case documents is complex, as these texts typically lack proper annotation. Fig. 1 shows a sample case document.

Figure 1: Sample case document

Text-based deep learning networks have a number of difficulties, including encoding lengthy documents without losing information, the slowness of gradient-based optimization techniques in dealing with high dimensional data, usage of insufficient data to train the DNN, and non-convex optimization in the Deep Neural Network (DNN).

One of the solutions for the above challenges is to enhance optimization algorithms. Optimization algorithms are generally used to train the deep learning model iteratively, resulting in either a maximum or minimum evaluation based on the objective function. They are used to find solutions for highly complex optimization problems. Conventional optimization algorithms like Adam, Gradient Descent, and stochastic optimizers use first-order derivatives which results in saddle points or flat regions of the loss landscape, leading to slow progress. Also, they suffer from the Curse of Dimensionality and are stuck in local optima. Nature-inspired optimization can be employed to resolve the aforementioned issues.

1.1 Benefits of Nature Inspired Metaheuristic Optimization

•   Metaheuristic algorithms deal with the optimal use of resources and time

•   Computation is less complex

•   Converges in less number of iterations

•   use stochastic and probabilistic mechanisms to avoid getting stuck in flat regions

It is difficult to educate a smart machine to predict the right judgment results due to the intricacy of court proceedings [8,9]. In the areas of text classification, Named Entity Recognition (NER) [10] sentiment analysis, and recommendation systems, NLP has produced outstanding results recently. Courts have accumulated a substantial amount of useful judgment document data while managing the case, which offers a research basis for applying NLP [11] to the legal sector and is anticipated to address flaws in the case-handling process. The Judgment Prediction task on Indian cases is more challenging for multiple reasons. Some of the challenges include the unstructured nature of case texts, the extraction of pertinent information from case facts to train the classifier models, and the lack of uniformity in the manner of case facts.

Our main contributions to this research are:

•   Retrieval of improved semantic similarity and entropy features during the feature extraction phase of the lemmatized case document.

•   Introduction of modified pelican optimization technique to update the weights of hidden layers in training the deep learning model for accurate prediction of judgment.

•   Experimental evaluation with preprocessed Madras High Court criminal cases using hybrid classifier models by developing an improved score fusion technique and performing comparative analysis with and without the proposed optimization method in the hybrid model.

The article is organized as follows: The literature survey is briefly described in Section 2. The proposed judgment prediction model is given in Section 3. An explanation of preprocessing, feature extraction, and prediction is given in Section 4. Experimental analysis is provided in Section 5. Section 6 provides a conclusion.

2  Related Works

Over several decades, research on LJP has advanced significantly. Using deep neural networks to solve LJP tasks is also gaining popularity among researchers. But most of the existing works use conventional optimizers in the classifier models which have more computation complexity and get stuck in local optima when used with real-time datasets [12,13]. Deep Learning models employed for prediction today frequently employ meta-heuristic optimization techniques inspired by nature. The pertinent literature about Deep Learning Models in Judgment Prediction is surveyed in this section in two different ways: Deep learning Models based on Legal Judgment Prediction and Deep learning models with nature-inspired Optimization.

2.1 Legal Judgement Prediction

In 2020, Shang Li et al. [14] introduced a Multi Attentive Neural Network (MANN), which executes the combined LJP task in an integrated architecture and learns from past judgment documents. MANN improves the capacity of the model by using both textual and contextual data to predict court rulings by combining many channels for feature extraction. It maximizes prediction accuracy with an attention mechanism to focus on case details. However, the approach relies on the input data standard and is incapable of holding cases with improper legal data or insufficient data.

In 2020, Guo et al. [15] suggested a novel technique called TenLa for predicting judgments in court cases. TenLa relies on a modifiable tensor decomposition procedure and an enhanced Lasso regression technique. Similarities between court cases are a significant indicator of verdict prediction in TenLa, which is mainly divided into three components termed ModTen, ConTen, and OLass. Furthermore, the ConTen intermediate tensor is proposed as an optimization approach for OLass. Tenla approaches are highly dimensional legal information that integrates tensor decomposition and lasso regression which employs better feature elimination and selection. However, the model relies on feature engineering, it does not perform better with high-dimensional, unstructured text data. Moreover, the approach is not conveyed better to other legal jurisdictions.

In 2020, Wang et al. [16] suggested a pre-training language method named Bidirectional Encoder Representations from Transformers (BERT) to train word embedding of case information in combination with Deep Learning (DL) model techniques like Long Short-Term Memory (LSTM), Deep Pyramid Convolutional Neural Network (DPCNN), Convolutional Neural Network (CNN) and Recurrent Convolutional Neural Network (RCNN) to detect outcomes in legal cases. The decision of a judge in a case is crucial to the legal system since it helps them decide what kind of criminals they are and how to punish them. This approach obtains better accuracy to predict judicial judgments with the use of BERT, a baseline transformer approach to find contextual relationships in legal data. However, these models are computationally expensive and require more resources to tune the parameters.

In 2022, Yang et al. [17] proposed a multi-view encoder fusing legal (MVE-FLK) a Multitask Legal judgment prediction model that used a multiclass multilabel classifier that infuses facts and legal keywords using word and sentence encoder along with an attention mechanism. Law articles and charges were predicted on CAIL small and CAIL big Chinese legal datasets. Data information loss still happens at the encoding stage. Furthermore, due to its greater reliance on keyword extraction, the model is unable to manage a variety of occurrences with inaccurate legal information.

In 2022, Alghazzawi et al. [18] presented LSTM with CNN, a new technique for predicting judicial case judgments. Important features are extracted from the case papers using the recursive feature elimination technique, which prioritizes the highest score. However, it is less effective when dealing with lengthy court cases.

In 2022, Lyu et al. [19] developed a Criminal Element Extraction Network (CEEN) for various discriminative criminal elements such as criminal, target, intentionality, and criminal behavior. Moreover, a reinforcement learning extractor is used to locate elements for various cases accurately. The model is experimented with the real-time dataset for judgment prediction and works only for criminal cases.

In 2023, Dal et al. [20] conceived a text regression technique to predict the amount of compensation from court rulings, as customers encounter issues with airlines and file claims for insignificant damages. It creates a few machine learning and natural language processing models. Additionally, the created model incorporates N-Grams Extraction, Feature Selection, Cross-Validation, Overfitting Avoidance, and Outliers Removal. Also, Attributes Extracted by the Legal Expert (AELE) is developed as a source for the text case. The integration of various components has a heavy impact on the performance of the developed prediction work. This model combines various contextual and legal domains for effective prediction that gives data about monetary damages in court cases. However, the model has subtle case-specific factors and oversimplifies intricate legal reasoning. Moreover, it is limited to predicting the compensation that does not translate to other case scenarios in different languages.

In 2024, Peng et al. [21] refined a framework known as Bidirectional Encoder Representations from Transformers (BERT) to predict the offense and penalty from Taiwan’s district court. The prediction of criminal charges and the prediction of sentences are the two stages of this activity. Penalties are predicted using training data, including injury and public endangerment decisions. Additionally, it uses a better way to get around BERT’s 512-token limit. The use of a bidirectional contextual framework increases the accuracy of prediction in different court cases. However, the computational cost is high due to the large datasets and the prediction is limited in certain countries because it focuses on Taiwanese court rulings.

In 2024, Latisha et al. [22] proposed a prediction system for criminal court decisions in Indonesia. The developed system is built by six Bidirectional Encoder Representations from Transformers (BERT) approach and Robustly Optimized BERT Pretraining Approach on the three established frameworks like BERT Base, Hierarchical BERT + Mean Pooling, and Hierarchical BERT + LSTM (Long Short-Term Memory). The prediction accuracy of BERT is improved due to its focus on legal text and case information for verdicts, criminal charges, and penalties. However, the approach may have difficulties with low-structured or improper legal statements.

In 2023, Zhang et al. [23] have established a supervised contrastive learning framework for predicting legal judgments. This approach is trained to distinguish the different articles of law enclosed with the same chapter and make the same charges for a similar article. The model is optimized by finding the cases with similar articles that permit for effective relationship between that fact description for the case and its related labels. The contrastive approach enhances the prediction accuracy by distinguishing the comparable and dissimilar legal classes. However, in some legal places, the approach needs more labeled data to improve the better performance. Moreover, the approach makes it more trouble to train the system and is less transparent to legal professionals.

In 2024, Sukanya et al. [24] empirically examined machine learning models for predicting legal judgments. Additionally, a hybrid CNN with a transformer model is proposed in this work to predict the binary judgments. The method first goes through word embeddings and preprocessing procedures. Real-time Madras High Court criminal cases from Manupatra were used for these studies. The developed hybrid CNN-Transformer Neural Network (TNN) model outperforms other Machine Learning (ML) and DL models which demonstrate the capability of integrating multiple models for better performance. However, the computational complexity of the model is more expensive with large datasets.

In 2024, Shelar et al. [25] established an advanced approach known as Deep Bi-LSTM for predicting legal judgments. The deep learning model is employed based on Texas wolf optimization which is termed (TWO-Bi-LSTM) model. First, the preprocessing process is carried out using judicial information. Then, feature extraction takes place with approaches like statistical features and Principal Component Analysis (PCA) for creating the extensive feature set. The developed model can predict legal judgment more effectively. However, the method may face challenges with high-dimensional, unstructured text data, as it relies heavily on feature engineering.

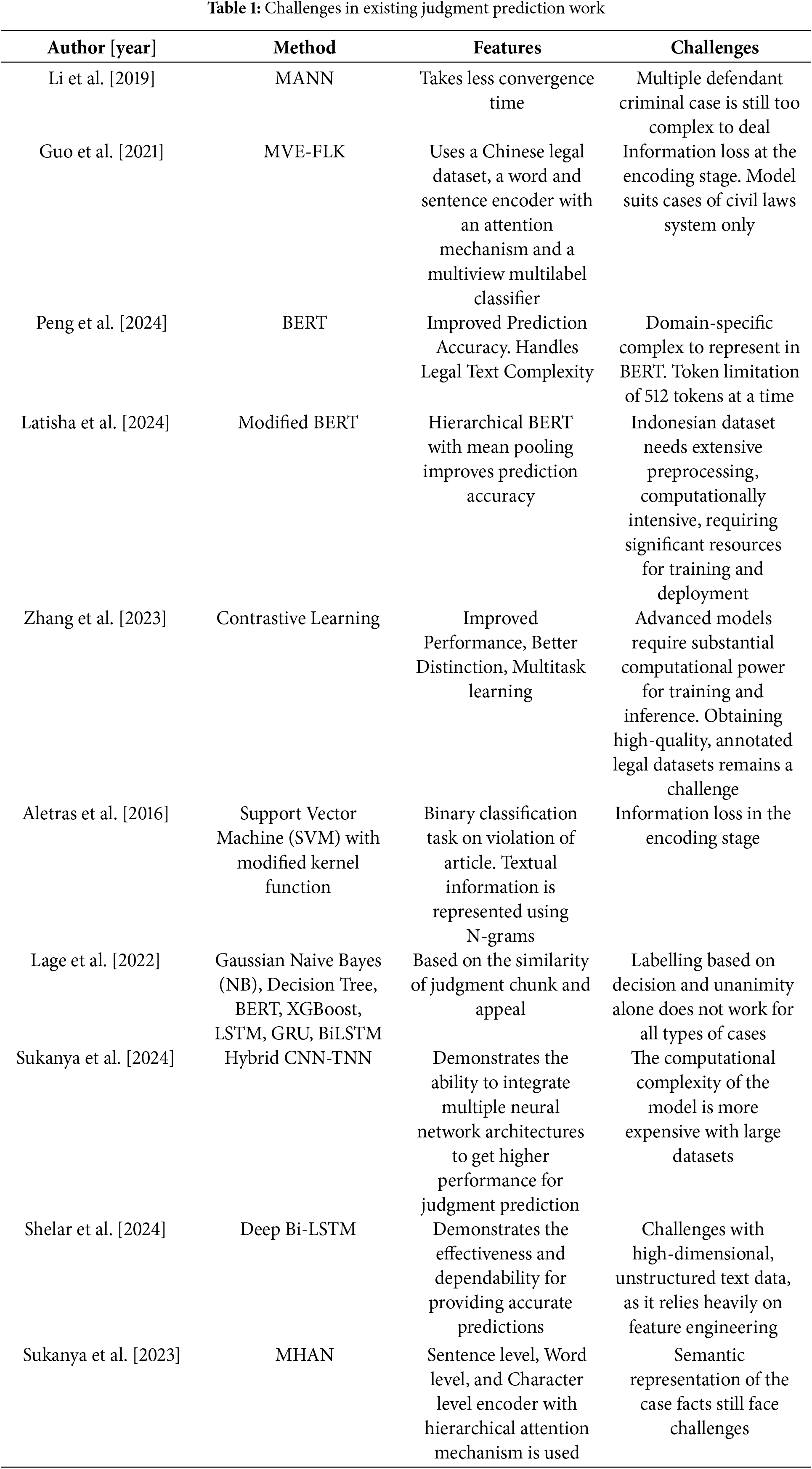
In 2023, Sukanya et al. [26] created the Modified Hierarchical-Attention Network (MHAN), a model for predicting judgment. For particular domain word embedding frameworks, it is specifically made. By combining the various characteristics with enhanced cosine similarity features, it implements the feature extraction procedure. The purpose of the hybrid Self Improved RNN is to forecast the court decision. Real-time criminal cases from the Supreme Court of India and the Madras High Court of India were used for the experimental studies. However, to improve performance and support system decisions, the method must be applied in a multi-input fashion. In 2022, Lage-Freitas et al. [27] outlined an approach to forecast the Brazilian court decisions. This model makes use of baseline deep learning models as well as several machine learning models. Using 4043 cases from a Brazilian court, this method is working as a prototype, with an F1 score of about 80.2%. The accuracy of the decision prediction is improved by considering various legal aspects, especially the Brazilian legal system. However, the model does not work effectively in other jurisdictions for various legal systems because it focuses more on the Brazilian setting. The summary of the existing work features and challenges is provided in Table 1.

Our proposed approach effectively addresses the unique challenges posed by existing strategies in legal judgment prediction (LJP). For instance, attention-mechanism-based models often have high computational costs and depend heavily on high-quality input data, limiting their scalability. Similarly, models that rely on preset feature engineering struggle to adapt to novel or unstructured legal data. While approaches employing BERT are highly effective, they face limitations due to their lack of jurisdiction-specific customization and significant computational demands. Moreover, methods dealing with unstructured legal materials and complex reasoning processes often encounter difficulties, and some models focusing on criminal case elements fail to generalize to broader legal contexts. Techniques involving multi-view encoders for legal keyword fusion, though innovative, can result in complex and less transparent applications.

To address these limitations, our work introduces a novel legal judgment prediction framework. The method enhances feature extraction by leveraging semantic similarity and entropy-based techniques to handle ambiguous legal data effectively. Additionally, the COLPO (Chaotic Opposition Learning-based Pelican Optimization) algorithm improves computational efficiency, ensuring better scalability. By employing versatile feature extraction methods, our approach is applicable across various legal domains. The hybrid strategy, integrating Bi-GRU and Deep Maxout with score-level fusion, achieves a balance between accuracy and efficiency while capturing sequential relationships and enhancing representational flexibility.

2.2 Nature-Inspired Optimization

The term “nature-inspired algorithms” refers to a group of cutting-edge approaches and strategies for solving problems using natural phenomena. Swarm intelligence (SI) optimization algorithms have long been a mainstay of approaches to problems involving global optimization because of their simplicity and flexibility in computation. Also, it provides a fine balance between exploration and exploitation over solution search space and finely solves global optimization problems. Nowadays, research in nature-inspired algorithms is growing faster based on different behaviors found such as foraging, hunting, etc. But most of them are applied to image data.

Very little existing literature work is available on the application of nature-inspired algorithms on text data. One of the limitations faced in the above algorithms is deriving local optimum for complex tasks which involves more computation and iteration. The most commonly used is the Sparrow Search Algorithm (SSA) by Xue et al. [28]. Table 2 lists the features and challenges of existing nature-inspired algorithms. In 2021, Ouoyang et al. [29] proposed the Learning Sparrow Search algorithm that uses a lens reverse strategy to overcome large randomness which results in a local optimum. Yan et al. [30] have done a clear analysis of the Sparrow Search Algorithm (SSA) regarding features and computations. It stated that though it has a fast convergence rate and high accuracy it faces some limitations such as a lower level of communication within the community, a weaker ability to jump out of the local optimum, a poorer ability to conduct global searches, and a rapidly dwindling diversity of its population.

Mostafa et al. [31] have proposed the mCOOT optimization algorithm based on Opposition Based Learning and Orthogonal Learning to overcome local minima for dimensionality reduction on datasets. Harish et al. [32] have implemented Spider Monkey Optimization which updates the weights based on Euclidean distance. The values are updated based on the positions and postures of the spider monkeys through communication. One of the restrictions is that there is no variation in the spacing between different data points and similar data points as it follows Euclidean distance. As no optimization algorithm can be guaranteed to be extremely effective at tackling every optimization issue, there is always a research gap between the optimization algorithm and the end product. Trojovský et al. [33] have proposed Pelican Optimization Algorithm (POA) and tested using 23 objective functions of unimodal and multimodal type. Also, a comparative study is done with 8 different nature-inspired algorithms on four real-world applications such as pressure vessel design, speed reducer, welded beam, and tension spring design. One of the greatest advantages of POA is high exploration power in search space. The stochastic nature of POA is unstable and solutions are not equal to global optimum for all optimization problems. Wang et al. [34] have implemented Adaptive Chaotic Grey Wolf Optimization (GWO) for increasing the productivity in Solid Oxide fuel cells by dynamically updating the adaptive weights using chaos with GWO in the multilayer of neural network for conversion of chemical energy into electrical energy. Since GWO suffers local optimization and slow convergence, they introduce chaos to select random values in the calculation of weights.

Although significant research has been conducted on legal judgment prediction using deep learning models, there remains a notable gap in optimizing these models for efficient exploration of the global search space to identify global optima consistently. Moreover, to the best of our knowledge, limited attention has been given to Indian court cases in this domain, with most studies focusing predominantly on Chinese cases. These studies often overlook the critical role of optimization during weight updates in the hidden layers of deep learning models when training on preprocessed textual data. Addressing this gap, our study explores the application of nature-inspired optimization techniques, specifically leveraging a modified pelican optimization algorithm within a hybrid deep learning framework, to enhance the performance of legal judgment prediction models using Indian court case data. Though Pelican optimization works well, its weakness lies in selecting the pelican agents (search agents) within the search range and in the way of selecting random numbers in the exploration phase. The above research gap is addressed in the proposed method COLPO by using a modified pelican optimization method with Opposition-Based Learning for tuning the weights in the hidden layer and experimenting on Madras High Court cases in English.

3  Proposed Methodology

The proposed methodology works with three main steps: Preprocessing, Feature Extraction, and Judgment prediction. This research proposes a hybrid classifier model that integrates BI-GRU and Deep Maxout neural networks, trained on a combination of enhanced legal text features such as improved semantic similarity and entropy of case facts. The empirical analysis was conducted using various deep learning models including Gated Recurrent Unit (GRU), Convolutional Neural Network (CNN), Recurrent Neural Network (RNN), Log-Short Term Memory (LSTM), Shallow Neural Network (SNN), Deep Neural Network (DNN), Recurrent Neural Network (RNN) with LSTM, CNN-LSTM, CNN-GRU, and Transformer-CNN, applied to Madras High Court cases, Sukanya et al. has found that the BiGRU model demonstrated the better performance in the context of analyzing lengthy case documents. Maxout is generally used for challenging tasks where flexible activation functions are beneficial. Also, it is used when specific tasks demand a dynamic and adaptable activation behavior and in a situation where overfitting issues are a concern. Consequently, we selected BiGRU integrated with deep maxout for the proposed methodology in this research article as it can remember information over long sequences without losing critical details and faces reduced vanishing gradient issues. The choice of hyperparameter settings plays a pivotal role in determining the performance of machine learning and deep learning models. Hyperparameters such as learning rate, batch size, number of hidden layers, dropout rate, and optimizer selection directly influence the training process, convergence speed, and model generalization. For instance, an improperly tuned hyperparameter can either slow down the convergence or cause the model to overshoot the optimal solution. So here, the hidden layer weights are optimized using a modified meta-heuristic approach. Specifically, the Pelican Optimization Algorithm was enhanced with Chaotic sequence generation instead of traditional random number calculation, along with the Opposition-Based Learning (OBL) concept to accelerate convergence toward the global minimum. The weights of the Deep Maxout and Bi-GRU classifiers are adjusted using the recently proposed Chaotic Opposition Learning based Pelican Optimization (COLPO) technique. The prediction accuracy is then increased by fusing the output scores of Deep Maxout and Bi-GRU utilizing better score level fusion. The outline of the suggested judgment prediction model is shown in Fig. 2.

Figure 2: Overall structure of judgement prediction model using COLPO

3.1 Preprocessing

Input text of the raw case documents is pre-processed using stopword removal, stemming, lemmatization and tokenization methods. The lemmatized case document is given as input into the word-level tokenizer. Compared to Glove and Word2vec, ElMo (Embeddings from Language Models) is employed as it can produce context-sensitive, dynamic embeddings [35].

3.2 Feature Extraction

ELMo first builds word representations using character-level Convolutional Neural Networks (CNNs). This facilitates processing words that are not in the vocabulary and records morphological details. The embedded ElMo vector acts as a function of a word which collects the entire sentence based on the current context. Every token has an ELMo vector value with size . Features like improved semantic similarity and entropy for case fact representation were calculated from the vectorized text representations. The extracted feature is denoted as which is a summation of improved Semantic similarity and entropy feature .

3.2.1 Improved Semantic Similarity

Existing text classification research works mostly use semantic similarity in NLP which is a predetermined metric, i.e., calculates cosine similarity to assess the likeness between case texts or documents based on its meaning. Conventional semantic similarity formula [36] is given in Eq. (1).

(1)

One drawback of cosine similarity is that it uses only direction and not the magnitude of its neighboring word. Eq. (2) defines enhanced semantic similarity following the suggested approach.

(2)

where is a correlation among normalized word i.e., Pearson correlation is calculated among each word in the document and keyword list and it is added as a new parameter in the existing semantic similarity formula. Pearson correlation is used above to bring the linear relationship between two vectors. The following Fig. 3 shows the improved semantic similarity between criminal case sentences.

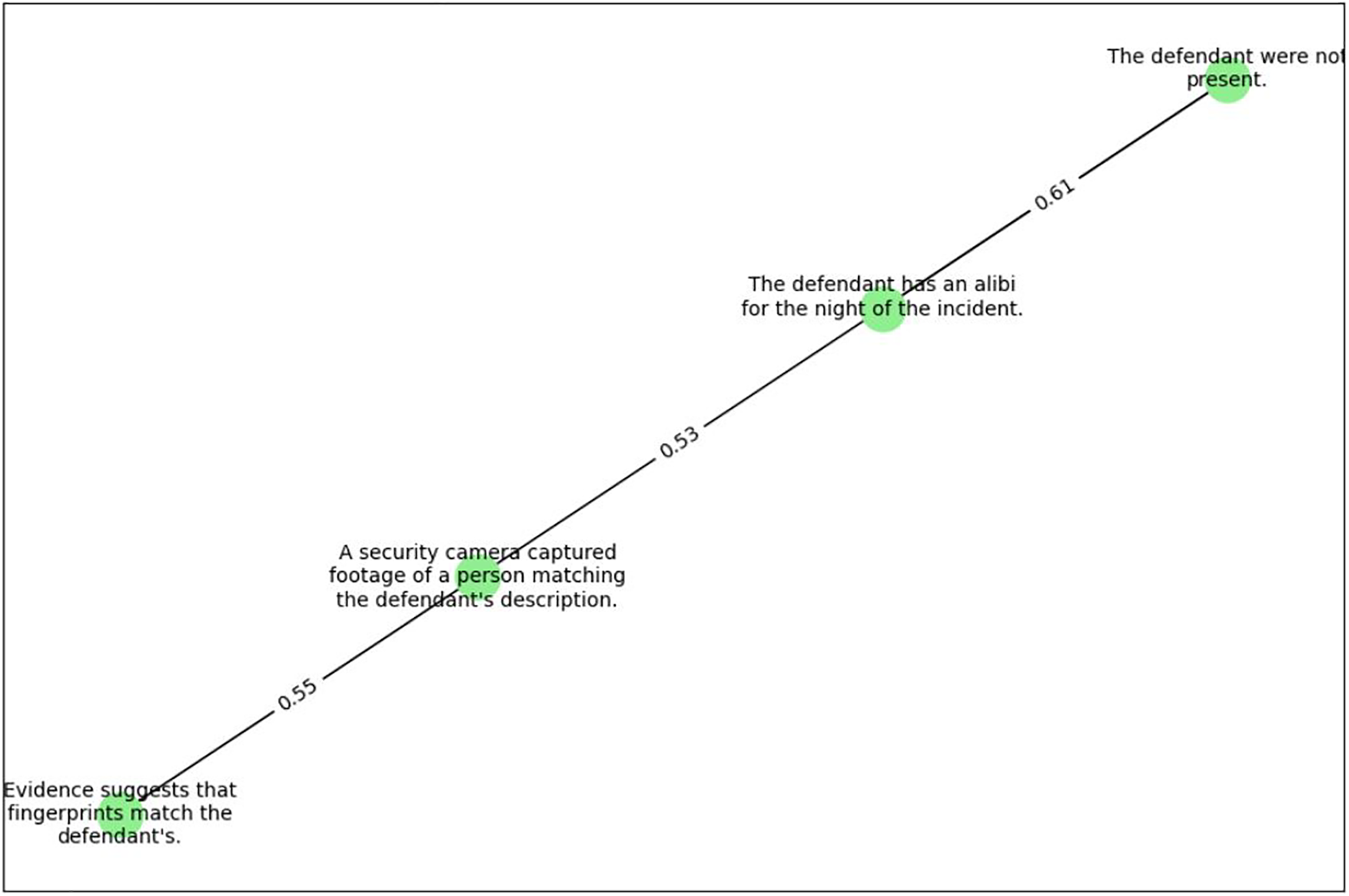
Figure 3: Improved semantic similarity on criminal case sentences

3.2.2 Entropy

Entropy is a measurement of the amount of uncertainty surrounding random variables. The formula for entropy is defined in Eq. (3).

(3)

where is the uncertainty of Z, represents the impurity by log to base 2 of the probability of a category and refers to the probability of category where the index refers to many possible categories. Here i = 2, as it denotes two categories such as allowed or dismissed. Adding entropy features along with improved semantic similarity features is useful for selecting irrelevant or less informative features.

The entropy measure and improved semantic similarity feature of the words are extracted from the tokenized vectors of the lemmatized case document. The summation of the improved semantic similarity and the entropy-based feature vectors is sent to the hybrid model for training. The impact of improved semantic similarity and entropy features extracted from the lemmatized document enhances the prediction accuracy comparatively rather than normal feature extraction.

3.3 Judgment Prediction

Although each has shortcomings, most current works process text documents using RNN, LSTM, and GRU because they are very good at processing sequential text. In this work, the features were trained by combining the BiGRU classifier with deep max out. Though BiGRUs can handle sequential data well, they are not ideal for processing lengthy documents due to their computational inefficiency, difficulty in retaining long-term dependencies, and potential loss of information in long sequences. The combination of a BiGRU and a Deep Maxout hybrid classifier results in a model that leverages the strengths of both architectures: capturing rich contextual information from sequential data via BiGRU and performing efficient, non-linear classification with Maxout. This hybrid approach offers improved performance, better generalization, and robustness, especially in tasks involving complex, high-dimensional sequential data.

The novel deep hybrid model that combines Deep Maxout and Bi-GRU classifiers is trained using the above features. Bi-GRU (Bidirectional Gated Recurrent Unit) and Deep Maxout were strategically included in the hybrid classifier because of their complimentary advantages in processing legal language. A particular kind of recurrent neural network called a Bi-GRU can recognize sequential dependencies in data, which is essential for comprehending the information flow in legal documents where context and the relationships between phrases in various textual sections are critical. Bi-GRU’s bidirectional feature enables the model to account for both past and future dependencies, which makes it especially useful for legal writings whose interpretation may be influenced by both earlier and later case facts. However, a feedforward neural network type called Deep Maxout enhances representational flexibility by enabling the model to learn a range of non-linear transformations, which makes it ideal for managing the intricate, subtle character of legal language. Deep Maxout improves the model’s capacity to represent intricate patterns and interactions in the data, but Bi-GRU is excellent at capturing temporal and sequential correlations. The hybrid classifier leverages the advantages of both designs by merging them. Deep Maxout provides flexibility and an improved ability to describe complex, non-linear relationships in the text, Bi-GRU guarantees that temporal dependencies inside legal situations are captured. When combined, they offer a strong foundation for examining legal texts, because precise judgment prediction depends on the intricate interactions between legal terminology as well as the order of events. The COLPO technique for adjusting the ideal classifier weights will be used to train the proposed prediction model. Then, the improved score level fusion (ISLF) technique is used to fuse the outputs of Bi-GRU and Deep Maxout classifiers. Fig. 4 represents the hybrid prediction model for legal judgment. The process is as follows: the features which is a summation of and are given as the input to both models separately. The learning weights in the hidden layer are optimized using a modified Pelican optimization algorithm to minimize the error rate shown in Fig. 5. The Pelican Optimization Algorithm stands out due to its simplicity, strong exploration-exploitation balance, and fast convergence, particularly for complex, high-dimensional, or multimodal optimization problems. Compared to other metaheuristic methods Pelican Optimization Algorithm often requires fewer iterations and less parameter tuning while being computationally efficient and scalable. Its reduced parameter sensitivity and ability to avoid premature convergence make it a strong alternative for a wide range of optimization tasks. The outcomes from both Bi-GRU and Deep maxout model are averaged to determine the final results. The following sections give a brief explanation of the hybrid model.

Figure 4: Hybrid prediction model for legal judgement

Figure 5: Solution encoding

Figure 6: Representation of chaotic sequence

3.3.1 Deep Maxout

Each neuron in a Maxout Neural Network [37] is part of a grouping of candidate items. It was chosen to employ a maximum value for neuron activation that exceeded elements. hidden layer's node is depicted as , and its components as . Eqs. (4) and (5) show a logical connection between them: Through the below layer’s forward propagation, is acquired:

(4)

(5)

Here, is layer's max-out activation vector, layer's weight matrix is which is tuned optimally by COLPO, layer's vector is , and layer's bias vector is . Due to the activation processes, the forward-propagation method of the max-out network is distinct from the feed-forward Neural Network. For backpropagation, for , additional weight will not be employed; It is only possible to use the weights related to the element that appears the most in each group.

3.3.2 Bi-GRU

Generally, a Gated Recurrent Unit serves as a good mechanism for artificial RNNs. However, GRUs have been demonstrated to perform effectively with smaller to medium-sized datasets. The calculation of the Bi-GRU network [20] for right is provided in Eqs. (6) to (9) and for the left is provided in Eqs. (10) to (14).

Right way:

(6)

(7)

(8)

(9)

Left way:

(10)

(11)

(12)

(13)

Result:

(14)

Here, is the reset gate, is the update gate, is reset memory, J is weight, optimally tuned by COLPO approach, represents the sigmoid function, is a network response based on recent and upcoming text, and W is a hidden state weight. Both the classifiers are trained using 80% of the lemmatized cases. The results of Bi-GRU and Deep Maxout are averaged, and this is used to predict if the case will be accepted or denied. Table 3 describes the parameters of the classifiers.

3.4 Colpo Method

The proposed hybrid model integrates a Bi-GRU and a Deep Maxout classifier for judgment prediction. These components are chosen from among the existing deep learning techniques because the RNN family, to which Bi-GRU belongs, is particularly effective in text analysis. Generally, error minimization has a significant impact on prediction accuracy in deep learning techniques. In this regard, emphasis has been placed on tuning the weights in the hidden layer of the deep learning model, using the nature-inspired modified pelican optimization method as they find global minima faster than conventional optimization algorithms. Eq. (15) defines the mathematical depiction of the specified objective function. The weights of Deep Max Out and Bi-GRU are provided as input to the COLPO algorithm. Herein, the total count of input is 10 and the problem size is 100. Algorithm 1 shows the detailed explanation of COLPO.

(15)

Among the recent metaheuristic optimization algorithms used, the Pelican Optimization Algorithm (POA) [38] is considered in this research to replace the conventional optimizer. The reason for using Pelican optimization is that it is computationally lighter and can dynamically adjust its behavior based on search space and current solution quality. The main goal of POA's design was to simulate pelican’s behavior and hunting skills in finding weights to avoid local minima in fewer iterations. On the other hand, POA suffers from premature convergence, in finding the position of search agents and parameter fine-tuning despite its smaller parameter set and robust exploration, exploitation, and adaption balance. The issues above in Pelican Optimization are resolved by implementing an Opposition-based Learning scheme to determine the neighboring location and using the concept of chaos sequence for generating random numbers.

The suggested method’s selection of Pelican Optimization (PO) and Opposition-Based Learning (OBL) is based on their capacity to improve accuracy and efficiency of global optimization. By taking advantage of opposition-based knowledge, OBL is renowned for increasing the convergence rate of optimization algorithms and enabling more efficient search space exploration. This idea ensures a more complete investigation of the solution space by assisting the model in avoiding local optima. The optimization process is further improved by integrating Pelican Optimization, a nature-inspired algorithm that balances exploration and exploitation by imitating pelican foraging behavior. Pelican Optimization can be used to optimize the weights of hybrid neural networks such as Deep Maxout and Bi-GRU since it has demonstrated promise in effectively traversing high-dimensional, complicated regions. Combining these two approaches gives the suggested model a strong global optimization process that improves forecast accuracy and guarantees quicker convergence, making it more effective than conventional optimization methods. To effectively train a hybrid neural network in the context of legal judgment prediction, OBL, and Pelican Optimization were chosen due to their complementary strengths. Pelican Optimization offers a potent mechanism for global search, while OBL speeds up convergence by investigating opposition-based solutions. Generally, nature-inspired optimization algorithms undergo three stages. Initialization, Exploration, and Exploitation.

3.4.1 Initialization

In this phase, search agents are initially distributed at random within a specific area, based on Eq. (16). According to our application following important parameters are initialized as population size (number of weights), lower bound and upper bound , the search space boundary D (100), objective function as Eq. (15) and maximum number of iterations (k).

(16)

where and . The proposed COLPO (Chaotic Opposition Learning Based Pelican Optimization method) makes use of the Opposition based learning concept, to find search opposites in global search space. As per the proposed COLPO method, an opposition solution is generated for the pelican position update given in Eq. (17).

(17)

where , is the search range of pelican and is a random number which is generated using chaotic cubic function [39] as per proposed COLPO. The points within the search range are selected using the Opposition-Based Learning concept uses opposite pairs in the objective function in Eq. (15). The infused OBL concept and random value generated using chaotic sequence produce optimal weights in the hidden layer.

Analysis of Chaotic Sequence over Random Numbers: Fig. 6 shows the chaotic sequence numbers generated using the logistic map function. It uses the parameters such as ‘r’ control parameter, x0 (initial value), and n (number of iterations) to generate the sequence numbers. The output of the resulting sequence appears to be random but is found in a deterministic way. By using the chaotic sequence mapping numbers instead of random numbers in the objective function of Pelican Optimization, random numbers are generated deterministically.

Minimal Computational Overhead: In many cases, especially for systems with straightforward governing equations, generating chaotic sequences involves less computational overhead than generating truly random values. This efficiency can be useful in settings where resources are limited.

Pseudorandomness with Deterministic Properties: Chaotic sequences are deterministic, which means that they can be replicated if the governing equations and the initial circumstances are known. In situations when reproducibility is sought, this trait may be helpful.

Embedded Randomness: To achieve a balance between randomness and determinism, chaotic systems can also incorporate random behavior into their dynamics. This capability can greatly benefit applications such as signal processing and random number generation. Naik et al. [40] have demonstrated how chaotic maps are used in pseudorandom number generation. We make use of a Logistic Cubic chaotic map. The initial set of population is fed into a chaotic map sequencer, which generates a chaotic series.

3.4.2 Exploration

Exploration in optimization algorithm is defined by authors as “collecting information” ie searching the feasible region in unexplored space. The capacity of the search agent to explore the search space is

(18)

increased by a randomly distributed prey, and Eq. (18) describes how the search agent updates its location after each iteration, where, represents the current iteration, is pelican in dimension, is a prey location in dimension, is at random either 1 or 2, is the fitness function value, and is the value of the objective function.

Analysis on Opposition Based Learning: Instead of solely focusing on a single candidate solution, OBL evaluates the opposite solution to enhance the exploration and exploitation of the search space. This can lead to faster convergence, better diversity of solutions, and improved performance in avoiding local optima. OBL is often integrated into metaheuristic algorithms to make them more efficient and robust [41–43]. The fitness function value for the search agents which are at different positions within the range 0 to 1 is calculated to get older fitness values as well as new fitness values for the initial search agents and opposite search agents. The main idea of Opposition-Based Learning (OBL) is to use the opposites for better/faster learning. If the search space is small, an exhaustive search can be done to find the global optimum, but it is tedious for a large search space. Opposites of the same nature also differ. One may be nearer to the solution and the other farther. The idea is to make a guessing point within the search space as a search agent create a symmetric-based opposite as another search agent and evaluate the fitness value based on the objective function. Fig. 7 represents the OBL concept in a square-shaped search space.

Figure 7: Opposition-based Learning in a square-shaped search space

While evaluating the fitness value, equations that involve the random number ‘r’ are mapped using chaotic sequence numbers generated by a chaotic cubic function. The creation of opposite search agents results in less number of iterations as well as minimizes the error rate.

3.4.3 Exploitation

It can be defined as the use of the information that is needed to produce a known-good result i.e., search of promising regions in the neighborhood. When the pelicans reach the water’s surface, they expand their wings to lift the fish upward and then scoop them up in their throat pouches. Here, the fitness values for both old and new positions of normal and opposition-based search agents are calculated and the minimum fitness value is updated as the new position based on the objective function. Eq. (19) simulates this pelican hunting behavior mathematically.

(19)

According to the proposed COLPO, pelican behavior is defined in Eq. (20).

(20)

where K is the maximum iteration, and is neighbor radius. OBL is a scheme that gives information about the weights and opposition weights. They are used in the field which uses estimates as exact solutions for complex problems. Nowadays research in swarm intelligence computation for the optimization concept is on the rise, as it gives a more promising result than traditional optimization which uses random values in weight computation. Improvements include fewer computations and iterations due to OBL-based swarm optimization methods as done by [44]. Table 4 represents the parameter settings of the optimization algorithms.

3.4.4 Time Complexity Analysis

The computational complexity of the proposed COLPO is computed in this section. The suggested COLPO’s computational complexity is based on four principles: initializing the algorithm, evaluating the fitness function, creating prey, and updating the solution. The algorithm’s initialization processes have a computational complexity of . During each iteration, each member of the population evaluates the objective function in both stages. Consequently, the computing complexity of the fitness function evaluation is . Given that prey is generated and evaluated at each iteration, the computational complexity of prey generation is . The number of N population members with dimensions needs to be updated twice in each cycle. As a result, is the computational complexity of updating solutions. The time complexity per iteration is . Thus is the time complexity of te suggested COLPO algorithm.

3.4.5 Space Complexity Analysis

The space complexity of COLPO mainly depends on the number of particles and the problem’s dimensionality . Each particle’s position and velocity vectors must be stored for COLPO to function; and is represented as . The spatial complexity is often proportional to the problem size and particle count. To store global optimal placements and other factors, the algorithm also needs more RAM. The amount of memory needed to store the particles’ locations, velocities, and personal bests determines the space complexity of COLPO. Consequently, can be used to represent the space complexity of the personal best position for COLPO. The space for the global best position is represented as and the space for the other variables is represented as . The space complexity of individual components in COLPO is represented as . Therefore, the total space complexity of the COLPO algorithm is .

3.5 Improved Score Level Fusion

Improved score level fusion is used to fuse the prediction scores of the Bi-GRU and Deep Maxout classifiers following the optimization procedure for adjusting their weights. The overall performance of the model is enhanced by using the score-level fusion. Eq. (22) is utilized to formulate the traditional score-level fusion.

(21)

(22)

Here, represents the score value of the sample , denotes the score normalization of the sample , represents the maximum score vector of the sample , denotes the minimum value of the score vector of the sample , and M represents the number of predicted outputs. However, the effectiveness of conventional score-level fusion relies on the accuracy and robustness of the individual classifiers. If one or more classifiers perform poorly, it can negatively impact the overall performance. To overcome this limitation, this work proposes improved score-level fusion as follows:

Step (i) Normalization: The predicted score of both Bi-GRU and Deep Maxout score was normalized by using the maximum absolute scaler as described in Eqs. (23) and (24).

(23)

(24)

Step (ii) After the normalization step, the improved score level fusion is carried out by a novel Logistic Sine Chaotic Map (LSCM). The logistic map and the sine map are both used in the chaotic map known as LSCM. Compared to the logistic map and sine map, this LSCM has a better random distribution and greater chaotic features. Eq. (25), which provides the mathematical formulation of LSCM.

(25)

Eq. (25) denotes the average of the target label, and represents the random variable. The term is formulated using Eq. (26).

(26)

Finally, the scores are fused based on the highest accuracy of both classifier predictions as represented in Eq. (27). if means

(27)

else if

(28)

where , i.e., LSCM, denotes the accuracy score of Bi-GRU, denotes the accuracy score of Deep Maxout. Our proposed LSCM-based score level fusion technique can combine the two classifiers to maximize the strengths to improve the prediction accuracy. The above LSCM-based score fusion mitigates the influence of quality scores and improves the overall accuracy of our model. This improved score level fusion is used to enhance the final prediction accuracy for legal judgment.

4  Dataset Description

4.1 Dataset 1-Madras High Court Database

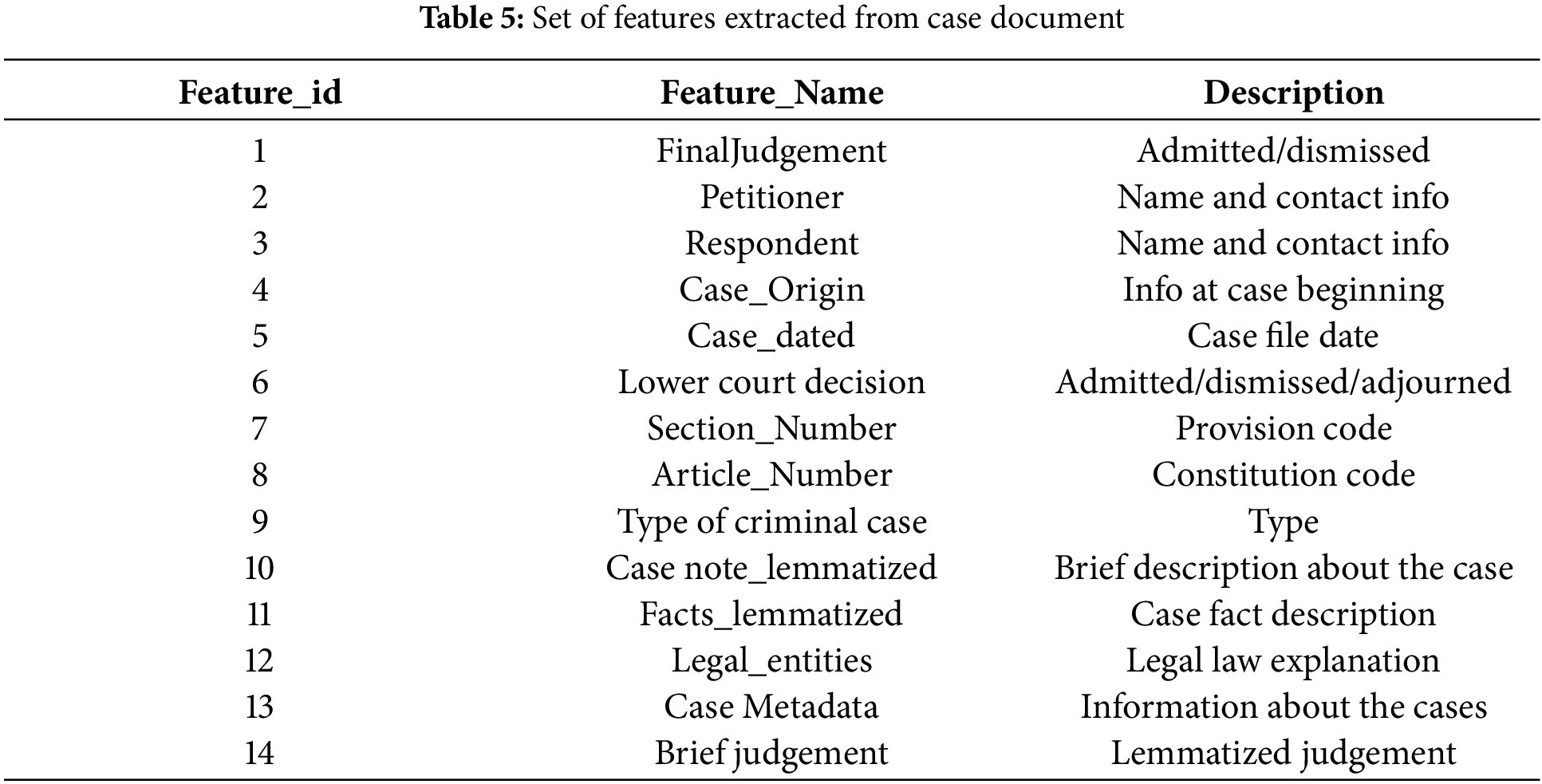
The experiments were conducted on around 1466 real-time Madras High Court criminal case documents web-scraped from the Manupatra [45] website. Each legal case document consists of a fact description, Charges, Sections, Articles, Penalty, and final judgment. Around 15 types of raw criminal cases are taken, web scraped, and converted into needed labels as case notes, facts, judgments, sections, and judgment labels as allowed or dismissed separately in a .csv file with the help of entity extractor and regular expressions. Table 5 shows the detailed set of features that can be utilized for judgment prediction.

The Fig. 8 shows the data sample of part of the lemmatized casefact without judgment, which is given as input into the proposed architecture from which tokenization and word embedding using Elmo is done for further feature extraction process. In the hybrid classifier model, of the whole dataset is used for training, and is used for testing. Accuracy, Recall, and F1 measures were used as metrics in the hybrid classifier model to evaluate our proposed method. Additionally, False Positive Rate and False Negative Rate were also measured.

Figure 8: Data sample of part of lemmatized case document

4.2 Dataset 2-Supreme Court of India Database

The Supreme Court of India dataset was gathered from [46]. It includes 1630 court case records in total. These documents bear two class labels, ‘acquitted’ (label 0) and ‘convict’ (label 1), which indicate the ’ final judgment. 1362 cases resulted in a conviction, while 268 instances resulted in acquittal out of the total 1630 cases. This dataset is a useful tool for researching trends and variables that affect the results of criminal trials since it compiles a range of court rulings and case facts from India’s highest court.

5  Experimental Results and Discussion

5.1 Simulation Procedure

In order to represent the features from raw case documents in machine learning techniques, the majority of the early efforts on legal judgment prediction in both English and Chinese cases used frequency-based approaches like count vectorizer and Term Frequency-Inverse Document Frequency (TF-IDF). In deep learning models, later word embeddings like word2vec and Glove were frequently employed to represent the characteristics for judgment prediction. The drawback here is that this word embedding has a predefined vocabulary that may not contain legally specific words. In this proposed method, customized ELMo word embedding is used with existing vocabulary and legal dictionaries to avoid out-of-vocabulary words. Using the preprocessed real-time Madras High Court criminal case dataset and the Supreme Court of India database, a series of experiments were carried out using the suggested strategy.

5.1.1 Evaluation Metrics

Evaluation metrics, such as accuracy, precision, sensitivity, specificity, False Negative Rate (FNR), False Positive Rate (FPR), Matthews Correlation Coefficient (MCC), F-measure, and Negative Predictive Value (NPV) are used to evaluate the performance of the proposed model to the baseline model. Also, the suggested COLPO model is compared with state-of-the-art deep learning models like hybrid CNN-TNN proposed by Sukanya et al., Deep Bi-LSTM by Shelar et al., and MHAN by Sukanya et al. in 2023 as well as conventional classifiers like Bi-GRU, Deep Maxout, CNN, Deep Belief Network (DBN), and LSTM. Additionally, statistical and convergence analyses are performed for the suggested COLPO model, which was compared to more well-known nature-inspired optimization methods such as the Pelican Optimization Algorithm (POA), Spider Mon-key Optimization (SMO), COOT, and Sparrow Search Algorithm (SSA).

5.2 Performance Analysis for Dataset 1

5.2.1 Positive Measure for Dataset 1

The performance analysis of positive indicators for Dataset 1 is shown in Figs. 9 and 10. The performance of the COLPO model is compared against both conventional classifiers like CNN, Deep Maxout, Bi-GRU, and LSTM, as well as state-of-the-art models like hybrid CNN-TNN [43], Deep Bi-LSTM [44], and MHAN [45]. In the entire training percentage, the recommended approach has demonstrated good prediction accuracy, sensitivity, precision, and specificity, as shown in the figure. This illustrates how successful the suggested work is at predicting judgment. The accuracy of almost all classifiers rises as the training percentage increases. Nevertheless, the classifier using the suggested COLPO approach outperformed the other extent classifiers in terms of accuracy, achieving 95.72% accuracy at training percentage = 90. The conventional classifiers, such as Bi-GRU (91.27%), Deep Maxout (91.50%), CNN (90.10%), DBN (89.76%), LSTM (87.92%), Deep Bi-LSTM (91.64%), Hybrid CNN-TNN (91.05%), and MHAN (91.89%), achieved comparatively poor accuracy in Fig. 9. The suggested model simultaneously attained a sensitivity of 97.13% in the 80% learning percentage, which is much better than the other well-known methods like Deep Bi-LSTM (92.21%), Hybrid CNN-TNN (94.16%), and MHAN (96.34%), respectively. Sensitivity indicates how well the model can forecast true positives for every category. When learning percentages were 60, 70, 80, and 90, the precision of the suggested model increased to 96.32%, 96.74%, 96.85%, and 97.55%. Thus, it is evident from the experiment that our suggested COLPO approach, which combines Opposition-Based Learning and Chaotic Sequence with enhanced score level fusion, has a higher prediction accuracy and is significantly more successful at making judgment predictions.

Figure 9: Accuracy and precision for Dataset 1

Figure 10: Specificity and sensitivity for Dataset 1

5.2.2 Analysis on Negative measure

The performance of COLPO model is compared against both conventional classifiers like CNN, Deep Maxout, Bi-GRU, and LSTM, as well as state-of-the-art models like hybrid CNN-TNN, Deep Bi-LSTM, and MHAN. The suggested model can be used to predict judgment with absolute confidence because its negative measure, False Negative Rate (FNR), is lower than that of the traditional methods. When compared to existing approaches like Deep Bi-LSTM = 7.785, the hybrid CNN-TNN = 5.834, and MHAN = 3.653, the proposed method’s FNR at 80% learning percentage is 2.863, which is very low. Additionally, the suggested method achieves an FPR of 2.935, whereas the Deep Bi-LSTM strategy likewise produces a maximum FPR of 8.493 at a 90% learning rate, with hybrid CNN-TNN being 9.537 and MHAN being 3.826. Therefore, the experiment’s results show that the recommended COLPO approach predicts judgments with low mistake rates and performs exceptionally well.

5.2.3 Analysis of Other Measures for Dataset 1

Classifiers like Deep Bi-LSTM, MHAN, and hybrid CNN-TNN have the lowest F-measures at an 80% learning rate, while the suggested approach has the highest F-measure, 97.16%. According to the NPV measure study, all classifiers achieved the maximal NPV, or over (about) 90% of NPV for all classifiers, at 90% of the training percentage. The recommended work, however, produced the highest NPV, 96.26%. Lastly, at 60%, 70%, 80%, and 90% of the learning rate, the MCC measure of the chosen work is 87.28%, 89.76%, 92.61%, and 94.56%, respectively. Since it consistently predicts the judgment with higher other metrics (F-measure, MCC, and NPV), the proposed COLPO classifier with the infusion of OBL and Chaotic sequence is therefore more effective.

5.3 Performance Analysis for Dataset 2

5.3.1 Analysis of Positive Measure for Dataset 2

Figs. 11 and 12 describe the performance analysis of positive measures for Dataset 2. In the Legal Judgment Prediction challenge, the COLPO model performs better than current classifiers on all important performance parameters. In comparison to models like Hybrid CNN-TNN [43] (93.73% at 80%) and more conventional models like Bi-GRU (84.94%) and CNN (69.30%), it obtains the highest accuracy, attaining 89.89% with 60% training data and improving to 94.25% at 90%. COLPO outperforms MHAN [45] (97%) and other models such as DeepMaxout (90.49%) in terms of precision, maintaining an impressive 97.50% with 60% training data and reaching 97.94% at 90%. With increased sensitivity value, it guarantees that it accurately detects the majority of true positives. The ability of COLPO to effectively identify true negatives while limiting false positives is further demonstrated by its excellent specificity, which outperforms other models such as Hybrid CNN-TNN and MHAN. Its specificity is 97.84% at 60% and 98.15% at 90%. COLPO provides a strong solution for categorizing legal situations, and its overall efficiency in positive metrics highlights its exceptional capability in legal judgment prediction.

Figure 11: Accuracy and precision

Figure 12: Specificity and sensitivity

5.3.2 Analysis of Negative Measure for Dataset 2

Important metrics for assessing the performance of the suggested COLPO model when compared to current classifiers are the False Negative Rate (FNR) and False Positive Rate (FPR). In all training data percentages, COLPO consistently exhibits the lowest FNR, with values as low as 3.47% at 60% and 2.25% at 90%. This suggests that COLPO successfully reduces the quantity of overlooked or incorrectly classified as negative true positive cases.

5.3.3 Analysis of Other Measures for Dataset 2

In every training data set, the COLPO model regularly beats the current classifiers on important metrics including F-measure, MCC, and NPV, proving its superior performance to strike a compromise between prediction accuracy and dependability. Starting at 90.95% at 60% and rising to 94.42% at 90%, COLPO has the greatest F-measure scores of any training data percentage. Additionally, COLPO is the most notable model when analyzing MCC, achieving 93.11% at 90%. Lastly, with NPV ratings as high as 97.44% at 90%, COLPO exhibits unparalleled performance. MHAN [45], on the other hand, performs admirably but attains somewhat lower NPV ratings, reaching a peak of 97.00% at 90%. NPV is lower for other classifiers like Bi-GRU and Deep Maxout, which have maximum values of 89.27% and 90.42%, respectively. Thus, the most dependable and well-rounded model for forecasting court rulings is COLPO, which performs exceptionally well across F-measure, MCC, and NPV.

5.4 Ablation Study on Datasets 1 and 2

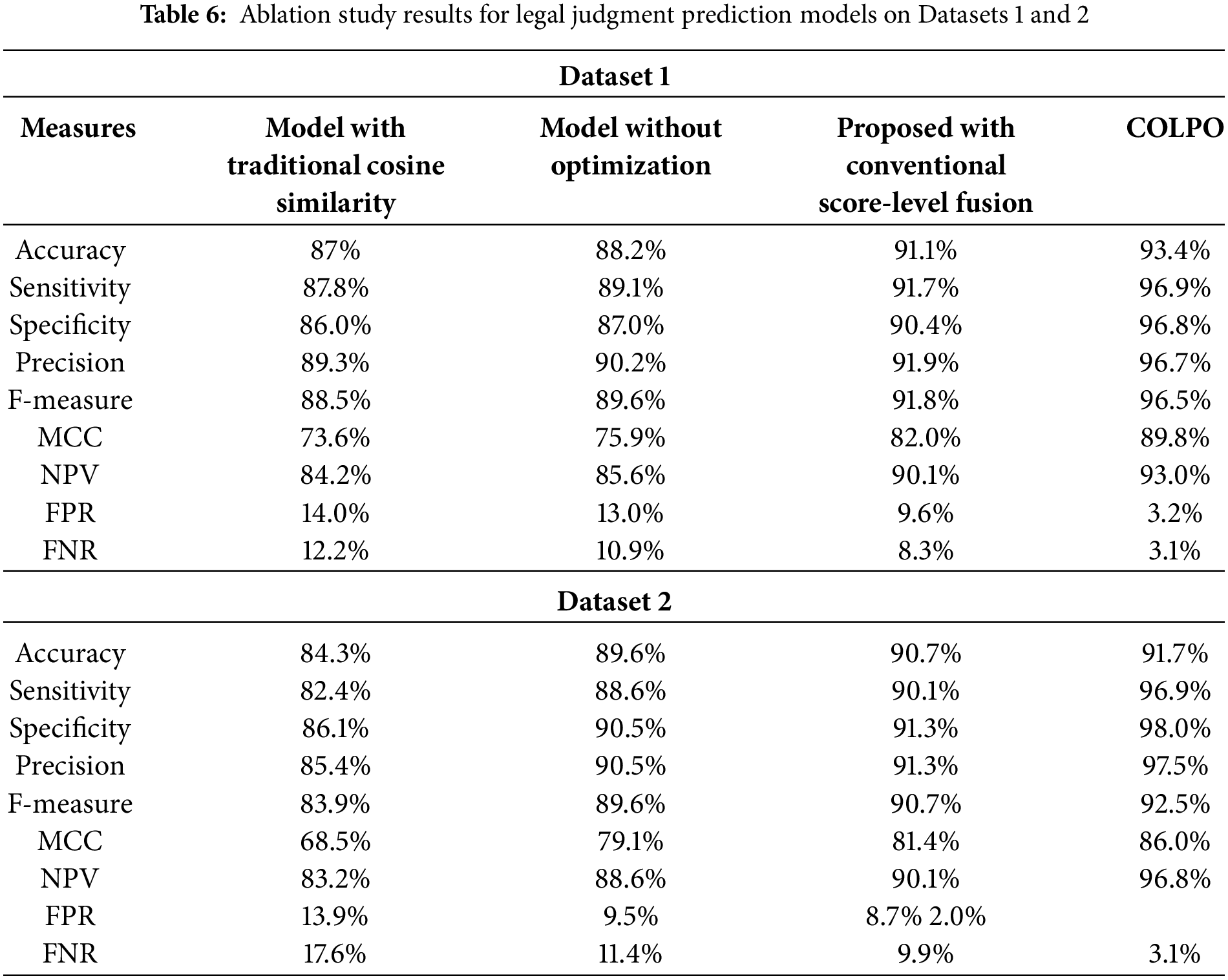
Table 6 compares the ablation study of suggested COLPO to that of the standard cosine similarity model and the model without optimization. Nine different performance metrics such as accuracy, FNR, F-measure, and others, are carried out to evaluate how well the suggested COLPO in hybrid classifier is performed. The accuracy of the model in Dataset 1 is 0.934, which is more than the accuracy of the models with score level fusion (0.911) and conventional cosine similarity (0.870). Dataset 1 achieved 0.969 for sensitivity and 0.968 for specificity, while Dataset 2 achieved 0.969 for sensitivity and 0.980 for specificity. Overall model balance is shown by the F-measure and MCC scores, which for the whole approach were 0.965 and 0.898 in Dataset 1 and 0.925 and 0.860 in Dataset 2, respectively. With NPV values of 0.930 in Dataset 1 and 0.968 in Dataset 2, the entire model also has the greatest NPV values, demonstrating its ability to properly predict acquittals. In conclusion, the entire model results in a considerable reduction in both FPR and FNR. FPR falls to as low as 0.032 in Dataset 1 and 0.020 in Dataset 2, while FNR falls to 0.031 in both datasets. The Proposed (Bi-GRU + Deep Maxout) with proposed COLPO for optimization is the most dependable and successful model for predicting judicial judgments across both datasets since it performs better overall in every category.

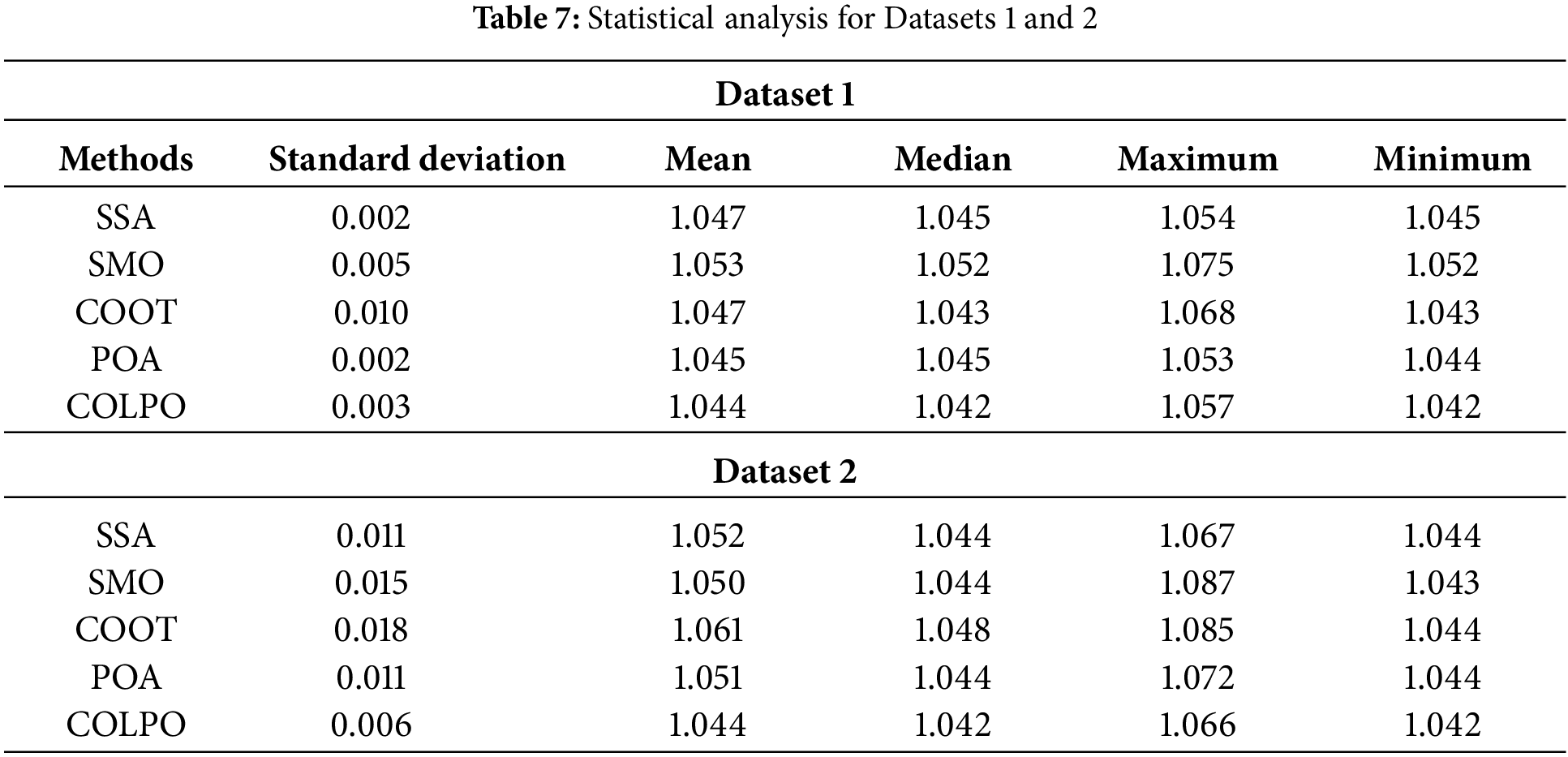
5.5 Statistical Analysis for Datasets 1 and 2

The optimization process is frequently conducted to ascertain the results in terms of statistical analysis because of its stochastic nature. The five distinct case scenarios used to contrast the suggested COLPO model with the traditional methods are listed in Table 7. Standard deviation, mean, maximum, median, and minimum are some examples of these situations. The suggested method’s mean value is 1.044, which is better than the baseline models, such as SSA = 1.047, SMO = 1.053, COOT = 1.047, and POA = 1.045. The suggested approach obtained the minimal median of 1.04 and 1.045 under median analysis. In terms of stability, COLPO performs better than alternative approaches for Dataset 2. With a standard deviation of 0.006, it achieves a mean fitness value of 1.044, comparable to the other approaches, but lower than SMO (0.015) and COOT (0.018), suggesting that COLPO is less susceptible to fluctuations. In Dataset 2, COLPO’s fitness range (maximum: 1.066, minimum: 1.042) is likewise constrained, demonstrating its dependability in delivering consistent outcomes. COLPO is a more dependable optimization technique since it routinely produces better stability than SSA and POA, which both exhibit reasonably stable performance. According to the statistical study, COLPO’s smaller fitness range and lower standard deviation indicate that it works well compared to existing approaches for stability and consistency across both datasets. These attributes imply that COLPO is more dependable in maximizing the model’s performance and can be regarded as the best option for tasks involving the prediction of legal decisions.

5.6 Convergence Evaluation for Datasets 1 and 2

Fig. 13 displays the convergence analysis of the suggested COLPO method with the traditional methods. The proposed method achieves significantly lower error and converges quickly compared to previous optimization algorithms. The first iteration has a higher convergence rate of 1.042 in accordance with the recommended method for Dataset 1, and a convergence value of 1.040 is then attained at iterations 5 to 9. It generated an astonishingly low convergence value of 1.038 in the last cycle, 10 to 50. Additionally, the convergence rates for the COOT, SMO, SSA, and POA during the 50th iteration are 1.058, 1.047, 1.045, and 1.044, respectively. According to Dataset 2, COLPO converges more quickly than alternative optimization techniques. COLPO rapidly stabilizes, achieving peak performance with less cost of 1.043 at the 20th to 50th iteration. Thus, it is evident that the COLPO technique that has been described has better judgment prediction with less error.

Figure 13: Convergence analysis for both Datasets 1 and 2

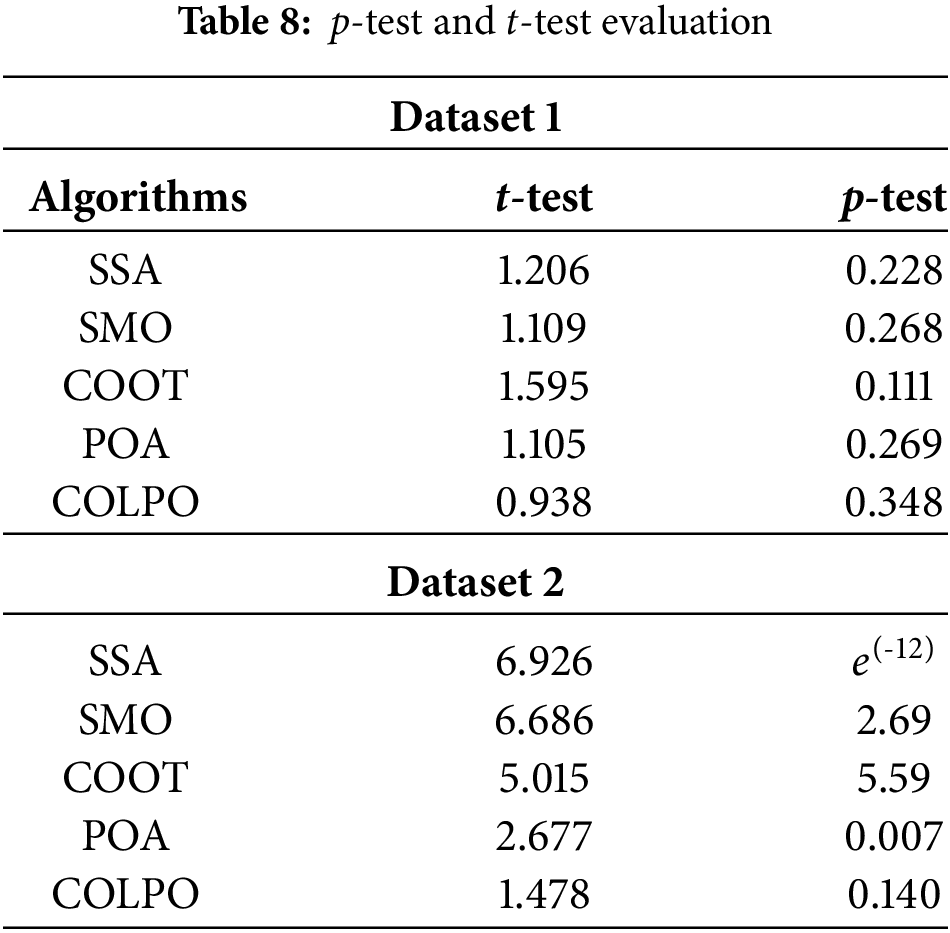
5.7 p-test and t-test Evaluation

Table 8 describes the p-test and t-test evaluation for Datasets 1 and 2. For the best model, the t-test must be low and the p-test must be high. In the t-test analysis, the COLPO model achieves a 0.938 value for Dataset 1 and a 1.478 value for Dataset 2 which is less when evaluated over conventional algorithms. Furthermore, in the p-test analysis, the proposed COLPO model obtains a 0.348 value for Dataset 1 and a 0.140 value for Dataset 2. Both findings are high when contrasted over conventional algorithms. Therefore, the suggested algorithm proves its statistical differences with better stability for Datasets 1 and 2 in the legal judgment prediction.

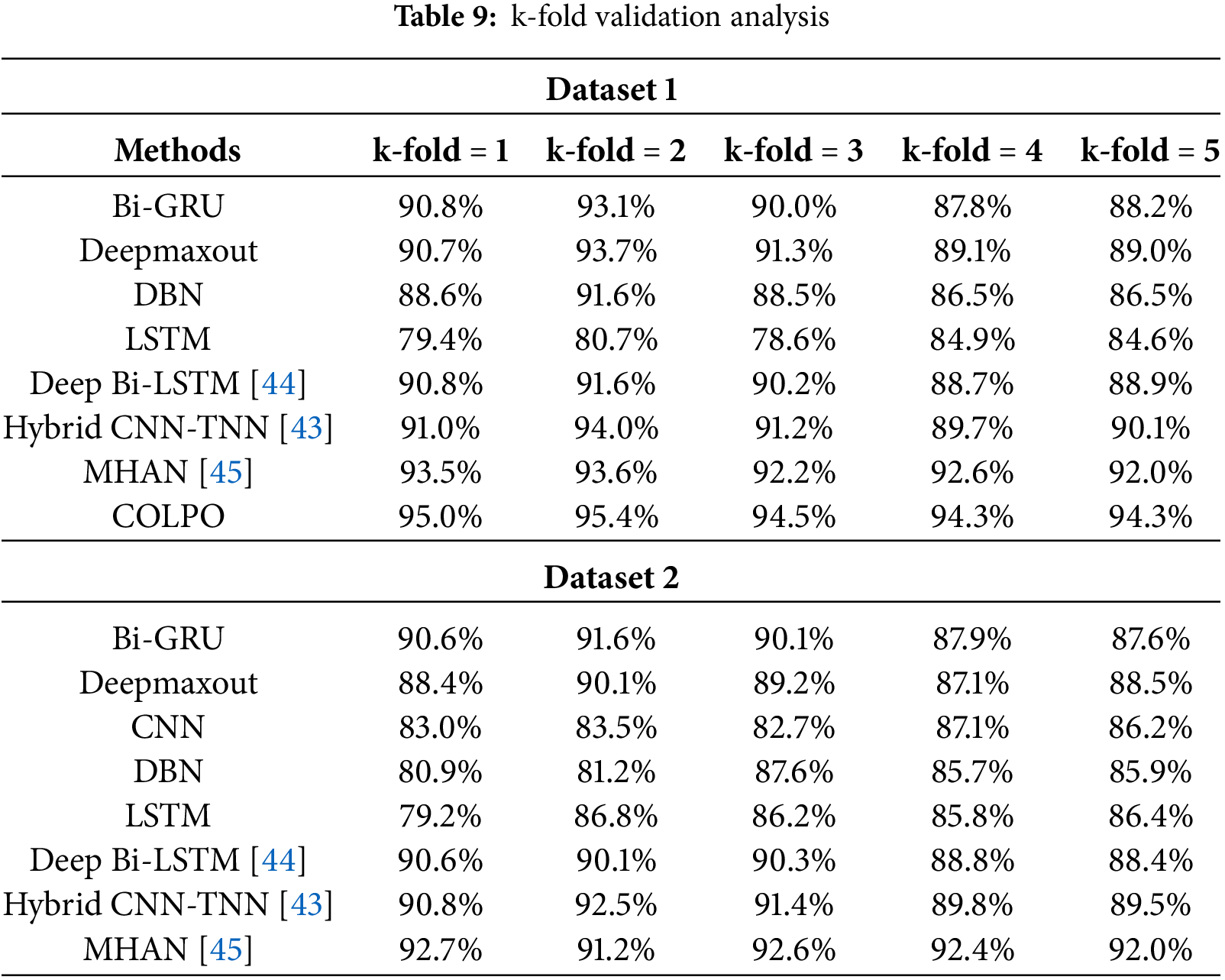
5.8 K-Fold Validation Evaluation

Table 9 describes a k-fold validation study that sheds light on how well different approaches performed on two distinct datasets. By dividing the data into several subsets (or “folds”) and evaluating the model across these various divisions, the method for assessing the reliability and robustness of machine learning models and avoiding overfitting problems is k-fold cross-validation. The findings for Dataset 1 indicate that all algorithms perform fairly consistently, with minor variations in accuracy as the number of folds rises. The proposed COLPO performs consistently across all validation sets, as evidenced by its maximum accuracy across all folds (varying from 0.943 to 0.950). Conversely, LSTM and CNN show less accuracy throughout the folds, with LSTM (0.786 to 0.849) and CNN (0.826 to 0.870) especially trailing the best-performing techniques. Similar patterns are seen with Dataset 2, although a little greater variation in the outcomes. These techniques are the most consistent and dependable across the folds, as evidenced by the fact that the proposed COLPO once again exhibits the best accuracy (ranging from 0.937 to 0.948), closely followed by MHAN (0.912 to 0.927). In both datasets, COLPO emerges as the best-performing model, exhibiting reliable and consistent outcomes across various data folds that demonstrate its efficiency in preventing overfitting issues for legal judgment prediction.

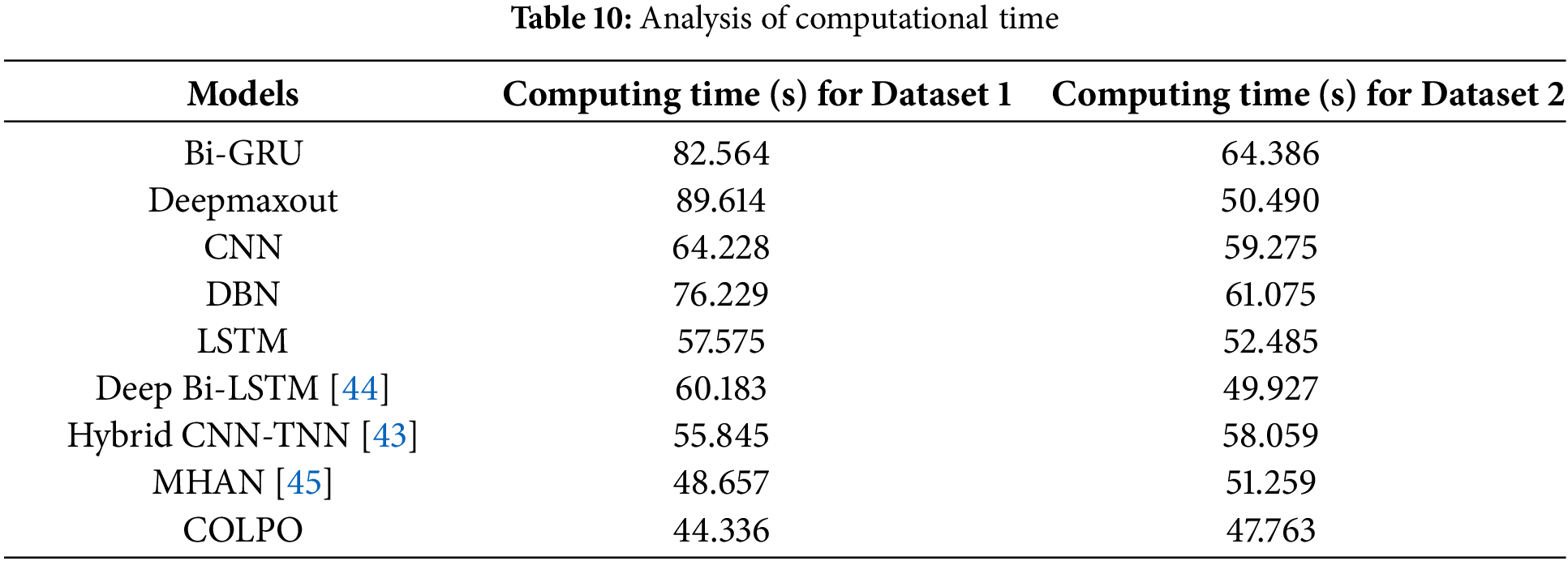
5.9 Computational Time Analysis

The computational time analysis presented in Table 10 demonstrates the effectiveness of diverse approaches when applied to two distinct datasets. Across all datasets, the suggested COLPO model has the quickest computation time, requiring 44.336 s for Dataset 1 and 47.763 s for Dataset 2. When compared to alternative approaches, this places COLPO as the model with the highest computational efficiency. With a considerable advantage over more intricate models like Bi-GRU (82.564 s), Deep Maxout (89.614 s), and Hybrid CNN-TNN (55.845 s), COLPO beats all other algorithms in Dataset 1. For Dataset 2, COLPO remains the fastest approach with 47.763 s, followed by CNN and LSTM, MHAN (51.259 s), and Deep Bi-LSTM (49.927 s). Thus, the COLPO is a very appropriate model for predicting judicial judgments because of its capacity to produce forecasts quickly while retaining competitive accuracy.

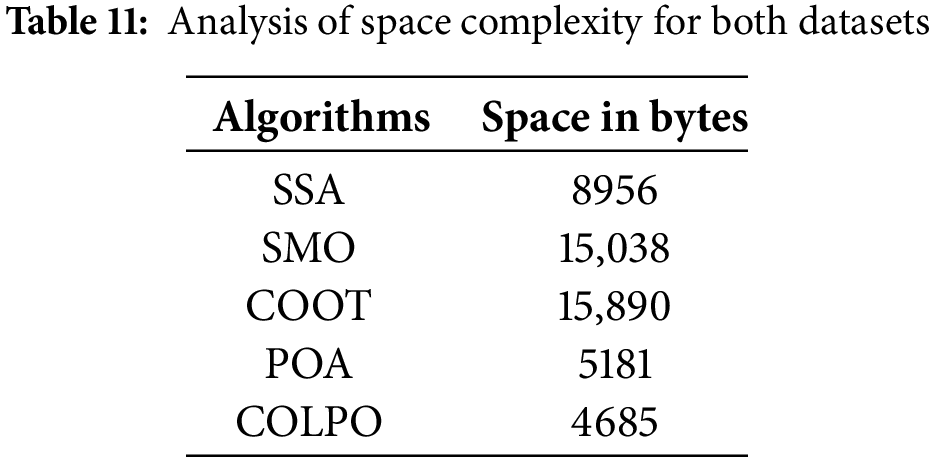
5.10 Space Complexity Analysis

The memory usage of different algorithms is highlighted by the space complexity study in Table 11, where COLPO once again shows an efficiency advantage. The space for the algorithms is the same for both datasets. COLPO is the least memory-intensive model of the mentioned algorithms, requiring only 4685 bytes of memory. Other models, such as SSA (8956 bytes), SMO (15,038 bytes), and COOT (15,890 bytes), use significantly more RAM in contrast. Although POA (5181 bytes) uses more memory than the suggested model, it is marginally more efficient than COLPO. Because COLPO makes effective use of its available space, it is not only computationally quick but also memory-light. Thus, the proposed COLPO method’s reduced space complexity makes it a desirable choice for judicial decision prediction, where managing massive amounts of data effectively is essential.

6  Conclusion

In this article, a modified COLPO technique has been proposed with a Bi-GRU Deep MaxOut classifier for judgment prediction on Madras High Court criminal cases. By providing more crucial information and minimizing information loss, improved semantic similarity and entropy features for the feature extraction phase improve the classifier model’s training and enable more accurate predictions. Additionally, to increase prediction accuracy, the prediction scores of the Deep Maxout and Bi-GRU classifiers are fused using the improved score level fusion. The experimental findings demonstrate that, for the fewest number of iterations, the proposed hybrid model trained using COLPO by adjusting classifier weights in the hidden layer outperforms baseline models. This COLPO method would act as a generalized model for all Indian court cases and the outline framework could be used for other legal systems which have Court cases in English. The evaluation factors considered for the experiment have provided more promising results than the other algorithms. Compared to other models using conventional optimization algorithms, OBL provides a more consistent method of achieving a good accuracy of 93.4%. The research work has used OBL to find opposition points from initial search agents to find the global optima in less time duration with the chaos concept in choosing random numbers in the Pelican Optimization Algorithm instead of choosing random values with a random number generator. Though POA works well with OBL, POA with orthogonal learning can be considered for future study of judgment prediction. The future scope of the research direction would be to enhance the proposed POA in other text-based applications so that it could be useful to society in many ways. Moreover, this work will involve adapting the model to different international legal systems and extending it to accommodate legal datasets from other nations and jurisdictions. This research aims to include a variety of legal codes, including common law, European Union, and US criminal law. The model will be improved to increase forecast accuracy in different domains such as family and civil law.

Acknowledgement: We thank the law school Head of the Department Dr. Ambika Nair and the librarian Dr. Tholkapian of VIT, Chennai Campus for the important details to be extracted from case facts and collecting datasets to a great extent.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: Conceptualization, G. Sukanya and J. Priyadarshini; methodology, G. Sukanya; software, G. Sukanya; validation, G. Sukanya and J. Priyadarshini; formal analysis, J. Priyadarshini; investigation, G. Sukanya and J. Priyadarshini; resources, G. Sukanya; data curation, G. Sukanya; writing—original draft preparation, G. Sukanya; writing—review & editing, G. Sukanya and J. Priyadarshini; visualization, G. Sukanya; supervision, J. Priyadarshini. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, priyadarshini.j@vit.ac.in, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Tong S, Yuan J, Zhang P, Li L. Legal Judgment Prediction via graph boosting with constraints. Inf Process Manag. 2024;61(3):103663. doi:10.1016/j.ipm.2024.103663. [Google Scholar] [CrossRef]

2. Zhang X. Legal challenges and responses to artificial intelligence-assisted decision-making in the international economic law system. Appl Math Nonlinear Sci. 2024;9(1). doi:10.2478/amns-2024-2506. [Google Scholar] [CrossRef]

3. Li S, Liu B, Ye L, Zhang H, Fang B. Element-aware legal judgment prediction for criminal cases with confusing charges. In: 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI); 2019 Nov; Portland, OR, USA: IEEE. p. 660–7. doi:10.1109/ICTAI.2019.00097. [Google Scholar] [CrossRef]

4. Dong Y, Li X, Shi J, Dong Y, Chen C. Graph contrastive learning networks with augmentation for legal judgment prediction. Artif Intell Law. 2024;23(1):155. doi:10.1007/s10506-024-09407-9. [Google Scholar] [CrossRef]

5. Agrawal A, Gans JS, Goldfarb A. Exploring the impact of artificial intelligence: prediction versus judgment. Inf Econ Policy. 2019;47(3):1–6. doi:10.1016/j.infoecopol.2019.05.001. [Google Scholar] [CrossRef]

6. Benedetto I, Koudounas A, Vaiani L, Pastor E, Cagliero L, Tarasconi F, et al. Boosting court judgment prediction and explanation using legal entities. Artif Intell Law. 2024. doi:10.1007/s10506-024-09397-8. [Google Scholar] [CrossRef]

7. Aletras N, Tsarapatsanis D, Preoţiuc-Pietro D, Lampos V. Predicting judicial decisions of the European Court of Human Rights: a natural language processing perspective. PeerJ Comput Sci. 2016;2(2):e93. doi:10.7717/peerj-cs.93. [Google Scholar] [CrossRef]

8. Xu Z, Li X, Li Y, Wang Z, Fanxu Y, Lai X. Multi-task legal judgement prediction combining a subtask of the seriousness of charges. In: Chinese Computational Linguistics: 19th China National Conference, CCL 2020; 2020 Oct 30–Nov 1; Haikou, China: Springer International Publishing. p. 415–29. [Google Scholar]

9. Zhu K, Guo R, Hu W, Li Z, Li Y. Legal judgment prediction based on multiclass information fusion. Complexity. 2020;2020(4):1–12. doi:10.1155/2020/3089189. [Google Scholar] [CrossRef]

10. Zhang Y, Wei X, Yu H. HD-LJP: a Hierarchical dependency-based legal judgment prediction framework for multi-task learning. Knowl Based Syst. 2024;299:112033. doi:10.1016/j.knosys.2024.112033. [Google Scholar] [CrossRef]

11. Feng G, Qin Y, Huang R, Chen Y. Criminal action graph: a semantic representation model of judgement documents for legal charge prediction. Inf Process Manag. 2023;60(5):103421. doi:10.1016/j.ipm.2023.103421. [Google Scholar] [CrossRef]

12. Cui J, Shen X, Wen S. A survey on legal judgment prediction: datasets, metrics, models and challenges. IEEE Access. 2023;11:102050–71. doi:10.1109/ACCESS.2023.3317083. [Google Scholar] [CrossRef]

13. He C, Tan TP, Zhang X, Xue S. Knowledge-enriched multi-cross attention network for legal judgment prediction. IEEE Access. 2023;11:87571–82. doi:10.1109/ACCESS.2023.3305259. [Google Scholar] [CrossRef]

14. Li S, Zhang H, Ye L, Guo X, Fang B. MANN: a multichannel attentive neural network for legal judgment prediction. IEEE Access. 2019;7:151144–55. doi:10.1109/ACCESS.2019.2945771. [Google Scholar] [CrossRef]

15. Guo X, Zhang H, Ye L, Li S. TenLa: an approach based on controllable tensor decomposition and optimized lasso regression for judgement prediction of legal cases. Appl Intell. 2021;51(4):2233–52. doi:10.1007/s10489-020-01912-z. [Google Scholar] [CrossRef]

16. Wang Y, Gao J, Chen J. Deep learning algorithm for judicial judgment prediction based on BERT. In: 2020 5th International Conference on Computing, Communication and Security (ICCCS); 2020; Patna, India: IEEE. doi:10.1109/ICCCS49678.2020.9277068. [Google Scholar] [CrossRef]

17. Yang S, Tong S, Zhu G, Cao J, Wang Y, Xue Z, et al. MVE-FLK: a multi-task legal judgment prediction via multi-view encoder fusing legal keywords. Knowl Based Syst. 2022;239(6):107960. doi:10.1016/j.knosys.2021.107960. [Google Scholar] [CrossRef]

18. Alghazzawi D, Bamasag O, Albeshri A, Sana I, Ullah H, Asghar MZ. Efficient prediction of court judgments using an LSTM+ CNN neural network model with an optimal feature set. Mathematics. 2022;10(5):683. doi:10.3390/math10050683. [Google Scholar] [CrossRef]

19. Lyu Y, Wang Z, Ren Z, Ren P, Chen Z, Liu X, et al. Improving legal judgment prediction through reinforced criminal element extraction. Inform Process Manag. 2022;59(1):102780. doi:10.1016/j.ipm.2021.102780. [Google Scholar] [CrossRef]

20. Dal Pont TR, Sabo IC, Hübner JF, Rover AJ. Regression applied to legal judgments to predict compensation for immaterial damage. PeerJ Comput Sci. 2023;9(1):e1225. doi:10.7717/peerj-cs.1225. [Google Scholar] [PubMed] [CrossRef]

21. Peng Y-T, Lei C-L. Using Bidirectional Encoder Representations from Transformers (BERT) to predict criminal charges and sentences from Taiwanese court judgments. PeerJ Comput Sci. 2024;10(4):e1841. doi:10.7717/peerj-cs.1841. [Google Scholar] [PubMed] [CrossRef]

22. Latisha S, Favian S, Suhartono D. Criminal court judgment prediction system built on modified BERT models. J Adv Inf Technol. 2024;15(2):288–98. doi:10.12720/jait.15.2.288-298. [Google Scholar] [CrossRef]

23. Zhang H, Dou Z, Zhu Y, Wen J-R. Contrastive learning for legal judgment prediction. ACM Trans Inf Syst. 2023;41(4):1–25. doi:10.1145/3580489. [Google Scholar] [CrossRef]

24. Sukanya G, Priyadarshini J. Hybrid CNN: an empirical analysis of machine learning models for predicting legal judgments. Int J Adv Comput Sci Appl. 2024;15(7). doi:10.14569/ijacsa.2024.01507124. [Google Scholar] [CrossRef]

25. Shelar A, Moharir M. Judgment prediction from legal documents using Texas wolf optimization based deep BiLSTM model. Intell Decis Technol. 2024;18(2):1557–76. doi:10.3233/IDT-230566. [Google Scholar] [CrossRef]

26. Sukanya G, Priyadarshini J. Modified Hierarchical-Attention Network model for legal judgment predictions. Data Knowl Eng. 2023;147(6):102203. doi:10.1016/j.datak.2023.102203. [Google Scholar] [CrossRef]

27. Lage-Freitas A, Allende-Cid H, Santana O, Oliveira-Lage L. Predicting Brazilian court decisions. PeerJ Comput Sci. 2022;8(2):e904. doi:10.7717/peerj-cs.904. [Google Scholar] [PubMed] [CrossRef]

28. Xue J, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm. Syst Sci Cont Eng. 2020;8(1):22–34. doi:10.1080/21642583.2019.1708830. [Google Scholar] [CrossRef]

29. Ouyang C, Zhu D, Qiu Y. Lens learning sparrow search algorithm. Math Probl Eng. 2021;2021(2):1–17. doi:10.1155/2021/9935090. [Google Scholar] [CrossRef]

30. Yan S, Liu W, Li X, Yang P, Wu F, Yan Z. Comparative study and improvement analysis of sparrow search algorithm. Wirel Commun Mob Comput. 2022;2022(12):1–15. doi:10.1155/2022/4882521. [Google Scholar] [CrossRef]

31. Mostafa RR, Hussien AG, Khan MA, Kadry S, Hashim FA. Enhanced coot optimization algorithm for dimensionality reduction. In: 2022 Fifth International Conference of Women in Data Science at Prince Sultan University (WiDS PSU); 2022 Mar; Riyadh, Saudi Arabia: IEEE. p. 43–8. doi:10.1109/WiDS-PSU54548.2022.00020. [Google Scholar] [CrossRef]

32. Sharma H, Hazrati G, Bansal JC. Spider monkey optimization algorithm. In: Bansal JC, Singh PK, Pal NR, editors. Evolutionary and swarm intelligence algorithms. Cham: Springer; 2019. p. 43–59. [Google Scholar]

33. Trojovský P, Dehghani M. Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications. Sensors. 2022;22(3):855. doi:10.3390/s22030855. [Google Scholar] [PubMed] [CrossRef]

34. Wang E, Xia J, Li J, Sun X, Li H. Parameters exploration of SOFC for dynamic simulation using adaptive chaotic grey wolf optimization algorithm. Energy. 2022;261(38):125146. doi:10.1016/j.energy.2022.125146. [Google Scholar] [CrossRef]

35. Alqaisi R, Ghanem W, Qaroush A. Extractive multi-document Arabic text summarization using evolutionary multi-objective optimization with K-medoid clustering. IEEE Access. 2020;8:228206–24. doi:10.1109/ACCESS.2020.3046494. [Google Scholar] [CrossRef]

36. Sohangir S, Wang D. Improved sqrt-cosine similarity measurement. J Big Data. 2017;4(1):1–13. doi:10.1186/s40537-017-0083-6. [Google Scholar] [CrossRef]

37. Cai M, Shi Y, Liu J. Deep maxout neural networks for speech recognition. In: Proceedings of the 2013 IEEE Automatic Speech Recognition and Understanding Workshop; 2013; Piscataway, NJ, USA: IEEE. p. 291–6. [Google Scholar]

38. Tuerxun W, Xu C, Haderbieke M, Guo L, Cheng Z. A wind turbine fault classification model using broad learning system optimized by improved pelican optimization algorithm. Machines. 2022;10(5):407. doi:10.3390/machines10050407. [Google Scholar] [CrossRef]

39. Gao J, Wang K, Lu S. The simulation analysis and constructing of the cubic logistic chaotic function family. ICIC Express Lett Part B: Appl. 2013;4(5):1327–34. [Google Scholar]

40. Naik R, Singh UR. A review on applications of chaotic maps in pseudo-random number generators and encryption. Ann Data Sci. 2024;11:25–50. doi:10.1007/s40745-021-00364-7. [Google Scholar] [CrossRef]

41. Cai Y, Guo C, Chen X. An improved sand cat swarm optimization with lens opposition-based learning and sparrow search algorithm. Sci Rep. 2024;14(1):30. doi:10.1038/s41598-024-71581-2. [Google Scholar] [PubMed] [CrossRef]

42. Sarkhel R, Chowdhury TM, Das M, Das N, Nasipuri M. A novel Harmony Search algorithm embedded with metaheuristic Opposition Based Learning. J Intell Fuzzy Syst. 2017;32(4):3189–99. doi:10.3233/JIFS-169262. [Google Scholar] [CrossRef]

43. Sarkhel R, Das N, Saha AK, Nasipuri M. An improved Harmony Search Algorithm embedded with a novel piecewise opposition based learning algorithm. Eng Appl Artif Intell. 2018;67(4):317–30. doi:10.1016/j.engappai.2017.09.020. [Google Scholar] [CrossRef]

44. Mahdavi S, Rahnamayan S, Deb K. Opposition based learning: a literature review. Swarm Evol Comput. 2018;39(8):1–23. doi:10.1016/j.swevo.2017.09.010. [Google Scholar] [CrossRef]

45. manupatra. [cited 2025 Jan 10]. Available from: https://www.manupatra.com/. [Google Scholar]

46. Supreme Court of India. [cited 2025 Jan 10]. Available from: https://www.sci.gov.in/judgements-judgement-date/. [Google Scholar]