 Open Access
Open Access
ARTICLE
A Synergistic Multi-Attribute Decision-Making Method for Educational Institutions Evaluation Using Similarity Measures of Possibility Pythagorean Fuzzy Hypersoft Sets
1 Department of Mathematics, University of Sargodha, Sargodha, 40100, Pakistan
2 Department of Mathematics, University of Management and Technology, Lahore, 54000, Pakistan
3 Department of Mathematics, College of Science, Qassim University, Buraydah, 51452, Saudi Arabia
* Corresponding Author: Salwa El-Morsy. Email:
(This article belongs to the Special Issue: Advances in Ambient Intelligence and Social Computing under uncertainty and indeterminacy: From Theory to Applications)
Computer Modeling in Engineering & Sciences 2025, 142(1), 501-530. https://doi.org/10.32604/cmes.2024.057865
Received 29 August 2024; Accepted 29 October 2024; Issue published 17 December 2024
Abstract
Due to the numerous variables to take into account as well as the inherent ambiguity and uncertainty, evaluating educational institutions can be difficult. The concept of a possibility Pythagorean fuzzy hypersoft set (pPyFHSS) is more flexible in this regard than other theoretical fuzzy set-like models, even though some attempts have been made in the literature to address such uncertainties. This study investigates the elementary notions of pPyFHSS including its set-theoretic operations union, intersection, complement, OR- and AND-operations. Some results related to these operations are also modified for pPyFHSS. Additionally, the similarity measures between pPyFHSSs are formulated with the assistance of numerical examples and results. Lastly, an intelligent decision-assisted mechanism is developed with the proposal of a robust algorithm based on similarity measures for solving multi-attribute decision-making (MADM) problems. A case study that helps the decision-makers assess the best educational institution is discussed to validate the suggested system. The algorithmic results are compared with the most pertinent model to evaluate the adaptability of pPyFHSS, as it generalizes the classical possibility fuzzy set-like theoretical models. Similarly, while considering significant evaluating factors, the flexibility of pPyFHSS is observed through structural comparison.Keywords
Educational institutions are essential in molding people and society. To cultivate the information, abilities, and values necessary for critical thinking, self-improvement, and well-informed decision-making, they offer an organized atmosphere. In addition to promoting academic excellence, they also help people develop their moral and intellectual capacities by promoting ethical behavior, social engagement, and cultural awareness. Educational institutions also stimulate research, innovation, and societal advancement, preparing the next generation for the difficulties of a world that is changing quickly [1,2]. The process of selecting an educational institution can be challenging because there are many different, interconnected factors involved. The relative significance of such features varies widely throughout individuals, making prioritization challenging. Furthermore, the decision-making process becomes more complex due to inherent uncertainties, which include future job prospects, the quality of education evolving, and individual adaptability to the institution’s environment. This results in a MADM problem with individualistic and improbable results [3,4]. Although numerous commendable attempts have been made to manage such uncertainties by developing theoretical frameworks, the Pythagorean fuzzy set (PyFS) [5] is unique in this sense. For membership function refinement, the fuzzy set (FS) [6] and intuitionistic fuzzy set (IFS) [7] are extended to develop the PyFS. The FS paved the way for more nuanced representations of vague and imprecise information by allowing elements to have partial memberships in sets. The IFS was projected to allow elements possessing dependent partial memberships and non-memberships to satisfy the condition that the sum must be within [0, 1]. The PyFS integrates the square sum of the membership and non-membership values within [0, 1], which offers more flexibility. Because PyFS now has more flexibility, it can better represent scenarios in which decision-makers are unsure or reluctant, which enhances modeling and decision-making accuracy in contexts marked by ambiguity and insufficient information. Garg [8] discussed decision-making applications based on geometric aggregation operators of generalized Pythagorean fuzzy set embedded with Einstein t-norm and t-conorm. Numerous scholars have investigated the representation and measurement of innate uncertainties in diverse fields, such as Qu et al. [9] presented intelligent and enhanced maximum expert consensus modeling embedded with dynamic feedback mechanisms to model inherent uncertainties. Sun et al. [10] previewed target signals using sliding mode control of discrete-time interval type-2 fuzzy Markov jump systems. Ge et al. [11] used a fuzzy neural network to model inherent uncertainties based on adaptive inventory control. Zhang et al. [12] developed observer-centered sliding mode control for fuzzy stochastic switching systems embedded with deception attacks. Xia et al. [13] discussed more results on fuzzy sampled-data stabilization of chaotic nonlinear systems. Gao et al. [14] investigated the representation and measurement of innate uncertainties in sliding mode control. These fields frequently deal with dynamic, complex environments where uncertainty results from various factors.
As the criteria or factors that direct the process, parameters are essential to decision-making. By offering a framework for comparison, these factors aid in the evaluation of various options and guarantee that choices are made under predetermined objectives or limitations. Parameters are important because they help make complex circumstances simpler by organizing and quantifying essential aspects. This makes it possible to make decisions that are more objective, consistent, and well-informed. Appropriately selected parameters can greatly improve the efficacy of decision-making by concentrating attention on the most important elements of the given problem. Molodtsov [15] introduced the idea of the soft set (SS) to equip FS, IFS, and PyFS with parameterization mode. Muthukumar et al. [16] discussed the problem of clinical diagnosis based on similarity measures of an intuitionistic fuzzy soft set (IFSS). Peng et al. [17] introduced Pythagorean fuzzy soft set (PyFSS) by integrating the theories of PyFS and SS. Kirişci et al. [18] discussed the clinical assessment-based algorithmic decisive method of PyFSS. Zulqarnain et al. [19] investigated supplier selection decisive issue based on aggregation operators of PyFSS. Using only generic parameters while making decisions can result in biased or incomplete results in several cases. Sub-parametric values are essential for an exhaustive examination since they offer more precise and in-depth insights into each parameter. By capturing the subtleties and complexity of the issue, these finer details make sure that all pertinent factors are taken into account. Decisions may be exaggerated or distorted as a result of essential elements being missed or misinterpreted when sub-parametric values are ignored. Consequently, it is crucial to incorporate both parameters and their sub-parametric values into the decision-making process to prevent dubious or biased results. To address this issue, Smarandache [20] introduced hypersoft set (HSS) by transforming the approximate mapping of SS to multi-argument approximate mapping, that considers the Cartesian product of sub-parametric valued based disjoint sets as domain and maps it to the collection of objects being evaluated. Researchers have recently shown a great deal of interest in the HSS because of its exceptional adaptability and versatility in handling scenarios involving sophisticated decision-making. Because of its versatility, HSS is especially useful in domains where a hierarchy of criteria influences decisions or where complicated, interconnected elements must be taken into account. The HSS is, therefore, emerging as a potent tool for handling a variety of issues in decision-making and related fields. Smarandache [21] introduced some new types of SS and HSS based on the indeterminate nature of parameters or sub-parametric values. Debnath [22] presented the notions of the fuzzy hypersoft set (FHSS) and its weightage operators. Musa et al. [23] discussed the evaluation of houses by proposing three algorithms based on aggregations of the N-hypersoft set (NHSS). Al-Quran et al. [24] discussed the evaluation of cars by proposing an algorithm based on the aggregations of bipolar fuzzy hypersoft set (BFHSS). Asaad et al. [25] discussed the recruitment of software engineers for a company by proposing a decisive framework based on aggregations of BFHSS. Sajid et al. [26] investigated the evaluation of solar panels based on the set-theoretic operations of the cubic intuitionistic fuzzy hypersoft set (CIFHSS). Hamid et al. [27] discussed mobile phone evaluation by proposing a decisive framework based on the integrated context of machine learning and FHSS. Saeed et al. [28] explored the similarity and entropy measures for FHSS and employed them for the evaluation of renewable energy resources. Rahman et al. [29] investigated operational risks based on supplier chain management based on set-theoretic operations of HSS mappings. Smarandache et al. [30] introduced the integrated context of HSS and game theory for decision-making systems. Siddique et al. [31] investigated the aggregation operators of a Pythagorean fuzzy hypersoft set (PyFHSS) for decision-making situations.
It is advisable to involve an impartial convener who can objectively evaluate the extent of partial acceptance of the approximations made by decision-makers to ensure neutrality and minimize bias in the decision-making process. By reducing the possible impact of individual preferences or prejudices that could distort the review process, this method promotes more impartial and equitable results. The convener increases the decision-making process’s legitimacy and dependability by offering an objective, outside viewpoint. Alkhazaleh et al. [32] introduced the possibility fuzzy soft set (pFSS) and they investigated the relevant operations and similarity measures of pFSS. They proposed a decisive framework for the diagnosis of dengue fever based on similarity measures of pFSS. Al-Sharqi et al. [33] explored the features of pFSS with interval-valued settings and investigated its operations and similarity measures. They proposed a decisive framework for the diagnosis of respiratory disease based on similarity measures of pFSS. Ponnalagu et al. [34] discussed cars evaluation problems using pFSS and expert set environments collectively. Ali [35] formulated similarity measures of bipolar pFSS by considering approximations of fuzzy parameters and applied the concepts in agricultural land selection scenarios. Bashir et al. [36] introduced the possibility of the intuitionistic fuzzy soft set (pIFSS) and investigated its set-theoretic operations, e.g., union, AND, intersection, and OR-operations. They designed a decision-assisted system for the evaluation of educational institutions. Selvachandran et al. [37] investigated its set-theoretic operations, e.g., union, AND, intersection, and OR-operations of pIFSS. They designed a decision-making framework for the recruitment process in the company. Garg et al. [38] investigated aggregation operators, information measures, and modified complex proportional assessment (COPRAS) under a pIFSS environment. Jia-Hua et al. [39] proposed the notions of possibility Pythagorean fuzzy soft set (pPyFSS) and investigated its operations like union, OR, intersection, and AND. They also proposed similarity measures for pPyFSS to apply in decision-making scenarios. Palanikumar et al. [40,41] discussed the notions of bipolar pPyFSS and pPyFSS with interval-valued settings. Rahman et al. [42] introduced the notions of several hybrids of HSS with possibility settings. They [43] employed the similarity measures of possibility fuzzy hypersoft set (pFHSS) in agri-automobile evaluation and HRM pattern recognition. Further, they [44] discussed decision-making scenarios based on the similarity measures of possibility intuitionistic fuzzy hypersoft set (pIFHSS). Sahoo et al. [45] and Bhatia et al. [46] applied different decision-making techniques to discuss the evaluation of educational institutions.
After careful analysis of the above-discussed literature, it is clear that the following important features are ignored:
1. Ignoring the biased tendency of the decision maker in decision-making is tantamount to questioning the validity of the decision. Therefore, the observations and opinions of the decision-makers must be evaluated with the help of an impartial expert.
2. Short-term decisions strengthen the credibility of decision-making, while long-term decisions undermine its credibility. Approximation of alternatives by decision-makers considering each attribute individually is not only a time-consuming but difficult process. However, if the same process is repeated with multiple arguments in mind, it will be completed in less time and more reliably.
3. Optimal membership and non-membership functions play a key role in controlling uncertainty based on incomplete and ambiguous information.
The proposed theoretical framework, the possibility Pythagorean fuzzy hypersoft set (pPyFHSS), collectively incorporates all of the above features. The idea of possibility degree is meant to deal with the first feature, the hypersoft setting is aimed at providing a multi-argument domain for the approximation of alternatives; the Pythagorean fuzzy setting provides the optimal and generalized membership and non-membership functions for controlling uncertainty. The pPyFHSS extends the notions of IFS, IFSS, FHSS, pFHSS, and pIFHSS. The extended range of pPyFHSS allows for a finer distinction in the degree of uncertainty. This is particularly useful in decision-making problems, where experts may need to express a more nuanced confidence or hesitation. In certain scenarios, the sum constraint of IFS, IFSS, and pIFHSS can be overly restrictive.
The salient contributions of the study are enlisted as:
1. By integrating the ideas of possibility degree, hypersoft set, and Pythagorean fuzzy set, a novel theoretical framework called pPyFHSS, is introduced that considers the possibility degree within [0, 1] to evaluate the acceptance level of approximations made by decision-makers. It helps reduce the prejudice of the decision makers or minimize their inclined impact on the decisions.
2. For the sake of the applicability of pPyFHSS in different fields of study, several fundamentals including axiomatic properties, aggregation operations, and types of pPyFHSS are investigated. Additionally, proofs of several essential theorems are also provided.
3. The formulation for similarity measures between two pPyFHSSs is developed and the related theorems are investigated. Additionally, the proposed formulation is explained with an illustration.
4. Based on the proposed similarity measures, a robust algorithm is proposed which is then validated by the prototype case study of educational institution evaluation.
The structure of this article is organized as in Section 2, and some fundamental definitions are discussed. The concept of pPyFHSS is introduced in Section 3, along with some of its intriguing properties. To address decision difficulties, a similarity measure for comparing two pPyFHSSs is proposed. Additionally, an algorithm for evaluating the optimum educational institution is provided in Section 4. At the end of this section, discussion is made on the comparison of the proposed model. Finally, Section 5 concludes with recommendations for future research.
Some basic definitions are provided here, which will be useful in the remaining portion of the work.
Definition 1. Reference [17] A pair (˘F,¨E) is called a SS over ¨U and ¨U be an initial universal set, where ˘F is a mapping ˘F:¨E→P¨U. For ¨E (parameters set), set of elements in the SS (˘F,¨E) that approximate η can be represented as ˘F(η) and P¨U indicates the power set of ¨U.
Definition 2. Reference [20] Let ¨x1,¨x2,...,¨xn for n⩾1, be n distinct attributes, whose corresponding sub attribute values are contained in the sets ¨Ξ1,¨Ξ2,¨Ξ3,...,¨Ξn respectively, with ¨Ξi ∩ ¨Ξj≠∅, for i≠j∈{1,2,3,...,n} such that ¨Ξ=¨Ξ1רΞ2רΞ3×...רΞn. Then the pair (˘F,¨Ξ), where: ˘F:¨Ξ→P¨U, is called HSS over ¨U.
Definition 3. Reference [22] A HSS (Ω,¨Ξ) is referred to as a FHSS over ¨U, where Ω:¨Ξ⟶F¨U, if Ω(¨ρ)={⟨¨ρ,Ω(¨ρ)(¨ℏ)⟩:¨ℏ∈¨U∧¨ρ∈¨Ξ=¨Ξ1רΞ2×...רΞn}, where, F¨U is the collection of all the fuzzy subsets on ¨U.
The following definition is the modified form of the definition presented in [31].
Definition 4. Let ¨x1,¨x2,¨x3,...,¨xn be the n distinct attributes whose corresponding sub-attributes are contained in disjoint sets ¨Ξ1,¨Ξ2,¨Ξ3,...,¨Ξn. A set pair (Ω,¨Ξ) is referred to as a PyFHSS over ¨U, if Ω:¨Ξ⟶PF¨U, where (Ω,¨Ξ)={⟨¨ρ,Ω(¨ρ)⟩:∀¨ρ∈¨Ξ=∏ni=1¨Ξi}, and Ω(¨ρ)={¨ℏiΩ(¨ρ)(¨ℏi):¨ℏi∈¨U∧∀¨ρ∈¨Ξ=∏ni=1¨Ξi},Ω(¨ρ)(¨ℏi)=⟨εΩ(¨ρ)(¨ℏi),τΩ(¨ρ)(¨ℏi)⟩⊆PF¨U (collection of all the Pythagorean fuzzy subset on ¨U), such that εΩ(¨ρ)(¨ℏi),τΩ(¨ρ)(¨ℏi)∈[0,1], and 0≤ε2Ω(¨ρ)(¨ℏi)+τ2Ω(¨ρ)(¨ℏi)≤1. Ω(¨ρ)(¨ℏi) is the Pythagorean value of ¨ℏi∈¨U in Ω(¨ρ).
Example 1. Let ¨U={¨ℏ1,¨ℏ2} be the universe of discourse and suppose that ¨x1=Teaching methodology, ¨x2=Subjects and ¨x3=Classes be the attributes and their corresponding non-overlapping attributes values are Teaching methodology=¨Ξ1={¨x11=project base,¨x12=class discussion}, Subjects=¨Ξ2={¨x21=Mathematics,¨x22=Computer Science,¨x23=Statistics} and Classes=¨Ξ3={¨x21=Master,¨x22=Bachelor}. If Ω:¨Ξ1רΞ2רΞ3⟶PF¨U and the Cartesian product is ¨Ξ=¨Ξ1רΞ2רΞ3 ={¨ρ1,¨ρ2,¨ρ3,¨ρ4,¨ρ5,¨ρ6,¨ρ7,¨ρ8,¨ρ9,¨ρ10,¨ρ11,¨ρ12} then Pythagorean fuzzy hypersoft set over ¨U is given as follows:
Ω(¨ρ1)={¨ℏ1(0.6,0.3),¨ℏ2(0.5,0.7)},Ω(¨ρ2)={¨ℏ1(0.6,0.7),¨ℏ2(0.7,0.5)},Ω(¨ρ3)={¨ℏ1(0.4,0.8),¨ℏ2(0.3,0.7)},Ω(¨ρ4)={¨ℏ1(0.6,0.5),¨ℏ2(0.5,0.6)},Ω(¨ρ5)={¨ℏ1(0.7,0.3),¨ℏ2(0.4,0.8)},Ω(¨ρ6)={¨ℏ1(0.5,0.4),¨ℏ2(0.6,0.5)},Ω(¨ρ7)={¨ℏ1(0.5,0.6),¨ℏ2(0.4,0.5)},Ω(¨ρ8)={¨ℏ1(0.2,0.5),¨ℏ2(0.3,0.9)},Ω(¨ρ9)={¨ℏ1(0.4,0.6),¨ℏ2(0.8,0.5)},Ω(¨ρ10)={¨ℏ1(0.7,0.4),¨ℏ2(0.7,0.2)},Ω(¨ρ11)={¨ℏ1(0.4,0.5),¨ℏ2(0.5,0.3)},Ω(¨ρ12)={¨ℏ1(0.5,0.7),¨ℏ2(0.4,0.7)},
and its parameterized family is:
(Ω,¨Ξ)={(¨ρ1,{⟨¨ℏ1(0.6,0.3)⟩,⟨¨ℏ2(0.5,0.7)⟩}),(¨ρ2,{⟨¨ℏ1(0.6,0.7)⟩,⟨¨ℏ20.7,0.5)⟩}),(¨ρ3,{⟨¨ℏ1(0.4,0.8)⟩,⟨¨ℏ2(0.3,0.7)⟩}),(¨ρ4,{⟨¨ℏ1(0.6,0.5)⟩,⟨¨ℏ2(0.5,0.6)⟩}),(¨ρ5,{⟨¨ℏ1(0.7,0.3)⟩,⟨¨ℏ2(0.4,0.8)⟩}),(¨ρ6,{⟨¨ℏ1(0.5,0.4)⟩,⟨¨ℏ2(0.6,0.5)⟩}),(¨ρ7,{⟨¨ℏ1(0.5,0.6)⟩,⟨¨ℏ2(0.4,0.5)⟩}),(¨ρ8,{⟨¨ℏ1(0.2,0.5)⟩,⟨¨ℏ2(0.3,0.9)⟩}),(¨ρ9,{⟨¨ℏ1(0.4,0.6)⟩,⟨¨ℏ2(0.8,0.5)⟩}),(¨ρ10,{⟨¨ℏ1(0.7,0.4)⟩,⟨¨ℏ2(0.7,0.2)⟩}),(¨ρ11,{⟨¨ℏ1(0.4,0.5)⟩,⟨¨ℏ2(0.5,0.3)⟩}),(¨ρ12,{⟨¨ℏ1(0.5,0.7)⟩,⟨¨ℏ2(0.4,0.7)⟩}).}
Definition 5. Reference [42] If ¨U be the universe of discourse and ¨x1,¨x2,¨x3,...,¨xn be n distinct attributes whose corresponding n distinct sub-attributes values are contained in disjoint sets ¨Ξ1,¨Ξ2,...,¨Ξn. Then (¨U,¨Ξ=¨Ξ1רΞ2×...¨Ξn) will be a hypersoft universe. Let Ω:¨Ξ⟶F¨U and μ be the fuzzy subset of ¨Ξ, i.e., μ:¨Ξ⟶F¨U. Let Ωμ:¨Ξ⟶F¨U×F¨U be the function defined as Ωμ(¨ρ)={⟨Ω(¨ρ)(¨ℏi),μ(¨ρ)(¨ℏi)⟩:∀¨ℏi∈¨U∧¨ρ∈¨Ξ=∏ni=1¨Ξi}, where; Ω(¨ρ)(¨ℏ),μ(¨ρ)(¨ℏ)⊆F¨U. Then Ωμ is referred to as a pFHSS over the hypersoft universe (¨U,¨Ξ).
In this section, we introduce the concept of pPyFHSS as an extension of the pFHSS model. The fundamental characteristics of the pPyFHSS are intended to control the ambiguity and uncertainty that are frequently encountered in MADM situations, like assessing educational institutions. When handling ambiguous data, the possibility degree-based option offers a layer of flexibility by assisting in evaluating the likelihood of different outcomes. Through the depiction of multi-argument qualities, the hypersoft setting extends conventional fuzzy models and captures intricate interdependencies in the decision-making process. Finally, decision-makers can more precisely indicate hesitation through membership and non-membership values in the Pythagorean fuzzy setting, which offers a more sophisticated treatment of uncertainty. Together, these characteristics improve the model’s capacity to manage complexity and ambiguity.
Definition 6. Let ¨x1,¨x2,¨x3,...,¨xn be a set of n distinct attributes and their corresponding sub-attributes values are contained in non-overlapping sets ¨Ξ1,¨Ξ2,...,¨Ξn and ¨Ξ=∏ni=1¨Ξi. Suppose that Ω:¨Ξ→PF¨U and m:¨Ξ⟶F¨U, where PF¨U and F¨U are the collection sets of all the Pythagorean fuzzy and fuzzy subsets on ¨U, respectively. If Ωm:¨Ξ→PF¨U×F¨U is a mapping defined as:
Ωm(¨ρ)={⟨¨ℏΩ(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ)⟩:¨ℏ∈¨U,∀¨ρ∈¨Ξ=n∏i=1¨Ξi},
then Ωm is said to be a pPyFHSS over the hypersoft universe (¨U,¨Ξ). For each parameter ¨ρ, it can be written as:
Ωm={(¨ρ,{⟨¨ℏΩ(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ)⟩:¨ℏ∈¨U}),∀¨ρ∈¨Ξ=n∏i=1¨Ξi},
where Ω(¨ρ)(¨ℏ)=⟨εΩ(¨ρ)(¨ℏ),τΩ(¨ρ)(¨ℏ)⟩⊆PF¨U and 0≤ε2Ω(¨ρ)(¨ℏ)+τ2Ω(¨ρ)(¨ℏ)≤1 with εΩ(¨ρ)(¨ℏ),τΩ(¨ρ)(¨ℏ)∈[0,1], such that Ω(¨ρ)(¨ℏ) is the Pythagorean fuzzy number of ¨ℏ∈¨U in Ωm(¨ρ). Also m(¨ρ)(¨ℏ)=μm(¨ρ)(¨ℏ)⊆F¨U with μm(¨ρ)(¨ℏ)∈[0,1], such that m(¨ρ)(¨ℏ) is the possibility membership grade of ¨ℏ∈¨U in Ωm(¨ρ).
Note: For convenience, it can be expressed as:
Ωm(¨ρ)={⟨(εΩ(¨ρ)(¨ℏ),τΨ(¨ρ)(¨ℏ)),μm(¨ρ)(¨ℏ)⟩:¨ℏ∈¨U,∀¨ρ∈¨Ξ=n∏i=1¨Ξi},
and collection of all pPyFHSS is symbolized by ˆΘˆλ.
Note: The difference between the above proposed mathematical framework, pPyFHSS, and the existing relevant frameworks like PyFHSS and pFHSS, is given as:
1. In PyFHSS, the possibility degree-based setting has been ignored, therefore, it is insufficient to reduce the prejudice of the decision makers or minimize their inclined impact on the decisions.
2. In pFHSS, the generalized membership and non-membership functions are ignored, therefore, it does not support the decision-makers to indicate hesitation more precisely through membership and non-membership values in the Pythagorean fuzzy setting, which offers a more sophisticated treatment of uncertainty.
Example 2. Let ¨U={¨ℏ1,¨ℏ2} be the set of two vehicles in auto showroom and ¨x1= luxury cars, ¨x2= sports cars, be the attributes and corresponding attributes values are luxury cars =¨Ξ1={¨x11=beautiful,¨x12=high safety}, sports cars =¨Ξ2={¨x21=expensive,¨x22=less space}. Their Cartesian product is ¨Ξ=∏ni=1¨Ξi=¨Ξ1רΞ2={¨ρ1,¨ρ2,¨ρ3,¨ρ4} is Ωm:¨Ξ→PF¨U×F¨U then the pPyFHSS can be constructed as:
Ωm(¨ρ1)={⟨¨ℏ1(0.9,0.4),0.51⟩,⟨¨ℏ2(0.7,0.4),0.61⟩},Ωm(¨ρ2)={⟨¨ℏ1(0.8,0.5),0.52⟩,⟨¨ℏ2(0.6,0.5),0.62⟩},
Ωm(¨ρ3)={⟨¨ℏ1(0.7,0.5),0.53⟩,⟨¨ℏ2(0.5,0.4),0.63⟩},Ωm(¨ρ4)={⟨¨ℏ1(0.6,0.4),0.54⟩,⟨¨ℏ2(0.4,0.3),0.64⟩},
Ωm={(¨ρ1,{⟨¨ℏ1(0.9,0.4),0.51⟩,⟨¨ℏ2(0.7,0.4),0.61⟩}),(¨ρ2,{⟨¨ℏ1(0.8,0.5),0.52⟩,⟨¨ℏ2(0.6,0.5),0.62⟩}),(¨ρ3,{⟨¨ℏ1(0.7,0.5),0.53⟩,⟨¨ℏ2(0.5,0.4),0.63⟩}),(¨ρ4,{⟨¨ℏ1(0.6,0.4),0.54⟩,⟨¨ℏ2(0.4,0.3),0.64⟩}).}(1)
In the matrix notion, data can be represented as follows:
Ωm=(⟨(0.9,0.4),0.51⟩⟨(0.7,0.4),0.61⟩⟨(0.8,0.5),0.52⟩⟨(0.6,0.5),0.62⟩⟨(0.7,0.5),0.53⟩⟨(0.5,0.4),0.63⟩⟨(0.6,0.4),0.54⟩⟨(0.4,0.3),0.64⟩).
Definition 7. If Ωm and Ψq be two pPyFHSSs defined over (¨U,¨Ξ), then Ψq is considered a subset of Ωm in terms of pPyFHSS if and only if q(¨ρ)(¨ℏ)⊆m(¨ρ)(¨ℏ) if μq(¨ρ)(¨ℏ)≤μm(¨ρ)(¨ℏ),Ψ(¨ρ)(¨ℏ)⊆Ω(¨ρ)(¨ℏ) if εΨ(¨ρ)(¨ℏ)≤εΩ(¨ρ)(¨ℏ) and τΨ(¨ρ)(¨ℏ)≥τΩ(¨ρ)(¨ℏ), ∀¨ℏ∈¨U and ∀¨ρ∈¨Ξ. This relationship is denoted as Ψq⊆Ωm.
Example 3. Consider that Ωm∈ˆΘˆλ over (¨U,¨Ξ) given in Example 2. Let Ψq be another pPyFHSS over (¨U,¨Ξ). Suppose that Ψq:¨Ξ→PF¨U×F¨U and defined as follows:
Ψq(¨ρ1)={⟨¨ℏ1(0.8,0.6),0.31⟩,⟨¨ℏ2(0.5,0.6),0.41⟩},Ψq(¨ρ2)={⟨¨ℏ1(0.7,0.8),0.32⟩,⟨¨ℏ2(0.4,0.8),0.42⟩},Ψq(¨ρ3)={⟨¨ℏ1(0.5,0.6),0.33⟩,⟨¨ℏ2(0.3,0.6),0.43⟩},Ψq(¨ρ4)={⟨¨ℏ1(0.4,0.8),0.34⟩,⟨¨ℏ2(0.2,0.7),0.44⟩}.
Ψq={(¨ρ1,{⟨¨ℏ1⟨0.8,0.6⟩,0.31⟩,⟨¨ℏ2⟨0.5,0.6⟩,0.41⟩}),(¨ρ2,{⟨¨ℏ1⟨0.7,0.8⟩,0.32⟩,⟨¨ℏ2⟨0.4,0.8⟩,0.42⟩}),(¨ρ3,{⟨¨ℏ1⟨0.5,0.6⟩,0.33⟩,⟨¨ℏ2⟨0.3,0.6⟩,0.43⟩}),(¨ρ4,{⟨¨ℏ1⟨0.4,0.8⟩,0.34⟩,⟨¨ℏ2⟨0.2,0.7⟩,0.44⟩}).}(2)
By comparing (1) and (2), we get Ψq⊆Ωm.
Definition 8. Suppose Ωm, Ψn∈ˆΘˆλ, then Ωm and Ψq are said to be equal pPyFHSS if and only if Ωm⊆Ψq, and Ωm⊇Ψq, which can be denoted by Ωm=Ψq.
Definition 9. If ¨U be the set of universe of discourse and ¨Ξi, for i∈{1,2,...,n} be the sub attributes values of attributes set ¨xi. Let Ωm be the pPyFHSS over (¨U,¨Ξ). Complement of Ωm can be be denoted as Ωcm and it is defined as Ωcm=(Ωc(¨ρ)(¨ℏ),mc(¨ρ)(¨ℏ)), where Ωc(¨ρ)(¨ℏ)=⟨τΩ(¨ρ)(¨ℏ),εΩ(¨ρ)(¨ℏ)⟩, and mc(¨ρ)(¨ℏ)=μmc(¨ρ)(¨ℏ)=μcm(¨ρ)(¨ℏ)=1−μm(¨ρ)(¨ℏ).
Note: From Definition 9, we observe that (Ωcm)c=Ωm.
Example 4. From Example 2, compliment of pPyFHSS Ωcm is written as:
Ωcm(¨ρ1)={⟨¨ℏ1(0.4,0.9),0.49⟩,⟨¨ℏ2(0.4,0.7),0.39⟩},Ωcm(¨ρ2)={⟨¨ℏ1(0.5,0.8),0.48⟩,⟨¨ℏ2(0.5,0.6),0.38⟩},
Ωcm(¨ρ3)={⟨¨ℏ1(0.5,0.7),0.47⟩,⟨¨ℏ2⟨0.4,0.5⟩,0.37⟩},Ωcm(¨ρ4)={⟨¨ℏ1(0.4,0.6),0.46⟩,⟨¨ℏ2(0.3,0.4),0.36⟩}.
Ωcm={(¨ρ1,{⟨¨ℏ1(0.4,0.9),0.49⟩,⟨¨ℏ2(0.4,0.7),0.39⟩}),(¨ρ2,{⟨¨ℏ1(0.5,0.8),0.48⟩,⟨¨ℏ2(0.5,0.6),0.38⟩}),(¨ρ3,{⟨¨ℏ1(0.5,0.7),0.47⟩,⟨¨ℏ2(0.4,0.5),0.37⟩}),(¨ρ4,{⟨¨ℏ1(0.4,0.6),0.46⟩,⟨¨ℏ2(0.3,0.4),0.36⟩}).}.
In the matrix notion, data can be represented as:
(Ωcm,¨Ξ)=(⟨(0.4,0.9),0.49⟩⟨(0.4,0.7),0.39⟩⟨(0.5,0.8),0.48⟩⟨(0.5,0.6),0.38⟩⟨(0.5,0.7),0.47⟩⟨(0.4,0.5),0.37⟩⟨(0.4,0.6),0.46⟩⟨(0.3,0.4),0.36⟩).
Definition 10. Suppose Ωm and Ψq be two pPyFHSSs over (¨U,¨Ξ). Then union and intersection operations on Ωm and Ψq are denoted as Ωm∪Ψq and Ωm ∩ Ψq respectively, and are defined by two mappings ℜr:¨Ξ→PF¨U×F¨U, and ζz:¨Ξ→PF¨U×F¨U. These two mappings give the same meanings such that
{ℜr(¨ρ)=(ℜ(¨ρ)(¨ℏ),r(¨ρ)(¨ℏ)):¨ℏ∈¨U,∀¨ρ∈¨Ξ=∏ni=1¨Ξi},
{ζz(¨ρ)=(ζ(¨ρ)(¨ℏ),z(¨ρ)(¨ℏ)):¨ℏ∈¨U,∀¨ρ∈¨Ξ=∏ni=1¨Ξi},
where ℜ(¨ρ)(¨ℏ)=Ω(¨ρ)(¨ℏ)∪Ψ(¨ρ)(¨ℏ) and r(¨ρ)(¨ℏ)=m(¨ρ)(¨ℏ)∪q(¨ρ)(¨ℏ). Also, ζ(¨ρ)(¨ℏ)=Ω(¨ρ)(¨ℏ) ∩ Ψ(¨ρ)(¨ℏ) and z(¨ρ)(¨ℏ)=m(¨ρ)(¨ℏ) ∩ q(¨ρ)(¨ℏ).
Example 5. Lets consider that Ωm, Ψq∈ˆΘˆλ over (¨U,¨Ξ), where they are explained as follows:
Ωm(¨ρ1)={⟨¨ℏ1(0.9,0.4),0.75⟩,⟨¨ℏ2(0.7,0.4),0.95⟩},
Ωm(¨ρ2)={⟨¨ℏ1(0.8,0.5),0.77⟩,⟨¨ℏ2(0.6,0.5),0.96⟩},
Ωm(¨ρ3)={⟨¨ℏ1(0.7,0.5),0.78⟩,⟨¨ℏ2(0.5,0.4),0.98⟩}.
and,Ψq(¨ρ1)={⟨¨ℏ1⟨0.8,0.6⟩,0.31⟩,⟨¨ℏ2(0.5,0.6),0.51⟩},
Ψq(¨ρ2)={⟨¨ℏ1(0.7,0.3),0.32⟩,⟨¨ℏ2(0.4,0.8),0.52⟩},
Ψq(¨ρ3)={⟨¨ℏ1(0.5,0.6),0.33⟩,⟨¨ℏ2(0.3,0.0.4),0.53⟩}.
By using Definition 10, union of these two functions is:
ℜ(¨ρ1)=Ω(¨ρ1)∪Ψ(¨ρ1)={⟨¨ℏ1(0.9,0.4),0.75⟩,⟨¨ℏ2(0.7,0.4),0.95⟩},
ℜ(¨ρ2)=Ω(¨ρ2)∪Ψ(¨ρ2)={⟨¨ℏ1(0.8,0.3),0.77⟩,⟨¨ℏ2(0.6,0.5),0.96⟩},
ℜ(¨ρ3)=Ω(¨ρ3)∪Ψ(¨ρ3)={⟨¨ℏ1(0.7,0.5),0.78⟩,⟨¨ℏ2(0.5,0.4),0.98⟩},
In the matrix notion, this can be represented as:
Ωm∪Ψq=(⟨(0.9,0.4),0.75⟩⟨(0.7,0.4),0.95⟩⟨(0.8,0.3),0.77⟩⟨(0.6,0.5),0.96⟩⟨(0.7,0.5),0.78⟩⟨(0.5,0.4),0.98⟩)
and intersection is:
ζz(¨ρ1)=Ω(¨ρ1) ∩ Ψ(¨ρ1)={⟨¨ℏ1(0.8,0.6),0.31⟩,⟨¨ℏ2(0.5,0.6),0.51⟩},
ζz(¨ρ2)=Ω(¨ρ2) ∩ Ψ(¨ρ2)={⟨¨ℏ1(0.7,0.5),0.32⟩,⟨¨ℏ2(0.5,0.6),0.52⟩},
ζz(¨ρ3)=Ω(¨ρ3) ∩ Ψ(¨ρ3)={⟨¨ℏ1(0.5,0.6),0.33⟩,⟨¨ℏ2(0.3,0.4),0.53⟩},
In the matrix notion, the intersection can be represented as:
Ωm ∩ Ψq=(⟨(0.8,0.6),0.31⟩⟨(0.5,0.6),0.51⟩⟨(0.7,0.5),0.32⟩⟨(0.5,0.6),0.52⟩⟨(0.5,0.6),0.33⟩⟨(0.3,0.4),0.53⟩).
Definition 11. A pPyFHSS ξθ(¨ρ)={(ξ(¨ρ)(¨ℏ),θ(¨ρ)(¨ℏ)):¨ℏ∈¨U,∀¨ρ∈¨Ξ=∏ni=1¨Ξi} is said to be possibility null Pythagorean fuzzy hypersoft set (pnPFHSS) over (¨U,¨Ξ) if ξθ:¨Ξ→PF¨U×F¨U, where ξ(¨ρ)(¨ℏ)=(εξ(¨ρ)(¨ℏ),τξ(¨ρ)(¨ℏ))=(0,1) and θ(¨ρ)(¨ℏ)=μθ(¨ρ)(¨ℏ)=0, ξθ={(¨ρ,⟨¨ℏ(0,1),0⟩):¨ℏ∈¨U,∀¨ρ∈¨Ξ=∏1i=1¨Ξi}.
Example 6. From Example 2, pnPFHSS Type-I over (¨U,¨Ξ), can be expressed as:
ξθ(¨ρ1)={⟨¨ℏ1(0,1),0⟩,⟨¨ℏ2(0,1),0⟩},ξθ(¨ρ2)={⟨¨ℏ1(0,1),0⟩,⟨¨ℏ2(0,1),0⟩},
ξθ(¨ρ3)={⟨¨ℏ1(0,1),0⟩,⟨¨ℏ2(0,1),0⟩},ξθ(¨ρ4)={⟨¨ℏ1(0,1),0⟩,⟨¨ℏ2(0,1),0⟩}
and in matrix notion is:
ξθ=(⟨(0,1),0⟩⟨(0,1),0⟩⟨(0,1),0⟩⟨(0,1),0⟩⟨(0,1),0⟩⟨(0,1),0⟩⟨(0,1),0⟩⟨(0,1),0⟩)
then ξθ is said to be a pnPFHSS.
Definition 12. A pPyFHSS ΓΛ(¨ρ)={(Γ(¨ρ)(¨ℏ),Λ(¨ρ)(¨ℏ)):¨ℏ∈¨U,∀¨ρ∈¨Ξ=∏ni=1¨Ξi}, is said to be possibility absolute Pythagorean fuzzy hypersoft set (paPFHSS) over (¨U,¨Ξ), if ΓΛ:¨Ξ→PF¨U×F¨U where Γ(¨ρ)(¨ℏ)=(εΓ(¨ρ)(¨ℏ),τΓ(¨ρ)(¨ℏ))=(1,0) and Λ(¨ρ)(¨ℏ)=μΛ(¨ρ)(¨ℏ)=1,
ΓΛ={(¨ρ,⟨¨ℏ(1,0),1⟩):¨ℏ∈¨U,∀¨ρ∈¨Ξ=∏ni=1¨Ξi}.
Example 7. Again from Example 2 paPFHSS over (¨U,¨Ξ), can be expressed as:
ΓΛ(¨ρ1)={⟨¨ℏ1(1,0),1⟩,⟨¨ℏ2(1,0),1⟩},ΓΛ(¨ρ2)={⟨¨ℏ1(1,0),1⟩,⟨¨ℏ2(1,0),1⟩},
ΓΛ(¨ρ3)={⟨¨ℏ1(1,0),1⟩,⟨¨ℏ2(1,0),1⟩},ΓΛ(¨ρ4)={⟨¨ℏ1(1,0),1⟩,⟨¨ℏ2(1,0),1⟩},
and in matrix notion is:ΓΛ=(⟨(1,0),1⟩⟨(1,0),1⟩⟨(1,0),1⟩⟨(1,0),1⟩⟨(1,0),1⟩⟨(1,0),1⟩⟨(1,0),1⟩⟨(1,0),1⟩).
Then ΓΛ is said to be the paPFHSS.
Theorem 1. If Ωm be a pPyFHSS over (¨U,¨Ξ) then the following properties hold:
1. (Ωm∪Ωm)⊇Ωm,Ωm⊆(Ωm ∩ Ωm)
2. Ωm=Ωm∪Ωm,Ωm=Ωm ∩ Ωm
3. Ωm∪ξθ=Ωm,Ωm ∩ ξθ=ξθ
4. Ωm∪ΓΛ=ΓΛ,Ωm ∩ ΓΛ=Ωm
Proof. By using Definitions 7 and 10, we will be able to prove these properties:
(1). For this, let Ωm∪Ωm=ℜr, where
ℜr(¨ρ)=(ℜ(¨ρ)(¨ℏ),r(¨ρ)(¨ℏ)),∀¨ρ∈¨Ξ=n∏i=1¨Ξi,∀¨ℏ∈¨U=(Ω(¨ρ)(¨ℏ)∪Ω(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ)∪m(¨ρ)(¨ℏ))=(Ω(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ))=Ωm(¨ρ)
Clearly, Ωm⊆ℜr=Ωm∪Ωm. Now, we will show that Ωm ∩ Ωm⊇Ωm. For this, let Ωm ∩ Ωm=ζz,
ζz(¨ρ)=(ζ(¨ρ)(¨ℏ),z(¨ρ)(¨ℏ)),∀¨ρ∈¨Ξ=n∏i=1¨Ξi,∀¨ℏ∈¨U=(Ω(¨ρ)(¨ℏ) ∩ Ω(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ) ∩ m(¨ρ)(¨ℏ))=(Ω(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ))=Ωm(¨ρ)
Clearly, Ωm⊆ζz=Ωm ∩ Ωm.
(2). Obvious from (1).
(3). For proving this Ωm∪ξθ=Ωm. Let Ωm∪ξθ=ℜr.
ℜr(¨ρ)=(ℜ(¨ρ)(¨ℏ),r(¨ρ)(¨ℏ))),∀¨ρ∈¨Ξ=n∏i=1¨Ξi=(Ω(¨ρ)(¨ℏ) ∪ ξ(¨ρ)(¨ℏ),m(¨ρ)(¨ℏ) ∪ θ(¨ρ)(¨ℏ))=(⟨max
Clearly,
Now, we will show that
(4). Obvious from (3). ◼
Theorem 2. Suppose
1.
2.
3.
4.
Proof. By using the Definition 10, we obtain these properties
(1). Let
Therefore,
(2). Obvious from (1).
(3). Since,
This implies,
(4). Obvious from (3). ◼
Theorem 3. If
1.
2.
3.
4.
5.
6.
Proof. The properties are a direct consequences of Definitions 9 and 10.
(1). Since
Therefore,
(2). Obvious from (1).
(3). For this, let
Therefore,
(4). Obvious from (3).
(5). To prove this, let
Therefore,
(6). Obvious from (5). ◼
Remark 1. Let
In subsequent sections, we introduce AND and OR operations for the pairs of pPyFHSS in the following manner:
Definition 13. If
Definition 14. If
Here,
Remark 2. If
Theorem 4. If
1.
2.
Proof. (1) From Definitions 13 and 9
This implies,
(2) To prove this, let
This implies,
3.1 Similarity Measure between Two pPyFHSSs
In this section, the idea of similarity measures between two pPyFHSSs is introduced, inspired by the concept of [8,16,39] as follows:
Definition 15. If
such that
Example 8. To find the similarity between two pPyFHSSs, consider
This implies,
This implies,
by using (16) and (17) in (4) and we obtain
By taking the values of
This implies,
By using Eqs. (18) and (19) in (4) and we have
It implies that
Theorem 5. If
1.
2.
3.
4.
5.
Proof. (1) For proving this we use the Definition 3
This implies,
(2) Since,
This implies, (6) and (7)
Hence,
(3) Let
This implies,
(4) Let
(5) Let
This implies that,
◼
4 Decision-Making Application of Similarity Measure
In life, decisions are always being made. For this reason, most real-world issues, including those involving politics, economics, management, technology, and daily living, require our decision-making. The educational outcomes to determine which institution of education is better. When choosing an institution to teach, teacher education is evaluated based on a variety of expert standards. There are numerous studies, mostly conducted, have looked into the factors that parents consider when choosing an institution that best fits their child’s needs and their expectations for the institution graduate. We find an element regarded to be involved in parental decision-making: The academic element is comprised of five distinct aspects namely Geographical Location, Academic Reputation, Operational Environment, Internship Opportunities, and faculty/staff. Our objective is to pick the best option from a wide range of options by comparing the expert assessment with the criteria.
4.1 Algorithm for Evaluation of Optimum Educational Institution
Input:
(i) Consider
(ii) Assume a collection of parameters
(iii) Categorize the n attributes into disjoints sub-attributes valued sets
Construction:
(iv)Determine the Cartesian product of non-overlapping attributes valued set i.e.,
(v) Construct the pPyFHSS by utilizing definition 6 in tabular representation and the views of decision-makers. Arrange the chosen Pythagorean fuzzy numbers in the first row corresponding to each attribute value
Computation:
(vi) Compute the values of
(vii) By taking
(viii) By taking
(ix) By multiply
Output:
(x) Find the maximum similarity measure, and
(xi) Select the educational institution with the maximum similarity measure as the optimal solution.
Fig. 1 is meant to briefly preview the steps of the proposed algorithm.
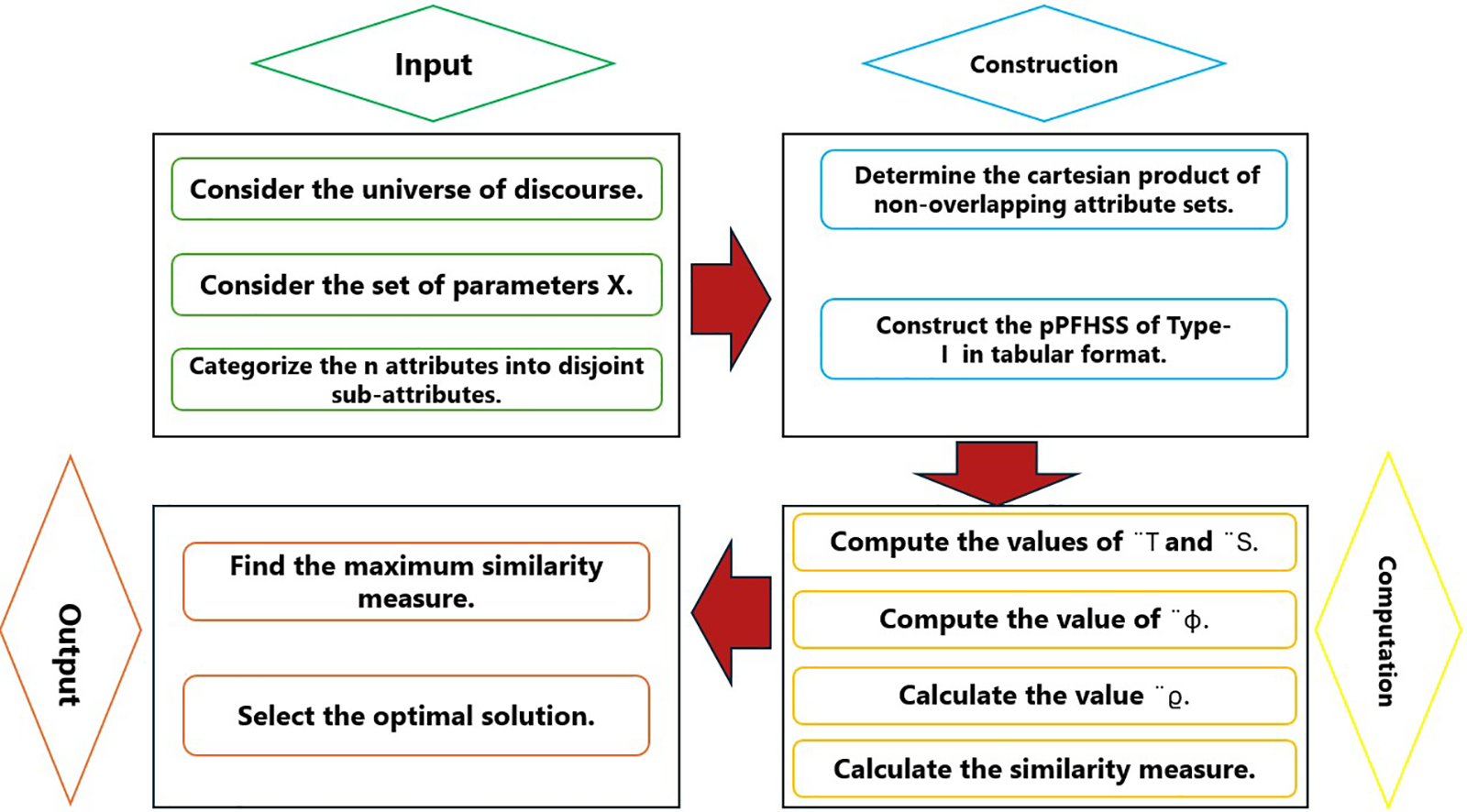
Figure 1: Algorithm construct for the proposed technique
Mrs. Emily has shifted from village to city and she intends to enroll her children in a good reputed educational institution. For the evaluation of educational institutions, she is accompanied by her friend who is well-known educationist (expert) in the area. They have considered the universal set






In this survey, in order to evaluate the educational institution which is the closest to the optimal educational institution, we should calculate the similarity measure of pPyFHSS in Tables 2–6 with the one in Table 1 in accordance with the definition 15. The bar of similarity measure should be based on the optimal educational institution. Typically, among all the five educational institutions, the one with a similarity measure above this bar is the best-suited one. The similarity measure computations for the educational profiles of
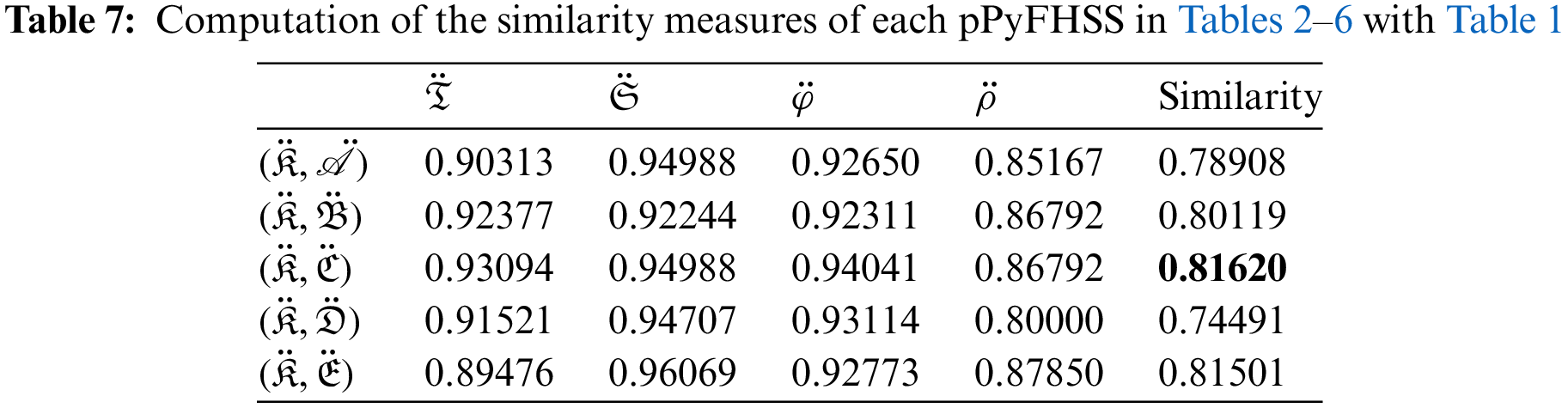

Figure 2: A graphical representation of scores of similarity measures corresponding to each educational institution shown in Table 7 (EIE represents the educational institution evaluation)
4.3 Comparison of the pPyFHSS Approach with PFHSS Approach without Generalizing the Parameter
In order to examine the impact of the possibility parameter, we shall reexamine the aforementioned survey study in this subsection by applying the PFHSS technique. The similarity measure for the aforementioned educational institutions’ evaluation is presented in Table 8. The possibility parameter significantly affects how the similarity measure of pPyFHSS is calculated, as can be seen from the preceding data. According to the similarity measure, it is found that the first, second, fourth, and fifth identify the educational institution with the maximum similarity measure as the optimal solution are significantly different from the optimum educational institution. We ought to select the third educational institution as a possible institution if the evaluator selects the threshold
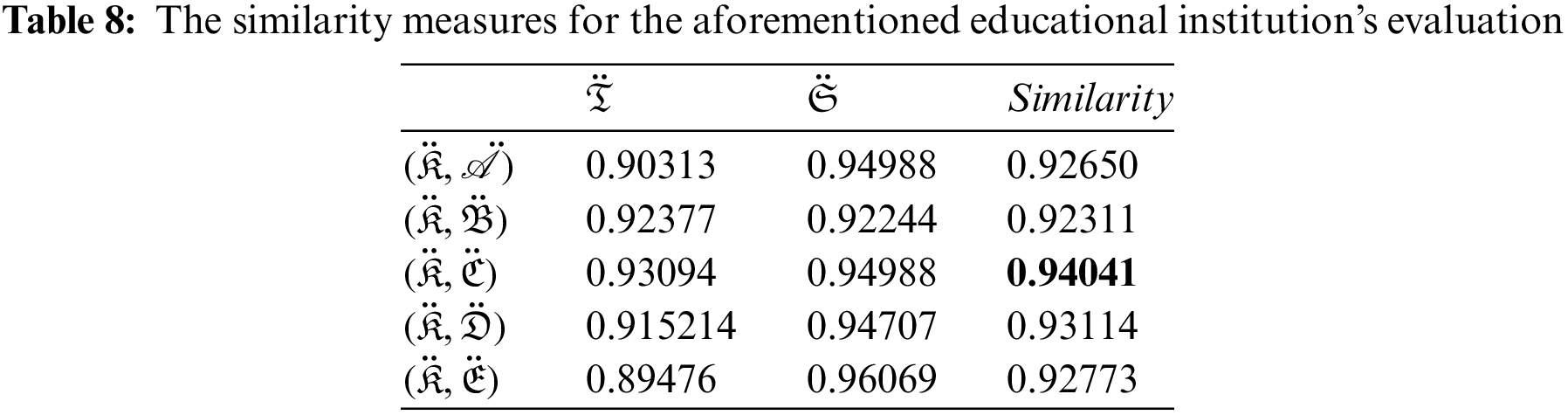

Figure 3: A graphical representation of comparison of similarity-based pPyFHSS with PFHSS
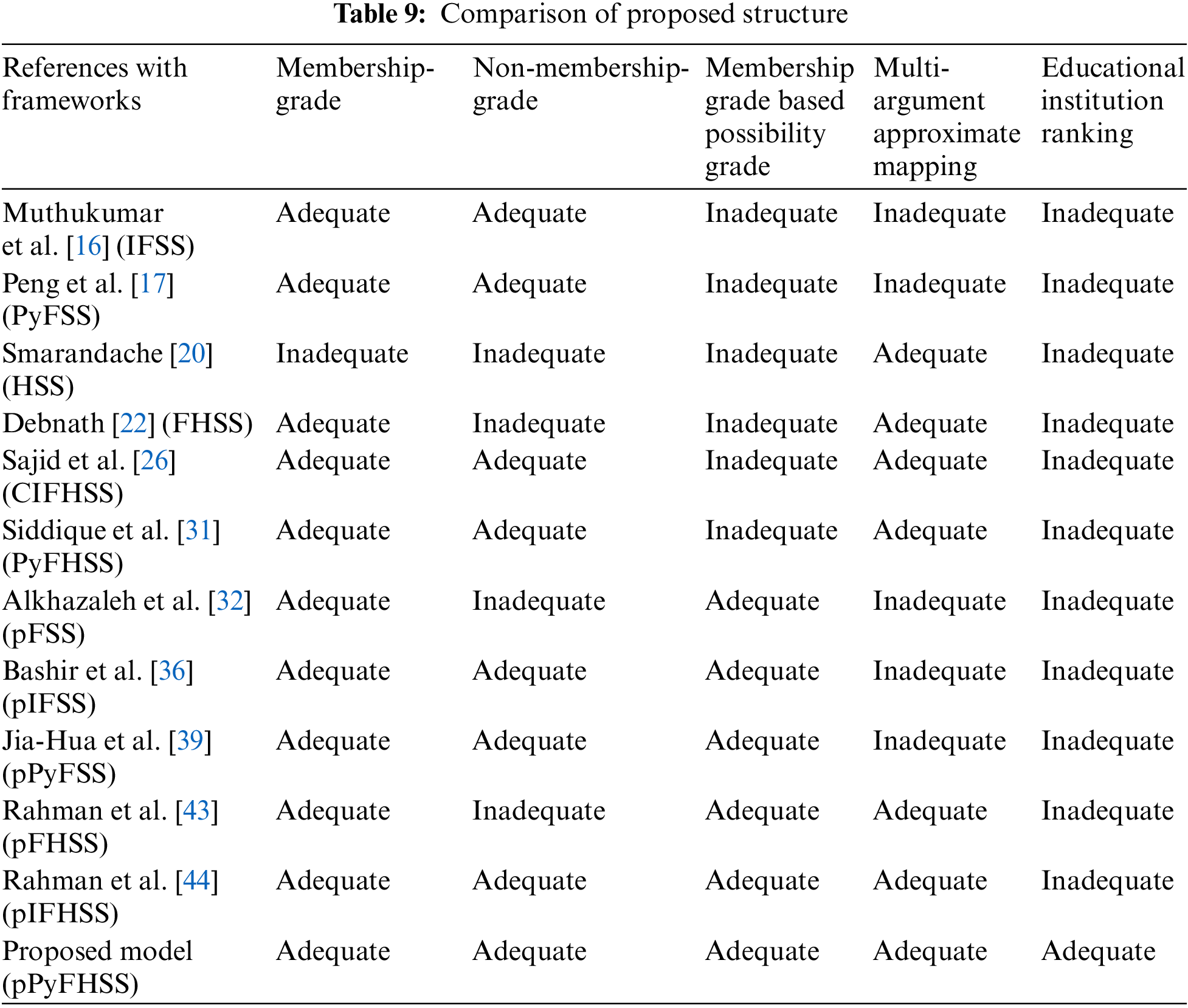
4.4 Flexibility Assessment through Structural Comparison
Many scholars have already discussed the evaluation of various educational institutions in the literature using Pythagorean hypersoft set-like structures. These methods employ fictional data with broad conclusions. In contrast, the suggested study evaluates and analyzes the challenges encountered by educational institutions using a synergistic strategy. Evaluation of educational institutions is actually a situation that needs further attribute partitioning into the corresponding sub-attribute values in the form of disjoint sets, which is something neglected by the existing methods. A classification like this guarantees accurate outcomes and decisions. To assess the structural differences between the proposed model and the most relevant existing models, a few attributes are thought to be sufficient. To minimize the possibility of biased decisions, the grade of possibility in the pPyFHSS model makes sure that expert opinions have been assessed under their level of acceptability. Table 9 illustrates this comparison in detail and shows how our suggested model fully combines all required components while existing models frequently lack key elements.
The significant preferential features of the proposed study are:
1. It has the proper arrangements to manage the biased tendency of the decision maker in decision-making to retain the validity of the decision. It has the settings to evaluate the observations and opinions of the decision-makers with the help of an impartial expert.
2. To strengthen the credibility of decision-making, it has a specific arrangement for short-term approximations. Decision-makers do not consider attributes one by one for the approximations of alternatives, rather, they have multiple arguments in mind for this purpose. That is accomplished in less time and more reliably.
3. It provides optimal and more generalized membership and non-membership functions that play a key role in controlling uncertainty based on incomplete and ambiguous information.
4. It embodies the characteristics and features of existing structures such as the possibility fuzzy hypersoft set (pFHSS), possibility intuitionistic fuzzy hypersoft set (pIFHSS), and the possibility Pythagorean fuzzy soft set (pPFSS). Thus, it is appropriate to consider pPyFHSS as a generalized form of all these structures.
The current study introduces a novel theoretical framework called pPyFHSS by generalizing existing models like pFHSS, pIFHSS, and pPFSS. This framework utilizes possible degree-based settings to cope with the biased tendency of decision-makers. The elementary notions of pPyFHSS, basic operations like union, intersection, AND-operations, OR-operations, etc., and essential theorems have been discussed with illustrations. Additionally, the formulation for similarity measures of pPyFHSS is developed and explained by numerical examples. Based on suggested similarity measures, an intelligent decision-assisted system has been developed with the proposal of an algorithm. The suggested steps of proposed algorithm are explained by a prototype case study for the evaluation of educational institutions. The flexibility of the pPyFHSS is checked through structure-based comparison. One of its limitations is that it utilizes possibility degree in terms of fuzzy membership value, but it is inadequate for those scenarios where falsity and indeterminacy are required to be considered for assessing the acceptance level through possibility degree. This work investigates the innovative use of the pPyFHSS model to enhance the educational institutions’ assessment procedure. In the past, assessing these kinds of organizations has included intricate decision-making processes involving the management of several criteria, frequently with ambiguous or contradicting data. With its special abilities, the pPyFHSS model offers a more accurate and adaptable method of tackling these problems. The model may be adjusted to the unique requirements and features of various educational institutions by incorporating parameterization, which increases its adaptability and effectiveness over current approaches. The pPyFHSS model has many sophisticated features that improve its ability to make decisions. These characteristics include the membership grade, which shows how effectively an institution satisfies specific requirements, and the nonmembership grade, which serves as a counterweight by demonstrating how much an institution falls short of those requirements. The model also presents the grade of possibility, which illustrates the likelihood of different scenarios and provides a sophisticated approach to managing uncertainty. The model provides a thorough evaluation framework by taking into account both individual criteria and the interactions between numerous criteria through the use of the single-argument approximate function and the multi-argument approximate function.
The ability to handle scenarios where the sum squares of the membership and nonmembership grades exceed one is one of the many notable advantages of the pPyFHSS model. This feature allows the model to represent uncertainty in a more realistic and complex way, which is helpful when making decisions in the real world. The pPyFHSS model is particularly well-suited for the complex evaluations required in the education sector because it offers a more accurate and scientific approach to evaluation by eliminating the constraints that hinder current approaches. Operational features and similarity measurements of the pPyFHSS model further verify its robustness. These features guarantee that the model operates consistently and dependably in a range of scenarios, offering a solid basis for its implementation in real-world scenarios. This study is all the more interesting and significant because this particular model has never been used to evaluate educational institutions. The results imply that the pPyFHSS model could produce assessments that are more accurate and trustworthy, providing a fresh viewpoint that has the potential to have a big influence on the evaluation of educational institutions.
The study recommends that future research may apply the pPyFHSS model to a broader range of educational institutions to further validate its effectiveness. This wider application would reinforce the model’s flexibility and robustness in a variety of circumstances. Insightful information regarding the relative benefits and drawbacks of the pPyFHSS model may also be provided by comparative studies with other complex models, which may lead to further advancements. These studies’ practical applicability would be further enhanced by incorporating real-world data, which would also ensure that the model meets the needs of decision-makers in the education sector.
Acknowledgement: The researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2024-9/1).
Funding Statement: The researchers is supported by the Deanship of Graduate Studies and Scientific Research at Qassim University (QU-APC-2024-9/1).
Author Contributions: Conceptualization, Khuram Ali Khan, Saba Mubeen Ishfaq, and Atiqe Ur Rahman; methodology, Saba Mubeen Ishfaq, Atiqe Ur Rahman, and Salwa El-Morsy; software, Saba Mubeen Ishfaq, and Atiqe Ur Rahman; validation, Khuram Ali Khan, Saba Mubeen Ishfaq, and Salwa El-Morsy; formal analysis, Khuram Ali Khan, Saba Mubeen Ishfaq, and Atiqe Ur Rahman; investigation, Khuram Ali Khan, Saba Mubeen Ishfaq, and Atiqe Ur Rahman; visualization, Khuram Ali Khan, and Salwa El-Morsy; supervision, Khuram Ali Khan, and Atiqe Ur Rahman; funding acquisition, Salwa El-Morsy. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. MacAllister J. What should educational institutions be for? Br J Educ Stud. 2016;64(3):375–91. doi:10.1080/00071005.2015.1131811. [Google Scholar] [CrossRef]
2. Chatterton P, Goddard J. The response of higher education institutions to regional needs. Eur J Educ. 2000;35(4):475–96. doi:10.1111/1467-3435.00041. [Google Scholar] [CrossRef]
3. Altbach PG, Reisberg L. Global trends and future uncertainties. Change: The Mag Higher Learn. 2018;50(3–4):63–7. doi:10.1080/00091383.2018.1509601. [Google Scholar] [CrossRef]
4. Waheed B, Khan FI, Veitch B, Hawboldt K. Uncertainty-based quantitative assessment of sustainability for higher education institutions. J Clean Prod. 2011;19(6–7):720–32. doi:10.1016/j.jclepro.2010.12.013. [Google Scholar] [CrossRef]
5. Yager RR. Pythagorean fuzzy subsets. In: 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013; Edmonton, AB, Canada: IEEE; p. 57–61. doi:10.1109/IFSA-NAFIPS.2013.6608375. [Google Scholar] [CrossRef]
6. Zadeh LA. Fuzzy sets. Inf Control. 1965;8(3):338–53. doi:10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
7. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi:10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
8. Garg H. Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst. 2017;32(6):597–630. doi:10.1002/int.21860. [Google Scholar] [CrossRef]
9. Qu S, Zhou Y, Ji Y, Dai Z, Wang Z. Robust maximum expert consensus modeling with dynamic feedback mechanism under uncertain environments. J Ind Manage Optim. 2024;21:524–52. doi:10.3934/jimo.2024093. [Google Scholar] [CrossRef]
10. Sun Q, Ren J, Zhao F. Sliding mode control of discrete-time interval type-2 fuzzy Markov jump systems with the preview target signal. Appl Math Comput. 2022;435:127479. doi:10.1016/j.amc.2022.127479. [Google Scholar] [CrossRef]
11. Ge J, Zhang S. Adaptive inventory control based on fuzzy neural network under uncertain environment. Complexity. 2020;2020(1):6190936. doi:10.1155/2020/6190936. [Google Scholar] [CrossRef]
12. Zhang N, Qi W, Pang G, Cheng J, Shi K. Observer-based sliding mode control for fuzzy stochastic switching systems with deception attacks. Appl Math Comput. 2022;427:127153. doi:10.1016/j.amc.2022.127153. [Google Scholar] [CrossRef]
13. Xia Y, Wang J, Meng B, Chen X. Further results on fuzzy sampled-data stabilization of chaotic nonlinear systems. Appl Math Comput. 2020;379:125225. doi:10.1016/j.amc.2020.125225. [Google Scholar] [CrossRef]
14. Gao M, Zhang L, Qi W, Cao J, Cheng J, Kao Y, et al. SMC for semi-Markov jump TS fuzzy systems with time delay. Appl Math Comput. 2020;374:125001. doi:10.1016/j.amc.2019.125001. [Google Scholar] [CrossRef]
15. Molodtsov D. Soft set theory-first results. Comput Math Appl. 1999;37:19–31. doi:10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
16. Muthukumar P, Krishnan GSS. A similarity measure of intuitionistic fuzzy soft sets and its application in medical diagnosis. Appl Soft Comput. 2016;41:148–56. doi:10.1016/j.asoc.2015.12.002. [Google Scholar] [CrossRef]
17. Peng X, Yang Y, Song J, Jiang Y. Pythagorean fuzzy soft set and its application. Comput Eng. 2015;41(7):224–9. [Google Scholar]
18. Kirişci M, Şimşek N. Decision making method related to Pythagorean Fuzzy Soft Sets with infectious diseases application. J King Saud Univ-Comput Inf Sci. 2022;34(8):5968–78. doi:10.1016/j.jksuci.2021.08.010. [Google Scholar] [CrossRef]
19. Zulqarnain RM, Xin XL, Garg H, Khan WA. Aggregation operators of pythagorean fuzzy soft sets with their application for green supplier chain management. J Intell Fuzzy Syst. 2021;40(3):5545–63. doi:10.3233/JIFS-202781. [Google Scholar] [CrossRef]
20. Smarandache F. Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 2018;22:168–70. doi:10.5281/zenodo.2838716. [Google Scholar] [CrossRef]
21. Smarandache F. New types of soft sets: hyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set. Int J Neutrosophic Sci. 2023;20(4):58–64. doi:10.54216/IJNS.200404. [Google Scholar] [CrossRef]
22. Debnath S. Fuzzy hypersoft sets and its weightage operator for decision making. J Fuzzy Ext Appl. 2021;2(2):163–70. doi:10.22105/jfea.2021.275132.1083. [Google Scholar] [CrossRef]
23. Musa SY, Mohammed RA, Asaad BA. N-hypersoft sets: an innovative extension of hypersoft sets and their applications. Symmetry. 2023;15(9):1795. doi:10.3390/sym15091795. [Google Scholar] [CrossRef]
24. Al-Quran A, Al-Sharqi F, Ullah K, Romdhini MU, Balti M, Alomair M. Bipolar fuzzy hypersoft set and its application in decision making. Int J Neutrosophic Sci. 2023;20(4):65–77. doi:10.54216/IJNS.200405. [Google Scholar] [CrossRef]
25. Asaad BA, Musa SY, Ameen ZA. Fuzzy bipolar hypersoft sets: a novel approach for decision-making applications. Math Comput Appl. 2024;29(4):50. doi:10.3390/mca29040050. [Google Scholar] [CrossRef]
26. Sajid M, Khan KA, Rahman AU, Bajri SA, Alburaikan A, Khalifa HAEW. A novel algorithmic multi-attribute decision-making framework for solar panel selection using modified aggregations of cubic intuitionistic fuzzy hypersoft set. Heliyon. 2024;10(17):e36508. doi:10.1016/j.heliyon.2024.e36508. [Google Scholar] [PubMed] [CrossRef]
27. Hamid MT, Abid M. Decision support system for mobile phone selection utilizing fuzzy hypersoft sets and machine learning. J Intell Manage Decis. 2024;3(2):104–15. doi:10.56578/jimd030204. [Google Scholar] [CrossRef]
28. Saeed MH, Saeed M, Rahman AU, Ahsan M, Mohammed MA, Marhoon HA, et al. Renewable energy resource management using an integrated robust decision making model under entropy and similarity measures of fuzzy hypersoft set. Heliyon. 2024;10(13):e33464. doi:10.1016/j.heliyon.2024.e33464. [Google Scholar] [CrossRef]
29. Rahman AU, Razaq A, Saeed M, Bajri SA, Alhabeeb SA, Khalifa HAEW. A risk analysis based multi-attribute decision-making framework for supply chain management using hypersoft mappings. IEEE Access. 2024;12:112261–77. doi:10.1109/ACCESS.2024.3441717. [Google Scholar] [CrossRef]
30. Smarandache F, Inthumathi V, Amsaveni M. Hypersoft sets in a game theory-based decision making model. Int J Neutrosophic Sci. 2024;24(1):74–86. doi:10.54216/IJNS.240107. [Google Scholar] [CrossRef]
31. Siddique I, Zulqarnain RM, Ali R, Jarad F, Iampan A. Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets. Comput Intell Neurosci. 2021;2021:2036506. doi:10.1155/2021/2036506. [Google Scholar] [PubMed] [CrossRef]
32. Alkhazaleh S, Salleh AR, Hassan N. Possibility fuzzy soft set. Adv Decis Sci. 2011;2011:479756. doi:10.1155/2011/479756. [Google Scholar] [CrossRef]
33. Al-Sharqi F, Al-Quran A, Romdhini MU. Decision-making techniques based on similarity measures of possibility interval fuzzy soft environment. Iraqi J Comput Sci Math. 2023;4(4):18–29. doi:10.52866/ijcsm. [Google Scholar] [CrossRef]
34. Ponnalagu K, Mounika P. A study on possibility fuzzy soft expert set. Int J Eng, Sci Math. 2018;7(2):256–62. [Google Scholar]
35. Ali G. Novel MCDM methods and similarity measures for extended fuzzy parameterized possibility fuzzy soft information with their applications. J Math. 2023;2023:5035347. doi:10.1155/2023/5035347. [Google Scholar] [CrossRef]
36. Bashir M, Razak Salleh A, Alkhazaleh S. Possibility intuitionistic fuzzy soft set. Adv Decis Sci. 2012;2012:404325. doi:10.1155/2012/404325. [Google Scholar] [CrossRef]
37. Selvachandran G, Salleh AR. Possibility intuitionistic fuzzy soft expert set theory and its application in decision making. Int J Math Math Sci. 2015;2015:314285. doi:10.1155/2015/314285. [Google Scholar] [CrossRef]
38. Garg H, Arora R. Algorithms based on COPRAS and aggregation operators with new information measures for possibility intuitionistic fuzzy soft decision-making. Math Probl Eng. 2020;2020(1):1563768. doi:10.1155/2020/1563768. [Google Scholar] [CrossRef]
39. Jia-Hua D, Zhang H, He Y. Possibility pythagorean fuzzy soft set and its application. J Intell Fuzzy Syst. 2019;36(1):413–21. doi:10.3233/JIFS-181649. [Google Scholar] [CrossRef]
40. Palanikumar M, Arulmozhi K. Possibility Pythagorean bipolar fuzzy soft sets and its application. Open J Discrete Appl Math. 2021;4(2):17–29. doi:10.30538/psrp-odam2021.0056. [Google Scholar] [CrossRef]
41. Palanikumar M, Arulmozhi K. Novel possibility Pythagorean interval valued fuzzy soft set method for a decision making. TWMS J Appl Eng Math. 2023;13(1):327–40. [Google Scholar]
42. Rahman AU, Smarandache F, Saeed M, Khan KA. Development of some new hybrid structures of hypersoft set with possibility-degree settings. In: Smarandache F, Jdid M, Vázquez MYL, editors. Neutrosophic and plithogenic inventory models for applied mathematics. New York: IGI Global; 2025. p. 1–31. doi:10.4018/979-8-3693-3204-7. [Google Scholar] [CrossRef]
43. Rahman AU, Saeed M, Garg H. An innovative decisive framework for optimized agri-automobile evaluation and HRM pattern recognition via possibility fuzzy hypersoft setting. Adv Mech Eng. 2022;14(10):16878132221132146. doi:10.1177/16878132221132146. [Google Scholar] [CrossRef]
44. Rahman AU, Saeed M, Khalifa HAEW, Afifi WA. Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math. 2022;7(3):3866–95. doi:10.3934/math.2022214. [Google Scholar] [CrossRef]
45. Sahoo D, Parida PK, Pati B. Efficient fuzzy multi-criteria decision-making for optimal college location selection: a comparative study of min-max fuzzy TOPSIS approach. Results Control Optim. 2024;15:100422. doi:10.1016/j.rico.2024.100422. [Google Scholar] [CrossRef]
46. Bhatia M, Arora HD, Chaudhary R, Kumar V. A study on the efficiency of divergence measure in fuzzy TOPSIS algorithm for multi-attribute decision making—a case study on university selection for admission. In: Kapur PK, Pham H, Singh G, Kumar V, editors. Reliability engineering for industrial processes. Cham: Springer; 2024. doi:10.1007/978-3-031-55048-5_18. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
