Dynamic Multi-Graph Spatio-Temporal Graph Traffic Flow Prediction in Bangkok: An Application of a Continuous Convolutional Neural Network

1  Introduction

In contemporary urban contexts, the challenge of traffic congestion has garnered significant attention, driving a heightened focus on the implementation of Intelligent Transportation Systems (ITS) to proactively address and manage congestion. As a result, accurate traffic prediction has emerged as a critical component in the ITS framework, aiming to enhance transportation safety, efficiency, and adaptability for both passengers and freight through the utilisation of advanced technology and comprehensive data analysis [1]. This deployment encompasses a range of strategies, including intersection management via traffic lights, dynamic routing facilitated by the Global Positioning System (GPS), real-time traveller information dissemination, and the integration of vehicle navigation and emergency notification systems. Furthermore, the integration of tracking systems for commercial vehicles serves to bolster logistics management and elevate goods security, facilitated by advancements in computing and communication technology [2].

Over the last decade, various methodologies have been extensively investigated from statistical, machine learning, and deep neural network perspectives. Nevertheless, there are ongoing practical hurdles in accurately predicting daily traffic flow due to inherent limitations. Recently, Graph Neural Networks (GNNs) have garnered significant attention, particularly in the domain of traffic prediction. Their adeptness in processing graph-structured data allows for the seamless updating of node representations through the aggregation of data from adjacent nodes. Consequently, GNNs have demonstrated efficacy and efficiency in a variety of tasks, including node classification and graph classification, as evidenced by several scholarly works [3–6]. Numerous academic endeavours have been undertaken to employ GNNs for extracting spatial characteristics within traffic networks, with spatio-temporal graph convolutional network (ST-GCN) [7] and decomposition convolutional recurrent neural networks (DCRNNs) [8] being notable examples. A prevailing approach in these studies involves the integration of GNNs with recurrent neural networks (RNNs) to capture spatial and temporal properties separately [9,10]. Furthermore, several investigations have sought to enhance recurrent architectures through the incorporation of convolutional structures, aiming to bolster training stability and efficiency [11,12].

Two persistently neglected problems arise in this domain. Firstly, the majority of approaches treat spatial and temporal patterns separately, neglecting the interplay between them. This limitation significantly restricts the representational capacity of the models. Secondly, while neural networks generally benefit from increased depth, GNNs show little improvement with added layers. Surprisingly, the optimal results are attained when cascading two-layer GNNs, with additional layers often yielding inferior performance [13,14]. Traditional GNNs suffer from the over-smoothing problem, wherein deeper layers cause all node representations to converge to the same value. This limitation severely constrains the depth of GNNs, hindering their potentiality to capture deeper and richer spatial properties. Despite the critical importance of considering network depth in spatial-temporal prediction to capture long-range dependencies, few works have addressed this aspect to date.

Existing research has primarily focused on capturing complex ST patterns through single or basic graph structures. However, these methods often struggle to represent the intricate relationships present in dynamic systems where multiple interacting entities and heterogeneous connections exist. Traditional ST models tend to overlook multi-scale interactions and the evolving nature of relationships in real-world phenomena, resulting in a limited understanding of temporal evolution and spatial dependencies. The motivation for this research lies in addressing these gaps by utilising a Dynamic Multi-Graph Spatio-Temporal framework, which allows for a more nuanced representation of dynamic systems. By integrating multiple graphs that capture diverse temporal and spatial relationships, this approach offers a richer, more accurate modelling of Ordinary Differential Equations (ODEs), ultimately leading to improved predictions and insights into complex dynamic processes.

In our model, we address the aforementioned challenges through several carefully designed components:

1.    To capture spatial correlations through dynamic multi-graph modelling, we develop three types of adjacency matrices: distance, pattern, and dynamic, derived from the spatial semantic similarities observed in traffic flow.

2.    We propose incorporating residual connections between layers to alleviate the issue of excessive smoothing. Additionally, prior research has shown that discrete layers with residual connections can be seen as a discrete form of ODE [15], which inspired the evolution of a continuous graph neural network (CGNN) [16]. In this study, we present CGNN featuring residual connections to tackle the problem of over-smoothing, allowing for the effective modelling of extended spatial-temporal dependencies.

3.    We developed a Dynamic Multi-Graph Spatial-Temporal Graph Neural Ordinary Differential Equation Networks (DMST-GNODE) model to concurrently capture spatial and temporal patterns using dynamic multi-graph modelling interactions and ODE. Finally, we compared DMST-GNODE with state-of-the-art baselines.

4.    To explore the potential applications of this model beyond traffic flow prediction, we consider several areas in ST data modelling where DMST-GNODE could be beneficial:

•   Disease Spread Prediction: Using ST data to predict the spread of diseases in different regions, which can help in planning and implementing preventive measures.

•   Natural Disaster Prediction: Predicting natural disasters like floods, earthquakes, and wildfires by analysing historical and real-time ST data.

•   Inventory Management: Using ST data to predict demand and optimise inventory levels across different regions, or

•   Renewable Energy Forecasting: Predicting the availability of renewable energy sources like solar and wind based on ST weather data.

The subsequent sections of this work are organised as follows: Section 2 provides a comprehensive review of related literature and existing studies pertaining to traffic flow prediction. Section 3 details the preliminary concepts necessary for understanding the proposed methodology. The methodology proposed for traffic flow prediction leveraging ST-GNN with multi-graph modelling and ODE. Sections 4–6 delineate the evaluation methodology employed and presents the results obtained. Lastly, Section 7 offers concluding remarks for the paper.

2  Related Works

2.1 Traffic Flow Predicting

Recently, considerable scholarly attention has been devoted to the task of traffic flow forecasting, which remains a pivotal concern within ITS [17]. This forecasting endeavor entails utilising ST data gleaned from diverse sensors to anticipate forthcoming traffic conditions. Traditional methodologies such as auto-regressive integrated moving average (ARIMA) [18,19], and support vector machine (SVM) [20–23]. However, owing to the inherent limitations in capturing intricate spatial-temporal relationships, there has been a pivot towards the adoption of deep neural network models. Noteworthy among these models is the fully connected long short-term memory (FC-LSTM) [22,24]. Likewise, spatio-temporal residual networks (ST-ResNet) [25] utilises a deep residual Convolutional Neural Network (CNN) to forecast citywide crowd movement, thereby underscoring the effectiveness of residual networks. Despite their commendable performance, these approaches are tailored for grid data and may not be suitable for scenarios involving graph-structured data in traffic environments.

2.2 Traditional Machine Learning to Traffic Predicting

In recent decades, scholars in fields like transportation systems [26], machine learning, statistics, and economics have developed numerous techniques for traffic forecasting [27]. These methods are typically categorised into two main approaches: knowledge-driven and data-driven. Knowledge-driven strategies aim to model and understand the transportation network using techniques like differential equations and numerical simulations [28,29]. While these models can accurately represent real traffic conditions, they rely on prior knowledge and detailed modelling, lack adaptability to different contexts, and require significant computational resources.

2.2.1 ARIMA

The ARIMA framework [18] is a statistical methodology that combines auto-regression, integration, and moving average parameters to account for auto-correlations observed in time series data. This model is defined by three hyper-parameters (p, d, q), each contributing significantly to improving the model’s precision. Specifically, p denotes the auto-regressive component, d represents integrated difference, and q indicates the moving average window size within the model equations.

2.2.2 Support Vector Regression (SVR)

SVR [20], much like ARIMA, specialises in short-term traffic flow prediction and functions as a supervised statistical learning model aimed at achieving an optimal global outcome. While short-term traffic prediction methods like ARIMA may be susceptible to disruption from random noise inherent in traffic data, SVR demonstrates proficiency in forecasting non-linear systems and exhibits faster convergence compared to traditional machine learning models for short-term traffic prediction. Using a principle akin to SVM, SVR addresses regression challenges with minimal deviation. Its core principle revolves around minimising errors and maximising margins by adjusting the hyperplane [27] to personalise predictions.

2.3 Deep Learning to Traffic Predicting

2.3.1 Graph Neural Networks (GNNs)

GNNs, as identified in previous studies by [14,30,31], are a category of neural networks specifically designed to operate within graph structures, which are mathematical structures consist nodes and edges symbolising entities and their interconnections. GNNs serve the purpose of learning graph representations and executing various tasks, including node classification, link prediction, and graph classification [14]. Their functionality revolves around aggregating information from neighbouring nodes and updating node representations [32] accordingly. Traffic flow forecasting involves predicting traffic volume or speed across different locations and time intervals. Traditional approaches to traffic flow forecasting rely on statistical models, time series analysis, and Machine Learning (ML) methods like SVR. Nonetheless, these techniques encounter challenges in capturing spatial dependencies and correlations inherent in traffic data, which are pivotal for crucial for accurate predictions. GNNs offer a solution by handling multiple data streams, such as traffic flow, weather conditions, and road network topology, and comprehensively capturing their intricate interrelations. By conceptualising traffic topology as a graph, GNNs adeptly capture spatial dependencies among traffic data, thereby addressing the limitations of traditional methods [30]. GNNs are capable of understanding complex associations among entities and drawing insights from data structured as graphs, showing effectiveness across various prediction tasks at different network levels [33]. They are generally grouped into four main categories: recurrent, convolutional, graph auto-encoders, and ST models [30]. Given the inherent spatio-temporal characteristics of traffic prediction, the focus primarily lies on ST-GNNs, although elements from other GNN types have also been integrated into traffic forecasting studies.

2.3.2 Spatio-Temporal Graph Convolutional Network (ST-GCN)

ST-GCNs are designed to address the complex nature of ST data, particularly in the context of traffic forecasting. These networks effectively capture both spatial and temporal dependencies by using graph convolutions for spatial relationships and temporal convolutions for sequential data.

The spatial method in the context of ST-GCN involves using GCNs to capture spatial dependencies in traffic networks. This paragraph describes the key concepts and mathematical formulations. The traffic network is represented as a graph 𝒢=(𝒱, ℰ), where 𝒱 is the set of nodes (e.g., traffic sensors or road segments), ℰ is the set of edges representing the connectivity between nodes, and 𝒲 is the weighted adjacency matrix, where 𝒲ij denotes the weight of the edge between nodes i and j. The convolution operation on a graph is defined in the spectral domain using the graph Laplacian. The normalised graph Laplacian is given by:

L=In−D−12𝒲D−12=UΛUT∈Rn×n,

where In is an identity matrix, D∈Rn×n is the diagonal degree matrix with Dii=∑j𝒲ij, Λ∈Rn×n is the diagonal matrix of eigenvalues of L. Next, we define the notation of graph convolution operator, that is ∗𝒢, based on the conception of the spectral graph convolution, as the multiplication of a signal x∈Rn with a filter θ,

Θ∗𝒢x=θ (L) x=Θ (UΛUT) x=UΘ (Λ) UTx,

where U is the matrix of eigenvectors, and filter Θ (Λ) is also a diagonal matrix.

The temporal method in the context of ST-GCN involves capturing temporal dependencies in traffic data using CNNs along the time axis. RNNs have been widely used for time-series analysis, but they suffer from time-consuming iterations and complex gate mechanisms. Instead, temporal convolutional networks (TCNs) offer several advantages, such as parallel training and simpler architectures. In the temporal convolutional layer, a 1-D convolution with a kernel of width Kt is applied along the time axis. For each node in the graph 𝒢, the input is treated as a sequence of length M with Ci channels, denoted as Y∈RM×Ci. The convolutional kernel ϕ∈RKt×Ci×2Co maps the input to an output sequence [P,Q]∈R(M−Kt+1)×2Co, where P and Q are split into equal-sized channels. Gated Linear Units (GLUs) are used. The temporal gated convolution is defined as:

ϕ∗TY=P⊙σ(Q)∈R(M−Kt+1)×Co,

where P, Q denote the input of gates in GLU, respectively, ⊙ denotes the element-wise Hadamard product, and σ(Q) is the sigmoid activation function applied to Q. The gates σ(Q) control which parts of the input P are relevant for the next layer. Residual connections are implemented among stacked temporal convolutional layers to prevent vanishing gradients and improve training stability. The residual connection for the l-th layer can be expressed as:

v(l+1)=σ (ϕ(l)∗Tv(l))+v(l),

where v(l) is the input to the l-th layer, and v(l+1) is the output of the l-th layer after applying the residual connection.

In ST-GCN combine temporal convolutions and graph convolutions, each block contains two temporal convolutional layers and one spatial graph convolutional layer in between. The overall architecture is designed to capture both spatial and temporal dependencies. The output of the l-th spatio-temporal convolutional block is given by:

v(l+1)=σ (ϕ(l,2)∗T (θ(l)∗𝒢 (ϕ(l,1)∗Tv(l))))+v(l),

where ϕ(l, 1) and ϕ(l, 2) are the temporal convolutional kernels, and θ(l) is the graph convolutional kernel.

In contrast to CNNs operating in Euclidean space, GNNs are capable of sampling and aggregating data in unordered and irregular spaces, making them more effective for handling graph-structured data. As GNNs have gained popularity, several variants have been developed, including graph convolutional networks (GCNs) [4], Chebyshev networks (ChebNet) [34], graph attention networks (GAT) [35], and diffusion convolutional neural networks (DCNN) [36]. GCNs are particularly popular and widely applied in tasks like graph structure classification and recommendation systems. Due to the spatial nature of traffic information, which fits well with graph structures, GCNs have become essential for extracting the inherent spatial characteristics of this data. Consequently, their ongoing development has positioned ST-GNN as the leading model for traffic prediction. Despite the numerous variations of ST-GNN, they can generally be categorised into two types: RNN-based [37] models and CNN-based models.

One type of RNN-based ST-GNN model captures temporal features using an RNN and incorporates graph convolution, either replacing or directly adding it to the RNN’s linear layer, to capture spatial features. Notable examples include T-GCN [10] and GCRNN [8], which both employ Gated Recurrent Unit (GRU) [38] for temporal features and GCN for spatial features, enabling the comprehensive capture of spatio-temporal features. However, the convolutional kernel sharing and GCN sharing present limitations, leading to the exploration of other GNNs for improved learning. For instance, Li et al. [8] introduced the DCRNN model, which utilises the random wandering of DCNN on the graph to capture spatial features and Seq2Seq for temporal features, enhancing the model’s flexibility and efficiency. Given the dynamic nature of traffic flow data, predictions may vary at each step, prompting [39] to propose Traffic Graph Convolutional-LSTM (TGC-LSTM), which combines GCN and LSTM [40], optimising graph convolution workflow with a free-flow reachability matrix. Guo et al. [41] constructed OGCRNN, which builds on GCRNN by optimising the Laplace matrix during graph convolution based on data variation, thereby obtaining dynamic spatio-temporal features. These advancements allow for dynamic adjustments in spatio-temporal correlations. Additionally, the A3T-GCN model [42] introduces attention mechanisms to T-GCN, accounting for dynamic data changes during feature acquisition. Despite these improvements, RNNs have inherent limitations due to parameter sharing at each time step, resulting in a reduced ability to capture the complex dynamics of temporal correlations. Attention Enhanced Graph Convolutional-LSTM (AGC-LSTM) [43] is a method that combines graph convolutional and LSTM networks with attention mechanisms. This approach effectively captures spatial-temporal patterns, leading to more accurate traffic flow predictions for real-time management. Building on these advancements, Dynamic Hypergraph Structure Learning (DyHSL) [44] offers a more flexible and adaptive approach. By representing traffic flow data as a hypergraph, it effectively captures complex multi-way interactions and temporal correlations. Unlike traditional models, this method dynamically adjusts its structure, allowing it to better learn evolving traffic patterns and provide more accurate forecasts in ever-changing traffic environments.

Numerous ST-GNN models employing CNN have been devised, aiming to capture both temporal and spatial features effectively. A prominent example is ST-GCN [7], which utilises CNN with GLU gating for temporal features and GCN for spatial features. However, the limited convolution kernel range of CNN results in a diminished perceptual field, hampering long-term prediction accuracy. Addressing this issue [45] introduced graph WaveNet, employing dilation convolution to enhance long sequence prediction accuracy. Additionally, it introduces a self-learning adjacency matrix to adaptively adjust to dynamic changes, marking the first instance of adaptive adjacency matrix utilisation in traffic prediction. Other models, such as Attribute-augmented Spatio-Temporal Graph Convolutional Network (ASTGCN) [46], incorporate attention mechanisms to mitigate the small perceptual field problem. ASTGCN integrates attention and GCN to model dynamic spatio-temporal correlations, while Graph Multi-Attention Network (GMAN) [47] replaces CNN and GCN entirely with attention mechanisms, emphasising the interplay between temporal and spatial information. Subsequent models like DGCN [48] and Multi-Scale Adaptive Spatial-Temporal Graph Convolutional Network (MASTGCN) [49] build upon ASTGCN and GMAN with enhancements, demonstrating strong performance in trajectory prediction and traffic data imputation as well [32,50,51].

2.3.3 Continuous Convolutional Neural Networks (CCNNs)

Neural ODE models, as introduced by [15], represent continuous dynamic systems by parameterise the derivative of the hidden state with a neural network, instead of using discrete sequences of hidden layers. The CGNN [16] expands this concept to graph-structured data, forming a continuous message-passing layer through derivatives that incorporate representations of both current and initial nodes. A crucial innovation in counteracting the over-smoothing effect is the use of a restart distribution, which serves as an inspiration for our work. They illustrate that a simple GCN can be interpreted as a discretization of a specific type of ODE, thereby describing the continuous dynamics of node representations and facilitating the development of deeper networks. To our knowledge, there is currently no research on graph ODEs within the scope of spatio-temporal prediction.

3  Preliminary

Definition 1. (Dynamic Multi-Graph Traffic Network: 𝒢). We characterise the road network through a graphical framework denoted as 𝒢=(𝒱, ℰ, 𝒲), where 𝒱∈RN denotes the set of vertices signifying N nodes, N represents the number of nodes, ℰ∈RN×N signifies the set of edges connecting any node pairs, and 𝒲=RN×N symbolises the adjacency matrix enumerating the weights of node pairs. Between eij∈ℰ denotes a particular road segment connecting vi∈𝒱 and vj∈𝒱, while wij∈𝒲 represents the directed weight associated with this connection, where i and j are positive integers. In this paper, three distinct road network graphs are delineated across various semantics: the distance graph (𝒢dis), the pattern graph (𝒢pat), and the dynamic graph (𝒢dyn).

Definition 2. (Graph Tensor Ω). We give the observation of node i at time t as Ωti∈RF, F represents the length of an observation vector. Ωt=(ωt1, ωt2,…,ωtN)∈RN×F signifies the observations of all nodes at time t. Moreover, Ω=(Ω1,Ω1,…,Ωt)∈RT×N×F indicates the observations of all nodes across all time instances.

3.1 Problem Construction

With the tensor Ω observed within a traffic network 𝒢, the objective of traffic forecasting is to acquire a mapping function f that translates historical 𝒯 observations into predictions of future 𝒯⊚ traffic observations.

[Ωt−T+1v, Ωt−T+2v,…, Ωtv;𝒢dis, 𝒢pat, 𝒢dyn]→f[Ωt+1⊚v, Ωt+2⊚v,…,Ωt+𝒯⊚⊚v].

3.2 Neural ODE

Initially, we examine GNNs featuring residual connections [52,53] implemented through addition, which can be expressed as:

xk+1=xk+fk(xk),(1)

where xk is the states of the graph in the k-th layer, fk(⋅) is any differentiable function defined on the graph, whose output has the same shape as its input, k∈{0, 1,…,K}, and xk∈R. These iterative updates can be seen as an Euler discretization of a continuous transformation [54]. In the limit, we describe the continuous dynamics of hidden units with ODE defined by a neural network:

dz(τ)d(τ)=f(z(τ),τ).(2)

We utility z(τ) in the continuous case and xk in the discrete case to the present hidden states of a graph. Starting from the input layer x0, we can define the output layer xT to be the solution to this ODE initial value problem at some time T. This value can be computed by a black-box differential equation solver, which evaluates the hidden unit dynamics f wherever necessary to determine the solution with the desired accuracy.

The forward propagation of GNNs featuring discrete layers can be expressed as:

x0=input,x1=x0+f0(x0),…,xK−1+fK−1(xK−1),(3)

where K is the total number of layers. After traversing through all K layers, the final layer, such as a fully-connected layer commonly used for classification tasks, is applied to the output xK. The initial traversal of graph-ODE (GODE) entails:

z(T)=z(0)+∫τ=0Tdz (τ)dτdτ=input+∫τ=0Tf (z (τ),τ) dτ,(4)

where z(0)=input and T is the integration time, corresponding to the number of layers K in the discrete case.

In this study, we begin with an initial input denoted as z(0), and we define the integration time T, which corresponds to the number of layers K in the discrete scenario. The evolution of states, represented by z, follows a model based on solving GODE. Subsequently, an output layer is applied to z at time T. The forward integration process can be executed using various ODE solvers, such as the Euler, Runge-Kutta methods, etc. [55–57].

3.3 Tensor Calculation

A tensor 𝒯 can be examined as a multidimensional array and a tensor matrix multiplication is provided on some mode fiber, for instance,

(𝒯×2M)ilk=∑j=1n2𝒯ilk⋅Mjl,(5)

where 𝒯∈Rn1×n2×n3, M∈Rn2×n2′, 𝒯×2M∈Rn1×2′×n3′, and ×2 denotes the tensor-matrix multiplication is conducted on mode-2, i.e., the second subscript. Some importance properties of tensor-matrix multiplication that will be applied in this work as follows:

•   𝒯×iM1×iM2=𝒯×i(M1M2);

•   𝒯×iM1×jM2=𝒯×jM1×iM2, i≠j.

3.4 DMST-GDODE Model

The DMST-GNODE model integrates MST-GCN [58] with the input data and adjacency matrix, along with a GODE [59] that includes both an integrator and a solver. This combination forms the DMST-GNODE model as depicted in Fig. 1.

Figure 1: Framework of the dynamic multi-graph spatio-temporal graph neural ordinary differential equation network (DMST-GNODE)

The structure of the DMST-GNODE model. It comprises three primary components: Input Module: This module collects raw traffic flow data stored in a No-SQL database. It normalises the traffic flow data using the Inverse Box-Cox transformation method [60].

GODE Module: This component is primarily composed of three parts: two STGNODE layers made up of multiple STGNODE blocks, a max-pooling layer, and an output layer. Each STGNODE block (refer to Fig. 2) includes three TCN blocks and a tensor-based ODE solver in between, which is designed to capture complex, long-range spatial-temporal relationships. The graphs–Distance graph (𝒢dis), which focuses on representing physical spatial connections by mapping the Euclidean distances between nodes and effectively reflecting how their geographic proximity influences traffic flow; Pattern graph (𝒢pat), which captures similarities in traffic behaviour across different nodes, identifying connections where traffic patterns, such as peak periods or congestion trends, resemble each other even if they are not geographically close; and finally, Dynamic graph (𝒢dyn), which models how these relationships evolve over time, adapting to changes in traffic conditions, weather, or road incidents, thus providing a time-sensitive view of traffic flow interactions–are fed into the solver separately to extract features from different perspectives.

Figure 2: STGODE layer

Spatio-Temporal Module: This module comprises two ST-Convolutional blocks and a fully connected layer at the end. Each ST-Convolutional block contains two Temporal-Convolutional layers with a Spatial-Convolutional layer in the middle (see Fig. 3). The Spatial-Convolutional layer operates on the graph by accounting for spatial dependencies between nodes, while the Temporal-Convolutional layers focus on extracting temporal dependencies from consecutive graph representations. Specifically, the Temporal-Convolutional layer uses a 1-D convolution with a kernel of width Zt, followed by a GLU activation. Finally, an output layer integrates these comprehensive features to generate the final prediction. Detailed descriptions of the model will be provided in the following sections.

Figure 3: ST-Convolutional block

3.5 Scalability and Computational Complexity of the DMST-GDODE Model

The scalability of the DMST-GDODE model is a critical aspect of its practical implementation, especially in the context of large-scale traffic flow forecasting. The model employs a tensor-based approach, which allows it to handle spatial and temporal information simultaneously. This integrated handling of spatio-temporal data can scale effectively across different sizes of networks and datasets:

1.    Graphs: The use of distance, pattern, and dynamic graphs allows DMST-GDODE to capture various spatial semantics, enhancing the accuracy and scalability of predictions by leveraging different perspectives of the traffic network.

2.    Temporal Convolutions: The temporal convolution process efficiently handles the time-series nature of traffic data, enabling the model to scale well with the temporal dimension of the dataset.

3.    Tensor-Based Computation: Leveraging tensor-based operations to handle spatio-temporal data allows the DMST-GDODE model to utilise modern hardware accelerators like GPUs, significantly improving processing speed and scalability.

4.    Parallelisation: The DMST-GDODE model employs a “sandwich” structure, consisting of TCN blocks and an ODE solver, allowing for efficient parallel computation. The TCN blocks use dilated convolutions, which expand the receptive field without significantly increasing the computational burden, making it suitable for processing large-scale data.

The computational complexity of the DMST-GDODE model is addressed through its modular design and efficient use of convolution operations:

1.    Graph Convolutions: The spatial convolution stage uses graph convolution operations over adjacency matrices. These operations are computationally intensive, they are optimised through techniques.

2.    Temporal Convolutions: The two-stage temporal convolution process helps in efficiently handling the time-series nature of traffic data, allowing the model to scale well with the temporal dimension of the dataset.

3.    Full Connection Stage: The integration of external factors (such as calendar and weather conditions) through a fully connected neural network ensures that the model comprehensively accounts for all relevant factors without significantly increasing computational overhead.

4.    TCNs: The TCN blocks use dilated convolutions to capture long-term temporal dependencies. For a TCN block with more than one layer, a dilation factor, and input sequence length are employed. Residual connections in TCN blocks help mitigate the vanishing gradient problem, supporting deeper network structures.

5.    ODE Solver: The ODE solver within the DMST-GDODE model operates on the hidden states represented as tensors. Given the nature of ODE solvers, the computational complexity can vary depending on the solver used.

6.    Handling Over-Smoothing: The DMST-GDODE model addresses the over-smoothing problem common in deeper GCNs by incorporating residual connections and leveraging the continuous nature of ODEs. This not only improves model stability but also enhances computational efficiency by preventing excessive smoothing of features across layers, which would otherwise increase complexity due to repeated aggregations.

3.6 Adjacency Matrix of Dynamic Multi-Graph Modelling

In this our model, we utilise three types of adjacency matrices. Drawing from ST-GCN [58], we define the adjacency matrix of distance graph (𝒲dis) as:

𝒲dis=(0𝒲dis(1,2)…𝒲dis(1,𝒱)𝒲dis(2,1)0…𝒲dis(2,𝒱)⋮⋱⋮𝒲dis(𝒱,1)𝒲dis(𝒱,2)…0),(6)

𝒲dis(i, j)={0,i, j is not directly connected,1,i, j is directly connected.(7)

Next, we delineate the adjacency matrix of the pattern graph (𝒲pat) based on a statistical perspective commonly applied in the business domain.

𝒲pat=(0𝒲pat(1,2)…𝒲pat(1,𝒱)𝒲pat(2,1)0…𝒲pat(2,𝒱)⋮⋱⋮𝒲pat(𝒱,1)𝒲pat(𝒱,2)…0),(8)

𝒲pat=exp⁡ (scal (i, j))∑i≠jexp⁡ (scal (i, j)),(9)

scal (i, j)=1−|dist (i, j)−mileage (i)|−min (|dist (i, Γ)−mileage (i) |)max (|dist (i, Γ)−mileage (i) |),(10)

where dist (i, j) represents the cartographic distance between node i and j, while mileage (i) provides the average mileage of vehicles departing from node i. Here, Γ refers to nodes other than the focal node i. Last one, we establish the adjacency matrix of the elastic graph (𝒲dyn) based on a latent relational perspective as follows:

𝒲dyn=(0𝒲dyn(1,2)…𝒲dyn(1,𝒱)𝒲dyn(2,1)0…𝒲dyn(2,𝒱)⋮⋱⋮𝒲dyn(𝒱,1)𝒲dyn(𝒱,2)…0),(11)

𝒲dyn(i,j)=βi∗βj,i,j∈𝒱,(12)

where its element 𝒲dyn (i, j)∈𝒲dyn represents the intrinsic relationship between node i and j, acquired through a fully connected neural network, ∗ denoted by multiply between the element βi and βj. The weight vector (β1, β2,…,βi,…,β𝒱)T is represented, where each βi∈(0, 1) for a node i is initialised from a normal distribution. Utilising gradient descent and back-propagation, βi undergoes progressive updates until the spatial relationship is acquired.

3.7 Customised Numerical Integration and Solver of ODE

GNNs enhance node representations by combining attributes obtained from both the nodes and their adjacent nodes through a graph convolution process. The traditional formulation of this convolution process can be articulated.

𝒢k+1=GCN (𝒢k)=ψ (𝒲^𝒢kℛ),(13)

where 𝒢k∈RN×C represents the input of the preceding graph convolutional layer (k-th graph), 𝒲^∈RN×N signifies the normalised adjacency matrix, ψ is threshold to control adjacency metric, and ℛ∈RC×C′ stands for a trainable parameter matrix that captures the interactions among various features. However, traditional GCNs are prone to over-smoothing as network depth increases [13,14], greatly limiting their capability to capture long-range dependencies. To address this drawback, we propose our innovative DMST-GNODE block.

To enable interactions between the adjacency matrices and modules, we draw inspiration from the effectiveness of the CGNN [16] and explore a more robust discrete dynamic function:

𝒢k+1=𝒢k×1𝒲^×2𝒰×3ℛ+𝒢0.(14)

In this setup, 𝒢k∈RN×T×F serves as a space-time tensor, capturing the latent embedding of the node from the previous layer. The ×i operation denotes metric multiplication performed on mode i. Here, 𝒲^ is the adjusted adjacency matrix, 𝒰 represents the temporal transformation matrix, and ℛ stands for the feature transformation matrix. 𝒢0 represents the initial input of the GCN, which can be obtained through an alternative neural network. Drawing inspiration from the CGNN method, a reset distribution 𝒢0 is employed to mitigate over-smoothing concerns. In particular, the expansion of Eq. (14) is presented.

𝒢k=∑i=0k(𝒢0×1𝒲^i×2𝒰i×3ℛi).(15)

In this context, it is evident that the resultant representation 𝒢k amalgamates information across all layers. This implies that the ultimate outputs gather data from no more than k-order neighbours while retaining the initial features. To underscore the importance of the restart distribution, consider an alternative scenario where there is no 𝒢0 component.

𝒢k+1=𝒢k×1𝒲^×2𝒰×3ℛ,(16)

where the final outcome will be:

𝒢n=𝒢0×1𝒲^n×2𝒰n×3ℛn.(17)

Consider the matrix 𝒲^ as a straightforward illustration. Assuming 𝒲^ undergoes eigenvalue decomposition as 𝒲^=𝒵𝒟𝒵T, where 𝒟=diag (γ1, γ2,…,γm) represents a diagonal matrix. Evidently,

𝒲^n=𝒵diag (γ1,γ2,…,γm)𝒵T=𝒲^1n𝒵diag (1,(γ2γ1)n,…,(γmγ1)n)𝒵T→𝒲^1n𝒵diag (1, 0,…,0)𝒵T.(18)

As the value of n approaches infinity with γ1>γ2>⋯>γm, the diagonal elements tend towards zero except for the largest one. This significant reduction in diagonal values results in substantial loss of information. The residual structure represented by Eq. (14) possesses considerable potency but presents challenges in training owing to its substantial parameter count. Consequently, our objective is to broaden the discrete formulation into a continuous framework. Conceptually, this involves substituting the discrete variable n with a continuous counterpart i, and reinterpreting the expansion equation as a Riemann sum [61] over the interval from 0 to n on i.

𝒢n=∑i=0n(𝒢0×1𝒲^i×2𝒰i×3ℛi)=∑i=1n+1(𝒢0×1𝒲^(i−1)×Δτ×2𝒰(i−1)×Δτ×3ℛ(i−1)×ΔτΔτ).(19)

In the limit as n approaches infinity, we express the following integral, where Δτ=τ+1n+1 and τ=n:

𝒢(τ)=∫0τ+1𝒢0×1𝒲^φ×2𝒰φ×3ℛφdφ.(20)

The pivotal aspect lies in converting the remaining structure into ODE format. It is evident that we are already in possession of an ODE as follows:

d𝒢(τ)dτ=𝒢0×1𝒲^τ+1×2𝒰τ+1×3ℛτ+1.(21)

However, calculating 𝒲^τ+1, 𝒰τ+1, and ℛτ+1 becomes challenging, particularly when τ is not an integer. Inspired by the research presented in [16], we derive the subsequent corollary (see proof in Appendix A).

Corollary 1. The discrete alteration outlined in Eq. (14) represents a discretized form of the subsequent ODE.

d𝒢(τ)dτ=𝒢(τ)×1ln⁡𝒲^+𝒢(τ)×2ln⁡𝒰+𝒢(τ)×3 ln⁡ℛ+𝒢0,(22)

where 𝒢0=f(𝒳) represents the result generated by preceding networks.

In this paper, we simplify the logarithm function by employing its first-order Taylor expansion [62], represented as ln⁡P≈P−1. This simplification yields a more straightforward expression.

d𝒢(τ)dτ=𝒢(τ)×1(𝒲^−1)+𝒢(τ)×2(𝒰−1)+𝒢(τ)×3(ℛ−1)+𝒢0.(23)

The ODE mentioned previously can be resolved analytically, as indicated by the following corollary (see proof in Appendix A).

Corollary 2. The equation presented in (23) is solved analytically as follows:

𝒢(τ)=𝒢(τ)×1e(𝒲^−1)τ×2e(𝒰−1)τ×3e(ℛ−1)τ+∫0τ𝒢(τ)×1e(𝒲^−1)(τ−φ)×2e(𝒰−1)(τ−φ)×3e(ℛ−1)(τ−φ)dφ.(24)

Finally, our DMST-GNODE framework is influenced by neural ODEs [15]. Here, we present the continuous expression of the hidden representation:

𝒢(τ)=ODESolver (d𝒢 (τ)dτ, 𝒢0, τ),(25)

where

d𝒢(τ)dτ=𝒢(τ)×1(𝒲^−1)+𝒢(τ)×2(𝒰−1)+𝒢(τ)×3(ℛ−1)+𝒢0.

In our model, 𝒢0 represents the initial value sourced from the upstream network, and the ODESolver is specifically selected as the Runge-Kutta solver. Runge-Kutta solvers are known for their stability compared to Euler solvers, making them essential for precisely tracking nuanced variations and attributes of action sequences. Furthermore, the Runge-Kutta solver offers superior accuracy in handling nonlinear and rapidly changing action sequences, enabling more precise capture of details and significant features in actions. Considering these factors, it is well-suited for our model’s requirements.

4  Evaluation Metrics

Compared of Evaluation metric with baselines: The effectiveness of the models is contingent upon the degree of error or, in certain scenarios, the accuracy of the model in classification tasks. However, in regression analysis, the focus is on how well the model fits the provided data. Evaluation of the model can be conducted utilising metrics such as root mean square error (RMSE), mean absolute error (MAE), and accuracy Accuracy. Here, within a specific day, 𝒱 denotes the set of nodes in the road network; at node v∈𝒱, Ω⊚v and Ωv denote the predicted traffic flow and the ground truth, respectively.

(i)   RMSE quantifies the deviation between an estimator and the true value of an estimated parameter. It calculates the mean of the squared differences between the predicted values and the actual values. RMSE is frequently employed in regression analysis to assess the predictive accuracy of a model [63], as detailed below:

RMSE=1𝒱∑v=1𝒱(Ω⊚v−Ωv)2.(26)

(ii)   MAE measures the average magnitude of errors in a set of predictions, ignoring their direction. It is determined by calculating the average of the absolute differences between predicted values and actual values, offering a way to evaluate the accuracy of a regression model [64]. The formula for computing the MAE is given by:

MAE=1𝒱∑v=1𝒱(Ω⊚v−Ωv).(27)

(iii) For evaluating the accuracy of a regression model, the Frobenius norm provides a method to measure the magnitude of the disparity between the ground truth and foretasted values, expressed as ‖Ω−Ω⊚‖, where

Accuracy=1−‖Ω−Ω⊚‖‖Ω‖.(28)

5  Experimental Settings

We evaluate the performance of our proposed model by employing comprehensive real datasets collected from traffic monitoring in Bangkok (BKK)1. This datasets comprises traffic data gathered from speed detectors installed on various road segments throughout Bangkok. Data was collected from 50 selected sensors over a two-month period, from 01 January 2024, to 29 February 2024 and real-word datasets (PeMS08 and Los_Loop). The traffic data are collected and reported by each detector at twenty-min intervals. All studies employ a one-hour historical time window to predict traffic conditions for the subsequent 20, 40, or 60 min.

The baseline models were compared with DMST-GNODE. First, ARIMA [18] is a widely recognised statistical tool for analysing time series data. Next, SVR [20] is a type of machine learning model that applies the principles of SVM to regression problems, allowing for the prediction of continuous values. FC-LSTM [22] integrates CNN with LSTM networks, enhancing FC-LSTM by embedding convolutional layers to capture both spatial and temporal relationships. TGC-LSTM [40] merges GCN with LSTM networks. AST-GCN [46] is an Attention-based ST-GCN that uses spatial and temporal attention mechanisms to capture spatial-temporal dynamics. To ensure a fair comparison, only recent components for modelling periodicity are considered. MAST-GCN [49] is a model designed to capture and analyse spatial and temporal relationships across multiple attributes. ST-GCN [7] is a ST-GCN that employs graph convolution to capture spatial dependencies and 1-D convolution to capture temporal correlations. After that, MST-GCN [58] is a network that integrates multiple graphs to capture various spatial dependencies and utilises graph convolution. Finally, Spatial-Temporal Graph Ordinary Differential Equation Networks (ST-NODE) [65] captures and analyses dynamic spatial and temporal relationships in data, leveraging continuous-time dynamics for improved prediction and understanding of complex processes.

The research was conducted using 20 computing nodes, each equipped with a 10-core 2.40 GHz Intel Xeon Processor (Skylake, IBRS (Intel, Malaysia)) featuring 32 MB L3 cache and 500 GB RAM, and running Ubuntu 20+ LTS. Whenever feasible, computations were performed concurrently to maximise efficiency.

6  Experiment Results

In our experimental assessment, we utilise a specific dataset. To facilitate comparison, we showcase the effectiveness of our suggested methodologies in contrast to baseline models and conventional techniques using the dataset, as outlined in Table 1. Within the presented results, Time denotes various prediction horizons. We gauge model performance using MAE and RMSE metrics, where lower values indicate superior performance, while Accuracy is expected to increase for enhanced performance, as shown in Figs. 4–12.

Figure 4: Visualisation of RMSE (vehicles per times) performance within 20 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 5: Visualisation of RMSE (vehicles per times) performance within 40 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 6: Visualisation of RMSE (vehicles per times) performance within 60 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 7: Visualisation of MAE (vehicles per times) performance within 20 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 8: Visualisation of MAE (vehicles per times) performance within 40 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 9: Visualisation of MAE (vehicles per times) performance within 60 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 10: Visualisation of Accuracy (vehicles per times) performance within 20 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 11: Visualisation of Accuracy (vehicles per times) performance within 40 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

Figure 12: Visualisation of Accuracy (vehicles per times) performance within 60 min, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown

In the baselines, Table 1 outcomes indicate a decline in accuracy scores with an increase in prediction duration from 20 to 60 min. Our study presents the empirical findings of our DMST-GNODE model, consistently demonstrating reduced error rates and increased accuracy compared to the baseline models across all prediction time-frames. Our results indicate that incorporating the multi-graph improves performance consistently across all time horizons compared to ST-GCN. However, combining the ODE technique with the ST-GCN model diminishes performance relative to using ST-GCN alone. The fusion of the multi-graph approach with ODE techniques outperforms ST-GCN. When extending the forecasting horizon from 20 to 60 min, ST-GCN experienced a notable 42.73% increase in RMSE. Conversely, the DMST-GNODE model demonstrated a reduction in RMSE from 6.3142 to 5.7631, marking a significant 9.5626% decrease in RMSE over a 60-min prediction period. This indicates a considerable enhancement in long-term prediction accuracy compared to ST-GCN.

Secondly, we compare the performance of DMST-GNODE and several baseline models on the PeMS08 and Los_Loop datasets, respectively. The metrics used for evaluation are RMSE, MAE, and Accuracy across different time intervals. In Table 2, the DMST-GNODE model consistently shows superior performance, with the lowest RMSE and MAE values and the highest Accuracy across all time intervals on the PeMS08 dataset. Similarly, in Table 3, the DMST-GNODE model outperforms others on the Los_Loop dataset, particularly noticeable at 20 and 60 time intervals, where it achieves the lowest error metrics and highest Accuracy. These results highlight the effectiveness of the DMST-GNODE model in providing accurate and reliable predictions compared to traditional and other baselines.

Moreover, we compared the MAE, RMSE, and Accuracy of the DMST-GNODE model with those of the baseline methods, and found that DMST-GNODE consistently outperformed all five methods. This demonstrates that DMST-GNODE is more effective at managing spatio-temporal correlations and integrating multi-graph networks with ODEs. The experimental results using the Bangkok dataset are presented in Figs. 4–12, where (A) ARIMA, (B) SVR, (C) FC-LSTM, (D) TGC-LSTM, (E) AST-GCN, (F) MAST-GCN, (G) ST-GCN, (H) MST-GCN, (I) ST-NODE, and (J) DMST-GNODE are shown.

The Fig. 13 of plots provides insights into the training and validation loss and accuracy over 600 epochs for a neural network model. The left plot shows a steady decline in both training and validation loss, indicating effective learning and reduction in errors throughout the epochs. Despite some fluctuations, the general downward trend demonstrates that the model is progressively improving its predictions. The right plot reveals a corresponding increase in training and validation accuracy, signifying enhanced performance in classifying or predicting outcomes as training progresses. The overlapping trends between training and validation metrics suggest that the model maintains a good balance between learning from the training data and generalising to unseen validation data, with minimal over-fitting. The predictive performance for two specific nodes, as illustrated in Figs. 14 and 15, shows that our DMST-GNODE and MST-GCN models more accurately match the real data, particularly in the larger traffic network. In summary, DMST-GNODE achieves high predictive accuracy by capturing spatial features from multiple perspectives. Fig. 16 illustrates a portion of the traffic network, displaying selected nodes and a heat map representing the vehicle outflow during a specific time interval.

Figure 13: The training and validation loss and accuracy over 600 epochs for DMST-GNODE model

Figure 14: Visualisation of 20-min predictions for Node 12

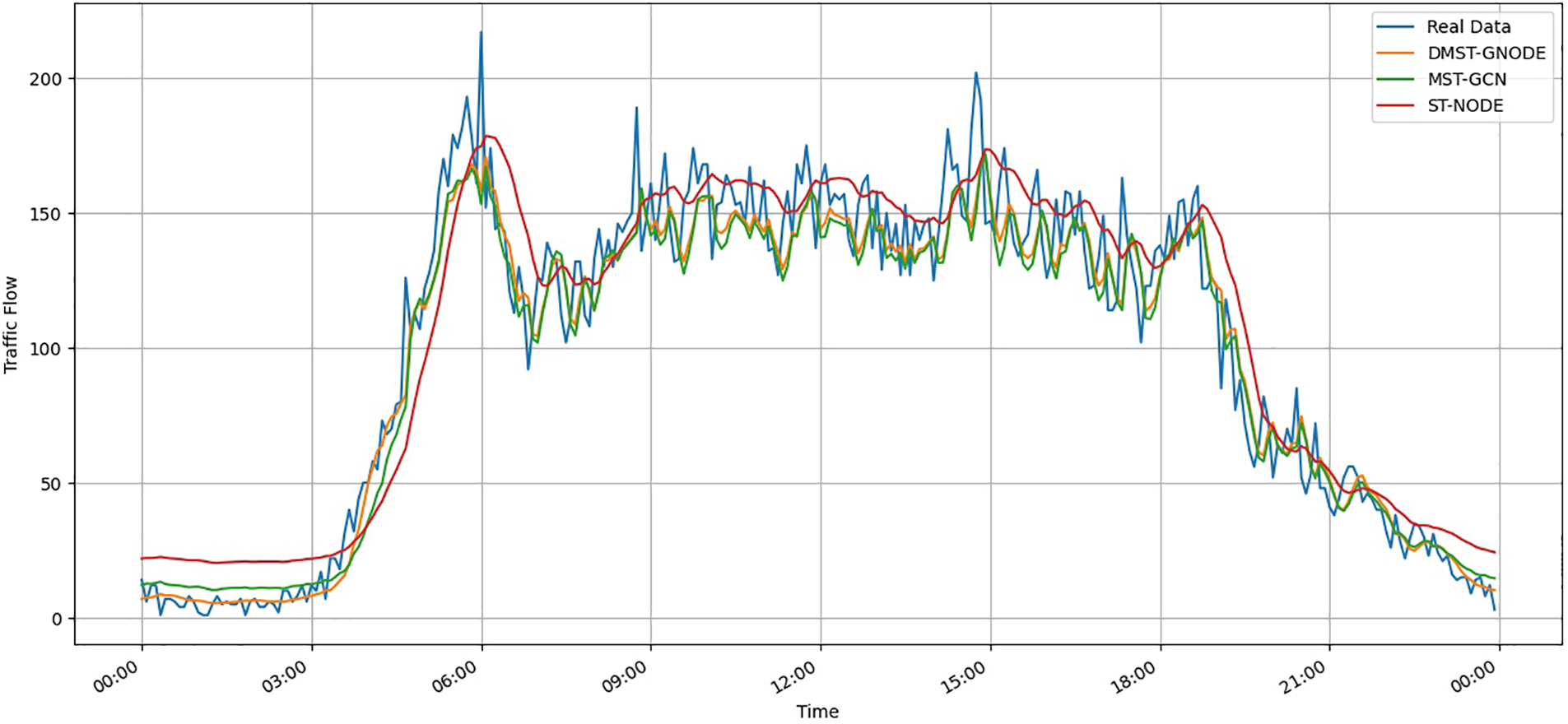
Figure 15: Visualisation of 20-min predictions for Node 13

Figure 16: Visualisation of 20-min predictions of DMST-GNODE

Finally, our analysis of how key parameters affect a model’s performance offers essential guidance for fine-tuning models for various applications. Effective data normalisation strategies address data imbalances, enhancing predictive accuracy and stability. Fine-tuning these strategies by implementing normalisation techniques that adjust for imbalanced data distributions can significantly improve model performance. In multi-graph construction, each graph captures different spatial semantics: the geographic graph uses physical connectivity, the influential graph is based on historical statistical influence, and the elastic graph dynamically learns inherent relationships. Experimenting with various graph construction techniques, such as using semantic adjacency matrices to account for contextually similar nodes, can capture more relevant spatial relationships. Temporal convolution, including stages like GLU, is crucial for capturing dynamic temporal relationships in traffic data, essential for accurate traffic pattern predictions. Adjusting the depth and dilation rates of temporal convolutional layers enables the model to capture both short-term and long-term dependencies. Incorporating external features, such as weather conditions and calendar data, enhances the model’s ability to account for factors influencing traffic flow. Tailoring these features based on the application context–such as including weather data, holidays, and special events for traffic prediction–further improves model robustness. Optimising model architecture involves experimenting with the number of layers and incorporating residual connections to mitigate over-smoothing, while utilising ODE solvers to model continuous dynamic systems. Finally, fine-tuning model training parameters, including the number of epochs, learning rate, and convolution kernel sizes, through hyper-parameter tuning techniques like grid search or Bayesian optimisation, can optimise model convergence and overall performance.

7  Conclusions

In summary, we introduced the DMST-GNODE technique to enhance the efficacy of ST-GCN in forecasting traffic flow. Our assessment compared its effectiveness with both baseline models and conventional approaches. Through experimental analysis on a multiple datasets, we consistently found that the integration of a multi-graph network and ODE yielded superior performance compared to baseline models and traditional machine learning methods across various prediction time-frames. These results underscore the improved overall performance and higher accuracy of the DMST-GNODE model in comparison to leading contemporary models.

However, several limitations warrant discussion for future research and practical implementations: (1) The framework requires multiple tensor operations that scale with the number of nodes and edges in the graph. Each temporal convolutional block within the DMST-GNODE model involves several layers of computation, contributing to the overall complexity. The use of dilated convolutions and residual connections, although beneficial for capturing long-term dependencies, adds to the computational burden due to the increased number of parameters and the necessity for back-propagation through time; (2) The data used for network-wide traffic flow prediction is highly imbalanced, with a long-tail distribution, which leads to large predictive errors at these critical points; (3) The elastic graph, which captures dynamic inherent semantics through self-learning, needs periodic retraining to maintain accuracy. This requirement for continuous updates can be resource-intensive and requires robust infrastructure for ongoing data collection and processing; (4) The sensitivity of the model to various parameters highlights the need for robust parameter tuning methods. Automated hyper-parameter optimisation techniques could be explored to streamline this process and enhance model performance. (5) Finally, the DMST-GNODE model captures temporal dynamics across multiple graphs; however, it does not inherently enforce time-reversal symmetry like TANGO [66], which may limit its accuracy in certain scenarios. Nevertheless, DMST-GNODE remains a feasible option and could enhance the modelling of complex systems, particularly where time-reversal symmetry and dynamic multi-agent interactions are crucial.

Addressing these limitations through future research efforts will be essential to further improve the efficacy and applicability of DMST-GNODE model, ultimately contributing to more efficient and ITS.

Acknowledgement: The authors—P.P. (pongsakon.p@rumail.ru.ac.th), W.S.-d. (weerapan.s@rumail.ru.ac.th), M.K. (marisa.k@rumail.ru.ac.th), W.S. (weerawat.s@rumail.ru.ac.th), and A.A. (aphirak.apt@gmail.com) would like to thank you for the financial support of this research through Ramkhamhaeng University and the Intelligent Transport System (ITS) for actual datasets acquired from traffic monitoring in Bangkok (BKK), Thailand.

Funding Statement: The authors would like to thank you for the financial support of this research through Ramkhamhaeng University, without a specific grant number.

Author Contributions: Conceptualization, Pongsakon Promsawat, Weerapan Sae-dan, Marisa Kaewsuwan, Weerawat Sudsutad, and Aphirak Aphithana; methodology, Pongsakon Promsawat, Weerapan Sae-dan, Marisa Kaewsuwan, Weerawat Sudsutad, and Aphirak Aphithana; software, Pongsakon Promsawat, and Weerapan Sae-dan; validation, Pongsakon Promsawat, and Weerapan Sae-dan; formal analysis, Pongsakon Promsawat, Weerapan Sae-dan, Marisa Kaewsuwan, Weerawat Sudsutad, and Aphirak Aphithana; investigation, Pongsakon Promsawat, and Weerapan Sae-dan; resources, Pongsakon Promsawat, and Weerapan Sae-dan; data curation, Pongsakon Promsawat, and Weerapan Sae-dan; writing—original draft preparation, Pongsakon Promsawat, Weerapan Sae-dan, Marisa Kaewsuwan, Weerawat Sudsutad, and Aphirak Aphithana; writing—review and editing, Pongsakon Promsawat, Weerapan Sae-dan, Marisa Kaewsuwan, Weerawat Sudsutad, and Aphirak Aphithana; visualization, Pongsakon Promsawat, and Weerapan Sae-dan; supervision, Weerapan Sae-dan; project administration, Pongsakon Promsawat, and Weerapan Sae-dan; funding acquisition, Pongsakon Promsawat. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All traffic flow datasets were collected from the Intelligent Transport System (ITS) in Thailand.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1Intelligent Transport System (ITS) in Thailand.

References

1. Guo XJ, Zhu Q. A traffic flow forecasting model based on BP neural network. In: 2009 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS2009; Shenzhen, China; vol. 3, p. 311–4. doi:10.1109/PEITS.2009.5406865. [Google Scholar] [CrossRef]

2. Damadam S, Zourbakhsh M, Javidan R, Faroughi A. An intelligent IoT based traffic light management system: deep reinforcement learning. Smart Cities. 2022;5(4):1293–311. doi:10.3390/smartcities5040066. [Google Scholar] [CrossRef]

3. Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs. Adv Neural Inf Process Syst. 2017;30:1024–34. doi:10.1016/j.heliyon.2024.e31873. [Google Scholar] [CrossRef]

4. Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:16090290. 2016. [Google Scholar]

5. Long Q, Jin Y, Song G, Li Y, Lin W. Graph structural-topic neural network. In: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020; CA, USA; p. 1065–73. doi:10.1145/3394486.3403150. [Google Scholar] [CrossRef]

6. Long Q, Wang Y, Du L, Song G, Jin Y, Lin W. Hierarchical community structure preserving network embedding: a subspace approach. In: Proceedings of the 28th ACM International Conference on Information and Knowledge Management, 2019; Beijing, China; p. 409–18. doi:10.1145/3357384.3357947. [Google Scholar] [CrossRef]

7. Yu B, Yin H, Zhu Z. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting. arXiv preprint arXiv:170904875. 2017. [Google Scholar]

8. Li Y, Yu R, Shahabi C, Liu Y. Diffusion convolutional recurrent neural network: data-driven traffic forecasting. arXiv preprint arXiv:170701926. 2017. [Google Scholar]

9. Pan Z, Liang Y, Wang W, Yu Y, Zheng Y, Zhang J. Urban traffic prediction from spatio-temporal data using deep meta learning. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2019; Anchorage, AK, USA; p. 1720–30. doi:10.1145/3292500.3330884. [Google Scholar] [CrossRef]

10. Zhao L, Song Y, Zhang C, Liu Y, Wang P, Lin T, et al. T-GCN: a temporal graph convolutional network for traffic prediction. IEEE Trans Intell Transp Syst. 2019;21(9):3848–58. doi:10.1109/TITS.2019.2935152. [Google Scholar] [CrossRef]

11. Fang S, Zhang Q, Meng G, Xiang S, Pan C. GSTNet: global spatial-temporal network for traffic flow prediction. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI-192019; p. 2286–93. doi:10.24963/ijcai.2019/317. [Google Scholar] [CrossRef]

12. Zhang Q, Chang J, Meng G, Xiang S, Pan C. Spatio-temporal graph structure learning for traffic forecasting. Proc AAAI Conf Artif Intell. 2020;34:1177–85. doi:10.1609/aaai.v34i01.5470. [Google Scholar] [CrossRef]

13. Li Q, Han Z, Wu XM. Deeper insights into graph convolutional networks for semi-supervised learning. Proc AAAI Conf Artif Intell. 2018;32(1). doi:10.1609/aaai.v32i1.11604. [Google Scholar] [CrossRef]

14. Zhou J, Cui G, Hu S, Zhang Z, Yang C, Liu Z, et al. Graph neural networks: a review of methods and applications. AI Open. 2020;1:57–81. doi:10.1016/j.aiopen.2021.01.001. [Google Scholar] [CrossRef]

15. Chen RT, Rubanova Y, Bettencourt J, Duvenaud DK. Neural ordinary differential equations. Adv Neural Inf Process Syst. 2018;31:6571–83 [Google Scholar]

16. Xhonneux LP, Qu M, Tang J. Continuous graph neural networks. In: International Conference on Machine Learning, 2020; San Francisco, CA, USA: PMLR; p. 10432–41. doi:10.48550/arXiv.1912.00967. [Google Scholar] [CrossRef]

17. Choosakun A, Chaiittipornwong Y, Yeom C. Development of the cooperative intelligent transport system in Thailand: a prospective approach. Infrastructures. 2021;6(3):36. doi:10.3390/infrastructures6030036. [Google Scholar] [CrossRef]

18. Suwardo, Madzlan N, Ibrahim K. Arima models for bus travel time prediction. 2010. Available from: https://api.semanticscholar.org/CorpusID:14520621. [Accessed 2024]. [Google Scholar]

19. Zhang L, Liu Q, Yang W, Wei N, Dong D. An improved k-nearest neighbor model for short-term traffic flow prediction. Proc Soc Behav Sci. 2013;96:653–62. doi:10.1016/j.sbspro.2013.08.076. [Google Scholar] [CrossRef]

20. Valente JM, Maldonado S. SVR-FFS: a novel forward feature selection approach for high-frequency time series forecasting using support vector regression. Expert Syst Appl. 2020;160:113729. doi:10.1016/j.eswa.2020.113729. [Google Scholar] [CrossRef]

21. Jeong YS, Byon YJ, Castro-Neto MM, Easa SM. Supervised weighting-online learning algorithm for short-term traffic flow prediction. IEEE Trans Intell Transp Syst. 2013;14(4):1700–7. doi:10.1109/TITS.2013.2267735. [Google Scholar] [CrossRef]

22. Van Lint J, Van Hinsbergen C. Short-term traffic and travel time prediction models. Artif Intell Appl Crit Transp Issues. 2012;22(1):22–41. [Google Scholar]

23. Williams BM, Hoel LA. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results. J Transp Eng. 2003;129(6):664–72. doi:10.1061/(ASCE)0733-947X(2003)129:6(664). [Google Scholar] [CrossRef]

24. Shi X, Chen Z, Wang H, Yeung DY, Wong WK, Wc Woo. Convolutional LSTM network: a machine learning approach for precipitation nowcasting. Adv Neural Inf Process Syst. 2015;28:802–10 [Google Scholar]

25. Zhang J, Zheng Y, Qi D. Deep spatio-temporal residual networks for citywide crowd flows prediction. Proc AAAI Conf Artif Intell. 2017;31(1). doi:10.1609/aaai.v31i1.10735. [Google Scholar] [CrossRef]

26. Smith BL, Demetsky MJ. Traffic flow forecasting: comparison of modeling approaches. J Transp Eng. 1997;123(4):261–6. doi:10.1061/(ASCE)0733-947X(1997)123:4(261). [Google Scholar] [CrossRef]

27. Wu T, Xie K, Song G, Hu C. A multiple SVR approach with time lags for traffic flow prediction. In: 2008 11th International IEEE Conference on Intelligent Transportation Systems, 2008; Beijing, China; p. 228–33. doi:10.1109/ITSC.2008.4732663. [Google Scholar] [CrossRef]

28. Chowdhury D, Santen L, Schadschneider A. Statistical physics of vehicular traffic and some related systems. Phys Rep. 2000;329(4–6):199–329. doi:10.1016/S0370-1573(99)00117-9. [Google Scholar] [CrossRef]

29. Saidallah M, El Fergougui A, Elalaoui AE. A comparative study of urban road traffic simulators. MATEC Web Conf. 2016;81:05002. doi:10.1051/matecconf/20168105002. [Google Scholar] [CrossRef]

30. Wu Z, Pan S, Chen F, Long G, Zhang C, Yu PS. A comprehensive survey on graph neural networks. IEEE Trans Neural Netw Learn Syst. 2019;32:4–24. doi:10.1109/TNNLS.2020.2978386. [Google Scholar] [PubMed] [CrossRef]

31. Zhang Z, Cui P, Zhu W. Deep learning on graphs: a survey. IEEE Trans Knowl Data Eng. 2022;34(1):249–70. doi:10.1109/TKDE.2020.2981333. [Google Scholar] [CrossRef]

32. Jiang W, Luo J. Graph neural network for traffic forecasting: a survey. Expert Syst Appl. 2022;207:117921. doi:10.1016/j.eswa.2022.117921. [Google Scholar] [CrossRef]

33. Jiang W, Zhang L. Geospatial data to images: a deep-learning framework for traffic forecasting. Tsinghua Sci Technol. 2018;24(1):52–64. doi:10.26599/TST.2018.9010033. [Google Scholar] [CrossRef]

34. Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv Neural Inf Process Syst. 2016;29:3844–52. doi:10.48550/arXiv.1606.09375. [Google Scholar] [CrossRef]

35. Velickovic P, Cucurull G, Casanova A, Romero A, Lio P, Bengio Y, et al. Graph attention networks. Stat. 2017;1050(20):10–48550. [Google Scholar]

36. Atwood J, Towsley D. Diffusion-convolutional neural networks. Adv Neural Inf Process Syst. 2016;29:2001–9 [Google Scholar]

37. Van Lint J, Hoogendoorn SP, van Zuylen HJ. Freeway travel time prediction with state-space neural networks: modeling state-space dynamics with recurrent neural networks. Transp Res Rec. 2002;1811(1):30–9. doi:10.3141/1811-04. [Google Scholar] [CrossRef]

38. Chung J, Gulcehre C, Cho K, Bengio Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:14123555. 2014. [Google Scholar]

39. Cui Z, Henrickson K, Ke R, Wang Y. Traffic graph convolutional recurrent neural network: a deep learning framework for network-scale traffic learning and forecasting. IEEE Trans Intell Transp Syst. 2019;21(11):4883–94. doi:10.1109/TITS.2019.2950416. [Google Scholar] [CrossRef]

40. Tian Y, Pan L. Predicting short-term traffic flow by long short-term memory recurrent neural network. In: 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCityChengdu, China, 2015, IEEE; p. 153–8. doi:10.1109/SmartCity.2015.63. [Google Scholar] [CrossRef]

41. Guo K, Hu Y, Qian Z, Liu H, Zhang K, Sun Y, et al. Optimized graph convolution recurrent neural network for traffic prediction. IEEE Trans Intell Transp Syst. 2020;22(2):1138–49. doi:10.1109/TITS.2019.2963722. [Google Scholar] [CrossRef]

42. Bai J, Zhu J, Song Y, Zhao L, Hou Z, Du R, et al. A3T-GCN: attention temporal graph convolutional network for traffic forecasting. ISPRS Int J Geo Inf. 2021;10(7):485. doi:10.3390/ijgi10070485. [Google Scholar] [CrossRef]

43. Zhang Y, Xu S, Zhang L, Jiang W, Alam S, Xue D. Short-term multi-step-ahead sector-based traffic flow prediction based on the attention-enhanced graph convolutional LSTM network (AGC-LSTM). Neural Comput Appl. 2024;31:1–20. doi:10.1007/s00521-024-09827-3. [Google Scholar] [CrossRef]

44. Zhao Y, Luo X, Ju W, Chen C, Hua XS, Zhang M. Dynamic hypergraph structure learning for traffic flow forecasting. In: 2023 IEEE 39th International Conference on Data Engineering (ICDE2023; Anaheim, CA, USA: IEEE; p. 2303–16. doi:10.1109/ICDE55515.2023.00178. [Google Scholar] [CrossRef]

45. Wu Z, Pan S, Long G, Jiang J, Zhang C. Graph wavenet for deep spatial-temporal graph modeling. arXiv preprint arXiv:190600121. 2019. [Google Scholar]

46. Guo S, Lin Y, Feng N, Song C, Wan H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. Proc AAAI Conf Artif Intell. 2019;33:922–9. doi:10.1609/aaai.v33i01.3301922. [Google Scholar] [CrossRef]

47. Zheng C, Fan X, Wang C, Qi J. Gman: a graph multi-attention network for traffic prediction. Proc AAAI Conf Artif Intell. 2020;34:1234–41. doi:10.1609/aaai.v34i01.5477. [Google Scholar] [CrossRef]

48. Guo K, Hu Y, Qian Z, Sun Y, Gao J, Yin B. Dynamic graph convolution network for traffic forecasting based on latent network of Laplace matrix estimation. IEEE Trans Intell Transportation Syst. 2020;23(2):1009–18. doi:10.1109/TITS.2020.3019497. [Google Scholar] [CrossRef]

49. Hu J, Chen L. Multi-attention based spatial-temporal graph convolution networks for traffic flow forecasting. In: 2021 International Joint Conference on Neural Networks (IJCNN2021; Shenzhen, China: IEEE; p. 1–7. doi:10.1109/IJCNN52387.2021.9534054. [Google Scholar] [CrossRef]

50. Liang Y, Zhao Z, Sun L. Dynamic spatiotemporal graph convolutional neural networks for traffic data imputation with complex missing patterns. arXiv preprint arXiv:210908357. 2021. [Google Scholar]

51. Ye J, Zhao J, Ye K, Xu C. How to build a graph-based deep learning architecture in traffic domain: a survey. IEEE Trans Intell Transp Syst. 2020;23(5):3904–24. doi:10.1109/TITS.2020.3043250. [Google Scholar] [CrossRef]

52. Xu K, Li C, Tian Y, Sonobe T, Kawarabayashi K, Jegelka S. Representation learning on graphs with jumping knowledge networks. In: International Conference on Machine Learning, 2018; Stockhelm, Sweden: PMLR; p. 5453–62. [Google Scholar]

53. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016; Las Vegas, NV, USA; p. 770–8. doi:10.1109/CVPR.2016.90. [Google Scholar] [CrossRef]

54. Fey M, Lenssen JE. Fast graph representation learning with PyTorch Geometric. arXiv preprint arXiv:190302428. 2019. [Google Scholar]

55. Fried I. Numerical solution of differential equations. San Diego, CA, USA: Academic Press; 2014. [Google Scholar]

56. Brown PN, Byrne GD, Hindmarsh AC. VODE: a variable-coefficient ODE solver. SIAM J Sci Stat Comput. 1989;10(5):1038–51. doi:10.1137/0910062. [Google Scholar] [CrossRef]

57. Ascher UM, Ruuth SJ, Spiteri RJ. Implicit-explicit Runge-Kutta methods for time-dependent partial differential equations. Appl Numer Math. 1997;25(2–3):151–67. doi:10.1016/S0168-9274(97)00056-1. [Google Scholar] [CrossRef]

58. Ding W, Zhang T, Wang J, Zhao Z. Multi-graph spatio-temporal graph convolutional network for traffic flow prediction. arXiv preprint arXiv:230805601.2023. [Google Scholar]

59. Zhuang J, Dvornek N, Li X, Duncan JS. Ordinary differential equations on graph networks. 2019. http://paperswithcode.com. [Accessed 2024]. [Google Scholar]

60. Sakia RM. The Box-Cox transformation technique: a review. J R Stat Soc Ser D Stat. 1992;41(2):169–78. doi:10.2307/2348250. [Google Scholar] [CrossRef]

61. Hughes-Hallett D, Gleason AM, McCallum WG. Calculus: single and multivariable. Hoboken, NJ, USA: John Wiley & Sons; 2020. [Google Scholar]

62. Taylor B. Methodus incrementorum directa & inversa. London, UK: Inny; 1717. [Google Scholar]

63. Pasolli L, Notarnicola C, Bruzzone L. Multiobjective model selection for non-linear regression techniques. In: 2010 IEEE International Geoscience and Remote Sensing Symposium, 2010; Honolulu, HI, USA: IEEE; p. 268–71. doi:10.1109/IGARSS.2010.5649190. [Google Scholar] [CrossRef]

64. Chicco D, Warrens MJ, Jurman G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput Sci. 2021;7:e623. doi:10.7717/peerj-cs.623. [Google Scholar] [PubMed] [CrossRef]

65. Fang Z, Long Q, Song G, Xie K. Spatial-temporal graph ode networks for traffic flow forecasting. In: Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, 2021, Singapore; p. 364–73. doi:10.1145/3447548.3467430. [Google Scholar] [CrossRef]

66. Huang Z, Zhao W, Gao J, Hu Z, Luo X, Cao Y, et al. TANGO: time-reversal latent GraphODE for multi-agent dynamical systems. arXiv preprint arXiv:231006427. 2023. [Google Scholar]

Appendix A

Proof of Corollary 1: Commencing from Eq. (21), we examine the secondary derivation of 𝒢τ employing derivative principles

d2𝒢(τ)d2τ=d𝒢(τ)dτ×1ln⁡𝒲^+d𝒢(τ)dτ×2ln⁡𝒰+d𝒢(τ)dτ×3ln⁡ℛ.(A1)

Then, by performing integration with respect to τ on both sides of (A1), we have

d𝒢(τ)dτ=𝒢(τ)×1ln⁡𝒲^+𝒢(τ)×2ln⁡𝒰+𝒢(τ)×3ln⁡ℛ+β.(A2)

In order to address the constant β, we combine Eqs. (21) and (A2), it follows that

β=𝒢0×1𝒲^τ+1×2𝒰τ+1×3ℛτ+1−(𝒢(τ)×1ln⁡𝒲^+𝒢(τ)×2ln⁡𝒰+𝒢(τ)×3ln⁡ℛ).(A3)

By approaching the limit as τ tends towards −1, we can readily ascertain that β equals 𝒢0. Consequently, the proof is completed. ■

Proof of Corollary 2: Let

𝒢⊛(τ)=𝒢(τ)×1e(𝒲^−1)τ×2e(𝒰−1)τ×3e(ℛ−1)τ.(A4)

Subsequently, it follows that

d𝒢⊛(τ)dτ=𝒢0×1e(𝒲^−1)τ×2e(𝒰−1)τ×3e(ℛ−1)τ,(A5)

and this steps from Eq. (23). By integrating Eq. (A4) on both sides, we arrive at the subsequent outcome.

𝒢⊛(τ)=𝒢0⊛+∫0τ𝒢0×1e(𝒲^−1)κ×2e(𝒰−1)κ×3e(ℛ−1)φdκ.(A6)

Therefore, 𝒢(τ) can be expressed

𝒢(τ)=𝒢(τ)×1e(𝒲^−1)τ×2e(𝒰−1)τ×3e(ℛ−1)τ+∫0τ𝒢(τ)×1e(𝒲^−1)(τ−κ)×2e(𝒰−1)(τ−κ)×3e(ℛ−1)(τ−κ)dκ.(A7)

The proof is completed. ■