Solid Waste Management: A MADM Approach Using Fuzzy Parameterized Possibility Single-Valued Neutrosophic Hypersoft Expert Settings

1  Introduction

Significant risks to human well-being are associated with the economy, society, and environment posed by the fast urban population growth. The buildup of material waste and the challenge of locating appropriate sites for its management and disposal rank among the most urgent problems. Numerous issues, including a lack of space, poor infrastructure, and the environmental risks associated with inappropriate waste management, exacerbate this issue. To maintain sustainable urban development and the well-being of the populace and ecosystem, these issues require immediate attention [1,2]. The problem of solid waste management, which is commonly perceived as a multi-criteria decision-making (MCDM) problem [3,4], entails assessing multiple criteria to determine the best possible solutions. However, it is better to approach it as a multi-attribute decision-making (MADM) problem because of the complexity that multiple parameters and sub-parameters introduce. This enables a more methodical analysis that concentrates on particular characteristics that influence the results of decisions. Prioritizing features, balancing economic, environmental, and social factors, and incorporating stakeholder preferences are all important issues to take into consideration in this situation as they are essential to making wise decisions [5,6]. The main research challenges are (a) how to address expert concerns about approximating different options, (b) how to deal with the inherent ambiguity of attributes and sub-attributes, and (c) how to support experts in freely expressing their opinions, even when those opinions are somewhat vague. Fuzzy parameterization and possibility-graded settings are crucial tools for addressing these problems. These ideas offer a methodical approach to handling expert subjectivity and uncertainty in decision-making. The main objective of the study is to integrate fuzzy set-based numerical frameworks to address these research questions, providing a mathematical approach to expert judgment and model ambiguity. To give readers a better understanding of the suggested method, this section also provides an overview of the theoretical methodology and addresses the motivational factors and background of the study. For researchers, coping with informative ambiguity and uncertainty has been a critical issue. However, various structures, such as the single-valued neutrosophic set (SV-NS) suggested by Wang et al. [7], have been designed to handle this kind of imprecision and incompleteness. The SV-NS is a unique application of the neutrosophic set (NS) [8], allowing it to be used in a variety of academic disciplines. Although it requires more processing than established structures [9–11] its advantages, such as flexibility and dependability, set it apart. The three main parts true, indeterminate, and false belongings grades are operators that take the range [0, 1] as a co-domain and the set of items under inspection as a domain. These parts are free as opposed to the aforementioned structures, and their sum must fall inside the range [0, 3]. There have been numerous studies on SV-NS reported up to this point. However, it is important to note the research done by the researchers [12–15], about the preparations of various measures and their use in different problems. Biswas et al. [16] have proposed a novel way for different techniques by using the various operations of SV-NS. Farid et al. [17,18] have covered usages of decision-related issues utilizing the aggregation operators of SV-NS. With time, it has been noticed that there are some real-world circumstances where specifications play a crucial role. As a result, the idea of soft sets (SS) [19] was developed to offer a parameterization tool for dealing with such circumstances. Then different structures have been developed by the combination of SS with neutrosophic set to form neutrosophic soft set (NSS) [20] and the single-valued neutrosophic soft set (SV-NSS) [21] are introduced since these two structures are unable to handle circumstances needing an approximate soft setting. By providing lower and upper approximations, Marei [22] applies the SV-NSS concept to rough sets to manage data roughness. Debnath [23] introduced a brand-new idea known as inverse SV-NSS to examine its use in decision-related issues by utilizing its operational advantages. When it came to handling situations when there were numerous expert opinions in a single soft set model, the soft set-like structures that had been developed for single expert opinions entirely broke down. This posed a significant obstacle when making decisions. The concept of a soft expert set (SeS) was provided by Alkhazaleh et al. [24] as a solution to the problem of managing different expert opinions in a model. In actuality, they included the viewpoints of several specialists in the domain set. The opinions of the experts have been employed to manage the uncertainty in the parameters. These viewpoints have been interpreted with precision. Then Alkhazaleh et al. [25] also used this arrangement in a fuzzy environment by introducing a fuzzy soft expert set. This was the combination of a fuzzy and soft expert environment. In 2015, Broumi et al. [26] made use of the combination by developing the intuitionistic fuzzy soft expert set. After this Şahin et al. [27] developed the structure of the neutrosophic expert set. The soft set cannot deal with the domain having multiple arguments because it is only for dealing with a domain having a single argument. As a result, a new technique of function with the domain of multiple arguments, which is used to create the hypersoft set (HSS) [28] is suggested. These functions regard the order pairing of disjoint subclasses with attribute values as its domain and approximate alternatives. Kamaci [29] investigated the creation of a new combination of HSS and rough set associated procedures. The different researchers explored the different methods and aggregation operations in a neutrosophic HSS context [30,31]. Saqlain et al. [32] suggested some new structures by using the combination of SV-NS and HSS. Ihsan et al. [33,34] presented and applied concepts of neutrosophic soft sets with the combination of hypersoft expert sets (HSES) [35] in decision-related issues in the direction of authorizing the multiple crucial judgments of specialists. The contributions of researchers [36,37] concerning the use of aim-situation systems, combination methods of uncertain situations, and fuzzy forecasting methods are important and worthy of mention. To deal with the informational hesitant temperament, the idea of possibility degree [38] has been proposed as an alternative to the theory of probability. According to Zadeh [39], the fuzzy set (FS)’s various properties serve as the basis for the idea of possibility degree. Fedrizzi [40] managed numerous optimization modules in a mixed setting of FSs and the idea of possibility degree. The emphasis on the amplifying of distinct characteristics of these ideas was made by Dubois et al. [41]. Many academics are quite interested in the idea of possibility degree for measuring approximation-based uncertainty. To evaluate the study limitations and inevitable nature of the provided work, a few pertinent types of literature are evaluated in the following paragraphs. Fuzzy SS and the idea of possibility degree were merged by Alkhazaleh et al. [42] to define possibility fuzzy SS, where each approximation is given a specific possibility grade. The purpose of this grade is to evaluate how precise approximations are. They also talked about how to use it based on how similarity measures are created. The possibility intuitionistic fuzzy soft set was established by Bashir et al. [43] by expanding the idea of a possibility fuzzy soft set. By utilizing the suggested similarity measures between them, Karaaslan [44] contributed to the construction of the possible NSS and explained in different situations. In the literature, Zhao et al. [45] made a new combination of the idea of possibility degree with different structures of neutrosophic sets. They put up an algorithm by using the different operations of this new structure and used it for different purposes. Rahman et al. [46,47] developed some new structures of the idea of possibility degree. Their aggregation processes and similarity metrics were described. They also used the suggested ideas for decision-related issues like recognition and medical diagnosis. It has been noted that selectors may not always be certain of the attributes to select on a preference basis while making decisions. Put differently, they don’t think the settings were chosen with certainty. Fuzzy parameterization, which is intended to evaluate the unsure attitude of decision-makers towards the choice of parameters, is used to manage this scenario. This evaluation is carried out by computing their approximations once a certain fuzzy membership grade has been attached to the parameters. Fuzzy parameterization was employed in a fuzzy soft set context by researchers [48–50] leading to the development of the fuzzy parameterized fuzzy soft set concepts. They talked about the applications for making decisions based on these put-up ideas. This concept was developed by Sulukan et al. [51] to form a new hybrid of fuzzy parameterization and the decision-related issues were covered based on performance values. In Deli’s [52] discussion of several models employing these unsure attributes, he linked the concepts of parameterization and HSS. Qu et al. [53] addressed the resolution of several problems characterized by uncertainty, focusing on approaches that manage ambiguous and imprecise information. The contributions of scholars [54–56] are worth noting regarding the quantification of uncertainties, and indeterminacies.

The greatest environmental change caused by the massive increase in human population is urbanization, which has a detrimental effect on the environment’s capacity to retain its natural stability. As per reports, a substantial quantity of solid waste, which is garbage collected from farms, businesses, municipalities, and other hazardous sources, is generated in every urban area due to various activities conducted by humans and other related species. For municipal administrations, figuring out how to handle and dispose of this much solid waste has proven to be a challenging task. The 3R (Reduce, Reuse, Recycle) method cannot, even when applied for this purpose, get rid of solid waste, including different kinds of materials that fall under specific categories. This specific kind of solid waste is typically handled by land-filling, incineration, and composting, among other well-known methods. But installing all these systems also means considering a lot of other factors, some of which might be social, political, economic, ecological, or environmental. Solid waste can contain a significant amount of organic compounds that can be used to create premium fertilizer for exceptional agricultural yields because it includes both industrial and agricultural waste. Similarly, setting up incinerators is a great way to generate energy, and you can dispose of the waste they generate by putting it in the appropriate type of landfill. Solid waste management and disposal have become recognized as intricate, multidisciplinary issues that need to be taken into account from social, technical, economic, and environmental perspectives.

Since several criteria and sub-criteria are involved, selecting suitable locations is also thought to be an essential step in putting any solid waste settlement techniques (SWST) into place (i.e., which are described in Fig. 1). Price, consistency, practicality, air problem mechanism, and its related factors were taken into consideration by Ekmekçioǧlu et al. [57] and Yildirim et al. [58] while determining the best location for solid waste management.

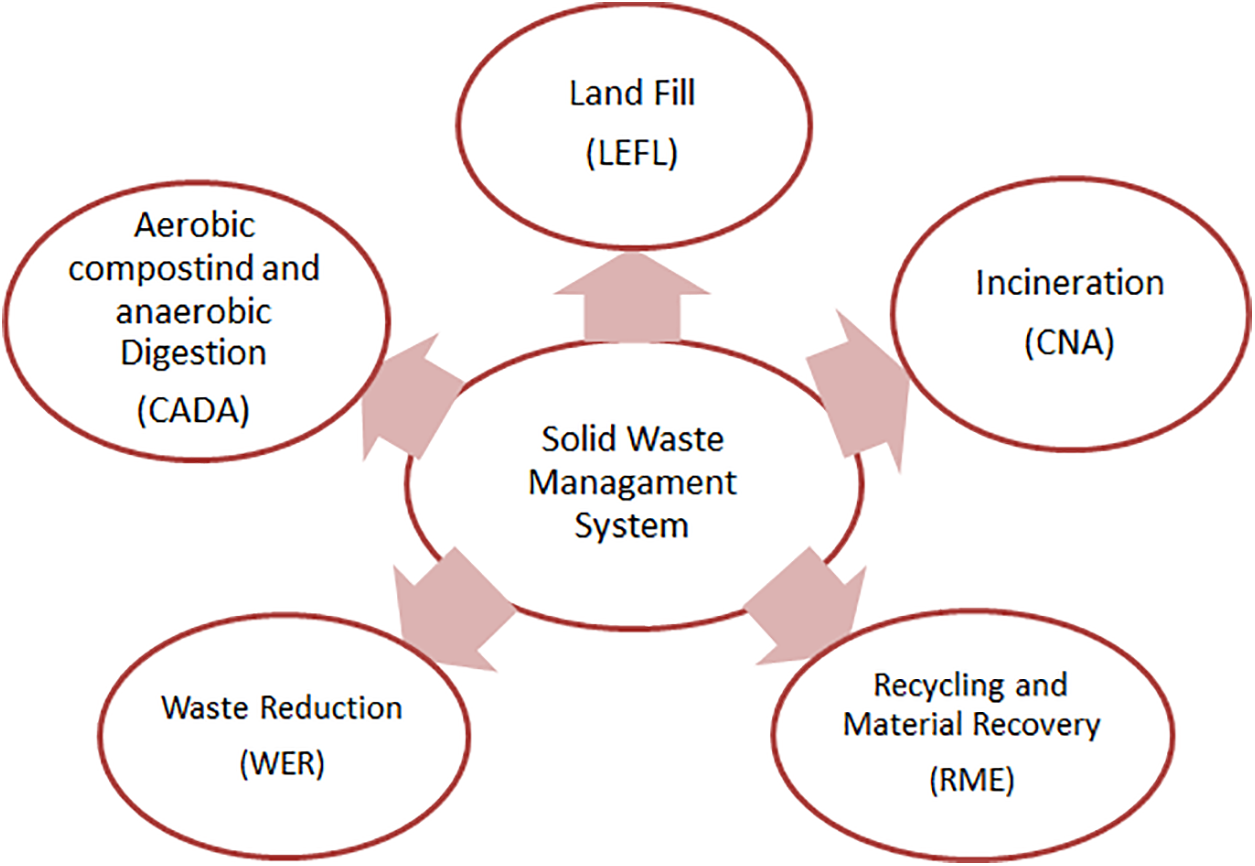
Figure 1: Solid waste management system

Since the participation of numerous attributes and sub-attributes, they have viewed the solid waste management challenge as an MCDM. Different techniques have been employed in many research studies to date to solve various environmental issues. In a Pythagorean hesitant fuzzy environment, researchers like using various techniques, Ghosh et al. [59] solved a multi-purpose material mobility issue for solid waste management. Luo et al. [60] used different techniques to evaluate the optimal selection of sites for the installation of an incineration plant. The choice of dump sites was covered by Liu et al. [61] utilizing an integrated strategy involving information skills. By using MADM, a contribution to recycling for environmentally friendly growth was made by Wang et al. [62]. It has been noted that the choice of solid waste site selection attributes and sub-attributes is illogical and vague. As a result, this issue has been covered extensively by authors who used decision-making techniques in contexts resembling fuzzy sets. But more notable and pertinent to this investigation are the studies of Rahimi et al. [63], Liu et al. [64], Mallick [65], Torabi-Kaveh et al. [66], Karasan et al. [67], Ali et al. [68], Hanine et al. [69,70], and Kahraman et al. [71]. To select a suitable solid waste site in uncertain environments, various techniques for decision-making have been applied in these structures. Max-min operators of neutrosophic hypersoft sets have recently been employed by Jafar et al. [72] to choose sites for SWST. A careful examination of the aforementioned research contributions reveals that the subsequent issues cannot be solved together by any analytical framework to solve the solid waste management issue:

(a). Since a typical theoretical approach offers an organized framework for the analysis of complex systems, it is necessary to address parameters and their sub-parametric values simultaneously. Using this method allows for the systematic consideration of interdependencies between parameters and their sub-levels, which facilitates more accurate problem modeling and assessment. This approach ensures a more comprehensive and effective decision-making process by allowing the identification of important factors, the measurement of their effects, and the creation of solutions that account for the intricate relationships between parameters.

(b). Since fuzzy parameterization enables the representation of imprecise information, it is essential for assessing the uncertain and ambiguous nature of multi-argument tuples. Each tuple’s fuzzy membership grade allows for the quantification of the data’s inherent uncertainty and vagueness. With values that are not strictly binary but rather fall within a range that reflects differing degrees of truth or relevance, this approach allows for a more flexible analysis. In situations of uncertainty, fuzzy parameterization enables more accurate modeling and decision-making by offering a nuanced understanding of complex systems.

(c). Since it measures how plausible or feasible these approximations are, the idea of possibility grades is crucial for assessing the degree to which decision-makers approximations are accepted. Rather than giving a definitive answer, possibility grades provide a means to handle uncertainty by assigning values that reflect how likely or possible a given approximation is. This enables more informed and adaptable decision-making in complex and uncertain environments by enabling decision-makers to evaluate and compare various options or solutions based on their potential effectiveness.

(d). A single-valued neutrosophic setting, or a three-dimensional membership function, allows decision-makers to independently express their opinions along various dimensions of analysis, capturing various aspects of the decision-making process. A composite “true grade” reflecting the decisions made by the decision-makers is produced by the function that results from the representation of individual criteria or attributes by each dimension. Because this method takes into account different viewpoints and levels of uncertainty, it can approximate the objects or scenarios being evaluated in a more nuanced manner.

The issue of choosing the solid waste site is a MADM problem, as was earlier mentioned. Thus, if the aforementioned crucial elements are taken into account as a whole, a reliable decision support framework can be created, which ultimately results in the development of a new conceptual framework to satisfy this requirement. The purpose of this study is to present the concepts of ρ^-set, which are fully able to address the previously described issues as one unit. These research’s significant contributions include but are not limited to:

(1). A unique mathematical structure, called ρ^-set, is constructed and characterized to address the potential decision-making concerns related to the degree of possibility, employing a specific degree to parameters, and different settings like SV-NS and hypersoft approximate mapping. By addressing these challenges collectively, it is qualified to aid in the creation of a reliable selecting framework.

(2). By calculating their pertinent fuzzy parameterized grades using the necessary criteria, the inspected attributes and sub-attributes uncertain behaviors are assessed.

(3). A mathematical approach is used to establish the important possibility degrees of alternatives to check the calculation of substitutes related to attributes and sub-attributes depending upon the opinions offered by the experts.

(4). Sanchez’s method, a well-known strategy for making decisions, is altered in the ρ^-set setting.

(5). The ρ^-set aggregates and the modified Sanchez’s approach are combined to create a decision-assisted framework. A strong site selection algorithm is then proposed to control solid waste.

Three main sections comprise the remainder of the paper. To make sure readers are familiar with the fundamental terms used throughout the study, Section 2 offers a review of key terminology and concepts from the pertinent literature. In Section 3, the methodology is presented in detail, including the steps and real-world application of the suggested technique, making it easy to understand how the approach functions. Section 4 presents a discussion of the obtained results, comparison, and sensitivity analysis. Lastly, Section 5 highlights the study’s contributions and possible ramifications while providing a succinct synopsis of the research findings and key conclusions.

2  Fundamental Knowledge

This part attempts to go over a few keywords for a correct comprehension of the study that is being presented. The subsequent parts of the paper represent Θ, ω^, Υ, and Ξ as the initial universe of objects, collection of parameters, collection of experts and their opinions, respectively.

Definition 2.1. [7] Consider three different functions βs,βn, and βi defined from Θ to unit closed interval. These are the representation for membership, non-membership and indeterminate functions respectively. If the condition 0≤βs(ϖ)+βi(ϖ)+βn(ϖ)≤3 is satisfied for ϖ∈Θ. Then a set NSV={ϖ,≺βs(ϖ),βi(ϖ),βn(ϖ)≻ϖ∈Θ} is named as a SV-NS set.

Definition 2.2. [35] If ω^1, ω^2, ω^3,…,ω^n, are sub-attribute-valued non-overlapping collections corresponding n different attributes and let Ω be the cartesian product of ω^1, ω^2, ω^3,…,ω^n, and Π=Ω×Υ×Ξ, then HSES represented by Γ can be defined as Γ={(δ,πΓ)∣δ∈Π} where πΓ:Π→Θ.

3  Materials and Methods

This section provides a quick description of the stages included in the approved methodology.

3.1 Notions of Proposed Theoretical Model, i.e., ρ^-set

This research area aims to characterize and elucidate the basic ideas behind the Λ-set. To help with understanding, illustrative examples will be provided in addition to these concepts.

Definition 3.1. If ω^1, ω^2, ω^3,…, ω^n, are sub-attribute-valued non-overlapping collections corresponding n different attributes and Ω=ω^1×ω^2×ω^3×,…,×ω^n, and Π=ΩF×Υ×Ξ={π1,π2,π3,…πn}, and ΩF={t1/ξ(t1),t2/ξ(t2),t3/ξ(t3),…,tn/ξ(tn)} is a fuzzy set over Ω such that ξ:Ω→[0,1], then a ρ^-set Λ can be stated as: Λ={π,Ψ(π)} with Ψ:Π→(PSVN)Θ defined by

Ψ(π)={(α/η(α),ϑ(π)(α)):α∈Θ;π∈Π}. Thus a ρ^-set Λ can be characterized as

Λ(π)={(π,{(α/η(π)(α),ϑ(π)(α)):α∈Θ}):π∈Π}. Where η:Π→(PSVN)Θ and ϑ:Π→FΘ and the symbols η(π)(α), ϑ(π)(α) represent for the neutrosophic and possibility values of α, respectively.

Example 3.1. Consider the collection of computers as a set of universe Θ={α1,α2,α3,α4}. A commercial bank wants to buy a computer for its use in the office. Bank manager calls an expert committee Υ={e˙1,e˙2} having expertise in computer selection. These experts decide some parameters ω^ = {p1=RAM,p2=ROM} to buy this thing. After the division of the parameters into sub-parameters with different classes such as Ram = {p11=4GB,p12=8GB} and ROM = {p21=32GB,p22=64GB}. Then Ω={t1=(4,32),t2=(4,64),t3=(8,32),t4=(8,64)}. Now Ω×Υ×Ξ={π1=(t1,e˙1,1),π2=(t1,e˙2,1),π3=(t2,e˙1,1),π4=(t2,e˙2,1),π5=(t3,e˙1,1),π6=(t3,e˙2,1),π7=(t4,e˙1,1),π8=(t4,e˙2,1),π9=(t1,e˙1,0),π10=(t1,e˙2,0),π11=(t2,e˙1,0),π12=(t2,e˙2,0),π13=(t3,e˙1,0),π14=(t3,e˙2,0),π15=(t4,e˙1,0),π16=(t4,e˙2,0)}. After the experts opinions, the sub-classes π1=(t1,e˙1,1),π7=(t4,e˙1,1),π14=(t2,e˙2,0),π18=(t4,e˙2,0)} are selected for the further process. Then the ρ^-set can be described as

ψ(t10.3,e˙1,1)={(α1⟨0.2,0.4,0.9⟩,0.3),(α2⟨0.3,0.7,0.8⟩,0.4),(α3⟨0.4,0.5,0.7⟩,0.6),(α4⟨0.5,0.4,0.7⟩,0.2)},ψ(t10.4,e˙1,0)={(α1⟨0.2,0.3,0.9⟩,0.7),(α2⟨0.3,0.4,0.8⟩,0.8),(α3⟨0.4,0.3,0.7⟩,0.5),(α4⟨0.5,0.9,0.7⟩,0.7)},ψ(t20.5,e˙2,1)={(α1⟨0.2,0.8,0.9⟩,0.2),(α2⟨0.3,0.9,0.8⟩,0.3),(α3⟨0.1,0.5,0.9⟩,0.7),(α4⟨0.1,0.7,0.9⟩,0.6)},ψ(t20.6,e˙2,0)={(α1⟨0.1,0.4,0.8⟩,0.1),(α3⟨0.1,0.8,0.2⟩,0.5),(α3⟨0.3,0.4,0.7⟩,0.5),(α7⟨0.5,0.3,0.8⟩,0.3)}.

OrΛ={ψ(t10.3,e˙1,1)={(α1⟨0.2,0.4,0.9⟩,0.3),(α2⟨0.3,0.7,0.8⟩,0.4),(α3⟨0.4,0.5,0.7⟩,0.6),(α4⟨0.5,0.4,0.7⟩,0.2)},ψ(t10.4,e˙1,0)={(α1⟨0.2,0.3,0.9⟩,0.7),(α2⟨0.3,0.4,0.8⟩,0.8),(α3⟨0.4,0.3,0.7⟩,0.5),(α4⟨0.5,0.9,0.7⟩,0.7)},ψ(t20.5,e˙2,1)={(α1⟨0.2,0.8,0.9⟩,0.2),(α2⟨0.3,0.9,0.8⟩,0.3),(α3⟨0.1,0.5,0.9⟩,0.7),(α4⟨0.1,0.7,0.9⟩,0.6)},ψ(t20.6,e˙2,0)={(α1⟨0.1,0.4,0.8⟩,0.1),(α3⟨0.1,0.8,0.2⟩,0.5),(α3⟨0.3,0.4,0.7⟩,0.5),(α7⟨0.5,0.3,0.8⟩,0.3)}}.

In above representation α1⟨0.2,0.4,0.9⟩,0.3, the values 0.2, 0.4, 0.9 have the meaning of true, indeterminate, and false belongings of α1, and the whole representation (α1⟨0.2,0.4,0.9⟩,0.3) gives the meaning of possibility value for the membership level for α1 is the 0.3 (i.e., 30 percent).

3.2 The Choice of Attributes and Their Fuzzy Parameterized Grades (Values)

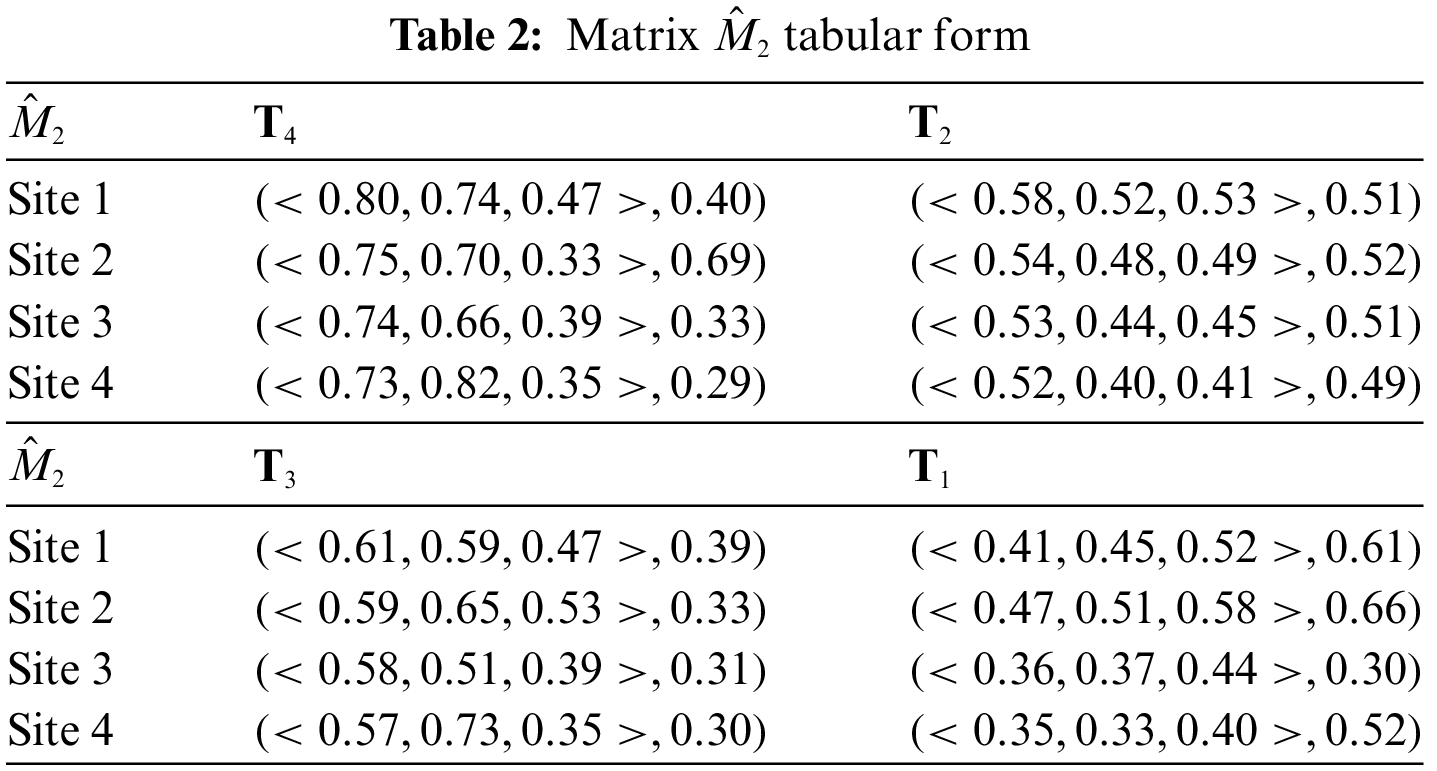
In any MADM problem, the procedure of choosing the characteristic is crucial. As a substitute, a smart technique for the selection of attributes may result in the dependability and flexibility of any MADM-based structure. A few well-known methods of gathering data on the choice of factors required for the estimation of the items to the bottom investigation include group surveys, surveys distributed to residents, in-depth analyses of previous research published in the literature, consultations with pertinent parties and specialists, etc. According to the acknowledged quantitative technique, i.e., the hypersoft expert setup, attributes, and the associated sub-attribute values are required to roughly estimate the assessment of some sites for solid waste governance. This is vital in terms of the significance of the research. The availability of adequate pertinent works makes the “literature review” the most appropriate and approachable source in this study for the choice of grades of parameters that go with them. The values for the qualities and sub-attributes are obtained from Jafar et al. [72] while keeping in mind the research’s slogan. Consequently, we have only considered those characteristics that were determined to be most applicable and essential for MADM-based solid waste governance through peer research to provide a basic structure for MADM-based solid waste administration. By doing this, the computational hassle that results from including the Cartesian product is avoided. The following is a description of the qualities and their operating features:

1.    Economic Values: Numerous elements have a direct bearing on a project’s finance and other economic features. Without considering the project’s associated economic issues, its viability cannot be approved. These elements could consist of land costs, building costs, operational costs, building costs, etc.

2.    Air Quality Index (AQI): It is a crucial measurement tool used to examine and evaluate the air quality in a specific location. Since SWST has a significant impact on air quality, when making decisions about the best SWST and locations for solid waste supervisors, it is crucial to take AQI into account. The AQI levels have been qualitatively categorized by specialists based on linguistic phrases that aid in comprehending the appropriateness of the SWST for solid waste supervisors. Fig. 2 displays the phrases that go along with them.

3.    Distance from Locality: It is yet another crucial element that significantly influences the choice of the location for solid waste management. A distance of fewer than one kilometer is usually not considered acceptable; nevertheless, a gradual increase up to three kilometer raises the acceptability threshold. It has an equal impact on each SWST’s level of appropriateness. Owing to the air pollution caused by Southwest, the locations, which are situated less than a kilometer away from the populace, can facilitate the propagation of various illnesses. On the other hand, locations farther than 3 km away may result in higher carrier costs.

4.    Land Inclination: The area’s slope must be evaluated for the site to manage solid waste. The best case scenario is for the region chosen to be free of slope, but because entirely level lands aren’t always available, inclination up to 9 percent may be compromised. For the majority of SWSTs, it is regarded as the most important geographical feature. Fig. 3 displays the language classifications for land inclination values.

Figure 2: Categories of air quality index

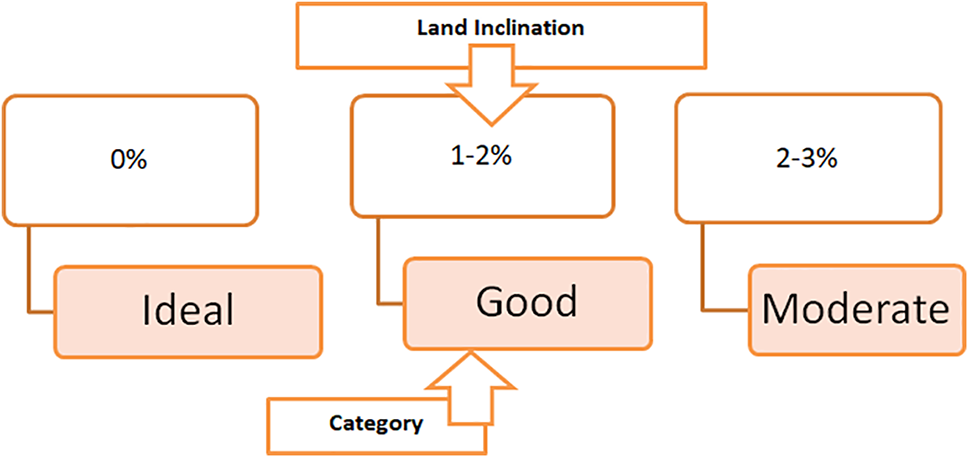
Figure 3: Categories of land inclination

3.3 Modification of Sanchez’s Method

Sanchez’s method, a decision-making strategy covered in [73], is used in this section, with some adjustments, to choose a suitable site for solid waste management using hypothetical values in a ρ^-set setting. The idea of modified Sanchez’s method as discussed by Rahman et al. [74] is also followed due to hypersoft settings. The lack of a tool to link options with sub-characteristics scored pairs in any of the other decision-making approaches results in a computational challenge because complex operators for aggregation must be included. Sanchez’s approach, on the other hand, has less computing complexity because of its simple phases. It connects options, decision-makers’ perspectives, and sub-attribute pairs using fundamental principles that everyone can comprehend, regardless of their level of mathematics experience.

Consider the set of sites as a universe of discourse denoted by as H¨={s1,s2,s3,…,sr} with two more sets of experts Υ and their opinions Ξ={1=agree,0=disagree}. If ω^1, ω^2, ω^3,…,ω^n, are sub-attribute-valued non-overlapping collections corresponding n different attributes and let Ω be the cartesian product of ω^1, ω^2, ω^3,…,ω^n, and Π=Ω×Υ×Ξ={k1,k2,k3,…,kn} be the set of triplets. Let a group of decision-makers be selected for the decision of problem and denoted by D^={d1,d2,d3,…,dm} and the set of SWSTs is represented by Λ^={Ψ^1,Ψ^1,Ψ^1,…,Ψ^k}. The phases of this revised technique are as follows, starting with the core sets’ suppositions:

1.    Construction of two ρ^-sets and their representation in two different matrices M^1=[cij]r×n and M^2=[dij]r×k. The first matrix M^1 is chosen for values of ρ^-set and M^1 is selected for the opinions of decision-makers.

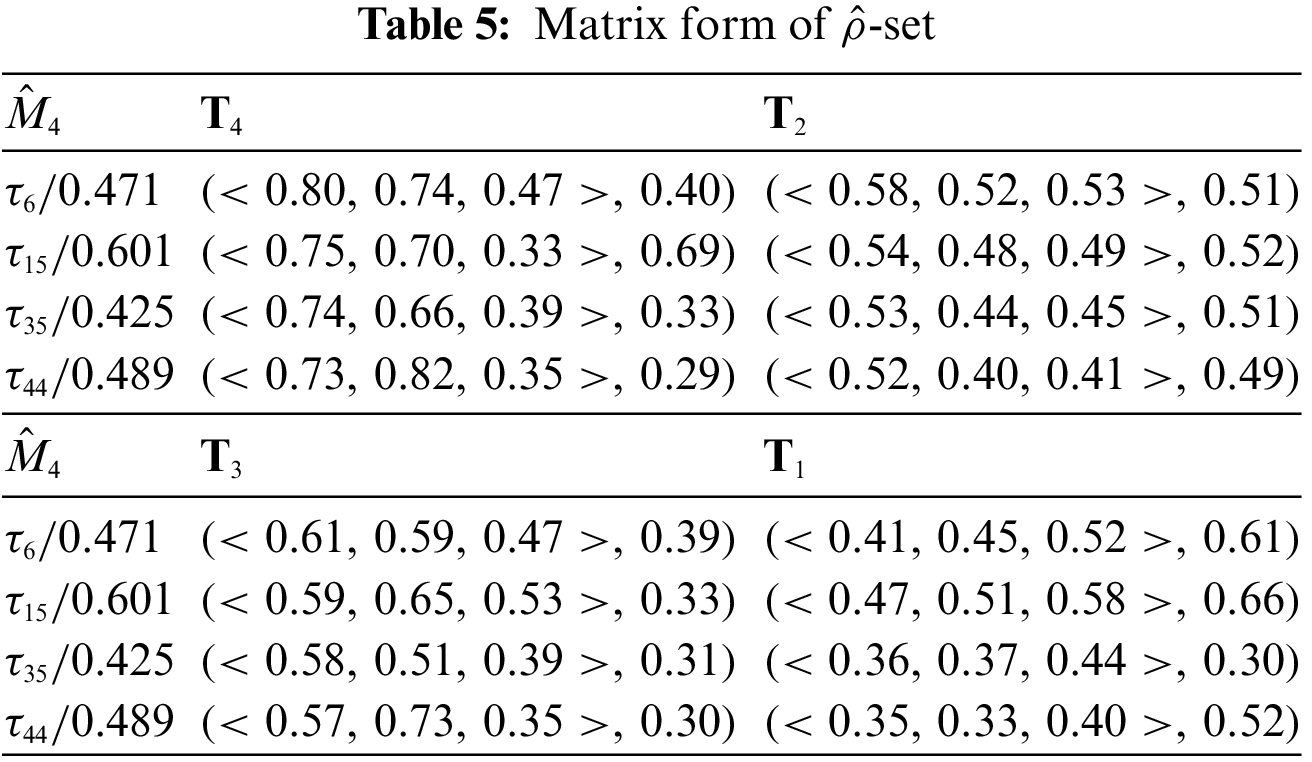
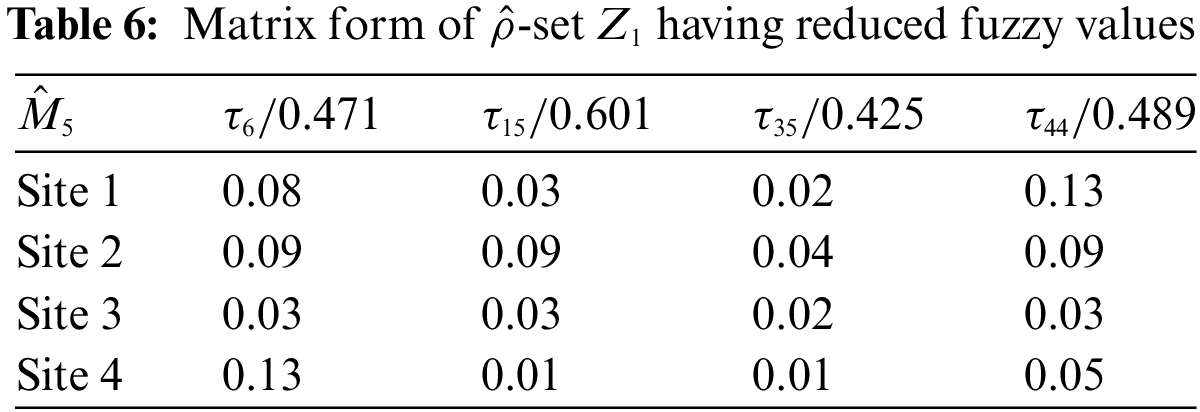
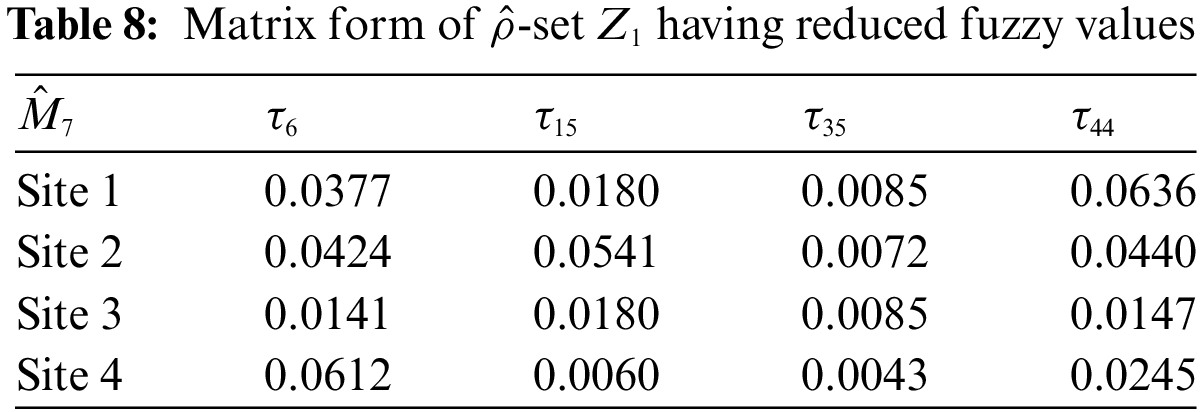
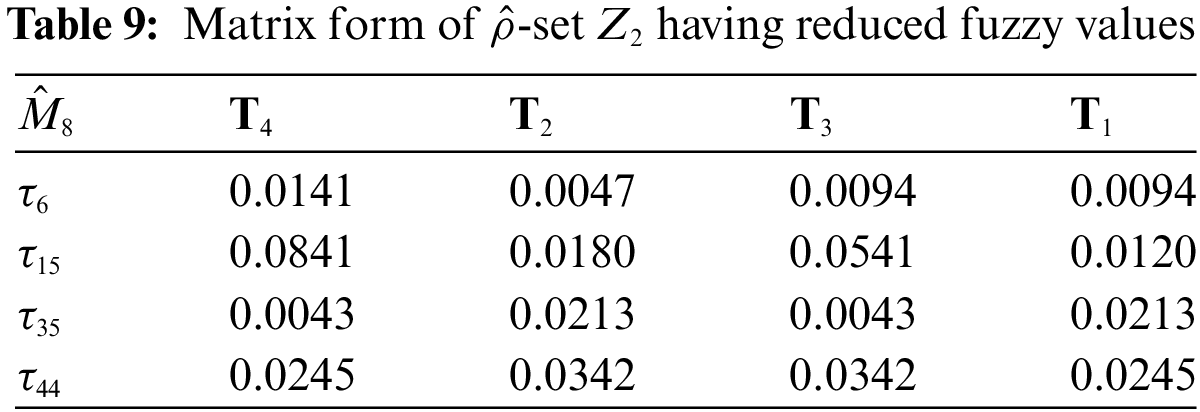
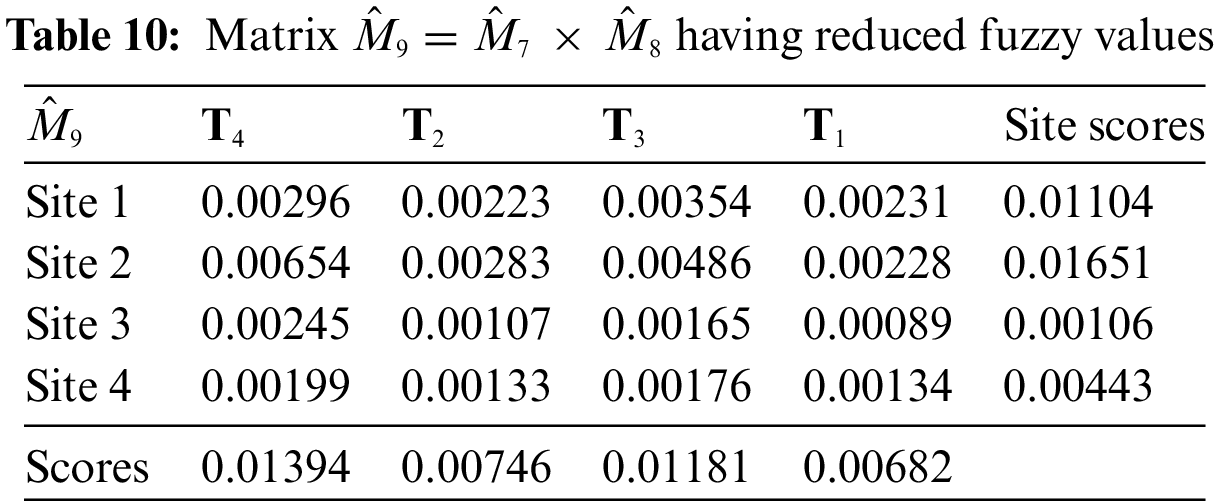
2.    First change the values of possibility single-valued neutrosophic hypersoft expert sets (PSV-NHSES) into reduced fuzzy grades by using any proper numerical method and then put them in two new different matrices M^3, M^4.

3.    Multiplication of fuzzy parameterized grades with each row or column and obtain two new matrices M^5, and M^6.

4.    Find the simple product (product of matrix) of two matrices M^5, and M^6 to get the decision-matrix M^7.

3.4 Criteria for Fuzzy Parameterization

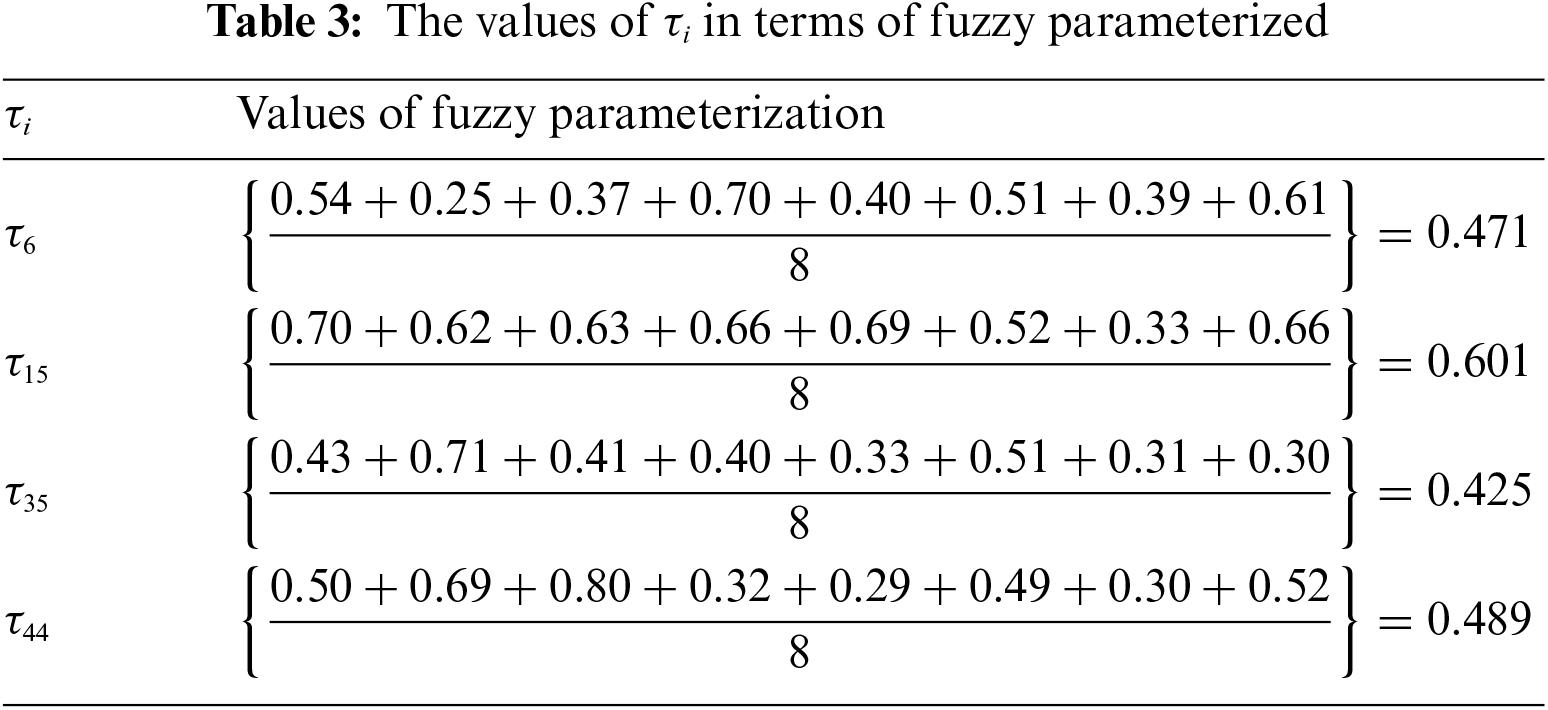
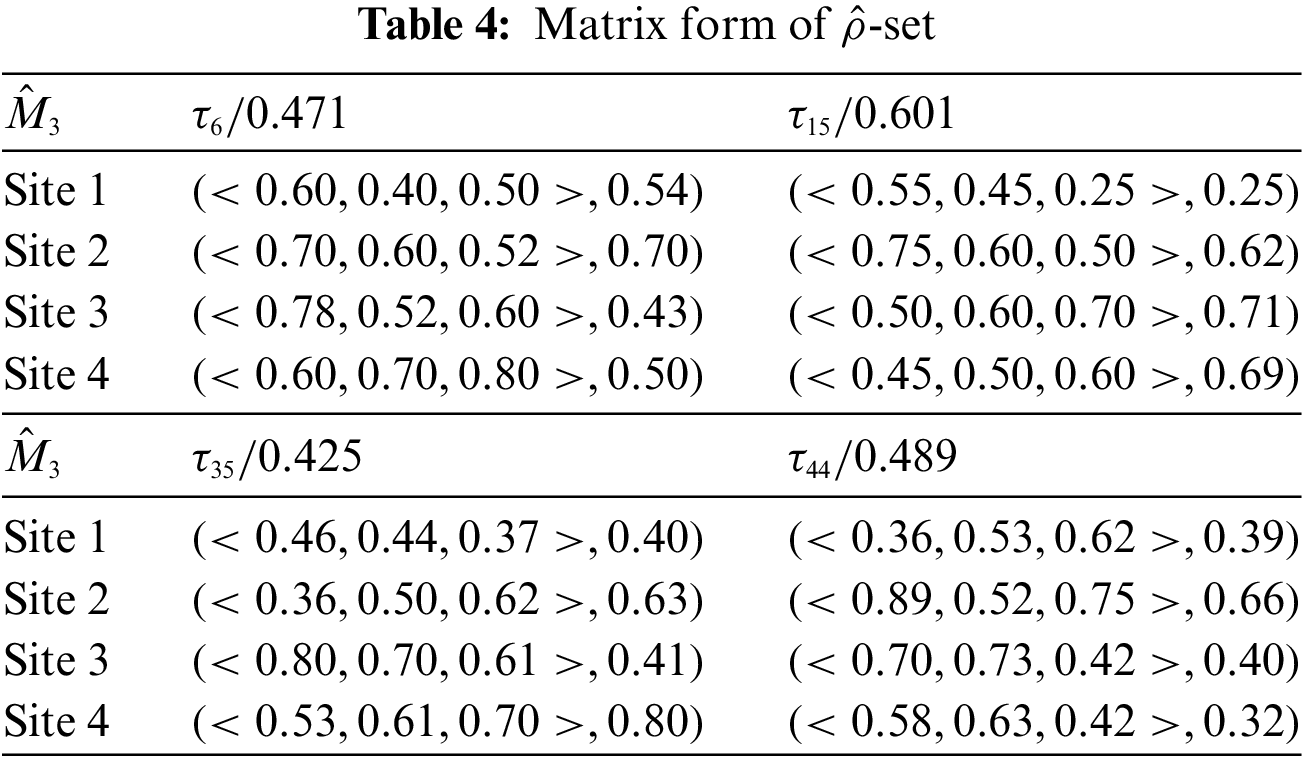
Rahman et al. [74] presented a formula for the calculation of fuzzy parameterized degrees. In this section, we followed that formula with partial modification. Let the decision-makers assigned possibility grades to the approximation of substitutes be

∂={λ1(σ),λ2(σ),λ3(σ),…,λm(σ)}. Then the fuzzy parameterized value of each element σ of Π=Ω×Υ×Ξ can be calculated by using the suitable criteria

χ(σ)=∑i=1mλi(σ)|∂|=λ1(σ)+λ2(σ)+,…,+λm(σ)m.(1)

3.5 Problem Declaration

The environmental problems brought on by the fast rise in population of a particular city X within its authority are of great concern to both the Ministry of Environment and Municipal Corporations. The administration of the Ministry of Environment calls for a combined meeting of the officers from both departments. A committee is established which is comprised of four experts Ei, i=1,2,3,4 from both departments with E1 as convener of the committee. The committee has decided on a few guidelines and sub-guidelines for carrying out the given assignment. Following the attributes and sub-attributes selected, the individuals of the committee are directed to visit different parts of the city to choose a few areas for closer inspection. They are advised to provide their thoughts about the sites and SWSTs together. The E1 has the power to determine potential grades for the evaluation of the level of acceptance of submitted viewpoints.

3.6 Suggested Algorithm

Now, a recommended algorithm is made to carry out the committee’s work. This algorithm is the modified form of an algorithm proposed by Rahman et al. [74] and it incorporates the MADM, the modified Sanchez’s approach, and the ρ^-set configuration.

The flowchart depicting Algorithm’s brief description is shown in Fig. 4.

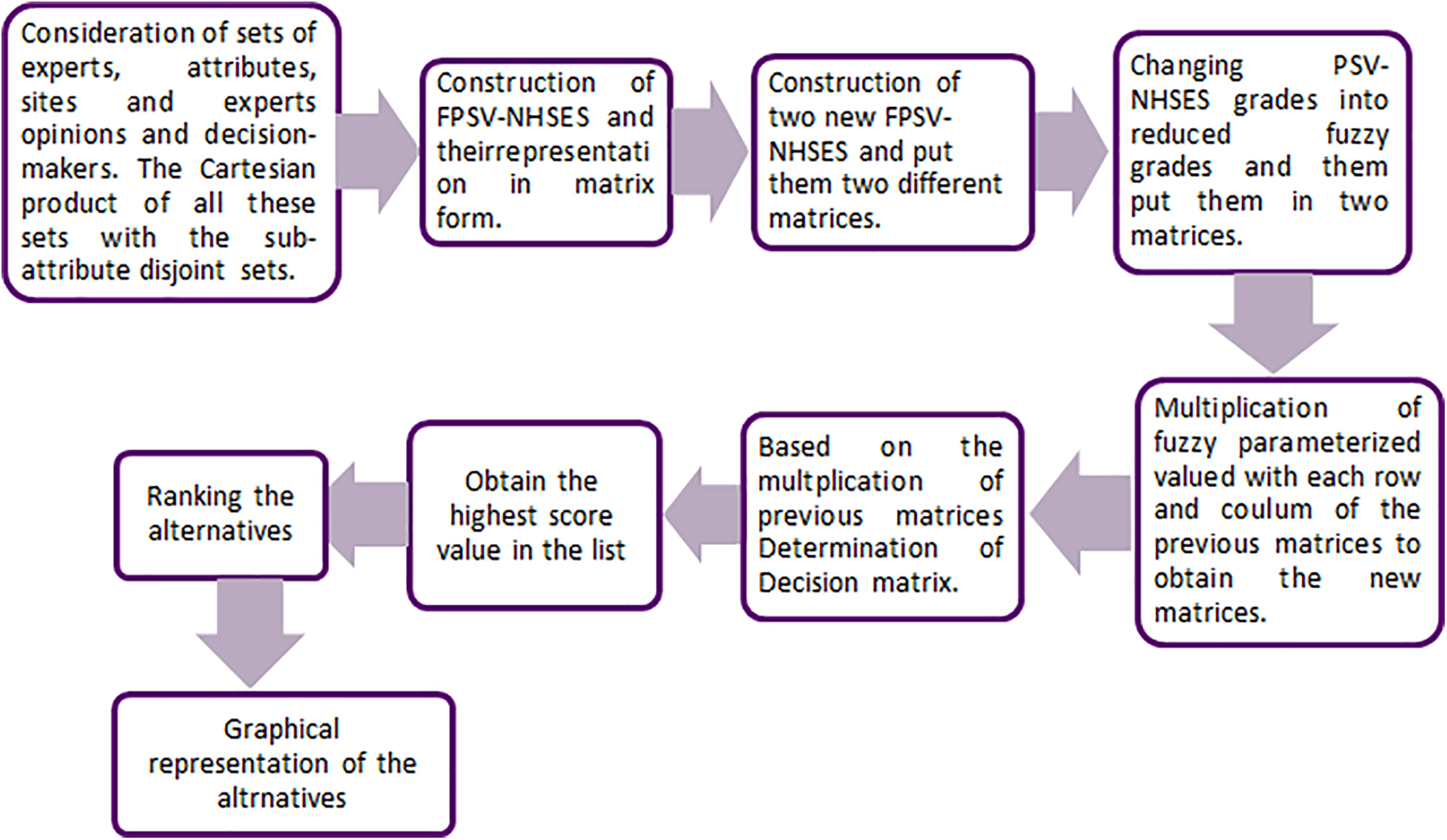
Figure 4: Flow chart of algorithm

3.7 Case Study: Explanation of Proposed Algorithm

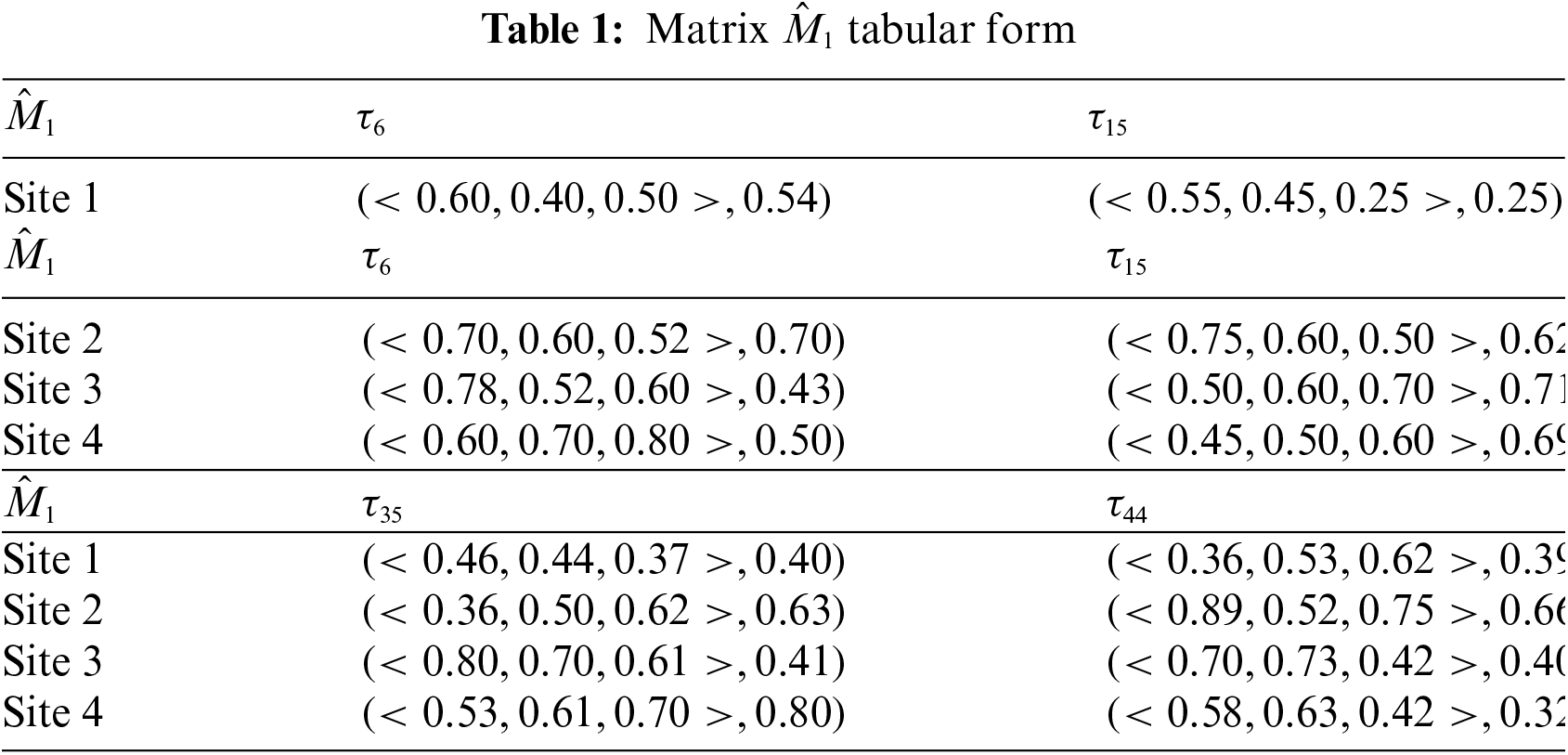
This part uses the next example to illustrate each stage of the suggested algorithm. The case study discussed by Rahman et al. [74] has been followed for hypersoft expert settings.

Example 3.2. As mentioned in Section 3.6, the assessment committee is composed of four individuals (experts): E1, E2, E3, and E4. These individuals are arranged in the set {E1;E2;E3;E4}. The participants went to a lot of locations, but just four designated as {Site1;Site2;Site3;Site4} were carefully examined. “T1”, “T2”, “T3”, and “T4” are the four SWST that are evaluated and added to the set. In the set {p1,p2,p3,p4}, let every member of the committee decide upon the variables: “Air quality index (p1)”, “Distance from the locality (p2)”, “Economical values (p3)”, and “Inclination of land (p4).” After the careful study, the sub-classes values of attributes lying in the different sets ω^1={20,30,40}, ω^2={1,1.5,2km}, and ω^3={lesscostly,costly,morecostly}, ω^4={1percent,2percent,3percent}. Let Ω=ω^1×ω^2×ω^3×ω^4 and then ω^×Υ×Ξ={τ1,τ2,τ3,…,τ641}. If the different values like 20, 30 are selected in ω^1, 1, 1.5 km, in ω^2, more costly and 2 percent are selected in ω^3 and ω^4 respectively on the basis of preference. After a long discussion, four tuples τ6,τ15,τ35,τ44 have been selected for further process. Now, every decision-maker aside from the “E1” shares their thoughts regarding sites, sub-attribute  tuples, and SWSTs in terms of single-valued neutrosophic soft expert (SV-NHSES) values. As the committee’s chairman, the “E1” assigns appropriate possibility grades to the decision-makers SV-NHSES valued opinions. As a result, two PSV-NHSESs are created and displayed using matrix notations, M^1 and M^2, which are found in Tables 1 and 2. Based on the possible grades that “E1” offered for each of τ6,τ15,τ35,τ44, their corresponding fuzzy parameterized grades are now determined using Eq. (1), which is listed in Table 3 along with a detailed explanation of the computations. Now, two ρ^-sets, M^1 and M^2, are formed using these computed fuzzy parameterized grades. This is done by substituting fuzzy parameterized sub-parametric tuples for the sub-parametric tuples τ6/0.471, τ15/0.601, τ35/0.425, τ44/0.489. Then, these sets are reported in Tables 4 and 5, respectively, and expressed in matrix notations M^3 and M^4. The mathematical criterion is applied to convert the PSV-NHSS entries of M^3 and M^4 into reduced fuzzy values |[(φt−φi−φf)+λ]/3|, which yields fuzzy parameterized fuzzy hypersoft expert sets (FP-FHSESs) Z1 and Z2. Following that, these sets are shown in matrix notations, with M^5 and M^6 being tabulated in Tables 6 and 7, respectively. As per the algorithm’s Step 3(ii), the matrices M^5 and M^6 undergo transformations to become M^7 and M^8, respectively. These new matrices are then summarised in Tables 8 and 9. The typical matrix product (also known as the decision matrix) of M^7 and M^8 is now found and given the designation M^9. Table 10 tabulates the data. The highest values found in every column of M^9 are indicated to arrive at a distinct conclusion.

4  Result and Discussion

This section is meant to discuss the sensitivity analysis of the results obtained and their comparison with the existing models.

4.1 Comparison and Discussion

Regarding the effectiveness of the provided method, this study is an attempt by the authors to give the transdisciplinary solid waste management problem based on MADM a mathematical component. As such, it is imperative to utilize an appropriate mathematical method with little processing overhead. The proposed algorithm meets this criterion. Even people without a strong background in mathematics can easily understand it thanks to its simple and basic computation-based techniques. Initially, the computed outcomes of the proposed algorithm are analyzed, followed by a discussion of their comparison with the computed outcomes of other pertinent structures that have been established previously. Examining the computed values in the decision matrix allows one to make the following significant findings. Studies that are significant, pertinent, and closely related to the suggested subject are taken into consideration for comparative analysis. After looking into the minimum (maximum) operators, distance and similarity metrics, and neutrosophic HSES, they created an algorithm to deal with solid waste management issues. While it is commendable that efforts are being made to tackle a significant problem with the environment, the efforts have shortcomings that include:

1.    Fuzzy parameterization is not explained as a practical method to assess the ambiguities that administrators need to take into account while choosing characteristics or sub-attributes.

2.    Since experts are permitted to freely describe their professional views in a multidimensional triad-based membership operator, they may occasionally be unclear. However, it needs to be controlled to avoid this ambiguity. One of the decision-makers ought to be named the coordinator in this situation. This person will have the authority to assess the estimates and offer each a possible grade. Stated differently, no thought is given to a framework based on grades.

3.    Relatively little is discussed regarding the correctness of sites and SWSTs for solid waste management. A quantitative overview is given in place of an explanation for the autonomous ordering determined by rating numbers, maintaining the interdependence of the sites and SWSTs.

The recommended approach is superior because it addresses the aforementioned constraints by employing a stable and consistent ranking system based on results as depicted in Table 11. A few more evaluating elements are included in Table 12 to further highlight to readers the beneficial potential of the suggested investigation. The calculated outcomes of the suggested methodology have low values of numerical. A numerical calculable condition states that a result is more accurate and dependable the smaller its numerical value. In light of this, the suggested structure has produced trustworthy results when compared to pertinent structures [72]. In a similar way Table 12, presents a structural comparison of the proposed structure to evaluate its favorable characteristics and adjustability. This is done by taking some assessing features into consideration. Certain evaluating parameters have been used in Table 12 for a comparison point of view. Such parameters are consideration of fuzzy parameterization, fuzzy membership values, consideration of possibility values, having a multi-argument approximate function, single-valued neutrosophic setting, solid waste site selection, and the usage of multi-decisive opinions.

4.2 Sensitivity Analysis

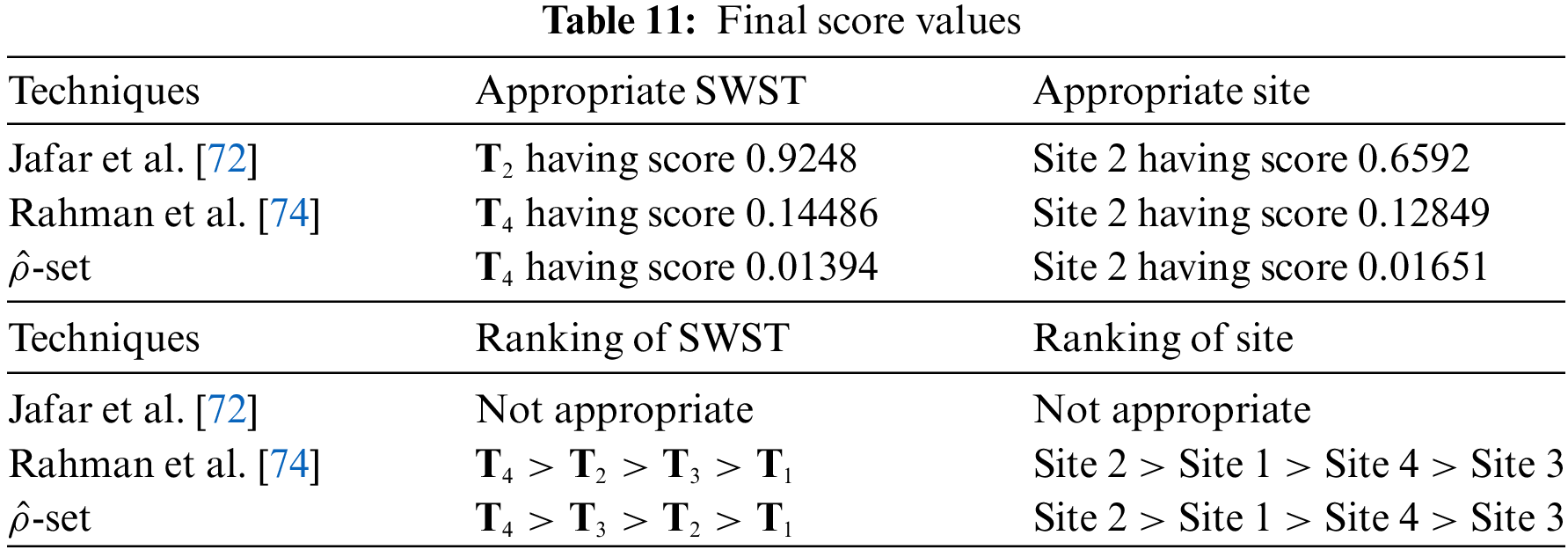
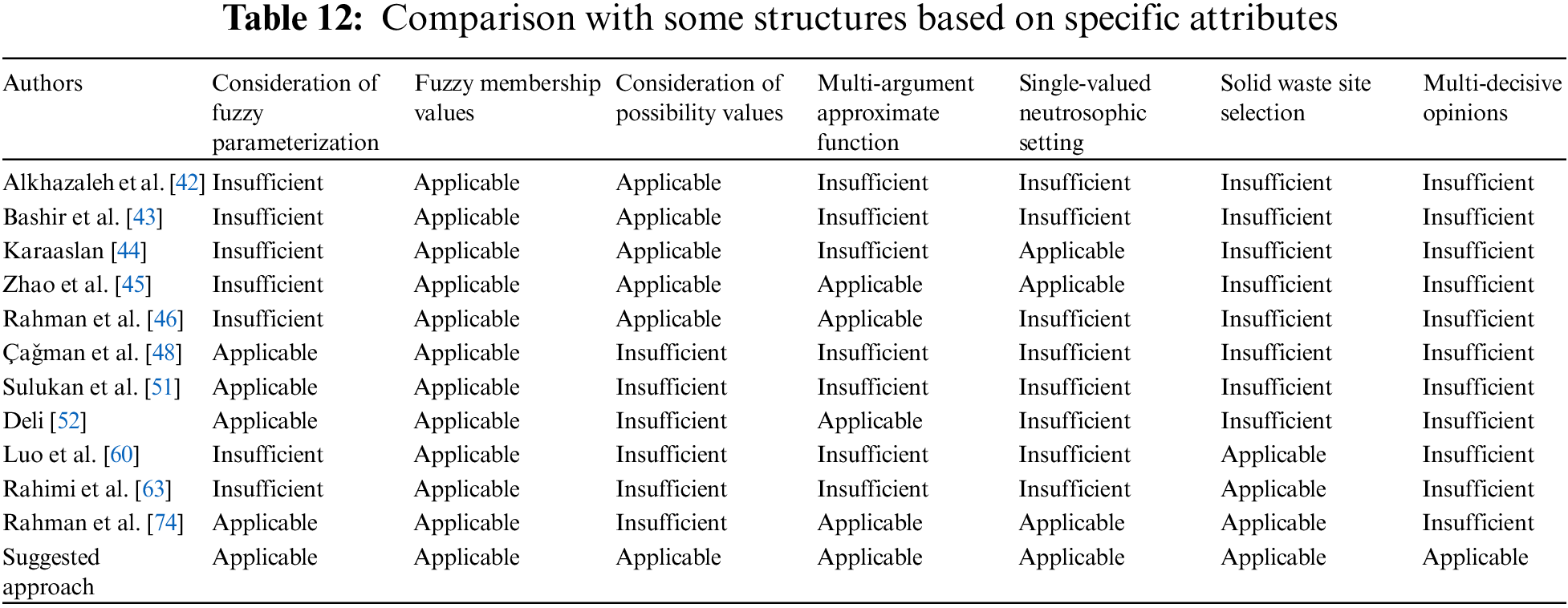
Sensitivity analysis for SWSTs based on ρ^-sets includes determining how changes to input parameters and subparameters affect the outputs of the structure. This is carried out to assess the consistency and reliability of the results and to determine which elements have the most impact on the final result. By doing sensitivity analysis, decision-makers can determine which aspects are most crucial to the solid waste management program’s performance and adjust their plan accordingly. Sensitivity analysis results can also help decision-makers allocate funds and resources more prudently. Policymakers may opt to augment their funding for waste minimization and recycling programs. We use the idea of Pythagorean means to compute the scores of sites and SWSTs to evaluate the sensitivity of the generated scores as shown in Table 10. Consequently, we have the subsequent three cases:

1.    Case 1: Table 10 computations are altered to produce Table 13 if the idea of the arithmetic mean is used to calculate the score values of sites and SWSTs.

2.    Case 2: Table 10 calculations are altered to produce Table 14 if the geometric mean idea is used to calculate the score values of sites and SWSTs.

3.    Case 3: Table 10 calculations are altered to produce Table 15 if the harmonic mean idea is used to calculate the score values of sites and SWSTs.

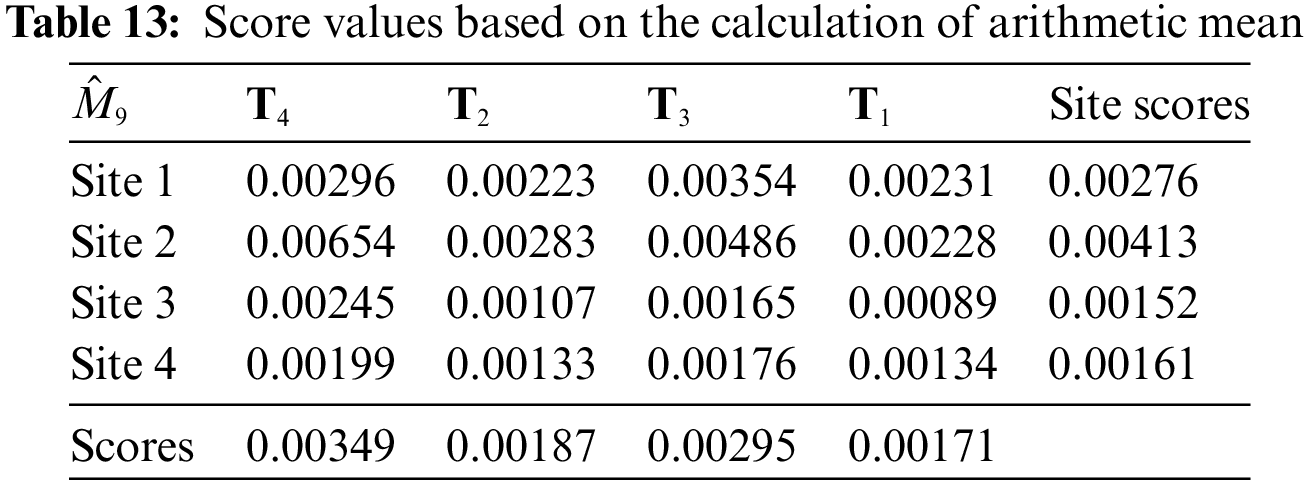
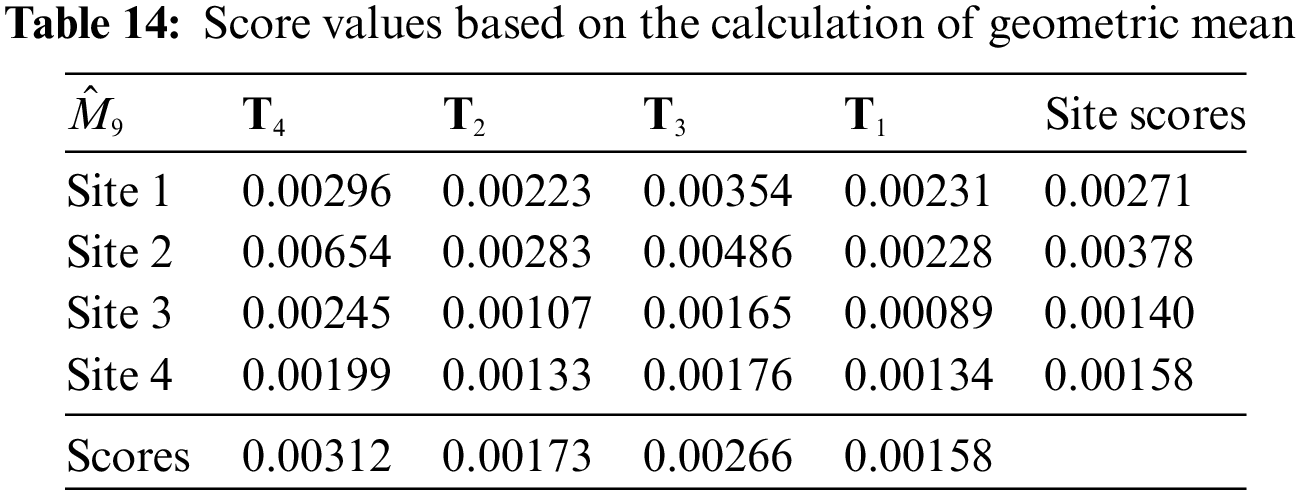
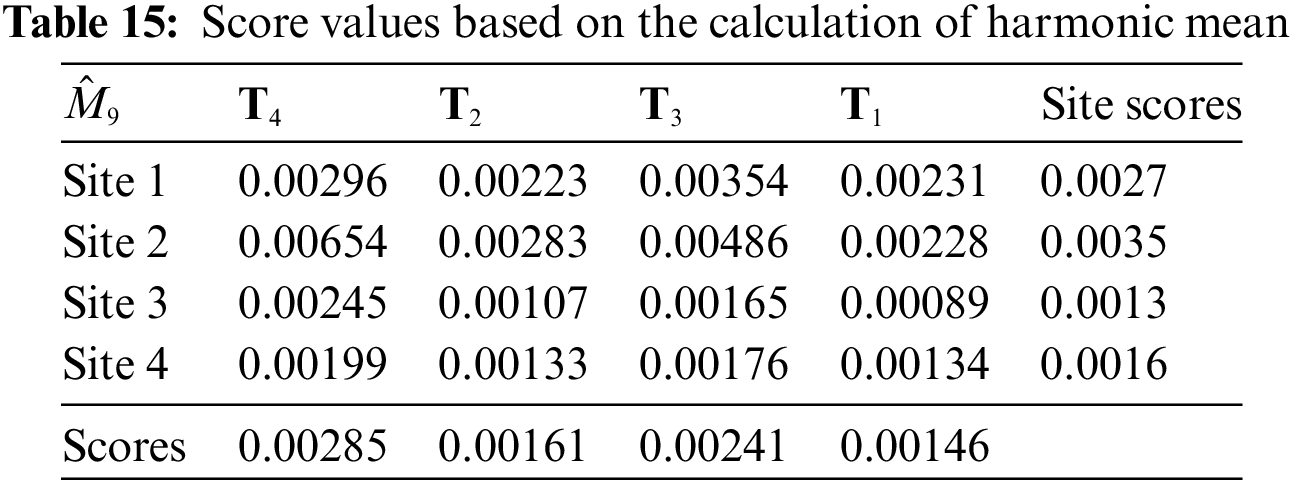
Table 16 readily demonstrates the consistency of the ranking outcomes for both sites and SWSTs.

5  Conclusion

This study has provided a novel approach to the selection of suitable SWSTs and locations for the management of solid waste collected from multiple sources within a city. By defining the concepts of ρ^-set, the anticipated ambiguities regarding the attributes, sub-characteristics valued pairs, expert advice based on approximations of substitutes regarding attributes, and sub-attribute grade pairs are addressed. To connect the SWSTs, sites, and sub-attribute valued pairs in the context of the ρ^-set, the traditional method, also known as Sanchez’s method, is modified. To make this adjustment, a ρ^-set matrix representation is used. An explanation and simple example are provided for a method that combines the ideas of ρ^-set and Sanchez’s approach to find the best SWST and location for solid waste control. This approach takes into account the fact that the solid waste management problem is a MADM problem. Two different opinions about the outcomes that were obtained have been expressed: (a) The interdependencies between sites and SWSTs are taken into account when answering the question, “Which of the sites is the most appropriate for any kind of SWST?” (b) The rankings of the site and the SWST are analyzed as independent variables. By comparing the proposed strategy with the most relevant, previously developed structure, it is examined. It is concluded that because of the new approach’s flexibility and reliability in effectively managing uncertainty, it has more positive aspects than previous research. Although this study uses pseudo data on expert opinions and other relevant variables to give a general impression, it can be successfully applied to some case study-based efforts using real data sets.

This work focuses on the fuzzy parameterized degree of sub-characteristic pairs to approximate alternatives; however, numerous other scenarios may require the use of neutrosophic, intuitionistic fuzzy, or picture fuzzy parameterizations of sub-characteristic pairs to evaluate their ambiguous and imprecise characteristics. Since the study employs Sanchez’s technique and expert-graded ideas to measure and estimate SWST with sites, other decision-making methodologies that provide true, value-based feedback from experts through review are also appropriate for these kinds of analyses. Additionally, to give some basic context, researchers only considered the characteristics that the peer literature evaluation deemed most important for MADM-based solid waste development. This avoids mathematical difficulties with the Cartesian product in a hypersoft expert setting. The writers plan to build upon this basic framework in the future by taking into account sets of traits or criteria, making it more global in scope, and utilizing machine learning and other pertinent computer-assisted software. This is because adding more criteria creates numerical challenges that necessitate the use of artificial intelligence and machine learning. Applied mathematics and artificial intelligence are both included in this research.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R404), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R404), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: Conceptualization, Tmader Alballa, Muhammad Ihsan, and Atiqe Ur Rahman; methodology, Muhammad Ihsan, Atiqe Ur Rahman, Noorah Ayed Alsorayea, and Hamiden Abd El-Wahed Khalifa; software, Muhammad Ihsan, Atiqe Ur Rahman, and Noorah Ayed Alsorayea; validation, Tmader Alballa, Muhammad Ihsan, Noorah Ayed Alsorayea, and Hamiden Abd El-Wahed Khalifa; formal analysis, Tmader Alballa, Muhammad Ihsan, and Atiqe Ur Rahman; investigation, Tmader Alballa, Muhammad Ihsan, and Atiqe Ur Rahman; visualization, Tmader Alballa, Noorah Ayed Alsorayea, and Hamiden Abd El-Wahed Khalifa; supervision, Tmader Alballa, and Atiqe Ur Rahman; funding acquisition, Tmader Alballa, and Hamiden Abd El-Wahed Khalifa. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Nanda S, Berruti F. Municipal solid waste management and landfilling technologies: a review. Environ Chem Lett. 2021;19(2):1433–56. doi:10.1007/s10311-020-01100-y. [Google Scholar] [CrossRef]

2. Guerrero LA, Maas G, Hogland W. Solid waste management challenges for cities in developing countries. Waste Manage. 2013;33(1):220–32. doi:10.1016/j.wasman.2012.09.008. [Google Scholar] [PubMed] [CrossRef]

3. Soltani A, Hewage K, Reza B, Sadiq R. Multiple stakeholders in multi-criteria decision-making in the context of municipal solid waste management: a review. Waste Manage. 2015;35:318–28. doi:10.1016/j.wasman.2014.09.010. [Google Scholar] [PubMed] [CrossRef]

4. Garcia-Garcia G. Using multi-criteria decision-making to optimise solid waste management. Curr Opin Green Sustain Chem. 2022;37:100650. doi:10.1016/j.cogsc.2022.100650. [Google Scholar] [CrossRef]

5. MacDonald ML. A multi-attribute spatial decision support system for solid waste planning. Comput Environ Urban Syst. 1996;20(1):1–17. doi:10.1016/S0198-9715(96)00006-3. [Google Scholar] [CrossRef]

6. Yadav V, Kalbar PP, Karmakar S, Dikshit AK. A two-stage multi-attribute decision-making model for selecting appropriate locations of waste transfer stations in urban centers. Waste Manage. 2020;114:80–8. doi:10.1016/j.wasman.2020.05.024. [Google Scholar] [PubMed] [CrossRef]

7. Wang H, Smarandache F, Zhang Y, Sunderraman R. Single valued neutrosophic sets. Rev Air Force Acad. 2010;1(10):410–3. [Google Scholar]

8. Smarandache F. Neutrosophy neutrosophic probability, set and logic: analytic synthesis synthetic analysis. New Mexico, USA: American Research Press; 1998. [Google Scholar]

9. Zadeh LA. Fuzzy sets. Inform Control. 1965;8(3):338–53. doi:10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]

10. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. [Google Scholar]

11. Cuong BC. Picture fuzzy sets. J Comput Sci Cybern. 2014;30:409–20. [Google Scholar]

12. Şahin R, Küçük A. Subsethood measure for single valued neutrosophic sets. J Intell Fuzzy Syst. 2015;29(2):525–30. doi:10.3233/IFS-141304. [Google Scholar] [CrossRef]

13. Huang HL. New distance measure of single-valued neutrosophic sets and its application. Int J Intell Syst. 2016;31(10):1021–32. doi:10.1002/int.21815. [Google Scholar] [CrossRef]

14. Pramanik S, Dalapati S, Alam S, Smarandache F, Roy TK. NS-cross entropy-based MAGDM under single-valued neutrosophic set environment. Information. 2018;9(2):37. doi:10.3390/info9020037. [Google Scholar] [CrossRef]

15. Aydoǧdu A. On similarity and entropy of single valued neutrosophic sets. Gen Math Notes. 2015;29(1):67–74. [Google Scholar]

16. Biswas P, Pramanik S, Giri BC. TOPSIS method for multiattribute group decision-making under single-valued neutrosophic environment. Neural Comput Appl. 2016;27(3):727–37. doi:10.1007/s00521-015-1891-2. [Google Scholar] [CrossRef]

17. Farid HMA, Riaz HMA. Single-valued neutrosophic Einstein interactive aggregation operators with applications for material selection in engineering design: case study of cryogenic storage tank. Complex Intell Syst. 2022;8(3):2131–49. doi:10.1007/s40747-021-00626-0. [Google Scholar] [CrossRef]

18. Farid HMA, Garg H, Riaz M, Santos-García G. Multi-criteria group decision-making algorithm based on single-valued neutrosophic Einstein prioritized aggregation operators and its applications. Manage Decis. 2022;61(2):382–420. [Google Scholar]

19. Molodtsov D. Soft set theory–first results. Comput Math Appl. 1999;37:19–31. doi:10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]

20. Maji PK. Neutrosophic soft set. Annals Fuzzy Math Inform. 2013;5(1):2287–623. [Google Scholar]

21. Jana C, Pal M. A robust single-valued neutrosophic soft aggregation operators in multi-criteria decision-making. Symmetry. 2019;11(1):110. doi:10.3390/sym11010110. [Google Scholar] [CrossRef]

22. Marei E. Single valued neutrosophic soft approach to rough sets, theory and application. Neutrosophic Set Syst. 2018;20:76–85. [Google Scholar]

23. Debnath S. Inverse single-valued neutrosophic soft set and its application. In: Handbook of research on advances and applications of fuzzy sets and logic. New York: IGI Global; 2022. p. 716–40. [Google Scholar]

24. Alkhazaleh S, Salleh AR. Soft expert sets. Adv Decis Sci. 2011;2011:757868–1. doi:10.1155/2011/757868. [Google Scholar] [CrossRef]

25. Alkhazaleh S, Salleh AR. Fuzzy soft expert set and its application. Appl Math. 2014;5:1349–68. doi:10.4236/am.2014.59127. [Google Scholar] [CrossRef]

26. Broumi S, Smarandache F. Intuitionistic fuzzy soft expert sets and its application in decision making. J New Theory. 2015;1:89–105. [Google Scholar]

27. Şahin M, Alkhazaleh S, Ulucay V. Neutrosophic soft expert sets. Appl Math. 2015;6(1):116–27. doi:10.4236/am.2015.61012. [Google Scholar] [CrossRef]

28. Smarandache F. Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 2018;22:168–70. [Google Scholar]

29. Kamaci H. On hybrid structures of hypersoft sets and rough sets. Int J Mod Sci Technol. 2021;6(4):69–82. [Google Scholar]

30. Jafar MN, Saeed M, Ghani T. Entropy and correlation coefficients of neutrosophic and interval-valued neutrosophic hypersoft set with application of multi-attributive problems. Neutrosophic Sets Syst. 2022;49:341–63. doi:10.5281/zenodo.6426421. [Google Scholar] [CrossRef]

31. Zulqarnain RM, Xin XL, Saqlain M, Smarandache F. Generalized aggregate operators on neutrosophic hypersoft set. Neutrosophic Sets Syst. 2020;36(1):271–81. doi:10.5281/zenodo.4065445. [Google Scholar] [CrossRef]

32. Saqlain M, Jafar N, Moin S, Saeed M, Broumi S. Single and multi-valued neutrosophic hypersoft set and tangent similarity measure of single valued neutrosophic hypersoft sets. Neutrosophic Sets Syst. 2020;32(1):317–29. doi:10.5281/zenodo.3723165. [Google Scholar] [CrossRef]

33. Ihsan M, Saeed M, Rahman AU. Neutrosophic hypersoft expert set: theory and applications. Neutrosophic Sets Syst. 2022;50(1):26. [Google Scholar]

34. Ihsan M, Rahman AU, Saeed M. Single valued neutrosophic hypersoft expert set with application in decision making. Neutrosophic Sets Syst. 2021;47:451–71. [Google Scholar]

35. Ihsan M, Rahman AU, Saeed M. Hypersoft expert set with application in decision making for recruitment process. Neutrosophic Sets Syst. 2021;42:191–208. [Google Scholar]

36. Kropat E, Weber GW. Fuzzy target-environment networks and fuzzy-regression approaches. Numer Algebra, Control Optim. 2018;8(2):135–55. doi:10.3934/naco.2018008. [Google Scholar] [CrossRef]

37. Kropat E, Özmen A, Weber GW, Meyer-Nieberg S, Defterli O. Fuzzy prediction strategies for gene-environment networks-fuzzy regression analysis for two-modal regulatory systems. RAIRO-Oper Res. 2016;50(2):413–35. doi:10.1051/ro/2015044. [Google Scholar] [CrossRef]

38. Cresswell MJ, Hughes GE. A new introduction to modal logic. London: Routledge; 1996. doi:10.4324/9780203028100. [Google Scholar] [CrossRef]

39. Zadeh LA. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978;1(1):3–28. doi:10.1016/0165-0114(78)90029-5. [Google Scholar] [CrossRef]

40. Fedrizzi M. Introduction to fuzzy sets and possibility theory. In: Optimization models using fuzzy sets and possibility theory. Dordrecht: Springer; 1987. p. 13–26. doi:10.1007/978-94-009-3869-4-2. [Google Scholar] [CrossRef]

41. Dubois D, Prade H. Possibility theory, probability theory and multiple-valued logics: a clarification. Ann Math Artif Intell. 2001;32(1):35–66. doi:10.1023/A:1016740830286. [Google Scholar] [CrossRef]

42. Alkhazaleh S, Salleh AR, Hassan N. Possibility fuzzy soft set. Adv Decis Sci. 2011;2011:1–18. doi:10.1155/2011/479756. [Google Scholar] [CrossRef]

43. Bashir M, Salleh AR, Alkhazaleh S. Possibility intuitionistic fuzzy soft set. Adv Decis Sci. 2012;2012:1–24. doi:10.1155/2012/404325. Article ID 404325. [Google Scholar] [CrossRef]

44. Karaaslan F. Similarity measure between possibility neutrosophic soft sets and its applications. Univ Politeh Buch Sci Bull Ser A. 2016;78(3):155–62. doi:10.5281/zenodo.32275. [Google Scholar] [CrossRef]

45. Zhao J, Li B, Rahman AU, Saeed M. An intelligent multiplecriteria decision-making approach based on sv-neutrosophic hypersoft set with possibility degree setting for investment selection. Manage Decis. 2022;61:472–85. doi:10.1108/md-04-2022-0462. [Google Scholar] [CrossRef]

46. Rahman AU, Saeed M, Khalifa HAEW, Afifi WA. Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math. 2022;7(3):3866–95. doi:10.3934/math.2022214. [Google Scholar] [CrossRef]

47. Rahman AU, Saeed M, Mohammed MA, Krishnamoorthy S, Kadry S, Eid F. An integrated algorithmic madm approach for heart disease diagnosis based on neutrosophic hypersoft set with possibility degree-based setting. Life. 2022;12(5):729. doi:10.3390/life12050729. [Google Scholar] [PubMed] [CrossRef]

48. Çaǧman N, Çıtak F, Enginoğlu S. Fuzzy parameterized fuzzy soft set theory and its applications. Turkish J Fuzzy Syst. 2010;1(1):21–35. [Google Scholar]

49. Zhu KY, Zhan J. Fuzzy parameterized fuzzy soft sets and decision making. Int J Mach Learn Cybern. 2016;7(6):1207–12. doi:10.1007/s13042-015-0449-z. [Google Scholar] [CrossRef]

50. Riaz M, Hashmi MR. Certain applications of fuzzy parameterized fuzzy soft sets in decision-making problems. Int J Algebra Stat. 2016;5(2):135–46. doi:10.20454/ijas.2016.1181. [Google Scholar] [CrossRef]

51. Sulukan E, Çaǧman N, Aydin T. Fuzzy parameterized intuitionistic fuzzy soft sets and their application to a performance-based value assignment problem. J New Theory. 2019;29:79–88. [Google Scholar]

52. Deli I. Hybrid set structures under uncertainly parameterized hypersoft sets, theory and applications. In: Smarandache F, Saeed M, Abdel-Baset M, Saqlain M, editors. Theory and application of hypersoft set. Brussels: Pons Publishing House; 2021. p. 24–49. [Google Scholar]

53. Qu S, Zhou Y, Ji Y, Dai Z, Wang Z. Robust maximum expert consensus modeling with dynamic feedback mechanism under uncertain environments. J Ind Manage Optim. 2024;21(1):524–52. [Google Scholar]

54. Debnath S. Fuzzy hypersoft sets and its weightage operator for decision making. J Fuzzy Ext Appl. 2021;2(2):163–70. [Google Scholar]

55. Smarandache F. A study on neutrosophic soft set and neutrosophic hypersoft set. J Fuzzy Ext Appl. 2024. doi:10.22105/jfea.2024.422349.1316. [Google Scholar] [CrossRef]

56. Smarandache F. Soft set product extended to hypersoft set and indetermsoft set cartesian product extended to indetermhypersoft set. J Fuzzy Ext Appl. 2022;3(4):313–6. [Google Scholar]

57. Ekmekçioğlu M, Kaya T, Kahraman C. Fuzzy multi-criteria disposal method and site selection for municipal solid waste. Waste Manage. 2010;30(8–9):1729–36. doi:10.1016/j.wasman.2010.02.031. [Google Scholar] [PubMed] [CrossRef]

58. Yildirim VM, Bediroglu TS, Colak HE. Municipal solid waste landfill site selection using multi-criteria decision making and GIS: case study of Bursa Province. J Environ Eng Landsc Manage. 2018;26(2):107–19. doi:10.3846/16486897.2017.1364646. [Google Scholar] [CrossRef]

59. Ghosh S, Küfer KH, Roy SK, Weber GW. Carbon mechanism on sustainable multi-objective solid transportation problem for waste management in Pythagorean hesitant fuzzy environment. Complex Intell Syst. 2022;8(5):4115–43. doi:10.1007/s40747-022-00686-w. [Google Scholar] [CrossRef]

60. Luo C, Ju Y, Santibanez Gonzalez EDR, Dong P, Wang A. The waste-to-energy incineration plant site selection based on hesitant fuzzy linguistic best-worst method ANP and double parameters TOPSIS approach: a case study in China. Energy. 2020;211:118564. doi:10.1016/j.energy.2020.118564. [Google Scholar] [CrossRef]

61. Liu KM, Lin SH, Hsieh JC, Tzeng GH. Improving the food waste composting facilities site selection for sustainable development using a hybrid modified MADM model. Waste Manage. 2018;75:44–59. doi:10.1016/j.wasman.2018.02.017. [Google Scholar] [PubMed] [CrossRef]

62. Wang G, Qin L, Li G, Chen L. Landfill site selection using spatial information technologies and AHP: a case study in Beijing, China. J Environ Manage. 2009;90(8):2414–21. doi:10.1016/j.jenvman.2008.12.008. [Google Scholar] [PubMed] [CrossRef]

63. Rahimi SH, Monavari A, Hafezalkotob SM, Rahimi AR. Sustainable landfill site selection for municipal solid waste based on a hybrid decision-making approach: fuzzy group BWM-MULTIMOORA-GIS. J Clean Prod. 2020;248:119–86. doi:10.1016/j.jclepro.2019.119186. [Google Scholar] [CrossRef]

64. Liu HC, You JX, Fan XJ, Chen YZ. Site selection in waste management by the VIKOR method using linguistic assessment. Appl Soft Comput. 2014;21:453–61. doi:10.1016/j.asoc.2014.04.004. [Google Scholar] [CrossRef]

65. Mallick J. Municipal solid waste landfill site selection based on fuzzy-AHP and geoinformation techniques in Asir region Saudi Arabia. Sustainability. 2021;13(3):1538. doi:10.3390/su13031538. [Google Scholar] [CrossRef]

66. Torabi-Kaveh M, Babazadeh R, Mohammadi SD, Zaresefat M. Landfill site selection using combination of GIS and fuzzy AHP, a case study: Iranshahr, Iran. Waste Manage Res. 2016;34(5):438–48. doi:10.1177/0734242x16633777. [Google Scholar] [PubMed] [CrossRef]

67. Karasan A, Ilbahar E, Kahraman C. A novel pythagorean fuzzy AHP and its application to landfill site selection problem. Soft Comput. 2019;23(21):10953–68. doi:10.1007/s00500-018-3649-0. [Google Scholar] [CrossRef]

68. Ali SA, Ahmad A. Suitability analysis for municipal landfill site selection using fuzzy analytic hierarchy process and geospatial technique. Environ Earth Sci. 2020;79(10):1–27. doi:10.1007/s12665-020-08970-z. [Google Scholar] [CrossRef]

69. Hanine M, Boutkhoum O, Maknissi AE, Tikniouine A, Agouti T. Decision making under uncertainty using PEES-fuzzy AHP-fuzzy TOPSIS methodology for landfill location selection. Environ Syst Decis. 2016;36(4):351–67. doi:10.1007/s10669-016-9609-2. [Google Scholar] [CrossRef]

70. Hanine MB, Tikniouine O, Agouti T. Comparison of fuzzy AHP and fuzzy TODIM methods for landfill location selection. SpringerPlus. 2016;5(1):1–30. doi:10.1186/s40064-016-2131-7. [Google Scholar] [PubMed] [CrossRef]

71. Kahraman C, Cebi S, Onar SC, Oztaysi B. A novel trapezoidal intuitionistic fuzzy information axiom approach: an application to multicriteria landfill site selection. Eng Appl Artif Intell. 2018;67:157–72. doi:10.1016/j.engappai.2017.09.009. [Google Scholar] [CrossRef]

72. Jafar MN, Saeed M, Khan KM, Alamri FS, Khalifa HAEW. Distance and similarity measures using max-min operators of neutrosophic hypersoft sets with application in site selection for solid waste management systems. IEEE Access. 2022;10:11220–35. doi:10.1109/access.2022.3144306. [Google Scholar] [CrossRef]

73. Sanchez E. Inverse of fuzzy relations, application to possibility distributions and medical diagnosis. Fuzzy Sets Syst. 1979;2(1):75–86. doi:10.1016/0165-0114(79)90017-4. [Google Scholar] [CrossRef]

74. Rahman AU, Saeed M, Mohammed MA, Abdulkareem KH, Nedoma J, Martinek R. Fppsv-NHSS: fuzzy parameterized possibility single valued neutrosophic hypersoft set to site selection for solid waste management. Appl Soft Comput. 2023;140:110273. doi:10.1016/j.asoc.2023.110273. [Google Scholar] [CrossRef]