A Novel Self-Supervised Learning Network for Binocular Disparity Estimation

1  Introduction

The integration of artificial intelligence (AI) and advanced imaging techniques in surgical robotics has emerged as a transformative force in modern healthcare, particularly in the realm of minimally invasive surgery. Recent advancements in deep learning algorithms have significantly enhanced the capabilities of surgical imaging systems, enabling more precise 3D reconstruction of anatomical structures and improved real-time decision support during procedures [1–3]. These AI-driven innovations are addressing longstanding challenges in surgical robotics, such as accurate depth perception in endoscopic imagery, robust feature extraction from monotonous tissue textures, and adaptive responses to dynamic intraoperative environments [4–6]. The synergy between AI and surgical imaging not only augments the surgeon’s visual capabilities but also lays the foundation for more autonomous and intelligent surgical systems, potentially revolutionizing surgical outcomes and patient care [7–9]. As the field progresses, there is a growing emphasis on developing sophisticated algorithms that can overcome the unique challenges posed by endoscopic environments, including specular reflections, varying illumination conditions, and the need for real-time processing of high-dimensional data [10,11].

A critical component in the advancement of surgical robotics is the accurate stereo matching of images, which is essential for robots to perform surgeries with enhanced safety and precision [12–14]. The robust capabilities of convolutional neural networks in computer vision [15] have led researchers to reframe stereo matching as a deep learning task. By leveraging large training datasets, these approaches have significantly improved upon traditional stereo matching methods [16]. However, early deep learning methods were often limited to specific processes within the stereo matching task and couldn’t directly generate disparity images from left-right image pairs. This segmented approach was prone to cumulative errors and did not fully capitalize on the learning potential of deep neural networks.

To address these limitations, researchers have developed end-to-end stereo matching methods [17–19]. These approaches typically employ a single network to process stereo images comprehensively. A notable example is the DispNet model proposed by Mayer et al. [20], which builds upon the optical flow estimation network FlowNet [21] to directly predict disparities from left-right image pairs. In 2017, Kendall et al. introduced a novel end-to-end binocular disparity regression framework (GC-Net) [22], which utilizes a twin network for feature extraction and constructs a 4D matching cost volume. This framework employs differentiable modules throughout, enabling end-to-end disparity regression with clear matching significance. Further advancements were made by Chang et al. in 2018 with the introduction of PSMNet [23], which incorporates a spatial pyramid pooling module and dilated convolutions to enhance the network’s receptive field and reduce false matches.

The evolution of neural network architectures has played a crucial role in these advancements. The U-Net architecture, proposed by Ronneberger et al. in 2015 [24], introduced a symmetric encoder-decoder structure that has become fundamental in many image processing tasks. Building upon this work, Goutcher et al. [25] developed an encoder-decoder network in 2021 that utilizes a shared binocular platform to process left-right images concurrently, improving feature consistency and enabling simultaneous depth estimation and object segmentation. The design of such a shared platform is able to improve the expressiveness and consistency of features, which can help to perform subsequent segmentation and depth estimation more accurately. In the processing stage, the network performs both object segmentation and depth estimation. With this joint processing, the network is able to simultaneously generate a set of depth estimation results with respect to the left camera distance in a single forward propagation and generate object recognition segmentation figures for the left-right camera images.

Despite these advancements, the unique challenges posed by endoscopic images, such as specular reflections and monotonous textures, continue to hinder accurate three-dimensional reconstruction of lesions by surgical robots. This limitation impedes the progress towards more intelligent and autonomous surgical systems. To address these specific challenges, our study proposes a novel end-to-end disparity estimation model designed to enhance robustness against specular reflections and lighting interferences common in endoscopic imagery.

Our approach introduces several innovations. First, we employ a Pseudo-Siamese neural network structure that leverages multi-scale image information and combines features at different scales to improve the network’s resilience. Second, we incorporate pyramid dilated convolutions to extract and fuse features from the same hidden layer using various dilation rates. This technique allows for a more comprehensive capture of contextual information. Additionally, we propose a Pseudo-Siamese structure-based disparity regression model that simplifies the comparison between left and right images, facilitating easier network convergence and improving both the accuracy and efficiency of the algorithm. This work additionally adds a disparity smoothing loss term to the loss function to increase the disparity image’s accuracy even further. Following detailed experiment, it was determined that the proposed binocular disparity estimation model outperforms two common fully convolutional networks [26,27] in the disparity estimation task of endoscopic images. This improvement has been achieved without major adjustments to the network parameters, highlighting the efficiency of our approach.

2  Method

This research proposes an end-to-end binocular disparity estimation network model. To enable network training on endoscopic image datasets without ground truth depth values, we utilize left-right view reconstruction to facilitate self-supervised training. Specifically, the disparity map generated by the encoder-decoder is used to sample from the original left and right images, reconstructing the corresponding views to form a reconstruction loss function. This approach allows the network to be trained effectively.

The model framework, as illustrated in Fig. 1, consists of three main components: encoder-decoder, spatial transformation module, and loss function.

Figure 1: Self-supervised binocular disparity estimation network framework

The encoder-decoder can directly estimate disparity from the input left-right image pairs without requiring additional processing steps. The spatial transformation module uses the disparity map to project one perspective in the stereo image to another, effectively realizing view reconstruction. To enhance the accuracy of disparity estimation, we incorporate relevant constraints from traditional stereo matching into the loss function. Considering the unique characteristics of endoscopic images, we have made targeted designs in each module of our model. The self-supervised nature of our approach, leveraging left-right view reconstruction, enables the model to learn and improve performance without relying on real depth supervision.

This approach of independent processing of left and right images preserves stereoscopic information more effectively compared to dual-channel networks. It enables the network to learn view-specific features, which are subsequently compared in later stages. This methodology enhances the accuracy of disparity estimation, particularly when addressing challenges common in endoscopic images such as monotonous textures and reflective surfaces.

2.1 Encoder-Decoder Model

In previous work, Chen et al. [28] proposed a deep reasoning method that combines monocular and stereo cues. They used a two-way network with shared weights to process monocular and stereo cues. Unlike their method, our Pseudo-Siamese structure does not share weights, allowing each sub-network to specialize in its own view. This structure uses two-dimensional convolution for disparity estimation of left and right stereo images, without dividing the feature extraction module, correlation calculation module, and cost aggregation module, and performs stereo matching in the form of a black box model.

This encoder-decoder consists of two subnetworks with the same structure but no shared weights. Its structure is shown in Fig. 2.

Figure 2: Pseudo-Siamese encoder-decoder structure

The structure of each sub-network of the encoder-decoder shown in Fig. 2 consists of an encoder in the first half, which is composed of several convolutional blocks and dilated convolutional blocks. After each convolutional block, a Rectified Linear Unit (ReLU) is used as the activation function. The second half of the structure is the decoder, which is composed of several deconvolution-convolution blocks.

For regions in endoscopic images where textures are either repetitive or sparse, contextual information in the image is helpful. The encoder proposed in this study uses a convolutional kernel with a large receptive field only in the first layer to convolve the image. For the remaining parts, dilated convolutions, which can increase the receptive field without adding training parameters, are combined with regular convolutions to downsample the image. This approach helps the network integrate information over a larger area.

To enhance the model’s perception of contextual information in the image, a pyramid dilated convolution module is incorporated into the encoder to fuse semantic information at different scales. As shown in Fig. 3, each pyramid dilated convolution consists of three dilated convolutions with different dilation rates and a convolutional layer with a kernel size of 1×1.

Figure 3: Pyramid dilated convolution

By using dilated convolutions with dilation rates of 2, 3, and 6, different ranges of contextual information can be captured, and a 1×1 convolution is then used to fuse the features from different dilated convolution layers. This convolutional layer is also followed by a ReLU activation function. Additionally, to reduce the loss of spatial information due to pooling, the encoder minimizes the use of pooling layers, employing max pooling only in the final layer of the encoder.

2.2 Spatial Transformation Module

The model is proposed for the absence of real parallax value. As is shown in Fig. 4, P is an arbitrary point in space, its image point in the left endoscopic image Il is Pl, and its image point in the right endoscopic image Ir is Pr.

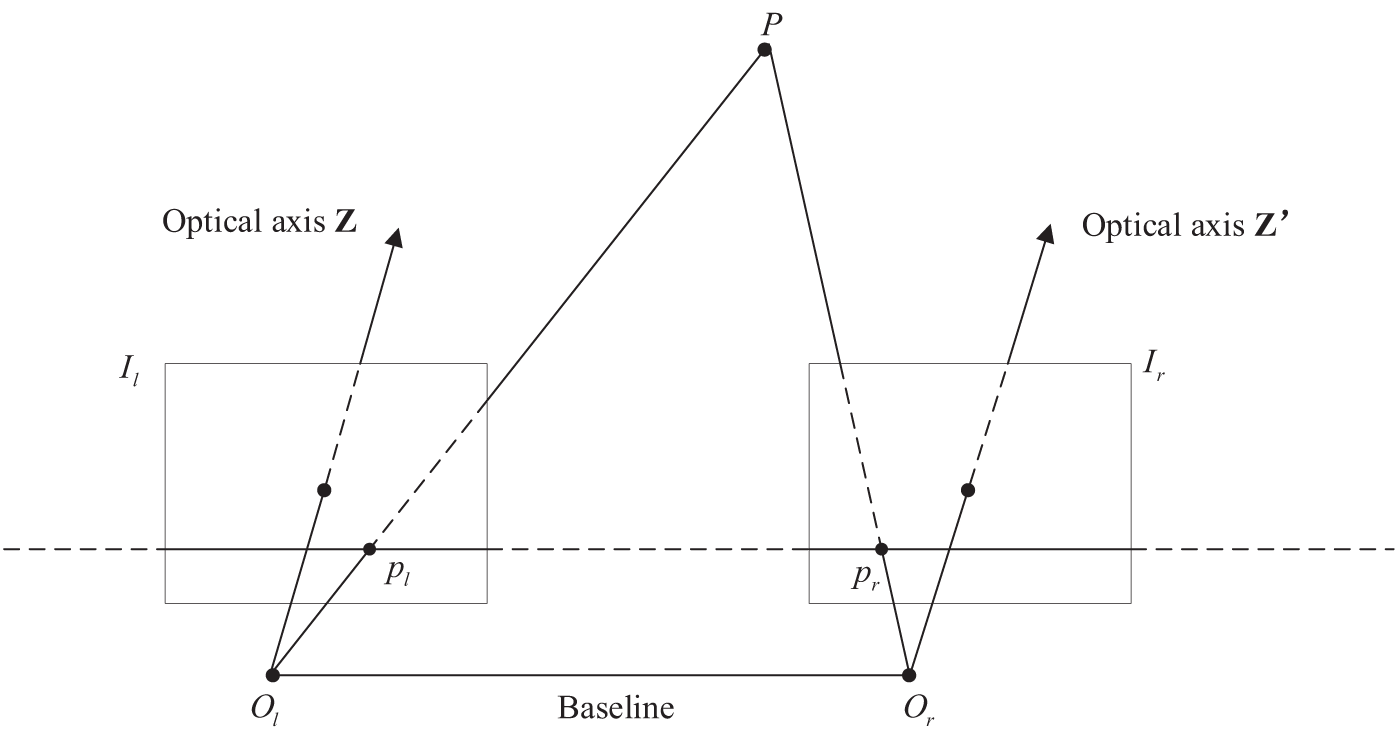
Figure 4: Standard stereo vision system

First, the supervised information training network generates images based on the spatial conversion relationship between the left-right perspectives in stereo vision. The network training is then guided by the differences between the reconstructed figure and the source figure. Finally, we use a linear sampling function to transform the source image into another view.

According to the stereo vision system model shown in Fig. 4, let the pixel coordinate of point P in the right figure be (ur,vr), the disparity image dr of the right image is defined as Eq. (1):

IR(ur,vr)=IL(ur+dr(ur,vr),vr)(1)

Among them, the dr pixel disparity value at the pixel coordinate (u,v) in the disparity figure represents the difference between the point at (u,v) in the right figure and the pixel intensity of the corresponding point in the left figure.

The method used in this study is one of the simplest image interpolation methods—one-dimensional linear interpolation.

Assume that the image coordinate of a point P in the right picture is (u,v), and it can be known from Fig. 3 and Eq. (1) that the coordinate of P in the left picture is (u+d(u,v),v). When u+d(u,v) is not an integer, according to the one-dimensional linear interpolation method, it is necessary to first find the nearest integer to u + d(u,v), u1, u2. That is, u1, u2 is the solution of Eq. (2):

argminu~|u~−(u+d(u,v))|s.t.u~∈Z(2)

Take the pixel values at (u1,v) and (u2,v) for weighted summation and assign it to the pixel point whose coordinate is (u,v) in the right figure. The weighted summation formula is shown in Eq. (3):

IR(u,v)=u+d(u,v)−u1u2−u1IL(u2,v)+u2−u−d(u,v)u2−u1IL(u1,v)(3)

During training, the network generates images by sampling pixels from stereo image pairs. In this study, the fully differentiable linear sampler is seamlessly integrated into the image generation module to sample the input image and output the weighted sum of the two input pixels as the output pixel.

2.3 Loss Function

The loss function is given in Eq. (4):

Loss=αrecLrec+αlrLlr+αsLs(4)

Among them, αrec, αlr and αs are hyperparameters, Lrec represents reconstruction loss, Llr represents left and right parallax consistency loss, and Ls represents parallax smoothing loss.

2.3.1 Reconstruction Loss Lrec

Previously, we have estimated the parallax of the image using the codec. However, since the images input to the network are the corrected left-right images, they only have parallax in the horizontal direction, so it is necessary to set a spatial transformation module using linear interpolation transformation in the network to transform the images using the parallax value. Simply put, after coordinate translation, the corresponding image needs to be linearly sampled to generate a new perspective, and the mean square error between the generated figure and the original figure is used to calculate the reconstruction loss. The loss function is shown in Eq. (5):

L2=1HW∑u=1W∑v=1H[I′(u,v)−I(u,v)]2(5)

Among them, H and W respectively represent the height and width of the figure, u and v respectively represent the number of columns and rows of pixels in the figure, I′ is the reconstructed figure, and I is the source figure.

The whole reconstruction loss is the sum of the reconstruction error L2l of the left figure and the reconstruction error L2r of the right figure as shown in Eq. (6):

Lrec=L2l+L2r(6)

2.3.2 Left and Right Parallax Consistency Loss Llr

Let the pixel coordinate of the space point P in the left figure be (ul,vl), and its pixel coordinate in the right figure is (ur,vr), the parallax image dl based on the left figure is defined as Eq. (7):

IL(ul,vl)=IR(ul−dl(ul,vl),vl)(7)

Therefore, using the left parallax image dl, when the space point P is transformed from the left figure to the right figure, the coordinate transformed to the right figure is (ul−dl(ul,vl),vl). When the right parallax image is used to transform the coordinate to the left figure, the transformed coordinate is (ul−dl(ul,vl)+dr(ul−dl(ul,vl),vl),vl), which should be equal to (ul,vl), so Eq. (8) can be obtained by simple derivation:

ul−dl(ul,vl)+dr(ul−dl(ul,vl),vl)=ul⇒dl(ul,vl)−dr(ul−dl(ul,vl),vl)=0(8)

The parallax consistency condition expressed by the above equation is used as a constraint term to add to the loss function, as shown in Eq. (9):

Llr=1HW∑u,v(dl(u,v)−dr(u−dl(u,v),u))2(9)

where H and W represent the height and width of the figure, respectively, and dl and dr represent the left and right parallax images, respectively.

2.3.3 Parallax Smoothing Loss Ls

To improve parallax accuracy, this study uses the gradient value of the original figure as the weight of the parallax smoothing term in the smoothing loss function term. The image gradient calculation formula is shown in Eq. (10):

{∂uI(u,v)=I(u+1,v)−I(u−1,v)∂vI(u,v)=I(u,v+1)−I(u,v−1)(10)

Among them, ∂uI(u,v) represents the gradient value at the pixel coordinate (u,v) in the horizontal direction. From Eq. (10), we can know that the gradient value at this place is the difference between the pixel values at the adjacent pixel coordinates before and after it.

Since the pixel value of each pixel point represents the disparity value at that point, when there is a small change in depth within the region of interest, the corresponding disparity value changes less. Consequently, the grayscale change in the disparity map is also small. This phenomenon is captured by the parallax smoothing loss function, as shown in Eq. (11):

Lsl=1HW∑u,v|∂udu,vl|e−‖∂uIu,vl‖+|∂vdu,vl|e−‖∂vIu,vl‖(11)

where ∂udu,vl represents the gradient of the disparity image in the horizontal direction, Lsl represents the smoothing term of the left disparity map, and the loss composition of the smoothing term of the right parallax is similar to Eq. (11), which is also composed of the gradient of the parallax map and the gradient of the initial right image.

The parallax smoothing term shown in Eq. (11) will suppress the areas where the parallax changes sharply and is more sensitive to the areas (edge areas) with large gradients in the original image.

3  Dataset and Preprocessing

The dataset used in this study is derived from stereo endoscope videos captured by the Da Vinci surgical robot, provided by Imperial College London. The dataset comprises two main components: real heart video data [29] and simulated silicone heart video sequences [30].

As the original video formats are not directly suitable for training our neural network model, a series of preprocessing steps were necessary to prepare the data for our experiments. These steps aimed to extract individual frames and create consistent datasets for both the real and simulated heart scenarios.

3.1 Real Heart Video Processing

The original video contains both left and right views within the same frame, with a frame width of 720 pixels. Each frame is split into two separate 360 × 288 pixel left and right views. Through frame-by-frame extraction, 1550 frames are obtained for each of the left and right views.

Fig. 5 illustrates sample frames from the processed real heart dataset, showing corresponding left and right views.

Figure 5: Sample frames from the real heart dataset

3.2 Silicone Heart Video Processing

The original data consists of two separate videos, one for the left view and one for the right view, each with a frame size of 360 × 288 pixels and a duration of 1 min 37 s. Frames are directly extracted from each video without the need for splitting. This process yielded 2425 frames for each of the left and right views.

Fig. 6 presents sample frames from the processed silicone heart dataset, displaying corresponding left and right views from the separate videos.

Figure 6: Sample frames from the silicone heart dataset

3.3 Dataset Construction

To ensure consistency in our experiments, we standardized the dataset sizes for both video types:

a)   Training set: First 1000 frames from each view (left and right)

b)   Test set: Last 500 frames from each view (left and right)

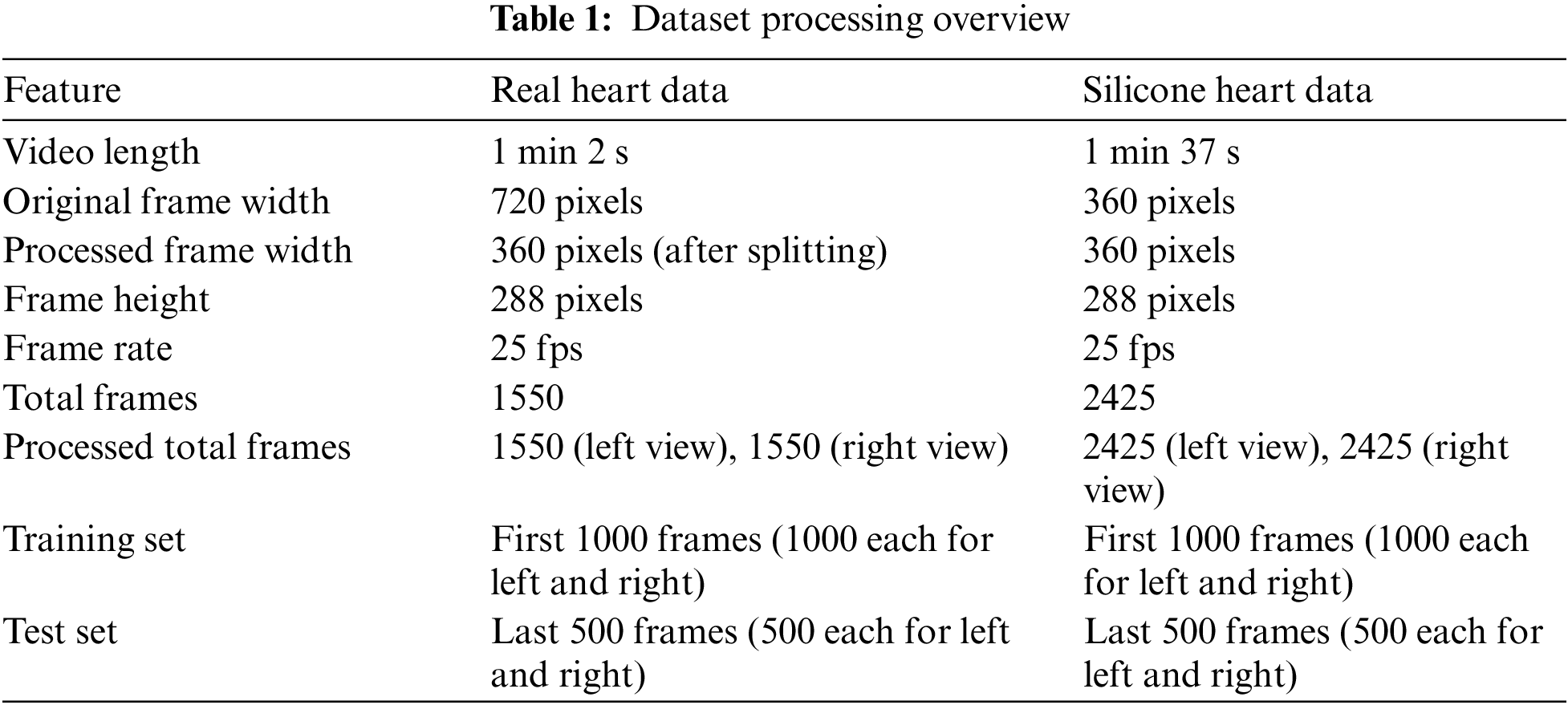
This preprocessing approach allows us to create uniform datasets from videos of different lengths and formats. By extracting and preparing the frames in this manner, we ensure that our model can be trained and evaluated on consistent data, facilitating fair comparisons between real and simulated scenarios. The Table 1 summarizes the key features of our preprocessed dataset.

This comprehensive preprocessing of the video data into standardized image sets lays the foundation for robust model training and evaluation. It ensures that our experimental results will be reliable and comparable across both real and simulated endoscopic scenarios.

4  Experiments and Results

The experiment is carried out in the TensorFlow deep learning framework. The image resolution of the input network is 288 pixels high and 360 pixels wide. Adam optimizer is used. This optimizer has small memory and has a fast convergence speed. The initial learning rate is 0.0001. The default value of other parameters such as the exponential decay rate of the optimizer is β1=0.9, β2=0.999, epsilon=10−8. The experimental platform environment information is shown in Table 2.

4.1 Hyperparameters Experiment

To find the appropriate loss term coefficient, this section tests the selection of the left-right parallax consistency loss function coefficient and the coefficient in front of the parallax image smoothing loss respectively. When the coefficient in front of the reconstruction loss term is fixed at 0.5. The oot means square error (RMSE) of the model obtained by comparing different smoothing coefficients and left-right parallax consistency coefficients in parallax estimation is shown in Fig. 7.

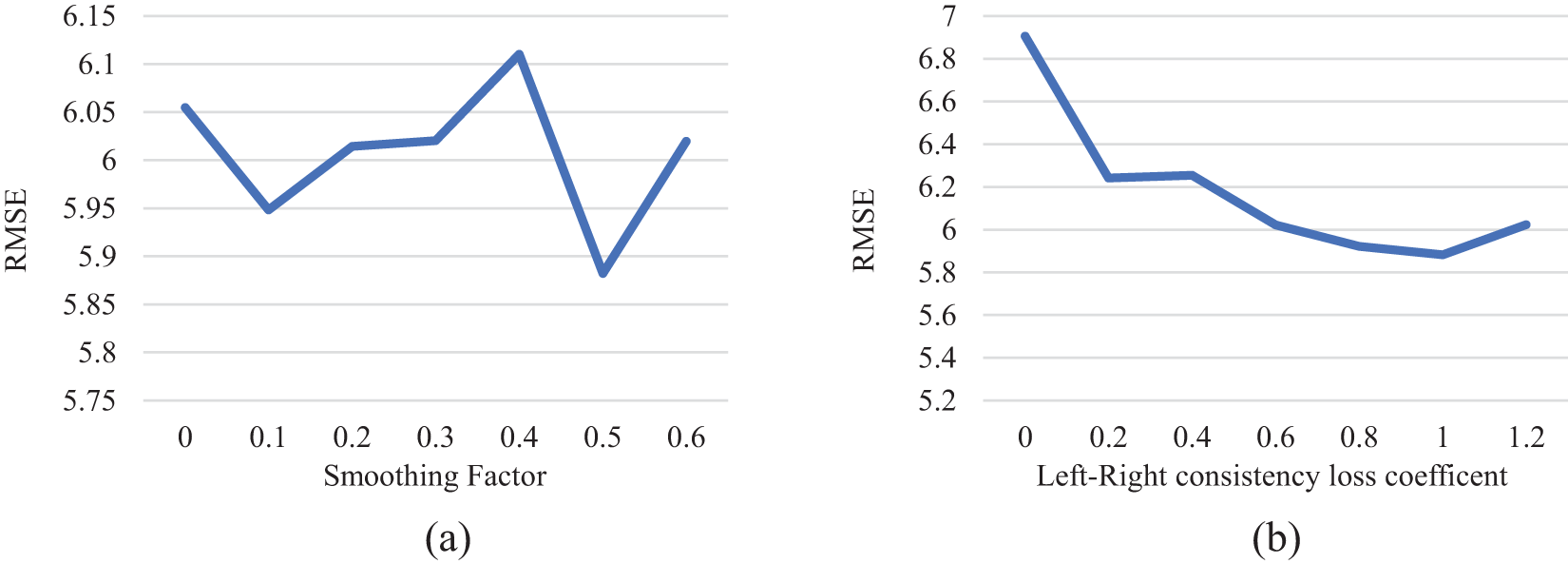
Figure 7: Experiment of smoothing coefficient and left-right consistency loss term coefficient. (a) The RMES of the loss coefficients of different smoothing terms on the test set; (b) Root mean square error of different left and right consistency loss on the test set

Analysis of Fig. 7 reveals the fluctuation of the RMSE on the test set in response to varying coefficient values. The RMSE reaches its minimum when the coefficient of the disparity smoothness loss term αs=0.5 and when the coefficient of the left-right disparity consistency loss function αlr=1. Consequently, in subsequent experiments, these optimal values (αs=0.5 and αlr=1) are employed to configure the model’s loss function.

4.2 Structure Experiment of Pseudo-Siamese Neural Network

This group of experiments compared the Pseudo-Siamese neural network structure designed in the study with the dual channel image matching network structure. The dual channel matching network structure is shown in Fig. 8. Its encoder-decoder structure is almost the same as the encoding and decoding structure of the Pseudo-Siamese neural network, but in Pseudo-Siamese neural network, the left-right images are input to each sub-network separately, while in the dual channel image matching network structure, they are input together. In the dual channel image matching network structure, the input is the left and right views, and the output is two parallax images.

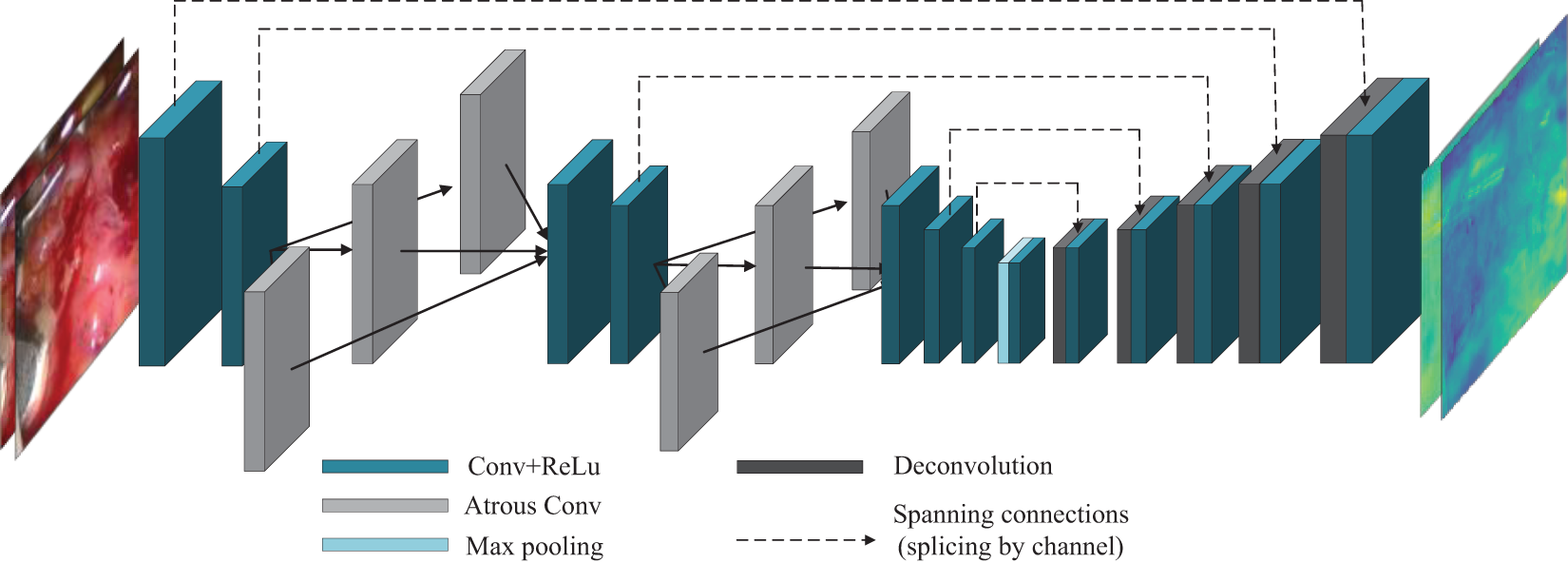
Figure 8: Schematic diagram of dual channel structure

The Pseudo-Siamese neural network and dual channel network are used to predict the 1001st frame of the silica gel heart dataset and real heart dataset, respectively. Fig. 9 shows the experiment results.

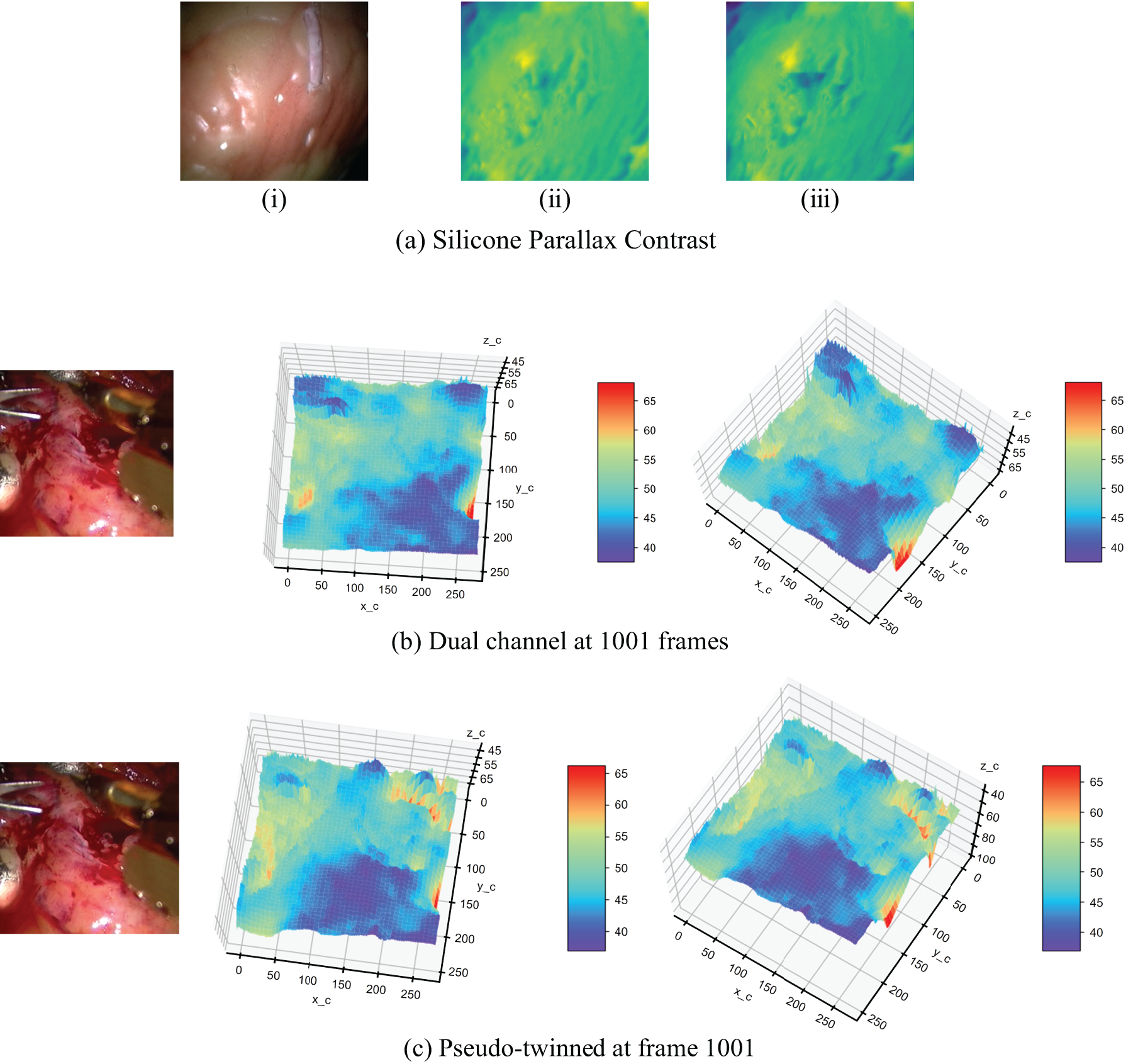
Figure 9: Structure comparison experiment of dual channel network and pseudo twin neural network. (a) Parallax contrast on silica heart; (i): Original Right View Image; (ii): Right Disparity from Dual-Channel Network; (iii): Right Disparity from Pseudo-Siamese Neural Network; (b) The depth estimated by the dual channel network on the real heart in frame 1001; (c) The estimated depth of the pseudo twin neural network structure on the real heart in frame 1001

Fig. 9 presents a comparative analysis of disparity maps generated by dual-channel and pseudo-twin neural network structures. In Fig. 9a, the silica gel heart model reveals that the pseudo-twin structure produces more defined depth transition edges. This enhanced edge definition suggests superior performance in capturing subtle depth variations, a critical factor in surgical environments. Fig. 9b,c extends this comparison to real heart data, where the pseudo-twin structure demonstrates improved accuracy in representing the complex topography of the heart’s inner surfaces. The pseudo-twin structure more accurately shows the tendency of the inner extension depth of the inner circle of the endoscopic image. This observation underscores the structure’s aptitude for handling the intricate geometries typical in endoscopic scenarios.

4.3 Pyramid Dilated Convolution Module Experiment

To assess the effectiveness of pyramid dilated convolution in reducing light reflection-induced mismatches, we compared our proposed model with a modified U-net [31] model. Both models were evaluated on silica gel and real heart datasets. The key difference between the models is their convolutional architecture. Our model uses a pyramid dilation convolution module for multi-scale contextual information, while the U-net uses standard convolution layers.

We modified the U-net to maintain consistent input and output dimensions, crucial for dense disparity map estimation. This involved adapting the decoder section to upsample outputs to match encoder feature map dimensions. Fig. 10 shows disparity estimation results for both models on the 1001st frame of the silica gel heart dataset and a corresponding real heart dataset frame. This comparison demonstrates each model’s performance in handling endoscopic imagery challenges, especially specular reflections and illumination variations.

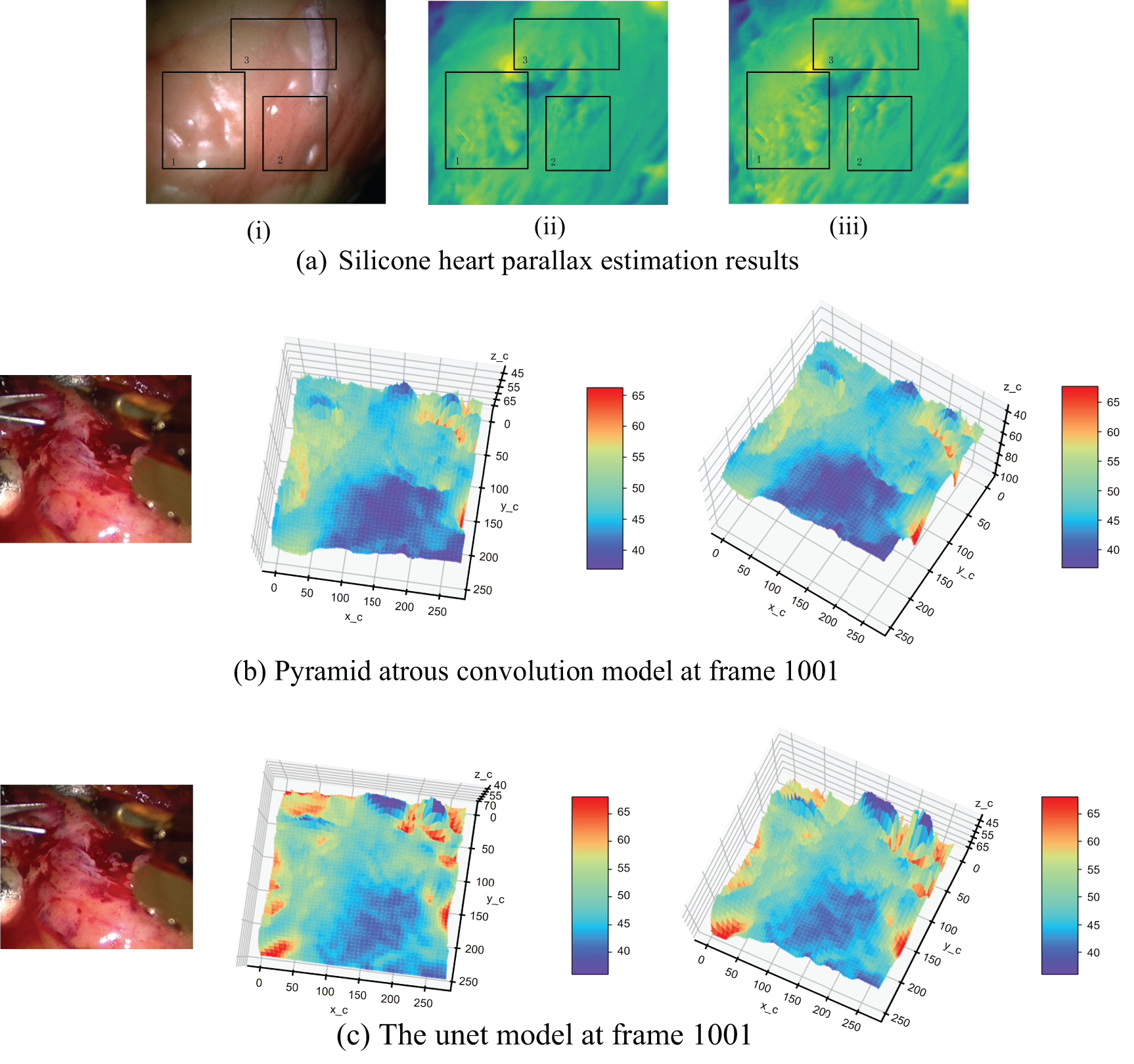
Figure 10: Pyramid cavity convolution experiment. (a) The parallax estimation results of the encoder and decoder with pyramid dilated convolution model and U-net structure in frame 1001; (i): Original Right View of Silicone Heart; (ii): Estimated Result by the Encoder-Decoder Designed in This Part; (iii): Estimated Result by U-net as Encoder-Decoder; (b) The depth estimation results of pyramid cavity convolution model on the real heart in frame 1001; (c) Depth estimation results of U-net model on the real heart in frame 1001

Fig. 10 offers insights into the efficacy of our pyramid dilated convolution model compared to the U-net model. The disparity maps in Fig. 10a highlight a key advantage of our approach: reduced sensitivity to specular reflections. In areas prone to intense reflections (highlighted in rectangle 1), our model maintains consistency in depth estimation, whereas the U-net model shows more pronounced artifacts. This resilience to reflection-induced interference is particularly valuable in the context of endoscopic imaging, where wet, reflective surfaces are common. However, the disparity map estimated using the U-net model shows many depth changes in this region that do not exist. This indicates that the pyramid dilated convolution model is more accurate in the region of specular reflection caused by illumination.

Fig. 10b,c reveals the depth estimation consequences of the pyramid dilated convolution model and the U-net model on real data, respectively. In the real heart surface with obvious light reflection (inside the ellipse), the depth point cloud obtained by using the pyramid dilated convolution model is more consistent with the trend of gentle surface change in the actual situation, while there is a sharp depth jump in the U-net model.

4.4 Smooth Constraint Experiment

In the classical stereo matching process, the parallax image obtained after parallax calculation often needs further post-processing to eliminate noise points, process occluded areas, and smooth the parallax image. This section compares the experimental results of using the parallax smoothing loss penalty term to train the network proposed in this study with those without smoothing term. Fig. 11 shows the parallax map of the model on the silica gel heart image pair in frame 1001 and the estimated three-dimensional point cloud map on the real heart in frame 1025 before and after adding the smooth term loss function. Fig. 11a shows the right viewing angle, the parallax without smoothing loss, and the parallax using smoothing loss from left to right. The Fig. 11b,c shows the results without and with smoothing loss, respectively.

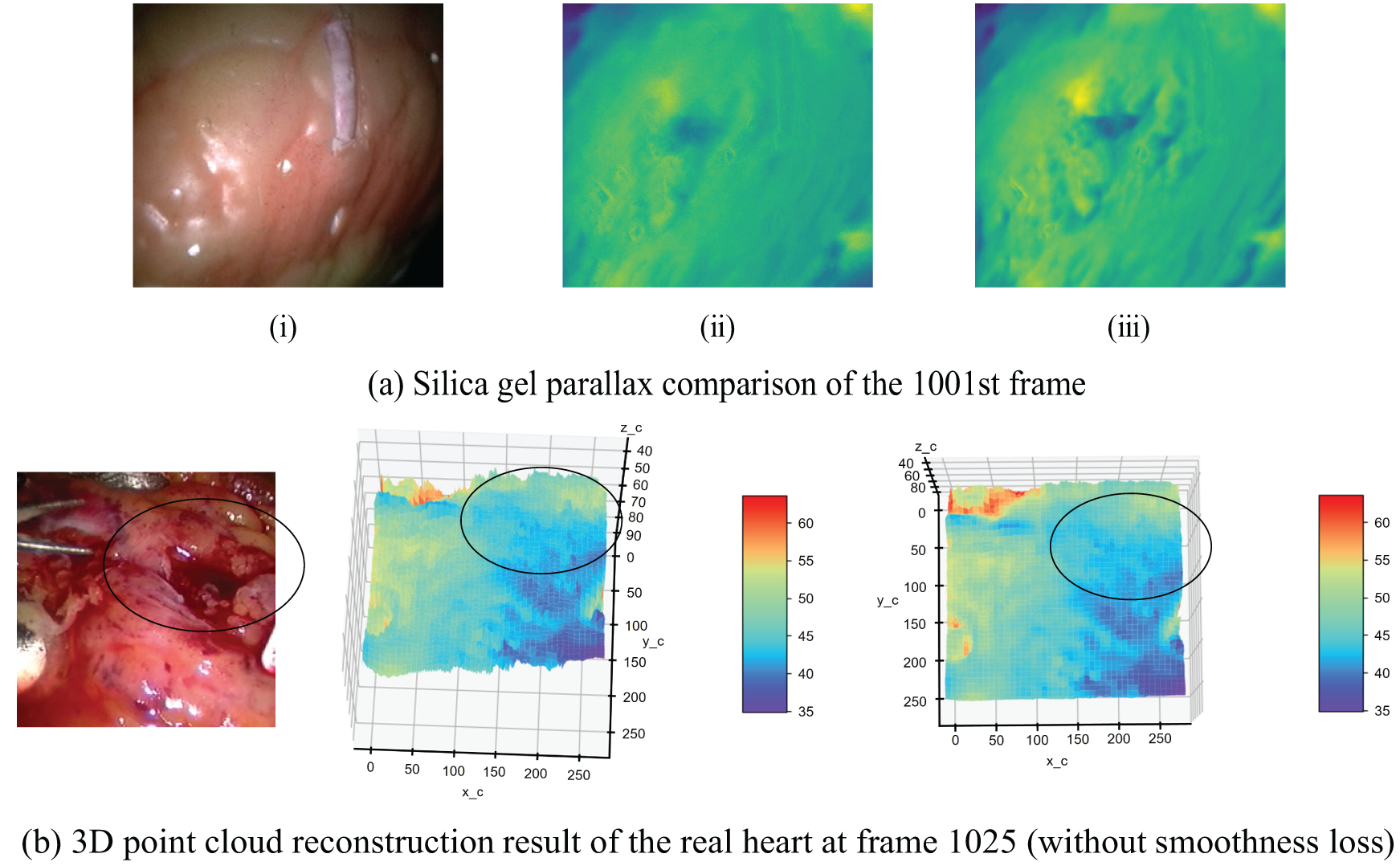
Figure 11: Comparison of model results before and after adding smoothing loss term. (a) Comparison of cardiac parallax estimation results in frame 1001; (i): Ground Truth Right Image; (ii): Model Without Smoothness Loss; (iii): Model with Smoothness Loss; (b) Comparison of 3D point cloud results of real heart in frame 1025 (without smoothness loss); (c) Comparison of 3D point cloud results of real heart in frame 1025 (with smoothness loss)

The impact of our smoothing constraint is evident in Fig. 11. Fig. 11a demonstrates that this constraint enhances the model’s ability to capture fine surface details, particularly noticeable on the real heart surface. Fig. 11b,c further illustrates the model’s robustness in challenging conditions, such as areas of low pixel intensity caused by blood occlusion (indicated by the black circle). In these regions, our model maintains a more coherent depth estimation, aligning closer with the expected anatomical structure.

The region within the black circle in the image has lower pixel intensity due to blood occlusion. Models trained without the smoothness term exhibit depth values in this area that are more influenced by the image’s pixel intensity. However, after incorporating the smoothness loss term, the estimated depth values produced by the trained model align more closely with the depth perception of the eyes.

4.5 Comparison of Other Network Structures

To further study the capability of the model, another image classification network ResNet50 [32] is used in this section. The network structure is deeper, and the training parameters are more than those designed in this section. After training on the silica gel heart data set, the silica gel heart data of frame 1001 is predicted. The comparison between the right parallax diagram and the structure results is shown in Fig. 12.

Figure 12: Comparison of the pyramid dilated convolution model with ResNet results. (a) Original right disparity; (b) Right disparity estimated by the proposed structure in this paper; (c) Right disparity estimated by the ResNet50 network

As can be seen from Fig. 12, the disparity image estimated by using the residual network ResNet50 has more noise and the gridding is more obvious, which may be caused by the small amount of data in the dataset. The following compares the above control experiments using RMES to analyze the network performance quantitatively.

Table 3 shows the RMSE and confidence interval (CI) of the reconstructed results from the real heart dataset for the control above experiments. This indicates that in the case of a small amount of data in the dataset, deep neural networks cannot play their advantages, and the proposed model is more effective.

Table 3 demonstrates that the encoder-decoder designed in this study achieves lower RMSE and overall error compared to both U-net and ResNet50 results. This validates the effectiveness of using dilated convolutions and reducing max pooling for disparity estimation in endoscopic images. Additionally, models using the Pseudo-Siamese neural network structure show reduced error compared to the dual-channel network model. Furthermore, among the Pseudo-Siamese structures, the U-net structure exhibits smaller errors than ResNet50, highlighting the advantages of U-net’s skip connections. These findings further support the efficacy of the pyramid dilated convolution model based on U-net improvements proposed in this study.

5  Discussion

The self-supervised learning network proposed in this study demonstrates advantages in binocular disparity estimation for endoscopic images. Through a series of experiments, we validated the model’s effectiveness in addressing the unique challenges present in endoscopic environments. Our results indicate that the Pseudo-Siamese neural network structure outperforms dual-channel matching networks in capturing depth variations of complex surfaces, such as the heart, confirming our hypothesis that independent processing of left and right images better preserves stereoscopic information. This approach differs from the U-net structure used by Wang et al. [26] for smoke removal in laparoscopic images, and the weight-sharing siamese network employed by Zhang et al. [27] for unsupervised binocular depth prediction in laparoscopic surgery. While these previous methods laid important groundwork, our non-weight-sharing approach demonstrates improved performance in depth estimation accuracy. Concurrently, the superior performance of pyramid dilated convolutions in mitigating lighting interferences, particularly specular reflections, underscores the importance of considering multi-scale contextual information in endoscopic image processing. The introduction of a smoothness constraint significantly enhanced the quality of disparity maps, especially in regions with low pixel intensity due to blood occlusion, highlighting the crucial role of considering both global structure and local consistency in disparity estimation. In practical application, the improvements in our model’s resilience to lighting interference translate directly into practical advantages in surgical environments. For instance, on reflective tissue surfaces or in areas obstructed by blood, our model maintains more consistent depth estimation, which is important for surgeons to accurately assess tissue depth during procedures.

Notably, our model demonstrates superior performance on small datasets compared to deeper networks like ResNet50, primarily due to four key factors. First, our architecture is specifically optimized for disparity estimation in endoscopic images, rather than general image classification tasks. Second, the model’s complexity is appropriately calibrated to our dataset size, capturing essential features without overfitting. Third, our pyramid dilated convolution efficiently extracts multi-scale information without the need for excessive network layers. Finally, our loss function incorporates task-specific constraints for disparity estimation, such as left-right consistency and smoothness, facilitating the learning of more meaningful features. This task-specific design contrasts with the more general approaches used in previous studies, allowing our model to excel in the specific context of endoscopic disparity estimation.

Despite the advancements presented in our study, several limitations warrant discussion. Our model’s performance may degrade under extreme lighting conditions, such as intense specular reflections or heavily shadowed areas. This degradation could be attributed to insufficient representation of such extreme cases in the training data or limited model capacity in handling highly non-linear light variations. We acknowledge that specular highlights in endoscopic images may violate view consistency assumptions, potentially compromising the accuracy of disparity estimation, especially when dealing with highly reflective instruments or moist tissue surfaces common in laparoscopic procedures. To address these challenges, our model employs two key strategies: First, the multi-scale features captured by pyramid dilated convolutions aid in distinguishing between specular highlights and actual surface features. Second, the incorporation of left-right consistency and smoothness losses provides additional constraints, reducing the impact of highlights. Despite these improvements, extreme specular highlights remain challenging.

The dataset used in this study comprises 1550 frames of real cardiac data and 2425 frames of simulated silicone heart data. While the scale of this dataset is relatively modest, it represents two critical scenarios: authentic surgical environments and controlled simulated settings. The real-world data captures actual surgical challenges, such as blood occlusion and tissue reflections, whereas the simulated data provides a benchmark with known geometric configurations. We acknowledge the limitations of our dataset in terms of size and diversity; however, it is sufficient to demonstrate the efficacy of our model in addressing the unique challenges inherent in endoscopic imagery. While our approach performs well on small datasets, it may require larger and more diverse training data to enhance generalization across varied anatomical structures and pathological conditions. Future work will focus on expanding the dataset to encompass a broader range of anatomical structures and pathological conditions.

To address these limitations, future research could explore more avenues. Such as, developing more sophisticated data augmentation techniques to simulate various extreme lighting conditions and surface reflections could enhance model robustness in challenging scenarios. Exploring different network structures to enhance the utilization of temporal information may improve model performance in dynamic scenes. To achieve real-time processing, model compression techniques or specialized hardware acceleration solutions could be investigated.

6  Conclusion

This study presents a novel self-supervised learning network for binocular disparity estimation in endoscopic imagery, specifically designed to address the challenges of minimally invasive surgery. Our approach integrates a Pseudo-Siamese neural network architecture with pyramid dilated convolutions to handle the complex visual environments encountered in surgical procedures, particularly the issues of monotonous texture and difficult feature extraction in endoscopic images.

The core of our model lies in its Pseudo-Siamese structure, which processes left and right images independently before comparison, allowing for better preservation of stereo information. We implemented pyramid dilated convolutions with varying dilation rates (2, 3, and 6) to capture multi-scale contextual information, crucial for dealing with specular reflections and monotonous textures common in endoscopic images. This approach generates multiple feature images, fusing various ranges of contextual information to enhance the model’s ability to extract features from endoscopic imagery. Our model employs a custom loss function that combines reconstruction loss, left-right consistency loss, and a smoothness term, each weighted to optimize performance. The left-right consistency constraint maintains consistent disparity estimation results, while the smoothness term enhances the quality of the disparity image. In the absence of real parallax as supervised information, we adopted a self-supervised approach, utilizing available left-right view images for training and disparity estimation.

Our experimental results provide strong evidence of the model’s efficacy. Quantitative analysis reveals superior performance compared to other architectures, with our model achieving an overall RMSE of 31.44049 on the real heart dataset, significantly lower than the dual-channel network (33.436127), U-net (32.859123), and ResNet50 (34.265533) structures. Notably, our model outperformed all tested alternatives in both left and right view RMSE, with values of 31.39589 and 29.58587, respectively. Qualitatively, our approach demonstrated enhanced edge definition in disparity maps compared to dual-channel networks, reduced artifacts in high-reflection areas compared to the U-net model, and improved depth consistency in low-contrast regions due to the incorporated smoothness constraint.

These results verify that our model can generate accurate disparity images and reconstruct source images with smaller errors. The proposed method demonstrates superior performance in handling the specific challenges of endoscopic imagery, including specular reflections, monotonous textures, and varying illumination conditions. It exhibits improved robustness in challenging conditions such as specular reflections and low-contrast areas, which are ubiquitous in surgical environments. The Pseudo-Siamese structure and pyramid dilated convolutions allow for better preservation of fine anatomical details, a crucial factor for surgical precision. Furthermore, our approach’s superior performance on small datasets makes it particularly suitable for medical applications where large, annotated datasets are often scarce.

However, it is important to acknowledge the limitations of this study. Firstly, while our model performs well on the datasets used, its generalizability to a wider range of surgical scenarios and anatomical structures remains to be fully explored. The dataset used in this study, comprising 1550 frames of real cardiac data and 2425 frames of simulated silicone heart data, while sufficient to demonstrate the efficacy of our approach, may not capture the full diversity of conditions encountered in various surgical procedures. Secondly, our model’s performance may degrade under extreme lighting conditions, such as intense specular reflections or heavily shadowed areas. This limitation could be attributed to insufficient representation of such extreme cases in the training data or limited model capacity in handling highly non-linear light variations. Thirdly, while our approach shows promise in real-time processing, further optimization may be necessary to meet the stringent latency requirements of live surgical applications. The current implementation may face challenges in scenarios requiring ultra-low latency response. Lastly, the model’s performance on highly dynamic scenes, where rapid movement of surgical instruments or tissue can occur, was not extensively tested in this study. This aspect requires further investigation.

Future work should focus on expanding the dataset to encompass a broader range of anatomical structures and pathological conditions, developing more sophisticated data augmentation techniques to simulate various extreme lighting conditions and surface reflections, and exploring different network structures to enhance the utilization of temporal information in dynamic scenes.

Acknowledgement: Authors thanks the support of Research Supporting Project Number (RSPD2024 R585), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: Supported by Sichuan Science and Technology Program (2023YFSY0026, 2023YFH0004). Supported by the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (No. RS-2022-00155885, Artificial Intelligence Convergence Innovation Human Resources Development (Hanyang University ERICA)).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Wenfeng Zheng, Bo Yang; data processing: Yu Zhou, Xiaobing Chen, Hongrong Chen; analysis and interpretation of results: Siyu Lu, Xiaobing Chen, Salman A. AlQahtani; draft manuscript preparation: Jiawei Tian, Yu Zhou, Siyu Lu; review and editing: Salman A. AlQahtani, Wenfeng Zheng, Bo Yang; funding acquisition: Jiawei Tian, Bo Yang, Salman A. AlQahtani, Wenfeng Zheng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this paper is open-source data provided by the Hamlyn Centre Laparoscopic/Endoscopic Video Datasets. This data can be found here: https://hamlyn.doc.ic.ac.uk/vision/ (accessed on 01 June 2024).

Ethics Approval: None.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ward TM, Mascagni P, Ban Y, Rosman G, Padoy N, Meireles O, et al. Computer vision in surgery. Surgery. 2021;169(5):1253–6. doi:10.1016/j.surg.2020.10.039. [Google Scholar] [PubMed] [CrossRef]

2. Mascagni P, Alapatt D, Sestini L, Altieri MS, Madani A, Watanabe Y, et al. Computer vision in surgery: from potential to clinical value. npj Digit Med. 2022;5(1):163. doi:10.1038/s41746-022-00707-5. [Google Scholar] [PubMed] [CrossRef]

3. Kitaguchi D, Takeshita N, Hasegawa H, Ito M. Artificial intelligence-based computer vision in surgery: recent advances and future perspectives. Ann Gastroenterol Surg. 2022;6(1):29–36. doi:10.1002/ags3.12513. [Google Scholar] [PubMed] [CrossRef]

4. Gumbs AA, Grasso V, Bourdel N, Croner R, Spolverato G, Frigerio I, et al. The advances in computer vision that are enabling more autonomous actions in surgery: a systematic review of the literature. Sensors. 2022;22(13):4918. doi:10.3390/s22134918. [Google Scholar] [PubMed] [CrossRef]

5. Gumbs AA, Frigerio I, Spolverato G, Croner R, Illanes A, Chouillard E, et al. Artificial intelligence surgery: how do we get to autonomous actions in surgery? Sensors. 2021;21(16):5526. doi:10.3390/s21165526. [Google Scholar] [PubMed] [CrossRef]

6. Guerrero DT, Asaad M, Rajesh A, Hassan A, Butler CE. Advancing surgical education: the use of artificial intelligence in surgical training. Am Surgeon. 2023;89(1):49–54. doi:10.1177/00031348221101503. [Google Scholar] [PubMed] [CrossRef]

7. Wang Z, Majewicz Fey A. Deep learning with convolutional neural network for objective skill evaluation in robot-assisted surgery. Int J Comput Ass Rad Surg. 2018;13:1959–70. doi:10.1007/s11548-018-1860-1. [Google Scholar] [PubMed] [CrossRef]

8. Kalli VDR. Advancements in deep learning for minimally invasive surgery: a journey through surgical system evolution. J Artif Intell Gen Sci. 2024;4(1):3006–4023. doi:10.60087/jaigs.vol4.issue1.p120. [Google Scholar] [CrossRef]

9. Kiyasseh D, Ma R, Haque TF, Miles BJ, Wagner C, Donoho DA, et al. A vision transformer for decoding surgeon activity from surgical videos. Nat Biomed Eng. 2023;7(6):780–96. doi:10.1038/s41551-023-01010-8. [Google Scholar] [PubMed] [CrossRef]

10. Lu S, Yang J, Yang B, Yin Z, Liu M, Yin L, et al. Analysis and design of surgical instrument localization algorithm. Comput Model Eng Sci. 2023;137(1):669–85. doi:10.32604/cmes.2023.027417. [Google Scholar] [CrossRef]

11. Rivas-Blanco I, Pérez-Del-Pulgar CJ, García-Morales I, Muñoz VF. A review on deep learning in minimally invasive surgery. IEEE Access. 2021;9:48658–78. doi:10.1109/ACCESS.2021.3068852. [Google Scholar] [CrossRef]

12. Liu Y, Tian J, Hu R, Yang B, Liu S, Yin L, et al. Improved feature point pair purification algorithm based on SIFT during endoscope image stitching. Front Neurorobot. 2022;16:840594. doi:10.3389/fnbot.2022.840594. [Google Scholar] [PubMed] [CrossRef]

13. Tian J, Ma B, Lu S, Yang B, Liu S, Yin Z. Three-dimensional point cloud reconstruction method of cardiac soft tissue based on binocular endoscopic images. Electronics. 2023;12(18):3799. doi:10.3390/electronics12183799. [Google Scholar] [CrossRef]

14. Portalés C, Gimeno J, Salvador A, García-Fadrique A, Casas-Yrurzum S. Mixed reality annotation of robotic-assisted surgery videos with real-time tracking and stereo matching. Comput Graph. 2023;110:125–40. doi:10.1016/j.cag.2022.12.006. [Google Scholar] [CrossRef]

15. Cheng K, You J, Wu S, Chen Z, Zhou Z, Guan J, et al. Artificial intelligence-based automated laparoscopic cholecystectomy surgical phase recognition and analysis. Surg Endosc. 2022;36(5):3160–8. doi:10.1007/s00464-021-08619-3. [Google Scholar] [PubMed] [CrossRef]

16. Penza V, Ciullo AS, Moccia S, Mattos LS, De Momi E. Endoabs dataset: endoscopic abdominal stereo image dataset for benchmarking 3d stereo reconstruction algorithms. Int J Med Robot Comput Assist Surg. 2018;14(5):e1926. doi:10.1002/rcs.1926. [Google Scholar] [PubMed] [CrossRef]

17. Brandao P, Psychogyios D, Mazomenos E, Stoyanov D, Janatka M. HAPNet: hierarchically aggregated pyramid network for real-time stereo matching. Comput Methods Biomech Biomed Eng: Imaging Vis. 2021;9(3):219–24. doi:10.1080/21681163.2020.1835561. [Google Scholar] [CrossRef]

18. Dinh VQ, Choi TJ. StereoPairFree: self-constructed stereo correspondence network from natural images. IEEE Intell Syst. 2023;38(1):19–33. doi:10.1109/MIS.2022.3193697. [Google Scholar] [CrossRef]

19. Zeng K, Wang Y, Wang W, Zhang H, Mao J, Zhu Q. Deep confidence propagation stereo network. IEEE Trans Intell Transp Syst. 2023;24(8):8097–108. doi:10.1109/TITS.2023.3264705. [Google Scholar] [CrossRef]

20. Mayer N, Ilg E, Hausser P, Fischer P, Cremers D, Dosovitskiy A, et al. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR2016 Jun 27–30; Las Vegas, NV, USA. [Google Scholar]

21. Dosovitskiy A, Fischer P, Ilg E, Häusser P, Hazirbas C, Golkov V, et al. FlowNet: learning optical flow with convolutional networks. In: 2015 IEEE International Conference on Computer Vision (ICCV); 2015 Dec 7–13; Santiago, Chile. [Google Scholar]

22. Kendall A, Martirosyan H, Dasgupta S, Henry P, Kennedy R, Bachrach A, et al. End-to-end learning of geometry and context for deep stereo regression. In: 2017 IEEE International Conference on Computer Vision (ICCV2017 Oct 22–29; Venice, Italy. [Google Scholar]

23. Chang JR, Chen YS. Pyramid stereo matching network. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018 Jun 18–23; Salt Lake City, Utah. [Google Scholar]

24. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, 2015; Munich, Germany: Springer International Publishing. [Google Scholar]

25. Goutcher R, Barrington C, Hibbard PB, Graham B. Binocular vision supports the development of scene segmentation capabilities: evidence from a deep learning model. J Vis. 2021;21(7):13. doi:10.1167/jov.21.7.13. [Google Scholar] [PubMed] [CrossRef]

26. Wang X-Z, Nie Y, Lu S-P, Zhang J. Deep convolutional network for stereo depth mapping in binocular endoscopy. IEEE Access. 2020;8:73241–9. doi:10.1109/ACCESS.2020.2987767. [Google Scholar] [CrossRef]

27. Zhang G, Huang Z, Lin J, Li Z, Cao E, Pang Y, et al. A 3D reconstruction based on an unsupervised domain adaptive for binocular endoscopy. Front Physiol. 2022;13:994343. doi:10.3389/fphys.2022.994343. [Google Scholar] [PubMed] [CrossRef]

28. Chen Z, Guo X, Li S, Yang Y, Yu J. Deep eyes: joint depth inference using monocular and binocular cues. Neurocomputing. 2021;453:812–24. doi:10.1016/j.neucom.2020.06.132. [Google Scholar] [CrossRef]

29. Stoyanov D, Mylonas GP, Deligianni F, Darzi A, Yang GZ. Soft-tissue motion tracking and structure estimation for robotic assisted MIS procedures. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2005, 2005; Palm Springs, CA, USA: Springer Berlin Heidelberg. [Google Scholar]

30. Stoyanov D, Scarzanella MV, Pratt P, Yang G-Z. Real-time stereo reconstruction in robotically assisted minimally invasive surgery. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010, 2010; Beijing, China: Springer Berlin Heidelberg. [Google Scholar]

31. Qin R, Huang X, Liu W, Xiao C. Pairwise stereo image disparity and semantics estimation with the combination of U-Net and pyramid stereo matching network. In: IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, 2019; IEEE. [Google Scholar]

32. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR2016 Jun 27–30; Las Vegas, NV, USA. [Google Scholar]