 Open Access
Open Access
ARTICLE
Global Piecewise Analysis of HIV Model with Bi-Infectious Categories under Ordinary Derivative and Non-Singular Operator with Neural Network Approach
1 Department of Mathematics and Statistics, College of Science, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, 13318, Saudi Arabia
2 Department of Mathematics, College of Science, King Saud University, Riyadh, 11989, Saudi Arabia
3 Department of Mathematics, Amity School of Applied Sciences, Amity University Rajasthan, Jaipur, 302002, India
4 School of Mathematical Sciences, Jiangsu University, Zhenjiang, 212013, China
5 Department of Computer Science and Mathematics, Lebanese American University, Beirut, 13-5053, Lebanon
* Corresponding Author: Mati ur Rahman. Email:
(This article belongs to the Special Issue: Innovative Applications of Fractional Modeling and AI for Real-World Problems)
Computer Modeling in Engineering & Sciences 2025, 142(1), 609-633. https://doi.org/10.32604/cmes.2024.056604
Received 25 July 2024; Accepted 17 October 2024; Issue published 17 December 2024
Abstract
This study directs the discussion of HIV disease with a novel kind of complex dynamical generalized and piecewise operator in the sense of classical and Atangana Baleanu (AB) derivatives having arbitrary order. The HIV infection model has a susceptible class, a recovered class, along with a case of infection divided into three sub-different levels or categories and the recovered class. The total time interval is converted into two, which are further investigated for ordinary and fractional order operators of the AB derivative, respectively. The proposed model is tested separately for unique solutions and existence on bi intervals. The numerical solution of the proposed model is treated by the piece-wise numerical iterative scheme of Newtons Polynomial. The proposed method is established for piece-wise derivatives under natural order and non-singular Mittag-Leffler Law. The cross-over or bending characteristics in the dynamical system of HIV are easily examined by the aspect of this research having a memory effect for controlling the said disease. This study uses the neural network (NN) technique to obtain a better set of weights with low residual errors, and the epochs number is considered 1000. The obtained figures represent the approximate solution and absolute error which are tested with NN to train the data accurately.Keywords
Viruses of HIV lie and transmit both in classical and modern world contents having various rates of infection. Among the sources of spreading of the said diseases from one man to another are through sexual meetings, used needles re-usages, drug usage, inherited through the mother, and by un-tested blood donations or transfusions. For stabilizing HIV infection transmission, there are various approaches including need-based HIV testing, usage of condoms during sex, circumcisions, usage of vaginal microbicides and antire-troviral (ARV) drug. To date, no cure or vaccination for HIV has been successfully discovered [1].
HIV infection is among the badly killing diseases, causing thousands of deaths all over the globe. Nearly thirty-eight million humans all over the world suffered from HIV in the year of 2019. After that, the virus has spread to each country of the globe. According to the statistics of the Health Ministry about 21,500 men were suffering from HIV in the African country of Morocco [1]. Among them,
In dealing with such infection, one of the significant tools is mathematical modeling whose benefits are to provide an esteemed prediction and feedback of any infection transmission whose viruses are contagious and invisible. Mathematical models of HIV are constructed by the scientific approval, given by analyzers, physicians and pharmacists along with the limit of spreading of the virus. So different HIV systems have been investigated by many authors [2–5]. Researchers have examined various models by applying different methodologies and explored the behaviors of each class and comparisons to real data [6–9]. Fractional calculus can be a useful technique in HIV disease modeling to capture the complex dynamics of the illness, particularly in areas where standard models are inadequate. It does, however, also provide new difficulties about the interpretation and complexity of mathematics [10–13]. Silva et al. [12] have considered an epidemiological system of HIV/AIDS transmissions including Pre-exposed Prophylaxis. In the same fashion, Li et al. [5] made a susceptible exposure in the Latent stage infection (SEI) level to draw the evolution of HIV. One of the Vivo deterministic problems has been discussed by Ngina et al. [7]. Shirazian et al. [11] have considered a mathematical method applied to express mathematically the procedure for medical tests and seeing the infection of HIV/AIDS.
The scholars have proposed a continuous system of five agents
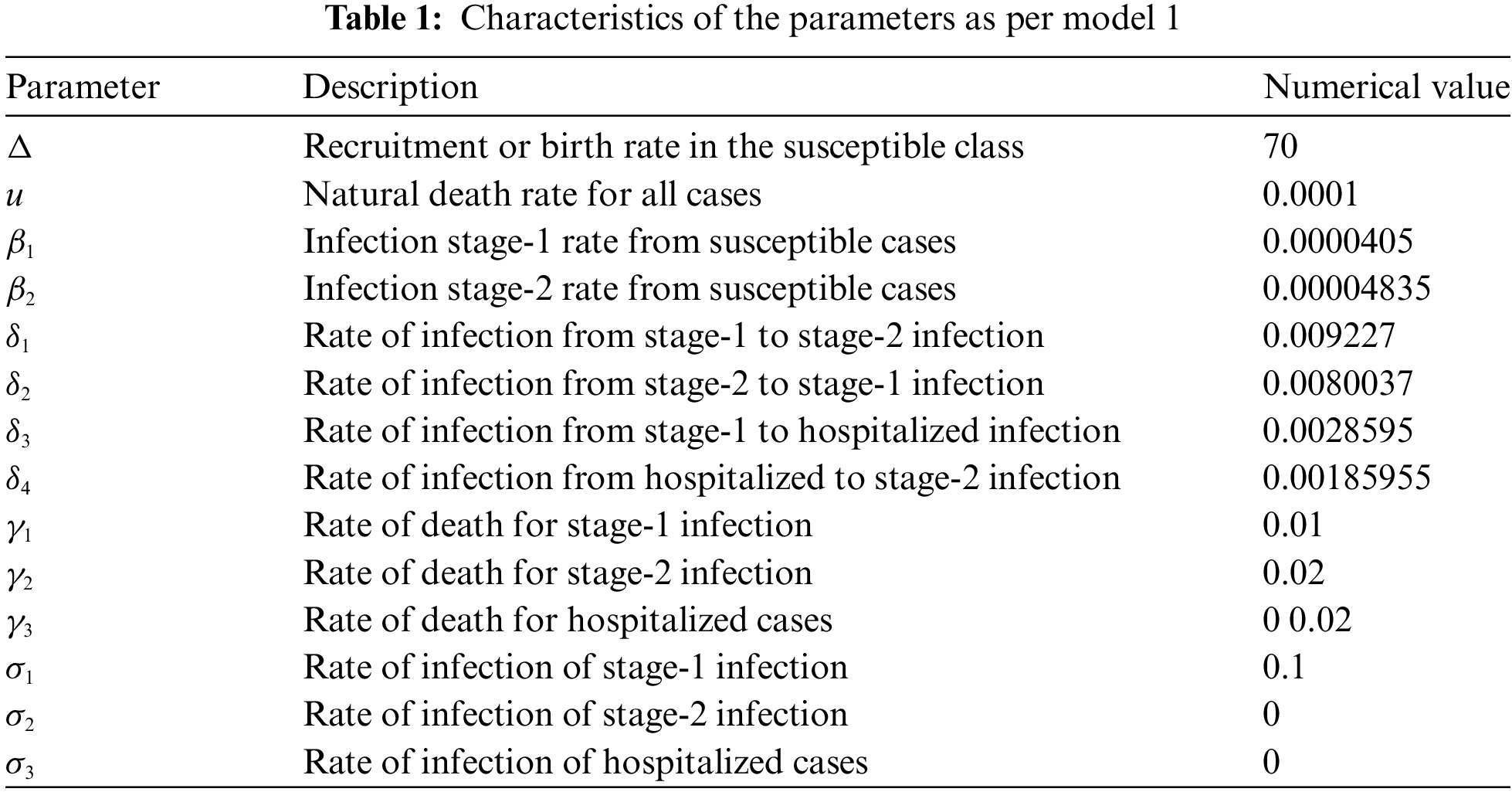
The used parameters are defined in Table 1 [1] along with numerical values.
Many sorts of derivatives have been developed in multiple attempts to understand cross-over dynamics and overcome discontinuities. These comprise fractal-fractional derivatives, derivatives of fractional order whose kernels show singularity and non-singularity, and other special cases of derivatives [14–17]. These methods, which offer sophisticated instruments for capturing the intricacies present in such dynamic processes, have all been designed to address particular facets of the behavior of the system [18–22]. These various derivative formulations enable a more sophisticated analysis of cross-over dynamics, allowing for the exploration of system transitions between multiple states or phases. Derivatives make it possible to model complicated, real-world processes more accurately and adaptably by taking into account both continuity and discontinuity [23–26]. This is particularly important in the domain of disease modeling, where a precise understanding of the dynamics of transitions, such as the HIV’s transition from latency to active infection, can result in more accurate forecasts and more potent interventions [27,28]. For analysis of the randomness or probabilistic in the scheme of stochastic equations having more real findings but up to now the cross-over dynamical behavior has not been investigated. Such behaviors are found in most infection models, like the heat flow, fluid dynamics, and many of the complex geometrical problems [22,29,30]. In fractional derivatives, the exponential and Mittag-Leffler mapping are not used to compute the time of crossover dynamics. Hence to treat such models, one of the novel schemes of piece-wise derivatives and antiderivatives has been formulated in [31]. A comprehensive framework incorporating global and classical piecewise derivatives was built by the concept’s authors. These derivatives were developed to model complicated systems, namely the dynamics of HIV infection. Keeping in view the said aspects, we will also discuss the said problem for at least one solution, uniqueness of solution, numerical solution, and stability analysis in the sense of classical and Atangana-Baleanu (AB) piecewise derivative. Further, such kind of operators are different and better than the other fractional operators. It removes the discontinuity on the whole interval by converting it into a sub-interval, it describes the crossover dynamics, AB operator has the non-singular kernel which removes the singularity of the given domain, it quickly gains the stability of any dynamical system on small fractional order, is more generalized than classical and other fractional operators. Moreover, the neural network (NN) approach is utilized and find different data sets for the considered model and the comparison of fractional and NN as well. The Eq. (1) is expressed in piece-wise derivative in the sense of classical and non-singular kernel operator as under.
where
where
1.1 Basis Properties of the Model
For any epidemiological problem, most of the authors assume that the total size of population N(t) is constant, in the rest of the paper, i.e.,
The transfer diagram may also be seen in [1].
Lemma 1.1. The set
is bounded in positive feasible region.
Proof. Adding all the five agents of Eq. (2) as follows:
or
On application of piece-wise integration we get
In the first interval if
Lemma 1.2. If the initial values of all the agent of the (2) is non-negative, i.e.,
Proof. The proof can be seen in [1]. ■
The free equilibrium point for the model (2) is
The Basic reproduction number for (2) [1] is
where
Now, in the next part of the article, we provide a few background definitions of the Caputo operator of derivative and integration along with the piecewise derivative concept.
Definition 2.1. The
While the integral can be written as
Definition 2.2. Choosing
and the integration is
here
Definition 2.3. Let
while the integration can be
here
Lemma 2.1. The solution of piece-wise derivable equation
is
This section will evaluate whether the piece-wise derivable problem under consideration has a unique solution and whether it exists or not. Based on the information provided in Lemma 2.1, we write the system (2) for this, and we further describe it as follows:
is
Consider
For the required result, we take the growth condition on the non-linear operator as
Theorem 3.1. Let
Proof. Let us assume a closed subset in both sub-intervals of
Next, let us suppose an operator
On some
The final equation suggests that
Next from (9), we obtain
Thus, in the interval
Further from (10) we get
Therefore, in the interval
Theorem 3.2. If
Proof. As previously, given a piece-wise continuous mapping
From (11), we have
It follows that
or
The presented problem, therefore, has a unique solution in the second sub-interval according to the Banach contraction theorem since
Ulam Hyers Stability
To obtain the Ulam-Hyers stability for the proposed model, we need to prove that a small perturbed term in the starting condition or the parameters of the system implies small perturbations in the solution of the system. It can be achieved by deriving that the operator
Definition 3.1. The proposed model (2) is called Ulam-Hyers stable, if for all
Let we have a unique solution
Next, if we chose an increasing operator
If
Remark 1. Assume that an operator
Lemma 3.1. Let the mapping
The solution of (17) is
Theorem 3.3. Lemma (3.1) implies that if
Proof. If
Case: 1 for
On more calculation
Case: 2
Using
We have
We use
Now, by Eqs. (21) and (22), we have
Thus, we finally say that the solution of (3) is Hyers-Ulam stable. Furthermore, if we write
So, we can say that the solution to the consider model (3) is G-H-U stable based on the fact that
In this part, we will now construct a numerical approach for the chosen piece-wise derivable model (2). For each of the two
Subsequently, we will demonstrate the methodology for model (24)’s first equation, and the remaining agents will follow the same process.
On
By expressing Eq. (25) in the Newton interpolation formula given in [31] as follows:
For the other three quantities, the Newton interpolation approach can be expressed as follows:
Our numerical simulation in Figs. 1 to 5, which uses the classical and global piece-wise AB derivative notion, is provided for the validation of the numerical method in this part. After splitting the interval into two sub-intervals, we verify that the first interval has an integer order derivative and compare it to Table 1’s available data for testing the second interval on various fractional orders in the sense of AB.
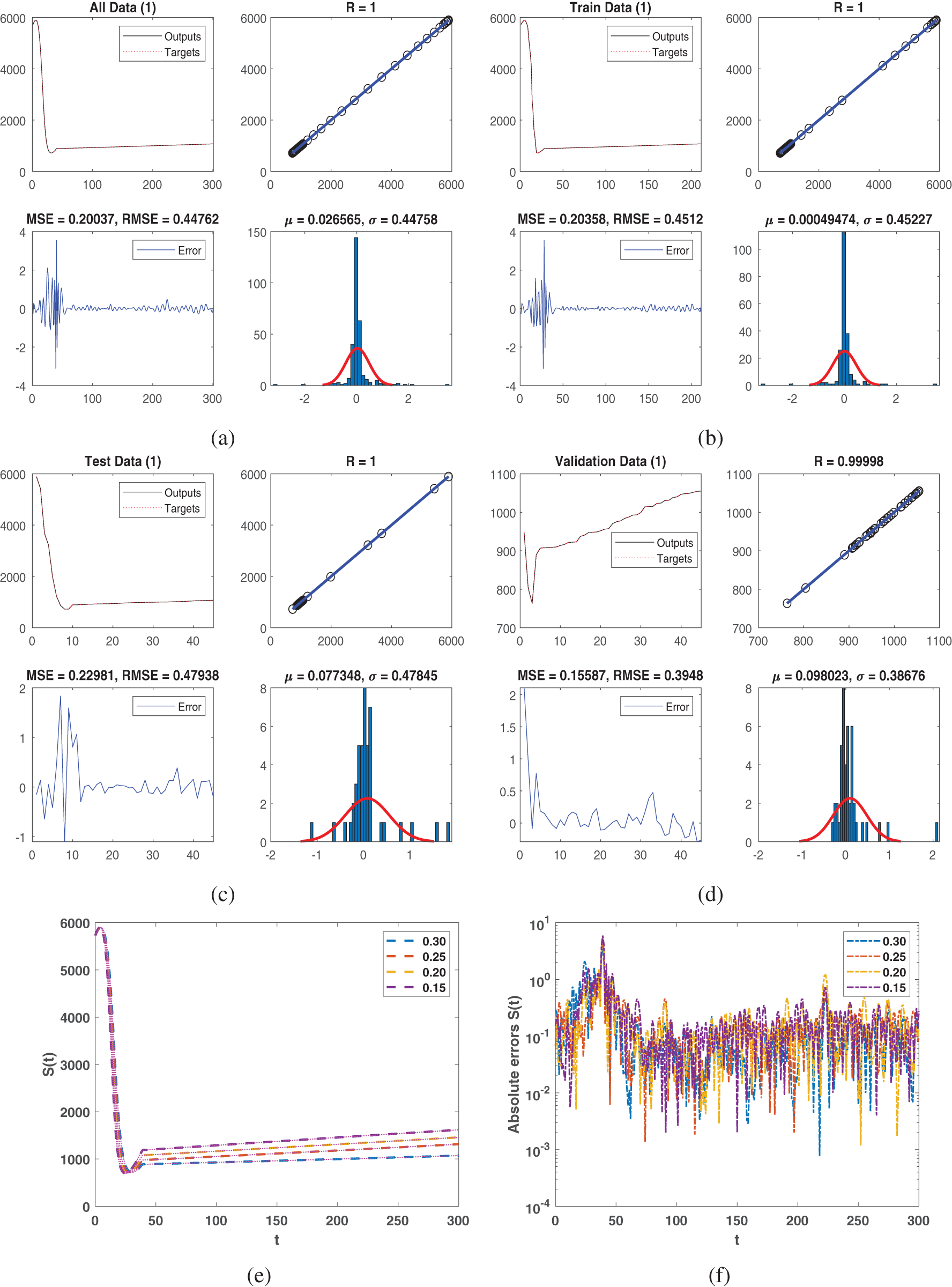
Figure 1: Piece-wise dynamical view of
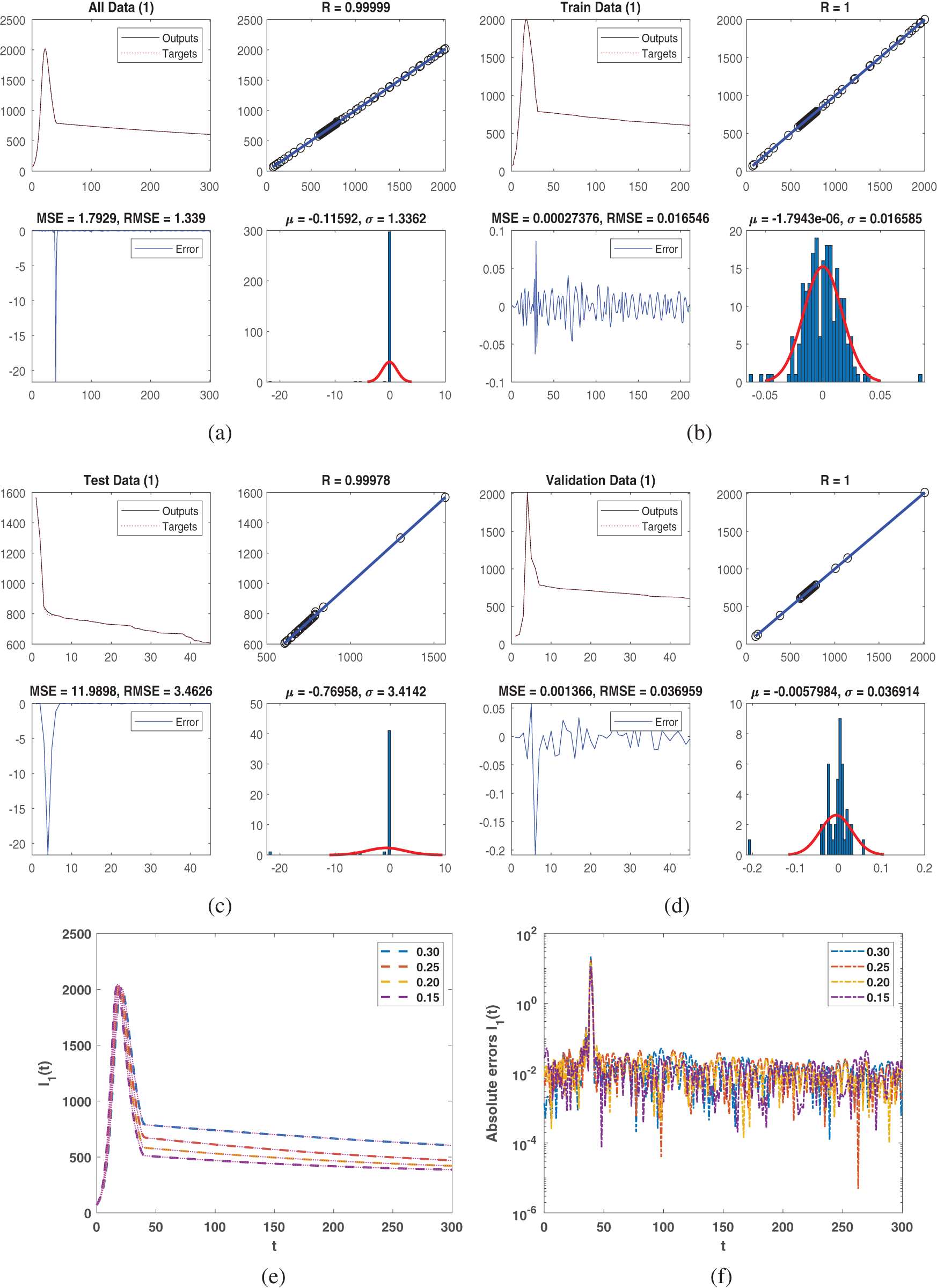
Figure 2: Piece-wise dynamical view of
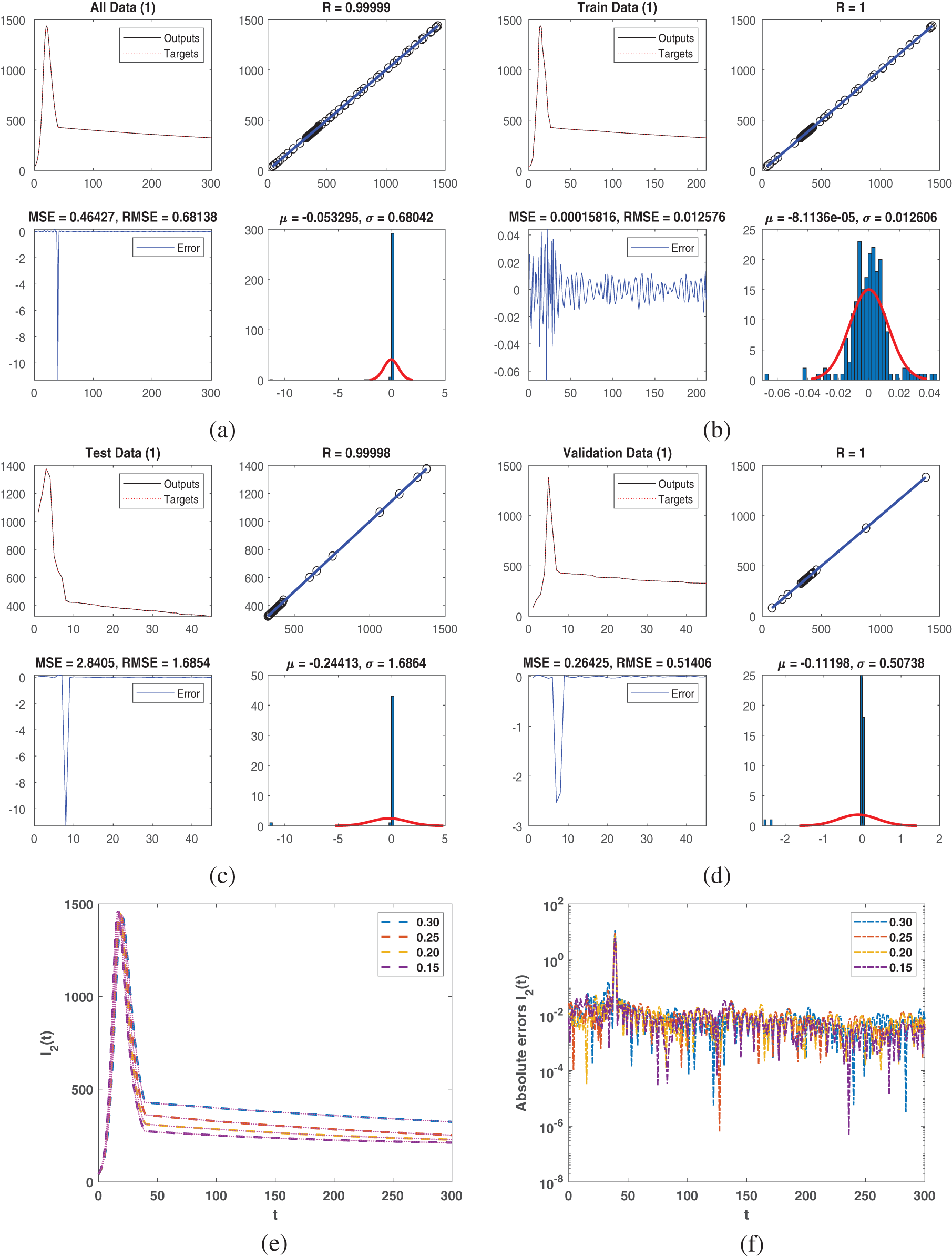
Figure 3: Piece-wise dynamical view of
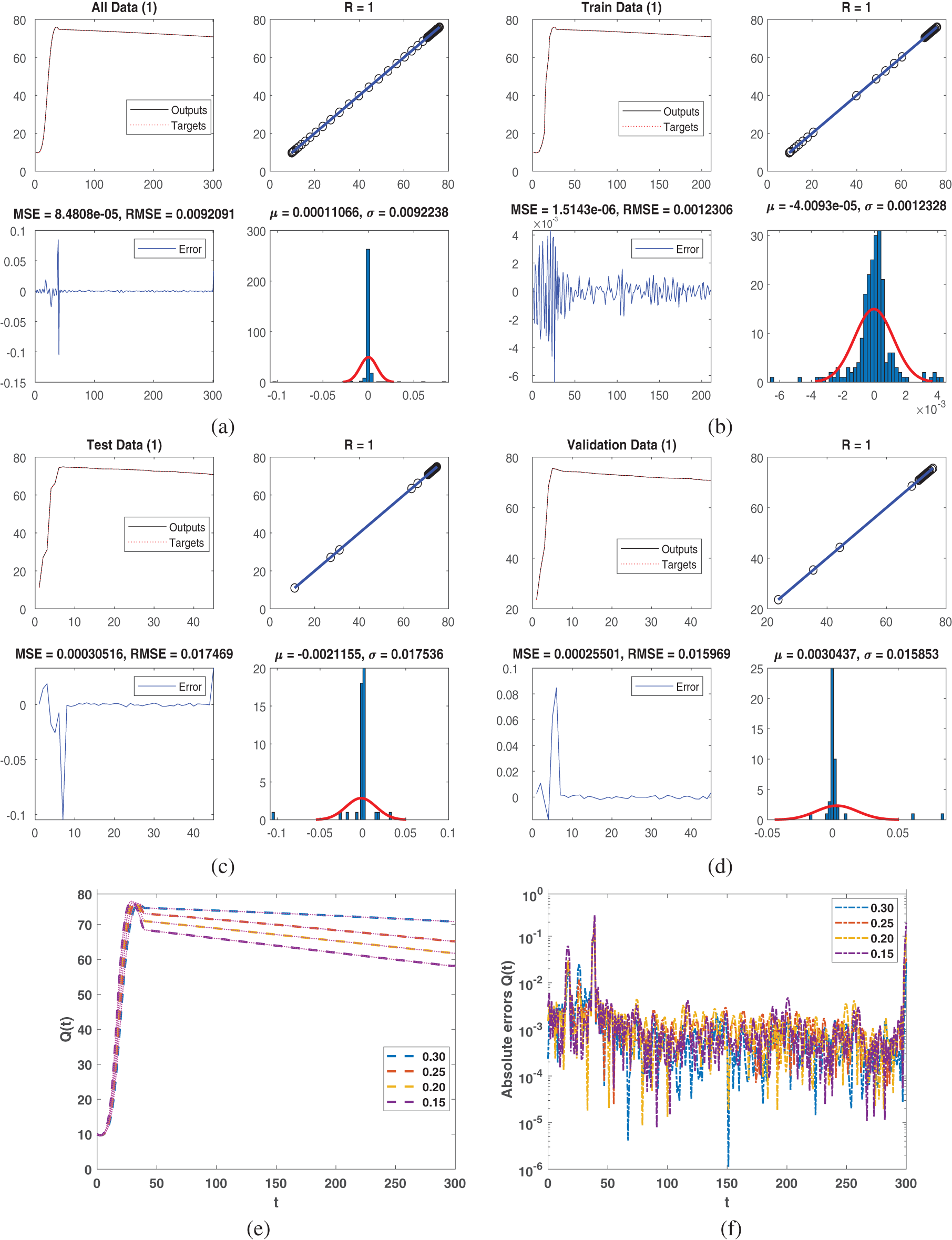
Figure 4: Piece-wise dynamical view of
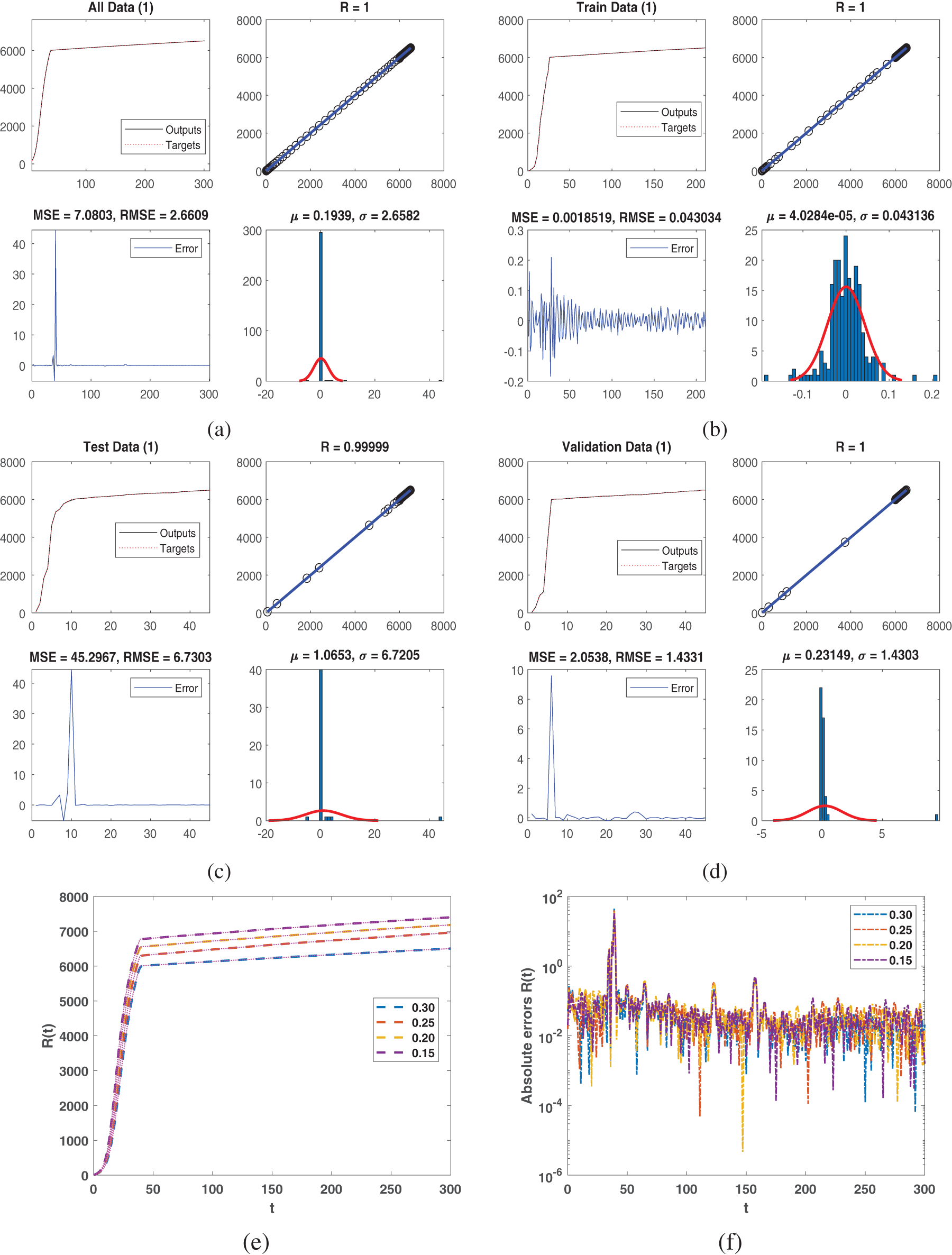
Figure 5: Piece-wise dynamical view of
Figs. 1–5 represent five agent populations in which the susceptible case decreases and then becomes stable as the other compartment increases on sub-intervals with bending from integer to fractional order. From
We address the piecewise Atangana-Baleanu-Caputo method with the NN approach for the previously mentioned model in this part. In this approach, we choose three types of hidden layers, including 10, 100, and 10 neurons for every layer to proceed the method onwards. Here, we applied the NN technique to obtain the performance of weight with low residual errors, and the epochs number is considered 1000. The obtained figures represented the approximate solution along with absolute error which we tested with NN to train the data accurately.
All data represented in Fig. 1a for class
All data represented in Fig. 2a for class
All data are used NN to obtain the class
All data are represented in Fig. 4a. NN was used to obtain the output for class
Fig. 5a represents all data. For class
The study analyzes a novel scheme of piece-wise derivable HIV infection with two two-stage infection models under the integer order derivative and AB operator, respectively. The considered system is treated on two sub-intervals by splitting the whole interval to establish the piece-wise dynamical system. The first interval is analyzed under integer order, while the second interval is processed under the global operator of AB derivative on different fractional orders. The uniqueness and existence in the form of theoretical results of both the intervals for the proposed model are proved using the analysis of fixed point theory. The numerical solution scheme for the model is also developed using Newton’s polynomial method for both sub-interval in integer order derivative and AB operator of fractional order
Acknowledgement: We are thankful to the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23066).
Funding Statement: This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23066).
Author Contributions: Ghaliah Alhamzi: Methodology, Writing—original draft, Formal analysis, Badr Saad T. Alkahtani: Conceptualization, Validation, Software, Ravi Shanker Dubey: Formal analysis, Validation, Software. Mati ur Rahman: Conceptualization, Supervision, Writing—original draft. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Sakkoum A, Lhous M, Magri EM. A mathematical simulation and optimal control of a VIH model with different infectious level. J Math Comput Sci. 2022;12:117. [Google Scholar]
2. Anderson RM. The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS. J Acquired Immune Def Synd. 1988;1(3):241–56. [Google Scholar] [PubMed]
3. Huo HF, Chen R, Wang XY. Modelling and stability of HIV/AIDS epidemic model with treatment. Appl Math Model. 2016;40(13–14):6550–9. doi:10.1016/j.apm.2016.01.054. [Google Scholar] [CrossRef]
4. Granich RM, Gilks CF, Dye C, De Cock KM, Williams BG. Universal voluntary HIV testing with immediate antiretroviral therapy as a strategy for elimination of HIV transmission: a mathematical model. Lancet. 2009;373(9657):48–57. doi:10.1016/S0140-6736(08)61697-9. [Google Scholar] [PubMed] [CrossRef]
5. Li Z, Teng Z, Miao H. Modeling and control for HIV/AIDS transmission in China based on data from 2004 to 2016. Comput Math Methods Med. 2017;2017(1):8935314. doi:10.1155/2017/8935314. [Google Scholar] [PubMed] [CrossRef]
6. May RM, Anderson RM. Commentary transmission dynamics of HIV infection. Nature. 1987;326:137–42. [Google Scholar] [PubMed]
7. Ngina P, Mbogo RW, Luboobi LS. Modelling optimal control of in-host HIV dynamics using different control strategies. Comput Math Methods Med. 2018;2018(1):9385080. doi:10.1155/2018/9385080. [Google Scholar] [PubMed] [CrossRef]
8. Singh R, Ali S, Jain M, Rakhee. Epidemic model of HIV/AIDS transmission dynamics with different latent stages based on treatment. Am J Appl Mathemat. 2016;13(2):222–34. doi:10.11648/j.ajam.20160405.14. [Google Scholar] [CrossRef]
9. Shen M, Xiao Y, Rong L. Global stability of an infection-age structured HIV-1 model linking within-host and between-host dynamics. Mathemat Biosci. 2015;263:37–50. doi:10.1016/j.mbs.2015.02.003. [Google Scholar] [PubMed] [CrossRef]
10. Shi S, Nguyen PK, Cabral HJ, Diez-Barroso R, Derry PJ, Kanahara SM, et al. Development of peptide inhibitors of HIV transmission. Bioact Mater. 2016;1(2):109–21. doi:10.1016/j.bioactmat.2016.09.004. [Google Scholar] [PubMed] [CrossRef]
11. Shirazian M, Farahi MH. Optimal control strategy for a fully determined HIV model. Intell Control Automat. 2010;1(1):15–9. doi:10.4236/ica.2010.11002. [Google Scholar] [CrossRef]
12. Silva CJ, Torres DF. Modeling and optimal control of HIV/AIDS prevention through PrEP. Discrete Contin Dyn Syst Ser S. 2017;11:119–41. [Google Scholar]
13. Umar M, Sabir Z, Amin F, Guirao JLG, Raja MAZ. Stochastic numerical technique for solving HIV infection model of CD4+ T cells. Eur Phys J Plus. 2020;135(5):403. doi:10.1140/epjp/s13360-020-00417-5. [Google Scholar] [CrossRef]
14. Işık E, Daşbaşı B. A compartmental fractional-order mobbing model and the determination of its parameters. Bull Biomathemat. 2023;1(2):153–76. doi:10.59292/bulletinbiomath.2023008. [Google Scholar] [CrossRef]
15. Bolaji B, Onoja T, Agbata C, Omede BI, Odionyenma UB. Dynamical analysis of HIV-TB co-infection transmission model in the presence of treatment for TB. Bull Biomathemat. 2024;2(1):21–56. doi:10.59292/bulletinbiomath.2024002. [Google Scholar] [CrossRef]
16. Kumar P, Erturk VS. Dynamics of cholera disease by using two recent fractional numerical methods. Mathemat Modell Numer Simulat Appl. 2021;1(2):102–11. doi:10.53391/mmnsa.2021.01.010. [Google Scholar] [CrossRef]
17. Ahmed I, Akgül A, Jarad F, Kumam P, Nonlaopon K. A Caputo-Fabrizio fractional-order cholera model and its sensitivity analysis. Mathemat Modell Numer Simulat Appl. 2023;3(2):170–87. doi:10.53391/mmnsa.1293162. [Google Scholar] [CrossRef]
18. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. J Thermal Sci. 2016;20(2):763–9. doi:10.2298/TSCI160111018A. [Google Scholar] [CrossRef]
19. Fatima B, Yavuz M, Rahman MU, Al-Duais FS. Modeling the epidemic trend of middle eastern respiratory syndrome coronavirus with optimal control. Math Biosci Eng. 2023;20(7):11847–74. doi:10.3934/mbe.2023527. [Google Scholar] [PubMed] [CrossRef]
20. Mahmood T, ur Rahman M, Arfan M, Kayani SI, Sun M. Mathematical study of Algae as a bio-fertilizer using fractal–fractional dynamic model. Mathemat Comput Simulat. 2023;203(2):207–22. doi:10.1016/j.matcom.2022.06.028. [Google Scholar] [CrossRef]
21. Mahmood T, Al-Duais FS, Sun M. Dynamics of Middle East respiratory syndrome coronavirus (MERS-CoV) involving fractional derivative with Mittag-Leffler kernel. Phys A: Statis Mech Appl. 2022;606(26):128144. doi:10.1016/j.physa.2022.128144. [Google Scholar] [PubMed] [CrossRef]
22. Atangana A, Araz Sİ. Nonlinear equations with global differential and integral operators: existence, uniqueness with application to epidemiology. Results Phys. 2021;20(2):103593. doi:10.1016/j.rinp.2020.103593. [Google Scholar] [CrossRef]
23. Haidong Q, ur Rahman M, Arfan M, Salimi M, Salahshour S, Ahmadian A. Fractal–fractional dynamical system of Typhoid disease including protection from infection. Eng Comput. 2023;39:1553–1562. [Google Scholar]
24. Mahmood T, Al-Duais FS, Sami A, Sun M. Analysis of tritrophic interaction with volatile compounds in plants with fractal fractional caputo operator. Fractals. 2023;31(10):2340082. doi:10.1142/S0218348X23400820. [Google Scholar] [CrossRef]
25. Awadalla M, Mu R, Al-Duais FS, Al-Bossly A, Abuasbeh K, Arab M. Exploring the role of fractal-fractional operators in mathematical modelling of corruption. Appl Mathemat Sci Eng. 2023;31(1):2233678. doi:10.1080/27690911.2023.2233678. [Google Scholar] [CrossRef]
26. Li B, Zhang T, Zhang C. Investigation of financial bubble mathematical model under fractal-fractional Caputo derivative. Fractals. 2023;31(5):14. doi:10.1142/S0218348X23500500. [Google Scholar] [CrossRef]
27. Baleanu D, Ghassabzade FA, Nieto JJ, Jajarmi A. On a new and generalized fractional model for a real cholera outbreak. Alexandria Eng J. 2022;61(11):9175–86. [Google Scholar]
28. Li B, Eskandari Z. Dynamical analysis of a discrete-time SIR epidemic model. J Frankl Inst. 2023;360(12):7989–8007. [Google Scholar]
29. Iwa LL, Nwajeri UK, Atede AO, Panle AB, Egeonu KU. Malaria and cholera co-dynamic model analysis furnished with fractional-order differential equations. Mathemat Modell Numer Simul Appl. 2023;3(1):33–57. [Google Scholar]
30. Atangana A, İğret Araz S. Mathematical model of COVID-19 spread in Turkey and South Africa: theory, methods, and applications. Adv Diff Equat. 2020;2020:1–89. [Google Scholar]
31. Atangana A, Araz Sİ. New concept in calculus: piecewise differential and integral operators. Chaos, Solit Fract. 2021;145:110638. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools