 Open Access
Open Access
ARTICLE
Insight Into the Separation-of-Variable Methods for the Closed-Form Solutions of Free Vibration of Rectangular Thin Plates
Institute of Solid Mechanics, Beihang University (BUAA), Beijing, 100191, China
* Corresponding Author: Yufeng Xing. Email:
Computer Modeling in Engineering & Sciences 2025, 142(1), 329-355. https://doi.org/10.32604/cmes.2024.056440
Received 23 July 2024; Accepted 11 November 2024; Issue published 17 December 2024
Abstract
The separation-of-variable (SOV) methods, such as the improved SOV method, the variational SOV method, and the extended SOV method, have been proposed by the present authors and coworkers to obtain the closed-form analytical solutions for free vibration and eigenbuckling of rectangular plates and circular cylindrical shells. By taking the free vibration of rectangular thin plates as an example, this work presents the theoretical framework of the SOV methods in an instructive way, and the bisection–based solution procedures for a group of nonlinear eigenvalue equations. Besides, the explicit equations of nodal lines of the SOV methods are presented, and the relations of nodal line patterns and frequency orders are investigated. It is concluded that the highly accurate SOV methods have the same accuracy for all frequencies, the mode shapes about repeated frequencies can also be precisely captured, and the SOV methods do not have the problem of missing roots as well.Keywords
The free vibration problems of rectangular plates can be classified into three categories according to boundary conditions (BCs), Category 1: all edges are simply supported and/or guided; Category 2: only two opposite edges are simply supported and/or guided; Category 3: BCs not falling into any of the above two categories. This classification is also suitable for the eigenbuckling problems of rectangular plates.
The problems of Categories 1 and 2 have the well-known Navier and Levy types of exact solutions that rigorously satisfy characteristic partial differential equations (PDEs) and BCs [1–5]. For the problems of Category 3, it is hard or even impossible to find exact solutions. To obtain analytical solutions to the problems of Category 3, several analytical methods have been developed from different perspectives since the 1950s, such as the Kantorovich-Krylov (K-K) method [6–10], the separation-of-variable (SOV) methods [11–15], the superposition method [16–19], the series expansion-based methods [20–24], the symplectic eigenfunction expansion method [25–29], and the dynamic stiffness method [30–34] for the plate assemblies.
Since the present work focuses on the SOV methods obtaining closed form eigensolutions, the motivations of the SOV methods are presented below. In the Navier method (an inverse method) and Levy method (a semi-inverse method), the separable mode function has the form of w(x, y) = φ(x)ψ(y), in which both φ(x) and ψ(y), or any one of them is constructed based on the simply supported BCs, limiting the application scope of the inverse methods. To extend the application of the Levy method, the direct SOV method [11] also using w(x, y) = φ(x)ψ(y) is proposed from a new perspective, wherein both unknown φ(x) and ψ(y) are solved simultaneously, and the closed-form solutions for the free vibration of rectangular plates with clamped adjacent edges were obtained for the first time. Afterwards, a few more powerful SOV methods are proposed based on the Rayleigh quotient, including the imSOV method [13], the vSOV method [12], the iSOV method [12], and the eSOV method [14]. Among them, the imSOV, iSOV, and eSOV methods are general ones, implying that they are suitable for rectangular plates and cylindrical shells with arbitrary homogeneous BCs.
In the SOV methods, mode functions have separable forms, like w(x, y) = φ(x)ψ(y). The relationships of the eigenvalues corresponding to spatial and temporal coordinates are achieved according to characteristic PDEs or/and the Rayleigh quotient. Transcendental eigenvalue equations are attained with the homogeneous BCs. Although there are several publications for each SOV method, there are no works about the following things: the general theoretical frameworks, the practical calculation method for natural frequencies and modes, the accuracy of frequencies of different orders, and the problem of missing frequencies or solution integrity.
In this context, this work presents the general methodology of how to solve the SOV solutions of characteristic PDEs, and how to obtain closed-form analytical solutions through the Rayleigh quotient. In addition, bisection-based solution procedures are presented to solve eigenvalue equations, and nodal line patterns which are used to check the accuracy and integrity of the SOV solutions are investigated. Note that the free vibration analysis of an isotropic rectangular thin plate is employed to achieve the objective of the present work.
The rest of this manuscript is organized as follows. Section 2 presents the theoretical framework of the SOV methods. After presenting the designing purposes and nonlinear eigenvalue equations of each SOV method, Section 3 gives the bisection-based solution procedures. Section 4 investigates the relations of nodal line patterns and frequency orders, as well as the accuracy and integrity of solutions. Section 5 compares the results of the SOV methods with those of the finite element method (FEM) and other methods, and conclusions are drawn in Section 6.
2 Theoretical Frameworks of the SOV Methods
The SOV methods are used to solve characteristic PDEs, the stationary value problems of the Rayleigh quotient, or both simultaneously. This section first presents the theoretical framework of the SOV methods, including the introduction of the characteristic PDEs and the Rayleigh quotient, as well as the methodology of finding SOV solutions based on them, and then demonstrates that all SOV methods come from the framework.
Fig. 1 shows a rectangular plate with length 2a, width 2b, and thickness h. According to the Kirchhoff plate theory [35], the displacement functions of thin plates have the forms as
U(x,y,z,t)=−z∂W(x,y,t)∂xV(x,y,z,t)=−z∂W(x,y,t)∂y
W(x,y,z,t)=W(x,y,t)(1)
where x, y are the coordinates of the middle surface, z is the coordinate of the thickness direction, and the origin of the coordinates is at the center of the middle surface; U, V, and W represent the displacements in the x, y and z directions, respectively, and only the deflection W is the independent variable according to Eq. (1).

Figure 1: A rectangular plate and the Cartesian coordinates
2.1 Characteristic Partial Differential Equations and Boundary Conditions
For a harmonic motion, the deflection W(x,y,t)=w(x,y)eiωt, where i=√−1, ω is the radial frequency, and w(x,y) is the mode function. The equation of the lateral translational motion for the free vibration of thin plates are [35]
∂Qx∂x+∂Qy∂y=−ρhω2w(2)
where ρ is the density, and h is the thickness; Qx and Qy are the transverse shear forces, which have the forms as
Qx=∂Mx∂x+∂Mxy∂y,Qy=∂Mxy∂x+∂My∂y(3)
Mx=−D(∂2w∂x2+ν∂2w∂y2),My=−D(∂2w∂y2+ν∂2w∂x2),Mxy=−D(1−ν)∂2w∂x∂y(4)
where Mx and My, and Mxy are the bending moments, and the twisting moment per unit length; D=Eh3/[12(1−ν2)] is the flexural rigidity, in which E is the Young’s modulus, and ν is the Poisson’s ratio. The equivalent shear forces have the forms asVx=Qx+∂Mxy∂y,Vy=Qy+∂Mxy∂x(5)
By substituting Eq. (4) into Eq. (3) and then into Eq. (2), the characteristic PDE is obtained as
D(∂4w∂x4+2∂4w∂x2∂y2+∂4w∂y4)−ρhω2w=0(6)
With the coordinate transformations ξ=x/a, η=y/b, Eq. (6) changes to
∂4w∂ξ4+2α2∂4w∂ξ2∂η2+α4∂4w∂η4=Ω4w(7)
where the aspect ratio α=a/b and the non-dimensional frequency Ω4=ω2(ρha4/D). All homogeneous BCs expressed in terms of w are listed in Table 1. Besides, symbolisms are used to denote the BCs of four edges. For example, “CSGF” indicates that the edges of ξ=−1, η=−1, ξ=1 and η=1 are clamped (C), simply supported (S), guided (G) and free (F) respectively, and other combinations of BCs can be interpreted in the same way.

2.2 Separation-of-Variable Solutions
This section introduces the general method of solving Eq. (7). Assuming that the closed-form mode function (deflection) w has the separable form as
w(ξ,η)=ϕ(ξ)ψ(η)(8)
then one can see from Table 1 that S, C, and G are separable, but F is not. Here ‘separable boundary condition’ implies that the boundary condition depends only on ϕ(ξ) or ψ(η). However, there is a special case: if a pair of opposite edges are S-S, G-G, or S-G, then even if the other two edges are free, their BCs are also separable. Section 3 will give an integration method to convert inseparable free BCs into separable ones.
Assuming the functions ϕ(ξ) or ψ(η) in Eq. (8) are as follows:
ϕ(ξ)=Aeμξ,ψ(η)=Beλη(9)
where μ and λ are the spatial eigenvalues concerning spatial coordinates ξ and η, respectively. With the substitution of Eq. (9) into Eq. (7), we have
(μ2+α2λ2)2=Ω4(10)
or
μ2+α2λ2=±Ω2(11)
which is the explicit relations of the two spatial eigenvalues μ and λ and the frequency Ω. One can see that there are four μ and four λ satisfying Eq. (10), and they can be written as
μ1,2≜±iα1,μ3,4≜±β1(12)
λ1,2≜±iα2,λ3,4≜±β2(13)
where α1, β1, α2, β2 are real numbers. Accordingly, the closed-form ϕ and ψ can be expressed as
ϕ(ξ)=A1cos(α1ξ)+A2sin(α1ξ)+A3cosh(β1ξ)+A4sinh(β1ξ)(14)
ψ(η)=B1cos(α2η)+B2sin(α2η)+B3cosh(β2η)+B4sinh(β2η)(15)
where A1−A4 and B1−B4 are the mode function coefficients. It should be emphasized that the mode functions in all SOV methods have the same expressions as given in Eqs. (8), (14) and (15), but each SOV method has a different technique to obtain α1, β1, α2, β2 and Ω. By substituting ϕ and ψ into the BCs of two pairs of opposite edges in Table 1, one can achieve A1−A4 and B1−B4 and two transcendental eigenvalue equations about α1, β1, α2, β2 and Ω. Solving for these five unknowns needs the other three equations, which are obtained below.
With the substitution of the four combinations (μ1,2,λ1,2), (μ1,2,λ3,4), (μ3,4,λ1,2), (μ3,4,λ3,4) into Eq. (10), one can have
α21+(αα2)2=Ω2(16)
−α21+(αβ2)2=±Ω2(17)
β21−(αα2)2=±Ω2(18)
β21+(αβ2)2=Ω2(19)
If the right-hand terms of Eqs. (17) and (18) are all equal to Ω2, or −Ω2, then using Eqs. (16)–(18) yields β21+α2β22=3Ω2, or β21+α2β22=−Ω2. These two equations contradict with Eq. (19), and this situation is denoted as Case 1. If the signs of the right-hand terms of Eqs. (17) and (18) are opposite, then Eq. (17) plus Eq. (18) and using (16) lead to Eq. (19), denoting this situation as Case 2.
Therefore, it can be seen that in Case 2, β21+α21=0 or β22+α22=0, having no non-trivial solutions, thus Case 2 is unrealistic and not considered further. In Case 1, the right-hand terms of Eqs. (17) and (18) should be equal to Ω2 since β21+α2β22=3Ω2 is more reasonable than β21+α2β22=−Ω2 in terms of Eq. (19), so Eqs. (17) and (18) should be
(αβ2)2=Ω2+α21(20)
β21=Ω2+(αα2)2(21)
The Eqs. (16), (20) and (21) are the three required equations. By using Eqs. (16), (20), (21) and two transcendental eigenvalue equations, one can determine α1, β1, α2, β2 and Ω. Besides, according to Eqs. (16), (20) and (21), we have
α21+β21=2Ω2(22)
(αβ2)2+(αα2)2=2Ω2(23)
Eq. (22) denotes the relation between Ω and two x-direction eigenvalues (α1, β1), and Eq. (23) stands for the relation between Ω and two y-direction eigenvalues (β2, α2).
For the problems of Category 1, Eq. (16) and two transcendental eigenvalue equations are solved together, and the solutions satisfy Eq. (7) and BCs exactly. For the problems of Category 2, Eqs. (16) and (20) or Eqs. (16) and (21) are solved together with two transcendental eigenvalue equations, and the results also satisfy Eq. (7) and BCs exactly. Therefore, the Navier method and the Levy method are the two special cases of the SOV methods.
For the problems of Category 3, three Eqs. (16), (20), (21) and two transcendental eigenvalue equations are solved concurrently, but Eq. (7) is not satisfied since Eq. (19) is not satisfied, implying that the obtained closed-form mode function w and the frequency Ω are not exact. There are two SOV methods solving Eqs. (16), (20), (21) and two transcendental eigenvalue equations. For the case without free edges, the constructed SOV method is the direct SOV method [11]. For the case with free edges, the constructed SOV method is the imSOV method [13], in which the expressions of separable free BCs are given in Section 2.3.
The Rayleigh quotient is generally used to derive characteristic PDEs of continuous systems and generalized eigenvalue equations of discrete systems and also serves as the foundation of FEM for dynamics problems. However, the present authors and coworkers found that the closed-form SOV analytical solutions can also be achieved through the Rayleigh quotient.
For free vibration, the Rayleigh quotient [36] has the form as
ω2=stUmaxT0(24)
where ‘st’ denotes ω2 is the stationary value of the quotient (Umax/T0); Umax is the maximum potential energy of a harmonic vibration; ω2T0 is the maximum kinetic energy; T0 is called the reference kinetic energy or the kinetic energy coefficient. For thin plates, we have
Umax=D2∬[(∂2w∂x2)2+2ν∂2w∂x2∂2w∂y2+(∂2w∂y2)2+2(1−ν)(∂2w∂x∂y)2]dxdy(25)
T0=12∬ρhw2dxdy(26)
By using the non-dimensional coordinates ξ and η, Eqs. (25) and (26) can be transformed into
Umax=abD2∬[1a4(∂2w∂ξ2)2+2νa2b2∂2w∂ξ2∂2w∂η2+1b4(∂2w∂η2)2+2(1−ν)a2b2(∂2w∂ξ∂η)2]dξdη(27)
T0=ab2ρh∬w2dξdη(28)
With the substitution of Eqs. (27) and (28) into Eq. (24), one can obtain the same PDE as Eq. (7) and the same natural BCs as those in Table 1.
When seeking the SOV solutions based on the Rayleigh quotient, Eqs. (8), (9) and Eqs. (12)–(15) are also used, and we assume that ψ is known but ϕ is unknown, or ψ is unknown but ϕ is known. When ψ is known and ϕ is unknown, Ωx is used to denote the corresponding frequency. When ψ is unknown and ϕ is known, Ωy is used to represent the corresponding frequency.
For the case with known ψ and unknown ϕ, according to Eqs. (27), (28) and (24), we can obtain the governing equation for ϕ, as
d4ϕdξ4+2α2[νS2S1−(1−ν)S3S1]d2ϕdξ2+(α4S4S1−Ω4x)ϕ=0(29)
and the boundary bending moment and equivalent shear force for the edges ξ=−1 and ξ=1, as
Mξ=abDa4(S1d2ϕdξ2+να2S2ϕ)Vξ=abDa4[S1d3ϕdξ3+α2(νS2−2(1−ν)S3)dϕdξ](30)
where the integral constants areS1=∫1−1ψ2dη,S2=∫1−1(ψd2ψdη2)dη,S3=∫1−1(dψdη)2dη,S4=∫1−1(d2ψdη2)2dη(31)
If an edge parallel to the y-axis is free, the separable free BCs can be obtained from Eq. (30), as
d2ϕdξ2+να2S2S1ϕ=0d3ϕdξ3+α2(νS2S1−2(1−ν)S3S1)dϕdξ=0(32)
By substituting the first expression in Eq. (9), or ϕ(ξ)=Aeμξ into Eq. (29), one can obtain the relation between μ and Ωx as
μ4+2α2[νS2S1−(1−ν)S3S1]μ2+(α4S4S1−Ω4x)=0(33)
the roots of which can be written in the same forms as those in Eq. (12), but here the spatial eigenvalues are
α1=α√√[νS2S1−(1−ν)S3S1]2−S4S1+Ω4xα4+[νS2S1−(1−ν)S3S1](34)
β1=α√√[νS2S1−(1−ν)S3S1]2−S4S1+Ω4xα4−[νS2S1−(1−ν)S3S1](35)
The expression of ϕ in terms of α1 and β1 has the same form as that in Eq. (14). Similarly, for the situation with unknown ψ and known ϕ, the governing equation for ψ can be achieved as
d4ψdη4+2α−2[νT2T1−(1−ν)T3T1]d2ψdη2+α−4(T4T1−Ω4y)ψ=0(36)
where
T1=∫1−1ϕ2dξ,T2=∫1−1(ϕd2ϕdξ2)dξ,T3=∫1−1(dϕdξ)2dξ,T4=∫1−1(d2ϕdξ2)2dξ(37)
The separable boundary bending moment and equivalent shear force for the edges η=−1 and η=1 are
Mη=abDb4(T1d2ψdη2+νT2α2ψ)Vη=abDb4[T1d3ψdη3+νT2−2(1−ν)T3α2dψdη](38)
The separable free BCs of an edge parallel to the x-axis can be obtained from Eq. (38), as
d2ψdη2+νT2α2T1ψ=0d3ψdη3+νT2−2(1−ν)T3α2T1dψdη=0(39)
With the substitution of the second expression in Eq. (9), or ψ(η)=Beλη into Eq. (36), the relation between λ and Ωy is obtained as
λ4+2α−2[νT2T1−(1−ν)T3T1]λ2+α−4(T4T1−Ω4y)=0(40)
whose roots have the forms of Eq. (13), and
α2=α−1√√[νT2T1−(1−ν)T3T1]2−T4T1+Ω4y+[νT2T1−(1−ν)T3T1](41)
β2=α−1√√[νT2T1−(1−ν)T3T1]2−T4T1+Ω4y−[νT2T1−(1−ν)T3T1](42)
The expression of ψ in terms of α2 and β2 is the same as that in Eq. (15).
The SOV methods based on the Rayleigh quotient include the iSOV method [12], the eSOV method [14], and the vSOV method [12]. In these three methods, the coefficients A1−A4 and B1−B4 and two transcendental eigenvalue equations can also be achieved by substituting ϕ and ψ into the simply support, clamp and guide BCs in Table 1 and the free BCs in Eqs. (32) and (39).
In the iSOV and eSOV methods, two transcendental eigenvalue equations and Eqs. (34), (35), (41), (42) are solved for α1, β1, α2, β2, Ωx and Ωy. In the vSOV method, Ωx=Ωy=Ω, and two transcendental eigenvalue equations and Eqs. (34), (35), (23), or two transcendental eigenvalue equations and Eqs. (41), (42), (22) are solved for α1, β1, α2, β2, Ω.
The iSOV and the eSOV methods are suitable for solving three Categories of problems. For the problems of Categories 1 and 2, the obtained solutions are exact; for the problems of Category 3, the solutions make the Rayleigh quotient take stationary value, implying that the solutions are the most accurate in the SOV function space. The vSOV method applies to the eigenproblem analysis of the rectangular plates without adjacent free edges.
3 SOV Methods and Bisection-Based Solution Procedures
In Section 2, the SOV methods have been formed based on the theoretical framework. This section first gives the purposes of proposing each SOV methods and then presents the corresponding eigenvalue equations. Then, the bisection-based solution procedures are provided for the imSOV method, the vSOV method, and the eSOV method respectively. Unlike the Newton iteration method, the bisection-based methods do not have the problem of choosing the initial values of solutions. The computational cost is discussed finally.
The imSOV method [13] is proposed to solve characteristic partial differential Eq. (7), which is a general method since it is capable of dealing with arbitrary homogeneous BCs. If an edge is free, its separable BCs are given in Eqs. (32) and (39).
This method uses Eqs. (16), (20), (21) and two transcendental equations to solve α1, β1, α2, β2 and Ω. The two transcendental equations can be attained through the substitution of ϕ(ξ) and ψ(η) into two pairs of BCs, as shown in Section 2.2. Here, taking a CCSS rectangular plate as an example, the two transcendental equations can be derived as
α1tanh2 β1=β1tan2 α1(43)
α2tanh2 β2=β2tan2 α2(44)
The bisection-based solution procedure for the imSOV method is as follows:
Preparation
1) To express α2 and β2 in terms of α1 and β1.
Eliminating Ω from Eqs. (16) and (21) generates
α22=β21−α212α2(45)
Then, with Eqs. (16), (20) and (45), one can have
β22=β21+3α212α2(46)
2) Substituting Eqs. (45) and (46) into Eq. (44) yields
√β21−α21tanh√2(β21+3α21)α2=√β21+3α21tan√2(β21−α21)α2(47)
Therefore, the original five Eqs. (16), (20), (21), (43) and (44) reduce to two nonlinear equations Eqs. (43) and (47), and the unknowns are α1 and β1.
Solution procedure
The flowchart of solving Eqs. (43) and (47) together is presented in Figs. 2 and 3, in which the non-zero small number ε is the initial value of α1; Δ is a small increment, and f1(α1,β1)=0 denotes Eq. (47) and f2(α1,β1)=0 stands for Eq. (43).
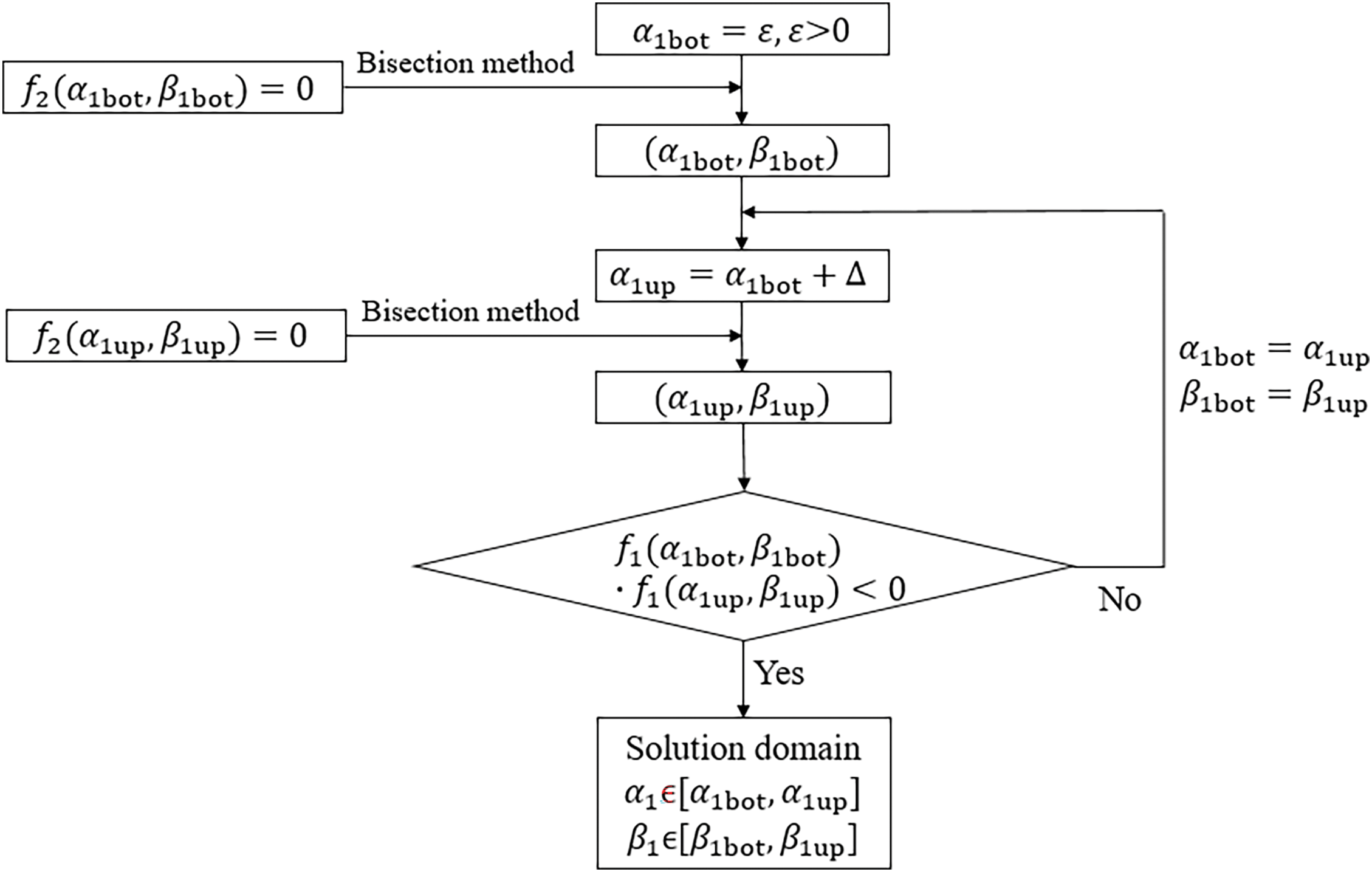
Figure 2: The procedure finding solution domains in the imSOV method
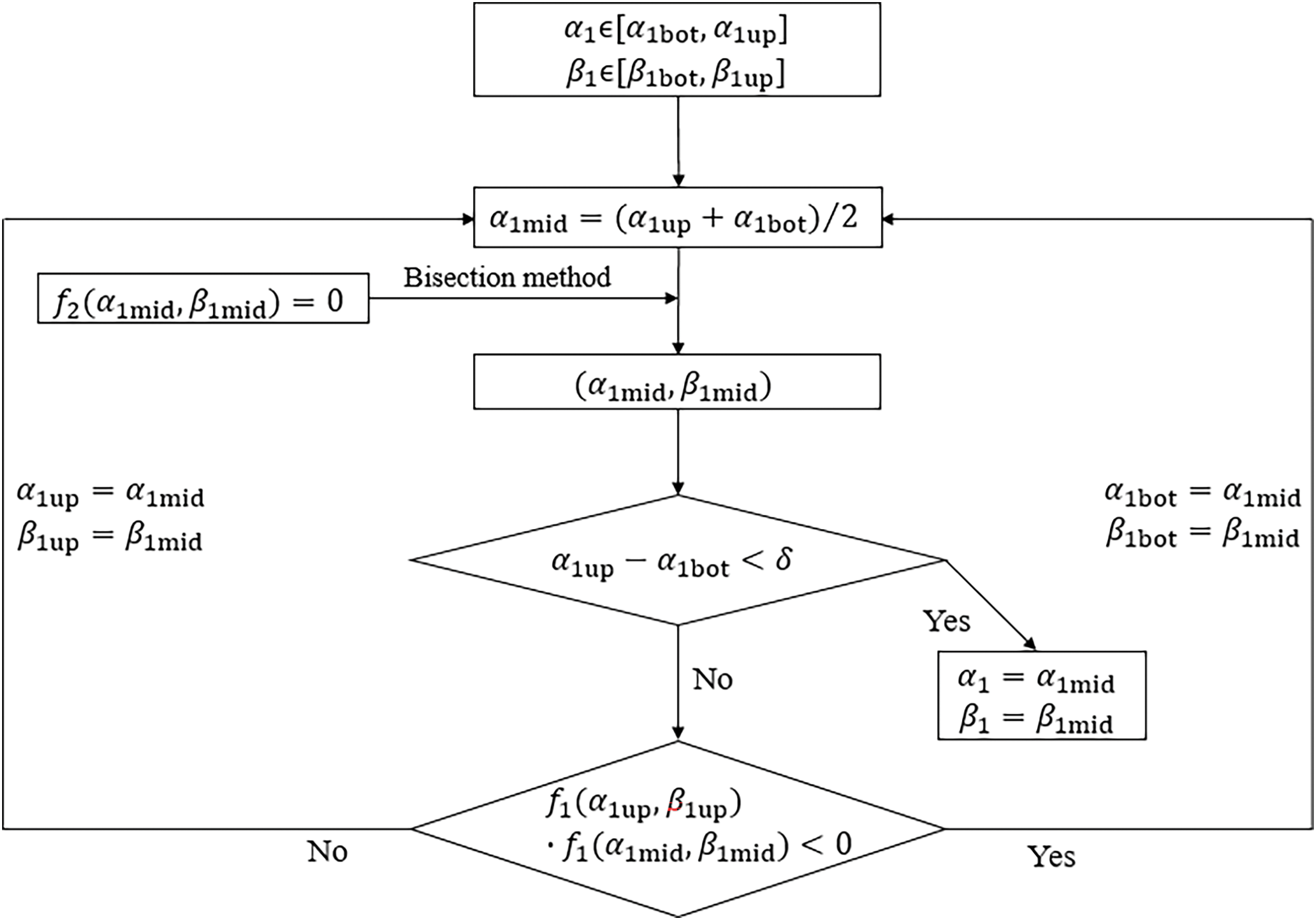
Figure 3: The process of calculating accurate results in each solution domain
Step 1 Find solution domains
The flowchart in Fig. 2 is used to search solution domains of Eq. (47), and a domain is represented by α1∈(α1bot,α1up), β1∈(β1bot,β1up).
It can be seen that by increasing the value of α1 gradually, one can find a set of (α1,β1) satisfying Eq. (43); then, one can select the solution domains of Eq. (47) from the set of (α1,β1) satisfying Eq. (43).
Step 2 Calculate accurate results
For each domain, the procedure shown in Fig. 3 is employed to calculate accurate solutions with the bisection method, in which δ, the solution precision of α1 and β1, is a number much smaller than Δ. Note that δ is also the solution precision when using the bisection method, for example, to solve β1bot for a given α1bot in Fig. 2. Finally, α2, β2 and Ω can be calculated through Eqs. (45), (46), and one of Eqs. (16), (20), (21).
It is noteworthy that the above solution procedure including two steps, finding solution domains and calculating accurate solutions, is also used in other SOV methods. If the imSOV method is used to deal with the plates with free corners, the solution procedure is the same as that of the eSOV method, refer to Section 3.3.
The vSOV method [12] is proposed to improve accuracy and extend the application of the direct SOV method [11]. The vSOV method can deal with rectangular plates without free corners (a free corner implies two adjacent edges are free). In addition to two transcendental eigenvalue equations, this method assumes Ωx=Ωy=Ω and solves either Eqs. (22), (41) and (42) or Eqs. (23), (34) and (35).
It can be seen that Eqs. (22) and (23) comes from Eq. (7) (a strong-form equation) and Eqs. (34) and (35), or (41) and (42) comes from Eq. (24) (a weak-form equation). So the vSOV method can be viewed as a mixed method, implying that the vSOV method is used to solve the strong-form Eq. (7) in the x or the y direction and obtain the stationary value of the Rayleigh quotient in the y or the x direction simultaneously.
It should be noteworthy that the vSOV method is the basis of the iSOV method [12] and the eSOV method [14]. Based on the bisection method, the solution procedures of the vSOV method are presented below for two cases.
Case1: Plates without free edges
Also take a CCSS plate as an example, and the transcendental equations are Eqs. (43) and (44). The coefficients A1−A4 of ϕ(ξ) are
A2=A1cotα1,A3=−A1cosα1coshβ1,A4=−A1cosα1sinhβ1(48)
Preparation
1) To express α2, β2 and Ω in terms of α1 and β1.
As shown in Eqs. (14) and (48), ϕ(ξ) is the explicit function of α1 and β1, then Eq. (37) shows that T1−T4 are the explicit functions of α1 and β1.
Besides, Eq. (22) shows that Ω is also the function of α1 and β1, so Eqs. (41) and (42) indicate that α2 and β2 are the explicit functions of α1 and β1.
2) Substituting Eqs. (41) and (42) into Eq. (44), one can have a transcendental equation about α1 and β1, which can be solved together with Eq. (43) for α1 and β1.
Solution procedure
The solution procedure is the same as that in Section 3.1, refer to Figs. 2 and 3.
Case2: Plates with one free edge or two opposite free edges
Here taking a CSSF plate as an example, the transcendental equation for the x direction is Eq. (43). According to the BCs of the edges η=−1 and η=1, the y-direction transcendental equation can be achieved as
β2(Ny2−α22)(Ny1+β22)tan2 α2=α2(Ny2+β22)(Ny1−α22)tanh2 β2(49)
where Ny1 and Ny2 are
{Ny1=νT2−2(1−ν)T3α2T1Ny2=νT2α2T1(50)
Preparation
1) To express α2, β2 and Ω in terms of α1 and β1.
Eq. (37) shows T1−T4 are the explicit functions of α1 and β1, and Ω can be calculated from Eq. (22) using α1 and β1, so α2 and β2 are the explicit functions of α1 and β1, refer to Eqs. (41) and (42).
2) By substituting Eqs. (41) and (42) into Eq. (49), one can obtain a transcendental equation regarding α1 and β1, which can be solved together with Eq. (43) for α1 and β1.
Solution procedure
The solution procedures of the vSOV method are the same as that of the imSOV method in Section 3.1.
The eSOV method [14] is proposed to improve accuracy and extend the application of the vSOV method [12], and it applies to any homogeneous BCs, so it is a general solution method. The eSOV method obtains the closed form eigensolutions by finding the stationary values of the Rayleigh quotient.
The method has nothing to do with Eq. (7). In this method, four Eqs. (34), (35), (41) and (42) in conjunction with two transcendental eigenvalue equations are solved to achieve the six unknowns α1, β1, α2, β2, Ωx and Ωy, in which Ωx and Ωy are independent each other in mathematical sense, but they are the same in physical sense, which can be proved through the Rayleigh quotient itself.
To simplify solution procedures, the four unknowns of α1, β1, α2 and β2 are solved first. By eliminating Ωx from Eqs. (34) and (35), we have
α21−β21=2α2[νS2S1−(1−ν)S3S1](51)
and eliminating Ωy from Eqs. (41) and (42) generates
α22−β22=2α−2[νT2T1−(1−ν)T3T1](52)
Then we only need to solve Eqs. (51), (52) and two transcendental equations for α1, β1, α2 and β2. After obtaining α1, β1, α2 and β2, one can use any one of Eqs. (34), (35), (41) and (42) to obtain the frequency Ω because of Ω=Ωx=Ωy.
Case1: Plates without free edges
Also taking the CCSS plate as an example, and the two transcendental equations are Eqs. (43) and (44). The mode function coefficients A1−A4 are given in Eq. (48), and B1−B4 are
B2=B1cotα2,B3=−B1cosα2coshβ2,B4=−B1cosα2sinhβ2(53)
Preparation
1) To express β2 in terms of α1, β1, and α2.
Eq. (52) can be reformed as
β22=α22−2α−2[νT2T1−(1−ν)T3T1](54)
which shows that β2 is an explicit function of α1,β1, and α2. Then ψ(η) in Eq. (15) and S1−S4 in Eq. (31) are also the explicit functions of α1,β1,α2.
2) By substituting Eq. (54) into Eq. (44), we have
α2tanh2√α22−2α−2[νT2T1−(1−ν)T3T1]=√α22−2α−2[νT2T1−(1−ν)T3T1]tan2α2(55)
Since T1−T4 are the explicit functions of α1 and β1, thus the y-direction transcendental Eq. (55) is an equation for α1,β1 and α2,
Solution procedure
After preparation, we can solve Eqs. (55), (43) and (51) for α1,β1,α2. Eqs. (43) and (55) are the transcendental equations, and Eq. (51) denotes the relation between the two-direction eigenvalues.
The procedure to find solution domains of Eqs. (55), (43) and (51) is presented in Fig. 4, wherein Eq. (43) is denoted by f2(α1,β1)=0, Eq. (55) is denoted by f1(α1,β1,α2)=0 and Eq. (51) is denoted by f3(α1,β1,α2)=0. The process of calculating accurate results is similar to that in Fig. 3. More explanations about Fig. 4 are given below:
1) Since Eq. (43) is only about α1 and β1, so to facilitate the solution procedure, for a given α1bot Eq. (43) is solved firstly to obtain β1bot with the bisection method.
2) With the known (α1bot,β1bot), Eq. (55) is a nonlinear equation of α2, which can be solved by the bisection method to obtain α2bot.
3) After having a group of (α1bot,β1bot,α2bot) satisfying Eqs. (43) and (55). By gradually increasing the value of α1 with the increment Δ, one can determine a group of (α1up,β1up,α2up), then the solution domain of Eq. (51) is obtained, which is α1∈(α1bot,α1up), β1∈(β1bot,β1up) and α2∈(α2bot,α2up).
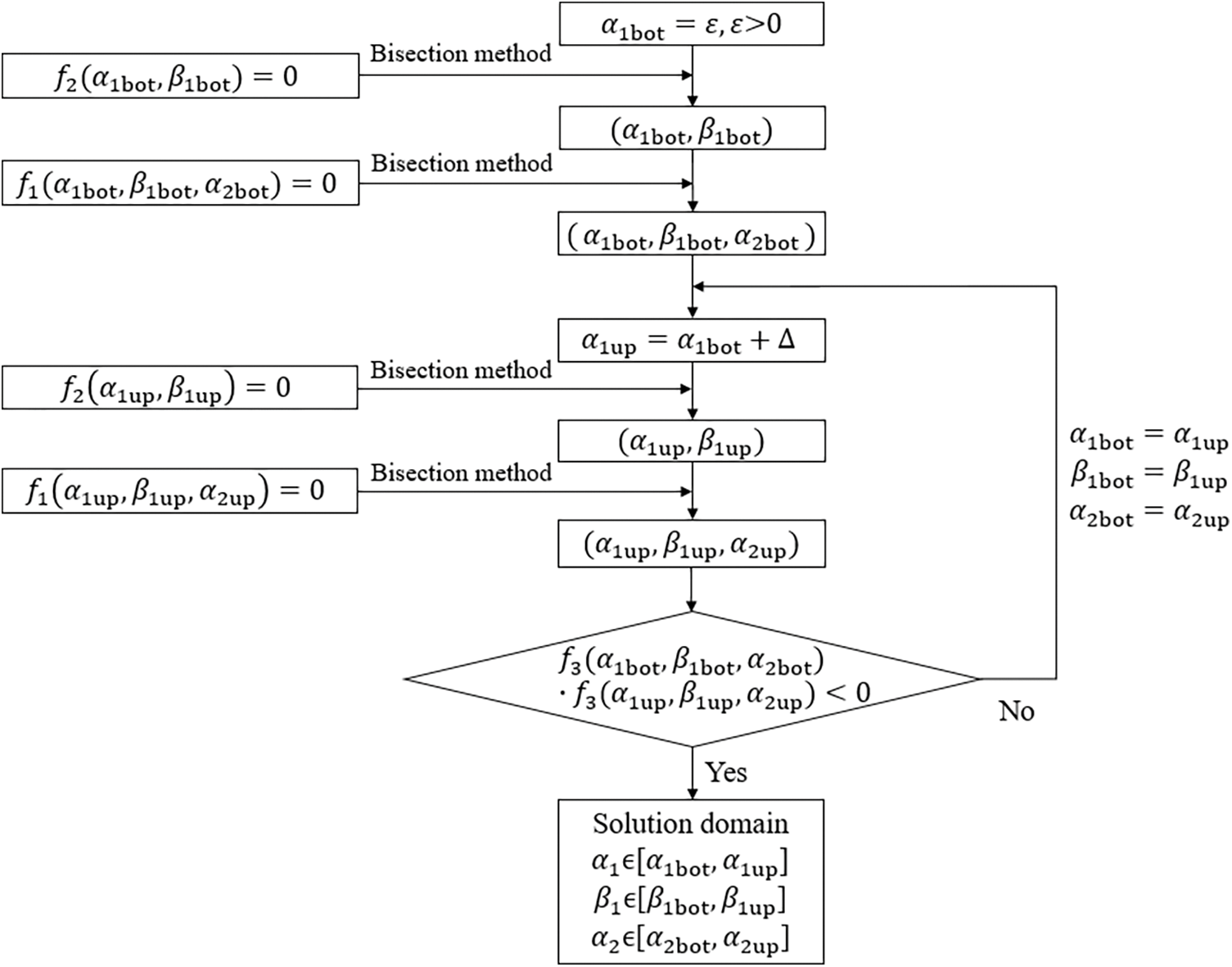
Figure 4: The procedure finding solution domains in the eSOV method
Case2: Plates with one free edge or two opposite edges free
The situation with one free edge is considered first. Similar to the vSOV method, the CSSF plate is taken as an example too. Eqs. (43) and (49) are the two transcendental equations. The coefficients A1−A4 are given in Eq. (48), and the coefficients B1−B4 are
B2=B1cotα2,B3=−B1cosα2coshβ2Ny2−α22Ny2+β22,B4=−B1cosα2sinhβ2Ny2−α22Ny2+β22(56)
Preparation
1) As shown in Section 3.1, β1 can be achieved from Eq. (43) for a given α1 with the bisection method, and T1−T4 are the explicit functions of α1 and β1.
2) Ny1 and Ny2 are also the explicit functions of α1 and β1 according to Eq. (50), from which we have
Ny1+Ny2=2α−2[νT2T1−(1−ν)T3T1](57)
From Eqs. (52) and (57), one can obtain
β22=α22−Ny1−Ny2(58)
Substituting Eq. (58) into Eq. (49) to eliminate β2 generates
√α22−Ny1−Ny2(Ny2−α22)2tan2α2=α2(Ny1−α22)2tanh(2√α22−Ny1−Ny2)(59)
which is a nonlinear equation for α1,β1,α2. Then from Eqs. (58), (56), (15) and (31), one can see that β2, B1−B4, ψ(η) and S1−S4 are also the explicit functions of α1,β1,α2.
Solution procedure
Solving Eqs. (43), (59) and (51) can give α1,β1,α2. Among these three equations, Eqs. (43) and (59) are the transcendental equations corresponding to two coordinate directions respectively, and Eq. (51) establishes the eigenvalue relation of two directions. The process for finding the solution domains of these three equations is the same as that shown in Fig. 4. Then a similar process as that in Fig. 3 can be used to calculate accurate results.
Case3: Plates with free corners
Taking a SSFF plate as an example, the y-direction transcendental equation is Eq. (49), and the x-direction transcendental equation is similar to Eq. (49), as
β1(Nx2−α21)(Nx1+β21)tan2α1=α1(Nx2+β21)(Nx1−α21)tanh2 β1(60)
where Nx1 and Nx2 are the variables from the free BCs of the edges ξ=−1 and ξ=1, as
Nx1=α2νS2−2(1−ν)S3S1(61)
Nx2=α2νS2S1(62)
The mode function coefficients B1−B4 are listed in Eq. (56), and A1−A4 are
A2=A1cotα1,A3=−A1cosα1coshβ1Nx2−α21Nx2+β21,A4=−A1cosα1sinhβ1Nx2−α21Nx2+β21(63)
Preparation
1) Deal with the eigenvalue equations in the x direction.
From Eqs. (61) and (62), we have
Nx1+Nx2=2α2[νS2S1−(1−ν)S3S1](64)
Then from Eqs. (51) and (64), one can obtain
α21−β21=Nx1+Nx2(65)
By substituting Eq. (65) into Eq. (60), we have
β1(Nx2−α21)2tan2α1=α1(Nx2+β21)2tanh2 β1(66)
which is a quadratic equation of Nx2. By using the root formula, Nx2 can be obtained, which is the explicit function of α1,β1, then the coefficient A1−A4 and the integrals T1−T4 are the explicit functions of α1,β1.
2) Deal with the eigenvalue equations in the y direction, and the work is the same as that in Section 3.2.
3) From Eqs. (65) and (66), we know that both Nx1 and Nx2 are the explicit functions of α1,β1. It can be seen from 2) that S1−S4 are the explicit functions of α1,β1andα2. By substituting S1−S4,Nx1,Nx2 into Eqs. (61) and (62), we have two nonlinear equations for α1,β1,α2.
Solution procedure
In the above preparation, one has obtained three nonlinear equations, including Eqs. (59), (61) and (62). Among them, Eq. (59) is the y-direction transcendental equation, and Eqs. (61) and (62) relate the eigenvalues of the x and y directions.
The solution domains of these three equations can be found with the procedure in Fig. 5, in which f1=0, f2=0 and f3=0 stand for Eqs. (59), (62) and (61), respectively. By increasing the value of α1 gradually, one can find a set of (α1,β1,α2) satisfying Eqs. (59) and (62); then by using the bisection method again, one can find (α1,β1,α2) satisfying Eq. (61) from the set of (α1,β1,α2). Finally, the closed-form solutions are achieved.
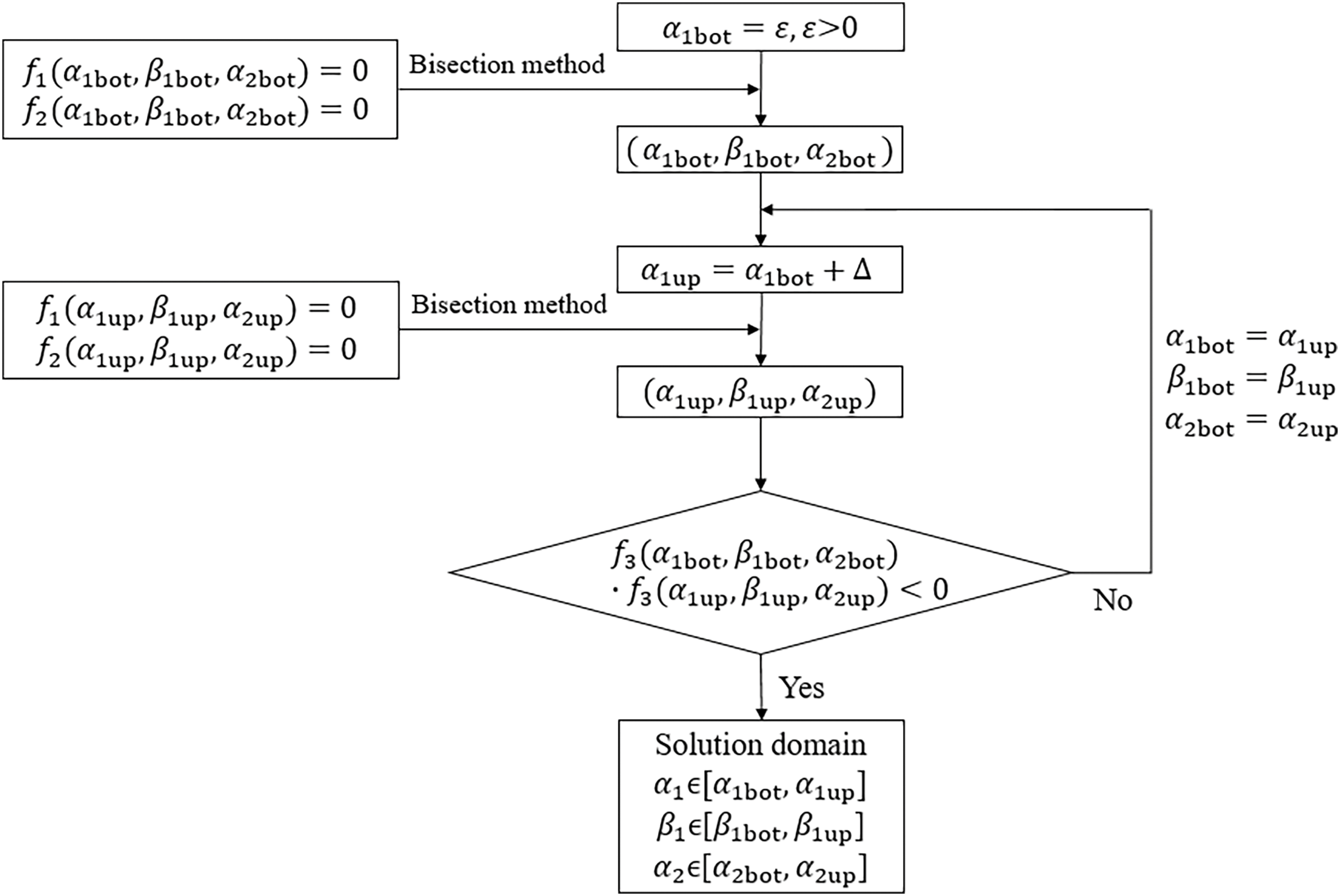
Figure 5: The procedure finding solution domains for SSFF plates in the eSOV method
In addition to the above solution procedures, an iteration method can also be used here. If (α1, β1, Ωx) are obtained with the assumed (α2, β2, Ωy), then (α2, β2, Ωy) can be updated with the obtained (α1, β1, Ωx), then updating (α2, β2, Ωy) again, the iteration ends if |Ωy−Ωx|/Ωx is small enough. This iteration solution method is the iSOV method [12].
The SOV methods are analytical methods, which can be used to solve characteristic PDEs or the stationary value of the Rayleigh quotient, not requiring to discretize spatial domain like FEM. To obtain frequencies and modes, only a few closed-form transcendental and algebraic eigenvalue equations need to be solved, as shown in Sections 3.1–3.3. So, the SOV methods are efficient and economical, and solving programs can be implemented on regular PCs.
In previous publications (for example, [11–15]), the Newton iteration method was used to solve eigenvalue equations. If initial values are appropriate, convergence can be reached after 3 or 4 iterations. But the initial values of solutions should be close to solutions, otherwise the solutions cannot be found, or the solutions are not expected, implying that selecting initial values is a troublesome issue especially when solving solutions of many orders.
To avoid the issue of selecting initial values, the bisection-based solution procedures are presented in this work as alternative methods to the Newton method, as shown in Sections 3.1–3.3. The procedures include two steps, searching solution intervals and calculating accurate solutions, and the bisection approach is used in the two steps.
4 Nodal Line Patterns and the Solution Integrity
This section gives the nodal line equations, from which the nodal line geometrical configurations or patterns can be obtained. Besides, with the help of the nodal line patterns, the solution integrity of the SOV methods is qualitatively discussed.
The SOV methods have the advantage that they have separable and explicit equations of nodal lines. The nodal line equations can be achieved by assuming the mode function w(ξ,η) in Eq. (8) is equal to zero, that is
w(ξ,η)=ϕ(ξ)ψ(η)=0(67)
then the nodal line equations are
ϕ(ξ)=0(68)
ψ(η)=0(69)
Solving the above two equations yields the positions of nodal lines within a plate. Since ϕ(ξ) is just a function of ξ and ψ(η) is just a function of η, then the nodal lines determined by Eqs. (68) and (69) are straight lines parallel to plate edges. That is, the nodal lines of ϕ(ξ)=0 are perpendicular to the x-axis, and the ones of ψ(η)=0 perpendicular to the y-axis. Besides, at the intersections of the nodal lines, ϕ(ξ)=ψ(η)=0. In the SOV methods, Eq. (68) and Eq. (69) are applicable to arbitrary homogeneous BCs.
According to Eqs. (14), (15), (68) and (69) can be rewritten as
ϕ(ξ)=A1cos(α1ξ)+A2sin(α1ξ)+A3cosh(β1ξ)+A4sinh(β1ξ)=0(70)
ψ(η)=B1cos(α2η)+B2sin(α2η)+B3cosh(β2η)+B4sinh(β2η)=0(71)
where A1−A4, B1−B4, α1,α2, β1,β2 can be obtained through the procedures provided in Section 3, so the forms of these two equations are explicit. A mode of a plate has no or many nodal lines, and the feature of a mode shape depends on the positions of nodal lines. The nodal line pattern of a mode is a geometry graph including all nodal lines inside a plate.
In the following, a simply supported plate is considered to show how to determine the positions of nodal lines. According to Eqs. (14) and (15) and the simply supported BCs, see Table 1, we can obtain the eigenvalue equations and mode function coefficients as follows:
sin2 α1=0sin2 α2=0}⇒α1=mπ2α2=mπ2}(72)
A1=sinα1,A2=cosα1,A3=A4=0
B1=sinα2,B2=cosα2,B3=B4=0(73)
where m,n=1,2,3,⋯ are the numbers of half waves in the x and y directions, respectively. Then using Eqs. (70) and (71) generates the equations of nodal lines as
ϕ(ξ)=sinmπ2cos(mπ2ξ)+cosmπ2sin(mπ2ξ)=sinmπ2(1+ξ)=0(74)
ψ(η)=sinnπ2cos(nπ2η)+cosnπ2sin(nπ2η)=sinnπ2(1+η)=0(75)
where ξ∈(−1,1), η∈(−1,1). Given m and n, one can calculate the nodal line positions and the number of nodal lines from Eqs. (74) and (75). For example, if m = 2, then ξ=0 and there is only one nodal line; if m = 3, then ξ=±1/3 and there are two nodal lines. The number of nodal lines is equal to the number of half waves minus one.
The nodal line patterns of the SSSS and CCSS isotropic square plates (α=1) are shown in Figs. 6 and 7 respectively, where the values (i, j) = (m – 1, n – 1), wherein i and j represent the numbers of nodal lines perpendicular to the x-axis and the y-axis, respectively. By observing the nodal line patterns and the frequency orders, one can find that for these two square plates, the correspondences between the numbers of nodal lines and the frequency orders are the same, but the positions of nodal lines are different. For the SSSS plate, the nodal lines distribute evenly within the plate, while for the CCSS plate, the nodal lines no longer distribute evenly, further away from the clamped edges parallel to them, refer to the two patterns of (2, 2) in Figs. 6, 7. It can be seen that the sizes of square ① and square ② in Fig. 6 are the same, while in Fig. 7 square ① is larger than square ②.
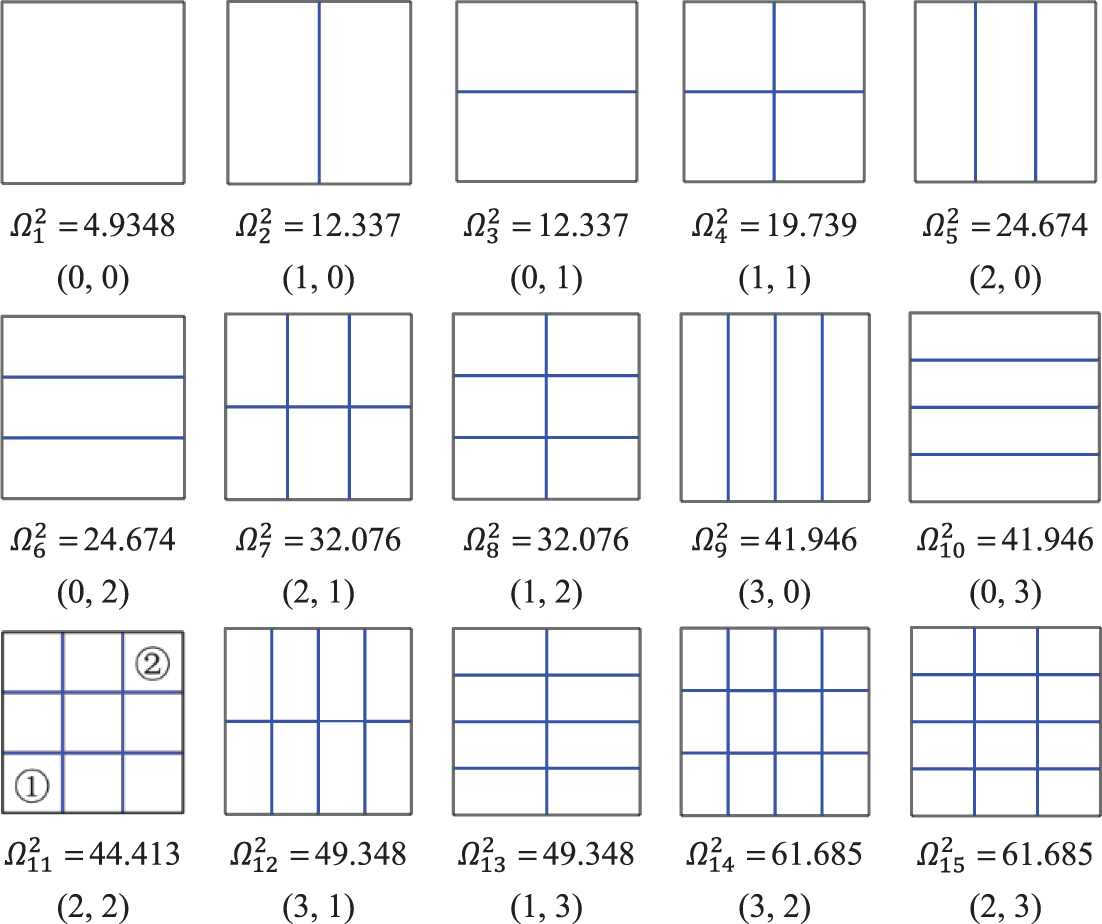
Figure 6: Nodal line patterns of the SSSS square plate for the first 15 modes
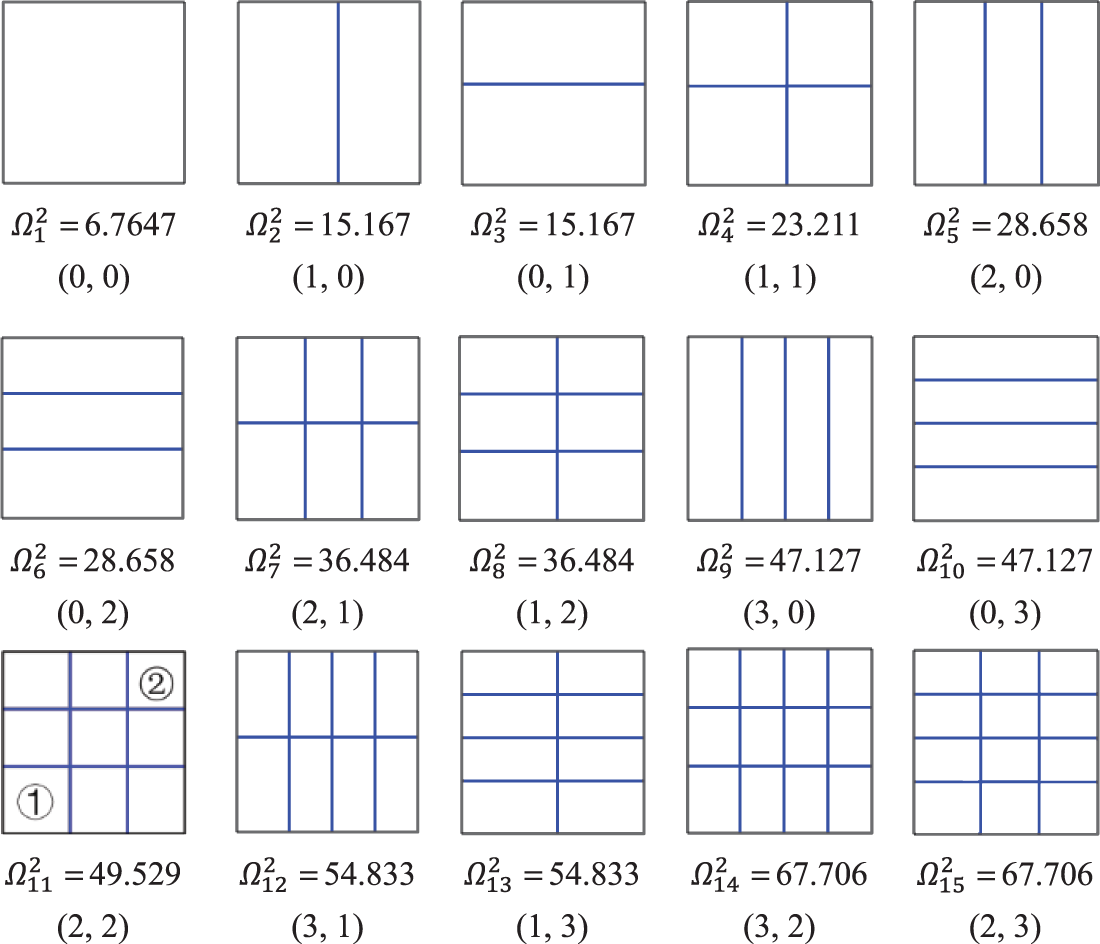
Figure 7: Nodal line patterns of the CCSS square plate for the first 15 modes
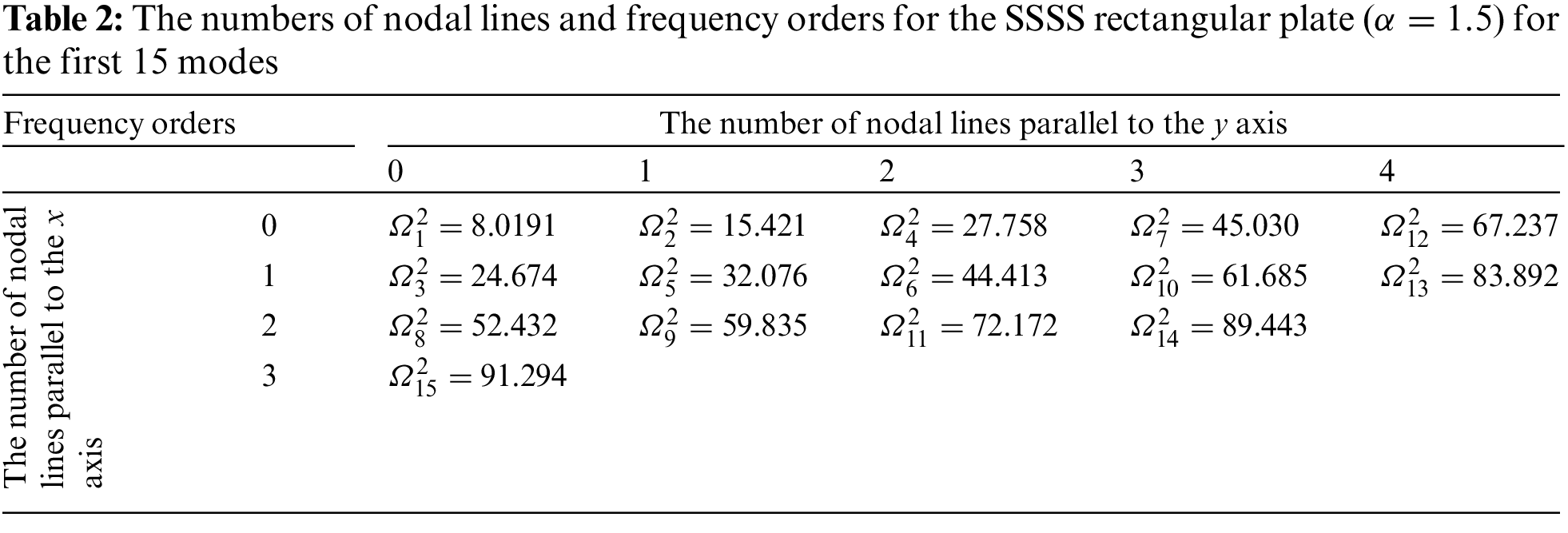
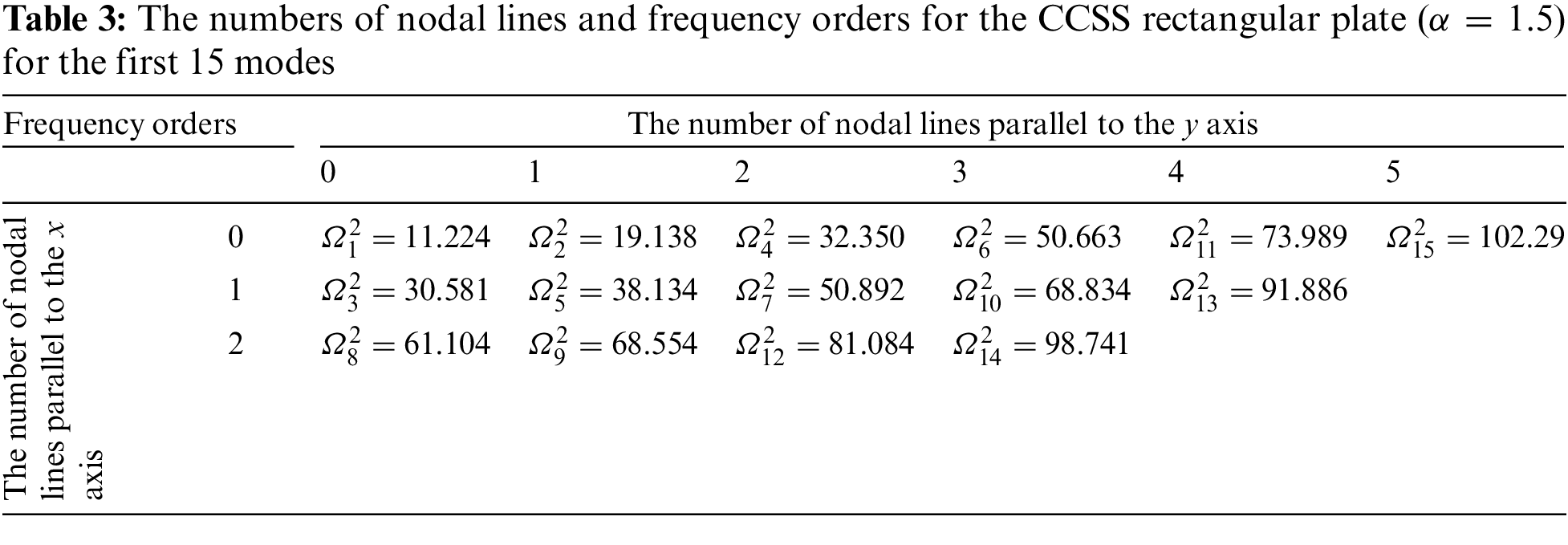
For comparison, Tables 2, 3 present the relationships between the numbers of nodal lines and the frequency orders for the SSSS and CCSS rectangular plates (α=1.5) respectively. For the two rectangular plates, the correspondences between the nodal line patterns and frequency orders are different. For example, the frequency of order 15 for the SSSS plate corresponds to the pattern (0, 3), while the frequency of the same order for the CCSS plate corresponds to the pattern (5, 0).
Besides, Figs. 6, 7 show that the nodal lines in the SOV methods are straight, even though for repeated frequencies, such as the two frequencies with patterns of (1, 0) and (0, 1). But the combinations of two modes having straight nodal lines that are parallel to plate edges can produce the modes having diagonal or curved nodal lines, also refer to the modes plotted in Section 5. Here the SSSS square plate is taken as an example to show the combining results. For clarity’s sake, the first pair of repeated frequencies corresponding to the patterns of (1, 0) and (0, 1), or (m, n) = (2, 1) and (1, 2), is taken into account below. The two-mode functions are
w(ξ,η)|(m,n)=(2,1)=ϕ(ξ)|m=2ψ(η)|n=1=−sin(πξ)cos(π2η)w(ξ,η)|(m,n)=(1,2)=ϕ(ξ)|m=1ψ(η)|n=2=−sin(πη)cos(π2ξ)(76)
Then by letting the two combinations of the two modes equal to zero, we have
w(ξ,η)|(m,n)=(2,1)+w(ξ,η)|(m,n)=(1,2)=−4cosπη2cosπξ2cosπ(ξ−η)4sinπ(ξ+η)4=0w(ξ,η)|(m,n)=(2,1)−w(ξ,η)|(m,n)=(1,2)=−4cosπη2cosπξ2cosπ(ξ+η)4sinπ(ξ−η)4=0(77)
Since ξ=±1 and η=±1 are not the required nodal lines for the simply supported plate, hence we obtain two equations of nodal lines from Eq. (77), as
ξ+η=0ξ−η=0(78)
which correspond to two diagonal nodal lines for the repeated frequencies.
As for other BCs, the above combining method can also be used to achieve the modes with diagonal or curved nodal lines corresponding to repeated frequencies.
4.2 Solution Accuracy and Integrity
For the problems of Categories 1 and 2, the SOV methods achieve the Navier and Levy solutions respectively, and the solutions are exact. For the problems of Category 3, one generally believes that there are no SOV exact solutions, and even believes that there are no closed-form solutions. To obtain the SOV and closed-form solutions of the problems of Category 3, the SOV methods are proposed, and the solutions are found to be highly accurate [12]. It is noteworthy that the nSOV method in [12] was renamed as the vSOV method after it was proposed. The imSOV method [12] has the same accuracy as the direct SOV method [11], and the iSOV method almost has the same accuracy as the eSOV method. In Section 5, the results of the SOV methods are compared with those of the FEM, and their high accuracy and versatility are validated.
According to the Rayleigh quotient, if the modes obtained by two methods have the same nodal line patterns, then the frequencies obtained by the two methods have the same accuracy, and the accuracy of the frequencies is one order higher than that of the modes. Through the numerical comparisons in [12] and [15], etc., also refer to Figs. 8 and 9 in Section 5, one can see that the SOV methods generate the same nodal line patterns as the referenced FEM, so the SOV methods are highly accurate, even though for the inseparable problems of Category 3.
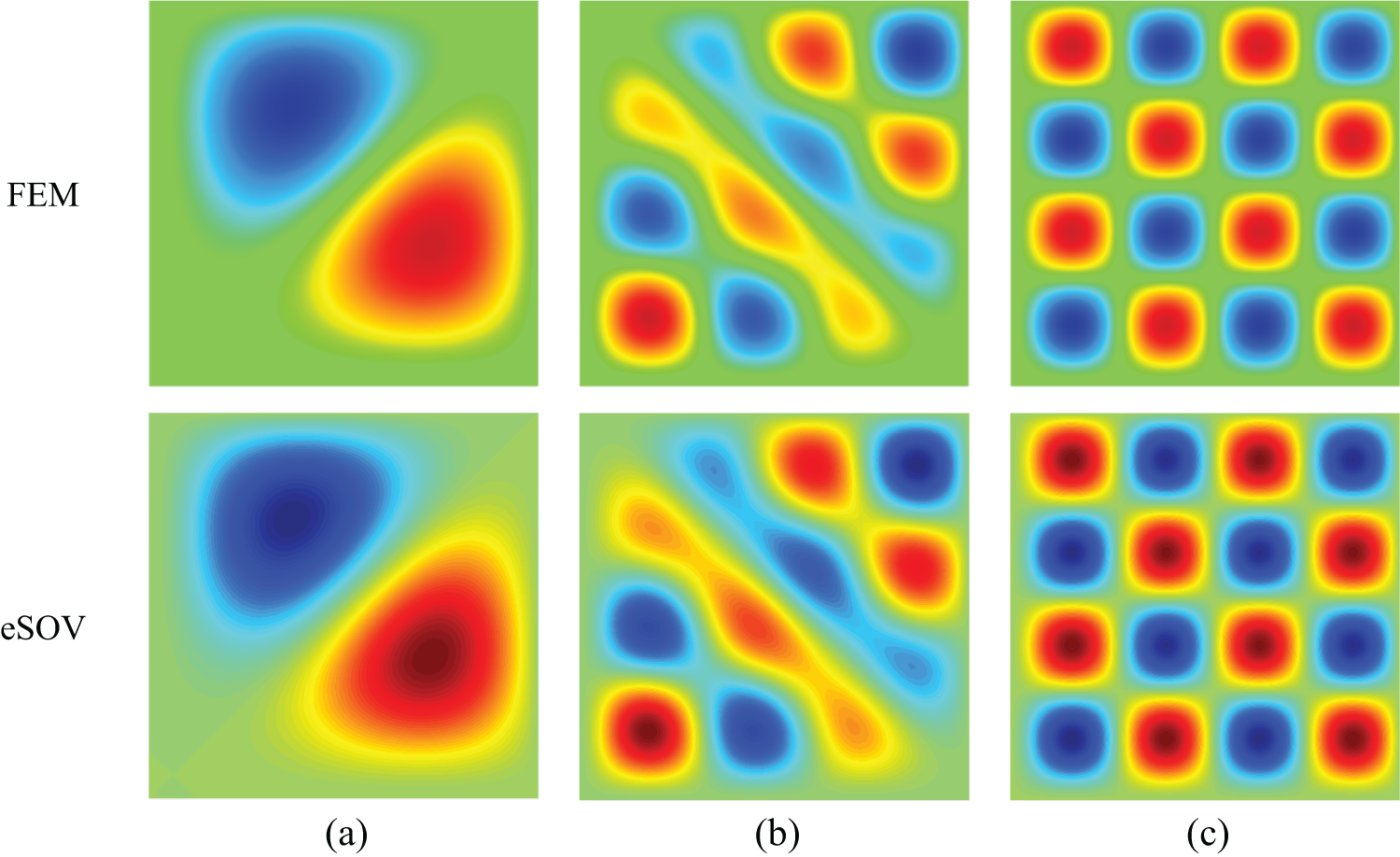
Figure 8: Some modes for the CCSS square plate. (a) Mode 2; (b) Mode 15; (c) Mode 20
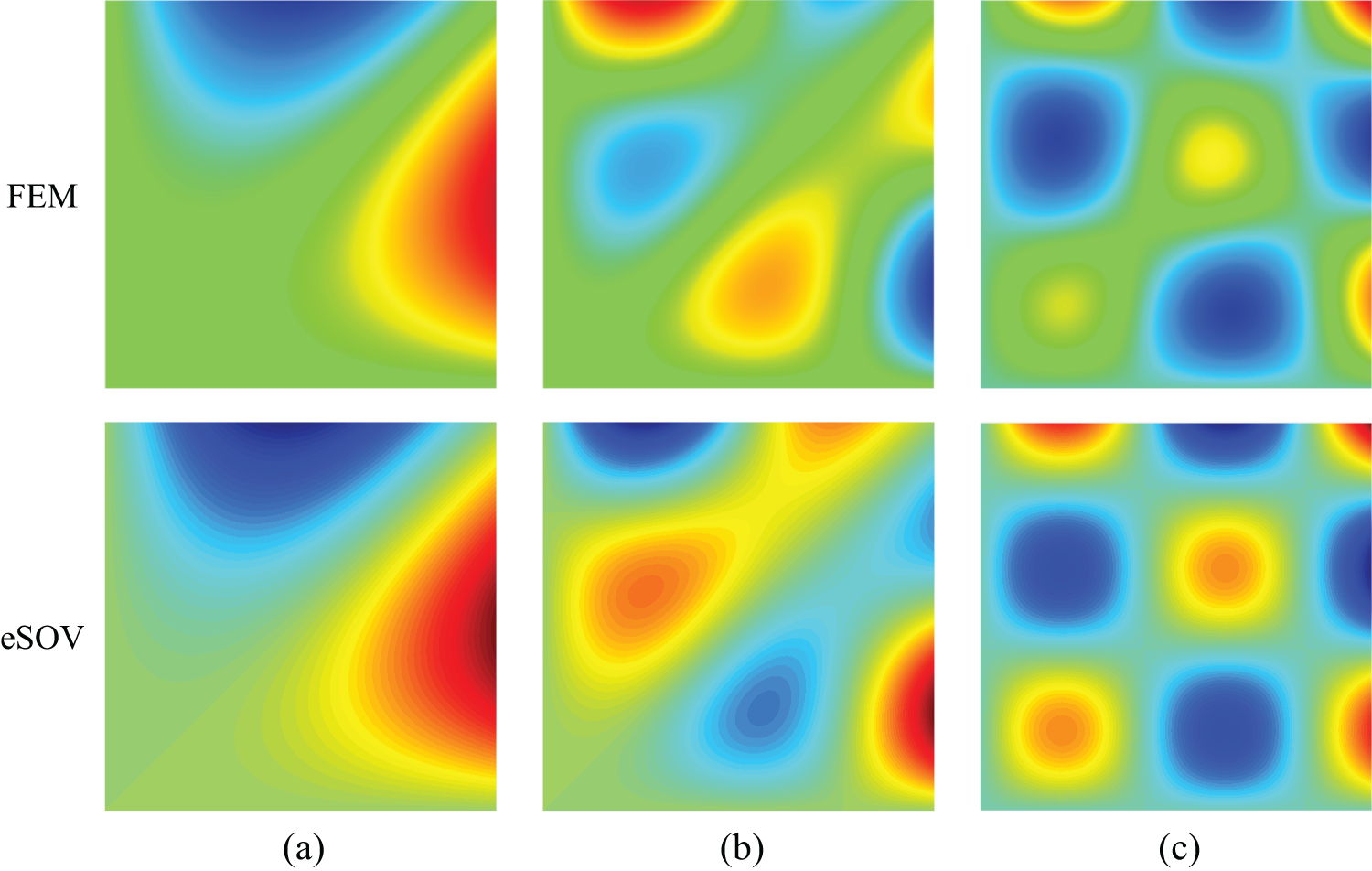
Figure 9: Some modes for the SSFF square plate. (a) Mode 2; (b) Mode 7; (c) Mode 11
In addition, the closed-form analytical solutions obtained by the SOV methods are simple and have explicit forms, therefore, it is necessary to check the integrity of the simple solutions or if there is a problem with missing roots. This can be fulfilled by counting the numbers of the nodal lines of modes.
It can be seen from Figs. 6 and 7 and Tables 2 and 3 that for both square and rectangular plates, the numbers of the vertical (parallel to the y-axis) and horizontal (parallel to the x-axis) nodal lines increase one by one with the frequency order, indicating that the SOV methods have no problem missing frequencies. This also ensures that the SOV methods have the same accuracy for the frequencies of different orders.
To show the high accuracy of the SOV methods and the effectiveness of the proposed bisection-based procedures for solving eigenvalue equations, this section compares the frequencies and modes obtained by the SOV methods and the FEM, as well as several non-SOV methods including the method of superposition [37,38], the spectral dynamic stiffness method (S-DSM) [39], the Galerkin method [40] and the symplectic superposition method [41].
The FEM’s results are achieved by NASTRAN using 200 × 200 (for Tables 4, 5, Figs. 8, 9) and 250 × 500 (for Table 6) bending panel elements. In calculation, ν=0.33, a = 1 and the thickness length ratio h/2a=1/200. The results of the SOV methods are calculated by the bisection-based solution procedures given in Section 3.
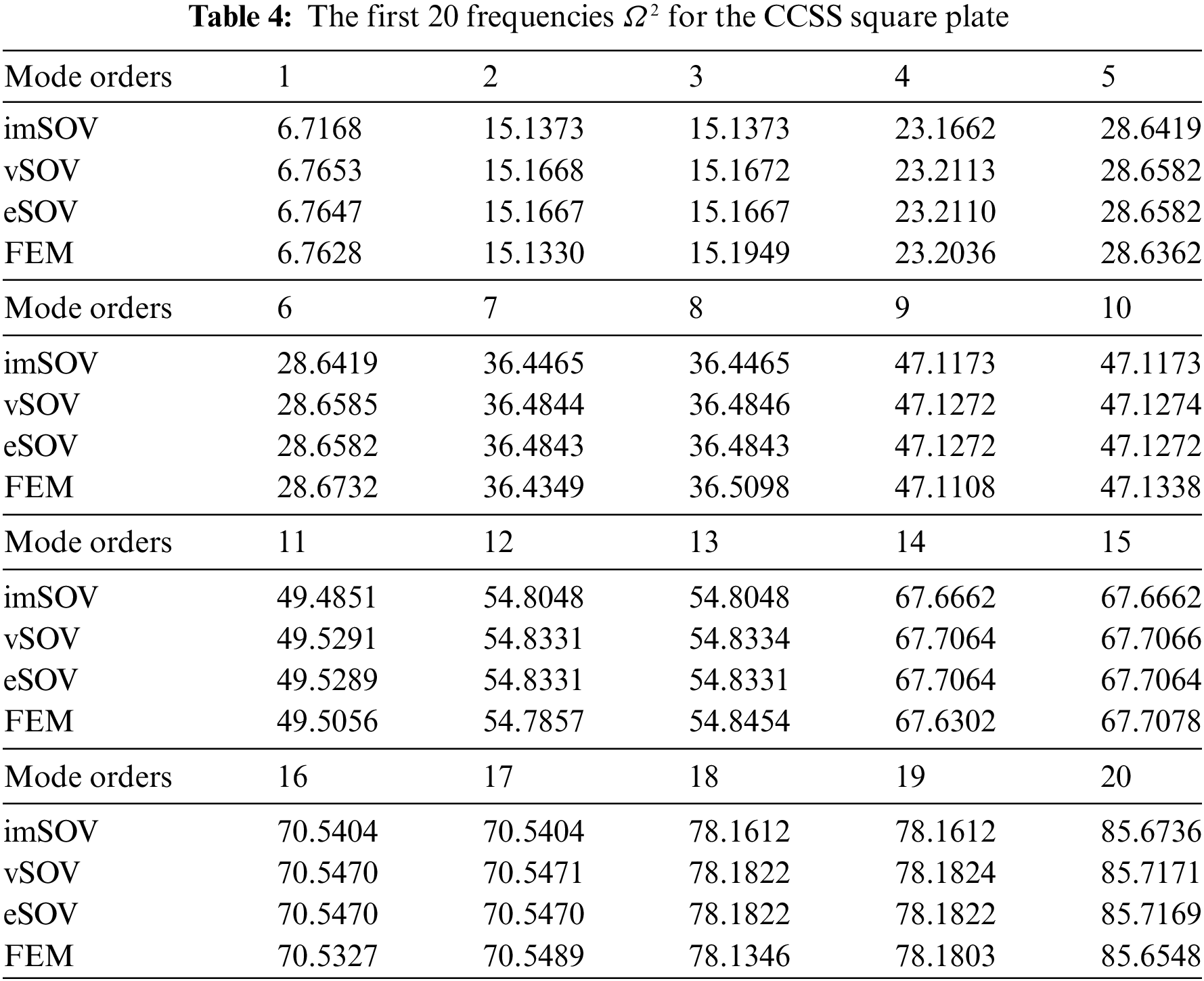
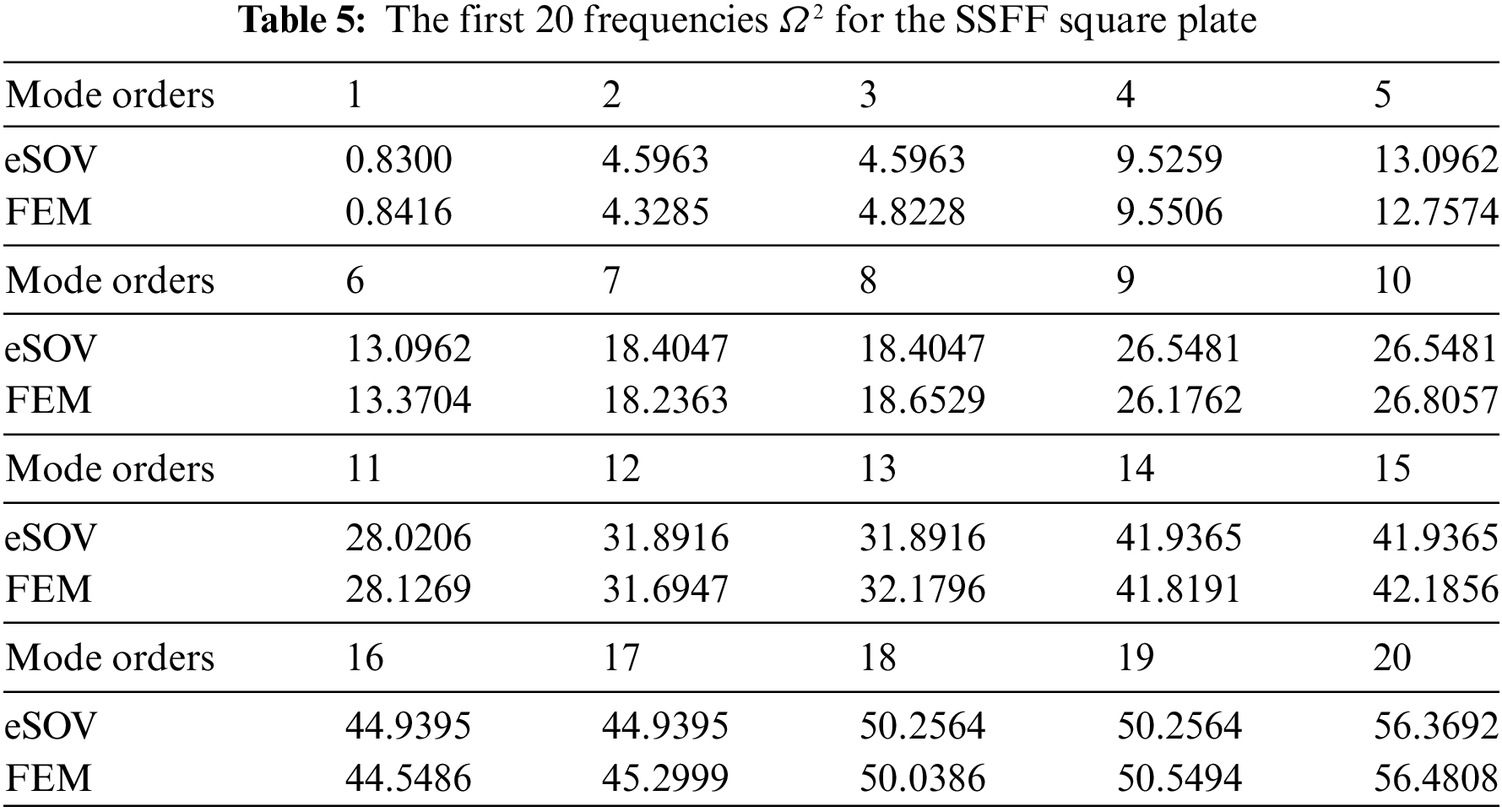
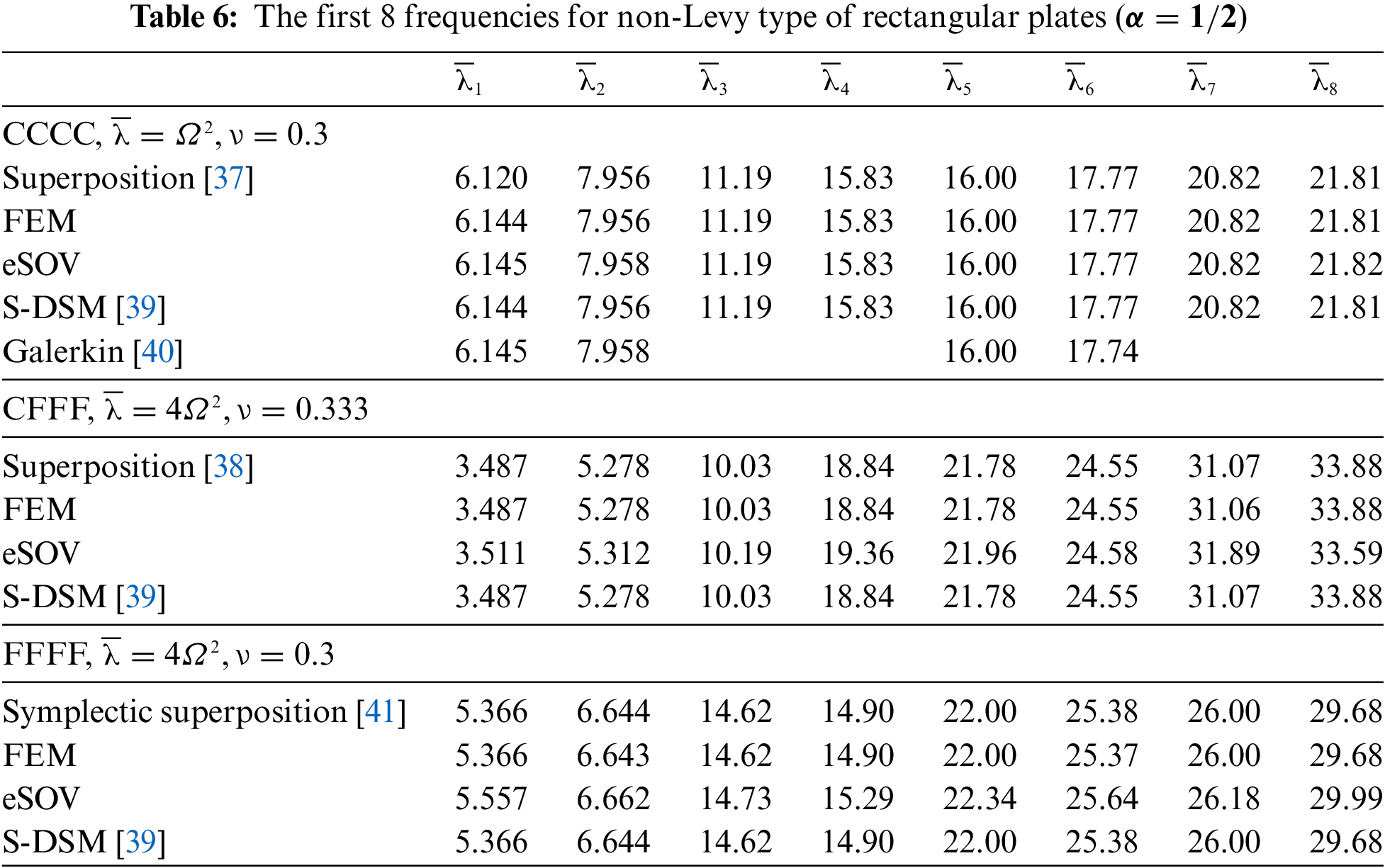
Tables 4 and 5 compare the first 20 frequencies Ω2=ωa2√ρh/D of the CCSS and SSFF square plates, Table 6 compares the first 8 frequencies of the clamped, free and cantilever rectangular plates (α=1/2), and Figs. 8 and 9 compare some mode shapes.
It can be seen from Tables 4–6 that the SOV methods are quite accurate, especially when the plates have no free edges (for example, the CCSS and CCCC plates), and in general, the accuracy of the SOV methods holds with the increase in mode orders (for instance, from the first to twenty orders). Since the CCSS and SSFF square plates are diagonal symmetrical, the SOV methods obtain repeated frequencies, while the FEM does not.
Besides, the nodal lines of the modes obtained by the SOV methods are straight lines even though for repeated frequencies, as mentioned in Section 4. However, when there are repeated frequencies, modes can have diagonal and curved nodal lines. In this situation, one can also see that the SOV methods can accurately capture this kind of modes by using the combining method as explained in Section 4.1. For example, Tables 4 and 5 show that the 2nd, the 7th, and the 15th frequencies are repeated frequencies, and Figs. 8 and 9 show that the nodal lines of the corresponding modes obtained by the eSOV method are also curves, as those obtained by NASTRAN.
The SOV methods provide a general approach for obtaining closed-form analytical solutions to characteristic problems involving rectangular plates and cylindrical shells. This work introduces three notable contributions and observations.
The theoretical framework of the SOV methods is presented in a thought-provoking manner, outlining the construction principles and methodologies behind these techniques. Based on the concept of finding the stationary value of the Rayleigh quotient, the vSOV method, the eSOV method, and the iSOV method were developed to achieve precise solutions. Additionally, using a different concept, the imSOV method was formulated to directly solve characteristic partial differential equations. Similar theoretical frameworks can also be established for the SOV methods used in solving eigenvalue problems of circular cylindrical shells and the eigenbuckling problems of rectangular plates.
Beyond the theoretical framework, this work presents a few bisection-based procedures for solving nonlinear eigenvalue equations, accompanied by flowcharts to illustrate implementation steps. In these procedures, the bisection method is initially applied to identify solution intervals and subsequently used to determine accurate solutions within each interval, thus avoiding the issue of missing roots. Unlike the Newton iteration method, these procedures are self-starting, eliminating the need to choose initial values for eigenvalues of different orders. Numerical results confirm the effectiveness of the proposed procedures.
Lastly, the explicit equations for nodal lines are provided, and the integrity of the solutions along with the patterns of nodal line modes are examined. It is concluded that, while the SOV methods produce straight nodal lines, diagonal and curved lines can also be accurately represented by the combining approaches for repeated frequencies. Moreover, by counting the nodal lines, it is observed that the SOV methods do not miss any modes, achieving consistent accuracy across frequencies and modes of various orders.
The closed-form solutions obtained by the SOV methods are highly accurate but are not exact except in cases where at least two opposite edges are simply supported/ guided. Furthermore, the SOV methods are not suitable for anisotropic rectangular plates and cylindrical shells.
Acknowledgement: None.
Funding Statement: This study is supported by the National Natural Science Foundation of China (12172023).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yufeng Xing; analysis and interpretation of results: Yufeng Xing, Ye Yuan; draft manuscript preparation: Gen Li, Ye Yuan. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Srinivas S, Rao AK. Bending, vibration and buckling of simply supported thick orthotropic rectangular plates and laminates. Int J Solids Struct. 1970;6(11):1463–81. doi:10.1016/0020-7683(70)90076-4. [Google Scholar] [CrossRef]
2. Bert CW, Malik M. Frequency equations and modes of free vibrations of rectangular plates with various edge conditions. Proc Inst Mech Eng Part C J Mech Eng Sci. 1994;208(5):307–19. doi:10.1243/PIME_PROC_1994_208_133_02. [Google Scholar] [CrossRef]
3. Hosseini-Hashemi S, Fadaee M, Rokni Damavandi Taher H. Exact solutions for free flexural vibration of Lévy-type rectangular thick plates via third-order shear deformation plate theory. Appl Math Model. 2011;35(2):708–27. doi:10.1016/j.apm.2010.07.028. [Google Scholar] [CrossRef]
4. Brischetto S. Exact elasticity solution for natural frequencies of functionally graded simply-supported structures. Comput Model Eng Sci. 2013;95:391–430. doi:10.3970/cmes.2013.095.391. [Google Scholar] [CrossRef]
5. Eisenberger M, Godoy LA. Navier type exact analytical solutions for vibrations of thin-walled shallow shells with rectangular planform. Thin-Walled Struct. 2021;160:107356. doi:10.1016/j.tws.2020.107356. [Google Scholar] [CrossRef]
6. Kantorovich LV, Krylov VI. Approximate methods of higher analysis. New York: Interscience Publishers; 1958. [Google Scholar]
7. Kerr AD. An extended Kantorovich method for the solution of eigenvalue problems. Int J Solids Struct. 1969;5(6):559–72. doi:10.1016/0020-7683(69)90028-6. [Google Scholar] [CrossRef]
8. Rafiefar M, Moeenfard H. Analytical modeling of variable thickness cylindrical shallow shells using extended Kantorovich method. Eur J Mech A/Solids. 2022;96(1968):104727. doi:10.1016/j.euromechsol.2022.104727. [Google Scholar] [CrossRef]
9. Singhatanadgid P, Singhanart T. The Kantorovich method applied to bending, buckling, vibration, and 3D stress analyses of plates: a literature review. Mech Adv Mater Struct. 2019;26(2):170–88. doi:10.1080/15376494.2017.1365984. [Google Scholar] [CrossRef]
10. Zafarabadi MMM, Aghdam MM, Araujo AL. Buckling and free vibration of grid-stiffened composite conical panels using Extended Kantorovich Method. Thin-Walled Struct. 2024;200:111845. doi:10.1016/j.tws.2024.111845. [Google Scholar] [CrossRef]
11. Xing Y, Liu B. New exact solutions for free vibrations of rectangular thin plates by symplectic dual method. Acta Mech Sin. 2009;25(2):265–70. doi:10.1007/s10409-008-0208-4. [Google Scholar] [CrossRef]
12. Xing Y, Sun Q, Liu B, Wang Z. The overall assessment of closed-form solution methods for free vibrations of rectangular thin plates. Int J Mech Sci. 2018;140(208):455–70. doi:10.1016/j.ijmecsci.2018.03.013. [Google Scholar] [CrossRef]
13. Xing Y, Wang Z. An improved separation-of-variable method for the free vibration of orthotropic rectangular thin plates. Compos Struct. 2020;252:112664. doi:10.1016/j.compstruct.2020.112664. [Google Scholar] [CrossRef]
14. Xing Y, Wang Z. An extended separation-of-variable method for the free vibration of orthotropic rectangular thin plates. Int J Mech Sci. 2020;182:105739. doi:10.1016/j.ijmecsci.2020.105739. [Google Scholar] [CrossRef]
15. Xing Y, Li G, Yuan Y. A review of the analytical solution methods for the eigenvalue problems of rectangular plates. Int J Mech Sci. 2022;221:107171. doi:10.1016/j.ijmecsci.2022.107171. [Google Scholar] [CrossRef]
16. Timoshenko S. Theory of plates and shells. New York: McGraw-Hill Book Company; 1940. [Google Scholar]
17. Gorman DJ, Sharma RK. A comprehensive approach to the free vibration analysis of rectangular plates by use of the method of superposition. J Sound Vib. 1976;47(1):126–8. doi:10.1016/0022-460X(76)90414-4. [Google Scholar] [CrossRef]
18. Gorman DJ. Free in-plane vibration analysis of rectangular plates by the method of superposition. J Sound Vib. 2004;272(3–5):831–51. doi:10.1016/S0022-460X(03)00421-8. [Google Scholar] [CrossRef]
19. Gorman DJ, Yu SD. A review of the superposition method for computing free vibration eigenvalues of elastic structures. Comput Struct. 2012;104–105(4):27–37. doi:10.1016/j.compstruc.2012.02.018. [Google Scholar] [CrossRef]
20. Hurlebaus S, Gaul L, Wang JS. An exact series solution for calculating the eigenfrequencies of orthotropic plates with completely free boundary. J Sound Vib. 2001;244(5):747–59. doi:10.1006/jsvi.2000.3541. [Google Scholar] [CrossRef]
21. Zhang S, Xu L, Li R. New exact series solutions for transverse vibration of rotationally-restrained orthotropic plates. Appl Math Model. 2019;65(3):348–60. doi:10.1016/j.apm.2018.08.033. [Google Scholar] [CrossRef]
22. Bhaskar K, Kaushik B. Simple and exact series solutions for flexure of orthotropic rectangular plates with any combination of clamped and simply supported edges. Compos Struct. 2004;63(1):63–8. doi:10.1016/S0263-8223(03)00132-6. [Google Scholar] [CrossRef]
23. Tenenbaum J, Eisenberger M. Analytic solution for buckling of rectangular isotropic plates with internal point supports. Thin-Walled Struct. 2021;163(2):107640. doi:10.1016/j.tws.2021.107640. [Google Scholar] [CrossRef]
24. Deutsch A, Eisenberger M. Benchmark analytic in-plane vibration frequencies of orthotropic rectangular plates. J Sound Vib. 2022;541(5):117248. doi:10.1016/j.jsv.2022.117248. [Google Scholar] [CrossRef]
25. Zhong WX. A new systematic methodology for theory of elasticity. China: Dalian University of Technology Press; 1995. [Google Scholar]
26. Lim CW, Lü CF, Xiang Y, Yao W. On new symplectic elasticity approach for exact free vibration solutions of rectangular Kirchhoff plates. Int J Eng Sci. 2009;47(1):131–40. doi:10.1016/j.ijengsci.2008.08.003. [Google Scholar] [CrossRef]
27. Hu Z, Zheng X, An D, Zhou C, Yang Y, Li R. New analytic buckling solutions of side-cracked rectangular thin plates by the symplectic superposition method. Int J Mech Sci. 2021;191:106051. doi:10.1016/j.ijmecsci.2020.106051. [Google Scholar] [CrossRef]
28. Shi Y, An D, Wu Z, Liang L, Chen L, Li R. Symplectic analytical solutions for free vibration of elastically line-hinged orthotropic rectangular plates with rotationally restrained edges. Appl Math Model. 2024;136(1–2):115629. doi:10.1016/j.apm.2024.08.001. [Google Scholar] [CrossRef]
29. Zheng X, Xu D, Ni Z, Zhou C, An D, Wang B, et al. New benchmark free vibration solutions of non-Lévy-type thick rectangular plates based on third-order shear deformation theory. Compos Struct. 2021;268(3):113955. doi:10.1016/j.compstruct.2021.113955. [Google Scholar] [CrossRef]
30. Banerjee JR. Dynamic stiffness formulation for structural elements: a general approach. Comput Struct. 1997;63(1):101–3. doi:10.1016/S0045-7949(96)00326-4. [Google Scholar] [CrossRef]
31. Wittrick WH, Williams FW. Buckling and vibration of anisotropic or isotropic plate assemblies under combined loadings. Int J Mech Sci. 1974;16(4):209–39. doi:10.1016/0020-7403(74)90069-1. [Google Scholar] [CrossRef]
32. Wei Z, Yin X, Yu S, Wu W. Dynamic stiffness formulation for transverse and in-plane vibration of rectangular plates with arbitrary boundary conditions based on a generalized superposition method. Int J Mech Mater Des. 2021;17(1):119–35. doi:10.1007/s10999-020-09515-9. [Google Scholar] [CrossRef]
33. Liu X, Liu X, Adhikari S. Exact dynamic stiffness formulations and vibration response analysis of orthotropic viscoelastic plate built-up structures. Comput Struct. 2024;302(11):107455. doi:10.1016/j.compstruc.2024.107455. [Google Scholar] [CrossRef]
34. Liu X, Li Y, Lin Y, Banerjee JR. Spectral dynamic stiffness theory for free vibration analysis of plate structures stiffened by beams with arbitrary cross-sections. Thin-Walled Struct. 2021;160(2):107391. doi:10.1016/j.tws.2020.107391. [Google Scholar] [CrossRef]
35. Ventsel E. Thin plates and shells: theory, analysis, and applications. New York: CRC Press; 2001. [Google Scholar]
36. Meirovitch L. Elements of vibration analysis. New York: McGraw-Hill Book Company; 1986. [Google Scholar]
37. Gorman DJ. Free-vibration analysis of rectangular plates with clamped-simply supported edge conditions by the method of superposition. J Appl Mech. 1977;44(4):743–9. doi:10.1115/1.3424166. [Google Scholar] [CrossRef]
38. Gorman DJ. Free vibration analysis of cantilever plates by the method of superposition. J Sound Vib. 1976;49(4):453–67. doi:10.1016/0022-460X(76)90828-2. [Google Scholar] [CrossRef]
39. Liu X, Banerjee JR. Free vibration analysis for plates with arbitrary boundary conditions using a novel spectral-dynamic stiffness method. Comput Struct. 2016;164(4):108–26. doi:10.1016/j.compstruc.2015.11.005. [Google Scholar] [CrossRef]
40. Ng SF, Araar Y. Free vibration and buckling analysis of clamped rectangular plates of variable thickness by the Galerkin method. J Sound Vib. 1989;135(2):263–74. doi:10.1016/0022-460X(89)90725-6. [Google Scholar] [CrossRef]
41. Li R, Wang B, Li G, Tian B. Hamiltonian system-based analytic modeling of the free rectangular thin plates’ free vibration. Appl Math Model. 2016;40(2):984–92. doi:10.1016/j.apm.2015.06.019. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
