 Open Access
Open Access
ARTICLE
Artificial Circulation System Algorithm: A Novel Bio-Inspired Algorithm
1 Department of Biomedical Technologies, Dokuz Eylül University, Izmir, 35390, Turkey
2 Department of Biomedical Engineering, Iskenderun Technical University, Iskenderun, 31200, Turkey
3 Department of Computer Engineering, Dokuz Eylül University, Izmir, 35390, Turkey
4 Department of Statistics and Computer Sciences, Karadeniz Technical University, Trabzon, 61080, Turkey
* Corresponding Author: Nermin Özcan. Email:
(This article belongs to the Special Issue: Advances in Swarm Intelligence Algorithms)
Computer Modeling in Engineering & Sciences 2025, 142(1), 635-663. https://doi.org/10.32604/cmes.2024.055860
Received 09 July 2024; Accepted 11 October 2024; Issue published 17 December 2024
Abstract
Metaheuristics are commonly used in various fields, including real-life problem-solving and engineering applications. The present work introduces a novel metaheuristic algorithm named the Artificial Circulatory System Algorithm (ACSA). The control of the circulatory system inspires it and mimics the behavior of hormonal and neural regulators involved in this process. The work initially evaluates the effectiveness of the suggested approach on 16 two-dimensional test functions, identified as classical benchmark functions. The method was subsequently examined by application to 12 CEC 2022 benchmark problems of different complexities. Furthermore, the paper evaluates ACSA in comparison to 64 metaheuristic methods that are derived from different approaches, including evolutionary, human, physics, and swarm-based. Subsequently, a sequence of statistical tests was undertaken to examine the superiority of the suggested algorithm in comparison to the 7 most widely used algorithms in the existing literature. The results show that the ACSA strategy can quickly reach the global optimum, avoid getting trapped in local optima, and effectively maintain a balance between exploration and exploitation. ACSA outperformed 42 algorithms statistically, according to post-hoc tests. It also outperformed 9 algorithms quantitatively. The study concludes that ACSA offers competitive solutions in comparison to popüler methods.Keywords
Supplementary Material
Supplementary Material FileOptimization is the systematic process of identifying and selecting the most optimal choices and determining the suitable solutions to minimize or maximize the desired outcome when addressing a problem. This process is widely employed in various domains to address real life problems, as well as in engineering applications [1–3].
Deterministic methods are commonly employed for solving optimization problems. Nevertheless, deterministic approaches may be constrained by the nature of the problem or the intricacy of the model [4]. For instance, the nonlinearity inherent in real-life problems can restrict the applicability of linear deterministic models. Furthermore, the utilization of gradient information in certain deterministic approaches may present challenges due to the non-differentiability of objective functions in numerous real-life problems. Additionally, gradient-based methods incur a substantial computational expense [5]. Complicated problems with a large number of possible outcomes may cause deterministic methods to become trapped in suboptimal solutions. The drawbacks mentioned above have prompted the investigation of stochastic optimization techniques as a viable alternative to deterministic methods. Stochastic optimization methods are a class of techniques that introduce randomness as opposed to deterministic methods [6]. Heuristics are straightforward and pragmatic, but they frequently become trapped at local optima. Meta-heuristic (MH) methods are high-level stochastic methods and are problem-independent. They assess based on objective functions and do not require the calculation of derivatives [7]. Typically, they are not greedy and are open to considering more optimal solutions. Due to this rationale, MH optimization methods have gained significant popularity over the past two decades, resulting in the proposal of numerous new techniques [8–12].
Methods in the field of MH draw inspiration from natural phenomena and can be classified into eight distinct categories based on their sources of inspiration. (1) Evolution-based methods are methodologies that rely on the principles of natural evolution. The Genetic Algorithm (GA) is the most widely used method in this category, drawing inspiration from Darwin’s theory of evolution [13]. Evolutionary Strategy (ES) [14], Differential Evolution (DE) [15], and Coral Reefs Optimization (CRO) [16] are additional well-known methods based on evolutionary principles. (2) Swarm-based methods imitate the social behavior of groups of animals. Particle Swarm Optimization (PSO), a widely used swarm-based technique, was created by Kennedy and Eberhart. It draws inspiration from the collective behavior of bird flocks [17]. Two additional widely-used conventional techniques in this classification are Ant Colony Optimization (ACO) [18] and Artificial Bee Colony (ABC) [19]. These techniques are derived from the cooperative behavior of ants and bees when searching for food. The intriguing social interactions among animals have captured the interest of researchers, leading to the development of innovative techniques in this field in recent years [20–22]. Grey Wolf Optimization (GWO) [23], Whale Optimization Algorithm (WOA) [24], Bat-inspired Algorithm (BA) [25], Grasshopper Optimization Algorithm (GOA) [26], and Elephant Herding Optimization (EHO) [27] are among the various innovative approaches. Another set of MH techniques (3) comprises physics-based methods that draw inspiration from the fundamental laws of physics governing the universe. The most ancient and widely used technique within this category is Simulated Annealing (SA) [28]. Electromagnetic Field Optimization (EFO) [29], Nuclear Reaction Optimization (NRO) [30], Atom Search Optimization (ASO) [31], and Equilibrium Optimizer (EO) [32] are additional techniques that draw inspiration from the principles of physics. (4) Certain researchers have devised methodologies centered around human behavior. The techniques mentioned, such as Culture Algorithm (CA) [33], Brain Storm Optimization (BSO) [34], Search And Rescue Optimization (SARO) [35], Life Choice-based Optimization (LCO) [36], Forensic Based Investigation Optimization (FBIO) [37], Social Ski-Driver Optimization (SSDO) [38], Student Psychology Based Optimization (SPBO) [39], serve as examples of these optimization methods. Additionally, there are also (5) bio-based [40–42], (6) system-based [43–45], (7) math-based [46–48] and (8) music-based [49] methods.
Real-life problems can vary significantly due to their association with distinct domains, resulting in varying levels of complexity. Although the problem may be fundamentally identical, having different inputs and dimensions can amplify the magnitude and intricacy of the problem. This can result in varying outcomes, even when using the same optimization technique. While MH methods share similarities, they vary in the mathematical, probabilistic, or stochastic processes they employ to optimize candidate solutions in algorithmic procedures. Methods based on various bases and stochastic processes in MH demonstrate distinct behaviors when applied to the same problem, enabling the identification of a superior solution. The proliferation of multiple methods in the field of MH can be attributed to their distinct exploration and exploitation behaviors, as they do not always converge to a global minimum. While a method may demonstrate favorable outcomes on one or multiple problems, it may not achieve success on every problem. This statement is substantiated by the No Free Lunch (NFL) theorem, [50] which establishes that there cannot exist a single optimization technique capable of solving all optimization problems. This theorem has stimulated the advancement of novel techniques and has motivated researchers to investigate innovative approaches. This research is motivated by this particular reason.
This paper presents a highly effective MH approach for solving optimization problems in various fields. The newly proposed method is referred to as the Artificial Circulatory System Algorithm (ACSA). It draws inspiration from the precise control and immediate adjustment and improvement of blood pressure and blood volume in the human circulatory system. The algorithm incorporates regulators in its mathematical framework that emulate neural and hormonal systems, akin to its source of inspiration, and enhances the optimization process at each iteration using these regulators. The study’s particulars are examined in different parts. Section 2 provides an overview of related works in the literature, discussing and comparing their working principles. The proposed method’s originality and contribution to the literature have been demonstrated in this direction. The details of the proposed ACSA algorithm are thoroughly discussed in Section 3. Section 4 outlines the experimental procedures employed in the algorithm and presents the corresponding results. Section 5 presents a concise overview of the study and the outcomes achieved.
2 Releated Work and Novelity of ACSA
As stated in Section 1, numerous MS algorithms have been suggested in the literature. While these algorithms may vary in terms of their sources of inspiration and mathematical modeling, they share commonalities in how they approach the problem and produce solutions. These methods can be categorized as individual-based and population-based.
Hill Climbing (HC), SA [28], and Tabu Search (TS) [51] techniques initiate with a randomly generated solution and strive to optimize it by iteratively enhancing the solution. The simulated annealing method employs a stochastic approach by incorporating a cooling component, which enhances its exploration capability in comparison to the other two approaches. Nevertheless, it is widely recognized that individual-based techniques exhibit a significant prevalence of getting stuck local optima.
GA [13], PSO [17], and ACO [18] are methods that rely on populations to search for multiple solutions. Population-based algorithms exhibit greater resistance to becoming trapped in local optima as a result of their ability to optimize many solutions. Population-based algorithms operate on the principle that every individual in the population is subjected to the same conditions and strives to get the optimal answer with a similar level of randomness. While most MS algorithms follow this strategy, examples of alternative algorithms are Moth-Flame Optimisation (MFO) [52], and WOA [24]. Some experts contend that having a leader with diverse duties and tasks, who guides individuals toward the optimal solution, enhances the speed of convergence. In algorithms such as GWO [23], Pathfinder algorithm [53], EHO [27], and Naked Mole-Rat Algorithm (NMRA) [54], a hierarchical structure is present with a leader steering the population. Another progressive strategy that has experienced growth in recent years is segmenting the population into smaller cohorts with distinct objectives and responsibilities, and subsequently pursuing the search process with these cohorts. Researchers contend that by following this approach, the exploration and exploitation stages are more effectively managed and the occurrence of local minima is prevented. The SPBO [39] utilizes four categories to facilitate the optimization process: best students, good students, average students, and students who try to improve randomly. The Artificial Ecosystem-based Optimisation (AEO) algorithm [46] is another approach that seeks to enhance performance by drawing inspiration from three energy transfer mechanisms: production, consumption, and decomposition.
On the other hand, MH algorithms utilize a position vector that represents the optimal solution or potential solutions. The key differentiating factor between the strategies is in the derivation of a mathematical model from the source of inspiration and its subsequent utilization in the solution update phase. In PSO [17], this procedure entails the particles possessing a velocity and converging towards the optimal position using this velocity vector. Several population-based optimization techniques rely on an optimization process that use a velocity vector, which is comparable to the PSO algorithm. In the ACO algorithm [18], the source of motivation is represented by a chemical substance called pheromone, which gradually dissipates as time passes. GOA employs a distinct methodology by using many factors such as social behavior, gravity, and wind speed to accurately track the movement of locusts [26]. These phenomena enable candidate solutions to acquire new positions from pre-existing positions.
The ACSA algorithm is a population-based optimization strategy. It employs a distinct mechanism for updating positions that is dissimilar to the velocity vector approach utilized by PSO [17]. As a result, it distinguishes itself from other approaches like BA [25], Wind Driven Optimization (WDO) [55], ASO [31] and Human Conception Optimizer (HCO) [56]. The method is unique and draws inspiration from a distinct source compared to other MS algorithms. The mathematical representation of the concept of stimulation in the regulation of blood pressure diverges significantly from the formulation of current methodologies. Neural and hormonal regulators have distinct functions and duties when it comes to inspiration. They explore the search space using a population of several specialized groupings. However, unlike other methods that target certain groups within the search space, this method not only prioritizes finding the best solution but also emphasizes the importance of considering the impact of the worst solutions and avoiding potential local minimums during the exploration phase. The suggested algorithm stands out from existing MS approaches due to its distinctive features, including inspiration and mathematical expression, population separation, and optimization strategy. These distinctions contribute to the novelty of the proposed method. Outlined below are the contributions of the research to the existing literature:
• A comprehensive description of the mathematical principles underlying ACSA is provided to establish a strong foundation for simulating the algorithm.
• In order to showcase the efficacy of ACSA, the algorithm underwent thorough evaluation into demanding benchmark functions. This study employed 16 conventional benchmark functions, namely unimodal, multimodal, convex, and separable, to evaluate convergence and the exploration-exploitation performances of the system. This phase is intended to showcase ACSA’s flexibility in addressing various problem types.
• The application and evaluation of ACSA on 12 CEC 2022 functions (unimodal, multimodal, hybrid, and composite) introduced at the Congress on Evolutionary Computing (CEC 2022) aimed to assess its capacity to handle the complex search environment of high-dimensional and composite functions.
• The performance of ACSA is evaluated by comparing it with 64 established MH mechanisms documented in the literature. The results of the comparison with the 7 most frequently cited techniques in the literature are also provided.
• The present work employed statistical tests, namely the Friedman Rank test and Sign Test, to assess the superiority of the obtained results.
This section provides a comprehensive analysis of the proposed ACSA. Section 3.1 describes the algorithm’s source of inspiration. Section 3.2 presents information on the modeling of regulators’ behavior. Section 3.3 provides a comprehensive explanation of the stimulation function and the specific parameters used in the algorithm. Section 3.4 outlines the conduct of the regulators throughout the exploration and exploitation stages.
The circulatory system is a fundamental system that maintains balance in the human body. This system transports the necessary nutrients and oxygen to the tissues and cells of the body. Additionally, it distributes hormones to specific areas of the body when necessary. Furthermore, it eliminates any remaining chemicals from the cells. Ensuring the uninterrupted flow of blood is crucial for maintaining optimal wellness and vitality levels. Consequently, the circulation of blood is carefully controlled to adequately supply the requirements of various tissues and organs. While the details of circulatory processes are intricate, this study specifically examines the regulation of arterial pressure and blood volume to create a structural model. This complex control mechanism involves multiple components, but fundamentally, two systems are responsible for regulating it. Fig. 1 depicts the systems within the human body, providing insight into the operational principles of the algorithm.
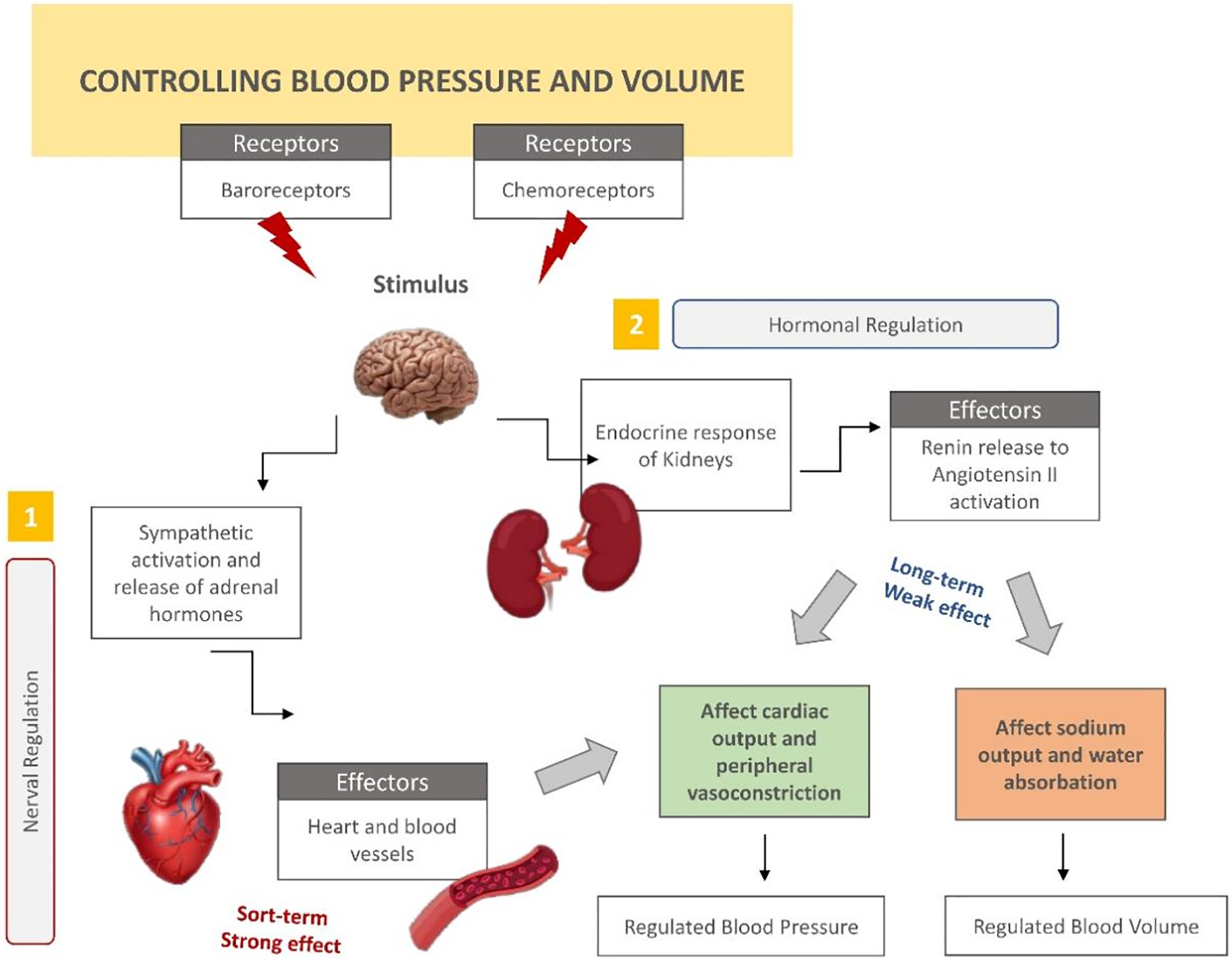
Figure 1: Management and control of the human circulatory system
The initial response to any alteration in blood pressure, regardless of the cause, is the activation of nerve regulation. The autonomic nervous system activates the nerve fibers around the blood vessels, causing them to either constrict or dilate in response to certain requirements. Neural control systems effectively regulate certain functions, but their long-term effectiveness is limited by the deactivation of the baroreceptors they interact with. The circulation must reach its usual level in order for it to be considered sufficient. At this point, the hormonal system, which serves as a regulatory mechanism over extended periods of time, becomes active. Hormonal regulation is comparatively slower than nerve control because it involves the sequential steps of secretion, transport, and the attainment of a certain hormone concentration. Aside from its chemical impact on blood vessels, hormone regulation also plays a secondary role in governing the reabsorption of water and salt in the body by exerting influence on local regulatory systems within the kidney. When needed, it facilitates the reabsorption of salt and water into the bloodstream, so increasing the volume of blood in the body. Alternatively, it decreases the surplus quantity of blood by promoting the outflow of water from the kidneys, thereby stabilizing blood pressure. Hormonal regulation is a comparatively slower but extremely precise process of adjustment. Unlike the nervous system, it may take several weeks or months to fully accomplish.
The crucial phase in MS techniques is the modeling of the source of inspiration. These mathematical or logical expressions are essential for updating the positions of randomly initialized candidate solutions and generating improved solutions. ACSA employs neurological and hormonal regulatory systems akin to inspiration in order to optimize an optimization issue. The term “optimisation” as used here refers to the highest or lowest point of any given problem, which is also known as the optimum point. Fig. 2 depicts regulators that are randomly distributed on a basic minimization problem.
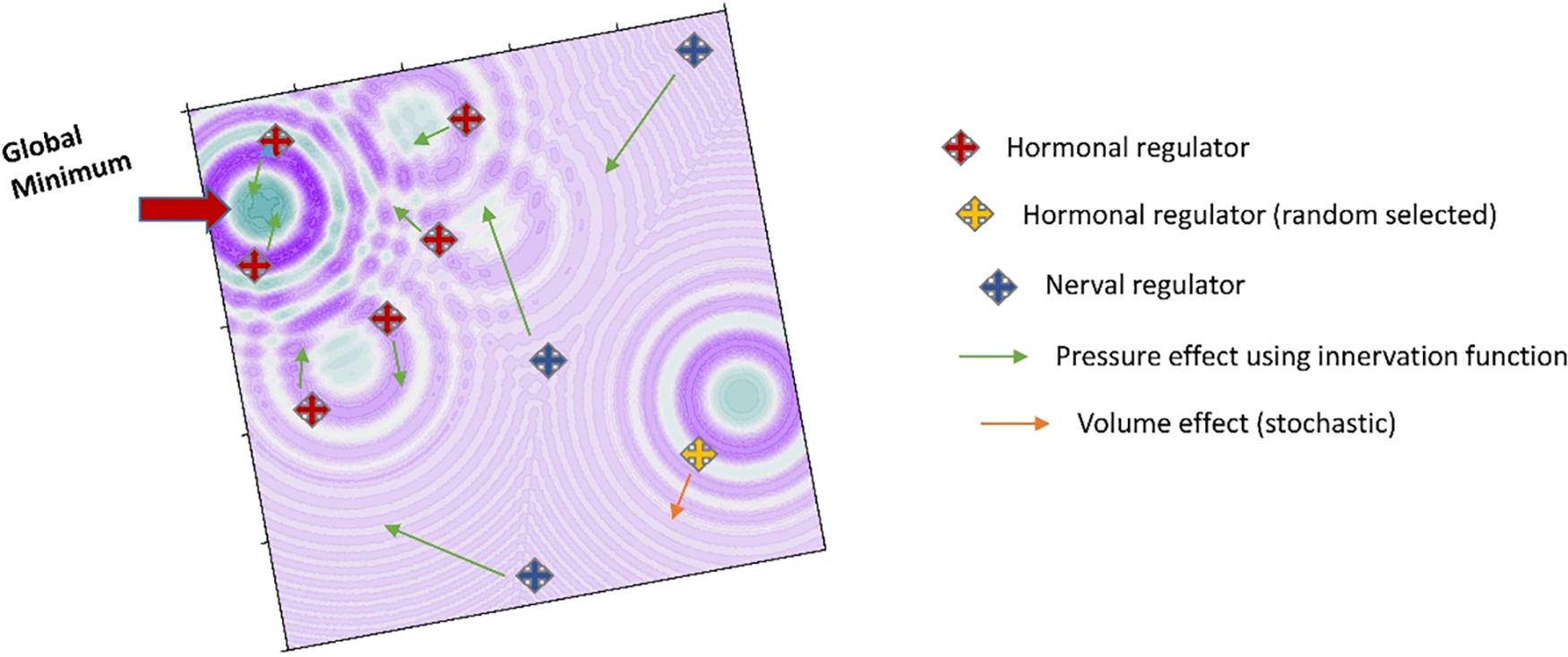
Figure 2: Simulation of regulator behaviour in a search space
The regulators, which are initially positioned randomly in the search area, are optimized at each iteration to achieve the optimal value. The optimization procedure is carried out using three distinct techniques. Neural regulators and certain hormonal regulators employ a stimulation function to regulate blood pressure, as stated in Section 4.1. Hormonal and neuronal regulators have distinct effects because of their own unique parameters, despite their identical formulation. Neural regulators exhibit a strong inclination to avoid the worst candidate solution and explore the search space by making significant leaps. Hormonal regulators, however, persist in the pursuit of improved solutions by exploring the vicinity of the best candidate solution with a lower effect. The third mechanism involves the activity of some hormonal regulators that mimic the regulation of blood volume discussed in Section 4.1. These regulators do not take advantage of the stimulation function, but instead seek to enhance the more advantageous solutions provided by the neural regulators by utilizing their own location information. The algorithm operates on the fundamental premise of iteratively repeating these mechanisms in order to approximate the optimal answer. The mathematical formulations of these notions and the parameters employed are thoroughly examined in the subsequent sections.
3.3 Stimulation Function and Model Parameters
Parameter identification is a crucial stage in designing optimization algorithms. If the appropriate parameters are not used, the optimization model may exhibit unwanted behavior, which can have a negative impact on the optimization process. There are essentially two categories of parameters: tuneable parameters and fixed parameters. The user has the freedom to choose tuneable parameters within a specified range, whereas fixed parameters are predetermined values derived from theoretical understanding or experimental computations. The fixed parameter method lacks human input in the optimization process and may not yield results in all problems. Tuneable parameters offer versatility in terms of their capacity to adjust to the problem, but the process of configuring the parameters may be time-consuming.
ACSA technique utilizes a formulation to articulate the neuronal and chemical stimulation of the regulators. This formulation bears resemblance to the sigmoid function [57], although it is an expansion of this function. The stimulation function
where
• In a particular investigation [58], an animal experiment was conducted to investigate the effects of spinal anesthesia on the transmission of nerve impulses. The results showed that the artery pressure decreased from 100 mm of mercury to 50 mm of mercury. Following a period of time, the introduction of a drug that stimulates the nervous system resulted in the constriction of the blood vessels, leading to an elevation in blood pressure that exceeded its typical level within a timeframe of 1–3 min. The study demonstrates that the impact begins immediately after the drug is activated and frequently results in a pressure increase of up to double the normal values over a span of 5–10 s. In a separate investigation [59], a standard experiment was conducted to analyze the impact of the Renin-Angiotensin system on arterial pressure during bleeding. The hormonal system enhances venous return to the heart by constricting the blood arteries, resulting in an increase in blood pressure from 50 mm of mercury to 83 mm of mercury. Using the given numerical data, the values of Ea, representing the magnitude of change in blood pressure (change amount divided by initial value), and Es, representing the period (1/hour) during which the change should take place, were computed.
• NHrate and S parameters are tunable parameters that can be determined based on the specific problem at hand, providing flexibility unlike the other two parameters. Table 1 displays the predetermined values for the parameters Ea ve Es, as well as the acceptable ranges of values for the parameters NHrate and S.

The range of NHrate values is from 0.1 to 0.9. Nearing a value of 1 results in an increase in the quantity of neural regulators. This impacts the ecological equilibrium between exploration and exploitation. S’s range of values is from 0.01 to 0.5. The rate at which the positions of the regulators are scaled during position update is determined by this factor. These parameters were established through preliminary studies conducted during the designing of the algorithm. Nevertheless, it is necessary to establish adjustable parameters through a meticulous analysis based on the specific problem that will be addressed. These limitations of the study are acknowledged and it is anticipated that future research will focus on parameter optimization.
3.4 Exploration and Exploitation Phases
The majority of nature-inspired MH algorithms for solving optimization problems initiate the exploration of the search space by generating a random population. The process of seeking the optimal solution is achieved through the tendencies of exploration and exploitation. Exploration involves seeking new, more optimal areas within randomly dispersed candidate solutions, whereas exploitation entails examining these areas to enhance current optimal solutions.
The regulators indicated in Section 3.2, referred to as candidate solutions, function as two distinct categories: neurological and hormonal. The objective is to further investigate the exploration process using neural regulators and to exploit potential optimal solutions through the use of hormone regulators. The population’s position is updated in two categories based on the type of regulators, as outlined below:
1. Neural regulators: Exhibit similar behavior to the inspiration source, searching the search space with a more considerable stimulation value. This type of regulator seeks to find the candidate solutions that are the worst relative to the target value of the regulators in the population to the current best candidate solution while adhering to the average value of the regulators of a similar type. Its goal is to find better candidate solutions by scanning the neighborhood of the worst solutions over a larger area. The mathematical calculation expresses the position update of neural regulators in Eq. (2).
where
2. Hormonal regulators: These regulators behave similarly to the inspiration and have the property of making the system regulated by neural control better and more stable. Their candidate solutions have a better objective value compared to neural regulators. The goal is to find the best candidate solution by scanning around the suitable solutions in smaller steps. They are involved in two functions, the first of which, similar to neural regulators, uses the stimulation function. It tries to find the current best-candidate solution for the population based on the average value of hormonal regulators. The other function is that the candidate solution converges to the population mean based on some randomness. The mathematical calculations express the position update of hormonal regulators in Eqs. (3) and (4), respectively. A randomization-dependent process governs the function of the regulator.
where
The ACSA, as previously said, is an algorithm that governs the circulatory system by employing several control mechanisms. The algorithm can be expressed using pseudo-code, as illustrated in Algorithm 1 and the algorithm flowchart is depicted in Fig. 3. The ACSA algorithm commences by generating a random initial population, similar to other MH approaches. Each regulator type iteratively changes its candidate solutions based on its objective function, employing mathematical computations and parameters. This method enhances the potential solutions with every update. Following each iteration of solution updates, the algorithm verifies the positions of the population to guarantee that the solutions remain inside the boundaries of the search space. If a solution is discovered outside the designated region, it is limited to remain within the defined search space. During each iteration, the fitness values of the regulators are computed with respect to the goal function. The regulator with the highest fitness value is then identified as the best solution within the population.
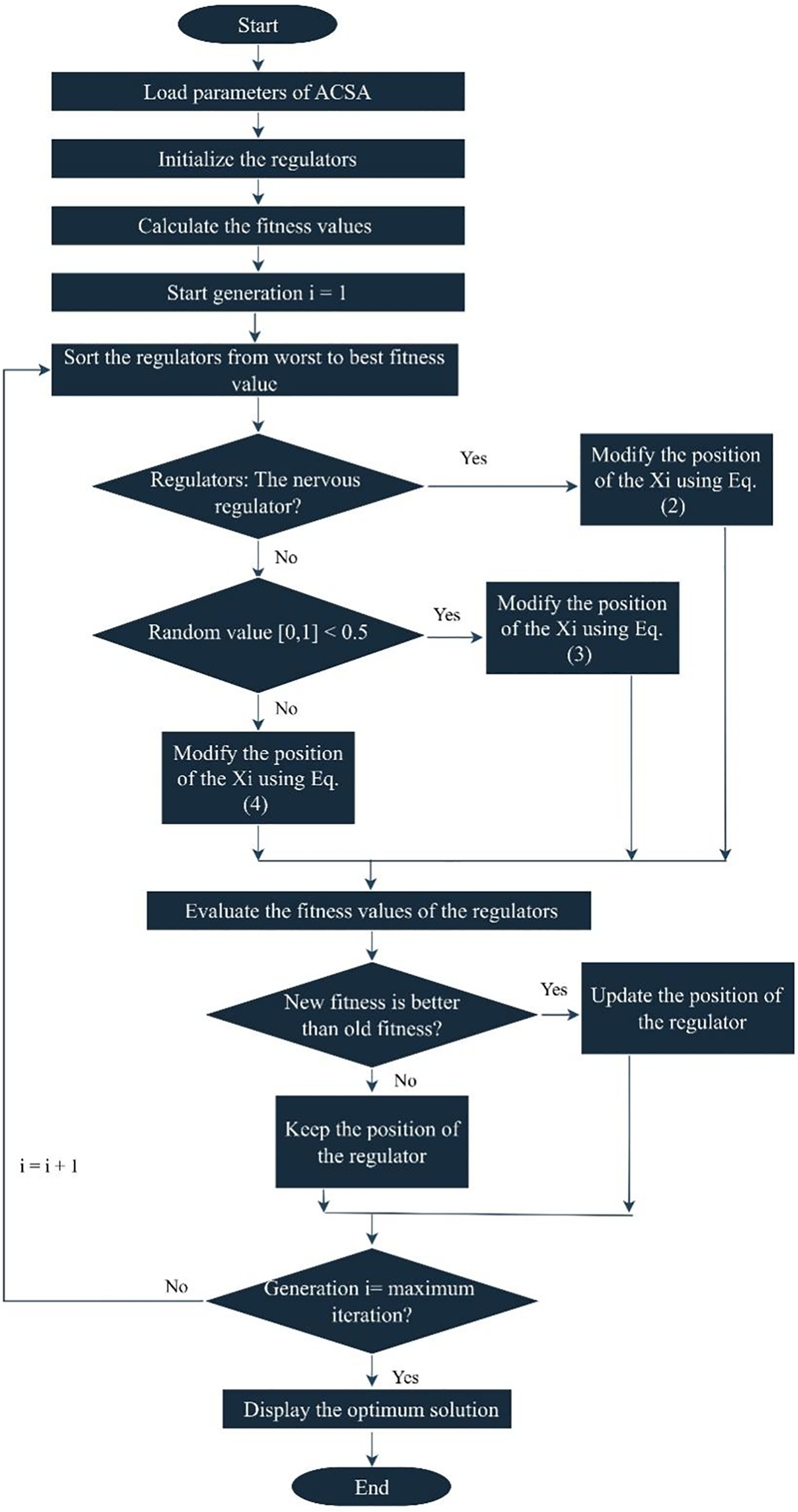
Figure 3: Flowchart of the ACSA

This section presents an analysis of the outcomes obtained from the proposed methodology. The experimental method involves conducting tests on the model using benchmark functions and subsequently comparing its performance with other widely-used optimization strategies. The subsequent sections provide a comprehensive description of the experimental procedure, the test functions. The methods were implemented using Python version 3.10. The simulations were conducted on a PC equipped with an 12th Intel Core i5 CPU, 16 GB of RAM, and Intel UHD Graphics 730.
In addition to the fundamental libraries, the Opfunu library [60] was utilized for the benchmark functions throughout the testing phase. During the comparison phase, the Mealpy library [61] was utilized for optimization techniques. All experiments in the experimental method were conducted under identical conditions to minimize the potential for software-induced superiority
MH algorithms are commonly tested using mathematical functions that have known optimal values. Nevertheless, employing test functions with distinct qualities yields crucial insights into the attributes of the techniques. For instance, a unimodal function lacks local solutions and possesses only one global solution. These functions offer data regarding the rate at which the methods converge. Contrarily, multimodal functions possess several local solutions, suggesting that the models are either trapped or deliberately avoiding local optima. Conversely, when the search process relies on two or more interconnected factors, it becomes more challenging compared to a situation when only one variable is involved. Obtaining the optimal solution for non-separable functions is more challenging compared to separable ones. Furthermore, several characteristics of mathematical functions, such as convexity and continuity, play a crucial role in assessing the strengths and weaknesses of the model.
There are numerous benchmark functions available in the literature that researchers use to evaluate their models [62]. This study utilizes two sets of benchmark functions with distinct features to evaluate the efficiency of the proposed algorithm. The initial set consists of 16 functions chosen from the standard benchmark functions commonly used to compare well-established algorithms in the literature [63]. These functionalities are determined by considering the aforementioned features. The characteristics of the functions are shown in Table 2. The second group comprises composite functions specifically designed by the researchers to more accurately imitate genuine optimization situations. Composite test functions are created by manipulating, rotating, or combining various functions of traditional benchmark functions. This group, published under the name CEC [64–66] and attracting the attention of many researchers in different years, is from the year 2022 and includes 12 composite benchmark functions. The characteristics of the functions are displayed in Table 3. In brief, rather than concentrating on analogous problem types, our objective was to determine whether the model is capable of handling problems of diverse nature and complexity. The benchmark functions were selected accordingly.


The tables present the characteristics, minimum values, upper and lower limits, and dimension numbers of the benchmark functions. Furthermore, it is possible to look at the Opfunu library [60], which is applied for mathematical formulations and other comprehensive information.
Furthermore, a thorough investigation was carried out to compare the effectiveness of the suggested optimization technique. A comprehensive set of 64 MH optimization algorithms were developed, encompassing evolutionary-based, human-based, physics-based, swarm-based, and systems approach methods. The statistical methods in the subsequent subsections were used to evaluate each approach on all test functions and compare them with ACSA. Every parameter of the methods is taken to be the default value provided by the library used in the experiments. All code of algorithms and results are available online (https://github.com/Nrmnzcn/ACSA-Algorithm-Results) (accessed on 11 October 2024). In order to ensure traceability, the study incorporates the outcomes of the 7 most widely used algorithms. When selecting algorithms, the researchers used the keywords ‘metaheuristic’, ‘bioinspired’, and ‘optimization’ in Web of Science (WoS) to identify the most frequently cited algorithms. Specific details regarding the chosen optimization algorithms can be found in Table 4. Furthermore, all approaches were simulated precisely under identical conditions while implementing the benchmark functions. The process was executed in 50 iterations using a 100 search agent.
MH methods are stochastic techniques, begin with some initial populations distributed randomly in the search space. Furthermore, the algorithm frameworks ensure the preservation of randomness while updating the population. While this facilitates the discovery of novel solutions, it can also represent a drawback as they may not consistently yield identical outcomes. Executing these algorithms solely once and providing commentary on their outcomes results in untrustworthy deductions. Therefore, when assessing the outcomes of these approaches, they are executed with a designated number of repetitions that can be deemed statistically significant, and the mean results are then compared. Within our study, we conducted 25 repetitions of each test function for ACSA and all other MH approaches.
The following section analyzes the qualitative outcomes of the suggested approach and offers a graphical comparison of the model with other optimization algorithms.
4.2 Qualitative Results and Discussion
4.2.1 Analysis of the Proposed Model
Classical test functions were employed in the initial phase of the experimental procedure to closely examine the behavior of the proposed model. The rationale behind this is that these functions possess a two-dimensional spatial structure, enabling the graphical observation of the search histories of the populations of these functions. In this work, our objective was to examine the performance of the proposed method on problems with various characteristics, including modality, convexity, and separability, among the well-known test functions in the literature. Fig. 4 displays four distinct diagrams representing five classical benchmark functions.
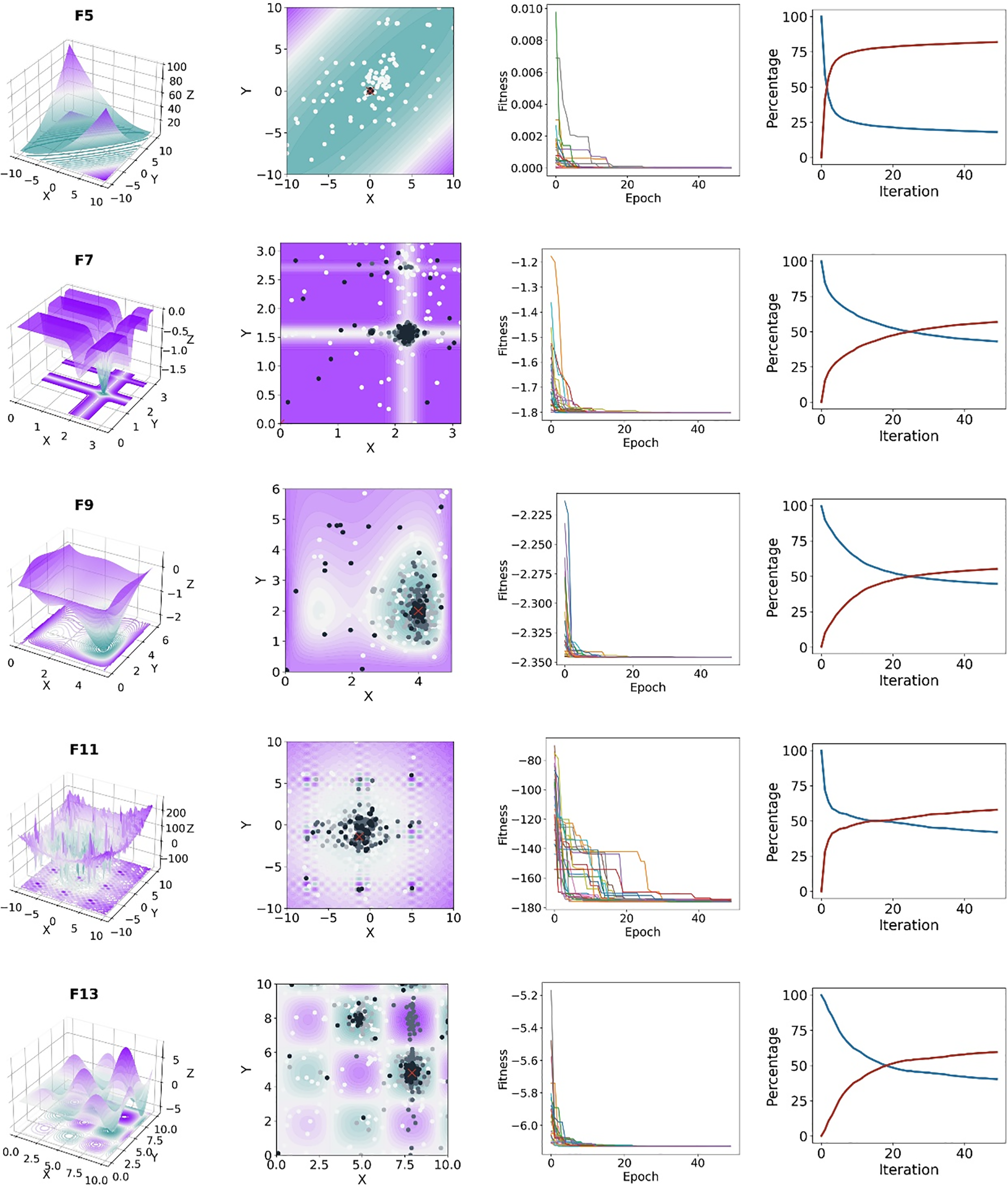
Figure 4: Behaviours of the proposed model on the classical benchmark function
The initial diagram graphically illustrates the benchmark functions in three dimensions, specifically within the lower and upper bound bands. It enables the investigation of the complexity of the problem and the local minimum points. The second graphical representation displays the search history, illustrating the locations of the regulators within the population at four distinct iterations. The white symbol denotes the 0th iteration, while the black symbol represents the final iteration. The intermediate colors correspond to the positions of the regulators in the intermediate iterations. The blue and purple hues correspond to the maximum and minimum points of the functions in terms of topography. The third diagram displays the curves of convergence for the functions. A convergence curve is a graphical representation of the time-dependent variation of the fitness value on each iteration. This chart presents the outcomes of 25 iterations of the suggested model on the benchmark functions. The convergence curves enable the observation of the speed with which the models can reach the minimum during the iterations, the presence of consistent stable behavior in each run, and the attainment of the global minimum. The last diagram is the graph representing exploration and exploitation. This graph provides detailed information on the equilibrium between exploration and exploitation in the model. The exploration and exploitation graph shows how fast the global minimum is approached. Exploration continues in problems characterized by a higher number of local minimum traps.
Upon examination of the search history diagrams in Fig. 4, it is evident that the regulators, while initially distributed randomly in the search space, converge towards the global minimum based on the number of iterations. The clustering of the data on the optimal point in the last iteration (shown by the black colour) provides evidence for this. The unimodal function F5 exhibits a strong clustering of grey and black points around the global minimum. Within multimodal functions, it is evident that the regulators persist in their search processes with respect to local minima. Upon study of the convergence curves, it is evident that the model exhibits the highest level of stability on the test functions F9 and F13. For the F11 function, despite experiencing temporary stagnation at the local minima, the algorithm consistently achieved the optimal value for all trials prior to the completion of the iteration. Furthermore, during the initial stages of the iteration number, the model converged towards the optimal value. This observation serves as evidence of the model’s rapid convergence rate.
Through analysis of the exploration and exploitation diagrams, it becomes evident that the model converged towards the optimal value during the initial iterations for the F5 function. This is apparent from the evident rapid decrease of the exploration curve (blue) and the corresponding increase of the exploitation curve (red). In the case of the other functions, while the equilibrium between exploration and exploitation is attained, this procedure is characterized by a slower pace and the exploration process is sustained throughout the iterations. It is typical for the proposed model to exhibit varying behavior for functions with distinct characteristics. Considering the overall landscape, it can be stated that the model consistently converges to the global minimum for all functions, irrespective of their unimodal/multimodal, convex/concave, separable/unseparable nature. Furthermore, it demonstrates rapid convergence and maintains a stable behavior.
4.2.2 Comparison of the Proposed Model with Other Optimization Algorithms
Although Fig. 4 demonstrates the efficacy of the proposed approach, Figs. 5 and 6 provide convergence curves based on all benchmark functions of 8 optimization algorithms, including the proposed method, to confirm the success of the model in solving optimization problems. Every curve is generated by taking the average of 25 repetitions. The graphs display the time cost of the function, determined by the number of iterations, on the x-axis and the best fitness value achieved over the iterations on the y-axis. Conclusions derived from the graphs are as follows:
1. SA exhibits the poorest convergence in nearly all of the test functions. Given that there is no disparity regarding the type of test functions, it can be inferred that this algorithm is the least successful among the competing approaches.
2. The ACO algorithm exhibited a competitive behavior, particularly in certain specific classical test functions. Nevertheless, in the majority of cases, it was unable to achieve the global minimum due to being trapped in local minima. The PSO algorithm also exhibited similar behavior to the ACO method.
3. The proposed ACSA model demonstrates rapid convergence on the classical test functions and outperforms the other 7 optimization methods. It may be stated that it retains this stability in the majority of the CEC 2022 test functions, but, the same level of success was not attained in the 10-dimensional C5, C10-12 functions.
4. The algorithms GWO, WOA, and ABC demonstrate stability in the majority of the test functions and can be considered as possible competitors to the proposed ACSA model. Although WOA demonstrated strong performance in the classical test functions, it exhibited poor performance in the CEC 2022 test functions. In comparison to WOA, GWO exhibits superior performance in 10-dimensional CEC 2022 functions, but its effectiveness is diminished in classical test functions.
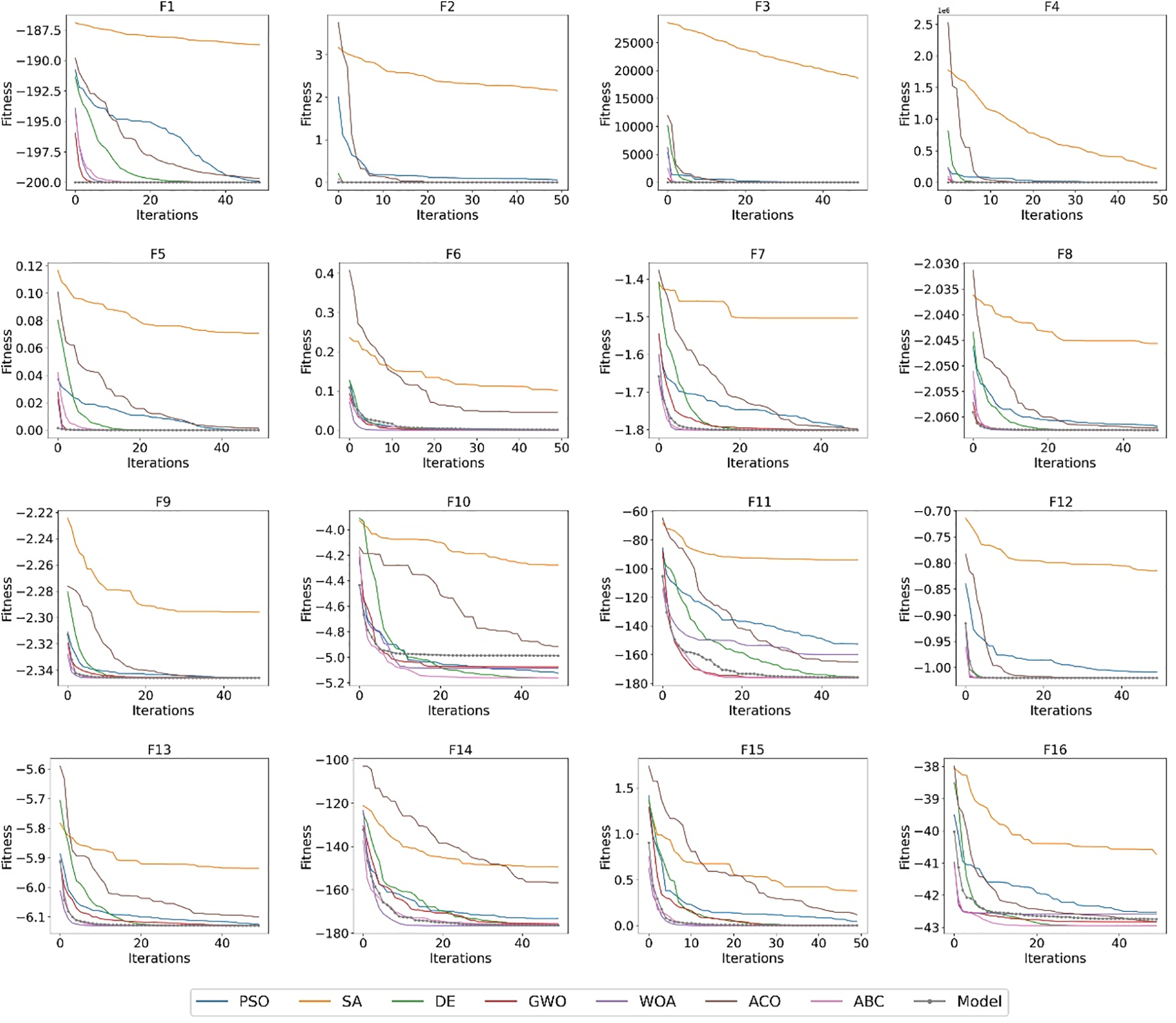
Figure 5: Comparison of convergence characteristics of optimizers obtained on classical benchmark functions

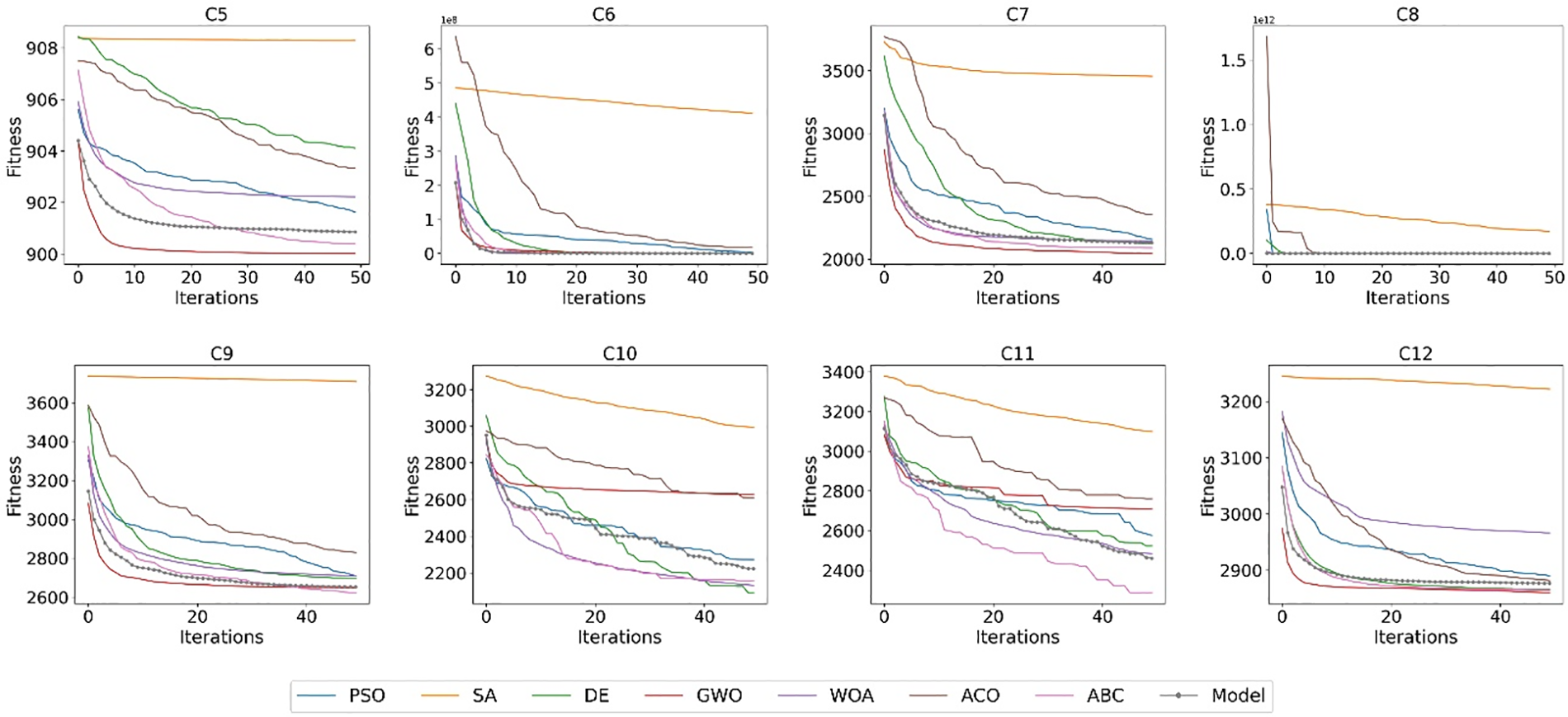
Figure 6: Comparison of convergence characteristic of optimizers obtained on CEC 2022 benchmark functions
4.3 Quantitative Results and Discussion
The aforementioned results provide qualitative evidence of the effectiveness of ACSA in solving optimization problems. Furthermore, they enable us to evaluate ACSA in relation to other optimization algorithms in terms of its speed of convergence and proximity to the minimum. Nevertheless, the qualitative results fail to provide us with precise information regarding the global minima of these algorithms. To comprehensively evaluate the superiority of the methods, this subsection presents and quantitatively discusses the results of the test functions.
This section presents an analysis of the optimal values obtained from 50 iterations for both the classical and CEC 2022 test functions of each model. The mean and standard deviation measures of the experimental results for 25 iterations of each algorithm are presented in Tables 5 and 6. The global minimums of the test functions exhibit varying values owing to the inherent characteristics of the problems. These values are documented in Tables 2 and 3. To enhance readability in analyzing the results, the optimal values assigned to all test functions are standardized to a range of 0 to 1. Standardization enables us to effectively compare the outcomes of various test functions. 0 denotes the optimal model, which is the approach that is in closest proximity to the minimum result. Conversely, 1 represents the least optimal model, which is the approach capable of generating the farthest solution to the minimum result.
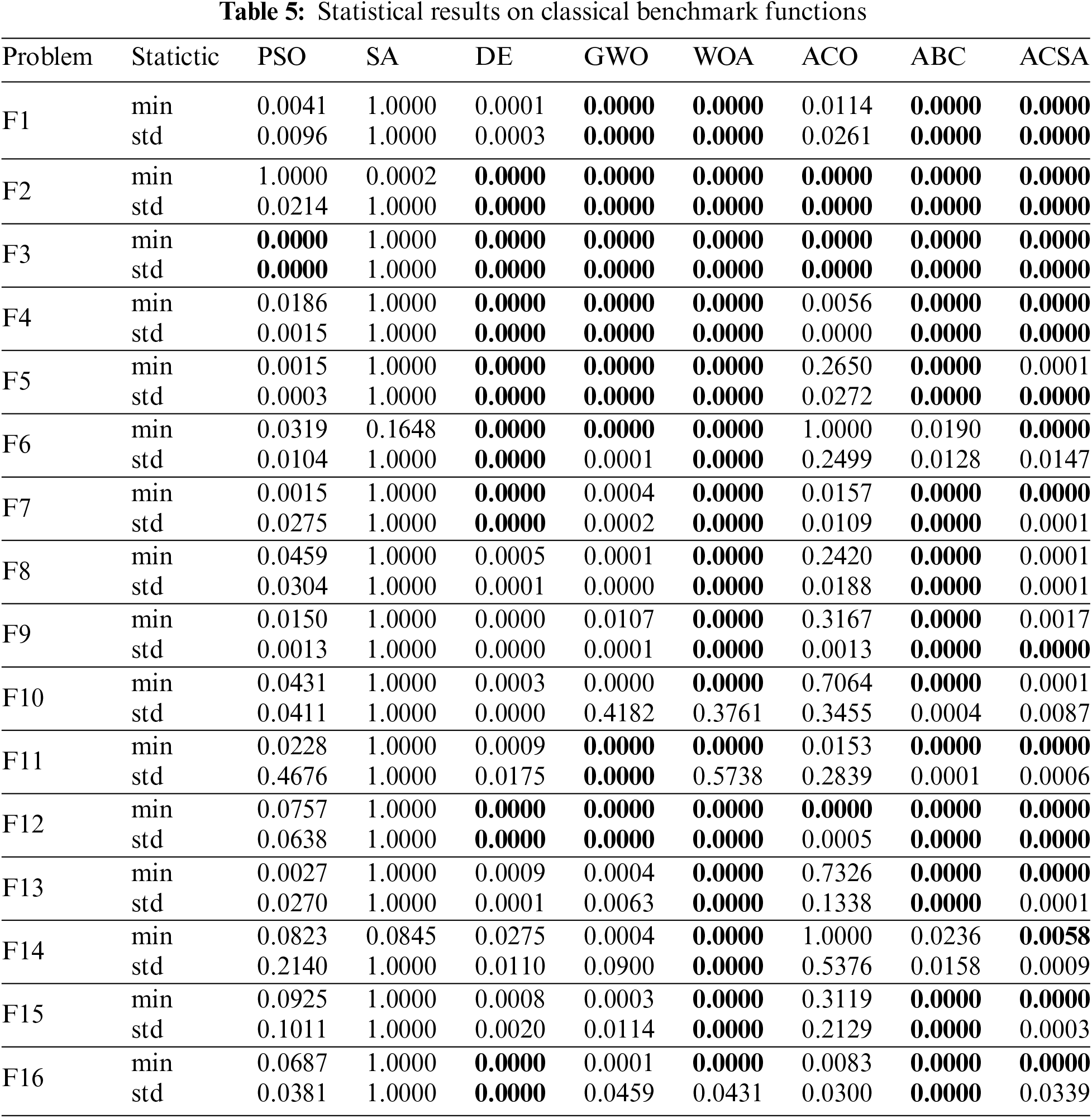
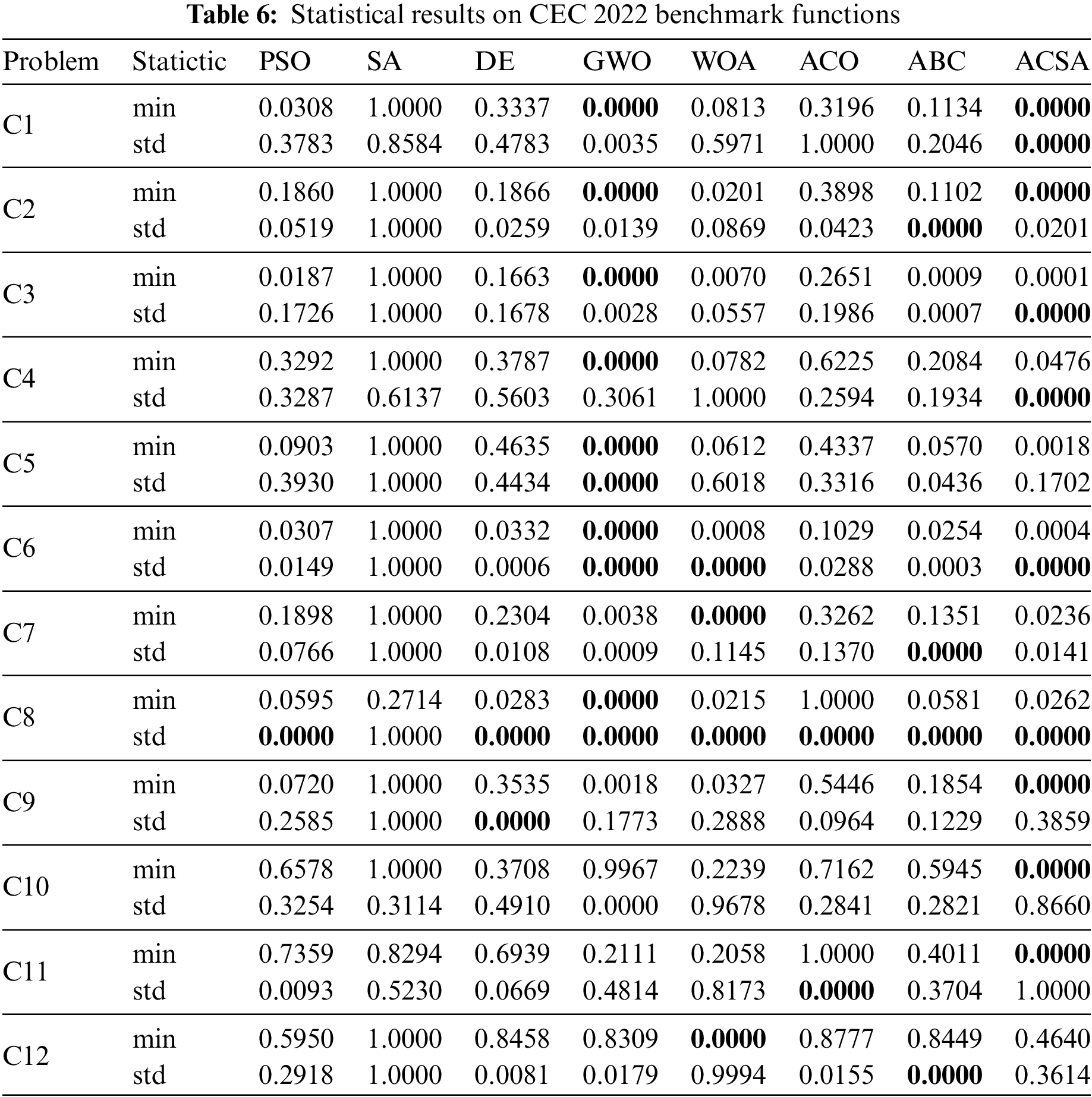
The data presented in Table 5 indicates that when solving two-dimensional classical test functions, the ACSA algorithm achieved the global minimum in 11 out of 16 functions. When examined based on the nature of the test functions, the level of success is greater for unimodal functions in comparison to multimodal functions. Furthermore, the low values of the standard deviation suggest that it consistently performs proficiently in all runs and provides a reliable strategy. Compared to ACSA, WOA and ABC algorithms, on average, approached the minimum value in a greater number of test functions. Within the CEC 2022 test group, the ACSA algorithm achieved the global minimum in functions C1-C2, and C9-11, as shown in Table 6. Within this test group, the dominant algorithm is GWO.
A further salient aspect is that there exist multiple approaches that achieve the minimum value in classical test functions. Nevertheless, several models encountered difficulties in achieving the global minimum in CEC 2022 functions. This can be understood as the observation that composite test functions containing multimodal characteristics present greater challenges compared to classical test functions. The proposed algorithm yields scores on multimodal test functions that are remarkably near to the global minimum. Hence, it can be asserted that ACSA demonstrates strong performance in addressing such complex issues.
Comparing algorithms based on mean and standard deviation over 25 independent trials allows us to comment on the general behavior of optimization methods. Nevertheless, just because a model gives good results on average does not necessarily mean that it achieves the best results. Thus, although it is unlikely, it is still possible that superiority occurs by chance. In order to assess the effectiveness of the optimization techniques and provide a thorough analysis, the following subsections compare the outcomes of all trials of the models. Since 25 is considered a small sample due to the number of samples, non-parametric tests are preferred. In the literature, it is common to use a similar non-parametric method for the comparison of models [3,39]. Furthermore, the results underwent normality testing prior to the application of statistical tests. Due to the absence of a normal distribution, the nonparametric Friedman rank test and sign test methods were employed.
4.3.2 Multiple Comparisons: Friedman Rank Test
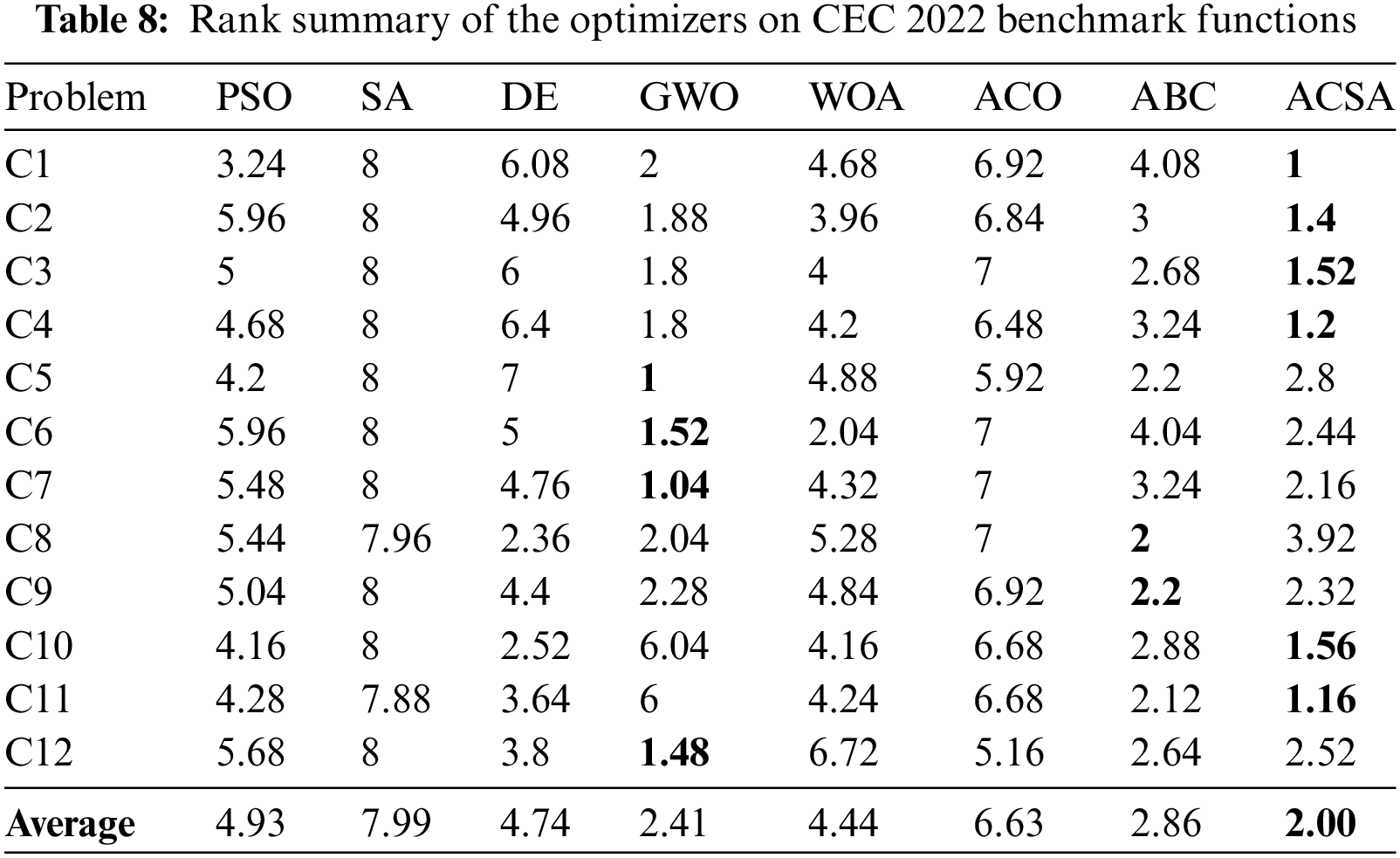
The Friedman test is a commonly used statistical test that helps to determine the better method among two or more algorithms. To minimize randomness, the iterations of each problem are sorted from from the smallest to the biggest before applying the Friedman test. The test compares the algorithms based on their performance, with Rank 1 indicating the best performance, followed by Rank 2, and go on. In the case of a tie, the average ranking is used. Therefore, the average rank for all test functions is calculated for each algorithm [69]. The Friedman ranking results for different test groups are tabulated in Tables 7 and 8.
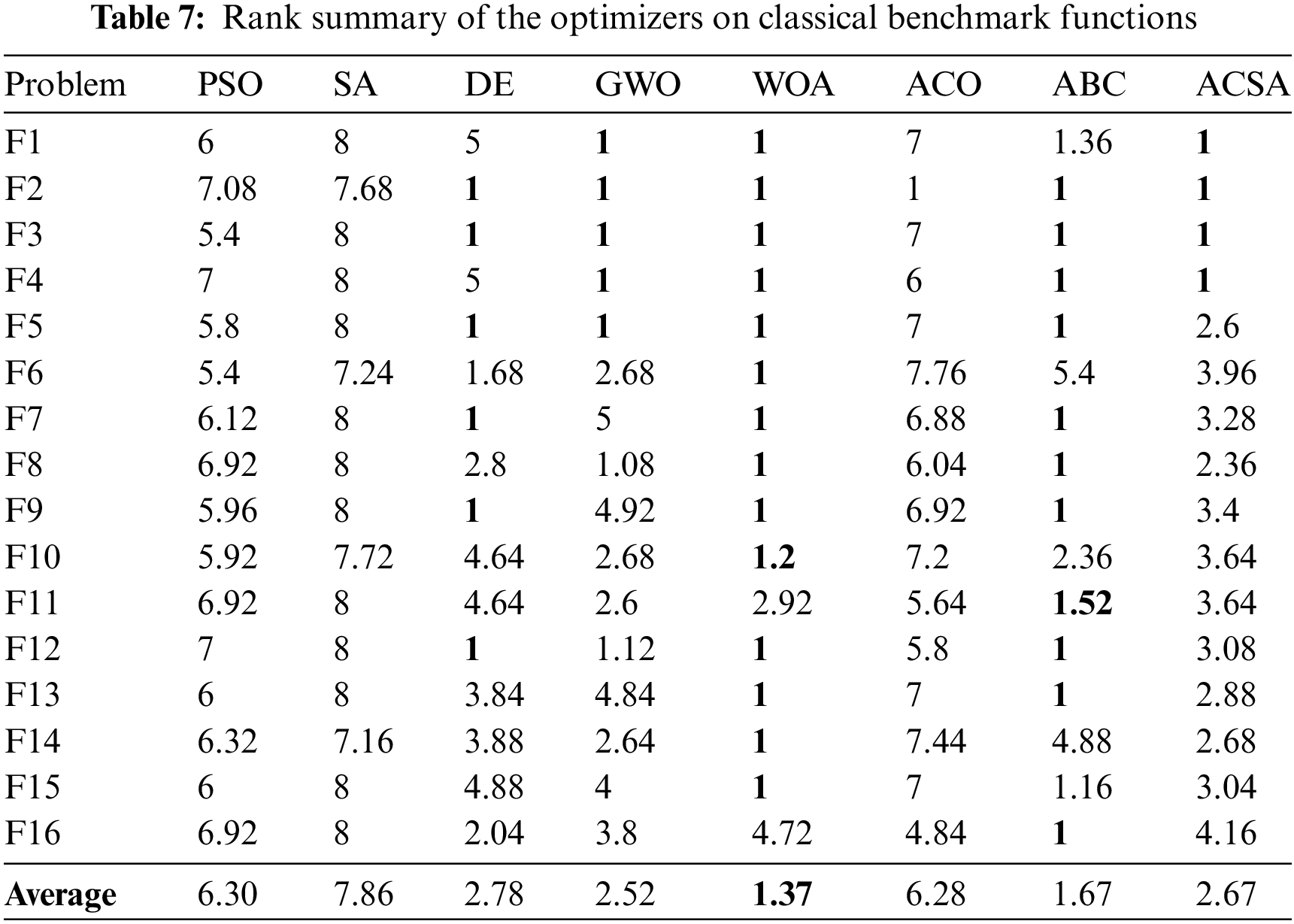
Upon analysis of Table 7, it is evident that the rank value of ACSA at F1-F4 functions is 1. The mean rank value for all classical functions is 2.679. Six optimization methods, including ACSA, all rank first for the F2 function, indicating that the function achieves the global optimum in all iterations of the algorithms and can be considered a straightforward problem to solve. For the classical test functions, the WOA algorithm has a better ranking than ACSA.
Table 8 demonstrates that ACSA has achieved the highest ranking in four out of the CEC 2022 test functions. The functions C2, C4, and C7 can be characterized as having a competitive approach, but function C8 does not exhibit the same level of performance. The performance of the ACSA algorithm in this test group is superior, achieving a ranking of 2.00, while GWO’s ranking is 2.41.
The first chapter highlights that while an efficient optimization algorithm may excel in problem-solving, it is not capable of achieving the same level of success for every problem. Upon examining Sections 4.3.1 and 4.3.2, it becomes evident that the WOA approach, which has proven effective in classical test functions, is unable to achieve the same level of performance in CEC 2022 functions. Furthermore, GWO, which performs above average in classical test functions, demonstrates greater resilience towards multidimensional composite functions. These findings provide evidence in favor of the NFL theorem. Therefore, an extra test was necessary to assess the effectiveness of the ACSA and thoroughly prove its superiority compared to other approaches. The sign test is a testing method that enables pairwise comparison. Further information about this test can be found in the following subsection.
4.3.3 Pairwise Comparisons: The Sign Test
A sign test is a statistical method used to assess the disparity between two samples. This method is often favored for small sample sizes or when the data does not conform to the normal distribution. In the application of the sign test, the initial step is to compute the difference between the observations. Differences are categorized as either positive or negative. Differences equal to zero are disregarded. The test statistic is computed by considering the count of positive and negative signs, and the outcomes are assessed at a significance level, often 5%.
As referenced in the preceding sections, the optimization outcomes were computed through 25 iterations. Given the limited size of the sample, the sign test was employed in the study. This test allows for the derivation of two distinct conclusions: Firstly, the p value is determined by comparing the fitness values obtained by the methods in each simulation. This approach allows for the observation of whether the proposed method can achieve results that are significantly different from those obtained by the compared methods. Secondly, we compared a total of 700 experimental results for 16 classical test functions (400 results for 25 trials) and 12 CEC 2022 test functions (300 results for 25 trials) by recording both positive and negative signs. This enables the acquisition of a numerical score regarding the overall performance by the comparison of all the outcomes of the methods. Comparing algorithms using similar scoring is a commonly favored method in the relevant literature [37]. Given that all the test functions explored in the work are minimization problems, the approach that achieves the lowest value is deemed more effective. Hence, a positive sign signifies that the minimum outcome of ACSA is inferior to the methods being compared, whereas a negative sign indicates that ACSA has achieved a more optimal value in problem-solving. To summarize, the winner in 700 runs was determined by taking into account the negative sign in the comparison between ACSA and the other approach. Results are displayed in Table 9.
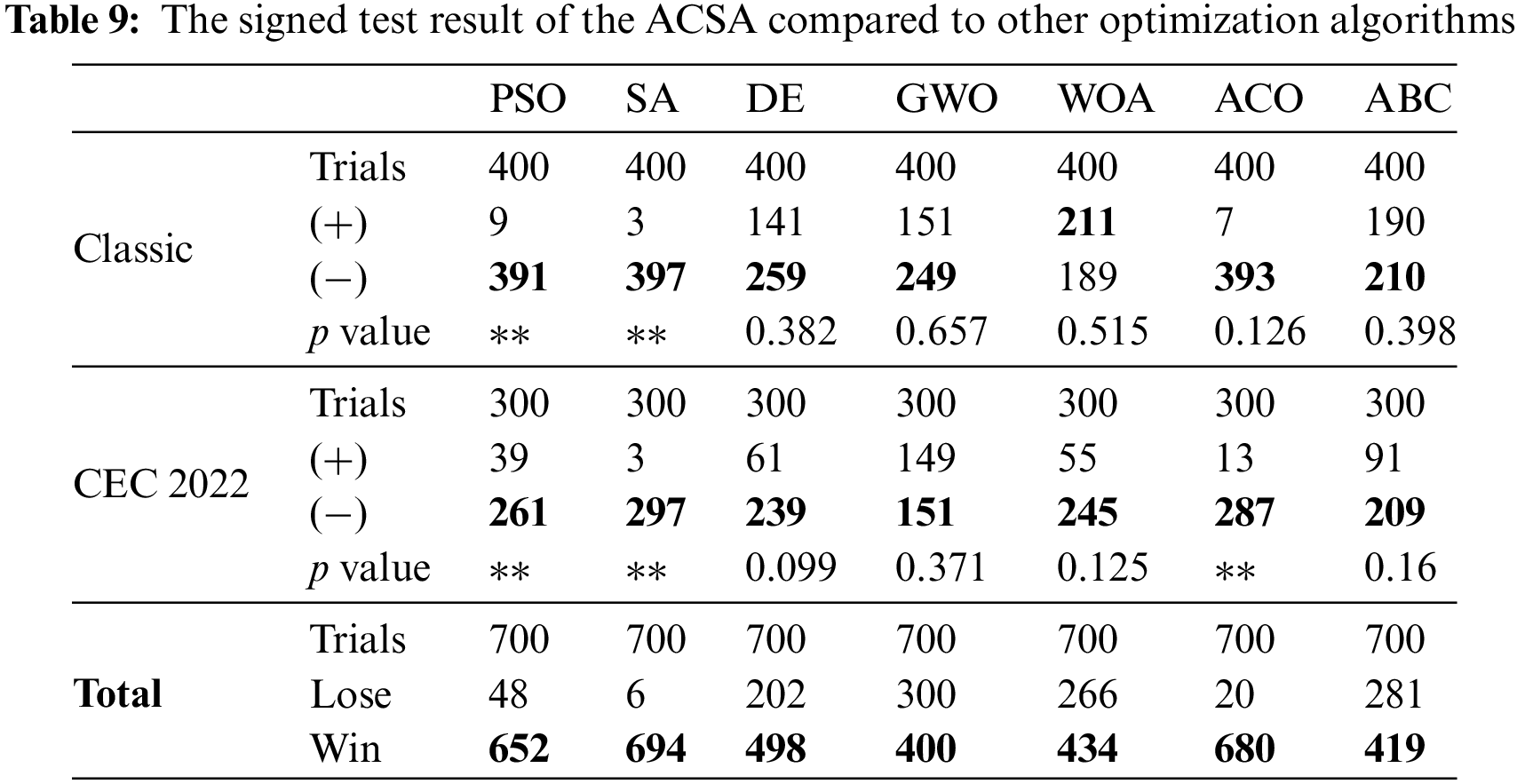
‘**’ denotes a statistically significant difference between ACSA and the algorithm being compared, with a 95% confidence interval. This means that the optimal result of the proposed method performs significantly better than the other algorithm. It is evident that the magnitude of this difference is greatest for the SA algorithm. Although ACSA may not differ significantly from other optimizers in some problems, the minimum results achieved by ACSA are generally numerically superior. The numerical superiority of WOA and ABC for classical test functions, and GWO for composite functions, over ACSA in achieving the optimal value has been demonstrated. Nevertheless, when taking into account the cumulative score derived from all test functions, it becomes evident that ACSA outperforms other widely used optimizers in the literature.
Special information regarding the computer configuration used for the experimental investigations can be found in Section 4. Specific metrics were employed to quantify the algorithmic efficiency of the system. Determining the complexity of an algorithm is a crucial measure for evaluating its performance. The population initialization procedure of the proposed ACSA has a time complexity of O(n g × n r), where n g denotes the number of generations and n r denotes the number of regulator sizes. Nevertheless, the mean running time of the suggested ACSA and other algorithms is provided in Fig. 7. ACSA demonstrates a shorter time cost compared to the other 5 methods.
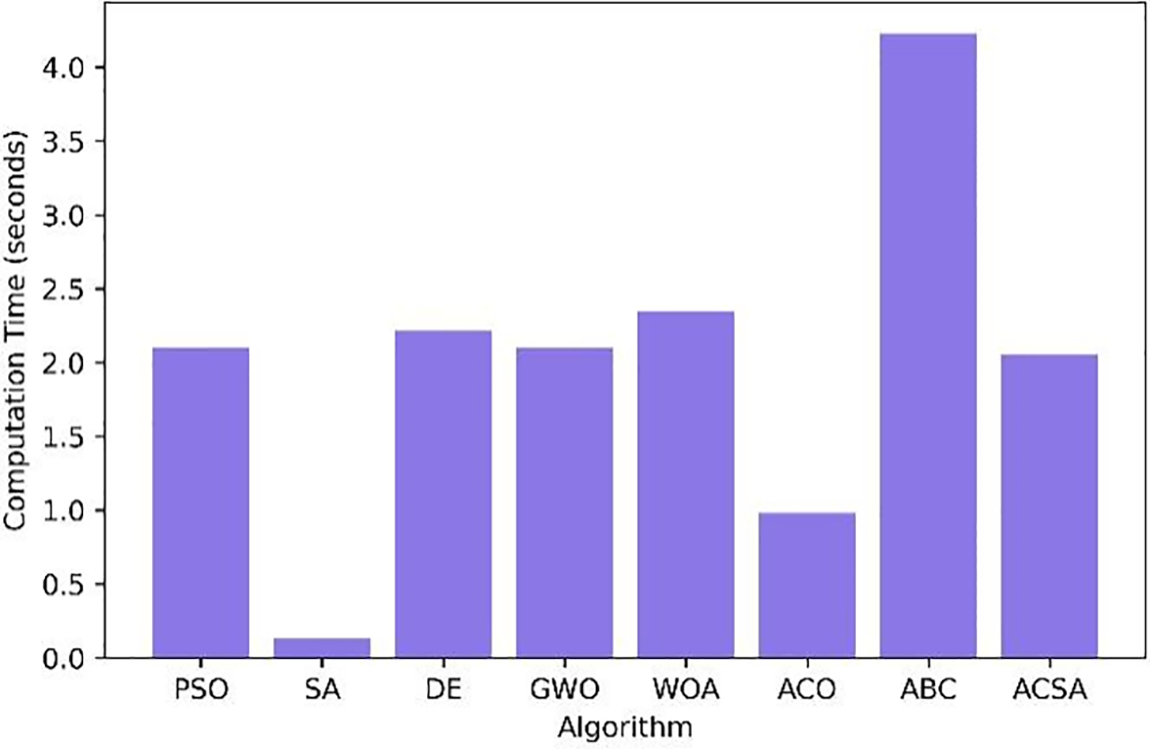
Figure 7: Average running time of metaheuristics algorithms
The present work introduces a novel optimization algorithm that draws inspiration from natural phenomena. The proposed ACSA method is based on the behavior of neural and hormonal regulators in the blood circulation system to address optimization problems. This study mathematically models the excitation behavior of regulators in maintaining an equilibrium state during the control of arterial pressure and blood volume. The approach establishes fixed values for the theoretical parameters that will impact the overall performance, while also incorporating adjustable parameters to deal with various optimization problems.
Several sets of tests were conducted to evaluate the performance of the proposed algorithm. The ACSA was initially evaluated using sixteen commonly used benchmark functions from the literature. This paper presents a qualitative analysis of the algorithm performance using search history, convergence curves, and exploration-exploitation diagrams. The present experiment and the subsequent discussions provide evidence in favor of the following conclusions:
• The search process, initiated at random, exhibits significant improvement throughout the iterations based on the fitness value of the problem. The regulators effectively target and investigate promising areas within the search space.
• The exploration and exploitation characteristic of different types of regulators guarantees the maintenance of a balanced search process. Despite the observation of fast convergence, the algorithm typically avoids being trapped in the local optimum and instead persists in searching for the global optimum.
Following the initial experiment, the algorithm was executed using two distinct categories of benchmark functions. The classical benchmark functions were set as two-dimensional and the CEC 2022 benchmark functions were set as ten-dimensional. The objective of this study was to assess the efficacy of the model on functions of varying degrees of difficulty. Furthermore, the ACSA algorithm was compared against 7 well-known optimization techniques in the literature using equal experimental conditions on these test functions. Comparative statistical analyses, including pairwise comparison tests (sign test), multiple comparison tests (Friedman rank test), and qualitative convergence curves, were employed to evaluate the approaches. The findings and discussions of the second experiment support the following conclusions:
• The speed of convergence and the global optimum attainment of the ACSA is satisfactory for problems involving two-dimensional classical test functions and above average for composite test functions.
• When solving problems with composite test functions, the ACSA can significantly outperform on a range of test functions when the difficulty level increases. It can be interpreted as robustness to challenging problems.
• In several aspects, ACSA surpassed the optimization algorithms documented in the literature.
Experimental results proved that the optimal values obtained by the ACSA method are more accurate than many of the defacto standard optimization methods. We have measured the performance of an algorithm by utilizing the absolute difference between the well-known optimal value and the optimal result produced by the algorithm. The distribution of the differences does not fit the normal distribution according to the Shapiro-Wilk Test at significance level
Nevertheless, ACSA has certain constraints similar to well-known MH algorithms. For instance, it cannot demonstrate superior success in every problem. Given its stochastic characterization, it does not ensure the optimal outcome; instead, it generates candidate optimal solutions. Furthermore, it needs precise parameter optimization tailored to the problem. Owing to these factors, additional evaluation studies are necessary to investigate the full extent of the algorithm’s capacity to address optimization problems.
Thorough comparisons with other meta-discoveries using intricate test functions and real-world problems will reveal the intricate strengths and weaknesses of the algorithm. Hence, a potential area of future study could involve the advancement of enhanced iterations (multi-objective or discrete) of the suggested approach to address diverse intricate problems. Another research possibility could be to examine the sensitivity of the parameters and explore the adjustable parameters of the suggested algorithm and their influence on preserving the ideal equilibrium between the exploration and exploitation stages of the algorithm optimization process.
Acknowledgement: The authors like to convey their sincere thanks to the journal editor and reviewers for their constructive criticism, which enhanced the content and quality of our paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Nermin Özcan, Semih Utku; analysis and interpretation of results: Nermin Özcan, Semih Utku, Tolga Berber; draft manuscript preparation: Nermin Özcan. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Supplementary Materials: The supplementary material is available online at https://doi.org/10.32604/cmes.2024.055860.
References
1. Altay EV, Altay O, Özçevik Y. A comparative study of metaheuristic optimization algorithms for solving real-world engineering design problems. Comput Model Eng Sci. 2024;139(1):1039–94. doi:10.32604/cmes.2023.029404. [Google Scholar] [CrossRef]
2. Li Y, Xiong G, Mirjalili S, Wagdy Mohamed A. Optimal equivalent circuit models for photovoltaic cells and modules using multi-source guided teaching-learning-based optimization. Ain Shams Eng J. 2024;292(22):102988. doi:10.1016/j.asej.2024.102988. [Google Scholar] [CrossRef]
3. Raja BD, Patel VK, Yildiz AR, Kotecha P. Performance of scientific law-inspired optimization algorithms for constrained engineering applications. Eng Optim. 2023;55(10):1798–1812. doi:10.1080/0305215X.2022.2127698. [Google Scholar] [CrossRef]
4. Lu C, Gao L, Li X, Hu C, Yan X, Gong W. Chaotic-based grey wolf optimizer for numerical and engineering optimization problems. Memetic Comput. 2020;12(4):371–98. doi:10.1007/s12293-020-00313-6. [Google Scholar] [CrossRef]
5. Su H, Zhao D, Heidari AA, Liu L, Zhang X, Mafarja M, et al. RIME: a physics-based optimization. Neurocomputing. 2023;532(5):183–214. doi:10.1016/j.neucom.2023.02.010. [Google Scholar] [CrossRef]
6. Savsani P, Savsani V. Passing vehicle search (PVSa novel metaheuristic algorithm. Appl Math Model. 2016;40(5–6):3951–78. doi:10.1016/j.apm.2015.10.040. [Google Scholar] [CrossRef]
7. Trojovský P, Dehghani M. A new human-based metaheuristic approach for solving optimization problems. Comput Model Eng Sci. 2023;137(2):1695–730. doi:10.32604/cmes.2023.028314. [Google Scholar] [CrossRef]
8. Abdollahzadeh B, Gharehchopogh FS, Khodadadi N, Mirjalili S. Mountain gazelle optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Adv Eng Softw. 2022;174(3):103282. doi:10.1016/j.advengsoft.2022.103282. [Google Scholar] [CrossRef]
9. Liang Z, Shu T, Ding Z. A novel improved whale optimization algorithm for global optimization and engineering applications. Mathematics. 2024;12(5):636. doi:10.3390/math12050636. [Google Scholar] [CrossRef]
10. Ghasemi M, Golalipour K, Zare M, Mirjalili S, Trojovský P, Abualigah L, et al. Flood algorithm (FLAan efficient inspired meta-heuristic for engineering optimization. J Supercomput. 2024;80(15):22913–3017. doi:10.1007/s11227-024-06291-7. [Google Scholar] [CrossRef]
11. Wang X, Snášel V, Mirjalili S, Pan JS, Kong L, Shehadeh HA. Artificial Protozoa Optimizer (APOa novel bio-inspired metaheuristic algorithm for engineering optimization. Knowl-Based Syst. 2024;295(5):111737. doi:10.1016/j.knosys.2024.111737. [Google Scholar] [CrossRef]
12. Oladejo SO, Ekwe SO, Mirjalili S. The hiking optimization algorithm: a novel human-based metaheuristic approach. Knowl-Based Syst. 2024;296(4):111880. doi:10.1016/j.knosys.2024.111880. [Google Scholar] [CrossRef]
13. Holland JH. Genetic algorithms. Sci Am. 1992;267(1):66–72. [Google Scholar]
14. Schwefel HP. Evolution strategies: a familiy of non-linear optimization techniques based on imitating some principles of organic evolution. Ann Oper Res. 1984;1(2):165–7. doi:10.1007/BF01876146. [Google Scholar] [CrossRef]
15. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]
16. Salcedo-Sanz S, Del Ser J, Landa-Torres I, Gil-López S, Portilla-Figueras JA. The coral reefs optimization algorithm: a novel metaheuristic for efficiently solving optimization problems. Sci World J. 2014;2014(8):1–15. doi:10.1155/2014/739768. [Google Scholar] [CrossRef]
17. Eberhart R, Kennedy J. New optimizer using particle swarm theory. In: Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 1995; Nagoya, Japan. doi:10.1109/MHS.1995.494215. [Google Scholar] [CrossRef]
18. Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern Part B. 1996;26(1):29–41. doi:10.1109/3477.484436. [Google Scholar] [CrossRef]
19. Karaboğa D. An idea based on honey bee swarm for numerical optimization. In: Technical report-TR06. 2005. Available from: https://abc.erciyes.edu.tr/pub/tr06_2005.pdf. [Accessed 2024]. [Google Scholar]
20. Abdollahzadeh B, Gharehchopogh FS, Mirjalili S. African vultures optimization algorithm: a new nature-inspired metaheuristic algorithm for global optimization problems. Comput Ind Eng. 2021;158(4):107408. doi:10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]
21. Alzoubi S, Abualigah L, Sharaf M, Daoud MS, Khodadadi N, Jia H. Synergistic swarm optimization algorithm. Comput Model Eng Sci. 2024;139(3):2557–604. doi:10.32604/cmes.2023.045170. [Google Scholar] [CrossRef]
22. Ghiaskar A, Amiri A, Mirjalili S. Polar fox optimization algorithm: a novel meta-heuristic algorithm. Neural Comput Applic. 2024;36(33):20983–1022. doi:10.1007/s00521-024-10346-4. [Google Scholar] [CrossRef]
23. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]
24. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]
25. Yang XS. A new metaheuristic batinspired algorithm. In: González JR, Pelta DA, Cruz C, Terrazas G, Krasnogor N, editors. Nature inspired cooperative strategies for optimization. Berlin: Springer; 2010. p. 65–74. doi:10.1007/978-3-642-12538-6_6. [Google Scholar] [CrossRef]
26. Saremi S, Mirjalili S, Lewis A. Grasshopper optimisation algorithm: theory and application. Adv Eng Softw. 2017;105:30–47. doi:10.1016/j.advengsoft.2017.01.004. [Google Scholar] [CrossRef]
27. Wang GG, Deb S, Coelho LDS. Elephant herding optimization. In: 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), 2015; Bali, Indonesia. doi:10.1109/ISCBI.2015.8. [Google Scholar] [CrossRef]
28. Laarhoven VPJM, Aarts EHL. Simulated annealing: theory and applications. Dordrecht: Springer; 1987. p. 33–8. doi:10.1007/978-94-015-7744-1. [Google Scholar] [CrossRef]
29. Abedinpourshotorban H, Mariyam Shamsuddin S, Beheshti Z, Jawawi DNA. Electromagnetic field optimization: a physics-inspired metaheuristic optimization algorithm. Swarm Evol Comput. 2015;26:8–22. doi:10.1016/j.swevo.2015.07.002. [Google Scholar] [CrossRef]
30. Wei Z, Huang C, Wang X, Han T, Li Y. Nuclear reaction optimization: a novel and powerful physics-based algorithm for global optimization. IEEE Access. 2019;7:1–9. doi:10.1109/ACCESS.2019.2918406. [Google Scholar] [CrossRef]
31. Zhao W, Wang L, Zhang Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl-Based Syst. 2019;163(4598):283–304. doi:10.1016/j.knosys.2018.08.030. [Google Scholar] [CrossRef]
32. Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: a novel optimization algorithm. Knowl-Based Syst. 2020;191:105190. doi:10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]
33. Reynolds R. An Introduction to Cultural Algorithms. 1994. Available from: https://www.researchgate.net/publication/201976967_An_Introduction_to_Cultural_Algorithms. [Accessed 2024]. [Google Scholar]
34. Shi Y. Brain storm optimization algorithm. In: Lecture notes in computer science. 2011; p. 303–9. doi:10.1007/978-3-642-21515-5_36. [Google Scholar] [CrossRef]
35. Shabani A, Asgarian B, Gharebaghi SA, Salido MA, Giret A. A new optimization algorithm based on search and rescue operations. Math Probl Eng. 2019;2019(1):23. doi:10.1155/2019/2482543. [Google Scholar] [CrossRef]
36. Khatri A, Gaba A, Rana KPS, Kumar V. A novel life choice-based optimizer. Soft Comput. 2020;24(12):9121–41. doi:10.1007/s00500-019-04443-z. [Google Scholar] [CrossRef]
37. Chou JS, Nguyen NM. FBI inspired meta-optimization. Appl Soft Comput J. 2020;93:106339. doi:10.1016/j.asoc.2020.106339. [Google Scholar] [CrossRef]
38. Tharwat A, Gabel T. Parameters optimization of support vector machines for imbalanced data using social ski driver algorithm. Neural Comput Appl. 2020;32(11):6925–38. doi:10.1007/s00521-019-04159-z. [Google Scholar] [CrossRef]
39. Das B, Mukherjee V, Das D. Student psychology based optimization algorithm: a new population based optimization algorithm for solving optimization problems. Adv Eng Softw. 2020;146(4):102804. doi:10.1016/j.advengsoft.2020.102804. [Google Scholar] [CrossRef]
40. Li S, Chen H, Wang M, Heidari AA, Mirjalili S. Slime mould algorithm: a new method for stochastic optimization. Futur Gener Comput Syst. 2020;111(Supplement C):300–23. doi:10.1016/j.future.2020.03.055. [Google Scholar] [CrossRef]
41. Dhiman G, Kumar V. Seagull optimization algorithm: theory and its applications for large-scale industrial engineering problems. Knowl-Based Syst. 2019;165(25):169–96. doi:10.1016/j.knosys.2018.11.024. [Google Scholar] [CrossRef]
42. Li MD, Zhao H, Weng XW, Han T. A novel nature-inspired algorithm for optimization: virus colony search. Adv Eng Softw. 2016;92(3):65–88. doi:10.1016/j.advengsoft.2015.11.004. [Google Scholar] [CrossRef]
43. Villaseñor C, Arana-Daniel N, Alanis AY, López-Franco C, Hernandez-Vargas EA. Germinal center optimization algorithm. Int J Comput Intell Syst. 2018;12(1):13–27. doi:10.2991/ijcis.2018.25905179. [Google Scholar] [CrossRef]
44. Eskandar H, Sadollah A, Bahreininejad A, Hamdi M. Water cycle algorithm–a novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput Struct. 2012;110-111(1):151–66. doi:10.1016/j.compstruc.2012.07.010. [Google Scholar] [CrossRef]
45. Zhao W, Wang L, Zhang Z. Artificial ecosystem-based optimization: a novel nature-inspired meta-heuristic algorithm. Neural Comput Appl. 2020;32(13):9383–425. doi:10.1007/s00521-019-04452-x. [Google Scholar] [CrossRef]
46. Abualigah L, Diabat A, Mirjalili S, Abd Elaziz M, Gandomi AH. The arithmetic optimization algorithm. Comput Methods Appl Mech Eng. 2021;376(2):113609. doi:10.1016/j.cma.2020.113609. [Google Scholar] [CrossRef]
47. Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl-Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]
48. Qais MH, Hasanien HM, Turky RA, Alghuwainem S, Tostado-Véliz M, Jurado F. Circle search algorithm: a geometry-based metaheuristic optimization algorithm. Mathematics. 2022;10(10):1–27. doi:10.3390/math10101626. [Google Scholar] [CrossRef]
49. Geem ZW, Kim HJ. A new heuristic optimization algorithm: harmony search. Optimization. 2015;51-70(2):60–8. doi:10.1177/003754970107600201. [Google Scholar] [CrossRef]
50. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]
51. Glover F. Tabu search: a tutorial. Interfaces. 1990;20(4):74–94. doi:10.1287/inte.20.4.74. [Google Scholar] [CrossRef]
52. Mirjalili S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl-Based Syst. 2015;89:228–49. doi:10.1016/j.knosys.2015.07.006. [Google Scholar] [CrossRef]
53. Yapici H, Cetinkaya N. A new meta-heuristic optimizer: pathfinder algorithm. Appl Soft Comput J. 2019;78(2):545–68. doi:10.1016/j.asoc.2019.03.012. [Google Scholar] [CrossRef]
54. Salgotra R, Singh U. The naked mole-rat algorithm. Neural Comput Appl. 2019;31(12):8837–57. doi:10.1007/s00521-019-04464-7. [Google Scholar] [CrossRef]
55. Bayraktar Z, Komurcu M, Bossard JA, Werner DH. The wind driven optimization technique and its application in electromagnetics. IEEE Trans Antennas Propag. 2013;61(5):2745–57. doi:10.1109/TAP.2013.2238654. [Google Scholar] [CrossRef]
56. Acharya D, Das DK. A novel human conception optimizer for solving optimization problems. Nat Sci Reports. 2022;12(1):1–20. doi:10.1038/s41598-022-25031-6. [Google Scholar] [CrossRef]
57. Dombi J, Jónás T. Generalizing the sigmoid function using continuous-valued logic. Fuzzy Sets Syst. 2022;449(11):79–99. doi:10.1016/j.fss.2022.02.010. [Google Scholar] [CrossRef]
58. Hall JE. Nervous regulation of the circulation, and rapid control of arterial pressure. In: Textbook of medical physiology. Netherlands: Elsevier; 2011. [Google Scholar]
59. Hall JE. Role of the kidneys in long-term control of arterial pressure and in hypertension: the integrated system for arterial pressure regulation. In: Textbook of medical physiology. Netherlands: Elsevier; 2011. [Google Scholar]
60. Thieu NV. OPFUNU (Optimization benchmark functions in numpy). 2020. Available from: https://github.com/thieu1995/opfunu. [Accessed 2024]. [Google Scholar]
61. Thieu NV, Mirjalili S. An open-source library for latest meta-heuristic algorithms in Python. J Syst Archit. 2023;139(12):102871. doi:10.1016/j.sysarc.2023.102871. [Google Scholar] [CrossRef]
62. Thieu NV. Opfunu: an open-source python library for optimization benchmark functions. J Open Res Softw. 2024;12(1):8. doi:10.5334/jors.508. [Google Scholar] [CrossRef]
63. Jamil M, Yang XS. A literature survey of benchmark functions for global optimization problems. Int J Math Model Numer Optim. 2013;4(2):150–94. doi:10.1504/IJMMNO.2013.055204. [Google Scholar] [CrossRef]
64. Suganthan PN, Hansen N, Liang JJ, Deb K, Chen YP, Auger A, et al. Problem definitions and evaluation criteria for the CEC, 2005 special session on real-parameter optimization. Natural Comput. 2005;341–57. [Google Scholar]
65. Wu G, Mallipeddi R, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization. Available from: https://www.researchgate.net/publication/317228117_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2017_Competition_and_Special_Session_on_Constrained_Single_Objective_Real-Parameter_Optimization. [Accessed 2024]. [Google Scholar]
66. Liang JJ, Suganthan PN, Qu BY, Gong DW, Yue CT. Problem definitions and evaluation criteria for the CEC, 2020 special session and competition on single objective bound constrained numerical optimization. In: Technical report 201912. doi:10.13140/RG.2.2.31746.02247. [Google Scholar] [CrossRef]
67. Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–80. doi:10.1126/science.220.4598.671. [Google Scholar] [PubMed] [CrossRef]
68. Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. J Glob Optim. 2007;39(3):459–71. doi:10.1007/s10898-007-9149-x. [Google Scholar] [CrossRef]
69. Derrac J, García S, Molina D, Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput. 2011;1(1):3–18. doi:10.1016/j.swevo.2011.02.002. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF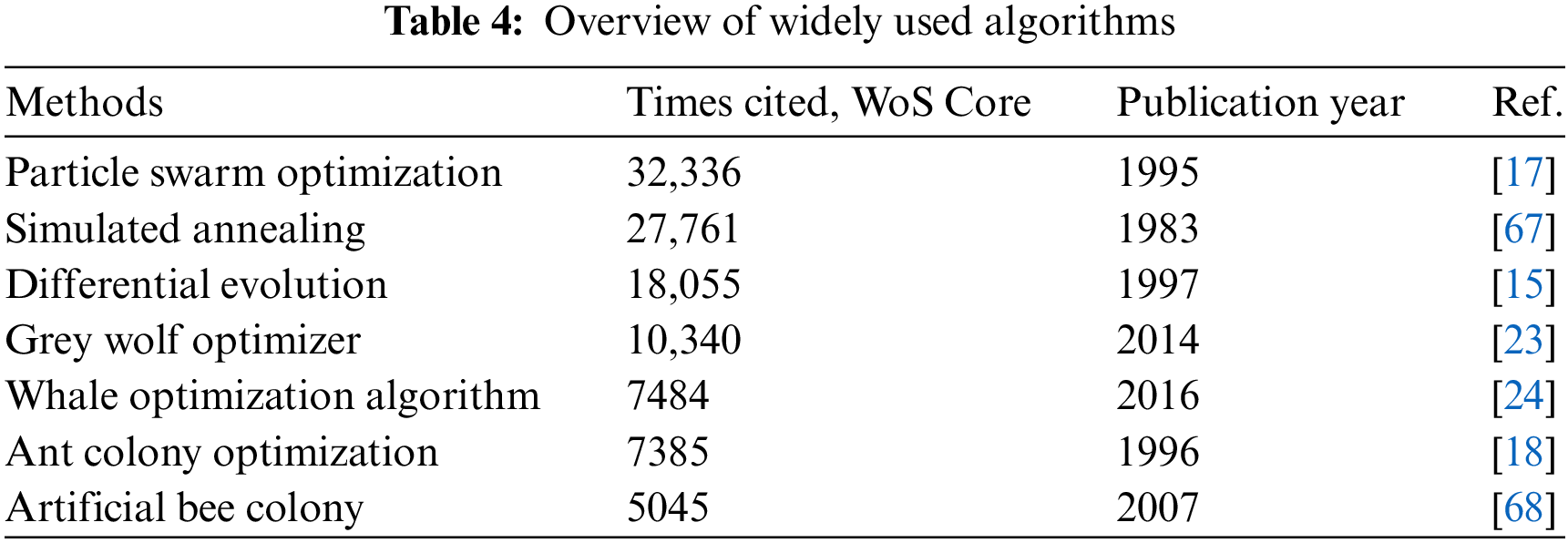
 Downloads
Downloads
 Citation Tools
Citation Tools