Parameter Optimization of Tuned Mass Damper Inerter via Adaptive Harmony Search

1  Introduction

Due to the increasing human population, industrialization, and technology, the number of cities and the density of people living in cities are increasing daily. This situation affects city construction, and more earthquake-resistant structures are being built in earthquake zones. There are various factors in the design of buildings in these cities. Among these, time-dependent loads such as wind and earthquake, which are relatively difficult to determine, play an important role. These effects cause loss of life, economic damages, and equipment losses. In order to ensure safety against these effects, various measures have been taken from past to present, and solutions have been developed using different technologies over time to minimize the damage caused. As a result of aiming to protect the structures from dynamic effects such as earthquakes and wind, structural control systems, which are one way to change the structures’ stiffness and damping, are used. Thus, the design engineer can minimize damage distribution by using control systems.

Control systems, which have many application examples, especially in developed and developing countries, can only obtain effective results by appropriately selecting the properties of the parts that make up the control systems, considering their intended use. For this purpose, scientific studies on control systems started in the 1920s [1]. The studies have accelerated considerably in the last 20–25 years with the development of computer technology and related iterative methods.

Structural vibration is one of the biggest problems faced by structures and is usually caused by wind, earthquake, traffic, or heavy machinery operations. As a result of structural vibration, severe damage to structures can occur. For example, the Takoma Bridge collapsed due to vibrations caused by wind. One of the control methods developed to ensure the safety of the various excitations is to add control devices to the building. The purpose of the structural control system is to reduce the vibration with an external control force and to increase the lateral integrity of the building [2]. The performance of the structural control system depends on different factors. Some of these factors are the characteristics of the structure and the design of the control system [3].

Structural control systems consist of active, semi-active, hybrid, and passive control systems. The active control system uses sensors to measure excitation and structural responses and actuators to control unwanted vibrations. The control forces are developed based on sensor feedback measuring the structure’s response [4]. The motion of the structure generates the control force in a semi-active control system, which is usually powered by a tiny external power source whose magnitude can be changed externally [4]. By combining the high performance of active devices with the durability of passive devices, hybrid actuators solve the drawbacks and restrictions of single controllers [5]. Passive control uses passive devices for structural control. In passive systems, energy is distributed by producing a relative motion according to the movement of the structure [4].

There are three groups of passive control systems. These are the base isolation system, energy dissipation, and energy transfer. Tuned mass damper inerter (TMDI) is in the energy transfer group. The tuned mass dampers (TMD), of which TMDI is a subgroup, were first proposed by Frahm [6] to reduce the effect of the dangerous vibration on the ship’s keel in 1909. The TMD, described in 1934 [7], is a passive energy damper widely employed to control resonance vibrations. In this study, a TMDI, which is a branch of passive control systems, is analyzed. In the rest of the paper, the study details are given, and summarized information about the necessary scientific studies on this subject from past to present and their contents are presented.

TMDI was first improved by Marian et al. [8] by combining the Two-Tip Flywheel (TTF) device “inertia” with the TMD. Thus, a new configuration for passive vibration control was proposed in their study. Marian et al. [9] concluded in their study that adding an inerter to the TMDI configuration can improve the performance of TMD in vibration control by deriving analytical closed-form solutions. Giaralis et al. [10] performed a standard numerical optimization study for a 74-storey building subjected to vortex shedding effects by optimizing the stiffness, damping, and inerter parameters of the TMDI system. As a result, using TMDI, a lighter structure can be obtained to meet the prescribed serviceability criteria of the building. Siami et al. [11] modeled a five-degree of freedom (5DOF) structure to improve the performance of Michelangelo Buonarroti’s famous sculpture and protect it from external vibration. This model investigated the effect of devices such as TMD and TMDI on this structure’s vibration reduction. It is concluded that the TMDI system is more effective in reducing the vibration of the sculpture than the TMD. Giaralis et al. [12] demonstrated the robustness of TMDI by applying it to an SDOF system excited with white noise excitation and obtained closed-form formulations of the optimal parameters. Pietrosanti et al. [13] demonstrated that the optimally designed TMDI system outperforms TMD by considering earthquake base excitation for displacement and acceleration minimization and dissipated energy maximization. De Domenico et al. [14] proposed an advanced base isolation system with TMDIs to reduce the displacement demand of foundation isolation systems due to the concentration of earthquake-induced displacement at the isolation level. It was shown that by installing a TMDI at the isolation floor, TMDIs can significantly reduce the displacement of foundation-isolated buildings. Xu et al. [15] observed a TMDI to control long-span bridges’ unwanted vortex-induced vibration (VIV). Based on the results, the TMDI system performs better in reducing the vortex-induced vibration responses of the bridge deck than the conventional TMD system. Sarkar et al. [16] installed TMDI in an engine section to reduce the vibrations of floating offshore wind turbine (FOWT) towers. It was concluded that TMDI reduces tower oscillation at a higher rate than a simple TMD system. Lara-Valencia et al. [17] studied the design of an optimal TMDI through an exhaustive search process on multiple performance indices. The results obtained from the numerical example they developed for the proposed optimization procedure showed that the devices designed based on exhaustive search optimization reduced the peak displacement. Pietrosanti et al. [18] applied a methodology to perform the optimal design of a TMDI with a generalized 2DOF model and a multi-degree-of-freedom structure. As a result, it is shown that the TMDI system improves the performances obtained with the classical TMD. Weber et al. [19] investigated the vibration reduction of high wind-excitation buildings equipped with TMDI. In the study, the overall performance of the TMDI system was evaluated based on the function of the ground to which the inerter is grounded, and it was stated that the ground to which the inerter is grounded is directly related to the TMDI performance. The best performance was achieved when the inerter was grounded to the ground. De Angelis et al. [20] investigated the optimal design of a TMDI for pedestrian bridges. By modeling the pedestrian bridge in reduced order, the study has made TMDI a very efficient control system for pedestrian bridges. Su et al. [21], with their proposed approach to TMDI, reduced wind and seismic induced responses using closed-form solutions by up to 60% and 55%, respectively, and provided guidance for determining the optimal parameters of TMDI systems. Bian et al. [22] investigated the optimum design of the TMDI system for vibration control of circular elements in structures to control the structure’s vibration. The results obtained from different optimization schemes show that the TMD system has vibration control performance and validity. Zahedin et al. [23] proposed the use of a hybrid control system (HCS) combining a base isolation system (BIS) with TMDI to reduce the seismic response of cylindrical tanks and investigated its multi-objective optimization. The optimally designed HCS significantly reduced the base shear, convective, and thrust displacements compared to the conventional design. Djerouni et al. [24] designed TMDI to minimize the peak of frequency response functions of the inter-story shear of adjacent buildings in ground motion excitation. The results showed that TMDI is effective in response reduction. Prakash et al. [25] optimized the tuning frequency ratio and damping of the TMDI in a damped structure subjected to constant white noise earthquake excitation. As a result, the optimally designed TMDI reduced the acceleration and displacement response of the structure. Jangid [26] found the optimum values of the damping and tuning frequency ratio in the base-isolated structure and demonstrated the effectiveness of TMDI and that the inertia increases as the mass ratio increases. Cao et al. [27] proposed multiple-tuned mass dampers-inerters (MTMDI) to control the structure’s response. The study results showed that the MTMDI installed in a single-degree-of-freedom (SDOF) structure makes it robust against earthquakes. Elias et al. [28] optimized the parameters of TMDI considering the soil structure interaction (SSI). The results indicated that TMDI optimization is important to improve the structure’s seismic performance. Djerouni et al. [29] optimized TMDIs to control the displacement of structures affected by near-fault ground motions. The results revealed that the optimized TMDI effectively controlled the structure’s response. Chen et al. [30] proposed a set of closed-form formulas for the optimal design of the TMDI system. The proposed closed formulas were analyzed with the frequency domain and time domain of a building and showed superior performance.

In this study, the seismic responses of the building equipped with a TMDI device on different floors are examined using the Adaptive Harmony Search (AHS) optimization algorithm, and their performance in the time domain is compared to the performance of conventional TMD. At the same time, the optimal physical parameters of the TMDI system are also obtained. Thus, the values of the TMDI that will minimize the structure’s response to the earthquake load are obtained. Various earthquake records are used in time-history analyses that are considered in the determination of the objective function of the optimization in all iterative processes. Compared to close-form methods, the methodology is effective considering different time-history analyses of different earthquake data and multiple vibration modes.

2  Material and Methods

2.1 Tuned Mass Damper Inerter (TMDI)

TMDIs are effective systems that minimize the negative responses of the structure. However, for TMDI systems to work effectively in the structure, various parameters can be adjusted to maximize the system performance and minimize reactions such as displacement and acceleration.

The increase of the mass of TMD is limited due to reasons such as structural space and manufacturing price. The larger the additional mass, the better the vibration reduction performance of the TMD, but the additional mass is limited [22]. For this reason, the concept of the “inerter”, introduced by Smith in 2002, has two independently movable terminals that develop an internal force proportional to the relative acceleration of their terminals, as shown in Fig. 1. The inerter is a mechanical element that can increase the mass by converting linear motion into rotation. TMDI takes advantage of the mass amplification effect of the inerter possessed by a two-terminal flywheel device to achieve better performance than TMD [9]. TMDI uses mass amplification, called inertia, to improve the vibration suppression properties of the TMD [31]. Through the mass amplification effect of the inerter, the performance of the energy dissipator can be significantly improved, and the structure’s vibration can be effectively controlled [22]. Inerters also have some physical mass. For example, the physical mass of a rack and pinion inertia with an inertia of 700 is 3.5 kg [32].

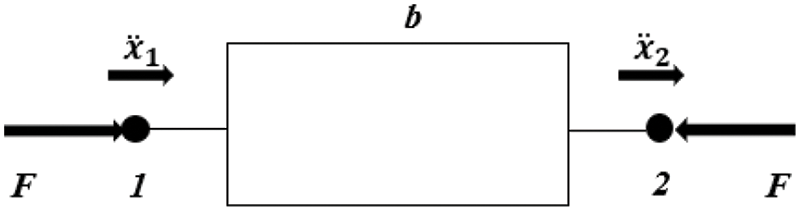
Figure 1: Schematic drawing of the inerter [8]

Where x¨1 and x¨2 are the accelerations and b is the inerter (kg) [8].

Although the inerter concept, introduced in 2002, was first used for research in electrical engineering, the use of inerters to improve the vibration control performance of dampers began in the 1990s [33,34]. Because it is also possible to obtain mechanical components such as rack and pinion gears and others with the same properties in civil engineering [35]. An inerter was initially developed for the suspension systems of Formula 1 cars [36]. Based on the definition of inertia, the relationship in Eq. (1) is valid [37,38].

F=b(x¨1−x¨2)(1)

The equation given by Eq. (1), for TMDI, the inertial force produced by the inertial device proportional to the relative acceleration of its terminals, is written as Eq. (2).

Finerter=b(x¨tmdi−x¨f)(2)

where x¨tmdi is the second derivative of the displacement of the auxiliary oscillating mass, x¨f is the second derivative of the displacement of the ground to which the inerter attaches the auxiliary mass. Hence, the inerter contributes to the mass-dependent inerter force of the primary structure [39].

A mechanical schematic of an inerter consisting of a flywheel connected to the rack and pinion with a gear is shown in Fig. 2. The rack [40] is the rod usually used to convert circular motion into linear motion. The circular gear that passes to this rod is called a pawn. The flywheel provides the energy.

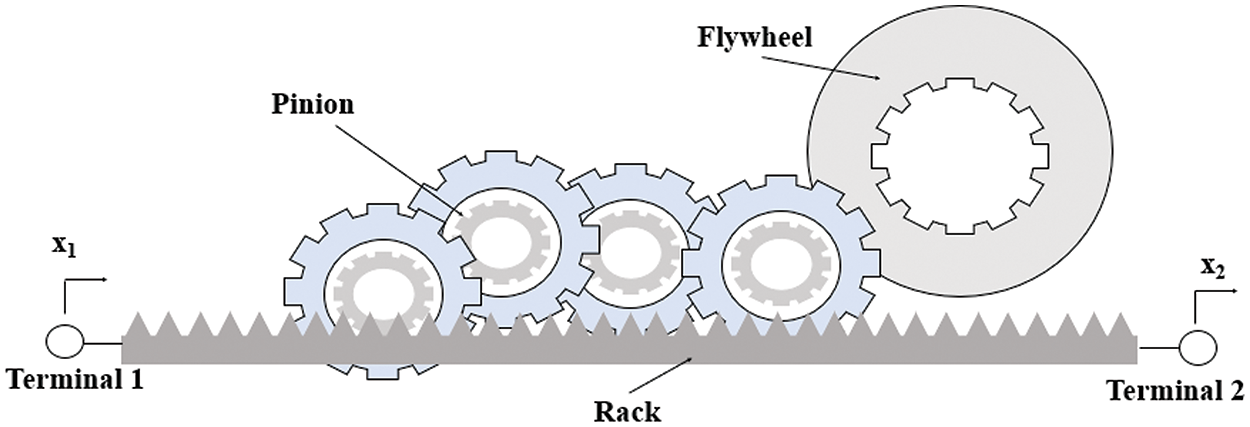
Figure 2: Schematic illustration of an inertial with four gears, rack, and pinion [41]

b=mfγf2γpr2(∏k=1nrk2rpk2)(3)

where mf is mass of the gear and γf is radius of the gear. γpr is the radius of the flywheel pinion. rk and rpk (k = 1,2, ..., n) are the radii of the kth gear and its corresponding pinion, respectively, connecting the rack to the gear pinion [41,42].

A vibration-damping device that directs the mass of the TMD to the ground was first introduced in 2014 by Marian and Giaralis, called as “Tuned Mass Damping Inerter” (TMDI). A TMDI-attached single degree of freedom (SDOF) structure is shown in Fig. 3.

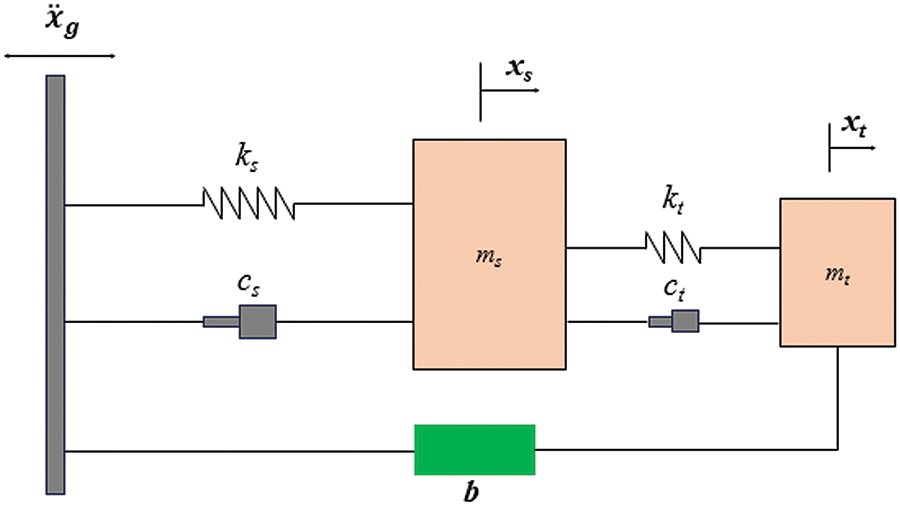
Figure 3: A TMDI attached SDOF system [42]

Where ms, ks and cs is the mass, stiffness and damping of the structure.

The TMDI device consists of a system that have mass (mt), stiffness (kt), and damping (ct) called TMD, and it has an inerter device with inertia b. The inerter device connects the ground and the auxiliary mass through. The vibration of the structure resonates the TMD. TMD dissipates the incident energy by damping it. The TMD system can be characterized using the parameters of natural frequency (wtmd) and damping ratio (ξtmd). The expression of these two parameters is shown in Eqs. (4) and (5) [25].

wtmd=ksms(4)

ξtmd=cs2msws(5)

The damping ratio of the TMDI and natural frequency of the TMDI are expressed in Eqs. (6) and (7).

ξtmdi=ctmdi2(mtmdi+b)wtmdi(6)

wtmdi=ktmdimtmdi+b(7)

where ξtmdi is the damping ratio of the system, mtmdi is the mass of the TMDI system, wtmdi is the natural frequency of the TMDI system, ctmdi is the damping coefficient of the TMDI system, and ktmdi is the stiffness of the TMDI system.

The optimum parameters of TMDI are investigated within the scope of the study, and in the following section, information about the studies in the literature on this subject is presented.

This study investigates a new TMDI design strategy based on a simplified model developed for vibration control of tall buildings to maintain high efficiency in designing TMDI parameters. In order to minimize the displacement and acceleration responses at the top floor of the structure, TMDI parameters were optimized using Adaptive Harmony Search (AHS), and the results were compared.

In order to obtain the best performance for the TMDI, the appropriate optimization of its parameters is required. This study uses structural dynamics to optimize the parameters of TMDI. The equations of motion of the structure with TMDI were solved using MATLAB Simulink (2018) [43].

2.2 Optimization

Optimization is the process of reaching the best solution among existing solutions, which has existed since human existence. An optimization problem is a problem with more than one suitable solution. An optimization problem generally consists of design variables, constraints, and objective functions. Optimization for the computation of complex problems has become one of the areas most intensively studied by the current artificial intelligence community.

The solution to many real-world problems is complex due to their limitations and various variables. The solution of engineering problems cannot be calculated directly since the optimum design variables impact the analysis of design constraints. This leads to the need for highly efficient methods for solving increasingly complex numerical optimization problems. For example, design cost problems in engineering often require methods to find the optimum from many available solutions [44]. The easiest way to solve a nonlinear problem is to use iterative solution trials, which can take a very long time. Iterative algorithms are essentially metaheuristics. Each process has objective functions that will minimize or maximize the objectives that it must meet [45].

Metaheuristic term was coined by Glover [46] and represents a well-defined class of algorithms for solving complex optimization problems [47]. Recently, many metaheuristic algorithms have been successfully applied to solve challenging problems. One of the reasons for the widespread use of these algorithms is that they can reach the optimum solution to enormous problems in a short time.

Metaheuristic algorithms have many applications. They can be applied in processes such as finding the shortest way to get to a place, obtaining the minimum cost for the delivery of goods in the field of logistics, optimally assigning workers to tasks during the organization of night shifts in a hospital, finding the minimum cost of the optimum distribution of aircraft crew. In the same problem, metaheuristic algorithms can perform differently due to the different searching processes and updating candidate solutions. Therefore, many optimization algorithms have been developed to find better solutions to optimization problems. In the literature, there are many metaheuristics inspired by nature. Optimization algorithms are inspired by the honey badger’s intelligent foraging behavior [48] or the principle of buoyancy applied upwards to an object partially or completely immersed in liquid [49]. Fig. 4 shows the stages in which the positions of the honey badgers are updated. In the digging phase, the honey badger digs and walks around, mimicking the heart shape, as shown in Fig. 4a. In the second phase, the search for honey, the honey badger accelerates with increasing density [48], as shown in Fig. 4b, obeying the Inverse Square Law.

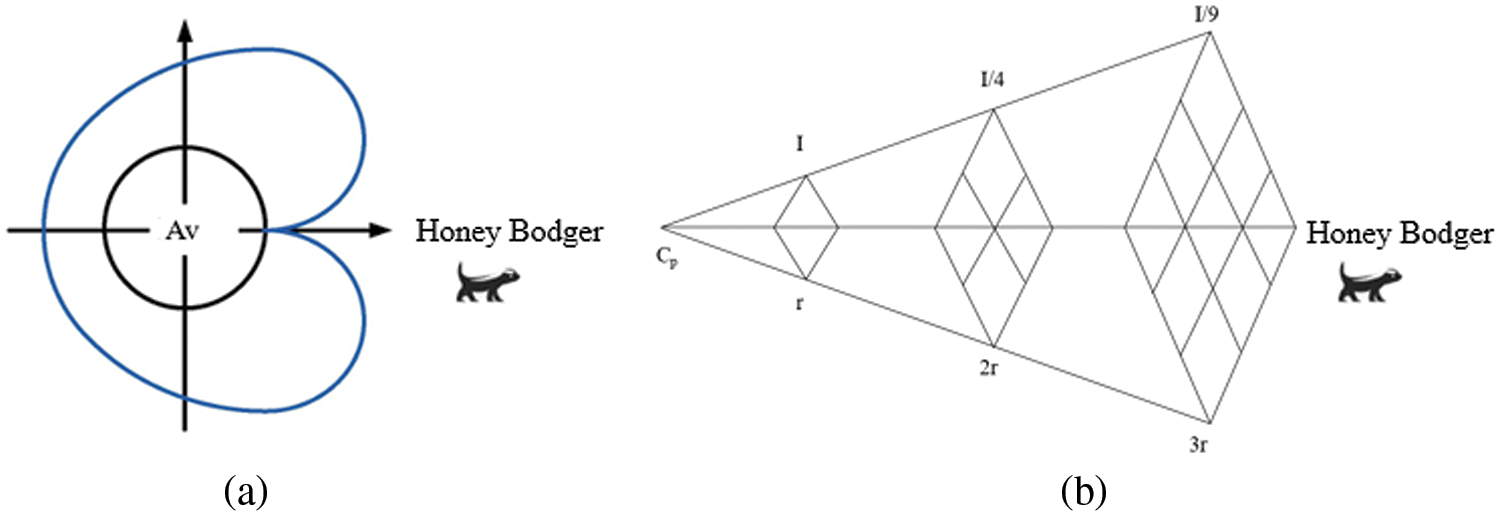
Figure 4: (a) Cardioid movement of the honey badger. (b) Inverse square law [48,50]

In this study, the properties of the TMDI system, which are explored as separate cases at the 10th, 9th, and 5th floor of a 10-storey superstructure, are optimized under 44 earthquake records, including FEMA [51] far fault records. The aim of the study is to present an optimal system with high structural control performance. The seismic data were utilized to the structure through MATLAB Simulink (Matlab R2018a, 2018). Adaptive Harmony Search (AHS) was used in the optimization, and the optimum algorithm parameters were obtained. The optimization process was implemented for three cases using the critical earthquake component.

Existing metaheuristic algorithms cannot solve all optimization problems [52]. The lack of a single algorithm with perfect characteristics that can simultaneously solve all optimization problems leads to the continuous development of new optimization algorithms. Therefore, new or improved optimization algorithms are always needed to better solve current and future problems that are too complex to be solved by existing methods [53]. In this study, a variant of the Harmony Search algorithm that was proposed by Geem et al. [54] was used. The goal of the HS algorithm is to optimize the objective function (cost, benefit, or efficiency) of the problem. The musician searches for optimal states determined by the value of the objective function, such as an optimization algorithm when continuously tuning the instrument to find the most beautiful harmony [55]. HS has been successfully applied to the engineering problems [56–60]. The main components of HS are harmony memory size (HMS), harmony memory consideration ratio (HMCR), pitch adjustment ratio (PAR), and stopping criterion. These parameters are responsible for exploration and exploitation.

The harmony search method has five steps. In the first step, the optimization problem is introduced, and the algorithm parameters are initialized. In Step 2, the initial harmony memory (HM) matrix is constructed via the process of randomization of design variables In Step 3, a new harmony vector is generated according to specific rules of HS. In Step 4, initial and new solutions are compared, and the best one is added to HM. If the termination criterion is met in Step 5, the iteration is stopped. If not, Steps 3 and 4 are reiterated [61].

HS uses some tuning parameters such as HMS, HMCR and PAR. In conventional HS, fixed values are assigned to the tuning parameters. Improved/modified HS algorithms were developed recently to increase the method’s efficiency [62]. For this reason, techniques independent of parameterization were also developed for the HS algorithm [63]. Since the time HS was proposed, with the efforts of scientists worldwide, good results have been achieved in the implementation and solution of optimization problems by improving the algorithm parameters, introducing new mechanisms and strategies, and others [64]. It is like the artist finalizing his/her unfinished work by changing it according to the audience’s opinions. For example, Kaveh et al. [65] developed an improved harmony search algorithm (Improved Harmony Search-IHS) for cost optimization of composite floor systems. Kayabekir et al. [66] optimized active tuned mass dampers (ATMDs) with the Modified Harmony Search algorithm, which is an updated version of the parameters of HS.

Saka et al. [63] developed an adaptive harmony search algorithm (AHS) for design code optimization of steel structures. Unlike HS, their proposed AHS automatically updates the HMCR and PAR values depending on the experience gained during the design process. The algorithm changes the harmony values by considering the HMCR and PAR parameters obtained from the design process. Therefore, the algorithm automatically selects the changing characteristics of a design space to strike a balance between exploration and exploitation search for the most successful optimization process. AHS eliminates the problem of having to perform analyses with different values of parameters, making the algorithm more general and applicable to the optimal design of large-sized steel structures [63]. In order to increase the convergence capacity, an attempt has been made to reduce the dependency on parameters to provide harmony to the problem optimization.

2.3 Adaptive Harmony Search (AHS)

Since the parameters are fixed in the harmony search algorithm, it cannot show harmony to changing conditions during the search, AHS, one of the developed algorithms, has a similar general framework to HS, except for the updating of the parameters. AHS has similar steps to classical HS, but instead of the fixed HMCR and PAR the updated HMCR and PAR values are used in each search step. With AHS, the dependency on parameters can be reduced and the convergence capacity can be increased. HMCR and PAR parameters were adapted to create AHS. Firstly, HMCR and PAR parameters are given initial values. It was then reduced using these initial values. In this case, optimum results are sought in a smaller range around the current solution by reducing the PAR. As HMCR decreases, the convergence to the best solution, the local search phase, increases. Eqs. (8) and (9) show the HMCR and PAR calculation in iterations.

HMCR=HMCRinitial(1−tmt)(8)

PAR=PARinitial(1−tmt)(9)

where mt is the maximum number of iterations and the number of iterations is shown with t. HMCR and PAR initial values are called HMCRinitial and PARinitial, respectively. The main parameters of the AHS are harmony memory size (HMS), HMCR, PAR and stopping criteria.

2.3.1 Initializing the Optimization Problem and Control Parameters

First, the parameters to be used in AHs are assigned. HMS, HMCR and PAR are the algorithm parameters. The values of the parameters are determined according to the problem to be solved. The stopping criterion (maxiter) is defined. The next step is taken after the design variables and their lower and upper limit ranges are defined.

2.3.2 Starting Harmony Memory

A harmony memory (HM) is created with randomly generated design variables within the defined solution space. The algorithm calculates the objective function values corresponding to each solution using Eq. (10).

HM=[x11x22…f(x1)x11x22…f(x2)⋮⋮⋮⋮x1HMSx2HMS…f(xHMS)](10)

The objective function is calculated by changing the rows of the HM matrix. Where x1 and x2 are the design variables and f(x) is the objective function.

xi,new=xi,min+rand()×(xi,max−xi,min)(11)

where xi is the newly produced i, xi,min and xi,max are the limit values of the design variables, respectively, and rand is a number between 0–1.

2.3.3 Generating a New Harmony Vector

HMCR randomly selects the newly created decision variable from the existing solution space. How the selection process will be done is given in Eqs. (12) and (13). k is a randomly selected solution (Eq. (14)).

xi,new=xi,min+rand()×(xi,max−xi,min)if HMCR>r1(12)

xi,new=xi,k+rand()×PAR(xi,max−xi,min)if HMCR≤r1(13)

k=ceil(rand×HMS)(14)

2.3.4 Updating Harmony Memory

Those in the newly created harmony memory are compared in terms of the values of the objective functions. If the newly created fit vector is better than the worst harmony, the worst harmony vector is replaced by the new harmony vector.

2.3.5 Evaluation of the Search Process

The steps of creating a new harmony vector and updating the harmony memory (2.3.3 and 2.3.4) are repeated until the defined stopping criterion is reached.

Fig. 5 shows the flow chart of AHS. For the selection of the current solution, the best solution (BSCR) parameters are defined by considering the ratio that defines the probability of using the best solution. Thanks to BSCR, modifying the algorithm using the best available solution solves the vibration problem involving random vibration of seismic excitations [66].

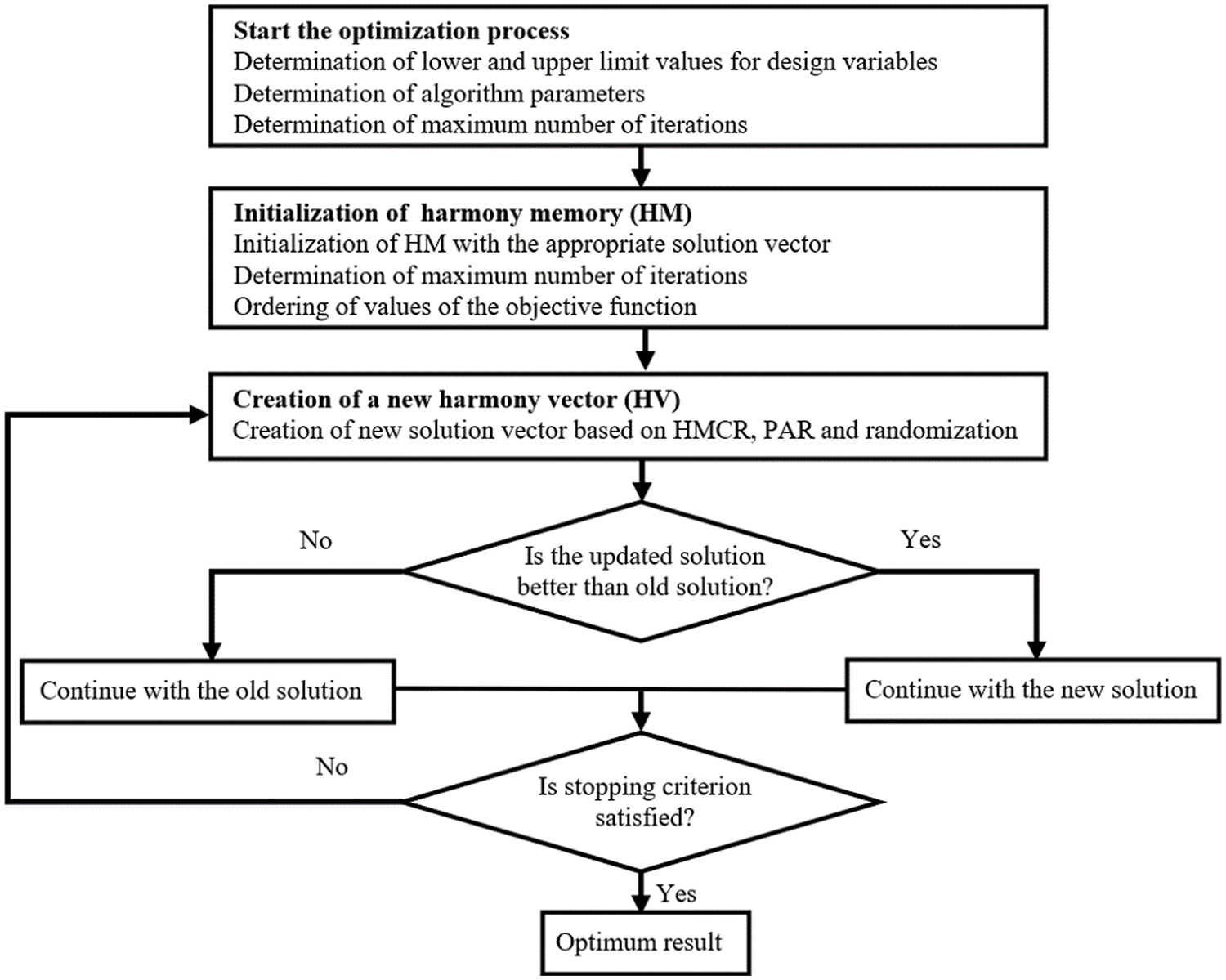
Figure 5: Flow chart of AHS

2.4 Equation of Motion for the TMDI System

This study proposes an approach for the seismic design of a 10-storey shear building equipped with the 10th floor with TMD, the 10th floor with TMDI, the 9th floor with TMDI, and the 5th floor with TMDI. The proposed approach aims to obtain optimum TMDI parameters based on minimizing the displacement response and acceleration response of the structure. The structure whose response will be examined consists of a 10-degree-of-freedom structure with mass, stiffness, and damping ratio ms, ks, and ξs, respectively. TMD with mass, stiffness, and damping ratio mtmd, ktmd, and ξtmd, respectively, and a TMDI with mass, stiffness, and damping ratio mtmdi, ktmdi, and ξtmdi.

The structure’s motion equation was shown in matrix using the mass, stiffness and damping properties obtained through TMDI and was modeled in MATLAB Simulink. Considering one degree for lateral movement of each floor, an n-storey building can be described with n degrees. By applying TMDI above, the system becomes a system with n + 1 degrees of freedom (Fig. 6).

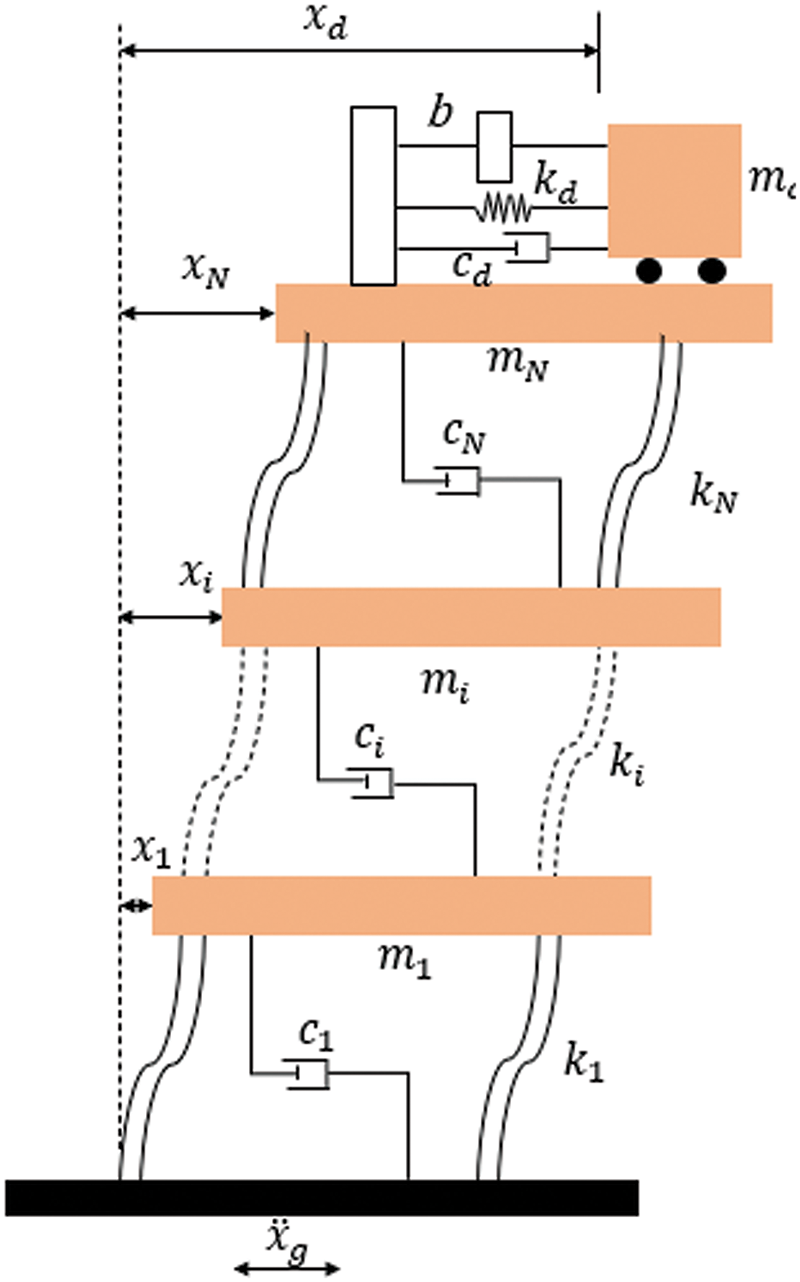
Figure 6: Shear-type frame structure equipped with TMDI [67]

The structure’s motion equation was formed in matrix form using the mass, stiffness, and damping properties obtained through TMDI and was modeled in MATLAB Simulink. Considering one degree for lateral movement of each floor, n-storey building can be described with n degrees. By applying TMDI above, the system becomes a system with n + 1 degrees of freedom, as seen in Fig. 6.

In buildings under the influence of earthquakes, TMDs are generally positioned on top floor since the first mode shape has the maximum amplitude at the top floor. The equations of motion of the N-storey shear building controlled by the TMDI system are expressed as in Eq. (15). The equation of motion can be expressed as a single matrix equation as shown in Eq. (15). In Eq. (15), the matrices of mass (M), stiffness (K) and damping (C) are combined with the corresponding derivative of their displacements relative to the ground for each floor and the displacement vector (x(t)) including TMDI (xtmdi). is multiplied. Earthquake forces coming to the floor; A unit vector [1] is used to define M and the ground acceleration resulting from earthquakes by multiplying it with the external excitation defined as X¨g. The dot operator (˙) on the vectors indicates the derivative with respect to time t. x(t) and -M [1] are the ground displacement and load vector, respectively. The parameters of the TMDI system are shown as mtmdi, ktmdi, and ctmdi, which are the mass, stiffness, and damping of the TMDI system, respectively. All matrices and vectors of Eq. (15) are shown in Eqs. (16)–(18):

Mx¨(t)+Cx˙(t)+Kx(t)=−M[1]X¨g(15)

M, C, and K in Eqs. (16)–(18) are mass, damping, and stiffness matrices, respectively.

M=[M10…0000M2…00⋮⋮⋮⋱⋮⋮⋮00…MN−1+b0−b00…0MN000…−b0Mtmdi+b](16)

K=[(K1+K2)−K2−K2(K2+K3)⋯⋮⋮⋮⋱⋮00⋯KN+Ktmdi−Ktmdi00⋯−KtmdiKtmdi](17)

C=[(C1+C2)−C2−C2(C2+C3)⋯⋮⋮⋱⋮⋮⋯CN+Ctmdi−Ctmdi−CtmdiCtmdi](18)

The matrices in Eqs. (16)–(18) are formularized as three diagonal stiffness matrices specific to shear frame structures. The components of the response vectors are shown in Eq. (19).

X=[X1X2⋮Xtmdi],X˙=[X˙1X˙2⋮X˙tmdi],X¨=[X¨1X¨2⋮X¨tmdi](19)

2.5 Optimization Problem

A ten-storey shear building was selected to investigate AHP to optimize TMDI parameters. The uniform mass of the building is 360 t, its stiffness is 650 MN/m, and the damping coefficient is 6.2 MNs/m on each floor. The objective function was chosen as the displacement of the top floor of the building to analyze the problem using AHP. The structural response was simulated using MATLAB Simulink under seismic excitation and solved using the optimization algorithm. In the TMDI optimization problem, the design variables are the mass (mtmdi), period (Ttmdi), damping (ctmdi), and inerter (b) of the TMDI system. Explicit constraints are defined as the mass, stiffness, and damping values of the TMDI system, and the design constraint is set as the maximum inter-storey drift of the TMDI (stroke capacity limit of the damping system). After the initial values and constraint limits of the problem were determined, the maximum floor displacement relative to the ground was calculated with MATLAB based on 44 different earthquake records, and the maximum ceiling displacement was defined as the objective function for minimization. Finally, optimum TMDI parameters for minimum upper displacement were obtained.

Optimization problem with TMDI has four design variables, as shown by Eq. (20). In the TMDI optimization problem, the design variables are the mass (mtmdi), period (Ttmdi), damping (ctmdi) and inerter (b) of the TMDI system. The calculation of the period (Ttmdi) and damping ratio (ξtmdi) of the TMDI system is given in Eqs. (21) and (22).

X={mtmdiTtmdiξtmdib}T(20)

Ttmdi=2πmtmdiktmdi(21)

ξtmdi=ctmdi2(mtmdi+b)mtmdiktmdi(22)

The natural angular frequency of the structure, the natural angular frequency of the TMDI system, and the stiffness calculation, which are among the equations required for the analysis and written in the codes, are calculated with Eqs. (23)–(25), respectively.

ws=km(23)

wtmdi=ktmdimtmdi(24)

ktmdi=mtmdi×wd,opt2(25)

The purpose of optimization in the method used is to minimizes the structure’s response. The answer is the displacement of the upper layer (xN) where the TMDI is placed. The objective function is calculated using the values of randomly generated design variables in each iteration and population. The first objective function for an N-storey building is formulated as Eq. (26).

f(x)=min(max|X|)(26)

The objective function is limited to a function (g1) that will limit the movement (displacement) of the TMDI. It is formulated as Eq. (27). In Eq. (27), xtmdi refers to the maximum displacement value of the floor where TMDI is located, and xN refers to the floor below it. Due to this constraint, the stroke capacity limitation value (stmax) determined by the user is not exceeded. In Eq. (27), xtmdi refers to the maximum displacement value of the floor where TMDI is located, and xN refers to the lower floor where the control system is not located.

g1=max(|xtmdi−xN|)TMDI′limax(|xN|)TMDI′siz<stmax(27)

stmax is a value that defined by the user for TMDI’s stroke capacity limitation. In Eq. (27), the only restriction for this problem is normalization based on the uncontrolled structure.

The primary purpose of this study is to propose the design of the optimum TMDI system for seismic vibration control of structures exposed to earthquakes. To achieve this goal, the optimum parameters of the TMDI system in terms of mass, stiffness, damping ratio, and inerter are determined by minimizing the maximum absolute value of the displacement of the top floor (Eq. (27)). Thus, with the control system, values that will minimize the response of the structure will be obtained.

2.6 Optimization with Adaptive Harmony Search Algorithm

As the first step in optimization, algorithm parameters, design constants, ranges of design variables, earthquake excitations, and limit values entered by the user are defined. In this optimization problem, the design constants are the mass, stiffness, and damping values of the structure. Simulation time and stroke capacity limitation (stmax) according to the time of earthquake excitations are values entered by the user. The design parameters of the algorithm are harmony memory size (HMS), Initial Harmony Memory Considering Rate (HMCR), initial pitch adjusting rate (PAR), population number (pn) and the best solution considering rate (BSCR).

In the optimum setting of TMDI, four different design parameters were considered, which will minimize the value of the objective function is the displacement of the upper floor. Optimization aims to find out the optimum mass, optimum period, optimum damping ratio, and optimum b inerter value of the TMDI system. These four features of the TMDI system were taken as design variables.

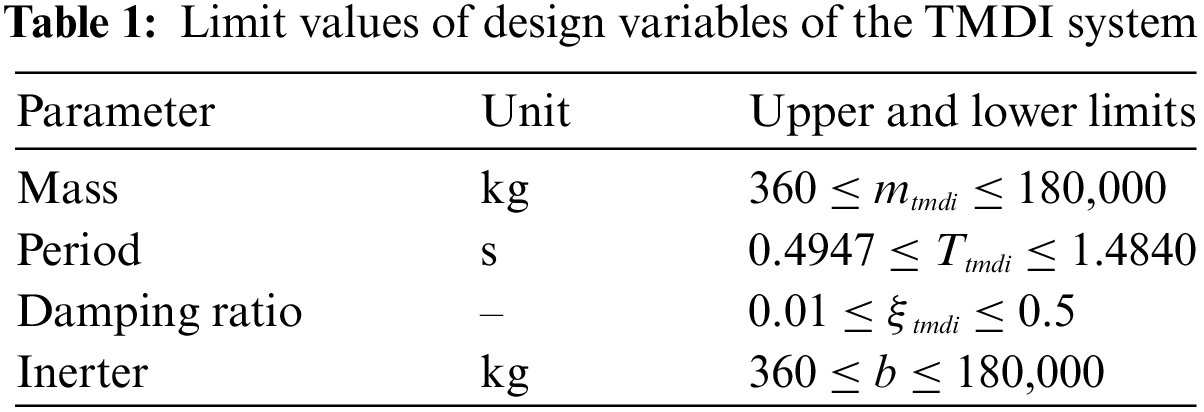
The range of the period of TMDI (Ttmdi), one of the design variables, is between 0.5 and 1.5 times that of the structure (Eqs. (28) and (29)). The period value of TMDI is spaced around the critical period of the structure.

Ttmdimin=0.5×Tn(28)

Ttmdimax=1.5×Tn(29)

In Eqs. (28) and (29), Ttmdi,min and Ttmdi,max are the lower and upper limits of the TMDI period.

Design constants are defined in a metaheuristic-based optimization process. In this method, the earthquake record data and the ranges of the design variables are fixed. Design variables are physical parameters of the TMDI system. The mass of the TMDI system is defined in proportion to the total mass of the building.

The inerter (b) of the TMDI system is between 1% and 5% of that of the structure (Eqs. (30) and (31)).

bmin=0.01×mn(30)

bmax=0.05×mn(31)

The lower and upper limits of the damping ratio of TMDI are given in Eqs. (32) and (33).

ξmin=0.01(32)

ξmax=0.5(33)

In Eqs. (32) and (33), ξmin and ξmax are the lower and upper limits of TMDI damping.

Table 1 represents the limit values of the design variables of the TMDI system.

2.7 Simulation of TMDI System with MATLAB Simulink

MATLAB/Simulink is useful for modeling systems with equations and combining them with other systems. Using MATLAB/Simulink, many systems can be simulated without writing code. Simulink can be accessed by using the Simulink shortcut button in MATLAB. Its extension is Simulink Models (.slx).

In the simulation study conducted with MATLAB/Simulink blocks, models of uncontrolled and controlled cutting buildings were proposed. The cycle of the motion equations (Eq. (34)) was modeled in Simulink using MATLAB/Simulink block diagrams. Since the structure’s response will be modeled, one of the responses is selected. In this study, acceleration response was selected, and Eq. (34) was modeled. The equations of acceleration include velocity and displacement. The 1st and 2nd integrals of acceleration are present in the equation. Acceleration value (Eq. (35)) was given as input to the control system created in MATLAB/Simulink environment, and displacement was obtained as output. Fig. 7 shows the simulation of the uncontrolled shear building model via Simulink. Fig. 8 shows the simulation of the TMDI-controlled shear building.

Mx¨(t)+Cx˙(t)+Kx(t)=−M[1]X¨g(34)

x¨(t)=−M[1]X¨g−Cx˙(t)−Kx(t)M(35)

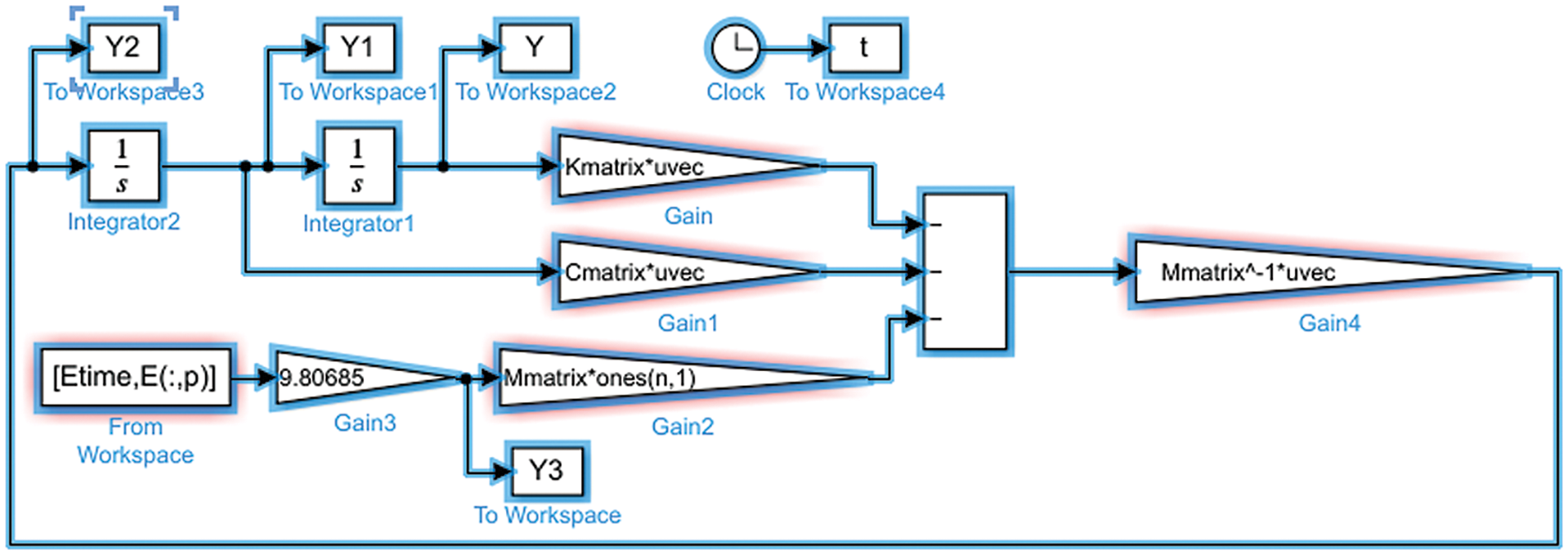
Figure 7: MATLAB/Simulink simulation of the uncontrolled shear building model

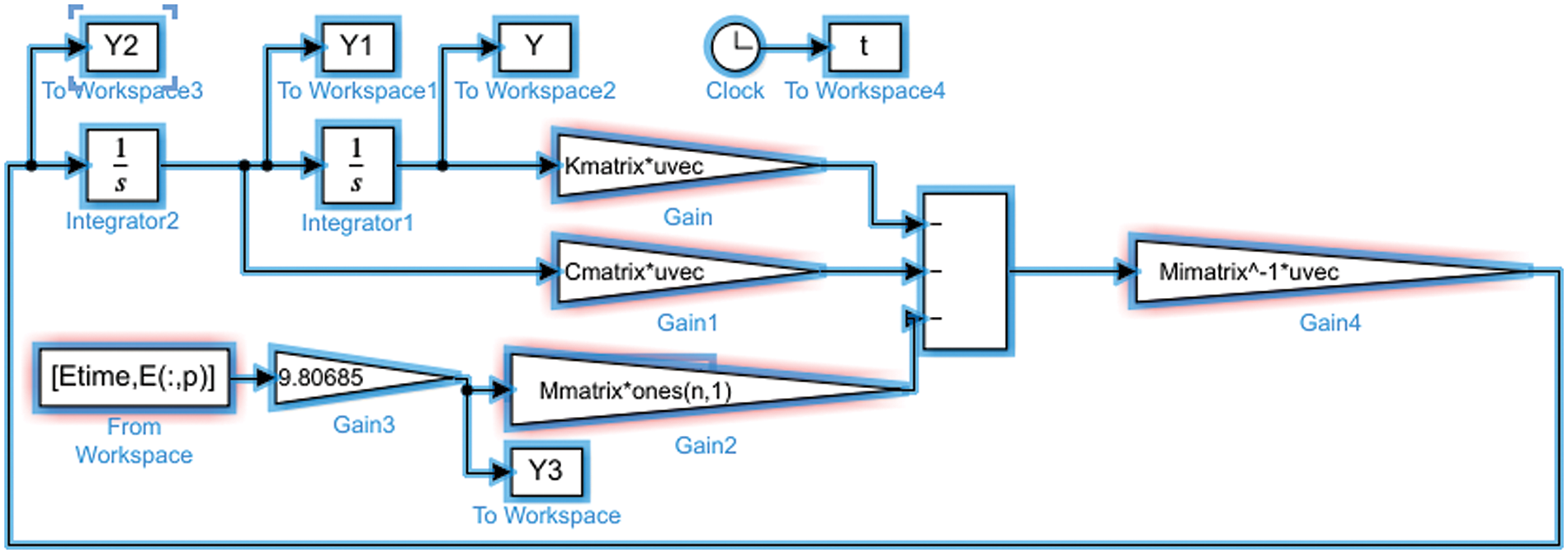
Figure 8: MATLAB/Simulink simulation of TMDI-controlled shear building

When TMDI is added, b is added to the equation. This situation is expressed with Mimatrix in Gain4 (Fig. 8).

3  Results

To examine the TMDI, 44 earthquake records previously recorded (FEMA) were used, and the structure was designed as 10 floors. In the study, analyses were conducted with different stroke capacity limitations and different mass ratio values for 4 different cases: the cutting building with TMD placed on the top floor, the cutting building with TMDI positioned on the top floor, the cutting building with TMDI positioned on the 9th floor, and the cutting building with TMDI positioned on the 5th floor. The shear building analyzed is shown in Fig. 9.

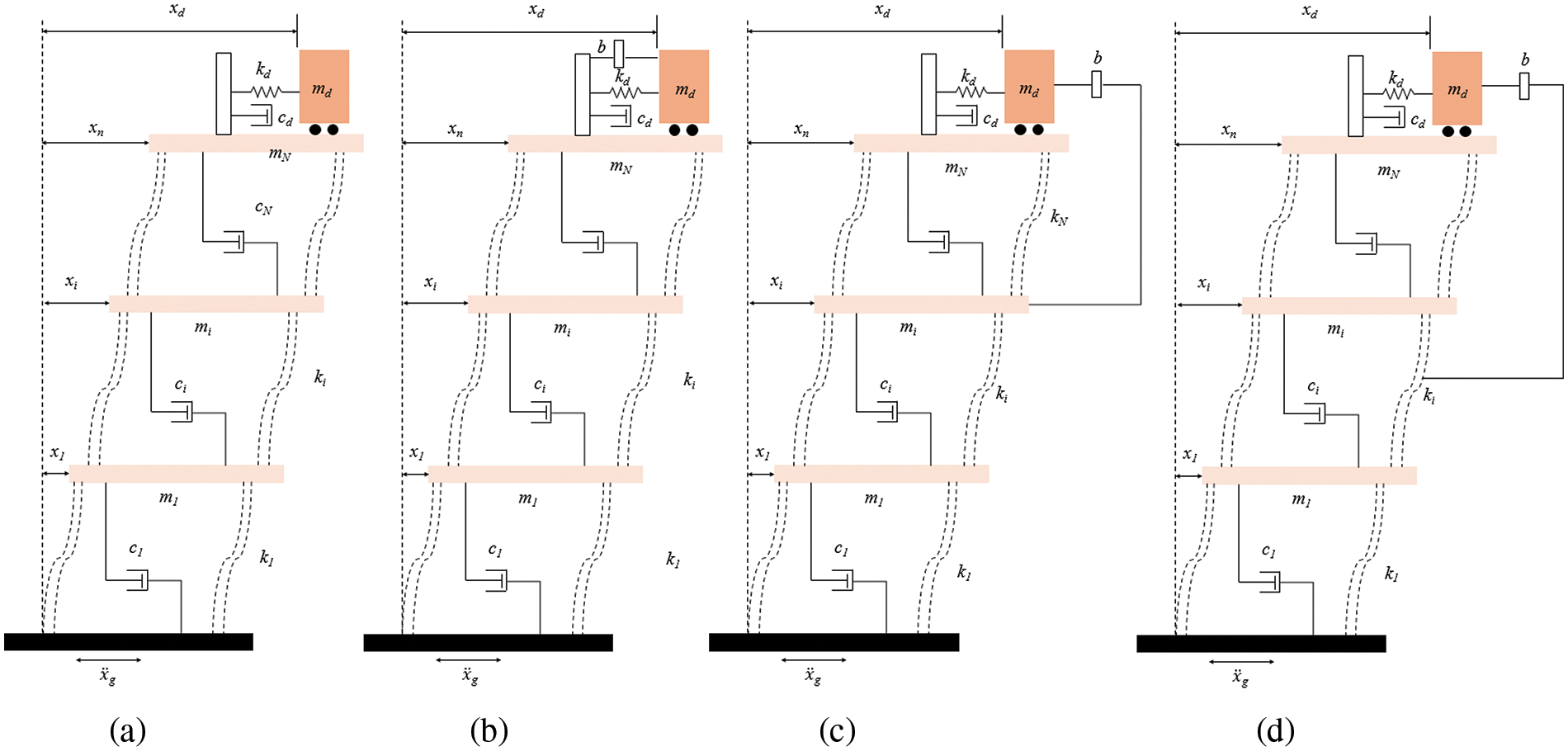
Figure 9: (a) Building with TMD positioned on the top floor (b) Building positioned as TMDI on the top floor (c) System where the inerter force is connected to the 9th floor (d) System where the inerter force is connected to the 5th floor

The features of the building are listed in Table 2.

Past earthquake records were used and tested while analyzing the time domain. The earthquake records used is listed in Table 3. To examine the TMDI performance, firstly, in a 10-storey building, the maximum displacements under the earthquake records were given as a warning to the system, the maximum acceleration values occurring in the system were obtained, and AHP was used. The AHS algorithm was analyzed on an IntelI CoreI I7-5005U CPU @ 2.00 GHz (4 Cores) PC. MATLAB program was used for the results, which were obtained based on the time domain. The number of iterations used in the analysis is 5000. The description and numerical values of the parameters of the AHS algorithm are listed in Table 4. Using BSCR 30% prevented getting stuck in the local optimum solution.

3.1 Optimum Results Achieved with AHS Algorithm Optimization

Optimum TMDI parameters with the Adaptive Harmony Search (AHS) algorithm created by changing the HMCR and PAR parameters depending on the iterations given in Eqs. (8) and (9), were obtained and compared with the parameters and response values obtained by TMD. The optimization process was conducted for different stmax values of 0.5, 1, 1.5, and 2 and for different mass ratio values of 0.01, 0.02, and 0.05.

Case 1, where the TMD system is connected to the top floor of the building (10th floor), Case 2, where the TMDI system is connected to the top floor of the building (10th floor), Case 3, where the TMDI system is connected to the lower floor of the top floor of the building (9th floor), Case 4 refers to the situation where the TMDI system is connected to the 5th floor of the building.

Table 5 shows the optimum TMD and TMDI system results at different locations for stmax = 0.5% and 1% mass ratio.

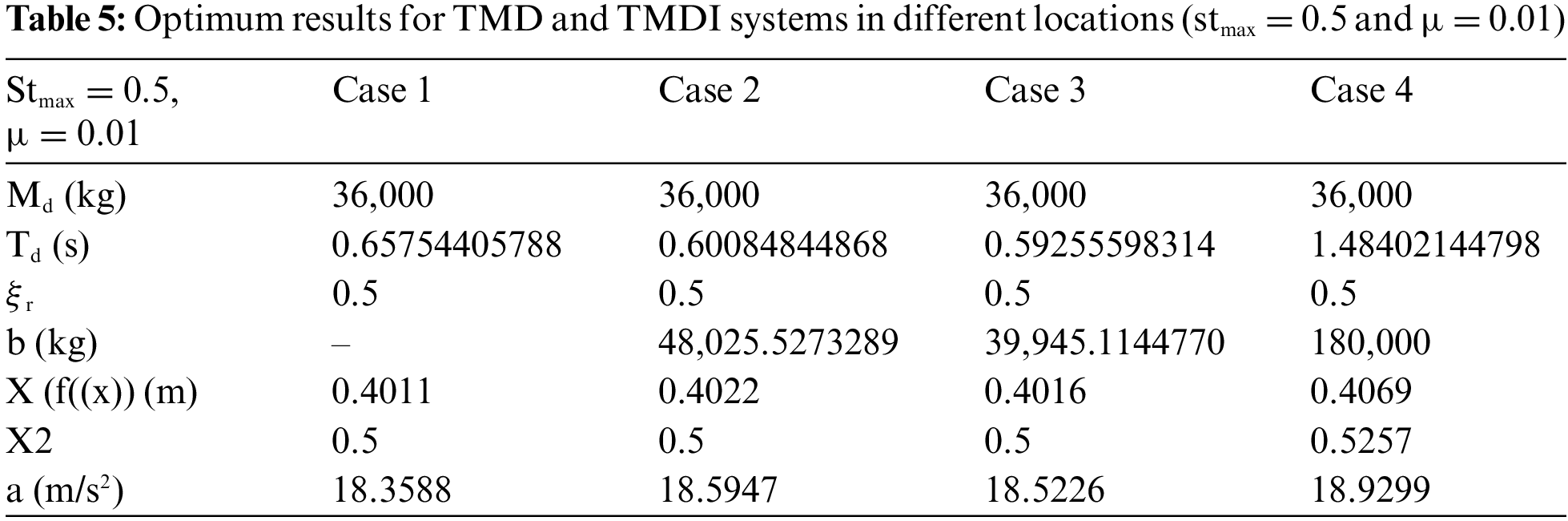
Table 5 indicates that for the case where the stroke capacity limitation is 0.5 (stmax = 0.5) and the maximum system mass is 1% of the system’s mass (µ = 0.01), TMD, TMDI 10th floor, TMDI 9th floor, and TMDI 5. The optimum mass of the system for the first floor is equal to the upper limit value defined for the mass (1% of the building mass). The optimum period values for four different situations are close to each other, but a higher period value is reached in the case of TMDI on the 5th floor. The damping ratio also equals the upper limit value defined for the damping ratio in four cases. The X2 is the ratio of the TMD or TMDI displacement to its maximum uncontrolled displacement. When the TMDI is compared for the b value, if there is an inerter on the lower or upper floor, it is seen from Table 5 that a lower b value is obtained by positioning the TMDI on the 9th floor. X2 in Table 5 is the ratio of TMD or TMDI displacement to its maximum uncontrolled displacement. The value of X2 is the same for the first three cases and is higher in the fourth case.

Table 6 shows the optimum TMD and TMDI system results at different locations for stmax = 0.5% and 2% mass ratio.

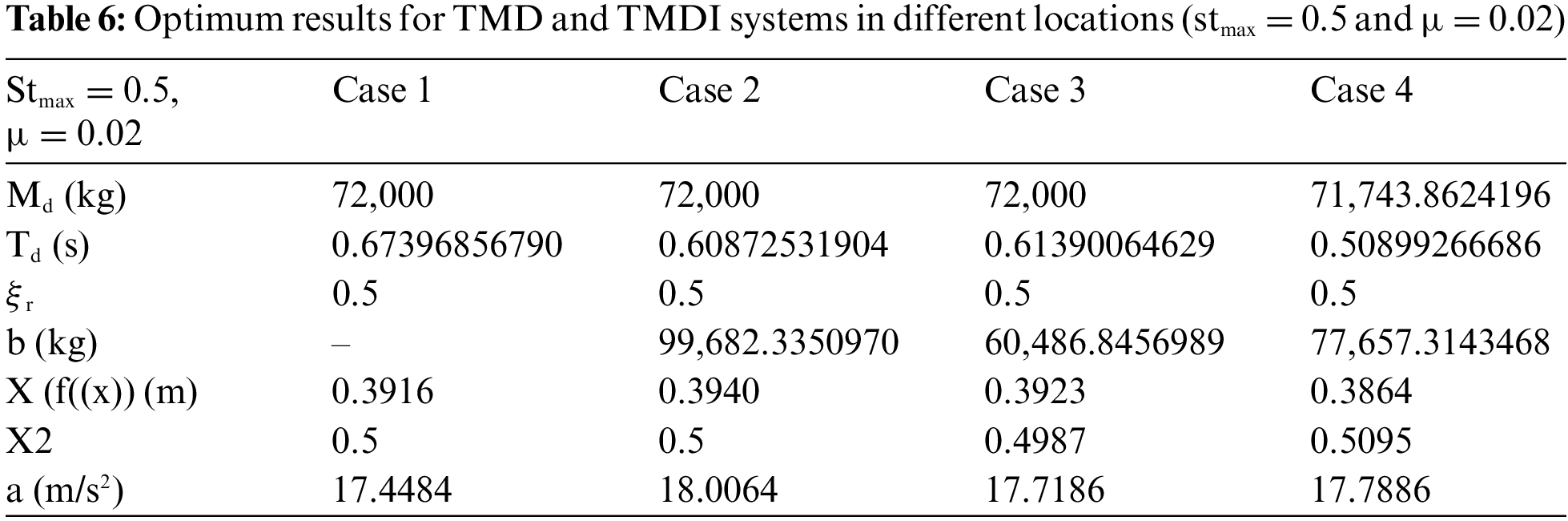
Table 6 indicates that for the case where the stroke capacity limitation is 0.5 (stmax = 0.5) and the maximum system mass is 2% of the mass of the system (µ = 0.02), the system is optimum for TMD, TMDI 10th floor and TMDI 9th floor. The mass equals the upper limit value defined for the mass (2% of the building mass). In the case where the TMDI system is located on the 5th floor, it is very close to 2% of the system’s mass. The optimum period values for four different situations are close to each other. The damping ratio also equals the upper limit value defined for the damping ratio in four cases.

When the TMDI is compared for the b value, if there is an inerter on the lower or upper floor, Table 6 reveals that a lower b value is obtained by positioning the TMDI on the 9th floor, and the X2 value is very close to each other for four different situations.

Table 7 shows the optimum TMD and TMDI system results at different locations for stmax = 0.5% and 5% mass ratio.

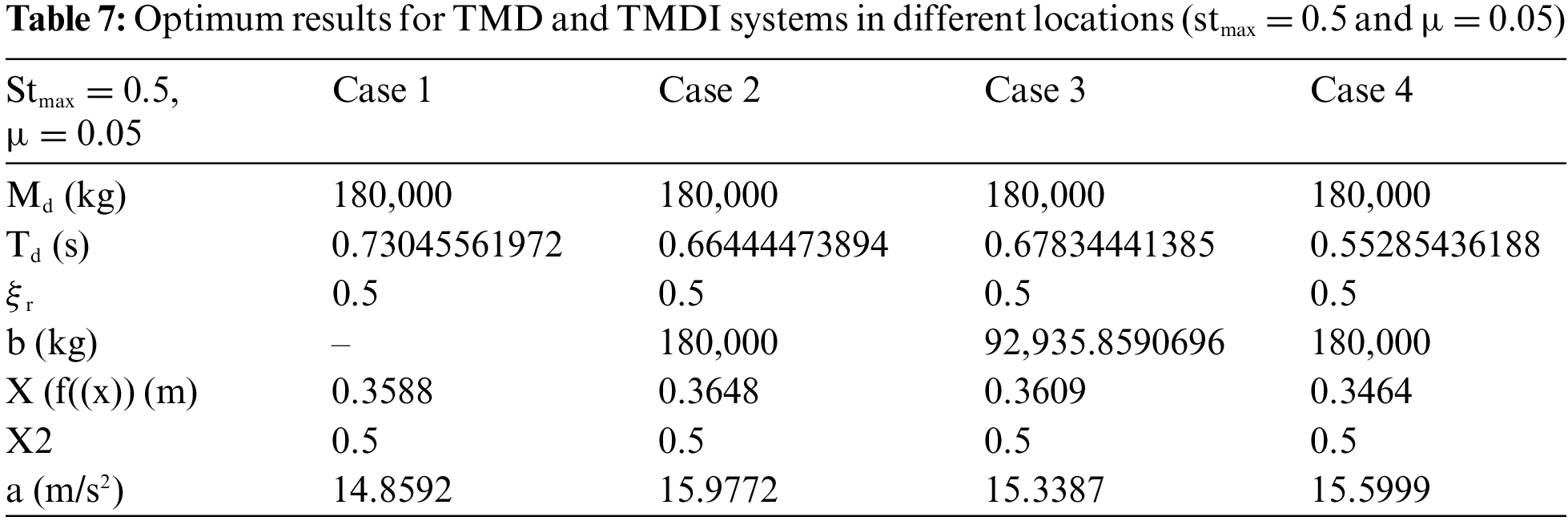
Table 7 demonstrates that for the case where the stroke capacity limitation is 0.5 (stmax = 0.5) and the maximum system mass is 5% of the system’s mass (µ = 0.05), TMD, TMDI 10th floor, TMDI 9th floor, and TMDI 5. The optimum mass of the system for the first floor is equal to the upper limit value defined for the mass (5% of the building mass). The optimum period values for four different situations are close to each other. The damping ratio also equals the upper limit value defined for the damping ratio in four cases.

When the TMDI is compared for the b value, if there is an inerter on the lower or upper floor, Table 7 shows that a lower b value is obtained by positioning the TMDI on the 9th floor, and X2 values are equal for four cases.

Table 8 shows the optimum TMD and TMDI system results at different locations for stmax = 1% and 5% mass ratio.

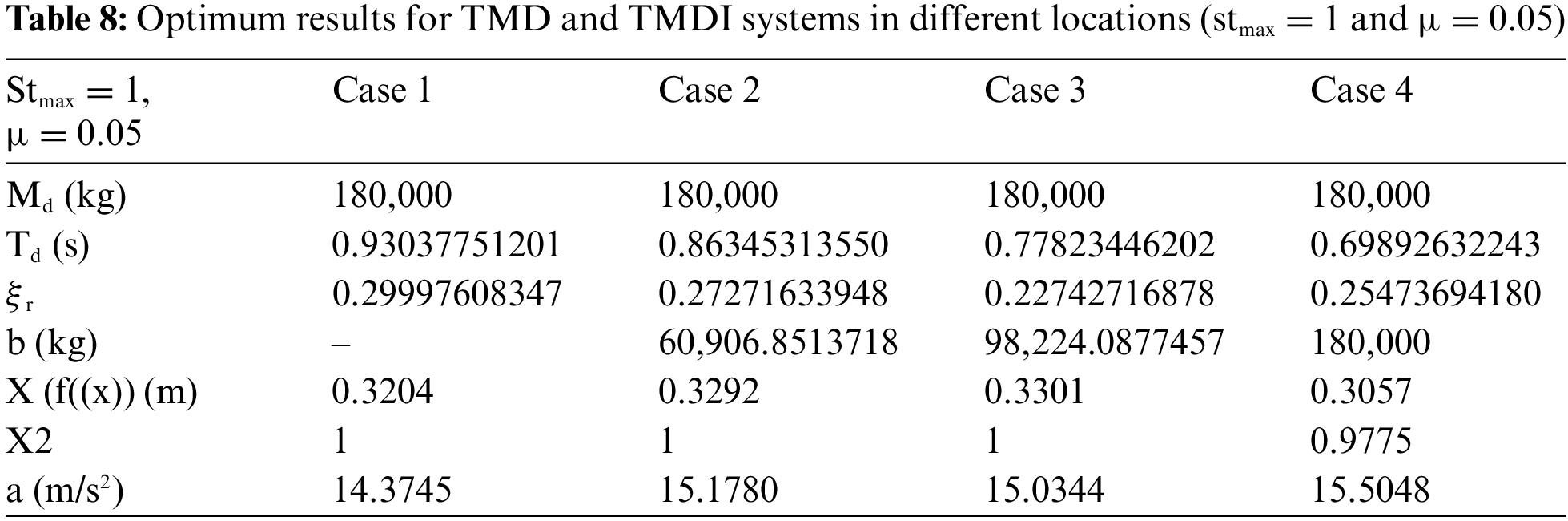
Table 8 illustrates that for the case where the stroke capacity limitation is 1 (stmax = 1) and the maximum system mass is 5% of the mass of the system (µ = 0.05), TMD, TMDI 10th floor, TMDI 9th floor, and the optimum mass of the TMDI system for the 5th floor is equal to the upper limit value defined for the mass (5% of the building mass). The optimum period values for four different situations are close to each other. The lowest damping ratio value was achieved by connecting TMDI to the lower floor.

When the TMDI is compared for the b value, if there is an inerter on the lower or upper floor, Table 8 reveals that a lower b value is obtained by positioning the TMDI on the 10th floor, and X2 values are equal for the first case, but less in the fourth case.

Table 9 shows the optimum TMD and TMDI system results at different locations for stmax = 1.5% and 5% mass ratio.

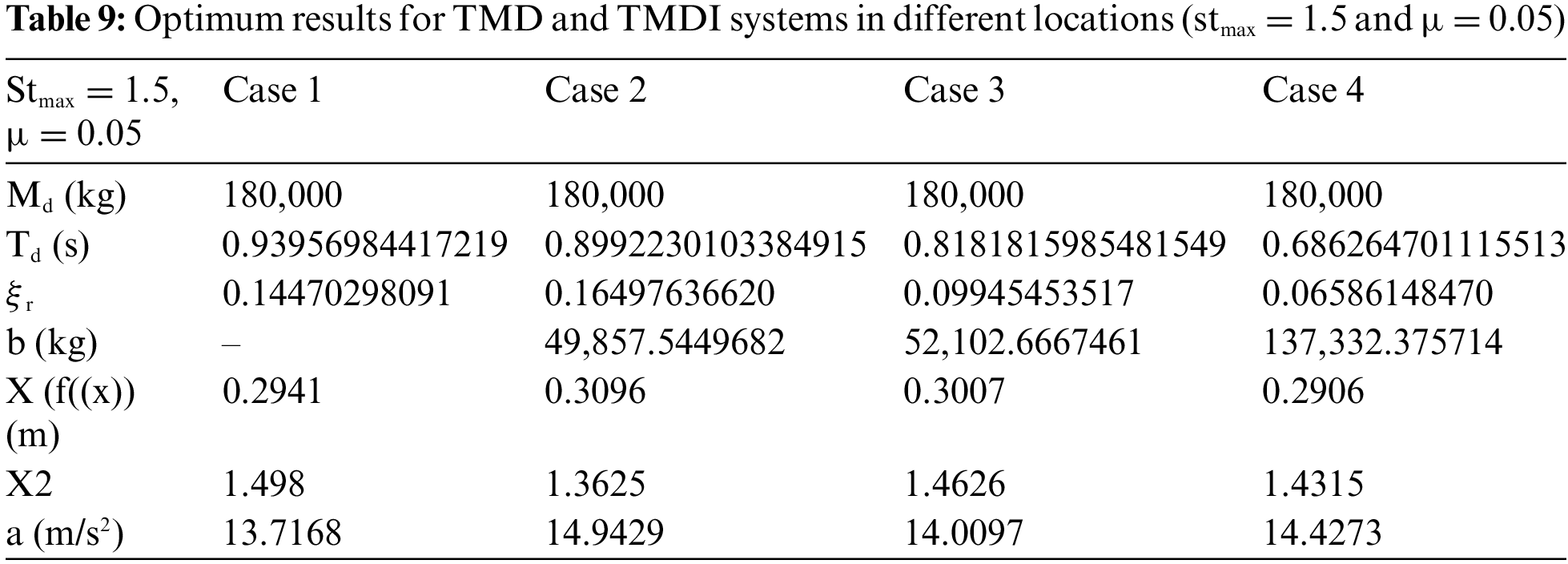
Table 9 indicates that for the case where the stroke capacity limitation is 1.5 (stmax = 1.5) and the maximum system mass is 5% of the mass of the system (µ = 0.05), TMD, TMDI 10th floor, TMDI 9th floor, and TMDI 5 It is seen that the optimum mass of the system for the first floor is equal to the upper limit value defined for the mass (5% of the building mass). The optimum period values for four different situations are close to each other. The lowest damping ratio value was achieved by connecting TMDI to the 5th floor.

When the TMDI is compared for the b value, if there is an inerter on the lower or upper floor, Table 9 shows that a lower b value is obtained by positioning the TMDI on the 10th floor and X2 values are close to each other for four cases.

Table 10 shows the optimum TMD and TMDI system results for stmax = 2% and 5% mass ratio at different locations.

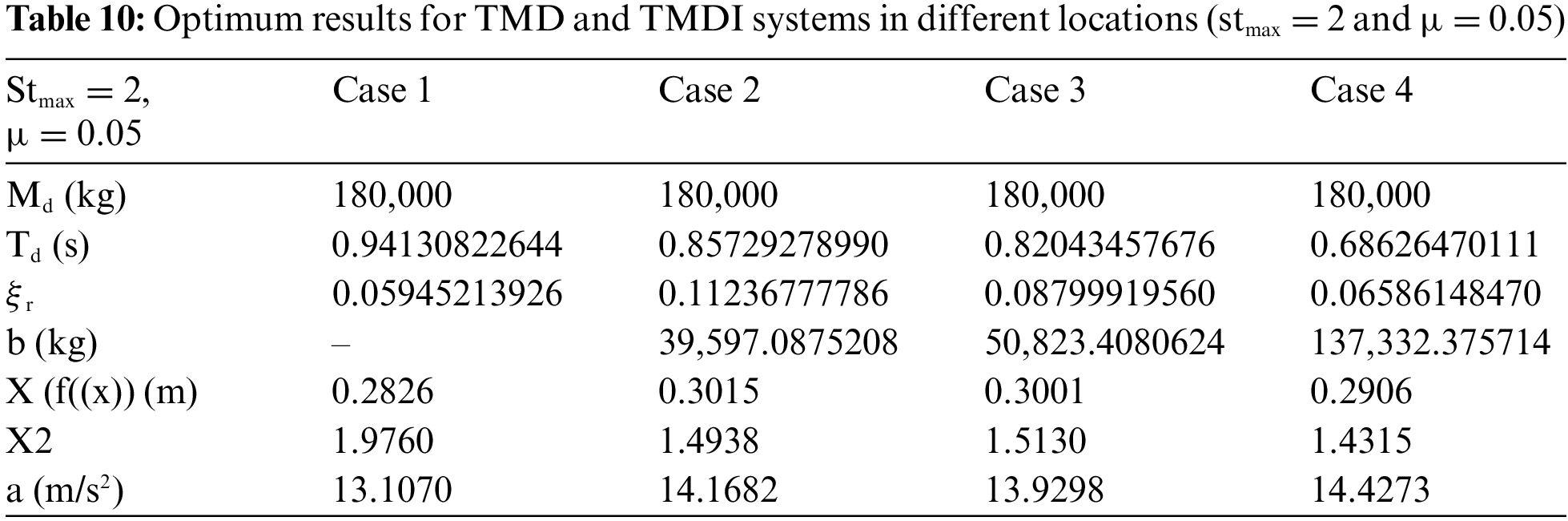
Table 10 demonstrates that for the case where the stroke capacity limitation is 2 (stmax = 2) and the maximum system mass is 5% of the mass of the system (µ = 0.05), TMD, TMDI 10th floor, TMDI 9th floor, and the optimum mass of the TMDI system for the 5th floor is equal to the upper limit value defined for the mass (5% of the building mass). The optimum period values for four different situations are close to each other. The lowest damping was achieved by positioning the TMD on the 10th floor.

When the TMDI is compared for the b value, if there is an inerter on the lower or upper floor, Table 10 shows that a lower b value is obtained by positioning the TMDI on the 10th floor, and the lowest X2 value is reached by connecting TMDI to the 5th floor.

Uncontrolled situation and four different cases (Case 1-TMD system is connected to the top floor of the building (10th floor), Case 2-TMDI system is connected to the top floor of the building (10th floor), Case 3-TMDI system is connected to the bottom floor of the building. Displacement graphs of the 6th earthquake record for different stmax and mass ratio (µ) values for the cases where the building is connected to the 9th floor (9th floor), Case 4-TMDI system is connected to the 5th floor of the building) are in Fig. 10, total acceleration graphs are shown in Fig. 11.

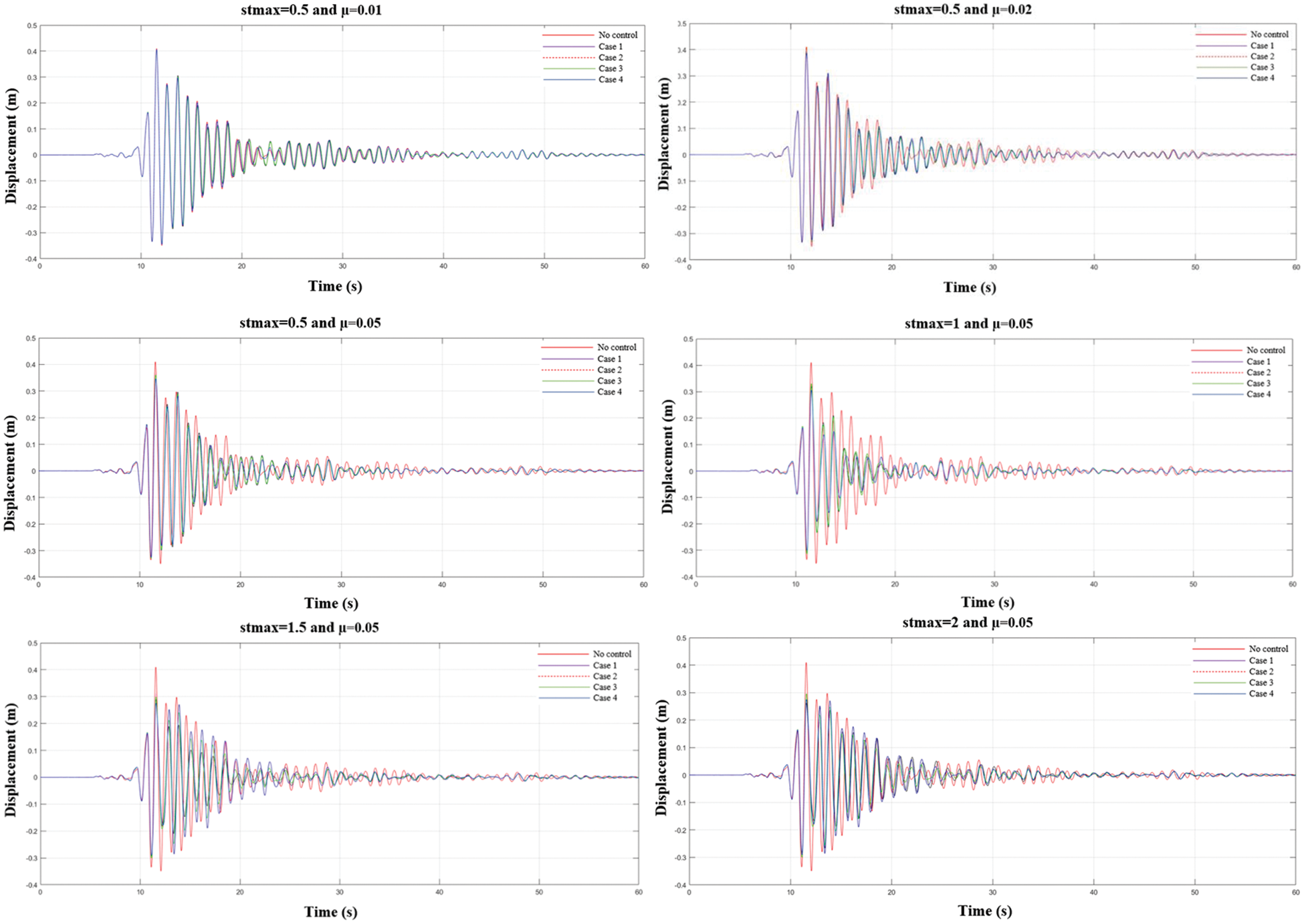
Figure 10: Displacement graphs of the 6th earthquake record for different stmax and mass ratio (µ) values for the cases

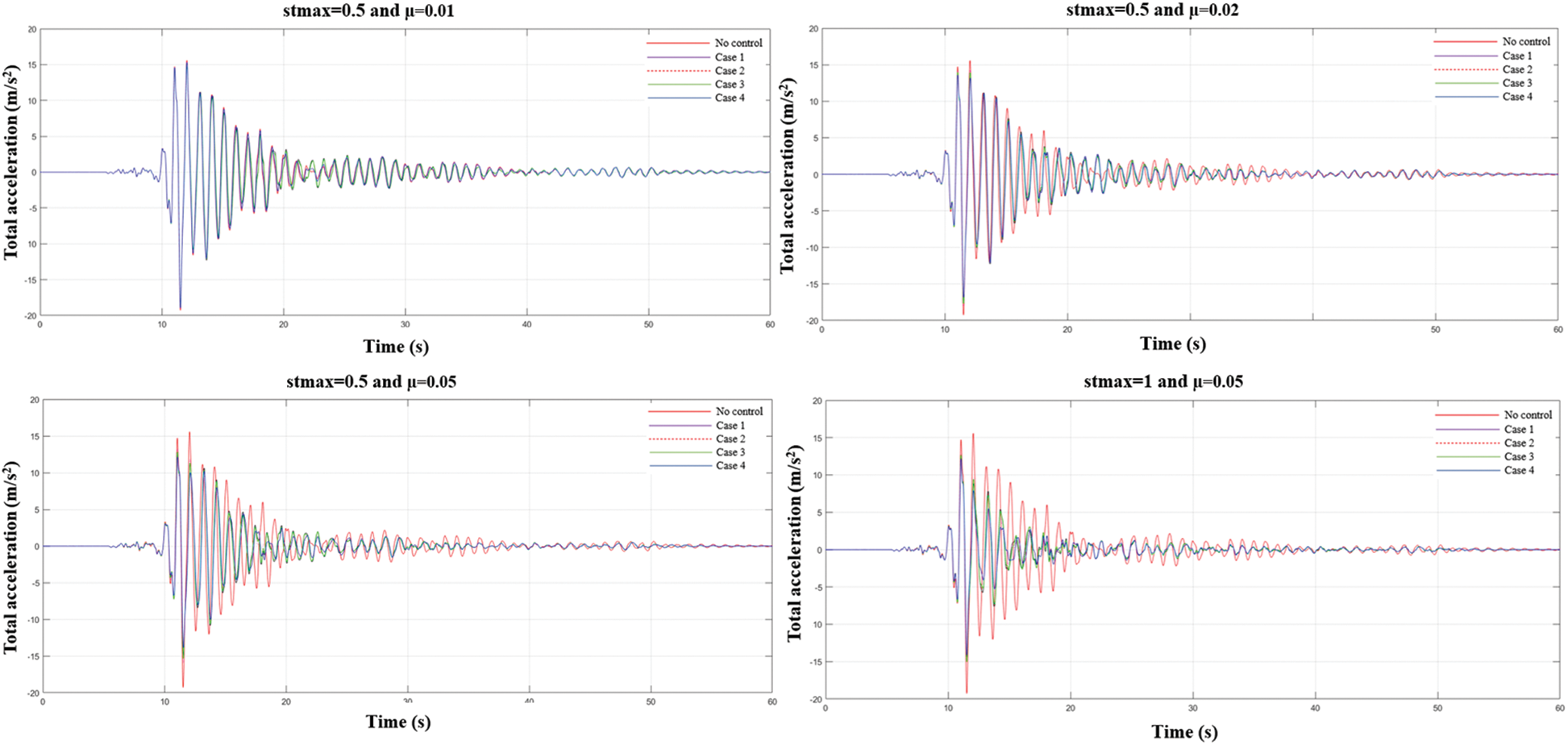
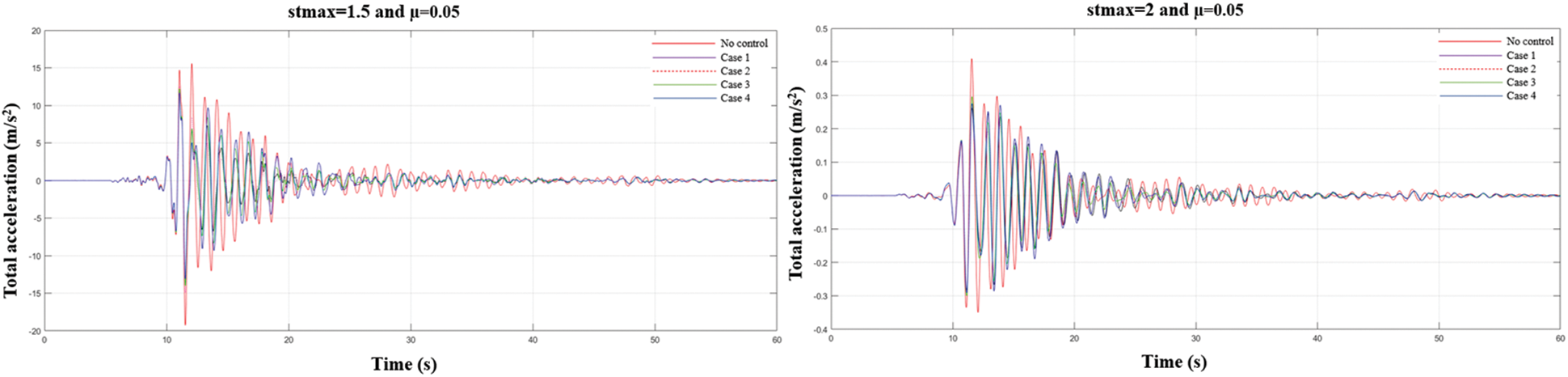
Figure 11: Total acceleration graphs of the 6th earthquake record for different stmax and mass ratio (µ) values for the cases

4  Discussion

The optimization of TMDI under earthquake loads was conducted in this study using earthquake records. The data obtained from the optimum design of the TMDI with metaheuristic algorithms were analyzed and compared, and the values that will minimize the TMDI’s response to the structure’s earthquake load were obtained. Table 11 is created by combining the displacement and acceleration values.

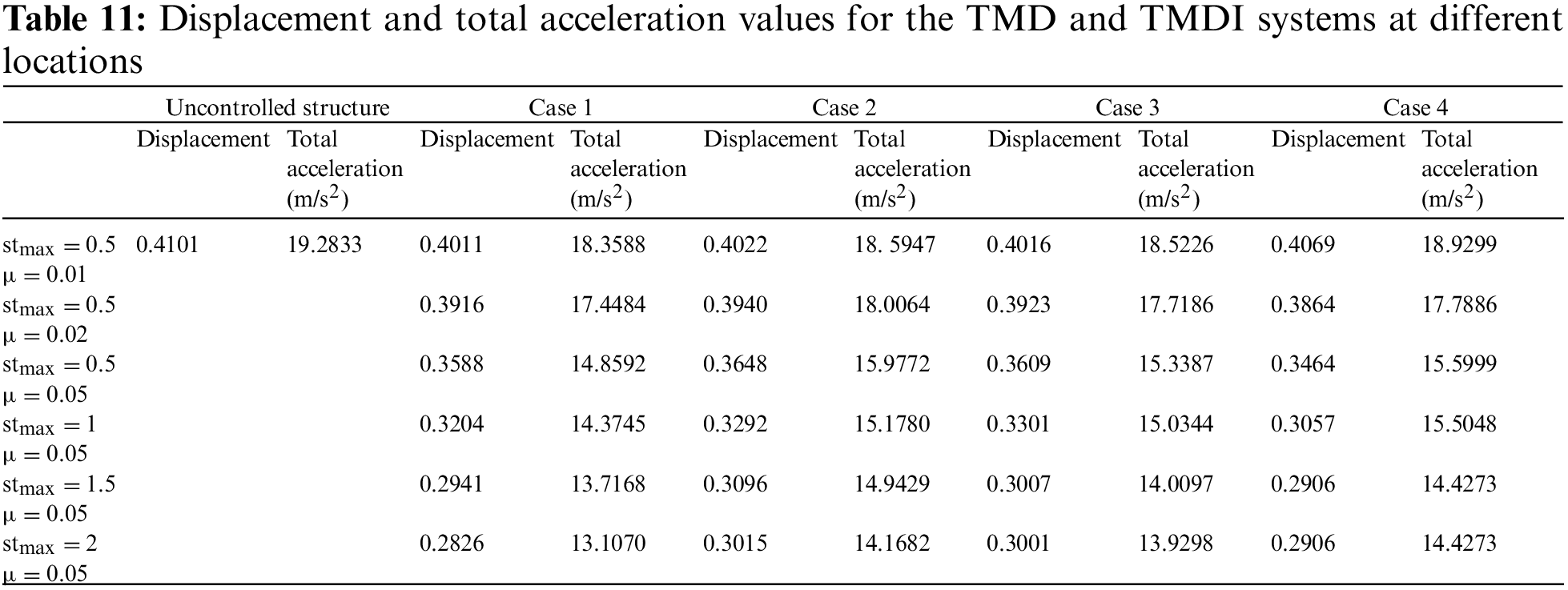
Table 11 reveals that the displacement value, which is 0.4101 m in the uncontrolled system, is 0.4011 m for stmax = 0.5 and µ = 0.01, 0.3916 m for stmax = 0.5 and µ = 0.02, 0.3588 m for stmax = 0.5 and µ = 0.05, 0.3204 m for stmax = 1 and µ = 0.05, 0.2941 m for stmax = 1.5 and µ = 0.05, and 0.2826 m for stmax = 2 and µ = 0.05. The system appears to perform effectively.

The least displacement and total acceleration reduction are when the TMDI system is connected to the upper floor (Case 2), the stmax value is 0.5, and the mass ratio is 1%. At these stmax and mass ratio values where the displacement and total acceleration values are reduced the least, the displacement reduction for Case 1 is 2.19%, the displacement reduction is 1.92% for Case 2, the displacement reduction is 2.07% for Case 3, the displacement reduction is 0.78% for Case 4. The total acceleration reduction for Case 1 is 4.79%, the total acceleration reduction for Case 2 is 3.57%, the total acceleration reduction for Case 3 is 3.94%, and the total acceleration reduction for Case 4 is 1.83%.

The maximum displacement and total acceleration reduction is in the TMD system (Case 1) when the stmax value is 2, and the mass ratio is 5%. At these stmax and mass ratio values, where the displacement and total acceleration values are reduced the most, the displacement reduction is 31.08% for Case 1, and the displacement reduction is 26.48% for Case 2, the displacement reduction is 26.82% for Case 3, the displacement reduction is 29.13% for Case 4. The total acceleration reduction for Case 1 is 32.02%, the total acceleration reduction for Case 2 is 26.52%, the total acceleration reduction for Case 3 is 27.76%, and the total acceleration reduction for Case 4 is 25.18%.

Upon investigating the change in mass ratio, displacement values of 0.4016 m for stmax = 0.5 and µ = 0.01, 0.3923 m for stmax = 0.5 and µ = 0.02, and 0.3609 m for µ = 0.05 were obtained. Acceleration values of 18.5226 m/s2 for stmax = 0.5 and µ = 0.01, 17.7186 m/s2 for stmax = 0.5 and µ = 0.02, and 15.3387 m/s2 for stmax = 0.5 and µ = 0.05 were obtained. For Case 4, different mass ratios were examined in the TMDI system at the same stmax value (stmax = 0.5). Displacement values of 0.4069 m for stmax = 0.5 and µ = 0.01, 0.3864 m for stmax = 0.5 and µ = 0.02, and 0.3464 m for µ = 0.05 were obtained. These results showed that increasing the mass ratio reduces displacement and total acceleration. Bekdaş et al. [68] indicated that in the problem they solved in their study, it is possible to reduce the objective function value by 20.5% and 63.8%, respectively, using a mass ratio between 1% and 40%.

In displacement reduction, the best performance is shown by Case 4, where the TMDI system is positioned on the 5th floor, except for stmax = –µ = 0.01 and stmax = 2–µ = 0.05. For example, in the case of the structure tested for stmax = 1 and µ = 0.05, it is possible to minimize the maximum upper floor displacement by 25.45% with the TMDI system, while TMD is effective by 21.87%. TMD and TMDI connected to the 5th floor reduce the total acceleration by 25.45% and 19.59%, respectively.

After examining the parameters, the optimum TMDI mass equals the upper limit values defined in the program (36,000 kg for µ = 0.01, 72,000 kg for µ = 0.02, 180,000 kg for µ = 0.05). The optimum TMDI period value indicated that as the stmax value increases, the period value also increases, depending on the stmax and mass ratio (µ). For example, the optimum TMDI period for the inerter connected to the 10th floor (Case 2) is 0.6644 s for stmax = 0.5 and µ = 0.05, and 0.8572 s for stmax = 2 and µ = 0.05. In contrast to the period, the optimum TMDI damping ratio decreases inversely as stmax increases. For example, the optimum TMDI damping ratio for the inerter connected to the 10th floor (Case 2) is 0.5000 s for stmax = 0.5 and µ = 0.05 and is 0.1123 for stmax = 2 and µ = 0.05. After examining the optimum inerter (b) value, the b value decreases as stmax increases. For example, for the inerter connected to the 10th floor (Case 2), the optimum inerter value is 180,000 kg for stmax = 0.5 and µ = 0.05 and is 39,597.0875 kg for stmax = 2 and µ = 0.05. The damping ratio and inerter values are inversely proportional to the stroke capacity limitation (stmax). As stmax increases, movement becomes easier as the arm can extend further. In cases where the stmax limit value is exceeded, optimization is optimized to the smallest physically possible collapse value.

5  Conclusions

Mass damping devices are frequently used in high-rise buildings in earthquake zones and effectively protect structures from dynamic stimuli. The emergence of the TMDI system was influenced by issues such as the need for a large mass to be effective against earthquakes. The inerter can create a virtual mass larger than the real mass of the device and thus meet the real mass requirement. The TMDI system is obtained by combining the TMD with an inerter device that acts as a mass amplifier to minimize the TMD mass in seismically excited systems.

TMD and TMDI systems exhibit similar control performance in analyses using far-fault records. When TMDI is examined, more effective control performance is obtained when the inerter is connected to the lower floors than when the inerter is connected to the upper floors. Since TMD and TMDI, which are examined in three different cases, show similar performances, they can suit different building types and earthquake records. The TMDI system is effective in reducing displacements under critical stimulation. Both systems have positive and negative aspects. Therefore, it can be decided which system to use by examining the structural situation.

However, there is no significant difference in terms of displacement reduction between connecting the TMDI system to the 10th floor (Case 2), 9th floor (Case 3), and 5th floor (Case 4) and connecting the TMD system to the 10th floor. In displacement reduction, the best performance is shown by Case 4, where the TMDI system is positioned on the 5th floor, except for stmax = 0.5 and µ = 0.01, and stmax = 2 and µ = 0.05. TMD and TMDI systems are equally effective in reducing displacement. TMD and TMDI perform very closely to each other.

When the TMDI system is compared within itself in terms of displacement reduction according to the floor to which the inerter is connected, the case of connecting the inerter force to the 5th floor (Case 4) gives better results. Also, normalized TMDI displacement (X2) is generally less in Case 4.

As a result of this study, the control efficiency of TMD and TMDI systems is very sensitive to the mass ratio. To increase the control efficiency of these control systems, a large mass ratio (2%–5%) is generally required. It is also concluded that TMD and TMDI systems reduce the displacement by 21.87% and 25.45%, respectively. Reducing the displacement indicates that damage due to earthquakes will be minimized. Therefore, using control systems such as TMDI will have a protective effect on the structure. The performance of the control systems increases as the arm extension limit value (stmax) increases with the same mass ratio. The inerter is a mechanical element that can increase mass by converting linear motion into rotation, opening up new possibilities for reducing the mass fraction of the TMD. In the future, lighter control systems can be achieved by optimally modifying the properties of the inerter used in the TMDI system. In future studies, newly developed optimization techniques can be employed to ensure the structure’s safety against dynamic effects, and a comparative analysis can be made using the findings of this study. The performance of TMDI can be analyzed by changing the number of stories in the building. Further improvements in the design and performance of TMDI can be achieved using new methods emerging with technological development.

As a limitation of the system, the connection location of the inerter device plays a vital role in the design. While the placement of the device is optimal for upper stories, the connection of the inerter is best suited for lower stories or the ground. This complicates the control system application, and a specified design must be provided according to the architecture and design of the structure.

Acknowledgement: The authors are highly supported by all reviewers and journal editors with their valuable comments which are very useful in improving our study.

Funding Statement: This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy, Republic of Korea (RS-2024-00441420; RS-2024-00442817).

Author Contributions: The background and theory of the problem were developed by Gebrail Bekdaş, Yaren Aydın and Sinan Melih Nigdeli. The text was written by Yaren Aydın, Gebrail Bekdaş and Sinan Melih Nigdeli. The analysis codes were generated by Yaren Aydın, Gebrail Bekdaş and Sinan Melih Nigdeli, Yaren Aydın, Gebrail Bekdaş and Sinan Melih Nigdeli verified the results. The figures were drawn by Yaren Aydın. Research direction was supervised by Zong Woo Geem. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data can be delivered upon reasonable request by mailing to the corresponding authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Den Hartog JPXL. The lowest natural frequency of circular arcs. The London, Edinburgh, and Dublin Phi Magaz J Sci. 1928;5(28):400–8. doi:10.1080/14786440208564480. [Google Scholar] [CrossRef]

2. Kim SB, Yun CB. Sliding mode fuzzy control: theory and verification on a benchmark structure. Earthq Eng & Struct Dynam. 2000;29(11):1587–608. doi:10.1002/1096-9845(200011)29:. [Google Scholar] [CrossRef]

3. Yi F, Dyke SJ. Structural control systems: performance assessment. In: Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No. 00CH36334), 2000, June; Chicago, IL, USA: IEEE. vol. 1, p. 14–8. [Google Scholar]

4. Symans MD, Constantinou MC. Semi-active control systems for seismic protection of structures: a state-of-the-art review. Eng Struct. 1999;21(6):469–87. doi:10.1016/S0141-0296(97)00225-3. [Google Scholar] [CrossRef]

5. Yu W, Thenozhi S. Active structural control with stable fuzzy PID techniques. New York City, NY, USA: Springer International Publishing; 2016. doi:10.1007/978-3-319-28025-7. [Google Scholar] [CrossRef]

6. Frahm H. Improved means for damping the vibrations of bodies; 1909. Patent No. GB190923828. Available from: https://patents.google.com/patent/US989958A/en. [Accessed 2024]. [Google Scholar]

7. Den Hartog JP. The amplitudes of non-harmonic vibrations. J Franklin Inst. 1933;216(4):459–73. doi:10.1016/S0016-0032(33)90915-1. [Google Scholar] [CrossRef]

8. Marian L, Giaralis A. Optimal design of inerter devices combined with TMDs for vibration control of buildings exposed to stochastic seismic excitation. In: Safety, reliability, risk and life-cycle performance of structures and infrastructures. London, UK: CRC Press; 2013. p. 1025–32. [Google Scholar]

9. Marian L, Giaralis A. Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probab Eng Mech. 2014;38(6):156–64. doi:10.1016/j.probengmech.2014.03.007. [Google Scholar] [CrossRef]

10. Giaralis A, Petrini F. Wind-induced vibration mitigation in tall buildings using the tuned mass-damper-inerter. J Struct Eng. 2017;143(9):4017127. doi:10.1061/(ASCE)ST.1943-541X.0001863. [Google Scholar] [CrossRef]

11. Siami A, Cigada A, Karimi HR, Zappa E, Sabbioni E. Using inerter-based isolator for passive vibration control of Michelangelo’s Rondanini Pietà. IFAC-PapersOnLine. 2017;50(1):13372–7. doi:10.1016/j.ifacol.2017.08.2259. [Google Scholar] [CrossRef]

12. Giaralis A, Marian L. Use of inerter devices for weight reduction of tuned mass-dampers for seismic protection of multi-story building: the Tuned Mass-Damper-Interter (TMDI). Active and Passive Smart Struct Integ Syst. 2016;9799:415–24. doi:10.1117/12.2219324. [Google Scholar] [CrossRef]

13. Pietrosanti D, De Angelis M, Basili M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthq Eng & Struct Dynam. 2017;46(8):1367–88. doi:10.1002/eqe.2861. [Google Scholar] [CrossRef]

14. De Domenico D, Ricciardi G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq Eng & Struct Dynam. 2018;47(5):1169–92. doi:10.1002/eqe.3011. [Google Scholar] [CrossRef]

15. Xu K, Bi K, Han Q, Li X, Du X. Using tuned mass damper inerter to mitigate vortex-induced vibration of long-span bridges: analytical study. Eng Struct. 2019;182:101–11. doi:10.1016/j.engstruct.2018.12.067. [Google Scholar] [CrossRef]

16. Sarkar S, Fitzgerald B. Vibration control of spar-type floating offshore wind turbine towers using a tuned mass-damper-inerter. Struct Control Health Monit. 2020;27(1):e2471. doi:10.1002/stc.2471. [Google Scholar] [CrossRef]

17. Lara-Valencia LA, Farbiarz-Farbiarz Y, Valencia-González Y. Design of a tuned mass damper inerter (TMDI) based on an exhaustive search optimization for structural control of buildings under seismic excitations. Shock Vib. 2020;2020(2):1–19. doi:10.1155/2020/8875268. [Google Scholar] [CrossRef]

18. Pietrosanti D, De Angelis M, Basili M. A generalized 2-DOF model for optimal design of MDOF structures controlled by Tuned Mass Damper Inerter (TMDI). Int J Mech Sci. 2020;185(7):105849. doi:10.1016/j.ijmecsci.2020.105849. [Google Scholar] [CrossRef]

19. Weber F, Huber P, Borchsenius F, Braun C. Performance of TMDI for tall building damping. Actuators. 2020;9(4):139. doi:10.3390/act9040139. [Google Scholar] [CrossRef]

20. De Angelis M, Petrini F, Pietrosanti D. Optimal design of the ideal grounded tuned mass damper inerter for comfort performances improvement in footbridges with practical implementation considerations. Struct Control Health Monit. 2021;28(9):e2800. doi:10.1002/stc.2800. [Google Scholar] [CrossRef]

21. Su N, Xia Y, Peng S. Filter-based inerter location dependence analysis approach of Tuned mass damper inerter (TMDI) and optimal design. Eng Struct. 2020;250(10):113459. doi:10.1016/j.engstruct.2021.113459. [Google Scholar] [CrossRef]

22. Bian Y, Liu X, Sun Y, Zhong Y. Optimized design of a tuned mass damper inerter (TMDI) applied to circular section members of transmission towers. Buildings. 2022;12(8):1154. doi:10.3390/buildings12081154. [Google Scholar] [CrossRef]

23. Zahedin Labaf D, De Angelis M, Basili M. Multi-objective optimal design and seismic assessment of an inerter-based hybrid control system for storage tanks. Bull Earthq Eng. 2023;21(3):1481–507. doi:10.1007/s10518-022-01457-1. [Google Scholar] [CrossRef]

24. Djerouni S, Elias S, Abdeddaim M, Domenico DD. Effectiveness of optimal shared multiple tuned mass damper inerters for pounding mitigation of adjacent buildings. Pract Period Struct Design Constr. 2023;28(1):4022063. doi:10.1061/(ASCE)SC.1943-5576.0000732. [Google Scholar] [CrossRef]

25. Prakash S, Jangid RS. Optimum parameters of tuned mass damper-inerter for damped structure under seismic excitation. Int J Dyn Control. 2022;10(5):1322–36. doi:10.1007/s40435-022-00911-x. [Google Scholar] [CrossRef]

26. Jangid RS. Optimum parameters and performance of tuned mass damper-inerter for base-isolated structures. Smart Struct Syst, An Int J. 2022;29(4):549–60. doi:10.12989/sss.2022.29.4.549. [Google Scholar] [CrossRef]

27. Cao L, Li C, Chen X. Performance of multiple tuned mass dampers-inerters for structures under harmonic ground acceleration. Smart Struct Syst, An Int J. 2020;26(1):49–61. doi:10.12989/sss.2020.26.1.049. [Google Scholar] [CrossRef]

28. Elias S, Djerouni S. Optimum tuned mass damper inerter under near-fault pulse-like ground motions of buildings including soil-structure interaction. J Build Eng. 2024;85(2):108674. doi:10.1016/j.jobe.2024.108674. [Google Scholar] [CrossRef]

29. Djerouni S, Ounis A, Elias S, Abdeddaim M, Rupakhety R. Optimization and performance assessment of tuned mass damper inerter systems for control of buildings subjected to pulse-like ground motions. Structures. 2022;38:139–56. doi:10.1016/j.istruc.2022.02.007. [Google Scholar] [CrossRef]

30. Chen B, Zhang Z, Hua X. Equal modal damping-based optimal design of a grounded tuned mass-damper-inerter for flexible structures. Struct Control Health Monit. 2022;29(12):e3106. doi:10.1002/stc.3106. [Google Scholar] [CrossRef]

31. Giaralis A, Taflanidis AA. Reliability-based design of tuned mass-damper-inerter (TMDI) equipped multi-storey frame buildings under seismic excitation. In: 12th International Conference on Applications of Statistics and Probability in Civil Engineering, ICASP 2015, 2015; Vancouver, BC, Canada: University of British Columbia Library. [Google Scholar]

32. Papageorgiou C, Houghton NE, Smith MC. Experimental testing and analysis of inerter devices. J Dyn Sys Meas Control. Jan 2009;131(1):011001. doi:10.1115/1.3023120. [Google Scholar] [CrossRef]

33. Arakaki T, Kuroda H, Arima F, Inoue Y, Baba K. Development of seismic devices applied to ball screw: part 1 Basic performance test of RD-series. J Technol Des. 1999;5:239–44 (In Japanese). [Google Scholar]

34. Soong T. State-of-the-art review: active structural control in civil engineering. Eng Struct. 1988;10(2):74–84. doi:10.1016/0141-0296(88)90033-8. [Google Scholar] [CrossRef]

35. Liu X, Li S, Wu C, Zhong Y, Bian Y. Research on vibration control of power transmission lines-TMDI based on colliding bodies optimization. Buildings. 2022;12(12):2200. doi:10.3390/buildings12122200. [Google Scholar] [CrossRef]

36. Lazar IF, Neild SA, Wagg DJ. Inerter-based vibration suppression systems for laterally and base-excited structures. In: Proceedings of EURODYN, 2014; Sheffield; p. 1525–30. [Google Scholar]

37. Smith MC. Synthesis of mechanical networks: the Inerter. IEEE Trans Automat Contr. 2002;47(10):1648–62. doi:10.1109/TAC.2002.803532. [Google Scholar] [CrossRef]

38. Li C, Liang M, Wang Y, Dong Y. Vibration suppression using two-terminal flywheel. Part I: modeling and characterization. J Vib Control. 2012;18(8):1096–105. doi:10.1177/107754631141954. [Google Scholar] [CrossRef]

39. Abd-Elhamed A, Alkhatib S, Dagher MA. Closed-form solutions to investigate the nonlinear response of foundations supporting operating machines under blast loads. J Low Freq Noise, Vib Active Cont. 2023;42(3):1162–87. doi:10.1177/14613484231174856. [Google Scholar] [CrossRef]

40. Rack and Pinion Gears and Their Uses. 2024. Available from: https://www.makinaegitimi.com/kremayer-disli-nedir-kremayer-dislinin-kullanim-alanlari/. [Accessed 2024]. [Google Scholar]

41. Marian L, Giaralis A. The tuned mass-damper-inerter for harmonic vibrations suppression, attached mass reduction, and energy harvesting. Smart Struct Syst. 2017;19(6):665–78. doi:10.12989/sss.2017.19.6.665. [Google Scholar] [CrossRef]

42. Kaveh A, Fahimi Farzam M, Hojat Jalali H, Maroofiazar R. Robust optimum design of a tuned mass damper inerter. Acta Mech. 2020;231(9):3871–96. doi:10.1007/s00707-020-02720-9. [Google Scholar] [CrossRef]

43. The MathWorks. Matlab R2018a. Natick, MA, USA; 2018. [Google Scholar]

44. Hayyolalam V, Kazem AAP. Black widow optimization algorithm: a novel meta-heuristic approach for solving engineering optimization problems. Eng Appl Artif Intell. 2020;87(1):103249. doi:10.1016/j.engappai.2019.103249. [Google Scholar] [CrossRef]

45. Kayabekir A, Bekdaş G, Nigdeli S. Brief information about metaheuristic methods: history and theory of metaheuristics. IGI Global. 2020, pp. 36–70. doi:10.4018/978-1-7998-2664-4.ch002. [Google Scholar] [CrossRef]

46. Glover F. Future paths for integer programming and links to artificial intelligence. Comput & Operat Res. 1986;13(5):533–49. doi:10.1016/0305-0548(86)90048-1. [Google Scholar] [CrossRef]

47. Gharehchopogh FS. Quantum-inspired metaheuristic algorithms: comprehensive survey and classification. Artif Intell Rev. 2023;56(6):5479–543. doi:10.1007/s10462-022-10280-8. [Google Scholar] [CrossRef]

48. Hashim FA, Houssein EH, Hussain K, Mabrouk MS, Al-Atabany W. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems. Math Comput Simul. 2022;192(2):84–110. doi:10.1016/j.matcom.2021.08.013. [Google Scholar] [CrossRef]

49. Hashim FA, Hussain K, Houssein EH, Mabrouk MS, Al-Atabany W. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Appl Intell. 2021;51(3):1531–51. doi:10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]

50. Majumdar P, Mitra S, Bhattacharya D. Honey Badger algorithm using lens opposition based learning and local search algorithm. Evol Syst. 2023;15:1–2. doi:10.1007/s12530-023-09495-z. [Google Scholar] [CrossRef]

51. FEMA P-695. Quantification of building seismic performance factors. Washington, DC, USA: US Department of Homeland Security, FEMA; 2009. [Google Scholar]

52. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]

53. Gupta S, Deep K. A novel random walk grey wolf optimizer. Swarm Evol Comput. 2019;44(4):101–12. doi:10.1016/j.swevo.2018.01.001. [Google Scholar] [CrossRef]

54. Geem ZW, Kim JH, Loganathan GV. A new heuristic optimization algorithm: harmony search. Simulation. 2001;76(2):60–8. doi:10.1177/003754970107600201. [Google Scholar] [CrossRef]

55. Li H, Liu X, Huang Z, Zeng C, Zou P, Chu Z, et al. Newly emerging nature-inspired optimization-algorithm review, unified framework, evaluation, and behavioural parameter optimization. IEEE Access. 2020;8:72620–49. doi:10.1109/ACCESS.2020.2987689. [Google Scholar] [CrossRef]

56. Geem ZW. Optimal cost design of water distribution networks using harmony search. Eng Optim. 2006;38(3):259–77. doi:10.1080/03052150500467430. [Google Scholar] [CrossRef]

57. Bekdaş G, Nigdeli SM. Estimating optimum parameters of tuned mass dampers using harmony search. Eng Struct. 2011;33(9):2716–23. doi:10.1016/j.engstruct.2011.05.024. [Google Scholar] [CrossRef]

58. Akin A, Saka MP. Harmony search algorithm based optimum detailed design of reinforced concrete plane frames subject to ACI 318-05 provisions. Comput & Struct. 2015;147(10):79–95. doi:10.1016/j.compstruc.2014.10.003. [Google Scholar] [CrossRef]

59. Uray E, Çarbaş S. Dynamic loads and different soil characteristics examination on optimum design of cantilever retaining walls utilizing harmony search algorithm. Int J Eng Appl Sci. 2021;13(4):140–54. doi:10.24107/ijeas.1033802. [Google Scholar] [CrossRef]

60. Bekdaş G, Cakiroglu C, Kim S, Geem ZW. Optimal dimensions of post-tensioned concrete cylindrical walls using harmony search and ensemble learning with SHAP. Sustainability. 2023;15(10):7890. doi:10.3390/su15107890. [Google Scholar] [CrossRef]

61. Lee KS, Geem ZW. A new structural optimization method based on the harmony search algorithm. Comput & Struct. 2004;82(9–10):781–98. doi:10.1016/j.compstruc.2004.01.002. [Google Scholar] [CrossRef]

62. Degertekin SO. Improved harmony search algorithms for sizing optimization of truss structures. Comput & Struct. 2010;92(2):229–41. doi:10.1016/j.compstruc.2011.10.022. [Google Scholar] [CrossRef]

63. Saka MP, Hasançebi O. Adaptive harmony search algorithm for design code optimization of steel structures. In: Harmony search algorithms for structural design optimization. Berlin, Heidelberg: Springer Berlin Heidelberg; 2009. p. 79–120. doi:10.1007/978-3-642-03450-3_3. [Google Scholar] [CrossRef]

64. Qin F, Zain AM, Zhou KQ. Harmony search algorithm and related variants: a systematic review. Swarm Evol Comput. 2022;74(7):101126. doi:10.1016/j.swevo.2022.101126. [Google Scholar] [CrossRef]

65. Kaveh A, Abadi ASM. Cost optimization of a composite floor system using an improved harmony search algorithm. J Constr Steel Res. 2010;66(5):664–9. doi:10.1016/j.jcsr.2010.01.009. [Google Scholar] [CrossRef]

66. Kayabekir AE, Bekdaş G, Nigdeli SM, Geem ZW. Optimum design of PID controlled active tuned mass damper via modified harmony search. Appl Sci. 2020;10(8):2976. doi:10.3390/app10082976. [Google Scholar] [CrossRef]

67. Nigdeli SM, Bekdaş G. Tuning and position optimization of mass dampers for seismic structures, harmony search algorithm. In: Proceedings of the 3rd International Conference on Harmony Search Algorithm (ICHSA 2017). Singapore: Springer; 2017. p. 232–9. doi:10.1007/978-981-10-3728-3_23. [Google Scholar] [CrossRef]

68. Bekdas G, Nigdeli SM. Mass ratio factor on optimum TMD design in frequency domain. Int J Theor Appl Mech. 2018;3:68–73. [Google Scholar]