 Open Access
Open Access
ARTICLE
Unsteady Flow of Hybrid Nanofluid with Magnetohydrodynamics-Radiation-Natural Convection Effects in a U-Shaped Wavy Porous Cavity
1 Department of Engineering, West Tehran Branch, Islamic Azad University, Tehran, 1468763785, Iran
2 Department of Mechanical Engineering, College of Engineering, University of Ha’il, Ha’il City, 81451, Saudi Arabia
3 Fakulti Teknologi dan Kejuruteraan Mekanikal, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, Durian Tunggal, Melaka, 76100, Malaysia
4 Department of Mathematics, Faculty of Science, Aswan University, Aswan, 81528, Egypt
5 Department of Mathematics, Faculty of Science, Assuit University, Assuit, 71515, Egypt
6 Basic and Applied Sciences Department, College of Engineering and Technology, Arab Academy for Science & Technology and Maritime Transport (AASTMT), Aswan Branch, 81511, Aswan, Egypt
7 Department of Chemical and Materials Engineering, College of Engineering, Northern Border University, Arar, 91431, Saudi Arabia
* Corresponding Author: Najiyah Safwa Khashi’ie. Email:
Computer Modeling in Engineering & Sciences 2024, 141(3), 2225-2251. https://doi.org/10.32604/cmes.2024.056676
Received 27 July 2024; Accepted 20 September 2024; Issue published 31 October 2024
Abstract
In this paper, the unsteady magnetohydrodynamic (MHD)-radiation-natural convection of a hybrid nanofluid within a U-shaped wavy porous cavity is investigated. This problem has relevant applications in optimizing thermal management systems in electronic devices, solar energy collectors, and other industrial applications where efficient heat transfer is very important. The study is based on the application of a numerical approach using the Finite Difference Method (FDM) for the resolution of the governing equations, which incorporates the Rosseland approximation for thermal radiation and the Darcy-Brinkman-Forchheimer model for porous media. It was found that the increase of Hartmann number (Ha) causes a reduction of the average Nusselt number (Nu), with a maximum decrease of 25% observed as Ha increases from 0 to 50. In addition, the influence of the wall’s wave amplitude and the heat source length on the heat transfer rate was quantified, and it was revealed that at high wave amplitude, the average Nu increases by up to 15%. These findings suggest that manipulating magnetic field strength and cavity geometry can significantly enhance thermal performance. The novelty of this is related to the exploration of a U-shaped wavy cavity, which is not covered in previous studies, and to the detailed examination of the combined effects of magnetic fields, radiation, and hybrid nanofluids.Keywords
Nomenclature
| bb | Length of the specific section at the wall (bottom) |
| B0B0 | Strength (constant) of the magnetic field |
| BB | Heat source length |
| DD | Location (dimensionless) of the left heater |
| DaDa | Darcy number |
| u,vu,v | Velocities of the nanofluid in the x−x− and y−y−directions |
| gg | Gravitational acceleration |
| HH | Side length of the cavity |
| HaHa | Hartmann number |
| kk | Thermal conductivity |
| KK | Permeability of the porous media |
| NumNum | Average Nusselt number of heat source |
| NusNus | Local Nusselt number |
| pp | Fluid pressure |
| PrPr | Prandtl number |
| Q0Q0 | Heat generation coefficient |
| Heat generation parameter | |
| RaRa | Rayleigh number |
| RdRd | Thermal radiation parameter |
| TT | Temperature |
| TcTc | Cold wall temperature |
| ThTh | Heated wall temperature |
| αα | Inclined angle of the magnetic field |
| αeff, hnfαeff, hnf | Effective thermal diffusion of the hybrid nanofluid |
| αeff, fαeff, f | Effective thermal diffusion of the base fluid |
| ββ | Thermal expansion coefficient |
| μμ | Dynamic viscosity |
| εε | Porosity of the Alumina ceramic |
| λλ | Specific wavelength of wavy cavity |
| γγ | Darcy permeability parameter |
| σσ | Electrical conductivity |
| ϕϕ | Volumetric concentration of the nanofluid |
| ΦΦ | Inclination angle of the cavity |
Energy consumption has increased significantly during the past few decades. Tremendous efforts have been made to pacify the ever-increasing consumption rate or find an appropriate, cheap, and environment-friendly energy resource. Using nanotechnology is one of the main candidates for increasing the performance of systems. Nanofluids seem promising candidates for energy consumption reduction strategies due to their improved thermo-physical properties. In recent years, the study of nanofluids has garnered significant attention within the scientific community due to their superior thermal properties and potential applications in various engineering fields. Nanofluids, which are fluids embedded with nanoscale particles, have been extensively researched for their ability to enhance heat transfer in comparison to conventional fluids. This enhancement is primarily due to the increased thermal conductivity imparted by the nanoparticles. The nanofluids utilizations are successfully investigated in different industries and applications, including combustion [1,2], lubrication [3], medicine [4], heat exchangers [5], heating and tempering processes [6], microelectronic cooling [7] and refrigeration [8].
Early research efforts focused on the theoretical and experimental analysis of nanofluids, laying the groundwork for understanding their unique properties. However, as computational techniques have advanced, the numerical solution of nanofluid flow has become a critical area of study. Recent studies have explored a wide range of configurations, including flow over flat plates, through channels, and around complex geometries. These investigations have employed various numerical methods, such as finite difference, finite volume, and finite element methods, to solve the governing equations of nanofluid flow. One area of particular interest is the study of boundary layer flow, where the presence of nanoparticles can significantly alter the thermal boundary layer and, consequently, the overall heat transfer characteristics. Researchers have applied numerical techniques to solve the nonlinear partial differential equations governing boundary layer flow, often incorporating effects such as variable viscosity, thermal radiation, and magnetic fields to better understand the behavior of nanofluids under practical conditions. Nawaz et al. [9] modified the Adams–Bashforth method and applied this scheme to the mixed convection flow problem inside a square cavity with the simultaneous effects of thermal radiation and magnetic. Meanwhile, Cengizci et al. [10] incorporated the pressure-stabilizing/Petrov–Galerkin (PSPG) and the streamline-upwind/Petrov–Galerkin (SUPG) into the Galerkin finite element method (GFEM) formulation in order to solve the magnetohydrodynamic (MHD)-natural convection problem in the nanofluid-filled quadrantal cavity. Other references that highlighted the numerical schemes to solve nanofluid flow problems can be found here (see [11–15]).
The effects of hybrid nanofluids on heat transfer performances were recently investigated under different conditions. For example, Abdel Nour et al. [16] considered the natural convection of alumina-copper-water hybrid nanofluids under a magnetic field in a porous cavity. The porosity and nanoparticle concentration were in the range of 0.1–0.9, and 0%–0.08%, respectively. A Ra of 103 to 106, a Da range of 10−5 to 10−2, and a Ha range of 0 to 100 were set in their simulations. It was concluded that the convective heat transfer mechanism is stronger at higher Ras. Mliki et al. [17] utilized the Lattice Boltzmann Method (LBM) to investigate the natural convection of hybrid nanofluids of Al2O3-CuO suspended in water in a heated incinerator-shaped cavity under magnetic force effects. Their findings show that Ra and Ha have a direct and reverse effect on the heat transfer rate, respectively. The same trend was also observed for the entropy generation. The use of nanoparticles was found to be beneficial in enhancing heat transfer and reducing the produced irreversibility. A numerical investigation of radiation effects on unsteady MHD hybrid nanofluids’ natural convection in an inclined wavy porous 2D enclosure was performed by Nabwey et al. [18]. A square obstacle was also included in the cavity. They found out that the heat transfer was enhanced by increasing the domain porosity, especially at higher rates of heat fluxes.
Ashorynejad et al. [19] simulated the free convection of hybrid nanofluids in wavy open cavities under Lorentz force effects by using the LBM. It was noticed that the heat transfer is reversely proportional to Ha. Meanwhile, Ra and nanoparticle volume fraction have direct effects on heat transfer. Sajjadi et al. [20] studied the effects of various parameters on the heat transfer during the natural convection of hybrid nanofluids subjected to a magnetic field using the double Multiple-Relaxation-Time (MRT) Lattice Boltzmann Method (LBM). The results indicate a clear rise in the Nu as both Ra and nanoparticle volume concentration increase. Similarly, the Darcy number and porosity directly affect the rate of heat transfer.
Ahmed et al. [21] delved into a numerical investigation of the intricate interplay between two distinct heat transfer mechanisms—surface thermal radiation and natural convection—in a micropolar fluid laden with Al2O3 and Cu nanoparticles, confined within a porous cavity under the influence of magnetic field inclination. Their study incorporated entropy analysis and employed both the first and second laws of thermodynamics to comprehensively scrutinize the physical system. The governing equations describing the 2-D steady-state flow were solved using the Alternating Direction Implicit (ADI) method within the framework of the finite volume method. The parameters considered in the investigation include the heat source length (0.2 ≤ B ≤ 0.8), heat generation/absorption (−2 ≤ Q ≤ 2), radiation factor (0 ≤ Rd ≤ 1.0), vortex viscosity parameter (0 ≤ k ≤ 2), Hartmann number (0 ≤ Ha ≤ 100), and inclination angle (0 ≤ θ ≤ π). Graphical representations of the computed results illustrated noteworthy trends, such as the impact of the vortex parameter (k) on the average Nusselt number and the role of the total solid volume fraction in influencing heat transfer. Moreover, their results highlighted the reinforcing effect of the radiation factor (Rd) on global entropy generation within the system. They found that the radiation parameter amplifies the convective processes, thereby elevating the nanofluid flow dynamics and enhancing the rate of heat transfer.
Roy [22] applied multiple heat sources to an enclosure filled with hybrid nanofluids under MHD natural convection conditions. He employed the finite difference method for the governing equations and validated the results against experimental and numerical data. The validation shows a good agreement. His results indicate significant alterations in flow patterns with variations in the magnetic field parameter, angle of the magnetic field, number and width of heat sources, and Rayleigh number. The stream function’s intensity is pronounced for higher Rayleigh numbers and smaller magnetic field parameters. Notably, when the volume fraction of Cu nanoparticles exceeds 6%, distinct patterns in streamlines and isotherms emerge compared to lower values. Additionally, as the number of heat sources, magnetic field angle, and Rayleigh number increase, the average Nusselt number is found to rise. Tayebi et al. [23] also conducted an interesting numerical analysis on the MHD natural convection of hybrid nanofluid of Al2O3-Cu/water in a square cavity, while a wavy circular conductive cylinder presents in the center of the domain.
They employed the Corcione correlations to calculate the effective thermal conductivity and viscosity of the hybrid nanofluid, incorporating the Brownian motion of nanoparticles. Then, a comprehensive numerical parametric study was conducted, exploring various values of nanoparticle volumetric concentration, Hartmann number, Rayleigh number, and the ratio of fluid to solid thermal conductivities. Their findings emphasize the significant influence of the corrugated conductive block in regulating both convective flow characteristics and the heat transfer rate within the system. Rashad et al. [24] also investigated the effect of multiple heat sources from the bottom and the center of a triangular cavity filled with hybrid nanofluids under MHD natural convection process. The inclined side of the cavity underwent isothermal cooling, while the remaining sides were thermally insulated. The numerical solution employed the finite difference method with the stream function-vorticity formulation for the governing equations. The problem involved several key parameters, including the size and position of the heater element (B = 0.2–0.8 and D = 0.3–0.7), the Rayleigh number (Ra = 102–106), the Hartmann number (Ha = 0–100), the volume fraction of suspended nanoparticles (ϕ = 0–0.2), and the heat generation parameter (Q = 0–6). Their results highlight a substantial impact of increasing the volume fraction of the hybrid nanofluid when natural convection is minimal.
Numerous studies have explored the convection of nanofluids in confined spaces. Most of them used Al2O3/Cu/water as hybrid nanofluids under different heating conditions and various cavity geometries [25–27]. Geometries including square [28], cylinder [29], triangular [30], trapezoidal [31], etc. However, there’s a noticeable gap in understanding the unsteady magnetohydrodynamic (MHD) natural convection of hybrid nanofluids. This research aims to bridge that gap by numerically investigating the impact of radiation on unsteady natural convection in MHD hybrid nanofluids. The study focuses on a unique scenario: a U-shaped square wavy porous cavity under a constant inclined magnetic field. It’s worth mentioning that the cavity is partially heated, and the flow is primarily driven by buoyancy forces.
Fig. 1 depicts the layout of the computational domain considered in the current investigation, featuring a U-shaped cavity with a side length denoted as H. The vertical walls of this cavity exhibit a wavy pattern with a specific wavelength, λ. The cavity is filled with a porous medium saturated with an Al2O3-Cu/water hybrid nanofluid. The sinusoidal right and left walls are cooled at a temperature denoted as Tc. Meanwhile, a specific section along the bottom wall, indicated by a length ‘b’, experiences heating at a temperature Th, where Th is greater than Tc. The rest of the enclosure’s walls are assumed to be adiabatic, meaning they do not exchange heat with their surroundings. The force of gravity acts downward in the cavity, and a constant magnetic field denoted as B0, exerts its influence at an angle Φ along the horizontal axis.
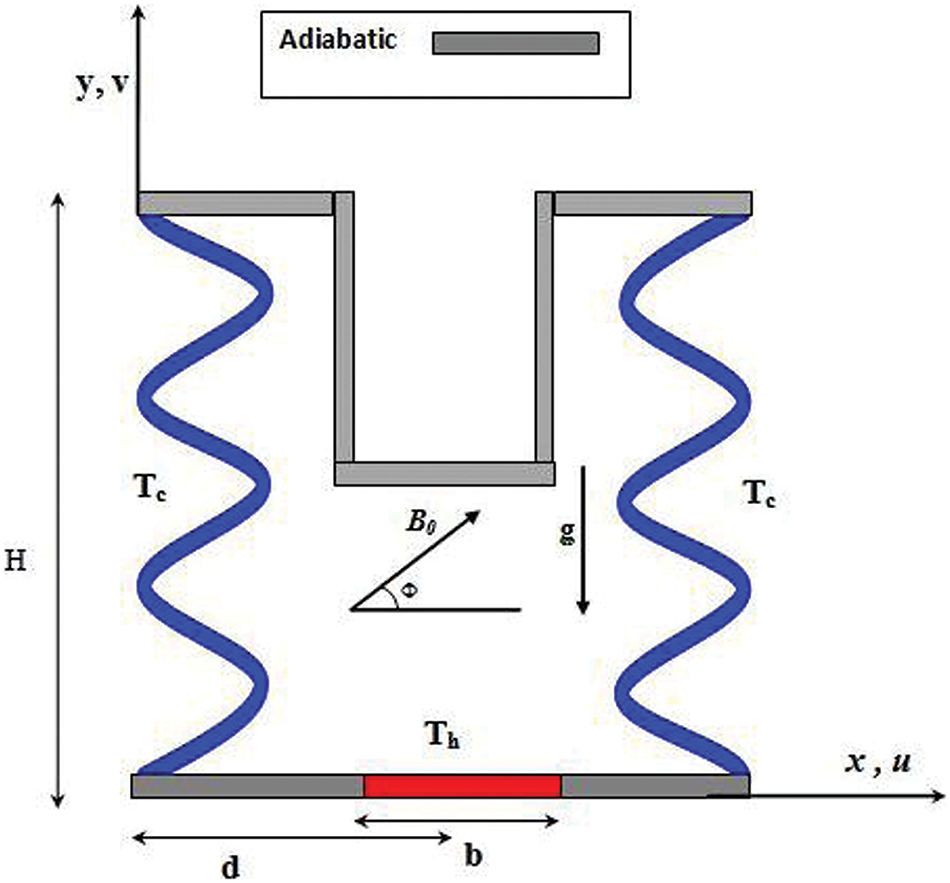
Figure 1: The considered model configuration
The hybrid nanofluid (Al2O3-Cu/water) is Newtonian, and the flow is laminar, unsteady, and incompressible. Table 1 includes some of the properties of the host fluid and nanoparticles. The density variation was approximated using the Boussinesq approximation. Therefore, the governing equations are as follows (see Nabwey et al. [18]):
∂u∂x+∂v∂y=0∂u∂x+∂v∂y=0(1)
1ε2(∂u∂t+u∂u∂x+v∂u∂y)=−1ρhnf∂p∂x+νhnfε(∂2u∂x2+∂2u∂y2)+gβhnf(T−Tc)sin α−νhnfKu+σhnfB20ρhnf(v sin Φ cos Φ−u sin2Φ)(2)
1ε2(∂v∂t+u∂v∂x+v∂v∂y)=−1ρhnf∂p∂y+νhnf(∂2v∂x2+∂2v∂y2)+gβhnf(T−Tc) cos α−νhnfKν+σhnfB20ρhnf(u sin Φ cos Φ−v cos2Φ)(3)
1ε(∂T∂t+u∂T∂x+v∂T∂y)=[αeff.hnf+16σ∗T3c3k∗(ρcp)hnf].∇2T+Q0ε(ρcp)hnf(4)
The considered boundary conditions are (see Nabwey et al. [18]):
t<0:u=v=T=0, 0≤x≤H, 0≤y≤H
t≥0:u=v=0, 0≤y≤H, 0≤x≤H at all walls
T=Th, D−0.5B≤yH≤D+0.5B, ∂T∂x=0,otherwise at wall x=0(5)
T=Tc, x=H−AH[1− cos (2πλyH)], 0≤y≤H
T=Tcx=AH[1− cos (2πλyH)], 0≤y≤H
Several expressions for the thermo-physical properties of nanofluids exist in the literature. In this work, a specific formulation that depends on the nanoparticles’ volume concentration only is adopted:
a) The thermal diffusions of the hybrid nanofluid and porous media are expressed as:
αeff, hnf=keff, hnf(ρcp)hnf(6)
αeff, f=keff, f(ρcp)f(7)
with:keff,hnf=εkhnf+(1−ε)ks(8)
keff,f=εkf+(1−ε)ks(9)
b) Density (see [32]):
ρhnf=ϕAl2O3ρAl2O3+ϕCuρCu+(1−ϕ)ρbf(10)
With: ϕ=ϕAl2O3+ϕCu.
c) The heat capacity:
(ρCp)hnf=ϕAl2O3(ρCp)Al2O3+ϕCu(ρCp)Cu+(1−ϕ)(ρCp)bf(11)
d) The thermal expansion coefficient:
(ρβ)hnf=ϕAl2O3(ρβ)Al2O3+ϕCu(ρβ)Cu+(1−ϕ)(ρβ)bf(12)
e) Thermal diffusivity, αnf of the nanofluid is defined as:
αnf=knf(ρcp)nf(13)
f) Thermal conductivity [33]:
khnfkbf=((ϕAl2O3kAl2O3+ϕCukCu)ϕ+2kbf+2(ϕAl2O3kAl2O3+ϕCukCu)−2ϕkbf)×((ϕAl2O3kAl2O3+ϕCukCu)ϕ+2kbf−(ϕAl2O3kAl2O3+ϕCukCu)+ϕkbf)−1(14)
g) Dynamic viscosity:
μhnf=μbf(1−(ϕAl2O3+ϕCu))2.5(15)
h) Electrical conductivity [34]:
σhnfσbf=1+3((ϕAl2O3σAl2O3+ϕCuσCu)σbf−(ϕAl2O3+ϕCu))((ϕAl2O3σAl2O3+ϕCuσCu)ϕσbf+2)−((ϕAl2O3σAl2O3+ϕCuσCu)σbf−(ϕAl2O3+ϕCu))(16)
There are some dimensionless parameters as follows:
X=xH, Y=yH,U=uHαf, V=vHαf, P=pH2ρnfα2f, θ=T−TcTh−Tc, τ=αfH2t(17)
By plugging the defined dimensionless parameters into Eqs. (1) to (5), the governing equations will be converted to:
∂U∂X+∂V∂Y=0(18)
1ε2(∂U∂τ+U∂U∂X+V∂U∂Y)=−∂P∂X+vhnfεvf Pr (∂2U∂X2+∂2U∂Y2)+RaβhnfβfPrθ sin α−vhnfvfPrDa+Ha2. Pr .σhnfσf(V sin Φ cos Φ−U sin2Φ)(19)
1ε2(∂V∂τ+U∂V∂X+V∂V∂Y)=−∂P∂Y+vhnfεvf Pr (∂2V∂X2+∂2V∂Y2)+Ra βhnfβfPrθ cos α−vhnfvfPrDa+Ha2 Pr σhnfσf(U sin Φ cos Φ−V cos2Φ)(20)
1ε(∂θ∂τ+U∂θ∂X+V∂θ∂Y)=αeff.hnfαeff.f(1+Rd)(∂2θ∂X2+∂2θ∂Y2)+(ρcp)f(ρcp)hnf.Q(21)
where some dimensionless numbers like Prandtl, Rayleigh, Hartman, and Radiation parameters are defined as follows:Pr=νfαf, Ra=gβf(Th−Tc)H3αfνf, Ha=B0H√σfμf, Rd=16σ∗T3c3knfk∗(22)
The boundary conditions are expressed as:
τ≺0:U=V=θ=0, 0≤X≤1, 0≤Y≤1,
τ≥0:U=V=0, 0≤Y≤1, 0≤X≤1 at all walls
θ=1, D−0.5B≤Y≤D+0.5B
∂θ∂X=0, otherwise at wall, X=0
θ=0, X=1−A[1−cos(2πλY)], 0≤Y≤1
θ=0, X=A[1−cos(2πλY)], 0≤Y≤1(23)
The local Nu is:
Nus=−knfkf(1+Rd)(∂θ∂X)X=0(24)
The average Nu is:
Num=1B∫D+0.5∗BD−0.5∗BNusdY(25)
Table 1 shows the properties of the selected bf (base fluid) and np (nanoparticles).
3 Numerical Technique and Validation
An iterative Finite Difference Method (FDM) is used to solve the governing equations. The convective terms were approximated by using a second-order upwind finite difference scheme. The first point in the solution methodology is writing the previous system in the following general form:
U∂Ω∂X+V∂Ω∂Y=ΓΩ∇2Ω+SΩ(26)
Here it should be mentioned that S refers to the source terms (including the pressure gradients and buoyancy terms in the momentum equations). The central differences scheme is used to estimate the first and second derivatives as:
∂Ω∂X=Ωi+1, j−Ωi−1, jXi+1−Xi−1, ∂Ω∂Y=Ωi, j+1−Ωi, j−1YJ+1−YJ−1∂2Ω∂X2+∂2Ω∂Y2=Ωi+1, j−2Ωi, j+Ωi−1, j(ΔX)2+Ωi, j−1−2Ωi, j+Ωi, j+1(ΔY)2(27)
Eq. (27) refers to the dependent variables U, V, N and θ and ΔX=Xi+1−Xi, ΔY=Yj+1−Yj, Using the previous forms, the following algebraic system is obtained:
ApΩi, j=AEΩi+1, j+AWΩi−1, j+ANΩi, j+1+ASΩi, j−1+SP(28)
Eq. (29) shows the FD approximation of the energy equation (see Nabwey et al. [18]):
θn+1i, j=θni, j+Δτσ{(αnfαf)[θni+1,j−2θni,j+θni−1,j(ΔX)2+θni,j+1−2θni,j+θni,j−1(ΔY)2]+ Q(ρcp)f(ρcp)nfθni,j−Uni,jθni+1,j−θni−1,j2ΔX−Vni, jθni, j+1−θni, j−12ΔY}(29)
A grid of 61 × 61 and a time step of 10−6 were considered to perform all the computations. To ensure the validity of the numerical model, a comparison with the findings of Ghasemi et al. [35] is performed (see Fig. 2). The comparison shows a very good concordance.
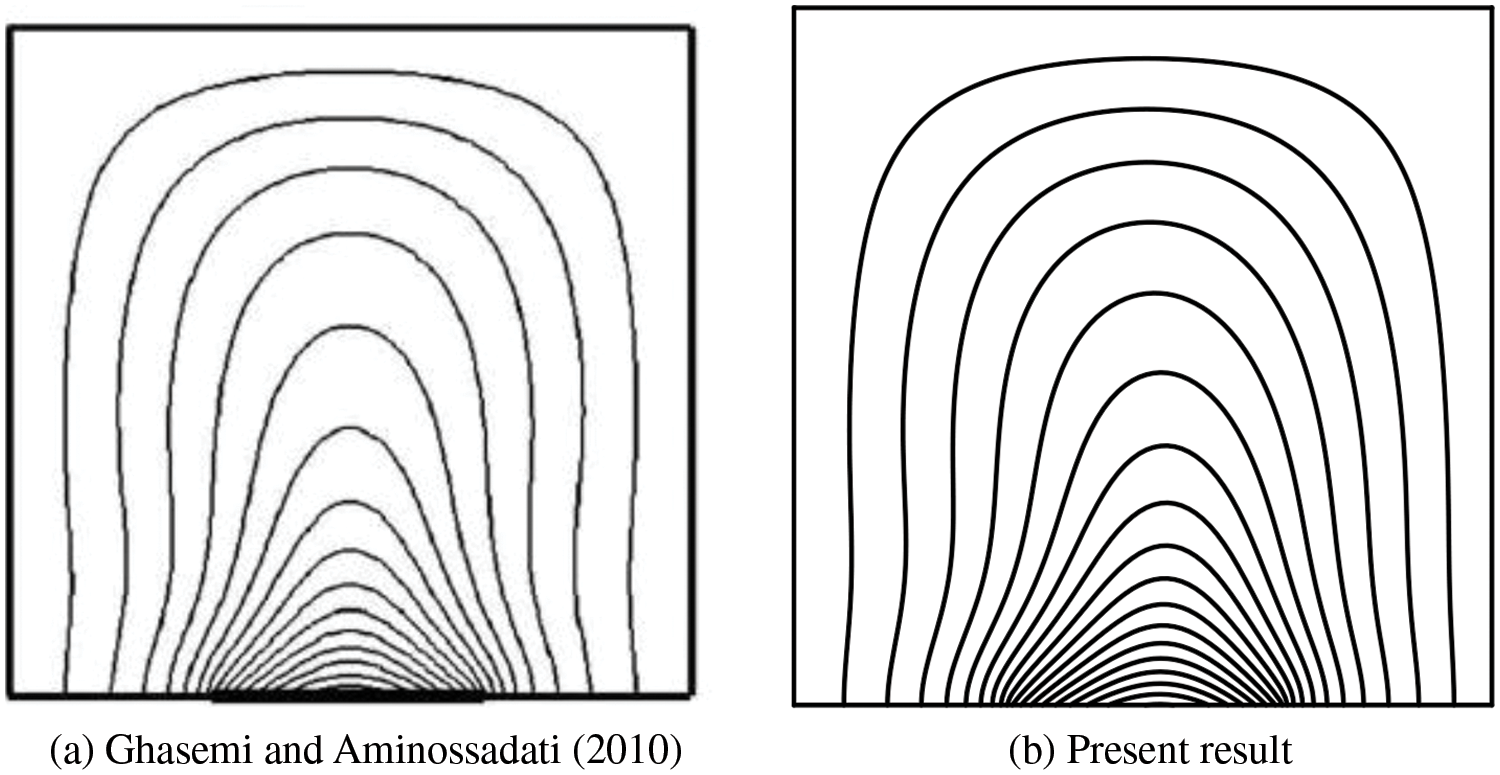
Figure 2: Validation of the temperature field with the results of Ghasemi et al. [35] for B = 0.4, Ra=105, ϕ=0.1, D=0.5
The simulation results of this work, including the flow structure, temperature field, and local and average Nu, are provided in this section. Fig. 3 shows the streamlines and isotherms of the hybrid nanofluids at different wave amplitudes of the walls. The results show that the higher amplitudes increase the significance of streamlines and reduce the significance of the isotherms. The variation of the local Nu vs. the x direction at different amplitudes is presented in Fig. 4. At the lowest amount of the amplitude (0.05), which is the closest value to a straight wall, the local Nu is minimum at the center, and it rises sharply by getting far from the center of the domain. The trend changes at higher amplitudes. The minimum local Nu moves from the center to the left corner. While, the maximum local Nu is still on both walls. The average Nu against nanoparticle volume concentration at different amplitudes is shown in Fig. 5. The higher the amplitudes, the higher average Nu. A possible reason could be the more significant streamlines at higher amplitudes.
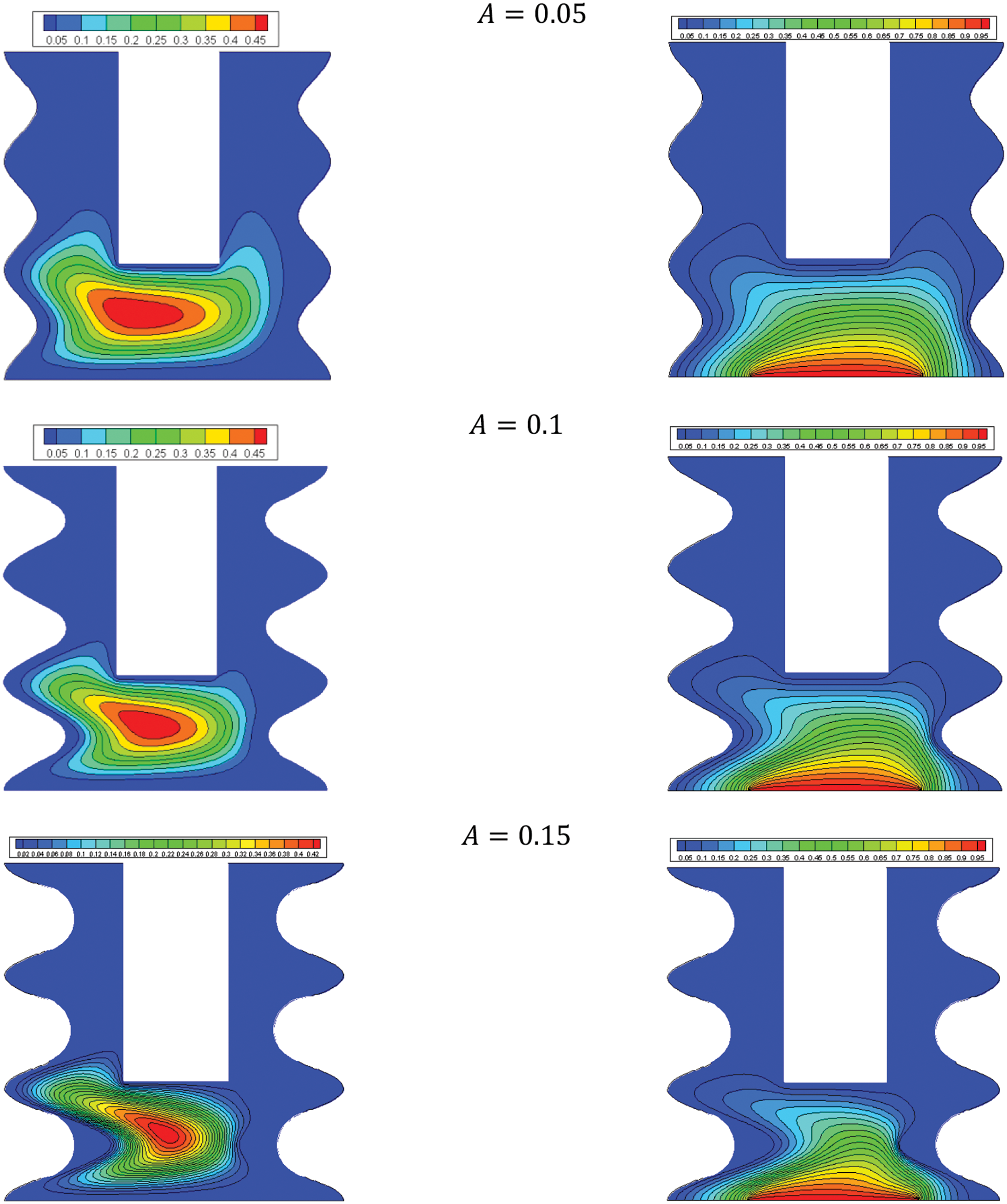
Figure 3: Effect of A on the flow structure (left) and temperature field (right) for: Ha = 10, φ = 0.05, Q = 1, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
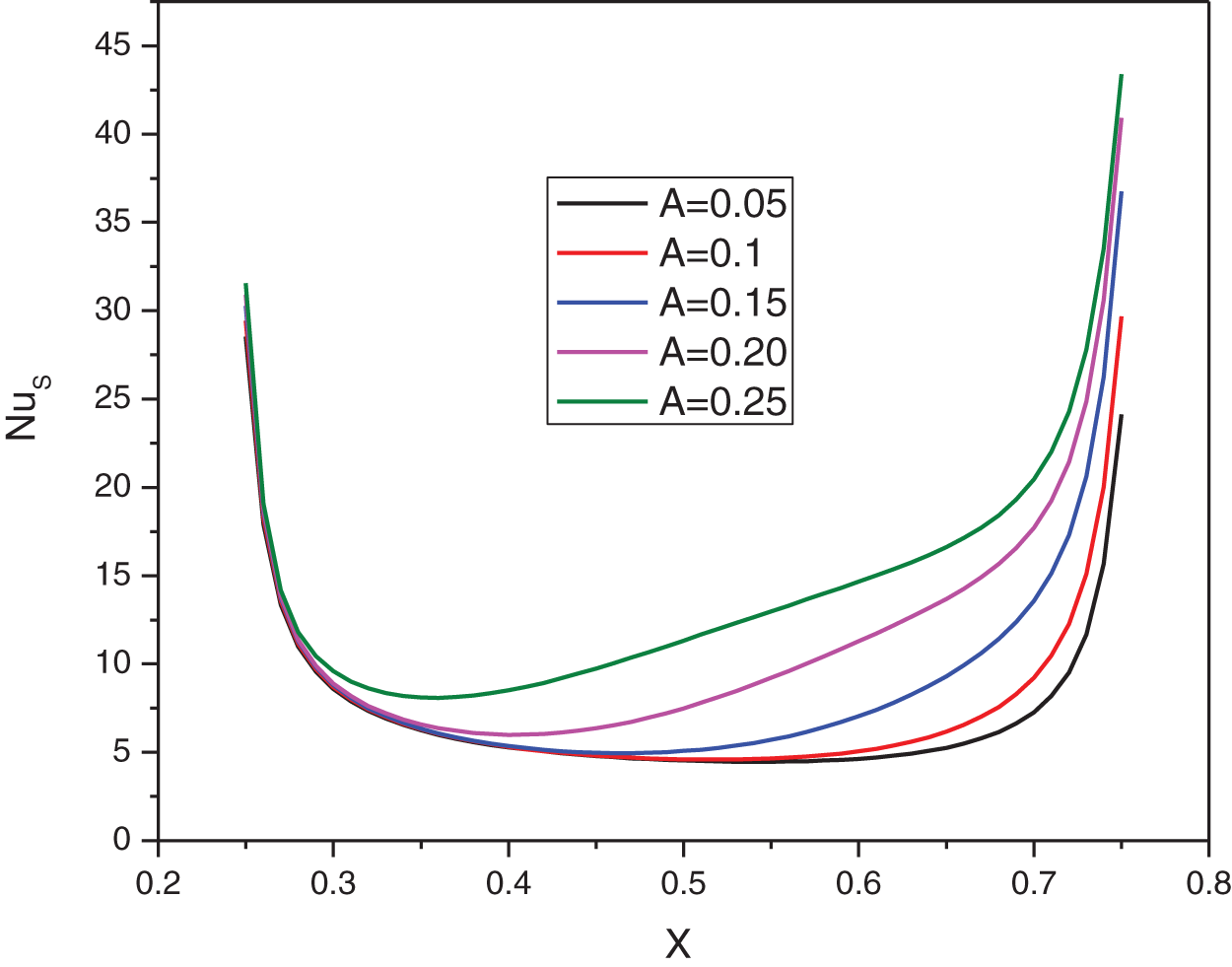
Figure 4: Effect of A on the local Nu for: Ha = 10, φ = 0.05, Q = 1, B = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
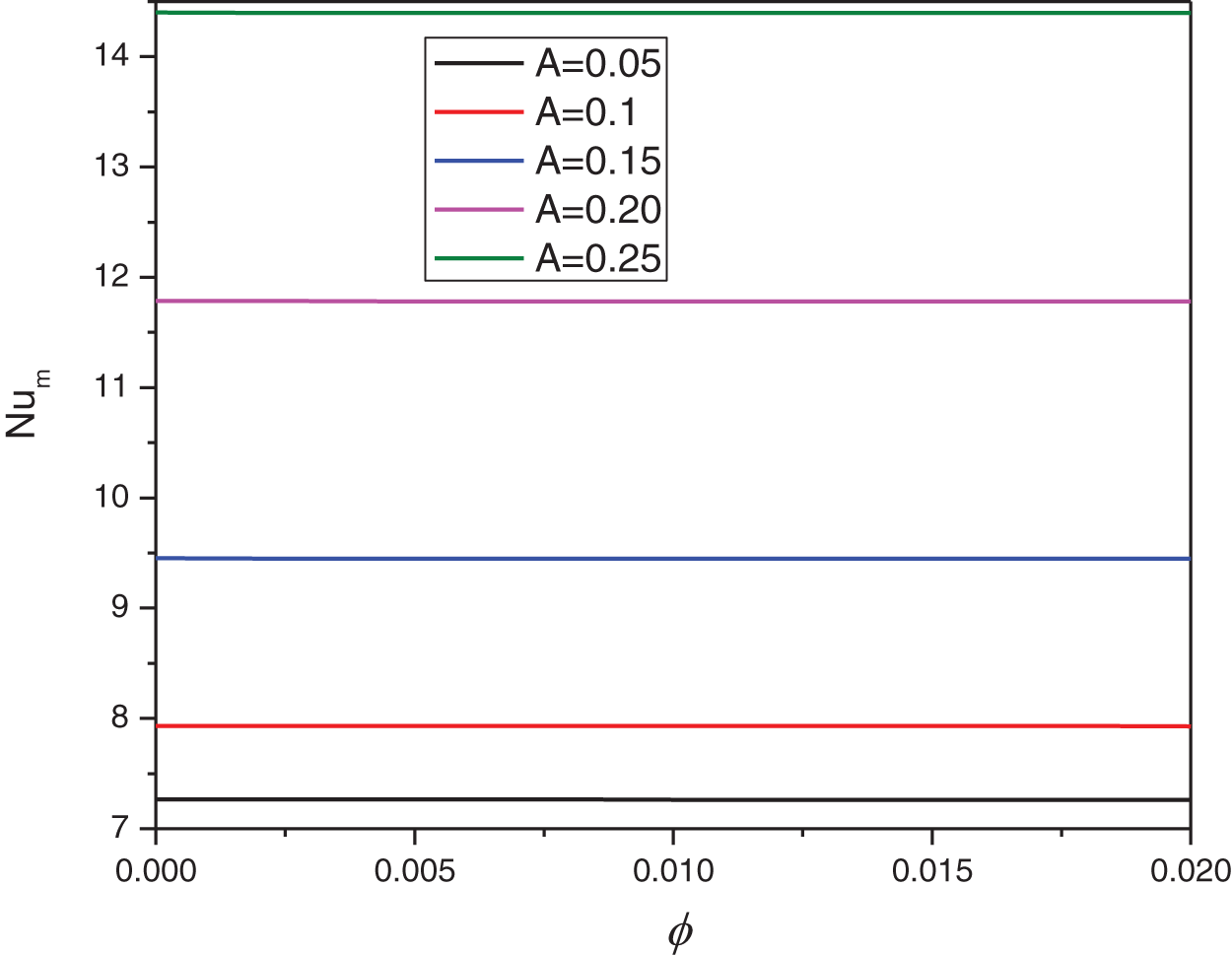
Figure 5: Effect of A on the average Nu for Ha = 10, φ = 0.05, Q = 1, B = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
Fig. 6 shows the streamlines and isotherms by changing the dimensionless heat source length at the bottom. It was observed that the streamlines are more significant by increasing the dimension less heat source length. A more uniform temperature distribution is expected with a larger heat source. This is shown in the results.
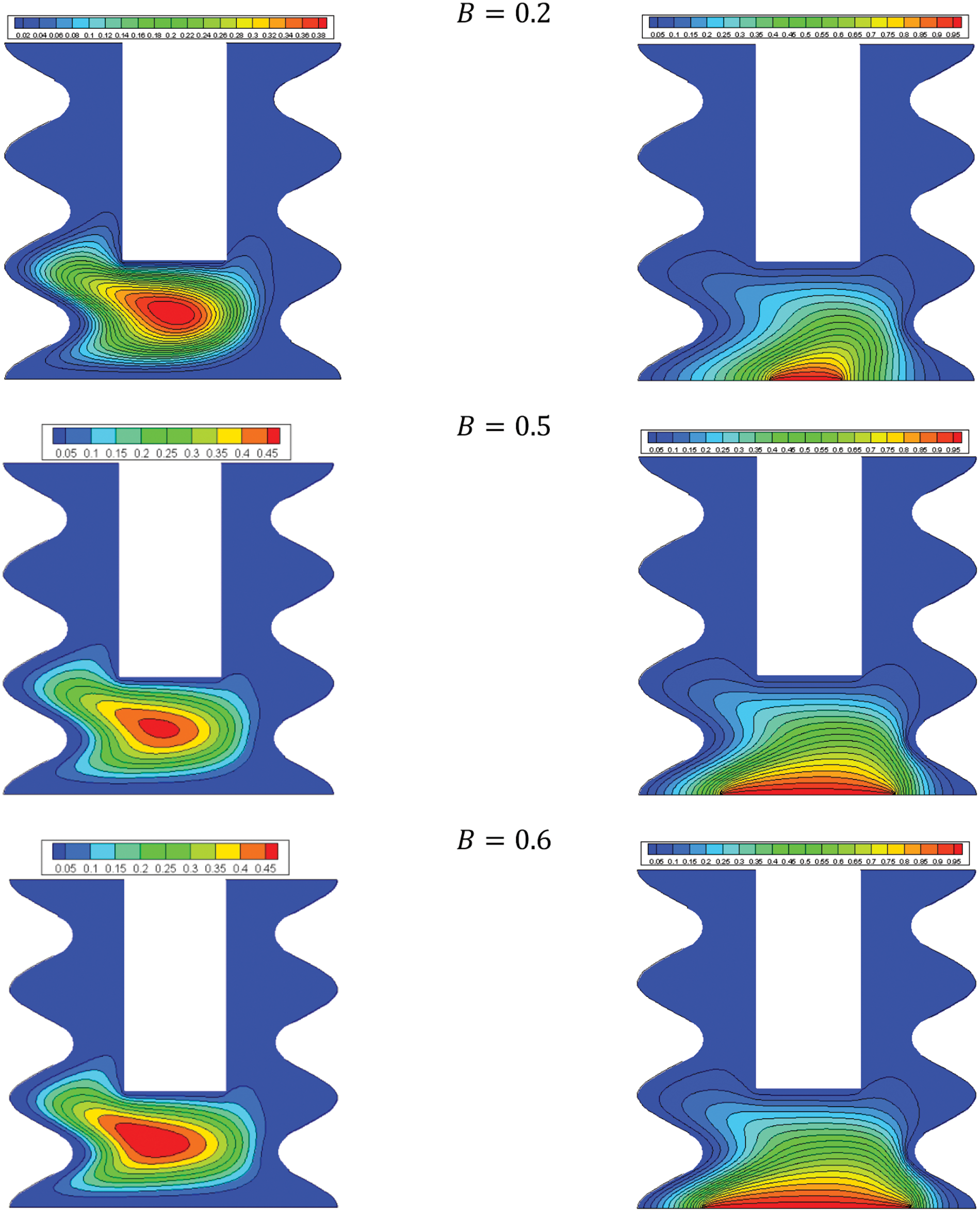
Figure 6: Effect of B on the flow structure (left) and temperature field (right) for: Ha = 10, φ = 0.05, Q = 1, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
Fig. 7 demonstrates the local Nu variation vs. x direction for different heat source lengths. The minimum local Nu is achieved at the center of the domain (x = 0.5) for all the studied cases, and it is increased sharply by changing the location at both directions. The sharp rise is however encountered at the edges of the heat source. The same trend (U-shape) was observed at different heat source lengths. Nevertheless, the minimum local Nu decreased with any increase in the heat source length. On the other hand, the maximum local Nu increased by increasing the heat source dimensions.
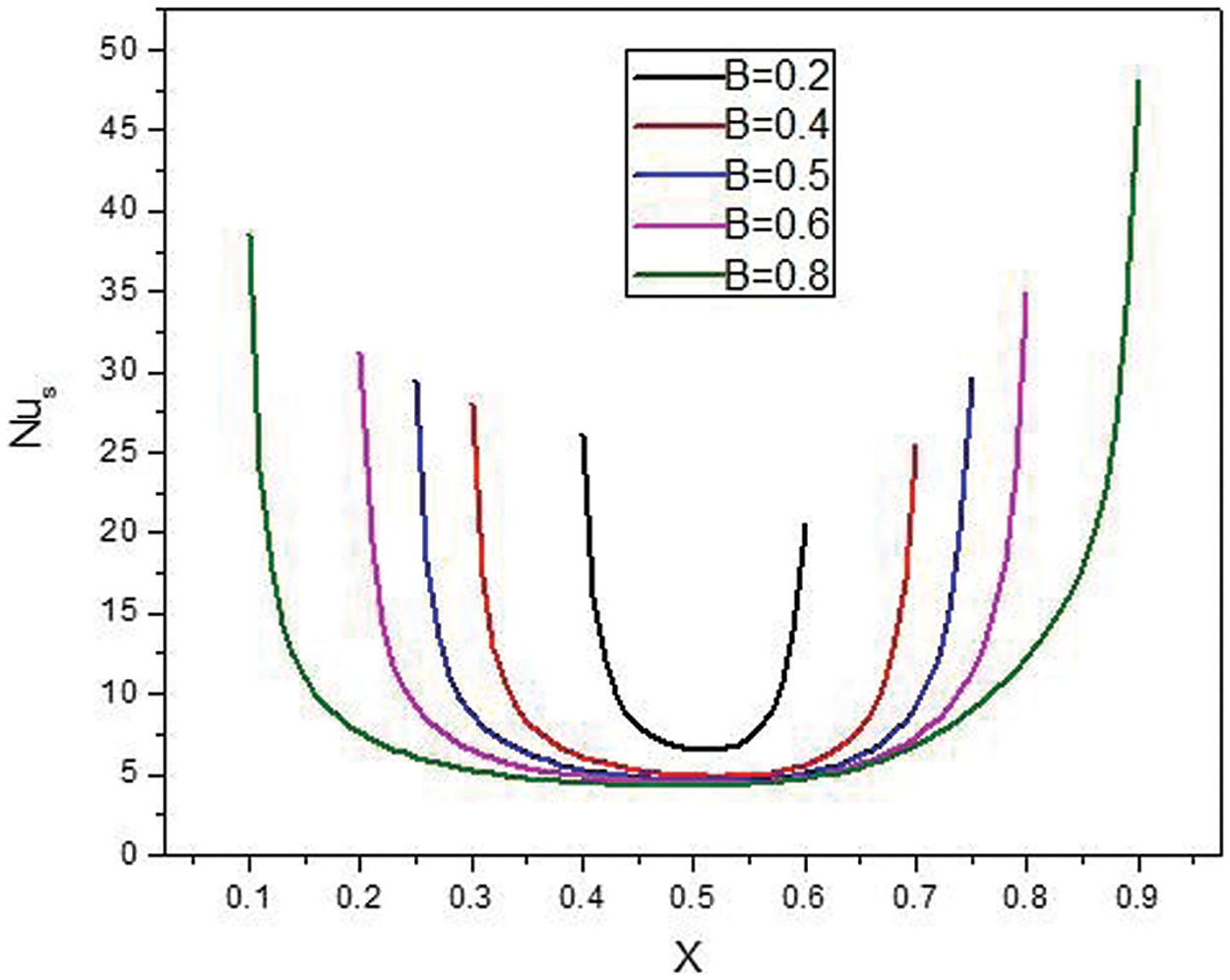
Figure 7: Effect of B on the local Nu for: Ha = 10, φ = 0.05, Q = 1, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
The average Nu against the nanoparticle volume concentration for various dimensionless heat source lengths is shown in Fig. 8. The findings show that the average Nu is not dependent on the nanoparticle load. However, it is a strong function of the heat source length. The smaller the dimensionless heat source, the higher amount of average Nu. Fig. 9 shows the streamlines (left) an isotherms of the hybrid nanofluids (right) for various Ha. As it is shown, increasing Ha does not change the streamlines and isotherms significance considerably. Increasing Ha means increasing the effect of the magnetic field order of magnitude on the flow. Therefore, the magnitude of the magnetic field does not significantly affect the streamlines and isotherms.
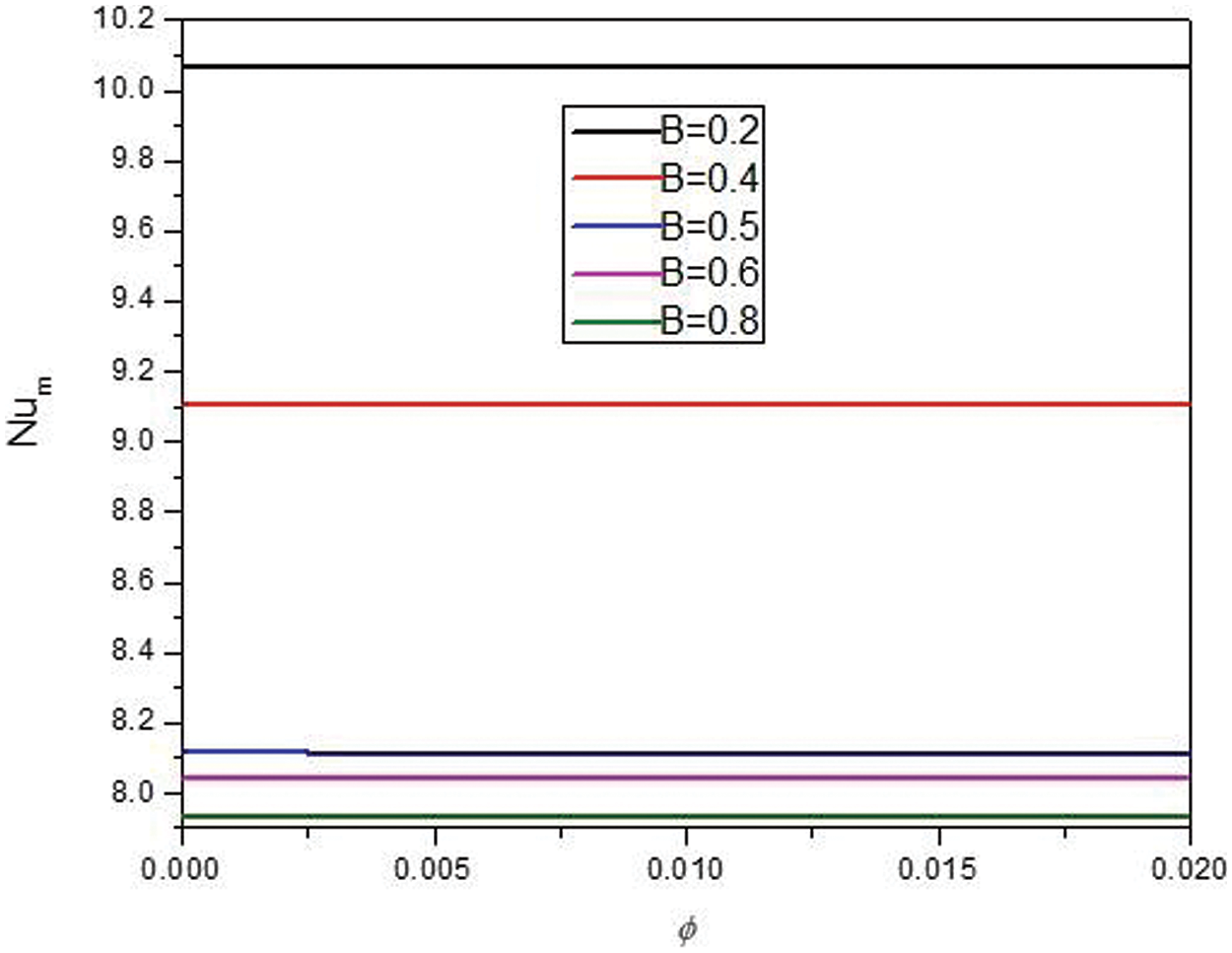
Figure 8: Effect of B on the average Nu for: Ha = 10, φ = 0.05, Q = 1, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
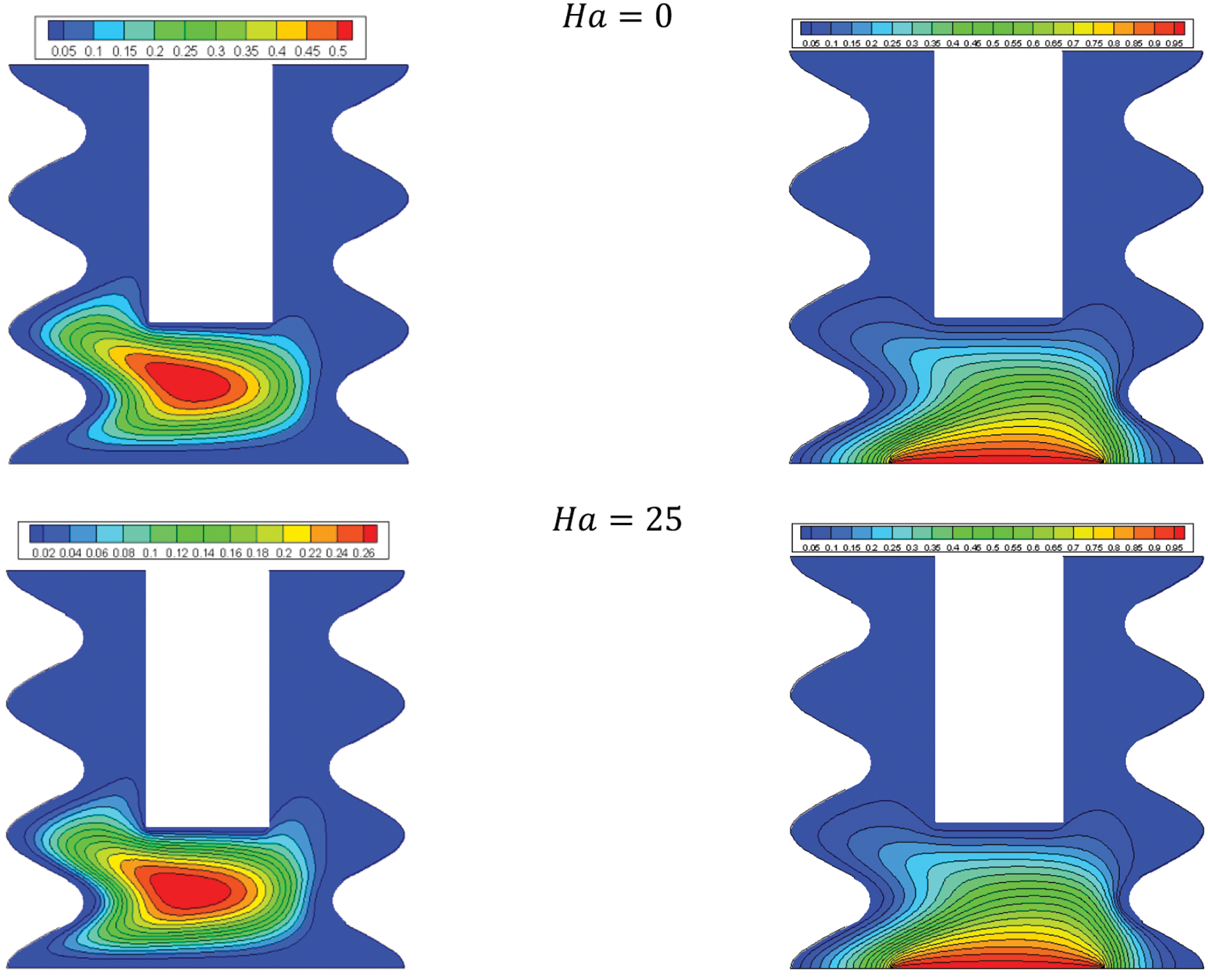
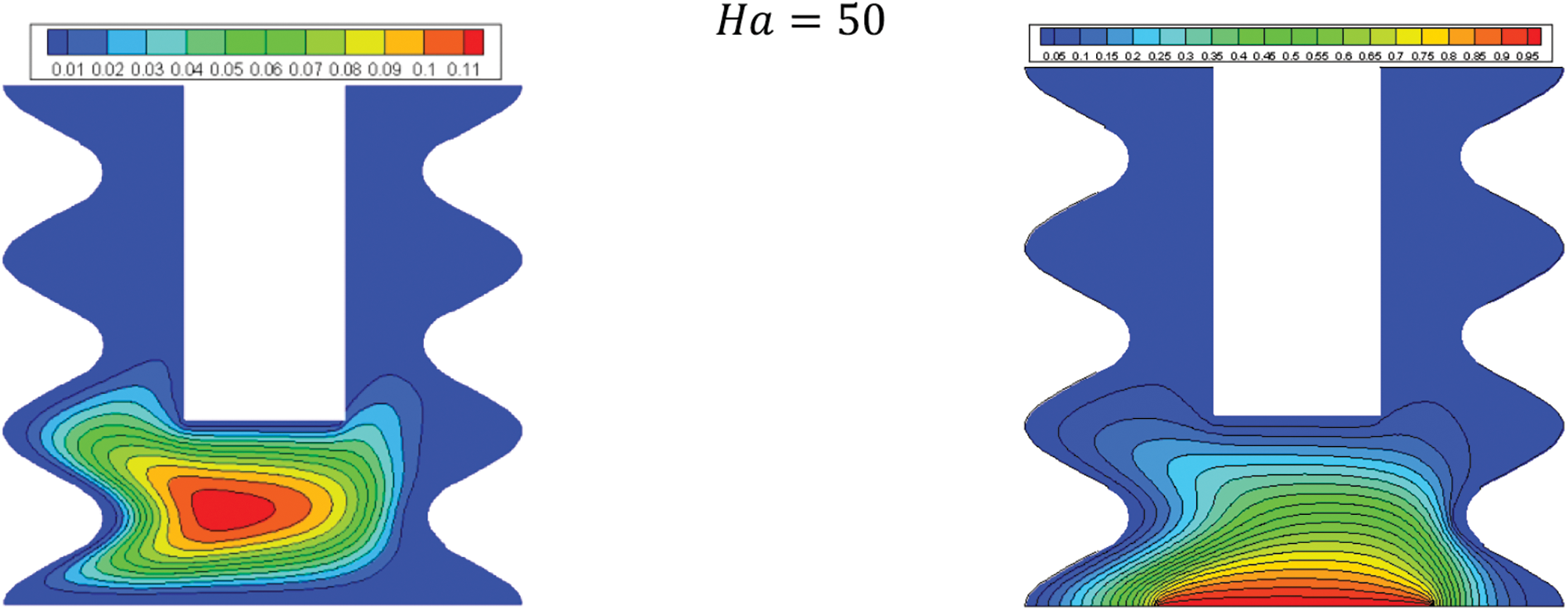
Figure 9: Effect of Ha on the flow structure (left), temperature field (right) for: φ = 0.05, Q = 1, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
The variation of the local Nusselt number (Nu) along the x-direction at different Hartmann numbers (Ha) is illustrated in Fig. 10. The local Nu reaches its minimum value at the center of the cavity and increases sharply as one moves away from the center, consistent with the behavior observed in previous cases. Interestingly, while Ha does not significantly influence the local Nu distribution, it has a substantial impact on the average Nu. As Ha increases, the average Nu decreases. This behavior suggests that a magnetic field (indicated by higher Ha values) suppresses convective heat transfer, allowing conduction to become the dominant heat transfer mechanism. Without a magnetic field (Ha = 0), the viscous forces are less effective in counteracting the convective currents, leading to a higher average Nu.
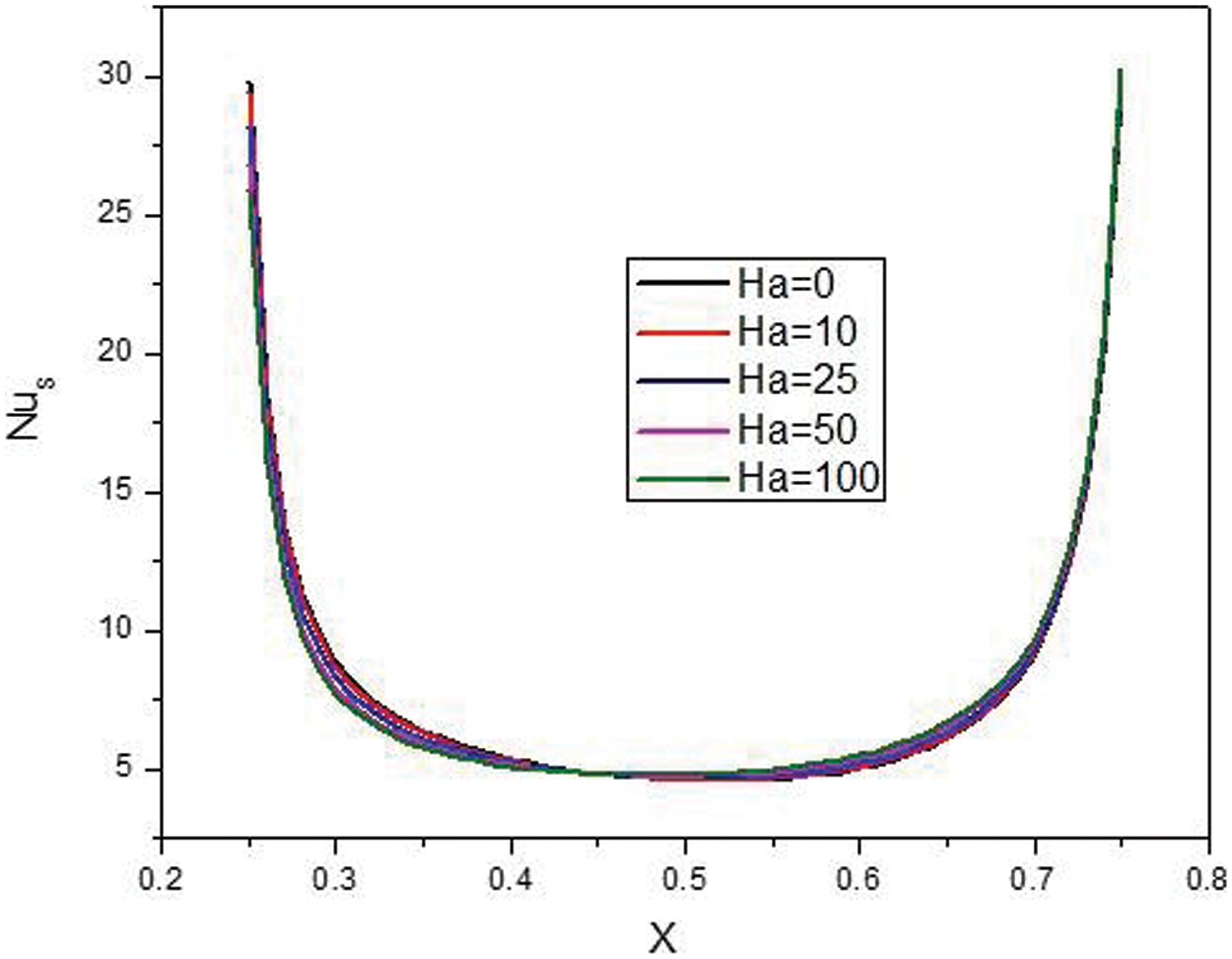
Figure 10: Effect of Ha local Nu for: φ = 0.05, Q = 1, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
Another key observation is the impact of nanoparticle concentration on heat transfer. As shown in Fig. 11, increasing the nanoparticle volume fraction results in a decrease in the average Nu. This effect is more pronounced at lower Ha values, implying that the magnetic field moderates the influence of nanoparticles on the flow dynamics. Physically, this could be because, at lower Ha, the nanoparticles enhance the effective viscosity of the nanofluid, thereby reducing the convective heat transfer rate. However, as Ha increases, the magnetic forces dampen fluid motion, diminishing the nanoparticles’ ability to alter the flow field significantly. Furthermore, the simulation results reveal that the streamline patterns and isotherms of the nanofluids remain largely unaffected by thermal radiation. However, thermal radiation exerts a noticeable influence on both local and average Nu, as depicted in Figs. 12 and 13. Higher radiation levels lead to an increase in both local and average Nu, which can be attributed to thermal radiation enhancing the energy transport within the fluid, thereby boosting the overall heat transfer rate. This finding underscores the importance of considering radiative effects in applications where high precision in thermal management is required.

Figure 11: Effect of Ha average Nu for: φ = 0.05, Q = 1, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
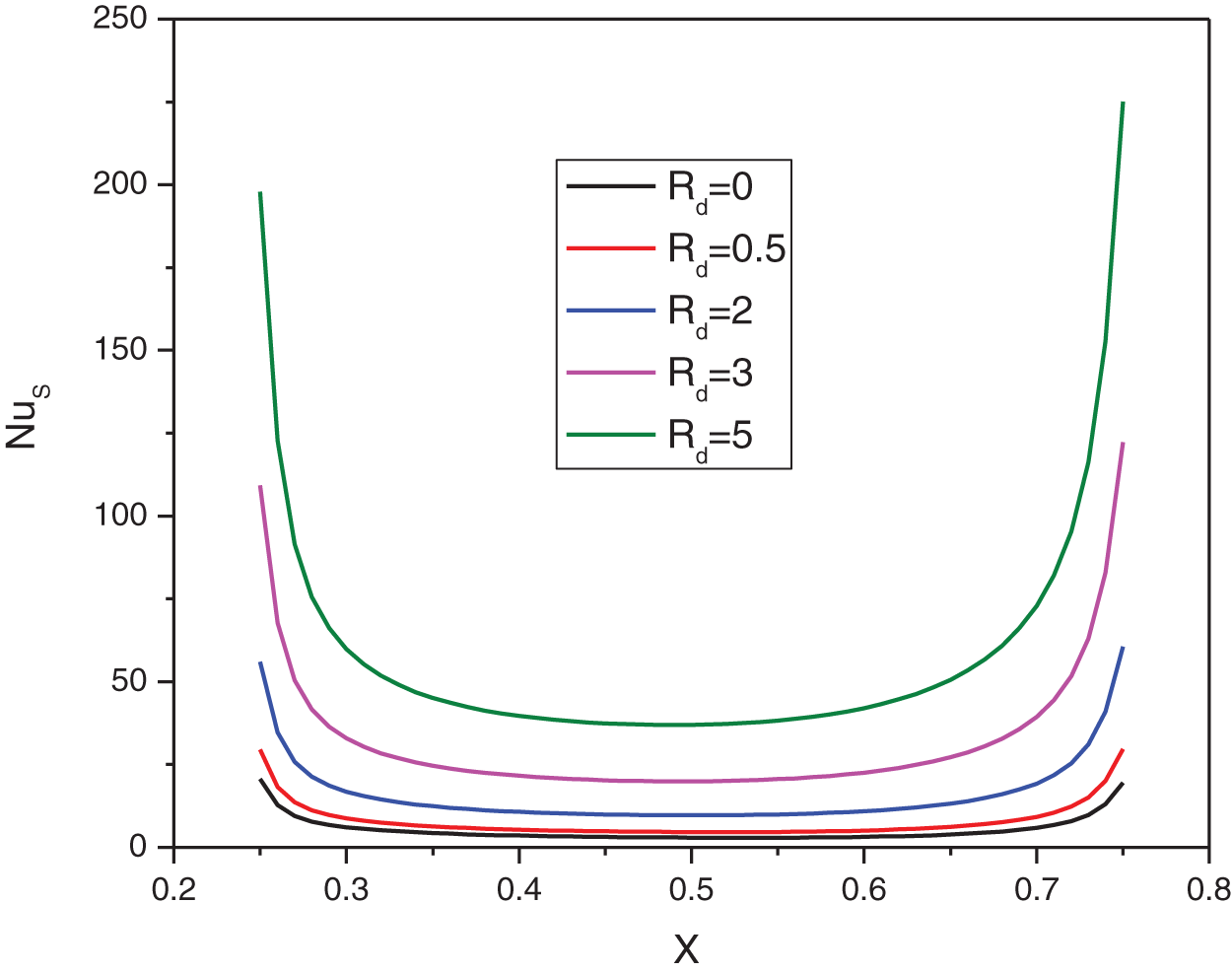
Figure 12: Effect of Rd on the local Nu for: Ha = 10, φ = 0.05, Q = 1, B = 0.5, D = 0.5, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
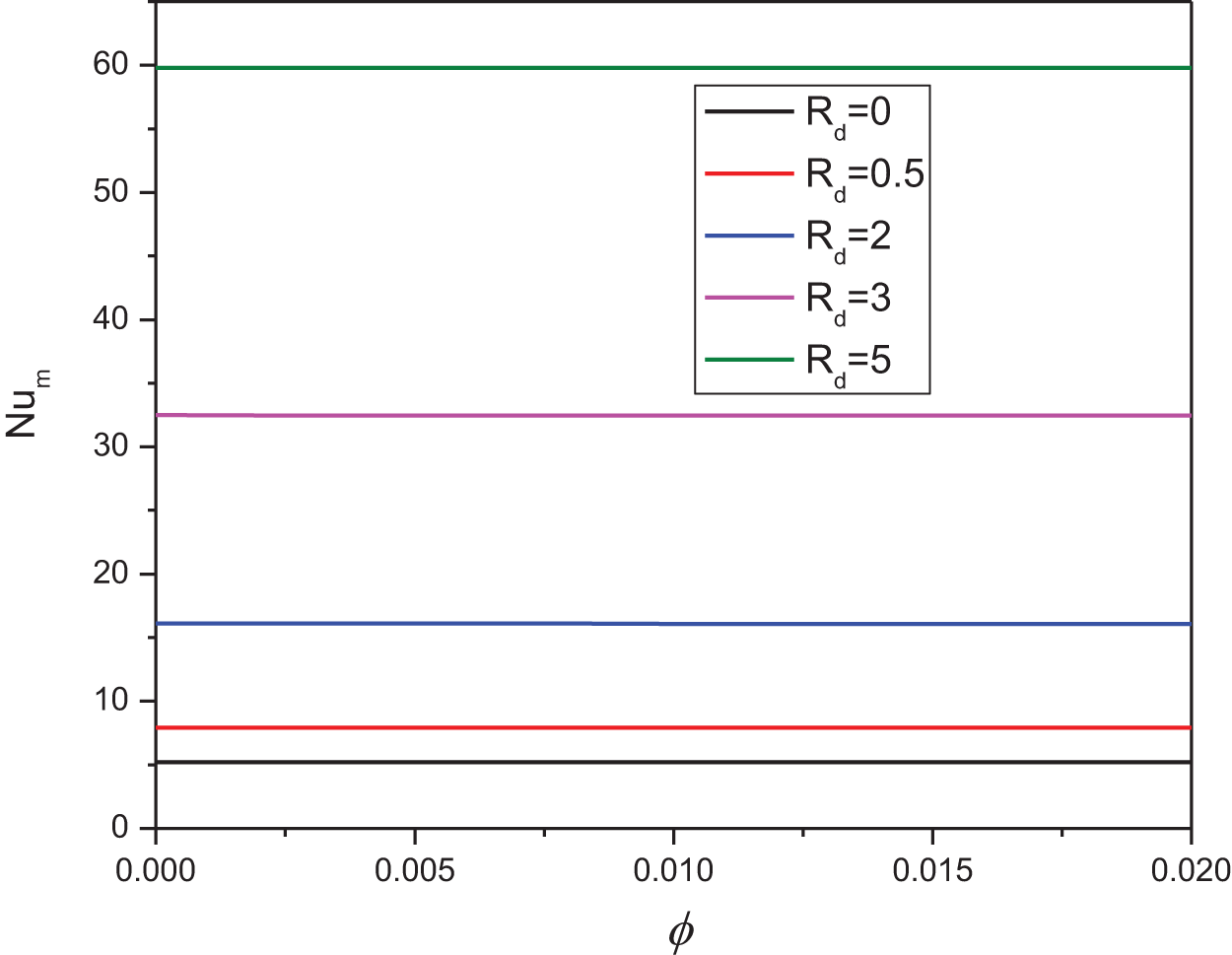
Figure 13: Effect of Rd on the average Nu for: Ha = 10, φ = 0.05, Q = 1, B = 0.5, D = 0.5, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
Fig. 14 shows the effect of heat absorption (negative values) or generation (positive values) on the streamlines and isotherms of the hybrid nanofluids. While the flow pattern and the significance of the streamlines are not dependent on heat absorption or generation, the isotherms and the temperature fields heavily depend on heat absorption or generation. Fig. 15 also shows that the minimum local Nu for heat generation is less than that of a heat absorption case. Fig. 16 proves that the nanoparticle volume concentration is not considerably effective the average Nu at a given amount of heat absorption or generation.
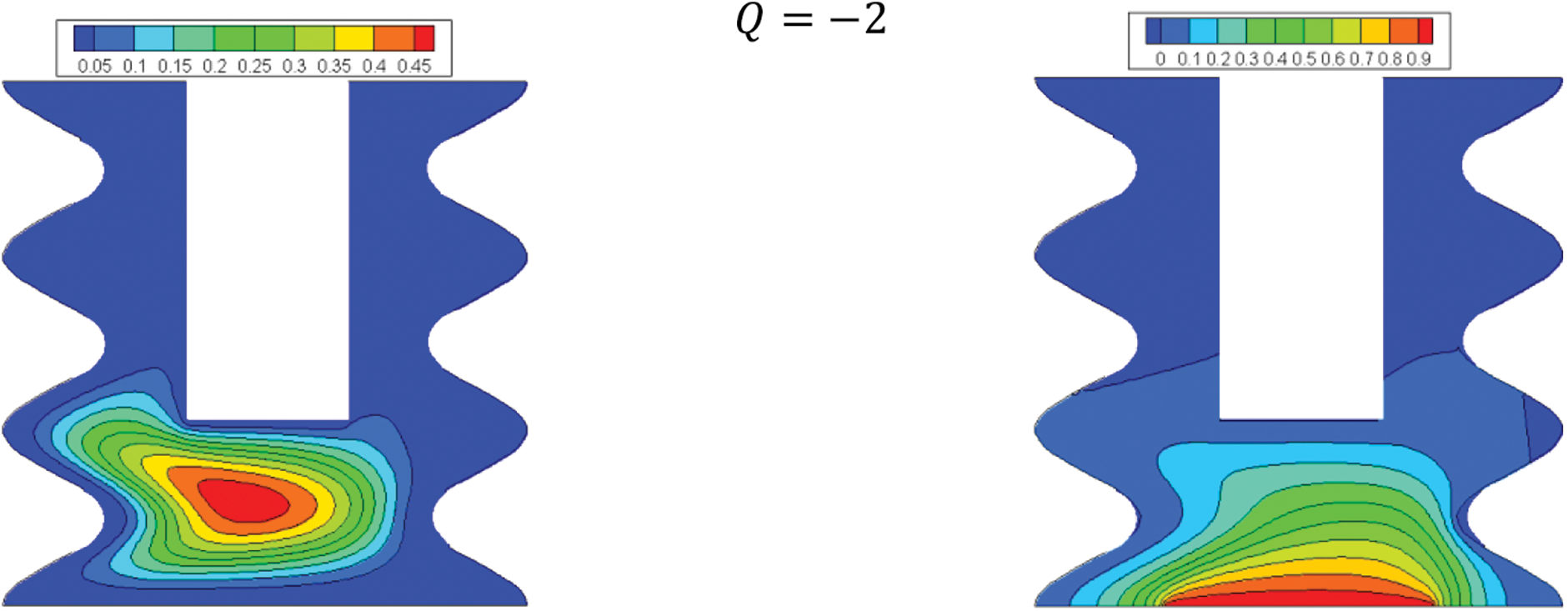
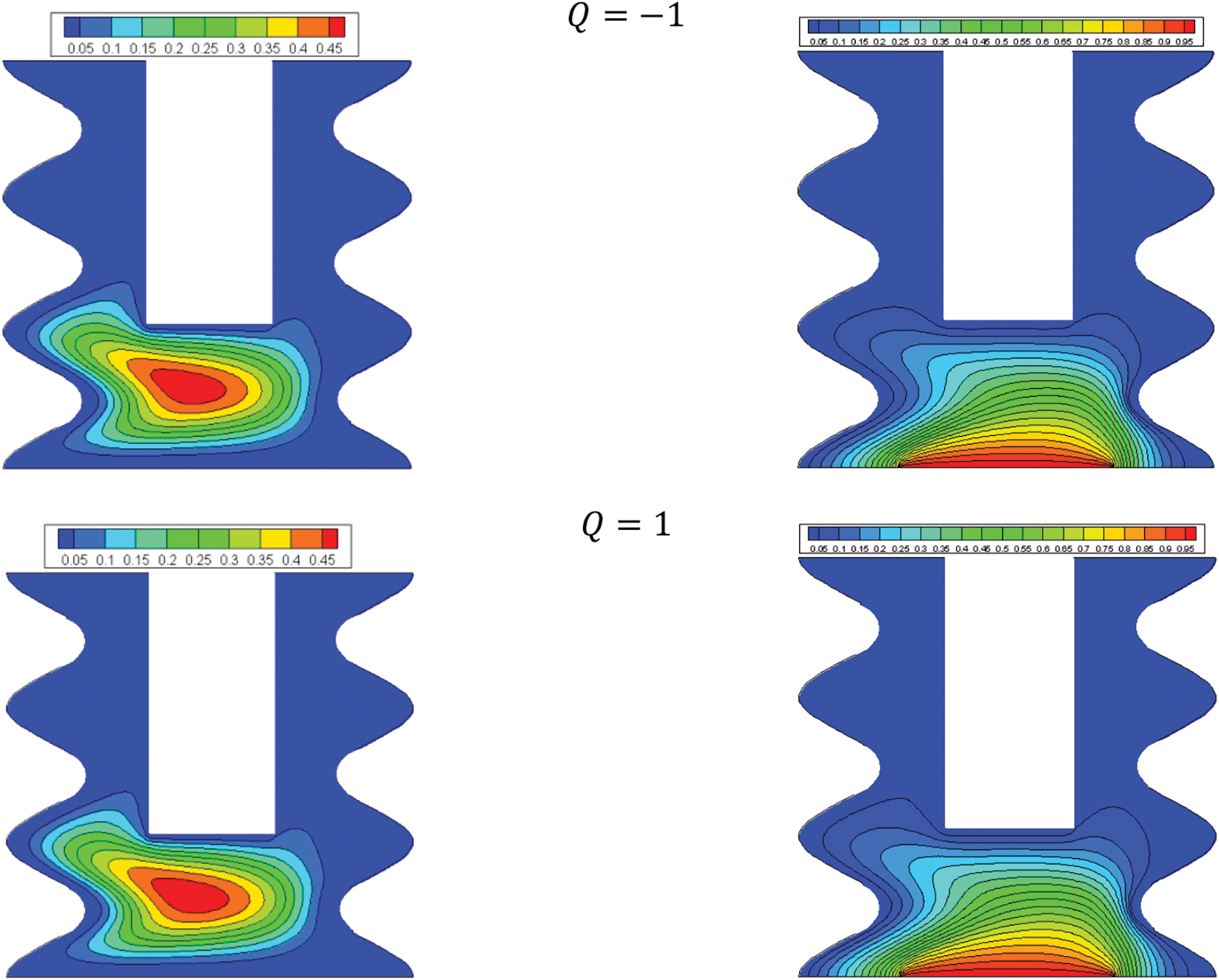
Figure 14: Effect of Q on the flow structure (left) and temperature field (right) for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
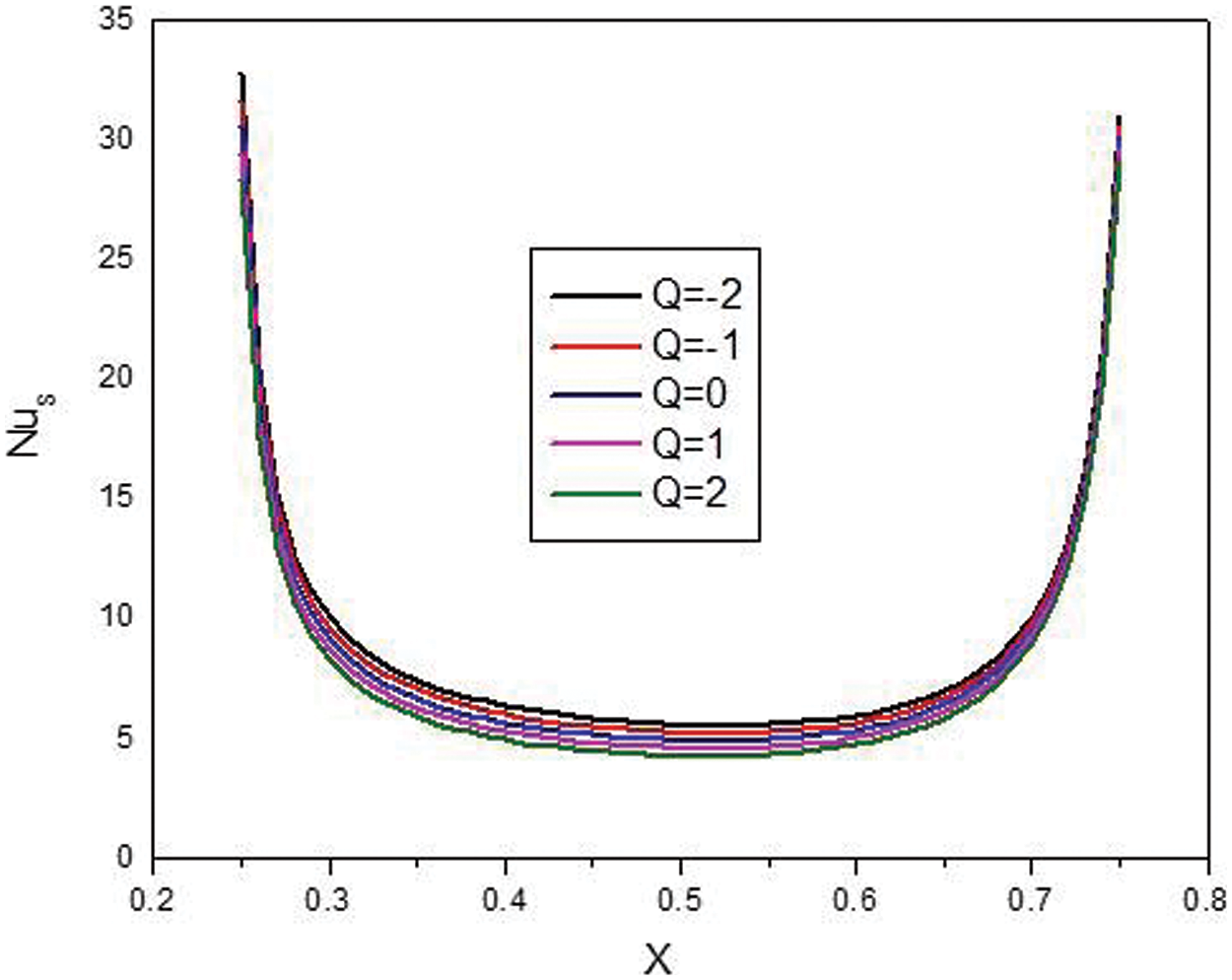
Figure 15: Effect of Q on the local Nu for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
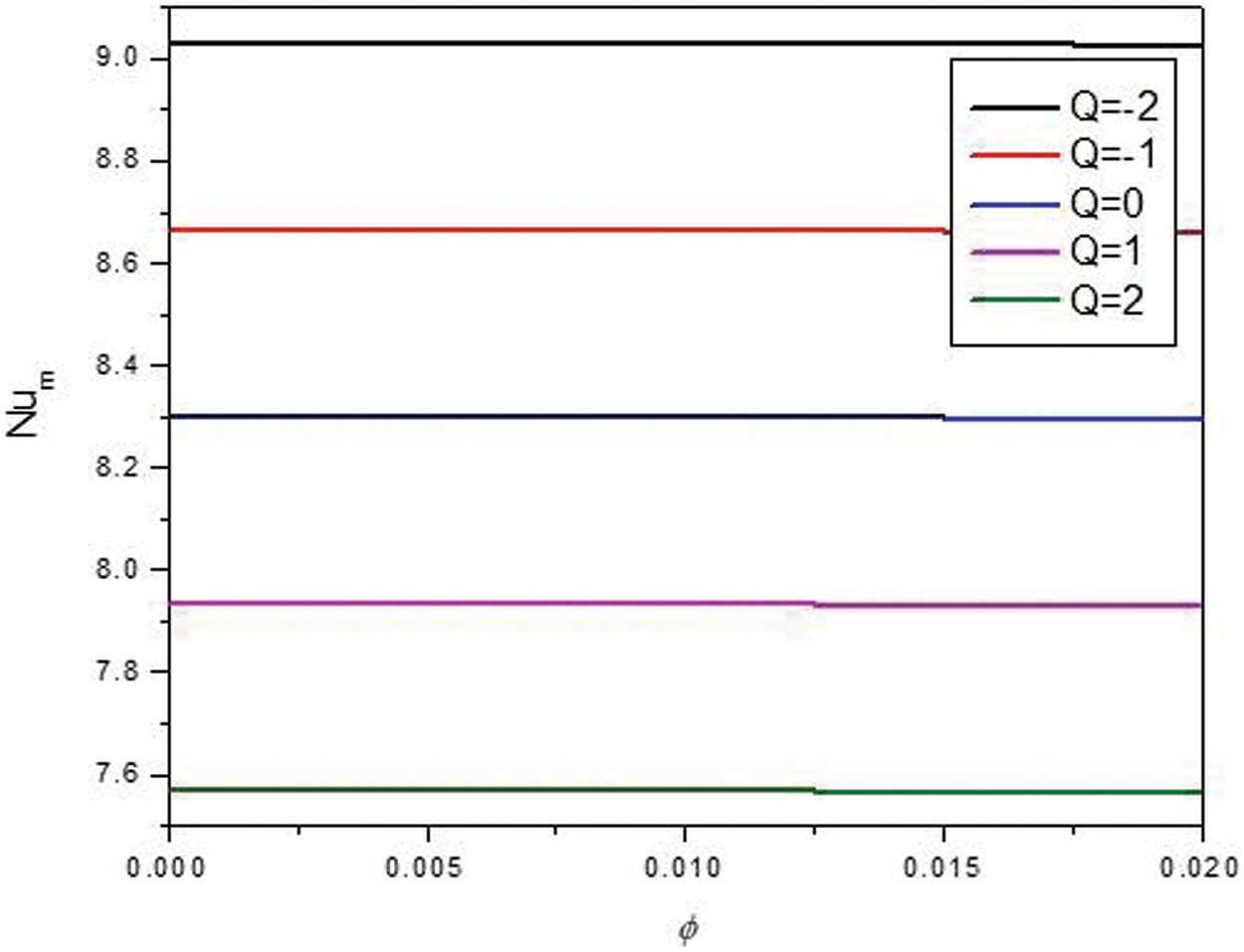
Figure 16: Effect of Q on the average Nu for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Ra = 105, Φ = 60°, φCu = φAl2O3 = φ/2
The effects of Ra on the flow and temperature fields are shown in Fig. 17. Varying Ra does not affect the significance of the streamlines. The flow pattern remains almost unchanged at different Ras. However, it affects the isotherms significance and pattern. Fig. 18 demonstrates that increasing Ra does not change the previously observed trend of the local Nu, except for Ra of 105. In this case, the local Nu is considerably higher than in the other cases, especially in the left corner. Fig. 19 shows that the average Nu is almost fixed vs. the nanoparticles volume fraction at each given Ra. However, the average Nu decreases slightly with any increase in the nanoparticle load, only at Ra of 105. A general observation is that the higher Ras yields higher average Nu.
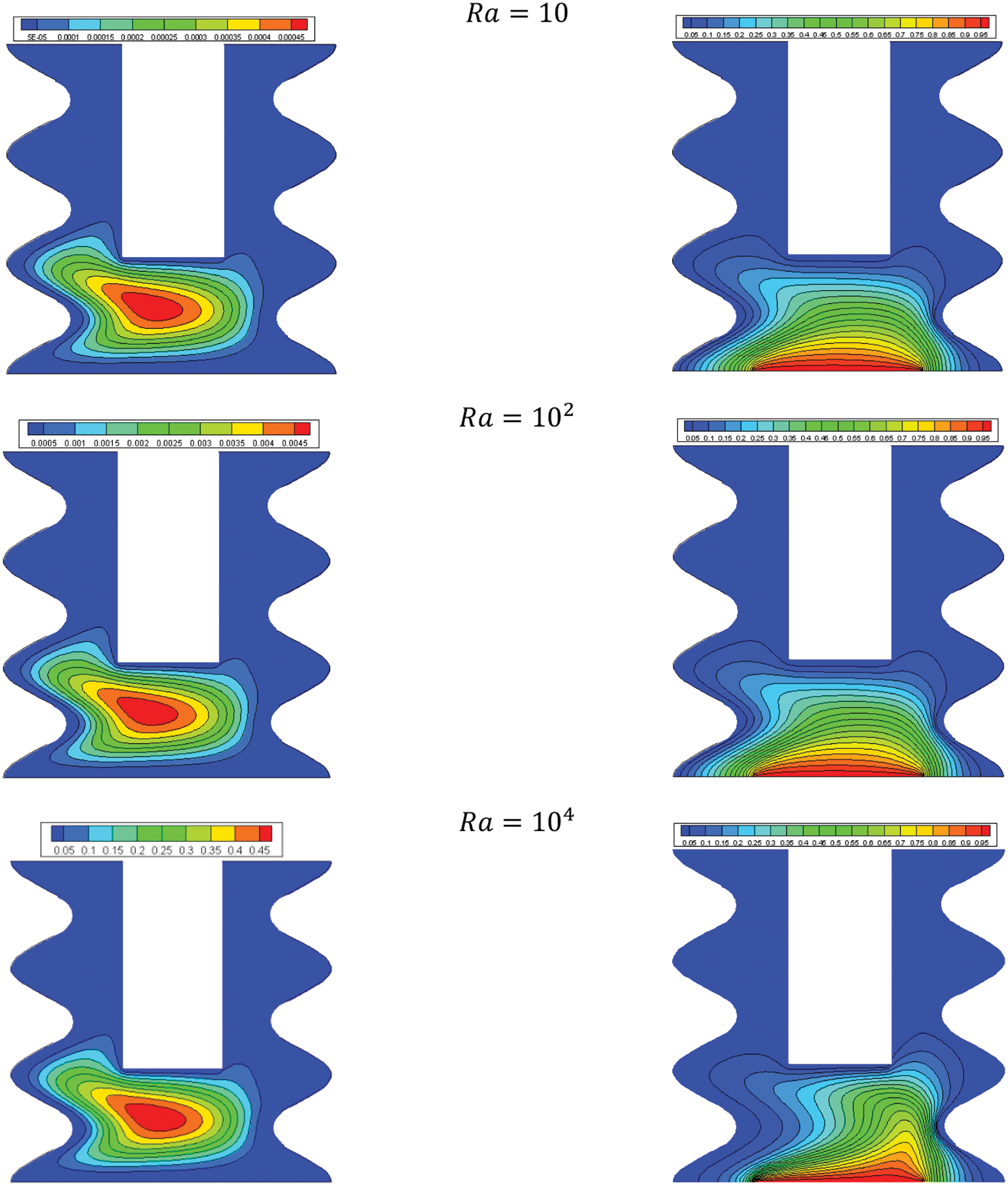
Figure 17: Effect of Ra on the flow structure (left) and temperature field (right) for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Φ = 60°, φCu = φAl2O3 = φ/2
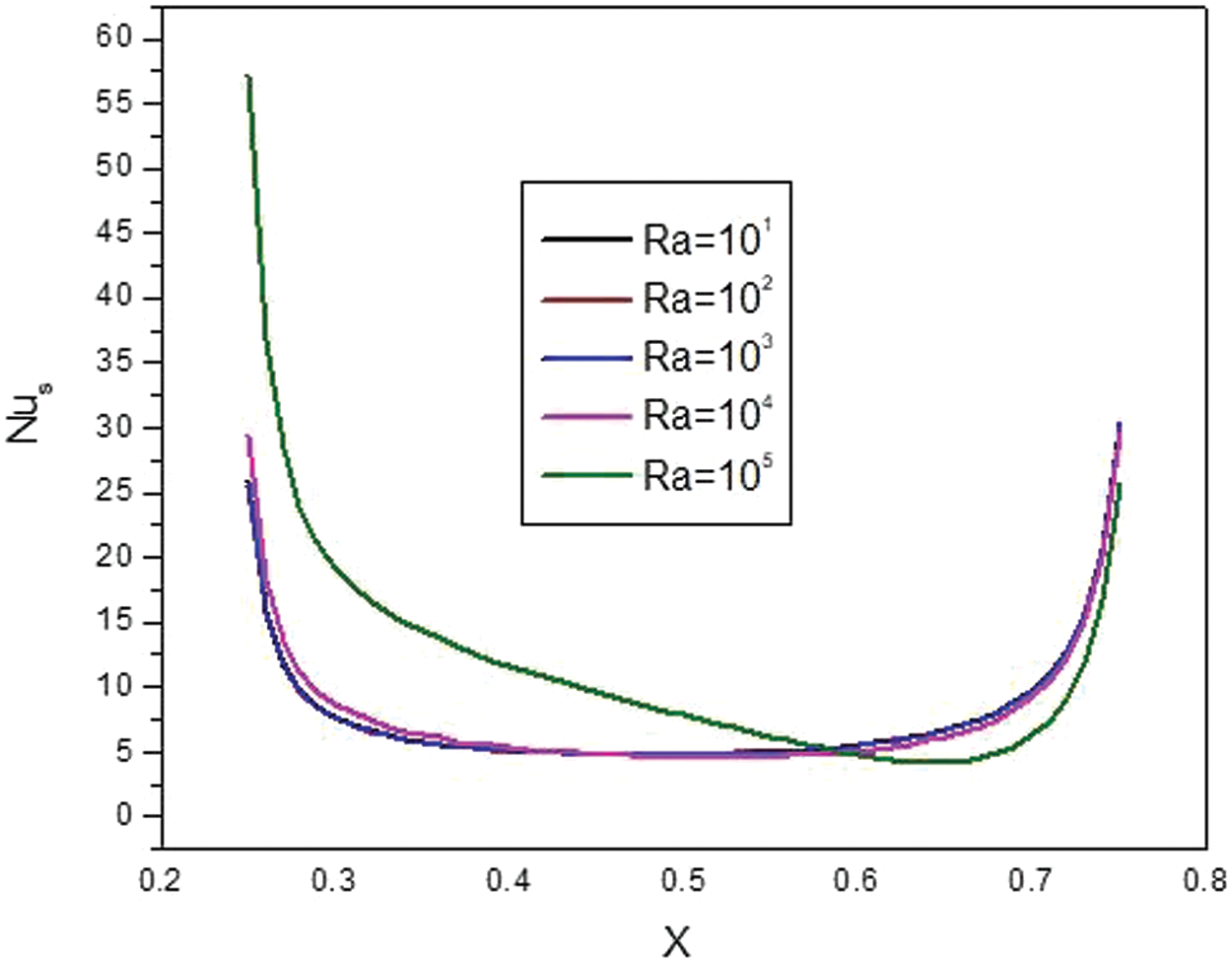
Figure 18: Effect of Ra on the local Nu for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Φ = 60°, φCu = φAl2O3 = φ/2
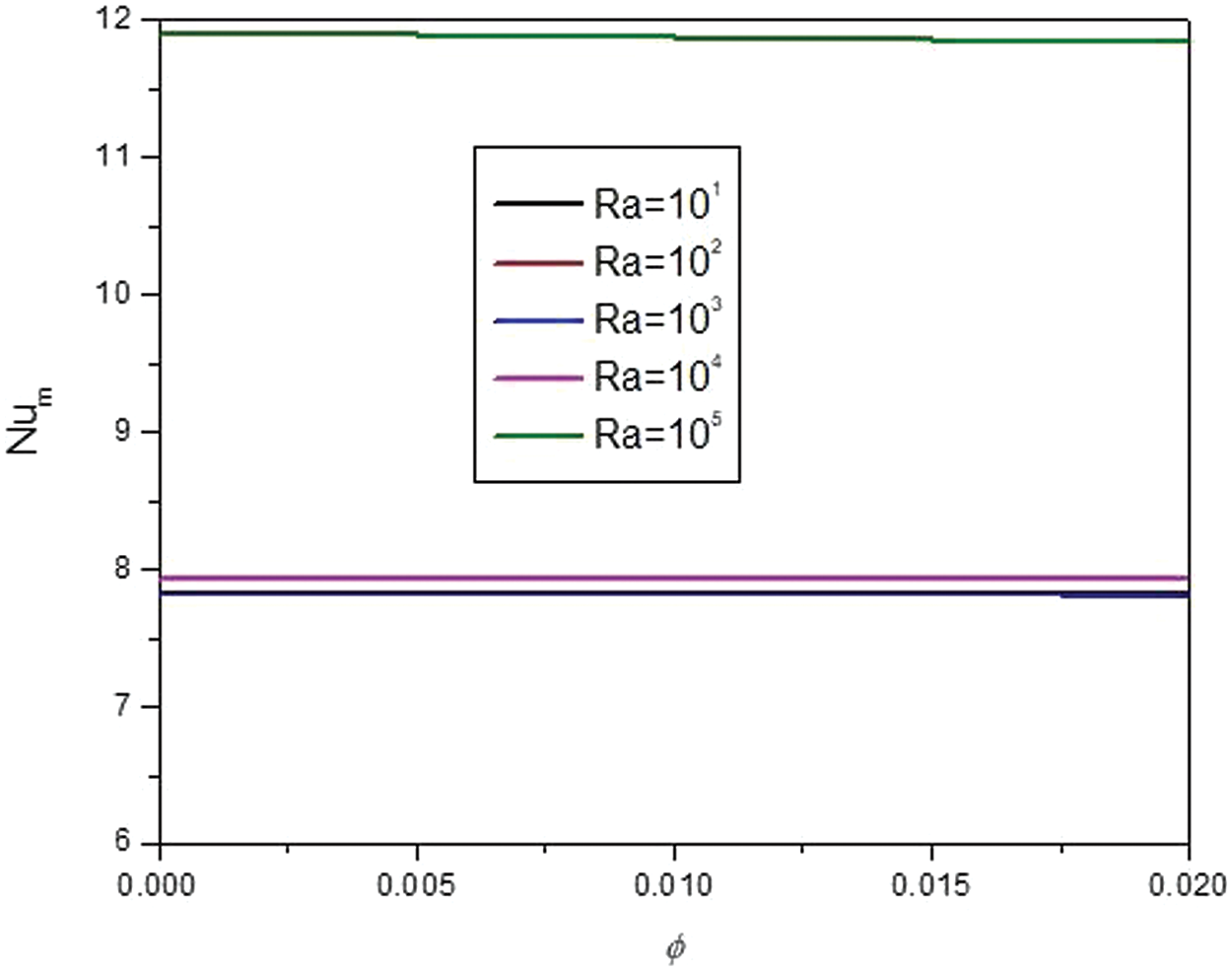
Figure 19: Effect of Ra on the average Nu for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, λ = 3, α = 45°, Φ = 60°, φCu = φAl2O3 = φ/2
Fig. 20 represents the temperature and flow fields of the hybrid nanofluid for various wavelengths of the walls. Although the streamlines’ significance is not affected heavily by changing the wavelength, the flow pattern is changed considerably. The flow pattern is elongated to the left at higher values of wavelength. The same trend was observed for the isotherms. The lower values of wavelengths, the more uniform temperature field. Fig. 21 shows a similar trend of the local Nu against the direction: the minimum value at the center and the maximum at both walls. Changing the wavelength does not change the local Nu considerably. The average Nu is almost constant with any change in the nanoparticles’ volume fraction at each given wavelength. However, a higher value of wavelength leads to a higher average Nu (see Fig. 22).
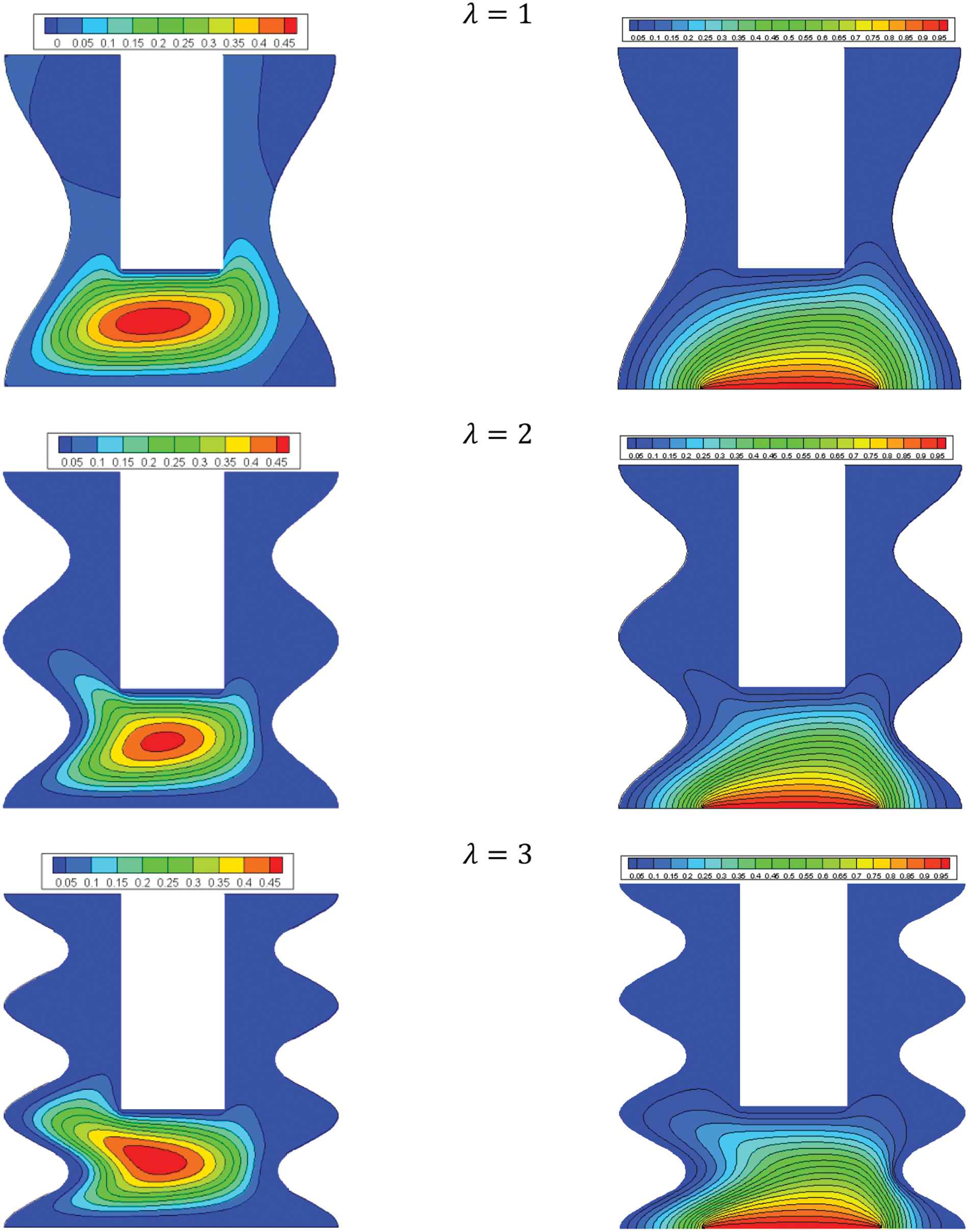
Figure 20: Effect of λ on the flow structure (left) and temperature field (right) for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, Ra = 105, α = 45° Φ = 60°, φCu = φAl2O3 = φ/2
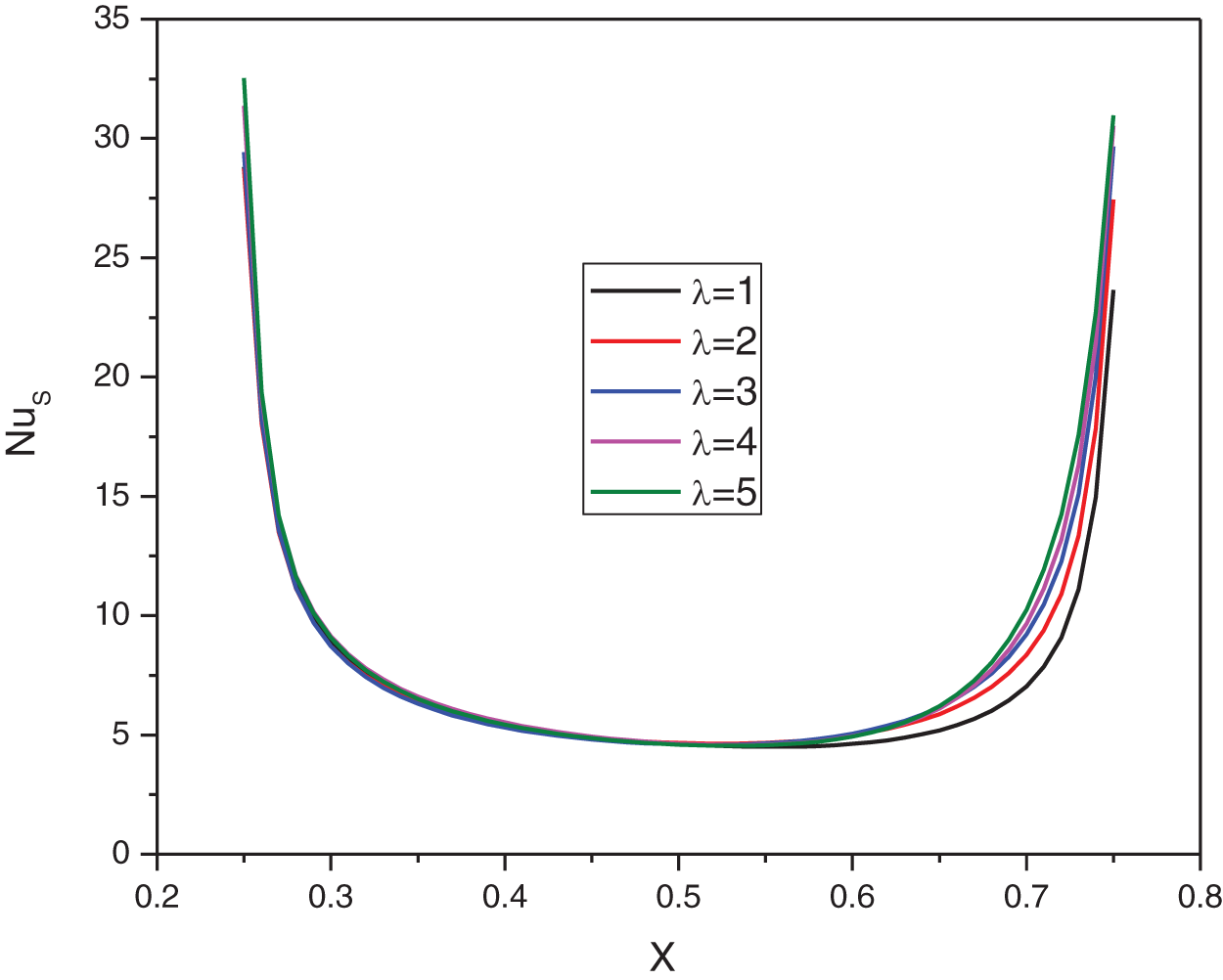
Figure 21: Effect of λ on the local Nu for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, Ra = 105, α = 45°, Φ = 60°, φCu = φAl2O3 = φ/2
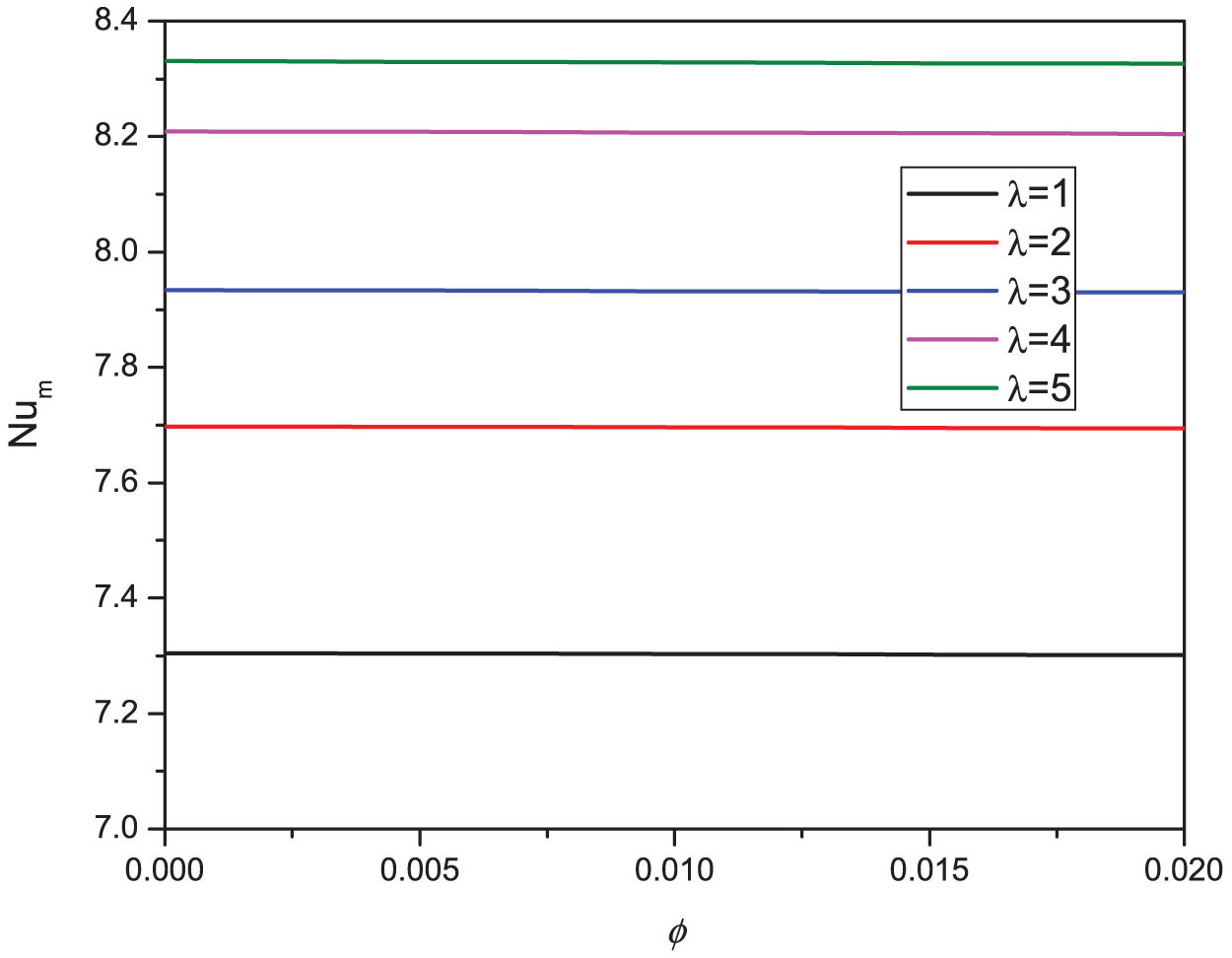
Figure 22: Effect of λ on the average Nu for: Ha = 10, φ = 0.05, B = 0.5, D = 0.5, Rd = 1, Ra = 105,α = 45°, Φ = 60°, φCu = φAl2O3 = φ/2
A series of numerical simulations were conducted in order to study the natural convection and radiation of alumina-copper/water hybrid nanofluids in a U-shaped wavy square porous cavity under a constant inclined magnetic field. The results are analyzed and provided in regard to flow structures, temperature fields, and heat transfer rates at various operational conditions by changing the wave amplitude of the wall, wall’s wavelength, Ha number, Ra number, heat source length, heat absorption/generation, and thermal radiation. The main conclusions are as follows:
– The higher amplitudes of the wall increase the significance of streamlines and reduce the significance of the isotherms.
– The higher the amplitudes, the higher average Nu.
– The streamlines are more significant by increasing the dimension less heat source length. A more uniform temperature distribution is expected with a larger heat source.
– The minimum values of the local Nu are achieved at the center of the domain (x = 0.5) for all of the studied cases, and it is increased sharply by changing the location at both directions. The sharp rise, however, occurs at the walls.
– The average Nu does not change with any change in the nanoparticles volume fraction, in most cases.
– Increasing Ha does not considerably affect the temperature fields and flow structures.
– The average Nu is heavily dependent on Ha. The higher Ha, the lower is the heat transfer.
– The flow pattern remains almost unchanged at different Ras. However, it affects the isotherms’ significance and pattern.
– A higher value of wavelength leads to a higher average Nu.
The primary limitations of this study include the assumption of a constant and inclined magnetic field and a homogeneous, isotropic porous medium, which may not fully capture real-world conditions. Our future research will address these aspects to broaden the study’s scope and relevance.
Acknowledgement: The authors extend their appreciation to Universiti Teknikal Malaysia Melaka for the research support.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2024-2505-08”.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and mathematical formulation: Taher Armaghani, Lioua Kolsi, Najiyah Safwa Khashi’ie; data collection: Taher Armaghani, Lioua Kolsi, Ahmed Muhammed Rashad, Muhammed Ahmed Mansour, Taha Salah; analysis and interpretation of results: Taher Armaghani, Lioua Kolsi, Najiyah Safwa Khashi’ie; draft manuscript preparation: Taher Armaghani, Lioua Kolsi, Najiyah Safwa Khashi’ie, Ahmed Muhammed Rashad, Aboulbaba Eladeb. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that no conflicts of interest to report regarding the present study.
References
1. Sabet Sarvestany N, Farzad A, Ebrahimnia-Bajestan E, Mir M. Effects of magnetic nanofluid fuel combustion on the performance and emission characteristics. J Dispers Sci Technol. 2014 Nov 2;35(12):1745–50. doi:10.1016/j.heliyon.2023.e21367. [Google Scholar] [CrossRef]
2. Basu S, Miglani A. Combustion and heat transfer characteristics of nanofluid fuel droplets: a short review. Int J Heat Mass Transf. 2016 May 1;96:482–503. doi:10.1016/j.ijheatmasstransfer.2016.01.053. [Google Scholar] [CrossRef]
3. Zeinali Heris S, Razbani MA, Estellé P, Mahian O. Rheological behavior of zinc-oxide nanolubricants. J Dispers Sci Technol. 2015 Aug 3;36(8):1073–9. doi:10.1080/01932691.2014.945595. [Google Scholar] [CrossRef]
4. Ghasemi SE, Vatani M, Hatami M, Ganji DD. Analytical and numerical investigation of nanoparticle effect on peristaltic fluid flow in drug delivery systems. J Mol Liq. 2016 Mar 1;215:88–97. doi:10.1016/j.molliq.2015.12.001. [Google Scholar] [CrossRef]
5. Molana M. On the nanofluids application in the automotive radiator to reach the enhanced thermal performance: a review. Am J Heat Mass Transf. 2017;4(4):168–87. doi:10.7726/ajhmt.2017.1015. [Google Scholar] [CrossRef]
6. Ghasemiasl R, Molana M, Armaghani T, Saffari Pour M. The effects of hot blocks geometry and particle migration on heat transfer and entropy generation of a novel I-shaped porous enclosure. Sustainability. 2021 Jun 26;13(13):7190. doi:10.3390/su13137190. [Google Scholar] [CrossRef]
7. Asadi A, Rafizadeh S, Molana M, Ghasemiasl R, Armaghani T. Two-phase study of nanofluids mixed convection and entropy generation in an I-shaped porous cavity with triangular hot block and different aspect ratios. Math Methods Appl Sci. 2020 Dec 10. doi:10.1002/mma.7006. [Google Scholar] [CrossRef]
8. Molana M, Wang H. A critical review on numerical study of nanorefrigerant heat transfer enhancement. Powder Technol. 2020 May 15;368:18–31. doi:10.1016/j.powtec.2020.04.044. [Google Scholar] [CrossRef]
9. Nawaz Y, Arif MS. Modified class of explicit and enhanced stability region schemes: application to mixed convection flow in a square cavity with a convective wall. Int J Numer Methods Fluids. 2021 Jun;93(6):1759–87. doi:10.1002/fld.4951. [Google Scholar] [CrossRef]
10. Cengizci S, Öztop HF, Mülayim G. Natural convection in nanofluid-filled quadrantal cavities under magnetic field: application of the SUPS formulation. Numer Heat Transfer Part B: Fundam. 2024 Jun;20:1–23. doi:10.1080/10407790.2024.2370515. [Google Scholar] [CrossRef]
11. Rashid U, Lu D, Iqbal Q. Nanoparticles impacts on natural convection nanofluid flow and heat transfer inside a square cavity with fixed a circular obstacle. Case Stud Therm Eng. 2023 Apr 1;44:102829. doi:10.1016/j.csite.2023.102829. [Google Scholar] [CrossRef]
12. Arif MS, Shatanawi W, Nawaz Y. Modified finite element study for heat and mass transfer of electrical MHD non-Newtonian boundary layer nanofluid flow. Mathematics. 2023 Feb 20;11(4):1064. doi:10.3390/math11041064. [Google Scholar] [CrossRef]
13. Hashemi-Tilehnoee M, Seyyedi SM, Del Barrio EP, Sharifpur M. Analysis of natural convection and the generation of entropy within an enclosure filled with nanofluid-packed structured pebble beds subjected to an external magnetic field and thermal radiation. J Energy Storage. 2023 Dec 20;73:109223. doi:10.1016/j.est.2023.109223. [Google Scholar] [CrossRef]
14. Thirumalaisamy K, Reddy AS. Numerical computation on MHD natural convective ternary nanofluid flow and heat transfer in a porous square cavity: marker-and-cell technique. Int J Numer Methods Heat Fluid Flow. 2023 Aug 17;33(10):3425–66. doi:10.1108/HFF-04-2023-0167. [Google Scholar] [CrossRef]
15. Khan SA, Yasmin S, Imran M, Muhammad T, Alhushaybari A, Farooq U, et al. Computational analysis of natural convection with water based nanofluid in a square cavity with partially active side walls: applications to thermal storage. J Mol Liq. 2023 Jul 15;382:122003. doi:10.1016/j.molliq.2023.122003. [Google Scholar] [CrossRef]
16. Abdel-Nour Z, Aissa A, Mebarek-Oudina F, Rashad AM, Ali HM, Sahnoun M, et al. Magnetohydrodynamic natural convection of hybrid nanofluid in a porous enclosure: numerical analysis of the entropy generation. J Therm Anal Calorim. 2020 Sep;141:1981–92. doi:10.1007/s10973-020-09690-z. [Google Scholar] [CrossRef]
17. Mliki B, Abbassi MA. Entropy generation of MHD natural convection heat transfer in a heated incinerator using hybrid-nanoliquid. Propuls Power Res. 2021 Jun 1;10(2):143–54. doi:10.1016/j.jppr.2021.01.002. [Google Scholar] [CrossRef]
18. Nabwey HA, Rashad AM, Reddy PB, Jakeer S, Mansour MA, Salah T. Radiative effects on unsteady MHD natural convection flow in an inclined wavy porous cavity using hybrid nanofluid containing a square obstacle. Alex Eng J. 2023 Feb 15;65:921–37. doi:10.1016/j.aej.2022.10.004. [Google Scholar] [CrossRef]
19. Ashorynejad HR, Shahriari A. MHD natural convection of hybrid nanofluid in an open wavy cavity. Results Phys. 2018 Jun 1;9:440–55. doi:10.1016/j.rinp.2018.02.045. [Google Scholar] [CrossRef]
20. Sajjadi H, Delouei AA, Izadi M, Mohebbi R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT-Fe3O4/water hybrid nanofluid. Int J Heat Mass Transf. 2019 Apr 1;132:1087–104. doi:10.1016/j.ijheatmasstransfer.2018.12.060. [Google Scholar] [CrossRef]
21. Ahmed SE, Mansour MA, Mahdy A. Analysis of natural convection-radiation interaction flow in a porous cavity with Al2O3-Cu water hybrid nanofluid: entropy generation. Arab J Sci Eng. 2022 Dec;47(12):15245–59. doi:10.1007/s13369-021-06495-6. [Google Scholar] [CrossRef]
22. Roy NC. MHD natural convection of a hybrid nanofluid in an enclosure with multiple heat sources. Alex Eng J. 2022 Feb 1;61(2):1679–94. doi:10.1016/j.aej.2021.06.076. [Google Scholar] [CrossRef]
23. Tayebi T, Chamkha AJ. Magnetohydrodynamic natural convection heat transfer of hybrid nanofluid in a square enclosure in the presence of a wavy circular conductive cylinder. J Therm Sci Eng Appl. 2020 Jun 1;12(3):31009. doi:10.1115/1.4044857. [Google Scholar] [CrossRef]
24. Rashad AM, Chamkha AJ, Ismael MA, Salah T. Magnetohydrodynamics natural convection in a triangular cavity filled with a Cu-Al2O3/water hybrid nanofluid with localized heating from below and internal heat generation. J Heat Transf. 2018 Jul 1;140(7):72502. doi:10.1115/1.4039213. [Google Scholar] [CrossRef]
25. Revnic C, Groşan T, Sheremet M, Pop I. Numerical simulation of MHD natural convection flow in a wavy cavity filled by a hybrid Cu-Al2O3-water nanofluid with discrete heating. Appl Math Mech. 2020 Sep;41:1345–58. doi:10.1007/s10483-020-2652-8. [Google Scholar] [CrossRef]
26. Mansour MA, Siddiqa S, Gorla RS, Rashad AM. Effects of heat source and sink on entropy generation and MHD natural convection of Al2O3-Cu/water hybrid nanofluid filled with square porous cavity. Therm Sci Eng Prog. 2018 Jun 1;6:57–71. doi:10.1063/1.4981911. [Google Scholar] [CrossRef]
27. Tayebi T, Chamkha AJ. Effects of various configurations of an inserted corrugated conductive cylinder on MHD natural convection in a hybrid nanofluid-filled square domain. J Therm Anal Calorim. 2021 Jan;143(2):1399–411. doi:10.1007/s10973-020-10206-y. [Google Scholar] [CrossRef]
28. Çiçek O, Baytaş AF, Baytaş AC. Entropy generation minimization of hybrid nanofluid mixed convection flow in lid-driven square enclosure with heat-generating porous layer on inner walls. Int J Numer Methods Heat Fluid Flow. 2024 Feb 23;34(2):629–65. doi:10.1108/HFF-05-2023-0281. [Google Scholar] [CrossRef]
29. Tayebi T, Chamkha AJ. Entropy generation analysis due to MHD natural convection flow in a cavity occupied with hybrid nanofluid and equipped with a conducting hollow cylinder. J Therm Anal Calorim. 2020 Feb;139(3):2165–79. doi:10.1007/s10973-019-08651-5. [Google Scholar] [CrossRef]
30. Amine BM, Redouane F, Mourad L, Jamshed W, Eid MR, Al-Kouz W. Magnetohydrodynamics natural convection of a triangular cavity involving Ag-MgO/water hybrid nanofluid and provided with rotating circular barrier and a quarter circular porous medium at its right-angled corner. Arab J Sci Eng. 2021 Dec;46(12):12573–97. doi:10.1007/s13369-021-06015-6. [Google Scholar] [CrossRef]
31. Alomari MA, Al-Farhany K, Hashem AL, Al-Dawody MF, Redouane F, Olayemi OA. Numerical study of MHD natural convection in trapezoidal enclosure filled with (50% MgO-50% Ag/Water) hybrid nanofluid: heated sinusoidal from below. Int J Heat Technol. 2021 Aug 1;39(4):1271–9. doi:10.18280/ijht.390425. [Google Scholar] [CrossRef]
32. Solyaev YO, Lurie SA, Semenov NA. Generalized Einstein’s and Brinkman’s solutions for the effective viscosity of nanofluids. J Appl Phys. 2020 Jul 21;128(3):035102. doi:10.1063/5.0014288. [Google Scholar] [CrossRef]
33. Xuan Y, Roetzel W. Conceptions for heat transfer correlation of nanofluids. Int J Heat Mass Transf. 2000 Oct 1;43(19):3701–7. doi:10.1016/S0017-9310(99)00369-5. [Google Scholar] [CrossRef]
34. Maxwell JC. A treatise on electricity and magnetism. Nature. 1873;7(182):478–480. doi:10.1038/007478a0. [Google Scholar] [CrossRef]
35. Ghasemi B, Aminossadati SM. Mixed convection in a lid-driven triangular enclosure filled with nanofluids. Int Commun Heat Mass Transf. 2010 Oct 1;37(8):1142–8. doi:10.1016/j.icheatmasstransfer.2010.06.020. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
