Transient Thermal Distribution in a Wavy Fin Using Finite Difference Approximation Based Physics Informed Neural Network

Nomenclature

1  Introduction

Thermal engineering is the study of the creation, conversion, and exchange of heat between physical systems. Advanced electrical devices often overcome significant thermal obstacles caused by high heat generation or reduced surface area for heat dissipation. Therefore, it is necessary to employ heat transfer augmentation strategies. Heat transfer improvement technologies primarily aim to boost heat transmission while reducing the size of equipment. Heat augmentation techniques are utilised in many industrial processes, such as regulating temperature in evaporators, thermal power plants, and air conditioning units. The advancement of electronic part incorporation and the future improvement of the energy and miniaturisation level of microelectronic components are both governed by the need for high-power dissipation. As a result, heat transfer surfaces are frequently utilised in various engineering sectors, notably tube heat exchangers, and nuclear technologies. In the study of heat transfer, fins are surfaces extending from an object to develop the heat transfer rate from its surface to the environment. Several researchers studied heat transfer in extended surfaces with the consideration of different conditions. Sarwe et al. [1] studied the thermal characteristics of the annular convective fin using a semi-numerical scheme. Das et al. [2] estimated the heat generation and effect of magnetic response in a permeable fin using the inverse methodology. Goud et al. [3] debriefed temperature variance in a dovetail fin wetted with ternary hybrid nanofluid. The heat transmission in convective-radiative longitudinal fin with heat source was elaborated by Gouran et al. [4] using the least square method. Abdulrahman et al. [5] studied the temperature variance in permeable fin wetted with nanofluid using the power series method. Many researchers studied the unsteady heat transfer and convective mechanism of different profiled fins [6–9].

Heat transmission by convection is also crucial in cases where the convective heat transfer coefficient plays a crucial role and cannot be ignored [10–14]. The best approach to enhance the performance of fin-and-tube heat exchangers is to optimise the air-side fin design and increase heat transmission. This is due to the fact that the air side of such heat exchangers experiences the majority of the resistance to thermal energy. The usual approach to improving air-side heat transfer is to utilise wavy or slot fins. There have been numerous research studies on the efficiency of wavy fin-and-tube heat exchangers for air-side heat transfer. Using novel compound designs, Sadeghianjahromi et al. [15] researched strategies to increase heat transmission in wavy fin-and-tube heat exchangers. The heat transport in a heat exchanger with wavy fins in a sand-dust environment was studied by Miao et al. [16]. A plate-fin heat exchanger with a wavy fin was the subject of substantial performance and optimisation conducted by Cui et al. [17]. The numerical simulation was conducted by Okon et al. [18] to study the thermal variation in a wavy-designed fin arrangement for a straight fin array. Using numerical simulation, Xu et al. [19] investigated the heat transfer characteristics of wavy fins in plate-fin heat exchangers for hydrogen liquefaction. The neural network (NN) has emerged as one of the artificial intelligence methods evoked by the human brain conception for rendering computers and machines resemble human beings. A NN comprises several neurons connected by the necessary number of linkages. Neural network layouts can vary depending on the type of neuron or how the neurons are interconnected. It is more sophisticated and advantageous than traditional regression and statistical procedures and can simulate complicated correlations without prior assumptions. Numerous problems involving classification, regression, and general estimation can be resolved with NN [20–24].

Physics-informed neural networks (PINNs) are a specific sort of neural network architecture that uses independent data such as position and time as input to accurately predict dependent field variables, such as temperature, in this particular case. The core of the system is founded around the neural networks’ capacity to approximate universal functions, were explained by Hornik et al. [25]. By employing automated differentiation, it is feasible to calculate the loss associated with the governing equations effectively, as illustrated by Baydin et al. [26]. PINNs have the capability to reduce the overall loss by evaluating it at specific locations within the domain, known as sparse collocation points, without the need for meshes. The mathematical expression of PINNs in its most comprehensive form combines a cost function that efficiently incorporates prior knowledge of the underlying physics. Like any other neural network model, PINN has the ability to precisely reproduce the underlying phenomena and, at the same time, reduce the cost. In this analysis, the Limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method by Liu et al. [27] minimized the cost function. The L-BFGS algorithm is a part of the Quasi-Newton techniques family and is a gradient-based second-order optimisation algorithm. Wang et al. [28] addressed various forward and inverse problems that involve partial differential equations (PDEs) but are limited in the understanding of how these constrained neural networks function during training using gradient descent. Parisi et al. [29] proposed an unsupervised neural network for a chemical engineering fixed-bed solid-gas reactor. Like Runge-Kutta, the neural network delivered solutions throughout the integration domain with low error. Raissi et al. [30] used data to study nonlinear PDEs. The brain networks obey physical principles in which data-efficient discrete and continuous time models approximate spatiotemporal functions. These methods enable perfect implicit Runge-Kutta time-stepping using data. Li et al. [31] estimated Fanning friction and Nusselt numbers using completely connected layers to transform spatial coordinates and design parameters into physical fields. Conservation rules are more loss function interpretable and mesh construction flexible than convolutional neural network models. Merdasi et al. [32] examined pressure-driven microchannel mixed electroosmotic flow using PINN.

The wavy fin was identified as one of the modified fins often utilised in many industrial purposes owing to its efficient heat transmission and pressure-dropping capabilities, alongside its resistivity to dust adherence, especially in a rigorous working situation. The wavy-structured fin surface can enhance the heat exchangers’ operational efficiency. However, the study of thermal dissipation in the wavy fin is rarely investigated, leading the current study to investigate heat transfer analysis in the convective wavy fin. Even though designs for apparatus with extended surfaces depend on steady-state analysis and are appropriate for many applications, consideration of the transient behaviour is sometimes essential. The unsteady response of fins is crucial in a variety of advanced devices, including heat exchangers, automatic control equipment, and motors. So, investigating the unsteady heat transmission within a wavy fin under the convective influence is the main objective of this scrutiny. Furthermore, the finite difference method integrated with physics informed neural network (FDM-PINN) strategy has been adopted to discuss the thermal model of the transient wavy fin. The governing PDE is converted into dimensionless form via non-dimensional variables and solved numerically using the finite difference scheme. Moreover, the numerically obtained FDM results are compared against novel FDM-PINN outcomes using graphical illustrations to analyze the effectiveness of the data-independent neural network technique. The results indicate that the data-independent FDM-PINN outcomes can capture the intricate nature of the current problem effectively compared to numerical results. The versatility of the proposed PINN model is observed to be an efficient procedure for studying the heat transfer behaviour of wavy fins.

2  Mathematical Formulation

Consider a wavy fin of width w and height 2H as revealed in Fig. 1. The time-dependent thermal variation in a wavy-shaped rectangular fin is studied in this work with the surface heat dissipation to the surrounding temperature Tamb. The wavy fin’s base is maintained at temperature Tb and the fin is of a wavy structure along the ⌢x-axis. In this scrutiny, convective heat transfer analysis is carried out in a wavy fin, which is associated with the convective heat transfer coefficient ⌢h(T) and can be denoted as

h⌢(T)=hb(T−TambTb−Tamb)m.(1)

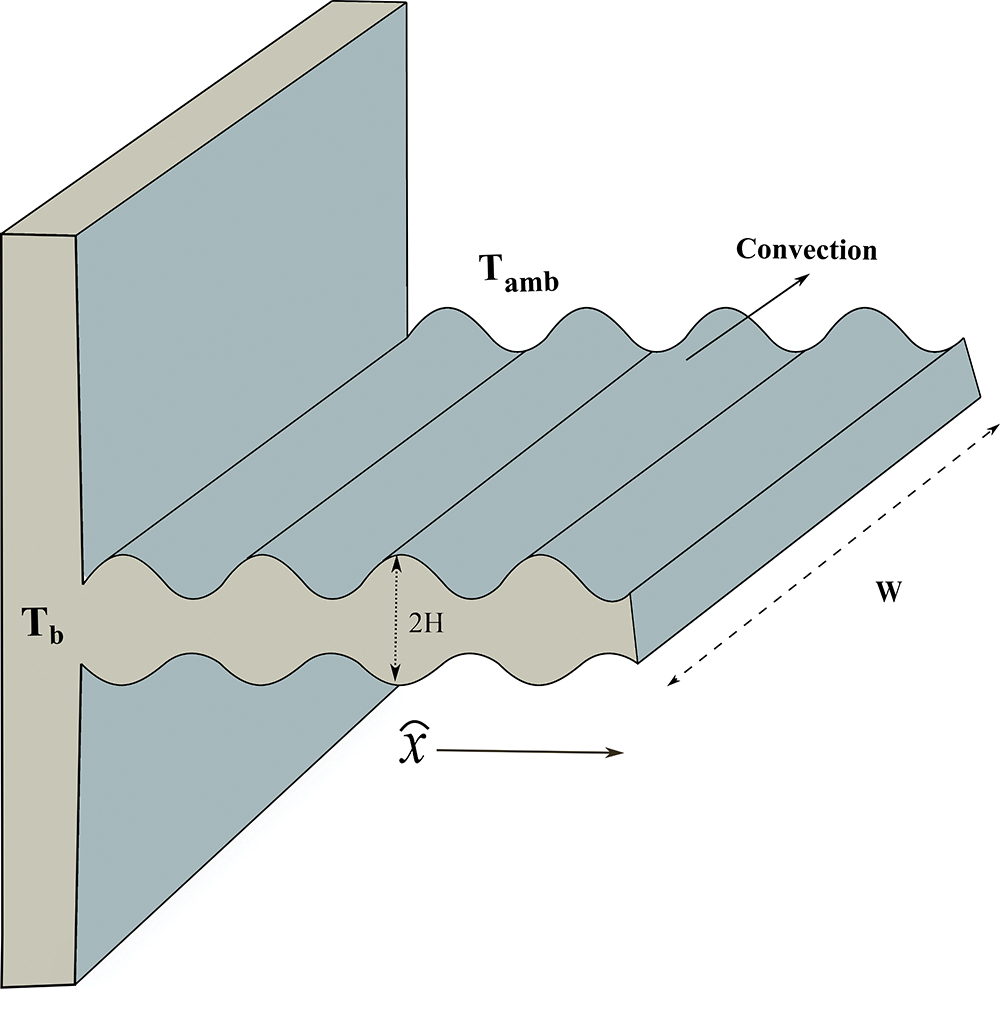
Figure 1: Physical model of a wavy fin

In addition, thermal conductivity may be linearly related to temperature in many engineering applications and is given as

k⌢(T)=ka{1+Υ(T−Tamb)}.(2)

The unsteady energy equation for the wavy fin losing heat by convection can be stated as (see [6] and [33]):

ρcp∂T∂τ⌢=∂∂x⌢[k⌢(T)∂T∂x⌢]−[∂Sarea∂x⌢]h⌢(T)Carea(T−Tamb)+[k⌢(T)Carea∂Carea∂x⌢]∂T∂x⌢.(3)

The corresponding initial condition and boundary condition (IC and BC) are specified as follows:

T=0 at τ⌢=0, x⌢>0,

T=Tb at x⌢=0, τ⌢>0,

∂T∂x⌢=0 at x⌢=L,τ⌢>0.(4)

The cross-sectional area is given by

Carea=2H0∫0w{1+δsin⁡[2πn(x⌢L)+φ]}dz.(5)

and

H=H0{1+δsin⁡[2πn(x⌢L)+φ]}.(6)

Also, the fin surface area is presented by

Sarea=2w∫0L1+(dHdx⌢)2dx⌢.(7)

From Eqs. (1) and (2), Eq. (3) can be expressed as

ρcp∂T∂τ⌢=∂∂x⌢[ka{1+Υ(T−Tamb)}∂T∂x⌢]−[∂Sarea∂x⌢]hb(T−Tamb)m+1Carea(Tb−Tamb)m+ka{1+Υ(T−Tamb)}∂T∂x⌢[1Carea∂Carea∂x⌢].(8)

For solving the corresponding heat equation numerically, Eq. (8) is required to be non-dimensional. The subsequent non-dimensional variables are provided in this context:

X=x⌢L,τ∗=kaτ⌢ρcpL2,Θ=T−TambTb−Tamb,β=Υ(Tb−Tamb),Nc=hbL2kaH0,arL=H0L.(9)

By using the above non-dimensional variables, the Eq. (8) will be transformed to

∂Θ∂τ∗=∂∂X[{(1+βΘ)}∂Θ∂X]+(1+βΘ)[2πδncos⁡(2πnX+φ)1+δsin⁡(2πnX+φ)]∂Θ∂X−Nc[1+4(πarLδn)2cos2⁡(2πnX+φ)1+δsin⁡(2πnX)]Θm+1=0,(10)

and the modified IC and BC are

Θ=0 at τ∗=0, X>0,

Θ=1 at X=0,τ∗>0,

∂Θ∂X=0 at X=1, τ∗>0.(11)

The above equations are numerically solved using FDM, and the FDM results are used for comparison purposes to check the reliability of the FDM-PINN. Thus, the FDM procedure described in [34,35] is avoided here. In FDM, computational approximations commonly incorporate basic arithmetic operations on adjacent grid points. This is computationally simpler and more robust than approaches that might involve solving large, complicated equations or executing sophisticated integrations.

3  Physics-Informed Neural Network-Integrated with Finite Difference Method

In designing physics-guided networks, automatic differentiation is an essential technique that significantly facilitates the computation of residuals for the loss term. This is accomplished by processing derivatives of outputs concerning inputs. This strategy eliminates the requirement for a manual back-propagation rule because the chain rule is utilised in solving derivatives. To compute derivatives across space-time orders, contemporary deep learning systems readily include automated differentiation as an alternative to complicated derivations or numerical discretisation. This section concisely explains the governing equations and loss functions that act as inputs for PINN training specific to the current study. Integrating PINN with the FDM provides a novel approach for solving PDEs. This method combines the computational efficiency of FDM with the data-independent capabilities of PINN. PDEs are discretised, and the applications of finite difference approximations and scaling to high-dimensional problems are used to estimate the derivatives. The PINNs can learn the underlying physics from the PDEs and use neural networks to impose on the differential equation. They are adaptive and have the ability to adjust to high-dimensional problems. In addition, incorporating physics-based restrictions from FDM into the construction of the PINN, a hybrid technique, improves the neural network’s interpretability and generalisation capabilities. This hybrid technique offers opportunities to increase scalability, accuracy, and efficiency for handling real-world issues by combining machine learning and numerical methodologies. The combination of these two methodologies may achieve the stated improvements. The non-dimensional heat equation for a wavy fin with a convective effect from Eq. (10) is considered for the PINN training, and Fig. 2 gives a schematic illustration of the FDM-PINN framework.

EqFDM−PINN=Θi,j+1−Θi,jΔτ∗−β(Θi+1,j−Θi−1,j2ΔX)2−{(1+βΘi,j)}Θi+1,j−2Θi,j+Θi−1,jΔX2−(1+βΘi,j)[2πδncos⁡(2πnX+φ)1+δsin⁡(2πnX+φ)]Θi+1,j−Θi−1,j2ΔX+Nc[1+4(πarLδn)2cos2⁡(2πnX+φ)1+δsin⁡(2πnX)]Θi,jm+1(12)

LossEq=1N r∑j=1N r‖EqFDM−PINN(Xjr,τ∗jr)‖2.(13)

Loss0a=1N a∑j=1N a‖Θη(Xj0,τj∗0)−Θ0a(Xj0)‖2.(14)

Lossb1=1N b1∑j=1N b1‖Θη(Xjb1,τj∗b1)−Θb1(Xjb1,τj∗b1)‖2Lossb2=1N b2∑j=1N b2‖∂XΘη(Xjb2,τj∗b2)−Θb2(Xjb2,τj∗b2)‖2.(15)

Losstotal=LossEq+Loss0a+Lossb1+Lossb2.(16)

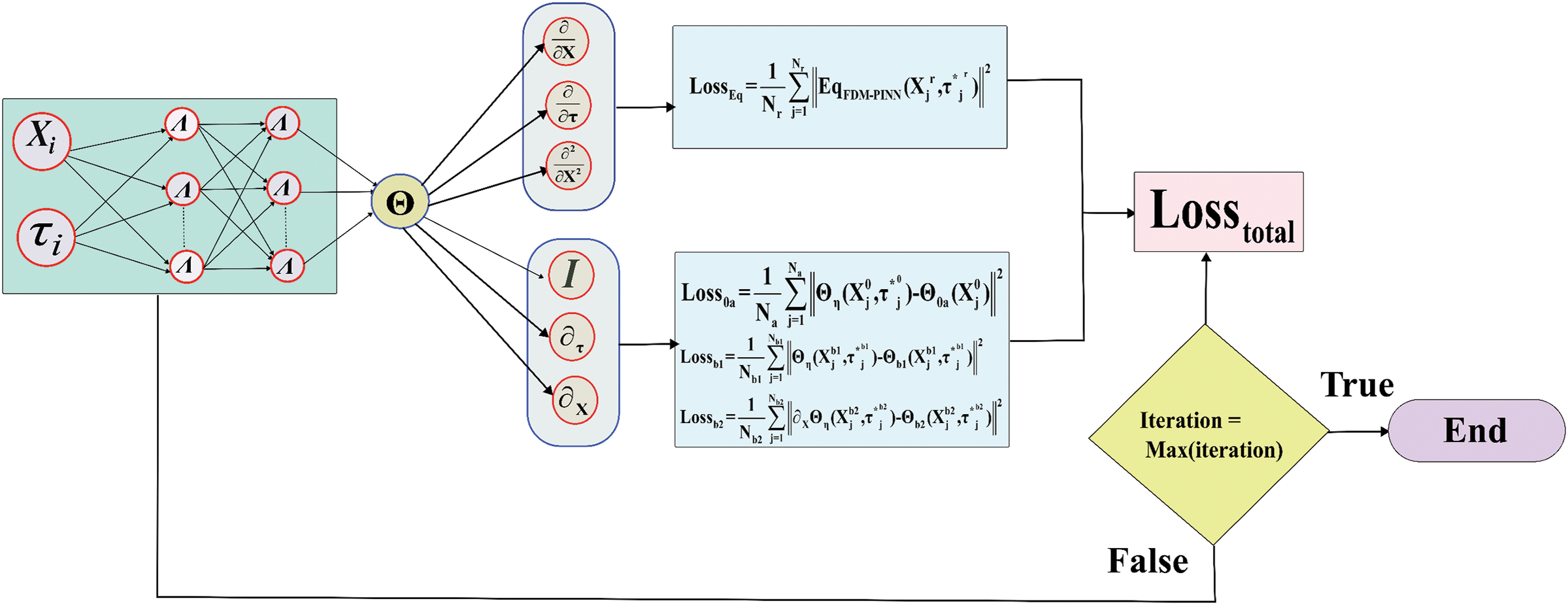
Figure 2: Pictorial design of applied FDM-PINN

The finite discretisation of the heat transfer equation is represented by Eq. (12), and the losses for the conditions are calculated using Eqs. (13)–(16). The working algorithm for the proposed method is given as below:

Step 1: Build the PINN model using a fully connected neural network architecture.

Step 2: Choose the collocation points inside the domain and generate the background mesh.

Step 3: Rearrange the governing equations into equations with finite differences that are appropriate for the implementation.

Step 4: The finite difference loss term will indicate the difference between the computed and real values based on the discretised equations.

Step 5: Choose the boundary condition points on the domain randomly.

Step 6: Define the boundary loss term, which takes into account the difference between the model’s predictions and the observed boundary conditions.

Step 7: Define the model’s parameters, including the weights and biases of the neural network.

Step 8: Adjust the network’s parameters using G gradient descent iterations.

Step 9: To efficiently change the model parameters to reduce the loss function and to update the parameters for each iteration (g = 1 to G), use optimisation techniques like Adam and L-BFGS.

Step 10: As the best-fit solution discovered throughout the iterative optimisation process, return the optimised settings.

Comprehensive information is provided regarding the model’s network architecture and training procedure by utilising deep neural networks (DNNs) to automatically differentiate and approximate functional relationships. Using the loss function, the PINN model offers a physically robust framework for predicting periodic heat transport in wavy fin structures. Although the framework offers a viable method of simulating both linear and nonlinear PDEs, it is important to note that implementing these models requires carefully modifying critical hyperparameters during the first training cycle. The model’s loss function, in contrast to techniques that are only driven by data, incisively combines the capabilities of DNN with physical constraints. This significantly improves the model’s ability to adhere to the physical constraints that govern heat transport behaviour and reduces the challenges associated with limited data availability. The learning rate is crucial in optimising the progress based on the total number of training epochs. The number of neurons in the hidden layers is a crucial determinant of the model’s ability to recognize intricate patterns in the input accurately. Regularisation affects dropout rates and regularisation weight, decreasing overfitting by either penalising complex models or randomly eliminating connections during training. Additionally, the convergence and performance of the model are significantly impacted by the total number of training epochs allotted to the dataset analysis. Iterative testing and validation using a range of datasets are frequently performed to find the optimal values for these hyperparameters. This study uses a four-layered network with 500 neurons per layer, a learning rate of 1E−08, and 100,000 training epochs to solve the heat equation using a self-updating weights and bias technique. To obtain the optimal output values, various optimisers are investigated, including gradient descent, Adam, and L-BFGS. L-BFGS shows faster convergence with less iterations than Adam. However, when L-BFGS alone is insufficient to achieve convergence, a combination of L-BFGS and Adam is required due to the vulnerability to local minima with high instability, ascribed to second-order derivatives in the loss function. In order to successfully mitigate loss, a combination of L-BFGS and Adam is used in this study after a predefined number of loops. Also, the proposed FDM-PINN has several advantages compared to traditional FDM, such as:

•   Traditional FDM requires time steps and grid spacing to avoid numerical diffusion and instability. Whereas, the FDM-PINN’s can estimate the solution smoothly even with coarse discretisation reducing numerical instability and strengthening solutions.

•   FDM-PINN uses collocation points to discretise but instead requires less grid fineness than standard FDM. As the neural network in FDM-PINN learns the physical principles to interpolate and approximate the solution, the grid points are less significant since the network may reflect the solution’s behaviour with fewer discretisation points.

•   By choosing regions with quick solution changes, FDM-PINN optimises processing resources. Instead of increasing grid density everywhere, like FDM, FDM-PINN can focus collocation points or training on critical areas while keeping a coarser grid in less sensitive areas. This flexibility reduces discretisation without compromising precision.

4  Validation of FDM-PINN Results

This section examines the verification of the FDM-PINN’s computational results under different conditions. For this purpose, the results are displayed in tables and graphical form.

Table 1 presents the validation of FDM-PINN results against numerical outcomes at different time instants represented by τ∗=0.5 and τ∗=0.8 for Nc=2. The table compares the numerical values with those obtained from FDM-based PINN predictions, showcasing the absolute error between the two, where each row corresponds to a different spatial location. The numerical column represents the reference values obtained through the numerical technique, and the FDM-PINN column displays the predictions generated by the deep learning model. The absolute error column quantifies the discrepancy between the numerical and FDM-PINN results, notably the absolute errors for all spatial locations are relatively small indicating a high level of agreement between the FDM-PINN predictions and the numerical results. This validation underscores the efficacy of the PINN approach in accurately capturing the underlying physics and providing reliable predictions, demonstrating its potential as a valuable tool for solving complex scientific and engineering problems.

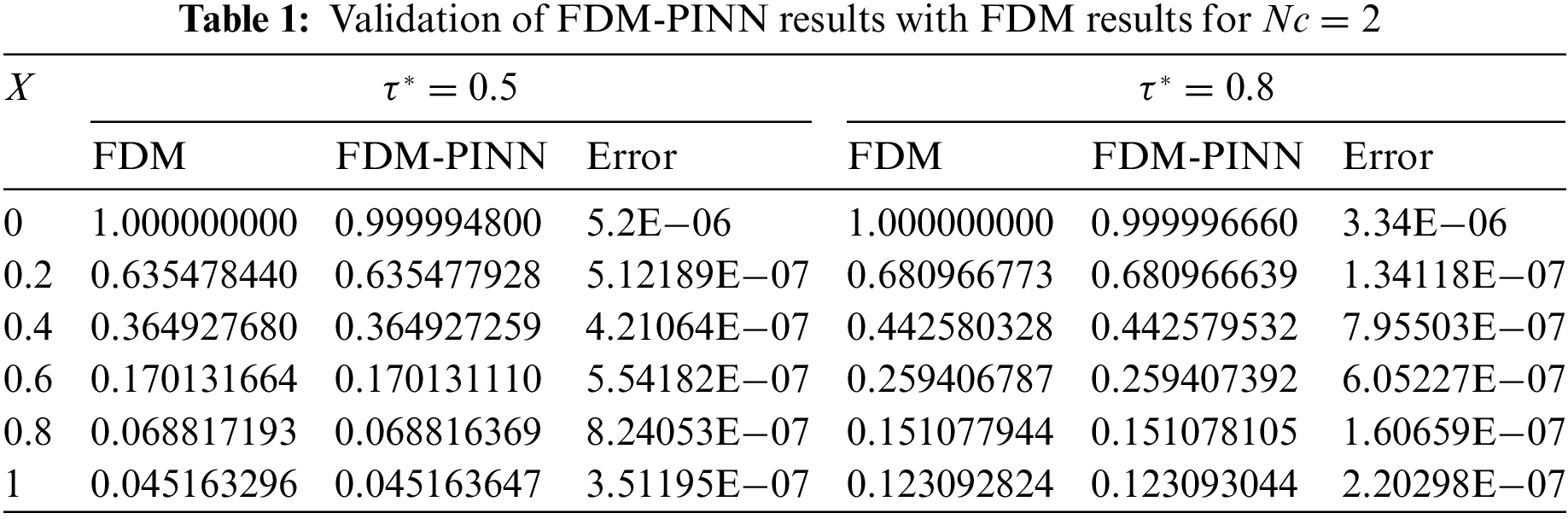
Table 2 presents a comparative analysis between FDM and FDM-PINN solutions, focusing on their performance when β=0.5 at time instance τ∗=0.5 and τ∗=0.8 and compares the predictions at various X positions. Each model’s prediction is accompanied by its corresponding absolute error, measuring the difference between the model’s output and the numerical values. Notably, the results highlight the excellent correlation of FDM-PINN with FDM by generating minimal errors. Both achieve consistently lower absolute errors across all spatial locations. However, this observation underscores the efficacy of FDM-PINN as a robust and reliable approach for solving unsteady heat transfer problem.

Table 3 provides a comprehensive illustration of traditional FDM and FDM-PINN outcomes, by comparing the results with the published work of Khaled [33]. The computational values of Θ(1) are listed in the table for different values of Nc and the significance of the considered methods are assessed by providing the absolute error results. In precise, the absolute error produced by comparing the results of [33] and FDM is indicated by ErrorFDM whereas ErrorFDM−PINN denotes the absolute error between [33] and FDM-PINN outcomes. It can be observed that both methodologies display minimal absolute error rates, representing good agreement with the reference values. FDM-PINN’s neural network is trained to understand the fundamental physical rules controlling the problem, therefore enabling it to interpolate and approximatively estimate the response more freely throughout the whole domain. The network can capture the behaviour of the solution even with fewer discretisation points, hence reducing the reliance on the number of grid points. By efficiently generalising the solution over the domain, the network lowers the necessity for significant discretisation. By allowing FDM-PINN to dynamically concentrate on regions of interest where the solution changes rapidly, allowing for more effective use of computing resources becomes feasible. FDM requires the grid density to be consistently increasing across, whereas the FDM-PINN can devote additional collocation points or training emphasis on critical areas while maintaining a coarser grid in less sensitive regions. Although it still employs some discretisation through collocation points, the FDM-PINN method lacks the fine grid necessary in conventional FDM. This flexibility lowers the total discretisation need while yet maintaining great accuracy. Thus, FDM requires more extensive discretization to achieve accurate results because it depends heavily on the density of the grid and time steps. In contrast, FDM-PINN reduces this requirement by leveraging the neural network’s ability to learn and generalize the solution across the domain, making it a more efficient method for solving complex thermal distribution problems with fewer discretization points. FDM-PINN indeed involves hyperparameter tuning, which can consume additional time. However, this investment should be weighed against the long-term benefits of the model. For instance, once the hyperparameters are optimized, the FDM-PINN model can be applied to a wide range of similar problems with minimal additional tuning.

In scenarios where data independence and physics-informed constraints play a crucial role by incorporating domain-specific knowledge through the finite difference method, FDM-PINN offers enhanced predictive capabilities, making it a preferred choice over traditional data-driven methods like artificial neural networks. To further comprehend the effectiveness of the utilised FDM-PINN, temperature results are assessed for several values of thermal parameters considering the various time instances, as displayed in Figs. 3–6. The assessment of FDM and FDM-PINN findings for Nc(2,4,6,8) at τ∗=0.5 and τ∗=0.8 is given in Figs. 3 and 4, respectively. Also, Figs. 5 and 6 are presented to divulge the association of the FDM and FDM-PINN results with τ∗=0.5 and τ∗=0.8 for β(−0.5,0,0.5,0.7). The implemented FDM-PINN procedure is effective, as evidenced by the strong concordance in all these figures.

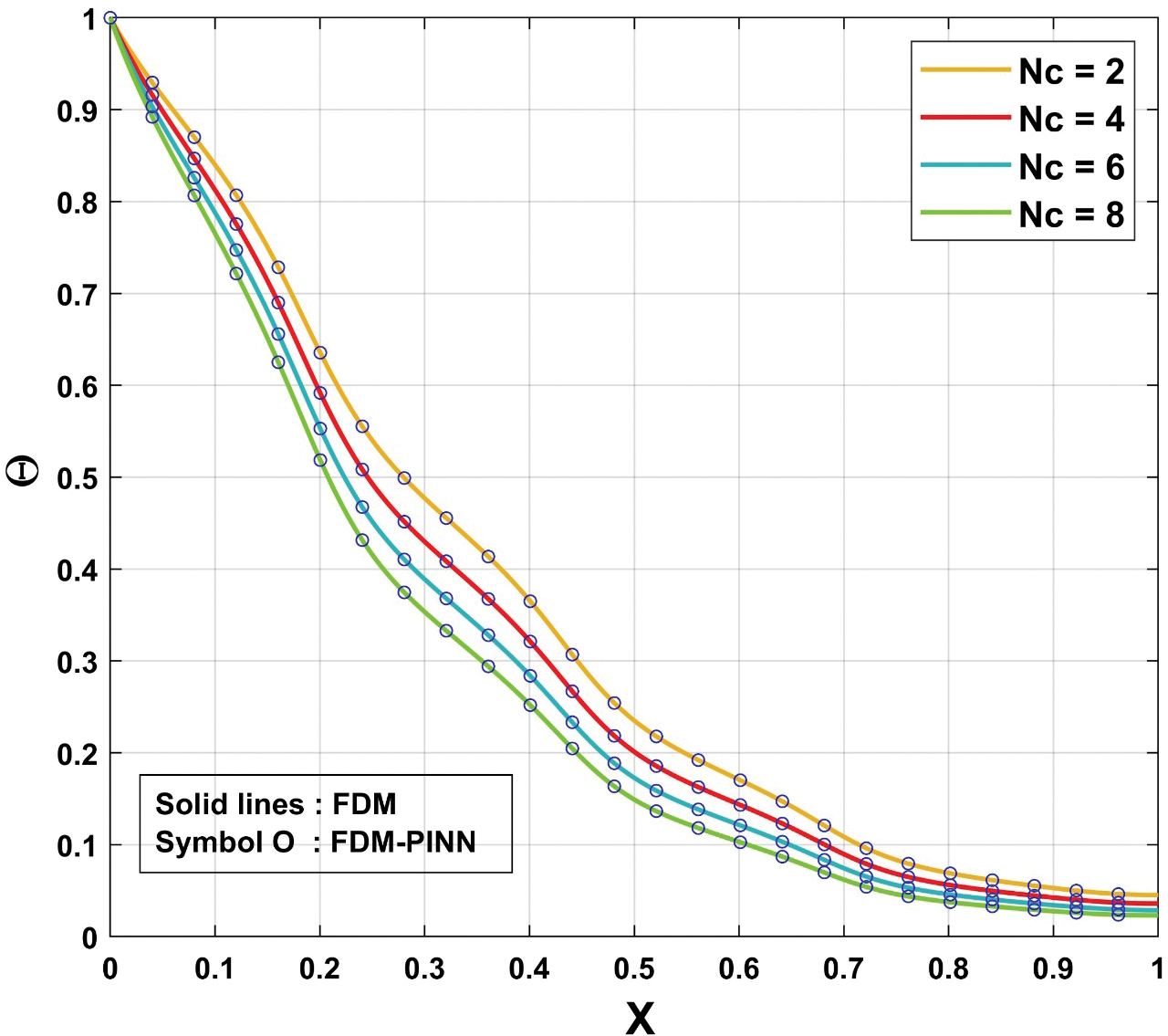
Figure 3: Comparison of FDM and FDM-PINN results for various Nc values at τ∗=0.5

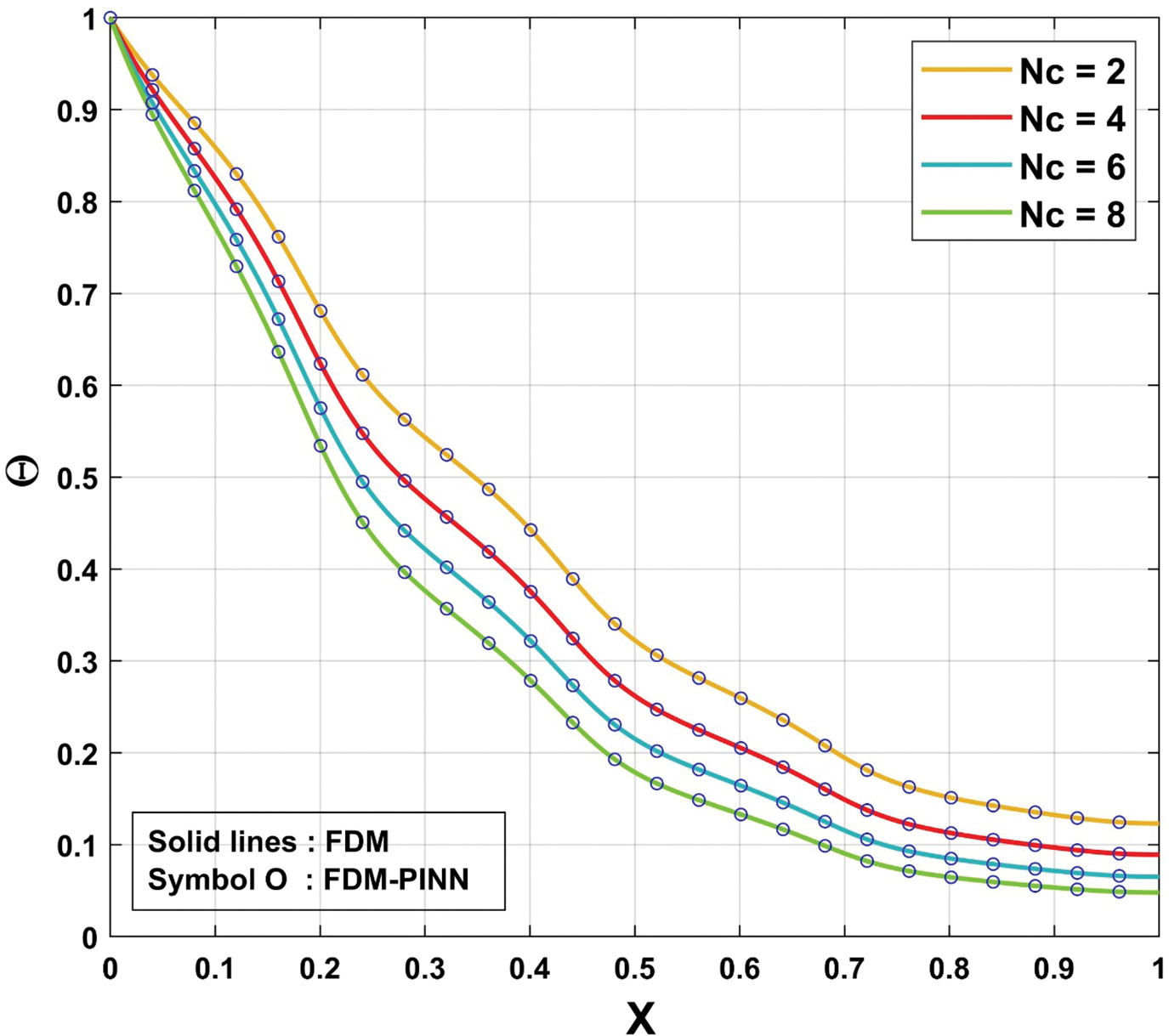
Figure 4: Comparison of FDM and FDM-PINN results for various Nc values at τ∗=0.8

Figure 5: Comparison of FDM and FDM-PINN results for various β values at τ∗=0.5

Figure 6: Comparison of FDM and FDM-PINN results for various β values at τ∗=0.8

5  Results and Discussion

The temperature distribution for the unsteady state is analyzed, and the influence of time is assessed using PINN analysis. The unsteady temperature variance in a wavy fin is considered in this present research. A dimensional transient temperature equation for the wavy fin is developed and Eq. (10) is the non-dimensional form of Eq. (3), obtained using suitable dimensionless variables. Further, the obtained non-dimensional equation is solved using FDM-PINN. This section investigates the dynamic temperature distribution in a fin with a wavy shape, considering several factors such as thermal conductivity, time, convective-conductive properties, and the fin’s aspect ratio. The graphical representation illustrates these factor’s impact on the wavy fin’s temperature profile. The wavy fin’s thermal distribution varies as time changes. In Figs. 7 to 9, differences in the time τ∗ show the deflection in the temperature profile of the wavy fin. The temperature curve for time τ∗=0.3 and τ∗=0.5 is indicated by solid lines and dashed lines respectively. Variation of temperature distribution in a wavy fin with different values of the fin’s aspect ratio is exhibited in Fig. 7a. Wavy fins temperature profile shows the decrement nature as the values of arL (0.1, 0.3, 0.5, 0.7) increase. Fig. 7b illustrates the characteristics of Θ for various scales of convective-conductive parameter. It is seen that the temperature in a wavy fin escalates for the decrease in the values of Nc. Physically, an increase in Nc (1, 2, 3, 4) values supports the intensification, and simultaneously effective cooling takes place. Thus, the temperature of wavy fin decreases. The upshot of the thermal conductivity parameter on the temperature profile of the wavy fin is displayed in Fig. 8a. As the thermal conductivity parameter rises, the temperature distribution in the wavy fin increases simultaneously. In particular, when the values of β becomes higher (0.1, 0.3, 0.5, 0.7), the heat conduction through fin length amplifies, enhancing the wavy fin’s temperature variation. Fig. 8b shows the temperature fluctuation in a wavy fin with respect to time. As the values of τ∗ upsurges, i.e., τ∗=(0.05,0.1,0.2,0.3), thermal distribution in a wavy fin also increases. The transient temperature distribution in a wavy fin rises gradually as time escalates. Also, the temperature dispersion in the fin with the time variation is shown in Fig. 9 as a contour graph. In precise, Fig. 9a–d demonstrates the variation in transient temperature with the time scales τ∗=0.01, τ∗=0.2, τ∗=0.8, and τ∗=2, respectively. These figures indicate that the temperature increases with increasing changes in time. Fig. 10a–d illustrates the thermal dispersion in the fin for dimensionless time τ∗=0.2, and τ∗=0.3 with different values of Nc. In particular, Fig. 10a,b indicates the thermal variation in the fin for τ∗=0.2, and τ∗=0.3 with Nc=1. The variation in the temperature of the fin with the change in time τ∗=0.2, and τ∗=0.3 is represented in Fig. 10c,d for Nc=2. The thermal variation in the fin is analyzed by considering the non-dimensional X and τ∗coordinate. It is observed from these figures that the thermal dispersion varies dynamically with the change in time. From all these figures, it is obvious that the temperature is found to be high at the fin’s base (X=0) and it decreases along the non-dimensional X to accomplish the minimum temperature at the fin’s tip (X=1). Moreover, the thermal distribution increases with increase in time as denoted by the upper surface deviation in Fig. 10b,d.

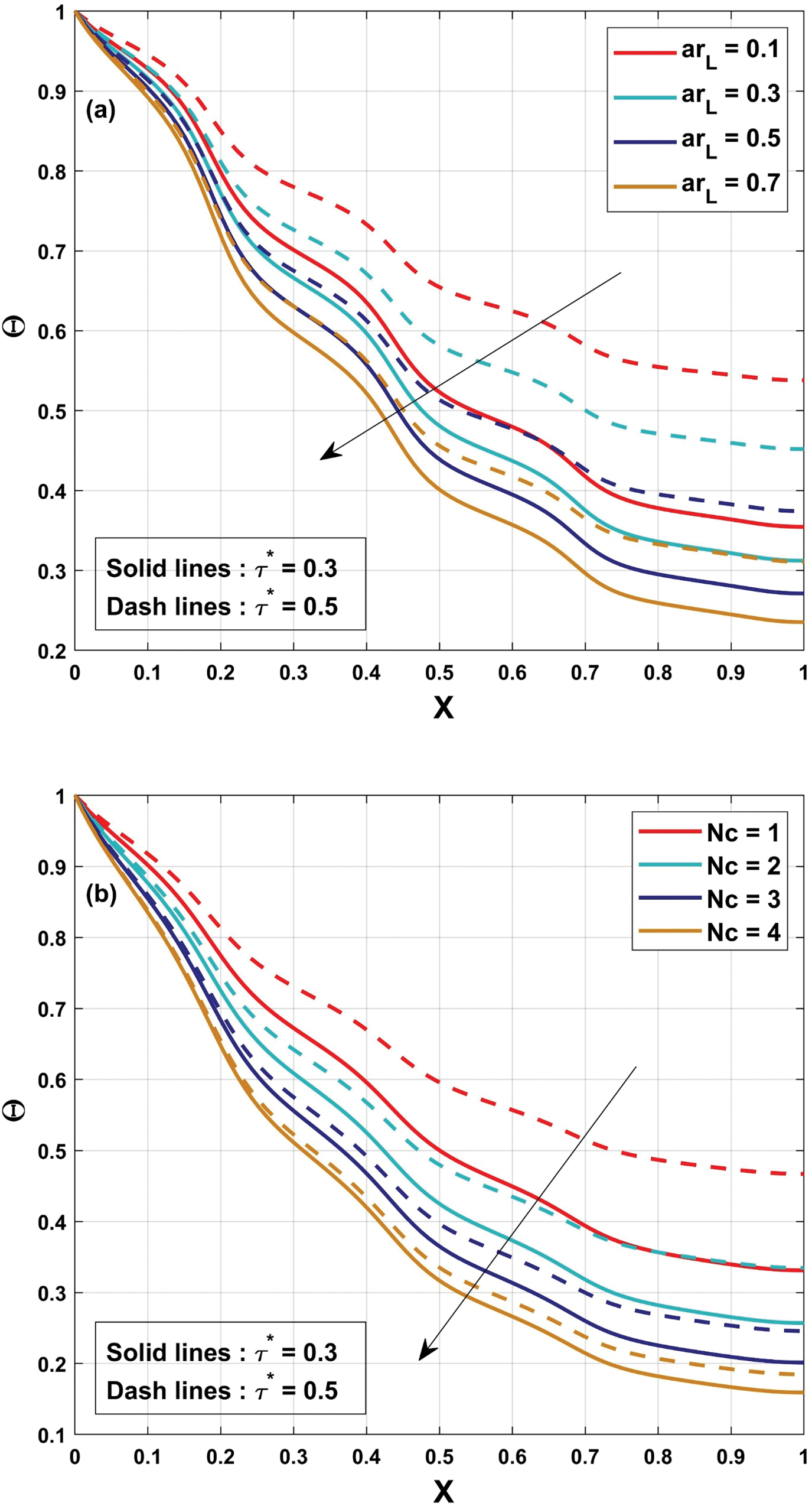
Figure 7: (a) Nature of Θ for variation in arL (b) Nature of Θ for variation in Nc

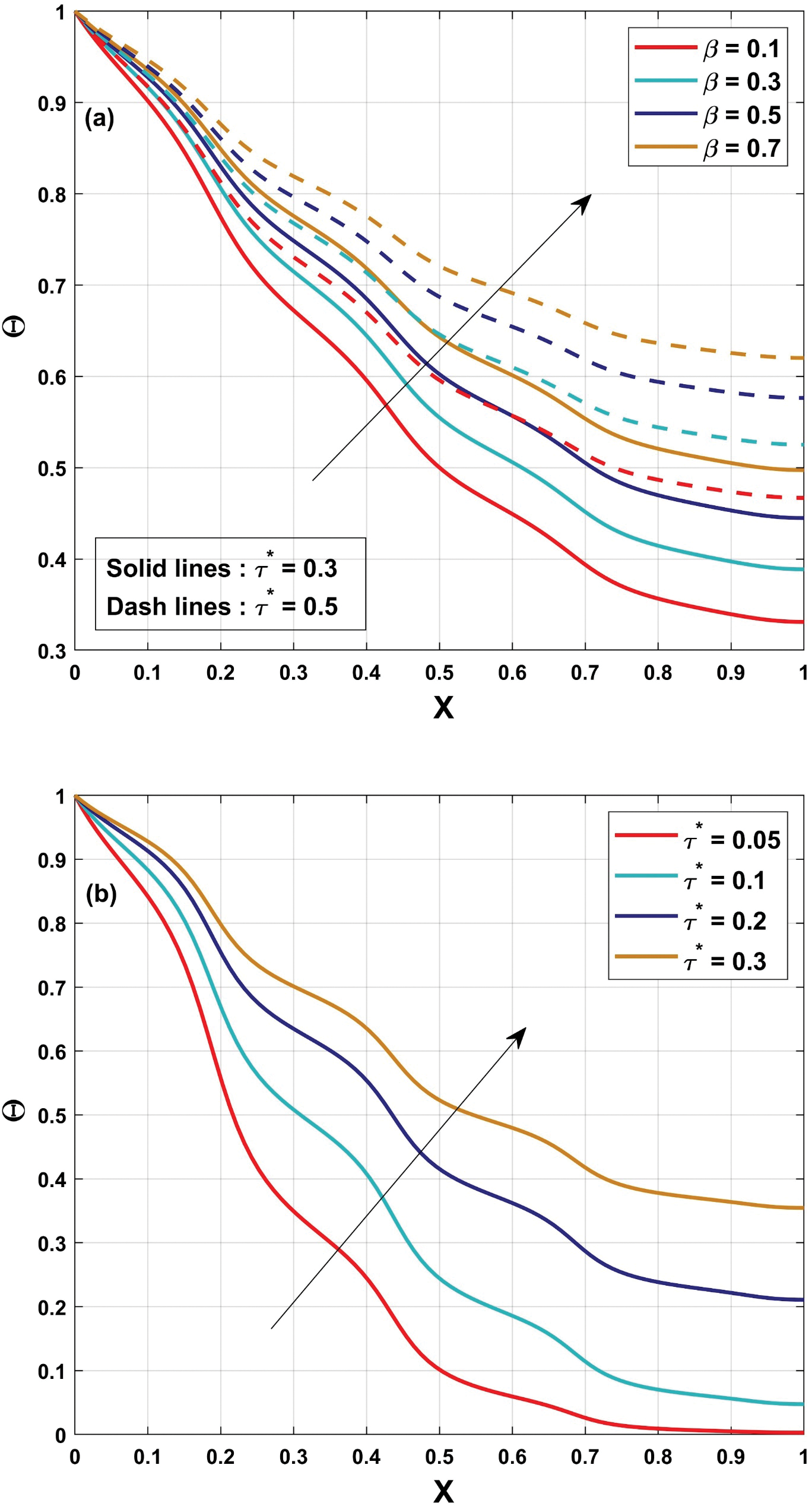
Figure 8: (a) Nature of Θ for variation in β (b) Nature of Θ for variation in τ∗

Figure 9: Thermal distribution in a wavy fin for variation in X with different τ∗ (a) Non-dimensional time τ∗=0.01 (b) Non-dimensional time τ∗=0.2 (c) Non-dimensional time τ∗=0.8 (d) Non-dimensional time τ∗=2

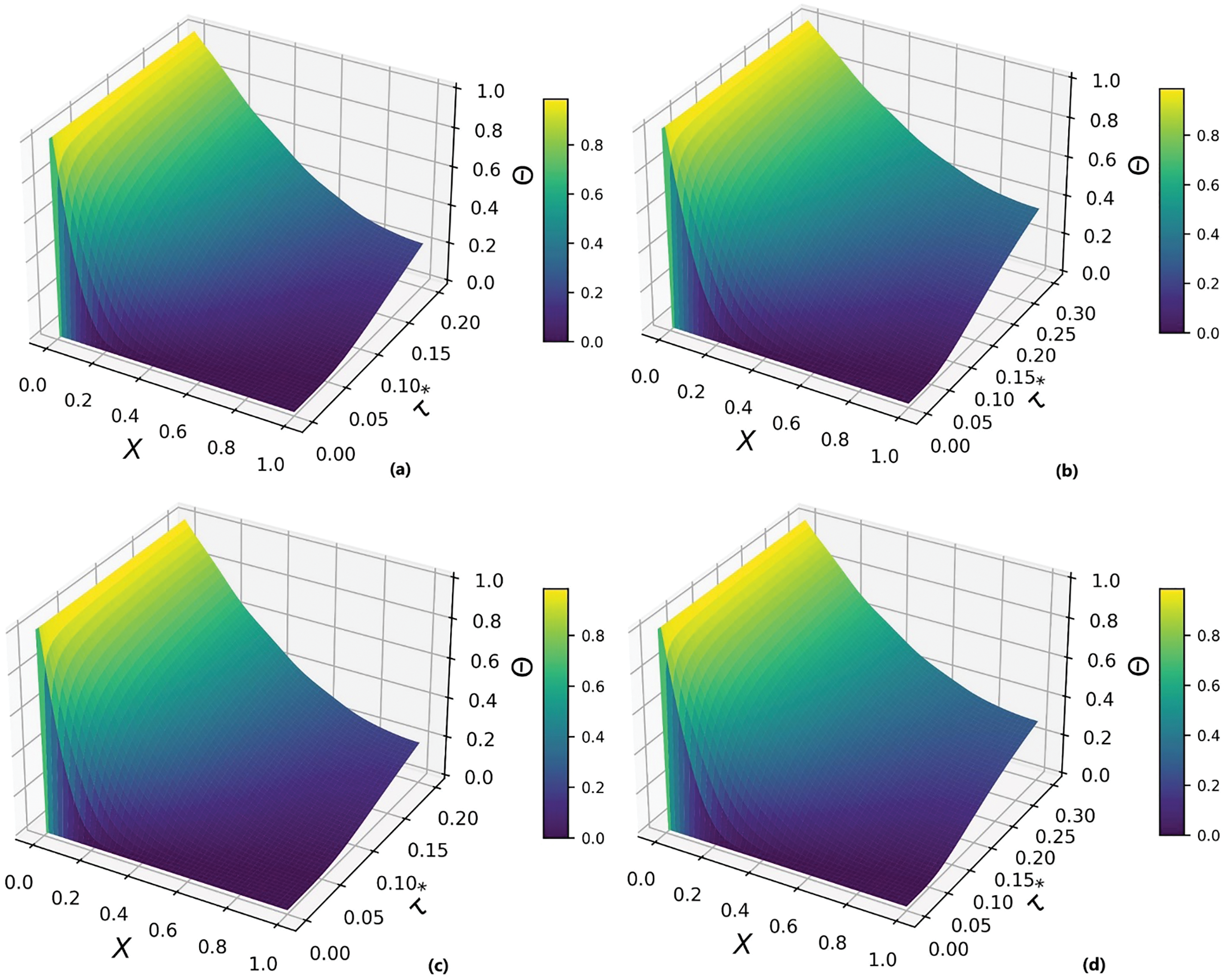
Figure 10: Three-dimensional representation of FDM-PINN results for with different τ∗ and Nc (a) Non-dimensional time τ∗=0.2 with Nc=1 (b) Non-dimensional time τ∗=0.3 with Nc=1 (c) Non-dimensional time τ∗=0.2 with Nc=2 (d) Non-dimensional time τ∗=0.3 with Nc=2

6  Conclusions

A mathematical representation of the unsteady heat transmission of a wavy fin is presented in the current analysis. Additionally, the wavy fin is subjected to the impact of convective heat dissipation. Also, the present investigation is designed to employ FDM-PINN in developing an unsteady thermal model of the wavy fin. Solutions to transient heat transfer problems alter with time, and when temperatures drop sharply, the discretization process might add stiffness to the system. In this case, PINNs might not be able to capture the dynamic changes with a moderate number of collocation points concerning the behaviour of the temperature distribution. The increase in collocation points leads to increased computational cost, which affects the overall performance of the procedure is one of the limitation of the study. This limitation can be resolved in future using different optimization techniques. The results of the current comprehensive examination are laid out below:

•   The wavy fin’s temperature distribution is strongly influenced by the associated parameters. The reduction in the temperature dispersion of the fin is caused by an elevation in the convective-conductive variable.

•   Thermal variance rises with higher non-dimensional time values. Further, enhanced variation is observed in the thermal curves with an increase in the time for all considered parameters.

•   Developments in the thermal conductivity parameter induce a decrease in the heat transmission rate and an increase in thermal dissipation.

•   The thermal effectiveness of wavy fins has been determined to be improved due to increased surface area and improved heat transfer mechanisms, relying on the fin operational conditions.

•   The FDM-PINN model’s ability to capture and depict the complex dynamics of heat transfer is demonstrated by the absolute errors ranging from 10−6 to 10−7.

•   The outcomes of numerical methods closely match the FDM-PINN outcomes, indicating a convergence of numerical solutions.

•   In contrast to conventional machine learning methods, the PINN methodology does not rely on training data and is not susceptible to generalisability constraints.

•   The FDM-PINN exhibits proficiency in effectively solving nonlinear thermal equations, setting itself apart from data-driven methods that depend on data dependencies.

•   The results accomplished from the proposed FDM-PINN technique were compared to the findings of the available work, and a stronger agreement in outcomes was observed due to minimal errors attributable to the influence of thermal factors.

Acknowledgement: The authors would like to thank the Researchers Supporting Project number (RSPD2024R526), King Saud University, Riyadh, Saudi Arabi.

Funding Statement: This study was supported by the Researchers Supporting Project number (RSPD2024R526), King Saud University, Riyadh, Saudi Arabi.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Kumar Chandan, Sara Salem Alzaid; data collection: Badr Saad T. Alkahtani; analysis and interpretation of results: Badr Saad T. Alkahtani, Kumar Chandan, Ravikumar Shashikala Varun Kumar; draft manuscript preparation: Sara Salem Alzaid, Kumar Chandan, Ravikumar Shashikala Varun Kumar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and analysed during the current study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Sarwe DU, Kulkarni VS. Thermal behaviour of annular hyperbolic fin with temperature dependent thermal conductivity by differential transformation method and Pade approximant. Phys Scr. 2021 Jul;96(10):105213. doi:10.1088/1402-4896/ac0c94. [Google Scholar] [CrossRef]

2. Das R, Kundu B. Simultaneous estimation of heat generation and magnetic field in a radial porous fin from surface temperature information. Int Commun Heat Mass Transf. 2021 Oct 1;127:105497. doi:10.1016/j.icheatmasstransfer.2021.105497. [Google Scholar] [CrossRef]

3. Goud JS, Srilatha P, Varun Kumar RS, Kumar KT, Khan U, Raizah Z, et al. Role of ternary hybrid nanofluid in the thermal distribution of a dovetail fin with the internal generation of heat. Case Stud Therm Eng. 2022 Jul 1;35(1):102113. doi:10.1016/j.csite.2022.102113. [Google Scholar] [CrossRef]

4. Gouran S, Ghasemi SE, Mohsenian S. Effect of internal heat source and non-independent thermal properties on a convective-radiative longitudinal fin. Alex Eng J. 2022 Nov 1;61(11):8545–54. doi:10.1016/j.aej.2022.01.063. [Google Scholar] [CrossRef]

5. Abdulrahman A, Gamaoun F, Varun Kumar RS, Khan U, Singh Gill H, Nagaraja KV, et al. Study of thermal variation in a longitudinal exponential porous fin wetted with TiO2−SiO2/hexanol hybrid nanofluid using hybrid residual power series method. Case Stud Therm Eng. 2023 Mar 1;43:102777. doi:10.1016/j.csite.2023.102777. [Google Scholar] [CrossRef]

6. Pasha AV, Jalili P, Ganji DD. Analysis of unsteady heat transfer of specific longitudinal fins with Temperature-dependent thermal coefficients by DTM. Alex Eng J. 2018 Dec 1;57(4):3509–21. doi:10.1016/j.aej.2017.11.019. [Google Scholar] [CrossRef]

7. Ndlovu PL, Moitsheki RJ. Analysis of transient heat transfer in radial moving fins with temperature-dependent thermal properties. J Therm Anal Calorim. 2019 Nov 1;138(4):2913–21. doi:10.1007/s10973-019-08306-5. [Google Scholar] [CrossRef]

8. Wang KJ, Shi F. A new fractal model of the convective-radiative fins with temperature-dependent thermal conductivity. Therm Sci. 2023;27(4):2831–7. doi:10.2298/TSCI220917207W. [Google Scholar] [CrossRef]

9. Din ZU, Ali A, De la Sen M, Zaman G. Entropy generation from convective-radiative moving exponential porous fins with variable thermal conductivity and internal heat generations. Sci Rep. 2022 Feb 2;12(1):1791. doi:10.1038/s41598-022-05507-1 [Google Scholar] [PubMed] [CrossRef]

10. Huang Y, Li XF. Exact and approximate solutions of convective-radiative fins with temperature-dependent thermal conductivity using integral equation method. Int J Heat Mass Transf. 2020 Apr 1;150(5):119303. doi:10.1016/j.ijheatmasstransfer.2019.119303. [Google Scholar] [CrossRef]

11. Ullah I, Ullah S, Ali A, Shah SI, Weera W, Alam MM. Heat transfer analysis from moving convection-radiative triangular porous fin exposed to heat generation. Case Stud Therm Eng. 2022 Oct 1;38:102177. doi:10.1016/j.csite.2022.102177. [Google Scholar] [CrossRef]

12. Sowmya G, Gireesha BJ, Madhu M. Analysis of a fully wetted moving fin with temperature-dependent internal heat generation using the finite element method. Heat Transfer. 2020;49(4):1939–54. doi:10.1002/htj.21701. [Google Scholar] [CrossRef]

13. Adnan, AlBaidani MM, Mishra NK, Alam MM, Eldin SM, AL-Zahrani AA, et al. Numerical analysis of magneto-radiated annular fin natural-convective heat transfer performance using advanced ternary nanofluid considering shape factors with heating source. Case Stud Therm Eng. 2023 Apr 1;44(4):102825. doi:10.1016/j.csite.2023.102825. [Google Scholar] [CrossRef]

14. Din ZU, Ali A, Ullah S, Zaman G, Shah K, Mlaiki N. Investigation of heat transfer from convective and radiative stretching/shrinking rectangular fins. Math Probl Eng. 2022;2022(1):1026698. doi:10.1155/2022/1026698. [Google Scholar] [CrossRef]

15. Sadeghianjahromi A, Kheradmand S, Nemati H, Wang CC. Heat transfer enhancement of wavy fin-and-tube heat exchangers via innovative compound designs. Int J Therm Sci. 2020 Mar 1;149:106211. doi:10.1016/j.ijthermalsci.2019.106211. [Google Scholar] [CrossRef]

16. Miao L, Wang Y, Kavtaradze R, Guo F, Li Y. Investigation of the heat transfer and flow characteristics in wavy fins of compact heat exchanger in a sand-dust environment. Int J Heat Mass Transf. 2021 Apr 1;168(8):120879. doi:10.1016/j.ijheatmasstransfer.2020.120879. [Google Scholar] [CrossRef]

17. Cui M, Song R. Comprehensive performance investigation and optimization of a plate fin heat exchanger with wavy fins. Therm Sci. 2022;26(3):2261–73. doi:10.2298/TSCI210718322C. [Google Scholar] [CrossRef]

18. Okon JO, Effiom SO. Numerical simulation of the thermal performance of a wavy fin configuration for a straight fin array. Sci Afr. 2022 Jul 1;16(6):e01265. doi:10.1016/j.sciaf.2022.e01265. [Google Scholar] [CrossRef]

19. Xu P, Wen J, Wang S, Chen Q, Li Y. Numerical simulation on flow and heat transfer performances of serrated and wavy fins in plate-fin heat exchanger for hydrogen liquefaction. Int J Hydrogen Energy. 2023 Jun 29;48(54):20680–93. doi:10.1016/j.ijhydene.2023.01.088. [Google Scholar] [CrossRef]

20. Sun Y, Bai Q, Zhao X, Tao M. Predicting the reflection coefficient of a viscoelastic coating containing a cylindrical cavity based on an artificial neural network model. Comput Model Eng Sci. 2021;130(2):1149–70. doi:10.32604/cmes.2022.017760. [Google Scholar] [CrossRef]

21. Pirhadi N, Wan X, Lu J, Hu J, Ahmad M, Tahmoorian F. Seismic liquefaction resistance based on strain energy concept considering fine content value effect and performance parametric sensitivity analysis. Comput Model Eng Sci. 2022;135(1):733–54. doi:10.32604/cmes.2022.022207. [Google Scholar] [CrossRef]

22. Faiz Z, Ahmed I, Baleanu D, Javeed S. A novel fractional dengue transmission model in the presence of wolbachia using stochastic based artificial neural network. Comput Model Eng Sci. 2024;139(2):1217–38. doi:10.32604/cmes.2023.029879. [Google Scholar] [CrossRef]

23. Wu G, Huang S, Liu T, Yang Z, Wu Y, Wei G, et al. Numerical study of the biomechanical behavior of a 3D printed polymer esophageal stent in the esophagus by bp neural network algorithm. Comput Model Eng Sci. 2023;138(3):2709–25. doi:10.32604/cmes.2023.031399. [Google Scholar] [CrossRef]

24. Ren Z, Wang D, Kondo G. Axial compressive capacity prediction and optimal design of circular UHPC-filled steel tube based on hybrid symbolic regression—neural network model. Structures. 2024 Oct 1;68:107084. doi:10.1016/j.istruc.2024.107084. [Google Scholar] [CrossRef]

25. Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989 Jan 1;2(5):359–66. doi:10.1016/0893-6080(89)90020-8. [Google Scholar] [CrossRef]

26. Baydin AG, Pearlmutter BA, Radul AA, Siskind JM. Automatic differentiation in machine learning: a survey. J Mach Learn Res. 2018;18(153):1–43. [Google Scholar]

27. Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Math Program. 1989 Aug 1;45(1):503–28. [Google Scholar]

28. Wang S, Yu X, Perdikaris P. When and why PINNs fail to train: a neural tangent kernel perspective. J Comput Phys. 2022 Jan 15;449:110768. [Google Scholar]

29. Parisi DR, Mariani MC, Laborde MA. Solving differential equations with unsupervised neural networks. Chem Eng Process Process Intensif. 2003 Aug 1;42(8):715–21. [Google Scholar]

30. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys. 2019 Feb 1;378:686–707. [Google Scholar]

31. Li Y, Liu T, Xie Y. Thermal fluid fields reconstruction for nanofluids convection based on physics-informed deep learning. Sci Rep. 2022 Jul 22;12(1):12567. doi:10.1038/s41598-022-16463-1 [Google Scholar] [PubMed] [CrossRef]

32. Merdasi A, Ebrahimi S, Yang X, Kunz R. Physics Informed Neural Network application on mixing and heat transfer in combined electroosmotic-pressure driven flow. Chem Eng Process—Process Intensif. 2023 Nov 1;193:109540. [Google Scholar]

33. Khaled AA. Thermal performance of six different types of wavy-fins. Int J Numer Methods Heat Fluid Flow. 2015 Jan 1;25(4):892–911. doi:10.1108/HFF-06-2014-0174. [Google Scholar] [CrossRef]

34. Benito JJ, Ureña F, Gavete L. Solving parabolic and hyperbolic equations by the generalized finite difference method. J Comput Appl Math. 2007 Dec 15;209(2):208–33. doi:10.1016/j.cam.2006.10.090. [Google Scholar] [CrossRef]

35. Ruan C, Dong C, Zhang Z, Chen B, Liu Z. Finite difference-peridynamic differential operator for solving transient heat conduction problems. Comput Model Eng Sci. 2024;140(3):2707–28. doi:10.32604/cmes.2024.050003. [Google Scholar] [CrossRef]