Using the Novel Wolverine Optimization Algorithm for Solving Engineering Applications

1  Introduction

Optimization problems are classified as those that have multiple possible solutions. Optimization involves the task of identifying the best solution from the various options available for a given problem [1]. Each optimization problem can be mathematically described through three fundamental components: (i) decision variables, (ii) constraints, and (iii) the objective function. The core aim of an optimization task is to identify the most suitable values for the decision variables, which will either maximize or minimize the objective function. This process must be carried out while ensuring that all specified constraints are strictly adhered to. The decision variables represent the choices or inputs that can be adjusted, the constraints define the limitations or conditions that must be met, and the objective function quantifies the goal of the optimization, guiding the search toward the best possible solution [2]. Numerous optimization challenges in various fields such as science, mathematics, engineering, and practical applications require the use of suitable techniques to achieve at least near-optimal solutions. The strategies for solving these optimization problems are categorized into two main groups: deterministic and stochastic approaches [3].

Two types of deterministic methods, namely gradient-based and non-gradient-based, have been effective in addressing linear, convex, continuous, differentiable, and low-dimensional optimization problems [4,5]. However, as problems become more complex and dimensions increase, deterministic approaches become less efficient due to being trapped in local optima. In particular, the majority of practical optimization challenges exhibit characteristics such as non-linearity, lack of convexity, discontinuity, non-differentiability, and high dimensionality. The challenges posed by these types of optimization problems for deterministic methods have led researchers to investigate stochastic strategies [6].

Metaheuristic algorithms stand as a highly effective stochastic method for managing optimization tasks. Operating via random search within the problem-solving domain and employing trial and error processes along with random operators, these algorithms can yield suitable solutions for optimization problems. Their appeal lies in the simplicity of their concepts, easy implementation, lack of dependency on problem types, avoidance of the derivation process, and effectiveness in addressing non-linear, non-convex, discontinuous, non-differentiable, and high-dimensional problems, as well as problems involving discrete and unknown variables. These advantages have contributed to the widespread adoption of metaheuristic algorithms [7]. Metaheuristic algorithms begin by generating a set number of candidate solutions randomly to form the algorithm’s population. These solutions are then enhanced through the updating steps of the iterative algorithm. Once the algorithm has completed the execution, the best candidate solution, which has been refined over multiple iterations, is put forth as the solution to the problem [8].

Metaheuristic algorithms employ random search techniques, which inherently lack the guarantee of finding the absolute global optimum. However, the solutions generated by these algorithms are often deemed quasi-optimal, as they tend to be close to the global optimum. This proximity to the best possible solution is generally sufficient for practical purposes, especially in complex and high-dimensional problems, where exact solutions are computationally infeasible. To tackle the challenge of obtaining solutions that are as close as possible to the global optimum, researchers have devised a multitude of metaheuristic algorithms. These algorithms are designed to enhance the efficiency and effectiveness of the search process, balancing exploration and exploitation to navigate the solution space more intelligently and improve the likelihood of approaching the global optimum [9].

Metaheuristic algorithms should incorporate both global and local levels within their random search mechanism. The global search involves exploration, allowing the algorithm to thoroughly traverse the problem-solving space to locate the primary optimum and avoid becoming trapped in a local optimum. Meanwhile, the local search involves exploitation, facilitating the algorithm’s ability to pinpoint solutions closer to the global optimum by meticulously examining nearby solutions and promising areas. Maintaining a balance between exploration and exploitation during the search process within the problem-solving space is crucial for the success of metaheuristic algorithms in the optimization process [10].

The primary concern in the research is whether there is a need for the development of new metaheuristic algorithms, given the current existing algorithms. This question is addressed by the No Free Lunch (NFL) theorem [11], which suggests that due to the stochastic nature of metaheuristic algorithm optimization processes, a consistent performance across all problems cannot be expected. In other words, according to the NFL theorem, the effectiveness of a metaheuristic algorithm in solving one set of optimization problems does not ensure the same effectiveness in solving other optimization problems. This indicates that, while a metaheuristic algorithm might find the best solution for one optimization problem, it could struggle with another problem by only finding a subpar solution. The NFL theorem emphasizes that the effectiveness of a metaheuristic algorithm in solving an optimization problem is not guaranteed. Rather than assuming success, the theorem highlights the need for continuous exploration of metaheuristic algorithms. It encourages researchers to keep pushing the boundaries by developing new and improved algorithms to tackle optimization problems. This ongoing pursuit ensures that better solutions can be found, as no single algorithm can be universally successful across all problems. The theorem serves as a reminder that the search for optimal solutions is an ever-evolving challenge.

Based on the NFL theorem, it is not possible to claim that any single metaheuristic algorithm is the best optimizer for all optimization problems. This limitation stems from three primary reasons.

Firstly, the inherent randomness in the search process of metaheuristic algorithms often leads to discrepancies between the solutions they produce and the true optimal solution of a problem. This issue becomes particularly significant when dealing with optimization problems where the optimal solution is unknown. In such cases, determining the absolute optimality of an algorithm is a fundamental challenge. Consequently, there is a need to design new and more efficient metaheuristic algorithms to address these problems more effectively, thereby enhancing solution accuracy and improving overall algorithm efficiency.

Secondly, many practical optimization problems possess specific characteristics that align closely with the search behaviors of certain metaheuristic algorithms. As a result, these algorithms can be highly effective for optimization problems that share a similar nature to their search mechanisms. However, the same algorithm may exhibit weaker performance when applied to optimization problems of a completely different nature. Since different metaheuristic algorithms are inspired by varying sources and exhibit distinct search behaviors, each algorithm tends to be suitable for only certain types of problems. This specialization means that existing optimization algorithms may struggle to effectively solve newly emerging or highly complex problems, highlighting the need for continuous innovation in the development of metaheuristic techniques.

The third reason is that the development of new metaheuristic algorithms allows to achieve better values than existing algorithms for optimization problems. The development of a new metaheuristic algorithm is a valuable opportunity to share knowledge with the aim of tackling challenging optimization problems, especially in real-world applications. Normally, a new metaheuristic algorithm is expected to be able to perform the optimization process efficiently by using specific operators and strategies. According to this, these reasons and the concept of the NFL theorem are the main motivations of the authors in order to design a new metaheuristic algorithm to provide more effective solutions for optimization problems.

However, the development of metaheuristic algorithms remains a worrisome challenge. This is the concern that the field of study of metaheuristic algorithms will move away from scientific accuracy. Therefore, researchers should use tests and analyzes to ensure that the algorithms they develop have significant improvements compared to existing algorithms. All this confirms that the development of newer metaheuristic algorithms is still a necessity in science, but also a challenge [12].

This article brings a fresh perspective by introducing the Wolverine Optimization Algorithm (WoOA), a new metaheuristic algorithm with practical applications for solving optimization problems. The key highlights of this research are as follows:

•   WoOA is designed based on simulating the natural wolverine behaviors in the wild.

•   The concept behind WoOA draws from the wolverine’s foraging approach, encompassing both scavenging and hunting.

•   The WoOA theory is described and mathematically modeled in two strategies (i) scavenging and (ii) hunting.

•   The scavenging strategy is modeled in a phase (i) exploration based on the simulation of wolverine movement towards carcasses.

•   The hunting strategy is modeled in two phases (i) exploration based on the simulation of the wolverine’s movement towards the location of live prey and (ii) exploitation based on the simulation of the process of chasing and fighting between the wolverine and the prey.

•   The performance of WoOA for solving optimization problems is evaluated in handling the Congress on Evolutionary Computation (CEC) 2017 test suite.

•   The effectiveness of WoOA for handling optimization tasks in real-world applications is challenged in solving twenty-two constrained optimization problems from the CEC 2011 test suite as well as four engineering design problems.

•   The quality of WoOA in the optimization process is compared with the performance of twelve well-known metaheuristic algorithms.

The paper is organized as follows: Section 2 contains the literature review, followed by the introduction and modeling of the Wolverine Optimization Algorithm (WoOA) in Section 3. Section 4 presents simulation studies and results, while Section 5 investigates the effectiveness of WoOA in solving real-world applications. Finally, Section 6 includes some conclusions and suggestions for future research.

2  Literature Review

Metaheuristic techniques have emerged by taking cues from diverse natural phenomena, biological theories, genetic mechanisms, human conduct, and evolutionary theories. Each category harnesses completely different mechanisms and concepts to address optimization problems. For instance, swarm-based approaches draw from the collective behavior observed in natural systems, such as flocks of birds or schools of fish, while evolutionary-based approaches mimic biological evolution and genetic algorithms. Physics-based approaches leverage physical laws and phenomena to guide the search process, and human-based approaches incorporate elements of human thinking and decision-making. By drawing on such diverse sources, these techniques provide varied and innovative solutions to optimization challenges, showcasing how different strategies can be applied to achieve effective problem-solving.

Swarm-based metaheuristic algorithms are inspired by the collective behavior observed in various natural systems, where groups of organisms work together in coordinated patterns. These algorithms simulate the interaction and cooperation found in swarms of creatures such as insects, birds, and fish to solve optimization problems. For example, Particle Swarm Optimization (PSO) [13] mimics the way flocks of birds or schools of fish move collectively in search of food. Similarly, Ant Colony Optimization (ACO) [14] draws from the foraging behaviors of ants, while the Artificial Bee Colony (ABC) [15] algorithm is inspired by the food search strategies of honeybees. The Firefly Algorithm (FA) [16] on the other hand, is based on the flashing patterns of fireflies. Each of these algorithms utilizes the inherent collaborative and adaptive behaviors of these natural systems to effectively explore and exploit the solution space. The Pelican Optimization Algorithm (POA) is created by mimicking the hunting strategy of pelicans as they catch fish in the sea [17]. The Reptile Search Algorithm (RSA) is crafted with inspiration from the hunting patterns of crocodiles [18]. In the nature, various actions such as foraging, hunting, migration, digging, and chasing are notable behaviors exhibited by living organisms. These behaviors have inspired the development of algorithms like: Orca Predation Algorithm (OPA) [19], Whale Optimization Algorithm (WOA) [20], Coati Optimization Algorithm (COA) [21], Pufferfish Optimization Algorithm (POA) [9], Tunicate Swarm Algorithm (TSA) [22], Honey Badger Algorithm (HBA) [23], White Shark Optimizer (WSO) [24], Golden Jackal Optimization (GJO) [25], Grey Wolf Optimizer (GWO) [26], Marine Predator Algorithm (MPA) [27], and African Vultures Optimization Algorithm (AVOA) [28].

Evolutionary-based metaheuristic algorithms are grounded in genetic and biological principles, drawing from concepts such as survival of the fittest, natural selection, and Darwin’s theory of evolution. These algorithms mimic the process of biological evolution to address optimization problems, utilizing mechanisms such as reproduction, genetic inheritance, and random evolutionary operations. Key examples in this category include the Genetic Algorithm (GA) [29] and Differential Evolution (DE) [30]. Specifically, they incorporate selection processes that mimic the survival of the fittest, mutation operations that introduce genetic diversity, and crossover techniques that combine genetic information from parent solutions to create offspring. By leveraging these evolutionary strategies, GA and DE effectively explore the solution space and evolve towards increasingly optimal solutions over successive generations. The human immune system’s way of handling germs and illnesses has been a model for the development of the Artificial Immune System (AIS) [31]. Some other evolutionary-based metaheuristic algorithms are: Evolution Strategy (ES) [32], One-to-One Based Optimizer (OOBO) [33], Genetic Programming (GP) [34], and Cultural Algorithm (CA) [35].

Physics-based metaheuristic algorithms draw inspiration from various natural concepts such as laws, forces, transformations, processes, and phenomena. The well-known algorithm called Simulated Annealing (SA) is a prime example of this category, as it takes inspiration from the physical process of metal annealing, where metals are subjected to heat to melt, and then slowly cooled to form perfect crystals [36]. The development of algorithms such as the Spring Search Algorithm (SSA) [37], the Gravitational Search Algorithm (GSA) [38], and the Momentum Search Algorithm (MSA) [39] is rooted in harnessing physical forces and adhering to Newton’s laws of motion. For instance, SSA leverages the elastic force of springs, GSA operates on the principle of gravitational attraction force, and MSA utilizes momentum force as its guiding principle. These algorithms simulate the behavior of physical phenomena to drive their optimization processes, offering unique perspectives and approaches to problem-solving in various domains. Concepts related to the universe and cosmology have served as a key source of inspiration in the development of algorithms such as the Black Hole Algorithm (BHA) [40] and the Multi-Verse Optimizer (MVO) [41]. Some other physics-based metaheuristic algorithms are: Optical Microscope Algorithm (OMA) [42], Electro-Magnetism Optimization (EMO) [43], Equilibrium Optimizer (EO) [44], Henry Gas Optimization (HGO) [45], Water Cycle Algorithm (WCA) [46], Archimedes Optimization Algorithm (AOA) [47], Lichtenberg Algorithm (LA) [48], Thermal Exchange Optimization (TEO) [49], and Nuclear Reaction Optimization (NRO) [50].

Human-based metaheuristic algorithms are designed to replicate various aspects of human behavior, including communication, decision-making, interactions, and cognitive processes. These algorithms model the way people handle complex tasks and make decisions to tackle optimization problems. One notable example is the Teaching-Learning Based Optimization (TLBO) algorithm, which is inspired by the dynamics of educational environments. TLBO mimics the interaction between teachers and students in a classroom, where teachers impart knowledge and students learn through exchange and feedback [51]. Another example is the Mother Optimization Algorithm (MOA), which is based on parenting strategies observed in Eshrat’s mother as she nurtures and guides her children [52]. Additionally, the Doctor and Patient Optimization (DPO) algorithm draws from the interactions between medical professionals and patients, reflecting the therapeutic processes involved in treatment [53]. Other human-based metaheuristic algorithms include War Strategy Optimization (WSO), which models strategies used in military conflicts [54] and Gaining Sharing Knowledge-based Algorithm (GSK), which simulates the exchange and accumulation of knowledge among individuals [55]. The Coronavirus Herd Immunity Optimizer (CHIO) is inspired by the concepts of herd immunity in disease control [56], while the Ali Baba and the Forty Thieves Algorithm (AFT) is inspired by the legendary tale of resourceful problem-solving and strategy [57].

In Table 1, a review study on metaheuristic algorithms is presented. In the literature, it is acknowledged that no metaheuristic algorithm has been developed by simulating the natural behaviors of wolverines in the wild. However, the wolverine’s clever methods of scavenging and hunting could serve as a valuable source of inspiration for creating a novel optimizer. Addressing this void in the research on metaheuristic algorithms, the paper introduces a new algorithm that models wolverine feeding strategies in the nature, as discussed in the following section.

3  Wolverine Optimization Algorithm (WoOA)

This section delves into the underlying inspiration for the creation of the Wolverine Optimization Algorithm (WoOA) and provides an in-depth explanation of how its implementation steps are mathematically formulated to address optimization problems. It explores the natural behaviors and strategies of wolverines that serve as the foundation for WoOA, highlighting the unique aspects that differentiate this algorithm from others. Additionally, it offers a comprehensive overview of the mathematical modeling process used to translate these biological inspirations into effective computational procedures for optimizing various types of problems.

3.1 Inspiration of WoOA

The wolverine, the largest land-dwelling species in the Mustelidae family, is primarily found in remote areas of subarctic and alpine tundra in the Northern Hemisphere as well as in the Northern boreal forests. An image of the wolverine is shown in Fig. 1.

Figure 1: Wolverine taken from: free media Wikimedia Commons

Among the natural behaviors of wolverine in the wild, the feeding strategies of this animal are much more prominent. The wolverine feeds in two ways: (i) scavenging and (ii) hunting. In the scavenging strategy, the wolverine finds the carrion and feeds on it by following the tracks of other predators. In the hunting strategy, the wolverine attacks the live prey and after a process of chasing and fighting, kills the prey and feeds on it. These two wolverine’s feeding strategies are intelligent processes whose mathematical modeling is employed to design the proposed WoOA approach that is discussed below.

3.2 Algorithm Initialization

The proposed WoOA approach is an evolutionary algorithm based on a population of wolverines. By leveraging the search capabilities of its members in addressing problems, WoOA is capable of generating effective solutions for optimization tasks through an iterative process. Each wolverine, as a member of WoOA, defines decision variables based on its position within the problem-solving space. In essence, every wolverine represents a potential solution to the problem, which is delineated using a vector in mathematical terms. Together, these wolverines form the WoOA population, and their collective behavior is mathematically represented using a matrix as per Eq. (1). The initial positioning of the wolverines in the problem-solving space is randomized through Eq. (2) at the start of the algorithm execution.

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,d⋯x1,m⋮⋱⋮⋰⋮xi,1⋯xi,d⋯xi,m⋮⋰⋮⋱⋮xN,1⋯xN,d⋯xN,m]N×m(1)

xi,d=lbd+r⋅(ubd−lbd)(2)

In this scenario, X represents the population matrix of the WoOA, Xi denotes the ith wolverine (which is essentially a potential solution), xi,d signifies its value in the dth dimension within the search space (i.e., decision variable). The variable N indicates the number of wolverines, while m represents the total number of decision variables. On the other hand, r is a random number in the interval [0,1], lbd, and ubd denote a lower bound and an upper bound on the dth decision variable, respectively.

According to this concept, the position of each wolverine within the space intended for problem-solving serves as a plausible solution to the given problem. Based on this understanding, the suggested values of each wolverine for the decision variables aids in the assessment of the problem’s objective function. These evaluated values for the objective function could then be effectively showcased in a vector form:

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1(3)

where F is the vector of the evaluated objective function values and Fi is the evaluated objective function value based on the ith wolverine.

The assessed values of the objective function provide valuable insights into the quality of the potential solutions. The best evaluated value of the objective function represents the top individual in the population (in other words, the best potential solution), while the worst evaluated value corresponds to the worst individual in the population (i.e., the worst potential solution). Since the position of wolverines in the problem-solving space is updated in each iteration of WoOA, the objective function is re-evaluated for each wolverine in every iteration. As a result, the top individual in the population should be regularly updated in every iteration by comparing the evaluated values of the objective function.

3.3 Mathematical Modelling of WoOA

The WoOA approach’s design involves updating the position of the population members in the problem-solving space by simulating the natural feeding behavior of the wolverine. The wolverine has two strategies for feeding: (i) scavenging and (ii) hunting. In the scavenging strategy, wolverines feed on abandoned carrion by moving along the path of other predators that leave the remains of their kills. In the hunting strategy, the wolverine first attacks the prey and after going through a fighting process, finally kills the prey and feeds on it. In the design of WoOA, it is assumed that in each iteration, each wolverine randomly chooses one of these two strategies with equal probability, and based on the simulation of the selected strategy, its position in the problem-solving space is updated. Using Eq. (4), the wolverine simulates its decision-making process to determine whether to scavenge or hunt for food. This means that in every iteration, each wolverine’s position is updated solely based on either the first or second strategy.

Update process for i′th wolverine Xi:{based on scavenging strategy,rp≤0.5based on hunting strategy,else(4)

Here, rp is a random number from the interval [0,1].

3.3.1 Strategy 1: Scavenging Strategy (Exploration Phase)

The first WoOA strategy involves updating the location of the population members in the problem-solving space through simulating the natural feeding behavior of the wolverine on carrion. In this strategy, the wolverine to get the carrion, follows the path of other predators who have left the rest of their kills. Simulating the wolverine’s movement in response to predators results in a radically different approach to exploring the solution space. This technique introduces significant variations in the positions of the population members, effectively altering their trajectories within the problem-solving domain. By adopting this strategy, the algorithm achieves a more comprehensive exploration of potential solutions. These extensive positional adjustments not only broaden the search area but also enhance the algorithm’s capacity to uncover diverse and optimal solutions. Consequently, the method improves the algorithm’s ability to perform a thorough global search, enabling it to better navigate complex problem spaces and discover innovative solutions. The scavenging strategy has an exploration phase based on simulating the wolverine’s movement in obtaining carrion.

In the WoOA design, the location of other members with a better objective function value is considered as the predators’ position who are aiming to release the rest of their kills for each wolverine, as specified in Eq. (5).

CPi={Xk:Fk<Fi and k≠i},where i=1,2,…,N and k∈{1,2,…,N}(5)

where CPi is the set of candidate predators’ locations for the ith wolverine, Xk is the population member with a better objective function value than the ith wolverine, and Fk is its objective function value.

In the design of WoOA, it is presumed that the wolverine chooses the position of a predator from the CPi set at random and then moves towards it. A schematic of this natural behavior of the wolverine during selection and moving towards the location of the predator that left its food remains is shown in Fig. 2. As the wolverine moves towards the selected predator with the goal of reaching the carrion, a new suggested position for the respective member has been computed using Eq. (6). If the objective function value is enhanced, this suggested position supersedes the previous position of the corresponding member according to Eq. (7).

xi,jS1=xi,j+ri,j⋅(SPi,j−Ii,j⋅xi,j),(6)

Xi={XiS1,FiS1≤Fi,Xi,else,(7)

where SPi represents the chosen predator for the ith wolverine, while SPi,j denotes the jth dimension of this predator. XiS1 refers to the newly computed position of the ith wolverine based on the scavenging strategy employed in the proposed WoOA. Similarly, xi,jS1 is the jth dimension of this new position. The term FiS1 indicates the objective function value associated with the ith wolverine at its new position. Additionally, ri,j are random numbers uniformly drawn from the interval [0,1], and Ii,j are binary random numbers that can be either 1 or 2.

Figure 2: Diagram of wolverine’s movement during scavenging strategy

3.3.2 Strategy 2: Hunting Strategy (Exploration and Exploitation Phases)

The second strategy of WoOA involves updating the position of the population members in the problem-solving space by simulating the natural hunting behavior of the wolverine. This process mirrors the wolverine’s typical approach to hunting, where it first attacks live prey, then engages in a fight and chase before securing and feeding on its kill. The population members’ update based on this hunting strategy consists of two phases: (i) exploration through simulating the wolverine’s movement towards the prey and (ii) exploitation by simulating the fight and chase process between the wolverine and its prey.

•   Phase 1: Attack (exploration phase)

During this phase of the WoOA, the population’s location within the problem-solving space is adjusted as a result of simulating the process of a wolverine attacking its prey. By imitating the wolverine’s movements during a hunt, significant changes are introduced to the population’s position, thereby enhancing the exploration capabilities of WoOA in navigating through the problem-solving area. When designing the WoOA, the position of the best population member is likened to the prey’s location. The schematic of this natural behavior of a wolverine during the attack towards the prey is shown in Fig. 3. Through simulating the wolverine’s approach towards the best member (the “prey”) for each member of WoOA, a new potential position is computed using Eq. (8). Subsequently, if the objective function demonstrates an improvement, this newly proposed position replaces the previous one for the corresponding member, as described in Eq. (9).

xi,jP1=xi,j+ri,j⋅(Preyj−Ii,j⋅xi,j),(8)

Xi={XiP1,FiP1≤Fi,Xi,else,(9)

where Prey is the best population member as prey, Preyj is its jth dimension, XiP1 signifies the newly computed position for the ith wolverine, determined by the first phase of the hunting strategy in the proposed WoOA. Similarly, xi,jP1 refers to the jth dimension of this new position. FiP1 indicates the objective function value of the ith wolverine at this new position. Additionally, ri,j are random values sampled from the interval [0,1], and Ii,j are binary numbers randomly assigned as either 1 or 2.

•   Phase 2: Fighting and chasing (exploitation phase)

Figure 3: Diagram of wolverine’s movement during attack towards the prey

During this WoOA phase, the population members’ locations in the problem-solving space are adjusted through simulating the hunt and pursuit interactions between the wolverine and its prey. By simulating the movements of the wolverine during chasing, small changes are introduced to the positions of the population members, thereby enhancing the WoOA’s capability for local search within the problem-solving space. The design of the WoOA assumes that these interactions occur in close proximity to the hunting location. The schematic of this natural behavior of wolverine during the process of chasing prey is shown in Fig. 4. Through modeling the wolverine’s movements during the hunt and pursuit, a new position is calculated for each WoOA member using Eq. (10). If this new position improves the objective function value, as per Eq. (11), it replaces the member’s previous position.

xi,jP2=xi,j+(1−2ri,j)⋅ubj−lbjt(10)

Xi={XiP2,FiP2≤FiXi,else(11)

where XiP2 denotes the new position determined for the ith wolverine based on the second phase of the hunting strategy employed in the proposed WoOA. xi,jP2 represents the jth dimension of this updated position. FiP2 indicates the objective function value associated with the ith wolverine at its new position. Additionally, ri,j are random numbers sampled from the interval [0,1], and t denotes the iteration counter.

Figure 4: Diagram of wolverine’s movement while fighting and chasing with prey

3.4 Repetition Process, Pseudo-Code, and Flowchart of WoOA

After recalibrating the positions of all wolverines within the problem-solving space, the first iteration of WoOA is finalized. Following this, utilizing the updated values, the algorithm proceeds to the subsequent iteration, continuously adjusting the wolverines’ positions until the algorithm’s final iteration, based on Eqs. (4) to (11). Each iteration involves updating the best candidate solution by comparing assessed values for the objective function. Upon the algorithm’s complete execution, the ultimate best solution uncovered throughout its iterations is unveiled as the WoOA solution for the assigned predicament. The implementation steps of WoOA are visually depicted in a flowchart in Fig. 5, and its pseudo-code is revealed in Algorithm 1.

Figure 5: Flowchart of WoOA

3.5 Computational Complexity of WoOA

The computational complexity of the Wolverine Optimization Algorithm (WoOA) is crucial to understand its efficiency and scalability in solving optimization problems. Here, we analyze the factors that contribute to its complexity and compare its running times with other metaheuristic algorithms.

Factors Influencing the Computational Complexity

1.    Population Size (N)

•   WoOA initializes a population of N candidate solutions in each iteration. The size of this population significantly affects the algorithm’s performance and convergence speed.

2.    Number of Decision Variables (m)

•   The complexity of evaluating each candidate solution depends on the number of decision variables m. As m increases, the search space grows exponentially, impacting the time required to evaluate potential solutions.

3.    Number of Iterations (T)

•   WoOA iteratively refines its solutions over T iterations. The total number of iterations influences how thoroughly the algorithm explores and exploits the search space.

4.    Objective Function Evaluation (O(f))

•   Evaluating the fitness of each candidate solution involves calculating the objective function f. The computational effort required for O(f) depends on the complexity of f, including its mathematical formulation and any constraints.

Time Complexity Analysis

The time complexity per iteration of WoOA can be approximated as O(N⋅O(f)), where:

•   N is the population size.

•   O(f) represents the computational effort to evaluate the objective function for each candidate solution.

Therefore, over T iterations, the total time complexity of WoOA is O(T⋅N⋅O(f)). This formulation captures the algorithm’s dependence on the number of iterations, population size, and the computational complexity of the objective function evaluation.

3.6 Applying WoOA to Constrained Optimization Challenges

Many real-world optimization problems are subject to constraints that must be managed to find feasible solutions. To address these types of constrained problems using the Wolverine Optimization Algorithm (WoOA), two distinct strategies are employed to handle solutions that do not meet the required constraints.

Replacement with Feasible Solutions: When an updated solution fails to satisfy the problem’s constraints, it is completely removed from the population of solutions. In its place, a new solution is generated randomly, ensuring it adheres to all constraints. This approach ensures that the algorithm maintains a population of feasible solutions throughout its execution.

Penalty Coefficient Method: If a solution does not meet the problem’s constraints, a penalty is added to its objective function value. This penalty makes the solution’s objective function worse, thereby signaling the algorithm that this solution is less optimal compared to others. The penalty effectively discourages the selection of infeasible solutions by making their objective function values less competitive.

Both strategies help in maintaining the effectiveness of the WoOA in solving constrained optimization problems by either ensuring feasibility through replacement or penalizing infeasible solutions to guide the search towards feasible and optimal solutions.

4  Simulation Studies and Results

This section assesses the effectiveness of WoOA in addressing optimization problems using the CEC 2017 test suite.

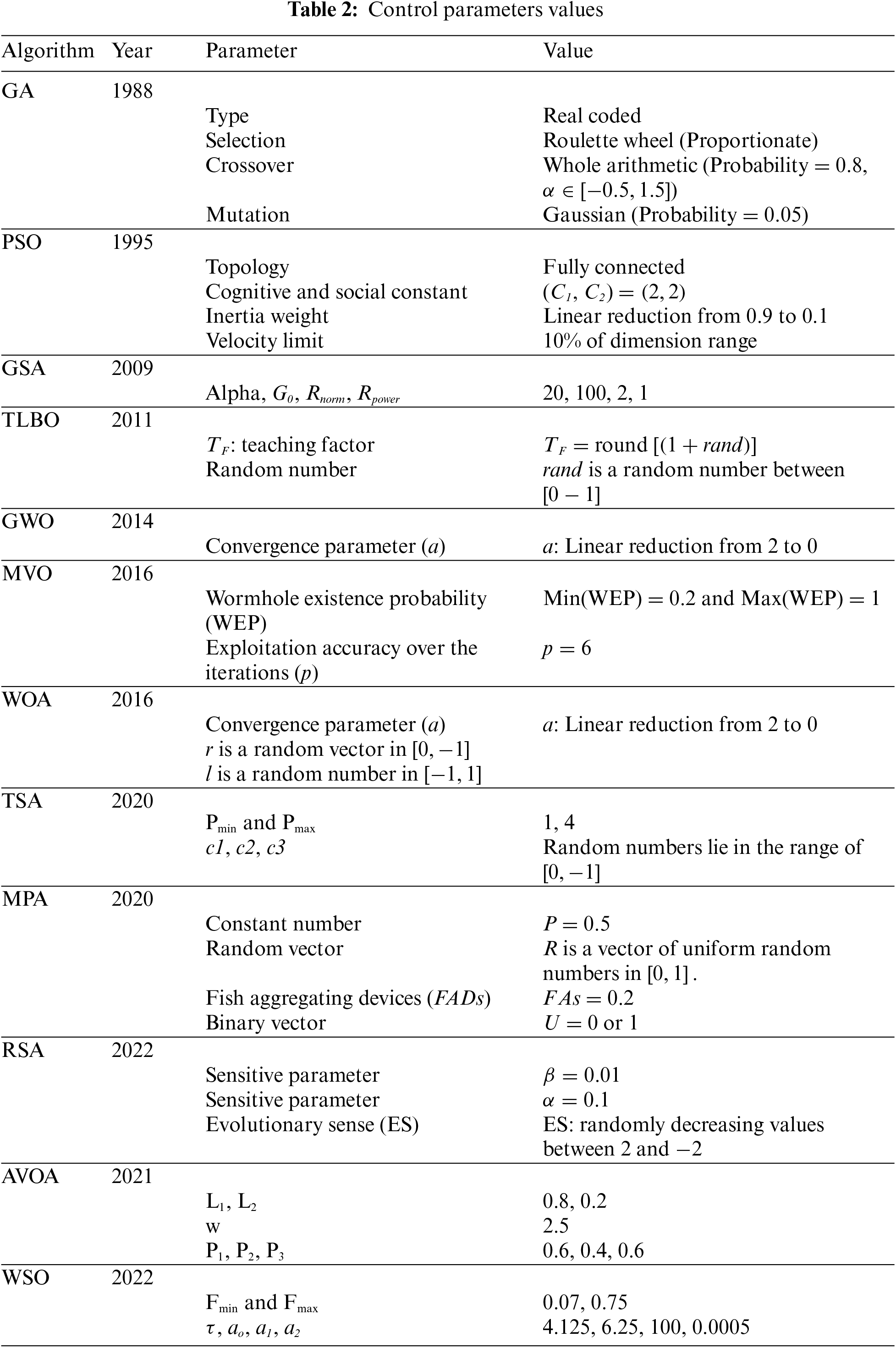
4.1 Benchmark Functions and Compared Algorithm

The effectiveness of WoOA in managing optimization tasks has been compared to twelve well-known metaheuristic algorithms, including: GA [29], PSO [13], GSA [38], TLBO [51], MVO [41], GWO [26], WOA [20], MPA [27], TSA [22], RSA [18], AVOA [28], and WSO [24]. Table 2 provides the defined values for the control parameters of the metaheuristic algorithms. Experiments have been implemented on the software MATLAB R2022a using a 64-bit Core i7 processor with 3.20 GHz and 16 GB main memory. The optimization results obtained from applying these algorithms to benchmark functions are detailed, showcasing six statistical measures for the assessment: mean, best, worst, standard deviation (std), median, and rank. The mean index values have been employed as a ranking standard for the metaheuristic algorithms in addressing each of the benchmark functions.

4.2 Evaluation CEC 2017 Test Suite

In this section, we evaluate the performance of the Wolverine Optimization Algorithm (WoOA) alongside other competing algorithms by applying them to the CEC 2017 test suite, with problem dimensions set at 10, 30, 50, and 100. The CEC 2017 test suite encompasses a total of thirty benchmark functions. These functions are categorized into several groups: three unimodal functions (C17-F1 through C17-F3), seven multimodal functions (C17-F4 through C17-F10), ten hybrid functions (C17-F11 through C17-F20), and ten composition functions (C17-F21 through C17-F30). For a comprehensive description and further details regarding the CEC 2017 test suite, please refer to [59].

In the process of evaluating the Wolverine Optimization Algorithm (WoOA) using the CEC 2017 test suite, function C17-F2 was omitted due to its erratic behavior. This exclusion was necessary to ensure the reliability and consistency of the results. Here, we explain the criteria for this exclusion and discuss its potential impact on the overall conclusions of the study.

Criteria for Exclusion of C17-F2

Function C17-F2 was excluded based on the following criteria:

1.    Erratic Behavior

•   During preliminary testing, C17-F2 exhibited significant numerical instabilities, leading to inconsistent and unreliable results. This erratic behavior could be due to issues in the function’s formulation or implementation, which made it an outlier compared to the other benchmark functions.

2.    Unpredictable Performance

•   The erratic nature of C17-F2 resulted in unpredictable performance outcomes, which did not align with the consistent patterns observed in other benchmark functions. This unpredictability hindered the ability to make fair and meaningful comparisons between WoOA and other algorithms.

3.    Impact on Statistical Validity

•   Including a function with such a behavior could distort the statistical analysis and overall performance evaluation. To maintain the integrity of the study, it was crucial to exclude functions that could potentially bias the results due to their inherent instability.

Impact on Overall Conclusions

The exclusion of C17-F2 might raise concerns about the comprehensiveness of the study, but the following points explain why this exclusion does not undermine the overall conclusions:

1.    Representation of Benchmark Functions

•   The CEC 2017 test suite comprises thirty benchmark functions, covering a wide range of optimization scenarios, including unimodal, multimodal, hybrid, and composition functions. With the exclusion of C17-F2, the remaining twenty-nine functions still provide a robust and comprehensive assessment of WoOA’s performance.

2.    Consistency of Results

•   The consistent superior performance of WoOA across multiple benchmark functions and problem dimensions (10, 30, 50, and 100) indicates that the exclusion of a single erratic function does not significantly alter the overall findings. WoOA demonstrated strong capabilities in exploration, exploitation, and maintaining a balance between the two throughout the search process.

3.    Statistical Significance

•   Statistical analyses, including the Wilcoxon rank sum test, were conducted on the results obtained from the remaining benchmark functions. These analyses confirmed WoOA’s significant statistical superiority over the twelve competing algorithms. The exclusion of C17-F2, therefore, does not compromise the statistical validity of these findings.

4.    Transparency and Integrity

•   By explicitly stating the exclusion and providing the reasons for it, the study maintains transparency and integrity. Researchers and practitioners can understand the rationale behind the decision and trust the reliability of the reported results.

Function C17-F2 was omitted from the evaluation due to its erratic behavior, which led to inconsistent and unreliable performance outcomes. The exclusion was necessary to maintain the reliability and consistency of the results. Despite this omission, the comprehensive assessment of WoOA using the remaining twenty-nine benchmark functions from the CEC 2017 test suite provides robust and statistically significant evidence of WoOA’s superior performance. The study’s transparency in reporting this exclusion further reinforces the integrity of the findings.

The CEC 2017 test suite is a standard set of benchmark functions to measure the abilities of metaheuristic algorithms in exploration, exploitation, and balancing them during the search process. Functions C17-F1 to C17-F3 are of unimodal type. Since these types of functions have only one global optimum and no local optimum, they are suitable criteria for testing the exploitation ability of metaheuristic algorithms. The functions C17-F4 to C17-F10 are selected from the multimodal type and have a large number of local optima. For this reason, these functions are suitable criteria for testing the exploration ability of metaheuristic algorithms for a comprehensive scanning of the problem-solving space. Functions C17-F11 to C17-F20 are selected from the hybrid type, where each function consists of several subcomponents. These types of functions can be a combination of unimodal and multimodal functions. For this reason, hybrid functions are suitable options to simultaneously investigate the exploration and exploitation capabilities of metaheuristic algorithms. Functions C17-F21 to C17-F30 are of composition type. These types of functions employ the hybrid functions as the basic functions and are considered as complex optimization problems. In an experimental level, the complexity of composition functions is increased significantly because of their shifted and rotated characteristics.

The WoOA methodology, along with several competing algorithms, was tested using the CEC 2017 benchmark functions across fifty-one independent runs. Each run involved 10,000·m function evaluations (FEs), where the population size (N) was set to 30. The results of these experiments are detailed in Tables 3 through 6, which compare the performance of WoOA against other algorithms.

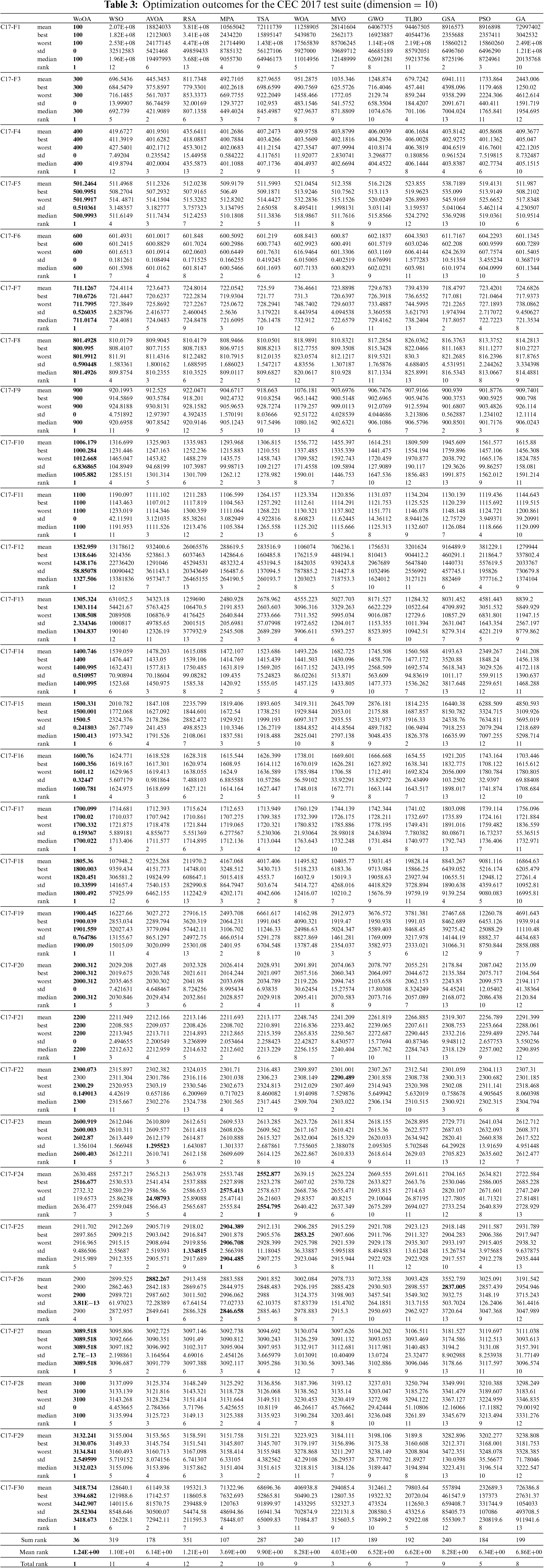
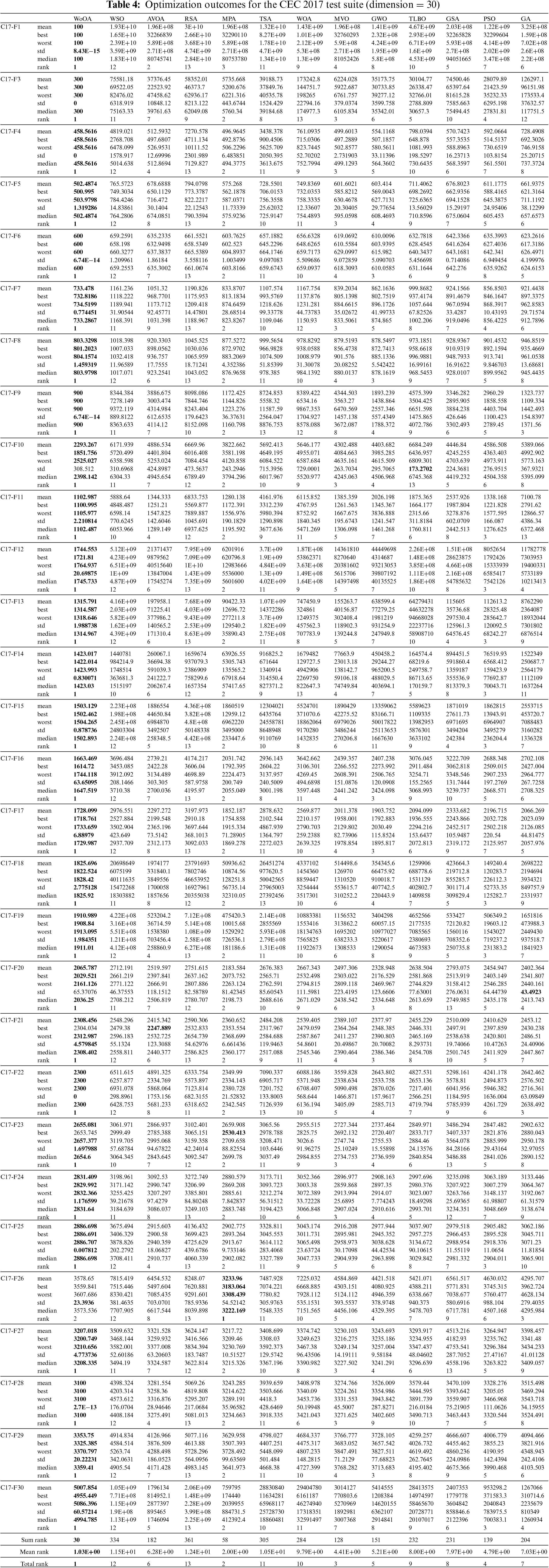
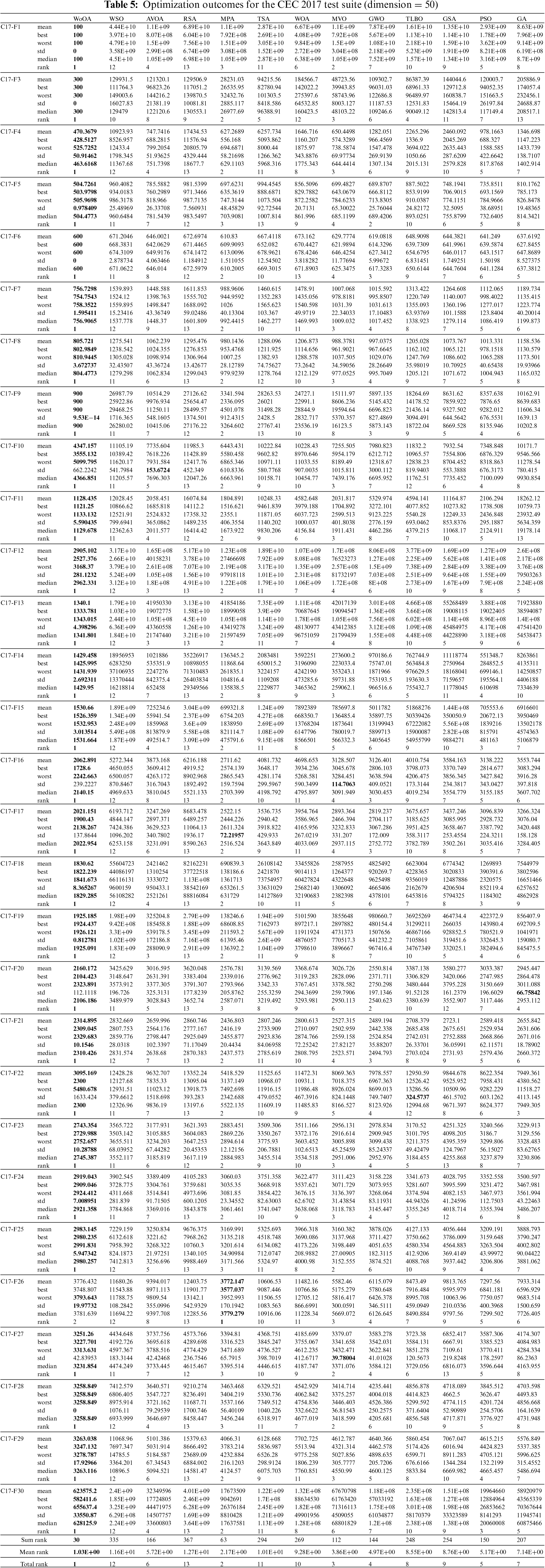
The performance of WoOA shows notable variation across different problem dimensions. For a problem dimension of 10 (m = 10), WoOA excelled as the top optimizer for functions C17-F1, C17-F3 through C17-F21, C17-F23, C17-F24, and C17-F26 through C17-F30. When the problem dimension increased to 30 (m = 30), WoOA continued to outperform competitors for functions C17-F1, C17-F3 through C17-F25, and C17-F27 through C17-F30. At a dimension of 50 (m = 50), WoOA maintained its superior performance for functions C17-F1, C17-F3 through C17-F25, and C17-F27 through C17-F30. Even for a higher dimension of 100 (m = 100), WoOA was identified as the best optimizer for functions C17-F1 and C17-F3 through C17-F30.

This consistent performance across different dimensions underscores the robustness and versatility of the WoOA approach in solving a wide range of optimization problems.

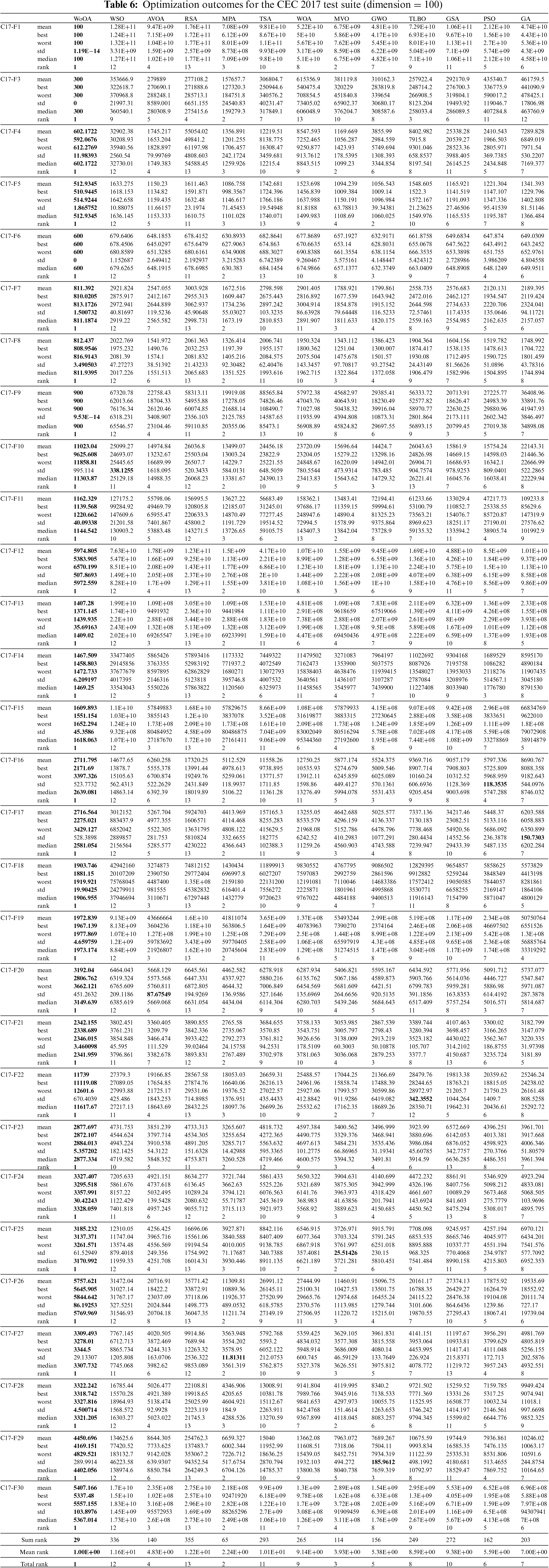
Additionally, Figs. 6–9 illustrate the convergence curves derived from the metaheuristic algorithms. Convergence curves plot the best objective function value found over the iterations for each algorithm. They provide insight into how quickly and effectively each algorithm finds near-optimal solutions.

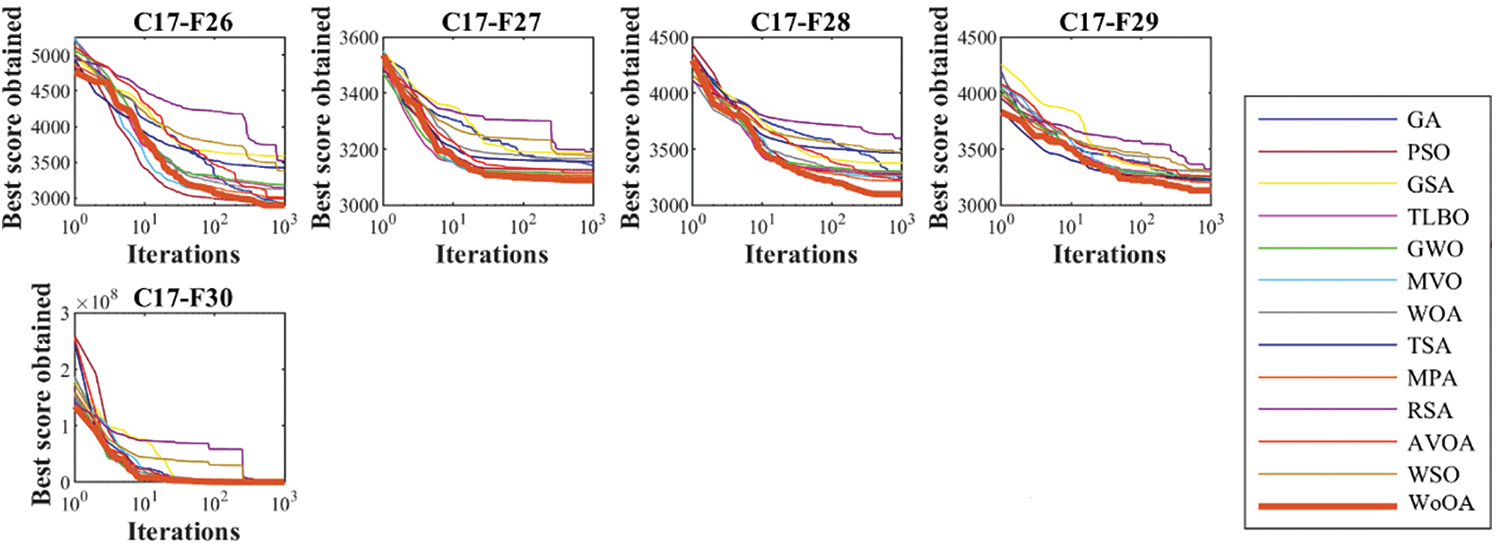
Figure 6: Convergence curves of the algorithms for the CEC 2017 test suite (dimension = 10)

Figure 7: Convergence curves of the algorithms for the CEC 2017 test suite (dimension = 30)

Figure 8: Convergence curves of the algorithms for the CEC 2017 test suite (dimension = 50)

Figure 9: Convergence curves of the algorithms for the CEC 2017 test suite (dimension = 100)

a)   Convergence Behavior

•   WoOA Convergence Pattern

•   WoOA’s curve shows a rapid initial decrease in the objective function value, indicating effective exploration and quick identification of promising solution areas.

•   As the iterations progress, the curve flattens, suggesting that WoOA shifts focus from exploration to exploitation, refining solutions near the optimum.

•   Comparison with Other Algorithms

•   Algorithms with steeper initial declines are also effective in exploration but may differ in how they balance exploration and exploitation.

•   Algorithms with flatter curves throughout may struggle with exploration, converging more slowly or getting trapped in local optima.

b)   Rate of Convergence

The rate of convergence is determined by how quickly an algorithm reduces the objective function value over time.

•   Initial Convergence Rate

•   WoOA shows a steep initial slope, demonstrating a high convergence rate at the beginning. This suggests that WoOA is efficient in rapidly exploring the search space and identifying good regions early in the optimization process.

•   Algorithms with similar steep initial slopes indicate competitive initial exploration capabilities.

•   Later Stages Convergence Rate

•   In later iterations, WoOA’s convergence curve gradually becomes flatter. This indicates a reduced convergence rate, typical as the algorithm switches from exploitation to fine-tune solutions.

•   Some competing algorithms might maintain a slightly higher convergence rate later, indicating continuous improvements. However, if the slope is too flat, it might suggest premature convergence.

Key Observations:

•   Effectiveness in Exploration

•   WoOA’s rapid initial convergence indicates strong exploration abilities, quickly finding promising areas in the search space.

•   Competitors with less steep initial slopes may not explore as effectively early on.

•   Effectiveness in Exploitation

•   The gradual flattening of WoOA’s curve indicates effective exploitation, focusing on refining the solutions and improving precision.

•   Competing algorithms with a flatter overall curve may either fail to transition effectively from exploration to exploitation or may not balance these phases well.

•   Overall Performance

•   WoOA demonstrates a strong balance between exploration and exploitation, achieving rapid initial improvements and continuing to fine-tune solutions effectively.

•   The overall shape and steepness of WoOA’s convergence curve suggest that it performs well across different phases of the optimization process compared to the other algorithms.

WoOA’s convergence curve reflects a robust optimization performance, characterized by a high initial convergence rate due to effective exploration and a sustained convergence rate during exploitation phases. This balance allows WoOA to consistently find near-optimal solutions efficiently. When compared to other metaheuristic algorithms, WoOA exhibits a superior performance in terms of both rapid initial convergence and steady improvements, making it a strong candidate for solving complex optimization problems in CEC 2017.

Upon analyzing the optimization results, it is apparent that WoOA has delivered successful outcomes in addressing optimization issues, showcasing its strong abilities in both exploration and exploitation while maintaining a balance between the two during the search process. The simulation results clearly indicate WoOA’s superiority, as it performs remarkably well for various benchmark functions and ranks as the top optimizer overall in handling the CEC 2017 test suite for problem dimensions equal to 10, 30, 50, and 100.

4.3 Statistical Analysis

In this section, we expand upon the initial statistical analysis to include additional measures to ascertain the statistical significance of WoOA’s performance compared to other algorithms. Specifically, we will employ the Wilcoxon rank sum test, the t-test, and the Friedman test to provide a comprehensive evaluation.

4.3.1 Wilcoxon Rank Sum Test

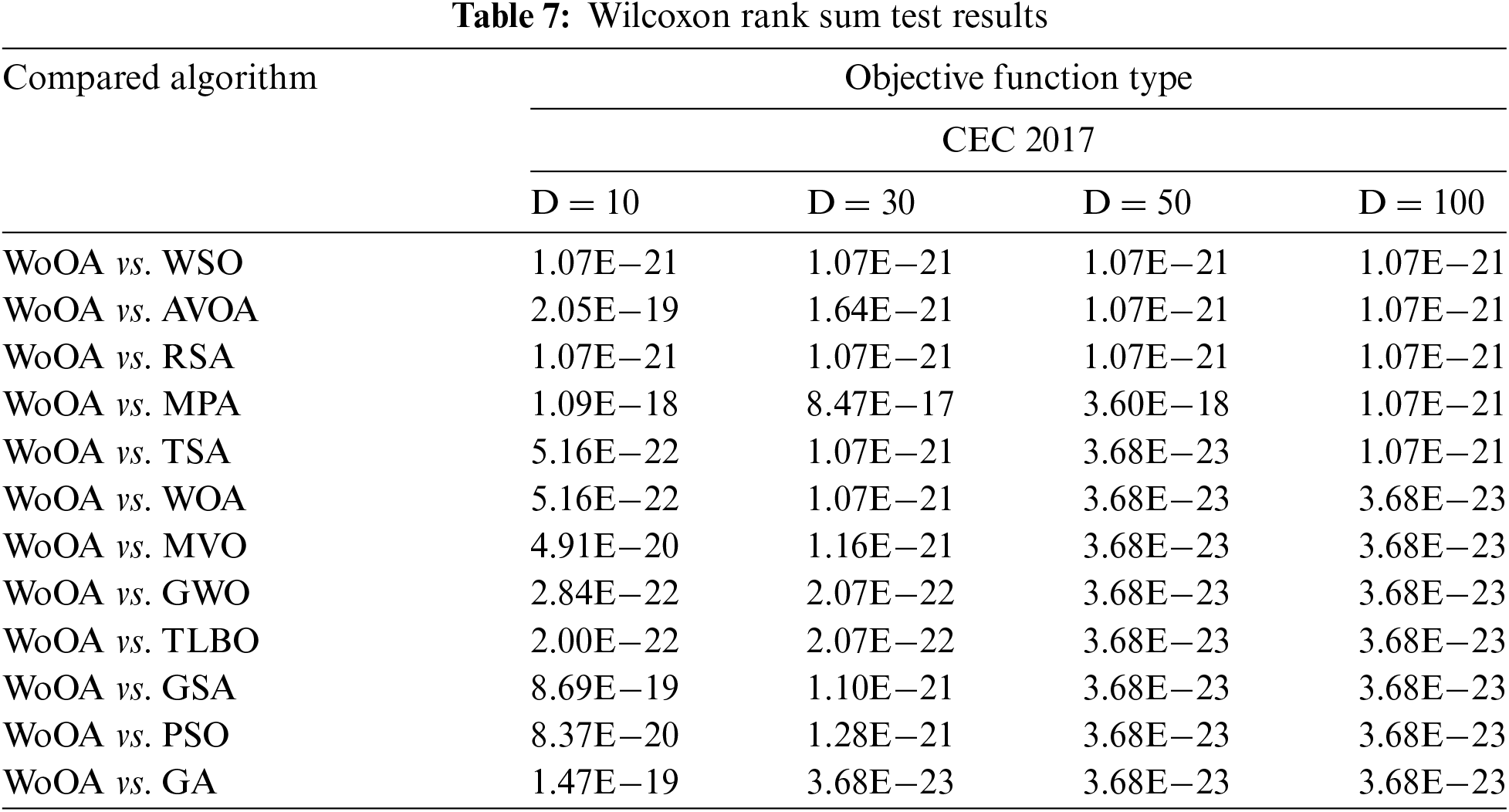
The Wilcoxon rank sum test [60] is a non-parametric test that effectively identifies significant differences between the means of two sets of data. The presence of a notable difference in the performance of two metaheuristic algorithms is assessed using a metric known as the p-value in the Wilcoxon rank sum test.

Table 7 reports the outcomes of the statistical analysis measuring the effectiveness of WoOA vs. other algorithms in managing the CEC 2017 test suite, using the Wilcoxon rank sum test. According to the findings, WoOA demonstrates a notable statistical superiority when the p-value is below 0.05 when compared to alternative algorithms. The statistical analysis reveals that WoOA significantly outperforms all twelve alternative algorithms when handling the CEC 2017 test suite.

4.3.2 t-test

The t-test is used to compare the means of two groups and determine whether they are statistically different from each other [61]. We use the paired t-test to compare WoOA’s performance with each of the twelve competing algorithms on the CEC 2017 test suite for the dimensions 10, 30, 50, and 100. The results obtained from the t-test are reported in Table 8. The t-test results indicate that WoOA’s performance is statistically significantly better than the compared algorithms across different dimensions.

4.3.3 Friedman Test

The Friedman test is a non-parametric test used to detect differences in treatments across multiple test attempts [62]. We apply this test to determine whether there are significant differences in the performance rankings of the algorithms. The results obtained from the implementation of the Friedman test are reported in Table 9. The Friedman test results confirm that there are statistically significant differences in the performance rankings of the algorithms across all dimensions.

4.4 Compatibility of WoOA with Changes in Dimensions

The Wolverine Optimization Algorithm (WoOA) demonstrates a robust performance across various problem dimensions (10, 30, 50, and 100). This adaptability to different dimensionalities is a testament to the algorithm’s flexible and efficient design. In this section, we will explain and discuss the compatibility of WoOA with changes in the dimensions by referring to its mathematical model and the special advantages highlighted in the earlier sections.

a)   Mathematical Model and Strategies

WoOA is inspired by the natural behaviors of the wolverines, specifically their scavenging and hunting techniques. The algorithm’s mathematical model integrates these behaviors into two main strategies: scavenging and hunting. These strategies facilitate exploration and exploitation in the search space, ensuring that the algorithm remains effective across different dimensionalities.

•   Scavenging Strategy (Exploration Phase)

•   This strategy simulates wolverines moving towards carrion left by other predators. It allows WoOA to perform a broad exploration of the search space, preventing premature convergence to local optima. The mathematical formulation ensures that this exploration phase is effective regardless of the dimensionality of the problem.

•   Hunting Strategy (Exploitation Phase)

•   The hunting strategy is divided into two parts: exploration (approaching the prey) and exploitation (pursuit and combat with the prey). This dual approach enables WoOA to fine-tune solutions and converge towards the global optimum efficiently. The algorithm’s ability to switch between exploration and exploitation phases dynamically helps it adapt to different dimensionalities.

b)   Special Advantages of WoOA

The WoOA has several inherent advantages that contribute to its compatibility with varying dimensions:

•   No Control Parameters

•   Unlike many metaheuristic algorithms, WoOA does not rely on specific control parameters. This parameter-free nature simplifies its application and ensures consistent performance across different problem dimensions without the need for an extensive parameter tuning.

•   Balancing Exploration and Exploitation

•   WoOA’s design effectively balances exploration and exploitation throughout the search process. This balance is crucial for handling high-dimensional problems where the search space is vast, and finding the global optimum requires a thorough exploration and precise exploitation.

•   High-Speed Convergence

•   The algorithm’s ability to rapidly converge to suitable solutions, especially in complex, high-dimensional problems, is a significant advantage. This high-speed convergence is facilitated by WoOA’s dynamic adaptation of its strategies based on the dimensionality and nature of the problem.

c)   Implementation and Performance across Dimensions

The implementation details and performance results from the CEC 2017 test suite provide empirical evidence of WoOA’s compatibility with different dimensions:

•   CEC 2017 Test Suite

•   The WoOA was tested on a comprehensive set of benchmark functions from the CEC 2017 test suite, with problem dimensions set at 10, 30, 50, and 100. The test suite includes unimodal, multimodal, hybrid, and composition functions, providing a diverse range of optimization challenges.

•   Performance Metrics

•   The algorithm’s performance was assessed using six statistical measures: mean, best, worst, standard deviation (std), median, and rank. Across all dimensions, WoOA consistently ranked as the top optimizer for most benchmark functions, demonstrating its robustness and adaptability.

•   Scalability

•   The results indicate that WoOA scales well with increasing dimensions. The algorithm maintained its superior performance even as the dimensionality increased from 10 to 100, showcasing its capability to handle large-scale optimization problems effectively.

The Wolverine Optimization Algorithm (WoOA) is highly compatible with changes in dimensionality due to its innovative design and strategic approach. Its parameter-free nature, effective balance between exploration and exploitation, and high-speed convergence contribute to its robustness across various problem dimensions. The empirical results from the CEC 2017 test suite further validate WoOA’s adaptability and superior performance in both low-dimensional and high-dimensional optimization problems. This adaptability makes WoOA a versatile and powerful tool for tackling a wide range of optimization challenges.

5  WoOA for Real-World Applications

One of the primary applications of metaheuristic algorithms is tackling real-world optimization problems. In this section, we thoroughly evaluate the effectiveness of the Wolverine Optimization Algorithm (WoOA) in solving a diverse set of optimization problems. Specifically, we assess WoOA’s capability to address twenty-two constrained optimization problems from the CEC 2011 test suite. Additionally, we extend our evaluation to include four complex engineering design problems, providing a comprehensive analysis of WoOA’s performance for practical, real-world scenarios. This assessment will demonstrate how well WoOA can navigate and optimize under various constraints and conditions inherent in these problems.

5.1 Evaluation for the CEC 2011 Test Suite

The application of metaheuristic algorithms in solving real-world optimization problems is crucial. In this section, we assess the effectiveness of WoOA in addressing twenty-two constrained optimization problems from the CEC 2011 test suite. Details and full descriptions of the twenty-two constrained optimization problems can be found in [63]. The choice of the CEC 2011 test suite for evaluating WoOA is justified based on its reputation, relevance to real-world applications, ability to facilitate a comparative analysis, and the specific challenges it presents that align with the strengths of WoOA. By using this established benchmark, the study ensures a rigorous and meaningful evaluation of WoOA’s performance, providing valuable insights into its practical utility and effectiveness in solving constrained optimization problems.

The WoOA approach, alongside various competing algorithms, was thoroughly tested on the CEC-2011 benchmark functions across twenty-five separate implementations. Each implementation comprised 150,000 function evaluations (FEs). In this experiment, the population size (N) is considered to be equal to 30. The comprehensive results of these tests are detailed in Table 10, and further illustrated through boxplot diagrams in Fig. 10, which present the performance metrics of all metaheuristic algorithms applied to this test suite. The evaluation results reveal that WoOA has excelled in tackling the complex optimization challenges posed by the CEC 2011 test suite. The algorithm showcased its adeptness at exploration and exploitation, effectively balancing these critical aspects throughout the search process. Notably, WoOA outperformed all other algorithms for solving the problems C11-F1 through C11-F22, demonstrating its superior capability in optimizing these functions.

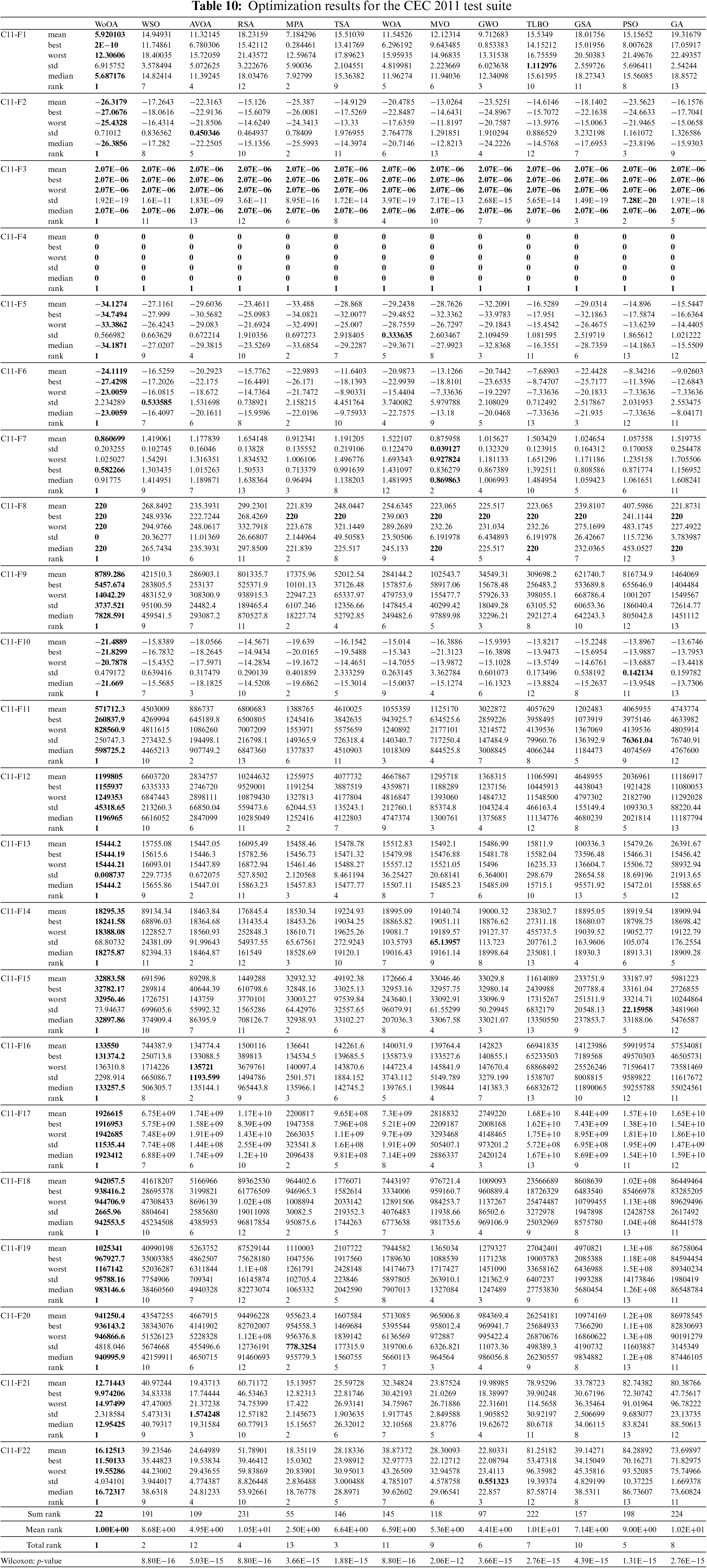
Figure 10: Boxplot diagrams of WoOA and the competing algorithms performances for the CEC 2011 test suite

A detailed comparison of the simulation outcomes highlights that WoOA consistently achieved better results than its competitors. This significant performance advantage underscores WoOA’s effectiveness and reliability in addressing a diverse array of optimization problems within the CEC 2011 test suite. It achieved superior results for most optimization problems and was ranked as the top optimizer. Additionally, the statistical analysis showed that WoOA holds a significant statistical superiority over alternative algorithms for handling the CEC 2011 test suite.

5.2 Optimizing Pressure Vessel Design Parameters

Pressure vessel design with the schematic shown in Fig. 11 is a real-world application in engineering with the aim of minimizing construction cost. The mathematical model of this design is fully available in [64].

Figure 11: Schematic of the pressure vessel design

The performance outcomes of the WoOA approach, compared to other competing algorithms for optimizing the pressure vessel design, are comprehensively detailed in Tables 11 and 12. Fig. 12 presents the convergence curve of WoOA, illustrating its progress toward finding the optimal solution for the pressure vessel design problem.

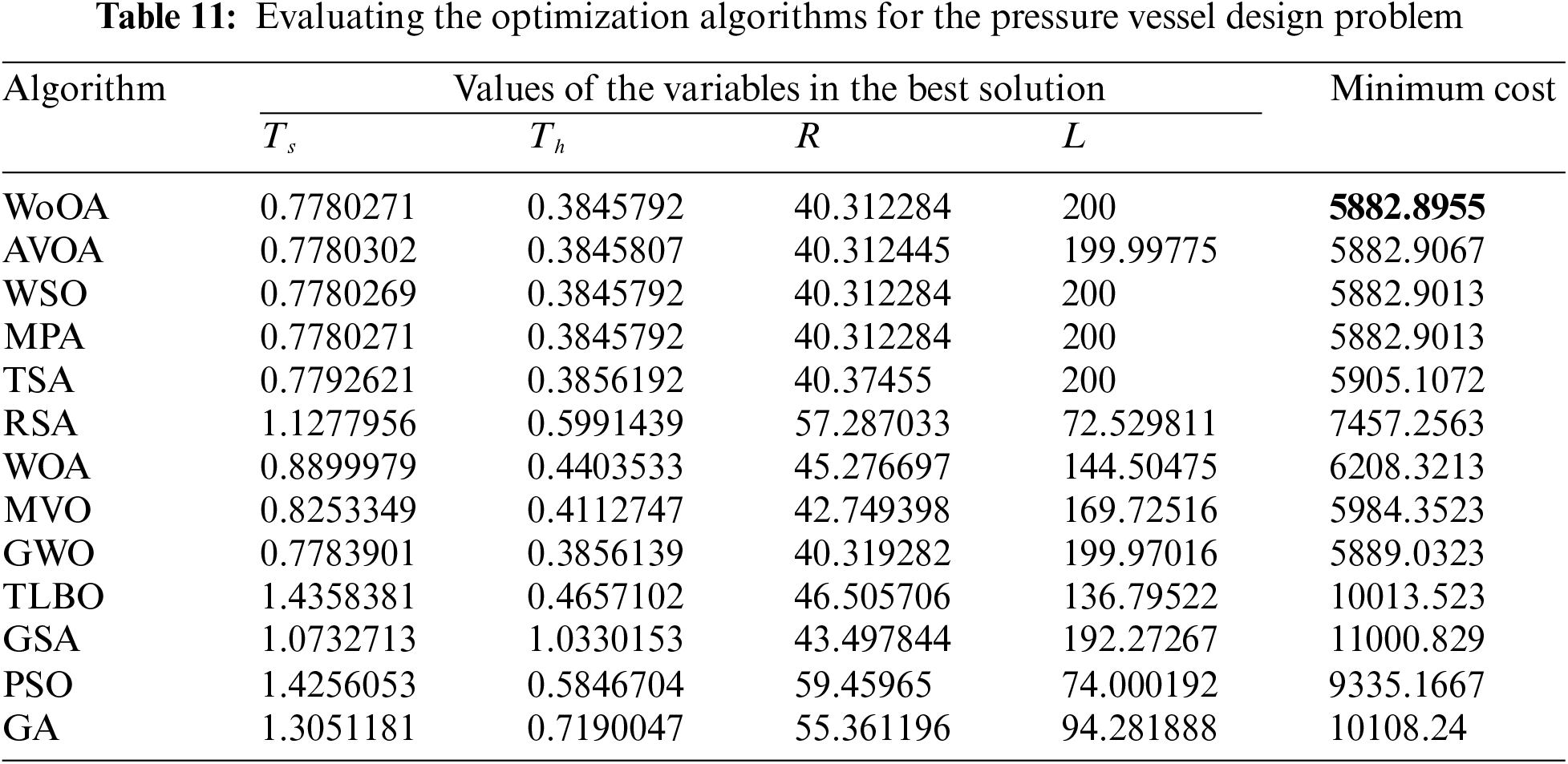
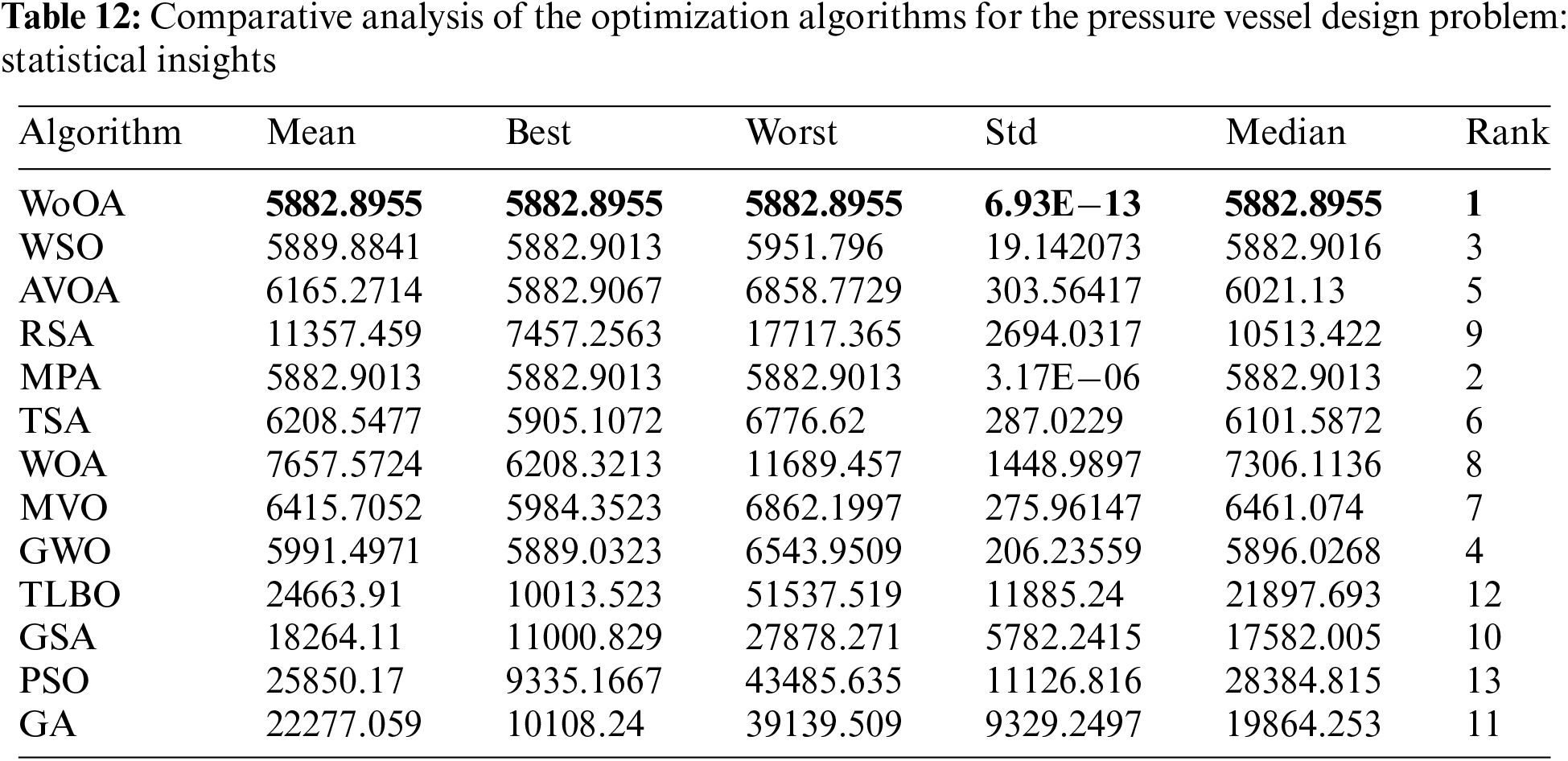
Figure 12: Convergence analysis of WoOA in optimizing pressure vessel design

From the analysis, WoOA achieved the most effective design, with the optimal values for the design variables being (0.7780271, 0.3845792, 40.312284, 200), and the corresponding objective function value being (5882.8955). These results indicate that WoOA not only met but exceeded expectations in this optimization task.

The simulation results further demonstrate that WoOA has outperformed other algorithms in terms of statistical indicators related to the pressure vessel design. This superior performance highlights WoOA’s ability to deliver better optimization results, providing a completely different and more efficient approach to solving the pressure vessel design problem compared to its competitors.

5.3 Optimizing Speed Reducer Design Parameters

The speed reducer design with the schematic shown in Fig. 13 is a real-world application in engineering with the aim of minimizing the weight of the speed reducer. The mathematical model of this design is fully available in [65,66].

Figure 13: Schematic of the speed reducer design

The effectiveness of the WoOA approach, as well as several competing algorithms, in optimizing the speed reducer design is thoroughly documented in Tables 13 and 14. Fig. 14 visually represents the convergence curve of WoOA, showcasing its progress toward the optimal solution for the speed reducer design.

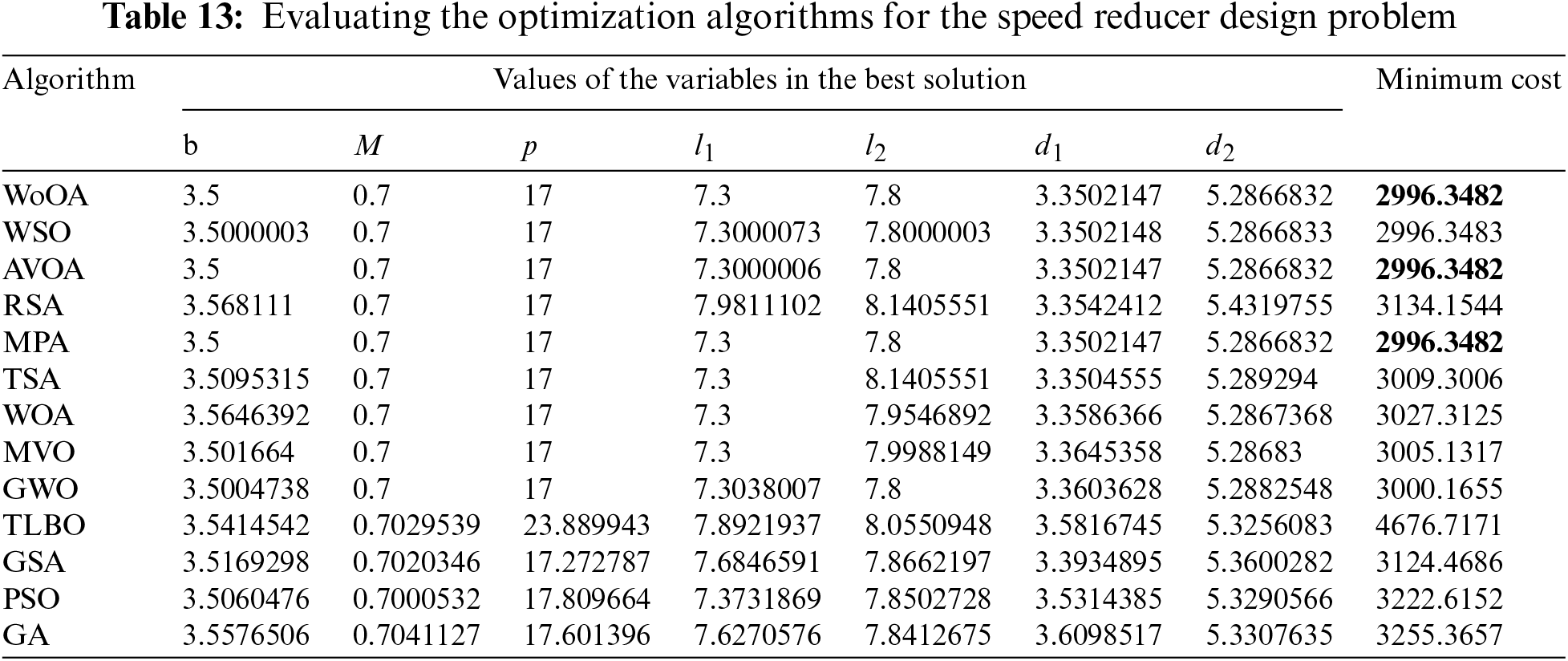
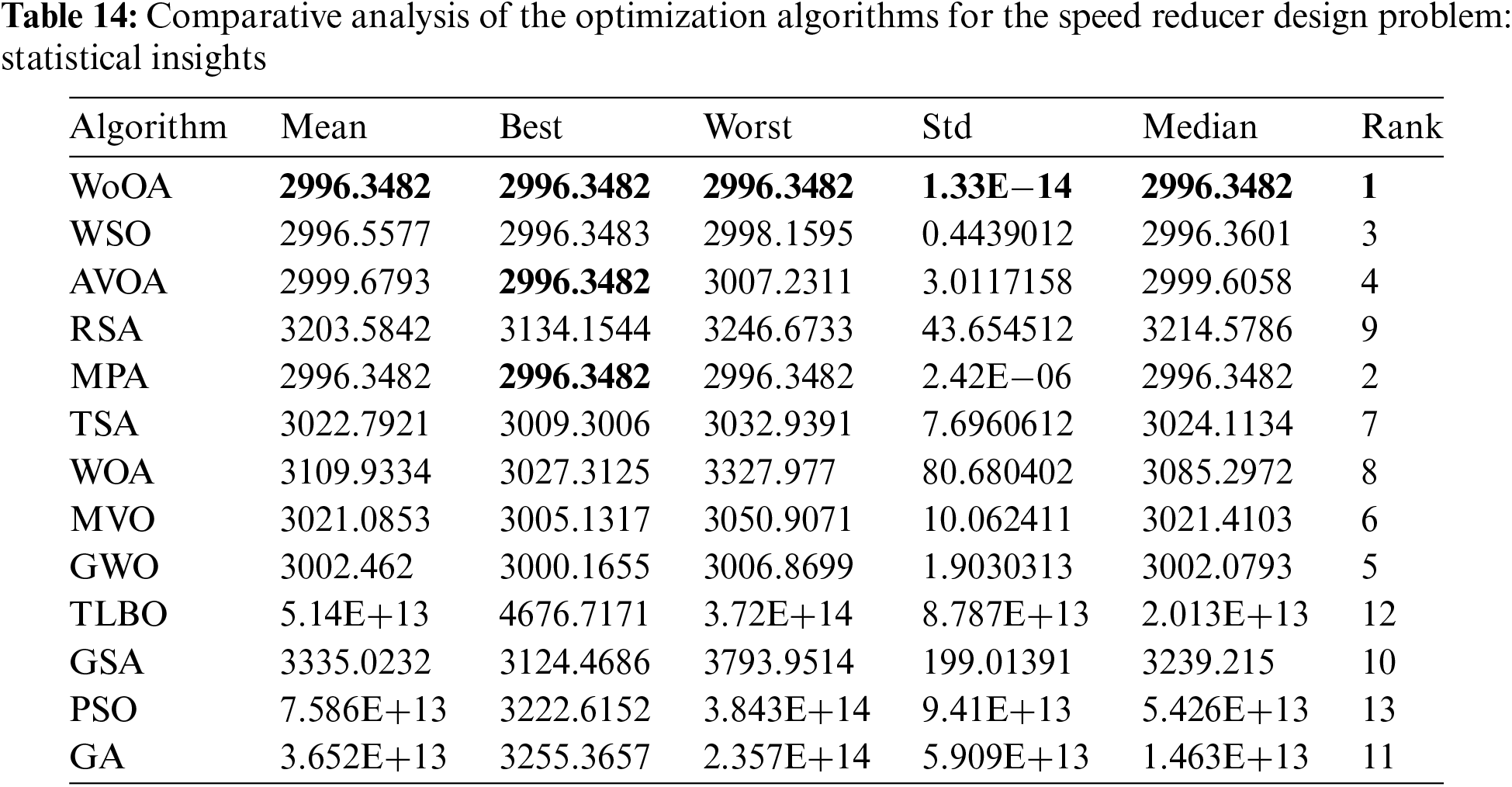
Figure 14: WoOA’s performance convergence curve for the speed reducer design

The data reveals that WoOA achieved the most effective design configuration, with the optimal values for the design variables being (3.5, 0.7, 17, 7.3, 7.8, 3.3502147, 5.2866832) and the objective function value at (2996.3482). This optimal design indicates a significant improvement over the results obtained by other algorithms.

A detailed analysis of the simulation results highlights that WoOA demonstrated superior performance compared to its competitors. The algorithm not only achieved better results for key statistical indicators but also showcased a completely different level of efficiency and precision in optimizing the speed reducer design. This distinction underscores WoOA’s effectiveness and reliability in solving complex design optimization problems.

5.4 Optimizing Welded Beam Design Parameters

The welded beam design with the schematic shown in Fig. 15 is a real-world application in engineering with the aim of minimizing the fabrication cost of the welded beam. The mathematical model of this design is fully available in [20].

Figure 15: Schematic of the welded beam design

The results obtained from using WoOA and the competing algorithms in order to address the welded beam design are presented in Tables 15 and 16. Fig. 16 illustrates the convergence curve of WoOA throughout the optimization process for this particular design challenge. According to the obtained results, WoOA successfully identified the best design configuration with the design variable values of (0.2057296, 3.4704887, 9.0366239, 0.2057296) and an objective function value of (1.7246798). Upon comparing the simulation results, it becomes apparent that WoOA has demonstrated a superior performance in optimizing welded beam designs compared with the competing algorithms, as evidenced by the improved statistical indicators it has provided.

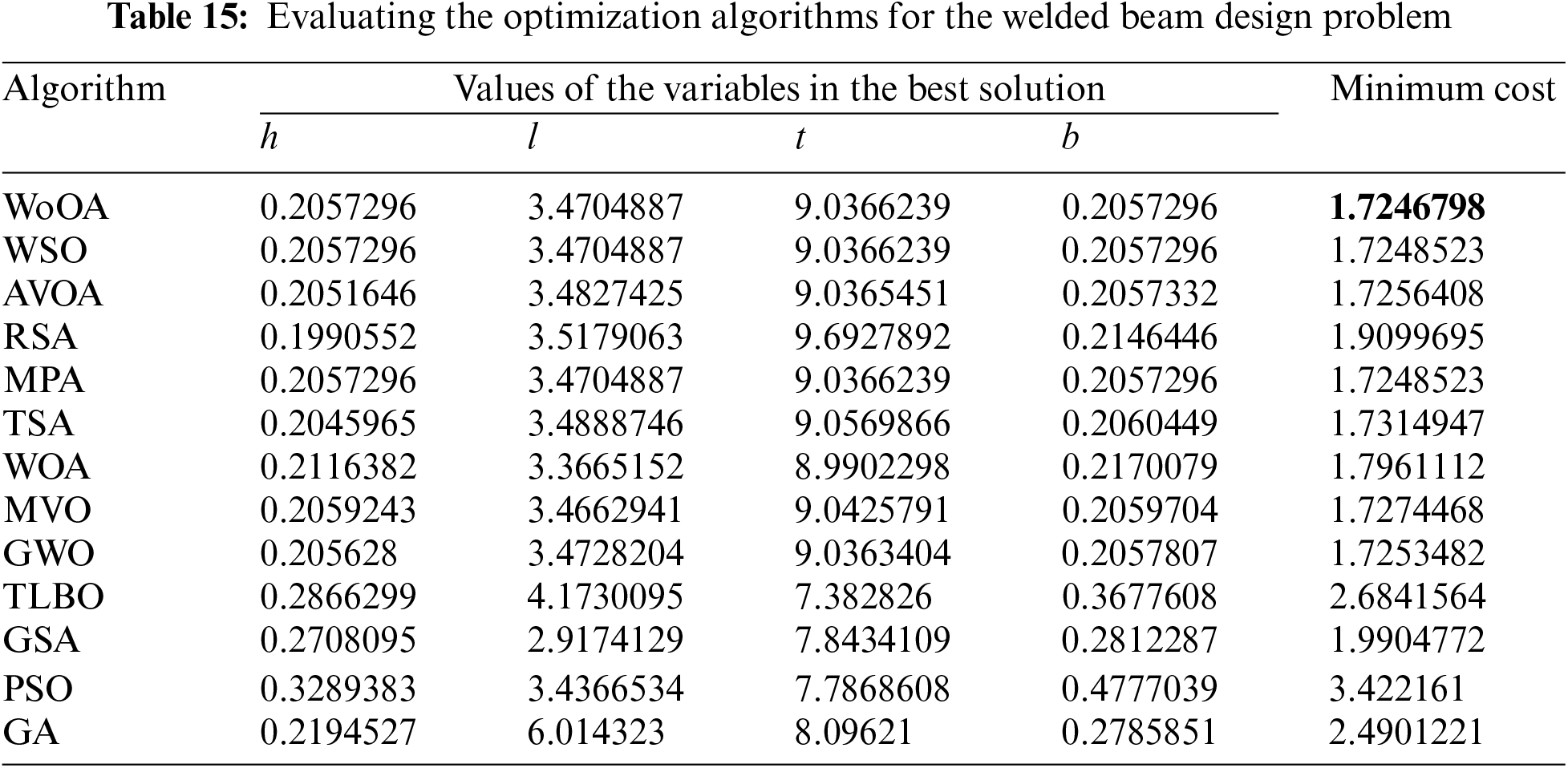
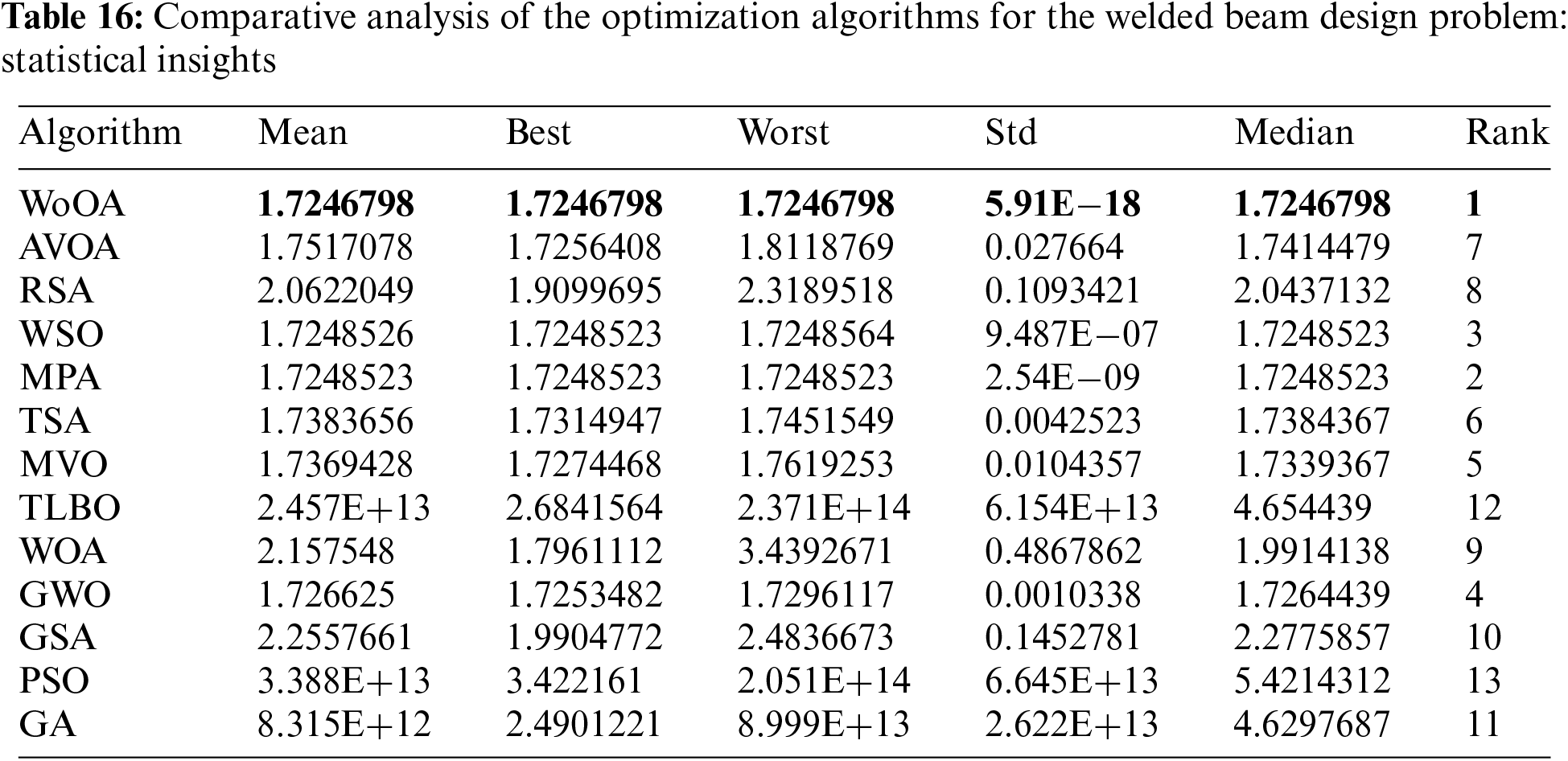
Figure 16: WoOA’s performance convergence curve for the welded beam design

5.5 Optimizing Tension/Compression Spring Design Parameters

The tension/compression spring design with the schematic shown in Fig. 17 is a real-world application in engineering with the aim of minimizing the construction cost. The mathematical model of this design is fully available in [20].

Figure 17: Schematic of the tension/compression spring design

The outcomes derived from utilizing the Wolverine Optimization Algorithm (WoOA) and various competing algorithms for optimizing the design of a tension/compression spring are detailed in Tables 17 and 18. Fig. 18 illustrates the convergence curve of WoOA as it approaches the best solution for this spring design task. According to the results, WoOA successfully identified the best design configuration with the design variable values of (0.0516891, 0.3567177, 11.288966) and an objective function value of (0.0126019). These findings underscore the effectiveness of WoOA in achieving a superior design optimization for tension/compression springs. The analysis of the simulation results indicates that WoOA has provided a superior performance in dealing with the tension/compression spring design by achieving better results for the statistical indicators compared to the competing algorithms.

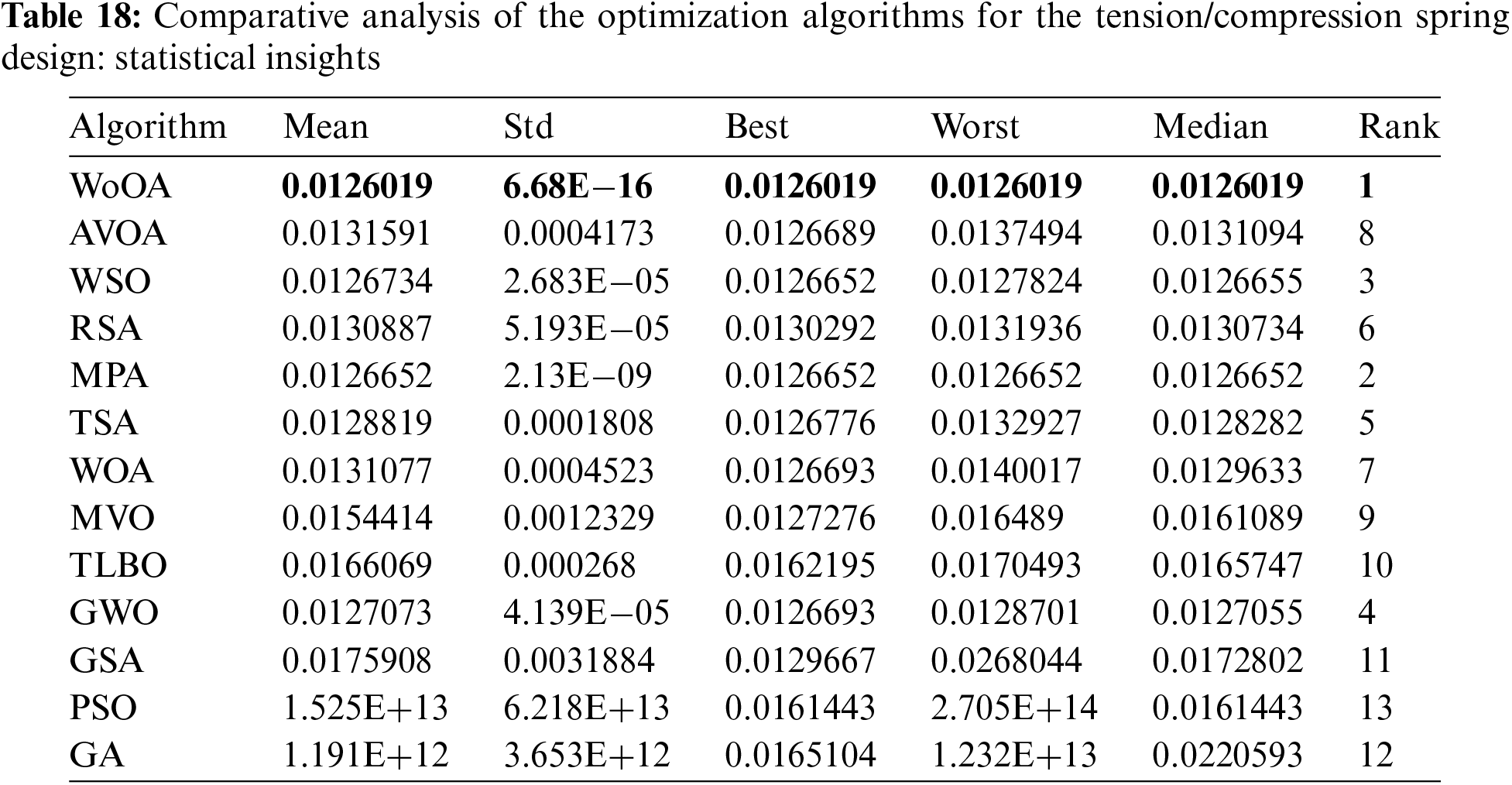
Figure 18: WoOA’s performance convergence curve for the tension/compression spring

6  Conclusions and Future Works

This study introduced a novel bio-inspired algorithm, called Wolverine Optimization Algorithm (WoOA), which mimics the natural behavior of wolverines. The inspiration for WoOA is drawn from the feeding habits of wolverines, which include scavenging for carrion and actively hunting prey. The algorithm incorporates two main strategies: scavenging and hunting. The scavenging strategy simulates the wolverine’s search for carrion, reflecting an exploration phase. The hunting strategy, on the other hand, involves both exploration, reflecting the wolverine’s attack on prey, and exploitation, reflecting the chase and confrontation between the wolverine and its prey. The effectiveness of WoOA in addressing optimization issues was assessed using the CEC 2017 test suite. The optimization findings demonstrated WoOA’s strong capability in the exploration, exploitation, and balancing of these aspects during the search process within the problem-solving domain. WoOA’s results were compared against twelve established metaheuristic algorithms, and the simulations revealed the superiority of the WoOA, outperforming most benchmark functions and earning the top rank as the best optimizer among its competitors. Through a statistical analysis, it was verified that the superiority of WoOA is statistically significant. Applying WoOA to twenty-two constrained scenarios from the CEC 2011 suite and four complex engineering design challenges demonstrated that the suggested method effectively and sufficiently performs optimization tasks for real-world applications.

The WoOA approach offers a range of distinct advantages for tackling global optimization problems. Firstly, WoOA’s design is completely different from many other algorithms in that it operates without any control parameters. This means that users are spared from the often complex and time-consuming task of setting and tuning these parameters. Secondly, WoOA demonstrates exceptional effectiveness across a broad spectrum of optimization problems, encompassing various scientific fields and intricate high-dimensional challenges. Its performance in such diverse contexts highlights its robustness and versatility. A third notable advantage of WoOA is its remarkable ability to balance exploration and exploitation throughout the search process. This balance enables the algorithm to converge rapidly, delivering highly suitable values for decision variables, particularly in complex optimization scenarios. This ability to maintain a dynamic equilibrium between exploring new solutions and refining existing ones is crucial for efficient problem-solving. Additionally, WoOA excels in addressing real-world optimization applications. Its powerful performance in practical scenarios underscores its capability to handle practical constraints and deliver effective solutions in real-world settings. However, despite these strengths, WoOA also has some limitations. As a stochastic algorithm, it does not guarantee achieving the global optimum. The inherent randomness in the algorithm’s search process means that while it can find highly effective solutions, it cannot ensure that these solutions are globally optimal. Moreover, according to the No Free Lunch (NFL) theorem, there are no absolute assurances regarding the success or failure of WoOA for every possible optimization problem. The theorem implies that no single algorithm is universally best for all problems, and WoOA’s effectiveness may vary depending on the specific nature of the problem being addressed. Finally, there is always the possibility that future advancements in metaheuristic algorithms could result in methods that outperform WoOA. Newer algorithms could offer improved performance or address certain problem types more effectively, making it crucial for WoOA to be continually assessed and compared with emerging techniques.

Along with the introduction of WoOA, this paper presents several research suggestions for future work. The design of binary and multi-purpose versions of WoOA are among the most significant research potentials of this study. Employing WoOA to address optimization tasks in various sciences and real-world applications is another suggestion of this study for further work.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tareq Hamadneh, Belal Batiha, Omar Alsayyed, Kei Eguchi, Mohammad Dehghani; data collection: Belal Batiha, Frank Werner, Kei Eguchi, Zeinab Monrazeri, Tareq Hamadneh; analysis and interpretation of results: Omar Alsayyed, Kei Eguchi, Mohammad Dehghani, Frank Werner, Tareq Hamadneh; draft manuscript preparation: Tareq Hamadneh, Zeinab Monrazeri, Omar Alsayyed, Belal Batiha, Mohammad Dehghani. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zhao S, Zhang T, Ma S, Chen M. Dandelion optimizer: a nature-inspired metaheuristic algorithm for engineering applications. Eng Appl Artif Intell. 2022;114:105075. doi:10.1016/j.engappai.2022.105075. [Google Scholar] [CrossRef]

2. Sergeyev YD, Kvasov D, Mukhametzhanov M. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci Rep. 2018;8(1):1–9. doi:10.1038/s41598-017-18940-4 [Google Scholar] [PubMed] [CrossRef]

3. Liberti L, Kucherenko S. Comparison of deterministic and stochastic approaches to global optimization. Int Trans Operat Res. 2005;12(3):263–85. doi:10.1111/j.1475-3995.2005.00503.x. [Google Scholar] [CrossRef]

4. Qawaqneh H. New contraction embedded with simulation function and cyclic (α, β)-admissible in metric-like spaces. Int J Math Comput Sci. 2020;15(4):1029–44. [Google Scholar]

5. Hamadneh T, Athanasopoulos N, Ali M editors. Minimization and positivity of the tensorial rational Bernstein form. In: 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT-Proceedings), 2019; Amman, Jordan: IEEE. [Google Scholar]

6. Mousavi A, Uihlein A, Pflug L, Wadbro E. Topology optimization of broadband acoustic transition section: a comparison between deterministic and stochastic approaches. Struct Multidiscipl Optim. 2024;67(5):67. doi:10.1007/s00158-024-03784-0. [Google Scholar] [CrossRef]

7. Tomar V, Bansal M, Singh P. Metaheuristic algorithms for optimization: a brief review. Eng Proc. 2024;59(1):238. doi:10.3390/engproc2023059238. [Google Scholar] [CrossRef]

8. de Armas J, Lalla-Ruiz E, Tilahun SL, Voß S. Similarity in metaheuristics: a gentle step towards a comparison methodology. Nat Comput. 2022;21(2):265–87. doi:10.1007/s11047-020-09837-9. [Google Scholar] [CrossRef]

9. Al-Baik O, Alomari S, Alssayed O, Gochhait S, Leonova I, Dutta U, et al. Pufferfish optimization algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems. Biomimetics. 2024;9(2):65. doi:10.3390/biomimetics9020065 [Google Scholar] [PubMed] [CrossRef]

10. Bai J, Li Y, Zheng M, Khatir S, Benaissa B, Abualigah L, et al. A sinh cosh optimizer. Knowl-Based Syst. 2023;282:111081. [Google Scholar]

11. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evolut Comput. 1997;1(1):67–82. doi:10.1016/j.knosys.2023.111081. [Google Scholar] [CrossRef]

12. Sörensen K. Metaheuristics—the metaphor exposed. Int Trans Operat Res. 2015;22(1):3–18. doi:10.1111/itor.12001. [Google Scholar] [CrossRef]

13. Kennedy J, Eberhart Reditors. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks, 1995 Nov 27–1995 Dec 1; Perth, WA, Australia: IEEE. [Google Scholar]

14. Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern Part B (Cybern). 1996;26(1):29–41. doi:10.1109/3477.484436 [Google Scholar] [PubMed] [CrossRef]

15. Karaboga D, Basturk Beditors. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In: International Fuzzy Systems Association World Congress, 2007; Berlin, Heidelberg: Springer. [Google Scholar]

16. Yang X-S. Firefly algorithm, stochastic test functions and design optimisation. Int J Bio-Inspired Comput. 2010;2(2):78–84. doi:10.1504/IJBIC.2010.032124 [Google Scholar] [PubMed] [CrossRef]

17. Trojovský P, Dehghani M. Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications. Sensors. 2022;22(3):855. doi:10.3390/s22030855 [Google Scholar] [PubMed] [CrossRef]

18. Abualigah L, Abd Elaziz M, Sumari P, Geem ZW, Gandomi AH. Reptile search algorithm (RSAa nature-inspired meta-heuristic optimizer. Expert Syst Appl. 2022;191:116158. doi:10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]

19. Jiang Y, Wu Q, Zhu S, Zhang L. Orca predation algorithm: a novel bio-inspired algorithm for global optimization problems. Expert Syst Appl. 2022;188:116026. doi:10.1016/j.eswa.2021.116026. [Google Scholar] [CrossRef]

20. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95:51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

21. Dehghani M, Montazeri Z, Trojovská E, Trojovský P. Coati optimization algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl-Based Syst. 2023;259:110011. doi:10.1016/j.knosys.2022.110011. [Google Scholar] [CrossRef]

22. Kaur S, Awasthi LK, Sangal AL, Dhiman G. Tunicate swarm algorithm: a new bio-inspired based metaheuristic paradigm for global optimization. Eng Appl Artif Intell. 2020;90:103541. doi:10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]

23. Hashim FA, Houssein EH, Hussain K, Mabrouk MS, Al-Atabany W. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems. Math Comput Simul. 2022;192:84–110. doi:10.1016/j.matcom.2021.08.013. [Google Scholar] [CrossRef]

24. Braik M, Hammouri A, Atwan J, Al-Betar MA, Awadallah MA. White shark optimizer: a novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl-Based Syst. 2022;243:108457. doi:10.1016/j.knosys.2022.108457. [Google Scholar] [CrossRef]

25. Chopra N, Ansari MM. Golden jackal optimization: a novel nature-inspired optimizer for engineering applications. Expert Syst Appl. 2022;198:116924. doi:10.1016/j.eswa.2022.116924. [Google Scholar] [CrossRef]

26. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

27. Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine predators algorithm: a nature-inspired metaheuristic. Expert Syst Appl. 2020;152:113377. doi:10.1016/j.eswa.2020.113377. [Google Scholar] [CrossRef]

28. Abdollahzadeh B, Gharehchopogh FS, Mirjalili S. African vultures optimization algorithm: a new nature-inspired metaheuristic algorithm for global optimization problems. Comput Indus Eng. 2021;158:107408. doi:10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]

29. Goldberg DE, Holland JH. Genetic algorithms and machine learning. Mach Learn. 1988;3(2):95–9. doi:10.1023/A:1022602019183. [Google Scholar] [CrossRef]

30. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]

31. De Castro LN, Timmis JI. Artificial immune systems as a novel soft computing paradigm. Soft Comput. 2003;7(8):526–44. doi:10.1007/s00500-002-0237-z. [Google Scholar] [CrossRef]

32. Beyer H-G, Schwefel H-P. Evolution strategies—a comprehensive introduction. Nat Comput. 2002;1(1):3–52. doi:10.1023/A:1015059928466. [Google Scholar] [CrossRef]

33. Dehghani M, Trojovská E, Trojovský P, Malik OP. OOBO: a new metaheuristic algorithm for solving optimization problems. Biomimetics. 2023;8(6):468. doi:10.3390/biomimetics8060468 [Google Scholar] [PubMed] [CrossRef]

34. Koza JR. Genetic programming as a means for programming computers by natural selection. Stat Comput. 1994;4:87–112. doi:10.1007/BF00175355. [Google Scholar] [CrossRef]

35. Reynolds RGeditor. An introduction to cultural algorithms. In: Proceedings of the Third Annual Conference on Evolutionary Programming, 1994; San Diego, CA, USA: World Scientific. [Google Scholar]

36. Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–80. doi:10.1126/science.220.4598.67. [Google Scholar] [CrossRef]

37. Dehghani M, Montazeri Z, Dhiman G, Malik O, Morales-Menendez R, Ramirez-Mendoza RA, et al. A spring search algorithm applied to engineering optimization problems. Appl Sci. 2020;10(18):6173. doi:10.3390/app10186173. [Google Scholar] [CrossRef]

38. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

39. Dehghani M, Samet H. Momentum search algorithm: a new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Appl Sci. 2020;2(10):1–15. doi:10.1007/s42452-020-03511-6. [Google Scholar] [CrossRef]

40. Hatamlou A. Black hole: a new heuristic optimization approach for data clustering. Inf Sci. 2013;222:175–84. doi:10.1016/j.ins.2012.08.023. [Google Scholar] [CrossRef]

41. Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput App. 2016;27(2):495–513. doi:10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]

42. Cheng M-Y, Sholeh MN. Optical microscope algorithm: a new metaheuristic inspired by microscope magnification for solving engineering optimization problems. Knowl-Based Syst. 2023;279:110939. doi:10.1016/j.knosys.2023.110939. [Google Scholar] [CrossRef]

43. Cuevas E, Oliva D, Zaldivar D, Pérez-Cisneros M, Sossa H. Circle detection using electro-magnetism optimization. Inf Sci. 2012;182(1):40–55. doi:10.1016/j.ins.2010.12.024. [Google Scholar] [CrossRef]

44. Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: a novel optimization algorithm. Knowl-Based Syst. 2020;191:105190. doi:10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]

45. Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S. Henry gas solubility optimization: a novel physics-based algorithm. Future Gen Comput Syst. 2019;101:646–67. doi:10.1016/j.future.2019.07.015. [Google Scholar] [CrossRef]

46. Eskandar H, Sadollah A, Bahreininejad A, Hamdi M. Water cycle algorithm-A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput Struct. 2012;110:151–66. doi:10.1016/j.compstruc.2012.07.010. [Google Scholar] [CrossRef]

47. Hashim FA, Hussain K, Houssein EH, Mabrouk MS, Al-Atabany W. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Appl Intell. 2021;51(3):1531–51. doi:10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]

48. Pereira JLJ, Francisco MB, Diniz CA, Oliver GA, Cunha SSJr, Gomes GF. Lichtenberg algorithm: a novel hybrid physics-based meta-heuristic for global optimization. Expert Syst Appl. 2021;170:114522. doi:10.1016/j.eswa.2020.114522. [Google Scholar] [CrossRef]

49. Kaveh A, Dadras A. A novel meta-heuristic optimization algorithm: thermal exchange optimization. Adv Eng Softw. 2017;110:69–84. doi:10.1016/j.advengsoft.2017.03.014. [Google Scholar] [CrossRef]

50. Wei Z, Huang C, Wang X, Han T, Li Y. Nuclear reaction optimization: a novel and powerful physics-based algorithm for global optimization. IEEE Access. 2019;7:66084–109. [Google Scholar]

51. Rao RV, Savsani VJ, Vakharia D. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput-Aided Des. 2011;43(3):303–15. doi:10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]

52. Matoušová I, Trojovský P, Dehghani M, Trojovská E, Kostra J. Mother optimization algorithm: a new human-based metaheuristic approach for solving engineering optimization. Sci Rep. 2023;13(1):10312. doi:10.1038/s41598-023-37537-8 [Google Scholar] [PubMed] [CrossRef]

53. Dehghani M, Mardaneh M, Guerrero JM, Malik OP, Ramirez-Mendoza RA, Matas J, et al. A new Doctor and Patient optimization algorithm: an application to energy commitment problem. Appl Sci. 2020;10(17):5791. doi:10.3390/app10175791. [Google Scholar] [CrossRef]

54. Ayyarao TL, RamaKrishna N, Elavarasam RM, Polumahanthi N, Rambabu M, Saini G, et al. War strategy optimization algorithm: a new effective metaheuristic algorithm for global optimization. IEEE Access. 2022;10(17):25073–105. doi:10.1109/ACCESS.2022.3153493. [Google Scholar] [CrossRef]

55. Mohamed AW, Hadi AA, Mohamed AK. Gaining-sharing knowledge based algorithm for solving optimization problems: a novel nature-inspired algorithm. Int J Mach Learn Cybern. 2020;11(7):1501–29. doi:10.1007/s13042-019-01053-x. [Google Scholar] [CrossRef]

56. Al-Betar MA, Alyasseri ZAA, Awadallah MA, Abu Doush I. Coronavirus herd immunity optimizer (CHIO). Neural Comput App. 2021;33(10):5011–42. doi:10.1007/s00521-020-05296-6 [Google Scholar] [PubMed] [CrossRef]

57. Braik M, Ryalat MH, Al-Zoubi H. A novel meta-heuristic algorithm for solving numerical optimization problems: ali Baba and the forty thieves. Neural Comput App. 2022;34(1):409–55. doi:10.1007/s00521-021-06392-x. [Google Scholar] [CrossRef]

58. Dehghani M, Trojovský P. Serval optimization algorithm: a new bio-inspired approach for solving optimization problems. Biomimetics. 2022;7(4):204. doi:10.3390/biomimetics7040204 [Google Scholar] [PubMed] [CrossRef]

59. Awad N, Ali M, Liang J, Qu B, Suganthan P, Definitions P. Evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. In: Technol report. Singapore: Nanyang Technological University; 2016. [Google Scholar]

60. Wilcoxon F. Individual comparisons by ranking methods. In: Breakthroughs in statistics. New York, NY: Springer; 1992. p. 196–202. [Google Scholar]

61. Kim TK. T test as a parametric statistic. Korean J Anesthesiol. 2015;68(6):540–6. doi:10.4097/kjae.2015.68.6.540 [Google Scholar] [PubMed] [CrossRef]

62. Daniel WW. Friedman two-way analysis of variance by ranks. Appl Nonparametric Stat. 1990;262–74. [Google Scholar]

63. Das S, Suganthan PN. Problem definitions and evaluation criteria for CEC 2011 competition on testing evolutionary algorithms on real world optimization problems. Kolkata: Jadavpur University, Nanyang Technological University; 2010. p. 341–59. [Google Scholar]

64. Kannan B, Kramer SN. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J Mech Des. 1994;116(2):405–11. doi:10.1115/1.2919393. [Google Scholar] [CrossRef]

65. Gandomi AH, Yang X-S. Benchmark problems in structural optimization. In: Computational optimization, methods and algorithms. Berlin, Heidelberg: Springer; 2011. p. 259–81. [Google Scholar]

66. Mezura-Montes E, Coello CACeditors. Useful infeasible solutions in engineering optimization with evolutionary algorithms. In: Mexican International Conference on Artificial Intelligence, 2005; Berlin, Heidelberg: Springer. [Google Scholar]