 Open Access
Open Access
ARTICLE
Computational Investigation of Brownian Motion and Thermophoresis Effect on Blood-Based Casson Nanofluid on a Non-linearly Stretching Sheet with Ohmic and Viscous Dissipation Effects
1 Department of Applied Mathematics, M. J. P. Rohilkhand University, Bareilly, 243006, Uttar Pradesh, India
2 Fakulti Teknologi dan Kejuruteraan Mekanikal, Universiti Teknikal Malaysia, Melaka, Durian Tunggal, 76100, Malaysia
3 Forecasting and Engineering Technology Analysis (FETA) Research Group, Universiti Teknikal Malaysia, Melaka, Durian Tunggal, 76100, Malaysia
* Corresponding Author: Nurul Amira Zainal. Email:
Computer Modeling in Engineering & Sciences 2024, 141(2), 1137-1163. https://doi.org/10.32604/cmes.2024.055493
Received 28 June 2024; Accepted 20 August 2024; Issue published 27 September 2024
Abstract
Motivated by the widespread applications of nanofluids, a nanofluid model is proposed which focuses on uniform magnetohydrodynamic (MHD) boundary layer flow over a non-linear stretching sheet, incorporating the Casson model for blood-based nanofluid while accounting for viscous and Ohmic dissipation effects under the cases of Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST). The study employs a two-phase model for the nanofluid, coupled with thermophoresis and Brownian motion, to analyze the effects of key fluid parameters such as thermophoresis, Brownian motion, slip velocity, Schmidt number, Eckert number, magnetic parameter, and non-linear stretching parameter on the velocity, concentration, and temperature profiles of the nanofluid. The proposed model is novel as it simultaneously considers the impact of thermophoresis and Brownian motion, along with Ohmic and viscous dissipation effects, in both CST and PST scenarios for blood-based Casson nanofluid. The numerical technique built into MATLAB’s bvp4c module is utilized to solve the governing system of coupled differential equations, revealing that the concentration of nanoparticles decreases with increasing thermophoresis and Brownian motion parameters while the temperature of the nanofluid increases. Additionally, a higher Eckert number is found to reduce the nanofluid temperature. A comparative analysis between CST and PST scenarios is also undertaken, which highlights the significant influence of these factors on the fluid’s characteristics. The findings have potential applications in biomedical processes to enhance fluid velocity and heat transfer rates, ultimately improving patient outcomes.Graphic Abstract
Keywords
Nomenclature
| Fw | Suction parameter (-) |
| ςp | Slip parameter (-) |
| η | Scaled similarity parameter (-) |
| ϕ | Scaled concentration (-) |
| θ | Dimensionless temperature (-) |
| μ | Fluid viscosity coefficient (kgm/s) |
| τ | Cauchy stress tensor (N/m2) |
| ν | Dynamic fluid viscosity (N/s2) |
| ρf | Density of fluid (kg/m3) |
| ρp | Density of nanofluid (kg/m3) |
| α | Thermal diffusivity (m2/s) |
| (ρc)p | Thermal capacitance of nanofluid (J/K) |
| cf | Thermal capacitance of fluid (J/K) |
| cf | Drag coefficient (-) |
| κ | Heat transfer coefficient (W/m2K) |
| C∞ | Local nanoparticles volume ratio (mol/m3) |
| T∞ | Temperature far away from sheet (K) |
| DT | Heat-induced migration coefficient (-) |
| DB | Particle diffusivity (-) |
| f | Dimensionless potential function (-) |
| uw | Deformation velocity of sheet (m/s) |
| Tw | Uniform temperature across stretching sheet (K) |
| Cw | Nanoparticle abundance on stretched surface (mol/m3) |
| a,d | Constants (-) |
| r | Parameter of surface temperature (-) |
| Shx | Local Sherwood number (-) |
| Nux | Local Nusselt number (-) |
| Cf | Local skin friction coefficient (-) |
| Nt | Thermal migration coefficient (-) |
| Nb | Brownian diffusion coefficient (-) |
| Sc | Mass transport number (-) |
| Ec | Thermal efficiency index (-) |
| M | Magnetic flux density (-) |
| Pr | Prandtl number (-) |
| p | Pressure of the fluid (kg/ms2) |
| β | Casson fluid component (-) |
| T | Fluid thermal state (K) |
| u,v | Transverse and longitudinal velocity (m/s) |
| qw | Local thermal energy transfer (J/s) |
| qm | Local mass transport rate (m/s) |
| τw | Wall shear stress (N/m2) |
Blood flow is the dynamic movement of blood throughout the circulatory system, vital for supplying nutrients and oxygen to tissues and organs while removing byproducts [1]. However, disruptions in blood flow can lead to a range of associated diseases and health complications. Conditions such as hypertension, atherosclerosis, and thrombosis can impair blood flow by narrowing blood vessels, increasing clot formation, or raising blood pressure [2]. These diseases can have serious consequences, including heart attacks, strokes, and organ damage. Thus, maintaining proper control over blood flow is crucial for overall health and well-being. Control mechanisms, such as regulation of blood pressure, vascular tone, and clotting factors, play a pivotal role in ensuring ample blood perfusion to fulfill the body’s metabolic needs. A better understanding of blood flow control is essential for preventing and managing cardiovascular diseases and optimizing health outcomes [3]. Additionally, advancements in medical technology and therapies aimed at improving blood flow regulation continue to be a focus of research and clinical practice. The Casson fluid model [4] is a rheological model commonly used to describe the fluidic behavior of multiphase fluids, particularly those with non-Newtonian characteristics. This model extends beyond the simple Newtonian fluid model by considering the presence of yield stress below which the fluid does not flow. Instead, it behaves like a solid until a certain threshold of stress is exceeded, at which point it transitions to a fluid-like behavior with a constant viscosity. The Casson fluid model is particularly useful in describing the flow of materials such as paints, gels, and biological fluids like blood, which exhibit non-Newtonian behavior. Blood is regarded as a Casson fluid due to its unique rheological properties [5]. Unlike simple Newtonian fluids, blood displays a nonlinear relationship between shear stress and shear rate, with its viscosity varying depending on factors such as shear rate, temperature, and hematocrit levels. Additionally, blood exhibits a yield stress, requiring a certain amount of force to initiate flow. Below this threshold, blood behaves as a non-flowing, structured fluid akin to a solid, while above it, it flows as a viscous liquid. This behavior is crucial for understanding blood flow dynamics in the circulatory system, where the Casson fluid model provides a more accurate representation compared to traditional Newtonian models. By regarding blood as a Casson fluid, researchers and clinicians can better interpret hemodynamic parameters, design medical devices, and develop computational models to simulate blood flow in health and disease [6]. On the other hand, nanotechnology, a cutting-edge field at the intersection of science, engineering, and technology, focuses on the manipulation of matter at the nanoscale, typically ranging from 1 to 100 nanometers. Its importance lies in its potential to revolutionize various industries and address pressing global challenges. Mauter et al. [7] and Wiek et al. [8] discussed the role of nanotechnology in global challenges for sustainable development. In medicine, nanotechnology offers promising avenues for targeted drug delivery, early disease detection, and precise imaging techniques, thus improving treatment efficacy while minimizing side effects [9]. Qi et al. [10] conducted an experimental investigation focusing on nanofluids’ flow behavior and heat transfer properties within double-tube heat exchangers, emphasizing thermal efficiency. Nanostructured particles, when engineered appropriately and dispersed in blood, can modulate various aspects of blood flow, including viscosity, rheology, and clotting behavior. Moreover, nanofluids containing functionalized nanoparticles can be advanced contrast agents for medical imaging techniques [11], enabling high-resolution visualization of blood vessels and tissue perfusion.
Brownian motion and thermophoresis effects play crucial roles in the behavior of nanoparticles within blood flow, presenting both challenges and opportunities in biomedical applications [12]. Brownian motion [13] refers to the random motion of particles suspended in a fluid due to collisions with surrounding molecules. In blood flow, nanoparticles experience Brownian motion, which affects their dispersion, distribution, and interaction with cells and tissues. Thermophoresis [14], on the other hand, is the migration of particles in response to temperature gradients within a fluid. In blood flow, thermophoresis effects can arise due to variations in temperature along blood vessels, influencing the movement of nanoparticles. Understanding and controlling these phenomena is essential for designing effective nanoparticle-based therapies and diagnostic tools. The importance of considering Brownian motion and thermophoresis effects lies in their impact on the targeting, delivery, and retention of nanoparticles in specific tissues or organs [15]. Zuberi et al. [16] investigated the effect of Brownian motion and thermophoresis on blood-based Casson nanofluid. Researchers can develop nanoparticle formulations with enhanced circulation times, improved targeting efficiency, and reduced off-target effects, thereby advancing precision medicine and personalized healthcare by utilizing these effects. Recently, Madhura et al. [17] conducted a numerical study on magnetohydrodynamics (MHD) Carreau nanofluid with thermophoresis and Brownian motion effects. In blood flow with nanoparticles, viscous and Ohmic dissipation effects [18] play significant roles, impacting the overall dynamics and efficiency of circulation. Viscous dissipation occurs due to the internal friction between blood components and the vessel walls as the fluid moves, leading to the conversion of mechanical energy into heat. Tang et al. [19] investigated the characteristics of blood flow using Au-nanofluid in a stenotic artery with porous walls and accounting for the viscous dissipation effect. This dissipation affects the flow velocity profile, pressure distribution, and energy expenditure within the circulatory system. On the other hand, Ohmic dissipation arises from the electrical resistance encountered by nanoparticles in blood, particularly metallic nanoparticles, when exposed to electromagnetic fields or currents [20]. These effects contribute to the heating of nanoparticles, potentially influencing their behavior, distribution, and therapeutic efficacy. The understanding and quantification of these dissipation mechanisms are essential for optimizing nanoparticle-based therapies and diagnostic techniques in blood flow applications. Under Ohmic heating, Yusuf explored the study of entropy generation for the convective flow of unsteady MHD flow over a vertical stretching sheet [21]. Siddiqui et al. [22] explored the film flow of nano-micropolar fluids, taking into account dissipation effects. By undertaking viscous and Ohmic dissipation effects, researchers can refine nanoparticle formulations, design efficient delivery strategies, and enhance treatment outcomes while minimizing unwanted side effects, thereby advancing precision medicine and personalized healthcare [23,24].
Fluid flow over-stretching sheets represent a class of fundamental problems in fluid mechanics with diverse applications in engineering and industrial processes. These problems involve the study of flow dynamics over a solid surface that is continuously stretched or contracted [25,26]. Cortell [27] investigated the 2-dimensional boundary layer flow of Newtonian fluid across a stretching surface, a pioneering inquiry that spurred considerable attention toward the flow of fluid on stretching surfaces. Researchers such as Alahmadi et al. [28], Raza et al. [29], Pandey et al. [30], and Boujelbene et al. [31] have explored various theoretical and computational models to elucidate slip flow phenomena. An interesting study conducted by Reddy et al. [32] is the “Computational investigation of chemical reaction and thermal diffusion Brinkman flow over an oscillating absorbent plate.” The modeling of blood flow over-stretching sheets enables researchers to gain valuable insights into the mechanics of cardiovascular conditions such as atherosclerosis, aneurysms, and arterial stenosis.
The investigation of blood flow over a stretching sheet with constant surface temperature or particular surface temperature, particularly in the presence of nanoparticles, holds significant importance in biomedical engineering and healthcare applications [33]. A better understanding of behavior of blood over such surfaces under different temperature conditions is crucial for optimizing various medical procedures and devices. For instance, in hyperthermia treatments for cancer therapy, maintaining a constant surface temperature on the stretching sheet can help precisely control the heating of nanoparticles within the blood, enhancing the effectiveness of localized tumor treatment while minimizing damage to healthy tissues [34–36]. Similarly, in diagnostic applications such as thermal imaging for detecting vascular abnormalities, controlling the surface temperature of the stretching sheet enables accurate interpretation of temperature distributions within the blood vessels, aiding in the early detection of diseases. Yazdi et al. [37] and Sk et al. [38] have explored the slip flow and heat transfer over non-linear permeable stretching surfaces, considering chemical reactions and magnetic field. These investigations have revealed that the slip velocity and temperature profiles are significantly influenced by the stretching parameter, chemical reaction rate, and magnetic field strength. Further, numerical investigations by Rana et al. [39] and Qayyum et al. [40] have been conducted to examine the flow and heat transfer of nanofluids over nonlinearly stretching sheets. These studies have demonstrated that the nanofluid velocity and temperature profiles are influenced by the stretching parameter, nanoparticle volume fraction, and viscous dissipation. Chaudhary et al. [41] have investigated the MHD blood-nanofluid flow through non-linearly stretched sheet, taking into account heat generation and permeable media. The heat transfer analysis of Radiative-Marangoni convective flow in nanofluids has been examined by Zari et al. [42] considering Lorentz force and porosity effect. Recently, Hou et al. [43] investigated the application of a hybrid model and ferrofluids in fluid flow and heat transfer using the finite element method. Makkar et al. [44] numerically investigated the MHD flow of fluid with double diffusive effects along with Ohmic and viscous dissipation. The impact of Brownian motion and thermophoresis for thermal and chemically reacting nanofluid (Casson) has been explored by Tawade et al. [45]. Researchers can advance the influence of Brownian motion and thermophoresis for improving drug delivery, ultimately enhancing patient outcomes [46–49]. The motivation for the current study stems from the critical need to comprehensively understand the intricate dynamics of blood flow with nanoparticles in physiological conditions. Blood is a complex non-Newtonian fluid, and incorporating nanoparticles further complicates its behavior. This pioneering study bridges a critical research gap by meticulously incorporating Ohmic and viscous dissipation effects in the blood-based Casson nanofluid flow analysis over a non-linearly stretching surface. The omission of these crucial factors in previous studies has led to a significant knowledge deficit, as Ohmic dissipation plays a vital role in regulating heat transfer processes. In contrast, viscous dissipation influences the fluid’s rheological behavior, thereby affecting the overall dynamics of blood flow. By accounting for these effects, this study provides a more comprehensive understanding of the complex interactions between nanoparticles and blood, ultimately enabling the optimization of nanoparticle-based therapies and medical devices. Notably, this investigation exhibits a dual nature, as it is employed in both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) cases, thereby offering a more nuanced appreciation of the intricate relationships between temperature, fluid dynamics, and heat transfer in blood-based nanofluids. The novelty of this study lies in its thorough examination of the interplay between Ohmic and viscous dissipation, Brownian motion, and thermophoresis in blood-based Casson nanofluids for two different cases of CST and PST, a topic that has not been explored previously. To the best of our knowledge, no such study has been conducted yet, making this research a groundbreaking contribution to the field of biomedical engineering and nanofluid dynamics. The governing partial differential equations are transformed into nonlinear ordinary differential equations via similarity transformations, enabling numerical solutions using MATLAB’s bvp4c module. This framework holds promise for regulating heat transfer processes in designing biomedical devices, targeted drug delivery, treatment of tumors by hyperthermia and treatment of other diseases.
The present study delves into the dynamics of Casson nanofluid flow adjacent to a stretching sheet, characterized by a velocity profile denoted by ub=axn, where a represents a constant and the parameter n embodies the non-linear variation in stretching. Flow is analyzed within the upper half-plane bounded by the x-axis, where the y-coordinate is orthogonal to the stretching surface. The initiation of Casson nanofluid flow is triggered by the stretching action exerted on the sheet. Fig. 1 illustrates the geometry of the problem. The Casson nanofluid’s Cauchy stress tensor rheological equation is given by
τ=τ0+μγ,(1)
τij=2{eij(μB+py√2π),πC<πeij(μB+py√2πC),πC>π.(2)
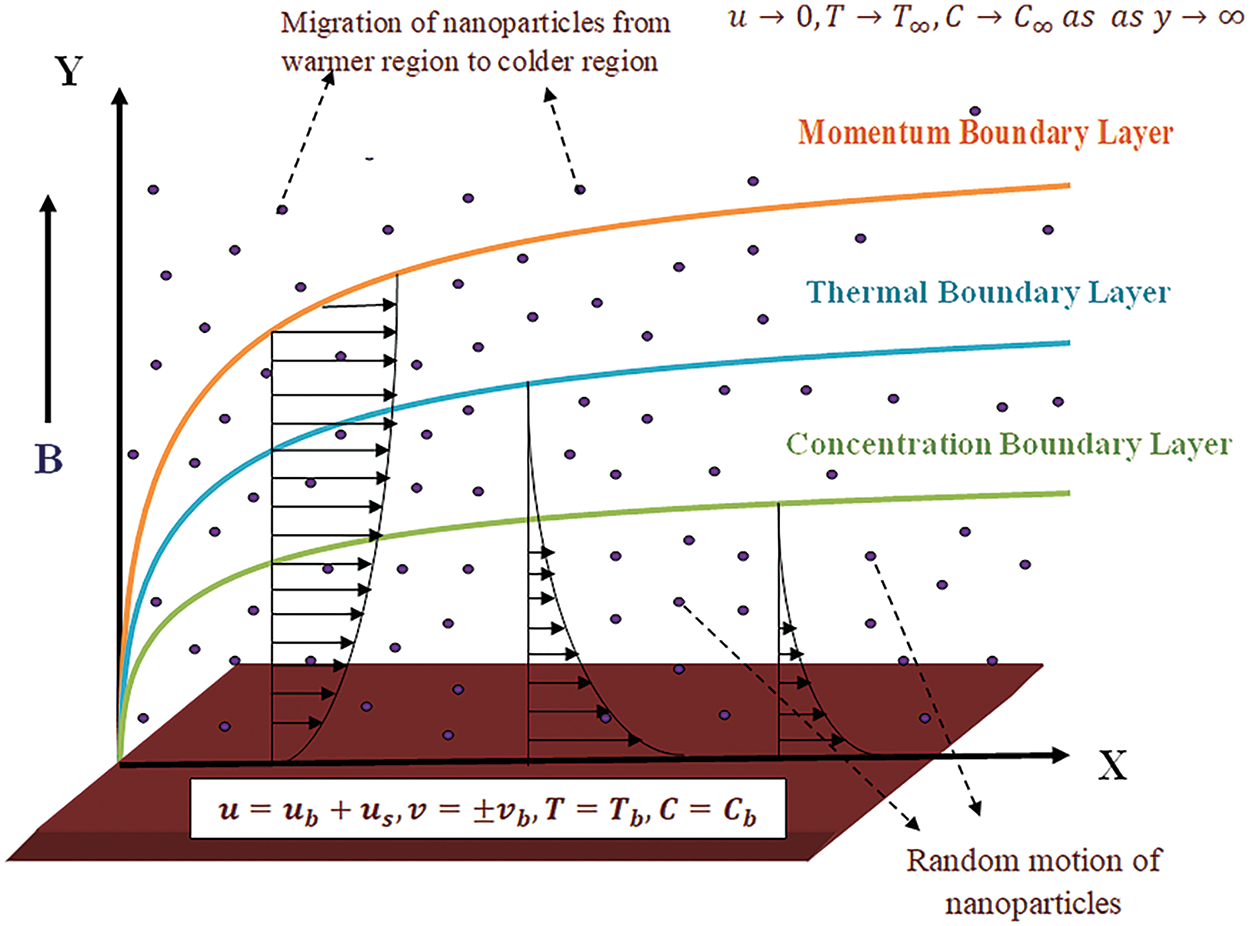
Figure 1: Physical geometry of the problem
A power-proportional relationship between velocity and the distance of a point from the slit on the plate is established to approximate the boundary layer flow of the nanofluid. The temperature at the stretching surface remains constant, as defined by
T=Tb=T∞+dxr,(3)
where T∞ represents the fluid’s temperature at a very large distance from the surface, d represents the positive constant and r is the parameter of surface temperature. The distinct values of the parameter of surface temperature enable the dual nature of the study. The case of CST is obtained using r=0. For r>0, the case of PST befalls [27]. The approximation of the boundary layer under the given assumptions is dictated by the following differential equations [27,44,45]:
∂u∂x+∂v∂y=0,(4)
u∂u∂x+v∂u∂y=ν(1+1β)∂2u∂y2−σB(x)2ρu,(5)
u∂T∂x+v∂T∂y=α∂2T∂y2+τ[DB∂C∂y∂T∂y+(DT/T∞)(∂T∂y)2]+(1+1β)μ(ρc)f(∂u∂y)2+σB2(ρc)fu2},(6)
u∂C∂x+v∂C∂y=(DT/T∞)∂2C∂y2+DB∂2C∂y2,(7)
under boundary conditions
u=ub+us,v=±vb,T=Tb,C=Cb when y=0u→0,T→T∞,C→C∞ when y→∞}.(8)
In this context, the vector (u,v,0) denotes the fluid velocity, where ν symbolizes the kinematic viscosity, α embodies the thermal diffusivity, β signifies the Casson fluid parameter, and τ=((ρc)f/(ρc)p)−1 delineates the proportionality quotient between the heat capacities intrinsic to the nanoparticles and those pertinent to the fluid medium. Additionally, ρf designates the density of the base fluid, C represents the volumetric fraction of nanoparticles, ρp denotes the density of nanoparticles, DB refers to the Brownian diffusion coefficient, DT represents the Thermophoretic diffusion coefficient, vb corresponds to suction, and the symbol us represents the slip velocity, which exhibits direct correlation with the boundary shear stress at the locus y = 0.
us=L∂u∂y|y=0.(9)
Here L is the proportionality constant and is termed as slip length.
η=y√a(n+1)2vxn−12,u=axnf′(η)v=−√av(n+1)2xa−12(f+(n−1n+1)ηf′)θ(η)=T−T∞Tw−T∞,ϕ(η)=C−C∞Cw−C∞},(10)
Non-linear coupled differential equations are formulated based on the boundary layer Eqs. (5)–(7), yielding the following expressions:
(1+1β)f′′′+ff′′−(2nn+1)f′2−(2n+1)Mf′=0,(11)
1Prθ′′+fθ′−(2rn+1)f′θ+Nbθ′ϕ′+Ntθ′2+(1+1β)f′′2+(2n+1)MScf′2=0,(12)
ϕ′′+12Scfϕ′+NtNbθ′′=0,(13)
and boundary conditions in (8) becomes
f=Fw,f′=1+ζp f′′,θ=1,ϕ=1when η=0f′→0,θ→0,ϕ→0when η→∞}.(14)
In this notation, derivatives with respect to η are indicated by primes, where Sc=νDB signifies the Schmidt number and Pr=vα represents the Prandtl number, M=σ(B0)2ax(n−1) constitute the magnetic parameter, Nt=(ρc)bDT(Tw−T∞)(ρc)fvT∞ expresses thermal drift coefficient, Nb=(ρc)pDB(Cw−C∞)(ρc)fr is Brownian motion parameter, ζp=l√a(n+1)2νxn−1 is slip parameter and Fw=−vw√αΔ−1|k(n+1)2 is suction parameter and Ec=u2wCp(Tw−T∞) is Eckert number. Now, introducing the non-linear term as [37]
P(n,x)=xn−1(n+1)2.
This parameter forces us to find local solution. Reconstructing Fw and ζp in terms of non-linear term P(n,x) yields fw and ζ free from n and x as follows:
Fw=fw√P(n,x).(15)
Here ζ=l√ay represents slip parameter and fw=−vw√ay represents suction based on P(n,x) which becomes totally free from n and x. Hence, it is possible to define these parameters (fw and ζ) in a form that avoids the problems caused by their dependence on n and x. Consequently, by fixing the x-coordinate values while varying n, the localization of the similarity solution can accurately yield diverse outcomes for the involved parameters.
Integrating the engineered physical parameters and the variables of interest for analysis—namely, the Nusselt number, Sherwood number, and skin friction—the designated parameters for the posed problem are delineated as follows:
Nux=xqwk(Tw−T∞)Shx=xqmDB(Cw−C∞)Cfx=τwρu2w},(16)
where
qw=−k(Tw−T∞)xn−12√a(n+1)2νθ′(0)qm=−DB(Cw−C∞)xn−12√a(n+1)2νϕ′(0)τw=x3n−12(1+1β)aμ√a(n+1)2νf′′(0)}.(17)
These terms represent, respectively, the heat flux localized at a specific point, the mass flux concentrated in a particular area, and the wall shear stress exerted on the surface of the expanding sheet. The non-dimensional form of the skin friction, Nusselt number and Sherwood number are described as follows:
Re1/2xCf=f′′(0)Re−1/2xNux=−θ′(0)Re1/2xShx=ϕ′(0)}.(18)
where Re1/2x is the local Reynold’s number.
The analytical solution of the boundary value problem (BVP), as outlined in Eqs. (11)–(13), is not possible due to high nonlinearity. Therefore, the Eqs. (11)–(13) are first converted to a first-order system and then executed using the bvp4c module of the computational software MATLAB. The bvp4c module of MATLAB is a powerful tool for solving boundary value problems (BVPs) arising from ordinary differential equations (ODEs). This module is based on the collocation method, which is a well-established technique for solving BVPs. One of the major advantages of the bvp4c module is its ability to easily handle complex BVPs. It can also solve problems with multiple solutions, singularities, and discontinuities, making it a versatile tool for a wide range of applications. Additionally, the bvp4c solver is highly efficient and can solve large-scale problems quickly and accurately. Another significant advantage of bvp4c is its stability. The solver uses an adaptive mesh refinement strategy, which ensures that the solution is computed with high accuracy and stability. This is particularly important for problems that exhibit sensitive dependence on initial conditions or have multiple solutions. The bvp4c solver is also robust and can handle problems with stiff or oscillatory behavior. In light of its several advantages, bvp4c module of MATLAB is employed to find the solution of the equations governing the stated model. To enable solution using bvp4c, Eqs. (11)–(13) are transformed into a system of first-order differential equations using the suitably defined transformations.
Considering
f=y1,f′=y1′=y2,f′′=y2′=y3,f′′′=y3′,θ=y4,θ′=y4′=y5,θ′′=y5′,ϕ=y6,ϕ′=y6′=y7,ϕ′′=y7′},(19)
the first-order system becomes
(y′1y′2y′3y′4y′5y′6y′7)=(y2y3−ff′′+(2nn+1)f′2+(2n+1)Mf′(1+1β)y5Pr∗(−fθ′+(2rn+1)f′θ−Nbθ′ϕ′−Ntθ′2−(1+1β)f′′2−(2n+1)MScf′2)y7−12Scfϕ′−NtNbθ′′),(20)
with boundary conditions
y1(0)=Fw,y2(0)=1+ζpy3(0),y4(0)=1,y6(0)=1y2(∞)=0,y4(∞)=0,y6(∞)=0}.(21)
The system of first-order differential equations obtained in Eq. (20), along with boundary conditions in Eq. (21), is utilized within the bvp4c built-in routine, which implements the collocation technique in MATLAB, facilitating the acquisition of numerical results. Tolerance of numerical values is taken up to order 10−6. The infinity condition is applied when the velocity, temperature, and concentration do not significantly vary at a huge but finite value.
4 Numerical Results and Discussion
The current investigation embarks on the numerical resolution of differential Eqs. (11) to (13) while adhering to the boundary conditions (14). This endeavor employs collocation method inbuilt in bvp4c module of computational software MATLAB. The investigation encompasses scenarios involving both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) for comparative analysis. Herein, r=0 denotes CST while r>0 indicates PST. The outcomes are graphically depicted to delineate the impacts of various physical parameters. The ranges of significant physical parameters necessary for numerical resolution are specified as follows: Casson parameter: 0.2≤β≤0.5, Slip parameter: 0≤ζ≤3, Non-linear stretching parameter: 0.75≤n≤3, Brownian motion parameter: 0.5≤Nb≤2, Thermophoresis parameter: 0≤Nt≤1.2, Magnetic parameter: 0.8≤M≤1.4, Eckert number: 0≤Ec≤0.3, and Schmidt number: 1.1≤Sc≤2. The values of the Prandtl number (Pr) and the suction parameter (fw) are maintained at constant levels of 25 and 0.2, respectively, unless explicitly stated otherwise. Figs. 2–19 encapsulate the intricate interplay of diverse paramount parameters on the intricate velocity, temperature, and concentration profiles characterizing the nanofluid, spanning across both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) settings. Specifically, Figs. 2–4 elucidate the multifaceted impact engendered by slip parameter ς on the velocity, temperature, and concentration of Casson nanofluid, showcasing distinct responses under both CST and PST conditions. Figs. 5–7 unveil the profound influence of the non-linear stretching parameter n on the intricate velocity, temperature, and concentration profiles of Casson nanofluid, offering insights under both CST and PST settings. Figs. 8–10 delve into the discernible ramifications triggered by the Casson parameter β on the intricate velocity, temperature, and concentration distributions, underscoring disparities under both constant and prescribed surface temperatures. Moreover, the graphical representations captured in Figs. 11–13 meticulously delineate the nuanced impacts orchestrated by the magnetic parameter M on the intricate velocity, temperature, and concentration profiles within the realm of stagnant and prescribed surface temperature conditions. Further insights into the intricate temperature and concentration distributions of Casson nanofluid under both PST and CST configurations, under the influences of the Brownian motion parameter Nb, and the Thermophoresis parameter Nt, are elaborated through the graphical depictions in Figs. 14–17. Furthermore, Figs. 18 and 19 provide a comprehensive exposition of the intricate influences wielded by the Eckert number Ec and the Schmidt number Sc on the temperature and concentration profiles of the nanofluid.
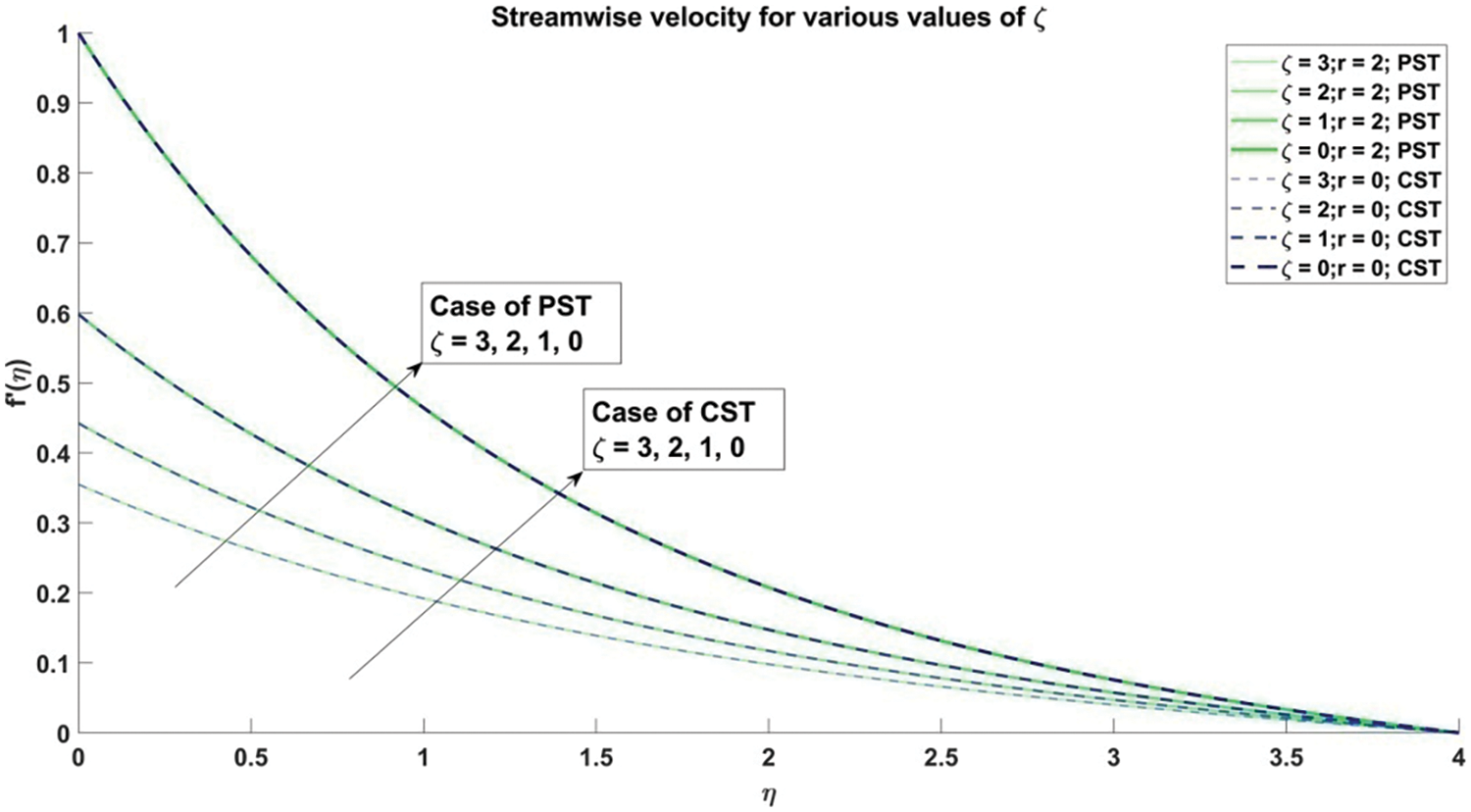
Figure 2: Stream-wise velocities corresponding to different values of ζ
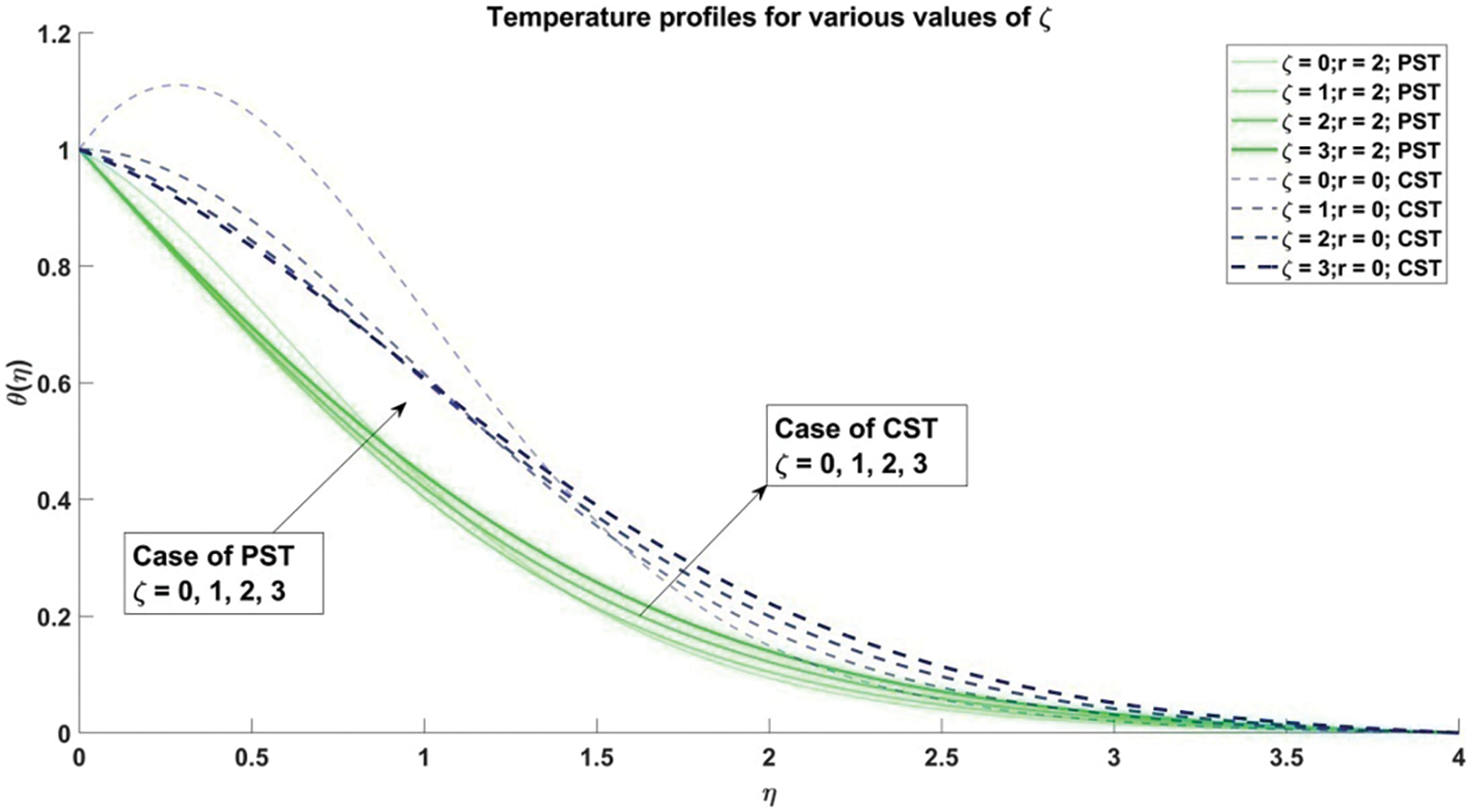
Figure 3: Temperature profiles corresponding to different values of slip parameter
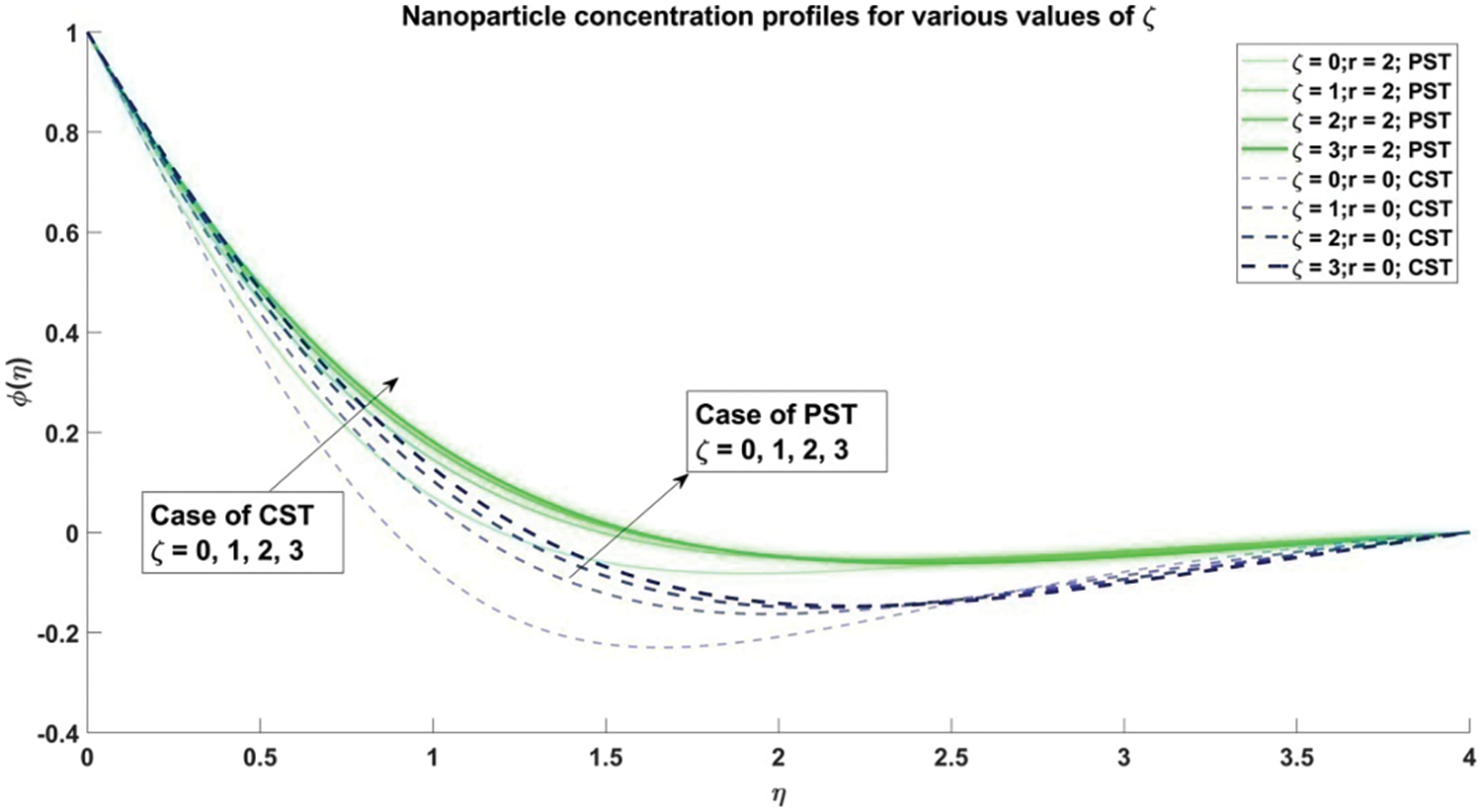
Figure 4: Concentration gradients of nanoparticles corresponding to various configurations of slip parameter
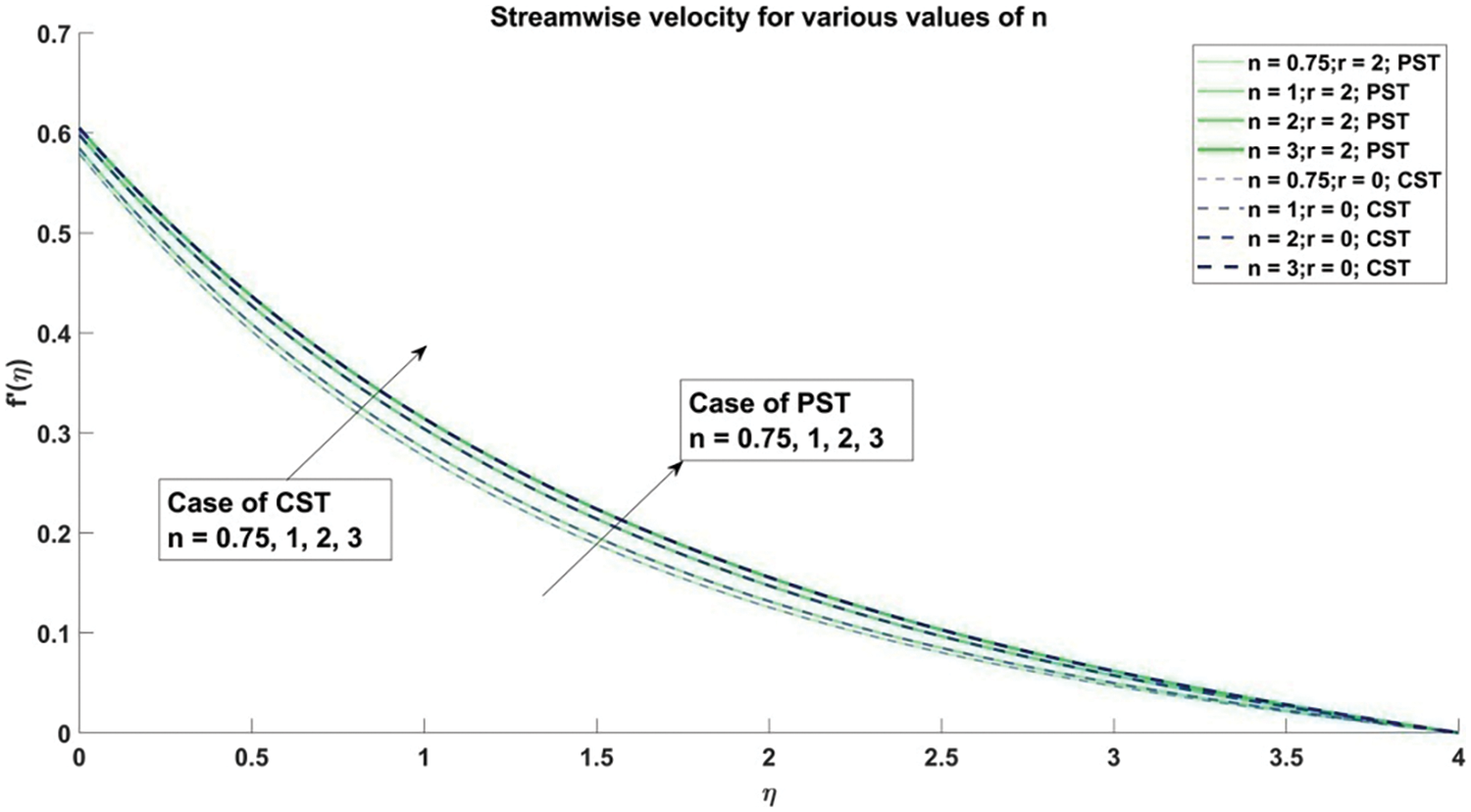
Figure 5: Stream-wise velocity corresponding to different values of n
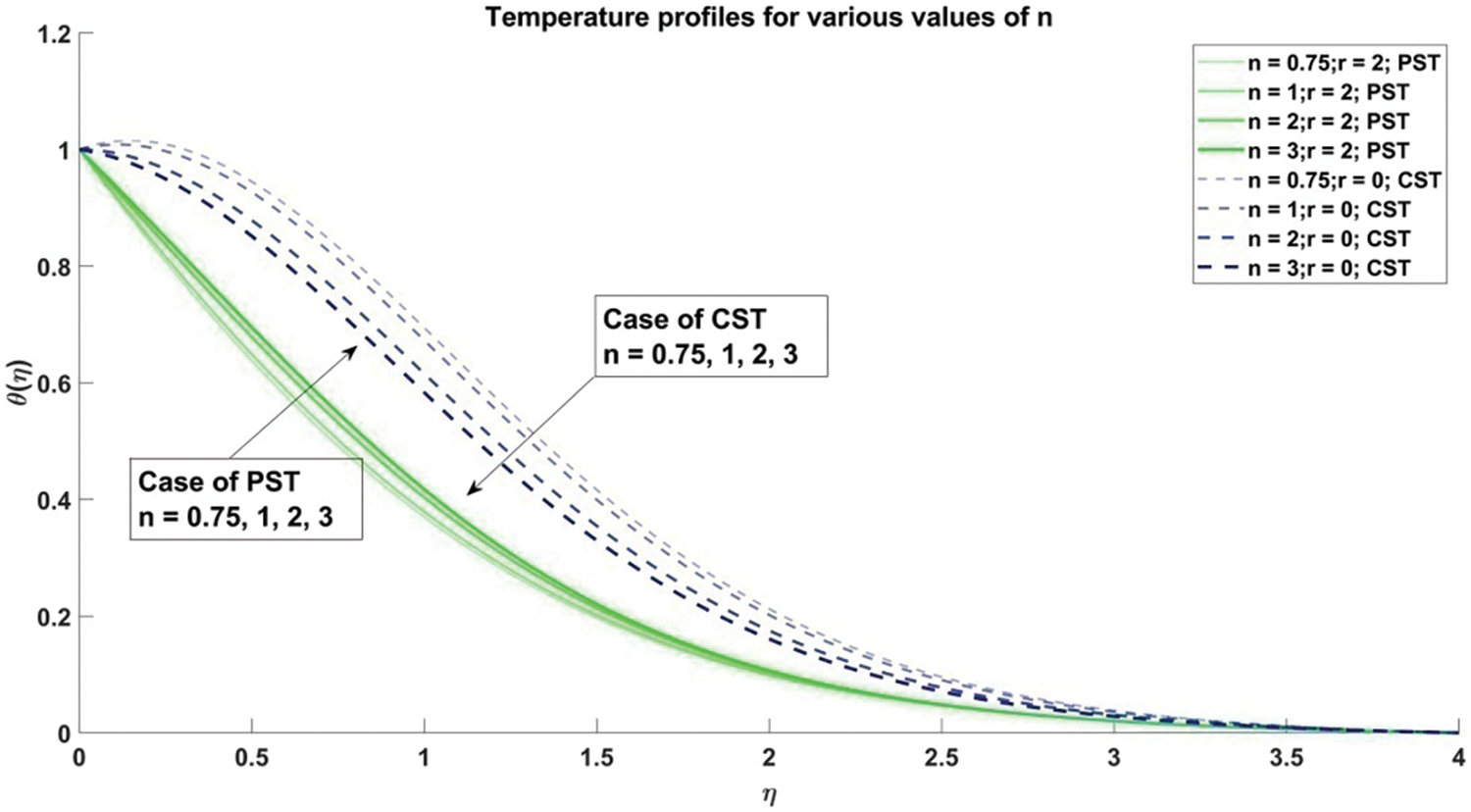
Figure 6: Profiles of temperature corresponding to different values of n
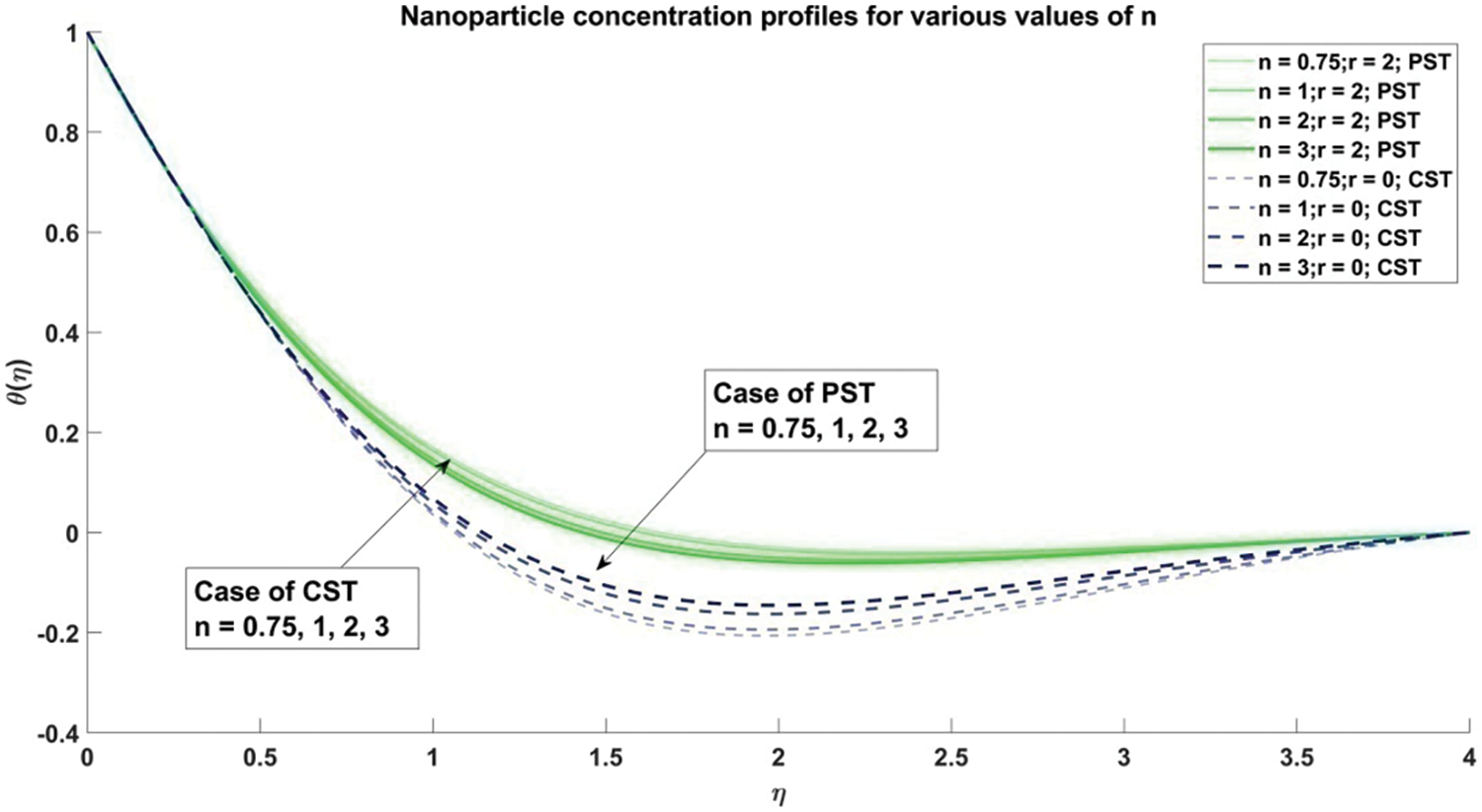
Figure 7: Profiles of concentration corresponding to different values of n
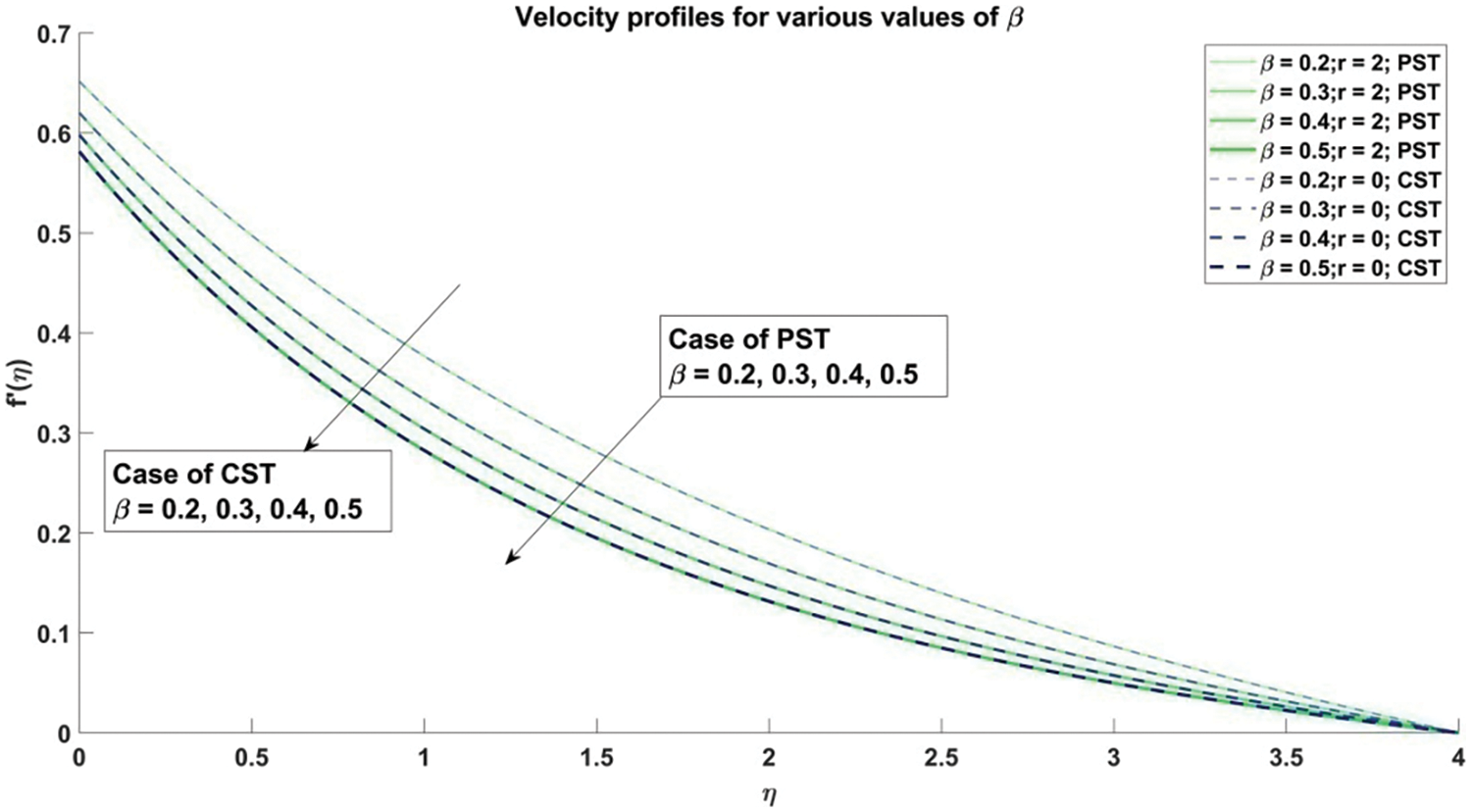
Figure 8: Profiles for velocity corresponding to different values of β
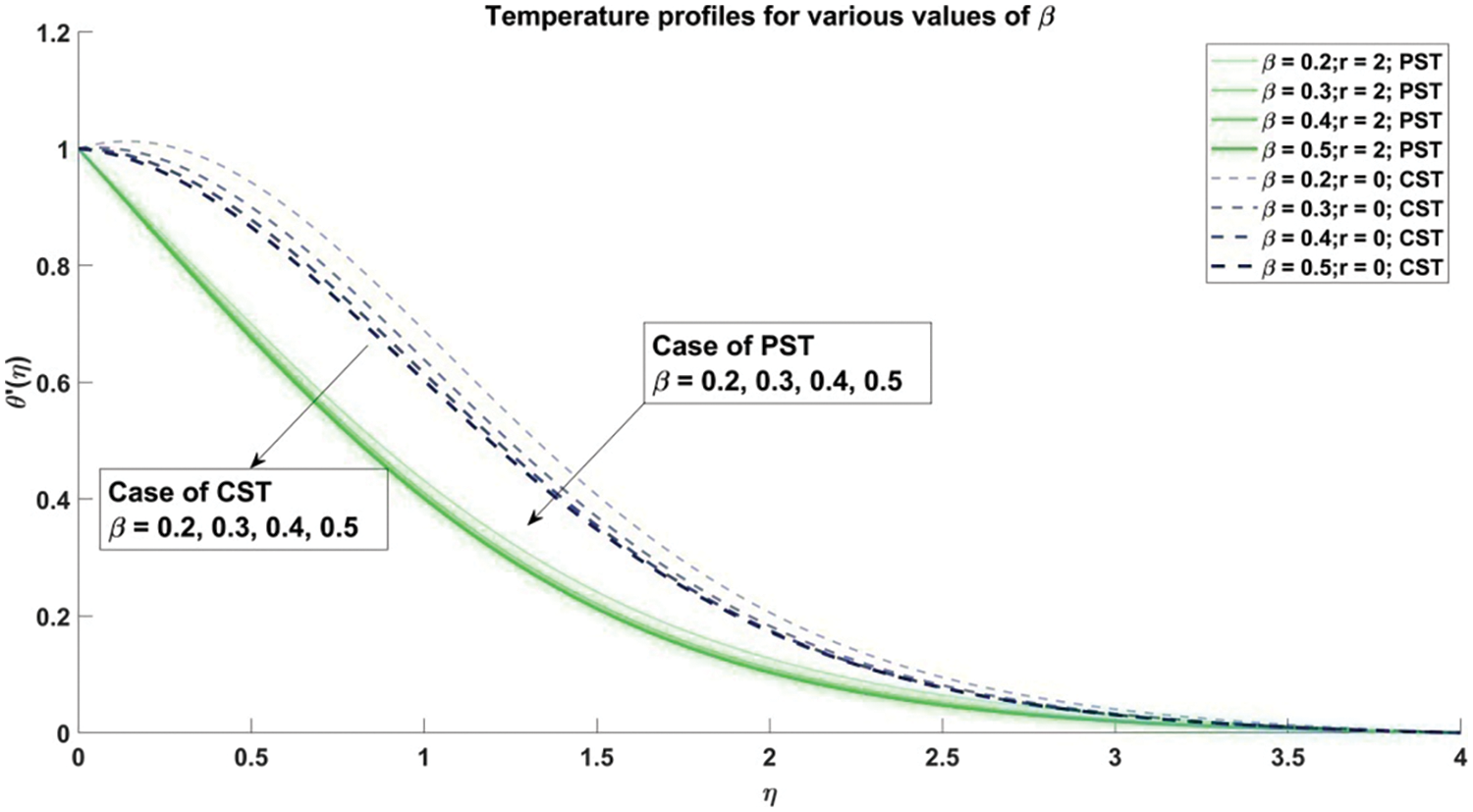
Figure 9: Profiles for temperature corresponding to different values of β
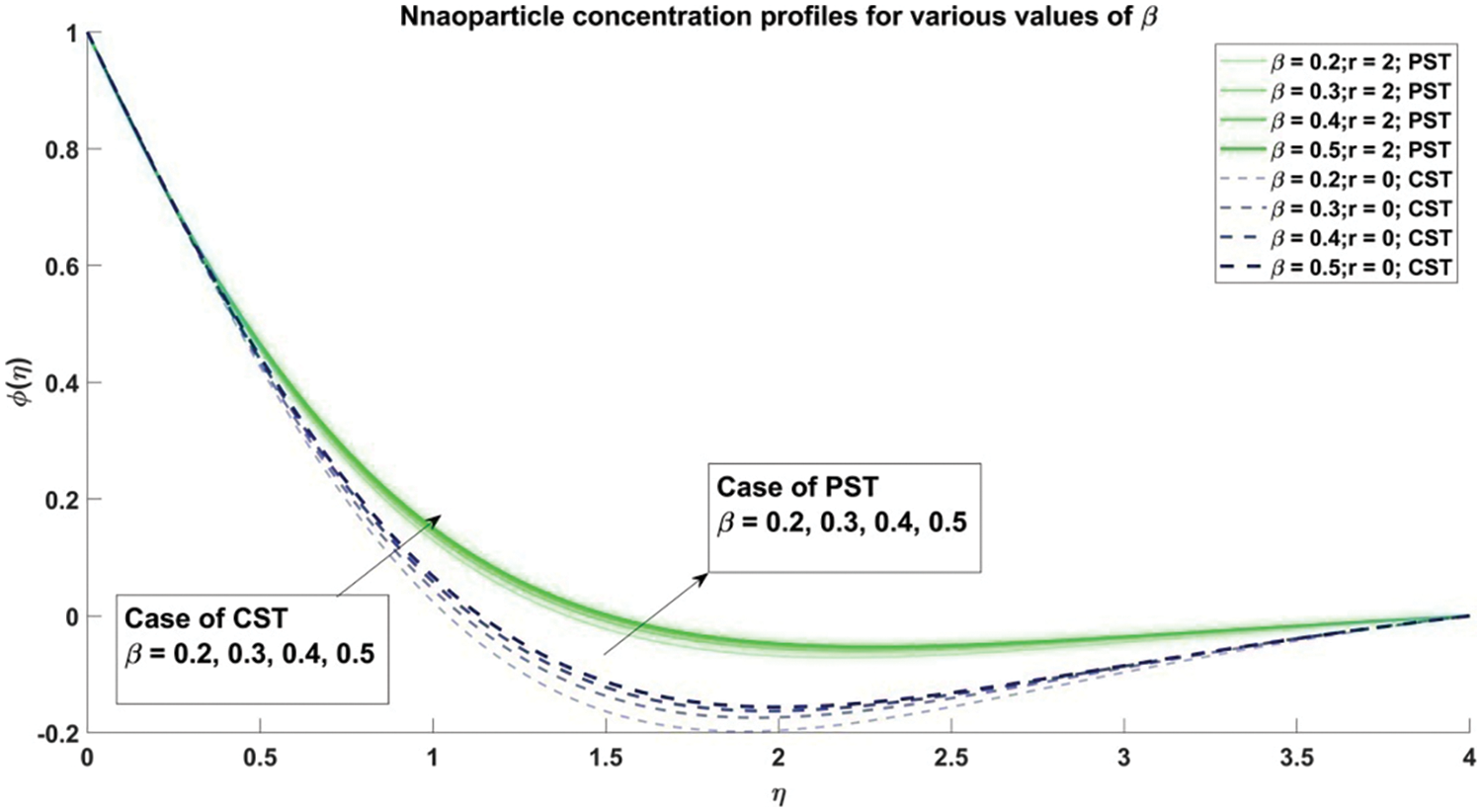
Figure 10: Profiles for nanoparticle concentration corresponding to different values of β
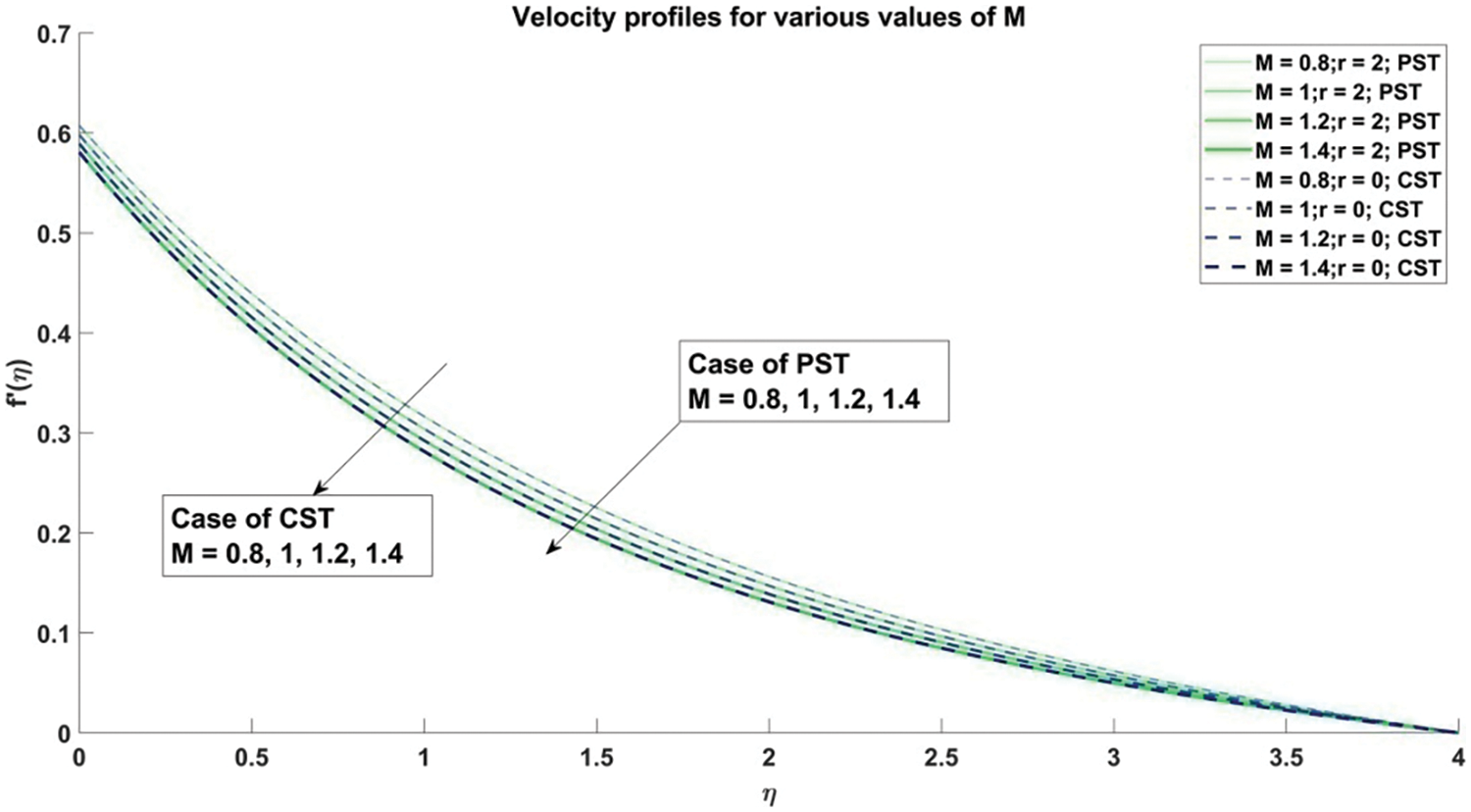
Figure 11: Profiles for velocity corresponding to different values of M
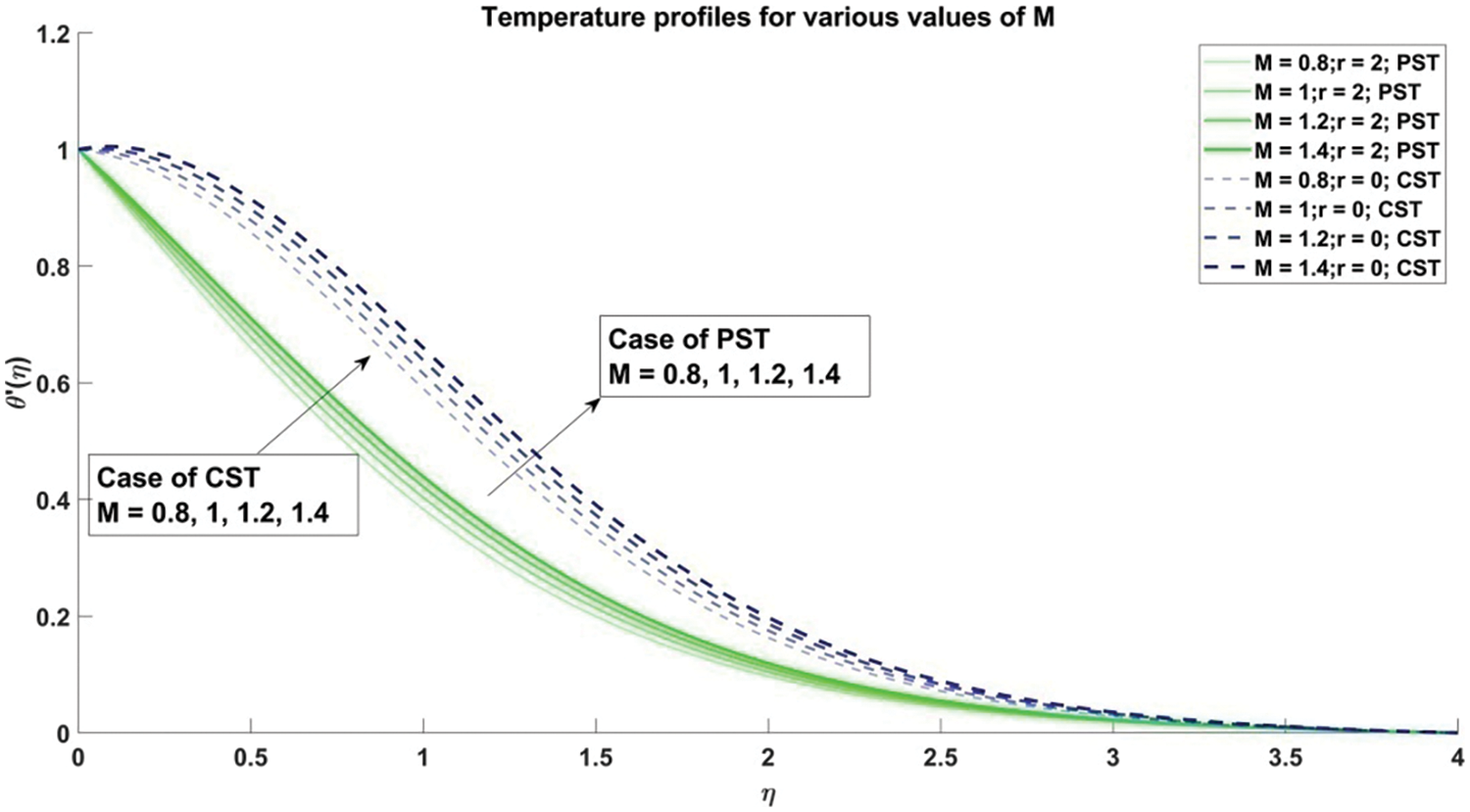
Figure 12: Profiles for temperature corresponding to different values of M
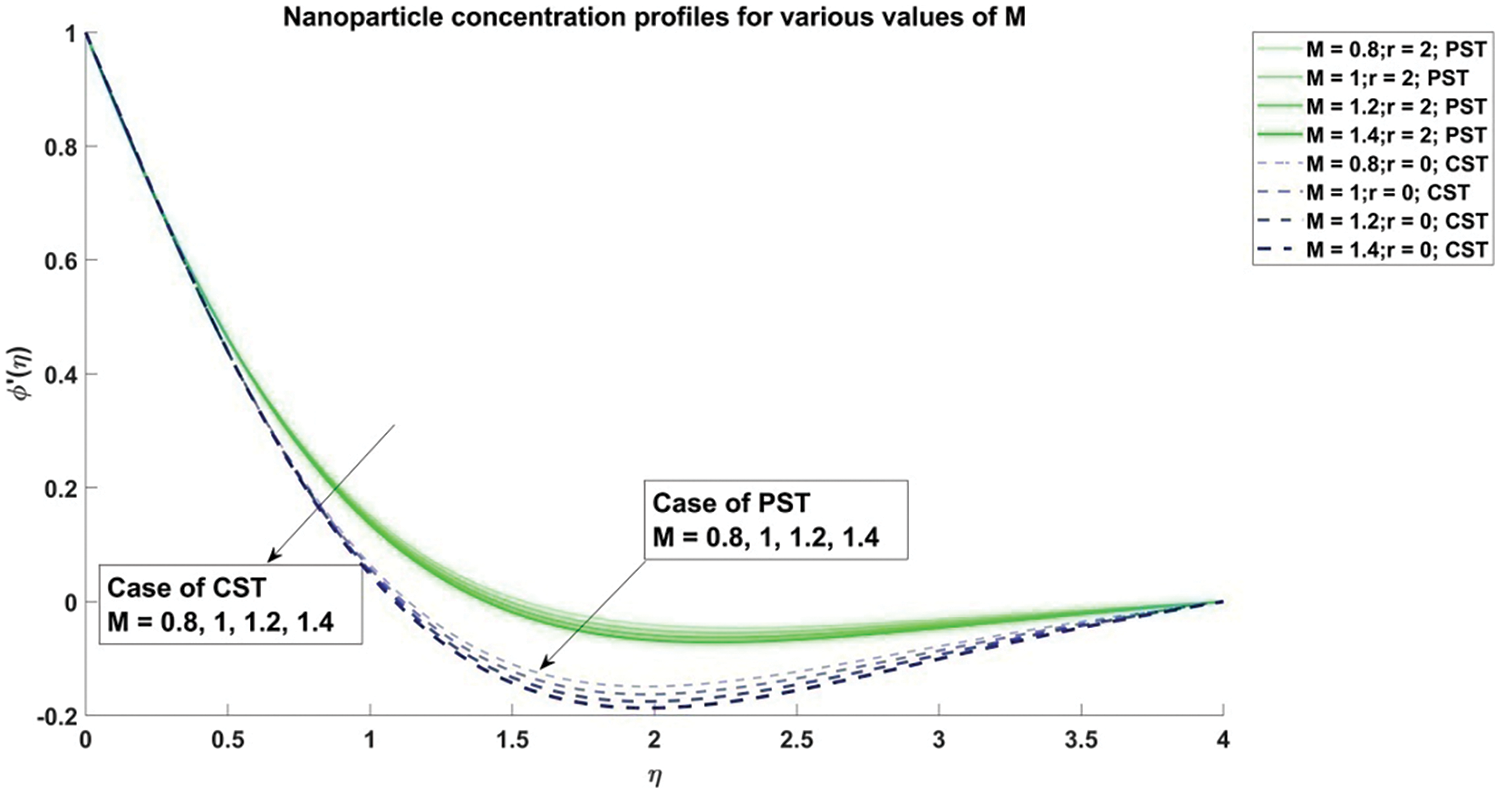
Figure 13: Profiles for nanoparticle concentration corresponding to different values of M
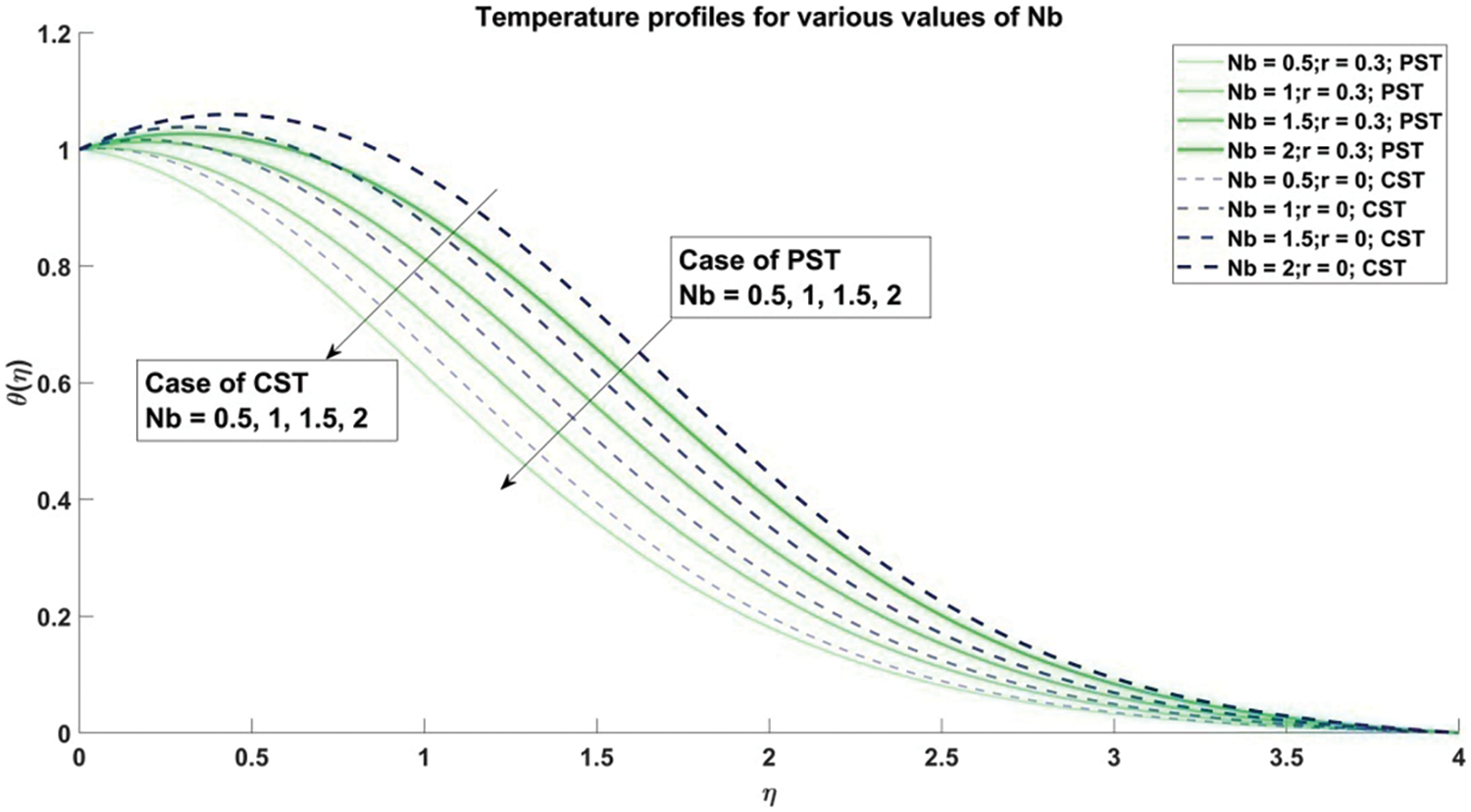
Figure 14: Profiles of temperature corresponding to different values of Nb
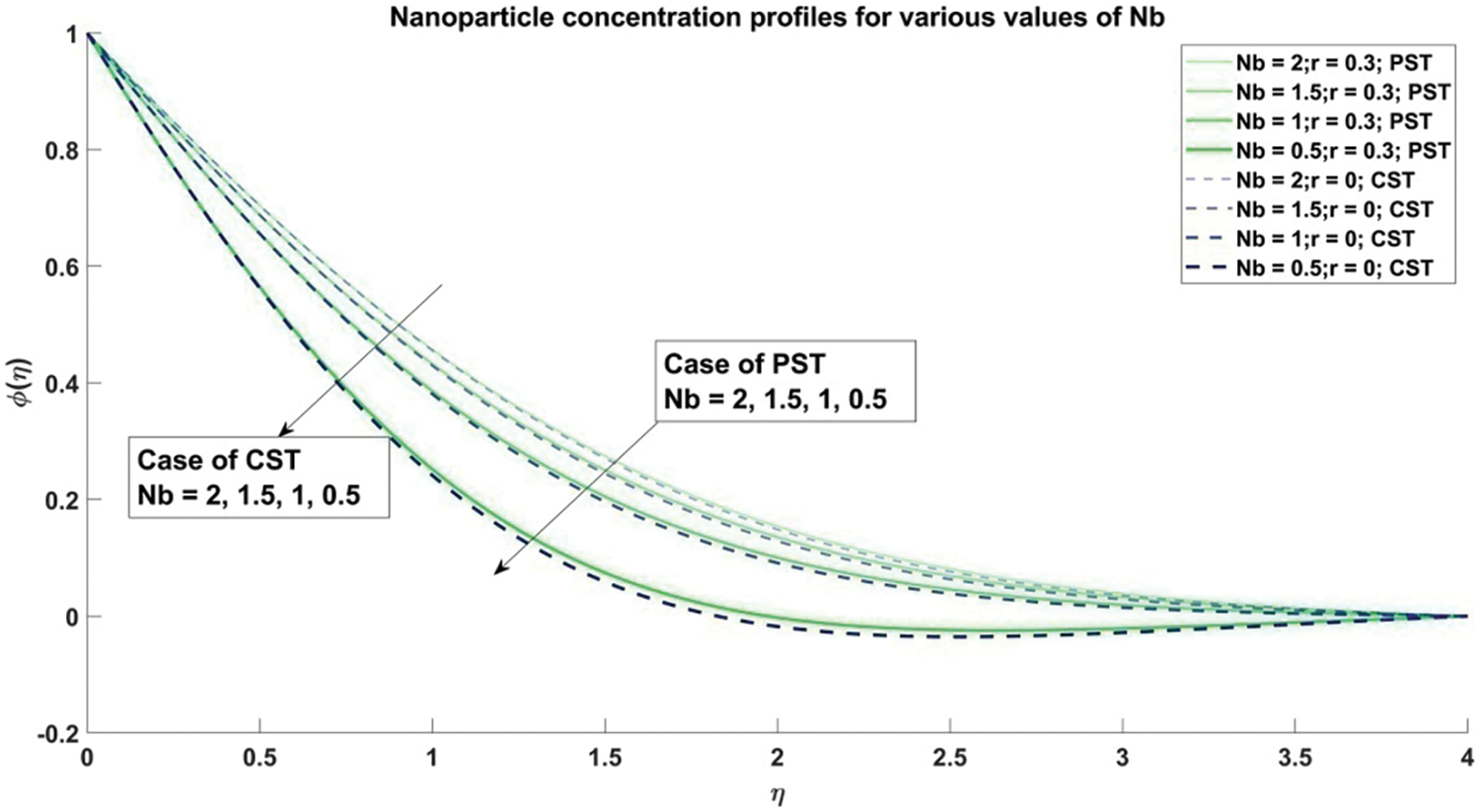
Figure 15: Nanoparticle concentration profiles corresponding to different values of Nb
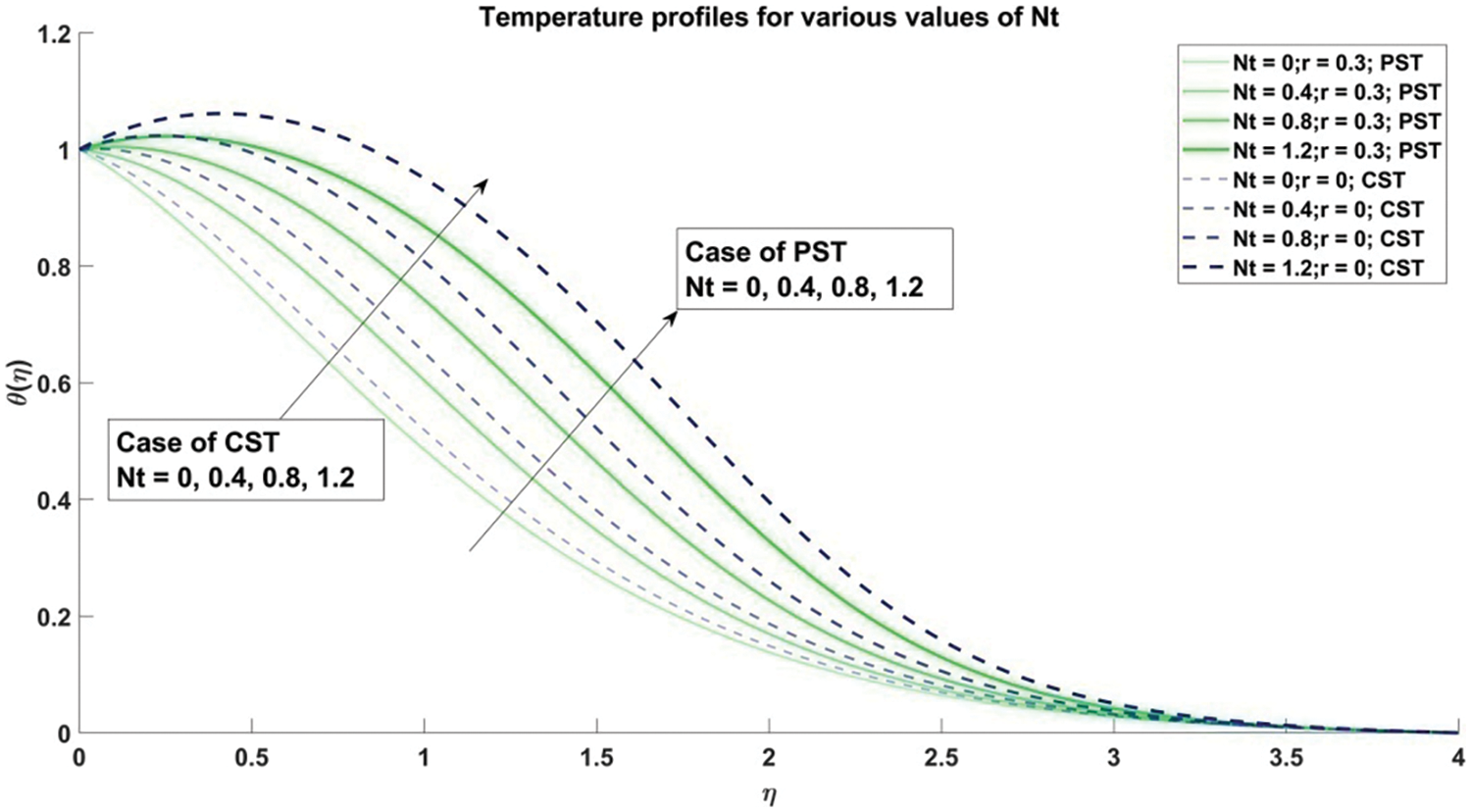
Figure 16: Profiles of temperature corresponding to different values of Nt
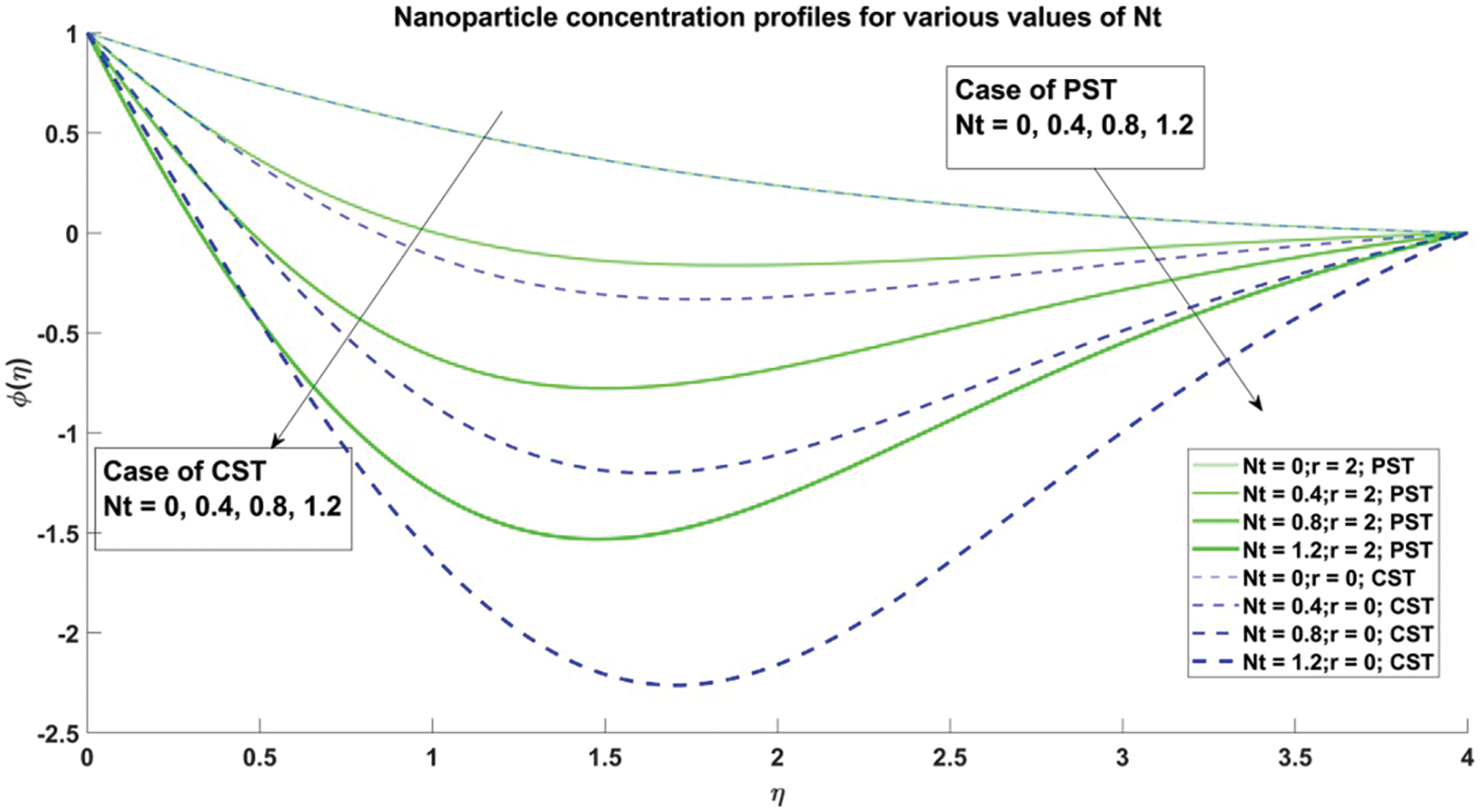
Figure 17: Profiles for nanoparticle concentration corresponding to different values of Nt
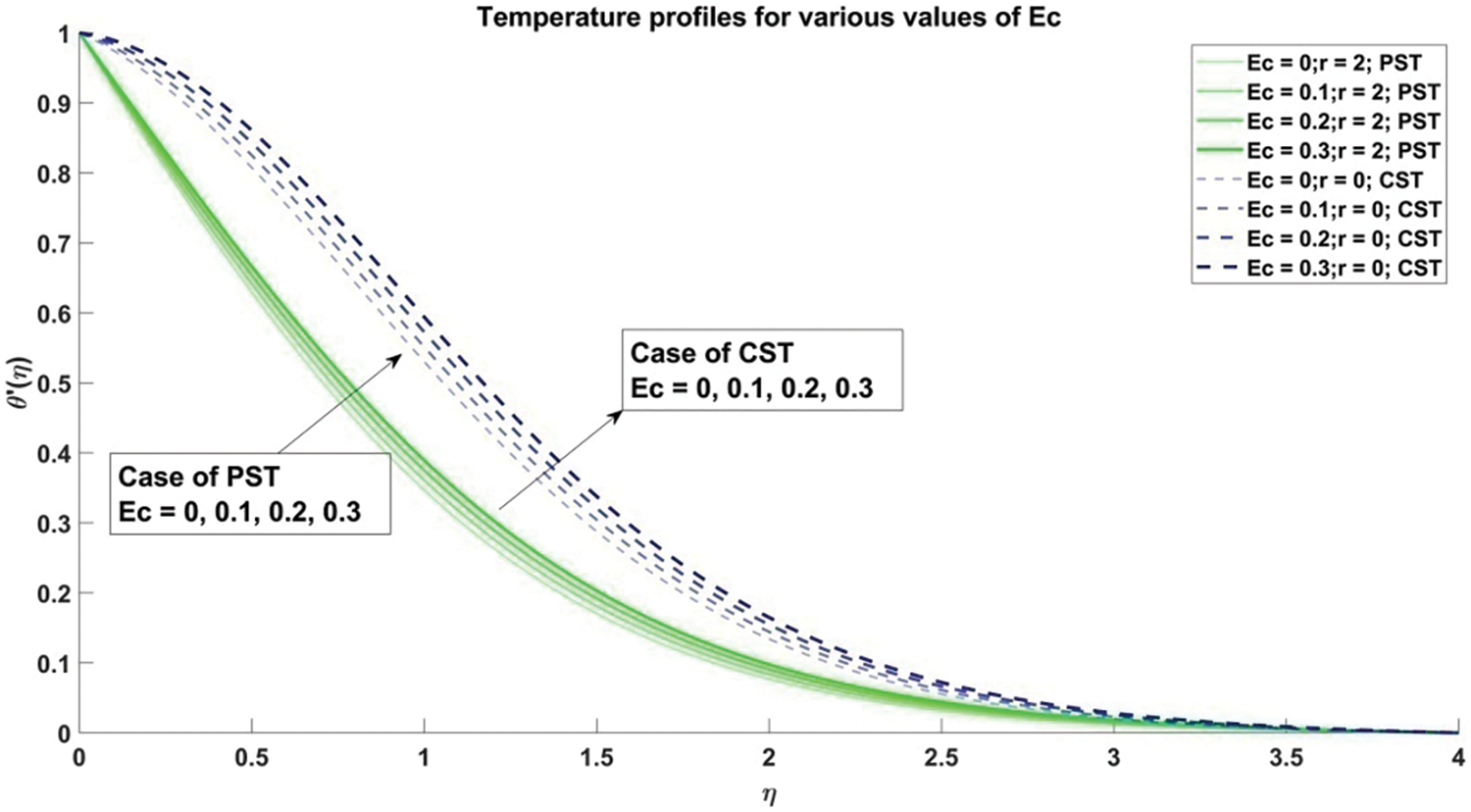
Figure 18: Profiles for temperature corresponding to different values of Ec
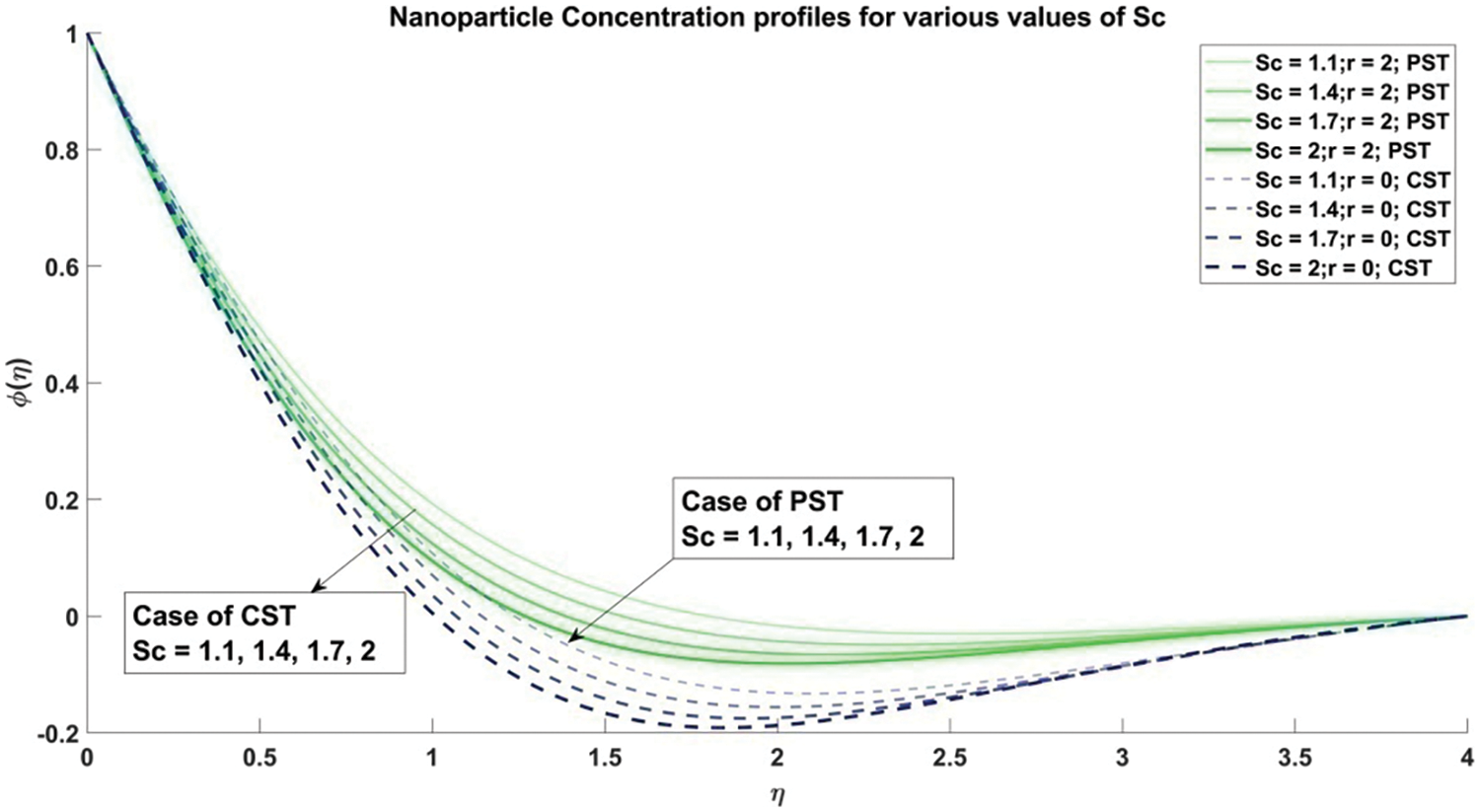
Figure 19: Profiles for nanoparticle concentration corresponding to different values of Sc
Fig. 2 presents a detailed exploration into the intricate ramifications of the slip parameter on the streamwise velocity characteristics of Casson nanofluid. Spanning across both Prescribed Surface Temperature (PST) and Constant Surface Temperature (CST) regimes, this graph meticulously examines the diverse magnitudes of the slip parameter, denoted by ζ. A consistent influence of slip parameter ζ on the fluid velocity is discerned, irrespective of the prevailing surface temperature conditions. Notably, higher values of the slip parameter engender a discernible reduction in the velocity profiles of the nanofluid. This is because the slip parameter represents the degree to which the fluid can slip along the boundary surface. As the slip parameter increases, the resistance to fluid motion at the boundary decreases, leading to a reduced velocity gradient at the wall. This reduction in the velocity gradient causes a corresponding decrease in the overall velocity of the nanofluid. Furthermore, the presence of thermophoresis and Brownian motion enhances the random motion of nanoparticles, which further disrupts the organized flow, leading to an additional decrease in velocity. Fig. 3 delves into the intricate impact of slip parameter ζ on the temperature profiles of the nanofluid under both PST and CST scenarios. The graph intricately illustrates the diminishing boundary layer thickness with the escalating velocity slip parameter ζ, attributed to the thermal jump phenomenon exhibited by fluid particles, accentuated by the presence of a magnetic field. Consequently, amplifying the velocity slip parameter heralds a decline in the temperature distribution of nanoparticles, thereby augmenting the rate of heat transfer and elevating the local Nusselt number. Moreover, the temperature distribution is observed to be higher under CST conditions than in PST settings. The higher temperature distribution observed under CST conditions is primarily due to the constant temperature difference that drives more efficient heat retention within the fluid, leading to a higher overall temperature in the system. The scrutiny of slip parameter ζ on the concentration profiles of nanofluid is further scrutinized in Fig. 4. It is perceptible that as the velocity slip parameter (ζ) experiences an augmentation, the concentration of nanoparticles at the stretching surface also intensifies, consequently leading to a reduction in the local Sherwood number. This decrease occurs because the Sherwood number is inversely related to the concentration gradient at the surface. When nanoparticles accumulate, the gradient becomes less steep, indicating a lower rate of mass transfer. Additionally, the concentration profiles under Prescribed Surface Temperature (PST) are more pronounced compared to those observed under Constant Surface Temperature (CST). Under PST condition, the temperature at the surface varies, which creates a non-uniform temperature distribution along the surface. This variation leads to a more significant thermal gradient, influencing the diffusion and convection of nanoparticles differently along the surface. The variable temperature distribution enhances thermophoretic forces, which drive nanoparticles from warmer to cooler regions, potentially leading to a higher nanoparticle concentration gradient near the surface. In Fig. 5, the profound impact of the non-linear stretching parameter n on nanofluid velocity profiles is meticulously delineated. The presence of the non-linear stretching parameter n engenders a discernable diminishment in nanofluid velocity owing to supplementary disruptions within various fluid layers. Consequently, the velocity gradient (f′(η)) experiences an augmentation. It is notable that the velocity remains consistent across both Prescribed Surface Temperature (PST) and Constant Surface Temperature (CST) scenarios. This consistency is due to the fact that the velocity is not influenced by the PST parameter r. Fig. 6 sheds light on the intricate influence of the non-linear stretching parameter n on the temperature distribution of Casson nanofluid. As the non-linearity of the stretching sheet intensifies, the thickness of the momentum boundary layer experiences a decrement, thereby expanding the breadth of the thermal boundary layer and elevating the fluid temperature for increasing values of the non-linear stretching parameter n under PST conditions. Conversely, under CST conditions, the augmentation in the thickness of the momentum surface layer concomitant with ascending magnitudes of non-linear stretching parameter engenders a discernible diminution in temperature, owing to the escalating non-linearity of the stretching parameter. Lastly, Fig. 7 intricately portrays variations in concentration profiles attributable to non-linear stretching parameter n for PST and CST scenarios. The depicted concentration profiles suggest an upward trend in nanofluid concentration with increasing non-linearity of the stretching parameter. This is because, with high stretching rate, the boundary layer becomes thin which becomes less effective in dispersal of nanoparticles resulting in higher concentration. However, concentration profiles are observed to be higher for PST compared to CST, primarily due to the more pronounced suction effect under CST condition. These variations in velocity, temperature and concentration due to the different parameters can be utilized in designing microfluidic devices for blood-based diagnostics, where precise control of fluid flow is necessary for accurate measurements and analyses.
Fig. 8 provides a comprehensive elucidation of the profound influence wielded by the Casson parameter β on the velocity profiles of nanofluid, meticulously considering both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) scenarios. A discernible correlation emerges, wherein heightened values of the Casson fluid parameter β correspond with a notable reduction in the velocity profile. This graphical representation effectively illustrates how augmenting the Casson fluid parameter β precipitates a decrement in the yield stress, thus impeding the unimpeded motion of fluid particles and subsequently diminishing the boundary layer thickness. Consequently, fluid velocity undergoes a discernible reduction, consequently resulting in a decline in the skin friction coefficient. The marginal disparity observed between PST and CST scenarios concerning the effect of the Casson parameter on nanofluid velocity is inconsequential. This is because, in both the cases of PST and CST, the primary role of the Casson parameter is to alter the viscosity and flow resistance of the nanofluid, affecting how easily the fluid can move. Since this effect is intrinsic to the fluid’s properties and is not directly impacted by the thermal boundary conditions, the velocity profiles exhibit only a marginal difference between the two cases. In Fig. 9, a meticulous examination unfolds the ramifications of the Casson parameter β on temperature distribution under both prescribed and constant surface temperature regimes. Notably, a decreasing trend is observed where the temperature registers lower values under PST than CST for a given value β. Furthermore, this graph effectively illustrates that augmentation in the value of the Casson parameter β precipitates a reduction in velocity, consequently diminishing the rate of thermal transfer and ultimately lowering the fluid temperature. Therefore, as the Casson fluid parameter β experiences an increase, the fluid temperature undergoes a subsequent decrease.
The scrutiny of the Casson fluid parameter β on nanoparticle concentration profiles is encapsulated in Fig. 10. Herein, it is discerned that an augmentation in the Casson fluid parameter β amplifies the viscous behavior inherent in fluid flow, consequently augmenting the concentration of nanoparticles due to the prevalence of this dominant viscous nature. This influence manifests more prominently in the case of uniform flow. Additionally, viscosity assumes greater significance in the scenario of prescribed surface temperature compared to constant surface temperature, thus resulting in lower nanoparticle concentration values for constant surface temperature for identical β values. The main reason for this consequence is temperature-dependent nature of viscosity. The variations in temperature under PST condition causes non-uniform changes in viscosity across the surface, affecting the flow behavior and nanoparticle distribution. In areas where the surface temperature is higher, reduced viscosity enhances the fluid flow, facilitating the dispersion and movement of nanoparticles. Fig. 11 delineates the influence of the magnetic parameter on the velocity profiles of the Casson nanofluid. It is elucidated that the presence of the magnetic parameter M imposes constraints on the unimpeded motion of fluid particles owing to the generation of the Lorentz force induced by the magnetic field. This magnetic behavior can be harnessed to regulate the blood flow.
The decrement in velocity distribution is thus attributed to an escalation in the value of the magnetic parameter M because of the increased effect of Lorentz force. Notably, no substantial disparity is observed in velocity profiles between CST and PST scenarios. The lack of substantial disparity in velocity profiles between CST and PST scenarios with increasing magnetic parameters is due to the fact that the influence of Lorentz force on flow resistance is independent of the thermal boundary conditions. In Fig. 12, temperature profiles for various values of magnetic parameters are meticulously illustrated for both CST and PST scenarios. As the magnetic parameter M undergoes an escalation, the velocity profile diminishes owing to the generation of the Lorentz force, intensifying the boundary width and heat transportation rate and ultimately elevating the fluid temperature. This Lorentz force is observed to be more pronounced in the case of CST than PST, thus yielding higher temperature profiles for CST settings. The Lorentz force is more pronounced in the case of CST because the consistent surface temperature creates a stable and uniform interaction between the magnetic field and the fluid, leading to a more pronounced magnetic drag force. This stability allows the Lorentz force to have a more significant and consistent impact on the fluid flow than the variable conditions in PST. Fig. 13 intricately elucidates the ramifications of the magnetic parameter M on the concentration profiles of the nanofluid. Herein, as the magnetic parameter M experiences an augmentation, the mass transfer rate escalates, consequently leading to a decline in nanoparticle concentration. Concentration profiles exhibit higher values for prescribed surface temperatures compared to constant surface temperatures, which can be attributed to the localized heating and reduced convective transport, ultimately resulting in higher nanoparticle concentration.
Fig. 14 meticulously elucidates the intricate repercussions of Brownian motion parameter Nb on the temperature profiles of the nanofluid, under both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) conditions. The Brownian motion parameter manifests a positive effect on the temperature profiles, indicating a surge in temperature with escalating values of Nb. This phenomenon arises from the collisions between suspended nanoparticles, inducing Brownian motion, which augments the width of the boundary layer and consequently elevates the fluid temperature for larger Brownian motion parameter values. This, in turn, precipitates a decrement in the local Nusselt number. It is noteworthy that the Brownian motion parameter has a more pronounced effect under Constant Surface Temperature (CST) condition as compared to Prescribed Surface Temperature (PST) conditions. This is because, under Constant Surface Temperature (CST) condition, the temperature remains uniform, leading to a consistent thermal environment that enhances the effect of Brownian motion throughout the fluid. In contrast, the Prescribed Surface Temperature (PST) condition involves variable temperature, which disrupts the uniform influence of Brownian motion and reduces its overall impact.
In Fig. 15, a meticulous examination analyzes how the Brownian motion parameter Nb influences the concentration profiles. The augmentation in Brownian motion parameter values precipitates high-speed collisions between fluid particles and nanoparticles, culminating in a reduction in concentration profiles. The influence of the Brownian motion parameter remains consistent across both PST and CST scenarios. The reason for the consistent influence of the Brownian motion parameter on concentration profiles across both Prescribed Surface Temperature (PST) and Constant Surface Temperature (CST) scenarios can be attributed to the dependence of Brownian motion on the thermal energy of the nanoparticles, which affects their random movement. Since this random motion results from the nanoparticle’s thermal energy and is relatively independent of the specific thermal boundary conditions at the surface, its effect on concentration profiles remains similar in both PST and CST settings. Fig. 16 delves into the impact of the thermophoresis parameter Nt on fluid temperature. Elevated values of the thermophoresis parameter herald a diminution in nanoparticle conduction, subsequently dampening the temperature gradient. This engenders an expansion in the width of the boundary layer, prompting ultrafine nanoparticles to migrate from hotter to cooler regions, thereby elevating the temperature profiles. This effect is observed to be more accentuated under constant surface temperature conditions compared to prescribed surface temperature conditions. This is because varying temperatures in PST conditions create a less uniform thermal environment, which moderates the effect of nanoparticle migration and, hence, temperature profile changes.
In Fig. 17, concentration profiles for various values of the thermophoresis parameter Nt under both CST and PST scenarios are meticulously illustrated. During thermophoresis, particles exert force on one another, instigating their migration from hotter to colder regions and intensifying the nanoparticle volume fraction. Thus, the concentration of the nanofluid exhibits a decremental trend concomitant with the augmentation of the thermophoresis parameter Nt. Also, the constant temperature creates a stable thermal gradient, leading to a more effective and consistent thermophoretic effect, which drives nanoparticles more efficiently from hotter to cooler regions. This consistent gradient enhances the removal of nanoparticles from the surface, resulting in a more rapid decrease in concentration in case of CST as compared to PST. Fig. 18 elucidates the influence of the Eckert number on the temperature profiles of the nanofluid. The amplified values of the Eckert number precipitate a diminution in temperature profiles for both CST and PST scenarios. The Eckert number epitomizes the ratio of heat dissipation potential to advective movement, predominantly catalyzing the conversion of kinetic energy into thermal energy. Elevated values of the Eckert number instigate an upsurge in the thermal buoyancy effect, consequently lowering fluid temperature. Notably, higher temperature profiles are observed for escalating values of the Eckert number under CST compared to PST. In CST conditions, where the surface temperature is constant, the heat generated by viscous dissipation is more uniformly absorbed by the fluid, leading to a higher overall temperature profile. In contrast, under PST condition, the temperature at the surface varies, leading to less consistent absorption of viscous heating and a more variable thermal environment. This variability supports the increase in temperature profiles with rising Eckert number compared to the steady conditions of CST. Lastly, Fig. 19 highlights the impact of Schmidt number on concentration profiles. As the value of the physical parameter Sc intensifies, there is a corresponding decline in mass diffusivity, culminating in a reduction in the concentration of nanoparticles. Concentration profiles are observed to be higher under PST compared to CST settings. This is because as the Schmidt number increases, the mass diffusivity decreases relative to the momentum diffusivity, which means that the fluid’s ability to mix or spread out nanoparticles is reduced. In PST condition, where the surface temperature varies, the resulting non-uniform temperature gradient can exacerbate the effects of reduced mass diffusivity by creating localized areas of higher nanoparticle accumulation. This leads to higher concentration profiles. In contrast, under CST condition, the temperature is uniform, which generally promotes more effective mixing and dispersal of nanoparticles, reducing concentration profiles compared to the more variable conditions in PST settings.
Table 1 presents the validation of the current results by comparing the computed Nusselt number with values reported in existing studies, specifically for the parameters Nb=0,Nt=0,M=0,ζ=0. This benchmarking process is crucial as it not only corroborates the accuracy and reliability of the present findings but also instills confidence in the methods and models employed in this study. The current results are found to be in good agreement with established results. Thus the current model of nanofluid is credible and thus provides a solid foundation for further exploration and application.
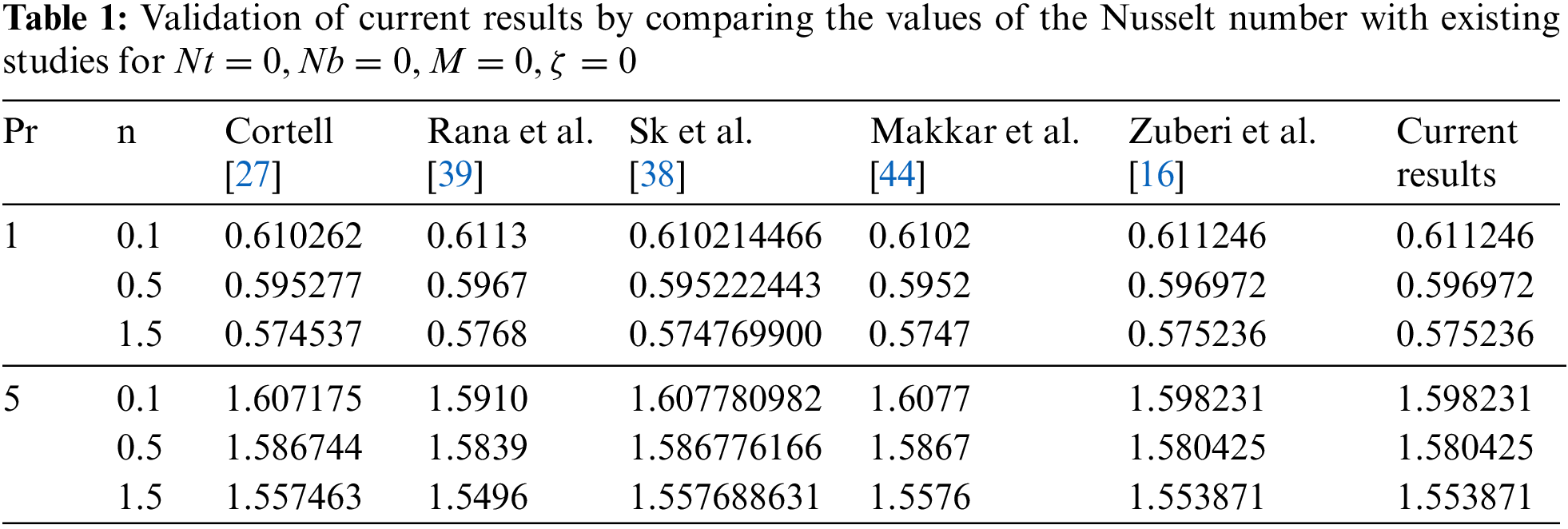
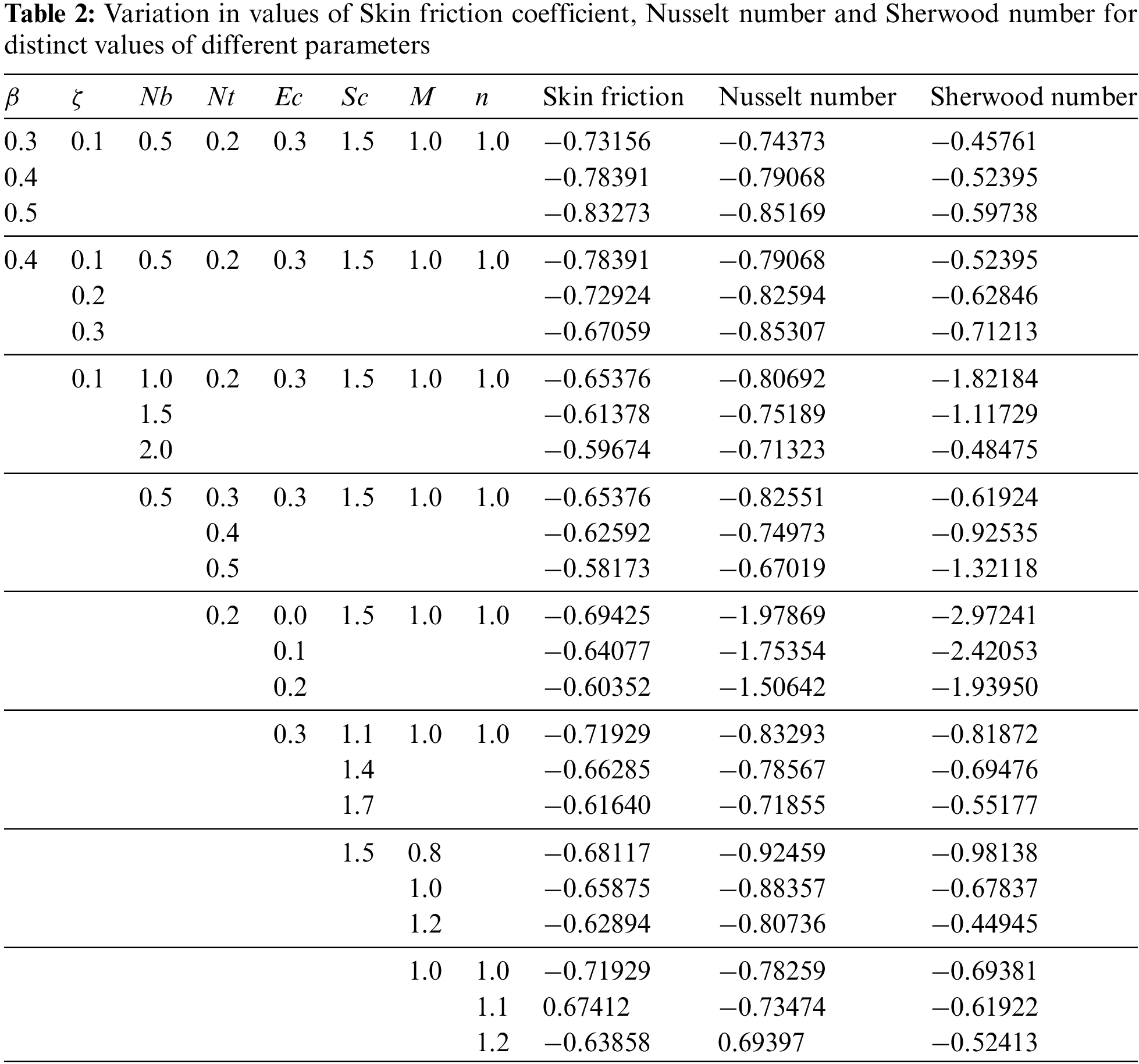
Table 2 delves into the variations in the values of the Skin Friction Coefficient, Nusselt number, and Sherwood number for distinct parameter settings, including β, ζ, Nb, Nt, Ec, Sc, M, and n. These parameters significantly influence the fluid dynamics and heat transfer characteristics of nanofluid flow, which have far-reaching implications in real-world scenarios, particularly in medicine and health. The slip parameter ζ influences nanoparticle transport efficiency in drug delivery systems, while the non-linear stretching parameter n affects dispersion in tissue engineering. The Casson parameter β is vital for managing the viscosity of blood-like fluids in diagnostic and therapeutic contexts. The brownian motion parameter Nb enhances nanoparticle distribution in targeted therapies, and thermophoresis parameter Nt controls their accumulation in hyperthermia treatments. The Eckert number Ec helps to manage the heat distribution in thermal therapies, while the Schmidt number Sc optimizes drug release and contrast agent dispersion. Hence, by carefully adjusting these parameters, advancement in the field of biomedicine can be achieved with more precise and effective treatments, enhancing therapeutic outcomes and diagnostic accuracy. The understanding of impact of these parameters can also enhance the design of drug delivery systems, where precise control of fluid flow and heat transfer is essential for maintaining the stability and efficacy of pharmaceuticals. Furthermore, these insights can be applied to biomedical engineering, such as in the cooling of electronic medical devices or in the development of advanced cooling systems for hyperthermia treatment, where managing heat dissipation is crucial. Hence, the current study not only advances theoretical modeling but also opens avenues for practical applications in enhancing patient care and treatment efficiency.
The present investigation delves into the intricate dynamics of mass, heat, and concentration transfer exhibited by a magnetohydrodynamic (MHD) Casson nanofluid interacting with a non-linearly stretched sheet. Emphasizing the inclusion of viscous and Ohmic dissipation effects, the study offers insights into the temperature distribution, volume fraction of nanoparticles, and the velocity profile of MHD Casson fluid flow. Moreover, the investigation meticulously explores both the scenarios of Constant Surface Temperature (CST) and Particular Surface Temperature (PST). Leveraging similarity conversion techniques, the governing partial differential equations are transformed into ordinary differential equations, necessitating a numerical exploration of the problem using the bvp4c module within MATLAB. Key conclusions drawn from the present analysis are summarized as follows:
1) As the magnetic parameter (M) ascends, the skin friction coefficient undergoes escalation owing to the augmented generation of the Lorentz force. Consequently, this phenomenon engenders an enhancement in both the local Nusselt number and Sherwood number, particularly notable with higher values of M.
2) Observations reveal a decline in the velocity profile as the Casson fluid parameter (β) and velocity slip parameter (ζ) escalate, juxtaposed with an upsurge in the velocity profile associated with an increase in the non-linear stretching parameter (n). Remarkably, the velocity profiles exhibit similarity between the scenarios of Prescribed Surface Temperature (PST) and Constant Surface Temperature (CST).
3) The interplay of the parameter of slip and curved deformation parameter manifests in the thermal boundary layer thickness, where an escalation is observed for Prescribed Surface Temperature (PST), leading to an increase in temperature profiles. Conversely, for Constant Surface Temperature (CST), a reduction in the thermal boundary layer thickness ensues, consequently resulting in a decline in temperature profiles.
4) The concentration of nanoparticles exhibits a decline as the values of the Brownian motion parameter and thermophoresis parameter escalate, observed consistently across both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) scenarios.
5) The temperature of the nanofluid demonstrates a notable increase corresponding to the escalation of both the Brownian motion parameter and thermophoresis parameter across both Constant Surface Temperature (CST) and Prescribed Surface Temperature (PST) conditions.
6) As the Schmidt number (Sc) decreases, the ability of nanoparticles to spread out decreases, which ultimately reduces the concentration of nanoparticles.
7) The rise in the values of the viscous dissipation parameter (Eckert number (Ec)) results in a decrease in the temperature of the nanofluid due to efficient heat dissipation at the boundary. Since the heat absorbed by the nanofluid is more pronounced in case of CST as compared to PST, therefore the temperature profiles are higher for CST compared to PST.
The study lacks the experimental validation. Also, the shape and size of nanoparticles have not been taken into account. Further, the results of the stated model are valid only for non-linear stretching sheet. Thus, the study can be explored further by taking into account the parameters of shape and size of nanoparticles. Also, the case of flow over shrinking sheet can be discussed, which will enhance our understanding of surface dynamics in various contexts. Moreover, the experimental validation by medical experts will benchmark the simulated results of the governing stated model.
Acknowledgement: The authors wish to extend their profound gratitude to Universiti Teknikal Malaysia Melaka (UTeM) for the unconditional support that enabled this research to be conducted. Also, the authors would like to express sincere thanks to all contributors whose hard work, knowledge, and teamwork were crucial to the accomplishment of this research.
Funding Statement: This research was funded by Universiti Teknikal Malaysia Melaka and Ministry of Higher Education (MoHE) Malaysia, grant number FRGS/1/2024/FTKM/F00586.
Author Contributions: The authors confirm their contribution to the paper as follows: Study conception and design: Haris Alam Zuberi, Madan Lal, Nurul Amira Zainal; Data collection: Haris Alam Zuberi, Madan Lal, Shivangi Verma, Nurul Amira Zainal; Analysis and interpretation of results: Haris Alam Zuberi, Madan Lal, Nurul Amira Zainal; Draft manuscript preparation: Haris Alam Zuberi, Madan Lal, Shivangi Verma, Nurul Amira Zainal. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Jacob M, Chappell D, Becker BF. Regulation of blood flow and volume exchange across the microcirculation. Critical Care. 2016;20:1–13. [Google Scholar]
2. Caplan RM. Heart disease and hypertension. In: Long life strategy: a guide for living a longer, healthier, and more fulfilling life. Switzerland AG: Springer; 2024. p. 109–24. [Google Scholar]
3. Faghy MA, Tatler A, Chidley C, Fryer S, Stoner L, Laddu D, et al. The physiologic benefits of optimizing cardiorespiratory fitness and physical activity–from the cell to systems level in a post-pandemic world. Prog Cardiovasc Dis. 2024;33:49–54. [Google Scholar]
4. Srivastava L, Srivastava V. Peristaltic transport of blood: Casson model—II. J Biomech. 1984;17(11):821–9. [Google Scholar] [PubMed]
5. Ali F, Sheikh NA, Khan I, Saqib M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: a fractional model. J Magn Magn Mater. 2017;423:327–36. [Google Scholar]
6. Pandey R, Kumar M, Majdoubi J, Rahimi-Gorji M, Srivastav VK. A review study on blood in human coronary artery: numerical approach. Comput Methods Programs Biomed. 2020;187:105243. [Google Scholar] [PubMed]
7. Mauter MS, Zucker I, Perreault F, Werber JR, Kim JH, Elimelech M. The role of nanotechnology in tackling global water challenges. Nat Sustain. 2018;1(4):166–75. doi:10.1038/s41893-018-0046-8. [Google Scholar] [CrossRef]
8. Wiek A, Foley RW, Guston DH. Nanotechnology for sustainability: what does nanotechnology offer to address complex sustainability problems?. In: Nanotechnology for sustainable development. Switzerland AG: Springer; 2014. p. 371–90. [Google Scholar]
9. Saxer T, Holme MN. Challenges in cardiovascular treatments using nanotechnology-based approaches. Nanosci Nanotechnol Human Health. 2016;51–70. [Google Scholar]
10. Qi C, Luo T, Liu M, Fan F, Yan Y. Experimental study on the flow and heat transfer characteristics of nanofluids in double-tube heat exchangers based on thermal efficiency assessment. Energy Convers Manag. 2019;197(39):111877. doi:10.1016/j.enconman.2019.111877. [Google Scholar] [CrossRef]
11. Kim J, Lee N, Hyeon T. Recent development of nanoparticles for molecular imaging. Philos Trans Royal Society A: Math, Phys Eng Sci. 2017;375(2107):20170022. doi:10.1098/rsta.2017.0022. [Google Scholar] [PubMed] [CrossRef]
12. Bhaumik B, Changdar S, De S. Combined impact of Brownian motion and thermophoresis on nanoparticle distribution in peristaltic Nanofluid flow in an asymmetric channel. Int J Ambient Energy. 2022;43(1):5064–75. doi:10.1080/01430750.2021.1934539. [Google Scholar] [CrossRef]
13. Mörters P, Peres Y. Brownian motion. Cambridge, UK: Cambridge University Press; 2010, vol. 30. [Google Scholar]
14. Piazza R, Parola A. Thermophoresis in colloidal suspensions. J Phys: Condens Matter. 2008;20(15):153102. doi:10.1088/0953-8984/20/15/153102. [Google Scholar] [CrossRef]
15. Dubey A, Vasu B, Anwar Bég O, Gorla RS, Kadir A. Computational fluid dynamic simulation of two-fluid non-Newtonian nanohemodynamics through a diseased artery with a stenosis and aneurysm. Comput Methods Biomech Biomed Eng. 2020;23(8):345–71. doi:10.1080/10255842.2020.1729755. [Google Scholar] [PubMed] [CrossRef]
16. Zuberi HA, Lal M, Verma S, Zainal NA. Computational investigation of brownian motion and thermophoresis effect on blood-based casson nanofluid on a non-linearly stretching sheet. J Adv Res Numer Heat Transfer. 2024;18(1):49–67. doi:10.37934/arnht.18.1.4967. [Google Scholar] [CrossRef]
17. Madhura KR, Babitha. Numerical study on magnetohydrodynamics micropolar Carreau nanofluid with Brownian motion and thermophoresis effect. Int J Model Simul. 2023 Jul;16:1–4. doi:10.1080/02286203.2023.2234240. [Google Scholar] [CrossRef]
18. Reddy SBV, Ashwathnarayana DP, Mysore J, Chandrashekhar DV. Ohmic and viscous dissipation effect on free and forced convective flow of casson fluid in a channel. Biointerface Res Appl Chem. 2021;12(1):132–48. doi:10.33263/BRIAC. [Google Scholar] [CrossRef]
19. Tang TQ, Rooman M, Vrinceanu N, Shah Z, Alshehri A. Blood flow of Au-nanofluid using Sisko model in stenotic artery with porous walls and viscous dissipation effect. Micromachines. 2022;13(8):1303. doi:10.3390/mi13081303. [Google Scholar] [PubMed] [CrossRef]
20. Das S, Pal T, Jana R. Electromagnetic hybrid nano-blood pumping via peristalsis through an endoscope having blood clotting in presence of Hall and ion slip currents. BioNanoScience. 2021;11(3):848–70. doi:10.1007/s12668-021-00853-2. [Google Scholar] [CrossRef]
21. Yusuf TA. Analysis of entropy generation in nonlinear convection flow of unsteady magneto-nanofluid configured by vertical stretching sheet with Ohmic heating. Int J Ambient Energy. 2023 Dec 31;44(1):2319–35. doi:10.1080/01430750.2023.2236103. [Google Scholar] [CrossRef]
22. Siddiqui AA, Turkyilmazoglu M. Film flow of nano-micropolar fluid with dissipation effect. Comput Model Eng Sci. 2024 Jul 8;140(3):2487–512. doi:10.32604/cmes.2024.050525. [Google Scholar] [CrossRef]
23. Hsu HJ, Bugno J, Lee Sr, Hong S. Dendrimer-based nanocarriers: a versatile platform for drug delivery. Wiley Interdiscip Rev: Nanomed Nanobiotechnology. 2017;9(1):e1409. doi:10.1002/wnan.1409. [Google Scholar] [PubMed] [CrossRef]
24. Kumar R. Lipid-based nanoparticles for drug-delivery systems. In: Nanocarriers for drug delivery. Amsterdam, Netherland: Elsevier; 2019. p. 249–84. [Google Scholar]
25. Nazar R, Amin N, Filip D, Pop I. Stagnation point flow of a micropolar fluid towards a stretching sheet. Int J Non-Linear Mech. 2004;39(7):1227–35. [Google Scholar]
26. Crane LJ. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP. 1970;21:645–7. [Google Scholar]
27. Cortell R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl Math Comput. 2007;184(2):864–73. [Google Scholar]
28. Alahmadi RA, Raza J, Mushtaq T, Abdelmohsen SA, Gorji R, Hassan M, et al. Optimization of MHD flow of radiative micropolar nanofluid in a channel by RSM: sensitivity analysis. Mathematics. 2023;11(4):939. [Google Scholar]
29. Raza J, Al-Khaled K, Dero S, Lund LA, Khan SU, Khan MI, et al. Heat and mass transfer phenomenon for micropolar nanofluid with microrotation effects: nonsimilarity simulations. Int J Mod Phys B. 2023;37(19):2350183. [Google Scholar]
30. Pandey AK, Kumar M. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alexandria Eng J. 2017;56(1):55–62. [Google Scholar]
31. Boujelbene M, Rehman S, Alqahtani S, Eldin SM. Optimizing thermal characteristics and entropy degradation with the role of Nanofluid flow configuration through an inclined channel. Alexandria Eng J. 2023;69:85–107. [Google Scholar]
32. Reddy BP, Shamshuddin MD, Salawu SO, Sademaki LJ. Computational analysis of transient thermal diffusion and propagation of chemically reactive magneto-nanofluid, Brinkman-type flow past an oscillating absorbent plate. Partial Differ Equ Appl Math. 2024 Jun 14;11:100761. [Google Scholar]
33. Thiriet M. Biology and mechanics of blood flows: part II: mechanics and medical aspects. New York, USA: Springer Science & Business Media; 2007. [Google Scholar]
34. Wang Y, Li H, Guo Y, Lee WN. Bidirectional ultrasound elastographic imaging framework for non-invasive assessment of the non-linear behavior of a physiologically pressurized artery. Ultrasoun Med Biol. 2019;45(5):1184–96. [Google Scholar]
35. Wajihah SA, Sankar D. A review on non-Newtonian fluid models for multi-layered blood rheology in constricted arteries. Arch Appl Mech. 2023;93(5):1771–96. doi:10.1007/s00419-023-02368-6. [Google Scholar] [PubMed] [CrossRef]
36. Saeed A, Khan N, Gul T, Kumam W, Alghamdi W, Kumam P. The flow of blood-based hybrid nanofluids with couple stresses by the convergent and divergent channel for the applications of drug delivery. Molecules. 2021;26(21):6330. doi:10.3390/molecules26216330. [Google Scholar] [PubMed] [CrossRef]
37. Yazdi MH, Abdullah S, Hashim I, Sopian K. Slip MHD liquid flow and heat transfer over non-linear permeable stretching surface with chemical reaction. Int J Heat Mass Transf. 2011 Jul 1;54(15–16):3214–25. doi:10.1016/j.ijheatmasstransfer.2011.04.009. [Google Scholar] [CrossRef]
38. Sk MT, Das K, Kundu PK. Effect of magnetic field on slip flow of nanofluid induced by a non-linear permeable stretching surface. Appl Therm Eng. 2016 Jul 5;104(3):758–66. doi:10.1016/j.applthermaleng.2016.05.129. [Google Scholar] [CrossRef]
39. Rana P, Bhargava R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: a numerical study. Commun Nonlinear Sci Numer Simul. 2012 Jan 1;17(1):212–26. doi:10.1016/j.cnsns.2011.05.009. [Google Scholar] [CrossRef]
40. Qayyum M, Riaz MB, Afzal S. Analysis of blood flow of unsteady Carreau-Yasuda nanofluid with viscous dissipation and chemical reaction under variable magnetic field. Heliyon. 2023 Jun 1;9(6):e16522. [Google Scholar]
41. Chaudhary S, Singh A, Kumar D, Baleanu D. Numerical analysis for MHD blood-nanofluid flow through a non-linearly stretched sheet interpolated in a permeable medium along heat generation. Case Stud Therm Eng. 2023 Dec 1;52:103786. [Google Scholar]
42. Zari I, Gul T, Dosmagulova K, Khan TS, Haq S. Heat transfer analysis of radiative-marangoni convective flow in nanofluid comprising Lorentz forces and porosity effects. Adv Theory Nonlinear Anal its Appl. 2023;7(1):61–81. [Google Scholar]
43. Hou E, Nazir U, Naz S, Sohail M, Nadeem M, Lee JR, et al. Novel analysis of two kinds hybrid models in ferro martial inserting variable Lorentz force past a heated disk: an implementation of finite element method. Comput Model Eng Sci. 2023;135(2):1393–411. doi:10.32604/cmes.2022.022500. [Google Scholar] [CrossRef]
44. Makkar V, Poply V, Goyal R, Sharma N. Numerical investigation of mhd casson nanofluid flow towards a non linear stretching sheet in presence of double-diffusive effects along with viscous and ohmic dissipation. J Therma Eng. 2021;7(2):1–17. [Google Scholar]
45. Tawade JV, Guled C, Noeiaghdam S, Fernandez-Gamiz U, Govindan V, Balamuralitharan S. Effects of thermophoresis and Brownian motion for thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet. Results Eng. 2022;15(3):100448. doi:10.1016/j.rineng.2022.100448. [Google Scholar] [CrossRef]
46. Hussain S, Rasheed K, Ali A, Vrinceanu N, Alshehri A, Shah Z. A sensitivity analysis of MHD nanofluid flow across an exponentially stretched surface with non-uniform heat flux by response surface methodology. Sci Rep. 2022;12(1):18523. doi:10.1038/s41598-022-22970-y. [Google Scholar] [PubMed] [CrossRef]
47. Gao S, Yang X, Xu J, Qiu N, Zhai G. Nanotechnology for boosting cancer immunotherapy and remodeling tumor microenvironment: the horizons in cancer treatment. ACS Nano. 2021;15(8):12567–603. doi:10.1021/acsnano.1c02103. [Google Scholar] [PubMed] [CrossRef]
48. Mitchell MJ, Billingsley MM, Haley RM, Wechsler ME, Peppas NA, Langer R. Engineering precision nanoparticles for drug delivery. Nat Rev Drug Discov. 2021;20(2):101–24. doi:10.1038/s41573-020-0090-8. [Google Scholar] [PubMed] [CrossRef]
49. Bao G, Mitragotri S, Tong S. Multifunctional nanoparticles for drug delivery and molecular imaging. Annu Rev Biomed Eng. 2013;15(1):253–82. doi:10.1146/annurev-bioeng-071812-152409. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
