AI-Powered Image Security: Utilizing Autoencoders for Advanced Medical Image Encryption

1  Introduction

In this digital age, with the widespread use of smart healthcare and electronic health record systems, securing medical images has become critically important. Medical images that contain private information about patients can be attacked, modified, and tampered with [1]. To protect the privacy of the patients, the information in these images should be effectively secured [2]. Image encryption algorithms can come in handy in this regard. Image encryption converts the images into a format that conceals the information and protects it from cyber-attacks and unauthorized access [3,4]. An efficient image encryption algorithm should have two most important properties, i.e., confusion and permutation [5,6]. The confusion part of the encryption scheme focuses on changing the values of the pixels and the permutation part of the scheme focuses on mixing the positions of the pixels. A carefully designed encryption scheme consisting of these two properties can effectively secure medicalimages [7,8].

Recently, artificial intelligence has been used in cryptography in many ways. Artificial intelligence-based autoencoders are extensively being used in image encryption applications. One of the important applications of autoencoders is using them as a dimensionality reduction tool [9]. Autoencoders are type of neural network that encode the large-size input images to their low-size equivalent images. By design, these networks learn to compress data (encode) into a lower-dimensional space and then reconstruct it back (decode) to its original form, with as little loss of information as possible. This process of encoding followed by decoding helps to discover and preserve the most important features in the data. Autoencoders are particularly effective because they are trained to minimize the reconstruction error, encouraging the model to capture and prioritize the most salient features of the data. This ability to reduce dimensionality while retaining significant information makes autoencoders valuable tools in areas like image processing, where reducing the size of data can significantly enhance computational efficiency without sacrificing critical content. When designing an encryption algorithm, it is important to ensure that, in addition to being secure, it encrypts large images efficiently and with good encryption speeds [10]. Hence, the motivation of this paper is to design an image encryption scheme that protects medical images with high security while efficiently handling large high-definition (HD) images and providing fast encryption speed.

This paper introduces a novel convolutional autoencoder-based image encryption scheme designed specifically for medical images. The proposed architecture of the convolutional autoencoder converts HD medical images into their low-resolution equivalents but keeps all the important information. These low-resolution equivalents are then encrypted and transmitted resulting in fast encryption and decryption speeds. The proposed encryption scheme consists of four stages of encryption. The first two stages involve permutation and the next two stages involve confusion. The proposed scheme is specifically designed to protect medical images and to facilitate fast encryption, transmission, and decryption of the input images. The procedural flowchart of the proposed scheme mentioning all components is depicted in Fig. 1.

Figure 1: Flowchart of the proposed artificial intelligence-driven encryption scheme

The main contributions of this paper are:

1.    A novel AI-based convolutional autoencoder is proposed. This autoencoder encodes the HD medical images into lower dimensional space to facilitate fast encryption and transmission of medical images over various communication channels.

2.    A novel four-stage medical image encryption is proposed. The first two stages involve two permutation modules that ensure the disruption of the correlation within the medical images. The last two stages involve two modules of confusion which makes the proposed scheme resistant to statistical and known-plaintext attacks.

The rest of the paper is organized as follows. A detailed literature review is presented in Section 2 which summarises the latest work related to this paper and highlights the research gap. Section 3 presents the design of the autoencoder. Section 4 entails the proposed medical image encryption scheme. The results are presented in Section 5, which is followed by a clear and concise conclusion in Section 6.

2  Related Work

The necessity for secure transmission and storage of medical images in telemedicine and related fields has resulted in the development of various cryptographic schemes. These systems aim to safeguard sensitive patient information from unauthorized access and misuse. For instance, a novel encryption system for digital medical images using DNA cryptography and dual hyper-chaotic maps is proposed in [11]. This scheme utilizes DNA encoding for the encryption stage and performs selective pixel encryption. This technique ensures fast encryption/decryption phases and results in efficient protection of medical images. In a similar attempt to protect medical images, the authors in [12] also follow the approach of elective encryption. They have utilized chaotic maps in conjunction with DNA encryption to protect medical images and the results portray secure encryption. Moreover, different chaotic maps have been utilized in [13]. The authors have utilized Chen’s chaotic system and Henon map and used it with Brownian motion. The authors claim that it is a lightweight encryption system and evaluation shows commendable statistical security results. Furthermore, hybrid chaotic maps have also been utilized to protect medical images, for example, the authors in [14] use a two-dimensional Logistic-Sine-Coupling map with the Arnlod’s cap map. Utilization of these two maps together results in a secure encryption scheme with close-to-ideal results. Moreover, medical images have also been encrypted in the frequency domain, like the authors in [15] propose a frequency domain encryption scheme and utilize wavelet transform in conjunction with DNA encryption. They also proposed a key generation module using 3D Lorenz map. The authors performed several security evaluations and the scheme performed very well.

Speaking of the application of autoencoders in image encryption schemes, several encryption schemes have utilized autoencoders, such as the authors in [9] present a convolutional autoencoder-based encryption scheme that utilizes DNA encryption to encrypt images. The autoencoder reconstructs images exceptionally well and the evaluation of the encryption scheme also showcases close to ideal results. Besides in another paper [16], a deep autoencoder has been used to maintain uniform distribution and to ensure randomness created by the encryption scheme. Furthermore, autoencoders have also been utilized in conjunction with chaotic maps in [17]. The logistic map is used for image scrambling and the autoencoder is used for dimensionality reduction. In addition, autoencoders have also been used as image-scrambling adversaries in [18]. The proposed scheme utilizes asymmetric encryption. The autoencoder is a Cycle-Consistent Generative Adversarial Network (CycleGAN) network and results in a secure encryption system. Besides, the autoencoders have also been used in an encryption scheme proposed in [19]. The autoencoder is used for semantic feature extraction, which follows a carefully designed encryption scheme. This scheme also utilizes an attention mechanism which is used to optimise the compression mechanism. Results indicate a high level of security and effective image compression. While most of the papers focus on dimensionality reduction, the architecture of the autoencoders is not lightweight. This paper focuses on proposing a new architecture that is lightweight and offers exact reconstruction of input images.

3  Design of the Proposed AI Autoencoder

In this paper, an autoencoder is proposed for the effective compression of high-resolution medical images before encryption to facilitate fast encryption-decryption stages. The architecture of the proposed autoencoder is given in Fig. 2 and Table 1. The autoencoder has been trained on two public datasets, i.e., the ‘COVID-19 Pakistani Patients X-ray Image Dataset’ [20,21] and the ‘Brain MRI Images for Brain Tumor Detection’ [22], both are publicly available on Kaggle. The training performance is given in the accuracy and loss curves in Fig. 3. The curves show that the autoencoder exhibits almost 99% accuracy. The following subsections entail the modeling of the proposed autoencoder.

Figure 2: Architecture of the proposed AI autoencoder; (a) AI Encoder. (b) AI Decoder

Figure 3: Training performance of the AI autoencoder; (a) Accuracy curves. (b) Loss curves

3.1 Mathematical Modelling of the Autoencoder Architecture

A comprehensive mathematical modeling of the proposed autoencoder including the encoder and decoder is given as follows:

Design of the Encoder

The autoencoder begins with an input layer receiving an RGB image of dimensions 512×512×3, denoted by the tensor X∈R512 ×  512 × 3. This foundational layer facilitates the extraction of features by subsequent layers.

X∈R512 × 512 × 3(1)

The first convolutional layer employs 128 filters, each of size 3×3 and stride 1. This layer applies these filters to generate feature maps, using the Rectified Linear Unit (ReLU) activation function to introduce non-linearity. The mathematical operation for this convolutional layer is captured by:

Z1[i,j,k]=ReLU(∑m=−11∑n=−11∑c=13X[i+m,j+n,c]⋅W1[m,n,c,k]+b1[k])(2)

The parameter count for this layer is computed considering the number of filters, the dimensions of each filter, and the number of input channels:

Parameters=Number of Filters×(Filter Height×Filter Width×Input Channels+1)=128×(3×3×3+1)=3,488(3)

A max pooling layer follows, with a 2×2 kernel and stride of 2, reducing the spatial dimensions to 256×256 and minimizing the potential for overfitting by downsampling feature maps:

Z2[i, j, k]=max0≤m, n<2Z1[2i+m, 2j+n, k](4)

Further, the third convolutional layer continues the feature extraction process. The third layer uses 64 filters with 3×3 kernels and a stride of 1, enhancing the detail of the features:

Z3[i, j, k]=ReLU(∑m=−11∑n=−11∑c=1128Z2[i+m, j+n, c]⋅W3[m, n, c, k]+b3[k])(5)

Including the effects of stride on the output dimensions, this layer helps further reduce dimensionality efficiently, which can be generally calculated as:

Output Dimension=⌊Input Dimension−Filter Size+2×PaddingStride⌋+1(6)

Another max pooling layer reduces dimensions to 128×128, further compressing the data:

Z4[i, j, k]=max0≤m, n<2Z3[2i+m, 2j+n, k](7)

Subsequent layers, including further convolutional stages and dense layers, process and transform the compressed feature maps into a more abstract representation, suitable for the encoding process:

Z5[i, j, k]=ReLU(∑m=−11∑n=−11∑c=164Z4[i+m, j+n, c]⋅W5[m, n, c, k]+b5[k])(8)

Z6[i, j, k]=ReLU(∑m=−11∑n=−11∑c=132Z5[2i+m, 2j+n, c]⋅W6[m, n, c, k]+b6[k])(9)

The encoded feature map is flattened and processed through dense layers, transforming the learned features into a compressed form that captures the essence of the input data:

Z7=vec(Z6)(10)

Z8=ReLU(W8Z7+b8)(11)

Design of the Decoder

Decoder layers, including convolutional transpose operations, reconstruct the original image from the compressed representation:

Z9=ReLU(W9Z8+b9)(12)

Z10=reshape(Z9,(64×64×32))(13)

Z11[i, j, k]=ReLU(∑m=−11∑n=−11Z10[i/2+m, j/2+n, c]⋅W11[m, n, c, k]+b11[k])(14)

Z12[i, j, k]=ReLU(∑m=−11∑n=−11Z11[i/2+m, j/2+n, c]⋅W12[m, n, c, k]+b12[k])(15)

Z13[i, j, k]=Z12[i/2, j/2, k](16)

Finally, the output layer consists of a convolutional transpose layer that uses three filters to reconstruct the RGB channels of the final output image, returning it to its original dimensions and appearance:

Y[i, j, k]=ReLU(∑m=−11∑n=−11Z14[i+m, j+n, c]⋅W15[m, n, c, k]+b15[k])(17)

4  The Proposed Medical Encryption Scheme

The proposed AI-driven encryption scheme comprises two important constituents, i.e., the novel AI-based autoencoder and the proposed medical image encryption scheme. The design of the autoencoder was explained in the previous section. The following subsections entail the design and implementation of the encryption scheme. The proposed encryption scheme is a four-stage encryption scheme. There are two stages of permutation and two stages of confusion. This four-stage encryption scheme ensures effective encryption. The detailed flowchart of the proposed medical image encryption scheme is given in Fig. 4.

Figure 4: Flowchart of the proposed medical image encryption scheme

1.    Hashing the Input: The first step is to read the encoded image and to apply the 256-bit Secure Hash Algorithm (SHA-256) hash to generate a unique hash. This unique hash is used to create three secret keys and a seed matrix. The secret keys control the permutation and the confusion process and the seed matrix is used in the fourth stage of the encryption. SHA-256 generates a 256-bit hash value from any input data. The algorithm processes a block size of 512 bits and outputs a hash of 256 bits. The input message undergoes padding to make its length a multiple of 512 bits. The steps include:

       (a)  Append a ‘1’ bit to the message.

       (b)  Append ‘0’ bits until the message length is 448 modulo 512.

       (c)  Append the original message length as a 64-bit number.

       The SHA-256 function uses several logical functions and bitwise operations:

      •   Ch(x, y, z)=(x∧y)⊕(¬x∧z)

      •   Maj(x, y, z)=(x∧y)⊕(x∧z)⊕(y∧z)

      •   Σ0(x)=ROTR2(x)⊕ROTR13(x)⊕ROTR22(x)

      •   Σ1(x)=ROTR6(x)⊕ROTR11(x)⊕ROTR25(x)

      •   σ0(x)=ROTR7(x)⊕ROTR18(x)⊕SHR3(x)

      •   σ1(x)=ROTR17(x)⊕ROTR19(x)⊕SHR10(x)

       The following steps are followed while generating the hash:

       (a)  Initialize the hash values h0, h1,…,h7.

       (b)  Expand the 512-bit block into a 64-word schedule using the σ functions.

       (c)  For each round, update the working variables and mix them into the intermediate hash values using the Σ and Ch, Maj functions along with round constants.

       (d)  After processing all blocks, concatenate the intermediate hash values to form the final hash.

2.    Initialization of the Chaotic Map: In this step, the logistic chaotic map is initialized by setting its control parameter and initial conditions. The logistic map equation used is:

xn+1=r⋅xn⋅(1−xn);

       This map takes input from the unique hash and generates the three secret keys and the seed matrix.

3.    Encryption Stage 1: Chaotic Column Shuffling: The first secret key derived from the logistic map sequence is used to shuffle the columns of the image. This shuffling is based on a permutation generated by sorting the outputs of several iterations of the map. The following steps are involved in the encryption stage 1:

      •   Selecting an initial value x0, obtained from the hash function:

x0=hash value

      •   Iterating the logistic map for N iterations to reach the chaotic regime:

xi+1=r⋅xi⋅(1−xi)for i=0, 1, 2,…,N−1

      •   Recording the values after discarding initial transients to form sequence S:

S=[xk, xk+1,…,xk+M−1]

    where k is the number of initial values discarded, and M is the number of columns to be shuffled.

      •   Converting the chaotic sequence to column indices for a matrix with m columns:

indexi=⌊xi⋅m⌋for i=k, k+1,…,k+M−1

      •   In this step, for a matrix A of dimensions n×m where n is the number of rows and m is the number of columns, the columns are shuffled as follows:

A′[:,i]=A[:,indexi]for each column i

    This reorders the columns based on the indices generated from the logistic map sequence. Following is the example of the encryption stage 1 on a matrix A with 5 columns (m=5), with initial conditions of the logistic maps as r=3.9, and x0=0.5. Then:

x1=3.9⋅0.5⋅(1−0.5)=0.975x2=3.9⋅0.975⋅(1−0.975)=0.09350625⋮

    The values from the chaotic indices are:

index1=⌊0.975⋅5⌋=4index2=⌊0.09350625⋅5⌋=0⋮

    The columns are shuffled accordingly:

A′[:,0]=A[:,4]A′[:,1]=A[:,0]⋮

    This process repeats for all columns of the image.

4.  Encryption Stage 2: Row Permutation: In this stage, a permutation key from the logistic map, i.e., the secret key 2 is used to permute the rows of the column-permuted image in a similar way done in stage 1.

Q[:,j]=P[τ(j),:]

    where τ is a permutation of the rows based on the chaotic sequence.

5.  Encryption Stage 3: Dynamic S-Box Substitution: In this stage, a dynamic S-box substitution is applied, and the secret key 3, which is also generated from the chaotic map, is utilized to select any one of the 3 S-boxes. The values from the selected s-box replace pixels in the row and column-shifted image. This substitution process ensures confusion the image.

R[i, j]=Sk[P[i, j]]

    where Sk is selected from a set of predefined S-boxes based on the key. The substitution process is performed as follows:

   •   Producing a chaotic sequence to select S-boxes:

xi+1=r⋅xi⋅(1−xi)

   •   Maping each xi to one of three S-boxes S1, S2, S3.

   •   Converting each pixel p to 8-bit binary, then splitting into Most Significant Bits (MSB) and Least Significant Bits (LSB), converting back to decimal, and calculating the S-box index:

MSBdec=decimal value of MSB,LSBdec=decimal value of LSB

   S-box index=MSBdec×LSBdec

   •   Substituting by using the selected S-box:

p′=Sindexi[S-box index]

6.  Encryption Stage 4: Seed Matrix Addition: The final encryption layer involves bitwise Exclusive OR (XOR) with a seed matrix derived from the logistic map to enhance security:

S[i, j]=R[i, j]⊕M[i, j]

    where M is the seed matrix, adding another layer of confusion and diffusion.

5  Results and Analysis

The proposed encryption scheme has been evaluated for various statistical security parameters to validate its security characteristics. Histogram analysis, correlation analysis, entropy analysis, correlation analysis, and other statistical parameters, such as energy, contrast, and homogeneity have been evaluated. The visual encryption results of four stages are given in Fig. 5.

Figure 5: Encryption results of four-stage encryption scheme. (a) to (e) Plaintext images. (f) to (j) Stage 1. (k) to (o) Stage 2. (p) to (t) Stage 3. (u) to (y) Stage 4

5.1 Histogram Analysis

The histogram of an image represents the frequency of occurrence of intensity levels within the image. This information is crucial for attackers as it can be used to extract concealed information from an encrypted image. Therefore, an ideal secure encryption scheme should result in a flat or uniformly distributed histogram, meaning that all intensity levels occur an equal number of times. As shown in the histogram analysis in Fig. 6, the histograms of the ciphertext images are uniformly distributed, depicting that all pixel intensities from 0 to 255 occur an equal number of times. Hence, the original information regarding the frequency of occurrence cannot be retrieved. These histograms demonstrate the effectiveness of the proposed encryption scheme.

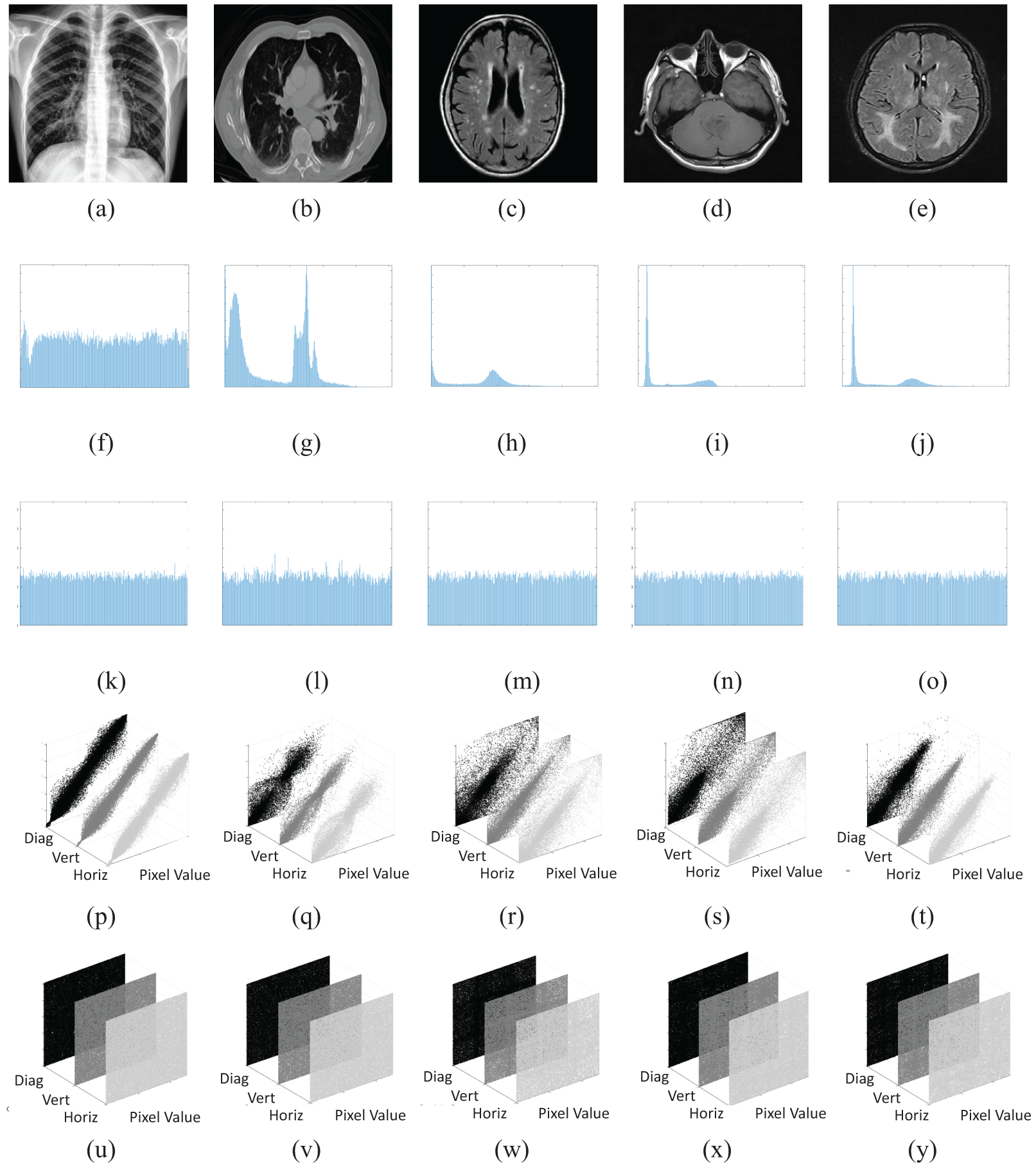
Figure 6: Histogram and correlation analysis. (a) to (e) Plaintext images. (f) to (j) Histogram of plaintext images. (k) to (o) Histogram of ciphertext images. (p) to (t) Correlation of plaintext images. (u) to (y) Correlation analysis of ciphertext images

5.2 Correlation Analysis

Correlation within an image indicates the patterns and shapes present in the image. Areas with defined patterns and shapes exhibit high correlation, whereas areas where pixels are not correlated with each other display low correlation values. An ideally encrypted image should correlate close to zero, indicating that no pixel is related to its neighbor. The correlation plots of an ideally encrypted image should be widely scattered, demonstrating the disrupted correlation throughout the image. As illustrated in Fig. 6, the correlation plots are widely scattered depicting that neighboring pixels in the cipher image are not correlated, validating the effectiveness of the proposed encryption scheme. Moreover, it can be seen in Table 2 that the correlation within the image is ideally close to zero. The table presents the correlation of plaintext and ciphertext images individually by calculating the Gray Level Co-occurrence Matrix (GLCM) and the correlation between the plaintext and ciphertext images as well.

5.3 Entropy Analysis

Entropy, or information entropy, measures the amount of randomness in an image. The greater the randomness, the more secure the encrypted image is. For a grayscale image, the ideally encrypted image should have an entropy of 8, which indicates that there is maximum randomness in the image, making it difficult to retrieve any information. As shown in Table 3, the entropy of the ciphertext images is ideally close to 8.

5.4 Contrast Analysis

Contrast in an image indicates how rapidly the intensity changes between two pixels or within a certain area. In regions where there are distinct shapes, the contrast is usually low because the pixels are related to each other to form a shape. Conversely, areas where colors change abruptly exhibit high contrast. An ideally encrypted image should have high contrast, indicating that no two pixels are related and the intensity of every neighboring pixel is completely different from each other. As shown in Table 4, the contrast of the ciphertext images is very high, validating the effectiveness of the proposed encryption scheme.

5.5 Energy Analysis

The energy of an image refers to the uniformity and repetition of pixels within it. High energy indicates the presence of patterns and shapes, while low energy values suggest that the pixels are unrelated and there are no distinct shapes in an image. Therefore, ideally, the energy of a well-encrypted image should be low. This can be validated through Table 5, which shows that the energy values of the encrypted images are quite low.

5.6 Homogeneity Analysis

Homogeneity measures the consistency and smoothness of patterns across an image. High homogeneity indicates smooth areas with distinct shapes, whereas low homogeneity corresponds to areas with no consistent relationship among pixels. An ideal encrypted image should have low homogeneity, indicating that the pixel values are less correlated. This can be validated by the results in Table 6, which show that all homogeneity values are very low, depicting secure encryption.

6  Conclusion

This paper introduced an innovative AI-driven encryption scheme specifically tailored for securing medical images. The process starts by utilizing an AI-based autoencoder that compresses high-resolution images into lower-resolution versions while preserving essential diagnostic information. These compressed images then undergo a sophisticated four-stage encryption process, involving permutation and confusion techniques, to enhance security. The permutation stages disrupt the image structure, effectively safeguarding against statistical attacks, while the confusion stages obscure the pixel values, making unauthorized decryption challenging. The effectiveness of this encryption strategy was rigorously validated through extensive security and performance evaluations. Results from these tests demonstrated that the scheme effectively maintained the confidentiality and integrity of the medical images during storage and transmission. This robust encryption approach thus ensures that sensitive medical data is protected against various cyber threats, making it highly suitable for real-world application in healthcare settings where data security is paramount. Moreover, a possible limitation of the scheme could be the scalability issue. As the volume of data increases, especially in large healthcare systems generating vast amounts of medical images, the training process could take more time.

Acknowledgement: None.

Funding Statement: The author received no specific funding for this research.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Ahmed ST, Hammood DA, Chisab RF, Al-Naji A, Chahl J. Medical image encryption: a comprehensive review. Computers. 2023;12(8):160. doi: 10.3390/computers12080160. [Google Scholar] [CrossRef]

2. Lai Q, Hu G, Erkan U, Toktas A. High-efficiency medical image encryption method based on 2D logistic-Gaussian hyperchaotic map. Appl Math Comput. 2023;442:127738. [Google Scholar]

3. Zhou NR, Hu LL, Huang ZW, Wang MM, Luo GS. Novel multiple color images encryption and decryption scheme based on a bit-level extension algorithm. Expert Syst Appl. 2024;238:122052. doi: 10.1016/j.eswa.2023.122052. [Google Scholar] [CrossRef]

4. Abbasi SF, Ahmad J, Khan JS, Khan MA, Sheikh SA. Visual meaningful encryption scheme using intertwinning logistic map. In: Intelligent Computing: proceedings of the 2018 Computing Conference, 2019; Cham: Springer; vol. 2, p. 764–73. [Google Scholar]

5. Khan MS, Ahmad J, Ali H, Pitropakis N, Al-Dubai A, Ghaleb B, et al. SRSS: a new chaos-based single-round single S-box image encryption scheme for highly auto-correlated data. In: 2023 International Conference on Engineering and Emerging Technologies (ICEET), 2023; Istanbul, Turkey; p. 1–6. [Google Scholar]

6. Khan MS, Ahmad J, Al-Dubai A, Ghaleb B, Pitropakis N, Buchanan WJ. RNA-TransCrypt: Image encryption using chaotic RNA encoding, novel transformative substitution, and tailored cryptographic operations. 2024. doi:10.48550/arXiv.2401.04707. [Google Scholar] [CrossRef]

7. Khan MS, Ahmad J, Al-Dubai A, Jaroucheh Z, Pitropakis N, Buchanan WJ, et al. PermutEx: feature-extraction-based permutation—a new diffusion scheme for image encryption algorithms. In: 2023 IEEE 28th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), 2023; Edinburgh, UK; p. 188–93. [Google Scholar]

8. Ali H, Khan MS, Driss M, Ahmad J, Buchanan WJ, Pitropakis N. CellSecure: securing image data in industrial internet-of-things via cellular automata and chaos-based encryption. In: 2023 IEEE 98th Vehicular Technology Conference (VTC2023-Fall), 2023; Hong Kong, China: IEEE; p. 1–6. [Google Scholar]

9. Ahmed F, Rehman MU, Ahmad J, Khan MS, Boulila W, Srivastava G, et al. A DNA based colour image encryption scheme using a convolutional autoencoder. ACM T Multim Comput. 2023;19(3s):1–21. doi:10.1145/3570165. [Google Scholar] [CrossRef]

10. Alawida M, Teh JS, Alshoura W. A new image encryption algorithm based on DNA state machine for UAV data encryption. Drones. 2023;7(1):38. doi:10.3390/drones7010038. [Google Scholar] [CrossRef]

11. Akkasaligar PT, Biradar S. Selective medical image encryption using DNA cryptography. Inform Secur J: A Glob Perspect. 2020;29(2):91–101. doi:10.1080/19393555.2020.1718248. [Google Scholar] [CrossRef]

12. Kamal ST, Hosny KM, Elgindy TM, Darwish MM, Fouda MM. A new image encryption algorithm for grey and color medical images. IEEE Access. 2021;9:37855–65. doi:10.1109/ACCESS.2021.3063237. [Google Scholar] [CrossRef]

13. Masood F, Driss M, Boulila W, Ahmad J, Rehman SU, Jan SU, et al. A lightweight chaos-based medical image encryption scheme using random shuffling and XOR operations. Wirel Pers Commun. 2022;127(2):1405–32. doi:10.1007/s11277-021-08584-z. [Google Scholar] [CrossRef]

14. Jain K, Aji A, Krishnan P. Medical image encryption scheme using multiple chaotic maps. Pattern Recognit Lett. 2021;152:356–64. doi:10.1016/j.patrec.2021.10.033. [Google Scholar] [CrossRef]

15. Banu SA, Amirtharajan R. A robust medical image encryption in dual domain: chaos-DNA-IWT combined approach. Med Biol Eng Comput. 2020;58:1445–58. doi:10.1007/s11517-020-02178-w. [Google Scholar] [PubMed] [CrossRef]

16. Sang Y, Sang J, Alam MS. Image encryption based on logistic chaotic systems and deep autoencoder. Pattern Recognit Lett. 2022;153:59–66. doi:10.1016/j.patrec.2021.11.025. [Google Scholar] [CrossRef]

17. Ameen Suhail K, Sankar S. Image compression and encryption combining autoencoder and chaotic logistic map. Iran J Sci Technol, Trans A: Sci. 2020;44(4):1091–100. doi:10.1007/s40995-020-00905-4. [Google Scholar] [CrossRef]

18. Bao Z, Xue R, Jin Y. Image scrambling adversarial autoencoder based on the asymmetric encryption. Multimed Tools Appl. 2021;80(18):28265–301. doi:10.1007/s11042-021-11043-3. [Google Scholar] [CrossRef]

19. Wang B, Lo KT. Autoencoder-based joint image compression and encryption. J Inf Secur Appl. 2024;80:103680. doi:10.1016/j.jisa.2023.103680. [Google Scholar] [CrossRef]

20. Khan MS. COVID-19 Pakistani patients X-ray image dataset. 2021. Available from: https://www.kaggle.com/datasets/muhammadshahbazkhan/covid19-pakistani-patients-xray-image-dataset. [Accessed 2024]. [Google Scholar]

21. Umair M, Khan MS, Ahmed F, Baothman F, Alqahtani F, Alian M, et al. Detection of COVID-19 using transfer learning and grad-CAM visualization on indigenously collected X-ray dataset. Sensors. 2021;21(17):5813. doi:10.3390/s21175813. [Google Scholar] [PubMed] [CrossRef]

22. Chakrabarty N. Brain MRI images for brain tumor detection. 2019. Available from: https://www.kaggle.com/datasets/navoneel/brain-mri-images-for-brain-tumor-detection. [Accessed 2024]. [Google Scholar]