 Open Access
Open Access
ARTICLE
An Improved Artificial Rabbits Optimization Algorithm with Chaotic Local Search and Opposition-Based Learning for Engineering Problems and Its Applications in Breast Cancer Problem
1 Department of Software Engineering, Firat University, Elazig, 23119, Turkey
2 Department of Computer Engineering, Firat University, Elazig, 23119, Turkey
3 Department of Computer Engineering, Urmia Branch, Islamic Azad University, Urmia, 44867-57159, Iran
* Corresponding Author: Farhad Soleimanian Gharehchopogh. Email:
Computer Modeling in Engineering & Sciences 2024, 141(2), 1067-1110. https://doi.org/10.32604/cmes.2024.054334
Received 25 May 2024; Accepted 22 August 2024; Issue published 27 September 2024
Abstract
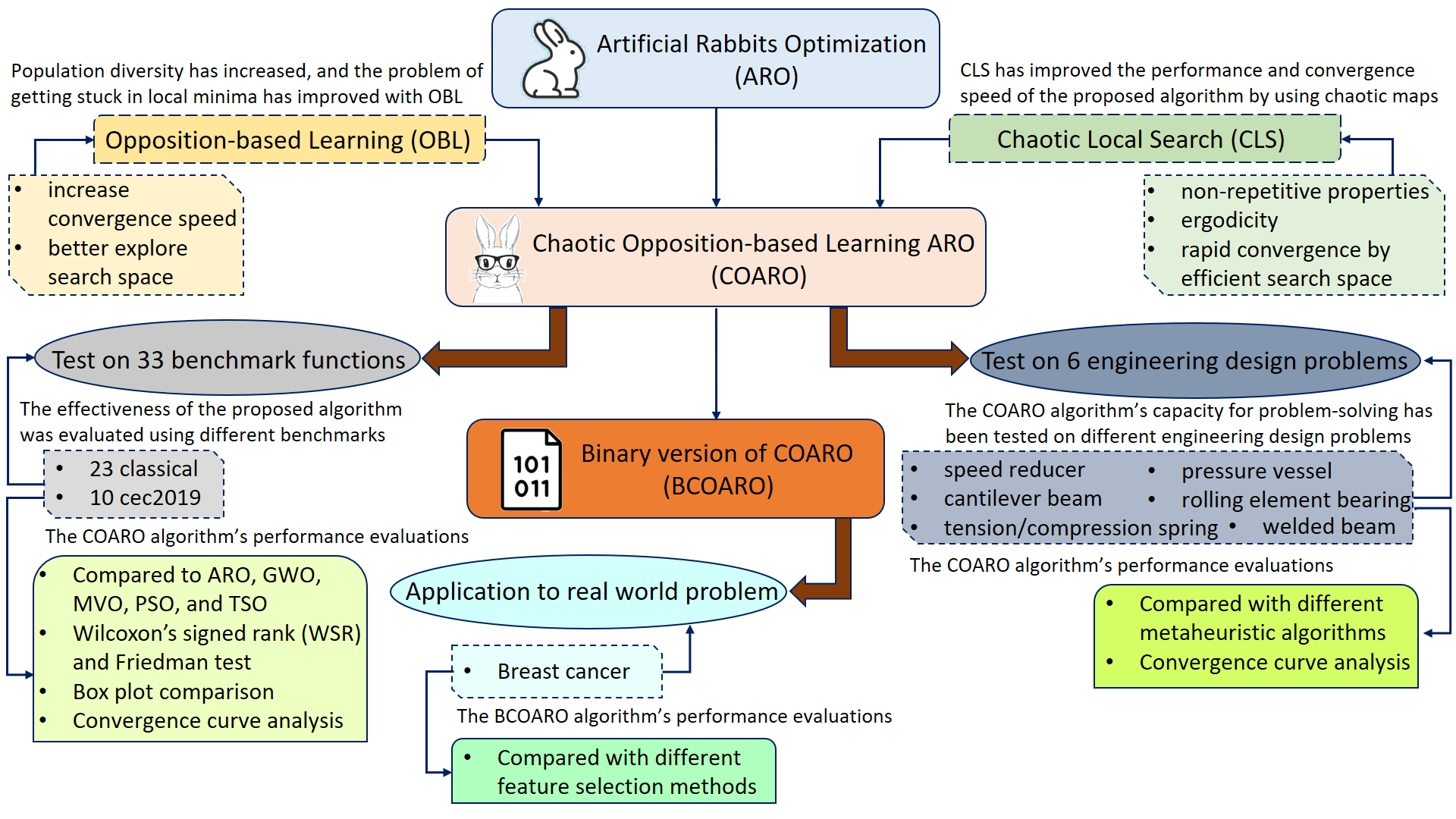
Artificial rabbits optimization (ARO) is a recently proposed biology-based optimization algorithm inspired by the detour foraging and random hiding behavior of rabbits in nature. However, for solving optimization problems, the ARO algorithm shows slow convergence speed and can fall into local minima. To overcome these drawbacks, this paper proposes chaotic opposition-based learning ARO (COARO), an improved version of the ARO algorithm that incorporates opposition-based learning (OBL) and chaotic local search (CLS) techniques. By adding OBL to ARO, the convergence speed of the algorithm increases and it explores the search space better. Chaotic maps in CLS provide rapid convergence by scanning the search space efficiently, since their ergodicity and non-repetitive properties. The proposed COARO algorithm has been tested using thirty-three distinct benchmark functions. The outcomes have been compared with the most recent optimization algorithms. Additionally, the COARO algorithm’s problem-solving capabilities have been evaluated using six different engineering design problems and compared with various other algorithms. This study also introduces a binary variant of the continuous COARO algorithm, named BCOARO. The performance of BCOARO was evaluated on the breast cancer dataset. The effectiveness of BCOARO has been compared with different feature selection algorithms. The proposed BCOARO outperforms alternative algorithms, according to the findings obtained for real applications in terms of accuracy performance, and fitness value. Extensive experiments show that the COARO and BCOARO algorithms achieve promising results compared to other metaheuristic algorithms.Graphic Abstract
Keywords
In today’s world, real-world optimization problems have become more complex. Their difficulty has increased due to developments in various application fields such as engineering, medicine, computer science, and manufacturing design. These problems include complexities such as multi-objective, non-linear, multi-dimensional, multi-disciplinary, and non-convex regions [1]. Practical and dependable optimization algorithms can be developed to solve these problems. Classical optimization methods based on gradient information, including calculating first and second derivatives, cannot provide satisfactory results reasonably for solving such issues [2]. These methods require a large number of complex mathematical calculations. In these methods, issues with convergence speed and getting stuck at the local optimum point may be encountered. Complex implementation, mathematical calculations, difficult convergence for discrete optimization problems, etc., are some disadvantages of classical optimization methods [3].
In recent years, researchers have taken great interest in metaheuristic approaches to eliminate the shortcomings of classical optimization methods and solve complex optimization problems with high efficiency and accuracy. Metaheuristic algorithms aim to find the optimal or approximate solution to complex optimization problems under limited conditions by using search methods inspired by different natural methods. These search strategies help find nearly optimal solutions by effectively searching the search space. Metaheuristic algorithms are not problem-specific and are flexible to solve various optimization problems [4]. They are stochastic algorithms that start the search process with random solutions. They have low computational complexity. Additionally, these algorithms can escape local optima due to randomness-based search strategies. In recent years, metaheuristic algorithms have been successfully used to solve various optimization problems in many research areas, such as image segmentation [5], robotic and path planning [6], medical application [7], sensor networks [8], water resources management [9], thin-walled structures [10], Internet of Things (IoT) [11], bioinformatics [12], and engineering problems [13]. Metaheuristic algorithms can be examined in different categories: physics, social, music, swarm, chemistry, biology, sports, mathematics, and hybrid-based.
Artificial Rabbits Optimization (ARO) is a new metaheuristic optimization method presented in 2022 [14]. ARO mimics rabbits’ natural foraging and hiding behaviors. The problem of falling into local optima and premature convergence are the main drawbacks of ARO. These limitations restrict the exploration of the search space and prevent finding the global optimum. The random initialization of the rabbits, the initial population in ARO, and the imbalance between exploration and exploitation also affect the algorithm’s performance. Chaotic opposition-based learning ARO (COARO), an improved version of ARO, has been proposed to overcome these limitations and improve the effectiveness of ARO. The COARO algorithm is proposed by combining the strengths of chaotic local search (CLS) and opposition-based learning (OBL) and incorporating ten different chaotic maps into the optimization process. CLS ensures that solution quality increases by directing the local search around the global best solution. Adding OBL to the algorithm improves the initial population and enhances the problem of getting stuck in local minima.
The effectiveness of the proposed algorithm was evaluated using different benchmarks. The COARO algorithm’s performance is compared to that of ARO, Grey Wolf Optimization (GWO), Multi-Verse Optimizer (MVO), Particle Swarm Optimization (PSO), and Transient Search Optimization (TSO). Performance comparison of the COARO algorithm was supported by Wilcoxon’s signed rank (WSR) and Friedman tests. Box plot comparison has been employed to check the proposed COARO algorithm’s consistency. The COARO algorithm’s capacity for problem-solving has been tested on six different engineering design problems, including pressure vessel, rolling element bearing design, cantilever beam, speed reducer, welded beam, and tension/compression spring. Simulation results indicate that the COARO algorithm outperforms ARO in most cases. It has also been observed that COARO achieves promising results compared to recent optimization algorithms. Furthermore, the paper proposes the binary version of the COARO algorithm (BCOARO) to solve the issue of feature selection in classification tasks. The V-shaped transfer function is integrated into the algorithm to convert the continuous COARO algorithm into a binary version. The BCOARO algorithm’s performance is compared using different feature selection methods.
The significant contributions of the paper are:
• This paper introduces COARO, which is proposed to eliminate the shortcomings of ARO and improve its performance.
• COARO algorithm is proposed by adding CLS with OBL to the original ARO and incorporating ten different chaotic maps into the optimization process. CLS has improved the performance and convergence speed of the proposed algorithm by using chaotic maps. Additionally, with the use of OBL, population diversity has increased, and the problem of getting stuck in local minima has improved.
• The effectiveness of the proposed algorithm was evaluated using different benchmarks. The COARO algorithm’s performance is compared to ARO, GWO, MVO, PSO, and TSO. Performance comparison of the COARO algorithm was supported by Wilcoxon’s signed rank (WSR) and Friedman tests. Box plot comparison has been employed to check the proposed COARO algorithm’s consistency.
• The COARO algorithm’s capacity for problem-solving has been tested on six engineering design problems, including pressure vessel, rolling element bearing design, cantilever beam, speed reducer, welded beam, and tension/compression spring.
• This paper also proposes a binary COARO algorithm (BCOARO) version. It has been tested on the breast cancer dataset, and the results have been compared with different feature selection methods.
The structure of the paper is as follows: The ARO algorithm’s mathematical model is described in Section 2. In Section 3, the proposed COARO algorithm is explained. CLS, OBL, and an overview of COARO and its complexity are detailed. Section 4 evaluates the proposed COARO algorithm using unimodal, multimodal, fixed-dimension multimodal, and CEC2019 functions. This section also compares the COARO algorithm’s performance to various metaheuristic algorithms in the literature. In the same section, performance assessments of WSR and Friedman statistical tests are made. The results of COARO algorithms on six different engineering problems are examined in this section. Section 5 concludes with a discussion of future research and conclusions.
2 The Mathematical Model of ARO Algorithm
ARO algorithm was developed with a mathematical model inspired by the survival strategies of rabbits in nature [15]. Rabbits’ survival strategies are based on exploration and exploitation. The first behavior, the exploration strategy, is described as detour foraging [16]. Rabbits aim to minimize the chance of being caught by digging many burrows to protect themselves from predators and mislead them. In this respect, the second behavior, the exploitation strategy, is described as random hiding. Depending on their energy state, rabbits must adaptively switch between circuitous foraging and random hiding strategies. In this respect, the third behavior, the switch from exploration to exploitation strategy, is described as energy shrink [17].
2.1 Detour Foraging (Exploration)
Rabbits prefer far places rather than near nests when searching for food. The location of each search individual tends to update towards the other search individual picked at random in the swarm. This behavior is a clear indication of the detour foraging behavior of the ARO [18]. The following is the mathematical model of rabbits’ detour foraging:
here, i, j = 1, … , n and j ≠ i. k = 1, … , d and l = 1, … , ⌈r3 ⋅ d ⌉. The ith rabbit’s potential location at a time (t+1) is
2.2 Random Hiding (Exploitation)
Rabbits dig tunnels around their caves to protect themselves from predators. According to the ARO algorithm, a rabbit always digs d tunnels around it in each dimension of the search space, and it always picks one of the caves at random to hide in to lessen the likelihood of being attacked [18]. The following is defined ofjth nest of the ith rabbit:
here, i = 1, … , n, j = 1, … , d, and k = 1, … , d. According to Eq. (7), a rabbit creates burrows in its immediate neighborhood in all directions. H defines the hiding parameter and iteratively decreases linearly from 1 to 1/T with a random perturbation [19]. The random selection of one of the rabbit’s burrows for shelter is rejected to avoid being caught by predators [14]. The following is described as the mathematical model for this random hiding strategy:
here, i = 1, … , n and k = 1, … , d defines a randomly chosen burrow to hide from its d burrows. r4 and r5 define two random numbers in (0, 1). Using Eq. (11), the ith search individual updates its location toward one of the caves from its d burrows that were randomly chosen. Following the successful completion of either detour foraging or random hiding, the ith rabbit’s position is updated in Eq. (14):
When the position of ith rabbit is checked according to Eq. (14), when the candidate position is better than the current position, the rabbit will leave its current position and move to the candidate positions determined by Eqs. (1) and (11).
2.3 Energy Decline (from Exploration to Exploitation)
Modeling the transition from the exploration process associated with detour foraging to the exploitation stage associated with random hiding includes an energy component. The energy factor designed in ARO is given in Eq. (15).
here, r represents a random number in (0, 1). A(t), the energy factor, tends to decrease towards zero as the number of iterations increases. The ARO pseudo-code is provided in Algorithm 1.

3 The Proposed COARO Algorithm
In this section, the proposed COARO algorithm is presented, which combines CLS and OBL techniques to improve the performance of the ARO algorithm and overcome its difficulties. The section includes general information about CLS and OBL techniques, the motivation for integrating them into ARO, and the general structure of the COARO algorithm.
3.1 Chaotic Local Search (CLS)
The term “chaos” describes the highly unexpected behavior of a complex system [20]. Mathematically, chaos is deterministic randomness found in a nonlinear, dynamic, and non-converging [21]. Due to this definition, it can be assumed that the source of randomness is chaotic systems. An optimization algorithm’s search strategy is often implemented within the search space based on random values. Chaos maps use a function to relate or match the chaos behavior in the optimization method based on a parameter. This way, optimization algorithms based on chaotic maps can scan the search space more dynamically and generally. Chaotic maps, which are used as an alternative to random number generators in the search space, often obtain better results than them. Although chaos has an unexpected behavior structure, it also has harmony within. Local optima can be avoided when randomness is adjusted by utilizing chaotic maps in optimization algorithms. A chaotic local search-based search strategy is introduced to enhance ARO’s ability to obtain optimal global solutions. In this study, the chaotic maps given in Table 1 are used.
3.2 Opposition-Based Learning (OBL)
OBL proposed by Tizoosh is used to improve the search capability of algorithms and increase the convergence speed [22]. Classical metaheuristic algorithms start the search process with a randomly generated population containing solutions to the problem to be tested. In this case, the algorithm’s convergence rate may be reduced and the calculation time may increase. To overcome this problem, the OBL strategy considering inverse solutions is introduced. OBL calculates an inverse solution
3.3 The Overview of Proposed COARO
As with all metaheuristic algorithms, ARO suffers from inefficient search, premature convergence, and local optima problems. To overcome these problems, the COARO algorithm was proposed by adding CLS and OBL techniques to the ARO algorithm. CLS is integrated into the ARO algorithm with the advantages of nonlinear dynamics and advanced exploration. In this way, ARO’s performance and convergence speed has increased with the proposed COARO algorithm. In addition, COARO’s convergence speed and performance has been increased by OBL’s ability to increase diversity and bring it closer to the global optimal solution.
The algorithm’s performance is not stable since a randomly generated initial population is used in the ARO algorithm. The initial population can be generated using chaotic maps, considering its ergodicity and unpredictability characteristics. Therefore, in the COARO algorithm, the OBL and CLS strategies are combined to create a more reliable initial population when initializing the rabbit population. Eq. (17) refers to generating rabbit population X with chaotic maps.
The chij value is the chaotic map value calculated using the equations in Table 1.

Local optimum traps, inefficient search, and early convergence are some of the issues that optimization algorithms may encounter. Chaotic maps are employed to increase the success of global optimal searching, accelerate the search, and avoid being mired in the local optimum. As mentioned in the ARO algorithm, predators frequently pursue and attack rabbits. As a result, for rabbits to survive, they need to locate a secure hiding area. The rabbits’ random selection of burrow
In the Eq. (18), CM refers to the value produced by the chaotic maps in Table 1. Furthermore, CLS and OBL approaches are also used to optimize the positions of the rabbits in this stage of COARO. If the rabbit’s position remains the same or changes slightly, the algorithm will fall into the local optimum. The CLS in Eq. (17) was used to eliminate this issue. As a result of the algorithm finding a better location, the chaotic local search is terminated and OBL is applied. The COARO pseudo-code is provided in Algorithm 2.

3.4 Computational Complexity of COARO
In this section, the complexity of the proposed COARO algorithm is examined. The complexity of the COARO adheres to initializing the search agents and evaluating the fitness function. The search agents are updated based on the value of the fitness function, chaotic local search, and opposition-based learning strategies. The initialization stage of the search agent has an O(n*d) complexity, where n is the population number and d is the number of dimensions. The complexity cost for evaluating the fitness functions of all search agents is O(n*T); here, T represents the max iteration numbers. The complexity cost of updating the search agents based on the fitness function value is O(n*T*d). The complexity cost of CLS and OBL strategies is O(n*T). Consequently, the overall complexity cost of COARO is calculated as O(n*T*d).
The experimental test results and evaluations that were utilized to gauge how well the suggested COARO algorithm performed are included in this section. Six different engineering design problems and 33 benchmark functions—including unimodal, multimodal, fixed-dimension multimodal, and CEC2019 functions—are used to assess it. The performance of the COARO algorithm is evaluated by comparing the results obtained with COARO algorithms for 23 classical and 10 CEC2019 benchmark functions with ARO and the well-known GWO, MVO, PSO, and TSO algorithms. Additionally, the evaluation of performance is supported by WSR and Friedman tests. The experimental results obtained in this paper were carried out in the MATLAB R2021b environment, and the test results were taken on a machine with Core i7 4.7 GHz CPU, 16 GB memory, and GeForce GTX4060 GPU.
4.1 The Performance Comparison for Classical and CEC2019 Benchmark Functions
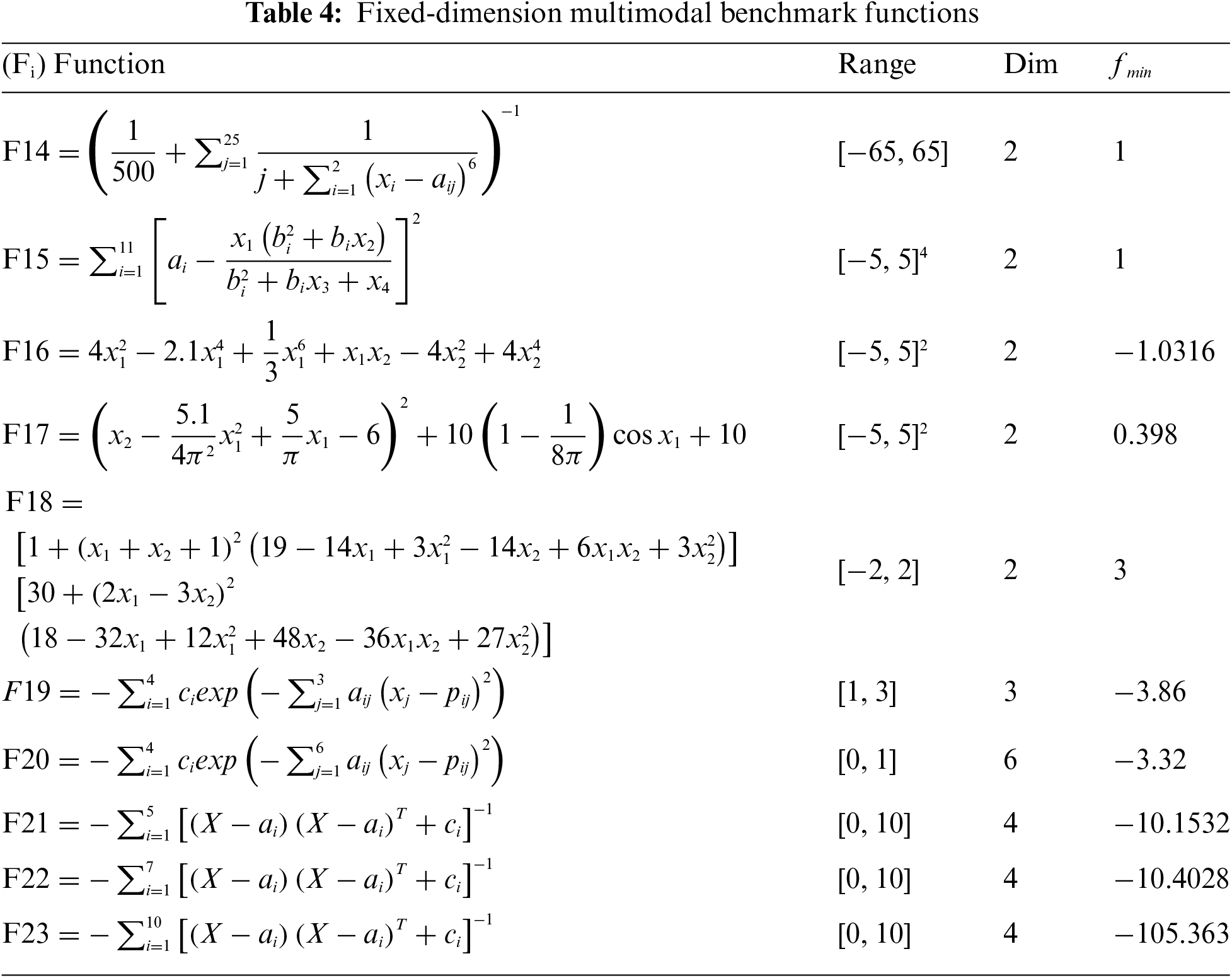
This section uses 33 benchmark functions to assess the efficacy of the proposed COARO. F1–F7 are unimodal functions used to measure the local exploitation capacity of the algorithm. F8–F13 functions are used to evaluate the algorithm’s exploration ability. F14–F23 functions assess the algorithm’s ability to explore fixed-dimension optimization problems. Mathematical expressions for these functions are shown in Tables 2–4.


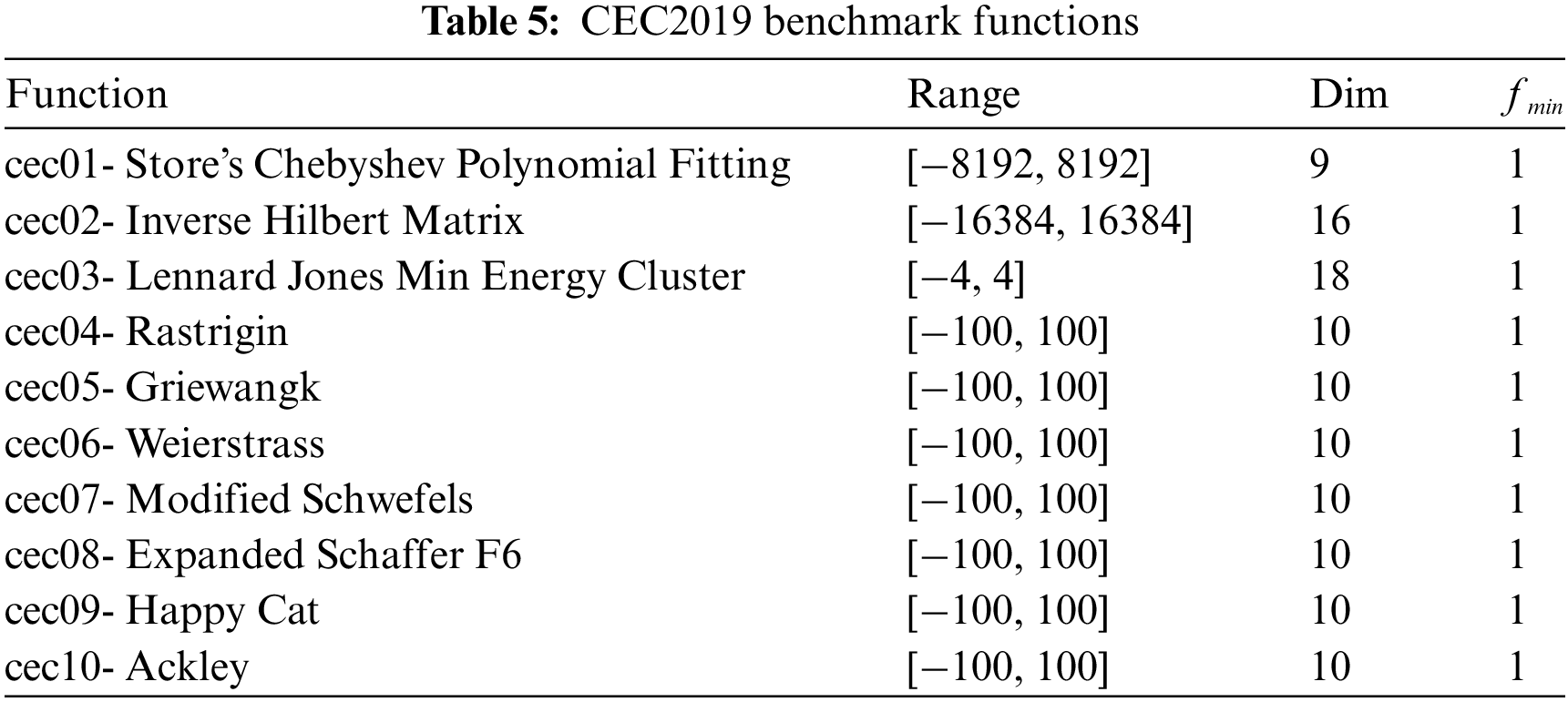
In this study, CEC2019 benchmark functions were also used to evaluate the performance of the COARO algorithm. These functions are minimization problems. cec01–cec03 are uncomplicated problems with different dimensions and ranges. cec04–cec10 are rotated and shifted and have the same dimension and range. Mathematical expressions, dimensions, ranges, and minimum values of function for CEC2019 functions are indicated in Table 5.
Before performing the experimental tests, the running parameters of the metaheuristic algorithms were adjusted. For a fair evaluation, the max iteration number was chosen as 1000 and the number of population was 50. Metaheuristic algorithms were executed 30 times in all experiments. Specific parameter values of GWO, MVO, PSO, and TSO algorithms were derived based on parameter values widely utilized in the literature and these values are included in Table 6.

The best, mean, standard deviation (SD), and Friedman mean rank (MR) values obtained for the classical and CEC2019 benchmark functions with the COARO and ARO algorithms are given in Tables 7 and 8, respectively.
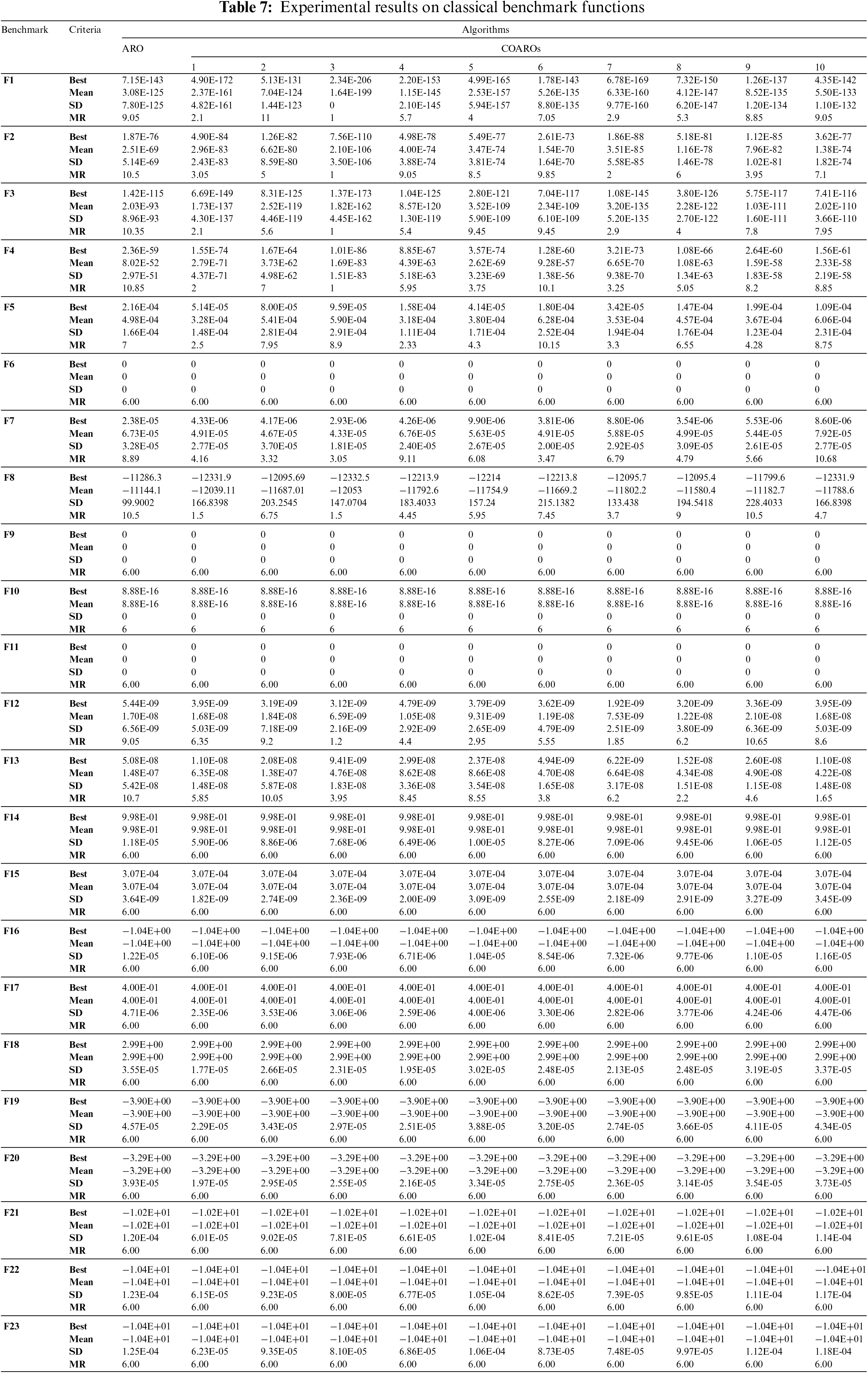
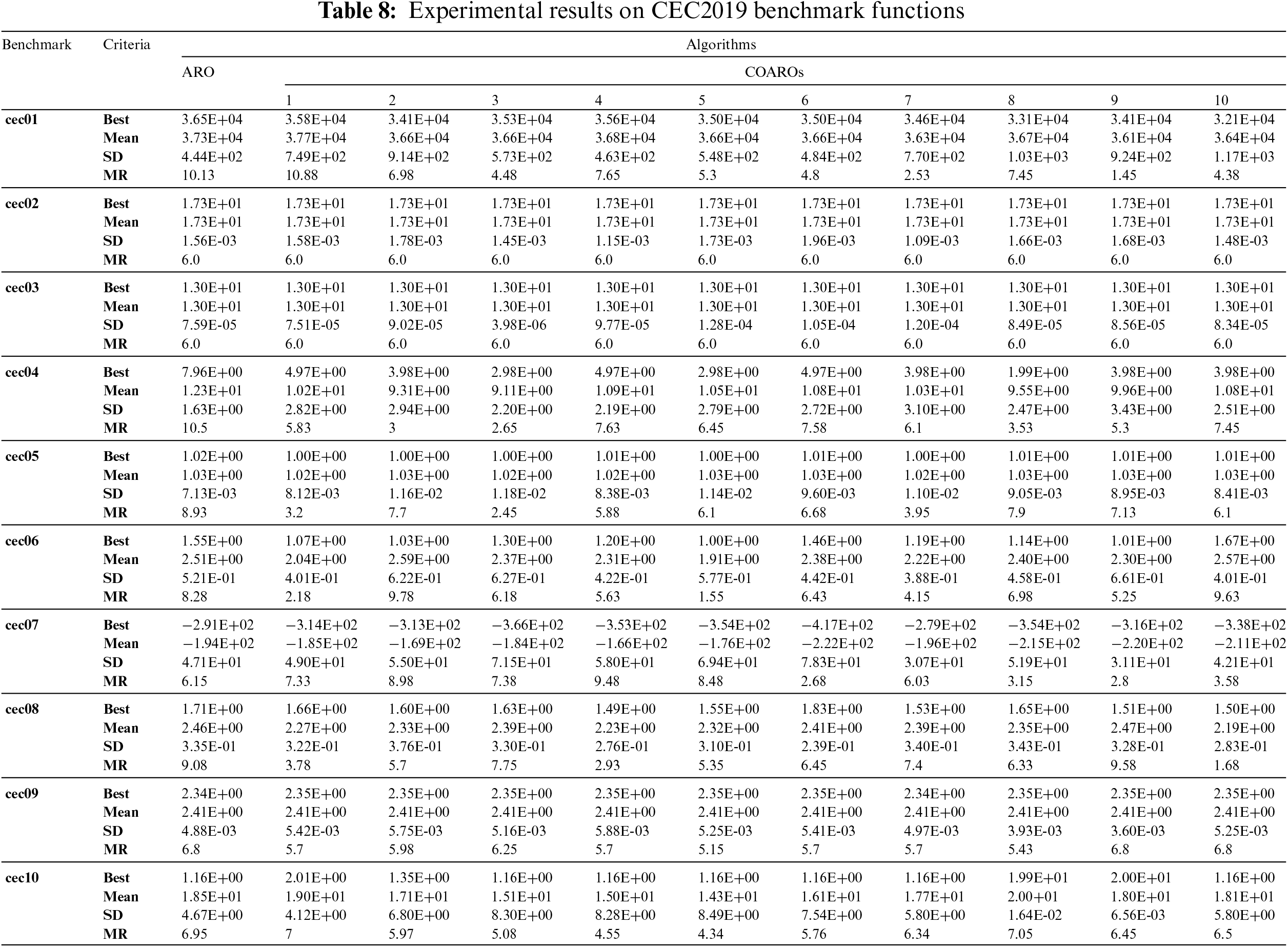
Table 7 analysis reveals that for unimodal functions, the proposed COARO method performs better than ARO. The best results have been achieved with COARO3 for F1–F4 and F7, and COARO4 for F5, according to MR values. It is observed that for the F6 function, the suggested COARO algorithm and ARO yield the same value. In multimodal benchmark functions, COARO3 for F8 and F12 functions and COARO10 for F13 function showed the best performance. The proposed COARO algorithm and ARO achieve similar performance for F9–F11. It is observed that for fixed-dimension multimodal benchmark functions, the proposed COARO algorithms with ten chaotic maps perform similarly to the ARO algorithm.
Table 8 shows that the proposed COARO algorithm and ARO achieve similar results for cec02 and cec03. Additionally, it is observed that COARO9 for cec01, COARO3 for cec04 and cec05, COARO5 for cec06, cec09 and cec10, COARO6 for cec07 and COARO10 for cec08 achieved the best results.
Based on the above analyses, combining CLS and OBL techniques and adding 10 chaotic maps to the optimization process, providing efficiency in determining global solutions, contributed to the COARO algorithm achieving promising results compared to the ARO algorithm in the classical and CEC2019 benchmark functions. Additionally, the results include validation of enhanced exploration advantage, increased diversity, and the ability to find better global resolution.
By integrating CLS into the COARO algorithm, dynamic behaviors are added to the movement rules, allowing rabbits to better explore the search space. With CLS, it is also possible to reduce the possibility of getting stuck in local optima and increase the convergence speed by maintaining a balance between exploration and exploitation. The addition of OBL to COARO provides the ability to explore opposing directions based on existing solutions. OBL encourages rabbits to explore opposite directions and discover potentially different but feasible solutions, rather than simply advancing towards optimal solutions. Exploring opposite directions has allowed COARO to discover solutions that ARO might have overlooked. Thus, the robustness of COARO is increased by providing alternative search areas. These gains are supported by the effective experimental results obtained in Tables 7 and 8.
The average Friedman MR values for the classic and CEC2019 benchmark functions are shown in Table 9. According to Table 9, the best performance for classical benchmark functions was achieved with the COARO3 algorithm. According to the same table, COARO1 achieved the second-best performance by following the COARO3 algorithm. The best performance for CEC2019 benchmark functions was achieved with the COARO3 and COARO7 algorithms. These algorithms are followed by the COARO5 algorithm with a close value.

Fast convergence of metaheuristic algorithms to the optimal solution is crucial to its effectiveness. Figs. 1 and 2 show the convergence graphs of the some classic and CEC2019 benchmark functions for COARO and ARO, respectively. Convergence curves show that the behavior of the proposed COARO algorithm and ARO varies throughout iterations for given functions.
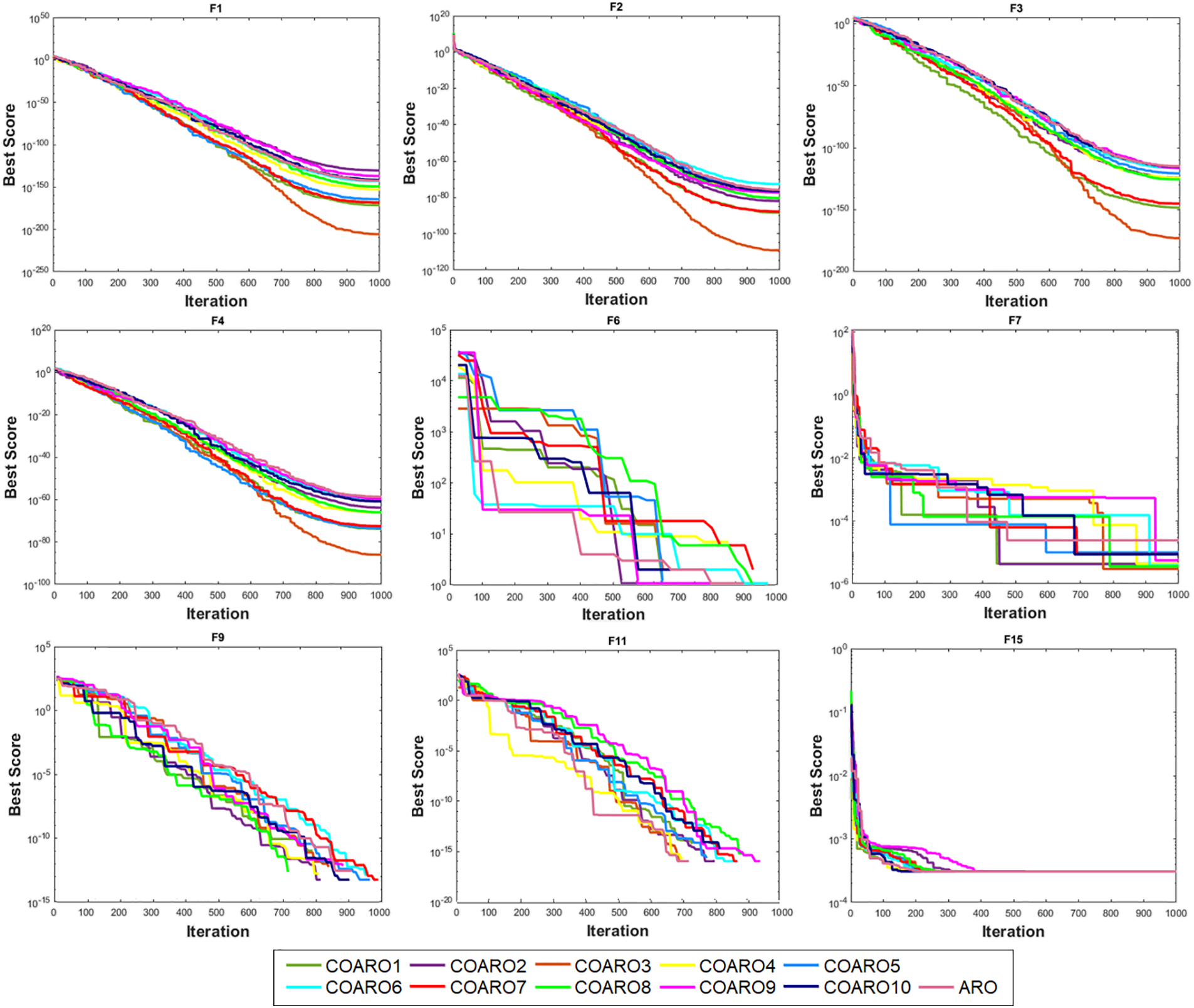
Figure 1: Convergence curve of some classical benchmark functions for COAROs and ARO
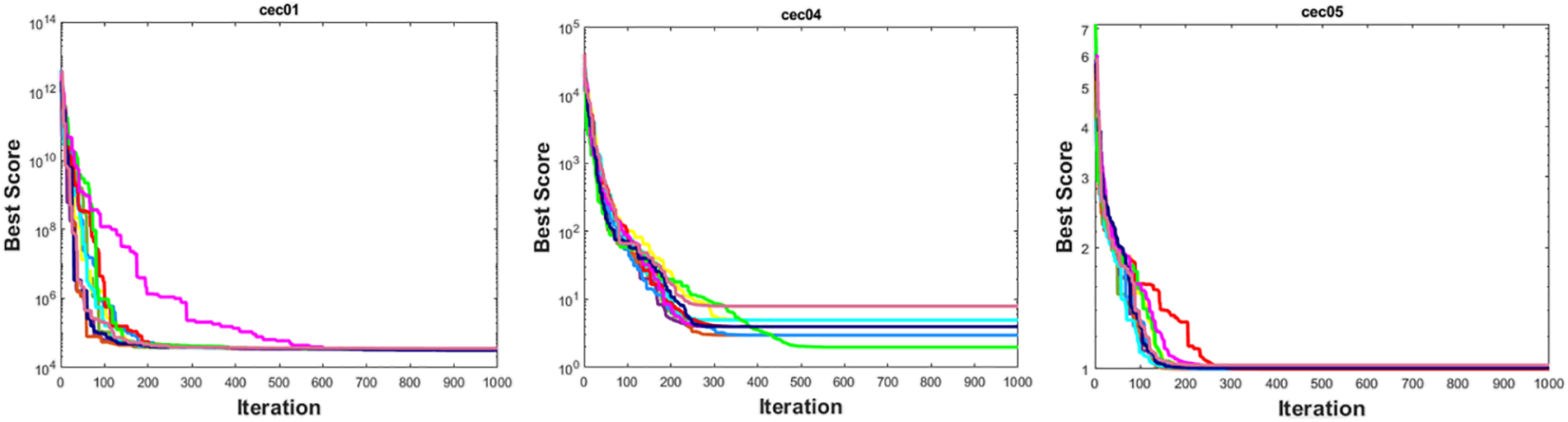
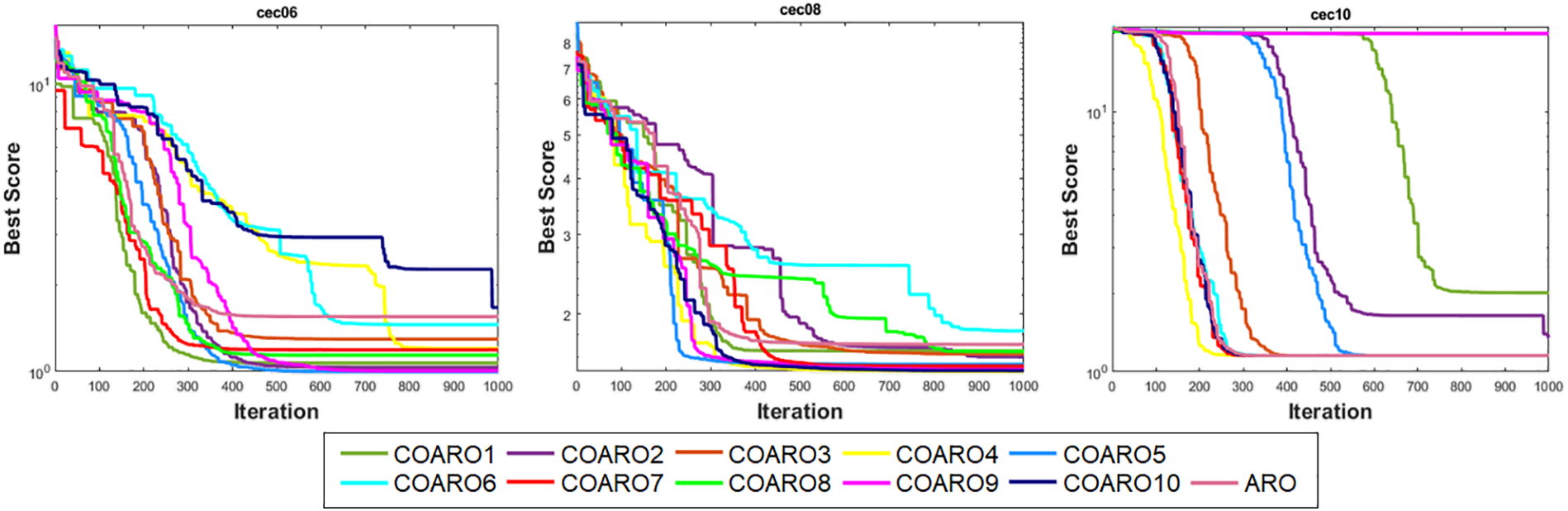
Figure 2: Convergence curve of some CEC2019 benchmark functions for COAROs and ARO
In addition to ARO, four cutting-edge metaheuristic algorithms: GWO, MVO, PSO, and TSO are employed to assess the performance of the proposed COARO algorithm. Statistical results such as best, mean and SD values obtained for the classic and CEC2019 benchmark functions are given in Tables 10 and 11. Examining the mean values in Table 10, it can be said that in 22 of the 23 classical benchmark functions except for F8, the COARO performs better than the other metaheuristic algorithms. Likewise, according to Table 11, the proposed COARO algorithm achieved superior performances than other algorithms for CEC2019 benchmark functions, except for the cec09 function. Figs. 3 and 4 show the convergence graphs of the some classical and CEC2019 benchmark functions for COARO and competitive algorithms. When Figs. 3 and 4 are examined, it has been noticed that the COARO algorithm’s convergence speed is faster than the ARO, GWO, MVO, PSO, and TSO algorithms.
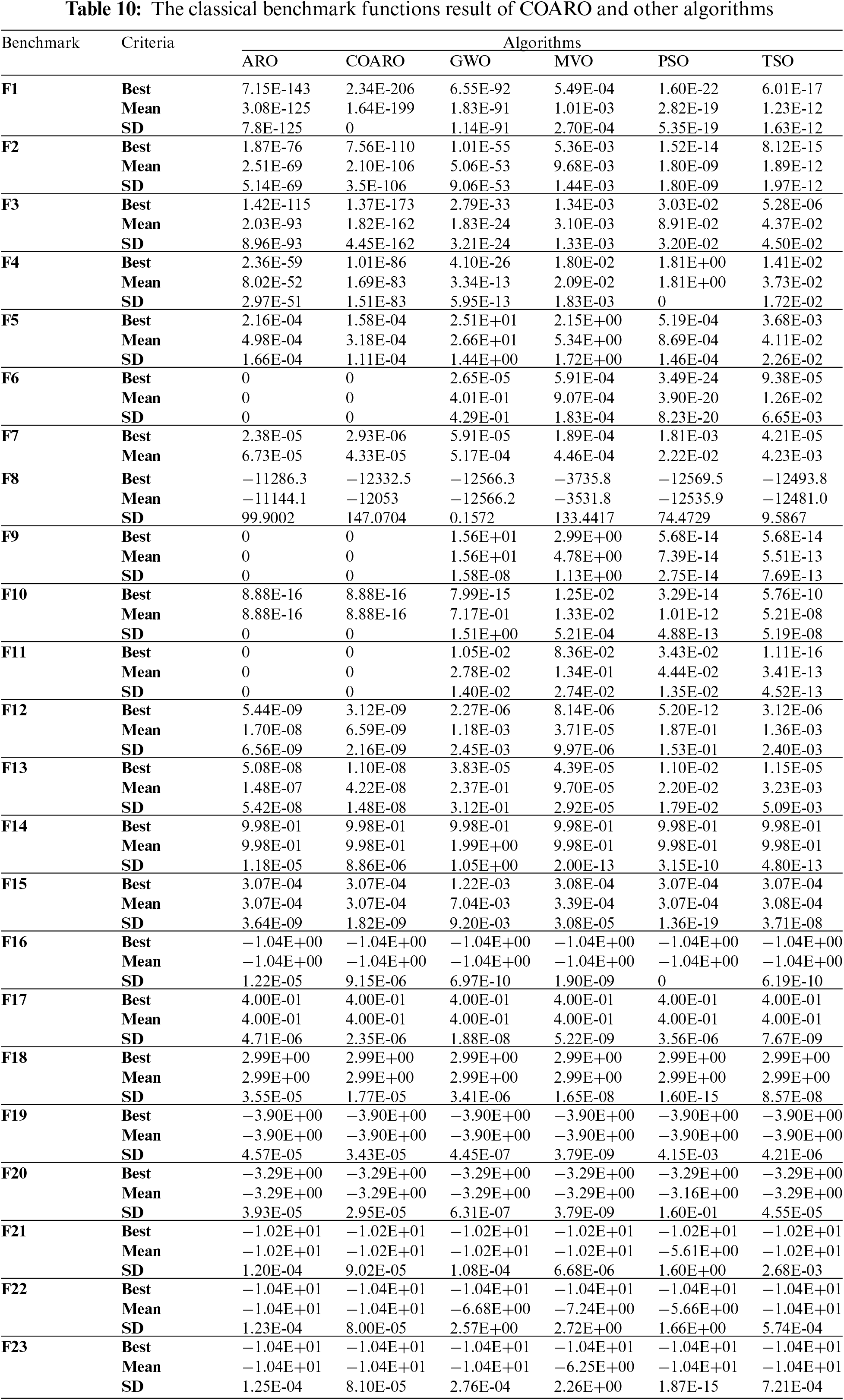
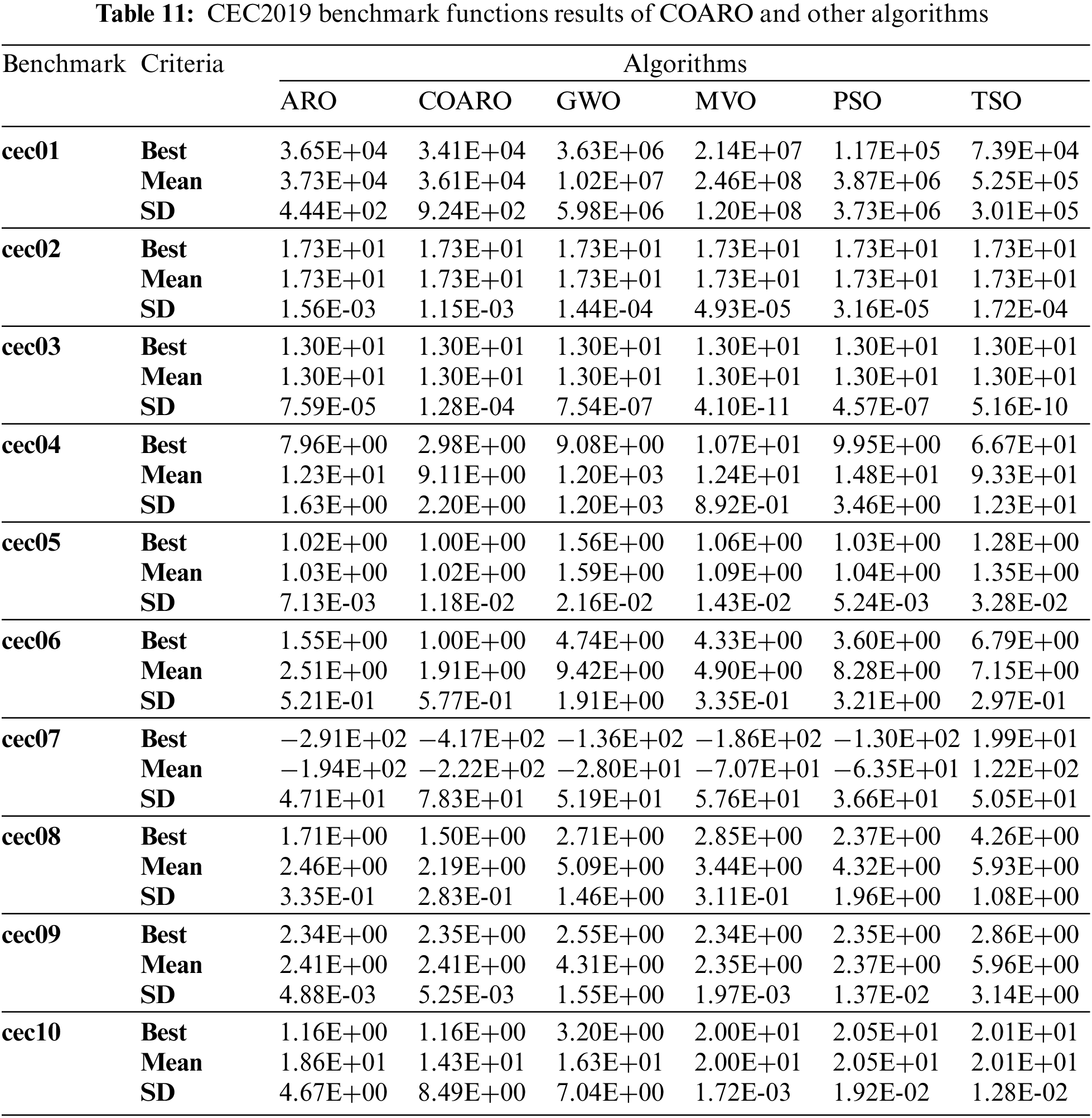
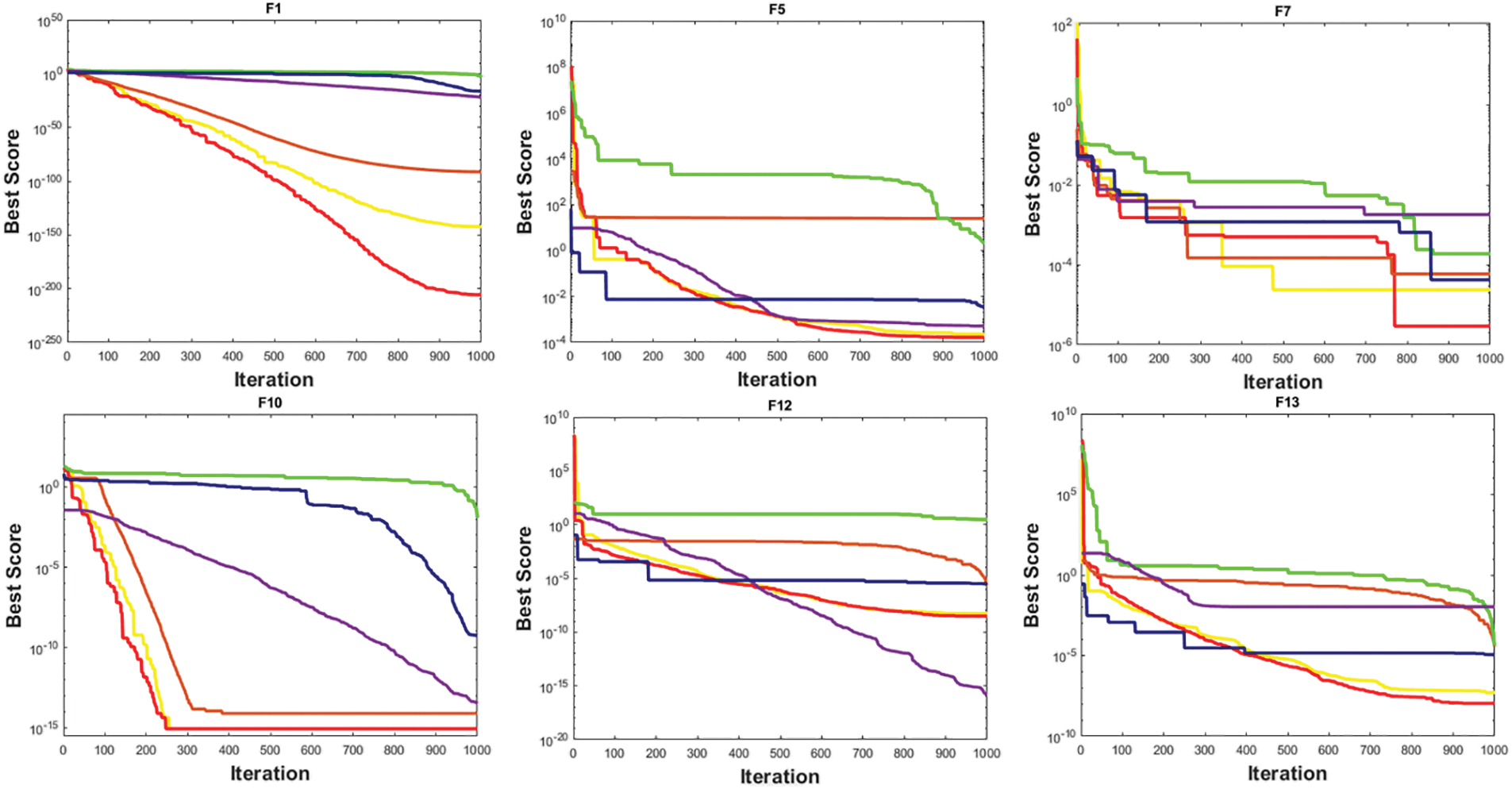
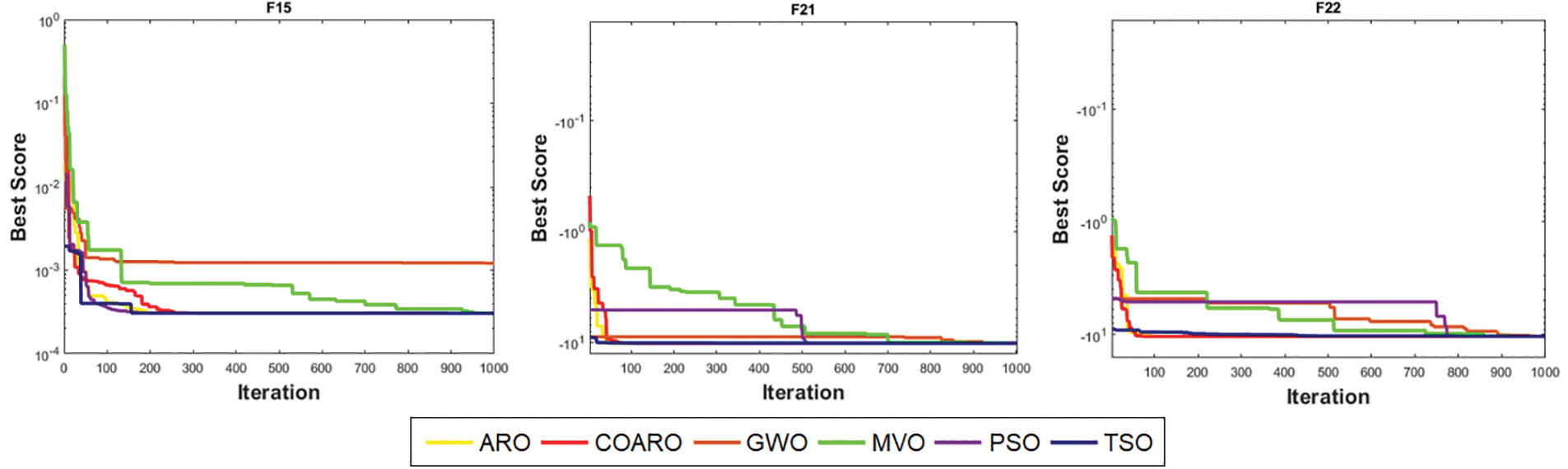
Figure 3: Convergence curve of some classical benchmark functions for all algorithms

Figure 4: Convergence curve of some CEC2019 benchmark functions for all algorithms
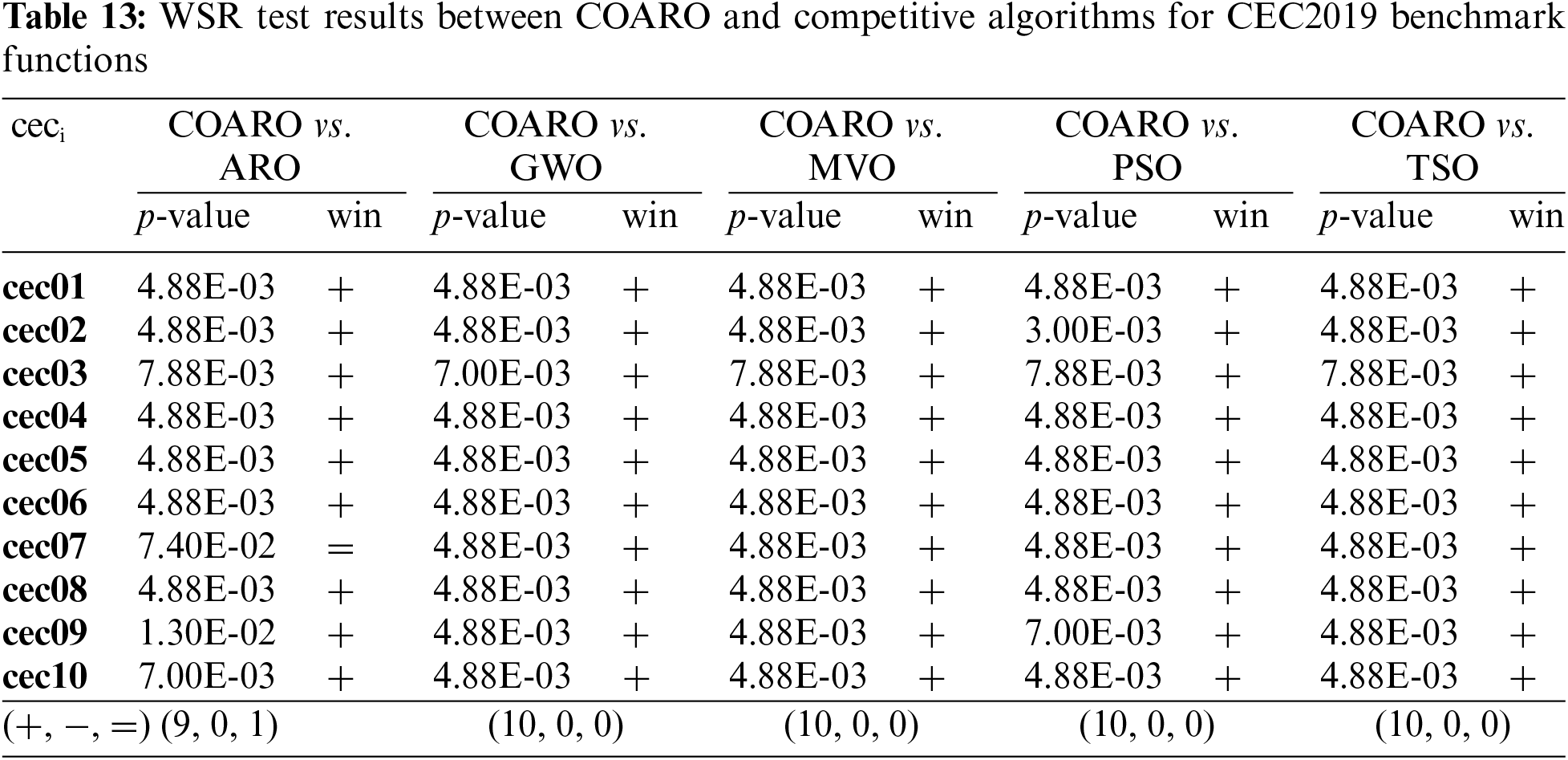
The proposed COARO algorithm has achieved promising results for the classical and CEC2019 benchmark functions. However, whether there is a notable distinction between the COARO algorithm and ARO, GWO, MVO, PSO, and TSO should be tested. Therefore, the WSR statistical test has been used to differentiate between COARO and competitive algorithms. To verify the effectiveness of the COARO algorithm, the WSR test was applied after 30 runs at a 95% confidence level. In the evaluations, the maximum number of iterations was chosen as 1000. There is a discernible difference between the compared algorithms if the p-value determined by the comparisons is less than 0.05. Otherwise, there aren’t any notable distinctions between the two metaheuristic algorithms. Tables 12 and 13 provide the outcomes of the WSR test for the standard and CEC2019 benchmark functions comparing COARO and competitor algorithms. In these tables, “+” indicates the superiority of the proposed COARO algorithm, “–” demonstrates the proposed COARO algorithm is worse than the competitive metaheuristic algorithm, and “=” means that COARO and the compared algorithm obtained the same values.
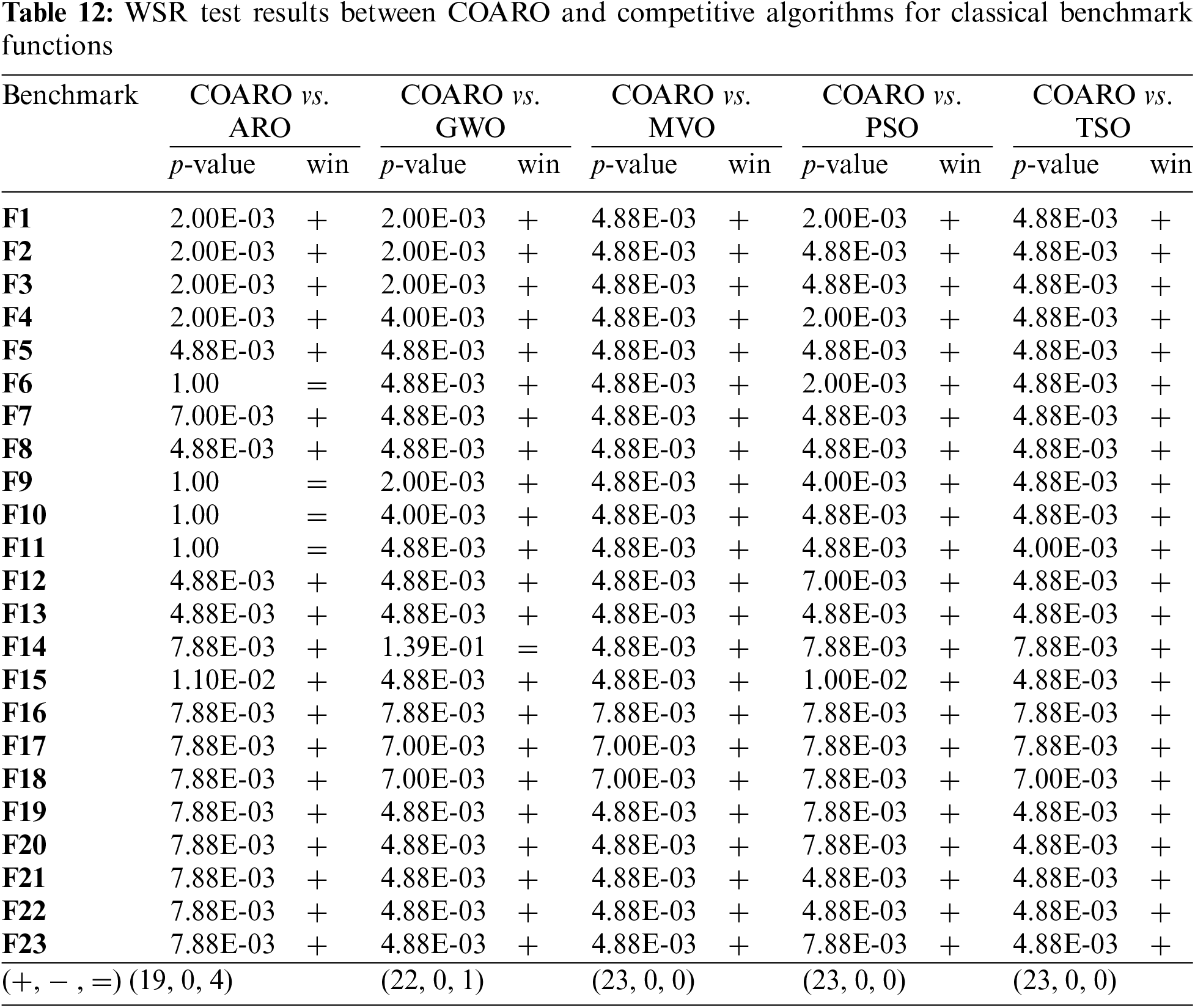
Except for the F9–F11 benchmark functions, the proposed COARO algorithm beat the ARO algorithm, according to the WSR statistical test results in Table 12. The p-values obtained for the F9-F11 indicate that the difference between COARO and ARO is insignificant. Moreover, the results of the COARO algorithm are significantly better than the GWO algorithm, except for the F14 function. The results of the COARO algorithm are better than the remaining three metaheuristic algorithms (MVO, PSO, and TSO) for all classical benchmark functions.
Except for the cec07 function, Table 13 shows that the proposed COARO algorithm performs better than the ARO algorithm. The p-values obtained for COARO and the other four competitive algorithms show that COARO performs better than the different algorithms.
Figs. 5 and 6 show the boxplots of the proposed COARO, ARO, GWO, MVO, PSO, and TSO algorithms for the classical and CEC2019 functions, respectively. The x-axis represents the metaheuristic algorithms being compared. Boxplots have been used to evaluate the distribution of results from the COARO, ARO, GWO, MVO, PSO, and TSO algorithms.
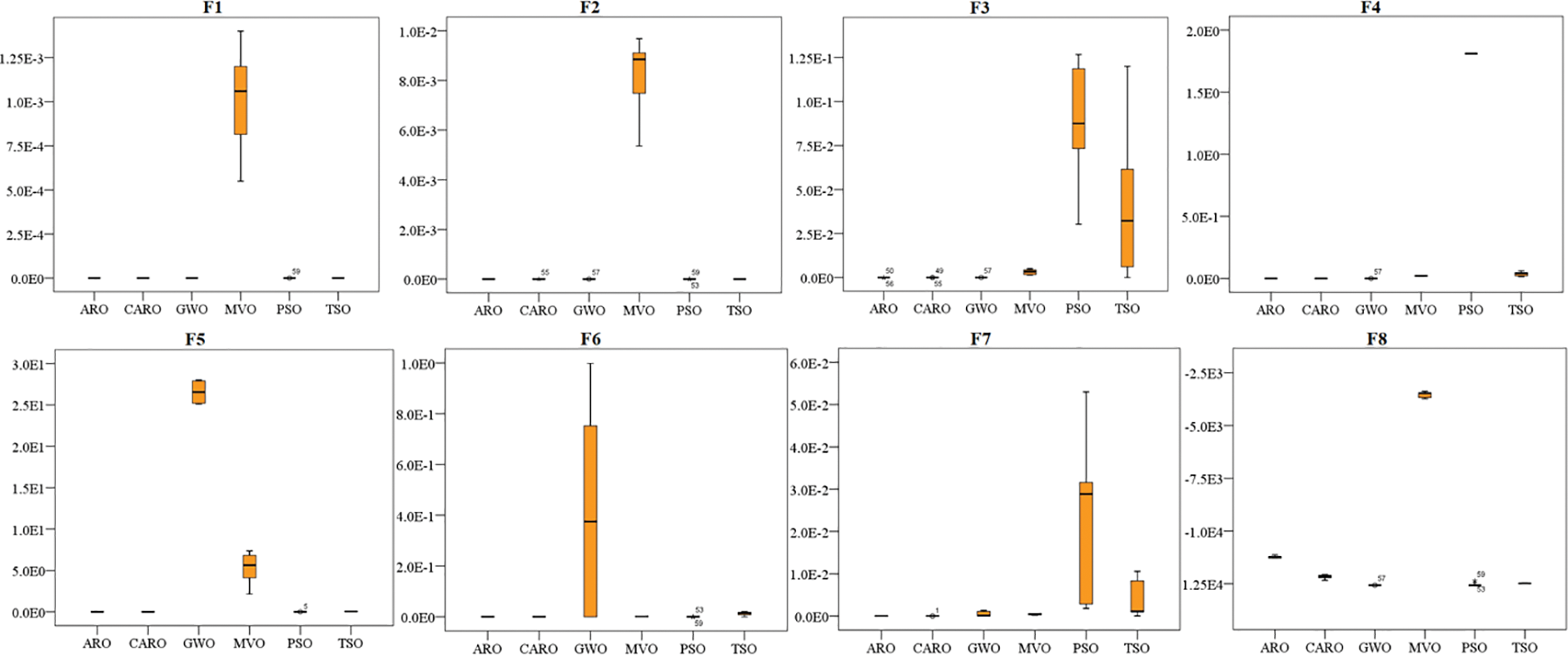
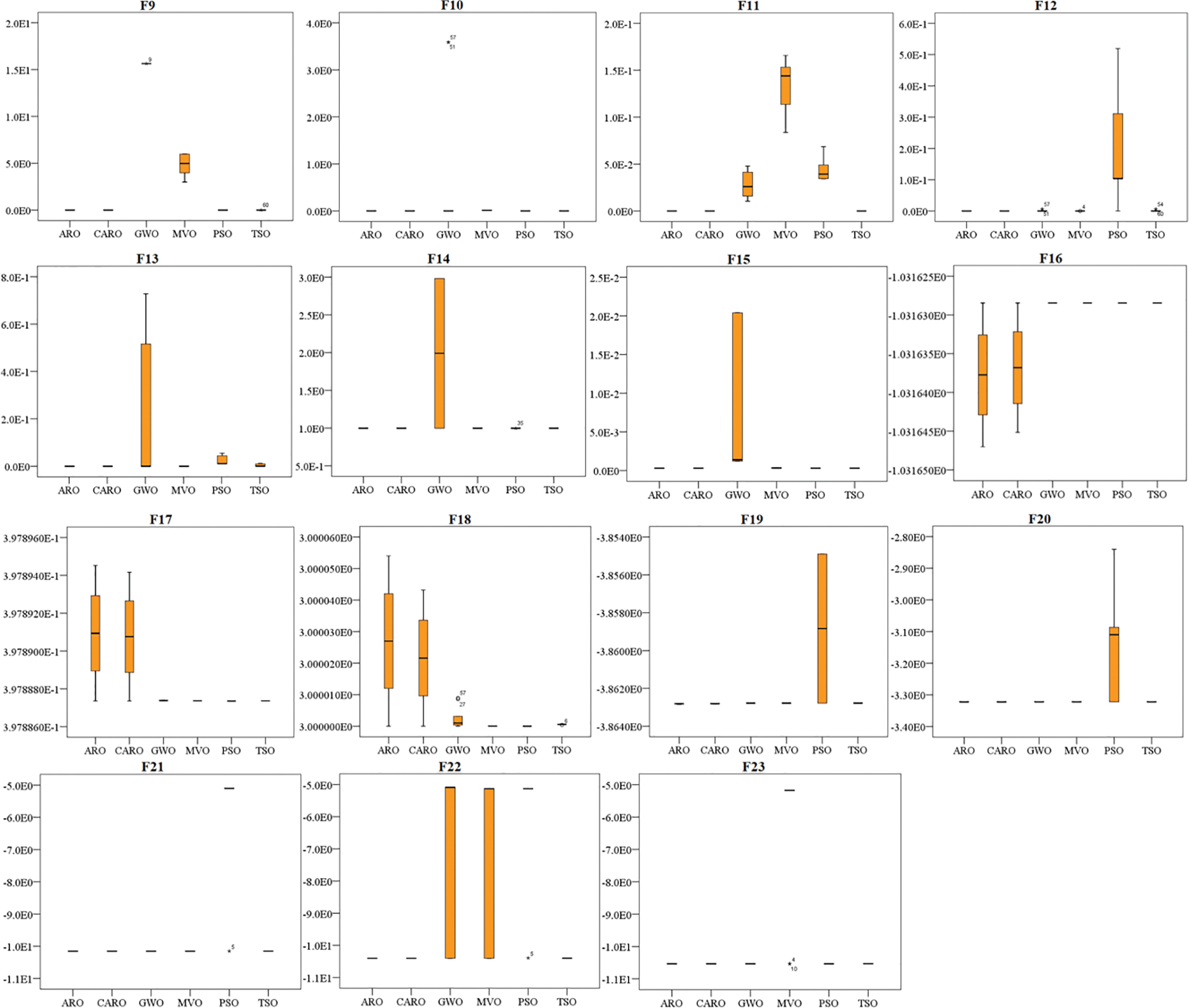
Figure 5: Boxplot of classical benchmark function (y-axis indicates values of fitness function)
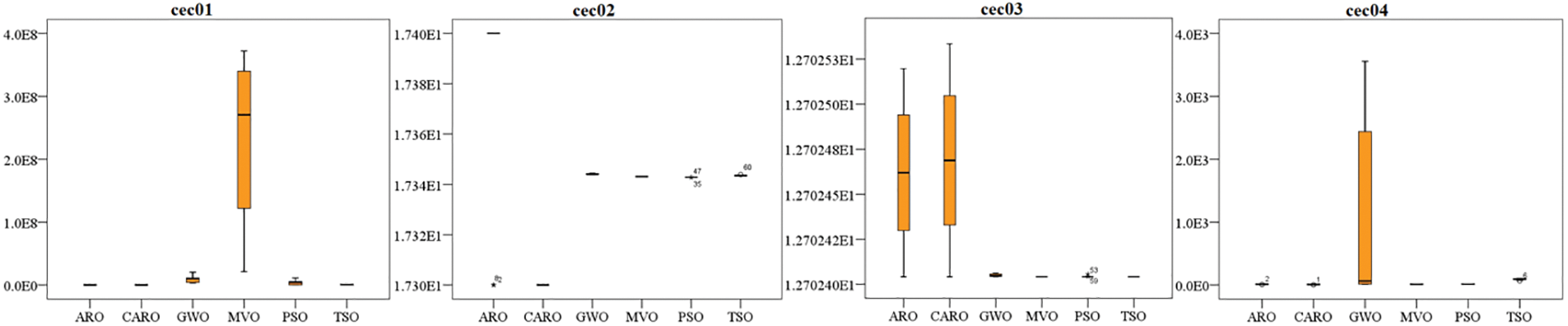
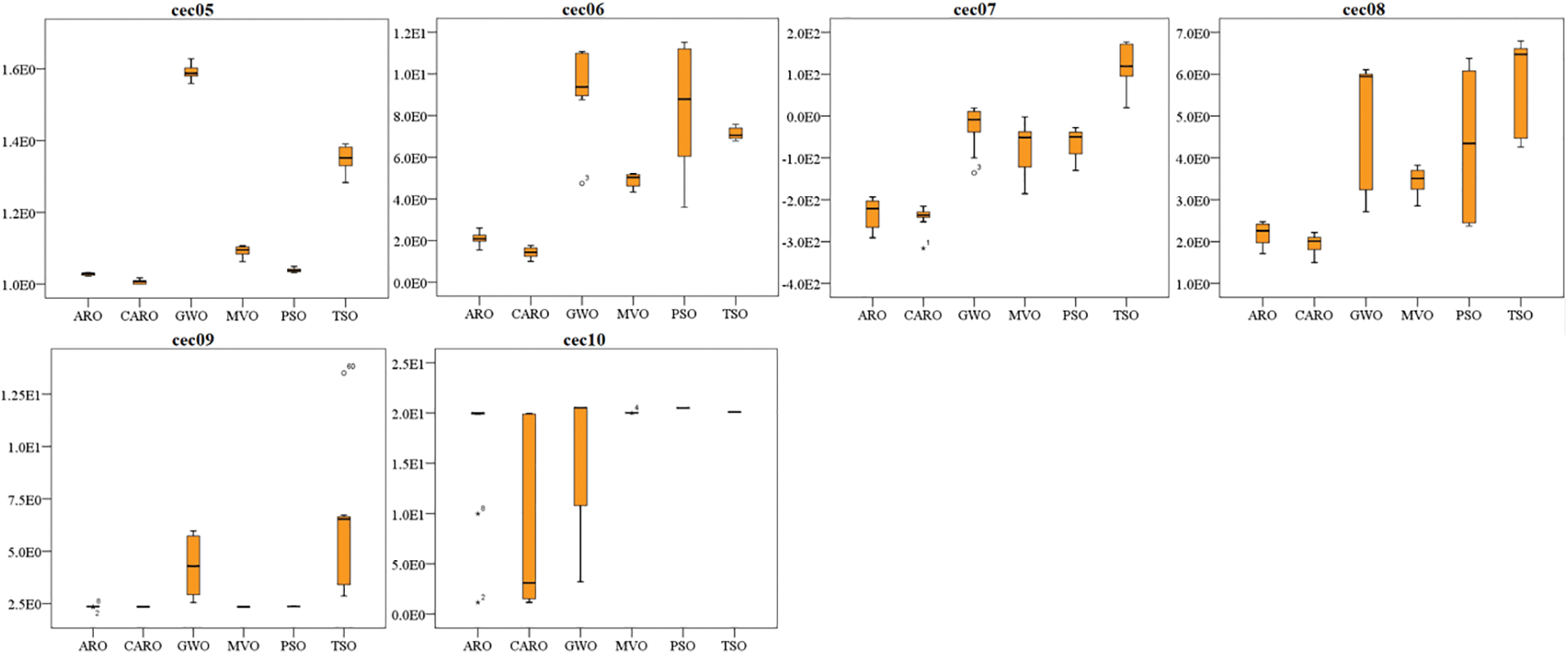
Figure 6: Boxplot of CEC2019 benchmark function (y-axis indicates values of fitness function)
OBL and CLS are strategies used to enhance the COARO algorithm. Considering the results of COARO in the Classic and CEC2019 benchmark functions, it can be concluded that the proposed COARO algorithm provides effectiveness and efficiency in determining global solutions by combining CLS and OBL techniques and adding ten chaotic maps to the optimization process. These improvements are due to CLS’s advantage of nonlinear dynamics and advanced exploration and OBL’s ability to increase diversity and bring closer to the global solution.
COARO has achieved promising results on the classic and CEC2019 benchmark functions. The proposed algorithm may exhibit different performances under different conditions. For example, in noisy environments, noise on the objective function may lead to incorrect fitness values, affecting the quality of the solutions obtained by the COARO algorithm. It can make it difficult for the algorithm to distinguish between real improvements and fluctuations caused by randomness due to noise. This can result in convergence to seemingly good but suboptimal solutions with random fluctuations. As a different example, in Dynamic Optimization Problems, the algorithm must be constantly adapted to meet new conditions since the optimization criteria, constraints, and variables change over time. Additionally, the algorithm needs to explore and exploit the changing environment efficiently.
4.2 Application of the COARO for Engineering Design Problems
This section uses six well-known engineering design problems to assess the COARO algorithm’s problem-solving abilities. Detailed information and mathematical formulations on engineering design problems can be found in [23]. Each engineering issue’s population and maximum iteration numbers are 30 and 500, respectively. For every engineering problem, all optimization algorithms have been performed 30 times. The results achieved by COARO for each engineering problem are compared with different metaheuristic algorithms.
Reducing the cost of creating the welded beam is the aim of this minimization problem. The welded beam problem has four variables: weld thickness (h), attached part to bar length (l), bar height (t), and bar thickness (b).
Consider x = [x1 x2 x3 x4] = [h l t b]
Table 14 compares the ARO algorithm’s outcomes and the suggested COARO algorithms applied to the welded beam.
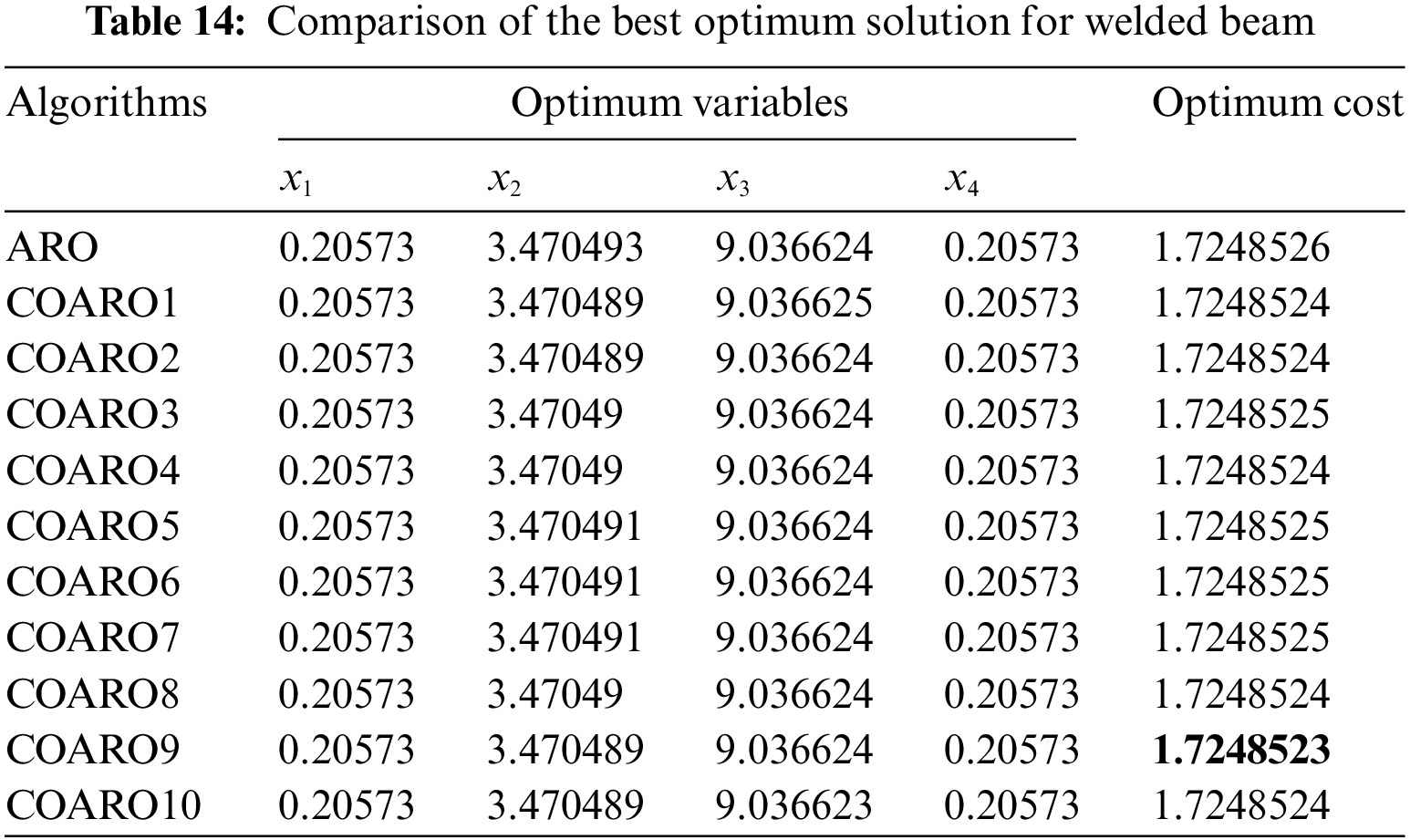
As seen from Table 14, the COARO9 algorithm achieved better performance than others for the welded beam with the decision variable values (0.20573, 3.470489, 9.036624, 0.20573) and the corresponding objective function value equal to 1.7248523. The statistical outcomes of the proposed COARO algorithms and ARO algorithm are given in Table 15.
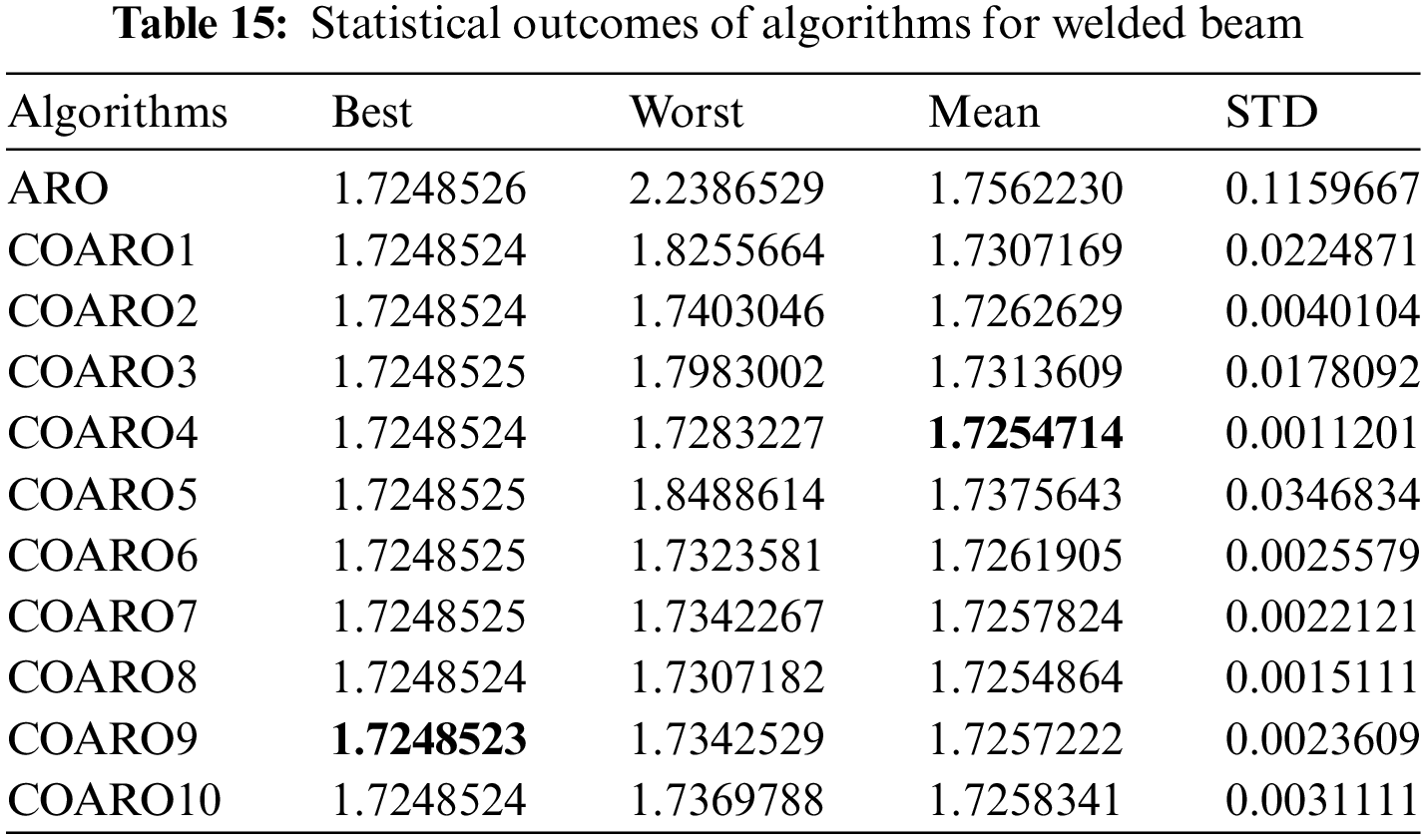
The different criteria outcomes of the used algorithms are displayed in Table 15. Upon examining Table 15, it is evident that the COARO9 algorithm outperforms the other algorithms about the best value, whereas the COARO4 algorithm outperforms the others regarding the mean value. Fig. 7a shows the convergence graphs of the ARO algorithm on the welded beam and proposed COARO algorithms.
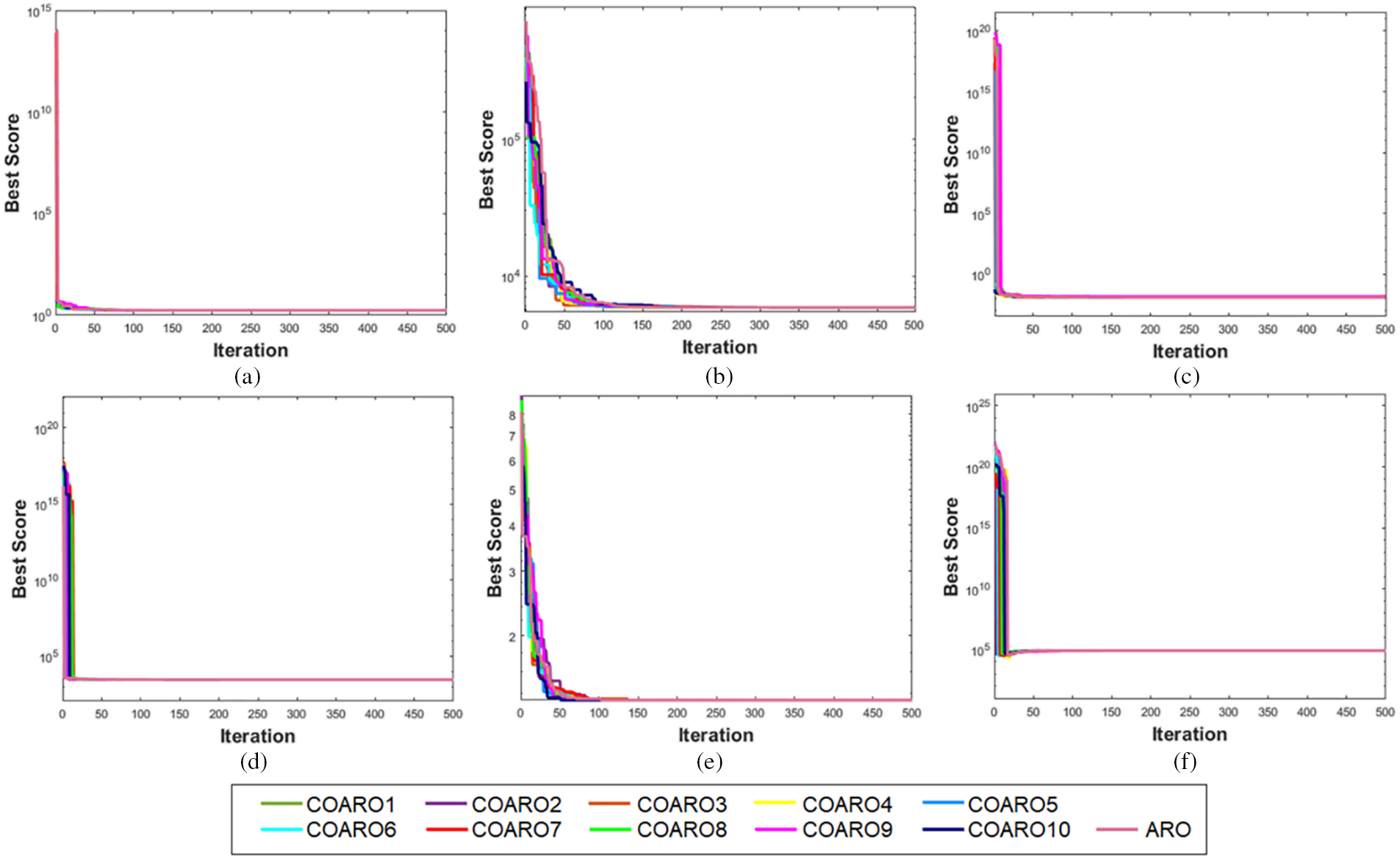
Figure 7: Convergence graphs of engineering design problems (a) Welded beam (b) Pressure vessel (c) Tension/Compression spring (d) Speed reducer (e) Cantilever beam (f) Rolling element bearing
This minimization problem aims to reduce the total cost of a cylindrical vessel, including the cost of materials, welding, and forming. The problem has four variables: head thickness (Th), length of the cylindrical vessel without head (L), shell thickness (Ts), and internal radius (R).
Consider x = [x1 x2 x3 x4] = [Ts, Th, R, L]
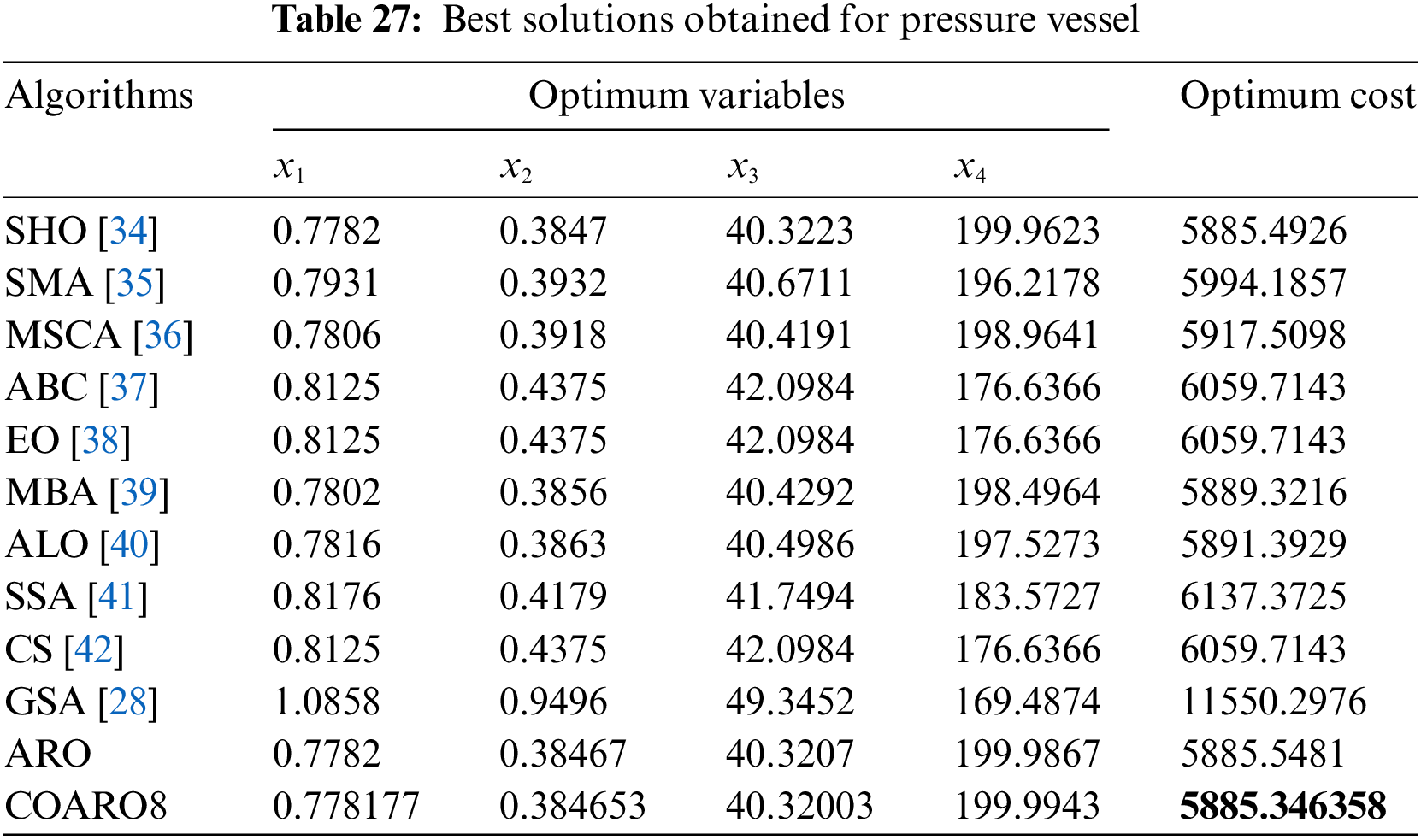
Table 16 compares the pressure vessel results using the ARO and proposed COARO algorithms.
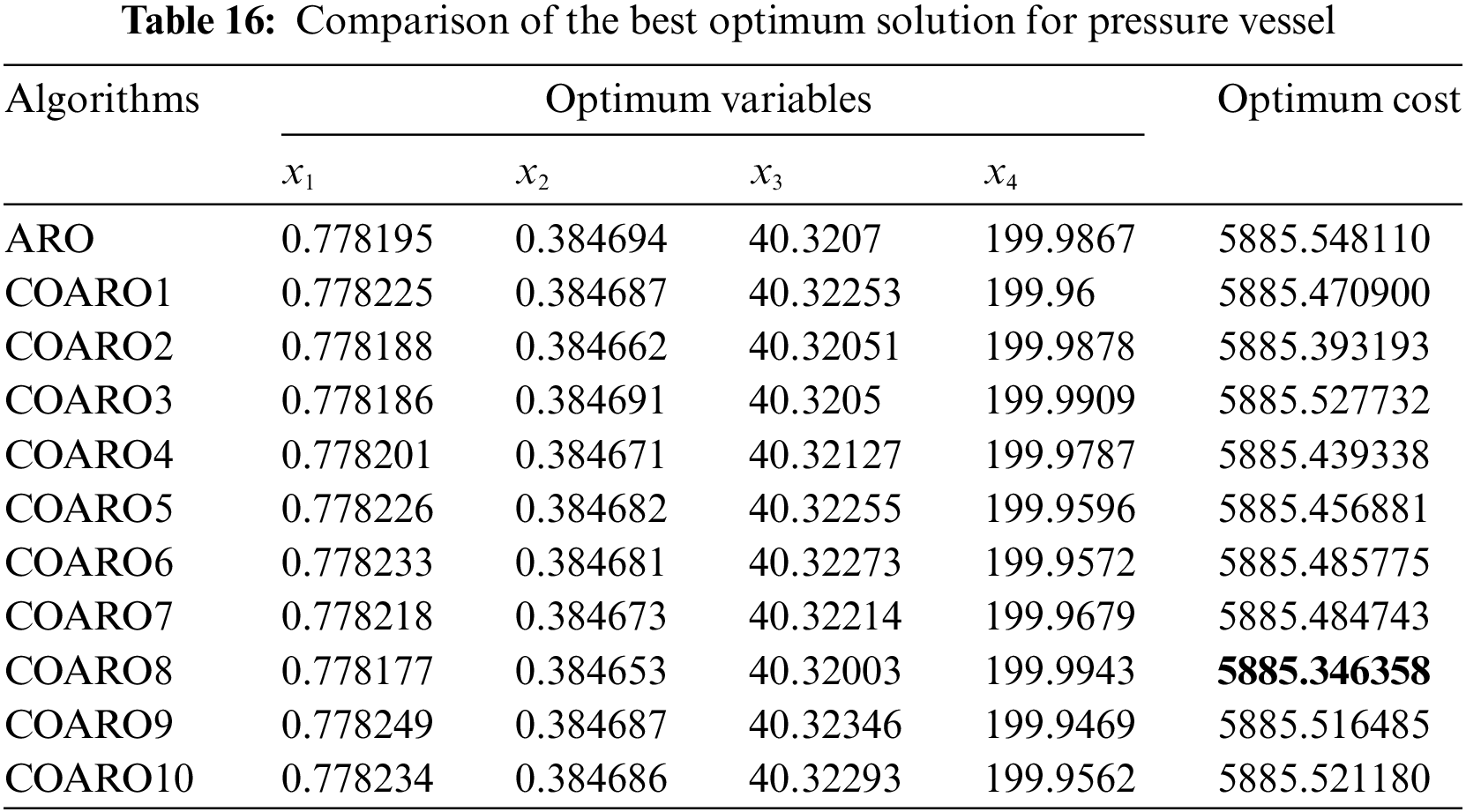
As seen from Table 16, the COARO8 algorithm achieved better performance than others for the pressure vessel with the decision variable values (0.778177, 0.384653, 40.32003, 199.9943) and the corresponding objective function value equal to 5885.346358. The statistical outcomes of the proposed COARO algorithms and ARO algorithm are given in Table 17.
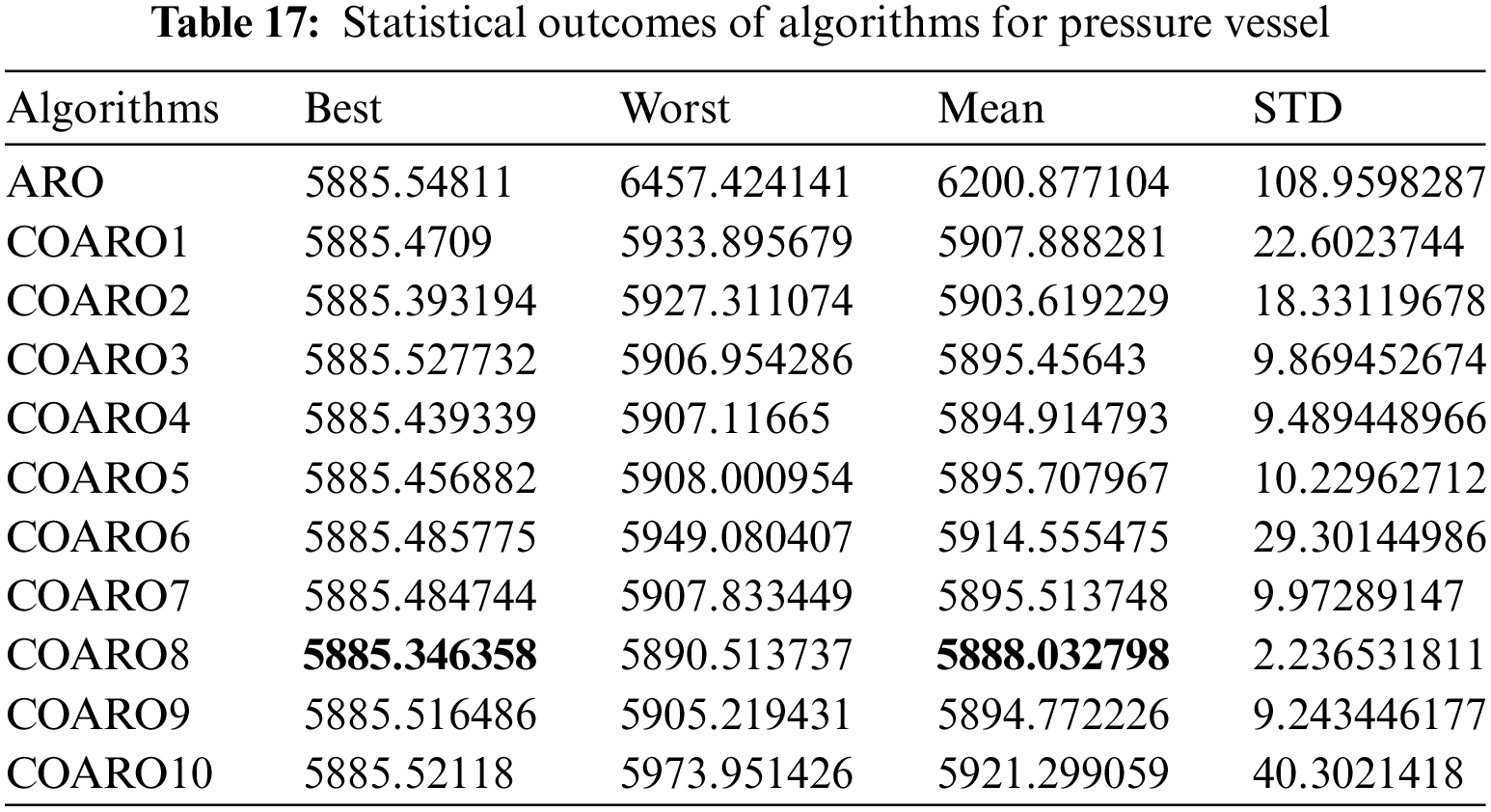
Table 17 displays the different criteria outcomes of the used algorithms. Upon closer inspection, the COARO8 algorithm outperforms the others in terms of best and mean values. Fig. 7b shows the convergence graphs of the ARO algorithm on the pressure vessel and the proposed COARO algorithm.
4.2.3 Tension/Compression Spring
This minimization problem aims to reduce the weight of this engineering problem. Three variables are involved in this problem: the number of active coils (P), wire diameter (d), and mean coil diameter (D).
Consider x = [x1 x2 x3] = [d, D, N]
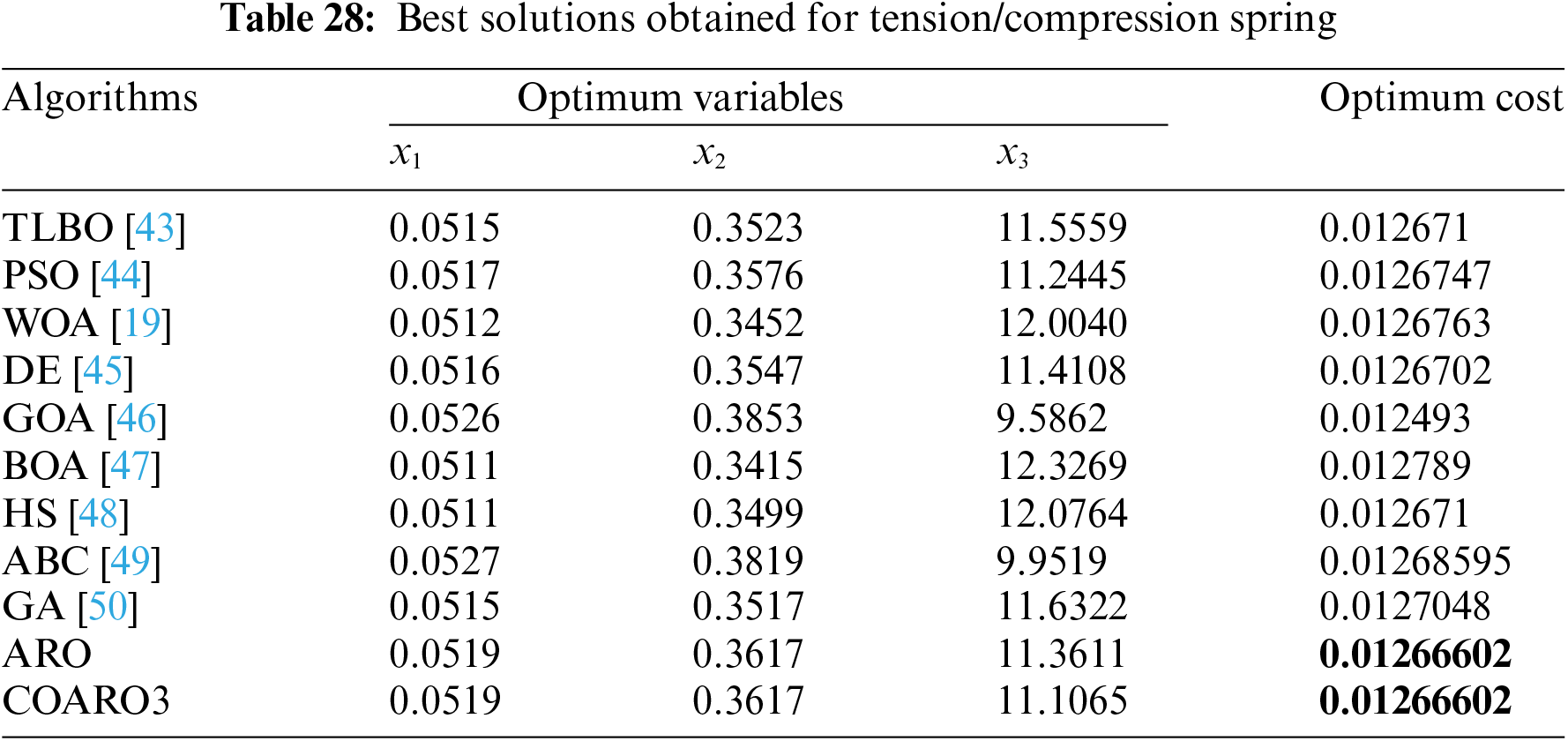
Table 18 compares the outcomes produced on the tension/compression spring using the ARO and proposed COARO algorithms.
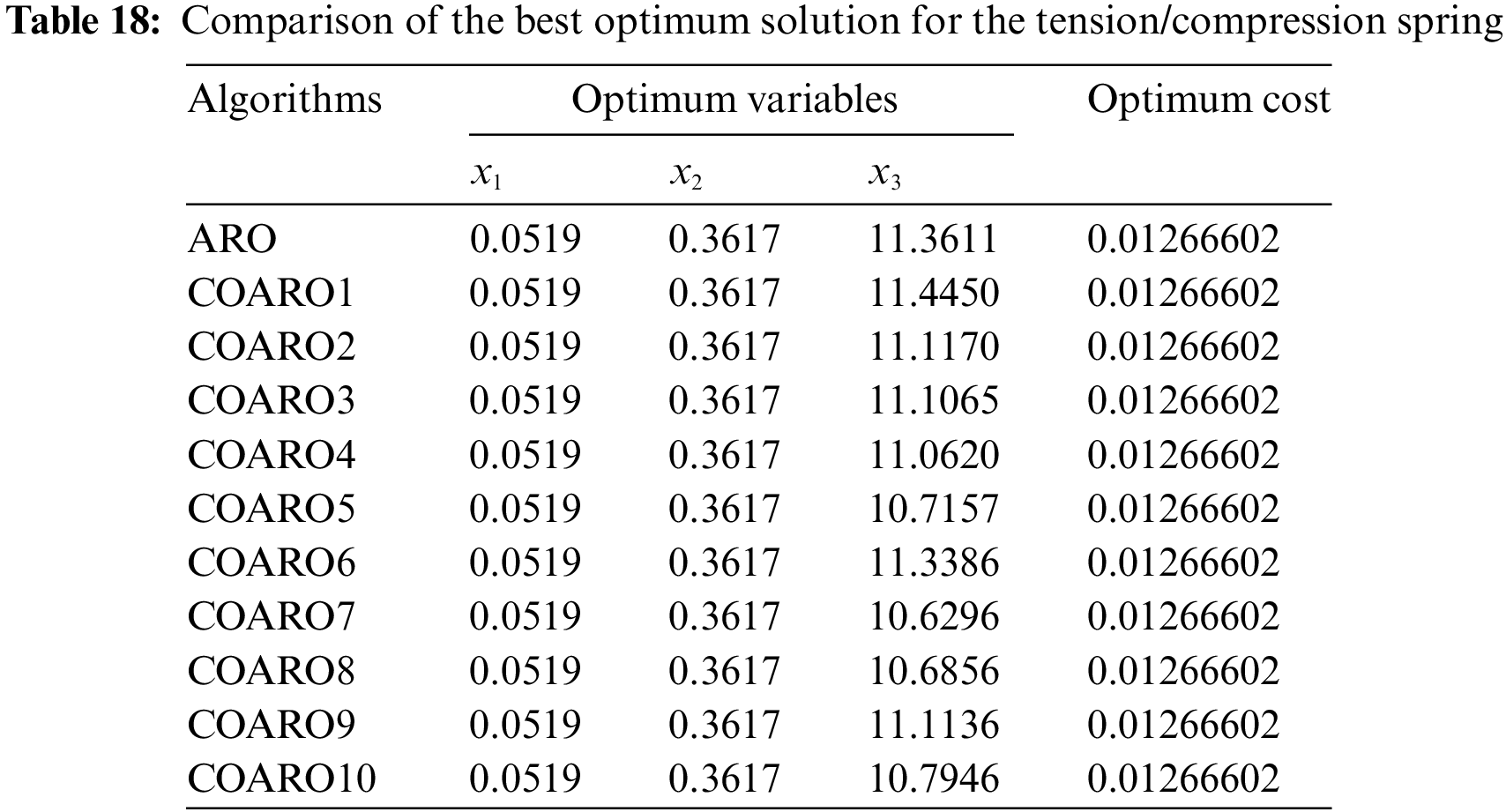
Table 18 shows the best ARO results, and the proposed COARO algorithms are relatively similar. Table 19 gives the statistical outcomes of the proposed COARO algorithms and the ARO algorithm.
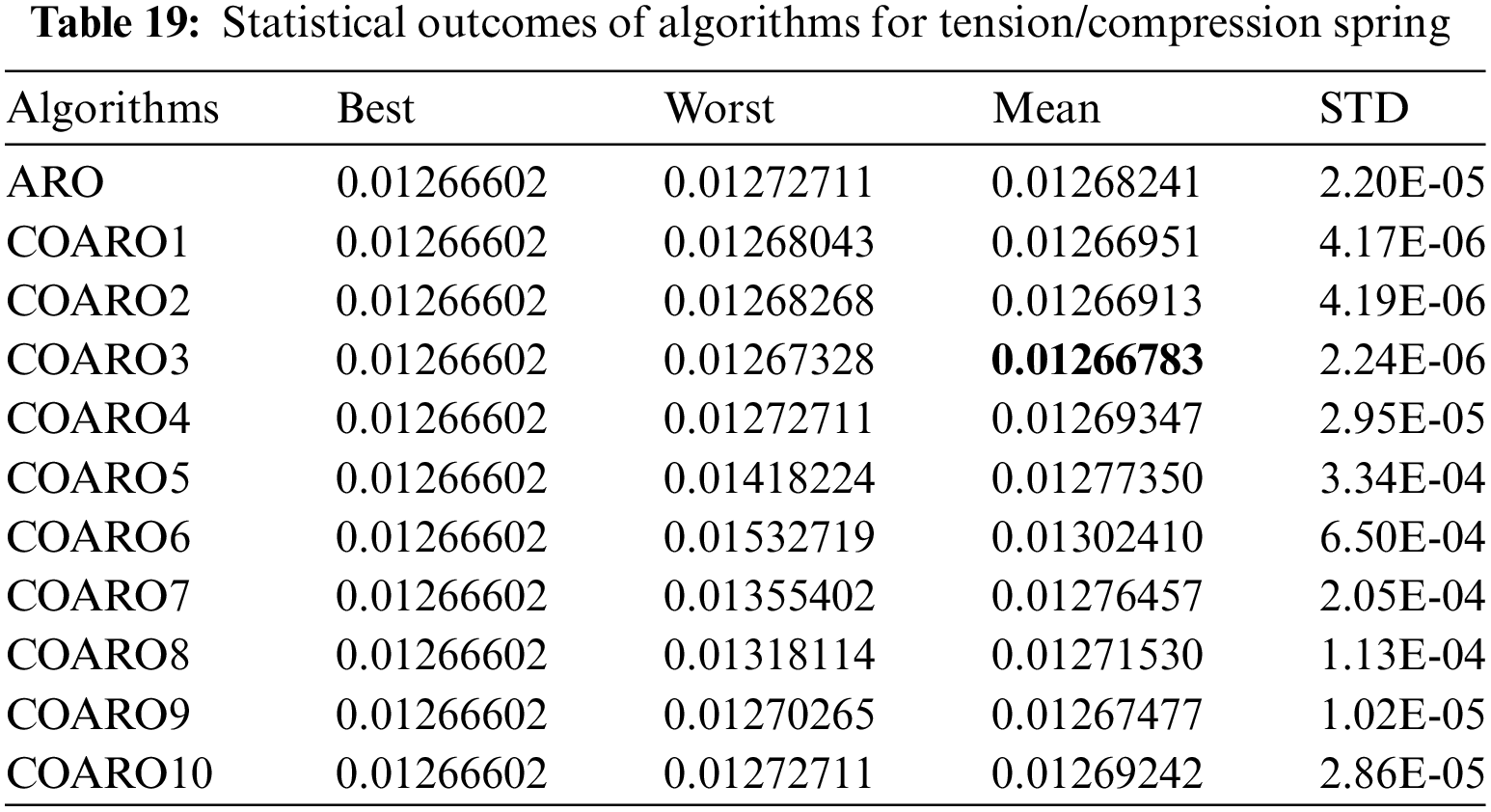
Table 19 displays the different criteria outcomes of the employed algorithms. According to Table 19, the COARO3 algorithm is more successful regarding mean value. The convergence graphs of the proposed COARO algorithms and the ARO algorithm on the tension/compression spring are illustrated in Fig. 7c.
The main goal of the speed reducer is to reduce its weight. The problem has seven variables, such as the face width (x1), the tooth’s module (x2), the number of teeth on the pinion (x3), the diameter of the first shaft (x6), the diameter of the second shaft (x7), the length of the first shaft between bearings (x4), and the length of the second shaft between bearings (x5).
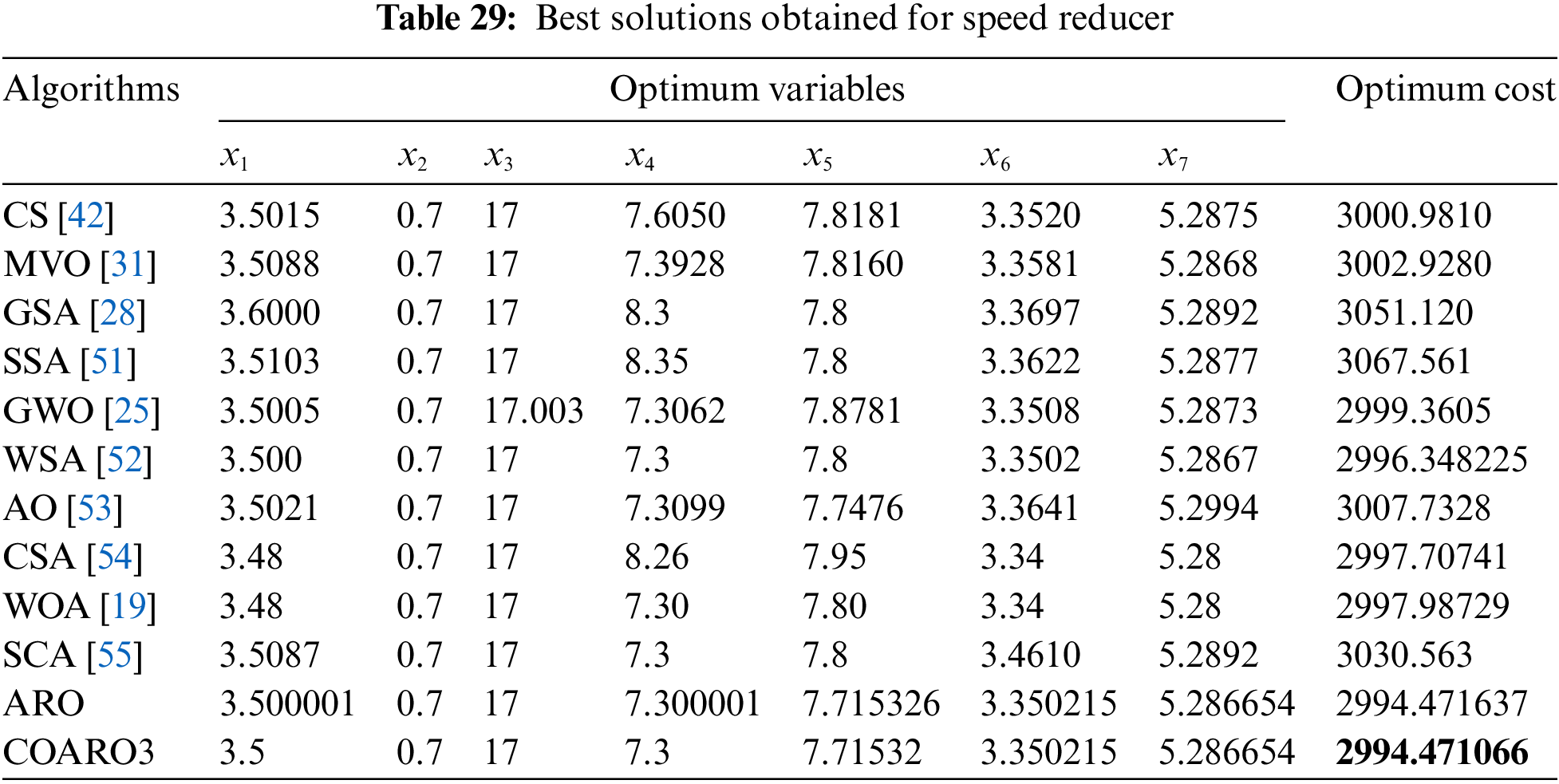
Table 20 compares the outcomes produced by the ARO algorithm and the proposed COARO algorithms on the speed reducer.
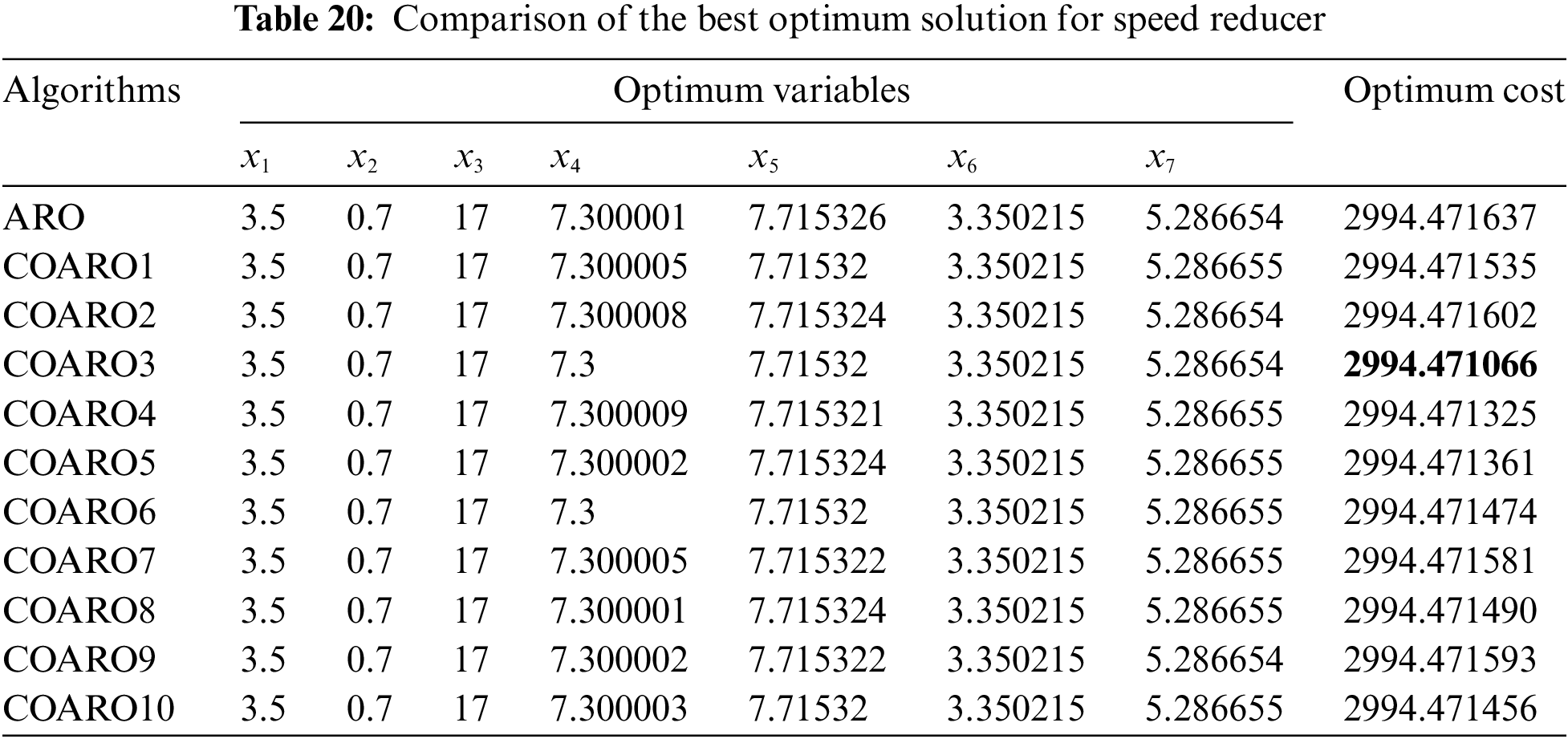
As seen from Table 20, the COARO3 algorithm achieved better performance than others for the speed reducer with the decision variable values (3.5, 0.7, 17, 7.3, 7.71532, 3.350215, 5.286654) and the corresponding objective function value equal to 2994.471066. The statistical outcomes of the proposed COARO algorithms and ARO algorithm are given in Table 21.
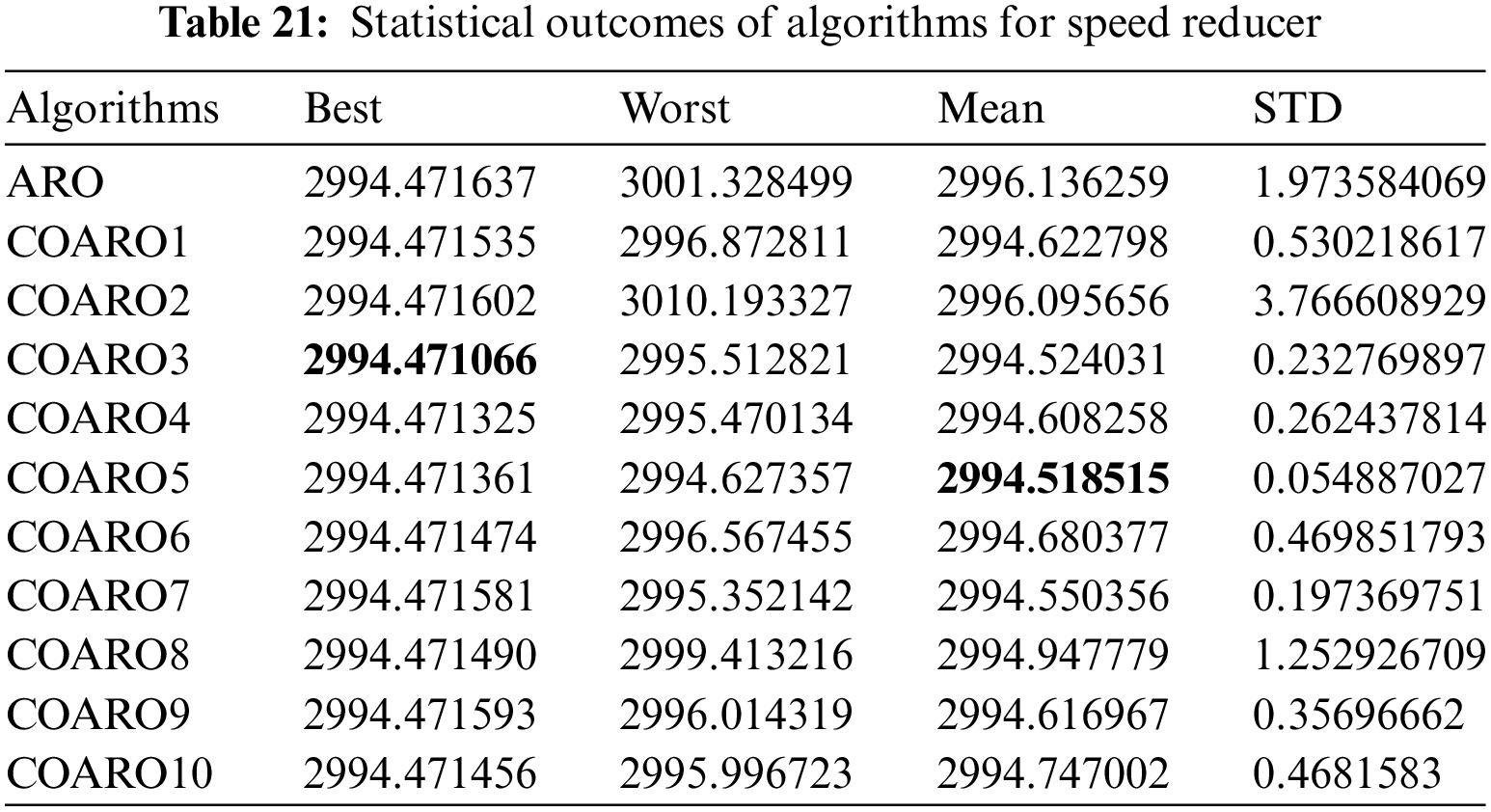
Table 21 displays the different criteria outcomes of the employed algorithms. The COARO3 algorithm beats the others in terms of greatest value, while the COARO5 algorithm beats the others in terms of mean value. The proposed COARO algorithm and the ARO algorithm’s convergence curves on the speed reducer are displayed in Fig. 7d.
This problem uses a hollow square portion to decrease the cantilever beam’s total weight. This problem has five decision variables: x1, x2, x3, x4, and x5.
Table 22 compares the outcomes produced on the cantilever beam using the ARO and proposed COARO algorithms.
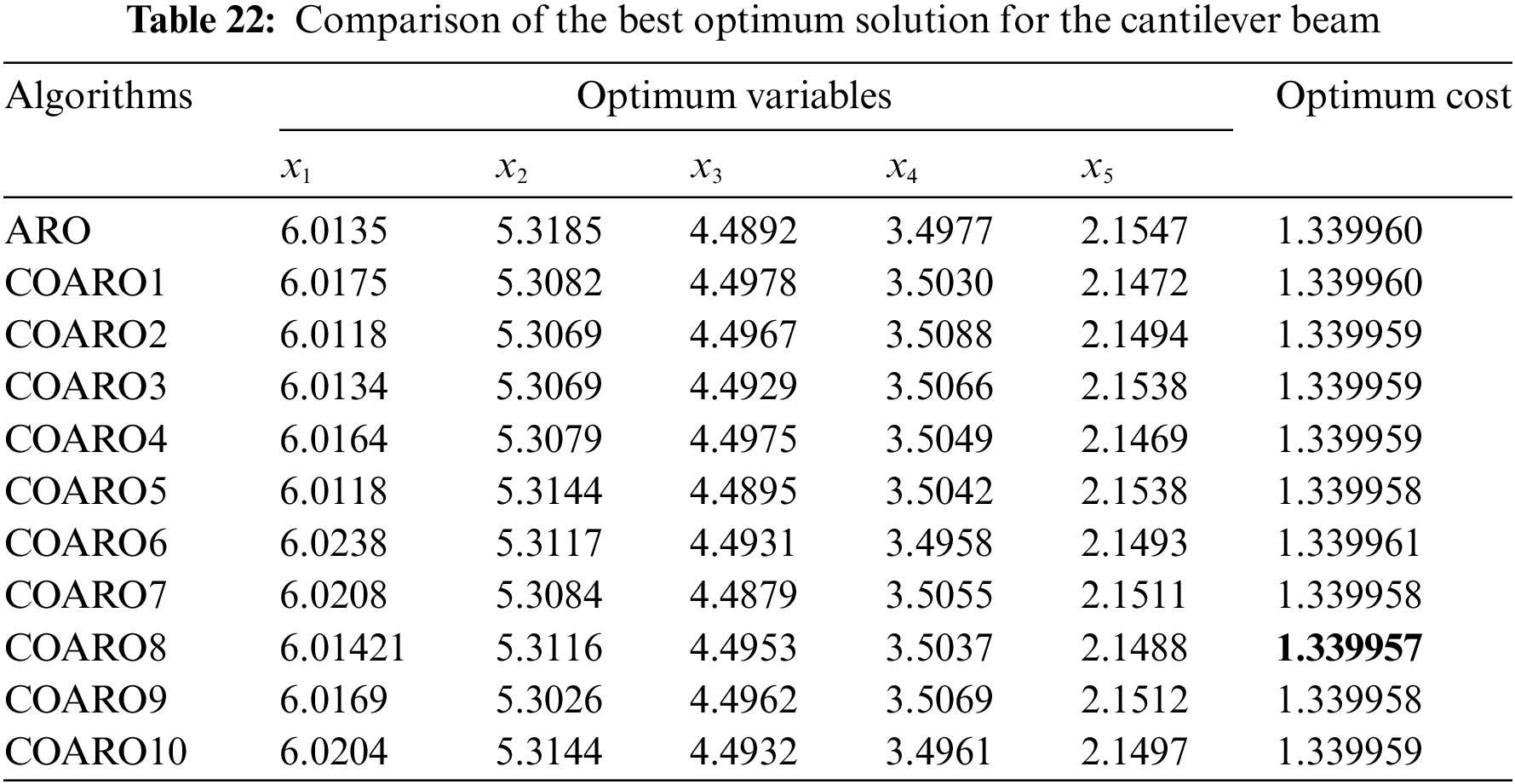
As seen from Table 22, the COARO8 algorithm achieved better performance than others for the cantilever beam with the decision variable values (6.01421, 5.3116, 4.4953, 3.5037, 2.1488) and the corresponding objective function value equal to 1.339957. The statistical outcomes of the proposed COARO algorithms and ARO algorithm are given in Table 23.
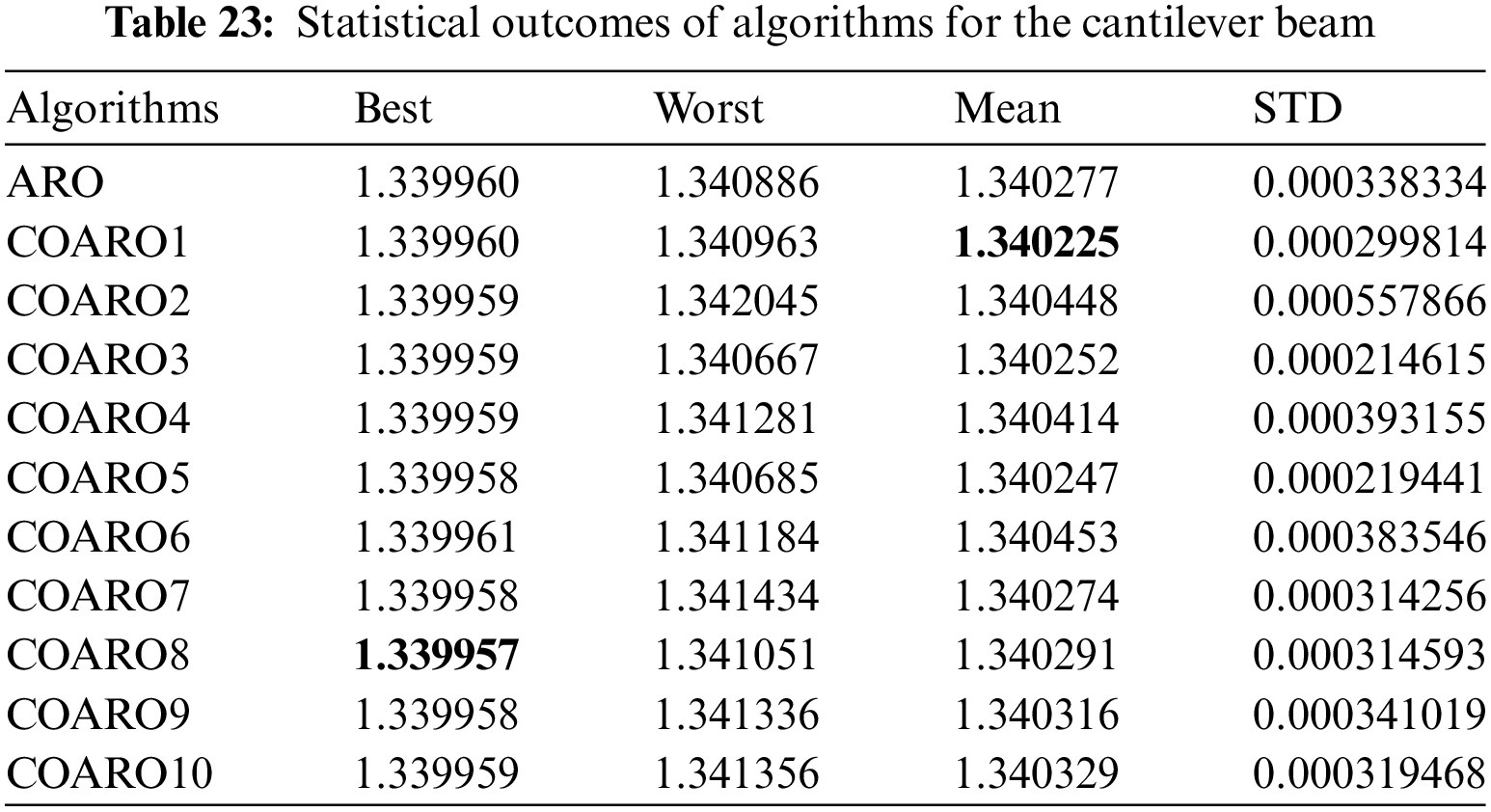
Table 23 displays the different criteria outcomes of the used algorithms. Examining Table 23 reveals that the COARO8 algorithm outperforms the others regarding the best value, while the COARO1 method outperforms the others regarding the mean value. Fig. 7e shows the convergence graphs of the ARO algorithm on the cantilever beam and the proposed COARO algorithm.
The rolling element bearing problem aims to maximize the load capacity by considering ten design variables and nine constraints. Table 24 compares the rolling element-bearing results using the ARO and the proposed COARO algorithms.
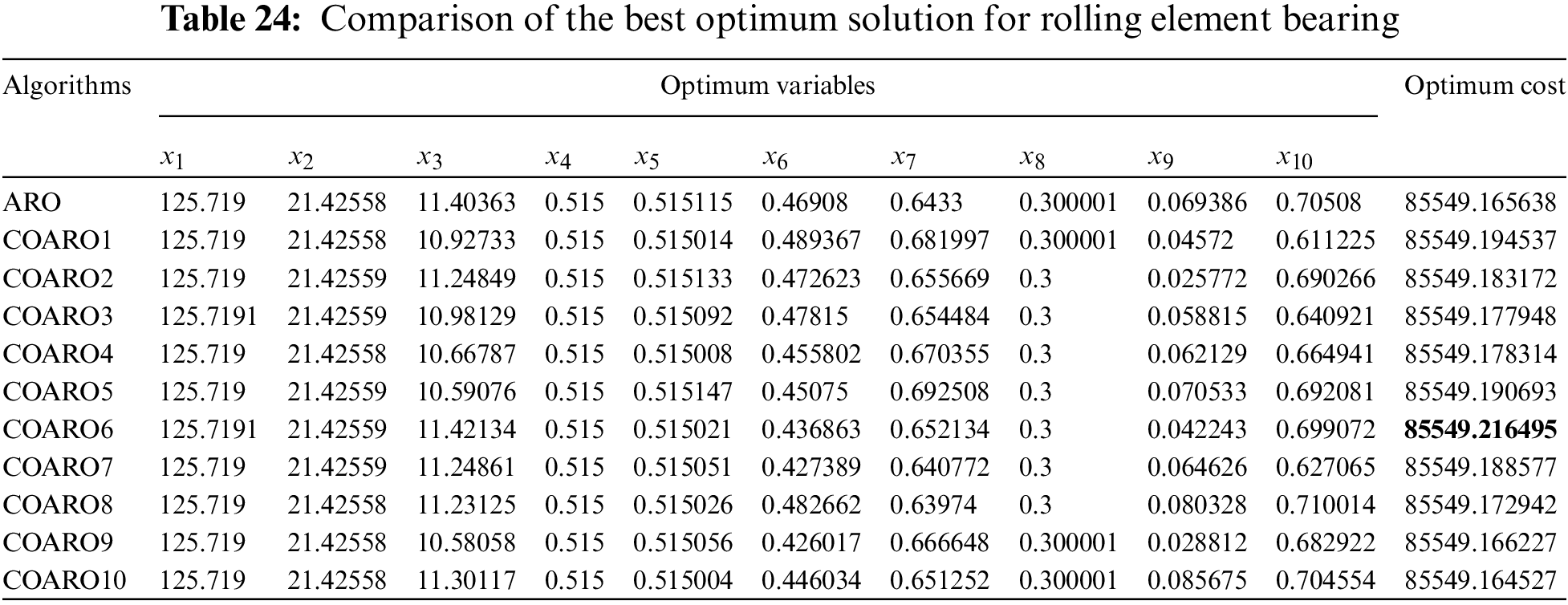
As seen from Table 24, the COARO6 algorithm achieved better performance than other algorithms for the rolling element bearing with the decision variable values (125.7191, 21.42559, 11.42134, 0.515, 0.515021, 0.436863, 0.652134, 0.3, 0.042243, 0.699072) and the corresponding objective function value equal to 85549.216495. The statistical outcomes of the proposed COARO algorithms and ARO algorithm are given in Table 25.
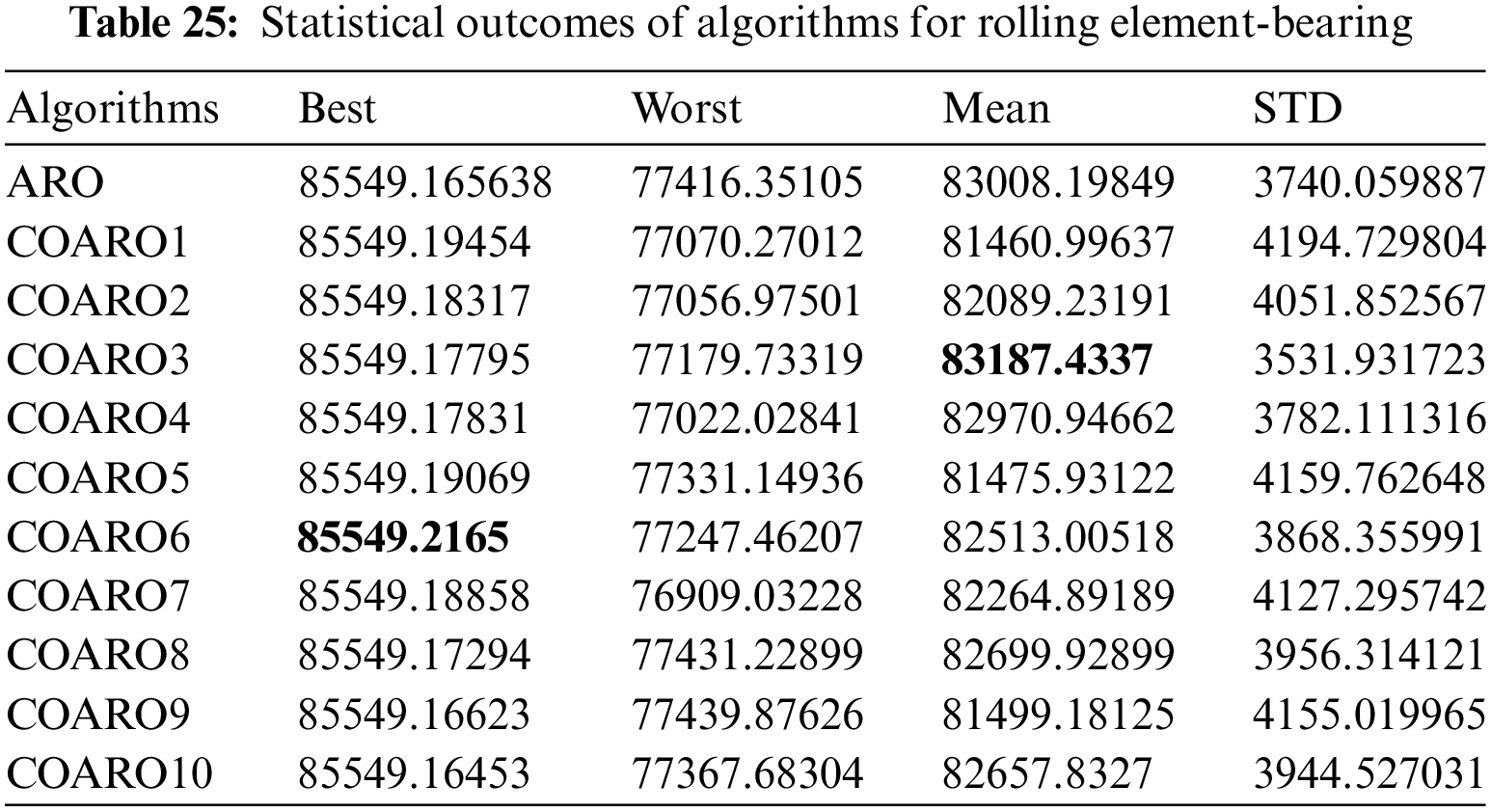
The different criteria outcomes of the employed algorithms are displayed in Table 25. Table 25 clearly shows that the COARO3 algorithm performs better than the others in terms of mean value, while the COARO6 algorithm performs better than the others in terms of best value. Fig. 7f shows the convergence graphs of the ARO algorithm on the rolling element bearing and the proposed COARO algorithms.
4.3 Analysis of COARO for Engineering Design Problems with Other Metaheuristic Algorithms
Many metaheuristic algorithms have found the best solution for the welded beam. The best cost and relevant decision variables obtained from the proposed COARO algorithm and other compared metaheuristic algorithms for the welded beam are given in Table 26.
Upon examining Table 26, it can be noted that the COARO9 method performs better than both ARO and the competitive optimization techniques. The literature has employed a variety of metaheuristic algorithms to determine the best solution for the pressure vessel. ARO and the proposed COARO algorithm were compared with ten different algorithms in the literature. Table 27 presents the optimal cost and pertinent choice variables derived from the proposed COARO algorithm and other comparative metaheuristic algorithms for the pressure vessel. The potential applications of the COARO algorithm in various fields, such as image processing, wireless sensor networks, and decision support systems, are inspiring.
Upon examining Table 27, it’s clear that the COARO8 method competes favorably with ARO and other competitive optimization techniques. The literature has employed various metaheuristic methods to find the best tension/compression spring solution. Nine different approaches from the literature were compared with ARO and the proposed COARO algorithm. Table 28 presents the optimal cost and relevant choice factors for the tension/compression spring derived from the proposed COARO algorithm and other comparative metaheuristic algorithms.
Upon examining Table 28, it can be noted that the algorithms for COARO3 and ARO performed better than those for competitive optimization. Numerous metaheuristic algorithms have been used in the literature to find the optimal solution for the speed reducer. Nine different approaches from the literature were compared with ARO and the proposed COARO algorithm. The best cost and relevant decision variables obtained from the proposed COARO algorithm and other compared metaheuristic algorithms for the speed reducer are given in Table 29.
Upon closer inspection of Table 30, it’s evident that the COARO3 algorithms outperform ARO and other competitive optimization algorithms. The literature has employed various metaheuristic methods to find the best cantilever beam solution. ARO and the proposed COARO algorithm were compared with four different algorithms in the literature. Table 30 gives the best cost and relevant decision variables obtained from the proposed COARO algorithm and other compared metaheuristic algorithms for the cantilever beam.
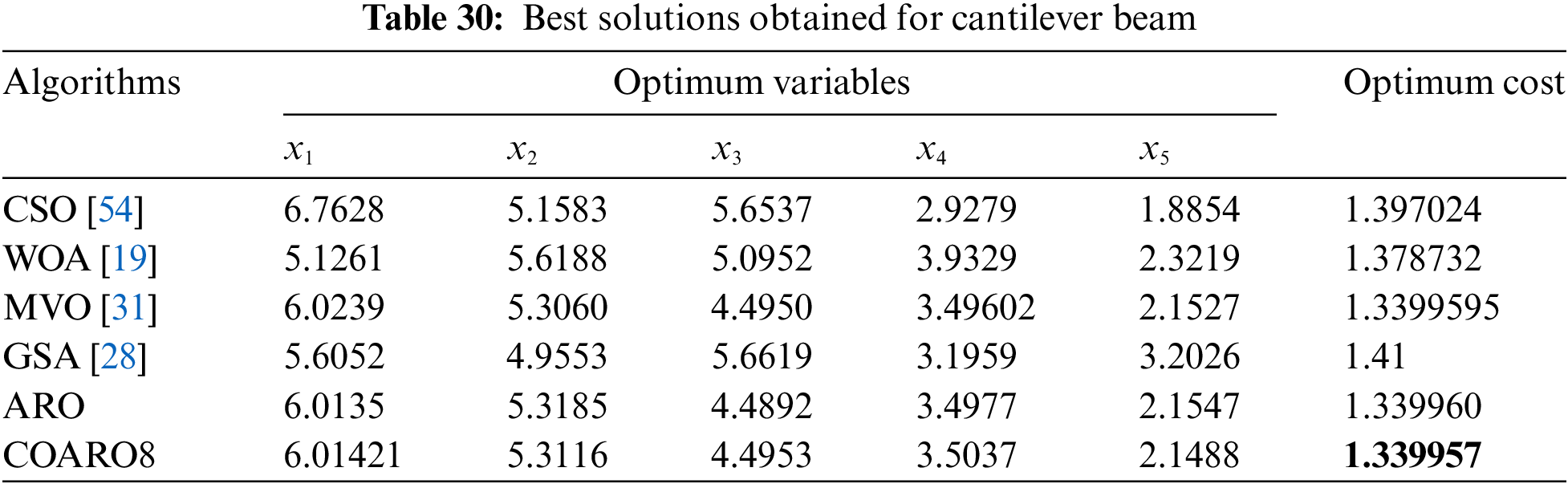
Upon closer inspection of Table 30, it can be shown that the COARO8 algorithms perform better than both ARO and the competitive optimization algorithms. The literature has employed various metaheuristic methods to determine the rolling element bearing the ideal solution. ARO and the proposed COARO algorithm were compared with five different algorithms in the literature. The best cost and relevant decision variables obtained from the proposed COARO algorithm and other compared metaheuristic algorithms for the rolling element bearing are given in Table 31.
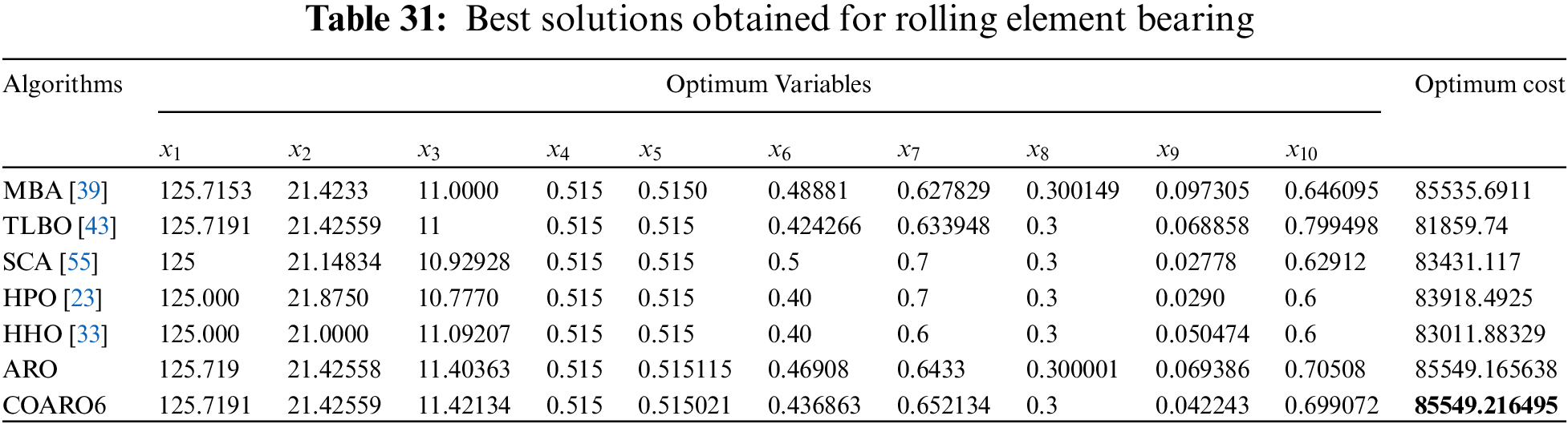
Upon closer inspection of Table 31, it can be shown that the COARO6 algorithms perform better than both ARO and the competitive optimization algorithms. In addition to all the evaluations in this section, the proposed COARO algorithm performs better for six engineering design problems than other metaheuristic algorithms.
Performance of BCOARO for Feature Selection in Breast Cancer Problem. The BCOARO algorithm shows promising results in feature selection for the breast cancer dataset, instilling hope for its potential in real-world applications. This section uses the breast cancer dataset to analyze the performance of binary COARO algorithms. This analysis’s main objective is to assess the proposed continuous COARO algorithm’s (BCOARO) binary version’s applicability in the real world and its efficiency in feature selection for the breast cancer dataset. It is also to compare its performance with different algorithms on this dataset. The breast cancer dataset used to consider the BCOARO algorithm performance contains a total of 569 data, 212 of which are malignant and 357 of which are benign [56]. It consists of 31 features in Table 32 in the breast cancer dataset.
The results obtained for the breast cancer dataset with the BCOARO algorithm are compared with those of the ARO, WOA, BGWO, BASO, HGSO, and BHHO algorithms. For a fair evaluation, the maximum iteration number was set to 100, and the number of populations was 30 for all algorithms. Table 33 displays the accuracy and fitness values acquired using these algorithms.
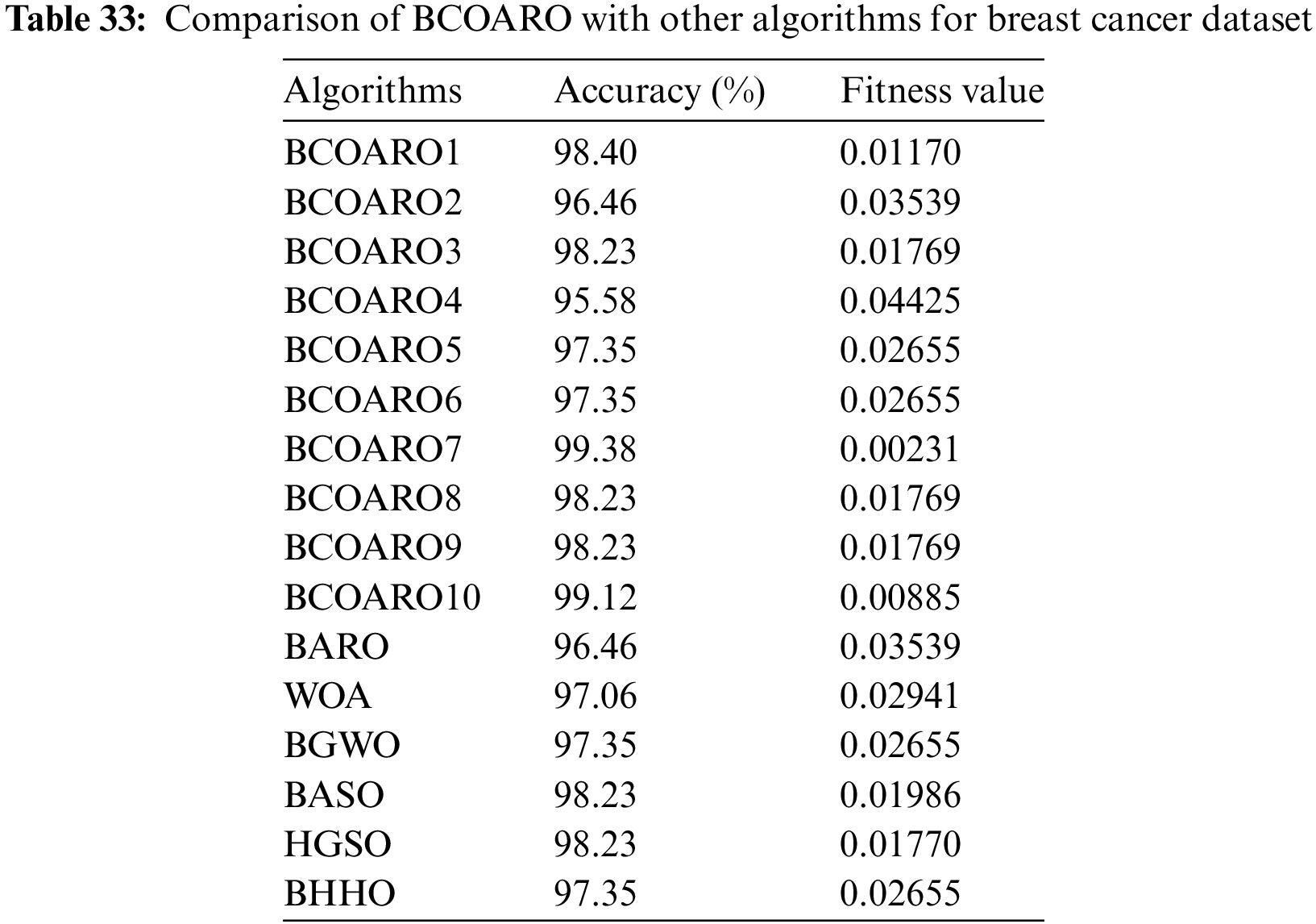
A graphical representation of accuracy values is presented in Fig. 8. According to Fig. 8, BCOARO7 achieved the highest accuracy value, BCOARO10 had the second highest accuracy value, and BCOARO4 showed the lowest. According to Table 33, the BCOARO7 algorithm has a superior result to other algorithms in terms of 99.38% accuracy. Likewise, BCOARO7, which uses a sine chaotic map, is more successful than other compared algorithms with a fitness value of 0.00231. Since the sine map introduces a specific form of nonlinearity, unlike other chaotic maps, it exhibits different behavioral patterns and obtains different statistical results. Therefore, the 99.38% accuracy and 0.00231 fitness value obtained from the experimental results showed that BCOARO7 demonstrated an outlier and practical value and that its performance was replicability. The second-best algorithm for feature selection in the breast cancer dataset is the BCOARO10 algorithm, with an accuracy value of 99.12%. The fitness function value of this algorithm is 0.00885.
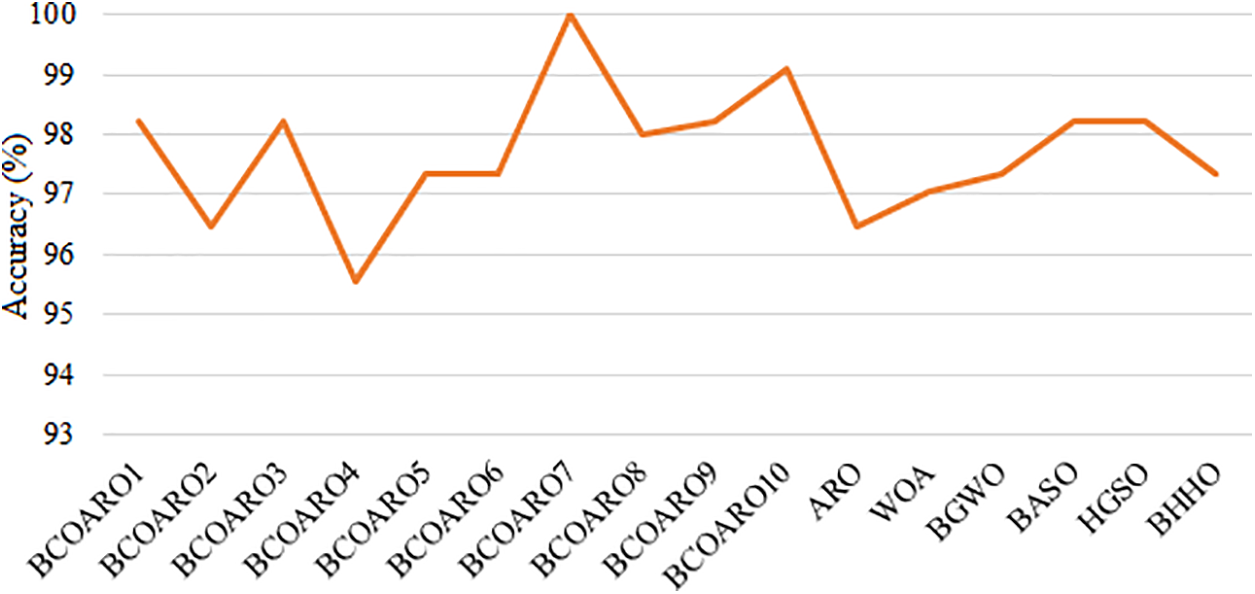
Figure 8: Comparison of accuracy values for breast cancer dataset
The detour foraging and random hiding habits of rabbits in the wild inspired the biology-based metaheuristic algorithm known as the ARO algorithm. This paper proposed an enhanced COARO by integrating the concept of CLS and OBL and incorporating ten different chaotic maps into the optimization process of ARO. CLS ensures that solution quality increases by directing the local search around the global best solution. Adding OBL to the algorithm improves the initial population and enhances the problem of getting stuck in local minima. The concept of chaos is a very effective technique to overcome the issues of optimization algorithms, such as local optimum traps, early convergence, and inefficient search. The findings showed that the COARO algorithm outperformed ARO in reaching the optimal solution for 33 benchmark functions, including unimodal, multimodal, fixed-dimension multimodal, and CEC2019 functions. Furthermore, the literature compares the performance of the COARO algorithm with four popular metaheuristic algorithms: GWO, MVO, PSO, and TSO. As a result of the comparison, the COARO algorithm achieved better results than competitive algorithms. We evaluated the proposed COARO algorithm’s performance on six engineering design problems. It is superior to other algorithms for engineering design problems. Additionally, a binary version of the COARO algorithm was developed, and its performance was evaluated as a feature selection method for an actual application. As a result of the analysis performed on the breast cancer dataset, it was observed that the results obtained with the BCOARO algorithm were promising.
Although it has the advantage of efficiently managing different types of applications, the proposed COARO algorithm has limitations. First of all, the first limitation that all metaheuristic methods have is that, according to the No-Free-Lunch theorem, there is the possibility of developing newer algorithms that achieve more effective performance than COARO. Another limitation is that although the COARO algorithm achieved successful performance for the optimization problems examined in this study, it does not guarantee successful performance for different optimization problems. This means that the COARO algorithm may still need changes and improvements. The proposed COARO algorithm can be applied to future research fields, such as image processing, wireless sensor networks, decision support systems, the Internet of Things, and logistics. Further study may focus on creating parallel or multi-objective versions of the proposed algorithm to address various optimization issues.
Acknowledgement: The authors thank the reviewers for their valuable comments, which significantly improved this paper.
Funding Statement: This article was funded by Firat University Scientific Research Projects Management Unit for the scientific research project of Feyza Altunbey Özbay, numbered MF.23.49.
Author Contributions: The authors confirm their contribution to the paper as follows: Methodology: Feyza Altunbey Özbay, Erdal Özbay and Farhad Soleimanian Gharehchopogh; Software: Feyza Altunbey Özbay, Erdal Özbay and Farhad Soleimanian Gharehchopogh; Validation: Feyza Altunbey Özbay; Formal analysis and investigation: Feyza Altunbey Özbay, Erdal Özbay and Farhad Soleimanian Gharehchopogh; Writing—original draft preparation: Feyza Altunbey Özbay, Erdal Özbay and Farhad Soleimanian Gharehchopogh; Writing—review and editing: Farhad Soleimanian Gharehchopogh; Visualization: Feyza Altunbey Özbay, Erdal Özbay and Farhad Soleimanian Gharehchopogh; Supervision: Feyza Altunbey Özbay, Erdal Özbay and Farhad Soleimanian Gharehchopogh. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: We use the available breast cancer dataset for evaluation: https://www.kaggle.com/datasets/yasserh/breast-cancer-dataset/ (accessed on 24 May 2024).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that there are no conflicts of interest to report regarding the present study.
References
1. Gharehchopogh FS, Gholizadeh H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm Evol Comput. 2019;48(8):1–24. doi:10.1016/j.swevo.2019.03.004. [Google Scholar] [CrossRef]
2. Özbay FA. A modified seahorse optimization algorithm based on chaotic maps for solving global optimization and engineering problems. Eng Sci Technol, Int J. 2023;41(1):101408. doi:10.1016/j.jestch.2023.101408. [Google Scholar] [CrossRef]
3. Gharehchopogh FS, Shayanfar H, Gholizadeh H. A comprehensive survey on symbiotic organisms search algorithms. Artif Intell Rev. 2020;53(3):2265–312. doi:10.1007/s10462-019-09733-4. [Google Scholar] [CrossRef]
4. Kiani F, Anka FA, Erenel F. PSCSO: enhanced sand cat swarm optimization inspired by the political system to solve complex problems. Adv Eng Softw. 2023;178(5):103423. doi:10.1016/j.advengsoft.2023.103423. [Google Scholar] [CrossRef]
5. Shajin FH, Aruna Devi B, Prakash NB, Sreekanth GR, Rajesh P. Sailfish optimizer with Levy flight, chaotic and opposition-based multi-level thresholding for medical image segmentation. Soft Comput. 2023;27(17):12457–82. doi:10.1007/s00500-023-07891-w. [Google Scholar] [CrossRef]
6. Kiani F, Seyyedabbasi A, Aliyev R, Shah MA, Gulle MU. 3D path planning method for multi-UAVs inspired by grey wolf algorithms. J Int Technol. 2021;22(4):743–55. doi:10.53106/160792642021072204003. [Google Scholar] [CrossRef]
7. Özbay E. An active deep learning method for diabetic retinopathy detection in segmented fundus images using artificial bee colony algorithm. Artif Intell Rev. 2023;56(4):3291–318. doi:10.1007/s10462-022-10231-3. [Google Scholar] [CrossRef]
8. Seyyedabbasi A, Dogan G, Kiani F. HEEL: a new clustering method to improve wireless sensor network lifetime. IET Wirel Sens Syst. 2020;10(3):130–6. doi:10.1049/iet-wss.2019.0153. [Google Scholar] [CrossRef]
9. Bhavya R, Elango L. Ant-inspired metaheuristic algorithms for combinatorial optimization problems in water resources management. Water. 2023;15(9):1712. doi:10.3390/w15091712. [Google Scholar] [CrossRef]
10. Xu S, Li W, Li L, Li T, Ma C. Crashworthiness design and multi-objective optimization for bio-inspired hierarchical thin-walled structures. Comput Model Eng Sci. 2022;131(2):929–47. doi:10.32604/cmes.2022.018964. [Google Scholar] [CrossRef]
11. Nematzadeh S, Torkamanian-Afshar M, Seyyedabbasi A, Kiani F. Maximizing coverage and maintaining connectivity in WSN and decentralized IoT: an efficient metaheuristic-based method for environment-aware node deployment. Neural Comput Appl. 2023;35(1):611–41. doi:10.1007/s00521-022-07786-1. [Google Scholar] [CrossRef]
12. Gonzalez-Sanchez B, Vega-Rodríguez MA, Santander-Jiménez S. A multi-objective butterfly optimization algorithm for protein-encoding. Appl Soft Comput. 2023;139(1):110269. doi:10.1016/j.asoc.2023.110269. [Google Scholar] [CrossRef]
13. Trojovský P, Dehghani M. Migration algorithm: a new human-based metaheuristic approach for solving optimization problems. Comput Model Eng Sci. 2023;137(2):1695–730. doi:10.32604/cmes.2023.028314. [Google Scholar] [CrossRef]
14. Wang L, Cao Q, Zhang Z, Mirjalili S, Zhao W. Artificial rabbits optimization: a new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng Appl Artif Intell. 2022;114(4):105082. doi:10.1016/j.engappai.2022.105082. [Google Scholar] [CrossRef]
15. Riad AJ, Hasanien HM, Turky RA, Yakout AH. Identifying the PEM fuel cell parameters using an artificial rabbit optimization algorithm. Sustainability. 2023;15(5):4625. doi:10.3390/su15054625. [Google Scholar] [CrossRef]
16. Siddiqui SA, Gerini F, Ikram A, Saeed F, Feng X, Chen Y. Rabbit meat—production, consumption and consumers’ attitudes and behavior. Sustainability. 2008;15(3):2008. doi:10.3390/su15032008. [Google Scholar] [CrossRef]
17. Dobos P, Kulik LN, Pongrácz P. The amicable rabbit-interactions between pet rabbits and their caregivers based on a questionnaire survey. Appl Anim Behav Sci. 2023;260:105869. doi:10.1016/j.applanim.2023.105869. [Google Scholar] [CrossRef]
18. Elshahed M, Tolba MA, El-Rifaie AM, Ginidi A, Shaheen A, Mohamed SA. An artificial rabbits’ optimization to allocate PVSTATCOM for ancillary service provision in distribution systems. Mathematics. 2023;11(2):339. doi:10.3390/math11020339. [Google Scholar] [CrossRef]
19. Seyedali M, Andrew L. The whale optimization algorithm. Adv in Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]
20. Kiani F, Nematzadeh S, Anka FA, Findikli MA. Chaotic sand cat swarm optimization. Mathematics. 2023;11(10):2340. doi:10.3390/math11102340. [Google Scholar] [CrossRef]
21. dos Santos Coelho L, Mariani VC. Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization. Expert Syst Appl. 2008;34(3):1905–13. doi:10.1016/j.eswa.2007.02.002. [Google Scholar] [CrossRef]
22. Tizhoosh HR. Opposition-based learning: a new scheme for machine intelligence. In: International Conference on Computational Intelligence for Modeling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, IEEE, (CIMCA-IAWTIC’06); 2005; Vienna, Austria. p. 695–701. [Google Scholar]
23. Naruei I, Keynia F, Sabbagh Molahosseini A. Hunter-prey optimization: algorithm and applications. Soft Comput. 2022;26(3):1279–314. doi:10.1007/s00500-021-06401-0. [Google Scholar] [CrossRef]
24. Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S. Henry gas solubility optimization: a novel physics-based algorithm. Future Gener Comput Syst. 2019;101(4):646–67. doi:10.1016/j.future.2019.07.015. [Google Scholar] [CrossRef]
25. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]
26. Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]
27. Abualigah L, Diabat A, Mirjalili S, Abd Elaziz M, Gandomi AH. The arithmetic optimization algorithm. Comput Methods Appl Mech Eng. 2021;376(2):113609. doi:10.1016/j.cma.2020.113609. [Google Scholar] [CrossRef]
28. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]
29. Peña-Delgado AF, Peraza-Vázquez H, Almazán-Covarrubias JH, Torres Cruz N, García-Vite PM, Morales-Cepeda AB, et al. A novel bio-inspired algorithm applied to selective harmonic elimination in a three-phase eleven-level inverter. Math Probl Eng. 2020;2020:1–10. doi:10.1155/2020/8856040. [Google Scholar] [CrossRef]
30. Dhiman G, Kumar V. Spotted hyena optimizer: a novel bio-inspired based metaheuristic technique for engineering applications. Adv Eng Softw. 2017;114(10):48–70. doi:10.1016/j.advengsoft.2017.05.014. [Google Scholar] [CrossRef]
31. Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl. 2016;27(2):495–513. doi:10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]
32. Abualigah L, Abd Elaziz M, Sumari P, Geem ZW, Gandomi AH. Reptile Search Algorithm (RSA): a nature-inspired meta-heuristic optimizer. Expert Syst Appl. 2022;191(11):116158. doi:10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]
33. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris hawks optimization: algorithm and applications. Future Gener Comput Syst. 2019;97:849–72. doi:10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]
34. Zhao S, Zhang T, Ma S, Wang M. Sea-horse optimizer: a novel nature-inspired meta-heuristic for global optimization problems. Appl Intell. 2023;53(10):11833–60. doi:10.1007/s10489-022-03994-3. [Google Scholar] [CrossRef]
35. Li S, Chen H, Wang M, Heidari AA, Mirjalili S. Slime mould algorithm: a new method for stochastic optimization. Future Gener Comput Syst. 2020;111(Supplement C):300–23. doi:10.1016/j.future.2020.03.055. [Google Scholar] [CrossRef]
36. Shang C, Zhou T-T, Liu S. Optimization of complex engineering problems using modified sine cosine algorithm. Sci Rep. 2022;12(1):20528. doi:10.1038/s41598-022-24840-z. [Google Scholar] [PubMed] [CrossRef]
37. Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm. Appl Soft Comput. 2008;8(1):687–97. doi:10.1016/j.asoc.2007.05.007. [Google Scholar] [CrossRef]
38. Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: a novel optimization algorithm. Knowl Based Syst. 2020;191:105190. doi:10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]
39. Sadollah A, Bahreininejad A, Eskandar H, Hamdi M. Mine blast algorithm: a new population-based algorithm for solving constrained engineering optimization problems. Appl Soft Comput. 2013;13(5):2592–612. doi:10.1016/j.asoc.2012.11.026. [Google Scholar] [CrossRef]
40. Trivedi IN, Bhoye M, Parmar SA, Jangir P, Jangir N, Kumar A. Ant-Lion optimization algorithm for solving Real Challenging Constrained Engineering optimization problems. In: International Conference on Computing, Communication & Automation, 2016; Greater Noida, India, IEEE. doi:10.13140/RG.2.1.2929.2409. [Google Scholar] [CrossRef]
41. Mokeddem D. A new improved salp swarm algorithm using logarithmic spiral mechanism enhanced with chaos for global optimization. Evol Intell. 2022;15(3):1745–75. doi:10.1007/s12065-021-00587-w. [Google Scholar] [CrossRef]
42. Gandomi AH, Yang X-S, Alavi AH. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng with Comput. 2013;29(1):17–35. doi:10.1007/s00366-011-0241-y. [Google Scholar] [CrossRef]
43. Yu K, Wang X, Wang Z. An improved teaching-learning-based optimization algorithm for numerical and engineering optimization problems. J Intell Manuf. 2016;27(4):831–43. doi:10.1007/s10845-014-0918-3. [Google Scholar] [CrossRef]
44. Fakhouri HN, Hudaib A, Sleit A. Hybrid particle swarm optimization with sine cosine algorithm and nelder-mead simplex for solving engineering design problems. Arab J Sci Eng. 2020;45(4):3091–109. doi:10.1007/s13369-019-04285-9. [Google Scholar] [CrossRef]
45. Li L-J, Huang Z, Liu F, Wu Q. A heuristic particle swarm optimizer for optimization of pin connected structures. Comput Struct. 2007;85(7–8):340–9. doi:10.1016/j.compstruc.2006.11.020. [Google Scholar] [CrossRef]
46. Saremi S, Mirjalili S, Lewis A. Grasshopper optimisation algorithm: theory and application. Adv Eng Softw. 2017;105:30–47. doi:10.1016/j.advengsoft.2017.01.004. [Google Scholar] [CrossRef]
47. Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput. 2019;23(3):715–34. doi:10.1007/s00500-018-3102-4. [Google Scholar] [CrossRef]
48. Lee KS, Geem ZW. A new meta-heuristic algorithm for continuous engineering optimization: harmony search theory and practice. Comput Methods Appl Mech Eng. 2005;194(36–38):3902–33. doi:10.1016/j.cma.2004.09.007. [Google Scholar] [CrossRef]
49. Akay B, Karaboga D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J Intell Manuf. 2012;23(4):1001–14. doi:10.1007/s10845-010-0393-4. [Google Scholar] [CrossRef]
50. Coello CAC. Use of a self-adaptive penalty approach for engineering optimization problems. Comput Ind. 2000;41(2):113–27. doi:10.1016/S0166-3615(99)00046-9. [Google Scholar] [CrossRef]
51. Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM. Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw. 2017;114:163–91. doi:10.1016/j.advengsoft.2017.07.002. [Google Scholar] [CrossRef]
52. Baykasoğlu A, Akpinar Ş. Weighted Superposition Attraction (WSA): a swarm intelligence algorithm for optimization problems–Part 2: constrained optimization. Appl Soft Comput. 2015;37(2):396–415. doi:10.1016/j.asoc.2015.08.052. [Google Scholar] [CrossRef]
53. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-Qaness MA, Gandomi AH. Aquila optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng. 2021;157(11):107250. doi:10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]
54. Chu S-C, Tsai P-W, and Pan J-S, Eds. Cat swarm optimization. In: PRICAI 2006: Trends in Artificial Intelligence: 9th Pacific Rim International Conference on Artificial Intelligence, 2006 Aug 7–11; Guilin, China: Springer. [Google Scholar]
55. Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]
56. Yasser MH. Breast cancer dataset 2021. Available from: https://www.kaggle.com/datasets/yasserh/breast-cancer-dataset/. [Accessed 2024]. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF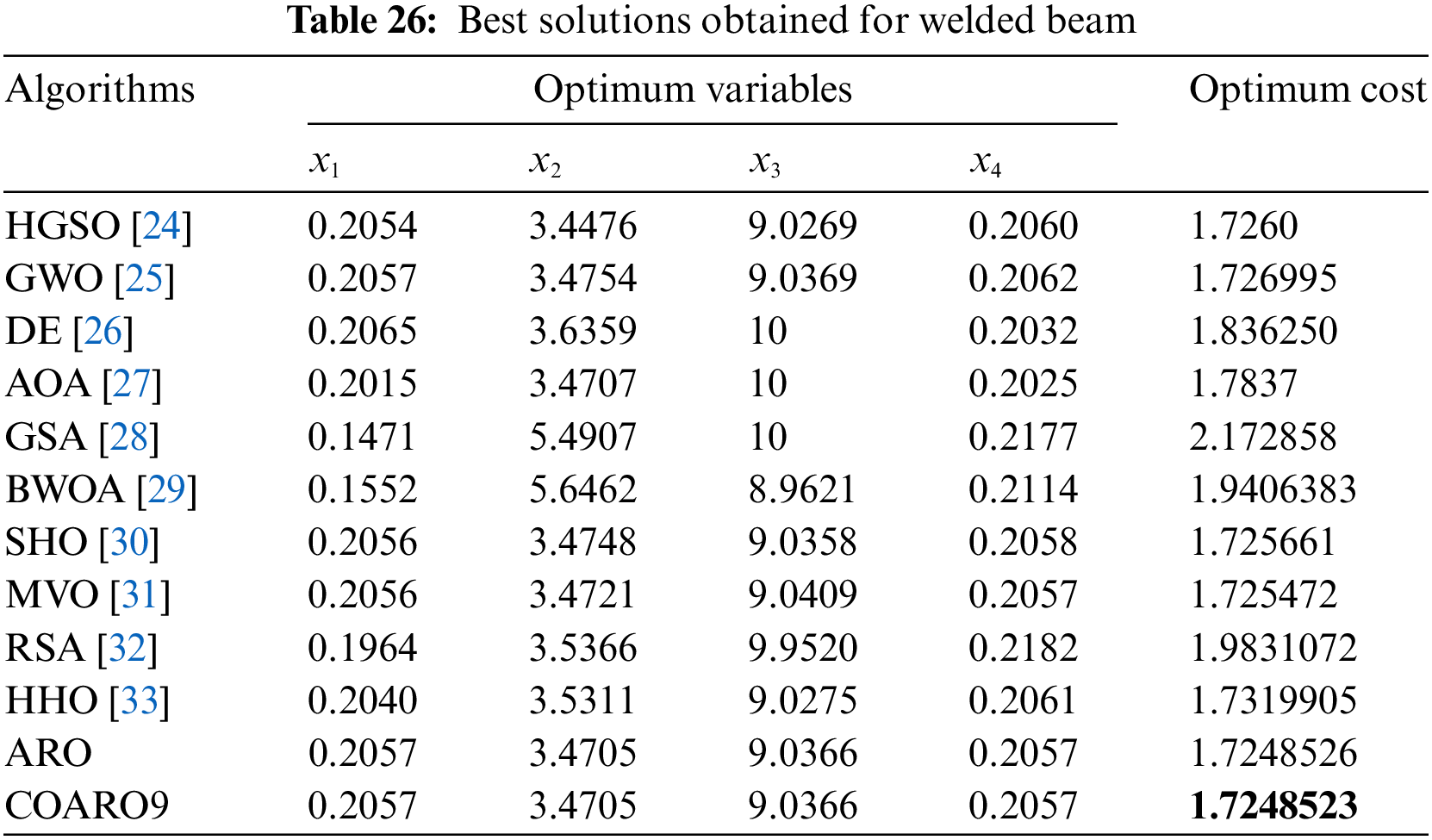
 Downloads
Downloads
 Citation Tools
Citation Tools