Task Offloading and Trajectory Optimization in UAV Networks: A Deep Reinforcement Learning Method Based on SAC and A-Star

1  Introduction

With the growth of artificial intelligence, the proliferation of intelligent terminal devices has led to a surge in data generation. This surge has imposed significant pressure on transmission networks and cloud computing centers. To address this challenge, mobile edge computing (MEC) has emerged as a solution, enabling devices to offload computing tasks to edge-deployed computing servers [1]. This approach not only alleviates the burden on transmission networks and cloud computing centers but also shortens the transmission distance between the computing server and terminal devices (TDs), thereby reducing communication transmission delays and enhancing user experience. Although edge computing offload effectively harnesses the abundant computing resources on edge servers, it also introduces additional communication overheads, including transmission energy consumption and communication delays. Consequently, multiplexing schemes, multiple input and multiple outputs (MIMO), and others have been proposed and thoroughly investigated. Literature [2] has developed a design method for MEC systems incorporating large-scale MIMO communication. The offloading performance of edge computing is intimately tied to the deployment of servers. In terms of the deployment of computing servers at the network’s periphery, a significant proportion of these servers are situated proximate to factories, warehouses, vehicles, and unmanned aerial vehicles (UAVs) [3], facilitating the provision of computing and processing services tailored to user’s requirements. To minimize energy consumption and task delays, Liao et al. [4] explored a MEC system encompassing servers and numerous mobile devices with computing requirements. Within this framework, an online algorithm known as dual reinforcement learning computing offload (DRLCO) is introduced. To facilitate task computation for vehicle users, Zhou et al. [5] investigated a vehicle MEC network that supports multi-user caching. In the scheme, one of the edge servers (ES) possesses caching and computing capabilities, the challenges of delay, energy consumption, and profitability that impact system performance are formulated as a binary integer programming problem. Unfortunately, the feasibility of resource allocation schemes for edge computing based on ground mobile devices is significantly compromised in constrained deployment environments, primarily due to the neglect of edge server location layout.

To address the limitations of ground-based edge computing in constrained deployment environments, edge computing schemes leveraging UAVs have been introduced. These UAV-based edge computing solutions [6,7] distinguish themselves from traditional ground-based approaches [8,9] by redefining the deployment of computing resources. Ground-based edge computing primarily distributes computing capabilities to devices at the network periphery, whereas UAV-based edge computing integrates computing power within the UAV systems, enabling direct provision of computational resources to users. This approach offers several unique advantages, particularly the high flexibility of UAV deployments. In scenarios involving natural disasters, such as typhoons and earthquakes, where roads become impassable, UAVs can seamlessly access areas with limited network coverage, promptly delivering computing services to affected users. Furthermore, during periods of excessive load or unavailability of ground-based computing servers, UAVs can be rapidly deployed to designated regions, fulfilling temporary computational demands and enhancing the resilience of edge computing systems. However, the batteries carried by drones possess limited energy capacity. When IoT devices are widely distributed on the ground, UAVs need to fly from one position to another to ensure reliable computation offloading for all IoT devices, which consumes a significant amount of energy. Limited energy capacity greatly restricts the service time of drones.

To reduce the energy consumption of UAV-enhanced edge computing, Li et al. [10] proposed a near-end strategy optimization algorithm to dynamically learn the offloading strategy and trajectory design strategy. In their scheme, the system’s energy consumption had been reduced through the joint optimization of the flight trajectory and computing resources of the UAV. However, the solution only analyzed the application scenarios of a single UAV. To mitigate energy consumption in scenarios involving multiple UAVs, Luo et al. [11] introduced a collaborative search framework leveraging edge computing. Within this framework, they presented a cooperative target search strategy known as Uncertainty Minimization-based Multi-UAV Cooperative Target Search. Nevertheless, the simulation of this approach overlooked the crucial aspect of collision avoidance during the UAVs’ movements, rendering its credibility limited. To reduce system energy consumption, Li et al. [12] proposed an MEC scheme assisted by multiple UAVs, where the UAVs collaborate to provide services to Internet of Things (IoT) devices. This approach avoided the issue of collision avoidance by directly specifying the optimized deployment locations for the UAVs. However, it is regrettable that the scheme did not consider the mobility and trajectory optimization of the UAVs, leading to a potential decrease in its effectiveness when ground-based IoT devices are mobile. To address the joint optimization challenge posed by queue-based computing offloading and adaptive computing resource allocation, Goudarzi et al. [13] introduced a computing resource allocation model leveraging cooperative evolutionary computation. The simulation results assert that their method satisfies task computing constraints while mitigating energy consumption in UAVs and mobile nodes. Nevertheless, the scheme neglected the pivotal aspect of collision avoidance for UAVs, and the experimental setup omitted trajectory optimization, thereby significantly limiting the practical viability of the scheme.

Moreover, the communication between UAVs and ground devices predominantly utilizes the line-of-sight transmission mode, characterized by its broadcast nature. This mode of communication renders UAVs vulnerable to eavesdropping by adversaries, thereby posing significant security challenges. In actual drone operation, the drone systems employ various sensor modules, including cameras, global positioning systems (GPS), and optical flow sensor modules to gather data and facilitate communication. However, these modules generate a significant volume of sensitive information, which adversaries may intercept during transmission through various means, rendering communication between drones and users vulnerable to security risks like interference and eavesdropping attacks. To safeguard the communication security of drones and mitigate threats such as GPS deception, where control of drones can be deceived by transmitting falsified coordinates, precautions must be taken. Sharma et al. have compiled a summary of existing electromagnetic wave interference attacks and their respective countermeasures [14]. Similarly, Kim et al. have consolidated various research findings on the effects of intentional electromagnetic interference (IEMI) on these sensor modules [15]. Consequently, the importance of safeguarding communication security between UAVs and ground devices has garnered increasing attention. However, it is regrettable to note that the aforementioned studies have overlooked this crucial factor, leaving a gap in ensuring secure communication in practical applications. Considering different enabling techniques for UAV-enabled MEC, the state-of-art solutions to the above-mentioned problems are reviewed as follows.

2  Related Works

To provide secure services, Karmakar et al. [16] proposed an intelligent mechanism called FairLearn. And, a fairness optimization problem was developed to maximize the average achievable confidentiality rate during the operation cycle of UAVs, and a deep neural network (DNN) based model was used to solve this problem. However, the maximum confidentiality rate achieved in the scheme is subject to constraints such as system latency and energy consumption. Consequently, while striving to maximize the confidentiality rate, it is noteworthy that the latency may not be optimized, potentially compromising user experience. To bolster the security of UAV-enabled MEC, Li et al. [17] introduced an alternative algorithm leveraging successive convex approximation. This algorithm jointly optimizes task allocation, the transmission power of individual devices, and the trajectory of the UAV, thereby minimizing the total energy consumption of the UAV. However, this scheme does not directly consider variables such as system latency and security throughput. To overcome the issue of malicious nodes overhearing the relay transmission of dual role UAV (DUAV), Wang et al. [18] developed a joint optimization of DUAV’s hover position, transmission power, and calculation rate allocation, and DUAV’s transmission duration and calculation offloading. However, while their scheme primarily aimed to minimize the overall energy consumption of DUAV and all cell-edge users (CEUs), it neglected the UAV’s flight trajectory and energy utilization. By comprehensively considering task offloading, resource allocation, and security assurance, He et al. [19] proposed an iterative algorithm based on relaxation and rounding and Lagrange methods to minimize the task processing delay. However, it neglected to enhance the secure transmission rate while striving to minimize system latency. Wei et al. [20] comprehensively considered the hovering energy consumption, flight energy consumption, and edge computing processing energy consumption of the UAV, and proposed a deep Q network (DQN) framework algorithm based on deep reinforcement learning to enable the UAV to perform as many tasks as possible on the trajectory to the destination. However, the security of user data offloading and transmission to drones has not been considered.

Under the constraints of secure offloading rate and computation delay, Gu et al. [21] proposed an edge computing scheme that jointly optimizes the allocation of computation and communication resources. Unfortunately, the energy consumption of UAV flight is not included in the system model. To improve security computing efficiency, the authors of [22,23] proposed efficient offloading schemes for UAV-assisted MEC. However, the energy consumption and impact of obstacles during UAV flight are not included in the system model, thus limiting their effectiveness. To enhance the secure computing capability of the edge networks, the authors of [24,25] proposed secure communication schemes for UAV-based MEC systems. While their schemes employed continuous convex approximation and block coordinate descent (BCD) methods to improve the average secure computing capability of the system, they neglected the crucial factors of UAV trajectory planning and flight energy consumption in the presence of obstacles.

2.1 Motivations and Contributions

The above researches have the following shortcomings: First, the joint optimization schemes aim to maximize system security benefits by jointly optimizing various parameters such as the UAV flight path and offloading ratio. Nevertheless, it is noteworthy that maximizing system security benefits may not necessarily translate into optimal system latency, energy consumption, or the secure offloading rate between UAVs and users. This potential trade-off could lead to compromised user experience and information security during the offloading process. Secondly, in the joint optimization problem involving the secure offloading rate between UAVs and users, system delay, and system energy consumption, the treatment of system energy consumption is insufficient. The analysis of system energy consumption fails to consider and differentiate the significance of the relationship between UAV hovering energy consumption, flight energy consumption, edge task processing energy consumption, and the secure offloading rate. This oversight resulted in an inadequate assessment of the overall system energy consumption, potentially compromising efficiency and sustainability.

To address these challenges, we introduce a novel algorithm termed the A* Soft Actor-Critic (SAC) algorithm. This algorithm leverages a task-offloading function to determine the optimal hovering position and task-offloading ratio for the UAV. This approach aims to maximize system efficiency, encompassing system energy consumption, user delay, and secure offloading rate during hovering flight. By doing so, we ensure an enhanced user experience and improved information security while minimizing the aggregate hovering energy consumption and task processing energy expenditure. Furthermore, our algorithm incorporates path-planning techniques to identify the optimal trajectory for the UAVs to reach the designated hover points. This optimization reduces the flight energy consumption of the UAVs, thereby leading to lower overall energy consumption for the entire process, ultimately translating into reduced system energy consumption.

The main contributions of this paper are as follows:

1)   The energy consumption profile of a UAV encompasses multiple components: hovering flight, constant speed flight, and task execution. Notably, only the energy expended during task execution holds a direct correlation with delay and the secure transmission rate of data. Therefore, we construct the optimization problem that aims to maximize system benefits, encompassing energy consumption of task execution, user delay, and secure data transmission rate. This optimization is achieved through a concerted effort to refine the hovering positions of the UAVs and adjust the task offloading ratio. Furthermore, given the fixed energy expenditure during hovering flight, the energy used by the UAV during constant-speed flight is solely determined by the path traversed from its starting point to the optimized hovering position. This leads us to formulate an optimal path problem for the UAVs, one that aims to minimize energy consumption during constant-speed flight. This optimization considers not only the energy efficiency of the UAV but also factors such as potential collisions with obstacles and inter-UAV collisions, ensuring a safe and energy-efficient flight trajectory.

2)   Owing to the intricate, high-dimensional nature of the state and action spaces within the task offloading model, coupled with their dynamic and non-discrete characteristics, maximizing system benefits presents a nonlinear programming challenge that often falls into the category of Nondeterministic Polynomial-time (NP) hard problems. To address this complexity, we propose an innovative A*SAC algorithm, which builds upon the SAC and A* algorithms to tackle both the NP-hard system benefit optimization and the optimal path planning for UAVs. The A*SAC algorithm is employed to maximize system benefits through the meticulous adjustment of the task offloading function. Additionally, the algorithm’s path planning function ensures the establishment of an optimal collision-free trajectory for the UAV to navigate towards its optimal hovering position. By leveraging the strengths of A*SAC, our approach not only addresses the computational challenges associated with high-dimensional state and action spaces but also ensures the efficient and safe navigation of UAVs in dynamic environments.

3)   Simulation results show that our proposed A*SAC algorithm can greatly improve the system’s utility, and establish the optimal hovering position of the UAVs and the optimal user offloading ratio. Specifically, it exhibits an average improvement of 13.18% in terms of different computing task sizes, an average improvement of 3.05% in terms of different task complexity, 25.61% higher on average in terms of the power of electromagnetic wave interference intrusion into UAVs emitted by different auxiliary UAVs, and 35.78% higher on average in terms of the maximum computing frequency of different auxiliary UAVs. During the performance verification of path planning, diverse obstacle environments were meticulously established to simulate real-world conditions. Notably, each UAV demonstrated its ability to effectively identify and traverse the optimal collision avoidance path, ensuring a safe and efficient journey to the designated endpoint.

The remaining parts of this article are as follows. In Section 3, the system model and optimization problem of this article are proposed. In Section 4, we introduce the A*SAC algorithm based on SAC and A*. Simulation analysis is presented in Section 5. Finally, we summarized our work in Section 6.

3  Problem Statement

3.1 System Model

As shown in Fig. 1, in this paper, we consider a security edge computing system enhanced by multiple UAVs, which includes auxiliary UAVs, invading UAVs, user equipment, and several obstacle areas R1. The auxiliary UAVs serve as edge computing servers, aiding users in carrying out computational tasks, and they are also capable of communicating with each other. As mobile eavesdroppers, invading UAVs hover and fly to intercept the offloading information transmitted from user devices to auxiliary UAVs. The auxiliary UAV is equipped with two antennas. One receiving antenna is utilized to capture offloading signals from the user, while the other transmitting antenna emits interference signals aimed at the invading UAV. Both the user and the invading UAV possess antennas dedicated to transmission and eavesdropping, respectively. In obstacle-ridden areas, UAVs are unable to traverse and must therefore detour, restricted to flying or hovering within designated P ∗ P areas. This article focuses on a multiple access channel scenario, where all users can concurrently transmit their signals using the same channel [26]. Additionally, it is presumed that the auxiliary UAV has accurate knowledge of each user’s position and the channel status information for all links within the multi-UAV edge computing system, either through synthetic aperture radar (SAR) or other means [27].

Figure 1: System model diagram

3.2 Communication Model

Based on the aforementioned system model, the set of auxiliary UAVs is set to M1={1,2,3,⋯,ς}, where ς is the total number of auxiliary UAVs; the set of invading UAVs is set to M2={1,2,3,⋯,ξ}, where ξ is the total number of invading UAVs; the set of user devices is set to N={1,2,3,⋯,ζ}, where ζ is the total number of user devices. Table 1 enumerates the primary symbols and their corresponding physical meanings that will be utilized throughout the text.

In this article, the vertical height of the user devices remains fixed, meaning that we solely consider the horizontal positions of the user devices. The position of the user device i is represented by ni=(xi,yi), where i∈N. The vertical height of the auxiliary UAV j is represented by zj, and the horizontal position is represented by mj=(xj,yj), where j∈M1. The vertical height of the invading UAV u is represented by zu, and the horizontal position is represented by qu=(xu,yu), where u∈M2. For air-to-ground channels, assuming that the Doppler frequency shift in communication can be compensated by the receiving end, the channel quality depends on the link between the UAV and the user. Since the UAV links are all LoS (Line of Sight) [28], the channel power gain between user device i and auxiliary UAV j can be expressed as

kij=β1d−2=β1zj2+∥mj−ni∥2.(1)

where i∈N, j∈M1, β1=gtgr(λ4πd0)2, parameter β1 represents the received power with a transmission power of 1W at a reference distance of d0=1m, with gt and gr representing the transmission gain of the user antenna and the reception gain of the UAV antenna, respectively, and λ representing the wavelength of the transmission signal.

The uplink transmission rate between user device i and auxiliary UAV j is expressed as

rij=log2(1+pikijχpjam+σ2).(2)

where i∈N, j∈M1, parameter pi denotes the transmission power of user i, and σ2 denotes the noise power, and χ is the self-interference coefficient, and pjam is the power of the auxiliary UAV to emit electromagnetic wave interference and invade the UAV. This also causes the auxiliary UAV to generate a self-interference noise signal of χ×pjam. The channel power gain between user device i and intrusion UAV u can be expressed as

kiu=β1d−2=β1zu2+∥qu−ni∥2(3)

where i∈N, j∈M1, β1=gtgr(λ4πd0)2. Similarly, in the air channel between the auxiliary and invasive UAVs, the channel power gain between the invasive UAV u and the auxiliary UAV j can be expressed as

kju=β2d−2=β2(zj−zu)2+∥qu−mj∥2(4)

where j∈M1, u∈M2, β2=grgr(λ4πd0)2, parameter β2 represents the channel gain between the auxiliary UAV and the invading UAV at the reference distance of d0=1m. The uplink transmission rate between user device i and intrusion UAV u can be expressed as

riu=log2(1+pikiukjupjam+σ2)(5)

where i∈N, u∈M2. We do not take into account the information security threats that arise during the local computing process executed by user devices, but solely focus on the information security issues that occur during the process of offloading tasks to auxiliary UAVs. The secure offloading rate from user device i to auxiliary UAV j [29–31] can be expressed as

Rijsec=[rij−riumax]+(6)

where i∈N2, j∈M1, u∈M2, parameter riumax represents the maximum transmission rate of eavesdropping on user device i in the intrusion UAV, [X]+=Δmax(X,0).

3.3 Time Delay Model

In the entire MEC system, user device i needs to regularly process computationally intensive tasks Wi=(Di,Ci), where Di represents the size of the task and Ci denotes the number of CPU cycles required to process this data. For user device i, the overall data computation procedure is bifurcated into dual components: local computation executed by the user device itself and computation carried out by auxiliary UAVs. Here εi1 and εij denote the task offloading proportions for user device i. This signifies that the total data volume of user device i is partitioned such that a fraction εi1×Di is processed locally by the user device, while another portion εij×Di is offloaded to auxiliary UAV j. It should be noted that the sum of these fractions complies with the unity condition, i.e., εi1+∑j∈M1εij=1. At this point, the local computing latency of user device i can be expressed as

Tiloc=εi1×Di×Cif0(7)

where i∈N1, parameter f0 is the local calculation frequency of the user, and by default, the local calculation frequency of each user is the same. The transmission bandwidth of each user in the channel is denoted by B, then the transmission delay from user device i to the auxiliary UAV j can be expressed as

Ti1ul=εij×DiB×rij(8)

where i∈N1. The latency incurred by the auxiliary UAV j during the execution of offloaded tasks can be expressed as

Ti1c=εij×Di×Cifij(9)

where i∈N1, parameter fij represents the calculation frequency assigned by the auxiliary UAV j to user i.

The proportional distribution of computing resources of auxiliary UAV to the offloaded task satisfies the following expression:

∑i=1N1εij×fij=fmaxUAV(10)

where fmaxUAV represents the total computing resources of the auxiliary UAV.

3.4 Energy Consumption Model

In the MEC system, it is assumed that the user equipment (UE) draws power directly from a stable energy source, hence its energy expenditure is not under consideration within our analysis. Our primary focus lies in the energy consumption attributed to the auxiliary UAV. The UAV’s energy consumption can be bifurcated into two principal categories: the energy consumed for maintaining flight operations and the energy expended during the execution of offloaded tasks. The component of flight energy consumption primarily encompasses the energetic demands associated with both hovering and uniform-speed flight maneuvers. The energy consumption for the hovering flight of the auxiliary UAV j can be expressed as [20]

EjU=nr×(Mg)322Lπβ2×TjU(11)

where nr is the number of rotors, g is the gravity constant, L is the fluid density in the air, β is the radius of the rotor disk, M is the total weight of the UAV, and TjU is the duration of hovering flight.

The energy consumption of the auxiliary UAV j during constant speed flight [20] can be expressed as

EjFX=κ×‖VjFX‖2(12)

where κ=0.5Mjδj, δj is the duration of the motion of the auxiliary UAV j, Mj is the total mass of the auxiliary UAV j, and VjFX is the velocity vector.

The energy consumption incurred by UAVs during task execution comprises three distinct aspects: Firstly, energy cost associated with the transmission of electromagnetic waves for the purpose of interference against potential intruders. Secondly, energy consumption is generated during the reception process of user-offloaded data. Lastly, computational energy expenditure results from the calculating offloaded tasks. The interference energy consumption generated by auxiliary UAVs transmitting electromagnetic waves to user equipment can be expressed as

Ejijam=pjam×Ti1ul(13)

Let pu denotes the power of the legitimate UAV to receive offloaded data, then the transmission power consumed by UAV j during the process of receiving offloaded data from user i can be expressed as

Ejiul=pu×Ti1ul(14)

The calculated power of the UAV is pic=υ×(fij)3, where υ denotes the power consumption coefficient, whose value depends on the CPU chip structure of the UAV edge server [32]. Therefore, the computational energy consumption incurred by the auxiliary UAV j for an offloaded task from user i can be expressed as

Ejic=pic×Ti1c=υ×εi×Di×Ci×(fij)2(15)

The energy consumption associated with the execution of tasks by the auxiliary UAV j can be expressed as

Ej1=∑i=1N1(Ejijam+Ejiul+Ejic)(16)

Then, the total energy consumption of the auxiliary UAV j can be expressed as

Ej=EjFX+EjU+Ej1(17)

3.5 Problem Formulation

In this multi-UAV secure communication edge computing system, the optimization objective of this paper is to minimize the system energy consumption, which is composed of UAV hovering energy consumption, UAV uniform flight energy consumption, and UAV edge task processing energy consumption, while simultaneously reducing user delay and enhancing the security of offloaded information. However, UAV hovering energy consumption and uniform flight energy consumption are not directly related to user delay and UAV secure data transmission rates. If the hovering and uniform flight energy consumption were forcibly optimized together with the secure data transmission rate, the resulting optimization might not be the most optimal. Therefore, we combine user delay, UAV secure data transmission rate, and UAV edge task processing energy consumption into a system utility maximization optimization problem. In this optimization problem, we consider UAV hovering energy consumption and uniform flight energy consumption as constraints. This enables the UAVs to hover at the location that maximizes system utility for data processing, thereby enhancing user experience. Additionally, to ensure that the multi-UAV system has sufficient energy to hover at the optimal location for processing, it is imperative to minimize the uniform flight energy consumption as much as possible. Since uniform flight energy consumption is closely related to flight paths and collision avoidance, the problem of minimizing uniform flight energy consumption is transformed into a minimum collision-avoidance path planning problem, which is optimized separately.

In the UAV-based edge computing system, the joint optimization of the secure offloading rate, system delay, and system energy consumption between UAVs and users usually takes the delay or energy consumption as a constraint. It is conceivable that the optimality of the system’s delay, energy consumption, or the secure offloading rate between UAVs and users may not be achieved when the system security benefits are maximized. Consequently, this could potentially impact the user experience and the security of the offloaded information. To address this issue, we focus on solving the secure communication problem by incorporating the energy consumption associated with edge computing task execution by auxiliary UAVs. Furthermore, we define the system benefit as as the difference between the average secure offloading rate from each user device to each auxiliary UAV, the average delay of each user device, and the average energy consumption of edge computing task execution of each auxiliary UAV, that is

η1=1N11M1∑i=1N1∑j=1M1Rijsec−(1N1∑i=1N1Ti+1M1∑j=1M1Ej1)(18)

The optimization problem can be modeled as problem P1:

maxqu,εij,fij⁡η1.(19)

s.t.

C1:εi1,εij∈[0,1].(20)

C2:εi1+∑j∈M1εij=1.(21)

C3:xi,yi,xj,yj,xu,yu∈[0,P].(22)

C4:∑i=1N1εij×fij=fmaxUAV.(23)

C5:Ej<E.(24)

C6:xj,yj∉R1.(25)

Constraints C1 and C2 indicate that the task is executed in collaboration between the user and the UAV. Constraint C3 is to ensure that users, auxiliary UAVs, and intrusion UAVs maintain a constant flight speed or hover within the designated P ∗ P area. Constraint C4 ensures that the allocation of total available resources of the auxiliary UAV is commensurate with the size of the task data offloaded by the user. It further ensures the optimal utilization of computing resources, thereby avoiding any wastage. Constraint C5 ensures that the UAV possesses sufficient energy to maintain a uniform speed towards the position with the highest safety benefit, and to hover at that position, thereby improving communication and computing services for user devices. Constraint C6 ensures that the auxiliary UAV avoids obstacles.

At this point, a direct solution to problem P1 is not feasible due to several reasons. Firstly, the average secure offloading rate from user devices to auxiliary UAVs, the average delay of each user device, and the average energy consumption of each auxiliary UAV, all under constraint conditions, exhibit relatively low values. These factors are intricately linked to the hovering position and user offloading ratio of the UAV, making it susceptible to abrupt fluctuations in the optimization target value during adjustments to these parameters. Consequently, identifying the optimal target value corresponding to specific hovering positions and user offloading ratios becomes challenging.

Secondly, the optimization objective aims to enhance the average secure offloading rate from user devices to auxiliary UAVs while minimizing the average latency of each user device and the average energy consumption of each auxiliary UAV. However, under the given constraints, the values of these metrics remain relatively small. A direct solution approach may result in scenarios where the optimization objective value reaches an optimal or maximum point at a specific UAV hovering position and user offloading ratio but at the cost of elevated average secure offloading rates and increased average delays for user devices. Thus, it leads to higher average energy consumption for auxiliary UAVs. Therefore, a more sophisticated approach is required to effectively address the problem P1.

Here, we will transform the original optimization problem P1 into an equivalent problem P2:

maxqu,εij,fij⁡η2.(26)

η2=1N1∑i=1N1∑j=1M1Rijsec−(∑i=1N1Ti+∑j=1M1Ej1).(27)

s.t. (20)(21)(22)(23)(24)(25).(28)

The system benefits are not only related to the user’s offloading strategy but also to the position of the auxiliary UAV. As the number of users increases, the action space of the joint strategy expands exponentially. So, we propose an A*SAC algorithm, which integrates SAC and A*, to effectively tackle this challenging optimization task.

4  A*SAC algorithm

In recent years, the advancement of artificial intelligence has led to a surge of interest in machine learning frameworks, which can effectively harness crucial information in unpredictable environments. Consequently, there has been a growing trend to integrate machine learning with edge computing, and many scholars have achieved good results. The state space and action space of the edge computing network model proposed in this paper are characterized by high-dimensional, dynamic, and non-discrete actions. The traditional multi-objective optimization algorithms usually rely on a comprehensive search of space or building models to estimate the optimal strategy. In high-dimensional, dynamic, and non-discrete environments, the computational load and storage requirements increase sharply, which makes it difficult for traditional methods to deal with all possible state and action combinations and find a globally optimal solution. In this paper, we construct our algorithm based on deep reinforcement learning to optimize the target value.

Single-agent or multi-agent algorithms based on deep reinforcement learning, such as Deep Deterministic Policy Gradient (DDPG) [33,34], SAC [35–37], and Proximal Policy Optimization (PPO) [38], have different effects in different environments. In this paper, we employ a single-agent algorithm to optimize the target value. The choice of this algorithm is multifaceted. Firstly, the optimization objective is intricately related to the positioning of the UAV, obstacle locations, and the dimensions of the flight area. Utilizing a single-agent algorithm based on PPO for objective value optimization may result in the auxiliary UAV’s position straying outside the designated constraint area, potentially interfering with the random strategy learning of PPO and ultimately leading to suboptimal results [39]. Using a single agent algorithm based on DDPG to optimize the target value may encounter difficulties in balancing exploration and exploitation, often converging to suboptimal solutions [40]. Secondly, SAC exhibits a high degree of exploration and robustness, enabling it to effectively explore the optimal strategy from the vast action space in complex and dynamic environments. Furthermore, it can be utilized to solve the optimization problem aimed at maximizing system benefits. For path planning problems, consider that A* algorithm [41,42] is a heuristic algorithm for path and graph search. The A* algorithm can select suitable heuristic functions based on specific needs. For example, Manhattan distance, Euclidean distance, and others can be utilized in different scenarios, showcasing strong adaptability. Additionally, heuristic functions serve to diminish the search space, aiding algorithms in selecting paths more intelligently and obviating the need for a complete search of the entire graph, thereby achieving high efficiency. The implementation of the A* algorithm follows clear steps and has a structured process that can be integrated with other algorithms and techniques, such as dynamic programming and local optimization. This characteristic renders it highly efficient in finding the shortest path and enables its application in solving the minimum collision avoidance path planning problem.

As the secure data transmission rate does not directly correlate with UAV energy consumption at constant speed, energy consumption is not directly optimized for maximizing system benefits. Instead, latency, secure offloading rate, and system benefits’ size depend on the UAV hovering position and task offloading proportion. To optimize UAV energy consumption during uniform flight, we focus on optimizing the flight path. Obtaining optimal hovering position, offloading ratio, and flight path with deep reinforcement learning algorithms like PPO, DDPG, and SAC is challenging. Thus, we combine SAC with A* to propose the A*SAC algorithm for solving these issues.

4.1 Markov Decision Process

The A*SAC algorithm is a deep reinforcement learning algorithm that requires transforming problem P2 into a Markov decision process (MDP) before solving the optimization problem. The Markov decision process corresponding to problem P2 is represented by a tuple ρ={S,A,P,R}, where S represents the state space, A represents the action space, P represents the state transition matrix, and R represents the reward function. The specific description of each element is as follows:

1) State space: If the state space of the system at time t is st, then st can be represented as st={mjt,εi1t,εijt,Ejt}. mjt represents the horizontal position of the auxiliary UAV j at time t, εi1t represents the proportion of local task processing by user device i at time t, εijt represents the proportion of task offloaded from user device i to auxiliary UAV j, and Ejt represents the remaining energy of auxiliary UAV j at time t.

2) Action space: To make the most of the available resources of UAVs and user devices, it is necessary to make appropriate action decisions based on the different states of each time slot t. Let the action space of the system at time t be at, define the action space as at={Aitd→d,Aijtd→uav,Ejt,mjt}, and satisfy

Aitd→d+∑j=1M1Aijtd→uav=1.(29)

where Aitd→d represents the proportion of task volume of user device i calculated locally. Aijtd→uav represents the proportion of task volume offloaded from user device i to auxiliary UAV j. mjt represents the horizontal position of the auxiliary UAV j at time t, and Ejt represents the remaining energy of the auxiliary UAV j at time t.

3) State transition matrix: The state transition probability in state transition matrix P represents the probability of the system moving to the next state st+1 after taking action at at state st.

4) Reward function: Every time the agent acts, the environment automatically assigns a reward. To maximize the system benefit η2, in this paper, we define the reward function as the system benefit η2. Apart from the four elements mentioned above, there is a hyperparameter γ. Denoting γ as the future reward weight, its value is in [0,1]. The choice of γ influences whether the system favors short-term or long-term rewards.

4.2 A*SAC Algorithm Framework

After defining the Markov decision process for the system, we proceed to demonstrate how to use the A*SAC algorithm based on SAC and A* to learn the task partitioning strategy for each user device and hovering flight strategy for auxiliary UAVs, and identify the optimal path for the UAVs. The framework of the proposed A*SAC algorithm based on SAC and A* is shown in Fig. 2. It comprises eight modules: environment, Agent 1, Agent 2, experience buffer, the A* algorithm, participant network, criticism network, and target network of criticism network. In the framework of the A*SAC algorithm, Agent 1 first inputs the environmental state st into the participant network to derive the action at, then this action at is relayed back to the environment. The environment will change accordingly to obtain the next environmental state st+1 and corresponding reward rt. Then Agent 1 inputs the updated environmental state st+1 into the participant network to acquire the subsequent action at+1. This newly obtained action at+1 is once again feedback to the environment, leading to further modifications in its state. These modifications yield the next environmental state st+2 and associated reward rt+1. Similarly, subsequent states st+2,⋯,st+n, actions at+2,⋯,at+n, and rewards rt+2,⋯,rt+n can be obtained. During the change process, the (st,at,rt,st+1) is stored in the replay pool, up to a predefined maximum capacity. When the replay pool does not reach its minimum storage threshold, the action at+2,⋯,at+n will be obtained by the initially initialized participant network. Once the playback pool attains its minimum storage capacity, G tuples {(si,ai,ri,si+1)}i=1,...,G is randomly sampled from the playback pool. For each tuple, the target network performs a calculation as follows

Figure 2: A*SAC algorithm framework

yi=ri+γminj=1,2Qωj(si+1,ai+1)−αlog⁡πθ(ai+1|si+1).(30)

The minimum loss function for j=1,2 can be expressed as follows:

L=1N∑i=1N(yi−Qωj(si,ai))2.(31)

Then, the two Critic networks can be updated. Due to the environment of continuous action space, the strategy output of the SAC algorithm is the mean and standard deviation of the Gaussian distribution. Therefore, it is necessary to employ reparameterization techniques to sample action a~i, and then use the following loss function (32) to update the current Actor network.

Lπ(θ)=1N∑i=1N(αlog⁡πθ(a~i|si)−minj=1,2⁡Qωj(si,ai)).(32)

The coefficient α of the entropy regularization term can be updated through loss function (33).

L(α)=Esi∼G,ai∼(•|st)[−αlog⁡π(at|st)−αH0].(33)

finally, update the target network

ω1−←τω1+(1−τ)ω1−.(34)

ω2−←τω2+(1−τ)ω2−.(35)

Proceed with the aforementioned procedure iteratively until either convergence is attained or the pre-established threshold of training iterations is achieved.

The collision avoidance A* algorithm in the framework will first randomly select an auxiliary drone to calculate the total cost, actual cost, and heuristic estimation cost of the path nodes based on Formula (36), to obtain the optimal path. Similarly, obtain the optimal path for the next auxiliary drone.

f(n)=g(n)+h(n).(36)

where f(n) is the total cost from the starting point to node n. g(n) is the actual cost. h(n) is the heuristic estimation cost from node n to the target node. After getting the individual optimal path for each auxiliary UAV, a comparative analysis is conducted between the optimal path points of these UAVs to ascertain whether there exist instances where two or more UAVs would converge at a singular path point concurrently. If simultaneous arrival at any path point is not projected, the presently computed paths are the optimal trajectories for each auxiliary UAV. Otherwise, a remedial strategy is invoked wherein the trajectory of one auxiliary UAV is fixed, while the coinciding path point is reclassified as a novel obstacle for the other UAVs within their navigational landscape. The other auxiliary UAVs will recalculate their trajectories and search for alternative optimal paths through an iterative process that continues until all path intersections between the auxiliary UAVs are avoided. The total computational complexity of A*SAC is O(T⋅K⋅G⋅L1⋅L22+R2R3), where T is the total number of training time steps, K is the number of updates in each step, G is the batch size of each update, L1 is the number of layers in the neural network, L2 is the number of neurons in each layer, R2 is the branching factor for each node, that is, the number of possible child nodes for each node, and R3 is the depth of the shortest path from the starting point to the target node. In practical applications, the appropriate network size can be selected based on the specific scenario task, and the appropriate computing resources can be selected based on the current computational complexity so that the algorithm can complete the task within an acceptable time. The pseudocode of the proposed algorithm is illustrated in Algorithm 1.

5  Simulation

5.1 Parameter Settings

In this paper, we employ Python 3.10 software for simulation experiments, and the simulation environment parameters are set according to references [23,33,43]. In an open and obstructed environment, 9 users, 2 auxiliary UAVs, and 1 invasive UAV are distributed in a square area of 400m×400m. Each user device needs to regularly process computationally intensive tasks, and their horizontal positions are shown in Fig. 3. The auxiliary UAVs and intrusion UAVs maintain fixed height, and zj=100m, zu=120m. Auxiliary UAVs 1 and 2 are capable of flying within the designated 400m×400m area, providing users with computing resources, while strictly avoiding obstacles. The fundamental task volumes are configured as follows: User Equipments 1, 2, 4, 5, and 8 are each allocated 20 Kbit, User Equipments 3 and 9 are set to 30 Kbit, while User Equipments 6 and 7 are assigned 40 Kbit.

Figure 3: Simulation environment area map

Given that the two Critic neural networks have the same structure, Table 2 lists the simulation parameters used by the Actor network and the two Critic networks in the A*SAC algorithm. The remaining simulation parameters are shown in Table 3.

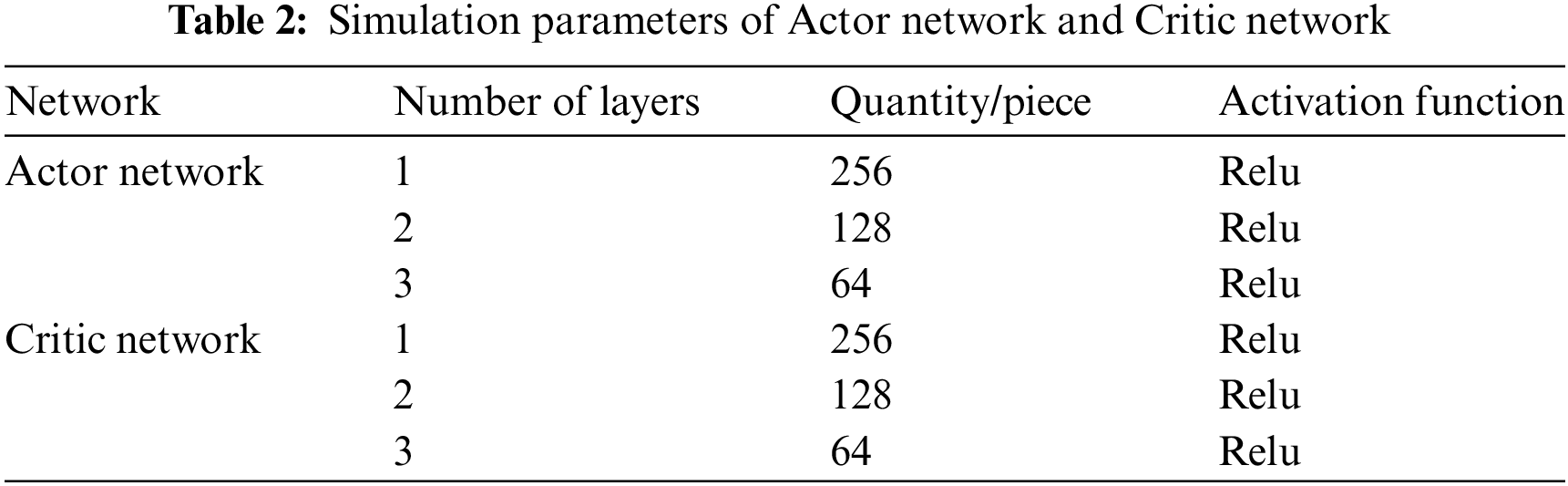
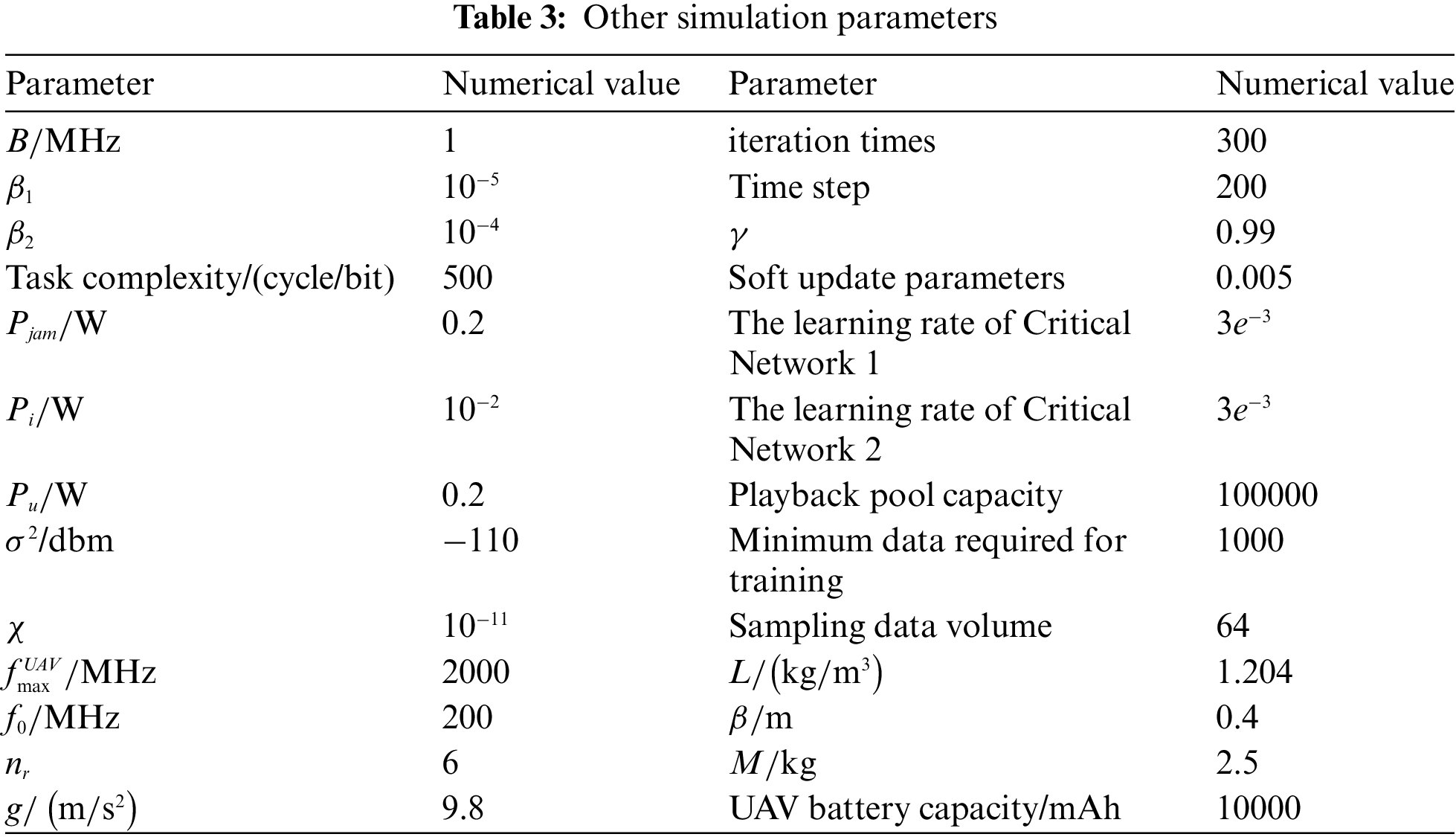
5.2 Analysis of Simulation Results

Due to the intimate interplay between path planning and the optimal hovering position of drones, in this paper, we initially assess the task offloading performance of the A*SAC algorithm and then evaluate the algorithm’s path planning performance. In terms of task offloading performance, the proposed A*SAC algorithm was first analyzed for its performance at different learning rates. To evaluate the efficiency of task offloading, we compare the performance of our proposed algorithm with DDPG [33,34], PPO [38,39], DDQN [44], and Advantage Actor-Critic (A2C) [45] algorithms in terms of task volume and complexity. Then, the adaptability of the A*SAC algorithm to diverse obstacle-laden environments was analyzed by deploying it across a range of such environments. The ability of path planning obstacle avoidance of the A*SAC algorithm in different obstacle-laden environments was analyzed. Furthermore, when multiple UAVs start from the same point and navigate to different endpoints, collisions may occur between them. To test the algorithm’s collision avoidance capability in path planning, additional special obstacle environments were set up.

For handling the user offloading ratio and drone horizontal hover position in the action space, the continuous action space algorithm directly outputs continuous actions from the Actor network, which are then used to calculate the remaining energy based on the offloading ratio and horizontal hover position. For the discrete action space algorithm, this article discretizes the user offloading ratio into increments of 0.05, with a range from 0 to 1. The difference between the local ratio and the offloading ratio is a certain multiple of 0.05. Similarly, the horizontal hovering position of the drone is discretized in units of 1 m, allowing it to move up, down, left, or right by exactly 1 m at a time. The remaining energy is subsequently calculated based on the selected offloading ratio and horizontal hovering position.

In the field of UAV-based edge computing, due to the high dimensionality, dynamic nature, and non-discrete characteristics of the environment’s state space and action space, it is difficult for traditional methods to find the optimal strategy. Consequently, many researchers have turned to deep reinforcement learning algorithms in search of the optimal strategy. DDPG excels in task allocation, resource management, and collaborative control owing to its proficiency in handling continuous action spaces and deterministic strategies. Meanwhile, PPO has significant advantages in resource management, dynamic environment adaptation, and multi-task coordination, attributed to its stability, efficient sample utilization, and versatility in both discrete and continuous action spaces. Therefore, DDPG and PPO have become widely adopted in UAV-based edge computing as common and typical algorithms. To underscore the performance of our proposed algorithm, a comparison with these schemes would serve as a more compelling validation.

(1) The impact of learning rate

In the A*SAC algorithm framework, it can be seen that the Actor outputs actions and interacts with the environment to obtain data for algorithm training, which is closely related to the Actor-network. Therefore, we evaluated the impact of different learning rates on algorithm performance. Fig. 4 shows the convergence of the algorithm at various learning rates.

Figure 4: Convergence graphs of algorithms at various learning rates

Fig. 4 illustrates the convergence of the algorithm across varied learning rates. Firstly, it can be observed that all curves converge to different values after about 15 iterations. As the number of iterations increases, the curve with a learning rate of 4e−4 begins to decline at the 55th iteration, rises at the 150th iteration, and ultimately re-converges. The curve with a learning rate of 2e−4 initially declines and then gradually rises after 200 iterations, finally converging. The main reason is that after a certain number of iterations of the algorithm, the Actor network outputs actions that interact with the environment to obtain data for subsequent algorithm training. The sampled training data interferes with the algorithm’s training to a certain extent, leading to a decrease in efficiency. Specifically, the Actor network of the algorithm in this article outputs actions that interact with the environment, act upon the environment to obtain rewards, and collect data for the subsequent training of the algorithm. This data is first stored in the experience replay pool and then sampled for model training. When the learning rates for Actor network Ir of the algorithm are set to 2e−4 and 4e−4, respectively, the quality of the early collected data is higher, enabling the agent to quickly improve its performance, thus forming the first peak. However, as the training progresses, the quality of the collected data deteriorates, leading to poorer performance of the model trained on this data. This results in fluctuations and degradation in performance. Subsequently, when some high-quality data is collected again, the performance improves once more, forming a second peak. Nevertheless, due to the prior exposure to poor-quality data, the algorithm gradually converges to a value that is inferior to its initial peak performance. This indicates that the algorithm is unstable at these two learning rates, as it is prone to performance degradation despite being able to converge after a certain number of iterations. As the number of iterations increases, the algorithm is not greatly affected by the curves with learning rates of 3e−4, 9e−5 and 7e−4. Consequently, a learning rate of 3e−4 is elected, given its superior convergence return and relative stability amidst prolonged iterations.

In addition, we can observe that the algorithm’s convergence graph is remarkably smooth. Firstly, this is attributed to the A*SAC algorithm’s encouragement of exploration through maximizing the strategy’s entropy, which prevents it from getting stuck in local optima during training, thus enhancing algorithm stability. Secondly, the soft updating of the target strategy leads to smoother updates of policy parameters, minimizing drastic fluctuations. Lastly, the A*SAC algorithm employs two value networks to reduce estimated variance, further smoothing the learning curve.

(2) Convergence analysis of algorithms

Setting the Actor learning rate of the algorithm to 3e−4, and setting the task complexity to 800, with a task volume 10 times the basic task volume, can yield Figs. 5–7. From Fig. 5, it can be observed that the algorithm converges to a good system benefit after about 10 iterations, and the convergence speed is very fast. Fig. 6 shows the optimal offloading strategy for the user’s task when the algorithm converges to the optimal system benefit. From Fig. 6, it can be observed that users 1 and 7 execute more than 50% of the data locally, tending to execute locally. Users 2, 4, 5, and 6 tend to offload half of their data to the UAV for execution and half to execute locally. Users 3, 8, and 9 execute more than 60% of their data on the UAV, tending to offload it for execution. Fig. 7 shows the optimal path diagram of the UAV when the algorithm converges to the optimal system benefit. It can be seen that UAV 1 and UAV 2 have established their respective hovering positions and corresponding trajectories.

Figure 5: Convergence graph

Figure 6: User task offloading situation corresponding to optimal benefits

Figure 7: The optimal path trajectory for auxiliary UAVs

(3) The impact of different task volumes on system efficiency

Fig. 8 presents a comparative analysis of the system performance exhibited by five distinct algorithms when subjected to varying task sizes. From Fig. 8, it can be observed that the system benefits of all algorithms gradually decrease with the increase of task size. This is mainly because as the task size increases, the calculation time and offloading transmission time of all user tasks will increase, leading to an increase in latency and calculation energy consumption of auxiliary UAVs. However, the average secure offloading rate of each auxiliary UAV is only directly related to the hovering position of the UAV when the power is fixed. Upon an increase in task size, the average secure offloading rate remains relatively stable, which consequently results in a gradual decrease in system benefits. From Fig. 8, it can also be seen that when the task volume of each user gradually increases from 5 times the basic task volume to 10 times, our algorithm achieves the highest average system efficiency. Specifically, it outperforms DDPG by an average of 13.18%. The allocation of resources and the selection of UAV hover positions still exert a substantial influence on the user latency and average secure offloading rate in system benefits. The DDPG scheme gradually progressively becomes entrapped in local optima. The random strategy of PPO learning can sometimes lead to the positioning of auxiliary UAVs beyond the prescribed constraint area, thereby introducing significant interference to the optimization of benefits.

Figure 8: The variation of total benefits with the number of tasks under different algorithms

(4) The impact of different task complexity on system efficiency

Fig. 9 compares the system performance of our algorithm to other algorithms under different task complexities. From Fig. 9, it can be observed that the system benefits of all algorithms gradually decrease with the increase of task complexity. This is mainly because as task complexity increases, the calculation time of all user tasks will increase, leading to an increase in latency and calculation energy consumption of auxiliary UAVs. The average secure offloading rate of each auxiliary UAV is only directly related to the hovering position of the UAV when the power is fixed. As the task complexity increases, the average secure offloading rate remains relatively stable, which leads to a gradual decrease in system efficiency. From Fig. 9, it can also be observed that as the task complexity gradually increases from 500 to 1000, our algorithm achieves the highest average system efficiency, surpassing DDPG by an average of 3.05%.

Figure 9: The variation of total benefits with task complexity under different algorithms

(5) The impact of maximum calculation frequency of different auxiliary UAVs on system efficiency

Fig. 10 illustrates a comparative analysis of the system performance of our proposed scheme relative to five alternative algorithms, under different maximum computational frequencies for auxiliary UAVs. From Fig. 10, it can be observed that the system efficiency of all algorithms gradually increases with the increase of the maximum calculation frequency of the UAVs. As the maximum computing frequency of auxiliary UAVs increases, the user task computation time will gradually decrease, leading to a gradual reduction in latency for all users and the computation energy consumption of auxiliary UAVs. The average secure offloading rate of each auxiliary UAV is directly related to the hovering position of the UAV when the power is fixed. As the maximum calculation frequency of the auxiliary UAV increases, the average secure offloading rate remains relatively stable, thus gradually enhancing the system’s efficiency. From Fig. 10, it can also be observed that as the maximum calculation frequency of the auxiliary UAVs gradually increases from 1600 to 2600, the average system efficiency achieved by our algorithm remains superior, exhibiting an average improvement of 35.78% compared to DDPG. This is mainly because DDPG can not effectively avoid local optima during both resource allocation and the designation of hover positions for UAVs.

Figure 10: The variation of total benefits with the maximum calculation frequency of auxiliary UAVs under different algorithms

(6) The impact of the power of different auxiliary UAVs emitting electromagnetic wave interference to invade UAVs on system efficiency

Fig. 11 illustrates a comparative analysis of the system’s performance under our proposed scheme vs. that of five distinct algorithms, all designed to facilitate UAVs in emitting electromagnetic wave interference to disrupt adversarial UAVs. Observably, Fig. 11 illustrates a universal decrement in system benefits across all algorithms as the transmit power of auxiliary UAVs deploying electromagnetic wave interference to target UAVs escalates. This observed trend primarily stems from the escalation in the power of the auxiliary UAVs transmitting electromagnetic wave interference towards target UAVs, which in turn triggers an increment in both the energy consumed for task computations and the energy expended on reception and transmission processes across all auxiliary UAVs. At the same time, the average secure offloading rate of each auxiliary UAV will also change with the power and hovering position of the UAV. However, the change in the average safe offloading rate is not as significant as the increase in energy consumption, which leads to a gradual decrease in system efficiency. From Fig. 11, it can also be observed that when the power of the auxiliary UAV transmitting electromagnetic wave interference to invade the UAV gradually increases from 0.2 to 0.8, the average system efficiency of the algorithm is the highest, with an average system efficiency 25.61% higher than DDPG, indicating good performance. Among them, DDPG is mainly due to the increasing power of auxiliary UAVs emitting electromagnetic wave interference to invade UAVs, and the relationship between the task calculation energy consumption and reception transmission energy consumption of all auxiliary UAVs and the average safe offloading rate of each auxiliary UAV will become increasingly complex. This gradually leads to the DDPG algorithm falling into local optima, while PPO is still because the random learning strategy may cause the position of the auxiliary UAV to be outside the constraint area, which may interfere with the optimization of efficiency to a certain extent.

Figure 11: The variation of total benefits with the power of auxiliary UAVs emitting electromagnetic wave interference and invading UAVs under different algorithms

(7) The impact of different obstacle environments on the algorithm’s path-planning ability

To highlight the path planning ability of the algorithm, the endpoints of UAV 1 and UAV 2 were set in opposite directions and the same direction, and tested separately. In the opposite direction, two different obstacle environments as shown in Fig. 12 were added to test the algorithm’s path planning ability. In the same direction, to more intuitively see the collision avoidance path of the UAV, the endpoints of UAV 1 and UAV 2 were set to the same position, and the path planning ability of the algorithm was tested.

Figure 12: Two different obstacle environment maps. (a) Map 1. (b) Map 2

In the opposite direction, the starting points of UAVs 1 and 2 are set to (200, 200), the endpoint of UAV 1 is set to (10, 10), and the endpoint of UAV 2 is set to (400, 400). After simulation, Fig. 13a–c are presented. From Fig. 13, it can be observed that the algorithm can find the optimal path to the endpoint in three different obstacle environments and has good performance. In the same direction, the starting points of UAVs 1 and 2 are set to (5, 25), and the ending points of UAVs 1 and 2 are set to (45, 25). After simulation, Fig. 14a–c are presented. From Fig. 14a, it can be seen that UAVs 1 and 2 find the same optimal path when searching separately. If they fly along this path, each point will reach and collide at the same time. To avoid collisions, it can be observed from Fig. 14b that the algorithm first fixes the optimal path of UAV 1, then sets the optimal path of UAV 1 as a new obstacle, and searches for the optimal path of UAV 2 again. Finally, from Fig. 14c, it can be observed that the optimal path found for UAV 2 is adjacent to the trajectory of UAV 1.

Figure 13: Flight trajectories of two auxiliary UAVs in three different obstacle maps. (a) Flight trajectory 1. (b) Flight trajectory 2. (c) Flight trajectory 3

Figure 14: The optimal path for avoiding collisions between UAV 1 and UAV 2. (a) The optimal path for UAV 1 and UAV 2 when searching separately. (b) Set a new obstacle to simultaneously reach a path point and search for the optimal path for UAV 2. (c) The final path of UAV 1 and UAV 2

To further observe the path planning ability of our proposed algorithm, we selected three more complex environments, namely Fig. 15a–c, to test its path planning ability. The differences between the three maps are as follows: the channel in Fig. 15a allows multiple drones to traverse simultaneously, the channel in Fig. 15b prohibits drones from passing through, and the channel in Fig. 15c allows only a single drone to pass through. From Fig. 15a–c, it is evident that our algorithm has successfully identified the shortest path to the endpoint in each map. In Fig. 15a, Drones 1 and 2 chose to traverse the lower channel due to its shorter route to the endpoint. In Fig. 15b, Drones 1 and 2 were unable to pass through the closed channel, their paths were re-planned. Lastly, in Fig. 15c, Drone 2 chose to take an alternative path to reach the endpoint, as the two UAVs were unable to pass through the channel simultaneously.

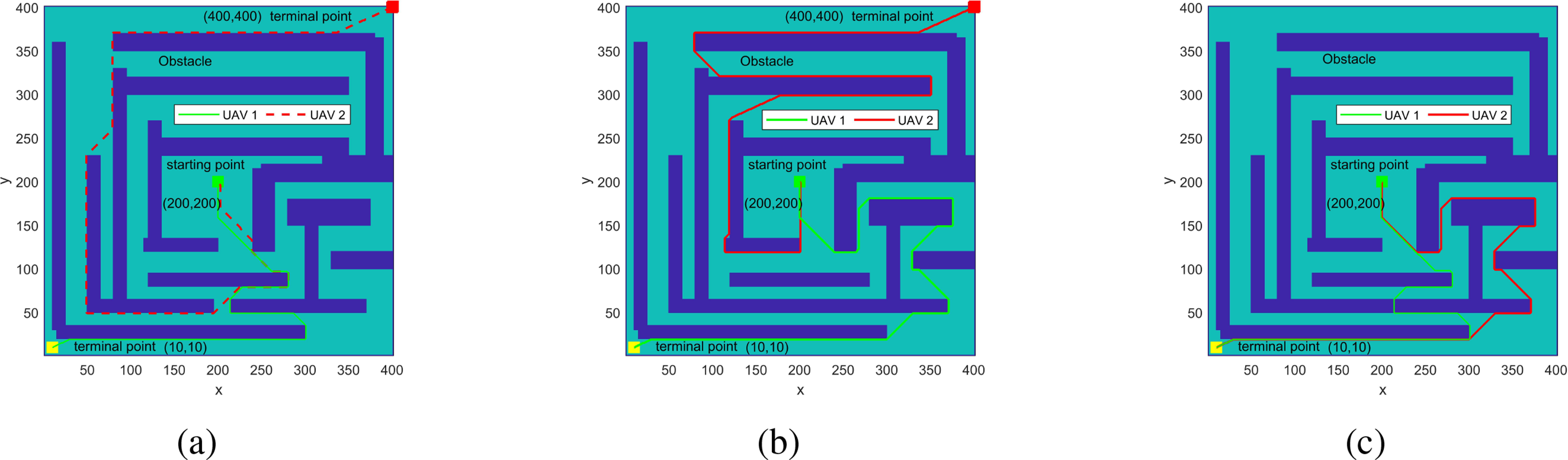
Figure 15: Flight trajectories of two auxiliary drones. (a) Flight trajectory 1. (b) Flight trajectory 2. (c) Flight trajectory 3

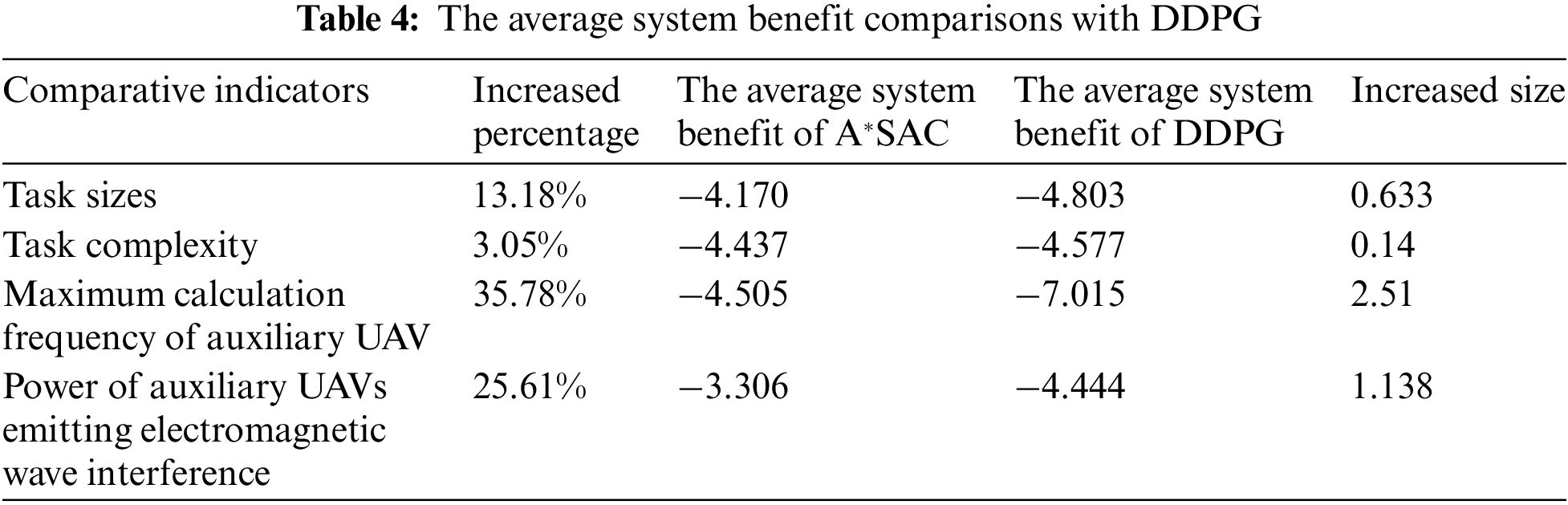
The improvement represented by percentages in this article is calculated based on the average system benefits obtained from 200 experiments conducted under the same indicator. Table 4 presents the data comparison between our proposed solution and the suboptimal solution DDPG from four aspects: Task sizes, Task complexity, Maximum calculation frequency of auxiliary UAV, and Power of auxiliary UAV emitting electromagnetic wave interference. From Table 4, it can be seen that our algorithm consistently outperforms DDPG. Especially, in terms of the maximum calculation frequency of the auxiliary UAV, the system benefits of our A*SAC algorithm are 35.78% greater than those of DDPG.

The A*SAC algorithm proposed in this article primarily modifies the SAC framework. To implement our scheme in a specific environment, the following steps need to be noted. Firstly, it is necessary to incorporate our improved A* algorithm into the relevant position of the SAC algorithm framework, and adapt the state S, action A, and reward function R in our algorithm to align with the specific environment. Secondly, one can initially set the learning rate and iteration times of the algorithm according to the parameters in this article. If the algorithm fails to converge after iterations and remains in an ascending phase, consider increasing the iteration count until convergence is achieved. Alternatively, if the algorithm exhibits a trend of non-convergent, such as rising, falling, and rising again, you can adjust the learning rate either upwards or downwards to identify a more suitable learning rate for the algorithm. The A*SAC algorithm is a deep reinforcement learning algorithm, and its overall framework resembles the SAC algorithm framework. The core idea of both algorithms is to foster exploration by maximizing the entropy of the strategy. Not only do they employ two Q-networks to estimate the value function and mitigate bias in value function estimation, but they also utilize offline strategies for training optimization. This renders the algorithm independent of the specific environment model, instead learning strategies through interaction with the environment, which is both stable and more exploratory, making them applicable in both complex and relatively simple environments. Both References [35] and [37] emphasize this aspect. Thus, our A*SAC algorithm can operate under more dynamic or less controlled conditions.

The A*SAC algorithm proposed in this article has the advantages of strong robustness, high sample utilization efficiency, strong stability, and high path planning efficiency. Specifically, in strategy optimization, the A*SAC algorithm introduces a maximum entropy objective function to enhance its robustness in complex environments. In addition, A*SAC adopts offline strategy learning, significantly improving sample utilization efficiency. By using a dual Q-network, A*SAC reduces the bias problem in Q-value estimation, thereby improving the stability of the algorithm. Combined with the A* algorithm, A*SAC can intelligently select paths and achieve high efficiency in path planning. Compared to deep reinforcement learning algorithms such as DDQN, A2C, DDPG, SAC, etc., the most obvious advantage of our scheme is that it incorporates A* algorithm, making it capable of performing multi-objective optimization and path planning optimization simultaneously. Compared with the A* algorithm, it has multi-objective optimization capability.

6  Conclusion

With the increasing popularity of UAVs in MEC, information security, and flight safety have become increasingly important for UAV-based edge computing systems. In this paper, we present a task offloading optimization problem along with a UAV path planning method, tailored for obstacle-ridden UAV-based edge computing systems. Furthermore, to efficiently solve the above problems, we propose an innovative A*SAC algorithm, which integrates the SAC and A* algorithms. The A*SAC algorithm is employed to maximize system benefits through the meticulous adjustment of the task offloading function. Additionally, our scheme ensures the establishment of a collision-free trajectory for the UAVs to navigate towards their optimal hovering positions.

Simulation results show that our proposed scheme not only addresses the task offloading challenges but also ensures the efficient and safe navigation of UAVs in obstacle-ridden environments. Notably, it achieves an average improvement of 13.18% across varying computing task sizes. In terms of electromagnetic wave interference intrusions emitted by different auxiliary UAVs, our scheme demonstrates a significant improvement of 25.61% in resisting such intrusions. Furthermore, it enhances the maximum computing frequency of various auxiliary UAVs by an average of 35.78%. Remarkably, each UAV employing our scheme exhibits proficiency in identifying and traversing the optimal collision-avoidance path, thereby ensuring a safe and efficient journey to the designated destination.

Acknowledgement: The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers and editors, which have improved the presentation.

Funding Statement: This work was supported by the Central University Basic Research Business Fee Fund Project (J2023–027), Open Fund of Key Laboratory of Flight Techniques and Flight Safety, CAAC (No. FZ2022KF06) and China Postdoctoral Science Foundation (No. 2022M722248).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Jianhua Liu, Peng Xie; data collection: Jianhua Liu, Peng Xie, Jiajia Liu, Xiaoguang Tu; analysis and interpretation of results: Jianhua Liu, Peng Xie, Jiajia Liu, Xiaoguang Tu; draft manuscript preparation: Jianhua Liu, Peng Xie. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu B, Luo Z, Chen H, Li C. A survey of state-of-the-art on edge computing: theoretical models, technologies, directions, and development paths. IEEE Access. 2022;10:54038–63. doi:10.1109/ACCESS.2022.3176106. [Google Scholar] [CrossRef]

2. Ding C, Wang J, Zhang H, Lin M, Wang J. Joint MU-MIMO precoding and resource allocation for mobile-edge computing. IEEE Trans Wirel Commun. 2021;20(3):1639–54. doi:10.1109/TWC.2020.3035153. [Google Scholar] [CrossRef]

3. Abrar M, Ajmal U, Almohaimeed Z, Gui X, Akram R, Masroor R. Energy efficient UAV-enabled mobile edge computing for IoT devices: a review. IEEE Access. 2021;9:127779–98. doi:10.1109/ACCESS.2021.3112104. [Google Scholar] [CrossRef]

4. Liao L, Lai Y, Yang F, Zeng W. Online computation offloading with double reinforcement learning algorithm in mobile edge computing. J Parallel Distr Com. 2023;171:28–39. doi:10.1016/j.jpdc.2022.09.006. [Google Scholar] [CrossRef]

5. Zhou W, Xia J, Zhou F, Fan L, Lei X, Nallanathan A, et al. Profit maximization for cache-enabled vehicular mobile edge computing networks. IEEE Trans Veh Technol. 2023;72(10):13793–98. doi:10.1109/TVT.2023.3275365. [Google Scholar] [CrossRef]

6. Hoa NT, Van Dai D, Lan L, Luong NC, Van Le D, Niyato D. Deep reinforcement learning for multi-hop offloading in UAV-assisted edge computing. IEEE Trans Veh Technol. 2023;72(12):16917–22. doi:10.1109/TVT.2023.3292815. [Google Scholar] [CrossRef]

7. Akter S, Kim DY, Yoon S. Task Offloading in multi-access edge computing enabled UAV-aided emergency response operations. IEEE Access. 2023;11:23167–88. doi:10.1109/ACCESS.2023.3252575. [Google Scholar] [CrossRef]

8. Kong X, Duan G, Hou M, Shen G, Wang H, Yan X, et al. Deep reinforcement learning-based energy-efficient edge computing for internet of vehicles. IEEE Trans Ind Inform. 2022;18(9):6308–16. doi:10.1109/TII.2022.3155162. [Google Scholar] [CrossRef]

9. Acheampong A, Zhang Y, Xu X. A parallel computing based model for online binary computation offloading in mobile edge computing. Comput Commun. 2023;203:248–61. doi:10.1016/j.comcom.2023.03.004. [Google Scholar] [CrossRef]

10. Li B, Xie W, Ye Y, Liu L, Fei Z. FlexEdge: digital twin-enabled task offloading for UAV-aided vehicular edge computing. IEEE Trans Veh Technol. 2023;72(8):11086–91. doi:10.1109/TVT.2023.3262261. [Google Scholar] [CrossRef]

11. Luo Q, Luan TH, Shi W, Fan P. Edge computing enabled energy-efficient multi-UAV cooperative target search. IEEE Trans Veh Technol. 2023;72(6):7757–71. doi:10.1109/TVT.2023.3238040. [Google Scholar] [CrossRef]

12. Li F, Luo J, Qiao Y, Li Y. Joint UAV deployment and task offloading scheme for multi-UAV-assisted edge computing. Drones. 2023;7(5):284. doi:10.3390/drones7050284. [Google Scholar] [CrossRef]

13. Goudarzi S, Soleymani SA, Wang W, Xiao P. UAV-enabled mobile edge computing for resource allocation using cooperative evolutionary computation. IEEE Trans Aero Elec Sys. 2023;59(5):5134–47. doi:10.1109/TAES.2023.3251967. [Google Scholar] [CrossRef]

14. Sharma J, Mehra PS. Secure communication in IOT-based UAV networks: a systematic survey. Internet Things. 2023;23:100883–95. doi:10.1016/j.iot.2023.100883. [Google Scholar] [CrossRef]

15. Kim S, Lee E, Hong IP, Yook JG. Review of intentional electromagnetic interference on UAV sensor modules and experimental study. Sensors. 2022;22(6):2384. doi:10.3390/s22062384. [Google Scholar] [PubMed] [CrossRef]

16. Karmakar R, Kaddoum G, Akhrif O. A novel federated learning-based smart power and 3D trajectory control for fairness optimization in secure UAV-assisted MEC services. IEEE Trans Mobile Comput. 2023;23(5):4832–48. doi:10.1109/TMC.2023.3298935. [Google Scholar] [CrossRef]

17. Li Y, Fang Y, Qiu L. Joint computation offloading and communication design for secure UAV-enabled MEC systems. In: 2021 IEEE Wireless Communications and Networking Conference (WCNC), 2021; Nanjing, China; p. 1–6. doi:10.1109/WCNC49053.2021.9417457. [Google Scholar] [CrossRef]

18. Wang T, Li Y, Wu Y. Energy-efficient UAV assisted secure relay transmission via cooperative computation offloading. IEEE Trans Green Commun. 2021;5(4):1669–83. doi:10.1109/TGCN.2021.3099523. [Google Scholar] [CrossRef]

19. He Y, Zhai D, Huang F, Wang D, Tang X, Zhang R. Joint task offloading, resource allocation, and security assurance for mobile edge computing-enabled UAV-assisted VANETs. Remote Sens. 2021;13(8):1547–57. doi:10.3390/rs13081547. [Google Scholar] [CrossRef]

20. Wei X, Cai L, Wei N, Zou P, Zhang J, Subramaniam S. Joint UAV trajectory planning, DAG task scheduling, and service function deployment based on DRL in UAV-empowered edge computing. IEEE Internet Things J. 2023;10(14):12826–38. doi:10.1109/JIOT.2023.3257291. [Google Scholar] [CrossRef]

21. Gu X, Zhang G, Gu J. Offloading optimization for energy-minimization secure UAV-Edge-computing Systems. In: 2021 IEEE Wireless Communications and Networking Conference (WCNC), 2021; Nanjing, China; p. 1–6. doi:10.1109/WCNC49053.2021.9417527. [Google Scholar] [CrossRef]

22. Ding Y, Feng Y, Lu W, Zheng S, Zhao N, Meng L, et al. Online edge learning offloading and resource management for UAV-assisted MEC secure communications. IEEE J Sel Top Signal Process. 2023;17(1):54–65. doi:10.1109/JSTSP.2022.3222910. [Google Scholar] [CrossRef]

23. Lu W, Ding Y, Gao Y, Hu S, Wu Y, Zhao N, et al. Resource and trajectory optimization for secure communications in dual unmanned aerial vehicle mobile edge computing systems. IEEE Trans Ind Inform. 2022;18(4):2704–13. doi:10.1109/TII.2021.3087726. [Google Scholar] [CrossRef]

24. Zhou Y, Pan C, Yeoh PL, Wang K, Elkashlan M, Vucetic B, et al. Secure communications for UAV-enabled mobile edge computing systems. IEEE Trans Commun. 2020;68(1):376–88. doi:10.1109/TCOMM.2019.2947921. [Google Scholar] [CrossRef]

25. Lu W, Ding Y, Gao Y, Chen Y, Zhao N, Ding Z, et al. Secure NOMA-based UAV-MEC network towards a flying eavesdropper. IEEE Trans Commun. 2022;70(5):3364–76. doi:10.1109/TCOMM.2022.3159703. [Google Scholar] [CrossRef]

26. Zhang G, Wu Q, Cui M, Zhang R. Securing UAV communications via joint trajectory and power control. IEEE Trans Wirel Commun. 2019;18(2):1376–89. doi:10.1109/TWC.2019.2892461. [Google Scholar] [CrossRef]

27. Chen X, Jiao L, Li W, Fu X. Efficient multi-user computation offloading for mobile-edge cloud computing. IEEE ACM Trans Netw. 2016;24(5):2795–808. doi:10.1109/TNET.2015.2487344. [Google Scholar] [CrossRef]

28. Liu Y, Yan J, Zhao X. Deep reinforcement learning based latency minimization for mobile edge computing with virtualization in maritime UAV communication network. IEEE Trans Veh Technol. 2022;71(4):4225–36. doi:10.1109/TVT.2022.3141799. [Google Scholar] [CrossRef]

29. Wyner AD. The wire-tap channel. Bell Syst Tech J. 1975;54(8):1355–87. doi:10.1002/J.1538-7305.1975.TB02040.X. [Google Scholar] [CrossRef]

30. Gopala PK, Lai L, El Gamal H. On the secrecy capacity of fading channels. IEEE Trans Inf Theory. 2008;54(10):4687–98. doi:10.1109/TIT.2008.928990. [Google Scholar] [CrossRef]

31. Lei H, Zhang J, Park K, Xu P, Zhang Z, Pan G, et al. Secrecy outage of max-min TAS scheme in MIMO-NOMA systems. IEEE Trans Veh Technol. 2018;67(8):6981–90. doi:10.1109/TVT.2018.2824310. [Google Scholar] [CrossRef]

32. Wang Y, Sheng M, Wang X, Wang L, Li J. Mobile-edge computing: partial computation offloading using dynamic voltage scaling. IEEE Trans Commun. 2016;64(10):4268–82. doi:10.1109/TCOMM.2016.2599530. [Google Scholar] [CrossRef]

33. Cheng Z, Min M, Liwang M, Huang L, Gao Z. Multiagent DDPG-based joint task partitioning and power control in fog computing networks. IEEE Internet Things J. 2022;9(1):104–16. doi:10.1109/JIOT.2021.3091508. [Google Scholar] [CrossRef]

34. Kumar AS, Zhao L, Fernando X. Task Offloading and resource allocation in vehicular networks: a lyapunov-based deep reinforcement learning approach. IEEE Trans Veh Technol. 2023;72(10):13360–73. doi:10.1109/TVT.2023.3271613. [Google Scholar] [CrossRef]

35. Zheng Y, Zhou H, Chen R, Jiang K, Cao Y. SAC-based computation offloading and resource allocation in vehicular edge computing. In: IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), 2022; New York, NY, USA; p. 1–6. doi:10.1109/INFOCOMWKSHPS54753.2022.9798187. [Google Scholar] [CrossRef]

36. Zhao X, Zhao T, Wang F, Wu Y, Li M. Sac-based uav mobile edge computing for energy minimization and secure data transmission. Ad Hoc Netw. 2024;157:103435–45. doi:10.1016/j.adhoc.2024.103435. [Google Scholar] [CrossRef]

37. Wang J, Sun Y, Wang B, Ushio T. Mission-aware UAV deployment for post-disaster scenarios: a worst-case SAC-based approach. IEEE Trans Veh Technol. 2024;73(2):2712–27. doi:10.1109/TVT.2023.3319480. [Google Scholar] [CrossRef]

38. Guan Y, Zou S, Peng H, Ni W, Sun Y, Gao H. Cooperative UAV trajectory design for disaster area emergency communications: a multiagent PPO method. IEEE Internet Things J. 2024;11(5):8848–59. doi:10.1109/JIOT.2023.3320796. [Google Scholar] [CrossRef]

39. Yang S, Liu J, Zhang F, Li F, Chen X, Fu X. Caching-enabled computation offloading in multi-region MEC network via deep reinforcement learning. IEEE Internet Things J. 2022;9(21):21086–98. doi:10.1109/JIOT.2022.3176289. [Google Scholar] [CrossRef]

40. Fujimoto S, Gu SS. A minimalist approach to offline reinforcement learning. Adv Neural Inf Process Syst. 2021;34:20132–45. doi:10.48550/arXiv.2106.06860. [Google Scholar] [CrossRef]

41. Tang G, Tang C, Claramunt C, Hu X, Zhou P. Geometric A-star algorithm: an improved A-star algorithm for AGV path planning in a port environment. IEEE Access. 2021;9:59196–210. doi:10.1109/ACCESS.2021.3070054. [Google Scholar] [CrossRef]

42. Tang XR, Zhu YK, Jiang XX. Improved A-star algorithm for robot path planning in static environment. J Phys Conf Ser. 2021;1792(1):12067–76. doi:10.1088/1742-6596/1792/1/012067. [Google Scholar] [CrossRef]

43. Dorling K, Heinrichs J, Messier G, Magierowski S. Vehicle routing problems for drone delivery. IEEE Trans Syst Man Cybern Syst. 2017;47(1):70–85. doi:10.1109/TSMC.2016.2582745. [Google Scholar] [CrossRef]

44. Peng Y, Liu Y, Li D, Zhang H. Deep reinforcement learning based freshness-aware path planning for UAV-assisted edge computing networks with device mobility. Remote Sens. 2022;14(16):4016–24. doi:10.3390/rs14164016. [Google Scholar] [CrossRef]

45. Sun Y, Zhang X. A2C learning for tasks segmentation with cooperative computing in edge computing networks. In: 2022 IEEE Global Communications Conference, 2022; Rio de Janeiro, Brazil; p. 2236–41. doi:10.1109/GLOBECOM48099.2022.10000948. [Google Scholar] [CrossRef]