Far and Near Optimization: A New Simple and Effective Metaphor-Less Optimization Algorithm for Solving Engineering Applications

1  Introduction

Currently, numerous optimization challenges are prevalent in science, engineering, mathematics, and practical applications, requiring suitable methodologies [1,2]. Typically, each optimization problem consists of three basic components: decision variables, constraints, and an objective function. The main goal in optimization is to find the optimal values for the decision variables, ensuring that the objective function is optimized within the constraints [3,4].

Metaheuristic algorithms are recognized as effective problem-solving tools designed to tackle optimization challenges. These algorithms employ random search techniques within the problem domain, along with stochastic operators, to provide feasible solutions for optimization problems [5]. They are valued for their simple conceptualization, ease of implementation, and ability to address various optimization problems, including non-convex, non-linear, non-derivative, discontinuous, and NP-hard problems, as well as navigating through discrete and unexplored search spaces [6]. The operational process of metaheuristic algorithms typically begins with randomly generating a set of feasible solutions, forming the algorithm population. Through iterative refinement processes, these solutions are improved via algorithmic update mechanisms. Upon completion of the algorithm’s execution, the most optimal solution obtained during the iterations is presented as the solution to the problem [7].

For metaheuristic algorithms to conduct an efficient search in the problem-solving space, they need to effectively manage the search process at both global and local levels. Global search, achieved through exploration, allows the algorithm to avoid getting trapped in local optima by thoroughly scanning the problem-solving space to identify the main optimum region. On the other hand, local search, through exploitation, enables the algorithm to converge towards potentially better solutions by closely examining the vicinity of discovered solutions and promising areas within the problem-solving space. In addition to exploration and exploitation, the success of a metaheuristic algorithm in facilitating an efficient search relies on maintaining a fine balance between these two strategies throughout the search process [8].

Because of the random nature of stochastic search methods, metaheuristic algorithms cannot guarantee reaching the global optimum. Therefore, solutions obtained from these algorithms are commonly labeled as quasi-optimal. This built-in uncertainty, along with researchers’ desire to attain quasi-optimal solutions closer to the global optimum, has driven the creation of various metaheuristic algorithms [9].

The main research question revolves around whether the existing metaheuristic algorithms adequately address the challenges in science, or if there’s a necessity for the development of newer ones. The No Free Lunch (NFL) theorem, as posited in reference [10], provides insight into this question by stating that the effectiveness of a metaheuristic algorithm in solving a specific set of optimization problems doesn’t guarantee similar success across all optimization problems. Hence, there’s no assured success or failure of a metaheuristic algorithm on any given optimization problem. According to the NFL theorem, no single metaheuristic algorithm can be deemed as the ultimate optimizer for all optimization tasks. This theorem, by continually stimulating the exploration and advancement of metaheuristic algorithms, encourages researchers to seek more efficient solutions for optimization problems through the design of newer algorithms.

This paper presents a novel contribution by introducing the Far and Near Optimization (FNO) metaheuristic algorithm, aimed at addressing optimization challenges across various scientific disciplines. Literature review shows that many metaheuristic algorithms have been designed so far. In most of these algorithms, researchers have tried to manage the search process by improving the state of exploration and exploitation in such a way as to achieve more effective solutions for optimization problems. In fact, the proper management of local and global search is the main key to the success of metaheuristic algorithms. This challenge of balancing exploration and exploitation has been the main motivation of the authors of this paper to design a dedicated algorithm that specifically deals with the design of the local and global search process. Therefore, it can be stated that the main source of inspiration for the authors in designing the proposed FNO approach was balancing exploration and exploitation.

In this new approach, the authors have used two basic mechanisms to change the position of the population members in the search space.

The first mechanism is the movement of each FNO member towards the farthest member of the population. In this mechanism, with the aim of increasing the discovery power of the algorithm in order to manage the global search, extensive changes are made in the position of each member of the population. These large displacements have a significant impact on the comprehensive scanning of the search space and prevent the algorithm from getting stuck in local optima. The important point in this process is that updating the population based on movement towards the best member is avoided. Because the excessive dependence of the update process based on the position of the best member can lead to the algorithm getting stuck early in inappropriate local optimal solutions.

The second mechanism is the movement of each FNO member towards the nearest member of the population. In this mechanism, small changes are made in the position of each population member with the aim of increasing the ability to exploit FNO in order to manage local search. These small displacements are effective in accurate scanning near the obtained solutions with the aim of obtaining possible better solutions and converging towards the global optimum.

Although based on the best knowledge obtained from the literature review, the originality of the proposed FNO approach is confirmed, however, the authors describe the differences of the proposed approach with one of the recently published algorithms called Giant Armadillo Optimization (GAO) [11]. GAO is a swarm-based algorithm inspired by the natural behavior of the giant armadillo in the wild. The main idea in FNO design is to move giant armadillo towards termite mounds and then dig in that position.

The first difference between proposed FNO approach and GAO is the source of design inspiration. As the title of the paper suggests, FNO is a population-based yet metaphor-free algorithm. But GAO is inspired by nature and wildlife in its design.

The second difference between FNO and GAO is in the design of the exploration phase. In the GAO design, each member of the population is directed to a position in the problem solving space that has a better objective function value compared to the corresponding member. Therefore, in GAO, it does not matter whether the location of the destination member is far or near. Meanwhile, in the design of the exploration phase in FNO, each member of the population moves towards the member farthest from itself. In this mechanism, the criterion for selecting the position of the destination member is the greatest distance to the corresponding member.

The third difference between FNO and GAO is related to the design of the exploitation phase. In GAO, in order to manage the local search, it is assumed that the movement range of each member becomes smaller and more limited during the iterations of the algorithm. This is while in FNO design, local search management is independent of algorithm iterations. The exploitation phase in FNO is designed in such a way that each member of the population moves towards the member closest to itself.

In general, it can be said that FNO is different from GAO from the point of view of source of inspiration in design, theory, mathematical model, exploration phase design, and exploitation phase design.

FNO has several advantages compared to other algorithms, which are described below:

I.  Balanced Exploration and Exploitation

•     Enhanced Global Search: FNO leverages the exploration phase by moving towards the farthest member, which helps in thoroughly exploring the search space and avoiding local optima.

•     Improved Local Search: The exploitation phase involves moving towards the nearest member, which refines the search around promising areas to find the optimal solution.

II.  Dynamic Population Update

•     Adaptive Strategy: FNO dynamically updates population members based on their distances, allowing for a more adaptive and responsive search process.

•     Efficient Convergence: The dual-phase approach ensures that the algorithm does not prematurely converge and maintains a good balance between exploration and exploitation throughout the optimization process.

III.  Mathematical Rigor

•     Clear Theoretical Foundation: The FNO algorithm is mathematically modeled and well-defined, providing a clear understanding of its working principles and mechanisms.

•     Predictable Behavior: The mathematical formulation allows for predictable and consistent behavior of the algorithm across different optimization problems.

IV.  Performance on Benchmark Functions

•     Superior Results: Comparative analyses show that FNO often outperforms other well-known metaheuristic algorithms in solving benchmark optimization problems.

•     Statistical Significance: The performance improvements offered by FNO are not only observed empirically but are also statistically significant, providing robust evidence of its effectiveness.

V.  Versatility and Applicability

•     Wide Range of Problems: FNO has demonstrated effectiveness across various problem domains, including both unconstrained and constrained optimization problems.

•     Real-World Applications: The algorithm has been successfully applied to real-world engineering design problems, showcasing its practical utility.

VI.  Scalability

•     Handling High-Dimensional Problems: FNO is capable of handling optimization problems with a large number of decision variables, making it suitable for complex, high-dimensional tasks.

•     Scalable Complexity: Despite its quadratic time complexity with respect to the number of population members, the algorithm remains computationally feasible for a wide range of practical applications.

VII.  Robustness and Reliability

•     Consistent Performance: FNO consistently provides high-quality solutions across different types of optimization problems, indicating its robustness.

•     Reliability: The algorithm’s ability to balance exploration and exploitation ensures that it reliably finds good solutions without getting stuck in suboptimal regions.

The FNO algorithm offers several advantages over other metaheuristic algorithms, including a balanced approach to exploration and exploitation, dynamic and adaptive population updates, strong mathematical foundations, superior performance on benchmark functions, versatility in application, scalability to high-dimensional problems, and overall robustness and reliability. These advantages make FNO a powerful and effective tool for tackling a wide variety of optimization challenges.

The key contributions of this research are outlined as follows:

•   The main idea in the design of FNO is to effectively update the population member of the algorithm in the problem-solving space by applying the concept of global search based on movement towards the farthest member and local search based on movement towards the nearest member.

•   The theory of FNO is stated and its implementation steps are mathematically modeled in two phases of exploration and exploitation.

•   Novel Approach: The paper introduces a new metaheuristic algorithm named Far and Near Optimization, designed to address various optimization challenges in scientific disciplines.

•   Balance between Exploration and Exploitation: FNO emphasizes a balanced approach to global and local search by employing distinct mechanisms for exploration (movement towards the farthest member) and exploitation (movement towards the nearest member).

•   Exploration Phase: The algorithm enhances global search capability by moving each population member towards the farthest member, which helps in avoiding local optima and ensures thorough exploration of the search space.

•   Exploitation Phase: FNO improves local search by moving each population member towards the nearest member, enabling precise scanning near discovered solutions to find potentially better solutions and converge towards the global optimum.

•   Clear Theoretical Foundation: The FNO algorithm is mathematically modeled, providing a well-defined and understandable framework for its working principles and mechanisms.

•   Mathematical Rigor: The paper provides a detailed mathematical formulation of the FNO algorithm, ensuring predictable and consistent behavior across different optimization problems.

•   Consistent Performance: FNO consistently provides high-quality solutions across different types of optimization problems, indicating its robustness.

•   Reliability: The algorithm’s balanced exploration and exploitation ensure that it reliably finds good solutions without getting stuck in suboptimal regions.

Below outlines the structure of this paper: Section 2 presents the review of relevant literature. In Section 3, we introduce and model the FNO approach. Section 4 covers simulation studies and their results. Section 5 examines the efficacy of FNO in addressing real-world applications. Finally, Section 6 offers conclusions and suggestions for future research.

2  Literature Review

Metaheuristic algorithms draw inspiration from a range of natural and evolutionary phenomena, including biology, genetics, physics, and human behaviors. As a result, these algorithms are categorized into five groups based on their underlying sources of inspiration: swarm-based, evolutionary-based, physics-based, and human-based.

Swarm-based metaheuristic algorithms take inspiration from the collective behaviors observed in diverse natural swarms, encompassing birds, animals, aquatic creatures, insects, and other organisms within their habitats. Notable examples include Particle Swarm Optimization (PSO) [12], Artificial Bee Colony (ABC) [13], Ant Colony Optimization (ACO) [14], and Firefly Algorithm (FA) [15]. PSO mirrors the coordinated movements of bird and fish flocks during foraging. ABC replicates the collaborative endeavors of bee colonies in locating new food sources. ACO is grounded in the efficient pathfinding capabilities of ants between their nest and food sites. FA is crafted based on the light signaling interactions among fireflies for communication and mate attraction. In the realm of natural behaviors exhibited by wild organisms, strategies like hunting, foraging, migration, chasing, digging, and searching prominently feature and have inspired the design of swarm-based metaheuristic algorithms such as: Arctic Puffin Optimization (APO) [16], Remora Optimization Algorithm (ROA) [17], Sand Cat Swarm Optimization (SCSO) [18,19], Giant Armadillo Optimization (GAO) [11], African Vultures Optimization Algorithm (AVOA) [20], Golden Jackal Optimization (GJO) [21], White Shark Optimizer (WSO) [22], Tunicate Swarm Algorithm (TSA) [23], Whale Optimization Algorithm (WOA) [24], Grey Wolf Optimizer (GWO) [25], Marine Predator Algorithm (MPA) [26], Honey Badger Algorithm (HBA) [27], and Reptile Search Algorithm (RSA) [28].

Evolutionary-based metaheuristic algorithms find their inspiration in principles from biological sciences and genetics, with a particular emphasis on concepts like natural selection, survival of the fittest, and Darwin’s evolutionary theory. Prominent examples include Genetic Algorithm (GA) [29] and Differential Evolution (DE) [30], which are deeply rooted in genetic principles, reproduction processes, and the application of evolutionary operators such as selection, mutation, and crossover. Furthermore, Artificial Immune System (AIS) [31] has been developed, drawing inspiration from the human body’s defense mechanisms against pathogens and diseases.

Physics-based metaheuristic algorithms draw inspiration from a wide array of forces, laws, phenomena, transformations, and other fundamental concepts within physics. Simulated Annealing (SA) [32] is a notable example, inspired by the process of metal annealing, where metals are heated and gradually cooled to achieve an optimal crystal structure. Moreover, algorithms like Spring Search Algorithm (SSA) [33] Momentum Search Algorithm (MSA) [34] and Gravitational Search Algorithm (GSA) [35] have been developed based on the emulation of physical forces. SSA employs spring tensile force modeling and Hooke’s law, MSA is founded on impulse force modeling, and GSA integrates gravitational attraction force modeling. Noteworthy physics-based methods include the Multi-Verse Optimizer (MVO) [36], Archimedes Optimization Algorithm (AOA) [37], Thermal Exchange Optimization (TEO) [38], Electro-Magnetism Optimization (EMO) [39], Water Cycle Algorithm (WCA) [40], Black Hole Algorithm (BHA) [41], Equilibrium Optimizer (EO) [42], and Lichtenberg Algorithm (LA) [43].

Human-based metaheuristic algorithms draw inspiration from diverse aspects of human behavior, encompassing communication, decision-making, thought processes, interactions, and choices observed in personal and social contexts. Teaching-Learning Based Optimization (TLBO) [44] serves as a prime example, inspired by the dynamics of education within classrooms, where knowledge exchange occurs among teachers and students as well as between students themselves. The Mother Optimization Algorithm (MOA) is introduced, drawing inspiration from the care provided by mothers to their children [45]. Poor and Rich Optimization (PRO) [46] is formulated based on economic activities observed among individuals of different socioeconomic backgrounds, with the aim of improving their financial situations. Conversely, Doctor and Patient Optimization (DPO) [47] simulates therapeutic interactions between healthcare providers and patients in hospital settings. Other notable human-based metaheuristic algorithms include War Strategy Optimization (WSO) [48], Ali Baba and the Forty Thieves (AFT) [49], Coronavirus Herd Immunity Optimizer (CHIO) [50], and Gaining Sharing Knowledge based Algorithm (GSK) [51].

In addition to the mentioned groupings, many researchers are interested in combining several algorithms and developing hybrid versions of them to benefit from the advantages of existing algorithms at the same time. Also, designing improved versions of existing algorithms has become a research motivation for researchers. WOA-SCSO is a hybrid metaheuristic algorithm that is derived from the combination of WOA and SCSO [52]. The nonlinear chaotic honey badger algorithm (NCHBA) is an improved version of the honey badger algorithm, which is designed to balance exploration and exploitation in this algorithm [53]. Some other hybrid metaheuristic algorithms are: hybrid PSO-GA [54], hybrid GWO-WOA [55], hybrid GA-PSO-TLBO [56], and hybrid TSA-PSO [57].

Table 1 lists an overview of metaheuristic algorithms and their grouping.

3  Far and Near Optimization

This section elucidates the theory behind the FNO approach and subsequently delineates its implementation steps through mathematical modeling.

3.1 Inspiration of FNO

Metaheuristic algorithms represent stochastic approaches to problem-solving within optimization tasks, primarily relying on random search techniques in the problem-solving domain. Two fundamental principles guiding this search process are exploration and exploitation. In the development of FNO, these principles are harnessed to update the algorithm’s population position within the problem-solving space. Each member of the population undergoes identification of both the farthest and nearest members based on distance calculations. Steering a population member towards the farthest counterpart enhances the algorithm’s exploration capacity for global search within the problem-solving space. Hence, within the FNO framework, a population update phase is dedicated to moving each member towards the farthest counterpart. Conversely, directing a population member towards the nearest counterpart enhances the algorithm’s exploitation capacity for local search within the problem-solving space. Accordingly, within the FNO framework, a separate population update phase is allocated for moving each member towards its closest counterpart.

3.2 Algorithm Initialization

The proposed FNO methodology constitutes a population-based metaheuristic algorithm, leveraging the search capabilities of its members within the problem-solving space to attain viable solutions for optimization problems through an iterative process. Each member within the FNO framework derives values for decision variables based on its position in the problem-solving space. Consequently, each FNO member serves as a candidate solution to the problem, represented mathematically as a vector. As a result, the algorithm population, comprising these vectors, can be mathematically represented as a matrix, as indicated by Eq. (1). The initial positions of the population members within the problem-solving space are randomly initialized using Eq. (2).

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,d⋯x1,m⋮⋱⋮⋰⋮xi,1⋯xi,d⋯xi,m⋮⋰⋮⋱⋮xN,1⋯xN,d⋯xN,m]N×m(1)

xi,d=lbd+r⋅(ubd−lbd)(2)

Here, X is the FNO population matrix, Xi is the ith FNO member (candidate solution), xi,d is its dth dimension in search space (decision variable), N is the number of population members, m is the number of decision variables, r is a random number in interval [0,1], lbd, and ubd are the lower bound and upper bound of the dth. decision variable, respectively.

In alignment with each FNO member serving as a potential solution to the problem, the objective function of the problem can be assessed. Consequently, the array of evaluated objective function values can be depicted utilizing a matrix, as outlined in Eq. (3).

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1(3)

Here, F is the vector of evaluated objective function and Fi is the evaluated objective function based on the ith FNO member.

The assessed objective function values provide crucial insights into the quality of population members and potential solutions. The best evaluated objective function value corresponds to the top-performing member within the population, while the worst value corresponds to the least effective member. It should also be explained that since optimization problems fall into two groups of minimization and maximization, the concept of the best and worst value of the objective function is different. In minimization problems, the best value of the objective function corresponds to the lowest evaluated value for the objective function and the worst value of the objective function corresponds to the highest evaluated value for the objective function. On the other hand, in maximization problems, the meaning of the best value of the objective function is the highest value evaluated for the objective function, and the meaning of the worst value of the objective function is the lowest value evaluated for the objective function.

As the position of population members in the problem-solving space is updated in each iteration, new objective function values are computed accordingly. Consequently, throughout each iteration, the top-performing member must also be updated based on comparisons of objective function values. Upon completion of the algorithm’s execution, the position of the top-performing member within the population is presented as the solution to the problem.

3.3 Mathematical Modelling of FNO

Within the FNO framework, the adjustment of each population member’s position occurs by moving towards both the farthest and nearest member from itself. The distance between each member and another is computed using Eq. (4).

Di,j=∑d=1m(Xi,d−Xj,d)2,i=1,2,…,N, and i≠j, d=1,2,3,…,m(4)

Here, Di,j is the distance between the ith and jth population members from each other. According to Eq. (4), the highest calculated value for Di corresponds to the farthest member (FMi) and the lowest calculated value for Di corresponds to the nearest member (NMi) for the ith member.

3.3.1 Phase 1: Moving to the Farthest Member (Exploration)

In the initial phase of FNO, the adjustment of population member positions in the problem-solving space is orchestrated by directing each member towards the farthest counterpart. This modeling process instigates significant alterations in the positions of population members within the problem-solving space, thereby enhancing FNO’s capacity for global search and exploration.

The calculation of a new position for each population member is based on the modeling of their movement towards the farthest counterpart, as outlined in Eq. (5). Subsequently, if an improvement in the objective function value is observed at this new position, it supersedes the previous position of the corresponding member, as per Eq. (6).

xi,dP1=xi,d+ri,d⋅(FMi,d−I⋅xi,d),(5)

Xi={XiP1,FiP1≤Fi, for minimization problemsXiP1,FiP1≥Fi, for maximization problemsXi,else(6)

Here, FMi is the farthest member for ith population member, FMi,d is the its dth dimension, XiP1 is the new position calculated for the ith population member based on exploration phase of FNO, xi,dP1 is its dth dimension, FiP1 is its objective function value, ri,d are random numbers from the interval [0,1], and I is number which is randomly selected as 1 or 2.

3.3.2 Phase 2: Moving to the Nearest Member (Exploitation)

In the subsequent phase of FNO, adjustments to population member positions within the problem-solving space are made by guiding each member towards its nearest counterpart. This modeling procedure induces subtle alterations in the positions of population members, thereby enhancing FNO’s capacity for local search management and exploitation.

Utilizing the modeling of each FNO member’s movement towards its nearest counterpart, a fresh position for every population member is computed, as specified in Eq. (7). Subsequently, if an enhancement in the objective function value is observed at this new position, it supplants the previous position of the corresponding member, in accordance with Eq. (8).

xi,dP2=xi,d+ri,d⋅(NMi,d−I⋅xi,d),(7)

Xi={XiP2,FiP2≤Fi, for minimization problemsXiP2,FiP2≥Fi, for maximization problemsXi,else(8)

Here, NMi is the nearest member for ith population member, NMi,d is the its dth dimension, XiP2 is the new position calculated for the ith population member based on exploitation phase of FNO, xi,dP2 is its dth dimension, FiP2 is its objective function value, ri,d are random numbers from the interval [0,1], and I is number which is randomly selected as 1 or 2.

3.4 Repetition Process, Pseudocode, and Flowchart of FNO

The initial iteration of FNO concludes with the updating of all population members through the first and second phases. Subsequently, based on the updated values for both the algorithm population and the objective function, the algorithm progresses to the next iteration, and the updating process persists using Eqs. (4) to (8) until the final iteration is reached. Throughout each iteration, the best solution attained is updated and preserved. Upon the culmination of the FNO execution, the best solution acquired during the algorithm’s iterations is provided as the solution for the given problem. The procedural steps of FNO are depicted in a flowchart in Fig. 1, while its pseudocode is outlined in Algorithm 1.

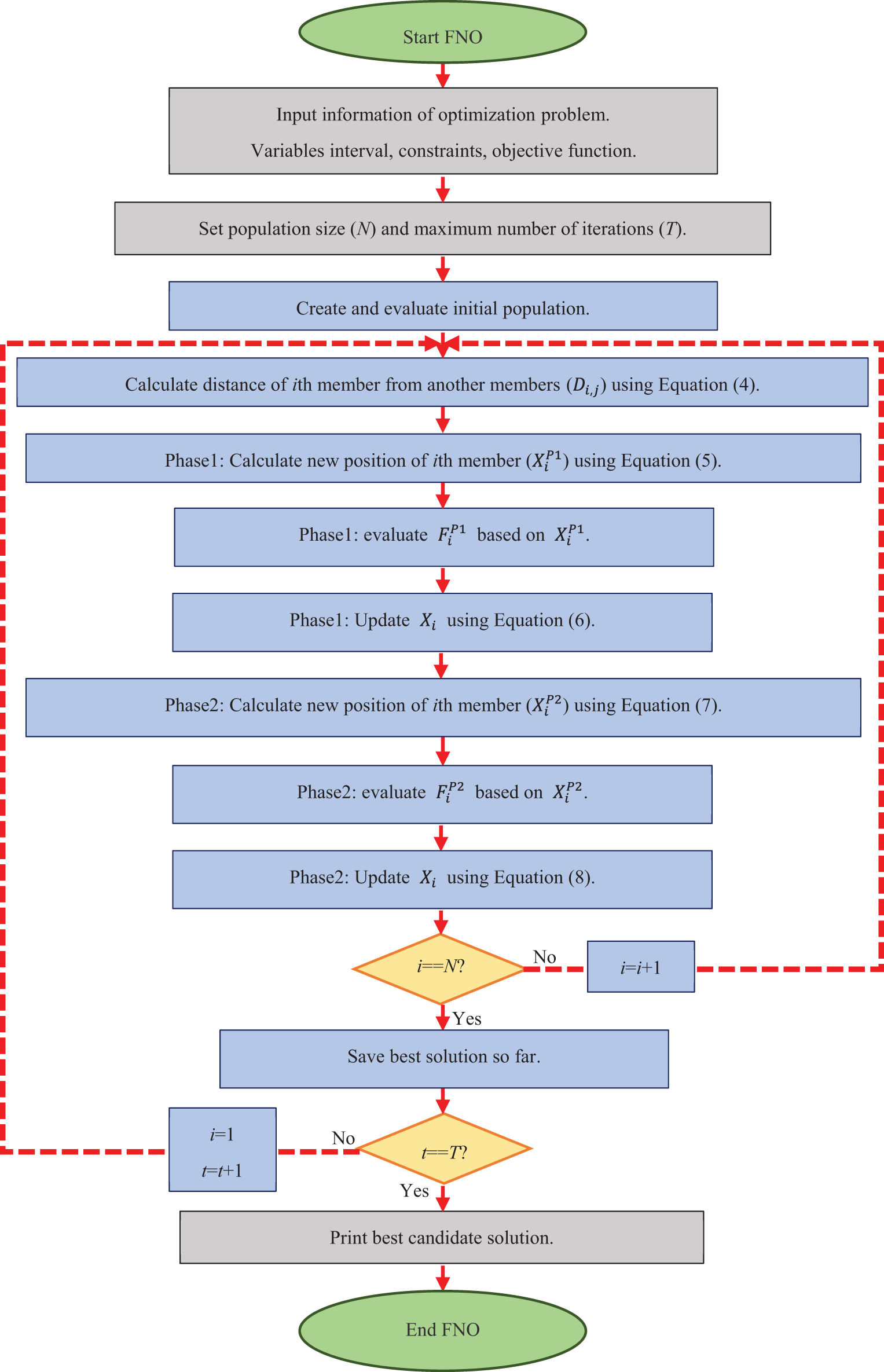
Figure 1: Flowchart of FNO

3.5 Theoretical Analysis of Time Complexity

To understand the efficiency and scalability of the FNO algorithm, we need to analyze its time complexity. The analysis is broken down into the key steps involved in each iteration of the algorithm.

I)  Initialization Phase

•     Population Initialization: Generating the initial population of N members, each with m decision variables.

∘   Time Complexity: O(N⋅m)

II)  Distance Calculation Phase

•     Distance Calculation: For each member, distances to all other N−1 members need to be calculated. Each distance calculation involves m dimensions.

∘   Time Complexity: O(N2.m)

III)  Exploration Phase (Moving to the Farthest Member)

•     Identify Farthest Member: For each member, determine the farthest member from the distance matrix.

∘   Time Complexity: O(N2)

•     Update Position: For each member, update its position towards the farthest member, which involves m dimensions.

∘   Time Complexity: O(N⋅m)

•     Evaluate Objective Function: For each member’s new position, compute the objective function.

∘   Time Complexity: O(N)

IV)  Exploitation Phase (Moving to the Nearest Member)

•     Identify Nearest Member: For each member, determine the nearest member from the distance matrix.

∘   Time Complexity: O(N2)

•     Update Position: For each member, update its position towards the nearest member, which involves m dimensions.

∘   Time Complexity: O(N⋅m)

•     Evaluate Objective Function: For each member’s new position, compute the objective function.

∘   Time Complexity: O(N)

V)  Iterative Process

The above phases are repeated for T iterations.

3.6 Overall Time Complexity

Combining the complexities of each phase, the total time complexity per iteration is:

O(N.m)+O(N2.m)+O(N2)+O(N.m)+O(N)+O(N2)+O(N.m)+O(N)

Simplifying, we get:

O(N2+m)+O(N2)

Since O(N2+m) dominates O(N2) when m ≥ 1, the overall time complexity per iteration is:

O(N2.m)

For T iterations, the overall time complexity becomes:

O(T.N2.m)

The time complexity of the FNO algorithm per iteration is (N2.m), and for T iterations, it is O(T.N2.m). This analysis indicates that the algorithm scales quadratically with the number of population members N and linearly with the number of decision variables m. The number of iterations T also linearly affects the total computational cost.

3.7 Population Diversity, Exploration, and Exploitation Analysis

Population diversity in the FNO pertains to the spread of individuals within the solution space, which is crucial for tracking the algorithm’s search dynamics. This metric reveals whether the algorithm’s focus is on exploring new solutions (exploration) or refining existing ones (exploitation). Evaluating FNO’s population diversity allows for an assessment and adjustment of the algorithm’s balance between exploration and exploitation. Several researchers have proposed different ways to define diversity. For instance, Pant introduced a method to calculate diversity using the following equations [58]:

Diversity=1N∑i=1N∑d=1m(xi,d−x¯d)2,(9)

x¯d=1N∑i=1Nxi,d(10)

where N is the population size, m represents the number of dimensions in the problem space, and xi,d is the mean value of the population in the dth dimension. Consequently, the percentages of exploration and exploitation at each iteration can be determined using the following equations:

Exploration=DiversityDiversitymax,(11)

Exploitation=|Diversity−Diversitymax|Diversitymax(12)

This subsection delves into the analysis of population diversity, as well as exploration and exploitation, using twenty-three standard benchmarks. These include seven unimodal functions (F1 to F7) and sixteen multimodal functions (F8 to F23), with detailed descriptions available in [59].

Fig. 2 demonstrates the ratio of exploration to exploitation throughout the iterations of the FNO, providing visual insights into how the algorithm navigates between global and local search strategies. Additionally, Table 2 presents the outcomes of the population diversity analysis, alongside exploration and exploitation metrics.

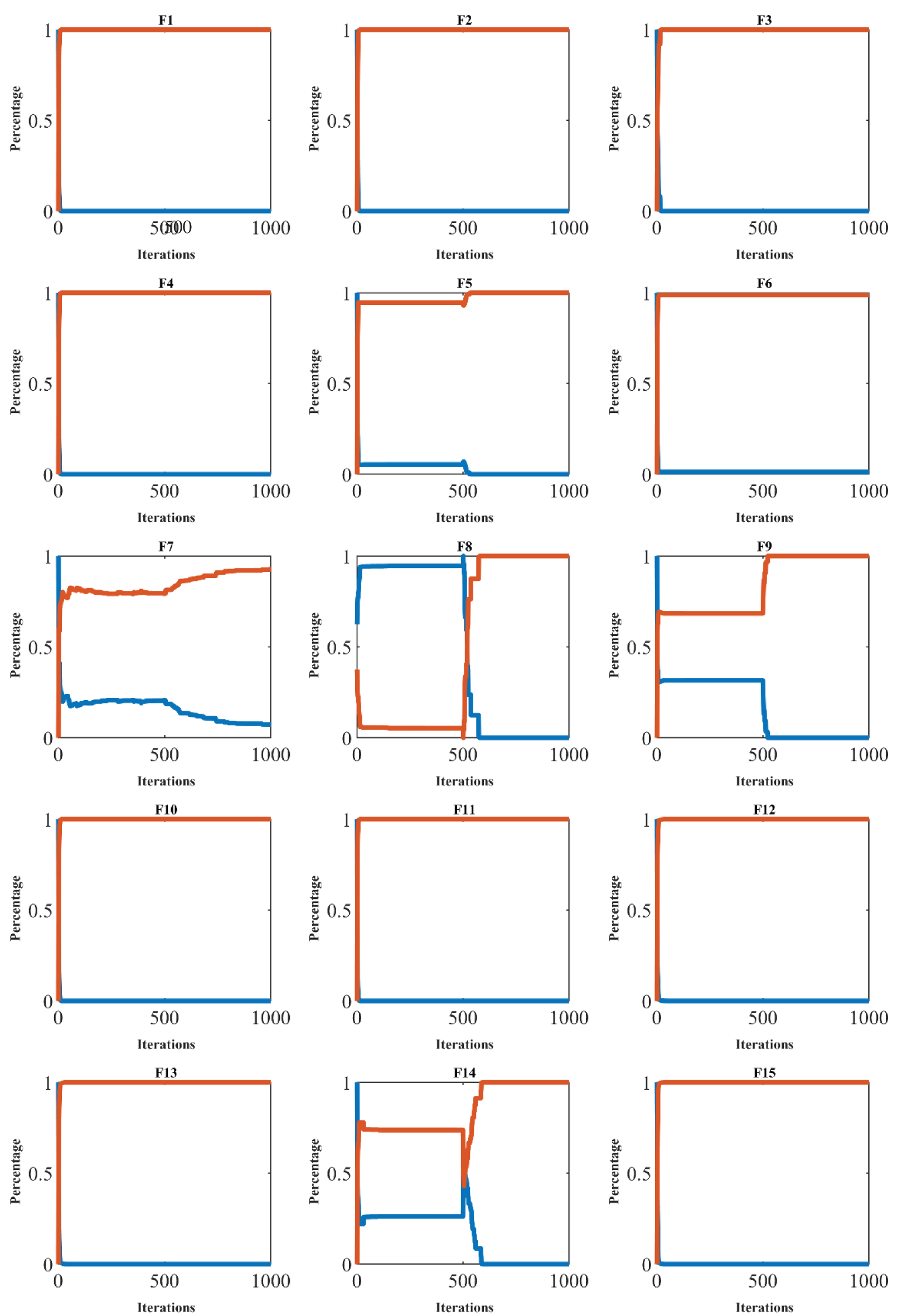
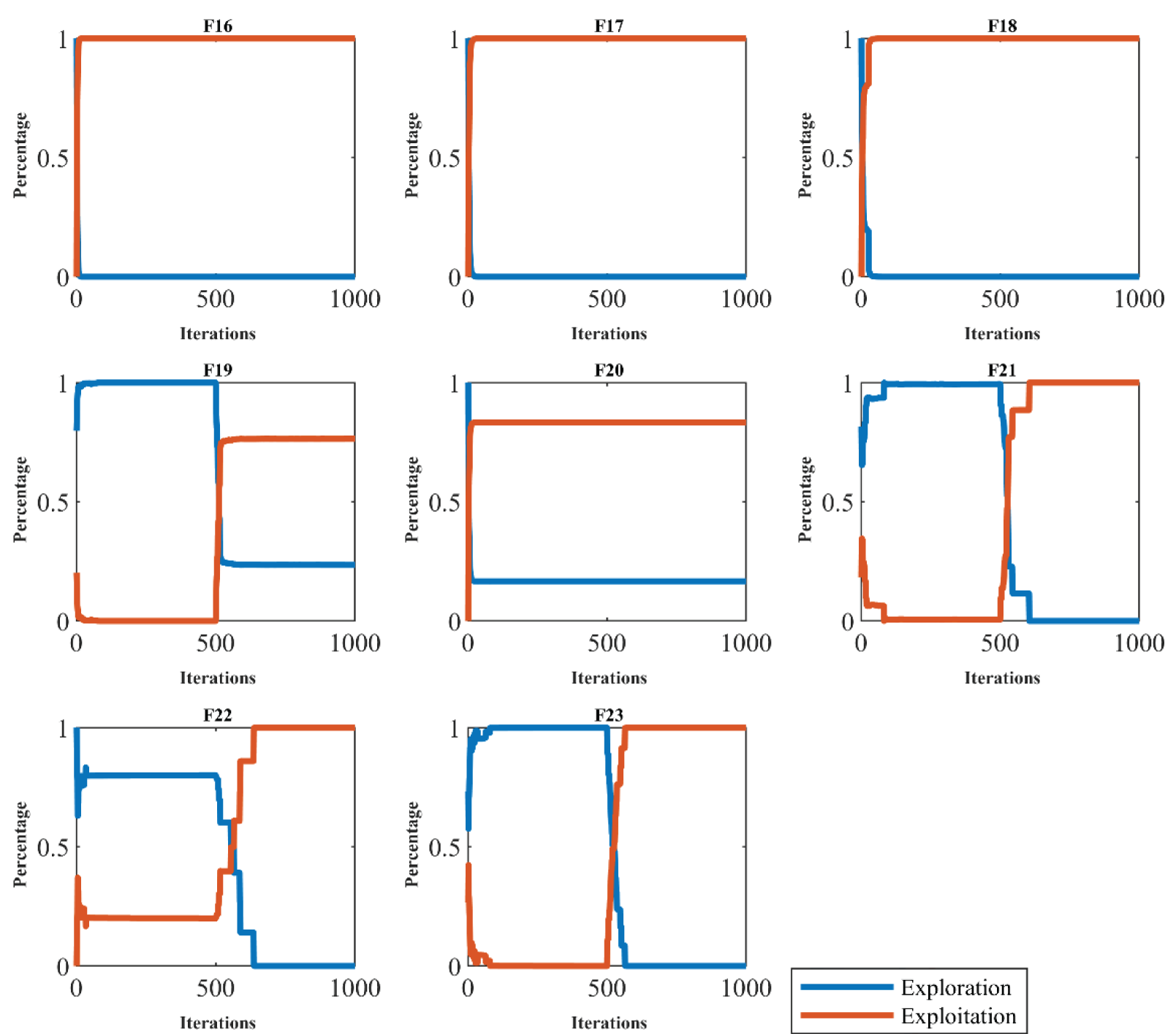
Figure 2: Exploration and exploitation of the FNO

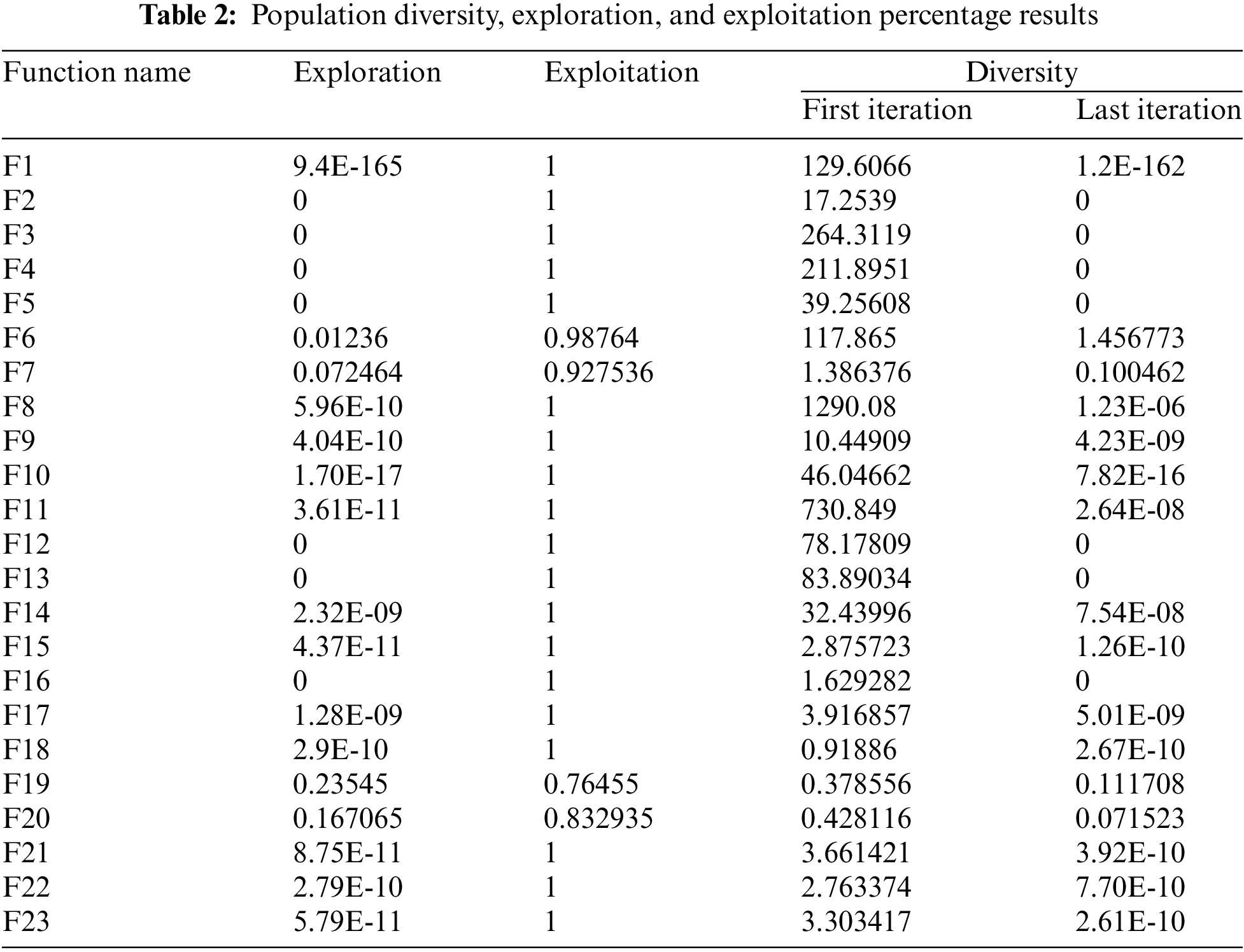
The simulation results highlight that FNO maintains high population diversity at the initial iterations, which gradually decreases as the iterations progress. This pattern indicates a shift from exploration to exploitation over time. Furthermore, the exploration-exploitation ratio for FNO frequently aligns closely with 0.00% exploration and 100% exploitation by the final iterations. These findings validate that the FNO effectively manages the balance between exploration and exploitation through its diverse population, ensuring robust performance across the iterative search process.

4  Simulation Studies and Results

In this section, the performance of the proposed FNO approach to solve optimization problems is evaluated. For this purpose, CEC 2017 test suite [59] for problem dimensions equal to 10, 30, 50, and 100, as well as to address CEC 2020 [60] have been selected.

4.1 Performance Comparison

The performance of FNO has been assessed by comparing its results with those of twelve established metaheuristic algorithms: GA, GSA, MVO, GWO, MPA, TSA, RSA, AVOA, and WSO. Table 3 specifies the parameter settings for each competing metaheuristic algorithm. To tackle the challenges posed by the CEC 2017 test suite, FNO and each competing algorithm were subjected to 51 independent runs, each consisting of 10,000·m (where m represents the number of variables) function evaluations (FEs). The optimization outcomes are evaluated using six statistical measures: mean, best, worst, standard deviation (std), median, and rank. The mean values serve as the basis for ranking the metaheuristic algorithms in their performance across the benchmark functions.

4.2 Evaluation CEC 2017 Test Suite

In this section, we assess the performance of FNO alongside competitor algorithms in addressing the CEC 2017 test suite across problem dimensions of 10, 30, 50, and 100. This test suite comprises thirty benchmark functions, encompassing unimodal, multimodal, hybrid, and composition functions. Specifically, it includes three unimodal functions (C17-F1 to C17-F3), seven multimodal functions (C17-F4 to C17-F10), ten hybrid functions (C17-F11 to C17-F20), and ten composition functions (C17-F21 to C17-F30). Notably, function C17-F2 is excluded from simulation studies due to its erratic behavior. Detailed information on the CEC 2017 test suite is accessible at [59]. The outcomes of applying metaheuristic algorithms to the CEC 2017 test suite are presented in Tables 4 to 7. Additionally, boxplot diagrams illustrating the performance of metaheuristic algorithms across the CEC 2017 test suite are depicted in Figs. 3 to 6.

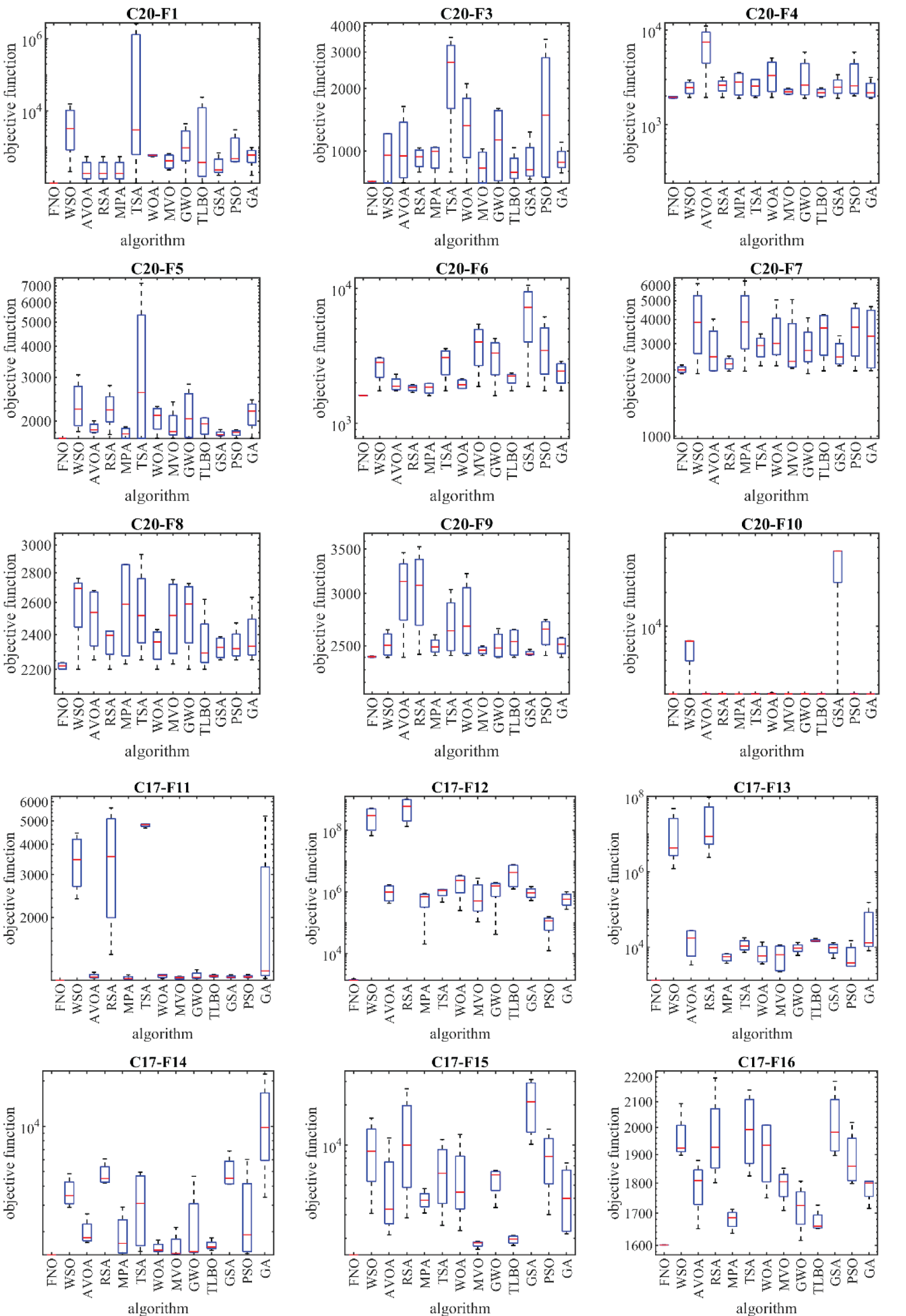
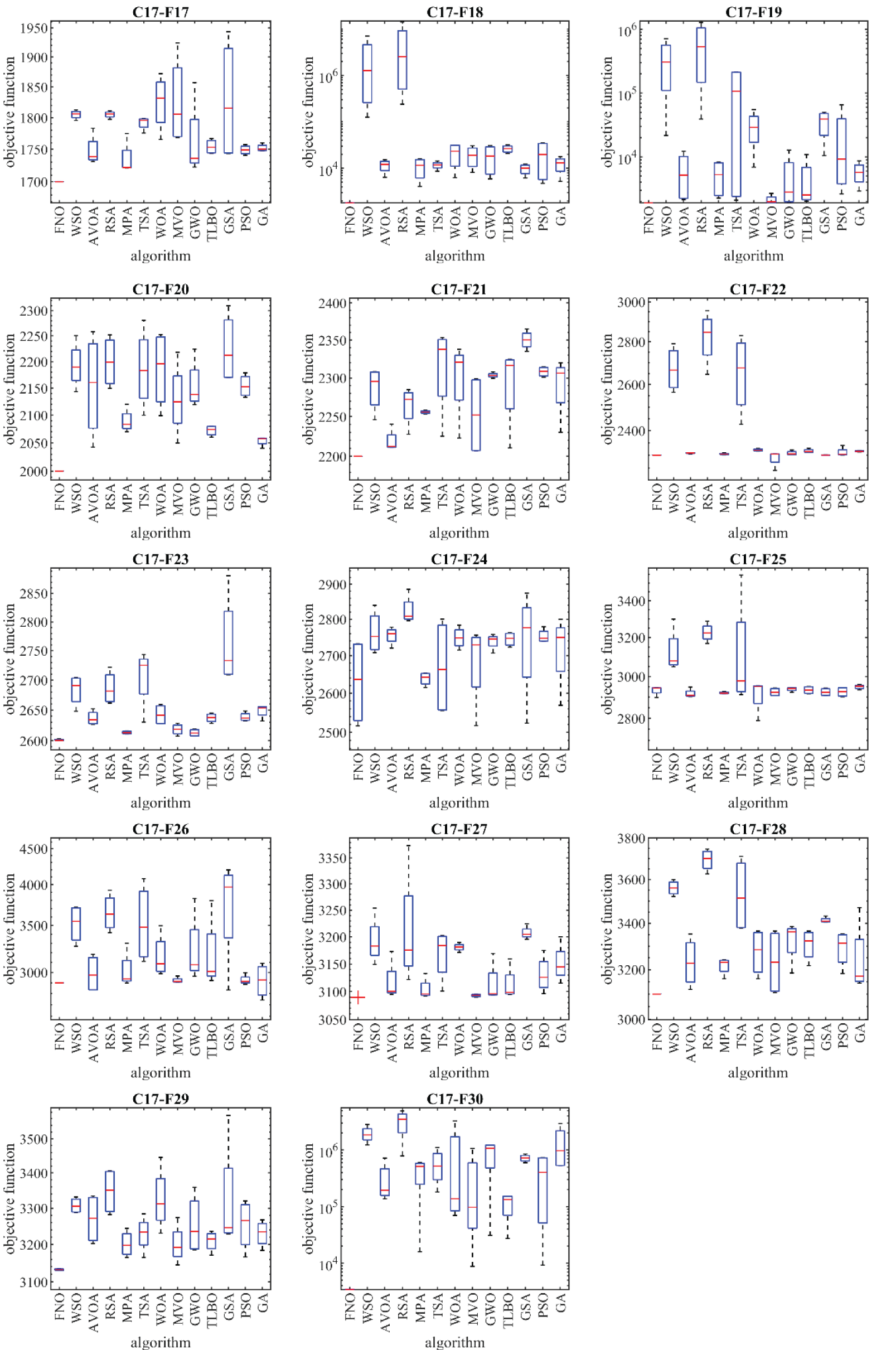
Figure 3: Boxplot diagrams of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 10)

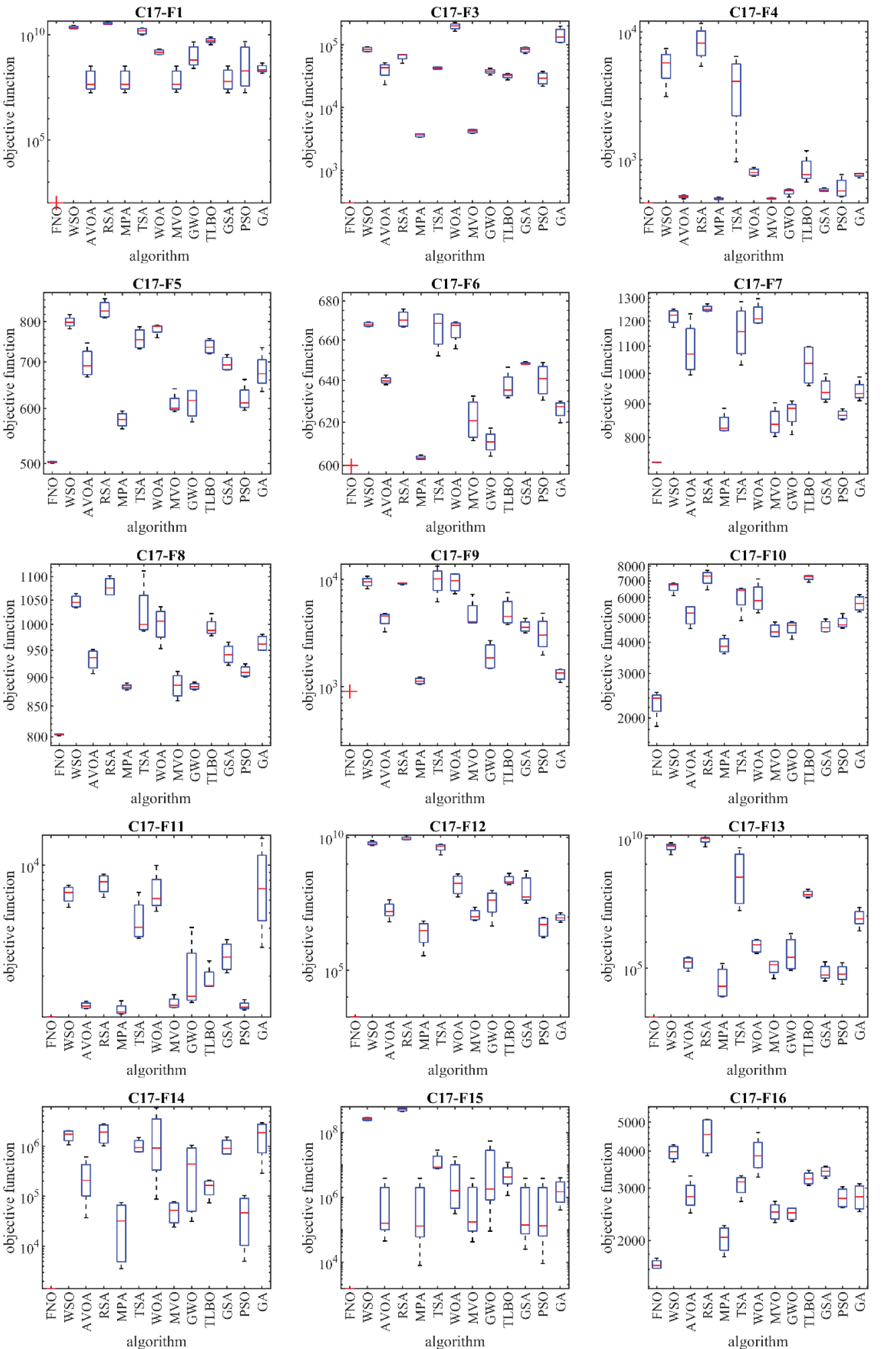
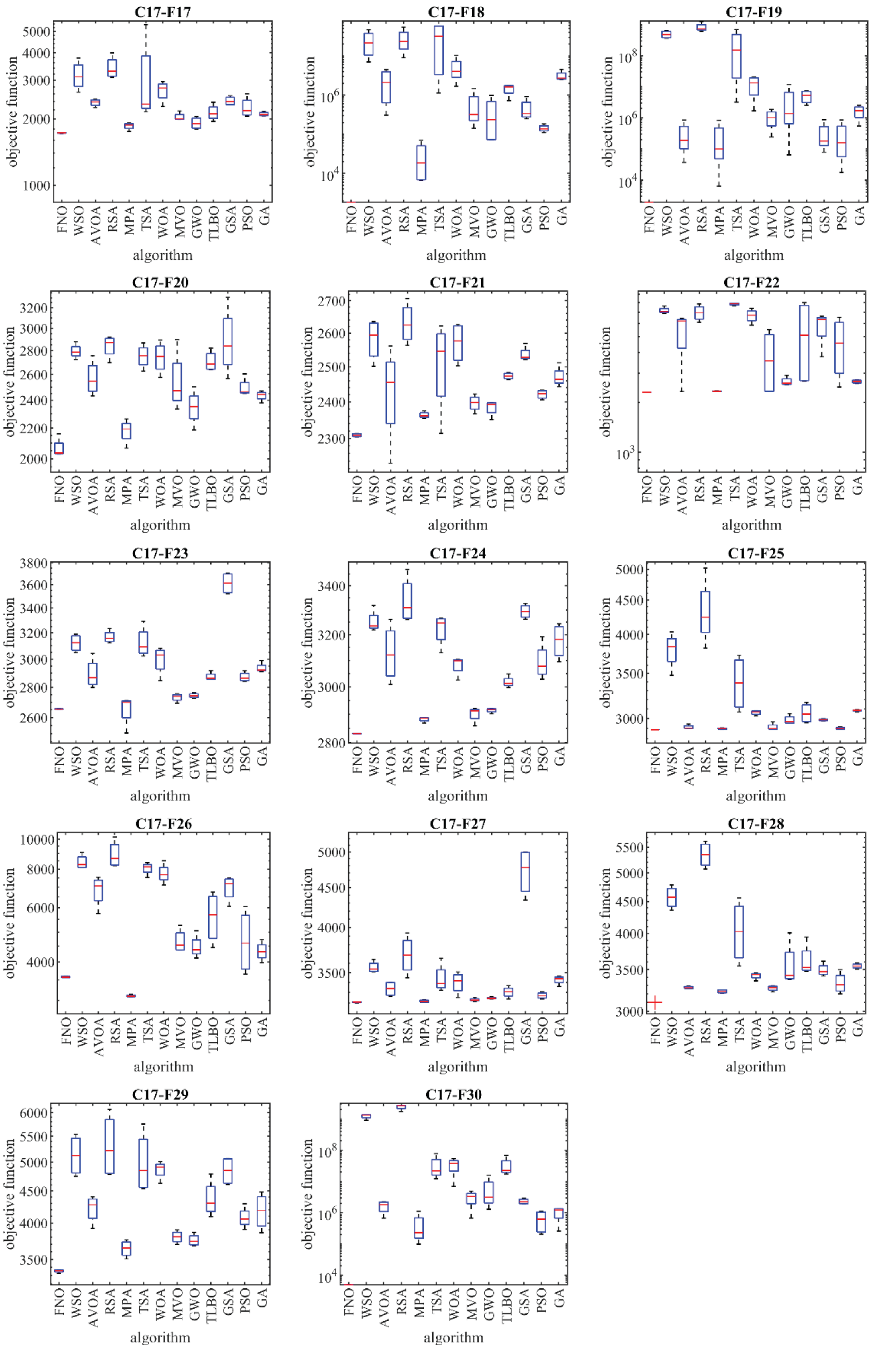
Figure 4: Boxplot diagrams of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 30)

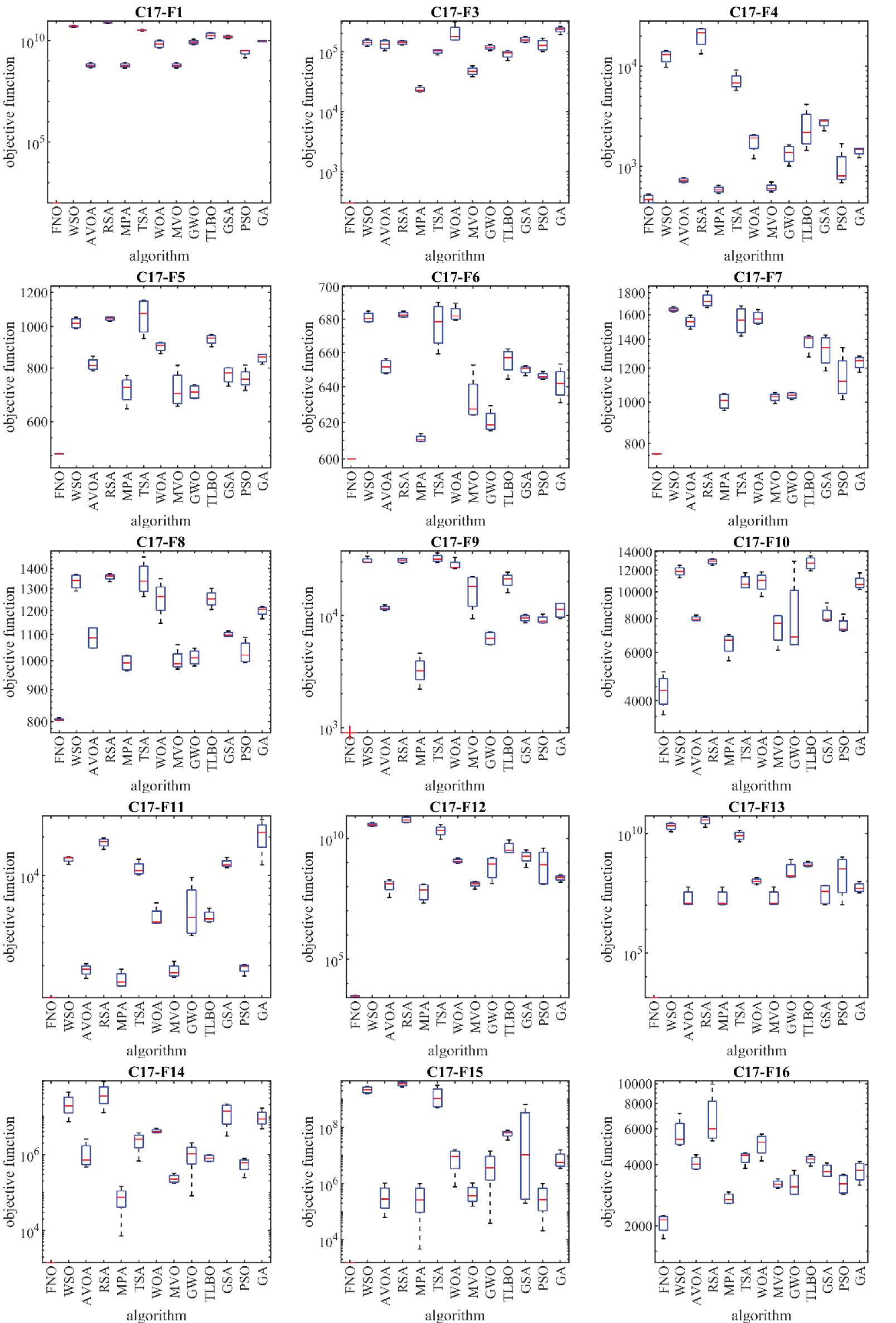
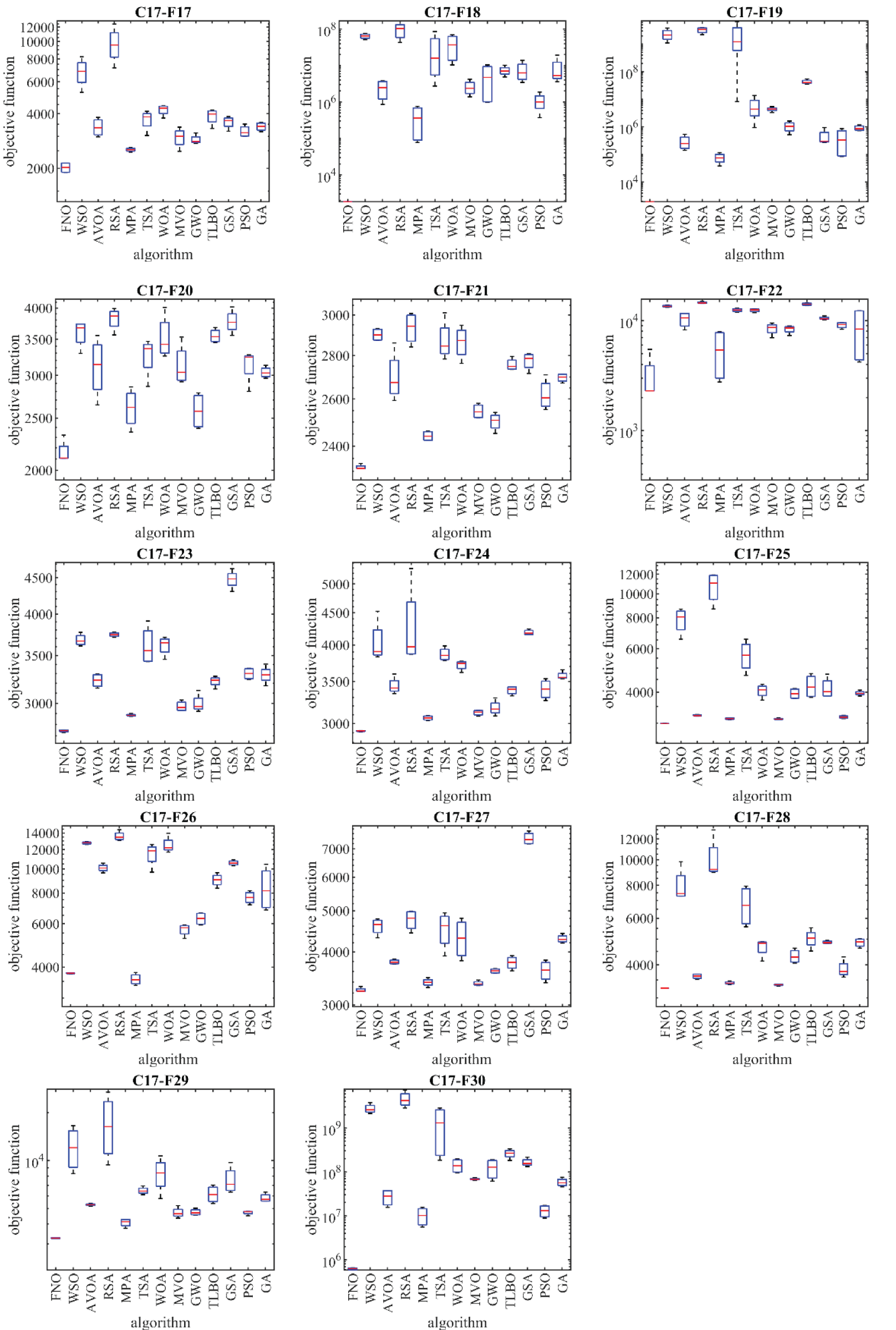
Figure 5: Boxplot diagrams of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 50)

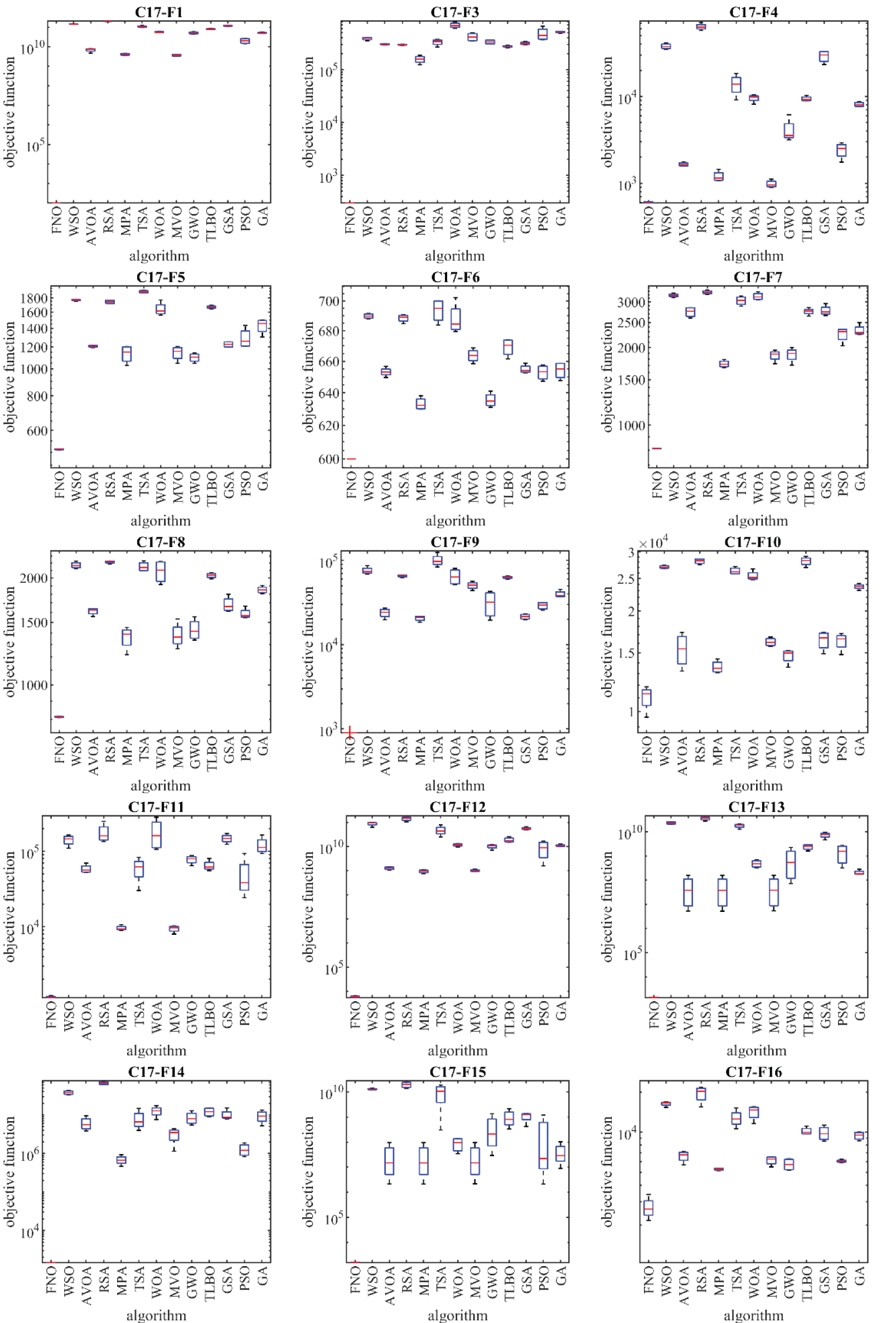
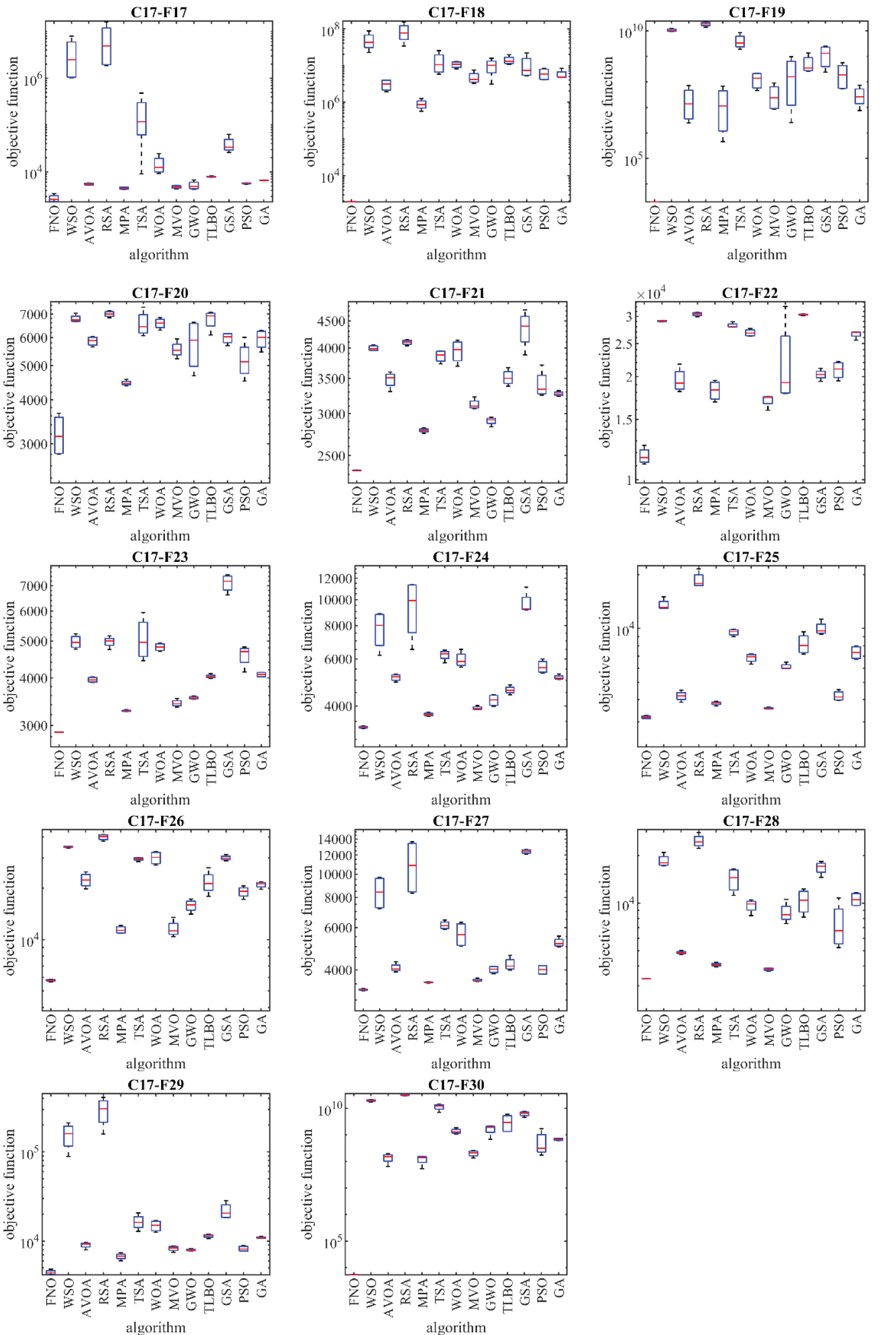
Figure 6: Boxplot diagrams of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 100)

According to the optimization outcomes, when tackling the CEC 2017 test suite with problem dimensions equal to 10 (m = 10), the proposed FNO approach emerges as the top-performing optimizer for functions C17-F1, C17-F3 to C17-F21, C17-F23, C17-F24, and C17-F26 to C17-F30. In the case of problem dimensions equal to 30 (m = 30), FNO proves to be the foremost optimizer for functions C17-F1, C17-F3 to C17-F22, C17-F24, C17-F25, and C17-F27 to C17-F30. Likewise, for problem dimensions of 50 (m = 50), FNO exhibits superiority as the primary optimizer for functions C17-F1, C17-F3 to C17-F25, and C17-F27 to C17-F30. Lastly, for problem dimensions of 100 (m = 100), FNO stands out as the premier optimizer for functions C17-F1, and C17-F3 to C17-F30.

The optimization outcomes highlight FNO’s exceptional ability in exploration, exploitation, and maintain a harmonious balance between these strategies throughout the search procedure, resulting in the discovery of viable solutions for the benchmark functions. Examination of the simulation results reveals FNO’s superior performance in tackling the challenges presented by the CEC 2017 test suite when compared to its competitors. FNO consistently outperforms other algorithms across a significant portion of the benchmark functions, earning the top rank as the most effective optimizer.

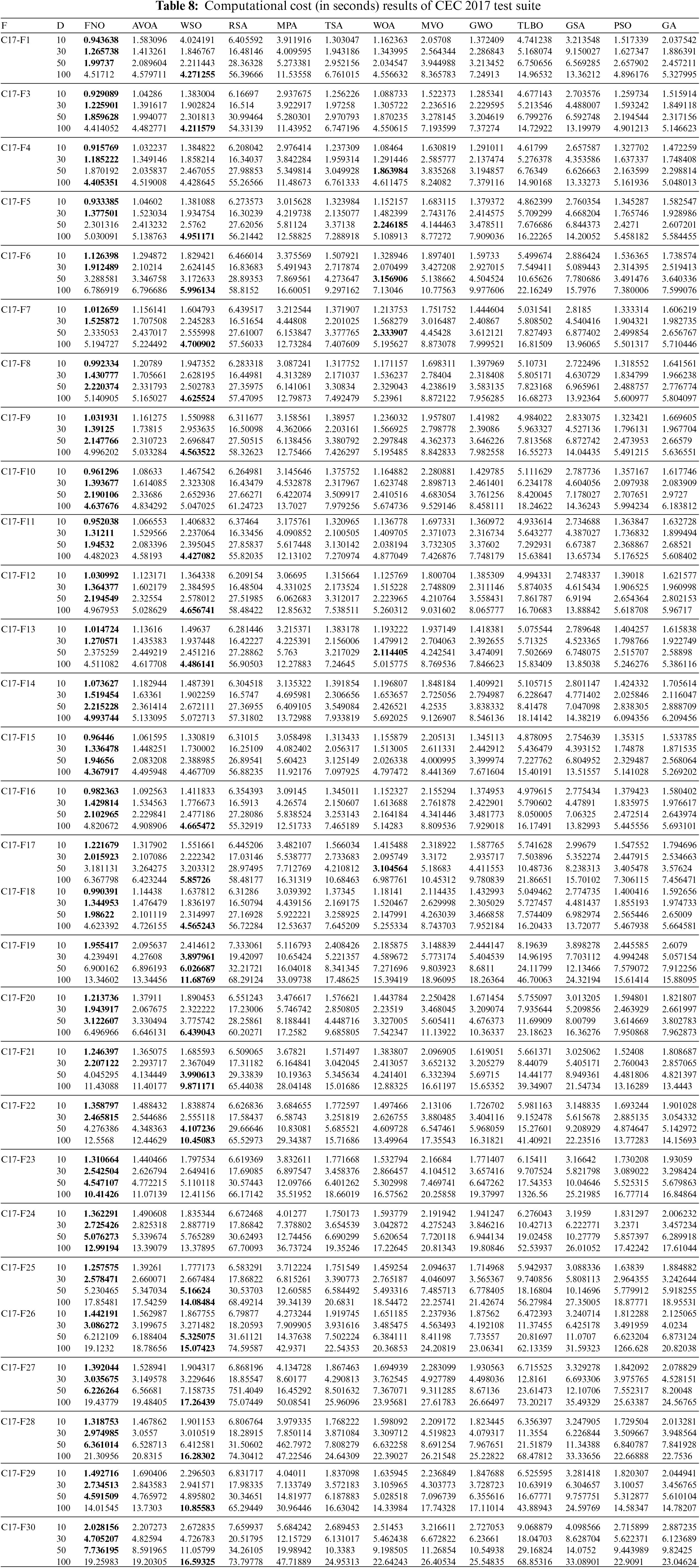
In addition to comparing the proposed approach of FNO and competing algorithms using statistical indicators and boxplot diagrams, it is valuable to present a comparison analysis of the computational cost and convergence speed between FNO and other competing metaheuristic algorithms. For this purpose, the results obtained from the analysis of the computational cost between FNO and competing algorithms in handling the CEC 2017 test suite for dimensions 10, 30, 50, and 100 are reported in Table 8. In order to analyze the computational cost of each algorithm in handling each benchmark function, the average execution time of each algorithm (in seconds) in different implementations on a benchmark function has been used. It should be mentioned that the experiments have been implemented on the software MATLAB R2022a using a 64-bit Core i7 processor with 3.20 GHz and 16 GB main memory. In fact, the results reported in Table 8 show that each algorithm needs a few seconds on average to run an implementation on each of the benchmark functions. The findings show that FNO has a lower computational cost compared to competing algorithms in most of the benchmark functions.

Also, with the aim of analyzing the convergence speed between FNO and competing algorithms, the convergence curves obtained from the performance of metaheuristic algorithms are drawn in Figs. 7 to 10. The findings show that FNO has different mechanisms to achieve the optimal solution during algorithm iterations. What is evident is that FNO, by balancing exploration and exploitation, has been able to handle most of the CEC 2017 test suite benchmark functions in a reasonable number of iterations.

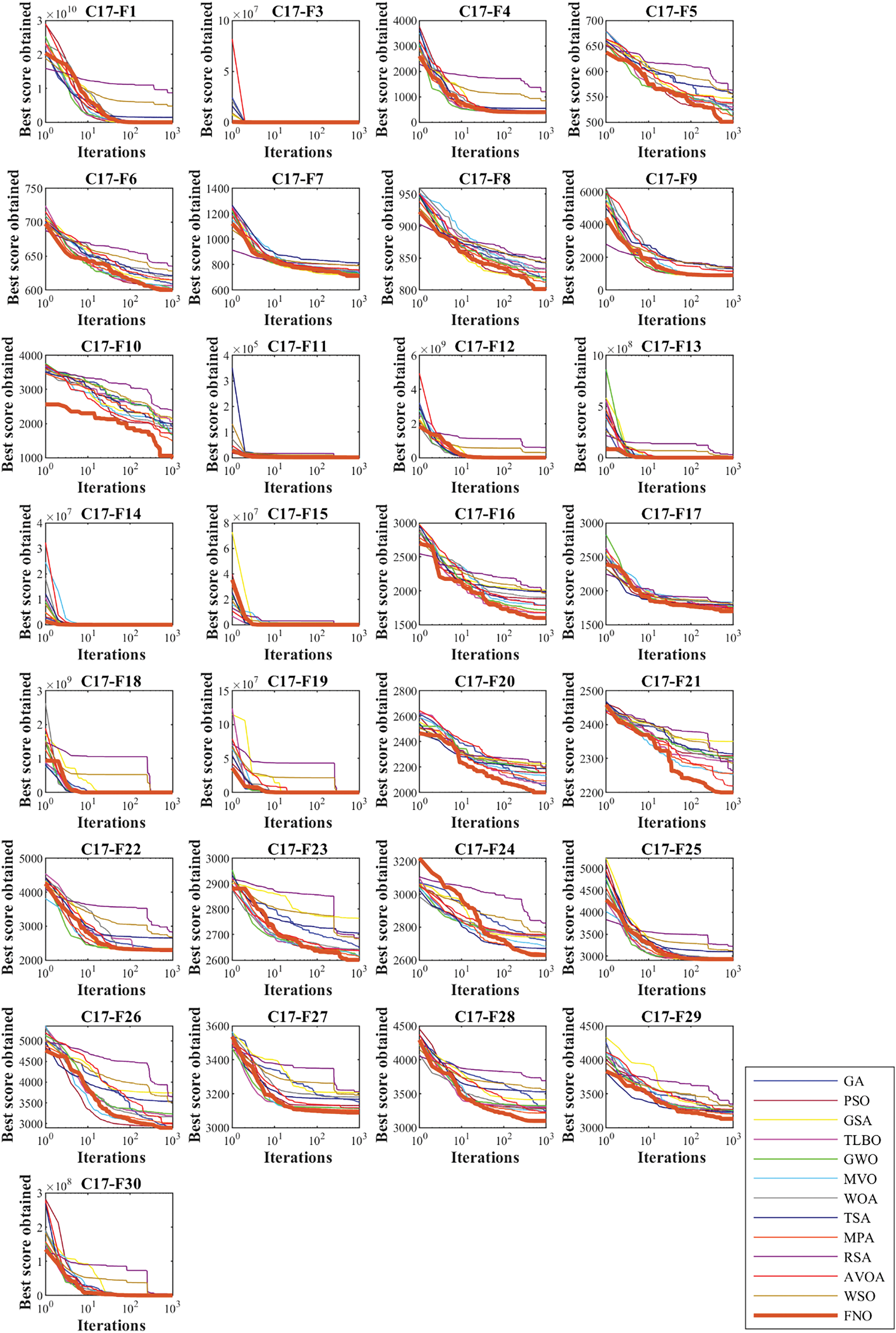
Figure 7: Convergence curves of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 10)

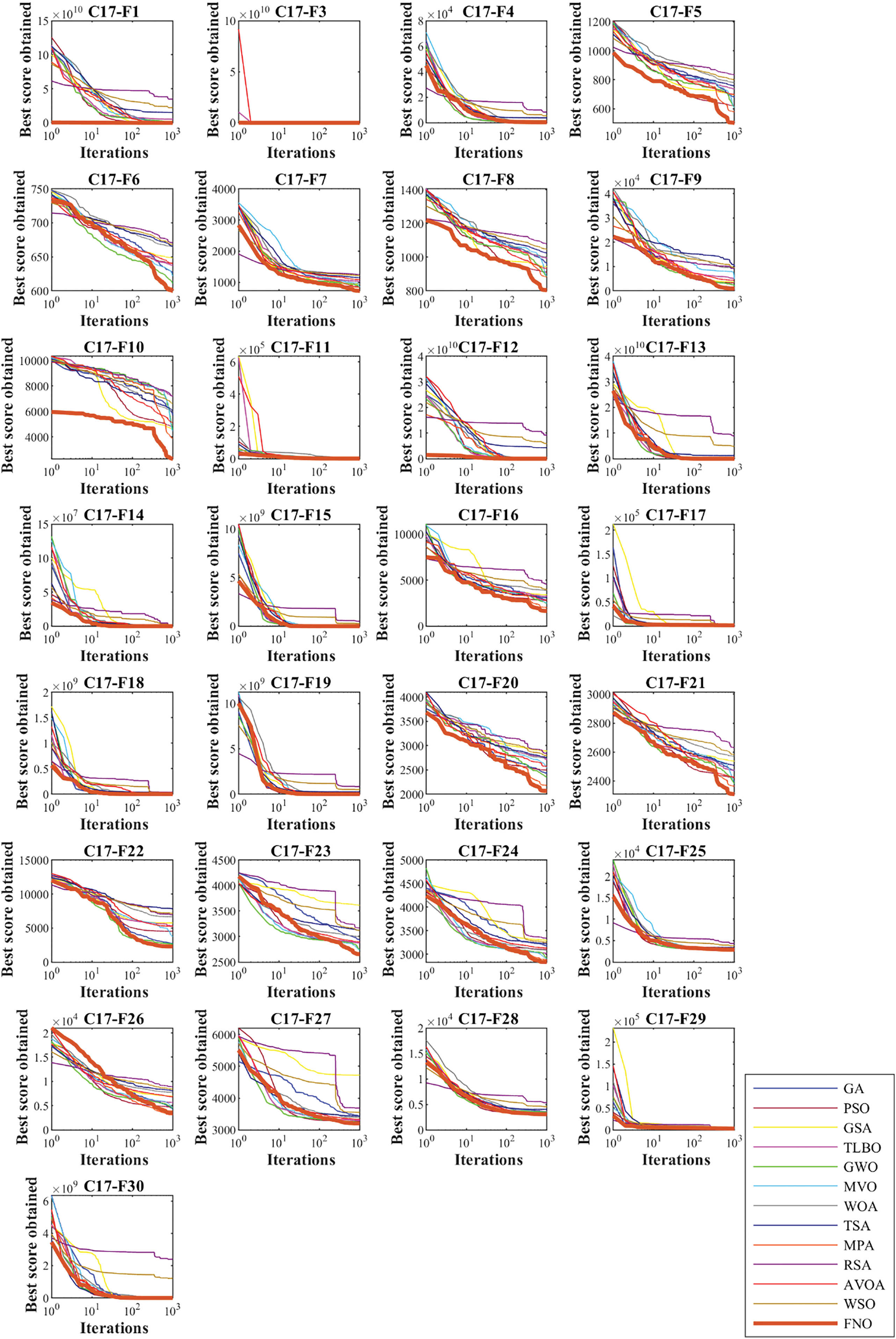
Figure 8: Convergence curves of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 30)

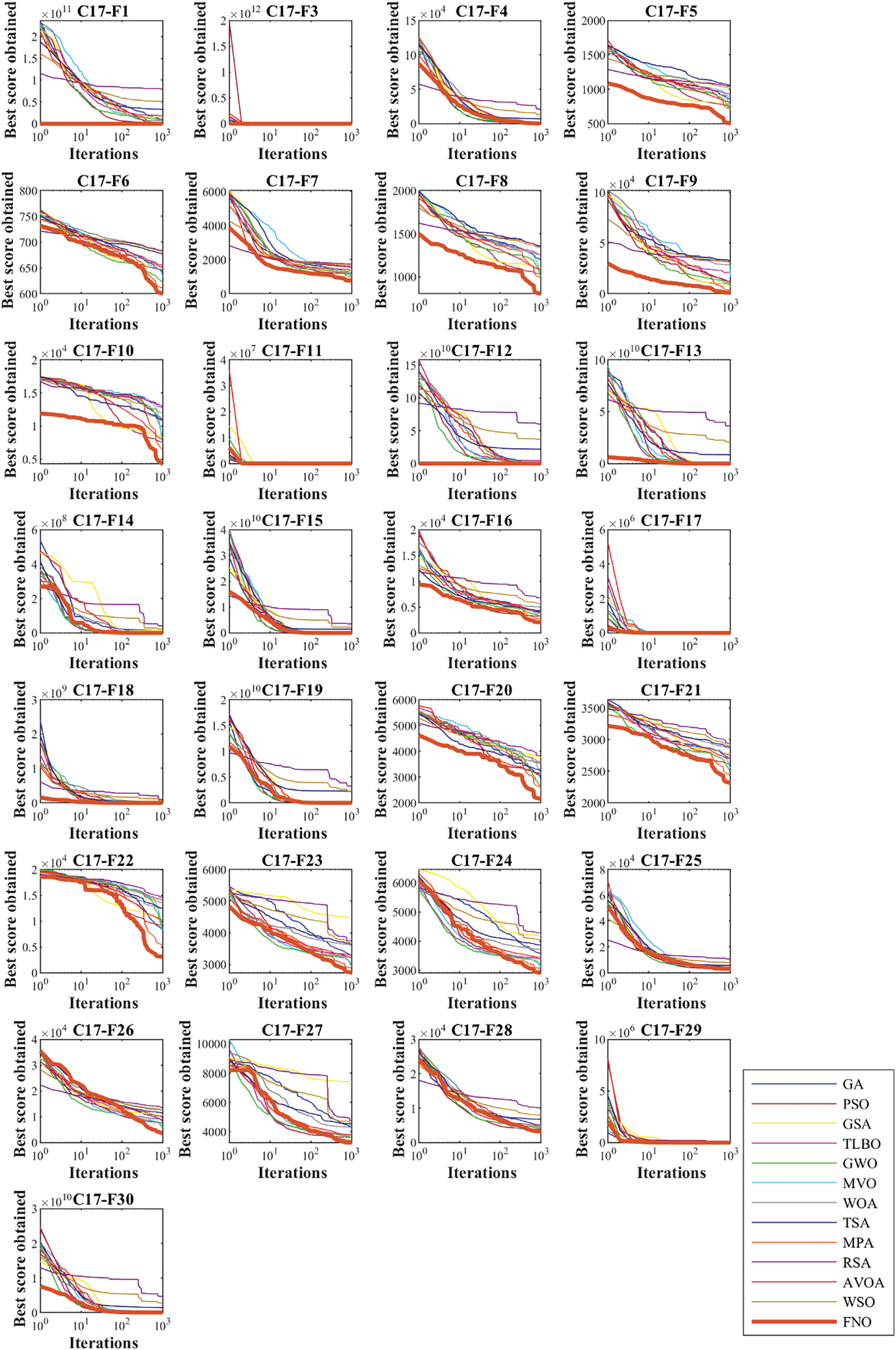
Figure 9: Convergence curves of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 50)

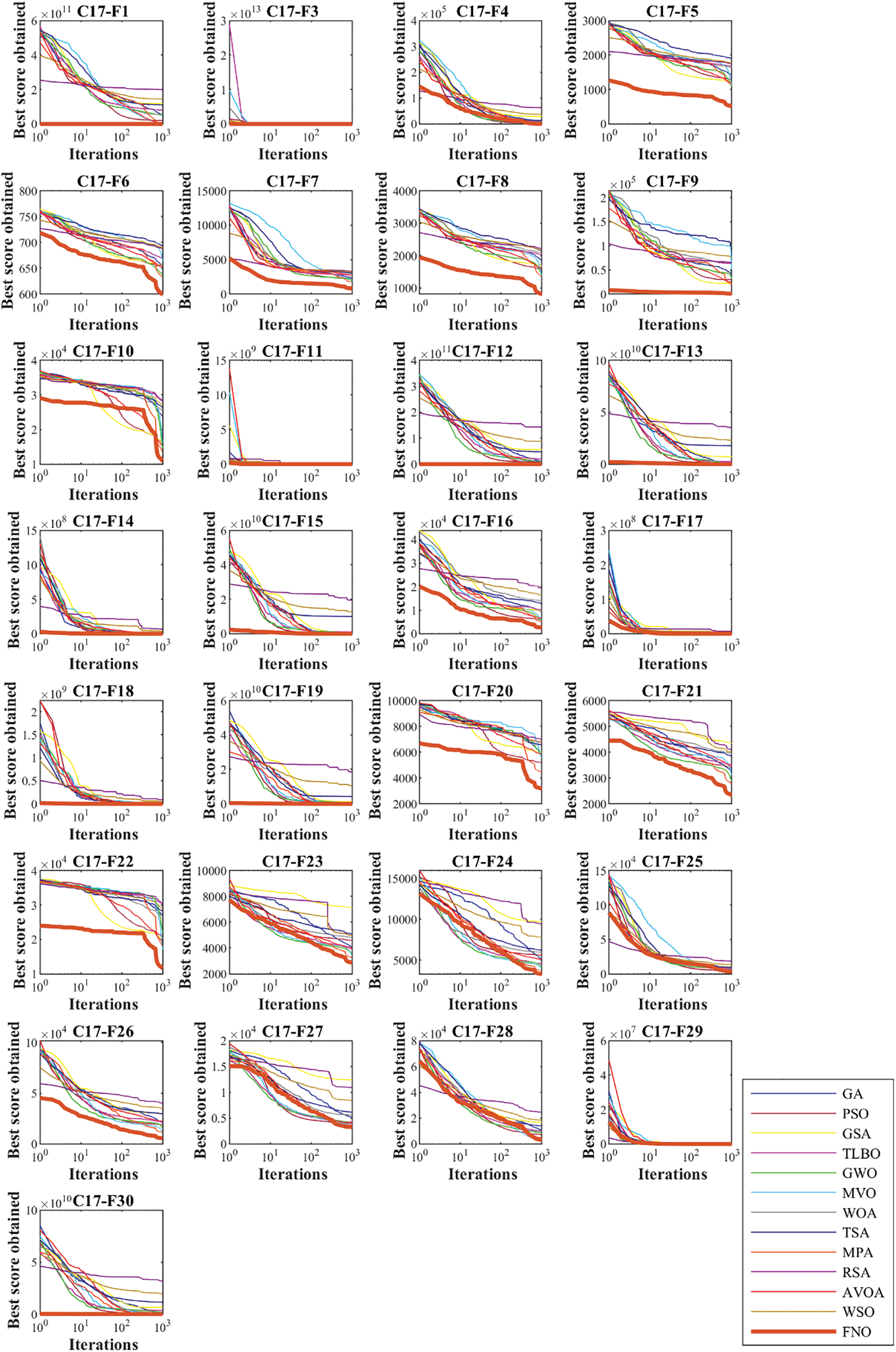
Figure 10: Convergence curves of FNO and competitor algorithms performances on CEC 2017 test suite (dimension = 100)

4.3 Evaluation of CEC 2020 Test Suite

In this sub-section, the effectiveness of the proposed approach to address CEC 2020 is challenged. This test suite consists of ten bound-constrained numerical optimization benchmark functions. Among these, C20-F1 is unimodal, C20-F2 to C20-F4 is basic, C20-F5 to C20-F7 is hybrid, and C20-F8 to C20-F10 is composition. Complete information of CEC 2020 is provided in detail on [60].

The implementation results of the proposed FNO approach and competing algorithms are reported in Table 9. Boxplot diagrams obtained from metaheuristic algorithms are drawn in Fig. 11. Based on the obtained results, FNO has been the first best optimizer to handle all 10 functions C20-F1 to C20-F10. The simulation findings show that FNO has provided superior performance for handling CEC 2020 by providing better results in each benchmark function compared to competing algorithms.

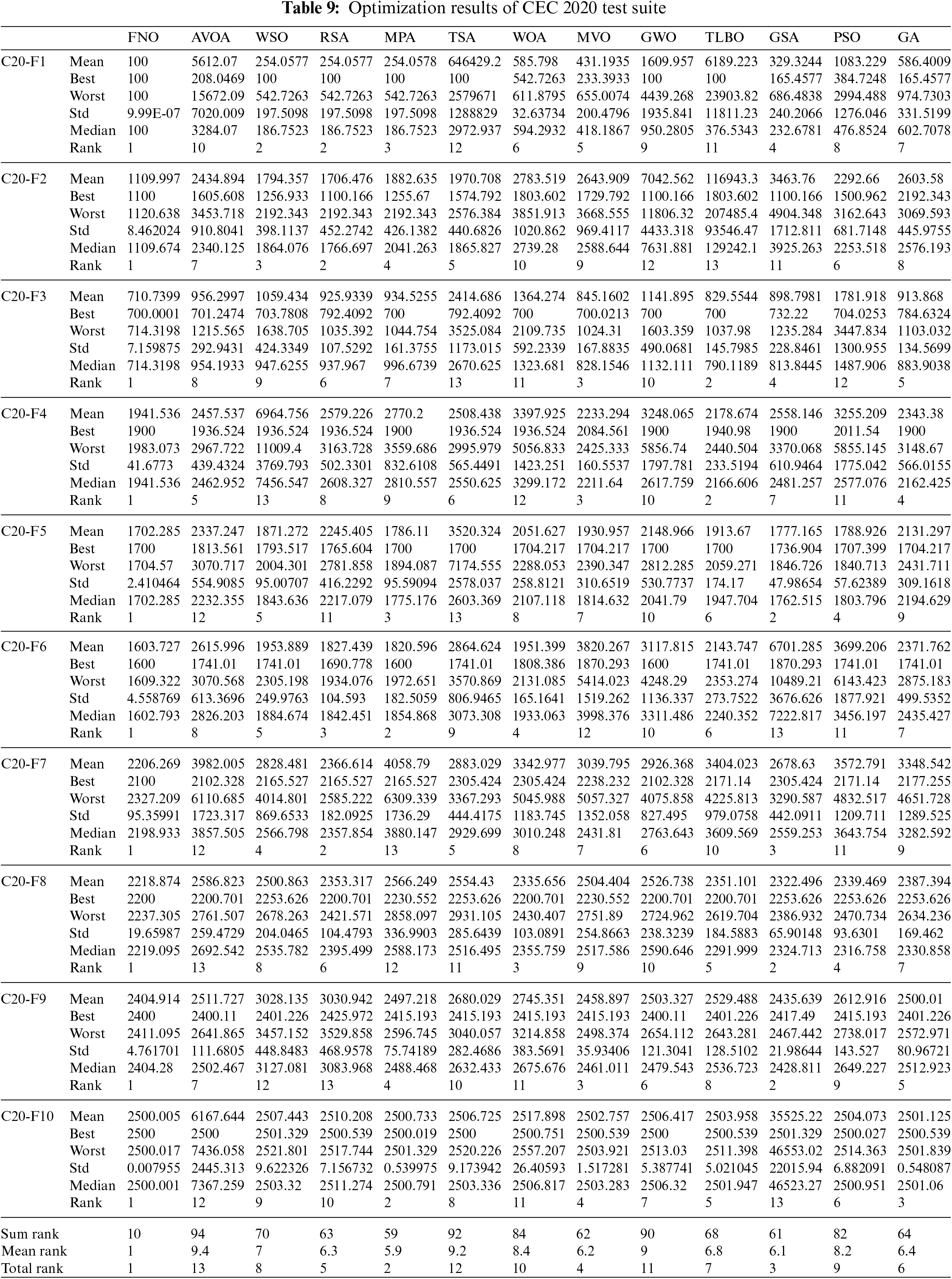
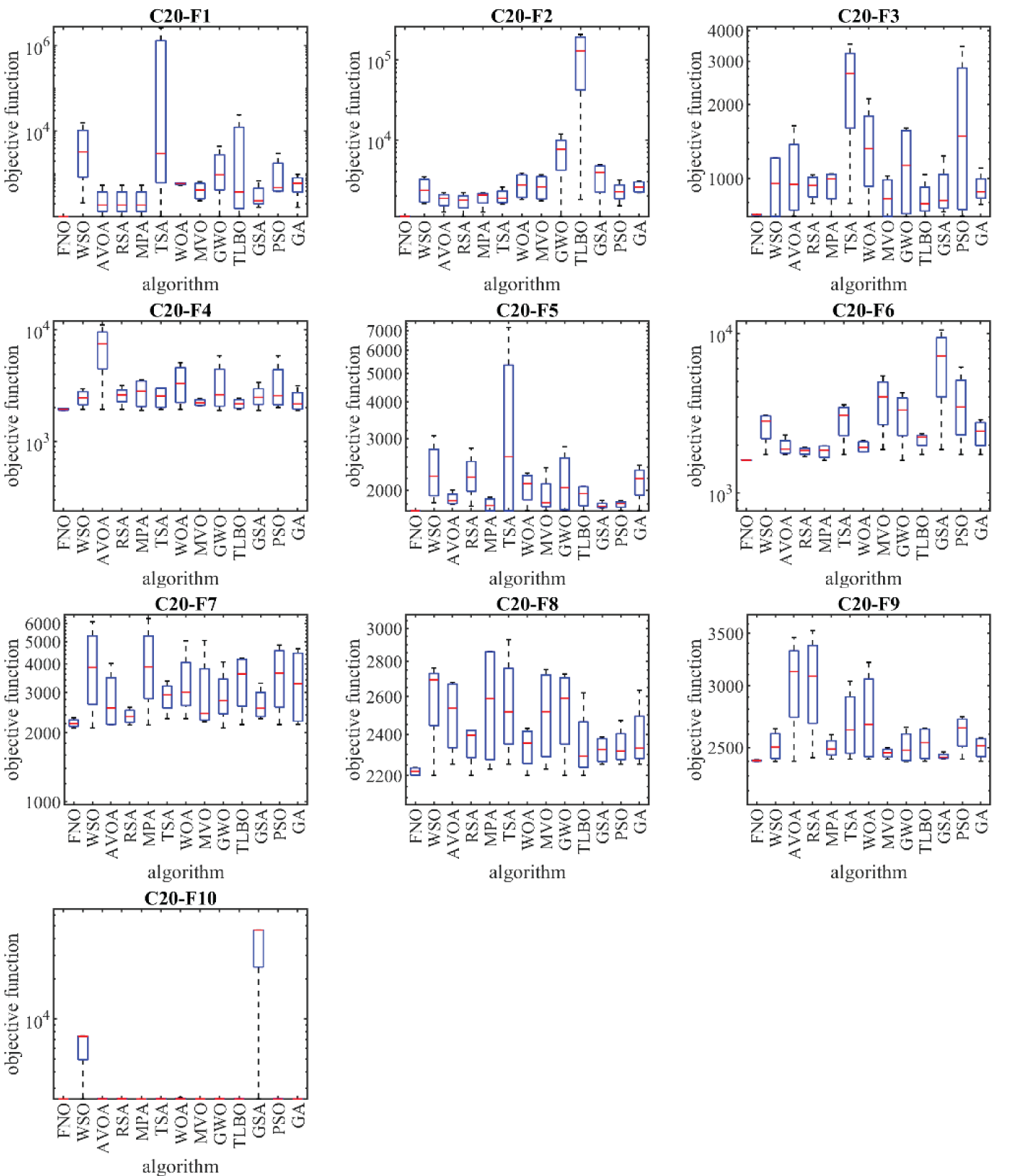
Figure 11: Boxplot diagrams of FNO and competitor algorithms performances on CEC 2020 test suite

4.4 Statistical Analysis

In this section, a statistical analysis is conducted to determine whether FNO exhibits a significant advantage over competitor algorithms. To address this inquiry, the Wilcoxon rank sum test [61] is utilized, a non-parametric test renowned for discerning significant differences between the means of two data samples. In the Wilcoxon rank sum test, the presence or absence of a noteworthy discrepancy in performance between two metaheuristic algorithms is gauged using a parameter known as the p-value. The results of applying the Wilcoxon rank sum test to evaluate FNO’s performance against each competitor algorithm are documented in Table 10.

Based on the outcomes of the statistical analysis, instances where the p-value falls below 0.05 indicate that FNO demonstrates a statistically significant superiority over the corresponding competitor algorithm. Consequently, it is evident that FNO outperforms all twelve competitor algorithms significantly across problem dimensions equal to 10, 30, 50, and 100 when handling the CEC 2017 test suite. Also, the findings indicate that FNO has a significant statistical advantage compared to competing algorithms for handling the CEC 2020 test suite.

5  FNO for Real-World Applications

In this section, we examine the efficacy of the proposed FNO methodology in tackling real-world optimization challenges. To achieve this, we have selected a subset of twenty-two constrained optimization problems from the CEC 2011 test suite, along with four engineering design problems, for assessment. As in the previous section, here the simulation results are reported using six statistical indicators: mean, best, worst, std, median, and rank. It should be noted that the values of the “mean” index are the criteria used to rank the algorithms in handling each of the CEC 2011 test suite problems as well as each of the engineering design problems.

CEC 2011 test suite has been used in many algorithms recently published in similar articles, in order to judge the efficiency of designed metaheuristic algorithms. This test suite consists of twenty-two constrained optimization problems from real world applications. For this reason, in this paper, CEC 2011 test suite has been chosen to evaluate the effectiveness of the proposed FNO approach in handling optimization problems in real world applications.

In order to adapt the proposed approach of FNO to deal with constrained optimization problems, there are different solutions. In this study, the method of penalty coefficient is used. In this case, for a candidate FNO solution, a penalty value is added to the objective function for each of the constraints that are not satisfied. As a result, automatically this inappropriate corresponding solution will not be placed as a solution in the output. However, it is possible that during the update process in the next iteration, a new solution will be produced that satisfies the constraints.

5.1 Evaluation of CEC 2011 Test Suite

In this section, we assess the performance of FNO and competitor algorithms in tackling the CEC 2011 test suite, comprising twenty-two constrained optimization problems derived from real-world applications. A comprehensive description and detailed information on the CEC 2011 test suite can be found in [62]. The proposed FNO approach and each of the competitor algorithms is implemented on the CEC 2011 functions in twenty-five independent implementations where each implementation contains 150,000 FEs. The implementation outcomes of FNO and competitor algorithms on the CEC 2011 test suite are documented in Table 11, while boxplot diagrams illustrating the performance of metaheuristic algorithms are presented in Fig. 12.

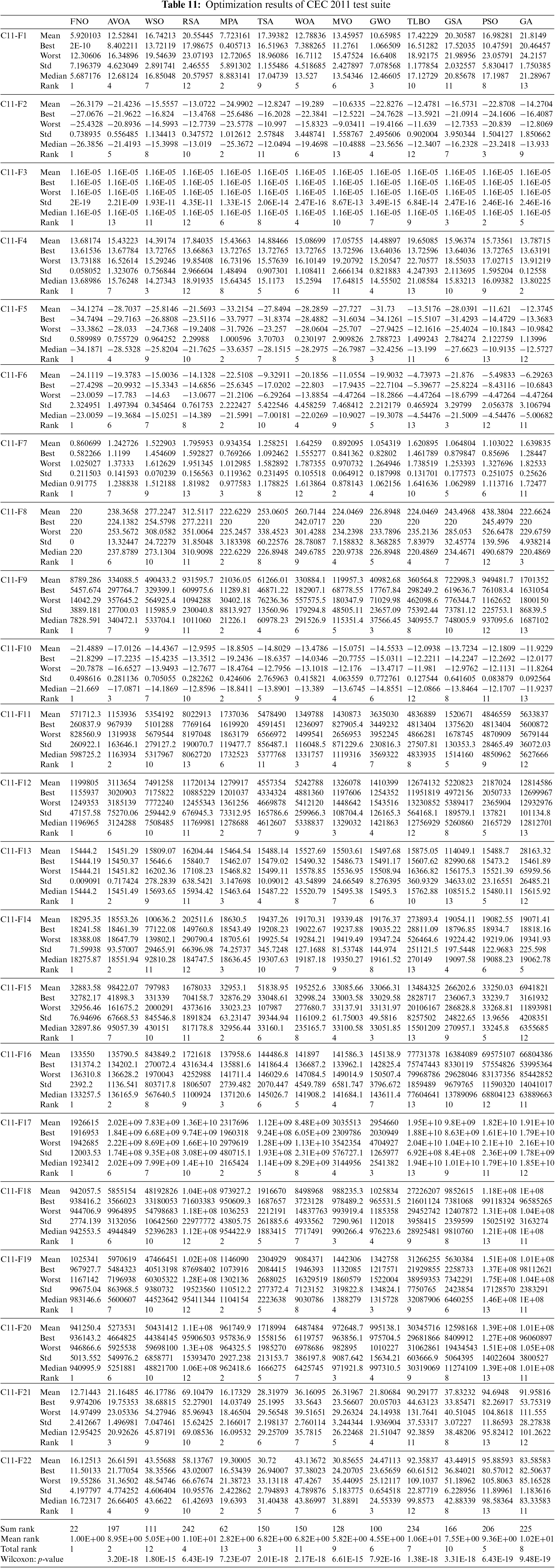
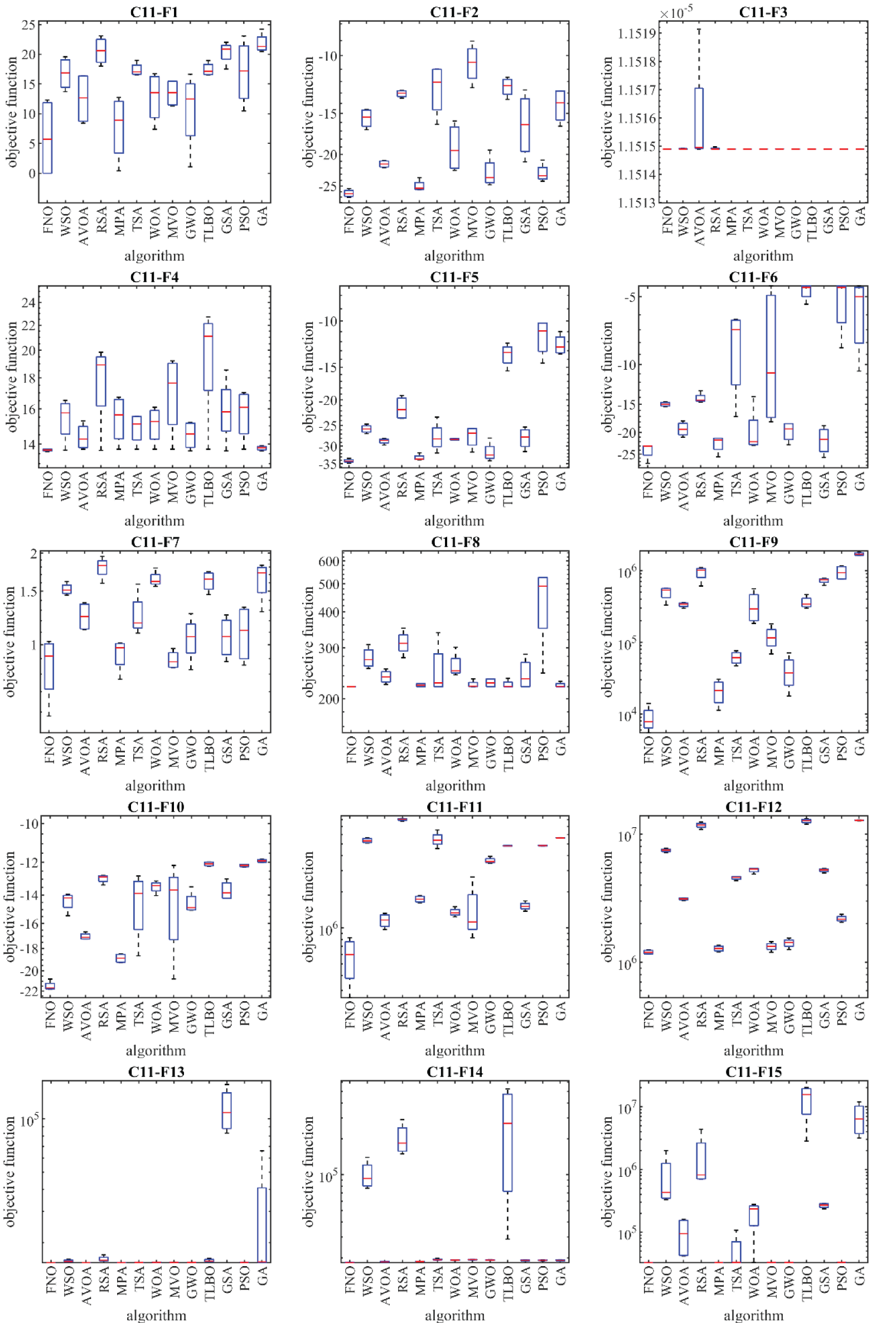
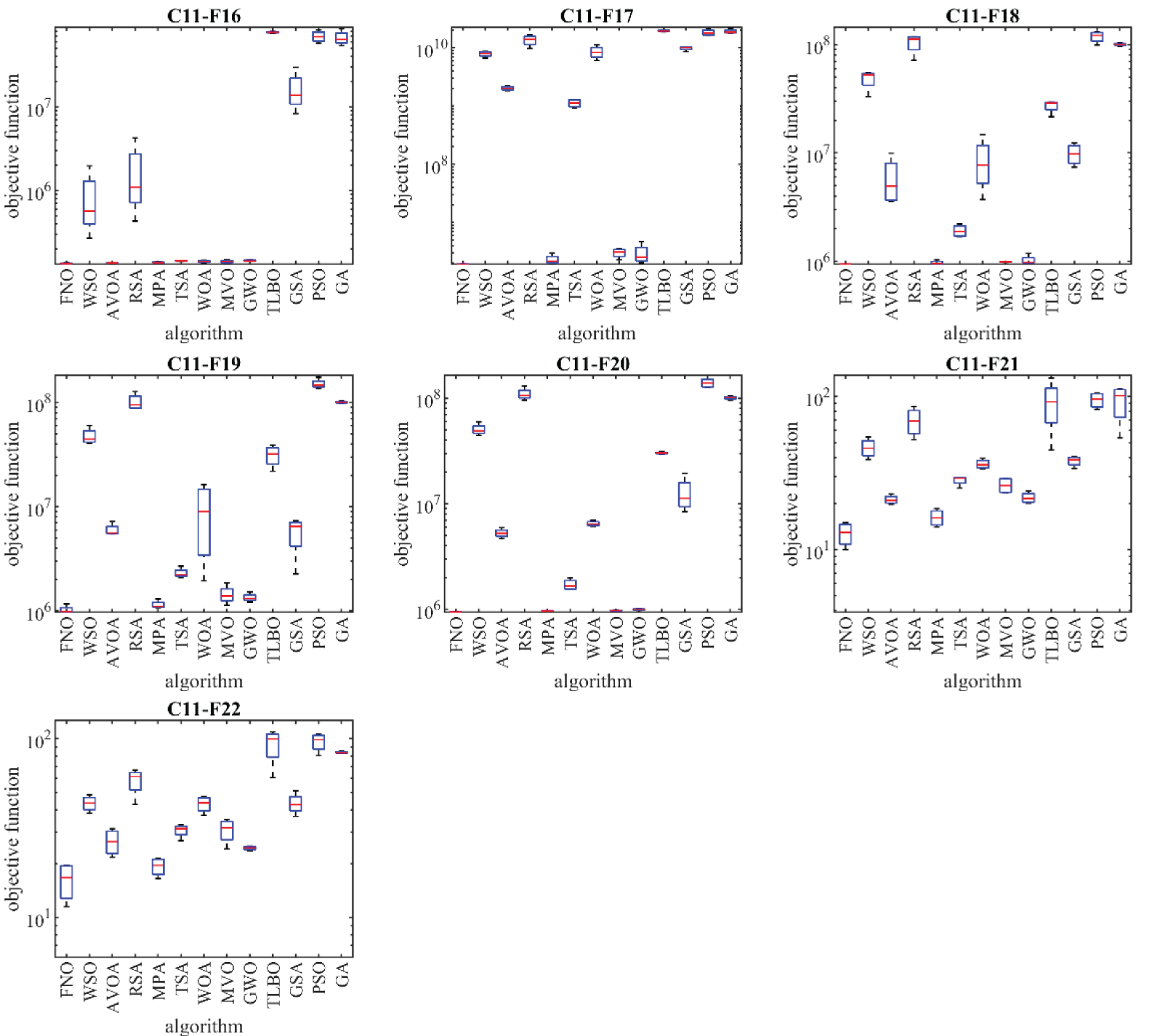
Figure 12: Boxplot diagrams of FNO and competitor algorithms performances on CEC 2011 test suite

Based on the optimization results, FNO emerges as the top-performing optimizer for optimization problems C11-F1 to C11-F22, demonstrating its adeptness in exploration, exploitation, and maintaining a balance between the two throughout the search process. The simulation results indicate FNO’s superior performance in handling the CEC 2011 test suite, achieving superior results across most optimization problems and securing the top rank as the first best optimizer compared to competitor algorithms. Additionally, the p-value results obtained using the Wilcoxon rank sum test affirm that FNO exhibits a statistically significant superiority over all twelve competitor algorithms in handling the CEC 2011 test suite.

5.2 Pressure Vessel Design Problem

Designing pressure vessels is a pertinent optimization task in real-world applications, as illustrated in Fig. 13, with the objective of minimizing construction costs. The mathematical model for this design is outlined as follows [63]:

Consider: X=[x1,x2,x3,x4]=[Ts,Th,R,L].

Minimize: f(x)=0.6224x1x3x4+1.778x2x32+3.1661x12x4+19.84x12x3.

Subject to:

g1(x)=−x1+0.0193x3≤0,   g2(x)=−x2+0.00954x3≤0,

g3(x)=−πx32x4−43πx33+1296000≤0,   g4(x)=x4−240≤0.

With

0≤x1,x2≤100 and 10≤x3,x4≤200.

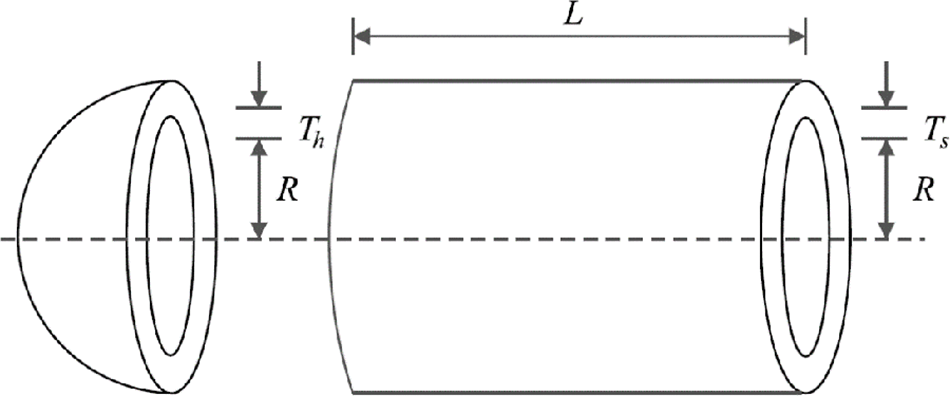
Figure 13: Schematic of pressure vessel design

The implementation outcomes of FNO and rival algorithms in addressing pressure vessel design are detailed in Tables 12 and 13. Fig. 14 illustrates the convergence curve of FNO during the attainment of the optimal design for this problem.

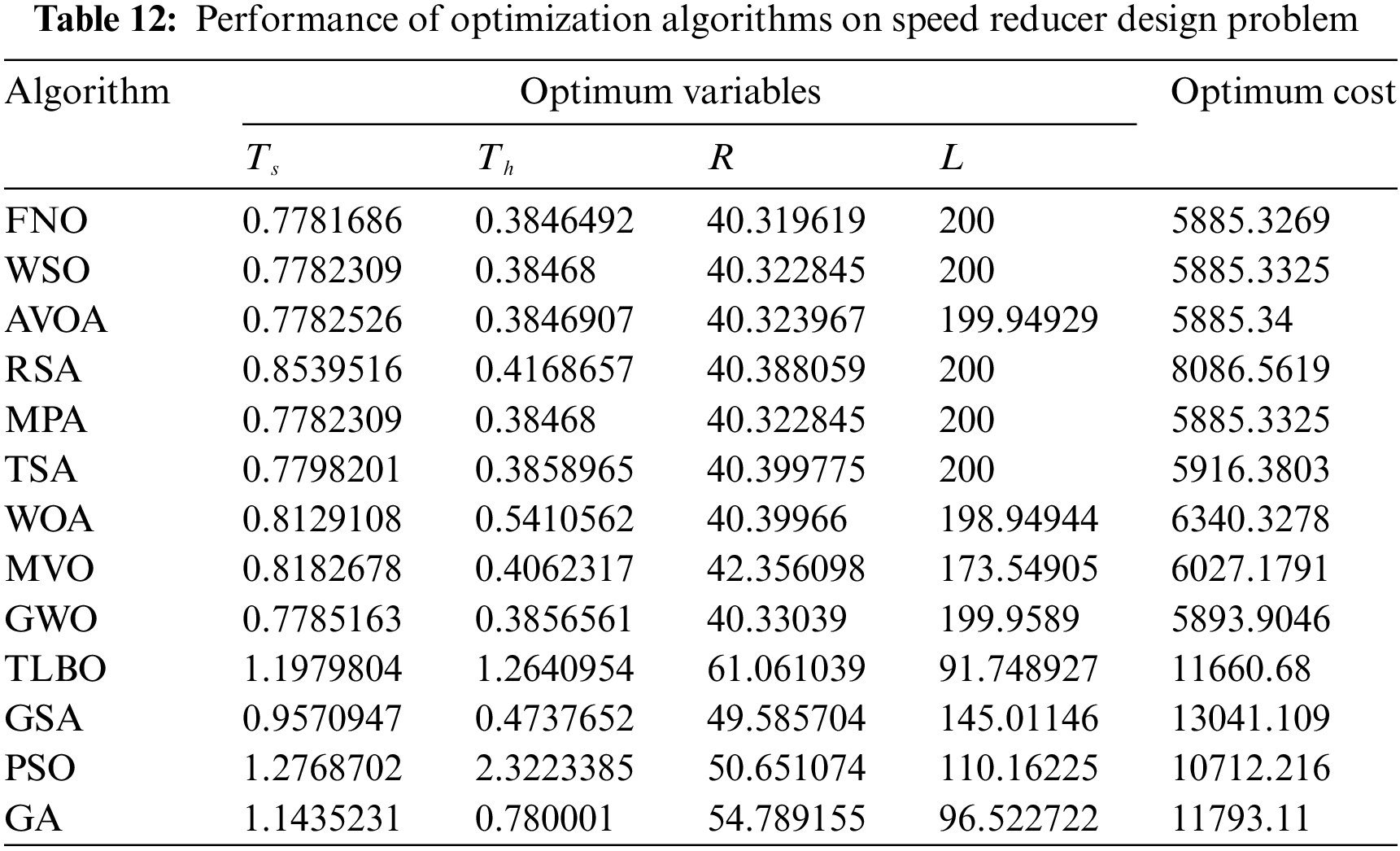
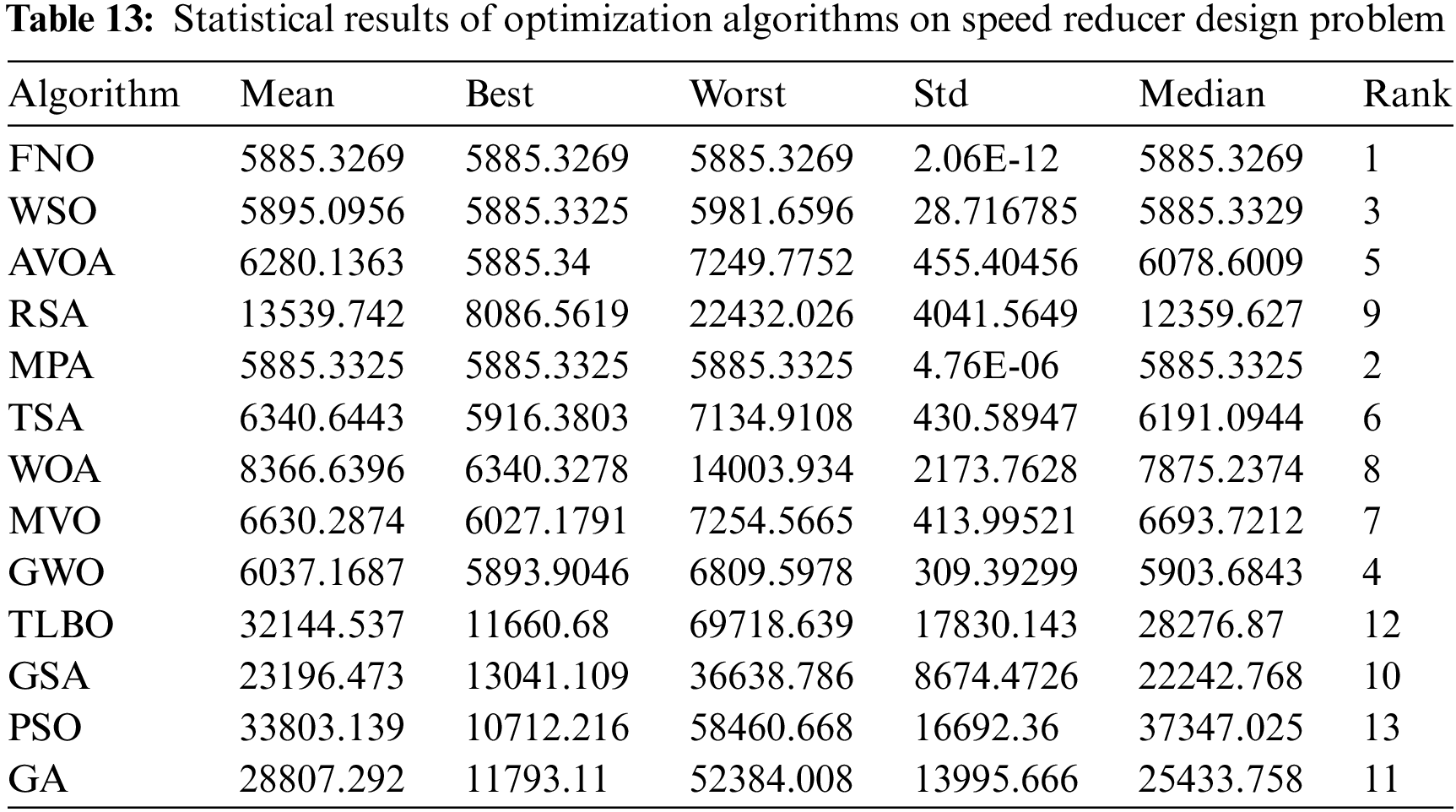
Figure 14: FNO’s performance convergence curve on pressure vessel design

According to the findings, FNO has delivered the optimal design with design variable values of (0.7781686, 0.3846492, 40.319619, 200), and an objective function value of 5885.3269. Examination of the simulation outcomes highlights the superior performance of FNO in handling pressure vessel design compared to rival algorithms.

5.3 Speed Reducer Design Problem

The optimization task of speed reducer design finds practical application in real-world scenarios, as depicted in Fig. 15, with the objective of minimizing the weight of the speed reducer. The mathematical model for this design is outlined as follows [64,65]:

Consider: X=[x1,x2,x3,x4,x5,x6,x7]=[b,m,p,l1,l2,d1,d2].

Minimize: f(x)=0.7854x1x22(3.3333x32+14.9334x3−43.0934)−1.508x1(x62+x72)+7.4777(x63+x73)+0.7854(x4x62+x5x72).

Subject to:

g1(x)=27x1x22x3−1≤0,   g2(x)=397.5x1x22x32−1≤0,

g3(x)=1.93x43x2x3x64−1≤0,   g4(x)=1.93x53x2x3x74−1≤0,

g5(x)=1110x63(745x4x2x3)2+16.9⋅106−1≤0,

g6(x)=185x73(745x5x2x3)2+157.5⋅106−1≤0,

g7(x)=x2x340−1≤0,   g8(x)=5x2x1−1≤0,

g9(x)=x112x2−1≤0,   g10(x)=1.5x6+1.9x4−1≤0,

g11(x)=1.1x7+1.9x5−1≤0.

With

2.6≤x1≤3.6,0.7≤x2≤0.8,17≤x3≤28,7.3≤x4≤8.3,7.8≤x5≤8.3,2.9≤x6≤3.9,and 5≤x7≤5.5.

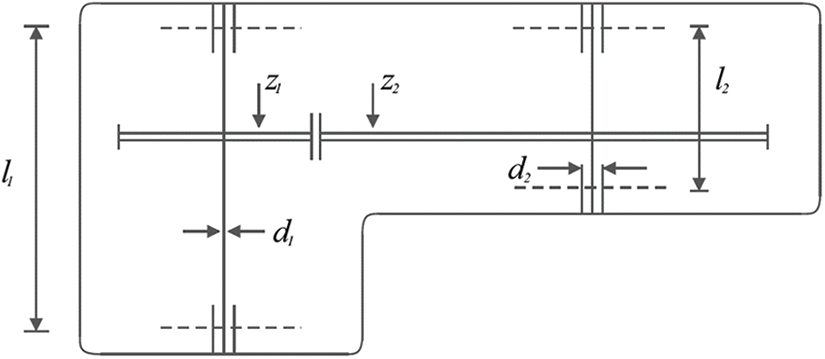
Figure 15: Schematic of speed reducer design

The outcomes of employing FNO and rival algorithms to optimize speed reducer design are presented in Tables 14 and 15. Fig. 16 illustrates the convergence curve of FNO during the attainment of the optimal design for this problem.

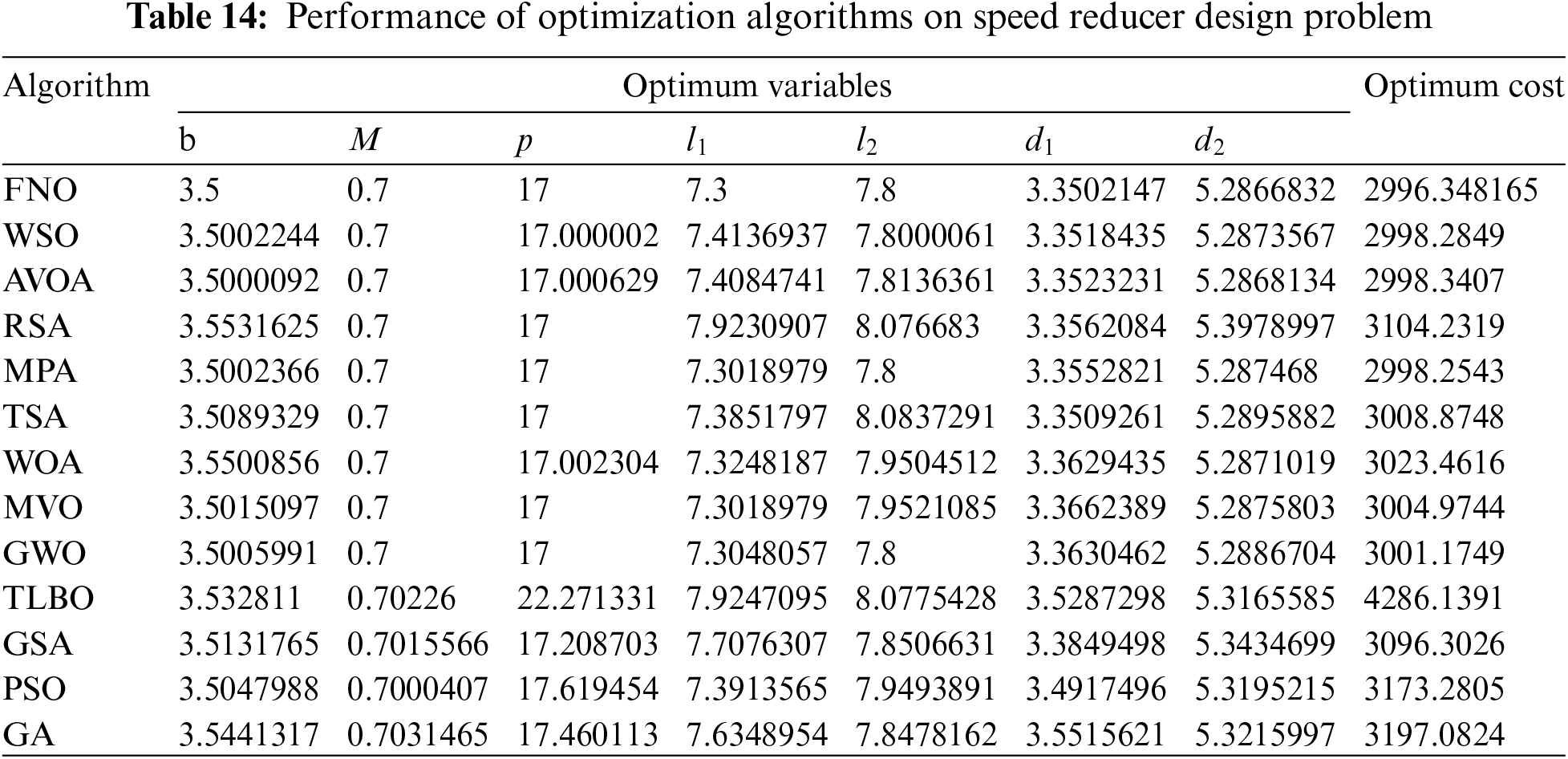
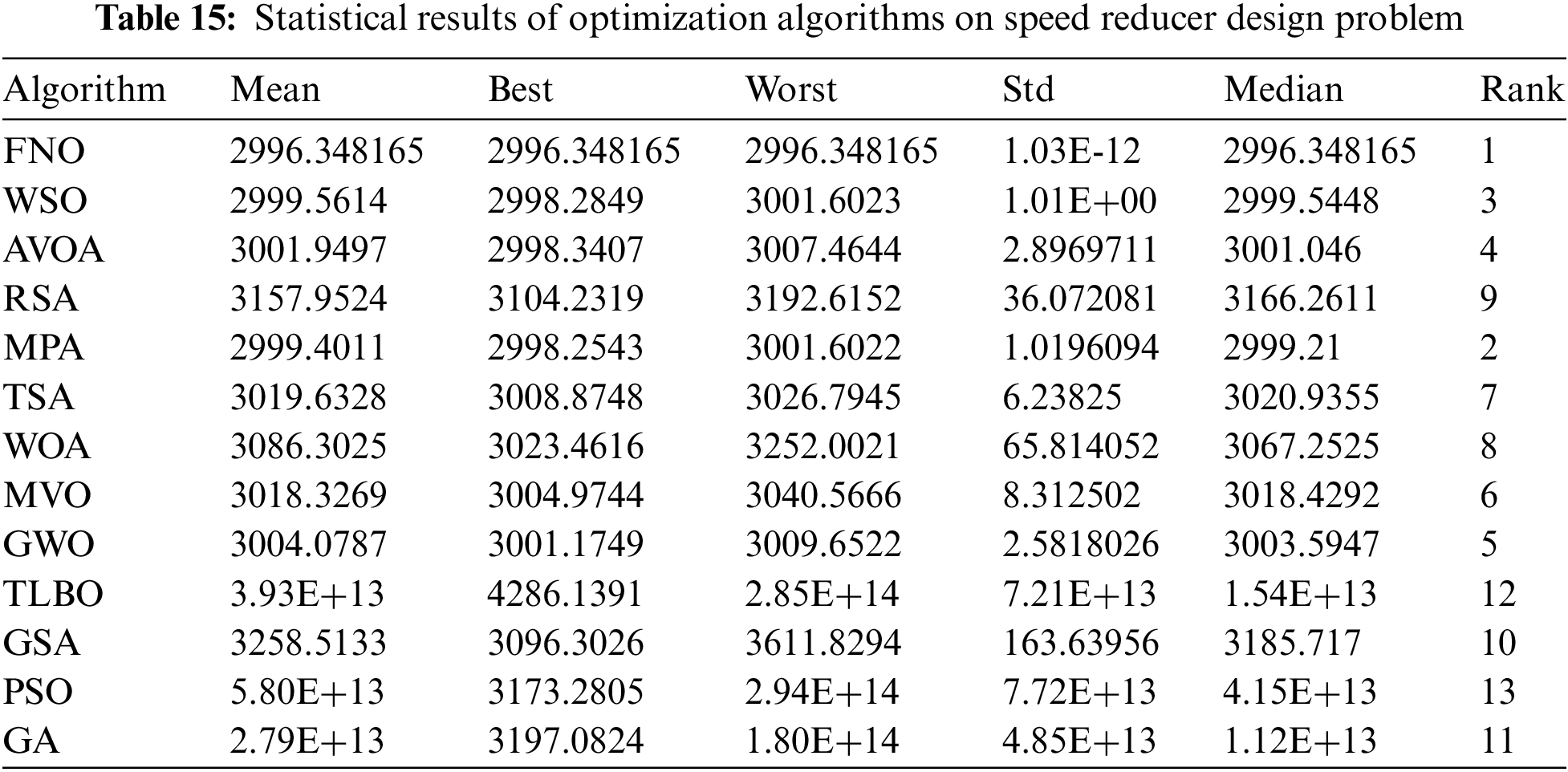
Figure 16: FNO’s performance convergence curve on speed reducer design

According to the findings, FNO has yielded the optimal design with design variable values of (3.5, 0.7, 17, 7.3, 7.8, 3.3502147, 5.2866832), and an objective function value of 2996.348165. Analysis of the simulation results underscores the superior performance of FNO in addressing speed reducer design when compared to rival algorithms.

5.4 Welded Beam Design

The optimization challenge of welded beam design holds significance in real-world applications, as depicted in Fig. 17, with the aim of minimizing the fabrication cost of the welded beam. The mathematical model for this design is articulated as follows [24]:

Consider: X=[x1,x2,x3,x4]=[h,l,t,b].

Minimize: f(x)=1.10471x12x2+0.04811x3x4(14.0+x2).

Subject to:

g1(x)=τ(x)−13600≤0,   g2(x)=σ(x)−30000≤0,

g3(x)=x1−x4≤0,   g4(x)=0.10471x12+0.04811x3x4(14+x2)−5.0≤0,

g5(x)=0.125−x1≤0,   g6(x)=δ(x)−0.25≤0,

g7(x)=6000−pc(x)≤0.

where

τ(x)=(τ′)2+(2ττ′)x22R+(τ′′)2,   τ′=60002x1x2,   τ′′=MRJ,

M=6000(14+x22),   R=x224+(x1+x32)2,

J=2x1x22[x2212+(x1+x32)2],   σ(x)=504000x4x32,

δ(x)=65856000(30⋅106)x4x33,   pc(x)=4.013(30⋅106)x3x431176(1−x3112).

With

0.1≤x1,x4≤2  and  0.1≤x2,x3≤10.

Figure 17: Schematic of welded beam design

Tables 16 and 17 present the outcomes of addressing welded beam design using FNO alongside rival algorithms. Fig. 18 illustrates the convergence curve of FNO as it achieves the optimal design for this problem.

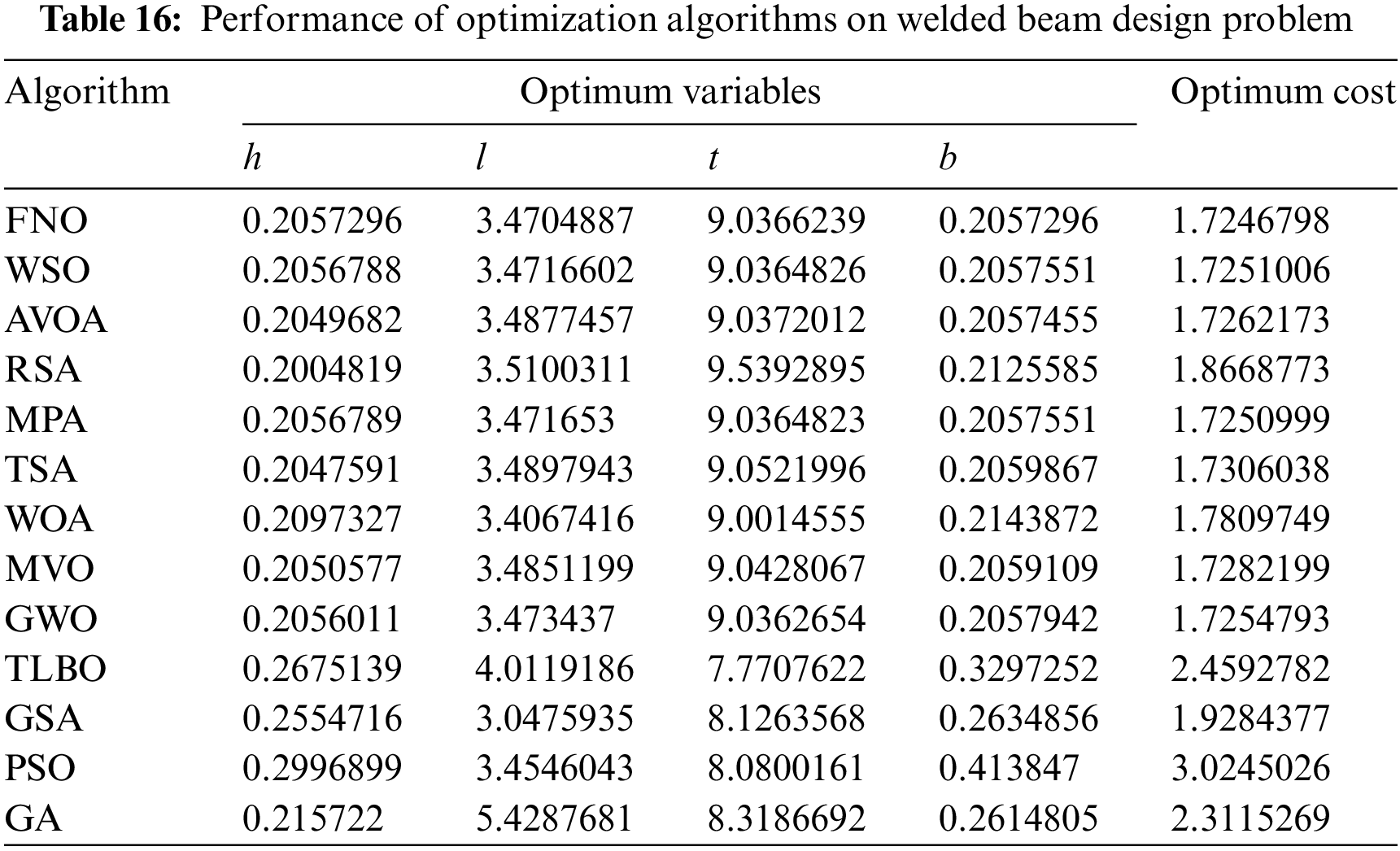
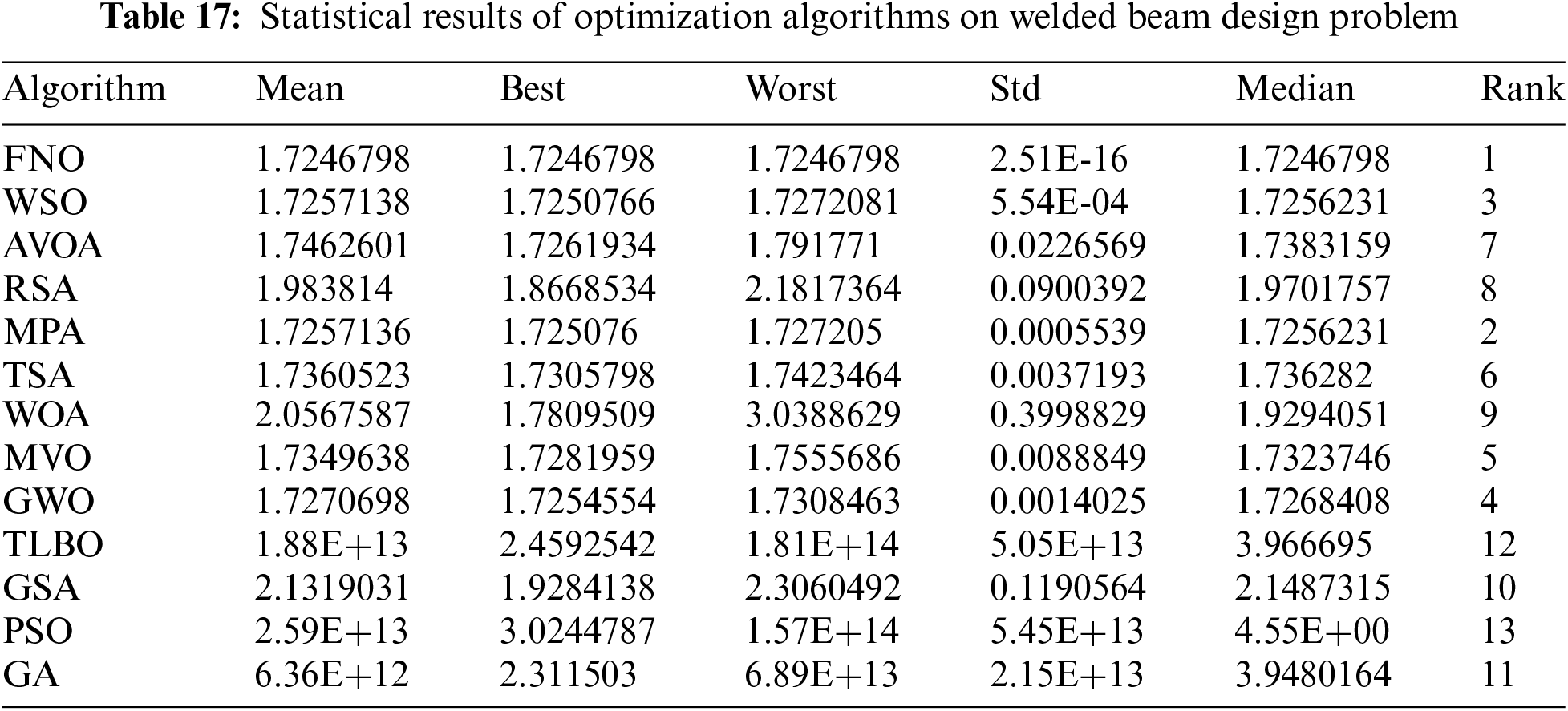
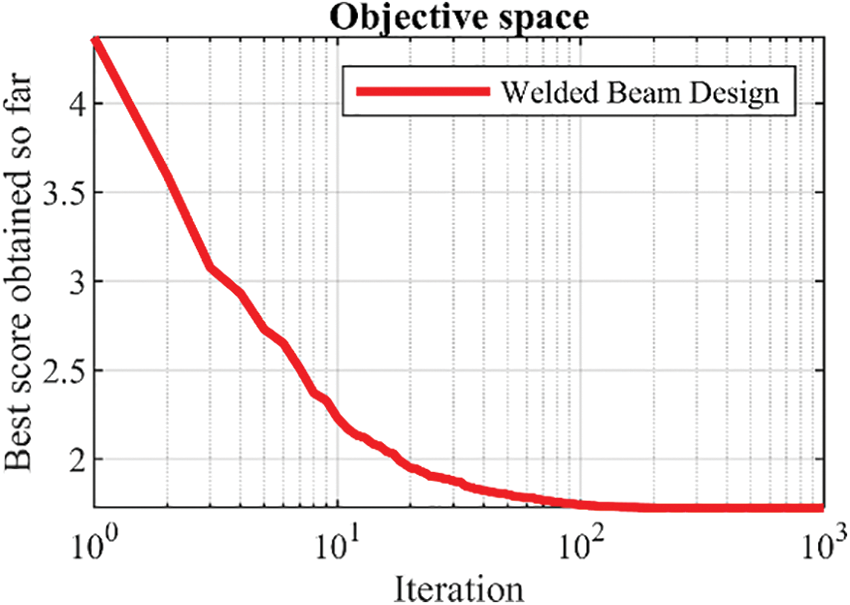
Figure 18: FNO’s performance convergence curve on welded beam design

As per the results obtained, FNO has delivered the optimal design with design variable values of (0.2057296, 3.4704887, 9.0366239, 0.2057296), and an objective function value of 1.7246798. Analysis of the simulation outcomes reveals the superior performance of FNO in optimizing welded beam design compared to rival algorithms.

5.5 Tension/Compression Spring Design

The optimization challenge of tension/compression spring design holds practical relevance in real-world scenarios, as depicted in Fig. 19, with the goal of minimizing the weight of the tension/compression spring. The mathematical model for this design is articulated as follows [24]:

Consider: X=[x1,x2,x3]=[d,D,P].

Minimize: f(x)=(x3+2)x2x12.

Subject to:

g1(x)=1−x23x371785x14≤0,   g2(x)=4x22−x1x212566(x2x13)+15108x12−1≤0,

g3(x)=1−140.45x1x22x3≤0,   g4(x)=x1+x21.5−1≤0. 

With

0.05≤x1≤2,0.25≤x2≤1.3   and   2≤x3≤15.

Tables 18 and 19 depict the outcomes of employing FNO and competitor algorithms to address tension/compression spring design. Fig. 20 showcases the convergence curve of FNO as it attains the optimal design for this problem.

Figure 19: Schematic of tension/compression spring design

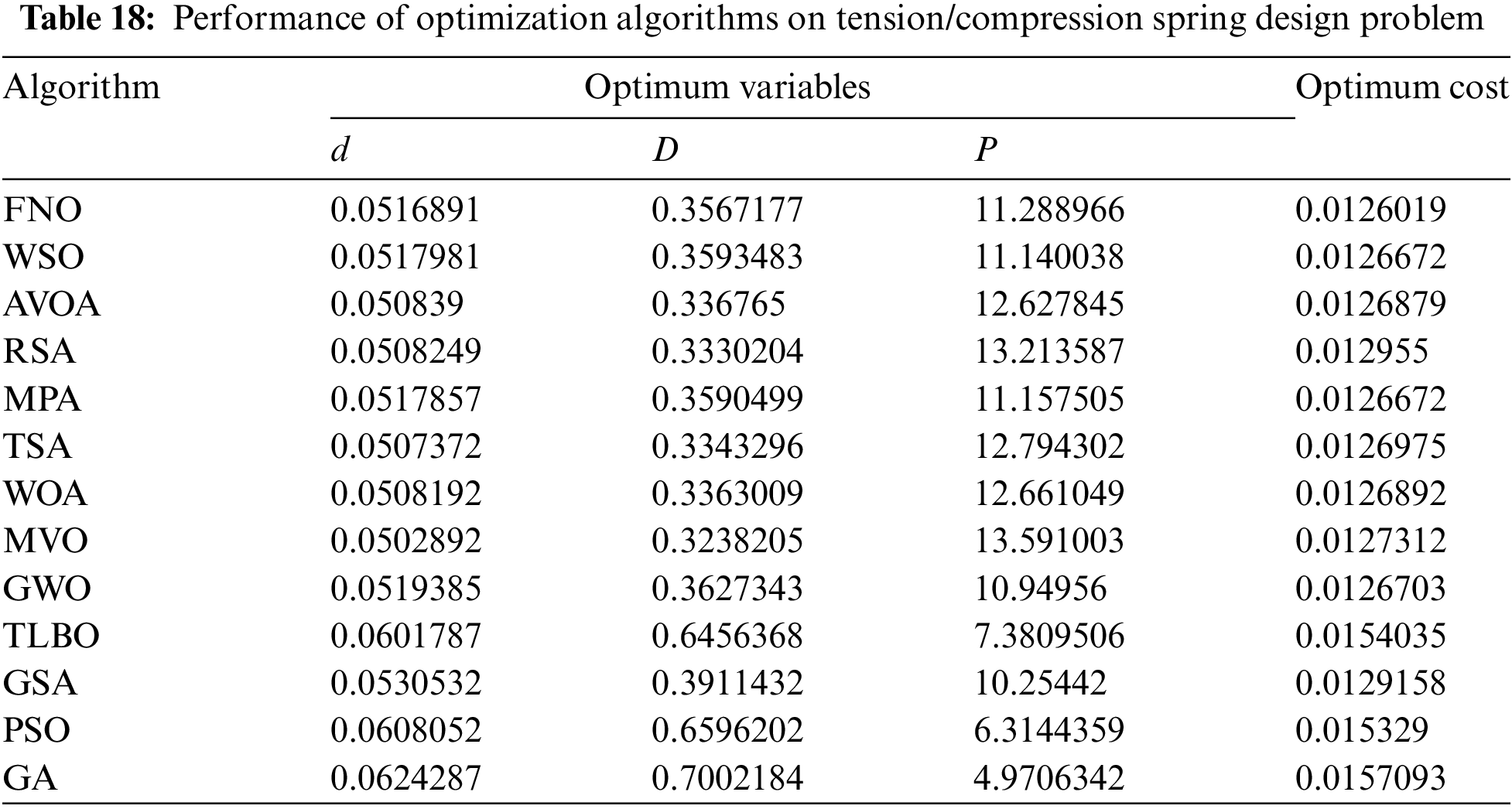
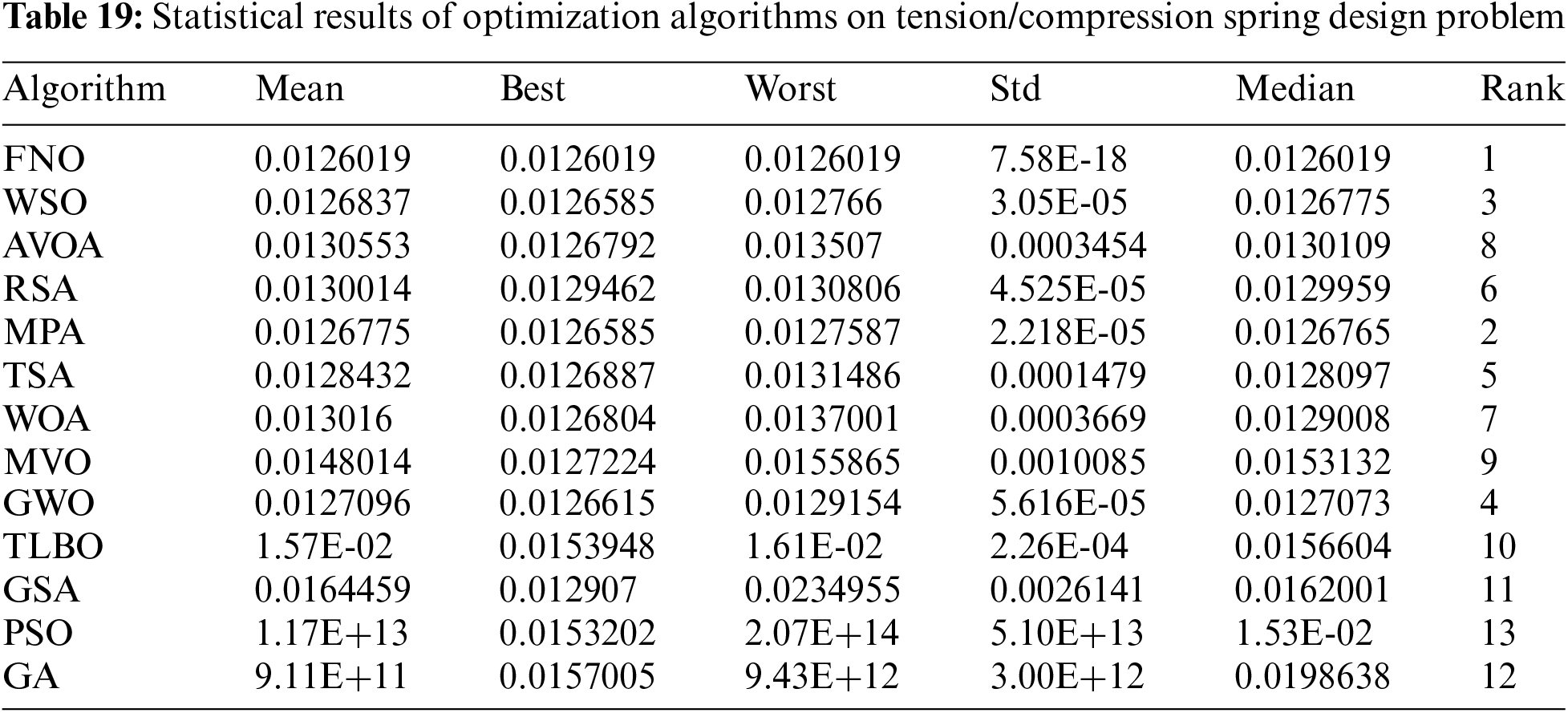
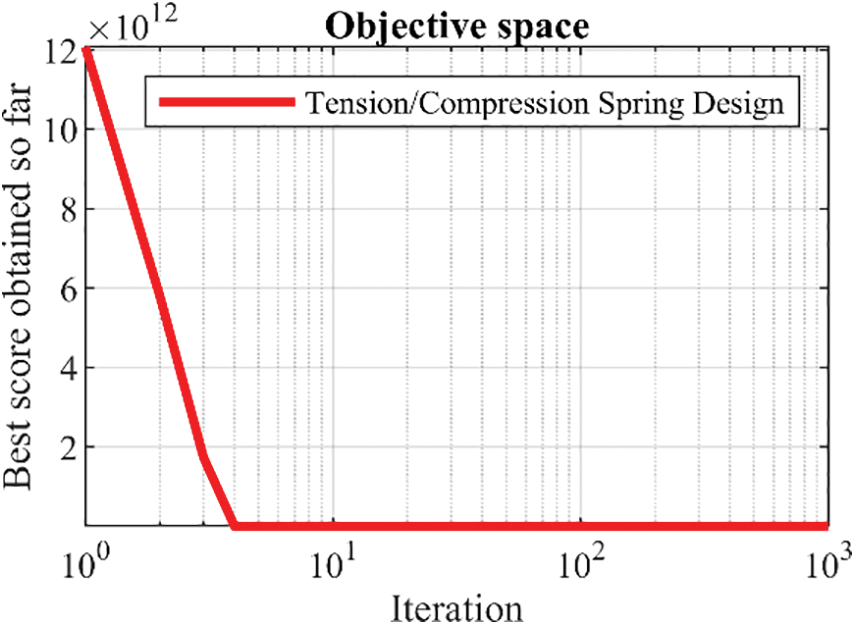
Figure 20: FNO’s performance convergence curve on tension/compression spring

According to the findings, FNO has achieved the optimal design with design variable values of (0.0516891, 0.3567177, 11.288966), and an objective function value of 0.0126019. Analysis of the simulation results underscores the superior performance of FNO in handling tension/compression spring design compared to competitor algorithms.

6  Conclusions and Future Works

This paper introduced a novel metaheuristic algorithm called Far and Near Optimization, tailored for addressing optimization challenges across various scientific domains. FNO’s core concept drew inspiration from global and local search strategies, dynamically updating population members within the problem-solving space by navigating towards both the farthest and nearest members, respectively. The theoretical underpinnings of FNO were elucidated and mathematically formulated in two distinct phases: (i) exploration based on the simulation of the movement of the population member towards the farthest member from itself and (ii) exploitation based on simulating the movement of the population member towards nearest member from itself. FNO’s performance was rigorously assessed on the CEC 2017 test suite across problem dimensions of 10, 30, 50, and 100, as well as to address CEC 2020. The optimization results underscored FNO’s adeptness in exploration, exploitation, and maintaining a delicate balance between the two throughout the search process, yielding effective solutions across various benchmark functions. The effectiveness of FNO in addressing optimization problems was assessed by comparing it with twelve widely recognized metaheuristic algorithms. The results of the simulation and statistical analysis indicated that FNO consistently outperformed most competitor algorithms across various benchmark functions, securing the top rank as the premier optimizer. This superiority is statistically significant and underscores FNO’s exceptional performance. Furthermore, FNO’s efficacy in real-world applications was evaluated through the resolution of twenty-two constrained optimization problems from the CEC 2011 test suite and four engineering design problems. The results demonstrated FNO’s effectiveness in tackling optimization tasks in practical scenarios.

While the FNO algorithm has shown promise in balancing exploration and exploitation, it has several shortcomings, including computational complexity, parameter sensitivity, risk of premature convergence, complexity in mathematical modeling, and limited experimental validation. Potential improvements include enhancing computational efficiency, adopting adaptive parameter tuning, mitigating premature convergence through hybridization and diversification strategies, simplifying the mathematical modeling, and conducting extensive experimental validation. These enhancements can help make FNO a more robust, efficient, and widely applicable optimization algorithm.

The introduction of the proposed FNO approach presents numerous avenues for future research endeavors. One particularly noteworthy proposal is the development of binary and multi-objective versions of FNO. Additionally, exploring the utilization of FNO for solving optimization problems across various scientific disciplines and real-world applications stands as another promising research direction.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tareq Hamadneh, Khalid Kaabneh, Kei Eguchi; data collection: Tareq Hamadneh, Zeinab Monrazeri, Omar Alssayed, Kei Eguchi, Mohammad Dehghani; analysis and interpretation of results: Khalid Kaabneh, Omar Alssayed, Zeinab Monrazeri, Tareq Hamadneh, Mohammad Dehghani; draft manuscript preparation: Omar Alssayed, Zeinab Monrazeri, Kei Eguchi, Mohammad Dehghani. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are available in the article and their references are cited.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Al-Nana AA, Batiha IM, Momani S. A numerical approach for dealing with fractional boundary value problems. Mathematics. 2023;11(19):4082. doi:10.3390/math11194082. [Google Scholar] [CrossRef]

2. Hamadneh T, Athanasopoulos N, Ali M. Minimization and positivity of the tensorial rational Bernstein form. In: 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), 2019; Amman, Jordan; IEEE. [Google Scholar]

3. Sergeyev YD, Kvasov D, Mukhametzhanov M. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci Rep. 2018;8(1):1–9. doi:10.1038/s41598-017-18940-4. [Google Scholar] [PubMed] [CrossRef]

4. Qawaqneh H. New contraction embedded with simulation function and cyclic (α, β)-admissible in metric-like spaces. Int J Math Comput Sci. 2020;15(4):1029–44. [Google Scholar]

5. Alshanti WG, Batiha IM, Hammad MMA, Khalil R. A novel analytical approach for solving partial differential equations via a tensor product theory of Banach spaces. Partial Differ Equ Appl Math. 2023;8(2):100531. doi:10.1016/j.padiff.2023.100531. [Google Scholar] [CrossRef]

6. Liñán DA, Contreras-Zarazúa G, Sánchez-Ramírez E, Segovia-Hernández JG, Ricardez-Sandoval LA. A hybrid deterministic-stochastic algorithm for the optimal design of process flowsheets with ordered discrete decisions. Comput Chem Eng. 2024;180:108501. doi:10.1016/j.compchemeng.2023.108501. [Google Scholar] [CrossRef]

7. de Armas J, Lalla-Ruiz E, Tilahun SL, Voß S. Similarity in metaheuristics: a gentle step towards a comparison methodology. Nat Comput. 2022;21(2):265–87. doi:10.1007/s11047-020-09837-9. [Google Scholar] [CrossRef]

8. Zhao W, Wang L, Zhang Z, Fan H, Zhang J, Mirjalili S, et al. Electric eel foraging optimization: a new bio-inspired optimizer for engineering applications. Expert Syst Appl. 2024;238:122200. doi:10.1016/j.eswa.2023.122200. [Google Scholar] [CrossRef]

9. Kumar G, Saha R, Conti M, Devgun T, Thomas R. GREPHRO: nature-inspired optimization duo for Internet-of-Things. Int Things. 2024;25:101067. doi:10.1016/j.iot.2024.101067. [Google Scholar] [CrossRef]

10. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. [Google Scholar]

11. Alsayyed O, Hamadneh T, Al-Tarawneh H, Alqudah M, Gochhait S, Leonova I, et al. Giant armadillo optimization: a new bio-inspired metaheuristic algorithm for solving optimization problems. Biomimetics. 2023;8(8):619. doi:10.3390/biomimetics8080619. [Google Scholar] [PubMed] [CrossRef]

12. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks, 1995 Nov 27–Dec 1; Perth, WA, Australia; IEEE. [Google Scholar]

13. Karaboga D, Basturk B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In: International Fuzzy Systems Association World Congress, 2007; Berlin, Heidelberg; Springer. [Google Scholar]

14. Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern B Cybern. 1996;26(1):29–41. doi:10.1109/3477.484436. [Google Scholar] [PubMed] [CrossRef]

15. Yang XSed. Firefly algorithms for multimodal optimization. In: International Symposium on Stochastic Algorithms, 2009; Berlin, Heidelberg; Springer. [Google Scholar]

16. Wang WC, Tian WC, Xu DM, Zang HF. Arctic puffin optimization: a bio-inspired metaheuristic algorithm for solving engineering design optimization. Adv Eng Softw. 2024;195:103694. doi:10.1016/j.advengsoft.2024.103694. [Google Scholar] [CrossRef]

17. Jia H, Peng X, Lang C. Remora optimization algorithm. Expert Syst Appl. 2021;185:115665. doi:10.1016/j.eswa.2021.115665. [Google Scholar] [CrossRef]

18. Wu D, Rao H, Wen C, Jia H, Liu Q, Abualigah L. Modified sand cat swarm optimization algorithm for solving constrained engineering optimization problems. Math. 2022;10(22):4350. doi:10.3390/math10224350. [Google Scholar] [CrossRef]

19. Seyyedabbasi A, Kiani F. Sand cat swarm optimization: a nature-inspired algorithm to solve global optimization problems. Eng Comput. 2023;39(4):2627–51. doi:10.1007/s00366-022-01604-x. [Google Scholar] [CrossRef]

20. Abdollahzadeh B, Gharehchopogh FS, Mirjalili S. African vultures optimization algorithm: a new nature-inspired metaheuristic algorithm for global optimization problems. Comput Ind Eng. 2021;158:107408. doi:10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]

21. Chopra N, Ansari MM. Golden jackal optimization: a novel nature-inspired optimizer for engineering applications. Expert Syst Appl. 2022;198:116924. doi:10.1016/j.eswa.2022.116924. [Google Scholar] [CrossRef]

22. Braik M, Hammouri A, Atwan J, Al-Betar MA, Awadallah MA. White Shark Optimizer: a novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl-Based Syst. 2022;243:108457. doi:10.1016/j.knosys.2022.108457. [Google Scholar] [CrossRef]

23. Kaur S, Awasthi LK, Sangal AL, Dhiman G. Tunicate Swarm Algorithm: a new bio-inspired based metaheuristic paradigm for global optimization. Eng Appl Artif Intell. 2020;90:103541. doi:10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]

24. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95:51–67. [Google Scholar]

25. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

26. Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine Predators Algorithm: a nature-inspired metaheuristic. Expert Syst Appl. 2020;152:113377. doi:10.1016/j.eswa.2020.113377. [Google Scholar] [CrossRef]

27. Hashim FA, Houssein EH, Hussain K, Mabrouk MS, Al-Atabany W. Honey Badger Algorithm: new metaheuristic algorithm for solving optimization problems. Math Comput Simul. 2022;192:84–110. doi:10.1016/j.matcom.2021.08.013. [Google Scholar] [CrossRef]

28. Abualigah L, Abd Elaziz M, Sumari P, Geem ZW, Gandomi AH. Reptile Search Algorithm (RSA): a nature-inspired meta-heuristic optimizer. Expert Syst Appl. 2022;191:116158. doi:10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]

29. Goldberg DE, Holland JH. Genetic algorithms and machine learning. Mach Learn. 1988;3(2):95–9. doi:10.1023/A:1022602019183. [Google Scholar] [CrossRef]

30. Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]

31. De Castro LN, Timmis JI. Artificial immune systems as a novel soft computing paradigm. Soft Comput. 2003;7(8):526–44. doi:10.1007/s00500-002-0237-z. [Google Scholar] [CrossRef]

32. Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–80. doi:10.1126/science.220.4598.671. [Google Scholar] [PubMed] [CrossRef]

33. Dehghani M, Montazeri Z, Dhiman G, Malik O, Morales-Menendez R, Ramirez-Mendoza RA, et al. A spring search algorithm applied to engineering optimization problems. Appl Sci. 2020;10(18):6173. doi:10.3390/app10186173. [Google Scholar] [CrossRef]

34. Dehghani M, Samet H. Momentum search algorithm: a new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Appl Sci. 2020;2(10):1–15. doi:10.1007/s42452-020-03511-6. [Google Scholar] [CrossRef]

35. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

36. Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl. 2016;27(2):495–513. doi:10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]

37. Hashim FA, Hussain K, Houssein EH, Mabrouk MS, Al-Atabany W. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Appl Intell. 2021;51(3):1531–51. doi:10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]

38. Kaveh A, Dadras A. A novel meta-heuristic optimization algorithm: thermal exchange optimization. Adv Eng Softw. 2017;110:69–84. doi:10.1016/j.advengsoft.2017.03.014. [Google Scholar] [CrossRef]

39. Cuevas E, Oliva D, Zaldivar D, Pérez-Cisneros M, Sossa H. Circle detection using electro-magnetism optimization. Inf Sci. 2012;182(1):40–55. doi:10.1016/j.ins.2010.12.024. [Google Scholar] [CrossRef]

40. Eskandar H, Sadollah A, Bahreininejad A, Hamdi M. Water cycle algorithm–a novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput Struct. 2012;110:151–66. doi:10.1016/j.compstruc.2012.07.010. [Google Scholar] [CrossRef]

41. Hatamlou A. Black hole: a new heuristic optimization approach for data clustering. Inf Sci. 2013;222:175–84. doi:10.1016/j.ins.2012.08.023. [Google Scholar] [CrossRef]

42. Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: a novel optimization algorithm. Knowl-Based Syst. 2020;191:105190. doi:10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]

43. Pereira JLJ, Francisco MB, Pereira HD, Abraham A. Elephant search algorithm: a bio-inspired metaheuristic algorithm for optimization problems. Memet Comput. 2020;12(4):375–88. doi:10.1109/ICDIM.2015.7381893. [Google Scholar] [CrossRef]

44. Bouchekara HREH, Belazzoug M, Kouzou A, Tlemçani C. HHO–A novel Harris Hawks Optimization algorithm for solving engineering optimization problems. Appl Intell. 2022;52(3):3484–520. [Google Scholar]

45. Santos Coelho L, Mariani VC. Firefly algorithm approach based on chaotic Tinkerbell map applied to multivariable PID controller tuning. Comput Math Appl. 2013;64(8):2371–82. doi:10.1016/j.camwa.2012.05.007. [Google Scholar] [CrossRef]

46. Lin Y, Gen M. Auto-tuning strategy for parameter settings of meta-heuristics based on ordinal transformation and scale transformation. Expert Syst Appl. 2009;36(4):7461–71. [Google Scholar]

47. Blum C, Roli A. Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM Comput Surv. 2003;35(3):268–308. [Google Scholar]

48. Nguyen TT, Memarmoghaddam H, Abraham A, Zhang M. Metaheuristics: advances and trends. J Ambient Intell Humaniz Comput. 2020;11:853–5. [Google Scholar]

49. Braik M, Ryalat MH, Al-Zoubi H. A novel meta-heuristic algorithm for solving numerical optimization problems: Ali Baba and the forty thieves. Neural Comput Appl. 2022;34(1):409–55. doi:10.1007/s00521-021-06392-x. [Google Scholar] [CrossRef]

50. Glover F. Tabu search—part I. ORSA J Comput. 1989;1(3):190–206. doi:10.1287/ijoc.1.3.190. [Google Scholar] [CrossRef]

51. Salcedo-Sanz S, Del Ser J, Landa-Torres I, Gil-Lopez S, Portilla-Figueras A. The coral reefs optimization algorithm: a novel metaheuristic for efficiently solving optimization problems. Sci World J. 2014;2014:1–15. doi:10.1155/2014/739768. [Google Scholar] [PubMed] [CrossRef]

52. Coello Coello CA. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: a survey of the state of the art. Comput Methods Appl Mech Eng. 2002;191(11–12):1245–87. doi:10.1016/S0045-7825(01)00323-1. [Google Scholar] [CrossRef]

53. Ali MZ, Awad NH, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on real-parameter optimization. J Simul. 2017;32(1):1–35. doi:10.1007/s11548-006-0027-7. [Google Scholar] [CrossRef]

54. Glover F. Heuristics for integer programming using surrogate constraints. Decis Sci. 1977;8(1):156–66. doi:10.1111/j.1540-5915.1977.tb01074.x. [Google Scholar] [CrossRef]

55. Price KV, Storn RM, Lampinen JA. Differential evolution: a practical approach to global optimization. Springer Berlin, Heidelberg: Springer; 2006. [Google Scholar]

56. Gao W, Liu S. A modified artificial bee colony algorithm. Comput Oper Res. 2011;39(3):687–97. doi:10.1016/j.cor.2011.06.007. [Google Scholar] [CrossRef]

57. Luke S. Essentials of metaheuristics. 2nd ed. San Francisco, CA, USA: Lulu; 2013. [Google Scholar]

58. Bäck T, Fogel DB, Michalewicz Z. Handbook of evolutionary computation. Boca Raton: IOP Publishing Ltd.; 1997. [Google Scholar]

59. Simon D. Evolutionary optimization algorithms: biologically-inspired and population-based approaches to computer intelligence. Hoboken, New Jersey: Wiley; 2013. [Google Scholar]

60. Goldberg DE. Genetic algorithms in search, optimization, and machine learning. Boston, USA: Addison-Wesley; 1989. [Google Scholar]

61. Yao X. Progress in evolutionary computation. Springer Berlin, Heidelberg: Springer; 1995. [Google Scholar]

62. Bonabeau E, Dorigo M, Theraulaz G. Swarm intelligence: from natural to artificial systems. New York, USA: Oxford University Press; 1999. [Google Scholar]

63. Kannan B, Kramer SN. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J Mech Des. 1994;116(2):405–11. doi:10.1115/1.2919393. [Google Scholar] [CrossRef]

64. Wolpert DH, Macready WG. Coevolutionary free lunches. IEEE Trans Evol Comput. 2005;9(6):721–35. doi:10.1109/TEVC.2005.856205. [Google Scholar] [CrossRef]

65. Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evol Comput. 2001;9(2):159–95. doi:10.1162/106365601750190398. [Google Scholar] [PubMed] [CrossRef]