A Two-Stage Scenario-Based Robust Optimization Model and a Column-Row Generation Method for Integrated Aircraft Maintenance-Routing and Crew Rostering

1  Introduction

Operational resources management plays a critical role in various industries, especially in the air transport and aviation industry, with its challenging characteristics such as high operating costs, variable demand, heavy traffic, and strict regulations. Since the early 1980s, with the passage of the Airline Liberation Act, a heavily competitive environment has become an integral part of this industry [1]. In this environment and under the practical regulations imposed by the International Air Transportation Association (IATA), airlines must manage the efficiency of their resources. They should provide a design and schedule planning that complies with real world scale constraints as well as crew and aircraft-related restrictions and regulations.

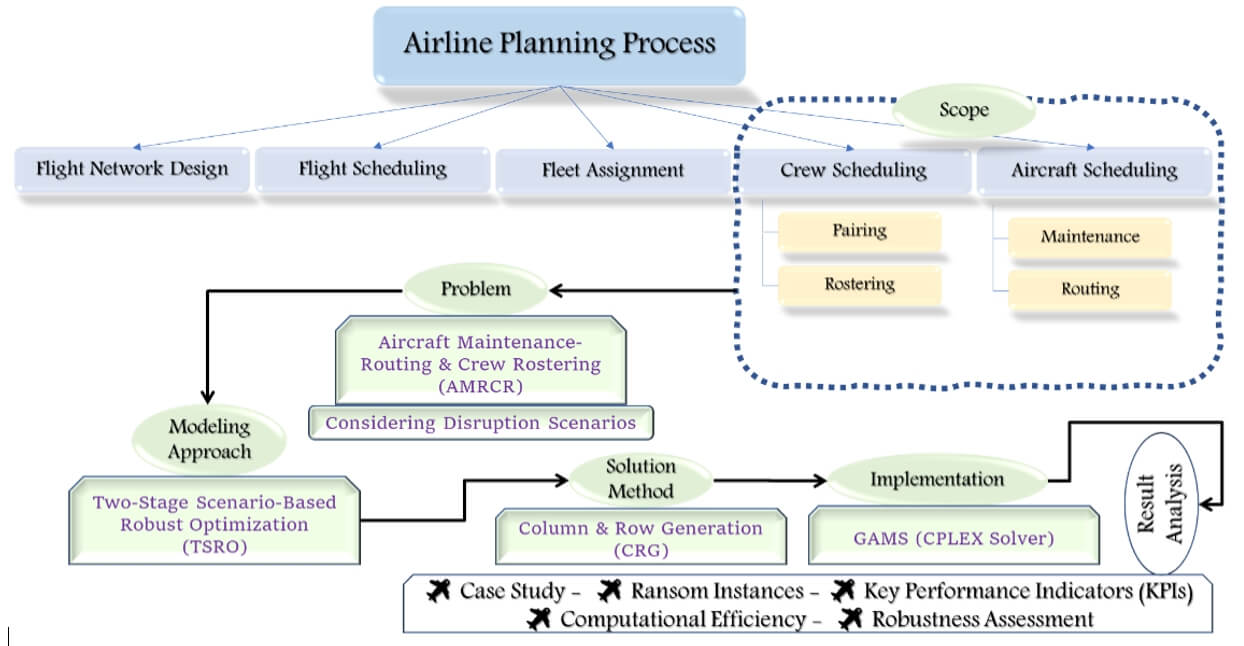
Entrance to the air transportation business and aviation industries requires a route network and a sufficient aircraft fleet. Based on the strategic decisions related to route network design and fleet planning, the airline schedule planning process starts. It is mainly classified into four influencing sub-problems, illustrated in Fig. 1. The first two sub-problems are schedule design (flight scheduling) and fleet assignment decision, which generally occur at the tactical level. The next is Aircraft Maintenance Routing (AMR). The final sub-problem is crew scheduling, which itself comprises smaller sub-problems such as crew pairing and crew rostering [2,3].

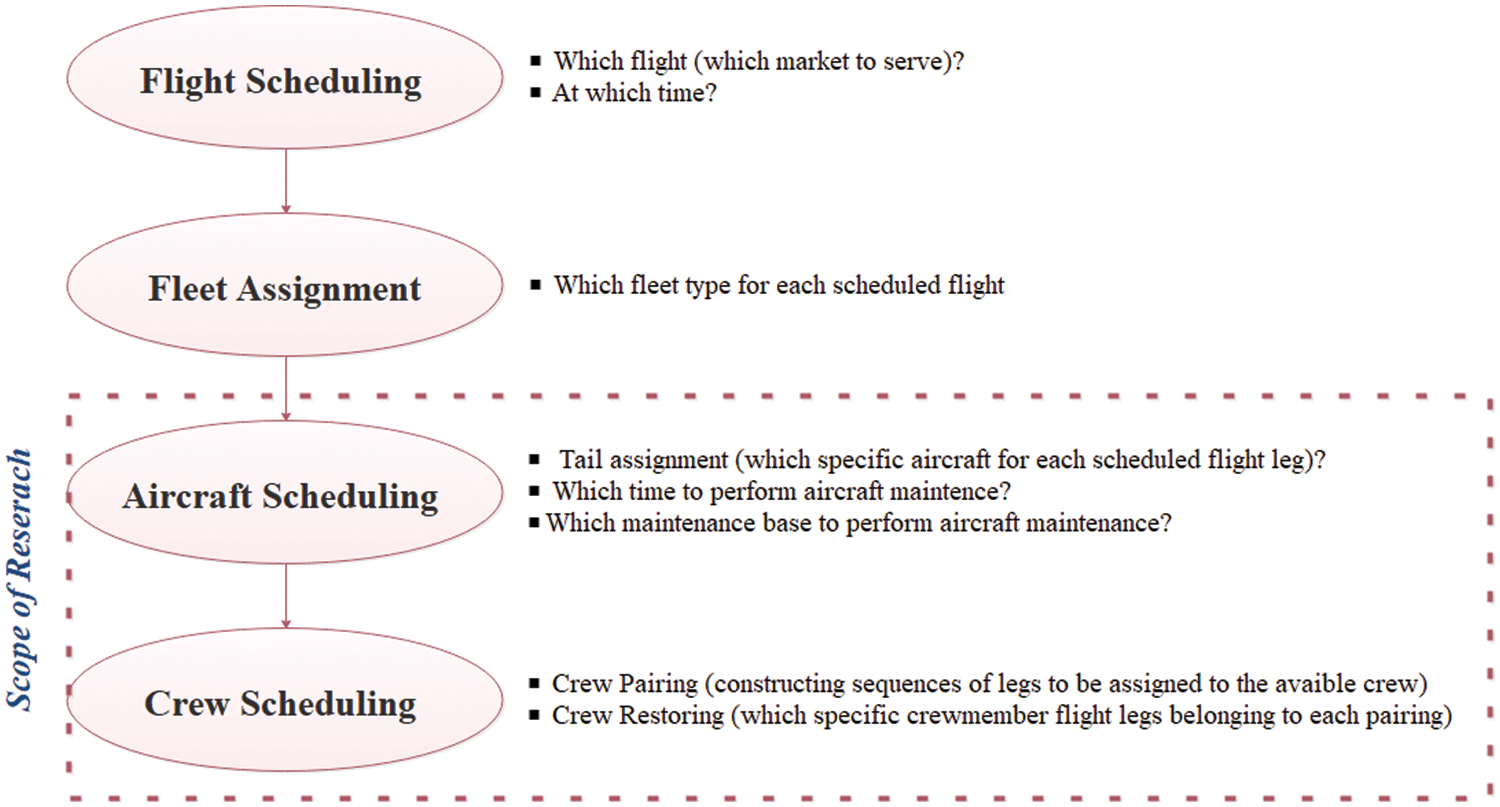
Figure 1: Airline schedule planning process

Flight scheduling provides the daily or weekly repetitive pattern of flights by determining the origin-destination cities of each flight and flight departure-arrival time. It depends largely on market demand forecast, current aircraft performance characteristics, available workforce, regulations, and the behavior of the competing airlines. Following flight scheduling, fleet assignment is performed. Regarding the fleet type, the number of aircraft in each fleet, and the scheduled flight legs, fleet assignment seeks an assignment of the available fleet to the scheduled flights such that maximum revenue or some other objective is obtained [4,5].

After fleet assignment, aircraft routing is accomplished under the restrictions, related rules, and aircraft maintenance regulations. Considering the operating costs of each aircraft, scheduled flight, maintenance base locations, and protocols governing aircraft maintenance, AMR assigns an aircraft to the scheduled flight, known as tail assignment, such that the aircraft operating cost is minimized.

Crew scheduling terminates the airline planning process. It must consider many airline workforce regulations, which contribute significantly to operating costs. Because of its complexity, it is usually divided into two phases: (I) crew pairing and (II) crew rostering (or assignment). Firstly, anonymous pairing/rotations are constructed based on scheduled flight legs such that the crew requirement for each flight is satisfied. A pairing is a sequence of legs with a specific number of crew members. Next, crew rostering assigns the available individual crewmembers to the flight legs of each pairing, having other considerations such as ground duties, night rest, crew bases, reserve-duty, off-duty blocks, and crew preferences [6].

In optimizing airline operations and flight schedule planning, operations research techniques, especially mathematical programming, have been widely used. This contribution has been to the extent that operations research departments have been established in many airlines [7]. These departments have been involved in the formation of an important professional body in the international federation of operations research society, called the airlines group (AGIFORS; see www.agifors.org, accessed on 01 June 2023, for more details).

For the sake of global optimality, although optimizing each of the four sub-problems in airline planning reduces cost and increases airline productivity, new researches usually solve two or more sub-problems in an integrated manner. In addition to avoiding the infeasibility of the solutions obtained in the hierarchical structure, the integration can provide the best solution for the airline.

Based on the optimal decisions of aircraft routing and crew scheduling and by fixing the forecasted revenue of the scheduled flight tickets, maximum profitability is achieved by the minimized total cost. After fuel costs, flight crew costs have the largest share of the total cost [2]. In other words, aircraft and crew scheduling have the most significant potential to reduce avoidable costs in flight plans. This fact has motivated various researchers to address an integrated planning of the fleet, aircraft, and crew.

Delays and disruptions in airline operations cause additional costs for airlines, air-travel passengers, and the economy. Airlines strive to reduce these costs by constructing schedules that are easier to rearrange when a disruption occurs [8]. Along with the integration of the airline planning process, airline disruption management is of great importance. Airline disruption is when a scheduled flight is either delayed or must be canceled because of a 48-h delay from its initial departure time. Referring to the Regulations of air passenger protection, flight disruption is the collective term for the airlines’ disruption that prevents passengers from completing their itineraries on time [9]. To mitigate the effect of flight disruptions and have a robust plan for aircraft and crew operations, it is so beneficial that airlines simulate and consider possible flight disruptions in the AMR and crew scheduling phases of airline planning. This approach enables airlines to optimally react when disruption occurs.

Our research is motivated by the limitations of sequential approaches to airline operational challenges, particularly regarding aircraft maintenance routing and crew scheduling. These approaches often lead to suboptimal outcomes. Additionally, disruptions significantly impact initial schedules and incur substantial costs due to a lack of robustness. This research proposes an integrated and robust model for airline operational decisions. Our primary aims are twofold: firstly, to achieve global optimality through integrated decision-making, and secondly, to ensure robustness against potential disruptions by providing resilience strategies. Furthermore, the proposed solution framework incorporates a decomposition-based column and row generation method, ensuring computational efficiency.

To address the above-mentioned considerations, we develop an integrated model to jointly specify aircraft maintenance routing and assign crewmembers to the scheduled flights in the generated pairing. The model considers multiple locations for airline maintenance and crew bases. To deal with the flight disruptions, a scenario-based robust optimization approach is applied, whose here-and-now variables are the initial resource assignment and its wait-and-see or scenario-dependent variables are the options of rescheduling or canceling the flight when a disruption occurs. Furthermore, to tackle the model complexity and make it more tractable, we apply the column and row generation method to solve the model with an acceptable run-time and computational performance.

In summary, the main innovations of this research are as follows:

a)    Integration of decision-making in airline operational planning, including crew scheduling, routing, and aircraft scheduling. This integration enhances five significant key performance indicators (KPI): I. Number of delayed flights per week, II. Number of canceled flights per week, III. Average delay time, IV. Average profit under disruption, V. Minimum profit under disruption.

b)    Incorporation of additional daily, weekly, and monthly operational constraints for resources, enhancing real-world applicability.

c)    Addressing possible disruption scenarios in the initial schedule (with varying intensities) and establishing robustness in the model against uncertainty arising from these disruptions.

d)    Development of a tractable two-stage robust optimization model, and finally, employing the decomposition-based column and row generation method to enhance computational efficiency in solving the model.

The rest of this paper is structured as follows. Section 2 reviews the recent literature and clarifies the research gaps and our contributions. Section 3 describes the problem in detail. Section 4 formulates the problem using the minimax robust optimization model. The column and row generation method is explained in Section 5. Section 6 validates the proposed solution using a numerical study and evaluates its performance and robustness in tackling disruption. Section 7 provides some concluding remarks and also suggestions for future research.

2  Literature Review

In this section, we review the literature on aircraft scheduling (the AMR problem) and crew scheduling (pairing and rostering decisions) to identify the research gap and clarify the contribution of our study. For a complete review of airline planning, the readers can refer to [10–13]. In one of the first studies in airline operational resource management, Cordeau et al. [14] considered the aircraft routing and crew scheduling problems simultaneously to minimize the time required for the crewmembers and the aircraft to be ready for the next flight after landing so that it can perform both flights. They used the Benders decomposition approach to solve the model.

Sandhu et al. [15] proposed an integrated model for fleet and crew planning and scheduling. They ignored the constraints of aircraft maintenance and solved the model using two approaches, one uses Lagrange relaxation with a column generation algorithm and the other uses benders decomposition.

Papadakos [16] developed an integrated model for the joint decisions of fleet assignment, aircraft maintenance routing, and crew scheduling problems. Because of the problem’s complexity, he applied a new algorithm based on Benders decomposition and column generation to solve the model, where the restriction on the number of available aircraft was also removed from the constraints. Souai et al. [17] examined crew pairing and crew rostering in an integrated model. They considered constraints such as the return of the crew to the home base after three days of flight, the maximum flight time in one day (duty), and the rest period between two consecutive flights. Weide et al. [18] developed a similar model with some new constraints, including the minimum time required for crew pairing.

Salazar-González [19] presented a new model integrating crew pairing, aircraft routing, and fleet assignment. Their model was based on the set assumptions and they solved it using the column generation algorithm. Sanchez et al. [4] developed a solution method for the same problem in which all of the above constraints were checked for just one day of flying. The novelty of their approach was the inclusion of maintenance constraints during the day without considering the diversity of fleet type and crew and maintenance bases.

Integration of decisions in the planning process, dealing with uncertainty/disruption, and focusing on robust integrated solutions constitute a common research scope in many applications and industries [20–22]. For example, in the field of multi-factory production networks, Razavi Al-e-hashem et al. [23] developed a novel robust and integrated model for integrated maintenance planning and scheduling that addresses disruption cost. Shao et al. [24] developed a mathematical model for the joint decisions of fleet assignment, aircraft routing, and crew scheduling. They used the Benders decomposition approach along with several strategies that accelerate run-time to reach the solution. An interactive optimization mechanism was proposed by [25] to model aircraft routing with generalized maintenance constraints. They presented a mixed-integer program that considers the full range of aircraft maintenance requirements. Yadegari et al. [26] presented a fuzzy mathematical model solved using an interactive approach to integrate allocation and routing decisions in a two-echelon transportation system.

For the coordination of aircraft maintenance routing and maintenance employees, a bi-level programming model, known as the leader-follower or Stackelberg game, was presented by [27]. It was solved using an Ant colony optimization algorithm. Ben et al. [28] developed a nonlinear model using the reformulation-linearization technique (RLL) for the formulation of a robust and integrated airline aircraft routing and crew pairing problem. They used the Monte Carlo simulation method to evaluate the solution’s robustness.

For the operational aircraft maintenance routing problem with all the operational requirements, Cui et al. [29] presented a mixed-integer linear programming (MILP) formulation and heuristic solution algorithm. Also, Haouari et al. [30] developed a set-partitioning formulation that generates a set of optimal pairings that covers all the daily scheduled flights under various crew regulations, safety rules, and airline policies. They introduced a novel compact polynomial-sized model formulation, which could be linearized by set-partitioning formulation.

To make the crew pairing part of crew scheduling robust against delays and disruptions in airline operations, Antunes et al. [8] proposed a robust optimization model that does not require detailed information about delay distributions. Their proposed model can make an acceptable trade-off between the particular cost of the scheduled flight legs and the expected delay and cancelation costs. Chen et al. [31] developed an evolutionary multi-objective optimization model based on a genetic algorithm and a non-dominated sorting mechanism to deal with the scheduling and rescheduling of joint aircraft routing and crew pairing. Recently, to optimize aviation maintenance planning, Korba et al. [32] presented an algorithmic approach that can be easily adopted by airlines and the same industries. Also, Teymouri et al. [33] developed an adaptive large neighborhood searching (ALNS) method to reduce the complexity of the AMR problem so that large-scale instances can be solved with more computational efficiency. Our research exhibits some thematic overlap with the work. However, several key distinctions exist in our research focus and methodological approaches:

a)    Focus: while Teymouri et al. [33] prioritized crew scheduling decisions, our research emphasizes Aircraft Maintenance Routing (AMR) while concurrently considering crew rostering.

b)    Disruption Management: the paper above focuses on revenue management during disruptions. In contrast, our study prioritizes rescheduling and building resilience to disruptions.

c)    Operational Constraints: our work incorporates additional daily, weekly, and monthly operational constraints for crew and aircraft resources, enhancing the model’s real-world applicability.

d)    Methodology: the problem formulation (optimization model) and solution approaches employed in our work differ significantly. We propose an efficiently formulated model that leverages the Compact Relaxation Generation (CRG) method for improved effectiveness. Conversely, the referenced paper utilizes an approximation method based on metaheuristics (ALNS).

We should note that the last method is inexact while we apply a decomposition-based exact method utilizing column-row cut generation.

Finally, Table 1 summarizes the recent literature on aircraft and crew schedule planning subproblems, integrated or individually. We compare our study with some of the newest research of the literature in five dimensions: (I) decisions in aircraft scheduling, (II) decisions in crew scheduling, (III) inclusion of possible disruptions and uncertainty modeling, (IV) solution robustness, and (V) methodology.

3  Problem Description

Given a set of scheduled flights, the number of available aircraft, crew groups in the airline, and a set of pre-generated possible daily pairing, we address an integrated airline planning problem considering both aircraft maintenance routing and crew rostering (AMRCR). Before we describe the problem, let us review some terminologies required to proceed further. As illustrated in Fig. 2, the crewmembers are assigned to their crew home/base, where their service starts/ends. A consecutive series of flights a crew group performs on a single day is called a crew duty. A paring is then a sequence of flight legs, including one or more duties, so the final duty’s end is exactly the crew home where the first duty begins. We should note that daily paring is a daily duty that starts and ends at the same crew base. Usually, explanatory meetings called crew briefing and de-briefing are held before and after each pairing or duty to justify everything. The rest time between two flights during the duty is a sit-time, while long breaks between two duties are called a rest-period.

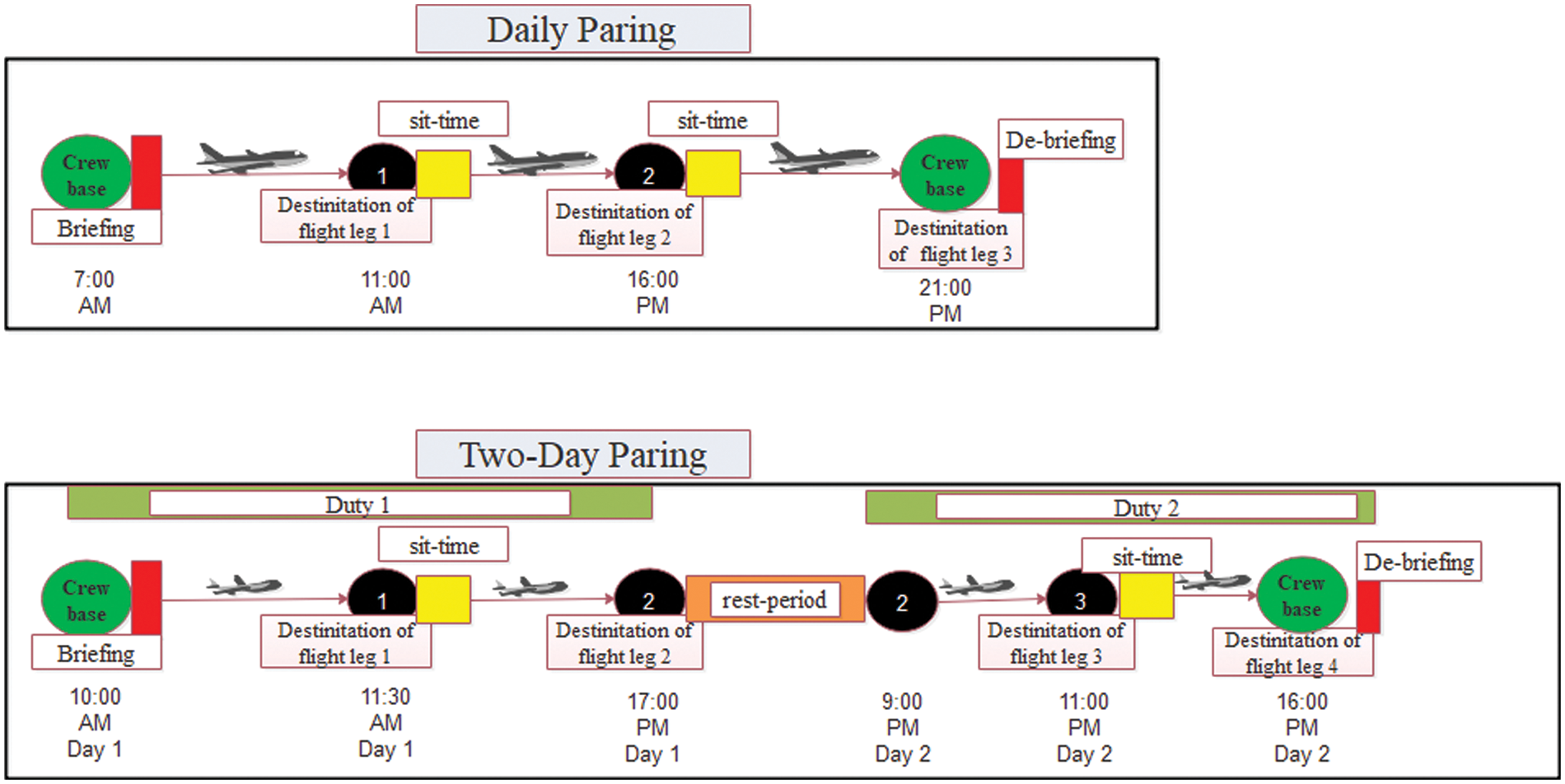
Figure 2: Schematic representation of some crew scheduling terminologies in a daily and two-day pairing

In the AMRCR problem, it is assumed that the network design and flight time schedules have already been determined, and the airline seeks to discover the optimal aircraft routing and crew scheduling so that the aircraft maintenance and crew rostering regulations are satisfied. Regarding the rules and regulations for pilots and aircraft, the planning should be done such that besides covering all scheduled flights, its total cost is minimized. This cost mainly includes the flight operating costs, i.e., the cost of using each aircraft (capital, fuel, etc.), the cost of the flight crew, and the cost of the aircraft maintenance during the flight. Moreover, cancellation and delay costs are also considered when a disruption affects the scheduled flights.

According to IATA regulations and some airline policies, each aircraft cannot fly more than the maximum time under a limited planning horizon. This time is independent of the type of pilots. Crew considerations and aircraft maintenance regulations are also considered in this research.

Assume that the weekly flight schedule is generated by solving flight scheduling and fleet assignment problems at the tactical level. Considering the daily pairings produced for daily flights at the crew pairing phase, the AMRCR problem seeks to find the best tail assignment, aircraft routing, and crew rostering decisions such that the minimum cost is obtained at the end of the week. In this regard, several rules and constraints are considered as follows: (1) each aircraft should be maintained at least once a week, (2) the maximum daily utilization of each aircraft is constrained, (3) the maximum number of flight legs assigned to each crewmember in a weakly rostering is limited, (4) the maximum flight time of each crewmember in a monthly rostering is limited.

As mentioned above, the AMRCR problem accounts for the possible disruptions that cause delays in the start of flights and affect the initial scheduling. To properly model this, like recent research of [33], we assume a normal situation and five disruptions as follows:

Scenario 0: (No disruption or negligible) In this case, the aircraft can take off after the initial preparation steps without the need for additional stops.

Scenario 1: (Very slight disruption) less than 10 min delay in the flight.

Scenario 2: (Slight disruption) 10 to 20 min delay in the flight.

Scenario 3: (Typical disruption) 30 min delay in the flight.

Scenario 4: (Severe disruption) a delay of approximately 60 min (1 h).

Scenario 5: (Very severe disruption) a delay of more than 1 h.

In the AMRCR problem, although some decisions, such as allocating aircraft to flights and assigning crews to pairings, must be determined before a disruption scenario occurs, other decisions, such as the route for the aircraft and the cancellation of some flights, depending on the scenario that occurs. Therefore, in short, the objective of the AMRRC problem is to find the optimal value for the first-stage variables (tail and crew assignment before the disruption scenario occurs) and the second-stage variables (rerouting, cancelation option, and flight rescheduling after the disruption scenario realizes) so that the cost is minimized. The following section presents the mathematical formulation of this problem using the scenario-based robust optimization approach. To address the AMRCR issue, our proposed solution framework, depicted in Fig. 3, initiates with a two-stage robust optimization model. Subsequently, we employ an innovative decomposition-oriented approach involving column and row generation techniques to ensure scalability and computational efficiency, particularly for handling large-scale instances. The following sections provide detailed explanations of each component within the framework illustration.

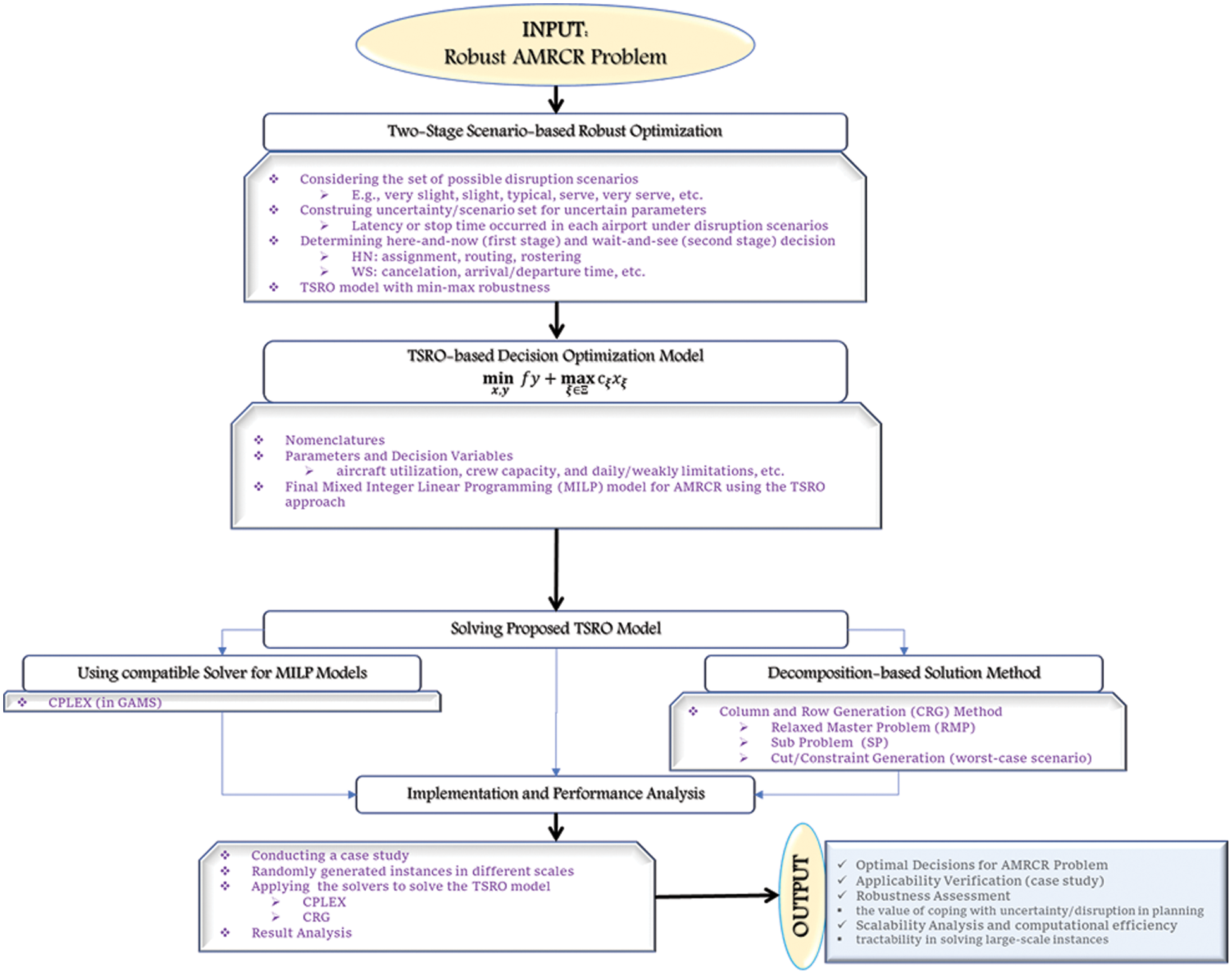
Figure 3: Illustration of the proposed methodology and solution framework to solve the AMRCR problem

4  Mathematical Modelling of the Robust AMRCR Problem

This section briefly explains the scenario-based robust optimization approach and then applies it to formulate the AMRRC problem under disruption. Two-stage scenario-based robust optimization addresses decision-making problems under uncertainty, where decisions are made in two stages. In the first stage, decisions are made with incomplete information about the future. In the second stage, recourse actions are taken after the uncertainty is revealed. This approach aims to find resilient solutions to the worst-case scenario within the uncertainty set. A scenario-based robust optimization approach is proposed regarding the uncertainty associated with disruptions in airline schedules, which is typically expressed as a set of plausible scenarios and usually focuses on robustness performance in worst-case conditions. Additionally, since this study considers adaptive decisions, such as canceling some flights and rescheduling under disruptions, in addition to the first-stage (here-and-now) decisions, there are also adaptive second-stage (wait-and-see) decisions. Therefore, we employ the two-stage scenario-based robust optimization approach to cope with the uncertainty of the AMRCR problem.

4.1 Two-Stage Scenario-Based Robust Optimization Approach

Consider the following uncertain optimization model:

[minx,y⁡ c(u)x+f(u)y,s.t.A(u)x+D(u)y≥b(u),K(u)y≤e(u),x∈X,y∈Y,u∈U.(1)

In which U indicates the uncertainty set, where for any u∈U, the parameters have deterministic values. To cope with uncertainty, the robust optimization (RO) paradigm considers the following worst-case model:

RO := minx∈X(u),y∈Y(u)⁡maxu∈U⁡c(u)x+f(u)y.(2)

Two-Stage Scenario-Based Robust Optimization (TSRO) is an application of the adjustable RO approach that divides the decision variables into the first stage or here-and-now variables and the second stage or wait-and-see variables.

Despite the classic RO models, the second stage variables are allowed here to adapt when the uncertainty scenario changes. In the RO model (2), let us define y variables as here-and-now variables and x variables as wait-and-see ones, and assume that the uncertainty set U is a finite set as Ξ={1,2,3,…,N<∞}. Furthermore, consider f(u), A(u), K(u), and e(u) as certain parameters. The TSRO model then can be formulated as follows:

TSRO := [minx,y fy+maxξ∈Ξ⁡ cξxξ,s.t.Axξ+Dξy≥bξ,for all ξ∈Ξ,Ky≤e,for all ξ∈Ξxξ∈X,y∈Y.(3)

The scenario-based RO approach, especially the TSRO model, has recently been used for various problems such as resource management, scheduling, supply chain network planning, transportation system design, etc., [36–38]. Since possible disruptions are included in the AMRCR problem as a finite set of scenarios and adaptive variables such as cancellation and rescheduling options are considered, we apply the TSRO model (3) to formulate the problem such that the minimum cost in the worst case is achieved.

There are several ways to create a scenario set Ξ. Two common methods are Sample Average Approximation (SAA) and Fuzzy C-Means (FCM). SAA uses known probability distributions of uncertain parameters to generate disruption scenarios. However, to make solving the model easier, only a few likely scenarios are considered at an iteration. FCM, on the other hand, is an unsupervised machine learning technique that can use historical data to generate scenarios. The number of scenarios you choose (like the 6 mentioned) depends on how many groups (clusters) the data can be divided into.

4.2 Problem Formulation Based on the TSRO Approach

Objective function

min Cost=(∑f∈F∑a∈A∑d∈DFCfdxf,ad+maxξ∈Ξ⁡[∑f∈F∑d∈D(CCfd−FCfd)yf,ξd+∑f∈F∑d∈DDCfdDelayf,ξd])(4)

Constraints

∑a∈Axf,ad=1 ∀ d∈D,f∈Fd(5)

∑c∈Cwp,cd=1 ∀ d∈D,p∈Pd,f∈Fp(6)

wp,cd≤∑a∈AQc,axf,ad ∀ d∈D,p∈Pd,f∈Fp,c∈C(7)

yf,ξd≤∑a∈Axf,ad ∀ d∈D,f∈Fd,ξ∈Ξ(8)

∑i∈N∑j∈Ma∑d∈Dra,i,j,ξd≥1 ∀ a∈A,ξ∈Ξ(9)

ra,Ofd,Dfd,ξd≥xf,ad−yf,ξd ∀ d∈D,a∈A,f∈Fd,ξ∈Ξ(10)

ata,j,ξd≥dta,i,ξd+∑f∈OUTid:Dfd=jDurfra,i,j,ξd ∀ d∈D,a∈A,i,j∈N,ξ∈Ξ(11)

dta,n,ξd≥ata,n,ξd+Gn+∑f∈OUTnd(xf,ad−yf,ξd)Ln,f,ξd ∀ d∈D,a∈A,n∈Nξ∈Ξ(12)

dta,Ofd,ξd≥Depf−(1−[yf,ξd−xf,ad])bigM  ∀ d∈D,a∈A,f∈Fdξ∈Ξ(13)

Delayf,ξd≥ata,Dfd,ξd−Arrf−(1−[yf,ξd−xf,ad])bigM  ∀ d∈D,a∈A,n∈Nξ∈Ξ(14)

Delayf,ξd≤ MaxDf ∀ d∈D,f∈F,ξ∈Ξ(15)

∑f∈FDurfxf,ad≤MaxUa ∀ a∈A,d∈D(16)

∑p∈P∑d∈D|FPpd|wp,cd≤MaxNF  ∀ c∈C(17)

4∑p∈P∑f∈Fp∑d∈DDurfwp,cd≤MaxST  ∀ c∈C(18)

[xf,ad∈{0,1},wp,cd∈{0,1},yf,ξd∈{0,1},ra,i,j,ξd∈{0,1}Delayf,ξd≥0,ata,n,ξd≥0,dta,n,ξd≥0(19)

Considering notations of mathematical model collected in Table 2, Eq. (4) shows the objective function of the AMRRC model based on the TSRO approach, in which the total cost in the worst-case disruption scenario is minimized. Constraint (5) indicates that only one aircraft must be assigned to each flight leg. Similarly, Constraint (6) ensures that each pairing of flights must be assigned only to one crew group. Constraint (7) ensures that if a crew group is assigned to a paring, they must be qualified to perform all the corresponding flights. Constraint (8) states that canceling a flight requires that it be on the original schedule. Constraint (9) guarantees that each aircraft must be maintained at maintenance bases at least once a week. Constraint (10) indicates that for scheduled flights that have not been canceled (xf,ad−yf,ξd=1), the aircraft assigned to it must depart from the origin of the flight destination. Constraint (11) focuses on the arrival time to each node, while Constraints (12) and (13) determine the departure time from each node on the flight network. Constraint (14) calculates the delay, while Constraint (15) controls its maximum limit. In Constraint (16), we consider the maximum daily utilization of each aircraft. Constraints (17) and (18) indicate the maximum number of flights per week and maximum flight/sky time per month for each crew group rostering. Finally, Constraint (19) shows the range of variables.

The proposed TSRO model (4)–(19) is a MILP, which can be solved by some MILP optimization solvers such as CPLEX and Gurobi. However, we apply a decomposition-based solution method in the next section to guarantee tractability and computational performance in large-scale instances.

5  Solution Method

In this section, we describe the column and constraint method and use it to solve the proposed model for the AMRCR problem.

5.1 Column and Row Generation Method

The column-and-row generation (CRG) method, also known as column and constraint generation, was first proposed by [39] in the context of scenario-based robust optimization problems. As some recent research has shown, the CRG method has performed well in dealing with the TSRO model, and we apply it to the proposed TSRO model of this paper.

The CRG method is an efficient technique for solving two-stage robust optimization models, dealing with uncertainty by considering multiple possible scenarios that could unfold in the second stage. It tackles the challenge of handling a potentially large number of scenarios by iteratively solving a restricted version of the problem and dynamically adding only the most relevant scenarios and constraints. The main principal components of the CRG method in solving the TSRO model are as follows:

a)    Relaxed Master Problem: a simplified version of the original robust model, typically considering only the initial scenario. It includes decision variables for the first stage (decisions made before knowing the actual scenario) and crucial information from selected scenarios.

b)    Sub-problem (SP): SP focuses on a single scenario not yet addressed in the master problem. It identifies additional decision variables and constraints specific to that scenario to potentially improve the solution.

c)    Iteration: if profitable deviations are found, corresponding decision variables and constraints are incorporated into the master problem. This enhances the solution by enabling better first-stage decisions that are adaptable to various scenarios. The master problem is then resolved with the updated information.

d)    Stopping Criteria: the iterative process continues until a stopping criterion is met, such as a threshold on the optimality gap between the worst-case cost and the best feasible solution found.

Computational efficiency, focus on relevant scenarios, and scalability are among the main benefits of the CRG method. However, limited control over scenario selection is known as one of the main disadvantages of this method.

To explain the mechanism of the CRG method, let us return to the compact TSRO model (3). Consider Ξ∗⊂Ξ as a subset of possible scenarios indicating system disruptions/uncertainties. Because some constraints were removed, it is clear that the solution of the relaxed master problem (RMP) model (20) is a lower bound of the main problem (3). Given a fixed value for the first-stage variables y¯, obtained by solving the RMP model (20), the TSRO model (3) can be decomposed into |Ξ| distinct scenarios, denoted as the sub-problem (SP) model, leading to an upper bound for the TSRO model (3).

Considering the lower bound generator (20) and the upper bound generators (21), the CRG method starts by solving the RMP model (20) regarding an initial subset of scenarios (Ξ∗). Then, based on the RMP solution for the first stage variable y¯, the SP model (21) is solved for each scenario, and some upper bounds are obtained. Let us consider ξ¯ as the worst scenario with the largest objective function and its objective value as an upper bound. If the relative gap between the upper bound and the lower bound is negligible, then the CRG stopes; otherwise, Ξ∗ is updated by adding a worst-case scenario (Ξ∗←Ξ∗∪{ξ¯}).

CRGRMP := [miny,x fy+ϕs.t.ϕ≥cξxξ ∀ ξ∈Ξ∗⊂ΞKy≤eAxξ+Dξy≥bξ ∀ ξ∈Ξ∗⊂Ξxξ∈X,y∈Y(20)

CRGSP(ξ) := [minx Zξ=cξxξs.t.Axξ≤bξ−Dξy¯∀ξ∈Ξxξ∈X(21)

The procedure then iterates by a new Ξ∗ for the RMP model. Finally, the iterative procedure of the CRG method stops when the termination criterion occurs. In the CRG method, for the new scenario ξ¯, ϕ≥cξxξ and Axξ+Dξy≥bξ constraints are optimality (column) cut and feasibility (row) cut, respectively [40,41]. The proposed CRG method is summarized below.

5.2 CRG Method for Solving the TSRO Model

As explained in the previous section, the formulation of the RMP and SP are the two main components of the CRG method. Thus, in the following, we clarify them for the proposed TSRO model.

Relaxed Master Problem (RMP) of CRG

min ∑f∈F∑a∈A∑d∈DFCfdxf,ad+ϕ(22)

∑a∈Axf,ad=1 ∀ d∈D,f∈Fd(23)

∑c∈Cwp,cd=1 ∀ d∈D,p∈Pd,f∈Fp(24)

wp,cd≤∑a∈AQc,axf,ad ∀ d∈D,p∈Pd,f∈Fp,c∈C(25)

∑f∈FDurfxf,ad≤MaxUa ∀ a∈A,d∈D(26)

∑p∈P∑d∈P|FPpd|wp,cd≤MaxNF  ∀ c∈C(27)

4∑p∈P∑f∈Fp∑d∈PDurfwp,cd≤MaxST  ∀ c∈C(28)

xf,ad∈[0,1],wp,cd∈[0,1](29)

Sub-Problem (SP) of CRG

min Zξ=∑f∈F⁡∑d∈D⁡(CCfd−FCfd)yf,ξd+∑f∈F⁡∑d∈D⁡DCfdDelayf,ξd(30)

yf,ξd≤∑a∈Axf,ad¯ ∀ d∈D,f∈Fd,ξ∈Ξ(31)

∑i∈N∑j∈Ma∑d∈Dra,i,j,ξd≥1 ∀ a∈A,ξ∈Ξ(32)

ra,Ofd,Dfd,ξd+yf,ξd≥xf,ad¯ ∀ d∈D,a∈A,f∈Fd,ξ∈Ξ(33)

ata,j,ξd≥dta,i,ξd+∑f∈OUTid:Dfd=jDurfra,i,j,ξd ∀ d∈D,a∈A,i,j∈N,ξ∈Ξ(34)

dta,n,ξd≥ata,n,ξd+Gn+∑f∈OUTnd(xf,ad¯−yf,ξd)Ln,f,ξd ∀ d∈D,a∈A,n∈N ξ∈Ξ(35)

dta,Ofd,ξd≥Depf−(1−[yf,ξd−xf,ad¯])bigM  ∀ d∈D,a∈A,f∈Fd ξ∈Ξ(36)

Delayf,ξd≥ata,Dfd,ξd−Arrf−(1−[yf,ξd−xf,ad¯])bigM  ∀ d∈D,a∈A,n∈N ξ∈Ξ(37)

Delayf,ξd≤ MaxDf ∀ d∈D,f∈F,ξ∈Ξ(38)

[yf,ξd∈[0,1],ra,i,j,ξd∈[0,1]Delayf,ξd≥0,ata,n,ξd≥0,dta,n,ξd≥0(39)

Column Cuts

ϕ≥∑f∈F∑d∈D(CCfd−FCfd)yf,ξd+∑f∈F∑d∈DDCfdDelayf,ξd ∀ ξ∈Ξ∗(40)

Row Cuts

yf,ξd≤∑a∈Axf,ad ∀ d∈D,f∈Fd,ξ∈Ξ∗(41)

∑i∈N∑j∈Ma∑d∈Dra,i,j,ξd≥1 ∀ a∈A,ξ∈Ξ∗(42)

ra,Ofd,Dfd,ξd≥xf,ad−yf,ξd ∀ d∈D,a∈A,f∈Fd,ξ∈Ξ∗(43)

ata,j,ξd≥dta,i,ξd+∑f∈OUTid:Dfd=jDurfra,i,j,ξd ∀ d∈D,a∈A,i,j∈N,ξ∈Ξ∗(44)

dta,n,ξd≥ata,n,ξd+Gn+∑f∈OUTnd(xf,ad−yf,ξd)Ln,f,ξd ∀ d∈D,a∈A,n∈Nξ∈Ξ∗(45)

dta,Ofd,ξd≥Depf−(1−[yf,ξd−xf,ad])bigM  ∀ d∈D,a∈A,f∈Fdξ∈Ξ∗(46)

Delayf,ξd≥ata,Dfd,ξd−Arrf−(1−[yf,ξd−xf,ad])bigM  ∀ d∈D,a∈A,n∈Nξ∈Ξ∗(47)

[UB=min{UB,maxξ∈ΞZξ∗+∑f∈F∑a∈A∑d∈DFCfdxf,ad¯}LB=∑f∈F∑a∈A∑d∈DFCfdxf,ad¯+ϕ(48)

6  Computational Experiments

In this section, we first provide a case example of one of the major Iranian airlines to validate the performance of the proposed TSRO model and the proposed solution method. Then, the price of robustness is measured using some criteria. Finally, we evaluate the computational performance of the proposed CRG method for random problem instances with different scales. The numerical studies are implemented in GAMS software www.gams.com (accessed on 01 June 2023) using CPLEX solver (v.12.6). Each experiment has been performed by a 64-bit 2.8 GHz Intel® Core™ i7 processor computer using 8 GB of RAM.

6.1 A Case Example

As an operational case example of the proposed AMRCR problem, we consider a part of the domestic route network of an Iranian airline www.mahan.aero/en (accessed on 01 June 2023) for some of the provinces with high air traffic density that are connected to Tehran as the main hub (Fig. 4). This domestic flight network includes 20 origin-destination cities (|N| = 20), 40 flights out of the 90 daily flights, 30 crews (|C| = 30), ten aircraft fleets (|A| = 10), and one maintenance bases (|M| = 1) in Tehran. Table 3 shows the scales of these numerical instances.

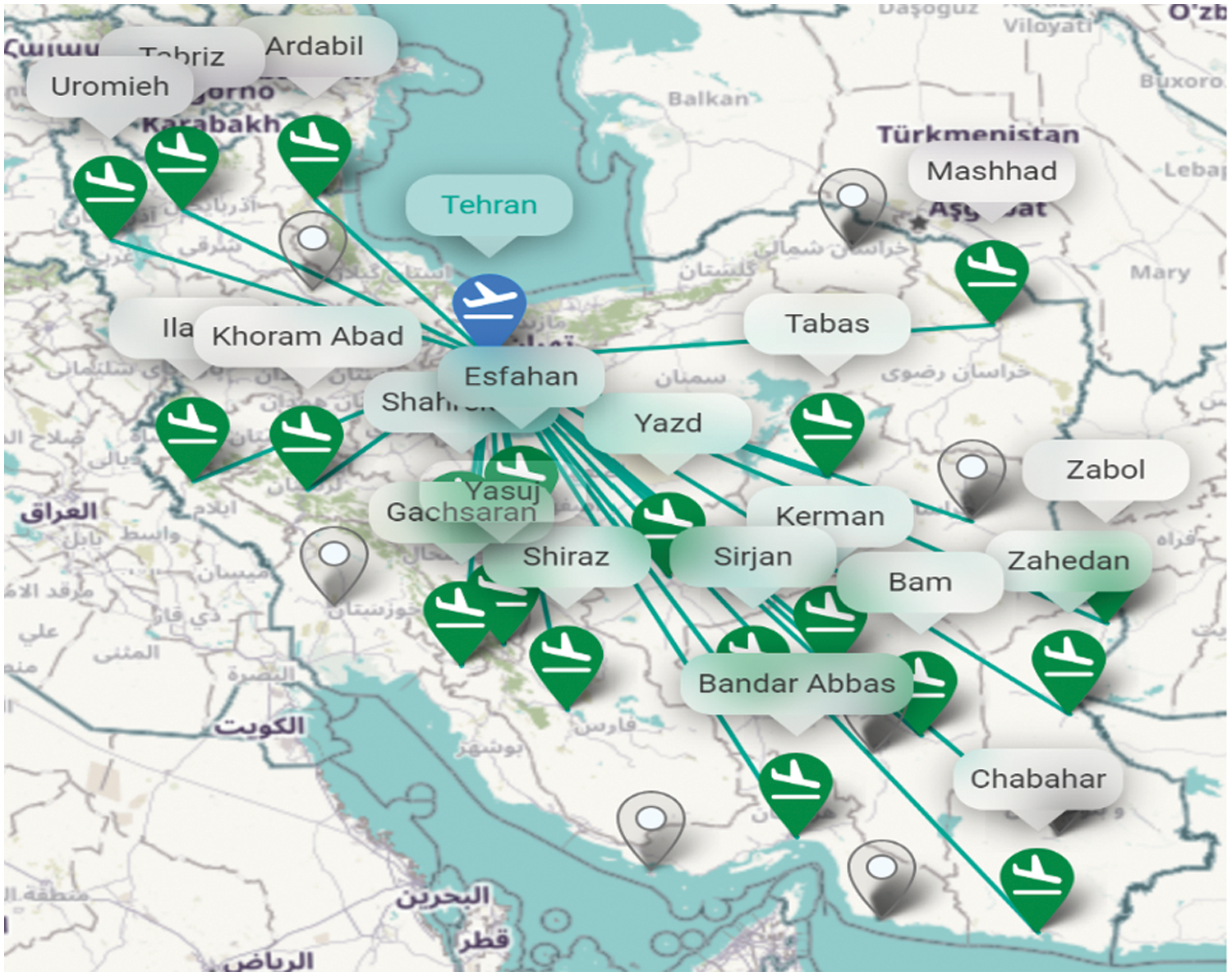
Figure 4: The route network of the scheduled flights in a case example of the AMRCR problem

For this network, a possible pairing is generated daily, and the crewmembers and aircraft must be stationed at the crew home at the end of the daily duty. The basic parameters of the AMRCR problem, MaxDf, MaxUa, MaxNF and MaxST are set in Table 4. The other parameters are randomly generated from the corresponding standards for the airlines.

In the proposed model, the total cost of the pre-planned flights is calculated. This cost is then subtracted from the revenue of the flights to determine the profit. To model the uncertainty of the price of each flight, a random number ρfd∼U(20,50) is generated as the price of that flight (xf,ad∗=1). The revenue will then be ∑f∈F∑a∈A∑d∈Dρfdxf,ad∗. Accordingly, the profit equals ∑f∈F∑a∈A∑d∈Dρfdxf,ad∗−Cost∗, where Cost* is the minimum cost of the proposed model. In the following subsections, we evaluate the performance of the proposed TSRO model in solving this numerical study and that of the proposed CRG method in solving the problem instances of different scales.

6.2 Key Performance Indicators for Model Assessment

To evaluate the proposed TSRO model, which solves the AMRCR problem in an integrated and robust manner, five key performance indicators (KPIs) are considered as follows:

a)   Number of delayed flights per week (KPI-1).

b)   Number of canceled flights per week (KPI-2).

c)   Average delay time (KPI-3).

d)   Average profit under disruption (KPI-4).

e)   Minimum profit under disruption (KPI-5).

where the first three ones are Lesser-is-Better and the last two ones are Greater-is-Better indicators.

In selecting the aforementioned KPIs, we considered the following considerations:

a)   These indicators offer a multifaceted evaluation of airline performance, encompassing both financial profitability and customer satisfaction aspects by addressing factors such as minimizing flight delays and cancellations.

b)   KPIs are well-established in the air transport industry and aligned with the research objectives.

c)   KPIs are simply calculable and actionable.

d)   KPIs provide a comprehensive and balanced view of airline performance.

e)   Furthermore, these KPIs serve as symbolic representations of sustainability performance and long-term profitability for airlines.

To evaluate the performance of the TSRO model, we compare it with two models: (1) the Nominal model, which does not consider uncertainty, and (2) the Sequential model, which does not consider integration. Table 5 and Fig. 5 display the results of these three models in terms of the defined KPIs. It can be seen from the Spider plot in Fig. 6 that the proposed TSRO model has substantially improved the solutions at all indicators compared with those of the non-integrated and non-robust models.

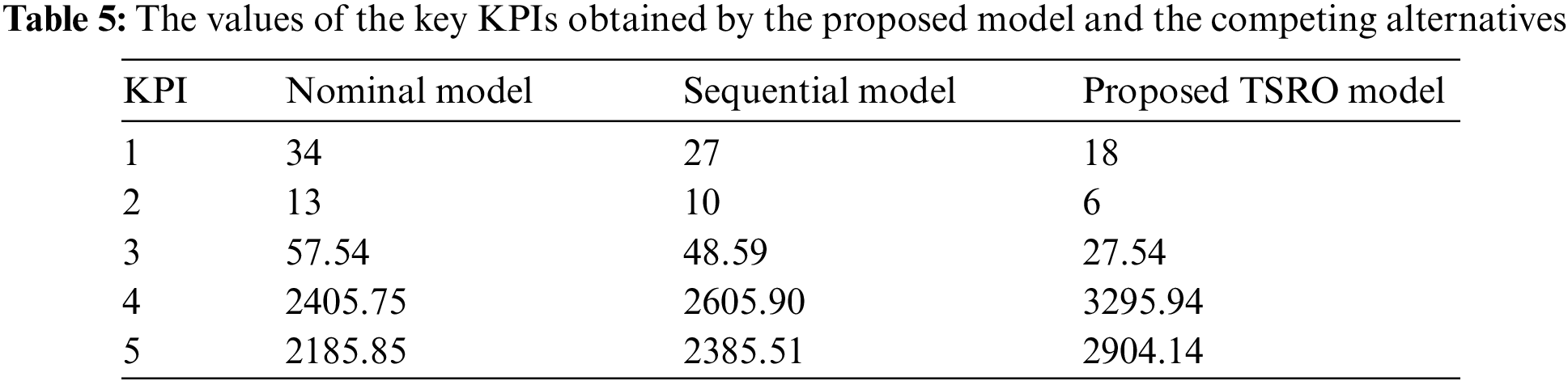
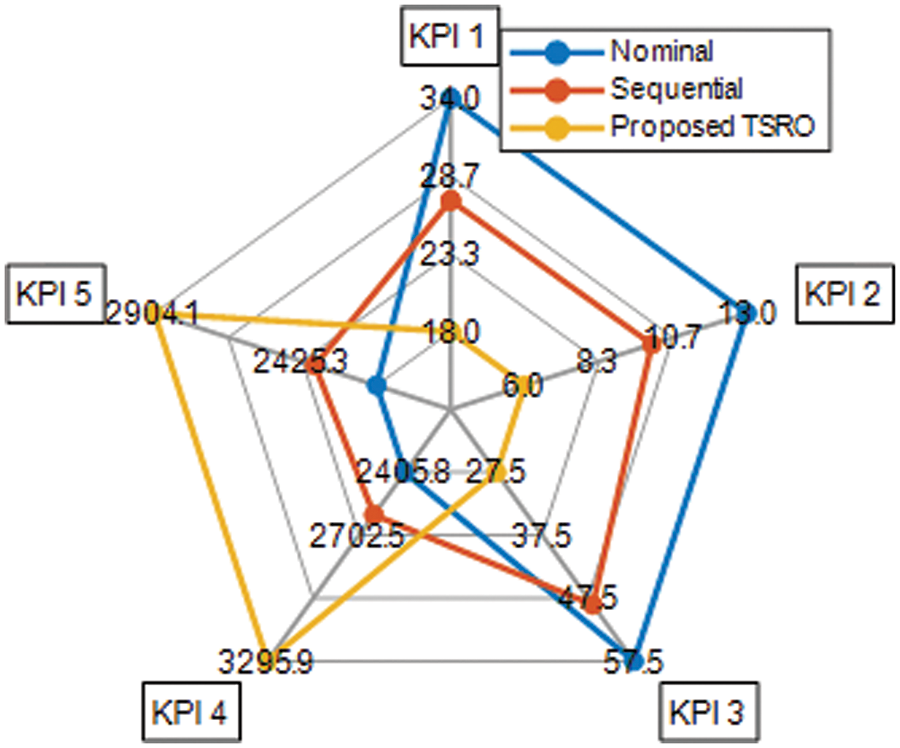
Figure 5: The comparison of the proposed TSRO model w.r.t. the five key KPIs

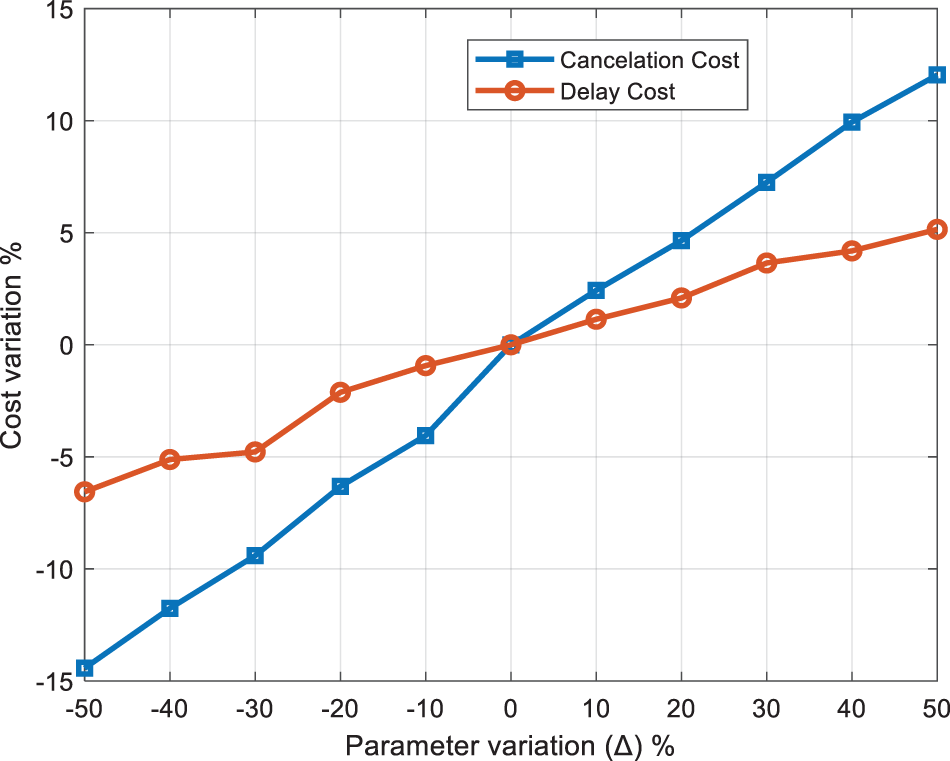
Figure 6: The cost variation w.r.t. to delay cost (DCfd) and cancelation cost (CCfd)

6.3 Sensitivity Analysis of Delay and Cancelation Costs

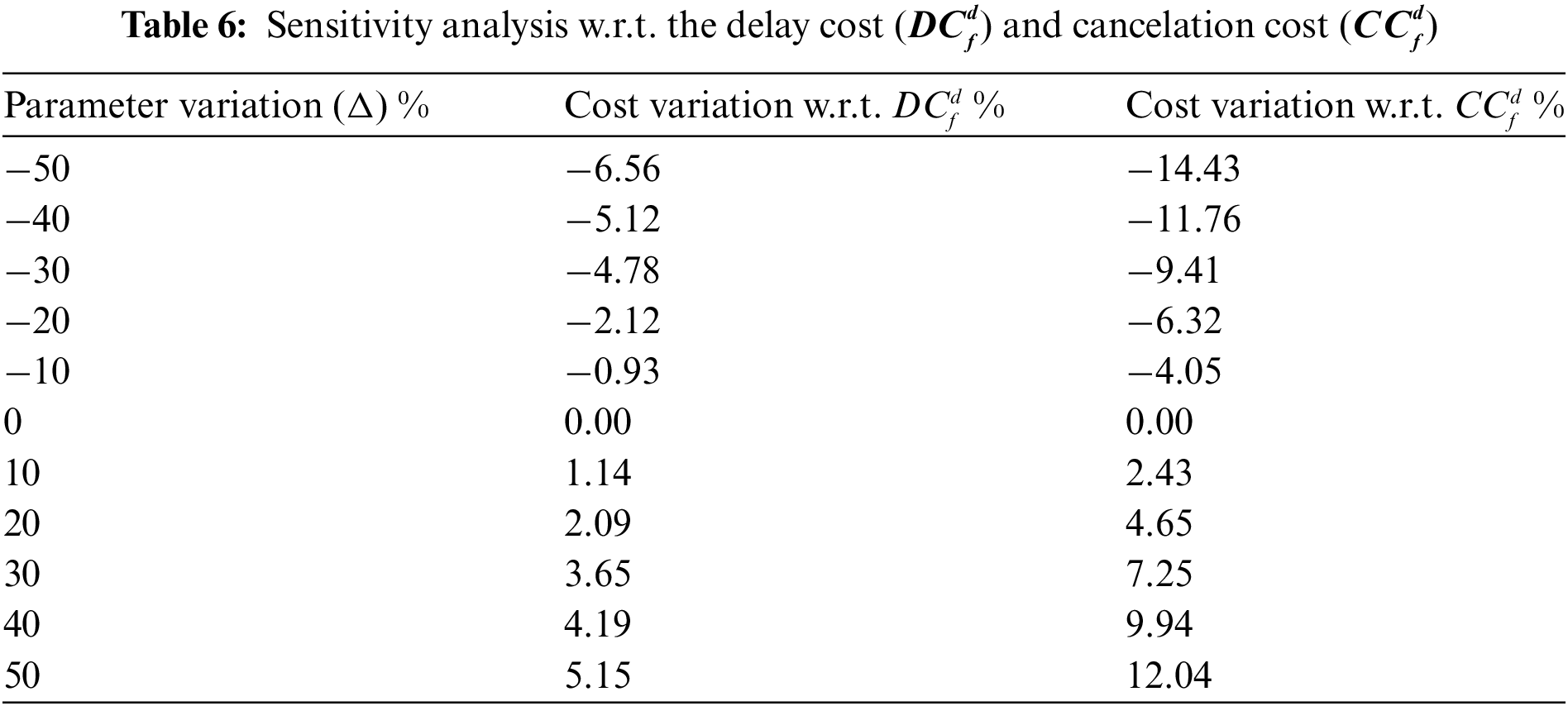
In this section, we analyze the sensitivity of the proposed AMRCR problem cost to two important and influential parameters, the cancelation cost (CCfd) and the unit penalty cost for the delay of each flight (DCfd). For this, the following values are considered for these parameters:

CCfdNEW=(1+Δ100)CCfd

DCfdNEW=(1+Δ100)DCfd

where −50≤Δ≤50 indicates the percentage of change in each parameter. From Table 6, it can be seen that a direct relationship exists, where the cost goes up with the increase of the two parameters. Fig. 6 shows that the objective function is more sensitive to CCfd than to DCfd. The reason for this can be attributed to the second-stage variables, which are related to the cancelation of a scheduled flight. In case of the increase or decrease of DCfd, the second-stage variables are affected drastically, and thus the objective function is more sensitive to its changes.

6.4 The Value of Robustness

In this section, to measure the value of robustness of the proposed TSRO model, both the solutions obtained from our model and the nominal model (in which the disruption scenarios and uncertainty are not considered) are called in 10 realizations of the problem and their profit in each realization is recorded. So, we show the robustness value of the proposed model through two measures: Average Profit and Minimum Profit. Moreover, the box plot of the profits verifies the lower standard deviation of the proposed robust model. Table 7 compares the proposed TRSO model with a nominal/non-robust model using randomly simulated data. The results indicate that the robust model performs better in both average and minimum measures. To further illustrate the robustness and reduced profit fluctuation, Fig. 7 illustrates the results using a box plot, which visually confirms the robustness of the proposed TRSO approach.

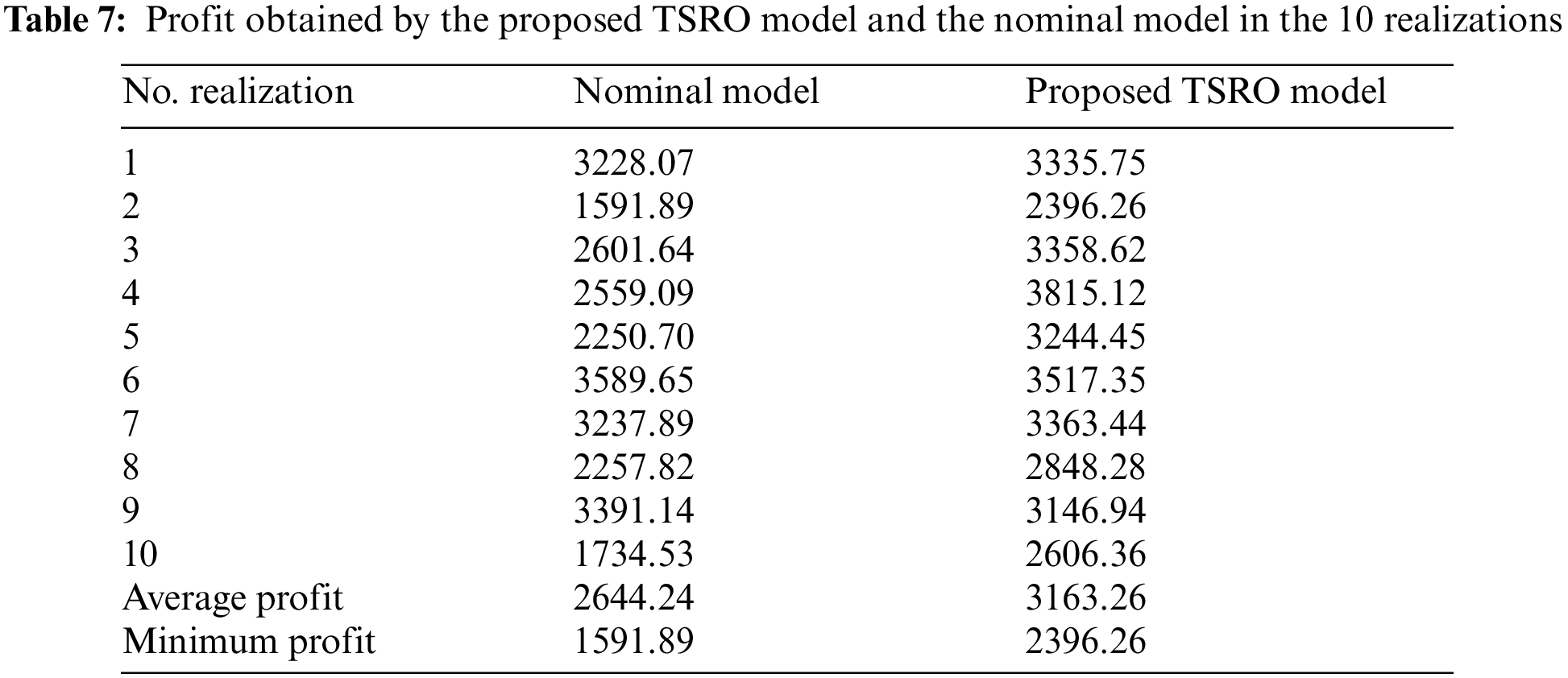
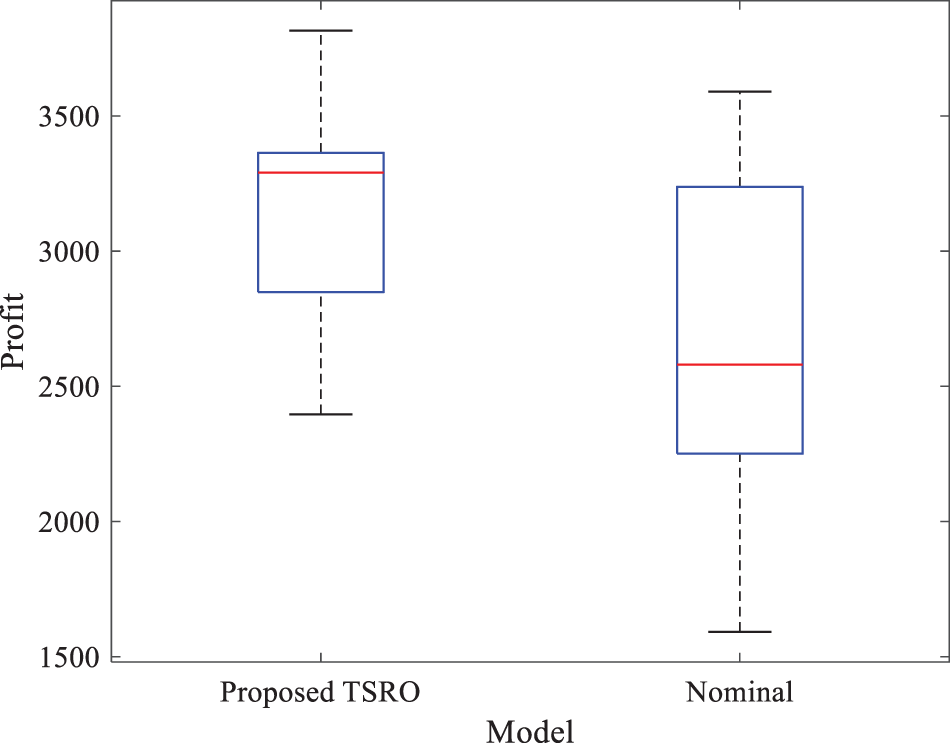
Figure 7: The robustness of the proposed TSRO model and the nominal model

6.5 Performance Evolution of the Proposed CRG Method

In this section, we evaluated the effectiveness of the proposed decomposition-based CRG in addressing the TSRO model across problem instances of varying scales. While the TSRO model was originally formulated as a MILP that the CPLEX solver can solve exactly, solving large-scale problems using this traditional method may be time-consuming and may result in an optimality gap. Consequently, we employed the CRG method to mitigate both the computational time and the occurrence of optimality gaps for larger instances.

Table 8 shows 20 test problems of different scales that the CPLEX solver and the proposed CRG method solved, with a maximum time of 3600 s. The numerical results show that CPLEX and CRG methods have similar and close to optimal performance for small-scale instances. However, the proposed TSRO model does not have an acceptable computational efficiency in large-scale problems. In contrast, the proposed CRG method can reduce the computational time and optimality gap to a sufficient extent. This fact can be seen in the last column of Table 8. Moreover, Fig. 8 shows that the CRG method significantly reduces the execution time of the model compared to that of the CPLEX.

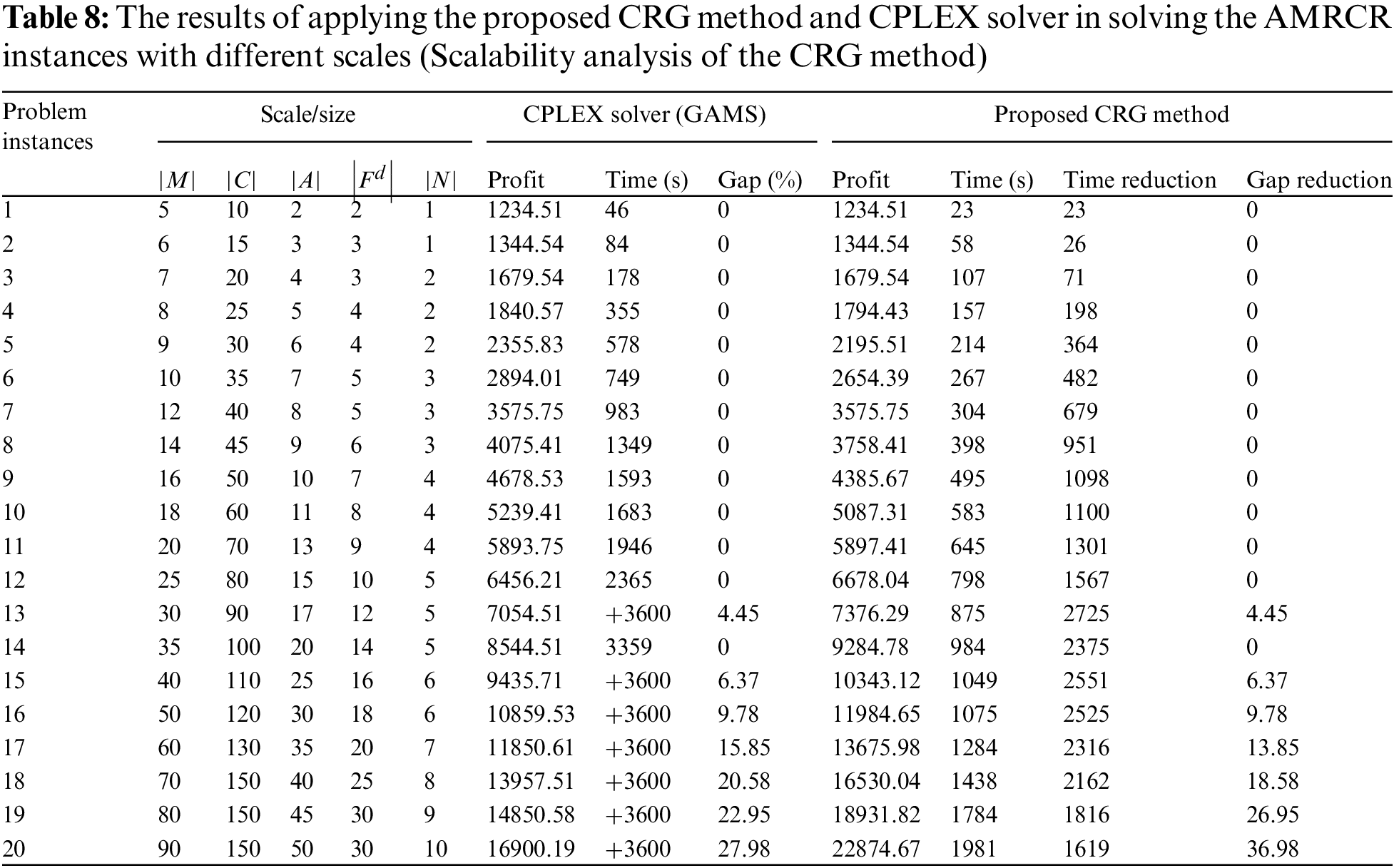
Figure 8: The run-time of the proposed CRG method and CPLEX solver

6.6 Impact of the Main Operational Parameters

As we mentioned in Table 4, the operational parameters of the AMRCR problem are the Maximum possible delay (MaxDf), Maximum utilization of aircraft (MaxUa), Maximum number of flight legs (MaxNF), and Maximum flight/sky time (MaxST), where their current value is 120, 500, 20, and 1500, respectively. In this section, we analyze the impact of these parameters on the two key KPIs, average profit and average delay time. Table 9 shows the numerical results of the sensitivity analysis. Figs. 9 and 10 illustrate the impacts on the profit and delay time, respectively. What can be driven is that the MaxUa has the maximum impact on the profit while the delay time remains almost constant. MaxDf can increase the profit. However, it simultaneously increases delay time. In contrast, MaxNF not only improves the profit but also reduces the delay. Finally, MaxST affects the profit and delay time like MaxDf but with less change in the KPIs.

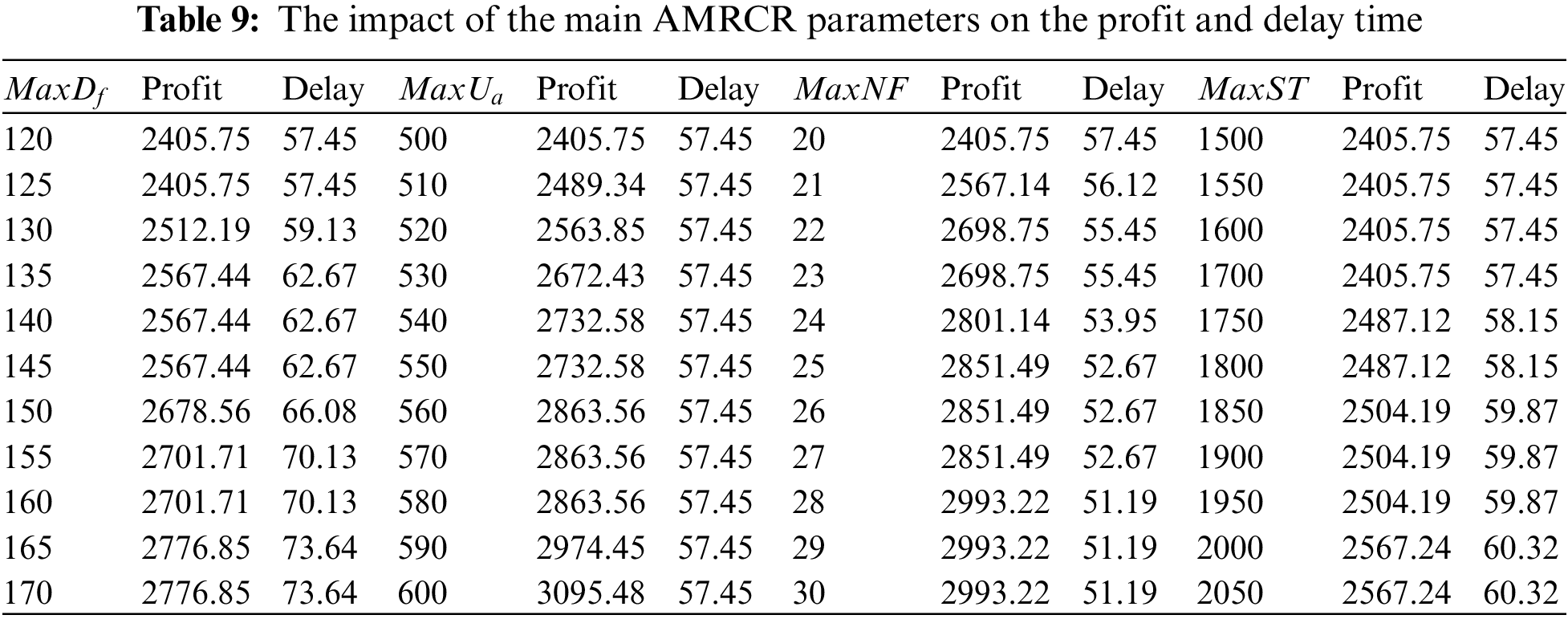
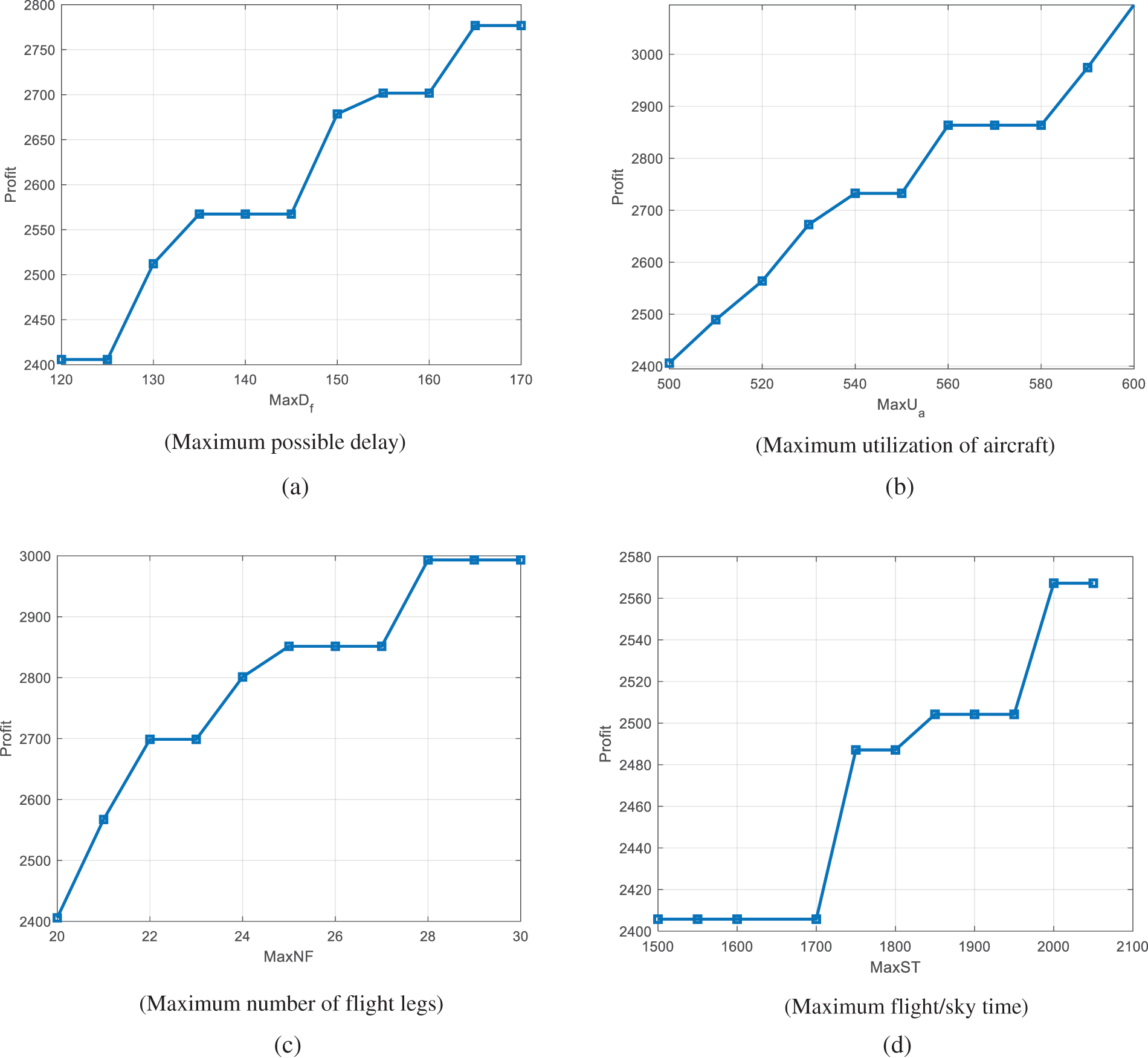
Figure 9: The impact of the main operational parameter on the profit

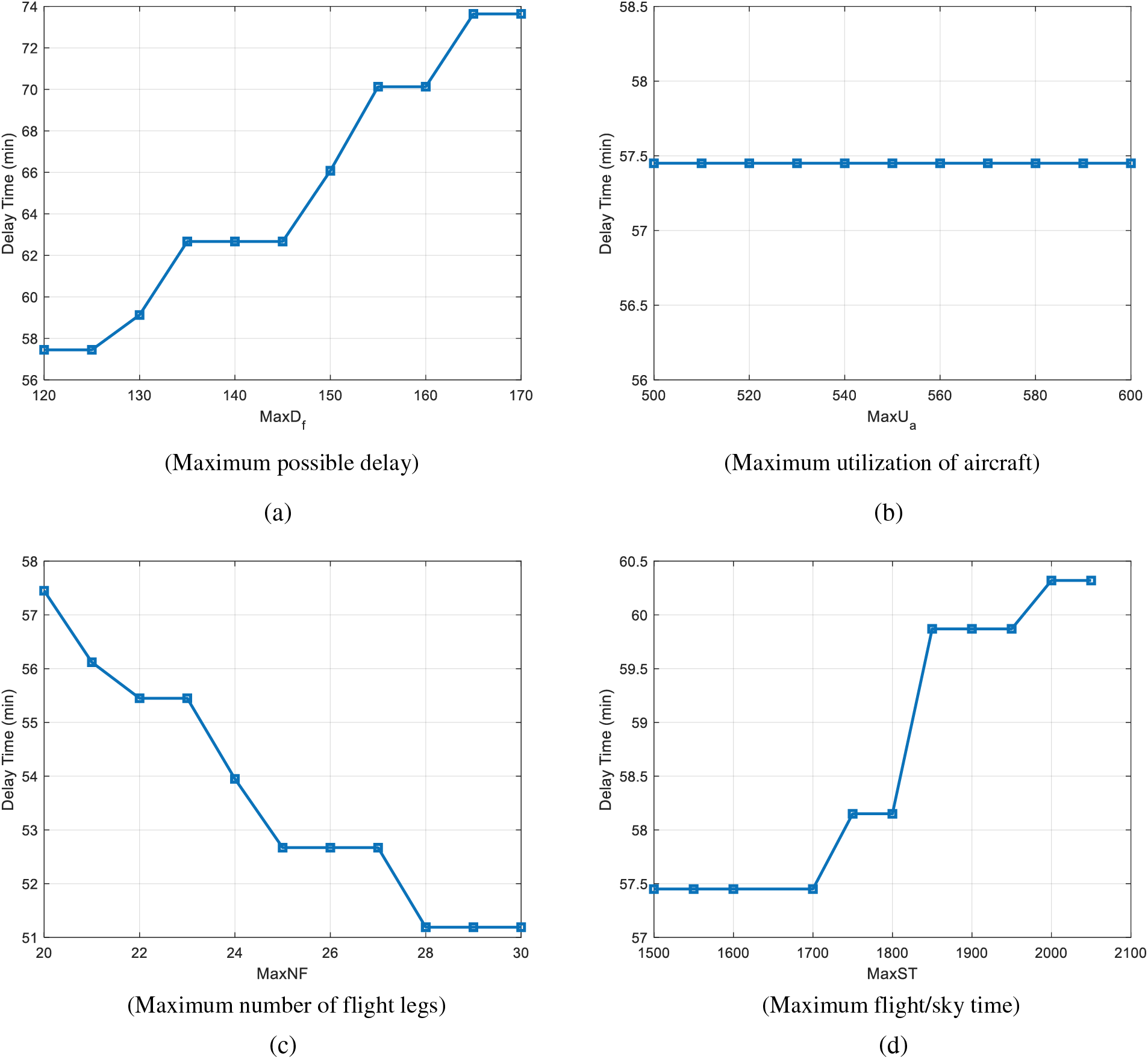
Figure 10: The impact of the main operational parameters on the delay time

7  Conclusion

In this research, to minimize an airline’s operating costs in making a set of pre-planned flights, we presented an integrated model for the integrated aircraft maintenance-routing and crew rostering (AMRCR) problem. In this problem, some disruption scenarios in the flight schedule were considered and formulated using the TSRO model as a MILP model.

This paper presents a novel approach to the airline AMRCR problem. This integrated approach significantly improves key performance indicators (KPIs) such as reduced flight delays and cancellations, improved on-time performance, and increased profitability even under disruptive scenarios. The model incorporates various daily, weekly, and monthly operational constraints for resources to enhance real-world applicability. Additionally, the model addresses potential disruptions by considering the initial schedule’s various intensities. This leads to a robust model that can handle unexpected events. Although the proposed TSRO model was formulated as a MILP and could be solved for small-scale problems using the CPLEX solver, we used the column and row generation (CRG) method. Five KPIs were considered to evaluate the proposed model: delayed and canceled flights, average cost, and average profit. The results confirmed that the proposed model significantly improves the considered KPIs compared with the two classic approaches in the literature, the nominal model and the sequential model. The analysis of the robustness value, using the realization-based method, showed that the proposed model could increase both the average and minimum profits compared with the nominal model (in which uncertainty and disruption scenarios were not considered). Moreover, the box-plot-based analysis indicated the stability of the proposed model.

Finally, to evaluate the performance of the proposed CRG method in solving the AMRCR problems, several instances of different scales were generated and solved by CPLEX solver and the CRG method. The numerical results showed that both methods solved the problem of small scales without an optimality gap but for large-scale instances. In contrast, the model cannot be solved by CPLEX solver; the CRG method was computationally efficient and could provide a solution close to the optimum in an acceptable time.

While our study strives to provide robust solutions to the addressed problem, it is essential to recognize certain constraints and potential drawbacks inherent in our approach. One limitation of our framework lies in the simplifying assumptions to model complex aviation operations. For instance, our model may not fully capture all intricacies of real-world scenarios, such as variations in weather conditions or unexpected disruptions beyond the scope of our defined disruption scenarios. Furthermore, while our model offers computational efficiency, scalability challenges may exist when applied to larger-scale instances or dynamic operational environments. Future research directions could focus on incorporating more sophisticated modeling techniques and enhancing the adaptability of our approach to dynamic operational environments. Furthermore, for the development of this research, it is suggested that the decisions related to demand recapture for canceled flights be considered in the problem modeling. Also, to have more integrated decision-making systems for airlines, the tactical decisions related to the design of the flight schedule can be influenced by the operational decisions of the AMRCR.

Acknowledgement: None.

Funding Statement: The authors declare that the content of this paper has never entitled them to a specific funding resource.

Author Contributions: The authors confirm contribution to the paper as follows: problem definition and its conceptions: Khalilallah Memarzadeh, Mohammad Fallah and Hamed Kazemipoor; modeling and solution mythology: Khalilallah Memarzadeh, Hamed Kazemipoor, Babak Farhang Moghaddam; implementation and result analysis: Khalilallah Memarzadeh and Mohammad Fallah. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The values assigned for developed models’ major parameters, including MaxDf, MaxUa, MaxNF and MaxST, are shown in Table 4. The other parameters are allocated randomly generated numbers, with their lower and upper bound values being thoroughly discussed in Section 6.1.

Ethics Approval: This article does not contain any studies with human participants or animals performed by any of the authors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study. More details about the data that support the findings of this study are available authors upon the official and reasonable requests.

References

1. Eltoukhy A, Chan FTS, Chung SH. Airline schedule planning: a review and future directions. Ind Manag Data Syst. 2017;117(6):1201–43. [Google Scholar]

2. Bazargan M. Airline operations and scheduling. London: Routledge; 2016. doi:10.4324/9781315566474. [Google Scholar] [CrossRef]

3. Lohatepanont M, Barnhart C. Airline schedule planning: integrated models and algorithms for schedule design and fleet assignment. Transp Sci. 2004;38(1):19–32. doi:10.1287/trsc.1030.0026. [Google Scholar] [CrossRef]

4. Sanchez DT, Boyacı B, Zografos KG. An optimisation framework for airline fleet maintenance scheduling with tail assignment considerations. Transp Res Part B Methodol. 2020;133:142–64. doi:10.1016/j.trb.2019.12.008. [Google Scholar] [CrossRef]

5. Zhou L, Liang Z, Chou C-A, Chaovalitwongse WA. Airline planning and scheduling: models and solution methodologies. Front Eng Manag. 2020;7(1):1–26. doi:10.1007/s42524-020-0093-5. [Google Scholar] [CrossRef]

6. Kohl N, Karisch SE. Airline crew rostering: problem types, modeling, and optimization. Ann Oper Res. 2004;127(1):223–57. [Google Scholar]

7. Barnhart C, Smith B. Quantitative problem solving methods in the airline industry. Springer; 2012. vol. 169, no. 1. [Google Scholar]

8. Antunes D, Vaze V, Antunes AP. A robust pairing model for airline crew scheduling. Transp Sci. 2019;53(6):1751–71. doi:10.1287/trsc.2019.0897. [Google Scholar] [CrossRef]

9. Su Y, Xie K, Wang H, Liang Z, Chaovalitwongse WA, Pardalos PM. Airline disruption management: a review of models and solution methods. Engineering. 2021;7(4):435–47. doi:10.1016/j.eng.2020.08.021. [Google Scholar] [CrossRef]

10. Hassan LK, Santos BF, Vink J. Airline disruption management: a literature review and practical challenges. Comput Oper Res. 2021;127:105137. doi:10.1016/j.cor.2020.105137. [Google Scholar] [CrossRef]

11. Kasirzadeh A, Saddoune M, Soumis F. Airline crew scheduling: models, algorithms, and data sets. EURO J Transp Logist. 2017;6(2):111–37. doi:10.1007/s13676-015-0080-x. [Google Scholar] [CrossRef]

12. Ruan JH, Wang ZX, Chan FTS, Patnaik S, Tiwari MK. A reinforcement learning-based algorithm for the aircraft maintenance routing problem. Expert Syst Appl. 2021;169:114399. [Google Scholar]

13. Wen X, Sun X, Sun Y, Yue X. Airline crew scheduling: models and algorithms. Transp Res Part E Logist Transp Rev. 2021;149:102304. doi:10.1016/j.tre.2021.102304. [Google Scholar] [CrossRef]

14. Cordeau J-F, Stojković G, Soumis F, Desrosiers J. Benders decomposition for simultaneous aircraft routing and crew scheduling. Transport Sci. 2001;35(4):375–88. [Google Scholar]

15. Sandhu R, Klabjan D. Integrated airline fleeting and crew-pairing decisions. Oper Res. 2007;55(3):439–56. doi:10.1287/opre.1070.0395. [Google Scholar] [CrossRef]

16. Papadakos N. Integrated airline scheduling. Comput Oper Res. 2009;36(1):176–95. doi:10.1016/j.cor.2007.08.002. [Google Scholar] [CrossRef]

17. Souai N, Teghem J. Genetic algorithm based approach for the integrated airline crew-pairing and rostering problem. Eur J Oper Res. 2009;199(3):674–83. doi:10.1016/j.ejor.2007.10.065. [Google Scholar] [CrossRef]

18. Weide O, Ryan D, Ehrgott M. An iterative approach to robust and integrated aircraft routing and crew scheduling. Comput Oper Res. 2010;37(5):833–44. doi:10.1016/j.cor.2009.03.024. [Google Scholar] [CrossRef]

19. Salazar-González J-J. Approaches to solve the fleet-assignment, aircraft-routing, crew-pairing and crew-rostering problems of a regional carrier. Omega. 2014;43:71–82. doi:10.1016/j.omega.2013.06.006. [Google Scholar] [CrossRef]

20. Azad N, Aazami A, Papi A, Jabbarzadeh A. A two-phase genetic algorithm for incorporating environmental considerations with production, inventory and routing decisions in supply chain networks. In: Proceedings of the Genetic and Evolutionary Computation Conference Companion; 2019 Jul 13; Prague, Czech Republic. p. 41–2. [Google Scholar]

21. Feng J, Nan J, Sun K, Deng X, Guan L, Zhou H. Hierarchical two-stage robust planning for demand-side energy storage with dynamic carbon incentive mechanism. Appl Sci. 2023;13(11):6524. doi:10.3390/app13116524. [Google Scholar] [CrossRef]

22. Jabbarzadeh A, Pishvaee M, Papi A. A multi-period fuzzy mathematical programming model for crude oil supply chain network design considering budget and equipment limitations. J Ind Syst Eng. 2016;9:88–107. [Google Scholar]

23. Razavi Al-e-hashem SA, Papi A, Pishvaee MS, Rasouli M. Robust maintenance planning and scheduling for multi-factory production networks considering disruption cost: a bi-objective optimization model and a metaheuristic solution method. Oper Res. 2022;22(5):4999–5034. doi:10.1007/s12351-022-00733-x. [Google Scholar] [CrossRef]

24. Shao S, Sherali HD, Haouari M. A novel model and decomposition approach for the integrated airline fleet assignment, aircraft routing, and crew pairing problem. Transp Sci. 2017;51(1):233–49. doi:10.1287/trsc.2015.0623. [Google Scholar] [CrossRef]

25. Safaei N, Jardine AKS. Aircraft routing with generalized maintenance constraints. Omega. 2018;80(1):111–22. doi:10.1016/j.omega.2017.08.013. [Google Scholar] [CrossRef]

26. Yadegari Z, Molana SMH, Kashan AH, Najafi SE. Designing a fuzzy mathematical model for a two-echelon allocation-routing problem by applying route conditions: a new interactive fuzzy approach. Decis Mak Appl Manag Eng. 2024;7(2):172–96. doi:10.31181/dmame180101p. [Google Scholar] [CrossRef]

27. Eltoukhy A, Wang ZX, Chan FTS, Chung SH. Joint optimization using a leader-follower Stackelberg game for coordinated configuration of stochastic operational aircraft maintenance routing and maintenance staffing. Comput Ind Eng. 2018;125:46–68. doi:10.1016/j.cie.2018.08.012. [Google Scholar] [CrossRef]

28. Ben AM, Mansour FZ, Haouari M. Robust integrated maintenance aircraft routing and crew pairing. J Air Transp Manag. 2018;73:15–31. doi:10.1016/j.jairtraman.2018.07.007. [Google Scholar] [CrossRef]

29. Cui R, Dong X, Lin Y. Models for aircraft maintenance routing problem with consideration of remaining time and robustness. Comput Ind Eng. 2019;137:106045. doi:10.1016/j.cie.2019.106045. [Google Scholar] [CrossRef]

30. Haouari M, Zeghal Mansour F, Sherali HD. A new compact formulation for the daily crew pairing problem. Transp Sci. 2019;53(3):811–28. [Google Scholar]

31. Chen CH, Chou FI, Chou JH. Multiobjective evolutionary scheduling and rescheduling of integrated aircraft routing and crew pairing problems. IEEE Access. 2020;8:35018–30. doi:10.1109/Access.6287639. [Google Scholar] [CrossRef]

32. Korba P, Šváb P, Vereš M, Lukáč J. Optimizing aviation maintenance through algorithmic approach of real-life data. Appl Sci. 2023;13(6):3824. doi:10.3390/app13063824. [Google Scholar] [CrossRef]

33. Teymouri A, Sahebi H, Pishvaee M. Airline operational crew-aircraft planning considering revenue management: a robust optimization model under disruption. Int J Ind Eng Comput. 2023;14(2):381–402. [Google Scholar]

34. Parmentier A, Meunier F. Aircraft routing and crew pairing: updated algorithms at Air France. Omega. 2020;93(1):102073. doi:10.1016/j.omega.2019.05.009. [Google Scholar] [CrossRef]

35. Bulbul KG, Kasimbeyli R. Augmented Lagrangian based hybrid subgradient method for solving aircraft maintenance routing problem. Comput Oper Res. 2021;132:105294. doi:10.1016/j.cor.2021.105294. [Google Scholar] [CrossRef]

36. Hajiagha SHR, Mahdiraji HA, Behnam M, Nekoughadirli B, Joshi R. A scenario-based robust time–cost tradeoff model to handle the effect of COVID-19 on supply chains project management. Oper Manag Res. 2021;15(1):357–77. [Google Scholar]

37. Rezaei M, Chaharsooghi SK, Kashan AH, Babazadeh R. Optimal design and planning of biodiesel supply chain network: a scenario-based robust optimization approach. Int J Energy Environ Eng. 2020;11(1):111–28. doi:10.1007/s40095-019-00316-1. [Google Scholar] [CrossRef]

38. Tosarkani BM, Amin SH, Zolfagharinia H. A scenario-based robust possibilistic model for a multi-objective electronic reverse logistics network. Int J Prod Econ. 2020;224(12):107557. doi:10.1016/j.ijpe.2019.107557. [Google Scholar] [CrossRef]

39. Zeng B, Zhao L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper Res Lett. 2013;41(5):457–61. doi:10.1016/j.orl.2013.05.003. [Google Scholar] [CrossRef]

40. Tönissen DD, Arts JJ, Shen Z-JM. A column-and-constraint generation algorithm for two-stage stochastic programming problems. TOP. 2021;29:1–18. doi:10.1007/s11750-021-00593-2. [Google Scholar] [CrossRef]

41. Wang Z, Qi M. Robust service network design under demand uncertainty. Transp Sci. 2020;54(3):676–89. doi:10.1287/trsc.2019.0935. [Google Scholar] [CrossRef]