FedAdaSS: Federated Learning with Adaptive Parameter Server Selection Based on Elastic Cloud Resources

1  Introduction

In recent years, artificial intelligence (AI) technology has made significant progress, and its application scope is constantly expanding, covering various fields such as smart homes, voice assistants, and intelligent decision-making. However, with the widespread promotion of AI applications, the issue of privacy protection has attracted widespread attention [1]. Many countries and regions have established corresponding laws and regulations to ensure user privacy, and strictly restrict the use and processing of data [2]. This undoubtedly poses a challenge to the development of artificial intelligence applications. In response to this concern, federated learning (FL) has gradually evolved into a privacy-preserving machine learning paradigm. In this paradigm, mobile devices and Internet of Things (IoT) clients distributed in different geographical regions can collaborate to train machine learning models while keeping their respective data on local devices. FL is widely used for a variety of tasks. Examples include speech recognition, handwriting recognition, and text prediction in the consumer Internet, as well as collaboration between medical, industrial [3], and communications [4] entities.

In FL training, there are numerous and widely distributed devices, coupled with a certain degree of heterogeneity in system performance, which leads to significant differences in the success probability of each client participating in training (hereinafter referred to as engagement). In addition, the client data participating in federated learning training varies in scale [5], and the data distribution also exhibits non-independent identically distributed (non-IID) characteristics [6]. These characteristics result in significant performance loss in federated learning, affecting round-to-accuracy performance, and there is an issue of optimization target deviation [7,8].

Existing FL optimization methods mainly aim to reduce communication costs and improve training efficiency by fine-tuning client selection strategies [9], local updates [10,11], and communication compression [12–16] strategies. However, these methods have not fully addressed the problem of low engagement. On the other hand, decentralized [17] and asynchronous methods [18–21] can increase engagement, but synchronization costs are high and convergence speed is slow.

The client selection mechanism has been widely studied and applied to improve training efficiency reduce communication overhead, and increase the robustness of FL training. The first is the system utility perspective. Client selection reduces communication pressure on the parameter server, reducing unnecessary communication and network load, especially in bandwidth-constrained environments. Mobile devices may have limited computing and storage resources. By selecting clients with sufficient resources for training, the training process can run smoothly without overburdening resource-constrained devices. The second is to improve the statistical performance of FL training. Client data may be heterogeneous, i.e., different clients may have different data characteristics. By selecting clients that represent the overall data distribution, a better-performing global model can be trained. At the same time, by selecting clients with high data quality and high computing power to participate in training, the convergence speed of the model can be accelerated.

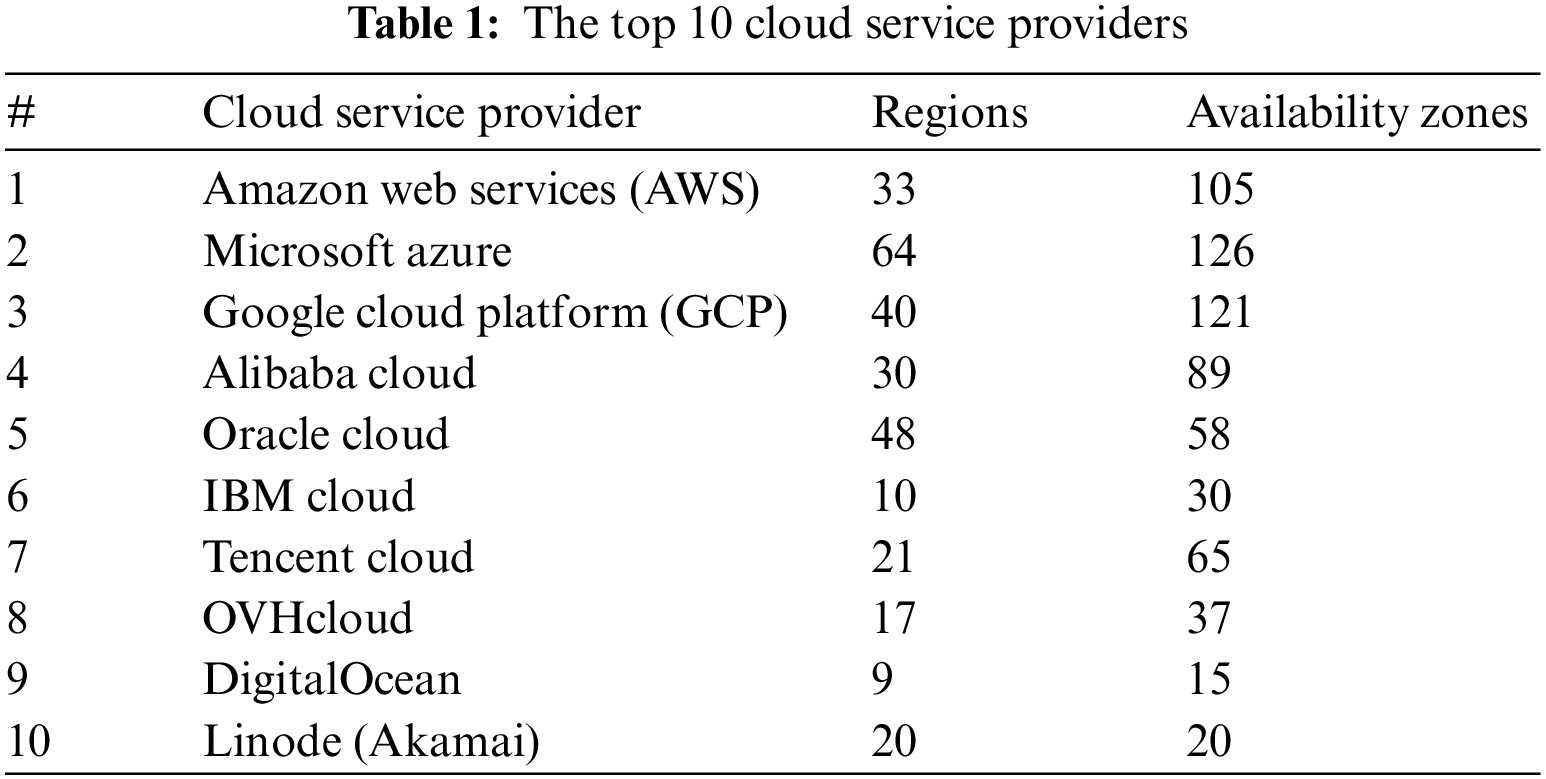
With the development of 5G/6G networks and the integration of computing resources through cloud computing, edge computing and other methods, mobile user-oriented application development can design more flexible paradigms [22,23]. Based on the widespread distribution of cloud computing resources worldwide (as shown in Table 1), effective utilization of these resources can optimize the federated learning process. The parameter server of FL can be set and migrated by a specific server selection mechanism, which ensures that the overall usage cost does not increase. Selecting the optimal parameter server according to geographical distribution, network state, and computing resources can reduce the communication delay of FL training and reduce resource competition, which has been widely verified in general distributed tasks. On the other hand, we found that server selection can improve the FL training process from a statistical utility perspective. This is reflected in two aspects: first, it can extend the client selection strategy (co-selection), and second, it can be combined with client selection as an orthogonal method (server selection after client selection), thereby improving the overall client participation and the training efficiency of federated learning.

We propose an adaptive server selection algorithm FedAdaSS, which differs from the traditional approach of having a unique fixed parameter server. We adopt an adaptive strategy to select the optimal server as the parameter server in each training round to optimize the training effect. The server selection mechanism can be incorporated into existing federated learning training algorithms as an orthogonal mechanism. In addition to improving FL from system performance as in classical distributed computing, we have also demonstrated that it can improve statistical performance while also expanding the client selection policy space.

Optimizing server selection is a challenging task. In theory, the optimal choice requires us to obtain global prior knowledge in advance. However, in the actual training process, we cannot know the current set of clients in advance. Relying solely on the optimal set of clients per round to select servers can reduce wall clock time, but it cannot effectively alleviate the problem of optimization target offset. To this end, this article proposes an adaptive random shuffle strategy that estimates the utility of the client system and server in each round and then approximately selects the nearest server to accelerate the training process.

After rigorous theoretical analysis, we have confirmed that the FedAdaSS algorithm converges under strong convexity and L-smooth assumptions. Within the FLSim framework, we compared FedAdaSS with the Federated Averaging with random reshuffling (FedAvg+RR) and confirmed that optimizing the server selection mechanism can reduce the training #round-to-accuracy by 12%–20%. Under communication optimization strategies such as small number of participants and the large number of local steps, this optimization method shows significant advantages. In addition, when comparing different engagement levels, FedAdaSS can effectively mitigate the performance loss caused by low engagement, reducing the loss indicator by 50%.

The key contributions of our work are the following:

•   We propose a basic framework for optimizing FL with elastic cloud resources, and analyze the optimization objectives and trade-offs for server selection.

•   We propose the FedAdaSS algorithm, which is an adaptive server selection algorithm with dynamic client random shuffling to overcome the problems of dynamic joining and low commitment of clients, thereby increasing the statistical performance, and theoretically analyzing its convergence.

•   We evaluate the adaptability of server selection to common FL optimization methods and the performance improvement it brings through comparative experiments.

2  Related Work

2.1 Federated Learning

Federated Learning is a distributed machine learning approach that allows multiple participants (typically devices or organizations) to work together to train a global machine learning model while maintaining the privacy of their respective data [6]. The key benefit of this approach is that it eliminates the need to centralize data in a single location, thereby reducing the risk of data leakage and reducing the need for centralized storage and computational resources [10].

Due to the size of the population and the diversity of user data and devices in FL, each round of training runs on a customer terminal set (with hundreds of participants), typically requiring hundreds of rounds (of a few minutes each) and several days to complete. For example, in the case of the Gboard keyboard, Google conducted weeks of federated training on natural language processing (NLP) models on 1.5 million devices [6,24]. Due to the large number of devices wide geographical distribution, and certain heterogeneity of system performance, each client shows great differences in the success probability of participating in training. Furthermore, client data involved in federated learning training differ in size and have a non-IID distribution. These factors cause federation learning performance to suffer a large loss, affect round-to-accuracy performance, and cause optimization target bias. To address these issues during the cross-device FL training process, existing methods can be classified into server-centric methods that focus on reducing communication overhead, and client-centric methods that focus on improving user engagement.

2.2 System Performance Optimization in FL

In the general paradigm of cross-device FL, the unique parameter server broadcasts the model parameters in each training round and aggregates the model parameters returned by the clients. However, due to resource constraints, methods such as multiple local updates, client selection, and communication compression have been proposed to meet the requirements of the parameter server.

The goal of the local update policy is to reduce the frequency of communication and to utilize the client’s computational resources as much as possible [25], where each device performs multiple local steps before passing its updates back to the central server. One representative method is the Federated Averaging algorithm [20], which is an adaption of local-update to parallel stochastic gradient descent (SGD). The client involved in the training of each round runs a certain number of SGD steps based on its local data and sends back the local updated parameters to the server, then the pseudo-gradient for the global model is aggregated from each returned update. Recently, such methods have attracted a lot of attention, both in terms of theoretical guarantees [11,26], as well as in terms of optimization for real-world scenarios [1,27–29].

To address network bandwidth constraints and client heterogeneity, FL client selection is an emerging topic. FL client selection determines which client devices are selected in each training round. Effective FL client selection schemes can significantly improve model accuracy, increase fairness, improve robustness, and reduce training overhead [9]. For example, the paper [30] proposed a client selection framework called Oort, which improves the time-to-accuracy performance of model training by prioritizing those clients that have the greatest benefit in improving model accuracy and can perform training quickly. In addition, Oort allows developers to specify data distribution requirements during model testing and improve test duration efficiency by carefully selecting clients that meet those requirements.

Communication compression in FL is also a strategy that reduces data transmission between client devices and the central server during the training process. Quantization is a popular method that reduces the precision of model updates, making their transmission size smaller [31,32]. Sketching, as introduced by [33], provides a more concise alternative by summarizing updates using compact data structures. This enables approximate, yet significantly smaller representations of the original data.

2.3 Framework Optimization in FL

The training time scheduled by the parameter server is difficult to match with the idle time of the device, and the effective engagement rate of the client is low. Therefore, new frameworks of FL such as asynchronous distributed training [34] as well as decentralized federated learning methods have also been widely studied.

For asynchronous FL, the server updates the global model whenever it receives a local update. The authors in [35] found empirically that the asynchronous approach is robust to participants joining in the middle of training rounds and when the federation includes participating devices with heterogeneous processing capabilities. A new asynchronous federation optimization algorithm was proposed in [36] to improve the flexibility and scalability of federation learning, where each newly received local update is adaptively weighted according to its staleness, which is defined as the difference between the current epoch and the iteration to which the received update belongs. Furthermore, the authors also prove the convergence guarantee for a restricted family of non-convex problems. However, the current hyperparameters of the FedAsync algorithm still need to be tuned to ensure convergence in different environments. As such, the algorithm is still unable to generalize to the dynamic computational constraints of heterogeneous devices. Synchronous FL is still the most commonly used method today due to the uncertain reliability of asynchronous FL [37].

Decentralized federated learning is another way to maximize the possibility of the participant, which distributes the aggregation of model parameters between the neighboring participants [21,38,39]. Decentralized Federated Learning uses a P2P communication method, it deals with a dynamic and heterogeneous topology where participants often change their location or role in the federation. A study compared the communication efficiency of decentralized algorithms, such as gossip learning, with centralized FL [21]. It found that the best gossip variant had comparable overall performance to the best centralized FL algorithm. Another challenge in decentralized FL is imbalance heterogeneity, replacement of weight averaging with mutual knowledge distillation [40] was proposed to tackle class imbalance.

2.4 Limitations of Current Works

Existing system performance optimization methods, whose core goal is to reduce communication overhead, mainly use multiple local updates, client selection, and communication compression methods, but these methods are assumed to have better results when all clients effectively complete training and all have a high probability of participation. In the actual system, the client, due to its task, can not do more than an effective synchronization to the free time for training, so the total training engagement is low, slowing down the total training time; on the other hand, due to the client’s data distribution of the phenomenon of non-IID, low engagement leads to the intensification of this imbalance phenomenon, which makes the distribution of training data is different from the distribution of the objective function, resulting in the training objective bias.

The methods proposed to solve the low engagement problem, such as asynchronous training and P2P training, have not been widely used in practical systems due to their characteristics, longer convergence times, and higher communication costs. Therefore, to solve the above contradiction, we propose a federated learning framework based on elastic cloud server resources, which improves the participation of clients and extends the policy framework of client selection by providing server selection when client selection, and on this basis, we propose a server selection method that supports dynamic client RR, FedAdaSS, which proves that server selection can be used as an orthogonal method to existing state-of-the-art (SOTA) methods and provides statistical performance improvement.

3  Overview

In this paper, the standard formulation of Federated Learning is considered as a finite sum minimization problem:

minx∈Rd[f(x)≜1|𝒞|∑c∈𝒞fc(x)],(1)

where 𝒞 is the client set. fc(x)=Eξ∼𝒟c[l(x;ξ)] corresponds to the average local loss of the current model parameterized by x∈Rd over the training data 𝒟c located on client c. In the real scenario, the participants are mainly geographically distributed and have numerous mobile devices. When these devices participate in training, it is difficult to ensure that each mobile client can continuously and stably participate in the training process due to the variety of usage scenarios and user behaviors.

We assume that the FL training organizer has automatic control over the creation and destruction of server resources. Modern cloud platforms have their application programming interface (API) to support the automatization, and many interfaces can hide the differences between multiple clouds and provide a unified resource lifecycle control interface. During the training process, there is a global orchestrator role that can be performed by a separate server. The orchestrator selects the server responsible for the next round of training (parameter broadcasting and aggregation) and the participating clients, i.e., the orchestrator is responsible for maintaining and updating the FL state information.

Since servers in the same region on the cloud platform have relatively consistent network and computing resources. For simplicity, we assume that each region of one cloud has one selectable server, as shown in Fig. 1, and the selection described in this article includes the entire lifecycle process of creation, maintenance, and eventual destruction.

Figure 1: Elastic cloud resources controlled by orchestrator

As shown in Fig. 2, the basic framework of FL includes server selection. The FL task is planned by the orchestrator as a whole, where the server set is all cloud servers available for selection (as mentioned earlier, including the entire lifecycle management), and the client set is all mobile clients participating in FL. This article mainly discusses learning and training tasks in a synchronous federation that involves multiple global rounds. In each round, the orchestrator selects the parameter server for that round, which is responsible for parameter distribution and aggregation. Then, some kind of client selection mechanism selects some clients to participate in the training. After the selected server distributes the model parameters to the clients, the clients use local data to perform several rounds of local steps, typically the SGD process. Then the parameter server collects the results returned by the clients, usually the clients that successfully returned within a certain time threshold, and calculates the weighted average of the returned weights as the result of this round. The above steps are repeated until the model meets a certain requirement, such as a fixed number of rounds, or the accuracy reaches a threshold.

Figure 2: The architecture of federated learning with server selection

Due to factors such as location distance and network quality, the bandwidth between clients and servers in different regions is different, the success rate of participating in training is also different, and the distribution of server training success rate among different clients is also different. We can assume that the success rate of clients under the same server is approximately a power-law distribution. Server selection based on optimized latency can improve the wall time of FL training. At the same time, server selection can cooperate with client selection, which not only expands the policy space of client selection but also further improves the effect of client selection with the existing state of the art, thus statistically improving training efficiency.

4  Server Selection Method in Federated Learning

4.1 General Optimization Objectives of FL

In the system design process of federated learning, the first metric to focus on is time-to-accuracy, which has two main influencing factors, (i) System utility factors: the training process includes the actual available performance of both client-side and server-side participants, and the quality of network among them. These physical metrics will affect the actual running time of the system. (ii) Algorithm and data factors: by adjusting the hyper-parameters in the training process, as well as the use of client selection algorithms, as a way to affect the round-to-accuracy performance of the training, to further reduce the training time in the same environment and system setup.

To achieve the above objectives. From a system optimization perspective, the main constraints are the unreliability of computing resources of clients and restricted network resources. Client selection methods are firstly involved to ensure that the training can be carried out continuously, and secondly, to reduce the communication overhead, methods such as local update and communication compression are further used.

From the client’s perspective, the primary constraint is the lack of engagement; due to the uncontrollable synchronization of training time and the passive selection mechanism from the parameter server, the client’s arithmetic availability and training time cannot occur simultaneously, resulting in the client arithmetic that participates in federated learning to be a very small fraction of the total arithmetic. In addition, due to possible single-point-of-failure issues and privacy considerations, the use of distributed algorithms can provide better hence protection. Therefore, clients expect to use asynchronous or decentralized methods to achieve this goal.

4.2 Optimal Server Selection Requirements

All servers that can be created by cloud platforms in different regions are taken as a server set, and the orchestrator selects one server as a parameter server, which is responsible for parameter broadcasting, collecting local update results from different clients, and calculating the final result of this round. To illustrate the importance of server selection, we discuss the requirements for optimal server selection in a state-of-the-art client selection scenario.

Concerning all data samples for training planning, Random Reshuffling of the training data at the beginning of each epoch is a successful technique for optimizing the empirical risk minimization process in standard SGD process analysis. In FL training, the current state-of-the-art approach also introduces the RR process, but the difference is that this process is defined on the client arrangement, as shown in Fig. 3, which requires that in a meta-epoch consisting of multiple rounds of global training, each client is selected at most once, and in the next meta-epoch all clients are randomly reshuffled to enter training.

Figure 3: Random reshuffling of clients in FL training scheduling

To further increase the round-to-accuracy performance, we can utilize the importance sampling method to prioritize high-utility clients [30,41], where the importance of each data point’s contribution to training can be quantified using the L2-norm of the gradient. Assuming that each client x has a training sample set of Bx, the importance of each client can be defined as

Ux≜|Bx|1|Bx|∑k∈Bx‖∇f(k)‖2.(2)

Optimal server selection can be quantified as selecting the most efficient server. After selecting clients by RR and quantifying the utility per client, we can compute the utility of each server. Due to the different geographic distributions of clients and servers, the network states of different client-server combinations are inconsistent. Assuming that the success rate of the training process between different clients and servers is defined as P(x, y), and assuming that the set of clients in each round is Ct, and the selected server corresponding to each round is yr, the final utility of a server and client co-selection in one meta-epoch is defined as the expectation the importance value sum of all client participated in training:

Util≜∑t=1R∑x∈CrP(x,y)Ux,⋃t=1RCt=𝒞 and Ci∩Cj=∅,∀i≠j.(3)

The client sets in each round of one meta-epoch do not intersect, and the union of the client sets Ct in each round covers all clients.

The optimal server selection mechanism should be the one that maximizes the utility in Eq. (3). In addition, the timing of the federated learning training provided by the parameter server from the client’s perspective should be matched as closely as possible with the time available for the client’s arithmetic, thus minimizing the partial participant problem. This requirement is equivalent to maximizing the number of FL client participants, consistent with the optimization goal.

4.3 Trade-Offs and Adaptive Server Selection Method

4.3.1 Adaptive Clients Random Reshuffling

In cross-device FL deployment, client joining and exiting are unpredictable. We cannot obtain the client set in advance, nor can we guarantee that it will remain unchanged during training. As a result, it is not possible to reshuffle all clients beforehand and select the optimal server in advance. There is no strict meta-epoch boundary in this case, so we cannot obtain a meta-epoch client permutation in advance according to the RR defined on the static client set. Therefore, we introduce an adaptive client random reshuffling method in FedAdaSS.

As shown in Fig. 4, before each round of training, FedAdaSS will update the current set of clients, remove the clients selected in previous rounds, and randomly select clients from the remaining set for this round. Server selection will also depend on the results of the current round of client selection. We approximate that choosing the optimal server in each round achieves a global relative superiority. The algorithm implements random reshuffle by dynamically maintaining the remaining unselected clients. trained clients are added to the set Cignored at the end of each round, and K clients are randomly selected from the set Cactive∖Cignored at the beginning of the round. when Cactive∖Cignored is empty, it can be approximated as the end of a global epoch, and reset Cignored to the empty set and continue the above steps.

Figure 4: The main loop and adaptive random reshuffling of clients in FedAdaSS

4.3.2 Server Selection with Utility Estimation

For the utility computation of clients and sever, Util(c) takes the value from the gradient obtained in the current round, and we can not get the utility of each client in advance before choosing the current server and training. However, due to the adaptive reshuffling process, each client only participates in training once per epoch, while the sequential relationship between client utilities, due to the positive correlation between utility and data size, does not change significantly over the multiple training epochs. Thus, our updated client utility for each epoch can be used as an estimate of that client’s utility for the next epoch of server selection.

4.3.3 Division of Roles and Cooperation in the Procedure

After introducing the two main computational processes in the Algorithm 1, we will introduce the interaction process in the FedAdaSS algorithm. As described in Section 3, we split the roles in FedAdaSS into orchestrator, parameter server, and client.

The orchestrator is responsible for maintaining the client collection and the server collection. The server collection is obtained during initialization, and the currently available clients are updated before each round of client selection. The orchestrator arranges each round of FL training in turn. In a given round t, the orchestrator first computes and selects the server st and clients Ct of the current round, and initializes the server st using the result and the parameters of the model of the previous round. Its communication overhead is not large, corresponding to a constant multiple (maybe including the intermediate state of optimization) of the communication between the server and one client. Then, FedAvg is executed between the server and the client, and the orchestrator retrieves the training results for that round from the server.

The server is initialized by the orchestrator through the cloud platform API, and the server obtains the client set of the current round and the current model parameters during initialization. Thereafter, the server process is similar to that in generic FL, where the server broadcasts the current model parameters xt to all clients in Ct. Each client performs multiple local steps, returning resulting model parameters Ctc and client utility Util(c). The server then computes xt+1←xt−ηg/|Ct|⋅∑c∈CtΔtc and returns all results to the orchestrator. The orchestrator then ends the life cycle of the server. The system implementation and training method of the client are consistent with the general federated learning process, and there is no need to provide redundant additional descriptions here.

5  Convergence Analysis

5.1 Preliminaries

The loss function of client c is composed of single losses fcj(x) where j corresponds to j-th data points with the current model parameterized by x. We assume that client c has access to an oracle that, when given input (j, x), returns the gradients ∇fcj(x) as an output. We donate [l]≜{1,2,…,l} for any l∈N. To show the convergence of our methods, we adopt the standard assumptions in convex optimization, which are commonly used in the previous works [42].

Assumption 1. The functions fcj(x) are Lc-smooth for all c∈C,j∈[|Dc|]; i.e., there is an Lc>0 such that for any c, j, x, y

‖∇fcj(x)−fcj(x)‖ ≤Lc‖x−y‖.(4)

Assumption 2. The functions fcj(x) are μc-strongly convex for all c∈C,j∈[|Dc|]; i.e., there is an μc>0 such that for any c, j, x, y

〈∇fcj(x),y−x〉≤−(fcj(x)−fcj(y)+μc2∥x−y∥).(5)

FedAdaSS introduces the RR of clients, and analysis of existing RR shows that it cannot converge to a certain exact value. Through analysis of the shuffling radius upper bound brought by RR, it can be proved that it converges to a certain neighborhood related to σrad2. We use the notions of shuffling variance, introduced by Mishchenko et al. [43] for the analysis, Given a static stepsize η>0 and a permutation π of [n], the intermediate points x∗1,x∗2,…,x∗n is

x∗i≜x∗−η∑j=1i∇fπj(x∗),i=1,…,n.(6)

The shuffling radius σrad2(η) is

σrad2(η)≜maxi∈[n][1η2Eπ[Dfπi(x∗i,x∗)]],(7)

where Df(x,y)=f(x)−f(y)−⟨∇f(y),x−y⟩ is the Bregman divergence associated with f. Due to our use of dynamic client rearrangement, the corresponding shuffling radius is equivalent to the RR process of each data point. With the combination of L-smooth of f and the definition of x∗i, we could get the bound of shuffling radius (for a detailed proof, see Appendix A).

Lemma 1. (Shuffling radius bounds). For all η>0, we get the upper bound of shuffling radius σrad2.

σrad2≤nLmax2(n‖∇f(x*)‖2+12σ*2),(8)

where σ*2 is the gradient variance at the optimum σ*2≜1n∑i∈[n]‖∇fi(x*)−∇f(x*)‖2. Since f is Lmax-smooth and ∇f(x*)=0, we get that

σrad2≤nLmax4σ*2.(9)

5.2 Convergence Guarantees

After defining the variance quantities and assuming that each fcj is μ-strongly convex which is commonly satisfied in machine learning applications as in l2 regularized linear regression and l2 regularized logistic regression, we can get the result that the optimization term decreases linearly. The exponential is the product of the number of data points of each client N, the number of communication rounds in each global epoch R, and the number of global epochs T. Since the cohort and data points on each client are sampled without replacement for each round, the statistical term scales proportionally to the squared step size η2. The formal statement of the theorem follows.

Theorem 1. Assume that functions fcj are Lc-smooth and μc-strongly convex for each c and j. If η≤1Lmax, then the iterates generated by the Algorithm 1 satisfy

E[ ‖xT−x*‖2 ]≤(1−ημ)NRT‖x0−x*‖2+2η2μσrad2.(10)

The results show the exponential rate of convergence to a neighborhood of size 2η2μσrad2 and can be adjusted to accommodate dynamic client shuffling, with the only requisite modification being the alteration of the rates and convergence analysis. Detailed proof can be found in the Appendix B.

6  Evaluation

6.1 Experimental Methodology

To demonstrate that FedAdaSS can effectively provide both random reshuffling and partial participant mitigation in large-scale client scenarios, we perform experimental verification in addition to theoretical analysis. Due to the lack of large-scale client validation conditions, we use simulation experiments for validation and expand FLSim [44] to provide a server selection mechanism as the experimental framework, simulating 10 candidate servers in the experiment. We used the CIFAR10 dataset to simulate 100 clients and split the data into IID and non-IID methods for experiments. The non-IID group splits the sample size according to a power law distribution. To account for the heterogeneity of clients, as shown in Fig. 5, we generate the training success probability of each client to one server according to the power law distribution. In the comparative experiment, to demonstrate the performance of server selection under different network conditions, we set the average success rate of client generation to p = 75%–95%.

Figure 5: Distribution of probability of successful communication

6.2 Comparisons Results

To demonstrate the improvement of statistical utility in FL process by server selection and to enhance existing client selection methods, we choose the state-of-the-art method, i.e., client RR (FedAvg+RR), as a comparison. The overall results show that FedAdaSS can reduce the number of rounds to reach the same accuracy value (#round-to-accuracy) by approximately 12% to 20% under the same environmental parameters,

Next, we will compare different environmental parameters (IID/non-IID, average success rate p, number of clients per round k, local steps N) to study the characteristics and causes of server selection performance improvement.

6.2.1 Increasing Training Speed

Fig. 6 compares the decline curves of the loss function for different numbers of participants in each training round. It can be seen that as the number of participants increases, the loss function decreases faster. This indicates that increasing the number of participants can reduce the #round-to-accuracy. Under the same k setting, it can be seen that FedAdaSS accelerates training speed by 5%–10%, which is more significant at low engagement levels.

Figure 6: Training loss of FedAdaSS and FedAvg+RR

In addition, as shown in Fig. 7, under the setting of non-IID, a lower number of training clients has a greater impact on convergence. At this time, adding server selection can also accelerate convergence speed by 10%–20%. This improvement is more significant with the fewer number of clients and less engagement.

Figure 7: Accuracy of aggregation of each training round on non-IID data and with p = 75% and p = 90%

6.2.2 Mitigating Low Engagement of Clients

Fig. 8 compares the accuracy training curves under the same machine learning parameter configuration but different communication success probability settings. It can be seen that compared to the FedAvg+RR method, the FedAdaSS method has a smaller negative impact on the decrease in engagement. Due to the dropout strategy, the actual number of client participants is the same under different methods. However, under the same method, the impact of low engagement may not have been added to the training, resulting in a reduction in effective training data. It can be seen that after joining the server selection, the decrease in accuracy under the same setting was alleviated by increasing the participation opportunities of these low-probability clients, resulting in a 3% increase in tie values. In addition, under the high local steps setting set to reduce communication overhead, the impact of low engagement on #round-to-accuracy is more pronounced, resulting in an increase of about 50% in #round-to-accuracy. At this point, using FedAdaSS can reduce this loss to about 20%.

Figure 8: Final average accuracy of the training and round-to-accuracy with different settings of the probability of successful communication (p = 75%–95%)

In summary, FedAdaSS can firstly improve client engagement compared to the singular server method, thus increasing the number of clients involved in training per round, thus reducing rounds to accuracy. Second, FedAdaSS improves the fairness of each client’s participation, allowing the random reshuffling process to cover a larger number of clients, making it possible to achieve a better gradient representation in a global epoch, and thus reducing round-to-accuracy. And since the number of local steps in FL is relatively large, adding RR can effectively improve the training performance. Therefore, it is demonstrated that FedAdaSS can be effectively combined with existing methods to accelerate the training process of federated learning.

7  Conclusions

Federated learning training involves a large number of geographically distributed devices, and the heterogeneity of system performance leads to significant differences in clients’ engagement levels. In addition, the client’s data have different scales and distributions, which are not independent and identically distributed, resulting in significant performance loss in federated learning, affecting the round-to-accuracy performance, and there is an optimization target bias problem. We propose a basic framework for optimizing using optional computing power servers in federated learning and analyze the optimization objectives and trade-offs for server selection. A self-adaptive server selection algorithm FedAdaSS with random shuffling is proposed to overcome the dynamic joining and low engagement issues of clients, and its effectiveness is theoretically analyzed. Through comparative experiments, we demonstrate that FedAdaSS can reduce round to accuracy and alleviate performance losses caused by low engagement.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant U22B2005, Grant 62372462.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Yuwei Xu, Baokang Zhao; data collection: Huan Zhou, Baokang Zhao; analysis and interpretation of results: Yuwei Xu, Huan Zhou; draft manuscript preparation: Yuwei Xu, Baokang Zhao, Jinshu Su. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data used in the experimental process was generated using the FLSim simulator, which is perfectly reproducible following the instructions of Section 6.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Bao G, Guo P. Federated learning in cloud-edge collaborative architecture: key technologies, applications and challenges. J Cloud Comput. 2022;11:4. [Google Scholar]

2. Kotsehub N, Baughman M, Chard R, Hudson N, Patros P, Rana O, et al. FLoX: federated learning with FaaS at the edge. In: 2022 IEEE 18th International Conference on e-Science (e-Science); 2022; Salt Lake City, UT, USA: IEEE. p. 11–20. [Google Scholar]

3. Wang X, Garg S, Lin H, Hu J, Kaddoum G, Piran MJ, et al. Toward accurate anomaly detection in industrial internet of things using hierarchical federated learning. IEEE Internet Things J. 2022 May;9:7110–9. doi: 10.1109/JIOT.2021.3074382. [Google Scholar] [CrossRef]

4. Wang X, Hu J, Lin H, Garg S, Kaddoum G, Piran MJ, et al. QoS and privacy-aware routing for 5G-enabled industrial internet of things: a federated reinforcement learning approach. IEEE Trans Ind Inform. 2022 Jun;18:4189–97. doi: 10.1109/TII.2021.3124848. [Google Scholar] [CrossRef]

5. Bonawitz K, Eichner H, Grieskamp W, Huba D, Ingerman A, Ivanov V, et al. Towards federated learning at scale: system design. Proc Mach Learni Syst. 2019;1:374–88. [Google Scholar]

6. Banabilah S, Aloqaily M, Alsayed E, Malik N, Jararweh Y. Federated learning review: fundamentals, enabling technologies, and future applications. Inform Process Manag. 2022 Nov;59:103061. doi: 10.1016/j.ipm.2022.103061. [Google Scholar] [CrossRef]

7. Sattler F, Wiedemann S, Muller KR, Samek W. Robust and communication-efficient federated learning from non-i.i.d. data. IEEE Trans Neural Netw Learn Syst. 2020 Sep;31:3400–13. doi: 10.1109/TNNLS.5962385. [Google Scholar] [CrossRef]

8. Luo K, Li X, Lan Y, Gao M. GradMA: a gradient-memory-based accelerated federated learning with alleviated catastrophic forgetting. In: 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023; Vancouver, BC, Canada: IEEE. p. 3708–17. [Google Scholar]

9. Fu L, Zhang H, Gao G, Zhang M, Liu X. Client selection in federated learning: principles, challenges, and opportunities. IEEE Internet Things J. 2023;10:1 [Google Scholar]

10. Gholami P, Seferoglu H. DIGEST: fast and communication efficient decentralized learning with local updates. IEEE Trans Mach Learn Commun Netw. 2024;1. [Google Scholar]

11. Glasgow M, Yuan H, Ma T. Sharp bounds for federated averaging (Local SGD) and continuous perspective. In: International Conference on Artificial Intelligence and Statistics; 2022; PMLR. p. 9050–90. [Google Scholar]

12. Yang HH, Liu Z, Quek TQS, Poor HV. Scheduling policies for federated learning in wireless networks. IEEE Trans Commun. 2020 Jan;68:317–33. doi: 10.1109/TCOMM.26. [Google Scholar] [CrossRef]

13. Foley P, Sheller MJ, Edwards B, Pati S, Riviera W, Sharma M, et al. OpenFL: the open federated learning library. Phys Med Biol. 2022 Nov;67:214001. doi: 10.1088/1361-6560/ac97d9. [Google Scholar] [PubMed] [CrossRef]

14. Oh K, Zhang M, Chandra A, Weissman J. Network cost-aware geo-distributed data analytics system. IEEE Trans Parallel Distrib Syst. 2022 Jun;33:1407–20. doi: 10.1109/TPDS.2021.3108893. [Google Scholar] [CrossRef]

15. Chahoud M, Otoum S, Mourad A. On the feasibility of federated learning towards on-demand client deployment at the edge. Inf Process Manag. 2023 Jan;60:103150. doi: 10.1016/j.ipm.2022.103150. [Google Scholar] [CrossRef]

16. Grudzień M, Malinovsky G, Richtárik P. Improving accelerated federated learning with compression and importance sampling. arXiv preprint arXiv:2306.03240, 2023. doi:10.48550/ARXIV.2306.03240. [Google Scholar] [CrossRef]

17. Li Z, Lu J, Luo S, Zhu D, Shao Y, Li Y, et al. Towards effective clustered federated learning: a peer-to-peer framework with adaptive neighbor matching. IEEE Trans Big Data. 2022:1–16. [Google Scholar]

18. Guan Y, Liu X, Ren T, Niu J. Enabling communication-efficient federated learning via distributed compressed sensing. In: IEEE INFOCOM 2023-IEEE Conference on Computer Communications; 2023; New York City, NY, USA: IEEE. p. 1–10. [Google Scholar]

19. Zhang F, Liu X, Lin S, Wu G, Zhou X, Jiang J, et al. No one idles: Efficient heterogeneous federated learning with parallel edge and server computation. In: International Conference on Machine Learning; 2023; Honolulu, Hawaii, USA: PMLR. p. 41399–413. [Google Scholar]

20. McMahan B, Moore E, Ramage D, Hampson S, Arcas BA. Communication-efficient learning of deep networks from decentralized data. In: Artificial intelligence and statistics; 2017; PMLR. p. 1273–82. [Google Scholar]

21. Beltrán ETM, Pérez MQ, Sánchez PMS, Bernal SL, Bovet G, Pérez MG, et al. Decentralized federated learning: fundamentals, state of the art, frameworks, trends, and challenges. IEEE Commun Surv Tutorials. 2023;25:2983–3013. doi: 10.1109/COMST.2023.3315746. [Google Scholar] [CrossRef]

22. Barbarossa S, Sardellitti S, Lorenzo PD. Communicating while computing: distributed mobile cloud computing over 5G heterogeneous networks. IEEE Signal Process Mag. 2014 Nov;31:45–55. doi: 10.1109/MSP.2014.2334709. [Google Scholar] [CrossRef]

23. Messaoud S, Bradai A, Ahmed OB, Quang PTA, Atri M, Hossain MS. Deep federated Q-learning-based network slicing for industrial IoT. IEEE Trans Ind Inform. 2021 Aug;17:5572–82. doi: 10.1109/TII.2020.3032165. [Google Scholar] [CrossRef]

24. Hard A, Rao K, Mathews R, Ramaswamy S, Beaufays F, Augenstein S, et al. Federated learning for mobile keyboard prediction. arXiv preprint arXiv: 81103604. 2018 Nov. [Google Scholar]

25. Zhang T, Gao L, He C, Zhang M, Krishnamachari B, Avestimehr AS. Federated learning for the internet of things: applications, challenges, and opportunities. IEEE Internet of Things Magazine. 2022 Mar;5:24–9. doi: 10.1109/IOTM.004.2100182. [Google Scholar] [CrossRef]

26. Li X, Huang K, Yang W, Wang S, Zhang Z. On the convergence of fedavg on non-iid data. arXiv preprint arXiv:190702189. 2019. [Google Scholar]

27. Lim WYB, Luong NC, Hoang DT, Jiao Y, Liang YC, Yang Q, et al. Federated learning in mobile edge networks: a comprehensive survey. IEEE Commun Surv Tutorials. 2020 Feb;22:2031–63. doi: 10.1109/COMST.9739. [Google Scholar] [CrossRef]

28. Roy S, Chergui H, Sanabria-Russo L, Verikoukis C. A cloud native SLA-driven stochastic federated learning policy for 6G zero-touch network slicing. In: ICC 2022—IEEE International Conference on Communications; 2022; Seoul, Republic of Korea: IEEE. p. 4269–74. [Google Scholar]

29. Shi W, Zhou S, Niu Z, Jiang M, Geng L. Joint device scheduling and resource allocation for latency constrained wireless federated learning. IEEE Trans Wirel Commun. 2021 Jan;20:453–67. doi: 10.1109/TWC.7693. [Google Scholar] [CrossRef]

30. Lai F, Zhu X, Madhyastha HV, Chowdhury M. Oort: efficient federated learning via guided participant selection. In: 15th USENIX Symposium on Operating Systems Design and Implementation (OSDI 21); 2021; p. 19–35. [Google Scholar]

31. Reisizadeh A, Mokhtari A, Hassani H, Jadbabaie A, Pedarsani R. FedPAQ: a communication-efficient federated learning method with periodic averaging and quantization. In: International Conference on Artificial Intelligence and Statistics; 2020; PMLR. p. 2021–31. [Google Scholar]

32. Shlezinger N, Chen M, Eldar YC, Poor HV, Cui S. UVeQFed: universal vector quantization for federated learning. IEEE Trans Signal Process. 2021;69:500–14. doi: 10.1109/TSP.78. [Google Scholar] [CrossRef]

33. Rothchild D, Panda A, Ullah E, Ivkin N, Stoica I, Braverman V, et al. FetchSGD: communication-efficient federated learning with sketching. In: International Conference on Machine Learning; 2020; PMLR. p. 8253–65. [Google Scholar]

34. Lian X, Zhang W, Zhang C, Liu J. Asynchronous decentralized parallel stochastic gradient descent. In: International Conference on Machine Learning; 2018; Stockholm, Sweden: PMLR. p 3043–52. [Google Scholar]

35. Sprague MR, Jalalirad A, Scavuzzo M, Capota C, Neun M, Do L, et al. Asynchronous federated learning for geospatial applications. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases; 2018; Dublin, Ireland: Springer. p. 21–8. [Google Scholar]

36. Xie C, Koyejo S, Gupta I. Asynchronous federated optimization. arXiv preprint arXiv:190 303934. 2013 Mar. [Google Scholar]

37. Kairouz P, McMahan HB, Avent B, Bellet A, Bennis M, Bhagoji AN, et al. Advances and open problems in federated learning. Found Trends Mach Learn. 2021;14:1–210. doi: 10.1561/2200000083. [Google Scholar] [CrossRef]

38. Lalitha A, Kilinc OC, Javidi T, Koushanfar F. Peer-to-peer federated learning on graphs. arXiv preprint arXiv:190111173. 2019 Jan. [Google Scholar]

39. Warnat-Herresthal S, Schultze H, Shastry KL, Manamohan S, Mukherjee S, Garg V, et al. Swarm learning for decentralized and confidential clinical machine learning. Nature. 2021 Jun;594:265–70. doi: 10.1038/s41586-021-03583-3. [Google Scholar] [PubMed] [CrossRef]

40. Li C, Li G, Varshney PK. Decentralized federated learning via mutual knowledge transfer. IEEE Internet Things J. 2022 Jan;9:1136–47. doi: 10.1109/JIOT.2021.3078543. [Google Scholar] [CrossRef]

41. Wang S, Yang S, Li H, Zhang X, Zhou C, Xu C, et al. PyramidFL: a fine-grained client selection framework for effiicient federated learning. In: 28th ACM Annual International Conference on Mobile Computing and Networking, MobiCom 2022; 2022; Sydney, NSW, Australia: Association for Computing Machinery. p. 542–55. [Google Scholar]

42. Horváth S, Sanjabi M, Xiao L, Richtárik P, Rabbat M. Fedshuffle: recipes for better use of local work in federated learning. arXiv preprint arXiv: 220413169. 2022. [Google Scholar]

43. Mishchenko K, Khaled A, Richtárik P. Random reshuffling: simple analysis with vast improvements. Adv Neural Inf Process Syst. 2020;33:17309–20. [Google Scholar]

44. Meta. Federated Learning Simulator (FLSim). Meta Res. 2022 Jun. Available from: https://github.com/facebookresearch/FLSim. [Accessed 2022]. [Google Scholar]

45. Mishchenko K, Khaled A, Richtárik P. Proximal and federated random reshuffling. In: International Conference on Machine Learning; 2022; Baltimore, MD, USA: PMLR. p. 15718–49. [Google Scholar]

Appendix A. Proof of Lemma Shuffling Radius Bounds

Proof 1. First, we have to introduce the lemma appears in [43,45], which describes the variance of sampling multiple vectors from a finite set of vectors without replacement. Supposed that there are vectors X1,…,Xn∈Rd. We define the average as X¯ and the population variance as σ2. Xπ1,…,Xπk are sampled uniformly from {X1,…,Xn} without replacement, and X¯π is their average. The average and variance of sampling is

E[X¯π]=X¯,

E[‖X¯π−X¯‖2]=n−kk(n−1)σ2.(11)

Since fc is Lc-smooth and the definition of x∗i, we can get the bound from Bregman divergence in Eq. (7).

E[Dfπi(x∗i,x∗)]≤E[Lπi2‖x∗i−x∗‖2]≤Lmax2E[‖x∗i−x∗‖2]=η2Lmax2E[‖∑j∈[i]∇fπj(x∗)‖2]=η2Lmaxi22E[‖1i∑j∈[i]∇fπj(x∗)‖2].(12)

Let Xc≜∇fc(x∗), then we have X¯π=1j∑j∈[i]Xπj and X¯=∇f(x∗), with Eq. (11) we get

E[Dfπi(x∗i,x∗)]≤η2Lmaxi22E[‖X¯π‖2]=η2Lmaxi22(‖∇f(x∗)‖2+n−ii(n−i)σ∗2).(13)

With definition of shuffling radius and i ≤ n, we get

σrad2≤nLmax2(n‖∇f(x∗)‖2+12σ∗2).(14)

■

Appendix B. Proof of Theorem 5.1

Proof 2. Using μ-convexity and L-smoothness of f, we have:

μ2‖xm,∗k−xm,tk‖2≤Dfm(xm,∗k,xm,tk)

E[‖∇fm(xm,tk)−∇fm(x∗)‖]≤2LDfm(xm,tk,x∗).

With the inequality, we have:

E[‖xm,tk,j+1−xm,∗k,j+1‖2]≤(1−ημ)E[‖xm,tk,j−xm,∗k,j‖2]+2ηE[Dfm(xm,tk,j,x∗)]−2η(1−ηL)E[Dfm(xm,tk,j,x∗)].(15)

Using the definition of σrad2 and η≤1L, we get following bound:

E[‖xm,tk,j+1−xm,∗k,j+1‖2]≤(1−ημ)E[‖xm,tk,j−xm,∗k,j‖2]+2η3σrad2.(16)

Unrolling the recursion, we have:

E[‖xm,tk,n−xm,∗k,n‖2]≤(1−ημ)NE[‖xtk−x∗k‖]+2η3σrad2∑j=0N−1(1−ημ)j.(17)

With the K recursion of epochs and clients selection involved:

E[‖xtk+1−x∗k+1‖2]=E[‖1C∑m∈Ctxm,tk−1C∑m∈Ctxm,∗k‖2]≤1C∑m∈CtE[‖xm,tk−xm,∗k‖2]≤1C∑m∈Ct((1−ημ)NE[‖xtk−x∗k‖2]+2μ3σrad2∑j=0N−1(1−ημ)j)=(1−ημ)NE[‖xtk−x∗k‖2]+2μ3σrad2∑j=0N−1(1−ημ)j.(18)

Since xt+1=xtK and x∗=x∗K, the recursion index r can be unrolled:

E[‖xt+1−x∗‖2]=E[‖xtK−x∗K‖2]≤(1−ημ)NKE[‖xt−x∗‖2]+2μ3σrad2∑j=0N−1(1−ημ)j∑k=0K−1(1−ημ)kN.(19)

Unroll the recursion for index t and apply the property described before:

E[‖xT−x∗‖2]≤(1−ημ)NKT‖x0−x∗‖2+2μ3σrad2∑j=0N−1(1−ημ)j∑k=0K−1(1−ημ)kN∑t=0T−1(1−ημ)tKN≤(1−ημ)NKT‖x0−x∗‖2+2μ3σrad2∑j=0NKT−1(1−ημ)j≤(1−ημ)NKT‖x0−x∗‖2+2η2μσrad2.(20)

■