DPAL-BERT: A Faster and Lighter Question Answering Model

Highlight

1. A novel Distillation model on PAL-BERT (DPAL-BERT) is proposed for the question-answering task.

2. BiLSTM is adopted as the student model to shorten inference time.

3. The PAL-BERT model is used as the teacher model to achieve high accuracy.

4. DPAL-BERT achieves competitive performance and significantly reduces the inference time.

1  Introduction

In natural language processing (NLP) tasks, deep learning (DL) has gathered considerable attention and is currently widely used. The advent of pre-trained language models in recent years has significantly enhanced the technology of question-answering systems. After pre-training the question-answering system, its transfer learning ability will be stronger, and its application range will be wider. In the training process of the Question Answering Model, complex models and many computing resources are needed to extract information from large and highly redundant datasets. In the experiment, the best models are often large-scale, such as Chat Generative Pre-trained Transformer (ChatGPT) [1], BERT [2], or even integrated by multiple models [3].

Deploying large models in service environments faces several common challenges, which can significantly impede their practicality and efficiency [4–6]. These challenges include: 1. Slower inference speed, leading to delays in obtaining results and reduced system responsiveness. 2. High demands on deployment resources, such as memory, make the process resource-intensive. 3. Stringent constraints are required during deployment to achieve low latency and efficient use of computing resources, necessitating careful optimization and planning. Due to the rapid development of portable equipment, some special application situations, such as devices with little memory and low computing capacity, do not support the online calculation of large models. Hence, it becomes imperative to downscale the model to ensure performance [7,8].

Currently, the prevalent techniques for compressing models can be broadly categorized into four groups: (1) parameter pruning and quantization [9], which mainly deletes redundant parameters in the model; (2) low-rank factorization [10], which uses tensor factorization to estimate the parameters of neural networks; (3) transferred/compact convolutional filters [11], designed a particular structure of convolutional filters, which can reduce parameter space and save memory; (4) knowledge distillation.

General experience holds that similar scale models must be maintained to retain similar knowledge [12]. This indicates that the parameters of a model determine the amount of knowledge contained in the data captured by the model. This understanding is correct, but the relationship between the parameter quantity contained in a model and the knowledge quantity that can be captured from the original data is not a stable linear relationship but a curve form in which, as the parameter quantity increases, the marginal return gradually decreases. In contrast, even when two models possess identical structures and equivalent parameters, they can assimilate different types of knowledge when trained on the same dataset. One of the critical factors is the selection of training methods. An appropriate training method can help the model capture as much knowledge as possible with a few parameters. This is the primary idea used in knowledge distillation [6,13,14].

Knowledge distillation fundamentally represents a technique for compressing models [14]. The fundamental concept of knowledge distillation is to direct the training of a lightweight model using the trained complex model as a guide and then get a lightweight model with the effect as close as possible to the complex model while simultaneously reducing the computational burden, decreasing the model scale and training time. The complex structure of the teacher network can train a suitable probability distribution, and the small model is the student network. The output probability distribution is employed to fit the distribution of the teacher network to realize knowledge transfer and performance improvement. In general, no distinction will be made between the models used in training and deployment, but there are some inconsistencies between training and deployment.

Hinton et al. [13] put forward the approach of relevant knowledge distillation as early as 2014. He proposed that using a “soft label” to perform model distillation can improve the effect of the “student” model. He reported that the classification prediction probability obtained by the complex model after training, although cross-entropy is chosen as a loss function, its score in the correct category considered by the model will be particularly large, while the score in other categories will be particularly low. However, this value with a particularly low score still has a relative role; that is, it can represent the correlation between classes, which cannot be reflected in the original annotation data. For example, in the MNIST handwritten data recognition dataset, the handwritten font “2” is often very similar to the handwritten font “3”, but people will only tell it that it corresponds to the label “2”. Such a hard label results in the model not considering the correlation between handwritten font “2” and “3” in the input data. Hence, this study designs the concept of “t” (temperature) in the loss function to make a corresponding scaling for the probability value predicted by the model to enlarge the score results of other categories in the model and then let the student model learn this corresponding feature in the distillation stage, to increase the loss of accuracy.

Growing model parameters and slower training speed of pre-training language models make more scholars begin to study the related work of lightweight pre-training language models. The researcher of the hugging face proposed the distill BERT model and performed the corresponding knowledge distillation strategy based on BERT [15]. Finally, under the condition of reducing the parameters of BERT by 40%, it can still maintain the original accuracy of BERT by 97% and improve the prediction speed by 60%. The study proposes that in the knowledge distillation stage, in addition to continuing to follow the “soft label” strategy proposed by Hinton, adding the hidden layer vector between “teacher BERT” and “student BERT” can also improve the effect of “student BERT”. Huawei Noah Ark laboratory has proposed the “TinyBERT” [16] model, which has made corresponding innovations in the relevant characteristics involved in the knowledge distillation strategy. When calculating the loss function, TinyBERT not only considers the “soft label”, which believes that the parameters of BERT in the output layer, the hidden layer vector in the transformer structure, and the attention vector positively affect knowledge distillation. Scholars of Huawei Noah’s Ark believe that BERT’s original “pre-training fine-tuning” model will cause some difficulty in knowledge distillation, and its semantic difference between the pre-training stage and fine-tuning [17] stage will result in a “teacher model” that single-stage knowledge distillation cannot learn well. Therefore, TinyBERT proposed a two-sided knowledge distillation strategy. Finally, the model parameters of TinyBERT are 7.5 times lower than the original BERT, and the prediction speed is 9.4 times faster. On average, TinyBERT is only 3% lower than the original BERT in nine downstream natural language processing tasks.

This study combines the advantages of the high accuracy of the PAL-BERT model [18] with the short inference time of a small-scale model as BiLSTM [19]. The internal knowledge information of a large model PAL-BERT is transferred to a small model using the method of knowledge distillation to shorten the inference time without compromising model performance.

2  Dataset

The Standard Question Answering Dataset (SQuAD) [20] is widely acknowledged as a benchmark in machine reading comprehension. The dataset comprises a diverse array of elements, including articles, the corresponding fragments within those articles, and questions paired with answers that are directly related to these fragments. Therefore, SQuAD 1.1 and SQuAD 2.0 are used as English datasets. Compared to version 1.1, SQuAD 2.0 expands some simple manually written negative samples other than automatically generated ones. In addition, machine reading comprehension models must account for the presence of unanswerable questions. These models should be capable of determining if a question can be answered based on the provided context. If the context does not support the question, the model should refrain from providing an answer, enhancing the model’s practical application value. The so-called “sample” is a problem corresponding to a fragment in an article. In version 2.0, the proportion of samples of the SQuAD dataset in the training dataset is about 2:1, and the proportion of articles that do not contain negative samples and articles that contain negative samples is also 2:1. However, the development set and test set remove those articles that do not contain negative samples in version 1.1, making the proportion about 1:1. The number and distribution of samples of SQuAD are shown in Table 1.

The new dataset version includes manually labeled “unanswerable” questions, serving as diverse negative samples. Even if these negative samples have no correct answers, the model can still pay attention to some relevant texts and give predicted fragments, which seem correct but often wrong, thus increasing the difficulty of the whole task.

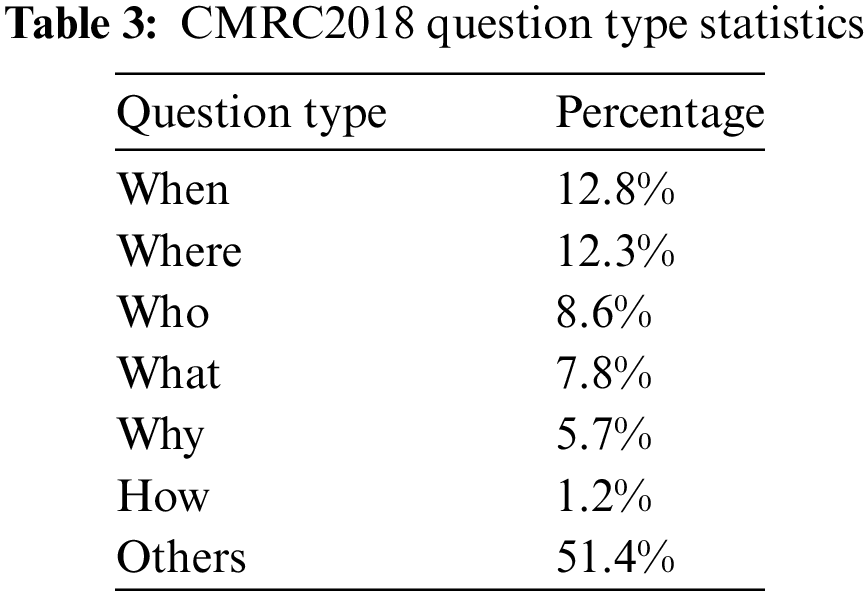
In addition, the Chinese machine reading comprehension dataset CMRC 2018 [21] is also used in this research. The dataset content is sourced from Chinese Wikipedia, with manually crafted questions. The training set comprises about 10,000 pieces of data. The preprocessed data portion is listed in Table 2. Given the gaps between Chinese and English, it is also a supplement for non-English cases. Every article provides multiple relevant questions, each accompanied by several manually annotated reference answers. The six problem types are displayed in Table 3.

3  Method

3.1 Knowledge Distillation

3.1.1 Soft Label-Based Knowledge Distillation

In the process of knowledge distillation, this study calls the original large model teacher model, the new small model student model, the label in the training set hard label, the probability output predicted by the teacher model soft label, and temperature (T) is employed to adjust the hyperparameters of the soft label, as depicted in Fig. 1.

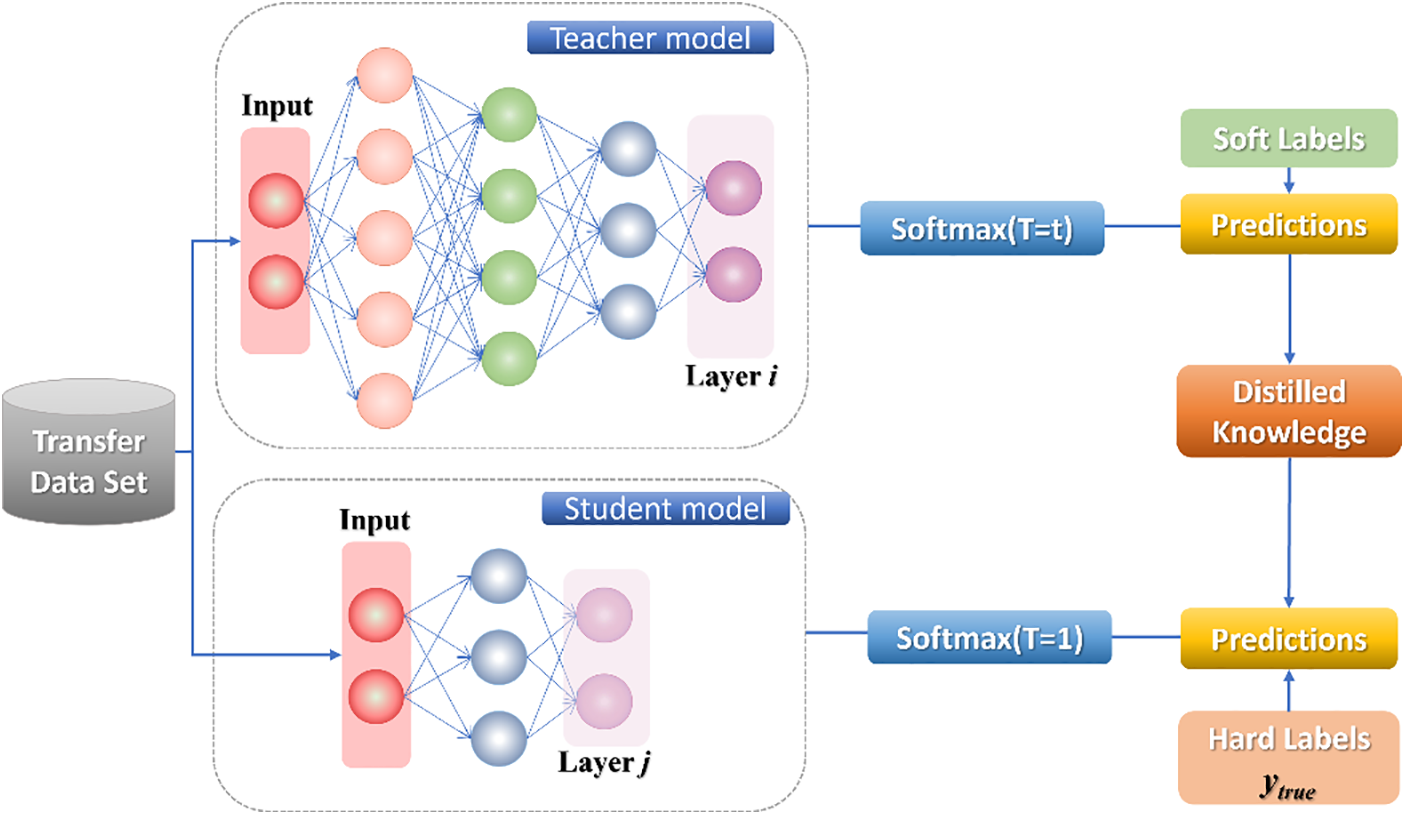
Figure 1: Soft label-based knowledge distillation

When training the student model, the KL divergence within the probability distribution of the output category is added to the loss function for classification tasks. The teacher model output T can be expressed as PT=softmax(aT), where aT is the previous layer output of SoftMax, and student model output S can be described as PS=softmax(aS), where aS is the previous layer output. Knowledge distillation makes the output of the student model PS close to that of the teacher model PT through loss function. Due to the operation of softmax(aT), the model’s output for a specific class can exhibit a high probability value nearing 1, while simultaneously displaying low probabilities nearing 0 for other classes, so that the output is close to single heat coding. Therefore, a temperature parameter τ≥1 is usually added to the operation to make the output distribution more average. At the same time, smoothing the output of the teacher and student model can obtain as follows:

PτT=softmax(aTτ)(1)

PτS=softmax(aSτ)(2)

The loss function of knowledge distillation can be expressed as follows:

Lkd(WS)=(1−α)∗H(Ytrue,PS)+α∗KL(PτT∥PτS)=(1−α)∗H(Ytrue,PS)+α∗(H(PτT,PτS)−H(PτT))(3)

where WS is the parameter of the student model; Ytrue is the distribution of real labels; KL,H are divergence and cross-entropy; α,α∈[0,1] is a hyperparameter, controlling the ratio of the cross entropy between the model output distribution and the actual label and the diversity within the student model output and the teacher model output.

3.1.2 Representation-Based Knowledge Distillation

The schematic diagram depicting knowledge distillation based on representation is given in Fig. 2. This approach compares the output representations of the teacher model’s second layer and the student model’s second layer. The dimensions of these representations can differ, and the corresponding relationships between the dimensions can also vary. In order to address this, a linear regression can be performed to align the output representation of the student model with that of the teacher model. The loss function for knowledge distillation, as depicted in Eq. (4), captures this alignment process.

Lrepj(WT,WS)=UTi(x;WT)UTi(x;WT)2−USj(x;Ws)∗WrUSj(x;Ws)∗Wr22(4)

where WT,Ws are parameters of the teacher model and student model, respectively; UTi,USj are the calculation functions of the teacher model and student model for input x to Transformer output of layer i and layer j; Wr is regression parameter matrix.

Figure 2: Representation-based knowledge distillation

3.1.3 Attention-Based Knowledge Distillation

The second norm of the feature vector at different positions of the picture output in the convolution layer can represent the attention distribution of the model to the picture [22]. The self-attention layer in the transformer structure contains the attention distribution of each input word to all other words in the text. In a self-attention layer, the attention distribution matrix for all input words is A∈Rl×l, where l is the input text length.

The loss of knowledge distillation between the attention matrix of the output of layer i of the teacher model and the attention matrix of the output of layer j of the student model is as shown in Eq. (5).

Lattnj(WT,Ws)=‖AttnTi(x;WT)−AttnSj(x;WS)‖2(5)

where AttnTi,AttnSj are the calculation functions of the teacher model and student model for self-attention input to layer and layer, respectively.

The schematic diagram of attention-based knowledge distillation is shown in Fig. 3.

Figure 3: Schematic diagram of attention-based knowledge distillation

Combined with these three knowledge distillation methods, this study simultaneously adds the losses of the above three knowledge distillations to the training objectives so the student model can learn the teacher model from multiple angles. The loss of mixed knowledge distillation is given in Eq. (6).

L(WT,Ws)=Lkd(Ws)+β∑jηjLrepj(WT,Ws)+γ∑jηjLattnj(WT,Ws)(6)

where β,γ are hyperparameters controlling the proportion of the loss of middle layer representation and attention in the final loss function, respectively; ηj,ηj∈[0,1] is the weight of knowledge distillation loss in different layers.

3.2 Design of Knowledge Distillation Model Based on PAL-BERT

3.2.1 Distillation Scheme

Although ALBERT (A Lite BERT)-based models have considerably fewer parameters than the original BERT model, they are still too large for practical online applications. In addition, although ALBERT’s model compression is evident during training, it does not reduce inference time during the inference stage. For offline data processing scenarios, where time requirements are generally less demanding, the ALBERT [23] model can be effectively employed due to its significant performance gains. However, further compression of the model is crucial to reduce inference time for online tasks. This study optimizes the PAL-BERT model using the method of knowledge distillation, reducing inference time while preserving accuracy as much as possible. PAL-BERT is a first-order pruning model proposed based on the ALBERT model, demonstrating outstanding performance in question-answering tasks. PAL-BERT can provide good efficiency while maintaining high performance, which is ideal for teacher models as it requires processing a large amount of input data and generating high-quality outputs for student model learning.

At present, most knowledge distillation based on a pre-training language model often needs to be carried out in the pre-training stage or fine-tuning stage. For example, the knowledge distillation strategy adopted in distilling BERT is to distill knowledge while pre-training, and the obtained student model is directly used for fine-tuning each downstream task. In TinyBERT [16], it proposes a two-stage distillation strategy. In the pre-training task stage, knowledge distillation is performed through large-scale unsupervised corpus to obtain the student model in the general field. Then, during fine-tuning, the general student model obtained in the previous step is employed for knowledge distillation to obtain the student model finally used for specific downstream tasks.

This study refers to the knowledge distillation strategy of the above literature [24–26], and combined with the current QA scene, it is considered that the distillation strategy can be conducted in the fine-tuning stage. The specific process uses the original pre-training model to get the teacher model in the downstream task fine-tuning and then keeps all the trainable parameters unchanged. Then, the trained teacher model is employed to facilitate the training of the student model, enabling the latter to acquire the pre-existing knowledge possessed by the former. Unlike previous methods that perform knowledge distillation during pre-training, this paper introduces a strategy that applies distillation during the fine-tuning stage for QA. This approach is more efficient because the already pre-trained model requires less time to adapt to the task. The fine-tuning process allows the model to concentrate on QA-specific patterns, enhancing the distillation’s relevance and effectiveness. Additionally, distillation in pre-training aims to maintain model portability, which is unnecessary for our focused QA scenario. By distilling knowledge directly related to QA during fine-tuning, this study ensures that only the essential knowledge is transferred, optimizing the training process.

In this process, the teacher model is the source of knowledge and success for the student model, which acts as the recipient. The specific structure is depicted in Fig. 4. Distillation loss refers to loss calculated with both the student and teacher models, which are the representation loss and attention loss, while student loss refers to loss only correlated with the student model, which is Lkd.

Figure 4: Knowledge distillation structure

The knowledge distillation process typically comprises two stages: the original model training stage and the small model training stage. During the former, the focus is on training the teacher model, characterized by its complexity and ability to effectively capture information from the original data. It can even consist of multiple separately trained models. In the latter stage, the objective is to train the student models, which are typically smaller with fewer parameters and a simpler model structure.

The teacher model used in this study is PAL-BERT, and the student models include BiLSTM and TextCNN [27]. The distillation model based on PAL-BERT is named DPAL-BERT.

3.2.2 Data Augmentation

In the task of knowledge distillation, a small dataset cannot effectively let the teacher network express all its information. Therefore, many unlabeled data with the prediction results of the teacher network are needed to expand the dataset so that effective knowledge can be fully displayed.

Data augmentation in NLP is much more difficult than in image processing. Image data can generate near-natural images by rotating, adding noise, or other deformations. However, if a sentence in natural language processing is manually operated, the fluency of the sentence becomes lower, and this approach does not play a prominent role in NLP.

In order to expand the amount of data, the method of modifying sentences is employed in a manner similar to the occlusion language model in BERT. It referred to the data augmentation method in [28] and made some modifications. There are three data augmentation methods:

1. Masking. For each word in the text, a symbol <mask> would replace it with a certain probability pmask. It helps to understand the contribution of different words in the text to the label.

2. Replacing. For a word in the text, it is replaced with another randomly sampled synonym with a certain probability psyn.

3. N-gram sampling. For text data, an n-gram is randomly sampled with a certain probability png, n ranges from 1 to 5. This method randomly selects a sequence of n consecutive words (an n-gram) from the text, and all other words are masked or removed. It is an extreme masking approach.

The specific use process is as follows: for the text to be processed, each position is iterated based on the uniform distribution. For each word 𝜔, a real number Xi is randomly generated between 0 and 1. If Xi<pmask, it will be masked. If pmask<Xi<pmask+psyn, it will be replaced. Provide for masking and replacing both operations; once one rule is satisfied, the other is ignored. After the iteration, the processed samples are sampled at all locations with probability png Finally the comprehensive example is extended to the dataset as unlabeled data. For each data, this study iterates it n times to obtain up to n samples and discards the repeated samples.

4  Experiments and Results

For experiments, two variants of DPAL-VERT models are built: DPAL-BERT-Bi and DPAL-BERT-C. Both models adopt the PAL-BERT model [18] as the teacher network. BiLSTM [19] and TextCNN [27] are used as the student network for constructing DPAL-BERT-Bi and DPAL-BERT-C, respectively. For the parameters of the data augmentation part, pmask=psyn=0.1,png=0.25,n=10.

4.1 Optimizing Random Masking for Adjacent Word Segmentations

This section introduces an optimization technique involving the application of masks to adjacent word segments instead of random individual words. The masking step is to sample a subset Y from the word set X and replace it with another word set. In ALBERT, a subset is randomly selected to find out Y, and the selection of each word is independent. The subset Y accounts for 15% of the word set X. 80% of the words in the subset Y are substituted by [MASK], and 10% of the words are replaced by random words according to the unigram distribution, leaving 10% unchanged.

In this study, the model subset Y is obtained by selecting adjacent word segmentation, and the scale and masking method of the model are unchanged. Specifically, for each word sequence X=(x1,…,xn), words are selected by iteratively sampling the word segmentation of the text until the masking scale (15% of the whole word set) is reached and a subset is formed. The process begins by sampling the length of each word segment from a geometric distribution I∼Geo(p), where p is set to 0.2. This sampling determines the number of words in each segment. To ensure manageable segments, the maximum allowable length of any given word segment is ten words. The geometric distribution is skewed and tends to shorten word segmentation, with an average word segmentation length of 3.8 words. The starting point of word segmentation is randomly selected. Combined with the above text length, the subset Y can be obtained by sampling.

4.2 Ablation Study on T and α

In the distillation model, two hyperparameters T and α must be determined during the experiment. Grid search is applied to find the best α∈[0.1,0.2,…,0.9] and T∈[1,2,3] with DPAL-BERT-Bi model to find the best hyperparameters. The experimental results of the impact of two parameters on the final accuracy are listed in Table 4.

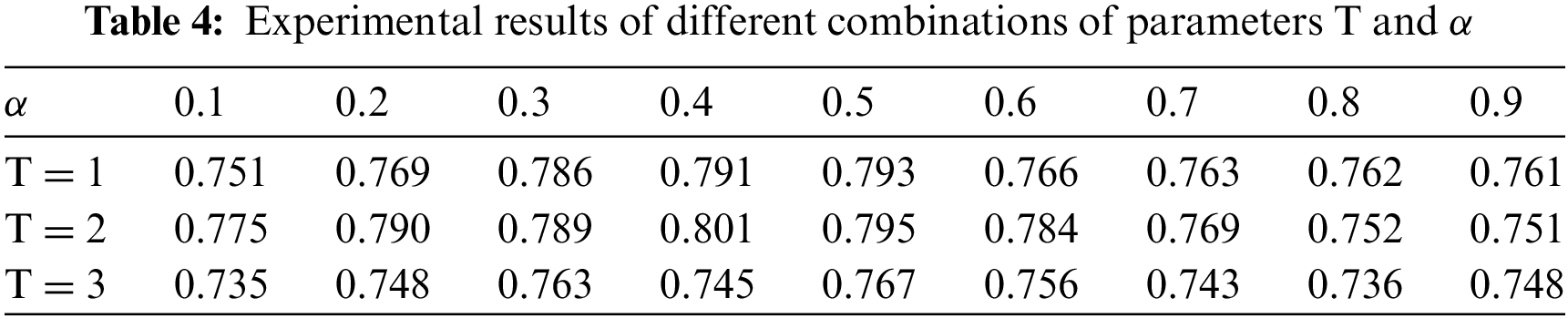
Fig. 5 indicates that the optimal configuration for the hyperparameters is achieved with a combination of T=2 and α=0.5. Hence, these values are adopted as the standard settings for these hyperparameters in all subsequent experiments.

Figure 5: Model performance on varying T and α

The impact of varying the temperature parameter, particularly when it is increased to 3, can be understood in terms of its effect on the student network’s attention to negative labels during training. When the temperature is low, less attention is paid to negative labels, especially those significantly lower than the average value. However, as the temperature rises, the relative importance of these negative labels increases, causing the student network to focus more on them.

Although negative labels contain helpful information, particularly those with values significantly above the average, the training process of the teacher network often introduces substantial noise in these labels. This noise tends to reduce the reliability of information from negative labels, especially as their values decrease. Hence, an excessively high-temperature value can lead to a decrease in the student network’s accuracy.

The following selection rules can be applied to optimize the use of the temperature parameter in training: 1. A higher temperature should be used when learning from negative labels that carry meaningful information. 2. A lower temperature is preferable to minimize the influence of noise on negative labels.

The data augmentation technique employed in this study can generate a substantial volume of unlabeled data, significantly expanding the dataset used for training. The impact of data augmentation on the performance is shown in Table 5.

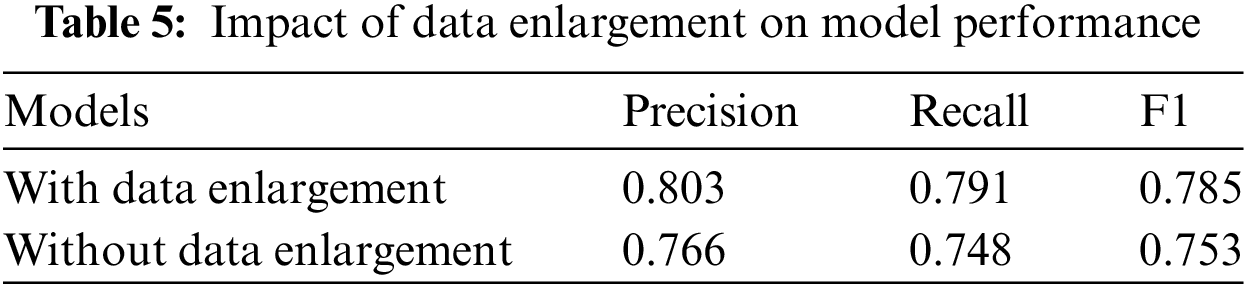
Table 5 indicates that incorporating data augmentation, coupled with the addition of unlabeled data to the training process, results in a performance improvement, with an accuracy increase of approximately 4%. This shows that applying unlabeled data augmentation in knowledge distillation is very necessary. A plausible explanation for this enhancement is that using a large volume of unlabeled data allows for a more comprehensive representation of relevant knowledge from the larger model. Then, the smaller model can learn more effectively, improving overall performance. The effectiveness of this approach is further evidenced by the prediction results on the SQuAD 2.0 and CMRC 2018 development sets, as detailed in Tables 6 and 7, respectively.

4.3 Model Performance of DPAL-BERT

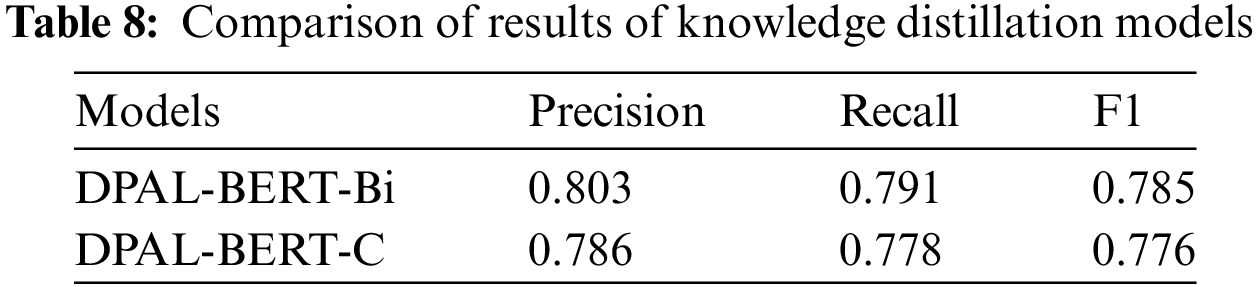
To evaluate the model performance and robustness of the proposed DPAL-BERT, two variants of DPAL-BERT models, DPAL-BERT-Bi and DPAL-BERT-C, are tested in the CMRC dataset. Results are given in Table 8.

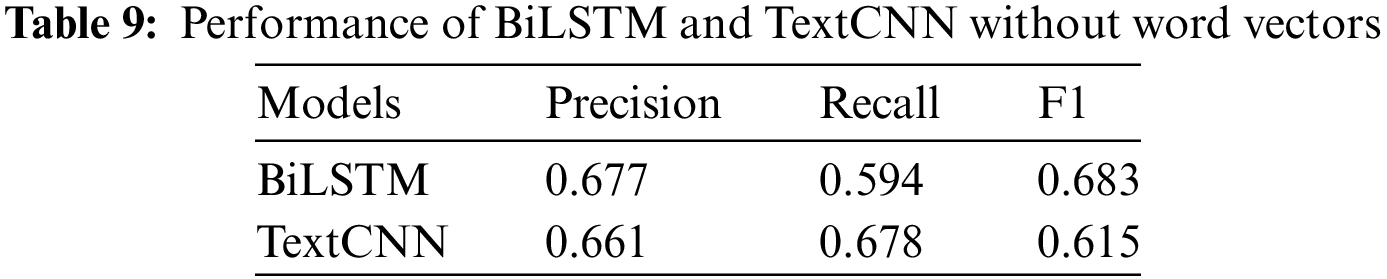
BiLSTM and TextCNN are trained from scratch without a word vector to evaluate the effectiveness of knowledge distillation. The obtained results are listed in Table 9. This study reveals that knowledge distillation significantly outperforms the small models trained without word vectors. BiLSTM and TextCNN, when trained directly on the dataset, achieve a maximum accuracy of only 67.7%. It indicates the challenges small models face in capturing the intricacies of diverse samples. In contrast, after applying knowledge distillation, the accuracy of the distilled models exceeds 80%, which is nearly 13% higher than the small models and about 4% higher than traditional models utilizing word vectors. Through the above experiments, the knowledge distillation demonstrates a remarkable efficiency in enhancing the accuracy of smaller models.

4.4 Inference Speed Comparison

Table 10 compares the number of parameters and inference time between the distilled model DPAL-BERT-Bi and the teacher model PAL-BERT. The inference time is the duration required to process the dataset using the trained models. For a fair comparison, the batch size for both models is set to 32. The results reveal that the DPAL-BERT-Bi model has nearly 20 times fewer parameters than the PAL-BERT model. In addition, its inference time is substantially lower. Specifically, the distilled model’s inference process is approximately 423 times faster than that of the PAL-BERT model.

5  Discussion

The knowledge distillation method has many advantages, such as shallowing the depth of the model, significantly reducing the computational cost, and directly accelerating the model without specific hardware requirements. Developing more methods based on knowledge distillation and exploring how to improve its performance is paramount. Using the method of knowledge distillation, the PAL-BERT model was employed as the teacher network, with BiLSTM and TextCNN serving as the student networks to develop two models, DPAL-BERT-Bi and DPAL-BERT-C, and the effectiveness of the method was verified through experiments.

Knowledge distillation successfully facilitates knowledge transfer from the large model PAL-BERT to the small models such as BiLSTM and TextCNN. After knowledge distillation, the accuracy is 13% higher than training directly on the small model. However, it is essential to acknowledge the inherent limitations in the representational capacity of smaller models compared to more complex ones like ALBERT. Although a significant portion of knowledge from PAL-BERT is transferred to BiLSTM, some knowledge remains untransferred. This limitation is represented in the performance of the distilled small models, which, despite being markedly better than the outcomes of direct training or traditional word vectorization, still do not match the performance level of PAL-BERT.

Nevertheless, the primary advantage of the proposed DPAL-BERT is the substantial reduction in inference time while retaining as much computational accuracy as possible. The distilled model requires only the computation time typical of smaller models, significantly speeding up the inference process compared to the original large model. DPAL-BERT-Bi, which employs knowledge distillation, reduces its parameter count by nearly 20 times compared to the original model, and the inference speed increases by approximately 423 times.

6  Conclusion

This study applies knowledge distillation to BERT-based models to reduce the inference time. Based on PAL-BERT, the DPAL-BERT-Bi and DPAL-BERT-C models are introduced. Experiments show a significant improvement in model performance compared to smaller models trained from scratch without using word vectors. There is an enhancement in effectiveness compared to smaller models trained either directly or after using word vectors. Although the performance after distillation is slightly lower than PAL-BERT, the model’s inference time is greatly reduced. This acceleration is especially beneficial for online applications, where the slight trade-off in performance is outweighed by substantial gains in processing speed.

However, there are still some limitations in the research. In terms of knowledge distillation, this study only uses soft labels, but in the following research, other features in the model can be introduced, such as hidden layer vector in the transformer or feature representation of the embedded layer. These can be further studied in combination with question-answering scenarios.

Acknowledgement: The authors extend their appreciation to the Distinguished Scientist Fellowship Program (DSPF), King Saud University, Riyadh, Saudi Arabi.

Funding Statement: This study was supported by Sichuan Science and Technology Program (2023YFSY0026, 2023YFH0004).

Author Contributions: Conceptualization: Wenfeng Zheng; methodology: Zhuohang Cai; software: Zhuohang Cai; formal analysis: Ahmed AlSanad, and Salman A. AlQahtani; data curation: Zhuohang Cai, Zhengtong Yin, Xiaobing Chen, Xiaolu Li, and Lei Wang; writing—original draft preparation: Lirong Yin, Siyu Lu, and Wenfeng Zheng; writing—review and editing: Lirong Yin, Siyu Lu, Ruiyang Wang, and Wenfeng Zheng; funding acquisition: Wenfeng Zheng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Radford A, Narasimhan K, Salimans T, Sutskever I. Improving language understanding by generative pre-training. OpenAI. 2018. [Google Scholar]

2. Devlin J, Chang MW, Lee K, Toutanova K. BERT: pre-training of deep bidirectional transformers for language understanding. Minneapolis, Minnesota: Association for Computational Linguistics; 2019. p. 4171–4186. doi:10.18653/v1/N19-1423. [Google Scholar] [CrossRef]

3. Zaib M, Zhang WE, Sheng QZ, Mahmood A, Zhang Y. Conversational question answering: a survey. Knowl Inf Syst. 2022;64:3151–95. doi:10.1007/s10115-022-01744-y. [Google Scholar] [CrossRef]

4. Lan W, Cheung YM, Jiang J, Hu Z, Li M. Compact neural network via stacking hybrid units. IEEE Trans Pattern Anal Mach Intell. 2024;46(1):103–16. doi:10.1109/TPAMI.2023.3323496. [Google Scholar] [PubMed] [CrossRef]

5. Menghani G. Efficient deep learning: a survey on making deep learning models smaller, faster, and better. ACM Comput Surv. 2023;55(12):259. doi:10.1145/3578938. [Google Scholar] [CrossRef]

6. Huang Y, Hao Y, Xu J, Xu B. Compressing speaker extraction model with ultra-low precision quantization and knowledge distillation. Neural Netw. 2022;154(1):13–21. doi:10.1016/j.neunet.2022.06.026. [Google Scholar] [PubMed] [CrossRef]

7. Choudhary T, Mishra V, Goswami A, Sarangapani J. A comprehensive survey on model compression and acceleration. Artif Intell Rev. 2020;53(7):5113–55. doi:10.1007/s10462-020-09816-7. [Google Scholar] [CrossRef]

8. Mo Y, Wu Y, Yang X, Liu F, Liao Y. Review the state-of-the-art technologies of semantic segmentation based on deep learning. Neurocomputing. 2022;493:626–46. doi:10.1016/j.neucom.2022.01.005. [Google Scholar] [CrossRef]

9. Liang T, Glossner J, Wang L, Shi S, Zhang X. Pruning and quantization for deep neural network acceleration: a survey. Neurocomputing. 2021;461(18):370–403. doi:10.1016/j.neucom.2021.07.045. [Google Scholar] [CrossRef]

10. Swaminathan S, Garg D, Kannan R, Andres F. Sparse low rank factorization for deep neural network compression. Neurocomputing. 2020;398(11):185–96. doi:10.1016/j.neucom.2020.02.035. [Google Scholar] [CrossRef]

11. Guo S, Lai B, Yang S, Zhao J, Shen F. Sensitivity pruner: filter-level compression algorithm for deep neural networks. Pattern Recogn. 2023;140(2):109508. doi:10.1016/j.patcog.2023.109508. [Google Scholar] [CrossRef]

12. Gou J, Sun L, Yu B, Du L, Ramamohanarao K, Tao D. Collaborative knowledge distillation via multiknowledge transfer. IEEE Trans Neural Netw Learn Syst. 2024;35(5):6718–30. doi:10.1109/TNNLS.2022.3212733. [Google Scholar] [PubMed] [CrossRef]

13. Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network. 2015. doi:10.48550/arXiv.1503.02531. [Google Scholar] [CrossRef]

14. Gou J, Yu B, Maybank SJ, Tao D. Knowledge distillation: a survey. Int J Comput Vis. 2021;129(6):1789–819. doi:10.1007/s11263-021-01453-z. [Google Scholar] [CrossRef]

15. Sanh V, Debut L, Chaumond J, Wolf T. DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter. 2019. doi:10.48550/arXiv.1910.01108. [Google Scholar] [CrossRef]

16. Jiao X, Yin Y, Shang L, Jiang X, Chen X, Li L, et al. Tinybert: distilling bert for natural language understanding. In: Findings of the Association for Computational Linguistics: EMNLP 2020; 2020. p. 4163–74. doi:10.18653/v1/2020.findings-emnlp.372. [Google Scholar] [CrossRef]

17. Jiao X, Chang H, Yin Y, Shang L, Jiang X, Chen X, et al. Improving task-agnostic BERT distillation with layer mapping search. Neurocomputing. 2021;461:194–203. doi:10.1016/j.neucom.2021.07.050. [Google Scholar] [CrossRef]

18. Zheng W, Lu S, Cai Z, Wang R, Wang L, Yin L. PAL-BERT: an improved question answering model. Comp Model Eng. 2023;139(3):2729–45. doi:10.32604/cmes.2023.046692. [Google Scholar] [CrossRef]

19. Wang H, Zhang Y, Liang J, Liu L. DAFA-BiLSTM: deep autoregression feature augmented bidirectional LSTM network for time series prediction. Neural Netw. 2023;157(2):240–56. doi:10.1016/j.neunet.2022.10.009. [Google Scholar] [PubMed] [CrossRef]

20. Rajpurkar P, Zhang J, Lopyrev K, Liang P. SQuAD: 100,000+ questions for machine comprehension of text. In: Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing; 2016 Nov; Austin, TX, USA: Association for Computational Linguistics. p. 2383–92. doi:10.18653/v1/D16-1264. [Google Scholar] [CrossRef]

21. Cui Y, Liu T, Che W, Xiao L, Chen Z, Ma W, et al. A span-extraction dataset for chinese machine reading comprehension. In: Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP); 2019; Hong Kong, China. p. 5883–9. doi:10.18653/v1/D19-1600. [Google Scholar] [CrossRef]

22. Gou J, Sun L, Yu B, Wan S, Ou W, Yi Z. Multilevel attention-based sample correlations for knowledge distillation. IEEE T Ind Inform. 2023;19(5):7099–109. doi:10.1109/TII.2022.3209672. [Google Scholar] [CrossRef]

23. Lan Z, Chen M, Goodman S, Gimpel K, Sharma P, Soricut R. ALBERT: a lite BERT for self-supervised learning of language representations; In: The Eighth International Conference on Learning Representations; 2020. [Google Scholar]

24. Peters ME, Ruder S, Smith NA. To tune or not to tune? Adapting pretrained representations to diverse tasks. In: Proceedings of the 4th Workshop on Representation Learning for NLP (RepL4NLP-2019); 2019 Aug; Florence, Italy. p. 7–14. doi:10.18653/v1/W19-4302. [Google Scholar] [CrossRef]

25. Clark K, Luong MT, Manning CD, Le QV. Semi-supervised sequence modeling with cross-view training. In: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing; 2018 Oct 31–Nov 4; Brussels, Belgium. p. 1914–25. [Google Scholar]

26. Li K, Wigington C, Tensmeyer C, Morariu VI, Zhao H, Varun M, et al. Improving cross-domain detection with self-supervised learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023; Vancouver, BC, Canada. p. 4746–55. [Google Scholar]

27. Jiang X, Song C, Xu Y, Li Y, Peng Y. Research on sentiment classification for netizens based on the BERT-BiLSTM-TextCNN model. PeerJ Comput Sci. 2022;8(3):e1005. doi:10.7717/peerj-cs.1005. [Google Scholar] [PubMed] [CrossRef]

28. Tang R, Lu Y, Liu L, Mou L, Vechtomova O, Lin J. Distilling task-specific knowledge from BERT into simple neural networks. 2019. doi:10.48550/arXiv.1903.12136. [Google Scholar] [CrossRef]