BHJO: A Novel Hybrid Metaheuristic Algorithm Combining the Beluga Whale, Honey Badger, and Jellyfish Search Optimizers for Solving Engineering Design Problems

1  Introduction

Optimization is a fundamental problem-solving approach that aims to find the best possible solution from a set of feasible configurations [1]. It plays a crucial role in various domains, including engineering [2], economics [3], logistics [4], and data analysis [5]. The complexity of real-world optimization problems often arises from large search spaces, non-linear relationships, and multiple conflicting objectives [6].

To tackle such challenging optimization problems, researchers have developed a diverse range of techniques, including metaheuristic algorithms [7]. Metaheuristics are high-level problem-solving strategies that guide the search process by iteratively exploring and exploiting the search space to find optimal or near-optimal solutions [8]. Unlike exact optimization methods that guarantee optimal solutions but are limited to small-scale problems, metaheuristics are capable of handling large-scale and complex optimization problems [8].

Metaheuristic algorithms draw inspiration from natural phenomena, social behaviors, and physical processes to create intelligent search strategies [9]. These algorithms iteratively improve a population of candidate solutions by iteratively applying exploration and exploitation techniques. Exploration involves searching new regions of the search space to discover potential solutions, while exploitation focuses on refining and exploiting promising solutions to improve their quality [10]. A good balance between exploration and exploitation is essential for the success of metaheuristic algorithms in solving optimization problems [11]. Exploration allows the algorithm to search widely across the search space, uncovering diverse regions and potentially finding better solutions. It helps prevent the algorithm from getting stuck in local optimums and promotes global exploration. On the other hand, exploitation focuses on intensively exploiting the promising regions of the search space, refining and improving the solutions to converge towards optimal or near-optimal solutions. Balancing these two aspects ensures that the algorithm maintains a healthy exploration to discover new regions while exploiting the discovered promising solutions effectively. A well-balanced approach enables the algorithm to avoid premature convergence and thoroughly explore the search space to find high-quality solutions [9].

Metaheuristic algorithms can be broadly categorized into two groups based on their search strategy: population-based algorithms and individual-based algorithms [12]. Typically, population-based algorithms maintain a population of candidate solutions and explore the search space collectively, exchanging information between individuals to guide the search process. Examples of population-based algorithms include genetic algorithms [13] and particle swarm optimization [14]. On the other hand, individual-based algorithms, also known as trajectory-based algorithms, focus on improving a single solution or trajectory by iteratively modifying it through exploration and exploitation. Examples of individual-based algorithms include simulated annealing [15] and tabu search [16]. These algorithms often rely on a memory mechanism to keep track of previously visited regions and avoid getting trapped in local optimums.

Metaheuristic algorithms have demonstrated their effectiveness and versatility in solving a wide range of optimization problems in various fields. They have been successfully applied in areas such as engineering design [17], scheduling [18], resource allocation [19], data mining [20], and image processing and segmentation [21]. The ability of metaheuristic algorithms to handle complex, non-linear, and multi-objective optimization problems makes them particularly useful in real-world applications where traditional optimization techniques may fail to provide satisfactory results.

In this paper, we focus on the combination of three well-known metaheuristic algorithms, namely the beluga whale optimization [22], the honey badger algorithm [23], and the jellyfish search optimizer [24], to design a hybrid metaheuristic algorithm. We aim to leverage the strengths of these individual algorithms and propose a novel hybrid approach that improves optimization performance. The main contributions of this research work are:

1.    After conducting an in-depth analysis of the three metaheuristics used to design the BHJO algorithm, we have concluded that the Beluga Whale Optimization (BWO) and the Honey Badger Algorithm (HBA) algorithms exhibit promising exploitation capabilities and stable exploration phases, although their balance between exploration and exploitation is suboptimal. Conversely, the Jellyfish Search (JS) algorithm demonstrates commendable exploration capacity and a well-balanced approach to exploration and exploitation, but its exploitation capability remains weak.

2.    We incorporated Opposition-Based Learning into the BHJO algorithm to enhance its exploration capabilities and prevent it from getting trapped in local optimums.

3.    We proposed a new balancing mechanism between exploration and exploitation, and it is very promising.

The organization of the remaining sections in the paper can be summarized in the following sentences. Section 2 reviews some recent metaheuristic algorithms and discusses their inspirations, highlighting the advancements in the field. Section 3 focuses on the working principle of the BHJO algorithm, providing a detailed explanation of its approach and highlighting its key features. Section 4presents the experimental study conducted to evaluate the performance of the BHJO algorithm, including the methodology, benchmarks, and performance metrics employed. The results are analyzed and discussed in detail. Finally, Section 5 concludes the paper by summarizing the key findings, discussing their implications, and suggesting future directions for further research and improvements in hybrid metaheuristic algorithms.

2  Related Work

In this section, we provide an overview of several popular metaheuristic algorithms that have significantly contributed to the optimization field and have been published between 2020 and 2023. These algorithms have been extensively studied and applied in various domains to tackle complex optimization problems. The review focuses on highlighting the key features and principles of each algorithm. While the list is not exhaustive, it encompasses some of the most widely recognized and influential metaheuristics.

The Golden Eagle Optimizer (GEO) [25] is an optimization algorithm inspired by the hunting behavior and characteristics of golden eagles. The Mountain Gazelle Optimizer (MGO) [26] takes cues from the social life and hierarchy of wild mountain gazelles. The Artificial Ecosystem-based Optimization (AEO) [27] emulates the flow of energy in an ecosystem on the earth and mimics three unique behaviors of living organisms: production, consumption, and decomposition. The Dandelion Optimizer (DO) [28] reflects the process of dandelion seed long-distance flight relying on the wind: the rising stage, the descending stage, and the landing stage. The Archerfish Hunting Optimizer (AHO) [29] mimics the shooting and jumping behaviors of archerfish when hunting aerial insects. The African Vultures Optimization Algorithm (AVOA) [30] models after the African vultures’ foraging and navigation behaviors. The Artificial Gorilla Troops Optimizer (GTO) [31] follows in the footsteps of the gorillas’ collective lifestyle. The Beluga Whale Optimization [22] is inspired by the behaviors of pair swim, prey, and whale fall of Beluga whales. The Elephant Clan Optimization (ECO) [32] evokes the most essential individual and collective behaviors of elephants, such as powerful memories and high capabilities for learning. The Cheetah Optimizer (CO) [33] recreates the hunting strategies of cheetahs: searching, sitting and waiting, and attacking. The Bear Smell Search Algorithm (BSSA) [34] imitates both dynamic behaviors of bears: the sense of smell mechanism and the way bears move in search of food. The Gaining-Sharing Knowledge-based (GSK) [35] algorithm mimics the process of gaining and sharing knowledge during the human life span.

The Nutcracker Optimization Algorithm (NOA) [36] draws inspiration from two distinct behaviors of Clark’s nutcrackers: search for seeds and storage in appropriate caches, and search for the hidden caches marked at different angles using markers. The Artificial Lizard Search Optimization (ALSO) [37] adopts the dynamic foraging behavior of Agama lizards and their effective way of capturing prey. The Red Deer Algorithm (RDA) [38] echoes the mating behavior of Scottish red deer in breeding seasons. The Ebola Optimization Search Algorithm (EOSA) [39] replicates the propagation mechanism of the Ebola virus disease. The Solar System Algorithm (SSA) [40] recreates the orbiting behaviors of some objects found in the solar system: i.e., the sun, planets, moons, stars, and black holes. The Siberian Tiger Optimization (STO) [41] imitates the natural behavior of the Siberian tiger during hunting and fighting. The Coati Optimization Algorithm (COA) [42] models the two natural behaviors of coatis: attacking and hunting iguanas and escaping from predators. The Artificial Rabbits Optimization (ARO) [43] simulates the survival strategies of rabbits in nature, including detour foraging and random hiding. The Red Piranha Optimization (RPO) [44] was inspired by the cooperation and organized teamwork of the piranha fish when hunting or saving their eggs. The Giza Pyramids Construction (GPC) [45] is based on the movements of the workers and pushing the stone blocks on the ramp when building the pyramids. The Sea-Horse Optimizer (SHO) [46] emulates the movement, predation, and breeding behaviors of sea horses in nature. The Aphid-Ant Mutualism (AAM) [47] mirrors the unique relationship between aphids and ants’ species which is called mutualism.

The White Shark Optimizer (WSO) [48] mimics the behaviors of great white sharks, including their senses of hearing and smell, while navigating and foraging. The Circulatory System Based Optimization (CSBO) [49] simulates the function of the body’s blood vessels with two distinctive circuits: pulmonary and systemic circuits. The Reptile Search Algorithm (RSA) [50] replicates the hunting behavior of Crocodiles: encircling, which is performed by high walking, and hunting, which is performed by hunting coordination. The Blood Coagulation Algorithm (BCA) [51] draws inspiration from the cooperative behavior of thrombocytes and their intelligent strategy of clot formation. The Color Harmony Algorithm (CHA) [52] mirrors the search behavior by combining harmonic colors based on their relative positions around the hue circle in the Munsell color system and harmonic templates. The Leopard Seal Optimization (LSO) [53] adopts the hunting strategy of the leopard seals. The Osprey Optimization Algorithm (OOA) [54] echoes the behavior of osprey in nature when hunting fish from the seas after detecting its position, then carries it to a suitable position to eat it. The Green Anaconda Optimization (GAO) [55] is inspired by the mechanism of recognizing the position of females by males during mating seasons and hunting strategies of green anacondas. The Subtraction-Average-Based Optimizer (SABO) [56] takes inspiration from the use of the subtraction average of searcher agents to update the position of population members in the search space. The Honey Badger Algorithm [23] simulates the behaviour of a honey badger when digging and finding honey. The Jellyfish Search [24] optimizer is motivated by the behavior of jellyfish in the ocean: following the ocean current, motions inside a jellyfish swarm, and convergence into jellyfish bloom.

Table 1 provides a detailed analysis of the metaheuristic algorithms discussed previously. It evaluates these algorithms by counting the instances of three fundamental steps that typically constitute metaheuristics: exploration, exploitation, and local minimum avoidance. This will allow readers to identify potential weaknesses in a specific algorithm. For instance, algorithms lacking the local minimum avoidance step can be located, suggesting a potential area for enhancement by incorporating this crucial phase. The first to third columns of Table 1 present information about the algorithm, and the fourth to sixth columns present the number of exploration, exploitation, and local minimum avoidance phases within each algorithm.

It is important to note that designing a new metaheuristic algorithm capable of effectively balancing the exploration of the search space with the exploitation of promising solutions, while also accurately determining the optimal times for each, is an extremely challenging task. Most hybridization efforts in the literature are geared towards addressing this issue by creating new hybrid algorithms that merge complementary strategies–for instance, combining a method with strong exploration but weak exploitation with one that excels in exploitation but not in exploration [57]. Additionally, the temporal complexity of these hybrid algorithms must be carefully considered. Hastily or poorly constructed hybrid models can significantly impair the efficiency of hybrid optimizers, underlining the necessity for meticulous development and evaluation.

It is worth emphasizing that the No-Free-Lunch (NFL) theorem [58] in optimization states that when considering the performance of optimization algorithms across all possible problem instances, no single algorithm can outperform all others on average. In other words, no universally superior algorithm can solve every optimization problem efficiently. The NFL theorem has implications for the field of metaheuristics and the existence of a large number of proposed algorithms. Since no single algorithm can be universally superior, researchers propose different metaheuristic algorithms to address specific problem characteristics and structures.

By developing a diverse set of metaheuristics, researchers aim to create algorithms that are tailored to specific problem domains and can exploit problem-specific information effectively. Different algorithms may have strengths and weaknesses that make them more suitable for particular problem types or classes. Therefore, the existence of a large number of metaheuristics can be seen as a way to cover a broad range of problem instances and improve the chances of finding a suitable algorithm for a given problem. Furthermore, the NFL theorem emphasizes the importance of algorithm selection and design for optimization problems. It suggests that the performance of an algorithm is intricately tied to the problem it is applied to. Therefore, the development of new metaheuristics aims to explore different search strategies, operators, or mechanisms that may be better suited for certain problem types or offer improvements over existing algorithms.

In summary, the No-Free-Lunch theorem implies that there is no universally superior optimization algorithm. This motivates the development of a large number of metaheuristic algorithms to address specific problem characteristics and improve the chances of finding suitable algorithms for various problem instances. The diversity of metaheuristics reflects the understanding that different algorithms may excel in different problem domains, and the search for the best algorithm for a specific problem requires careful consideration and experimentation.

3  Proposed Hybrid Algorithm

In this section, we provide a comprehensive explanation of the hybrid algorithm that we have proposed. Section 3.1 presents the source of inspiration that guided the development of our algorithm. Section 3.2 outlines the mathematical model underlying the BHJO algorithm. Finally, Section 3.3 presents the pseudo-code implementation of our algorithm along with a discussion of its time complexity.

3.1 Source of Inspiration

To elucidate the working principle of the proposed hybrid algorithm, a comprehensive understanding of the algorithms utilized in its design is provided. Section 3.1.1 focuses on elucidating the fundamental concept and workings of the BWO algorithm. Similarly, Section 3.1.2 delves into the underlying principles and mechanisms of the HBA algorithm. Finally, Section 3.1.3 provides a detailed account of the underlying idea behind the JS algorithm. By addressing the working principles of these constituent algorithms, a holistic understanding of the hybrid algorithm’s operation is attained, thereby facilitating its effective application and potential future enhancements.

3.1.1 Beluga Whale Optimization

Beluga whales are marine mammals that belong to the whale family. They inhabit the Arctic and subarctic oceans and are characterized by their medium size. Beluga whales are known for their sociability, keen sensory perception, and distinct behaviors, including swimming with raised pectoral fins, synchronized diving and surfacing, and the release of bubbles from their blowholes. They have an omnivorous diet, consuming various prey such as fish and invertebrates, and often cooperate in groups for hunting and feeding. However, they face threats from natural predators like orcas and polar bears, as well as human activities. Additionally, when beluga whales die, their bodies sink to the ocean floor (known as a whale fall), creating a food source for deep-sea organisms1. The mathematical formulation of the exploration, the exploitation, and the concept of whale fall (i.e., local optimum avoidance) with the BWO algorithm is depicted in Fig. 1 and will be further elucidated in the following sections.

Figure 1: Behaviour of beluga whales [22]

The various symbols utilized in the equations about the BWO algorithm can be elucidated as follows:

•   N: The population size.

•   D: The dimensionality of the search space.

•   LB: The lower bound of the search space.

•   UB: The upper bound of the search space.

•   Tmax: The maximum number of iterations.

•   t: The current iteration.

•   Xi,jt: The position of the ith agent on the jth dimension at the iteration t.

•   Xit: The position of the ith agent at the iteration t.

•   ρ: A random number drawn from the range {1,…,D}.

•   r: A random number drawn from the range {1,…,N}.

•   r1, r2, r3, r4, r5, r6, r7, α, and B0: Random numbers drawn from the uniform distribution.

•   Xbestt: The best solution in the current population.

•   υ and ν: Random numbers drawn from the Gaussian distribution.

•   β: A constant number set to 1.5.

•   Γ: The Gamma function.

•   LF: The lévy flight.

1) Initialization Phase: Eq. (1) is employed to initialize the different agents within the initial population of the BWO algorithm.

Xi, j0=α(UB−LB)+LB , i∈{1,…,N} , j∈{1,…,D}(1)

2) Exploration Phase: The locations of search agents are determined by the paired swimming behavior, where two beluga whales swim together in a synchronized or mirrored manner. This approach allows search agents to explore the search space more efficiently and effectively, leading to the discovery of new and potentially better solutions. The positions of the different agents are updated using Eq. (2).

{Xi, jt+1=Xi, ρt+(Xr, 1t−Xi, ρt)(1+r1)sin⁡(2πr2),j=2kXi, jt+1=Xi, ρt+(Xr, 1t−Xi, ρt)(1+r1)cos⁡(2πr2),j=2k+1(2)

3) Exploitation Phase: The search agents share information about their current positions and consider the best solution, as well as other nearby solutions, when updating their locations. This mechanism helps the agents efficiently move towards promising regions of the search space. The exploitation phase also includes the lévy flight [59]. This strategy helps enhance search agents’ convergence towards the global solution of the search space. The positions of agents are updated using Eq. (3).

Xit+1=r3Xbestt−r4Xit+2r4(1−tTmax)LF(Xrt−Xit)(3)

LF=0.05(υ×σ|ν|1β)

σ=(Γ(1+β)×sin⁡(π×β2)Γ(1+β2)×β×2β−12)1β

4) Balance between Exploration and Exploitation: During the search process, the balance between the exploration and exploitation phases is determined by a swapping factor, denoted as Bf, which is calculated using Eq. (4). Therefore, if the value of Bf is greater than or equal to a specific threshold (e.g., 0.5), the search space is explored using Eq. (2); otherwise, the search space is exploited using Eq. (3).

Bf=B0(1−t2Tmax)(4)

5) Whale Fall: The whale fall phase represents the concept of beluga whales’ dying and becoming a food source for other creatures. In the BWO algorithm, the whale fall phase serves as a random operator to introduce diversity and prevent the search process from getting trapped in local optimums. The mathematical model of this step is expressed through Eq. (5).

Xit+1=r5Xit−r6Xrt+r7Xstep(5)

Xstep=(UB−LB)exp⁡(−C2tTmax)

C2=2×Wf×N

Wf=0.1−0.05tTmax(6)

3.1.2 Honey Badger Algorithm

Honey badgers are captivating mammals renowned for their fearless and tenacious nature. They inhabit semi-deserts and rainforests across Africa, Southwest Asia, and the Indian subcontinent. With their distinct black and white fluffy fur, honey badgers typically measure between 60 to 77 centimeters in length and weigh around 7 to 13 kilograms. Their survival primarily relies on two modes: the digging mode and the honey mode. In the digging mode, honey badgers utilize their keen sense of smell to locate prey and engage in digging to capture it. In the honey mode, they take advantage of birds to identify beehives and obtain honey2. The mathematical formulation and associated concepts about the HBA algorithm are elaborated upon in the following sections.

The different symbols utilized in the equations related to the HBA algorithm can be described as follows:

•   N: The population size.

•   D: The dimensionality of the search space.

•   LB: The lower bound of the search space.

•   UB: The upper bound of the search space.

•   Tmax: The maximum number of iterations.

•   t: The current iteration.

•   r1, r2, r3, r4, r5, r6, and r7: Random numbers drawn from the uniform distribution.

•   Xprey: The global best position so far found.

•   β: A constant number replicating the ability of a honey badger to get food.

•   di: The distance between the ith honey badger and Xprey.

•   F: A flag number that alters the search direction. It is used to avoid getting stuck in local optimums.

•   C´: A constant number greater than or equal to 1.

1) Initialization Phase: Eq. (7) is employed to initialize the different agents within the first population of the HBA algorithm.

Xi, j0=r1(UB−LB)+LB , i∈{1,…,N} , j∈{1,…,D}(7)

2) Smell Intensity: The intensity in the HBA algorithm is associated with the concentration strength of the prey’s smell and its distance from a honey badger. The symbol Ii represents the smell intensity of the prey in relation to the i th honey badger. This intensity is determined using the Inverse Square Law [60], as illustrated in Fig. 2, and is defined by Eq. (8).

Ii=r2S4πdi2(8)

S=(Xit−Xi+1t)2

di=Xprey−Xit

Figure 2: The inverse square law (I is the smell intensity, S is the prey’s location, and r is a random number drawn from the uniform distribution) [23]

3) Density Factor: The density factor α is a randomizer that ensures the smooth transition from exploration to exploitation. Eq. (9) is used to compute α.

α=C´×exp⁡(−tTmax)(9)

4) Exploration Phase: In nature, honey badgers dig like-cardioid shapes to surround and catch prey. Fig. 3 shows the form of a two-dimensional shape that has a heart-shaped curve. The exploration phase of the HBA algorithm is formulated using Eq. (10).

Xit+1=(1+FβIi)Xprey+Fr3αdi|cos⁡(2πr4)(1−cos⁡(2πr5))|(10)

F={−1,r6≤0.51,r6>0.5

Figure 3: The digging behavior of honey badgers in nature to surround and catch prey [23]

5) Exploitation Phase: The exploitation phase is depicted by honey badgers’ behaviors as they approach beehives, when following honey-guide birds. It is mathematically represented by Eq. (11).

Xit+1=Xprey+Fr7αdi(11)

3.1.3 Jellyfish Search Optimizer

Jellyfish, also known as medusae, are fascinating marine organisms that inhabit various depths and temperatures of water worldwide. They display an array of shapes, sizes, and colors, owing to their soft, translucent, and gelatinous composition. Typically, jellyfish possess a distinct bell-shaped body, contributing to their unique appearance. The size and form of the bell can significantly differ among jellyfish species. Additionally, jellyfish have developed a multitude of adaptation mechanisms to thrive in their oceanic environment. These mechanisms include specialized structures for hunting prey, such as elongated tentacles equipped with stinging cells known as nematocysts. Jellyfish employ two primary hunting strategies: passive swarming and active swarming. In the former, specific jellyfish follow the movement of a school of organisms, while in the latter, individuals hunt alone. During periods of non-hunting, jellyfish drift along with the ocean currents3. The behaviors of jellyfish are illustrated in Fig. 4. The mathematical formulation of exploration and exploitation concepts about the JS algorithm will be expounded upon in the following sections.

Figure 4: The behaviours of jellyfish in the ocean [24]

The symbols employed in the equations about the JS algorithm can be explained as follows:

•   N: The population size.

•   D: The dimensionality of the search space.

•   LB: The lower bound of the search space.

•   UB: The upper bound of the search space.

•   Tmax: The maximum number of iterations.

•   t: The current iteration.

•   Xbestt: The local best solution so far found.

•   β: A number replicating the distribution coefficient.

•   r1, r2, r3, r4, and r5: Random numbers drawn from the uniform distribution.

•   γ: A strictly positive number replicating the motion coefficient, and it is related to the length of motion around jellyfish’s locations.

1) Initialization Phase: The initial population in the majority of metaheuristic algorithms is generally initialized randomly. However, this approach presents two significant drawbacks: a slow convergence and a tendency to get trapped in local optimums due to reduced population diversity. To address these issues and enhance diversity within the initial population, the authors of the JS algorithm conducted tests using various chaotic maps [61–63]. The findings revealed that the logistic map [64] produces a more diverse initial population compared to random initialization, thereby mitigating the problem of premature convergence [62,65]. Eq. (12) is utilized to initialize the different individuals within the initial population of the JS algorithm. It is worth pointing out that the values φ1, j are random numbers drawn from the uniform distribution and should satisfy the constraint: φ1,j∉{0, 0.25, 0.5, 0.75, 1}.

Xi, j0=φi, j(UB−LB)+LB , i∈{1,…,N} , j∈{1,…,D}(12)

φi+1, j=4φi, j(1−φi, j)

2) Exploration Phase: Jellyfish utilize ocean currents to conserve energy and move efficiently. In the JS algorithm, this behavior is reflected in the exploration of the search space and the generation of new random candidate solutions. Consequently, the positions of individuals are updated using Eq. (13).

Xit+1=Xit+r1(Xbestt−βr2M)(13)

M=1N(X1t+…+XNt)

3) Exploitation Phase: Jellyfish navigate within the swarm to search for food. In the JS algorithm, this corresponds to the exploitation of the search space. There are two distinct behaviors observed: a jellyfish either moves randomly in search of food independently or moves towards a better solution. These mechanisms are referred to as passive motion and active motion, respectively [66,67].

1.    Passive Motion: The different agents in a specific population update their locations using Eq. (14).

Xit+1=Xit+γr3(UB−LB)(14)

2.    Active Motion: To simulate this kind of movement, we randomly select two locations p and q. If the solution at the location p is better than q, then q moves towards p and vice versa. Hence, the different agents within a given population update their locations using Eq. (15). This exploitation mechanism has proven to be very efficient, according to the work reported in [68].

Xit+1=Xit+r4Δ→(15)

Δ→={Xpt−Xqt,f(Xpt)<f(Xqt)Xqt−Xpt,f(Xpt)≥f(Xqt)

4) Time Control Mechanism: The JS algorithm incorporates a time control model that facilitates the transition between exploration and exploitation phases, as well as between passive and active motions. This time control mechanism is mathematically modeled by Eq. (16) and visually illustrated in Fig. 5.

c(t)=|(2r5−1)×(1−tTmax)|(16)

Figure 5: Time control mechanism used in the JS algorithm [24]

3.2 Mathematical Model of the BHJO Algorithm

By combining the previous algorithms, we aim to design a more robust and efficient hybrid metaheuristic algorithm that can leverage the advantages and strengths of each one. Hybrid nature-inspired approaches involve combining different optimization algorithms to enhance their performance. There are two manners of hybridization, namely high-level and low-level [69]. In the first type, the algorithms to be hybridized are applied consecutively, whereas in the second type, the similar steps of each algorithm are merged.

It is worth emphasizing that the exploration and exploitation abilities of the aforementioned algorithms–namely, the Beluga Whale Optimization [22], the Honey Badger algorithm [23], and the Jellyfish Search Optimizer [24]–are quite good. However, the results reported in [22–24] indicate the following observations: (i) the exploitation of the BWO algorithm is better than its exploration; (ii) the exploitation of the HBA algorithm is better than its exploration; and iii) the exploration of the JS algorithm is better than its exploitation.

We have adopted a low-level hybridization approach to design the BHJO algorithm. Specifically, the exploration phases of the BWO, HBA, and JS algorithms are combined to form the exploration component of the BHJO optimizer. On the other hand, the exploitation phases of the BWO and HBA metaheuristics are utilized to design the exploitation component of the BHJO algorithm. The key to success often lies in finding the right combination that effectively balances the trade-off between exploration and exploitation. Exploration involves generating new solutions and discovering promising regions, while exploitation aims to improve existing solutions and avoid local optimums.

3.2.1 Initialization Phase

To improve the diversity of the population, the logistic map has been used to generate chaotic sequences [70]. This can enhance the global search ability of the BHJO algorithm by allowing it to explore the search space more effectively. Eq. (12) is employed to create the first population of our algorithm.

3.2.2 Exploration Phase

The exploration phase of the BHJO algorithm is composed of two strategies, namely the first exploration strategy and the second exploration strategy. In the first strategy, we combine the exploration of the HBA and the JS algorithms. In the second strategy, we use the exploration of the BWO algorithm. To switch between the first and second strategies, we employ the following technique: First, we assume a uniform random number; next, if this number is less than 0.5, we apply the first strategy; otherwise, we apply the second strategy.

1) First Exploration Strategy: We utilize Eq. (17) to perform the first exploration strategy. This equation is designed by merging Eqs. (10) and (13). The factor Bf is computed using Eq. (18).

Xit+1=r1Xprey+FIiΔ→diBf|cos⁡(2πr2)(1−cos⁡(2πr3))|(17)

2) Second Exploration Strategy: We employ Eq. (2) to execute the second exploration strategy.

3.2.3 Exploitation Phase

The exploitation phase of the BHJO algorithm works with two strategies, namely first exploitation strategy and the second exploitation strategy. In the first strategy, we employ the exploitation of the BWO algorithm. In the second strategy, we use the exploitation of the HBA algorithm. To switch between the first and second strategies, we use the following technique: First, we assume a uniform random number; next, if this number is greater than 1−Bf, we apply the first strategy; otherwise, we apply the second strategy. The factor Bf is computed using Eq. (18).

1) First Exploitation Strategy: We use Eq. (3) to carry out the first exploitation strategy.

2) Second Exploitation Strategy: We apply Eq. (11) to realize the second exploitation strategy.

3.2.4 Balance between Exploration and Exploitation

In most metaheuristic algorithms, the optimizers explore and then exploit the search space. This approach has several disadvantages. For instance, during the exploration phase, the algorithm searches a wide range of solutions to identify promising areas in the search space, but it may fail to find optimal or near-optimal solutions; or the exploitation phase, which focuses on intensifying the search in selected regions, can lead the algorithm to prematurely converge to a suboptimal solution, without exploring other regions of the search space that may contain better solutions. Therefore, we propose a novel search mechanism that allows for exploration across a wide range of solutions to identify promising areas in the research domain; and simultaneously, it intensifies research in those promising areas to ensure an effective balance between exploration and exploitation, ultimately leading to the discovery of optimal or near-optimal solutions. Fig. 6 depicts the curve of balancing between exploration and exploitation, which is defined by Eq. (18).

Bf=|(r1C−1)(1+mcos⁡(2πftTmax)cos⁡(2πft))|(18)

where C, f, and m are constant numbers set to 2, 5, and −3, respectively; and r1 is a uniform random number.

Figure 6: The curve of balancing between exploration and exploitation phases in the BHJO algorithm

3.2.5 Local Optimum Avoidance

To enhance the BHJO algorithm’s capability to avoid getting stuck in local optimums, we utilize Eq. (5).

3.2.6 Opposition-Based Learning

The Combined Opposition-Based Learning (COBL) [71] is a novel research strategy that integrates two variants of opposition-based learning: Lens Opposition-Based Learning [72] and Random Opposition-Based Learning [73]. This research strategy is renowned for its ability to accelerate the convergence speed of metaheuristics by incorporating the concept of lens opposition, which entails generating an opposite solution based on the lens formed between the current solution and the global best solution. By integrating COBL into the BHJO algorithm, we can effectively mitigate the issues of local optimums and premature convergence. COBL is given by Eq. (19). It is worth emphasizing that Eq. (19) is applied each time a candidate solution is created or updated.

X˘i={LB+UB−r1Xi,q<0.5LB+UB2+LB+UB2k−Xik,q≥0.5(19)

where q is a uniform random number and k is a scale factor set to 12000 according to [71].

3.3 Pseudo-Code and Time Complexity of the BHJO Algorithm

Algorithm 1 describes the different steps of the proposed BHJO algorithm. Theoretically, the computational complexity of the BHJO algorithm is an important metric to assess its performance. It includes three processes: fitness evaluation, initialization of the first population, and updating the positions of search agents. First, the time complexity of the fitness evaluation is O(D)∼O(n). Second, the time complexity of the initialization of the first population is O(max{N, N×D})∼O(n2). Finally, the time complexity of the swarming behavior is O(Tmax×N×D)∼O(n3). From the previous time complexities, we conclude that the time complexity of BHJO is O(n3). For further clarity, Fig. 7 provides the flowchart of the proposed algorithm.

Figure 7: The flowchart of the proposed BHJO algorithm

4  Experimental Results and Discussion

In this section, we delve into the experimental study, which aims to evaluate the performance of the BHJO algorithm on different fronts. Section 4.1 focuses on scrutinizing the BHJO algorithm’s performance on benchmark test functions or Unconstrained Optimization Problems (UOPs), allowing us to assess its effectiveness and efficiency in solving standard optimization problems. Moving on to Section 4.2, our attention shifts to investigating the BHJO algorithm’s performance on engineering design problems or Constrained Optimization Problems (COPs). This analysis enables us to gauge its applicability and robustness in tackling real-world optimization challenges specific to the field of engineering design. Through these comprehensive evaluations, we aim to gain insights into the BHJO algorithm’s strengths, weaknesses, and potential areas of improvement.

The experiments were conducted using a computer system with the following hardware and software configuration. The computer is equipped with an Intel(R) Core(TM) i7-9750H CPU running at a base frequency of 2.60 GHz and a maximum turbo frequency of 4.50 GHz. The installed RAM capacity is 16 GB, providing ample memory for running complex algorithms and processing large computational loads. The operating system used is Windows 11 Home, which provides a stable and user-friendly environment for conducting the experiments. The experiments were implemented using the MATLAB R2020b programming language, known for its extensive mathematical and scientific computing capabilities. Furthermore, statistical analyses were conducted using IBM SPSS Statistics, a widely used software package for analyzing and interpreting data, facilitating robust statistical analysis.

4.1 Performance of the BHJO Algorithm on UOPs

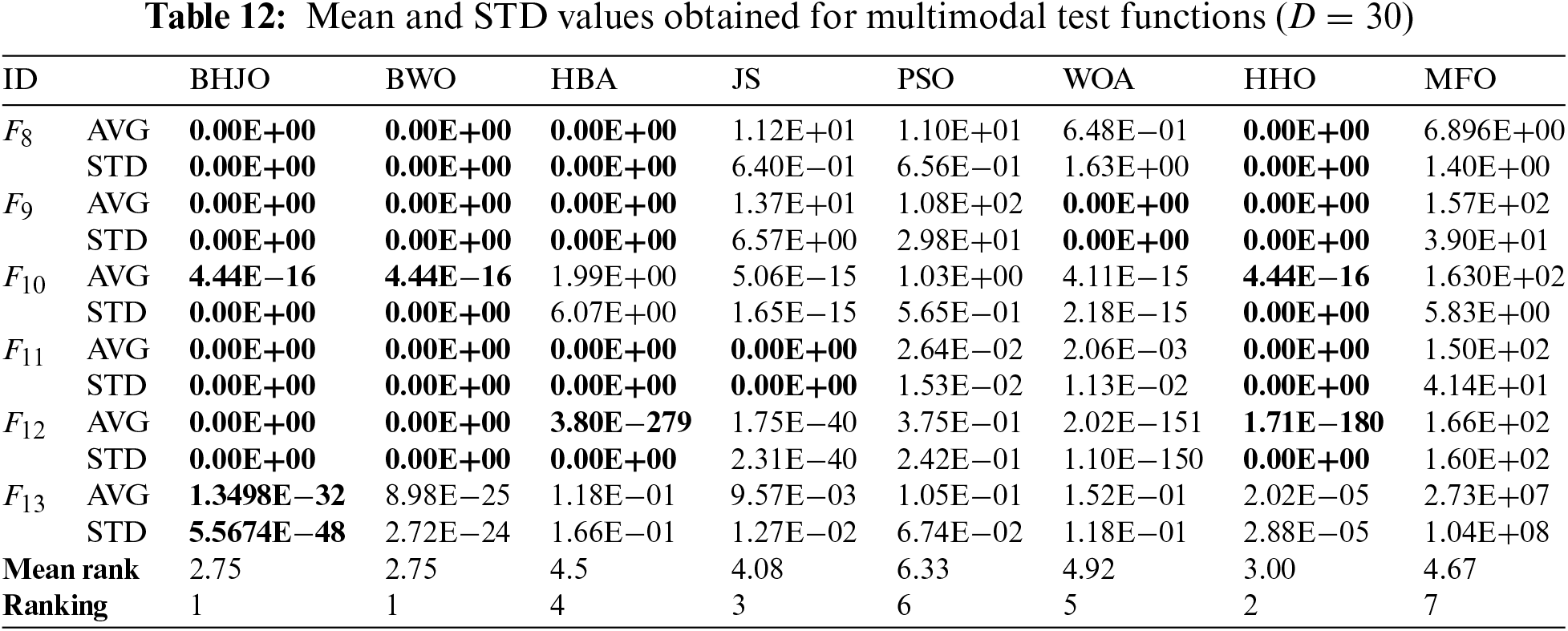
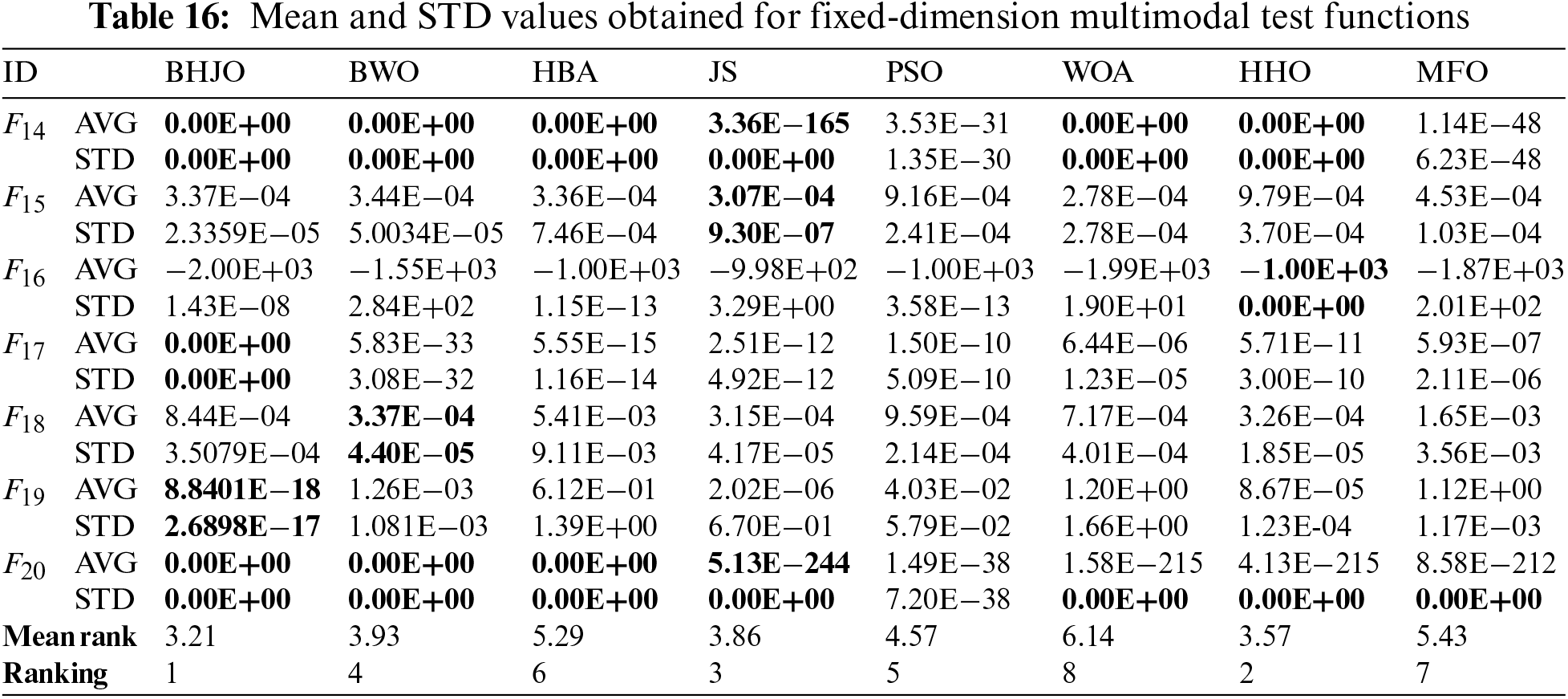
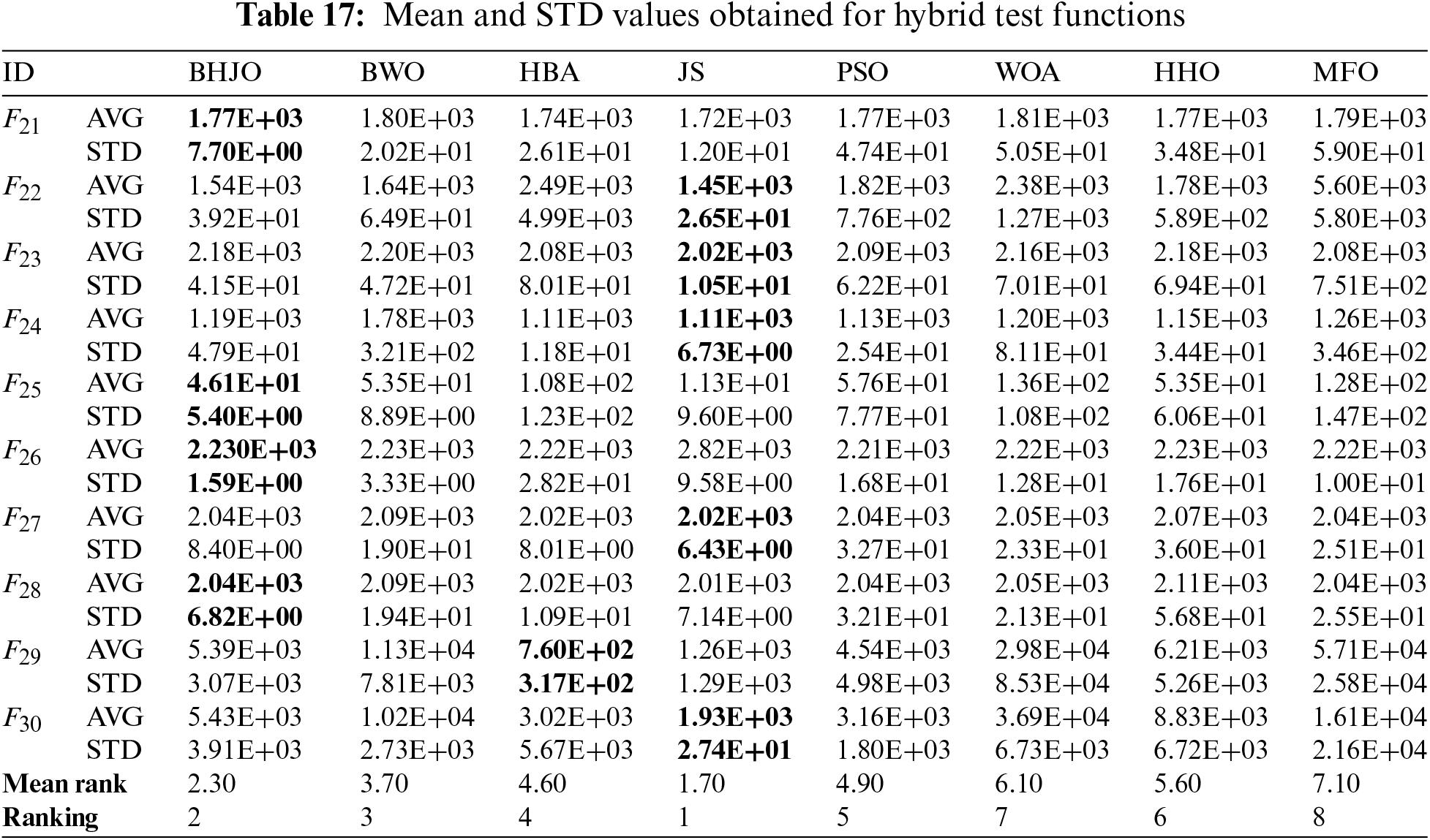
To evaluate the effectiveness of the BHJO algorithm, a collection of 40 well-established benchmark test functions from the existing literature is selected [74,75]. The set covers four types of functions: unimodal, multimodal, hybrid, and composition functions. Tables 2–6 provide an overview of the details of each function, including their mathematical expressions, dimensions, ranges, and global optimums. Unimodal functions {F1,…,F7} have only one global optimum and are used to assess the exploitation ability of optimization methods. On the other hand, multimodal functions {F8,…,F20} possess several local optimums and are employed to evaluate the exploration ability of optimization methods, specifically the avoidance of local optimums and the prevention of premature convergence. Finally, the hybrid and composition functions {F21,…,F40} are known to be very challenging and difficult. They have a large number of local optimums and are used to evaluate the well-balanced trade-off between exploration and exploitation in metaheuristic algorithms.

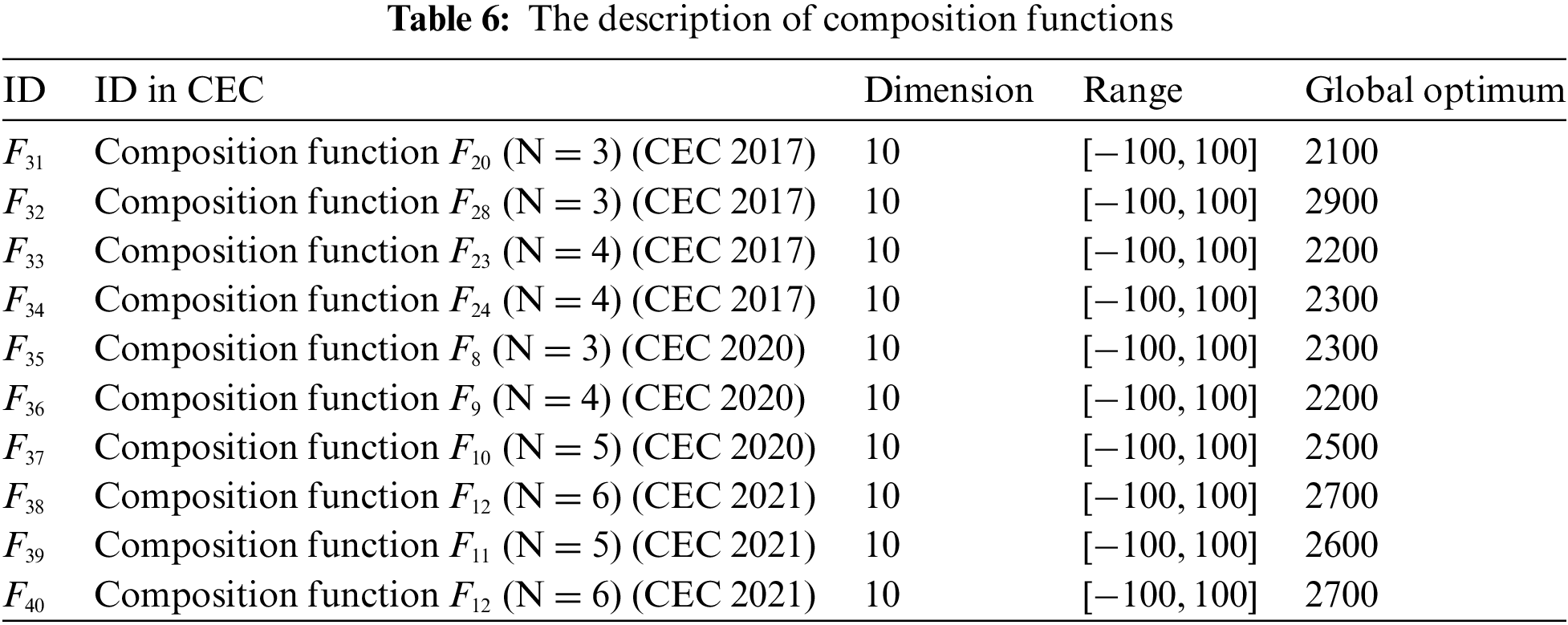
To validate the performance of the BHJO algorithm, the obtained results are compared to seven state-of-the-art optimization algorithms; namely, BWO [22], HBA [23], JS [24], WOA (Whale Optimization Algorithm) [76], MFO (Moth-Flame Optimization) [77], PSO (Particle Swarm Optimization) [14], and HHO (Harris Hawks Optimization) [78]. These algorithms are relatively new, but they have shown outstanding performance when compared to many optimizers. The population size for all the optimizers is set to 30. In addition, each algorithm was run 30 times to minimize the variance, and each run was iterated 1000 iterations to ensure the validity of the law of large numbers. The parameter settings for the algorithms utilized were obtained from their respective papers. These settings were chosen based on the authors’ recommendations and empirical evaluations, ensuring consistency and comparability with the existing literature. By adopting the parameter settings from the original papers, we aimed to establish a reliable basis for evaluating and comparing the performance of our algorithm against the established state-of-the-art methods. The values used in the BHJO algorithm are taken from the three algorithms utilized for its conception. The decision to adopt specific parameter settings for the BHJO algorithm was based on extensive testing. The parameters m, f, and C were varied across three values each–−3, −2, −1 for m; 4, 5, 6 for f; and 1, 2, 3 for C–resulting in 27 unique combinations. Analysis showed that the configuration presented in Table 7 optimally balanced exploration and exploitation during the swarming process. Additionally, to maintain comparability with established research, we adopted the Wf and C´ values directly from the seminal paper. Despite experimenting with different population sizes–30, 50, and 100–it became evident that variations in population size did not significantly impact the performance of the hybrid algorithm. Consequently, we selected a population size of 30 for all optimizers, as this size is sufficient for the engineering design problems detailed in Section 4.2 and represents nearly the median value considered in these cases. Due to space constraints in this paper, not all experimental results could be included. By employing these specific parameter settings, we aim to ensure fair and comprehensive comparisons among the algorithms in our study, ultimately providing valuable insights into their performance and effectiveness. Table 7 provides a detailed overview of these parameters and their respective values.

Tables 8 to 18 report the mean and standard deviation (STD) values averaged over 30 runs for each configuration consisting of an optimization algorithm and a test function. First, Tables 8 to 15 provide the aforementioned measurements for both unimodal and multimodal test functions across varying dimensions, specifically for dimensions 30, 50, 100, and 1000. Then, Table 16 presents the same statistical indicators for the fixed-dimension multimodal test functions across the corresponding dimensions. Finally, Tables 17 and 18 show the same statistical metrics for the hybrid and composition test functions. The standard deviation values will be utilized in various statistical tests aiming to uncover any discernible variations between the algorithms concerning their performance. In this context, it is worth emphasizing that the smaller the standard deviation value, the closer to optimal the solution obtained by the optimizer. The ideal scenario occurs when the standard deviation value equals zero, indicating that the metaheuristic algorithm has successfully obtained the global optimum when applied to the corresponding test function. Thus, the values highlighted in bold font represent the best or optimal solutions.

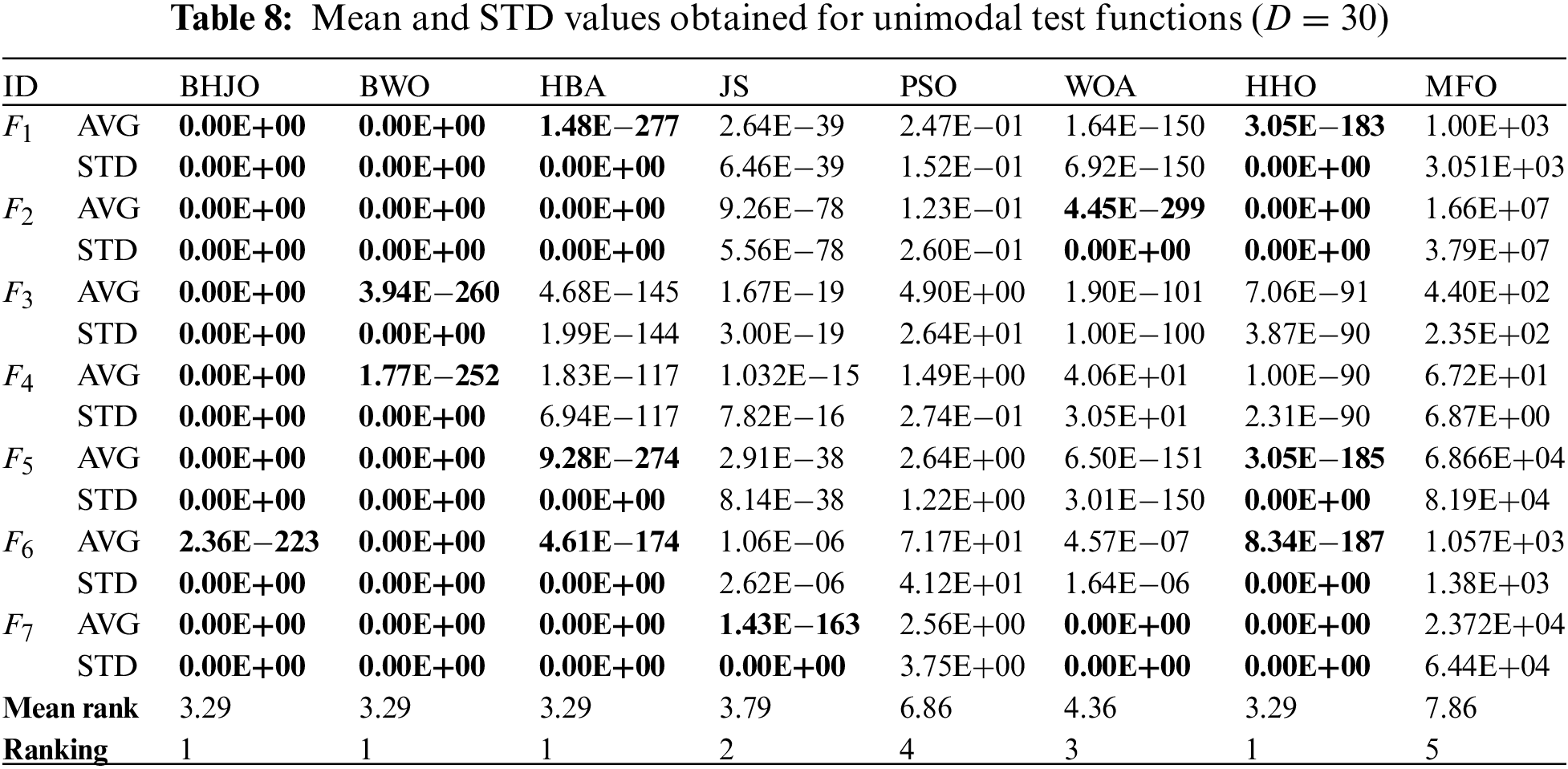
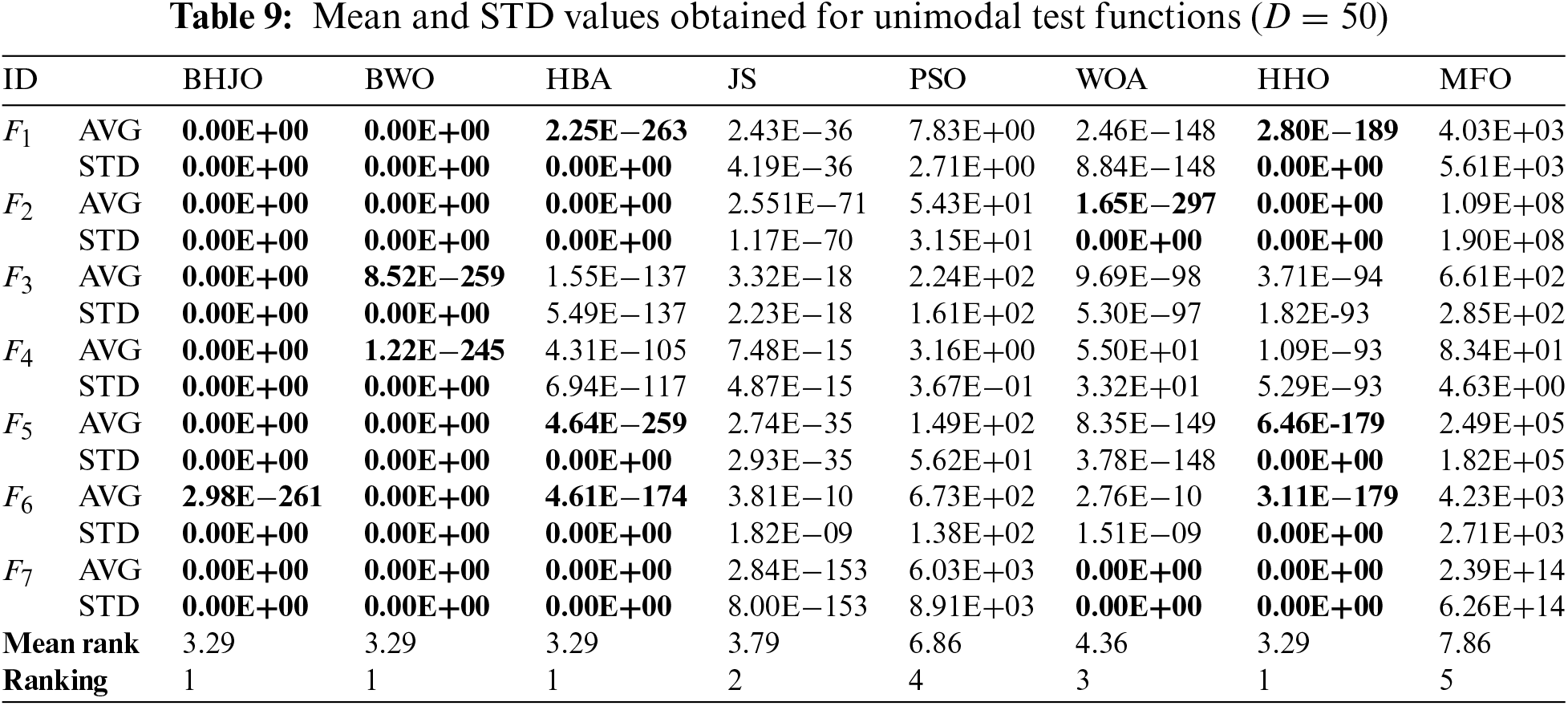
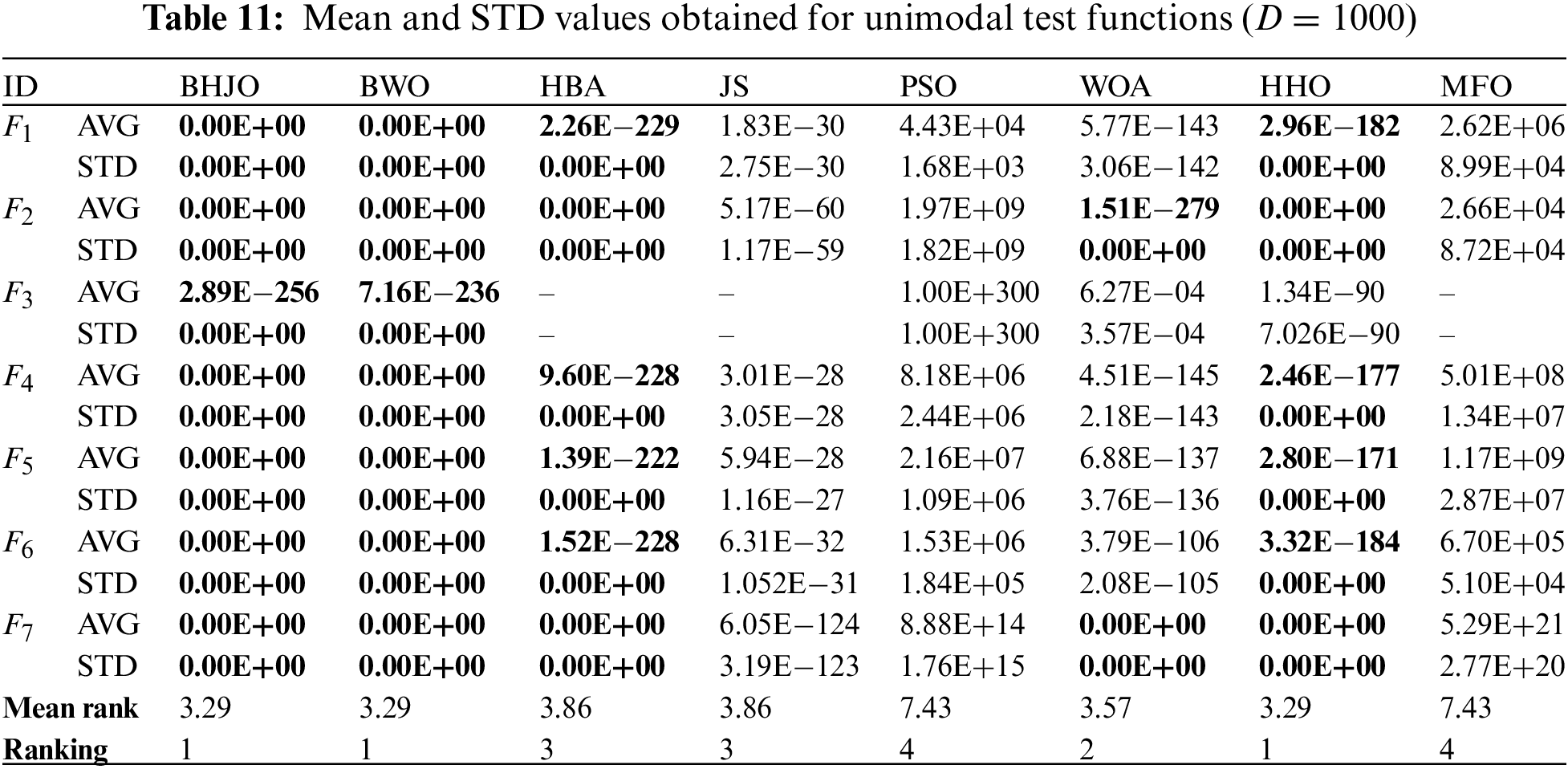
Then, we performed eleven Friedman tests using the standard deviation values reported in Tables 8 to 18, with a significance level of 0.05. The p-values computed by the Friedman test are reported in Table 19. It is important to note that if the p-value is equal to or less than 0.05, it is concluded that there is a significant difference in performance between the algorithms of the comparative study. Conversely, if the p-value is greater than 0.05, it indicates that all the algorithms exhibit similar performance. Upon observation, we find that all the p-values, except for experiment 9, are less than or equal to 0.05, indicating a difference in performance among the algorithms. Therefore, we will proceed to conduct the post-hoc Dunn’s test for these cases to analyze their performance more comprehensively.

Upon examining the last and penultimate lines of Tables 8 to 18, presenting the mean ranks and the rankings respectively, a distinct pattern emerges regarding the performance of the BHJO algorithm. Notably, the BHJO algorithm achieves the highest score in the first position for a remarkable nine out of the eleven cases studied. In addition, it secures the second position in one case and the third position in another case. Specifically:

•   First, the BHJO algorithm excels in cases dedicated to analyzing unimodal test functions, consistently ranking first. This remarkable performance highlights its exceptional exploitation capability, establishing it as the top-performing algorithm among those considered in the comparative study.

•   Furthermore, in the context of multimodal test functions, the BHJO algorithm secures the first position in four out of five cases and the third position in one case. The case where the BHJO algorithm ranks third will be further investigated in the post-hoc Dunn’s test.

•   Finally, when confronted with hybrid test functions, the algorithm ranks second, and when faced with composition test functions, it emerges as the frontrunner, securing the first position. The case in which the BHJO algorithm attains a second-place ranking will undergo additional investigation in the post-hoc Dunn’s test.

The post-hoc Dunn’s test, also known as Dunn’s multiple comparison tests, is a statistical test used to compare multiple groups or conditions after performing a non-parametric test, such as the Friedman test or the Kruskal-Wallis test. It allows for pairwise comparisons between the groups to determine if there are significant differences between them. Dunn’s test utilizes rank-based methods and applies appropriate adjustments for multiple comparisons, such as the Bonferroni correction or the Holm-Bonferroni method. This test helps to identify specific group differences and provides further insights into the significance of those differences. Tables 20 to 29 report the significance values that have been adjusted by the Bonferroni correction for multiple tests. In this analysis, the significance of differences between algorithms is indicated by the p-values, with bold font highlighting cases where the algorithm in the row demonstrates superior performance compared to that in the corresponding column. On the other hand, p-values presented in normal font signify instances where both algorithms exhibit similar performance.

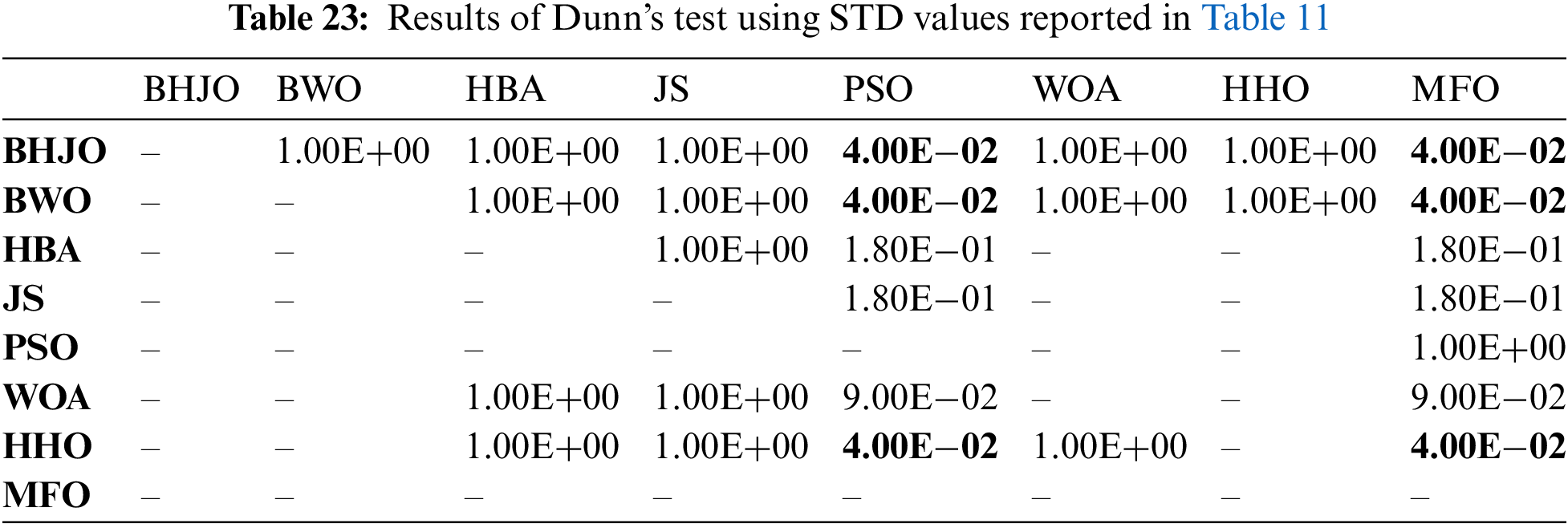
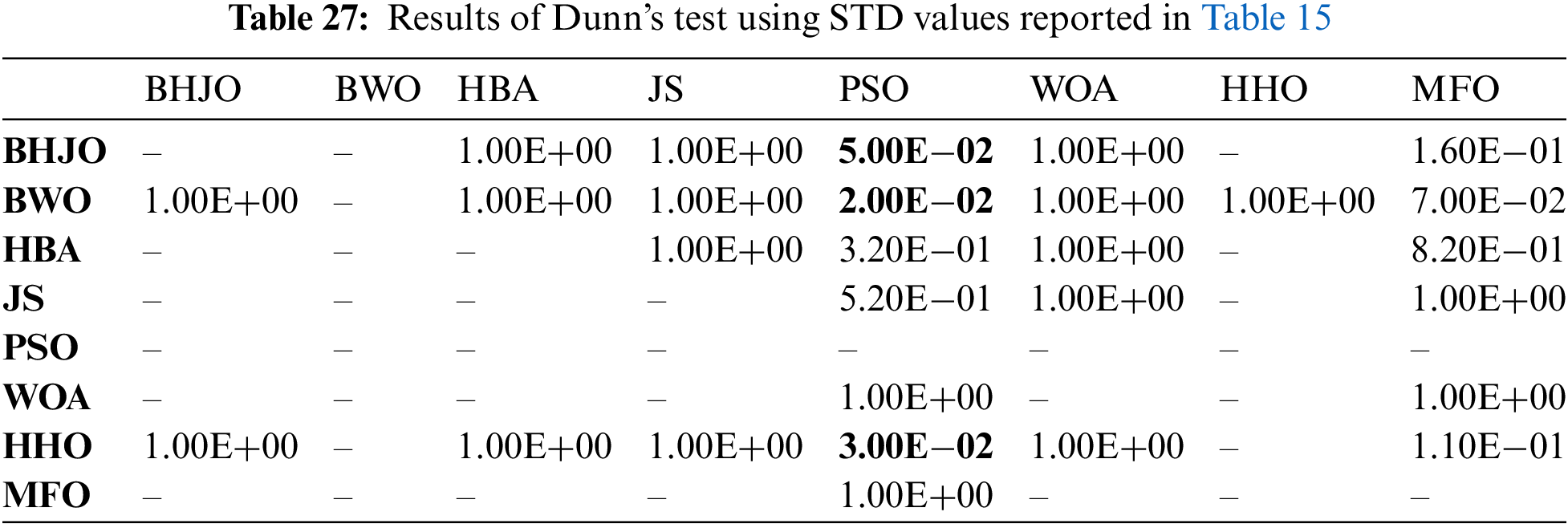
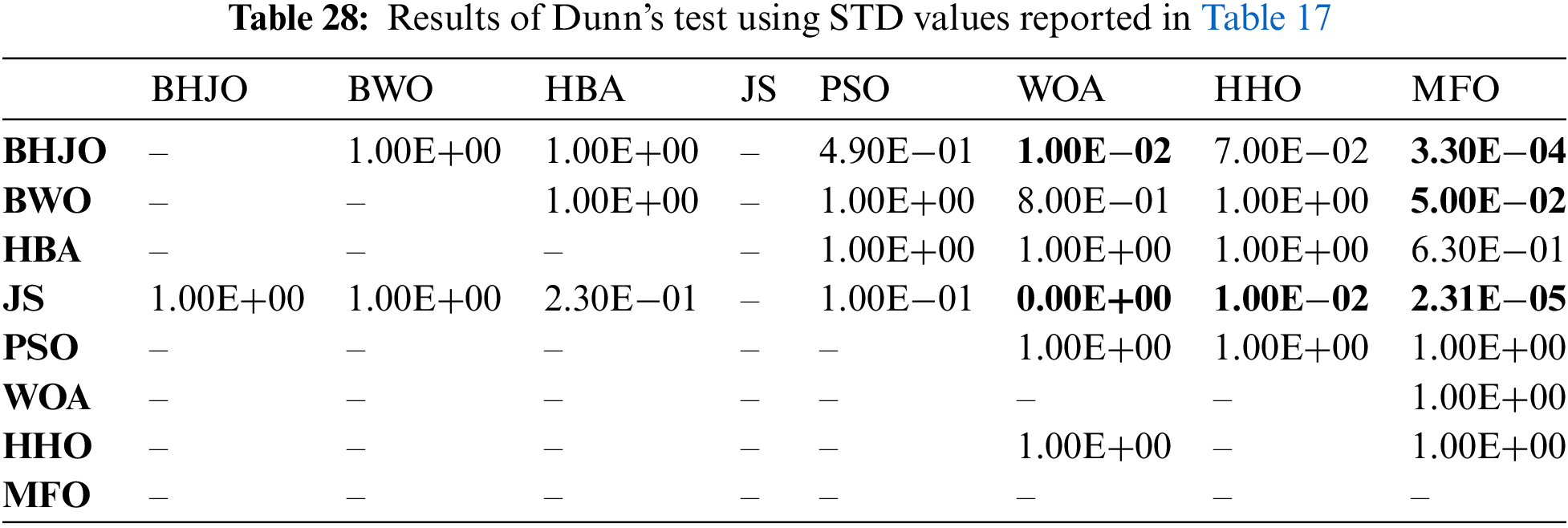
Now, let us consider the cases previously mentioned where the BHJO algorithm did not secure the first rank. Referring to Table 15, it becomes evident that the BHJO algorithm occupies the third position, trailing behind the BWO and HHO algorithms, respectively. In Table 27, the p-values are both 1, indicating that the BHJO, BWO, and HHO algorithms demonstrate similar performance. Shifting our focus to Tables 17, the BHJO algorithm is seen as the second-best, following the JS algorithm. Furthermore, Table 28 reveals a p-value of 1, suggesting comparable performance between the BHJO and JS algorithms.

4.2 Performance of the BHJO Algorithm on COPs

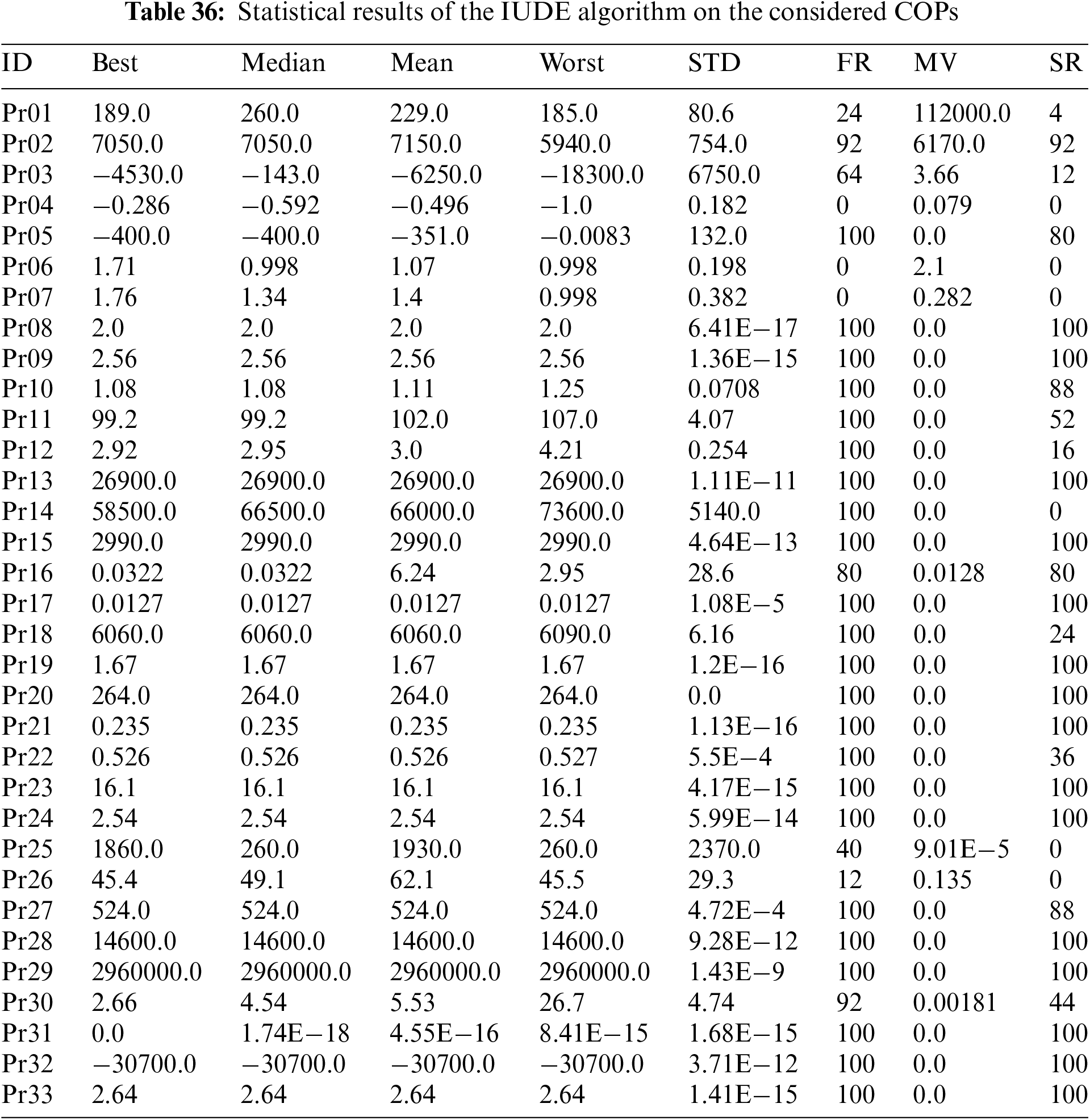
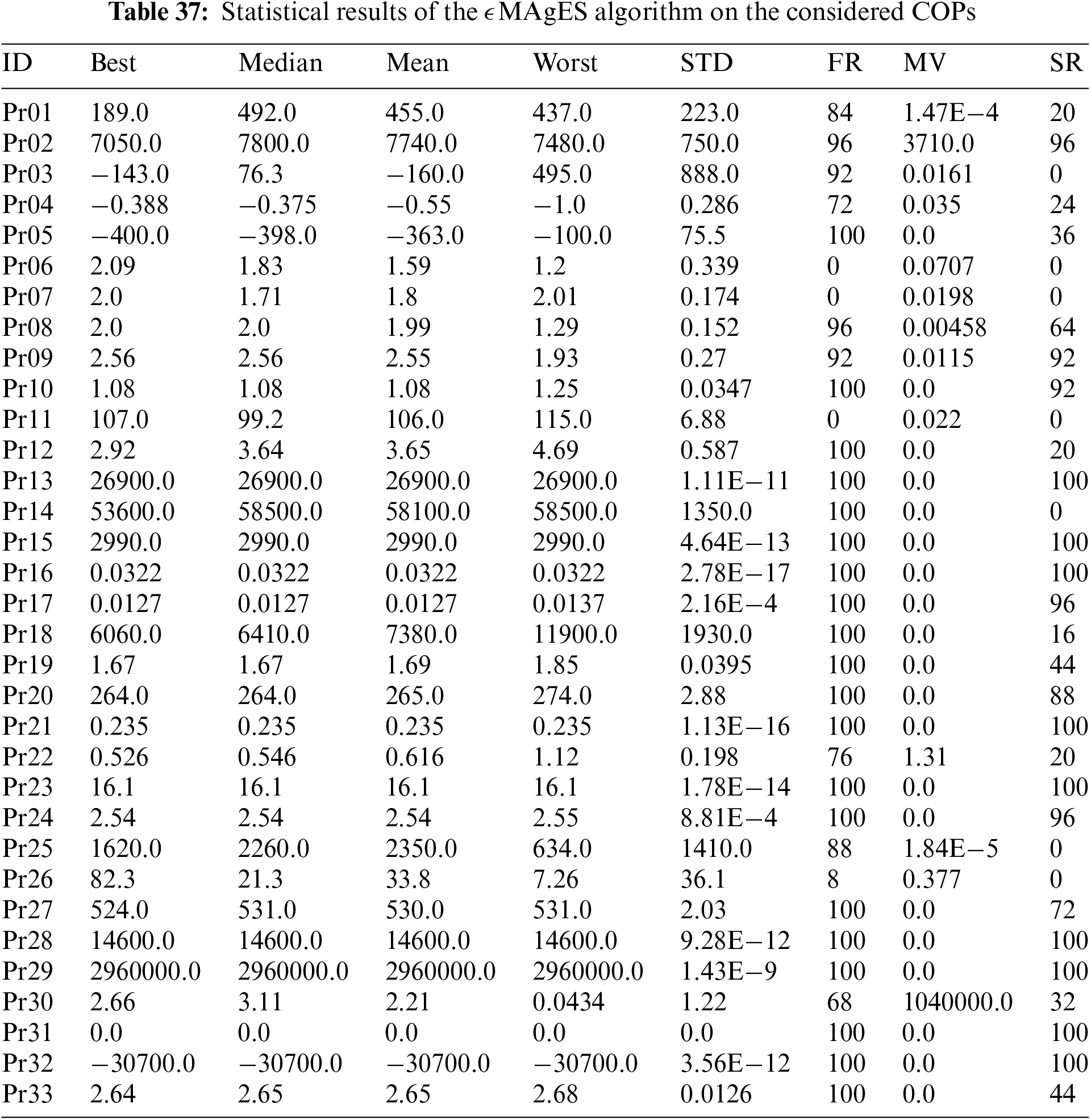
This section focuses on evaluating the effectiveness of the BHJO algorithm in tackling a range of 33 distinct engineering design problems [79]. The specific details and characteristics of these constrained optimization problems can be found in Tables 30–32. Furthermore, to assess the performance of the BHJO algorithm, a comparative analysis is conducted against five optimization algorithms, denoted as BWO [22], HBA [23], the Improved Unified Differential Evolution (IUDE) [80], the Matrix Adaptation Evolution Strategy (ϵ MAgES) [81], and the Improved Success-History based Adaptive Differential Evolution with Linear Population Size Reduction and ϵ-level control (iLSHADE  ϵ) [82]. For each combination of algorithm and design problem, the experiments are repeated 25 times, and the resulting statistical measures, including minimum, maximum, median, mean, and standard deviation values, are documented. Tables 33–38 summarize these comprehensive statistical indicators, providing valuable insights into the relative performance of the algorithms across the evaluated design problems. In addition, we calculate three other performance metrics [79]:

1.    The Feasibility Rate (FR), which represents the ratio of runs where at least one feasible solution is achieved within the maximum function evaluations out of the total number of runs.

2.    The Mean constraint Violation (MV), which is computed using Eq. (20).

MV=∑i=1Mmax(gi(X), 0)+∑j=1Nmax(|hj(X)|−10−4, 0)M+N(20)

3.    The Success Rate (SR), which indicates the ratio of runs where an algorithm successfully obtains a feasible solution X that satisfies the constrained f(X)−f(X∗)≤10−8 within the maximum function evaluations out of all the runs performed.

To assess and compare the performance of different optimizers on the set of 33 constrained optimization problems, we employ a comprehensive Evaluation Metric (EM), which will be calculated using Eq. (21). This equation incorporates a weighted sum of various key metrics, namely the best value attained throughout all optimization runs, the feasibility rate, the mean constraint violation, and the success rate. To emphasize the significance of each metric in the computation of EM, they are multiplied by specific coefficients: c1, c2, c3, and c4, reflecting their relative importance. By employing this multifaceted evaluation approach, we aim to gain a holistic understanding of the optimizers’ effectiveness in addressing the considered constrained optimization problems.

EM=c1×Best+c2×FR+c3×MV+c4×SR(21)

To evaluate the significance of the obtained EM values and determine whether there exists a notable difference in performance among the algorithms examined in this comparative study, we subject the EM values to the Friedman test at a significance level of 0.05. The resulting p-value is 7.42⋅10−11, indicating statistical evidence of performance discrepancies among the considered algorithms. This finding signifies that at least one algorithm exhibits a distinct level of performance compared to the others, warranting further investigation and analysis to identify the specific variations in their optimization capabilities.

To conduct a more detailed analysis of the performance differences among the optimizers, we further apply the post-hoc Dunn’s test to the EM values. The resulting mean ranks, as presented in Table 39, provide valuable insights into the relative performance of each algorithm. Notably, the BHJO algorithm achieved the highest rank, indicating that it exhibits the best overall performance compared to the other optimizers under consideration. To delve deeper into the statistical significance of these performance disparities, we present the corresponding p-values in Table 40, enabling a comprehensive investigation and further exploration of the observed variations.

5  Conclusion and Future Directions

In conclusion, this research paper presented a hybrid algorithm, BHJO, which combines the Beluga Whale Optimization, Honey Badger Algorithm, and Jellyfish Search optimizer. Through a meticulous analysis of the exploration and exploitation capabilities of these metaheuristics, their strengths, and weaknesses were identified and leveraged in the development of the BHJO optimizer. In other words, after a thorough evaluation of the three metaheuristics foundational to the BHJO algorithm, we have identified several strengths. The BWO and the HBA both show promising results in terms of exploitation and maintaining stability during exploration phases. However, they could benefit from an improved balance between these two aspects. On the other hand, the JS excels in exploration, offering a commendable balance between exploration and exploitation, although it does fall short in its exploitation capabilities. Collectively, these attributes contribute to the overall effectiveness of the BHJO algorithm, making each component valuable in its own right despite some areas needing enhancement, and this is shown via the thorough experimental study. Additionally, the incorporation of Opposition-Based Learning further enhanced the algorithm’s performance and solution quality. Extensive evaluations on both unconstrained and constrained optimization problems demonstrated the efficacy and versatility of the BHJO algorithm across diverse domains. Comparative analyses against renowned algorithms confirmed the algorithm’s competitiveness. Furthermore, the statistical analysis through the Friedman post hoc Dunn’s test revealed significant performance differences, highlighting the superiority of the BHJO optimizer in solving complex optimization problems. Overall, this research introduces a promising hybrid algorithm with immense potential for addressing challenging optimization tasks and contributes to the advancement of metaheuristic algorithms. In the interest of a balanced discussion, it is important to acknowledge some limitations of the BHJO algorithm. Firstly, the algorithm includes multiple parameters that require meticulous adjustment to reach optimal performance, a process that is both time-consuming and dependent on extensive experimental or simulation efforts. Additionally, the BHJO algorithm is computationally demanding, largely due to its integration of several heuristic strategies, each of which independently consumes significant resources. Moreover, there is a risk of the algorithm becoming trapped in local optima, as there are no definitive guarantees regarding the effectiveness of its swarming process. By addressing these concerns, the effectiveness of the BHJO algorithm can be significantly enhanced, leading to improved performance and reliability.

In the future, several directions can be pursued to further enhance the BHJO algorithm. For example, exploring the integration of machine learning techniques, such as deep learning or reinforcement learning, into the BHJO algorithm can provide opportunities for improved learning capabilities and adaptive behavior. This future direction aims to advance the algorithm’s versatility, efficiency, and applicability in solving a wider range of optimization problems.

Acknowledgement: The authors present their appreciation to King Saud University for funding the publication of this research through Researchers Supporting Program (RSPD2024R809), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: The research is funded by the Researchers Supporting Program at King Saud University (RSPD2024R809).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Farouq Zitouni; data collection: Farouq Zitouni, Fatima Zohra Khechiba, Khadidja Kherchouche; analysis and interpretation of results: Farouq Zitouni, Fatima Zohra Khechiba, Khadidja Kherchouche; draft manuscript preparation: Farouq Zitouni, Saad Harous, Abdulaziz S. Almazyad, Ali Wagdy Mohamed, Guojiang Xiong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1Encyclopedia of Life: https://eol.org/, accessed on 05 April 2023.

2Encyclopedia of Life: https://eol.org/, accessed on 05 April 2023.

3Encyclopedia of Life: https://eol.org/, accessed on 05 April 2023.

References

1. Mohamed A, Oliva D, Suganthan PN. Handbook of nature-inspired optimization algorithms: the state of the art. In: Studies in systems, decision and control, Cham: Springer; 2022. vol. 212. [Google Scholar]

2. Ye H, Gu Y, Zhang X, Wang S, Tan F, Zhang J, et al. Fast optimization for Betatron radiation from laser wakefield acceleration based on Bayesian optimization. Results Phys. 2022;43:106116. doi:10.1016/j.rinp.2022.106116. [Google Scholar] [CrossRef]

3. Abaluck J, Gruber J. When less is more: improving choices in health insurance markets. Rev Econ Stud. 2023;90(3):1011–40. doi:10.1093/restud/rdac050. [Google Scholar] [CrossRef]

4. Weinberg SJ, Sanches F, Ide T, Kamiya K, Correll R. Supply chain logistics with quantum and classical annealing algorithms. Sci Rep. 2023;13(1):4770. doi:10.1038/s41598-023-31765-8. [Google Scholar] [PubMed] [CrossRef]

5. Nicoletti A, Martino M, Karimi A. A data-driven approach to power converter control via convex optimization. In: 1st IEEE Conference on Control Technology and Applications, 2017; Kohala Coast, Hawaii; p. 1466–71. [Google Scholar]

6. Krentel MW. The complexity of optimization problems. In: Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing, 1986; New York, NY, USA: Association for Computing Machinery; p. 69–76. doi:10.1145/12130.12138. [Google Scholar] [CrossRef]

7. Okwu MO, Tartibu LK. Metaheuristic optimization: nature-inspired algorithms swarm and computational intelligence, theory and applications. In: Studies in computational intelligence, Cham: Springer; 2021. vol. 927. [Google Scholar]

8. Kaul S, Kumar Y. Nature-inspired metaheuristic algorithms for constraint handling: challenges, issues, and research perspective. In: Constraint handling in metaheuristics and applications. Singapore: Springer; 2021. p. 55–80. [Google Scholar]

9. Chou X, Gambardella LM, Montemanni R. A metaheuristic algorithm for the probabilistic orienteering problem. In: Proceedings of the 2019 2nd International Conference on Machine Learning and Machine Intelligence, 2019; New York, NY, USA: Association for Computing Machinery; p. 30–34. doi:10.1145/3366750.3366761. [Google Scholar] [CrossRef]

10. Tsai CW, Chiang MC. Handbook of metaheuristic algorithms: from fundamental theories to advanced applications. Elsevier; 2023. p. 71–76. https://books.google.dz/books?id=P6umEAAAQBAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false. [Accessed 2024]. [Google Scholar]

11. Keller AA. Multi-objective optimization in theory and practice II: Metaheuristic algorithms. Bentham Science Publishers; 2019. p. 54–81. https://books.google.dz/books?id=3uyRDwAAQBAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false. [Accessed 2024]. [Google Scholar]

12. Carbas S, Toktas A, Ustun D. Introduction and overview: nature-inspired metaheuristic algorithms for engineering optimization applications. In: Nature-inspired metaheuristic algorithms for engineering optimization applications, Singapore: Springer Singapore; 2021. p. 1–9. doi:10.1007/978-981-33-6773-9_1. [Google Scholar] [CrossRef]

13. Holland JH. Genetic algorithms. Sci Am. 1992;267(1):66–73. doi:10.1038/scientificamerican0792-66. [Google Scholar] [CrossRef]

14. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks, 1995; Perth, WA, Australia: IEEE; vol. 4, p. 1942–8. [Google Scholar]

15. Bertsimas D, Tsitsiklis J. Simulated annealing. Stat Sci. 1993;8(1):10–5. [Google Scholar]

16. Glover F. Tabu search: a tutorial. Interfaces. 1990;20(4):74–94. [Google Scholar]

17. Greiner D, Periaux J, Quagliarella D, Magalhaes-Mendes J, Galván B. Evolutionary algorithms and metaheuristics: applications in engineering design and optimization. Math Probl Eng. 2018;2018:1–4. [Google Scholar]

18. Xhafa F, Abraham A. Metaheuristics for scheduling in industrial and manufacturing applications. Springer Berlin, Heidelberg: Springer; 2008. vol. 128. [Google Scholar]

19. Jain DK, Tyagi SKS, Neelakandan S, Prakash M, Natrayan L. Metaheuristic optimization-based resource allocation technique for cybertwin-driven 6G on IoE environment. IEEE Trans Ind Inform. 2021;18(7):4884–92. [Google Scholar]

20. Dhaenens C, Jourdan L. Metaheuristics for data mining: survey and opportunities for big data. Ann Oper Res. 2022;314(1):117–40. [Google Scholar]

21. Monteiro ACB, França RP, Estrela VV, Razmjooy N, Iano Y, Negrete PDM. Metaheuristics applied to blood image analysis. In: Metaheuristics and optimization in computer and electrical engineering. Springer; 2020. p. 117–135. [Google Scholar]

22. Zhong C, Li G, Meng Z. Beluga whale optimization: a novel nature-inspired metaheuristic algorithm. Knowl Based Syst. 2022;251:109215. [Google Scholar]

23. Hashim FA, Houssein EH, Hussain K, Mabrouk MS, Al-Atabany W. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems. Math Comput Simul. 2022;192:84–110. [Google Scholar]

24. Chou JS, Truong DN. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl Math Comput. 2021;389:125535. [Google Scholar]

25. Mohammadi-Balani A, Nayeri MD, Azar A, Taghizadeh-Yazdi M. Golden eagle optimizer: a nature-inspired metaheuristic algorithm. Comput Ind Eng. 2021;152:107050. [Google Scholar]

26. Abdollahzadeh B, Gharehchopogh FS, Khodadadi N, Mirjalili S. Mountain gazelle optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Adv Eng Softw. 2022;174:103282. [Google Scholar]

27. Zhao W, Wang L, Zhang Z. Artificial ecosystem-based optimization: a novel nature-inspired meta-heuristic algorithm. Neural Comput Appl. 2020;32:9383–425. [Google Scholar]

28. Zhao S, Zhang T, Ma S, Chen M. Dandelion optimizer: a nature-inspired metaheuristic algorithm for engineering applications. Eng Appl Artif Intell. 2022;114:105075. [Google Scholar]

29. Zitouni F, Harous S, Belkeram A, Hammou LEB. The archerfish hunting optimizer: a novel metaheuristic algorithm for global optimization. Arab J Sci Eng. 2022;47(2):2513–53. [Google Scholar]

30. Abdollahzadeh B, Gharehchopogh FS, Mirjalili S. African vultures optimization algorithm: a new nature-inspired metaheuristic algorithm for global optimization problems. Comput Ind Eng. 2021;158:107408. [Google Scholar]

31. Abdollahzadeh B, Soleimanian Gharehchopogh F, Mirjalili S. Artificial gorilla troops optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Int J Intell Syst. 2021;36(10):5887–958. [Google Scholar]

32. Jafari M, Salajegheh E, Salajegheh J. Elephant clan optimization: a nature-inspired metaheuristic algorithm for the optimal design of structures. Appl Soft Comput. 2021;113:107892. [Google Scholar]

33. Akbari MA, Zare M, Azizipanah-Abarghooee R, Mirjalili S, Deriche M. The cheetah optimizer: a nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci Rep. 2022;12(1):10953. [Google Scholar] [PubMed]

34. Ghasemi-Marzbali A. A novel nature-inspired meta-heuristic algorithm for optimization: bear smell search algorithm. Soft Comput. 2020;24(17):13003–35. [Google Scholar]

35. Mohamed AW, Hadi AA, Mohamed AK. Gaining-sharing knowledge based algorithm for solving optimization problems: a novel nature-inspired algorithm. Int J Mach Learn Cybern. 2020;11(7):1501–29. [Google Scholar]

36. Abdel-Basset M, Mohamed R, Jameel M, Abouhawwash M. Nutcracker optimizer: a novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl Based Syst. 2023;262:110248. [Google Scholar]

37. Kumar N, Singh N, Vidyarthi DP. Artificial lizard search optimization (ALSOa novel nature-inspired meta-heuristic algorithm. Soft Comput. 2021;25(8):6179–201. [Google Scholar]

38. Fathollahi-Fard AM, Hajiaghaei-Keshteli M, Tavakkoli-Moghaddam R. Red deer algorithm (RDAa new nature-inspired meta-heuristic. Soft Comput. 2020;24:14637–65. [Google Scholar]

39. Oyelade ON, Ezugwu AES, Mohamed TI, Abualigah L. Ebola optimization search algorithm: a new nature-inspired metaheuristic optimization algorithm. IEEE Access. 2022;10:16150–77. [Google Scholar]

40. Zitouni F, Harous S, Maamri R. The solar system algorithm: a novel metaheuristic method for global optimization. IEEE Access. 2020;9:4542–65. [Google Scholar]

41. Trojovský P, Dehghani M, Hanuš P. Siberian tiger optimization: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems. IEEE Access. 2022;10:132396–431. [Google Scholar]

42. Dehghani M, Montazeri Z, Trojovská E, Trojovský P. Coati optimization algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl Based Syst. 2023;259:110011. [Google Scholar]

43. Wang L, Cao Q, Zhang Z, Mirjalili S, Zhao W. Artificial rabbits optimization: a new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng Appl Artif Intell. 2022;114:105082. [Google Scholar]

44. Rabie AH, Saleh AI, Mansour NA. Red piranha optimization (RPOa natural inspired meta-heuristic algorithm for solving complex optimization problems. J Ambient Intell Humaniz Comput. 2023;14(6):7621–48. [Google Scholar] [PubMed]

45. Harifi S, Mohammadzadeh J, Khalilian M, Ebrahimnejad S. Giza pyramids construction: an ancient-inspired metaheuristic algorithm for optimization. Evol Intell. 2021;14:1743–61. [Google Scholar]

46. Zhao S, Zhang T, Ma S, Wang M. Sea-horse optimizer: a novel nature-inspired meta-heuristic for global optimization problems. Appl Intell. 2023;53(10):11833–60. [Google Scholar]

47. Eslami N, Yazdani S, Mirzaei M, Hadavandi E. Aphid–ant mutualism: a novel nature-inspired metaheuristic algorithm for solving optimization problems. Math Comput Simul. 2022;201:362–95. [Google Scholar]

48. Braik M, Hammouri A, Atwan J, Al-Betar MA, Awadallah MA. White shark optimizer: a novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl Based Syst. 2022;243:108457. [Google Scholar]

49. Ghasemi M, Akbari MA, Jun C, Bateni SM, Zare M, Zahedi A, et al. Circulatory system based optimization (CSBOan expert multilevel biologically inspired meta-heuristic algorithm. Eng Appl Comput Fluid Mech. 2022;16(1):1483–525. [Google Scholar]

50. Abualigah L, Abd Elaziz M, Sumari P, Geem ZW, Gandomi AH. Reptile search algorithm (RSAa nature-inspired meta-heuristic optimizer. Expert Syst Appl. 2022;191:116158. [Google Scholar]

51. Yadav D. Blood coagulation algorithm: a novel bio-inspired meta-heuristic algorithm for global optimization. Mathematics. 2021;9(23):3011. [Google Scholar]

52. Zaeimi M, Ghoddosian A. Color harmony algorithm: an art-inspired metaheuristic for mathematical function optimization. Soft Comput. 2020;24:12027–66. [Google Scholar]

53. Rabie AH, Mansour NA, Saleh AI. Leopard seal optimization (LSOA natural inspired meta-heuristic algorithm. Commun Nonlinear Sci Numer Simul. 2023;125:107338. [Google Scholar]

54. Dehghani M, Trojovský P. Osprey optimization algorithm: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front Mech Eng. 2023;8:1126450. [Google Scholar]

55. Dehghani M, Trojovský P, Malik OP. Green anaconda optimization: a new bio-inspired metaheuristic algorithm for solving optimization problems. Biomimetics. 2023;8(1):121. [Google Scholar] [PubMed]

56. Trojovský P, Dehghani M. Subtraction-average-based optimizer: a new swarm-inspired metaheuristic algorithm for solving optimization problems. Biomimetics. 2023;8(2):149. [Google Scholar] [PubMed]

57. Zitouni F, Harous S, Maamri R. A novel quantum firefly algorithm for global optimization. Arab J Sci Eng. 2021;46(9):8741–59. [Google Scholar]

58. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. [Google Scholar]

59. Viswanathan G, Afanasyev V, Buldyrev SV, Havlin S, Da Luz M, Raposo E, et al. Lévy flights in random searches. Phys A: Stat Mech Appl. 2000;282(1–2):1–12. [Google Scholar]

60. Adelberger EG, Heckel BR, Nelson AE. Tests of the gravitational inverse-square law. Annu Rev Nucl Part Sci. 2003;53(1):77–121. [Google Scholar]

61. Xiang T, Liao X, Wong Kw. An improved particle swarm optimization algorithm combined with piecewise linear chaotic map. Appl Math Comput. 2007;190(2):1637–45. doi:10.1016/j.amc.2007.02.103. [Google Scholar] [CrossRef]

62. Chou JS, Ngo NT. Modified firefly algorithm for multidimensional optimization in structural design problems. Struct Multidiscipl Optim. 2017;55:2013–28. doi:10.1007/s00158-016-1624-x. [Google Scholar] [CrossRef]

63. Kaveh A, Mahdipour Moghanni R, Javadi S. Optimum design of large steel skeletal structures using chaotic firefly optimization algorithm based on the Gaussian map. Struct Multidiscipl Optim. 2019;60:879–94. doi:10.1007/s00158-019-02263-1. [Google Scholar] [CrossRef]

64. Gandomi AH, Yang XS, Talatahari S, Alavi AH. Firefly algorithm with chaos. Commun Nonlinear Sci Numer Simul. 2013;18(1):89–98. doi:10.1016/j.cnsns.2012.06.009. [Google Scholar] [CrossRef]

65. Kıran MS, Fındık O. A directed artificial bee colony algorithm. Appl Soft Comput. 2015;26:454–62. doi:10.1016/j.asoc.2014.10.020. [Google Scholar] [CrossRef]

66. Fossette S, Gleiss AC, Chalumeau J, Bastian T, Armstrong CD, Vandenabeele S, et al. Current-oriented swimming by jellyfish and its role in bloom maintenance. Curr Biol. 2015;25(3):342–7. doi:10.1016/j.cub.2014.11.050. [Google Scholar] [PubMed] [CrossRef]

67. Zavodnik D. Spatial aggregations of the swarming jellyfish Pelagia noctiluca (Scyphozoa). Mar Biol. 1987;94(2):265–9. doi:10.1007/BF00392939. [Google Scholar] [CrossRef]

68. Gaidhane PJ, Nigam MJ. A hybrid grey wolf optimizer and artificial bee colony algorithm for enhancing the performance of complex systems. J Comput Sci. 2018;27:284–302. doi:10.1016/j.jocs.2018.06.008. [Google Scholar] [CrossRef]

69. Talbi EG. A taxonomy of hybrid metaheuristics. J Heuristics. 2002;8:541–64. doi:10.1023/A:1016540724870. [Google Scholar] [CrossRef]

70. Liu Y, Li X. A hybrid mobile robot path planning scheme based on modified gray wolf optimization and situation assessment. J Robot. 2022;2022:1–9. doi:10.1155/2022/4167170. [Google Scholar] [CrossRef]

71. Xiao Y, Guo Y, Cui H, Wang Y, Li J, Zhang Y. IHAOAVOA: an improved hybrid aquila optimizer and African vultures optimization algorithm for global optimization problems. Math Biosci Eng. 2022;19(11):10963–1017. [Google Scholar] [PubMed]

72. Xiao Y, Sun X, Guo Y, Li S, Zhang Y, Wang Y. An improved gorilla troops optimizer based on lens opposition-based learning and adaptive β-hill climbing for global optimization. Comput Model Eng Sci. 2022;131(2):815–50. doi:10.32604/cmes.2022.019198. [Google Scholar] [CrossRef]

73. Tizhoosh H. Opposition-based learning: a new scheme for machine intelligence. In: Paper presented at the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), 2005;Vienna, Austria. [Google Scholar]

74. Digalakis JG, Margaritis KG. On benchmarking functions for genetic algorithms. Int J Comput Math. 2001;77(4):481–506. [Google Scholar]

75. Yao X, Liu Y, Lin G. Evolutionary programming made faster. IEEE Trans Evol Comput. 1999;3(2):82–102. [Google Scholar]

76. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95:51–67. [Google Scholar]

77. Mirjalili S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst. 2015;89:228–49. [Google Scholar]

78. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris hawks optimization: algorithm and applications. Future Gener Comput Syst. 2019;97:849–72. [Google Scholar]

79. Kumar A, Wu G, Ali MZ, Mallipeddi R, Suganthan PN, Das S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol Comput. 2020; 56:100693. [Google Scholar]

80. Trivedi A, Srinivasan D, Biswas N. An improved unified differential evolution algorithm for constrained optimization problems. In: Proceedings of 2018 IEEE Congress on Evolutionary Computation, 2018; Rio de Janeiro, Brazil: IEEE. doi:10.1109/CEC.2017.7969446. [Google Scholar] [CrossRef]

81. Hellwig M, Beyer HG. A matrix adaptation evolution strategy for constrained real-parameter optimization. In: 2018 IEEE Congress on Evolutionary Computation (CEC), 2018; Rio de Janeiro, Brazil: IEEE; p. 1–8. doi:10.1109/CEC.2018.8477950. [Google Scholar] [CrossRef]

82. Fan Z, Fang Y, Li W, Yuan Y, Wang Z, Bian X. LSHADE44 with an improved epsilon constraint-handling method for solving constrained single-objective optimization problems. In: 2018 IEEE Congress on Evolutionary Computation (CEC), 2018; Rio de Janeiro, Brazil: IEEE; p. 1–8. doi:10.1109/CEC.2018.8477943. [Google Scholar] [CrossRef]